2013 University of New South Wales School Mathematics Competition
|
|
|
- Myra Barker
- 5 years ago
- Views:
Transcription
1 Parabola Volume 49, Issue (201) 201 University of New South Wales School Mathematics Competition Junior Division Problems and s Problem 1 Suppose that x, y, z are non-zero integers with no common factor except 1 such that x 2 + y 2 = z 2. Prove that exactly one of these integers is a multiple of 5. Let x, y, z Z, x, y, z 0 gcd(x, y, z) = 1. Now x mod 5 x mod 5 2x mod 5 So, if x y mod 5, then z 2 = x 2 + y 2 2x 2 mod 5 is possible if and only if This contradicts to x y z 0 mod 5. gcd(x, y, z) = 1. So x y mod 5. Thus, we have x 2 + y (in some order) 1 (0.1) or (0.2) or (0.) or (0.4) Since z 2 is impossible, (0.4) cannot occur. So either (0.1), (0.2) or (0.) occurs. In (0.1) or (0.2) exactly one of x, y 0 mod 5; and in (0.) neither of x, y mod 5 and z 0 mod 5. 1
2 Problem 2 How many integers between 100 and have exactly three identical digits in their decimal representation. For example, 1112 and are such numbers but is not. The only 6-digit number in the range is fails the condition so the required numbers have, 4 or 5 digits. Let α represents the number of integers with repeating 0 and β the number of integers with repeating non-zero digit. For the integers computed by α, the leading digit is non-zero, so α = α 4 + α 5, where α j is the number of j-digit integers counted by α. So ( ) j 1 α j = }{{} 9 P (8, j 4), }{{} A }{{} C B where A stands for the choice for the leading digit; B stands for the choice of the places for the repeating zero; and C represents filling the remaining j 4 positions with other digits with no repetitions. So, we compute α = α 4 + α 5 = = = 9 = 297. ( ) 4 8 We split the integers counted by β into three subgroups: β = β + β 4 + β 5, where β j is the number of j-digit integers within β. Within integers counted by β, repeating digit may or may not include leading digit, so we compute β j = 9 }{{} A [ }{{} 1 B + 8 }{{} B ( ) j 1 2 }{{} C ( ) j 1 2 } {{ } C P (9, j ) }{{} D P (8, j 4) }{{} D ],
3 where A chooses the non-zero repeating digit; B puts that digit into the leading position; C chooses two other positions for the remaining repeating digits; D fills the rest with no repetition; B chooses another non-zero digit for the leading position; C chooses positions for the repeating digit; D fills the rest with no repetition. Skipping some elementary computations, we conclude that Problem β = 6516 and α + β = Find the number which is divisible by 2 and 9 and which has 14 divisors (including 1 and the number itself). 2. Show that there are multiple solutions in the case when the number has 15 divisors. Let be factorisation of n into distinct primes such that all α j > 0 and r 2. So n = 2 α 1 α 2 p α... p αr r 2 < < p <... < p r 2 n α 1 1 n α 2 2 Observe that the number of divisors of n is d(n) = (α 1 + 1)(α 2 + 1)... (α r + 1) and α and α If d(n) = 14 = 2 7, then r = 2 and α = 2, α = 7. So α 1 = 1 and α 2 = 6 and n = = If d(n) = 15 = 5, then r = 2 and α = and α = 5
4 or So or α = 5 and α =. α 1 = 2, α 2 = 4 and n = = 24 α 1 = 4, α 2 = 2 and n = = 144. Problem 4 1. The plan of an art museum is an equilateral triangle consisting of 6 triangular exhibition halls (see the diagram). Each hall has passages into all adjacent halls. Prove that you can visit at most 1 halls if you plan to enter each hall at most once. 2. Subject to the condition that each hall is visited at most once, find the largest number of halls that can be visited in the case that the museum is an equilateral triangle and that it has k 2 exhibition halls, where k is an integer. This problem is also in the Senior Division. See the solution given there. Problem 5 We wish to label the vertices of a regular polygon with 45 sides using the digits 0, 1,..., 9. Can this be done such that for every pair of digits there is an edge labelled by these digits? Such labelling cannot be done. A digit a forms 9 pairs with other digits. To accommodate these pairs, the digit a must be next to at least 5 vertices. So, at least 50 vertices are required. Problem 6 You are given n different weights and a balance. On every move, you add one more weight to one of the sides of the balance. 4
5 1. Prove that there is a strategy such that the left hand side of the balance is lower after the first move; the right hand side of the balance is lower after the second move; the left hand side is lower after the third move; and so on. 2. We assign the word LRLRLR... to the strategy above. The letter L means that the left hand side is lower; the letter R means that the right hand side is lower. For any word of length n of letters L and R, find a strategy which will correspond to that word according to the rules above. The strategy is based on the following lemma. Lemma Let m 1 < m 2 <... < m k. If then and S odd = m 1 + m +... and S even = m 2 + m , S even > S odd S odd > S even if k even if k odd. That is, the sum which has the heaviest weight is the largest. Proof of Lemma The proof has two parts. If k is even, then we add the following inequalities: m 1 < m 2 m < m 4 m k 1 < m k On the other hand, if k is odd, then we add the following inequalities 0 < m 1 m 2 < m m k 1 < m k Now the required strategy is described as follows. It is convenient to describe the strategy in reverse. That is, we give the final distribution of weights first and then we explain how to choose the weight to remove on each step until the balance is empty Let be the weights; m 1 < m 2 <... < m n 5
6 2. put all odd indexed weights on one side of the balance and all even indexed weights on the other side such that the heaviest weight is on the left hand side, if the last letter of the word is L ; or the right hand side if the letter is R ;. on every move, you remove the last letter from the word and a weight from the balance as follows: (a) you remove the heaviest if the letter at the back changes from L to R or from R to L ; (b) otherwise, you remove the lightest weight if the letter at the back of the word does not change. 6
7 Senior Division Problems and s Problem 1 In this problem you may assume the following result. Ptolemy s Theorem: If ABCD is a cyclic quadrilateral, that is a quadrilateral inscribed in a circle, then BD AC = AD BC + AB DC. B C A D Suppose ABCDE is a regular pentagon inscribed in a circle. Let P be any point on the arc BC. Prove that P A + P D = P B + P C + P E. A B E P O C D Since we have to prove P A + P D = P B + P C + P E 7
8 we may assume (by applying a dilation) that AB = BC = CD = DE = EA = 1. The five diagonals of the regular pentagon have the same length so assume that AC = BD = CE = DA = EB = d. With six points on the circle there are ( ) 6 = 15 4 quadruples of points to which Ptolemy s Theorem can be applied. Fortunately the 5 sets corresponding to the points of that pentagon give the same equation. Consider the quadrilateral ABCD: The exact value of d, is not needed. Apply Ptolemy s Theorem to P BAE: and to P CDE: Add (0.6) and (0.7) AC BD = AB CD + AD BC d 2 = 1 + d (0.5) d = 1 2 (1 + 5), P A BE = P B AE + P E AB, P A d = P B + P E (0.6) P D CE = P C DE + P E CD, P D d = P C + P E. (0.7) Apply Ptolemy s to P AED: so Substitute in (0.8) P B + P C + 2P E = P A d + P D d (0.8) P E AD = P A ED + P D AE, P E d = P A + P D, P E = 1 d P A + 1 d P D. P B + P C + P E = P A(d 1 d ) + P D(d 1 d ). But from (0.5) and as required. d 1 d = 1 P B + P C + P E + P A + P D 8
9 Problem 2 1. The plan of an art museum is an equilateral triangle consisting of 6 triangular exhibition halls (see the diagram). Each hall has passages into all adjacent halls. Prove that you can visit at most 1 halls if you plan to enter each hall at most once. 2. Subject to the condition that each hall is visited at most once, find the largest number of halls that can be visited in the case that the museum is an equilateral triangle and that it has k 2 exhibition halls, where k is an integer. Starting from the top and working systematically along each row it appears that one can only visit 6 5 = 1 rooms. Let a k be the number of rooms which can be visited, then apparently and for k, in general, k = a k = a k = k 2 (k 1) = k 2 k + 1. Indeed, the method described above shows that a 6 1 and a k k 2 k + 1, in general. To see that 1 is the most possible, colour the up triangles red and the down triangles white. 9
10 Each path must go... RWRW... There are 21 red triangles and 15 white triangles so a maximal path can contain no more than 16 red and 15 white triangles, so a 6 1. Thus, a 6 = 1. If there are k 2 exhibition halls, then the number of red halls is and the number of white halls is So the maximal possible path visits k = 1 k(k + 1) (k 1) = 1 k(k 1). 2 halls. 1 2 k(k 1) k(k 1) + 1 = k2 k + 1 Problem Given an integer n, find the largest integer k such that k is a factor of 2 n + 1. Give an argument to justify your answer. For a few initial values of n, we have Thus, we hypothesise n = 0 : =, n = 1 : = = 9, n = 2 : = = k = n
11 and a proof by induction is available. Assume with n 2 and (, A n ) = 1. Then, 2 n = (2 n ) n + 1 = n+1 A n = ( 2 n + 1 ) ( (2 n ) 2 2 n + 1 ) = n+1 A n ( ( n+1 A n 1) 2 ( n+1 A n 1) + 1 ) = n+1 A n ( n+1 ( n+1 A n 2A n A n ) + ) = n+2 A n ( n ( n+1 A n A n ) + 1 ) which is divisible by exactly n+2 but not n+ as required. Since k = n + 1 for n = 0, 1, 2,... the proof by induction is complete. Problem 4 Suppose that x 1, x 2, x and y 1, y 2, y are positive real numbers such that 0 < x 1 y 1 < x 2 y 2 < x y and Prove that x 1 + x 2 + x y 1 + y 2 + y. 1 x x x 1 y y y. Unfortunately this question is wrong as can be seen by taking x 1 small relative to y 1, y 2 and y. For example, let (x 1, x 2, x ) = (1, 4, 4) with 1 x x x = 2 and then (y 1, y 2, y ) = (2,, 4) with 1 y y y = 1 12, 0 < x 1 y 1 < x 2 y 2 < x y, x 1 + x 2 + x y 1 + y 2 + y and 1 x x x > 1 y y y. 11
12 Problem 5 Each of the numbers x 1,..., x n is either 1 or 1 and furthermore Prove that n is a multiple of 4. Let Clearly, x 1 x 2 + x 2 x x n 1 x n + x n x 1 = 0. y 1 = x 1 x 2, y 2 = x 2 x,..., y n = x n x 1. y j = ±1, j = 1, 2,..., n. Now the sum of an odd number of odd numbers is odd, so if then n is even. n y j = 0, j=1 Let us show that n is a multiple of 4. If n y j = 0 with n = 2k, then k of the y j s are 1 and k of the y j s are 1. Consider, j=1 y 1 y 2... y n = x 2 1x x 2 n = 1, since each x 2 j = 1. Thus, the number of negative y j s, which is k, is even. So n = 2k is a multiple of 4. Alternative We may assume x 1 = 1. Consider the signs of x 1, x 2,..., x n, x 1 as The number of negative y j s is the number of times + or + occurs in the sequence. Clearly + and + occur the same number of times so k is even, and n = 2k is a multiple of 4. Problem 6 Seven people have access to a bank vault. The vault is secured with a number of locks, and for each lock, some but not all of the seven people have a key. Find the minimal number of locks needed so that any 4 of them can open the vault whereas any of them cannot. For the minimal number of locks, specify the required distribution of the keys among the people. 12
13 The required number of locks is n = ( ) 7 = 5. Assume first that we have some amount of locks installed and some distribution of keys between the people such that the conditions of the problem are met. That is, every group of three people cannot open the vault and any group of four can open the vault. In this case, for every group of three people, there is a unique lock such that this group cannot open this lock, i.e., none in the group has a key to the lock. Indeed, if this was not so, that is, if there was two different groups of three people, say A and B, and a lock, say L, such that both A and B cannot open the lock L, then, by joining a person from B to the group A, we end up with a group of four people which cannot open the lock L. This is in contradiction with the assumption above. Hence, every group of three people has at least one unique lock associated with it. There are ( 7 ) groups of people and so the number of locks is at least ( ) 7 = 5. This number of locks is sufficient to ensure the requirement of the problem. Indeed, given that that we install ( 7 ) locks, we associate uniquely a lock with a group of three people and we give keys to this lock to everyone but the associated group of three. 1
Hanoi Open Mathematical Competition 2017
 Hanoi Open Mathematical Competition 2017 Junior Section Saturday, 4 March 2017 08h30-11h30 Important: Answer to all 15 questions. Write your answers on the answer sheets provided. For the multiple choice
Hanoi Open Mathematical Competition 2017 Junior Section Saturday, 4 March 2017 08h30-11h30 Important: Answer to all 15 questions. Write your answers on the answer sheets provided. For the multiple choice
This class will demonstrate the use of bijections to solve certain combinatorial problems simply and effectively.
 . Induction This class will demonstrate the fundamental problem solving technique of mathematical induction. Example Problem: Prove that for every positive integer n there exists an n-digit number divisible
. Induction This class will demonstrate the fundamental problem solving technique of mathematical induction. Example Problem: Prove that for every positive integer n there exists an n-digit number divisible
International Mathematical Olympiad. Preliminary Selection Contest 2004 Hong Kong. Outline of Solutions 3 N
 International Mathematical Olympiad Preliminary Selection Contest 004 Hong Kong Outline of Solutions Answers:. 8. 0. N 4. 49894 5. 6. 004! 40 400 7. 6 8. 7 9. 5 0. 0. 007. 8066. π + 4. 5 5. 60 6. 475 7.
International Mathematical Olympiad Preliminary Selection Contest 004 Hong Kong Outline of Solutions Answers:. 8. 0. N 4. 49894 5. 6. 004! 40 400 7. 6 8. 7 9. 5 0. 0. 007. 8066. π + 4. 5 5. 60 6. 475 7.
1 Hanoi Open Mathematical Competition 2017
 1 Hanoi Open Mathematical Competition 017 1.1 Junior Section Question 1. Suppose x 1, x, x 3 are the roots of polynomial P (x) = x 3 6x + 5x + 1. The sum x 1 + x + x 3 is (A): 4 (B): 6 (C): 8 (D): 14 (E):
1 Hanoi Open Mathematical Competition 017 1.1 Junior Section Question 1. Suppose x 1, x, x 3 are the roots of polynomial P (x) = x 3 6x + 5x + 1. The sum x 1 + x + x 3 is (A): 4 (B): 6 (C): 8 (D): 14 (E):
number. However, unlike , three of the digits of N are 3, 4 and 5, and N is a multiple of 6.
 C1. The positive integer N has six digits in increasing order. For example, 124 689 is such a number. However, unlike 124 689, three of the digits of N are 3, 4 and 5, and N is a multiple of 6. How many
C1. The positive integer N has six digits in increasing order. For example, 124 689 is such a number. However, unlike 124 689, three of the digits of N are 3, 4 and 5, and N is a multiple of 6. How many
1. Suppose that a, b, c and d are four different integers. Explain why. (a b)(a c)(a d)(b c)(b d)(c d) a 2 + ab b = 2018.
 New Zealand Mathematical Olympiad Committee Camp Selection Problems 2018 Solutions Due: 28th September 2018 1. Suppose that a, b, c and d are four different integers. Explain why must be a multiple of
New Zealand Mathematical Olympiad Committee Camp Selection Problems 2018 Solutions Due: 28th September 2018 1. Suppose that a, b, c and d are four different integers. Explain why must be a multiple of
40th International Mathematical Olympiad
 40th International Mathematical Olympiad Bucharest, Romania, July 999 Determine all finite sets S of at least three points in the plane which satisfy the following condition: for any two distinct points
40th International Mathematical Olympiad Bucharest, Romania, July 999 Determine all finite sets S of at least three points in the plane which satisfy the following condition: for any two distinct points
International Mathematics TOURNAMENT OF THE TOWNS
 International Mathematics TOURNAMENT OF THE TOWNS Senior A-Level Paper Fall 2011 1 Pete has marked at least 3 points in the plane such that all distances between them are different A pair of marked points
International Mathematics TOURNAMENT OF THE TOWNS Senior A-Level Paper Fall 2011 1 Pete has marked at least 3 points in the plane such that all distances between them are different A pair of marked points
SMT 2011 General Test and Solutions February 19, F (x) + F = 1 + x. 2 = 3. Now take x = 2 2 F ( 1) = F ( 1) = 3 2 F (2)
 SMT 0 General Test and Solutions February 9, 0 Let F () be a real-valued function defined for all real 0, such that ( ) F () + F = + Find F () Answer: Setting =, we find that F () + F ( ) = Now take =,
SMT 0 General Test and Solutions February 9, 0 Let F () be a real-valued function defined for all real 0, such that ( ) F () + F = + Find F () Answer: Setting =, we find that F () + F ( ) = Now take =,
2011 Olympiad Solutions
 011 Olympiad Problem 1 Let A 0, A 1, A,..., A n be nonnegative numbers such that Prove that A 0 A 1 A A n. A i 1 n A n. Note: x means the greatest integer that is less than or equal to x.) Solution: We
011 Olympiad Problem 1 Let A 0, A 1, A,..., A n be nonnegative numbers such that Prove that A 0 A 1 A A n. A i 1 n A n. Note: x means the greatest integer that is less than or equal to x.) Solution: We
Sydney University Mathematical Society Problems Competition Solutions.
 Sydney University Mathematical Society Problems Competition 005 Solutions 1 Suppose that we look at the set X n of strings of 0 s and 1 s of length n Given a string ɛ = (ɛ 1,, ɛ n ) X n, we are allowed
Sydney University Mathematical Society Problems Competition 005 Solutions 1 Suppose that we look at the set X n of strings of 0 s and 1 s of length n Given a string ɛ = (ɛ 1,, ɛ n ) X n, we are allowed
Singapore Mathematical Society
 Singapore Mathematical Society Interschool Mathematical Competition 1990 Part A Saturday, 23 June 1990 100Q-1100 Attempt as many questions as you can. No calculators are allowed. Circle your answers on
Singapore Mathematical Society Interschool Mathematical Competition 1990 Part A Saturday, 23 June 1990 100Q-1100 Attempt as many questions as you can. No calculators are allowed. Circle your answers on
The Alberta High School Mathematics Competition Solution to Part I, 2014.
 The Alberta High School Mathematics Competition Solution to Part I, 2014. Question 1. When the repeating decimal 0.6 is divided by the repeating decimal 0.3, the quotient is (a) 0.2 (b) 2 (c) 0.5 (d) 0.5
The Alberta High School Mathematics Competition Solution to Part I, 2014. Question 1. When the repeating decimal 0.6 is divided by the repeating decimal 0.3, the quotient is (a) 0.2 (b) 2 (c) 0.5 (d) 0.5
The sum x 1 + x 2 + x 3 is (A): 4 (B): 6 (C): 8 (D): 14 (E): None of the above. How many pairs of positive integers (x, y) are there, those satisfy
 Important: Answer to all 15 questions. Write your answers on the answer sheets provided. For the multiple choice questions, stick only the letters (A, B, C, D or E) of your choice. No calculator is allowed.
Important: Answer to all 15 questions. Write your answers on the answer sheets provided. For the multiple choice questions, stick only the letters (A, B, C, D or E) of your choice. No calculator is allowed.
CAREER POINT. PRMO EXAM-2017 (Paper & Solution) Sum of number should be 21
 PRMO EXAM-07 (Paper & Solution) Q. How many positive integers less than 000 have the property that the sum of the digits of each such number is divisible by 7 and the number itself is divisible by 3? Sum
PRMO EXAM-07 (Paper & Solution) Q. How many positive integers less than 000 have the property that the sum of the digits of each such number is divisible by 7 and the number itself is divisible by 3? Sum
First selection test. a n = 3n + n 2 1. b n = 2( n 2 + n + n 2 n),
 First selection test Problem. Find the positive real numbers a, b, c which satisfy the inequalities 4(ab + bc + ca) a 2 + b 2 + c 2 3(a 3 + b 3 + c 3 ). Laurenţiu Panaitopol Problem 2. Consider the numbers
First selection test Problem. Find the positive real numbers a, b, c which satisfy the inequalities 4(ab + bc + ca) a 2 + b 2 + c 2 3(a 3 + b 3 + c 3 ). Laurenţiu Panaitopol Problem 2. Consider the numbers
Problems and Solutions
 46 th Canadian Mathematical Olympiad Wednesday, April 2, 204 Problems and Solutions. Let a, a 2,..., a n be positive real numbers whose product is. Show that the sum a a 2 + + a ( + a )( + a 2 ) + a 3
46 th Canadian Mathematical Olympiad Wednesday, April 2, 204 Problems and Solutions. Let a, a 2,..., a n be positive real numbers whose product is. Show that the sum a a 2 + + a ( + a )( + a 2 ) + a 3
EGMO 2016, Day 1 Solutions. Problem 1. Let n be an odd positive integer, and let x1, x2,..., xn be non-negative real numbers.
 EGMO 2016, Day 1 Solutions Problem 1. Let n be an odd positive integer, and let x1, x2,..., xn be non-negative real numbers. Show that min (x2i + x2i+1 ) max (2xj xj+1 ), j=1,...,n i=1,...,n where xn+1
EGMO 2016, Day 1 Solutions Problem 1. Let n be an odd positive integer, and let x1, x2,..., xn be non-negative real numbers. Show that min (x2i + x2i+1 ) max (2xj xj+1 ), j=1,...,n i=1,...,n where xn+1
Non-standard MMC problems
 Non-standard MMC problems Carl Joshua Quines 1 Algebra 1. (15S/9B/E6) A quadratic function f(x) satisfies f(0) = 30 and f(2) = 0. Determine all the zeros of f(x). [2 and 15] 2. (15S/IVB/E6) What is the
Non-standard MMC problems Carl Joshua Quines 1 Algebra 1. (15S/9B/E6) A quadratic function f(x) satisfies f(0) = 30 and f(2) = 0. Determine all the zeros of f(x). [2 and 15] 2. (15S/IVB/E6) What is the
Pre RMO Exam Paper Solution:
 Paper Solution:. How many positive integers less than 000 have the property that the sum of the digits of each such number is divisible by 7 and the number itself is divisible by 3? Sum of Digits Drivable
Paper Solution:. How many positive integers less than 000 have the property that the sum of the digits of each such number is divisible by 7 and the number itself is divisible by 3? Sum of Digits Drivable
Olimpiada Matemática de Centroamérica y el Caribe
 Olimpiada Matemática de Centroamérica y el Caribe 1st Centromerican 1999 Problem A1 A, B, C, D, E each has a unique piece of news. They make a series of phone calls to each other. In each call, the caller
Olimpiada Matemática de Centroamérica y el Caribe 1st Centromerican 1999 Problem A1 A, B, C, D, E each has a unique piece of news. They make a series of phone calls to each other. In each call, the caller
CDS-I 2019 Elementary Mathematics (Set-C)
 1 CDS-I 019 Elementary Mathematics (Set-C) Direction: Consider the following for the next three (03) items : A cube is inscribed in a sphere. A right circular cylinder is within the cube touching all the
1 CDS-I 019 Elementary Mathematics (Set-C) Direction: Consider the following for the next three (03) items : A cube is inscribed in a sphere. A right circular cylinder is within the cube touching all the
2017 Harvard-MIT Mathematics Tournament
 Team Round 1 Let P(x), Q(x) be nonconstant polynomials with real number coefficients. Prove that if P(y) = Q(y) for all real numbers y, then P(x) = Q(x) for all real numbers x. 2 Does there exist a two-variable
Team Round 1 Let P(x), Q(x) be nonconstant polynomials with real number coefficients. Prove that if P(y) = Q(y) for all real numbers y, then P(x) = Q(x) for all real numbers x. 2 Does there exist a two-variable
The Pigeonhole Principle
 The Pigeonhole Principle 2 2.1 The Pigeonhole Principle The pigeonhole principle is one of the most used tools in combinatorics, and one of the simplest ones. It is applied frequently in graph theory,
The Pigeonhole Principle 2 2.1 The Pigeonhole Principle The pigeonhole principle is one of the most used tools in combinatorics, and one of the simplest ones. It is applied frequently in graph theory,
 FROSH-SOPH 2 PERSON COMPETITION LARGE PRINT QUESTION 1 ICTM 2017 STATE DIVISION AA 1. Determine the sum of all distinct positive integers between 8 and 16 inclusive that can be expressed in one and only
FROSH-SOPH 2 PERSON COMPETITION LARGE PRINT QUESTION 1 ICTM 2017 STATE DIVISION AA 1. Determine the sum of all distinct positive integers between 8 and 16 inclusive that can be expressed in one and only
11 th Philippine Mathematical Olympiad Questions, Answers, and Hints
 view.php3 (JPEG Image, 840x888 pixels) - Scaled (71%) https://mail.ateneo.net/horde/imp/view.php3?mailbox=inbox&inde... 1 of 1 11/5/2008 5:02 PM 11 th Philippine Mathematical Olympiad Questions, Answers,
view.php3 (JPEG Image, 840x888 pixels) - Scaled (71%) https://mail.ateneo.net/horde/imp/view.php3?mailbox=inbox&inde... 1 of 1 11/5/2008 5:02 PM 11 th Philippine Mathematical Olympiad Questions, Answers,
UNC Charlotte 2006 Comprehensive
 March 6, 2006. What is the sum of the digits of the integer solution to 4? (A) 5 (B) 6 (C) 8 (D) 9 (E) 4 + 27 x = 2. In a box there are red and blue balls. If you select a handful of them with eyes closed,
March 6, 2006. What is the sum of the digits of the integer solution to 4? (A) 5 (B) 6 (C) 8 (D) 9 (E) 4 + 27 x = 2. In a box there are red and blue balls. If you select a handful of them with eyes closed,
BRITISH COLUMBIA SECONDARY SCHOOL MATHEMATICS CONTEST, 2017 Junior Preliminary Problems & Solutions
 BRITISH COLUMBIA SECONDARY SCHOOL MATHEMATICS CONTEST, 017 Junior Preliminary Problems & s 1. If x is a number larger than, which of the following expressions is the smallest? (A) /(x 1) (B) /x (C) /(x
BRITISH COLUMBIA SECONDARY SCHOOL MATHEMATICS CONTEST, 017 Junior Preliminary Problems & s 1. If x is a number larger than, which of the following expressions is the smallest? (A) /(x 1) (B) /x (C) /(x
3. A square has 4 sides, so S = 4. A pentagon has 5 vertices, so P = 5. Hence, S + P = 9. = = 5 3.
 JHMMC 01 Grade Solutions October 1, 01 1. By counting, there are 7 words in this question.. (, 1, ) = 1 + 1 + = 9 + 1 + =.. A square has sides, so S =. A pentagon has vertices, so P =. Hence, S + P = 9..
JHMMC 01 Grade Solutions October 1, 01 1. By counting, there are 7 words in this question.. (, 1, ) = 1 + 1 + = 9 + 1 + =.. A square has sides, so S =. A pentagon has vertices, so P =. Hence, S + P = 9..
T-2 In the equation A B C + D E F = G H I, each letter denotes a distinct non-zero digit. Compute the greatest possible value of G H I.
 2016 ARML Local Problems and Solutions Team Round Solutions T-1 All the shelves in a library are the same length. When filled, two shelves side-by-side can hold exactly 12 algebra books and 10 geometry
2016 ARML Local Problems and Solutions Team Round Solutions T-1 All the shelves in a library are the same length. When filled, two shelves side-by-side can hold exactly 12 algebra books and 10 geometry
37th United States of America Mathematical Olympiad
 37th United States of America Mathematical Olympiad 1. Prove that for each positive integer n, there are pairwise relatively prime integers k 0, k 1,..., k n, all strictly greater than 1, such that k 0
37th United States of America Mathematical Olympiad 1. Prove that for each positive integer n, there are pairwise relatively prime integers k 0, k 1,..., k n, all strictly greater than 1, such that k 0
BRITISH COLUMBIA COLLEGES High School Mathematics Contest 2003 Solutions
 BRITISH COLUMBIA COLLEGES High School Mathematics Contest 3 Solutions Junior Preliminary. Solve the equation x = Simplify the complex fraction by multiplying numerator and denominator by x. x = = x = (x
BRITISH COLUMBIA COLLEGES High School Mathematics Contest 3 Solutions Junior Preliminary. Solve the equation x = Simplify the complex fraction by multiplying numerator and denominator by x. x = = x = (x
4 a b 1 1 c 1 d 3 e 2 f g 6 h i j k 7 l m n o 3 p q 5 r 2 s 4 t 3 3 u v 2
 Round Solutions Year 25 Academic Year 201 201 1//25. In the hexagonal grid shown, fill in each space with a number. After the grid is completely filled in, the number in each space must be equal to the
Round Solutions Year 25 Academic Year 201 201 1//25. In the hexagonal grid shown, fill in each space with a number. After the grid is completely filled in, the number in each space must be equal to the
SMT China 2014 Team Test Solutions August 23, 2014
 . Compute the remainder when 2 30 is divided by 000. Answer: 824 Solution: Note that 2 30 024 3 24 3 mod 000). We will now consider 24 3 mod 8) and 24 3 mod 25). Note that 24 3 is divisible by 8, but 24
. Compute the remainder when 2 30 is divided by 000. Answer: 824 Solution: Note that 2 30 024 3 24 3 mod 000). We will now consider 24 3 mod 8) and 24 3 mod 25). Note that 24 3 is divisible by 8, but 24
UNIVERSITY OF MICHIGAN UNDERGRADUATE MATH COMPETITION 28 APRIL 7, 2011
 UNIVERSITY OF MICHIGAN UNDERGRADUATE MATH COMPETITION 28 APRIL 7, 20 Instructions. Write on the front of your blue book your student ID number. Do not write your name anywhere on your blue book. Each question
UNIVERSITY OF MICHIGAN UNDERGRADUATE MATH COMPETITION 28 APRIL 7, 20 Instructions. Write on the front of your blue book your student ID number. Do not write your name anywhere on your blue book. Each question
SUMS PROBLEM COMPETITION, 2000
 SUMS ROBLEM COMETITION, 2000 SOLUTIONS 1 The result is well known, and called Morley s Theorem Many proofs are known See for example HSM Coxeter, Introduction to Geometry, page 23 2 If the number of vertices,
SUMS ROBLEM COMETITION, 2000 SOLUTIONS 1 The result is well known, and called Morley s Theorem Many proofs are known See for example HSM Coxeter, Introduction to Geometry, page 23 2 If the number of vertices,
Exercises for Unit V (Introduction to non Euclidean geometry)
 Exercises for Unit V (Introduction to non Euclidean geometry) V.1 : Facts from spherical geometry Ryan : pp. 84 123 [ Note : Hints for the first two exercises are given in math133f07update08.pdf. ] 1.
Exercises for Unit V (Introduction to non Euclidean geometry) V.1 : Facts from spherical geometry Ryan : pp. 84 123 [ Note : Hints for the first two exercises are given in math133f07update08.pdf. ] 1.
Solution: By direct calculation, or observe that = = ( ) 2222 = =
 1 Fillins 1. Find the last 4 digits of 3333 6666. Solution: 7778. By direct calculation, or observe that 3333 6666 = 9999 2222 = (10000 1) 2222 = 22220000 2222 = 22217778. 2. How many ways are there to
1 Fillins 1. Find the last 4 digits of 3333 6666. Solution: 7778. By direct calculation, or observe that 3333 6666 = 9999 2222 = (10000 1) 2222 = 22220000 2222 = 22217778. 2. How many ways are there to
46th ANNUAL MASSACHUSETTS MATHEMATICS OLYMPIAD. A High School Competition Conducted by. And Sponsored by FIRST-LEVEL EXAMINATION SOLUTIONS
 46th ANNUAL MASSACHUSETTS MATHEMATICS OLYMPIAD 009 00 A High School Competition Conducted by THE MASSACHUSETTS ASSOCIATION OF MATHEMATICS LEAGUES (MAML) And Sponsored by THE ACTUARIES CLUB OF BOSTON FIRST-LEVEL
46th ANNUAL MASSACHUSETTS MATHEMATICS OLYMPIAD 009 00 A High School Competition Conducted by THE MASSACHUSETTS ASSOCIATION OF MATHEMATICS LEAGUES (MAML) And Sponsored by THE ACTUARIES CLUB OF BOSTON FIRST-LEVEL
HANOI OPEN MATHEMATICAL COMPETITON PROBLEMS
 HANOI MATHEMATICAL SOCIETY NGUYEN VAN MAU HANOI OPEN MATHEMATICAL COMPETITON PROBLEMS HANOI - 2013 Contents 1 Hanoi Open Mathematical Competition 3 1.1 Hanoi Open Mathematical Competition 2006... 3 1.1.1
HANOI MATHEMATICAL SOCIETY NGUYEN VAN MAU HANOI OPEN MATHEMATICAL COMPETITON PROBLEMS HANOI - 2013 Contents 1 Hanoi Open Mathematical Competition 3 1.1 Hanoi Open Mathematical Competition 2006... 3 1.1.1
How to prove it (or not) Gerry Leversha MA Conference, Royal Holloway April 2017
 How to prove it (or not) Gerry Leversha MA Conference, Royal Holloway April 2017 My favourite maxim It is better to solve one problem in five different ways than to solve five problems using the same method
How to prove it (or not) Gerry Leversha MA Conference, Royal Holloway April 2017 My favourite maxim It is better to solve one problem in five different ways than to solve five problems using the same method
1. The sides of a triangle are in the ratio 3 : 5 : 9. Which of the following words best describes the triangle?
 UNIVERSITY OF NORTH CAROLINA CHARLOTTE 999 HIGH SCHOOL MATHEMATICS CONTEST March 8, 999 The sides of a triangle are in the ratio : 5 : 9 Which of the following words best describes the triangle? (A) obtuse
UNIVERSITY OF NORTH CAROLINA CHARLOTTE 999 HIGH SCHOOL MATHEMATICS CONTEST March 8, 999 The sides of a triangle are in the ratio : 5 : 9 Which of the following words best describes the triangle? (A) obtuse
Joe Holbrook Memorial Math Competition
 Joe Holbrook Memorial Math Competition 8th Grade Solutions October 9th, 06. + (0 ( 6( 0 6 ))) = + (0 ( 6( 0 ))) = + (0 ( 6)) = 6 =. 80 (n ). By the formula that says the interior angle of a regular n-sided
Joe Holbrook Memorial Math Competition 8th Grade Solutions October 9th, 06. + (0 ( 6( 0 6 ))) = + (0 ( 6( 0 ))) = + (0 ( 6)) = 6 =. 80 (n ). By the formula that says the interior angle of a regular n-sided
1) (JUNIOR 1 and SENIOR 1) Let n be a positive integer. Show that n n
 All Problems on the Prize Exams Spring 2016 The source for each problem is listed below when available; but even when the source is given, the formulation of the problem may have been changed. Solutions
All Problems on the Prize Exams Spring 2016 The source for each problem is listed below when available; but even when the source is given, the formulation of the problem may have been changed. Solutions
Georgia Tech High School Math Competition
 Georgia Tech High School Math Competition Multiple Choice Test February 28, 2015 Each correct answer is worth one point; there is no deduction for incorrect answers. Make sure to enter your ID number on
Georgia Tech High School Math Competition Multiple Choice Test February 28, 2015 Each correct answer is worth one point; there is no deduction for incorrect answers. Make sure to enter your ID number on
Mathematical Olympiad for Girls
 UKMT UKMT UKMT United Kingdom Mathematics Trust Mathematical Olympiad for Girls Organised by the United Kingdom Mathematics Trust These are polished solutions and do not illustrate the process of failed
UKMT UKMT UKMT United Kingdom Mathematics Trust Mathematical Olympiad for Girls Organised by the United Kingdom Mathematics Trust These are polished solutions and do not illustrate the process of failed
HANOI OPEN MATHEMATICS COMPETITON PROBLEMS
 HANOI MATHEMATICAL SOCIETY NGUYEN VAN MAU HANOI OPEN MATHEMATICS COMPETITON PROBLEMS 2006-2013 HANOI - 2013 Contents 1 Hanoi Open Mathematics Competition 3 1.1 Hanoi Open Mathematics Competition 2006...
HANOI MATHEMATICAL SOCIETY NGUYEN VAN MAU HANOI OPEN MATHEMATICS COMPETITON PROBLEMS 2006-2013 HANOI - 2013 Contents 1 Hanoi Open Mathematics Competition 3 1.1 Hanoi Open Mathematics Competition 2006...
SOLUTIONS, what is the value of f(4)?
 005 Georgia Tech High School Mathematics Competition Junior-Varsity Multiple-Choice Examination Version A Problem : If f(x) = x4 x +x x SOLUTIONS, what is the value of f(4)? (A) 6 (B) 70 (C) 78 (D) 8 (E)
005 Georgia Tech High School Mathematics Competition Junior-Varsity Multiple-Choice Examination Version A Problem : If f(x) = x4 x +x x SOLUTIONS, what is the value of f(4)? (A) 6 (B) 70 (C) 78 (D) 8 (E)
PURPLE COMET MATH MEET April 2012 MIDDLE SCHOOL - SOLUTIONS
 PURPLE COMET MATH MEET April 2012 MIDDLE SCHOOL - SOLUTIONS Copyright c Titu Andreescu and Jonathan Kane Problem 1 Evaluate 5 4 4 3 3 2 2 1 1 0. Answer: 549 The expression equals 625 64 9 2 1 = 549. Problem
PURPLE COMET MATH MEET April 2012 MIDDLE SCHOOL - SOLUTIONS Copyright c Titu Andreescu and Jonathan Kane Problem 1 Evaluate 5 4 4 3 3 2 2 1 1 0. Answer: 549 The expression equals 625 64 9 2 1 = 549. Problem
20th Bay Area Mathematical Olympiad. BAMO 2018 Problems and Solutions. February 27, 2018
 20th Bay Area Mathematical Olympiad BAMO 201 Problems and Solutions The problems from BAMO- are A E, and the problems from BAMO-12 are 1 5. February 27, 201 A Twenty-five people of different heights stand
20th Bay Area Mathematical Olympiad BAMO 201 Problems and Solutions The problems from BAMO- are A E, and the problems from BAMO-12 are 1 5. February 27, 201 A Twenty-five people of different heights stand
Baltic Way 2008 Gdańsk, November 8, 2008
 Baltic Way 008 Gdańsk, November 8, 008 Problems and solutions Problem 1. Determine all polynomials p(x) with real coefficients such that p((x + 1) ) = (p(x) + 1) and p(0) = 0. Answer: p(x) = x. Solution:
Baltic Way 008 Gdańsk, November 8, 008 Problems and solutions Problem 1. Determine all polynomials p(x) with real coefficients such that p((x + 1) ) = (p(x) + 1) and p(0) = 0. Answer: p(x) = x. Solution:
CHMMC 2015 Individual Round Problems
 CHMMC 05 Individual Round Problems November, 05 Problem 0.. The following number is the product of the divisors of n. What is n? 6 3 3 Solution.. In general, the product of the divisors of n is n # of
CHMMC 05 Individual Round Problems November, 05 Problem 0.. The following number is the product of the divisors of n. What is n? 6 3 3 Solution.. In general, the product of the divisors of n is n # of
13 th Annual Harvard-MIT Mathematics Tournament Saturday 20 February 2010
 13 th Annual Harvard-MIT Mathematics Tournament Saturday 0 February 010 1. [3] Suppose that x and y are positive reals such that Find x. x y = 3, x + y = 13. 3+ Answer: 17 Squaring both sides of x y =
13 th Annual Harvard-MIT Mathematics Tournament Saturday 0 February 010 1. [3] Suppose that x and y are positive reals such that Find x. x y = 3, x + y = 13. 3+ Answer: 17 Squaring both sides of x y =
First selection test
 First selection test Problem 1. Let ABC be a triangle right at C and consider points D, E on the sides BC, CA, respectively such that BD = AE = k. Lines BE and AC CD AD intersect at point O. Show that
First selection test Problem 1. Let ABC be a triangle right at C and consider points D, E on the sides BC, CA, respectively such that BD = AE = k. Lines BE and AC CD AD intersect at point O. Show that
Taiwan International Mathematics Competition 2012 (TAIMC 2012)
 Section. (5 points each) orrect nswers: Taiwan International Mathematics ompetition 01 (TIM 01) World onference on the Mathematically Gifted Students ---- the Role of Educators and Parents Taipei, Taiwan,
Section. (5 points each) orrect nswers: Taiwan International Mathematics ompetition 01 (TIM 01) World onference on the Mathematically Gifted Students ---- the Role of Educators and Parents Taipei, Taiwan,
Math Wrangle Practice Problems
 Math Wrangle Practice Problems American Mathematics Competitions November 19, 2010 1. Find the sum of all positive two-digit integers that are divisible by each of their digits. 2. A finite set S of distinct
Math Wrangle Practice Problems American Mathematics Competitions November 19, 2010 1. Find the sum of all positive two-digit integers that are divisible by each of their digits. 2. A finite set S of distinct
MeritPath.com. Problems and Solutions, INMO-2011
 Problems and Solutions, INMO-011 1. Let,, be points on the sides,, respectively of a triangle such that and. Prove that is equilateral. Solution 1: c ka kc b kb a Let ;. Note that +, and hence. Similarly,
Problems and Solutions, INMO-011 1. Let,, be points on the sides,, respectively of a triangle such that and. Prove that is equilateral. Solution 1: c ka kc b kb a Let ;. Note that +, and hence. Similarly,
International Mathematical Olympiad. Preliminary Selection Contest 2011 Hong Kong. Outline of Solutions
 International Mathematical Olympiad Preliminary Selection Contest Hong Kong Outline of Solutions Answers:.. 76... 6. 7.. 6.. 6. 6.... 6. 7.. 76. 6. 7 Solutions:. Such fractions include. They can be grouped
International Mathematical Olympiad Preliminary Selection Contest Hong Kong Outline of Solutions Answers:.. 76... 6. 7.. 6.. 6. 6.... 6. 7.. 76. 6. 7 Solutions:. Such fractions include. They can be grouped
(A) 2S + 3 (B) 3S + 2 (C) 3S + 6 (D) 2S + 6 (E) 2S + 12
 1 The sum of two numbers is S Suppose 3 is added to each number and then each of the resulting numbers is doubled What is the sum of the final two numbers? (A) S + 3 (B) 3S + (C) 3S + 6 (D) S + 6 (E) S
1 The sum of two numbers is S Suppose 3 is added to each number and then each of the resulting numbers is doubled What is the sum of the final two numbers? (A) S + 3 (B) 3S + (C) 3S + 6 (D) S + 6 (E) S
2008 Euclid Contest. Solutions. Canadian Mathematics Competition. Tuesday, April 15, c 2008 Centre for Education in Mathematics and Computing
 Canadian Mathematics Competition An activity of the Centre for Education in Mathematics and Computing, University of Waterloo, Waterloo, Ontario 008 Euclid Contest Tuesday, April 5, 008 Solutions c 008
Canadian Mathematics Competition An activity of the Centre for Education in Mathematics and Computing, University of Waterloo, Waterloo, Ontario 008 Euclid Contest Tuesday, April 5, 008 Solutions c 008
Baltic Way Riga, Latvia. Problems and solutions
 Baltic Way 013 Riga, Latvia Problems and solutions Problems and solutions Baltic Way 013 Problem 1 Let n be a positive integer. Assume that n numbers are to be chosen from the table 0 1 n 1 n n + 1 n 1......
Baltic Way 013 Riga, Latvia Problems and solutions Problems and solutions Baltic Way 013 Problem 1 Let n be a positive integer. Assume that n numbers are to be chosen from the table 0 1 n 1 n n + 1 n 1......
nx + 1 = (n + 1)x 13(n + 1) and nx = (n + 1)x + 27(n + 1).
 1. (Answer: 630) 001 AIME SOLUTIONS Let a represent the tens digit and b the units digit of an integer with the required property. Then 10a + b must be divisible by both a and b. It follows that b must
1. (Answer: 630) 001 AIME SOLUTIONS Let a represent the tens digit and b the units digit of an integer with the required property. Then 10a + b must be divisible by both a and b. It follows that b must
Computer Science Foundation Exam
 Computer Science Foundation Exam May 6, 2016 Section II A DISCRETE STRUCTURES NO books, notes, or calculators may be used, and you must work entirely on your own. SOLUTION Question Max Pts Category Passing
Computer Science Foundation Exam May 6, 2016 Section II A DISCRETE STRUCTURES NO books, notes, or calculators may be used, and you must work entirely on your own. SOLUTION Question Max Pts Category Passing
Gauss School and Gauss Math Circle 2017 Gauss Math Tournament Grade 7-8 (Sprint Round 50 minutes)
 Gauss School and Gauss Math Circle 2017 Gauss Math Tournament Grade 7-8 (Sprint Round 50 minutes) 1. Compute. 2. Solve for x: 3. What is the sum of the negative integers that satisfy the inequality 2x
Gauss School and Gauss Math Circle 2017 Gauss Math Tournament Grade 7-8 (Sprint Round 50 minutes) 1. Compute. 2. Solve for x: 3. What is the sum of the negative integers that satisfy the inequality 2x
1 Sequences and Summation
 1 Sequences and Summation A sequence is a function whose domain is either all the integers between two given integers or all the integers greater than or equal to a given integer. For example, a m, a m+1,...,
1 Sequences and Summation A sequence is a function whose domain is either all the integers between two given integers or all the integers greater than or equal to a given integer. For example, a m, a m+1,...,
1. Let g(x) and h(x) be polynomials with real coefficients such that
 1. Let g(x) and h(x) be polynomials with real coefficients such that g(x)(x 2 3x + 2) = h(x)(x 2 + 3x + 2) and f(x) = g(x)h(x) + (x 4 5x 2 + 4). Prove that f(x) has at least four real roots. 2. Let M be
1. Let g(x) and h(x) be polynomials with real coefficients such that g(x)(x 2 3x + 2) = h(x)(x 2 + 3x + 2) and f(x) = g(x)h(x) + (x 4 5x 2 + 4). Prove that f(x) has at least four real roots. 2. Let M be
Comprehensive Mathematics Contest
 Comprehensive Mathematics Contest Elon University Mathematics and Statistics Department Saturday, March 17, 2018 Multiple Choice 1. Let a and b be lengths of the major and minor axis of the ellipse given
Comprehensive Mathematics Contest Elon University Mathematics and Statistics Department Saturday, March 17, 2018 Multiple Choice 1. Let a and b be lengths of the major and minor axis of the ellipse given
SOUTH AFRICAN TERTIARY MATHEMATICS OLYMPIAD
 SOUTH AFRICAN TERTIARY MATHEMATICS OLYMPIAD. Determine the following value: 7 August 6 Solutions π + π. Solution: Since π
SOUTH AFRICAN TERTIARY MATHEMATICS OLYMPIAD. Determine the following value: 7 August 6 Solutions π + π. Solution: Since π
not to be republished NCERT REAL NUMBERS CHAPTER 1 (A) Main Concepts and Results
 REAL NUMBERS CHAPTER 1 (A) Main Concepts and Results Euclid s Division Lemma : Given two positive integers a and b, there exist unique integers q and r satisfying a = bq + r, 0 r < b. Euclid s Division
REAL NUMBERS CHAPTER 1 (A) Main Concepts and Results Euclid s Division Lemma : Given two positive integers a and b, there exist unique integers q and r satisfying a = bq + r, 0 r < b. Euclid s Division
Problem 1. Solve the equation 3 x + 9 x = 27 x. Solution: 3 x + 3 2x = 3 3x. Denote: y = 3 x, then. y + y 2 = y 3. y 3 y 2 y = 0. y(y 2 y 1) = 0.
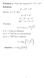 Problem 1. Solve the equation 3 x + 9 x = 7 x. Solution: 3 x + 3 x = 3 3x. Denote: y = 3 x, then Therefore, y + y = y 3. y 3 y y = 0. y(y y 1) = 0. y = 0 or y = 1 ± 5. i) 3 x = 0 has no solutions, ii)
Problem 1. Solve the equation 3 x + 9 x = 7 x. Solution: 3 x + 3 x = 3 3x. Denote: y = 3 x, then Therefore, y + y = y 3. y 3 y y = 0. y(y y 1) = 0. y = 0 or y = 1 ± 5. i) 3 x = 0 has no solutions, ii)
Problems and Solutions: INMO-2012
 Problems and Solutions: INMO-2012 1. Let ABCD be a quadrilateral inscribed in a circle. Suppose AB = 2+ 2 and AB subtends 135 at the centre of the circle. Find the maximum possible area of ABCD. Solution:
Problems and Solutions: INMO-2012 1. Let ABCD be a quadrilateral inscribed in a circle. Suppose AB = 2+ 2 and AB subtends 135 at the centre of the circle. Find the maximum possible area of ABCD. Solution:
2016 EF Exam Texas A&M High School Students Contest Solutions October 22, 2016
 6 EF Exam Texas A&M High School Students Contest Solutions October, 6. Assume that p and q are real numbers such that the polynomial x + is divisible by x + px + q. Find q. p Answer Solution (without knowledge
6 EF Exam Texas A&M High School Students Contest Solutions October, 6. Assume that p and q are real numbers such that the polynomial x + is divisible by x + px + q. Find q. p Answer Solution (without knowledge
x = y +z +2, y = z +x+1, and z = x+y +4. C R
 1. [5] Solve for x in the equation 20 14+x = 20+14 x. 2. [5] Find the area of a triangle with side lengths 14, 48, and 50. 3. [5] Victoria wants to order at least 550 donuts from Dunkin Donuts for the
1. [5] Solve for x in the equation 20 14+x = 20+14 x. 2. [5] Find the area of a triangle with side lengths 14, 48, and 50. 3. [5] Victoria wants to order at least 550 donuts from Dunkin Donuts for the
Organization Team Team ID#
 1. [4] A random number generator will always output 7. Sam uses this random number generator once. What is the expected value of the output? 2. [4] Let A, B, C, D, E, F be 6 points on a circle in that
1. [4] A random number generator will always output 7. Sam uses this random number generator once. What is the expected value of the output? 2. [4] Let A, B, C, D, E, F be 6 points on a circle in that
NEW YORK CITY INTERSCHOLASTIC MATHEMATICS LEAGUE Senior A Division CONTEST NUMBER 1
 Senior A Division CONTEST NUMBER 1 PART I FALL 2011 CONTEST 1 TIME: 10 MINUTES F11A1 Larry selects a 13-digit number while David selects a 10-digit number. Let be the number of digits in the product of
Senior A Division CONTEST NUMBER 1 PART I FALL 2011 CONTEST 1 TIME: 10 MINUTES F11A1 Larry selects a 13-digit number while David selects a 10-digit number. Let be the number of digits in the product of
8 th Grade Exam Scoring Format: 3 points per correct response -1 each wrong response 0 for blank answers
 Pellissippi State Middle School Mathematics Competition 8 th Grade Exam Scoring Format: 3 points per correct response -1 each wrong response 0 for blank answers Directions: For each multiple-choice problem
Pellissippi State Middle School Mathematics Competition 8 th Grade Exam Scoring Format: 3 points per correct response -1 each wrong response 0 for blank answers Directions: For each multiple-choice problem
International Mathematics TOURNAMENT OF THE TOWNS
 International Mathematics TOURNAMENT OF THE TOWNS Senior A-Level Paper Fall 2010 1 1 There are 100 points on the plane All 4950 pairwise distances between two points have been recorded (a) A single record
International Mathematics TOURNAMENT OF THE TOWNS Senior A-Level Paper Fall 2010 1 1 There are 100 points on the plane All 4950 pairwise distances between two points have been recorded (a) A single record
Year 1: Fall. Year 1: Spring. HSB Topics - 2 Year Cycle
 Year 1: Fall Pigeonhole 1 Pigeonhole 2 Induction 1 Induction 2 Inequalities 1 (AM-GM) Geometry 1 - Triangle Area Ratio Theorem (TART) Contest (Math Battle) Geometry 2 - Inscribed Quadrilaterals, Ptolemy
Year 1: Fall Pigeonhole 1 Pigeonhole 2 Induction 1 Induction 2 Inequalities 1 (AM-GM) Geometry 1 - Triangle Area Ratio Theorem (TART) Contest (Math Battle) Geometry 2 - Inscribed Quadrilaterals, Ptolemy
Individual Solutions
 Individual s November 19, 017 1. A dog on a 10 meter long leash is tied to a 10 meter long, infinitely thin section of fence. What is the minimum area over which the dog will be able to roam freely on
Individual s November 19, 017 1. A dog on a 10 meter long leash is tied to a 10 meter long, infinitely thin section of fence. What is the minimum area over which the dog will be able to roam freely on
Number Theory Solutions Packet
 Number Theory Solutions Pacet 1 There exist two distinct positive integers, both of which are divisors of 10 10, with sum equal to 157 What are they? Solution Suppose 157 = x + y for x and y divisors of
Number Theory Solutions Pacet 1 There exist two distinct positive integers, both of which are divisors of 10 10, with sum equal to 157 What are they? Solution Suppose 157 = x + y for x and y divisors of
 Q 1 Find the square root of 729. 6. Squares and Square Roots Q 2 Fill in the blank using the given pattern. 7 2 = 49 67 2 = 4489 667 2 = 444889 6667 2 = Q 3 Without adding find the sum of 1 + 3 + 5 + 7
Q 1 Find the square root of 729. 6. Squares and Square Roots Q 2 Fill in the blank using the given pattern. 7 2 = 49 67 2 = 4489 667 2 = 444889 6667 2 = Q 3 Without adding find the sum of 1 + 3 + 5 + 7
MIDDLE SCHOOL - SOLUTIONS. is 1. = 3. Multiplying by 20n yields 35n + 24n + 20 = 60n, and, therefore, n = 20.
 PURPLE COMET! MATH MEET April 208 MIDDLE SCHOOL - SOLUTIONS Copyright c Titu Andreescu and Jonathan Kane Problem Find n such that the mean of 7 4, 6 5, and n is. Answer: 20 For the mean of three numbers
PURPLE COMET! MATH MEET April 208 MIDDLE SCHOOL - SOLUTIONS Copyright c Titu Andreescu and Jonathan Kane Problem Find n such that the mean of 7 4, 6 5, and n is. Answer: 20 For the mean of three numbers
UNCC 2001 Comprehensive, Solutions
 UNCC 2001 Comprehensive, Solutions March 5, 2001 1 Compute the sum of the roots of x 2 5x + 6 = 0 (A) (B) 7/2 (C) 4 (D) 9/2 (E) 5 (E) The sum of the roots of the quadratic ax 2 + bx + c = 0 is b/a which,
UNCC 2001 Comprehensive, Solutions March 5, 2001 1 Compute the sum of the roots of x 2 5x + 6 = 0 (A) (B) 7/2 (C) 4 (D) 9/2 (E) 5 (E) The sum of the roots of the quadratic ax 2 + bx + c = 0 is b/a which,
1966 IMO Shortlist. IMO Shortlist 1966
 IMO Shortlist 1966 1 Given n > 3 points in the plane such that no three of the points are collinear. Does there exist a circle passing through (at least) 3 of the given points and not containing any other
IMO Shortlist 1966 1 Given n > 3 points in the plane such that no three of the points are collinear. Does there exist a circle passing through (at least) 3 of the given points and not containing any other
Solutions to Practice Final
 s to Practice Final 1. (a) What is φ(0 100 ) where φ is Euler s φ-function? (b) Find an integer x such that 140x 1 (mod 01). Hint: gcd(140, 01) = 7. (a) φ(0 100 ) = φ(4 100 5 100 ) = φ( 00 5 100 ) = (
s to Practice Final 1. (a) What is φ(0 100 ) where φ is Euler s φ-function? (b) Find an integer x such that 140x 1 (mod 01). Hint: gcd(140, 01) = 7. (a) φ(0 100 ) = φ(4 100 5 100 ) = φ( 00 5 100 ) = (
= 10 such triples. If it is 5, there is = 1 such triple. Therefore, there are a total of = 46 such triples.
 . Two externally tangent unit circles are constructed inside square ABCD, one tangent to AB and AD, the other to BC and CD. Compute the length of AB. Answer: + Solution: Observe that the diagonal of the
. Two externally tangent unit circles are constructed inside square ABCD, one tangent to AB and AD, the other to BC and CD. Compute the length of AB. Answer: + Solution: Observe that the diagonal of the
High School Mathematics Contest Spring 2006 Draft March 27, 2006
 High School Mathematics Contest Spring 2006 Draft March 27, 2006 1. Going into the final exam, which will count as two tests, Courtney has test scores of 80, 81, 73, 65 and 91. What score does Courtney
High School Mathematics Contest Spring 2006 Draft March 27, 2006 1. Going into the final exam, which will count as two tests, Courtney has test scores of 80, 81, 73, 65 and 91. What score does Courtney
Junior Mathematical Olympiad
 UKMT UKMT UKMT United Kingdom Mathematics Trust Junior Mathematical Olympiad Organised by the United Kingdom Mathematics Trust s These are polished solutions and do not illustrate the process of exploration
UKMT UKMT UKMT United Kingdom Mathematics Trust Junior Mathematical Olympiad Organised by the United Kingdom Mathematics Trust s These are polished solutions and do not illustrate the process of exploration
MAT246H1S - Concepts In Abstract Mathematics. Solutions to Term Test 1 - February 1, 2018
 MAT246H1S - Concepts In Abstract Mathematics Solutions to Term Test 1 - February 1, 2018 Time allotted: 110 minutes. Aids permitted: None. Comments: Statements of Definitions, Principles or Theorems should
MAT246H1S - Concepts In Abstract Mathematics Solutions to Term Test 1 - February 1, 2018 Time allotted: 110 minutes. Aids permitted: None. Comments: Statements of Definitions, Principles or Theorems should
Gordon solutions. n=1 1. p n
 Gordon solutions 1. A positive integer is called a palindrome if its base-10 expansion is unchanged when it is reversed. For example, 121 and 7447 are palindromes. Show that if we denote by p n the nth
Gordon solutions 1. A positive integer is called a palindrome if its base-10 expansion is unchanged when it is reversed. For example, 121 and 7447 are palindromes. Show that if we denote by p n the nth
2007 Shortlist JBMO - Problems
 Chapter 1 007 Shortlist JBMO - Problems 1.1 Algebra A1 Let a be a real positive number such that a 3 = 6(a + 1). Prove that the equation x + ax + a 6 = 0 has no solution in the set of the real number.
Chapter 1 007 Shortlist JBMO - Problems 1.1 Algebra A1 Let a be a real positive number such that a 3 = 6(a + 1). Prove that the equation x + ax + a 6 = 0 has no solution in the set of the real number.
1. Prove that for every positive integer n there exists an n-digit number divisible by 5 n all of whose digits are odd.
 32 nd United States of America Mathematical Olympiad Proposed Solutions May, 23 Remark: The general philosophy of this marking scheme follows that of IMO 22. This scheme encourages complete solutions.
32 nd United States of America Mathematical Olympiad Proposed Solutions May, 23 Remark: The general philosophy of this marking scheme follows that of IMO 22. This scheme encourages complete solutions.
Screening Test Gauss Contest NMTC at PRIMARY LEVEL V & VI Standards Saturday, 27th August, 2016
 THE ASSOCIATION OF MATHEMATICS TEACHERS OF INDIA Screening Test Gauss Contest NMTC at PRIMARY LEVEL V & VI Standards Saturday, 7th August, 06 :. Fill in the response sheet with your Name, Class and the
THE ASSOCIATION OF MATHEMATICS TEACHERS OF INDIA Screening Test Gauss Contest NMTC at PRIMARY LEVEL V & VI Standards Saturday, 7th August, 06 :. Fill in the response sheet with your Name, Class and the
SOLUTIONS FOR IMO 2005 PROBLEMS
 SOLUTIONS FOR IMO 005 PROBLEMS AMIR JAFARI AND KASRA RAFI Problem. Six points are chosen on the sides of an equilateral triangle AB: A, A on B; B, B on A;, on AB. These points are the vertices of a convex
SOLUTIONS FOR IMO 005 PROBLEMS AMIR JAFARI AND KASRA RAFI Problem. Six points are chosen on the sides of an equilateral triangle AB: A, A on B; B, B on A;, on AB. These points are the vertices of a convex
BRITISH COLUMBIA SECONDARY SCHOOL MATHEMATICS CONTEST,
 BRITISH COLUMBIA SECONDARY SCHOOL MATHEMATICS CONTEST, 014 Solutions Junior Preliminary 1. Rearrange the sum as (014 + 01 + 010 + + ) (013 + 011 + 009 + + 1) = (014 013) + (01 011) + + ( 1) = 1 + 1 + +
BRITISH COLUMBIA SECONDARY SCHOOL MATHEMATICS CONTEST, 014 Solutions Junior Preliminary 1. Rearrange the sum as (014 + 01 + 010 + + ) (013 + 011 + 009 + + 1) = (014 013) + (01 011) + + ( 1) = 1 + 1 + +
HIGH SCHOOL - PROBLEMS
 PURPLE COMET! MATH MEET April 2017 HIGH SCHOOL - PROBLEMS Copyright c Titu Andreescu and Jonathan Kane Problem 1 Paul starts at 1 and counts by threes: 1, 4, 7, 10,.... At the same time and at the same
PURPLE COMET! MATH MEET April 2017 HIGH SCHOOL - PROBLEMS Copyright c Titu Andreescu and Jonathan Kane Problem 1 Paul starts at 1 and counts by threes: 1, 4, 7, 10,.... At the same time and at the same
Hanoi Open Mathematical Competition 2016
 Hanoi Open Mathematical Competition 2016 Junior Section Saturday, 12 March 2016 08h30-11h30 Question 1. If then m is equal to 2016 = 2 5 + 2 6 + + 2 m, (A): 8 (B): 9 (C): 10 (D): 11 (E): None of the above.
Hanoi Open Mathematical Competition 2016 Junior Section Saturday, 12 March 2016 08h30-11h30 Question 1. If then m is equal to 2016 = 2 5 + 2 6 + + 2 m, (A): 8 (B): 9 (C): 10 (D): 11 (E): None of the above.
Some Basic Logic. Henry Liu, 25 October 2010
 Some Basic Logic Henry Liu, 25 October 2010 In the solution to almost every olympiad style mathematical problem, a very important part is existence of accurate proofs. Therefore, the student should be
Some Basic Logic Henry Liu, 25 October 2010 In the solution to almost every olympiad style mathematical problem, a very important part is existence of accurate proofs. Therefore, the student should be
1999 Solutions Fermat Contest (Grade 11)
 Canadian Mathematics Competition n activity of The Centre for Education in Mathematics and Computing, University of Waterloo, Waterloo, Ontario 999 s Fermat Contest (Grade ) for the wards 999 Waterloo
Canadian Mathematics Competition n activity of The Centre for Education in Mathematics and Computing, University of Waterloo, Waterloo, Ontario 999 s Fermat Contest (Grade ) for the wards 999 Waterloo
2017 Math Olympics Level I Solutions
 Saginaw Valley State University 017 Math Olympics Level I Solutions 1. What is the last (least significant) digit of 017? (a) 0 (b) (c) 4 (d) 6 (e) 8 Solution (b): Looking at the first few powers of :
Saginaw Valley State University 017 Math Olympics Level I Solutions 1. What is the last (least significant) digit of 017? (a) 0 (b) (c) 4 (d) 6 (e) 8 Solution (b): Looking at the first few powers of :
