A proof of Atiyah s conjecture on configurations of four points in Euclidean three-space
|
|
|
- Nathaniel Bryant
- 5 years ago
- Views:
Transcription
1 ISSN (on line) (printed) 885 Geometry & Topology Volume 5 (200) Published: 26 November 200 G G G G T TT G TT T G T G T GG TT G GG G GG T T T TT A proof of Atiyah s conjecture on configurations of four points in Euclidean three-space Michael Eastwood Paul Norbury Pure Mathematics Department Adelaide University South Australia meastwoo@maths.adelaide.edu.au, pnorbury@maths.adelaide.edu.au Abstract From any configuration of finitely many points in Euclidean three-space, Atiyah constructed a determinant and conjectured that it was always non-zero. In this article we prove the conjecture for the case of four points. AMS Classification numbers Primary: 5M04 Secondary: 70G25 Keywords Atiyah s conjecture, configuration space Proposed: Walter Neumann Received: 26 October 200 Seconded: Ralph Cohen, Steven Ferry Revised: 0 November 200 c Geometry & Topology Publications
2 886 Michael Eastwood and Paul Norbury Consider n distinct points in Euclidean three-space. Fixing attention on one of these points, the others give rise to n points on its sphere of vision. Thinking of this as the Riemann sphere gives a monic polynomial of degree n, having as its zeroes the points not equal to the point chosen to be. We may regard its coefficients as a complex n-vector (for degree d < n, its first n d coefficients are deemed to be zero). Repeating this exercise for each of the n points gives n such vectors and hence an n n matrix. In [, 2], Atiyah conjectured that a matrix constructed in this way cannot be singular. In [3], Atiyah and Sutcliffe amass a great deal of numerical evidence for this conjecture and formulate a series of further conjectures based on the geometry that their numerical studies apparently reveal. In spite of overwhelming evidence in its favour, the basic conjecture, as stated above, remains surprisingly resistant. The case n = 3 is not too hard: a geometric argument is given in [] and an algebraic one in [2]. In this article we establish the case n = 4. Normalisation In describing Atiyah s conjecture above we used only the directions defined by pairsof pointsamongst the n points. Itturnsout to befar morenatural to keep track of scale as well as direction, in particular in order to see what happens if we rotate the sphere of directions in R 3, obtaining a different identification with the Riemann sphere. We will use the Hopf mapping C 2 w w 2 h ( w 2 w 2 2 )/2 w w 2 R C = R 3 as follows. This mapping intertwines the action of SU(2) on C 2 with the action of SO(3) on R 3 and descends to an isomorphism from CP to the sphere of rays through the origin in R 3. Therefore, for each point in R 3 \{0}, we may choose a corresponding point in C 2 \{0} defined up to phase. Their symmetric tensor product lies in n C 2 = C n and is also well-defined up to phase. We may regard this as normalising, up to phase, the complex n-vectors appearing in our initial formulation of Atiyah s conjecture. If we now construct the columns of an n n matrix M in this way, then detm is well-defined up to phase and detm 2 is invariant under Euclidean motions.
3 Atiyah s Conjecture 887 Following Atiyah and Sutcliffe [3], we may normalize det M further. Consider the mapping C 2 w σ w 2 C 2, w 2 w observing that h(σ(w)) = h(w) for all w C 2. Also note that σ(e iθ w) = e iθ σ(w) and σ(σ(w)) = w. () Fix an ordering for our original n points in R 3. Each pair of these points contributestwice to detm, oncewhenthelater pointisviewed fromtheearlier and once when this view is reversed. We mandate using w and σ(w), respectively, in lifting to C 2. By virtue of (), both the phase ambiguity w e iθ w and the ordering ambiguity cancel from detm. In conclusion, detm is invariant under Euclidean motions. It is easy to check that detm is replaced by its complex conjugate under reflection. In particular, if all points lie in a plane then the determinant is real. For further details see [2, 3]. We shall call detm, normalised in this way, the Atiyah determinant. In [3] a scale invariant normalisation D is used. The two normalisations are related by detm = D (2r ij ) where r ij is the distance between the i th and j th points. We are free to use Euclidean motions to place points in convenient locations. Let us do this to verify the conjecture when n = 3, choosing the three points in R C to be 0 0 i>j 0 a 0 z with a real. They form a triangle with side lengths a, b = z, and c = a z. We may use the following a a h 0 b a a b h 0 z z a a a b z b h 0 a h 0 z c c z a a z c c h 0 z a h 0 a z
4 888 Michael Eastwood and Paul Norbury in computing detm. We obtain ab ac z(a z) abc a z +ab a( z a)+ac zc+b(a z) a z a( z a) bc where = a((z + z)(c a b)+2b(a+b+3c)) = (a 2 +b 2 c 2 )(c a b)+2ab(a+b+3c) = d 3 (a,b,c)+8abc, d 3 (a,b,c) = (a+b c)(b+c a)(c+a b). (2) The triangle inequalities imply that d 3 (a,b,c) 0 with equality if and only if the points lie on a line. Therefore detm 8abc > 0 and, in particular, is non-zero, as required. 2 The case n = 4 Theorem For any four points in R 3, the Atiyah determinant is non-zero. Proof Choose the four points in R 3 = R C to be r. z z 2 z 3 0 Put z ij = z i z j for i > j and label the distances between points by r ij. We define z 4 = 0 so that z 4j = z j. Thus, r 2 ij = z ij 2 for i < 4 and r 2 4j = r 2 + z 4j 2. For j < i < 4 the vector running from the j th point to the i th point may be lifted to w = r ij, with σ(w) = z ij. rij z ij rij r ij Similarly, if we put R 4j = r 4j +r for j < 4, then w = R4j R 4j z 4j and σ(w) = R4j z 4j R 4j lift to C 2 the vectors in R 3 joining the j th point to the 4 th point and vice versa. For each of the four points, the coefficients of the corresponding third
5 Atiyah s Conjecture 889 degree polynomial give the following four vectors: v = v 2 = v 4 = v 3 = r2 r 3 R 4 r32 R 42 r 2 R43 r 3 r 32 R4 R 42 R 43 r 2 r 3 R 4 r 2 r 3 z 4 +r 2 R 4 z 3 +r 3 R 4 z 2 r 2 z 3 z 4 +r 3 z 2 z 4 +R 4 z 2 z 3 z 2 z 3 z 4 r 32 R 42 z 2 r 32 z 2 z 42 +r 32 R 42 r 2 z 2 R 42 z 32 r 32 r 2 z 42 z 2 z 32 z 42 +R 42 z 32 r 2 z 32 r 2 z 42 z 3 z 32 R 43 z 3 z 32 z 43 z 3 R 43 r 32 z 32 R 43 r 3 z 3 r 32 z 43 z 32 r 3 z 43 +R 43 r 3 r 32 r 3 r 32 z 43 z 4 z 42 z 43 z 4 z 42 R 43 +z 4 z 43 R 42 +z 42 z 43 R 4 z 4 R 42 R 43 z 42 R 4 R 43 z 43 R 4 R 42 R 4 R 42 R 43 and we may take M to be the matrix with column vectors v i. Hence, detm = P/(r 2 r 3 r 32 R 4 R 42 R 43 ) where P is a polynomial consisting of monomials each of which contains one of r 2 ij, r ijz ij, r ij z ij, or z ij z ij for each j < i < 4, and one of R 2 4j, R 4jz 4j, R 4j z 4j, or z 4j z 4j. Since z ij z ij = r 2 ij, each monomial is divisible by r ij and, since z 4j 2 = R 4j (r 4j r), each monomial is divisible by R 4j. Therefore, we can divide by the factor of r 2 r 3 r 32 R 4 R 42 R 43 leaving monomials with one of r ij, z ij or z ij for each j < i < 4, and one of (r 4j +r), z 4j, z 4j or (r 4j r). It follows that detm is now expressed as a homogeneous degree 6 polynomial in r, r ij, z ij and z ij for j < i 4. Recall that det M is invariant under Euclidean motions. Moreover, the six distances r ij determine our configuration of four points. Also, notice that these distances are constrained only by triangle inequalities. Hence, the Atiyah determinant detm may be regarded as a function of the independent variables r ij. We claim that R(detM) is a polynomial in r ij (homogeneous of degree 6). detm 2 is a polynomial in r ij (homogeneous of degree 2).
6 890 Michael Eastwood and Paul Norbury Having done this we shall use the triangle inequalities on the four faces of our configuration to show that, in fact, R(detM) > 0. This is more than sufficient to finish the proof. It is convenient to set z ij = z ji and r ij = r ji when j > i. The monomials in our expression for detm contain an equal number of z ij and z kl. Consider the product z ij z kl. There are two cases: (i) {i,j} and {k,l} have an element in common (suppose l = j): z ij z kj = (/2) ( r 2 ij +r2 kj r2 ki) +2Aijk (3) where A ijk, defined by (3), equals plus or minus the area of the ijk th triangle under the projection R 3 = R C C onto the complex plane; (ii) {i,j,k,l} = {,2,3,4}: z ij z kl = z ij z kj z kj z kl /r 2 kj and we can rewrite the numerator as in (i). We claim that all quadratic expressions in the A ijk may be written as polynomials in the r ij and r 2. Specifically, when all four points lie in the complex plane, then one may verify that 6A ijk A ijl = 2r 2 ij (r2 ik +r2 il r2 kl ) (r2 ij +r2 ik r2 jk )(r2 ij +r2 il r2 jl ) (4) and when the fourth point lies off the plane (r > 0), we replace r 2 4j by r2 4j r2. Now, observe that our formulae so far for R(detM) and (I(detM)) 2 involve only quadratics expressions in A ijk. If we substitute according to (4) and its non-planar version, we obtain rational expressions for R(det M) and (I(detM)) 2 in the seven quantities in r ij and r, the denominator being a polynomial in the six variables r ij. Recall that a reflection such as r r conjugates detm. Hence, we may drop all odd powers of r in the numerators, to obtain polynomials in r ij and r 2. Finally, we eliminate r 2 from these expressions. This is possible by writing the volume V of the tetrahedron with vertices our four points in two different ways. On the one hand 44V 2 = r 4 2r 2 43 r 2 2r 4 43 r 2 32r 4 4 r 4 32r 2 4 r 4 3r 2 42 r 2 3r r 2 2r 2 43r 2 3 +r 2 2r 2 43r 2 4 r 2 2r 2 42r 2 4 +r 2 2r 2 42r r 2 2r 2 42r 2 3 +r 2 2r 2 32r 2 43 r 2 2r 2 32r 2 3 +r 2 32r 2 42r 2 4 +r 2 3 r2 42 r2 4 +r2 32 r2 43 r2 4 r2 32 r2 42 r2 43 +r2 32 r2 42 r2 3 +r 2 3 r2 42 r2 43 +r2 32 r2 3 r2 4 r2 3 r2 43 r2 4 +r2 2 r2 32 r2 4.
7 Atiyah s Conjecture 89 On the other hand, let A denote the area of the triangular base in C. Then 6A 2 = 2r 2 2r r 2 2r r 2 3r 2 32 r 4 2 r 4 3 r 4 32 and V = ra/3. We may therefore replace r 2 by 9V 2 /A 2, as required. Thus, we may conclude that R(detM) and (I(detM)) 2 are rational functions of the variables r ij but, if we now clear any common factors, we claim they are, in fact, polynomials. To see this, notice that in (ii) we had a choice when we introduced z kj z kj /rkj 2. We could have insisted that {k,j} {,2,3}. Then the denominators of R(detM) and (I(detM)) 2 would not involve r 4j. However, detm does not see the ordering of our four points. Hence, if r 4j are omitted from the denominators, then so are all variables r ij, as required. It remains to calculate these polynomials. We did this using Maple and found that R(detM) is a homogeneous polynomial of degree 6 with 226 terms and detm 2 is a homogeneous degree 2 polynomial with 4500 terms. We claim that R(detM) > 0. To see this, we can rewrite the output of the Maple calculation as follows: R(detM) = 64r 2 r 3 r 32 r 4 r 42 r 43 4d 3 (r 2 r 43,r 3 r 42,r 32 r 4 ) +2av ( r 4 ((r 42 +r 43 ) 2 r 2 32 )d 3(r 2,r 3,r 32 ) ) +288V 2. Here, d 3 (a,b,c) is the polynomial (2) and av denotes the operation of averaging a polynomial in r ij under the action of S 4 on the vertices of our tetrahedron: for example, av(r 2 ) = (r 2 +r 3 +r 32 +r 4 +r 42 +r 43 )/6 av(r 2 r 43 ) = (r 2 r 43 +r 3 r 42 +r 4 r 32 )/3. The final two terms are non-negative since the triangle inequality gives (r 42 +r 43 ) 2 r 2 32 and d 3 (r 2,r 3,r 32 ) 0, and the square of the volume is non-negative. To estimate the other terms we may use the easily verified inequality In conclusion, abc d 3 (a,b,c), a,b,c 0. R(detM) 60r 2 r 3 r 32 r 4 r 42 r 43 > 0, as required. This is nearly enough for a stronger conjecture of Atiyah and Sutcliffe [3, Conjecture 2] that detm 64r 2 r 3 r 32 r 4 r 42 r 43. The program is at: ftp://ftp.maths.adelaide.edu.au/meastwood/maple/points
8 892 Michael Eastwood and Paul Norbury A third conjecture of Atiyah and Sutcliffe [3, Conjecture 3] can be expressed in the four point case in terms of polynomials in the edge lengths as: detm 2 4 (d 3 (r ij,r ik,r jk )+8r ij r ik r jk ) where the product runs over the four faces of the tetrahedron and the left hand side is known explicitly. We have been unable to prove this conjecture even in the case that the four points lie in a plane (in which case detm can be replaced by the simpler expression R(det M) given above). 3 The planar case Atiyah s basic conjecture is unresolved in general, even when the n points lie in a plane (in which case recall that detm is real). Reasoning analogous to the case of four points gives the following. Theorem 2 The Atiyah determinant of n points in a plane can be expressed as a rational function in the distances between the points. Proof Again, we can express z ij z kl as a rational function in the r ij and A ijk. It is no longer true that quadratic expressions in the A ijk are polynomials in the r ij. Instead they are rational functions in the r ij. This uses the same trick of introducing new points in common between two triangles in order to apply (4): A ijk A lmn = (A ijka ijn )(A imn A lmn ) A ijn A imn. In the general four point case, the distances r ij acted as variables. The denominator was too small to be appropriately symmetrical and therefore had to divide the numerator, leaving a polynomial rather than a rational function. In the planar case (and also in the general case with more than four points), the distances between points satisfy a set of polynomial constraints. Symmetry arguments are no longer valid and expressions for the determinant are no longer unique. We suspect, however, that there is a polynomial expression. Acknowledgements Support from the Australian Research Council and the Mathematical Sciences Research Institute is gratefully acknowledged. Research at MSRI is supported in part by NSF grant DMS
9 Atiyah s Conjecture 893 References [] M F Atiyah, The geometry of classical particles, Surveys in Differential Geometry vol. 7, International Press (200) to appear [2] M F Atiyah, Configurations of points, Phil. Trans. Roy. Soc. Lond. A359(200) to appear [3] M F Atiyah, P M Sutcliffe, The geometry of point particles, hep-th/00579
A matrix over a field F is a rectangular array of elements from F. The symbol
 Chapter MATRICES Matrix arithmetic A matrix over a field F is a rectangular array of elements from F The symbol M m n (F ) denotes the collection of all m n matrices over F Matrices will usually be denoted
Chapter MATRICES Matrix arithmetic A matrix over a field F is a rectangular array of elements from F The symbol M m n (F ) denotes the collection of all m n matrices over F Matrices will usually be denoted
ELEMENTARY LINEAR ALGEBRA
 ELEMENTARY LINEAR ALGEBRA K R MATTHEWS DEPARTMENT OF MATHEMATICS UNIVERSITY OF QUEENSLAND First Printing, 99 Chapter LINEAR EQUATIONS Introduction to linear equations A linear equation in n unknowns x,
ELEMENTARY LINEAR ALGEBRA K R MATTHEWS DEPARTMENT OF MATHEMATICS UNIVERSITY OF QUEENSLAND First Printing, 99 Chapter LINEAR EQUATIONS Introduction to linear equations A linear equation in n unknowns x,
a 11 x 1 + a 12 x a 1n x n = b 1 a 21 x 1 + a 22 x a 2n x n = b 2.
 Chapter 1 LINEAR EQUATIONS 11 Introduction to linear equations A linear equation in n unknowns x 1, x,, x n is an equation of the form a 1 x 1 + a x + + a n x n = b, where a 1, a,, a n, b are given real
Chapter 1 LINEAR EQUATIONS 11 Introduction to linear equations A linear equation in n unknowns x 1, x,, x n is an equation of the form a 1 x 1 + a x + + a n x n = b, where a 1, a,, a n, b are given real
TRIANGLE CENTERS DEFINED BY QUADRATIC POLYNOMIALS
 Math. J. Okayama Univ. 53 (2011), 185 216 TRIANGLE CENTERS DEFINED BY QUADRATIC POLYNOMIALS Yoshio Agaoka Abstract. We consider a family of triangle centers whose barycentric coordinates are given by quadratic
Math. J. Okayama Univ. 53 (2011), 185 216 TRIANGLE CENTERS DEFINED BY QUADRATIC POLYNOMIALS Yoshio Agaoka Abstract. We consider a family of triangle centers whose barycentric coordinates are given by quadratic
The Matrix Representation of a Three-Dimensional Rotation Revisited
 Physics 116A Winter 2010 The Matrix Representation of a Three-Dimensional Rotation Revisited In a handout entitled The Matrix Representation of a Three-Dimensional Rotation, I provided a derivation of
Physics 116A Winter 2010 The Matrix Representation of a Three-Dimensional Rotation Revisited In a handout entitled The Matrix Representation of a Three-Dimensional Rotation, I provided a derivation of
Linear Algebra. Min Yan
 Linear Algebra Min Yan January 2, 2018 2 Contents 1 Vector Space 7 1.1 Definition................................. 7 1.1.1 Axioms of Vector Space..................... 7 1.1.2 Consequence of Axiom......................
Linear Algebra Min Yan January 2, 2018 2 Contents 1 Vector Space 7 1.1 Definition................................. 7 1.1.1 Axioms of Vector Space..................... 7 1.1.2 Consequence of Axiom......................
Proof of Atiyah's conjecture for two special types of configurations
 Electronic Journal of Linear Algebra Volume 9 Volume 9 (2002) Article 14 2002 Proof of Atiyah's conjecture for two special types of configurations Dragomir Z. Djokovic dragomir@herod.uwaterloo.ca Follow
Electronic Journal of Linear Algebra Volume 9 Volume 9 (2002) Article 14 2002 Proof of Atiyah's conjecture for two special types of configurations Dragomir Z. Djokovic dragomir@herod.uwaterloo.ca Follow
Chapter 12. The cross ratio Klein s Erlanger program The projective line. Math 4520, Fall 2017
 Chapter 12 The cross ratio Math 4520, Fall 2017 We have studied the collineations of a projective plane, the automorphisms of the underlying field, the linear functions of Affine geometry, etc. We have
Chapter 12 The cross ratio Math 4520, Fall 2017 We have studied the collineations of a projective plane, the automorphisms of the underlying field, the linear functions of Affine geometry, etc. We have
Clifford Algebras and Spin Groups
 Clifford Algebras and Spin Groups Math G4344, Spring 2012 We ll now turn from the general theory to examine a specific class class of groups: the orthogonal groups. Recall that O(n, R) is the group of
Clifford Algebras and Spin Groups Math G4344, Spring 2012 We ll now turn from the general theory to examine a specific class class of groups: the orthogonal groups. Recall that O(n, R) is the group of
1 Differentiable manifolds and smooth maps. (Solutions)
 1 Differentiable manifolds and smooth maps Solutions Last updated: March 17 2011 Problem 1 The state of the planar pendulum is entirely defined by the position of its moving end in the plane R 2 Since
1 Differentiable manifolds and smooth maps Solutions Last updated: March 17 2011 Problem 1 The state of the planar pendulum is entirely defined by the position of its moving end in the plane R 2 Since
The moduli space of binary quintics
 The moduli space of binary quintics A.A.du Plessis and C.T.C.Wall November 10, 2005 1 Invariant theory From classical invariant theory (we refer to the version in [2]), we find that the ring of (SL 2 )invariants
The moduli space of binary quintics A.A.du Plessis and C.T.C.Wall November 10, 2005 1 Invariant theory From classical invariant theory (we refer to the version in [2]), we find that the ring of (SL 2 )invariants
QUATERNIONS AND ROTATIONS
 QUATERNIONS AND ROTATIONS SVANTE JANSON 1. Introduction The purpose of this note is to show some well-known relations between quaternions and the Lie groups SO(3) and SO(4) (rotations in R 3 and R 4 )
QUATERNIONS AND ROTATIONS SVANTE JANSON 1. Introduction The purpose of this note is to show some well-known relations between quaternions and the Lie groups SO(3) and SO(4) (rotations in R 3 and R 4 )
Quivers of Period 2. Mariya Sardarli Max Wimberley Heyi Zhu. November 26, 2014
 Quivers of Period 2 Mariya Sardarli Max Wimberley Heyi Zhu ovember 26, 2014 Abstract A quiver with vertices labeled from 1,..., n is said to have period 2 if the quiver obtained by mutating at 1 and then
Quivers of Period 2 Mariya Sardarli Max Wimberley Heyi Zhu ovember 26, 2014 Abstract A quiver with vertices labeled from 1,..., n is said to have period 2 if the quiver obtained by mutating at 1 and then
THE ENVELOPE OF LINES MEETING A FIXED LINE AND TANGENT TO TWO SPHERES
 6 September 2004 THE ENVELOPE OF LINES MEETING A FIXED LINE AND TANGENT TO TWO SPHERES Abstract. We study the set of lines that meet a fixed line and are tangent to two spheres and classify the configurations
6 September 2004 THE ENVELOPE OF LINES MEETING A FIXED LINE AND TANGENT TO TWO SPHERES Abstract. We study the set of lines that meet a fixed line and are tangent to two spheres and classify the configurations
1 Differentiable manifolds and smooth maps. (Solutions)
 1 Differentiable manifolds and smooth maps Solutions Last updated: February 16 2012 Problem 1 a The projection maps a point P x y S 1 to the point P u 0 R 2 the intersection of the line NP with the x-axis
1 Differentiable manifolds and smooth maps Solutions Last updated: February 16 2012 Problem 1 a The projection maps a point P x y S 1 to the point P u 0 R 2 the intersection of the line NP with the x-axis
Algebra I. Course Outline
 Algebra I Course Outline I. The Language of Algebra A. Variables and Expressions B. Order of Operations C. Open Sentences D. Identity and Equality Properties E. The Distributive Property F. Commutative
Algebra I Course Outline I. The Language of Algebra A. Variables and Expressions B. Order of Operations C. Open Sentences D. Identity and Equality Properties E. The Distributive Property F. Commutative
Homework set 5 - Solutions
 Homework set 5 - Solutions Math 469 Renato Feres 1. Hall s textbook, Exercise 4.9.2, page 105. Show the following: (a) The adjoint representation and the standard representation are isomorphic representations
Homework set 5 - Solutions Math 469 Renato Feres 1. Hall s textbook, Exercise 4.9.2, page 105. Show the following: (a) The adjoint representation and the standard representation are isomorphic representations
ELEMENTARY LINEAR ALGEBRA
 ELEMENTARY LINEAR ALGEBRA K. R. MATTHEWS DEPARTMENT OF MATHEMATICS UNIVERSITY OF QUEENSLAND Second Online Version, December 1998 Comments to the author at krm@maths.uq.edu.au Contents 1 LINEAR EQUATIONS
ELEMENTARY LINEAR ALGEBRA K. R. MATTHEWS DEPARTMENT OF MATHEMATICS UNIVERSITY OF QUEENSLAND Second Online Version, December 1998 Comments to the author at krm@maths.uq.edu.au Contents 1 LINEAR EQUATIONS
GROUP THEORY PRIMER. New terms: so(2n), so(2n+1), symplectic algebra sp(2n)
 GROUP THEORY PRIMER New terms: so(2n), so(2n+1), symplectic algebra sp(2n) 1. Some examples of semi-simple Lie algebras In the previous chapter, we developed the idea of understanding semi-simple Lie algebras
GROUP THEORY PRIMER New terms: so(2n), so(2n+1), symplectic algebra sp(2n) 1. Some examples of semi-simple Lie algebras In the previous chapter, we developed the idea of understanding semi-simple Lie algebras
MTH 1310, SUMMER 2012 DR. GRAHAM-SQUIRE. A rational expression is just a fraction involving polynomials, for example 3x2 2
 MTH 1310, SUMMER 2012 DR. GRAHAM-SQUIRE SECTION 1.2: PRECALCULUS REVIEW II Practice: 3, 7, 13, 17, 19, 23, 29, 33, 43, 45, 51, 57, 69, 81, 89 1. Rational Expressions and Other Algebraic Fractions A rational
MTH 1310, SUMMER 2012 DR. GRAHAM-SQUIRE SECTION 1.2: PRECALCULUS REVIEW II Practice: 3, 7, 13, 17, 19, 23, 29, 33, 43, 45, 51, 57, 69, 81, 89 1. Rational Expressions and Other Algebraic Fractions A rational
(x 1, y 1 ) = (x 2, y 2 ) if and only if x 1 = x 2 and y 1 = y 2.
 1. Complex numbers A complex number z is defined as an ordered pair z = (x, y), where x and y are a pair of real numbers. In usual notation, we write z = x + iy, where i is a symbol. The operations of
1. Complex numbers A complex number z is defined as an ordered pair z = (x, y), where x and y are a pair of real numbers. In usual notation, we write z = x + iy, where i is a symbol. The operations of
Hyperbolic Transformations
 C H A P T E R 17 Hyperbolic Transformations Though the text of your article on Crystal Symmetry and Its Generalizations is much too learned for a simple, selfmade pattern man like me, some of the text-illustrations
C H A P T E R 17 Hyperbolic Transformations Though the text of your article on Crystal Symmetry and Its Generalizations is much too learned for a simple, selfmade pattern man like me, some of the text-illustrations
10. Cartan Weyl basis
 10. Cartan Weyl basis 1 10. Cartan Weyl basis From this point on, the discussion will be restricted to semi-simple Lie algebras, which are the ones of principal interest in physics. In dealing with the
10. Cartan Weyl basis 1 10. Cartan Weyl basis From this point on, the discussion will be restricted to semi-simple Lie algebras, which are the ones of principal interest in physics. In dealing with the
PHYS 705: Classical Mechanics. Rigid Body Motion Introduction + Math Review
 1 PHYS 705: Classical Mechanics Rigid Body Motion Introduction + Math Review 2 How to describe a rigid body? Rigid Body - a system of point particles fixed in space i r ij j subject to a holonomic constraint:
1 PHYS 705: Classical Mechanics Rigid Body Motion Introduction + Math Review 2 How to describe a rigid body? Rigid Body - a system of point particles fixed in space i r ij j subject to a holonomic constraint:
CHAPTER 8. Smoothing operators
 CHAPTER 8 Smoothing operators Lecture 8: 13 October, 2005 Now I am heading towards the Atiyah-Singer index theorem. Most of the results proved in the process untimately reduce to properties of smoothing
CHAPTER 8 Smoothing operators Lecture 8: 13 October, 2005 Now I am heading towards the Atiyah-Singer index theorem. Most of the results proved in the process untimately reduce to properties of smoothing
THE HOMOTOPY TYPE OF THE SPACE OF RATIONAL FUNCTIONS
 THE HOMOTOPY TYPE OF THE SPACE OF RATIONAL FUNCTIONS by M.A. Guest, A. Kozlowski, M. Murayama and K. Yamaguchi In this note we determine some homotopy groups of the space of rational functions of degree
THE HOMOTOPY TYPE OF THE SPACE OF RATIONAL FUNCTIONS by M.A. Guest, A. Kozlowski, M. Murayama and K. Yamaguchi In this note we determine some homotopy groups of the space of rational functions of degree
SOME SPECIAL KLEINIAN GROUPS AND THEIR ORBIFOLDS
 Proyecciones Vol. 21, N o 1, pp. 21-50, May 2002. Universidad Católica del Norte Antofagasta - Chile SOME SPECIAL KLEINIAN GROUPS AND THEIR ORBIFOLDS RUBÉN HIDALGO Universidad Técnica Federico Santa María
Proyecciones Vol. 21, N o 1, pp. 21-50, May 2002. Universidad Católica del Norte Antofagasta - Chile SOME SPECIAL KLEINIAN GROUPS AND THEIR ORBIFOLDS RUBÉN HIDALGO Universidad Técnica Federico Santa María
Algebra 1.5 Year Long. Content Skills Learning Targets Assessment Resources & Technology CEQ: Chapters 1 2 Review
 St. Michael Albertville High School Teacher: Mindi Sechser Algebra 1.5 Year Long August 2015 CEQ: Chapters 1 2 Review Variables, Function A. Simplification of Patterns, and Graphs Expressions LT1. I can
St. Michael Albertville High School Teacher: Mindi Sechser Algebra 1.5 Year Long August 2015 CEQ: Chapters 1 2 Review Variables, Function A. Simplification of Patterns, and Graphs Expressions LT1. I can
The complex projective line
 17 The complex projective line Now we will to study the simplest case of a complex projective space: the complex projective line. We will see that even this case has already very rich geometric interpretations.
17 The complex projective line Now we will to study the simplest case of a complex projective space: the complex projective line. We will see that even this case has already very rich geometric interpretations.
GROUP THEORY PRIMER. New terms: tensor, rank k tensor, Young tableau, Young diagram, hook, hook length, factors over hooks rule
 GROUP THEORY PRIMER New terms: tensor, rank k tensor, Young tableau, Young diagram, hook, hook length, factors over hooks rule 1. Tensor methods for su(n) To study some aspects of representations of a
GROUP THEORY PRIMER New terms: tensor, rank k tensor, Young tableau, Young diagram, hook, hook length, factors over hooks rule 1. Tensor methods for su(n) To study some aspects of representations of a
Study Guide for Math 095
 Study Guide for Math 095 David G. Radcliffe November 7, 1994 1 The Real Number System Writing a fraction in lowest terms. 1. Find the largest number that will divide into both the numerator and the denominator.
Study Guide for Math 095 David G. Radcliffe November 7, 1994 1 The Real Number System Writing a fraction in lowest terms. 1. Find the largest number that will divide into both the numerator and the denominator.
Partial Fraction Decompositions
 Partial Fraction Rational Functions Partial Fraction Finding Partial Fractions Integrating Partial Fraction Eamples Rational Functions Definition Eample A function of the type P/Q, where both P and Q are
Partial Fraction Rational Functions Partial Fraction Finding Partial Fractions Integrating Partial Fraction Eamples Rational Functions Definition Eample A function of the type P/Q, where both P and Q are
Three Descriptions of the Cohomology of Bun G (X) (Lecture 4)
 Three Descriptions of the Cohomology of Bun G (X) (Lecture 4) February 5, 2014 Let k be an algebraically closed field, let X be a algebraic curve over k (always assumed to be smooth and complete), and
Three Descriptions of the Cohomology of Bun G (X) (Lecture 4) February 5, 2014 Let k be an algebraically closed field, let X be a algebraic curve over k (always assumed to be smooth and complete), and
Mathematics that Every Physicist should Know: Scalar, Vector, and Tensor Fields in the Space of Real n- Dimensional Independent Variable with Metric
 Mathematics that Every Physicist should Know: Scalar, Vector, and Tensor Fields in the Space of Real n- Dimensional Independent Variable with Metric By Y. N. Keilman AltSci@basicisp.net Every physicist
Mathematics that Every Physicist should Know: Scalar, Vector, and Tensor Fields in the Space of Real n- Dimensional Independent Variable with Metric By Y. N. Keilman AltSci@basicisp.net Every physicist
Linear Algebra March 16, 2019
 Linear Algebra March 16, 2019 2 Contents 0.1 Notation................................ 4 1 Systems of linear equations, and matrices 5 1.1 Systems of linear equations..................... 5 1.2 Augmented
Linear Algebra March 16, 2019 2 Contents 0.1 Notation................................ 4 1 Systems of linear equations, and matrices 5 1.1 Systems of linear equations..................... 5 1.2 Augmented
18.06 Professor Johnson Quiz 1 October 3, 2007
 18.6 Professor Johnson Quiz 1 October 3, 7 SOLUTIONS 1 3 pts.) A given circuit network directed graph) which has an m n incidence matrix A rows = edges, columns = nodes) and a conductance matrix C [diagonal
18.6 Professor Johnson Quiz 1 October 3, 7 SOLUTIONS 1 3 pts.) A given circuit network directed graph) which has an m n incidence matrix A rows = edges, columns = nodes) and a conductance matrix C [diagonal
Limits of Functions (a, L)
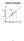 Limits of Functions f(x) (a, L) L f(x) x a x x 20 Informal Definition: If the values of can be made as close to as we like by taking values of sufficiently close to [but not equal to ] then we write or
Limits of Functions f(x) (a, L) L f(x) x a x x 20 Informal Definition: If the values of can be made as close to as we like by taking values of sufficiently close to [but not equal to ] then we write or
Algebra 1.5. Content Skills Learning Targets Assessment Resources & Technology CEQ:
 St. Michael Albertville High School Teacher: Mindi Sechser Algebra 1.5 September 2015 Content Skills Learning Targets Assessment Resources & Technology CEQ: Chapters 1 3 Review Variables, Function Patterns,
St. Michael Albertville High School Teacher: Mindi Sechser Algebra 1.5 September 2015 Content Skills Learning Targets Assessment Resources & Technology CEQ: Chapters 1 3 Review Variables, Function Patterns,
In Z: x + 3 = 2 3x = 2 x = 1 No solution In Q: 3x = 2 x 2 = 2. x = 2 No solution. In R: x 2 = 2 x = 0 x = ± 2 No solution Z Q.
 THE UNIVERSITY OF NEW SOUTH WALES SCHOOL OF MATHEMATICS AND STATISTICS MATH 1141 HIGHER MATHEMATICS 1A ALGEBRA. Section 1: - Complex Numbers. 1. The Number Systems. Let us begin by trying to solve various
THE UNIVERSITY OF NEW SOUTH WALES SCHOOL OF MATHEMATICS AND STATISTICS MATH 1141 HIGHER MATHEMATICS 1A ALGEBRA. Section 1: - Complex Numbers. 1. The Number Systems. Let us begin by trying to solve various
5.1 Monomials. Algebra 2
 . Monomials Algebra Goal : A..: Add, subtract, multiply, and simplify polynomials and rational expressions (e.g., multiply (x ) ( x + ); simplify 9x x. x Goal : Write numbers in scientific notation. Scientific
. Monomials Algebra Goal : A..: Add, subtract, multiply, and simplify polynomials and rational expressions (e.g., multiply (x ) ( x + ); simplify 9x x. x Goal : Write numbers in scientific notation. Scientific
Chapter 10: Rational Functions and the Riemann Sphere. By a rational function we mean a function f which can be expressed in the form
 Chapter 10: Rational Functions and the Riemann Sphere By a rational function we mean a function f which can be expressed in the form f(z) = p(z) q(z) = a nz n +a n 1 z n 1 + +a 1 z +a 0 b m z m +b m 1
Chapter 10: Rational Functions and the Riemann Sphere By a rational function we mean a function f which can be expressed in the form f(z) = p(z) q(z) = a nz n +a n 1 z n 1 + +a 1 z +a 0 b m z m +b m 1
PURE Math Residents Program Gröbner Bases and Applications Week 3 Lectures
 PURE Math Residents Program Gröbner Bases and Applications Week 3 Lectures John B. Little Department of Mathematics and Computer Science College of the Holy Cross June 2012 Overview of this week The research
PURE Math Residents Program Gröbner Bases and Applications Week 3 Lectures John B. Little Department of Mathematics and Computer Science College of the Holy Cross June 2012 Overview of this week The research
5.3 The Upper Half Plane
 Remark. Combining Schwarz Lemma with the map g α, we can obtain some inequalities of analytic maps f : D D. For example, if z D and w = f(z) D, then the composition h := g w f g z satisfies the condition
Remark. Combining Schwarz Lemma with the map g α, we can obtain some inequalities of analytic maps f : D D. For example, if z D and w = f(z) D, then the composition h := g w f g z satisfies the condition
ELEMENTARY LINEAR ALGEBRA
 ELEMENTARY LINEAR ALGEBRA K R MATTHEWS DEPARTMENT OF MATHEMATICS UNIVERSITY OF QUEENSLAND Second Online Version, December 998 Comments to the author at krm@mathsuqeduau All contents copyright c 99 Keith
ELEMENTARY LINEAR ALGEBRA K R MATTHEWS DEPARTMENT OF MATHEMATICS UNIVERSITY OF QUEENSLAND Second Online Version, December 998 Comments to the author at krm@mathsuqeduau All contents copyright c 99 Keith
Dr. Relja Vulanovic Professor of Mathematics Kent State University at Stark c 2008
 MATH-LITERACY MANUAL Dr. Relja Vulanovic Professor of Mathematics Kent State University at Stark c 2008 2 Algebraic Epressions 2.1 Terms and Factors 29 2.2 Types of Algebraic Epressions 32 2.3 Transforming
MATH-LITERACY MANUAL Dr. Relja Vulanovic Professor of Mathematics Kent State University at Stark c 2008 2 Algebraic Epressions 2.1 Terms and Factors 29 2.2 Types of Algebraic Epressions 32 2.3 Transforming
1 Euclidean geometry. 1.1 The metric on R n
 1 Euclidean geometry This chapter discusses the geometry of n-dimensional Euclidean space E n, together with its distance function. The distance gives rise to other notions such as angles and congruent
1 Euclidean geometry This chapter discusses the geometry of n-dimensional Euclidean space E n, together with its distance function. The distance gives rise to other notions such as angles and congruent
ALGEBRAIC EXPRESSIONS AND POLYNOMIALS
 MODULE - ic Epressions and Polynomials ALGEBRAIC EXPRESSIONS AND POLYNOMIALS So far, you had been using arithmetical numbers, which included natural numbers, whole numbers, fractional numbers, etc. and
MODULE - ic Epressions and Polynomials ALGEBRAIC EXPRESSIONS AND POLYNOMIALS So far, you had been using arithmetical numbers, which included natural numbers, whole numbers, fractional numbers, etc. and
Quantum Symmetries in Free Probability Theory. Roland Speicher Queen s University Kingston, Canada
 Quantum Symmetries in Free Probability Theory Roland Speicher Queen s University Kingston, Canada Quantum Groups are generalizations of groups G (actually, of C(G)) are supposed to describe non-classical
Quantum Symmetries in Free Probability Theory Roland Speicher Queen s University Kingston, Canada Quantum Groups are generalizations of groups G (actually, of C(G)) are supposed to describe non-classical
nx ~p Us x Uns2"'-1,» i
 PROCEEDINGS OF THE AMERICAN MATHEMATICAL SOCIETY Volume 96, Number 4, April 1986 LOOP SPACES OF FINITE COMPLEXES AT LARGE PRIMES C. A. MCGIBBON AND C. W. WILKERSON1 ABSTRACT. Let X be a finite, simply
PROCEEDINGS OF THE AMERICAN MATHEMATICAL SOCIETY Volume 96, Number 4, April 1986 LOOP SPACES OF FINITE COMPLEXES AT LARGE PRIMES C. A. MCGIBBON AND C. W. WILKERSON1 ABSTRACT. Let X be a finite, simply
Construction of `Wachspress type' rational basis functions over rectangles
 Proc. Indian Acad. Sci. (Math. Sci.), Vol. 110, No. 1, February 2000, pp. 69±77. # Printed in India Construction of `Wachspress type' rational basis functions over rectangles P L POWAR and S S RANA Department
Proc. Indian Acad. Sci. (Math. Sci.), Vol. 110, No. 1, February 2000, pp. 69±77. # Printed in India Construction of `Wachspress type' rational basis functions over rectangles P L POWAR and S S RANA Department
A GEOMETRIC VIEW OF RATIONAL LANDEN TRANSFORMATIONS
 Bull. London Math. Soc. 35 (3 93 3 C 3 London Mathematical Society DOI:./S4693393 A GEOMETRIC VIEW OF RATIONAL LANDEN TRANSFORMATIONS JOHN HUBBARD and VICTOR MOLL Abstract In this paper, a geometric interpretation
Bull. London Math. Soc. 35 (3 93 3 C 3 London Mathematical Society DOI:./S4693393 A GEOMETRIC VIEW OF RATIONAL LANDEN TRANSFORMATIONS JOHN HUBBARD and VICTOR MOLL Abstract In this paper, a geometric interpretation
SUMS PROBLEM COMPETITION, 2000
 SUMS ROBLEM COMETITION, 2000 SOLUTIONS 1 The result is well known, and called Morley s Theorem Many proofs are known See for example HSM Coxeter, Introduction to Geometry, page 23 2 If the number of vertices,
SUMS ROBLEM COMETITION, 2000 SOLUTIONS 1 The result is well known, and called Morley s Theorem Many proofs are known See for example HSM Coxeter, Introduction to Geometry, page 23 2 If the number of vertices,
Math 3108: Linear Algebra
 Math 3108: Linear Algebra Instructor: Jason Murphy Department of Mathematics and Statistics Missouri University of Science and Technology 1 / 323 Contents. Chapter 1. Slides 3 70 Chapter 2. Slides 71 118
Math 3108: Linear Algebra Instructor: Jason Murphy Department of Mathematics and Statistics Missouri University of Science and Technology 1 / 323 Contents. Chapter 1. Slides 3 70 Chapter 2. Slides 71 118
h-vectors OF SMALL MATROID COMPLEXES
 h-vectors OF SMALL MATROID COMPLEXES JESÚS A. DE LOERA, YVONNE KEMPER, STEVEN KLEE Abstract. Stanley conjectured in 1977 that the h-vector of a matroid simplicial complex is a pure O-sequence. We give
h-vectors OF SMALL MATROID COMPLEXES JESÚS A. DE LOERA, YVONNE KEMPER, STEVEN KLEE Abstract. Stanley conjectured in 1977 that the h-vector of a matroid simplicial complex is a pure O-sequence. We give
4. Noether normalisation
 4. Noether normalisation We shall say that a ring R is an affine ring (or affine k-algebra) if R is isomorphic to a polynomial ring over a field k with finitely many indeterminates modulo an ideal, i.e.,
4. Noether normalisation We shall say that a ring R is an affine ring (or affine k-algebra) if R is isomorphic to a polynomial ring over a field k with finitely many indeterminates modulo an ideal, i.e.,
Again we return to a row of 1 s! Furthermore, all the entries are positive integers.
 Lecture Notes Introduction to Cluster Algebra Ivan C.H. Ip Updated: April 4, 207 Examples. Conway-Coxeter frieze pattern Frieze is the wide central section part of an entablature, often seen in Greek temples,
Lecture Notes Introduction to Cluster Algebra Ivan C.H. Ip Updated: April 4, 207 Examples. Conway-Coxeter frieze pattern Frieze is the wide central section part of an entablature, often seen in Greek temples,
Power sums and Homfly skein theory
 ISSN 1464-8997 (on line) 1464-8989 (printed) 235 Geometry & Topology Monographs Volume 4: Invariants of knots and 3-manifolds (Kyoto 2001) Pages 235 244 Power sums and Homfly skein theory Hugh R. Morton
ISSN 1464-8997 (on line) 1464-8989 (printed) 235 Geometry & Topology Monographs Volume 4: Invariants of knots and 3-manifolds (Kyoto 2001) Pages 235 244 Power sums and Homfly skein theory Hugh R. Morton
CSC Linear Programming and Combinatorial Optimization Lecture 12: The Lift and Project Method
 CSC2411 - Linear Programming and Combinatorial Optimization Lecture 12: The Lift and Project Method Notes taken by Stefan Mathe April 28, 2007 Summary: Throughout the course, we have seen the importance
CSC2411 - Linear Programming and Combinatorial Optimization Lecture 12: The Lift and Project Method Notes taken by Stefan Mathe April 28, 2007 Summary: Throughout the course, we have seen the importance
Spring Nikos Apostolakis
 Spring 07 Nikos Apostolakis Review of fractions Rational expressions are fractions with numerator and denominator polynomials. We need to remember how we work with fractions (a.k.a. rational numbers) before
Spring 07 Nikos Apostolakis Review of fractions Rational expressions are fractions with numerator and denominator polynomials. We need to remember how we work with fractions (a.k.a. rational numbers) before
ON TOTALLY REAL SUBMANIFOLDS IN A NEARLY KÄHLER MANIFOLD *
 PORTUGALIAE MATHEMATICA Vol. 58 Fasc. 2 2001 Nova Série ON TOTALLY REAL SUBMANIFOLDS IN A NEARLY KÄHLER MANIFOLD * Zhong Hua Hou Abstract: Let M m be a totally real submanifold of a nearly Kähler manifold
PORTUGALIAE MATHEMATICA Vol. 58 Fasc. 2 2001 Nova Série ON TOTALLY REAL SUBMANIFOLDS IN A NEARLY KÄHLER MANIFOLD * Zhong Hua Hou Abstract: Let M m be a totally real submanifold of a nearly Kähler manifold
1.1.1 Algebraic Operations
 1.1.1 Algebraic Operations We need to learn how our basic algebraic operations interact. When confronted with many operations, we follow the order of operations: Parentheses Exponentials Multiplication
1.1.1 Algebraic Operations We need to learn how our basic algebraic operations interact. When confronted with many operations, we follow the order of operations: Parentheses Exponentials Multiplication
Instructional Unit Basic Statistics Algebra II #309 Unit Content Objective Performance Indicator Performance Task State Standards Code:
 Algebra II Instructional Unit Basic Statistics -Displaying data with dotplots and The students will be -Use scientific or graphing -Classroom discussion 2.1.11.A stemplots. able to evaluate calculator
Algebra II Instructional Unit Basic Statistics -Displaying data with dotplots and The students will be -Use scientific or graphing -Classroom discussion 2.1.11.A stemplots. able to evaluate calculator
Quadratics. Shawn Godin. Cairine Wilson S.S Orleans, ON October 14, 2017
 Quadratics Shawn Godin Cairine Wilson S.S Orleans, ON Shawn.Godin@ocdsb.ca October 14, 2017 Shawn Godin (Cairine Wilson S.S.) Quadratics October 14, 2017 1 / 110 Binary Quadratic Form A form is a homogeneous
Quadratics Shawn Godin Cairine Wilson S.S Orleans, ON Shawn.Godin@ocdsb.ca October 14, 2017 Shawn Godin (Cairine Wilson S.S.) Quadratics October 14, 2017 1 / 110 Binary Quadratic Form A form is a homogeneous
EXPONENT REVIEW!!! Concept Byte (Review): Properties of Exponents. Property of Exponents: Product of Powers. x m x n = x m + n
 Algebra B: Chapter 6 Notes 1 EXPONENT REVIEW!!! Concept Byte (Review): Properties of Eponents Recall from Algebra 1, the Properties (Rules) of Eponents. Property of Eponents: Product of Powers m n = m
Algebra B: Chapter 6 Notes 1 EXPONENT REVIEW!!! Concept Byte (Review): Properties of Eponents Recall from Algebra 1, the Properties (Rules) of Eponents. Property of Eponents: Product of Powers m n = m
Dot Products, Transposes, and Orthogonal Projections
 Dot Products, Transposes, and Orthogonal Projections David Jekel November 13, 2015 Properties of Dot Products Recall that the dot product or standard inner product on R n is given by x y = x 1 y 1 + +
Dot Products, Transposes, and Orthogonal Projections David Jekel November 13, 2015 Properties of Dot Products Recall that the dot product or standard inner product on R n is given by x y = x 1 y 1 + +
Extra Problems for Math 2050 Linear Algebra I
 Extra Problems for Math 5 Linear Algebra I Find the vector AB and illustrate with a picture if A = (,) and B = (,4) Find B, given A = (,4) and [ AB = A = (,4) and [ AB = 8 If possible, express x = 7 as
Extra Problems for Math 5 Linear Algebra I Find the vector AB and illustrate with a picture if A = (,) and B = (,4) Find B, given A = (,4) and [ AB = A = (,4) and [ AB = 8 If possible, express x = 7 as
Lecture 13 The Fundamental Forms of a Surface
 Lecture 13 The Fundamental Forms of a Surface In the following we denote by F : O R 3 a parametric surface in R 3, F(u, v) = (x(u, v), y(u, v), z(u, v)). We denote partial derivatives with respect to the
Lecture 13 The Fundamental Forms of a Surface In the following we denote by F : O R 3 a parametric surface in R 3, F(u, v) = (x(u, v), y(u, v), z(u, v)). We denote partial derivatives with respect to the
Intrinsic products and factorizations of matrices
 Available online at www.sciencedirect.com Linear Algebra and its Applications 428 (2008) 5 3 www.elsevier.com/locate/laa Intrinsic products and factorizations of matrices Miroslav Fiedler Academy of Sciences
Available online at www.sciencedirect.com Linear Algebra and its Applications 428 (2008) 5 3 www.elsevier.com/locate/laa Intrinsic products and factorizations of matrices Miroslav Fiedler Academy of Sciences
APPENDIX A. Background Mathematics. A.1 Linear Algebra. Vector algebra. Let x denote the n-dimensional column vector with components x 1 x 2.
 APPENDIX A Background Mathematics A. Linear Algebra A.. Vector algebra Let x denote the n-dimensional column vector with components 0 x x 2 B C @. A x n Definition 6 (scalar product). The scalar product
APPENDIX A Background Mathematics A. Linear Algebra A.. Vector algebra Let x denote the n-dimensional column vector with components 0 x x 2 B C @. A x n Definition 6 (scalar product). The scalar product
22m:033 Notes: 3.1 Introduction to Determinants
 22m:033 Notes: 3. Introduction to Determinants Dennis Roseman University of Iowa Iowa City, IA http://www.math.uiowa.edu/ roseman October 27, 2009 When does a 2 2 matrix have an inverse? ( ) a a If A =
22m:033 Notes: 3. Introduction to Determinants Dennis Roseman University of Iowa Iowa City, IA http://www.math.uiowa.edu/ roseman October 27, 2009 When does a 2 2 matrix have an inverse? ( ) a a If A =
LESSON 9.1 ROOTS AND RADICALS
 LESSON 9.1 ROOTS AND RADICALS LESSON 9.1 ROOTS AND RADICALS 67 OVERVIEW Here s what you ll learn in this lesson: Square Roots and Cube Roots a. Definition of square root and cube root b. Radicand, radical
LESSON 9.1 ROOTS AND RADICALS LESSON 9.1 ROOTS AND RADICALS 67 OVERVIEW Here s what you ll learn in this lesson: Square Roots and Cube Roots a. Definition of square root and cube root b. Radicand, radical
Permutations and Polynomials Sarah Kitchen February 7, 2006
 Permutations and Polynomials Sarah Kitchen February 7, 2006 Suppose you are given the equations x + y + z = a and 1 x + 1 y + 1 z = 1 a, and are asked to prove that one of x,y, and z is equal to a. We
Permutations and Polynomials Sarah Kitchen February 7, 2006 Suppose you are given the equations x + y + z = a and 1 x + 1 y + 1 z = 1 a, and are asked to prove that one of x,y, and z is equal to a. We
a. Define a function called an inner product on pairs of points x = (x 1, x 2,..., x n ) and y = (y 1, y 2,..., y n ) in R n by
 Real Analysis Homework 1 Solutions 1. Show that R n with the usual euclidean distance is a metric space. Items a-c will guide you through the proof. a. Define a function called an inner product on pairs
Real Analysis Homework 1 Solutions 1. Show that R n with the usual euclidean distance is a metric space. Items a-c will guide you through the proof. a. Define a function called an inner product on pairs
A geometric interpretation of Milnor s triple linking numbers
 ISSN 1472-2739 (on-line) 1472-2747 (printed) 557 Algebraic & Geometric Topology Volume 3 (2003) 557 568 Published: 19 June 2003 ATG A geometric interpretation of Milnor s triple linking numbers Blake Mellor
ISSN 1472-2739 (on-line) 1472-2747 (printed) 557 Algebraic & Geometric Topology Volume 3 (2003) 557 568 Published: 19 June 2003 ATG A geometric interpretation of Milnor s triple linking numbers Blake Mellor
MATHEMATICS Lecture. 4 Chapter.8 TECHNIQUES OF INTEGRATION By Dr. Mohammed Ramidh
 MATHEMATICS Lecture. 4 Chapter.8 TECHNIQUES OF INTEGRATION By TECHNIQUES OF INTEGRATION OVERVIEW The Fundamental Theorem connects antiderivatives and the definite integral. Evaluating the indefinite integral,
MATHEMATICS Lecture. 4 Chapter.8 TECHNIQUES OF INTEGRATION By TECHNIQUES OF INTEGRATION OVERVIEW The Fundamental Theorem connects antiderivatives and the definite integral. Evaluating the indefinite integral,
ELEMENTARY LINEAR ALGEBRA
 ELEMENTARY LINEAR ALGEBRA K. R. MATTHEWS DEPARTMENT OF MATHEMATICS UNIVERSITY OF QUEENSLAND Corrected Version, 7th April 013 Comments to the author at keithmatt@gmail.com Chapter 1 LINEAR EQUATIONS 1.1
ELEMENTARY LINEAR ALGEBRA K. R. MATTHEWS DEPARTMENT OF MATHEMATICS UNIVERSITY OF QUEENSLAND Corrected Version, 7th April 013 Comments to the author at keithmatt@gmail.com Chapter 1 LINEAR EQUATIONS 1.1
A.1 Appendix on Cartesian tensors
 1 Lecture Notes on Fluid Dynamics (1.63J/2.21J) by Chiang C. Mei, February 6, 2007 A.1 Appendix on Cartesian tensors [Ref 1] : H Jeffreys, Cartesian Tensors; [Ref 2] : Y. C. Fung, Foundations of Solid
1 Lecture Notes on Fluid Dynamics (1.63J/2.21J) by Chiang C. Mei, February 6, 2007 A.1 Appendix on Cartesian tensors [Ref 1] : H Jeffreys, Cartesian Tensors; [Ref 2] : Y. C. Fung, Foundations of Solid
Fundamentals of Engineering Analysis (650163)
 Philadelphia University Faculty of Engineering Communications and Electronics Engineering Fundamentals of Engineering Analysis (6563) Part Dr. Omar R Daoud Matrices: Introduction DEFINITION A matrix is
Philadelphia University Faculty of Engineering Communications and Electronics Engineering Fundamentals of Engineering Analysis (6563) Part Dr. Omar R Daoud Matrices: Introduction DEFINITION A matrix is
On Q-derived Polynomials
 On Q-derived Polynomials R.J. Stroeker Econometric Institute, EUR Report EI 2002-0 Abstract A Q-derived polynomial is a univariate polynomial, defined over the rationals, with the property that its zeros,
On Q-derived Polynomials R.J. Stroeker Econometric Institute, EUR Report EI 2002-0 Abstract A Q-derived polynomial is a univariate polynomial, defined over the rationals, with the property that its zeros,
The Spinor Representation
 The Spinor Representation Math G4344, Spring 2012 As we have seen, the groups Spin(n) have a representation on R n given by identifying v R n as an element of the Clifford algebra C(n) and having g Spin(n)
The Spinor Representation Math G4344, Spring 2012 As we have seen, the groups Spin(n) have a representation on R n given by identifying v R n as an element of the Clifford algebra C(n) and having g Spin(n)
A degree bound for codimension two lattice ideals
 Journal of Pure and Applied Algebra 18 (003) 01 07 www.elsevier.com/locate/jpaa A degree bound for codimension two lattice ideals Leah H. Gold Department of Mathematics, Texas A& M University, College
Journal of Pure and Applied Algebra 18 (003) 01 07 www.elsevier.com/locate/jpaa A degree bound for codimension two lattice ideals Leah H. Gold Department of Mathematics, Texas A& M University, College
Cohomology of some configuration spaces and associated bundles
 Cohomology of some configuration spaces and associated bundles untitled t Page of Printed: Friday, July 8, 005 :7: PM 誕生日おめでとうの男 Laurence R. Taylor University of Notre Dame July, 005 For any space X, F
Cohomology of some configuration spaces and associated bundles untitled t Page of Printed: Friday, July 8, 005 :7: PM 誕生日おめでとうの男 Laurence R. Taylor University of Notre Dame July, 005 For any space X, F
Fractions, Projective Representation, Duality, Linear Algebra and Geometry
 Fractions, Projective Representation, Duality, Linear Algebra and Geometry Vaclav Skala Department of Computer Science and Engineering, Faculty of Applied Sciences, University of West Bohemia, Univerzitni
Fractions, Projective Representation, Duality, Linear Algebra and Geometry Vaclav Skala Department of Computer Science and Engineering, Faculty of Applied Sciences, University of West Bohemia, Univerzitni
Vectors. January 13, 2013
 Vectors January 13, 2013 The simplest tensors are scalars, which are the measurable quantities of a theory, left invariant by symmetry transformations. By far the most common non-scalars are the vectors,
Vectors January 13, 2013 The simplest tensors are scalars, which are the measurable quantities of a theory, left invariant by symmetry transformations. By far the most common non-scalars are the vectors,
5. Grassmannians and the Space of Trees In this lecture we shall be interested in a very particular ideal. The ambient polynomial ring C[p] has ( n
![5. Grassmannians and the Space of Trees In this lecture we shall be interested in a very particular ideal. The ambient polynomial ring C[p] has ( n 5. Grassmannians and the Space of Trees In this lecture we shall be interested in a very particular ideal. The ambient polynomial ring C[p] has ( n](/thumbs/89/97533670.jpg) 5. Grassmannians and the Space of Trees In this lecture we shall be interested in a very particular ideal. The ambient polynomial ring C[p] has ( n d) variables, which are called Plücker coordinates: C[p]
5. Grassmannians and the Space of Trees In this lecture we shall be interested in a very particular ideal. The ambient polynomial ring C[p] has ( n d) variables, which are called Plücker coordinates: C[p]
LMI MODELLING 4. CONVEX LMI MODELLING. Didier HENRION. LAAS-CNRS Toulouse, FR Czech Tech Univ Prague, CZ. Universidad de Valladolid, SP March 2009
 LMI MODELLING 4. CONVEX LMI MODELLING Didier HENRION LAAS-CNRS Toulouse, FR Czech Tech Univ Prague, CZ Universidad de Valladolid, SP March 2009 Minors A minor of a matrix F is the determinant of a submatrix
LMI MODELLING 4. CONVEX LMI MODELLING Didier HENRION LAAS-CNRS Toulouse, FR Czech Tech Univ Prague, CZ Universidad de Valladolid, SP March 2009 Minors A minor of a matrix F is the determinant of a submatrix
k=0 /D : S + S /D = K 1 2 (3.5) consistently with the relation (1.75) and the Riemann-Roch-Hirzebruch-Atiyah-Singer index formula
 20 VASILY PESTUN 3. Lecture: Grothendieck-Riemann-Roch-Hirzebruch-Atiyah-Singer Index theorems 3.. Index for a holomorphic vector bundle. For a holomorphic vector bundle E over a complex variety of dim
20 VASILY PESTUN 3. Lecture: Grothendieck-Riemann-Roch-Hirzebruch-Atiyah-Singer Index theorems 3.. Index for a holomorphic vector bundle. For a holomorphic vector bundle E over a complex variety of dim
Linear Algebra (part 1) : Matrices and Systems of Linear Equations (by Evan Dummit, 2016, v. 2.02)
 Linear Algebra (part ) : Matrices and Systems of Linear Equations (by Evan Dummit, 206, v 202) Contents 2 Matrices and Systems of Linear Equations 2 Systems of Linear Equations 2 Elimination, Matrix Formulation
Linear Algebra (part ) : Matrices and Systems of Linear Equations (by Evan Dummit, 206, v 202) Contents 2 Matrices and Systems of Linear Equations 2 Systems of Linear Equations 2 Elimination, Matrix Formulation
Symmetries and Polynomials
 Symmetries and Polynomials Aaron Landesman and Apurva Nakade June 30, 2018 Introduction In this class we ll learn how to solve a cubic. We ll also sketch how to solve a quartic. We ll explore the connections
Symmetries and Polynomials Aaron Landesman and Apurva Nakade June 30, 2018 Introduction In this class we ll learn how to solve a cubic. We ll also sketch how to solve a quartic. We ll explore the connections
Chapter 7 Rational Expressions, Equations, and Functions
 Chapter 7 Rational Expressions, Equations, and Functions Section 7.1: Simplifying, Multiplying, and Dividing Rational Expressions and Functions Section 7.2: Adding and Subtracting Rational Expressions
Chapter 7 Rational Expressions, Equations, and Functions Section 7.1: Simplifying, Multiplying, and Dividing Rational Expressions and Functions Section 7.2: Adding and Subtracting Rational Expressions
Lecture 7. Quaternions
 Matthew T. Mason Mechanics of Manipulation Spring 2012 Today s outline Motivation Motivation have nice geometrical interpretation. have advantages in representing rotation. are cool. Even if you don t
Matthew T. Mason Mechanics of Manipulation Spring 2012 Today s outline Motivation Motivation have nice geometrical interpretation. have advantages in representing rotation. are cool. Even if you don t
Cyclic Central Configurations in the Four-Body Problem
 Cyclic Central Configurations in the Four-Body Problem Gareth E. Roberts Department of Mathematics and Computer Science College of the Holy Cross Josep Cors (Universitat Politècnica de Catalunya) NSF DMS-0708741
Cyclic Central Configurations in the Four-Body Problem Gareth E. Roberts Department of Mathematics and Computer Science College of the Holy Cross Josep Cors (Universitat Politècnica de Catalunya) NSF DMS-0708741
ON THE LOCAL VERSION OF THE CHERN CONJECTURE: CMC HYPERSURFACES WITH CONSTANT SCALAR CURVATURE IN S n+1
 Kragujevac Journal of Mathematics Volume 441 00, Pages 101 111. ON THE LOCAL VERSION OF THE CHERN CONJECTURE: CMC HYPERSURFACES WITH CONSTANT SCALAR CURVATURE IN S n+1 S. C. DE ALMEIDA 1, F. G. B. BRITO,
Kragujevac Journal of Mathematics Volume 441 00, Pages 101 111. ON THE LOCAL VERSION OF THE CHERN CONJECTURE: CMC HYPERSURFACES WITH CONSTANT SCALAR CURVATURE IN S n+1 S. C. DE ALMEIDA 1, F. G. B. BRITO,
Quantum Field Theory III
 Quantum Field Theory III Prof. Erick Weinberg January 19, 2011 1 Lecture 1 1.1 Structure We will start with a bit of group theory, and we will talk about spontaneous symmetry broken. Then we will talk
Quantum Field Theory III Prof. Erick Weinberg January 19, 2011 1 Lecture 1 1.1 Structure We will start with a bit of group theory, and we will talk about spontaneous symmetry broken. Then we will talk
MATH Linear Algebra
 MATH 304 - Linear Algebra In the previous note we learned an important algorithm to produce orthogonal sequences of vectors called the Gramm-Schmidt orthogonalization process. Gramm-Schmidt orthogonalization
MATH 304 - Linear Algebra In the previous note we learned an important algorithm to produce orthogonal sequences of vectors called the Gramm-Schmidt orthogonalization process. Gramm-Schmidt orthogonalization
Optimistic limits of the colored Jones polynomials
 Optimistic limits of the colored Jones polynomials Jinseok Cho and Jun Murakami arxiv:1009.3137v9 [math.gt] 9 Apr 2013 October 31, 2018 Abstract We show that the optimistic limits of the colored Jones
Optimistic limits of the colored Jones polynomials Jinseok Cho and Jun Murakami arxiv:1009.3137v9 [math.gt] 9 Apr 2013 October 31, 2018 Abstract We show that the optimistic limits of the colored Jones
Computing syzygies with Gröbner bases
 Computing syzygies with Gröbner bases Steven V Sam July 2, 2008 1 Motivation. The aim of this article is to motivate the inclusion of Gröbner bases in algebraic geometry via the computation of syzygies.
Computing syzygies with Gröbner bases Steven V Sam July 2, 2008 1 Motivation. The aim of this article is to motivate the inclusion of Gröbner bases in algebraic geometry via the computation of syzygies.
Massachusetts Institute of Technology Department of Economics Statistics. Lecture Notes on Matrix Algebra
 Massachusetts Institute of Technology Department of Economics 14.381 Statistics Guido Kuersteiner Lecture Notes on Matrix Algebra These lecture notes summarize some basic results on matrix algebra used
Massachusetts Institute of Technology Department of Economics 14.381 Statistics Guido Kuersteiner Lecture Notes on Matrix Algebra These lecture notes summarize some basic results on matrix algebra used
Faculty of Engineering, Mathematics and Science School of Mathematics
 Faculty of Engineering, Mathematics and Science School of Mathematics JS & SS Mathematics SS Theoretical Physics SS TSM Mathematics Module MA3429: Differential Geometry I Trinity Term 2018???, May??? SPORTS
Faculty of Engineering, Mathematics and Science School of Mathematics JS & SS Mathematics SS Theoretical Physics SS TSM Mathematics Module MA3429: Differential Geometry I Trinity Term 2018???, May??? SPORTS
CHAPTER 6. Direct Methods for Solving Linear Systems
 CHAPTER 6 Direct Methods for Solving Linear Systems. Introduction A direct method for approximating the solution of a system of n linear equations in n unknowns is one that gives the exact solution to
CHAPTER 6 Direct Methods for Solving Linear Systems. Introduction A direct method for approximating the solution of a system of n linear equations in n unknowns is one that gives the exact solution to
