MATHEMATICS IV 2 MARKS. 5 2 = e 3, 4
|
|
|
- Alice Clark
- 5 years ago
- Views:
Transcription
1 MATHEMATICS IV MARKS. If c epesents cicle with dius 6, find the vlue of c. R 9 f c ; g, f 6 9 c 6 c c. Find the eccenticit of the hpeol Eqution of the hpeol Hee, nd + e + e 5 e 5 e. Find the distnce etween the two points in plne whose pol coodintes e (, /6 (, /) Distnce etween the points P, 6 nd Q, is Hint: cos 5 cos (6 5) PQ cos( ) () () ()()cos cos 6 cos 5 + sin 6 sin cos5 6 units. Stte the Simpson s ule fo numeicl Integtion of function f() ove the intevl [, ] dividing [, ] into n su-intevls. Let P {, + h, + h,... n + nh }, whee h (n is n even intege) e ptitions of [, ]. n Let,,,... n e the vlues of f() t,,,... n espectivel. h f() d n 5... n... n. 5. Find the vete nd focus of the pol Eqution of the pol X ( ) 6 Comping with ( h) ( + k) We get h, k, 6 Coodintes of the focus e (h, k + ) Vete of the pol (h, k),., (, ) 6. Find the cente nd eccenticit of the hpeol Eqution of the hpeol is ( + 8) 6( + ) 6 9( ) 6( + + ) ( + ) 6( + ) ( ) ( ) 6 9 ( h) ( k) Compe with, we get h, k 6, 9 Cente of the hpeol (h, k) (, ) Eccenticit e Tking the oigin s the pole nd the positive -is s the initil, convet into pol fom. Eqution of the cuve in Ctesin fom is Put sin, cos, we get ( sin ) ( cos )
2 cos sin cot cosec is the eqution in pol fom. 8. Find e d. e d e d 9. Evlute: Put 9 t d (). e d d d.e () e d.e e + c e ( ) + c 8 d. 8 Then 9 8 d dt (o) 8 d 9 dt Now, 8 d 8 dt 9 9.tn (t) C tn ( ) C t Evlute: Let f(i) Then I / cos 5/ ( ) d. 5 / 5 / sin ( ) cos ( ) / 5 / cos () d... () 5 / 5 / sin () cos () / 5 / cos d 5 / 5 / sin cos I f() d f( ) d / 5 / sin d... () 5 / 5 / sin sin Adding () nd () I / / 5 / 5 / cos () sin () d 5 / 5 / 5 / 5 / sin () cos () sin () sin () / / 5 / 5 / cos sin / 5 / 5 / d d [] sin cos I I / 5 / cos d. 5 / 5 / sin cos. Stte Tpezoidl ule fo Numeicl integtion of function f(), ove the intevl [, ] dividing [, ] into n su intevls. Let P {, + h, + h,... n + h } Whee h, e pticin of [, ] dividing [, ] into n equl pts. n Let,,... n e the vlues of f() t,,... n espectivel. Then Tpezoidl ule h f() d [( + n ) + ( n )]. d. If the eqution epesents hpeol, find the limits of c (whee c is n el constnt). 9 c 5 c Given eqution is 9 c 5 c This eqution epesents hpeol, then 9 c > nd 5 c < 9 > c nd 5 < c 5 < c < 9. Find the length of the pependicul fom the pole to the stight line 6 cos + sin.
3 Eqution of the given line in the pol fom is 6 (i.e.,) 6 cos sin cos + sin 6 cos cos 6 Pependicul distnce fom pole to the given lines is p 6 units.. Evlute: ( )e cos (e ) d Put. e t Then [. e + e ()] d dt e ( + ) d dt Now e ( ) dt d sec cos (e ) (t) dt tn (t) + c tn (e ) + c cos t 5. Evlute: ( ) d, >, >,,. ( ) ( ) + ( ) + ( ) d d d d d d d Hint: d c, >, log c c c log log log log log log log log 6. Clculte d Simpson s ule dividing [, ] into 6 equls intevls. f(),, n 6 h 6 n 6 6 X f() B Simpson s ule f() d h [ + ( n ) + ( n ) + n ] h ( + 6 ) + ( ) + ( + ) [(8 + 8) + ( ) + ( + )] (6 8 ) Otin the pmetic equtions of the cicle epesented Cente of the cicle (h, k) (, ) nd dius () h k c The pmetic equtions of cicle with cente (h, k) nd dius () e given h + cos ; k + sin, whee < (i.e.,) + cos ; + sin 8. Find the eqution of tngents to the ellipse + 8, which e pependicul to + + Slope of the given line + + is The tngent is pependicul to the line + + Slope of the tngent is m Eqution of the tngent is m m... () Eqution of the ellipse is, Hee, 8, m 8 Fom () equtions of tngents e () () 8 9. If the eccenticit of the hpeol is 5, find the eccenticit of its conjugte hpeol.
4 Eqution of the hpeol is e e Eqution of the conjugte hpeol is... () e 6, () Find the length of the ltus ectum nd eccenticit of the conic ( + 7 cos ) 8 Eqution of the conic is ( + 7 cos ) cos cos Comping with + e cos ; we get l, e 7 Length of the ltus ectum l Eccenticit e 7.. If e cos, pove tht + If e cos( + c), then n n e cos c ntn Put,, c nd n, then e cos e cos ( + ) e cos + d. Evlute: e cos d, R cosh sinh cosh () sinh () cosh sinh cosh() sinh() d e cos[ + tn ()] Hint: cos h () sin h () [(cos h() sin h())] d cos h() d sin h() d sin h cos h + c. Find the e cut off etween nd The given pol meet, the X is t A(, ) nd Y is t P(, ) nd Q(, ) The pol is smmeticl ut X is Requied e Ae of OAP P(, ) 8 6 ( ) d 8. sq. units. O A X Q(, ). Find the eqution of the hpeol with eccenticit, focus (, ) nd the coesponding diecti is +. S(, ) is the focus
5 Eqution of the diectid is + e P(, ) is n point on the hpeol. Dwn PM pependicul to the diecti PM 5 B Def SP e. PM SP e.pm ( ) + ( ) ( ) 5 5( ) ( ) Eqution of the hpeol is M + + P(, ) S(, ) n 5. Otin: ( ) d, n Let I n ( ) d f() d f( ) d n I n n n ( ) d ( ) d ( ) d n n n n. n (n ) (n ) n n n n (n )(n ) n I. (n )(n ) 6. Find the e ounded +, X-is nd the odintes nd. Ae equied is A d 8 7 ( ) d sq. units 8 6 Y X X Y 7. Find the eqution of the cicle whose etemities of the dimete e (, ) nd (, 5). Hee (, ) (, ), (, ) (, 5) Eqution of the cicle hving A(, ) nd B(, ) s ends of the dimete is ( )( ) + ( )( ) The eqution of the equied cicle is ( )( ) + ( )( 5) (i.e.,) Show tht the line + is tngent to the pol 6. Also find the point of contct. Eqution of the line is () +... () is eqution of tngent in tems of m slope 6 Hee 6 Comping equtions () nd () we get m ; m Hee m + is tngent to 6 () Point of contct is,, (,) m m. 9. Find the pole of the line 6 with espect to the ellipse +. Eqution of the ellipse is +, Hee, Pole of the line 6 is n m,, l, m 6, n n
6 m ( 6) 7, n ( ) n ( ) Pole (7, ).. Find the e of the tingle fomed the points (, ), 5 5, nd,. 6 The e of the tingle fomed (, ), (, ) nd (, ) is sin( ) Requied e of the tingle fomed (, ), 5 5, nd, 6 is 5 ( 5)()sin ().sin(7 ) ()( ) 6 sq. units.. Find the n th deivtive of e + 5,. Let e + 5. Then n D n [e + 5. ] (e + 5 ) n + n C (e + 5 ) n ( ) + n C (e + 5 ) n ( ) n. (e + 5 ) + (n) n. e + 5 (n)(n ) () +. n e + 5 () e + 5. n [9 + 6n + (n)(n )].. Find the e ounded sin, is, nd. Y Requied e sin d cos cos + cos ( ) + + sq. units tn (). d on R {}. tn () d d tn d (tn ). d d tn. d d tn d tn n n C. Evlute: / sin d X - / sin( ), if We hve sin sin(), if / / / sin d sin d sin d sin( ) d sin() d / / / / sin() d sin d cos / cos cos cos cos cos / + 5. Evlute: d d Hint: 6 f () d f() C f() d Find the e enclosed etween the cuves,.
7 Given equtions e... ()... () Eliminting, we get X ( ) (o) (o) Points of intesection e O(, ), A(, ) Ae of the egion A 8 ( ) d. sq. units A(, ) X 7. If point P is moving such tht the lengths of tngents dwn fom P to + + nd e in the tio :, then find the eqution of the locus of P. Let P(, ) e n point on the locus. PT, PT e the lengths of tngents fom P to the given cicles. PT Then we hve PT (i.e.,) PT PT 8 B squing on oth sides 8 (o) 6 6 Locus of P(, ) is ( + ) + 8 / 8. Evlute: 6 sin cos d / sin cos d Using Simpson s ule find ppoimtel d tking equl intevls. Let,,, n h.5 n P {,.5,.5,.75, } i B Simpson s Rule h d [( + ) + ( + ) + ].5.5 d. 7 [5 + (.65) + (.5)] 8. [5 + ( ) + (.5)]. Show tht the line l + m + n is noml to the cicle S, if nd onl if gl + mf n. Eqution of the cicle is S (i.e.,) + + g + f + c The line l + m + n is noml to the cicle S, if the cente of the cicle ( g, f) lies on l + m + n l( g) + m( f) + n gl + mf n. Find the vlue of k, if the lines + + nd + k e conjugte with espect to the pol 8 The pole of the line + + w..t the pol n m () () is P,, P(6, 6) The lines e conjugte, P(6, 6) lies on + k
8 6 ( 6) + k k. Find the eqution of the hpeol efeed to its es s es of co-odintes whose distnce etween foci is 6 nd eccenticit is. Given e e 6 e (e ) ( ) Eqution of the hpeol is i.e.,.. Find the e cut off etween, +. The points of intesection of nd + e otined fom + ( )( ), Point of intesection e (, ), (, ) Requied e of the egion A ( ) d (9 8 ) sq. units. X Y O X. Evlute: cos + sin + d Put tn Then d Now dt t d cos sin t ; sin t t nd cos t dt dt t t t ( t) t t log + t + C log tn C Y e (+ ) 5. Find d on R { } ( + ) e ( ) e ( ) d ( ) ( ) ( ) e e d e. C C ( ). d Hint: e [f() + f()] d e. f() + C 6. Evlute: log d + Let f() log f( ) log log f() f( ) f() is odd log d. MARKS. Find the midpoint of the chod of the cicle intecepted the line. Eqution to the cicle is its cente is (, ) Eqution of the chod AB is... () Let M e the midpoint of AB
9 CM AB Slope of AB Slope of CM C B Eqution of CM is + ( ) + g + o Solve X we get co-odintes of M 7 9 /5, /5, M, 5 5. A M. Show tht the cicles c ; c touch if +. c Given the cicles e c... () c... () the eqution of dicl is of () nd (_ is The cicles () nd () touch ech othe if the dicl is is common tngent. Pependicul distnce fom cente (, ) to is equl to dius. c c. ( c) ( + ) c( + ) c.. Show tht the poles of the tngents to the cicle ( h) + with espect to the cicle + lie on the cuve ( h) ( + ). Let P( ) e the pole The pol of P() ) w..t. the cicle + is +... () It is tngent to the cicle ( h) +, then pependicul distnce fom cente (h, ) dius h squing oth sides we get (h ) Hence locus e ( h) ( + )... Find the eqution to the cicle which psses though the points (, ), (6, 5) nd whose cente lies on the line + 6. Let the eqution of the cicle e + + g + f + c it psses though the points (, ) (6, 5) + + g() + f() + c 8g + f + c 7... () nd g(6) + f(5) + c g + f + c 6... () cente ( g, f) lies on + 6 ( g) + ( f) 6 g + f () Fom () nd () 8g + f + c 7 g + f + c 6 Solving we get g, f, c 5 Hence equied eqution of cicle e Show tht the e of the tingle fomed the tngent t ( ) to the cicle + with the coodinte is is sq. units. Eqution of the tngent to the cicle X + t ( ) is +... () Since e of tingle fomed the line + + c c With co-odintes is is Ae of the tingle fomed the tngent + ( ) with co-odinte is is
10 Ae sq. units. 6. Find the eqution of the cicle which pss though the oigin nd is othogonl to the given two cicles + 6 ; Let the eqution of the cicle e + + g + f + c... () Since it psses though oigin c () cuts the cicle + 6 nd othogonll. g( ) + f( ) c... () g( 8) + f( ) c +... () Solving () nd () we get g 7/, f 8/9 Requied eqution e Find the vlue of C, if the cicle nd + + c cut ech othe othogonll nd + + c cut ech othe othogonll. gg + ff c + c ( 8)() 6( ) + c 6 + c c If the pol of p with espect to + touches the pol. Show tht the locus of p is + Let P(, ) e n point on the locus. Then pol of P(, ) w..t the cicle + is S + (o) +... () It touches the pol c m () Hence locus of p(, ) is + 9. If the pol of the point p w..t. the pol touches the cicle +. Find the locus of the point P. Let P(, ) e n point on the locus. The pol of P w..t. the pol is ( + )... () It touches the cicle +, then d Hence locus of P(, ) is.. Show tht the eqution of the chod joining the points P() nd Q() on the ellipse + is cos + sin cos. P() P( cos, sin ) Q() Q( cos, sin ) e two points on the ellipse Eqution of the chod joining the points P() nd Q() is (sin sin ) ( sin ) ( cos ) (cos cos ) sin sin cos. ( cos ) sin.sin cos sin cos o cos sin cos.
11 . Find the eqution of the noml t P() on the ellipse cos, sin d d sin, d d cos d tn d d d tn (slope of Noml) +. Eqution of Noml e sin tn ( cos ) cos sin cos sin. sin cos ( ) sin cos sin cos o is equied eqution of Noml. cos sin. Find the eccenticit, foci nd length of the ltus ectum of the given ellipse ; e foci ( e, ) 8, 7, Length of ltus ectum (6) If l + m + n epesents the eqution of the noml to the hpeol ( + ). m n Eqution of the hpeol is Eqution of the noml is sec tn +... () But eqution of the given line l + m + n... () Comping () nd () we get sec nd tn n m n m n ( ). m n (sec tn ) sec mtn n, show tht. If the lines l + m + n, l + m + n e conjugte with espect to the hpeol then pove tht ll mm nn. Two stight lines e side to e conjugte, if pole of line w..t. hpeol lies on the othe l + m + n... () l + m + n... () Pole of l + m + n w..t. hpeol Since the lines e conjugte is n m m n n n ll + mm + nn ll mm nn which is equied condition. m ; n, 5. Show tht the locus of point of intesection of the tngents of hpeol which e inclined t 5 to ech othe is ( + ) ( + ). Eqution of pi of tngents is S.S S Let P( ) e locus points S:
12 ( ).( ) ( ) Now enging eqution we get [ ] + [ ] + + ( ) tn h (ngle etween tngents) h tn ( + ) (h ) ( )( ) [ + ] [ + ] Hence locus e ( + ) ( + ). 6. If PSQ is focl chod of conic whose focus is S nd the length of the semi-ltus ectum is l, then show tht +. SP SQ Let the eqution of the conic e e cos. Let P(, ), Q( + ) e the ends of the focl chod e cos nd e cos( + ) + e cos e cos + + e cos 7. Pove tht the eqution cos + sin epesents cicle. Given cos + sin Put cos sin which is cicle. 8. Pove tht the cicle cos ( ) nd sin ( ) e othogonl. Eqution of the fist cicle is cos ( ) Its cente A, Eqution of the second cuve is sin( ) cos ( ) cos Its cente B, These two cicles psses though the pole O OA + OB AB + cos( ) cos AB OA + OB Hence cicles cut othogonll. cos 9. Find the equtions of stight lines pssing though the point, nd pllel nd pependicul to the given stight line cos + sin. Let the eqution of line pllel to cos sin e k cos sin It psses though the point k cos sin ( ) k () k,
13 Hence eqution of line is cos sin Let the eqution of the line to cos sin is R cos sin it psses though the point, k cos sin k Hence the eqution of line is cos sin. If cos (m log ), then show tht + + m nd hence deduce tht n+ + (n + ) n + + (m + n ) n. cos (m log ) sin(m log ). m m. sin(m log ) Diffeentiting w..t.. +. m cos (m log ). m + m cos(m log ) m + + m Diffeentiting n times w.. to, leinitz s theoem ( ) n + ( ) n + m n + ( ) n. + nc ( ) n () + nc. ( ) n ). + [( ) n. + nc.( ) n ] + m n n(n ). n + + n n n + n + + n + m n. n + + (n + ) n + + (n n + n + m ) n. n + + (n + ) n + + (m + n ) n. sin + cos. Find: sin + cos d. Let N A d (D) + 8(D) d sin + cos A( cos sin ) + B( sin + cos )... () Eqution coeffs. of sin nd cos, we get A + B A + B Solve, we get A,B Fom () sin + cos (cos sin) 8 (sin cos ) 5 5 sin cos (cos sin) 8 d d d sin cos 5 sin cos 5 log sin cos 8 () c 5 5 d. Evlute: 5 + sin d I d 5 sin dt t Put tn t d,sin t t dt dt dt dt. 8t t 5 5t 8t t t 6 t 5 t 5 t 5tn dt t tn c tn c.. Evlute: 6 + d 8 Put t d dt. d dt.
14 8 t (t ) d. dt dt 6 t t dt dt t [t tn (t)] + c 8 d [ tn ( )] + c 6 d. Find: + sin + cos Put tn t Then d dt t t nd sin t dt t d t t sin cos t ( t ) t nd cos t dt dt log tn c t t t t. 5. Evlute: + d I d d d 9..sin + C 9 6. If n is positive intege nd I n tn n d, show tht I n I n tn n d tn n. tn d tn n (sec ) d tn n sec d tn n d I 5 tn 5 d n tn I n n tn tn tn I tn tn I + tn d tn tn + log sec + c. (tn) n n I n nd hence evlute I 5. log(+ ) 7. Find: d + I I / log( ) d log( tn ).sec d putting tn tn / log( tn ) d / / tn log tn d log d tn / [log log( tn ) log. I I log I 8 log
15 / 8. If I n I n I n n tn d, then pove tht I n + I n / / / n n n tn d tn.tn d tn (sec ) d / / n n tn sec d tn d / I n + I n I I I / n tn I n n tn d I n / I d I. / nd lso evlute: n tn d. n- 9. If I n sec n sec tn n 6 d, then show tht I n + I n nd find the vlue of n n sec d. I n sec n d sec n. sec d d (sec n ). sec d d sec n sec d d sec n. tn (n ) sec n sec. tn d sec n tn (n )I n + (n )I n (n )I n sec n tn + (n )I n I n n sec tn (n ) n n I n sec d sec d 5 5 / / 6 / sec d Solve: ( + ) d + ( + ) d ( + )d + ( + ) d d d d d ln ln C. C. /. Solve: ( ) d + 5 d ( ) d + 5 d d 5 d I.F. e d d e d ln e 5 5. d d 5 C 5( ) + c.
16 . Solve: e d + e d e d + e d e. e d + e.e d e.d e d e d e d e e c. 7 MARKS. Find the eqution of the cicle which psses though the oigin nd elongs to the coil sstem of which (, ), (, ) e limiting points. Eqution of the cicle of which (, ) s limiting point is ( ) + ( ) i.e., () Eqution of the cicle of which (, ) s limiting point is ( ) + ( ) () Rdicl is of () nd () is 6 + Eqution of the coil sstem will e 5 + L ( + + 5) + (6 + ) It psses though the oigin ( + + 5) + ( + ) ¼ Hence the eqution of the equied cicle is ( + + 5) + (6 + ) o ( + ) 7 Definition: A sstem of cicles of which eve pi of cicles hs the sme dicl is is clled sstem of coil cicles o coil sstem. Eqution of the coil sstem in its simplest fom: Let + + g + f + c epesents the memes of the coil sstem fo diffeent vlue of g, f nd c Let the line of centes e the -is nd the common dicl is e the -is. The centes of ll cicles of the sstem lie on the -is its odintes e zeo (i.e. f ). Let the equtions of n two cicles e of the sstem X + + g + c... () X + + g + c... () Rdicl is of () nd () is (g g ) + (c c ) Rdicl is lies on -is c c o c c Let c c c The cicles () nd () ecomes X + + g + c... () X + + g + c... () Simill n othe cicles of the sstem with () nd () will e + + g + c Hence the eqution of coil sstem of cicles in simplest fom is c whee is pmete. C is constnt.. If (, ) is limiting point of the coil sstem of which is meme, find the othe limiting point. Eqution of the cicle coesponding to the limiting point (, ) is ( ) + ( + ) X () Anothe cicle of the sstem is The dicl is of the sstem is S S (i.e) Eqution of the coil sstem is S + L ( ) + ( ) whee is pmete. Its cente (, ) Rdius ( ) (9 ) Fo limiting point dius o Othe limiting point is (, ).. Find the eqution of the cicle cutting the two cicles nd othogonll nd touching the line + Let eqution of the cicle cuts the given cicle othogonll is + + g + f + c it cuts othogonll g() + f() c + 8 g c () it cuts othogonll g( ) + f() c + 8 8g c () Fom () nd () g c 9 it touches the line + d f 8f g f (f ) g t c f 8
17 f o f 8 Equtions of the cicles e + 8 nd Find the limiting points of the coil sstem detemined the cicles nd Eqution of the cicles e nd Rdicl is of the given cicles is 5 5 Eqution of the coil sstem is 5 + L ( + + 6) + ( 5) + ( ) ( + ) 5 its cente is c(, + ) Rdius ( ) ( ) ( 5 ) Fo limiting points, dius ( + ) ( + ), Hence limiting points e L ( +, ) (, ); L ( +, ) (, ). 5. If the two cicles pssing though the points (, ), (, ) nd touching the line m + c cut ech othe othogonll, then show tht c ( + m ). Let the eqution of n cicle e + + g + f + k... () Given () psses though the points(, ), (, ) + f + k... () f + k... () Solving () nd () : f nd k Given () touches the line m + c o m + c m( g) c g k m ( mg + c) (m + )(g + ) ( k ) g + cgm + (m + ) c. Let g g e the oots of the qudtic in g. g g ( + m ) c... () The equtions of the two cicles e + + g... (5) nd + + g... (6) (5) nd (6) cut ech othe othogonll if (g g + ) g g ( + m ) c o ( + m ) c 6. Show tht the locus of poles of ll the tngents to the pol with espect to the pol is the pol. Let P(, ) e the pole. The pol of P(, ) w..t the pol is ( + ).... () It is tngent to the pol c (o). m Hence the locus of P(, ) is. 7. Deive the eqution of the pol in its stndd fom. S e the locus nd ZZ e the Z diection of the pol. A is the mid point of SZ. Let SA AZ Tke A s the oigin nd AS s -is AS co-odintes of S e (, ). Tke AY s -is A(, ). Suppose P(, ) e n point on the pol M Dw PM to ZZ Dw PN to -is PM ZN ZA + AN + Fom the definition of the pol Z SP PM SP PM ( ) + ( + ) ( + ) ( ) : This is the stndd eqution of the pol. P N A (, ) S 8. Fine the condition tht the line m + c is tngent to the pol.
18 Let P(, ) e point on the pol the line m + c meets the pol t P. Eqution of the tngent t P(, ) is ( + ) +... () But the line is m + c () nd () epesent the sme line m c m + c P(, ) c nd m m P(, ) lies on the pol m c m c which is the equied condition. m A 9. Tngents e dwn to the pol t points whose scisse e in the tio k :. Pove tht the intesect on the cuve (k / + k / ). Let the tngents t R(t ) nd Q(t ) on the pol intesect t P) ) Eqution of the tngent t R(t ) is t + t... () Eqution of the tngent t Q(t ) is t + t... () The point of intesection of () nd () is (t t, (t + t )) t t... () (t + t )... () Given scisse of R(t ) nd Q(t ) e in the tio k : t : t k : t kt Now eliminting t, t, t fom () () (5) We get the locus of P(, ) Fom () t t (kt ) t B (5); t k Fom () (t + t ) t t tt k k k k B using (6) [(k) / + k / ] Locus of P(, ) is (k / + k / ).. If P is point on the ellipse + Let S nd S e the foci of the ellipse P e n point on the ellipse PM nd PM e pependiculs fom P to SP SP diectices l nd l espectivel. Fom definition of the ellipse e, PM PM e SP e(pm) SP e(pm) SP + SP e(pm + PM) e(mm) e (distnce etween the two diectices) e e Mjo is of stndd ellipse. SP + SP length of mjo is, which is constnt fo given ellipse.. Find: d., show tht SP + SP (constnt) whee S nd S e the foci. ( )( ) d d ( + )( + ) d ( ) ( ) d + c. Evlute: d + ( )d d I M Z l A S B B S A l M Z
19 d ln d ln ( ) ( ) ln tn c. cos. Evlute: cos + sin d I cos d cos sin Numeto A(denominto) + B d d (denominto) cos A( cos + sin ) + B( sin + cos ) A + B, A B solving them we get A (cos sin) ( sin cos ) 5 5 d cos sin ;B 5 5. d sin cos d log cos + sin + c. 5 5 cos sin 5 5 sin. Show tht: d + cos. I I I sin d ( )sin( ) d cos cos ( ) I sin d I cos ( sin) d tn cos cos / 5. If I n I n I n n tn d, then pove tht I n + I n / / / n n n n tn d tn.tn d tn (sec ) d / / n n tn sec d tn d / I n + I n I I I I / n tn I n n tn d I n / Io d. / / nd lso evlute: tn d. m n m Show tht I m, n sin cos d I m, n nd hence find the vlue of m + n sin cos d. I m, n / / m n m n sin cos sin.sin.cos d
20 / / m n d m n sin sin.cos d (sin ) sin.cos dd d / m cos n () m cos n sin (). (m ) sin cos. d n n + m n / / sin n n.cos.cos d m n m m sin cos ( cos ) d Im,n Im,n n n m m I m, n I m, n n n m I m, n I n m,n I 7 5 sin.cos d f() d f( ) d 7 5 sin ( )cos ( ) d I I 7. Find the e of the egion ounded the ellipse Eqution of the ellipse is + nd deduce the e of the cicle. B (, ) Y Ae of the egion ounded the ellipse (Ae egion OAB) d d A (, ) A (, ) sin Cicle e, when B 8. Show tht the e ounded, + nd -is... () Ae of shded potion A OAB + A ABC d d ( ) d d, + nd -is is ( ) ( ) sin sin sq. units sq. units O sq. units. A C 9. Solve the diffeentil eqution ( + ) d d + ( + ) ( + ) d d + ( + ) d d
21 d d ln( ) ln lnc c. Solve: d d d d d d d d ln + c ln + c. Solve: ( + )d + ( + )d ( + )d + ( + )d d d d d ln + ln + + c c.
Lesson-5 ELLIPSE 2 1 = 0
 Lesson-5 ELLIPSE. An ellipse is the locus of point which moves in plne such tht its distnce from fied point (known s the focus) is e (< ), times its distnce from fied stright line (known s the directri).
Lesson-5 ELLIPSE. An ellipse is the locus of point which moves in plne such tht its distnce from fied point (known s the focus) is e (< ), times its distnce from fied stright line (known s the directri).
, MATHS H.O.D.: SUHAG R.KARIYA, BHOPAL, CONIC SECTION PART 8 OF
 DOWNLOAD FREE FROM www.tekoclsses.com, PH.: 0 903 903 7779, 98930 5888 Some questions (Assertion Reson tpe) re given elow. Ech question contins Sttement (Assertion) nd Sttement (Reson). Ech question hs
DOWNLOAD FREE FROM www.tekoclsses.com, PH.: 0 903 903 7779, 98930 5888 Some questions (Assertion Reson tpe) re given elow. Ech question contins Sttement (Assertion) nd Sttement (Reson). Ech question hs
STD: XI MATHEMATICS Total Marks: 90. I Choose the correct answer: ( 20 x 1 = 20 ) a) x = 1 b) x =2 c) x = 3 d) x = 0
 STD: XI MATHEMATICS Totl Mks: 90 Time: ½ Hs I Choose the coect nswe: ( 0 = 0 ). The solution of is ) = b) = c) = d) = 0. Given tht the vlue of thid ode deteminnt is then the vlue of the deteminnt fomed
STD: XI MATHEMATICS Totl Mks: 90 Time: ½ Hs I Choose the coect nswe: ( 0 = 0 ). The solution of is ) = b) = c) = d) = 0. Given tht the vlue of thid ode deteminnt is then the vlue of the deteminnt fomed
B.A. (PROGRAMME) 1 YEAR MATHEMATICS
 Gdute Couse B.A. (PROGRAMME) YEAR MATHEMATICS ALGEBRA & CALCULUS PART B : CALCULUS SM 4 CONTENTS Lesson Lesson Lesson Lesson Lesson Lesson Lesson : Tngents nd Nomls : Tngents nd Nomls (Pol Co-odintes)
Gdute Couse B.A. (PROGRAMME) YEAR MATHEMATICS ALGEBRA & CALCULUS PART B : CALCULUS SM 4 CONTENTS Lesson Lesson Lesson Lesson Lesson Lesson Lesson : Tngents nd Nomls : Tngents nd Nomls (Pol Co-odintes)
NORMALS. a y a y. Therefore, the slope of the normal is. a y1. b x1. b x. a b. x y a b. x y
 LOCUS 50 Section - 4 NORMALS Consider n ellipse. We need to find the eqution of the norml to this ellipse t given point P on it. In generl, we lso need to find wht condition must e stisfied if m c is to
LOCUS 50 Section - 4 NORMALS Consider n ellipse. We need to find the eqution of the norml to this ellipse t given point P on it. In generl, we lso need to find wht condition must e stisfied if m c is to
/ 3, then (A) 3(a 2 m 2 + b 2 ) = 4c 2 (B) 3(a 2 + b 2 m 2 ) = 4c 2 (C) a 2 m 2 + b 2 = 4c 2 (D) a 2 + b 2 m 2 = 4c 2
 SET I. If the locus of the point of intersection of perpendiculr tngents to the ellipse x circle with centre t (0, 0), then the rdius of the circle would e + / ( ) is. There re exctl two points on the
SET I. If the locus of the point of intersection of perpendiculr tngents to the ellipse x circle with centre t (0, 0), then the rdius of the circle would e + / ( ) is. There re exctl two points on the
Ellipse. 1. Defini t ions. FREE Download Study Package from website: 11 of 91CONIC SECTION
 FREE Downlod Stud Pckge from wesite: www.tekoclsses.com. Defini t ions Ellipse It is locus of point which moves in such w tht the rtio of its distnce from fied point nd fied line (not psses through fied
FREE Downlod Stud Pckge from wesite: www.tekoclsses.com. Defini t ions Ellipse It is locus of point which moves in such w tht the rtio of its distnce from fied point nd fied line (not psses through fied
MATHEMATICS PAPER IIB COORDINATE GEOMETRY AND CALCULUS. Note: This question paper consists of three sections A,B and C. SECTION A
 MATHEMATICS PAPER IIB COORDINATE GEOMETRY AND CALCULUS. TIME : 3hrs M. Mrks.75 Note: This question pper consists of three sections A,B nd C. SECTION A VERY SHORT ANSWER TYPE QUESTIONS. X = ) Find the eqution
MATHEMATICS PAPER IIB COORDINATE GEOMETRY AND CALCULUS. TIME : 3hrs M. Mrks.75 Note: This question pper consists of three sections A,B nd C. SECTION A VERY SHORT ANSWER TYPE QUESTIONS. X = ) Find the eqution
 JEE Advnced Mths Assignment Onl One Correct Answer Tpe. The locus of the orthocenter of the tringle formed the lines (+P) P + P(+P) = 0, (+q) q+q(+q) = 0 nd = 0, where p q, is () hperol prol n ellipse
JEE Advnced Mths Assignment Onl One Correct Answer Tpe. The locus of the orthocenter of the tringle formed the lines (+P) P + P(+P) = 0, (+q) q+q(+q) = 0 nd = 0, where p q, is () hperol prol n ellipse
PARABOLA EXERCISE 3(B)
 PARABOLA EXERCISE (B). Find eqution of the tngent nd norml to the prbol y = 6x t the positive end of the ltus rectum. Eqution of prbol y = 6x 4 = 6 = / Positive end of the Ltus rectum is(, ) =, Eqution
PARABOLA EXERCISE (B). Find eqution of the tngent nd norml to the prbol y = 6x t the positive end of the ltus rectum. Eqution of prbol y = 6x 4 = 6 = / Positive end of the Ltus rectum is(, ) =, Eqution
CONIC SECTIONS. Chapter 11
 CONIC SECTIONS Chpter. Overview.. Sections of cone Let l e fied verticl line nd m e nother line intersecting it t fied point V nd inclined to it t n ngle α (Fig..). Fig.. Suppose we rotte the line m round
CONIC SECTIONS Chpter. Overview.. Sections of cone Let l e fied verticl line nd m e nother line intersecting it t fied point V nd inclined to it t n ngle α (Fig..). Fig.. Suppose we rotte the line m round
Prerna Tower, Road No 2, Contractors Area, Bistupur, Jamshedpur , Tel (0657) ,
 R Pen Towe Rod No Conttos Ae Bistupu Jmshedpu 8 Tel (67)89 www.penlsses.om IIT JEE themtis Ppe II PART III ATHEATICS SECTION I (Totl ks : ) (Single Coet Answe Type) This setion ontins 8 multiple hoie questions.
R Pen Towe Rod No Conttos Ae Bistupu Jmshedpu 8 Tel (67)89 www.penlsses.om IIT JEE themtis Ppe II PART III ATHEATICS SECTION I (Totl ks : ) (Single Coet Answe Type) This setion ontins 8 multiple hoie questions.
1 Using Integration to Find Arc Lengths and Surface Areas
 Novembe 9, 8 MAT86 Week Justin Ko Using Integtion to Find Ac Lengths nd Sufce Aes. Ac Length Fomul: If f () is continuous on [, b], then the c length of the cuve = f() on the intevl [, b] is given b s
Novembe 9, 8 MAT86 Week Justin Ko Using Integtion to Find Ac Lengths nd Sufce Aes. Ac Length Fomul: If f () is continuous on [, b], then the c length of the cuve = f() on the intevl [, b] is given b s
The Formulas of Vector Calculus John Cullinan
 The Fomuls of Vecto lculus John ullinn Anlytic Geomety A vecto v is n n-tuple of el numbes: v = (v 1,..., v n ). Given two vectos v, w n, ddition nd multipliction with scl t e defined by Hee is bief list
The Fomuls of Vecto lculus John ullinn Anlytic Geomety A vecto v is n n-tuple of el numbes: v = (v 1,..., v n ). Given two vectos v, w n, ddition nd multipliction with scl t e defined by Hee is bief list
Mathematics. Area under Curve.
 Mthemtics Are under Curve www.testprepkrt.com Tle of Content 1. Introduction.. Procedure of Curve Sketching. 3. Sketching of Some common Curves. 4. Are of Bounded Regions. 5. Sign convention for finding
Mthemtics Are under Curve www.testprepkrt.com Tle of Content 1. Introduction.. Procedure of Curve Sketching. 3. Sketching of Some common Curves. 4. Are of Bounded Regions. 5. Sign convention for finding
PhysicsAndMathsTutor.com
 PhsicsAMthsTuto.com 6. The hpeol H hs equtio, whee e costts. The lie L hs equtio m c, whee m c e costts. Leve lk () Give tht L H meet, show tht the -cooites of the poits of itesectio e the oots of the
PhsicsAMthsTuto.com 6. The hpeol H hs equtio, whee e costts. The lie L hs equtio m c, whee m c e costts. Leve lk () Give tht L H meet, show tht the -cooites of the poits of itesectio e the oots of the
r a + r b a + ( r b + r c)
 AP Phsics C Unit 2 2.1 Nme Vectos Vectos e used to epesent quntities tht e chcteized b mgnitude ( numeicl vlue with ppopite units) nd diection. The usul emple is the displcement vecto. A quntit with onl
AP Phsics C Unit 2 2.1 Nme Vectos Vectos e used to epesent quntities tht e chcteized b mgnitude ( numeicl vlue with ppopite units) nd diection. The usul emple is the displcement vecto. A quntit with onl
KEY CONCEPTS. satisfies the differential equation da. = 0. Note : If F (x) is any integral of f (x) then, x a
 KEY CONCEPTS THINGS TO REMEMBER :. The re ounded y the curve y = f(), the -is nd the ordintes t = & = is given y, A = f () d = y d.. If the re is elow the is then A is negtive. The convention is to consider
KEY CONCEPTS THINGS TO REMEMBER :. The re ounded y the curve y = f(), the -is nd the ordintes t = & = is given y, A = f () d = y d.. If the re is elow the is then A is negtive. The convention is to consider
P 1 (x 1, y 1 ) is given by,.
 MA00 Clculus nd Bsic Liner Alger I Chpter Coordinte Geometr nd Conic Sections Review In the rectngulr/crtesin coordintes sstem, we descrie the loction of points using coordintes. P (, ) P(, ) O The distnce
MA00 Clculus nd Bsic Liner Alger I Chpter Coordinte Geometr nd Conic Sections Review In the rectngulr/crtesin coordintes sstem, we descrie the loction of points using coordintes. P (, ) P(, ) O The distnce
GEOMETRY Properties of lines
 www.sscexmtuto.com GEOMETRY Popeties of lines Intesecting Lines nd ngles If two lines intesect t point, ten opposite ngles e clled veticl ngles nd tey ve te sme mesue. Pependicul Lines n ngle tt mesues
www.sscexmtuto.com GEOMETRY Popeties of lines Intesecting Lines nd ngles If two lines intesect t point, ten opposite ngles e clled veticl ngles nd tey ve te sme mesue. Pependicul Lines n ngle tt mesues
Radial geodesics in Schwarzschild spacetime
 Rdil geodesics in Schwzschild spcetime Spheiclly symmetic solutions to the Einstein eqution tke the fom ds dt d dθ sin θdϕ whee is constnt. We lso hve the connection components, which now tke the fom using
Rdil geodesics in Schwzschild spcetime Spheiclly symmetic solutions to the Einstein eqution tke the fom ds dt d dθ sin θdϕ whee is constnt. We lso hve the connection components, which now tke the fom using
Time : 3 hours 03 - Mathematics - March 2007 Marks : 100 Pg - 1 S E CT I O N - A
 Time : hours 0 - Mthemtics - Mrch 007 Mrks : 100 Pg - 1 Instructions : 1. Answer ll questions.. Write your nswers ccording to the instructions given below with the questions.. Begin ech section on new
Time : hours 0 - Mthemtics - Mrch 007 Mrks : 100 Pg - 1 Instructions : 1. Answer ll questions.. Write your nswers ccording to the instructions given below with the questions.. Begin ech section on new
Math 4318 : Real Analysis II Mid-Term Exam 1 14 February 2013
 Mth 4318 : Rel Anlysis II Mid-Tem Exm 1 14 Febuy 2013 Nme: Definitions: Tue/Flse: Poofs: 1. 2. 3. 4. 5. 6. Totl: Definitions nd Sttements of Theoems 1. (2 points) Fo function f(x) defined on (, b) nd fo
Mth 4318 : Rel Anlysis II Mid-Tem Exm 1 14 Febuy 2013 Nme: Definitions: Tue/Flse: Poofs: 1. 2. 3. 4. 5. 6. Totl: Definitions nd Sttements of Theoems 1. (2 points) Fo function f(x) defined on (, b) nd fo
π,π is the angle FROM a! TO b
 Mth 151: 1.2 The Dot Poduct We hve scled vectos (o, multiplied vectos y el nume clled scl) nd dded vectos (in ectngul component fom). Cn we multiply vectos togethe? The nswe is YES! In fct, thee e two
Mth 151: 1.2 The Dot Poduct We hve scled vectos (o, multiplied vectos y el nume clled scl) nd dded vectos (in ectngul component fom). Cn we multiply vectos togethe? The nswe is YES! In fct, thee e two
Physical Security Countermeasures. This entire sheet. I m going to put a heptadecagon into game.
 Phsicl Secuit Countemesues This entie sheet Telmo, AHI I m going to put heptdecgon into gme. Cssie Hung Mechnicl lockpicking is mechnicked geometic constuctions with compss nd stightedge. Ech lock will
Phsicl Secuit Countemesues This entie sheet Telmo, AHI I m going to put heptdecgon into gme. Cssie Hung Mechnicl lockpicking is mechnicked geometic constuctions with compss nd stightedge. Ech lock will
Linear Inequalities: Each of the following carries five marks each: 1. Solve the system of equations graphically.
 Liner Inequlities: Ech of the following crries five mrks ech:. Solve the system of equtions grphiclly. x + 2y 8, 2x + y 8, x 0, y 0 Solution: Considerx + 2y 8.. () Drw the grph for x + 2y = 8 by line.it
Liner Inequlities: Ech of the following crries five mrks ech:. Solve the system of equtions grphiclly. x + 2y 8, 2x + y 8, x 0, y 0 Solution: Considerx + 2y 8.. () Drw the grph for x + 2y = 8 by line.it
Class Summary. be functions and f( D) , we define the composition of f with g, denoted g f by
 Clss Summy.5 Eponentil Functions.6 Invese Functions nd Logithms A function f is ule tht ssigns to ech element D ectly one element, clled f( ), in. Fo emple : function not function Given functions f, g:
Clss Summy.5 Eponentil Functions.6 Invese Functions nd Logithms A function f is ule tht ssigns to ech element D ectly one element, clled f( ), in. Fo emple : function not function Given functions f, g:
HYPERBOLA. AIEEE Syllabus. Total No. of questions in Ellipse are: Solved examples Level # Level # Level # 3..
 HYPERBOLA AIEEE Sllus. Stndrd eqution nd definitions. Conjugte Hperol. Prmetric eqution of te Hperol. Position of point P(, ) wit respect to Hperol 5. Line nd Hperol 6. Eqution of te Tngent Totl No. of
HYPERBOLA AIEEE Sllus. Stndrd eqution nd definitions. Conjugte Hperol. Prmetric eqution of te Hperol. Position of point P(, ) wit respect to Hperol 5. Line nd Hperol 6. Eqution of te Tngent Totl No. of
Given P(1,-4,-3), convert to cylindrical and spherical values;
 CHAPTER 1 Poblems Pob. 1.1 Pob. 1.2 () Given P(1,-4,-3), convet to cylindicl nd spheicl vlues; 4 x y = + = + = = 1 ( 4) 17 4.123. 1 y 1 4 = tn = tn = 284.04. x 1 P(,, ) = (4.123, 284.04, 3). Spheicl :
CHAPTER 1 Poblems Pob. 1.1 Pob. 1.2 () Given P(1,-4,-3), convet to cylindicl nd spheicl vlues; 4 x y = + = + = = 1 ( 4) 17 4.123. 1 y 1 4 = tn = tn = 284.04. x 1 P(,, ) = (4.123, 284.04, 3). Spheicl :
Thomas Whitham Sixth Form
 Thoms Whithm Sith Form Pure Mthemtics Unit C Alger Trigonometry Geometry Clculus Vectors Trigonometry Compound ngle formule sin sin cos cos Pge A B sin Acos B cos Asin B A B sin Acos B cos Asin B A B cos
Thoms Whithm Sith Form Pure Mthemtics Unit C Alger Trigonometry Geometry Clculus Vectors Trigonometry Compound ngle formule sin sin cos cos Pge A B sin Acos B cos Asin B A B sin Acos B cos Asin B A B cos
1. The sphere P travels in a straight line with speed
 1. The sphee P tels in stight line with speed = 10 m/s. Fo the instnt depicted, detemine the coesponding lues of,,,,, s mesued eltie to the fixed Oxy coodinte system. (/134) + 38.66 1.34 51.34 10sin 3.639
1. The sphee P tels in stight line with speed = 10 m/s. Fo the instnt depicted, detemine the coesponding lues of,,,,, s mesued eltie to the fixed Oxy coodinte system. (/134) + 38.66 1.34 51.34 10sin 3.639
1. If y 2 2x 2y + 5 = 0 is (A) a circle with centre (1, 1) (B) a parabola with vertex (1, 2) 9 (A) 0, (B) 4, (C) (4, 4) (D) a (C) c = am m.
 SET I. If y x y + 5 = 0 is (A) circle with centre (, ) (B) prbol with vertex (, ) (C) prbol with directrix x = 3. The focus of the prbol x 8x + y + 7 = 0 is (D) prbol with directrix x = 9 9 (A) 0, (B)
SET I. If y x y + 5 = 0 is (A) circle with centre (, ) (B) prbol with vertex (, ) (C) prbol with directrix x = 3. The focus of the prbol x 8x + y + 7 = 0 is (D) prbol with directrix x = 9 9 (A) 0, (B)
FP3 past questions - conics
 Hperolic functions cosh sinh = sinh = sinh cosh cosh = cosh + sinh rcosh = ln{ + } ( ) rsinh = ln{ + + } + rtnh = ln ( < ) FP3 pst questions - conics Conics Ellipse Prol Hperol Rectngulr Hperol Stndrd
Hperolic functions cosh sinh = sinh = sinh cosh cosh = cosh + sinh rcosh = ln{ + } ( ) rsinh = ln{ + + } + rtnh = ln ( < ) FP3 pst questions - conics Conics Ellipse Prol Hperol Rectngulr Hperol Stndrd
Eigen Values and Eigen Vectors of a given matrix
 Engineering Mthemtics 0 SUBJECT NAME SUBJECT CODE MATERIAL NAME MATERIAL CODE : Engineering Mthemtics I : 80/MA : Prolem Mteril : JM08AM00 (Scn the ove QR code for the direct downlod of this mteril) Nme
Engineering Mthemtics 0 SUBJECT NAME SUBJECT CODE MATERIAL NAME MATERIAL CODE : Engineering Mthemtics I : 80/MA : Prolem Mteril : JM08AM00 (Scn the ove QR code for the direct downlod of this mteril) Nme
Lecture 10. Solution of Nonlinear Equations - II
 Fied point Poblems Lectue Solution o Nonline Equtions - II Given unction g : R R, vlue such tht gis clled ied point o the unction g, since is unchnged when g is pplied to it. Whees with nonline eqution
Fied point Poblems Lectue Solution o Nonline Equtions - II Given unction g : R R, vlue such tht gis clled ied point o the unction g, since is unchnged when g is pplied to it. Whees with nonline eqution
Electric Field F E. q Q R Q. ˆ 4 r r - - Electric field intensity depends on the medium! origin
 1 1 Electic Field + + q F Q R oigin E 0 0 F E ˆ E 4 4 R q Q R Q - - Electic field intensity depends on the medium! Electic Flux Density We intoduce new vecto field D independent of medium. D E So, electic
1 1 Electic Field + + q F Q R oigin E 0 0 F E ˆ E 4 4 R q Q R Q - - Electic field intensity depends on the medium! Electic Flux Density We intoduce new vecto field D independent of medium. D E So, electic
Physics 505 Fall 2005 Midterm Solutions. This midterm is a two hour open book, open notes exam. Do all three problems.
 Physics 55 Fll 5 Midtem Solutions This midtem is two hou open ook, open notes exm. Do ll thee polems. [35 pts] 1. A ectngul ox hs sides of lengths, nd c z x c [1] ) Fo the Diichlet polem in the inteio
Physics 55 Fll 5 Midtem Solutions This midtem is two hou open ook, open notes exm. Do ll thee polems. [35 pts] 1. A ectngul ox hs sides of lengths, nd c z x c [1] ) Fo the Diichlet polem in the inteio
The Area of a Triangle
 The e of Tingle tkhlid June 1, 015 1 Intodution In this tile we will e disussing the vious methods used fo detemining the e of tingle. Let [X] denote the e of X. Using se nd Height To stt off, the simplest
The e of Tingle tkhlid June 1, 015 1 Intodution In this tile we will e disussing the vious methods used fo detemining the e of tingle. Let [X] denote the e of X. Using se nd Height To stt off, the simplest
13.5. Torsion of a curve Tangential and Normal Components of Acceleration
 13.5 osion of cuve ngentil nd oml Components of Acceletion Recll: Length of cuve '( t) Ac length function s( t) b t u du '( t) Ac length pmetiztion ( s) with '( s) 1 '( t) Unit tngent vecto '( t) Cuvtue:
13.5 osion of cuve ngentil nd oml Components of Acceletion Recll: Length of cuve '( t) Ac length function s( t) b t u du '( t) Ac length pmetiztion ( s) with '( s) 1 '( t) Unit tngent vecto '( t) Cuvtue:
Drill Exercise Find the coordinates of the vertices, foci, eccentricity and the equations of the directrix of the hyperbola 4x 2 25y 2 = 100.
 Drill Exercise - 1 1 Find the coordintes of the vertices, foci, eccentricit nd the equtions of the directrix of the hperol 4x 5 = 100 Find the eccentricit of the hperol whose ltus-rectum is 8 nd conjugte
Drill Exercise - 1 1 Find the coordintes of the vertices, foci, eccentricit nd the equtions of the directrix of the hperol 4x 5 = 100 Find the eccentricit of the hperol whose ltus-rectum is 8 nd conjugte
Einstein Classes, Unit No. 102, 103, Vardhman Ring Road Plaza, Vikas Puri Extn., Outer Ring Road New Delhi , Ph. : ,
 CA Vectos & Thei Repesenttion : CB MV VECTORS Vecto quntities e specified y definite mgnitude nd definite diections A vecto is genelly epesented y diected line segment, sy AB A is clled the initil point
CA Vectos & Thei Repesenttion : CB MV VECTORS Vecto quntities e specified y definite mgnitude nd definite diections A vecto is genelly epesented y diected line segment, sy AB A is clled the initil point
R(3, 8) P( 3, 0) Q( 2, 2) S(5, 3) Q(2, 32) P(0, 8) Higher Mathematics Objective Test Practice Book. 1 The diagram shows a sketch of part of
 Higher Mthemtics Ojective Test Prctice ook The digrm shows sketch of prt of the grph of f ( ). The digrm shows sketch of the cuic f ( ). R(, 8) f ( ) f ( ) P(, ) Q(, ) S(, ) Wht re the domin nd rnge of
Higher Mthemtics Ojective Test Prctice ook The digrm shows sketch of prt of the grph of f ( ). The digrm shows sketch of the cuic f ( ). R(, 8) f ( ) f ( ) P(, ) Q(, ) S(, ) Wht re the domin nd rnge of
k ) and directrix x = h p is A focal chord is a line segment which passes through the focus of a parabola and has endpoints on the parabola.
 Stndrd Eqution of Prol with vertex ( h, k ) nd directrix y = k p is ( x h) p ( y k ) = 4. Verticl xis of symmetry Stndrd Eqution of Prol with vertex ( h, k ) nd directrix x = h p is ( y k ) p( x h) = 4.
Stndrd Eqution of Prol with vertex ( h, k ) nd directrix y = k p is ( x h) p ( y k ) = 4. Verticl xis of symmetry Stndrd Eqution of Prol with vertex ( h, k ) nd directrix x = h p is ( y k ) p( x h) = 4.
Optimization. x = 22 corresponds to local maximum by second derivative test
 Optimiztion Lectue 17 discussed the exteme vlues of functions. This lectue will pply the lesson fom Lectue 17 to wod poblems. In this section, it is impotnt to emembe we e in Clculus I nd e deling one-vible
Optimiztion Lectue 17 discussed the exteme vlues of functions. This lectue will pply the lesson fom Lectue 17 to wod poblems. In this section, it is impotnt to emembe we e in Clculus I nd e deling one-vible
9.4 The response of equilibrium to temperature (continued)
 9.4 The esponse of equilibium to tempetue (continued) In the lst lectue, we studied how the chemicl equilibium esponds to the vition of pessue nd tempetue. At the end, we deived the vn t off eqution: d
9.4 The esponse of equilibium to tempetue (continued) In the lst lectue, we studied how the chemicl equilibium esponds to the vition of pessue nd tempetue. At the end, we deived the vn t off eqution: d
Homework 3 MAE 118C Problems 2, 5, 7, 10, 14, 15, 18, 23, 30, 31 from Chapter 5, Lamarsh & Baratta. The flux for a point source is:
 . Homewok 3 MAE 8C Poblems, 5, 7, 0, 4, 5, 8, 3, 30, 3 fom Chpte 5, msh & Btt Point souces emit nuetons/sec t points,,, n 3 fin the flux cuent hlf wy between one sie of the tingle (blck ot). The flux fo
. Homewok 3 MAE 8C Poblems, 5, 7, 0, 4, 5, 8, 3, 30, 3 fom Chpte 5, msh & Btt Point souces emit nuetons/sec t points,,, n 3 fin the flux cuent hlf wy between one sie of the tingle (blck ot). The flux fo
PhysicsAndMathsTutor.com
 PhysicsAMthsTuto.com . M 6 0 7 0 Leve lk 6 () Show tht 7 is eigevlue of the mti M fi the othe two eigevlues of M. (5) () Fi eigevecto coespoig to the eigevlue 7. *M545A068* (4) Questio cotiue Leve lk *M545A078*
PhysicsAMthsTuto.com . M 6 0 7 0 Leve lk 6 () Show tht 7 is eigevlue of the mti M fi the othe two eigevlues of M. (5) () Fi eigevecto coespoig to the eigevlue 7. *M545A068* (4) Questio cotiue Leve lk *M545A078*
( ) ( ) ( ) ( ) ( ) # B x ( ˆ i ) ( ) # B y ( ˆ j ) ( ) # B y ("ˆ ( ) ( ) ( (( ) # ("ˆ ( ) ( ) ( ) # B ˆ z ( k )
 Emple 1: A positie chge with elocit is moing though unifom mgnetic field s shown in the figues below. Use the ight-hnd ule to detemine the diection of the mgnetic foce on the chge. Emple 1 ˆ i = ˆ ˆ i
Emple 1: A positie chge with elocit is moing though unifom mgnetic field s shown in the figues below. Use the ight-hnd ule to detemine the diection of the mgnetic foce on the chge. Emple 1 ˆ i = ˆ ˆ i
7.5-Determinants in Two Variables
 7.-eteminnts in Two Vibles efinition of eteminnt The deteminnt of sque mti is el numbe ssocited with the mti. Eve sque mti hs deteminnt. The deteminnt of mti is the single ent of the mti. The deteminnt
7.-eteminnts in Two Vibles efinition of eteminnt The deteminnt of sque mti is el numbe ssocited with the mti. Eve sque mti hs deteminnt. The deteminnt of mti is the single ent of the mti. The deteminnt
Parabola Exercise 1 2,6 Q.1 (A) S(0, 1) directric x + 2y = 0 PS = PM. x y x y 2y 1 x 2y Q.2 (D) y 2 = 18 x. 2 = 3t. 2 t 3 Q.
 Prbol Exercise Q. (A) S(0, ) directric x + y = 0 PS = PM x y x y 5 5 x y y x y Q. (D) y = 8 x (t, t) t t = t t 8 4 8 t,t, 4 9 4,6 Q. (C) y 4 x 5 Eqution of directrix is x + = 0 x 0 5 Q.4 y = 8x M P t,t
Prbol Exercise Q. (A) S(0, ) directric x + y = 0 PS = PM x y x y 5 5 x y y x y Q. (D) y = 8 x (t, t) t t = t t 8 4 8 t,t, 4 9 4,6 Q. (C) y 4 x 5 Eqution of directrix is x + = 0 x 0 5 Q.4 y = 8x M P t,t
D Properties and Measurement
 APPENDIX D. Review of Alge, Geomet, nd Tigonomet A D Popetie nd Meuement D. Review of Alge, Geomet, nd Tigonomet Alge Popetie of Logitm Geomet Plne Anltic Geomet Solid Anltic Geomet Tigonomet Li of Function
APPENDIX D. Review of Alge, Geomet, nd Tigonomet A D Popetie nd Meuement D. Review of Alge, Geomet, nd Tigonomet Alge Popetie of Logitm Geomet Plne Anltic Geomet Solid Anltic Geomet Tigonomet Li of Function
Appendix D: Formulas, Properties and Measurements
 Appendi D: Fomul, Popetie nd Meuement Review of Alge, Geomet, nd Tigonomet Unit of Meuement D. REVIEW OF ALGEBRA, GEOMETRY, AND TRIGONOMETRY Alge Popetie of Logitm Geomet Plne Anltic Geomet Solid Anltic
Appendi D: Fomul, Popetie nd Meuement Review of Alge, Geomet, nd Tigonomet Unit of Meuement D. REVIEW OF ALGEBRA, GEOMETRY, AND TRIGONOMETRY Alge Popetie of Logitm Geomet Plne Anltic Geomet Solid Anltic
Friedmannien equations
 ..6 Fiedmnnien equtions FLRW metic is : ds c The metic intevl is: dt ( t) d ( ) hee f ( ) is function which detemines globl geometic l popety of D spce. f d sin d One cn put it in the Einstein equtions
..6 Fiedmnnien equtions FLRW metic is : ds c The metic intevl is: dt ( t) d ( ) hee f ( ) is function which detemines globl geometic l popety of D spce. f d sin d One cn put it in the Einstein equtions
SUBJECT: MATHEMATICS ANSWERS: COMMON ENTRANCE TEST 2012
 MOCK TEST 0 SUBJECT: MATHEMATICS ANSWERS: COMMON ENTRANCE TEST 0 ANSWERS. () π π Tke cos - (- ) then sin [ cos - (- )]sin [ ]/. () Since sin - + sin - y + sin - z π, -; y -, z - 50 + y 50 + z 50 - + +
MOCK TEST 0 SUBJECT: MATHEMATICS ANSWERS: COMMON ENTRANCE TEST 0 ANSWERS. () π π Tke cos - (- ) then sin [ cos - (- )]sin [ ]/. () Since sin - + sin - y + sin - z π, -; y -, z - 50 + y 50 + z 50 - + +
MATH 155/GRACEY CH. 10 PRACTICE. SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question.
 MATH /GRACEY CH. PRACTICE Name SHORT ANSWER. Wite the wod o phase that best completes each statement o answes the question. At the given point, find the line that is nomal to the cuve at the given point.
MATH /GRACEY CH. PRACTICE Name SHORT ANSWER. Wite the wod o phase that best completes each statement o answes the question. At the given point, find the line that is nomal to the cuve at the given point.
CHAPTER 7 Applications of Integration
 CHAPTER 7 Applitions of Integtion Setion 7. Ae of Region Between Two Cuves.......... Setion 7. Volume: The Disk Method................. Setion 7. Volume: The Shell Method................ Setion 7. A Length
CHAPTER 7 Applitions of Integtion Setion 7. Ae of Region Between Two Cuves.......... Setion 7. Volume: The Disk Method................. Setion 7. Volume: The Shell Method................ Setion 7. A Length
JUST THE MATHS UNIT NUMBER INTEGRATION APPLICATIONS 12 (Second moments of an area (B)) A.J.Hobson
 JUST THE MATHS UNIT NUMBE 13.1 INTEGATION APPLICATIONS 1 (Second moments of n re (B)) b A.J.Hobson 13.1.1 The prllel xis theorem 13.1. The perpendiculr xis theorem 13.1.3 The rdius of grtion of n re 13.1.4
JUST THE MATHS UNIT NUMBE 13.1 INTEGATION APPLICATIONS 1 (Second moments of n re (B)) b A.J.Hobson 13.1.1 The prllel xis theorem 13.1. The perpendiculr xis theorem 13.1.3 The rdius of grtion of n re 13.1.4
Topics for Review for Final Exam in Calculus 16A
 Topics fo Review fo Finl Em in Clculus 16A Instucto: Zvezdelin Stnkov Contents 1. Definitions 1. Theoems nd Poblem Solving Techniques 1 3. Eecises to Review 5 4. Chet Sheet 5 1. Definitions Undestnd the
Topics fo Review fo Finl Em in Clculus 16A Instucto: Zvezdelin Stnkov Contents 1. Definitions 1. Theoems nd Poblem Solving Techniques 1 3. Eecises to Review 5 4. Chet Sheet 5 1. Definitions Undestnd the
Mark Scheme (Results) January 2008
 Mk Scheme (Results) Jnuy 00 GCE GCE Mthemtics (6679/0) Edecel Limited. Registeed in Englnd nd Wles No. 4496750 Registeed Office: One90 High Holbon, London WCV 7BH Jnuy 00 6679 Mechnics M Mk Scheme Question
Mk Scheme (Results) Jnuy 00 GCE GCE Mthemtics (6679/0) Edecel Limited. Registeed in Englnd nd Wles No. 4496750 Registeed Office: One90 High Holbon, London WCV 7BH Jnuy 00 6679 Mechnics M Mk Scheme Question
Review Exercises for Chapter 4
 _R.qd // : PM Pge CHAPTER Integrtion Review Eercises for Chpter In Eercises nd, use the grph of to sketch grph of f. To print n enlrged cop of the grph, go to the wesite www.mthgrphs.com... In Eercises
_R.qd // : PM Pge CHAPTER Integrtion Review Eercises for Chpter In Eercises nd, use the grph of to sketch grph of f. To print n enlrged cop of the grph, go to the wesite www.mthgrphs.com... In Eercises
Integration Techniques
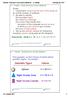
 Integrtion Techniques. Integrtion of Trigonometric Functions Exmple. Evlute cos x. Recll tht cos x = cos x. Hence, cos x Exmple. Evlute = ( + cos x) = (x + sin x) + C = x + 4 sin x + C. cos 3 x. Let u
Integrtion Techniques. Integrtion of Trigonometric Functions Exmple. Evlute cos x. Recll tht cos x = cos x. Hence, cos x Exmple. Evlute = ( + cos x) = (x + sin x) + C = x + 4 sin x + C. cos 3 x. Let u
EECE 260 Electrical Circuits Prof. Mark Fowler
 EECE 60 Electicl Cicuits Pof. Mk Fowle Complex Numbe Review /6 Complex Numbes Complex numbes ise s oots of polynomils. Definition of imginy # nd some esulting popeties: ( ( )( ) )( ) Recll tht the solution
EECE 60 Electicl Cicuits Pof. Mk Fowle Complex Numbe Review /6 Complex Numbes Complex numbes ise s oots of polynomils. Definition of imginy # nd some esulting popeties: ( ( )( ) )( ) Recll tht the solution
Lecture 11: Potential Gradient and Capacitor Review:
 Lectue 11: Potentil Gdient nd Cpcito Review: Two wys to find t ny point in spce: Sum o Integte ove chges: q 1 1 q 2 2 3 P i 1 q i i dq q 3 P 1 dq xmple of integting ove distiution: line of chge ing of
Lectue 11: Potentil Gdient nd Cpcito Review: Two wys to find t ny point in spce: Sum o Integte ove chges: q 1 1 q 2 2 3 P i 1 q i i dq q 3 P 1 dq xmple of integting ove distiution: line of chge ing of
Mathematical Reflections, Issue 5, INEQUALITIES ON RATIOS OF RADII OF TANGENT CIRCLES. Y.N. Aliyev
 themtil efletions, Issue 5, 015 INEQULITIES ON TIOS OF DII OF TNGENT ILES YN liev stt Some inequlities involving tios of dii of intenll tngent iles whih inteset the given line in fied points e studied
themtil efletions, Issue 5, 015 INEQULITIES ON TIOS OF DII OF TNGENT ILES YN liev stt Some inequlities involving tios of dii of intenll tngent iles whih inteset the given line in fied points e studied
dx was area under f ( x ) if ( ) 0
 13. Line Integls Line integls e simil to single integl, f ( x) dx ws e unde f ( x ) if ( ) 0 Insted of integting ove n intevl [, ] (, ) f xy ds f x., we integte ove cuve, (in the xy-plne). **Figue - get
13. Line Integls Line integls e simil to single integl, f ( x) dx ws e unde f ( x ) if ( ) 0 Insted of integting ove n intevl [, ] (, ) f xy ds f x., we integte ove cuve, (in the xy-plne). **Figue - get
CET MATHEMATICS 2013
 CET MATHEMATICS VERSION CODE: C. If sin is the cute ngle between the curves + nd + 8 t (, ), then () () () Ans: () Slope of first curve m ; slope of second curve m - therefore ngle is o A sin o (). The
CET MATHEMATICS VERSION CODE: C. If sin is the cute ngle between the curves + nd + 8 t (, ), then () () () Ans: () Slope of first curve m ; slope of second curve m - therefore ngle is o A sin o (). The
SCORE JEE (Advanced)
 SLUTIN. ns. (D) L : x + y 0 S L : x + y 0 L : x + y 7 0 Point of intersection of L 0 & L 0 is (,9) Point of intersection of L 0 & L 0 is (0,) line perpendiculr to L nd pssing through (, 9) isx y + 0...
SLUTIN. ns. (D) L : x + y 0 S L : x + y 0 L : x + y 7 0 Point of intersection of L 0 & L 0 is (,9) Point of intersection of L 0 & L 0 is (0,) line perpendiculr to L nd pssing through (, 9) isx y + 0...
AP Calculus AB Exam Review Sheet B - Session 1
 AP Clcls AB Em Review Sheet B - Session Nme: AP 998 # Let e the nction given y e.. Find lim nd lim.. Find the solte minimm vle o. Jstiy tht yo nswe is n solte minimm. c. Wht is the nge o? d. Conside the
AP Clcls AB Em Review Sheet B - Session Nme: AP 998 # Let e the nction given y e.. Find lim nd lim.. Find the solte minimm vle o. Jstiy tht yo nswe is n solte minimm. c. Wht is the nge o? d. Conside the
ELECTRO - MAGNETIC INDUCTION
 NTRODUCTON LCTRO - MAGNTC NDUCTON Whenee mgnetic flu linked with cicuit chnges, n e.m.f. is induced in the cicuit. f the cicuit is closed, cuent is lso induced in it. The e.m.f. nd cuent poduced lsts s
NTRODUCTON LCTRO - MAGNTC NDUCTON Whenee mgnetic flu linked with cicuit chnges, n e.m.f. is induced in the cicuit. f the cicuit is closed, cuent is lso induced in it. The e.m.f. nd cuent poduced lsts s
ELLIPSE. Standard equation of an ellipse referred to its principal axes along the co-ordinate axes is. ( a,0) A'
 J-Mthemtics LLIPS. STANDARD QUATION & DFINITION : Stndrd eqution of n ellipse referred to its principl es long the co-ordinte es is > & = ( e ) = e. Y + =. where where e = eccentricit (0 < e < ). FOCI
J-Mthemtics LLIPS. STANDARD QUATION & DFINITION : Stndrd eqution of n ellipse referred to its principl es long the co-ordinte es is > & = ( e ) = e. Y + =. where where e = eccentricit (0 < e < ). FOCI
4.3 Area of a Sector. Area of a Sector Section
 ea of a Secto Section 4. 9 4. ea of a Secto In geomety you leaned that the aea of a cicle of adius is π 2. We will now lean how to find the aea of a secto of a cicle. secto is the egion bounded by a cental
ea of a Secto Section 4. 9 4. ea of a Secto In geomety you leaned that the aea of a cicle of adius is π 2. We will now lean how to find the aea of a secto of a cicle. secto is the egion bounded by a cental
Electric Potential. and Equipotentials
 Electic Potentil nd Euipotentils U Electicl Potentil Review: W wok done y foce in going fom to long pth. l d E dl F W dl F θ Δ l d E W U U U Δ Δ l d E W U U U U potentil enegy electic potentil Potentil
Electic Potentil nd Euipotentils U Electicl Potentil Review: W wok done y foce in going fom to long pth. l d E dl F W dl F θ Δ l d E W U U U Δ Δ l d E W U U U U potentil enegy electic potentil Potentil
u(r, θ) = 1 + 3a r n=1
 Mth 45 / AMCS 55. etuck Assignment 8 ue Tuesdy, Apil, 6 Topics fo this week Convegence of Fouie seies; Lplce s eqution nd hmonic functions: bsic popeties, computions on ectngles nd cubes Fouie!, Poisson
Mth 45 / AMCS 55. etuck Assignment 8 ue Tuesdy, Apil, 6 Topics fo this week Convegence of Fouie seies; Lplce s eqution nd hmonic functions: bsic popeties, computions on ectngles nd cubes Fouie!, Poisson
This immediately suggests an inverse-square law for a "piece" of current along the line.
 Electomgnetic Theoy (EMT) Pof Rui, UNC Asheville, doctophys on YouTube Chpte T Notes The iot-svt Lw T nvese-sque Lw fo Mgnetism Compe the mgnitude of the electic field t distnce wy fom n infinite line
Electomgnetic Theoy (EMT) Pof Rui, UNC Asheville, doctophys on YouTube Chpte T Notes The iot-svt Lw T nvese-sque Lw fo Mgnetism Compe the mgnitude of the electic field t distnce wy fom n infinite line
MH CET 2018 (QUESTION WITH ANSWER)
 ( P C M ) MH CET 8 (QUESTION WITH ANSWER). /.sec () + log () - log (3) + log () Ans. () - log MATHS () 3 c + c C C A cos + cos c + cosc + + cosa ( + cosc ) + + cosa c c ( + + ) c / / I tn - in sec - in
( P C M ) MH CET 8 (QUESTION WITH ANSWER). /.sec () + log () - log (3) + log () Ans. () - log MATHS () 3 c + c C C A cos + cos c + cosc + + cosa ( + cosc ) + + cosa c c ( + + ) c / / I tn - in sec - in
15 - TRIGONOMETRY Page 1 ( Answers at the end of all questions )
 - TRIGONOMETRY Pge P ( ) In tringle PQR, R =. If tn b c = 0, 0, then Q nd tn re the roots of the eqution = b c c = b b = c b = c [ AIEEE 00 ] ( ) In tringle ABC, let C =. If r is the inrdius nd R is the
- TRIGONOMETRY Pge P ( ) In tringle PQR, R =. If tn b c = 0, 0, then Q nd tn re the roots of the eqution = b c c = b b = c b = c [ AIEEE 00 ] ( ) In tringle ABC, let C =. If r is the inrdius nd R is the
MATHEMATICS PART A. 1. ABC is a triangle, right angled at A. The resultant of the forces acting along AB, AC
 FIITJEE Solutions to AIEEE MATHEMATICS PART A. ABC is tringle, right ngled t A. The resultnt of the forces cting long AB, AC with mgnitudes AB nd respectively is the force long AD, where D is the AC foot
FIITJEE Solutions to AIEEE MATHEMATICS PART A. ABC is tringle, right ngled t A. The resultnt of the forces cting long AB, AC with mgnitudes AB nd respectively is the force long AD, where D is the AC foot
MATHEMATICS (Part II) (Fresh / New Course)
 Sig. of Supdt... MRD-XII-(A) MATHEMATICS Roll No... Time Allowed : Hrs. MATHEMATICS Totl Mrks: 00 NOTE : There re THREE sections in this pper i.e. Section A, B nd C. Time : 0 Mins. Section A Mrks: 0 NOTE
Sig. of Supdt... MRD-XII-(A) MATHEMATICS Roll No... Time Allowed : Hrs. MATHEMATICS Totl Mrks: 00 NOTE : There re THREE sections in this pper i.e. Section A, B nd C. Time : 0 Mins. Section A Mrks: 0 NOTE
JEE(MAIN) 2018 TEST PAPER WITH SOLUTIONS (HELD ON SUNDAY 08 th APRIL, 2018) PART B MATHEMATICS ALLEN
 . The integal sin cos 5 5 (sin cos sin sin cos cos ) is equal to () ( tan ) C () cot C () cot C () ( tan ) C (whee C is a constant of integation) Ans. () Let I sin cos d [(sin cos )(sin cos )] sin cos
. The integal sin cos 5 5 (sin cos sin sin cos cos ) is equal to () ( tan ) C () cot C () cot C () ( tan ) C (whee C is a constant of integation) Ans. () Let I sin cos d [(sin cos )(sin cos )] sin cos
Physics 604 Problem Set 1 Due Sept 16, 2010
 Physics 64 Polem et 1 Due ept 16 1 1) ) Inside good conducto the electic field is eo (electons in the conducto ecuse they e fee to move move in wy to cncel ny electic field impessed on the conducto inside
Physics 64 Polem et 1 Due ept 16 1 1) ) Inside good conducto the electic field is eo (electons in the conducto ecuse they e fee to move move in wy to cncel ny electic field impessed on the conducto inside
1. If * is the operation defined by a*b = a b for a, b N, then (2 * 3) * 2 is equal to (A) 81 (B) 512 (C) 216 (D) 64 (E) 243 ANSWER : D
 . If * is the opertion defined by *b = b for, b N, then ( * ) * is equl to (A) 8 (B) 5 (C) 6 (D) 64 (E) 4. The domin of the function ( 9)/( ),if f( ) = is 6, if = (A) (0, ) (B) (-, ) (C) (-, ) (D) (, )
. If * is the opertion defined by *b = b for, b N, then ( * ) * is equl to (A) 8 (B) 5 (C) 6 (D) 64 (E) 4. The domin of the function ( 9)/( ),if f( ) = is 6, if = (A) (0, ) (B) (-, ) (C) (-, ) (D) (, )
SOLUTIONS TO CONCEPTS CHAPTER 11
 SLUTINS T NEPTS HPTE. Gvittionl fce of ttction, F.7 0 0 0.7 0 7 N (0.). To clculte the gvittionl fce on t unline due to othe ouse. F D G 4 ( / ) 8G E F I F G ( / ) G ( / ) G 4G 4 D F F G ( / ) G esultnt
SLUTINS T NEPTS HPTE. Gvittionl fce of ttction, F.7 0 0 0.7 0 7 N (0.). To clculte the gvittionl fce on t unline due to othe ouse. F D G 4 ( / ) 8G E F I F G ( / ) G ( / ) G 4G 4 D F F G ( / ) G esultnt
Answers to test yourself questions
 Answes to test youself questions opic Descibing fields Gm Gm Gm Gm he net field t is: g ( d / ) ( 4d / ) d d Gm Gm Gm Gm Gm Gm b he net potentil t is: V d / 4d / d 4d d d V e 4 7 9 49 J kg 7 7 Gm d b E
Answes to test youself questions opic Descibing fields Gm Gm Gm Gm he net field t is: g ( d / ) ( 4d / ) d d Gm Gm Gm Gm Gm Gm b he net potentil t is: V d / 4d / d 4d d d V e 4 7 9 49 J kg 7 7 Gm d b E
 THEORY OF EQUATIONS OBJECTIVE PROBLEMS. If the eqution x 6x 0 0 ) - ) 4) -. If the sum of two oots of the eqution k is -48 ) 6 ) 48 4) 4. If the poduct of two oots of 4 ) -4 ) 4) - 4. If one oot of is
THEORY OF EQUATIONS OBJECTIVE PROBLEMS. If the eqution x 6x 0 0 ) - ) 4) -. If the sum of two oots of the eqution k is -48 ) 6 ) 48 4) 4. If the poduct of two oots of 4 ) -4 ) 4) - 4. If one oot of is
BINOMIAL THEOREM SOLUTION. 1. (D) n. = (C 0 + C 1 x +C 2 x C n x n ) (1+ x+ x 2 +.)
 BINOMIAL THEOREM SOLUTION. (D) ( + + +... + ) (+ + +.) The coefficiet of + + + +... + fo. Moeove coefficiet of is + + + +... + if >. So. (B)... e!!!! The equied coefficiet coefficiet of i e -.!...!. (A),
BINOMIAL THEOREM SOLUTION. (D) ( + + +... + ) (+ + +.) The coefficiet of + + + +... + fo. Moeove coefficiet of is + + + +... + if >. So. (B)... e!!!! The equied coefficiet coefficiet of i e -.!...!. (A),
HIGHER SCHOOL CERTIFICATE EXAMINATION MATHEMATICS 4 UNIT (ADDITIONAL) Time allowed Three hours (Plus 5 minutes reading time)
 HIGHER SCHOOL CERTIFICATE EXAMINATION 999 MATHEMATICS UNIT (ADDITIONAL) Time llowed Three hours (Plus 5 minutes reding time) DIRECTIONS TO CANDIDATES Attempt ALL questions ALL questions re of equl vlue
HIGHER SCHOOL CERTIFICATE EXAMINATION 999 MATHEMATICS UNIT (ADDITIONAL) Time llowed Three hours (Plus 5 minutes reding time) DIRECTIONS TO CANDIDATES Attempt ALL questions ALL questions re of equl vlue
School of Electrical and Computer Engineering, Cornell University. ECE 303: Electromagnetic Fields and Waves. Fall 2007
 School of Electicl nd Compute Engineeing, Conell Univesity ECE 303: Electomgnetic Fields nd Wves Fll 007 Homewok 4 Due on Sep. 1, 007 by 5:00 PM Reding Assignments: i) Review the lectue notes. ii) Relevnt
School of Electicl nd Compute Engineeing, Conell Univesity ECE 303: Electomgnetic Fields nd Wves Fll 007 Homewok 4 Due on Sep. 1, 007 by 5:00 PM Reding Assignments: i) Review the lectue notes. ii) Relevnt
General Physics II. number of field lines/area. for whole surface: for continuous surface is a whole surface
 Genel Physics II Chpte 3: Guss w We now wnt to quickly discuss one of the moe useful tools fo clculting the electic field, nmely Guss lw. In ode to undestnd Guss s lw, it seems we need to know the concept
Genel Physics II Chpte 3: Guss w We now wnt to quickly discuss one of the moe useful tools fo clculting the electic field, nmely Guss lw. In ode to undestnd Guss s lw, it seems we need to know the concept
Collection of Formulas
 Collection of Fomuls Electomgnetic Fields EITF8 Deptment of Electicl nd Infomtion Technology Lund Univesity, Sweden August 8 / ELECTOSTATICS field point '' ' Oigin ' Souce point Coulomb s Lw The foce F
Collection of Fomuls Electomgnetic Fields EITF8 Deptment of Electicl nd Infomtion Technology Lund Univesity, Sweden August 8 / ELECTOSTATICS field point '' ' Oigin ' Souce point Coulomb s Lw The foce F
Fourier-Bessel Expansions with Arbitrary Radial Boundaries
 Applied Mthemtics,,, - doi:./m.. Pulished Online My (http://www.scirp.og/jounl/m) Astct Fouie-Bessel Expnsions with Aity Rdil Boundies Muhmmd A. Mushef P. O. Box, Jeddh, Sudi Ai E-mil: mmushef@yhoo.co.uk
Applied Mthemtics,,, - doi:./m.. Pulished Online My (http://www.scirp.og/jounl/m) Astct Fouie-Bessel Expnsions with Aity Rdil Boundies Muhmmd A. Mushef P. O. Box, Jeddh, Sudi Ai E-mil: mmushef@yhoo.co.uk
Chapter 4 Kinematics in Two Dimensions
 D Kinemtic Quntities Position nd Velocit Acceletion Applictions Pojectile Motion Motion in Cicle Unifom Cicul Motion Chpte 4 Kinemtics in Two Dimensions D Motion Pemble In this chpte, we ll tnsplnt the
D Kinemtic Quntities Position nd Velocit Acceletion Applictions Pojectile Motion Motion in Cicle Unifom Cicul Motion Chpte 4 Kinemtics in Two Dimensions D Motion Pemble In this chpte, we ll tnsplnt the
St Andrew s Academy Mathematics Department Higher Mathematics VECTORS
 St ndew s cdemy Mthemtics etment Highe Mthemtics VETORS St ndew's cdemy Mths et 0117 1 Vectos sics 1. = nd = () Sketch the vectos nd. () Sketch the vectos nd. (c) Given u = +, sketch the vecto u. (d) Given
St ndew s cdemy Mthemtics etment Highe Mthemtics VETORS St ndew's cdemy Mths et 0117 1 Vectos sics 1. = nd = () Sketch the vectos nd. () Sketch the vectos nd. (c) Given u = +, sketch the vecto u. (d) Given
U>, and is negative. Electric Potential Energy
 Electic Potentil Enegy Think of gvittionl potentil enegy. When the lock is moved veticlly up ginst gvity, the gvittionl foce does negtive wok (you do positive wok), nd the potentil enegy (U) inceses. When
Electic Potentil Enegy Think of gvittionl potentil enegy. When the lock is moved veticlly up ginst gvity, the gvittionl foce does negtive wok (you do positive wok), nd the potentil enegy (U) inceses. When
Chapter 4 Two-Dimensional Motion
 D Kinemtic Quntities Position nd Velocit Acceletion Applictions Pojectile Motion Motion in Cicle Unifom Cicul Motion Chpte 4 Two-Dimensionl Motion D Motion Pemble In this chpte, we ll tnsplnt the conceptul
D Kinemtic Quntities Position nd Velocit Acceletion Applictions Pojectile Motion Motion in Cicle Unifom Cicul Motion Chpte 4 Two-Dimensionl Motion D Motion Pemble In this chpte, we ll tnsplnt the conceptul
( ) D x ( s) if r s (3) ( ) (6) ( r) = d dr D x
 SIO 22B, Rudnick dpted fom Dvis III. Single vile sttistics The next few lectues e intended s eview of fundmentl sttistics. The gol is to hve us ll speking the sme lnguge s we move to moe dvnced topics.
SIO 22B, Rudnick dpted fom Dvis III. Single vile sttistics The next few lectues e intended s eview of fundmentl sttistics. The gol is to hve us ll speking the sme lnguge s we move to moe dvnced topics.
Coordinate Geometry. = k2 e 2. 1 e + x. 1 e. ke ) 2. We now write = a, and shift the origin to the point (a, 0). Referred to
 Coodinate Geomet Conic sections These ae pane cuves which can be descibed as the intesection of a cone with panes oiented in vaious diections. It can be demonstated that the ocus of a point which moves
Coodinate Geomet Conic sections These ae pane cuves which can be descibed as the intesection of a cone with panes oiented in vaious diections. It can be demonstated that the ocus of a point which moves
SSC TIER II (MATHS) MOCK TEST - 31 (SOLUTION)
 007, OUTRM LINES, ST FLOOR, OOSITE MUKHERJEE NGR OLIE STTION, DELHI-0009 SS TIER II (MTHS) MOK TEST - (SOLUTION). () We know tht x + y + z xyz (x + y + z) (x + y + z xy yz zx) (x + y + z)[(x + y + z) (xy
007, OUTRM LINES, ST FLOOR, OOSITE MUKHERJEE NGR OLIE STTION, DELHI-0009 SS TIER II (MTHS) MOK TEST - (SOLUTION). () We know tht x + y + z xyz (x + y + z) (x + y + z xy yz zx) (x + y + z)[(x + y + z) (xy
Homework: Study 6.2 #1, 3, 5, 7, 11, 15, 55, 57
 Gols: 1. Undestnd volume s the sum of the es of n infinite nume of sufces. 2. Be le to identify: the ounded egion the efeence ectngle the sufce tht esults fom evolution of the ectngle ound n xis o foms
Gols: 1. Undestnd volume s the sum of the es of n infinite nume of sufces. 2. Be le to identify: the ounded egion the efeence ectngle the sufce tht esults fom evolution of the ectngle ound n xis o foms
Calculus AB. For a function f(x), the derivative would be f '(
 lculus AB Derivtive Formuls Derivtive Nottion: For function f(), the derivtive would e f '( ) Leiniz's Nottion: For the derivtive of y in terms of, we write d For the second derivtive using Leiniz's Nottion:
lculus AB Derivtive Formuls Derivtive Nottion: For function f(), the derivtive would e f '( ) Leiniz's Nottion: For the derivtive of y in terms of, we write d For the second derivtive using Leiniz's Nottion:
PARABOLA. moves such that PM. = e (constant > 0) (eccentricity) then locus of P is called a conic. or conic section.
 wwwskshieducioncom PARABOLA Le S be given fixed poin (focus) nd le l be given fixed line (Direcrix) Le SP nd PM be he disnce of vrible poin P o he focus nd direcrix respecively nd P SP moves such h PM
wwwskshieducioncom PARABOLA Le S be given fixed poin (focus) nd le l be given fixed line (Direcrix) Le SP nd PM be he disnce of vrible poin P o he focus nd direcrix respecively nd P SP moves such h PM
