Problem 4.4 and 6.16 of Devore discuss the Rayleigh Distribution, whose pdf is x, x > 0; x x 0. x 2 f(x; θ) dx x=0. pe p dp.
|
|
|
- Peregrine Marshall
- 5 years ago
- Views:
Transcription
1 Math Treibergs Blade Stress Example: Estimate Parameter of Rayleigh Distribution. Name: Example June 15, 2011 Problem 4.4 and 6.16 of Devore discuss the Rayleigh Distribution, whose pdf is ) x ( f(x; θ) = θ exp x2, x > 0; 2θ 0. x 0. The expectation of X 2 is found by substituting p = x 2 /(2θ) so dp = x/θ dx and d dp ( (1 + p)e p ) = pe p so E(X 2 ) = = x 2 f(x; θ) dx x=0 x 3 2 x=0 θ e x /2θ dx = 2θ p=0 pe p dp = 2θ [ (1 + p)e p] p= = 2θ. Hence for a random sample X 1,...,X n from this distribution, Thus an unbiased estimator for θ is ( 1 n E 2n i=1 ˆθ = 1 2n X 2 i ) n Xi 2. We apple the estimate to the data from the article Blade Fatigue Life... J. Solar Energy, 1982, to get an estimte of θ and superimpose the pdf onto the density histogram. We also find a way to generate Rayleigh random variables. Suppose that the cdf is F (x) = P(X x), which is strictly increasing on x > 0. Then if U Unif(0, 1) is a standard uniform RV then Y = F 1 (U) is a Rayliegh RV. To tee this, i=1 = θ. p=0 P(Y y) = P ( F 1 (U)) y ) = P (U F (y)) = F (y) because, for numbers 0 m 1, for uniform variables, P(U m) = m. Thus the simulation can be carried out because we can find F (x) for Rayleigh RV s. F (x) = = = = x f(x; θ) dx 0 x x 2 0 θ e x /2θ dx x 2 /(2θ) e p dp p=0 [ e p] p=x 2 /(2θ) p=0 = 1 e x2 /(2θ). 1
2 Finally, we observe that a Rayleigh RV is a special case of the Weibull distribution. W Weibull(α, β) has a pdf ( ( ) α ) α x dweibull(x; α, β) = β α xα 1 exp, x > 0; β 0. x 0. Thus by setting α = 2 and β = 2θ, we see that f(x; θ) = dweibull(x, 2, 2θ). R Session: R version ( ) Copyright (C) 2010 The R Foundation for Statistical Computing ISBN R is free software and comes with ABSOLUTELY NO WARRANTY. You are welcome to redistribute it under certain conditions. Type license() or licence() for distribution details. Natural language support but running in an English locale R is a collaborative project with many contributors. Type contributors() for more information and citation() on how to cite R or R packages in publications. Type demo() for some demos, help() for on-line help, or help.start() for an HTML browser interface to help. Type q() to quit R. [R.app GUI 1.34 (5589) i386-apple-darwin9.8.0] [Workspace restored from /home/1004/ma/treibergs/.rdata] > ######################### DOWLOAD A BUNCH OF COLORS ########################## > library(rcolorbrewer) > colr <- c(brewer.pal(9,"set1"),brewer.pal(8,"set2")) > > ######################### ENTER THE RAYLEIGH PDF ############################# > f <- function(x,theta){ x*exp(-x^2/(2*theta))/theta} > > xs <- seq(0,10,.099) > # Maximum of f(x,1) at fmax. for j > 1 maximum of f(x,j) is less than fmax. > fmax <- exp(-.5) 2
3 > plot(xs,f(xs,1), type="n", ylab=expression(f(x,theta)), xlab="x", + main=expression(paste("pdf for Rayleigh Distribution ", + f(x,theta)==(x/theta)*exp(-x^2/(2*theta)))), ylim=c(-.02,fmax+.02)) > for(j in 1:10) + { + lines(xs, f(xs,j), col = colr[j]) + } > abline(h=0,col=8);abline(v=0,col=8) > abline(h=(1:6)/10,col=8,lty=3);abline(v=1:10,col=8,lty=3) > legend(6.5,.55, legend = 1:10, fill = colr[1:10], bg="white", + title=expression(theta=="")) > # M3074Rayleigh1.pdf 3
4 pdf for Rayleigh Distribution f(x, θ) = (x θ)exp( x 2 (2θ)) f(x, θ) θ = x > ################ ENTER VIBRATION DATA ######################################### > # Devore 6.15 Vibratory Stress of turbine Blade from > # Blade Fatigue Life\ldots {\it J.~Solar Energy}, 1982 > Stress <- scan() 1: : : Read 10 items 4
5 > Stress [1] > > ################## ESTIMATOR THETA HAT ######################################### > thetahat <-.5*mean(Stress^2) > # Plot histogram of "Stress" and density using estimated "thetahat" > hist(stress, breaks = "FD", freq = FALSE, + main = paste("stress Histogram, Density f(x,theta^), theta^ =", thetahat)) > lines(xxs, f(xxs,thetahat), col=2) > # M3074Rayleigh2.pdf 5
6 Stress Histogram, Density f(x,theta^), theta^ = Density Stress > ##################### SIMULATING Rayleigh rv s ################################ > # method works using cdf > # F(x) = P(X <= x). > # F^(-1)(p) = inverse of F > th3 <- 3 > Finv <- function(p){sqrt(-2*th3*log(1-p))} > # sapply( numbers, function ) evaluates the "function" on each of the "numbers." > hist(sapply(runif(1000),"finv"), xlab="x", freq = FALSE, + main = paste("histogram of Simulated Rayleigh RVs theta =", th3), col=colr[15]) 6
7 > xxxs<-seq(0,7,.097) > lines(xxxs,f(xxxs,th3),col=2) > # M3074Rayleigh3.pdf Histogram of Simulated Rayleigh RVs theta = 3 Density x > th3 <- 9 > Finv <- function(p){sqrt(-2*th3*log(1-p))} > xxxs<-seq(0,12,.097) 7
8 > hist(sapply(runif(1000),"finv"), xlab="x", freq=false, + main = paste("histogram of Simulated Rayleigh RVs theta =", th3), col=colr[16]) > lines(xxxs, f(xxxs,th3), col = 6) > # M3074Rayleigh4.pdf Histogram of Simulated Rayleigh RVs theta = 9 Density x > ###################### TEST IF RAYLEIGH EQUALS WEIBULL ########################### > # Compute difference f(x,theta) - dweibull(x,2,sqrt(2*theta) for several x,theta > s <- matrix(numeric(50), ncol=5, dimnames = list((1:10)/2, 1:5)) 8
9 > > for(i in 1:10) + { + for(j in 1:5) + { + s[i,j]<-f(i/2,j)-dweibull(i/2,2,sqrt(2*j)) + } + } > s e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e-17 > # Hmmmmmm! Very small differences! > > ############### USE WEIBULL TO SIMULATE RAYLEIGH RV #################### > hist( rweibull(1000,2,sqrt(2*th3)), xlab = "x", freq = FALSE, + main=paste("hist. Random Weibull, (alpha,beta) = (", 2, ",", sqrt(2*th3), + ")"),col=colr[15]) > lines(xxxs, dweibull(xxxs, 2, sqrt(2*th3)), col = colr[4]) > # M3074Rayleigh5.pdf 9
10 Hist. Random Weibull, (alpha,beta) = ( 2, ) Density x 10
X = S 2 = 1 n. X i. i=1
 Math 3070 1. Treibergs Horse Kick Example: Confidence Interval for Poisson Parameter Name: Example July 3, 2011 The Poisson Random Variable describes the number of occurences of rare events in a period
Math 3070 1. Treibergs Horse Kick Example: Confidence Interval for Poisson Parameter Name: Example July 3, 2011 The Poisson Random Variable describes the number of occurences of rare events in a period
f Simulation Example: Simulating p-values of Two Sample Variance Test. Name: Example June 26, 2011 Math Treibergs
 Math 3070 1. Treibergs f Simulation Example: Simulating p-values of Two Sample Variance Test. Name: Example June 26, 2011 The t-test is fairly robust with regard to actual distribution of data. But the
Math 3070 1. Treibergs f Simulation Example: Simulating p-values of Two Sample Variance Test. Name: Example June 26, 2011 The t-test is fairly robust with regard to actual distribution of data. But the
Carapace Example: Confidence Intervals in the Wilcoxon Sign-rank Test
 Math 3080 1. Treibergs Carapace Example: Confidence Intervals in the Wilcoxon Sign-rank Test Name: Example April 19, 2014 In this discussion, we look at confidence intervals in the Wilcoxon Sign-Rank Test
Math 3080 1. Treibergs Carapace Example: Confidence Intervals in the Wilcoxon Sign-rank Test Name: Example April 19, 2014 In this discussion, we look at confidence intervals in the Wilcoxon Sign-Rank Test
Munitions Example: Negative Binomial to Predict Number of Accidents
 Math 37 1. Treibergs Munitions Eample: Negative Binomial to Predict Number of Accidents Name: Eample July 17, 211 This problem comes from Bulmer, Principles of Statistics, Dover, 1979, which is a republication
Math 37 1. Treibergs Munitions Eample: Negative Binomial to Predict Number of Accidents Name: Eample July 17, 211 This problem comes from Bulmer, Principles of Statistics, Dover, 1979, which is a republication
Horse Kick Example: Chi-Squared Test for Goodness of Fit with Unknown Parameters
 Math 3080 1. Treibergs Horse Kick Example: Chi-Squared Test for Goodness of Fit with Unknown Parameters Name: Example April 4, 014 This R c program explores a goodness of fit test where the parameter is
Math 3080 1. Treibergs Horse Kick Example: Chi-Squared Test for Goodness of Fit with Unknown Parameters Name: Example April 4, 014 This R c program explores a goodness of fit test where the parameter is
Spectrophotometer Example: One-Factor Random Effects ANOVA
 Math 3080 1. Treibergs Spectrophotometer Example: One-Factor Random Effects ANOVA Name: Example Jan. 22, 2014 Today s example was motivated from problem.14.9 of Walpole, Myers, Myers and Ye, Probability
Math 3080 1. Treibergs Spectrophotometer Example: One-Factor Random Effects ANOVA Name: Example Jan. 22, 2014 Today s example was motivated from problem.14.9 of Walpole, Myers, Myers and Ye, Probability
Straw Example: Randomized Block ANOVA
 Math 3080 1. Treibergs Straw Example: Randomized Block ANOVA Name: Example Jan. 23, 2014 Today s example was motivated from problem 13.11.9 of Walpole, Myers, Myers and Ye, Probability and Statistics for
Math 3080 1. Treibergs Straw Example: Randomized Block ANOVA Name: Example Jan. 23, 2014 Today s example was motivated from problem 13.11.9 of Walpole, Myers, Myers and Ye, Probability and Statistics for
R version ( ) Copyright (C) 2009 The R Foundation for Statistical Computing ISBN
 Math 3070 1. Treibergs Design of a Binomial Experiment: Programming Conditional Statements Name: Example May 20, 2011 How big a sample should we test in order that the Type I and Type II error probabilities
Math 3070 1. Treibergs Design of a Binomial Experiment: Programming Conditional Statements Name: Example May 20, 2011 How big a sample should we test in order that the Type I and Type II error probabilities
Pumpkin Example: Flaws in Diagnostics: Correcting Models
 Math 3080. Treibergs Pumpkin Example: Flaws in Diagnostics: Correcting Models Name: Example March, 204 From Levine Ramsey & Smidt, Applied Statistics for Engineers and Scientists, Prentice Hall, Upper
Math 3080. Treibergs Pumpkin Example: Flaws in Diagnostics: Correcting Models Name: Example March, 204 From Levine Ramsey & Smidt, Applied Statistics for Engineers and Scientists, Prentice Hall, Upper
Gas Transport Example: Confidence Intervals in the Wilcoxon Rank-Sum Test
 Math 3080 1. Treibergs Gas Transport Example: Confidence Intervals in the Wilcoxon Rank-Sum Test Name: Example April 19, 014 In this discussion, we look at confidence intervals in the Wilcoxon Rank-Sum
Math 3080 1. Treibergs Gas Transport Example: Confidence Intervals in the Wilcoxon Rank-Sum Test Name: Example April 19, 014 In this discussion, we look at confidence intervals in the Wilcoxon Rank-Sum
R version ( ) Copyright (C) 2009 The R Foundation for Statistical Computing ISBN
 Math 3070 1. Tibergs Simulating the Sampling Distribution of the t-statistic Name: Eample May 20, 2011 How well does a statistic behave when the assumptions about the underlying population fail to hold?
Math 3070 1. Tibergs Simulating the Sampling Distribution of the t-statistic Name: Eample May 20, 2011 How well does a statistic behave when the assumptions about the underlying population fail to hold?
R version ( ) Copyright (C) 2009 The R Foundation for Statistical Computing ISBN
 Math 3070 1. Treibergs Extraterrestial Life Example: One-Sample CI and Test of Proportion Name: Example May 31, 2011 The existence of intelligent life on other planets has fascinated writers, such as H.
Math 3070 1. Treibergs Extraterrestial Life Example: One-Sample CI and Test of Proportion Name: Example May 31, 2011 The existence of intelligent life on other planets has fascinated writers, such as H.
Math Treibergs. Turbine Blade Example: 2 6 Factorial Name: Example Experiment with 1 4 Replication February 22, 2016
 Math 3080 1. Treibergs Turbine Blade Example: 2 6 actorial Name: Example Experiment with 1 4 Replication ebruary 22, 2016 An experiment was run in the VPI Mechanical Engineering epartment to assess various
Math 3080 1. Treibergs Turbine Blade Example: 2 6 actorial Name: Example Experiment with 1 4 Replication ebruary 22, 2016 An experiment was run in the VPI Mechanical Engineering epartment to assess various
R version ( ) Copyright (C) 2009 The R Foundation for Statistical Computing ISBN
 Math 3080 1. Treibergs Spray Data: 2 3 Factorial with Multiple Replicates Per ell ANOVA Name: Example April 7, 2010 Data File Used in this Analysis: # Math 3081-1 Spray Data April 17,2010 # Treibergs #
Math 3080 1. Treibergs Spray Data: 2 3 Factorial with Multiple Replicates Per ell ANOVA Name: Example April 7, 2010 Data File Used in this Analysis: # Math 3081-1 Spray Data April 17,2010 # Treibergs #
R version ( ) Copyright (C) 2009 The R Foundation for Statistical Computing ISBN
 Math 3080 1. Treibergs Bread Wrapper Data: 2 4 Incomplete Block Design. Name: Example April 26, 2010 Data File Used in this Analysis: # Math 3080-1 Bread Wrapper Data April 23, 2010 # Treibergs # # From
Math 3080 1. Treibergs Bread Wrapper Data: 2 4 Incomplete Block Design. Name: Example April 26, 2010 Data File Used in this Analysis: # Math 3080-1 Bread Wrapper Data April 23, 2010 # Treibergs # # From
Natural language support but running in an English locale
 R version 3.2.1 (2015-06-18) -- "World-Famous Astronaut" Copyright (C) 2015 The R Foundation for Statistical Computing Platform: x86_64-apple-darwin13.4.0 (64-bit) R is free software and comes with ABSOLUTELY
R version 3.2.1 (2015-06-18) -- "World-Famous Astronaut" Copyright (C) 2015 The R Foundation for Statistical Computing Platform: x86_64-apple-darwin13.4.0 (64-bit) R is free software and comes with ABSOLUTELY
Beam Example: Identifying Influential Observations using the Hat Matrix
 Math 3080. Treibergs Beam Example: Identifying Influential Observations using the Hat Matrix Name: Example March 22, 204 This R c program explores influential observations and their detection using the
Math 3080. Treibergs Beam Example: Identifying Influential Observations using the Hat Matrix Name: Example March 22, 204 This R c program explores influential observations and their detection using the
(1) (AE) (BE) + (AB) + (CE) (AC) (BE) + (ABCE) +(DE) (AD) (BD) + (ABDE) + (CD) (ACDE) (BCDE) + (ABCD)
 Math 3080 1. Treibergs Peanut xample: 2 5 alf Replication Factorial xperiment Name: xample Feb. 8, 2014 We describe a 2 5 experimental design with one half replicate per cell. It comes from a paper by
Math 3080 1. Treibergs Peanut xample: 2 5 alf Replication Factorial xperiment Name: xample Feb. 8, 2014 We describe a 2 5 experimental design with one half replicate per cell. It comes from a paper by
Math Treibergs. Peanut Oil Data: 2 5 Factorial design with 1/2 Replication. Name: Example April 22, Data File Used in this Analysis:
 Math 3080 1. Treibergs Peanut Oil Data: 2 5 Factorial design with 1/2 Replication. Name: Example April 22, 2010 Data File Used in this Analysis: # Math 3080-1 Peanut Oil Data April 22, 2010 # Treibergs
Math 3080 1. Treibergs Peanut Oil Data: 2 5 Factorial design with 1/2 Replication. Name: Example April 22, 2010 Data File Used in this Analysis: # Math 3080-1 Peanut Oil Data April 22, 2010 # Treibergs
STAT 753 Homework 3 SOLUTIONS
 STAT 753 Homework 3 SOLUTIONS. Y Weibull distribution W (α, ). The survival function is given by S Y (y) = P r(y y) = e ( y α), y 0, α, > 0. (a) Cumulative distribution and its inverse functions. The cumulative
STAT 753 Homework 3 SOLUTIONS. Y Weibull distribution W (α, ). The survival function is given by S Y (y) = P r(y y) = e ( y α), y 0, α, > 0. (a) Cumulative distribution and its inverse functions. The cumulative
Basic Data Analysis. Stephen Turnbull Business Administration and Public Policy Lecture 9: June 6, Abstract. Regression and R.
 July 22, 2013 1 ohp9 Basic Data Analysis Stephen Turnbull Business Administration and Public Policy Lecture 9: June 6, 2013 Regression and R. Abstract Regression Correlation shows the statistical strength
July 22, 2013 1 ohp9 Basic Data Analysis Stephen Turnbull Business Administration and Public Policy Lecture 9: June 6, 2013 Regression and R. Abstract Regression Correlation shows the statistical strength
Prof. Thistleton MAT 505 Introduction to Probability Lecture 13
 Prof. Thistleton MAT 55 Introduction to Probability Lecture 3 Sections from Text and MIT Video Lecture: Sections 5.4, 5.6 http://ocw.mit.edu/courses/electrical-engineering-and-computer-science/6-4- probabilisticsystems-analysis-and-applied-probability-fall-2/video-lectures/lecture-8-continuousrandomvariables/
Prof. Thistleton MAT 55 Introduction to Probability Lecture 3 Sections from Text and MIT Video Lecture: Sections 5.4, 5.6 http://ocw.mit.edu/courses/electrical-engineering-and-computer-science/6-4- probabilisticsystems-analysis-and-applied-probability-fall-2/video-lectures/lecture-8-continuousrandomvariables/
Continuous random variables
 Continuous random variables Continuous r.v. s take an uncountably infinite number of possible values. Examples: Heights of people Weights of apples Diameters of bolts Life lengths of light-bulbs We cannot
Continuous random variables Continuous r.v. s take an uncountably infinite number of possible values. Examples: Heights of people Weights of apples Diameters of bolts Life lengths of light-bulbs We cannot
Math 362, Problem set 1
 Math 6, roblem set Due //. (4..8) Determine the mean variance of the mean X of a rom sample of size 9 from a distribution having pdf f(x) = 4x, < x
Math 6, roblem set Due //. (4..8) Determine the mean variance of the mean X of a rom sample of size 9 from a distribution having pdf f(x) = 4x, < x
Joint Probability Distributions and Random Samples (Devore Chapter Five)
 Joint Probability Distributions and Random Samples (Devore Chapter Five) 1016-345-01: Probability and Statistics for Engineers Spring 2013 Contents 1 Joint Probability Distributions 2 1.1 Two Discrete
Joint Probability Distributions and Random Samples (Devore Chapter Five) 1016-345-01: Probability and Statistics for Engineers Spring 2013 Contents 1 Joint Probability Distributions 2 1.1 Two Discrete
Definition 1.1 (Parametric family of distributions) A parametric distribution is a set of distribution functions, each of which is determined by speci
 Definition 1.1 (Parametric family of distributions) A parametric distribution is a set of distribution functions, each of which is determined by specifying one or more values called parameters. The number
Definition 1.1 (Parametric family of distributions) A parametric distribution is a set of distribution functions, each of which is determined by specifying one or more values called parameters. The number
Chapter 3 sections. SKIP: 3.10 Markov Chains. SKIP: pages Chapter 3 - continued
 Chapter 3 sections 3.1 Random Variables and Discrete Distributions 3.2 Continuous Distributions 3.3 The Cumulative Distribution Function 3.4 Bivariate Distributions 3.5 Marginal Distributions 3.6 Conditional
Chapter 3 sections 3.1 Random Variables and Discrete Distributions 3.2 Continuous Distributions 3.3 The Cumulative Distribution Function 3.4 Bivariate Distributions 3.5 Marginal Distributions 3.6 Conditional
f (1 0.5)/n Z =
 Math 466/566 - Homework 4. We want to test a hypothesis involving a population proportion. The unknown population proportion is p. The null hypothesis is p = / and the alternative hypothesis is p > /.
Math 466/566 - Homework 4. We want to test a hypothesis involving a population proportion. The unknown population proportion is p. The null hypothesis is p = / and the alternative hypothesis is p > /.
Mathematical Statistics 1 Math A 6330
 Mathematical Statistics 1 Math A 6330 Chapter 2 Transformations and Expectations Mohamed I. Riffi Department of Mathematics Islamic University of Gaza September 14, 2015 Outline 1 Distributions of Functions
Mathematical Statistics 1 Math A 6330 Chapter 2 Transformations and Expectations Mohamed I. Riffi Department of Mathematics Islamic University of Gaza September 14, 2015 Outline 1 Distributions of Functions
(U 338-E) 2018 Nuclear Decommissioning Cost Triennial Proceeding A Workpapers
 (U 338-E) 2018 Nuclear Decommissioning Cost Triennial Proceeding A.18-03-009 Workpapers 2018 SCE Trust Fund Contributions and Financial Assumptions SCE-06 Chapter II: Burial Escalation Rate Calculation
(U 338-E) 2018 Nuclear Decommissioning Cost Triennial Proceeding A.18-03-009 Workpapers 2018 SCE Trust Fund Contributions and Financial Assumptions SCE-06 Chapter II: Burial Escalation Rate Calculation
Distributions of Functions of Random Variables. 5.1 Functions of One Random Variable
 Distributions of Functions of Random Variables 5.1 Functions of One Random Variable 5.2 Transformations of Two Random Variables 5.3 Several Random Variables 5.4 The Moment-Generating Function Technique
Distributions of Functions of Random Variables 5.1 Functions of One Random Variable 5.2 Transformations of Two Random Variables 5.3 Several Random Variables 5.4 The Moment-Generating Function Technique
1 Solution to Problem 2.1
 Solution to Problem 2. I incorrectly worked this exercise instead of 2.2, so I decided to include the solution anyway. a) We have X Y /3, which is a - function. It maps the interval, ) where X lives) onto
Solution to Problem 2. I incorrectly worked this exercise instead of 2.2, so I decided to include the solution anyway. a) We have X Y /3, which is a - function. It maps the interval, ) where X lives) onto
Generalized Linear Models in R
 Generalized Linear Models in R NO ORDER Kenneth K. Lopiano, Garvesh Raskutti, Dan Yang last modified 28 4 2013 1 Outline 1. Background and preliminaries 2. Data manipulation and exercises 3. Data structures
Generalized Linear Models in R NO ORDER Kenneth K. Lopiano, Garvesh Raskutti, Dan Yang last modified 28 4 2013 1 Outline 1. Background and preliminaries 2. Data manipulation and exercises 3. Data structures
ECE 650. Some MATLAB Help (addendum to Lecture 1) D. Van Alphen (Thanks to Prof. Katz for the Histogram PDF Notes!)
 ECE 65 Some MATLAB Help (addendum to Lecture 1) D. Van Alphen (Thanks to Prof. Katz for the Histogram PDF Notes!) Obtaining Probabilities for Gaussian RV s - An Example Let X be N(1, s 2 = 4). Find Pr(X
ECE 65 Some MATLAB Help (addendum to Lecture 1) D. Van Alphen (Thanks to Prof. Katz for the Histogram PDF Notes!) Obtaining Probabilities for Gaussian RV s - An Example Let X be N(1, s 2 = 4). Find Pr(X
Week 9 The Central Limit Theorem and Estimation Concepts
 Week 9 and Estimation Concepts Week 9 and Estimation Concepts Week 9 Objectives 1 The Law of Large Numbers and the concept of consistency of averages are introduced. The condition of existence of the population
Week 9 and Estimation Concepts Week 9 and Estimation Concepts Week 9 Objectives 1 The Law of Large Numbers and the concept of consistency of averages are introduced. The condition of existence of the population
Connexions and the Gumbel Distribution
 Connexions and the Gumbel Distribution Myron Hlynka Department of Mathematics and Statistics University of Windsor Windsor, ON, Canada. October, 2016 Myron Hlynka (University of Windsor) Connexions and
Connexions and the Gumbel Distribution Myron Hlynka Department of Mathematics and Statistics University of Windsor Windsor, ON, Canada. October, 2016 Myron Hlynka (University of Windsor) Connexions and
0 otherwise. Page 100 Exercise 9: Suppose that a random variable X has a discrete distribution with the following p.m.f.: { c. 2 x. 0 otherwise.
 Stat 42 Solutions for Homework Set 4 Page Exercise 5: Suppose that a box contains seven red balls and three blue balls. If five balls are selected at random, without replacement, determine the p.m.f. of
Stat 42 Solutions for Homework Set 4 Page Exercise 5: Suppose that a box contains seven red balls and three blue balls. If five balls are selected at random, without replacement, determine the p.m.f. of
Data Modeling & Analysis Techniques. Probability & Statistics. Manfred Huber
 Data Modeling & Analysis Techniques Probability & Statistics Manfred Huber 2017 1 Probability and Statistics Probability and statistics are often used interchangeably but are different, related fields
Data Modeling & Analysis Techniques Probability & Statistics Manfred Huber 2017 1 Probability and Statistics Probability and statistics are often used interchangeably but are different, related fields
LANGEBIO - BIOSTATISTICS
 LANGEBIO - BIOSTATISTICS OCTAVIO MARTÍNEZ DE LA VEGA 7. Continuous Random Variables So far we have been studying random variables which result from counting. However, in many cases we measure something
LANGEBIO - BIOSTATISTICS OCTAVIO MARTÍNEZ DE LA VEGA 7. Continuous Random Variables So far we have been studying random variables which result from counting. However, in many cases we measure something
Matematisk statistik allmän kurs, MASA01:A, HT-15 Laborationer
 Lunds universitet Matematikcentrum Matematisk statistik Matematisk statistik allmän kurs, MASA01:A, HT-15 Laborationer General information on labs During the rst half of the course MASA01 we will have
Lunds universitet Matematikcentrum Matematisk statistik Matematisk statistik allmän kurs, MASA01:A, HT-15 Laborationer General information on labs During the rst half of the course MASA01 we will have
Statistics Assignment 2 HET551 Design and Development Project 1
 Statistics Assignment HET Design and Development Project Michael Allwright - 74634 Haddon O Neill 7396 Monday, 3 June Simple Stochastic Processes Mean, Variance and Covariance Derivation The following
Statistics Assignment HET Design and Development Project Michael Allwright - 74634 Haddon O Neill 7396 Monday, 3 June Simple Stochastic Processes Mean, Variance and Covariance Derivation The following
1 Probability and Random Variables
 1 Probability and Random Variables The models that you have seen thus far are deterministic models. For any time t, there is a unique solution X(t). On the other hand, stochastic models will result in
1 Probability and Random Variables The models that you have seen thus far are deterministic models. For any time t, there is a unique solution X(t). On the other hand, stochastic models will result in
Generating pseudo- random numbers
 Generating pseudo- random numbers What are pseudo-random numbers? Numbers exhibiting statistical randomness while being generated by a deterministic process. Easier to generate than true random numbers?
Generating pseudo- random numbers What are pseudo-random numbers? Numbers exhibiting statistical randomness while being generated by a deterministic process. Easier to generate than true random numbers?
Chapter 3. Chapter 3 sections
 sections 3.1 Random Variables and Discrete Distributions 3.2 Continuous Distributions 3.4 Bivariate Distributions 3.5 Marginal Distributions 3.6 Conditional Distributions 3.7 Multivariate Distributions
sections 3.1 Random Variables and Discrete Distributions 3.2 Continuous Distributions 3.4 Bivariate Distributions 3.5 Marginal Distributions 3.6 Conditional Distributions 3.7 Multivariate Distributions
Explore the data. Anja Bråthen Kristoffersen
 Explore the data Anja Bråthen Kristoffersen density 0.2 0.4 0.6 0.8 Probability distributions Can be either discrete or continuous (uniform, bernoulli, normal, etc) Defined by a density function, p(x)
Explore the data Anja Bråthen Kristoffersen density 0.2 0.4 0.6 0.8 Probability distributions Can be either discrete or continuous (uniform, bernoulli, normal, etc) Defined by a density function, p(x)
MIT Spring 2015
 MIT 18.443 Dr. Kempthorne Spring 2015 MIT 18.443 1 Outline 1 MIT 18.443 2 Batches of data: single or multiple x 1, x 2,..., x n y 1, y 2,..., y m w 1, w 2,..., w l etc. Graphical displays Summary statistics:
MIT 18.443 Dr. Kempthorne Spring 2015 MIT 18.443 1 Outline 1 MIT 18.443 2 Batches of data: single or multiple x 1, x 2,..., x n y 1, y 2,..., y m w 1, w 2,..., w l etc. Graphical displays Summary statistics:
STAT 801: Mathematical Statistics. Distribution Theory
 STAT 81: Mathematical Statistics Distribution Theory Basic Problem: Start with assumptions about f or CDF of random vector X (X 1,..., X p ). Define Y g(x 1,..., X p ) to be some function of X (usually
STAT 81: Mathematical Statistics Distribution Theory Basic Problem: Start with assumptions about f or CDF of random vector X (X 1,..., X p ). Define Y g(x 1,..., X p ) to be some function of X (usually
t x 1 e t dt, and simplify the answer when possible (for example, when r is a positive even number). In particular, confirm that EX 4 = 3.
 Mathematical Statistics: Homewor problems General guideline. While woring outside the classroom, use any help you want, including people, computer algebra systems, Internet, and solution manuals, but mae
Mathematical Statistics: Homewor problems General guideline. While woring outside the classroom, use any help you want, including people, computer algebra systems, Internet, and solution manuals, but mae
Chapter 3 sections. SKIP: 3.10 Markov Chains. SKIP: pages Chapter 3 - continued
 Chapter 3 sections Chapter 3 - continued 3.1 Random Variables and Discrete Distributions 3.2 Continuous Distributions 3.3 The Cumulative Distribution Function 3.4 Bivariate Distributions 3.5 Marginal Distributions
Chapter 3 sections Chapter 3 - continued 3.1 Random Variables and Discrete Distributions 3.2 Continuous Distributions 3.3 The Cumulative Distribution Function 3.4 Bivariate Distributions 3.5 Marginal Distributions
Probability measures A probability measure, P, is a real valued function from the collection of possible events so that the following
 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike License. Your use of this material constitutes acceptance of that license and the conditions of use of materials on this
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike License. Your use of this material constitutes acceptance of that license and the conditions of use of materials on this
Explore the data. Anja Bråthen Kristoffersen Biomedical Research Group
 Explore the data Anja Bråthen Kristoffersen Biomedical Research Group density 0.2 0.4 0.6 0.8 Probability distributions Can be either discrete or continuous (uniform, bernoulli, normal, etc) Defined by
Explore the data Anja Bråthen Kristoffersen Biomedical Research Group density 0.2 0.4 0.6 0.8 Probability distributions Can be either discrete or continuous (uniform, bernoulli, normal, etc) Defined by
Math 494: Mathematical Statistics
 Math 494: Mathematical Statistics Instructor: Jimin Ding jmding@wustl.edu Department of Mathematics Washington University in St. Louis Class materials are available on course website (www.math.wustl.edu/
Math 494: Mathematical Statistics Instructor: Jimin Ding jmding@wustl.edu Department of Mathematics Washington University in St. Louis Class materials are available on course website (www.math.wustl.edu/
Statistics 3657 : Moment Approximations
 Statistics 3657 : Moment Approximations Preliminaries Suppose that we have a r.v. and that we wish to calculate the expectation of g) for some function g. Of course we could calculate it as Eg)) by the
Statistics 3657 : Moment Approximations Preliminaries Suppose that we have a r.v. and that we wish to calculate the expectation of g) for some function g. Of course we could calculate it as Eg)) by the
Chapter 2. Continuous random variables
 Chapter 2 Continuous random variables Outline Review of probability: events and probability Random variable Probability and Cumulative distribution function Review of discrete random variable Introduction
Chapter 2 Continuous random variables Outline Review of probability: events and probability Random variable Probability and Cumulative distribution function Review of discrete random variable Introduction
1. Point Estimators, Review
 AMS571 Prof. Wei Zhu 1. Point Estimators, Review Example 1. Let be a random sample from. Please find a good point estimator for Solutions. There are the typical estimators for and. Both are unbiased estimators.
AMS571 Prof. Wei Zhu 1. Point Estimators, Review Example 1. Let be a random sample from. Please find a good point estimator for Solutions. There are the typical estimators for and. Both are unbiased estimators.
MAS223 Statistical Inference and Modelling Exercises
 MAS223 Statistical Inference and Modelling Exercises The exercises are grouped into sections, corresponding to chapters of the lecture notes Within each section exercises are divided into warm-up questions,
MAS223 Statistical Inference and Modelling Exercises The exercises are grouped into sections, corresponding to chapters of the lecture notes Within each section exercises are divided into warm-up questions,
Math 70 Homework 2 Michael Downs. 2(w i b) 0 = (w i b) 0 = 0 = b = 1 n. w i b 2 = nb = = z iz i 2z iaˆd i + ˆd 2 i
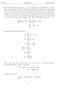 1. I show that minimizing n x i b aĉ i 2 with x i, b, a R n and a 2 = 1 is the same as maximizing the variance of Za. The problem here is finding an n-dimensional best fit line with direction vector a
1. I show that minimizing n x i b aĉ i 2 with x i, b, a R n and a 2 = 1 is the same as maximizing the variance of Za. The problem here is finding an n-dimensional best fit line with direction vector a
Package gumbel. February 15, 2013
 Package gumbel February 15, 2013 Type Package Title Gumbel copula Version 1.04 Date 2012-07-31 Author Anne-Lise Caillat, Christophe Dutang, V eronique Larrieu and Triet Nguyen Maintainer Christophe Dutang
Package gumbel February 15, 2013 Type Package Title Gumbel copula Version 1.04 Date 2012-07-31 Author Anne-Lise Caillat, Christophe Dutang, V eronique Larrieu and Triet Nguyen Maintainer Christophe Dutang
p. 6-1 Continuous Random Variables p. 6-2
 Continuous Random Variables Recall: For discrete random variables, only a finite or countably infinite number of possible values with positive probability (>). Often, there is interest in random variables
Continuous Random Variables Recall: For discrete random variables, only a finite or countably infinite number of possible values with positive probability (>). Often, there is interest in random variables
Closed book and notes. 60 minutes. Cover page and four pages of exam. No calculators.
 IE 230 Seat # Closed book and notes. 60 minutes. Cover page and four pages of exam. No calculators. Score Exam #3a, Spring 2002 Schmeiser Closed book and notes. 60 minutes. 1. True or false. (for each,
IE 230 Seat # Closed book and notes. 60 minutes. Cover page and four pages of exam. No calculators. Score Exam #3a, Spring 2002 Schmeiser Closed book and notes. 60 minutes. 1. True or false. (for each,
AMS 132: Discussion Section 2
 Prof. David Draper Department of Applied Mathematics and Statistics University of California, Santa Cruz AMS 132: Discussion Section 2 All computer operations in this course will be described for the Windows
Prof. David Draper Department of Applied Mathematics and Statistics University of California, Santa Cruz AMS 132: Discussion Section 2 All computer operations in this course will be described for the Windows
MATH 180A - INTRODUCTION TO PROBABILITY PRACTICE MIDTERM #2 FALL 2018
 MATH 8A - INTRODUCTION TO PROBABILITY PRACTICE MIDTERM # FALL 8 Name (Last, First): Student ID: TA: SO AS TO NOT DISTURB OTHER STUDENTS, EVERY- ONE MUST STAY UNTIL THE EXAM IS COMPLETE. ANSWERS TO THE
MATH 8A - INTRODUCTION TO PROBABILITY PRACTICE MIDTERM # FALL 8 Name (Last, First): Student ID: TA: SO AS TO NOT DISTURB OTHER STUDENTS, EVERY- ONE MUST STAY UNTIL THE EXAM IS COMPLETE. ANSWERS TO THE
Density and Distribution Estimation
 Density and Distribution Estimation Nathaniel E. Helwig Assistant Professor of Psychology and Statistics University of Minnesota (Twin Cities) Updated 04-Jan-2017 Nathaniel E. Helwig (U of Minnesota) Density
Density and Distribution Estimation Nathaniel E. Helwig Assistant Professor of Psychology and Statistics University of Minnesota (Twin Cities) Updated 04-Jan-2017 Nathaniel E. Helwig (U of Minnesota) Density
Math438 Actuarial Probability
 Math438 Actuarial Probability Jinguo Lian Department of Math and Stats Jan. 22, 2016 Continuous Random Variables-Part I: Definition A random variable X is continuous if its set of possible values is an
Math438 Actuarial Probability Jinguo Lian Department of Math and Stats Jan. 22, 2016 Continuous Random Variables-Part I: Definition A random variable X is continuous if its set of possible values is an
STAT 430/510: Lecture 10
 STAT 430/510: Lecture 10 James Piette June 9, 2010 Updates HW2 is due today! Pick up your HW1 s up in stat dept. There is a box located right when you enter that is labeled "Stat 430 HW1". It ll be out
STAT 430/510: Lecture 10 James Piette June 9, 2010 Updates HW2 is due today! Pick up your HW1 s up in stat dept. There is a box located right when you enter that is labeled "Stat 430 HW1". It ll be out
Estimation of Quantiles
 9 Estimation of Quantiles The notion of quantiles was introduced in Section 3.2: recall that a quantile x α for an r.v. X is a constant such that P(X x α )=1 α. (9.1) In this chapter we examine quantiles
9 Estimation of Quantiles The notion of quantiles was introduced in Section 3.2: recall that a quantile x α for an r.v. X is a constant such that P(X x α )=1 α. (9.1) In this chapter we examine quantiles
Lecture 4. Continuous Random Variables and Transformations of Random Variables
 Math 408 - Mathematical Statistics Lecture 4. Continuous Random Variables and Transformations of Random Variables January 25, 2013 Konstantin Zuev (USC) Math 408, Lecture 4 January 25, 2013 1 / 13 Agenda
Math 408 - Mathematical Statistics Lecture 4. Continuous Random Variables and Transformations of Random Variables January 25, 2013 Konstantin Zuev (USC) Math 408, Lecture 4 January 25, 2013 1 / 13 Agenda
ST745: Survival Analysis: Parametric
 ST745: Survival Analysis: Parametric Eric B. Laber Department of Statistics, North Carolina State University January 13, 2015 ...the statistician knows... that in nature there never was a normal distribution,
ST745: Survival Analysis: Parametric Eric B. Laber Department of Statistics, North Carolina State University January 13, 2015 ...the statistician knows... that in nature there never was a normal distribution,
Frequency Analysis & Probability Plots
 Note Packet #14 Frequency Analysis & Probability Plots CEE 3710 October 0, 017 Frequency Analysis Process by which engineers formulate magnitude of design events (i.e. 100 year flood) or assess risk associated
Note Packet #14 Frequency Analysis & Probability Plots CEE 3710 October 0, 017 Frequency Analysis Process by which engineers formulate magnitude of design events (i.e. 100 year flood) or assess risk associated
Test Problems for Probability Theory ,
 1 Test Problems for Probability Theory 01-06-16, 010-1-14 1. Write down the following probability density functions and compute their moment generating functions. (a) Binomial distribution with mean 30
1 Test Problems for Probability Theory 01-06-16, 010-1-14 1. Write down the following probability density functions and compute their moment generating functions. (a) Binomial distribution with mean 30
Chapter 4 Multiple Random Variables
 Review for the previous lecture Theorems and Examples: How to obtain the pmf (pdf) of U = g ( X Y 1 ) and V = g ( X Y) Chapter 4 Multiple Random Variables Chapter 43 Bivariate Transformations Continuous
Review for the previous lecture Theorems and Examples: How to obtain the pmf (pdf) of U = g ( X Y 1 ) and V = g ( X Y) Chapter 4 Multiple Random Variables Chapter 43 Bivariate Transformations Continuous
SOLUTIONS TO MATH68181 EXTREME VALUES AND FINANCIAL RISK EXAM
 SOLUTIONS TO MATH68181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question A1 a) The marginal cdfs of F X,Y (x, y) = [1 + exp( x) + exp( y) + (1 α) exp( x y)] 1 are F X (x) = F X,Y (x, ) = [1
SOLUTIONS TO MATH68181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question A1 a) The marginal cdfs of F X,Y (x, y) = [1 + exp( x) + exp( y) + (1 α) exp( x y)] 1 are F X (x) = F X,Y (x, ) = [1
A Probability Primer. A random walk down a probabilistic path leading to some stochastic thoughts on chance events and uncertain outcomes.
 A Probability Primer A random walk down a probabilistic path leading to some stochastic thoughts on chance events and uncertain outcomes. Are you holding all the cards?? Random Events A random event, E,
A Probability Primer A random walk down a probabilistic path leading to some stochastic thoughts on chance events and uncertain outcomes. Are you holding all the cards?? Random Events A random event, E,
System Identification, Lecture 4
 System Identification, Lecture 4 Kristiaan Pelckmans (IT/UU, 2338) Course code: 1RT880, Report code: 61800 - Spring 2016 F, FRI Uppsala University, Information Technology 13 April 2016 SI-2016 K. Pelckmans
System Identification, Lecture 4 Kristiaan Pelckmans (IT/UU, 2338) Course code: 1RT880, Report code: 61800 - Spring 2016 F, FRI Uppsala University, Information Technology 13 April 2016 SI-2016 K. Pelckmans
Math Spring Practice for the Second Exam.
 Math 4 - Spring 27 - Practice for the Second Exam.. Let X be a random variable and let F X be the distribution function of X: t < t 2 t < 4 F X (t) : + t t < 2 2 2 2 t < 4 t. Find P(X ), P(X ), P(X 2),
Math 4 - Spring 27 - Practice for the Second Exam.. Let X be a random variable and let F X be the distribution function of X: t < t 2 t < 4 F X (t) : + t t < 2 2 2 2 t < 4 t. Find P(X ), P(X ), P(X 2),
Continuous Random Variables. and Probability Distributions. Continuous Random Variables and Probability Distributions ( ) ( ) Chapter 4 4.
 UCLA STAT 11 A Applied Probability & Statistics for Engineers Instructor: Ivo Dinov, Asst. Prof. In Statistics and Neurology Teaching Assistant: Christopher Barr University of California, Los Angeles,
UCLA STAT 11 A Applied Probability & Statistics for Engineers Instructor: Ivo Dinov, Asst. Prof. In Statistics and Neurology Teaching Assistant: Christopher Barr University of California, Los Angeles,
Package emg. R topics documented: May 17, 2018
 Package emg May 17, 2018 Type Package Title Exponentially Modified Gaussian (EMG) Distribution Version 1.0.7 Date 2018-05-17 Author Shawn Garbett, Mark Kozdoba Maintainer Shawn Garbett
Package emg May 17, 2018 Type Package Title Exponentially Modified Gaussian (EMG) Distribution Version 1.0.7 Date 2018-05-17 Author Shawn Garbett, Mark Kozdoba Maintainer Shawn Garbett
MATH 4426 HW7 solutions. April 15, Recall, Z is said to have a standard normal distribution (denoted Z N(0, 1)) if its pdf is
 MATH 446 HW7 solutions April 5, 5 Recall, Z is said to have a standard normal distribution (denoted Z N(, )) if its pdf is f Z (z) = p e z /,z (, ). Table A. (pp.697-698) tabulates values of its cdf (denoted.)
MATH 446 HW7 solutions April 5, 5 Recall, Z is said to have a standard normal distribution (denoted Z N(, )) if its pdf is f Z (z) = p e z /,z (, ). Table A. (pp.697-698) tabulates values of its cdf (denoted.)
MA : Introductory Probability
 MA 320-001: Introductory Probability David Murrugarra Department of Mathematics, University of Kentucky http://www.math.uky.edu/~dmu228/ma320/ Spring 2017 David Murrugarra (University of Kentucky) MA 320:
MA 320-001: Introductory Probability David Murrugarra Department of Mathematics, University of Kentucky http://www.math.uky.edu/~dmu228/ma320/ Spring 2017 David Murrugarra (University of Kentucky) MA 320:
CHAPTER 6 SOME CONTINUOUS PROBABILITY DISTRIBUTIONS. 6.2 Normal Distribution. 6.1 Continuous Uniform Distribution
 CHAPTER 6 SOME CONTINUOUS PROBABILITY DISTRIBUTIONS Recall that a continuous random variable X is a random variable that takes all values in an interval or a set of intervals. The distribution of a continuous
CHAPTER 6 SOME CONTINUOUS PROBABILITY DISTRIBUTIONS Recall that a continuous random variable X is a random variable that takes all values in an interval or a set of intervals. The distribution of a continuous
Math Review Sheet, Fall 2008
 1 Descriptive Statistics Math 3070-5 Review Sheet, Fall 2008 First we need to know about the relationship among Population Samples Objects The distribution of the population can be given in one of the
1 Descriptive Statistics Math 3070-5 Review Sheet, Fall 2008 First we need to know about the relationship among Population Samples Objects The distribution of the population can be given in one of the
Chapter 2. Random Variable. Define single random variables in terms of their PDF and CDF, and calculate moments such as the mean and variance.
 Chapter 2 Random Variable CLO2 Define single random variables in terms of their PDF and CDF, and calculate moments such as the mean and variance. 1 1. Introduction In Chapter 1, we introduced the concept
Chapter 2 Random Variable CLO2 Define single random variables in terms of their PDF and CDF, and calculate moments such as the mean and variance. 1 1. Introduction In Chapter 1, we introduced the concept
Math 152. Rumbos Fall Solutions to Assignment #12
 Math 52. umbos Fall 2009 Solutions to Assignment #2. Suppose that you observe n iid Bernoulli(p) random variables, denoted by X, X 2,..., X n. Find the LT rejection region for the test of H o : p p o versus
Math 52. umbos Fall 2009 Solutions to Assignment #2. Suppose that you observe n iid Bernoulli(p) random variables, denoted by X, X 2,..., X n. Find the LT rejection region for the test of H o : p p o versus
Topic 4: Continuous random variables
 Topic 4: Continuous random variables Course 003, 2018 Page 0 Continuous random variables Definition (Continuous random variable): An r.v. X has a continuous distribution if there exists a non-negative
Topic 4: Continuous random variables Course 003, 2018 Page 0 Continuous random variables Definition (Continuous random variable): An r.v. X has a continuous distribution if there exists a non-negative
MIT Spring 2015
 Assessing Goodness Of Fit MIT 8.443 Dr. Kempthorne Spring 205 Outline 2 Poisson Distribution Counts of events that occur at constant rate Counts in disjoint intervals/regions are independent If intervals/regions
Assessing Goodness Of Fit MIT 8.443 Dr. Kempthorne Spring 205 Outline 2 Poisson Distribution Counts of events that occur at constant rate Counts in disjoint intervals/regions are independent If intervals/regions
Continuous Distributions
 Chapter 3 Continuous Distributions 3.1 Continuous-Type Data In Chapter 2, we discuss random variables whose space S contains a countable number of outcomes (i.e. of discrete type). In Chapter 3, we study
Chapter 3 Continuous Distributions 3.1 Continuous-Type Data In Chapter 2, we discuss random variables whose space S contains a countable number of outcomes (i.e. of discrete type). In Chapter 3, we study
Continuous Random Variables. and Probability Distributions. Continuous Random Variables and Probability Distributions ( ) ( )
 UCLA STAT 35 Applied Computational and Interactive Probability Instructor: Ivo Dinov, Asst. Prof. In Statistics and Neurology Teaching Assistant: Chris Barr Continuous Random Variables and Probability
UCLA STAT 35 Applied Computational and Interactive Probability Instructor: Ivo Dinov, Asst. Prof. In Statistics and Neurology Teaching Assistant: Chris Barr Continuous Random Variables and Probability
W = 2 log U 1 and V = 2πU 2, We need the (absolute) determinant of the partial derivative matrix ye (1/2)(x2 +y 2 ) x x 2 +y 2.
 Stat 591 Homework 05 Solutions 1. (a) First, let X be a random variable with distribution function F, and assume that F is strictly increasing and continuous. Define U = F (X); the claim is that U Unif(0,
Stat 591 Homework 05 Solutions 1. (a) First, let X be a random variable with distribution function F, and assume that F is strictly increasing and continuous. Define U = F (X); the claim is that U Unif(0,
Chapter 2 Continuous Distributions
 Chapter Continuous Distributions Continuous random variables For a continuous random variable X the probability distribution is described by the probability density function f(x), which has the following
Chapter Continuous Distributions Continuous random variables For a continuous random variable X the probability distribution is described by the probability density function f(x), which has the following
Modeling Uncertainty in the Earth Sciences Jef Caers Stanford University
 Probability theory and statistical analysis: a review Modeling Uncertainty in the Earth Sciences Jef Caers Stanford University Concepts assumed known Histograms, mean, median, spread, quantiles Probability,
Probability theory and statistical analysis: a review Modeling Uncertainty in the Earth Sciences Jef Caers Stanford University Concepts assumed known Histograms, mean, median, spread, quantiles Probability,
EE/CpE 345. Modeling and Simulation. Fall Class 9
 EE/CpE 345 Modeling and Simulation Class 9 208 Input Modeling Inputs(t) Actual System Outputs(t) Parameters? Simulated System Outputs(t) The input data is the driving force for the simulation - the behavior
EE/CpE 345 Modeling and Simulation Class 9 208 Input Modeling Inputs(t) Actual System Outputs(t) Parameters? Simulated System Outputs(t) The input data is the driving force for the simulation - the behavior
Generating Random Numbers
 Generating Random Numbers Seungchul Baek Department of Mathematics and Statistics, UMBC STAT 633: Statistical Computing 1 / 67 Introduction Simulation is a very powerful tool for statisticians. It allows
Generating Random Numbers Seungchul Baek Department of Mathematics and Statistics, UMBC STAT 633: Statistical Computing 1 / 67 Introduction Simulation is a very powerful tool for statisticians. It allows
Smoking Habits. Moderate Smokers Heavy Smokers Total. Hypertension No Hypertension Total
 Math 3070. Treibergs Final Exam Name: December 7, 00. In an experiment to see how hypertension is related to smoking habits, the following data was taken on individuals. Test the hypothesis that the proportions
Math 3070. Treibergs Final Exam Name: December 7, 00. In an experiment to see how hypertension is related to smoking habits, the following data was taken on individuals. Test the hypothesis that the proportions
Quiz #2 A Mighty Fine Review
 Quiz #2 A Mighty Fine Review February 27: A reliable adventure; a day like all days filled with those events that alter and change the course of history and you will be there! What is a Quiz #2? Three
Quiz #2 A Mighty Fine Review February 27: A reliable adventure; a day like all days filled with those events that alter and change the course of history and you will be there! What is a Quiz #2? Three
MATH : EXAM 2 INFO/LOGISTICS/ADVICE
 MATH 3342-004: EXAM 2 INFO/LOGISTICS/ADVICE INFO: WHEN: Friday (03/11) at 10:00am DURATION: 50 mins PROBLEM COUNT: Appropriate for a 50-min exam BONUS COUNT: At least one TOPICS CANDIDATE FOR THE EXAM:
MATH 3342-004: EXAM 2 INFO/LOGISTICS/ADVICE INFO: WHEN: Friday (03/11) at 10:00am DURATION: 50 mins PROBLEM COUNT: Appropriate for a 50-min exam BONUS COUNT: At least one TOPICS CANDIDATE FOR THE EXAM:
Power laws. Leonid E. Zhukov
 Power laws Leonid E. Zhukov School of Data Analysis and Artificial Intelligence Department of Computer Science National Research University Higher School of Economics Structural Analysis and Visualization
Power laws Leonid E. Zhukov School of Data Analysis and Artificial Intelligence Department of Computer Science National Research University Higher School of Economics Structural Analysis and Visualization
Review 1: STAT Mark Carpenter, Ph.D. Professor of Statistics Department of Mathematics and Statistics. August 25, 2015
 Review : STAT 36 Mark Carpenter, Ph.D. Professor of Statistics Department of Mathematics and Statistics August 25, 25 Support of a Random Variable The support of a random variable, which is usually denoted
Review : STAT 36 Mark Carpenter, Ph.D. Professor of Statistics Department of Mathematics and Statistics August 25, 25 Support of a Random Variable The support of a random variable, which is usually denoted
2 Random Variable Generation
 2 Random Variable Generation Most Monte Carlo computations require, as a starting point, a sequence of i.i.d. random variables with given marginal distribution. We describe here some of the basic methods
2 Random Variable Generation Most Monte Carlo computations require, as a starting point, a sequence of i.i.d. random variables with given marginal distribution. We describe here some of the basic methods
Transformations of Standard Uniform Distributions
 Transformations of Standard Uniform Distributions We have seen that the R function runif uses a random number generator to simulate a sample from the standard uniform distribution UNIF(0, 1). All of our
Transformations of Standard Uniform Distributions We have seen that the R function runif uses a random number generator to simulate a sample from the standard uniform distribution UNIF(0, 1). All of our
Chapter Learning Objectives. Probability Distributions and Probability Density Functions. Continuous Random Variables
 Chapter 4: Continuous Random Variables and Probability s 4-1 Continuous Random Variables 4-2 Probability s and Probability Density Functions 4-3 Cumulative Functions 4-4 Mean and Variance of a Continuous
Chapter 4: Continuous Random Variables and Probability s 4-1 Continuous Random Variables 4-2 Probability s and Probability Density Functions 4-3 Cumulative Functions 4-4 Mean and Variance of a Continuous
