*********************************************************
|
|
|
- Deirdre Louise Page
- 5 years ago
- Views:
Transcription
1 Problems Ted Eisenberg, Section Editor ********************************************************* This section of the Journl offers reders n opportunit to exchnge interesting mthemticl problems nd solutions Plese send them to Ted Eisenberg, Deprtment of Mthemtics, Ben-Gurion Universit, Beer-Shev, Isrel or fx to: Questions concerning proposls nd/or solutions cn be sent e-mil to <eisenbt@0net> Solutions to previousl stted problems cn be seen t < Solutions to the problems stted in this issue should be posted before Mrch 5, 09 55: Proposed b Kenneth Korbin, New York, NY For ever prime number P, there is circle with dimeter 4P 4 + In ech of these circles, it is possible to inscribe tringle with integer length sides nd with re (P (P + (P (P Find the sides of the tringles if P nd if P 554: Proposed b Michel Brozinsk, Centrl Islip, NY A billird tble whose sides obe the lw of reflection is in the shpe of right tringle ABC with legs of length nd b where > b nd hpotenuse c A bll is shot from the right ngle nd rebounds off the hpotenuse t point P on pth prllel to leg CB tht hits let CA t point Q Find the rtio AQ QC 555: Proposed b Dniel Sitru, Ntionl Economic College Theodor Costescu, Drobet Turnu-Severin, Mehedinti, Romni Find rel vlues for x nd such tht: 4 sin (x cos x + 4 cos 556: Proposed b Ionnis D Sfiks, Ntionl nd Kpodistrin Universit of Athens, Greece The lengths of the sides of right tringle re, 6 nd 0 Determine the number of stright lines which simultneousl hlve the re nd the perimeter of the tringle 557: Proposed b José Luis Díz-Brrero, Brcelon Tech, Brcelon, Spin Let, b nd c be positive rel numbers such tht + b + c Prove tht for ll rel α > 0, holds: ( α+ b α α b α + bα+ c α b α c α + cα+ α c α α
2 ( α+ α + bα+ b α + cα+ c α ( α b α c α α b α c α 558: Proposed b Ovidiu Furdui, Technicl Universit of Cluj-Npoc, Cluj-Npoc, Romni Let > 0 Clculte dxd x 6 (x + Solutions 5505: Proposed b Kenneth Korbin, New York, NY Given Primitive Pthgoren Triple (, b, c with b > Express in terms of nd b the sides of Heronin Tringle with re b(b (A Heronin Tringle is tringle with ech side length nd re n integer Solution b Stnle Rbinowitz, Chelmsford, MA One w of doing this would be to form n obtuse tringle ABC s shown with bse of length b nd ltitude of length b, so tht the re of ABC is b(b s desired If the line segment from B to D, the foot of the ltitude from C, hs length, then hpotenuse BC in BDC would hve length c, since this tringle would be similr to n b c right tringle, scled up b Then AD would hve length b, nd b the Pthgoren Theorem, AC would hve length + b Thus, ABC is the desired Heronin Tringle, with sides b, + b, nd + b C + b c b A b B D Solution b Anthon J Bevelcqu, Universit of North Dkot, Grnd Forks, ND Given primitive Pthgoren triple (, b, c with b >, let x b, + b, z + b Note tht c nd z c Since c 4 b > 0 we hve c >
3 We clculte x + + z (b + c + ( + b 4 + c > 0, x + z (b c + c (b + c(c > 0, nd x + z (b + c ( + b (c > 0 Thus x + > z, x + z >, nd + z > x so (x,, z gives the sides of Heronin tringle Let s be the semiperimeter nd A the re of this tringle B Heron s formul we hve A s(s x(s (s z We hve s x + + z b + c, s x b + c (b c +, s b + c c b c, nd s z b + c ( + b c So A (b + c(c + (b c(c [(b (c ][(c ( ] Now (b (c b 4 b + 4 ( + b b 4 b b (b nd (c ( (c 4 (b
4 so A b (b Thus if (, b, c is primitive Pthgoren triple with b > then (x,, z with x b, + b, z + b is Heronin tringle with re b(b NB For prticulr (, b, c there cn be other Heronin tringles with re b(b For exmple, for the primitive Pthgoren triple (5,, we re looking for Heronin tringle with re 440 The formuls bove give the tringle (69, 0, 69, but (4, 0, 07 is nother tringle with re 440 Solution b Tre Smith, Angelo Stte Universit, Sn Angelo, TX Let x b, + b, nd z + b be the lengths of the three sides of the tringle We first observe tht ll of these re positive integers; x nd z obviousl so, nd since + b c, so tht The perimeter of the tringle is + b c c x + + z (b + ( + b + ( + b (c 4 + c + c c + c 4 Then the semiperimeter is s c + c Appling Heron s formul to find the re A, we hve A s(s x(s (s z s(s (b (s ( + b (s ( + b s(s (c 4 (s c(s c (c + c ((c + c (c 4 ((c + c c((c + c c (c + c (c + (c c (c [(c + (c ][(c + ][(c + (c ][(c ] (c (c 4 b (b 4
5 Thus A b(b Editor s Comment : Dvid Stone nd John Hopkins of Georgi Southern Universit dded the following comment to their solution to this problem: So how did we find x,, z? We first tired the simplest possible exmple; (, b, c (, 5, After some lgebr nd some computer help, we found the tringle (x,, z (69, 69, 0 hs the pproprite re From this we conjectured the form for rbitrr x,, z x 69 c 69 5 b z 0 5 c Then it onl required simple lgebr to verif this construction Some Excel computtions lso led us to the broder result (when b < The perfect exmple of computing power ssisting person! Also solved b Brin D Besle, Presbterin College, Clinton, SC; Ed Gr, Highlnd Bech, FL; Ionnis D Sfiks, Ntionl nd Kpodistrin Universit of Athens, Greece; Dvid Stone nd John Hwkins, Georgi Southern Universit, Sttesboro, GA, nd the proposer 5506: Proposed b Dniel Sitru, Theodor Costescu Ntionl Economic College, Drobet Turnu-Severin, Mehedinti, Romni [ ( 00 ( ] Find Ω det Solution b Michel Btille, Ronen, Frnce ( ( ( ( Let A, B, O 5 5 5, I It is redil checked tht AB BA O nd A + B 6I Since AB BA, the binomil theorem gives 00 ( 00 (A + B 00 A k B 00 k ( k Now, if k {,,, 50}, then k0 A k B 00 k A k B k B 00 k (AB k B 00 k O B 00 k O (note tht A k B k (AB k since AB BA nd similrl, if k {5, 5,, 99}, then A k B 00 k A k 00 (AB 00 k O As result, ( gives (A + B 00 A 00 + B 00, tht is, 6 00 I A 00 + B 00 We cn conclude: Ω det(6 00 I 6 00 Solution b Jeremih Brtz, Universit of North Dkot, Grnd Forks, ND Observe ( ([ 5 ] [ ] 00 5 [ 5 5 ] ( [ 5 ] [ 5 ] 99 ( [ ]
6 nd ( ([ 5 It follows tht [ ( Ω det ] [ ] 00 [ ( ] ] ( [ 5 ] [ 5 [( det ] 99 ( [ ] ] 6 00 Solution b Dvid A Huckb, Angelo Stte Universit, Sn Angelo, TX ( ( Let A nd B Mtrices A nd B re ech smmetric, hence orthogonll digonlizble Solving the eqution det (λi A 0 ields λ 0 nd λ 6 s the eigenvlues of A Solving the eqution (λi A x ( 0 successivel for λ 0 nd λ 6 ields 5 ( x 6 nd x 6 5 s corresponding unit eigenvectors So ( (0 ( A Similrl, ( (0 ( B Since for both A nd B the mtrix of eigenvectors is orthogonl, we hve ( 5 A 00 (0 ( B 00 ( (0 ( So Ω det [ ( A 00 + B 00] det ( ( ( ( 6 99, nd ( ( ( ( Solution 4 b Ionnis D Sfiks, Ntionl nd Kpodistrin Universit of Athens, Greece A w to clculte A n for mtrix is to use the Hmilton-Cle Theorem: A Tr(A A + det A I 0 ( ( For exmple, if we hve mtrix A (or A with det A 0 nd Tr(A +, then the Hmilton-Cle theorem becomes: A Tr(A ( + A 6
7 A ( + A ( + A, A n ( + A n ( + n A So we hve: ( nd finll we hve: Ω det ( 00 ( ( 5 ( , ( ( ( ( ( ( 00 (( ( ( 00 ( det ( , 5 ( ( , 5 0 ( Solution 5 b Polo Perfetti, Deprtment of Mthemtics, Tor Vergt Universit, Rome, Itl Let c 6 We know tht ( ( ( ( 5 5/c /c 0 0 5/c /c AΛA 5 5 /c 5/c 0 6 /c 5/c Thus ( ( ( /c 5/c 0 0 5/c /c 0 6 ( /c 5/c BΛB 5/c /c Ω AΛ 00 A + BΛ 00 B ( AΛ 00 A ( BΛ 00 B ( Ω det Also solved b Arkd Alt, Sn Jose, CA; Ashlnd Universit Undergrdute Problem Solving Group, Ashlnd Universit, Ashlnd, Ohio; Brin D Besle, Presbterin College, Clinton, SC; Anthon J 7
8 Bevelcqu, Universit of North Dkot, Grnd Forks, ND; Dionne Bile, Elsie Cmpbell nd Chrles Diminnie, Angelo Ste Universit, Sn Angelo, TX; Pt Costello, Estern Kentuck Universit, Richmond, KY; Dvid Diminnie, Texs Instruments Inc, Dlls, TX; Michel Fleski, Universit Center, MI; Bruno Slgueiro Fnego Viveiro, Spin; Ed Gr, Highlnd Bech, FL; Kee-Wi Lu, Hong Kong, Chin; Moti Lev, Rehovot, Isrel; Crl Libis, Columbi Southern Universit, Ornge Bech, AL; Ismil Mmmdzd (student, ADA Universit, Bku, Azerbijn; Pedro Pntoj, Ntl/RN, Brzil; Rvi Prksh, Oxford Universit Press; New Delhi, Indi; Neculi Stnciu George Emil Plde School, Buzău, Romni nd Titu Zvonru, Comănesti, Romni; Henr Ricrdo (four different proofs, Westchester Are Mth Circle, NY; Tre Smith, Angelo Stte Universit, Sn Angelo, TX; Albert Stdler, Herrliberg, Switzerlnd; Dvid Stone nd John Hwkins, Georgi Southern Universit, Sttesboro, GA; Mrin Ursărescu, Romn Vodă College, Romn, Romni; Dniel Văcru, Pitesti, Romni, nd the proposer 5507: Proposed b Dvid Benko, Universit of South Albm, Mobile, AL A cr is driving forwrd on the rel xis strting from the origin Its position t time 0 t is s(t Its speed is decresing function: v(t, 0 t Given tht the drive hs finite pth (tht is lim t s <, tht v(t/v(t hs rel limit c s t, find ll possible vlues of c Solution b Moti Lev, Rehovot, Isrel We will show tht the set of ll possible vlues of c, is the intervl [ 0, ], ie, 0 c Let us summrize the conditions on the speed function v (t: v (t 0, v (t is decresing function for ll t 0, 0 v (t dt < v(t 4 lim t v(t c, c is rel number Since v(t 0, then clerl c 0 Since v (t is decresing function, then c It follows tht 0 c Now we show tht c cn ttin n vlue in the intervl [ 0, ] Let r be rel number nd r > Then v (t +t r stisfies ll four requirements from the speed function, in prticulr nd 0 dt <, for r >, + tr v (t lim t v (t lim + t r t + r t r r c It follows tht c ( 0, To see tht c cn ttin lso the vlue zero, choose v (t e t To see tht c cn ttin lso the vlue, choose v (t { ln t ln t, for 0 t,, for < t 8
9 Then v (t stisfies ll the four requirements from the speed function, in prticulr nd 0 v (t dt ln + ln, v (t lim t v (t lim t ln t t t ln (t To finish the proof, we hve to show tht c / (, ] Suppose lim t v(t v(t c, then for ever ε > 0, there is rel number t 0 such tht t > t 0 implies v(t v(t > c ε Now we define stircse function s (t, s follows: s (t : (c ε k v (t 0, for k t 0 t 0 t < k t 0, k,, Since the function v (t is positive decresing function for ll t 0, then v (t s (t, hence t 0 v (t dt Integrting the stircse function, we get k t 0 s (t dt s (t dt v (t 0 (c ε k k v (t 0 (c ε ( (c ε k t 0 If c ε then t 0 s (t dt diverges nd so t 0 v (t dt diverges We conclude tht if c > then t 0 v (t dt diverges, contrdicting propert of the speed function Solution b Kee-Wi Lu, Hong Kong, Chin k0 We show tht 0 c ( Let lim s(t L < Then lim s(t L nd 0 s(t < s(t < L for t > 0 Hence, t t b L Hôpitl s rule, we hve lim t L s(t L s(t lim t ds(t dt ds(t dt lim t v(t v(t c Thus ( holds B tking s(t e t, s(t (t + ln(c ln, s(t ln( + e c 0, 0 < c <, c we see tht ech c in ( is in fct dmissible Solution b Albert Stdler, Herrliberg, Switzerlnd We clim tht the set C of possible vlues of c is the closed intervl 9 ccording s [ 0, ]
10 Indeed, if v(t v 0 e t, then v(t is decresing function, v(t lim 0 So 0 C t v(t If nd v(t nd lim t c > v(t v(t lim t then c/ C v 0 + t ln ( + t + t ln ( + t + t ln ( + t So then v(t is decresing function, 0 v(tdt <, nd 0 v(tdt < ( 0, ] C It remins to prove tht if v(t Suppose if possible tht lim t v(t c, where c > c / Let ɛ : > 0 Then there is number T T (ɛ > 0 such tht ɛ < v(t c < ɛ, whenever t > T We conclude v(tn tht T v(rtdt T v(tdt > (c ɛ T v(tdt (c ɛ which is contrdiction, nd the proof is complete Also solved b the proposer 5508: Proposed b Pedro Pntoj, Ntl RN, Brzil T v(tdt (+ɛ Let, b, c be positive rel numbers such tht + b + c Find the minimum vlue of f(, b, c b + b + b bc + c + c c + Solution b Solution b Dionne Bile, Elsie Cmpbell, nd Chrles Diminnie, Angelo Stte Universit, Sn Angelo, TX To begin, we note tht since, b, c > 0 nd + b + c, the Arithmetic - Geometric Men Inequlit implies tht + b + c ( + b + c ( + b + c As result of (, we hve + b + c + b + bc + c + b + b c + c ( + b + ( b + bc + ( c + c + b + b c + c 4 b + b 4 c + c 4 + b + b c + c T v(tdt > ( b + b c + c ( ( + b + c + b + c + (b + bc + c ( b + b c + c + (b + bc + c ( b + b + ( b c + bc + ( c + c ( T v(tdt, 0
11 Then, using propert (, the convexit of g (x on (0,, nd Jensen s Theorem, x we obtin f (, b, c b + b + b bc + c + c c + g (b + b + bg (bc + c + cg (c + g [ (b + b + b (bc + c + c (c + ] g [( b + b + ( b c + bc + ( c + c ] ( b + b + (b c + bc + (c + c f (,, It follows tht( under the conditions, b, c > 0 nd + b + c, the minimum vlue of f (, b, c is f,, Solution b Dvid E Mnes, Oneont, NY We will show tht the minimum vlue of f is B the Arithmetic Men-Geometric Men inequlit, we get f(, b, c b( + b c(b + c (c + ( + (b + (c + We gin use the AM-GM inequlit to obtin ( + + (b + + (c + ( + (b + (c + ( + b + c + 6 Hence, so tht f(, b, c ( + (b + (c + (/ ( + (b + (c + with equlit if nd onl if b c Solution b Bruno Slgueiro Fnego, Viveiro, Spin From Bergström s nd the Arithmetic men -Geometric men inequlities, ( ( ( b ( c b c b f(, b, c + + c b + + c + b + c + b c + + b + + c + b + c +
12 b b c c Equlit is ttined iff it occurs in those two inequlities, tht is, iff b c b + c b + b c + nd b b c c These lst identities re true if nd onl if b c, tht is, if nd onl if b c In this cse equlit is lso obtined in Bergström s inequlit So, the minimum vlue of f(, b, c is, nd this occurs if nd onl if b c Solution 4 b Arkd Alt, Sn Jose,CA ( Since + b (( ( ( b 0 then triples ( b + ( b b (b + ( + +, b b +, c, c +, b, re greed in order nd, therefore, b the c Rerrngement Inequlit ( cc + ( cc + b ( + b cc + cc + cc Also, b Cuch Inequlit ( + cc cc cc + 9 cc + Thus, f(, b, c nd since f(,, we m conclude tht min f(, b, c Solution 5 b Ionnis D Sfiks, Ntionl nd Kpodistrin Universit of Athens, Greece Since c b, then we hve: f(, b, c b + b + b b( b + ( b + b ( b + Tht mens tht we m ssume the function: g(, b b + b b (b + ( + b + + b + ( + b 5 To find the sttionr points of g(, b, work out g nd g nd set both to zero b This gives two equtions for two unknowns nd b We m solve these equtions for nd b (often there is more thn one solution Let (x, be sttionr point If g > 0 nd g bb > 0 t (x, then (x, is minimum point So, g ( + b (6 + b 5 ( + b 5 b( + + b (b + ( + b + b + b + ( + b 5
13 g b (b ( + + b( + 6b (b + ( + b (b + ( + b + ( + b 5 (,, we hve: [ nd for (, b nd for (, b min g(, b min b + b (,, we hve: [ min g(, b min b + b b (b + ( + b + + b ] ( + b 5 b (b + ( + b + + b ] ( + b 5 Solution 6 b Albert Stdler, Herrliberg, Switzerlnd We will prove tht the minimum vlue equls nd the minimum is ssumed if nd onl if b c / To tht end we must prove tht f(, b, c ( + b + c b + b( + b + c + ( + b + c b + b( + b + c + ( + b + c b + b( + b + c We cler denomintors nd get the equivlent inequlit ( + b ( + b 5, 0 4 b +4 b +8 4 c +4 4 c 4 bc+5 4 b c+ 4 bc +8 b c ( ccl ccl ccl ccl ccl ccl ccl ccl B the (weightedam-gm inequlit, 4 bc, 4 b + 4 c ccl ccl ccl 5 b 5 ( b + c 5 b c, ccl ccl ccl 4 c ( 4 c + 6 b4 + 6 c4 b bc, ccl ccl ccl 9 ccl 4 b 7 b c, 9 ccl b 7 b c, 6 ccl 4 c 8 b c, 4 ccl 5 c b c, nd ( follows if we dd the lst seven inequlities In ll seven inequlities equlit holds if nd onl if b c
14 Comment b Stnle Rbinowitz of Chelmsford, MA Problems such s this re esil solvble b computer lgebr sstems these ds For exmple; the Mthemtic commnd Minimize [{/( b + b + b/(b c + c + c/(c +, > 0&& b > 0&&c > 0&&{ + b + c }, {, b responds b sing tht the minimum vlue is nd occurs when b c Also solved b Konul Aliev (student, ADA Universit, Bku, Azerbijn; Michel Btille, Rouen, Frnce; Ed Gr, Highlnd Bech, FL; Trn Hong (student, Co Lnh School, Dong Thp, Vietnm; Snong Hureri, Rttnkosinsomphothow School, Nkon, Pthom, Thilnd; Sern Ibrhimov, Bku Stte Universit, Msilli, Azerbijn; Kee-Wi Lu, Hong Kong, Chin; Moti Lev, Rehovot, Isrel; Polo Perfetti, Deprtment of Mthemtics, Tor Vergt Universit, Rome, Itl; Stnle Rbinowitz of Chelmsford, MA; Neculi Stnciu George Emil Plde School, Buză, Romni nd Titu Zvonru, Comănesti, Romni; Dniel Văcru, Pitesti, Romni; Nicusor Zlot Trin Vui Technicl College, Focsni, Romni, nd the proposer 5509: Proposed b José Luis Díz-Brrero, Brcelon Tech, Brcelon, Spin Let x,, z be positive rel numbers tht dd up to one nd such tht 0 < x, z, z x < π Prove tht ( ( ( z x x cos + cos + z cos < z x 5 5 Solution b Michel Btille, Rouen, Frnce The Cuch-Schwrz inequlit provides ( x cos + ( z cos + z x z cos ( ( x ( ( z (x++z / cos + cos + cos z x Since x + + z, it follows tht the left-hnd side L of the proposed inequlit stisfies ( ( ( ( z x / L cos + cos + cos z x Thus, it suffices to show tht ( ( ( z x cos + cos + cos < z x 9 5 ( Now, Jensen s inequlit pplied to the cosine function, which is concve on (0, π, ields ( /z + z/x + x/ ( ( z cos + cos + cos z x ( x cos ( ( x / 4
15 But we hve z z x x /z+z/x+x/ (b AM-GM nd 0 < /z+z/x+x/ < π π, hence ( /z + z/x + x/ cos cos( (since the cosine function is decresing on (0, π Then ( gives cos ( ( ( z + cos z x + cos x cos( There just remins to remrk tht cos( < 06 5 to obtin the desired inequlit ( Solution b Trn Hong (student, Co Lnh School, Dong Thp, Vietnm LHS BCS ( ( z ( x x + + z cos + cos + cos z x ( ( z ( x cos + cos + cos z x ( Let f(t cos t, t 0, π f (t cos t < 0 ( Using Jensen s we hve: ( ( ( z ( x z f + f + f f z x + z x + x ( z cos + z x + x cos( {( cos(, 7 < 5 5, 46 Solution b Dvid E Mnes, Oneont, NY Let J x cos ( z + cos ( ( z x + z cos x We will show tht J cos < 5 5 B the Cuch-Schwrz inequlit, one obtins ( ( ( z x J x cos + cos + z cos z x ( ( ( z x x + + z cos + cos + cos z x ( ( ( z x cos + cos + cos z x At the risk of being redundnt, note tht ( J cos (x + + z ( cos z z cc cc (x + + z cos ( ( z + (x + + z cos + (x + + z cos z x ( x 5
16 Since the cosine function is concve on the intervl (0, π/, it follows b Jensen s inequlit tht for ech of the following terms in the cclic sum under the squre root sign, we get Therefore, J ( ( z x cos + cos + z cos z x ( ( z cos + z cos z x ( ( z z cos + x cos + cos z x cos ( x z + z x + zx ( ( x x cos z + z x + xz ( ( x + x cos cos z + z x + x ( x cos( + z + x cos ( + cos z + z x + x + cos For the first term, x z + z x + zx, in prentheses bove, observe tht using the Arithmetic Men-Geometric Men inequlit, one obtins ( x z + z x z x xz, ( z x + zx xz x z, ( zx + x x z x z z Summing the bove terms ields x z + z x + zx x + + z ( Using the Cuch-Schwrz inequlit in the Engel-Titu form for the second term in prentheses in J bove, one immeditel obtins z + z x + x ( + z + x z + x + ( Since the cosine function is decresing on the ( intervl [0, π/] nd s result of inequlities ( nd (, it follows tht cos x z + z x + zx cos nd ( cos z + z x + x cos Therefore, ( ( ( z x J x cos + cos + z cos z x cos Finll, note tht for ech of the bove steps the inequlities become equlities if nd onl if x z Solution 4 b Dniel Văcru, Pitesti, Romni One hs x cos z + cos zx + z cos x x + + z cos }{{} z + cos zx + cos x cos z + cos z x + cos x 6
17 sin ( π ( π + sin z x z ( π + sin x {}}{ < (π z ( π + x z ( π + x π ( z + z x + x The inequlit under the brce is true becuse sin x < x, x ( 0, π On the other hnd, one knows tht z + z x + x b the MA-MG inequlit Therefore one hs x cos z cos + zx cos + x < π ( π ( < (5 5 Also solved b Bruno Slgueiro Fnego, Viveiro, Spin; Ed Gr, Highlnd Bech, FL; Kee-Wi Lu, Hong Kong, Chin; Moti Lev, Rehovot, Isrel; Polo Perfetti, Deprtment of Mthemtics, Tor Vergt Universit, Rome, Itl; Ionnis D Sfiks, Ntionl nd Kpodistrin Universit of Athens, Greece; Albert Stdler, Herrliberg, Switzerlnd nd the proposer 550: Proposed b Ovidiu Furdui nd Alin Sîntămărin both t the Technicl Universit of Cluj-Npoc, Cluj-Npoc, Romni Clculte [4 n (ζ(n ], n where ζ denotes the Riemnn zet function Solution b Albert Stdler, Herrliberg, Switzerlnd (4 n (ζ(n n ( ( 4 n n m m n n m ( n m m n ( n m ( m ( m m m 4 m 4 m ( m m Solution b Polo Perfetti, Deprtment of Mthemtics, Tor Vergt Universit, Rome, Itl 7
18 [4 n (ζ(n ] n k n lim n k + lim n k 4 n k n k [4 n k n ] n 4 k ( 4 n [ k k n [ k + ] k + k k ] + lim 4 k 4 k n n k n k [ k k n k n ] + lim n n k [ k ] + k + Solution b Moti Lev, Rehovot, Isrel Let Then S : (4 n (ζ (n, S N : n S N n N (4 n (ζ (n n (( N ( n N k n k n ( k n N n k n k 4 k 4 ( k k N n k n N S lim N S N k k 4 k 4 ( k k + k k k k5 Now, s bonus, let us evlute prmetrized version of the bove sum: Then S (t : S (t N n (t n (ζ (n tn n, S N (t : (( N t n n ( N t n k n k n k n k n ( tn N n k n n k N n t n k n N t n n N t n k n k S (t lim S (t N t N k t 8 k (t n (ζ (n tn n N t n n n t k t ( ( t N k
19 Let us ssume tht t is not positive integer nd stisfies the inequlit t >, then ψ (t + ψ ( t + k, t t k where ψ (t is the Digmm function ψ ( z + ψ (z + π cot (πz k t ( cot (πt t t k S (t t t ( π cot (πt t t t t t 5t4 5t + 4 πt ( t 4 5t + 4 cot (πt (t 4 5t + 4 We summrize our result s follows, 5t 4 5t + 4 πt ( t 4 5t + 4 cot (πt (t 4 5t, t < + 4 S (t 5t 4 5t + 4 πt ( t 4 5t + 4 cot (πt lim t (t 4 5t 5, t, + 4 5t 4 5t + 4 πt ( t 4 5t + 4 cot (πt lim t (t 4 5t + 4 5, t Remrk: The function S (t, s defined bove, is continuous in the intervl t < Reference: Borwein, Jonthn; Brdle, Dvid M; Crndll, Richrd (000 Computtionl Strtegies for the Riemnn Zet Function J Comp App Mth ( : Solution 4 b Kee-Wi Lu, Hong Kong, Chin Denote the sum of the problem b S so tht S k n n k ( n k Since the summnds re positive, so interchnging the order of summtion, we hve ( n S 4 k k 4 For n integer M, we hve 4 k k M k 4 ( k 5 M+ k + k It follows tht S 5 9 km k
20 Comment b Editor : Ed Gr of Highlnd Bech, FL wrote: I didn t know n recursive formul tht would help, so I did the sum b brute force, computing the sum of the first 0 terms, getting result of 088This roused m curiosit, so I went to Wolfrm-lph nd sought the sum for gret number of terms, like 00 nd 00 It becme cler tht the nswer is 08 forever Converting this to frction, we get beutiful nswer of 5/4 He continued on sing tht he did not ctull solve the problem This is being mentioned here s ver useful heuristic for getting feel for the problem, nd s cvet tht there re n infinite number of different ws to express closed form representtion for specific deciml Also solved b Michel Btille, Rouen, Frnce; Bruno Slgueiro Fnego, Viveiro, Spin; Ionnis D Sfiks, Ntionl nd Kpodistrin Universit of Athens, Greece, nd the proposer Me Culp Mr Wgner-Krnkel of St Mr s Universit in Sn Antonio, TX should hve been credited with hving solved problem
*********************************************************
 Prolems Ted Eisenerg, Section Editor ********************************************************* This section of the Journl offers reders n opportunity to echnge interesting mthemticl prolems nd solutions.
Prolems Ted Eisenerg, Section Editor ********************************************************* This section of the Journl offers reders n opportunity to echnge interesting mthemticl prolems nd solutions.
*********************************************************
 Problems Ted Eisenberg, Section Editor ********************************************************* This section of the Journl offers reders n opportunity to echnge interesting mthemticl problems nd solutions
Problems Ted Eisenberg, Section Editor ********************************************************* This section of the Journl offers reders n opportunity to echnge interesting mthemticl problems nd solutions
SOLUTIONS A 2 + B 2 = AB + BA = 2 4
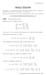 SOLUTIONS /4 SOLUTIONS No problem is ever permnently closed The editor is lwys plesed to consider for publiction new solutions or new insights on pst problems Sttements of the problems in this section
SOLUTIONS /4 SOLUTIONS No problem is ever permnently closed The editor is lwys plesed to consider for publiction new solutions or new insights on pst problems Sttements of the problems in this section
Number 12 Spring 2019
 Number 2 Spring 209 ROMANIAN MATHEMATICAL MAGAZINE Avilble online www.ssmrmh.ro Founding Editor DANIEL SITARU ISSN-L 250-0099 ROMANIAN MATHEMATICAL MAGAZINE PROBLEMS FOR JUNIORS JP.66. If, b [0; + ) nd
Number 2 Spring 209 ROMANIAN MATHEMATICAL MAGAZINE Avilble online www.ssmrmh.ro Founding Editor DANIEL SITARU ISSN-L 250-0099 ROMANIAN MATHEMATICAL MAGAZINE PROBLEMS FOR JUNIORS JP.66. If, b [0; + ) nd
Two Interesting Integer Parameters of Integer-sided Triangles
 Forum Geometricorum Volume 17 (2017) 411 417. FORUM GEOM ISSN 1534-1178 Two Interesting Integer Prmeters of Integer-sided Tringles Jose A. De l Cruz nd John F. Goehl, Jr. Abstrct. When tringle is described
Forum Geometricorum Volume 17 (2017) 411 417. FORUM GEOM ISSN 1534-1178 Two Interesting Integer Prmeters of Integer-sided Tringles Jose A. De l Cruz nd John F. Goehl, Jr. Abstrct. When tringle is described
Lecture notes. Fundamental inequalities: techniques and applications
 Lecture notes Fundmentl inequlities: techniques nd pplictions Mnh Hong Duong Mthemtics Institute, University of Wrwick Emil: m.h.duong@wrwick.c.uk Februry 8, 207 2 Abstrct Inequlities re ubiquitous in
Lecture notes Fundmentl inequlities: techniques nd pplictions Mnh Hong Duong Mthemtics Institute, University of Wrwick Emil: m.h.duong@wrwick.c.uk Februry 8, 207 2 Abstrct Inequlities re ubiquitous in
Exam 2, Mathematics 4701, Section ETY6 6:05 pm 7:40 pm, March 31, 2016, IH-1105 Instructor: Attila Máté 1
 Exm, Mthemtics 471, Section ETY6 6:5 pm 7:4 pm, Mrch 1, 16, IH-115 Instructor: Attil Máté 1 17 copies 1. ) Stte the usul sufficient condition for the fixed-point itertion to converge when solving the eqution
Exm, Mthemtics 471, Section ETY6 6:5 pm 7:4 pm, Mrch 1, 16, IH-115 Instructor: Attil Máté 1 17 copies 1. ) Stte the usul sufficient condition for the fixed-point itertion to converge when solving the eqution
*********************************************************
 Problems Ted Eisenberg, Section Editor ********************************************************* This section of the Journal offers readers an opportunity to exchange interesting mathematical problems
Problems Ted Eisenberg, Section Editor ********************************************************* This section of the Journal offers readers an opportunity to exchange interesting mathematical problems
DETERMINANTS. All Mathematical truths are relative and conditional. C.P. STEINMETZ
 DETERMINANTS Chpter 4 All Mthemticl truths re reltive nd conditionl. C.P. STEINMETZ 4. Introduction In the previous chpter, we hve studied bout mtrices nd lgebr of mtrices. We hve lso lernt tht sstem of
DETERMINANTS Chpter 4 All Mthemticl truths re reltive nd conditionl. C.P. STEINMETZ 4. Introduction In the previous chpter, we hve studied bout mtrices nd lgebr of mtrices. We hve lso lernt tht sstem of
Higher Checklist (Unit 3) Higher Checklist (Unit 3) Vectors
 Vectors Skill Achieved? Know tht sclr is quntity tht hs only size (no direction) Identify rel-life exmples of sclrs such s, temperture, mss, distnce, time, speed, energy nd electric chrge Know tht vector
Vectors Skill Achieved? Know tht sclr is quntity tht hs only size (no direction) Identify rel-life exmples of sclrs such s, temperture, mss, distnce, time, speed, energy nd electric chrge Know tht vector
42nd International Mathematical Olympiad
 nd Interntionl Mthemticl Olympid Wshington, DC, United Sttes of Americ July 8 9, 001 Problems Ech problem is worth seven points. Problem 1 Let ABC be n cute-ngled tringle with circumcentre O. Let P on
nd Interntionl Mthemticl Olympid Wshington, DC, United Sttes of Americ July 8 9, 001 Problems Ech problem is worth seven points. Problem 1 Let ABC be n cute-ngled tringle with circumcentre O. Let P on
Algebra & Functions (Maths ) opposite side
 Instructor: Dr. R.A.G. Seel Trigonometr Algebr & Functions (Mths 0 0) 0th Prctice Assignment hpotenuse hpotenuse side opposite side sin = opposite hpotenuse tn = opposite. Find sin, cos nd tn in 9 sin
Instructor: Dr. R.A.G. Seel Trigonometr Algebr & Functions (Mths 0 0) 0th Prctice Assignment hpotenuse hpotenuse side opposite side sin = opposite hpotenuse tn = opposite. Find sin, cos nd tn in 9 sin
SOLUTIONS FOR ADMISSIONS TEST IN MATHEMATICS, COMPUTER SCIENCE AND JOINT SCHOOLS WEDNESDAY 5 NOVEMBER 2014
 SOLUTIONS FOR ADMISSIONS TEST IN MATHEMATICS, COMPUTER SCIENCE AND JOINT SCHOOLS WEDNESDAY 5 NOVEMBER 014 Mrk Scheme: Ech prt of Question 1 is worth four mrks which re wrded solely for the correct nswer.
SOLUTIONS FOR ADMISSIONS TEST IN MATHEMATICS, COMPUTER SCIENCE AND JOINT SCHOOLS WEDNESDAY 5 NOVEMBER 014 Mrk Scheme: Ech prt of Question 1 is worth four mrks which re wrded solely for the correct nswer.
13.3 CLASSICAL STRAIGHTEDGE AND COMPASS CONSTRUCTIONS
 33 CLASSICAL STRAIGHTEDGE AND COMPASS CONSTRUCTIONS As simple ppliction of the results we hve obtined on lgebric extensions, nd in prticulr on the multiplictivity of extension degrees, we cn nswer (in
33 CLASSICAL STRAIGHTEDGE AND COMPASS CONSTRUCTIONS As simple ppliction of the results we hve obtined on lgebric extensions, nd in prticulr on the multiplictivity of extension degrees, we cn nswer (in
USA Mathematical Talent Search Round 1 Solutions Year 21 Academic Year
 1/1/21. Fill in the circles in the picture t right with the digits 1-8, one digit in ech circle with no digit repeted, so tht no two circles tht re connected by line segment contin consecutive digits.
1/1/21. Fill in the circles in the picture t right with the digits 1-8, one digit in ech circle with no digit repeted, so tht no two circles tht re connected by line segment contin consecutive digits.
Log1 Contest Round 3 Theta Individual. 4 points each 1 What is the sum of the first 5 Fibonacci numbers if the first two are 1, 1?
 008 009 Log1 Contest Round Thet Individul Nme: points ech 1 Wht is the sum of the first Fiboncci numbers if the first two re 1, 1? If two crds re drwn from stndrd crd deck, wht is the probbility of drwing
008 009 Log1 Contest Round Thet Individul Nme: points ech 1 Wht is the sum of the first Fiboncci numbers if the first two re 1, 1? If two crds re drwn from stndrd crd deck, wht is the probbility of drwing
*********************************************************
 Problems Ted Eisenberg, Section Editor ********************************************************* This section of the Journal offers readers an opportunity to exchange interesting mathematical problems
Problems Ted Eisenberg, Section Editor ********************************************************* This section of the Journal offers readers an opportunity to exchange interesting mathematical problems
MAA 4212 Improper Integrals
 Notes by Dvid Groisser, Copyright c 1995; revised 2002, 2009, 2014 MAA 4212 Improper Integrls The Riemnn integrl, while perfectly well-defined, is too restrictive for mny purposes; there re functions which
Notes by Dvid Groisser, Copyright c 1995; revised 2002, 2009, 2014 MAA 4212 Improper Integrls The Riemnn integrl, while perfectly well-defined, is too restrictive for mny purposes; there re functions which
6.2 The Pythagorean Theorems
 PythgorenTheorems20052006.nb 1 6.2 The Pythgoren Theorems One of the best known theorems in geometry (nd ll of mthemtics for tht mtter) is the Pythgoren Theorem. You hve probbly lredy worked with this
PythgorenTheorems20052006.nb 1 6.2 The Pythgoren Theorems One of the best known theorems in geometry (nd ll of mthemtics for tht mtter) is the Pythgoren Theorem. You hve probbly lredy worked with this
*********************************************************
 Problems Ted Eisenberg, Section Editor ********************************************************* This section of the Journal offers readers an opportunity to echange interesting mathematical problems and
Problems Ted Eisenberg, Section Editor ********************************************************* This section of the Journal offers readers an opportunity to echange interesting mathematical problems and
Integral points on the rational curve
 Integrl points on the rtionl curve y x bx c x ;, b, c integers. Konstntine Zeltor Mthemtics University of Wisconsin - Mrinette 750 W. Byshore Street Mrinette, WI 5443-453 Also: Konstntine Zeltor P.O. Box
Integrl points on the rtionl curve y x bx c x ;, b, c integers. Konstntine Zeltor Mthemtics University of Wisconsin - Mrinette 750 W. Byshore Street Mrinette, WI 5443-453 Also: Konstntine Zeltor P.O. Box
UniversitaireWiskundeCompetitie. Problem 2005/4-A We have k=1. Show that for every q Q satisfying 0 < q < 1, there exists a finite subset K N so that
 Problemen/UWC NAW 5/7 nr juni 006 47 Problemen/UWC UniversitireWiskundeCompetitie Edition 005/4 For Session 005/4 we received submissions from Peter Vndendriessche, Vldislv Frnk, Arne Smeets, Jn vn de
Problemen/UWC NAW 5/7 nr juni 006 47 Problemen/UWC UniversitireWiskundeCompetitie Edition 005/4 For Session 005/4 we received submissions from Peter Vndendriessche, Vldislv Frnk, Arne Smeets, Jn vn de
JEE(MAIN) 2015 TEST PAPER WITH SOLUTION (HELD ON SATURDAY 04 th APRIL, 2015) PART B MATHEMATICS
 JEE(MAIN) 05 TEST PAPER WITH SOLUTION (HELD ON SATURDAY 0 th APRIL, 05) PART B MATHEMATICS CODE-D. Let, b nd c be three non-zero vectors such tht no two of them re colliner nd, b c b c. If is the ngle
JEE(MAIN) 05 TEST PAPER WITH SOLUTION (HELD ON SATURDAY 0 th APRIL, 05) PART B MATHEMATICS CODE-D. Let, b nd c be three non-zero vectors such tht no two of them re colliner nd, b c b c. If is the ngle
MATH STUDENT BOOK. 10th Grade Unit 5
 MATH STUDENT BOOK 10th Grde Unit 5 Unit 5 Similr Polygons MATH 1005 Similr Polygons INTRODUCTION 3 1. PRINCIPLES OF ALGEBRA 5 RATIOS AND PROPORTIONS 5 PROPERTIES OF PROPORTIONS 11 SELF TEST 1 16 2. SIMILARITY
MATH STUDENT BOOK 10th Grde Unit 5 Unit 5 Similr Polygons MATH 1005 Similr Polygons INTRODUCTION 3 1. PRINCIPLES OF ALGEBRA 5 RATIOS AND PROPORTIONS 5 PROPERTIES OF PROPORTIONS 11 SELF TEST 1 16 2. SIMILARITY
Improper Integrals. Type I Improper Integrals How do we evaluate an integral such as
 Improper Integrls Two different types of integrls cn qulify s improper. The first type of improper integrl (which we will refer to s Type I) involves evluting n integrl over n infinite region. In the grph
Improper Integrls Two different types of integrls cn qulify s improper. The first type of improper integrl (which we will refer to s Type I) involves evluting n integrl over n infinite region. In the grph
ARITHMETIC OPERATIONS. The real numbers have the following properties: a b c ab ac
 REVIEW OF ALGEBRA Here we review the bsic rules nd procedures of lgebr tht you need to know in order to be successful in clculus. ARITHMETIC OPERATIONS The rel numbers hve the following properties: b b
REVIEW OF ALGEBRA Here we review the bsic rules nd procedures of lgebr tht you need to know in order to be successful in clculus. ARITHMETIC OPERATIONS The rel numbers hve the following properties: b b
MORE FUNCTION GRAPHING; OPTIMIZATION. (Last edited October 28, 2013 at 11:09pm.)
 MORE FUNCTION GRAPHING; OPTIMIZATION FRI, OCT 25, 203 (Lst edited October 28, 203 t :09pm.) Exercise. Let n be n rbitrry positive integer. Give n exmple of function with exctly n verticl symptotes. Give
MORE FUNCTION GRAPHING; OPTIMIZATION FRI, OCT 25, 203 (Lst edited October 28, 203 t :09pm.) Exercise. Let n be n rbitrry positive integer. Give n exmple of function with exctly n verticl symptotes. Give
Overview of Calculus I
 Overview of Clculus I Prof. Jim Swift Northern Arizon University There re three key concepts in clculus: The limit, the derivtive, nd the integrl. You need to understnd the definitions of these three things,
Overview of Clculus I Prof. Jim Swift Northern Arizon University There re three key concepts in clculus: The limit, the derivtive, nd the integrl. You need to understnd the definitions of these three things,
A BRIEF INTRODUCTION TO UNIFORM CONVERGENCE. In the study of Fourier series, several questions arise naturally, such as: c n e int
 A BRIEF INTRODUCTION TO UNIFORM CONVERGENCE HANS RINGSTRÖM. Questions nd exmples In the study of Fourier series, severl questions rise nturlly, such s: () (2) re there conditions on c n, n Z, which ensure
A BRIEF INTRODUCTION TO UNIFORM CONVERGENCE HANS RINGSTRÖM. Questions nd exmples In the study of Fourier series, severl questions rise nturlly, such s: () (2) re there conditions on c n, n Z, which ensure
Definite integral. Mathematics FRDIS MENDELU
 Definite integrl Mthemtics FRDIS MENDELU Simon Fišnrová Brno 1 Motivtion - re under curve Suppose, for simplicity, tht y = f(x) is nonnegtive nd continuous function defined on [, b]. Wht is the re of the
Definite integrl Mthemtics FRDIS MENDELU Simon Fišnrová Brno 1 Motivtion - re under curve Suppose, for simplicity, tht y = f(x) is nonnegtive nd continuous function defined on [, b]. Wht is the re of the
Abstract inner product spaces
 WEEK 4 Abstrct inner product spces Definition An inner product spce is vector spce V over the rel field R equipped with rule for multiplying vectors, such tht the product of two vectors is sclr, nd the
WEEK 4 Abstrct inner product spces Definition An inner product spce is vector spce V over the rel field R equipped with rule for multiplying vectors, such tht the product of two vectors is sclr, nd the
Chapter 4 Contravariance, Covariance, and Spacetime Diagrams
 Chpter 4 Contrvrince, Covrince, nd Spcetime Digrms 4. The Components of Vector in Skewed Coordintes We hve seen in Chpter 3; figure 3.9, tht in order to show inertil motion tht is consistent with the Lorentz
Chpter 4 Contrvrince, Covrince, nd Spcetime Digrms 4. The Components of Vector in Skewed Coordintes We hve seen in Chpter 3; figure 3.9, tht in order to show inertil motion tht is consistent with the Lorentz
Physics 116C Solution of inhomogeneous ordinary differential equations using Green s functions
 Physics 6C Solution of inhomogeneous ordinry differentil equtions using Green s functions Peter Young November 5, 29 Homogeneous Equtions We hve studied, especilly in long HW problem, second order liner
Physics 6C Solution of inhomogeneous ordinry differentil equtions using Green s functions Peter Young November 5, 29 Homogeneous Equtions We hve studied, especilly in long HW problem, second order liner
Diophantine Steiner Triples and Pythagorean-Type Triangles
 Forum Geometricorum Volume 10 (2010) 93 97. FORUM GEOM ISSN 1534-1178 Diophntine Steiner Triples nd Pythgoren-Type Tringles ojn Hvl bstrct. We present connection between Diophntine Steiner triples (integer
Forum Geometricorum Volume 10 (2010) 93 97. FORUM GEOM ISSN 1534-1178 Diophntine Steiner Triples nd Pythgoren-Type Tringles ojn Hvl bstrct. We present connection between Diophntine Steiner triples (integer
Algebra Of Matrices & Determinants
 lgebr Of Mtrices & Determinnts Importnt erms Definitions & Formule 0 Mtrix - bsic introduction: mtrix hving m rows nd n columns is clled mtrix of order m n (red s m b n mtrix) nd mtrix of order lso in
lgebr Of Mtrices & Determinnts Importnt erms Definitions & Formule 0 Mtrix - bsic introduction: mtrix hving m rows nd n columns is clled mtrix of order m n (red s m b n mtrix) nd mtrix of order lso in
1. On some properties of definite integrals. We prove
 This short collection of notes is intended to complement the textbook Anlisi Mtemtic 2 by Crl Mdern, published by Città Studi Editore, [M]. We refer to [M] for nottion nd the logicl stremline of the rguments.
This short collection of notes is intended to complement the textbook Anlisi Mtemtic 2 by Crl Mdern, published by Città Studi Editore, [M]. We refer to [M] for nottion nd the logicl stremline of the rguments.
Definite integral. Mathematics FRDIS MENDELU. Simona Fišnarová (Mendel University) Definite integral MENDELU 1 / 30
 Definite integrl Mthemtics FRDIS MENDELU Simon Fišnrová (Mendel University) Definite integrl MENDELU / Motivtion - re under curve Suppose, for simplicity, tht y = f(x) is nonnegtive nd continuous function
Definite integrl Mthemtics FRDIS MENDELU Simon Fišnrová (Mendel University) Definite integrl MENDELU / Motivtion - re under curve Suppose, for simplicity, tht y = f(x) is nonnegtive nd continuous function
Linear Inequalities: Each of the following carries five marks each: 1. Solve the system of equations graphically.
 Liner Inequlities: Ech of the following crries five mrks ech:. Solve the system of equtions grphiclly. x + 2y 8, 2x + y 8, x 0, y 0 Solution: Considerx + 2y 8.. () Drw the grph for x + 2y = 8 by line.it
Liner Inequlities: Ech of the following crries five mrks ech:. Solve the system of equtions grphiclly. x + 2y 8, 2x + y 8, x 0, y 0 Solution: Considerx + 2y 8.. () Drw the grph for x + 2y = 8 by line.it
Lecture 1. Functional series. Pointwise and uniform convergence.
 1 Introduction. Lecture 1. Functionl series. Pointwise nd uniform convergence. In this course we study mongst other things Fourier series. The Fourier series for periodic function f(x) with period 2π is
1 Introduction. Lecture 1. Functionl series. Pointwise nd uniform convergence. In this course we study mongst other things Fourier series. The Fourier series for periodic function f(x) with period 2π is
Functions of bounded variation
 Division for Mthemtics Mrtin Lind Functions of bounded vrition Mthemtics C-level thesis Dte: 2006-01-30 Supervisor: Viktor Kold Exminer: Thoms Mrtinsson Krlstds universitet 651 88 Krlstd Tfn 054-700 10
Division for Mthemtics Mrtin Lind Functions of bounded vrition Mthemtics C-level thesis Dte: 2006-01-30 Supervisor: Viktor Kold Exminer: Thoms Mrtinsson Krlstds universitet 651 88 Krlstd Tfn 054-700 10
1 The Riemann Integral
 The Riemnn Integrl. An exmple leding to the notion of integrl (res) We know how to find (i.e. define) the re of rectngle (bse height), tringle ( (sum of res of tringles). But how do we find/define n re
The Riemnn Integrl. An exmple leding to the notion of integrl (res) We know how to find (i.e. define) the re of rectngle (bse height), tringle ( (sum of res of tringles). But how do we find/define n re
f(x) dx, If one of these two conditions is not met, we call the integral improper. Our usual definition for the value for the definite integral
 Improper Integrls Every time tht we hve evluted definite integrl such s f(x) dx, we hve mde two implicit ssumptions bout the integrl:. The intervl [, b] is finite, nd. f(x) is continuous on [, b]. If one
Improper Integrls Every time tht we hve evluted definite integrl such s f(x) dx, we hve mde two implicit ssumptions bout the integrl:. The intervl [, b] is finite, nd. f(x) is continuous on [, b]. If one
Notes on length and conformal metrics
 Notes on length nd conforml metrics We recll how to mesure the Eucliden distnce of n rc in the plne. Let α : [, b] R 2 be smooth (C ) rc. Tht is α(t) (x(t), y(t)) where x(t) nd y(t) re smooth rel vlued
Notes on length nd conforml metrics We recll how to mesure the Eucliden distnce of n rc in the plne. Let α : [, b] R 2 be smooth (C ) rc. Tht is α(t) (x(t), y(t)) where x(t) nd y(t) re smooth rel vlued
1. Extend QR downwards to meet the x-axis at U(6, 0). y
 In the digrm, two stright lines re to be drwn through so tht the lines divide the figure OPQRST into pieces of equl re Find the sum of the slopes of the lines R(6, ) S(, ) T(, 0) Determine ll liner functions
In the digrm, two stright lines re to be drwn through so tht the lines divide the figure OPQRST into pieces of equl re Find the sum of the slopes of the lines R(6, ) S(, ) T(, 0) Determine ll liner functions
The Dirac distribution
 A DIRAC DISTRIBUTION A The Dirc distribution A Definition of the Dirc distribution The Dirc distribution δx cn be introduced by three equivlent wys Dirc [] defined it by reltions δx dx, δx if x The distribution
A DIRAC DISTRIBUTION A The Dirc distribution A Definition of the Dirc distribution The Dirc distribution δx cn be introduced by three equivlent wys Dirc [] defined it by reltions δx dx, δx if x The distribution
Recitation 3: More Applications of the Derivative
 Mth 1c TA: Pdric Brtlett Recittion 3: More Applictions of the Derivtive Week 3 Cltech 2012 1 Rndom Question Question 1 A grph consists of the following: A set V of vertices. A set E of edges where ech
Mth 1c TA: Pdric Brtlett Recittion 3: More Applictions of the Derivtive Week 3 Cltech 2012 1 Rndom Question Question 1 A grph consists of the following: A set V of vertices. A set E of edges where ech
*********************************************************
 Problems Ted Eisenberg, Section Editor ********************************************************* This section of the Journal offers readers an opportunity to echange interesting mathematical problems and
Problems Ted Eisenberg, Section Editor ********************************************************* This section of the Journal offers readers an opportunity to echange interesting mathematical problems and
Convergence of Fourier Series and Fejer s Theorem. Lee Ricketson
 Convergence of Fourier Series nd Fejer s Theorem Lee Ricketson My, 006 Abstrct This pper will ddress the Fourier Series of functions with rbitrry period. We will derive forms of the Dirichlet nd Fejer
Convergence of Fourier Series nd Fejer s Theorem Lee Ricketson My, 006 Abstrct This pper will ddress the Fourier Series of functions with rbitrry period. We will derive forms of the Dirichlet nd Fejer
Chapter 3. Vector Spaces
 3.4 Liner Trnsformtions 1 Chpter 3. Vector Spces 3.4 Liner Trnsformtions Note. We hve lredy studied liner trnsformtions from R n into R m. Now we look t liner trnsformtions from one generl vector spce
3.4 Liner Trnsformtions 1 Chpter 3. Vector Spces 3.4 Liner Trnsformtions Note. We hve lredy studied liner trnsformtions from R n into R m. Now we look t liner trnsformtions from one generl vector spce
The Riemann-Lebesgue Lemma
 Physics 215 Winter 218 The Riemnn-Lebesgue Lemm The Riemnn Lebesgue Lemm is one of the most importnt results of Fourier nlysis nd symptotic nlysis. It hs mny physics pplictions, especilly in studies of
Physics 215 Winter 218 The Riemnn-Lebesgue Lemm The Riemnn Lebesgue Lemm is one of the most importnt results of Fourier nlysis nd symptotic nlysis. It hs mny physics pplictions, especilly in studies of
Math 61CM - Solutions to homework 9
 Mth 61CM - Solutions to homework 9 Cédric De Groote November 30 th, 2018 Problem 1: Recll tht the left limit of function f t point c is defined s follows: lim f(x) = l x c if for ny > 0 there exists δ
Mth 61CM - Solutions to homework 9 Cédric De Groote November 30 th, 2018 Problem 1: Recll tht the left limit of function f t point c is defined s follows: lim f(x) = l x c if for ny > 0 there exists δ
7. Indefinite Integrals
 7. Indefinite Integrls These lecture notes present my interprettion of Ruth Lwrence s lecture notes (in Herew) 7. Prolem sttement By the fundmentl theorem of clculus, to clculte n integrl we need to find
7. Indefinite Integrls These lecture notes present my interprettion of Ruth Lwrence s lecture notes (in Herew) 7. Prolem sttement By the fundmentl theorem of clculus, to clculte n integrl we need to find
AP Calculus Multiple Choice: BC Edition Solutions
 AP Clculus Multiple Choice: BC Edition Solutions J. Slon Mrch 8, 04 ) 0 dx ( x) is A) B) C) D) E) Divergent This function inside the integrl hs verticl symptotes t x =, nd the integrl bounds contin this
AP Clculus Multiple Choice: BC Edition Solutions J. Slon Mrch 8, 04 ) 0 dx ( x) is A) B) C) D) E) Divergent This function inside the integrl hs verticl symptotes t x =, nd the integrl bounds contin this
Sections 5.2: The Definite Integral
 Sections 5.2: The Definite Integrl In this section we shll formlize the ides from the lst section to functions in generl. We strt with forml definition.. The Definite Integrl Definition.. Suppose f(x)
Sections 5.2: The Definite Integrl In this section we shll formlize the ides from the lst section to functions in generl. We strt with forml definition.. The Definite Integrl Definition.. Suppose f(x)
Advanced Calculus: MATH 410 Uniform Convergence of Functions Professor David Levermore 11 December 2015
 Advnced Clculus: MATH 410 Uniform Convergence of Functions Professor Dvid Levermore 11 December 2015 12. Sequences of Functions We now explore two notions of wht it mens for sequence of functions {f n
Advnced Clculus: MATH 410 Uniform Convergence of Functions Professor Dvid Levermore 11 December 2015 12. Sequences of Functions We now explore two notions of wht it mens for sequence of functions {f n
AQA Further Pure 2. Hyperbolic Functions. Section 2: The inverse hyperbolic functions
 Hperbolic Functions Section : The inverse hperbolic functions Notes nd Emples These notes contin subsections on The inverse hperbolic functions Integrtion using the inverse hperbolic functions Logrithmic
Hperbolic Functions Section : The inverse hperbolic functions Notes nd Emples These notes contin subsections on The inverse hperbolic functions Integrtion using the inverse hperbolic functions Logrithmic
*********************************************************
 Problems Ted Eisenberg, Section Editor ********************************************************* This section of the Journal offers readers an opportunity to exchange interesting mathematical problems
Problems Ted Eisenberg, Section Editor ********************************************************* This section of the Journal offers readers an opportunity to exchange interesting mathematical problems
Jim Lambers MAT 169 Fall Semester Lecture 4 Notes
 Jim Lmbers MAT 169 Fll Semester 2009-10 Lecture 4 Notes These notes correspond to Section 8.2 in the text. Series Wht is Series? An infinte series, usully referred to simply s series, is n sum of ll of
Jim Lmbers MAT 169 Fll Semester 2009-10 Lecture 4 Notes These notes correspond to Section 8.2 in the text. Series Wht is Series? An infinte series, usully referred to simply s series, is n sum of ll of
The margin is too narrow to contain a truly remarkable proof.
 The mrgin is too nrrow to contin trul remrkble proof. Pierre de Fermt B For HP & KP Abstrct. The im of this pper is to tr for Fermt s lost proof. Introduction In bout 637 Pierre de Fermt, French mthemticin,
The mrgin is too nrrow to contin trul remrkble proof. Pierre de Fermt B For HP & KP Abstrct. The im of this pper is to tr for Fermt s lost proof. Introduction In bout 637 Pierre de Fermt, French mthemticin,
Convex Sets and Functions
 B Convex Sets nd Functions Definition B1 Let L, +, ) be rel liner spce nd let C be subset of L The set C is convex if, for ll x,y C nd ll [, 1], we hve 1 )x+y C In other words, every point on the line
B Convex Sets nd Functions Definition B1 Let L, +, ) be rel liner spce nd let C be subset of L The set C is convex if, for ll x,y C nd ll [, 1], we hve 1 )x+y C In other words, every point on the line
We divide the interval [a, b] into subintervals of equal length x = b a n
![We divide the interval [a, b] into subintervals of equal length x = b a n We divide the interval [a, b] into subintervals of equal length x = b a n](/thumbs/80/80533932.jpg) Arc Length Given curve C defined by function f(x), we wnt to find the length of this curve between nd b. We do this by using process similr to wht we did in defining the Riemnn Sum of definite integrl:
Arc Length Given curve C defined by function f(x), we wnt to find the length of this curve between nd b. We do this by using process similr to wht we did in defining the Riemnn Sum of definite integrl:
On some Hardy-Sobolev s type variable exponent inequality and its application
 Trnsctions of NAS of Azerbijn Issue Mthemtics 37 4 2 27. Series of Phsicl-Technicl nd Mthemticl Sciences On some Hrd-Sobolev s tpe vrible exponent inequlit nd its ppliction Frmn I. Mmedov Sli M. Mmmdli
Trnsctions of NAS of Azerbijn Issue Mthemtics 37 4 2 27. Series of Phsicl-Technicl nd Mthemticl Sciences On some Hrd-Sobolev s tpe vrible exponent inequlit nd its ppliction Frmn I. Mmedov Sli M. Mmmdli
UNIFORM CONVERGENCE MA 403: REAL ANALYSIS, INSTRUCTOR: B. V. LIMAYE
 UNIFORM CONVERGENCE MA 403: REAL ANALYSIS, INSTRUCTOR: B. V. LIMAYE 1. Pointwise Convergence of Sequence Let E be set nd Y be metric spce. Consider functions f n : E Y for n = 1, 2,.... We sy tht the sequence
UNIFORM CONVERGENCE MA 403: REAL ANALYSIS, INSTRUCTOR: B. V. LIMAYE 1. Pointwise Convergence of Sequence Let E be set nd Y be metric spce. Consider functions f n : E Y for n = 1, 2,.... We sy tht the sequence
UNIFORM CONVERGENCE. Contents 1. Uniform Convergence 1 2. Properties of uniform convergence 3
 UNIFORM CONVERGENCE Contents 1. Uniform Convergence 1 2. Properties of uniform convergence 3 Suppose f n : Ω R or f n : Ω C is sequence of rel or complex functions, nd f n f s n in some sense. Furthermore,
UNIFORM CONVERGENCE Contents 1. Uniform Convergence 1 2. Properties of uniform convergence 3 Suppose f n : Ω R or f n : Ω C is sequence of rel or complex functions, nd f n f s n in some sense. Furthermore,
Problem Set 9. Figure 1: Diagram. This picture is a rough sketch of the 4 parabolas that give us the area that we need to find. The equations are:
 (x + y ) = y + (x + y ) = x + Problem Set 9 Discussion: Nov., Nov. 8, Nov. (on probbility nd binomil coefficients) The nme fter the problem is the designted writer of the solution of tht problem. (No one
(x + y ) = y + (x + y ) = x + Problem Set 9 Discussion: Nov., Nov. 8, Nov. (on probbility nd binomil coefficients) The nme fter the problem is the designted writer of the solution of tht problem. (No one
Math 113 Fall Final Exam Review. 2. Applications of Integration Chapter 6 including sections and section 6.8
 Mth 3 Fll 0 The scope of the finl exm will include: Finl Exm Review. Integrls Chpter 5 including sections 5. 5.7, 5.0. Applictions of Integrtion Chpter 6 including sections 6. 6.5 nd section 6.8 3. Infinite
Mth 3 Fll 0 The scope of the finl exm will include: Finl Exm Review. Integrls Chpter 5 including sections 5. 5.7, 5.0. Applictions of Integrtion Chpter 6 including sections 6. 6.5 nd section 6.8 3. Infinite
7.2 The Definite Integral
 7.2 The Definite Integrl the definite integrl In the previous section, it ws found tht if function f is continuous nd nonnegtive, then the re under the grph of f on [, b] is given by F (b) F (), where
7.2 The Definite Integrl the definite integrl In the previous section, it ws found tht if function f is continuous nd nonnegtive, then the re under the grph of f on [, b] is given by F (b) F (), where
Form 5 HKCEE 1990 Mathematics II (a 2n ) 3 = A. f(1) B. f(n) A. a 6n B. a 8n C. D. E. 2 D. 1 E. n. 1 in. If 2 = 10 p, 3 = 10 q, express log 6
 Form HK 9 Mthemtics II.. ( n ) =. 6n. 8n. n 6n 8n... +. 6.. f(). f(n). n n If = 0 p, = 0 q, epress log 6 in terms of p nd q.. p q. pq. p q pq p + q Let > b > 0. If nd b re respectivel the st nd nd terms
Form HK 9 Mthemtics II.. ( n ) =. 6n. 8n. n 6n 8n... +. 6.. f(). f(n). n n If = 0 p, = 0 q, epress log 6 in terms of p nd q.. p q. pq. p q pq p + q Let > b > 0. If nd b re respectivel the st nd nd terms
How do we solve these things, especially when they get complicated? How do we know when a system has a solution, and when is it unique?
 XII. LINEAR ALGEBRA: SOLVING SYSTEMS OF EQUATIONS Tody we re going to tlk bout solving systems of liner equtions. These re problems tht give couple of equtions with couple of unknowns, like: 6 2 3 7 4
XII. LINEAR ALGEBRA: SOLVING SYSTEMS OF EQUATIONS Tody we re going to tlk bout solving systems of liner equtions. These re problems tht give couple of equtions with couple of unknowns, like: 6 2 3 7 4
Numerical Linear Algebra Assignment 008
 Numericl Liner Algebr Assignment 008 Nguyen Qun B Hong Students t Fculty of Mth nd Computer Science, Ho Chi Minh University of Science, Vietnm emil. nguyenqunbhong@gmil.com blog. http://hongnguyenqunb.wordpress.com
Numericl Liner Algebr Assignment 008 Nguyen Qun B Hong Students t Fculty of Mth nd Computer Science, Ho Chi Minh University of Science, Vietnm emil. nguyenqunbhong@gmil.com blog. http://hongnguyenqunb.wordpress.com
Theoretical foundations of Gaussian quadrature
 Theoreticl foundtions of Gussin qudrture 1 Inner product vector spce Definition 1. A vector spce (or liner spce) is set V = {u, v, w,...} in which the following two opertions re defined: (A) Addition of
Theoreticl foundtions of Gussin qudrture 1 Inner product vector spce Definition 1. A vector spce (or liner spce) is set V = {u, v, w,...} in which the following two opertions re defined: (A) Addition of
A LEVEL TOPIC REVIEW. factor and remainder theorems
 A LEVEL TOPIC REVIEW unit C fctor nd reminder theorems. Use the Fctor Theorem to show tht: ) ( ) is fctor of +. ( mrks) ( + ) is fctor of ( ) is fctor of + 7+. ( mrks) +. ( mrks). Use lgebric division
A LEVEL TOPIC REVIEW unit C fctor nd reminder theorems. Use the Fctor Theorem to show tht: ) ( ) is fctor of +. ( mrks) ( + ) is fctor of ( ) is fctor of + 7+. ( mrks) +. ( mrks). Use lgebric division
15 - TRIGONOMETRY Page 1 ( Answers at the end of all questions )
 - TRIGONOMETRY Pge P ( ) In tringle PQR, R =. If tn b c = 0, 0, then Q nd tn re the roots of the eqution = b c c = b b = c b = c [ AIEEE 00 ] ( ) In tringle ABC, let C =. If r is the inrdius nd R is the
- TRIGONOMETRY Pge P ( ) In tringle PQR, R =. If tn b c = 0, 0, then Q nd tn re the roots of the eqution = b c c = b b = c b = c [ AIEEE 00 ] ( ) In tringle ABC, let C =. If r is the inrdius nd R is the
Chapter 1: Fundamentals
 Chpter 1: Fundmentls 1.1 Rel Numbers Types of Rel Numbers: Nturl Numbers: {1, 2, 3,...}; These re the counting numbers. Integers: {... 3, 2, 1, 0, 1, 2, 3,...}; These re ll the nturl numbers, their negtives,
Chpter 1: Fundmentls 1.1 Rel Numbers Types of Rel Numbers: Nturl Numbers: {1, 2, 3,...}; These re the counting numbers. Integers: {... 3, 2, 1, 0, 1, 2, 3,...}; These re ll the nturl numbers, their negtives,
than 1. It means in particular that the function is decreasing and approaching the x-
 6 Preclculus Review Grph the functions ) (/) ) log y = b y = Solution () The function y = is n eponentil function with bse smller thn It mens in prticulr tht the function is decresing nd pproching the
6 Preclculus Review Grph the functions ) (/) ) log y = b y = Solution () The function y = is n eponentil function with bse smller thn It mens in prticulr tht the function is decresing nd pproching the
Indefinite Integral. Chapter Integration - reverse of differentiation
 Chpter Indefinite Integrl Most of the mthemticl opertions hve inverse opertions. The inverse opertion of differentition is clled integrtion. For exmple, describing process t the given moment knowing the
Chpter Indefinite Integrl Most of the mthemticl opertions hve inverse opertions. The inverse opertion of differentition is clled integrtion. For exmple, describing process t the given moment knowing the
Lecture 3 ( ) (translated and slightly adapted from lecture notes by Martin Klazar)
 Lecture 3 (5.3.2018) (trnslted nd slightly dpted from lecture notes by Mrtin Klzr) Riemnn integrl Now we define precisely the concept of the re, in prticulr, the re of figure U(, b, f) under the grph of
Lecture 3 (5.3.2018) (trnslted nd slightly dpted from lecture notes by Mrtin Klzr) Riemnn integrl Now we define precisely the concept of the re, in prticulr, the re of figure U(, b, f) under the grph of
Torsion in Groups of Integral Triangles
 Advnces in Pure Mthemtics, 01,, 116-10 http://dxdoiorg/1046/pm011015 Pulished Online Jnury 01 (http://wwwscirporg/journl/pm) Torsion in Groups of Integrl Tringles Will Murry Deprtment of Mthemtics nd Sttistics,
Advnces in Pure Mthemtics, 01,, 116-10 http://dxdoiorg/1046/pm011015 Pulished Online Jnury 01 (http://wwwscirporg/journl/pm) Torsion in Groups of Integrl Tringles Will Murry Deprtment of Mthemtics nd Sttistics,
Section - 2 MORE PROPERTIES
 LOCUS Section - MORE PROPERTES n section -, we delt with some sic properties tht definite integrls stisf. This section continues with the development of some more properties tht re not so trivil, nd, when
LOCUS Section - MORE PROPERTES n section -, we delt with some sic properties tht definite integrls stisf. This section continues with the development of some more properties tht re not so trivil, nd, when
Properties of the Riemann Integral
 Properties of the Riemnn Integrl Jmes K. Peterson Deprtment of Biologicl Sciences nd Deprtment of Mthemticl Sciences Clemson University Februry 15, 2018 Outline 1 Some Infimum nd Supremum Properties 2
Properties of the Riemnn Integrl Jmes K. Peterson Deprtment of Biologicl Sciences nd Deprtment of Mthemticl Sciences Clemson University Februry 15, 2018 Outline 1 Some Infimum nd Supremum Properties 2
Best Approximation in the 2-norm
 Jim Lmbers MAT 77 Fll Semester 1-11 Lecture 1 Notes These notes correspond to Sections 9. nd 9.3 in the text. Best Approximtion in the -norm Suppose tht we wish to obtin function f n (x) tht is liner combintion
Jim Lmbers MAT 77 Fll Semester 1-11 Lecture 1 Notes These notes correspond to Sections 9. nd 9.3 in the text. Best Approximtion in the -norm Suppose tht we wish to obtin function f n (x) tht is liner combintion
5.7 Improper Integrals
 458 pplictions of definite integrls 5.7 Improper Integrls In Section 5.4, we computed the work required to lift pylod of mss m from the surfce of moon of mss nd rdius R to height H bove the surfce of the
458 pplictions of definite integrls 5.7 Improper Integrls In Section 5.4, we computed the work required to lift pylod of mss m from the surfce of moon of mss nd rdius R to height H bove the surfce of the
5.3 The Fundamental Theorem of Calculus, Part I
 59 C HAPTER 5 THE INTEGRAL θ b 87. Suppose tht f nd g re continuous functions such tht, for ll, Z Z f./d g./d Give n intuitive rgument showing tht f./ g./.eplin our ide with grph. Let R f./d R g./d.considerwhthppenss
59 C HAPTER 5 THE INTEGRAL θ b 87. Suppose tht f nd g re continuous functions such tht, for ll, Z Z f./d g./d Give n intuitive rgument showing tht f./ g./.eplin our ide with grph. Let R f./d R g./d.considerwhthppenss
STUDY GUIDE FOR BASIC EXAM
 STUDY GUIDE FOR BASIC EXAM BRYON ARAGAM This is prtil list of theorems tht frequently show up on the bsic exm. In mny cses, you my be sked to directly prove one of these theorems or these vrints. There
STUDY GUIDE FOR BASIC EXAM BRYON ARAGAM This is prtil list of theorems tht frequently show up on the bsic exm. In mny cses, you my be sked to directly prove one of these theorems or these vrints. There
Math Calculus with Analytic Geometry II
 orem of definite Mth 5.0 with Anlytic Geometry II Jnury 4, 0 orem of definite If < b then b f (x) dx = ( under f bove x-xis) ( bove f under x-xis) Exmple 8 0 3 9 x dx = π 3 4 = 9π 4 orem of definite Problem
orem of definite Mth 5.0 with Anlytic Geometry II Jnury 4, 0 orem of definite If < b then b f (x) dx = ( under f bove x-xis) ( bove f under x-xis) Exmple 8 0 3 9 x dx = π 3 4 = 9π 4 orem of definite Problem
State space systems analysis (continued) Stability. A. Definitions A system is said to be Asymptotically Stable (AS) when it satisfies
 Stte spce systems nlysis (continued) Stbility A. Definitions A system is sid to be Asymptoticlly Stble (AS) when it stisfies ut () = 0, t > 0 lim xt () 0. t A system is AS if nd only if the impulse response
Stte spce systems nlysis (continued) Stbility A. Definitions A system is sid to be Asymptoticlly Stble (AS) when it stisfies ut () = 0, t > 0 lim xt () 0. t A system is AS if nd only if the impulse response
50. Use symmetry to evaluate xx D is the region bounded by the square with vertices 5, Prove Property 11. y y CAS
 68 CHAPTE MULTIPLE INTEGALS 46. e da, 49. Evlute tn 3 4 da, where,. [Hint: Eploit the fct tht is the disk with center the origin nd rdius is smmetric with respect to both es.] 5. Use smmetr to evlute 3
68 CHAPTE MULTIPLE INTEGALS 46. e da, 49. Evlute tn 3 4 da, where,. [Hint: Eploit the fct tht is the disk with center the origin nd rdius is smmetric with respect to both es.] 5. Use smmetr to evlute 3
1 Part II: Numerical Integration
 Mth 4 Lb 1 Prt II: Numericl Integrtion This section includes severl techniques for getting pproimte numericl vlues for definite integrls without using ntiderivtives. Mthemticll, ect nswers re preferble
Mth 4 Lb 1 Prt II: Numericl Integrtion This section includes severl techniques for getting pproimte numericl vlues for definite integrls without using ntiderivtives. Mthemticll, ect nswers re preferble
Lecture 3: Curves in Calculus. Table of contents
 Mth 348 Fll 7 Lecture 3: Curves in Clculus Disclimer. As we hve textook, this lecture note is for guidnce nd supplement only. It should not e relied on when prepring for exms. In this lecture we set up
Mth 348 Fll 7 Lecture 3: Curves in Clculus Disclimer. As we hve textook, this lecture note is for guidnce nd supplement only. It should not e relied on when prepring for exms. In this lecture we set up
ODE: Existence and Uniqueness of a Solution
 Mth 22 Fll 213 Jerry Kzdn ODE: Existence nd Uniqueness of Solution The Fundmentl Theorem of Clculus tells us how to solve the ordinry differentil eqution (ODE) du = f(t) dt with initil condition u() =
Mth 22 Fll 213 Jerry Kzdn ODE: Existence nd Uniqueness of Solution The Fundmentl Theorem of Clculus tells us how to solve the ordinry differentil eqution (ODE) du = f(t) dt with initil condition u() =
Math Advanced Calculus II
 Mth 452 - Advnced Clculus II Line Integrls nd Green s Theorem The min gol of this chpter is to prove Stoke s theorem, which is the multivrible version of the fundmentl theorem of clculus. We will be focused
Mth 452 - Advnced Clculus II Line Integrls nd Green s Theorem The min gol of this chpter is to prove Stoke s theorem, which is the multivrible version of the fundmentl theorem of clculus. We will be focused
HOMEWORK SOLUTIONS MATH 1910 Sections 7.9, 8.1 Fall 2016
 HOMEWORK SOLUTIONS MATH 9 Sections 7.9, 8. Fll 6 Problem 7.9.33 Show tht for ny constnts M,, nd, the function yt) = )) t ) M + tnh stisfies the logistic eqution: y SOLUTION. Let Then nd Finlly, y = y M
HOMEWORK SOLUTIONS MATH 9 Sections 7.9, 8. Fll 6 Problem 7.9.33 Show tht for ny constnts M,, nd, the function yt) = )) t ) M + tnh stisfies the logistic eqution: y SOLUTION. Let Then nd Finlly, y = y M
Euler-Maclaurin Summation Formula 1
 Jnury 9, Euler-Mclurin Summtion Formul Suppose tht f nd its derivtive re continuous functions on the closed intervl [, b]. Let ψ(x) {x}, where {x} x [x] is the frctionl prt of x. Lemm : If < b nd, b Z,
Jnury 9, Euler-Mclurin Summtion Formul Suppose tht f nd its derivtive re continuous functions on the closed intervl [, b]. Let ψ(x) {x}, where {x} x [x] is the frctionl prt of x. Lemm : If < b nd, b Z,
Chapter 6 Notes, Larson/Hostetler 3e
 Contents 6. Antiderivtives nd the Rules of Integrtion.......................... 6. Are nd the Definite Integrl.................................. 6.. Are............................................ 6. Reimnn
Contents 6. Antiderivtives nd the Rules of Integrtion.......................... 6. Are nd the Definite Integrl.................................. 6.. Are............................................ 6. Reimnn
ASYMPTOTIC BEHAVIOR OF INTERMEDIATE POINTS IN CERTAIN MEAN VALUE THEOREMS. II
 STUDIA UNIV. BABEŞ BOLYAI, MATHEMATICA, Volume LV, Number 3, September 2010 ASYMPTOTIC BEHAVIOR OF INTERMEDIATE POINTS IN CERTAIN MEAN VALUE THEOREMS. II TIBERIU TRIF Dedicted to Professor Grigore Ştefn
STUDIA UNIV. BABEŞ BOLYAI, MATHEMATICA, Volume LV, Number 3, September 2010 ASYMPTOTIC BEHAVIOR OF INTERMEDIATE POINTS IN CERTAIN MEAN VALUE THEOREMS. II TIBERIU TRIF Dedicted to Professor Grigore Ştefn
Math 1431 Section M TH 4:00 PM 6:00 PM Susan Wheeler Office Hours: Wed 6:00 7:00 PM Online ***NOTE LABS ARE MON AND WED
 Mth 43 Section 4839 M TH 4: PM 6: PM Susn Wheeler swheeler@mth.uh.edu Office Hours: Wed 6: 7: PM Online ***NOTE LABS ARE MON AND WED t :3 PM to 3: pm ONLINE Approimting the re under curve given the type
Mth 43 Section 4839 M TH 4: PM 6: PM Susn Wheeler swheeler@mth.uh.edu Office Hours: Wed 6: 7: PM Online ***NOTE LABS ARE MON AND WED t :3 PM to 3: pm ONLINE Approimting the re under curve given the type
New Expansion and Infinite Series
 Interntionl Mthemticl Forum, Vol. 9, 204, no. 22, 06-073 HIKARI Ltd, www.m-hikri.com http://dx.doi.org/0.2988/imf.204.4502 New Expnsion nd Infinite Series Diyun Zhng College of Computer Nnjing University
Interntionl Mthemticl Forum, Vol. 9, 204, no. 22, 06-073 HIKARI Ltd, www.m-hikri.com http://dx.doi.org/0.2988/imf.204.4502 New Expnsion nd Infinite Series Diyun Zhng College of Computer Nnjing University
Math 1102: Calculus I (Math/Sci majors) MWF 3pm, Fulton Hall 230 Homework 2 solutions
 Mth 1102: Clculus I (Mth/Sci mjors) MWF 3pm, Fulton Hll 230 Homework 2 solutions Plese write netly, nd show ll work. Cution: An nswer with no work is wrong! Do the following problems from Chpter III: 6,
Mth 1102: Clculus I (Mth/Sci mjors) MWF 3pm, Fulton Hll 230 Homework 2 solutions Plese write netly, nd show ll work. Cution: An nswer with no work is wrong! Do the following problems from Chpter III: 6,
Self-similarity and symmetries of Pascal s triangles and simplices mod p
 Sn Jose Stte University SJSU ScholrWorks Fculty Publictions Mthemtics nd Sttistics Februry 2004 Self-similrity nd symmetries of Pscl s tringles nd simplices mod p Richrd P. Kubelk Sn Jose Stte University,
Sn Jose Stte University SJSU ScholrWorks Fculty Publictions Mthemtics nd Sttistics Februry 2004 Self-similrity nd symmetries of Pscl s tringles nd simplices mod p Richrd P. Kubelk Sn Jose Stte University,
Some estimates on the Hermite-Hadamard inequality through quasi-convex functions
 Annls of University of Criov, Mth. Comp. Sci. Ser. Volume 3, 7, Pges 8 87 ISSN: 13-693 Some estimtes on the Hermite-Hdmrd inequlity through qusi-convex functions Dniel Alexndru Ion Abstrct. In this pper
Annls of University of Criov, Mth. Comp. Sci. Ser. Volume 3, 7, Pges 8 87 ISSN: 13-693 Some estimtes on the Hermite-Hdmrd inequlity through qusi-convex functions Dniel Alexndru Ion Abstrct. In this pper
