Probabilistic Graphical Models
|
|
|
- Gerard Payne
- 5 years ago
- Views:
Transcription
1 School of Comuter Scece Probablstc rahcal Models Parameter Est. fully observed Bs Erc Xg X X X X Lecture 7 February 5 04 X X 3 X X X 3 X 3 Readg: KF-cha 7 X 4 X 4 Erc CMU
2 Learg rahcal Models The goal: ve set of deedet samles assgmets of radom varables fd the best the most lely? Bayesa etwor both DA ad CPDs E B E B R A C R A C Structural learg BEACR=TFFTF BEACR=TFTTF.. BEACR=FTTTF E e e e e B b b b b PA EB Parameter learg Erc CMU
3 Learg rahcal Models Scearos: comletely observed Ms drected udrected artally or uobserved Ms drected udrected a oe research toc Estmato rcles: Mamal lelhood estmato MLE Bayesa estmato Mamal codtoal lelhood Mamal "Marg" Mamum etroy We use learg as a ame for the rocess of estmatg the arameters ad some cases the toology of the etwor from data. Erc CMU
4 ML Structural Learg for comletely observed Ms E R B A C Data M M Erc CMU
5 Two Otmal aroaches Otmal here meas the emloyed algorthms guaratee to retur a structure that mamzes the objectves e.g. LogL May heurstcs used to be oular but they rovde o guaratee o attag otmalty terretablty or eve do ot have a elct objectve E.g.: structured EM Module etwor greedy structural search etc. We wll lear two classes of algorthms for guarateed structure learg whch are lely to be the oly ow methods ejoyg such guaratee but they oly aly to certa famles of grahs: Trees: The Chow-Lu algorthm ths lecture Parwse MRFs: covarace selecto eghborhood-selecto later Erc CMU
6 Structural Search How may grahs over odes? O How may trees over odes? O! But t turs out that we ca fd eact soluto of a otmal tree uder MLE! Trc: MLE score decomosable to edge-related elemets Trc: a tree each ode has oly oe aret! Chow-lu algorthm Erc CMU
7 Iformato Theoretc Iterretato of ML M M cout M D D log ˆ log log log log ; l From sum over data ots to sum over cout of varable states Erc CMU
8 Iformato Theoretc Iterretato of ML co'd H M I M M M M M D D ˆ ˆ ˆ log ˆ ˆ ˆ ˆ log ˆ ˆ ˆ ˆ ˆ log ˆ ˆ log ˆ ˆ log ; l Decomosable score ad a fucto of the grah structure Erc CMU
9 Chow-Lu tree learg algorthm Objecto fucto: l ; D log ˆ D M Iˆ M Hˆ C M Iˆ Chow-Lu: For each ar of varable ad j Comute emrcal dstrbuto: Comute mutual formato: ˆ X Iˆ X X X j j cout j M j j log ˆ ˆ j j ˆ ˆ Defe a grah wth ode Edge Ij gets weght Iˆ X X j Erc CMU
10 Chow-Lu algorthm co'd Objecto fucto: Chow-Lu: Otmal tree B Comute mamum weght sag tree Drecto B: c ay ode as root do breadth-frst-search to defe drectos I-equvalece: H M I M D D ˆ ˆ ˆ log ; l I M C ˆ A B C D E C A E B D E C D A B E C I D C I C A I B A I C Erc CMU
11 Structure Learg for geeral grahs Theorem: The roblem of learg a B structure wth at most d arets s P-hard for ay fed d Most structure learg aroaches use heurstcs Elot score decomosto Two heurstcs that elot decomosto dfferet ways reedy search through sace of ode-orders Local search of grah structures Erc CMU
12 Z ML Parameter Est. for comletely observed Ms of gve structure X The data: { z z z z } Erc CMU
13 Parameter Learg Assume s ow ad fed from eert desg from a termedate outcome of teratve structure learg oal: estmate from a dataset of deedet detcally dstrbuted d trag cases D = {... }. I geeral each trag case =... M s a vector of M values oe er ode the model ca be comletely observable.e. every elemet s ow o mssg values o hdde varables or artally observable.e. s.t. s ot observed. I ths lecture we cosder learg arameters for a B wth gve structure ad s comletely observable l ; D log D log log Erc CMU
14 Revew of desty estmato Ca be vewed as sgle-ode grahcal models M: 3 Istaces of eoetal famly dst. Buldg blocs of geeral M MLE ad Bayesa estmate Erc CMU
15 Beroull dstrbuto: Ber Multomal dstrbuto: Mult Multomal dcator varable:. w.. ad ] [ where [...6] [...6] j j j j j j j X X X X X X X X X X T C A j j T C A j X P j de the dce - face} where { Dscrete Dstrbutos 0 P for for P Erc CMU
16 Multomal dstrbuto: Mult Cout varable: Dscrete Dstrbutos j j K where K K K K!!!!!!!! Erc CMU
17 Eamle: multomal model Data: We observed d de rolls K-sded: D={5 K 3} Reresetato: Ut bass vectors: Model: How to wrte the lelhood of a sgle observato? The lelhood of datasetd={ }: K K P P } th roll the de the de - sde of where { P P... ad {0} where K K ad w.. } {...K X K 3 M: Erc CMU
18 MLE: costraed otmzato wth Lagrage multlers Objectve fucto: l ; D logp D log log We eed to mamze ths subject to the costra Costraed cost fucto wth a Lagrage multler K l log Tae dervatves wrt l 0 MLE or Suffcet statstcs K The couts are suffcet statstcs of data D K MLE Frequecy as samle mea Erc CMU
19 Bayesa estmato: Drchlet dstrbuto: Posteror dstrbuto of : otce the somorhsm of the osteror to the ror such a ror s called a cojugate ror Posteror mea estmato: C P - - P d C d D 3 M: Drchlet arameters ca be uderstood as seudo-couts Erc CMU
20 More o Drchlet Pror: Where s the ormalze costat C come from? Itegrato by arts s the gamma fucto: For regers Margal lelhood: Posteror closed-form: Posteror redctve rate: K K d d C K 0 dt e t t! }... { C C d C P }... { Dr }... { C C d C Erc CMU
21 Sequetal Bayesa udatg Start wth Drchlet ror P Dr : Observe ' samles wth suffcet statstcs '. Posteror becomes: P ' Dr : ' Observe aother " samles wth suffcet statstcs ". Posteror becomes: P ' " Dr : ' " So sequetally absorbg data ay order s equvalet to batch udate. Erc CMU
22 Herarchcal Bayesa Models are the arameters for the lelhood are the arameters for the ror. We ca have hyer-hyer-arameters etc. We sto whe the choce of hyer-arameters maes o dfferece to the margal lelhood; tycally mae hyerarameters costats. Where do we get the ror? Itellget guesses Emrcal Bayes Tye-II mamum lelhood comutg ot estmates of : MLE arg ma Erc CMU
23 Lmtato of Drchlet Pror: Erc CMU
24 - Log Partto Fucto - ormalzato Costat log log e ~ ~ 0 K K K K K e C e L μ Σ The Logstc ormal Pror Pro: co-varace structure Co: o-cojugate we wll dscuss how to solve ths later Erc CMU
25 Logstc ormal Destes Erc CMU
26 Cotuous Dstrbutos Uform Probablty Desty Fucto / b a for a b 0 elsewhere ormal aussa Probablty Desty Fucto f / e The dstrbuto s symmetrc ad s ofte llustrated as a bell-shaed curve. Two arameters mea ad stadard devato determe the locato ad shae of the dstrbuto. The hghest ot o the ormal curve s at the mea whch s also the meda ad mode. The mea ca be ay umercal value: egatve zero or ostve. Multvarate aussa X ; / / e T X X Erc CMU
27 MLE for a multvarate-aussa It ca be show that the MLE for µ ad Σ s where the scatter matr s The suffcet statstcs are ad T. ote that X T X= T may ot be full ra eg. f <D whch case Σ ML s ot vertble S T ML ML MLE MLE T ML ML T T ML ML S K T T T X Erc CMU
28 Bayesa arameter estmato for a aussa There are varous reasos to ursue a Bayesa aroach We would le to udate our estmates sequetally over tme. We may have ror owledge about the eected magtude of the arameters. The MLE for Σ may ot be full ra f we do t have eough data. We wll restrct our atteto to cojugate rors. We wll cosder varous cases order of creasg comlety: Kow σ uow µ Kow µ uow σ Uow µ ad σ Erc CMU
29 Bayesa estmato: uow µ ow σ ormal Pror: Jot robablty: Posteror: 0 / e / P 0 ~ ad / / / / / / ~ where 3 M: Samle mea 0 / e e / / P ~ / ~ e ~ / P Erc CMU
30 Bayesa estmato: uow µ ow σ The osteror mea s a cove combato of the ror ad the MLE wth weghts roortoal to the relatve ose levels. The recso of the osteror /σ s the recso of the ror /σ 0 lus oe cotrbuto of data recso /σ for each observed data ot. Sequetally udatg the mea µ = 0.8 uow σ = 0. ow Effect of sgle data ot Uformatve vague/ flat ror σ ~ / / / / / / Erc CMU
31 Other scearos Kow µ uow λ = /σ The cojugate ror for λ s a amma wth shae a 0 ad rate verse scale b 0 The cojugate ror for σ s Iverse-amma Uow µ ad uow σ The cojugate ror s ormal-iverse-amma Sem cojugate ror Multvarate case: The cojugate ror s ormal-iverse-wshart Erc CMU
32 Estmato of codtoal desty Ca be vewed as two-ode grahcal models Istaces of LIM Q Q Buldg blocs of geeral M MLE ad Bayesa estmate X X See sulemetary sldes Erc CMU
33 MLE for geeral Bs If we assume the arameters for each CPD are globally deedet ad all odes are fully observed the the loglelhood fucto decomoses to a sum of local terms oe er ode: l ; D log D log log X = X 5 =0 X =0 X 5 = Erc CMU
34 Plates A late s a macro that allows subgrahs to be relcated X X X For d echageable data the lelhood s X D We ca rereset ths as a Bayes et wth odes. The rules of lates are smle: reeat every structure a bo a umber of tmes gve by the teger the corer of the bo e.g. udatg the late de varable e.g. as you go. Dulcate every arrow gog to the late ad every arrow leavg the late by coectg the arrows to each coy of the structure. Erc CMU
35 Decomosable lelhood of a B Cosder the dstrbuto defed by the drected acyclc M: Ths s eactly le learg four searate small Bs each of whch cossts of a ode ad ts arets. X X X X X X 3 X X X 3 X 3 X 4 X 4 Erc CMU
36 MLE for Bs wth tabular CPDs Assume each CPD s rereseted as a table multomal where def X j X ote that case of multle arets wll have a comoste state ad the CPD wll be a hgh-dmesoal table The suffcet statstcs are couts of famly cofguratos The log-lelhood s Usg a Lagrage multler j to eforce we get: j j j def j X j l ; D log log j j ML j j j j' j j' j Erc CMU
37 How to defe arameter ror? Earthquae Burglary Factorzato: M X Rado Alarm Call Local Dstrbutos defed by e.g. multomal arameters: j j Assumtos eger & Hecerma 9799: Comlete Model Equvalece lobal Parameter Ideedece Local Parameter Ideedece Lelhood ad Pror Modularty? Erc CMU
38 lobal & Local Parameter Ideedece lobal Parameter Ideedece For every DA model: Earthquae Burglary M m Rado Alarm Local Parameter Ideedece For every ode: q j j P deedet of Call Call AlarmYES P O Call Alarm Erc CMU
39 Parameter Ideedece rahcal Vew lobal Parameter Ideedece X X Local Parameter Ideedece samle X X samle Provded all varables are observed all cases we ca erform Bayesa udate each arameter deedetly!!! Erc CMU
40 Whch PDFs Satsfy Our Assumtos? eger & Hecerma 9799 Dscrete DA Models: Drchlet ror: aussa DA Models: ormal ror: ormal-wshart ror: C P - - Mult ~ j ormal ~ j ' e / /. where W tr e W W / / W w w w w c ormal W W Erc CMU
41 Parameter sharg A X X X 3 X T Cosder a tme-varat statoary st -order Marov model Ital state robablty vector: State trasto robablty matr: The jot: The log-lelhood: Aga we otmze each arameter searately s a multomal frequecy vector ad we've see t before What about A? X : def A j X def X j t X T T X t X t t t T l ; D log log t t A t Erc CMU t
42 Learg a Marov cha trasto matr A s a stochastc matr: j Each row of A s multomal dstrbuto. So MLE of A j s the fracto of trastos from to j Aj A ML j # # j T t j t t T t t Alcato: f the states X t rereset words ths s called a bgram laguage model Sarse data roblem: If j dd ot occur data we wll have A j =0 the ay future sequece wth word ar j wll have zero robablty. A stadard hac: bacoff smoothg or deleted terolato ~ A A t ML Erc CMU
43 Bayesa laguage model lobal ad local arameter deedece A A ' X X X 3 X T A The osteror of A ad A ' s factorzed deste v-structure o X t because X t- acts le a multleer Assg a Drchlet ror to each row of the trasto matr: A Bayes j def # j ' j D A # ML j where # We could cosder more realstc rors e.g. mtures of Drchlets to accout for tyes of words adjectves verbs etc. Erc CMU
44 Eamle: HMM: two scearos Suervsed learg: estmato whe the rght aswer s ow Eamles: IVE: IVE: a geomc rego = where we have good eermetal aotatos of the C slads the caso layer allows us to observe hm oe eveg as he chages dce ad roduces 0000 rolls Usuervsed learg: estmato whe the rght aswer s uow Eamles: IVE: IVE: the orcue geome; we do t ow how frequet are the C slads there ether do we ow ther comosto 0000 rolls of the caso layer but we do t see whe he chages dce QUESTIO: Udate the arameters of the model to mamze P - -- Mamal lelhood ML estmato Erc CMU
45 Recall defto of HMM Trasto robabltes betwee ay two states y y y 3... y T j yt yt a j A A A 3... A T or a a a. yt yt ~ Multomal M I Start robabltes ~ Multomal. y M Emsso robabltes assocated wth each state b b b. t yt ~ Multomal K I or geeral:. y ~ f I t t Erc CMU
46 Suervsed ML estmato ve = for whch the true state ath y = y y s ow Defe: A j B = # tmes state trasto j occurs y = # tmes state y emts We ca show that the mamum lelhood arameters are: a b ML j ML # j # # # T t T t j t t T y t t T What f s cotuous? We ca treat t y t : t : T : as T observatos of e.g. a aussa ad aly learg rules for aussa y y t t y t y t ' A j' j B B A ' j' Erc CMU
47 Suervsed ML estmato ctd. Ituto: Whe we ow the uderlyg states the best estmate of s the average frequecy of trastos & emssos that occur the trag data Drawbac: ve lttle data there may be overfttg: P s mamzed but s ureasoable 0 robabltes VERY BAD Eamle: ve 0 caso rolls we observe = y = F F F F F F F F F F The: a FF = ; a FL = 0 b F = b F3 =.; b F =.3; b F4 = 0; b F5 = b F6 =. Erc CMU
48 Pseudocouts Soluto for small trag sets: Add seudocouts A j B = # tmes state trasto j occurs y + R j = # tmes state y emts + S R j S j are seudocouts reresetg our ror belef Total seudocouts: R = j R j S = S --- "stregth" of ror belef --- total umber of magary staces the ror Larger total seudocouts strog ror belef Small total seudocouts: just to avod 0 robabltes --- smoothg Ths s equvalet to Bayesa est. uder a uform ror wth "arameter stregth" equals to the seudocouts Erc CMU
49 Summary: Learg M For fully observed B the log-lelhood fucto decomoses to a sum of local terms oe er ode; thus learg s also factored Structural learg Chow lu eghborhood selecto Learg sgle-ode M desty estmato: eoetal famly dst. Tycal dscrete dstrbuto Tycal cotuous dstrbuto Cojugate rors Learg two-ode B: LIM Codtoal Desty Est. Classfcato Learg B wth more odes Local oeratos Erc CMU
50 Sulemetal revew: Erc CMU
51 Two ode fully observed Bs Codtoal mtures Lear/Logstc Regresso Classfcato eeratve ad dscrmatve aroaches Q X Q X Erc CMU
52 Classfcato: oal: Wsh to lear f: X Y eeratve: Modelg the jot dstrbuto of all data Dscrmatve: Modelg oly ots at the boudary Erc CMU
53 Codtoal aussa The data: y y y y 3 3 Both odes are observed: Y s a class dcator vector M: Y X y mult y : X s a codtoal aussa varable wth a class-secfc mea y e - / y - y : Erc CMU y
54 Data log-lelhood MLE log log ; y y y D θ l ; ma y D rg a MLE MLE θ l the fracto of samles of class m MLE MLE y y y D ; ma arg θ l the average of samles of class m MLE of codtoal aussa M: Y X Erc CMU
55 Pror: Posteror mea Bayesa est. Bsyesa estmato of codtoal aussa M: Y X : Dr P : ormal P K Bayes ML Bayes ad / / / / / / ML Bayes Erc CMU
56 Classfcato aussa Dscrmatve Aalyss: The jot robablty of a datum ad t label s: ve a datum we redct ts label usg the codtoal robablty of the label gve the datum: Ths s basc ferece troduce evdece ad the ormalze / - - e y y y ' ' / ' / - - e - - e y Y X Erc CMU
57 Trasductve classfcato ve X what s ts corresodg Y whe we ow the aswer for a set of trag data? Frequetst redcto: we ft ad from data frst ad the Bayesa: we comute the osteror dst. of the arameters frst M: Y X K Y X ' ' ' y y Erc CMU
58 Lear Regresso The data: y y y y Both odes are observed: X s a ut vector Y s a resose vector we frst cosder y as a geerc cotuous resose vector the we cosder the secal case of classfcato where y s a dscrete dcator 3 3 Y X A regresso scheme ca be used to model y drectly rather tha y Erc CMU
59 A dscrmatve robablstc model Let us assume that the target varable ad the uts are related by the equato: where ε s a error term of umodeled effects or radom ose ow assume that ε follows a aussa 0σ the we have: By deedece assumto: T y e ; T y y T y y L e ; Erc CMU
60 Lear regresso Hece the log-lelhood s: T l log y Do you recogze the last term? Yes t s: T J y It s same as the MSE! Erc CMU
61 A reca: LMS udate rule Pros: o-le low er-ste cost Cos: coordate maybe slow-covergg Steeest descet Pros: fast-covergg easy to mlemet Cos: a batch ormal equatos t t * t t y T t Pros: a sgle-shot algorthm! Easest to mlemet. Cos: eed to comute seudo-verse X T X - eesve umercal ssues e.g. matr s sgular.. T t y T T X X X y Erc CMU
62 Bayesa lear regresso Erc CMU
63 Smle Ms are the buldg blocs of comle Bs Desty estmato Parametrc ad oarametrc methods Regresso Lear codtoal mture oarametrc Classfcato eeratve ad dscrmatve aroach X X Q X X Y Q X Erc CMU
CS 2750 Machine Learning Lecture 5. Density estimation. Density estimation
 CS 750 Mache Learg Lecture 5 esty estmato Mlos Hausrecht mlos@tt.edu 539 Seott Square esty estmato esty estmato: s a usuervsed learg roblem Goal: Lear a model that rereset the relatos amog attrbutes the
CS 750 Mache Learg Lecture 5 esty estmato Mlos Hausrecht mlos@tt.edu 539 Seott Square esty estmato esty estmato: s a usuervsed learg roblem Goal: Lear a model that rereset the relatos amog attrbutes the
Learning Graphical Models
 School of omuter Scece Statstcal learg wth basc grahcal models robablstc Grahcal Models -78 Lecture 7 Oct 8 7 Recetor A Recetor B ase ase D ase E 3 4 5 Erc g Gee G TF F 6 7 Gee H 8 Readg: J-ha. 56 F-ha.
School of omuter Scece Statstcal learg wth basc grahcal models robablstc Grahcal Models -78 Lecture 7 Oct 8 7 Recetor A Recetor B ase ase D ase E 3 4 5 Erc g Gee G TF F 6 7 Gee H 8 Readg: J-ha. 56 F-ha.
Parameter Estimation
 arameter Estmato robabltes Notatoal Coveto Mass dscrete fucto: catal letters Desty cotuous fucto: small letters Vector vs. scalar Scalar: la Vector: bold D: small Hgher dmeso: catal Notes a cotuous state
arameter Estmato robabltes Notatoal Coveto Mass dscrete fucto: catal letters Desty cotuous fucto: small letters Vector vs. scalar Scalar: la Vector: bold D: small Hgher dmeso: catal Notes a cotuous state
Lecture 3 Probability review (cont d)
 STATS 00: Itroducto to Statstcal Iferece Autum 06 Lecture 3 Probablty revew (cot d) 3. Jot dstrbutos If radom varables X,..., X k are depedet, the ther dstrbuto may be specfed by specfyg the dvdual dstrbuto
STATS 00: Itroducto to Statstcal Iferece Autum 06 Lecture 3 Probablty revew (cot d) 3. Jot dstrbutos If radom varables X,..., X k are depedet, the ther dstrbuto may be specfed by specfyg the dvdual dstrbuto
Point Estimation: definition of estimators
 Pot Estmato: defto of estmators Pot estmator: ay fucto W (X,..., X ) of a data sample. The exercse of pot estmato s to use partcular fuctos of the data order to estmate certa ukow populato parameters.
Pot Estmato: defto of estmators Pot estmator: ay fucto W (X,..., X ) of a data sample. The exercse of pot estmato s to use partcular fuctos of the data order to estmate certa ukow populato parameters.
Generative classification models
 CS 75 Mache Learg Lecture Geeratve classfcato models Mlos Hauskrecht mlos@cs.ptt.edu 539 Seott Square Data: D { d, d,.., d} d, Classfcato represets a dscrete class value Goal: lear f : X Y Bar classfcato
CS 75 Mache Learg Lecture Geeratve classfcato models Mlos Hauskrecht mlos@cs.ptt.edu 539 Seott Square Data: D { d, d,.., d} d, Classfcato represets a dscrete class value Goal: lear f : X Y Bar classfcato
Bayes (Naïve or not) Classifiers: Generative Approach
 Logstc regresso Bayes (Naïve or ot) Classfers: Geeratve Approach What do we mea by Geeratve approach: Lear p(y), p(x y) ad the apply bayes rule to compute p(y x) for makg predctos Ths s essetally makg
Logstc regresso Bayes (Naïve or ot) Classfers: Geeratve Approach What do we mea by Geeratve approach: Lear p(y), p(x y) ad the apply bayes rule to compute p(y x) for makg predctos Ths s essetally makg
Lecture 3 Naïve Bayes, Maximum Entropy and Text Classification COSI 134
 Lecture 3 Naïve Baes, Mamum Etro ad Tet Classfcato COSI 34 Codtoal Parameterzato Two RVs: ItellgeceI ad SATS ValI = {Hgh,Low}, ValS={Hgh,Low} A ossble jot dstrbuto Ca descrbe usg cha rule as PI,S PIPS
Lecture 3 Naïve Baes, Mamum Etro ad Tet Classfcato COSI 34 Codtoal Parameterzato Two RVs: ItellgeceI ad SATS ValI = {Hgh,Low}, ValS={Hgh,Low} A ossble jot dstrbuto Ca descrbe usg cha rule as PI,S PIPS
Parametric Density Estimation: Bayesian Estimation. Naïve Bayes Classifier
 arametrc Dest Estmato: Baesa Estmato. Naïve Baes Classfer Baesa arameter Estmato Suose we have some dea of the rage where arameters should be Should t we formalze such ror owledge hoes that t wll lead
arametrc Dest Estmato: Baesa Estmato. Naïve Baes Classfer Baesa arameter Estmato Suose we have some dea of the rage where arameters should be Should t we formalze such ror owledge hoes that t wll lead
Machine Learning. Tutorial on Basic Probability. Lecture 2, September 15, 2006
 Mache Learg -7/5 7/5-78, 78, all 6 Tutoral o asc robablty Erc g f Lecture, Setember 5, 6 Readg: Cha. &, C & Cha 5,6, TM What s ths? Classcal AI ad ML research gored ths heomea The roblem a eamle: you wat
Mache Learg -7/5 7/5-78, 78, all 6 Tutoral o asc robablty Erc g f Lecture, Setember 5, 6 Readg: Cha. &, C & Cha 5,6, TM What s ths? Classcal AI ad ML research gored ths heomea The roblem a eamle: you wat
Econometric Methods. Review of Estimation
 Ecoometrc Methods Revew of Estmato Estmatg the populato mea Radom samplg Pot ad terval estmators Lear estmators Ubased estmators Lear Ubased Estmators (LUEs) Effcecy (mmum varace) ad Best Lear Ubased Estmators
Ecoometrc Methods Revew of Estmato Estmatg the populato mea Radom samplg Pot ad terval estmators Lear estmators Ubased estmators Lear Ubased Estmators (LUEs) Effcecy (mmum varace) ad Best Lear Ubased Estmators
STK4011 and STK9011 Autumn 2016
 STK4 ad STK9 Autum 6 Pot estmato Covers (most of the followg materal from chapter 7: Secto 7.: pages 3-3 Secto 7..: pages 3-33 Secto 7..: pages 35-3 Secto 7..3: pages 34-35 Secto 7.3.: pages 33-33 Secto
STK4 ad STK9 Autum 6 Pot estmato Covers (most of the followg materal from chapter 7: Secto 7.: pages 3-3 Secto 7..: pages 3-33 Secto 7..: pages 35-3 Secto 7..3: pages 34-35 Secto 7.3.: pages 33-33 Secto
Overview. Basic concepts of Bayesian learning. Most probable model given data Coin tosses Linear regression Logistic regression
 Overvew Basc cocepts of Bayesa learg Most probable model gve data Co tosses Lear regresso Logstc regresso Bayesa predctos Co tosses Lear regresso 30 Recap: regresso problems Iput to learg problem: trag
Overvew Basc cocepts of Bayesa learg Most probable model gve data Co tosses Lear regresso Logstc regresso Bayesa predctos Co tosses Lear regresso 30 Recap: regresso problems Iput to learg problem: trag
2. Independence and Bernoulli Trials
 . Ideedece ad Beroull Trals Ideedece: Evets ad B are deedet f B B. - It s easy to show that, B deedet mles, B;, B are all deedet ars. For examle, ad so that B or B B B B B φ,.e., ad B are deedet evets.,
. Ideedece ad Beroull Trals Ideedece: Evets ad B are deedet f B B. - It s easy to show that, B deedet mles, B;, B are all deedet ars. For examle, ad so that B or B B B B B φ,.e., ad B are deedet evets.,
Chapter 5 Properties of a Random Sample
 Lecture 6 o BST 63: Statstcal Theory I Ku Zhag, /0/008 Revew for the prevous lecture Cocepts: t-dstrbuto, F-dstrbuto Theorems: Dstrbutos of sample mea ad sample varace, relatoshp betwee sample mea ad sample
Lecture 6 o BST 63: Statstcal Theory I Ku Zhag, /0/008 Revew for the prevous lecture Cocepts: t-dstrbuto, F-dstrbuto Theorems: Dstrbutos of sample mea ad sample varace, relatoshp betwee sample mea ad sample
Nonparametric Density Estimation Intro
 Noarametrc Desty Estmato Itro Parze Wdows No-Parametrc Methods Nether robablty dstrbuto or dscrmat fucto s kow Haes qute ofte All we have s labeled data a lot s kow easer salmo bass salmo salmo Estmate
Noarametrc Desty Estmato Itro Parze Wdows No-Parametrc Methods Nether robablty dstrbuto or dscrmat fucto s kow Haes qute ofte All we have s labeled data a lot s kow easer salmo bass salmo salmo Estmate
UNIVERSITY OF OSLO DEPARTMENT OF ECONOMICS
 UNIVERSITY OF OSLO DEPARTMENT OF ECONOMICS Postpoed exam: ECON430 Statstcs Date of exam: Jauary 0, 0 Tme for exam: 09:00 a.m. :00 oo The problem set covers 5 pages Resources allowed: All wrtte ad prted
UNIVERSITY OF OSLO DEPARTMENT OF ECONOMICS Postpoed exam: ECON430 Statstcs Date of exam: Jauary 0, 0 Tme for exam: 09:00 a.m. :00 oo The problem set covers 5 pages Resources allowed: All wrtte ad prted
ρ < 1 be five real numbers. The
 Lecture o BST 63: Statstcal Theory I Ku Zhag, /0/006 Revew for the prevous lecture Deftos: covarace, correlato Examples: How to calculate covarace ad correlato Theorems: propertes of correlato ad covarace
Lecture o BST 63: Statstcal Theory I Ku Zhag, /0/006 Revew for the prevous lecture Deftos: covarace, correlato Examples: How to calculate covarace ad correlato Theorems: propertes of correlato ad covarace
Chapter 4 (Part 1): Non-Parametric Classification (Sections ) Pattern Classification 4.3) Announcements
 Aoucemets No-Parametrc Desty Estmato Techques HW assged Most of ths lecture was o the blacboard. These sldes cover the same materal as preseted DHS Bometrcs CSE 90-a Lecture 7 CSE90a Fall 06 CSE90a Fall
Aoucemets No-Parametrc Desty Estmato Techques HW assged Most of ths lecture was o the blacboard. These sldes cover the same materal as preseted DHS Bometrcs CSE 90-a Lecture 7 CSE90a Fall 06 CSE90a Fall
å 1 13 Practice Final Examination Solutions - = CS109 Dec 5, 2018
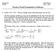 Chrs Pech Fal Practce CS09 Dec 5, 08 Practce Fal Examato Solutos. Aswer: 4/5 8/7. There are multle ways to obta ths aswer; here are two: The frst commo method s to sum over all ossbltes for the rak of
Chrs Pech Fal Practce CS09 Dec 5, 08 Practce Fal Examato Solutos. Aswer: 4/5 8/7. There are multle ways to obta ths aswer; here are two: The frst commo method s to sum over all ossbltes for the rak of
Entropy, Relative Entropy and Mutual Information
 Etro Relatve Etro ad Mutual Iformato rof. Ja-Lg Wu Deartmet of Comuter Scece ad Iformato Egeerg Natoal Tawa Uverst Defto: The Etro of a dscrete radom varable s defed b : base : 0 0 0 as bts 0 : addg terms
Etro Relatve Etro ad Mutual Iformato rof. Ja-Lg Wu Deartmet of Comuter Scece ad Iformato Egeerg Natoal Tawa Uverst Defto: The Etro of a dscrete radom varable s defed b : base : 0 0 0 as bts 0 : addg terms
Unsupervised Learning and Other Neural Networks
 CSE 53 Soft Computg NOT PART OF THE FINAL Usupervsed Learg ad Other Neural Networs Itroducto Mture Destes ad Idetfablty ML Estmates Applcato to Normal Mtures Other Neural Networs Itroducto Prevously, all
CSE 53 Soft Computg NOT PART OF THE FINAL Usupervsed Learg ad Other Neural Networs Itroducto Mture Destes ad Idetfablty ML Estmates Applcato to Normal Mtures Other Neural Networs Itroducto Prevously, all
STK3100 and STK4100 Autumn 2017
 SK3 ad SK4 Autum 7 Geeralzed lear models Part III Covers the followg materal from chaters 4 ad 5: Sectos 4..5, 4.3.5, 4.3.6, 4.4., 4.4., ad 4.4.3 Sectos 5.., 5.., ad 5.5. Ørulf Borga Deartmet of Mathematcs
SK3 ad SK4 Autum 7 Geeralzed lear models Part III Covers the followg materal from chaters 4 ad 5: Sectos 4..5, 4.3.5, 4.3.6, 4.4., 4.4., ad 4.4.3 Sectos 5.., 5.., ad 5.5. Ørulf Borga Deartmet of Mathematcs
ENGI 4421 Joint Probability Distributions Page Joint Probability Distributions [Navidi sections 2.5 and 2.6; Devore sections
 ENGI 441 Jot Probablty Dstrbutos Page 7-01 Jot Probablty Dstrbutos [Navd sectos.5 ad.6; Devore sectos 5.1-5.] The jot probablty mass fucto of two dscrete radom quattes, s, P ad p x y x y The margal probablty
ENGI 441 Jot Probablty Dstrbutos Page 7-01 Jot Probablty Dstrbutos [Navd sectos.5 ad.6; Devore sectos 5.1-5.] The jot probablty mass fucto of two dscrete radom quattes, s, P ad p x y x y The margal probablty
Random Variables. ECE 313 Probability with Engineering Applications Lecture 8 Professor Ravi K. Iyer University of Illinois
 Radom Varables ECE 313 Probablty wth Egeerg Alcatos Lecture 8 Professor Rav K. Iyer Uversty of Illos Iyer - Lecture 8 ECE 313 Fall 013 Today s Tocs Revew o Radom Varables Cumulatve Dstrbuto Fucto (CDF
Radom Varables ECE 313 Probablty wth Egeerg Alcatos Lecture 8 Professor Rav K. Iyer Uversty of Illos Iyer - Lecture 8 ECE 313 Fall 013 Today s Tocs Revew o Radom Varables Cumulatve Dstrbuto Fucto (CDF
Lecture 9. Some Useful Discrete Distributions. Some Useful Discrete Distributions. The observations generated by different experiments have
 NM 7 Lecture 9 Some Useful Dscrete Dstrbutos Some Useful Dscrete Dstrbutos The observatos geerated by dfferet eermets have the same geeral tye of behavor. Cosequetly, radom varables assocated wth these
NM 7 Lecture 9 Some Useful Dscrete Dstrbutos Some Useful Dscrete Dstrbutos The observatos geerated by dfferet eermets have the same geeral tye of behavor. Cosequetly, radom varables assocated wth these
CHAPTER VI Statistical Analysis of Experimental Data
 Chapter VI Statstcal Aalyss of Expermetal Data CHAPTER VI Statstcal Aalyss of Expermetal Data Measuremets do ot lead to a uque value. Ths s a result of the multtude of errors (maly radom errors) that ca
Chapter VI Statstcal Aalyss of Expermetal Data CHAPTER VI Statstcal Aalyss of Expermetal Data Measuremets do ot lead to a uque value. Ths s a result of the multtude of errors (maly radom errors) that ca
2SLS Estimates ECON In this case, begin with the assumption that E[ i
 SLS Estmates ECON 3033 Bll Evas Fall 05 Two-Stage Least Squares (SLS Cosder a stadard lear bvarate regresso model y 0 x. I ths case, beg wth the assumto that E[ x] 0 whch meas that OLS estmates of wll
SLS Estmates ECON 3033 Bll Evas Fall 05 Two-Stage Least Squares (SLS Cosder a stadard lear bvarate regresso model y 0 x. I ths case, beg wth the assumto that E[ x] 0 whch meas that OLS estmates of wll
Summary of the lecture in Biostatistics
 Summary of the lecture Bostatstcs Probablty Desty Fucto For a cotuos radom varable, a probablty desty fucto s a fucto such that: 0 dx a b) b a dx A probablty desty fucto provdes a smple descrpto of the
Summary of the lecture Bostatstcs Probablty Desty Fucto For a cotuos radom varable, a probablty desty fucto s a fucto such that: 0 dx a b) b a dx A probablty desty fucto provdes a smple descrpto of the
Machine Learning. Introduction to Regression. Le Song. CSE6740/CS7641/ISYE6740, Fall 2012
 Mache Learg CSE6740/CS764/ISYE6740, Fall 0 Itroducto to Regresso Le Sog Lecture 4, August 30, 0 Based o sldes from Erc g, CMU Readg: Chap. 3, CB Mache learg for apartmet hutg Suppose ou are to move to
Mache Learg CSE6740/CS764/ISYE6740, Fall 0 Itroducto to Regresso Le Sog Lecture 4, August 30, 0 Based o sldes from Erc g, CMU Readg: Chap. 3, CB Mache learg for apartmet hutg Suppose ou are to move to
Training Sample Model: Given n observations, [[( Yi, x i the sample model can be expressed as (1) where, zero and variance σ
 Stat 74 Estmato for Geeral Lear Model Prof. Goel Broad Outle Geeral Lear Model (GLM): Trag Samle Model: Gve observatos, [[( Y, x ), x = ( x,, xr )], =,,, the samle model ca be exressed as Y = µ ( x, x,,
Stat 74 Estmato for Geeral Lear Model Prof. Goel Broad Outle Geeral Lear Model (GLM): Trag Samle Model: Gve observatos, [[( Y, x ), x = ( x,, xr )], =,,, the samle model ca be exressed as Y = µ ( x, x,,
Lecture 7. Confidence Intervals and Hypothesis Tests in the Simple CLR Model
 Lecture 7. Cofdece Itervals ad Hypothess Tests the Smple CLR Model I lecture 6 we troduced the Classcal Lear Regresso (CLR) model that s the radom expermet of whch the data Y,,, K, are the outcomes. The
Lecture 7. Cofdece Itervals ad Hypothess Tests the Smple CLR Model I lecture 6 we troduced the Classcal Lear Regresso (CLR) model that s the radom expermet of whch the data Y,,, K, are the outcomes. The
Bayesian belief networks
 Lecture 14 ayesa belef etworks los Hauskrecht mlos@cs.ptt.edu 5329 Seott Square Desty estmato Data: D { D1 D2.. D} D x a vector of attrbute values ttrbutes: modeled by radom varables { 1 2 d} wth: otuous
Lecture 14 ayesa belef etworks los Hauskrecht mlos@cs.ptt.edu 5329 Seott Square Desty estmato Data: D { D1 D2.. D} D x a vector of attrbute values ttrbutes: modeled by radom varables { 1 2 d} wth: otuous
Dr. Shalabh Department of Mathematics and Statistics Indian Institute of Technology Kanpur
 Aalyss of Varace ad Desg of Exermets-I MODULE II LECTURE - GENERAL LINEAR HYPOTHESIS AND ANALYSIS OF VARIANCE Dr Shalabh Deartmet of Mathematcs ad Statstcs Ida Isttute of Techology Kaur Tukey s rocedure
Aalyss of Varace ad Desg of Exermets-I MODULE II LECTURE - GENERAL LINEAR HYPOTHESIS AND ANALYSIS OF VARIANCE Dr Shalabh Deartmet of Mathematcs ad Statstcs Ida Isttute of Techology Kaur Tukey s rocedure
Chain Rules for Entropy
 Cha Rules for Etroy The etroy of a collecto of radom varables s the sum of codtoal etroes. Theorem: Let be radom varables havg the mass robablty x x.x. The...... The roof s obtaed by reeatg the alcato
Cha Rules for Etroy The etroy of a collecto of radom varables s the sum of codtoal etroes. Theorem: Let be radom varables havg the mass robablty x x.x. The...... The roof s obtaed by reeatg the alcato
Probability and Statistics. What is probability? What is statistics?
 robablt ad Statstcs What s robablt? What s statstcs? robablt ad Statstcs robablt Formall defed usg a set of aoms Seeks to determe the lkelhood that a gve evet or observato or measuremet wll or has haeed
robablt ad Statstcs What s robablt? What s statstcs? robablt ad Statstcs robablt Formall defed usg a set of aoms Seeks to determe the lkelhood that a gve evet or observato or measuremet wll or has haeed
CS 2750 Machine Learning. Lecture 8. Linear regression. CS 2750 Machine Learning. Linear regression. is a linear combination of input components x
 CS 75 Mache Learg Lecture 8 Lear regresso Mlos Hauskrecht mlos@cs.ptt.edu 539 Seott Square CS 75 Mache Learg Lear regresso Fucto f : X Y s a lear combato of put compoets f + + + K d d K k - parameters
CS 75 Mache Learg Lecture 8 Lear regresso Mlos Hauskrecht mlos@cs.ptt.edu 539 Seott Square CS 75 Mache Learg Lear regresso Fucto f : X Y s a lear combato of put compoets f + + + K d d K k - parameters
Introduction to local (nonparametric) density estimation. methods
 Itroducto to local (oparametrc) desty estmato methods A slecture by Yu Lu for ECE 66 Sprg 014 1. Itroducto Ths slecture troduces two local desty estmato methods whch are Parze desty estmato ad k-earest
Itroducto to local (oparametrc) desty estmato methods A slecture by Yu Lu for ECE 66 Sprg 014 1. Itroducto Ths slecture troduces two local desty estmato methods whch are Parze desty estmato ad k-earest
Chapter 4 Multiple Random Variables
 Revew for the prevous lecture: Theorems ad Examples: How to obta the pmf (pdf) of U = g (, Y) ad V = g (, Y) Chapter 4 Multple Radom Varables Chapter 44 Herarchcal Models ad Mxture Dstrbutos Examples:
Revew for the prevous lecture: Theorems ad Examples: How to obta the pmf (pdf) of U = g (, Y) ad V = g (, Y) Chapter 4 Multple Radom Varables Chapter 44 Herarchcal Models ad Mxture Dstrbutos Examples:
Lecture Notes Types of economic variables
 Lecture Notes 3 1. Types of ecoomc varables () Cotuous varable takes o a cotuum the sample space, such as all pots o a le or all real umbers Example: GDP, Polluto cocetrato, etc. () Dscrete varables fte
Lecture Notes 3 1. Types of ecoomc varables () Cotuous varable takes o a cotuum the sample space, such as all pots o a le or all real umbers Example: GDP, Polluto cocetrato, etc. () Dscrete varables fte
Bayesian belief networks
 Lecture 19 ayesa belef etworks los Hauskrecht mlos@cs.ptt.edu 539 Seott Square Varous ferece tasks: robablstc ferece Dagostc task. from effect to cause eumoa Fever redcto task. from cause to effect Fever
Lecture 19 ayesa belef etworks los Hauskrecht mlos@cs.ptt.edu 539 Seott Square Varous ferece tasks: robablstc ferece Dagostc task. from effect to cause eumoa Fever redcto task. from cause to effect Fever
Point Estimation: definition of estimators
 Pot Estmato: defto of estmators Pot estmator: ay fucto W (X,..., X ) of a data sample. The exercse of pot estmato s to use partcular fuctos of the data order to estmate certa ukow populato parameters.
Pot Estmato: defto of estmators Pot estmator: ay fucto W (X,..., X ) of a data sample. The exercse of pot estmato s to use partcular fuctos of the data order to estmate certa ukow populato parameters.
Channel Models with Memory. Channel Models with Memory. Channel Models with Memory. Channel Models with Memory
 Chael Models wth Memory Chael Models wth Memory Hayder radha Electrcal ad Comuter Egeerg Mchga State Uversty I may ractcal etworkg scearos (cludg the Iteret ad wreless etworks), the uderlyg chaels are
Chael Models wth Memory Chael Models wth Memory Hayder radha Electrcal ad Comuter Egeerg Mchga State Uversty I may ractcal etworkg scearos (cludg the Iteret ad wreless etworks), the uderlyg chaels are
CS 3710 Advanced Topics in AI Lecture 17. Density estimation. CS 3710 Probabilistic graphical models. Administration
 CS 37 Avace Topcs AI Lecture 7 esty estmato Mlos Hauskrecht mlos@cs.ptt.eu 539 Seott Square CS 37 robablstc graphcal moels Amstrato Mterm: A take-home exam week ue o Weesay ovember 5 before the class epes
CS 37 Avace Topcs AI Lecture 7 esty estmato Mlos Hauskrecht mlos@cs.ptt.eu 539 Seott Square CS 37 robablstc graphcal moels Amstrato Mterm: A take-home exam week ue o Weesay ovember 5 before the class epes
Bayesian Classification. CS690L Data Mining: Classification(2) Bayesian Theorem: Basics. Bayesian Theorem. Training dataset. Naïve Bayes Classifier
 Baa Classfcato CS6L Data Mg: Classfcato() Referece: J. Ha ad M. Kamber, Data Mg: Cocepts ad Techques robablstc learg: Calculate explct probabltes for hypothess, amog the most practcal approaches to certa
Baa Classfcato CS6L Data Mg: Classfcato() Referece: J. Ha ad M. Kamber, Data Mg: Cocepts ad Techques robablstc learg: Calculate explct probabltes for hypothess, amog the most practcal approaches to certa
Multivariate Transformation of Variables and Maximum Likelihood Estimation
 Marquette Uversty Multvarate Trasformato of Varables ad Maxmum Lkelhood Estmato Dael B. Rowe, Ph.D. Assocate Professor Departmet of Mathematcs, Statstcs, ad Computer Scece Copyrght 03 by Marquette Uversty
Marquette Uversty Multvarate Trasformato of Varables ad Maxmum Lkelhood Estmato Dael B. Rowe, Ph.D. Assocate Professor Departmet of Mathematcs, Statstcs, ad Computer Scece Copyrght 03 by Marquette Uversty
Bayes Estimator for Exponential Distribution with Extension of Jeffery Prior Information
 Malaysa Joural of Mathematcal Sceces (): 97- (9) Bayes Estmator for Expoetal Dstrbuto wth Exteso of Jeffery Pror Iformato Hadeel Salm Al-Kutub ad Noor Akma Ibrahm Isttute for Mathematcal Research, Uverst
Malaysa Joural of Mathematcal Sceces (): 97- (9) Bayes Estmator for Expoetal Dstrbuto wth Exteso of Jeffery Pror Iformato Hadeel Salm Al-Kutub ad Noor Akma Ibrahm Isttute for Mathematcal Research, Uverst
TESTS BASED ON MAXIMUM LIKELIHOOD
 ESE 5 Toy E. Smth. The Basc Example. TESTS BASED ON MAXIMUM LIKELIHOOD To llustrate the propertes of maxmum lkelhood estmates ad tests, we cosder the smplest possble case of estmatg the mea of the ormal
ESE 5 Toy E. Smth. The Basc Example. TESTS BASED ON MAXIMUM LIKELIHOOD To llustrate the propertes of maxmum lkelhood estmates ad tests, we cosder the smplest possble case of estmatg the mea of the ormal
STK3100 and STK4100 Autumn 2018
 SK3 ad SK4 Autum 8 Geeralzed lear models Part III Covers the followg materal from chaters 4 ad 5: Cofdece tervals by vertg tests Cosder a model wth a sgle arameter β We may obta a ( α% cofdece terval for
SK3 ad SK4 Autum 8 Geeralzed lear models Part III Covers the followg materal from chaters 4 ad 5: Cofdece tervals by vertg tests Cosder a model wth a sgle arameter β We may obta a ( α% cofdece terval for
Chapter 14 Logistic Regression Models
 Chapter 4 Logstc Regresso Models I the lear regresso model X β + ε, there are two types of varables explaatory varables X, X,, X k ad study varable y These varables ca be measured o a cotuous scale as
Chapter 4 Logstc Regresso Models I the lear regresso model X β + ε, there are two types of varables explaatory varables X, X,, X k ad study varable y These varables ca be measured o a cotuous scale as
BASIC PRINCIPLES OF STATISTICS
 BASIC PRINCIPLES OF STATISTICS PROBABILITY DENSITY DISTRIBUTIONS DISCRETE VARIABLES BINOMIAL DISTRIBUTION ~ B 0 0 umber of successes trals Pr E [ ] Var[ ] ; BINOMIAL DISTRIBUTION B7 0. B30 0.3 B50 0.5
BASIC PRINCIPLES OF STATISTICS PROBABILITY DENSITY DISTRIBUTIONS DISCRETE VARIABLES BINOMIAL DISTRIBUTION ~ B 0 0 umber of successes trals Pr E [ ] Var[ ] ; BINOMIAL DISTRIBUTION B7 0. B30 0.3 B50 0.5
CHAPTER 6. d. With success = observation greater than 10, x = # of successes = 4, and
 CHAPTR 6 Secto 6.. a. We use the samle mea, to estmate the oulato mea µ. Σ 9.80 µ 8.407 7 ~ 7. b. We use the samle meda, 7 (the mddle observato whe arraged ascedg order. c. We use the samle stadard devato,
CHAPTR 6 Secto 6.. a. We use the samle mea, to estmate the oulato mea µ. Σ 9.80 µ 8.407 7 ~ 7. b. We use the samle meda, 7 (the mddle observato whe arraged ascedg order. c. We use the samle stadard devato,
Continuous Random Variables: Conditioning, Expectation and Independence
 Cotuous Radom Varables: Codtog, xectato ad Ideedece Berl Che Deartmet o Comuter cece & Iormato geerg atoal Tawa ormal Uverst Reerece: - D.. Bertsekas, J.. Tstskls, Itroducto to robablt, ectos 3.4-3.5 Codtog
Cotuous Radom Varables: Codtog, xectato ad Ideedece Berl Che Deartmet o Comuter cece & Iormato geerg atoal Tawa ormal Uverst Reerece: - D.. Bertsekas, J.. Tstskls, Itroducto to robablt, ectos 3.4-3.5 Codtog
3. Basic Concepts: Consequences and Properties
 : 3. Basc Cocepts: Cosequeces ad Propertes Markku Jutt Overvew More advaced cosequeces ad propertes of the basc cocepts troduced the prevous lecture are derved. Source The materal s maly based o Sectos.6.8
: 3. Basc Cocepts: Cosequeces ad Propertes Markku Jutt Overvew More advaced cosequeces ad propertes of the basc cocepts troduced the prevous lecture are derved. Source The materal s maly based o Sectos.6.8
STRONG CONSISTENCY FOR SIMPLE LINEAR EV MODEL WITH v/ -MIXING
 Joural of tatstcs: Advaces Theory ad Alcatos Volume 5, Number, 6, Pages 3- Avalable at htt://scetfcadvaces.co. DOI: htt://d.do.org/.864/jsata_7678 TRONG CONITENCY FOR IMPLE LINEAR EV MODEL WITH v/ -MIXING
Joural of tatstcs: Advaces Theory ad Alcatos Volume 5, Number, 6, Pages 3- Avalable at htt://scetfcadvaces.co. DOI: htt://d.do.org/.864/jsata_7678 TRONG CONITENCY FOR IMPLE LINEAR EV MODEL WITH v/ -MIXING
ENGI 3423 Simple Linear Regression Page 12-01
 ENGI 343 mple Lear Regresso Page - mple Lear Regresso ometmes a expermet s set up where the expermeter has cotrol over the values of oe or more varables X ad measures the resultg values of aother varable
ENGI 343 mple Lear Regresso Page - mple Lear Regresso ometmes a expermet s set up where the expermeter has cotrol over the values of oe or more varables X ad measures the resultg values of aother varable
IS 709/809: Computational Methods in IS Research. Simple Markovian Queueing Model
 IS 79/89: Comutatoal Methods IS Research Smle Marova Queueg Model Nrmalya Roy Deartmet of Iformato Systems Uversty of Marylad Baltmore Couty www.umbc.edu Queueg Theory Software QtsPlus software The software
IS 79/89: Comutatoal Methods IS Research Smle Marova Queueg Model Nrmalya Roy Deartmet of Iformato Systems Uversty of Marylad Baltmore Couty www.umbc.edu Queueg Theory Software QtsPlus software The software
Special Instructions / Useful Data
 JAM 6 Set of all real umbers P A..d. B, p Posso Specal Istructos / Useful Data x,, :,,, x x Probablty of a evet A Idepedetly ad detcally dstrbuted Bomal dstrbuto wth parameters ad p Posso dstrbuto wth
JAM 6 Set of all real umbers P A..d. B, p Posso Specal Istructos / Useful Data x,, :,,, x x Probablty of a evet A Idepedetly ad detcally dstrbuted Bomal dstrbuto wth parameters ad p Posso dstrbuto wth
X ε ) = 0, or equivalently, lim
 Revew for the prevous lecture Cocepts: order statstcs Theorems: Dstrbutos of order statstcs Examples: How to get the dstrbuto of order statstcs Chapter 5 Propertes of a Radom Sample Secto 55 Covergece
Revew for the prevous lecture Cocepts: order statstcs Theorems: Dstrbutos of order statstcs Examples: How to get the dstrbuto of order statstcs Chapter 5 Propertes of a Radom Sample Secto 55 Covergece
UNIVERSITY OF OSLO DEPARTMENT OF ECONOMICS
 UNIVERSITY OF OSLO DEPARTMENT OF ECONOMICS Exam: ECON430 Statstcs Date of exam: Frday, December 8, 07 Grades are gve: Jauary 4, 08 Tme for exam: 0900 am 00 oo The problem set covers 5 pages Resources allowed:
UNIVERSITY OF OSLO DEPARTMENT OF ECONOMICS Exam: ECON430 Statstcs Date of exam: Frday, December 8, 07 Grades are gve: Jauary 4, 08 Tme for exam: 0900 am 00 oo The problem set covers 5 pages Resources allowed:
STA 108 Applied Linear Models: Regression Analysis Spring Solution for Homework #1
 STA 08 Appled Lear Models: Regresso Aalyss Sprg 0 Soluto for Homework #. Let Y the dollar cost per year, X the umber of vsts per year. The the mathematcal relato betwee X ad Y s: Y 300 + X. Ths s a fuctoal
STA 08 Appled Lear Models: Regresso Aalyss Sprg 0 Soluto for Homework #. Let Y the dollar cost per year, X the umber of vsts per year. The the mathematcal relato betwee X ad Y s: Y 300 + X. Ths s a fuctoal
Functions of Random Variables
 Fuctos of Radom Varables Chapter Fve Fuctos of Radom Varables 5. Itroducto A geeral egeerg aalyss model s show Fg. 5.. The model output (respose) cotas the performaces of a system or product, such as weght,
Fuctos of Radom Varables Chapter Fve Fuctos of Radom Varables 5. Itroducto A geeral egeerg aalyss model s show Fg. 5.. The model output (respose) cotas the performaces of a system or product, such as weght,
Artificial Intelligence Learning of decision trees
 Artfcal Itellgece Learg of decso trees Peter Atal atal@mt.bme.hu A.I. November 21, 2016 1 Problem: decde whether to wat for a table at a restaurat, based o the followg attrbutes: 1. Alterate: s there a
Artfcal Itellgece Learg of decso trees Peter Atal atal@mt.bme.hu A.I. November 21, 2016 1 Problem: decde whether to wat for a table at a restaurat, based o the followg attrbutes: 1. Alterate: s there a
Chapter 3 Sampling For Proportions and Percentages
 Chapter 3 Samplg For Proportos ad Percetages I may stuatos, the characterstc uder study o whch the observatos are collected are qualtatve ature For example, the resposes of customers may marketg surveys
Chapter 3 Samplg For Proportos ad Percetages I may stuatos, the characterstc uder study o whch the observatos are collected are qualtatve ature For example, the resposes of customers may marketg surveys
( ) = ( ) ( ) Chapter 13 Asymptotic Theory and Stochastic Regressors. Stochastic regressors model
 Chapter 3 Asmptotc Theor ad Stochastc Regressors The ature of eplaator varable s assumed to be o-stochastc or fed repeated samples a regresso aalss Such a assumpto s approprate for those epermets whch
Chapter 3 Asmptotc Theor ad Stochastc Regressors The ature of eplaator varable s assumed to be o-stochastc or fed repeated samples a regresso aalss Such a assumpto s approprate for those epermets whch
best estimate (mean) for X uncertainty or error in the measurement (systematic, random or statistical) best
 Error Aalyss Preamble Wheever a measuremet s made, the result followg from that measuremet s always subject to ucertaty The ucertaty ca be reduced by makg several measuremets of the same quatty or by mprovg
Error Aalyss Preamble Wheever a measuremet s made, the result followg from that measuremet s always subject to ucertaty The ucertaty ca be reduced by makg several measuremets of the same quatty or by mprovg
Qualifying Exam Statistical Theory Problem Solutions August 2005
 Qualfyg Exam Statstcal Theory Problem Solutos August 5. Let X, X,..., X be d uform U(,),
Qualfyg Exam Statstcal Theory Problem Solutos August 5. Let X, X,..., X be d uform U(,),
Parametric Density Estimation: Bayesian Estimation. Naïve Bayes Classifier
 arametrc Dest Estmato: Baesa Estmato. Naïve Baes Classfer Baesa arameter Estmato Suppose we have some dea of the rage where parameters θ should be Should t we formalze such pror owledge hopes that t wll
arametrc Dest Estmato: Baesa Estmato. Naïve Baes Classfer Baesa arameter Estmato Suppose we have some dea of the rage where parameters θ should be Should t we formalze such pror owledge hopes that t wll
Naïve Bayes MIT Course Notes Cynthia Rudin
 Thaks to Şeyda Ertek Credt: Ng, Mtchell Naïve Bayes MIT 5.097 Course Notes Cytha Rud The Naïve Bayes algorthm comes from a geeratve model. There s a mportat dstcto betwee geeratve ad dscrmatve models.
Thaks to Şeyda Ertek Credt: Ng, Mtchell Naïve Bayes MIT 5.097 Course Notes Cytha Rud The Naïve Bayes algorthm comes from a geeratve model. There s a mportat dstcto betwee geeratve ad dscrmatve models.
Ordinary Least Squares Regression. Simple Regression. Algebra and Assumptions.
 Ordary Least Squares egresso. Smple egresso. Algebra ad Assumptos. I ths part of the course we are gog to study a techque for aalysg the lear relatoshp betwee two varables Y ad X. We have pars of observatos
Ordary Least Squares egresso. Smple egresso. Algebra ad Assumptos. I ths part of the course we are gog to study a techque for aalysg the lear relatoshp betwee two varables Y ad X. We have pars of observatos
Part I: Background on the Binomial Distribution
 Part I: Bacgroud o the Bomal Dstrbuto A radom varable s sad to have a Beroull dstrbuto f t taes o the value wth probablt "p" ad the value wth probablt " - p". The umber of "successes" "" depedet Beroull
Part I: Bacgroud o the Bomal Dstrbuto A radom varable s sad to have a Beroull dstrbuto f t taes o the value wth probablt "p" ad the value wth probablt " - p". The umber of "successes" "" depedet Beroull
Logistic regression (continued)
 STAT562 page 138 Logstc regresso (cotued) Suppose we ow cosder more complex models to descrbe the relatoshp betwee a categorcal respose varable (Y) that takes o two (2) possble outcomes ad a set of p explaatory
STAT562 page 138 Logstc regresso (cotued) Suppose we ow cosder more complex models to descrbe the relatoshp betwee a categorcal respose varable (Y) that takes o two (2) possble outcomes ad a set of p explaatory
22 Nonparametric Methods.
 22 oparametrc Methods. I parametrc models oe assumes apror that the dstrbutos have a specfc form wth oe or more ukow parameters ad oe tres to fd the best or atleast reasoably effcet procedures that aswer
22 oparametrc Methods. I parametrc models oe assumes apror that the dstrbutos have a specfc form wth oe or more ukow parameters ad oe tres to fd the best or atleast reasoably effcet procedures that aswer
= 2. Statistic - function that doesn't depend on any of the known parameters; examples:
 of Samplg Theory amples - uemploymet househol cosumpto survey Raom sample - set of rv's... ; 's have ot strbuto [ ] f f s vector of parameters e.g. Statstc - fucto that oes't epe o ay of the ow parameters;
of Samplg Theory amples - uemploymet househol cosumpto survey Raom sample - set of rv's... ; 's have ot strbuto [ ] f f s vector of parameters e.g. Statstc - fucto that oes't epe o ay of the ow parameters;
Lecture 9: Tolerant Testing
 Lecture 9: Tolerat Testg Dael Kae Scrbe: Sakeerth Rao Aprl 4, 07 Abstract I ths lecture we prove a quas lear lower boud o the umber of samples eeded to do tolerat testg for L dstace. Tolerat Testg We have
Lecture 9: Tolerat Testg Dael Kae Scrbe: Sakeerth Rao Aprl 4, 07 Abstract I ths lecture we prove a quas lear lower boud o the umber of samples eeded to do tolerat testg for L dstace. Tolerat Testg We have
Estimation of Stress- Strength Reliability model using finite mixture of exponential distributions
 Iteratoal Joural of Computatoal Egeerg Research Vol, 0 Issue, Estmato of Stress- Stregth Relablty model usg fte mxture of expoetal dstrbutos K.Sadhya, T.S.Umamaheswar Departmet of Mathematcs, Lal Bhadur
Iteratoal Joural of Computatoal Egeerg Research Vol, 0 Issue, Estmato of Stress- Stregth Relablty model usg fte mxture of expoetal dstrbutos K.Sadhya, T.S.Umamaheswar Departmet of Mathematcs, Lal Bhadur
Chapter 4 Multiple Random Variables
 Revew o BST 63: Statstcal Theory I Ku Zhag, /0/008 Revew for Chapter 4-5 Notes: Although all deftos ad theorems troduced our lectures ad ths ote are mportat ad you should be famlar wth, but I put those
Revew o BST 63: Statstcal Theory I Ku Zhag, /0/008 Revew for Chapter 4-5 Notes: Although all deftos ad theorems troduced our lectures ad ths ote are mportat ad you should be famlar wth, but I put those
Maximum Likelihood Estimation
 Marquette Uverst Maxmum Lkelhood Estmato Dael B. Rowe, Ph.D. Professor Departmet of Mathematcs, Statstcs, ad Computer Scece Coprght 08 b Marquette Uverst Maxmum Lkelhood Estmato We have bee sag that ~
Marquette Uverst Maxmum Lkelhood Estmato Dael B. Rowe, Ph.D. Professor Departmet of Mathematcs, Statstcs, ad Computer Scece Coprght 08 b Marquette Uverst Maxmum Lkelhood Estmato We have bee sag that ~
Discrete Mathematics and Probability Theory Fall 2016 Seshia and Walrand DIS 10b
 CS 70 Dscrete Mathematcs ad Probablty Theory Fall 206 Sesha ad Walrad DIS 0b. Wll I Get My Package? Seaky delvery guy of some compay s out delverg packages to customers. Not oly does he had a radom package
CS 70 Dscrete Mathematcs ad Probablty Theory Fall 206 Sesha ad Walrad DIS 0b. Wll I Get My Package? Seaky delvery guy of some compay s out delverg packages to customers. Not oly does he had a radom package
Module 7. Lecture 7: Statistical parameter estimation
 Lecture 7: Statstcal parameter estmato Parameter Estmato Methods of Parameter Estmato 1) Method of Matchg Pots ) Method of Momets 3) Mamum Lkelhood method Populato Parameter Sample Parameter Ubased estmato
Lecture 7: Statstcal parameter estmato Parameter Estmato Methods of Parameter Estmato 1) Method of Matchg Pots ) Method of Momets 3) Mamum Lkelhood method Populato Parameter Sample Parameter Ubased estmato
Lecture 8: Linear Regression
 Lecture 8: Lear egresso May 4, GENOME 56, Sprg Goals Develop basc cocepts of lear regresso from a probablstc framework Estmatg parameters ad hypothess testg wth lear models Lear regresso Su I Lee, CSE
Lecture 8: Lear egresso May 4, GENOME 56, Sprg Goals Develop basc cocepts of lear regresso from a probablstc framework Estmatg parameters ad hypothess testg wth lear models Lear regresso Su I Lee, CSE
Lecture Note to Rice Chapter 8
 ECON 430 HG revsed Nov 06 Lecture Note to Rce Chapter 8 Radom matrces Let Y, =,,, m, =,,, be radom varables (r.v. s). The matrx Y Y Y Y Y Y Y Y Y Y = m m m s called a radom matrx ( wth a ot m-dmesoal dstrbuto,
ECON 430 HG revsed Nov 06 Lecture Note to Rce Chapter 8 Radom matrces Let Y, =,,, m, =,,, be radom varables (r.v. s). The matrx Y Y Y Y Y Y Y Y Y Y = m m m s called a radom matrx ( wth a ot m-dmesoal dstrbuto,
X X X E[ ] E X E X. is the ()m n where the ( i,)th. j element is the mean of the ( i,)th., then
![X X X E[ ] E X E X. is the ()m n where the ( i,)th. j element is the mean of the ( i,)th., then X X X E[ ] E X E X. is the ()m n where the ( i,)th. j element is the mean of the ( i,)th., then](/thumbs/83/87696552.jpg) Secto 5 Vectors of Radom Varables Whe workg wth several radom varables,,..., to arrage them vector form x, t s ofte coveet We ca the make use of matrx algebra to help us orgaze ad mapulate large umbers
Secto 5 Vectors of Radom Varables Whe workg wth several radom varables,,..., to arrage them vector form x, t s ofte coveet We ca the make use of matrx algebra to help us orgaze ad mapulate large umbers
Statistical modelling and latent variables (2)
 Statstcal modellg ad latet varables (2 Mxg latet varables ad parameters statstcal erece Trod Reta (Dvso o statstcs ad surace mathematcs, Departmet o Mathematcs, Uversty o Oslo State spaces We typcally
Statstcal modellg ad latet varables (2 Mxg latet varables ad parameters statstcal erece Trod Reta (Dvso o statstcs ad surace mathematcs, Departmet o Mathematcs, Uversty o Oslo State spaces We typcally
Continuous Distributions
 7//3 Cotuous Dstrbutos Radom Varables of the Cotuous Type Desty Curve Percet Desty fucto, f (x) A smooth curve that ft the dstrbuto 3 4 5 6 7 8 9 Test scores Desty Curve Percet Probablty Desty Fucto, f
7//3 Cotuous Dstrbutos Radom Varables of the Cotuous Type Desty Curve Percet Desty fucto, f (x) A smooth curve that ft the dstrbuto 3 4 5 6 7 8 9 Test scores Desty Curve Percet Probablty Desty Fucto, f
D KL (P Q) := p i ln p i q i
 Cheroff-Bouds 1 The Geeral Boud Let P 1,, m ) ad Q q 1,, q m ) be two dstrbutos o m elemets, e,, q 0, for 1,, m, ad m 1 m 1 q 1 The Kullback-Lebler dvergece or relatve etroy of P ad Q s defed as m D KL
Cheroff-Bouds 1 The Geeral Boud Let P 1,, m ) ad Q q 1,, q m ) be two dstrbutos o m elemets, e,, q 0, for 1,, m, ad m 1 m 1 q 1 The Kullback-Lebler dvergece or relatve etroy of P ad Q s defed as m D KL
Construction and Evaluation of Actuarial Models. Rajapaksha Premarathna
 Costructo ad Evaluato of Actuaral Models Raapaksha Premaratha Table of Cotets Modelg Some deftos ad Notatos...4 Case : Polcy Lmtu...4 Case : Wth a Ordary deductble....5 Case 3: Maxmum Covered loss u wth
Costructo ad Evaluato of Actuaral Models Raapaksha Premaratha Table of Cotets Modelg Some deftos ad Notatos...4 Case : Polcy Lmtu...4 Case : Wth a Ordary deductble....5 Case 3: Maxmum Covered loss u wth
The expected value of a sum of random variables,, is the sum of the expected values:
 Sums of Radom Varables xpected Values ad Varaces of Sums ad Averages of Radom Varables The expected value of a sum of radom varables, say S, s the sum of the expected values: ( ) ( ) S Ths s always true
Sums of Radom Varables xpected Values ad Varaces of Sums ad Averages of Radom Varables The expected value of a sum of radom varables, say S, s the sum of the expected values: ( ) ( ) S Ths s always true
Recall MLR 5 Homskedasticity error u has the same variance given any values of the explanatory variables Var(u x1,...,xk) = 2 or E(UU ) = 2 I
 Chapter 8 Heterosedastcty Recall MLR 5 Homsedastcty error u has the same varace gve ay values of the eplaatory varables Varu,..., = or EUU = I Suppose other GM assumptos hold but have heterosedastcty.
Chapter 8 Heterosedastcty Recall MLR 5 Homsedastcty error u has the same varace gve ay values of the eplaatory varables Varu,..., = or EUU = I Suppose other GM assumptos hold but have heterosedastcty.
Block-Based Compact Thermal Modeling of Semiconductor Integrated Circuits
 Block-Based Compact hermal Modelg of Semcoductor Itegrated Crcuts Master s hess Defese Caddate: Jg Ba Commttee Members: Dr. Mg-Cheg Cheg Dr. Daqg Hou Dr. Robert Schllg July 27, 2009 Outle Itroducto Backgroud
Block-Based Compact hermal Modelg of Semcoductor Itegrated Crcuts Master s hess Defese Caddate: Jg Ba Commttee Members: Dr. Mg-Cheg Cheg Dr. Daqg Hou Dr. Robert Schllg July 27, 2009 Outle Itroducto Backgroud
Lecture Notes 2. The ability to manipulate matrices is critical in economics.
 Lecture Notes. Revew of Matrces he ablt to mapulate matrces s crtcal ecoomcs.. Matr a rectagular arra of umbers, parameters, or varables placed rows ad colums. Matrces are assocated wth lear equatos. lemets
Lecture Notes. Revew of Matrces he ablt to mapulate matrces s crtcal ecoomcs.. Matr a rectagular arra of umbers, parameters, or varables placed rows ad colums. Matrces are assocated wth lear equatos. lemets
MIMA Group. Chapter 4 Non-Parameter Estimation. School of Computer Science and Technology, Shandong University. Xin-Shun SDU
 Grou M D L M Chater 4 No-Parameter Estmato X-Shu Xu @ SDU School of Comuter Scece ad Techology, Shadog Uversty Cotets Itroducto Parze Wdows K-Nearest-Neghbor Estmato Classfcato Techques The Nearest-Neghbor
Grou M D L M Chater 4 No-Parameter Estmato X-Shu Xu @ SDU School of Comuter Scece ad Techology, Shadog Uversty Cotets Itroducto Parze Wdows K-Nearest-Neghbor Estmato Classfcato Techques The Nearest-Neghbor
Mean is only appropriate for interval or ratio scales, not ordinal or nominal.
 Mea Same as ordary average Sum all the data values ad dvde by the sample sze. x = ( x + x +... + x Usg summato otato, we wrte ths as x = x = x = = ) x Mea s oly approprate for terval or rato scales, ot
Mea Same as ordary average Sum all the data values ad dvde by the sample sze. x = ( x + x +... + x Usg summato otato, we wrte ths as x = x = x = = ) x Mea s oly approprate for terval or rato scales, ot
Chapter 5 Properties of a Random Sample
 Lecture 3 o BST 63: Statstcal Theory I Ku Zhag, /6/006 Revew for the revous lecture Cocets: radom samle, samle mea, samle varace Theorems: roertes of a radom samle, samle mea, samle varace Examles: how
Lecture 3 o BST 63: Statstcal Theory I Ku Zhag, /6/006 Revew for the revous lecture Cocets: radom samle, samle mea, samle varace Theorems: roertes of a radom samle, samle mea, samle varace Examles: how
Feature Selection: Part 2. 1 Greedy Algorithms (continued from the last lecture)
 CSE 546: Mache Learg Lecture 6 Feature Selecto: Part 2 Istructor: Sham Kakade Greedy Algorthms (cotued from the last lecture) There are varety of greedy algorthms ad umerous amg covetos for these algorthms.
CSE 546: Mache Learg Lecture 6 Feature Selecto: Part 2 Istructor: Sham Kakade Greedy Algorthms (cotued from the last lecture) There are varety of greedy algorthms ad umerous amg covetos for these algorthms.
Assignment 5/MATH 247/Winter Due: Friday, February 19 in class (!) (answers will be posted right after class)
 Assgmet 5/MATH 7/Wter 00 Due: Frday, February 9 class (!) (aswers wll be posted rght after class) As usual, there are peces of text, before the questos [], [], themselves. Recall: For the quadratc form
Assgmet 5/MATH 7/Wter 00 Due: Frday, February 9 class (!) (aswers wll be posted rght after class) As usual, there are peces of text, before the questos [], [], themselves. Recall: For the quadratc form
Supervised learning: Linear regression Logistic regression
 CS 57 Itroducto to AI Lecture 4 Supervsed learg: Lear regresso Logstc regresso Mlos Hauskrecht mlos@cs.ptt.edu 539 Seott Square CS 57 Itro to AI Data: D { D D.. D D Supervsed learg d a set of eamples s
CS 57 Itroducto to AI Lecture 4 Supervsed learg: Lear regresso Logstc regresso Mlos Hauskrecht mlos@cs.ptt.edu 539 Seott Square CS 57 Itro to AI Data: D { D D.. D D Supervsed learg d a set of eamples s
Lecture 3. Sampling, sampling distributions, and parameter estimation
 Lecture 3 Samplg, samplg dstrbutos, ad parameter estmato Samplg Defto Populato s defed as the collecto of all the possble observatos of terest. The collecto of observatos we take from the populato s called
Lecture 3 Samplg, samplg dstrbutos, ad parameter estmato Samplg Defto Populato s defed as the collecto of all the possble observatos of terest. The collecto of observatos we take from the populato s called
6.867 Machine Learning
 6.867 Mache Learg Problem set Due Frday, September 9, rectato Please address all questos ad commets about ths problem set to 6.867-staff@a.mt.edu. You do ot eed to use MATLAB for ths problem set though
6.867 Mache Learg Problem set Due Frday, September 9, rectato Please address all questos ad commets about ths problem set to 6.867-staff@a.mt.edu. You do ot eed to use MATLAB for ths problem set though
Application of Generating Functions to the Theory of Success Runs
 Aled Mathematcal Sceces, Vol. 10, 2016, o. 50, 2491-2495 HIKARI Ltd, www.m-hkar.com htt://dx.do.org/10.12988/ams.2016.66197 Alcato of Geeratg Fuctos to the Theory of Success Rus B.M. Bekker, O.A. Ivaov
Aled Mathematcal Sceces, Vol. 10, 2016, o. 50, 2491-2495 HIKARI Ltd, www.m-hkar.com htt://dx.do.org/10.12988/ams.2016.66197 Alcato of Geeratg Fuctos to the Theory of Success Rus B.M. Bekker, O.A. Ivaov
