Algorithms and Data Structures 2014 Exercises week 5
|
|
|
- Claire Scott
- 6 years ago
- Views:
Transcription
1 Algorithms and Data Structures 014 Exercises week 5 October, 014 Exercises marked by ( ) are hard, but they might show up on the exam. Exercises marked by ( ) are even harder, but they will not be on the exam. 1. Consider the following function: } void example(int A[], int N) { /* N is the size of the array */ Node p; for (int i = 1; i <= N; i++) p = insert(a,n,i,p); convert(p,a,1); Assuming T insert = O(lg N) and T convert = O(N ), analyze the execution time of the function example in the worst case. Answer. First, we note that the for loop executes N times, no matter what. Then, we write T (n), the execution time function for example: T (N) c 1 (N + 1) + (c lg N)N + c 3 N Here, the comes from the fact that we know T insert = O(lg N) and T convert = O(N ), which means T insert c lg N and T convert c 3 N for some constants c and c 3. Now we can see that T (N) O(N ), because N is the greatest factor in T (N) above, but let us show that indeed T (N) CN (for almost all N). T (N) c 1 (N + 1) + (c lg N)N + c 3 N = c 1 N + c 1 + (c lg N)N + c 3 N c 1 N + c 1 N + (c N)N + c 3 N N N, 1 N, lg N N, for N > 0. = (c 1 + c + c 3 ) N C 1
2 . For each of the following bounds on T, draw a recursion tree and guess the least O-order. Then prove that T is in that O-order using the substitution method. (a) T (n) T (n 1) + n for n 1 (Bubblesort) (b) T (n) T ( n ) + 37 for n 1 (Binary search) (c) (**) T (n) T ( n ) + 1 for n 1 (d) ( ) T (n) T ( 3n 4 ) + 1n for n 1 (Lucky quicksort) (e) ( ) T (n) n + T ( n 5 ) + T ( 3n 4 ) for n 1 (Linearselect) Answer (a) The tree is just a line with n + 1 levels and each level i costs i (let us assume that level 0 costs c 0 ). The total cost c 0 + n i=1 i = c 0 + (n + n)/, where c 0 is the value we assume for T (0) (in the sum you need arithmetic progression formula). We conjecture that T (n) O(n ). Wenow prove it using the substitution method: T (n) T (n 1) + n = c(n 1) + n Induction Hypothesis = cn cn + c + n cn For the last equation to hold we need n c (1 c). (c) Drawing the tree one observes that the tree has lg(n)+1 levels and each level i costs i c for c = 1. This means that the total cost is n c (here you need geometric progression formula). Let us prove the the algorithm is in O(n). This example shows that the substitution method is sometimes not easy to use. If we try to use it here what happens is: T (n) T ( n ) + 1 = c( n ) + 1 Induction Hypothesis cn For the last equation to hold we need c n + 1 0, which is impossible if n 0 and c 0. You could now think that the conjecture O(n) is wrong, which is in fact not true. We can prove it using a different method.
3 I did it by first considering the case n = m. For m, we have T ( m ) T ( m 1 ) + 1 T () m 1 + 1( m ) = T () m 1 + 1( m 1 1) (T () + 1) m 1 (T () + 1) m.... m 1 times Given any n >, there exist m, r N such that m+1 n, m 1 and n = m + r. And thus T (n) = T ( m + r) T ( m+1 ) (T () + 1) m+1 = (T () + 4) m (T () + 4)n, which shows T O(n). 3. For the following problems provide a naive solution and the corresponding dynamic programming solution (either using memoization or the bottom up approach). For each problem analyze the time complexity of both the naive solutions and the DP solution. Write clearly what are the subproblems and what is the number of subproblems you need to solve in order to find the solution of the original problem. (a) Wouter loves to go to the Casino. Tonight the main game is the following. Greta, the assistant, puts down at each round a sequence of cards that have random real numbers printed in them A[1],... A[n]. Each player chooses a contiguous subsequence A[i], A[i+1],..., A[j]. You win if you choose the subsequence for which the sum of elements in the subsequence is maximized. E.g. {5, 5, 3,, 7} should return subsequence {3,, 7}. Answer The naive solution would be: take all possible contiguous subsequences of the given array and compute their sum, then select the max. What is the complexity? For the DP solution, we look at subsequences ending at j (the subproblems are maximum sum of a subsequence ending at j, we can then re-use sums already computed): 3
4 MaxSum(j) A[j] if j=0 = max( MaxSum(j 1) + A[j] Extend window ending at position j-1, A[j] start a new window at position j ) otherwise With each element of MaxSum, you also keep the starting element of the sum (the same as for MaxSum(j 1) or j if you restart). At the end, scan MaxSum for the maximum value and return it together with the starting and ending indexes. Alternatively, you could keep track of the maximum value as you create MaxSum. The array MaxSum has size n and evaluating each element takes constant. Scanning MaxSum also takes O(n) so in total we have a O(n) algorithm. (b) At some point Greta decided to change the rules and asked the players to, given a sequence of n cards A[1],... A[n] (still with real numbers), pick a subsequence of cards (not necessarily contiguous) of maximum length, so that the values in the cards the player picked form a strictly increasing sequence. (c) At the end of his visit to the Casino Wouter changes the casino chips he has into real money. Imagine that the Casino s cashier has n types of coins of values v 1 < v <... < v n (all natural numbers). Assume v 1 = 1, so you can always make change for any amount of chips. Wouter hates to carry coins so he asks the cashier to give him as few coins as possible. Give an algorithm which makes change for any amount with as few coins as possible. (d) (*) Greta s aunt wants to build a new fence to protect her chickens. She was given by her neighbour who just finish renovating his house a truck with n types of rectangular 3-D bricks. She measured all the bricks and registered for each type i, the height h i, the width w i and the depth d i (all real numbers). She then wondered what would be the highest stack of bricks that she could build, having as rule that one can only stack a brick on top of another one if the dimensions of the base of the lower brick are each strictly larger than those of the base of the higher brick. Of course, you can rotate a brick so that any of the 6 sides functions as its base. It is also allowed to use multiple times the the same type of brick. 4. The (always used as example) Fibonacci recurrence f(n + 1) = f(n) + f(n 1) can be represented in the form a matrix as follows: ( ) ( ) ( ) 1 1 f(n) f(n + 1) = 1 0 f(n 1) f(n) where ( ) ( f(0) 1 =. f(1) 1) 4
5 ( ) 1 1 Let A =. One can easily observe that in order to compute f(n+1) 1 0 we can use the equality ( ) ( ) ( ) f(n) f(n + 1) A = = A n f(1) f(n 1) f(n) f(0) So all that we have to do is compute the n th power of the matrix A. Provide a O(lg n) time algorithm that does this. Answer Hint: use recursive doubling; to find A n, one can do A n/ A n/ (take care if n is odd). 5. (**) Hacker team (Kleinberg & Tardos): Suppose you are managing a consulting team of expert computer hackers, and each week you have to choose a job for them to undertake. The set of possible jobs is divided into those that are low-stress (e.g. setting up a Web site for a class at the local elementary school) and those that are high-stress (e.g., protecting the dean s most valuable secrets.) The basic question each week is whether to take on a low-stress job or a high-stress job. If you select a low-stress job for your team in week i, then you get a revenue of l i > 0 dollars; if you select a high-stress job, you get a revenue of h i > 0 dollars. High-stress jobs typically pay more. The catch, however, is that in order for the team to take on a high-stress job in week i, it is required that they do no job (of either type) in week i 1; they need a full week of prep time to get ready for the crushing stress level. On the other hand, it is okay for them to take a low-stress job in week i even if they have done a job (of either type) in week i 1. So, given a sequence of n weeks, a plan is specified by a choice of low-stress, high-stress or none for each of the n weeks, with the property that if high-stress is chosen for week i > 1, then none has to be chosen for week i 1. (It is okay to choose a high-stress job in week 1.) The value of the plan is determined in the natural way; for each i, you add l i to the value if you choose low-stress in week i, and you add h i to the value if you choose high-stress in week i. (You add 0 if you choose none in week i.) Given sets of values l 1, l,..., l n and h 1, h,..., h n, find a plan of maximum value (such a plan is called optimal.) Give an efficient algorithm to take the input values and return the value of an optimal plan. 5
Algorithms and Data Structures 2016 Week 5 solutions (Tues 9th - Fri 12th February)
 Algorithms and Data Structures 016 Week 5 solutions (Tues 9th - Fri 1th February) 1. Draw the decision tree (under the assumption of all-distinct inputs) Quicksort for n = 3. answer: (of course you should
Algorithms and Data Structures 016 Week 5 solutions (Tues 9th - Fri 1th February) 1. Draw the decision tree (under the assumption of all-distinct inputs) Quicksort for n = 3. answer: (of course you should
Analysis of Algorithms CMPSC 565
 Analysis of Algorithms CMPSC 565 LECTURES 38-39 Randomized Algorithms II Quickselect Quicksort Running time Adam Smith L1.1 Types of randomized analysis Average-case analysis : Assume data is distributed
Analysis of Algorithms CMPSC 565 LECTURES 38-39 Randomized Algorithms II Quickselect Quicksort Running time Adam Smith L1.1 Types of randomized analysis Average-case analysis : Assume data is distributed
Analysis of Algorithms I: Asymptotic Notation, Induction, and MergeSort
 Analysis of Algorithms I: Asymptotic Notation, Induction, and MergeSort Xi Chen Columbia University We continue with two more asymptotic notation: o( ) and ω( ). Let f (n) and g(n) are functions that map
Analysis of Algorithms I: Asymptotic Notation, Induction, and MergeSort Xi Chen Columbia University We continue with two more asymptotic notation: o( ) and ω( ). Let f (n) and g(n) are functions that map
Chapter 4 Divide-and-Conquer
 Chapter 4 Divide-and-Conquer 1 About this lecture (1) Recall the divide-and-conquer paradigm, which we used for merge sort: Divide the problem into a number of subproblems that are smaller instances of
Chapter 4 Divide-and-Conquer 1 About this lecture (1) Recall the divide-and-conquer paradigm, which we used for merge sort: Divide the problem into a number of subproblems that are smaller instances of
1 Terminology and setup
 15-451/651: Design & Analysis of Algorithms August 31, 2017 Lecture #2 last changed: August 29, 2017 In this lecture, we will examine some simple, concrete models of computation, each with a precise definition
15-451/651: Design & Analysis of Algorithms August 31, 2017 Lecture #2 last changed: August 29, 2017 In this lecture, we will examine some simple, concrete models of computation, each with a precise definition
Quick Sort Notes , Spring 2010
 Quick Sort Notes 18.310, Spring 2010 0.1 Randomized Median Finding In a previous lecture, we discussed the problem of finding the median of a list of m elements, or more generally the element of rank m.
Quick Sort Notes 18.310, Spring 2010 0.1 Randomized Median Finding In a previous lecture, we discussed the problem of finding the median of a list of m elements, or more generally the element of rank m.
CS 577 Introduction to Algorithms: Strassen s Algorithm and the Master Theorem
 CS 577 Introduction to Algorithms: Jin-Yi Cai University of Wisconsin Madison In the last class, we described InsertionSort and showed that its worst-case running time is Θ(n 2 ). Check Figure 2.2 for
CS 577 Introduction to Algorithms: Jin-Yi Cai University of Wisconsin Madison In the last class, we described InsertionSort and showed that its worst-case running time is Θ(n 2 ). Check Figure 2.2 for
CS325: Analysis of Algorithms, Fall Midterm
 CS325: Analysis of Algorithms, Fall 2017 Midterm I don t know policy: you may write I don t know and nothing else to answer a question and receive 25 percent of the total points for that problem whereas
CS325: Analysis of Algorithms, Fall 2017 Midterm I don t know policy: you may write I don t know and nothing else to answer a question and receive 25 percent of the total points for that problem whereas
6.854 Advanced Algorithms
 6.854 Advanced Algorithms Homework Solutions Hashing Bashing. Solution:. O(log U ) for the first level and for each of the O(n) second level functions, giving a total of O(n log U ) 2. Suppose we are using
6.854 Advanced Algorithms Homework Solutions Hashing Bashing. Solution:. O(log U ) for the first level and for each of the O(n) second level functions, giving a total of O(n log U ) 2. Suppose we are using
Algorithm Design and Analysis
 Algorithm Design and Analysis LECTURE 9 Divide and Conquer Merge sort Counting Inversions Binary Search Exponentiation Solving Recurrences Recursion Tree Method Master Theorem Sofya Raskhodnikova S. Raskhodnikova;
Algorithm Design and Analysis LECTURE 9 Divide and Conquer Merge sort Counting Inversions Binary Search Exponentiation Solving Recurrences Recursion Tree Method Master Theorem Sofya Raskhodnikova S. Raskhodnikova;
Fall 2017 November 10, Written Homework 5
 CS1800 Discrete Structures Profs. Aslam, Gold, & Pavlu Fall 2017 November 10, 2017 Assigned: Mon Nov 13 2017 Due: Wed Nov 29 2017 Instructions: Written Homework 5 The assignment has to be uploaded to blackboard
CS1800 Discrete Structures Profs. Aslam, Gold, & Pavlu Fall 2017 November 10, 2017 Assigned: Mon Nov 13 2017 Due: Wed Nov 29 2017 Instructions: Written Homework 5 The assignment has to be uploaded to blackboard
CS 170 Algorithms Fall 2014 David Wagner MT2
 CS 170 Algorithms Fall 2014 David Wagner MT2 PRINT your name:, (last) SIGN your name: (first) Your Student ID number: Your Unix account login: cs170- The room you are sitting in right now: Name of the
CS 170 Algorithms Fall 2014 David Wagner MT2 PRINT your name:, (last) SIGN your name: (first) Your Student ID number: Your Unix account login: cs170- The room you are sitting in right now: Name of the
Data Structures and Algorithms
 Data Structures and Algorithms Spring 2017-2018 Outline 1 Sorting Algorithms (contd.) Outline Sorting Algorithms (contd.) 1 Sorting Algorithms (contd.) Analysis of Quicksort Time to sort array of length
Data Structures and Algorithms Spring 2017-2018 Outline 1 Sorting Algorithms (contd.) Outline Sorting Algorithms (contd.) 1 Sorting Algorithms (contd.) Analysis of Quicksort Time to sort array of length
Lecture 7: Dynamic Programming I: Optimal BSTs
 5-750: Graduate Algorithms February, 06 Lecture 7: Dynamic Programming I: Optimal BSTs Lecturer: David Witmer Scribes: Ellango Jothimurugesan, Ziqiang Feng Overview The basic idea of dynamic programming
5-750: Graduate Algorithms February, 06 Lecture 7: Dynamic Programming I: Optimal BSTs Lecturer: David Witmer Scribes: Ellango Jothimurugesan, Ziqiang Feng Overview The basic idea of dynamic programming
Concrete models and tight upper/lower bounds
 Lecture 3 Concrete models and tight upper/lower bounds 3.1 Overview In this lecture, we will examine some simple, concrete models of computation, each with a precise definition of what counts as a step,
Lecture 3 Concrete models and tight upper/lower bounds 3.1 Overview In this lecture, we will examine some simple, concrete models of computation, each with a precise definition of what counts as a step,
Midterm Exam. CS 3110: Design and Analysis of Algorithms. June 20, Group 1 Group 2 Group 3
 Banner ID: Name: Midterm Exam CS 3110: Design and Analysis of Algorithms June 20, 2006 Group 1 Group 2 Group 3 Question 1.1 Question 2.1 Question 3.1 Question 1.2 Question 2.2 Question 3.2 Question 3.3
Banner ID: Name: Midterm Exam CS 3110: Design and Analysis of Algorithms June 20, 2006 Group 1 Group 2 Group 3 Question 1.1 Question 2.1 Question 3.1 Question 1.2 Question 2.2 Question 3.2 Question 3.3
What we have learned What is algorithm Why study algorithm The time and space efficiency of algorithm The analysis framework of time efficiency Asympt
 Lecture 3 The Analysis of Recursive Algorithm Efficiency What we have learned What is algorithm Why study algorithm The time and space efficiency of algorithm The analysis framework of time efficiency
Lecture 3 The Analysis of Recursive Algorithm Efficiency What we have learned What is algorithm Why study algorithm The time and space efficiency of algorithm The analysis framework of time efficiency
Binomial Coefficient Identities/Complements
 Binomial Coefficient Identities/Complements CSE21 Fall 2017, Day 4 Oct 6, 2017 https://sites.google.com/a/eng.ucsd.edu/cse21-fall-2017-miles-jones/ permutation P(n,r) = n(n-1) (n-2) (n-r+1) = Terminology
Binomial Coefficient Identities/Complements CSE21 Fall 2017, Day 4 Oct 6, 2017 https://sites.google.com/a/eng.ucsd.edu/cse21-fall-2017-miles-jones/ permutation P(n,r) = n(n-1) (n-2) (n-r+1) = Terminology
MA008/MIIZ01 Design and Analysis of Algorithms Lecture Notes 3
 MA008 p.1/37 MA008/MIIZ01 Design and Analysis of Algorithms Lecture Notes 3 Dr. Markus Hagenbuchner markus@uow.edu.au. MA008 p.2/37 Exercise 1 (from LN 2) Asymptotic Notation When constants appear in exponents
MA008 p.1/37 MA008/MIIZ01 Design and Analysis of Algorithms Lecture Notes 3 Dr. Markus Hagenbuchner markus@uow.edu.au. MA008 p.2/37 Exercise 1 (from LN 2) Asymptotic Notation When constants appear in exponents
Algorithms And Programming I. Lecture 5 Quicksort
 Algorithms And Programming I Lecture 5 Quicksort Quick Sort Partition set into two using randomly chosen pivot 88 31 25 52 14 98 62 30 23 79 14 31 2530 23 52 88 62 98 79 Quick Sort 14 31 2530 23 52 88
Algorithms And Programming I Lecture 5 Quicksort Quick Sort Partition set into two using randomly chosen pivot 88 31 25 52 14 98 62 30 23 79 14 31 2530 23 52 88 62 98 79 Quick Sort 14 31 2530 23 52 88
Taking Stock. IE170: Algorithms in Systems Engineering: Lecture 3. Θ Notation. Comparing Algorithms
 Taking Stock IE170: Algorithms in Systems Engineering: Lecture 3 Jeff Linderoth Department of Industrial and Systems Engineering Lehigh University January 19, 2007 Last Time Lots of funky math Playing
Taking Stock IE170: Algorithms in Systems Engineering: Lecture 3 Jeff Linderoth Department of Industrial and Systems Engineering Lehigh University January 19, 2007 Last Time Lots of funky math Playing
Analysis of Algorithms - Using Asymptotic Bounds -
 Analysis of Algorithms - Using Asymptotic Bounds - Andreas Ermedahl MRTC (Mälardalens Real-Time Research Center) andreas.ermedahl@mdh.se Autumn 004 Rehersal: Asymptotic bounds Gives running time bounds
Analysis of Algorithms - Using Asymptotic Bounds - Andreas Ermedahl MRTC (Mälardalens Real-Time Research Center) andreas.ermedahl@mdh.se Autumn 004 Rehersal: Asymptotic bounds Gives running time bounds
Introduction to Induction (LAMC, 10/14/07)
 Introduction to Induction (LAMC, 10/14/07) Olga Radko October 1, 007 1 Definitions The Method of Mathematical Induction (MMI) is usually stated as one of the axioms of the natural numbers (so-called Peano
Introduction to Induction (LAMC, 10/14/07) Olga Radko October 1, 007 1 Definitions The Method of Mathematical Induction (MMI) is usually stated as one of the axioms of the natural numbers (so-called Peano
CSE 21 Practice Exam for Midterm 2 Fall 2017
 CSE 1 Practice Exam for Midterm Fall 017 These practice problems should help prepare you for the second midterm, which is on monday, November 11 This is longer than the actual exam will be, but good practice
CSE 1 Practice Exam for Midterm Fall 017 These practice problems should help prepare you for the second midterm, which is on monday, November 11 This is longer than the actual exam will be, but good practice
Sorting and Searching. Tony Wong
 Tony Wong 2017-03-04 Sorting Sorting is the reordering of array elements into a specific order (usually ascending) For example, array a[0..8] consists of the final exam scores of the n = 9 students in
Tony Wong 2017-03-04 Sorting Sorting is the reordering of array elements into a specific order (usually ascending) For example, array a[0..8] consists of the final exam scores of the n = 9 students in
Chapter 2. Recurrence Relations. Divide and Conquer. Divide and Conquer Strategy. Another Example: Merge Sort. Merge Sort Example. Merge Sort Example
 Recurrence Relations Chapter 2 Divide and Conquer Equation or an inequality that describes a function by its values on smaller inputs. Recurrence relations arise when we analyze the running time of iterative
Recurrence Relations Chapter 2 Divide and Conquer Equation or an inequality that describes a function by its values on smaller inputs. Recurrence relations arise when we analyze the running time of iterative
CS 4407 Algorithms Lecture 2: Iterative and Divide and Conquer Algorithms
 CS 4407 Algorithms Lecture 2: Iterative and Divide and Conquer Algorithms Prof. Gregory Provan Department of Computer Science University College Cork 1 Lecture Outline CS 4407, Algorithms Growth Functions
CS 4407 Algorithms Lecture 2: Iterative and Divide and Conquer Algorithms Prof. Gregory Provan Department of Computer Science University College Cork 1 Lecture Outline CS 4407, Algorithms Growth Functions
CPSC 320 Sample Final Examination December 2013
 CPSC 320 Sample Final Examination December 2013 [10] 1. Answer each of the following questions with true or false. Give a short justification for each of your answers. [5] a. 6 n O(5 n ) lim n + This is
CPSC 320 Sample Final Examination December 2013 [10] 1. Answer each of the following questions with true or false. Give a short justification for each of your answers. [5] a. 6 n O(5 n ) lim n + This is
More Asymptotic Analysis Spring 2018 Discussion 8: March 6, 2018
 CS 61B More Asymptotic Analysis Spring 2018 Discussion 8: March 6, 2018 Here is a review of some formulas that you will find useful when doing asymptotic analysis. ˆ N i=1 i = 1 + 2 + 3 + 4 + + N = N(N+1)
CS 61B More Asymptotic Analysis Spring 2018 Discussion 8: March 6, 2018 Here is a review of some formulas that you will find useful when doing asymptotic analysis. ˆ N i=1 i = 1 + 2 + 3 + 4 + + N = N(N+1)
SEQUENCES, MATHEMATICAL INDUCTION, AND RECURSION
 CHAPTER 5 SEQUENCES, MATHEMATICAL INDUCTION, AND RECURSION One of the most important tasks of mathematics is to discover and characterize regular patterns, such as those associated with processes that
CHAPTER 5 SEQUENCES, MATHEMATICAL INDUCTION, AND RECURSION One of the most important tasks of mathematics is to discover and characterize regular patterns, such as those associated with processes that
INDIAN INSTITUTE OF TECHNOLOGY KHARAGPUR Design and Analysis of Algorithms Department of Mathematics MA21007/Assignment-2/Due: 18 Aug.
 INDIAN INSTITUTE OF TECHNOLOGY KHARAGPUR Design and Analysis of Algorithms Department of Mathematics MA21007/Assignment-2/Due: 18 Aug. 2015 Problem 1. Computing Fibonacci Numbers The Fibonacci numbers
INDIAN INSTITUTE OF TECHNOLOGY KHARAGPUR Design and Analysis of Algorithms Department of Mathematics MA21007/Assignment-2/Due: 18 Aug. 2015 Problem 1. Computing Fibonacci Numbers The Fibonacci numbers
Outline. We will cover (over the next few weeks) Induction Strong Induction Constructive Induction Structural Induction
 Outline We will cover (over the next few weeks) Induction Strong Induction Constructive Induction Structural Induction Induction P(1) ( n 2)[P(n 1) P(n)] ( n 1)[P(n)] Why Does This Work? I P(1) ( n 2)[P(n
Outline We will cover (over the next few weeks) Induction Strong Induction Constructive Induction Structural Induction Induction P(1) ( n 2)[P(n 1) P(n)] ( n 1)[P(n)] Why Does This Work? I P(1) ( n 2)[P(n
Analysis of Algorithms. Randomizing Quicksort
 Analysis of Algorithms Randomizing Quicksort Randomizing Quicksort Randomly permute the elements of the input array before sorting OR... modify the PARTITION procedure At each step of the algorithm we
Analysis of Algorithms Randomizing Quicksort Randomizing Quicksort Randomly permute the elements of the input array before sorting OR... modify the PARTITION procedure At each step of the algorithm we
CS-141 Exam 2 Review October 19, 2016 Presented by the RIT Computer Science Community
 CS-141 Exam 2 Review October 19, 2016 Presented by the RIT Computer Science Community http://csc.cs.rit.edu Linked Lists 1. You are given the linked list: 1 2 3. You may assume that each node has one field
CS-141 Exam 2 Review October 19, 2016 Presented by the RIT Computer Science Community http://csc.cs.rit.edu Linked Lists 1. You are given the linked list: 1 2 3. You may assume that each node has one field
1 Introduction (January 21)
 CS 97: Concrete Models of Computation Spring Introduction (January ). Deterministic Complexity Consider a monotonically nondecreasing function f : {,,..., n} {, }, where f() = and f(n) =. We call f a step
CS 97: Concrete Models of Computation Spring Introduction (January ). Deterministic Complexity Consider a monotonically nondecreasing function f : {,,..., n} {, }, where f() = and f(n) =. We call f a step
Intermediate Math Circles March 11, 2009 Sequences and Series
 1 University of Waterloo Faculty of Mathematics Centre for Education in Mathematics and Computing Intermediate Math Circles March 11, 009 Sequences and Series Tower of Hanoi The Tower of Hanoi is a game
1 University of Waterloo Faculty of Mathematics Centre for Education in Mathematics and Computing Intermediate Math Circles March 11, 009 Sequences and Series Tower of Hanoi The Tower of Hanoi is a game
Asymptotic Analysis and Recurrences
 Appendix A Asymptotic Analysis and Recurrences A.1 Overview We discuss the notion of asymptotic analysis and introduce O, Ω, Θ, and o notation. We then turn to the topic of recurrences, discussing several
Appendix A Asymptotic Analysis and Recurrences A.1 Overview We discuss the notion of asymptotic analysis and introduce O, Ω, Θ, and o notation. We then turn to the topic of recurrences, discussing several
Week 5: Quicksort, Lower bound, Greedy
 Week 5: Quicksort, Lower bound, Greedy Agenda: Quicksort: Average case Lower bound for sorting Greedy method 1 Week 5: Quicksort Recall Quicksort: The ideas: Pick one key Compare to others: partition into
Week 5: Quicksort, Lower bound, Greedy Agenda: Quicksort: Average case Lower bound for sorting Greedy method 1 Week 5: Quicksort Recall Quicksort: The ideas: Pick one key Compare to others: partition into
CPSC 320 (Intermediate Algorithm Design and Analysis). Summer Instructor: Dr. Lior Malka Final Examination, July 24th, 2009
 CPSC 320 (Intermediate Algorithm Design and Analysis). Summer 2009. Instructor: Dr. Lior Malka Final Examination, July 24th, 2009 Student ID: INSTRUCTIONS: There are 6 questions printed on pages 1 7. Exam
CPSC 320 (Intermediate Algorithm Design and Analysis). Summer 2009. Instructor: Dr. Lior Malka Final Examination, July 24th, 2009 Student ID: INSTRUCTIONS: There are 6 questions printed on pages 1 7. Exam
Strong Induction (Second Principle) Example: There are two piles of cards, players take turn: each turn: one player removes any number of cards from
 Strong Induction (Second Principle) Example: There are two piles of cards, players take turn: each turn: one player removes any number of cards from 1 pile (any of the two). The player who removes the
Strong Induction (Second Principle) Example: There are two piles of cards, players take turn: each turn: one player removes any number of cards from 1 pile (any of the two). The player who removes the
Exercise Sheet #1 Solutions, Computer Science, A M. Hallett, K. Smith a k n b k = n b + k. a k n b k c 1 n b k. a k n b.
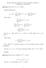 Exercise Sheet #1 Solutions, Computer Science, 308-251A M. Hallett, K. Smith 2002 Question 1.1: Prove (n + a) b = Θ(n b ). Binomial Expansion: Show O(n b ): (n + a) b = For any c 1 > b = O(n b ). Show
Exercise Sheet #1 Solutions, Computer Science, 308-251A M. Hallett, K. Smith 2002 Question 1.1: Prove (n + a) b = Θ(n b ). Binomial Expansion: Show O(n b ): (n + a) b = For any c 1 > b = O(n b ). Show
Central Algorithmic Techniques. Iterative Algorithms
 Central Algorithmic Techniques Iterative Algorithms Code Representation of an Algorithm class InsertionSortAlgorithm extends SortAlgorithm { void sort(int a[]) throws Exception { for (int i = 1; i < a.length;
Central Algorithmic Techniques Iterative Algorithms Code Representation of an Algorithm class InsertionSortAlgorithm extends SortAlgorithm { void sort(int a[]) throws Exception { for (int i = 1; i < a.length;
The maximum-subarray problem. Given an array of integers, find a contiguous subarray with the maximum sum. Very naïve algorithm:
 The maximum-subarray problem Given an array of integers, find a contiguous subarray with the maximum sum. Very naïve algorithm: Brute force algorithm: At best, θ(n 2 ) time complexity 129 Can we do divide
The maximum-subarray problem Given an array of integers, find a contiguous subarray with the maximum sum. Very naïve algorithm: Brute force algorithm: At best, θ(n 2 ) time complexity 129 Can we do divide
b + O(n d ) where a 1, b > 1, then O(n d log n) if a = b d d ) if a < b d O(n log b a ) if a > b d
 CS161, Lecture 4 Median, Selection, and the Substitution Method Scribe: Albert Chen and Juliana Cook (2015), Sam Kim (2016), Gregory Valiant (2017) Date: January 23, 2017 1 Introduction Last lecture, we
CS161, Lecture 4 Median, Selection, and the Substitution Method Scribe: Albert Chen and Juliana Cook (2015), Sam Kim (2016), Gregory Valiant (2017) Date: January 23, 2017 1 Introduction Last lecture, we
Asymptotic Running Time of Algorithms
 Asymptotic Complexity: leading term analysis Asymptotic Running Time of Algorithms Comparing searching and sorting algorithms so far: Count worst-case of comparisons as function of array size. Drop lower-order
Asymptotic Complexity: leading term analysis Asymptotic Running Time of Algorithms Comparing searching and sorting algorithms so far: Count worst-case of comparisons as function of array size. Drop lower-order
Math 391: Midterm 1.0 Spring 2016
 Math 391: Midterm 1.0 Spring 2016 James Skon skonjp@kenyon.edu Test date: October 5 Submission Instructions: Give all your assumptions. Show all your work. Be as complete as possible. Grading Problem 1
Math 391: Midterm 1.0 Spring 2016 James Skon skonjp@kenyon.edu Test date: October 5 Submission Instructions: Give all your assumptions. Show all your work. Be as complete as possible. Grading Problem 1
Computational Complexity. This lecture. Notes. Lecture 02 - Basic Complexity Analysis. Tom Kelsey & Susmit Sarkar. Notes
 Computational Complexity Lecture 02 - Basic Complexity Analysis Tom Kelsey & Susmit Sarkar School of Computer Science University of St Andrews http://www.cs.st-andrews.ac.uk/~tom/ twk@st-andrews.ac.uk
Computational Complexity Lecture 02 - Basic Complexity Analysis Tom Kelsey & Susmit Sarkar School of Computer Science University of St Andrews http://www.cs.st-andrews.ac.uk/~tom/ twk@st-andrews.ac.uk
Computational Complexity - Pseudocode and Recursions
 Computational Complexity - Pseudocode and Recursions Nicholas Mainardi 1 Dipartimento di Elettronica e Informazione Politecnico di Milano nicholas.mainardi@polimi.it June 6, 2018 1 Partly Based on Alessandro
Computational Complexity - Pseudocode and Recursions Nicholas Mainardi 1 Dipartimento di Elettronica e Informazione Politecnico di Milano nicholas.mainardi@polimi.it June 6, 2018 1 Partly Based on Alessandro
CSCI 3110 Assignment 6 Solutions
 CSCI 3110 Assignment 6 Solutions December 5, 2012 2.4 (4 pts) Suppose you are choosing between the following three algorithms: 1. Algorithm A solves problems by dividing them into five subproblems of half
CSCI 3110 Assignment 6 Solutions December 5, 2012 2.4 (4 pts) Suppose you are choosing between the following three algorithms: 1. Algorithm A solves problems by dividing them into five subproblems of half
The PRIMES 2014 problem set
 Dear PRIMES applicant! The PRIMES 24 problem set This is the PRIMES 24 problem set. Please send us your solutions as part of your PRIMES application by December, 24. For complete rules, see http://web.mit.edu/primes/apply.shtml
Dear PRIMES applicant! The PRIMES 24 problem set This is the PRIMES 24 problem set. Please send us your solutions as part of your PRIMES application by December, 24. For complete rules, see http://web.mit.edu/primes/apply.shtml
Week 7 Solution. The two implementations are 1. Approach 1. int fib(int n) { if (n <= 1) return n; return fib(n 1) + fib(n 2); } 2.
 Week 7 Solution 1.You are given two implementations for finding the nth Fibonacci number(f Fibonacci numbers are defined by F(n = F(n 1 + F(n 2 with F(0 = 0 and F(1 = 1 The two implementations are 1. Approach
Week 7 Solution 1.You are given two implementations for finding the nth Fibonacci number(f Fibonacci numbers are defined by F(n = F(n 1 + F(n 2 with F(0 = 0 and F(1 = 1 The two implementations are 1. Approach
CS 350 Midterm Algorithms and Complexity
 It is recommended that you read through the exam before you begin. Answer all questions in the space provided. Name: Answer whether the following statements are true or false and briefly explain your answer
It is recommended that you read through the exam before you begin. Answer all questions in the space provided. Name: Answer whether the following statements are true or false and briefly explain your answer
Quicksort. Recurrence analysis Quicksort introduction. November 17, 2017 Hassan Khosravi / Geoffrey Tien 1
 Quicksort Recurrence analysis Quicksort introduction November 17, 2017 Hassan Khosravi / Geoffrey Tien 1 Announcement Slight adjustment to lab 5 schedule (Monday sections A, B, E) Next week (Nov.20) regular
Quicksort Recurrence analysis Quicksort introduction November 17, 2017 Hassan Khosravi / Geoffrey Tien 1 Announcement Slight adjustment to lab 5 schedule (Monday sections A, B, E) Next week (Nov.20) regular
Problem Set 2 Solutions
 Introduction to Algorithms October 1, 2004 Massachusetts Institute of Technology 6.046J/18.410J Professors Piotr Indyk and Charles E. Leiserson Handout 9 Problem Set 2 Solutions Reading: Chapters 5-9,
Introduction to Algorithms October 1, 2004 Massachusetts Institute of Technology 6.046J/18.410J Professors Piotr Indyk and Charles E. Leiserson Handout 9 Problem Set 2 Solutions Reading: Chapters 5-9,
CS 2110: INDUCTION DISCUSSION TOPICS
 CS 110: INDUCTION DISCUSSION TOPICS The following ideas are suggestions for how to handle your discussion classes. You can do as much or as little of this as you want. You can either present at the board,
CS 110: INDUCTION DISCUSSION TOPICS The following ideas are suggestions for how to handle your discussion classes. You can do as much or as little of this as you want. You can either present at the board,
CS Analysis of Recursive Algorithms and Brute Force
 CS483-05 Analysis of Recursive Algorithms and Brute Force Instructor: Fei Li Room 443 ST II Office hours: Tue. & Thur. 4:30pm - 5:30pm or by appointments lifei@cs.gmu.edu with subject: CS483 http://www.cs.gmu.edu/
CS483-05 Analysis of Recursive Algorithms and Brute Force Instructor: Fei Li Room 443 ST II Office hours: Tue. & Thur. 4:30pm - 5:30pm or by appointments lifei@cs.gmu.edu with subject: CS483 http://www.cs.gmu.edu/
MIDTERM I CMPS Winter 2013 Warmuth
 test I 1 MIDTERM I CMPS 101 - Winter 2013 Warmuth With Solutions NAME: Student ID: This exam is closed book, notes, computer and cell phone. Show partial solutions to get partial credit. Make sure you
test I 1 MIDTERM I CMPS 101 - Winter 2013 Warmuth With Solutions NAME: Student ID: This exam is closed book, notes, computer and cell phone. Show partial solutions to get partial credit. Make sure you
CS 598RM: Algorithmic Game Theory, Spring Practice Exam Solutions
 CS 598RM: Algorithmic Game Theory, Spring 2017 1. Answer the following. Practice Exam Solutions Agents 1 and 2 are bargaining over how to split a dollar. Each agent simultaneously demands share he would
CS 598RM: Algorithmic Game Theory, Spring 2017 1. Answer the following. Practice Exam Solutions Agents 1 and 2 are bargaining over how to split a dollar. Each agent simultaneously demands share he would
Data selection. Lower complexity bound for sorting
 Data selection. Lower complexity bound for sorting Lecturer: Georgy Gimel farb COMPSCI 220 Algorithms and Data Structures 1 / 12 1 Data selection: Quickselect 2 Lower complexity bound for sorting 3 The
Data selection. Lower complexity bound for sorting Lecturer: Georgy Gimel farb COMPSCI 220 Algorithms and Data Structures 1 / 12 1 Data selection: Quickselect 2 Lower complexity bound for sorting 3 The
CS 4104 Data and Algorithm Analysis. Recurrence Relations. Modeling Recursive Function Cost. Solving Recurrences. Clifford A. Shaffer.
 Department of Computer Science Virginia Tech Blacksburg, Virginia Copyright c 2010,2017 by Clifford A. Shaffer Data and Algorithm Analysis Title page Data and Algorithm Analysis Clifford A. Shaffer Spring
Department of Computer Science Virginia Tech Blacksburg, Virginia Copyright c 2010,2017 by Clifford A. Shaffer Data and Algorithm Analysis Title page Data and Algorithm Analysis Clifford A. Shaffer Spring
Algorithms. Quicksort. Slide credit: David Luebke (Virginia)
 1 Algorithms Quicksort Slide credit: David Luebke (Virginia) Sorting revisited We have seen algorithms for sorting: INSERTION-SORT, MERGESORT More generally: given a sequence of items Each item has a characteristic
1 Algorithms Quicksort Slide credit: David Luebke (Virginia) Sorting revisited We have seen algorithms for sorting: INSERTION-SORT, MERGESORT More generally: given a sequence of items Each item has a characteristic
Heaps Induction. Heaps. Heaps. Tirgul 6
 Tirgul 6 Induction A binary heap is a nearly complete binary tree stored in an array object In a max heap, the value of each node that of its children (In a min heap, the value of each node that of its
Tirgul 6 Induction A binary heap is a nearly complete binary tree stored in an array object In a max heap, the value of each node that of its children (In a min heap, the value of each node that of its
CS2223 Algorithms D Term 2009 Exam 3 Solutions
 CS2223 Algorithms D Term 2009 Exam 3 Solutions May 4, 2009 By Prof. Carolina Ruiz Dept. of Computer Science WPI PROBLEM 1: Asymptoptic Growth Rates (10 points) Let A and B be two algorithms with runtimes
CS2223 Algorithms D Term 2009 Exam 3 Solutions May 4, 2009 By Prof. Carolina Ruiz Dept. of Computer Science WPI PROBLEM 1: Asymptoptic Growth Rates (10 points) Let A and B be two algorithms with runtimes
Review Of Topics. Review: Induction
 Review Of Topics Asymptotic notation Solving recurrences Sorting algorithms Insertion sort Merge sort Heap sort Quick sort Counting sort Radix sort Medians/order statistics Randomized algorithm Worst-case
Review Of Topics Asymptotic notation Solving recurrences Sorting algorithms Insertion sort Merge sort Heap sort Quick sort Counting sort Radix sort Medians/order statistics Randomized algorithm Worst-case
Name Class Date. Geometric Sequences and Series Going Deeper. Writing Rules for a Geometric Sequence
 Name Class Date 5-3 Geometric Sequences and Series Going Deeper Essential question: How can you write a rule for a geometric sequence and find the sum of a finite geometric series? In a geometric sequence,
Name Class Date 5-3 Geometric Sequences and Series Going Deeper Essential question: How can you write a rule for a geometric sequence and find the sum of a finite geometric series? In a geometric sequence,
CS161: Algorithm Design and Analysis Recitation Section 3 Stanford University Week of 29 January, Problem 3-1.
 CS161: Algorithm Design and Analysis Recitation Section 3 Stanford University Week of 29 January, 2018 Problem 3-1. (Quicksort Median-of-3 Partition) One way to improve the randomized quicksort procedure
CS161: Algorithm Design and Analysis Recitation Section 3 Stanford University Week of 29 January, 2018 Problem 3-1. (Quicksort Median-of-3 Partition) One way to improve the randomized quicksort procedure
3.1 Induction: An informal introduction
 Chapter 3 Induction and Recursion 3.1 Induction: An informal introduction This section is intended as a somewhat informal introduction to The Principle of Mathematical Induction (PMI): a theorem that establishes
Chapter 3 Induction and Recursion 3.1 Induction: An informal introduction This section is intended as a somewhat informal introduction to The Principle of Mathematical Induction (PMI): a theorem that establishes
Section Summary. Sequences. Recurrence Relations. Summations Special Integer Sequences (optional)
 Section 2.4 Section Summary Sequences. o Examples: Geometric Progression, Arithmetic Progression Recurrence Relations o Example: Fibonacci Sequence Summations Special Integer Sequences (optional) Sequences
Section 2.4 Section Summary Sequences. o Examples: Geometric Progression, Arithmetic Progression Recurrence Relations o Example: Fibonacci Sequence Summations Special Integer Sequences (optional) Sequences
Advanced Analysis of Algorithms - Midterm (Solutions)
 Advanced Analysis of Algorithms - Midterm (Solutions) K. Subramani LCSEE, West Virginia University, Morgantown, WV {ksmani@csee.wvu.edu} 1 Problems 1. Solve the following recurrence using substitution:
Advanced Analysis of Algorithms - Midterm (Solutions) K. Subramani LCSEE, West Virginia University, Morgantown, WV {ksmani@csee.wvu.edu} 1 Problems 1. Solve the following recurrence using substitution:
CS 161 Summer 2009 Homework #2 Sample Solutions
 CS 161 Summer 2009 Homework #2 Sample Solutions Regrade Policy: If you believe an error has been made in the grading of your homework, you may resubmit it for a regrade. If the error consists of more than
CS 161 Summer 2009 Homework #2 Sample Solutions Regrade Policy: If you believe an error has been made in the grading of your homework, you may resubmit it for a regrade. If the error consists of more than
CS Data Structures and Algorithm Analysis
 CS 483 - Data Structures and Algorithm Analysis Lecture II: Chapter 2 R. Paul Wiegand George Mason University, Department of Computer Science February 1, 2006 Outline 1 Analysis Framework 2 Asymptotic
CS 483 - Data Structures and Algorithm Analysis Lecture II: Chapter 2 R. Paul Wiegand George Mason University, Department of Computer Science February 1, 2006 Outline 1 Analysis Framework 2 Asymptotic
TTIC / CMSC Algorithms. Lectures 1 and 2 + background material
 TTIC 31010 / CMSC 37000 - Algorithms Lectures 1 and 2 + background material Avrim Blum Toyota Technological Institute at Chicago January 7, 2019 ii Contents 1 Introduction to Algorithms, and the Divide
TTIC 31010 / CMSC 37000 - Algorithms Lectures 1 and 2 + background material Avrim Blum Toyota Technological Institute at Chicago January 7, 2019 ii Contents 1 Introduction to Algorithms, and the Divide
ECS 20: Discrete Mathematics for Computer Science UC Davis Phillip Rogaway June 12, Final Exam
 ECS 20: Discrete Mathematics for Computer Science Handout F UC Davis Phillip Rogaway June 12, 2000 Final Exam Instructions: Read the questions carefully; maybe I m not asking what you assume me to be asking!
ECS 20: Discrete Mathematics for Computer Science Handout F UC Davis Phillip Rogaway June 12, 2000 Final Exam Instructions: Read the questions carefully; maybe I m not asking what you assume me to be asking!
csci 210: Data Structures Program Analysis
 csci 210: Data Structures Program Analysis 1 Summary Summary analysis of algorithms asymptotic analysis big-o big-omega big-theta asymptotic notation commonly used functions discrete math refresher READING:
csci 210: Data Structures Program Analysis 1 Summary Summary analysis of algorithms asymptotic analysis big-o big-omega big-theta asymptotic notation commonly used functions discrete math refresher READING:
In-Class Soln 1. CS 361, Lecture 4. Today s Outline. In-Class Soln 2
 In-Class Soln 1 Let f(n) be an always positive function and let g(n) = f(n) log n. Show that f(n) = o(g(n)) CS 361, Lecture 4 Jared Saia University of New Mexico For any positive constant c, we want to
In-Class Soln 1 Let f(n) be an always positive function and let g(n) = f(n) log n. Show that f(n) = o(g(n)) CS 361, Lecture 4 Jared Saia University of New Mexico For any positive constant c, we want to
Weighted Activity Selection
 Weighted Activity Selection Problem This problem is a generalization of the activity selection problem that we solvd with a greedy algorithm. Given a set of activities A = {[l, r ], [l, r ],..., [l n,
Weighted Activity Selection Problem This problem is a generalization of the activity selection problem that we solvd with a greedy algorithm. Given a set of activities A = {[l, r ], [l, r ],..., [l n,
Math Circle: Recursion and Induction
 Math Circle: Recursion and Induction Prof. Wickerhauser 1 Recursion What can we compute, using only simple formulas and rules that everyone can understand? 1. Let us use N to denote the set of counting
Math Circle: Recursion and Induction Prof. Wickerhauser 1 Recursion What can we compute, using only simple formulas and rules that everyone can understand? 1. Let us use N to denote the set of counting
Algorithms Design & Analysis. Analysis of Algorithm
 Algorithms Design & Analysis Analysis of Algorithm Review Internship Stable Matching Algorithm 2 Outline Time complexity Computation model Asymptotic notions Recurrence Master theorem 3 The problem of
Algorithms Design & Analysis Analysis of Algorithm Review Internship Stable Matching Algorithm 2 Outline Time complexity Computation model Asymptotic notions Recurrence Master theorem 3 The problem of
Fast Sorting and Selection. A Lower Bound for Worst Case
 Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 0 Fast Sorting and Selection USGS NEIC. Public domain government image. A Lower Bound
Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 0 Fast Sorting and Selection USGS NEIC. Public domain government image. A Lower Bound
CS 350 Algorithms and Complexity
 1 CS 350 Algorithms and Complexity Fall 2015 Lecture 15: Limitations of Algorithmic Power Introduction to complexity theory Andrew P. Black Department of Computer Science Portland State University Lower
1 CS 350 Algorithms and Complexity Fall 2015 Lecture 15: Limitations of Algorithmic Power Introduction to complexity theory Andrew P. Black Department of Computer Science Portland State University Lower
CSC236 Week 3. Larry Zhang
 CSC236 Week 3 Larry Zhang 1 Announcements Problem Set 1 due this Friday Make sure to read Submission Instructions on the course web page. Search for Teammates on Piazza Educational memes: http://www.cs.toronto.edu/~ylzhang/csc236/memes.html
CSC236 Week 3 Larry Zhang 1 Announcements Problem Set 1 due this Friday Make sure to read Submission Instructions on the course web page. Search for Teammates on Piazza Educational memes: http://www.cs.toronto.edu/~ylzhang/csc236/memes.html
CS60007 Algorithm Design and Analysis 2018 Assignment 1
 CS60007 Algorithm Design and Analysis 2018 Assignment 1 Palash Dey and Swagato Sanyal Indian Institute of Technology, Kharagpur Please submit the solutions of the problems 6, 11, 12 and 13 (written in
CS60007 Algorithm Design and Analysis 2018 Assignment 1 Palash Dey and Swagato Sanyal Indian Institute of Technology, Kharagpur Please submit the solutions of the problems 6, 11, 12 and 13 (written in
CSEP 521 Applied Algorithms. Richard Anderson Winter 2013 Lecture 1
 CSEP 521 Applied Algorithms Richard Anderson Winter 2013 Lecture 1 CSEP 521 Course Introduction CSEP 521, Applied Algorithms Monday s, 6:30-9:20 pm CSE 305 and Microsoft Building 99 Instructor Richard
CSEP 521 Applied Algorithms Richard Anderson Winter 2013 Lecture 1 CSEP 521 Course Introduction CSEP 521, Applied Algorithms Monday s, 6:30-9:20 pm CSE 305 and Microsoft Building 99 Instructor Richard
Algorithm Analysis Recurrence Relation. Chung-Ang University, Jaesung Lee
 Algorithm Analysis Recurrence Relation Chung-Ang University, Jaesung Lee Recursion 2 Recursion 3 Recursion in Real-world Fibonacci sequence = + Initial conditions: = 0 and = 1. = + = + = + 0, 1, 1, 2,
Algorithm Analysis Recurrence Relation Chung-Ang University, Jaesung Lee Recursion 2 Recursion 3 Recursion in Real-world Fibonacci sequence = + Initial conditions: = 0 and = 1. = + = + = + 0, 1, 1, 2,
Data structures Exercise 1 solution. Question 1. Let s start by writing all the functions in big O notation:
 Data structures Exercise 1 solution Question 1 Let s start by writing all the functions in big O notation: f 1 (n) = 2017 = O(1), f 2 (n) = 2 log 2 n = O(n 2 ), f 3 (n) = 2 n = O(2 n ), f 4 (n) = 1 = O
Data structures Exercise 1 solution Question 1 Let s start by writing all the functions in big O notation: f 1 (n) = 2017 = O(1), f 2 (n) = 2 log 2 n = O(n 2 ), f 3 (n) = 2 n = O(2 n ), f 4 (n) = 1 = O
Chapter 5. Divide and Conquer CLRS 4.3. Slides by Kevin Wayne. Copyright 2005 Pearson-Addison Wesley. All rights reserved.
 Chapter 5 Divide and Conquer CLRS 4.3 Slides by Kevin Wayne. Copyright 2005 Pearson-Addison Wesley. All rights reserved. 1 Divide-and-Conquer Divide-and-conquer. Break up problem into several parts. Solve
Chapter 5 Divide and Conquer CLRS 4.3 Slides by Kevin Wayne. Copyright 2005 Pearson-Addison Wesley. All rights reserved. 1 Divide-and-Conquer Divide-and-conquer. Break up problem into several parts. Solve
INF2220: algorithms and data structures Series 1
 Universitetet i Oslo Institutt for Informatikk I. Yu, D. Karabeg INF2220: algorithms and data structures Series 1 Topic Function growth & estimation of running time, trees (Exercises with hints for solution)
Universitetet i Oslo Institutt for Informatikk I. Yu, D. Karabeg INF2220: algorithms and data structures Series 1 Topic Function growth & estimation of running time, trees (Exercises with hints for solution)
Algorithm Analysis Divide and Conquer. Chung-Ang University, Jaesung Lee
 Algorithm Analysis Divide and Conquer Chung-Ang University, Jaesung Lee Introduction 2 Divide and Conquer Paradigm 3 Advantages of Divide and Conquer Solving Difficult Problems Algorithm Efficiency Parallelism
Algorithm Analysis Divide and Conquer Chung-Ang University, Jaesung Lee Introduction 2 Divide and Conquer Paradigm 3 Advantages of Divide and Conquer Solving Difficult Problems Algorithm Efficiency Parallelism
Park School Mathematics Curriculum Book 9, Lesson 2: Introduction to Logarithms
 Park School Mathematics Curriculum Book 9, Lesson : Introduction to Logarithms We re providing this lesson as a sample of the curriculum we use at the Park School of Baltimore in grades 9-11. If you d
Park School Mathematics Curriculum Book 9, Lesson : Introduction to Logarithms We re providing this lesson as a sample of the curriculum we use at the Park School of Baltimore in grades 9-11. If you d
V. Adamchik 1. Recurrences. Victor Adamchik Fall of 2005
 V. Adamchi Recurrences Victor Adamchi Fall of 00 Plan Multiple roots. More on multiple roots. Inhomogeneous equations 3. Divide-and-conquer recurrences In the previous lecture we have showed that if the
V. Adamchi Recurrences Victor Adamchi Fall of 00 Plan Multiple roots. More on multiple roots. Inhomogeneous equations 3. Divide-and-conquer recurrences In the previous lecture we have showed that if the
Economics 3012 Strategic Behavior Andy McLennan October 20, 2006
 Economics 301 Strategic Behavior Andy McLennan October 0, 006 Lecture 11 Topics Problem Set 9 Extensive Games of Imperfect Information An Example General Description Strategies and Nash Equilibrium Beliefs
Economics 301 Strategic Behavior Andy McLennan October 0, 006 Lecture 11 Topics Problem Set 9 Extensive Games of Imperfect Information An Example General Description Strategies and Nash Equilibrium Beliefs
Divide and Conquer Algorithms. CSE 101: Design and Analysis of Algorithms Lecture 14
 Divide and Conquer Algorithms CSE 101: Design and Analysis of Algorithms Lecture 14 CSE 101: Design and analysis of algorithms Divide and conquer algorithms Reading: Sections 2.3 and 2.4 Homework 6 will
Divide and Conquer Algorithms CSE 101: Design and Analysis of Algorithms Lecture 14 CSE 101: Design and analysis of algorithms Divide and conquer algorithms Reading: Sections 2.3 and 2.4 Homework 6 will
CS 361, Lecture 14. Outline
 Bucket Sort CS 361, Lecture 14 Jared Saia University of New Mexico Bucket sort assumes that the input is drawn from a uniform distribution over the range [0, 1) Basic idea is to divide the interval [0,
Bucket Sort CS 361, Lecture 14 Jared Saia University of New Mexico Bucket sort assumes that the input is drawn from a uniform distribution over the range [0, 1) Basic idea is to divide the interval [0,
CS173 Running Time and Big-O. Tandy Warnow
 CS173 Running Time and Big-O Tandy Warnow CS 173 Running Times and Big-O analysis Tandy Warnow Today s material We will cover: Running time analysis Review of running time analysis of Bubblesort Review
CS173 Running Time and Big-O Tandy Warnow CS 173 Running Times and Big-O analysis Tandy Warnow Today s material We will cover: Running time analysis Review of running time analysis of Bubblesort Review
PUTNAM TRAINING MATHEMATICAL INDUCTION. Exercises
 PUTNAM TRAINING MATHEMATICAL INDUCTION (Last updated: December 11, 017) Remark. This is a list of exercises on mathematical induction. Miguel A. Lerma 1. Prove that n! > n for all n 4. Exercises. Prove
PUTNAM TRAINING MATHEMATICAL INDUCTION (Last updated: December 11, 017) Remark. This is a list of exercises on mathematical induction. Miguel A. Lerma 1. Prove that n! > n for all n 4. Exercises. Prove
CS 170 Algorithms Spring 2009 David Wagner Final
 CS 170 Algorithms Spring 2009 David Wagner Final PRINT your name:, (last) SIGN your name: (first) PRINT your Unix account login: Your TA s name: Name of the person sitting to your left: Name of the person
CS 170 Algorithms Spring 2009 David Wagner Final PRINT your name:, (last) SIGN your name: (first) PRINT your Unix account login: Your TA s name: Name of the person sitting to your left: Name of the person
Introduction to Fall 2009 Artificial Intelligence Final Exam
 CS 188 Introduction to Fall 2009 Artificial Intelligence Final Exam INSTRUCTIONS You have 3 hours. The exam is closed book, closed notes except a two-page crib sheet. Please use non-programmable calculators
CS 188 Introduction to Fall 2009 Artificial Intelligence Final Exam INSTRUCTIONS You have 3 hours. The exam is closed book, closed notes except a two-page crib sheet. Please use non-programmable calculators
BMT 2016 Orthogonal Polynomials 12 March Welcome to the power round! This year s topic is the theory of orthogonal polynomials.
 Power Round Welcome to the power round! This year s topic is the theory of orthogonal polynomials. I. You should order your papers with the answer sheet on top, and you should number papers addressing
Power Round Welcome to the power round! This year s topic is the theory of orthogonal polynomials. I. You should order your papers with the answer sheet on top, and you should number papers addressing
Task Type Grouping Strategy. Scaffolding Task Individual/Partner Task. Practice Task Individual/Partner Task. Scaffolding Task Individual/Partner Task
 SELECTED TASKS The following tasks represent the level of depth, rigor, and complexity expected of all Coordinate Algebra students. These tasks, or tasks of similar depth and rigor, should be used to demonstrate
SELECTED TASKS The following tasks represent the level of depth, rigor, and complexity expected of all Coordinate Algebra students. These tasks, or tasks of similar depth and rigor, should be used to demonstrate
Written Homework #1: Analysis of Algorithms
 Written Homework #1: Analysis of Algorithms CIS 121 Fall 2016 cis121-16fa-staff@googlegroups.com Due: Thursday, September 15th, 2015 before 10:30am (You must submit your homework online via Canvas. A paper
Written Homework #1: Analysis of Algorithms CIS 121 Fall 2016 cis121-16fa-staff@googlegroups.com Due: Thursday, September 15th, 2015 before 10:30am (You must submit your homework online via Canvas. A paper
