CS 161 Summer 2009 Homework #2 Sample Solutions
|
|
|
- Randall McDaniel
- 5 years ago
- Views:
Transcription
1 CS 161 Summer 2009 Homework #2 Sample Solutions Regrade Policy: If you believe an error has been made in the grading of your homework, you may resubmit it for a regrade. If the error consists of more than an error in addition of points, please include with your homework a detailed explanation of which problems you think you deserve more points on and why. We reserve the right to regrade your entire homework, so your final grade may either increase or decrease. Problem 1 [24 points] Remarks: (1) You need to specify the constant ɛ and c in formal proof; (2) To apply case 3 of Master Theorem, you need to check regularity condition first. (a) (3 points) T (n) = 3T (n/2) + n log n Answer: T (n) = Θ(n log 2 3 ). We will apply case 1 of the Master Theorem. Since f(n) = n log n and n log b a = n log 2 3 n We can pick ɛ = 0.1 to satisfy the conditions of the theorem. Therefore T (n) = Θ(n log 2 3 ). (b) (3 points) T (n) = 5T (n/5) + n/ log n Answer: T (n) = Θ(n log log n). We have a = 5, b = 5, f(n) = n/ log n. So n log b a = n. None of the Master Theorem cases may be applied here, since f(n) is neither polynomially bigger or smaller than n, and is not equal to Θ(n log k n) for any k 0. Therefore, we will solve this problem by algebraic substitution. T (n) = 5T (n/5) + n/ log n = 5(5T (n/25) + (n/5)/ log(n/5)) + n/ log n = 25T (n/25) + n/ log(n/5) + n/ log n... i 1 = 5 i T (n/5 i ) + (n/ log(n/5 j )) j=0 1
2 2 When i = log 5 n, then first term reduces to 5 log 5 n T (1), so we have log 5 n 1 T (n) = nθ(1) + (n/ log(n/5 j )) j=0 log 5 n 1 = Θ(n) + n (1/(log n j log 5)) j=0 log 5 n 1 = Θ(n) + n/ log 5 (1/(log 5 n j)) j=0 log 5 n = Θ(n) + n log 5 2 (1/k) This is the harmonic sum, so we have T (n) = Θ(n) + c 2 n ln(log 5 n) + Θ(1) = Θ(n log log n) (c) (3 points) T (n) = 4T (n/2) + n 2 n Answer: T (n) = Θ(n 2 n). We will use case 3 of the Master Theorem, Since f(n) = n 2 n = n 2.5 and n log b a = n log 2 4 = n 2. We can pick ɛ = 0.1 to satisfy the conditions of the theorem. Moreover if c = 0.9 we can verify that 4(n/2) 2.5 c n 2.5. Therefore the premises for case 3 hold and we conclude that T (n) = Θ(n 2 n). (d) (3 points) T (n) = 3T (n/3 + 5) + n/2 Answer: T (n) = Θ(n log n). We will solve the problem by guess-and-check. By induction, T (n) is a monotonically increasing function. Thus, for the lower bound, since T (n/3) T (n/3 + 5), using case 2 of the Master Theorem, we have T (n) = Ω(n log n). For the upper bound, we can show T (n) = O(n log n). For the base cases n 30, we can choose a sufficiently large constant d 1 such that T (n) < d 1 n log n. For the inductive step, assume for all k < n, that T (n) < d 1 n log n. Then for k = n > 30, we have n/3 + 5 < n 15, then T (n) = 3T (n/3 + 5) + n/2 < 3T (n 15) + n/2 k=1 < 3(3T ((n 15)/3 + 5) + (n 15)/2) + n/2 < 9T (n/3) + 3(n 15)/2 + n/2 < 9d 1 (n/3) log(n/3) + 2n 45/2 < 3d 1 n log(n/3) + 2n 45/2 < 3d 1 n log n
3 CS161 Homework #2 Sample Solutions 3 The last line holds for n 1 and d 1 > 2 3 log 3. Thus we can proof by induction that 2 T (n) < cn log n for all n, where c = max{d 1, 3d 1, log 3 }. Therefore, T (n) = O(n log n) and T (n) = Θ(n log n). (e) (3 points) T (n) = 2T (n/2) + n/ log n Answer: T (n) = Θ(n log log n). Similar to part(b). (f) (3 points) T (n) = T (n/2) + T (n/4) + T (n/8) + n Answer: T (n) = Θ(n). We solve this problem by guess-and-check. The total size on each level of the recurrence tree is less than n, so we guess that f(n) = n will dominate. Base case, for n 0 = 1, we have T (n) = n. Inductive step: Assume for all i < n that c 1 n T (i) c 2 n. Then, c 1 n/2 + c 1 n/4 + c 1 n/8 + kn T (n) c 2 n/2 + c 2 n/4 + c 2 n/8 + kn c 1 n(7/8 + k/c 1 ) T (n) c 2 n(7/8 + k/c 2 ) If c 1 8k and c 2 8k, then c 1 n T (n) c 2 n. So, T (n) = Θ(n). (g) (3 points) T (n) = T (n 1) + 1/n Answer: T (n) = Θ(log n). We solve this problem by algebraic substitution. (j) (3 points) T (n) = nt ( n) + n T (n) = T (n 1) + 1/n = T (n 2) + 1/(n 1) + 1/n... = Θ(1) + n 1/i i=1 = Θ(1) + ln n Answer: T (n) = Θ(n log log n). We solve it by algebraic substitution. T (n) = nt ( n) + n = n 1/2 (n 1/4 T (n 1/4 + n 1/2 )) + n = n 3/4 T (n 1/4 ) + 2n = n 3/4 (n 1/8 T (n 1/8 + n 1/4 )) + 2n = n 7/8 T (n 1/8 ) + 3n... = n 1 1/2k T (n 1/2k ) + kn
4 4 When n 1/2k falls under 2, we have k > log log n. We then have T (n) = n 1 1/ log n T (2)+ n log log n = Θ(n log log n). Problem 2 [5 points] Answer: a = 48. A : T (n) = 7T (n/2) + n 2. We have a = 7, b = 2, f(n) = n 2. Apply case 1 of the Master Theorem, we get T (n) = Θ(n log 2 7 ). A : T (n) = at (n/4) + n 2. We have a = a, b = 4, f(n) = n 2. If log 2 7 > log 4 a > 2, Apply case 1 of the Master Theorem, we will get T (n) = Θ(n log 4a ) < Θ(n log 27 ) = T (n). Solving the inequation, we get a < 49. When log 4 a 2, by case 2 and case 3 of the Master Theorem, we won t get a faster algorithm than A. Problem 3 [30 points] (a) (10 points) Insertion-Sort: O(kn). Define an inversion in A as a pair (i, j) where i < j and A[i] > A[j]. If every element is within k slots from its proper position, then there are at most O(kn) inversions. Thus the running time for Insertion-Sort is O(n + I) = O(kn), where I is the number of inversions in A. The reason is because I is exactly number of shifting operations we need in Insertion- Sort. For the inner loop of the algorithm, each element A[i] is shifted left as many times as l i where l i is number of elements j so that j < i and A[j] > A[i]. Therefore number of shif ting operations needed = = n i=1 l i n {(j, i) (j, i) is an inversion in A, j} i=1 = total number of inversions in A Now consider the outer loop of the Insertion-Sort algorithm. It iterates n times as the index traverses the array and it is independent of the number of inversions. Therefore the total running time of Insertion-Sort is O(I + n) = O(kn). Merge-Sort: Θ(n log n). Same Recurrence function T (n) = 2T (n/2) + Θ(n). QuickSort: Best-case scenario, rewrite recurrence as T (n) = T (k) + T (n k) + Θ(n). The depth
5 CS161 Homework #2 Sample Solutions 5 of the recurrence tree is n/k. Thus T (n) = O(n 2 /k). When k << n, it is close to O(n 2 ). Worst-case scenario (sorted), rewrite recurrence as T (n) = T (1) + T (n 1) + Θ(n). Thus T (n) = O(n 2 ). (b) (5 points) O(kn). The idea of the bubble-sort algorithm is, starting from the left, compare adjacent items and keep bubbling the larger one to the right until all items reach their proper positions. From 3(a), we know there are at most O(kn) inversions. After each swap operation in line 6, the number of inversion will decrease by one. Thus line 6 will be executed at most O(kn) times, which is the bottle-neck of the running time. (c) (10 points) For the solution to this problem, we are going to use a heap. We assume that we have a heap with the following subroutines: Make-Heap() returns a new empty heap. Insert(H, key, value) inserts the key/value pair into the heap. Extract-Min(H) removes the key/value pair with the smallest key from the heap, returning the value. We consider A as a set of sorted lists. In particular, notice that A[i] < A[i + 2k + 1], for all i n 2k 1. That s because the element at slot i can at most move forwards during sorting to slot i + k and the element at slot i + 2k + 1 can at most move backwards during sorting to slot i + k + 1. For simplicity, assume n is divided by 2k. We divide the array A into 2k lists defined as follows: A 1 = [A[1], A[2k + 1], A[4k + 1],..., A[n (2k 1)]] A 2 = [A[2], A[2k + 2], A[4k + 2],..., A[n (2k 2)]]... A 2k = [A[2k], A[4k], A[6k],..., A[n]] Each of these lists is sorted, and of size n. We can sort these lists in O(n log k) time using the Sort-K-Sorted algorithm below.
6 6 Algorithm 1 Sort-K-Sorted(A, n, k) 1: H = Make-Heap() 2: for i = 1 to 2k do 3: Insert(H, A[i], i) 4: end for 5: for i = 1 to n do 6: j=extract-min(h) 7: B[i] = A[j] 8: if j + 2k n then 9: Insert(H, A[j + 2k], j) 10: end if 11: end for 12: return B Running time analysis: Since there are never more than 2k element in the heap, Each Extract-Min and Insert operation requires O(log k) time. The second loop is is repeated n times, resulting in an O(n log k) running time. (d) (5 points) The key invariant is to show that after every iteration of the loop, the heap contains the smallest element in every list. A formal induction proof is required here. Alternative Solution: Recall we already know how to merge two sorted lists that contain n elements in O(n) time. It is possible, then to merge the lists in a tournament. For example, for 2k = 8, where A + B means to merge lists A and B: Round 1: (A 1 + A 2 ), (A 3 + A 4 ), (A 5 + A 6 ), (A 7 + A 8 ) Round 2: (A 1 + A 2 + A 3 + A 4 ), (A 5 + A 6 + A 7 + A 8 ) Round 3: (A 1 + A 2 + A 3 + A 4 + A 5 + A 6 + A 7 + A 8 ) Notice that there are log k merge steps, each of which merges n elements and hence has a cost of O(n). This leads to the total running time of O(n log k). Problem 4 [15 points] (a) (5 points) Merge-Sort is the most amenable one because you can give a machine a part of the array in any order. QuickSort and Insertion-Sort are bad because one iteration depends on the state of the array based on previous iterations, which is complicated to communicate between machines. (b) (5 points) Split the array into m = 2 i subarrays. Call Merge-Sort on each subarray on separate machine. Once machines start to returning answers, use free machines to merge subarrys that are adjacent to each other.
7 CS161 Homework #2 Sample Solutions 7 (c) (5 points) Running time: O((n/m) log(n/m) + n). Since we are splitting the array into m = 2 i parts, each call of Merge-Sort on a subarray of size n/m will take O((n/m) log(n/m)).then we need to merge m sorted array into a big one, which will take linear time O(n). Thus the total time is O((n/m) log(n/m) + n). Alternative Solution: At the Merge step, we can use m/2 machines to merge all pairs of sorted subarrays, then m/4 machines for the next merge step, etc. This will give the same Big-O running time. Problem 5 [8 points] Insertion-Sort: Stable. We can prove it using the following loop invariant: At the start of each interaction of the for loop of lines 1-8 (page 17 of CLRS), if A[a] = A[b], a < b j 1 and distinct, then A[a] appeared before A[b] in teh initial array. Proof by induction is omitted here. Merge-Sort: Stable. We can prove it by induction on the fact that Merge-Sort (page 29 and 32 on CLRS) is stable. Base case: When we call Merge-Sort with indices p and r such that p r (therefore p == r), we return the same array. So calling Merge-Sort on an array of size one returns the same array, which is stable. Induction: We assume that calling Merge-Sort on an array of size less than n returns a stably sorted array. We then show that if we call Merge-Sort on an array of size n, we also return a stably sorted array. Each call of Merge-Sort contains two calls to Merge- Sort on half arrays, and in addition, merges these two subarrays and returns. Since we assume that the calls to Merge-Sort on smaller arrys return stably sorted arrays, we only need to show that the Merge step on two stably sorted arrays returns a stable array. if A[i] = A[j], i < j in the initial array, we need f(i) < f(j) in the new array, where f is the function which gives the new positions in the sorted array. If i and j are in the same half of the recursive Merge-Sort call, then by assumption, it hold. If i and j are in different subarrays, then we know that i is in the left subarray and j is in the right subarray since i < j. In the Merge step, we take the elements from the left subarray while it is less than or equal to the right subarray element (line 13). Therefore, we will take element i before taking element j and f(i) < f(j), the claim we are trying to prove. Bubble-Sort: Stable. Formal proof by induction is omitted here. The key point is that equal value elements are not swapped (line 5 in the pseudocode in Problem 3(b)). QuickSort: NOT stable. To make it stable, we can add a new field to each array element, which indicates the index of that element in the original array. Then, when we
8 8 sort, we can sort on the condition (line 4 on page 146 of CLRS) A[j] > x OR A[j] == x AND index(a[j]) < index(x). At the end of the sort, we are guaranteed to have all the elements in sorted order, and for any i < j, such that A[i] equals A[j], we will have index(a[j]) < index(a[i]) so the sort will be stable. Extra Credit [5 points] We will give a proof using the decision-tree technique. We already know that sorting the array requires Ω(n log n) comparisons. If k > n/2, then n log n = Ω(n log k), and the proof is complete. For the remainder of this proof, assume that k n/2. Our goal is to provide a lower-bound on the number of leaves in a decision tree for an algorithm that sorts an array in which every element is within k slots of its proper position. We therefore provide a lower bound on the number of possible permutations that satisfy this condition. First, break the array of size n into n/k blocks, each of size k, and the remainder of size n (mod k). For each block, there exist k! permutations, resulting in at least (k!) n/k total permutations of the entire array. None of these permutations move an element more than k slots. Notice that this undercounts the total number of permutations, since no element moves from one k-element block to another, and we ignore permutations of elements in the remainder block. We therefore conclude that the decision tree has at least (k!) n/k leaves. Since the decision tree is a binary tree, we can then conclude that the height of the decision tree is log((k!) n/k ) n/k log(k!) n/k c 1 k log k c 1 (n k) log k c 1 n log k/2 = Ω(n log k) The last step follows because of our assumption that k n/2.
Solutions. Problem 1: Suppose a polynomial in n of degree d has the form
 Assignment 1 1. Problem 3-1 on p. 57 2. Problem 3-2 on p. 58 3. Problem 4-5 on p. 86 4. Problem 6-1 on p. 142 5. Problem 7-4 on p. 162 6. Prove correctness (including halting) of SelectionSort (use loop
Assignment 1 1. Problem 3-1 on p. 57 2. Problem 3-2 on p. 58 3. Problem 4-5 on p. 86 4. Problem 6-1 on p. 142 5. Problem 7-4 on p. 162 6. Prove correctness (including halting) of SelectionSort (use loop
Week 5: Quicksort, Lower bound, Greedy
 Week 5: Quicksort, Lower bound, Greedy Agenda: Quicksort: Average case Lower bound for sorting Greedy method 1 Week 5: Quicksort Recall Quicksort: The ideas: Pick one key Compare to others: partition into
Week 5: Quicksort, Lower bound, Greedy Agenda: Quicksort: Average case Lower bound for sorting Greedy method 1 Week 5: Quicksort Recall Quicksort: The ideas: Pick one key Compare to others: partition into
Quicksort (CLRS 7) We previously saw how the divide-and-conquer technique can be used to design sorting algorithm Merge-sort
 Quicksort (CLRS 7) We previously saw how the divide-and-conquer technique can be used to design sorting algorithm Merge-sort Partition n elements array A into two subarrays of n/2 elements each Sort the
Quicksort (CLRS 7) We previously saw how the divide-and-conquer technique can be used to design sorting algorithm Merge-sort Partition n elements array A into two subarrays of n/2 elements each Sort the
CS 577 Introduction to Algorithms: Strassen s Algorithm and the Master Theorem
 CS 577 Introduction to Algorithms: Jin-Yi Cai University of Wisconsin Madison In the last class, we described InsertionSort and showed that its worst-case running time is Θ(n 2 ). Check Figure 2.2 for
CS 577 Introduction to Algorithms: Jin-Yi Cai University of Wisconsin Madison In the last class, we described InsertionSort and showed that its worst-case running time is Θ(n 2 ). Check Figure 2.2 for
Lecture 1: Asymptotics, Recurrences, Elementary Sorting
 Lecture 1: Asymptotics, Recurrences, Elementary Sorting Instructor: Outline 1 Introduction to Asymptotic Analysis Rate of growth of functions Comparing and bounding functions: O, Θ, Ω Specifying running
Lecture 1: Asymptotics, Recurrences, Elementary Sorting Instructor: Outline 1 Introduction to Asymptotic Analysis Rate of growth of functions Comparing and bounding functions: O, Θ, Ω Specifying running
Data structures Exercise 1 solution. Question 1. Let s start by writing all the functions in big O notation:
 Data structures Exercise 1 solution Question 1 Let s start by writing all the functions in big O notation: f 1 (n) = 2017 = O(1), f 2 (n) = 2 log 2 n = O(n 2 ), f 3 (n) = 2 n = O(2 n ), f 4 (n) = 1 = O
Data structures Exercise 1 solution Question 1 Let s start by writing all the functions in big O notation: f 1 (n) = 2017 = O(1), f 2 (n) = 2 log 2 n = O(n 2 ), f 3 (n) = 2 n = O(2 n ), f 4 (n) = 1 = O
Computational Complexity - Pseudocode and Recursions
 Computational Complexity - Pseudocode and Recursions Nicholas Mainardi 1 Dipartimento di Elettronica e Informazione Politecnico di Milano nicholas.mainardi@polimi.it June 6, 2018 1 Partly Based on Alessandro
Computational Complexity - Pseudocode and Recursions Nicholas Mainardi 1 Dipartimento di Elettronica e Informazione Politecnico di Milano nicholas.mainardi@polimi.it June 6, 2018 1 Partly Based on Alessandro
Recommended readings: Description of Quicksort in my notes, Ch7 of your CLRS text.
 Chapter 1 Quicksort 1.1 Prerequisites You need to be familiar with the divide-and-conquer paradigm, standard notations for expressing the time-complexity of an algorithm, like the big-oh, big-omega notations.
Chapter 1 Quicksort 1.1 Prerequisites You need to be familiar with the divide-and-conquer paradigm, standard notations for expressing the time-complexity of an algorithm, like the big-oh, big-omega notations.
COMP Analysis of Algorithms & Data Structures
 COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 4 - Jan. 10, 2018 CLRS 1.1, 1.2, 2.2, 3.1, 4.3, 4.5 University of Manitoba Picture is from the cover of the textbook CLRS. 1 /
COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 4 - Jan. 10, 2018 CLRS 1.1, 1.2, 2.2, 3.1, 4.3, 4.5 University of Manitoba Picture is from the cover of the textbook CLRS. 1 /
COMP Analysis of Algorithms & Data Structures
 COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 4 - Jan. 14, 2019 CLRS 1.1, 1.2, 2.2, 3.1, 4.3, 4.5 University of Manitoba Picture is from the cover of the textbook CLRS. COMP
COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 4 - Jan. 14, 2019 CLRS 1.1, 1.2, 2.2, 3.1, 4.3, 4.5 University of Manitoba Picture is from the cover of the textbook CLRS. COMP
Data Structures and Algorithms CSE 465
 Data Structures and Algorithms CSE 465 LECTURE 8 Analyzing Quick Sort Sofya Raskhodnikova and Adam Smith Reminder: QuickSort Quicksort an n-element array: 1. Divide: Partition the array around a pivot
Data Structures and Algorithms CSE 465 LECTURE 8 Analyzing Quick Sort Sofya Raskhodnikova and Adam Smith Reminder: QuickSort Quicksort an n-element array: 1. Divide: Partition the array around a pivot
Quicksort. Where Average and Worst Case Differ. S.V. N. (vishy) Vishwanathan. University of California, Santa Cruz
 Quicksort Where Average and Worst Case Differ S.V. N. (vishy) Vishwanathan University of California, Santa Cruz vishy@ucsc.edu February 1, 2016 S.V. N. Vishwanathan (UCSC) CMPS101 1 / 28 Basic Idea Outline
Quicksort Where Average and Worst Case Differ S.V. N. (vishy) Vishwanathan University of California, Santa Cruz vishy@ucsc.edu February 1, 2016 S.V. N. Vishwanathan (UCSC) CMPS101 1 / 28 Basic Idea Outline
CS 4407 Algorithms Lecture 2: Iterative and Divide and Conquer Algorithms
 CS 4407 Algorithms Lecture 2: Iterative and Divide and Conquer Algorithms Prof. Gregory Provan Department of Computer Science University College Cork 1 Lecture Outline CS 4407, Algorithms Growth Functions
CS 4407 Algorithms Lecture 2: Iterative and Divide and Conquer Algorithms Prof. Gregory Provan Department of Computer Science University College Cork 1 Lecture Outline CS 4407, Algorithms Growth Functions
Big O 2/14/13. Administrative. Does it terminate? David Kauchak cs302 Spring 2013
 /4/3 Administrative Big O David Kauchak cs3 Spring 3 l Assignment : how d it go? l Assignment : out soon l CLRS code? l Videos Insertion-sort Insertion-sort Does it terminate? /4/3 Insertion-sort Loop
/4/3 Administrative Big O David Kauchak cs3 Spring 3 l Assignment : how d it go? l Assignment : out soon l CLRS code? l Videos Insertion-sort Insertion-sort Does it terminate? /4/3 Insertion-sort Loop
CSCI 3110 Assignment 6 Solutions
 CSCI 3110 Assignment 6 Solutions December 5, 2012 2.4 (4 pts) Suppose you are choosing between the following three algorithms: 1. Algorithm A solves problems by dividing them into five subproblems of half
CSCI 3110 Assignment 6 Solutions December 5, 2012 2.4 (4 pts) Suppose you are choosing between the following three algorithms: 1. Algorithm A solves problems by dividing them into five subproblems of half
Review Of Topics. Review: Induction
 Review Of Topics Asymptotic notation Solving recurrences Sorting algorithms Insertion sort Merge sort Heap sort Quick sort Counting sort Radix sort Medians/order statistics Randomized algorithm Worst-case
Review Of Topics Asymptotic notation Solving recurrences Sorting algorithms Insertion sort Merge sort Heap sort Quick sort Counting sort Radix sort Medians/order statistics Randomized algorithm Worst-case
Data Structures and Algorithms
 Data Structures and Algorithms Spring 2017-2018 Outline 1 Sorting Algorithms (contd.) Outline Sorting Algorithms (contd.) 1 Sorting Algorithms (contd.) Analysis of Quicksort Time to sort array of length
Data Structures and Algorithms Spring 2017-2018 Outline 1 Sorting Algorithms (contd.) Outline Sorting Algorithms (contd.) 1 Sorting Algorithms (contd.) Analysis of Quicksort Time to sort array of length
CIS 121 Data Structures and Algorithms with Java Spring Big-Oh Notation Monday, January 22/Tuesday, January 23
 CIS 11 Data Structures and Algorithms with Java Spring 018 Big-Oh Notation Monday, January /Tuesday, January 3 Learning Goals Review Big-Oh and learn big/small omega/theta notations Discuss running time
CIS 11 Data Structures and Algorithms with Java Spring 018 Big-Oh Notation Monday, January /Tuesday, January 3 Learning Goals Review Big-Oh and learn big/small omega/theta notations Discuss running time
MA008/MIIZ01 Design and Analysis of Algorithms Lecture Notes 3
 MA008 p.1/37 MA008/MIIZ01 Design and Analysis of Algorithms Lecture Notes 3 Dr. Markus Hagenbuchner markus@uow.edu.au. MA008 p.2/37 Exercise 1 (from LN 2) Asymptotic Notation When constants appear in exponents
MA008 p.1/37 MA008/MIIZ01 Design and Analysis of Algorithms Lecture Notes 3 Dr. Markus Hagenbuchner markus@uow.edu.au. MA008 p.2/37 Exercise 1 (from LN 2) Asymptotic Notation When constants appear in exponents
Asymptotic Algorithm Analysis & Sorting
 Asymptotic Algorithm Analysis & Sorting (Version of 5th March 2010) (Based on original slides by John Hamer and Yves Deville) We can analyse an algorithm without needing to run it, and in so doing we can
Asymptotic Algorithm Analysis & Sorting (Version of 5th March 2010) (Based on original slides by John Hamer and Yves Deville) We can analyse an algorithm without needing to run it, and in so doing we can
Lecture 4. Quicksort
 Lecture 4. Quicksort T. H. Cormen, C. E. Leiserson and R. L. Rivest Introduction to Algorithms, 3rd Edition, MIT Press, 2009 Sungkyunkwan University Hyunseung Choo choo@skku.edu Copyright 2000-2018 Networking
Lecture 4. Quicksort T. H. Cormen, C. E. Leiserson and R. L. Rivest Introduction to Algorithms, 3rd Edition, MIT Press, 2009 Sungkyunkwan University Hyunseung Choo choo@skku.edu Copyright 2000-2018 Networking
Analysis of Algorithms CMPSC 565
 Analysis of Algorithms CMPSC 565 LECTURES 38-39 Randomized Algorithms II Quickselect Quicksort Running time Adam Smith L1.1 Types of randomized analysis Average-case analysis : Assume data is distributed
Analysis of Algorithms CMPSC 565 LECTURES 38-39 Randomized Algorithms II Quickselect Quicksort Running time Adam Smith L1.1 Types of randomized analysis Average-case analysis : Assume data is distributed
b + O(n d ) where a 1, b > 1, then O(n d log n) if a = b d d ) if a < b d O(n log b a ) if a > b d
 CS161, Lecture 4 Median, Selection, and the Substitution Method Scribe: Albert Chen and Juliana Cook (2015), Sam Kim (2016), Gregory Valiant (2017) Date: January 23, 2017 1 Introduction Last lecture, we
CS161, Lecture 4 Median, Selection, and the Substitution Method Scribe: Albert Chen and Juliana Cook (2015), Sam Kim (2016), Gregory Valiant (2017) Date: January 23, 2017 1 Introduction Last lecture, we
1 Divide and Conquer (September 3)
 The control of a large force is the same principle as the control of a few men: it is merely a question of dividing up their numbers. Sun Zi, The Art of War (c. 400 C.E.), translated by Lionel Giles (1910)
The control of a large force is the same principle as the control of a few men: it is merely a question of dividing up their numbers. Sun Zi, The Art of War (c. 400 C.E.), translated by Lionel Giles (1910)
Exercise Sheet #1 Solutions, Computer Science, A M. Hallett, K. Smith a k n b k = n b + k. a k n b k c 1 n b k. a k n b.
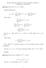 Exercise Sheet #1 Solutions, Computer Science, 308-251A M. Hallett, K. Smith 2002 Question 1.1: Prove (n + a) b = Θ(n b ). Binomial Expansion: Show O(n b ): (n + a) b = For any c 1 > b = O(n b ). Show
Exercise Sheet #1 Solutions, Computer Science, 308-251A M. Hallett, K. Smith 2002 Question 1.1: Prove (n + a) b = Θ(n b ). Binomial Expansion: Show O(n b ): (n + a) b = For any c 1 > b = O(n b ). Show
CS161: Algorithm Design and Analysis Recitation Section 3 Stanford University Week of 29 January, Problem 3-1.
 CS161: Algorithm Design and Analysis Recitation Section 3 Stanford University Week of 29 January, 2018 Problem 3-1. (Quicksort Median-of-3 Partition) One way to improve the randomized quicksort procedure
CS161: Algorithm Design and Analysis Recitation Section 3 Stanford University Week of 29 January, 2018 Problem 3-1. (Quicksort Median-of-3 Partition) One way to improve the randomized quicksort procedure
Analysis of Algorithms I: Asymptotic Notation, Induction, and MergeSort
 Analysis of Algorithms I: Asymptotic Notation, Induction, and MergeSort Xi Chen Columbia University We continue with two more asymptotic notation: o( ) and ω( ). Let f (n) and g(n) are functions that map
Analysis of Algorithms I: Asymptotic Notation, Induction, and MergeSort Xi Chen Columbia University We continue with two more asymptotic notation: o( ) and ω( ). Let f (n) and g(n) are functions that map
CS 310 Advanced Data Structures and Algorithms
 CS 310 Advanced Data Structures and Algorithms Runtime Analysis May 31, 2017 Tong Wang UMass Boston CS 310 May 31, 2017 1 / 37 Topics Weiss chapter 5 What is algorithm analysis Big O, big, big notations
CS 310 Advanced Data Structures and Algorithms Runtime Analysis May 31, 2017 Tong Wang UMass Boston CS 310 May 31, 2017 1 / 37 Topics Weiss chapter 5 What is algorithm analysis Big O, big, big notations
Inf 2B: Sorting, MergeSort and Divide-and-Conquer
 Inf 2B: Sorting, MergeSort and Divide-and-Conquer Lecture 7 of ADS thread Kyriakos Kalorkoti School of Informatics University of Edinburgh The Sorting Problem Input: Task: Array A of items with comparable
Inf 2B: Sorting, MergeSort and Divide-and-Conquer Lecture 7 of ADS thread Kyriakos Kalorkoti School of Informatics University of Edinburgh The Sorting Problem Input: Task: Array A of items with comparable
ECE250: Algorithms and Data Structures Analyzing and Designing Algorithms
 ECE50: Algorithms and Data Structures Analyzing and Designing Algorithms Ladan Tahvildari, PEng, SMIEEE Associate Professor Software Technologies Applied Research (STAR) Group Dept. of Elect. & Comp. Eng.
ECE50: Algorithms and Data Structures Analyzing and Designing Algorithms Ladan Tahvildari, PEng, SMIEEE Associate Professor Software Technologies Applied Research (STAR) Group Dept. of Elect. & Comp. Eng.
Reductions, Recursion and Divide and Conquer
 Chapter 5 Reductions, Recursion and Divide and Conquer CS 473: Fundamental Algorithms, Fall 2011 September 13, 2011 5.1 Reductions and Recursion 5.1.0.1 Reduction Reducing problem A to problem B: (A) Algorithm
Chapter 5 Reductions, Recursion and Divide and Conquer CS 473: Fundamental Algorithms, Fall 2011 September 13, 2011 5.1 Reductions and Recursion 5.1.0.1 Reduction Reducing problem A to problem B: (A) Algorithm
Introduction to Divide and Conquer
 Introduction to Divide and Conquer Sorting with O(n log n) comparisons and integer multiplication faster than O(n 2 ) Periklis A. Papakonstantinou York University Consider a problem that admits a straightforward
Introduction to Divide and Conquer Sorting with O(n log n) comparisons and integer multiplication faster than O(n 2 ) Periklis A. Papakonstantinou York University Consider a problem that admits a straightforward
Fundamental Algorithms
 Chapter 2: Sorting, Winter 2018/19 1 Fundamental Algorithms Chapter 2: Sorting Jan Křetínský Winter 2018/19 Chapter 2: Sorting, Winter 2018/19 2 Part I Simple Sorts Chapter 2: Sorting, Winter 2018/19 3
Chapter 2: Sorting, Winter 2018/19 1 Fundamental Algorithms Chapter 2: Sorting Jan Křetínský Winter 2018/19 Chapter 2: Sorting, Winter 2018/19 2 Part I Simple Sorts Chapter 2: Sorting, Winter 2018/19 3
Fundamental Algorithms
 Fundamental Algorithms Chapter 2: Sorting Harald Räcke Winter 2015/16 Chapter 2: Sorting, Winter 2015/16 1 Part I Simple Sorts Chapter 2: Sorting, Winter 2015/16 2 The Sorting Problem Definition Sorting
Fundamental Algorithms Chapter 2: Sorting Harald Räcke Winter 2015/16 Chapter 2: Sorting, Winter 2015/16 1 Part I Simple Sorts Chapter 2: Sorting, Winter 2015/16 2 The Sorting Problem Definition Sorting
CS361 Homework #3 Solutions
 CS6 Homework # Solutions. Suppose I have a hash table with 5 locations. I would like to know how many items I can store in it before it becomes fairly likely that I have a collision, i.e., that two items
CS6 Homework # Solutions. Suppose I have a hash table with 5 locations. I would like to know how many items I can store in it before it becomes fairly likely that I have a collision, i.e., that two items
CIS 121. Analysis of Algorithms & Computational Complexity. Slides based on materials provided by Mary Wootters (Stanford University)
 CIS 121 Analysis of Algorithms & Computational Complexity Slides based on materials provided by Mary Wootters (Stanford University) Today Sorting: InsertionSort vs MergeSort Analyzing the correctness of
CIS 121 Analysis of Algorithms & Computational Complexity Slides based on materials provided by Mary Wootters (Stanford University) Today Sorting: InsertionSort vs MergeSort Analyzing the correctness of
Solving recurrences. Frequently showing up when analysing divide&conquer algorithms or, more generally, recursive algorithms.
 Solving recurrences Frequently showing up when analysing divide&conquer algorithms or, more generally, recursive algorithms Example: Merge-Sort(A, p, r) 1: if p < r then 2: q (p + r)/2 3: Merge-Sort(A,
Solving recurrences Frequently showing up when analysing divide&conquer algorithms or, more generally, recursive algorithms Example: Merge-Sort(A, p, r) 1: if p < r then 2: q (p + r)/2 3: Merge-Sort(A,
Data Structures and Algorithms Chapter 3
 Data Structures and Algorithms Chapter 3 1. Divide and conquer 2. Merge sort, repeated substitutions 3. Tiling 4. Recurrences Recurrences Running times of algorithms with recursive calls can be described
Data Structures and Algorithms Chapter 3 1. Divide and conquer 2. Merge sort, repeated substitutions 3. Tiling 4. Recurrences Recurrences Running times of algorithms with recursive calls can be described
Divide & Conquer. Jordi Cortadella and Jordi Petit Department of Computer Science
 Divide & Conquer Jordi Cortadella and Jordi Petit Department of Computer Science Divide-and-conquer algorithms Strategy: Divide the problem into smaller subproblems of the same type of problem Solve the
Divide & Conquer Jordi Cortadella and Jordi Petit Department of Computer Science Divide-and-conquer algorithms Strategy: Divide the problem into smaller subproblems of the same type of problem Solve the
Math 391: Midterm 1.0 Spring 2016
 Math 391: Midterm 1.0 Spring 2016 James Skon skonjp@kenyon.edu Test date: October 5 Submission Instructions: Give all your assumptions. Show all your work. Be as complete as possible. Grading Problem 1
Math 391: Midterm 1.0 Spring 2016 James Skon skonjp@kenyon.edu Test date: October 5 Submission Instructions: Give all your assumptions. Show all your work. Be as complete as possible. Grading Problem 1
Analysis of Algorithms - Using Asymptotic Bounds -
 Analysis of Algorithms - Using Asymptotic Bounds - Andreas Ermedahl MRTC (Mälardalens Real-Time Research Center) andreas.ermedahl@mdh.se Autumn 004 Rehersal: Asymptotic bounds Gives running time bounds
Analysis of Algorithms - Using Asymptotic Bounds - Andreas Ermedahl MRTC (Mälardalens Real-Time Research Center) andreas.ermedahl@mdh.se Autumn 004 Rehersal: Asymptotic bounds Gives running time bounds
The maximum-subarray problem. Given an array of integers, find a contiguous subarray with the maximum sum. Very naïve algorithm:
 The maximum-subarray problem Given an array of integers, find a contiguous subarray with the maximum sum. Very naïve algorithm: Brute force algorithm: At best, θ(n 2 ) time complexity 129 Can we do divide
The maximum-subarray problem Given an array of integers, find a contiguous subarray with the maximum sum. Very naïve algorithm: Brute force algorithm: At best, θ(n 2 ) time complexity 129 Can we do divide
COMP 250: Quicksort. Carlos G. Oliver. February 13, Carlos G. Oliver COMP 250: Quicksort February 13, / 21
 COMP 250: Quicksort Carlos G. Oliver February 13, 2018 Carlos G. Oliver COMP 250: Quicksort February 13, 2018 1 / 21 1 1 https://xkcd.com/1667/ Carlos G. Oliver COMP 250: Quicksort February 13, 2018 2
COMP 250: Quicksort Carlos G. Oliver February 13, 2018 Carlos G. Oliver COMP 250: Quicksort February 13, 2018 1 / 21 1 1 https://xkcd.com/1667/ Carlos G. Oliver COMP 250: Quicksort February 13, 2018 2
Bucket-Sort. Have seen lower bound of Ω(nlog n) for comparisonbased. Some cheating algorithms achieve O(n), given certain assumptions re input
 Bucket-Sort Have seen lower bound of Ω(nlog n) for comparisonbased sorting algs Some cheating algorithms achieve O(n), given certain assumptions re input One example: bucket sort Assumption: input numbers
Bucket-Sort Have seen lower bound of Ω(nlog n) for comparisonbased sorting algs Some cheating algorithms achieve O(n), given certain assumptions re input One example: bucket sort Assumption: input numbers
Algorithms and Their Complexity
 CSCE 222 Discrete Structures for Computing David Kebo Houngninou Algorithms and Their Complexity Chapter 3 Algorithm An algorithm is a finite sequence of steps that solves a problem. Computational complexity
CSCE 222 Discrete Structures for Computing David Kebo Houngninou Algorithms and Their Complexity Chapter 3 Algorithm An algorithm is a finite sequence of steps that solves a problem. Computational complexity
Randomized Sorting Algorithms Quick sort can be converted to a randomized algorithm by picking the pivot element randomly. In this case we can show th
 CSE 3500 Algorithms and Complexity Fall 2016 Lecture 10: September 29, 2016 Quick sort: Average Run Time In the last lecture we started analyzing the expected run time of quick sort. Let X = k 1, k 2,...,
CSE 3500 Algorithms and Complexity Fall 2016 Lecture 10: September 29, 2016 Quick sort: Average Run Time In the last lecture we started analyzing the expected run time of quick sort. Let X = k 1, k 2,...,
CS 470/570 Divide-and-Conquer. Format of Divide-and-Conquer algorithms: Master Recurrence Theorem (simpler version)
 CS 470/570 Divide-and-Conquer Format of Divide-and-Conquer algorithms: Divide: Split the array or list into smaller pieces Conquer: Solve the same problem recursively on smaller pieces Combine: Build the
CS 470/570 Divide-and-Conquer Format of Divide-and-Conquer algorithms: Divide: Split the array or list into smaller pieces Conquer: Solve the same problem recursively on smaller pieces Combine: Build the
N/4 + N/2 + N = 2N 2.
 CS61B Summer 2006 Instructor: Erin Korber Lecture 24, 7 Aug. 1 Amortized Analysis For some of the data structures we ve discussed (namely hash tables and splay trees), it was claimed that the average time
CS61B Summer 2006 Instructor: Erin Korber Lecture 24, 7 Aug. 1 Amortized Analysis For some of the data structures we ve discussed (namely hash tables and splay trees), it was claimed that the average time
CS 4104 Data and Algorithm Analysis. Recurrence Relations. Modeling Recursive Function Cost. Solving Recurrences. Clifford A. Shaffer.
 Department of Computer Science Virginia Tech Blacksburg, Virginia Copyright c 2010,2017 by Clifford A. Shaffer Data and Algorithm Analysis Title page Data and Algorithm Analysis Clifford A. Shaffer Spring
Department of Computer Science Virginia Tech Blacksburg, Virginia Copyright c 2010,2017 by Clifford A. Shaffer Data and Algorithm Analysis Title page Data and Algorithm Analysis Clifford A. Shaffer Spring
1 Terminology and setup
 15-451/651: Design & Analysis of Algorithms August 31, 2017 Lecture #2 last changed: August 29, 2017 In this lecture, we will examine some simple, concrete models of computation, each with a precise definition
15-451/651: Design & Analysis of Algorithms August 31, 2017 Lecture #2 last changed: August 29, 2017 In this lecture, we will examine some simple, concrete models of computation, each with a precise definition
COMP Analysis of Algorithms & Data Structures
 COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 5 - Jan. 12, 2018 CLRS 1.1, 1.2, 2.2, 3.1, 4.3, 4.5 University of Manitoba Picture is from the cover of the textbook CLRS. 1 /
COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 5 - Jan. 12, 2018 CLRS 1.1, 1.2, 2.2, 3.1, 4.3, 4.5 University of Manitoba Picture is from the cover of the textbook CLRS. 1 /
Data Structures and Algorithms CSE 465
 Data Structures and Algorithms CSE 465 LECTURE 3 Asymptotic Notation O-, Ω-, Θ-, o-, ω-notation Divide and Conquer Merge Sort Binary Search Sofya Raskhodnikova and Adam Smith /5/0 Review Questions If input
Data Structures and Algorithms CSE 465 LECTURE 3 Asymptotic Notation O-, Ω-, Θ-, o-, ω-notation Divide and Conquer Merge Sort Binary Search Sofya Raskhodnikova and Adam Smith /5/0 Review Questions If input
Divide and conquer. Philip II of Macedon
 Divide and conquer Philip II of Macedon Divide and conquer 1) Divide your problem into subproblems 2) Solve the subproblems recursively, that is, run the same algorithm on the subproblems (when the subproblems
Divide and conquer Philip II of Macedon Divide and conquer 1) Divide your problem into subproblems 2) Solve the subproblems recursively, that is, run the same algorithm on the subproblems (when the subproblems
Algorithms Design & Analysis. Analysis of Algorithm
 Algorithms Design & Analysis Analysis of Algorithm Review Internship Stable Matching Algorithm 2 Outline Time complexity Computation model Asymptotic notions Recurrence Master theorem 3 The problem of
Algorithms Design & Analysis Analysis of Algorithm Review Internship Stable Matching Algorithm 2 Outline Time complexity Computation model Asymptotic notions Recurrence Master theorem 3 The problem of
Fall 2016 Test 1 with Solutions
 CS3510 Design & Analysis of Algorithms Fall 16 Section B Fall 2016 Test 1 with Solutions Instructor: Richard Peng In class, Friday, Sep 9, 2016 Do not open this quiz booklet until you are directed to do
CS3510 Design & Analysis of Algorithms Fall 16 Section B Fall 2016 Test 1 with Solutions Instructor: Richard Peng In class, Friday, Sep 9, 2016 Do not open this quiz booklet until you are directed to do
Ch01. Analysis of Algorithms
 Ch01. Analysis of Algorithms Input Algorithm Output Acknowledgement: Parts of slides in this presentation come from the materials accompanying the textbook Algorithm Design and Applications, by M. T. Goodrich
Ch01. Analysis of Algorithms Input Algorithm Output Acknowledgement: Parts of slides in this presentation come from the materials accompanying the textbook Algorithm Design and Applications, by M. T. Goodrich
1 Quick Sort LECTURE 7. OHSU/OGI (Winter 2009) ANALYSIS AND DESIGN OF ALGORITHMS
 OHSU/OGI (Winter 2009) CS532 ANALYSIS AND DESIGN OF ALGORITHMS LECTURE 7 1 Quick Sort QuickSort 1 is a classic example of divide and conquer. The hard work is to rearrange the elements of the array A[1..n]
OHSU/OGI (Winter 2009) CS532 ANALYSIS AND DESIGN OF ALGORITHMS LECTURE 7 1 Quick Sort QuickSort 1 is a classic example of divide and conquer. The hard work is to rearrange the elements of the array A[1..n]
Problem Set 2 Solutions
 Introduction to Algorithms October 1, 2004 Massachusetts Institute of Technology 6.046J/18.410J Professors Piotr Indyk and Charles E. Leiserson Handout 9 Problem Set 2 Solutions Reading: Chapters 5-9,
Introduction to Algorithms October 1, 2004 Massachusetts Institute of Technology 6.046J/18.410J Professors Piotr Indyk and Charles E. Leiserson Handout 9 Problem Set 2 Solutions Reading: Chapters 5-9,
CSCI Honor seminar in algorithms Homework 2 Solution
 CSCI 493.55 Honor seminar in algorithms Homework 2 Solution Saad Mneimneh Visiting Professor Hunter College of CUNY Problem 1: Rabin-Karp string matching Consider a binary string s of length n and another
CSCI 493.55 Honor seminar in algorithms Homework 2 Solution Saad Mneimneh Visiting Professor Hunter College of CUNY Problem 1: Rabin-Karp string matching Consider a binary string s of length n and another
P, NP, NP-Complete, and NPhard
 P, NP, NP-Complete, and NPhard Problems Zhenjiang Li 21/09/2011 Outline Algorithm time complicity P and NP problems NP-Complete and NP-Hard problems Algorithm time complicity Outline What is this course
P, NP, NP-Complete, and NPhard Problems Zhenjiang Li 21/09/2011 Outline Algorithm time complicity P and NP problems NP-Complete and NP-Hard problems Algorithm time complicity Outline What is this course
Analysis of Algorithms. Randomizing Quicksort
 Analysis of Algorithms Randomizing Quicksort Randomizing Quicksort Randomly permute the elements of the input array before sorting OR... modify the PARTITION procedure At each step of the algorithm we
Analysis of Algorithms Randomizing Quicksort Randomizing Quicksort Randomly permute the elements of the input array before sorting OR... modify the PARTITION procedure At each step of the algorithm we
CS483 Design and Analysis of Algorithms
 CS483 Design and Analysis of Algorithms Chapter 2 Divide and Conquer Algorithms Instructor: Fei Li lifei@cs.gmu.edu with subject: CS483 Office hours: Room 5326, Engineering Building, Thursday 4:30pm -
CS483 Design and Analysis of Algorithms Chapter 2 Divide and Conquer Algorithms Instructor: Fei Li lifei@cs.gmu.edu with subject: CS483 Office hours: Room 5326, Engineering Building, Thursday 4:30pm -
Lecture 2: Asymptotic Notation CSCI Algorithms I
 Lecture 2: Asymptotic Notation CSCI 700 - Algorithms I Andrew Rosenberg September 2, 2010 Last Time Review Insertion Sort Analysis of Runtime Proof of Correctness Today Asymptotic Notation Its use in analyzing
Lecture 2: Asymptotic Notation CSCI 700 - Algorithms I Andrew Rosenberg September 2, 2010 Last Time Review Insertion Sort Analysis of Runtime Proof of Correctness Today Asymptotic Notation Its use in analyzing
Sorting. Chapter 11. CSE 2011 Prof. J. Elder Last Updated: :11 AM
 Sorting Chapter 11-1 - Sorting Ø We have seen the advantage of sorted data representations for a number of applications q Sparse vectors q Maps q Dictionaries Ø Here we consider the problem of how to efficiently
Sorting Chapter 11-1 - Sorting Ø We have seen the advantage of sorted data representations for a number of applications q Sparse vectors q Maps q Dictionaries Ø Here we consider the problem of how to efficiently
Quiz 1 Solutions. Problem 2. Asymptotics & Recurrences [20 points] (3 parts)
![Quiz 1 Solutions. Problem 2. Asymptotics & Recurrences [20 points] (3 parts) Quiz 1 Solutions. Problem 2. Asymptotics & Recurrences [20 points] (3 parts)](/thumbs/87/95581149.jpg) Introduction to Algorithms October 13, 2010 Massachusetts Institute of Technology 6.006 Fall 2010 Professors Konstantinos Daskalakis and Patrick Jaillet Quiz 1 Solutions Quiz 1 Solutions Problem 1. We
Introduction to Algorithms October 13, 2010 Massachusetts Institute of Technology 6.006 Fall 2010 Professors Konstantinos Daskalakis and Patrick Jaillet Quiz 1 Solutions Quiz 1 Solutions Problem 1. We
Module 1: Analyzing the Efficiency of Algorithms
 Module 1: Analyzing the Efficiency of Algorithms Dr. Natarajan Meghanathan Professor of Computer Science Jackson State University Jackson, MS 39217 E-mail: natarajan.meghanathan@jsums.edu What is an Algorithm?
Module 1: Analyzing the Efficiency of Algorithms Dr. Natarajan Meghanathan Professor of Computer Science Jackson State University Jackson, MS 39217 E-mail: natarajan.meghanathan@jsums.edu What is an Algorithm?
Fall 2017 November 10, Written Homework 5
 CS1800 Discrete Structures Profs. Aslam, Gold, & Pavlu Fall 2017 November 10, 2017 Assigned: Mon Nov 13 2017 Due: Wed Nov 29 2017 Instructions: Written Homework 5 The assignment has to be uploaded to blackboard
CS1800 Discrete Structures Profs. Aslam, Gold, & Pavlu Fall 2017 November 10, 2017 Assigned: Mon Nov 13 2017 Due: Wed Nov 29 2017 Instructions: Written Homework 5 The assignment has to be uploaded to blackboard
Divide & Conquer. Jordi Cortadella and Jordi Petit Department of Computer Science
 Divide & Conquer Jordi Cortadella and Jordi Petit Department of Computer Science Divide-and-conquer algorithms Strategy: Divide the problem into smaller subproblems of the same type of problem Solve the
Divide & Conquer Jordi Cortadella and Jordi Petit Department of Computer Science Divide-and-conquer algorithms Strategy: Divide the problem into smaller subproblems of the same type of problem Solve the
Algorithms and Data Structures 2016 Week 5 solutions (Tues 9th - Fri 12th February)
 Algorithms and Data Structures 016 Week 5 solutions (Tues 9th - Fri 1th February) 1. Draw the decision tree (under the assumption of all-distinct inputs) Quicksort for n = 3. answer: (of course you should
Algorithms and Data Structures 016 Week 5 solutions (Tues 9th - Fri 1th February) 1. Draw the decision tree (under the assumption of all-distinct inputs) Quicksort for n = 3. answer: (of course you should
data structures and algorithms lecture 2
 data structures and algorithms 2018 09 06 lecture 2 recall: insertion sort Algorithm insertionsort(a, n): for j := 2 to n do key := A[j] i := j 1 while i 1 and A[i] > key do A[i + 1] := A[i] i := i 1 A[i
data structures and algorithms 2018 09 06 lecture 2 recall: insertion sort Algorithm insertionsort(a, n): for j := 2 to n do key := A[j] i := j 1 while i 1 and A[i] > key do A[i + 1] := A[i] i := i 1 A[i
A design paradigm. Divide and conquer: (When) does decomposing a problem into smaller parts help? 09/09/ EECS 3101
 A design paradigm Divide and conquer: (When) does decomposing a problem into smaller parts help? 09/09/17 112 Multiplying complex numbers (from Jeff Edmonds slides) INPUT: Two pairs of integers, (a,b),
A design paradigm Divide and conquer: (When) does decomposing a problem into smaller parts help? 09/09/17 112 Multiplying complex numbers (from Jeff Edmonds slides) INPUT: Two pairs of integers, (a,b),
Lecture 5: Loop Invariants and Insertion-sort
 Lecture 5: Loop Invariants and Insertion-sort COMS10007 - Algorithms Dr. Christian Konrad 11.01.2019 Dr. Christian Konrad Lecture 5: Loop Invariants and Insertion-sort 1 / 12 Proofs by Induction Structure
Lecture 5: Loop Invariants and Insertion-sort COMS10007 - Algorithms Dr. Christian Konrad 11.01.2019 Dr. Christian Konrad Lecture 5: Loop Invariants and Insertion-sort 1 / 12 Proofs by Induction Structure
5 + 9(10) + 3(100) + 0(1000) + 2(10000) =
 Chapter 5 Analyzing Algorithms So far we have been proving statements about databases, mathematics and arithmetic, or sequences of numbers. Though these types of statements are common in computer science,
Chapter 5 Analyzing Algorithms So far we have been proving statements about databases, mathematics and arithmetic, or sequences of numbers. Though these types of statements are common in computer science,
Algorithms. Quicksort. Slide credit: David Luebke (Virginia)
 1 Algorithms Quicksort Slide credit: David Luebke (Virginia) Sorting revisited We have seen algorithms for sorting: INSERTION-SORT, MERGESORT More generally: given a sequence of items Each item has a characteristic
1 Algorithms Quicksort Slide credit: David Luebke (Virginia) Sorting revisited We have seen algorithms for sorting: INSERTION-SORT, MERGESORT More generally: given a sequence of items Each item has a characteristic
Quick Sort Notes , Spring 2010
 Quick Sort Notes 18.310, Spring 2010 0.1 Randomized Median Finding In a previous lecture, we discussed the problem of finding the median of a list of m elements, or more generally the element of rank m.
Quick Sort Notes 18.310, Spring 2010 0.1 Randomized Median Finding In a previous lecture, we discussed the problem of finding the median of a list of m elements, or more generally the element of rank m.
Ch 01. Analysis of Algorithms
 Ch 01. Analysis of Algorithms Input Algorithm Output Acknowledgement: Parts of slides in this presentation come from the materials accompanying the textbook Algorithm Design and Applications, by M. T.
Ch 01. Analysis of Algorithms Input Algorithm Output Acknowledgement: Parts of slides in this presentation come from the materials accompanying the textbook Algorithm Design and Applications, by M. T.
1. [10 marks] Consider the following two algorithms that find the two largest elements in an array A[1..n], where n >= 2.
![1. [10 marks] Consider the following two algorithms that find the two largest elements in an array A[1..n], where n >= 2. 1. [10 marks] Consider the following two algorithms that find the two largest elements in an array A[1..n], where n >= 2.](/thumbs/73/68822500.jpg) CSC 6 H5S Homework Assignment # 1 Spring 010 Worth: 11% Due: Monday February 1 (at class) For each question, please write up detailed answers carefully. Make sure that you use notation and terminology
CSC 6 H5S Homework Assignment # 1 Spring 010 Worth: 11% Due: Monday February 1 (at class) For each question, please write up detailed answers carefully. Make sure that you use notation and terminology
CSCE 750, Spring 2001 Notes 2 Page 1 4 Chapter 4 Sorting ffl Reasons for studying sorting is a big deal pedagogically useful Λ the application itself
 CSCE 750, Spring 2001 Notes 2 Page 1 4 Chapter 4 Sorting ffl Reasons for studying sorting is a big deal pedagogically useful Λ the application itself is easy to understand Λ a complete analysis can often
CSCE 750, Spring 2001 Notes 2 Page 1 4 Chapter 4 Sorting ffl Reasons for studying sorting is a big deal pedagogically useful Λ the application itself is easy to understand Λ a complete analysis can often
Mergesort and Recurrences (CLRS 2.3, 4.4)
 Mergesort and Recurrences (CLRS 2.3, 4.4) We saw a couple of O(n 2 ) algorithms for sorting. Today we ll see a different approach that runs in O(n lg n) and uses one of the most powerful techniques for
Mergesort and Recurrences (CLRS 2.3, 4.4) We saw a couple of O(n 2 ) algorithms for sorting. Today we ll see a different approach that runs in O(n lg n) and uses one of the most powerful techniques for
Divide-and-conquer: Order Statistics. Curs: Fall 2017
 Divide-and-conquer: Order Statistics Curs: Fall 2017 The divide-and-conquer strategy. 1. Break the problem into smaller subproblems, 2. recursively solve each problem, 3. appropriately combine their answers.
Divide-and-conquer: Order Statistics Curs: Fall 2017 The divide-and-conquer strategy. 1. Break the problem into smaller subproblems, 2. recursively solve each problem, 3. appropriately combine their answers.
Divide & Conquer. CS 320, Fall Dr. Geri Georg, Instructor CS320 Div&Conq 1
 Divide & Conquer CS 320, Fall 2017 Dr. Geri Georg, Instructor georg@colostate.edu CS320 Div&Conq 1 Strategy 1. Divide the problem up into equal sized sub problems 2. Solve the sub problems recursively
Divide & Conquer CS 320, Fall 2017 Dr. Geri Georg, Instructor georg@colostate.edu CS320 Div&Conq 1 Strategy 1. Divide the problem up into equal sized sub problems 2. Solve the sub problems recursively
Selection and Adversary Arguments. COMP 215 Lecture 19
 Selection and Adversary Arguments COMP 215 Lecture 19 Selection Problems We want to find the k'th largest entry in an unsorted array. Could be the largest, smallest, median, etc. Ideas for an n lg n algorithm?
Selection and Adversary Arguments COMP 215 Lecture 19 Selection Problems We want to find the k'th largest entry in an unsorted array. Could be the largest, smallest, median, etc. Ideas for an n lg n algorithm?
Introduction to Algorithms 6.046J/18.401J
 Introduction to Algorithms 6.046J/8.40J Lecture Prof. Piotr Indyk Welcome to Introduction to Algorithms, Spring 08 Handouts. Course Information. Calendar 3. Signup sheet (PLEASE return at the end of this
Introduction to Algorithms 6.046J/8.40J Lecture Prof. Piotr Indyk Welcome to Introduction to Algorithms, Spring 08 Handouts. Course Information. Calendar 3. Signup sheet (PLEASE return at the end of this
Methods for solving recurrences
 Methods for solving recurrences Analyzing the complexity of mergesort The merge function Consider the following implementation: 1 int merge ( int v1, int n1, int v, int n ) { 3 int r = malloc ( ( n1+n
Methods for solving recurrences Analyzing the complexity of mergesort The merge function Consider the following implementation: 1 int merge ( int v1, int n1, int v, int n ) { 3 int r = malloc ( ( n1+n
Analysis of Algorithm Efficiency. Dr. Yingwu Zhu
 Analysis of Algorithm Efficiency Dr. Yingwu Zhu Measure Algorithm Efficiency Time efficiency How fast the algorithm runs; amount of time required to accomplish the task Our focus! Space efficiency Amount
Analysis of Algorithm Efficiency Dr. Yingwu Zhu Measure Algorithm Efficiency Time efficiency How fast the algorithm runs; amount of time required to accomplish the task Our focus! Space efficiency Amount
Homework 1 Submission
 Homework Submission Sample Solution; Due Date: Thursday, May 4, :59 pm Directions: Your solutions should be typed and submitted as a single pdf on Gradescope by the due date. L A TEX is preferred but not
Homework Submission Sample Solution; Due Date: Thursday, May 4, :59 pm Directions: Your solutions should be typed and submitted as a single pdf on Gradescope by the due date. L A TEX is preferred but not
Average Case Analysis. October 11, 2011
 Average Case Analysis October 11, 2011 Worst-case analysis Worst-case analysis gives an upper bound for the running time of a single execution of an algorithm with a worst-case input and worst-case random
Average Case Analysis October 11, 2011 Worst-case analysis Worst-case analysis gives an upper bound for the running time of a single execution of an algorithm with a worst-case input and worst-case random
An analogy from Calculus: limits
 COMP 250 Fall 2018 35 - big O Nov. 30, 2018 We have seen several algorithms in the course, and we have loosely characterized their runtimes in terms of the size n of the input. We say that the algorithm
COMP 250 Fall 2018 35 - big O Nov. 30, 2018 We have seen several algorithms in the course, and we have loosely characterized their runtimes in terms of the size n of the input. We say that the algorithm
CS Analysis of Recursive Algorithms and Brute Force
 CS483-05 Analysis of Recursive Algorithms and Brute Force Instructor: Fei Li Room 443 ST II Office hours: Tue. & Thur. 4:30pm - 5:30pm or by appointments lifei@cs.gmu.edu with subject: CS483 http://www.cs.gmu.edu/
CS483-05 Analysis of Recursive Algorithms and Brute Force Instructor: Fei Li Room 443 ST II Office hours: Tue. & Thur. 4:30pm - 5:30pm or by appointments lifei@cs.gmu.edu with subject: CS483 http://www.cs.gmu.edu/
Divide and Conquer. Arash Rafiey. 27 October, 2016
 27 October, 2016 Divide the problem into a number of subproblems Divide the problem into a number of subproblems Conquer the subproblems by solving them recursively or if they are small, there must be
27 October, 2016 Divide the problem into a number of subproblems Divide the problem into a number of subproblems Conquer the subproblems by solving them recursively or if they are small, there must be
CS 5321: Advanced Algorithms - Recurrence. Acknowledgement. Outline. Ali Ebnenasir Department of Computer Science Michigan Technological University
 CS 5321: Advanced Algorithms - Recurrence Ali Ebnenasir Department of Computer Science Michigan Technological University Acknowledgement Eric Torng Moon Jung Chung Charles Ofria Outline Motivating example:
CS 5321: Advanced Algorithms - Recurrence Ali Ebnenasir Department of Computer Science Michigan Technological University Acknowledgement Eric Torng Moon Jung Chung Charles Ofria Outline Motivating example:
CMPT 307 : Divide-and-Conqer (Study Guide) Should be read in conjunction with the text June 2, 2015
 CMPT 307 : Divide-and-Conqer (Study Guide) Should be read in conjunction with the text June 2, 2015 1 Introduction The divide-and-conquer strategy is a general paradigm for algorithm design. This strategy
CMPT 307 : Divide-and-Conqer (Study Guide) Should be read in conjunction with the text June 2, 2015 1 Introduction The divide-and-conquer strategy is a general paradigm for algorithm design. This strategy
Divide and Conquer Algorithms. CSE 101: Design and Analysis of Algorithms Lecture 14
 Divide and Conquer Algorithms CSE 101: Design and Analysis of Algorithms Lecture 14 CSE 101: Design and analysis of algorithms Divide and conquer algorithms Reading: Sections 2.3 and 2.4 Homework 6 will
Divide and Conquer Algorithms CSE 101: Design and Analysis of Algorithms Lecture 14 CSE 101: Design and analysis of algorithms Divide and conquer algorithms Reading: Sections 2.3 and 2.4 Homework 6 will
Concrete models and tight upper/lower bounds
 Lecture 3 Concrete models and tight upper/lower bounds 3.1 Overview In this lecture, we will examine some simple, concrete models of computation, each with a precise definition of what counts as a step,
Lecture 3 Concrete models and tight upper/lower bounds 3.1 Overview In this lecture, we will examine some simple, concrete models of computation, each with a precise definition of what counts as a step,
CPSC 320 Sample Final Examination December 2013
 CPSC 320 Sample Final Examination December 2013 [10] 1. Answer each of the following questions with true or false. Give a short justification for each of your answers. [5] a. 6 n O(5 n ) lim n + This is
CPSC 320 Sample Final Examination December 2013 [10] 1. Answer each of the following questions with true or false. Give a short justification for each of your answers. [5] a. 6 n O(5 n ) lim n + This is
Outline. 1 Introduction. 3 Quicksort. 4 Analysis. 5 References. Idea. 1 Choose an element x and reorder the array as follows:
 Outline Computer Science 331 Quicksort Mike Jacobson Department of Computer Science University of Calgary Lecture #28 1 Introduction 2 Randomized 3 Quicksort Deterministic Quicksort Randomized Quicksort
Outline Computer Science 331 Quicksort Mike Jacobson Department of Computer Science University of Calgary Lecture #28 1 Introduction 2 Randomized 3 Quicksort Deterministic Quicksort Randomized Quicksort
CS 5321: Advanced Algorithms Analysis Using Recurrence. Acknowledgement. Outline
 CS 5321: Advanced Algorithms Analysis Using Recurrence Ali Ebnenasir Department of Computer Science Michigan Technological University Acknowledgement Eric Torng Moon Jung Chung Charles Ofria Outline Motivating
CS 5321: Advanced Algorithms Analysis Using Recurrence Ali Ebnenasir Department of Computer Science Michigan Technological University Acknowledgement Eric Torng Moon Jung Chung Charles Ofria Outline Motivating
Topic 17. Analysis of Algorithms
 Topic 17 Analysis of Algorithms Analysis of Algorithms- Review Efficiency of an algorithm can be measured in terms of : Time complexity: a measure of the amount of time required to execute an algorithm
Topic 17 Analysis of Algorithms Analysis of Algorithms- Review Efficiency of an algorithm can be measured in terms of : Time complexity: a measure of the amount of time required to execute an algorithm
Problem. Problem Given a dictionary and a word. Which page (if any) contains the given word? 3 / 26
 Binary Search Introduction Problem Problem Given a dictionary and a word. Which page (if any) contains the given word? 3 / 26 Strategy 1: Random Search Randomly select a page until the page containing
Binary Search Introduction Problem Problem Given a dictionary and a word. Which page (if any) contains the given word? 3 / 26 Strategy 1: Random Search Randomly select a page until the page containing
Algorithms. Jordi Planes. Escola Politècnica Superior Universitat de Lleida
 Algorithms Jordi Planes Escola Politècnica Superior Universitat de Lleida 2016 Syllabus What s been done Formal specification Computational Cost Transformation recursion iteration Divide and conquer Sorting
Algorithms Jordi Planes Escola Politècnica Superior Universitat de Lleida 2016 Syllabus What s been done Formal specification Computational Cost Transformation recursion iteration Divide and conquer Sorting
