Right-handed screw dislocation in an isotropic solid
|
|
|
- Sharlene Wood
- 6 years ago
- Views:
Transcription
1 Dislocation Mechanics Elastic Popeties of Isolated Dislocations Ou study of dislocations to this point has focused on thei geomety and thei ole in accommodating plastic defomation though thei motion. We now tun to anothe impotant aspect of dislocations: thei elastic fields. The emakable thing about dislocations is that while they leave a cystal intenally pefect afte they have passed though the cystal, they poduce elastic distotions in the cystal as long as they ae pesent. Thei elastic fields detemine, to a lage extent, how they inteact with each othe and with othe stuctual defects in the cystal. Ou study of the elastic popeties of dislocations will assume that the mateial in which they ae found is elastically isotopic. While most cystals ae not elastically isotopic, the famewok that emeges by assuming elastic isotopy is still quite useful and even easonably accuate fo most cystals. Scew Dislocation in an Infinite Cylinde We wish to descibe the elastic field of a ight-handed scew dislocation in an elastically isotopic solid. The diagam shows an infinitely long cylinde containing a scew dislocation unning along its axis. The outside adius of the cylinde is R while the adius of the small hole at the coe is o. The coe mateial is assumed to be emoved to avoid singula stesses and stains, as discussed befoe. Right-handed scew dislocation in an isotopic solid The elastic field of a scew dislocation in an isotopic elastic solid, such as shown in the diagam, is a poblem of anti-plane stain, a two dimensional elastic field which is chaacteized by the conditions that 154
2 u z = f (x, y) g(z), u x = u y = 0 that is, thee ae only z displacements, u z, and they depend only on the in-plane coodinate positions, (x, y), and not on z. The govening equation fo anti-plane stain elasticity poblems is Laplace s equation, u z = u z x + u z y = 0. We need a displacement field u z (x, y) that satisfies this equation and also satisfies the Buges condition: u ( / s)ds = b. By inspection one can guess that the ight solution is u z = b = b y tan1 x. It is easy to demonstate that this solution satisfies Laplaces s equation: u z x = b 1 1+ y x u z y = b 1 1+ y x u z x u z y y x = b y x + y 1 x = b x x + y = b (x + y )(0) y(x) (x + y ) = b (x + y )(0) x(y) (x + y ) = b xy (x + y ) = b xy (x + y ), so that Laplace s equation is satisfied: u z = u z x + u z y = 0. Since we know the displacement field, it is a simple matte to compute the elastic stains and stesses aound the dislocation. By diffeentiating the displacement field we can calculate the stains: 155
3 xz = u x z + u z x = b y x + y yz = u y z + u z y = b x x + y. These ae the only non-zeo stain components. Now we use Hooke s law to compute the coesponding stesses xz = μ xz = μb y x + y yz = μ yz = μb. x x + y In cylindical coodinates we could calculate the stains and stesses as follows: z = 1 u z + u z = z = μ z = μb b. A simple way to deive this basic esult is to conside a thin shell of adius and thickness d suounding a unit length of dislocation. If this shell is unwapped and flattened out we have a ectangula sheet of height and unit width with a shea stain of z = b /. The coesponding shea stess is then z = μ z = μb /, the same esult obtained above. We note that the stesses nea a dislocation line depend linealy on the shea modulus and Buges vecto and invesely on the distance fom the dislocation line. Thus the elastic field is singula, with a singulaity of the fom ij 1. It is the singula natue of this field that equies us to emove the coe fom consideation. Obviously, the solution beaks down in the coe of the dislocation whee the stesses cannot go to infinity and must be bounded. Linea elasticity beaks down in the coe as atoms slide past each othe. It is sometimes useful to convet the stesses fom one coodinate system to anothe. Using the coodinates shown below, the shea stess in the cylindical coodinate system, z, can be witten as z = a zk a l kl = a zx a z xz + a zz a x zx + a zy a z yz + a zz a y zy, whee a zx is the cosine of the angle between the diections z and x and whee a z is the cosine of the angle between and z, etc., ie. the diection cosines. It is easy to see that the diection cosines fo this tansfomation ae 156
4 so that Cylindical-Catesian coodinate tansfomation a zx = 0,a zy = 0,a zz = 1 a x = sin,a y = cos,a z = 0, z = sin zx + cos zy, which, using cos = x / x + y and sin = y / x + y and xz = μb y x + y yz = μb, x x + y leads back to z = μb 1 x + y = μb. Scew Dislocation in a Finite Cylinde The above solution fo the stesses about a scew dislocation is valid if the cylinde is infinitely long and constained at its ends so that it does not twist. If, instead, the cylinde is of finite length and toque fee, then the cylinde will twist when the dislocation is ceated and the stess field will be modified. The following diagam shows a dislocated cylinde in a constained state and the twist associated with the toque-fee state. The twist that occus when the cylinde is made toque-fee is called the Eshelby twist, afte J.D. Eshelby who fist studied these popeties in the 1950s. As shown in the diagam, when the cylinde is constained, the shea stesses, z, that act on any section of the cylinde add up to a toque, T z, that acts in 157
5 the cylinde. The supescipt is meant to denote an infinitely long cylinde. If that toque is eleased (the equivalent of applying an equal but oppositely signed toque) then the cylinde will twist as shown in the diagam. The toque acting in the constained cylinde can be expessed appoximately as T z = R o 0 z ddi whee the fist tems in the integal epesent the shea stess and aea element, constituting a shea foce, and the last tem epesents the moment am length fom the oigin. Using the basic solution fom above, z = μb we have, fo R >> o, T z = R o 0 ( μb )ddi R = μb d = μb R o o μbr. If the end of the cylinde is fee (o if the cylinde is of finite length) a toque cannot exist in the cylinde. To satisfy this end condition the above solution must be coected by supeimposing an image toque, T z = T z = μbr /, which is equal and opposite to the above toque. Supeimposing this image toque causes the cylinde to twist, as shown in the figue. Scew dislocation in an infinitely long, constained cylinde and in a cylinde that is unconstained and toque fee. 158
6 Tosion of a cylindical ba. We can calculate the additional o image displacements, stains and stesses associated with the image toque by finding a solution fo pue tosion. By inspection we can guess that the displacement field fo pue tosion is u = Az whee A is a constant to be detemined and the displacements ae linea in both and z. The coesponding elastic stains ae z = u z = A = u u + 1 u = 0 with all othe components zeo. The coesponding shea stesses ae then z = μ z = μa. The coesponding image toque is then T z which is T z R = z ddi = (μa)ddi = μa 3 d o 0 = μa R4 4 4 o 4 R whee again we use R >> o. o 0 μa R4 R o 159
7 By setting this toque equal and opposite to the oiginal toque we can find the constant A, T z = T z = μbr = μa R4, so that, A = b R. We now have the coection o image solution fo a scew dislocation in a cylinde of finite length. u = b R z z = b R z = μb R. The full stess field fo a scew dislocation in a cylinde of finite length is now z = z + z = μb μb R = μb 1 R. We see that nea the coe of the dislocation, whee << R, the standad solution is ecoveed. But the image solution becomes moe and moe impotant fa away fom the coe. Note that the shea stess changes sign nea the oute bounday of the cylinde. One inteesting aspect of this solution is that a finite cylinde containing a scew dislocation along its coe is expected to twist. Using the image displacement field, we can calculate the citical length fo which one complete evolution would be expected by setting u ( = R) = R : u ( = R) = b R z c = R z c = R. b This kind of twisting has been obseved in PbSe nanowies ecently by J. Zhu, Y. Cui et al. Natue Nanotechnlogy (008). 160
8 Eshelby twist in a PbSe nanowie. A scew dislocation is found along the axis of the main nanowie. The nanowie banches ae fee of dislocations and ae not twisted. (J. Zhu, Y. Cui et al. Natue Nanotechnology (008)) Edge Dislocation in a Cylinde We now descibe the elastic field of a positive edge dislocation in an elastically isotopic solid. The diagam below shows an edge dislocation in a cylinde of adius R with a small hole at the coe of adius o. Edge dislocation The elastic field of an edge dislocation is a poblem of plane defomation, specifically, plane stain. Note that when the dislocation is ceated, the slab of mateial lying in the xy plane emains plana when the dislocation is fomed and the thickness of that slab neithe inceases of deceases when the distotion is ceated. So it is a poblem of plane-stain defomation (the stains ae all inplane). Fo two dimensional plane defomation poblems, including plane stain, 161
9 the govening equation that detemines the elastic field is the bi-hamonic equation 4 = x + y x + y = 0, whee is a potential, o stess function, the deivatives of which poduce the stesses xx = y yy = x xy = xy. It can be shown that stess functions that satisfy the bi-hamonic equation lead to displacements that ae compatible and stesses that satisfy the conditions of equilibium. So any stess function that satisfies the bi-hamonic equation and also the bounday conditions fo the poblem povides the coect elastic field fo that poblem. In tems of pola o cylindical coodinates, = = = Solution fo an Edge Dislocation 1. The geneal solution to the bi-hamonic equation fo an edge dislocation takes the fom = f( )sin f( )= B 3 A ln, whee B and A ae constants to be detemined fom the bounday conditions. Because the field is peiodic in the dependence of the stess function on sin can be anticipated. It is easy to show that this function satisfies the bi-hamonic equation. Since fo a dislocation in an infinite solid the stesses ae expected to go to zeo at, it follows that B = 0 fo a cylinde of infinite adius R. Also, it can be shown that the Buges condition, u ( / s)ds = b equies that the constant A be selected as A = μb ( 1 ), whee is Poisson s atio. To show this we would need to compute the stesses fom the stess function, calculate the stains using Hooke s law, integate the 16
10 stains the get the displacements and then, finally, equie that they satisfy the Buges condition. So the stess function fo a positive edge dislocation in an infinite solid is = μb ln sin = A ln sin, ( 1 ) o in the Catesian coodinates = Ayln x + y. Stesses aound a Positive Edge Dislocation Using the stess function, we can now calculate the stesses aound the dislocation: = = 1 ( Asin ) [ 1+ ln ]+ 1 (A ln )(sin) = Asin = = Asin [ 1+ ln ] = Asin = 1 = 1 ( A ln )cos = Acos 163
11 The moe familia expessions fo the stesses about a positive edge dislocation ae the ones expessed in the Catesian coodinate system. Using the equations above in the Catesian coodinates we can easily find xx = y 3x + y y = A (x + y ) yy = x ( ) ( ) =A y x y (x + y ) ( ) xy = xy = A x x y (x + y ). Fo this plane-stain poblem we can also compute the out-of-plane stesses zz = ( xx + yy )= Ay x + y, which, of couse, comes fom the condition that zz = 0. We may also want to know the hydostatic pessue at any point in the solid aound the dislocation p = 1 ( 3 xx + yy + zz )= A (1 + )y 3 (x + y ). Visualization of the Stess Field It is helpful to develop an intuition about the stesses aound a dislocation, so that one can anticipate how dislocations inteact with each othe and with othe defects. The diagam below shows the in-plane stess components about a positive edge dislocation, as descibed by the equations above. We note that the signs of some of the components can be guessed fom the natue of the distotion about the exta half plane. Notice that the shea stess, xy, is natually positive on the ight hand side of the dislocation while that stess component is negative on the left hand side, consistent with the solution. Those signs ae expected fom the way the exta half plane displaces mateial at its edge, as shown in the figue. Since the exta half plane is expected to ceate hydostatic compession whee it is pesent, we can anticipate that both xx and yy (and zz fo that matte) ae all negative above (and positive below) the dislocation. The hydostatic compession and tensions expected ae shown in the diagam. Because an exta half plane is inseted, one can futhe guess that xx would be negative (compession) eveywhee above the slip plane while it would be positive (tension) eveywhee below the slip plane. Othe components of the stess field cannot be easily guessed and the fact that some of the stess components change sign along the 45 degee lines cannot be pedicted intuitively. Fo example, yy on eithe side of the dislocation has a sign that is opposite that of xx in those 164
12 same egions. One might emembe this by noting that a shea stess and not a hydostatic stess is found on eithe side of the dislocation. Visualization of the stess field about a positive edge dislocation. Edge Dislocation in a Cylinde of Finite Radius The solution we have descibed is valid fo a positive edge dislocation in an infinite elastic solid. If we want to have a solution of an edge dislocation in a cylinde of finite adius, then coections need to be made to account fo the taction-fee cylindical sufaces, ( = R) = ( = R) = 0. We do this by choosing a non-zeo value fo the constant B in the above stess function, so that we have a coection stess function descibing the coection field: = B 3 sin. Fist calculate the coection stesses 165
13 = = Bsin = B sin 3 + B3 ( sin ), and = 1 = 1 B3 cos. = B cos We equie that ( = R)= ( = R) + ( = R) = 0 ( = R)= ( = R) + ( = R) = 0. Consideing the component, we have ( = R) + ( = R) = 0 Asin R + brsin = 0, which gives B = A R. Consideing the component, we have ( = R) + ( = R) = 0 Acos, BRcos = 0 R which, again, gives B = A R. 166
14 Thus, this value of B leads to a coection stess field that makes the tactions on the cylindical suface zeo. With this coection the shea stess field fo a positive edge dislocation in a cylinde of finite adius is = + = Acos Acos R = Acos 1 R. The coection is simila in fom to the coection fo the finite length of the cylinde fo a scew dislocation, except in this case the stess goes continuously to zeo and does not change sign with inceasing adial distance fom the coe. Stess Field fo a Staight Mixed Dislocation Using the pinciple of supeposition of solutions fo linea elastic poblems, we can easily descibe the stess field fo a mixed dislocation by supeimposing the fields of the scew and edge pats of that dislocation. Buges vectos fo a mixed dislocation In the z coodinate system the stess field of the mixed dislocation in an infinite solid can be expessed as whee 0 ij = z, 0 z zz = = Asin = = Acos 167
15 and A = μb e (1 ) = μbsin (1 ) z = z = μb s = μb cos. The supeposition of elastic solutions is justified fo linea elasticity. The displacements, stains and stesses fo diffeent solutions can be added o supeimposed without any inteactions. The enegies of diffeent elastic fields depend quadatically on the stesses o stains and cannot be added in this way. 168
2. Plane Elasticity Problems
 S0 Solid Mechanics Fall 009. Plane lasticity Poblems Main Refeence: Theoy of lasticity by S.P. Timoshenko and J.N. Goodie McGaw-Hill New Yok. Chaptes 3..1 The plane-stess poblem A thin sheet of an isotopic
S0 Solid Mechanics Fall 009. Plane lasticity Poblems Main Refeence: Theoy of lasticity by S.P. Timoshenko and J.N. Goodie McGaw-Hill New Yok. Chaptes 3..1 The plane-stess poblem A thin sheet of an isotopic
7.2.1 Basic relations for Torsion of Circular Members
 Section 7. 7. osion In this section, the geomety to be consideed is that of a long slende cicula ba and the load is one which twists the ba. Such poblems ae impotant in the analysis of twisting components,
Section 7. 7. osion In this section, the geomety to be consideed is that of a long slende cicula ba and the load is one which twists the ba. Such poblems ae impotant in the analysis of twisting components,
2 Governing Equations
 2 Govening Equations This chapte develops the govening equations of motion fo a homogeneous isotopic elastic solid, using the linea thee-dimensional theoy of elasticity in cylindical coodinates. At fist,
2 Govening Equations This chapte develops the govening equations of motion fo a homogeneous isotopic elastic solid, using the linea thee-dimensional theoy of elasticity in cylindical coodinates. At fist,
Stress, Cauchy s equation and the Navier-Stokes equations
 Chapte 3 Stess, Cauchy s equation and the Navie-Stokes equations 3. The concept of taction/stess Conside the volume of fluid shown in the left half of Fig. 3.. The volume of fluid is subjected to distibuted
Chapte 3 Stess, Cauchy s equation and the Navie-Stokes equations 3. The concept of taction/stess Conside the volume of fluid shown in the left half of Fig. 3.. The volume of fluid is subjected to distibuted
B. Spherical Wave Propagation
 11/8/007 Spheical Wave Popagation notes 1/1 B. Spheical Wave Popagation Evey antenna launches a spheical wave, thus its powe density educes as a function of 1, whee is the distance fom the antenna. We
11/8/007 Spheical Wave Popagation notes 1/1 B. Spheical Wave Popagation Evey antenna launches a spheical wave, thus its powe density educes as a function of 1, whee is the distance fom the antenna. We
LINEAR PLATE BENDING
 LINEAR PLATE BENDING 1 Linea plate bending A plate is a body of which the mateial is located in a small egion aound a suface in the thee-dimensional space. A special suface is the mid-plane. Measued fom
LINEAR PLATE BENDING 1 Linea plate bending A plate is a body of which the mateial is located in a small egion aound a suface in the thee-dimensional space. A special suface is the mid-plane. Measued fom
15 Solving the Laplace equation by Fourier method
 5 Solving the Laplace equation by Fouie method I aleady intoduced two o thee dimensional heat equation, when I deived it, ecall that it taes the fom u t = α 2 u + F, (5.) whee u: [0, ) D R, D R is the
5 Solving the Laplace equation by Fouie method I aleady intoduced two o thee dimensional heat equation, when I deived it, ecall that it taes the fom u t = α 2 u + F, (5.) whee u: [0, ) D R, D R is the
THE LAPLACE EQUATION. The Laplace (or potential) equation is the equation. u = 0. = 2 x 2. x y 2 in R 2
 THE LAPLACE EQUATION The Laplace (o potential) equation is the equation whee is the Laplace opeato = 2 x 2 u = 0. in R = 2 x 2 + 2 y 2 in R 2 = 2 x 2 + 2 y 2 + 2 z 2 in R 3 The solutions u of the Laplace
THE LAPLACE EQUATION The Laplace (o potential) equation is the equation whee is the Laplace opeato = 2 x 2 u = 0. in R = 2 x 2 + 2 y 2 in R 2 = 2 x 2 + 2 y 2 + 2 z 2 in R 3 The solutions u of the Laplace
AH Mechanics Checklist (Unit 2) AH Mechanics Checklist (Unit 2) Circular Motion
 AH Mechanics Checklist (Unit ) AH Mechanics Checklist (Unit ) Cicula Motion No. kill Done 1 Know that cicula motion efes to motion in a cicle of constant adius Know that cicula motion is conveniently descibed
AH Mechanics Checklist (Unit ) AH Mechanics Checklist (Unit ) Cicula Motion No. kill Done 1 Know that cicula motion efes to motion in a cicle of constant adius Know that cicula motion is conveniently descibed
Stress Intensity Factor
 S 47 Factue Mechanics http://imechanicaog/node/7448 Zhigang Suo Stess Intensity Facto We have modeled a body by using the linea elastic theoy We have modeled a cack in the body by a flat plane, and the
S 47 Factue Mechanics http://imechanicaog/node/7448 Zhigang Suo Stess Intensity Facto We have modeled a body by using the linea elastic theoy We have modeled a cack in the body by a flat plane, and the
A dual-reciprocity boundary element method for axisymmetric thermoelastodynamic deformations in functionally graded solids
 APCOM & ISCM 11-14 th Decembe, 013, Singapoe A dual-ecipocity bounday element method fo axisymmetic themoelastodynamic defomations in functionally gaded solids *W. T. Ang and B. I. Yun Division of Engineeing
APCOM & ISCM 11-14 th Decembe, 013, Singapoe A dual-ecipocity bounday element method fo axisymmetic themoelastodynamic defomations in functionally gaded solids *W. T. Ang and B. I. Yun Division of Engineeing
Lecture 8 - Gauss s Law
 Lectue 8 - Gauss s Law A Puzzle... Example Calculate the potential enegy, pe ion, fo an infinite 1D ionic cystal with sepaation a; that is, a ow of equally spaced chages of magnitude e and altenating sign.
Lectue 8 - Gauss s Law A Puzzle... Example Calculate the potential enegy, pe ion, fo an infinite 1D ionic cystal with sepaation a; that is, a ow of equally spaced chages of magnitude e and altenating sign.
EM Boundary Value Problems
 EM Bounday Value Poblems 10/ 9 11/ By Ilekta chistidi & Lee, Seung-Hyun A. Geneal Desciption : Maxwell Equations & Loentz Foce We want to find the equations of motion of chaged paticles. The way to do
EM Bounday Value Poblems 10/ 9 11/ By Ilekta chistidi & Lee, Seung-Hyun A. Geneal Desciption : Maxwell Equations & Loentz Foce We want to find the equations of motion of chaged paticles. The way to do
To Feel a Force Chapter 7 Static equilibrium - torque and friction
 To eel a oce Chapte 7 Chapte 7: Static fiction, toque and static equilibium A. Review of foce vectos Between the eath and a small mass, gavitational foces of equal magnitude and opposite diection act on
To eel a oce Chapte 7 Chapte 7: Static fiction, toque and static equilibium A. Review of foce vectos Between the eath and a small mass, gavitational foces of equal magnitude and opposite diection act on
working pages for Paul Richards class notes; do not copy or circulate without permission from PGR 2004/11/3 10:50
 woking pages fo Paul Richads class notes; do not copy o ciculate without pemission fom PGR 2004/11/3 10:50 CHAPTER7 Solid angle, 3D integals, Gauss s Theoem, and a Delta Function We define the solid angle,
woking pages fo Paul Richads class notes; do not copy o ciculate without pemission fom PGR 2004/11/3 10:50 CHAPTER7 Solid angle, 3D integals, Gauss s Theoem, and a Delta Function We define the solid angle,
Lecture 3. Announce: Office Hours to be held Tuesdays 1-3pm in I've discussed plane wave solutions. When seeking more general solutions to
 Lectue 3. Announce: Office Hous to be held Tuesdays 1-3pm in 4115 I've discussed plane wave solutions. When seeking moe geneal solutions to ρ && u = (λ + 2µ) ( u) µ ( u) many people will decouple the PDE
Lectue 3. Announce: Office Hous to be held Tuesdays 1-3pm in 4115 I've discussed plane wave solutions. When seeking moe geneal solutions to ρ && u = (λ + 2µ) ( u) µ ( u) many people will decouple the PDE
Flux. Area Vector. Flux of Electric Field. Gauss s Law
 Gauss s Law Flux Flux in Physics is used to two distinct ways. The fist meaning is the ate of flow, such as the amount of wate flowing in a ive, i.e. volume pe unit aea pe unit time. O, fo light, it is
Gauss s Law Flux Flux in Physics is used to two distinct ways. The fist meaning is the ate of flow, such as the amount of wate flowing in a ive, i.e. volume pe unit aea pe unit time. O, fo light, it is
Computational Methods of Solid Mechanics. Project report
 Computational Methods of Solid Mechanics Poject epot Due on Dec. 6, 25 Pof. Allan F. Bowe Weilin Deng Simulation of adhesive contact with molecula potential Poject desciption In the poject, we will investigate
Computational Methods of Solid Mechanics Poject epot Due on Dec. 6, 25 Pof. Allan F. Bowe Weilin Deng Simulation of adhesive contact with molecula potential Poject desciption In the poject, we will investigate
Lecture 5. Torsion. Module 1. Deformation Pattern in Pure Torsion In Circular Cylinder. IDeALab. Prof. Y.Y.KIM. Solid Mechanics
 Lectue 5. Tosion Module 1. Defomation Patten in Pue Tosion In Cicula Cylinde Defomation Patten Shafts unde tosion ae eveywhee. Candall, An Intoduction to the Mechanics of solid, Mc Gaw-Hill, 1999 1 Defomation
Lectue 5. Tosion Module 1. Defomation Patten in Pue Tosion In Cicula Cylinde Defomation Patten Shafts unde tosion ae eveywhee. Candall, An Intoduction to the Mechanics of solid, Mc Gaw-Hill, 1999 1 Defomation
EM-2. 1 Coulomb s law, electric field, potential field, superposition q. Electric field of a point charge (1)
 EM- Coulomb s law, electic field, potential field, supeposition q ' Electic field of a point chage ( ') E( ) kq, whee k / 4 () ' Foce of q on a test chage e at position is ee( ) Electic potential O kq
EM- Coulomb s law, electic field, potential field, supeposition q ' Electic field of a point chage ( ') E( ) kq, whee k / 4 () ' Foce of q on a test chage e at position is ee( ) Electic potential O kq
Physics 2A Chapter 10 - Moment of Inertia Fall 2018
 Physics Chapte 0 - oment of netia Fall 08 The moment of inetia of a otating object is a measue of its otational inetia in the same way that the mass of an object is a measue of its inetia fo linea motion.
Physics Chapte 0 - oment of netia Fall 08 The moment of inetia of a otating object is a measue of its otational inetia in the same way that the mass of an object is a measue of its inetia fo linea motion.
8 Separation of Variables in Other Coordinate Systems
 8 Sepaation of Vaiables in Othe Coodinate Systems Fo the method of sepaation of vaiables to succeed you need to be able to expess the poblem at hand in a coodinate system in which the physical boundaies
8 Sepaation of Vaiables in Othe Coodinate Systems Fo the method of sepaation of vaiables to succeed you need to be able to expess the poblem at hand in a coodinate system in which the physical boundaies
you of a spring. The potential energy for a spring is given by the parabola U( x)
 Small oscillations The theoy of small oscillations is an extemely impotant topic in mechanics. Conside a system that has a potential enegy diagam as below: U B C A x Thee ae thee points of stable equilibium,
Small oscillations The theoy of small oscillations is an extemely impotant topic in mechanics. Conside a system that has a potential enegy diagam as below: U B C A x Thee ae thee points of stable equilibium,
From Gravitational Collapse to Black Holes
 Fom Gavitational Collapse to Black Holes T. Nguyen PHY 391 Independent Study Tem Pape Pof. S.G. Rajeev Univesity of Rocheste Decembe 0, 018 1 Intoduction The pupose of this independent study is to familiaize
Fom Gavitational Collapse to Black Holes T. Nguyen PHY 391 Independent Study Tem Pape Pof. S.G. Rajeev Univesity of Rocheste Decembe 0, 018 1 Intoduction The pupose of this independent study is to familiaize
22.615, MHD Theory of Fusion Systems Prof. Freidberg Lecture 4: Toroidal Equilibrium and Radial Pressure Balance
 .615, MHD Theoy of Fusion Systems Pof. Feidbeg Lectue 4: Tooidal Equilibium and Radial Pessue Balance Basic Poblem of Tooidal Equilibium 1. Radial pessue balance. Tooidal foce balance Radial Pessue Balance
.615, MHD Theoy of Fusion Systems Pof. Feidbeg Lectue 4: Tooidal Equilibium and Radial Pessue Balance Basic Poblem of Tooidal Equilibium 1. Radial pessue balance. Tooidal foce balance Radial Pessue Balance
As is natural, our Aerospace Structures will be described in a Euclidean three-dimensional space R 3.
 Appendix A Vecto Algeba As is natual, ou Aeospace Stuctues will be descibed in a Euclidean thee-dimensional space R 3. A.1 Vectos A vecto is used to epesent quantities that have both magnitude and diection.
Appendix A Vecto Algeba As is natual, ou Aeospace Stuctues will be descibed in a Euclidean thee-dimensional space R 3. A.1 Vectos A vecto is used to epesent quantities that have both magnitude and diection.
Graphs of Sine and Cosine Functions
 Gaphs of Sine and Cosine Functions In pevious sections, we defined the tigonometic o cicula functions in tems of the movement of a point aound the cicumfeence of a unit cicle, o the angle fomed by the
Gaphs of Sine and Cosine Functions In pevious sections, we defined the tigonometic o cicula functions in tems of the movement of a point aound the cicumfeence of a unit cicle, o the angle fomed by the
Chapter 22 The Electric Field II: Continuous Charge Distributions
 Chapte The lectic Field II: Continuous Chage Distibutions A ing of adius a has a chage distibution on it that vaies as l(q) l sin q, as shown in Figue -9. (a) What is the diection of the electic field
Chapte The lectic Field II: Continuous Chage Distibutions A ing of adius a has a chage distibution on it that vaies as l(q) l sin q, as shown in Figue -9. (a) What is the diection of the electic field
Physics 235 Chapter 5. Chapter 5 Gravitation
 Chapte 5 Gavitation In this Chapte we will eview the popeties of the gavitational foce. The gavitational foce has been discussed in geat detail in you intoductoy physics couses, and we will pimaily focus
Chapte 5 Gavitation In this Chapte we will eview the popeties of the gavitational foce. The gavitational foce has been discussed in geat detail in you intoductoy physics couses, and we will pimaily focus
FE FORMULATIONS FOR PLASTICITY
 G These slides ae designed based on the book: Finite Elements in Plasticity Theoy and Pactice, D.R.J. Owen and E. Hinton, 970, Pineidge Pess Ltd., Swansea, UK. Couse Content: A INTRODUCTION AND OVERVIEW
G These slides ae designed based on the book: Finite Elements in Plasticity Theoy and Pactice, D.R.J. Owen and E. Hinton, 970, Pineidge Pess Ltd., Swansea, UK. Couse Content: A INTRODUCTION AND OVERVIEW
Physics 2B Chapter 22 Notes - Magnetic Field Spring 2018
 Physics B Chapte Notes - Magnetic Field Sping 018 Magnetic Field fom a Long Staight Cuent-Caying Wie In Chapte 11 we looked at Isaac Newton s Law of Gavitation, which established that a gavitational field
Physics B Chapte Notes - Magnetic Field Sping 018 Magnetic Field fom a Long Staight Cuent-Caying Wie In Chapte 11 we looked at Isaac Newton s Law of Gavitation, which established that a gavitational field
Nuclear and Particle Physics - Lecture 20 The shell model
 1 Intoduction Nuclea and Paticle Physics - Lectue 0 The shell model It is appaent that the semi-empiical mass fomula does a good job of descibing tends but not the non-smooth behaviou of the binding enegy.
1 Intoduction Nuclea and Paticle Physics - Lectue 0 The shell model It is appaent that the semi-empiical mass fomula does a good job of descibing tends but not the non-smooth behaviou of the binding enegy.
Supplementary material for the paper Platonic Scattering Cancellation for Bending Waves on a Thin Plate. Abstract
 Supplementay mateial fo the pape Platonic Scatteing Cancellation fo Bending Waves on a Thin Plate M. Fahat, 1 P.-Y. Chen, 2 H. Bağcı, 1 S. Enoch, 3 S. Guenneau, 3 and A. Alù 2 1 Division of Compute, Electical,
Supplementay mateial fo the pape Platonic Scatteing Cancellation fo Bending Waves on a Thin Plate M. Fahat, 1 P.-Y. Chen, 2 H. Bağcı, 1 S. Enoch, 3 S. Guenneau, 3 and A. Alù 2 1 Division of Compute, Electical,
Vector d is a linear vector function of vector d when the following relationships hold:
 Appendix 4 Dyadic Analysis DEFINITION ecto d is a linea vecto function of vecto d when the following elationships hold: d x = a xxd x + a xy d y + a xz d z d y = a yxd x + a yy d y + a yz d z d z = a zxd
Appendix 4 Dyadic Analysis DEFINITION ecto d is a linea vecto function of vecto d when the following elationships hold: d x = a xxd x + a xy d y + a xz d z d y = a yxd x + a yy d y + a yz d z d z = a zxd
On the Sun s Electric-Field
 On the Sun s Electic-Field D. E. Scott, Ph.D. (EE) Intoduction Most investigatos who ae sympathetic to the Electic Sun Model have come to agee that the Sun is a body that acts much like a esisto with a
On the Sun s Electic-Field D. E. Scott, Ph.D. (EE) Intoduction Most investigatos who ae sympathetic to the Electic Sun Model have come to agee that the Sun is a body that acts much like a esisto with a
A NEW VARIABLE STIFFNESS SPRING USING A PRESTRESSED MECHANISM
 Poceedings of the ASME 2010 Intenational Design Engineeing Technical Confeences & Computes and Infomation in Engineeing Confeence IDETC/CIE 2010 August 15-18, 2010, Monteal, Quebec, Canada DETC2010-28496
Poceedings of the ASME 2010 Intenational Design Engineeing Technical Confeences & Computes and Infomation in Engineeing Confeence IDETC/CIE 2010 August 15-18, 2010, Monteal, Quebec, Canada DETC2010-28496
Algebra-based Physics II
 lgebabased Physics II Chapte 19 Electic potential enegy & The Electic potential Why enegy is stoed in an electic field? How to descibe an field fom enegetic point of view? Class Website: Natual way of
lgebabased Physics II Chapte 19 Electic potential enegy & The Electic potential Why enegy is stoed in an electic field? How to descibe an field fom enegetic point of view? Class Website: Natual way of
Math 124B February 02, 2012
 Math 24B Febuay 02, 202 Vikto Gigoyan 8 Laplace s equation: popeties We have aleady encounteed Laplace s equation in the context of stationay heat conduction and wave phenomena. Recall that in two spatial
Math 24B Febuay 02, 202 Vikto Gigoyan 8 Laplace s equation: popeties We have aleady encounteed Laplace s equation in the context of stationay heat conduction and wave phenomena. Recall that in two spatial
Liquid gas interface under hydrostatic pressure
 Advances in Fluid Mechanics IX 5 Liquid gas inteface unde hydostatic pessue A. Gajewski Bialystok Univesity of Technology, Faculty of Civil Engineeing and Envionmental Engineeing, Depatment of Heat Engineeing,
Advances in Fluid Mechanics IX 5 Liquid gas inteface unde hydostatic pessue A. Gajewski Bialystok Univesity of Technology, Faculty of Civil Engineeing and Envionmental Engineeing, Depatment of Heat Engineeing,
Chapter 13 Gravitation
 Chapte 13 Gavitation In this chapte we will exploe the following topics: -Newton s law of gavitation, which descibes the attactive foce between two point masses and its application to extended objects
Chapte 13 Gavitation In this chapte we will exploe the following topics: -Newton s law of gavitation, which descibes the attactive foce between two point masses and its application to extended objects
17.1 Electric Potential Energy. Equipotential Lines. PE = energy associated with an arrangement of objects that exert forces on each other
 Electic Potential Enegy, PE Units: Joules Electic Potential, Units: olts 17.1 Electic Potential Enegy Electic foce is a consevative foce and so we can assign an electic potential enegy (PE) to the system
Electic Potential Enegy, PE Units: Joules Electic Potential, Units: olts 17.1 Electic Potential Enegy Electic foce is a consevative foce and so we can assign an electic potential enegy (PE) to the system
Math 2263 Solutions for Spring 2003 Final Exam
 Math 6 Solutions fo Sping Final Exam ) A staightfowad appoach to finding the tangent plane to a suface at a point ( x, y, z ) would be to expess the cuve as an explicit function z = f ( x, y ), calculate
Math 6 Solutions fo Sping Final Exam ) A staightfowad appoach to finding the tangent plane to a suface at a point ( x, y, z ) would be to expess the cuve as an explicit function z = f ( x, y ), calculate
2. Electrostatics. Dr. Rakhesh Singh Kshetrimayum 8/11/ Electromagnetic Field Theory by R. S. Kshetrimayum
 2. Electostatics D. Rakhesh Singh Kshetimayum 1 2.1 Intoduction In this chapte, we will study how to find the electostatic fields fo vaious cases? fo symmetic known chage distibution fo un-symmetic known
2. Electostatics D. Rakhesh Singh Kshetimayum 1 2.1 Intoduction In this chapte, we will study how to find the electostatic fields fo vaious cases? fo symmetic known chage distibution fo un-symmetic known
(read nabla or del) is defined by, k. (9.7.1*)
 9.7 Gadient of a scala field. Diectional deivative Some of the vecto fields in applications can be obtained fom scala fields. This is vey advantageous because scala fields can be handled moe easily. The
9.7 Gadient of a scala field. Diectional deivative Some of the vecto fields in applications can be obtained fom scala fields. This is vey advantageous because scala fields can be handled moe easily. The
Magnetic Dipoles Challenge Problem Solutions
 Magnetic Dipoles Challenge Poblem Solutions Poblem 1: Cicle the coect answe. Conside a tiangula loop of wie with sides a and b. The loop caies a cuent I in the diection shown, and is placed in a unifom
Magnetic Dipoles Challenge Poblem Solutions Poblem 1: Cicle the coect answe. Conside a tiangula loop of wie with sides a and b. The loop caies a cuent I in the diection shown, and is placed in a unifom
AST 121S: The origin and evolution of the Universe. Introduction to Mathematical Handout 1
 Please ead this fist... AST S: The oigin and evolution of the Univese Intoduction to Mathematical Handout This is an unusually long hand-out and one which uses in places mathematics that you may not be
Please ead this fist... AST S: The oigin and evolution of the Univese Intoduction to Mathematical Handout This is an unusually long hand-out and one which uses in places mathematics that you may not be
Lab 10: Newton s Second Law in Rotation
 Lab 10: Newton s Second Law in Rotation We can descibe the motion of objects that otate (i.e. spin on an axis, like a popelle o a doo) using the same definitions, adapted fo otational motion, that we have
Lab 10: Newton s Second Law in Rotation We can descibe the motion of objects that otate (i.e. spin on an axis, like a popelle o a doo) using the same definitions, adapted fo otational motion, that we have
SIO 229 Gravity and Geomagnetism. Lecture 6. J 2 for Earth. J 2 in the solar system. A first look at the geoid.
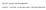 SIO 229 Gavity and Geomagnetism Lectue 6. J 2 fo Eath. J 2 in the sola system. A fist look at the geoid. The Thee Big Themes of the Gavity Lectues 1.) An ellipsoidal otating Eath Refeence body (mass +
SIO 229 Gavity and Geomagnetism Lectue 6. J 2 fo Eath. J 2 in the sola system. A fist look at the geoid. The Thee Big Themes of the Gavity Lectues 1.) An ellipsoidal otating Eath Refeence body (mass +
The Strain Compatibility Equations in Polar Coordinates RAWB, Last Update 27/12/07
 The Stain Compatibility Equations in Pola Coodinates RAWB Last Update 7//7 In D thee is just one compatibility equation. In D polas it is (Equ.) whee denotes the enineein shea (twice the tensoial shea)
The Stain Compatibility Equations in Pola Coodinates RAWB Last Update 7//7 In D thee is just one compatibility equation. In D polas it is (Equ.) whee denotes the enineein shea (twice the tensoial shea)
arxiv: v1 [physics.pop-ph] 3 Jun 2013
![arxiv: v1 [physics.pop-ph] 3 Jun 2013 arxiv: v1 [physics.pop-ph] 3 Jun 2013](/thumbs/89/100795062.jpg) A note on the electostatic enegy of two point chages axiv:1306.0401v1 [physics.pop-ph] 3 Jun 013 A C Tot Instituto de Física Univesidade Fedeal do io de Janeio Caixa Postal 68.58; CEP 1941-97 io de Janeio,
A note on the electostatic enegy of two point chages axiv:1306.0401v1 [physics.pop-ph] 3 Jun 013 A C Tot Instituto de Física Univesidade Fedeal do io de Janeio Caixa Postal 68.58; CEP 1941-97 io de Janeio,
OSCILLATIONS AND GRAVITATION
 1. SIMPLE HARMONIC MOTION Simple hamonic motion is any motion that is equivalent to a single component of unifom cicula motion. In this situation the velocity is always geatest in the middle of the motion,
1. SIMPLE HARMONIC MOTION Simple hamonic motion is any motion that is equivalent to a single component of unifom cicula motion. In this situation the velocity is always geatest in the middle of the motion,
Section 8.2 Polar Coordinates
 Section 8. Pola Coodinates 467 Section 8. Pola Coodinates The coodinate system we ae most familia with is called the Catesian coodinate system, a ectangula plane divided into fou quadants by the hoizontal
Section 8. Pola Coodinates 467 Section 8. Pola Coodinates The coodinate system we ae most familia with is called the Catesian coodinate system, a ectangula plane divided into fou quadants by the hoizontal
Electrostatics (Electric Charges and Field) #2 2010
 Electic Field: The concept of electic field explains the action at a distance foce between two chaged paticles. Evey chage poduces a field aound it so that any othe chaged paticle expeiences a foce when
Electic Field: The concept of electic field explains the action at a distance foce between two chaged paticles. Evey chage poduces a field aound it so that any othe chaged paticle expeiences a foce when
Chem 453/544 Fall /08/03. Exam #1 Solutions
 Chem 453/544 Fall 3 /8/3 Exam # Solutions. ( points) Use the genealized compessibility diagam povided on the last page to estimate ove what ange of pessues A at oom tempeatue confoms to the ideal gas law
Chem 453/544 Fall 3 /8/3 Exam # Solutions. ( points) Use the genealized compessibility diagam povided on the last page to estimate ove what ange of pessues A at oom tempeatue confoms to the ideal gas law
- 5 - TEST 1R. This is the repeat version of TEST 1, which was held during Session.
 - 5 - TEST 1R This is the epeat vesion of TEST 1, which was held duing Session. This epeat test should be attempted by those students who missed Test 1, o who wish to impove thei mak in Test 1. IF YOU
- 5 - TEST 1R This is the epeat vesion of TEST 1, which was held duing Session. This epeat test should be attempted by those students who missed Test 1, o who wish to impove thei mak in Test 1. IF YOU
ELASTIC ANALYSIS OF CIRCULAR SANDWICH PLATES WITH FGM FACE-SHEETS
 THE 9 TH INTERNATIONAL CONFERENCE ON COMPOSITE MATERIALS ELASTIC ANALYSIS OF CIRCULAR SANDWICH PLATES WITH FGM FACE-SHEETS R. Sbulati *, S. R. Atashipou Depatment of Civil, Chemical and Envionmental Engineeing,
THE 9 TH INTERNATIONAL CONFERENCE ON COMPOSITE MATERIALS ELASTIC ANALYSIS OF CIRCULAR SANDWICH PLATES WITH FGM FACE-SHEETS R. Sbulati *, S. R. Atashipou Depatment of Civil, Chemical and Envionmental Engineeing,
A Cross Section surface tension viscosity σ U 2 10 inertia gravity gd
 .5 Final Exam 005 SOLUTION Question U A Coss Section Photo emoved fo copyight easons. Souce: Figue 7l in Clanet, C. "Dynamics and stability of wate bells." J. Fluid Mech 40 (00): -47. R d Tooidal im U
.5 Final Exam 005 SOLUTION Question U A Coss Section Photo emoved fo copyight easons. Souce: Figue 7l in Clanet, C. "Dynamics and stability of wate bells." J. Fluid Mech 40 (00): -47. R d Tooidal im U
Article : 8 Article : 8 Stress Field. and. Singularity Problem
 Aticle : 8 Aticle : 8 Stess Field and Singulaity Poblem (fatigue cack gowth) Repeated load cycles cack development Time (cycles) Cack length 3 Weakening due to gowing cacks Cack length stess concentation
Aticle : 8 Aticle : 8 Stess Field and Singulaity Poblem (fatigue cack gowth) Repeated load cycles cack development Time (cycles) Cack length 3 Weakening due to gowing cacks Cack length stess concentation
$ i. !((( dv vol. Physics 8.02 Quiz One Equations Fall q 1 q 2 r 2 C = 2 C! V 2 = Q 2 2C F = 4!" or. r ˆ = points from source q to observer
 Physics 8.0 Quiz One Equations Fall 006 F = 1 4" o q 1 q = q q ˆ 3 4" o = E 4" o ˆ = points fom souce q to obseve 1 dq E = # ˆ 4" 0 V "## E "d A = Q inside closed suface o d A points fom inside to V =
Physics 8.0 Quiz One Equations Fall 006 F = 1 4" o q 1 q = q q ˆ 3 4" o = E 4" o ˆ = points fom souce q to obseve 1 dq E = # ˆ 4" 0 V "## E "d A = Q inside closed suface o d A points fom inside to V =
B da = 0. Q E da = ε. E da = E dv
 lectomagnetic Theo Pof Ruiz, UNC Asheville, doctophs on YouTube Chapte Notes The Maxwell quations in Diffeential Fom 1 The Maxwell quations in Diffeential Fom We will now tansfom the integal fom of the
lectomagnetic Theo Pof Ruiz, UNC Asheville, doctophs on YouTube Chapte Notes The Maxwell quations in Diffeential Fom 1 The Maxwell quations in Diffeential Fom We will now tansfom the integal fom of the
Physics 107 TUTORIAL ASSIGNMENT #8
 Physics 07 TUTORIAL ASSIGNMENT #8 Cutnell & Johnson, 7 th edition Chapte 8: Poblems 5,, 3, 39, 76 Chapte 9: Poblems 9, 0, 4, 5, 6 Chapte 8 5 Inteactive Solution 8.5 povides a model fo solving this type
Physics 07 TUTORIAL ASSIGNMENT #8 Cutnell & Johnson, 7 th edition Chapte 8: Poblems 5,, 3, 39, 76 Chapte 9: Poblems 9, 0, 4, 5, 6 Chapte 8 5 Inteactive Solution 8.5 povides a model fo solving this type
Fracture Mechanics: Linear Elastic Fracture Mechanics 2/2
 Task 6 - Safety Review and Licensing On the Job Taining on Stess Analysis Factue Mechanics: Linea Elastic Factue Mechanics / Davide Mazzini Cio Santus Pisa (taly) June 15 July 14, 015 Table of content
Task 6 - Safety Review and Licensing On the Job Taining on Stess Analysis Factue Mechanics: Linea Elastic Factue Mechanics / Davide Mazzini Cio Santus Pisa (taly) June 15 July 14, 015 Table of content
Chapter 12. Kinetics of Particles: Newton s Second Law
 Chapte 1. Kinetics of Paticles: Newton s Second Law Intoduction Newton s Second Law of Motion Linea Momentum of a Paticle Systems of Units Equations of Motion Dynamic Equilibium Angula Momentum of a Paticle
Chapte 1. Kinetics of Paticles: Newton s Second Law Intoduction Newton s Second Law of Motion Linea Momentum of a Paticle Systems of Units Equations of Motion Dynamic Equilibium Angula Momentum of a Paticle
π(x, y) = u x + v y = V (x cos + y sin ) κ(x, y) = u y v x = V (y cos x sin ) v u x y
 F17 Lectue Notes 1. Unifom flow, Souces, Sinks, Doublets Reading: Andeson 3.9 3.12 Unifom Flow Definition A unifom flow consists of a velocit field whee V φ = uî + vθˆ is a constant. In 2-D, this velocit
F17 Lectue Notes 1. Unifom flow, Souces, Sinks, Doublets Reading: Andeson 3.9 3.12 Unifom Flow Definition A unifom flow consists of a velocit field whee V φ = uî + vθˆ is a constant. In 2-D, this velocit
Physics 161 Fall 2011 Extra Credit 2 Investigating Black Holes - Solutions The Following is Worth 50 Points!!!
 Physics 161 Fall 011 Exta Cedit Investigating Black Holes - olutions The Following is Woth 50 Points!!! This exta cedit assignment will investigate vaious popeties of black holes that we didn t have time
Physics 161 Fall 011 Exta Cedit Investigating Black Holes - olutions The Following is Woth 50 Points!!! This exta cedit assignment will investigate vaious popeties of black holes that we didn t have time
1 Spherical multipole moments
 Jackson notes 9 Spheical multipole moments Suppose we have a chage distibution ρ (x) wheeallofthechageiscontained within a spheical egion of adius R, as shown in the diagam. Then thee is no chage in the
Jackson notes 9 Spheical multipole moments Suppose we have a chage distibution ρ (x) wheeallofthechageiscontained within a spheical egion of adius R, as shown in the diagam. Then thee is no chage in the
d 2 x 0a d d =0. Relative to an arbitrary (accelerating frame) specified by x a = x a (x 0b ), the latter becomes: d 2 x a d 2 + a dx b dx c
 Chapte 6 Geneal Relativity 6.1 Towads the Einstein equations Thee ae seveal ways of motivating the Einstein equations. The most natual is pehaps though consideations involving the Equivalence Pinciple.
Chapte 6 Geneal Relativity 6.1 Towads the Einstein equations Thee ae seveal ways of motivating the Einstein equations. The most natual is pehaps though consideations involving the Equivalence Pinciple.
3. Electromagnetic Waves II
 Lectue 3 - Electomagnetic Waves II 9 3. Electomagnetic Waves II Last time, we discussed the following. 1. The popagation of an EM wave though a macoscopic media: We discussed how the wave inteacts with
Lectue 3 - Electomagnetic Waves II 9 3. Electomagnetic Waves II Last time, we discussed the following. 1. The popagation of an EM wave though a macoscopic media: We discussed how the wave inteacts with
4. Kruskal Coordinates and Penrose Diagrams.
 4. Kuskal Coodinates and Penose Diagams. 4.1. Removing a coodinate ingulaity at the chwazschild Radius. The chwazschild metic has a singulaity at = whee g 0 and g. Howeve, 00 we have aleady seen that a
4. Kuskal Coodinates and Penose Diagams. 4.1. Removing a coodinate ingulaity at the chwazschild Radius. The chwazschild metic has a singulaity at = whee g 0 and g. Howeve, 00 we have aleady seen that a
POISSON S EQUATION 2 V 0
 POISSON S EQUATION We have seen how to solve the equation but geneally we have V V4k We now look at a vey geneal way of attacking this poblem though Geen s Functions. It tuns out that this poblem has applications
POISSON S EQUATION We have seen how to solve the equation but geneally we have V V4k We now look at a vey geneal way of attacking this poblem though Geen s Functions. It tuns out that this poblem has applications
Applied Aerodynamics
 Applied Aeodynamics Def: Mach Numbe (M), M a atio of flow velocity to the speed of sound Compessibility Effects Def: eynolds Numbe (e), e ρ c µ atio of inetial foces to viscous foces iscous Effects If
Applied Aeodynamics Def: Mach Numbe (M), M a atio of flow velocity to the speed of sound Compessibility Effects Def: eynolds Numbe (e), e ρ c µ atio of inetial foces to viscous foces iscous Effects If
Hopefully Helpful Hints for Gauss s Law
 Hopefully Helpful Hints fo Gauss s Law As befoe, thee ae things you need to know about Gauss s Law. In no paticula ode, they ae: a.) In the context of Gauss s Law, at a diffeential level, the electic flux
Hopefully Helpful Hints fo Gauss s Law As befoe, thee ae things you need to know about Gauss s Law. In no paticula ode, they ae: a.) In the context of Gauss s Law, at a diffeential level, the electic flux
Entropy and Free Energy: Predicting the direction of spontaneous change The approach to Chemical equilibrium
 Lectue 8-9 Entopy and Fee Enegy: Pedicting the diection of spontaneous change The appoach to Chemical equilibium Absolute entopy and the thid law of themodynamics To define the entopy of a compound in
Lectue 8-9 Entopy and Fee Enegy: Pedicting the diection of spontaneous change The appoach to Chemical equilibium Absolute entopy and the thid law of themodynamics To define the entopy of a compound in
7.2. Coulomb s Law. The Electric Force
 Coulomb s aw Recall that chaged objects attact some objects and epel othes at a distance, without making any contact with those objects Electic foce,, o the foce acting between two chaged objects, is somewhat
Coulomb s aw Recall that chaged objects attact some objects and epel othes at a distance, without making any contact with those objects Electic foce,, o the foce acting between two chaged objects, is somewhat
Ch 30 - Sources of Magnetic Field! The Biot-Savart Law! = k m. r 2. Example 1! Example 2!
 Ch 30 - Souces of Magnetic Field 1.) Example 1 Detemine the magnitude and diection of the magnetic field at the point O in the diagam. (Cuent flows fom top to bottom, adius of cuvatue.) Fo staight segments,
Ch 30 - Souces of Magnetic Field 1.) Example 1 Detemine the magnitude and diection of the magnetic field at the point O in the diagam. (Cuent flows fom top to bottom, adius of cuvatue.) Fo staight segments,
Central Force Motion
 Cental Foce Motion Cental Foce Poblem Find the motion of two bodies inteacting via a cental foce. Examples: Gavitational foce (Keple poblem): m1m F 1, ( ) =! G ˆ Linea estoing foce: F 1, ( ) =! k ˆ Two
Cental Foce Motion Cental Foce Poblem Find the motion of two bodies inteacting via a cental foce. Examples: Gavitational foce (Keple poblem): m1m F 1, ( ) =! G ˆ Linea estoing foce: F 1, ( ) =! k ˆ Two
2 E. on each of these two surfaces. r r r r. Q E E ε. 2 2 Qencl encl right left 0
 Ch : 4, 9,, 9,,, 4, 9,, 4, 8 4 (a) Fom the diagam in the textbook, we see that the flux outwad though the hemispheical suface is the same as the flux inwad though the cicula suface base of the hemisphee
Ch : 4, 9,, 9,,, 4, 9,, 4, 8 4 (a) Fom the diagam in the textbook, we see that the flux outwad though the hemispheical suface is the same as the flux inwad though the cicula suface base of the hemisphee
Chapter 7-8 Rotational Motion
 Chapte 7-8 Rotational Motion What is a Rigid Body? Rotational Kinematics Angula Velocity ω and Acceleation α Unifom Rotational Motion: Kinematics Unifom Cicula Motion: Kinematics and Dynamics The Toque,
Chapte 7-8 Rotational Motion What is a Rigid Body? Rotational Kinematics Angula Velocity ω and Acceleation α Unifom Rotational Motion: Kinematics Unifom Cicula Motion: Kinematics and Dynamics The Toque,
Question Bank. Section A. is skew-hermitian matrix. is diagonalizable. (, ) , Evaluate (, ) 12 about = 1 and = Find, if
 Subject: Mathematics-I Question Bank Section A T T. Find the value of fo which the matix A = T T has ank one. T T i. Is the matix A = i is skew-hemitian matix. i. alculate the invese of the matix = 5 7
Subject: Mathematics-I Question Bank Section A T T. Find the value of fo which the matix A = T T has ank one. T T i. Is the matix A = i is skew-hemitian matix. i. alculate the invese of the matix = 5 7
Motion in One Dimension
 Motion in One Dimension Intoduction: In this lab, you will investigate the motion of a olling cat as it tavels in a staight line. Although this setup may seem ovesimplified, you will soon see that a detailed
Motion in One Dimension Intoduction: In this lab, you will investigate the motion of a olling cat as it tavels in a staight line. Although this setup may seem ovesimplified, you will soon see that a detailed
PHYS 110B - HW #7 Spring 2004, Solutions by David Pace Any referenced equations are from Griffiths Problem statements are paraphrased
 PHYS 0B - HW #7 Sping 2004, Solutions by David Pace Any efeenced euations ae fom Giffiths Poblem statements ae paaphased. Poblem 0.3 fom Giffiths A point chage,, moves in a loop of adius a. At time t 0
PHYS 0B - HW #7 Sping 2004, Solutions by David Pace Any efeenced euations ae fom Giffiths Poblem statements ae paaphased. Poblem 0.3 fom Giffiths A point chage,, moves in a loop of adius a. At time t 0
An Exact Solution of Navier Stokes Equation
 An Exact Solution of Navie Stokes Equation A. Salih Depatment of Aeospace Engineeing Indian Institute of Space Science and Technology, Thiuvananthapuam, Keala, India. July 20 The pincipal difficulty in
An Exact Solution of Navie Stokes Equation A. Salih Depatment of Aeospace Engineeing Indian Institute of Space Science and Technology, Thiuvananthapuam, Keala, India. July 20 The pincipal difficulty in
Why Professor Richard Feynman was upset solving the Laplace equation for spherical waves? Anzor A. Khelashvili a)
 Why Pofesso Richad Feynman was upset solving the Laplace equation fo spheical waves? Anzo A. Khelashvili a) Institute of High Enegy Physics, Iv. Javakhishvili Tbilisi State Univesity, Univesity St. 9,
Why Pofesso Richad Feynman was upset solving the Laplace equation fo spheical waves? Anzo A. Khelashvili a) Institute of High Enegy Physics, Iv. Javakhishvili Tbilisi State Univesity, Univesity St. 9,
ENGI 4430 Non-Cartesian Coordinates Page xi Fy j Fzk from Cartesian coordinates z to another orthonormal coordinate system u, v, ˆ i ˆ ˆi
 ENGI 44 Non-Catesian Coodinates Page 7-7. Conesions between Coodinate Systems In geneal, the conesion of a ecto F F xi Fy j Fzk fom Catesian coodinates x, y, z to anothe othonomal coodinate system u,,
ENGI 44 Non-Catesian Coodinates Page 7-7. Conesions between Coodinate Systems In geneal, the conesion of a ecto F F xi Fy j Fzk fom Catesian coodinates x, y, z to anothe othonomal coodinate system u,,
F Q E v B MAGNETOSTATICS. Creation of magnetic field B. Effect of B on a moving charge. On moving charges only. Stationary and moving charges
 MAGNETOSTATICS Ceation of magnetic field. Effect of on a moving chage. Take the second case: F Q v mag On moving chages only F QE v Stationay and moving chages dw F dl Analysis on F mag : mag mag Qv. vdt
MAGNETOSTATICS Ceation of magnetic field. Effect of on a moving chage. Take the second case: F Q v mag On moving chages only F QE v Stationay and moving chages dw F dl Analysis on F mag : mag mag Qv. vdt
Scattering in Three Dimensions
 Scatteing in Thee Dimensions Scatteing expeiments ae an impotant souce of infomation about quantum systems, anging in enegy fom vey low enegy chemical eactions to the highest possible enegies at the LHC.
Scatteing in Thee Dimensions Scatteing expeiments ae an impotant souce of infomation about quantum systems, anging in enegy fom vey low enegy chemical eactions to the highest possible enegies at the LHC.
Hydroelastic Analysis of a 1900 TEU Container Ship Using Finite Element and Boundary Element Methods
 TEAM 2007, Sept. 10-13, 2007,Yokohama, Japan Hydoelastic Analysis of a 1900 TEU Containe Ship Using Finite Element and Bounday Element Methods Ahmet Egin 1)*, Levent Kaydıhan 2) and Bahadı Uğulu 3) 1)
TEAM 2007, Sept. 10-13, 2007,Yokohama, Japan Hydoelastic Analysis of a 1900 TEU Containe Ship Using Finite Element and Bounday Element Methods Ahmet Egin 1)*, Levent Kaydıhan 2) and Bahadı Uğulu 3) 1)
( ) [ ] [ ] [ ] δf φ = F φ+δφ F. xdx.
![( ) [ ] [ ] [ ] δf φ = F φ+δφ F. xdx. ( ) [ ] [ ] [ ] δf φ = F φ+δφ F. xdx.](/thumbs/90/103689049.jpg) 9. LAGRANGIAN OF THE ELECTROMAGNETIC FIELD In the pevious section the Lagangian and Hamiltonian of an ensemble of point paticles was developed. This appoach is based on a qt. This discete fomulation can
9. LAGRANGIAN OF THE ELECTROMAGNETIC FIELD In the pevious section the Lagangian and Hamiltonian of an ensemble of point paticles was developed. This appoach is based on a qt. This discete fomulation can
Physics 111. Ch 12: Gravity. Newton s Universal Gravity. R - hat. the equation. = Gm 1 m 2. F g 2 1. ˆr 2 1. Gravity G =
 ics Announcements day, embe 9, 004 Ch 1: Gavity Univesal Law Potential Enegy Keple s Laws Ch 15: Fluids density hydostatic equilibium Pascal s Pinciple This week s lab will be anothe physics wokshop -
ics Announcements day, embe 9, 004 Ch 1: Gavity Univesal Law Potential Enegy Keple s Laws Ch 15: Fluids density hydostatic equilibium Pascal s Pinciple This week s lab will be anothe physics wokshop -
TheWaveandHelmholtzEquations
 TheWaveandHelmholtzEquations Ramani Duaiswami The Univesity of Mayland, College Pak Febuay 3, 2006 Abstact CMSC828D notes (adapted fom mateial witten with Nail Gumeov). Wok in pogess 1 Acoustic Waves 1.1
TheWaveandHelmholtzEquations Ramani Duaiswami The Univesity of Mayland, College Pak Febuay 3, 2006 Abstact CMSC828D notes (adapted fom mateial witten with Nail Gumeov). Wok in pogess 1 Acoustic Waves 1.1
But for simplicity, we ll define significant as the time it takes a star to lose all memory of its original trajectory, i.e.,
 Stella elaxation Time [Chandasekha 1960, Pinciples of Stella Dynamics, Chap II] [Ostike & Davidson 1968, Ap.J., 151, 679] Do stas eve collide? Ae inteactions between stas (as opposed to the geneal system
Stella elaxation Time [Chandasekha 1960, Pinciples of Stella Dynamics, Chap II] [Ostike & Davidson 1968, Ap.J., 151, 679] Do stas eve collide? Ae inteactions between stas (as opposed to the geneal system
I( x) t e. is the total mean free path in the medium, [cm] tis the total cross section in the medium, [cm ] A M
![I( x) t e. is the total mean free path in the medium, [cm] tis the total cross section in the medium, [cm ] A M I( x) t e. is the total mean free path in the medium, [cm] tis the total cross section in the medium, [cm ] A M](/thumbs/79/79663309.jpg) t I ( x) I e x x t Ie (1) whee: 1 t is the total mean fee path in the medium, [cm] N t t -1 tis the total coss section in the medium, [cm ] A M 3 is the density of the medium [gm/cm ] v 3 N= is the nuclea
t I ( x) I e x x t Ie (1) whee: 1 t is the total mean fee path in the medium, [cm] N t t -1 tis the total coss section in the medium, [cm ] A M 3 is the density of the medium [gm/cm ] v 3 N= is the nuclea
The Poisson bracket and magnetic monopoles
 FYST420 Advanced electodynamics Olli Aleksante Koskivaaa Final poject ollikoskivaaa@gmail.com The Poisson backet and magnetic monopoles Abstact: In this wok magnetic monopoles ae studied using the Poisson
FYST420 Advanced electodynamics Olli Aleksante Koskivaaa Final poject ollikoskivaaa@gmail.com The Poisson backet and magnetic monopoles Abstact: In this wok magnetic monopoles ae studied using the Poisson
ME 210 Applied Mathematics for Mechanical Engineers
 Tangent and Ac Length of a Cuve The tangent to a cuve C at a point A on it is defined as the limiting position of the staight line L though A and B, as B appoaches A along the cuve as illustated in the
Tangent and Ac Length of a Cuve The tangent to a cuve C at a point A on it is defined as the limiting position of the staight line L though A and B, as B appoaches A along the cuve as illustated in the
Static equilibrium requires a balance of forces and a balance of moments.
 Static Equilibium Static equilibium equies a balance of foces and a balance of moments. ΣF 0 ΣF 0 ΣF 0 ΣM 0 ΣM 0 ΣM 0 Eample 1: painte stands on a ladde that leans against the wall of a house at an angle
Static Equilibium Static equilibium equies a balance of foces and a balance of moments. ΣF 0 ΣF 0 ΣF 0 ΣM 0 ΣM 0 ΣM 0 Eample 1: painte stands on a ladde that leans against the wall of a house at an angle
LINEAR AND NONLINEAR ANALYSES OF A WIND-TUNNEL BALANCE
 LINEAR AND NONLINEAR ANALYSES O A WIND-TUNNEL INTRODUCTION BALANCE R. Kakehabadi and R. D. Rhew NASA LaRC, Hampton, VA The NASA Langley Reseach Cente (LaRC) has been designing stain-gauge balances fo utilization
LINEAR AND NONLINEAR ANALYSES O A WIND-TUNNEL INTRODUCTION BALANCE R. Kakehabadi and R. D. Rhew NASA LaRC, Hampton, VA The NASA Langley Reseach Cente (LaRC) has been designing stain-gauge balances fo utilization
Chapter 2: Basic Physics and Math Supplements
 Chapte 2: Basic Physics and Math Supplements Decembe 1, 215 1 Supplement 2.1: Centipetal Acceleation This supplement expands on a topic addessed on page 19 of the textbook. Ou task hee is to calculate
Chapte 2: Basic Physics and Math Supplements Decembe 1, 215 1 Supplement 2.1: Centipetal Acceleation This supplement expands on a topic addessed on page 19 of the textbook. Ou task hee is to calculate
Qualifying Examination Electricity and Magnetism Solutions January 12, 2006
 1 Qualifying Examination Electicity and Magnetism Solutions Januay 12, 2006 PROBLEM EA. a. Fist, we conside a unit length of cylinde to find the elationship between the total chage pe unit length λ and
1 Qualifying Examination Electicity and Magnetism Solutions Januay 12, 2006 PROBLEM EA. a. Fist, we conside a unit length of cylinde to find the elationship between the total chage pe unit length λ and
ASTR415: Problem Set #6
 ASTR45: Poblem Set #6 Cuan D. Muhlbege Univesity of Mayland (Dated: May 7, 27) Using existing implementations of the leapfog and Runge-Kutta methods fo solving coupled odinay diffeential equations, seveal
ASTR45: Poblem Set #6 Cuan D. Muhlbege Univesity of Mayland (Dated: May 7, 27) Using existing implementations of the leapfog and Runge-Kutta methods fo solving coupled odinay diffeential equations, seveal
Appendix A. Appendices. A.1 ɛ ijk and cross products. Vector Operations: δ ij and ɛ ijk
 Appendix A Appendices A1 ɛ and coss poducts A11 Vecto Opeations: δ ij and ɛ These ae some notes on the use of the antisymmetic symbol ɛ fo expessing coss poducts This is an extemely poweful tool fo manipulating
Appendix A Appendices A1 ɛ and coss poducts A11 Vecto Opeations: δ ij and ɛ These ae some notes on the use of the antisymmetic symbol ɛ fo expessing coss poducts This is an extemely poweful tool fo manipulating
