L(θ X) s 0 (1 θ 0) m s. (s/m) s (1 s/m) m s
|
|
|
- Joy Williams
- 5 years ago
- Views:
Transcription
1 Hw 4 (due March ) 83 The LRT statstcs s λ(x) sup θ θ 0 L(θ X) The lkelhood s L(θ) θ P x ( sup Θ L(θ X) θ) m P x ad ad the log-lkelhood s (θ) x log θ +(m x ) log( θ) Let S X Note that the ucostraed MLE s S/m, whle the MLE uder the ull hy- f S/m θ0, pothess s m(s/m, θ 0 ) Thus, λ(s) θ s 0 ( θ 0) m s θ s 0 ( θ 0) m s else, ad we reject H 0 f <c To shows that ths s equvalet to rejectg f s<b, we could show λ(s) s decreasg s so that λ(s) <coccurs for s>b>mθ 0 It s easer to work wth log λ(s), ad we have log λ(s) s log θ 0 +(m s) log( θ 0 ) s log(s/m) (m s) log((m s)/m) ad d log λ(s) log ds θ0 ( m s m ) s/m( θ 0 ) For s/m > θ 0, s/m (m s)/m < θ 0, so the fracto above s less tha, ad the log s less tha 0 Thus, λ s a decreasg fucto s ad λ(s) <cf ad oly f s>b θ Alteratvely, oe could work through the algebra We reject f s 0 ( θ 0) m s <c Whch correspods to θ0 x log +(m s/m x ) log θ 0 s/m log c x log c m log θ 0 s/m log θ 0 log θ 0 s/m s/m b 87(a) L(θ, λ x) e (P x θ)/λ I [θ, )(x ()) λ whch s creasg θ f x () θ (regardless of λ) So, the MLE of θ s ˆθ x () The log L P + x ˆθ 0 ad thus ˆλ x x λ λ λ 2 () Because log L P 2 λ 2 λ 2 x ˆθ λ 3 ( x x () < 0, we have ˆθ x ) 2 () ad ˆλ x x () as the urestrcted MLEs of θ ad λ Uder the restrcto θ 0, the MLE of θ (regardless of λ) s ˆθ 0 f x () > 0, 0 For else x () 9
2 x () > 0, substtutg ˆθ 0 0 ad maxmzg the lkelhood wth respect to λ, asabove, f yelds ˆλ x() 0, 0 x Therefore, λ(x) f x () > 0 where L( x, 0 x) L(ˆλ, ˆθ x) L( x,0 x) L(ˆλ,ˆθ x) (/ x) e x/ x (/ˆλ) e ( x x ())/( x x () ) So reject f λ(x) c s equvalet to rejectg f x () / x c x () x 85 From the Neyma-Pearso lemma, the UMP test rejects H 0 f f(x σ ) f(x σ 0 ) (2πσ2 ) /2 e P x2 /(2σ2 ) (2πσ 2 0) /2 e P σ0 exp x 2 x2 /(2σ2 0 ) (/σ 2 0 /σ 2 σ 2 ) for some k 0 After some algebra, ths s equvalet to rejectg f x 2 > 2 log(k(σ /σ 0 ) ) (/σ 2 0 /σ 2 ) Ths s the UMP test of sze α, where α P σ0 ( X2 >c) Note that X2 /σ 2 0 χ 2 Thus, c α P σ0 ( X 2 /σ 2 0 >c/σ 2 0)P (χ 2 >c/σ 2 0) So we must have c/σ 2 0 χ 2,α ad c σ 2 0χ 2,α 87 a The lkelhood fucto s L(µ, θ x,y)µ ( x ) µ θ m m θ j j y ad the loglkelhood fucto s (µ, θ) log µ +(µ ) log x + m log θ +(θ ) m j log y j Hece, the (ucostraed) MLEs are ˆµ P ad ˆθ m log x Pj Uder H 0, the lkelhood log y j s L(θ x,y)θ +m x j y j θ ad maxmzg wrt θ yelds the restrcted MLE, θ0 ˆ ˆθ ˆθ +m (+m) 0 P log x + P θˆ Hece the LRT statstc s λ(x,y) 0 j log y j ˆµ ˆθ ( m x θ ) ˆ 0 ˆµ j y j b Substtutg the formulas for ˆθ, ˆµ ad ˆθ 0 yelds ( x θ ) ˆ 0 ˆµ ( j y θ j) ˆ 0 ˆθ, ad λ(x,y) +m θˆ 0 ˆµ ˆθ ˆ m θ 0 θ0 ˆ m ˆµ ˆθ m+ m m+ m m m ( T ) m T Ths s a umodal fucto of T So, rejectg H 0 f λ(x,y) c s equvalet to rejectg f T c or T c 2, where c ad c 2 are approprately chose costats 0
3 c Smple trasformatos yeld log X exp(/µ) ad log Y exp(/θ) Therefore, T W/(W + V ) where W ad V are depedet, W Gamma(, /µ) ad V Gamma(m, /θ) Uder H 0, the scale parameters of W ad V are equal The, a smple geeralzato of Exercse 49b yelds T Beta(, m) The costats c ad c 2 are determed by the two equatos P (T c )+P (T c 2 )α ad ( c ) m c ( c 2 ) m c 2 03 (a)(e) a The ull hypothess s H 0 : p p 2, whch we ca wrte as H 0 : p p 2 0 To costruct the Wald test statstc, look at T mle uder H ŝe 0 Uder H 0, the mle of p p 2 s ˆp ˆp 2 S / + S 2 / 2 The varace of ths uder H 0 s se 2 (p p 2 ) p ( p ) + p 2( p 2 ) 2 p( p)(/ +/ 2 ) where we estmate p p p 2 uder H 0 as ˆp S +S Thus, the Wald test statstc s T ˆp ˆp 2 ˆp( ˆp)(/ +/ 2 ) Next wrte T ˆp ˆp 2 se(p) se(p) We kow that ˆp ˆp 2 se(ˆp) se(p) d T N(0, ) ad se(p) se(ˆp) p Usg Slutsky s Theorem, we have that T d T N(0, ) uder H 0 Usg the cotuous mappg theorem (e, trasformato theorem covergece dstrbuto), we the have that T 2 d χ 2 e We have that ˆp 34/40, ˆp 2 9/35, ˆp , ad T 836 Sce χ , , we ca reject H 0 at α 005 The p-value of the test s a Frst calculate the MLEs uder p p 2 p We have L(p x) p x p x 2 p x 3 3 p x 2p 3 P m x p Takg logs ad dfferetatg yeld the followg equatos for the MLEs: logl p logl p x + x 2 2(m x ) p 2p 3 p x x p 2p 3 p 0 where 3,, The solutos are ˆp x +x 2, ˆp 2m x for 3,,, ad m ˆp (m x )/m Except for the frst ad secod cells, we have expected observed, 0
4 sce both are equal to x Note that ths comes from the statemet the problem that the expected cell frequeces are the MLEs of mp, uder the assumpto that p p 2 Thus, the expected frequecy of a cell s mˆp m x x m,for 3,, For the frst two cells, expected mˆp (x + x 2 )/2 Hece, (obs exp) 2 exp, reduces to (x (x + x 2 )/2) 2 (x + x 2 )/2 + (x 2 (x + x 2 )/2) 2 (x + x 2 )/2 (x x 2 ) 2 x + x 2 b Now the hypothess about the codtoal probabltes s gve by H 0 : P(chage-tal p agree) P(chage-tal dsagree) or, terms of the parameters, H 0 : p +p 3 p 2 p 2 +p 4 Ths s the same as testg p p 4 p 2 p 3 whch s ot the same as p p f(x α, β) x α e x/β Thus, L(β) e x /β Γαβ α ad (β) α log β β α x /β The S(β) (β) α/β + x /β 2 (/β)( x/β α) ad (β) α/β 2 2 x /β 3 (/β 2 )(α 2 x/β) E( (β)) α/β 2 a Solvg S(β) (β) 0forβ gves us ˆβ MLE x Note that α (ˆβ MLE ) α 3 / x 2 < 0 b se(ˆβ MLE ) /I(ˆβ MLE ) x 2 /(α 3 ) Thus, a Wald statstc for testg H 0 : β β 0 s x/α β 0 x 2 /(α 3 ) 038 We wll use the outputs from 036: A score statstc for testg H 0 : β β 0 s S(β 0 ) (/β 0 )( x/β 0 α) ( x αβ 0 ) I(β0 ) α/β 2 0 αβ 2 0 Addtoal HW The lkelhood fucto ad log lkelhood fucto for (θ, σ 2 )are L(θ, σ 2 )(2πσ 2 ) /2 exp (X θ) 2 2σ 2 (θ, σ 2 ) 2 log(2πσ2 ) (X θ) 2 2σ 2 a Uder H 0, (θ 0,σ 2 ) σ 2 b I the whole parameter space, (θ,σ2 ) + 2σ 2 (X θ 0 ) 2 0 Thus, σ 2 2(σ 2 ) 2 (X θ) θ (X ˆθ) 2 (X X) 2 Thus, ˆθ X ad ˆσ 2 c The lkelhood rato statstc, λ( X), s λ( X) L(θ 0, σ 2 0) (2π σ2 ) /2 exp L(ˆθ, ˆσ 2 ) (2πˆσ 2 ) /2 exp 0 ad (θ,σ2 ) σ 2 σ 2 ˆσ 2 σ 2 2ˆσ 2 P (X θ 0 ) 2 2 σ 2 P (X ˆθ) 2 P (X θ 0 ) 2 2σ 2 + (X θ) 2 2(σ 2 ) 2 0 /2 (X X) 2 (X θ 0 ) 2 /2 2
5 d We ca smplfy λ( X) the followg way: λ( X) (X X) 2 /2 (X (X X) 2 /2 θ 0 ) 2 (X X) 2 + ( X θ 0 ) 2 + ( X θ 0 ) 2 P (X X) 2 /2 + T 2 where T (X) X θ 0 Thus, λ( X) <cs equvalet to the followgs: S /2 λ(x) <c + T <c T (X) 2 >k 2 ( )(c 2/ ) T (X) > k (X)2 Thus, rejectg H 0 whe λ(x) <c correspods to rejectg H 0 whe T (X) > k e Uder H 0, T (X) T, T dstrbuto wth parameters (I beleve that you ca prove t, as t s related to stat 607) f The level α lkelhood rato test s as follows : rejectg H 0 whe λ(x) < c where α P ( 2 log λ(x) >c ) uder H 0 Here, λ(x) <cs equvalet to T (X) > kad T (X) T uder H 0 where α P ( T (X) > t,α/2 ) Thus, k t,α/2 /2 3
Chapter 8. Hypothesis Testing. x=560
 Chapter 8 Hypothess Testg 8 Let X # of heads out of 000 If the co s far, the X bomal000, / So P X 560 000 x560 x x 000 000085, x where a computer was used to do the calculato For ths bomal, E X 000p 500
Chapter 8 Hypothess Testg 8 Let X # of heads out of 000 If the co s far, the X bomal000, / So P X 560 000 x560 x x 000 000085, x where a computer was used to do the calculato For ths bomal, E X 000p 500
Qualifying Exam Statistical Theory Problem Solutions August 2005
 Qualfyg Exam Statstcal Theory Problem Solutos August 5. Let X, X,..., X be d uform U(,),
Qualfyg Exam Statstcal Theory Problem Solutos August 5. Let X, X,..., X be d uform U(,),
LINEAR REGRESSION ANALYSIS
 LINEAR REGRESSION ANALYSIS MODULE V Lecture - Correctg Model Iadequaces Through Trasformato ad Weghtg Dr. Shalabh Departmet of Mathematcs ad Statstcs Ida Isttute of Techology Kapur Aalytcal methods for
LINEAR REGRESSION ANALYSIS MODULE V Lecture - Correctg Model Iadequaces Through Trasformato ad Weghtg Dr. Shalabh Departmet of Mathematcs ad Statstcs Ida Isttute of Techology Kapur Aalytcal methods for
TESTS BASED ON MAXIMUM LIKELIHOOD
 ESE 5 Toy E. Smth. The Basc Example. TESTS BASED ON MAXIMUM LIKELIHOOD To llustrate the propertes of maxmum lkelhood estmates ad tests, we cosder the smplest possble case of estmatg the mea of the ormal
ESE 5 Toy E. Smth. The Basc Example. TESTS BASED ON MAXIMUM LIKELIHOOD To llustrate the propertes of maxmum lkelhood estmates ad tests, we cosder the smplest possble case of estmatg the mea of the ormal
STAT 400 Homework 09 Spring 2018 Dalpiaz UIUC Due: Friday, April 6, 2:00 PM
 STAT Homework 9 Sprg 28 Dalpaz UIUC Due: Fray, Aprl 6, 2: PM Exercse f(x, θ) = θ e x/θ, x >, θ > Note that, the momets of ths strbuto are gve by E[X k ] = Ths wll be a useful fact for Exercses 2 a 3. x
STAT Homework 9 Sprg 28 Dalpaz UIUC Due: Fray, Aprl 6, 2: PM Exercse f(x, θ) = θ e x/θ, x >, θ > Note that, the momets of ths strbuto are gve by E[X k ] = Ths wll be a useful fact for Exercses 2 a 3. x
1 Solution to Problem 6.40
 1 Soluto to Problem 6.40 (a We wll wrte T τ (X 1,...,X where the X s are..d. wth PDF f(x µ, σ 1 ( x µ σ g, σ where the locato parameter µ s ay real umber ad the scale parameter σ s > 0. Lettg Z X µ σ we
1 Soluto to Problem 6.40 (a We wll wrte T τ (X 1,...,X where the X s are..d. wth PDF f(x µ, σ 1 ( x µ σ g, σ where the locato parameter µ s ay real umber ad the scale parameter σ s > 0. Lettg Z X µ σ we
UNIVERSITY OF OSLO DEPARTMENT OF ECONOMICS
 UNIVERSITY OF OSLO DEPARTMENT OF ECONOMICS Exam: ECON430 Statstcs Date of exam: Frday, December 8, 07 Grades are gve: Jauary 4, 08 Tme for exam: 0900 am 00 oo The problem set covers 5 pages Resources allowed:
UNIVERSITY OF OSLO DEPARTMENT OF ECONOMICS Exam: ECON430 Statstcs Date of exam: Frday, December 8, 07 Grades are gve: Jauary 4, 08 Tme for exam: 0900 am 00 oo The problem set covers 5 pages Resources allowed:
Summary of the lecture in Biostatistics
 Summary of the lecture Bostatstcs Probablty Desty Fucto For a cotuos radom varable, a probablty desty fucto s a fucto such that: 0 dx a b) b a dx A probablty desty fucto provdes a smple descrpto of the
Summary of the lecture Bostatstcs Probablty Desty Fucto For a cotuos radom varable, a probablty desty fucto s a fucto such that: 0 dx a b) b a dx A probablty desty fucto provdes a smple descrpto of the
Point Estimation: definition of estimators
 Pot Estmato: defto of estmators Pot estmator: ay fucto W (X,..., X ) of a data sample. The exercse of pot estmato s to use partcular fuctos of the data order to estmate certa ukow populato parameters.
Pot Estmato: defto of estmators Pot estmator: ay fucto W (X,..., X ) of a data sample. The exercse of pot estmato s to use partcular fuctos of the data order to estmate certa ukow populato parameters.
Likelihood Ratio, Wald, and Lagrange Multiplier (Score) Tests. Soccer Goals in European Premier Leagues
 Lkelhood Rato, Wald, ad Lagrage Multpler (Score) Tests Soccer Goals Europea Premer Leagues - 4 Statstcal Testg Prcples Goal: Test a Hpothess cocerg parameter value(s) a larger populato (or ature), based
Lkelhood Rato, Wald, ad Lagrage Multpler (Score) Tests Soccer Goals Europea Premer Leagues - 4 Statstcal Testg Prcples Goal: Test a Hpothess cocerg parameter value(s) a larger populato (or ature), based
M2S1 - EXERCISES 8: SOLUTIONS
 MS - EXERCISES 8: SOLUTIONS. As X,..., X P ossoλ, a gve that T ˉX, the usg elemetary propertes of expectatos, we have E ft [T E fx [X λ λ, so that T s a ubase estmator of λ. T X X X Furthermore X X X From
MS - EXERCISES 8: SOLUTIONS. As X,..., X P ossoλ, a gve that T ˉX, the usg elemetary propertes of expectatos, we have E ft [T E fx [X λ λ, so that T s a ubase estmator of λ. T X X X Furthermore X X X From
Special Instructions / Useful Data
 JAM 6 Set of all real umbers P A..d. B, p Posso Specal Istructos / Useful Data x,, :,,, x x Probablty of a evet A Idepedetly ad detcally dstrbuted Bomal dstrbuto wth parameters ad p Posso dstrbuto wth
JAM 6 Set of all real umbers P A..d. B, p Posso Specal Istructos / Useful Data x,, :,,, x x Probablty of a evet A Idepedetly ad detcally dstrbuted Bomal dstrbuto wth parameters ad p Posso dstrbuto wth
UNIVERSITY OF OSLO DEPARTMENT OF ECONOMICS
 UNIVERSITY OF OSLO DEPARTMENT OF ECONOMICS Postpoed exam: ECON430 Statstcs Date of exam: Jauary 0, 0 Tme for exam: 09:00 a.m. :00 oo The problem set covers 5 pages Resources allowed: All wrtte ad prted
UNIVERSITY OF OSLO DEPARTMENT OF ECONOMICS Postpoed exam: ECON430 Statstcs Date of exam: Jauary 0, 0 Tme for exam: 09:00 a.m. :00 oo The problem set covers 5 pages Resources allowed: All wrtte ad prted
Chapter 14 Logistic Regression Models
 Chapter 4 Logstc Regresso Models I the lear regresso model X β + ε, there are two types of varables explaatory varables X, X,, X k ad study varable y These varables ca be measured o a cotuous scale as
Chapter 4 Logstc Regresso Models I the lear regresso model X β + ε, there are two types of varables explaatory varables X, X,, X k ad study varable y These varables ca be measured o a cotuous scale as
Lecture Notes Types of economic variables
 Lecture Notes 3 1. Types of ecoomc varables () Cotuous varable takes o a cotuum the sample space, such as all pots o a le or all real umbers Example: GDP, Polluto cocetrato, etc. () Dscrete varables fte
Lecture Notes 3 1. Types of ecoomc varables () Cotuous varable takes o a cotuum the sample space, such as all pots o a le or all real umbers Example: GDP, Polluto cocetrato, etc. () Dscrete varables fte
STK4011 and STK9011 Autumn 2016
 STK4 ad STK9 Autum 6 Pot estmato Covers (most of the followg materal from chapter 7: Secto 7.: pages 3-3 Secto 7..: pages 3-33 Secto 7..: pages 35-3 Secto 7..3: pages 34-35 Secto 7.3.: pages 33-33 Secto
STK4 ad STK9 Autum 6 Pot estmato Covers (most of the followg materal from chapter 7: Secto 7.: pages 3-3 Secto 7..: pages 3-33 Secto 7..: pages 35-3 Secto 7..3: pages 34-35 Secto 7.3.: pages 33-33 Secto
9 U-STATISTICS. Eh =(m!) 1 Eh(X (1),..., X (m ) ) i.i.d
 9 U-STATISTICS Suppose,,..., are P P..d. wth CDF F. Our goal s to estmate the expectato t (P)=Eh(,,..., m ). Note that ths expectato requres more tha oe cotrast to E, E, or Eh( ). Oe example s E or P((,
9 U-STATISTICS Suppose,,..., are P P..d. wth CDF F. Our goal s to estmate the expectato t (P)=Eh(,,..., m ). Note that ths expectato requres more tha oe cotrast to E, E, or Eh( ). Oe example s E or P((,
ρ < 1 be five real numbers. The
 Lecture o BST 63: Statstcal Theory I Ku Zhag, /0/006 Revew for the prevous lecture Deftos: covarace, correlato Examples: How to calculate covarace ad correlato Theorems: propertes of correlato ad covarace
Lecture o BST 63: Statstcal Theory I Ku Zhag, /0/006 Revew for the prevous lecture Deftos: covarace, correlato Examples: How to calculate covarace ad correlato Theorems: propertes of correlato ad covarace
Bounds on the expected entropy and KL-divergence of sampled multinomial distributions. Brandon C. Roy
 Bouds o the expected etropy ad KL-dvergece of sampled multomal dstrbutos Brado C. Roy bcroy@meda.mt.edu Orgal: May 18, 2011 Revsed: Jue 6, 2011 Abstract Iformato theoretc quattes calculated from a sampled
Bouds o the expected etropy ad KL-dvergece of sampled multomal dstrbutos Brado C. Roy bcroy@meda.mt.edu Orgal: May 18, 2011 Revsed: Jue 6, 2011 Abstract Iformato theoretc quattes calculated from a sampled
MS exam problems Fall 2012
 MS exam problems Fall 01 (From: Rya Mart) 1. (Stat 401) Cosder the followg game wth a box that cotas te balls two red, three blue, ad fve gree. A player selects two balls from the box at radom, wthout
MS exam problems Fall 01 (From: Rya Mart) 1. (Stat 401) Cosder the followg game wth a box that cotas te balls two red, three blue, ad fve gree. A player selects two balls from the box at radom, wthout
Wu-Hausman Test: But if X and ε are independent, βˆ. ECON 324 Page 1
 Wu-Hausma Test: Detectg Falure of E( ε X ) Caot drectly test ths assumpto because lack ubased estmator of ε ad the OLS resduals wll be orthogoal to X, by costructo as ca be see from the momet codto X'
Wu-Hausma Test: Detectg Falure of E( ε X ) Caot drectly test ths assumpto because lack ubased estmator of ε ad the OLS resduals wll be orthogoal to X, by costructo as ca be see from the momet codto X'
Logistic regression (continued)
 STAT562 page 138 Logstc regresso (cotued) Suppose we ow cosder more complex models to descrbe the relatoshp betwee a categorcal respose varable (Y) that takes o two (2) possble outcomes ad a set of p explaatory
STAT562 page 138 Logstc regresso (cotued) Suppose we ow cosder more complex models to descrbe the relatoshp betwee a categorcal respose varable (Y) that takes o two (2) possble outcomes ad a set of p explaatory
CHAPTER 6. d. With success = observation greater than 10, x = # of successes = 4, and
 CHAPTR 6 Secto 6.. a. We use the samle mea, to estmate the oulato mea µ. Σ 9.80 µ 8.407 7 ~ 7. b. We use the samle meda, 7 (the mddle observato whe arraged ascedg order. c. We use the samle stadard devato,
CHAPTR 6 Secto 6.. a. We use the samle mea, to estmate the oulato mea µ. Σ 9.80 µ 8.407 7 ~ 7. b. We use the samle meda, 7 (the mddle observato whe arraged ascedg order. c. We use the samle stadard devato,
Chapter 4 (Part 1): Non-Parametric Classification (Sections ) Pattern Classification 4.3) Announcements
 Aoucemets No-Parametrc Desty Estmato Techques HW assged Most of ths lecture was o the blacboard. These sldes cover the same materal as preseted DHS Bometrcs CSE 90-a Lecture 7 CSE90a Fall 06 CSE90a Fall
Aoucemets No-Parametrc Desty Estmato Techques HW assged Most of ths lecture was o the blacboard. These sldes cover the same materal as preseted DHS Bometrcs CSE 90-a Lecture 7 CSE90a Fall 06 CSE90a Fall
X X X E[ ] E X E X. is the ()m n where the ( i,)th. j element is the mean of the ( i,)th., then
![X X X E[ ] E X E X. is the ()m n where the ( i,)th. j element is the mean of the ( i,)th., then X X X E[ ] E X E X. is the ()m n where the ( i,)th. j element is the mean of the ( i,)th., then](/thumbs/83/87696552.jpg) Secto 5 Vectors of Radom Varables Whe workg wth several radom varables,,..., to arrage them vector form x, t s ofte coveet We ca the make use of matrx algebra to help us orgaze ad mapulate large umbers
Secto 5 Vectors of Radom Varables Whe workg wth several radom varables,,..., to arrage them vector form x, t s ofte coveet We ca the make use of matrx algebra to help us orgaze ad mapulate large umbers
STK3100 and STK4100 Autumn 2018
 SK3 ad SK4 Autum 8 Geeralzed lear models Part III Covers the followg materal from chaters 4 ad 5: Cofdece tervals by vertg tests Cosder a model wth a sgle arameter β We may obta a ( α% cofdece terval for
SK3 ad SK4 Autum 8 Geeralzed lear models Part III Covers the followg materal from chaters 4 ad 5: Cofdece tervals by vertg tests Cosder a model wth a sgle arameter β We may obta a ( α% cofdece terval for
Maximum Likelihood Estimation
 Marquette Uverst Maxmum Lkelhood Estmato Dael B. Rowe, Ph.D. Professor Departmet of Mathematcs, Statstcs, ad Computer Scece Coprght 08 b Marquette Uverst Maxmum Lkelhood Estmato We have bee sag that ~
Marquette Uverst Maxmum Lkelhood Estmato Dael B. Rowe, Ph.D. Professor Departmet of Mathematcs, Statstcs, ad Computer Scece Coprght 08 b Marquette Uverst Maxmum Lkelhood Estmato We have bee sag that ~
Mu Sequences/Series Solutions National Convention 2014
 Mu Sequeces/Seres Solutos Natoal Coveto 04 C 6 E A 6C A 6 B B 7 A D 7 D C 7 A B 8 A B 8 A C 8 E 4 B 9 B 4 E 9 B 4 C 9 E C 0 A A 0 D B 0 C C Usg basc propertes of arthmetc sequeces, we fd a ad bm m We eed
Mu Sequeces/Seres Solutos Natoal Coveto 04 C 6 E A 6C A 6 B B 7 A D 7 D C 7 A B 8 A B 8 A C 8 E 4 B 9 B 4 E 9 B 4 C 9 E C 0 A A 0 D B 0 C C Usg basc propertes of arthmetc sequeces, we fd a ad bm m We eed
å 1 13 Practice Final Examination Solutions - = CS109 Dec 5, 2018
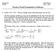 Chrs Pech Fal Practce CS09 Dec 5, 08 Practce Fal Examato Solutos. Aswer: 4/5 8/7. There are multle ways to obta ths aswer; here are two: The frst commo method s to sum over all ossbltes for the rak of
Chrs Pech Fal Practce CS09 Dec 5, 08 Practce Fal Examato Solutos. Aswer: 4/5 8/7. There are multle ways to obta ths aswer; here are two: The frst commo method s to sum over all ossbltes for the rak of
9.1 Introduction to the probit and logit models
 EC3000 Ecoometrcs Lecture 9 Probt & Logt Aalss 9. Itroducto to the probt ad logt models 9. The logt model 9.3 The probt model Appedx 9. Itroducto to the probt ad logt models These models are used regressos
EC3000 Ecoometrcs Lecture 9 Probt & Logt Aalss 9. Itroducto to the probt ad logt models 9. The logt model 9.3 The probt model Appedx 9. Itroducto to the probt ad logt models These models are used regressos
Ordinary Least Squares Regression. Simple Regression. Algebra and Assumptions.
 Ordary Least Squares egresso. Smple egresso. Algebra ad Assumptos. I ths part of the course we are gog to study a techque for aalysg the lear relatoshp betwee two varables Y ad X. We have pars of observatos
Ordary Least Squares egresso. Smple egresso. Algebra ad Assumptos. I ths part of the course we are gog to study a techque for aalysg the lear relatoshp betwee two varables Y ad X. We have pars of observatos
THE ROYAL STATISTICAL SOCIETY GRADUATE DIPLOMA
 THE ROYAL STATISTICAL SOCIETY EXAMINATIONS SOLUTIONS GRADUATE DIPLOMA PAPER II STATISTICAL THEORY & METHODS The Socety provdes these solutos to assst caddates preparg for the examatos future years ad for
THE ROYAL STATISTICAL SOCIETY EXAMINATIONS SOLUTIONS GRADUATE DIPLOMA PAPER II STATISTICAL THEORY & METHODS The Socety provdes these solutos to assst caddates preparg for the examatos future years ad for
Chapter 8. Inferences about More Than Two Population Central Values
 Chapter 8. Ifereces about More Tha Two Populato Cetral Values Case tudy: Effect of Tmg of the Treatmet of Port-We tas wth Lasers ) To vestgate whether treatmet at a youg age would yeld better results tha
Chapter 8. Ifereces about More Tha Two Populato Cetral Values Case tudy: Effect of Tmg of the Treatmet of Port-We tas wth Lasers ) To vestgate whether treatmet at a youg age would yeld better results tha
Lecture 3. Sampling, sampling distributions, and parameter estimation
 Lecture 3 Samplg, samplg dstrbutos, ad parameter estmato Samplg Defto Populato s defed as the collecto of all the possble observatos of terest. The collecto of observatos we take from the populato s called
Lecture 3 Samplg, samplg dstrbutos, ad parameter estmato Samplg Defto Populato s defed as the collecto of all the possble observatos of terest. The collecto of observatos we take from the populato s called
( ) = ( ) ( ) Chapter 13 Asymptotic Theory and Stochastic Regressors. Stochastic regressors model
 Chapter 3 Asmptotc Theor ad Stochastc Regressors The ature of eplaator varable s assumed to be o-stochastc or fed repeated samples a regresso aalss Such a assumpto s approprate for those epermets whch
Chapter 3 Asmptotc Theor ad Stochastc Regressors The ature of eplaator varable s assumed to be o-stochastc or fed repeated samples a regresso aalss Such a assumpto s approprate for those epermets whch
Multivariate Transformation of Variables and Maximum Likelihood Estimation
 Marquette Uversty Multvarate Trasformato of Varables ad Maxmum Lkelhood Estmato Dael B. Rowe, Ph.D. Assocate Professor Departmet of Mathematcs, Statstcs, ad Computer Scece Copyrght 03 by Marquette Uversty
Marquette Uversty Multvarate Trasformato of Varables ad Maxmum Lkelhood Estmato Dael B. Rowe, Ph.D. Assocate Professor Departmet of Mathematcs, Statstcs, ad Computer Scece Copyrght 03 by Marquette Uversty
Dimensionality Reduction and Learning
 CMSC 35900 (Sprg 009) Large Scale Learg Lecture: 3 Dmesoalty Reducto ad Learg Istructors: Sham Kakade ad Greg Shakharovch L Supervsed Methods ad Dmesoalty Reducto The theme of these two lectures s that
CMSC 35900 (Sprg 009) Large Scale Learg Lecture: 3 Dmesoalty Reducto ad Learg Istructors: Sham Kakade ad Greg Shakharovch L Supervsed Methods ad Dmesoalty Reducto The theme of these two lectures s that
ECONOMETRIC THEORY. MODULE VIII Lecture - 26 Heteroskedasticity
 ECONOMETRIC THEORY MODULE VIII Lecture - 6 Heteroskedastcty Dr. Shalabh Departmet of Mathematcs ad Statstcs Ida Isttute of Techology Kapur . Breusch Paga test Ths test ca be appled whe the replcated data
ECONOMETRIC THEORY MODULE VIII Lecture - 6 Heteroskedastcty Dr. Shalabh Departmet of Mathematcs ad Statstcs Ida Isttute of Techology Kapur . Breusch Paga test Ths test ca be appled whe the replcated data
Chapter 4 Multiple Random Variables
 Revew for the prevous lecture: Theorems ad Examples: How to obta the pmf (pdf) of U = g (, Y) ad V = g (, Y) Chapter 4 Multple Radom Varables Chapter 44 Herarchcal Models ad Mxture Dstrbutos Examples:
Revew for the prevous lecture: Theorems ad Examples: How to obta the pmf (pdf) of U = g (, Y) ad V = g (, Y) Chapter 4 Multple Radom Varables Chapter 44 Herarchcal Models ad Mxture Dstrbutos Examples:
The number of observed cases The number of parameters. ith case of the dichotomous dependent variable. the ith case of the jth parameter
 LOGISTIC REGRESSION Notato Model Logstc regresso regresses a dchotomous depedet varable o a set of depedet varables. Several methods are mplemeted for selectg the depedet varables. The followg otato s
LOGISTIC REGRESSION Notato Model Logstc regresso regresses a dchotomous depedet varable o a set of depedet varables. Several methods are mplemeted for selectg the depedet varables. The followg otato s
Analysis of Variance with Weibull Data
 Aalyss of Varace wth Webull Data Lahaa Watthaacheewaul Abstract I statstcal data aalyss by aalyss of varace, the usual basc assumptos are that the model s addtve ad the errors are radomly, depedetly, ad
Aalyss of Varace wth Webull Data Lahaa Watthaacheewaul Abstract I statstcal data aalyss by aalyss of varace, the usual basc assumptos are that the model s addtve ad the errors are radomly, depedetly, ad
STK3100 and STK4100 Autumn 2017
 SK3 ad SK4 Autum 7 Geeralzed lear models Part III Covers the followg materal from chaters 4 ad 5: Sectos 4..5, 4.3.5, 4.3.6, 4.4., 4.4., ad 4.4.3 Sectos 5.., 5.., ad 5.5. Ørulf Borga Deartmet of Mathematcs
SK3 ad SK4 Autum 7 Geeralzed lear models Part III Covers the followg materal from chaters 4 ad 5: Sectos 4..5, 4.3.5, 4.3.6, 4.4., 4.4., ad 4.4.3 Sectos 5.., 5.., ad 5.5. Ørulf Borga Deartmet of Mathematcs
STA302/1001-Fall 2008 Midterm Test October 21, 2008
 STA3/-Fall 8 Mdterm Test October, 8 Last Name: Frst Name: Studet Number: Erolled (Crcle oe) STA3 STA INSTRUCTIONS Tme allowed: hour 45 mutes Ads allowed: A o-programmable calculator A table of values from
STA3/-Fall 8 Mdterm Test October, 8 Last Name: Frst Name: Studet Number: Erolled (Crcle oe) STA3 STA INSTRUCTIONS Tme allowed: hour 45 mutes Ads allowed: A o-programmable calculator A table of values from
STATISTICAL PROPERTIES OF LEAST SQUARES ESTIMATORS. x, where. = y - ˆ " 1
 STATISTICAL PROPERTIES OF LEAST SQUARES ESTIMATORS Recall Assumpto E(Y x) η 0 + η x (lear codtoal mea fucto) Data (x, y ), (x 2, y 2 ),, (x, y ) Least squares estmator ˆ E (Y x) ˆ " 0 + ˆ " x, where ˆ
STATISTICAL PROPERTIES OF LEAST SQUARES ESTIMATORS Recall Assumpto E(Y x) η 0 + η x (lear codtoal mea fucto) Data (x, y ), (x 2, y 2 ),, (x, y ) Least squares estmator ˆ E (Y x) ˆ " 0 + ˆ " x, where ˆ
22 Nonparametric Methods.
 22 oparametrc Methods. I parametrc models oe assumes apror that the dstrbutos have a specfc form wth oe or more ukow parameters ad oe tres to fd the best or atleast reasoably effcet procedures that aswer
22 oparametrc Methods. I parametrc models oe assumes apror that the dstrbutos have a specfc form wth oe or more ukow parameters ad oe tres to fd the best or atleast reasoably effcet procedures that aswer
Lecture 02: Bounding tail distributions of a random variable
 CSCI-B609: A Theorst s Toolkt, Fall 206 Aug 25 Lecture 02: Boudg tal dstrbutos of a radom varable Lecturer: Yua Zhou Scrbe: Yua Xe & Yua Zhou Let us cosder the ubased co flps aga. I.e. let the outcome
CSCI-B609: A Theorst s Toolkt, Fall 206 Aug 25 Lecture 02: Boudg tal dstrbutos of a radom varable Lecturer: Yua Zhou Scrbe: Yua Xe & Yua Zhou Let us cosder the ubased co flps aga. I.e. let the outcome
Chapter 5 Properties of a Random Sample
 Lecture 6 o BST 63: Statstcal Theory I Ku Zhag, /0/008 Revew for the prevous lecture Cocepts: t-dstrbuto, F-dstrbuto Theorems: Dstrbutos of sample mea ad sample varace, relatoshp betwee sample mea ad sample
Lecture 6 o BST 63: Statstcal Theory I Ku Zhag, /0/008 Revew for the prevous lecture Cocepts: t-dstrbuto, F-dstrbuto Theorems: Dstrbutos of sample mea ad sample varace, relatoshp betwee sample mea ad sample
ENGI 3423 Simple Linear Regression Page 12-01
 ENGI 343 mple Lear Regresso Page - mple Lear Regresso ometmes a expermet s set up where the expermeter has cotrol over the values of oe or more varables X ad measures the resultg values of aother varable
ENGI 343 mple Lear Regresso Page - mple Lear Regresso ometmes a expermet s set up where the expermeter has cotrol over the values of oe or more varables X ad measures the resultg values of aother varable
X ε ) = 0, or equivalently, lim
 Revew for the prevous lecture Cocepts: order statstcs Theorems: Dstrbutos of order statstcs Examples: How to get the dstrbuto of order statstcs Chapter 5 Propertes of a Radom Sample Secto 55 Covergece
Revew for the prevous lecture Cocepts: order statstcs Theorems: Dstrbutos of order statstcs Examples: How to get the dstrbuto of order statstcs Chapter 5 Propertes of a Radom Sample Secto 55 Covergece
{ }{ ( )} (, ) = ( ) ( ) ( ) Chapter 14 Exercises in Sampling Theory. Exercise 1 (Simple random sampling): Solution:
 Chapter 4 Exercses Samplg Theory Exercse (Smple radom samplg: Let there be two correlated radom varables X ad A sample of sze s draw from a populato by smple radom samplg wthout replacemet The observed
Chapter 4 Exercses Samplg Theory Exercse (Smple radom samplg: Let there be two correlated radom varables X ad A sample of sze s draw from a populato by smple radom samplg wthout replacemet The observed
Lecture 7. Confidence Intervals and Hypothesis Tests in the Simple CLR Model
 Lecture 7. Cofdece Itervals ad Hypothess Tests the Smple CLR Model I lecture 6 we troduced the Classcal Lear Regresso (CLR) model that s the radom expermet of whch the data Y,,, K, are the outcomes. The
Lecture 7. Cofdece Itervals ad Hypothess Tests the Smple CLR Model I lecture 6 we troduced the Classcal Lear Regresso (CLR) model that s the radom expermet of whch the data Y,,, K, are the outcomes. The
THE ROYAL STATISTICAL SOCIETY 2016 EXAMINATIONS SOLUTIONS GRADUATE DIPLOMA MODULE 2
 THE ROYAL STATISTICAL SOCIETY 06 EXAMINATIONS SOLUTIONS GRADUATE DIPLOMA MODULE The Socety s provdg these solutos to assst caddates preparg for the examatos 07. The solutos are teded as learg ads ad should
THE ROYAL STATISTICAL SOCIETY 06 EXAMINATIONS SOLUTIONS GRADUATE DIPLOMA MODULE The Socety s provdg these solutos to assst caddates preparg for the examatos 07. The solutos are teded as learg ads ad should
The Mathematical Appendix
 The Mathematcal Appedx Defto A: If ( Λ, Ω, where ( λ λ λ whch the probablty dstrbutos,,..., Defto A. uppose that ( Λ,,..., s a expermet type, the σ-algebra o λ λ λ are defed s deoted by ( (,,...,, σ Ω.
The Mathematcal Appedx Defto A: If ( Λ, Ω, where ( λ λ λ whch the probablty dstrbutos,,..., Defto A. uppose that ( Λ,,..., s a expermet type, the σ-algebra o λ λ λ are defed s deoted by ( (,,...,, σ Ω.
Lecture Notes 15 Hypothesis Testing (Chapter 10)
 1 Itroductio Lecture Notes 15 Hypothesis Testig Chapter 10) Let X 1,..., X p θ x). Suppose we we wat to kow if θ = θ 0 or ot, where θ 0 is a specific value of θ. For example, if we are flippig a coi, we
1 Itroductio Lecture Notes 15 Hypothesis Testig Chapter 10) Let X 1,..., X p θ x). Suppose we we wat to kow if θ = θ 0 or ot, where θ 0 is a specific value of θ. For example, if we are flippig a coi, we
ESS Line Fitting
 ESS 5 014 17. Le Fttg A very commo problem data aalyss s lookg for relatoshpetwee dfferet parameters ad fttg les or surfaces to data. The smplest example s fttg a straght le ad we wll dscuss that here
ESS 5 014 17. Le Fttg A very commo problem data aalyss s lookg for relatoshpetwee dfferet parameters ad fttg les or surfaces to data. The smplest example s fttg a straght le ad we wll dscuss that here
Econometric Methods. Review of Estimation
 Ecoometrc Methods Revew of Estmato Estmatg the populato mea Radom samplg Pot ad terval estmators Lear estmators Ubased estmators Lear Ubased Estmators (LUEs) Effcecy (mmum varace) ad Best Lear Ubased Estmators
Ecoometrc Methods Revew of Estmato Estmatg the populato mea Radom samplg Pot ad terval estmators Lear estmators Ubased estmators Lear Ubased Estmators (LUEs) Effcecy (mmum varace) ad Best Lear Ubased Estmators
STATISTICAL INFERENCE
 (STATISTICS) STATISTICAL INFERENCE COMPLEMENTARY COURSE B.Sc. MATHEMATICS III SEMESTER ( Admsso) UNIVERSITY OF CALICUT SCHOOL OF DISTANCE EDUCATION CALICUT UNIVERSITY P.O., MALAPPURAM, KERALA, INDIA -
(STATISTICS) STATISTICAL INFERENCE COMPLEMENTARY COURSE B.Sc. MATHEMATICS III SEMESTER ( Admsso) UNIVERSITY OF CALICUT SCHOOL OF DISTANCE EDUCATION CALICUT UNIVERSITY P.O., MALAPPURAM, KERALA, INDIA -
Dr. Shalabh Department of Mathematics and Statistics Indian Institute of Technology Kanpur
 Aalyss of Varace ad Desg of Exermets-I MODULE II LECTURE - GENERAL LINEAR HYPOTHESIS AND ANALYSIS OF VARIANCE Dr Shalabh Deartmet of Mathematcs ad Statstcs Ida Isttute of Techology Kaur Tukey s rocedure
Aalyss of Varace ad Desg of Exermets-I MODULE II LECTURE - GENERAL LINEAR HYPOTHESIS AND ANALYSIS OF VARIANCE Dr Shalabh Deartmet of Mathematcs ad Statstcs Ida Isttute of Techology Kaur Tukey s rocedure
Chapter 7. Hypothesis Testing
 Chapter 7. Hypothesis Testing Joonpyo Kim June 24, 2017 Joonpyo Kim Ch7 June 24, 2017 1 / 63 Basic Concepts of Testing Suppose that our interest centers on a random variable X which has density function
Chapter 7. Hypothesis Testing Joonpyo Kim June 24, 2017 Joonpyo Kim Ch7 June 24, 2017 1 / 63 Basic Concepts of Testing Suppose that our interest centers on a random variable X which has density function
A New Family of Transformations for Lifetime Data
 Proceedgs of the World Cogress o Egeerg 4 Vol I, WCE 4, July - 4, 4, Lodo, U.K. A New Famly of Trasformatos for Lfetme Data Lakhaa Watthaacheewakul Abstract A famly of trasformatos s the oe of several
Proceedgs of the World Cogress o Egeerg 4 Vol I, WCE 4, July - 4, 4, Lodo, U.K. A New Famly of Trasformatos for Lfetme Data Lakhaa Watthaacheewakul Abstract A famly of trasformatos s the oe of several
THE ROYAL STATISTICAL SOCIETY 2016 EXAMINATIONS SOLUTIONS HIGHER CERTIFICATE MODULE 5
 THE ROYAL STATISTICAL SOCIETY 06 EAMINATIONS SOLUTIONS HIGHER CERTIFICATE MODULE 5 The Socety s provdg these solutos to assst cadtes preparg for the examatos 07. The solutos are teded as learg ads ad should
THE ROYAL STATISTICAL SOCIETY 06 EAMINATIONS SOLUTIONS HIGHER CERTIFICATE MODULE 5 The Socety s provdg these solutos to assst cadtes preparg for the examatos 07. The solutos are teded as learg ads ad should
Algorithms Theory, Solution for Assignment 2
 Juor-Prof. Dr. Robert Elsässer, Marco Muñz, Phllp Hedegger WS 2009/200 Algorthms Theory, Soluto for Assgmet 2 http://lak.formatk.u-freburg.de/lak_teachg/ws09_0/algo090.php Exercse 2. - Fast Fourer Trasform
Juor-Prof. Dr. Robert Elsässer, Marco Muñz, Phllp Hedegger WS 2009/200 Algorthms Theory, Soluto for Assgmet 2 http://lak.formatk.u-freburg.de/lak_teachg/ws09_0/algo090.php Exercse 2. - Fast Fourer Trasform
MEASURES OF DISPERSION
 MEASURES OF DISPERSION Measure of Cetral Tedecy: Measures of Cetral Tedecy ad Dsperso ) Mathematcal Average: a) Arthmetc mea (A.M.) b) Geometrc mea (G.M.) c) Harmoc mea (H.M.) ) Averages of Posto: a) Meda
MEASURES OF DISPERSION Measure of Cetral Tedecy: Measures of Cetral Tedecy ad Dsperso ) Mathematcal Average: a) Arthmetc mea (A.M.) b) Geometrc mea (G.M.) c) Harmoc mea (H.M.) ) Averages of Posto: a) Meda
hp calculators HP 30S Statistics Averages and Standard Deviations Average and Standard Deviation Practice Finding Averages and Standard Deviations
 HP 30S Statstcs Averages ad Stadard Devatos Average ad Stadard Devato Practce Fdg Averages ad Stadard Devatos HP 30S Statstcs Averages ad Stadard Devatos Average ad stadard devato The HP 30S provdes several
HP 30S Statstcs Averages ad Stadard Devatos Average ad Stadard Devato Practce Fdg Averages ad Stadard Devatos HP 30S Statstcs Averages ad Stadard Devatos Average ad stadard devato The HP 30S provdes several
Lecture Note to Rice Chapter 8
 ECON 430 HG revsed Nov 06 Lecture Note to Rce Chapter 8 Radom matrces Let Y, =,,, m, =,,, be radom varables (r.v. s). The matrx Y Y Y Y Y Y Y Y Y Y = m m m s called a radom matrx ( wth a ot m-dmesoal dstrbuto,
ECON 430 HG revsed Nov 06 Lecture Note to Rce Chapter 8 Radom matrces Let Y, =,,, m, =,,, be radom varables (r.v. s). The matrx Y Y Y Y Y Y Y Y Y Y = m m m s called a radom matrx ( wth a ot m-dmesoal dstrbuto,
CHAPTER 3 POSTERIOR DISTRIBUTIONS
 CHAPTER 3 POSTERIOR DISTRIBUTIONS If scece caot measure the degree of probablt volved, so much the worse for scece. The practcal ma wll stck to hs apprecatve methods utl t does, or wll accept the results
CHAPTER 3 POSTERIOR DISTRIBUTIONS If scece caot measure the degree of probablt volved, so much the worse for scece. The practcal ma wll stck to hs apprecatve methods utl t does, or wll accept the results
Functions of Random Variables
 Fuctos of Radom Varables Chapter Fve Fuctos of Radom Varables 5. Itroducto A geeral egeerg aalyss model s show Fg. 5.. The model output (respose) cotas the performaces of a system or product, such as weght,
Fuctos of Radom Varables Chapter Fve Fuctos of Radom Varables 5. Itroducto A geeral egeerg aalyss model s show Fg. 5.. The model output (respose) cotas the performaces of a system or product, such as weght,
ENGI 4421 Joint Probability Distributions Page Joint Probability Distributions [Navidi sections 2.5 and 2.6; Devore sections
 ENGI 441 Jot Probablty Dstrbutos Page 7-01 Jot Probablty Dstrbutos [Navd sectos.5 ad.6; Devore sectos 5.1-5.] The jot probablty mass fucto of two dscrete radom quattes, s, P ad p x y x y The margal probablty
ENGI 441 Jot Probablty Dstrbutos Page 7-01 Jot Probablty Dstrbutos [Navd sectos.5 ad.6; Devore sectos 5.1-5.] The jot probablty mass fucto of two dscrete radom quattes, s, P ad p x y x y The margal probablty
Statistics MINITAB - Lab 5
 Statstcs 10010 MINITAB - Lab 5 PART I: The Correlato Coeffcet Qute ofte statstcs we are preseted wth data that suggests that a lear relatoshp exsts betwee two varables. For example the plot below s of
Statstcs 10010 MINITAB - Lab 5 PART I: The Correlato Coeffcet Qute ofte statstcs we are preseted wth data that suggests that a lear relatoshp exsts betwee two varables. For example the plot below s of
Lecture 9: Tolerant Testing
 Lecture 9: Tolerat Testg Dael Kae Scrbe: Sakeerth Rao Aprl 4, 07 Abstract I ths lecture we prove a quas lear lower boud o the umber of samples eeded to do tolerat testg for L dstace. Tolerat Testg We have
Lecture 9: Tolerat Testg Dael Kae Scrbe: Sakeerth Rao Aprl 4, 07 Abstract I ths lecture we prove a quas lear lower boud o the umber of samples eeded to do tolerat testg for L dstace. Tolerat Testg We have
Chapter 9 Jordan Block Matrices
 Chapter 9 Jorda Block atrces I ths chapter we wll solve the followg problem. Gve a lear operator T fd a bass R of F such that the matrx R (T) s as smple as possble. f course smple s a matter of taste.
Chapter 9 Jorda Block atrces I ths chapter we wll solve the followg problem. Gve a lear operator T fd a bass R of F such that the matrx R (T) s as smple as possble. f course smple s a matter of taste.
b. There appears to be a positive relationship between X and Y; that is, as X increases, so does Y.
 .46. a. The frst varable (X) s the frst umber the par ad s plotted o the horzotal axs, whle the secod varable (Y) s the secod umber the par ad s plotted o the vertcal axs. The scatterplot s show the fgure
.46. a. The frst varable (X) s the frst umber the par ad s plotted o the horzotal axs, whle the secod varable (Y) s the secod umber the par ad s plotted o the vertcal axs. The scatterplot s show the fgure
Module 7. Lecture 7: Statistical parameter estimation
 Lecture 7: Statstcal parameter estmato Parameter Estmato Methods of Parameter Estmato 1) Method of Matchg Pots ) Method of Momets 3) Mamum Lkelhood method Populato Parameter Sample Parameter Ubased estmato
Lecture 7: Statstcal parameter estmato Parameter Estmato Methods of Parameter Estmato 1) Method of Matchg Pots ) Method of Momets 3) Mamum Lkelhood method Populato Parameter Sample Parameter Ubased estmato
ECON 5360 Class Notes GMM
 ECON 560 Class Notes GMM Geeralzed Method of Momets (GMM) I beg by outlg the classcal method of momets techque (Fsher, 95) ad the proceed to geeralzed method of momets (Hase, 98).. radtoal Method of Momets
ECON 560 Class Notes GMM Geeralzed Method of Momets (GMM) I beg by outlg the classcal method of momets techque (Fsher, 95) ad the proceed to geeralzed method of momets (Hase, 98).. radtoal Method of Momets
Lecture 4 Sep 9, 2015
 CS 388R: Radomzed Algorthms Fall 205 Prof. Erc Prce Lecture 4 Sep 9, 205 Scrbe: Xagru Huag & Chad Voegele Overvew I prevous lectures, we troduced some basc probablty, the Cheroff boud, the coupo collector
CS 388R: Radomzed Algorthms Fall 205 Prof. Erc Prce Lecture 4 Sep 9, 205 Scrbe: Xagru Huag & Chad Voegele Overvew I prevous lectures, we troduced some basc probablty, the Cheroff boud, the coupo collector
CHAPTER VI Statistical Analysis of Experimental Data
 Chapter VI Statstcal Aalyss of Expermetal Data CHAPTER VI Statstcal Aalyss of Expermetal Data Measuremets do ot lead to a uque value. Ths s a result of the multtude of errors (maly radom errors) that ca
Chapter VI Statstcal Aalyss of Expermetal Data CHAPTER VI Statstcal Aalyss of Expermetal Data Measuremets do ot lead to a uque value. Ths s a result of the multtude of errors (maly radom errors) that ca
Introduction to F-testing in linear regression models
 ECON 43 Harald Goldste, revsed Nov. 4 Itroducto to F-testg lear regso s (Lecture ote to lecture Frday 4..4) Itroducto A F-test usually s a test where several parameters are volved at oce the ull hypothess
ECON 43 Harald Goldste, revsed Nov. 4 Itroducto to F-testg lear regso s (Lecture ote to lecture Frday 4..4) Itroducto A F-test usually s a test where several parameters are volved at oce the ull hypothess
Analysis of Variance and Regression
 Chapter Aalyss of Varace ad Regresso a The frst order Taylor s seres approxmato s b If we choose gy g y y a Var[gY ] [g θ] VarY [g θ] vθ dg θ dθ dx, the vx d dθ θ a vx dx vθ, by the Fudametal Theorem of
Chapter Aalyss of Varace ad Regresso a The frst order Taylor s seres approxmato s b If we choose gy g y y a Var[gY ] [g θ] VarY [g θ] vθ dg θ dθ dx, the vx d dθ θ a vx dx vθ, by the Fudametal Theorem of
BASIC PRINCIPLES OF STATISTICS
 BASIC PRINCIPLES OF STATISTICS PROBABILITY DENSITY DISTRIBUTIONS DISCRETE VARIABLES BINOMIAL DISTRIBUTION ~ B 0 0 umber of successes trals Pr E [ ] Var[ ] ; BINOMIAL DISTRIBUTION B7 0. B30 0.3 B50 0.5
BASIC PRINCIPLES OF STATISTICS PROBABILITY DENSITY DISTRIBUTIONS DISCRETE VARIABLES BINOMIAL DISTRIBUTION ~ B 0 0 umber of successes trals Pr E [ ] Var[ ] ; BINOMIAL DISTRIBUTION B7 0. B30 0.3 B50 0.5
Unsupervised Learning and Other Neural Networks
 CSE 53 Soft Computg NOT PART OF THE FINAL Usupervsed Learg ad Other Neural Networs Itroducto Mture Destes ad Idetfablty ML Estmates Applcato to Normal Mtures Other Neural Networs Itroducto Prevously, all
CSE 53 Soft Computg NOT PART OF THE FINAL Usupervsed Learg ad Other Neural Networs Itroducto Mture Destes ad Idetfablty ML Estmates Applcato to Normal Mtures Other Neural Networs Itroducto Prevously, all
Recall MLR 5 Homskedasticity error u has the same variance given any values of the explanatory variables Var(u x1,...,xk) = 2 or E(UU ) = 2 I
 Chapter 8 Heterosedastcty Recall MLR 5 Homsedastcty error u has the same varace gve ay values of the eplaatory varables Varu,..., = or EUU = I Suppose other GM assumptos hold but have heterosedastcty.
Chapter 8 Heterosedastcty Recall MLR 5 Homsedastcty error u has the same varace gve ay values of the eplaatory varables Varu,..., = or EUU = I Suppose other GM assumptos hold but have heterosedastcty.
Investigation of Partially Conditional RP Model with Response Error. Ed Stanek
 Partally Codtoal Radom Permutato Model 7- vestgato of Partally Codtoal RP Model wth Respose Error TRODUCTO Ed Staek We explore the predctor that wll result a smple radom sample wth respose error whe a
Partally Codtoal Radom Permutato Model 7- vestgato of Partally Codtoal RP Model wth Respose Error TRODUCTO Ed Staek We explore the predctor that wll result a smple radom sample wth respose error whe a
Random Variables and Probability Distributions
 Radom Varables ad Probablty Dstrbutos * If X : S R s a dscrete radom varable wth rage {x, x, x 3,. } the r = P (X = xr ) = * Let X : S R be a dscrete radom varable wth rage {x, x, x 3,.}.If x r P(X = x
Radom Varables ad Probablty Dstrbutos * If X : S R s a dscrete radom varable wth rage {x, x, x 3,. } the r = P (X = xr ) = * Let X : S R be a dscrete radom varable wth rage {x, x, x 3,.}.If x r P(X = x
Solutions to Odd-Numbered End-of-Chapter Exercises: Chapter 17
 Itroucto to Ecoometrcs (3 r Upate Eto) by James H. Stock a Mark W. Watso Solutos to O-Numbere E-of-Chapter Exercses: Chapter 7 (Ths erso August 7, 04) 05 Pearso Eucato, Ic. Stock/Watso - Itroucto to Ecoometrcs
Itroucto to Ecoometrcs (3 r Upate Eto) by James H. Stock a Mark W. Watso Solutos to O-Numbere E-of-Chapter Exercses: Chapter 7 (Ths erso August 7, 04) 05 Pearso Eucato, Ic. Stock/Watso - Itroucto to Ecoometrcs
STA 108 Applied Linear Models: Regression Analysis Spring Solution for Homework #1
 STA 08 Appled Lear Models: Regresso Aalyss Sprg 0 Soluto for Homework #. Let Y the dollar cost per year, X the umber of vsts per year. The the mathematcal relato betwee X ad Y s: Y 300 + X. Ths s a fuctoal
STA 08 Appled Lear Models: Regresso Aalyss Sprg 0 Soluto for Homework #. Let Y the dollar cost per year, X the umber of vsts per year. The the mathematcal relato betwee X ad Y s: Y 300 + X. Ths s a fuctoal
ON THE USE OF OBSERVED FISHER INFORMATION IN WALD AND SCORE TEST
 N THE USE F BSERVED FISHER INFRMATIN IN WALD AND SCRE TEST Vasudeva Guddattu 1 & Arua Rao Abstract I the recet years there s a large alcato of large samle tests may scetfc vestgatos. The commoly used large
N THE USE F BSERVED FISHER INFRMATIN IN WALD AND SCRE TEST Vasudeva Guddattu 1 & Arua Rao Abstract I the recet years there s a large alcato of large samle tests may scetfc vestgatos. The commoly used large
Discrete Mathematics and Probability Theory Fall 2016 Seshia and Walrand DIS 10b
 CS 70 Dscrete Mathematcs ad Probablty Theory Fall 206 Sesha ad Walrad DIS 0b. Wll I Get My Package? Seaky delvery guy of some compay s out delverg packages to customers. Not oly does he had a radom package
CS 70 Dscrete Mathematcs ad Probablty Theory Fall 206 Sesha ad Walrad DIS 0b. Wll I Get My Package? Seaky delvery guy of some compay s out delverg packages to customers. Not oly does he had a radom package
COV. Violation of constant variance of ε i s but they are still independent. The error term (ε) is said to be heteroscedastic.
 c Pogsa Porchawseskul, Faculty of Ecoomcs, Chulalogkor Uversty olato of costat varace of s but they are stll depedet. C,, he error term s sad to be heteroscedastc. c Pogsa Porchawseskul, Faculty of Ecoomcs,
c Pogsa Porchawseskul, Faculty of Ecoomcs, Chulalogkor Uversty olato of costat varace of s but they are stll depedet. C,, he error term s sad to be heteroscedastc. c Pogsa Porchawseskul, Faculty of Ecoomcs,
THE ROYAL STATISTICAL SOCIETY 2010 EXAMINATIONS SOLUTIONS GRADUATE DIPLOMA MODULE 2 STATISTICAL INFERENCE
 THE ROYAL STATISTICAL SOCIETY 00 EXAMINATIONS SOLUTIONS GRADUATE DIPLOMA MODULE STATISTICAL INFERENCE The Socety provdes these solutos to assst caddates preparg for the examatos future years ad for the
THE ROYAL STATISTICAL SOCIETY 00 EXAMINATIONS SOLUTIONS GRADUATE DIPLOMA MODULE STATISTICAL INFERENCE The Socety provdes these solutos to assst caddates preparg for the examatos future years ad for the
Chapter 2 Supplemental Text Material
 -. Models for the Data ad the t-test Chapter upplemetal Text Materal The model preseted the text, equato (-3) s more properl called a meas model. ce the mea s a locato parameter, ths tpe of model s also
-. Models for the Data ad the t-test Chapter upplemetal Text Materal The model preseted the text, equato (-3) s more properl called a meas model. ce the mea s a locato parameter, ths tpe of model s also
f X (x i ;θ) = n ( n logx i = 0 = θml = n/ n logx i 1 θ +1 n n 2 < 0 for all θ (θ +1) n logx i 1 ESTIMATOR: = logx i θ n for all θ θ 2 < 0 2θ 2 x 3
 MATH 557 - EXERCISES SOLUTIONS 1 The lkelhoo the orgal parameterzato s ( ( 1 L (θ 1,θ x 1,x = θ x 1 1 x (1 θ 1 1 x 1 θ x 1 x (1 θ x If φ = θ /(1 θ, the θ = φ/(1+φ θ 1 = (φψ/(1+φψ. Ether by wrtg out the
MATH 557 - EXERCISES SOLUTIONS 1 The lkelhoo the orgal parameterzato s ( ( 1 L (θ 1,θ x 1,x = θ x 1 1 x (1 θ 1 1 x 1 θ x 1 x (1 θ x If φ = θ /(1 θ, the θ = φ/(1+φ θ 1 = (φψ/(1+φψ. Ether by wrtg out the
Asymptotics. Hypothesis Testing UMP. Asymptotic Tests and p-values
 of the secod half Biostatistics 6 - Statistical Iferece Lecture 6 Fial Exam & Practice Problems for the Fial Hyu Mi Kag Apil 3rd, 3 Hyu Mi Kag Biostatistics 6 - Lecture 6 Apil 3rd, 3 / 3 Rao-Blackwell
of the secod half Biostatistics 6 - Statistical Iferece Lecture 6 Fial Exam & Practice Problems for the Fial Hyu Mi Kag Apil 3rd, 3 Hyu Mi Kag Biostatistics 6 - Lecture 6 Apil 3rd, 3 / 3 Rao-Blackwell
Bayes (Naïve or not) Classifiers: Generative Approach
 Logstc regresso Bayes (Naïve or ot) Classfers: Geeratve Approach What do we mea by Geeratve approach: Lear p(y), p(x y) ad the apply bayes rule to compute p(y x) for makg predctos Ths s essetally makg
Logstc regresso Bayes (Naïve or ot) Classfers: Geeratve Approach What do we mea by Geeratve approach: Lear p(y), p(x y) ad the apply bayes rule to compute p(y x) for makg predctos Ths s essetally makg
BAYESIAN INFERENCES FOR TWO PARAMETER WEIBULL DISTRIBUTION
 Iteratoal Joural of Mathematcs ad Statstcs Studes Vol.4, No.3, pp.5-39, Jue 06 Publshed by Europea Cetre for Research Trag ad Developmet UK (www.eajourals.org BAYESIAN INFERENCES FOR TWO PARAMETER WEIBULL
Iteratoal Joural of Mathematcs ad Statstcs Studes Vol.4, No.3, pp.5-39, Jue 06 Publshed by Europea Cetre for Research Trag ad Developmet UK (www.eajourals.org BAYESIAN INFERENCES FOR TWO PARAMETER WEIBULL
7.0 Equality Contraints: Lagrange Multipliers
 Systes Optzato 7.0 Equalty Cotrats: Lagrage Multplers Cosder the zato of a o-lear fucto subject to equalty costrats: g f() R ( ) 0 ( ) (7.) where the g ( ) are possbly also olear fuctos, ad < otherwse
Systes Optzato 7.0 Equalty Cotrats: Lagrage Multplers Cosder the zato of a o-lear fucto subject to equalty costrats: g f() R ( ) 0 ( ) (7.) where the g ( ) are possbly also olear fuctos, ad < otherwse
Answer key to problem set # 2 ECON 342 J. Marcelo Ochoa Spring, 2009
 Aswer key to problem set # ECON 34 J. Marcelo Ochoa Sprg, 009 Problem. For T cosder the stadard pael data model: y t x t β + α + ǫ t a Numercally compare the fxed effect ad frst dfferece estmates. b Compare
Aswer key to problem set # ECON 34 J. Marcelo Ochoa Sprg, 009 Problem. For T cosder the stadard pael data model: y t x t β + α + ǫ t a Numercally compare the fxed effect ad frst dfferece estmates. b Compare
Bayesian Inferences for Two Parameter Weibull Distribution Kipkoech W. Cheruiyot 1, Abel Ouko 2, Emily Kirimi 3
 IOSR Joural of Mathematcs IOSR-JM e-issn: 78-578, p-issn: 9-765X. Volume, Issue Ver. II Ja - Feb. 05, PP 4- www.osrjourals.org Bayesa Ifereces for Two Parameter Webull Dstrbuto Kpkoech W. Cheruyot, Abel
IOSR Joural of Mathematcs IOSR-JM e-issn: 78-578, p-issn: 9-765X. Volume, Issue Ver. II Ja - Feb. 05, PP 4- www.osrjourals.org Bayesa Ifereces for Two Parameter Webull Dstrbuto Kpkoech W. Cheruyot, Abel
Multiple Choice Test. Chapter Adequacy of Models for Regression
 Multple Choce Test Chapter 06.0 Adequac of Models for Regresso. For a lear regresso model to be cosdered adequate, the percetage of scaled resduals that eed to be the rage [-,] s greater tha or equal to
Multple Choce Test Chapter 06.0 Adequac of Models for Regresso. For a lear regresso model to be cosdered adequate, the percetage of scaled resduals that eed to be the rage [-,] s greater tha or equal to
Multiple Regression. More than 2 variables! Grade on Final. Multiple Regression 11/21/2012. Exam 2 Grades. Exam 2 Re-grades
 STAT 101 Dr. Kar Lock Morga 11/20/12 Exam 2 Grades Multple Regresso SECTIONS 9.2, 10.1, 10.2 Multple explaatory varables (10.1) Parttog varablty R 2, ANOVA (9.2) Codtos resdual plot (10.2) Trasformatos
STAT 101 Dr. Kar Lock Morga 11/20/12 Exam 2 Grades Multple Regresso SECTIONS 9.2, 10.1, 10.2 Multple explaatory varables (10.1) Parttog varablty R 2, ANOVA (9.2) Codtos resdual plot (10.2) Trasformatos
MOLECULAR VIBRATIONS
 MOLECULAR VIBRATIONS Here we wsh to vestgate molecular vbratos ad draw a smlarty betwee the theory of molecular vbratos ad Hückel theory. 1. Smple Harmoc Oscllator Recall that the eergy of a oe-dmesoal
MOLECULAR VIBRATIONS Here we wsh to vestgate molecular vbratos ad draw a smlarty betwee the theory of molecular vbratos ad Hückel theory. 1. Smple Harmoc Oscllator Recall that the eergy of a oe-dmesoal
