Derivatives in General Relativity
|
|
|
- Delilah Ferguson
- 5 years ago
- Views:
Transcription
1 Derivatives in General Relativity One of the problems with curved space is in dealing with vectors how do you add a vector at one point in the surface of a sphere to a vector at a different point, and end up with a result that is still in the sphere? Even worse, how do you take the derivative of a vector in a spherical surface? That s easy in Euclidean space, because a vector at a point P can be naturally compared by simple translation to the vector at a nearby point Q. But in curved spacetime, we are trying to compare vectors at different points that may not even have the same tangent basis vectors! This document addresses this issue. In these sections, all the examples use 2-D or 3-D spaces (as opposed to a 4-D spacetime) to keep things simple and easier to visualize. In 2-D spaces or higher, all derivatives require that you specify a direction; you can either take the direction along an axis (which gives you the partial derivative), or along a line, etc. The concept of transport is used for derivatives on curved surfaces : take a scalar, vector, or tensor (SVT) at one point and (somehow) transport it to the same place as another SVT. If the two SVTs are the same, the derivative between the two points is zero. Otherwise, by comparing the SVTs, you can calculate the derivative. There are two basic types of derivatives for neighboring tangent spaces in general relativity : covariant derivatives and Lie derivatives. The Lie derivative evaluates the change of one SVT field along the direction of a separate vector field. A covariant derivative introduces an extra geometric structure (the affine connection, which requires a metric tensor) on the surface and evaluates the change in the SVT field using the connection. Path Tangent Vectors Tangent vector in general refers to any vector that is tangent to a curved surface at a point. However, when following along a worldline in spacetime, its path tangent vector points along the direction of travel. The path tangent vector T to a parameterized curve x a (λ) is given by T a (λ) = dx a / dλ (where x a represents position as a function of λ), so that (as usual) T = T a e a For example, let the path be a circle where R=1, parameterized by λ Then x 1 (λ) = x(λ) = cos λ x 2 (λ) = y(λ) = sin λ And the path tangent vector is : T x = dx / dλ = sin λ T y = dy / dλ = cos λ For the figure to the right, λ = 25, so T = (-0.4,0.9) as indicated by the black arrow. φ λ Derivative of a Scalar Field If e i is the i th basis vector and x i is the i th coordinate, then the gradient of a scalar field S=f(x,y,z) is a vector whose components are the derivative with respect to the coordinates : S/ x i = e i S/ x i
2 = e 1 S/ x 1 + e 2 S/ x 2 + e 3 S/ x 3 = ( S/ x 1, S/ x 2, S/ x 3 ) same thing in vector notation = ( S/ x, S/ y, S/ z) in Cartesian coordinates (for example) Note that / i is always accompanied by an e i whether it is shown or not! In Euclidean space, this is the gradient. The gradient of a scalar field at point P is a vector pointing perpendicular to the surface at P. In the figure to the right, the surface S=f(x,y) and the blue line is the gradient ( S/ x, S/ y) at a specific point (x,y). There are several notations used by various authors, and sometimes the e i is assumed : i S = S,i = i S = S/ x i = e i S/ x i For example, the surface of a sphere with a radius of 4 can be described by z = ±(4 x 2 y 2 ) 1/2, or in its more usual format, S : x 2 +y 2 +z 2 = 16. The normal to this function at the point P=( 1, 1, 1.41) is given by i S = ( S/ x, S/ y, S/ z) = (2x, 2y, 2z) which at P is the vector ( 2, 2, 2.82) In 4-D spacetime, due to the negative sign on the spatial coordinates, and the (sometimes implied) presence of c on the time coordinate, the correct definitions of the four-gradient are : Where (as usual) α could also be calculated by g µα µ The divergence of the gradient is called the Laplacian. The Laplacian of a scalar field is a scalar : S = e i (e j S/ x j )/ x i = e i e j 2 S/ x j x i = g ij S,ij And also goes by several different notations : = 2 = Δ = i i = i i = 2 The Laplacian of a vector is a vector : 2 V = g jk V i,jk e i
3 Directional Scalar Derivative The derivative along the coordinate axes can be generalized to a directional derivative of a scalar field in the direction of any unit vector u. The directional derivative of a scalar field S is : ( i S) u = u i ( S/ x i ) = u x S/ x + u y S/ y + u z S/ z in Cartesian coordinates This result is a scalar, which is the magnitude of the rate of change of the scalar field in the direction of u. If the vector is the path tangent vector T(λ) of a path x i (λ), then the derivative of S along the path is : T S = T i i S = T i ( S/ x i ) = ( S/ x i ) ( x i / λ) = S/ λ which is just the rate of change of the scalar field as you travel along the path. Derivative of a Vector Field The derivative of a vector field V = V α e α with respect to coordinate x β in Euclidean space with Cartesian coordinates is : V/ x β = (V α e α )/ x β = e α V α / x β = ( V 1 / x β, V 2 / x β, V 3 / x β ) for all β since the basis vectors do not vary and so e α / x β = 0. This is the ordinary partial derivative, but virtually all authors leave out the e β that goes along with the / β : V/ x β = (V α e α )/ x β e β = V α / x β (e α e β ) Which means that V/ x β is really a tensor! For example, if V = (V x (x,y,z), V y (x,y,z), V z (x,y,z)) : V x / x V y / x V z / x V/ x 1 V/ x = V x / y V y / y V z / y V/ x 2 V x / z V y / z V z / z V/ x 3 For the remaining sections, the e β term will also be left out for simplicity, but it should always be kept in mind that a term like V α / x β implies a tensor, because there are two non-summed indexes. There are several different notations for the ordinary partial derivative as well. And since index notation shows a vector V by its components V α, the notation V/ x β is not actually used. Again, sometimes the e α is merely implied : V α, β = β V α = V α / x β = e α V α / x β
4 Affine Connection Informally, an affine space is a vector space without an origin, so points in an affine space cannot be added together. However, a vector V may be added to a point P by placing the initial point of the vector at P and then transporting P to the end of the vector. An affine connection is a geometrical object which connects nearby tangent spaces in a surface (like taping two maps together along a common edge), and so permits tangent vector fields to be differentiated. The choice of an affine connection is equivalent to describing a way of differentiating vector fields which satisfies several reasonable properties (such as linearity and the product rule). An affine connection also defines the idea of parallel transport and geodesics. Conversely, specifying a method of parallel transport defines the connection. So affine connections are intimately tied together with all the concepts we have been discussing so far. The main invariant measures of an affine connection are its torsion and its curvature. There are infinitely many affine connections on a surface, but if the surface has a metric then there is a natural choice of affine connection, called the Levi-Civita connection, which has zero torsion. Then the value of the parameter used to describe a worldline is proportional to the worldline s path length (and also happens to represent its proper time if the worldline is timelike). [any worldline or only geodesics?] In local coordinates, the components of the Levi-Civita connection are called Christoffel symbols (next section), and because the Levi-Civita connection is unique, they can be calculated directly from the metric. For this reason, this type of connection is often called a metric connection. It should be noted that the zero-torsion condition is an assumption of general relativity, and there are extensions to general relativity which allow for torsion. Christoffel Symbols In any curvilinear coordinate system or non-euclidean space, the basis vectors change orientation with position, so the derivative of a vector field V = V α e α becomes : V/ x β = (V α e α )/ x β = ( V α / x β )e α + V α ( e α / x β ) Since e α / x β is itself a vector, it can be written as some linear combination of the basis vectors : e α / x β = Γ μ αβ e μ = Γ x αβe x + Γ y αβe y + Γ z αβe z in Cartesian coordinates, for example Γ is called a Christoffel symbol (of the second kind), affine connection, or metric connection. It provides the weights or coefficients to create e α / x β from the basis vectors e i. It is sometimes written as In terms of the covariant basis vectors e i and contravariant basis vectors e i the Christoffel symbol is defined as : Γ i jk = e i ( e j / x k ) ( the i th component of the j th basis wrt the k th axis ) where e i means to take the i th component of what follows ( = dot product along the e i axis). The Christoffel symbol measures how the basis vectors change as we move in a particular direction. Once we
5 know how the basis vectors change, then we can use this information to correct the ordinary derivative which we obtained using that basis, in order to obtain the covariant derivative in a curved surface (next section). The Christoffel symbol can also be defined in terms of the metric tensor : Γ a bc = g ai ( b g ci + c g ib i g bc ) / 2 Note that there can be many variations on this formula due to the nature of the Einstein notation, the multiple formats for the derivatives, and the symmetry of the metric tensor! In addition, the Riemann tensor described in GR1c can now be given in terms of the Christoffel symbol : And there are many variations on this formula as well, for all the same reasons, and the symmetry of the bottom indexes in Γ (see below), as well as the choice of contravariant/covariant indexes for R. Things to know about Christoffel symbols : Christoffel symbols are in the surface. Despite the notation used to describe them, Christoffel symbols are not actually tensors. Christoffel symbols appear when either the space is curved, or when non-cartesian coordinates are used in a Euclidean space. If torsion is zero (which is assumed in general relativity), the Christoffel symbol is symmetric in its bottom indexes, so Γ i jk = Γ i kj which means, for example : Γ α γβv γ X β is the exact thing same as Γ α βγv β X γ is exactly the same as Γ α βγv γ X β In Euclidean space with Cartesian coordinates, Γ i jk = 0 for all i,j,k because the basis vectors never change. Christoffel symbols are also all zero in the tangent plane (which is a local inertial frame and so a Minkowski spacetime) because the basis vectors do not change. Example In Euclidean 2-D polar coordinates (r,θ) the non-zero Christoffel symbols are : Γ θ rθ = 1/r Γ θ θr = 1/r Γ r θθ = r And so the coordinate derivatives e α / x β = Γ μ αβ e μ are : e r / r = Γ r rre r + Γ θ rre θ e θ / r = Γ r θre r + Γ θ θre θ Which simplifies to : e r / r = 0 e θ / r = e θ / r e r / θ = Γ r rθe r + Γ θ rθe θ e θ / θ = Γ r θθe r + Γ θ θθe θ e r / θ = e θ / r e θ / θ = r e r The figure below shows what each coordinate derivative means. The vector from the smaller value of r or θ is copied (as a dotted-line) over to the vector at the larger value. The difference between them (from the head of the dotted-line vector to the head of the solid-line vector) is e α / x β.
6 For reference, in Euclidean 3-D spherical coordinates [r,φ,θ], the non-zero Christoffel symbols are : Γ r θθ = r Γ r φφ = r sin 2 φ Γ θ φφ = sinθ cosφ Γ θ rθ = Γ θ θr = 1/r Γ φ rφ = Γ φ φr = 1/r Γ φ φθ = Γ φ θφ = cotφ Covariant Derivative In curved space, the covariant derivative is the change in the vector itself, plus the changes in the basis vectors. If M is a surface with curvilinear coordinates x i, and V is a tangent vector field to M at a point P, then (from the previous section) the derivative of V along the x β axis is : V/ x β = (V α e α )/ x β = ( V α / x β )e α + V α ( e α / x β ) But as we have seen, e α / x β = Γ μ αβe μ So we have : V/ x β = ( V α / x β )e α + V α Γ μ αβe μ Or (with a change to the dummy indexes in the second term, α μ) : V/ x β = ( V α / x β + V μ Γ α μβ)e α Which in Cartesian coordinates (for example) becomes : V/ x β = ( V x / x β + V x Γ x xβ + V y Γ x yβ + V z Γ x zβ)e x + ( V y / x β + V x Γ y xβ + V y Γ y yβ + V z Γ y zβ)e y + ( V z / x β + V x Γ z xβ + V y Γ z yβ + V z Γ z zβ)e z and is really three equations, one each for x β = x, y, z (which means it is a tensor!). This example is just to show how the notation works, since in Euclidean space with Cartesian coordinates every Γ i jk is zero.
7 The symbol β is often used to represent the covariant derivative in the x β direction or along the basis vector e β. And since index notation uses the components of the vector V, the most common notation is : β V α = V α / x β + Γ α μβv μ which returns only the α-component of the entire answer ( β V 1, β V 2, β V 3 ), so some authors use ( β V) α. And there is yet another notation, using just a semicolon : V α ;β Summing up, the covariant derivative can be expressed in any of the following ways : V α ;β = β V α = ( β V) α = ( V α / x β )e α + V α Γ μ αβe μ = ( V α / x β + V μ Γ α μβ)e α = V α / x β + Γ α μβv μ = β V α + V μ Γ α μβ = V α,β + Γ α μβv μ All of which stand for the amount of change in the α component of the covariant derivative of vector V when we move in the x β direction. And just to make things more confusing, D is also sometimes used for, as in D(V) or D β V. This actually comes in handy when you want to take the covariant derivative with respect to a path parameter, such as D/Dλ. In addition, some authors use D to indicate only the 3-D spatial covariant derivatives. What does all this mean? Let s say we want to find the amount of change in the β component of the covariant derivative of a vector v when we move in the x γ direction, or ( γ v) β : Since v is a function of its position in spacetime, the v β component will change just because we re moving in the x γ direction (in the figure above, the new v β is larger than the old v β ). The amount of this change is v β / x γ (this is just the ordinary partial derivative), and is the real change in the picture below.
8 Now look at the other basis vector e α ( α axis ) in the figure above. As we move in the x γ direction, e α changes because the space is not flat. We also need to know how much e α changes in the β direction. The following figure combines information from both the old and the new planes in the previous figure : So we need to add the change in e α to the real change in v β, and we need to scale the change in e α by [the part of v which lies along the direction of e α ( = v α )]. In other words, v α contributes a change to v β which is proportional to v α times [the component in the β direction of the change in e α as we move in the x γ direction]. This scaling factor in the brackets is just e β e α / x γ Γ β αγ. So the extra change due to e α is Γ β αγv α (for the specific values of α, β, γ no summing!). Now, the change to the e β basis vector will contribute Γ β βγv β and the change to e γ will contribute Γ β γγv γ, so summing over all of them with a dummy index μ gives us : ( γ V) β = V β / x γ + Γ β μγv μ QED (which is Latin for ta-daa!!! ) The covariant derivative turns a type (r,s) tensor into a type (r,s+1) tensor, increasing the rank by one. So for the above examples, it turns a (1,0) contravariant vector into a (1,1) tensor of rank 2. In general relativity, the covariant derivative is associated with the Levi-Civita affine connection. By definition, the Levi-Civita connection preserves the metric under parallel transport, therefore, the covariant derivative is zero when acting on the metric tensor (as well as its inverse). This means we can take the metric tensor (or its inverse) in and out of the derivative and use it to raise and lower indices : β V α = β (g αγ V γ ) = g αγ β V γ And it can be used to take the contravariant derivative : α V = g αβ β The covariant derivative can be extended to tensors of any rank For a type (1,0) contravariant vector field V a : For a type (0,1) covariant vector field V a : c V a = c V a + Γ a icv i c V a = c V a Γ i acv i
9 For a type (2,0) tensor field T ab : For a type (0,2) tensor field T ab : For a type (1,1) tensor field T a b : b For a type (1,1) tensor field T a : c T ab = c T ab + Γ a ict ib + Γ b ict ai c T ab = c T ab Γ i act ib Γ i bct ai c T a b = c T a b + Γ a ict i b Γ i bct a i c T b a = c T b a Γ i act b i + Γ b i ict a The pattern is : take the ordinary derivative, then add a Γ term for each contravariant letter and subtract a Γ term for each covariant letter. Things to know about covariant derivatives : Covariant derivatives are in the surface. The covariant derivative in Euclidean space with Cartesian coordinates is the same as the ordinary partial derivative, because the basis vectors never change. The covariant derivative of a scalar field V is the ordinary partial derivative : α V = V/ x α The covariant derivative of a vector field β V α = ( β V 1, β V 2, β V 3 ) is the partial derivative of V in the e β direction, and is often equated to the divergence (except that divergence returns a scalar value!). The covariant derivative of the metric tensor is zero everywhere on the surface : c g ab = 0 Note that α V β is a covariant derivative (because V β implies a vector), while α V is the gradient of the scalar V (no indexes). Directional Covariant Derivative We can generalize the covariant derivative by taking the derivative of V in the direction of another vector T (for example, the path tangent vector to some path x α (λ)). As before, let M be a surface, let V be a tangent vector to M at a point P, and let T(λ) be a path tangent vector at P. Then the directional covariant derivative (which is independent of the curve used to create T), is T V α = T β β T α = T β ( V α / x β + Γ α βγv γ ) e α The directional covariant derivative of a type (r,s) tensor is also of type (r,s). When a vector V moves along a path x α (λ) that has path tangent vectors T(λ), and T V α = 0 for all α, then V was parallel transported along the path. This is equivalent to moving V along the path so that it remains parallel to itself and does not change length. When the vector field V is described in terms of a parameter λ, the covariant derivative becomes : λ V α = ( γ V α )( x γ / λ) = ( V α / x γ + Γ α βγv β ) ( x γ / λ) = V α / λ + Γ α βγv β ( x γ / λ) A path that parallel-transports its own path tangent vector T(λ), T T α = 0, is a geodesic. This means that in addition to the path tangent vector remaining parallel to itself with constant length, the path appears straight within the surface. The figure below shows a couple path tangent vectors of a geodesic, with their components
10 along the tangent basis vectors e x = x and e y = y (note how they line up with their local lines of latitude and longitude) : It is now possible to give a mathematical definition of a non-rotating inertial frame : eo e i = 0 In particular, i=0 implies that there is no acceleration ( = inertial), and i=1 3 implies non-rotation. Lie Derivative and Lie Bracket While the covariant derivative requires an affine connection for transport, the Lie derivative uses the flow of another vector field to describe the direction of travel. If a vector field V is defined by a set of differential equations, then its congruence of curves (or just congruence ) is the family of solutions ( = the integrals of the equations), and is often parameterized. A single path in this congruence is a trajectory, whose tangent vector at each point is in turn the value of V at that point. The collection of tangent vectors (across all trajectories) is called a flow. For example, if V is defined by V x / θ = r sinθ V y / θ = r cosθ Then the solution to V is V x = r cosθ V y = r sinθ where r and θ are parameters. The last two equations result in a series of concentric circles as you vary r and θ. The concentric circles are the trajectories, the tangent vectors (some of which are shown in blue) are defined by ( r sinθ, r cosθ), and the set of all tangent vectors is the flow. A congruence in spacetime is a family of world lines. One example of a timelike geodesic congruence is the trajectories of many free-falling test particles. A null geodesic congruence could be a family of propagating light rays. But not all congruences have to be geodesics. The idea of Lie dragging a function along a congruence leads to a definition of the Lie derivative. Consider a small coordinate change in the surface that results from dragging along a trajectory of the vector field V, using its tangent vector at point P to point the way. After moving a small distance ε along the vector, we are now at point Q. Let U be some object (scalar/vector/tensor field) defined on the surface. There are two values we
11 can consider at Q : U evaluated at Q, and the value that results from dragging the value of U at P to the point Q thru the coordinate system. Since the surface is not flat, we need to subtract out coordinate transformation to get the actual change in U (as was true of the covariant derivative as well). These two different values at Q allow us to form the Lie derivative at Q. The Lie derivative is usually denoted by L V where V is the vector field along whose congruence the Lie derivative is taken. The Lie derivative takes a tensor of type (r,s) and creates a tensor of type (r,s). The Lie derivative of a scalar field S=f(x,y,z) is just the directional derivative of f along the vector field V : L V S = V a S,a = V a a S = V a ( S/ x a ) The Lie derivative of a (contravariant) vector field U is : L V U a = V i U a,i U i V a,i = V i ( U a / x i ) U i ( V a / x i ) and if U is covariant, just turn all the superscripts on U into subscripts. Another notation is the Lie bracket [X,Y] which is the Lie derivative of a pair of vector fields X and Y acting on a function f : [X,Y](f) = [X b ( Y a / x b ) Y b ( X a / x b )] f/ x a Note : a set of holonomic basis vectors e i satisfies [e i,e j ]=0 The Lie derivative of a tensor T is given by : L V T ab = T ai V i,b + T ib V i,a + V i T ab,i L V T ab = T ai ( V i / x b ) + T ib ( V i / x a ) + V i ( T ab / x i ) and the Lie derivative of the metric tensor is : L V g ab = b V a + a V b If the Lie derivative of an object is everywhere zero, the object possesses a symmetry : L V T = 0 means that T s structure is constant along the flows of V. This leads to the concept of Killing vectors, which are discussed in GR3x.
Curved Spacetime I. Dr. Naylor
 Curved Spacetime I Dr. Naylor Last Week Einstein's principle of equivalence We discussed how in the frame of reference of a freely falling object we can construct a locally inertial frame (LIF) Space tells
Curved Spacetime I Dr. Naylor Last Week Einstein's principle of equivalence We discussed how in the frame of reference of a freely falling object we can construct a locally inertial frame (LIF) Space tells
Basics of Special Relativity
 Basics of Special Relativity You must understand special relativity in order to really understand general relativity. Here s a brief summary of the basic ideas and terminology of special relativity (there
Basics of Special Relativity You must understand special relativity in order to really understand general relativity. Here s a brief summary of the basic ideas and terminology of special relativity (there
Tensors, and differential forms - Lecture 2
 Tensors, and differential forms - Lecture 2 1 Introduction The concept of a tensor is derived from considering the properties of a function under a transformation of the coordinate system. A description
Tensors, and differential forms - Lecture 2 1 Introduction The concept of a tensor is derived from considering the properties of a function under a transformation of the coordinate system. A description
3 Parallel transport and geodesics
 3 Parallel transport and geodesics 3.1 Differentiation along a curve As a prelude to parallel transport we consider another form of differentiation: differentiation along a curve. A curve is a parametrized
3 Parallel transport and geodesics 3.1 Differentiation along a curve As a prelude to parallel transport we consider another form of differentiation: differentiation along a curve. A curve is a parametrized
Georgia Tech PHYS 6124 Mathematical Methods of Physics I
 Georgia Tech PHYS 6124 Mathematical Methods of Physics I Instructor: Predrag Cvitanović Fall semester 2012 Homework Set #6a due Thursday, October 25, 2012 Notes for lectures 14 and 15: Calculus on smooth
Georgia Tech PHYS 6124 Mathematical Methods of Physics I Instructor: Predrag Cvitanović Fall semester 2012 Homework Set #6a due Thursday, October 25, 2012 Notes for lectures 14 and 15: Calculus on smooth
Contravariant and Covariant as Transforms
 Contravariant and Covariant as Transforms There is a lot more behind the concepts of contravariant and covariant tensors (of any rank) than the fact that their basis vectors are mutually orthogonal to
Contravariant and Covariant as Transforms There is a lot more behind the concepts of contravariant and covariant tensors (of any rank) than the fact that their basis vectors are mutually orthogonal to
carroll/notes/ has a lot of good notes on GR and links to other pages. General Relativity Philosophy of general
 http://pancake.uchicago.edu/ carroll/notes/ has a lot of good notes on GR and links to other pages. General Relativity Philosophy of general relativity. As with any major theory in physics, GR has been
http://pancake.uchicago.edu/ carroll/notes/ has a lot of good notes on GR and links to other pages. General Relativity Philosophy of general relativity. As with any major theory in physics, GR has been
Chapter 7 Curved Spacetime and General Covariance
 Chapter 7 Curved Spacetime and General Covariance In this chapter we generalize the discussion of preceding chapters to extend covariance to more general curved spacetimes. 145 146 CHAPTER 7. CURVED SPACETIME
Chapter 7 Curved Spacetime and General Covariance In this chapter we generalize the discussion of preceding chapters to extend covariance to more general curved spacetimes. 145 146 CHAPTER 7. CURVED SPACETIME
Curved spacetime and general covariance
 Chapter 7 Curved spacetime and general covariance In this chapter we generalize the discussion of preceding chapters to extend covariance to more general curved spacetimes. 219 220 CHAPTER 7. CURVED SPACETIME
Chapter 7 Curved spacetime and general covariance In this chapter we generalize the discussion of preceding chapters to extend covariance to more general curved spacetimes. 219 220 CHAPTER 7. CURVED SPACETIME
General Relativity I
 General Relativity I presented by John T. Whelan The University of Texas at Brownsville whelan@phys.utb.edu LIGO Livingston SURF Lecture 2002 July 5 General Relativity Lectures I. Today (JTW): Special
General Relativity I presented by John T. Whelan The University of Texas at Brownsville whelan@phys.utb.edu LIGO Livingston SURF Lecture 2002 July 5 General Relativity Lectures I. Today (JTW): Special
has a lot of good notes on GR and links to other pages. General Relativity Philosophy of general relativity.
 http://preposterousuniverse.com/grnotes/ has a lot of good notes on GR and links to other pages. General Relativity Philosophy of general relativity. As with any major theory in physics, GR has been framed
http://preposterousuniverse.com/grnotes/ has a lot of good notes on GR and links to other pages. General Relativity Philosophy of general relativity. As with any major theory in physics, GR has been framed
Lecture: Lorentz Invariant Dynamics
 Chapter 5 Lecture: Lorentz Invariant Dynamics In the preceding chapter we introduced the Minkowski metric and covariance with respect to Lorentz transformations between inertial systems. This was shown
Chapter 5 Lecture: Lorentz Invariant Dynamics In the preceding chapter we introduced the Minkowski metric and covariance with respect to Lorentz transformations between inertial systems. This was shown
Covariant Formulation of Electrodynamics
 Chapter 7. Covariant Formulation of Electrodynamics Notes: Most of the material presented in this chapter is taken from Jackson, Chap. 11, and Rybicki and Lightman, Chap. 4. Starting with this chapter,
Chapter 7. Covariant Formulation of Electrodynamics Notes: Most of the material presented in this chapter is taken from Jackson, Chap. 11, and Rybicki and Lightman, Chap. 4. Starting with this chapter,
Chapter 11. Special Relativity
 Chapter 11 Special Relativity Note: Please also consult the fifth) problem list associated with this chapter In this chapter, Latin indices are used for space coordinates only eg, i = 1,2,3, etc), while
Chapter 11 Special Relativity Note: Please also consult the fifth) problem list associated with this chapter In this chapter, Latin indices are used for space coordinates only eg, i = 1,2,3, etc), while
Vectors, metric and the connection
 Vectors, metric and the connection 1 Contravariant and covariant vectors 1.1 Contravariant vectors Imagine a particle moving along some path in the 2-dimensional flat x y plane. Let its trajectory be given
Vectors, metric and the connection 1 Contravariant and covariant vectors 1.1 Contravariant vectors Imagine a particle moving along some path in the 2-dimensional flat x y plane. Let its trajectory be given
Tensor Analysis in Euclidean Space
 Tensor Analysis in Euclidean Space James Emery Edited: 8/5/2016 Contents 1 Classical Tensor Notation 2 2 Multilinear Functionals 4 3 Operations With Tensors 5 4 The Directional Derivative 5 5 Curvilinear
Tensor Analysis in Euclidean Space James Emery Edited: 8/5/2016 Contents 1 Classical Tensor Notation 2 2 Multilinear Functionals 4 3 Operations With Tensors 5 4 The Directional Derivative 5 5 Curvilinear
Exact Solutions of the Einstein Equations
 Notes from phz 6607, Special and General Relativity University of Florida, Fall 2004, Detweiler Exact Solutions of the Einstein Equations These notes are not a substitute in any manner for class lectures.
Notes from phz 6607, Special and General Relativity University of Florida, Fall 2004, Detweiler Exact Solutions of the Einstein Equations These notes are not a substitute in any manner for class lectures.
UNIVERSITY OF DUBLIN
 UNIVERSITY OF DUBLIN TRINITY COLLEGE JS & SS Mathematics SS Theoretical Physics SS TSM Mathematics Faculty of Engineering, Mathematics and Science school of mathematics Trinity Term 2015 Module MA3429
UNIVERSITY OF DUBLIN TRINITY COLLEGE JS & SS Mathematics SS Theoretical Physics SS TSM Mathematics Faculty of Engineering, Mathematics and Science school of mathematics Trinity Term 2015 Module MA3429
PHZ 6607 Fall 2004 Homework #4, Due Friday, October 22, 2004
 Read Chapters 9, 10 and 20. PHZ 6607 Fall 2004 Homework #4, Due Friday, October 22, 2004 1. The usual metric of four-dimensional flat Minkowski-space in spherical-polar coordinates is ds 2 = dt 2 + dr
Read Chapters 9, 10 and 20. PHZ 6607 Fall 2004 Homework #4, Due Friday, October 22, 2004 1. The usual metric of four-dimensional flat Minkowski-space in spherical-polar coordinates is ds 2 = dt 2 + dr
Mathematical Relativity, Spring 2017/18 Instituto Superior Técnico
 Mathematical Relativity, Spring 2017/18 Instituto Superior Técnico 1. Starting from R αβµν Z ν = 2 [α β] Z µ, deduce the components of the Riemann curvature tensor in terms of the Christoffel symbols.
Mathematical Relativity, Spring 2017/18 Instituto Superior Técnico 1. Starting from R αβµν Z ν = 2 [α β] Z µ, deduce the components of the Riemann curvature tensor in terms of the Christoffel symbols.
2 General Relativity. 2.1 Curved 2D and 3D space
 22 2 General Relativity The general theory of relativity (Einstein 1915) is the theory of gravity. General relativity ( Einstein s theory ) replaced the previous theory of gravity, Newton s theory. The
22 2 General Relativity The general theory of relativity (Einstein 1915) is the theory of gravity. General relativity ( Einstein s theory ) replaced the previous theory of gravity, Newton s theory. The
Tensors - Lecture 4. cos(β) sin(β) sin(β) cos(β) 0
 1 Introduction Tensors - Lecture 4 The concept of a tensor is derived from considering the properties of a function under a transformation of the corrdinate system. As previously discussed, such transformations
1 Introduction Tensors - Lecture 4 The concept of a tensor is derived from considering the properties of a function under a transformation of the corrdinate system. As previously discussed, such transformations
Physics 6303 Lecture 2 August 22, 2018
 Physics 6303 Lecture 2 August 22, 2018 LAST TIME: Coordinate system construction, covariant and contravariant vector components, basics vector review, gradient, divergence, curl, and Laplacian operators
Physics 6303 Lecture 2 August 22, 2018 LAST TIME: Coordinate system construction, covariant and contravariant vector components, basics vector review, gradient, divergence, curl, and Laplacian operators
General Relativity and Differential
 Lecture Series on... General Relativity and Differential Geometry CHAD A. MIDDLETON Department of Physics Rhodes College November 1, 2005 OUTLINE Distance in 3D Euclidean Space Distance in 4D Minkowski
Lecture Series on... General Relativity and Differential Geometry CHAD A. MIDDLETON Department of Physics Rhodes College November 1, 2005 OUTLINE Distance in 3D Euclidean Space Distance in 4D Minkowski
Problem 1, Lorentz transformations of electric and magnetic
 Problem 1, Lorentz transformations of electric and magnetic fields We have that where, F µν = F µ ν = L µ µ Lν ν F µν, 0 B 3 B 2 ie 1 B 3 0 B 1 ie 2 B 2 B 1 0 ie 3 ie 2 ie 2 ie 3 0. Note that we use the
Problem 1, Lorentz transformations of electric and magnetic fields We have that where, F µν = F µ ν = L µ µ Lν ν F µν, 0 B 3 B 2 ie 1 B 3 0 B 1 ie 2 B 2 B 1 0 ie 3 ie 2 ie 2 ie 3 0. Note that we use the
I. HARTLE CHAPTER 8, PROBLEM 2 (8 POINTS) where here an overdot represents d/dλ, must satisfy the geodesic equation (see 3 on problem set 4)
 Physics 445 Solution for homework 5 Fall 2004 Cornell University 41 points) Steve Drasco 1 NOTE From here on, unless otherwise indicated we will use the same conventions as in the last two solutions: four-vectors
Physics 445 Solution for homework 5 Fall 2004 Cornell University 41 points) Steve Drasco 1 NOTE From here on, unless otherwise indicated we will use the same conventions as in the last two solutions: four-vectors
Covariant Formulation of Electrodynamics
 Chapter 7. Covariant Formulation of Electrodynamics Notes: Most of the material presented in this chapter is taken from Jackson, Chap. 11, and Rybicki and Lightman, Chap. 4. Starting with this chapter,
Chapter 7. Covariant Formulation of Electrodynamics Notes: Most of the material presented in this chapter is taken from Jackson, Chap. 11, and Rybicki and Lightman, Chap. 4. Starting with this chapter,
PHYM432 Relativity and Cosmology 6. Differential Geometry
 PHYM432 Relativity and Cosmology 6. Differential Geometry The central idea of general relativity is that gravity arrises from the curvature of spacetime. Gravity is Geometry matter tells space how to curve
PHYM432 Relativity and Cosmology 6. Differential Geometry The central idea of general relativity is that gravity arrises from the curvature of spacetime. Gravity is Geometry matter tells space how to curve
Solving the Geodesic Equation
 Solving the Geodesic Equation Jeremy Atkins December 12, 2018 Abstract We find the general form of the geodesic equation and discuss the closed form relation to find Christoffel symbols. We then show how
Solving the Geodesic Equation Jeremy Atkins December 12, 2018 Abstract We find the general form of the geodesic equation and discuss the closed form relation to find Christoffel symbols. We then show how
Syllabus. May 3, Special relativity 1. 2 Differential geometry 3
 Syllabus May 3, 2017 Contents 1 Special relativity 1 2 Differential geometry 3 3 General Relativity 13 3.1 Physical Principles.......................................... 13 3.2 Einstein s Equation..........................................
Syllabus May 3, 2017 Contents 1 Special relativity 1 2 Differential geometry 3 3 General Relativity 13 3.1 Physical Principles.......................................... 13 3.2 Einstein s Equation..........................................
Schwarschild Metric From Kepler s Law
 Schwarschild Metric From Kepler s Law Amit kumar Jha Department of Physics, Jamia Millia Islamia Abstract The simplest non-trivial configuration of spacetime in which gravity plays a role is for the region
Schwarschild Metric From Kepler s Law Amit kumar Jha Department of Physics, Jamia Millia Islamia Abstract The simplest non-trivial configuration of spacetime in which gravity plays a role is for the region
Vectors. January 13, 2013
 Vectors January 13, 2013 The simplest tensors are scalars, which are the measurable quantities of a theory, left invariant by symmetry transformations. By far the most common non-scalars are the vectors,
Vectors January 13, 2013 The simplest tensors are scalars, which are the measurable quantities of a theory, left invariant by symmetry transformations. By far the most common non-scalars are the vectors,
4.7 The Levi-Civita connection and parallel transport
 Classnotes: Geometry & Control of Dynamical Systems, M. Kawski. April 21, 2009 138 4.7 The Levi-Civita connection and parallel transport In the earlier investigation, characterizing the shortest curves
Classnotes: Geometry & Control of Dynamical Systems, M. Kawski. April 21, 2009 138 4.7 The Levi-Civita connection and parallel transport In the earlier investigation, characterizing the shortest curves
Properties of Traversable Wormholes in Spacetime
 Properties of Traversable Wormholes in Spacetime Vincent Hui Department of Physics, The College of Wooster, Wooster, Ohio 44691, USA. (Dated: May 16, 2018) In this project, the Morris-Thorne metric of
Properties of Traversable Wormholes in Spacetime Vincent Hui Department of Physics, The College of Wooster, Wooster, Ohio 44691, USA. (Dated: May 16, 2018) In this project, the Morris-Thorne metric of
Chapter 2. Coordinate Systems and Transformations
 Chapter 2 Coordinate Systems and Transformations A physical system has a symmetry under some operation if the system after the operation is observationally indistinguishable from the system before the
Chapter 2 Coordinate Systems and Transformations A physical system has a symmetry under some operation if the system after the operation is observationally indistinguishable from the system before the
Gravitation: Tensor Calculus
 An Introduction to General Relativity Center for Relativistic Astrophysics School of Physics Georgia Institute of Technology Notes based on textbook: Spacetime and Geometry by S.M. Carroll Spring 2013
An Introduction to General Relativity Center for Relativistic Astrophysics School of Physics Georgia Institute of Technology Notes based on textbook: Spacetime and Geometry by S.M. Carroll Spring 2013
CS 468, Lecture 11: Covariant Differentiation
 CS 468, Lecture 11: Covariant Differentiation Adrian Butscher (scribe: Ben Mildenhall) May 6, 2013 1 Introduction We have talked about various extrinsic and intrinsic properties of surfaces. Extrinsic
CS 468, Lecture 11: Covariant Differentiation Adrian Butscher (scribe: Ben Mildenhall) May 6, 2013 1 Introduction We have talked about various extrinsic and intrinsic properties of surfaces. Extrinsic
Mathematics that Every Physicist should Know: Scalar, Vector, and Tensor Fields in the Space of Real n- Dimensional Independent Variable with Metric
 Mathematics that Every Physicist should Know: Scalar, Vector, and Tensor Fields in the Space of Real n- Dimensional Independent Variable with Metric By Y. N. Keilman AltSci@basicisp.net Every physicist
Mathematics that Every Physicist should Know: Scalar, Vector, and Tensor Fields in the Space of Real n- Dimensional Independent Variable with Metric By Y. N. Keilman AltSci@basicisp.net Every physicist
Math review. Math review
 Math review 1 Math review 3 1 series approximations 3 Taylor s Theorem 3 Binomial approximation 3 sin(x), for x in radians and x close to zero 4 cos(x), for x in radians and x close to zero 5 2 some geometry
Math review 1 Math review 3 1 series approximations 3 Taylor s Theorem 3 Binomial approximation 3 sin(x), for x in radians and x close to zero 4 cos(x), for x in radians and x close to zero 5 2 some geometry
PAPER 309 GENERAL RELATIVITY
 MATHEMATICAL TRIPOS Part III Monday, 30 May, 2016 9:00 am to 12:00 pm PAPER 309 GENERAL RELATIVITY Attempt no more than THREE questions. There are FOUR questions in total. The questions carry equal weight.
MATHEMATICAL TRIPOS Part III Monday, 30 May, 2016 9:00 am to 12:00 pm PAPER 309 GENERAL RELATIVITY Attempt no more than THREE questions. There are FOUR questions in total. The questions carry equal weight.
Physics 209 Fall 2002 Notes 5 Thomas Precession
 Physics 209 Fall 2002 Notes 5 Thomas Precession Jackson s discussion of Thomas precession is based on Thomas s original treatment, and on the later paper by Bargmann, Michel, and Telegdi. The alternative
Physics 209 Fall 2002 Notes 5 Thomas Precession Jackson s discussion of Thomas precession is based on Thomas s original treatment, and on the later paper by Bargmann, Michel, and Telegdi. The alternative
Tensor Calculus, Part 2
 Massachusetts Institute of Technology Department of Physics Physics 8.962 Spring 2002 Tensor Calculus, Part 2 c 2000, 2002 Edmund Bertschinger. 1 Introduction The first set of 8.962 notes, Introduction
Massachusetts Institute of Technology Department of Physics Physics 8.962 Spring 2002 Tensor Calculus, Part 2 c 2000, 2002 Edmund Bertschinger. 1 Introduction The first set of 8.962 notes, Introduction
Lecture 3: Vectors. Any set of numbers that transform under a rotation the same way that a point in space does is called a vector.
 Lecture 3: Vectors Any set of numbers that transform under a rotation the same way that a point in space does is called a vector i.e., A = λ A i ij j j In earlier courses, you may have learned that a vector
Lecture 3: Vectors Any set of numbers that transform under a rotation the same way that a point in space does is called a vector i.e., A = λ A i ij j j In earlier courses, you may have learned that a vector
Ask class: what is the Minkowski spacetime in spherical coordinates? ds 2 = dt 2 +dr 2 +r 2 (dθ 2 +sin 2 θdφ 2 ). (1)
 1 Tensor manipulations One final thing to learn about tensor manipulation is that the metric tensor is what allows you to raise and lower indices. That is, for example, v α = g αβ v β, where again we use
1 Tensor manipulations One final thing to learn about tensor manipulation is that the metric tensor is what allows you to raise and lower indices. That is, for example, v α = g αβ v β, where again we use
Physics 325: General Relativity Spring Final Review Problem Set
 Physics 325: General Relativity Spring 2012 Final Review Problem Set Date: Friday 4 May 2012 Instructions: This is the third of three review problem sets in Physics 325. It will count for twice as much
Physics 325: General Relativity Spring 2012 Final Review Problem Set Date: Friday 4 May 2012 Instructions: This is the third of three review problem sets in Physics 325. It will count for twice as much
CHAPTER 4 GENERAL COORDINATES. 4.1 General coordinate transformations
 CHAPTER 4 GENERAL COORDINATES No one can understand the new law of gravitation without a thorough knowledge of the theory of invariants and of the calculus of variations J. J. Thomson Royal Society, 1919
CHAPTER 4 GENERAL COORDINATES No one can understand the new law of gravitation without a thorough knowledge of the theory of invariants and of the calculus of variations J. J. Thomson Royal Society, 1919
III. TRANSFORMATION RELATIONS
 III. TRANSFORMATION RELATIONS The transformation relations from cartesian coordinates to a general curvilinear system are developed here using certain concepts from differential geometry and tensor analysis,
III. TRANSFORMATION RELATIONS The transformation relations from cartesian coordinates to a general curvilinear system are developed here using certain concepts from differential geometry and tensor analysis,
1.4 LECTURE 4. Tensors and Vector Identities
 16 CHAPTER 1. VECTOR ALGEBRA 1.3.2 Triple Product The triple product of three vectors A, B and C is defined by In tensor notation it is A ( B C ) = [ A, B, C ] = A ( B C ) i, j,k=1 ε i jk A i B j C k =
16 CHAPTER 1. VECTOR ALGEBRA 1.3.2 Triple Product The triple product of three vectors A, B and C is defined by In tensor notation it is A ( B C ) = [ A, B, C ] = A ( B C ) i, j,k=1 ε i jk A i B j C k =
Tensors and Special Relativity
 Tensors and Special Relativity Lecture 6 1 Introduction and review of tensor algebra While you have probably used tensors of rank 1, i.e vectors, in special relativity, relativity is most efficiently expressed
Tensors and Special Relativity Lecture 6 1 Introduction and review of tensor algebra While you have probably used tensors of rank 1, i.e vectors, in special relativity, relativity is most efficiently expressed
Metrics and Curvature
 Metrics and Curvature How to measure curvature? Metrics Euclidian/Minkowski Curved spaces General 4 dimensional space Cosmological principle Homogeneity and isotropy: evidence Robertson-Walker metrics
Metrics and Curvature How to measure curvature? Metrics Euclidian/Minkowski Curved spaces General 4 dimensional space Cosmological principle Homogeneity and isotropy: evidence Robertson-Walker metrics
Gravitation: Special Relativity
 An Introduction to General Relativity Center for Relativistic Astrophysics School of Physics Georgia Institute of Technology Notes based on textbook: Spacetime and Geometry by S.M. Carroll Spring 2013
An Introduction to General Relativity Center for Relativistic Astrophysics School of Physics Georgia Institute of Technology Notes based on textbook: Spacetime and Geometry by S.M. Carroll Spring 2013
Special and General Relativity (PHZ 4601/5606) Fall 2018 Classwork and Homework. Every exercise counts 10 points unless stated differently.
 1 Special and General Relativity (PHZ 4601/5606) Fall 2018 Classwork and Homework Every exercise counts 10 points unless stated differently. Set 1: (1) Homework, due ( F ) 8/31/2018 before ( ) class. Consider
1 Special and General Relativity (PHZ 4601/5606) Fall 2018 Classwork and Homework Every exercise counts 10 points unless stated differently. Set 1: (1) Homework, due ( F ) 8/31/2018 before ( ) class. Consider
Spacetime and 4 vectors
 Spacetime and 4 vectors 1 Minkowski space = 4 dimensional spacetime Euclidean 4 space Each point in Minkowski space is an event. In SR, Minkowski space is an absolute structure (like space in Newtonian
Spacetime and 4 vectors 1 Minkowski space = 4 dimensional spacetime Euclidean 4 space Each point in Minkowski space is an event. In SR, Minkowski space is an absolute structure (like space in Newtonian
Relativistic Mechanics
 Physics 411 Lecture 9 Relativistic Mechanics Lecture 9 Physics 411 Classical Mechanics II September 17th, 2007 We have developed some tensor language to describe familiar physics we reviewed orbital motion
Physics 411 Lecture 9 Relativistic Mechanics Lecture 9 Physics 411 Classical Mechanics II September 17th, 2007 We have developed some tensor language to describe familiar physics we reviewed orbital motion
Is there a magnification paradox in gravitational lensing?
 Is there a magnification paradox in gravitational lensing? Olaf Wucknitz wucknitz@astro.uni-bonn.de Astrophysics seminar/colloquium, Potsdam, 26 November 2007 Is there a magnification paradox in gravitational
Is there a magnification paradox in gravitational lensing? Olaf Wucknitz wucknitz@astro.uni-bonn.de Astrophysics seminar/colloquium, Potsdam, 26 November 2007 Is there a magnification paradox in gravitational
General Relativity and Cosmology Mock exam
 Physikalisches Institut Mock Exam Universität Bonn 29. June 2011 Theoretische Physik SS 2011 General Relativity and Cosmology Mock exam Priv. Doz. Dr. S. Förste Exercise 1: Overview Give short answers
Physikalisches Institut Mock Exam Universität Bonn 29. June 2011 Theoretische Physik SS 2011 General Relativity and Cosmology Mock exam Priv. Doz. Dr. S. Förste Exercise 1: Overview Give short answers
GTR is founded on a Conceptual Mistake And hence Null and Void
 GTR is founded on a Conceptual Mistake And hence Null and Void A critical review of the fundamental basis of General Theory of Relativity shows that a conceptual mistake has been made in the basic postulate
GTR is founded on a Conceptual Mistake And hence Null and Void A critical review of the fundamental basis of General Theory of Relativity shows that a conceptual mistake has been made in the basic postulate
Physics 110. Electricity and Magnetism. Professor Dine. Spring, Handout: Vectors and Tensors: Everything You Need to Know
 Physics 110. Electricity and Magnetism. Professor Dine Spring, 2008. Handout: Vectors and Tensors: Everything You Need to Know What makes E&M hard, more than anything else, is the problem that the electric
Physics 110. Electricity and Magnetism. Professor Dine Spring, 2008. Handout: Vectors and Tensors: Everything You Need to Know What makes E&M hard, more than anything else, is the problem that the electric
Notes on Minkowski space-time
 Notes on Minkowski space-time Following Hermann Minkowski, the arena for special relativity is Minkowski space-time. The squared interval S between points X = (t, x, y, z) and X = (t, x, y, z ) is: S =
Notes on Minkowski space-time Following Hermann Minkowski, the arena for special relativity is Minkowski space-time. The squared interval S between points X = (t, x, y, z) and X = (t, x, y, z ) is: S =
An Introduction to Kaluza-Klein Theory
 An Introduction to Kaluza-Klein Theory A. Garrett Lisi nd March Department of Physics, University of California San Diego, La Jolla, CA 993-39 gar@lisi.com Introduction It is the aim of Kaluza-Klein theory
An Introduction to Kaluza-Klein Theory A. Garrett Lisi nd March Department of Physics, University of California San Diego, La Jolla, CA 993-39 gar@lisi.com Introduction It is the aim of Kaluza-Klein theory
Multidimensional Calculus: Mainly Differential Theory
 9 Multidimensional Calculus: Mainly Differential Theory In the following, we will attempt to quickly develop the basic differential theory of calculus in multidimensional spaces You ve probably already
9 Multidimensional Calculus: Mainly Differential Theory In the following, we will attempt to quickly develop the basic differential theory of calculus in multidimensional spaces You ve probably already
Rotational motion of a rigid body spinning around a rotational axis ˆn;
 Physics 106a, Caltech 15 November, 2018 Lecture 14: Rotations The motion of solid bodies So far, we have been studying the motion of point particles, which are essentially just translational. Bodies with
Physics 106a, Caltech 15 November, 2018 Lecture 14: Rotations The motion of solid bodies So far, we have been studying the motion of point particles, which are essentially just translational. Bodies with
Übungen zu RT2 SS (4) Show that (any) contraction of a (p, q) - tensor results in a (p 1, q 1) - tensor.
 Übungen zu RT2 SS 2010 (1) Show that the tensor field g µν (x) = η µν is invariant under Poincaré transformations, i.e. x µ x µ = L µ νx ν + c µ, where L µ ν is a constant matrix subject to L µ ρl ν ση
Übungen zu RT2 SS 2010 (1) Show that the tensor field g µν (x) = η µν is invariant under Poincaré transformations, i.e. x µ x µ = L µ νx ν + c µ, where L µ ν is a constant matrix subject to L µ ρl ν ση
PAPER 52 GENERAL RELATIVITY
 MATHEMATICAL TRIPOS Part III Monday, 1 June, 2015 9:00 am to 12:00 pm PAPER 52 GENERAL RELATIVITY Attempt no more than THREE questions. There are FOUR questions in total. The questions carry equal weight.
MATHEMATICAL TRIPOS Part III Monday, 1 June, 2015 9:00 am to 12:00 pm PAPER 52 GENERAL RELATIVITY Attempt no more than THREE questions. There are FOUR questions in total. The questions carry equal weight.
Geometry for Physicists
 Hung Nguyen-Schafer Jan-Philip Schmidt Tensor Analysis and Elementary Differential Geometry for Physicists and Engineers 4 i Springer Contents 1 General Basis and Bra-Ket Notation 1 1.1 Introduction to
Hung Nguyen-Schafer Jan-Philip Schmidt Tensor Analysis and Elementary Differential Geometry for Physicists and Engineers 4 i Springer Contents 1 General Basis and Bra-Ket Notation 1 1.1 Introduction to
Exercises in field theory
 Exercises in field theory Wolfgang Kastaun June 12, 2008 Vectors and Tensors Contravariant vector Coordinate independent definition, e.g. as tangent of a curve. A contravariant vector A is expressed with
Exercises in field theory Wolfgang Kastaun June 12, 2008 Vectors and Tensors Contravariant vector Coordinate independent definition, e.g. as tangent of a curve. A contravariant vector A is expressed with
Final Physics of Schwarzschild
 Physics 4 Lecture 32 Final Physics of Schwarzschild Lecture 32 Physics 4 Classical Mechanics II November 6th, 27 We have studied a lot of properties of the Schwarzschild metric I want to finish with a
Physics 4 Lecture 32 Final Physics of Schwarzschild Lecture 32 Physics 4 Classical Mechanics II November 6th, 27 We have studied a lot of properties of the Schwarzschild metric I want to finish with a
Christoffel Symbols. 1 In General Topologies. Joshua Albert. September 28, W. First we say W : λ n = x µ (λ) so that the world
 Christoffel Symbols Joshua Albert September 28, 22 In General Topoloies We have a metric tensor nm defined by, Note by some handy theorem that for almost any continuous function F (L), equation 2 still
Christoffel Symbols Joshua Albert September 28, 22 In General Topoloies We have a metric tensor nm defined by, Note by some handy theorem that for almost any continuous function F (L), equation 2 still
Classical differential geometry of two-dimensional surfaces
 Classical differential geometry of two-dimensional surfaces 1 Basic definitions This section gives an overview of the basic notions of differential geometry for twodimensional surfaces. It follows mainly
Classical differential geometry of two-dimensional surfaces 1 Basic definitions This section gives an overview of the basic notions of differential geometry for twodimensional surfaces. It follows mainly
Astr 2320 Tues. May 2, 2017 Today s Topics Chapter 23: Cosmology: The Big Bang and Beyond Introduction Newtonian Cosmology Solutions to Einstein s
 Astr 0 Tues. May, 07 Today s Topics Chapter : Cosmology: The Big Bang and Beyond Introduction Newtonian Cosmology Solutions to Einstein s Field Equations The Primeval Fireball Standard Big Bang Model Chapter
Astr 0 Tues. May, 07 Today s Topics Chapter : Cosmology: The Big Bang and Beyond Introduction Newtonian Cosmology Solutions to Einstein s Field Equations The Primeval Fireball Standard Big Bang Model Chapter
Contents. Motivation. 1 di 7 23/03/ :41
 1 di 7 23/03/2015 09:41 From Wikipedia, the free encyclopedia In mathematics, orthogonal coordinates are defined as a set of d coordinates q = (q 1, q 2,..., q d ) in which the coordinate surfaces all
1 di 7 23/03/2015 09:41 From Wikipedia, the free encyclopedia In mathematics, orthogonal coordinates are defined as a set of d coordinates q = (q 1, q 2,..., q d ) in which the coordinate surfaces all
Tutorial General Relativity
 Tutorial General Relativity Winter term 016/017 Sheet No. 3 Solutions will be discussed on Nov/9/16 Lecturer: Prof. Dr. C. Greiner Tutor: Hendrik van Hees 1. Tensor gymnastics (a) Let Q ab = Q ba be a
Tutorial General Relativity Winter term 016/017 Sheet No. 3 Solutions will be discussed on Nov/9/16 Lecturer: Prof. Dr. C. Greiner Tutor: Hendrik van Hees 1. Tensor gymnastics (a) Let Q ab = Q ba be a
Introduction to General Relativity
 Introduction to General Relativity Lectures by Igor Pesando Slides by Pietro Fré Virgo Site May 22nd 2006 The issue of reference frames Since oldest and observers antiquity the Who is at motion? The Sun
Introduction to General Relativity Lectures by Igor Pesando Slides by Pietro Fré Virgo Site May 22nd 2006 The issue of reference frames Since oldest and observers antiquity the Who is at motion? The Sun
MATH 423/ Note that the algebraic operations on the right hand side are vector subtraction and scalar multiplication.
 MATH 423/673 1 Curves Definition: The velocity vector of a curve α : I R 3 at time t is the tangent vector to R 3 at α(t), defined by α (t) T α(t) R 3 α α(t + h) α(t) (t) := lim h 0 h Note that the algebraic
MATH 423/673 1 Curves Definition: The velocity vector of a curve α : I R 3 at time t is the tangent vector to R 3 at α(t), defined by α (t) T α(t) R 3 α α(t + h) α(t) (t) := lim h 0 h Note that the algebraic
A5682: Introduction to Cosmology Course Notes. 2. General Relativity
 2. General Relativity Reading: Chapter 3 (sections 3.1 and 3.2) Special Relativity Postulates of theory: 1. There is no state of absolute rest. 2. The speed of light in vacuum is constant, independent
2. General Relativity Reading: Chapter 3 (sections 3.1 and 3.2) Special Relativity Postulates of theory: 1. There is no state of absolute rest. 2. The speed of light in vacuum is constant, independent
Week 6: Differential geometry I
 Week 6: Differential geometry I Tensor algebra Covariant and contravariant tensors Consider two n dimensional coordinate systems x and x and assume that we can express the x i as functions of the x i,
Week 6: Differential geometry I Tensor algebra Covariant and contravariant tensors Consider two n dimensional coordinate systems x and x and assume that we can express the x i as functions of the x i,
Introduction to General Relativity
 Introduction to General Relativity 1 Recall Newtonian gravitation: Clearly not Lorentz invariant, since Laplacian appears rather than d'alembertian. No attempt to find Lorentz invariant equations that
Introduction to General Relativity 1 Recall Newtonian gravitation: Clearly not Lorentz invariant, since Laplacian appears rather than d'alembertian. No attempt to find Lorentz invariant equations that
Uniformity of the Universe
 Outline Universe is homogenous and isotropic Spacetime metrics Friedmann-Walker-Robertson metric Number of numbers needed to specify a physical quantity. Energy-momentum tensor Energy-momentum tensor of
Outline Universe is homogenous and isotropic Spacetime metrics Friedmann-Walker-Robertson metric Number of numbers needed to specify a physical quantity. Energy-momentum tensor Energy-momentum tensor of
Physics 480/581. Homework No. 10 Solutions: due Friday, 19 October, 2018
 Physics 480/58 Homework No. 0 Solutions: due Friday, 9 October, 208. Using the coordinate bases for -forms, and their reciprocal bases for tangent vectors, and the usual form of the Schwarzschild metric,
Physics 480/58 Homework No. 0 Solutions: due Friday, 9 October, 208. Using the coordinate bases for -forms, and their reciprocal bases for tangent vectors, and the usual form of the Schwarzschild metric,
2.1 The metric and and coordinate transformations
 2 Cosmology and GR The first step toward a cosmological theory, following what we called the cosmological principle is to implement the assumptions of isotropy and homogeneity withing the context of general
2 Cosmology and GR The first step toward a cosmological theory, following what we called the cosmological principle is to implement the assumptions of isotropy and homogeneity withing the context of general
From An Apple To Black Holes Gravity in General Relativity
 From An Apple To Black Holes Gravity in General Relativity Gravity as Geometry Central Idea of General Relativity Gravitational field vs magnetic field Uniqueness of trajectory in space and time Uniqueness
From An Apple To Black Holes Gravity in General Relativity Gravity as Geometry Central Idea of General Relativity Gravitational field vs magnetic field Uniqueness of trajectory in space and time Uniqueness
2.2 Coordinate transformations
 2.2 Coordinate transformations Lets now think about more general spaces which have arbitrary curvature. Define a point P in some space, and another point a little further on called R. These points have
2.2 Coordinate transformations Lets now think about more general spaces which have arbitrary curvature. Define a point P in some space, and another point a little further on called R. These points have
THEODORE VORONOV DIFFERENTIAL GEOMETRY. Spring 2009
 [under construction] 8 Parallel transport 8.1 Equation of parallel transport Consider a vector bundle E B. We would like to compare vectors belonging to fibers over different points. Recall that this was
[under construction] 8 Parallel transport 8.1 Equation of parallel transport Consider a vector bundle E B. We would like to compare vectors belonging to fibers over different points. Recall that this was
Review and Notation (Special relativity)
 Review and Notation (Special relativity) December 30, 2016 7:35 PM Special Relativity: i) The principle of special relativity: The laws of physics must be the same in any inertial reference frame. In particular,
Review and Notation (Special relativity) December 30, 2016 7:35 PM Special Relativity: i) The principle of special relativity: The laws of physics must be the same in any inertial reference frame. In particular,
Curvilinear coordinates
 C Curvilinear coordinates The distance between two points Euclidean space takes the simplest form (2-4) in Cartesian coordinates. The geometry of concrete physical problems may make non-cartesian coordinates
C Curvilinear coordinates The distance between two points Euclidean space takes the simplest form (2-4) in Cartesian coordinates. The geometry of concrete physical problems may make non-cartesian coordinates
General Relativity ASTR 2110 Sarazin. Einstein s Equation
 General Relativity ASTR 2110 Sarazin Einstein s Equation Curvature of Spacetime 1. Principle of Equvalence: gravity acceleration locally 2. Acceleration curved path in spacetime In gravitational field,
General Relativity ASTR 2110 Sarazin Einstein s Equation Curvature of Spacetime 1. Principle of Equvalence: gravity acceleration locally 2. Acceleration curved path in spacetime In gravitational field,
Appendix to Lecture 2
 PHYS 652: Astrophysics 1 Appendix to Lecture 2 An Alternative Lagrangian In class we used an alternative Lagrangian L = g γδ ẋ γ ẋ δ, instead of the traditional L = g γδ ẋ γ ẋ δ. Here is the justification
PHYS 652: Astrophysics 1 Appendix to Lecture 2 An Alternative Lagrangian In class we used an alternative Lagrangian L = g γδ ẋ γ ẋ δ, instead of the traditional L = g γδ ẋ γ ẋ δ. Here is the justification
1.2 Euclidean spacetime: old wine in a new bottle
 CHAPTER 1 EUCLIDEAN SPACETIME AND NEWTONIAN PHYSICS Absolute, true, and mathematical time, of itself, and from its own nature, flows equably without relation to anything external... Isaac Newton Scholium
CHAPTER 1 EUCLIDEAN SPACETIME AND NEWTONIAN PHYSICS Absolute, true, and mathematical time, of itself, and from its own nature, flows equably without relation to anything external... Isaac Newton Scholium
NIL. Let M be R 3 equipped with the metric in which the following vector. fields, U = and. are an orthonormal basis.
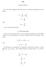 NIL KEVIN WHYTE Let M be R 3 equipped with the metric in which the following vector fields: U = x + y z V = y and W = z are an orthonormal basis. 1. Preliminaries Since we re given the metric via an orthonormal
NIL KEVIN WHYTE Let M be R 3 equipped with the metric in which the following vector fields: U = x + y z V = y and W = z are an orthonormal basis. 1. Preliminaries Since we re given the metric via an orthonormal
Math 265H: Calculus III Practice Midterm II: Fall 2014
 Name: Section #: Math 65H: alculus III Practice Midterm II: Fall 14 Instructions: This exam has 7 problems. The number of points awarded for each question is indicated in the problem. Answer each question
Name: Section #: Math 65H: alculus III Practice Midterm II: Fall 14 Instructions: This exam has 7 problems. The number of points awarded for each question is indicated in the problem. Answer each question
Physics 6303 Lecture 3 August 27, 2018
 Physics 6303 Lecture 3 August 27, 208 LAST TIME: Vector operators, divergence, curl, examples of line integrals and surface integrals, divergence theorem, Stokes theorem, index notation, Kronecker delta,
Physics 6303 Lecture 3 August 27, 208 LAST TIME: Vector operators, divergence, curl, examples of line integrals and surface integrals, divergence theorem, Stokes theorem, index notation, Kronecker delta,
INTRODUCING VECTORS: THE OLD AND THE NEW! The concept of a metric can be introduced as a fairly simple generalization of Pythagoras s theorem.
 INTRODUCING VECTORS: THE OLD AND THE NEW! The concept of a metric can be introduced as a fairly simple generalization of Pythagoras s theorem. But the definitions: - a vector is... a tensor is... a manifold
INTRODUCING VECTORS: THE OLD AND THE NEW! The concept of a metric can be introduced as a fairly simple generalization of Pythagoras s theorem. But the definitions: - a vector is... a tensor is... a manifold
Introduction and Vectors Lecture 1
 1 Introduction Introduction and Vectors Lecture 1 This is a course on classical Electromagnetism. It is the foundation for more advanced courses in modern physics. All physics of the modern era, from quantum
1 Introduction Introduction and Vectors Lecture 1 This is a course on classical Electromagnetism. It is the foundation for more advanced courses in modern physics. All physics of the modern era, from quantum
PHZ 6607 Special and General Relativity I Handout #1: The case for General Relativity
 Handout #1: The case for General Relativity General Relativity is an exceptionally powerful physical theory. Ultimately, it is also a theory about geometry, the geometry of a four dimensional spacetime.
Handout #1: The case for General Relativity General Relativity is an exceptionally powerful physical theory. Ultimately, it is also a theory about geometry, the geometry of a four dimensional spacetime.
Lecture 13 Notes, Electromagnetic Theory II Dr. Christopher S. Baird, faculty.uml.edu/cbaird University of Massachusetts Lowell
 Lecture 13 Notes, Electromagnetic Theory II Dr. Christopher S. Baird, faculty.uml.edu/cbaird University of Massachusetts Lowell 1. Covariant Geometry - We would like to develop a mathematical framework
Lecture 13 Notes, Electromagnetic Theory II Dr. Christopher S. Baird, faculty.uml.edu/cbaird University of Massachusetts Lowell 1. Covariant Geometry - We would like to develop a mathematical framework
Lorentz transformation
 13 Mar 2012 Equivalence Principle. Einstein s path to his field equation 15 Mar 2012 Tests of the equivalence principle 20 Mar 2012 General covariance. Math. Covariant derivative è Homework 6 is due on
13 Mar 2012 Equivalence Principle. Einstein s path to his field equation 15 Mar 2012 Tests of the equivalence principle 20 Mar 2012 General covariance. Math. Covariant derivative è Homework 6 is due on
The spacetime of special relativity
 1 The spacetime of special relativity We begin our discussion of the relativistic theory of gravity by reviewing some basic notions underlying the Newtonian and special-relativistic viewpoints of space
1 The spacetime of special relativity We begin our discussion of the relativistic theory of gravity by reviewing some basic notions underlying the Newtonian and special-relativistic viewpoints of space
A brief introduction to Semi-Riemannian geometry and general relativity. Hans Ringström
 A brief introduction to Semi-Riemannian geometry and general relativity Hans Ringström May 5, 2015 2 Contents 1 Scalar product spaces 1 1.1 Scalar products...................................... 1 1.2 Orthonormal
A brief introduction to Semi-Riemannian geometry and general relativity Hans Ringström May 5, 2015 2 Contents 1 Scalar product spaces 1 1.1 Scalar products...................................... 1 1.2 Orthonormal
Physics 411 Lecture 7. Tensors. Lecture 7. Physics 411 Classical Mechanics II
 Physics 411 Lecture 7 Tensors Lecture 7 Physics 411 Classical Mechanics II September 12th 2007 In Electrodynamics, the implicit law governing the motion of particles is F α = m ẍ α. This is also true,
Physics 411 Lecture 7 Tensors Lecture 7 Physics 411 Classical Mechanics II September 12th 2007 In Electrodynamics, the implicit law governing the motion of particles is F α = m ẍ α. This is also true,
Fundamental Cosmology: 4.General Relativistic Cosmology
 Fundamental Cosmology: 4.General Relativistic Cosmology Matter tells space how to curve. Space tells matter how to move. John Archibald Wheeler 1 4.1: Introduction to General Relativity Introduce the Tools
Fundamental Cosmology: 4.General Relativistic Cosmology Matter tells space how to curve. Space tells matter how to move. John Archibald Wheeler 1 4.1: Introduction to General Relativity Introduce the Tools
