Sequences and Series; Finite and Infinite
|
|
|
- Cory Lee
- 5 years ago
- Views:
Transcription
1 Sequeces ad Series; Fiite ad Ifiite Calculus 2, Veritas Prep. We are about to do the coolest theorem i calculus. Not the most importat theorem, mid you that s the FTC the coolest. We are about to do the coolest, weirdest, most mid-blowig theorem i all of first-year calculus. I have stories about this theorem that I d be fired if I told you. We are about to do Taylor s theorem. Taylor s theorem, roughly speakig, says that everythig is a polyomial. Trig fuctios, expoetial fuctios, logarithms, ratioal fuctios, all sorts of weird stuff they ca all just be thought of as polyomials (albeit possibly ifiitely-log polyomials). Ad that is woderful ad weird, because polyomials are really ice fuctios. They re cotiuous everywhere they have o holes or asymptotes they have derivatives everywhere we ca plug ay real umber i they re ice ad predictable ad curvy. They re so simple! Remember how easy graphig them is, compared to graphig ratioal fuctios? All you do is factor them! Or thik about how easy it is to evaluate a polyomial at ay radom poit you just plug i the umber, do a lot of arithmetic, ad evetually get it! You ca t do that with trig fuctios (uless you re lucky ad you wat to plug i, say π/2): if f(x) = x 2 + 3x + 5, ad I wat to fid f(2), I just plug 2 i for x: f(2) = = 5 if f(x) = l(x), ad I wat to fid f(2), I just plug 2 i for x: f(2) = l(2) =...um. I do t kow how to work this out as a decimal. Ayway. Taylor s theorem says that everythig is a polyomial. For istace, sie is a polyomial albeit a ifiitely-log oe: si(x) = x x3 3! + x5 5! x7 7! + x9 9! So is e x : e x = + x + x2 2! + x3 3! + x4 4! + This stuff is really cool! But before we start talkig about it fully, there are some prelimiaries we eed to take care of. Namely: Taylor series are a type of series, so we should probably talk about those, ad series are made of idividual terms (a sequece of terms, added together), so we should probably talk about those, too. Sequeces A sequece, i essece, is just a ordered list of umbers. Here are some examples of sequeces:, 2, 3, 4, 5, 6, 2, 3, 4, (the atural umbers) (fractios!),,, 3, 3, 3, 3, 3, 4, 9, 6, 36 2, 4, 6, 8, x, x 2, x 3, x 4, (it s flippig back ad forth!) (kid of borig) (squares!) (eve umbers!) (a sequece of fuctios, rather tha umbers!) If you re a math perso, please do t rui the fu by shoutig out some idiotic commet. Look, I kow the cops are goig to break up this party evetually ad cite us for violatig uiform covergece, ad the i the morig we ll all wake up with deadly hagovers as a result of havig approximated, say, l( + x) far outside its radius of covergece... but for ow, let us just believe i the beauty ad the glory of EVERYTHING BEING POLYNOMIALS. Because it is beautiful. Tomorrow will come whe it will.
2 Note that these are all examples of ifiite sequeces, i.e., sequeces that could go o forever. Questio: I ve listed, for each sequece, the first term, the secod term, the third term, etc., etc.,... what will the th term look like?, 2, 3, 4, 5, 6,,, 2, 3, 4,,,,,,,, ( ), 3, 3, 3, 3, 3, 3,, 4, 9, 6, 36, 2, 2, 4, 6, 8,, 2, x, x 2, x 3, x 4,, x, Aother way of thikig about a sequece ad this is the way we d formally defie it is that it s a fuctio, but whereas basically all of the fuctios we deal with ca take ay real umber as iput, a sequece ca oly take a atural umber as iput. It s a fuctio whose domai is oly the atural umbers (but whose rage could be all real umbers). Here s a picture of what the sequece f() = / looks like: If I wat to fully describe a sequece, the rather tha list terms, it s probably a better idea to just give the formula for the th term: S = or f() = is the sequece, 2, 3, 4, 5, 6,, S = or f() = is the sequece, 2. 3, 4,,, S = ( ) or f() = 2 is the sequece,,,,, ( ), S = 3 or f() = 3 is the sequece 3, 3, 3, 3, 3, 3, S = 2 or f() = 2 is the sequece, 4, 9, 6, 36, 2, S = 2 or f() = 2 is the sequece 2, 4, 6, 8,, 2, S = x or f() = x is the sequece x, x 2, x 3, x 4,, x, Note that I m usig the letter rather tha x because, well, mathematicias ted to use the letter (or sometimes k, or, less ofte, m, i, ad j) to represet atural umbers, whereas x teds to be used to 2
3 represet real umbers. Of course, that s ot a ecessary covetio; it s just usual practice. The cotext of the problem should make it clear whether a variable rages over all possible real umbers (like the x i f(x) = x 2 ) or over just the atural umbers (like the i S = 2). Remember that N is the symbol for the atural umbers, whereas R is the symbol for real umbers. By the facy expressio i the above graph N, I mea that is a atural umber, or, more literally, is a member of the set of atural umbers, with meaig is a elemet/member of. The mai questio we ca ask about a sequece is: does it coverge or diverge? Meaig: as, does the sequece either: a) approach some sigle, fiite umber (coverge), or b) ot? (diverge) Ad as a secodary questio: if it does coverge, what does it coverge to? For example: The sequece S =, i.e., the sequece, 2, 3, 4, diverges, because as, the sequece just keeps gettig bigger ad bigger, i.e., S. The sequece S = / (i.e.,, 2, 3, 4, ) coverges, because as, S 0. So it coverges, ad moreover, it coverges to 0. The sequece S = ( ), i.e., the sequece, 2, 3, 4, 5, coverges, because as, S 0, just as i the last example. Note that, because of the ( ), it bouces aroud it keeps alteratig betwee beig positive ad egative. But it still approaches 0. The sequece S = ( ), i.e., the sequece,,,,, diverges, because as, the limit of S does t exist. It keeps alteratig betwee + ad. It ever settles dow. The sequece of fuctios S = x /, i.e., the sequece, x, x /2, x /3, x /4, coverges to x 0, or just. Series So, those are sequeces. They re kid of cool, but ot that cool, because they re easy to deal with. If we wat to fid whether a sequece coverges, we just take a limit! Not too difficult. But what if we add all the terms i a sequece together? For istace: rather tha havig the sequece:, 2, 3, 4, what if we have the series: This is a very differet creature. We kow that the sequece coverges, but we do t kow whether the series (i which we add everythig together) coverges. More formally, a series, or a sum, is whe we add the terms of a sequece together, rather tha simply listig them. They could be fiite (I add together a fiite umber of terms) or ifiite (I add together a ifiite umber of terms). Here s a example of a fiite series: There are three differet ways we ca write series: I could show each term explicitly: I could write it as a sigle umber: = 50 k=4 or I could write it usig Σ-otatio for sums: = 5k You ve see -otatio before, but as a quick remider, it works somethig like this: k=4 k= 5k = }{{} 5 + the k= term the k=2 term {}}{ }{{} the k=3 term k= the k=4 term 3 {}}{ 5 4 = = 50
4 Or, more geerally: k=b f(k) = f(a) + f(a + ) + f(a + 2) + + f(b 2) + f(b ) + f(b) k=a Obviously, if I have a ifiite series, I ca t write every term explicitly there are a ifiite umber of them! But I ca ask the same questio I ask of sequeces: give a series, does it coverge or diverge? For series, this is a much harder questio to aswer 2. With sequeces, we ca just take a limit; with series, we have just a smatterig of ad hoc methods, some of which might or might ot work for a give series. There are some obvious cosideratios first. Cosider the ifiite series: = = Obviously this diverges. We re addig bigger ad bigger umbers! The sum is gettig bigger ad bigger! So clearly, if each of the idividual terms i the series icrease, the series will diverge. I fact, eve if each of the terms stay the same, the series diverges: = 5 = = So we ca say this: if the idividual terms of a series do ot decrease (i.e., icrease or remai costat), the sequece will diverge. But just because the terms of a series decrease, it is ot always the case that the series coverges. For example, cosider the two series: The terms i both of these series go to 0. But (for reasos which you re about to see) oe of these series coverges, ad the other diverges. Oe last thig: do t get the terms sequece ad series cofused. I do it all the time. Do t follow my example: This is a sequece:, 2, 3, 4, 5, 6,,, This is a series: A Cool, Simple Series Cosider the series: a = + a + a 2 + a 3 + a 4 + for some umber a; for istace, if a = /2, this becomes the series: ( ) = Also ote that it s really oly a iterestig questio to ask about ifiite series, sice fiite series obviously coverge to whatever they add up to. 4
5 There is a startlig result about this series: it coverges to a : a = + a + a 2 + a 3 + a 4 + = a So, for istace, i the case of a = /2, o matter how may terms we add, the series simply gets closer ad closer to 2: ( ) = = /2 = /2 = 2 Let s prove this. Imagie, for the sake of coveiece, we call this series S: S = + a + a 2 + a 3 + a 4 + The: what happes if we multiply both sides of this equatio by a? We ll have: as = a + a 2 + a 3 + a 4 + a 5 What if we cosider the quatity S as? This must be just: S {}}{{}}{ S as = ( + a + a 2 + a 3 + a 4 + ) ( a + a 2 + a 3 + a 4 + a 5 ) But if I combie those two paretheses, most early everythig will cacel out we ve got a a, ad a a; we ve got a a 2, ad a a 2, etc. The oly thig that will be left is : S as = as But we ca easily solve this for S: S( a) = S = a Ta-da! Now we ca deal with ay series of the form a. I fact, we have quite a bit of power, because most of our tests for covergece oly tell us whether a certai series coverges they do t tell us what such series coverge to. But this test does. For istace, if we have the series: which is really just the series: ( ) 2 3 we kow, usig this formula we just proved, that this series must coverge, ad it must coverge to 3: ( ) 2 = 3 2/3 = /3 = 3 Ufortuately (or fortuately, depedig o how you look at it), there s a pretty substatial caveat. Namely: what if we have the series 2 : (2) =
6 Does this series coverge? Certaily ot! It just keeps gettig bigger ad bigger! It goes to! But accordig to our theorem, it does coverge: (2) = 2 = This series is ot. You caot keep addig powers of two ad get. That is utterly ridiculous. You will keep gettig bigger ad bigger umbers. The problem is pervasive cosider a = : () = = So really, we should specify that i order for this series to coverge, a must be less tha. Ad, actually, we should say that a has to be betwee ad, because umbers below give us the same problem: ( ) = + = does t coverge! keeps flippig betwee 0 ad ( 2) = = does t coverge! gets bigger ad bigger, but with alteratig sigs So we should restate our theorem a little bit more precisely: a =, but oly if < a < a This type of series, by the way, is kow as a geometric series. Not that the ame really meas much, but other people use the ame, so you should probably kow it. Aother Type of Series Here s aother series: what if I have somethig like: or, writte i -otatio: = = (This is called the harmoic series, by the way.) Does this coverge? It might, sice the terms get smaller. It does t obviously diverge. But how do we deal with it? Allow me to suggest this: did the last series remid you at all of a itegral? a improper itegral? remember how weird it was that sometimes we have itegrals to that coverge? i.e., shapes that are ifiitely log but have fiite area? like, for example: x 2 = Ad if we have a series, it s kid of like addig up areas! Thik about it like this: remember that the sequece f() = / looks like this (just a buch of poits): 6
7 but if we tur each of these poits ito the top of rectagles, ad the fid the areas of all the rectagles, that s like the series : = So I guess we could make the aalogy: a series is to a sequece as a itegral is to a smooth curve. Ayway, what if we simultaeously cosider the fuctio f() = /, where ca be ay real umber (ot just a atural umber), ad the fid the area udereath that curve? 7
8 Clearly, there will be slightly less area udereath the curve / tha there is i the boxes (i.e., i the series ). Put differetly, we kow that: d < But we kow how to work out that itegral! We kow: d = [l()] = = l( ) l() = So the area udereath the curve / is ifiite... but the area udereath the boxes is greater tha the area uder the curve, meaig the boxes must have ifiite area, too, ad sice the boxes are the series, the series must be ifiite, too, ad thus the series diverges! so d < = < = = = I fact, we ca state this as a more geeral priciple: if if a a f() d diverges, the f() d coverges, the =a =a f() also diverges f() also coverges We could have use this test to figure out that the geometric series (our previous example) coverges: we 8
9 had the series 0 a, where 0 < a <, ad we kow: [ a d = l(a) a 0 ] = l(a) a l(a) a0 = l(a) 0 l(a) =, which is fiite l(a) so sice 0 a d coverges, 0 a must coverge, too. The disadvatage is that usig this test, we kow that it coverges, but we do t kow what it coverges to. It does t coverge to, because a) we l(a) already kow it coverges to /( a), ad clearly those two thigs are ot equal, ad b) this is because a itegral is ot precisely the same as a sum there s extra area i the boxes that the smooth curve of the itegral misses (look at the previous graph the area of the itegral ad of the sum are similar, but ot idetical). Plus, this test wo t always work. What if we have a series like? We ca t cosider!! d, because we have o idea how to atidifferetiate!. Likewise with, say, 0, sice we ca t atid- ( ) ifferetiate that, either. (Our rule for a x dx oly works whe a > 0, because otherwise the fuctio is really really bizarre ad somewhat itractable.) Aother Test For Covergece/Divergece Here s aother cool series: Ay idea what its formula is? No? It s a factorial! It s /!: =! = So the obvious questio we ca ask about this series, like about every other series, is: does it coverge? Each of the terms are gettig smaller, so it might. But we ca t come up with a ice little algebraic formula for its sum, like we could for a geometric series. We ca t treat it like a itegral ad see whether the itegral coverges, because we do t kow how to atidifferetiate! ad it s ot just that we do t kow how to, either, but that the very idea of atidifferetiatig (or differetiatig) such a fuctio makes o sese, because! is t a smooth curve like x 2 or e x. (What is 3.5!? Is it ? Is it 3 2? Does the questio ot eve make sese?) What we ll have to do is compare it to a series that we do kow coverges. I the last example, we made this argumet:. we kow that the itegral 2. we kow that the series 3. therefore, = = diverges. d diverges; is greater tha 9 d; 0
10 We ca make a similar argumet with /!. Here s what we kow: we kow that! is a skyrocketig fuctio it goes up really, really fast. Compare it, for example, with x 2 (or 2 ) ad 2 : 2 2! , It takes! slightly loger to get goig it s ot i first place util = 4 but after that, it zooms up. Which meas, of course, that /! is zoomig dow, zoomig dow to 0 far faster tha / 2 or /2. BUT WAIT. We kow that /2 coverges. That s just a geometric series: AND we kow that 2 =. ( ) = 2. /2 = /2 = 2 so the we kow that 2 >, at least after = 4! =4 2 > (Note how I chaged the s to start at 4. Not a big deal, though. I ll address it more i a momet.) Sice the /2 series coverges, ad sice /! is less tha /2, the /! series must coverge, too: =4 2 }{{} this coverges > =4! =4! }{{} so this must, too Of course, our origial questio was ot about /! whe starts at 4; our questio was about /! whe starts at. But this is t a cocer. If I just add the first few terms back i, I ll just be addig some fiite umber, ad that wo t all-of-sudde make the series diverge. Put more formally: the = term! = {}}{ }{{} the =2 term! = =4 the =3 term {}}{ 6 + We kow that the series from = 4 coverges, so addig 0/6 wo t make it diverge. It will still coverge, eve if we add 0/6. The sum from = will coverge to a slightly differet poit, yes (a poit 0/6! =4! 0
11 greater tha what the sum from = 4 coverges to), but sice we do t kow what the sum from = 4 coverges to i the first place, this does t really chage our situatio. The poit is: =! coverges. Ayway, the poit is, this is aother method we ca use to determie whether series coverge or diverge: we ca compare them to a series we kow somethig about. We might have a series that s always greater tha a series which diverges; therefore, we kow it diverges. We might have a series that s always smaller tha a series which coverges; therefore, we kow it coverges. (If we have a series that s always greater tha a series which coverges; we kow othig, sice the series could either coverge or diverge (the latter if it s too much greater tha the series that coverges). If we have a series that s always less tha a series that diverges, we kow othig, sice the series could either coverge or diverge (the latter if it s ot smaller eough tha the series which diverges).) Here is a simpler form of the two argumets we could make: ARGUMENT, VERY BRIEFLY: We have a series that s always smaller tha a series which coverges; therefore, we kow it coverges. ARGUMENT, SLIGHTLY MORE DETAILED:. we kow that series B coverges; 2. the terms of series B are always greater tha the terms of series A; 3. therefore series B is greater tha series A; 4. put differetly, series A is less tha series B; 5. therefore, sice series B coverges, series A also coverges. ARGUMENT, VERY BRIEFLY: We have a series that s always greater tha a series which diverges; therefore, we kow it diverges. ARGUMENT, SLIGHTLY MORE DETAILED:. we kow that series B diverges to ; 2. the terms of series B are always less tha the terms of series A; 3. therefore series B is less tha series A; 4. put differetly, series A is greater tha series B; 5. therefore, sice series B diverges, series A also diverges. We could use this sort of argumet for all sorts of differet series for example, we could have a series that we could t take a itegral of, because we do t kow how to atidifferetiate it, but we could compare it to oe we did kow how to atidifferetiate.
12 Fid a formula for the th term of the sequece: Problems.,,,, 2.,,,,, 3., 4, 9, 6, 25 4., 4, 9, 6, 25, 5. 0, 3, 8, 5, 24, 6. 3,,, 0,, 7., 5, 9, 3, , 6, 0, 4, 8, 9. 2, 3, 5, 7,, 3, 7, 9, 23, 29 For each of the followig sequeces, write out the first few terms, ad the determie whether it coverges or diverges. If it coverges, what does it coverge to? 0. S = ( ) ( S = ) 2. f() = (! 27. S = 2 ) ( ) 2 2. f() = ( ) S = 2 + ( ) 4. S = 2 + (0.) 28. f() = ( )+ 2 ( 29. S = ) 2 5. S = ( ) 6. f() = ( ) 7. S = + ( ) 8. S = f() = S = f() = f() = S = S = + ( ) ( 25. f() = ( ) ) 30. f() = si() 3. f() = si2 () S = + ( π 33. f() = si 2 + ) 34. f() = l() l( + ) 35. f() = f() = f() = l( + ) 38. f() = l() l(2) 39. f() = 8 / 40. f() = (0.03) / 2
13 Write out each of the followig sums (give i Σ-otatio): k=2 k=5 ( ) ( ) k 4. (3k + ) 43. k! k=3 42. k=3 (2 k ) 44. k=4 k=2 3 k Write each of the followig sums i Σ-otatio f(x ) x + f(x 2 ) x f(x ) x Which of the followig series coverge, ad which diverge? Why? For those that coverge, ca you determie what they coverge to? 49. ( ) cos(π) 70. = ( ( ) 5 = = = = ( 2 ) l() l(/) ) ( ) ( 2 ) = cos(π) 5 e e 2 ( ) 5 k 2 k 2 2 k 4 l k k ( ) + = = 2 3! 000 x ( ) x ( ) x 2 = l( k) k k k ( ) l + 3
14 = = = ( + ) + ( ) 2 / 2 /(+) ( ) l( + 2) l( + ) k k 2 + 3k + 2 e ke k2 k 2 2 k3 ( 2 ) 89. For what values of p does the series k p coverge? for what values of p does it diverge? 90. The followig is a sketch of a fractal, costructed by takig a square, drawig a square iside of it usig the midpoits as corers, drawig a square iside of that usig the midpoits as corers, ad so forth, ad ifiitum. Fid a) the total area eclosed by all the squares, ad b) the total perimeter of all the squares. 9. This is a famous fractal: Helge vo Koch s sowflake curve, kow geerally as the Koch curve or Koch sowflake. It is draw by takig a equilateral triagle, the pastig o three equilateral triagles i the ceterthird of each side, the pastig o equilateral triagles ito the ceter-third of the sides of the triagles costructed i the previous step, ad so forth. Show that a) the total area eclosed by the Koch curve is fiite (what is it?), but that b) its perimeter is ifiite. (Sorry the sketch is t better; go olie if you wat a clearer picture (ad aimatios!).) 4
Chapter 6: Numerical Series
 Chapter 6: Numerical Series 327 Chapter 6 Overview: Sequeces ad Numerical Series I most texts, the topic of sequeces ad series appears, at first, to be a side topic. There are almost o derivatives or itegrals
Chapter 6: Numerical Series 327 Chapter 6 Overview: Sequeces ad Numerical Series I most texts, the topic of sequeces ad series appears, at first, to be a side topic. There are almost o derivatives or itegrals
6.3 Testing Series With Positive Terms
 6.3. TESTING SERIES WITH POSITIVE TERMS 307 6.3 Testig Series With Positive Terms 6.3. Review of what is kow up to ow I theory, testig a series a i for covergece amouts to fidig the i= sequece of partial
6.3. TESTING SERIES WITH POSITIVE TERMS 307 6.3 Testig Series With Positive Terms 6.3. Review of what is kow up to ow I theory, testig a series a i for covergece amouts to fidig the i= sequece of partial
Chapter 6 Overview: Sequences and Numerical Series. For the purposes of AP, this topic is broken into four basic subtopics:
 Chapter 6 Overview: Sequeces ad Numerical Series I most texts, the topic of sequeces ad series appears, at first, to be a side topic. There are almost o derivatives or itegrals (which is what most studets
Chapter 6 Overview: Sequeces ad Numerical Series I most texts, the topic of sequeces ad series appears, at first, to be a side topic. There are almost o derivatives or itegrals (which is what most studets
Sequences A sequence of numbers is a function whose domain is the positive integers. We can see that the sequence
 Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece 1, 1, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet
Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece 1, 1, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet
A sequence of numbers is a function whose domain is the positive integers. We can see that the sequence
 Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece,, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet as
Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece,, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet as
Chapter 7: Numerical Series
 Chapter 7: Numerical Series Chapter 7 Overview: Sequeces ad Numerical Series I most texts, the topic of sequeces ad series appears, at first, to be a side topic. There are almost o derivatives or itegrals
Chapter 7: Numerical Series Chapter 7 Overview: Sequeces ad Numerical Series I most texts, the topic of sequeces ad series appears, at first, to be a side topic. There are almost o derivatives or itegrals
Infinite Sequences and Series
 Chapter 6 Ifiite Sequeces ad Series 6.1 Ifiite Sequeces 6.1.1 Elemetary Cocepts Simply speakig, a sequece is a ordered list of umbers writte: {a 1, a 2, a 3,...a, a +1,...} where the elemets a i represet
Chapter 6 Ifiite Sequeces ad Series 6.1 Ifiite Sequeces 6.1.1 Elemetary Cocepts Simply speakig, a sequece is a ordered list of umbers writte: {a 1, a 2, a 3,...a, a +1,...} where the elemets a i represet
Math 113 Exam 3 Practice
 Math Exam Practice Exam will cover.-.9. This sheet has three sectios. The first sectio will remid you about techiques ad formulas that you should kow. The secod gives a umber of practice questios for you
Math Exam Practice Exam will cover.-.9. This sheet has three sectios. The first sectio will remid you about techiques ad formulas that you should kow. The secod gives a umber of practice questios for you
Part I: Covers Sequence through Series Comparison Tests
 Part I: Covers Sequece through Series Compariso Tests. Give a example of each of the followig: (a) A geometric sequece: (b) A alteratig sequece: (c) A sequece that is bouded, but ot coverget: (d) A sequece
Part I: Covers Sequece through Series Compariso Tests. Give a example of each of the followig: (a) A geometric sequece: (b) A alteratig sequece: (c) A sequece that is bouded, but ot coverget: (d) A sequece
4x 2. (n+1) x 3 n+1. = lim. 4x 2 n+1 n3 n. n 4x 2 = lim = 3
 Exam Problems (x. Give the series (, fid the values of x for which this power series coverges. Also =0 state clearly what the radius of covergece is. We start by settig up the Ratio Test: x ( x x ( x x
Exam Problems (x. Give the series (, fid the values of x for which this power series coverges. Also =0 state clearly what the radius of covergece is. We start by settig up the Ratio Test: x ( x x ( x x
Math 21, Winter 2018 Schaeffer/Solis Stanford University Solutions for 20 series from Lecture 16 notes (Schaeffer)
 Math, Witer 08 Schaeffer/Solis Staford Uiversity Solutios for 0 series from Lecture 6 otes (Schaeffer) a. r 4 +3 The series has algebraic terms (polyomials, ratioal fuctios, ad radicals, oly), so the test
Math, Witer 08 Schaeffer/Solis Staford Uiversity Solutios for 0 series from Lecture 6 otes (Schaeffer) a. r 4 +3 The series has algebraic terms (polyomials, ratioal fuctios, ad radicals, oly), so the test
Z ß cos x + si x R du We start with the substitutio u = si(x), so du = cos(x). The itegral becomes but +u we should chage the limits to go with the ew
 Problem ( poits) Evaluate the itegrals Z p x 9 x We ca draw a right triagle labeled this way x p x 9 From this we ca read off x = sec, so = sec ta, ad p x 9 = R ta. Puttig those pieces ito the itegralrwe
Problem ( poits) Evaluate the itegrals Z p x 9 x We ca draw a right triagle labeled this way x p x 9 From this we ca read off x = sec, so = sec ta, ad p x 9 = R ta. Puttig those pieces ito the itegralrwe
Math 113 Exam 3 Practice
 Math Exam Practice Exam 4 will cover.-., 0. ad 0.. Note that eve though. was tested i exam, questios from that sectios may also be o this exam. For practice problems o., refer to the last review. This
Math Exam Practice Exam 4 will cover.-., 0. ad 0.. Note that eve though. was tested i exam, questios from that sectios may also be o this exam. For practice problems o., refer to the last review. This
Section 11.8: Power Series
 Sectio 11.8: Power Series 1. Power Series I this sectio, we cosider geeralizig the cocept of a series. Recall that a series is a ifiite sum of umbers a. We ca talk about whether or ot it coverges ad i
Sectio 11.8: Power Series 1. Power Series I this sectio, we cosider geeralizig the cocept of a series. Recall that a series is a ifiite sum of umbers a. We ca talk about whether or ot it coverges ad i
CHAPTER 10 INFINITE SEQUENCES AND SERIES
 CHAPTER 10 INFINITE SEQUENCES AND SERIES 10.1 Sequeces 10.2 Ifiite Series 10.3 The Itegral Tests 10.4 Compariso Tests 10.5 The Ratio ad Root Tests 10.6 Alteratig Series: Absolute ad Coditioal Covergece
CHAPTER 10 INFINITE SEQUENCES AND SERIES 10.1 Sequeces 10.2 Ifiite Series 10.3 The Itegral Tests 10.4 Compariso Tests 10.5 The Ratio ad Root Tests 10.6 Alteratig Series: Absolute ad Coditioal Covergece
Math 2784 (or 2794W) University of Connecticut
 ORDERS OF GROWTH PAT SMITH Math 2784 (or 2794W) Uiversity of Coecticut Date: Mar. 2, 22. ORDERS OF GROWTH. Itroductio Gaiig a ituitive feel for the relative growth of fuctios is importat if you really
ORDERS OF GROWTH PAT SMITH Math 2784 (or 2794W) Uiversity of Coecticut Date: Mar. 2, 22. ORDERS OF GROWTH. Itroductio Gaiig a ituitive feel for the relative growth of fuctios is importat if you really
Sequences, Series, and All That
 Chapter Te Sequeces, Series, ad All That. Itroductio Suppose we wat to compute a approximatio of the umber e by usig the Taylor polyomial p for f ( x) = e x at a =. This polyomial is easily see to be 3
Chapter Te Sequeces, Series, ad All That. Itroductio Suppose we wat to compute a approximatio of the umber e by usig the Taylor polyomial p for f ( x) = e x at a =. This polyomial is easily see to be 3
Ma 530 Infinite Series I
 Ma 50 Ifiite Series I Please ote that i additio to the material below this lecture icorporated material from the Visual Calculus web site. The material o sequeces is at Visual Sequeces. (To use this li
Ma 50 Ifiite Series I Please ote that i additio to the material below this lecture icorporated material from the Visual Calculus web site. The material o sequeces is at Visual Sequeces. (To use this li
Math 113 Exam 4 Practice
 Math Exam 4 Practice Exam 4 will cover.-.. This sheet has three sectios. The first sectio will remid you about techiques ad formulas that you should kow. The secod gives a umber of practice questios for
Math Exam 4 Practice Exam 4 will cover.-.. This sheet has three sectios. The first sectio will remid you about techiques ad formulas that you should kow. The secod gives a umber of practice questios for
Chapter 6 Infinite Series
 Chapter 6 Ifiite Series I the previous chapter we cosidered itegrals which were improper i the sese that the iterval of itegratio was ubouded. I this chapter we are goig to discuss a topic which is somewhat
Chapter 6 Ifiite Series I the previous chapter we cosidered itegrals which were improper i the sese that the iterval of itegratio was ubouded. I this chapter we are goig to discuss a topic which is somewhat
Roberto s Notes on Series Chapter 2: Convergence tests Section 7. Alternating series
 Roberto s Notes o Series Chapter 2: Covergece tests Sectio 7 Alteratig series What you eed to kow already: All basic covergece tests for evetually positive series. What you ca lear here: A test for series
Roberto s Notes o Series Chapter 2: Covergece tests Sectio 7 Alteratig series What you eed to kow already: All basic covergece tests for evetually positive series. What you ca lear here: A test for series
MA131 - Analysis 1. Workbook 2 Sequences I
 MA3 - Aalysis Workbook 2 Sequeces I Autum 203 Cotets 2 Sequeces I 2. Itroductio.............................. 2.2 Icreasig ad Decreasig Sequeces................ 2 2.3 Bouded Sequeces..........................
MA3 - Aalysis Workbook 2 Sequeces I Autum 203 Cotets 2 Sequeces I 2. Itroductio.............................. 2.2 Icreasig ad Decreasig Sequeces................ 2 2.3 Bouded Sequeces..........................
62. Power series Definition 16. (Power series) Given a sequence {c n }, the series. c n x n = c 0 + c 1 x + c 2 x 2 + c 3 x 3 +
 62. Power series Defiitio 16. (Power series) Give a sequece {c }, the series c x = c 0 + c 1 x + c 2 x 2 + c 3 x 3 + is called a power series i the variable x. The umbers c are called the coefficiets of
62. Power series Defiitio 16. (Power series) Give a sequece {c }, the series c x = c 0 + c 1 x + c 2 x 2 + c 3 x 3 + is called a power series i the variable x. The umbers c are called the coefficiets of
(A sequence also can be thought of as the list of function values attained for a function f :ℵ X, where f (n) = x n for n 1.) x 1 x N +k x N +4 x 3
 MATH 337 Sequeces Dr. Neal, WKU Let X be a metric space with distace fuctio d. We shall defie the geeral cocept of sequece ad limit i a metric space, the apply the results i particular to some special
MATH 337 Sequeces Dr. Neal, WKU Let X be a metric space with distace fuctio d. We shall defie the geeral cocept of sequece ad limit i a metric space, the apply the results i particular to some special
Sequences III. Chapter Roots
 Chapter 4 Sequeces III 4. Roots We ca use the results we ve established i the last workbook to fid some iterestig limits for sequeces ivolvig roots. We will eed more techical expertise ad low cuig tha
Chapter 4 Sequeces III 4. Roots We ca use the results we ve established i the last workbook to fid some iterestig limits for sequeces ivolvig roots. We will eed more techical expertise ad low cuig tha
Carleton College, Winter 2017 Math 121, Practice Final Prof. Jones. Note: the exam will have a section of true-false questions, like the one below.
 Carleto College, Witer 207 Math 2, Practice Fial Prof. Joes Note: the exam will have a sectio of true-false questios, like the oe below.. True or False. Briefly explai your aswer. A icorrectly justified
Carleto College, Witer 207 Math 2, Practice Fial Prof. Joes Note: the exam will have a sectio of true-false questios, like the oe below.. True or False. Briefly explai your aswer. A icorrectly justified
MAT1026 Calculus II Basic Convergence Tests for Series
 MAT026 Calculus II Basic Covergece Tests for Series Egi MERMUT 202.03.08 Dokuz Eylül Uiversity Faculty of Sciece Departmet of Mathematics İzmir/TURKEY Cotets Mootoe Covergece Theorem 2 2 Series of Real
MAT026 Calculus II Basic Covergece Tests for Series Egi MERMUT 202.03.08 Dokuz Eylül Uiversity Faculty of Sciece Departmet of Mathematics İzmir/TURKEY Cotets Mootoe Covergece Theorem 2 2 Series of Real
INTEGRATION BY PARTS (TABLE METHOD)
 INTEGRATION BY PARTS (TABLE METHOD) Suppose you wat to evaluate cos d usig itegratio by parts. Usig the u dv otatio, we get So, u dv d cos du d v si cos d si si d or si si d We see that it is ecessary
INTEGRATION BY PARTS (TABLE METHOD) Suppose you wat to evaluate cos d usig itegratio by parts. Usig the u dv otatio, we get So, u dv d cos du d v si cos d si si d or si si d We see that it is ecessary
Sequences. Notation. Convergence of a Sequence
 Sequeces A sequece is essetially just a list. Defiitio (Sequece of Real Numbers). A sequece of real umbers is a fuctio Z (, ) R for some real umber. Do t let the descriptio of the domai cofuse you; it
Sequeces A sequece is essetially just a list. Defiitio (Sequece of Real Numbers). A sequece of real umbers is a fuctio Z (, ) R for some real umber. Do t let the descriptio of the domai cofuse you; it
Sequences I. Chapter Introduction
 Chapter 2 Sequeces I 2. Itroductio A sequece is a list of umbers i a defiite order so that we kow which umber is i the first place, which umber is i the secod place ad, for ay atural umber, we kow which
Chapter 2 Sequeces I 2. Itroductio A sequece is a list of umbers i a defiite order so that we kow which umber is i the first place, which umber is i the secod place ad, for ay atural umber, we kow which
The Binomial Theorem
 The Biomial Theorem Robert Marti Itroductio The Biomial Theorem is used to expad biomials, that is, brackets cosistig of two distict terms The formula for the Biomial Theorem is as follows: (a + b ( k
The Biomial Theorem Robert Marti Itroductio The Biomial Theorem is used to expad biomials, that is, brackets cosistig of two distict terms The formula for the Biomial Theorem is as follows: (a + b ( k
Additional Notes on Power Series
 Additioal Notes o Power Series Mauela Girotti MATH 37-0 Advaced Calculus of oe variable Cotets Quick recall 2 Abel s Theorem 2 3 Differetiatio ad Itegratio of Power series 4 Quick recall We recall here
Additioal Notes o Power Series Mauela Girotti MATH 37-0 Advaced Calculus of oe variable Cotets Quick recall 2 Abel s Theorem 2 3 Differetiatio ad Itegratio of Power series 4 Quick recall We recall here
The Growth of Functions. Theoretical Supplement
 The Growth of Fuctios Theoretical Supplemet The Triagle Iequality The triagle iequality is a algebraic tool that is ofte useful i maipulatig absolute values of fuctios. The triagle iequality says that
The Growth of Fuctios Theoretical Supplemet The Triagle Iequality The triagle iequality is a algebraic tool that is ofte useful i maipulatig absolute values of fuctios. The triagle iequality says that
CHAPTER I: Vector Spaces
 CHAPTER I: Vector Spaces Sectio 1: Itroductio ad Examples This first chapter is largely a review of topics you probably saw i your liear algebra course. So why cover it? (1) Not everyoe remembers everythig
CHAPTER I: Vector Spaces Sectio 1: Itroductio ad Examples This first chapter is largely a review of topics you probably saw i your liear algebra course. So why cover it? (1) Not everyoe remembers everythig
Chapter 10: Power Series
 Chapter : Power Series 57 Chapter Overview: Power Series The reaso series are part of a Calculus course is that there are fuctios which caot be itegrated. All power series, though, ca be itegrated because
Chapter : Power Series 57 Chapter Overview: Power Series The reaso series are part of a Calculus course is that there are fuctios which caot be itegrated. All power series, though, ca be itegrated because
Math 10A final exam, December 16, 2016
 Please put away all books, calculators, cell phoes ad other devices. You may cosult a sigle two-sided sheet of otes. Please write carefully ad clearly, USING WORDS (ot just symbols). Remember that the
Please put away all books, calculators, cell phoes ad other devices. You may cosult a sigle two-sided sheet of otes. Please write carefully ad clearly, USING WORDS (ot just symbols). Remember that the
MA131 - Analysis 1. Workbook 3 Sequences II
 MA3 - Aalysis Workbook 3 Sequeces II Autum 2004 Cotets 2.8 Coverget Sequeces........................ 2.9 Algebra of Limits......................... 2 2.0 Further Useful Results........................
MA3 - Aalysis Workbook 3 Sequeces II Autum 2004 Cotets 2.8 Coverget Sequeces........................ 2.9 Algebra of Limits......................... 2 2.0 Further Useful Results........................
Math 106 Fall 2014 Exam 3.2 December 10, 2014
 Math 06 Fall 04 Exam 3 December 0, 04 Determie if the series is coverget or diverget by makig a compariso (DCT or LCT) with a suitable b Fill i the blaks with your aswer For Coverget or Diverget write
Math 06 Fall 04 Exam 3 December 0, 04 Determie if the series is coverget or diverget by makig a compariso (DCT or LCT) with a suitable b Fill i the blaks with your aswer For Coverget or Diverget write
Recitation 4: Lagrange Multipliers and Integration
 Math 1c TA: Padraic Bartlett Recitatio 4: Lagrage Multipliers ad Itegratio Week 4 Caltech 211 1 Radom Questio Hey! So, this radom questio is pretty tightly tied to today s lecture ad the cocept of cotet
Math 1c TA: Padraic Bartlett Recitatio 4: Lagrage Multipliers ad Itegratio Week 4 Caltech 211 1 Radom Questio Hey! So, this radom questio is pretty tightly tied to today s lecture ad the cocept of cotet
MATH 21 SECTION NOTES
 MATH SECTION NOTES EVAN WARNER. March 9.. Admiistrative miscellay. These weekly sectios will be for some review ad may example problems, i geeral. Attedace will be take as per class policy. We will be
MATH SECTION NOTES EVAN WARNER. March 9.. Admiistrative miscellay. These weekly sectios will be for some review ad may example problems, i geeral. Attedace will be take as per class policy. We will be
Infinite Series. Definition. An infinite series is an expression of the form. Where the numbers u k are called the terms of the series.
 Ifiite Series Defiitio. A ifiite series is a expressio of the form uk = u + u + u + + u + () 2 3 k Where the umbers u k are called the terms of the series. Such a expressio is meat to be the result of
Ifiite Series Defiitio. A ifiite series is a expressio of the form uk = u + u + u + + u + () 2 3 k Where the umbers u k are called the terms of the series. Such a expressio is meat to be the result of
4.3 Growth Rates of Solutions to Recurrences
 4.3. GROWTH RATES OF SOLUTIONS TO RECURRENCES 81 4.3 Growth Rates of Solutios to Recurreces 4.3.1 Divide ad Coquer Algorithms Oe of the most basic ad powerful algorithmic techiques is divide ad coquer.
4.3. GROWTH RATES OF SOLUTIONS TO RECURRENCES 81 4.3 Growth Rates of Solutios to Recurreces 4.3.1 Divide ad Coquer Algorithms Oe of the most basic ad powerful algorithmic techiques is divide ad coquer.
Lesson 10: Limits and Continuity
 www.scimsacademy.com Lesso 10: Limits ad Cotiuity SCIMS Academy 1 Limit of a fuctio The cocept of limit of a fuctio is cetral to all other cocepts i calculus (like cotiuity, derivative, defiite itegrals
www.scimsacademy.com Lesso 10: Limits ad Cotiuity SCIMS Academy 1 Limit of a fuctio The cocept of limit of a fuctio is cetral to all other cocepts i calculus (like cotiuity, derivative, defiite itegrals
Continuous Functions
 Cotiuous Fuctios Q What does it mea for a fuctio to be cotiuous at a poit? Aswer- I mathematics, we have a defiitio that cosists of three cocepts that are liked i a special way Cosider the followig defiitio
Cotiuous Fuctios Q What does it mea for a fuctio to be cotiuous at a poit? Aswer- I mathematics, we have a defiitio that cosists of three cocepts that are liked i a special way Cosider the followig defiitio
Math 113, Calculus II Winter 2007 Final Exam Solutions
 Math, Calculus II Witer 7 Fial Exam Solutios (5 poits) Use the limit defiitio of the defiite itegral ad the sum formulas to compute x x + dx The check your aswer usig the Evaluatio Theorem Solutio: I this
Math, Calculus II Witer 7 Fial Exam Solutios (5 poits) Use the limit defiitio of the defiite itegral ad the sum formulas to compute x x + dx The check your aswer usig the Evaluatio Theorem Solutio: I this
Topic 1 2: Sequences and Series. A sequence is an ordered list of numbers, e.g. 1, 2, 4, 8, 16, or
 Topic : Sequeces ad Series A sequece is a ordered list of umbers, e.g.,,, 8, 6, or,,,.... A series is a sum of the terms of a sequece, e.g. + + + 8 + 6 + or... Sigma Notatio b The otatio f ( k) is shorthad
Topic : Sequeces ad Series A sequece is a ordered list of umbers, e.g.,,, 8, 6, or,,,.... A series is a sum of the terms of a sequece, e.g. + + + 8 + 6 + or... Sigma Notatio b The otatio f ( k) is shorthad
( 1) n (4x + 1) n. n=0
 Problem 1 (10.6, #). Fid the radius of covergece for the series: ( 1) (4x + 1). For what values of x does the series coverge absolutely, ad for what values of x does the series coverge coditioally? Solutio.
Problem 1 (10.6, #). Fid the radius of covergece for the series: ( 1) (4x + 1). For what values of x does the series coverge absolutely, ad for what values of x does the series coverge coditioally? Solutio.
7 Sequences of real numbers
 40 7 Sequeces of real umbers 7. Defiitios ad examples Defiitio 7... A sequece of real umbers is a real fuctio whose domai is the set N of atural umbers. Let s : N R be a sequece. The the values of s are
40 7 Sequeces of real umbers 7. Defiitios ad examples Defiitio 7... A sequece of real umbers is a real fuctio whose domai is the set N of atural umbers. Let s : N R be a sequece. The the values of s are
AP Calculus Chapter 9: Infinite Series
 AP Calculus Chapter 9: Ifiite Series 9. Sequeces a, a 2, a 3, a 4, a 5,... Sequece: A fuctio whose domai is the set of positive itegers = 2 3 4 a = a a 2 a 3 a 4 terms of the sequece Begi with the patter
AP Calculus Chapter 9: Ifiite Series 9. Sequeces a, a 2, a 3, a 4, a 5,... Sequece: A fuctio whose domai is the set of positive itegers = 2 3 4 a = a a 2 a 3 a 4 terms of the sequece Begi with the patter
Series: Infinite Sums
 Series: Ifiite Sums Series are a way to mae sese of certai types of ifiitely log sums. We will eed to be able to do this if we are to attai our goal of approximatig trascedetal fuctios by usig ifiite degree
Series: Ifiite Sums Series are a way to mae sese of certai types of ifiitely log sums. We will eed to be able to do this if we are to attai our goal of approximatig trascedetal fuctios by usig ifiite degree
INFINITE SEQUENCES AND SERIES
 INFINITE SEQUENCES AND SERIES INFINITE SEQUENCES AND SERIES I geeral, it is difficult to fid the exact sum of a series. We were able to accomplish this for geometric series ad the series /[(+)]. This is
INFINITE SEQUENCES AND SERIES INFINITE SEQUENCES AND SERIES I geeral, it is difficult to fid the exact sum of a series. We were able to accomplish this for geometric series ad the series /[(+)]. This is
Once we have a sequence of numbers, the next thing to do is to sum them up. Given a sequence (a n ) n=1
 . Ifiite Series Oce we have a sequece of umbers, the ext thig to do is to sum them up. Give a sequece a be a sequece: ca we give a sesible meaig to the followig expressio? a = a a a a While summig ifiitely
. Ifiite Series Oce we have a sequece of umbers, the ext thig to do is to sum them up. Give a sequece a be a sequece: ca we give a sesible meaig to the followig expressio? a = a a a a While summig ifiitely
Calculus BC and BCD Drill on Sequences and Series!!! By Susan E. Cantey Walnut Hills H.S. 2006
 Calculus BC ad BCD Drill o Sequeces ad Series!!! By Susa E. Catey Walut Hills H.S. 2006 Sequeces ad Series I m goig to ask you questios about sequeces ad series ad drill you o some thigs that eed to be
Calculus BC ad BCD Drill o Sequeces ad Series!!! By Susa E. Catey Walut Hills H.S. 2006 Sequeces ad Series I m goig to ask you questios about sequeces ad series ad drill you o some thigs that eed to be
Statistics 511 Additional Materials
 Cofidece Itervals o mu Statistics 511 Additioal Materials This topic officially moves us from probability to statistics. We begi to discuss makig ifereces about the populatio. Oe way to differetiate probability
Cofidece Itervals o mu Statistics 511 Additioal Materials This topic officially moves us from probability to statistics. We begi to discuss makig ifereces about the populatio. Oe way to differetiate probability
Lecture 6: Integration and the Mean Value Theorem. slope =
 Math 8 Istructor: Padraic Bartlett Lecture 6: Itegratio ad the Mea Value Theorem Week 6 Caltech 202 The Mea Value Theorem The Mea Value Theorem abbreviated MVT is the followig result: Theorem. Suppose
Math 8 Istructor: Padraic Bartlett Lecture 6: Itegratio ad the Mea Value Theorem Week 6 Caltech 202 The Mea Value Theorem The Mea Value Theorem abbreviated MVT is the followig result: Theorem. Suppose
6 Integers Modulo n. integer k can be written as k = qn + r, with q,r, 0 r b. So any integer.
 6 Itegers Modulo I Example 2.3(e), we have defied the cogruece of two itegers a,b with respect to a modulus. Let us recall that a b (mod ) meas a b. We have proved that cogruece is a equivalece relatio
6 Itegers Modulo I Example 2.3(e), we have defied the cogruece of two itegers a,b with respect to a modulus. Let us recall that a b (mod ) meas a b. We have proved that cogruece is a equivalece relatio
Math 106 Fall 2014 Exam 3.1 December 10, 2014
 Math 06 Fall 0 Exam 3 December 0, 0 Determie if the series is coverget or diverget by makig a compariso DCT or LCT) with a suitable b Fill i the blaks with your aswer For Coverget or Diverget write Coverget
Math 06 Fall 0 Exam 3 December 0, 0 Determie if the series is coverget or diverget by makig a compariso DCT or LCT) with a suitable b Fill i the blaks with your aswer For Coverget or Diverget write Coverget
Discrete Mathematics for CS Spring 2007 Luca Trevisan Lecture 22
 CS 70 Discrete Mathematics for CS Sprig 2007 Luca Trevisa Lecture 22 Aother Importat Distributio The Geometric Distributio Questio: A biased coi with Heads probability p is tossed repeatedly util the first
CS 70 Discrete Mathematics for CS Sprig 2007 Luca Trevisa Lecture 22 Aother Importat Distributio The Geometric Distributio Questio: A biased coi with Heads probability p is tossed repeatedly util the first
Roberto s Notes on Infinite Series Chapter 1: Sequences and series Section 3. Geometric series
 Roberto s Notes o Ifiite Series Chapter 1: Sequeces ad series Sectio Geometric series What you eed to kow already: What a ifiite series is. The divergece test. What you ca le here: Everythig there is to
Roberto s Notes o Ifiite Series Chapter 1: Sequeces ad series Sectio Geometric series What you eed to kow already: What a ifiite series is. The divergece test. What you ca le here: Everythig there is to
Notes for Lecture 5. 1 Grover Search. 1.1 The Setting. 1.2 Motivation. Lecture 5 (September 26, 2018)
 COS 597A: Quatum Cryptography Lecture 5 (September 6, 08) Lecturer: Mark Zhadry Priceto Uiversity Scribe: Fermi Ma Notes for Lecture 5 Today we ll move o from the slightly cotrived applicatios of quatum
COS 597A: Quatum Cryptography Lecture 5 (September 6, 08) Lecturer: Mark Zhadry Priceto Uiversity Scribe: Fermi Ma Notes for Lecture 5 Today we ll move o from the slightly cotrived applicatios of quatum
Power Series: A power series about the center, x = 0, is a function of x of the form
 You are familiar with polyomial fuctios, polyomial that has ifiitely may terms. 2 p ( ) a0 a a 2 a. A power series is just a Power Series: A power series about the ceter, = 0, is a fuctio of of the form
You are familiar with polyomial fuctios, polyomial that has ifiitely may terms. 2 p ( ) a0 a a 2 a. A power series is just a Power Series: A power series about the ceter, = 0, is a fuctio of of the form
11.6 Absolute Convergence and the Ratio and Root Tests
 .6 Absolute Covergece ad the Ratio ad Root Tests The most commo way to test for covergece is to igore ay positive or egative sigs i a series, ad simply test the correspodig series of positive terms. Does
.6 Absolute Covergece ad the Ratio ad Root Tests The most commo way to test for covergece is to igore ay positive or egative sigs i a series, ad simply test the correspodig series of positive terms. Does
Series III. Chapter Alternating Series
 Chapter 9 Series III With the exceptio of the Null Sequece Test, all the tests for series covergece ad divergece that we have cosidered so far have dealt oly with series of oegative terms. Series with
Chapter 9 Series III With the exceptio of the Null Sequece Test, all the tests for series covergece ad divergece that we have cosidered so far have dealt oly with series of oegative terms. Series with
ENGI Series Page 6-01
 ENGI 3425 6 Series Page 6-01 6. Series Cotets: 6.01 Sequeces; geeral term, limits, covergece 6.02 Series; summatio otatio, covergece, divergece test 6.03 Stadard Series; telescopig series, geometric series,
ENGI 3425 6 Series Page 6-01 6. Series Cotets: 6.01 Sequeces; geeral term, limits, covergece 6.02 Series; summatio otatio, covergece, divergece test 6.03 Stadard Series; telescopig series, geometric series,
Seunghee Ye Ma 8: Week 5 Oct 28
 Week 5 Summary I Sectio, we go over the Mea Value Theorem ad its applicatios. I Sectio 2, we will recap what we have covered so far this term. Topics Page Mea Value Theorem. Applicatios of the Mea Value
Week 5 Summary I Sectio, we go over the Mea Value Theorem ad its applicatios. I Sectio 2, we will recap what we have covered so far this term. Topics Page Mea Value Theorem. Applicatios of the Mea Value
Math 120 Answers for Homework 23
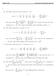 Math 0 Aswers for Homewor. (a) The Taylor series for cos(x) aroud a 0 is cos(x) x! + x4 4! x6 6! + x8 8! x0 0! + ( ) ()! x ( ) π ( ) ad so the series ()! ()! (π) is just the series for cos(x) evaluated
Math 0 Aswers for Homewor. (a) The Taylor series for cos(x) aroud a 0 is cos(x) x! + x4 4! x6 6! + x8 8! x0 0! + ( ) ()! x ( ) π ( ) ad so the series ()! ()! (π) is just the series for cos(x) evaluated
Math 105: Review for Final Exam, Part II - SOLUTIONS
 Math 5: Review for Fial Exam, Part II - SOLUTIONS. Cosider the fuctio f(x) = x 3 lx o the iterval [/e, e ]. (a) Fid the x- ad y-coordiates of ay ad all local extrema ad classify each as a local maximum
Math 5: Review for Fial Exam, Part II - SOLUTIONS. Cosider the fuctio f(x) = x 3 lx o the iterval [/e, e ]. (a) Fid the x- ad y-coordiates of ay ad all local extrema ad classify each as a local maximum
10.6 ALTERNATING SERIES
 0.6 Alteratig Series Cotemporary Calculus 0.6 ALTERNATING SERIES I the last two sectios we cosidered tests for the covergece of series whose terms were all positive. I this sectio we examie series whose
0.6 Alteratig Series Cotemporary Calculus 0.6 ALTERNATING SERIES I the last two sectios we cosidered tests for the covergece of series whose terms were all positive. I this sectio we examie series whose
Physics 116A Solutions to Homework Set #1 Winter Boas, problem Use equation 1.8 to find a fraction describing
 Physics 6A Solutios to Homework Set # Witer 0. Boas, problem. 8 Use equatio.8 to fid a fractio describig 0.694444444... Start with the formula S = a, ad otice that we ca remove ay umber of r fiite decimals
Physics 6A Solutios to Homework Set # Witer 0. Boas, problem. 8 Use equatio.8 to fid a fractio describig 0.694444444... Start with the formula S = a, ad otice that we ca remove ay umber of r fiite decimals
SOLUTIONS TO EXAM 3. Solution: Note that this defines two convergent geometric series with respective radii r 1 = 2/5 < 1 and r 2 = 1/5 < 1.
 SOLUTIONS TO EXAM 3 Problem Fid the sum of the followig series 2 + ( ) 5 5 2 5 3 25 2 2 This series diverges Solutio: Note that this defies two coverget geometric series with respective radii r 2/5 < ad
SOLUTIONS TO EXAM 3 Problem Fid the sum of the followig series 2 + ( ) 5 5 2 5 3 25 2 2 This series diverges Solutio: Note that this defies two coverget geometric series with respective radii r 2/5 < ad
Practice Problems: Taylor and Maclaurin Series
 Practice Problems: Taylor ad Maclauri Series Aswers. a) Start by takig derivatives util a patter develops that lets you to write a geeral formula for the -th derivative. Do t simplify as you go, because
Practice Problems: Taylor ad Maclauri Series Aswers. a) Start by takig derivatives util a patter develops that lets you to write a geeral formula for the -th derivative. Do t simplify as you go, because
University of Colorado Denver Dept. Math. & Stat. Sciences Applied Analysis Preliminary Exam 13 January 2012, 10:00 am 2:00 pm. Good luck!
 Uiversity of Colorado Dever Dept. Math. & Stat. Scieces Applied Aalysis Prelimiary Exam 13 Jauary 01, 10:00 am :00 pm Name: The proctor will let you read the followig coditios before the exam begis, ad
Uiversity of Colorado Dever Dept. Math. & Stat. Scieces Applied Aalysis Prelimiary Exam 13 Jauary 01, 10:00 am :00 pm Name: The proctor will let you read the followig coditios before the exam begis, ad
f t dt. Write the third-degree Taylor polynomial for G
 AP Calculus BC Homework - Chapter 8B Taylor, Maclauri, ad Power Series # Taylor & Maclauri Polyomials Critical Thikig Joural: (CTJ: 5 pts.) Discuss the followig questios i a paragraph: What does it mea
AP Calculus BC Homework - Chapter 8B Taylor, Maclauri, ad Power Series # Taylor & Maclauri Polyomials Critical Thikig Joural: (CTJ: 5 pts.) Discuss the followig questios i a paragraph: What does it mea
Practice Test Problems for Test IV, with Solutions
 Practice Test Problems for Test IV, with Solutios Dr. Holmes May, 2008 The exam will cover sectios 8.2 (revisited) to 8.8. The Taylor remaider formula from 8.9 will ot be o this test. The fact that sums,
Practice Test Problems for Test IV, with Solutios Dr. Holmes May, 2008 The exam will cover sectios 8.2 (revisited) to 8.8. The Taylor remaider formula from 8.9 will ot be o this test. The fact that sums,
JANE PROFESSOR WW Prob Lib1 Summer 2000
 JANE PROFESSOR WW Prob Lib Summer 000 Sample WeBWorK problems. WeBWorK assigmet Series6CompTests due /6/06 at :00 AM..( pt) Test each of the followig series for covergece by either the Compariso Test or
JANE PROFESSOR WW Prob Lib Summer 000 Sample WeBWorK problems. WeBWorK assigmet Series6CompTests due /6/06 at :00 AM..( pt) Test each of the followig series for covergece by either the Compariso Test or
Series Review. a i converges if lim. i=1. a i. lim S n = lim i=1. 2 k(k + 2) converges. k=1. k=1
 Defiitio: We say that the series S = Series Review i= a i is the sum of the first terms. i= a i coverges if lim S exists ad is fiite, where The above is the defiitio of covergece for series. order to see
Defiitio: We say that the series S = Series Review i= a i is the sum of the first terms. i= a i coverges if lim S exists ad is fiite, where The above is the defiitio of covergece for series. order to see
1. (25 points) Use the limit definition of the definite integral and the sum formulas 1 to compute
 Math, Calculus II Fial Eam Solutios. 5 poits) Use the limit defiitio of the defiite itegral ad the sum formulas to compute 4 d. The check your aswer usig the Evaluatio Theorem. ) ) Solutio: I this itegral,
Math, Calculus II Fial Eam Solutios. 5 poits) Use the limit defiitio of the defiite itegral ad the sum formulas to compute 4 d. The check your aswer usig the Evaluatio Theorem. ) ) Solutio: I this itegral,
Chapter 4. Fourier Series
 Chapter 4. Fourier Series At this poit we are ready to ow cosider the caoical equatios. Cosider, for eample the heat equatio u t = u, < (4.) subject to u(, ) = si, u(, t) = u(, t) =. (4.) Here,
Chapter 4. Fourier Series At this poit we are ready to ow cosider the caoical equatios. Cosider, for eample the heat equatio u t = u, < (4.) subject to u(, ) = si, u(, t) = u(, t) =. (4.) Here,
Sequences and Series of Functions
 Chapter 6 Sequeces ad Series of Fuctios 6.1. Covergece of a Sequece of Fuctios Poitwise Covergece. Defiitio 6.1. Let, for each N, fuctio f : A R be defied. If, for each x A, the sequece (f (x)) coverges
Chapter 6 Sequeces ad Series of Fuctios 6.1. Covergece of a Sequece of Fuctios Poitwise Covergece. Defiitio 6.1. Let, for each N, fuctio f : A R be defied. If, for each x A, the sequece (f (x)) coverges
Convergence: nth-term Test, Comparing Non-negative Series, Ratio Test
 Covergece: th-term Test, Comparig No-egative Series, Ratio Test Power Series ad Covergece We have writte statemets like: l + x = x x2 + x3 2 3 + x + But we have ot talked i depth about what values of x
Covergece: th-term Test, Comparig No-egative Series, Ratio Test Power Series ad Covergece We have writte statemets like: l + x = x x2 + x3 2 3 + x + But we have ot talked i depth about what values of x
Mathematical Induction
 Mathematical Iductio Itroductio Mathematical iductio, or just iductio, is a proof techique. Suppose that for every atural umber, P() is a statemet. We wish to show that all statemets P() are true. I a
Mathematical Iductio Itroductio Mathematical iductio, or just iductio, is a proof techique. Suppose that for every atural umber, P() is a statemet. We wish to show that all statemets P() are true. I a
f(x) dx as we do. 2x dx x also diverges. Solution: We compute 2x dx lim
 Math 3, Sectio 2. (25 poits) Why we defie f(x) dx as we do. (a) Show that the improper itegral diverges. Hece the improper itegral x 2 + x 2 + b also diverges. Solutio: We compute x 2 + = lim b x 2 + =
Math 3, Sectio 2. (25 poits) Why we defie f(x) dx as we do. (a) Show that the improper itegral diverges. Hece the improper itegral x 2 + x 2 + b also diverges. Solutio: We compute x 2 + = lim b x 2 + =
x a x a Lecture 2 Series (See Chapter 1 in Boas)
 Lecture Series (See Chapter i Boas) A basic ad very powerful (if pedestria, recall we are lazy AD smart) way to solve ay differetial (or itegral) equatio is via a series expasio of the correspodig solutio
Lecture Series (See Chapter i Boas) A basic ad very powerful (if pedestria, recall we are lazy AD smart) way to solve ay differetial (or itegral) equatio is via a series expasio of the correspodig solutio
Math 132, Fall 2009 Exam 2: Solutions
 Math 3, Fall 009 Exam : Solutios () a) ( poits) Determie for which positive real umbers p, is the followig improper itegral coverget, ad for which it is diverget. Evaluate the itegral for each value of
Math 3, Fall 009 Exam : Solutios () a) ( poits) Determie for which positive real umbers p, is the followig improper itegral coverget, ad for which it is diverget. Evaluate the itegral for each value of
Math 19B Final. Study Aid. June 6, 2011
 Math 9B Fial Study Aid Jue 6, 20 Geeral advise. Get plety of practice. There s a lot of material i this sectio - try to do as may examples ad as much of the homework as possible to get some practice. Just
Math 9B Fial Study Aid Jue 6, 20 Geeral advise. Get plety of practice. There s a lot of material i this sectio - try to do as may examples ad as much of the homework as possible to get some practice. Just
Ma 530 Introduction to Power Series
 Ma 530 Itroductio to Power Series Please ote that there is material o power series at Visual Calculus. Some of this material was used as part of the presetatio of the topics that follow. What is a Power
Ma 530 Itroductio to Power Series Please ote that there is material o power series at Visual Calculus. Some of this material was used as part of the presetatio of the topics that follow. What is a Power
The Comparison Tests. Examples. math 131 infinite series, part iii: comparison tests 18
 math 3 ifiite series, part iii: compariso tests 8 The Compariso Tests The idea behid the compariso tests is pretty simple. Suppose we have a series such as which we kow coverges by the p-series test. Now
math 3 ifiite series, part iii: compariso tests 8 The Compariso Tests The idea behid the compariso tests is pretty simple. Suppose we have a series such as which we kow coverges by the p-series test. Now
9.3 Power Series: Taylor & Maclaurin Series
 9.3 Power Series: Taylor & Maclauri Series If is a variable, the a ifiite series of the form 0 is called a power series (cetered at 0 ). a a a a a 0 1 0 is a power series cetered at a c a a c a c a c 0
9.3 Power Series: Taylor & Maclauri Series If is a variable, the a ifiite series of the form 0 is called a power series (cetered at 0 ). a a a a a 0 1 0 is a power series cetered at a c a a c a c a c 0
September 2012 C1 Note. C1 Notes (Edexcel) Copyright - For AS, A2 notes and IGCSE / GCSE worksheets 1
 September 0 s (Edecel) Copyright www.pgmaths.co.uk - For AS, A otes ad IGCSE / GCSE worksheets September 0 Copyright www.pgmaths.co.uk - For AS, A otes ad IGCSE / GCSE worksheets September 0 Copyright
September 0 s (Edecel) Copyright www.pgmaths.co.uk - For AS, A otes ad IGCSE / GCSE worksheets September 0 Copyright www.pgmaths.co.uk - For AS, A otes ad IGCSE / GCSE worksheets September 0 Copyright
x x x Using a second Taylor polynomial with remainder, find the best constant C so that for x 0,
 Math Activity 9( Due with Fial Eam) Usig first ad secod Taylor polyomials with remaider, show that for, 8 Usig a secod Taylor polyomial with remaider, fid the best costat C so that for, C 9 The th Derivative
Math Activity 9( Due with Fial Eam) Usig first ad secod Taylor polyomials with remaider, show that for, 8 Usig a secod Taylor polyomial with remaider, fid the best costat C so that for, C 9 The th Derivative
10.1 Sequences. n term. We will deal a. a n or a n n. ( 1) n ( 1) n 1 2 ( 1) a =, 0 0,,,,, ln n. n an 2. n term.
 0. Sequeces A sequece is a list of umbers writte i a defiite order: a, a,, a, a is called the first term, a is the secod term, ad i geeral eclusively with ifiite sequeces ad so each term Notatio: the sequece
0. Sequeces A sequece is a list of umbers writte i a defiite order: a, a,, a, a is called the first term, a is the secod term, ad i geeral eclusively with ifiite sequeces ad so each term Notatio: the sequece
CALCULUS BASIC SUMMER REVIEW
 CALCULUS BASIC SUMMER REVIEW NAME rise y y y Slope of a o vertical lie: m ru Poit Slope Equatio: y y m( ) The slope is m ad a poit o your lie is, ). ( y Slope-Itercept Equatio: y m b slope= m y-itercept=
CALCULUS BASIC SUMMER REVIEW NAME rise y y y Slope of a o vertical lie: m ru Poit Slope Equatio: y y m( ) The slope is m ad a poit o your lie is, ). ( y Slope-Itercept Equatio: y m b slope= m y-itercept=
PLEASE MARK YOUR ANSWERS WITH AN X, not a circle! 1. (a) (b) (c) (d) (e) 3. (a) (b) (c) (d) (e) 5. (a) (b) (c) (d) (e) 7. (a) (b) (c) (d) (e)
 Math 0560, Exam 3 November 6, 07 The Hoor Code is i effect for this examiatio. All work is to be your ow. No calculators. The exam lasts for hour ad 5 mi. Be sure that your ame is o every page i case pages
Math 0560, Exam 3 November 6, 07 The Hoor Code is i effect for this examiatio. All work is to be your ow. No calculators. The exam lasts for hour ad 5 mi. Be sure that your ame is o every page i case pages
Math 155 (Lecture 3)
 Math 55 (Lecture 3) September 8, I this lecture, we ll cosider the aswer to oe of the most basic coutig problems i combiatorics Questio How may ways are there to choose a -elemet subset of the set {,,,
Math 55 (Lecture 3) September 8, I this lecture, we ll cosider the aswer to oe of the most basic coutig problems i combiatorics Questio How may ways are there to choose a -elemet subset of the set {,,,
 FINALTERM EXAMINATION Fall 9 Calculus & Aalytical Geometry-I Questio No: ( Mars: ) - Please choose oe Let f ( x) is a fuctio such that as x approaches a real umber a, either from left or right-had-side,
FINALTERM EXAMINATION Fall 9 Calculus & Aalytical Geometry-I Questio No: ( Mars: ) - Please choose oe Let f ( x) is a fuctio such that as x approaches a real umber a, either from left or right-had-side,
Fall 2013 MTH431/531 Real analysis Section Notes
 Fall 013 MTH431/531 Real aalysis Sectio 8.1-8. Notes Yi Su 013.11.1 1. Defiitio of uiform covergece. We look at a sequece of fuctios f (x) ad study the coverget property. Notice we have two parameters
Fall 013 MTH431/531 Real aalysis Sectio 8.1-8. Notes Yi Su 013.11.1 1. Defiitio of uiform covergece. We look at a sequece of fuctios f (x) ad study the coverget property. Notice we have two parameters
P1 Chapter 8 :: Binomial Expansion
 P Chapter 8 :: Biomial Expasio jfrost@tiffi.kigsto.sch.uk www.drfrostmaths.com @DrFrostMaths Last modified: 6 th August 7 Use of DrFrostMaths for practice Register for free at: www.drfrostmaths.com/homework
P Chapter 8 :: Biomial Expasio jfrost@tiffi.kigsto.sch.uk www.drfrostmaths.com @DrFrostMaths Last modified: 6 th August 7 Use of DrFrostMaths for practice Register for free at: www.drfrostmaths.com/homework
Math F15 Rahman
 Math 2-009 F5 Rahma Week 0.9 Covergece of Taylor Series Sice we have so may examples for these sectios ad it s usually a simple matter of recallig the formula ad pluggig i for it, I ll simply provide the
Math 2-009 F5 Rahma Week 0.9 Covergece of Taylor Series Sice we have so may examples for these sectios ad it s usually a simple matter of recallig the formula ad pluggig i for it, I ll simply provide the
Lecture 3: Catalan Numbers
 CCS Discrete Math I Professor: Padraic Bartlett Lecture 3: Catala Numbers Week 3 UCSB 2014 I this week, we start studyig specific examples of commoly-occurrig sequeces of umbers (as opposed to the more
CCS Discrete Math I Professor: Padraic Bartlett Lecture 3: Catala Numbers Week 3 UCSB 2014 I this week, we start studyig specific examples of commoly-occurrig sequeces of umbers (as opposed to the more
1 Generating functions for balls in boxes
 Math 566 Fall 05 Some otes o geeratig fuctios Give a sequece a 0, a, a,..., a,..., a geeratig fuctio some way of represetig the sequece as a fuctio. There are may ways to do this, with the most commo ways
Math 566 Fall 05 Some otes o geeratig fuctios Give a sequece a 0, a, a,..., a,..., a geeratig fuctio some way of represetig the sequece as a fuctio. There are may ways to do this, with the most commo ways
