Lecture 3: Catalan Numbers
|
|
|
- Adele Pope
- 6 years ago
- Views:
Transcription
1 CCS Discrete Math I Professor: Padraic Bartlett Lecture 3: Catala Numbers Week 3 UCSB 2014 I this week, we start studyig specific examples of commoly-occurrig sequeces of umbers (as opposed to the more geeral coutig techiques we discussed for the past few weeks. Our first example of such a sequece are the Catala umbers: 1 Catala Numbers 1.1 Ascii Moutai Rages Questio. Suppose you have a umber of forward-slashes / ad backward-slashes \. A Ascii moutai rage is ay sequece made of these 2 slash marks, with forward slashes iterpreted as a icrease i altitude ad backward-slashes iterpreted as a decrease i altitude, so that We ed at the same height that we start. We ever dip below the height that we start at. Here are some Ascii moutai rages: /\ /\ /\ / \/\ /\ / \ / \ /\/ \ / \ /\ / \/\ / \ / \ /\/\/\/ \ / \/ \/\ Here are some sequeces that are ot moutai rages: /\/\/\/ /\ / /\ /\ / \ /\ / /\ /\/\/ \ / \ /\/\ /\/ \ / \ \/ \/ \/ \ Let M deote the total umber of moutai rages of legth 2. What is M, for ay? Aswer. We start by first collectig some data, to help us make a guess. I a sese, there is exactly oe possible moutai rage made out of 0 slash marks, i the same way that there is oe way to pick 0 thigs out of a set: so we say that M 0 1. More ituitively, there is exactly oe moutai rage made out of 2 slash marks; this is because our first move must be to place a / so that we icrease i altitude, which we must follow with a \ to go back dow to our startig height. There are two possible moutai rages made out of 4 slash marks: /\ 1
2 /\ /\/\ / \ There are five possible moutai rages made out of 6 slash marks: /\ /\ /\ / \ /\/\ /\/\/\ / \/\ /\/ \ / \ / \ With some time, you ca figure out that M 4 14 ad M 5 42, givig us the followig table: M It s hard to see a patter i the above data! So, istead, let s try to thik about how we actually make these moutais. Notice that with ay moutai,we must have the followig: We must start our moutai with a forward slash. Let s color it gree: /. We must at some poit i time retur back to our origial height via a backslash. Let s color the first such backslash that returs to our origial height red: \. Now, make the followig observatios: /\ / \ /\ / \/ \ /\/\ / \ / \ / \/ \ Betwee our gree forward-slash ad our red backslash, we have a moutai that starts at height 1 ad ever dips below height 1. After our red backslash, we have a moutai that starts ad eds at height 0. I other words, we have writte our origial moutai rage as the combiatio of two smaller moutais, oe of which we put o top of the /, \ marks ad the other of which we put to the right of the \ mark. Furthermore, This decompositio is uique: that is, give ay origial moutai rage, our process above is t ambiguous i how it breaks our moutai ito two smaller moutais! This process is reversible: give our two smaller moutais, we ca combie them by udoig our process to get back to our origial moutai rage! Cosequetly, if we wat to cout the total umber of large moutais, it suffices to cout all of the pairs of smaller moutais that ca create those larger moutais. I other words, we have a recursive relatioship! Specifically, because we ca break ay 2-legth moutai 2
3 dow ito some 2k-legth moutai o top of the /, \ marks, alog with a 2( 1 k- legth moutai after those marks, we have the followig recursive relatioship: 1 M M 0 M 1 + M 1 M M k M 1 k. This looks familiar! I fact, we ve oticed a relatioship like this before: last week, whe we studied geeratig fuctios, we saw that ( ( ( a x b x a k b k x for ay two formal power series a x, b x. I particular, this tells us that if we set F (x M x, we get ( ( ( F (x F (x M x M x M k M k k0 k0 k0 x Our recursive relatioship tells us that k0 M km k M +1 ; therefore, we have ( (F (x 2 M k M k x M +1 x x(f (x 2 k0 M +1 x +1 x(f (x F (x x(f (x 2 F (x M x M 0 + M x 1 So: we have a expressio for F (x! I particular, we have a quadratic-polyomialtype expressio for F (x: therefore, we kow that F (x has to algebraically satisfy this expressio! However, we kow the form of ay solutio to a quadratic of the form a? 2 + b? + c: it s give by the quadratic formula? b± b 2 4ac 2a. I particular, we have that F (x 1 ± 1 4x for our specific formal power series F (x. Now: remember whe we defied formal power series, ad I said that we d ever plug thigs ito them? I kida lied. We will almost ever plug thigs ito geeratig fuctios, ad wheever we do we will be careful to make sure that the ifiite sum we ve created actually coverges to somethig sesible ad that we re makig sese. But! Now is totally oe of the times where it makes sese to do this! Cosider what we ve got here: 3
4 O oe had, if we take ay formal power series o matter what it is! we ca always plug i x 0 to it ad get somethig well-defied. Specifically, if our formal power series is some A(x a x, settig x 0 is just sayig that every term other tha the a 0 term gets multiplied by 0 0; i other words, A(0 a 0! So o matter what our formal power series is, we kow that pluggig i 0 to it should give us its costat term. O the other had, for the problem we re curretly cosiderig, we kow that F (x 1± 1 4x. This is a little irritatig, i that we have this ± term: we re gettig two possible aswers for F (x, whe we really wat oe (after all, there is oly oe correct value for M, the umber of 2-legth moutai rages! So: what happes whe we plug i x 0 to 1± 1 4x? Well: if we have the +-brach, we get somethig of the form 2 0 at x 0; this is hopeless, as it will either equal 1 M 0 F (0 or could it eve equal 1 i the limit, as the top goes to 2 while the bottom goes to 0! Coversely, if we take the brach, we get somethig of the form 0 0 at x 0, which is... ot great, but better! I specific, if we take limits + use L Hopital, we ca see that 1 ( d 1 4x dx 1 1 4x 1 2 lim lim x 0 x 0 d dx ( lim (1 4x 1/2 4 1, x 0 2 which is right! So, we actually kow which of the two braches is right to cosider here: we must have F (x 1 1 4x. Cool! So. If this was a stadard geeratig-fuctios problem, we d fid some way to expad the right-had side as a power series, ad use this expasio to determie what the M s are! To do this, we re goig to eed ew tools, however: we have this 1 4x term, which we do t have tools for. Let s build them! 1.2 Detour: Newto s Geeralized Biomial Theorem Last week, we proved that for ay N, (x + y k0 ( x k y k. k We wat to uderstad (1 4x 1/2. A seemigly very dumb thig we could write to try to aswer this problem is the followig: 1/2 ( 1/2 (1 4x 1/2 1 k ( 4x (1/2 k. k k0 4
5 Surprisigly, this is actually correct! Let s make some defiitios, so we ca prove this: Defiitio. Take ay real umber r ot i the atural umbers, ad ay atural umber k. We defie the geeralized biomial coefficiet ( r k as follows: ( r k (r(r 1(r 2... (r (k 1. k! Notice that if r was a atural umber k, this is literally the same thig as the ormal biomial coefficiet! By covetio, if k 0, we set this expressio equal to 1. This lets us make the k terms make sese. To get the rest of the expressio, let s pull out some results from calculus: Defiitio. Take ay fuctio f(x. The Taylor series aroud 0 correspodig to f(x is the power series f ( (0 x,! where f ( (0 deotes the -th derivative of f(x evaluated at x 0. So. Suppose that we cosider the Taylor series for (x + y r, for ay o-atural real value r. To do this, we ll eed to fid the derivatives of this fuctio with respect to x. It is ot too hard to see that d dx ((x + yr r(x + y r 1 d dx (x + y r(x + yr 1 1 r(x + y r 1 d 2 dx 2 ((x + yr d ( r(x + y r 1 r(r 1(x + y r 2 d (x + y r(r 1(x + yr 2 dx dx d 3 dx 3 ((x + yr d ( r(r 1(x + y r 2 r(r 1(r 2(x + y r 3 dx. d dx ((x + yr d ( r(r 1... (r ( 2(x + y r 2 r(r 1... (r ( 1(x + y r. dx (The last step here is justified by iductio; we leave formal details to the reader! Do this iff you do t see why it s true. If you plug i x 0, you get that d dx ((x + yr r(r 1... (r ( 1(x + y r x0 r(r 1... (r ( 1y r, x0 5
6 ad therefore that the Taylor series correspodig to (x + y r is just f ( (0 x! r(r 1... (r ( 1 y r x.! The coefficiets here are precisely our geeralized biomial coefficiets! Therefore, we ve show that the Taylor series for (x + y r is actually ( r y r x, ad specifically that the Taylor series for (1 4x 1/2 is ( r ( 4x. From here, we eed a few quick results from calculus: we simply state them, ad leave their derivatio (because they ivolve more i-depth Taylor series maipulatios tha we wat to do here for the reader! Our Taylor series for (1 4x 1/2 coverges ad is equal to (1 4x 1/2 for values of x i ( 1/4, 1/4. Two power series are equal if ad oly if all of their coefficiets are equal! Therefore, we have M x F (x 1 1 4x 1 ( 4x. 1.3 Back to Moutais So we ca solve for the M coefficiets! We do this here. First, let s clea up our expressio above, by just doig some algebraic maipulatios. Nothig crazy happes here; try to read lie-by-lie ad make sure you follow our steps! 6
7 M x 1 ( 4x 1 ( 1/2 0 ( 4x 0 1 ( 4x ( 4x ( 4x +1 ( 4x ( 4x (1/2((1/ ((1/2 (( ( 4x ( + 1! (+1 terms {}}{ ( 1 4 x ( + 1! (+1 terms {}}{ ( 1 2 ( 1 4 x ( + 1! (2 1 ( ( 1 4 x ( + 1! (2 1 2 x ( + 1! Ok, let s breathe for a secod. The right-had side is certaily less awful tha before, but it s still ot as simple as possible. I particular, the (2 1 expressio is t ecessarily as simple as we d like! We ca fix this, with the followig clever trick; I call this out mostly because it s a maipulatio I ve see come up about oce every four-five moths, ad it s useful to have somewhere i your mid! Notice that 2! 2 (
8 Therefore, we have ad thus that (2 1 (2! 2!, M x (2 1 2 x ( + 1! (2! 2!( + 1! 2 x 1 (2! + 1 2!! 2 x ( 1 2 x + 1 That is... a far icer expressio. Also: it works! I theory, we should have M 1 for all, ad check it out: M 0 1 ( 2 0 1, M 1 1 ( ! !1! 1, M 2 1 ( ! !2! 2, M 3 1 ( ! !3! 5, M 4 1 ( ! !4! 14, M 5 1 ( ! !5! ( 2 Amazig! Math: it s ridiculous. 1.4 Alterate Derivatios Whe you get a aswer as simple as M 1 +1( 2, it suggests that there may be a ice combiatorial iterpretatio of this formula as it relates to moutais that is, some way i which we ca pick thigs out of 2 thigs, ad after scalig by 1/( + 1 to deal with overcoutig get our aswer! Pleasatly, this is true: there is a way to derive our closed-form forumla for M without geeratig fuctios! We preset this here, after the 8
9 geeratig fuctio solutio, because (while this is a much shorter solutio it is arguably oe that requires more cleveress: ulike the above, which was a (crazy applicatio of tools we kow, this oe ivolves either kowig the aswer M +1( 1 2 ahead of time or comig up with some surprisig isights ito moutai rages (or both! We do this here. First, let s chage our problem somewhat: cosider ay sequece made out of + 1 forward-slashes / ad backslashes \. Here, we re ot worryig about these sequeces formig proper moutai rages: i.e. we ca dip below our startig altitude. Moreover, we kow that after oe of these sequeces, we will be precisely oe uit higher tha we started, as we wet up + 1 times ad dow times. Imagie drawig these slashes o the iteger lattice Z 2, so that each forward slash coects some (a, b to (a + 1, b + 1, ad each backwards slash coects some (a, b to (a + 1, b Catala Numbers i Other Cotexts Not to kock the above derivatios, but they re actually ot what most mathematicias thik are the cool thigs here! Istead, cosider the recurrece relatio we studied to get these umbers: 1 C 0 C 1 1, C C k C ( 1 k The crazy thig about this recurrece is that there are literally hudreds of mathematical objects ad cocepts that reduce to this patter! O the homework you have six of these recurreces to study; we give oe more particularly beautiful example here. Let C deote the total umber of ways to take a + 2-sided regular covex polygo ca be cut ito triagles by drawig straight lies betwee vertices. There are fourtee ways to do this for 4, as draw below: k0 (Picture stole from Wikipedia I claim that this sequece satisfies the recurrece relatio described above. Our base cases, as typical, are automatic; C 0 is kid-of trivially 1, as there s exactly oe way (do othig to cut the o-existet 2-sided regular polygo ito triagles, while C 1 1 because there s exactly oe way (do othig! to cut a triagle ito... triagles. To get our recurrece relatio: Take ay regular + 2-go. How are we goig to break this ito smaller polygos? Well: if we ve divided our polygos ito triagles, this motivates us to thik about cuttig alog a triagle to get smaller polygos! 9
10 Specifically, take our polygo, ad pick out the triagle that uses the top edge: because we ve broke our polygo ito triagles, we kow that exactly oe such triagle exists! Split our polygo ito two polygos alog this triagle: because we create two ew edges from the chord-lies of this triagle, ad delete oe edge by gettig rid of the top edge, we must have C k C -1-k Split our polygo ito two polygos alog this triagle: because we create two ew edges from the chord-lies of this triagle, ad delete oe edge by gettig rid of the top edge, we must have edges, split over two polygos. So we have oe k + 2-go ad oe 1 k + 2-go! I other words, we have the recurrece as claimed. 1 C 0 C 1 1, C C k C ( 1 k k0 10
Infinite Sequences and Series
 Chapter 6 Ifiite Sequeces ad Series 6.1 Ifiite Sequeces 6.1.1 Elemetary Cocepts Simply speakig, a sequece is a ordered list of umbers writte: {a 1, a 2, a 3,...a, a +1,...} where the elemets a i represet
Chapter 6 Ifiite Sequeces ad Series 6.1 Ifiite Sequeces 6.1.1 Elemetary Cocepts Simply speakig, a sequece is a ordered list of umbers writte: {a 1, a 2, a 3,...a, a +1,...} where the elemets a i represet
6.3 Testing Series With Positive Terms
 6.3. TESTING SERIES WITH POSITIVE TERMS 307 6.3 Testig Series With Positive Terms 6.3. Review of what is kow up to ow I theory, testig a series a i for covergece amouts to fidig the i= sequece of partial
6.3. TESTING SERIES WITH POSITIVE TERMS 307 6.3 Testig Series With Positive Terms 6.3. Review of what is kow up to ow I theory, testig a series a i for covergece amouts to fidig the i= sequece of partial
P1 Chapter 8 :: Binomial Expansion
 P Chapter 8 :: Biomial Expasio jfrost@tiffi.kigsto.sch.uk www.drfrostmaths.com @DrFrostMaths Last modified: 6 th August 7 Use of DrFrostMaths for practice Register for free at: www.drfrostmaths.com/homework
P Chapter 8 :: Biomial Expasio jfrost@tiffi.kigsto.sch.uk www.drfrostmaths.com @DrFrostMaths Last modified: 6 th August 7 Use of DrFrostMaths for practice Register for free at: www.drfrostmaths.com/homework
A sequence of numbers is a function whose domain is the positive integers. We can see that the sequence
 Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece,, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet as
Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece,, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet as
Math 155 (Lecture 3)
 Math 55 (Lecture 3) September 8, I this lecture, we ll cosider the aswer to oe of the most basic coutig problems i combiatorics Questio How may ways are there to choose a -elemet subset of the set {,,,
Math 55 (Lecture 3) September 8, I this lecture, we ll cosider the aswer to oe of the most basic coutig problems i combiatorics Questio How may ways are there to choose a -elemet subset of the set {,,,
1 Generating functions for balls in boxes
 Math 566 Fall 05 Some otes o geeratig fuctios Give a sequece a 0, a, a,..., a,..., a geeratig fuctio some way of represetig the sequece as a fuctio. There are may ways to do this, with the most commo ways
Math 566 Fall 05 Some otes o geeratig fuctios Give a sequece a 0, a, a,..., a,..., a geeratig fuctio some way of represetig the sequece as a fuctio. There are may ways to do this, with the most commo ways
MA131 - Analysis 1. Workbook 2 Sequences I
 MA3 - Aalysis Workbook 2 Sequeces I Autum 203 Cotets 2 Sequeces I 2. Itroductio.............................. 2.2 Icreasig ad Decreasig Sequeces................ 2 2.3 Bouded Sequeces..........................
MA3 - Aalysis Workbook 2 Sequeces I Autum 203 Cotets 2 Sequeces I 2. Itroductio.............................. 2.2 Icreasig ad Decreasig Sequeces................ 2 2.3 Bouded Sequeces..........................
Sequences I. Chapter Introduction
 Chapter 2 Sequeces I 2. Itroductio A sequece is a list of umbers i a defiite order so that we kow which umber is i the first place, which umber is i the secod place ad, for ay atural umber, we kow which
Chapter 2 Sequeces I 2. Itroductio A sequece is a list of umbers i a defiite order so that we kow which umber is i the first place, which umber is i the secod place ad, for ay atural umber, we kow which
Lecture 6: Integration and the Mean Value Theorem. slope =
 Math 8 Istructor: Padraic Bartlett Lecture 6: Itegratio ad the Mea Value Theorem Week 6 Caltech 202 The Mea Value Theorem The Mea Value Theorem abbreviated MVT is the followig result: Theorem. Suppose
Math 8 Istructor: Padraic Bartlett Lecture 6: Itegratio ad the Mea Value Theorem Week 6 Caltech 202 The Mea Value Theorem The Mea Value Theorem abbreviated MVT is the followig result: Theorem. Suppose
4.3 Growth Rates of Solutions to Recurrences
 4.3. GROWTH RATES OF SOLUTIONS TO RECURRENCES 81 4.3 Growth Rates of Solutios to Recurreces 4.3.1 Divide ad Coquer Algorithms Oe of the most basic ad powerful algorithmic techiques is divide ad coquer.
4.3. GROWTH RATES OF SOLUTIONS TO RECURRENCES 81 4.3 Growth Rates of Solutios to Recurreces 4.3.1 Divide ad Coquer Algorithms Oe of the most basic ad powerful algorithmic techiques is divide ad coquer.
Sequences A sequence of numbers is a function whose domain is the positive integers. We can see that the sequence
 Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece 1, 1, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet
Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece 1, 1, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet
Section 1.1. Calculus: Areas And Tangents. Difference Equations to Differential Equations
 Differece Equatios to Differetial Equatios Sectio. Calculus: Areas Ad Tagets The study of calculus begis with questios about chage. What happes to the velocity of a swigig pedulum as its positio chages?
Differece Equatios to Differetial Equatios Sectio. Calculus: Areas Ad Tagets The study of calculus begis with questios about chage. What happes to the velocity of a swigig pedulum as its positio chages?
3.2 Properties of Division 3.3 Zeros of Polynomials 3.4 Complex and Rational Zeros of Polynomials
 Math 60 www.timetodare.com 3. Properties of Divisio 3.3 Zeros of Polyomials 3.4 Complex ad Ratioal Zeros of Polyomials I these sectios we will study polyomials algebraically. Most of our work will be cocered
Math 60 www.timetodare.com 3. Properties of Divisio 3.3 Zeros of Polyomials 3.4 Complex ad Ratioal Zeros of Polyomials I these sectios we will study polyomials algebraically. Most of our work will be cocered
The Binomial Theorem
 The Biomial Theorem Robert Marti Itroductio The Biomial Theorem is used to expad biomials, that is, brackets cosistig of two distict terms The formula for the Biomial Theorem is as follows: (a + b ( k
The Biomial Theorem Robert Marti Itroductio The Biomial Theorem is used to expad biomials, that is, brackets cosistig of two distict terms The formula for the Biomial Theorem is as follows: (a + b ( k
Seunghee Ye Ma 8: Week 5 Oct 28
 Week 5 Summary I Sectio, we go over the Mea Value Theorem ad its applicatios. I Sectio 2, we will recap what we have covered so far this term. Topics Page Mea Value Theorem. Applicatios of the Mea Value
Week 5 Summary I Sectio, we go over the Mea Value Theorem ad its applicatios. I Sectio 2, we will recap what we have covered so far this term. Topics Page Mea Value Theorem. Applicatios of the Mea Value
(A sequence also can be thought of as the list of function values attained for a function f :ℵ X, where f (n) = x n for n 1.) x 1 x N +k x N +4 x 3
 MATH 337 Sequeces Dr. Neal, WKU Let X be a metric space with distace fuctio d. We shall defie the geeral cocept of sequece ad limit i a metric space, the apply the results i particular to some special
MATH 337 Sequeces Dr. Neal, WKU Let X be a metric space with distace fuctio d. We shall defie the geeral cocept of sequece ad limit i a metric space, the apply the results i particular to some special
Zeros of Polynomials
 Math 160 www.timetodare.com 4.5 4.6 Zeros of Polyomials I these sectios we will study polyomials algebraically. Most of our work will be cocered with fidig the solutios of polyomial equatios of ay degree
Math 160 www.timetodare.com 4.5 4.6 Zeros of Polyomials I these sectios we will study polyomials algebraically. Most of our work will be cocered with fidig the solutios of polyomial equatios of ay degree
Math 120 Answers for Homework 23
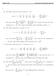 Math 0 Aswers for Homewor. (a) The Taylor series for cos(x) aroud a 0 is cos(x) x! + x4 4! x6 6! + x8 8! x0 0! + ( ) ()! x ( ) π ( ) ad so the series ()! ()! (π) is just the series for cos(x) evaluated
Math 0 Aswers for Homewor. (a) The Taylor series for cos(x) aroud a 0 is cos(x) x! + x4 4! x6 6! + x8 8! x0 0! + ( ) ()! x ( ) π ( ) ad so the series ()! ()! (π) is just the series for cos(x) evaluated
MATH 31B: MIDTERM 2 REVIEW
 MATH 3B: MIDTERM REVIEW JOE HUGHES. Evaluate x (x ) (x 3).. Partial Fractios Solutio: The umerator has degree less tha the deomiator, so we ca use partial fractios. Write x (x ) (x 3) = A x + A (x ) +
MATH 3B: MIDTERM REVIEW JOE HUGHES. Evaluate x (x ) (x 3).. Partial Fractios Solutio: The umerator has degree less tha the deomiator, so we ca use partial fractios. Write x (x ) (x 3) = A x + A (x ) +
Discrete Mathematics for CS Spring 2007 Luca Trevisan Lecture 22
 CS 70 Discrete Mathematics for CS Sprig 2007 Luca Trevisa Lecture 22 Aother Importat Distributio The Geometric Distributio Questio: A biased coi with Heads probability p is tossed repeatedly util the first
CS 70 Discrete Mathematics for CS Sprig 2007 Luca Trevisa Lecture 22 Aother Importat Distributio The Geometric Distributio Questio: A biased coi with Heads probability p is tossed repeatedly util the first
Lecture 7: Fourier Series and Complex Power Series
 Math 1d Istructor: Padraic Bartlett Lecture 7: Fourier Series ad Complex Power Series Week 7 Caltech 013 1 Fourier Series 1.1 Defiitios ad Motivatio Defiitio 1.1. A Fourier series is a series of fuctios
Math 1d Istructor: Padraic Bartlett Lecture 7: Fourier Series ad Complex Power Series Week 7 Caltech 013 1 Fourier Series 1.1 Defiitios ad Motivatio Defiitio 1.1. A Fourier series is a series of fuctios
Discrete Mathematics for CS Spring 2005 Clancy/Wagner Notes 21. Some Important Distributions
 CS 70 Discrete Mathematics for CS Sprig 2005 Clacy/Wager Notes 21 Some Importat Distributios Questio: A biased coi with Heads probability p is tossed repeatedly util the first Head appears. What is the
CS 70 Discrete Mathematics for CS Sprig 2005 Clacy/Wager Notes 21 Some Importat Distributios Questio: A biased coi with Heads probability p is tossed repeatedly util the first Head appears. What is the
GENERATING FUNCTIONS AND RANDOM WALKS
 GENERATING FUNCTIONS AND RANDOM WALKS SIMON RUBINSTEIN-SALZEDO 1 A illustrative example Before we start studyig geeratig fuctios properly, let us look a example of their use Cosider the umbers a, defied
GENERATING FUNCTIONS AND RANDOM WALKS SIMON RUBINSTEIN-SALZEDO 1 A illustrative example Before we start studyig geeratig fuctios properly, let us look a example of their use Cosider the umbers a, defied
September 2012 C1 Note. C1 Notes (Edexcel) Copyright - For AS, A2 notes and IGCSE / GCSE worksheets 1
 September 0 s (Edecel) Copyright www.pgmaths.co.uk - For AS, A otes ad IGCSE / GCSE worksheets September 0 Copyright www.pgmaths.co.uk - For AS, A otes ad IGCSE / GCSE worksheets September 0 Copyright
September 0 s (Edecel) Copyright www.pgmaths.co.uk - For AS, A otes ad IGCSE / GCSE worksheets September 0 Copyright www.pgmaths.co.uk - For AS, A otes ad IGCSE / GCSE worksheets September 0 Copyright
Combinatorics and Newton s theorem
 INTRODUCTION TO MATHEMATICAL REASONING Key Ideas Worksheet 5 Combiatorics ad Newto s theorem This week we are goig to explore Newto s biomial expasio theorem. This is a very useful tool i aalysis, but
INTRODUCTION TO MATHEMATICAL REASONING Key Ideas Worksheet 5 Combiatorics ad Newto s theorem This week we are goig to explore Newto s biomial expasio theorem. This is a very useful tool i aalysis, but
The Growth of Functions. Theoretical Supplement
 The Growth of Fuctios Theoretical Supplemet The Triagle Iequality The triagle iequality is a algebraic tool that is ofte useful i maipulatig absolute values of fuctios. The triagle iequality says that
The Growth of Fuctios Theoretical Supplemet The Triagle Iequality The triagle iequality is a algebraic tool that is ofte useful i maipulatig absolute values of fuctios. The triagle iequality says that
Worksheet on Generating Functions
 Worksheet o Geeratig Fuctios October 26, 205 This worksheet is adapted from otes/exercises by Nat Thiem. Derivatives of Geeratig Fuctios. If the sequece a 0, a, a 2,... has ordiary geeratig fuctio A(x,
Worksheet o Geeratig Fuctios October 26, 205 This worksheet is adapted from otes/exercises by Nat Thiem. Derivatives of Geeratig Fuctios. If the sequece a 0, a, a 2,... has ordiary geeratig fuctio A(x,
1 Approximating Integrals using Taylor Polynomials
 Seughee Ye Ma 8: Week 7 Nov Week 7 Summary This week, we will lear how we ca approximate itegrals usig Taylor series ad umerical methods. Topics Page Approximatig Itegrals usig Taylor Polyomials. Defiitios................................................
Seughee Ye Ma 8: Week 7 Nov Week 7 Summary This week, we will lear how we ca approximate itegrals usig Taylor series ad umerical methods. Topics Page Approximatig Itegrals usig Taylor Polyomials. Defiitios................................................
Chapter 6: Numerical Series
 Chapter 6: Numerical Series 327 Chapter 6 Overview: Sequeces ad Numerical Series I most texts, the topic of sequeces ad series appears, at first, to be a side topic. There are almost o derivatives or itegrals
Chapter 6: Numerical Series 327 Chapter 6 Overview: Sequeces ad Numerical Series I most texts, the topic of sequeces ad series appears, at first, to be a side topic. There are almost o derivatives or itegrals
1. n! = n. tion. For example, (n+1)! working with factorials. = (n+1) n (n 1) 2 1
 Biomial Coefficiets ad Permutatios Mii-lecture The followig pages discuss a few special iteger coutig fuctios You may have see some of these before i a basic probability class or elsewhere, but perhaps
Biomial Coefficiets ad Permutatios Mii-lecture The followig pages discuss a few special iteger coutig fuctios You may have see some of these before i a basic probability class or elsewhere, but perhaps
Bertrand s Postulate
 Bertrad s Postulate Lola Thompso Ross Program July 3, 2009 Lola Thompso (Ross Program Bertrad s Postulate July 3, 2009 1 / 33 Bertrad s Postulate I ve said it oce ad I ll say it agai: There s always a
Bertrad s Postulate Lola Thompso Ross Program July 3, 2009 Lola Thompso (Ross Program Bertrad s Postulate July 3, 2009 1 / 33 Bertrad s Postulate I ve said it oce ad I ll say it agai: There s always a
Lecture Overview. 2 Permutations and Combinations. n(n 1) (n (k 1)) = n(n 1) (n k + 1) =
 COMPSCI 230: Discrete Mathematics for Computer Sciece April 8, 2019 Lecturer: Debmalya Paigrahi Lecture 22 Scribe: Kevi Su 1 Overview I this lecture, we begi studyig the fudametals of coutig discrete objects.
COMPSCI 230: Discrete Mathematics for Computer Sciece April 8, 2019 Lecturer: Debmalya Paigrahi Lecture 22 Scribe: Kevi Su 1 Overview I this lecture, we begi studyig the fudametals of coutig discrete objects.
CHAPTER 10 INFINITE SEQUENCES AND SERIES
 CHAPTER 10 INFINITE SEQUENCES AND SERIES 10.1 Sequeces 10.2 Ifiite Series 10.3 The Itegral Tests 10.4 Compariso Tests 10.5 The Ratio ad Root Tests 10.6 Alteratig Series: Absolute ad Coditioal Covergece
CHAPTER 10 INFINITE SEQUENCES AND SERIES 10.1 Sequeces 10.2 Ifiite Series 10.3 The Itegral Tests 10.4 Compariso Tests 10.5 The Ratio ad Root Tests 10.6 Alteratig Series: Absolute ad Coditioal Covergece
Ma 530 Introduction to Power Series
 Ma 530 Itroductio to Power Series Please ote that there is material o power series at Visual Calculus. Some of this material was used as part of the presetatio of the topics that follow. What is a Power
Ma 530 Itroductio to Power Series Please ote that there is material o power series at Visual Calculus. Some of this material was used as part of the presetatio of the topics that follow. What is a Power
Lecture 6: Integration and the Mean Value Theorem
 Math 8 Istructor: Padraic Bartlett Lecture 6: Itegratio ad the Mea Value Theorem Week 6 Caltech - Fall, 2011 1 Radom Questios Questio 1.1. Show that ay positive ratioal umber ca be writte as the sum of
Math 8 Istructor: Padraic Bartlett Lecture 6: Itegratio ad the Mea Value Theorem Week 6 Caltech - Fall, 2011 1 Radom Questios Questio 1.1. Show that ay positive ratioal umber ca be writte as the sum of
10.1 Sequences. n term. We will deal a. a n or a n n. ( 1) n ( 1) n 1 2 ( 1) a =, 0 0,,,,, ln n. n an 2. n term.
 0. Sequeces A sequece is a list of umbers writte i a defiite order: a, a,, a, a is called the first term, a is the secod term, ad i geeral eclusively with ifiite sequeces ad so each term Notatio: the sequece
0. Sequeces A sequece is a list of umbers writte i a defiite order: a, a,, a, a is called the first term, a is the secod term, ad i geeral eclusively with ifiite sequeces ad so each term Notatio: the sequece
The Riemann Zeta Function
 Physics 6A Witer 6 The Riema Zeta Fuctio I this ote, I will sketch some of the mai properties of the Riema zeta fuctio, ζ(x). For x >, we defie ζ(x) =, x >. () x = For x, this sum diverges. However, we
Physics 6A Witer 6 The Riema Zeta Fuctio I this ote, I will sketch some of the mai properties of the Riema zeta fuctio, ζ(x). For x >, we defie ζ(x) =, x >. () x = For x, this sum diverges. However, we
Recitation 4: Lagrange Multipliers and Integration
 Math 1c TA: Padraic Bartlett Recitatio 4: Lagrage Multipliers ad Itegratio Week 4 Caltech 211 1 Radom Questio Hey! So, this radom questio is pretty tightly tied to today s lecture ad the cocept of cotet
Math 1c TA: Padraic Bartlett Recitatio 4: Lagrage Multipliers ad Itegratio Week 4 Caltech 211 1 Radom Questio Hey! So, this radom questio is pretty tightly tied to today s lecture ad the cocept of cotet
Random Models. Tusheng Zhang. February 14, 2013
 Radom Models Tusheg Zhag February 14, 013 1 Radom Walks Let me describe the model. Radom walks are used to describe the motio of a movig particle (object). Suppose that a particle (object) moves alog the
Radom Models Tusheg Zhag February 14, 013 1 Radom Walks Let me describe the model. Radom walks are used to describe the motio of a movig particle (object). Suppose that a particle (object) moves alog the
1+x 1 + α+x. x = 2(α x2 ) 1+x
 Math 2030 Homework 6 Solutios # [Problem 5] For coveiece we let α lim sup a ad β lim sup b. Without loss of geerality let us assume that α β. If α the by assumptio β < so i this case α + β. By Theorem
Math 2030 Homework 6 Solutios # [Problem 5] For coveiece we let α lim sup a ad β lim sup b. Without loss of geerality let us assume that α β. If α the by assumptio β < so i this case α + β. By Theorem
SYDE 112, LECTURE 2: Riemann Sums
 SYDE, LECTURE : Riema Sums Riema Sums Cosider the problem of determiig the area below the curve f(x) boud betwee two poits a ad b. For simple geometrical fuctios, we ca easily determie this based o ituitio.
SYDE, LECTURE : Riema Sums Riema Sums Cosider the problem of determiig the area below the curve f(x) boud betwee two poits a ad b. For simple geometrical fuctios, we ca easily determie this based o ituitio.
MATH 147 Homework 4. ( = lim. n n)( n + 1 n) n n n. 1 = lim
 MATH 147 Homework 4 1. Defie the sequece {a } by a =. a) Prove that a +1 a = 0. b) Prove that {a } is ot a Cauchy sequece. Solutio: a) We have: ad so we re doe. a +1 a = + 1 = + 1 + ) + 1 ) + 1 + 1 = +
MATH 147 Homework 4 1. Defie the sequece {a } by a =. a) Prove that a +1 a = 0. b) Prove that {a } is ot a Cauchy sequece. Solutio: a) We have: ad so we re doe. a +1 a = + 1 = + 1 + ) + 1 ) + 1 + 1 = +
The Random Walk For Dummies
 The Radom Walk For Dummies Richard A Mote Abstract We look at the priciples goverig the oe-dimesioal discrete radom walk First we review five basic cocepts of probability theory The we cosider the Beroulli
The Radom Walk For Dummies Richard A Mote Abstract We look at the priciples goverig the oe-dimesioal discrete radom walk First we review five basic cocepts of probability theory The we cosider the Beroulli
NUMERICAL METHODS COURSEWORK INFORMAL NOTES ON NUMERICAL INTEGRATION COURSEWORK
 NUMERICAL METHODS COURSEWORK INFORMAL NOTES ON NUMERICAL INTEGRATION COURSEWORK For this piece of coursework studets must use the methods for umerical itegratio they meet i the Numerical Methods module
NUMERICAL METHODS COURSEWORK INFORMAL NOTES ON NUMERICAL INTEGRATION COURSEWORK For this piece of coursework studets must use the methods for umerical itegratio they meet i the Numerical Methods module
Z ß cos x + si x R du We start with the substitutio u = si(x), so du = cos(x). The itegral becomes but +u we should chage the limits to go with the ew
 Problem ( poits) Evaluate the itegrals Z p x 9 x We ca draw a right triagle labeled this way x p x 9 From this we ca read off x = sec, so = sec ta, ad p x 9 = R ta. Puttig those pieces ito the itegralrwe
Problem ( poits) Evaluate the itegrals Z p x 9 x We ca draw a right triagle labeled this way x p x 9 From this we ca read off x = sec, so = sec ta, ad p x 9 = R ta. Puttig those pieces ito the itegralrwe
Recursive Algorithms. Recurrences. Recursive Algorithms Analysis
 Recursive Algorithms Recurreces Computer Sciece & Egieerig 35: Discrete Mathematics Christopher M Bourke cbourke@cseuledu A recursive algorithm is oe i which objects are defied i terms of other objects
Recursive Algorithms Recurreces Computer Sciece & Egieerig 35: Discrete Mathematics Christopher M Bourke cbourke@cseuledu A recursive algorithm is oe i which objects are defied i terms of other objects
Polynomial Functions and Their Graphs
 Polyomial Fuctios ad Their Graphs I this sectio we begi the study of fuctios defied by polyomial expressios. Polyomial ad ratioal fuctios are the most commo fuctios used to model data, ad are used extesively
Polyomial Fuctios ad Their Graphs I this sectio we begi the study of fuctios defied by polyomial expressios. Polyomial ad ratioal fuctios are the most commo fuctios used to model data, ad are used extesively
6 Integers Modulo n. integer k can be written as k = qn + r, with q,r, 0 r b. So any integer.
 6 Itegers Modulo I Example 2.3(e), we have defied the cogruece of two itegers a,b with respect to a modulus. Let us recall that a b (mod ) meas a b. We have proved that cogruece is a equivalece relatio
6 Itegers Modulo I Example 2.3(e), we have defied the cogruece of two itegers a,b with respect to a modulus. Let us recall that a b (mod ) meas a b. We have proved that cogruece is a equivalece relatio
Lesson 10: Limits and Continuity
 www.scimsacademy.com Lesso 10: Limits ad Cotiuity SCIMS Academy 1 Limit of a fuctio The cocept of limit of a fuctio is cetral to all other cocepts i calculus (like cotiuity, derivative, defiite itegrals
www.scimsacademy.com Lesso 10: Limits ad Cotiuity SCIMS Academy 1 Limit of a fuctio The cocept of limit of a fuctio is cetral to all other cocepts i calculus (like cotiuity, derivative, defiite itegrals
Understanding Samples
 1 Will Moroe CS 109 Samplig ad Bootstrappig Lecture Notes #17 August 2, 2017 Based o a hadout by Chris Piech I this chapter we are goig to talk about statistics calculated o samples from a populatio. We
1 Will Moroe CS 109 Samplig ad Bootstrappig Lecture Notes #17 August 2, 2017 Based o a hadout by Chris Piech I this chapter we are goig to talk about statistics calculated o samples from a populatio. We
Ma 530 Infinite Series I
 Ma 50 Ifiite Series I Please ote that i additio to the material below this lecture icorporated material from the Visual Calculus web site. The material o sequeces is at Visual Sequeces. (To use this li
Ma 50 Ifiite Series I Please ote that i additio to the material below this lecture icorporated material from the Visual Calculus web site. The material o sequeces is at Visual Sequeces. (To use this li
Chapter 6 Overview: Sequences and Numerical Series. For the purposes of AP, this topic is broken into four basic subtopics:
 Chapter 6 Overview: Sequeces ad Numerical Series I most texts, the topic of sequeces ad series appears, at first, to be a side topic. There are almost o derivatives or itegrals (which is what most studets
Chapter 6 Overview: Sequeces ad Numerical Series I most texts, the topic of sequeces ad series appears, at first, to be a side topic. There are almost o derivatives or itegrals (which is what most studets
7 Sequences of real numbers
 40 7 Sequeces of real umbers 7. Defiitios ad examples Defiitio 7... A sequece of real umbers is a real fuctio whose domai is the set N of atural umbers. Let s : N R be a sequece. The the values of s are
40 7 Sequeces of real umbers 7. Defiitios ad examples Defiitio 7... A sequece of real umbers is a real fuctio whose domai is the set N of atural umbers. Let s : N R be a sequece. The the values of s are
Math 113 Exam 3 Practice
 Math Exam Practice Exam will cover.-.9. This sheet has three sectios. The first sectio will remid you about techiques ad formulas that you should kow. The secod gives a umber of practice questios for you
Math Exam Practice Exam will cover.-.9. This sheet has three sectios. The first sectio will remid you about techiques ad formulas that you should kow. The secod gives a umber of practice questios for you
(3) If you replace row i of A by its sum with a multiple of another row, then the determinant is unchanged! Expand across the i th row:
 Math 50-004 Tue Feb 4 Cotiue with sectio 36 Determiats The effective way to compute determiats for larger-sized matrices without lots of zeroes is to ot use the defiitio, but rather to use the followig
Math 50-004 Tue Feb 4 Cotiue with sectio 36 Determiats The effective way to compute determiats for larger-sized matrices without lots of zeroes is to ot use the defiitio, but rather to use the followig
Sequences III. Chapter Roots
 Chapter 4 Sequeces III 4. Roots We ca use the results we ve established i the last workbook to fid some iterestig limits for sequeces ivolvig roots. We will eed more techical expertise ad low cuig tha
Chapter 4 Sequeces III 4. Roots We ca use the results we ve established i the last workbook to fid some iterestig limits for sequeces ivolvig roots. We will eed more techical expertise ad low cuig tha
MA131 - Analysis 1. Workbook 7 Series I
 MA3 - Aalysis Workbook 7 Series I Autum 008 Cotets 4 Series 4. Defiitios............................... 4. Geometric Series........................... 4 4.3 The Harmoic Series.........................
MA3 - Aalysis Workbook 7 Series I Autum 008 Cotets 4 Series 4. Defiitios............................... 4. Geometric Series........................... 4 4.3 The Harmoic Series.........................
Tennessee Department of Education
 Teessee Departmet of Educatio Task: Comparig Shapes Geometry O a piece of graph paper with a coordiate plae, draw three o-colliear poits ad label them A, B, C. (Do ot use the origi as oe of your poits.)
Teessee Departmet of Educatio Task: Comparig Shapes Geometry O a piece of graph paper with a coordiate plae, draw three o-colliear poits ad label them A, B, C. (Do ot use the origi as oe of your poits.)
Recurrence Relations
 Recurrece Relatios Aalysis of recursive algorithms, such as: it factorial (it ) { if (==0) retur ; else retur ( * factorial(-)); } Let t be the umber of multiplicatios eeded to calculate factorial(). The
Recurrece Relatios Aalysis of recursive algorithms, such as: it factorial (it ) { if (==0) retur ; else retur ( * factorial(-)); } Let t be the umber of multiplicatios eeded to calculate factorial(). The
II. Descriptive Statistics D. Linear Correlation and Regression. 1. Linear Correlation
 II. Descriptive Statistics D. Liear Correlatio ad Regressio I this sectio Liear Correlatio Cause ad Effect Liear Regressio 1. Liear Correlatio Quatifyig Liear Correlatio The Pearso product-momet correlatio
II. Descriptive Statistics D. Liear Correlatio ad Regressio I this sectio Liear Correlatio Cause ad Effect Liear Regressio 1. Liear Correlatio Quatifyig Liear Correlatio The Pearso product-momet correlatio
Once we have a sequence of numbers, the next thing to do is to sum them up. Given a sequence (a n ) n=1
 . Ifiite Series Oce we have a sequece of umbers, the ext thig to do is to sum them up. Give a sequece a be a sequece: ca we give a sesible meaig to the followig expressio? a = a a a a While summig ifiitely
. Ifiite Series Oce we have a sequece of umbers, the ext thig to do is to sum them up. Give a sequece a be a sequece: ca we give a sesible meaig to the followig expressio? a = a a a a While summig ifiitely
Combinatorially Thinking
 Combiatorially Thiig SIMUW 2008: July 4 25 Jeifer J Qui jjqui@uwashigtoedu Philosophy We wat to costruct our mathematical uderstadig To this ed, our goal is to situate our problems i cocrete coutig cotexts
Combiatorially Thiig SIMUW 2008: July 4 25 Jeifer J Qui jjqui@uwashigtoedu Philosophy We wat to costruct our mathematical uderstadig To this ed, our goal is to situate our problems i cocrete coutig cotexts
is also known as the general term of the sequence
 Lesso : Sequeces ad Series Outlie Objectives: I ca determie whether a sequece has a patter. I ca determie whether a sequece ca be geeralized to fid a formula for the geeral term i the sequece. I ca determie
Lesso : Sequeces ad Series Outlie Objectives: I ca determie whether a sequece has a patter. I ca determie whether a sequece ca be geeralized to fid a formula for the geeral term i the sequece. I ca determie
Math 475, Problem Set #12: Answers
 Math 475, Problem Set #12: Aswers A. Chapter 8, problem 12, parts (b) ad (d). (b) S # (, 2) = 2 2, sice, from amog the 2 ways of puttig elemets ito 2 distiguishable boxes, exactly 2 of them result i oe
Math 475, Problem Set #12: Aswers A. Chapter 8, problem 12, parts (b) ad (d). (b) S # (, 2) = 2 2, sice, from amog the 2 ways of puttig elemets ito 2 distiguishable boxes, exactly 2 of them result i oe
subcaptionfont+=small,labelformat=parens,labelsep=space,skip=6pt,list=0,hypcap=0 subcaption ALGEBRAIC COMBINATORICS LECTURE 8 TUESDAY, 2/16/2016
 subcaptiofot+=small,labelformat=pares,labelsep=space,skip=6pt,list=0,hypcap=0 subcaptio ALGEBRAIC COMBINATORICS LECTURE 8 TUESDAY, /6/06. Self-cojugate Partitios Recall that, give a partitio λ, we may
subcaptiofot+=small,labelformat=pares,labelsep=space,skip=6pt,list=0,hypcap=0 subcaptio ALGEBRAIC COMBINATORICS LECTURE 8 TUESDAY, /6/06. Self-cojugate Partitios Recall that, give a partitio λ, we may
Frequentist Inference
 Frequetist Iferece The topics of the ext three sectios are useful applicatios of the Cetral Limit Theorem. Without kowig aythig about the uderlyig distributio of a sequece of radom variables {X i }, for
Frequetist Iferece The topics of the ext three sectios are useful applicatios of the Cetral Limit Theorem. Without kowig aythig about the uderlyig distributio of a sequece of radom variables {X i }, for
Statistics 511 Additional Materials
 Cofidece Itervals o mu Statistics 511 Additioal Materials This topic officially moves us from probability to statistics. We begi to discuss makig ifereces about the populatio. Oe way to differetiate probability
Cofidece Itervals o mu Statistics 511 Additioal Materials This topic officially moves us from probability to statistics. We begi to discuss makig ifereces about the populatio. Oe way to differetiate probability
MAT1026 Calculus II Basic Convergence Tests for Series
 MAT026 Calculus II Basic Covergece Tests for Series Egi MERMUT 202.03.08 Dokuz Eylül Uiversity Faculty of Sciece Departmet of Mathematics İzmir/TURKEY Cotets Mootoe Covergece Theorem 2 2 Series of Real
MAT026 Calculus II Basic Covergece Tests for Series Egi MERMUT 202.03.08 Dokuz Eylül Uiversity Faculty of Sciece Departmet of Mathematics İzmir/TURKEY Cotets Mootoe Covergece Theorem 2 2 Series of Real
(ii) Two-permutations of {a, b, c}. Answer. (B) P (3, 3) = 3! (C) 3! = 6, and there are 6 items in (A). ... Answer.
 SOLUTIONS Homewor 5 Due /6/19 Exercise. (a Cosider the set {a, b, c}. For each of the followig, (A list the objects described, (B give a formula that tells you how may you should have listed, ad (C verify
SOLUTIONS Homewor 5 Due /6/19 Exercise. (a Cosider the set {a, b, c}. For each of the followig, (A list the objects described, (B give a formula that tells you how may you should have listed, ad (C verify
Infinite Series. Definition. An infinite series is an expression of the form. Where the numbers u k are called the terms of the series.
 Ifiite Series Defiitio. A ifiite series is a expressio of the form uk = u + u + u + + u + () 2 3 k Where the umbers u k are called the terms of the series. Such a expressio is meat to be the result of
Ifiite Series Defiitio. A ifiite series is a expressio of the form uk = u + u + u + + u + () 2 3 k Where the umbers u k are called the terms of the series. Such a expressio is meat to be the result of
In algebra one spends much time finding common denominators and thus simplifying rational expressions. For example:
 74 The Method of Partial Fractios I algebra oe speds much time fidig commo deomiators ad thus simplifyig ratioal epressios For eample: + + + 6 5 + = + = = + + + + + ( )( ) 5 It may the seem odd to be watig
74 The Method of Partial Fractios I algebra oe speds much time fidig commo deomiators ad thus simplifyig ratioal epressios For eample: + + + 6 5 + = + = = + + + + + ( )( ) 5 It may the seem odd to be watig
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
 Preface Here are the solutios to the practice problems for my otes. Some solutios will have more or less detail tha other solutios. As the difficulty level of the problems icreases less detail will go
Preface Here are the solutios to the practice problems for my otes. Some solutios will have more or less detail tha other solutios. As the difficulty level of the problems icreases less detail will go
The Phi Power Series
 The Phi Power Series I did this work i about 0 years while poderig the relatioship betwee the golde mea ad the Madelbrot set. I have fially decided to make it available from my blog at http://semresearch.wordpress.com/.
The Phi Power Series I did this work i about 0 years while poderig the relatioship betwee the golde mea ad the Madelbrot set. I have fially decided to make it available from my blog at http://semresearch.wordpress.com/.
Math 299 Supplement: Real Analysis Nov 2013
 Math 299 Supplemet: Real Aalysis Nov 203 Algebra Axioms. I Real Aalysis, we work withi the axiomatic system of real umbers: the set R alog with the additio ad multiplicatio operatios +,, ad the iequality
Math 299 Supplemet: Real Aalysis Nov 203 Algebra Axioms. I Real Aalysis, we work withi the axiomatic system of real umbers: the set R alog with the additio ad multiplicatio operatios +,, ad the iequality
Sequences, Series, and All That
 Chapter Te Sequeces, Series, ad All That. Itroductio Suppose we wat to compute a approximatio of the umber e by usig the Taylor polyomial p for f ( x) = e x at a =. This polyomial is easily see to be 3
Chapter Te Sequeces, Series, ad All That. Itroductio Suppose we wat to compute a approximatio of the umber e by usig the Taylor polyomial p for f ( x) = e x at a =. This polyomial is easily see to be 3
Riemann Sums y = f (x)
 Riema Sums Recall that we have previously discussed the area problem I its simplest form we ca state it this way: The Area Problem Let f be a cotiuous, o-egative fuctio o the closed iterval [a, b] Fid
Riema Sums Recall that we have previously discussed the area problem I its simplest form we ca state it this way: The Area Problem Let f be a cotiuous, o-egative fuctio o the closed iterval [a, b] Fid
Lecture Chapter 6: Convergence of Random Sequences
 ECE5: Aalysis of Radom Sigals Fall 6 Lecture Chapter 6: Covergece of Radom Sequeces Dr Salim El Rouayheb Scribe: Abhay Ashutosh Doel, Qibo Zhag, Peiwe Tia, Pegzhe Wag, Lu Liu Radom sequece Defiitio A ifiite
ECE5: Aalysis of Radom Sigals Fall 6 Lecture Chapter 6: Covergece of Radom Sequeces Dr Salim El Rouayheb Scribe: Abhay Ashutosh Doel, Qibo Zhag, Peiwe Tia, Pegzhe Wag, Lu Liu Radom sequece Defiitio A ifiite
INTEGRATION BY PARTS (TABLE METHOD)
 INTEGRATION BY PARTS (TABLE METHOD) Suppose you wat to evaluate cos d usig itegratio by parts. Usig the u dv otatio, we get So, u dv d cos du d v si cos d si si d or si si d We see that it is ecessary
INTEGRATION BY PARTS (TABLE METHOD) Suppose you wat to evaluate cos d usig itegratio by parts. Usig the u dv otatio, we get So, u dv d cos du d v si cos d si si d or si si d We see that it is ecessary
Math 2784 (or 2794W) University of Connecticut
 ORDERS OF GROWTH PAT SMITH Math 2784 (or 2794W) Uiversity of Coecticut Date: Mar. 2, 22. ORDERS OF GROWTH. Itroductio Gaiig a ituitive feel for the relative growth of fuctios is importat if you really
ORDERS OF GROWTH PAT SMITH Math 2784 (or 2794W) Uiversity of Coecticut Date: Mar. 2, 22. ORDERS OF GROWTH. Itroductio Gaiig a ituitive feel for the relative growth of fuctios is importat if you really
n outcome is (+1,+1, 1,..., 1). Let the r.v. X denote our position (relative to our starting point 0) after n moves. Thus X = X 1 + X 2 + +X n,
 CS 70 Discrete Mathematics for CS Sprig 2008 David Wager Note 9 Variace Questio: At each time step, I flip a fair coi. If it comes up Heads, I walk oe step to the right; if it comes up Tails, I walk oe
CS 70 Discrete Mathematics for CS Sprig 2008 David Wager Note 9 Variace Questio: At each time step, I flip a fair coi. If it comes up Heads, I walk oe step to the right; if it comes up Tails, I walk oe
MA131 - Analysis 1. Workbook 3 Sequences II
 MA3 - Aalysis Workbook 3 Sequeces II Autum 2004 Cotets 2.8 Coverget Sequeces........................ 2.9 Algebra of Limits......................... 2 2.0 Further Useful Results........................
MA3 - Aalysis Workbook 3 Sequeces II Autum 2004 Cotets 2.8 Coverget Sequeces........................ 2.9 Algebra of Limits......................... 2 2.0 Further Useful Results........................
Definitions and Theorems. where x are the decision variables. c, b, and a are constant coefficients.
 Defiitios ad Theorems Remember the scalar form of the liear programmig problem, Miimize, Subject to, f(x) = c i x i a 1i x i = b 1 a mi x i = b m x i 0 i = 1,2,, where x are the decisio variables. c, b,
Defiitios ad Theorems Remember the scalar form of the liear programmig problem, Miimize, Subject to, f(x) = c i x i a 1i x i = b 1 a mi x i = b m x i 0 i = 1,2,, where x are the decisio variables. c, b,
TR/46 OCTOBER THE ZEROS OF PARTIAL SUMS OF A MACLAURIN EXPANSION A. TALBOT
 TR/46 OCTOBER 974 THE ZEROS OF PARTIAL SUMS OF A MACLAURIN EXPANSION by A. TALBOT .. Itroductio. A problem i approximatio theory o which I have recetly worked [] required for its solutio a proof that the
TR/46 OCTOBER 974 THE ZEROS OF PARTIAL SUMS OF A MACLAURIN EXPANSION by A. TALBOT .. Itroductio. A problem i approximatio theory o which I have recetly worked [] required for its solutio a proof that the
NICK DUFRESNE. 1 1 p(x). To determine some formulas for the generating function of the Schröder numbers, r(x) = a(x) =
 AN INTRODUCTION TO SCHRÖDER AND UNKNOWN NUMBERS NICK DUFRESNE Abstract. I this article we will itroduce two types of lattice paths, Schröder paths ad Ukow paths. We will examie differet properties of each,
AN INTRODUCTION TO SCHRÖDER AND UNKNOWN NUMBERS NICK DUFRESNE Abstract. I this article we will itroduce two types of lattice paths, Schröder paths ad Ukow paths. We will examie differet properties of each,
MATH 21 SECTION NOTES
 MATH SECTION NOTES EVAN WARNER. March 9.. Admiistrative miscellay. These weekly sectios will be for some review ad may example problems, i geeral. Attedace will be take as per class policy. We will be
MATH SECTION NOTES EVAN WARNER. March 9.. Admiistrative miscellay. These weekly sectios will be for some review ad may example problems, i geeral. Attedace will be take as per class policy. We will be
David Vella, Skidmore College.
 David Vella, Skidmore College dvella@skidmore.edu Geeratig Fuctios ad Expoetial Geeratig Fuctios Give a sequece {a } we ca associate to it two fuctios determied by power series: Its (ordiary) geeratig
David Vella, Skidmore College dvella@skidmore.edu Geeratig Fuctios ad Expoetial Geeratig Fuctios Give a sequece {a } we ca associate to it two fuctios determied by power series: Its (ordiary) geeratig
Calculus BC and BCD Drill on Sequences and Series!!! By Susan E. Cantey Walnut Hills H.S. 2006
 Calculus BC ad BCD Drill o Sequeces ad Series!!! By Susa E. Catey Walut Hills H.S. 2006 Sequeces ad Series I m goig to ask you questios about sequeces ad series ad drill you o some thigs that eed to be
Calculus BC ad BCD Drill o Sequeces ad Series!!! By Susa E. Catey Walut Hills H.S. 2006 Sequeces ad Series I m goig to ask you questios about sequeces ad series ad drill you o some thigs that eed to be
Sequences. Notation. Convergence of a Sequence
 Sequeces A sequece is essetially just a list. Defiitio (Sequece of Real Numbers). A sequece of real umbers is a fuctio Z (, ) R for some real umber. Do t let the descriptio of the domai cofuse you; it
Sequeces A sequece is essetially just a list. Defiitio (Sequece of Real Numbers). A sequece of real umbers is a fuctio Z (, ) R for some real umber. Do t let the descriptio of the domai cofuse you; it
Chapter 7: Numerical Series
 Chapter 7: Numerical Series Chapter 7 Overview: Sequeces ad Numerical Series I most texts, the topic of sequeces ad series appears, at first, to be a side topic. There are almost o derivatives or itegrals
Chapter 7: Numerical Series Chapter 7 Overview: Sequeces ad Numerical Series I most texts, the topic of sequeces ad series appears, at first, to be a side topic. There are almost o derivatives or itegrals
( 1) n (4x + 1) n. n=0
 Problem 1 (10.6, #). Fid the radius of covergece for the series: ( 1) (4x + 1). For what values of x does the series coverge absolutely, ad for what values of x does the series coverge coditioally? Solutio.
Problem 1 (10.6, #). Fid the radius of covergece for the series: ( 1) (4x + 1). For what values of x does the series coverge absolutely, ad for what values of x does the series coverge coditioally? Solutio.
Math 113 Exam 3 Practice
 Math Exam Practice Exam 4 will cover.-., 0. ad 0.. Note that eve though. was tested i exam, questios from that sectios may also be o this exam. For practice problems o., refer to the last review. This
Math Exam Practice Exam 4 will cover.-., 0. ad 0.. Note that eve though. was tested i exam, questios from that sectios may also be o this exam. For practice problems o., refer to the last review. This
CALCULUS II. Sequences and Series. Paul Dawkins
 CALCULUS II Sequeces ad Series Paul Dawkis Table of Cotets Preface... ii Sequeces ad Series... 3 Itroductio... 3 Sequeces... 5 More o Sequeces...5 Series The Basics... Series Covergece/Divergece...7 Series
CALCULUS II Sequeces ad Series Paul Dawkis Table of Cotets Preface... ii Sequeces ad Series... 3 Itroductio... 3 Sequeces... 5 More o Sequeces...5 Series The Basics... Series Covergece/Divergece...7 Series
Math 61CM - Solutions to homework 3
 Math 6CM - Solutios to homework 3 Cédric De Groote October 2 th, 208 Problem : Let F be a field, m 0 a fixed oegative iteger ad let V = {a 0 + a x + + a m x m a 0,, a m F} be the vector space cosistig
Math 6CM - Solutios to homework 3 Cédric De Groote October 2 th, 208 Problem : Let F be a field, m 0 a fixed oegative iteger ad let V = {a 0 + a x + + a m x m a 0,, a m F} be the vector space cosistig
Math 451: Euclidean and Non-Euclidean Geometry MWF 3pm, Gasson 204 Homework 3 Solutions
 Math 451: Euclidea ad No-Euclidea Geometry MWF 3pm, Gasso 204 Homework 3 Solutios Exercises from 1.4 ad 1.5 of the otes: 4.3, 4.10, 4.12, 4.14, 4.15, 5.3, 5.4, 5.5 Exercise 4.3. Explai why Hp, q) = {x
Math 451: Euclidea ad No-Euclidea Geometry MWF 3pm, Gasso 204 Homework 3 Solutios Exercises from 1.4 ad 1.5 of the otes: 4.3, 4.10, 4.12, 4.14, 4.15, 5.3, 5.4, 5.5 Exercise 4.3. Explai why Hp, q) = {x
Fall 2018 Exam 2 PIN: 17 INSTRUCTIONS
 MARK BOX problem poits 0 0 HAND IN PART 0 3 0 NAME: Solutios 4 0 0 PIN: 6-3x % 00 INSTRUCTIONS This exam comes i two parts. () HAND IN PART. Had i oly this part. () STATEMENT OF MULTIPLE CHOICE PROBLEMS.
MARK BOX problem poits 0 0 HAND IN PART 0 3 0 NAME: Solutios 4 0 0 PIN: 6-3x % 00 INSTRUCTIONS This exam comes i two parts. () HAND IN PART. Had i oly this part. () STATEMENT OF MULTIPLE CHOICE PROBLEMS.
Revision Topic 1: Number and algebra
 Revisio Topic : Number ad algebra Chapter : Number Differet types of umbers You eed to kow that there are differet types of umbers ad recogise which group a particular umber belogs to: Type of umber Symbol
Revisio Topic : Number ad algebra Chapter : Number Differet types of umbers You eed to kow that there are differet types of umbers ad recogise which group a particular umber belogs to: Type of umber Symbol
Machine Learning for Data Science (CS 4786)
 Machie Learig for Data Sciece CS 4786) Lecture & 3: Pricipal Compoet Aalysis The text i black outlies high level ideas. The text i blue provides simple mathematical details to derive or get to the algorithm
Machie Learig for Data Sciece CS 4786) Lecture & 3: Pricipal Compoet Aalysis The text i black outlies high level ideas. The text i blue provides simple mathematical details to derive or get to the algorithm
Sequences, Mathematical Induction, and Recursion. CSE 2353 Discrete Computational Structures Spring 2018
 CSE 353 Discrete Computatioal Structures Sprig 08 Sequeces, Mathematical Iductio, ad Recursio (Chapter 5, Epp) Note: some course slides adopted from publisher-provided material Overview May mathematical
CSE 353 Discrete Computatioal Structures Sprig 08 Sequeces, Mathematical Iductio, ad Recursio (Chapter 5, Epp) Note: some course slides adopted from publisher-provided material Overview May mathematical
Chapter 7 COMBINATIONS AND PERMUTATIONS. where we have the specific formula for the binomial coefficients:
 Chapter 7 COMBINATIONS AND PERMUTATIONS We have see i the previous chapter that (a + b) ca be writte as 0 a % a & b%þ% a & b %þ% b where we have the specific formula for the biomial coefficiets: '!!(&)!
Chapter 7 COMBINATIONS AND PERMUTATIONS We have see i the previous chapter that (a + b) ca be writte as 0 a % a & b%þ% a & b %þ% b where we have the specific formula for the biomial coefficiets: '!!(&)!
Topic 1 2: Sequences and Series. A sequence is an ordered list of numbers, e.g. 1, 2, 4, 8, 16, or
 Topic : Sequeces ad Series A sequece is a ordered list of umbers, e.g.,,, 8, 6, or,,,.... A series is a sum of the terms of a sequece, e.g. + + + 8 + 6 + or... Sigma Notatio b The otatio f ( k) is shorthad
Topic : Sequeces ad Series A sequece is a ordered list of umbers, e.g.,,, 8, 6, or,,,.... A series is a sum of the terms of a sequece, e.g. + + + 8 + 6 + or... Sigma Notatio b The otatio f ( k) is shorthad
