Creating transformations for matrix obfuscation
|
|
|
- Miranda Clark
- 5 years ago
- Views:
Transcription
1 Creating transformations for matrix obfuscation Stephen Drape and Irina Voiculescu Oxford University Computing Laboratory August / 23
2 What is Obfuscation? An obfuscation is: a program transformation used to make programs `harder to understand' a technique for protecting intellectual property not encryption The area of obfuscation needs more research 2 / 23
3 Two Important Papers Christian Collberg, Clark Thomborson, and Douglas Low. A taxonomy of obfuscating transformations. Technical Report 148, Department of Computer Science, University of Auckland, July Boaz Barak, Oded Goldreich, Russell Impagliazzo, Steven Rudich, Amit Sahai, Salil P. Vadhan, and Ke Yang. On the (im)possibility of obfuscating programs. In Proceedings of the 21st Annual International Cryptology Conference on Advances in Cryptology, pages 118. Springer-Verlag, / 23
4 Attack models and static analysis It is impossible to create obfuscations that could withstand all possible attacks (such as static analyses). Should aim to produce obfuscations designed to withstand certain attacks this is the attack model. For example, restricting the usefulness of program slicing. Our attack model assumes that the attacker is trying to prove various program assertions. 4 / 23
5 Obfuscation as data renement Localised obfuscation: obfuscate certain parts of the program, such as particular methods or variables. Data renement obfuscation: obfuscate an abstract data-type (implicitly) obfuscate all the operations of the data-type specify a set of assertions that the data-type operations satisfy (as part of the attack model) obfuscation makes these assertions `harder to prove' 5 / 23
6 Obfuscation Equations To obfuscate a data-type D into E using an obfuscation O, we need an abstraction function af. For x :: D and y :: E: x y (x = af (y)) dti(y) An obfuscated function f O is correct with respect to f if it satises: We can rewrite this as ( x :: D; y :: E) x y f(x) f O (y) f af = af f O 6 / 23
7 Obfuscating matrices Matrices are essential in solving systems of equations, wavelets, graph theory, graphics. The focus of this work is on obfuscating matrices through Our work changing the matrix elements changing the pattern of the elements studies one established obfuscation develops a new obfuscation shows how matrices can be used to obfuscate numbers 7 / 23
8 Matrix Data-Type Matrix (α) scale :: α Matrix α Matrix α add :: Matrix α Matrix α Matrix α transpose :: Matrix α Matrix α mult :: Matrix α Matrix α Matrix α transpose transpose = id transpose (scale λ) = (scale λ) transpose transpose (mult(m, N)) = mult (transpose N, transpose M) add(m, N) = add(n, M) We will take Matrix (α) to be Q r c 8 / 23
9 Matrices Suppose that we want to split a matrix M r c into n matrices, called the split components, M M 0,..., M n 1 sp where M i has size r i c i for i : [0..n). We can characterise a split sp by dening: a choice function ch a family F of injective functions where F = {f t } t:[0..n) 9 / 23
10 Dening the splitting relationship We dene the relationship between M and the split components element-wise: M t (f t (i, j)) = M(i, j) where t = ch(i, j) The abstraction function for some split component M t is af (M t (i, j)) = M(f t 1 (i, j)) where f t 1 f t = id (which is valid as f t is injective). 10 / 23
11 Example Split We can dene a split, called the (k k)-square split (denoted by s k ) by ensuring that the rst component is a k k matrix. a (0,0)... a (0,k 1) a (0,k)... a (0,n 1) a (k 1,0)... a (k 1,k 1) a (k 1,k)... a (k 1,n 1) a (k,0)... a (k,k 1) a (k,k)... a (k,n 1) a (n 1,0)... a (n 1,k 1) a (n 1,k)... a (n 1,n 1) We will show the denitions of our matrix operations for this split. 11 / 23
12 Operations for split matrices If M M 0,..., M 3 sk and N N 0,..., N 3 sk then scale λ M scale λ M 0,..., scale λ M 3 sk add (M, N) add (M 0, N 0 ),..., add (M 3, N 3 ) sk M T M 0 T, M 2 T, M 1 T, M 3 T sk M N (M 0 N 0 ) + (M 1 N 2 ), (M 0 N 1 ) + (M 1 N 3 ), (M 2 N 0 ) + (M 3 N 2 ), (M 2 N 1 ) + (M 3 N 3 ) sk 12 / 23
13 Review of The obfuscated operations have a similar complexity to the original versions. We can use matrix splitting as an array obfuscation. It is hard to dene determinants and inverses for split matrices. The obfuscation changes the shape of the matrices but not the actual matrix values. 13 / 23
14 Polynomial bases Matrix A 1 y y x x stores p(x, y) = x 2 y 2 + 3xy 2 + 2y 2 + xy + 1 p(x, y) = ( 1 x x 2) y y 2 = XAY 14 / 23
15 Bernstein bases Can change the basis of the linear transformation using Bernstein polynomials Bk n(x) = ( n k) x k (1 x) n k, x [0, 1], k = 0,..., n. p B (x, y) = ( B 2 0 (x) B2 1 (x) B2 2 (x)) C B 2 0 (y) B 2 1 (y) B2 2(y) = ( 1 x x 2) C y y 2 = X U 2 C V 2 Y 15 / 23
16 Bernstein obfuscation of matrices Since XAY = p(x, y) = p B (x, y) = XU 2 CV 2 Y the Bernstein-form matrix corresponding to A = is C = U 2 1 AV 2 1 = and can be used as an obfuscation of A / 23
17 Operations for the Bernstein Obfuscation For a matrix S with dim(s) = (a + 1, b + 1), and a matrix T, it can be proved that scale B λ S = scale λ S add B (S, T) = S + T transpose B (S) = U b 1 V b T S T U a T V a 1 mult B (S, T) = S V b U b T inverse B (S) = U a 1 V a 1 S 1 U a 1 V a 1 det B (S) = det(u a ) det(s) det(v b ) 17 / 23
18 Review of the Bernstein obfuscation The obfuscated matrices have dierent structure. Determinants and inverses of matrices can be computed easily. The scaling and addition operations are not obfuscated. Any change of basis transformation would be suitable. We can generalise to more than two dimensions, or to arrays. There is an extra cost in computational complexity. 18 / 23
19 Using matrices to obfuscate numbers We can use matrices to obfuscate other data-types. To obfuscate a rational number data-type which contains the operations of addition, multiplication and reciprocal. We need matrix operations plus, times and recip such that, for rational numbers n and p, if n A and p C then n + p plus(a, C) n p times(a, C) n 1 recip(a) 19 / 23
20 Using determinants There are many ways in which to use matrices for the obfuscation of rational numbers. We show an obfuscation whose abstraction function is the determinant. We choose to obfuscate a number n by a 2 2 matrix which has 1 and n as eigenvalues. Here is one possible transformation (where a Q): ( ) a b n where b 0 n + 1 a (a 1)(n a) b 20 / 23
21 Obfuscated number operations ( ) ( ) ( ) a b e f a + e 1 bf plus(, ) = c d g h d + h (a+e 2)(d+h 1) bf ( ) ( ) (a + d)(e + h) + 1 bf a b e f times(, ) = c d g h 1 a d e h ( ) a b recip( ) = c d (a+d)(e+h)(a+d+e+h) bf d a+d 1 (a 1)(d 1) b(a+d 1) 2 b a a+d 1 21 / 23
22 Evaluation of techniques We have considered obfuscations at an appropriate level of abstraction: we are not concerned with implementation details. Our obfuscations can be evaluated against the assertion attack model: our obfuscations make the assertions harder to prove. To understand our matrix obfuscations, a human attacker needs, e.g., familiarity with the Bernstein basis and with the relationship between bi-variate polynomials and matrices. We can combine obfuscations to create more complicated obfuscations. 22 / 23
23 The Bernstein obfuscation allows us to devise obfuscations for a wider variety of matrix operations than matrix splitting did. However the Bernstein obfuscation can adversely aect the complexity of the matrix operations. There is usually a trade-o between the quality of the obfuscations and their complexity. Considering obfuscations at an abstract level creates the opportunity to devise more general obfuscations. 23 / 23
Creating transformations for matrix obfuscation
 Creating transformations for matrix obfuscation Stephen Drape and Irina Voiculescu Oxford University Computing Laboratory, Wolfosn Building, Parks Road, Oxford, UK, OX1 3QD {sjd,irina}@comlab.ox.ac.uk
Creating transformations for matrix obfuscation Stephen Drape and Irina Voiculescu Oxford University Computing Laboratory, Wolfosn Building, Parks Road, Oxford, UK, OX1 3QD {sjd,irina}@comlab.ox.ac.uk
Obfuscation without Multilinear Maps
 Obfuscation without Multilinear Maps Dingfeng Ye Peng Liu DCS Center Cyber Security Lab nstitute of nformation Engineering College of nformation Sciences and Technology Chinese Academy of Sciences Pennsylvania
Obfuscation without Multilinear Maps Dingfeng Ye Peng Liu DCS Center Cyber Security Lab nstitute of nformation Engineering College of nformation Sciences and Technology Chinese Academy of Sciences Pennsylvania
4.1 Eigenvalues, Eigenvectors, and The Characteristic Polynomial
 Linear Algebra (part 4): Eigenvalues, Diagonalization, and the Jordan Form (by Evan Dummit, 27, v ) Contents 4 Eigenvalues, Diagonalization, and the Jordan Canonical Form 4 Eigenvalues, Eigenvectors, and
Linear Algebra (part 4): Eigenvalues, Diagonalization, and the Jordan Form (by Evan Dummit, 27, v ) Contents 4 Eigenvalues, Diagonalization, and the Jordan Canonical Form 4 Eigenvalues, Eigenvectors, and
Answers and Solutions to Selected Homework Problems From Section 2.5 S. F. Ellermeyer. and B =. 0 2
 Answers and Solutions to Selected Homework Problems From Section 2.5 S. F. Ellermeyer 5. Since gcd (2; 4) 6, then 2 is a zero divisor (and not a unit) in Z 4. In fact, we see that 2 2 0 in Z 4. Thus 2x
Answers and Solutions to Selected Homework Problems From Section 2.5 S. F. Ellermeyer 5. Since gcd (2; 4) 6, then 2 is a zero divisor (and not a unit) in Z 4. In fact, we see that 2 2 0 in Z 4. Thus 2x
Vision 3D articielle Session 2: Essential and fundamental matrices, their computation, RANSAC algorithm
 Vision 3D articielle Session 2: Essential and fundamental matrices, their computation, RANSAC algorithm Pascal Monasse monasse@imagine.enpc.fr IMAGINE, École des Ponts ParisTech Contents Some useful rules
Vision 3D articielle Session 2: Essential and fundamental matrices, their computation, RANSAC algorithm Pascal Monasse monasse@imagine.enpc.fr IMAGINE, École des Ponts ParisTech Contents Some useful rules
Implicit Differentiation
 Implicit Differentiation Sometimes we have a curve in the plane defined by a function Fxy= (, ) 0 (1) that involves both x and y, possibly in complicated ways. Examples. We show below the graphs of the
Implicit Differentiation Sometimes we have a curve in the plane defined by a function Fxy= (, ) 0 (1) that involves both x and y, possibly in complicated ways. Examples. We show below the graphs of the
Lecture 2: Program Obfuscation - II April 1, 2009
 Advanced Topics in Cryptography Lecture 2: Program Obfuscation - II April 1, 2009 Lecturer: S. Goldwasser, M. Naor Scribe by: R. Marianer, R. Rothblum Updated: May 3, 2009 1 Introduction Barak et-al[1]
Advanced Topics in Cryptography Lecture 2: Program Obfuscation - II April 1, 2009 Lecturer: S. Goldwasser, M. Naor Scribe by: R. Marianer, R. Rothblum Updated: May 3, 2009 1 Introduction Barak et-al[1]
linearly indepedent eigenvectors as the multiplicity of the root, but in general there may be no more than one. For further discussion, assume matrice
 3. Eigenvalues and Eigenvectors, Spectral Representation 3.. Eigenvalues and Eigenvectors A vector ' is eigenvector of a matrix K, if K' is parallel to ' and ' 6, i.e., K' k' k is the eigenvalue. If is
3. Eigenvalues and Eigenvectors, Spectral Representation 3.. Eigenvalues and Eigenvectors A vector ' is eigenvector of a matrix K, if K' is parallel to ' and ' 6, i.e., K' k' k is the eigenvalue. If is
A Finite Element Method for an Ill-Posed Problem. Martin-Luther-Universitat, Fachbereich Mathematik/Informatik,Postfach 8, D Halle, Abstract
 A Finite Element Method for an Ill-Posed Problem W. Lucht Martin-Luther-Universitat, Fachbereich Mathematik/Informatik,Postfach 8, D-699 Halle, Germany Abstract For an ill-posed problem which has its origin
A Finite Element Method for an Ill-Posed Problem W. Lucht Martin-Luther-Universitat, Fachbereich Mathematik/Informatik,Postfach 8, D-699 Halle, Germany Abstract For an ill-posed problem which has its origin
Functional equations 1.
 Functional equations. What is a function? Technically speaking, it would be rather impossible to give a proper notion of a function. We will need to use other words, such as 'relation', 'map' or other,
Functional equations. What is a function? Technically speaking, it would be rather impossible to give a proper notion of a function. We will need to use other words, such as 'relation', 'map' or other,
Skills Practice Skills Practice for Lesson 10.1
 Skills Practice Skills Practice for Lesson.1 Name Date Higher Order Polynomials and Factoring Roots of Polynomial Equations Problem Set Solve each polynomial equation using factoring. Then check your solution(s).
Skills Practice Skills Practice for Lesson.1 Name Date Higher Order Polynomials and Factoring Roots of Polynomial Equations Problem Set Solve each polynomial equation using factoring. Then check your solution(s).
Integer Circuit Evaluation is PSPACE-complete. Ke Yang. Computer Science Department, Carnegie Mellon University, 5000 Forbes Ave.
 Integer Circuit Evaluation is PSPACE-complete Ke Yang Computer Science Department, Carnegie Mellon University, 5000 Forbes Ave., Pittsburgh, PA 15213, USA E-mail: yangke@cmu.edu Key Words: PSPACE, Integer
Integer Circuit Evaluation is PSPACE-complete Ke Yang Computer Science Department, Carnegie Mellon University, 5000 Forbes Ave., Pittsburgh, PA 15213, USA E-mail: yangke@cmu.edu Key Words: PSPACE, Integer
Linear Algebra, 4th day, Thursday 7/1/04 REU Info:
 Linear Algebra, 4th day, Thursday 7/1/04 REU 004. Info http//people.cs.uchicago.edu/laci/reu04. Instructor Laszlo Babai Scribe Nick Gurski 1 Linear maps We shall study the notion of maps between vector
Linear Algebra, 4th day, Thursday 7/1/04 REU 004. Info http//people.cs.uchicago.edu/laci/reu04. Instructor Laszlo Babai Scribe Nick Gurski 1 Linear maps We shall study the notion of maps between vector
IMC 2015, Blagoevgrad, Bulgaria
 IMC 05, Blagoevgrad, Bulgaria Day, July 9, 05 Problem. For any integer n and two n n matrices with real entries, B that satisfy the equation + B ( + B prove that det( det(b. Does the same conclusion follow
IMC 05, Blagoevgrad, Bulgaria Day, July 9, 05 Problem. For any integer n and two n n matrices with real entries, B that satisfy the equation + B ( + B prove that det( det(b. Does the same conclusion follow
Journal of the Association for Computing Machinery. On the (Im)possibility of Obfuscating Programs. For Peer Review
 On the (Im)possibility of Obfuscating Programs Journal: Journal of the ACM Manuscript ID: Manuscript Type: Date Submitted by the Author: JACM-0000-0 Paper -Jan-0 Complete List of Authors: Barak, Boaz;
On the (Im)possibility of Obfuscating Programs Journal: Journal of the ACM Manuscript ID: Manuscript Type: Date Submitted by the Author: JACM-0000-0 Paper -Jan-0 Complete List of Authors: Barak, Boaz;
Eigenvalues and Eigenvectors
 LECTURE 3 Eigenvalues and Eigenvectors Definition 3.. Let A be an n n matrix. The eigenvalue-eigenvector problem for A is the problem of finding numbers λ and vectors v R 3 such that Av = λv. If λ, v are
LECTURE 3 Eigenvalues and Eigenvectors Definition 3.. Let A be an n n matrix. The eigenvalue-eigenvector problem for A is the problem of finding numbers λ and vectors v R 3 such that Av = λv. If λ, v are
Lecture 12: Diagonalization
 Lecture : Diagonalization A square matrix D is called diagonal if all but diagonal entries are zero: a a D a n 5 n n. () Diagonal matrices are the simplest matrices that are basically equivalent to vectors
Lecture : Diagonalization A square matrix D is called diagonal if all but diagonal entries are zero: a a D a n 5 n n. () Diagonal matrices are the simplest matrices that are basically equivalent to vectors
Vector Space Basics. 1 Abstract Vector Spaces. 1. (commutativity of vector addition) u + v = v + u. 2. (associativity of vector addition)
 Vector Space Basics (Remark: these notes are highly formal and may be a useful reference to some students however I am also posting Ray Heitmann's notes to Canvas for students interested in a direct computational
Vector Space Basics (Remark: these notes are highly formal and may be a useful reference to some students however I am also posting Ray Heitmann's notes to Canvas for students interested in a direct computational
Math 291-2: Final Exam Solutions Northwestern University, Winter 2016
 Math 29-2: Final Exam Solutions Northwestern University, Winter 206 Determine whether each of the following statements is true or false f it is true, explain why; if it is false, give a counterexample
Math 29-2: Final Exam Solutions Northwestern University, Winter 206 Determine whether each of the following statements is true or false f it is true, explain why; if it is false, give a counterexample
LECTURE VI: SELF-ADJOINT AND UNITARY OPERATORS MAT FALL 2006 PRINCETON UNIVERSITY
 LECTURE VI: SELF-ADJOINT AND UNITARY OPERATORS MAT 204 - FALL 2006 PRINCETON UNIVERSITY ALFONSO SORRENTINO 1 Adjoint of a linear operator Note: In these notes, V will denote a n-dimensional euclidean vector
LECTURE VI: SELF-ADJOINT AND UNITARY OPERATORS MAT 204 - FALL 2006 PRINCETON UNIVERSITY ALFONSO SORRENTINO 1 Adjoint of a linear operator Note: In these notes, V will denote a n-dimensional euclidean vector
CCSS Math- Algebra. Domain: Algebra Seeing Structure in Expressions A-SSE. Pacing Guide. Standard: Interpret the structure of expressions.
 1 Domain: Algebra Seeing Structure in Expressions A-SSE Standard: Interpret the structure of expressions. H.S. A-SSE.1a. Interpret expressions that represent a quantity in terms of its context. Content:
1 Domain: Algebra Seeing Structure in Expressions A-SSE Standard: Interpret the structure of expressions. H.S. A-SSE.1a. Interpret expressions that represent a quantity in terms of its context. Content:
MAT116 Final Review Session Chapter 3: Polynomial and Rational Functions
 MAT116 Final Review Session Chapter 3: Polynomial and Rational Functions Quadratic Function A quadratic function is defined by a quadratic or second-degree polynomial. Standard Form f x = ax 2 + bx + c,
MAT116 Final Review Session Chapter 3: Polynomial and Rational Functions Quadratic Function A quadratic function is defined by a quadratic or second-degree polynomial. Standard Form f x = ax 2 + bx + c,
Section 3.6 Complex Zeros
 04 Chapter Section 6 Complex Zeros When finding the zeros of polynomials, at some point you're faced with the problem x = While there are clearly no real numbers that are solutions to this equation, leaving
04 Chapter Section 6 Complex Zeros When finding the zeros of polynomials, at some point you're faced with the problem x = While there are clearly no real numbers that are solutions to this equation, leaving
N.G.Bean, D.A.Green and P.G.Taylor. University of Adelaide. Adelaide. Abstract. process of an MMPP/M/1 queue is not a MAP unless the queue is a
 WHEN IS A MAP POISSON N.G.Bean, D.A.Green and P.G.Taylor Department of Applied Mathematics University of Adelaide Adelaide 55 Abstract In a recent paper, Olivier and Walrand (994) claimed that the departure
WHEN IS A MAP POISSON N.G.Bean, D.A.Green and P.G.Taylor Department of Applied Mathematics University of Adelaide Adelaide 55 Abstract In a recent paper, Olivier and Walrand (994) claimed that the departure
Introduction. A rational function is a quotient of polynomial functions. It can be written in the form
 RATIONAL FUNCTIONS Introduction A rational function is a quotient of polynomial functions. It can be written in the form where N(x) and D(x) are polynomials and D(x) is not the zero polynomial. 2 In general,
RATIONAL FUNCTIONS Introduction A rational function is a quotient of polynomial functions. It can be written in the form where N(x) and D(x) are polynomials and D(x) is not the zero polynomial. 2 In general,
Beal City High School Algebra 2A Curriculum and Alignment
 Beal City High School Algebra 2A Curriculum and Alignment UNIT 1 Linear Functions (Chapters 1-3) 1. Combine like terms, solve equations, solve inequalities, evaluate expressions(1-2,3,4) 2. Solve an equation
Beal City High School Algebra 2A Curriculum and Alignment UNIT 1 Linear Functions (Chapters 1-3) 1. Combine like terms, solve equations, solve inequalities, evaluate expressions(1-2,3,4) 2. Solve an equation
Mathematics High School Algebra
 Mathematics High School Algebra Expressions. An expression is a record of a computation with numbers, symbols that represent numbers, arithmetic operations, exponentiation, and, at more advanced levels,
Mathematics High School Algebra Expressions. An expression is a record of a computation with numbers, symbols that represent numbers, arithmetic operations, exponentiation, and, at more advanced levels,
Math Linear Algebra II. 1. Inner Products and Norms
 Math 342 - Linear Algebra II Notes 1. Inner Products and Norms One knows from a basic introduction to vectors in R n Math 254 at OSU) that the length of a vector x = x 1 x 2... x n ) T R n, denoted x,
Math 342 - Linear Algebra II Notes 1. Inner Products and Norms One knows from a basic introduction to vectors in R n Math 254 at OSU) that the length of a vector x = x 1 x 2... x n ) T R n, denoted x,
5 Eigenvalues and Diagonalization
 Linear Algebra (part 5): Eigenvalues and Diagonalization (by Evan Dummit, 27, v 5) Contents 5 Eigenvalues and Diagonalization 5 Eigenvalues, Eigenvectors, and The Characteristic Polynomial 5 Eigenvalues
Linear Algebra (part 5): Eigenvalues and Diagonalization (by Evan Dummit, 27, v 5) Contents 5 Eigenvalues and Diagonalization 5 Eigenvalues, Eigenvectors, and The Characteristic Polynomial 5 Eigenvalues
Solutions for Math 225 Assignment #5 1
 Solutions for Math 225 Assignment #5 1 (1) Find a polynomial f(x) of degree at most 3 satisfying that f(0) = 2, f( 1) = 1, f(1) = 3 and f(3) = 1. Solution. By Lagrange Interpolation, ( ) (x + 1)(x 1)(x
Solutions for Math 225 Assignment #5 1 (1) Find a polynomial f(x) of degree at most 3 satisfying that f(0) = 2, f( 1) = 1, f(1) = 3 and f(3) = 1. Solution. By Lagrange Interpolation, ( ) (x + 1)(x 1)(x
On the (Im)possibility of Obfuscating Programs
 On the (Im)possibility of Obfuscating Programs The Harvard community has made this article openly available. Please share how this access benefits you. Your story matters Citation Barak, Boaz, Oded Goldreich,
On the (Im)possibility of Obfuscating Programs The Harvard community has made this article openly available. Please share how this access benefits you. Your story matters Citation Barak, Boaz, Oded Goldreich,
MATA Y, Tutorial #11, Lucas Ashbury-Bridgwood
 MATA 018Y, Tutorial #11, Lucas Ashbury-Bridgwood 1 today Q5 pick-up + solution A11 Q5 pick-up 0:100:15 3 Q5 solution 0:150:35 A11.1 A11 #3e 0:300:50 0 Find the eigenvalues A and compute det A, det A 3
MATA 018Y, Tutorial #11, Lucas Ashbury-Bridgwood 1 today Q5 pick-up + solution A11 Q5 pick-up 0:100:15 3 Q5 solution 0:150:35 A11.1 A11 #3e 0:300:50 0 Find the eigenvalues A and compute det A, det A 3
Contents. 2 Partial Derivatives. 2.1 Limits and Continuity. Calculus III (part 2): Partial Derivatives (by Evan Dummit, 2017, v. 2.
 Calculus III (part 2): Partial Derivatives (by Evan Dummit, 2017, v 260) Contents 2 Partial Derivatives 1 21 Limits and Continuity 1 22 Partial Derivatives 5 23 Directional Derivatives and the Gradient
Calculus III (part 2): Partial Derivatives (by Evan Dummit, 2017, v 260) Contents 2 Partial Derivatives 1 21 Limits and Continuity 1 22 Partial Derivatives 5 23 Directional Derivatives and the Gradient
Homework For each of the following matrices, find the minimal polynomial and determine whether the matrix is diagonalizable.
 Math 5327 Fall 2018 Homework 7 1. For each of the following matrices, find the minimal polynomial and determine whether the matrix is diagonalizable. 3 1 0 (a) A = 1 2 0 1 1 0 x 3 1 0 Solution: 1 x 2 0
Math 5327 Fall 2018 Homework 7 1. For each of the following matrices, find the minimal polynomial and determine whether the matrix is diagonalizable. 3 1 0 (a) A = 1 2 0 1 1 0 x 3 1 0 Solution: 1 x 2 0
Math Camp Notes: Linear Algebra II
 Math Camp Notes: Linear Algebra II Eigenvalues Let A be a square matrix. An eigenvalue is a number λ which when subtracted from the diagonal elements of the matrix A creates a singular matrix. In other
Math Camp Notes: Linear Algebra II Eigenvalues Let A be a square matrix. An eigenvalue is a number λ which when subtracted from the diagonal elements of the matrix A creates a singular matrix. In other
Linear Algebra March 16, 2019
 Linear Algebra March 16, 2019 2 Contents 0.1 Notation................................ 4 1 Systems of linear equations, and matrices 5 1.1 Systems of linear equations..................... 5 1.2 Augmented
Linear Algebra March 16, 2019 2 Contents 0.1 Notation................................ 4 1 Systems of linear equations, and matrices 5 1.1 Systems of linear equations..................... 5 1.2 Augmented
Limits at Infinity. Horizontal Asymptotes. Definition (Limits at Infinity) Horizontal Asymptotes
 Limits at Infinity If a function f has a domain that is unbounded, that is, one of the endpoints of its domain is ±, we can determine the long term behavior of the function using a it at infinity. Definition
Limits at Infinity If a function f has a domain that is unbounded, that is, one of the endpoints of its domain is ±, we can determine the long term behavior of the function using a it at infinity. Definition
Group Theory. 1. Show that Φ maps a conjugacy class of G into a conjugacy class of G.
 Group Theory Jan 2012 #6 Prove that if G is a nonabelian group, then G/Z(G) is not cyclic. Aug 2011 #9 (Jan 2010 #5) Prove that any group of order p 2 is an abelian group. Jan 2012 #7 G is nonabelian nite
Group Theory Jan 2012 #6 Prove that if G is a nonabelian group, then G/Z(G) is not cyclic. Aug 2011 #9 (Jan 2010 #5) Prove that any group of order p 2 is an abelian group. Jan 2012 #7 G is nonabelian nite
Math 1270 Honors ODE I Fall, 2008 Class notes # 14. x 0 = F (x; y) y 0 = G (x; y) u 0 = au + bv = cu + dv
 Math 1270 Honors ODE I Fall, 2008 Class notes # 1 We have learned how to study nonlinear systems x 0 = F (x; y) y 0 = G (x; y) (1) by linearizing around equilibrium points. If (x 0 ; y 0 ) is an equilibrium
Math 1270 Honors ODE I Fall, 2008 Class notes # 1 We have learned how to study nonlinear systems x 0 = F (x; y) y 0 = G (x; y) (1) by linearizing around equilibrium points. If (x 0 ; y 0 ) is an equilibrium
On the (Im)possibility of Obfuscating Programs
 On the (Im)possibility of Obfuscating Programs Boaz Barak Oded Goldreich Russell Impagliazzo Steven Rudich Amit Sahai Salil Vadhan Ke Yang November 13, 2001 Abstract Informally, an obfuscator O is an (efficient,
On the (Im)possibility of Obfuscating Programs Boaz Barak Oded Goldreich Russell Impagliazzo Steven Rudich Amit Sahai Salil Vadhan Ke Yang November 13, 2001 Abstract Informally, an obfuscator O is an (efficient,
Algebra I Number and Quantity The Real Number System (N-RN)
 Number and Quantity The Real Number System (N-RN) Use properties of rational and irrational numbers N-RN.3 Explain why the sum or product of two rational numbers is rational; that the sum of a rational
Number and Quantity The Real Number System (N-RN) Use properties of rational and irrational numbers N-RN.3 Explain why the sum or product of two rational numbers is rational; that the sum of a rational
Course: Algebra MP: Reason abstractively and quantitatively MP: Model with mathematics MP: Look for and make use of structure
 Algebra Cluster: Interpret the structure of expressions. A.SSE.1: Interpret expressions that represent a quantity in terms of its context (Modeling standard). a. Interpret parts of an expression, such
Algebra Cluster: Interpret the structure of expressions. A.SSE.1: Interpret expressions that represent a quantity in terms of its context (Modeling standard). a. Interpret parts of an expression, such
Linear Algebra. Matrices Operations. Consider, for example, a system of equations such as x + 2y z + 4w = 0, 3x 4y + 2z 6w = 0, x 3y 2z + w = 0.
 Matrices Operations Linear Algebra Consider, for example, a system of equations such as x + 2y z + 4w = 0, 3x 4y + 2z 6w = 0, x 3y 2z + w = 0 The rectangular array 1 2 1 4 3 4 2 6 1 3 2 1 in which the
Matrices Operations Linear Algebra Consider, for example, a system of equations such as x + 2y z + 4w = 0, 3x 4y + 2z 6w = 0, x 3y 2z + w = 0 The rectangular array 1 2 1 4 3 4 2 6 1 3 2 1 in which the
Midterm Review. Name: Class: Date: ID: A. Short Answer. 1. For each graph, write the equation of a radical function of the form y = a b(x h) + k.
 Name: Class: Date: ID: A Midterm Review Short Answer 1. For each graph, write the equation of a radical function of the form y = a b(x h) + k. a) b) c) 2. Determine the domain and range of each function.
Name: Class: Date: ID: A Midterm Review Short Answer 1. For each graph, write the equation of a radical function of the form y = a b(x h) + k. a) b) c) 2. Determine the domain and range of each function.
1 The relation between a second order linear ode and a system of two rst order linear odes
 Math 1280 Spring, 2010 1 The relation between a second order linear ode and a system of two rst order linear odes In Chapter 3 of the text you learn to solve some second order linear ode's, such as x 00
Math 1280 Spring, 2010 1 The relation between a second order linear ode and a system of two rst order linear odes In Chapter 3 of the text you learn to solve some second order linear ode's, such as x 00
Comm. Korean Math. Soc. 13(1998), No. 1, pp SEMI-QUASITRIANGULARITY OF TOEPLITZ OPERATORS WITH QUASICONTINUOUS SYMBOLS In Hyoun Kim and Woo You
 Comm. Korean Math. Soc. 13(1998), No. 1, pp. 77-84 SEMI-QUASITRIANGULARITY OF TOEPLITZ OPERATORS WITH QUASICONTINUOUS SYMBOLS In Hyoun Kim and Woo Young Lee Abstract. In this note we show that if T ' is
Comm. Korean Math. Soc. 13(1998), No. 1, pp. 77-84 SEMI-QUASITRIANGULARITY OF TOEPLITZ OPERATORS WITH QUASICONTINUOUS SYMBOLS In Hyoun Kim and Woo Young Lee Abstract. In this note we show that if T ' is
Lecture Notes 20: Zero-Knowledge Proofs
 CS 127/CSCI E-127: Introduction to Cryptography Prof. Salil Vadhan Fall 2013 Lecture Notes 20: Zero-Knowledge Proofs Reading. Katz-Lindell Ÿ14.6.0-14.6.4,14.7 1 Interactive Proofs Motivation: how can parties
CS 127/CSCI E-127: Introduction to Cryptography Prof. Salil Vadhan Fall 2013 Lecture Notes 20: Zero-Knowledge Proofs Reading. Katz-Lindell Ÿ14.6.0-14.6.4,14.7 1 Interactive Proofs Motivation: how can parties
Horizontal and Vertical Asymptotes from section 2.6
 Horizontal and Vertical Asymptotes from section 2.6 Definition: In either of the cases f(x) = L or f(x) = L we say that the x x horizontal line y = L is a horizontal asymptote of the function f. Note:
Horizontal and Vertical Asymptotes from section 2.6 Definition: In either of the cases f(x) = L or f(x) = L we say that the x x horizontal line y = L is a horizontal asymptote of the function f. Note:
New concepts: Span of a vector set, matrix column space (range) Linearly dependent set of vectors Matrix null space
 Lesson 6: Linear independence, matrix column space and null space New concepts: Span of a vector set, matrix column space (range) Linearly dependent set of vectors Matrix null space Two linear systems:
Lesson 6: Linear independence, matrix column space and null space New concepts: Span of a vector set, matrix column space (range) Linearly dependent set of vectors Matrix null space Two linear systems:
Vector bundles in Algebraic Geometry Enrique Arrondo. 1. The notion of vector bundle
 Vector bundles in Algebraic Geometry Enrique Arrondo Notes(* prepared for the First Summer School on Complex Geometry (Villarrica, Chile 7-9 December 2010 1 The notion of vector bundle In affine geometry,
Vector bundles in Algebraic Geometry Enrique Arrondo Notes(* prepared for the First Summer School on Complex Geometry (Villarrica, Chile 7-9 December 2010 1 The notion of vector bundle In affine geometry,
Right Behavior. Left Behavior. Right Behavior
 U n i t 3 P a r t P a g e 1 Math 3 Unit 3 Part Day 1 Graphing Polynomial Functions Expression 9 x- 3x x + 4x 3 + x + x + 1 5x 4 + x + 10 X 5 + x + 5 3c + 4c /c Type of Function Left Behavior: Right Behavior:
U n i t 3 P a r t P a g e 1 Math 3 Unit 3 Part Day 1 Graphing Polynomial Functions Expression 9 x- 3x x + 4x 3 + x + x + 1 5x 4 + x + 10 X 5 + x + 5 3c + 4c /c Type of Function Left Behavior: Right Behavior:
Common Core State Standards for Mathematics - High School PARRC Model Content Frameworks Mathematics Algebra 2
 A Correlation of CME Project Algebra 2 Common Core 2013 to the Common Core State Standards for , Common Core Correlated to the Number and Quantity The Real Number System N RN Extend the properties of exponents
A Correlation of CME Project Algebra 2 Common Core 2013 to the Common Core State Standards for , Common Core Correlated to the Number and Quantity The Real Number System N RN Extend the properties of exponents
Lecture 9 : PPAD and the Complexity of Equilibrium Computation. 1 Complexity Class PPAD. 1.1 What does PPAD mean?
 CS 599: Algorithmic Game Theory October 20, 2010 Lecture 9 : PPAD and the Complexity of Equilibrium Computation Prof. Xi Chen Scribes: Cheng Lu and Sasank Vijayan 1 Complexity Class PPAD 1.1 What does
CS 599: Algorithmic Game Theory October 20, 2010 Lecture 9 : PPAD and the Complexity of Equilibrium Computation Prof. Xi Chen Scribes: Cheng Lu and Sasank Vijayan 1 Complexity Class PPAD 1.1 What does
Multi Variable Calculus
 Multi Variable Calculus Joshua Wilde, revised by Isabel Tecu, Takeshi Suzuki and María José Boccardi August 3, 03 Functions from R n to R m So far we have looked at functions that map one number to another
Multi Variable Calculus Joshua Wilde, revised by Isabel Tecu, Takeshi Suzuki and María José Boccardi August 3, 03 Functions from R n to R m So far we have looked at functions that map one number to another
1 Groups Examples of Groups Things that are not groups Properties of Groups Rings and Fields Examples...
 Contents 1 Groups 2 1.1 Examples of Groups... 3 1.2 Things that are not groups....................... 4 1.3 Properties of Groups... 5 2 Rings and Fields 6 2.1 Examples... 8 2.2 Some Finite Fields... 10
Contents 1 Groups 2 1.1 Examples of Groups... 3 1.2 Things that are not groups....................... 4 1.3 Properties of Groups... 5 2 Rings and Fields 6 2.1 Examples... 8 2.2 Some Finite Fields... 10
SOLVING QUADRATIC EQUATIONS IN DIMENSION 5 OR MORE WITHOUT FACTORING
 SOLVING QUADRATIC EQUATIONS IN DIMENSION 5 OR MORE WITHOUT FACTORING PIERRE CASTEL Abstract. Let Q be a 5 5 symmetric matrix with integral entries and with det Q 0, but neither positive nor negative denite.
SOLVING QUADRATIC EQUATIONS IN DIMENSION 5 OR MORE WITHOUT FACTORING PIERRE CASTEL Abstract. Let Q be a 5 5 symmetric matrix with integral entries and with det Q 0, but neither positive nor negative denite.
A PRIMER ON SESQUILINEAR FORMS
 A PRIMER ON SESQUILINEAR FORMS BRIAN OSSERMAN This is an alternative presentation of most of the material from 8., 8.2, 8.3, 8.4, 8.5 and 8.8 of Artin s book. Any terminology (such as sesquilinear form
A PRIMER ON SESQUILINEAR FORMS BRIAN OSSERMAN This is an alternative presentation of most of the material from 8., 8.2, 8.3, 8.4, 8.5 and 8.8 of Artin s book. Any terminology (such as sesquilinear form
Mathematics 206 Solutions for HWK 23 Section 6.3 p358
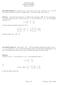 Mathematics 6 Solutions for HWK Section Problem 9. Given T(x, y, z) = (x 9y + z,6x + 5y z) and v = (,,), use the standard matrix for the linear transformation T to find the image of the vector v. Note
Mathematics 6 Solutions for HWK Section Problem 9. Given T(x, y, z) = (x 9y + z,6x + 5y z) and v = (,,), use the standard matrix for the linear transformation T to find the image of the vector v. Note
Rotation, scale and translation invariant digital image watermarking. O'RUANAIDH, Joséph John, PUN, Thierry. Abstract
 Proceedings Chapter Rotation, scale and translation invariant digital image watermarking O'RUANAIDH, Joséph John, PUN, Thierry Abstract A digital watermark is an invisible mark embedded in a digital image
Proceedings Chapter Rotation, scale and translation invariant digital image watermarking O'RUANAIDH, Joséph John, PUN, Thierry Abstract A digital watermark is an invisible mark embedded in a digital image
APPENDIX A. Background Mathematics. A.1 Linear Algebra. Vector algebra. Let x denote the n-dimensional column vector with components x 1 x 2.
 APPENDIX A Background Mathematics A. Linear Algebra A.. Vector algebra Let x denote the n-dimensional column vector with components 0 x x 2 B C @. A x n Definition 6 (scalar product). The scalar product
APPENDIX A Background Mathematics A. Linear Algebra A.. Vector algebra Let x denote the n-dimensional column vector with components 0 x x 2 B C @. A x n Definition 6 (scalar product). The scalar product
Chapter 3: Vector Spaces x1: Basic concepts Basic idea: a vector space V is a collection of things you can add together, and multiply by scalars (= nu
 Math 314 Topics for second exam Technically, everything covered by the rst exam plus Chapter 2 x6 Determinants (Square) matrices come in two avors: invertible (all Ax = b have a solution) and noninvertible
Math 314 Topics for second exam Technically, everything covered by the rst exam plus Chapter 2 x6 Determinants (Square) matrices come in two avors: invertible (all Ax = b have a solution) and noninvertible
Math 10b Ch. 8 Reading 1: Introduction to Taylor Polynomials
 Math 10b Ch. 8 Reading 1: Introduction to Taylor Polynomials Introduction: In applications, it often turns out that one cannot solve the differential equations or antiderivatives that show up in the real
Math 10b Ch. 8 Reading 1: Introduction to Taylor Polynomials Introduction: In applications, it often turns out that one cannot solve the differential equations or antiderivatives that show up in the real
Lecture 32: Taylor Series and McLaurin series We saw last day that some functions are equal to a power series on part of their domain.
 Lecture 32: Taylor Series and McLaurin series We saw last day that some functions are equal to a power series on part of their domain. For example f(x) = 1 1 x = 1 + x + x2 + x 3 + = ln(1 + x) = x x2 2
Lecture 32: Taylor Series and McLaurin series We saw last day that some functions are equal to a power series on part of their domain. For example f(x) = 1 1 x = 1 + x + x2 + x 3 + = ln(1 + x) = x x2 2
Chapter 2. Recurrence Relations. Divide and Conquer. Divide and Conquer Strategy. Another Example: Merge Sort. Merge Sort Example. Merge Sort Example
 Recurrence Relations Chapter 2 Divide and Conquer Equation or an inequality that describes a function by its values on smaller inputs. Recurrence relations arise when we analyze the running time of iterative
Recurrence Relations Chapter 2 Divide and Conquer Equation or an inequality that describes a function by its values on smaller inputs. Recurrence relations arise when we analyze the running time of iterative
EXAMPLES OF PROOFS BY INDUCTION
 EXAMPLES OF PROOFS BY INDUCTION KEITH CONRAD 1. Introduction In this handout we illustrate proofs by induction from several areas of mathematics: linear algebra, polynomial algebra, and calculus. Becoming
EXAMPLES OF PROOFS BY INDUCTION KEITH CONRAD 1. Introduction In this handout we illustrate proofs by induction from several areas of mathematics: linear algebra, polynomial algebra, and calculus. Becoming
COMPLEXITY OF LATTICE PROBLEMS A Cryptographic Perspective
 COMPLEXITY OF LATTICE PROBLEMS A Cryptographic Perspective THE KLUWER INTERNATIONAL SERIES IN ENGINEERING AND COMPUTER SCIENCE COMPLEXITY OF LATTICE PROBLEMS A Cryptographic Perspective Daniele Micciancio
COMPLEXITY OF LATTICE PROBLEMS A Cryptographic Perspective THE KLUWER INTERNATIONAL SERIES IN ENGINEERING AND COMPUTER SCIENCE COMPLEXITY OF LATTICE PROBLEMS A Cryptographic Perspective Daniele Micciancio
Linear Cryptanalysis. Kaisa Nyberg. Department of Computer Science Aalto University School of Science. S3, Sackville, August 11, 2015
 Kaisa Nyberg Department of Computer Science Aalto University School of Science s 2 r t S3, Sackville, August 11, 2015 Outline Linear characteristics and correlations Matsui s algorithms Traditional statistical
Kaisa Nyberg Department of Computer Science Aalto University School of Science s 2 r t S3, Sackville, August 11, 2015 Outline Linear characteristics and correlations Matsui s algorithms Traditional statistical
1.1. The analytical denition. Denition. The Bernstein polynomials of degree n are dened analytically:
 DEGREE REDUCTION OF BÉZIER CURVES DAVE MORGAN Abstract. This paper opens with a description of Bézier curves. Then, techniques for the degree reduction of Bézier curves, along with a discussion of error
DEGREE REDUCTION OF BÉZIER CURVES DAVE MORGAN Abstract. This paper opens with a description of Bézier curves. Then, techniques for the degree reduction of Bézier curves, along with a discussion of error
Tennessee s State Mathematics Standards - Algebra II
 Domain Cluster Standard Scope and Clarifications The Real Number System (N-RN) Extend the properties of exponents to rational exponents 1. Explain how the definition of the meaning of rational exponents
Domain Cluster Standard Scope and Clarifications The Real Number System (N-RN) Extend the properties of exponents to rational exponents 1. Explain how the definition of the meaning of rational exponents
Homework 7 Solutions to Selected Problems
 Homework 7 Solutions to Selected Prolems May 9, 01 1 Chapter 16, Prolem 17 Let D e an integral domain and f(x) = a n x n +... + a 0 and g(x) = m x m +... + 0 e polynomials with coecients in D, where a
Homework 7 Solutions to Selected Prolems May 9, 01 1 Chapter 16, Prolem 17 Let D e an integral domain and f(x) = a n x n +... + a 0 and g(x) = m x m +... + 0 e polynomials with coecients in D, where a
Better proofs for rekeying
 Better proofs for rekeying 1 D. J. Bernstein Security of AES-256 key k is far below 2 256 in most protocols: (AES k (0); : : : ; AES k (n 1)) is distinguishable from uniform with probability n(n 1)=2 129,
Better proofs for rekeying 1 D. J. Bernstein Security of AES-256 key k is far below 2 256 in most protocols: (AES k (0); : : : ; AES k (n 1)) is distinguishable from uniform with probability n(n 1)=2 129,
Pearson Mathematics Algebra 2 Common Core 2015
 A Correlation of Pearson Mathematics Algebra 2 Common Core 2015 to the Common Core State Standards for Bid Category 13-050-10 A Correlation of Pearson Common Core Pearson Number and Quantity The Real Number
A Correlation of Pearson Mathematics Algebra 2 Common Core 2015 to the Common Core State Standards for Bid Category 13-050-10 A Correlation of Pearson Common Core Pearson Number and Quantity The Real Number
Linear Finite State Machines 1. X. Sun E. Kontopidi M. Serra J. Muzio. Abstract
 The Concatenation and Partitioning of Linear Finite State Machines 1 X. Sun E. Kontopidi M. Serra J. Muzio Dept. of Electrical Engineering University of Alberta Edmonton, AB T6G 2G7 Dept. of Comp. Science
The Concatenation and Partitioning of Linear Finite State Machines 1 X. Sun E. Kontopidi M. Serra J. Muzio Dept. of Electrical Engineering University of Alberta Edmonton, AB T6G 2G7 Dept. of Comp. Science
VOYAGER INSIDE ALGEBRA CORRELATED TO THE NEW JERSEY STUDENT LEARNING OBJECTIVES AND CCSS.
 We NJ Can STUDENT Early Learning LEARNING Curriculum OBJECTIVES PreK Grades 8 12 VOYAGER INSIDE ALGEBRA CORRELATED TO THE NEW JERSEY STUDENT LEARNING OBJECTIVES AND CCSS www.voyagersopris.com/insidealgebra
We NJ Can STUDENT Early Learning LEARNING Curriculum OBJECTIVES PreK Grades 8 12 VOYAGER INSIDE ALGEBRA CORRELATED TO THE NEW JERSEY STUDENT LEARNING OBJECTIVES AND CCSS www.voyagersopris.com/insidealgebra
2 Garrett: `A Good Spectral Theorem' 1. von Neumann algebras, density theorem The commutant of a subring S of a ring R is S 0 = fr 2 R : rs = sr; 8s 2
 1 A Good Spectral Theorem c1996, Paul Garrett, garrett@math.umn.edu version February 12, 1996 1 Measurable Hilbert bundles Measurable Banach bundles Direct integrals of Hilbert spaces Trivializing Hilbert
1 A Good Spectral Theorem c1996, Paul Garrett, garrett@math.umn.edu version February 12, 1996 1 Measurable Hilbert bundles Measurable Banach bundles Direct integrals of Hilbert spaces Trivializing Hilbert
Correlation Attack to the Block Cipher RC5. and the Simplied Variants of RC6. 3 Fujitsu Laboratories LTD.
 Correlation Attack to the Block Cipher RC5 and the Simplied Variants of RC6 Takeshi Shimoyama 3, Kiyofumi Takeuchi y, Juri Hayakawa y 3 Fujitsu Laboratories LTD. 4-1-1 Kamikodanaka, Nakahara-ku, Kawasaki
Correlation Attack to the Block Cipher RC5 and the Simplied Variants of RC6 Takeshi Shimoyama 3, Kiyofumi Takeuchi y, Juri Hayakawa y 3 Fujitsu Laboratories LTD. 4-1-1 Kamikodanaka, Nakahara-ku, Kawasaki
Factors of Polynomials Factoring For Experts
 Factors of Polynomials SUGGESTED LEARNING STRATEGIES: Shared Reading, Activating Prior Knowledge, Discussion Group, Note-taking When you factor a polynomial, you rewrite the original polynomial as a product
Factors of Polynomials SUGGESTED LEARNING STRATEGIES: Shared Reading, Activating Prior Knowledge, Discussion Group, Note-taking When you factor a polynomial, you rewrite the original polynomial as a product
Math 42, Discrete Mathematics
 c Fall 2018 last updated 12/05/2018 at 15:47:21 For use by students in this class only; all rights reserved. Note: some prose & some tables are taken directly from Kenneth R. Rosen, and Its Applications,
c Fall 2018 last updated 12/05/2018 at 15:47:21 For use by students in this class only; all rights reserved. Note: some prose & some tables are taken directly from Kenneth R. Rosen, and Its Applications,
Recall, R is an integral domain provided: R is a commutative ring If ab = 0 in R, then either a = 0 or b = 0.
 Recall, R is an integral domain provided: R is a commutative ring If ab = 0 in R, then either a = 0 or b = 0. Examples: Z Q, R Polynomials over Z, Q, R, C The Gaussian Integers: Z[i] := {a + bi : a, b
Recall, R is an integral domain provided: R is a commutative ring If ab = 0 in R, then either a = 0 or b = 0. Examples: Z Q, R Polynomials over Z, Q, R, C The Gaussian Integers: Z[i] := {a + bi : a, b
Entrance Exam, Real Analysis September 1, 2017 Solve exactly 6 out of the 8 problems
 September, 27 Solve exactly 6 out of the 8 problems. Prove by denition (in ɛ δ language) that f(x) = + x 2 is uniformly continuous in (, ). Is f(x) uniformly continuous in (, )? Prove your conclusion.
September, 27 Solve exactly 6 out of the 8 problems. Prove by denition (in ɛ δ language) that f(x) = + x 2 is uniformly continuous in (, ). Is f(x) uniformly continuous in (, )? Prove your conclusion.
Chapter 2 Polynomial and Rational Functions
 Chapter 2 Polynomial and Rational Functions Overview: 2.2 Polynomial Functions of Higher Degree 2.3 Real Zeros of Polynomial Functions 2.4 Complex Numbers 2.5 The Fundamental Theorem of Algebra 2.6 Rational
Chapter 2 Polynomial and Rational Functions Overview: 2.2 Polynomial Functions of Higher Degree 2.3 Real Zeros of Polynomial Functions 2.4 Complex Numbers 2.5 The Fundamental Theorem of Algebra 2.6 Rational
A field trips costs $800 for the charter bus plus $10 per student for x students. The cost per student is represented by: 10x x
 LEARNING STRATEGIES: Activate Prior Knowledge, Shared Reading, Think/Pair/Share, Note Taking, Group Presentation, Interactive Word Wall A field trips costs $800 for the charter bus plus $10 per student
LEARNING STRATEGIES: Activate Prior Knowledge, Shared Reading, Think/Pair/Share, Note Taking, Group Presentation, Interactive Word Wall A field trips costs $800 for the charter bus plus $10 per student
In Exercises 1 12, list the all of the elements of the given set. 2. The set of all positive integers whose square roots are less than or equal to 3
 APPENDIX A EXERCISES In Exercises 1 12, list the all of the elements of the given set. 1. The set of all prime numbers less than 20 2. The set of all positive integers whose square roots are less than
APPENDIX A EXERCISES In Exercises 1 12, list the all of the elements of the given set. 1. The set of all prime numbers less than 20 2. The set of all positive integers whose square roots are less than
Bootstrapping Obfuscators via Fast Pseudorandom Functions
 Bootstrapping Obfuscators via Fast Pseudorandom Functions Benny Applebaum October 26, 2013 Abstract We show that it is possible to upgrade an obfuscator for a weak complexity class WEAK into an obfuscator
Bootstrapping Obfuscators via Fast Pseudorandom Functions Benny Applebaum October 26, 2013 Abstract We show that it is possible to upgrade an obfuscator for a weak complexity class WEAK into an obfuscator
A matrix over a field F is a rectangular array of elements from F. The symbol
 Chapter MATRICES Matrix arithmetic A matrix over a field F is a rectangular array of elements from F The symbol M m n (F ) denotes the collection of all m n matrices over F Matrices will usually be denoted
Chapter MATRICES Matrix arithmetic A matrix over a field F is a rectangular array of elements from F The symbol M m n (F ) denotes the collection of all m n matrices over F Matrices will usually be denoted
Section September 6, If n = 3, 4, 5,..., the polynomial is called a cubic, quartic, quintic, etc.
 Section 2.1-2.2 September 6, 2017 1 Polynomials Definition. A polynomial is an expression of the form a n x n + a n 1 x n 1 + + a 1 x + a 0 where each a 0, a 1,, a n are real numbers, a n 0, and n is a
Section 2.1-2.2 September 6, 2017 1 Polynomials Definition. A polynomial is an expression of the form a n x n + a n 1 x n 1 + + a 1 x + a 0 where each a 0, a 1,, a n are real numbers, a n 0, and n is a
Linear Algebra. Christos Michalopoulos. September 24, NTU, Department of Economics
 Linear Algebra Christos Michalopoulos NTU, Department of Economics September 24, 2011 Christos Michalopoulos Linear Algebra September 24, 2011 1 / 93 Linear Equations Denition A linear equation in n-variables
Linear Algebra Christos Michalopoulos NTU, Department of Economics September 24, 2011 Christos Michalopoulos Linear Algebra September 24, 2011 1 / 93 Linear Equations Denition A linear equation in n-variables
Positive Results and Techniques for Obfuscation
 Positive Results and Techniques for Obfuscation Benjamin Lynn Stanford University Manoj Prabhakaran Princeton University February 28, 2004 Amit Sahai Princeton University Abstract Informally, an obfuscator
Positive Results and Techniques for Obfuscation Benjamin Lynn Stanford University Manoj Prabhakaran Princeton University February 28, 2004 Amit Sahai Princeton University Abstract Informally, an obfuscator
Notes on the matrix exponential
 Notes on the matrix exponential Erik Wahlén erik.wahlen@math.lu.se February 14, 212 1 Introduction The purpose of these notes is to describe how one can compute the matrix exponential e A when A is not
Notes on the matrix exponential Erik Wahlén erik.wahlen@math.lu.se February 14, 212 1 Introduction The purpose of these notes is to describe how one can compute the matrix exponential e A when A is not
Linear Equations in One Variable *
 OpenStax-CNX module: m64441 1 Linear Equations in One Variable * Ramon Emilio Fernandez Based on Linear Equations in One Variable by OpenStax This work is produced by OpenStax-CNX and licensed under the
OpenStax-CNX module: m64441 1 Linear Equations in One Variable * Ramon Emilio Fernandez Based on Linear Equations in One Variable by OpenStax This work is produced by OpenStax-CNX and licensed under the
Matrices and Linear Algebra
 Contents Quantitative methods for Economics and Business University of Ferrara Academic year 2017-2018 Contents 1 Basics 2 3 4 5 Contents 1 Basics 2 3 4 5 Contents 1 Basics 2 3 4 5 Contents 1 Basics 2
Contents Quantitative methods for Economics and Business University of Ferrara Academic year 2017-2018 Contents 1 Basics 2 3 4 5 Contents 1 Basics 2 3 4 5 Contents 1 Basics 2 3 4 5 Contents 1 Basics 2
Rational Distance Problem for the Unit Square
 Rational Distance Problem for the Unit Square Ameet Sharma November 18, 015 ameet_n_sharma@hotmail.com Abstract We present a proof of the non-existence of points at a rational distance from all 4 corners
Rational Distance Problem for the Unit Square Ameet Sharma November 18, 015 ameet_n_sharma@hotmail.com Abstract We present a proof of the non-existence of points at a rational distance from all 4 corners
5 Quiver Representations
 5 Quiver Representations 5. Problems Problem 5.. Field embeddings. Recall that k(y,..., y m ) denotes the field of rational functions of y,..., y m over a field k. Let f : k[x,..., x n ] k(y,..., y m )
5 Quiver Representations 5. Problems Problem 5.. Field embeddings. Recall that k(y,..., y m ) denotes the field of rational functions of y,..., y m over a field k. Let f : k[x,..., x n ] k(y,..., y m )
A Questionable Distance-Regular Graph
 A Questionable Distance-Regular Graph Rebecca Ross Abstract In this paper, we introduce distance-regular graphs and develop the intersection algebra for these graphs which is based upon its intersection
A Questionable Distance-Regular Graph Rebecca Ross Abstract In this paper, we introduce distance-regular graphs and develop the intersection algebra for these graphs which is based upon its intersection
Numerical Solutions to PDE s
 Introduction Numerical Solutions to PDE s Mathematical Modelling Week 5 Kurt Bryan Let s start by recalling a simple numerical scheme for solving ODE s. Suppose we have an ODE u (t) = f(t, u(t)) for some
Introduction Numerical Solutions to PDE s Mathematical Modelling Week 5 Kurt Bryan Let s start by recalling a simple numerical scheme for solving ODE s. Suppose we have an ODE u (t) = f(t, u(t)) for some
Properties of Real Numbers
 Properties of Real Numbers Essential Understanding. Relationships that are always true for real numbers are called properties, which are rules used to rewrite and compare expressions. Two algebraic expressions
Properties of Real Numbers Essential Understanding. Relationships that are always true for real numbers are called properties, which are rules used to rewrite and compare expressions. Two algebraic expressions
The best expert versus the smartest algorithm
 Theoretical Computer Science 34 004 361 380 www.elsevier.com/locate/tcs The best expert versus the smartest algorithm Peter Chen a, Guoli Ding b; a Department of Computer Science, Louisiana State University,
Theoretical Computer Science 34 004 361 380 www.elsevier.com/locate/tcs The best expert versus the smartest algorithm Peter Chen a, Guoli Ding b; a Department of Computer Science, Louisiana State University,
Algebra 1 (Honors 7th and Advanced 8th)
 Readington Township Public Schools Algebra 1 (Honors 7th and Advanced 8th) Authored by: Megan Grocholske Reviewed by: Sarah Pauch Supervisor of Math, Science, and Technology Approval Date: September 25,
Readington Township Public Schools Algebra 1 (Honors 7th and Advanced 8th) Authored by: Megan Grocholske Reviewed by: Sarah Pauch Supervisor of Math, Science, and Technology Approval Date: September 25,
A NOTE ON A YAO S THEOREM ABOUT PSEUDORANDOM GENERATORS
 A NOTE ON A YAO S THEOREM ABOUT PSEUDORANDOM GENERATORS STÉPHANE BALLET AND ROBERT ROLLAND Abstract. The Yao s theorem gives an equivalence between the indistinguishability of a pseudorandom generator
A NOTE ON A YAO S THEOREM ABOUT PSEUDORANDOM GENERATORS STÉPHANE BALLET AND ROBERT ROLLAND Abstract. The Yao s theorem gives an equivalence between the indistinguishability of a pseudorandom generator
Math 110 Linear Algebra Midterm 2 Review October 28, 2017
 Math 11 Linear Algebra Midterm Review October 8, 17 Material Material covered on the midterm includes: All lectures from Thursday, Sept. 1st to Tuesday, Oct. 4th Homeworks 9 to 17 Quizzes 5 to 9 Sections
Math 11 Linear Algebra Midterm Review October 8, 17 Material Material covered on the midterm includes: All lectures from Thursday, Sept. 1st to Tuesday, Oct. 4th Homeworks 9 to 17 Quizzes 5 to 9 Sections
