Deutsches Institut für Wirtschaftsforschung 2017
|
|
|
- Leonard Gilmore
- 5 years ago
- Views:
Transcription
1 1707 Discussion Papers Deutsches Institut für Wirtschaftsforschung 017 Bayesian Inference for Structural Vector Autoregressions Identified by Markov-Switching Heteroskedasticity Helmut Lütkepohl and Tomasz Woźniak
2 Opinions expressed in this paper are those of the author(s) and do not necessarily reflect views of the institute. IMPRESSUM DIW Berlin, 017 DIW Berlin German Institute for Economic Research Mohrenstr Berlin Tel. +49 (30) Fax +49 (30) ISSN electronic edition Papers can be downloaded free of charge from the DIW Berlin website: Discussion Papers of DIW Berlin are indexed in RePEc and SSRN:
3 Bayesian Inference for Structural Vector Autoregressions Identified by Markov-Switching Heteroskedasticity Helmut Lütkepohl a,, Tomasz Woźniak b a DIW Berlin and Freie Universität Berlin b University of Melbourne November 9, 017 Abstract In order to identify structural shocks that affect economic variables, restrictions need to be imposed on the parameters of structural vector autoregressive (SVAR) models. Economic theory is the primary source of such restrictions. However, only over-identifying restrictions can be tested with statistical methods which limits the statistical validation of many just-identified SVAR models. In this study, Bayesian inference is developed for SVAR models in which the structural parameters are identified via Markov-switching heteroskedasticity. In such a model, restrictions that are just-identifying in the homoskedastic case, become over-identifying and can be tested. A set of parametric restrictions is derived under which the structural matrix is globally identified and a Savage-Dickey density ratio is used to assess the validity of the identification conditions. For that purpose, a new probability distribution is defined that generalizes the beta, F, and compound gamma distributions. As an empirical example, monetary models are compared using heteroskedasticity as an additional device for identification. The empirical results support models with money in the interest rate reaction function. Keywords: Identification Through Heteroskedasticity, Markov-Switching Models, Savage-Dickey Density Ratio, Monetary Policy Shocks, Divisia Money JEL classification: C11, C1, C3, E3 Corresponding author. Address: DIW Berlin, Mohrenstr. 58, Berlin, Germany, Phone: , Fax: , address: hluetkepohl@diw.de. 1
4 1. Introduction A central problem in structural vector autoregressive (SVAR) analysis is the identification of the structural parameters or, equivalently, the identification of the structural shocks of interest. The identifying assumptions are often controversial. In order to avoid imposing unnecessarily many restrictions, typically only just-identifying restrictions are formulated. In that case the data are not informative about the validity of the restrictions and they cannot be tested with statistical methods. Moreover, even if over-identifying restrictions are imposed, they can only be tested conditionally on a set of just-identifying restrictions. This state of the art has led some researchers to extract additional identifying information from the statistical properties of the data. Notably heteroskedasticity and conditional heteroskedasticity of the reduced form residuals have been used in this context. Using such additional information may enable the researcher to make the data speak on the validity of restrictions that cannot be tested in a conventional framework. One model that has been used repeatedly in applied studies lately to capture heteroskedasticity is based on a latent Markov process that drives the changes in volatility. The model was first proposed by Lanne, Lütkepohl & Maciejowska (010) for SVAR analysis with identification through heteroskedasticity and it was further developed by Herwartz & Lütkepohl (014). The SVAR model with Markov-switching heteroskedasticity (SVAR-MSH) is in widespread use (see, e.g., Netšunajev (013), Lütkepohl & Netšunajev (014, 017), Lütkepohl & Velinov (014), Velinov & Chen (015), Chen & Netšunajev (017) and (Kilian & Lütkepohl, 017, Chapter 14)). Some Bayesian methodology has been developed for its analysis by Kulikov & Netšunajev (013, 017), Lanne & Luoto (016) and Woźniak & Droumaguet (015). Apart from Woźniak & Droumaguet (015), all Bayesian approaches base inference for these models on draws from the posterior of the reduced form parameters and transform this output into the posterior draws of the structural model identified through heteroskedasticity. Hence their methodology can only be used to generate posterior draws for just-identified structural parameters which limits its applicability when over-identifying restrictions are of interest. Woźniak & Droumaguet (015) focus on a locally identified SVAR-MSH model and develop methods for drawing from the posterior of the structural parameters. The posterior distribution of the parameters of a locally identified model is multimodal, however, which allows a statistical model comparison, but severely limits the analysis of the structural parameters.
5 In the present study, a full Bayesian analysis framework is presented based on a globally identified SVAR-MSH model that facilitates both of the objectives mentioned above. The main additional contributions to the SVAR-MSH literature for identification through heteroskedasticity are as follows: (1) A set of parametric restrictions for global identification of the model is derived and the model is set up in an identified form such that the data become informative on the conditions required for identification through heteroskedasticity. Moreover, the model setup facilitates the Bayesian estimation of the structural parameters. () A procedure for investigating the restrictions for unique identification of the structural parameters based on a Savage-Dickey density ratio (SDDR) is proposed. For that purpose, a new probability distribution is defined that generalizes the beta, F, and compound gamma distributions. Thereby a Bayesian statistical procedure is obtained for investigating global identification of the SVAR-MSH model. A SDDR can also be used for assessing the heteroskedasticity of the structural shocks. (3) A fast Markov Chain Monte Carlo (MCMC) sampler is developed for the posterior distribution of the structural parameters and a method for computing the marginal data density (MDD) is provided which facilitates a full Bayesian model selection. The methods are illustrated by applying them for an empirical analysis of the role of a Divisia money aggregate in a monetary policy reaction function. In a frequentist SVAR analysis, Belongia & Ireland (015) find support for the hypothesis that Divisia monetary aggregates are important variables in the monetary policy rule. In their conventional SVAR models without accounting for heteroskedasticity they can only test over-identifying restrictions to validate their hypotheses. Using Belongia & Ireland (015) as a benchmark, the Bayesian methods developed in the current study for the SVAR-MSH model are applied for a broader statistical analysis of the identifying restrictions even for models that are not identified in Belongia & Ireland s framework. We find evidence that a money aggregate is an important factor determining the monetary policy. The remainder of this study is organized as follows. The next section presents the basic model framework and derives conditions for global identification of the structural parameters. Section 3 discusses the prior assumptions used for the structural parameters. The SDDR procedure for investigating the conditions for global identification of the structural parameters obtained from the volatility model is presented in Section 4 and the empirical illustration is discussed in Section 5. Conclusions follow in Section 6 and, finally, the computational details of the Gibbs sampler and 3
6 the estimation of the marginal data densities are presented in Appendix A, while Appendix B contains more details on the new distribution used in the SDDR procedure. Additional empirical results on the precision of our estimates are presented in Appendix C.. Identified Heteroskedastic Structural Vector Autoregressions.1. The Model In this section, a structural VAR model is introduced for the N-dimensional vector of observable variables y t in which the structural shocks are conditionally heteroskedastic. The structural-form model is given by A 0 y t = µ + A 1 y t A p y t p + u t, (1) where the structural matrix A 0 is assumed to be nonsingular with unit diagonal, denoted by diag(a 0 ) = ı N, where ı N is an N-dimensional vector of ones, and A 0 does not have other unit elements. In other words, there is one equation for each variable. This assumption is not restrictive for standard macroeconomic models, but it helps simplifying the identification conditions presented later on. The quantity µ is an N-dimensional vector of constant terms, A 1,..., A p denote N N autoregressive slope coefficient matrices, and u t is a contemporaneously and serially uncorrelated structural error term. The variances of the structural errors are assumed to change over time according to a latent process s t, t {1,..., T}, and the variance of u it conditional on the state s t is denoted as λ st,i. Moreover, conditionally on s t, the structural errors are assumed to be normally distributed with mean vector zero and diagonal covariance matrix, u t s t N(0, diag(λ st )), t {1,..., T}, () where λ st = (λ st,1,..., λ st,n) is an N-dimensional vector of variances associated with volatility state s t and diag(λ st ) denotes a diagonal matrix with main diagonal given by λ st. Later in this section, the heteroskedasticity of the data is used to identify the structural matrix A 0. The process s t for each t can take a discrete number of values, s t {1,..., M}. In the current study it is assumed to be an unobservable Markov process that defines a Markov-switching model as proposed by Lanne et al. (010). In principle, the uniqueness restrictions and their Bayesian verification procedure can also be used for other types of processes s t that describe the volatility 4
7 changes. The properties of the Markov process, s t, considered in the current study are fully governed by an M M matrix of transition probabilities P. The (i, j) th element of P is the probability of switching to state j at time t, given that at time t 1 the process is in state i, p ij = Pr [ s t = j s t 1 = i ], for i, j {1,..., M}, and M j=1 p ij = 1. Since the hidden Markov process has M states, also M vectors of the state-specific structural error variances, λ 1,..., λ M, have to be estimated. Such a flexible MS heteroskedastic process offers a range of possibilities of modeling particular patterns of changes in volatility in economic data (see Sims, Waggoner & Zha, 008; Woźniak & Droumaguet, 015). The heteroskedastic SVAR model presented so far allows for the statistical identification of all the N N free elements of the structural matrix A 0, as will be demonstrated shortly. Therefore, the matrix A 0 can be estimated in a heteroskedastic structural form model given by equations (1) and (). Any further restrictions imposed on the matrix A 0 over-identify the system, and thus, the data are informative about such restrictions... Identifying A 0 via Heteroskedasticity To see how statistical identification of the model is obtained via heteroskedasticity, it is useful to study the implied reduced-form model and its relation to the structural form. The reduced form of the model is obtained by multiplying the structural-form model in equation (1) by A 1 0 from the left. The reduced-form residuals are ɛ t = A 1 0 u t such that, for a uniquely determined matrix A 0, the structural errors are obtained from the reduced-form residuals as A 0 ɛ t = u t. Suppose that the M covariance matrices of the reduced-form residuals are denoted by Σ m, m {1,..., M}. Under the current assumptions, where only the variances of the structural errors are state dependent while the VAR structure is time-invariant, there exists a decomposition Σ m = A 1 0 diag (λ m) A 1 0, m {1,..., M}. (3) The following proposition shows that for M, the matrix A 0 is unique if there is enough heterogeneity in the changes of the variances. Proposition 1. Let Σ m, m {1,..., M} and M > 1, be positive definite matrices that can be decomposed as in equation (3). Then A 0 is unique iff i, j {1,..., N}, i j, there exists an 5
8 m {,..., M} such that λ m,i /λ 1,i λ m,j /λ 1,j. 1 Proof. Given that Σ m, m {1,..., M}, are positive definite symmetric, the same is true for the inverses and there exists a decomposition Σ 1 1 = CC, Σ 1 m = C diag(ω m ) C, m {,..., M}, (4) where ω m = (ω m,1,..., ω m,n ) is an N 1 vector of positive numbers such that ω m,n = λ m,n /λ 1,n. It follows from Proposition 1 of Lanne et al. (010) that C = [c ij ] is unique up to column sign changes and column ordering iff i, j {1,..., N}, i j, there exists an m {,..., M} such that ω m,i ω m,j. Defining A 0 = C diag(1/c 11,..., 1/c NN ) so that it has unit diagonal, A 0 is unique iff i, j {1,..., N}, i j, there exists an m {,..., M} such that ω m,i ω m,j. Replacing C by A 0 diag(c 11,..., c NN ) in (4) and taking inverses, the latter condition is seen to be equivalent to the condition for uniqueness of A 0 given in Proposition 1. Note that unlike C, the column (and row) signs of A 0 are determined by the unit main diagonal and, hence, this type of non-uniqueness of C does not affect A 0. Likewise, the rows of this matrix are fixed by the requirement of a unit diagonal because there are no other unit elements that would allow a permutation of rows of A 0. Proposition 1 implies that A 0 is globally identified if the conditions of the proposition are satisfied. This fact is an advantage of our model setup relative to the typical setup used in the related literature on identification via heteroskedasticity. In that literature, a so-called B-model is typically used which results in locally identified shocks, which are unique up to sign and ordering only (see Lütkepohl, 005). More precisely, the structural errors u t are assumed to be related to the reduced-form residuals ɛ t as u t = B 1 ɛ t such that we get a reduced-form covariance decomposition Σ 1 = BB, Σ m = B diag(λ m) B, m =,..., M. (5) The matrix B has a direct interpretation as the matrix of impact effects of the shocks on the variables. 1 Note that the standardization of the relative variances by the variances from the first state could be changed to variances from any other state. Our results do not depend on this choice. 6
9 No restrictions are imposed on the main diagonal of B and local uniqueness of B is obtained by normalizing the variances of the structural shocks associated with the first volatility state, that is, u t (s t = 1) N(0, I N ). The conditions for local uniqueness of this decomposition for any number of states M are derived in Lanne et al. (010). While such local identification results are sufficient for asymptotic theory in a frequentist framework, they are not convenient for Bayesian analysis because they complicate simulating posterior distributions. Thus, the setup of Proposition 1, with restricted diagonal elements of A 0, is particularly useful for Bayesian analysis. Moreover, estimation and inference of the unrestricted parameters of the matrix A 0 in the current model is separated from the scaling problem associated with the label switching of heteroskedastic states. In effect, the likelihood function and the posterior distribution have more regular shapes with fewer modes (see Woźniak & Droumaguet, 015, for the detailed analysis of the impact of label switching of the heteroskedastic states on the shape of the posterior distribution). The main condition of Proposition 1 is that there has to be some heterogeneity in the volatility changes. For example, if there are just two volatility states and all variances change proportionally, that is, for some scalar c, λ 1 = cλ, then λ,i /λ 1,i = λ,j /λ 1,j, so that the conditions of Proposition 1 are not satisfied. On the other hand, Proposition 1 implies that full identification may be obtained even if one of the structural shocks is homoskedastic. For example, in a two-dimensional model the conditions of Proposition 1 are satisfied if the first variance components λ 1,1 and λ,1 are equal (λ 1,1 = λ,1 ) as long as λ 1, and λ, are distict. Conditions for full identification could be formulated equivalently for parametrisation (5). In fact, instead of normalizing the diagonal elements of A 0, one could normalize the diagonal elements of B to obtain global identification. Such a normalization amounts to assuming that the k th shock has unit instantaneous impact on the k th variable. It is used by Stock & Watson (016) who list several of its advantages. However, a potential drawback is that such a normalization requires knowledge that the k th shock has a nonzero impact effect on the k th variable which may not be obvious in some situations. Thus, we prefer to work with a normalized A 0 matrix. The advantage of the conditions given in Proposition 1 for the variances in parametrization (3) is that they can be investigated by statistical methods because the data are informative about them. If the conditions for full identification in Proposition 1 are not satisfied, the changing volatility 7
10 may still offer some additional identifying information that implies sufficient curvature in the likelihood and, hence, in the posterior, to enable the data to discriminate between competing economic models. Note that the identification of the matrix A 0 using heteroskedasticity is only a statistical identification that allows to estimate all the elements of this matrix without imposing any further restrictions on the model. This method allows to fully identify the structural parameters. Therefore, the matrices A i for i {0,..., p} can be used to compute the structural impulse response functions. However, the structural-form errors do not have economic interpretations as such. In order to call any of the structural shocks, say a monetary policy shock, economic reasoning needs to be imposed. Still, it is useful to exploit such an identification of the shocks as it opens up the possibility for testing any further restrictions imposed on the model on the basis of economic considerations..3. Imposing Restrictions on the Matrix A 0 In order to obtain a flexible framework that facilitates the estimation of models with unrestricted or restricted matrix A 0, the approach proposed by Amisano & Giannini (1997), used also by Canova & Pérez Forero (015) is helpful. Let the r 1 vector α collect all of the unrestricted elements of the matrix A 0 column by column. Then we impose restrictions on the structural matrix A 0 by setting vec (A 0 ) = Qα + q, (6) where Q and q are respectively an N r matrix and an N 1 vector. Typically the elements of Q and q will be zeros and ones if zero restrictions are imposed on the off-diagonal elements of A 0 in addition to the restrictions due to normalizing the main diagonal. 3. Prior Distributions for Bayesian Analysis To facilitate the inference on the restrictions for the uniqueness of the matrix A 0 with ones on the main diagonal we estimate state-specific variances of the structural shocks in a parametrization that includes the variances of the structural shocks in the first state, λ 1, and M 1 vectors of relative variances, ω m = [λ m,i /λ 1,i ], for states m {,..., M}. Specifying independent inverse gamma distributions (IG) as prior distributions for the ω m s, given our assumptions about the distribution 8
11 of the error terms, leads to the full conditional posterior distributions for these parameters being of the same type. This setup is the basis for feasible computations of the SDDRs for the uniqueness conditions that are specified for relative variances. The choice of the parametrization, marginal prior and full conditional posterior distributions for the ω m s makes our framework general. Note that it does not dependent on the inference on the latent state variable s t. The details of Bayesian assessment of the uniqueness restrictions are given in Section 4. The variances of the structural shocks in the first state, λ 1,n, are a priori independently distributed as IG with parameters a λ and b λ set to 1 which makes the distribution quite spread out over a wide range. In fact, under this assumption the first and second moments of λ 1,n may be infinite which limits the impact of the prior distribution on the posterior distribution. The prior of each of the relative variances of structural shocks ω m,n, for m {,..., M}, follows independently an IG distribution with parameters a ω = 1 and b ω = a ω +, which ensures that the mode of the prior distribution is located at 1. This assumption implies that the state-specific variances for states,..., M have the same prior distributions similar to Woźniak & Droumaguet (015). At the mode of the prior distribution there is no heteroskedasticity and hence the rows of A 0 are not uniquely identified. The prior distribution for the unrestricted elements of the matrix A 0 collected in the vector α, conditionally on hyper-parameter γ α, is a normal distribution with mean vector zero and a diagonal covariance matrix γ α I r. To avoid making the prior more restrictive for some elements of A 0 than for others one could make sure that the variables entering the model have similar orders of magnitude. In macro models this is typically not a problem because many variables enter in logs or rates of change. The hyper-parameter γ α is interpreted as the level of shrinkage imposed on the structural parameters α and is also estimated. For that purpose, we define the marginal prior distribution of γ α to be IG with parameters a and b set to 1. The conditional prior distribution of the variable-specific constant term, µ n, n {1,..., N}, given a constant term specific hyper-parameter γ µ, is a univariate normal distribution with mean zero and variance γ µ. The marginal prior distribution for γ µ is IG with parameters a and b set to 1. To specify the prior distribution of the structural VAR slope parameters β = [A 1,..., A p ], let For the definition of the distribution, its properties, and the random numbers sampling algorithm see Bauwens, Richard & Lubrano (1999, Appendix B). 9
12 P = [ D 0 N N(p 1) ], where D is an N N diagonal matrix. Typically the diagonal elements of the matrix D are zeros for stationary variables and ones for persistent variables, as in the Minnesota prior, but they could also be other known quantities. of the equation-specific autoregressive parameters, β n Then the conditional prior distribution = [A 1.n,..., A p.n ], where A l.n is the n th row of matrix A l for l {1,..., p}, is a pn-variate normal distribution. It is conditioned on an autoregressive hyper-parameter γ β and the n th row of A 0, denoted by A 0.n. Its prior mean is equal to A 0.n P and its prior covariance matrix is equal to γ β H. The diagonal matrix H has the main diagonal set to the vector ( (1 ) 1 ı N, ( ) 1 ı N,..., (p ) 1 ı N), and thus it allows to impose a decaying pattern of prior variances for the subsequent lags as in the Minnesota prior of Doan, Litterman & Sims (1983). The prior distribution for γ β is IG with parameters a and b set to 1. Finally, denote by P m the m th row of the transition matrix P. The prior distributions for the rows of the transition probabilities matrix, P m, are set independently for each row and are given by M-dimensional Dirichlet distributions (D M ) as in Woźniak & Droumaguet (015). The parameters of these distributions, e m,k, for k {1,..., M}, are all set to 1 except the parameters corresponding to the diagonal elements of the matrix P of transition probabilities, denoted by e m,m, which are set to 10. This choice expresses the prior assumption that the volatility states are persistent over time. To summarize, the prior specification takes the following form: p(θ) = p ( ) ( ) ( ) ( ) M N γ α p γµ p γβ p α γα p (P m ) p ( ) ( ) M µ n γ µ p βn A 0.n, γ β p (λ1.n ) p (ω m.n ), m=1 n=1 m= (7) 10
13 where the specific prior distributions are: µ n γ µ N ( ) 0, γ µ ( β n A 0.n, γ β N pn A0.n P, γ β H ) ( ) α γ α N r 0r, γ α I r λ 1,n IG ( ) a λ, b λ ω m,n IG ( ) a ω, b ω γ α IG ( a, b ) γ µ IG ( a, b ) γ β IG ( a, b ) ( ) P m D M em1,..., e mm for n {1,..., N}, m {1,..., M} and m {,..., M}. The above choice of the prior distributions is practical. Priority is given to distributions that result in convenient and proper full conditional posterior distributions, and therefore, allow for the derivation of an efficient Gibbs sampler that is described in Appendix A. The hierarchical prior distributions for the constant terms, autoregressive slope parameters, and the structural matrix constitute a flexible framework in which the impact of the choice of the hyper-parameters of the prior distribution on inference is reduced, in line with Giannone, Lenza & Primiceri (015). 4. Bayesian Assessment of Identification Conditions and Heteroskedasticity In this section, we propose to use the Savage-Dickey Density Ratio (SDDR) (see Verdinelli & Wasserman, 1995, and references therein) to verify the identification conditions for the structural model considered in this paper. The SDDR is one of the methods to compute a Bayes factor. The Bayes factor itself, under the assumption of equal prior probabilities of the competing models, is interpreted as a posterior odds ratio of the model with restrictions versus the unrestricted model. Thus, a large value of the SDDR is evidence in favor of the restriction considered and a small SDDR provides evidence against the restriction. The identification requires sufficient variability in the conditional variances of the structural shocks. The uniqueness of the structural matrix A 0 11
14 can be assessed by verifying the equality restrictions for specific relative variances, such as: ω m,i = ω m,j. (8) If the restriction above holds for some i and j for all m {,..., M}, then the i th structural shock cannot be distinguished from the j th structural shock and the corresponding rows of matrix A 0 are not uniquely identified. Of course, identification through heteroskedasticity requires that there are at least two distinct volatility states. In other words, for heteroskedasticity of structural shock i, there must be two distinct variances λ m,i, m {1,..., M}, which translates to the requirement that at least one of the ω m,i, m {,..., M} is not equal to one. Thus, the homoskedasticity of the i th structural shock is assessed by verifying restrictions ω,i = = ω M,i = 1. (9) Both of the restrictions (8) and (9) can be verified as the data are informative about these features Identification Conditions We rewrite the restriction in equation (8) as ω m,i ω m,j = 1 (10) and use the SDDR to evaluate its validity. The SDDR for the restriction given in equation (10) is a ratio of the marginal posterior distribution to the marginal prior distribution of the left-hand side of the restriction both evaluated at the restricting value. Formally, SDDR = ( ) ωm,i p ω m,j = 1 Y ( ), (11) ωm,i p ω m,j = 1 where Y = (y 1,..., y T ) denotes the data. Small values of the SDDR provide evidence against the ratio ω m,i ω m,j being 1. Of course, this raises the question how small the SDDR has to be to indicate clear evidence against the restriction. Kass & Raftery (1995) discuss a scale for evaluating the size of the SDDR. We will use that scale in our empirical illustration in Section 5. 1
15 The SDDR is particularly suitable for the verification of the identification conditions because it does not require the estimation of the restricted models. Moreover, the SDDR can be easily computed as long as the densities of the full conditional posterior and the prior distributions of ω m,i ω m,j are of known analytical form. We propose a new distribution that is useful for such computations in the context of IG distributed relative variances of the structural shocks. Definition 1 (Inverse Gamma Ratio distribution). Let x and y be two strictly positive independent random variables distributed according to the following IG distributions: x IG (a 1, b 1 ) and y IG (a, b ), where a 1, a, b 1, and b are positive real numbers and the probability density function of the inverse gamma distribution is given by: ( ) a 1 ( ) a b { f IG (x; a, b) = Γ x a+ exp 1 } b, (1) x where Γ( ) denotes the gamma function. Then, the random variable z, defined as z = x/y, follows the Inverse Gamma Ratio (IGR) distribution with probability density function given by: ( a1 f IGR (z; a 1, a, b 1, b ) = B, a ) 1 a 1 a b 1 b z a (b 1 + b z) a 1 +a, (13) where B(, ) denotes the beta function. It is easy to show that the moments of the Inverse Gamma Ratio distribution are as follows. Moments of the IGR distribution. The expected value and the variance of the IGR distributed random variable z are respectively given by E[z] = b 1 b a a 1 Var[z] = ( b 1 b ) a (a 1 + a ) (a 1 ) (a 1 4) for a 1 >, (14) for a 1 > 4. (15) In general, the k th order non-central moment of z is given by E [ z k] = ( b1 b ) k B ( ) a 1 k, a +k B ( ) for a a 1, a 1 > k. (16) 13
16 The density given above generalizes the F distribution that is nested within our distribution family by setting a 1 = b 1 and a = b, as well as the compound gamma distribution derived by Dubey (1970) that is parametrized by three parameters a 1 /, a /, and b 1 /b. 3 For completeness of the derivations, Appendix B defines the Inverse Gamma 1 Ratio distribution of a random variable that is defined as a ratio of two independent inverse gamma 1-distributed random variables. The probability density function as well as the moments of that distribution are also established. These results may facilitate the computations if one prefers to parametrize the model in terms of the conditional standard deviations instead of conditional variances λ and ω. In Section 3 it was assumed that the parameters ω m,i and ω m,j are a priori independently distributed as IG. In effect, the denominator of the SDDR from equation (11) can be computed by simply evaluating the newly proposed distribution with parameters a 1 = a = a ω = 1 and b 1 = b = b ω = 3 at value z = 1. In Appendix A it is shown that, given the data, realizations of the Markov process, and other parameters, the relative variances are independently IG distributed. We use this feature to compute the numerator of the SDDR, apply the Rao-Blackwell tool of Gelfand & Smith (1990), and obtain ˆp ) = 1 Y = 1 ω m,j S ( ωm,i S s=1 ( ) f IGR 1; a (s) i,m, a(s) j,m, b(s) i,m, b(s), (17) j,m { } S where a (s) i,m, a(s) j,m, b(s) i,m, b(s) is a sample of S draws from the posterior distribution defined for j,m s=1 n {i, j} as follows: a (s) n,m = a ω + T (s) m, (18a) b (s) n,m = b ω + ( λ (s) 1,n ) 1 T t=1 ( (s) A 0,n y t µ (s) n A (s) 1,n y ) t 1 A (s) p,ny t p, (18b) where T (s) m is the number of observations classified as belonging to the m th state in the s th iteration of the sampling algorithm. According to the conditions stated in Section, the j th structural shock may not be identified 3 Further generalizations of the F, Beta, and compound gamma distributions were proposed by McDonald (1984) and McDonald & Xu (1995). The latter work is particularly relevant for our developments as it proposes the generalizations of the compound gamma distributions parametrized by four and five parameters. Their distributions explicitly nest the compound gamma distribution, however, none of them nests our Inverse Gamma Ratio or the Inverse Gamma 1 Ratio distribution. 14
17 if all the ratios ω m,i ω m,j to investigate whether ω m,i ω m,j are equal to 1. Hence, to establish possible identification problems, we have purpose. Let U i.j denote the event that ω m,i ω m,j = 1 holds for all m {,..., M}. The SDDR can be extended for that denominator of the SDDR for U i.j is computed simply as: m= = 1 holds for m {,..., M}. In such a case, the ˆp ( ) M ( ) ωm,i ( ) M 1 U i.j = p = 1 = f ω IGR 1; aω, a ω, b ω, b ω, (19) m,j where the last equality comes from the assumption of the invariance of the prior distribution with respect to m. The SDDR s numerator is computed as: ( ) ˆp U i.j Y = 1 S S M s=1 m= ( ) f IGR 1; a (s) i,m, a(s) j,m, b(s) i,m, b(s). (0) j,m The computations of the SDDRs presented above, given the output from the MCMC estimation, are fast and accurate, which emphasizes the advantages of the current setup. The verification of the identification conditions with the SDDRs requires the prior and full conditional posterior distributions for the relative variances of the structural shocks being IG- or IG1-distributed. The setup can be further generalized by assuming hierarchical prior distributions for the relative variances, ω m,n, and is independent on how the state variable s t is estimated. It is, therefore, easily applicable also to other regime-dependent heteroskedastic processes such as those considered by Woźniak & Droumaguet (015) and Markov-switching models with time-varying transition probabilities as considered by Sims et al. (008) and Chen & Netšunajev (017). Having a procedure for verifying the identification conditions emphasizes the benefits of applying Bayesian inference in this paper. Note that there does not exist a general, valid frequentist test of such conditions. In Bayesian inference the estimation of a model that is not identified does not pose any theoretical or practical obstacles. Therefore, using a standard way of verifying hypotheses, such as through the SDDR, is straightforward. Still, verification of the uniqueness is essential to understand the SVAR model identified through heteroskedasticity. 4.. Homoskedasticity If the identification conditions are confirmed, then heteroskedasticity is also established as a by-product. However, one may also be interested in testing the shocks individually or jointly for heteroskedasticity. 15
18 In a similar way as the SDDR can be used to verify the identification conditions, it can also be used to investigate the heteroskedasticity of the structural shocks. Denote by H i the event that the restrictions ω,i = = ω M,i = 1 hold, which is the condition for the homoskedasticity of the i th shock. The SDDR for assessing this hypothesis is given by SDDR = p (H i Y) p (H i ). (1) The elements of the SDDR in the equation above can be computed easily by M ˆp (H i ) = p ( ω m,i = 1 ) ( ) M 1 = f IG 1; aω, b ω () m= and ˆp ( Y ) M H i = p ( ω m,i = 1 Y ) = 1 S m= S M s=1 m= f IG ( 1; a (s) i,m, b(s) i,m), (3) where a (s) and b(s) are given in equation (18). i,m i,m The condition for joint homoskedasticity of several structural shocks can be assessed as well. Let J be a set of K N indicators that define the considered conjuction of homoskedasticity conditions: J = { j i {1,..., N} for i {1,..., K} : H j1 H jk }. Then, the joint homoskedasticity condition is denoted by H = H j1 H jk and the elements of the SDDR are computed as follows: M ˆp (H) = p ( ω m,i = 1 ) ( ) K(M 1) = f IG 1; aω, b ω (4) i J m= and ˆp ( H Y ) = i J m= M p ( ω m,i = 1 Y ) = 1 S S M s=1 i J m= f IG ( 1; a (s) i,m, b(s) i,m). (5) All the computations in this section are facilitated by the fact that ω m,n are a priori as well as conditionally a posteriori independent for m {,..., M} and n {1,..., N}. The proposed Bayesian SDDR for assessing homoskedasticity can be computed easily given the sample of draws from the posterior distribution and it does not pose any significant theoretical challenges (see, e.g., Frühwirth-Schnatter, 006). 16
19 cp gdp p u m1 FF Figure 1: Time series data taken from Belongia & Ireland (015). 5. Empirical Illustration 5.1. Background In this section we illustrate our Bayesian procedures by applying them to SVAR models that were considered by Belongia & Ireland (015) to study the role of Divisia monetary aggregates in monetary policy models. These authors find statistical support for the importance of Divisia monetary aggregates in the monetary policy rule. They document these relationships using Divisia measurements of several alternative monetary aggregates. In this paper, we focus on the particular role of the money aggregate M that, when properly represented by a Divisia measure, has the capability of explaining aggregate fluctuations to a large extent, as argued by Barnett (01). For that purpose, we review a number of identification schemes for the SVAR model some of which have been considered by Belongia & Ireland (015). We build VAR models for the following six quarterly U.S. variables: p t - log of GDP deflator, gdp t - log of real GDP, cp t - a measure of commodity prices defined as the spot index compiled now by the Commodity Research Bureau and earlier by the Bureau of Labor Statistics, FF t - federal funds rate, M t - M Divisia monetary aggregate to measure the flow of monetary services and m t its logarithm, uc t - user-cost measure, provided by Barnett et al. (013), that is the price dual to the Divisia monetary aggregate M t. These variables in exactly this order are collected in the vector y t, i.e., y t = (p t, gdp t, cp t, FF t, m t, uc t ). The series are plotted in Figure 1 for the sample period from 17
20 Table 1: Competing Monetary Policy Models Unrestricted 1 α 1 α 13 α 14 α 15 α 16 α 1 1 α 3 α 4 α 5 α 6 α 31 α 3 1 α 34 α 35 α 36 α 41 α 4 α 43 1 α 45 α 46 α 51 α 5 α 53 α 54 1 α 56 α 61 α 6 α 63 α 64 α 65 1 Recursive Scheme α α 31 α α 41 α 4 α α 51 α 5 α 53 α α 61 α 6 α 63 α 64 α 65 1 Taylor Rule with Money Taylor Rule without Money Money-Interest Rate Rule α α α α 31 α 3 1 α 34 α 35 α 36 α 31 α 3 1 α 34 α 35 α 36 α 31 α 3 1 α 34 α 35 α 36 α 41 α α 45 0 α 41 α α α α 56 1 α α 56 1 α α 56 α α 64 α 65 1 α α 64 α 65 1 α α 64 α 65 1 Note: Vector of variables at time t is y t = (p t, gdp t, cp t, FF t, m t, uc t ). The fourth row of each matrix specifies the monetary policy reaction function and identifies the fourth shock as the monetary policy shock. 1967Q1-013Q Alternative Identification Schemes Assuming that there is sufficient heterogeneity in the covariance structure of the VAR model, a full set of shocks can be identified by heteroskedasticity. No further restrictions are needed for A 0 in this case. In the following we refer to the model as unrestricted if it is identified purely by heteroskedasticity (see the first scheme in Table 1). A standard conventional identification scheme is a recursive model motivated by the work of Bernanke & Blinder (199), Sims (1986, 199) and others (see the second scheme in Table 1). It just-identifies the system in the conventional homoskedastic case. In the heteroskedastic case instead, the zero restrictions above the main diagonal are over-identifying and can be tested. This model identifies the monetary policy shock by imposing restrictions on the fourth row of the matrix A 0 such that the interest rate reacts to contemporaneous changes in the price level, output, and commodity prices. Note that the fourth equation of our model represents the interest rate reaction function. In a monetary model the interest rate equation is typically set up as a Taylor rule which assumes 4 We thank Belongia & Ireland for sharing their data set with us. 18
21 that the interest rate reacts to inflation and the output gap. In our model comparison we include a benchmark model inspired by Leeper & Roush (003) which is also discussed by Belongia & Ireland (015). In Table 1 the identification of the A 0 matrix from this work is described as Taylor Rule with Money. In addition to standard Taylor rule variables such as output gap and inflation, the interest rate equation also contains the Divisia monetary aggregate, meaning that monetary policy reacts to changes in the money stock. Additionally, this model identifies the fifth and sixth shocks as money demand and money supply shocks, respectively. The restrictions imposed on the last two rows of A 0 over-identify the model and, hence, they can be tested in a conventional setting as well as in our heteroskedastic setting. Belongia & Ireland are specifically interested in the role of the divisia money variable in the interest rate reaction function. Therefore they test two sets of over-identifying restrictions on the fourth row of A 0. First, they exclude the money aggregate from the Taylor rule by imposing the restriction α 45 = 0. This scheme is indicated as Taylor Rule without Money in Table 1. It corresponds to the standard monetary policy reaction function of Taylor (1993). Another specification considered by Belongia & Ireland (015) is denoted as Money-Interest Rate Rule in Table 1. It assumes that the interest rate reacts contemporaneously only to the money aggregate. Such a rule was advocated by Leeper & Roush (003) and used also in Leeper & Zha (003) and Sims & Zha (006). The restrictions α 41 = α 4 = 0 are over-identifying in this model and they were not rejected by Belongia & Ireland (015). There are some major differences in the comparison of the models proposed in the present paper and the analysis conducted by Belongia & Ireland (015). First of all, Belongia & Ireland did not allow for heteroskedasticity of the structural shocks. Consequently, they could only test the over-identifying specifications conditional on a set of just-identifying restrictions. Thus, their tests of the restrictions in the fourth row of A 0 are conditional on restrictions imposed in the other rows of A 0. By using the heteroskedasticity of the structural shocks we can test not only the restrictions imposed by Belongia & Ireland, but we can also test the restrictions in the fourth row and leave all other rows unrestricted because in the heteroskedastic case any of the zeros imposed on the matrix A 0 over-identify the model and, thus, the data are informative about them. In order to investigate the importance of the money aggregate in the interest rate equation, we estimate the models mentioned above with heteroskedastic structural shocks. We estimate models 19
22 with the full set of restrictions as presented in Table 1 and also test models in which all of the rows apart from the fourth row are unrestricted, as well as models where restrictions are imposed only on the last three rows which correspond to the monetary system. Finally, all of the models are confronted with a model solely identified by heteroskedasticity in which all the off-diagonal elements of matrix A 0 are estimated without any zero restrictions. Importantly, our approach allows us to statistically compare alternative monetary policy models that are not nested within one another. For instance, our Bayes factors allow us to compare the recursive model to each of the remaining monetary policy models despite the fact that neither of them is nested within the recursive one. We fit VAR models of order p = 4, as in Belongia & Ireland (015), to our full sample of quarterly data from 1967Q1-013Q4 and also to a reduced sample from 1967Q1-007Q4. Following Belongia & Ireland (015), the shorter sample is considered because it excludes the financial crisis period which could affect the structure of monetary policy in the US and, hence, it might lead to distortions in our analysis Assessing Heteroskedasticity We have fitted a two-state Markov process to capture possible changes in the volatility of the residuals. The estimated variances of the second regime relative to the variances in the first regime are shown in Table for all the different identification schemes imposed on A 0. Thus the quantities in the table are the estimated elements of ω. They are all distinct from one, indicating that the second regime indeed has different variances than regime 1. The marginal posterior regime probabilities of the second volatility state are depicted in Figure. They show that roughly the first part and the last part of the sample constitute the second volatility regime and the middle part from the first half of the 1980s to the beginning of the financial crisis constitute the first volatility regime. There is also a short period around the change of the millennium which is assigned to the second volatility state in the longer sample. Since the relative variances of the second volatility state are greater than one, this regime is clearly a high-volatility state. With respect to the dating and the interpretation the first state resembles the Greenspan state found by Sims & Zha (006) while the second one highly resembles the Burns and Volcker state (see, e.g., Woźniak & Droumaguet, 015). A similar classification of the volatility states is also obtained when the model is fitted only to the reduced sample ending in 007Q4. 0
23 Table : Estimated Relative Variances, ˆω, of Structural Shocks in Heteroskedastic Models Taylor Rule Taylor Rule Money- Unrestricted Recursive with Money without Money Interest Rate Sample period 1967Q1-013Q4 p t (1.081) (1.16) (1.301) (1.160) (1.1) gdp t (.90) (.016) (1.971) (.183) (.131) cp t (1.70) (1.71) (1.717) (1.547) (1.570) FF t (10.85) (8.70) (10.484) (10.007) (9.839) m t (1.970) (.517) (1.673) (1.909) (1.973) uc t (0.991) (1.59) (1.616) (1.586) (1.591) Sample period 1967Q1-007Q4 p t (1.167) (1.70) (1.16) (1.54) (1.0) gdp t (3.73) (.034) (1.991) (.151) (.9) cp t (0.99) (0.959) (0.940) (0.918) (0.91) FF t (13.908) (8.497) (10.773) (8.89) (9.598) m t (1.367) (1.375) (0.71) (0.810) (0.756) uc t (0.806) (0.917) (1.008) (0.94) (1.05) Note: The table reports posterior means and posterior standard deviations in parentheses of the structural shocks relative variances, ω, for the Markov-switching models with two states, M =. Thus, the assignment of states is reasonably similar in both samples and is, hence, not driven entirely by the potentially higher macroeconomic volatility during the financial crisis. In Table the posterior standard deviations of the relative variances are also presented. Partly they are quite large. Therefore one may wonder whether the two estimated volatility states are really clearly distinct. This question can be answered by our formal statistical tools. In Table 3 1
24 Sample from 1967Q1 to 013Q Sample from 1967Q1 to 007Q Figure : Marginal posterior probabilities of the second state for the best models with Markov-switching heteroskedasticity with states. we use SDDRs to assess whether the relative variances are actually 1. 5 Note that for our model with only two volatility regimes (M = ), the i th structural shock is heteroskedastic if ω,i 1. It turns out that all results for the longer sample show strong support for the relative variances to be different from 1 which implies heteroskedasticity of all structural shocks. For the shorter sample the evidence is still strong that at least some of the relative variances are not equal to 1, while some others may not be different from 1. Apart from the unrestricted model, in all other models the evidence is strong that at most one shock is homoskedastic and, hence, we may still have full identification through heteroskedasticity, as discussed in Section. In any case, the evidence for two distinct volatility states is very strong for both samples because, to confirm distinct covariance matrices in the two states, it is enough that one of the relative variances differs from 1. 5 In Appendix C we provide details on the precision of the estimated quantities. All results are sufficiently precise so as to ensure the qualitative validity of the results.
25 Table 3: Natural Logarithms of SDDRs for Assessing Heteroskedasticity Taylor Rule Taylor Rule Money- Unrestricted Recursive with Money without Money Interest Rate Sample period 1967Q1-013Q4 Hypothesis: ω,i = 1 p t gdp t cp t FF t m t uc t Hypothesis: ω,i = 1 for i = 1,..., N Sample period 1967Q1-007Q4 Hypothesis: ω,i = 1 p t gdp t cp t FF t m t uc t Hypothesis: ω,i = 1 for i = 1,..., N Note: The table reports natural logarithms of SDDRs for the hypothesis of homoskedasticity of individual structural shocks, as well as the hypothesis of joint homoskedasticity in the models with two volatility states, M =. Numbers in boldface denote SDDR values indicating very strong evidence against the hypothesis on a scale by Kass & Raftery (1995). The numerical standard errors for the SDDRs reported in this table are given in Appendix C Assessing Identification These results clearly indicate that there is time-varying volatility in the data that can be used for identification purposes. It is therefore of interest to know whether there is sufficient heteroskedasticity to ensure a fully identified model. As discussed in the earlier sections, in a model with two states, full identification requires that all of the relative variances, ω,n, n = 1,..., N, are distinct. Again we can use SDDRs to investigate this identification condition. In Table 4 the relevant SDDRs are given. For both samples they provide strong support for at least some distinct relative variances. 3
Bayesian Inference for Structural Vector Autoregressions Identified by Markov-Switching Heteroskedasticity
 Bayesian Inference for Structural Vector Autoregressions Identified by Markov-Switching Heteroskedasticity Helmut Lütkepohl a, Tomasz Woźniak Ib, a DIW Berlin and Freie Universität Berlin b University
Bayesian Inference for Structural Vector Autoregressions Identified by Markov-Switching Heteroskedasticity Helmut Lütkepohl a, Tomasz Woźniak Ib, a DIW Berlin and Freie Universität Berlin b University
Assessing Monetary Policy Models: Bayesian Inference for Heteroskedastic Structural VARs
 Assessing Monetary Policy Models: Bayesian Inference for Heteroskedastic Structural VARs Tomasz Woźniak a, Matthieu Droumaguet b a Department of Economics, University of Melbourne b Goldman Sachs, Hong
Assessing Monetary Policy Models: Bayesian Inference for Heteroskedastic Structural VARs Tomasz Woźniak a, Matthieu Droumaguet b a Department of Economics, University of Melbourne b Goldman Sachs, Hong
Structural Vector Autoregressions with Markov Switching. Markku Lanne University of Helsinki. Helmut Lütkepohl European University Institute, Florence
 Structural Vector Autoregressions with Markov Switching Markku Lanne University of Helsinki Helmut Lütkepohl European University Institute, Florence Katarzyna Maciejowska European University Institute,
Structural Vector Autoregressions with Markov Switching Markku Lanne University of Helsinki Helmut Lütkepohl European University Institute, Florence Katarzyna Maciejowska European University Institute,
Disentangling Demand and Supply Shocks in the Crude Oil Market
 95 Discussion Papers Deutsches Institut für Wirtschaftsforschung Disentangling Demand and Supply Shocks in the Crude Oil Market How to Check Sign Restrictions in Structural VARs Helmut Lütkepohl and Aleksei
95 Discussion Papers Deutsches Institut für Wirtschaftsforschung Disentangling Demand and Supply Shocks in the Crude Oil Market How to Check Sign Restrictions in Structural VARs Helmut Lütkepohl and Aleksei
Inference in VARs with Conditional Heteroskedasticity of Unknown Form
 Inference in VARs with Conditional Heteroskedasticity of Unknown Form Ralf Brüggemann a Carsten Jentsch b Carsten Trenkler c University of Konstanz University of Mannheim University of Mannheim IAB Nuremberg
Inference in VARs with Conditional Heteroskedasticity of Unknown Form Ralf Brüggemann a Carsten Jentsch b Carsten Trenkler c University of Konstanz University of Mannheim University of Mannheim IAB Nuremberg
Disentangling Demand and Supply Shocks in the Crude Oil Market: How to Check Sign Restrictions in Structural VARs
 September 27, 2011 Preliminary. Please do not quote. Disentangling Demand and Supply Shocks in the Crude Oil Market: How to Check Sign Restrictions in Structural VARs by Helmut Lütkepohl and Aleksei Netšunajev
September 27, 2011 Preliminary. Please do not quote. Disentangling Demand and Supply Shocks in the Crude Oil Market: How to Check Sign Restrictions in Structural VARs by Helmut Lütkepohl and Aleksei Netšunajev
Identification of Economic Shocks by Inequality Constraints in Bayesian Structural Vector Autoregression
 Identification of Economic Shocks by Inequality Constraints in Bayesian Structural Vector Autoregression Markku Lanne Department of Political and Economic Studies, University of Helsinki Jani Luoto Department
Identification of Economic Shocks by Inequality Constraints in Bayesian Structural Vector Autoregression Markku Lanne Department of Political and Economic Studies, University of Helsinki Jani Luoto Department
In this chapter, we explain the principle of identification by heteroskedasticity.
 Chapter 14 Identification by Heteroskedasticity or Non-Gaussianity 14.1 Introduction As we have seen in Chapters 8 and 10, the identification of structural VAR models typically relies on economically motivated
Chapter 14 Identification by Heteroskedasticity or Non-Gaussianity 14.1 Introduction As we have seen in Chapters 8 and 10, the identification of structural VAR models typically relies on economically motivated
Stargazing with Structural VARs: Shock Identification via Independent Component Analysis
 Stargazing with Structural VARs: Shock Identification via Independent Component Analysis Dmitry Kulikov and Aleksei Netšunajev Eesti Pank Estonia pst. 13 19 Tallinn Estonia phone: +372 668777 e-mail: dmitry.kulikov@eestipank.ee
Stargazing with Structural VARs: Shock Identification via Independent Component Analysis Dmitry Kulikov and Aleksei Netšunajev Eesti Pank Estonia pst. 13 19 Tallinn Estonia phone: +372 668777 e-mail: dmitry.kulikov@eestipank.ee
Identifying SVARs with Sign Restrictions and Heteroskedasticity
 Identifying SVARs with Sign Restrictions and Heteroskedasticity Srečko Zimic VERY PRELIMINARY AND INCOMPLETE NOT FOR DISTRIBUTION February 13, 217 Abstract This paper introduces a new method to identify
Identifying SVARs with Sign Restrictions and Heteroskedasticity Srečko Zimic VERY PRELIMINARY AND INCOMPLETE NOT FOR DISTRIBUTION February 13, 217 Abstract This paper introduces a new method to identify
Dynamic Factor Models and Factor Augmented Vector Autoregressions. Lawrence J. Christiano
 Dynamic Factor Models and Factor Augmented Vector Autoregressions Lawrence J Christiano Dynamic Factor Models and Factor Augmented Vector Autoregressions Problem: the time series dimension of data is relatively
Dynamic Factor Models and Factor Augmented Vector Autoregressions Lawrence J Christiano Dynamic Factor Models and Factor Augmented Vector Autoregressions Problem: the time series dimension of data is relatively
Online appendix to On the stability of the excess sensitivity of aggregate consumption growth in the US
 Online appendix to On the stability of the excess sensitivity of aggregate consumption growth in the US Gerdie Everaert 1, Lorenzo Pozzi 2, and Ruben Schoonackers 3 1 Ghent University & SHERPPA 2 Erasmus
Online appendix to On the stability of the excess sensitivity of aggregate consumption growth in the US Gerdie Everaert 1, Lorenzo Pozzi 2, and Ruben Schoonackers 3 1 Ghent University & SHERPPA 2 Erasmus
The PPP Hypothesis Revisited
 1288 Discussion Papers Deutsches Institut für Wirtschaftsforschung 2013 The PPP Hypothesis Revisited Evidence Using a Multivariate Long-Memory Model Guglielmo Maria Caporale, Luis A.Gil-Alana and Yuliya
1288 Discussion Papers Deutsches Institut für Wirtschaftsforschung 2013 The PPP Hypothesis Revisited Evidence Using a Multivariate Long-Memory Model Guglielmo Maria Caporale, Luis A.Gil-Alana and Yuliya
Web Appendix for The Dynamics of Reciprocity, Accountability, and Credibility
 Web Appendix for The Dynamics of Reciprocity, Accountability, and Credibility Patrick T. Brandt School of Economic, Political and Policy Sciences University of Texas at Dallas E-mail: pbrandt@utdallas.edu
Web Appendix for The Dynamics of Reciprocity, Accountability, and Credibility Patrick T. Brandt School of Economic, Political and Policy Sciences University of Texas at Dallas E-mail: pbrandt@utdallas.edu
Title. Description. var intro Introduction to vector autoregressive models
 Title var intro Introduction to vector autoregressive models Description Stata has a suite of commands for fitting, forecasting, interpreting, and performing inference on vector autoregressive (VAR) models
Title var intro Introduction to vector autoregressive models Description Stata has a suite of commands for fitting, forecasting, interpreting, and performing inference on vector autoregressive (VAR) models
Identification in Structural VAR models with different volatility regimes
 Identification in Structural VAR models with different volatility regimes Emanuele Bacchiocchi 28th September 2010 PRELIMINARY VERSION Abstract In this paper we study the identification conditions in structural
Identification in Structural VAR models with different volatility regimes Emanuele Bacchiocchi 28th September 2010 PRELIMINARY VERSION Abstract In this paper we study the identification conditions in structural
Identifying the Monetary Policy Shock Christiano et al. (1999)
 Identifying the Monetary Policy Shock Christiano et al. (1999) The question we are asking is: What are the consequences of a monetary policy shock a shock which is purely related to monetary conditions
Identifying the Monetary Policy Shock Christiano et al. (1999) The question we are asking is: What are the consequences of a monetary policy shock a shock which is purely related to monetary conditions
Data-Driven Inference on Sign Restrictions in Bayesian Structural Vector Autoregression. Markku Lanne and Jani Luoto. CREATES Research Paper
 Data-Driven Inference on Sign Restrictions in Bayesian Structural Vector Autoregression Markku Lanne and Jani Luoto CREATES Research Paper 2016-4 Department of Economics and Business Economics Aarhus University
Data-Driven Inference on Sign Restrictions in Bayesian Structural Vector Autoregression Markku Lanne and Jani Luoto CREATES Research Paper 2016-4 Department of Economics and Business Economics Aarhus University
Identifying Aggregate Liquidity Shocks with Monetary Policy Shocks: An Application using UK Data
 Identifying Aggregate Liquidity Shocks with Monetary Policy Shocks: An Application using UK Data Michael Ellington and Costas Milas Financial Services, Liquidity and Economic Activity Bank of England May
Identifying Aggregate Liquidity Shocks with Monetary Policy Shocks: An Application using UK Data Michael Ellington and Costas Milas Financial Services, Liquidity and Economic Activity Bank of England May
Confidence Bands for Impulse Responses
 134 Discussion Papers Deutsches Institut für Wirtschaftsforschung 214 Confidence Bands for Impulse Responses Bonferroni versus Wald Helmut Lütkepohl, Anna Staszewska-Bystrova, Peter Winker Opinions expressed
134 Discussion Papers Deutsches Institut für Wirtschaftsforschung 214 Confidence Bands for Impulse Responses Bonferroni versus Wald Helmut Lütkepohl, Anna Staszewska-Bystrova, Peter Winker Opinions expressed
Time-Varying Vector Autoregressive Models with Structural Dynamic Factors
 Time-Varying Vector Autoregressive Models with Structural Dynamic Factors Paolo Gorgi, Siem Jan Koopman, Julia Schaumburg http://sjkoopman.net Vrije Universiteit Amsterdam School of Business and Economics
Time-Varying Vector Autoregressive Models with Structural Dynamic Factors Paolo Gorgi, Siem Jan Koopman, Julia Schaumburg http://sjkoopman.net Vrije Universiteit Amsterdam School of Business and Economics
Estimating and Identifying Vector Autoregressions Under Diagonality and Block Exogeneity Restrictions
 Estimating and Identifying Vector Autoregressions Under Diagonality and Block Exogeneity Restrictions William D. Lastrapes Department of Economics Terry College of Business University of Georgia Athens,
Estimating and Identifying Vector Autoregressions Under Diagonality and Block Exogeneity Restrictions William D. Lastrapes Department of Economics Terry College of Business University of Georgia Athens,
Inference when identifying assumptions are doubted. A. Theory B. Applications
 Inference when identifying assumptions are doubted A. Theory B. Applications 1 A. Theory Structural model of interest: A y t B 1 y t1 B m y tm u t nn n1 u t i.i.d. N0, D D diagonal 2 Bayesian approach:
Inference when identifying assumptions are doubted A. Theory B. Applications 1 A. Theory Structural model of interest: A y t B 1 y t1 B m y tm u t nn n1 u t i.i.d. N0, D D diagonal 2 Bayesian approach:
Inference when identifying assumptions are doubted. A. Theory. Structural model of interest: B 1 y t1. u t. B m y tm. u t i.i.d.
 Inference when identifying assumptions are doubted A. Theory B. Applications Structural model of interest: A y t B y t B m y tm nn n i.i.d. N, D D diagonal A. Theory Bayesian approach: Summarize whatever
Inference when identifying assumptions are doubted A. Theory B. Applications Structural model of interest: A y t B y t B m y tm nn n i.i.d. N, D D diagonal A. Theory Bayesian approach: Summarize whatever
Estimating and Accounting for the Output Gap with Large Bayesian Vector Autoregressions
 Estimating and Accounting for the Output Gap with Large Bayesian Vector Autoregressions James Morley 1 Benjamin Wong 2 1 University of Sydney 2 Reserve Bank of New Zealand The view do not necessarily represent
Estimating and Accounting for the Output Gap with Large Bayesian Vector Autoregressions James Morley 1 Benjamin Wong 2 1 University of Sydney 2 Reserve Bank of New Zealand The view do not necessarily represent
Computational Macroeconomics. Prof. Dr. Maik Wolters Friedrich Schiller University Jena
 Computational Macroeconomics Prof. Dr. Maik Wolters Friedrich Schiller University Jena Overview Objective: Learn doing empirical and applied theoretical work in monetary macroeconomics Implementing macroeconomic
Computational Macroeconomics Prof. Dr. Maik Wolters Friedrich Schiller University Jena Overview Objective: Learn doing empirical and applied theoretical work in monetary macroeconomics Implementing macroeconomic
Identifying Monetary Policy Shocks via Changes in Volatility 1
 June 29, 2007 Identifying Monetary Policy Shocks via Changes in Volatility 1 Markku Lanne Department of Economics, P.O. Box 17 (Arkadiankatu 7), FI-00014 University of Helsinki, FINLAND email: markku.lanne@helsinki.fi
June 29, 2007 Identifying Monetary Policy Shocks via Changes in Volatility 1 Markku Lanne Department of Economics, P.O. Box 17 (Arkadiankatu 7), FI-00014 University of Helsinki, FINLAND email: markku.lanne@helsinki.fi
Katsuhiro Sugita Faculty of Law and Letters, University of the Ryukyus. Abstract
 Bayesian analysis of a vector autoregressive model with multiple structural breaks Katsuhiro Sugita Faculty of Law and Letters, University of the Ryukyus Abstract This paper develops a Bayesian approach
Bayesian analysis of a vector autoregressive model with multiple structural breaks Katsuhiro Sugita Faculty of Law and Letters, University of the Ryukyus Abstract This paper develops a Bayesian approach
Restrictions Search for Panel VARs
 1612 Discussion Papers Deutsches Institut für Wirtschaftsforschung 2016 Restrictions Search for Panel VARs Annika Schnücker Opinions expressed in this paper are those of the author(s) and do not necessarily
1612 Discussion Papers Deutsches Institut für Wirtschaftsforschung 2016 Restrictions Search for Panel VARs Annika Schnücker Opinions expressed in this paper are those of the author(s) and do not necessarily
A Non-Parametric Approach of Heteroskedasticity Robust Estimation of Vector-Autoregressive (VAR) Models
 Journal of Finance and Investment Analysis, vol.1, no.1, 2012, 55-67 ISSN: 2241-0988 (print version), 2241-0996 (online) International Scientific Press, 2012 A Non-Parametric Approach of Heteroskedasticity
Journal of Finance and Investment Analysis, vol.1, no.1, 2012, 55-67 ISSN: 2241-0988 (print version), 2241-0996 (online) International Scientific Press, 2012 A Non-Parametric Approach of Heteroskedasticity
Dynamic probabilities of restrictions in state space models: An application to the New Keynesian Phillips Curve
 Dynamic probabilities of restrictions in state space models: An application to the New Keynesian Phillips Curve Gary Koop Department of Economics University of Strathclyde Scotland Gary.Koop@strath.ac.uk
Dynamic probabilities of restrictions in state space models: An application to the New Keynesian Phillips Curve Gary Koop Department of Economics University of Strathclyde Scotland Gary.Koop@strath.ac.uk
Labor-Supply Shifts and Economic Fluctuations. Technical Appendix
 Labor-Supply Shifts and Economic Fluctuations Technical Appendix Yongsung Chang Department of Economics University of Pennsylvania Frank Schorfheide Department of Economics University of Pennsylvania January
Labor-Supply Shifts and Economic Fluctuations Technical Appendix Yongsung Chang Department of Economics University of Pennsylvania Frank Schorfheide Department of Economics University of Pennsylvania January
Inference in Bayesian Proxy-SVARs
 Inference in Bayesian Proxy-SVARs Jonas E. Arias Juan F. Rubio-Ramírez Daniel F. Waggoner October 30, 2018 Abstract Motivated by the increasing use of external instruments to identify structural vector
Inference in Bayesian Proxy-SVARs Jonas E. Arias Juan F. Rubio-Ramírez Daniel F. Waggoner October 30, 2018 Abstract Motivated by the increasing use of external instruments to identify structural vector
Structural Vector Autoregressions with Markov Switching: Identification via Heteroskedasticity
 Structural Vector Autoregressions with Markov Switching: Identification via Heteroskedasticity Aleksei Netšunajev Thesis submitted for assessment with a view to obtaining the degree of Doctor of Economics
Structural Vector Autoregressions with Markov Switching: Identification via Heteroskedasticity Aleksei Netšunajev Thesis submitted for assessment with a view to obtaining the degree of Doctor of Economics
WERE THERE REGIME SWITCHES IN US MONETARY POLICY? I. INTRODUCTION
 WERE THERE REGIME SWITCHES IN US MONETARY POLICY? ABSTRACT. A multivariate model, identifying monetary policy and allowing for simultaneity and regime switching in coefficients and variances, is confronted
WERE THERE REGIME SWITCHES IN US MONETARY POLICY? ABSTRACT. A multivariate model, identifying monetary policy and allowing for simultaneity and regime switching in coefficients and variances, is confronted
Vector Autoregressive Model. Vector Autoregressions II. Estimation of Vector Autoregressions II. Estimation of Vector Autoregressions I.
 Vector Autoregressive Model Vector Autoregressions II Empirical Macroeconomics - Lect 2 Dr. Ana Beatriz Galvao Queen Mary University of London January 2012 A VAR(p) model of the m 1 vector of time series
Vector Autoregressive Model Vector Autoregressions II Empirical Macroeconomics - Lect 2 Dr. Ana Beatriz Galvao Queen Mary University of London January 2012 A VAR(p) model of the m 1 vector of time series
Econometría 2: Análisis de series de Tiempo
 Econometría 2: Análisis de series de Tiempo Karoll GOMEZ kgomezp@unal.edu.co http://karollgomez.wordpress.com Segundo semestre 2016 IX. Vector Time Series Models VARMA Models A. 1. Motivation: The vector
Econometría 2: Análisis de series de Tiempo Karoll GOMEZ kgomezp@unal.edu.co http://karollgomez.wordpress.com Segundo semestre 2016 IX. Vector Time Series Models VARMA Models A. 1. Motivation: The vector
Computational statistics
 Computational statistics Markov Chain Monte Carlo methods Thierry Denœux March 2017 Thierry Denœux Computational statistics March 2017 1 / 71 Contents of this chapter When a target density f can be evaluated
Computational statistics Markov Chain Monte Carlo methods Thierry Denœux March 2017 Thierry Denœux Computational statistics March 2017 1 / 71 Contents of this chapter When a target density f can be evaluated
Bayesian Statistical Methods. Jeff Gill. Department of Political Science, University of Florida
 Bayesian Statistical Methods Jeff Gill Department of Political Science, University of Florida 234 Anderson Hall, PO Box 117325, Gainesville, FL 32611-7325 Voice: 352-392-0262x272, Fax: 352-392-8127, Email:
Bayesian Statistical Methods Jeff Gill Department of Political Science, University of Florida 234 Anderson Hall, PO Box 117325, Gainesville, FL 32611-7325 Voice: 352-392-0262x272, Fax: 352-392-8127, Email:
Monetary and Exchange Rate Policy Under Remittance Fluctuations. Technical Appendix and Additional Results
 Monetary and Exchange Rate Policy Under Remittance Fluctuations Technical Appendix and Additional Results Federico Mandelman February In this appendix, I provide technical details on the Bayesian estimation.
Monetary and Exchange Rate Policy Under Remittance Fluctuations Technical Appendix and Additional Results Federico Mandelman February In this appendix, I provide technical details on the Bayesian estimation.
Working Paper Series. A note on implementing the Durbin and Koopman simulation smoother. No 1867 / November Marek Jarocinski
 Working Paper Series Marek Jarocinski A note on implementing the Durbin and Koopman simulation smoother No 1867 / November 2015 Note: This Working Paper should not be reported as representing the views
Working Paper Series Marek Jarocinski A note on implementing the Durbin and Koopman simulation smoother No 1867 / November 2015 Note: This Working Paper should not be reported as representing the views
Oil price and macroeconomy in Russia. Abstract
 Oil price and macroeconomy in Russia Katsuya Ito Fukuoka University Abstract In this note, using the VEC model we attempt to empirically investigate the effects of oil price and monetary shocks on the
Oil price and macroeconomy in Russia Katsuya Ito Fukuoka University Abstract In this note, using the VEC model we attempt to empirically investigate the effects of oil price and monetary shocks on the
Bayesian Inference for DSGE Models. Lawrence J. Christiano
 Bayesian Inference for DSGE Models Lawrence J. Christiano Outline State space-observer form. convenient for model estimation and many other things. Bayesian inference Bayes rule. Monte Carlo integation.
Bayesian Inference for DSGE Models Lawrence J. Christiano Outline State space-observer form. convenient for model estimation and many other things. Bayesian inference Bayes rule. Monte Carlo integation.
Structural VAR Models and Applications
 Structural VAR Models and Applications Laurent Ferrara 1 1 University of Paris Nanterre M2 Oct. 2018 SVAR: Objectives Whereas the VAR model is able to capture efficiently the interactions between the different
Structural VAR Models and Applications Laurent Ferrara 1 1 University of Paris Nanterre M2 Oct. 2018 SVAR: Objectives Whereas the VAR model is able to capture efficiently the interactions between the different
MA Advanced Macroeconomics: 4. VARs With Long-Run Restrictions
 MA Advanced Macroeconomics: 4. VARs With Long-Run Restrictions Karl Whelan School of Economics, UCD Spring 2016 Karl Whelan (UCD) Long-Run Restrictions Spring 2016 1 / 11 An Alternative Approach: Long-Run
MA Advanced Macroeconomics: 4. VARs With Long-Run Restrictions Karl Whelan School of Economics, UCD Spring 2016 Karl Whelan (UCD) Long-Run Restrictions Spring 2016 1 / 11 An Alternative Approach: Long-Run
Robust Bayes Inference for Non-identified SVARs
 1/29 Robust Bayes Inference for Non-identified SVARs Raffaella Giacomini (UCL) & Toru Kitagawa (UCL) 27, Dec, 2013 work in progress 2/29 Motivating Example Structural VAR (SVAR) is a useful tool to infer
1/29 Robust Bayes Inference for Non-identified SVARs Raffaella Giacomini (UCL) & Toru Kitagawa (UCL) 27, Dec, 2013 work in progress 2/29 Motivating Example Structural VAR (SVAR) is a useful tool to infer
Bayesian Inference for DSGE Models. Lawrence J. Christiano
 Bayesian Inference for DSGE Models Lawrence J. Christiano Outline State space-observer form. convenient for model estimation and many other things. Bayesian inference Bayes rule. Monte Carlo integation.
Bayesian Inference for DSGE Models Lawrence J. Christiano Outline State space-observer form. convenient for model estimation and many other things. Bayesian inference Bayes rule. Monte Carlo integation.
Alternative Bayesian Estimators for Vector-Autoregressive Models
 Alternative Bayesian Estimators for Vector-Autoregressive Models Shawn Ni, Department of Economics, University of Missouri, Columbia, MO 65211, USA Dongchu Sun, Department of Statistics, University of
Alternative Bayesian Estimators for Vector-Autoregressive Models Shawn Ni, Department of Economics, University of Missouri, Columbia, MO 65211, USA Dongchu Sun, Department of Statistics, University of
Research Division Federal Reserve Bank of St. Louis Working Paper Series
 Research Division Federal Reserve Bank of St Louis Working Paper Series Kalman Filtering with Truncated Normal State Variables for Bayesian Estimation of Macroeconomic Models Michael Dueker Working Paper
Research Division Federal Reserve Bank of St Louis Working Paper Series Kalman Filtering with Truncated Normal State Variables for Bayesian Estimation of Macroeconomic Models Michael Dueker Working Paper
BEAR 4.2. Introducing Stochastic Volatility, Time Varying Parameters and Time Varying Trends. A. Dieppe R. Legrand B. van Roye ECB.
 BEAR 4.2 Introducing Stochastic Volatility, Time Varying Parameters and Time Varying Trends A. Dieppe R. Legrand B. van Roye ECB 25 June 2018 The views expressed in this presentation are the authors and
BEAR 4.2 Introducing Stochastic Volatility, Time Varying Parameters and Time Varying Trends A. Dieppe R. Legrand B. van Roye ECB 25 June 2018 The views expressed in this presentation are the authors and
Bayesian Inference for DSGE Models. Lawrence J. Christiano
 Bayesian Inference for DSGE Models Lawrence J. Christiano Outline State space-observer form. convenient for model estimation and many other things. Preliminaries. Probabilities. Maximum Likelihood. Bayesian
Bayesian Inference for DSGE Models Lawrence J. Christiano Outline State space-observer form. convenient for model estimation and many other things. Preliminaries. Probabilities. Maximum Likelihood. Bayesian
1. Introduction. Hang Qian 1 Iowa State University
 Users Guide to the VARDAS Package Hang Qian 1 Iowa State University 1. Introduction The Vector Autoregression (VAR) model is widely used in macroeconomics. However, macroeconomic data are not always observed
Users Guide to the VARDAS Package Hang Qian 1 Iowa State University 1. Introduction The Vector Autoregression (VAR) model is widely used in macroeconomics. However, macroeconomic data are not always observed
Granger-Causal-Priority and Choice of Variables in Vector Autoregressions
 Granger-Causal-Priority and Choice of Variables in Vector Autoregressions Marek Jarociński European Central Bank Bartosz Maćkowiak European Central Bank and CEPR First version: September 2011. This version:
Granger-Causal-Priority and Choice of Variables in Vector Autoregressions Marek Jarociński European Central Bank Bartosz Maćkowiak European Central Bank and CEPR First version: September 2011. This version:
Warwick Business School Forecasting System. Summary. Ana Galvao, Anthony Garratt and James Mitchell November, 2014
 Warwick Business School Forecasting System Summary Ana Galvao, Anthony Garratt and James Mitchell November, 21 The main objective of the Warwick Business School Forecasting System is to provide competitive
Warwick Business School Forecasting System Summary Ana Galvao, Anthony Garratt and James Mitchell November, 21 The main objective of the Warwick Business School Forecasting System is to provide competitive
ECON 4160: Econometrics-Modelling and Systems Estimation Lecture 9: Multiple equation models II
 ECON 4160: Econometrics-Modelling and Systems Estimation Lecture 9: Multiple equation models II Ragnar Nymoen Department of Economics University of Oslo 9 October 2018 The reference to this lecture is:
ECON 4160: Econometrics-Modelling and Systems Estimation Lecture 9: Multiple equation models II Ragnar Nymoen Department of Economics University of Oslo 9 October 2018 The reference to this lecture is:
Granger-Causal-Priority and Choice of Variables in Vector Autoregressions
 Granger-Causal-Priority and Choice of Variables in Vector Autoregressions Marek Jarociński European Central Bank Bartosz Maćkowiak European Central Bank and CEPR Abstract We derive a closed-form expression
Granger-Causal-Priority and Choice of Variables in Vector Autoregressions Marek Jarociński European Central Bank Bartosz Maćkowiak European Central Bank and CEPR Abstract We derive a closed-form expression
1 Teaching notes on structural VARs.
 Bent E. Sørensen February 22, 2007 1 Teaching notes on structural VARs. 1.1 Vector MA models: 1.1.1 Probability theory The simplest (to analyze, estimation is a different matter) time series models are
Bent E. Sørensen February 22, 2007 1 Teaching notes on structural VARs. 1.1 Vector MA models: 1.1.1 Probability theory The simplest (to analyze, estimation is a different matter) time series models are
Assessing Structural Convergence between Romanian Economy and Euro Area: A Bayesian Approach
 Vol. 3, No.3, July 2013, pp. 372 383 ISSN: 2225-8329 2013 HRMARS www.hrmars.com Assessing Structural Convergence between Romanian Economy and Euro Area: A Bayesian Approach Alexie ALUPOAIEI 1 Ana-Maria
Vol. 3, No.3, July 2013, pp. 372 383 ISSN: 2225-8329 2013 HRMARS www.hrmars.com Assessing Structural Convergence between Romanian Economy and Euro Area: A Bayesian Approach Alexie ALUPOAIEI 1 Ana-Maria
Econ 423 Lecture Notes: Additional Topics in Time Series 1
 Econ 423 Lecture Notes: Additional Topics in Time Series 1 John C. Chao April 25, 2017 1 These notes are based in large part on Chapter 16 of Stock and Watson (2011). They are for instructional purposes
Econ 423 Lecture Notes: Additional Topics in Time Series 1 John C. Chao April 25, 2017 1 These notes are based in large part on Chapter 16 of Stock and Watson (2011). They are for instructional purposes
Markov-Switching Models with Endogenous Explanatory Variables. Chang-Jin Kim 1
 Markov-Switching Models with Endogenous Explanatory Variables by Chang-Jin Kim 1 Dept. of Economics, Korea University and Dept. of Economics, University of Washington First draft: August, 2002 This version:
Markov-Switching Models with Endogenous Explanatory Variables by Chang-Jin Kim 1 Dept. of Economics, Korea University and Dept. of Economics, University of Washington First draft: August, 2002 This version:
1. Shocks. This version: February 15, Nr. 1
 1. Shocks This version: February 15, 2006 Nr. 1 1.3. Factor models What if there are more shocks than variables in the VAR? What if there are only a few underlying shocks, explaining most of fluctuations?
1. Shocks This version: February 15, 2006 Nr. 1 1.3. Factor models What if there are more shocks than variables in the VAR? What if there are only a few underlying shocks, explaining most of fluctuations?
Hypothesis Testing. Econ 690. Purdue University. Justin L. Tobias (Purdue) Testing 1 / 33
 Hypothesis Testing Econ 690 Purdue University Justin L. Tobias (Purdue) Testing 1 / 33 Outline 1 Basic Testing Framework 2 Testing with HPD intervals 3 Example 4 Savage Dickey Density Ratio 5 Bartlett
Hypothesis Testing Econ 690 Purdue University Justin L. Tobias (Purdue) Testing 1 / 33 Outline 1 Basic Testing Framework 2 Testing with HPD intervals 3 Example 4 Savage Dickey Density Ratio 5 Bartlett
1 Teaching notes on structural VARs.
 Bent E. Sørensen November 8, 2016 1 Teaching notes on structural VARs. 1.1 Vector MA models: 1.1.1 Probability theory The simplest to analyze, estimation is a different matter time series models are the
Bent E. Sørensen November 8, 2016 1 Teaching notes on structural VARs. 1.1 Vector MA models: 1.1.1 Probability theory The simplest to analyze, estimation is a different matter time series models are the
Lecture 5: Spatial probit models. James P. LeSage University of Toledo Department of Economics Toledo, OH
 Lecture 5: Spatial probit models James P. LeSage University of Toledo Department of Economics Toledo, OH 43606 jlesage@spatial-econometrics.com March 2004 1 A Bayesian spatial probit model with individual
Lecture 5: Spatial probit models James P. LeSage University of Toledo Department of Economics Toledo, OH 43606 jlesage@spatial-econometrics.com March 2004 1 A Bayesian spatial probit model with individual
Factor models. March 13, 2017
 Factor models March 13, 2017 Factor Models Macro economists have a peculiar data situation: Many data series, but usually short samples How can we utilize all this information without running into degrees
Factor models March 13, 2017 Factor Models Macro economists have a peculiar data situation: Many data series, but usually short samples How can we utilize all this information without running into degrees
Regime-Switching Cointegration
 Regime-Switching Cointegration Markus Jochmann Newcastle University Rimini Centre for Economic Analysis Gary Koop University of Strathclyde Rimini Centre for Economic Analysis July 2013 Abstract We develop
Regime-Switching Cointegration Markus Jochmann Newcastle University Rimini Centre for Economic Analysis Gary Koop University of Strathclyde Rimini Centre for Economic Analysis July 2013 Abstract We develop
Generalized Impulse Response Analysis: General or Extreme?
 MPRA Munich Personal RePEc Archive Generalized Impulse Response Analysis: General or Extreme? Kim Hyeongwoo Auburn University April 2009 Online at http://mpra.ub.uni-muenchen.de/17014/ MPRA Paper No. 17014,
MPRA Munich Personal RePEc Archive Generalized Impulse Response Analysis: General or Extreme? Kim Hyeongwoo Auburn University April 2009 Online at http://mpra.ub.uni-muenchen.de/17014/ MPRA Paper No. 17014,
Nonperforming Loans and Rules of Monetary Policy
 Nonperforming Loans and Rules of Monetary Policy preliminary and incomplete draft: any comment will be welcome Emiliano Brancaccio Università degli Studi del Sannio Andrea Califano andrea.califano@iusspavia.it
Nonperforming Loans and Rules of Monetary Policy preliminary and incomplete draft: any comment will be welcome Emiliano Brancaccio Università degli Studi del Sannio Andrea Califano andrea.califano@iusspavia.it
Generalized Impulse Response Analysis: General or Extreme?
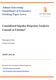 Auburn University Department of Economics Working Paper Series Generalized Impulse Response Analysis: General or Extreme? Hyeongwoo Kim Auburn University AUWP 2012-04 This paper can be downloaded without
Auburn University Department of Economics Working Paper Series Generalized Impulse Response Analysis: General or Extreme? Hyeongwoo Kim Auburn University AUWP 2012-04 This paper can be downloaded without
On Using Markov Switching Time Series Models to Verify Structural Identifying Restrictions and to Assess Public Debt Sustainability
 On Using Markov Switching Time Series Models to Verify Structural Identifying Restrictions and to Assess Public Debt Sustainability Anton Velinov Thesis submitted for assessment with a view to obtaining
On Using Markov Switching Time Series Models to Verify Structural Identifying Restrictions and to Assess Public Debt Sustainability Anton Velinov Thesis submitted for assessment with a view to obtaining
B y t = γ 0 + Γ 1 y t + ε t B(L) y t = γ 0 + ε t ε t iid (0, D) D is diagonal
 Structural VAR Modeling for I(1) Data that is Not Cointegrated Assume y t =(y 1t,y 2t ) 0 be I(1) and not cointegrated. That is, y 1t and y 2t are both I(1) and there is no linear combination of y 1t and
Structural VAR Modeling for I(1) Data that is Not Cointegrated Assume y t =(y 1t,y 2t ) 0 be I(1) and not cointegrated. That is, y 1t and y 2t are both I(1) and there is no linear combination of y 1t and
Illustrating the Implicit BIC Prior. Richard Startz * revised June Abstract
 Illustrating the Implicit BIC Prior Richard Startz * revised June 2013 Abstract I show how to find the uniform prior implicit in using the Bayesian Information Criterion to consider a hypothesis about
Illustrating the Implicit BIC Prior Richard Startz * revised June 2013 Abstract I show how to find the uniform prior implicit in using the Bayesian Information Criterion to consider a hypothesis about
Combining Macroeconomic Models for Prediction
 Combining Macroeconomic Models for Prediction John Geweke University of Technology Sydney 15th Australasian Macro Workshop April 8, 2010 Outline 1 Optimal prediction pools 2 Models and data 3 Optimal pools
Combining Macroeconomic Models for Prediction John Geweke University of Technology Sydney 15th Australasian Macro Workshop April 8, 2010 Outline 1 Optimal prediction pools 2 Models and data 3 Optimal pools
The Price Puzzle: Mixing the Temporary and Permanent Monetary Policy Shocks.
 The Price Puzzle: Mixing the Temporary and Permanent Monetary Policy Shocks. Ida Wolden Bache Norges Bank Kai Leitemo Norwegian School of Management BI September 2, 2008 Abstract We argue that the correct
The Price Puzzle: Mixing the Temporary and Permanent Monetary Policy Shocks. Ida Wolden Bache Norges Bank Kai Leitemo Norwegian School of Management BI September 2, 2008 Abstract We argue that the correct
Bayesian Structural VAR models: an extended approach. February 28, PRELIMINARY DO NOT CIRCULATE (most recent version available here)
 Bayesian Structural VAR models: an extended approach Martin Bruns Michele Piffer February 8, 18 - PRELIMINARY DO NOT CIRCULATE (most recent version available here) Abstract We provide an approach to derive
Bayesian Structural VAR models: an extended approach Martin Bruns Michele Piffer February 8, 18 - PRELIMINARY DO NOT CIRCULATE (most recent version available here) Abstract We provide an approach to derive
STA 4273H: Statistical Machine Learning
 STA 4273H: Statistical Machine Learning Russ Salakhutdinov Department of Statistics! rsalakhu@utstat.toronto.edu! http://www.utstat.utoronto.ca/~rsalakhu/ Sidney Smith Hall, Room 6002 Lecture 3 Linear
STA 4273H: Statistical Machine Learning Russ Salakhutdinov Department of Statistics! rsalakhu@utstat.toronto.edu! http://www.utstat.utoronto.ca/~rsalakhu/ Sidney Smith Hall, Room 6002 Lecture 3 Linear
Markov Switching Regular Vine Copulas
 Int. Statistical Inst.: Proc. 58th World Statistical Congress, 2011, Dublin (Session CPS057) p.5304 Markov Switching Regular Vine Copulas Stöber, Jakob and Czado, Claudia Lehrstuhl für Mathematische Statistik,
Int. Statistical Inst.: Proc. 58th World Statistical Congress, 2011, Dublin (Session CPS057) p.5304 Markov Switching Regular Vine Copulas Stöber, Jakob and Czado, Claudia Lehrstuhl für Mathematische Statistik,
Cointegrated VAR s. Eduardo Rossi University of Pavia. November Rossi Cointegrated VAR s Financial Econometrics / 56
 Cointegrated VAR s Eduardo Rossi University of Pavia November 2013 Rossi Cointegrated VAR s Financial Econometrics - 2013 1 / 56 VAR y t = (y 1t,..., y nt ) is (n 1) vector. y t VAR(p): Φ(L)y t = ɛ t The
Cointegrated VAR s Eduardo Rossi University of Pavia November 2013 Rossi Cointegrated VAR s Financial Econometrics - 2013 1 / 56 VAR y t = (y 1t,..., y nt ) is (n 1) vector. y t VAR(p): Φ(L)y t = ɛ t The
STRATHCLYDE DISCUSSION PAPERS IN ECONOMICS FORECASTING WITH MEDIUM AND LARGE BAYESIAN VARS GARY KOOP NO
 STRATHCLYDE DISCUSSION PAPERS IN ECONOMICS FORECASTING WITH MEDIUM AND LARGE BAYESIAN VARS BY GARY KOOP NO. 11-17 DEPARTMENT OF ECONOMICS UNIVERSITY OF STRATHCLYDE GLASGOW Forecasting with Medium and Large
STRATHCLYDE DISCUSSION PAPERS IN ECONOMICS FORECASTING WITH MEDIUM AND LARGE BAYESIAN VARS BY GARY KOOP NO. 11-17 DEPARTMENT OF ECONOMICS UNIVERSITY OF STRATHCLYDE GLASGOW Forecasting with Medium and Large
Financial Econometrics
 Financial Econometrics Multivariate Time Series Analysis: VAR Gerald P. Dwyer Trinity College, Dublin January 2013 GPD (TCD) VAR 01/13 1 / 25 Structural equations Suppose have simultaneous system for supply
Financial Econometrics Multivariate Time Series Analysis: VAR Gerald P. Dwyer Trinity College, Dublin January 2013 GPD (TCD) VAR 01/13 1 / 25 Structural equations Suppose have simultaneous system for supply
Essex Finance Centre Working Paper Series
 Essex Finance Centre Working Paper Series Working Paper No14: 12-216 Adaptive Minnesota Prior for High-Dimensional Vector Autoregressions Dimitris Korobilis and Davide Pettenuzzo Essex Business School,
Essex Finance Centre Working Paper Series Working Paper No14: 12-216 Adaptive Minnesota Prior for High-Dimensional Vector Autoregressions Dimitris Korobilis and Davide Pettenuzzo Essex Business School,
Shortfalls of Panel Unit Root Testing. Jack Strauss Saint Louis University. And. Taner Yigit Bilkent University. Abstract
 Shortfalls of Panel Unit Root Testing Jack Strauss Saint Louis University And Taner Yigit Bilkent University Abstract This paper shows that (i) magnitude and variation of contemporaneous correlation are
Shortfalls of Panel Unit Root Testing Jack Strauss Saint Louis University And Taner Yigit Bilkent University Abstract This paper shows that (i) magnitude and variation of contemporaneous correlation are
Outline. Clustering. Capturing Unobserved Heterogeneity in the Austrian Labor Market Using Finite Mixtures of Markov Chain Models
 Capturing Unobserved Heterogeneity in the Austrian Labor Market Using Finite Mixtures of Markov Chain Models Collaboration with Rudolf Winter-Ebmer, Department of Economics, Johannes Kepler University
Capturing Unobserved Heterogeneity in the Austrian Labor Market Using Finite Mixtures of Markov Chain Models Collaboration with Rudolf Winter-Ebmer, Department of Economics, Johannes Kepler University
Discussion of Bootstrap prediction intervals for linear, nonlinear, and nonparametric autoregressions, by Li Pan and Dimitris Politis
 Discussion of Bootstrap prediction intervals for linear, nonlinear, and nonparametric autoregressions, by Li Pan and Dimitris Politis Sílvia Gonçalves and Benoit Perron Département de sciences économiques,
Discussion of Bootstrap prediction intervals for linear, nonlinear, and nonparametric autoregressions, by Li Pan and Dimitris Politis Sílvia Gonçalves and Benoit Perron Département de sciences économiques,
Forecasting with Bayesian Global Vector Autoregressive Models
 Forecasting with Bayesian Global Vector Autoregressive Models A Comparison of Priors Jesús Crespo Cuaresma WU Vienna Martin Feldkircher OeNB Florian Huber WU Vienna 8th ECB Workshop on Forecasting Techniques
Forecasting with Bayesian Global Vector Autoregressive Models A Comparison of Priors Jesús Crespo Cuaresma WU Vienna Martin Feldkircher OeNB Florian Huber WU Vienna 8th ECB Workshop on Forecasting Techniques
Volatility. Gerald P. Dwyer. February Clemson University
 Volatility Gerald P. Dwyer Clemson University February 2016 Outline 1 Volatility Characteristics of Time Series Heteroskedasticity Simpler Estimation Strategies Exponentially Weighted Moving Average Use
Volatility Gerald P. Dwyer Clemson University February 2016 Outline 1 Volatility Characteristics of Time Series Heteroskedasticity Simpler Estimation Strategies Exponentially Weighted Moving Average Use
The Role of Aggregation in the Nonlinear Relationship between Monetary Policy and Output
 The Role of Aggregation in the Nonlinear Relationship between Monetary Policy and Output Luiggi Donayre Department of Economics Washington University in St. Louis August 2010 Abstract Within a Bayesian
The Role of Aggregation in the Nonlinear Relationship between Monetary Policy and Output Luiggi Donayre Department of Economics Washington University in St. Louis August 2010 Abstract Within a Bayesian
Regime-Switching Cointegration
 Regime-Switching Cointegration Markus Jochmann Newcastle University Rimini Centre for Economic Analysis Gary Koop University of Strathclyde Rimini Centre for Economic Analysis May 2011 Abstract We develop
Regime-Switching Cointegration Markus Jochmann Newcastle University Rimini Centre for Economic Analysis Gary Koop University of Strathclyde Rimini Centre for Economic Analysis May 2011 Abstract We develop
Bayesian Methods for Machine Learning
 Bayesian Methods for Machine Learning CS 584: Big Data Analytics Material adapted from Radford Neal s tutorial (http://ftp.cs.utoronto.ca/pub/radford/bayes-tut.pdf), Zoubin Ghahramni (http://hunch.net/~coms-4771/zoubin_ghahramani_bayesian_learning.pdf),
Bayesian Methods for Machine Learning CS 584: Big Data Analytics Material adapted from Radford Neal s tutorial (http://ftp.cs.utoronto.ca/pub/radford/bayes-tut.pdf), Zoubin Ghahramni (http://hunch.net/~coms-4771/zoubin_ghahramani_bayesian_learning.pdf),
A primer on Structural VARs
 A primer on Structural VARs Claudia Foroni Norges Bank 10 November 2014 Structural VARs 1/ 26 Refresh: what is a VAR? VAR (p) : where y t K 1 y t = ν + B 1 y t 1 +... + B p y t p + u t, (1) = ( y 1t...
A primer on Structural VARs Claudia Foroni Norges Bank 10 November 2014 Structural VARs 1/ 26 Refresh: what is a VAR? VAR (p) : where y t K 1 y t = ν + B 1 y t 1 +... + B p y t p + u t, (1) = ( y 1t...
A. Recursively orthogonalized. VARs
 Orthogonalized VARs A. Recursively orthogonalized VAR B. Variance decomposition C. Historical decomposition D. Structural interpretation E. Generalized IRFs 1 A. Recursively orthogonalized Nonorthogonal
Orthogonalized VARs A. Recursively orthogonalized VAR B. Variance decomposition C. Historical decomposition D. Structural interpretation E. Generalized IRFs 1 A. Recursively orthogonalized Nonorthogonal
Cross-sectional space-time modeling using ARNN(p, n) processes
 Cross-sectional space-time modeling using ARNN(p, n) processes W. Polasek K. Kakamu September, 006 Abstract We suggest a new class of cross-sectional space-time models based on local AR models and nearest
Cross-sectional space-time modeling using ARNN(p, n) processes W. Polasek K. Kakamu September, 006 Abstract We suggest a new class of cross-sectional space-time models based on local AR models and nearest
Working Paper SerieS. Granger-Causal-Priority and Choice of Variables in Vector Autoregressions. NO 1600 / october 2013
 Working Paper SerieS NO 1600 / october 2013 Granger-Causal-Priority and Choice of Variables in Vector Autoregressions Marek Jarociński and Bartosz Maćkowiak In 2013 all ECB publications feature a motif
Working Paper SerieS NO 1600 / october 2013 Granger-Causal-Priority and Choice of Variables in Vector Autoregressions Marek Jarociński and Bartosz Maćkowiak In 2013 all ECB publications feature a motif
Bootstrapping the Grainger Causality Test With Integrated Data
 Bootstrapping the Grainger Causality Test With Integrated Data Richard Ti n University of Reading July 26, 2006 Abstract A Monte-carlo experiment is conducted to investigate the small sample performance
Bootstrapping the Grainger Causality Test With Integrated Data Richard Ti n University of Reading July 26, 2006 Abstract A Monte-carlo experiment is conducted to investigate the small sample performance
November 2002 STA Random Effects Selection in Linear Mixed Models
 November 2002 STA216 1 Random Effects Selection in Linear Mixed Models November 2002 STA216 2 Introduction It is common practice in many applications to collect multiple measurements on a subject. Linear
November 2002 STA216 1 Random Effects Selection in Linear Mixed Models November 2002 STA216 2 Introduction It is common practice in many applications to collect multiple measurements on a subject. Linear
Forecasting with Bayesian Vector Autoregressions
 WORKING PAPER 12/2012 Forecasting with Bayesian Vector Autoregressions Sune Karlsson Statistics ISSN 1403-0586 http://www.oru.se/institutioner/handelshogskolan-vid-orebro-universitet/forskning/publikationer/working-papers/
WORKING PAPER 12/2012 Forecasting with Bayesian Vector Autoregressions Sune Karlsson Statistics ISSN 1403-0586 http://www.oru.se/institutioner/handelshogskolan-vid-orebro-universitet/forskning/publikationer/working-papers/
Index. Pagenumbersfollowedbyf indicate figures; pagenumbersfollowedbyt indicate tables.
 Index Pagenumbersfollowedbyf indicate figures; pagenumbersfollowedbyt indicate tables. Adaptive rejection metropolis sampling (ARMS), 98 Adaptive shrinkage, 132 Advanced Photo System (APS), 255 Aggregation
Index Pagenumbersfollowedbyf indicate figures; pagenumbersfollowedbyt indicate tables. Adaptive rejection metropolis sampling (ARMS), 98 Adaptive shrinkage, 132 Advanced Photo System (APS), 255 Aggregation
Online Appendix (Not intended for Publication): Decomposing the Effects of Monetary Policy Using an External Instruments SVAR
 Online Appendix (Not intended for Publication): Decomposing the Effects of Monetary Policy Using an External Instruments SVAR Aeimit Lakdawala Michigan State University December 7 This appendix contains
Online Appendix (Not intended for Publication): Decomposing the Effects of Monetary Policy Using an External Instruments SVAR Aeimit Lakdawala Michigan State University December 7 This appendix contains
Nowcasting Norwegian GDP
 Nowcasting Norwegian GDP Knut Are Aastveit and Tørres Trovik May 13, 2007 Introduction Motivation The last decades of advances in information technology has made it possible to access a huge amount of
Nowcasting Norwegian GDP Knut Are Aastveit and Tørres Trovik May 13, 2007 Introduction Motivation The last decades of advances in information technology has made it possible to access a huge amount of
1.2. Structural VARs
 1. Shocks Nr. 1 1.2. Structural VARs How to identify A 0? A review: Choleski (Cholesky?) decompositions. Short-run restrictions. Inequality restrictions. Long-run restrictions. Then, examples, applications,
1. Shocks Nr. 1 1.2. Structural VARs How to identify A 0? A review: Choleski (Cholesky?) decompositions. Short-run restrictions. Inequality restrictions. Long-run restrictions. Then, examples, applications,
