Analysis and geometry of the measurable Riemannian structure on the Sierpiński gasket
|
|
|
- Dominick Hicks
- 5 years ago
- Views:
Transcription
1 Analysis and geometry of the measurable Riemannian structure on the Sierpiński gasket Naotaka Kajino Abstract. This expository article is devoted to a survey of existent results concerning the measurable Riemannian structure on the Sierpiński gasket and to a brief account of the author s recent result on Weyl s eigenvalue asymptotics of its associated Laplacian. In particular, properties of the Hausdorff measure with respect to the canonical geodesic metric are described in some detail as a key step to the proof of Weyl s asymptotics. A complete characterization of minimal geodesics is newly proved and applied to invalidity of Ricci curvature lower bound conditions such as the curvature-dimension condition and the measure contraction property. Possibility of and difficulty in extending the results to other self-similar fractals are also discussed. Contents 1. Introduction 2 2. Sierpiński gasket and its standard Dirichlet form 4 3. Measurable Riemannian structure on the Sierpiński gasket 7 4. Geometry under the measurable Riemannian structure Short time asymptotics of the heat kernels Intricsic metrics and off-diagonal Gaussian behavior One-dimensional asymptotics at vertices On-diagonal asymptotics at almost every point Ahlfors regularity and singularity of Hausdorff measure Weyl s Laplacian eigenvalue asymptotics Connections to general theories on metric measure spaces Identification of Dirichlet form as Cheeger energy Invalidity of Ricci curvature lower bound Possible generalizations to other self-similar fractals Sierpiński gaskets 32 Version of August 20, Mathematics Subject Classification. Primary 28A80, 35P20, 53C23; Secondary 31C25, 37B10, 60J35. Key words and phrases. Sierpiński gasket, Dirichlet form, Kusuoka measure, measurable Riemannian structure, geodesic metric, heat kernel, Weyl s Laplacian eigenvalue asymptotics, Ricci curvature lower bound. The author was supported in part by SFB 701 of the German Research Council (DFG). 1
2 2 NAOTAKA KAJINO 9.2. Other nested fractals and Sierpiński carpets 33 Appendix A. Case of the standard Laplacian on the Sierpiński gasket 35 References Introduction The purpose of this expository article is to review known results concerning the measurable Riemannian structure on the Sierpiński gasket (Figure 1) and describe its connections to general theories of analysis and geometry on metric measure spaces. We also state the author s recent result on Weyl s eigenvalue asymptotics of its associated Laplacian and briefly explain the idea of its proof. In particular, we present various properties of the Hausdorff measure with respect to the canonical geodesic metric as the key facts for the proof of Weyl s asymptotics. The notion of the measurable Riemannian structure on the Sierpiński gasket was first introduced by Kigami [52] on the basis of Kusuoka s construction in [63] of weak gradients for Dirichlet forms on fractals. In [52], Kigami proved that the Sierpiński gasket can be embedded in R 2 by a certain harmonic map, whose image is now called the harmonic Sierpiński gasket (Figure 2), and that Kusuoka s weak gradients can be identified as the gradients with respect to the (measurable) Riemannian structure inherited from R 2 through this embedding. (A related result is also found in Hino [35].) These results are reviewed in Section 3 after a brief account of the Sierpiński gasket and its standard Dirichlet form in Section 2. Kigami further proved in [54] that the heat kernel associated with this Riemannian structure satisfies the two-sided Gaussian bound in terms of the natural geodesic metric, unlike typical fractal diffusions treated e.g. in [11, 60, 24, 7, 8] for whose transition densities (heat kernels) the two-sided sub-gaussian bounds hold. Later in [44] the author proved some more detailed asymptotics of this heat kernel such as Varadhan s asymptotic relation, together with an analytic characterization of the geodesic metric and slight generalizations and improvements of the results in [54]. These results are reviewed in Section 5 following a summary of basic geometric properties of the measurable Riemannian structure in Section 4, where we also newly prove a complete characterization of minimal geodesics (Theorem 4.19). Very recently, the author has also proved Weyl s Laplacian eigenvalue asymptotics for this case, which is to be treated in a forthcoming paper [47]. The proof of Weyl s asymptotics require some detailed properties of the Hausdorff measure with respect to the geodesic metric and this is reviewed in Section 6, along with the singularity of the Hausdorff measure to the energy measures. Then in Section 7, we give the statement of Weyl s asymptotics and sketch the idea of its proof. Since the situation of the measurable Riemannian structure on the Sierpiński gasket looks similar to that of Riemannian manifolds, it is natural to expect close connections to general theories of analysis and geometry on metric measure spaces which are not applicable to the case of typical fractal diffusions. In fact, Koskela and Zhou [58, Section 4] recently proved that the theory of differential calculus on metric measure spaces, established by Cheeger [17] and developed further by e.g. Shanmugalingam [81] and Keith [48, 49, 50], is applicable to the measurable Riemannian structure on the Sierpiński gasket. To be more precise, they prove that in this case the (1, 2)-Sobolev space equipped with a natural (1, 2)-seminorm, due
3 ANALYSIS AND GEOMETRY OF MEASURABLE RIEMANNIAN STRUCTURE ON S.G. 3 Figure 1. Sierpiński gasket Figure 2. Harmonic Sierpiński gasket to Cheeger [17, Section 2] and Shanmugalingam [81, Definition 2.5], coincides with the standard Dirichlet form on the Sierpiński gasket. This result is briefly reviewed in Subsection 8.1. On the other hand, the notions of Ricci curvature lower bound for general metric measure spaces due to Lott and Villani [71, 70], Sturm [86, 87] and Ohta [76] are not applicable to the case of the measurable Riemannian structure. More precisely, the (harmonic) Sierpiński gasket equipped with the natural geodesic metric and the Riemannian volume measure does not satisfy either the curvature dimension condition CD(k, N) of Lott and Villani [71, 70] and Sturm [86, 87] or the measure contraction property MCP(k, N) of Ohta [76] and Sturm [87] for any (k, N) R [1, ]. We prove this fact in Subsection 8.2 (Theorem 8.23) as an application of the characterization of minimal geodesics (Theorem 4.19) after a review of the precise definitions of CD(k, N) and MCP(k, N) and related results. Finally, we conclude this paper with a short discussion on possibility of (and difficulties in) extending the above-mentioned results to other self-similar fractals. In the appendix, we provide a brief review of important results for the Brownian motion and the standard Laplacian on the Sierpiński gasket, whose associated heat kernel is known to satisfy the two-sided sub-gaussian estimate and exhibit various oscillatory behavior. Those who are not familiar with these results are strongly recommended to read the appendix directly after Section 2. Notation. In this article, we adopt the following notation and conventions. (1) N = {1, 2, 3,... }, i.e. 0 N. (2) The cardinality (the number of all the elements) of a set A is denoted by #A. (3) We set sup := 0 and inf :=. We write a b := max{a, b}, a b := min{a, b}, a + := a 0 and a := (a 0) for a, b [, ]. We use the same notations also for functions. All functions treated in this paper are assumed to be [, ]-valued. (4) Let k N. The Euclidean inner product and norm on R k are denoted by, and respectively. For a continuous map γ : [a, b] R k, where a, b R, a b, let l R k(γ) be its length with respect to. Let R k k be the set of real k k matrices, which are also regarded as linear maps from R k to itself through the standard basis of R k, and set R k k 0 := R k k \{0 R k k}. For T R k k, let det T be its determinant, T its transpose, and T its Hilbert-Schmidt norm with respect to,. The real orthogonal group of degree k is denoted by O(k).
4 4 NAOTAKA KAJINO (5) Let E be a topological space. The Borel σ-field of E is denoted by B(E). We set C(E) := {f f : E R, f is continuous} and f := sup x E f(x), f C(E). For A E, its interior in E is denoted by int E A and its boundary in E by E A. (6) Let (E, ρ) be a metric space. For r (0, ), x K and A E, we set B r (x, ρ) := {y E ρ(x, y) < r}, diam ρ A := sup y,z A ρ(y, z) and dist ρ (x, A) := inf y A ρ(x, y). For f : E R we set Lip ρ f := sup x,y E, x y f(x) f(y) /ρ(x, y). 2. Sierpiński gasket and its standard Dirichlet form In this section, we briefly recall basic facts concerning the Sierpiński gasket and its standard Dirichlet form (resistance form). We mainly follow [44, Section 2] for the presentation of this section and refer the reader to [25, 53, 56, 82] for further details of each fact. Definition 2.1 (Sierpiński gasket). Let V 0 = {q 1, q 2, q 3 } R 2 be the set of the three vertices of an equilateral triangle, set S := {1, 2, 3}, and for i S define f i : R 2 R 2 by f i (x) := (x + q i )/2. The Sierpiński gasket (Figure 1) is defined as the self-similar set associated with {f i } i S, i.e. the unique non-empty compact subset K of R 2 that satisfies K = i S f i(k). For i S we set F i := f i K : K K. Define V m for m N inductively by V m := i S F i(v m 1 ) and set V := m N V m. Note that V m 1 V m for any m N. K is always regarded as equipped with the relative topology inherited from R 2, so that F i : K K is continuous for each i S and V is dense in K. Definition 2.2. (1) Let W 0 := { }, where is an element called the empty word, let W m := S m = {w 1... w m w i S for i {1,..., m}} for m N and W := m N {0} W m. For w W, the unique m N {0} with w W m is denoted by w and called the length of w. Also for i S and n N {0} we write i n := i... i W n. (2) We set Σ := S N = {ω 1 ω 2 ω 3... ω i S for i N}, and define the shift map σ : Σ Σ by σ(ω 1 ω 2 ω 3... ) := ω 2 ω 3 ω Also for i S we define σ i : Σ Σ by σ i (ω 1 ω 2 ω 3... ) := iω 1 ω 2 ω 3... and set i := iii... Σ. For ω = ω 1 ω 2 ω 3... Σ and m N {0}, we write [ω] m := ω 1... ω m W m. (3) For w = w 1... w m W, we set F w := F w1 F wm (F := id K ), K w := F w (K), σ w := σ w1 σ wm (σ := id Σ ) and Σ w := σ w (Σ). Associated with the triple (K, S, {F i } i S ) is a natural projection π : Σ K given by the following proposition, which is used to describe the topological structure of K. Proposition 2.3. There exists a unique continuous surjective map π : Σ K such that F i π = π σ i for any i S, and it satisfies {π(ω)} = m N K [ω] m for any ω Σ. Moreover, #π 1 (x) = 1 for x K \ V, π 1 (q i ) = {i } for i S, and for m N and each x V m \ V m 1 there exist w W m 1 and i, j S with i j such that π 1 (x) = {wij, wji }. Recall the following basic fact ([53, Proposition (2)]) meaning that V 0 should be considered as the boundary of K, which we will use below without further notice: if w, v W and Σ w Σ v = then K w K v = F w (V 0 ) F v (V 0 ). As studied in [5, 53, 82], a standard Dirichlet form (to be precise, a resistance form) (E, F) is defined on the Sierpiński gasket K, as follows. See [53, Chapter
5 ANALYSIS AND GEOMETRY OF MEASURABLE RIEMANNIAN STRUCTURE ON S.G. 5 2] and [56, Part 1] for general theory of resistance forms. A concise introduction to the theory of resistance forms is found in [82, Chapter 1], where the theory is illustrated by treating the particular case of the Sierpiński gasket in detail. Definition 2.4. Let m N {0}. We define a non-negative definite symmetric bilinear form E m : R Vm R Vm R on V m by (2.1) E m (u, v) := ) m (u(x) u(y))(v(x) v(y)), 2( 3 x,y V m, x m y where, for x, y V m, we write x m y if and only if x, y F w (V 0 ) for some w W m and x y. The usual definition of E m does not contain the factor 1/2 so that each edge in the graph (V m, m ) has resistance (3/5) m. Here it has been added for simplicity of the subsequent arguments; see Definition 3.1-(0) below. The factor 3/5, called the resistance scaling factor of the Sierpiński gasket, is specifically chosen for the sake of the validity of the following proposition. Proposition 2.5. Let m, n N {0}, m n. Then for each u R Vm, (2.2) E m (u, u) = min{e n (v, v) v R V n, v Vm = u} and there exists a unique function h m,n (u) R V n with h m,n (u) Vm = u such that E m (u, u) = E n (h m,n (u), h m,n (u)). Moreover, h m,n : R V m R V n is linear. Let u : V R. (2.2) implies that {E m (u Vm, u Vm )} m N {0} is non-decreasing and hence has the limit in [0, ]. Moreover, if lim m E m (u Vm, u Vm ) <, then it is not difficult to verify that u is uniformly continuous with respect to any metric on K compatible with the original (Euclidean) topology of K, so that u is uniquely extended to a continuous function on K. Based on these observations, we can prove the following theorem; see [53, Chapter 2 and Section 3.3] or [82, Chapter 1] for details. Let 1 := 1 K denote the constant function on K with value 1. (2.3) Theorem 2.6. Define F C(K) and E : F F R by F := {u C(K) lim m E (m) (u Vm, u Vm ) < }, E(u, v) := lim m E (m) (u Vm, v Vm ) R, u, v F. Then F is a dense subalgebra of C(K), E is a non-negative definite symmetric bilinear form on F, and (E, F) possesses the following properties: (1) {u F E(u, u) = 0} = {c1 c R} =: R1, and (F/R1, E) is a Hilbert space. (2) R E (x, y) := sup u F\R1 u(x) u(y) 2 /E(u, u) < for any x, y K and R E : K K [0, ) is a metric on K compatible with the original topology of K. (3) u + 1 F and E(u + 1, u + 1) E(u, u) for any u F. (4) F = {u C(K) u F i F for any i S}, and for any u, v F, (2.4) E(u, v) = 5 E(u F i, v F i ). 3 i S (E, F) is called the standard resistance form on the Sierpiński gasket, which is indeed a resistance form on K with resistance metric R E by Theorem 2.6-(1),(2),(3) and F being a dense subalgebra of C(K). Consequently we also have the following theorem by virtue of [56, Corollary 6.4, Theorems 9.4 and 10.4], where the strong
6 6 NAOTAKA KAJINO locality of (E, F) follows from (2.4) and E(1, 1) = 0. See [25, Section 1.1] for the notions of regular Dirichlet forms and their strong locality. Theorem 2.7. Let ν be a finite Borel measure on K with full support, i.e. such that ν(u) > 0 for any non-empty open subset U of K. Then (E, F) is a strongly local regular Dirichlet form on L 2 (K, ν), and its associated Markovian semigroup {Tt ν } t (0, ) on L 2 (K, ν) admits a continuous integral kernel p ν, i.e. a continuous function p ν = p ν (t, x, y) : (0, ) K K R such that for any f L 2 (K, ν) and any t (0, ), (2.5) Tt ν f = p ν (t,, y)f(y)dν(y) ν-a.e. K In the situation of Theorem 2.7, a standard monotone class argument easily shows that such p ν is unique and satisfies p ν (t, x, y) = p ν (t, y, x) 0 for any (t, x, y) (0, ) K K. Moreover, p ν is in fact (0, )-valued by [55, Theorem A.4]. ν is called the reference measure of the Dirichlet space (K, ν, E, F), and p ν is called the (continuous) heat kernel associated with (K, ν, E, F). See [56, Theorem 10.4] for other basic properties of p ν. Since we have a regular Dirichlet form (E, F) with compact state space K, by [25, (3.2.13) and (3.2.14)] we can define E-energy measures as in the following definition. Definition 2.8. The E-energy measure of u F is defined as the unique Borel measure µ u on K such that (2.6) fdµ u = E(uf, u) 1 2 E(u2, f) for any f F. K We also define λ u to be the unique Borel measure on Σ that satisfies λ u (Σ w ) = (5/3) w E(u F w, u F w ) for any w W, which exists by (2.4) and the Kolmogorov extension theorem. For u, v F we set µ u,v := (µ u+v µ u v )/4 and λ u,v := (λ u+v λ u v )/4, so that they are finite Borel signed measures on K and on Σ respectively and are symmetric and bilinear in (u, v) F F. Let u F. According to [36, Proposition 3.8] (see also [14, Theorem I.7.1.1]), the strong locality of (E, F) implies that the image measure µ u u 1 on (R, B(R)) is absolutely continuous with respect to the Lebesgue measure on R. In particular, µ u ({x}) = 0 for any x K. We also easily see the following proposition by using (2.4) and (2.6). Note that π(a) B(K) for any A B(Σ) by Proposition 2.3. Proposition 2.9. λ u,v = µ u,v π and λ u,v π 1 = µ u,v for any u, v F. The definition of the measurable Riemannian structure on the Sierpiński gasket involves certain harmonic functions. In the present setting, harmonic functions are formulated as follows. Definition (1) We define F B := {u F u K\B = 0} for each B K. (2) Let F be a closed subset of K. Then h F is called F -harmonic if and only if (2.7) E(h, h) = inf u F, u F =h F E(u, u) or equivalently, E(h, u) = 0, u F K\F. We set H F := {h F h is F -harmonic} and H m := H Vm for each m N {0}.
7 ANALYSIS AND GEOMETRY OF MEASURABLE RIEMANNIAN STRUCTURE ON S.G. 7 Note that H F is a linear subspace of F for any closed subset F of K and that H m 1 H m for any m N. Moreover, we easily have the following proposition by [56, Lemma 8.2 and Theorem 8.4]. Proposition Let F be a non-empty closed subset of K. (1) Let u F. Then there exists a unique h F (u) H F such that h F (u) F = u F. Moreover, h F : F H F is linear. (2) Let h H F. Then min F h h(x) max F h for any x K. (2.8) (2.9) Proposition 2.5 and (2.4) imply the following useful characterizations of H m. Proposition It holds that for any m N {0}, H m = {u F E(u, u) = E m (u Vm, u Vm )} = {u F u F w H 0 for any w W m }. For each h H 0, by virtue of h F w H 0, w W, h V can be, in principle, explicitly calculated from h V0 through simple matrix multiplications, as follows. Proposition 2.13 ([53, (3.2.3) and Example 3.2.6]). Define (2.10) A 1 := , A 2 := , A 3 := , which we regard as linear maps from R V0 to itself through the standard basis of R V0. Then for any u H 0 and any w = w 1... w m W, (2.11) u F w V0 = A wm A w1 (u V0 ). 3. Measurable Riemannian structure on the Sierpiński gasket This section is devoted to a brief introduction to the notion of the measurable Riemannian structure on the Sierpiński gasket and its basic properties. We continue to follow mainly [44, Section 2] and refer to [63, 52, 35] for further details. We first define a harmonic embedding Φ of K into R 2, through which we will regard K as a kind of Riemannian submanifold in R 2 to obtain its measurable Riemannian structure. We also introduce a measure µ which is regarded as the E-energy measure of the embedding Φ and will play the role of the Riemannian volume measure. See [90] for an attempt to generalize the framework of harmonic embeddings and their energy measures to other finitely ramified fractals. Recall that V 0 = {q 1, q 2, q 3 }. Definition 3.1. (0) We define h 1, h 2 F to be the V 0 -harmonic functions satisfying h 1 (q 1 ) = h 2 (q 1 ) = 0, h 1 (q 2 ) = h 1 (q 3 ) = 1 and h 2 (q 2 ) = h 2 (q 3 ) = 1/ 3, so that E(h 1, h 1 ) = E(h 2, h 2 ) = 1 (recall the factor 1/2 in (2.1)) and E(h 1, h 2 ) = 0 by (2.8), and h 1 F 1 = (3/5)h 1 and h 2 F 1 = (1/5)h 2 by (2.11). (1) We define a continuous map Φ : K R 2 and a compact subset K H of R 2 by (3.1) Φ(x) := (h 1 (x), h 2 (x)), x K and K H := Φ(K). K H is called the harmonic Sierpiński gasket (Figure 2). We also set ˆq i := Φ(q i ) for i S, so that {ˆq 1, ˆq 2, ˆq 3 } = Φ(V 0 ) is the set of vertices of an equilateral triangle. (2) We define finite Borel measures µ on K and λ on Σ by (3.2) µ := µ h1 + µ h2 and λ := λ h1 + λ h2,
8 8 NAOTAKA KAJINO respectively, so that λ = µ π and λ π 1 = µ by Proposition 2.9. µ is called the Kusuoka measure on the Sierpiński gasket. Notation. In what follows h 1, h 2 always denote the V 0 -harmonic functions given in Definition 3.1-(0). We often regard {h 1, h 2 } as an orthonormal basis of (H 0 /R1, E). Moreover, we set (3.3) u E := E(u, u), u F and S H0 := {h H 0 h E = 1}. The following proposition, which is in fact an easy consequence of Proposition 2.13, provides an alternative geometric definition of K H, and essentially as its corollary we also see the injectivity of Φ (Theorem 3.3), Proposition 3.4 below and that µ h has full support for any h H 0 \ R1. Proposition 3.2 ([52, 3]). Define ( ) 3/5 0 (3.4) T 1 :=, T 0 1/5 2 := ( 3/10 3/10 3/10 1/2 ), T 3 := ( ) 3/10 3/10 3/10 1/2 and set T w := T w1 T wm for w = w 1... w m W (T := ( ) ). Also for i S define H i : R 2 R 2 by H i (x) := ˆq i + T i (x ˆq i ). Then the following hold: (1) T 2 = R 2 3 π T 1 R 2 3 π and T 3 = R 2 3 π T 1 R 2 3 π, where R θ := ( ) cos θ sin θ sin θ cos θ for θ R. (2) For any w W, Tw := (T w ) is equal to the matrix representation of the linear map Fw : H 0 /R1 H 0 /R1, Fwh := h F w by the basis {h 1, h 2 } of H 0 /R1. (3) H i Φ = Φ F i and hence H i (Φ π) = (Φ π) σ i for any i S. In particular, K H = i S H i(k H ), i.e. K H is the self-similar set associated with {H i } i S. Theorem 3.3 ([52, Theorem 3.6]). Φ : K K H is a homeomorphism. Proposition 3.4. µ(k w ) = λ(σ w ) = (5/3) w T w 2 for any w W. Moreover, we have the following theorem due to Kusuoka [63] (see [44, Theorem 6.8] for an alternative simple proof based on (2.4) and the strong locality of (E, F)). Recall that σ : Σ Σ is the shift map defined by σ(ω 1 ω 2 ω 3... ) := ω 2 ω 3 ω Theorem 3.5 ([63, 6, Example 1]). λ is σ-ergodic, that is, λ σ 1 = λ and λ(a)λ(σ \ A) = 0 for any A B(Σ) with σ 1 (A) = A. We also remark the following fact due to Hino [35]. Theorem 3.6 ([35, Theorem 5.6]). Let h H 0 \ R1. Then µ and µ h are mutually absolutely continuous. Now we can introduce the measurable Riemannian structure on K, which is formulated as a Borel measurable map Z : K R 2 2, as follows. Recall that π Σ\π 1 (V \V 0 ) is injective by Proposition 2.3. Proposition 3.7 ([63, 1], [52, Proposition B.2]). Define Σ Z B(Σ) and K Z B(K) by { (3.5) Σ Z := ω Σ Z T [ω]m T } [ω] Σ(ω) := lim m m T [ω]m 2 exists in R 2 2, K Z := π(σ Z ). Then λ(σ \ Σ Z ) = µ(k \ K Z ) = 0, Z Σ (ω) is an orthogonal projection of rank 1 for any ω Σ Z, π 1 (V ) Σ Z and Z Σ (ω) = Z Σ (τ) for ω, τ π 1 (x), x V \ V 0. Hence setting Z x := Z Σ (ω), ω π 1 (x) for x K Z and Z x := ( ) for x K\KZ gives a well-defined Borel measurable map Z : K R 2 2, x Z x.
9 ANALYSIS AND GEOMETRY OF MEASURABLE RIEMANNIAN STRUCTURE ON S.G. 9 Theorem 3.8 ([52, 4]). Set CΦ 1 (K) := {v Φ v C1 (R 2 )}. Then for each u CΦ 1 (K), u := ( v) Φ is independent of a particular choice of v C1 (R 2 ) satisfying u = v Φ. Moreover, CΦ 1 (K) F, C1 Φ (K)/R1 is dense in (F/R1, E), and for any u, v CΦ 1 (K), (3.6) dµ u,v = Z u, Z v dµ and E(u, v) = Z u, Z v dµ. In view of Theorem 3.8, especially (3.6), we may regard Z as defining a onedimensional tangent space Im Z x of K at x with the metric inherited from R 2 for µ-a.e. x K in a measurable way, with µ considered as the associated Riemannian volume measure and Z u as the gradient vector field of u CΦ 1 (K). Then the Dirichlet space associated with this Riemannian structure is (K, µ, E, F). Remark 3.9. (1) By [52, Theorem B.5-(1)], Σ \ Σ Z is dense in Σ and hence K \ K Z is dense in K. In other words, there exists a dense set of points x of K where the notion of the tangent space Im Z x at x does not make sense. (2) Z KZ : K Z R 2 2 is discontinuous. Indeed, let n N {0} and set x n := F 1 n 3(q 2 ), so that lim n x n = q 1. Then it easily follows from (3.4) and (3.5) that Z q1 = ( ) and Zxn = ( ), which does not converge to ( ) = Zq1 as n. As a matter of fact, any u F admits a natural gradient vector field u, thereby (3.6) extended to functions in F, as in the following theorem whose essential part is due to Hino [35, Theorem 5.4]; see [44, Theorem 2.17] for details. Theorem Let h H 0 \ R1. Then for any u F the following hold: (1) For µ-a.e. x K, there exists u(x) Im Z x such that for any ω π 1 (x), (3.7) sup y K [ω]m u(y) u(x) u(x), Φ(y) Φ(x) = o( T[ω]m ) as m. Such u(x) Im Z x as in (3.7) is unique for each x K Z, and dµ u = u 2 dµ. (2) For µ h -a.e. x K, there exists du dh (x) R such that for any ω π 1 (x), (3.8) sup du u(y) u(x) (x)(h(y) h(x)) dh = o( h F [ω] m E ) as m. y K [ω] m Such du dh (x) R as in (3.8) is unique for each x K, and dµ u = ( du dh) 2dµ h. In fact, Theorem 3.10 has been recently improved by Koskela and Zhou [58] where the reminder estimates for the derivatives u and du dh are given in terms of the associated geodesic metrics; see Theorem 8.3 below. Remark (1) As mentioned in [44, Remark 2.20], the gradient vector field u in Theorem 3.10-(1) coincides with the weak gradient Y ( ; u) defined by Kusuoka [63, Lemma 5.1] (see also [54, Definition 4.11]). (2) The rank of the matrix Z, which is 1 µ-a.e. in the present case, is closely related to the martingale dimension of the associated diffusion process. The martingale dimension of a symmetric diffusion process is formally defined as the maximal number of martingale additive functionals which are independent in the sense of stochastic integral representation, and intuitively it corresponds to the maximal dimension of the tangent space over the state space. For the purpose of analytic characterization of martingale dimension, Kusuoka [63, 64] introduced the notion of index for certain strongly local symmetric regular Dirichlet forms on a certain K
10 10 NAOTAKA KAJINO class of self-similar fractals and identified it as the martingale dimension of the associated diffusion. Hino [35, Definitions 2.9, 3.3 and Theorem 3.4] has recently extended these results to general strongly local symmetric regular Dirichlet forms, where the index is defined through certain matrix-valued measurable maps similar to Z as above whose entries are the Radon-Nikodym derivatives of energy measures. The index of a non-degenerate elliptic symmetric diffusion on a smooth manifold is easily seen to be equal to the dimension of the manifold, whereas it is difficult to determine the exact value of the index for diffusions on fractals. In our case of the standard resistance form (E, F) on the Sierpiński gasket, it follows from rank Z = 1, µ-a.e., that the index is 1, and the same is true also for the k-dimensional Sierpiński gasket with k 3, as shown in [63, 6, Example 1]. Hino [34, 36] has recently proved that the index of a point-recurrent self-similar diffusion (to be precise, the index of the resistance form associated with a regular harmonic structure) on a post-critically finite self-similar set is always 1. This result in particular applies to Brownian motion on affine nested fractals, whose construction is essentailly due to Lindstrøm [69]; see [53, Section 3.8] and references therein in this regard. In the case of the canonical Dirichlet form on a generalized Sierpiński carpet, which was constructed in [6, 8, 65] and is known to be unique by [9], Hino has also proved in [36, Theorem 4.15] that the index is less than or equal to the spectral dimension d s of the carpet. Note that this result gives only an upper bound for the index, so that the exact value of the index for generalized Sierpiński carpets is still unknown, except when d s < 2, which implies that the index is 1. (A brief summary of important facts concerning the canonical Dirichlet form on generalized Sierpiński carpets, as well as pictures of some typical generalized Sierpiński carpets, is available in [46, Section 5].) (3) [35, Theorem 5.4], from which Theorem 3.10 follows, was stated and proved only for (regular harmonic structures on) post-critically finite self-similar sets. In fact, Hino [37, Theorem 3.4] has recently generalized it to general strongly local symmetric regular Dirichlet forms with finite index. See [37] for details. 4. Geometry under the measurable Riemannian structure This section is a brief summary of the results in [44, Section 3], which are slight improvements of those in [54, Sections 3 and 5] and concern basic geometric properties of K under the measurable Riemannian structure. We start with the definition of the canonical geodesic metrics associated with the Dirichlet spaces (K, µ, E, F) and (K, µ h, E, F), h H 0 \ R1. Definition 4.1. Let h H 0 \ R1. We define the harmonic geodesic metric ρ H on K and the h-geodesic metric ρ h on K by respectively (4.1) (4.2) ρ H (x, y) := inf{l H (γ) γ : [0, 1] K, γ is continuous, γ(0) = x, γ(1) = y}, ρ h (x, y) := inf{l h (γ) γ : [0, 1] K, γ is continuous, γ(0) = x, γ(1) = y} for x, y K, where we set l H (γ) := l R 2(Φ γ) and l h (γ) := l R (h γ) for each continuous map γ : [a, b] K, a, b R, a b. ρ H was first introduced by Kigami in [54, Section 5], and the author adopted his idea to define ρ h in [44]. As observed in [44, Section 3] and reviewed below, ρ h plays the role of the canonical geodesic metric for the Dirichlet space (K, µ h, E, F), as ρ H does for (K, µ, E, F), and (K, ρ h, µ h ) possesses most of the fundamental geometric
11 ANALYSIS AND GEOMETRY OF MEASURABLE RIEMANNIAN STRUCTURE ON S.G. 11 properties in common with (K, ρ H, µ). The generalization to (K, ρ h, µ h ), where in fact the constants involved are all independent of h S H0, played essential roles in the proofs of the main results of [44], and it does also in the proofs of the author s recent results in [47], which are reviewed in Sections 6 and 7 below. Remark 4.2. Note that ρ H is different from the harmonic metric ρ Φ on K introduced in [52, Definition 3.8], which is defined by (4.3) ρ Φ (x, y) := Φ(x) Φ(y), x, y K. ρ Φ is a metric on K compatible with the original topology of K by Theorem 3.3 and satisfies ρ Φ ρ H, but ρ H is not comparable to ρ Φ. Indeed, as noted in [54, p. 800, Remark], ρ Φ ( F1 n(q 2 ), F 1 n(q 3 ) ) /ρ H ( F1 n(q 2 ), F 1 n(q 3 ) ) = O(3 n ) as n. In practice, we need to relate the metrics ρ H and ρ h suitably to the cell structure of K to obtain various fundamental inequalities such as volume doubling property of measures and weak Poincaré inequality. In [55], Kigami proposed a systematic way of describing the geometry of a self-similar set using the cell-structure and applied it to establish reasonable sufficient conditions for sub-gaussian bounds of the heat kernel associated with a self-similar Dirichlet form. We follow his framework to describe the relation between the cell structure of K and the metrics ρ H and ρ h. Definitions 4.3, 4.4, 4.6, 4.8 and Proposition 4.5 below are adopted from [55]. Definition 4.3. (1) Let w, v W, w = w 1... w m, v = v 1... v n. We define wv W by wv := w 1... w m v 1... v n (w := w, v := v). We write w v if and only if w = vτ for some τ W. Note that Σ w Σ v = if and only if neither w v nor v w. (2) A finite subset Λ of W is called a partition of Σ if and only if Σ w Σ v = for any w, v Λ with w v and Σ = w Λ Σ w. (3) Let Λ 1, Λ 2 be partitions of Σ. We say that Λ 1 is a refinement of Λ 2, and write Λ 1 Λ 2, if and only if for each w 1 Λ 1 there exists w 2 Λ 2 such that w 1 w 2. If Λ 1 Λ 2, then we have a natural surjection Λ 1 Λ 2 by which w 1 Λ 1 is mapped to the unique w 2 Λ 2 such that w 1 w 2, and in particular, #Λ 1 #Λ 2. Definition 4.4. (1) A family S = {Λ s } s (0,1] of partitions of Σ is called a scale on Σ if and only if S satisfies the following three properties: (S1) Λ 1 = W 0 (= { }). Λ s1 Λ s2 for any s 1, s 2 (0, 1] with s 1 s 2. (S2) min{ w w Λ s } as s 0. (Sr) Each s (0, 1) admits ε (0, 1 s] such that Λ s = Λ s for any s (s, s + ε). (2) A function l : W (0, 1] is called a gauge function on W if and only if l(wi) l(w) for any (w, i) W S and lim m max{l(w) w W m } = 0. There is a natural one-to-one correspondence between scales on Σ and gauge functions on W, as in the following proposition. See [55, Section 1.1] for a proof. Proposition 4.5. (1) Let l be a gauge function on W. For s (0, 1], define (4.4) Λ s (l) := {w w = w 1... w m W, l(w 1... w m 1 ) > s l(w)} where l(w 1... w m 1 ) := 2 when w =. Then the collection S(l) := {Λ s (l)} s (0,1] is a scale on Σ. We call S(l) the scale induced by the gauge function l. (2) Let S = {Λ s } s (0,1] be a scale on Σ. Then there exists a unique gauge function l S on W such that S = S(l S ). We call l S the gauge function of the scale S.
12 12 NAOTAKA KAJINO Definition 4.6. Let S = {Λ s } s (0,1] be a scale on Σ. For s (0, 1] and x K, we define (4.5) K s (x, S) := K w, U s (x, S) := K w. w Λ s, x K w w Λ s, K w K s (x,s) K s (x, S) and U s (x, S) are clearly non-decreasing in s (0, 1], and it immediately follows from [53, Proposition 1.3.6] that {K s (x, S)} s (0,1] and {U s (x, S)} s (0,1] are fundamental systems of neighborhoods of x in K. Proposition 2.3 easily yields the following lemma. Lemma 4.7. Let S = {Λ s } s (0,1] be a scale on Σ, let s (0, 1], x K and w Λ s. Then #{v Λ s K v K s (x, S) } 6 and #{v Λ s K w K v } 4. Definition 4.8. Let S = {Λ s } s (0,1] be a scale on Σ. A metric ρ on K is called adapted to S if and only if there exist β 1, β 2 (0, ) such that (4.6) B β1 s(x, ρ) U s (x, S) B β2 s(x, ρ), (s, x) (0, 1] K. Lemma 4.9. Let S = {Λ s } s (0,1] be a scale on Σ with gauge function l and let ρ be a metric on K adapted to S. Then ρ is compatible with the original topology of K, and diam ρ K w β 2 l(w) for any w W, where β 2 (0, ) is as in (4.6). Proof. See [44, Lemma 3.7]. Next we define scales on Σ to which the metrics ρ H and ρ h, h S H0, are adapted (recall (3.3) for S H0 ). Definition (1) We define S H = {Λ H s } s (0,1] to be the scale on Σ induced by the gauge function l H : W (0, 1], l H (w) := T w 1 = (3/5) w µ(k w ) 1. (2) Let h S H0. We define S h = {Λ h s } s (0,1] to be the scale on Σ induced by the gauge function l h : W (0, 1], l h (w) := h F w E = (3/5) w µ h (K w ). As we will state in Theorem 4.15 below, ρ H and ρ h introduced in Definition 4.1, where h S H0, are indeed metrics on K adapted to S H and S h respectively and the infimums in (4.1) and (4.2) are achieved by a specific class of paths in K. The key to these results is the next theorem, which requires the following definition. Definition (1) For x, y R 2, we set xy := {x + t(y x) t [0, 1]}, which is also regarded as the map [0, 1] t (1 t)x + ty R 2. (2) Let m N {0} and x, y V m, x m y, where m is as in Definition 2.4. We define w(x, y) to be the unique w W m such that x, y F w (V 0 ). Note that xy K w(x,y). Theorem 4.12 ([89], [54, Theorem 5.4]). Set I := [ 1/ 3, 1/ 3]. Φ(q 2 q 3 ) = {(ϕ(t), t) t I} for some ϕ : I R, and the following hold: (1) ϕ is C 1 but not C 2, ϕ is strictly increasing and ϕ (±1/ 3) = ±1/ 3. (2) q 2 q 3 K Z and (ϕ (t), 1) Im Z Φ 1 (ϕ(t),t) for any t I. (3) K H {(s, t) R I s ϕ(t)}, or equivalently, h 1 ϕ h 2. Then Definition (1) Let m N {0}. A sequence Γ = {x k } N k=0 V m, where N N, is called an m-walk if and only if x k 1 m xk for k {1,..., N} and w(x k 1, x k ) w(x k, x k+1 ) for k {1,..., N 1}. For such Γ we define continuous maps Γ : [0, N] K and Γ : [0, l H (Γ)] K by (4.7) Γ(t) := (k t)x k 1 + (t k + 1)x k, t [k 1, k], k {1,..., N},
13 ANALYSIS AND GEOMETRY OF MEASURABLE RIEMANNIAN STRUCTURE ON S.G. 13 and Γ := Γ ϕ 1 Γ, where ϕ Γ is the homeomorphism ϕ Γ : [0, N] [0, l H (Γ)], ϕ Γ (t) := l H (Γ [0,t] ); note that l H (Γ) < by Theorem 4.12 and Proposition 3.2. (2) Let γ : [a, b] K be continuous, a, b R, a < b. For m N {0}, γ is called a harmonic m-geodesic if and only if γ(t) = Γ ( l H (Γ) b a) t a, t [a, b] for some m-walk Γ. γ is called a harmonic geodesic if and only if there exist n N {0} and {a m } m n, {b m } m n [a, b] with lim m a m = a and lim m b m = b such that a m+1 a m < b m b m+1 and γ [am,b m] is a harmonic m-geodesic for each m n. Then Theorem 4.12 together with Propositions 3.2 and 3.7 immediately yields the following proposition. Proposition If γ : [0, 1] K is a harmonic geodesic, then Φ γ (0,1) is C 1 and for any t (0, 1), γ(t) K Z, (Φ γ) (t) Im Z γ(t) and (Φ γ) (t) = l H (γ). Theorem 4.15 ([54, Theorems 5.1 and 5.11], [44, Propositions 3.15 and 3.16]). Let h S H0 and let h denote any one of H and h. (1) ρ h is a metric on K satisfying (4.8) B 2s/50 (x, ρ h) U s (x, S h ) B 10s (x, ρ h ), (s, x) (0, 1] K. (2) For each x, y K with x y, there exists a harmonic geodesic γ h xy : [0, 1] K such that γ h xy(0) = x, γ h xy(1) = y and ρ h (x, y) = l h (γ h xy). Moreover, if m N {0} and x, y V m then we can take a harmonic m-geodesic as γ h xy. Remark Let γ : [0, 1] K be a harmonic geodesic and let h H 0 \ R1. Then we easily see from Theorem 4.12 that the set {t (0, 1) (h γ) (t) = 0} is discrete (see [44, (3.15)]), so that ϕ h : [0, 1] [0, l h (γ)], ϕ h (t) := l h (γ [0,t] ), is strictly increasing. Therefore γ admits a parametrization by l h -length given by γ ϕ 1 h : l h(γ ϕ 1 h [0,t]) = t for any t [0, l h (γ)]. The proof of Theorem 4.15 is based on the following lemma, which in turn is an easy consequence of Theorem Lemma 4.17 ([54, Lemma 5.6], [44, Lemma 3.18]). Let h S H0 and let h denote any one of H and h. Let w W and x, y F w (V 0 ), x y. Then (4.9) l h (xy) = inf{l h (γ) γ : [0, 1] K w, γ is continuous, γ(0) = x, γ(1) = y}, 2 10 l h(w) l h (xy) 4 6 (4.10) 3 l h(w). The proof of (4.9) for l H utilizes the following theorem from convex geometry as well, which is quoted in [54, Theorem 5.2] without reference. Recall that a subset Γ of R 2 is called a Jordan curve if and only if it is homeomorphic to {x R 2 x = 1}. For such Γ, its length l R 2(Γ) with respect to the Euclidean norm is naturally defined, and according to the Jordan curve theorem (see e.g. [73, Section 4]), R 2 \Γ consists of two connected components whose boundaries in R 2 are both equal to Γ. Theorem Let C be a compact convex subset of R 2 with int R 2 C. (1) R 2C is a Jordan curve and l R 2( R 2C) <. (2) Let D be a compact subset of R 2 such that R 2D is a Jordan curve and C D. If C D, or equivalently if R 2C R 2D, then l R 2( R 2C) < l R 2( R 2D). Proof. (1) An elementary argument shows that R 2C is a Jordan curve (see e.g. [13, Theorems 6.7 and 11.9]), and it follows from (2) that l R 2( R 2C) <.
14 14 NAOTAKA KAJINO (2) Note that for q int R 2 D, R 2D regarded as a closed curve in R 2 \ {q} is not homotopic in R 2 \ {q} to a constant map, by virtue of the Schönflies theorem [73, Section 10, Theorem 4] saying that every injective continuous map from a Jordan curve to R 2 is the restriction of a homeomorphism from R 2 to R 2. On the basis of this fact, the assertion can be verified by using [13, Theorem 7.9] to approximate R 2C by convex polygons whose vertices belong to R 2C and by applying the arguments in [13, Proof of Theorem 7.11 and Exercise 7.4]. In fact, we can also prove the following characterization of shortest paths with respect to l H by using Theorems 4.12 and 4.18, as follows. Theorem Let γ : [0, 1] K be continuous and satisfy ρ H (γ(0), γ(1)) = l H (γ) > 0. Then there exist a unique harmonic geodesic γ : [0, 1] K and a unique non-decreasing continuous surjection ϕ γ : [0, 1] [0, 1] such that γ = γ ϕ γ. Moreover, if m N {0} and γ(0), γ(1) V m, then γ is a harmonic m-geodesic. Theorem 4.19 has important applications to the invalidity of various geometric conditions on (K, ρ H, µ) related to Ricci curvature lower bound; see Subsection 8.2 below. We need the following lemma for the proof of Theorem Lemma Let w W and x, y F w (V 0 ), x y. Let a, b R, a < b and let γ : [a, b] K w be a continuous injective map with γ(a) = x and γ(b) = y. If l H (γ) l H (xy), then γ([a, b]) = xy. Proof. Let C, D be the compact subsets of R 2 with int R 2 C = int R 2 D whose boundaries in R 2 are the Jordan curves Φ(x)Φ(y) Φ(xy) and Φ(x)Φ(y) Φ γ([a, b]), respectively. Then C is convex and C D by virtue of the rotational symmetry of K H, Proposition 3.2-(3), Theorem 4.12 and the Jordan curve theorem. Therefore if l H (γ) l H (xy), then l R 2( R 2D) l R 2( R 2C), hence R 2D = R 2C by Theorem 4.18-(2), and thus γ([a, b]) = xy. Proof of Theorem For uniqueness, let γ and ϕ γ be as in the assertion, so that ϕ γ (0) = 0, ϕ γ (1) = 1 and l H ( γ) = l H (γ). Let t [0, 1] and choose s [0, 1] so that t = l H (γ [0,s] )/l H (γ). Then l H (γ [0,t] ) = l H ( γ [0,ϕγ(t)]) = l H (γ)ϕ γ (t) by Proposition 4.14, hence t = ϕ γ (s) and γ(t) = γ(s), proving the uniqueness assertion. For existence, define a non-decreasing continuous surjection ϕ γ : [0, 1] [0, 1] by ϕ γ (t) := l H (γ [0,t] )/l H (γ). Since γ(s) = γ(t) for any s, t [a, b] with ϕ γ (s) = ϕ γ (t), there exists a unique map γ : [0, 1] K such that γ = γ ϕ γ, and then γ is continuous and l H ( γ [0,t] ) = tl H (γ) for any t [0, 1]. In particular, l H ( γ [s,t] ) > 0 for any s, t [0, 1] with s < t, which together with l H ( γ) = l H (γ) = ρ H (γ(0), γ(1)), γ(0) = γ(0) and γ(1) = γ(1) shows that γ is injective. To see that γ is a harmonic geodesic, set n := inf{m N {0} # γ 1 (V m ) 2} (n < by γ(0) γ(1)), and for m n set a m := min γ 1 (V m ) and b m := max γ 1 (V m ), so that a m+1 a m < b m b m+1 for any m n. The injectivity of γ easily yields lim m a m = 0, lim m b m = 1 and # γ 1 (V m ) <. Let m n, N := # γ 1 (V m ) 1 and let {t k } N k=0 be the strictly increasing enumeration of the elements of γ 1 (V m ), so that t 0 = a m and t N = b m. Also set x k := γ(t k ) for k {0,..., N} and Γ := {x k } N k=0 V m. We claim that Γ is an m-walk and that γ(t) = Γ ( l H (Γ) t a ) m b m a m for any t [am, b m ]. Indeed, let m k {1,..., N}. It easily follows from γ((t k 1, t k )) V m = that x k 1 xk and that
15 ANALYSIS AND GEOMETRY OF MEASURABLE RIEMANNIAN STRUCTURE ON S.G. 15 γ([t k 1, t k ]) K w(xk 1,x k ), and then we also have l H ( γ [tk 1,t k ]) = ρ H (x k 1, x k ) by l H ( γ) = ρ H ( γ(0), γ(1)). If k < N and w(x k 1, x k ) = w(x k, x k+1 ), then Lemma 4.20 implies l H (x k 1 x k+1 ) < l H ( γ [tk 1,t k+1 ]), contradicting l H ( γ) = ρ H ( γ(0), γ(1)). Thus Γ is an m-walk. Moreover, since l H ( γ [tk 1,t k ]) = ρ H (x k 1, x k ) l H (x k 1 x k ), Lemma 4.20 yields γ([t k 1, t k ]) = x k 1 x k, which together with l H ( γ [0,t] ) = tl H ( γ), t [0, 1], easily implies the above claim. Thus γ [am,b m] is a harmonic m-geodesic for any m n and hence γ is a harmonic geodesic. If m N {0} and γ(0), γ(1) V m, then m n, a m = 0 and b m = 1, so that γ is a harmonic m-geodesic. Remark If h H 0 \R1, then the assertions of Theorem 4.19 and Lemma 4.20 are not valid for l h and ρ h. Proof. Noting that min V0 h < max V0 h by Proposition 2.11-(2), let i, j S be such that h(q i ) = min V0 h and h(q j ) = max V0 h and let {k} = S \ {i, j}. We first assume h(q i ) + h(q j ) 2h(q k ). By considering h and q j instead of h and q i if necessary, we may assume that h(q i ) + h(q j ) < 2h(q k ). Let U be the connected component of h 1 ((, h(q k )) with q i U. Then Theorem 4.12 and the rotational symmetry of K H easily imply that h is strictly decreasing on q k q i and on q k F k n(q j ) for some n N. Therefore K k n \ {q k } U by the strong maximum principle [53, Theorem ] for h F k n, and hence ρ h (q i, x) = h(x) h(q i ) for any x K k n by [44, (4.13)] (see (5.8) below). A similar argument for h F k n together with [44, (4.13)] also implies that ρ h (q k, x) = h(q k ) h(x) for any x K k m for some m n. Thus by Theorem 4.15 and Remark 4.16, for any x K k m \ {q k } there exists a continuous injective map γ x : [0, 1] K with γ x (0) = q i, γ x (1/2) = x and γ x (1) = q k such that l h (γ x ) = h(q k ) h(q i ) = l h (q i q k ) = ρ h (q i, q k ). Now if x K k m \ w W F w (q 1 q 2 q 2 q 3 q 3 q 1 ), then the conclusions of Theorem 4.19 and Lemma 4.20 are not valid for γ x since γ((0, 1)) w W F w (q 1 q 2 q 2 q 3 q 3 q 1 ) and hence x γ((0, 1)) for any harmonic geodesic γ : [0, 1] K. If h(q i ) + h(q j ) = 2h(q k ), then since h H {qi,q j} by the axial symmetry of K and (E, F), it follows similarly to [44, Proposition 4.9] (see Proposition 5.8 below) that ρ h (q i, x) = h(x) h(q i ) and ρ h (q j, x) = h(q j ) h(x) for any x K. The rest of the proof goes in exactly the same way as in the previous paragraph. At the last of this section, we state the volume doubling property and the weak Poincaré inequality of (K, µ, E, F) and (K, µ h, E, F) under the metrics ρ H and ρ h, respectively. The following lemma is essential for the proofs of those properties. Lemma 4.22 ([44, Lemma 3.9], cf. [54, Section 3]). Let h S H0. (1) For any (w, i) W S, (4.11) (4.12) 1 15 µ(k w) µ(k wi ) 3 5 µ(k w), 1 15 µ h (K w ) µ h (K wi ) 3 5 µ h (K w ), (2) If w, v W satisfies w = v and K w K v, then 1 5 T w T wi 3 5 T w, 1 5 l h(w) l h (wi) 3 5 l h(w). (4.13) µ h (K w ) 9µ h (K v ), l h (w) 3l h (v) and l H (w) 3l H (v). Then we can verify the following proposition on the basis of Lemma 4.22 in exactly the same ways as [55, Proofs of Theorems and 1.4.3].
16 16 NAOTAKA KAJINO Proposition 4.23 ([44, Proposition 3.10], cf. [54, Theorem 6.2]). (1) There exists c G (0, ) such that for any g, h S H0, (4.14) µ g (K w ) c G µ g (K v ) whenever either w, v Λ H s or w, v Λ h s for some s (0, 1] and K w K v. (2) Let κ := log 5 15 and ˆκ := log 5/3 15. Then there exists c v (0, ) such that for any g, h S H0, any x K and any s, t (0, 1] with s t, ( t ) κν(us ( t )ˆκµ g (4.15) ν(u t (x, S)) c v (x, S)), µ g (U t (x, S)) c v (U s (x, S)), s s where (ν, S) denotes any one of (µ, S H ) and (µ h, S h ). Remark The powers κ and ˆκ in (4.15) are best possible. See [44, Remark 3.11] for details. Now we conclude the volume doubling property of (K, ρ H, µ) and (K, ρ h, µ h ) as an immediate consequence of Proposition 4.23-(2) and Theorem 4.15-(1). Theorem 4.25 ([54, Theorem 6.2], [44, Theorem 3.19]). As in Proposition 4.23-(2) let κ := log 5 15 and ˆκ := log 5/3 15. Then there exists c V (0, ) such that for any g, h H 0 \ R1, any x K and any r, s (0, ) with r s, ( s ) κν(br ( s )ˆκµ g (4.16) ν(b s (x, ρ)) c V (x, ρ)), µ g (B s (x, ρ)) c V (B r (x, ρ)), r r where (ν, ρ) denotes any one of (µ, ρ H ) and (µ h, ρ h ). Finally we state the weak Poincaré inequality of (K, µ, E, F) and (K, µ h, E, F). Proposition 4.26 ([44, Proposition 3.20]). Let c P := c 4 G with c G as in Proposition 4.23-(1). Let h H 0 \ R1 and let (ν, ρ) denote any one of (µ, ρ H ) and (µ h, ρ h ). Then for any (r, x) (0, ) K, with u ν,ρ r,x := ν(b r (x, ρ)) 1 B r (x,ρ) udν, (4.17) u u ν,ρ 2 dν c P r 2 ( µ u B250 2r (x, ρ) ), u F. B r (x,ρ) r,x Proposition 4.26 is easily proved by using Lemma 4.7, Theorem 4.15-(1), Lemma 4.22-(1), Proposition 4.23-(1) and the following fact implied by the definition of the resistance metric R E : for any w W and any x, y K w, (4.18) u(x) u(y) 2 ( R E F 1 w (x), Fw 1 (y) ) ( 3 ) w µ u E(u F w, u F w ) 3 (K w ); 5 note that we easily have diam RE K 3 by using [53, Lemma 3.3.5]. Notation. In what follows we will use the constants κ = log 5 15, ˆκ = log 5/3 15, c G and c V appearing in Proposition 4.23 and Theorem 4.25 without further notice. 5. Short time asymptotics of the heat kernels In this section, we review known results on short time asymptotic behavior of the heat kernels p µ and p µ h, h H 0 \R1, mainly following [44, Sections 4 6]. The results concern three different aspects of the asymptotics: off-diagonal Gaussian behavior, one-dimensional behavior at vertices and non-integer-dimensional µ-a.e. on-diagonal behavior, which are reviewed separately in each of the following three subsections.
17 ANALYSIS AND GEOMETRY OF MEASURABLE RIEMANNIAN STRUCTURE ON S.G Intricsic metrics and off-diagonal Gaussian behavior. Let us start this subsection with the following standard definition. Definition 5.1. Let ν be a finite Borel measure on K with full support. Define (5.1) ρ ν (x, y) = sup{u(x) u(y) u F, µ u ν}, x, y K. Clearly, ρ ν (x, y) = ρ ν (y, x) [0, ), ρ ν (x, x) = 0 and ρ ν (x, y) ρ ν (x, z) + ρ ν (z, y) for any x, y, z K; in fact, ρ ν (x, y) 2 ν(k)r E (x, y). ρ ν is called the intrinsic metric of the Dirichlet space (K, ν, E, F) or simply the ν-intrinsic metric on K. As suggested by the results of [84, 85, 78, 40], off-diagonal Gaussian behavior of the Markovian semigroup of a strong local Dirichlet space is described best by the associated intrinsic metric. On the other hand, it is highly non-trivial to give a reasonable geometric characterization of the intrinsic metric for concrete examples. For the canonical Dirichlet space associated with a smooth Riemannian manifold, it is not difficult to see that the intrinsic metric is equal to its Riemannian distance; see [75] and references therein for related results on Riemannian manifolds. The same is in fact true also for (K, µ, E, F) and (K, µ h, E, F), h H 0 \R1, as follows. Theorem 5.2 ([44, Theorem 4.2]). Let h H 0 \ R1 and let (ν, ρ) denote any one of (µ, ρ H ) and (µ h, ρ h ). Then ρ = ρ ν. Moreover, ρ(x, ) F and µ ρ(x, ) = ν for any x K. Then in view of Theorem 4.25 and Proposition 4.26, the general results of Sturm [84, 85] and Ramírez [78] together with ρ = ρ ν imply the following Gaussian bounds and Varadhan s asymptotic relation. Corollary 5.3 ([54, Theorem 6.3], [44, Corollary 4.3]). Let h H 0 \ R1 and let (ν, ρ) denote any one of (µ, ρ H ) and (µ h, ρ h ). Let n N. Then there exist c L, c U (0, ) determined solely by κ, c G, c V and c U (n) (0, ) determined solely by n, κ, c G, c V such that for any (t, x, y) (0, ) K K, exp ( ρ(x,y) 2 ) ( c c L t 1 + ρ(x,y) ) 2 κ/2 ( L ν ( B t (x, ρ)) p t exp ρ(x,y) ) 2 (5.2) 4t ν(t, x, y) c U ν ( B t (x, ρ)) ν (, B t (y, ρ)) (5.3) n t p ν (t, x, y) c U (n) ( 1 + ρ(x,y) ) 2 κ/2+n ( exp ρ(x,y) ) 2 t t n ν ( B t (x, ρ)) ν (. B t (y, ρ)) Corollary 5.4 ([44, Corollary 4.4]). Let h H 0 \ R1 and let (ν, ρ) denote any one of (µ, ρ H ) and (µ h, ρ h ). Then (5.4) lim t 0 4t log p ν (t, x, y) = ρ(x, y) 2, x, y K. Moreover, according to a recent result [58, Theorem 7.1] of Koskela and Zhou, we have the following asymptotic behavior of the logarithmic derivatives of the heat kernels by virtue of ρ(x, ) F and µ ρ(x, ) = ν, x K; see [72, 83] for the corresponding pointwise results for the heat kernels on Riemannian manifolds. Note that dist ρ (, A) F for any A K with A by Proposition 5.6 below. Corollary 5.5. Let h H 0 \ R1 and let (ν, ρ) denote any one of (µ, ρ H ) and (µ h, ρ h ). Then for any A B(K) with ν(a) > 0, µ 4t log T ν t 1 A converges weakly 4t
18 18 NAOTAKA KAJINO to µ distρ(,a) 2 as t 0, that is, for any f C(K), (5.5) lim fdµ 4t log T ν t 0 t 1 A = fµ distρ(,a) 2. K The proof of ρ ρ ν and that of ρ(x, ) F and µ ρ(x, ) = µ for x K are based on Theorem 3.10 and Theorem 4.15-(2), whereas the converse inequality ρ ν ρ is an immediate consequence of the following proposition. Proposition 5.6 ([44, Proposition 4.10]). Let h H 0 \R1 and let (ν, ρ) be any one of (µ, ρ H ) and (µ h, ρ h ). Then {u F µ u ν} = {u C(K) Lip ρ u 1}. Proposition 5.6 is proved by using Theorem 4.15-(2) and Proposition 5.8 below to reduce the proof to the case of the heat kernels on one-dimensional intervals. We need the following lemma for the statement of Proposition 5.8. Lemma 5.7 (cf. [56, Theorem 10.4]). Let ν be a finite Borel measure on K with full support, let U be a non-empty open subset of K and set ν U := ν B(U) and E U := E FU F U. Then (E U, F U ) is a strong local regular Dirichlet form on L 2 (U, ν U ) whose associated Markovian semigroup {T ν,u t } t (0, ) admits a unique continuous integral kernel p U ν = p U ν (t, x, y) : (0, ) U U [0, ), and p U ν is extended to a continuous function on (0, ) K K by setting p U ν := 0 on (0, ) (K K\U U). p U ν is called the heat kernel associated with (U, ν U, E U, F U ). Proposition 5.8 ([44, Proposition 4.9]). Let h H 0 \R1, i S, b (h(q i ), ) and set a := h(q i ). Suppose that the connected component U of h 1 ((, b)) with q i U satisfies U V 0 = {q i }. Let p [a,b) = p [a,b) (t, x, y) : (0, ) [a, b] [a, b] [0, ) be the heat kernel for d 2 /dx 2 on [a, b] with Neumann (reflecting) boundary condition at a and Dirichlet (absorbing) boundary condition at b. Then K (5.6) (5.7) (5.8) µ h (h U ) 1 = E(h, h i 1)1 [a,b] dx (dx is the Lebesgue measure on R), p U µ h (t, q i, x) = E(h, h i 1) 1 p [a,b) (t, a, h(x)), (t, x) (0, ) U, ρ h (q i, x) = ρ µ h (q i, x) = h(x) a, x U One-dimensional asymptotics at vertices. As observed from the picture of the harmonic Sierpiński gasket K H (Figure 2), for x V, sufficiently small neighborhoods of Φ(x) in K H are geometrically very close to the tangent line of K H at Φ(x). As reflections of this geometric intuition, the Kusuoka measure µ and the associated heat kernel p µ exhibit sharp one-dimensional behavior, as follows. Theorem 5.9 ([44, Theorem 5.3]). The limit lim r 0 µ(b r (x, ρ H ))/r =: 2ξ x (0, ) exists for any x V. Theorem 5.10 ([44, Theorem 5.8]). Let x V. Choose ζ x = (ζx, 1 ζx) 2 Im Z x so that ζ x = 1 and set h x := ζx(h 1 1 h 1 (x)1) + ζx(h 2 2 h 2 (x)1). Then there exist t x, r x, c x (0, ) such that for any δ (0, 1] and any (t, y) (0, t x ] B rx (x, ρ H ), (5.9) p µ(t, x, y) exp ( h x(y) ) 2 4t )exp ξ x 4πt c x,δ (t ( h ) x(y) 2 ˆκ δ κ h x (y) 2(ˆκ 1) 4(1+δ)t κ+1, ξ x 4πt where c x,δ := c x /δ 15 4 κ+ ˆκ In particular, lim t 0 4πtpµ (t, x, x) = 1/ξ x.
19 ANALYSIS AND GEOMETRY OF MEASURABLE RIEMANNIAN STRUCTURE ON S.G. 19 Theorem 5.11 ([44, Theorem 5.16]). Let x V and α ( 1, ). Then 1 (5.10) lim ρ t 0 t α/2 H (x, y) α p µ (t, x, y)dµ(y) = y α /4 e y2 dy. 4π K The key to the proofs of Theorems 5.9, 5.10 and 5.11 is again reduction to the direction of the tangent line Im Z x = Rζ x of K H at Φ(x), that is, to the case of µ hx, p and ρ µ h x h x, based on a suitable modification [44, Proposition 5.4] of Proposition 5.8 for h x on a sufficiently small neighborhood of x On-diagonal asymptotics at almost every point. As we saw in Subsections 5.1 and 5.2, the heat kernel p µ of (K, µ, E, F) satisfies the Gaussian bounds and Varadhan s asymptotic relation of exactly the same forms as those for the heat kernels on Riemannian manifolds, and p µ (t, x, x) is asymptotically equivalent to a constant multiple of 1/ 4πt as t 0 for each x V. On the other hand, we cannot expect such a smooth behavior of p µ (t, x, x) for generic x K. Indeed, we have the following result. Recall that λ = µ π. Note also that 2 log 25/3 5 = < 2. Theorem 5.12 ([44, Theorem 6.1 and Proposition 6.6]). Let h H 0 \ R1 and let (ν, ρ) denote any one of (µ, ρ H ) and (µ h, ρ h ). Define 1 (5.11) η := inf λ(σ w ) log T w and d loc := 2 + η 1 log 5 m N 2m 3. w W m Then η = and lim m 1 2m w W m λ(σ w ) log T w [ log 3 5, log 5) 3, d loc (1, 2 log 25/3 5] log ν(b r (x, ρ)) 2 log p ν (t, x, x) (5.12) lim = lim = d loc ν-a.e. x K. r 0 log r t 0 log t The key step for the proof of Theorem 5.12 is the following proposition, which can be verified by using Lemma 4.7, Proposition 4.23-(1), (4.8), (4.16) and (4.11). Proposition 5.13 ([44, Proposition 6.4]). Let x K and ω π 1 (x). Then 1 lim r 0 log µ(b r (x, ρ H ))/ log r exists if and only if lim m m log T [ω] m exists, and if either of these two limits exists then (5.13) lim r 0 log µ(b r (x, ρ H )) log r = 2 + R log 5 3 lim m 1 m log T [ω] m [1, 2 log 25/3 5]. It is immediate from (5.11) that η < log 3 5. Since η = lim m 1 m log T [ω] m for λ-a.e. ω Σ by the σ-ergodicity of λ (Theorem 3.5) and Kingman s subadditive ergodic theorem [21, Theorem ], Theorem 5.12 is now easily proved by using Proposition 5.13 (as well as its counterpart for (µ h, ρ h )) and (5.2). 6. Ahlfors regularity and singularity of Hausdorff measure In this and the next sections, we review the author s recent unpublished results to be treated in a forthcoming paper [47] which mainly concerns Weyl s Laplacian eigenvalue asymptotics for the Dirichlet space (K, µ, E, F). A crucial fact for Weyl s asymptotics is the Ahlfors regularity of (K, ρ H ) and of (K, ρ h ) uniform in h S H0, which we explain in some detail in this section as a preparation for the next section. We also see that the Hausdorff measures on (K, ρ H ) and (K, ρ h ) (of the appropriate dimension) are singular with respect to the Kusuoka measure µ.
20 20 NAOTAKA KAJINO Let us first recall the following standard notations and definitions. See e.g. [22, Chapters 2 and 3] and references therein for details of Hausdorff measure, Hausdorff dimension and box-counting dimension; note that the definitions there apply to any metric space although they are stated only for the Euclidean spaces. Notation. Let (E, ρ) be a metric space and let A E be non-empty. (1) For α (0, ), the α-dimensional Hausdorff measure on E with respect to ρ is denoted by H α ρ and the Hausdorff dimension of A with respect to ρ by dim H (A, ρ). (2) The lower and upper box-counting dimensions of A with respect to ρ are denoted by dim B (A, ρ) and dim B (A, ρ), respectively. If they are equal, their common value, called the box-counting dimension of A with respect to ρ, is denoted by dim B (A, ρ). Note that 0 dim H (A, ρ) dim B (A, ρ) dim B (A, ρ) by [22, (3.17)]. The following theorem was obtained in [44]. Recall (5.11) for the constant d loc. Theorem 6.1 ([44, Theorem 7.2 and Proposition 7.6]). Set d := dim H (K, ρ H ). Then d loc d 2 log 25/3 5 and H d ρ H (K) (0, ). Moreover, for any h S H0, (6.1) (6.2) d = dim B (K, ρ H ) = dim B (K, ρ h ), 3 10 s d #Λ h s #Λ H s 3 19 s d, s (0, 1]. The proof of (6.2) heavily relies on the rotational symmetry of K and (E, F), whereas (6.1) follows from (6.2) by virtue of Lemma 4.7, (4.8) and [43, Proposition 2.24]. In fact, we can further prove the following theorem which asserts that (K, ρ H ) and (K, ρ h ), h S H0, are Ahlfors regular with Hausdorff dimension d. Theorem 6.2. There exist c 6.1, c 6.2 (0, ) such that for any h S H0 and any (r, x) (0, 1] K, (6.3) c 6.1 r d H d ρ H (B r (x, ρ H )) c 6.2 r d, c 6.1 r d H d ρ h (B r (x, ρ h )) c 6.2 r d. In particular, d = dim H (K, ρ h ) for any h H 0 \ R1. The following propositions are the key steps for the proof of Theorem 6.2. Proposition 6.3. Let h S H0 and let Λ be a partition of Σ. Then (6.4) 3 29 w Λ h F w d E Proposition 6.4. There exist c 6.3, c 6.4 (0, ) such that for any h H 0 \ R1 and any w W, (6.5) (6.6) Λ h Fw/ h Fw E s/ h F w E c 6.3 T w d H d ρ H (K w ) c 6.4 T w d, c 6.3 h F w d E H d ρ h (K w ) c 6.4 h F w d E. Theorem 6.2 is now an easy consequence of Proposition 6.4 together with (4.8), Lemma 4.7 and Lemma 4.22-(1). Proposition 6.3 follows by applying (6.2) to with s := min v Λ h F v E for w Λ and using #Λ h Fw/ h Fw E s/ h F w E = #{v Λ h s v w} to sum up the resulting inequalities, which is possible since the constants in (6.2) is independent of h. Then we can also verify Proposition 6.4 on the basis of Proposition 6.3, Lemma 4.9 and the following lemma, by considering h F w / h F w E instead of h to localize the argument to K w (or alternatively, by using Lemma 7.6 below).
21 ANALYSIS AND GEOMETRY OF MEASURABLE RIEMANNIAN STRUCTURE ON S.G. 21 Lemma 6.5 (cf. [44, Lemma 7.8]). Let S = {Λ s } s (0,1] be a scale on Σ with gauge function l and let ρ be a metric on K adapted to S with β 1, β 2 (0, ) as in (4.6). Let α, δ, ε (0, ) and let Hρ,δ α be the α-dimensional pre-hausdorff measure on K with respect to ρ as defined in [22, (2.1)] and [53, Definition 1.5.1]. If δ (0, β 1 ) and Hρ,δ α (K) < ε, then there exists a partition Λ of Σ such that w Λ l(w)α < 4β1 α ε and max w Λ l(w) β1 1 δ. For h, h S H0 with E(h, h ) = 0, a monotone class argument using Proposition 6.4 easily shows that 2 d/2 c 6.3 c Hd ρ H Hρ d h + Hρ d 21 d/2 c 1 h 6.3 c 6.4Hρ d H. Then the following conjecture seems natural in view of Proposition 3.4, Theorem 3.6 and Proposition 6.4 although the author has no particular idea how to prove it. Conjecture 6.6. For any h H 0 \ R1, H d ρ H and H d ρ h are mutually absolutely continuous. Recall that d loc d by Theorem 6.1. In fact, here we have the strict inequality, which also implies the singularity of H d ρ H and H d ρ h, h H 0 \ R1, with respect to µ. Theorem 6.7. d loc < d. Corollary 6.8. H d ρ H is singular to µ, and so is H d ρ h for any h H 0 \ R1. Proof. Let h H 0 \R1 and let (ν, ρ) denote any one of (µ, ρ H ) and (µ h, ρ h ). Define K ν,ρ B(K) by d loc { (6.7) K ν,ρ := x K d loc lim log ν(b r (x, ρ)) = d }. loc r 0 log r Then µ ( K \ K ν,ρ ) ( d = 0 by Theorems 5.12 and 3.6, whereas dimh K ν,ρ, ρ ) = d loc loc d loc by [22, Proposition 4.9], ( where (4.16) is used to verify [22, Covering lemma 4.8] for (K, ρ), and hence Hρ d K ν,ρ ) d = 0 by d loc < d. Thus H d loc ρ is singular to µ. In the rest of this section, we briefly explain the idea of the proof of Theorem 6.7. A similar idea was also used in [33, Theorem 4.1 and Proof of Theorem 2.1] to establish singularity of energy measures on self-similar sets. For m N, we set (6.8) η m := 1 2(2 d) w W m ( 5 3 ) m Tw 2 log T w 2 H d ρ H (K w ), 1 so that lim m m η m = η by Theorem 5.12 and Proposition 6.4. Then for m, n N, η (m+1)n = ( 5 3 )(m+1)n Hρ d 2(2 d) H (K w ) Hd ρ H (K wv ) T wv 2 H d w W mn v W ρ H (K w ) Hρ d H (K wv ) log T wv 2 Hρ d H (K wv ) n ( 5 3 )(m+1)n Hρ d 2(2 d) H (K w ) ( 3 5 )n T w 2 H w W ρ d H (K w ) log ( 3 5 )n T w 2 Hρ d H (K w ) = η mn + n log 3 (6.9) 5 2 d, mn where the inequality is due to the convexity of the function (0, ) t t log t and v W n T wv 2 = (3/5) n T w 2. (6.9) in particular yields (6.10) log 3 5 η m = η = lim 2 dloc m m lim m 1 m ( η 1 + (m 1) log d ) = log d and hence d loc d, which was proved in [44, Proof of Theorem 7.2] by a different method.
22 22 NAOTAKA KAJINO Note that c T w 2 d T w 2 /Hρ d H (K w ) c T w 2 d for any w W by Proposition 6.4 and that the image Z(K Z ) of the map Z KZ : K Z R 2 2 is equal to the set of all orthogonal projections on R 2 of rank 1 by Theorem 4.12 and the rotational symmetry of K H. By using these facts and the definition of ( Z in Proposition 3.7, we can verify that if we fix a sufficiently large n N, then Twv 2 /Hρ d H (K wv ) ) v W n R Wn appearing in the first line of (6.9) is some uniform distance away from constant vectors for m large enough and for sufficiently many w W mn. Then the second line of (6.9) has to be smaller than the first by a uniform constant for m large enough, which together with the same limiting procedure as in (6.10) yields d loc < d. See [47] for the complete proof and further details. 7. Weyl s Laplacian eigenvalue asymptotics As already mentioned in the last section, our main concern in this section is Weyl s Laplacian eigenvalue asymptotics for the Dirichlet space (K, µ, E, F), which is the main result of the author s forthcoming paper [47]. Let us start with the following basic definition. See Lemma 5.7 above for the definitions of ν U, (E U, F U ), {T ν,u t } t (0, ) and p U ν. Definition 7.1. Let ν be a finite Borel measure on K with full support and let U be a non-empty open subset of K. Noting that the non-positive self-adjoint operator ν,u of (U, ν U, E U, F U ) (the generator of {T ν,u t } t (0, ) ) has discrete spectrum and that tr T ν,u t < for t (0, ) by [19, Theorem 2.1.4], let {λ ν,u n } n N be the non-decreasing enumeration of all the eigenvalues of ν,u, where each eigenvalue is repeated according to its multiplicity. The eigenvalue counting function N ν,u and the partition function Z ν,u of the Dirichlet space (U, ν U, E U, F U ) are defined respectively by, for λ R and t (0, ), (7.1) (7.2) Z ν,u (t) := tr T ν,u t N ν,u (λ) := #{n N λ ν,u n λ}, = e λν,u n t = e λt dn ν,u (λ) = n N R K p U ν (t, x, x)dν(x). In the situation of Definition 7.1, N ν,u (λ) < for λ R by lim n λ ν,u n =, N ν,u (λ) = 0 for λ (, 0) by λ ν,u 1 0, and Z ν,u is (0, )-valued and continuous. The main result of [47] is stated as follows. Theorem 7.2. There exist c N, c Z (0, ) such that for any non-empty open subset U of K with H d ρ H ( K U) = 0, N µ,u (λ) (7.3) lim = c λ λ d/2 N Hρ d H (U) and lim t d/2 Z µ,u (t) = c Z Hρ d t 0 H (U). Recall that for the eigenvalue counting function N U and the partition function Z U associated with the Dirichlet Laplacian on a non-empty open subset U of R k with vol k (U) <, where vol k denotes the Lebesgue measure on R k, it holds that N U (λ) (7.4) lim = (2π) k v λ λ k/2 k vol k (U) and lim t k/2 Z U (t) = (4π) k/2 vol k (U) t 0 with v k := vol k ({x R k x < 1}). See e.g. [15, 16, 66, 67, 68, 74] and references therein for known results concerning Weyl s asymptotics on Euclidean domains and Riemannian manifolds. According to Theorem 7.2, the Dirichlet Laplacian µ,u on a non-empty open subset U of K satisfies Weyl s eigenvalue asymptotics similar to
23 ANALYSIS AND GEOMETRY OF MEASURABLE RIEMANNIAN STRUCTURE ON S.G. 23 (7.4) unless K U is too rough, but the limit is given by a constant multiple of the Hausdorff measure Hρ d H which is, contrary to (7.4), singular to the Riemannian volume measure µ by Corollary 6.8. The rest of this section is devoted to a sketch of the proof of Theorem 7.2. The main idea of the proof is to follow the method due to Kigami and Lapidus [57] of obtaining a renewal equation for the eigenvalue counting function (or the partition function) from the self-similarity of (E, F) to apply a suitable renewal theorem. The problem in doing so for the present setting of (K, µ, E, F) is that the reference measure µ is not self-similar, but it can be resolved by incorporating the information on the pair {h 1 F w, h 2 F w } of V 0 -harmonic functions appearing in µ F w = (5/3) w ( µ h1 F w + µ h2 F w ) as the second variable, in the following way. Definition 7.3. Let M = ( ) a b c d R We define Φ M := MΦ : K R 2, (7.5) (7.6) µ M := µ ah1 +bh 2 + µ ch1 +dh 2, ρ M (x, y) := inf{l M (γ) γ : [0, 1] K, γ is continuous, γ(0) = x, γ(1) = y} for x, y K, where l M (γ) := l R 2(Φ M γ) for each continuous map γ : [a γ, b γ ] K, a γ, b γ R, a γ b γ. Note that Φ M (x) = ((ah 1 +bh 2 )(x), (ch 1 +dh 2 )(x)) for x K. Namely, we identify M = ( ) a b c d R with the pair {ah 1 + bh 2, ch 1 + dh 2 } of V 0 -harmonic functions and define the counterpart of Φ, µ, ρ H for M by replacing {h 1, h 2 } with {ah 1 +bh 2, ch 1 +dh 2 }. Then for M R with det M 0, Theorems 3.8 and 3.10-(1) are valid with Φ M, µ M, Z M := MZ 2 MZM in place of Φ, µ, Z (Theorem 3.10-(1) remains valid for det M = 0 if we set Z M := ( ) for MZ = 0); note that Z M (x) is the orthogonal projection onto M(Im Z x ) for each x K. We also define the corresponding scale on Σ as follows. Note that M 2 = ah 1 + bh 2 2 E + ch 1 + dh 2 2 E for M = ( ) a b c d R Definition 7.4. (1) We set S 2 2 := {M R 2 2 M = 1}. (2) Let M S 2 2. We define S M = {Λ M s } s (0,1] to be the scale on Σ induced by the gauge function l M : W (0, 1], l M (w) := MT w = (3/5) w µ M (K w ). Then for M S 2 2, by exactly the same proofs we still have Theorem 4.15 and Lemma 4.17 with M in place of h, and Lemma 4.22 and Proposition 4.23 with µ M, l M, S M = {Λ M s } s (0,1] in place of µ h, l h, S h = {Λ h s } s (0,1] and c G, c v the same. Consequently Theorem 4.25, Proposition 4.26, Theorem 5.2, Corollaries 5.3, 5.4, 5.5 and Proposition 5.6 hold for (ν, ρ) = (µ M, ρ M ), M R 2 2 0, with c V, c P, c L, c U, c U (n) unchanged. Theorem 4.19 and Lemma 4.20 with ρ M, l M in place of ρ H, l H are also valid for any M R with det M 0 by exactly the same proofs. Remark 7.5. Here we do not exclude the case of det M = 0 where µ M, ρ M, l M are equal to µ h, ρ h, l h for some h H 0 \ R1 with h E = M and l M, S M are equal to l h, S h when M S 2 2. This consideration is absolutely necessary for the proof of Theorem 7.2, whose reason will be described at the very end of this section. Noting that # K K w < for w W by K K w F w (V 0 ), we can easily verify the following lemma from Proposition 3.2 and the definitions of ρ M and H d ρ M. Lemma 7.6. H d ρ M F w = H d ρ MTw for any M R and any w W. The following proposition is a crucial step for the proof of Theorem 7.2.
24 24 NAOTAKA KAJINO Proposition 7.7. (1) There exist c 7.1, c 7.2 (0, ) such that (7.7) c 7.1 M d H d ρ M (K) c 7.2 M d, M R (2) Define T : R (0, ) by T(M) := Hρ d M (K) 1/d. Then T is continuous, and for any M R 2 2 0, any U O(2) and any a R \ {0}, (7.8) T(M) d = i S T(MT i ) d, T(UM) = T(M) and T(aM) = a T(M). Remark 7.8. (1) Let M R 2 2 0, det M 0 and c M := inf T R 2 2 MT / T, 0 so that c M > 0. Then a monotone class argument using (6.5), Lemma 7.6 and (7.7) easily shows that c c 7.1c d M Hd ρ H H d ρ M c c 7.2 M d H d ρ H. In particular, H d ρ M is singular to µ by Corollary 6.8. d (2) In fact, for each r, s (0, ) with r s, T is d+1-hölder continuous on {M R r M s} with respect to the norm metric. (3) The properties stated in Proposition 7.7-(2) characterizes T uniquely up to constant multiples: if T 0 : R [0, ) is continuous and satisfies (7.8) for any M R0 2 2, any U O(2) and any a R \ {0}, then T 0 = c 0 T for some c 0 [0, ). Proposition 7.7-(1) follows from Proposition 6.3, Lemma 6.5 and (4.8) with M in place of h, and (7.8) is immediate from Lemma 7.6 and the definition of T. On the other hand, the proof of the continuity of T at M R satisfying det M = 0 is quite involved and relies heavily on Theorem 4.15-(2). By virtue of Proposition 7.7, now we can associate to the function (t, M) Z µm,k\v 0 (t) a certain renewal equation to which Kesten s renewal theorem [51, Theorem 2] for functionals of Markov chains is applicable, as follows. Define (7.9) S T := {M R T(M) = 1} and M T := T(M) 1 M S T, M R 2 2 0, so that S T is compact by Proposition 7.7, and further define N : S T R N {0} and Z : S T (0, ) (0, ) by (7.10) N(M, λ) := N µm,k\v 0 (λ) and Z(M, t) := Z µm,k\v 0 (t). Let M S T. Then µ M c d/2 7.1 µ by (7.7) and hence λ µ M,K\V 0 1 c 2/d 7.1 λµ,k\v 0 1 > 0. Since N µm,k i\f i(v 0)(λ) = N µmti,k\v 0 (λ) = N ( (MT i ) T, T(MT i ) 2 λ ) for λ R and i S by (2.4) and µ M F i = (5/3)µ MTi, [53, Corollary 4.1.8] yields 0 N(M, λ) i S N ( (MT i ) T, T(MT i ) 2 λ ) = N µm,k\v 0 (λ) N µm,k\v 1 (λ) 3 for λ R, and hence for any t (0, ), (7.11) 0 Z(M, t) i S Z ( (MT i ) T, T(MT i ) 2 t ) 3. Now we define f, g : S T R R by f(m, s) := e ds Z(M, e 2s ) and (7.12) g(m, s) := e ds ( Z(M, e 2s ) i S Z ( (MT i ) T, T(MT i ) 2 e 2s)), so that for any (M, s) S T R, 0 g(m, s) 3e ds and (7.13) f(m, s) = g(m, s) + i S T(MT i ) d f ( (MT i ) T, s + log T(MT i ) ).
25 ANALYSIS AND GEOMETRY OF MEASURABLE RIEMANNIAN STRUCTURE ON S.G. 25 Since i S T(MT i) d = T(M) d = 1 by (7.8), we observe that the sum in (7.13) involves a conservative Markovian kernel (see Definition 8.2 below) P on (S T, B(S T )) given by (7.14) P(M, ) := i S T(MT i ) d δ (MTi ) T, M S T, where δ M (A) := 1 A (M), M S T, A S T. Then by considering a Markov chain X = (Ω, M, {X n } n N {0}, {P M } M ST ) on S T such that P M X1 1 = P(M, ) for M S T and another sequence {u n } n N of real random variables on (Ω, M) such that u n = log T(X n T i ) on {X n+1 = (X n T i ) T }, from (7.13) we obtain [ n 1 ] (7.15) f(m, s) = E M g(x k, s V k ) + E M [f(x n, s V n )] k=0 for any (M, s) S T R and any n N, where V n := n 1 k=0 u k. It is not difficult to see that 0 f(x n, s V n ) c 7.3 e ds (3/5) dn for n large enough (depending only on s) for some c 7.3 (0, ), and hence letting n in (7.15) results in [ ] (7.16) f(m, s) = E M g(x n, s V n ), (M, s) S T R. n=0 Kesten s renewal theorem [51, Theorem 2] asserts the convergence as s of a function of the form (7.16) to a finite limit which is independent of M. Therefore once the assumptions of [51, Theorem 2] are verified, we can conclude (7.3) for U = K w \ F w (V 0 ), w W, where the strict positivity of the limit is guaranteed by an a priori bound [44, Theorem 7.2] for Z µ h,k, h S H0, and then the extension to a general U is straightforward. The assumptions of [51, Theorem 2] consist of conditions [51, I.1 I.4] on the random variables {(X n, V n )} n N {0}, the direct Riemann integrability [51, Definition 1] of the function g : S T R R and the continuity of g. The direct Riemann integrability of g follows from the estimates λ µ M,K\V 0 1 c 2/d 7.1 λµ,k\v 0 1 > 0 and 0 g(m, s) 3e ds for (M, s) S T R, and for the sake of the continuity we need to consider the partition functions Z µm,k\v 0 and not the eigenvalue counting functions N µm,k\v 0. To verify part of the conditions [51, I.1 and I.2], we need the existence and the uniqueness of an invariant probability measure for P. The existence follows by the classical theorem of Krylov and Bogolioubov [59] (see [29, Theorem 1.10]) since S T is compact and P is a Feller Markovian kernel, i.e. Pu C(S T ) for any u C(S T ), by the continuity of T. The uniqueness is implied by a recent powerful result [94, Theorem 6.4] of Worm and Hille (see also [93, Theorem 7.4.6]). (To be precise, the uniqueness is assured only after taking the quotient ŠT := O(2)\S T of S T by the canonical left action O(2) S T (U, M) UM S T of O(2) on S T. Accordingly S T in the above argument has to be replaced by ŠT.) Note that the state space S T of the Markov chain X would not be compact if S 0 T := {M S T det M = 0} were removed. Moreover, since S 0 T is closed in S T and P-invariant (i.e. P(M, S 0 T ) = 1 for any M S 0 T ), the invariant measure for P has to be supported on S0 T (to be precise, P needs to be regarded as a Markovian kernel on (ŠT, B(ŠT))). For these reasons we cannot exclude S 0 T from the state space of the Markov chain X.
26 26 NAOTAKA KAJINO 8. Connections to general theories on metric measure spaces In this section, we briefly mention some connections to general theories of analysis and geometry on metric measure spaces. In Subsection 8.1, we state some recent results of Koskela and Zhou [58, Section 4] on connections to the theory of differential calculus on metric measure spaces initiated by Cheeger [17] and developed further by many people, e.g. Shanmugalingam [81] and Keith [48, 49, 50]. Subsection 8.2 concerns the theory of Ricci curvature lower bound for metric measure spaces established by Lott and Villani [71, 70] and Sturm [86, 87] and partially also by Ohta [76]. In fact, very recently there have been attempts to unify methods and ideas developed in those fields to establish differential calculus on an even wider range of metric measure spaces, e.g. Ambrosio, Gigli and Savaré [2, 3, 4], Gigli [27] and Koskela and Zhou [58]. There are also a huge number of other related results and it is beyond the author s ability to review even just the central achievements of these fields. For further details, we refer the reader to the above-mentioned works, monographs [31, 1, 91, 92] and references therein. We need the following definitions for the discussions below. Definition 8.1. Let (E, ρ) be a metric space and let γ : [a, b] E, a, b R, a b, be continuous. (1) The ρ-length l ρ (γ) of γ is defined by (8.1) l ρ (γ) := sup{ n k=1 ρ(γ(t k 1), γ(t k )) n N, {t k } n k=0 [a, b] is non-decreasing}. (2) Suppose l ρ (γ) < and define ϕ γ : [a, b] [0, l ρ (γ)] by ϕ γ (t) := l ρ (γ [a,t] ). Since γ(s) = γ(t) for any s, t [a, b] with ϕ γ (s) = ϕ γ (t), there exists a unique map γ ρ : [0, l ρ (γ)] E such that γ = γ ρ ϕ γ, and then γ ρ is continuous and l ρ (γ ρ [0,t] ) = t for any t [0, l ρ (γ)]. γ ρ is called the ρ-length parametrization of γ. (3) Suppose a < b. Then γ is called a minimal ρ-geodesic if and only if l ρ (γ [a,t] ) = t a b a t s ρ(γ(a), γ(b)) for any t [a, b], or equivalently ρ(γ(s), γ(t)) = b a ρ(γ(a), γ(b)) for any s, t [a, b]. Let G(E, ρ) denote the set of minimal ρ-geodesics with domain [0, 1], which is equipped with the metric ρ G(E,ρ) (γ 1, γ 2 ) := sup t [0,1] ρ(γ 1 (t), γ 2 (t)). Also recall the following standard definition. Definition 8.2. Let (E, B) be a measurable space. Then P : E B [0, 1] is called a Markovian kernel on (E, B) if and only if P(x, ) : B [0, 1] is a measure on (E, B) for any x E and P(, A) : E [0, 1] is B-measurable for any A B. Such P is called conservative if and only if P(x, E) = 1 for any x E Identification of Dirichlet form as Cheeger energy. In [17] Cheeger established a theory of differential calculus on a general metric measure space which admits the volume doubling property and the weak (1, p)-poincaré inequality (in terms of upper gradients) for some p [1, ). Since (K, ρ H, µ) and (K, ρ h, µ h ), h H 0 \ R1, satisfy the volume doubling property (Theorem 4.25) and the weak Poincaré inequality in terms of (the densities of) the E-energy measures (Proposition 4.26), it is natural to expect that Cheeger s results in [17] are applicable to them. Koskela and Zhou [58, Section 4] have recently proved that this is indeed the case, that Cheeger s Rademacher theorem [17, Theorem 4.38] takes an explicit form using Φ and h as the coordinate functions, and that the associated Cheeger 2- energies coincide with the Dirichlet form (E, F). To be precise, they have proved the following results. Recall Theorem 3.10 for the derivatives u and du dh of u F.
27 ANALYSIS AND GEOMETRY OF MEASURABLE RIEMANNIAN STRUCTURE ON S.G. 27 Theorem 8.3 ([58, Theorems 4.2 and 4.3]). Let h H 0 \R1 and u F. Then for µ-a.e. x K, or equivalently for µ h -a.e. x K (recall Theorem 3.6), (8.2) (8.3) u(y) u(x) = u(x), Φ(y) Φ(x) + o(ρ H (x, y)) as y x, u(y) u(x) = du dh (x)(h(y) h(x)) + o(ρ h(x, y)) as y x. Definition 8.4. Let (E, ρ) be a metric space. For f : E R, we define (8.4) Lip ρ f(x) := lim r 0 sup y B r (x,ρ)\{x} f(y) f(x), x E. ρ(x, y) Note that Lip ρ f : E [0, ] is Borel measurable if f C(E). Theorem 8.5 ([58, Theorems 4.1 and 4.3]). Let h H 0 \R1 and u F. Then (8.5) u = Lip ρh u µ-a.e. and du = Lip dh ρh u µ h -a.e. As a consequence, we obtain the identification of (E, F) as the Cheeger 2-energy and (1, 2)-Sobolev space, for which let us recall Cheeger s definitions in [17]. Definition 8.6 ([32]). Let (E, ρ) be a metric space and let f : E R. A Borel measurable function g : X [0, ] is called an upper ρ-gradient for f if and only if for any continuous map γ : [0, 1] E with l ρ (γ) <, (8.6) f(γ(1)) f(γ(0)) lρ(γ) 0 g(γ ρ (s))ds. Definition 8.7 ([17, Section 2]). Let (E, ρ) be a metric space and let m be a Borel measure on E such that m(b r (x, ρ)) (0, ) for any (r, x) (0, ) E. For p [1, ), we define the Cheeger p-energy Ch ρ,m p : L p (E, m) [0, ] by (8.7) g n is an upper ρ-gradient for an m-version Ch ρ,m p (f) := inf lim inf g p ndm n of f n for each n N for some {f n } n N E L p (E, m) with lim n E f n f p dm = 0 and the Cheeger (1, p)-sobolev space H 1,p (E, ρ, m) over (E, ρ, m) by (8.8) H 1,p (E, ρ, m) := {f L p (E, m) Ch ρ,m p (f) < }. Remark 8.8. (1) Ch ρ,m p was originally termed the upper gradient p-energy in [17]. Here we have followed the notation and terminology adopted in [2, 3, 27]. (2) Shanmugalingam [81, Definition 2.5] proposed another way of defining a (1, p)- Sobolev space under the same framework, independently of Cheeger s work [17, Section 2]. Her Sobolev space is denoted as N 1,p (E, ρ, m) and called the Newtonian space of index p [1, ), and she proved in [81, Theorem 4.10] that for p (1, ), H 1,p (E, ρ, m) = N 1,p (E, ρ, m) and they are equipped with exactly the same norm. Corollary 8.9. Let h H 0 \ R1. Then E(u, u) = Ch ρ H,µ 2 (u) = Ch ρ h,µ h 2 (u) for any u F and F = H 1,2 (K, ρ H, µ) = H 1,2 (K, ρ h, µ h ). Proof. On the basis of Theorem 4.25 and Proposition 4.26, the first assertion follows from (8.5), [48, Theorem 2], [17, Theorem 6.1] and [58, Theorem 2.2-(i)], whereas [58, Theorem 2.2-(i)] and [81, Theorem 4.10] yield the latter.
28 28 NAOTAKA KAJINO Remark Let M R and let Φ M, µ M, ρ M be as in Definition 7.3. Then Theorems 8.3, 8.5 and Corollary 8.9 with Φ M, µ M, ρ M in place of Φ, µ, ρ H are still valid with exactly the same proofs as those in [58, Section 4], where u is given by the version of Theorem 3.10-(1) for Φ M, µ M with Z and T [ω]m replaced by Z M := MZ 2 MZM (Z M := ( ) when MZ = 0) and MT[ω]m, respectively Invalidity of Ricci curvature lower bound. In the last decade, Lott and Villani [71, 70] and Sturm [86, 87] formulated Ricci curvature lower bound for general metric measure spaces and showed that for a complete Riemannian manifold equipped with Riemannian distance and volume, their formulations are equivalent to the usual lower bound of its Ricci curvature tensor. Around the same period, Ohta [76] and Sturm [87] proposed another formulation of Ricci curvature lower bound which is in principle weaker but easier to handle. Their main idea was to make use of notions from optimal transport theory, and they also derived various analytic and geometric consequences of their formulations. The purpose of this subsection is to show that (K, ρ H, µ) does not satisfy any of those conditions for Ricci curvature lower bound. We need to introduce several notions from optimal transport theory to state the Ricci bound conditions precisely. Throughout this subsection, we fix a complete separable metric space (E, ρ) and a Borel measure m on E such that m(e) > 0 and E = U E open in E, m(u)< U. Definition 8.11 (Wasserstein space). Let P(E) denote the set of all Borel probability measures on E. Let p [1, ) and define (8.9) (8.10) P p (E, ρ) := { ν P(E) E ρ(x, y)p dν(y) < for some (any) x E }, Wp ρ (ν 1, ν 2 ) p := inf { E E ρp dϖ ϖ P(E E), ϖ pr 1 j = ν j, j = 1, 2 } for ν 1, ν 2 P(E), where pr j : E E E is given by pr j (x 1, x 2 ) := x j. Then W ρ p is indeed a metric on P p (E, ρ) by [91, Theorem 7.3-(i)] and called the p-wasserstein distance over (E, ρ). (P p (E, ρ), W ρ p ) is called the p-wasserstein space over (E, ρ), which is a complete separable metric space by [92, Theorem 6.18]. Definition 8.12 (Relative entropy). For ν P(E), we write ν m if and only if ν is absolutely continuous with respect to m. We define the relative entropy Ent m : P 2 (E, ρ) [, ] with respect to m by (8.11) Ent m (ν) := { E dν dν dm log dm dm if ν m and E otherwise ( dν dν +dm dm log dm) <, for ν P 2 (E, ρ), and we set P 2 (E, ρ, m) := {v P 2 (E, ρ) Ent m (ν) < }. Definition 8.13 (Curvature-dimension condition, [86, Definition 4.5-(i)]). Let k R. We say that (E, ρ, m) satisfies the curvature-dimension condition CD(k, ) or (E, ρ, m) has curvature k if and only if for any ν 0, ν 1 P 2 (E, ρ, m) there exists a minimal W ρ 2 -geodesic α : [0, 1] P 2(E, ρ) such that α(0) = ν 0, α(1) = ν 1 and (8.12) Ent m (α(t)) (1 t) Ent m (α(0)) + t Ent m (α(1)) k 2 t(1 t)w ρ 2 (α(0), α(1))2 for any t [0, 1]. Note that α(t) P 2 (E, ρ, m) for any t [0, 1] for such α. The curvature-dimension condition CD(k, ) is a generalization of the notion of Ricci curvature lower bound adapted to the setting of a general metric measure space. Indeed, the following equivalence holds for complete Riemannian manifolds.
29 ANALYSIS AND GEOMETRY OF MEASURABLE RIEMANNIAN STRUCTURE ON S.G. 29 Theorem 8.14 ([80, Theorem 1.1], [86, Theorem 4.9]). Let (M, g) be a complete Riemannian manifold with Riemannian geodesic distance ρ g and Riemannian volume measure m g. Let k R. Then (M, ρ g, m g ) satisfies CD(k, ) if and only if Ric g kg, i.e. Ric g (v, v) kg(v, v) for any x M and any v T x M, where T x M denotes the tangent space of M at x and Ric g the Ricci curvature tensor of (M, g). Definition For A, B E and t [0, 1], we define { } (8.13) [A, B] ρ t := z E ρ(x, z) = tρ(x, y) and ρ(z, y) = (1 t)ρ(x, y). for some (x, y) A B Note that [A, B] ρ t ν P(E) B(E)ν if A, B B(E) by [20, III.13, III.17 and III.33], where B(E) ν denotes the completion of B(E) by ν. We also set [x, y] ρ t := [{x}, {y}] ρ t for x, y E and t [0, 1], so that [x, y] ρ t is a closed subset of E. Let A, B B(E) be such that m(a), m(b) (0, ) and set ν 0 := m(a) 1 1 A m and ν 1 := m(b) 1 1 B m. By [86, Lemma 2.11-(ii)], if ν 0, ν 1 P 2 (E, ρ) and α : [0, 1] P 2 (E, ρ) is a minimal W ρ 2 -geodesic with α(0) = ν 0 and α(1) = ν 1, then α(t)([a, B] ρ t ) = 1 for any t [0, 1]. Thus an application of Jensen s inequality to the left-hand side of (8.12), together with the lower semicontinuity of W ρ 2 under weak convergence ([92, Remark 6.12]), yields the following generalized Brunn-Minkowski inequality, which was new even for complete Riemannian manifolds. Proposition 8.16 (Brunn-Minkowski inequality, cf. [87, Proposition 2.1]). Let k R and suppose that (E, ρ, m) satisfies CD(k, ). Then for any A, B B(E) with m(a), m(b) (0, ) and any t [0, 1], (8.14) log m([a, B] ρ t ) (1 t) log m(a) + t log m(b) + k 2 t(1 t)w ρ 2 ( 1A m(a) m, ) 2 1 B m(b) m. Remark (1) Some time after [86], Sturm introduced in [87, Definition 1.3] a variant of the curvature-dimension condition for (E, ρ, m) denoted as CD(k, N), where k R and N [1, ). Roughly speaking, (E, ρ, m) satisfying CD(k, N) has Ricci curvature bounded from below by k and dimension at most N. Indeed, according to [87, Theorem 1.7], for (M, g), ρ g, m g as in Theorem 8.14, (M, ρ g, m g ) satisfies CD(k, N) if and only if Ric g kg and dim M N. As naturally expected from its meaning, if (E, ρ, m) satisfies CD(k, N) then it also satisfies CD(k, N ) for any k (, k] and any N [N, ) by [87, Proposition 1.6-(i)]. Moreover by [87, Proposition 1.6-(ii)], if k R, (E, ρ, m) satisfies CD(k, N) for some N [1, ) and m(e) <, then (E, ρ, m) also satisfies CD(k, ). (2) Independently of Sturm s work [86, 87], Lott and Villani [70, Definition 4.7] (see also [71, Definitions 5.12 and 5.13]) also defined the notion of (E, ρ, m) having N-Ricci curvature bounded below by k for k R and N [1, ], which is essentially the same as the curvature-dimension condition CD(k, N). As noted in [70, Remark 4.11], this notion gets weaker as K decreases and N increases. (In the main texts of [71, 70], the compactness of the metric space is assumed for the sake of simplicity, but many results there can be extended to the non-compact case; see [71, Appendix E] and [92, Chapters 29 and 30].) As remarked in [70, discussions before and after Lemma 4.14], for k R, N [1, ] and (E, ρ, m) with E compact and m(e) <, the condition of N-Ricci curvature bounded below by k implies CD(k, N). (3) An important feature of the notions of CD(k, N) and of N-Ricci curvature bounded below by k is that they are preserved under measured Gromov-Hausdorff
30 30 NAOTAKA KAJINO limits; see [86, Subsection 4.5], [87, Section 3], [71, Subsections 4.2, 5.3 and E.5] and [92, Chapter 29] for details. They also give rise to a lot of fundamental analytic and geometric consequences; see e.g. [87, Section 2], [71, Section 6], [70, Section 5] and [92, Chapter 30]. There is yet another formulation of Ricci curvature lower bound for (E, ρ, m) due to Ohta [76] and Sturm [87], which is given as follows. Definition 8.18 (Measure contraction property, [87, Section 5], cf. [76]). Let k R and N [1, ). (E, ρ, m) is said to satisfy the measure contraction property MCP(k, N) if and only if for each t (0, 1), for m-a.e. x E there exists a Markovian kernel P t,x on (E, B(E)) such that P t,x (y, [x, y] ρ t ) = 1 for m-a.e. y E and (8.15) where ς (t) k,n (8.16) ς (t) k,n (θ) := E ς (t) k,n (ρ(x, y))p t,x(y, )dm(y) m, : [0, ) (0, ] is defined by if kθ 2 (N 1)π 2, ( ( )) sin tθ k/(n 1) N 1 t sin ( θ k/(n 1) ) if 0 < kθ 2 < (N 1)π 2, t N if kθ 2 = 0, ( ( )) sinh tθ k/(n 1) N 1 t sinh ( θ k/(n 1) ) if kθ 2 < 0 for N > 1 and ς (t) k,1 (θ) := 1 (0, )(kθ 2 ) + t1 (,0] (kθ 2 ). Remark (1) Let t (0, 1), k, k R, k k and N, N [1, ), N N. Then it is easy to see that ς (t) k,n ς(t) k,n, so that MCP(k, N) implies MCP(k, N ). (2) Sturm s original version [87, Definition 5.1] of MCP(k, N) is slightly stronger than as in Definition 8.18, requiring additionally the Borel measurability of P t,x (y, ) in (x, y) E E and E ς(1 t) k,n (ρ(x, y))p t,x(y, )dm(x) m for m-a.e. y E. (3) MCP(k, N) as in Definition 8.18 is implied by Ohta s definition [76, Definition 2.1] of MCP(k, N) under his standing assumption in [76] that m(b r (x, ρ)) (0, ) for any (r, x) (0, ) E and (E, ρ) is a length space, i.e. for any x, y E, ρ(x, y) = inf{l ρ (γ) γ[0, 1] E, γ is continuous, γ(0) = x, γ(1) = y}. Indeed, this observation is easily verified by using [21, Theorems and ] (and m ( E \B π (N 1)/k (x, ρ) ) = 0 for any x E when k(n 1) > 0, which follows from [76, Theorem 4.3 and Lemma 4.4-(i)]). In principle, MCP(k, N) is weaker than CD(k, N) but still means Ricci curvature lower bound by k and dimension upper bound by N. Indeed, by [76, Corollary 2.7] or [87, Remark 5.3], if (E, ρ, m) satisfies MCP(k, N) then dim H (supp E [m], ρ) N, where supp E [m] := {x E m(u) > 0 for any open subset U of E with x U}. Furthermore CD(k, N) implies MCP(k, N) under certain geometric conditions on (E, ρ, m), and for a complete Riemannian manifold (M, g), MCP(k, N) corresponds to Ric g kg and dim M N in a weaker sense than CD(k, N) does, as follows. Theorem 8.20 ([87, Lemma 4.1 and Theorem 5.4]). Let k R, N [1, ) and suppose that (E, ρ, m) satisfies CD(k, N).
31 ANALYSIS AND GEOMETRY OF MEASURABLE RIEMANNIAN STRUCTURE ON S.G. 31 (1) If (E, ρ) is non-branching, i.e. x 1 = x 2 for any z, x 0, x 1, x 2 E with 2ρ(z, x i ) = ρ(x 0, x 1 ) = ρ(x 0, x 2 ), i {0, 1, 2}, then there exists a Borel measurable map γ : E E G(E, ρ) such that for m m-a.e. (x, y) E E, γ(x, y) is the unique minimal ρ-geodesic with γ(x, y)(0) = x and γ(x, y)(1) = y. (2) If a map γ : E E G(E, ρ) as in (1) exists, then (E, ρ, m) satisfies MCP(k, N). Theorem 8.21 ([76, Theorem 3.2 and Corollary 3.3], [87, Corollary 5.5]). Let (M, g) be a complete Riemannian manifold with Riemannian geodesic distance ρ g and Riemannian volume measure m g. (Note that (M, ρ g ) is non-branching.) Let k R. Then (M, ρ g, m g ) satisfies MCP(k, dim M) if and only if Ric g kg. Remark (1) In principle, MCP(k, N) should hold for a wider range of metric measure spaces than CD(k, N). Indeed, for (M, g), ρ g, m g as in Theorem 8.21, MCP(k, N) with dim M < N does not imply CD(k, N) nor Ric g kg in general, as noted in [87, Remark 5.6]. Furthermore for the (2n + 1)-dimensional Heisenberg group H n (R) := R 2n+1 equipped with the Carnot-Carathéodory metric and the Lebesgue measure, where n N, MCP(k, N) holds if and only (k, N) (, 0] [2n+3, ) by [42, Theorem 2.3 and Remark 3.3], whereas CD(k, N) does not hold for any (k, N) R [1, ] by [42, Theorem 3.2 and Remark 3.3]. Another advantage of MCP(k, N) is that it is easier to handle than CD(k, N). For example, MCP(k, N) is preserved by the operations of taking products and cones of metric measure spaces by [77, Proposition 3.3 and Theorem 4.2], but similar properties for CD(k, N) are not known except for products of non-branching compact CD(k, )-spaces due to [86, Proposition 4.16]. (2) Similarly to CD(k, N), MCP(k, N) is preserved by measured Gromov-Hausdorff limits; see [76, Section 6] and [87, Theorem 5.9 and Corollary 5.10]. MCP(k, N) also admits almost the same analytic and geometric consequences as CD(k, N); see [76, Sections 2, 4 and 5], [87, Sections 5 and 6] and [79, Section 3] for details. Now we turn to the case of the Sierpiński gasket K equipped with the harmonic geodesic metric ρ H and the Kusuoka measure µ. We have the following result. Theorem Let k R and N [1, ). Then (K, ρ H, µ) does not satisfy any one of CD(k, ), CD(k, N), MCP(k, N). The rest of this section is devoted to the proof of Theorem We start with the following easy lemma. Recall that we set xy := {(1 t)x + ty t [0, 1]} for x, y R 2 (Definition 4.11-(1)). Lemma Set := w W F w (q 1 q 2 q 2 q 3 q 3 q 1 ). Then µ( ) = 0. Proof. Let h H 0, w W, i S and S \ {i} = {j, k}. By [41, Lemma 4.2], (8.17) µ h (K vj K vk ) = µ h (K v ) µ h (K vi ) µ h (K v ), v W (see [38, Proposition 3.8] and [36, Proposition 5.27] for similar estimates in more general settings), and then an inductive use of (8.17) easily shows that µ h (F w (q j q k )) = lim µ ( ) ( 14 ) mµ h h m v {j,k} K m wv lim (K w ) = 0. m 15 Thus µ h ( ) = 0 and hence µ( ) = µ h1 ( ) + µ h2 ( ) = 0. The key to the proof of Theorem 8.23 is the following proposition, which is an easy consequence of Theorem 4.19.
32 32 NAOTAKA KAJINO Proposition Let A, B K and t (0, 1). Then [A, B] ρ H t (A B). Proof. Let z [A, B] ρ H t. Take (x, y) A B such that ρ H (x, z) = tρ H (x, y) and ρ H (z, y) = (1 t)ρ H (x, y). If x = y, then ρ H (x, z) = 0 and z = x = y A B. Assume x y, so that z {x, y}. By Theorem 4.15-(2), there exist harmonic geodesics γ xz : [0, t] K and γ zy : [t, 1] K such that γ xz (0) = x, γ xz (t) = z = γ zy (t), γ zy (1) = y, l H (γ xz ) = ρ H (x, z) = tρ H (x, y) and l H (γ zy ) = ρ H (z, y) = (1 t)ρ H (x, y). Define γ : [0, 1] K by γ [0,t] := γ xz and γ [t,1] := γ zy. Then γ is continuous, γ(0) = x, γ(t) = z, γ(1) = y and l H (γ) = l H (γ xz ) + l H (γ zy ) = ρ H (x, y). Now Theorem 4.19 implies that γ = γ ϕ γ for some harmonic geodesic γ : [0, 1] K and a non-decreasing continuous surjection ϕ γ : [0, 1] [0, 1], and then z = γ(ϕ γ (t)) by z {x, y} = { γ(0), γ(1)} and the definition of γ being a harmonic geodesic (Definition 4.13-(2)). Thus [A, B] ρ H t (A B). Proof of Theorem Let A, B B(K) be such that µ(a)µ(b) > 0 and µ(a B) = 0. Let t (0, 1). Then µ([a, B] ρ H t ) = 0 by Proposition 8.25 and Lemma 8.24, so that (8.14) does not hold and hence neither does CD(k, ) by Proposition [87, Proposition 1.6-(ii)] (see Remark 8.17-(1) above) further implies that (K, ρ H, µ) does not satisfy CD(k, N), either. For MCP(k, N), let t (0, 1), x K and suppose that there exists a Markovian kernel P t,x on (K, B(K)) satisfying (8.15) and P t,x (y, [x, y] ρ H t ) = 1, µ-a.e. y K. Then since [x, y] ρ H t for any K \ {x} by Proposition 8.25, P t,x (y, ) = 1 for µ-a.e. y K and hence (8.15) yields µ( ) K ς(t) k,n (ρ H(x, y))dµ(y) > 0, contradicting Lemma Therefore (K, ρ H, µ) does not satisfy MCP(k, N). Remark Unfortunately, the above proof of Theorem 8.23 does not work for (K, ρ h, µ h ), h H 0 \ R1, since the assertion of Theorem 4.19 is not valid for l h and ρ h by Remark Theorem 8.23 is quite likely to be true also for (K, ρ h, µ h ), but the author has no idea at this moment how to manage this case. On the other hand, for any M R with det M 0 and with µ M, ρ M, l M as in Definition 7.3, Theorem 4.19 with ρ M, l M in place of ρ H, l H is valid and hence Theorem 8.23 and Proposition 8.25 hold also for (K, ρ M, µ M ). 9. Possible generalizations to other self-similar fractals We conclude this paper with some remarks on possible generalizations to other self-similar fractals. In this paper, we have restricted our attention to the particular case of the 2-dimensional standard Sierpiński gasket. In fact, it is almost the only self-similar fractal that possesses all the required properties for the framework and the results of this paper. Extension to other self-similar fractals would be only partially possible and involve essential difficulties which would vary depending on each fractal. Below we illustrate the actual (complicated) situation by mentioning each of the concrete examples in Figure 3 separately Sierpiński gaskets. Let k N, k 3. The k-dimensional standard Sierpiński gasket is the direct k-dimensional analogue of the Sierpiński gasket. The results in [63, 52, 35] except those in [52, Lemma 4.2 and Appendix] are stated and proved including this case and therefore Section 3 is immediately extended to this case (with obvious changes). As shown in [54, Section 3] for the Kusuoka measure µ, Lemma 4.22 and Proposition 4.23 can be verified similarly with suitable changes of the constants. On the other hand, the proof of Lemma 4.17 for the
33 ANALYSIS AND GEOMETRY OF MEASURABLE RIEMANNIAN STRUCTURE ON S.G. 33 Sierpiński gasket heavily relied on the 2-dimensionality of the space, as is observed from its dependence on Theorem 4.18, and extension to the k-dimensional case is not straightforward at all. Since the proof of Theorem 4.15 was based on Lemma 4.17, it is still unclear how we can verify Theorem 4.15 for the k-dimensional case. Recall that Lemma 4.17 has two assertions (4.9) and (4.10). It seems possible to prove (4.9) by taking the projection of the harmonic k-dimensional Sierpiński gasket onto a suitable 2-dimensional subspace and then applying Theorem To the contrary, the lower inequality of (4.10) is not valid for the k-dimensional case. Indeed, if h is a V 0 -harmonic function taking 1 at x V 0, 1 at y V 0 and 0 on V 0 \ {x, y}, then h = 0 on the hyperplane containing V 0 \ {x, y}, from which we can easily show that the lower inequality of (4.10) does not hold. This degeneracy causes a lot of troubles in the proofs of various geometric inequalities and therefore extension to the k-dimensional case should require significant effort, although most of the results in this paper are quite likely to hold also for the k-dimensional case. Another possible extension is the case of the 2-dimensional level-l Sierpiński gasket with l 3 (see Figure 3 for a picture of the level-3 case; the Sierpiński gasket is regarded as the level-2 case). For simplicity we consider here the level-3 case only. Then the measurable Riemannian structure can be introduced in exactly the same manner, and by virtue of the 2-dimensionality and Theorem 4.18 we can prove Lemma 4.17, thereby Theorem 4.15, and also Theorems 4.19 and Interestingly, however, it is also possible to show that Lemma 4.22-(2) does not hold, on the basis of the denseness of vertices from which the space spreads away in three directions. Consequently Proposition 4.23 is not valid by [55, Theorems and 1.4.3] and hence neither is the volume doubling property (Theorem 4.25). Therefore by [55, Theorem 3.2.3], even the on-diagonal upper bound p µ (t, x, x) c U /µ ( B t (x, ρ H) ) of the heat kernel p µ is false in this case. It is an interesting challenging problem to establish a sharp two-sided estimate for the heat kernel p µ in this case, but the actual behavior of p µ is expected to be very wild and this problem should be difficult. On the other hand, it is still likely that we can extend Theorem 5.2 and the results in Sections 6 and 7 to this case, but the actual proofs will be much more involved. In the case of the (level-2) Sierpiński gasket, Lemma 4.22-(2) is used especially in the proof of the continuity of the function T : R (0, ) defined in Proposition 7.7-(2), and the extension to the level-3 case, where Lemma 4.22-(2) is invalid, will require a non-trivial improvement in the proof Other nested fractals and Sierpiński carpets. For most other nested fractals such as the N-polygasket with N 5, N/4 N (see [45, Subsection 5.2] for its precise definition), the snowflake and the Vicsek set shown in Figure 3, the situation is much worse than in the case of Sierpiński gaskets. The problem is that the harmonic structure is degenerate, i.e. non-constant V 0 -harmonic functions can be constant on some K w, or in other words, the family {A i } i S R (#V 0) (#V 0 ) of matrices defined by (2.11) contains non-invertible ones. In such cases it is highly non-trivial whether the Kusuoka measure µ := #V 0 1 i=1 µ hi, where {h i } #V 0 1 i=1 H 0 is arbitrarily chosen to be orthonormal in (H 0 /R1, E), is energy-dominant in the sense that µ u is absolutely continuous with respect to µ for any u F. The method of introducing a measurable Riemannian structure on the basis of µ makes sense only if µ is energy-dominant, which may or may not be the case depending on each self-similar fractal.
34 34 NAOTAKA KAJINO t t t t Figure 3. Typical self-similar fractals. From the upper left, threedimensional standard (level-2) Sierpin ski gasket, two-dimensional level-3 Sierpin ski gasket, pentagasket (5-polygasket), hexagasket (6-polygasket), nonagasket (9-polygasket), snowflake, the Vicsek set and Sierpin ski carpet. In each fractal except the last one, the set V0 of its boundary points is marked by solid circles. For example, in the case of the Vicsek set, any V0 -harmonic function is constant on each connected component of the complement of the two diagonals, so that the Kusuoka measure µ is supported only on the union of the diagonals, which is much smaller than the whole Vicsek set. For the N -polygasket with N 6= 6, 9 and the snowflake, it is still not known whether the Kusuoka measure µ is energy-dominant. On the other hand, in the case of the hexagasket (6-polygasket) and the nonagasket (9-polygasket), by virtue of their dihedral symmetry we can prove that the Kusuoka measure µ is energy-dominant, which was essentially stated and proved in [88, Section 7]. Therefore µ gives rise to a measurable Riemannian structure. We can extend Lemma 4.17 and thereby Theorem 4.15 to this case with a suitable notion of harmonic geodesics, whereas the degeneracy of the harmonic structure easily implies that Lemma 4.22-(2) and the lower inequalities in Lemma 4.22-(1) are not true. Consequently Proposition 4.23 and Theorem 4.25 do not ( hold and) hence neither does the on-diagonal upper bound pµ (t, x, x) cu /µ B t (x, ρh ) of the heat kernel pµ by [55, Theorem 3.2.3]. (To be precise, [55, Theorem 3.2.3] is not directly applicable to this case due to the lack of the lower inequalities in Lemma 4.22-(1), but we can still verify [55, Lemmas and 3.5.5] by using certain specific properties of the hexagasket and the nonagasket.) Similarly to the case of the 2-dimensional level-3 Sierpin ski gasket, it is likely that we can extend Theorem 5.2 and the results in Sections 6 and 7. In fact, since the linear map Fw : H0 /R1 H0 /R1, Fw h := h Fw, has rank one with the same image (same up to symmetry of the space) for most w W, just the usual renewal theorem [23, Section XI.1, Renewal theorem (Alternative form)] should suffice for the proof of Theorem 7.2 and therefore Proposition 7.7-(2) should not be required.
ON THE REGULARITY OF SAMPLE PATHS OF SUB-ELLIPTIC DIFFUSIONS ON MANIFOLDS
 Bendikov, A. and Saloff-Coste, L. Osaka J. Math. 4 (5), 677 7 ON THE REGULARITY OF SAMPLE PATHS OF SUB-ELLIPTIC DIFFUSIONS ON MANIFOLDS ALEXANDER BENDIKOV and LAURENT SALOFF-COSTE (Received March 4, 4)
Bendikov, A. and Saloff-Coste, L. Osaka J. Math. 4 (5), 677 7 ON THE REGULARITY OF SAMPLE PATHS OF SUB-ELLIPTIC DIFFUSIONS ON MANIFOLDS ALEXANDER BENDIKOV and LAURENT SALOFF-COSTE (Received March 4, 4)
Heat kernel asymptotics on the usual and harmonic Sierpinski gaskets. Cornell Prob. Summer School 2010 July 22, 2010
 Heat kernel asymptotics on the usual and harmonic Sierpinski gaskets Naotaka Kajino (Kyoto University) http://www-an.acs.i.kyoto-u.ac.jp/~kajino.n/ Cornell Prob. Summer School 2010 July 22, 2010 For some
Heat kernel asymptotics on the usual and harmonic Sierpinski gaskets Naotaka Kajino (Kyoto University) http://www-an.acs.i.kyoto-u.ac.jp/~kajino.n/ Cornell Prob. Summer School 2010 July 22, 2010 For some
9 Radon-Nikodym theorem and conditioning
 Tel Aviv University, 2015 Functions of real variables 93 9 Radon-Nikodym theorem and conditioning 9a Borel-Kolmogorov paradox............. 93 9b Radon-Nikodym theorem.............. 94 9c Conditioning.....................
Tel Aviv University, 2015 Functions of real variables 93 9 Radon-Nikodym theorem and conditioning 9a Borel-Kolmogorov paradox............. 93 9b Radon-Nikodym theorem.............. 94 9c Conditioning.....................
DOMAINS OF DIRICHLET FORMS AND EFFECTIVE RESISTANCE ESTIMATES ON P.C.F. FRACTALS. 1. Introduction
 DOMAINS OF DIRICHLET FORMS AND EFFECTIVE RESISTANCE ESTIMATES ON P.C.F. FRACTALS JIAXIN HU 1 AND XINGSHENG WANG Abstract. In this paper we consider post-critically finite self-similar fractals with regular
DOMAINS OF DIRICHLET FORMS AND EFFECTIVE RESISTANCE ESTIMATES ON P.C.F. FRACTALS JIAXIN HU 1 AND XINGSHENG WANG Abstract. In this paper we consider post-critically finite self-similar fractals with regular
Densely defined non-closable curl on topologically one-dimensional Dirichlet metric measure spaces
 Densely defined non-closable curl on topologically one-dimensional Dirichlet metric measure spaces Kansai Probability Seminar, Kyoto March 11, 2016 Universität Bielefeld joint with Alexander Teplyaev (University
Densely defined non-closable curl on topologically one-dimensional Dirichlet metric measure spaces Kansai Probability Seminar, Kyoto March 11, 2016 Universität Bielefeld joint with Alexander Teplyaev (University
DISTRIBUTION THEORY ON P.C.F. FRACTALS
 DISTRIBUTION THEORY ON P.C.F. FRACTALS LUKE G. ROGERS AND ROBERT S. STRICHARTZ Abstract. We construct a theory of distributions in the setting of analysis on post-critically finite self-similar fractals,
DISTRIBUTION THEORY ON P.C.F. FRACTALS LUKE G. ROGERS AND ROBERT S. STRICHARTZ Abstract. We construct a theory of distributions in the setting of analysis on post-critically finite self-similar fractals,
ICM 2014: The Structure and Meaning. of Ricci Curvature. Aaron Naber ICM 2014: Aaron Naber
 Outline of Talk Background and Limit Spaces Structure of Spaces with Lower Ricci Regularity of Spaces with Bounded Ricci Characterizing Ricci Background: s (M n, g, x) n-dimensional pointed Riemannian
Outline of Talk Background and Limit Spaces Structure of Spaces with Lower Ricci Regularity of Spaces with Bounded Ricci Characterizing Ricci Background: s (M n, g, x) n-dimensional pointed Riemannian
Part V. 17 Introduction: What are measures and why measurable sets. Lebesgue Integration Theory
 Part V 7 Introduction: What are measures and why measurable sets Lebesgue Integration Theory Definition 7. (Preliminary). A measure on a set is a function :2 [ ] such that. () = 2. If { } = is a finite
Part V 7 Introduction: What are measures and why measurable sets Lebesgue Integration Theory Definition 7. (Preliminary). A measure on a set is a function :2 [ ] such that. () = 2. If { } = is a finite
BOUNDARY VALUE PROBLEMS ON A HALF SIERPINSKI GASKET
 BOUNDARY VALUE PROBLEMS ON A HALF SIERPINSKI GASKET WEILIN LI AND ROBERT S. STRICHARTZ Abstract. We study boundary value problems for the Laplacian on a domain Ω consisting of the left half of the Sierpinski
BOUNDARY VALUE PROBLEMS ON A HALF SIERPINSKI GASKET WEILIN LI AND ROBERT S. STRICHARTZ Abstract. We study boundary value problems for the Laplacian on a domain Ω consisting of the left half of the Sierpinski
Spaces with Ricci curvature bounded from below
 Spaces with Ricci curvature bounded from below Nicola Gigli February 23, 2015 Topics 1) On the definition of spaces with Ricci curvature bounded from below 2) Analytic properties of RCD(K, N) spaces 3)
Spaces with Ricci curvature bounded from below Nicola Gigli February 23, 2015 Topics 1) On the definition of spaces with Ricci curvature bounded from below 2) Analytic properties of RCD(K, N) spaces 3)
Function spaces and stochastic processes on fractals I. Takashi Kumagai. (RIMS, Kyoto University, Japan)
 Function spaces and stochastic processes on fractals I Takashi Kumagai (RIMS, Kyoto University, Japan) http://www.kurims.kyoto-u.ac.jp/~kumagai/ International workshop on Fractal Analysis September 11-17,
Function spaces and stochastic processes on fractals I Takashi Kumagai (RIMS, Kyoto University, Japan) http://www.kurims.kyoto-u.ac.jp/~kumagai/ International workshop on Fractal Analysis September 11-17,
Part III. 10 Topological Space Basics. Topological Spaces
 Part III 10 Topological Space Basics Topological Spaces Using the metric space results above as motivation we will axiomatize the notion of being an open set to more general settings. Definition 10.1.
Part III 10 Topological Space Basics Topological Spaces Using the metric space results above as motivation we will axiomatize the notion of being an open set to more general settings. Definition 10.1.
Volume Doubling Measures and Heat Kernel Estimates on Self-Similar Sets. Jun Kigami
 Volume Doubling Measures and Heat Kernel Estimates on Self-Similar Sets Jun Kigami Author address: Graduate School of Informatics, Kyoto University, Kyoto 606-8501, Japan E-mail address: kigami@i.kyoto-u.ac.jp
Volume Doubling Measures and Heat Kernel Estimates on Self-Similar Sets Jun Kigami Author address: Graduate School of Informatics, Kyoto University, Kyoto 606-8501, Japan E-mail address: kigami@i.kyoto-u.ac.jp
Functional Analysis. Franck Sueur Metric spaces Definitions Completeness Compactness Separability...
 Functional Analysis Franck Sueur 2018-2019 Contents 1 Metric spaces 1 1.1 Definitions........................................ 1 1.2 Completeness...................................... 3 1.3 Compactness......................................
Functional Analysis Franck Sueur 2018-2019 Contents 1 Metric spaces 1 1.1 Definitions........................................ 1 1.2 Completeness...................................... 3 1.3 Compactness......................................
Topological properties
 CHAPTER 4 Topological properties 1. Connectedness Definitions and examples Basic properties Connected components Connected versus path connected, again 2. Compactness Definition and first examples Topological
CHAPTER 4 Topological properties 1. Connectedness Definitions and examples Basic properties Connected components Connected versus path connected, again 2. Compactness Definition and first examples Topological
Ricci Curvature and Bochner Formula on Alexandrov Spaces
 Ricci Curvature and Bochner Formula on Alexandrov Spaces Sun Yat-sen University March 18, 2013 (work with Prof. Xi-Ping Zhu) Contents Alexandrov Spaces Generalized Ricci Curvature Geometric and Analytic
Ricci Curvature and Bochner Formula on Alexandrov Spaces Sun Yat-sen University March 18, 2013 (work with Prof. Xi-Ping Zhu) Contents Alexandrov Spaces Generalized Ricci Curvature Geometric and Analytic
LECTURE 15: COMPLETENESS AND CONVEXITY
 LECTURE 15: COMPLETENESS AND CONVEXITY 1. The Hopf-Rinow Theorem Recall that a Riemannian manifold (M, g) is called geodesically complete if the maximal defining interval of any geodesic is R. On the other
LECTURE 15: COMPLETENESS AND CONVEXITY 1. The Hopf-Rinow Theorem Recall that a Riemannian manifold (M, g) is called geodesically complete if the maximal defining interval of any geodesic is R. On the other
1 Math 241A-B Homework Problem List for F2015 and W2016
 1 Math 241A-B Homework Problem List for F2015 W2016 1.1 Homework 1. Due Wednesday, October 7, 2015 Notation 1.1 Let U be any set, g be a positive function on U, Y be a normed space. For any f : U Y let
1 Math 241A-B Homework Problem List for F2015 W2016 1.1 Homework 1. Due Wednesday, October 7, 2015 Notation 1.1 Let U be any set, g be a positive function on U, Y be a normed space. For any f : U Y let
Self-similar Sets as Quotients of Shift Spaces Jun Kigami Kyoto University
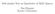 Self-similar Sets as Quotients of Shift Spaces Jun Kigami Kyoto University (One-sided) Shift space S: a finite set, symbols For w = w 1...w m W, Σ = S N = {w 1 w 2... i N,w i S} W m = S m = {w 1...w m
Self-similar Sets as Quotients of Shift Spaces Jun Kigami Kyoto University (One-sided) Shift space S: a finite set, symbols For w = w 1...w m W, Σ = S N = {w 1 w 2... i N,w i S} W m = S m = {w 1...w m
Metric Spaces and Topology
 Chapter 2 Metric Spaces and Topology From an engineering perspective, the most important way to construct a topology on a set is to define the topology in terms of a metric on the set. This approach underlies
Chapter 2 Metric Spaces and Topology From an engineering perspective, the most important way to construct a topology on a set is to define the topology in terms of a metric on the set. This approach underlies
i=1 α i. Given an m-times continuously
 1 Fundamentals 1.1 Classification and characteristics Let Ω R d, d N, d 2, be an open set and α = (α 1,, α d ) T N d 0, N 0 := N {0}, a multiindex with α := d i=1 α i. Given an m-times continuously differentiable
1 Fundamentals 1.1 Classification and characteristics Let Ω R d, d N, d 2, be an open set and α = (α 1,, α d ) T N d 0, N 0 := N {0}, a multiindex with α := d i=1 α i. Given an m-times continuously differentiable
MATH 205C: STATIONARY PHASE LEMMA
 MATH 205C: STATIONARY PHASE LEMMA For ω, consider an integral of the form I(ω) = e iωf(x) u(x) dx, where u Cc (R n ) complex valued, with support in a compact set K, and f C (R n ) real valued. Thus, I(ω)
MATH 205C: STATIONARY PHASE LEMMA For ω, consider an integral of the form I(ω) = e iωf(x) u(x) dx, where u Cc (R n ) complex valued, with support in a compact set K, and f C (R n ) real valued. Thus, I(ω)
Local and Non-Local Dirichlet Forms on the Sierpiński Carpet
 Local and Non-Local Dirichlet Forms on the Sierpiński Carpet Alexander Grigor yan and Meng Yang Abstract We give a purely analytic construction of a self-similar local regular Dirichlet form on the Sierpiński
Local and Non-Local Dirichlet Forms on the Sierpiński Carpet Alexander Grigor yan and Meng Yang Abstract We give a purely analytic construction of a self-similar local regular Dirichlet form on the Sierpiński
Empirical Processes: General Weak Convergence Theory
 Empirical Processes: General Weak Convergence Theory Moulinath Banerjee May 18, 2010 1 Extended Weak Convergence The lack of measurability of the empirical process with respect to the sigma-field generated
Empirical Processes: General Weak Convergence Theory Moulinath Banerjee May 18, 2010 1 Extended Weak Convergence The lack of measurability of the empirical process with respect to the sigma-field generated
Degenerate harmonic structures on fractal graphs.
 Degenerate harmonic structures on fractal graphs. Konstantinos Tsougkas Uppsala University Fractals 6, Cornell University June 16, 2017 1 / 25 Analysis on fractals via analysis on graphs. The motivation
Degenerate harmonic structures on fractal graphs. Konstantinos Tsougkas Uppsala University Fractals 6, Cornell University June 16, 2017 1 / 25 Analysis on fractals via analysis on graphs. The motivation
Laplace s Equation. Chapter Mean Value Formulas
 Chapter 1 Laplace s Equation Let be an open set in R n. A function u C 2 () is called harmonic in if it satisfies Laplace s equation n (1.1) u := D ii u = 0 in. i=1 A function u C 2 () is called subharmonic
Chapter 1 Laplace s Equation Let be an open set in R n. A function u C 2 () is called harmonic in if it satisfies Laplace s equation n (1.1) u := D ii u = 0 in. i=1 A function u C 2 () is called subharmonic
Energy on fractals and related questions: about the use of differential 1-forms on the Sierpinski Gasket and other fractals
 Energy on fractals and related questions: about the use of differential 1-forms on the Sierpinski Gasket and other fractals Part 2 A.Teplyaev University of Connecticut Rome, April May 2015 Main works to
Energy on fractals and related questions: about the use of differential 1-forms on the Sierpinski Gasket and other fractals Part 2 A.Teplyaev University of Connecticut Rome, April May 2015 Main works to
Sobolev Mappings between Manifolds and Metric Spaces
 Sobolev Mappings between Manifolds and Metric Spaces Piotr Haj lasz Abstract In connection with the theory of p-harmonic mappings, Eells and Lemaire raised a question about density of smooth mappings in
Sobolev Mappings between Manifolds and Metric Spaces Piotr Haj lasz Abstract In connection with the theory of p-harmonic mappings, Eells and Lemaire raised a question about density of smooth mappings in
Math 350 Fall 2011 Notes about inner product spaces. In this notes we state and prove some important properties of inner product spaces.
 Math 350 Fall 2011 Notes about inner product spaces In this notes we state and prove some important properties of inner product spaces. First, recall the dot product on R n : if x, y R n, say x = (x 1,...,
Math 350 Fall 2011 Notes about inner product spaces In this notes we state and prove some important properties of inner product spaces. First, recall the dot product on R n : if x, y R n, say x = (x 1,...,
Recall that if X is a compact metric space, C(X), the space of continuous (real-valued) functions on X, is a Banach space with the norm
 Chapter 13 Radon Measures Recall that if X is a compact metric space, C(X), the space of continuous (real-valued) functions on X, is a Banach space with the norm (13.1) f = sup x X f(x). We want to identify
Chapter 13 Radon Measures Recall that if X is a compact metric space, C(X), the space of continuous (real-valued) functions on X, is a Banach space with the norm (13.1) f = sup x X f(x). We want to identify
LAPLACIANS COMPACT METRIC SPACES. Sponsoring. Jean BELLISSARD a. Collaboration:
 LAPLACIANS on Sponsoring COMPACT METRIC SPACES Jean BELLISSARD a Georgia Institute of Technology, Atlanta School of Mathematics & School of Physics Collaboration: I. PALMER (Georgia Tech, Atlanta) a e-mail:
LAPLACIANS on Sponsoring COMPACT METRIC SPACES Jean BELLISSARD a Georgia Institute of Technology, Atlanta School of Mathematics & School of Physics Collaboration: I. PALMER (Georgia Tech, Atlanta) a e-mail:
CHAPTER 7. Connectedness
 CHAPTER 7 Connectedness 7.1. Connected topological spaces Definition 7.1. A topological space (X, T X ) is said to be connected if there is no continuous surjection f : X {0, 1} where the two point set
CHAPTER 7 Connectedness 7.1. Connected topological spaces Definition 7.1. A topological space (X, T X ) is said to be connected if there is no continuous surjection f : X {0, 1} where the two point set
Some SDEs with distributional drift Part I : General calculus. Flandoli, Franco; Russo, Francesco; Wolf, Jochen
 Title Author(s) Some SDEs with distributional drift Part I : General calculus Flandoli, Franco; Russo, Francesco; Wolf, Jochen Citation Osaka Journal of Mathematics. 4() P.493-P.54 Issue Date 3-6 Text
Title Author(s) Some SDEs with distributional drift Part I : General calculus Flandoli, Franco; Russo, Francesco; Wolf, Jochen Citation Osaka Journal of Mathematics. 4() P.493-P.54 Issue Date 3-6 Text
Spectral Theory, with an Introduction to Operator Means. William L. Green
 Spectral Theory, with an Introduction to Operator Means William L. Green January 30, 2008 Contents Introduction............................... 1 Hilbert Space.............................. 4 Linear Maps
Spectral Theory, with an Introduction to Operator Means William L. Green January 30, 2008 Contents Introduction............................... 1 Hilbert Space.............................. 4 Linear Maps
Topological properties of Z p and Q p and Euclidean models
 Topological properties of Z p and Q p and Euclidean models Samuel Trautwein, Esther Röder, Giorgio Barozzi November 3, 20 Topology of Q p vs Topology of R Both R and Q p are normed fields and complete
Topological properties of Z p and Q p and Euclidean models Samuel Trautwein, Esther Röder, Giorgio Barozzi November 3, 20 Topology of Q p vs Topology of R Both R and Q p are normed fields and complete
Heat kernels on metric spaces with doubling measure
 Heat kernels on metric spaces with doubling measure Alexander Grigor yan, Jiaxin Hu and Ka-Sing Lau Abstract. In this survey we discuss heat kernel estimates of self-similar type on metric spaces with
Heat kernels on metric spaces with doubling measure Alexander Grigor yan, Jiaxin Hu and Ka-Sing Lau Abstract. In this survey we discuss heat kernel estimates of self-similar type on metric spaces with
Boundary measures, generalized Gauss Green formulas, and mean value property in metric measure spaces
 Boundary measures, generalized Gauss Green formulas, and mean value property in metric measure spaces Niko Marola, Michele Miranda Jr, and Nageswari Shanmugalingam Contents 1 Introduction 2 2 Preliminaries
Boundary measures, generalized Gauss Green formulas, and mean value property in metric measure spaces Niko Marola, Michele Miranda Jr, and Nageswari Shanmugalingam Contents 1 Introduction 2 2 Preliminaries
A Concise Course on Stochastic Partial Differential Equations
 A Concise Course on Stochastic Partial Differential Equations Michael Röckner Reference: C. Prevot, M. Röckner: Springer LN in Math. 1905, Berlin (2007) And see the references therein for the original
A Concise Course on Stochastic Partial Differential Equations Michael Röckner Reference: C. Prevot, M. Röckner: Springer LN in Math. 1905, Berlin (2007) And see the references therein for the original
1 Inner Product Space
 Ch - Hilbert Space 1 4 Hilbert Space 1 Inner Product Space Let E be a complex vector space, a mapping (, ) : E E C is called an inner product on E if i) (x, x) 0 x E and (x, x) = 0 if and only if x = 0;
Ch - Hilbert Space 1 4 Hilbert Space 1 Inner Product Space Let E be a complex vector space, a mapping (, ) : E E C is called an inner product on E if i) (x, x) 0 x E and (x, x) = 0 if and only if x = 0;
CHAPTER 6. Differentiation
 CHPTER 6 Differentiation The generalization from elementary calculus of differentiation in measure theory is less obvious than that of integration, and the methods of treating it are somewhat involved.
CHPTER 6 Differentiation The generalization from elementary calculus of differentiation in measure theory is less obvious than that of integration, and the methods of treating it are somewhat involved.
USING FUNCTIONAL ANALYSIS AND SOBOLEV SPACES TO SOLVE POISSON S EQUATION
 USING FUNCTIONAL ANALYSIS AND SOBOLEV SPACES TO SOLVE POISSON S EQUATION YI WANG Abstract. We study Banach and Hilbert spaces with an eye towards defining weak solutions to elliptic PDE. Using Lax-Milgram
USING FUNCTIONAL ANALYSIS AND SOBOLEV SPACES TO SOLVE POISSON S EQUATION YI WANG Abstract. We study Banach and Hilbert spaces with an eye towards defining weak solutions to elliptic PDE. Using Lax-Milgram
HOPF S DECOMPOSITION AND RECURRENT SEMIGROUPS. Josef Teichmann
 HOPF S DECOMPOSITION AND RECURRENT SEMIGROUPS Josef Teichmann Abstract. Some results of ergodic theory are generalized in the setting of Banach lattices, namely Hopf s maximal ergodic inequality and the
HOPF S DECOMPOSITION AND RECURRENT SEMIGROUPS Josef Teichmann Abstract. Some results of ergodic theory are generalized in the setting of Banach lattices, namely Hopf s maximal ergodic inequality and the
WELL-POSEDNESS OF THE LAPLACIAN ON MANIFOLDS WITH BOUNDARY AND BOUNDED GEOMETRY
 WELL-POSEDNESS OF THE LAPLACIAN ON MANIFOLDS WITH BOUNDARY AND BOUNDED GEOMETRY BERND AMMANN, NADINE GROSSE, AND VICTOR NISTOR Abstract. Let M be a Riemannian manifold with a smooth boundary. The main
WELL-POSEDNESS OF THE LAPLACIAN ON MANIFOLDS WITH BOUNDARY AND BOUNDED GEOMETRY BERND AMMANN, NADINE GROSSE, AND VICTOR NISTOR Abstract. Let M be a Riemannian manifold with a smooth boundary. The main
RIEMANNIAN GEOMETRY COMPACT METRIC SPACES. Jean BELLISSARD 1. Collaboration:
 RIEMANNIAN GEOMETRY of COMPACT METRIC SPACES Jean BELLISSARD 1 Georgia Institute of Technology, Atlanta School of Mathematics & School of Physics Collaboration: I. PALMER (Georgia Tech, Atlanta) 1 e-mail:
RIEMANNIAN GEOMETRY of COMPACT METRIC SPACES Jean BELLISSARD 1 Georgia Institute of Technology, Atlanta School of Mathematics & School of Physics Collaboration: I. PALMER (Georgia Tech, Atlanta) 1 e-mail:
DIFFERENTIAL GEOMETRY, LECTURE 16-17, JULY 14-17
 DIFFERENTIAL GEOMETRY, LECTURE 16-17, JULY 14-17 6. Geodesics A parametrized line γ : [a, b] R n in R n is straight (and the parametrization is uniform) if the vector γ (t) does not depend on t. Thus,
DIFFERENTIAL GEOMETRY, LECTURE 16-17, JULY 14-17 6. Geodesics A parametrized line γ : [a, b] R n in R n is straight (and the parametrization is uniform) if the vector γ (t) does not depend on t. Thus,
The Lusin Theorem and Horizontal Graphs in the Heisenberg Group
 Analysis and Geometry in Metric Spaces Research Article DOI: 10.2478/agms-2013-0008 AGMS 2013 295-301 The Lusin Theorem and Horizontal Graphs in the Heisenberg Group Abstract In this paper we prove that
Analysis and Geometry in Metric Spaces Research Article DOI: 10.2478/agms-2013-0008 AGMS 2013 295-301 The Lusin Theorem and Horizontal Graphs in the Heisenberg Group Abstract In this paper we prove that
CHAPTER 3. Gauss map. In this chapter we will study the Gauss map of surfaces in R 3.
 CHAPTER 3 Gauss map In this chapter we will study the Gauss map of surfaces in R 3. 3.1. Surfaces in R 3 Let S R 3 be a submanifold of dimension 2. Let {U i, ϕ i } be a DS on S. For any p U i we have a
CHAPTER 3 Gauss map In this chapter we will study the Gauss map of surfaces in R 3. 3.1. Surfaces in R 3 Let S R 3 be a submanifold of dimension 2. Let {U i, ϕ i } be a DS on S. For any p U i we have a
Chapter 2 Metric Spaces
 Chapter 2 Metric Spaces The purpose of this chapter is to present a summary of some basic properties of metric and topological spaces that play an important role in the main body of the book. 2.1 Metrics
Chapter 2 Metric Spaces The purpose of this chapter is to present a summary of some basic properties of metric and topological spaces that play an important role in the main body of the book. 2.1 Metrics
n [ F (b j ) F (a j ) ], n j=1(a j, b j ] E (4.1)
![n [ F (b j ) F (a j ) ], n j=1(a j, b j ] E (4.1) n [ F (b j ) F (a j ) ], n j=1(a j, b j ] E (4.1)](/thumbs/81/82707553.jpg) 1.4. CONSTRUCTION OF LEBESGUE-STIELTJES MEASURES In this section we shall put to use the Carathéodory-Hahn theory, in order to construct measures with certain desirable properties first on the real line
1.4. CONSTRUCTION OF LEBESGUE-STIELTJES MEASURES In this section we shall put to use the Carathéodory-Hahn theory, in order to construct measures with certain desirable properties first on the real line
Banach Spaces V: A Closer Look at the w- and the w -Topologies
 BS V c Gabriel Nagy Banach Spaces V: A Closer Look at the w- and the w -Topologies Notes from the Functional Analysis Course (Fall 07 - Spring 08) In this section we discuss two important, but highly non-trivial,
BS V c Gabriel Nagy Banach Spaces V: A Closer Look at the w- and the w -Topologies Notes from the Functional Analysis Course (Fall 07 - Spring 08) In this section we discuss two important, but highly non-trivial,
MET Workshop: Exercises
 MET Workshop: Exercises Alex Blumenthal and Anthony Quas May 7, 206 Notation. R d is endowed with the standard inner product (, ) and Euclidean norm. M d d (R) denotes the space of n n real matrices. When
MET Workshop: Exercises Alex Blumenthal and Anthony Quas May 7, 206 Notation. R d is endowed with the standard inner product (, ) and Euclidean norm. M d d (R) denotes the space of n n real matrices. When
Pseudo-Poincaré Inequalities and Applications to Sobolev Inequalities
 Pseudo-Poincaré Inequalities and Applications to Sobolev Inequalities Laurent Saloff-Coste Abstract Most smoothing procedures are via averaging. Pseudo-Poincaré inequalities give a basic L p -norm control
Pseudo-Poincaré Inequalities and Applications to Sobolev Inequalities Laurent Saloff-Coste Abstract Most smoothing procedures are via averaging. Pseudo-Poincaré inequalities give a basic L p -norm control
Math 147, Homework 5 Solutions Due: May 15, 2012
 Math 147, Homework 5 Solutions Due: May 15, 2012 1 Let f : R 3 R 6 and φ : R 3 R 3 be the smooth maps defined by: f(x, y, z) = (x 2, y 2, z 2, xy, xz, yz) and φ(x, y, z) = ( x, y, z) (a) Show that f is
Math 147, Homework 5 Solutions Due: May 15, 2012 1 Let f : R 3 R 6 and φ : R 3 R 3 be the smooth maps defined by: f(x, y, z) = (x 2, y 2, z 2, xy, xz, yz) and φ(x, y, z) = ( x, y, z) (a) Show that f is
The Dirichlet s P rinciple. In this lecture we discuss an alternative formulation of the Dirichlet problem for the Laplace equation:
 Oct. 1 The Dirichlet s P rinciple In this lecture we discuss an alternative formulation of the Dirichlet problem for the Laplace equation: 1. Dirichlet s Principle. u = in, u = g on. ( 1 ) If we multiply
Oct. 1 The Dirichlet s P rinciple In this lecture we discuss an alternative formulation of the Dirichlet problem for the Laplace equation: 1. Dirichlet s Principle. u = in, u = g on. ( 1 ) If we multiply
CHAPTER 9. Embedding theorems
 CHAPTER 9 Embedding theorems In this chapter we will describe a general method for attacking embedding problems. We will establish several results but, as the main final result, we state here the following:
CHAPTER 9 Embedding theorems In this chapter we will describe a general method for attacking embedding problems. We will establish several results but, as the main final result, we state here the following:
Extreme points of compact convex sets
 Extreme points of compact convex sets In this chapter, we are going to show that compact convex sets are determined by a proper subset, the set of its extreme points. Let us start with the main definition.
Extreme points of compact convex sets In this chapter, we are going to show that compact convex sets are determined by a proper subset, the set of its extreme points. Let us start with the main definition.
The oblique derivative problem for general elliptic systems in Lipschitz domains
 M. MITREA The oblique derivative problem for general elliptic systems in Lipschitz domains Let M be a smooth, oriented, connected, compact, boundaryless manifold of real dimension m, and let T M and T
M. MITREA The oblique derivative problem for general elliptic systems in Lipschitz domains Let M be a smooth, oriented, connected, compact, boundaryless manifold of real dimension m, and let T M and T
Essential Spectra of complete manifolds
 Essential Spectra of complete manifolds Zhiqin Lu Analysis, Complex Geometry, and Mathematical Physics: A Conference in Honor of Duong H. Phong May 7, 2013 Zhiqin Lu, Dept. Math, UCI Essential Spectra
Essential Spectra of complete manifolds Zhiqin Lu Analysis, Complex Geometry, and Mathematical Physics: A Conference in Honor of Duong H. Phong May 7, 2013 Zhiqin Lu, Dept. Math, UCI Essential Spectra
An Introduction to Self Similar Structures
 An Introduction to Self Similar Structures Christopher Hayes University of Connecticut April 6th, 2018 Christopher Hayes (University of Connecticut) An Introduction to Self Similar Structures April 6th,
An Introduction to Self Similar Structures Christopher Hayes University of Connecticut April 6th, 2018 Christopher Hayes (University of Connecticut) An Introduction to Self Similar Structures April 6th,
CONTENTS. 4 Hausdorff Measure Introduction The Cantor Set Rectifiable Curves Cantor Set-Like Objects...
 Contents 1 Functional Analysis 1 1.1 Hilbert Spaces................................... 1 1.1.1 Spectral Theorem............................. 4 1.2 Normed Vector Spaces.............................. 7 1.2.1
Contents 1 Functional Analysis 1 1.1 Hilbert Spaces................................... 1 1.1.1 Spectral Theorem............................. 4 1.2 Normed Vector Spaces.............................. 7 1.2.1
CAPACITIES ON METRIC SPACES
 [June 8, 2001] CAPACITIES ON METRIC SPACES V. GOL DSHTEIN AND M. TROYANOV Abstract. We discuss the potential theory related to the variational capacity and the Sobolev capacity on metric measure spaces.
[June 8, 2001] CAPACITIES ON METRIC SPACES V. GOL DSHTEIN AND M. TROYANOV Abstract. We discuss the potential theory related to the variational capacity and the Sobolev capacity on metric measure spaces.
Harmonic Functions and Brownian motion
 Harmonic Functions and Brownian motion Steven P. Lalley April 25, 211 1 Dynkin s Formula Denote by W t = (W 1 t, W 2 t,..., W d t ) a standard d dimensional Wiener process on (Ω, F, P ), and let F = (F
Harmonic Functions and Brownian motion Steven P. Lalley April 25, 211 1 Dynkin s Formula Denote by W t = (W 1 t, W 2 t,..., W d t ) a standard d dimensional Wiener process on (Ω, F, P ), and let F = (F
1 Directional Derivatives and Differentiability
 Wednesday, January 18, 2012 1 Directional Derivatives and Differentiability Let E R N, let f : E R and let x 0 E. Given a direction v R N, let L be the line through x 0 in the direction v, that is, L :=
Wednesday, January 18, 2012 1 Directional Derivatives and Differentiability Let E R N, let f : E R and let x 0 E. Given a direction v R N, let L be the line through x 0 in the direction v, that is, L :=
Heat Kernel and Analysis on Manifolds Excerpt with Exercises. Alexander Grigor yan
 Heat Kernel and Analysis on Manifolds Excerpt with Exercises Alexander Grigor yan Department of Mathematics, University of Bielefeld, 33501 Bielefeld, Germany 2000 Mathematics Subject Classification. Primary
Heat Kernel and Analysis on Manifolds Excerpt with Exercises Alexander Grigor yan Department of Mathematics, University of Bielefeld, 33501 Bielefeld, Germany 2000 Mathematics Subject Classification. Primary
Spaces with Ricci curvature bounded from below
 Spaces with Ricci curvature bounded from below Nicola Gigli March 10, 2014 Lessons Basics of optimal transport Definition of spaces with Ricci curvature bounded from below Analysis on spaces with Ricci
Spaces with Ricci curvature bounded from below Nicola Gigli March 10, 2014 Lessons Basics of optimal transport Definition of spaces with Ricci curvature bounded from below Analysis on spaces with Ricci
Introduction to Real Analysis Alternative Chapter 1
 Christopher Heil Introduction to Real Analysis Alternative Chapter 1 A Primer on Norms and Banach Spaces Last Updated: March 10, 2018 c 2018 by Christopher Heil Chapter 1 A Primer on Norms and Banach Spaces
Christopher Heil Introduction to Real Analysis Alternative Chapter 1 A Primer on Norms and Banach Spaces Last Updated: March 10, 2018 c 2018 by Christopher Heil Chapter 1 A Primer on Norms and Banach Spaces
LECTURE 10: THE ATIYAH-GUILLEMIN-STERNBERG CONVEXITY THEOREM
 LECTURE 10: THE ATIYAH-GUILLEMIN-STERNBERG CONVEXITY THEOREM Contents 1. The Atiyah-Guillemin-Sternberg Convexity Theorem 1 2. Proof of the Atiyah-Guillemin-Sternberg Convexity theorem 3 3. Morse theory
LECTURE 10: THE ATIYAH-GUILLEMIN-STERNBERG CONVEXITY THEOREM Contents 1. The Atiyah-Guillemin-Sternberg Convexity Theorem 1 2. Proof of the Atiyah-Guillemin-Sternberg Convexity theorem 3 3. Morse theory
Local semiconvexity of Kantorovich potentials on non-compact manifolds
 Local semiconvexity of Kantorovich potentials on non-compact manifolds Alessio Figalli, Nicola Gigli Abstract We prove that any Kantorovich potential for the cost function c = d / on a Riemannian manifold
Local semiconvexity of Kantorovich potentials on non-compact manifolds Alessio Figalli, Nicola Gigli Abstract We prove that any Kantorovich potential for the cost function c = d / on a Riemannian manifold
RESEARCH STATEMENT MICHAEL MUNN
 RESEARCH STATEMENT MICHAEL MUNN Ricci curvature plays an important role in understanding the relationship between the geometry and topology of Riemannian manifolds. Perhaps the most notable results in
RESEARCH STATEMENT MICHAEL MUNN Ricci curvature plays an important role in understanding the relationship between the geometry and topology of Riemannian manifolds. Perhaps the most notable results in
08a. Operators on Hilbert spaces. 1. Boundedness, continuity, operator norms
 (February 24, 2017) 08a. Operators on Hilbert spaces Paul Garrett garrett@math.umn.edu http://www.math.umn.edu/ garrett/ [This document is http://www.math.umn.edu/ garrett/m/real/notes 2016-17/08a-ops
(February 24, 2017) 08a. Operators on Hilbert spaces Paul Garrett garrett@math.umn.edu http://www.math.umn.edu/ garrett/ [This document is http://www.math.umn.edu/ garrett/m/real/notes 2016-17/08a-ops
fy (X(g)) Y (f)x(g) gy (X(f)) Y (g)x(f)) = fx(y (g)) + gx(y (f)) fy (X(g)) gy (X(f))
 1. Basic algebra of vector fields Let V be a finite dimensional vector space over R. Recall that V = {L : V R} is defined to be the set of all linear maps to R. V is isomorphic to V, but there is no canonical
1. Basic algebra of vector fields Let V be a finite dimensional vector space over R. Recall that V = {L : V R} is defined to be the set of all linear maps to R. V is isomorphic to V, but there is no canonical
Chapter 1. Measure Spaces. 1.1 Algebras and σ algebras of sets Notation and preliminaries
 Chapter 1 Measure Spaces 1.1 Algebras and σ algebras of sets 1.1.1 Notation and preliminaries We shall denote by X a nonempty set, by P(X) the set of all parts (i.e., subsets) of X, and by the empty set.
Chapter 1 Measure Spaces 1.1 Algebras and σ algebras of sets 1.1.1 Notation and preliminaries We shall denote by X a nonempty set, by P(X) the set of all parts (i.e., subsets) of X, and by the empty set.
A LOCALIZATION PROPERTY AT THE BOUNDARY FOR MONGE-AMPERE EQUATION
 A LOCALIZATION PROPERTY AT THE BOUNDARY FOR MONGE-AMPERE EQUATION O. SAVIN. Introduction In this paper we study the geometry of the sections for solutions to the Monge- Ampere equation det D 2 u = f, u
A LOCALIZATION PROPERTY AT THE BOUNDARY FOR MONGE-AMPERE EQUATION O. SAVIN. Introduction In this paper we study the geometry of the sections for solutions to the Monge- Ampere equation det D 2 u = f, u
SHARP BOUNDARY TRACE INEQUALITIES. 1. Introduction
 SHARP BOUNDARY TRACE INEQUALITIES GILES AUCHMUTY Abstract. This paper describes sharp inequalities for the trace of Sobolev functions on the boundary of a bounded region R N. The inequalities bound (semi-)norms
SHARP BOUNDARY TRACE INEQUALITIES GILES AUCHMUTY Abstract. This paper describes sharp inequalities for the trace of Sobolev functions on the boundary of a bounded region R N. The inequalities bound (semi-)norms
Chapter 3. Riemannian Manifolds - I. The subject of this thesis is to extend the combinatorial curve reconstruction approach to curves
 Chapter 3 Riemannian Manifolds - I The subject of this thesis is to extend the combinatorial curve reconstruction approach to curves embedded in Riemannian manifolds. A Riemannian manifold is an abstraction
Chapter 3 Riemannian Manifolds - I The subject of this thesis is to extend the combinatorial curve reconstruction approach to curves embedded in Riemannian manifolds. A Riemannian manifold is an abstraction
HAUSDORFF DIMENSION AND ITS APPLICATIONS
 HAUSDORFF DIMENSION AND ITS APPLICATIONS JAY SHAH Abstract. The theory of Hausdorff dimension provides a general notion of the size of a set in a metric space. We define Hausdorff measure and dimension,
HAUSDORFF DIMENSION AND ITS APPLICATIONS JAY SHAH Abstract. The theory of Hausdorff dimension provides a general notion of the size of a set in a metric space. We define Hausdorff measure and dimension,
THE INVERSE FUNCTION THEOREM FOR LIPSCHITZ MAPS
 THE INVERSE FUNCTION THEOREM FOR LIPSCHITZ MAPS RALPH HOWARD DEPARTMENT OF MATHEMATICS UNIVERSITY OF SOUTH CAROLINA COLUMBIA, S.C. 29208, USA HOWARD@MATH.SC.EDU Abstract. This is an edited version of a
THE INVERSE FUNCTION THEOREM FOR LIPSCHITZ MAPS RALPH HOWARD DEPARTMENT OF MATHEMATICS UNIVERSITY OF SOUTH CAROLINA COLUMBIA, S.C. 29208, USA HOWARD@MATH.SC.EDU Abstract. This is an edited version of a
Topology. Xiaolong Han. Department of Mathematics, California State University, Northridge, CA 91330, USA address:
 Topology Xiaolong Han Department of Mathematics, California State University, Northridge, CA 91330, USA E-mail address: Xiaolong.Han@csun.edu Remark. You are entitled to a reward of 1 point toward a homework
Topology Xiaolong Han Department of Mathematics, California State University, Northridge, CA 91330, USA E-mail address: Xiaolong.Han@csun.edu Remark. You are entitled to a reward of 1 point toward a homework
Completely Symmetric Resistance Forms on the Stretched Sierpinski Gasket
 Completely Symmetric Resistance Forms on the Stretched Sierpinski Gasket P. Alonso Ruiz U. Freiberg J. Kigami Abstract The stretched Sierpinski gasket, SSG for short, is the space obtained by replacing
Completely Symmetric Resistance Forms on the Stretched Sierpinski Gasket P. Alonso Ruiz U. Freiberg J. Kigami Abstract The stretched Sierpinski gasket, SSG for short, is the space obtained by replacing
Kernel Method: Data Analysis with Positive Definite Kernels
 Kernel Method: Data Analysis with Positive Definite Kernels 2. Positive Definite Kernel and Reproducing Kernel Hilbert Space Kenji Fukumizu The Institute of Statistical Mathematics. Graduate University
Kernel Method: Data Analysis with Positive Definite Kernels 2. Positive Definite Kernel and Reproducing Kernel Hilbert Space Kenji Fukumizu The Institute of Statistical Mathematics. Graduate University
Connectedness. Proposition 2.2. The following are equivalent for a topological space (X, T ).
 Connectedness 1 Motivation Connectedness is the sort of topological property that students love. Its definition is intuitive and easy to understand, and it is a powerful tool in proofs of well-known results.
Connectedness 1 Motivation Connectedness is the sort of topological property that students love. Its definition is intuitive and easy to understand, and it is a powerful tool in proofs of well-known results.
THEOREMS, ETC., FOR MATH 516
 THEOREMS, ETC., FOR MATH 516 Results labeled Theorem Ea.b.c (or Proposition Ea.b.c, etc.) refer to Theorem c from section a.b of Evans book (Partial Differential Equations). Proposition 1 (=Proposition
THEOREMS, ETC., FOR MATH 516 Results labeled Theorem Ea.b.c (or Proposition Ea.b.c, etc.) refer to Theorem c from section a.b of Evans book (Partial Differential Equations). Proposition 1 (=Proposition
Finite-dimensional spaces. C n is the space of n-tuples x = (x 1,..., x n ) of complex numbers. It is a Hilbert space with the inner product
 Chapter 4 Hilbert Spaces 4.1 Inner Product Spaces Inner Product Space. A complex vector space E is called an inner product space (or a pre-hilbert space, or a unitary space) if there is a mapping (, )
Chapter 4 Hilbert Spaces 4.1 Inner Product Spaces Inner Product Space. A complex vector space E is called an inner product space (or a pre-hilbert space, or a unitary space) if there is a mapping (, )
Harmonic Functions and the Spectrum of the Laplacian on the Sierpinski Carpet
 Harmonic Functions and the Spectrum of the Laplacian on the Sierpinski Carpet Matthew Begué, Tristan Kalloniatis, & Robert Strichartz October 4, 2011 Norbert Wiener Center Seminar Construction of the Sierpinski
Harmonic Functions and the Spectrum of the Laplacian on the Sierpinski Carpet Matthew Begué, Tristan Kalloniatis, & Robert Strichartz October 4, 2011 Norbert Wiener Center Seminar Construction of the Sierpinski
Basic Properties of Metric and Normed Spaces
 Basic Properties of Metric and Normed Spaces Computational and Metric Geometry Instructor: Yury Makarychev The second part of this course is about metric geometry. We will study metric spaces, low distortion
Basic Properties of Metric and Normed Spaces Computational and Metric Geometry Instructor: Yury Makarychev The second part of this course is about metric geometry. We will study metric spaces, low distortion
g 2 (x) (1/3)M 1 = (1/3)(2/3)M.
 COMPACTNESS If C R n is closed and bounded, then by B-W it is sequentially compact: any sequence of points in C has a subsequence converging to a point in C Conversely, any sequentially compact C R n is
COMPACTNESS If C R n is closed and bounded, then by B-W it is sequentially compact: any sequence of points in C has a subsequence converging to a point in C Conversely, any sequentially compact C R n is
B. Appendix B. Topological vector spaces
 B.1 B. Appendix B. Topological vector spaces B.1. Fréchet spaces. In this appendix we go through the definition of Fréchet spaces and their inductive limits, such as they are used for definitions of function
B.1 B. Appendix B. Topological vector spaces B.1. Fréchet spaces. In this appendix we go through the definition of Fréchet spaces and their inductive limits, such as they are used for definitions of function
5 Measure theory II. (or. lim. Prove the proposition. 5. For fixed F A and φ M define the restriction of φ on F by writing.
 5 Measure theory II 1. Charges (signed measures). Let (Ω, A) be a σ -algebra. A map φ: A R is called a charge, (or signed measure or σ -additive set function) if φ = φ(a j ) (5.1) A j for any disjoint
5 Measure theory II 1. Charges (signed measures). Let (Ω, A) be a σ -algebra. A map φ: A R is called a charge, (or signed measure or σ -additive set function) if φ = φ(a j ) (5.1) A j for any disjoint
1 Continuity Classes C m (Ω)
 0.1 Norms 0.1 Norms A norm on a linear space X is a function : X R with the properties: Positive Definite: x 0 x X (nonnegative) x = 0 x = 0 (strictly positive) λx = λ x x X, λ C(homogeneous) x + y x +
0.1 Norms 0.1 Norms A norm on a linear space X is a function : X R with the properties: Positive Definite: x 0 x X (nonnegative) x = 0 x = 0 (strictly positive) λx = λ x x X, λ C(homogeneous) x + y x +
On John type ellipsoids
 On John type ellipsoids B. Klartag Tel Aviv University Abstract Given an arbitrary convex symmetric body K R n, we construct a natural and non-trivial continuous map u K which associates ellipsoids to
On John type ellipsoids B. Klartag Tel Aviv University Abstract Given an arbitrary convex symmetric body K R n, we construct a natural and non-trivial continuous map u K which associates ellipsoids to
Chapter 4. Inverse Function Theorem. 4.1 The Inverse Function Theorem
 Chapter 4 Inverse Function Theorem d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d dd d d d d This chapter
Chapter 4 Inverse Function Theorem d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d dd d d d d This chapter
1 Functional Analysis
 1 Functional Analysis 1 1.1 Banach spaces Remark 1.1. In classical mechanics, the state of some physical system is characterized as a point x in phase space (generalized position and momentum coordinates).
1 Functional Analysis 1 1.1 Banach spaces Remark 1.1. In classical mechanics, the state of some physical system is characterized as a point x in phase space (generalized position and momentum coordinates).
Line integrals of 1-forms on the Sierpinski gasket
 Line integrals of 1-forms on the Sierpinski gasket Università di Roma Tor Vergata - in collaboration with F. Cipriani, D. Guido, J-L. Sauvageot Cambridge, 27th July 2010 Line integrals of Outline The Sierpinski
Line integrals of 1-forms on the Sierpinski gasket Università di Roma Tor Vergata - in collaboration with F. Cipriani, D. Guido, J-L. Sauvageot Cambridge, 27th July 2010 Line integrals of Outline The Sierpinski
An introduction to some aspects of functional analysis
 An introduction to some aspects of functional analysis Stephen Semmes Rice University Abstract These informal notes deal with some very basic objects in functional analysis, including norms and seminorms
An introduction to some aspects of functional analysis Stephen Semmes Rice University Abstract These informal notes deal with some very basic objects in functional analysis, including norms and seminorms
Real Analysis Notes. Thomas Goller
 Real Analysis Notes Thomas Goller September 4, 2011 Contents 1 Abstract Measure Spaces 2 1.1 Basic Definitions........................... 2 1.2 Measurable Functions........................ 2 1.3 Integration..............................
Real Analysis Notes Thomas Goller September 4, 2011 Contents 1 Abstract Measure Spaces 2 1.1 Basic Definitions........................... 2 1.2 Measurable Functions........................ 2 1.3 Integration..............................
PICARD S THEOREM STEFAN FRIEDL
 PICARD S THEOREM STEFAN FRIEDL Abstract. We give a summary for the proof of Picard s Theorem. The proof is for the most part an excerpt of [F]. 1. Introduction Definition. Let U C be an open subset. A
PICARD S THEOREM STEFAN FRIEDL Abstract. We give a summary for the proof of Picard s Theorem. The proof is for the most part an excerpt of [F]. 1. Introduction Definition. Let U C be an open subset. A
A local time scaling exponent for compact metric spaces
 A local time scaling exponent for compact metric spaces John Dever School of Mathematics Georgia Institute of Technology Fractals 6 @ Cornell, June 15, 2017 Dever (GaTech) Exit time exponent Fractals 6
A local time scaling exponent for compact metric spaces John Dever School of Mathematics Georgia Institute of Technology Fractals 6 @ Cornell, June 15, 2017 Dever (GaTech) Exit time exponent Fractals 6
arxiv: v3 [math.ds] 9 Nov 2012
![arxiv: v3 [math.ds] 9 Nov 2012 arxiv: v3 [math.ds] 9 Nov 2012](/thumbs/92/108796755.jpg) Positive expansive flows Alfonso Artigue November 13, 2018 arxiv:1210.3202v3 [math.ds] 9 Nov 2012 Abstract We show that every positive expansive flow on a compact metric space consists of a finite number
Positive expansive flows Alfonso Artigue November 13, 2018 arxiv:1210.3202v3 [math.ds] 9 Nov 2012 Abstract We show that every positive expansive flow on a compact metric space consists of a finite number
The optimal partial transport problem
 The optimal partial transport problem Alessio Figalli Abstract Given two densities f and g, we consider the problem of transporting a fraction m [0, min{ f L 1, g L 1}] of the mass of f onto g minimizing
The optimal partial transport problem Alessio Figalli Abstract Given two densities f and g, we consider the problem of transporting a fraction m [0, min{ f L 1, g L 1}] of the mass of f onto g minimizing
A new proof of Gromov s theorem on groups of polynomial growth
 A new proof of Gromov s theorem on groups of polynomial growth Bruce Kleiner Courant Institute NYU Groups as geometric objects Let G a group with a finite generating set S G. Assume that S is symmetric:
A new proof of Gromov s theorem on groups of polynomial growth Bruce Kleiner Courant Institute NYU Groups as geometric objects Let G a group with a finite generating set S G. Assume that S is symmetric:
