Constraint Satisfaction. Algorithm Design (3) Constraint Satisfaction and Optimization. Formalization of Constraint Satisfaction Problems
|
|
|
- Alison French
- 5 years ago
- Views:
Transcription
1 Algorithm Desig (3) Costrait Satisfactio ad Optimizatio Taashi Chiayama School of Egieerig The Uiversity of Toyo Costrait Satisfactio Fidig a way that satisfies give coditios e.g. How to obtai eough credits without attedig Moday classes Ways are selectios of classes here Without attedig Moday classes A subsettig costrait o possible ways To obtai eough credits A iequality costrait o obtaied credits Implicit costraits: Two classes held i the same time slot caot be tae, etc Formalizatio of Costrait Satisfactio Problems Fidig a set of values < 1,, >, D that satisfies a coditio C( 1,, ) Solutios are ot ecessarily uique e.g. Iteger is greater tha 3 ad less tha 6 Domai of the variable is iteger Costraits: 3 < < 6 Solutios: = 4 ad = 5 No ewly added iformatio i the solutio The problem is to modify the costraits ito a simpler form The defiitio of beig simple may vary Classes of Costrait Satisfactio Problems Variable domais Fiite domais (oe of fiite umber of cadidates) Ifiite domais (iteger, real, comple, ) Structures (trees, graphs, ) usually decomposed ito compoets Kids of costraits Equality (liear, oliear, ) Iequality (total or partial order) Logical combiatio of multiple costraits 1
2 Iteger Domai, Equality Costraits Craes ad Turtles There are 5 aimals, craes ad/or turtles, ad the sum of their legs is 14. How may craes ad turtles are there? Variables ad y i iteger domai Costraits: + y = y = 14 Solutio: = 2, y = 3 Comple Domai, Equality Costraits Solvig quadratic equatios Variable domai is comple umbers Costrait is a quadratic equatio Costrait : a 2 b c 0 2 b b 4ac Solutio : 2a I geeral, solutios to costrait satisfactio problems restates the give iformatio i some other forms Real Domai, Iequality Costraits y Below this lie Iteger Domai, Iequality Costraits y The regio satisfyig the costrait Above this lie 2
3 Fiite Domai, Combiatorial Costraits Thesis defese: selectig slots, rooms, judges Domais of slots, rooms, judges are fiite Costraits: Each judge has his/her epertise area At oe time slot ad oe room, oly oe defese ca be doe Judges ca atted oe defese at a time All the defeses should be doe Most of combiatorial costrait satisfactio problems are NP-hard with epoetial compleity P, NP, NP-hard, NP-complete P: Problems that ca be solved withi time epressed as a polyomial of iput size NP: Problems for which whether a give value is a solutio or ot ca be told i polyomial time NP is from Nodetermiistic Polyomial time, meaig that odetermiistic Turig machies ca solve them i polyomial time NP-hard: Problems to which ay NP problems ca be trasformed i polyomial time NP-complete: NP-hard problems that are NP I short, the hardest subset of NP Whether P=NP or ot is still a ope problem P, NP, NP-hard, ad NP-complete Visually Eight Quees Problem Placig eight quees o a chess board so that oe of them offed oe aother P NP NP-hard NP-complete 3
4 A Simple Strategy for Combiatorial Costraits Geerate ad Test Geerate all possible combiatios systematically Test all of the geerated combiatios whether they satisfy the costraits Whe the umber of variables icreases, the umber of combiatios becomes huge Combiatorial Eplosio e.g. Ways to put 8 quees o a 8 by 8 board is 64 C 8 = Tree Structure of Geeratig Combiatios First selectio Secod selectio Third selectio Brach factor b # of selectios d # of combiatios = b d Solvig Combiatorial Costraits More Efficietly Reductio of tree geeratio: brach pruig Geeratio scheme that reflects the costraits Costrait chec before complete geeratio: bactracig Checig the possibility of satisfactio durig geeratio: forward checig If the costraits eforce a selectio, mae that decisio earlier: determiacy detectio Geeralizatio: Mae decisios earlier o selectios with less alteratives I Case of Eight Quees Geeratio scheme Oly oe quee i a row C ,777,216 No more quees o colums already with oe 8 8 8! 40,320 Bactracig Costrait checs made each time a quee is placed, rather tha after placig all the quees More devices are eeded for larger-scale problems 4
5 Forward Checig After several quees are placed, chec whether all the remaiig rows still have safe colums Irrespective of quees positios o these rows Determiacy Detectio After several quees are placed, if there is a row with a uique safe positio, place a quee there first Oly oe safe place left o this row No quees ca be placed o this row Optimizatio Problems Multiple solutios satisfyig the costraits may have relative merits Should choose the best solutio with the highest merits Merits should have a total order With a partial order, the best might ot eist Whe more tha oe aspects are to be cosidered, they should be combied ito oe sigle value with total order Formalizatio of Costrait Optimizatio Miimize (or maimize) the objective fuctio f( 1,, ) with values < 1,, >, D that satisfies a coditio C( 1,, ) A objective fuctio to be miimized is also called a cost fuctio A set of values < 1,, > that satisfies the costrait but may or may ot give the miimum (or maimum) of the objective fuctio is called a feasible solutio 5
6 Objective Fuctio Values of the objective fuctio should be compared i a total order Objective fuctios which do ot have umeric values ca be cosidered Numerical values, however, is desirable as some algorithms require them to wor For eample, values of objective fuctios for partial problems may be summed up to obtai the value for the whole problem Liear Programmig (LP) Miimizatio of liear objective fuctio uder liear iequality costrait y Area of feasible solutios Optimum solutio Iteger Programmig (IP) Liear Programmig i Iteger Domai Oly itegral solutios are feasible y Optimum solutio Combiatorial Optimizatio Maimizatio/miimizatio of objective fuctio uder combiatorial costraits o a fiite domai A variety of costraits No restrictio o objective fuctios Objective fuctios may be o-liear No efficiet geeral algorithm is ow Usually, some smoothess is assumed: Similar argumets result i similar values 6
7 Kapsac Problem: a Typical Combiatorial Optimizatio A apsac of some give capacity Goods of various sizes ad values Fid the highest-valued set of goods that fits i the apsac Formulatio of the Kapsac Problem Variables : Boolea variables idicatig whether or ot the item is icluded i the set Costrait: Sum of the sizes of items s should ot eceed the apsac capacity c (liear iequality) 1 ( s ) c Objective fuctio: Sum of the values v (liear) f ( 1,, ) ( v ) ma 1 Ca be regarded as a -dimesioal iteger programmig problem with 0-1 domai Travellig Salesma Problem: aother typical problem A umber of cities ad distaces betwee them are give The shortest route to visit all the cities should be foud Formulatio of TSP Variables : The -th city visited The domai is the set of cities (fiite domai) Costrait: Should visit all of cities { 1,..., } X Cost fuctio: Total travel distace f ( 1,..., ) d (, 1) 1 1 mi 7
8 Algorithms for Combiatorial Optimizatio Strict algorithms The strictly best solutio is to be foud i.e., No other feasible solutio is better Ofte requires large computatioal cost Approimate algorithms Fid a solutio close to the best i.e., Not ecessarily the real best A variety of defiitios o how close the obtaied solutio should be Ofte decreases the computatioal cost Simple Strict Algorithm: Geerate ad Evaluate Geerate all feasible solutios ad evaluate them 1. Geerate all feasible solutios systematically Efficiet algorithms for combiatorial costrait satisfactio may be used 2. Compute the objective fuctio for each 3. The solutio givig the maimum/miimum value is the optimum Simple ad easy to uderstad, but iefficiet whe there are a huge umber of feasible solutios, which is frequetly the case Compleity of Geerate-ad-Evaluate Scheme Huge umber of feasible solutios may eist Whe each selectio has b choices ad the umber of selectios (= tree depth) is d, there are b d leaves (epoetial) For a apsac problem with 10 items, there are 1024 feasible solutios; with 20 items, about oe millio; with 30, oe billio TSP with 10 cities, there are 362,880 feasible solutios; with 100 cities, the umber has 156 digits! Brach ad Boud The tree of feasible solutios is epaded i a depth-first order Durig tree epasio, if a ode is ow ever to have leaves better tha a already ow solutio, o further epasio below the ode is required If the merit upper boud of possible further choices is ow, the followig coditio ca be used to prue the braches below the ode [sum of merits of already chose part] + [upper boud of sum of merits of further choices] [merit of already ow solutio] 8
9 Brach ad Boud merit upper boud > + merit upper boud? ow solutio B&B for Kapsac Problems Decide whether to put a item ito the apsac i the descedig order of value per size, v /s The total value of the items i first m choices is m 1 ( v ) For all remaiig m items, value per size ever eceeds v m+1 /s m+1 ad thus a upper boud of the sum ca be give as v m1 s m1 S m s 1 Relaatio of Costraits Relaig IP to LP Some problems ca be more efficietly solved if costraits are relaed e.g., Wideig the domai of iteger programmig from iteger to real maes it a LP problem, for which we have efficiet algorithms The optimum of the origial problem ca ever be better tha that of the relaed problem A relaed problem gives a upper boud y optimum of iteger programmig optimum of liear programmig 9
10 Solvig Relaed Problems to Estimate Upper Bouds Durig tree search, choices ot made yet ca be cosidered to be a subproblem The solutio of a relaed subproblem gives a upper boud of the origial subproblem This iformatio ca be used for search pruig Useful whe Subproblems ca be clealy etracted, Relaed subproblems have optimum ot too much differet from the origial, ad Efficiet algorithms are ow Relaatio of Kapsac Problem to LP Origial Kapsac 1 ( s ) S ( 0or1) f (,, ) ( v ) ma 1 1 Relaed Kapsac 1 ( s ) S (0 1) f (,, ) ( v ) ma 1 1 This is a LP problem ad ca be solved i polyomial time Priciple of Optimality The optimum solutio of a subproblem forms a part of the optimum solutio of the whole problem If there eists a better solutio to a subproblem, replacig the part with that solutio improves the solutio of the whole problem Note: This is applicable oly whe subproblems are idepedet E.g., i TSP, optimum subroute for a subset of cities might ot be a part of the optimum route for all the cities; Start ad ed poits have to agree to merge the subroutes ito oe Dyamic Programmig (DP) A algorithm derived from the priciple of optimality 1. Solve small subproblems 2. Gradually combie solutios of subproblems 3. Record optimum solutios of subproblems to avoid recomputatio: memoizatio Coditios to apply dyamic programmig Subproblems should be mutually idepedet The umber of subproblems is small eough so that their optimum solutios ca be recorded 10
11 Optimizatio o State Trasitios A set of state S = { s 0, s 1,, s } Cost of trasitio from s i to s j is c i,j At time t, the state is t Miimize the total cost of trasitios from the iitial state s 0 to the fial state s f ( 0 1 0,, ) c t 0 t, t1 s, 0 s Optimum Solutio Epressed as Recurrece Equatios The cost sum after t = u ca be defied as 1 fu ( u,, ) c tu t, t 1 The followig recurrece formula is observed f ( mi u u 0 u mi u1 f ( 0,, f ( u u f,...,,, u1 ) f ( ) u1 u1 ),, f ( 0 ( u1,...,,, ) c ), u ) c u1, u u1 Computig Edit Distace Editig a Sequece Edit a character strig to mae aother A give fiite set of primitive editig operatios Deletio: Isertio: cost 3 ABCD ABD cost 4 ABD AYBD Replacemet: cost 5 AYBD XYBD Fid a sequece of operatios with the least cost to obtai the target strig A problem that completely fits the DP framewor States: Strigs beig edited Costs of primitive operatios are idepedet isertio deletio Record i each ode the miimum cost to reach there X Y B D A B C D I practice, oly a sigle row of memory is required at a time O( 2 ) time ad O() space 11
12 Matri Chai Multiplicatio: A More Comple DP Fidig the best order of computig matri multiplicatio chai Needs the product of may matrices Associativity allows ay computatio order ( A1 A2 A3 ) A4 A1 (A2 A3 A4 ) The order affects the computatioal cost The umber of scalar multiplicatios should be miimized The umber of possible orderig icreases epoetially proportioal to the umber of matrices p i-1 Matri Chai Multiplicatio Size of the matri A i is p i-1 p i Multiplyig a p q matri by a q r matri requires p q r scalar multiplicatios By A i, j, we mea the product A i A j A i, j has the size p i-1 p j p i A i = p i p i+1 A i+1 p i+1 p i+2 Ai+2 p i-1 p i+2 A i, i+2 Recurrece Equatio o Computatioal Cost With m i, j beig the least umber of scalar multiplicatios to obtai A i, As A i, j is obtaied by A i, A, j for some, we have the followig recurrece equatio m 0 mimi i j m p i, j,, j i1 p p j ; ; i j i j Matri Chai Computatio as DP Subproblems : Computig A i, j (1 i < j ) These subproblems are idepedet The umber of subproblems is O( 2 ) where is the umber of matrices Small eough to record 1. Mae a cost table of m i, j With iitial values of ifiity (cost uow) 2. Compute m i,j startig with m i,i+1 ad gradually wideig the rage 3. Whe m 1, is reached, trace bac the way it is computed 12
13 Matri Chai Computatio m 1,2 m 2,3 m 3,4 m 4,5 m 1,3 m 2,4 m 3,5 m 1,4 m 2,5 Approimatig Algorithms Algorithms, usually for NP-hard problems, that give solutios ot ecessarily optimal but hopefully acceptable (suboptimal) Polyomial-time approimatio Algorithms that repeatedly search for better solutios m 1,5 Polyomial-Time Approimatio By permittig (1+ ε) times the cost of the optimum solutio, computatioal time might be made proportioal to a polyomial of the problem size Computatioal compleity ca be polyomial for fied ε but rapidly becomes larger for smaller ε, for eample, O( 1/ε ), or eve O( ep(1/ε) ) Thus, the algorithms are ot practical for problems requirig small ε Iterative Improvemet Methods 1. Fid a iitial feasible solutio somehow, which should satisfy the costrait but may be far from optimal 2. The solutio is modified a bit without violatig the costraits, maig the et feasible solutio (eighbor solutio) 3. Repeat the process util some termiatio coditio is reached Small modificatios are epected to lead to a little better feasible solutios 13
14 Simple Iterative Improvemet I the step 2 of the previous page, always choose the best amog the eighbor solutios Simple ad efficiet Several ames Local Search Greedy Search Hill Climbig Local Search 1. If there eists a better feasible solutio i the eighborhood of the curret solutio, mae that solutio curret 2. Repeat this util there is o better solutios i the eighborhood Neighborhood: A set of feasible solutios that ca be easily derived from the curret solutio Usually, some of the variables comprisig the solutio are modified Neighborhoods too wide may icur high cost Should be able to cover all the feasible solutios K-Opt method: A Neighborhood Costructio Scheme for TSP paths i the solutio are cut ad With cities, eighborhood size is O( ) Commoly used are 2 ad 3 Or-Opt method: Aother Neighborhood for TSP s cities i the route are removed ad iserted agai at a differet positio Neighborhood size is O( 2 ) Commoly used s are 1 through 3 2-opt Or-opt 3-opt 14
15 Covergece to Local Optima Local search may result i a locally optimal solutio which is far from the global optimum cost iitial solutio oe of local optima solutio space The global optimum Summary Costrait satisfactio ad costrait optimizatio problems Combiatorial optimizatio Strict algorithms Pruig, forward checig, lower boud Dyamic programmig Approimate algorithms Algorithms with ow approimatio errors Iterative Improvemet But, local search may lead to a local optimum Net Wee Iterative improvemet methods that ca escape from local optima Are there geeral methods that are ot specific to problem domais? Metaheuristics 15
Integer Programming (IP)
 Iteger Programmig (IP) The geeral liear mathematical programmig problem where Mied IP Problem - MIP ma c T + h Z T y A + G y + y b R p + vector of positive iteger variables y vector of positive real variables
Iteger Programmig (IP) The geeral liear mathematical programmig problem where Mied IP Problem - MIP ma c T + h Z T y A + G y + y b R p + vector of positive iteger variables y vector of positive real variables
Markov Decision Processes
 Markov Decisio Processes Defiitios; Statioary policies; Value improvemet algorithm, Policy improvemet algorithm, ad liear programmig for discouted cost ad average cost criteria. Markov Decisio Processes
Markov Decisio Processes Defiitios; Statioary policies; Value improvemet algorithm, Policy improvemet algorithm, ad liear programmig for discouted cost ad average cost criteria. Markov Decisio Processes
Definitions and Theorems. where x are the decision variables. c, b, and a are constant coefficients.
 Defiitios ad Theorems Remember the scalar form of the liear programmig problem, Miimize, Subject to, f(x) = c i x i a 1i x i = b 1 a mi x i = b m x i 0 i = 1,2,, where x are the decisio variables. c, b,
Defiitios ad Theorems Remember the scalar form of the liear programmig problem, Miimize, Subject to, f(x) = c i x i a 1i x i = b 1 a mi x i = b m x i 0 i = 1,2,, where x are the decisio variables. c, b,
Optimization Methods MIT 2.098/6.255/ Final exam
 Optimizatio Methods MIT 2.098/6.255/15.093 Fial exam Date Give: December 19th, 2006 P1. [30 pts] Classify the followig statemets as true or false. All aswers must be well-justified, either through a short
Optimizatio Methods MIT 2.098/6.255/15.093 Fial exam Date Give: December 19th, 2006 P1. [30 pts] Classify the followig statemets as true or false. All aswers must be well-justified, either through a short
IP Reference guide for integer programming formulations.
 IP Referece guide for iteger programmig formulatios. by James B. Orli for 15.053 ad 15.058 This documet is iteded as a compact (or relatively compact) guide to the formulatio of iteger programs. For more
IP Referece guide for iteger programmig formulatios. by James B. Orli for 15.053 ad 15.058 This documet is iteded as a compact (or relatively compact) guide to the formulatio of iteger programs. For more
Notes on iteration and Newton s method. Iteration
 Notes o iteratio ad Newto s method Iteratio Iteratio meas doig somethig over ad over. I our cotet, a iteratio is a sequece of umbers, vectors, fuctios, etc. geerated by a iteratio rule of the type 1 f
Notes o iteratio ad Newto s method Iteratio Iteratio meas doig somethig over ad over. I our cotet, a iteratio is a sequece of umbers, vectors, fuctios, etc. geerated by a iteratio rule of the type 1 f
THE SOLUTION OF NONLINEAR EQUATIONS f( x ) = 0.
 THE SOLUTION OF NONLINEAR EQUATIONS f( ) = 0. Noliear Equatio Solvers Bracketig. Graphical. Aalytical Ope Methods Bisectio False Positio (Regula-Falsi) Fied poit iteratio Newto Raphso Secat The root of
THE SOLUTION OF NONLINEAR EQUATIONS f( ) = 0. Noliear Equatio Solvers Bracketig. Graphical. Aalytical Ope Methods Bisectio False Positio (Regula-Falsi) Fied poit iteratio Newto Raphso Secat The root of
CS537. Numerical Analysis and Computing
 CS57 Numerical Aalysis ad Computig Lecture Locatig Roots o Equatios Proessor Ju Zhag Departmet o Computer Sciece Uiversity o Ketucky Leigto KY 456-6 Jauary 9 9 What is the Root May physical system ca be
CS57 Numerical Aalysis ad Computig Lecture Locatig Roots o Equatios Proessor Ju Zhag Departmet o Computer Sciece Uiversity o Ketucky Leigto KY 456-6 Jauary 9 9 What is the Root May physical system ca be
Differentiable Convex Functions
 Differetiable Covex Fuctios The followig picture motivates Theorem 11. f ( x) f ( x) f '( x)( x x) ˆx x 1 Theorem 11 : Let f : R R be differetiable. The, f is covex o the covex set C R if, ad oly if for
Differetiable Covex Fuctios The followig picture motivates Theorem 11. f ( x) f ( x) f '( x)( x x) ˆx x 1 Theorem 11 : Let f : R R be differetiable. The, f is covex o the covex set C R if, ad oly if for
Optimization Methods: Linear Programming Applications Assignment Problem 1. Module 4 Lecture Notes 3. Assignment Problem
 Optimizatio Methods: Liear Programmig Applicatios Assigmet Problem Itroductio Module 4 Lecture Notes 3 Assigmet Problem I the previous lecture, we discussed about oe of the bech mark problems called trasportatio
Optimizatio Methods: Liear Programmig Applicatios Assigmet Problem Itroductio Module 4 Lecture Notes 3 Assigmet Problem I the previous lecture, we discussed about oe of the bech mark problems called trasportatio
TEACHER CERTIFICATION STUDY GUIDE
 COMPETENCY 1. ALGEBRA SKILL 1.1 1.1a. ALGEBRAIC STRUCTURES Kow why the real ad complex umbers are each a field, ad that particular rigs are ot fields (e.g., itegers, polyomial rigs, matrix rigs) Algebra
COMPETENCY 1. ALGEBRA SKILL 1.1 1.1a. ALGEBRAIC STRUCTURES Kow why the real ad complex umbers are each a field, ad that particular rigs are ot fields (e.g., itegers, polyomial rigs, matrix rigs) Algebra
NUMERICAL METHODS FOR SOLVING EQUATIONS
 Mathematics Revisio Guides Numerical Methods for Solvig Equatios Page 1 of 11 M.K. HOME TUITION Mathematics Revisio Guides Level: GCSE Higher Tier NUMERICAL METHODS FOR SOLVING EQUATIONS Versio:. Date:
Mathematics Revisio Guides Numerical Methods for Solvig Equatios Page 1 of 11 M.K. HOME TUITION Mathematics Revisio Guides Level: GCSE Higher Tier NUMERICAL METHODS FOR SOLVING EQUATIONS Versio:. Date:
Apply change-of-basis formula to rewrite x as a linear combination of eigenvectors v j.
 Eigevalue-Eigevector Istructor: Nam Su Wag eigemcd Ay vector i real Euclidea space of dimesio ca be uiquely epressed as a liear combiatio of liearly idepedet vectors (ie, basis) g j, j,,, α g α g α g α
Eigevalue-Eigevector Istructor: Nam Su Wag eigemcd Ay vector i real Euclidea space of dimesio ca be uiquely epressed as a liear combiatio of liearly idepedet vectors (ie, basis) g j, j,,, α g α g α g α
Practical Spectral Anaysis (continue) (from Boaz Porat s book) Frequency Measurement
 Practical Spectral Aaysis (cotiue) (from Boaz Porat s book) Frequecy Measuremet Oe of the most importat applicatios of the DFT is the measuremet of frequecies of periodic sigals (eg., siusoidal sigals),
Practical Spectral Aaysis (cotiue) (from Boaz Porat s book) Frequecy Measuremet Oe of the most importat applicatios of the DFT is the measuremet of frequecies of periodic sigals (eg., siusoidal sigals),
A widely used display of protein shapes is based on the coordinates of the alpha carbons - - C α
 Nice plottig of proteis: I A widely used display of protei shapes is based o the coordiates of the alpha carbos - - C α -s. The coordiates of the C α -s are coected by a cotiuous curve that roughly follows
Nice plottig of proteis: I A widely used display of protei shapes is based o the coordiates of the alpha carbos - - C α -s. The coordiates of the C α -s are coected by a cotiuous curve that roughly follows
Integer Linear Programming
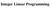 Iteger Liear Programmig Itroductio Iteger L P problem (P) Mi = s. t. a = b i =,, m = i i 0, iteger =,, c Eemple Mi z = 5 s. t. + 0 0, 0, iteger F(P) = feasible domai of P Itroductio Iteger L P problem
Iteger Liear Programmig Itroductio Iteger L P problem (P) Mi = s. t. a = b i =,, m = i i 0, iteger =,, c Eemple Mi z = 5 s. t. + 0 0, 0, iteger F(P) = feasible domai of P Itroductio Iteger L P problem
subject to A 1 x + A 2 y b x j 0, j = 1,,n 1 y j = 0 or 1, j = 1,,n 2
 Additioal Brach ad Boud Algorithms 0-1 Mixed-Iteger Liear Programmig The brach ad boud algorithm described i the previous sectios ca be used to solve virtually all optimizatio problems cotaiig iteger variables,
Additioal Brach ad Boud Algorithms 0-1 Mixed-Iteger Liear Programmig The brach ad boud algorithm described i the previous sectios ca be used to solve virtually all optimizatio problems cotaiig iteger variables,
(A sequence also can be thought of as the list of function values attained for a function f :ℵ X, where f (n) = x n for n 1.) x 1 x N +k x N +4 x 3
 MATH 337 Sequeces Dr. Neal, WKU Let X be a metric space with distace fuctio d. We shall defie the geeral cocept of sequece ad limit i a metric space, the apply the results i particular to some special
MATH 337 Sequeces Dr. Neal, WKU Let X be a metric space with distace fuctio d. We shall defie the geeral cocept of sequece ad limit i a metric space, the apply the results i particular to some special
CS321. Numerical Analysis and Computing
 CS Numerical Aalysis ad Computig Lecture Locatig Roots o Equatios Proessor Ju Zhag Departmet o Computer Sciece Uiversity o Ketucky Leigto KY 456-6 September 8 5 What is the Root May physical system ca
CS Numerical Aalysis ad Computig Lecture Locatig Roots o Equatios Proessor Ju Zhag Departmet o Computer Sciece Uiversity o Ketucky Leigto KY 456-6 September 8 5 What is the Root May physical system ca
w (1) ˆx w (1) x (1) /ρ and w (2) ˆx w (2) x (2) /ρ.
 2 5. Weighted umber of late jobs 5.1. Release dates ad due dates: maximimizig the weight of o-time jobs Oce we add release dates, miimizig the umber of late jobs becomes a sigificatly harder problem. For
2 5. Weighted umber of late jobs 5.1. Release dates ad due dates: maximimizig the weight of o-time jobs Oce we add release dates, miimizig the umber of late jobs becomes a sigificatly harder problem. For
Recursive Algorithms. Recurrences. Recursive Algorithms Analysis
 Recursive Algorithms Recurreces Computer Sciece & Egieerig 35: Discrete Mathematics Christopher M Bourke cbourke@cseuledu A recursive algorithm is oe i which objects are defied i terms of other objects
Recursive Algorithms Recurreces Computer Sciece & Egieerig 35: Discrete Mathematics Christopher M Bourke cbourke@cseuledu A recursive algorithm is oe i which objects are defied i terms of other objects
ROLL CUTTING PROBLEMS UNDER STOCHASTIC DEMAND
 Pacific-Asia Joural of Mathematics, Volume 5, No., Jauary-Jue 20 ROLL CUTTING PROBLEMS UNDER STOCHASTIC DEMAND SHAKEEL JAVAID, Z. H. BAKHSHI & M. M. KHALID ABSTRACT: I this paper, the roll cuttig problem
Pacific-Asia Joural of Mathematics, Volume 5, No., Jauary-Jue 20 ROLL CUTTING PROBLEMS UNDER STOCHASTIC DEMAND SHAKEEL JAVAID, Z. H. BAKHSHI & M. M. KHALID ABSTRACT: I this paper, the roll cuttig problem
Sequences, Mathematical Induction, and Recursion. CSE 2353 Discrete Computational Structures Spring 2018
 CSE 353 Discrete Computatioal Structures Sprig 08 Sequeces, Mathematical Iductio, ad Recursio (Chapter 5, Epp) Note: some course slides adopted from publisher-provided material Overview May mathematical
CSE 353 Discrete Computatioal Structures Sprig 08 Sequeces, Mathematical Iductio, ad Recursio (Chapter 5, Epp) Note: some course slides adopted from publisher-provided material Overview May mathematical
Chapter Vectors
 Chapter 4. Vectors fter readig this chapter you should be able to:. defie a vector. add ad subtract vectors. fid liear combiatios of vectors ad their relatioship to a set of equatios 4. explai what it
Chapter 4. Vectors fter readig this chapter you should be able to:. defie a vector. add ad subtract vectors. fid liear combiatios of vectors ad their relatioship to a set of equatios 4. explai what it
ACO Comprehensive Exam 9 October 2007 Student code A. 1. Graph Theory
 1. Graph Theory Prove that there exist o simple plaar triagulatio T ad two distict adjacet vertices x, y V (T ) such that x ad y are the oly vertices of T of odd degree. Do ot use the Four-Color Theorem.
1. Graph Theory Prove that there exist o simple plaar triagulatio T ad two distict adjacet vertices x, y V (T ) such that x ad y are the oly vertices of T of odd degree. Do ot use the Four-Color Theorem.
OPTIMAL ALGORITHMS -- SUPPLEMENTAL NOTES
 OPTIMAL ALGORITHMS -- SUPPLEMENTAL NOTES Peter M. Maurer Why Hashig is θ(). As i biary search, hashig assumes that keys are stored i a array which is idexed by a iteger. However, hashig attempts to bypass
OPTIMAL ALGORITHMS -- SUPPLEMENTAL NOTES Peter M. Maurer Why Hashig is θ(). As i biary search, hashig assumes that keys are stored i a array which is idexed by a iteger. However, hashig attempts to bypass
Inverse Matrix. A meaning that matrix B is an inverse of matrix A.
 Iverse Matrix Two square matrices A ad B of dimesios are called iverses to oe aother if the followig holds, AB BA I (11) The otio is dual but we ofte write 1 B A meaig that matrix B is a iverse of matrix
Iverse Matrix Two square matrices A ad B of dimesios are called iverses to oe aother if the followig holds, AB BA I (11) The otio is dual but we ofte write 1 B A meaig that matrix B is a iverse of matrix
x x x Using a second Taylor polynomial with remainder, find the best constant C so that for x 0,
 Math Activity 9( Due with Fial Eam) Usig first ad secod Taylor polyomials with remaider, show that for, 8 Usig a secod Taylor polyomial with remaider, fid the best costat C so that for, C 9 The th Derivative
Math Activity 9( Due with Fial Eam) Usig first ad secod Taylor polyomials with remaider, show that for, 8 Usig a secod Taylor polyomial with remaider, fid the best costat C so that for, C 9 The th Derivative
Castiel, Supernatural, Season 6, Episode 18
 13 Differetial Equatios the aswer to your questio ca best be epressed as a series of partial differetial equatios... Castiel, Superatural, Seaso 6, Episode 18 A differetial equatio is a mathematical equatio
13 Differetial Equatios the aswer to your questio ca best be epressed as a series of partial differetial equatios... Castiel, Superatural, Seaso 6, Episode 18 A differetial equatio is a mathematical equatio
8. Applications To Linear Differential Equations
 8. Applicatios To Liear Differetial Equatios 8.. Itroductio 8.. Review Of Results Cocerig Liear Differetial Equatios Of First Ad Secod Orders 8.3. Eercises 8.4. Liear Differetial Equatios Of Order N 8.5.
8. Applicatios To Liear Differetial Equatios 8.. Itroductio 8.. Review Of Results Cocerig Liear Differetial Equatios Of First Ad Secod Orders 8.3. Eercises 8.4. Liear Differetial Equatios Of Order N 8.5.
Introduction to Optimization Techniques. How to Solve Equations
 Itroductio to Optimizatio Techiques How to Solve Equatios Iterative Methods of Optimizatio Iterative methods of optimizatio Solutio of the oliear equatios resultig form a optimizatio problem is usually
Itroductio to Optimizatio Techiques How to Solve Equatios Iterative Methods of Optimizatio Iterative methods of optimizatio Solutio of the oliear equatios resultig form a optimizatio problem is usually
( ) ( ) ( ) ( ) ( + ) ( )
 LSM Nov. 00 Cotet List Mathematics (AH). Algebra... kow ad use the otatio!, C r ad r.. kow the results = r r + + = r r r..3 kow Pascal's triagle. Pascal's triagle should be eteded up to = 7...4 kow ad
LSM Nov. 00 Cotet List Mathematics (AH). Algebra... kow ad use the otatio!, C r ad r.. kow the results = r r + + = r r r..3 kow Pascal's triagle. Pascal's triagle should be eteded up to = 7...4 kow ad
Math 312 Lecture Notes One Dimensional Maps
 Math 312 Lecture Notes Oe Dimesioal Maps Warre Weckesser Departmet of Mathematics Colgate Uiversity 21-23 February 25 A Example We begi with the simplest model of populatio growth. Suppose, for example,
Math 312 Lecture Notes Oe Dimesioal Maps Warre Weckesser Departmet of Mathematics Colgate Uiversity 21-23 February 25 A Example We begi with the simplest model of populatio growth. Suppose, for example,
Solutions for the Exam 9 January 2012
 Mastermath ad LNMB Course: Discrete Optimizatio Solutios for the Exam 9 Jauary 2012 Utrecht Uiversity, Educatorium, 15:15 18:15 The examiatio lasts 3 hours. Gradig will be doe before Jauary 23, 2012. Studets
Mastermath ad LNMB Course: Discrete Optimizatio Solutios for the Exam 9 Jauary 2012 Utrecht Uiversity, Educatorium, 15:15 18:15 The examiatio lasts 3 hours. Gradig will be doe before Jauary 23, 2012. Studets
Polynomials with Rational Roots that Differ by a Non-zero Constant. Generalities
 Polyomials with Ratioal Roots that Differ by a No-zero Costat Philip Gibbs The problem of fidig two polyomials P(x) ad Q(x) of a give degree i a sigle variable x that have all ratioal roots ad differ by
Polyomials with Ratioal Roots that Differ by a No-zero Costat Philip Gibbs The problem of fidig two polyomials P(x) ad Q(x) of a give degree i a sigle variable x that have all ratioal roots ad differ by
The Method of Least Squares. To understand least squares fitting of data.
 The Method of Least Squares KEY WORDS Curve fittig, least square GOAL To uderstad least squares fittig of data To uderstad the least squares solutio of icosistet systems of liear equatios 1 Motivatio Curve
The Method of Least Squares KEY WORDS Curve fittig, least square GOAL To uderstad least squares fittig of data To uderstad the least squares solutio of icosistet systems of liear equatios 1 Motivatio Curve
The picture in figure 1.1 helps us to see that the area represents the distance traveled. Figure 1: Area represents distance travelled
 1 Lecture : Area Area ad distace traveled Approximatig area by rectagles Summatio The area uder a parabola 1.1 Area ad distace Suppose we have the followig iformatio about the velocity of a particle, how
1 Lecture : Area Area ad distace traveled Approximatig area by rectagles Summatio The area uder a parabola 1.1 Area ad distace Suppose we have the followig iformatio about the velocity of a particle, how
REGRESSION (Physics 1210 Notes, Partial Modified Appendix A)
 REGRESSION (Physics 0 Notes, Partial Modified Appedix A) HOW TO PERFORM A LINEAR REGRESSION Cosider the followig data poits ad their graph (Table I ad Figure ): X Y 0 3 5 3 7 4 9 5 Table : Example Data
REGRESSION (Physics 0 Notes, Partial Modified Appedix A) HOW TO PERFORM A LINEAR REGRESSION Cosider the followig data poits ad their graph (Table I ad Figure ): X Y 0 3 5 3 7 4 9 5 Table : Example Data
Dynamic Programming. Sequence Of Decisions
 Dyamic Programmig Sequece of decisios. Problem state. Priciple of optimality. Dyamic Programmig Recurrece Equatios. Solutio of recurrece equatios. Sequece Of Decisios As i the greedy method, the solutio
Dyamic Programmig Sequece of decisios. Problem state. Priciple of optimality. Dyamic Programmig Recurrece Equatios. Solutio of recurrece equatios. Sequece Of Decisios As i the greedy method, the solutio
Dynamic Programming. Sequence Of Decisions. 0/1 Knapsack Problem. Sequence Of Decisions
 Dyamic Programmig Sequece Of Decisios Sequece of decisios. Problem state. Priciple of optimality. Dyamic Programmig Recurrece Equatios. Solutio of recurrece equatios. As i the greedy method, the solutio
Dyamic Programmig Sequece Of Decisios Sequece of decisios. Problem state. Priciple of optimality. Dyamic Programmig Recurrece Equatios. Solutio of recurrece equatios. As i the greedy method, the solutio
The Simplex algorithm: Introductory example. The Simplex algorithm: Introductory example (2)
 Discrete Mathematics for Bioiformatics WS 07/08, G. W. Klau, 23. Oktober 2007, 12:21 1 The Simplex algorithm: Itroductory example The followig itroductio to the Simplex algorithm is from the book Liear
Discrete Mathematics for Bioiformatics WS 07/08, G. W. Klau, 23. Oktober 2007, 12:21 1 The Simplex algorithm: Itroductory example The followig itroductio to the Simplex algorithm is from the book Liear
We are mainly going to be concerned with power series in x, such as. (x)} converges - that is, lims N n
 Review of Power Series, Power Series Solutios A power series i x - a is a ifiite series of the form c (x a) =c +c (x a)+(x a) +... We also call this a power series cetered at a. Ex. (x+) is cetered at
Review of Power Series, Power Series Solutios A power series i x - a is a ifiite series of the form c (x a) =c +c (x a)+(x a) +... We also call this a power series cetered at a. Ex. (x+) is cetered at
6.003 Homework #3 Solutions
 6.00 Homework # Solutios Problems. Complex umbers a. Evaluate the real ad imagiary parts of j j. π/ Real part = Imagiary part = 0 e Euler s formula says that j = e jπ/, so jπ/ j π/ j j = e = e. Thus the
6.00 Homework # Solutios Problems. Complex umbers a. Evaluate the real ad imagiary parts of j j. π/ Real part = Imagiary part = 0 e Euler s formula says that j = e jπ/, so jπ/ j π/ j j = e = e. Thus the
Linear Programming and the Simplex Method
 Liear Programmig ad the Simplex ethod Abstract This article is a itroductio to Liear Programmig ad usig Simplex method for solvig LP problems i primal form. What is Liear Programmig? Liear Programmig is
Liear Programmig ad the Simplex ethod Abstract This article is a itroductio to Liear Programmig ad usig Simplex method for solvig LP problems i primal form. What is Liear Programmig? Liear Programmig is
μ are complex parameters. Other
 A New Numerical Itegrator for the Solutio of Iitial Value Problems i Ordiary Differetial Equatios. J. Suday * ad M.R. Odekule Departmet of Mathematical Scieces, Adamawa State Uiversity, Mubi, Nigeria.
A New Numerical Itegrator for the Solutio of Iitial Value Problems i Ordiary Differetial Equatios. J. Suday * ad M.R. Odekule Departmet of Mathematical Scieces, Adamawa State Uiversity, Mubi, Nigeria.
INTEGRATION BY PARTS (TABLE METHOD)
 INTEGRATION BY PARTS (TABLE METHOD) Suppose you wat to evaluate cos d usig itegratio by parts. Usig the u dv otatio, we get So, u dv d cos du d v si cos d si si d or si si d We see that it is ecessary
INTEGRATION BY PARTS (TABLE METHOD) Suppose you wat to evaluate cos d usig itegratio by parts. Usig the u dv otatio, we get So, u dv d cos du d v si cos d si si d or si si d We see that it is ecessary
Root Finding COS 323
 Root Fidig COS 323 Remider Sig up for Piazza Assigmet 0 is posted, due Tue 9/25 Last time.. Floatig poit umbers ad precisio Machie epsilo Sources of error Sesitivity ad coditioig Stability ad accuracy
Root Fidig COS 323 Remider Sig up for Piazza Assigmet 0 is posted, due Tue 9/25 Last time.. Floatig poit umbers ad precisio Machie epsilo Sources of error Sesitivity ad coditioig Stability ad accuracy
f(x) dx as we do. 2x dx x also diverges. Solution: We compute 2x dx lim
 Math 3, Sectio 2. (25 poits) Why we defie f(x) dx as we do. (a) Show that the improper itegral diverges. Hece the improper itegral x 2 + x 2 + b also diverges. Solutio: We compute x 2 + = lim b x 2 + =
Math 3, Sectio 2. (25 poits) Why we defie f(x) dx as we do. (a) Show that the improper itegral diverges. Hece the improper itegral x 2 + x 2 + b also diverges. Solutio: We compute x 2 + = lim b x 2 + =
2 DD2458 Popup HT Solution: Choose the activity which ends first and does not conflict with earlier chosen activities.
 DD2458, Problem Solvig ad Programmig Uder Pressure Lecture 1: Greedy algorithms ad dyamic programmig Date: 2008-09-01 Scribe(s: Marti Wedi ad Nilas Wagre Lecturer: Douglas Wiström This lecture cotais basic
DD2458, Problem Solvig ad Programmig Uder Pressure Lecture 1: Greedy algorithms ad dyamic programmig Date: 2008-09-01 Scribe(s: Marti Wedi ad Nilas Wagre Lecturer: Douglas Wiström This lecture cotais basic
Infinite Sequences and Series
 Chapter 6 Ifiite Sequeces ad Series 6.1 Ifiite Sequeces 6.1.1 Elemetary Cocepts Simply speakig, a sequece is a ordered list of umbers writte: {a 1, a 2, a 3,...a, a +1,...} where the elemets a i represet
Chapter 6 Ifiite Sequeces ad Series 6.1 Ifiite Sequeces 6.1.1 Elemetary Cocepts Simply speakig, a sequece is a ordered list of umbers writte: {a 1, a 2, a 3,...a, a +1,...} where the elemets a i represet
Find a formula for the exponential function whose graph is given , 1 2,16 1, 6
 Math 4 Activity (Due by EOC Apr. ) Graph the followig epoetial fuctios by modifyig the graph of f. Fid the rage of each fuctio.. g. g. g 4. g. g 6. g Fid a formula for the epoetial fuctio whose graph is
Math 4 Activity (Due by EOC Apr. ) Graph the followig epoetial fuctios by modifyig the graph of f. Fid the rage of each fuctio.. g. g. g 4. g. g 6. g Fid a formula for the epoetial fuctio whose graph is
PC5215 Numerical Recipes with Applications - Review Problems
 PC55 Numerical Recipes with Applicatios - Review Problems Give the IEEE 754 sigle precisio bit patter (biary or he format) of the followig umbers: 0 0 05 00 0 00 Note that it has 8 bits for the epoet,
PC55 Numerical Recipes with Applicatios - Review Problems Give the IEEE 754 sigle precisio bit patter (biary or he format) of the followig umbers: 0 0 05 00 0 00 Note that it has 8 bits for the epoet,
U8L1: Sec Equations of Lines in R 2
 MCVU U8L: Sec. 8.9. Equatios of Lies i R Review of Equatios of a Straight Lie (-D) Cosider the lie passig through A (-,) with slope, as show i the diagram below. I poit slope form, the equatio of the lie
MCVU U8L: Sec. 8.9. Equatios of Lies i R Review of Equatios of a Straight Lie (-D) Cosider the lie passig through A (-,) with slope, as show i the diagram below. I poit slope form, the equatio of the lie
Machine Learning Theory Tübingen University, WS 2016/2017 Lecture 11
 Machie Learig Theory Tübige Uiversity, WS 06/07 Lecture Tolstikhi Ilya Abstract We will itroduce the otio of reproducig kerels ad associated Reproducig Kerel Hilbert Spaces (RKHS). We will cosider couple
Machie Learig Theory Tübige Uiversity, WS 06/07 Lecture Tolstikhi Ilya Abstract We will itroduce the otio of reproducig kerels ad associated Reproducig Kerel Hilbert Spaces (RKHS). We will cosider couple
Zeros of Polynomials
 Math 160 www.timetodare.com 4.5 4.6 Zeros of Polyomials I these sectios we will study polyomials algebraically. Most of our work will be cocered with fidig the solutios of polyomial equatios of ay degree
Math 160 www.timetodare.com 4.5 4.6 Zeros of Polyomials I these sectios we will study polyomials algebraically. Most of our work will be cocered with fidig the solutios of polyomial equatios of ay degree
1. (25 points) Use the limit definition of the definite integral and the sum formulas 1 to compute
 Math, Calculus II Fial Eam Solutios. 5 poits) Use the limit defiitio of the defiite itegral ad the sum formulas to compute 4 d. The check your aswer usig the Evaluatio Theorem. ) ) Solutio: I this itegral,
Math, Calculus II Fial Eam Solutios. 5 poits) Use the limit defiitio of the defiite itegral ad the sum formulas to compute 4 d. The check your aswer usig the Evaluatio Theorem. ) ) Solutio: I this itegral,
ENGI 9420 Engineering Analysis Assignment 3 Solutions
 ENGI 9 Egieerig Aalysis Assigmet Solutios Fall [Series solutio of ODEs, matri algebra; umerical methods; Chapters, ad ]. Fid a power series solutio about =, as far as the term i 7, to the ordiary differetial
ENGI 9 Egieerig Aalysis Assigmet Solutios Fall [Series solutio of ODEs, matri algebra; umerical methods; Chapters, ad ]. Fid a power series solutio about =, as far as the term i 7, to the ordiary differetial
CSI 2101 Discrete Structures Winter Homework Assignment #4 (100 points, weight 5%) Due: Thursday, April 5, at 1:00pm (in lecture)
 CSI 101 Discrete Structures Witer 01 Prof. Lucia Moura Uiversity of Ottawa Homework Assigmet #4 (100 poits, weight %) Due: Thursday, April, at 1:00pm (i lecture) Program verificatio, Recurrece Relatios
CSI 101 Discrete Structures Witer 01 Prof. Lucia Moura Uiversity of Ottawa Homework Assigmet #4 (100 poits, weight %) Due: Thursday, April, at 1:00pm (i lecture) Program verificatio, Recurrece Relatios
Topic 1 2: Sequences and Series. A sequence is an ordered list of numbers, e.g. 1, 2, 4, 8, 16, or
 Topic : Sequeces ad Series A sequece is a ordered list of umbers, e.g.,,, 8, 6, or,,,.... A series is a sum of the terms of a sequece, e.g. + + + 8 + 6 + or... Sigma Notatio b The otatio f ( k) is shorthad
Topic : Sequeces ad Series A sequece is a ordered list of umbers, e.g.,,, 8, 6, or,,,.... A series is a sum of the terms of a sequece, e.g. + + + 8 + 6 + or... Sigma Notatio b The otatio f ( k) is shorthad
AP Calculus BC Review Applications of Derivatives (Chapter 4) and f,
 AP alculus B Review Applicatios of Derivatives (hapter ) Thigs to Kow ad Be Able to Do Defiitios of the followig i terms of derivatives, ad how to fid them: critical poit, global miima/maima, local (relative)
AP alculus B Review Applicatios of Derivatives (hapter ) Thigs to Kow ad Be Able to Do Defiitios of the followig i terms of derivatives, ad how to fid them: critical poit, global miima/maima, local (relative)
The Discrete Fourier Transform
 The Discrete Fourier Trasform Complex Fourier Series Represetatio Recall that a Fourier series has the form a 0 + a k cos(kt) + k=1 b k si(kt) This represetatio seems a bit awkward, sice it ivolves two
The Discrete Fourier Trasform Complex Fourier Series Represetatio Recall that a Fourier series has the form a 0 + a k cos(kt) + k=1 b k si(kt) This represetatio seems a bit awkward, sice it ivolves two
6.3 Testing Series With Positive Terms
 6.3. TESTING SERIES WITH POSITIVE TERMS 307 6.3 Testig Series With Positive Terms 6.3. Review of what is kow up to ow I theory, testig a series a i for covergece amouts to fidig the i= sequece of partial
6.3. TESTING SERIES WITH POSITIVE TERMS 307 6.3 Testig Series With Positive Terms 6.3. Review of what is kow up to ow I theory, testig a series a i for covergece amouts to fidig the i= sequece of partial
Review Problems 1. ICME and MS&E Refresher Course September 19, 2011 B = C = AB = A = A 2 = A 3... C 2 = C 3 = =
 Review Problems ICME ad MS&E Refresher Course September 9, 0 Warm-up problems. For the followig matrices A = 0 B = C = AB = 0 fid all powers A,A 3,(which is A times A),... ad B,B 3,... ad C,C 3,... Solutio:
Review Problems ICME ad MS&E Refresher Course September 9, 0 Warm-up problems. For the followig matrices A = 0 B = C = AB = 0 fid all powers A,A 3,(which is A times A),... ad B,B 3,... ad C,C 3,... Solutio:
Chapter 2 The Solution of Numerical Algebraic and Transcendental Equations
 Chapter The Solutio of Numerical Algebraic ad Trascedetal Equatios Itroductio I this chapter we shall discuss some umerical methods for solvig algebraic ad trascedetal equatios. The equatio f( is said
Chapter The Solutio of Numerical Algebraic ad Trascedetal Equatios Itroductio I this chapter we shall discuss some umerical methods for solvig algebraic ad trascedetal equatios. The equatio f( is said
NICK DUFRESNE. 1 1 p(x). To determine some formulas for the generating function of the Schröder numbers, r(x) = a(x) =
 AN INTRODUCTION TO SCHRÖDER AND UNKNOWN NUMBERS NICK DUFRESNE Abstract. I this article we will itroduce two types of lattice paths, Schröder paths ad Ukow paths. We will examie differet properties of each,
AN INTRODUCTION TO SCHRÖDER AND UNKNOWN NUMBERS NICK DUFRESNE Abstract. I this article we will itroduce two types of lattice paths, Schröder paths ad Ukow paths. We will examie differet properties of each,
Lecture 12: Spiral: Domain Specific HLS. James C. Hoe Department of ECE Carnegie Mellon University
 8 643 Lecture : Spiral: Domai Specific HLS James C. Hoe Departmet of ECE Caregie Mello Uiversity 8 643 F7 L S, James C. Hoe, CMU/ECE/CALCM, 07 Houseeepig Your goal today: see a eample of really highlevel
8 643 Lecture : Spiral: Domai Specific HLS James C. Hoe Departmet of ECE Caregie Mello Uiversity 8 643 F7 L S, James C. Hoe, CMU/ECE/CALCM, 07 Houseeepig Your goal today: see a eample of really highlevel
Lecture Overview. 2 Permutations and Combinations. n(n 1) (n (k 1)) = n(n 1) (n k + 1) =
 COMPSCI 230: Discrete Mathematics for Computer Sciece April 8, 2019 Lecturer: Debmalya Paigrahi Lecture 22 Scribe: Kevi Su 1 Overview I this lecture, we begi studyig the fudametals of coutig discrete objects.
COMPSCI 230: Discrete Mathematics for Computer Sciece April 8, 2019 Lecturer: Debmalya Paigrahi Lecture 22 Scribe: Kevi Su 1 Overview I this lecture, we begi studyig the fudametals of coutig discrete objects.
Different kinds of Mathematical Induction
 Differet ids of Mathematical Iductio () Mathematical Iductio Give A N, [ A (a A a A)] A N () (First) Priciple of Mathematical Iductio Let P() be a propositio (ope setece), if we put A { : N p() is true}
Differet ids of Mathematical Iductio () Mathematical Iductio Give A N, [ A (a A a A)] A N () (First) Priciple of Mathematical Iductio Let P() be a propositio (ope setece), if we put A { : N p() is true}
Chapter 2 The Monte Carlo Method
 Chapter 2 The Mote Carlo Method The Mote Carlo Method stads for a broad class of computatioal algorithms that rely o radom sampligs. It is ofte used i physical ad mathematical problems ad is most useful
Chapter 2 The Mote Carlo Method The Mote Carlo Method stads for a broad class of computatioal algorithms that rely o radom sampligs. It is ofte used i physical ad mathematical problems ad is most useful
Sequences A sequence of numbers is a function whose domain is the positive integers. We can see that the sequence
 Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece 1, 1, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet
Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece 1, 1, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet
Linear Differential Equations of Higher Order Basic Theory: Initial-Value Problems d y d y dy
 Liear Differetial Equatios of Higher Order Basic Theory: Iitial-Value Problems d y d y dy Solve: a( ) + a ( )... a ( ) a0( ) y g( ) + + + = d d d ( ) Subject to: y( 0) = y0, y ( 0) = y,..., y ( 0) = y
Liear Differetial Equatios of Higher Order Basic Theory: Iitial-Value Problems d y d y dy Solve: a( ) + a ( )... a ( ) a0( ) y g( ) + + + = d d d ( ) Subject to: y( 0) = y0, y ( 0) = y,..., y ( 0) = y
Chapter 9: Numerical Differentiation
 178 Chapter 9: Numerical Differetiatio Numerical Differetiatio Formulatio of equatios for physical problems ofte ivolve derivatives (rate-of-chage quatities, such as velocity ad acceleratio). Numerical
178 Chapter 9: Numerical Differetiatio Numerical Differetiatio Formulatio of equatios for physical problems ofte ivolve derivatives (rate-of-chage quatities, such as velocity ad acceleratio). Numerical
Kinetics of Complex Reactions
 Kietics of Complex Reactios by Flick Colema Departmet of Chemistry Wellesley College Wellesley MA 28 wcolema@wellesley.edu Copyright Flick Colema 996. All rights reserved. You are welcome to use this documet
Kietics of Complex Reactios by Flick Colema Departmet of Chemistry Wellesley College Wellesley MA 28 wcolema@wellesley.edu Copyright Flick Colema 996. All rights reserved. You are welcome to use this documet
15.083J/6.859J Integer Optimization. Lecture 3: Methods to enhance formulations
 15.083J/6.859J Iteger Optimizatio Lecture 3: Methods to ehace formulatios 1 Outlie Polyhedral review Slide 1 Methods to geerate valid iequalities Methods to geerate facet defiig iequalities Polyhedral
15.083J/6.859J Iteger Optimizatio Lecture 3: Methods to ehace formulatios 1 Outlie Polyhedral review Slide 1 Methods to geerate valid iequalities Methods to geerate facet defiig iequalities Polyhedral
A.1 Algebra Review: Polynomials/Rationals. Definitions:
 MATH 040 Notes: Uit 0 Page 1 A.1 Algera Review: Polyomials/Ratioals Defiitios: A polyomial is a sum of polyomial terms. Polyomial terms are epressios formed y products of costats ad variales with whole
MATH 040 Notes: Uit 0 Page 1 A.1 Algera Review: Polyomials/Ratioals Defiitios: A polyomial is a sum of polyomial terms. Polyomial terms are epressios formed y products of costats ad variales with whole
Generating subtour elimination constraints for the Traveling Salesman Problem
 IOSR Joural of Egieerig (IOSRJEN) ISSN (e): 2250-3021, ISSN (p): 2278-8719 Vol. 08, Issue 7 (July. 2018), V (I) PP 17-21 www.iosre.org Geeratig subtour elimiatio costraits for the Travelig Salesma Problem
IOSR Joural of Egieerig (IOSRJEN) ISSN (e): 2250-3021, ISSN (p): 2278-8719 Vol. 08, Issue 7 (July. 2018), V (I) PP 17-21 www.iosre.org Geeratig subtour elimiatio costraits for the Travelig Salesma Problem
15.081J/6.251J Introduction to Mathematical Programming. Lecture 21: Primal Barrier Interior Point Algorithm
 508J/65J Itroductio to Mathematical Programmig Lecture : Primal Barrier Iterior Poit Algorithm Outlie Barrier Methods Slide The Cetral Path 3 Approximatig the Cetral Path 4 The Primal Barrier Algorithm
508J/65J Itroductio to Mathematical Programmig Lecture : Primal Barrier Iterior Poit Algorithm Outlie Barrier Methods Slide The Cetral Path 3 Approximatig the Cetral Path 4 The Primal Barrier Algorithm
Analysis of Algorithms. Introduction. Contents
 Itroductio The focus of this module is mathematical aspects of algorithms. Our mai focus is aalysis of algorithms, which meas evaluatig efficiecy of algorithms by aalytical ad mathematical methods. We
Itroductio The focus of this module is mathematical aspects of algorithms. Our mai focus is aalysis of algorithms, which meas evaluatig efficiecy of algorithms by aalytical ad mathematical methods. We
Complex Analysis Spring 2001 Homework I Solution
 Complex Aalysis Sprig 2001 Homework I Solutio 1. Coway, Chapter 1, sectio 3, problem 3. Describe the set of poits satisfyig the equatio z a z + a = 2c, where c > 0 ad a R. To begi, we see from the triagle
Complex Aalysis Sprig 2001 Homework I Solutio 1. Coway, Chapter 1, sectio 3, problem 3. Describe the set of poits satisfyig the equatio z a z + a = 2c, where c > 0 ad a R. To begi, we see from the triagle
3.2 Properties of Division 3.3 Zeros of Polynomials 3.4 Complex and Rational Zeros of Polynomials
 Math 60 www.timetodare.com 3. Properties of Divisio 3.3 Zeros of Polyomials 3.4 Complex ad Ratioal Zeros of Polyomials I these sectios we will study polyomials algebraically. Most of our work will be cocered
Math 60 www.timetodare.com 3. Properties of Divisio 3.3 Zeros of Polyomials 3.4 Complex ad Ratioal Zeros of Polyomials I these sectios we will study polyomials algebraically. Most of our work will be cocered
On forward improvement iteration for stopping problems
 O forward improvemet iteratio for stoppig problems Mathematical Istitute, Uiversity of Kiel, Ludewig-Mey-Str. 4, D-24098 Kiel, Germay irle@math.ui-iel.de Albrecht Irle Abstract. We cosider the optimal
O forward improvemet iteratio for stoppig problems Mathematical Istitute, Uiversity of Kiel, Ludewig-Mey-Str. 4, D-24098 Kiel, Germay irle@math.ui-iel.de Albrecht Irle Abstract. We cosider the optimal
Beurling Integers: Part 2
 Beurlig Itegers: Part 2 Isomorphisms Devi Platt July 11, 2015 1 Prime Factorizatio Sequeces I the last article we itroduced the Beurlig geeralized itegers, which ca be represeted as a sequece of real umbers
Beurlig Itegers: Part 2 Isomorphisms Devi Platt July 11, 2015 1 Prime Factorizatio Sequeces I the last article we itroduced the Beurlig geeralized itegers, which ca be represeted as a sequece of real umbers
End-of-Year Contest. ERHS Math Club. May 5, 2009
 Ed-of-Year Cotest ERHS Math Club May 5, 009 Problem 1: There are 9 cois. Oe is fake ad weighs a little less tha the others. Fid the fake coi by weighigs. Solutio: Separate the 9 cois ito 3 groups (A, B,
Ed-of-Year Cotest ERHS Math Club May 5, 009 Problem 1: There are 9 cois. Oe is fake ad weighs a little less tha the others. Fid the fake coi by weighigs. Solutio: Separate the 9 cois ito 3 groups (A, B,
September 2012 C1 Note. C1 Notes (Edexcel) Copyright - For AS, A2 notes and IGCSE / GCSE worksheets 1
 September 0 s (Edecel) Copyright www.pgmaths.co.uk - For AS, A otes ad IGCSE / GCSE worksheets September 0 Copyright www.pgmaths.co.uk - For AS, A otes ad IGCSE / GCSE worksheets September 0 Copyright
September 0 s (Edecel) Copyright www.pgmaths.co.uk - For AS, A otes ad IGCSE / GCSE worksheets September 0 Copyright www.pgmaths.co.uk - For AS, A otes ad IGCSE / GCSE worksheets September 0 Copyright
Element sampling: Part 2
 Chapter 4 Elemet samplig: Part 2 4.1 Itroductio We ow cosider uequal probability samplig desigs which is very popular i practice. I the uequal probability samplig, we ca improve the efficiecy of the resultig
Chapter 4 Elemet samplig: Part 2 4.1 Itroductio We ow cosider uequal probability samplig desigs which is very popular i practice. I the uequal probability samplig, we ca improve the efficiecy of the resultig
Math 155 (Lecture 3)
 Math 55 (Lecture 3) September 8, I this lecture, we ll cosider the aswer to oe of the most basic coutig problems i combiatorics Questio How may ways are there to choose a -elemet subset of the set {,,,
Math 55 (Lecture 3) September 8, I this lecture, we ll cosider the aswer to oe of the most basic coutig problems i combiatorics Questio How may ways are there to choose a -elemet subset of the set {,,,
THE ASYMPTOTIC COMPLEXITY OF MATRIX REDUCTION OVER FINITE FIELDS
 THE ASYMPTOTIC COMPLEXITY OF MATRIX REDUCTION OVER FINITE FIELDS DEMETRES CHRISTOFIDES Abstract. Cosider a ivertible matrix over some field. The Gauss-Jorda elimiatio reduces this matrix to the idetity
THE ASYMPTOTIC COMPLEXITY OF MATRIX REDUCTION OVER FINITE FIELDS DEMETRES CHRISTOFIDES Abstract. Cosider a ivertible matrix over some field. The Gauss-Jorda elimiatio reduces this matrix to the idetity
Lecture Notes for Analysis Class
 Lecture Notes for Aalysis Class Topological Spaces A topology for a set X is a collectio T of subsets of X such that: (a) X ad the empty set are i T (b) Uios of elemets of T are i T (c) Fiite itersectios
Lecture Notes for Aalysis Class Topological Spaces A topology for a set X is a collectio T of subsets of X such that: (a) X ad the empty set are i T (b) Uios of elemets of T are i T (c) Fiite itersectios
Comparison Study of Series Approximation. and Convergence between Chebyshev. and Legendre Series
 Applied Mathematical Scieces, Vol. 7, 03, o. 6, 3-337 HIKARI Ltd, www.m-hikari.com http://d.doi.org/0.988/ams.03.3430 Compariso Study of Series Approimatio ad Covergece betwee Chebyshev ad Legedre Series
Applied Mathematical Scieces, Vol. 7, 03, o. 6, 3-337 HIKARI Ltd, www.m-hikari.com http://d.doi.org/0.988/ams.03.3430 Compariso Study of Series Approimatio ad Covergece betwee Chebyshev ad Legedre Series
CS 270 Algorithms. Oliver Kullmann. Growth of Functions. Divide-and- Conquer Min-Max- Problem. Tutorial. Reading from CLRS for week 2
 Geeral remarks Week 2 1 Divide ad First we cosider a importat tool for the aalysis of algorithms: Big-Oh. The we itroduce a importat algorithmic paradigm:. We coclude by presetig ad aalysig two examples.
Geeral remarks Week 2 1 Divide ad First we cosider a importat tool for the aalysis of algorithms: Big-Oh. The we itroduce a importat algorithmic paradigm:. We coclude by presetig ad aalysig two examples.
Lesson 10: Limits and Continuity
 www.scimsacademy.com Lesso 10: Limits ad Cotiuity SCIMS Academy 1 Limit of a fuctio The cocept of limit of a fuctio is cetral to all other cocepts i calculus (like cotiuity, derivative, defiite itegrals
www.scimsacademy.com Lesso 10: Limits ad Cotiuity SCIMS Academy 1 Limit of a fuctio The cocept of limit of a fuctio is cetral to all other cocepts i calculus (like cotiuity, derivative, defiite itegrals
+ au n+1 + bu n = 0.)
 Lecture 6 Recurreces - kth order: u +k + a u +k +... a k u k 0 where a... a k are give costats, u 0... u k are startig coditios. (Simple case: u + au + + bu 0.) How to solve explicitly - first, write characteristic
Lecture 6 Recurreces - kth order: u +k + a u +k +... a k u k 0 where a... a k are give costats, u 0... u k are startig coditios. (Simple case: u + au + + bu 0.) How to solve explicitly - first, write characteristic
Ma 530 Infinite Series I
 Ma 50 Ifiite Series I Please ote that i additio to the material below this lecture icorporated material from the Visual Calculus web site. The material o sequeces is at Visual Sequeces. (To use this li
Ma 50 Ifiite Series I Please ote that i additio to the material below this lecture icorporated material from the Visual Calculus web site. The material o sequeces is at Visual Sequeces. (To use this li
A NEW APPROACH TO SOLVE AN UNBALANCED ASSIGNMENT PROBLEM
 A NEW APPROACH TO SOLVE AN UNBALANCED ASSIGNMENT PROBLEM *Kore B. G. Departmet Of Statistics, Balwat College, VITA - 415 311, Dist.: Sagli (M. S.). Idia *Author for Correspodece ABSTRACT I this paper I
A NEW APPROACH TO SOLVE AN UNBALANCED ASSIGNMENT PROBLEM *Kore B. G. Departmet Of Statistics, Balwat College, VITA - 415 311, Dist.: Sagli (M. S.). Idia *Author for Correspodece ABSTRACT I this paper I
(c) Write, but do not evaluate, an integral expression for the volume of the solid generated when R is
 Calculus BC Fial Review Name: Revised 7 EXAM Date: Tuesday, May 9 Remiders:. Put ew batteries i your calculator. Make sure your calculator is i RADIAN mode.. Get a good ight s sleep. Eat breakfast. Brig:
Calculus BC Fial Review Name: Revised 7 EXAM Date: Tuesday, May 9 Remiders:. Put ew batteries i your calculator. Make sure your calculator is i RADIAN mode.. Get a good ight s sleep. Eat breakfast. Brig:
Lyapunov Stability Analysis for Feedback Control Design
 Copyright F.L. Lewis 008 All rights reserved Updated: uesday, November, 008 Lyapuov Stability Aalysis for Feedbac Cotrol Desig Lyapuov heorems Lyapuov Aalysis allows oe to aalyze the stability of cotiuous-time
Copyright F.L. Lewis 008 All rights reserved Updated: uesday, November, 008 Lyapuov Stability Aalysis for Feedbac Cotrol Desig Lyapuov heorems Lyapuov Aalysis allows oe to aalyze the stability of cotiuous-time
A New Solution Method for the Finite-Horizon Discrete-Time EOQ Problem
 This is the Pre-Published Versio. A New Solutio Method for the Fiite-Horizo Discrete-Time EOQ Problem Chug-Lu Li Departmet of Logistics The Hog Kog Polytechic Uiversity Hug Hom, Kowloo, Hog Kog Phoe: +852-2766-7410
This is the Pre-Published Versio. A New Solutio Method for the Fiite-Horizo Discrete-Time EOQ Problem Chug-Lu Li Departmet of Logistics The Hog Kog Polytechic Uiversity Hug Hom, Kowloo, Hog Kog Phoe: +852-2766-7410
( ) GENERATING FUNCTIONS
 GENERATING FUNCTIONS Solve a ifiite umber of related problems i oe swoop. *Code the problems, maipulate the code, the decode the aswer! Really a algebraic cocept but ca be eteded to aalytic basis for iterestig
GENERATING FUNCTIONS Solve a ifiite umber of related problems i oe swoop. *Code the problems, maipulate the code, the decode the aswer! Really a algebraic cocept but ca be eteded to aalytic basis for iterestig
CALCULATION OF FIBONACCI VECTORS
 CALCULATION OF FIBONACCI VECTORS Stuart D. Aderso Departmet of Physics, Ithaca College 953 Daby Road, Ithaca NY 14850, USA email: saderso@ithaca.edu ad Dai Novak Departmet of Mathematics, Ithaca College
CALCULATION OF FIBONACCI VECTORS Stuart D. Aderso Departmet of Physics, Ithaca College 953 Daby Road, Ithaca NY 14850, USA email: saderso@ithaca.edu ad Dai Novak Departmet of Mathematics, Ithaca College
Divide and Conquer. 1 Overview. 2 Multiplying Bit Strings. COMPSCI 330: Design and Analysis of Algorithms 1/19/2016 and 1/21/2016
 COMPSCI 330: Desig ad Aalysis of Algorithms 1/19/2016 ad 1/21/2016 Lecturer: Debmalya Paigrahi Divide ad Coquer Scribe: Tiaqi Sog 1 Overview I this lecture, a importat algorithm desig techique called divide-ad-coquer
COMPSCI 330: Desig ad Aalysis of Algorithms 1/19/2016 ad 1/21/2016 Lecturer: Debmalya Paigrahi Divide ad Coquer Scribe: Tiaqi Sog 1 Overview I this lecture, a importat algorithm desig techique called divide-ad-coquer
