Classical and Quantum Mechanics of a Charged Particle Moving in Electric and Magnetic Fields
|
|
|
- Claud Shelton
- 5 years ago
- Views:
Transcription
1 Classical Mechanics Classical and Quantum Mechanics of a Charged Particle Moving in Electric and Magnetic Fields In this section I describe the Lagrangian and the Hamiltonian formulations of classical mechanics of a charged particle moving in general electric and magnetic fields. The fields E(r, t) and B(r, t) may be time-dependent, but I take their time-dependence as given; the effects of a moving charged particle on the EM fields themselves will be explored in the second half of the classical electrodynamics class (PHY 352 L). In a purely electrostatic field E(r) the net force F = qe(r) acting on a charged particle is a potential force. Consequently, the Lagrangian and the Hamiltonian of the particle s dynamics involve the scalar potential V (r) rather then the electric field E itself, thus L(r, v) = m 2 v2 qv (r), (1) H(r, p) = p2 2m + qv (r). (2) Likewise, when we turn on a magnetic field B(r), the Lagrangian and the Hamiltonian involve the vector potential A(r) rather than magnetic field B itself. Specifically, the Lagrangian becomes L(r, v) = m 2 v2 qv (r) + qv A(r) (3) in MKSA units, or L(r, v) = m 2 v2 qv (r) + q v A(r) (4) c in Gauss units. Arguably, the vector-potential term in this Lagrangian is a relativistic correction to the scalar-potential term, but I don t want to get into special relativity in these notes. Instead, I am going to justify the Lagrangian (3) by showing that it leads to the Euler Lagrange equation of motion which agrees with the Newton s Second Law for the 1
2 usual electric+magnetic force, ma = F net = qe(r) + qv B(r). (5) But first, let me remind you that for the time-dependent electromagnetic fields B = A, (6) E = A V, (7) where the first equation assures B = 0, come hell or high water, while the second equation leads to the Induction Law E = A V = ( ) A 0 = B. (8) Now, with these relations in mind, let s derive the Euler-Lagrange equations of motion d ( ) L(r, v) v L(r, v) = + r (9) for the Lagrangian (3). The first step is the canonical momentum p def = L v = mv + qa(r). (10) Note: In the vector potential term qa(r), the r is the time-dependent particle s position rather than some fixed point in space. Making the time dependence explicit, we have p(t) = mv(t) + qa(r(t), t) (11) where the second argument of the vector potential allows for a time-dependent magnetic 2
3 field. Consequently, d A(r(t), t) = ( ) r + ( ) dr A = A + (v )A (12) and therefore dp = m dv + q A + (v )A. (13) On the other hand, the Euler Lagrange equation (9) for the Lagrangian (3) reads dp = + L r = q V + q (v A). (14) Equating the right hand sides of the last two formulae, we arrive at m dv + q A + (v )A = q V + q (v A) (15) and hence ma def = m dv ( = q V A ) ( ) + q (v A) (v )A. (16) In light of eq. (7), the first group of terms on the RHS here is simply the electric force qe. As to the second group of terms, it amounts to the Lorentz magnetic force qv B. Indeed, by the B(AC) C(AB) rule for a double vector product A (B C), we have v B = v ( A) = (v A) (v )A, (17) exactly as in eq. (16). Altogether, the Lagrangian (3) and hence eq. (16) gives a simple equation of motion for the charged particle in EM fields, ma(t) = qe(r, t) + qv(t) B(r, t). (18) Physically, we know this equation of motion is correct, and that s what justifies the Lagrangian (3). 3
4 Next, consider the classical Hamiltonian for the charged particle. By the usual rules of classical mechanics, the Hamiltonian follows from the Lagrangian as H(r, p) = L(r, v) v v L(r, v), (19) where the RHS should be re-expressed in terms of the position r and the canonical momentum p = L/ v rather than the position and the velocity. For the Lagrangian (3), the canonical momentum p = mv + qa(r) (10) is different from the usual kinematic momentum mv. Consequently, while H = p v L = mv 2 + qa v 1 2 mv2 + qv qv A = 1 2 mv2 + qv (r) (20) seems to be independent of the vector potential, this is an artefact of writing H as a function of the velocity and position. When we rewrite this Hamiltonian as a function of the canonical momentum instead of the velocity, the A dependence becomes manifest: v = p qa(r) m (21) and therefore H(r, p) = 1 ( ) 2 p qa(r) + qv (r). (22) 2m 4
5 Quantum Mechanics In quantum mechanics, the classical dynamical variables like positions and momenta become linear operators in the Hilbert space of quantum states. Some of these linear operators do not commute with each other, Â ˆB ˆBÂ. In particular, the position and the canonical momentum operators obey the canonical commutation relations ˆr iˆr j ˆr j ˆr i = 0, ˆp iˆp j ˆp j ˆp i = 0, ˆr iˆp j ˆp j ˆr i = i hδ i,j, (23) for i, j = x, y, z. In terms of the wave-functions of coordinates ψ(x, y, z), the position operators act by multiplication ˆxψ(x, y, z) = x ψ(x, y, z), ŷψ(x, y, z) = y ψ(x, y, z), ẑψ(x, y, z) = z ψ(x, y, z), while the canonical momenta act as space derivatives (24) ˆp x ψ(x, y, z) = i h ψ x, ˆp yψ(x, y, z) = i h ψ y, ˆp zψ(x, y, z) = i h ψ y. (25) Note that for a charged particle in EM fields, these derivative operators correspond to the canonical momenta p i = mv i + qa i (r) rather that to the kinematic momenta π i = mv i. The kinematic momenta ˆπ x,y,z act in a more complicated way as ˆπ i ψ(r) = i h ψ r i qa i (r) ψ(r), (26) or in vector notations ˆπψ(r) = i h ψ(r) qa(r)ψ(r). (27) Consequently, the classical Hamiltonian (22) of the charged particle becomes the quantum 5
6 Hamiltonian operator Ĥ = 1 ) 2 (ˆp qa(ˆr) + qv (ˆr), 2m Ĥψ(r) = 1 (28) ( ) 2ψ(r) i h qa(r) + qv (r)ψ(r). 2m This Hamiltonian operator governs the time-dependence of the wave function ψ(x, y, z, t) according to the Schrödinger equation i h 1 ( ) 2ψ(r, ψ(r, t) = Ĥψ(r, t) = i h qa(r, t) t) + qv (r, t)ψ(r, t). (29) 2m Gauge Transforms. The electric and the magnetic fields E(r, t) and B(r, t) do not uniquely determine the vector and the scalar potentials V (r, t) and A(r, t). Instead, the fields determine the potentials up to a gauge transform: Pick any function Λ(x, y, z, t) of space and time and let A(r, t) A (r, t) = A(r, t) + Λ(r, t), V (r, t) V (r, t) = V (r, t) Λ(r, t). (30) Regardless of Λ(r, t), the new potential A and V yield exactly the same electric and magnetic fields as the old potentials: E = V A ( = V Λ ) ( ) A + Λ = V A ( ( )) Λ + ( Λ) = E + 0, (31) B = A = ( A + Λ) = A + Λ = B + 0. (32) In classical mechanics, a gauge transform of the potentials has no effect on the equation of motion (5) for the charged particle. In quantum mechanics, a gauge transform also does not 6
7 have any effect on any physically measurable quantities. However, to keep the Schrödinger equation (29) working, a gauge transform (30) of the potentials should be accompanied by a local phase transform of the wave-function, ψ(x, y, z, t) ψ (x, y, z, t) = ψ(x, y, z, t) exp ( i q h Λ(x, y, z, t)). (33) To see how this works, let me show that the combined gauge transform (30) and the local phase transform (33) is a symmetry of the Schrödinger equation for any position-and-timedependent Λ(x, y, z, t). Let s start with the local phase transform (33) for a position-dependent Λ and consider what happens to the gradient of the wave function: ψ = (ψ exp ( i q h Λ)) q h Λ)) = ( ψ) exp ( i q h Λ) + ψ ( exp ( i = ( ψ) exp ( i q h Λ) + ψ (exp ( ) i q h Λ) i q h Λ = exp ( ) i q h Λ) ( ψ + i q h ( Λ) ψ. (34) Note that the gradient ψ does not transform covariantly, i.e. like ψ itself. Instead, there is an extra inhomogeneous term ( Λ)ψ inside the big ( ). To remedy this non-covariance, let s define the covariant derivative Dψ(r) = ψ(r) i q h A(r)ψ(r). (35) This derivative does transform covariantly under the local phase transforms (33), provided the vector potential A(r) is gauge-transformed for the same Λ(r). Indeed, [ ] Dψ = D ψ = ψ i q h A ψ note A as well as ψ here = exp ( ) i q h Λ) ( ψ + i q h ( Λ) ψ i q h ( ) ( A + Λ exp i q h Λ) ψ = exp ( ] i q h Λ) [ ψ + i q h ( Λ) ψ i q h A ψ i q h ( Λ) ψ = exp ( ] i q h Λ) [ ψ i q h A ψ (36) = exp ( i q h Λ) Dψ. 7
8 In the same way, for a time-dependent Λ(r, t), we define the covariant time derivative D t ψ(r, t) = ψ(r, t) + i q h V (r, t)ψ(r, t), (37) then after a combined phase and gauge transform [ Dt ψ(r, t) ] = exp ( i q h Λ(r, t)) D t ψ(r, t). (38) As an operator acting on the wave functions, the covariant gradient (35) or rather i h D is the kinematic momentum operator, ˆπ = ˆp qa(ˆr) = i h qa(r) = i h D. (39) Consequently, the Hamiltonian operator (28) for the charged particles can be written in terms of covariant derivatives as Ĥψ(r) = h2 2m D 2 ψ(r) + V (r)ψ(r). (40) Moreover, if we put the V ψ term on the other side of the time-dependent Schrödinger eqn. (29), we get i h h2 ψ(r, t) V (r, t)ψ(r, t) = D 2m 2 ψ(r, t) (41) where the left-hand side is the covariant time derivative i hd t ψ(r, t). Altogether, we get the covariant form of the Schrödinger equation i hd t ψ(r, t) = h2 2m D 2 ψ(r, t) (42) where both sides transform covariantly under the local phase transforms: [ ψ (x, y, z, t) = exp ( i q h Λ(x, y, z, t)) ψ(x, y, z, t), [ i hdt ψ(x, y, z, t) ] = exp ( i q h Λ(x, y, z, t)) [ i hd t ψ(x, y, z, t) ], [ h2 2m D 2 ψ(x, y, z, t) ] = exp ( i q h Λ(x, y, z, t)) h2 2m D 2 ψ(x, y, z, t) ]. (43) Therefore, if the wave function ψ(x, y, z, t) obeys the Schrödinger equation before the combined gauge/phase transform, then after the transform the new ψ (x, y, z, t) also obeys the 8
9 new Schrödinger equation. And that s why the local phase transform (33) should be accompanied by the gauge transform (30) and vice verse. This issue of the gauge/phase transforms may seem rather technical, but as I show in the next set of my notes, it leads to the Aharonov Bohm effect, helps explain how SQUID magnetometers work, and even explains how magnetic monopoles might work in quantum mechanics. For the moment, let me simply generalize the relation between the gauge and the phase transforms from ordinary quantum mechanics to quantum electrodynamics (QED) and other quantum field theories. In QED, instead of wave-functions of individual electrons we have the quantum electron field ˆΨ(x, y, z, t) which creates and annihilated electrons and positrons. But despite its operatorial nature, as a function of space and time coordinates or rather, as a 4-component array of such functions it obeys a linear Dirac equation i hd t ˆΨ + i hc α D ˆΨ mc 2 β ˆΨ = 0 (44) where D and D t are the covariant derivatives exactly as in eqs. (35) and (37) for q = e, and α x, α y, α z and β are 4 4 Dirac matrices, never mind their details. In light of the covariant derivatives in the Dirac equation, QED is invariant under local phase transforms of the electron field ˆΨ(r, t) accompanied by the gauge transforms of the EM potential fields ˆV (r, t) and Â(r, t). This invariance called the gauge symmetry is absolutely essential to QED and helps explain many of it key features, for example the exact masslessness of the photons. The gauge symmetry of QED can be generalized to more complicated local symmetries of other quantum field theories. For example, in QCD quantum chromodynamics, the theory of strong interactions there is a gauge symmetry mixing the 3 colors of the quarks, accompanied by a rather complicated transform of the EM-like gluon fields. Almost all features of QCD and hence of the strong interactions follow from this gauge symmetry, but the explanation is waay too complicated for this class. 9
Physics 452 Lecture 33: A Particle in an E&M Field
 Physics 452 Lecture 33: A Particle in an E&M Field J. Peatross In lectures 31 and 32, we considered the Klein-Gordon equation for a free particle. We would like to add a potential to the equation (since
Physics 452 Lecture 33: A Particle in an E&M Field J. Peatross In lectures 31 and 32, we considered the Klein-Gordon equation for a free particle. We would like to add a potential to the equation (since
Electric and Magnetic Forces in Lagrangian and Hamiltonian Formalism
 Electric and Magnetic Forces in Lagrangian and Hamiltonian Formalism Benjamin Hornberger 1/26/1 Phy 55, Classical Electrodynamics, Prof. Goldhaber Lecture notes from Oct. 26, 21 Lecture held by Prof. Weisberger
Electric and Magnetic Forces in Lagrangian and Hamiltonian Formalism Benjamin Hornberger 1/26/1 Phy 55, Classical Electrodynamics, Prof. Goldhaber Lecture notes from Oct. 26, 21 Lecture held by Prof. Weisberger
etc., etc. Consequently, the Euler Lagrange equations for the Φ and Φ fields may be written in a manifestly covariant form as L Φ = m 2 Φ, (S.
 PHY 396 K. Solutions for problem set #3. Problem 1a: Let s start with the scalar fields Φx and Φ x. Similar to the EM covariant derivatives, the non-abelian covariant derivatives may be integrated by parts
PHY 396 K. Solutions for problem set #3. Problem 1a: Let s start with the scalar fields Φx and Φ x. Similar to the EM covariant derivatives, the non-abelian covariant derivatives may be integrated by parts
Under evolution for a small time δt the area A(t) = q p evolves into an area
 Physics 106a, Caltech 6 November, 2018 Lecture 11: Hamiltonian Mechanics II Towards statistical mechanics Phase space volumes are conserved by Hamiltonian dynamics We can use many nearby initial conditions
Physics 106a, Caltech 6 November, 2018 Lecture 11: Hamiltonian Mechanics II Towards statistical mechanics Phase space volumes are conserved by Hamiltonian dynamics We can use many nearby initial conditions
Maxwell s equations. based on S-54. electric field charge density. current density
 Maxwell s equations based on S-54 Our next task is to find a quantum field theory description of spin-1 particles, e.g. photons. Classical electrodynamics is governed by Maxwell s equations: electric field
Maxwell s equations based on S-54 Our next task is to find a quantum field theory description of spin-1 particles, e.g. photons. Classical electrodynamics is governed by Maxwell s equations: electric field
Canonical Quantization
 Canonical Quantization March 6, 06 Canonical quantization of a particle. The Heisenberg picture One of the most direct ways to quantize a classical system is the method of canonical quantization introduced
Canonical Quantization March 6, 06 Canonical quantization of a particle. The Heisenberg picture One of the most direct ways to quantize a classical system is the method of canonical quantization introduced
Relativistic Quantum Mechanics
 Physics 342 Lecture 34 Relativistic Quantum Mechanics Lecture 34 Physics 342 Quantum Mechanics I Wednesday, April 30th, 2008 We know that the Schrödinger equation logically replaces Newton s second law
Physics 342 Lecture 34 Relativistic Quantum Mechanics Lecture 34 Physics 342 Quantum Mechanics I Wednesday, April 30th, 2008 We know that the Schrödinger equation logically replaces Newton s second law
E = φ 1 A The dynamics of a particle with mass m and charge q is determined by the Hamiltonian
 Lecture 9 Relevant sections in text: 2.6 Charged particle in an electromagnetic field We now turn to another extremely important example of quantum dynamics. Let us describe a non-relativistic particle
Lecture 9 Relevant sections in text: 2.6 Charged particle in an electromagnetic field We now turn to another extremely important example of quantum dynamics. Let us describe a non-relativistic particle
1 The Quantum Anharmonic Oscillator
 1 The Quantum Anharmonic Oscillator Perturbation theory based on Feynman diagrams can be used to calculate observables in Quantum Electrodynamics, like the anomalous magnetic moment of the electron, and
1 The Quantum Anharmonic Oscillator Perturbation theory based on Feynman diagrams can be used to calculate observables in Quantum Electrodynamics, like the anomalous magnetic moment of the electron, and
Problem 1(a): As discussed in class, Euler Lagrange equations for charged fields can be written in a manifestly covariant form as L (D µ φ) L
 PHY 396 K. Solutions for problem set #. Problem a: As discussed in class, Euler Lagrange equations for charged fields can be written in a manifestly covariant form as D µ D µ φ φ = 0. S. In particularly,
PHY 396 K. Solutions for problem set #. Problem a: As discussed in class, Euler Lagrange equations for charged fields can be written in a manifestly covariant form as D µ D µ φ φ = 0. S. In particularly,
1 The postulates of quantum mechanics
 1 The postulates of quantum mechanics The postulates of quantum mechanics were derived after a long process of trial and error. These postulates provide a connection between the physical world and the
1 The postulates of quantum mechanics The postulates of quantum mechanics were derived after a long process of trial and error. These postulates provide a connection between the physical world and the
PHY 396 K. Problem set #5. Due October 9, 2008.
 PHY 396 K. Problem set #5. Due October 9, 2008.. First, an exercise in bosonic commutation relations [â α, â β = 0, [â α, â β = 0, [â α, â β = δ αβ. ( (a Calculate the commutators [â αâ β, â γ, [â αâ β,
PHY 396 K. Problem set #5. Due October 9, 2008.. First, an exercise in bosonic commutation relations [â α, â β = 0, [â α, â β = 0, [â α, â β = δ αβ. ( (a Calculate the commutators [â αâ β, â γ, [â αâ β,
REVIEW. Quantum electrodynamics (QED) Quantum electrodynamics is a theory of photons interacting with the electrons and positrons of a Dirac field:
 Quantum electrodynamics (QED) based on S-58 Quantum electrodynamics is a theory of photons interacting with the electrons and positrons of a Dirac field: Noether current of the lagrangian for a free Dirac
Quantum electrodynamics (QED) based on S-58 Quantum electrodynamics is a theory of photons interacting with the electrons and positrons of a Dirac field: Noether current of the lagrangian for a free Dirac
Maxwell s equations. electric field charge density. current density
 Maxwell s equations based on S-54 Our next task is to find a quantum field theory description of spin-1 particles, e.g. photons. Classical electrodynamics is governed by Maxwell s equations: electric field
Maxwell s equations based on S-54 Our next task is to find a quantum field theory description of spin-1 particles, e.g. photons. Classical electrodynamics is governed by Maxwell s equations: electric field
The Particle-Field Hamiltonian
 The Particle-Field Hamiltonian For a fundamental understanding of the interaction of a particle with the electromagnetic field we need to know the total energy of the system consisting of particle and
The Particle-Field Hamiltonian For a fundamental understanding of the interaction of a particle with the electromagnetic field we need to know the total energy of the system consisting of particle and
FYS 3120: Classical Mechanics and Electrodynamics
 FYS 3120: Classical Mechanics and Electrodynamics Formula Collection Spring semester 2014 1 Analytical Mechanics The Lagrangian L = L(q, q, t), (1) is a function of the generalized coordinates q = {q i
FYS 3120: Classical Mechanics and Electrodynamics Formula Collection Spring semester 2014 1 Analytical Mechanics The Lagrangian L = L(q, q, t), (1) is a function of the generalized coordinates q = {q i
PHY 396 K. Solutions for homework set #9.
 PHY 396 K. Solutions for homework set #9. Problem 2(a): The γ 0 matrix commutes with itself but anticommutes with the space-indexed γ 1,2,3. At the same time, the parity reflects the space coordinates
PHY 396 K. Solutions for homework set #9. Problem 2(a): The γ 0 matrix commutes with itself but anticommutes with the space-indexed γ 1,2,3. At the same time, the parity reflects the space coordinates
Chapter 4: Quantum Electrodynamics
 Chapter 4: Quantum Electrodynamics This chapter provides a survey of quantum electrodynamics, the quantum theory of the electromagnetic field and its interaction with electrically charged particles, such
Chapter 4: Quantum Electrodynamics This chapter provides a survey of quantum electrodynamics, the quantum theory of the electromagnetic field and its interaction with electrically charged particles, such
Vector Potential for the Magnetic Field
 Vector Potential for the Magnetic Field Let me start with two two theorems of Vector Calculus: Theorem 1: If a vector field has zero curl everywhere in space, then that field is a gradient of some scalar
Vector Potential for the Magnetic Field Let me start with two two theorems of Vector Calculus: Theorem 1: If a vector field has zero curl everywhere in space, then that field is a gradient of some scalar
-state problems and an application to the free particle
 -state problems and an application to the free particle Sourendu Gupta TIFR, Mumbai, India Quantum Mechanics 1 2013 3 September, 2013 Outline 1 Outline 2 The Hilbert space 3 A free particle 4 Keywords
-state problems and an application to the free particle Sourendu Gupta TIFR, Mumbai, India Quantum Mechanics 1 2013 3 September, 2013 Outline 1 Outline 2 The Hilbert space 3 A free particle 4 Keywords
MSci EXAMINATION. Date: XX th May, Time: 14:30-17:00
 MSci EXAMINATION PHY-415 (MSci 4242 Relativistic Waves and Quantum Fields Time Allowed: 2 hours 30 minutes Date: XX th May, 2010 Time: 14:30-17:00 Instructions: Answer THREE QUESTIONS only. Each question
MSci EXAMINATION PHY-415 (MSci 4242 Relativistic Waves and Quantum Fields Time Allowed: 2 hours 30 minutes Date: XX th May, 2010 Time: 14:30-17:00 Instructions: Answer THREE QUESTIONS only. Each question
Aharonov Bohm Effect, Magnetic Monopoles, and Charge Quantization
 Aharonov Bohm Effect, Magnetic Monopoles, and Charge Quantization Aharonov Bohm Effect In classical mechanics, the motion of a charged particle depends only on the electric and magnetic tension fields
Aharonov Bohm Effect, Magnetic Monopoles, and Charge Quantization Aharonov Bohm Effect In classical mechanics, the motion of a charged particle depends only on the electric and magnetic tension fields
Preliminaries: what you need to know
 January 7, 2014 Preliminaries: what you need to know Asaf Pe er 1 Quantum field theory (QFT) is the theoretical framework that forms the basis for the modern description of sub-atomic particles and their
January 7, 2014 Preliminaries: what you need to know Asaf Pe er 1 Quantum field theory (QFT) is the theoretical framework that forms the basis for the modern description of sub-atomic particles and their
Quantum Field Theory 2 nd Edition
 Quantum Field Theory 2 nd Edition FRANZ MANDL and GRAHAM SHAW School of Physics & Astromony, The University of Manchester, Manchester, UK WILEY A John Wiley and Sons, Ltd., Publication Contents Preface
Quantum Field Theory 2 nd Edition FRANZ MANDL and GRAHAM SHAW School of Physics & Astromony, The University of Manchester, Manchester, UK WILEY A John Wiley and Sons, Ltd., Publication Contents Preface
6. QED. Particle and Nuclear Physics. Dr. Tina Potter. Dr. Tina Potter 6. QED 1
 6. QED Particle and Nuclear Physics Dr. Tina Potter Dr. Tina Potter 6. QED 1 In this section... Gauge invariance Allowed vertices + examples Scattering Experimental tests Running of alpha Dr. Tina Potter
6. QED Particle and Nuclear Physics Dr. Tina Potter Dr. Tina Potter 6. QED 1 In this section... Gauge invariance Allowed vertices + examples Scattering Experimental tests Running of alpha Dr. Tina Potter
1. Griffiths Suppose two spin-1/2 particles are known to be in the singlet configuration.
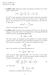 Physics 443 HW #7 Due March 12, 2008 1. Griffiths 4.50. Suppose two spin-1/2 particles are known to be in the singlet configuration. ( 00 = 1 2 ( + 1 2 1 2 1 2 +1 2 ) Let S a (1) be the component of the
Physics 443 HW #7 Due March 12, 2008 1. Griffiths 4.50. Suppose two spin-1/2 particles are known to be in the singlet configuration. ( 00 = 1 2 ( + 1 2 1 2 1 2 +1 2 ) Let S a (1) be the component of the
3 Quantization of the Dirac equation
 3 Quantization of the Dirac equation 3.1 Identical particles As is well known, quantum mechanics implies that no measurement can be performed to distinguish particles in the same quantum state. Elementary
3 Quantization of the Dirac equation 3.1 Identical particles As is well known, quantum mechanics implies that no measurement can be performed to distinguish particles in the same quantum state. Elementary
Joint Undergraduate Lecture Tour Higgs Physics and the Mystery of Mass. Heather Logan
 1 CAP-CASCA Joint Undergraduate Lecture Tour 2009 Heather Logan With thanks to St. Mary s U., Acadia U., St. Francis Xavier U., Mount Allison U., & U. de Moncton 2 The Large Hadron Collider (LHC) is a
1 CAP-CASCA Joint Undergraduate Lecture Tour 2009 Heather Logan With thanks to St. Mary s U., Acadia U., St. Francis Xavier U., Mount Allison U., & U. de Moncton 2 The Large Hadron Collider (LHC) is a
221A Lecture Notes Electromagnetic Couplings
 221A Lecture Notes Electromagnetic Couplings 1 Classical Mechanics The coupling of the electromagnetic field with a charged point particle of charge e is given by a term in the action (MKSA system) S int
221A Lecture Notes Electromagnetic Couplings 1 Classical Mechanics The coupling of the electromagnetic field with a charged point particle of charge e is given by a term in the action (MKSA system) S int
Coordinate and Momentum Representation. Commuting Observables and Simultaneous Measurements. January 30, 2012
 Coordinate and Momentum Representation. Commuting Observables and Simultaneous Measurements. January 30, 2012 1 Coordinate and Momentum Representations Let us consider an eigenvalue problem for a Hermitian
Coordinate and Momentum Representation. Commuting Observables and Simultaneous Measurements. January 30, 2012 1 Coordinate and Momentum Representations Let us consider an eigenvalue problem for a Hermitian
σ 2 + π = 0 while σ satisfies a cubic equation λf 2, σ 3 +f + β = 0 the second derivatives of the potential are = λ(σ 2 f 2 )δ ij, π i π j
 PHY 396 K. Solutions for problem set #4. Problem 1a: The linear sigma model has scalar potential V σ, π = λ 8 σ + π f βσ. S.1 Any local minimum of this potential satisfies and V = λ π V σ = λ σ + π f =
PHY 396 K. Solutions for problem set #4. Problem 1a: The linear sigma model has scalar potential V σ, π = λ 8 σ + π f βσ. S.1 Any local minimum of this potential satisfies and V = λ π V σ = λ σ + π f =
Lecture 9: Macroscopic Quantum Model
 Lecture 9: Macroscopic Quantum Model Outline 1. Development of Quantum Mechanics 2. Schrödinger's Equation Free particle With forces With Electromagnetic force 3. Physical meaning of Wavefunction Probability
Lecture 9: Macroscopic Quantum Model Outline 1. Development of Quantum Mechanics 2. Schrödinger's Equation Free particle With forces With Electromagnetic force 3. Physical meaning of Wavefunction Probability
Quantum Physics 2006/07
 Quantum Physics 6/7 Lecture 7: More on the Dirac Equation In the last lecture we showed that the Dirac equation for a free particle i h t ψr, t = i hc α + β mc ψr, t has plane wave solutions ψr, t = exp
Quantum Physics 6/7 Lecture 7: More on the Dirac Equation In the last lecture we showed that the Dirac equation for a free particle i h t ψr, t = i hc α + β mc ψr, t has plane wave solutions ψr, t = exp
Part III. Interacting Field Theory. Quantum Electrodynamics (QED)
 November-02-12 8:36 PM Part III Interacting Field Theory Quantum Electrodynamics (QED) M. Gericke Physics 7560, Relativistic QM 183 III.A Introduction December-08-12 9:10 PM At this point, we have the
November-02-12 8:36 PM Part III Interacting Field Theory Quantum Electrodynamics (QED) M. Gericke Physics 7560, Relativistic QM 183 III.A Introduction December-08-12 9:10 PM At this point, we have the
Attempts at relativistic QM
 Attempts at relativistic QM based on S-1 A proper description of particle physics should incorporate both quantum mechanics and special relativity. However historically combining quantum mechanics and
Attempts at relativistic QM based on S-1 A proper description of particle physics should incorporate both quantum mechanics and special relativity. However historically combining quantum mechanics and
Dirac Equation. Chapter 1
 Chapter Dirac Equation This course will be devoted principally to an exposition of the dynamics of Abelian and non-abelian gauge theories. These form the basis of the Standard Model, that is, the theory
Chapter Dirac Equation This course will be devoted principally to an exposition of the dynamics of Abelian and non-abelian gauge theories. These form the basis of the Standard Model, that is, the theory
Vacuum Energy and Effective Potentials
 Vacuum Energy and Effective Potentials Quantum field theories have badly divergent vacuum energies. In perturbation theory, the leading term is the net zero-point energy E zeropoint = particle species
Vacuum Energy and Effective Potentials Quantum field theories have badly divergent vacuum energies. In perturbation theory, the leading term is the net zero-point energy E zeropoint = particle species
Quantum Electrodynamics Test
 MSc in Quantum Fields and Fundamental Forces Quantum Electrodynamics Test Monday, 11th January 2010 Please answer all three questions. All questions are worth 20 marks. Use a separate booklet for each
MSc in Quantum Fields and Fundamental Forces Quantum Electrodynamics Test Monday, 11th January 2010 Please answer all three questions. All questions are worth 20 marks. Use a separate booklet for each
Lecture notes for FYS610 Many particle Quantum Mechanics
 UNIVERSITETET I STAVANGER Institutt for matematikk og naturvitenskap Lecture notes for FYS610 Many particle Quantum Mechanics Note 20, 19.4 2017 Additions and comments to Quantum Field Theory and the Standard
UNIVERSITETET I STAVANGER Institutt for matematikk og naturvitenskap Lecture notes for FYS610 Many particle Quantum Mechanics Note 20, 19.4 2017 Additions and comments to Quantum Field Theory and the Standard
Fermionic Algebra and Fock Space
 Fermionic Algebra and Fock Space Earlier in class we saw how harmonic-oscillator-like bosonic commutation relations [â α,â β ] = 0, [ ] â α,â β = 0, [ ] â α,â β = δ α,β (1) give rise to the bosonic Fock
Fermionic Algebra and Fock Space Earlier in class we saw how harmonic-oscillator-like bosonic commutation relations [â α,â β ] = 0, [ ] â α,â β = 0, [ ] â α,â β = δ α,β (1) give rise to the bosonic Fock
Lecture 8. September 21, General plan for construction of Standard Model theory. Choice of gauge symmetries for the Standard Model
 Lecture 8 September 21, 2017 Today General plan for construction of Standard Model theory Properties of SU(n) transformations (review) Choice of gauge symmetries for the Standard Model Use of Lagrangian
Lecture 8 September 21, 2017 Today General plan for construction of Standard Model theory Properties of SU(n) transformations (review) Choice of gauge symmetries for the Standard Model Use of Lagrangian
Quantum Field Theory. and the Standard Model. !H Cambridge UNIVERSITY PRESS MATTHEW D. SCHWARTZ. Harvard University
 Quantum Field Theory and the Standard Model MATTHEW D. Harvard University SCHWARTZ!H Cambridge UNIVERSITY PRESS t Contents v Preface page xv Part I Field theory 1 1 Microscopic theory of radiation 3 1.1
Quantum Field Theory and the Standard Model MATTHEW D. Harvard University SCHWARTZ!H Cambridge UNIVERSITY PRESS t Contents v Preface page xv Part I Field theory 1 1 Microscopic theory of radiation 3 1.1
YANG-MILLS GAUGE INVARIANT THEORY FOR SPACE CURVED ELECTROMAGNETIC FIELD. Algirdas Antano Maknickas 1. September 3, 2014
 YANG-MILLS GAUGE INVARIANT THEORY FOR SPACE CURVED ELECTROMAGNETIC FIELD Algirdas Antano Maknickas Institute of Mechanical Sciences, Vilnius Gediminas Technical University September 3, 04 Abstract. It
YANG-MILLS GAUGE INVARIANT THEORY FOR SPACE CURVED ELECTROMAGNETIC FIELD Algirdas Antano Maknickas Institute of Mechanical Sciences, Vilnius Gediminas Technical University September 3, 04 Abstract. It
Microscopic electrodynamics. Trond Saue (LCPQ, Toulouse) Microscopic electrodynamics Virginia Tech / 46
 Microscopic electrodynamics Trond Saue (LCPQ, Toulouse) Microscopic electrodynamics Virginia Tech 2015 1 / 46 Maxwell s equations for electric field E and magnetic field B in terms of sources ρ and j The
Microscopic electrodynamics Trond Saue (LCPQ, Toulouse) Microscopic electrodynamics Virginia Tech 2015 1 / 46 Maxwell s equations for electric field E and magnetic field B in terms of sources ρ and j The
Particle Physics. Michaelmas Term 2011 Prof. Mark Thomson. Handout 2 : The Dirac Equation. Non-Relativistic QM (Revision)
 Particle Physics Michaelmas Term 2011 Prof. Mark Thomson + e - e + - + e - e + - + e - e + - + e - e + - Handout 2 : The Dirac Equation Prof. M.A. Thomson Michaelmas 2011 45 Non-Relativistic QM (Revision)
Particle Physics Michaelmas Term 2011 Prof. Mark Thomson + e - e + - + e - e + - + e - e + - + e - e + - Handout 2 : The Dirac Equation Prof. M.A. Thomson Michaelmas 2011 45 Non-Relativistic QM (Revision)
Particle Physics Lecture 1 : Introduction Fall 2015 Seon-Hee Seo
 Particle Physics Lecture 1 : Introduction Fall 2015 Seon-Hee Seo Particle Physics Fall 2015 1 Course Overview Lecture 1: Introduction, Decay Rates and Cross Sections Lecture 2: The Dirac Equation and Spin
Particle Physics Lecture 1 : Introduction Fall 2015 Seon-Hee Seo Particle Physics Fall 2015 1 Course Overview Lecture 1: Introduction, Decay Rates and Cross Sections Lecture 2: The Dirac Equation and Spin
Mechanics Physics 151
 Mechanics Physics 151 Lecture 4 Continuous Systems and Fields (Chapter 13) What We Did Last Time Built Lagrangian formalism for continuous system Lagrangian L Lagrange s equation = L dxdydz Derived simple
Mechanics Physics 151 Lecture 4 Continuous Systems and Fields (Chapter 13) What We Did Last Time Built Lagrangian formalism for continuous system Lagrangian L Lagrange s equation = L dxdydz Derived simple
3.3 Lagrangian and symmetries for a spin- 1 2 field
 3.3 Lagrangian and symmetries for a spin- 1 2 field The Lagrangian for the free spin- 1 2 field is The corresponding Hamiltonian density is L = ψ(i/ µ m)ψ. (3.31) H = ψ( γ p + m)ψ. (3.32) The Lagrangian
3.3 Lagrangian and symmetries for a spin- 1 2 field The Lagrangian for the free spin- 1 2 field is The corresponding Hamiltonian density is L = ψ(i/ µ m)ψ. (3.31) H = ψ( γ p + m)ψ. (3.32) The Lagrangian
Derivation of Electro Weak Unification and Final Form of Standard Model with QCD and Gluons 1 W W W 3
 Derivation of Electro Weak Unification and Final Form of Standard Model with QCD and Gluons 1 W 1 + 2 W 2 + 3 W 3 Substitute B = cos W A + sin W Z 0 Sum over first generation particles. up down Left handed
Derivation of Electro Weak Unification and Final Form of Standard Model with QCD and Gluons 1 W 1 + 2 W 2 + 3 W 3 Substitute B = cos W A + sin W Z 0 Sum over first generation particles. up down Left handed
Particle Physics Dr. Alexander Mitov Handout 2 : The Dirac Equation
 Dr. A. Mitov Particle Physics 45 Particle Physics Dr. Alexander Mitov µ + e - e + µ - µ + e - e + µ - µ + e - e + µ - µ + e - e + µ - Handout 2 : The Dirac Equation Dr. A. Mitov Particle Physics 46 Non-Relativistic
Dr. A. Mitov Particle Physics 45 Particle Physics Dr. Alexander Mitov µ + e - e + µ - µ + e - e + µ - µ + e - e + µ - µ + e - e + µ - Handout 2 : The Dirac Equation Dr. A. Mitov Particle Physics 46 Non-Relativistic
The Klein Gordon Equation
 December 30, 2016 7:35 PM 1. Derivation Let s try to write down the correct relativistic equation of motion for a single particle and then quantize as usual. a. So take (canonical momentum) The Schrödinger
December 30, 2016 7:35 PM 1. Derivation Let s try to write down the correct relativistic equation of motion for a single particle and then quantize as usual. a. So take (canonical momentum) The Schrödinger
4. The Standard Model
 4. The Standard Model Particle and Nuclear Physics Dr. Tina Potter Dr. Tina Potter 4. The Standard Model 1 In this section... Standard Model particle content Klein-Gordon equation Antimatter Interaction
4. The Standard Model Particle and Nuclear Physics Dr. Tina Potter Dr. Tina Potter 4. The Standard Model 1 In this section... Standard Model particle content Klein-Gordon equation Antimatter Interaction
Introduction to Elementary Particles
 David Criffiths Introduction to Elementary Particles Second, Revised Edition WILEY- VCH WILEY-VCH Verlag GmbH & Co. KGaA Preface to the First Edition IX Preface to the Second Edition XI Formulas and Constants
David Criffiths Introduction to Elementary Particles Second, Revised Edition WILEY- VCH WILEY-VCH Verlag GmbH & Co. KGaA Preface to the First Edition IX Preface to the Second Edition XI Formulas and Constants
Dynamics of Relativistic Particles and EM Fields
 October 7, 2008 1 1 J.D.Jackson, Classical Electrodynamics, 3rd Edition, Chapter 12 Lagrangian Hamiltonian for a Relativistic Charged Particle The equations of motion [ d p dt = e E + u ] c B de dt = e
October 7, 2008 1 1 J.D.Jackson, Classical Electrodynamics, 3rd Edition, Chapter 12 Lagrangian Hamiltonian for a Relativistic Charged Particle The equations of motion [ d p dt = e E + u ] c B de dt = e
The Gauge Principle Contents Quantum Electrodynamics SU(N) Gauge Theory Global Gauge Transformations Local Gauge Transformations Dynamics of Field Ten
 Lecture 4 QCD as a Gauge Theory Adnan Bashir, IFM, UMSNH, Mexico August 2013 Hermosillo Sonora The Gauge Principle Contents Quantum Electrodynamics SU(N) Gauge Theory Global Gauge Transformations Local
Lecture 4 QCD as a Gauge Theory Adnan Bashir, IFM, UMSNH, Mexico August 2013 Hermosillo Sonora The Gauge Principle Contents Quantum Electrodynamics SU(N) Gauge Theory Global Gauge Transformations Local
Classical-quantum Correspondence and Wave Packet Solutions of the Dirac Equation in a Curved Spacetime
 Classical-quantum Correspondence and Wave Packet Solutions of the Dirac Equation in a Curved Spacetime Mayeul Arminjon 1,2 and Frank Reifler 3 1 CNRS (Section of Theoretical Physics) 2 Lab. Soils, Solids,
Classical-quantum Correspondence and Wave Packet Solutions of the Dirac Equation in a Curved Spacetime Mayeul Arminjon 1,2 and Frank Reifler 3 1 CNRS (Section of Theoretical Physics) 2 Lab. Soils, Solids,
Classical Field Theory
 April 13, 2010 Field Theory : Introduction A classical field theory is a physical theory that describes the study of how one or more physical fields interact with matter. The word classical is used in
April 13, 2010 Field Theory : Introduction A classical field theory is a physical theory that describes the study of how one or more physical fields interact with matter. The word classical is used in
7 Quantized Free Dirac Fields
 7 Quantized Free Dirac Fields 7.1 The Dirac Equation and Quantum Field Theory The Dirac equation is a relativistic wave equation which describes the quantum dynamics of spinors. We will see in this section
7 Quantized Free Dirac Fields 7.1 The Dirac Equation and Quantum Field Theory The Dirac equation is a relativistic wave equation which describes the quantum dynamics of spinors. We will see in this section
Chapter 10 Operators of the scalar Klein Gordon field. from my book: Understanding Relativistic Quantum Field Theory.
 Chapter 10 Operators of the scalar Klein Gordon field from my book: Understanding Relativistic Quantum Field Theory Hans de Vries November 11, 2008 2 Chapter Contents 10 Operators of the scalar Klein Gordon
Chapter 10 Operators of the scalar Klein Gordon field from my book: Understanding Relativistic Quantum Field Theory Hans de Vries November 11, 2008 2 Chapter Contents 10 Operators of the scalar Klein Gordon
Symmetry Groups conservation law quantum numbers Gauge symmetries local bosons mediate the interaction Group Abelian Product of Groups simple
 Symmetry Groups Symmetry plays an essential role in particle theory. If a theory is invariant under transformations by a symmetry group one obtains a conservation law and quantum numbers. For example,
Symmetry Groups Symmetry plays an essential role in particle theory. If a theory is invariant under transformations by a symmetry group one obtains a conservation law and quantum numbers. For example,
Introduction to particle physics Lecture 9: Gauge invariance
 Introduction to particle physics Lecture 9: Gauge invariance Frank Krauss IPPP Durham U Durham, Epiphany term 2010 1 / 17 Outline 1 Symmetries 2 Classical gauge invariance 3 Phase invariance 4 Generalised
Introduction to particle physics Lecture 9: Gauge invariance Frank Krauss IPPP Durham U Durham, Epiphany term 2010 1 / 17 Outline 1 Symmetries 2 Classical gauge invariance 3 Phase invariance 4 Generalised
Lecture 9 Quantum mechanical description of physical systems MATH-GA Mechanics
 Lecture 9 Quantum mechanical description of physical systems MATH-GA 2710.001 Mechanics 1 Limitations of classical mechanics There are several ways of motivating the study of quantum mechanics. A common
Lecture 9 Quantum mechanical description of physical systems MATH-GA 2710.001 Mechanics 1 Limitations of classical mechanics There are several ways of motivating the study of quantum mechanics. A common
Problem Set #5: 5.2, 5.4, 5.8, 5.12, 5.15, 5.19, 5.24, 5.27, 5.35 (Due Tuesday, April 8th)
 Chapter 5 Magnetostatics Problem Set #5: 5.2, 5.4, 5.8, 5.12, 5.15, 5.19, 5.24, 5.27, 5.35 (Due Tuesday, April 8th 5.1 Lorentz Force So far we were concerned with forces on test charges Q due to static
Chapter 5 Magnetostatics Problem Set #5: 5.2, 5.4, 5.8, 5.12, 5.15, 5.19, 5.24, 5.27, 5.35 (Due Tuesday, April 8th 5.1 Lorentz Force So far we were concerned with forces on test charges Q due to static
Electron-positron pairs can be produced from a photon of energy > twice the rest energy of the electron.
 Particle Physics Positron - discovered in 1932, same mass as electron, same charge but opposite sign, same spin but magnetic moment is parallel to angular momentum. Electron-positron pairs can be produced
Particle Physics Positron - discovered in 1932, same mass as electron, same charge but opposite sign, same spin but magnetic moment is parallel to angular momentum. Electron-positron pairs can be produced
Superintegrable 3D systems in a magnetic field and Cartesian separation of variables
 Superintegrable 3D systems in a magnetic field and Cartesian separation of variables in collaboration with L. Šnobl Czech Technical University in Prague GSD 2017, June 5-10, S. Marinella (Roma), Italy
Superintegrable 3D systems in a magnetic field and Cartesian separation of variables in collaboration with L. Šnobl Czech Technical University in Prague GSD 2017, June 5-10, S. Marinella (Roma), Italy
On Quantum Mechanics
 On Quantum Mechanics F.GHABOUSSI Department of Physics, University of Konstanz P.O. Box 5560, D 78434 Konstanz, Germany arxiv:quant-ph/9805079v3 2 Jun 1998 E-mail: ghabousi@kaluza.physik.uni-konstanz.de
On Quantum Mechanics F.GHABOUSSI Department of Physics, University of Konstanz P.O. Box 5560, D 78434 Konstanz, Germany arxiv:quant-ph/9805079v3 2 Jun 1998 E-mail: ghabousi@kaluza.physik.uni-konstanz.de
Functional determinants
 Functional determinants based on S-53 We are going to discuss situations where a functional determinant depends on some other field and so it cannot be absorbed into the overall normalization of the path
Functional determinants based on S-53 We are going to discuss situations where a functional determinant depends on some other field and so it cannot be absorbed into the overall normalization of the path
Le Modèle Standard et ses extensions
 Particules Élémentaires, Gravitation et Cosmologie Année 2007-08 08 Le Modèle Standard et ses extensions Cours I: 8 février f 2008 Théories de jauge : un rappel Programme du cours 2008 Théories de jauge:
Particules Élémentaires, Gravitation et Cosmologie Année 2007-08 08 Le Modèle Standard et ses extensions Cours I: 8 février f 2008 Théories de jauge : un rappel Programme du cours 2008 Théories de jauge:
A Modern Anatomy of Electron Mass. Abstract
 A Modern Anatomy of Electron Mass Xiangdong Ji and Wei Lu Department of Physics University of Maryland College Park, Maryland 20742 USA (UMD PP#98-093 DOE/ER/40762-145 February 1998) Abstract Motivated
A Modern Anatomy of Electron Mass Xiangdong Ji and Wei Lu Department of Physics University of Maryland College Park, Maryland 20742 USA (UMD PP#98-093 DOE/ER/40762-145 February 1998) Abstract Motivated
We start with some important background material in classical and quantum mechanics.
 Chapter Basics We start with some important background material in classical and quantum mechanics.. Classical mechanics Lagrangian mechanics Compared to Newtonian mechanics, Lagrangian mechanics has the
Chapter Basics We start with some important background material in classical and quantum mechanics.. Classical mechanics Lagrangian mechanics Compared to Newtonian mechanics, Lagrangian mechanics has the
Radiative Processes in Astrophysics
 Radiative Processes in Astrophysics 6. Relativistic Covariance & Kinematics Eline Tolstoy http://www.astro.rug.nl/~etolstoy/astroa07/ Practise, practise, practise... mid-term, 31st may, 9.15-11am As we
Radiative Processes in Astrophysics 6. Relativistic Covariance & Kinematics Eline Tolstoy http://www.astro.rug.nl/~etolstoy/astroa07/ Practise, practise, practise... mid-term, 31st may, 9.15-11am As we
The Strong Interaction and LHC phenomenology
 The Strong Interaction and LHC phenomenology Juan Rojo STFC Rutherford Fellow University of Oxford Theoretical Physics Graduate School course Lecture 2: The QCD Lagrangian, Symmetries and Feynman Rules
The Strong Interaction and LHC phenomenology Juan Rojo STFC Rutherford Fellow University of Oxford Theoretical Physics Graduate School course Lecture 2: The QCD Lagrangian, Symmetries and Feynman Rules
Pions are Special Contents Chiral Symmetry and Its Breaking Symmetries and Conservation Laws Goldstone Theorem The Potential Linear Sigma Model Wigner
 Lecture 3 Pions as Goldstone Bosons of Chiral Symmetry Breaking Adnan Bashir, IFM, UMSNH, Mexico August 2013 Hermosillo Sonora Pions are Special Contents Chiral Symmetry and Its Breaking Symmetries and
Lecture 3 Pions as Goldstone Bosons of Chiral Symmetry Breaking Adnan Bashir, IFM, UMSNH, Mexico August 2013 Hermosillo Sonora Pions are Special Contents Chiral Symmetry and Its Breaking Symmetries and
Loop corrections in Yukawa theory based on S-51
 Loop corrections in Yukawa theory based on S-51 Similarly, the exact Dirac propagator can be written as: Let s consider the theory of a pseudoscalar field and a Dirac field: the only couplings allowed
Loop corrections in Yukawa theory based on S-51 Similarly, the exact Dirac propagator can be written as: Let s consider the theory of a pseudoscalar field and a Dirac field: the only couplings allowed
On the non-relativistic limit of charge conjugation in QED
 arxiv:1001.0757v3 [hep-th] 20 Jun 2010 On the non-relativistic limit of charge conjugation in QED B. Carballo Pérez and M. Socolovsky Instituto de Ciencias Nucleares, Universidad Nacional Autónoma de México,
arxiv:1001.0757v3 [hep-th] 20 Jun 2010 On the non-relativistic limit of charge conjugation in QED B. Carballo Pérez and M. Socolovsky Instituto de Ciencias Nucleares, Universidad Nacional Autónoma de México,
Statistical physics and light-front quantization. JR and S.J. Brodsky, Phys. Rev. D70, (2004) and hep-th/
 Statistical physics and light-front quantization Jörg Raufeisen (Heidelberg U.) JR and S.J. Brodsky, Phys. Rev. D70, 085017 (2004) and hep-th/0409157 Introduction: Dirac s Forms of Hamiltonian Dynamics
Statistical physics and light-front quantization Jörg Raufeisen (Heidelberg U.) JR and S.J. Brodsky, Phys. Rev. D70, 085017 (2004) and hep-th/0409157 Introduction: Dirac s Forms of Hamiltonian Dynamics
REVIEW. Hamilton s principle. based on FW-18. Variational statement of mechanics: (for conservative forces) action Equivalent to Newton s laws!
 Hamilton s principle Variational statement of mechanics: (for conservative forces) action Equivalent to Newton s laws! based on FW-18 REVIEW the particle takes the path that minimizes the integrated difference
Hamilton s principle Variational statement of mechanics: (for conservative forces) action Equivalent to Newton s laws! based on FW-18 REVIEW the particle takes the path that minimizes the integrated difference
129 Lecture Notes Relativistic Quantum Mechanics
 19 Lecture Notes Relativistic Quantum Mechanics 1 Need for Relativistic Quantum Mechanics The interaction of matter and radiation field based on the Hamitonian H = p e c A m Ze r + d x 1 8π E + B. 1 Coulomb
19 Lecture Notes Relativistic Quantum Mechanics 1 Need for Relativistic Quantum Mechanics The interaction of matter and radiation field based on the Hamitonian H = p e c A m Ze r + d x 1 8π E + B. 1 Coulomb
Lecture 4: Equations of motion and canonical quantization Read Sakurai Chapter 1.6 and 1.7
 Lecture 4: Equations of motion and canonical quantization Read Sakurai Chapter 1.6 and 1.7 In Lecture 1 and 2, we have discussed how to represent the state of a quantum mechanical system based the superposition
Lecture 4: Equations of motion and canonical quantization Read Sakurai Chapter 1.6 and 1.7 In Lecture 1 and 2, we have discussed how to represent the state of a quantum mechanical system based the superposition
Lecture 7. both processes have characteristic associated time Consequence strong interactions conserve more quantum numbers then weak interactions
 Lecture 7 Conserved quantities: energy, momentum, angular momentum Conserved quantum numbers: baryon number, strangeness, Particles can be produced by strong interactions eg. pair of K mesons with opposite
Lecture 7 Conserved quantities: energy, momentum, angular momentum Conserved quantum numbers: baryon number, strangeness, Particles can be produced by strong interactions eg. pair of K mesons with opposite
The Dirac Field. Physics , Quantum Field Theory. October Michael Dine Department of Physics University of California, Santa Cruz
 Michael Dine Department of Physics University of California, Santa Cruz October 2013 Lorentz Transformation Properties of the Dirac Field First, rotations. In ordinary quantum mechanics, ψ σ i ψ (1) is
Michael Dine Department of Physics University of California, Santa Cruz October 2013 Lorentz Transformation Properties of the Dirac Field First, rotations. In ordinary quantum mechanics, ψ σ i ψ (1) is
YANG-MILLS THEORY. This theory will be invariant under the following U(1) phase transformations
 YANG-MILLS THEORY TOMAS HÄLLGREN Abstract. We give a short introduction to classical Yang-Mills theory. Starting from Abelian symmetries we motivate the transformation laws, the covariant derivative and
YANG-MILLS THEORY TOMAS HÄLLGREN Abstract. We give a short introduction to classical Yang-Mills theory. Starting from Abelian symmetries we motivate the transformation laws, the covariant derivative and
Lecture 5: Orbital angular momentum, spin and rotation
 Lecture 5: Orbital angular momentum, spin and rotation 1 Orbital angular momentum operator According to the classic expression of orbital angular momentum L = r p, we define the quantum operator L x =
Lecture 5: Orbital angular momentum, spin and rotation 1 Orbital angular momentum operator According to the classic expression of orbital angular momentum L = r p, we define the quantum operator L x =
d 3 k In the same non-relativistic normalization x k = exp(ikk),
 PHY 396 K. Solutions for homework set #3. Problem 1a: The Hamiltonian 7.1 of a free relativistic particle and hence the evolution operator exp itĥ are functions of the momentum operator ˆp, so they diagonalize
PHY 396 K. Solutions for homework set #3. Problem 1a: The Hamiltonian 7.1 of a free relativistic particle and hence the evolution operator exp itĥ are functions of the momentum operator ˆp, so they diagonalize
129 Lecture Notes More on Dirac Equation
 19 Lecture Notes More on Dirac Equation 1 Ultra-relativistic Limit We have solved the Diraction in the Lecture Notes on Relativistic Quantum Mechanics, and saw that the upper lower two components are large
19 Lecture Notes More on Dirac Equation 1 Ultra-relativistic Limit We have solved the Diraction in the Lecture Notes on Relativistic Quantum Mechanics, and saw that the upper lower two components are large
PY 351 Modern Physics - Lecture notes, 3
 PY 351 Modern Physics - Lecture notes, 3 Copyright by Claudio Rebbi, Boston University, October 2016. These notes cannot be duplicated and distributed without explicit permission of the author. Time dependence
PY 351 Modern Physics - Lecture notes, 3 Copyright by Claudio Rebbi, Boston University, October 2016. These notes cannot be duplicated and distributed without explicit permission of the author. Time dependence
Lectures April 29, May
 Lectures 25-26 April 29, May 4 2010 Electromagnetism controls most of physics from the atomic to the planetary scale, we have spent nearly a year exploring the concrete consequences of Maxwell s equations
Lectures 25-26 April 29, May 4 2010 Electromagnetism controls most of physics from the atomic to the planetary scale, we have spent nearly a year exploring the concrete consequences of Maxwell s equations
Electromagnetic. G. A. Krafft Jefferson Lab Jefferson Lab Professor of Physics Old Dominion University TAADI Electromagnetic Theory
 TAAD1 Electromagnetic Theory G. A. Krafft Jefferson Lab Jefferson Lab Professor of Physics Old Dominion University 8-31-12 Classical Electrodynamics A main physics discovery of the last half of the 2 th
TAAD1 Electromagnetic Theory G. A. Krafft Jefferson Lab Jefferson Lab Professor of Physics Old Dominion University 8-31-12 Classical Electrodynamics A main physics discovery of the last half of the 2 th
G : Quantum Mechanics II
 G5.666: Quantum Mechanics II Notes for Lecture 5 I. REPRESENTING STATES IN THE FULL HILBERT SPACE Given a representation of the states that span the spin Hilbert space, we now need to consider the problem
G5.666: Quantum Mechanics II Notes for Lecture 5 I. REPRESENTING STATES IN THE FULL HILBERT SPACE Given a representation of the states that span the spin Hilbert space, we now need to consider the problem
Quantization of a Scalar Field
 Quantization of a Scalar Field Required reading: Zwiebach 0.-4,.4 Suggested reading: Your favorite quantum text Any quantum field theory text Quantizing a harmonic oscillator: Let s start by reviewing
Quantization of a Scalar Field Required reading: Zwiebach 0.-4,.4 Suggested reading: Your favorite quantum text Any quantum field theory text Quantizing a harmonic oscillator: Let s start by reviewing
The Dirac Equation. Topic 3 Spinors, Fermion Fields, Dirac Fields Lecture 13
 The Dirac Equation Dirac s discovery of a relativistic wave equation for the electron was published in 1928 soon after the concept of intrisic spin angular momentum was proposed by Goudsmit and Uhlenbeck
The Dirac Equation Dirac s discovery of a relativistic wave equation for the electron was published in 1928 soon after the concept of intrisic spin angular momentum was proposed by Goudsmit and Uhlenbeck
DISCRETE SYMMETRIES IN NUCLEAR AND PARTICLE PHYSICS. Parity PHYS NUCLEAR AND PARTICLE PHYSICS
 PHYS 30121 NUCLEAR AND PARTICLE PHYSICS DISCRETE SYMMETRIES IN NUCLEAR AND PARTICLE PHYSICS Discrete symmetries are ones that do not depend on any continuous parameter. The classic example is reflection
PHYS 30121 NUCLEAR AND PARTICLE PHYSICS DISCRETE SYMMETRIES IN NUCLEAR AND PARTICLE PHYSICS Discrete symmetries are ones that do not depend on any continuous parameter. The classic example is reflection
arxiv: v2 [math-ph] 10 Aug 2011
![arxiv: v2 [math-ph] 10 Aug 2011 arxiv: v2 [math-ph] 10 Aug 2011](/thumbs/85/92996566.jpg) Classical mechanics in reparametrization-invariant formulation and the Schrödinger equation A. A. Deriglazov and B. F. Rizzuti Depto. de Matemática, ICE, Universidade Federal de Juiz de Fora, MG, Brazil
Classical mechanics in reparametrization-invariant formulation and the Schrödinger equation A. A. Deriglazov and B. F. Rizzuti Depto. de Matemática, ICE, Universidade Federal de Juiz de Fora, MG, Brazil
Lecture 10. September 28, 2017
 Lecture 10 September 28, 2017 The Standard Model s QCD theory Comments on QED calculations Ø The general approach using Feynman diagrams Ø Example of a LO calculation Ø Higher order calculations and running
Lecture 10 September 28, 2017 The Standard Model s QCD theory Comments on QED calculations Ø The general approach using Feynman diagrams Ø Example of a LO calculation Ø Higher order calculations and running
( ) ( ) ( ) Invariance Principles & Conservation Laws. = P δx. Summary of key point of argument
 Invariance Principles & Conservation Laws Without invariance principles, there would be no laws of physics! We rely on the results of experiments remaining the same from day to day and place to place.
Invariance Principles & Conservation Laws Without invariance principles, there would be no laws of physics! We rely on the results of experiments remaining the same from day to day and place to place.
Minimal coupling and Berry s phase
 Phys460.nb 63 5 Minimal coupling Berry s phase Q: For charged quantum particles (e.g. electrons), if we apply an E&M field (E or B), the particle will feel the field. How do we consider the effect E B
Phys460.nb 63 5 Minimal coupling Berry s phase Q: For charged quantum particles (e.g. electrons), if we apply an E&M field (E or B), the particle will feel the field. How do we consider the effect E B
Curves in the configuration space Q or in the velocity phase space Ω satisfying the Euler-Lagrange (EL) equations,
 Physics 6010, Fall 2010 Hamiltonian Formalism: Hamilton s equations. Conservation laws. Reduction. Poisson Brackets. Relevant Sections in Text: 8.1 8.3, 9.5 The Hamiltonian Formalism We now return to formal
Physics 6010, Fall 2010 Hamiltonian Formalism: Hamilton s equations. Conservation laws. Reduction. Poisson Brackets. Relevant Sections in Text: 8.1 8.3, 9.5 The Hamiltonian Formalism We now return to formal
Introduction to Path Integrals
 Introduction to Path Integrals Consider ordinary quantum mechanics of a single particle in one space dimension. Let s work in the coordinate space and study the evolution kernel Ut B, x B ; T A, x A )
Introduction to Path Integrals Consider ordinary quantum mechanics of a single particle in one space dimension. Let s work in the coordinate space and study the evolution kernel Ut B, x B ; T A, x A )
d 2 Area i K i0 ν 0 (S.2) when the integral is taken over the whole space, hence the second eq. (1.12).
 PHY 396 K. Solutions for prolem set #. Prolem 1a: Let T µν = λ K λµ ν. Regardless of the specific form of the K λµ ν φ, φ tensor, its antisymmetry with respect to its first two indices K λµ ν K µλ ν implies
PHY 396 K. Solutions for prolem set #. Prolem 1a: Let T µν = λ K λµ ν. Regardless of the specific form of the K λµ ν φ, φ tensor, its antisymmetry with respect to its first two indices K λµ ν K µλ ν implies
Quantum Field Theory II
 Quantum Field Theory II T. Nguyen PHY 391 Independent Study Term Paper Prof. S.G. Rajeev University of Rochester April 2, 218 1 Introduction The purpose of this independent study is to familiarize ourselves
Quantum Field Theory II T. Nguyen PHY 391 Independent Study Term Paper Prof. S.G. Rajeev University of Rochester April 2, 218 1 Introduction The purpose of this independent study is to familiarize ourselves
