Probability - Lecture 4
|
|
|
- Austin Holmes
- 5 years ago
- Views:
Transcription
1 1 Introduction Probability - Lecture 4 Many methods of computation physics and the comparison of data to a mathematical representation, apply stochastic methods. These ideas were first introduced in the theory of dilute gases, and later more fully developed in statistical mechanics. The application of statistical analysis is based on the observation that processes can be described by the laws of probability. The laws of probability are based on empirical observation. Any conclusion which results from a measurement is uncertain, and we use imprecise data to determine the value of some parameter or to establish a hypothesis. This has two possibilities when applying probabilities. 1. We wish to determine which theory is most compatible with the data. Thus the theory is conditioned by credibility and aesthetics. We have previously discussed Occam s razor, for example. 2. We wish to determine which values of a parameter set are more compatible with a theory. In this case, the measurement is conditioned by the theory. In the case of 1 above, the theory itself is determined by statistical analysis, so a firm conclusion cannot be made. In the case of 2, there is always some uncertainty in the measurement. In general, the application of statistics to analysis introduces uncertainty, either in the theory or in the parameters. 2 Definitions The outcome of any observation can depend on many parameters, some measured and some unknown. In any experiment, one tries to hold as many parameters constant, especially those which primarily effect the result. The fluctuation in parameters leads to uncertainty in the measurement and produces a range of results for a number of identical measurements. This range of values is called a statistical distribution. In a simple example, a perfect die is cast N times. Some of the unknowns are the way the die is held, thrown, and/or various environmental parameters. The resulting frequency of the integers that are observed, gives a distribution of discrete sample points. This is illustrated in Figure 1 1
2 N/ Figure 1: An example of a discrete probability distribution of a die thrown N times N = dx n(x) L X Figure 2: An example of a continuous distribution obtained by measuring a length On the other hand, suppose one obtains a distribution of measurements of the length of a rod. This distribution is continuous, and the area under the curve equals N. A continuous distribution is illustrated in Figure 2. The word random is used to describe the fluctuations in the results of processes described above. However, random is difficult to define. It is easiest to think in terms of the continuous distribution of a variant as in Figure 2, although application to a discrete example will also be obvious. Define the probability as the limit in the ratio of the number of times a particular observation occurs divided by the total number of observations, as the number of observations. In this case, a uniform distribution has equal probabilities for each observation for each interval of the variant. Thus suppose an interval, X, of the variant, X, where X is either discrete or continuous. Then the outcome of any observation which falls in the interval x is described as random. Although the results of an individual outcome cannot be predicted, a statistical distribution of a set of observations can be modeled and predicted. Note in the case of the discrete distribution, if the number of observations within any integer interval X = (n + 1) n is not equal, the distribution is not random. The above definitions are a frequentist approach to probability. This is the classical understanding of probability and statistics, and is closer to scientific reasoning since it can be determined independently of the observer. It is related to the frequency of the occurrence of an event, but it is restricted to repeatable observations. 2
3 There is another definition of probability called the Bayesian approach or subjective probability. The Bayesian approach is interpreted as the degree of belief that an observation will occur. For hypothesis testing and parameter estimation, the numerical results are essentially the same as the frequentist approach. However, an exact frequentist approach requires as input, probabilities of all data, including data observed and data not observed. Obviously an impossibility. An exact Bayesian approach requires an input of all prior beliefs of the observer, and this also is not possible and is subjective. For testing goodness of fit of a single hypothesis, one cannot obtain results in the Bayesian approach. On the other hand, decision theory is subjective, and cannot be handled by the frequentist. There is also confusion in the language of statistics. We apply the language of physics here, but that of the statistician is sometimes different. See Table 1 for examples. Table 1: Language comparison of definitions between a physicist and a statistician Physics Determine Estimate Data Data Size Statistics Estimate Guess Sample Population Finally the following ISO definitions are useful as these are the defined standard. Probability - Probability is the expectation of the occurrence of an event. It is a normalized number between 0 and 1. The number 0 means there is no chance of occurring, and the number 1 means that it will always occur. Event - a labeled occurrence written as X i where i is the event number. X is the total number of events in a set and X is the number of events outside the set X. Thus; P(X) + P(X) = 1. Uncertainty - Uncertainty is defined as the parameter associated with a measurement which characterizes the dispersion of values that could reasonably be attributed to the measurement. Note the word reasonably. Error - Error is the result of a measurement minus the true value of the parameter. As such, this is not really known as the true value of any measurement is unknown. 3
4 True Value - The true value is the exact value of a given parameter Mathematical Probability - The abstract mathematical concept defined by a set of laws or axioms (Kolmogorov axioms). For a set of events X i which are exclusive, ie if one occurs then no other event is possible, then the axioms state; 1. P(x i ) 0 2. P(X i or X j ) = P(X i ) + P(X j ) 3. i P(X i ) = 1 Frequentist Probability - For a set of n events which are observed during a total of N observations. Then; P(X) = lim N n N Obviously, this last axiom is not possible, but it does show that the freqentist approach requires repeatable experiments. Thus one cannot use the frequentist approach to predict whether the sun will rise tomorrow using the fact that it has risen for the last 4 million years. The reason the sun shines today is not why is shone yesterday. Bayesian Probability - Bayesian probability is based on the belief that an event will occur. This is defined by what is called the coherent bet. The coherent bet is a number between 0 and 1 which an observer places that an event will occur. It has the properties that; 1. The bet depends as much on the observer as the system under observation 2. It depends on the knowledge of the observer and can change as knowledge is gained 3 Examples The physical review has a new policy which is intended to increase the significance of the articles that are published. In a paper, experimenters fit their results using an incorrect 4
5 hypothesis, but extract a parameter with better precision than previously. The paper is published. Statistically the error is small, but the published result is completely incorrect. The stock market generates volumes of data and one can always find correlations if one selectively looks for them. These back testing models have been used by various money managers without knowledge of statistics. To prove irresponsible data mining, one statistician tested correlations of the stock market with the annual butter production in Bangladesh and reproduced the S&P return correctly 75% of the time. If he included the production of cheese in the US and the population of sheep in Bangladesh, he was correct 99% of the time over a 10 year period. Remember Garbage in = Garbage out As a final example, suppose a test for H1N1 virus has a probability of being 100% positive if someone has the H1N1 virus and a probability of 0.2% positive if someone does not have the virus. Does this mean a person with a positive test is 99.8% likely to have the virus? The answer is no. Look at this more closely. Suppose a population of 10 8 people and a chance of infection of 0.1% in this population. If everyone were tested one would find 10 5 infections, and [ ]x x10 5 positive tests in uninfected people. Then the probability that a positive test is a result of infection is; P(Infection/[H1N1 + H1N1]) = = 0.33 This later example requires an understanding of conditional probability which is discussed in the next section. 4 Combining Probabilities The best way to understand how probabilities are combined to visualize a combination of sets of elements. A pictorial diagram is shown in Figure refaunionb which illustrates the intersection of two sets A and B. Probability is defined as a continuous measure on the interval between 0 and 1. If an event has no chance of occurring it has probability 0, if it always occurs it has probability 1. Success is the occurrence of an observation, and a success of event X is given a probability, P(X). A failure is written P(X) so that as previously, P(X) + P(X) = 1 Then suppose two non-exclusive sets such as A and B in the figure. The probability of an event occurring which is contained in either A or B is given by; P(A or B) = P(A) + P(B) P(A B) 5
6 A B A B A B Figure 3: The intersection of the sets A B and the union of these sets A B Obviously the subtraction of P(A B) prevents double counting this intersection. For a number n of mutually exclusive events, X i we have; P(X) = i P(X i ) In set theory; P(X 1 X 2 X n ) = i P(X i ) As an example, suppose one asks for the probability of drawing a face card from a deck of cards with replacement and reshuffling before each card is drawn. The probability of drawing any card is 1/52 and as there are 4 cards the probability of drawing a jack is 4/52. There are 3 face cards so the probability of drawing a face card is (3x4)/52. The observation here is that drawing any card has the same probability, and is the occurrence of any draw is random. The probability of drawing the full set of cards is normalized to 1. The conditional probability of the occurrence of an event A given that event B has occurred is written, P(A/B). This is the probability that an event known to belong to the set B, is also in the set A. This is defined by; P(A and B) = P(A B) = P(A/B)P(B) = P(B/A)P(A) The sets A and B are independent if; P(A/B) = P(A) The occurrence of B is irrelevant to the occurrence of A. Thus if A is independent of B; 6
7 P(A B) = P(A) P(B) The expression that links P(A/B) to P(B/A) above is Bayes theorem. It is stated; P(A/B) = P(B/A) P(A) P(B) Then if A i are exclusive and exhaustive sets (ie each event must belong to one and only one of the sets A i ), then Bayes theorem becomes; P(A i /B) = P(B/A i) P(A i ) P(B/A i ) P(A i ) i The denominator is the normalization for all possibilities for the occurrence of B. Now as an example, suppose an experiment is designed to look for decays of a particle. It is desired to know if one counter is sufficient to detect the decay in the presence of a background. Let; P(B) be the probability of any event in the detector P(A) be the probability of the occurrence of the event which is sought P(B/A) is the probability that a true event gives a signal in the detector P(A/B) is the probability of a true event is an event is observed P(B) is measured by turning on the detector to observe events. P(A) is assumed known from other experiments. P(A/B) is calculated from measured efficiencies of the detector. This then determines P(A/B) the probability that is desired. However, when A or B is not a set of events but an hypothesis, then the interpretation is not so clear. This case will be discussed later. 5 Probability of a sequence of events Suppose one wants the probability of a sequence of successes in a probability set, ie the probability of P(X 1 ) and P(X 1 ) and and P(X N ). Begin by looking for the probability of when events, X 2, occurs after event 1, X 1. This is that part of X 2 which in included in 7
8 X 1, or X 1 X 2. P(X 1 X 2 ) = P(X 2 /X 1 )P(X 1 ) = P(X 1 /X 2 )P(X 2 ) In the above, P(X 2 /X 1 ) is the conditional probability that X 2 will occur after X 1 has occurred. This leads to the result; P(X 2 /X 1 ) = P(X 1 X 2 ) P(x 1 ) Note that this probability is normalized by the probability, P(X 1 ), ie the probability that both X 1 and X 2 occur divided by the probability that X 1 occurs. If the occurrence of X 1 and X 2 are independent, then; P(X 2 /X 1 ) = P(X 1)P(X 2 ) P(X 1 ) = P(X 2 ) In the general case when the occurrence of each event is independent; P(X T ) = P(X 1 )P(X 2 ) P(X N ) Consider the following example. We wish to find the probability of drawing a red jack from a randomly shuffled deck of cards. The fact that the card is a jack and the color is red are independent. Thus; P T = P(drawing a Jack)P(drawing a red card) = (4/52)(1/2) = 1/26 Obviously one could obtain this result by counting possibilities using the probability of drawing one card from a deck of only red cards, 2/52. This is a frequentist approach to obtaining the probability. Now suppose the events are not mutually exclusive. Previously we found; P(X 1 X 2 ) = P(X 1 ) + P(X 2 ) P(x 1 ) P(X 2 ) We use this to obtain the probability of 2 cards drawn with replacement from a randomly shuffled deck. We wish that at least one of the cards is a jack. The possibilities are shown in the probability tree in Table 2. Obviously there are 4 possibilities and three lead to success. We cannot add probabilities here because the probability of drawing one jack is not mutually exclusive in all draws, ie the first event is included in both X 1 and X 2. The result is most easily obtained by subtracting the double failure which is counted only once in Table 2, but we may also use the above equation to evaluate P(X 1 X 2 ). The probability of a failure to draw a jack is (1 4/52). A double failure to draw a jack is the square of this factor, so the probability of drawing at least one jack is; 8
9 P(at least 1 jack) = 1 [1 4/52] 2 = (2/13)[1 1/13] Then using the union of X 1 and X 2 one obtains; P(X 1 X 2 ) = P(X 1 ) + P(X 2 ) P(X 1 ) P(X 2 ) Substituting values; P(at least 1 jack) = [4/52] + [4/52] ([4/52][4/52]) = (2/13)[1 1/13] The last term is the probability of drawing 2 jacks and contains the overlap of the 2 sets, X 1 and X 2. 6 Bayes theorem We previously obtained an expression for the conditional probability of event X 2 when it occurs after event X 1. This was stated in Bayes theorem. P(X 2 /X 1 )P(X 1 ) = P(X 1 /X 2 )P(X 2 ) = P(X 1 X 2 ) Note that P(X 2 /X 1 ) can be different from P(X 1 /X 2 ). For example, the probability of a physics professor given all people wearing sandals is not the same as the probability of wearing sandals given all physics professors. Bayes theorem can be used to update beliefs (probabilities) using the axioms of combining probability. Return to the probability for drawing a jack. Let X 1 represent success on the first try and X 2 success on the second. Then ; P(X 1 /X 2 ) = P(X 1 X 2 ) P(X 1 ) = (4/51)(4/52) (4/52) = (4/52) Table 2: The probability tree of drawing a jack on 2 separate draws from a random deck with replacement First Draw Jack Drawn (success) Jack Drawn (success) Jack Drawn (failure) Jack Drawn (failure) Second Draw Jack Drawn (success) Jack not Drawn (failure) Jack Drawn (success) Jack Drawn (failure) 9
10 As expected the probability of drawing a jack on the second draw is independent of what happened on the first draw, assuming replacement and reshuffling. 7 Model Likelihood Now consider a model. M with parameters, w. We want to fit data by varying the parameters of the model. First determine the Likelihood (ie given a set of parameters w and a model, M, determine the probability of a data set, D). This is written P(D/wM), which is the probability of the data given the model and parameters.use Bayes theorem to write; P(w/DM) = P(D/wM)P(w/M) P(D/M) What we are trying to find is the probability of the parameter set given the model and the data. The term on the right is the Likelihood, P(D/wM) and P(w/M) is the probability distribution of the parameters without the data. The denominator is the normalization. P(D/M) = k P(D/w k M)P(w k /M) The above equation relates a prior probability, P(w/M), to a posterior probability P(w/DM) by conditioning the prior probability with the Likelihood. In most cases one can ignore the normalization term as we want the shape of the distribution. As another example, you meet a friend in a pub and agree that the one with the lowest value on a roll of a die will pay for the beer. The friend always wins. What is the probability that he cheats? There are two hypothesis, 1) Cheats (C), or 2) Honest (H). Begin by assuming that the probability of cheating is low. Propose that a cheater always wins, thus P(C) = 1 and honest behavior has a probability P(H) = (1/2). Assume the die is rolled n times. Thus P(w n /C) = (1/2) n. Use by Bayes theorem; P(C/w n ) = P(w n /C)P 0 (C) P(w n /C)P 0 (C) + P(w n /C)P 0 (H) In the above, P 0 are the initial assumptions. Thus; P(C/w n ) = 1 P 0 (C) 1 P 0 (C) + 2 n P 0 (H) Running the probabilities by updating the priors (P 0 ) Table 3 is produced. Thus Bayesian probability allows an updating probability as events are collected. Note that the result after a number of tries becomes independent of the initial guess. Finally look at the probability of throwing two dice one showing the number 1 and in addition the 10
11 sum of the numbers showing on the faces is an odd. We can do this by the frequentist approach using counting. Table 4 gives the 6 6 = 36 possibilities. In the Table 4, the bold faced pair of numbers show the possibilities of having an odd sum of the face value of the dice with at least one die that shows a 1. There are 6 possibilities out of a set of 36, so the probability is 1/6. Let A be an event when the sum of the numbers of dice is odd, P(A) = 1/2. Let B be an events having a number 1 showing in at least one die. Using Bayes theorem; P(A B) = P(A/B)P(B) = P(B/A)P(A) = (6/11)(11/36) = 1/6 Also we find that; P(A B) = (1/2) + 11/36 1/6 = 23/36 By counting, there are 36 possibilities and 6 3 = 18 events where the sum of the faces is odd, and 11 have at least one ace. Also 6 events have one ace and the sum of the faces is odd. Then P(A) = 18/36 and P(B) = 11/36 Table 3: The probability of cheating when throwing dice and always winning P 0 (C) un-normalized P(C/w n ) n = 5 n = 10 n = 15 n = Table 4: Possible outcomes when rolling 2 dice
12 8 Combinatorial analysis Consider a set of N events, X i, which are labeled, X 1, X 2, X N. Choose k of these to form a population of events. Make the choice with replacement so that each selection has N possibilities. The number of possible populations is N k. If the choice is made without replacement, there are N possible, (N 1) second choices, etc. Thus there are, N(N 1) (N k + 1) possible populations. Thus we also see that the number of ways N elements can be reordered is N! (N elements chosen without replacement). What is the probability that no event appears twice in a population (ie no repetition of elements occurs in a set)?. P = N(N 1) (N k + 1) N k As the above expression will be used many times in the future introduce the notation; P = (N) k N k = N(N 1) (N k + 1) N k As an example, random numbers were once selected from the final digits in numbers extracted from a set of mathematical tables with many decimal places. You may test to see if 10 numbers are random by comparing the probability that three (or any reasonable number) of digits are different when selecting a number of sequential digits from some table. One could also select numbers from a non-repeating fraction or some irrational number like π or e. The probability that one obtains 3 different numbers is P 3 = = 0.72 To perform a sequence test for randomness, consider the number, e = The first 800 decimals form 160 groups of 5 digits each. Arrange these in 16 groups of ten, 5 digit numbers. The number of subgroups in each of the 16 groups which have all 5 digits different are shown in Table 5. Table 5: The number of subgroups which have 5 separate digits as selected from the sample of 160 groups of 5 digits extracted from the first 800 digits representing e Group Number Group Number Group Number Group Number Number w/o repeats Number w/o repeats Number w/o repeats Number w/o repeats
13 The total number of sub-groups with different digits is (sum of the numbers) 52 and there are 160 such groups, so the probability for a group to not have a repeating number is; P T = 52/160 = Then apply the combinatorial probability as previously developed. P Tc = (10) = = This test, at least to its statistical accuracy, indicates the number string is random. Now consider the birthdays of k people which form a sample size from the number of days in a year. Assume all years have 365 days and that birthdays are equally probable on any day. The probability that in this sample size all birthdays are different is ; P D = (365) k (365) k For k = 23 we find that P D = 1/2. Thus for 23 people the probability of at least 2 people having the same birthday is 1 P D = 1/2 Suppose we choose k elements of a population of size N. We know that there are (N) k samples. Now the k elements can be arranged in k! ways. If X is the number of populations of size K the number of ordered samples is X k! (number of samples times the number of ways to order them). X k! = (N) k X = (N) k k! = N(N 1) (N K + 1) k! = ( N k The last term defines the( binomial ) coefficient. Out of a group of N elements we can choose N a group of k elements in different ways. The elements are indistinguishable. k ( ) 52 As an example, there are = 2, 598, 960 different ways to distribute cards in 5 card 5 stud poker. What( is the) probability that a hand contains 5 different card values? The cards 13 can be chosen in ways and there are 4 suits for each card. Thus; 5 ) ) P C = ( ( ) =
14 As another example, suppose 5 balls (1,2,3,4,5), and pick 3. This results in the following combinations; (123), (134), (145), (234), (245), (345), (124), (125), (135) The above also has a multiplication factor if the balls are reordered within each selection. This gives at total 10 3! = 60 possibilities but only 10 distinguishable ones if the balls are indistinguishable within each group of 3. We count the number of possibilities by recognizing that we can choose the first ball in 5 ways, the second in (5-1=4) ways, and the third in (5-1-1=3) ways. Thus we write the possibilities as; N T = = 60 To generalize, write this as ; ( ) ( N 5 N T = = k 3 ) = ! = 10 Then there are 3! = 6 ways to reorder the balls within each group. Using the frequency definition of probability, we develop probability distributions for various ways to distribute a set of events into cells. In the case that the balls are distinguishable; P = 3! (5 4 3/3!) = 6/10 9 Occupancy Problems Use the model of placing k elements into N cells to determine the probability of various occupancy distributions (ie the probability of finding a particular distribution of k elements among N cells. There are N k possible distributions each with an equal probability of 1/N k. Cell occupancy is defined by the notation, k = k 1 + k 2 + k N. Here k i represents the number of elements in the i th cell. The elements are indistinguishable. The resulting distributions are indistinguishable only if the ordered n-tuples (k 1, k 2,, k N ) are identical. We wish to find the number of possible distributions. Graphically let * represent an element and let a cell be represented by the space between two vertical lines. An example of a distribution is ; In the graphical representation above, the total number of interior lines is 7 and the total number of * is also k = 7. There are N = 8 cells with occupancy (3, 1, 0, 0, 0, 1, 0, 2). Thus we obtain a particular distribution by selecting k positions out of a possible (N 1) + k 14
15 ( ) N + k 1 places. From previous considerations this yields; distributions. In the case k when only one particle per cell is allowed, the n k ( < N ) and the number of ways to put k N elements in N cells with no more than 1 per cell is. k As an example, the partial derivatives of a function do not depend on the order in which they( are taken. Let ) each variable correspond to a cell and select k derivatives. Thus there N + k 1 are partial derivatives of k k th order. Thus a function of 3 variables has 15 derivatives of 4 th order. ( ) ( ) N + k Number = = = 15 k 4 Finally consider the number of ways a population of N elements can be divided into k ordered parts having elements k 1, k 2, k j with k j = N. This is given by; j Number = N! k 1!k 2! k j! It there is to be no( order) with in the groups, choose k 1 elements out of the N, so the number N of populations is;. When this is continued for all populations; k ( )( ) ( ) N N k1 N k1 k 2 k1 k 2 k ( ) 3 N k1 k j 2. k j 1 As an example 52 cards are partitioned into 4 equal groups. Thus one has; Number = 52! (13!)(13!)(13!)(13!) There are then 4! ways to distribute one ace to each group. ( ), ( ), ( ), ( ) This leaves 48 cards which must be divided among the 4 groups as described above. The probability is then; P = 4![(48!)/(12!)]4 (52!)/(13!) =
16 10 Moments Suppose we have a set of N random events, X i, and probability of their occurrance f i. The mean value of these events is defined by; µ = (1/N) N i=1 f i X i Then define the moments of this set of events as; µ r = (1/N) N i=1 f i [X i µ] r Thus when 0 = 1 by completeness; µ 0 = (1/N) N For other moments; i=1 f i = 1 µ 1 = (1/N) N i=1 µ 2 = (1/N) N i=1 f i [X i µ] = 0 f i [X i µ] 2 = σ 2 The spread of the distribution of events is measured by the variance, σ 2. The 3 rd and 4 th moments measure the asymmetry and central peak relative to the distribution tails. A symmetrical distribution has µ 3 = 0. Postitive or negative values represent asymmetric tails to right or left, respectively. This moment is called the skew of the distribution. The 4 th moment divided by µ 2 is called the Kurtosis - peakness - of the central value of the distribution with respect to the tails. As an example suppose one has a distribution of events from a roll of a die. This produces a number from 1 to 6 with probability 1/6. A large number of events would equally populate all possible numbers. Thus the mean, µ = (1/N) j(1/6) = 21N 6N = 3.5. The variance is µ 2 = (1/N) (j 3.5) 2 (1/6) = The moments of a discrete distribution as discussed above can be extended to a continuous distribution. In this case f i f(x) and X i g(x). The function, f(x) is a probability density function. Then; dxf(x) = 1 dxf(x) g(x) = E(g) 16
17 E(g) is the expectation value of the function, g(x). The expectation value for the random variable, X, is µ = dxx f(x) The variance is; σ 2 = E([x µ] 2 ) = E(x 2 ) µ 2 The standard deviation is the square root of the variance, σ = σ 2. The variance may not always exist as the integral may not converge. 17
Sample Space: Specify all possible outcomes from an experiment. Event: Specify a particular outcome or combination of outcomes.
 Chapter 2 Introduction to Probability 2.1 Probability Model Probability concerns about the chance of observing certain outcome resulting from an experiment. However, since chance is an abstraction of something
Chapter 2 Introduction to Probability 2.1 Probability Model Probability concerns about the chance of observing certain outcome resulting from an experiment. However, since chance is an abstraction of something
Discrete Mathematics and Probability Theory Spring 2016 Rao and Walrand Note 14
 CS 70 Discrete Mathematics and Probability Theory Spring 2016 Rao and Walrand Note 14 Introduction One of the key properties of coin flips is independence: if you flip a fair coin ten times and get ten
CS 70 Discrete Mathematics and Probability Theory Spring 2016 Rao and Walrand Note 14 Introduction One of the key properties of coin flips is independence: if you flip a fair coin ten times and get ten
7.1 What is it and why should we care?
 Chapter 7 Probability In this section, we go over some simple concepts from probability theory. We integrate these with ideas from formal language theory in the next chapter. 7.1 What is it and why should
Chapter 7 Probability In this section, we go over some simple concepts from probability theory. We integrate these with ideas from formal language theory in the next chapter. 7.1 What is it and why should
Econ 325: Introduction to Empirical Economics
 Econ 325: Introduction to Empirical Economics Lecture 2 Probability Copyright 2010 Pearson Education, Inc. Publishing as Prentice Hall Ch. 3-1 3.1 Definition Random Experiment a process leading to an uncertain
Econ 325: Introduction to Empirical Economics Lecture 2 Probability Copyright 2010 Pearson Education, Inc. Publishing as Prentice Hall Ch. 3-1 3.1 Definition Random Experiment a process leading to an uncertain
Probability COMP 245 STATISTICS. Dr N A Heard. 1 Sample Spaces and Events Sample Spaces Events Combinations of Events...
 Probability COMP 245 STATISTICS Dr N A Heard Contents Sample Spaces and Events. Sample Spaces........................................2 Events........................................... 2.3 Combinations
Probability COMP 245 STATISTICS Dr N A Heard Contents Sample Spaces and Events. Sample Spaces........................................2 Events........................................... 2.3 Combinations
Fundamentals of Probability CE 311S
 Fundamentals of Probability CE 311S OUTLINE Review Elementary set theory Probability fundamentals: outcomes, sample spaces, events Outline ELEMENTARY SET THEORY Basic probability concepts can be cast in
Fundamentals of Probability CE 311S OUTLINE Review Elementary set theory Probability fundamentals: outcomes, sample spaces, events Outline ELEMENTARY SET THEORY Basic probability concepts can be cast in
Lecture 3 Probability Basics
 Lecture 3 Probability Basics Thais Paiva STA 111 - Summer 2013 Term II July 3, 2013 Lecture Plan 1 Definitions of probability 2 Rules of probability 3 Conditional probability What is Probability? Probability
Lecture 3 Probability Basics Thais Paiva STA 111 - Summer 2013 Term II July 3, 2013 Lecture Plan 1 Definitions of probability 2 Rules of probability 3 Conditional probability What is Probability? Probability
Lecture Notes 1 Basic Probability. Elements of Probability. Conditional probability. Sequential Calculation of Probability
 Lecture Notes 1 Basic Probability Set Theory Elements of Probability Conditional probability Sequential Calculation of Probability Total Probability and Bayes Rule Independence Counting EE 178/278A: Basic
Lecture Notes 1 Basic Probability Set Theory Elements of Probability Conditional probability Sequential Calculation of Probability Total Probability and Bayes Rule Independence Counting EE 178/278A: Basic
Probability (Devore Chapter Two)
 Probability (Devore Chapter Two) 1016-345-01: Probability and Statistics for Engineers Fall 2012 Contents 0 Administrata 2 0.1 Outline....................................... 3 1 Axiomatic Probability 3
Probability (Devore Chapter Two) 1016-345-01: Probability and Statistics for Engineers Fall 2012 Contents 0 Administrata 2 0.1 Outline....................................... 3 1 Axiomatic Probability 3
Probability Theory. Introduction to Probability Theory. Principles of Counting Examples. Principles of Counting. Probability spaces.
 Probability Theory To start out the course, we need to know something about statistics and probability Introduction to Probability Theory L645 Advanced NLP Autumn 2009 This is only an introduction; for
Probability Theory To start out the course, we need to know something about statistics and probability Introduction to Probability Theory L645 Advanced NLP Autumn 2009 This is only an introduction; for
Preliminary Statistics Lecture 2: Probability Theory (Outline) prelimsoas.webs.com
 1 School of Oriental and African Studies September 2015 Department of Economics Preliminary Statistics Lecture 2: Probability Theory (Outline) prelimsoas.webs.com Gujarati D. Basic Econometrics, Appendix
1 School of Oriental and African Studies September 2015 Department of Economics Preliminary Statistics Lecture 2: Probability Theory (Outline) prelimsoas.webs.com Gujarati D. Basic Econometrics, Appendix
MATH MW Elementary Probability Course Notes Part I: Models and Counting
 MATH 2030 3.00MW Elementary Probability Course Notes Part I: Models and Counting Tom Salisbury salt@yorku.ca York University Winter 2010 Introduction [Jan 5] Probability: the mathematics used for Statistics
MATH 2030 3.00MW Elementary Probability Course Notes Part I: Models and Counting Tom Salisbury salt@yorku.ca York University Winter 2010 Introduction [Jan 5] Probability: the mathematics used for Statistics
18.600: Lecture 3 What is probability?
 18.600: Lecture 3 What is probability? Scott Sheffield MIT Outline Formalizing probability Sample space DeMorgan s laws Axioms of probability Outline Formalizing probability Sample space DeMorgan s laws
18.600: Lecture 3 What is probability? Scott Sheffield MIT Outline Formalizing probability Sample space DeMorgan s laws Axioms of probability Outline Formalizing probability Sample space DeMorgan s laws
I - Probability. What is Probability? the chance of an event occuring. 1classical probability. 2empirical probability. 3subjective probability
 What is Probability? the chance of an event occuring eg 1classical probability 2empirical probability 3subjective probability Section 2 - Probability (1) Probability - Terminology random (probability)
What is Probability? the chance of an event occuring eg 1classical probability 2empirical probability 3subjective probability Section 2 - Probability (1) Probability - Terminology random (probability)
STT When trying to evaluate the likelihood of random events we are using following wording.
 Introduction to Chapter 2. Probability. When trying to evaluate the likelihood of random events we are using following wording. Provide your own corresponding examples. Subjective probability. An individual
Introduction to Chapter 2. Probability. When trying to evaluate the likelihood of random events we are using following wording. Provide your own corresponding examples. Subjective probability. An individual
2) There should be uncertainty as to which outcome will occur before the procedure takes place.
 robability Numbers For many statisticians the concept of the probability that an event occurs is ultimately rooted in the interpretation of an event as an outcome of an experiment, others would interpret
robability Numbers For many statisticians the concept of the probability that an event occurs is ultimately rooted in the interpretation of an event as an outcome of an experiment, others would interpret
Review Counting Principles Theorems Examples. John Venn. Arthur Berg Counting Rules 2/ 21
 Counting Rules John Venn Arthur Berg Counting Rules 2/ 21 Augustus De Morgan Arthur Berg Counting Rules 3/ 21 Algebraic Laws Let S be a sample space and A, B, C be three events in S. Commutative Laws:
Counting Rules John Venn Arthur Berg Counting Rules 2/ 21 Augustus De Morgan Arthur Berg Counting Rules 3/ 21 Algebraic Laws Let S be a sample space and A, B, C be three events in S. Commutative Laws:
Probability Theory and Random Variables
 Probability Theory and Random Variables One of the most noticeable aspects of many computer science related phenomena is the lack of certainty. When a job is submitted to a batch oriented computer system,
Probability Theory and Random Variables One of the most noticeable aspects of many computer science related phenomena is the lack of certainty. When a job is submitted to a batch oriented computer system,
Probability Experiments, Trials, Outcomes, Sample Spaces Example 1 Example 2
 Probability Probability is the study of uncertain events or outcomes. Games of chance that involve rolling dice or dealing cards are one obvious area of application. However, probability models underlie
Probability Probability is the study of uncertain events or outcomes. Games of chance that involve rolling dice or dealing cards are one obvious area of application. However, probability models underlie
Review Basic Probability Concept
 Economic Risk and Decision Analysis for Oil and Gas Industry CE81.9008 School of Engineering and Technology Asian Institute of Technology January Semester Presented by Dr. Thitisak Boonpramote Department
Economic Risk and Decision Analysis for Oil and Gas Industry CE81.9008 School of Engineering and Technology Asian Institute of Technology January Semester Presented by Dr. Thitisak Boonpramote Department
Deep Learning for Computer Vision
 Deep Learning for Computer Vision Lecture 3: Probability, Bayes Theorem, and Bayes Classification Peter Belhumeur Computer Science Columbia University Probability Should you play this game? Game: A fair
Deep Learning for Computer Vision Lecture 3: Probability, Bayes Theorem, and Bayes Classification Peter Belhumeur Computer Science Columbia University Probability Should you play this game? Game: A fair
Discrete Random Variables
 Discrete Random Variables An Undergraduate Introduction to Financial Mathematics J. Robert Buchanan 2014 Introduction The markets can be thought of as a complex interaction of a large number of random
Discrete Random Variables An Undergraduate Introduction to Financial Mathematics J. Robert Buchanan 2014 Introduction The markets can be thought of as a complex interaction of a large number of random
CMPSCI 240: Reasoning about Uncertainty
 CMPSCI 240: Reasoning about Uncertainty Lecture 2: Sets and Events Andrew McGregor University of Massachusetts Last Compiled: January 27, 2017 Outline 1 Recap 2 Experiments and Events 3 Probabilistic Models
CMPSCI 240: Reasoning about Uncertainty Lecture 2: Sets and Events Andrew McGregor University of Massachusetts Last Compiled: January 27, 2017 Outline 1 Recap 2 Experiments and Events 3 Probabilistic Models
Probability Year 10. Terminology
 Probability Year 10 Terminology Probability measures the chance something happens. Formally, we say it measures how likely is the outcome of an event. We write P(result) as a shorthand. An event is some
Probability Year 10 Terminology Probability measures the chance something happens. Formally, we say it measures how likely is the outcome of an event. We write P(result) as a shorthand. An event is some
Single Maths B: Introduction to Probability
 Single Maths B: Introduction to Probability Overview Lecturer Email Office Homework Webpage Dr Jonathan Cumming j.a.cumming@durham.ac.uk CM233 None! http://maths.dur.ac.uk/stats/people/jac/singleb/ 1 Introduction
Single Maths B: Introduction to Probability Overview Lecturer Email Office Homework Webpage Dr Jonathan Cumming j.a.cumming@durham.ac.uk CM233 None! http://maths.dur.ac.uk/stats/people/jac/singleb/ 1 Introduction
Recitation 2: Probability
 Recitation 2: Probability Colin White, Kenny Marino January 23, 2018 Outline Facts about sets Definitions and facts about probability Random Variables and Joint Distributions Characteristics of distributions
Recitation 2: Probability Colin White, Kenny Marino January 23, 2018 Outline Facts about sets Definitions and facts about probability Random Variables and Joint Distributions Characteristics of distributions
Probability & Random Variables
 & Random Variables Probability Probability theory is the branch of math that deals with random events, processes, and variables What does randomness mean to you? How would you define probability in your
& Random Variables Probability Probability theory is the branch of math that deals with random events, processes, and variables What does randomness mean to you? How would you define probability in your
Probability Year 9. Terminology
 Probability Year 9 Terminology Probability measures the chance something happens. Formally, we say it measures how likely is the outcome of an event. We write P(result) as a shorthand. An event is some
Probability Year 9 Terminology Probability measures the chance something happens. Formally, we say it measures how likely is the outcome of an event. We write P(result) as a shorthand. An event is some
What is Probability? Probability. Sample Spaces and Events. Simple Event
 What is Probability? Probability Peter Lo Probability is the numerical measure of likelihood that the event will occur. Simple Event Joint Event Compound Event Lies between 0 & 1 Sum of events is 1 1.5
What is Probability? Probability Peter Lo Probability is the numerical measure of likelihood that the event will occur. Simple Event Joint Event Compound Event Lies between 0 & 1 Sum of events is 1 1.5
Basic notions of probability theory
 Basic notions of probability theory Contents o Boolean Logic o Definitions of probability o Probability laws Why a Lecture on Probability? Lecture 1, Slide 22: Basic Definitions Definitions: experiment,
Basic notions of probability theory Contents o Boolean Logic o Definitions of probability o Probability laws Why a Lecture on Probability? Lecture 1, Slide 22: Basic Definitions Definitions: experiment,
MAE 493G, CpE 493M, Mobile Robotics. 6. Basic Probability
 MAE 493G, CpE 493M, Mobile Robotics 6. Basic Probability Instructor: Yu Gu, Fall 2013 Uncertainties in Robotics Robot environments are inherently unpredictable; Sensors and data acquisition systems are
MAE 493G, CpE 493M, Mobile Robotics 6. Basic Probability Instructor: Yu Gu, Fall 2013 Uncertainties in Robotics Robot environments are inherently unpredictable; Sensors and data acquisition systems are
Topic 3: Introduction to Probability
 Topic 3: Introduction to Probability 1 Contents 1. Introduction 2. Simple Definitions 3. Types of Probability 4. Theorems of Probability 5. Probabilities under conditions of statistically independent events
Topic 3: Introduction to Probability 1 Contents 1. Introduction 2. Simple Definitions 3. Types of Probability 4. Theorems of Probability 5. Probabilities under conditions of statistically independent events
Mathematical Probability
 Mathematical Probability STA 281 Fall 2011 1 Introduction Engineers and scientists are always exposed to data, both in their professional capacities and in everyday activities. The discipline of statistics
Mathematical Probability STA 281 Fall 2011 1 Introduction Engineers and scientists are always exposed to data, both in their professional capacities and in everyday activities. The discipline of statistics
Probability and distributions. Francesco Corona
 Probability Probability and distributions Francesco Corona Department of Computer Science Federal University of Ceará, Fortaleza Probability Many kinds of studies can be characterised as (repeated) experiments
Probability Probability and distributions Francesco Corona Department of Computer Science Federal University of Ceará, Fortaleza Probability Many kinds of studies can be characterised as (repeated) experiments
With Question/Answer Animations. Chapter 7
 With Question/Answer Animations Chapter 7 Chapter Summary Introduction to Discrete Probability Probability Theory Bayes Theorem Section 7.1 Section Summary Finite Probability Probabilities of Complements
With Question/Answer Animations Chapter 7 Chapter Summary Introduction to Discrete Probability Probability Theory Bayes Theorem Section 7.1 Section Summary Finite Probability Probabilities of Complements
A Event has occurred
 Statistics and probability: 1-1 1. Probability Event: a possible outcome or set of possible outcomes of an experiment or observation. Typically denoted by a capital letter: A, B etc. E.g. The result of
Statistics and probability: 1-1 1. Probability Event: a possible outcome or set of possible outcomes of an experiment or observation. Typically denoted by a capital letter: A, B etc. E.g. The result of
n N CHAPTER 1 Atoms Thermodynamics Molecules Statistical Thermodynamics (S.T.)
 CHAPTER 1 Atoms Thermodynamics Molecules Statistical Thermodynamics (S.T.) S.T. is the key to understanding driving forces. e.g., determines if a process proceeds spontaneously. Let s start with entropy
CHAPTER 1 Atoms Thermodynamics Molecules Statistical Thermodynamics (S.T.) S.T. is the key to understanding driving forces. e.g., determines if a process proceeds spontaneously. Let s start with entropy
Probability the chance that an uncertain event will occur (always between 0 and 1)
 Quantitative Methods 2013 1 Probability as a Numerical Measure of the Likelihood of Occurrence Probability the chance that an uncertain event will occur (always between 0 and 1) Increasing Likelihood of
Quantitative Methods 2013 1 Probability as a Numerical Measure of the Likelihood of Occurrence Probability the chance that an uncertain event will occur (always between 0 and 1) Increasing Likelihood of
LECTURE 1. 1 Introduction. 1.1 Sample spaces and events
 LECTURE 1 1 Introduction The first part of our adventure is a highly selective review of probability theory, focusing especially on things that are most useful in statistics. 1.1 Sample spaces and events
LECTURE 1 1 Introduction The first part of our adventure is a highly selective review of probability theory, focusing especially on things that are most useful in statistics. 1.1 Sample spaces and events
Chapter 2.5 Random Variables and Probability The Modern View (cont.)
 Chapter 2.5 Random Variables and Probability The Modern View (cont.) I. Statistical Independence A crucially important idea in probability and statistics is the concept of statistical independence. Suppose
Chapter 2.5 Random Variables and Probability The Modern View (cont.) I. Statistical Independence A crucially important idea in probability and statistics is the concept of statistical independence. Suppose
Statistics for Business and Economics
 Statistics for Business and Economics Basic Probability Learning Objectives In this lecture(s), you learn: Basic probability concepts Conditional probability To use Bayes Theorem to revise probabilities
Statistics for Business and Economics Basic Probability Learning Objectives In this lecture(s), you learn: Basic probability concepts Conditional probability To use Bayes Theorem to revise probabilities
Fourier and Stats / Astro Stats and Measurement : Stats Notes
 Fourier and Stats / Astro Stats and Measurement : Stats Notes Andy Lawrence, University of Edinburgh Autumn 2013 1 Probabilities, distributions, and errors Laplace once said Probability theory is nothing
Fourier and Stats / Astro Stats and Measurement : Stats Notes Andy Lawrence, University of Edinburgh Autumn 2013 1 Probabilities, distributions, and errors Laplace once said Probability theory is nothing
PROBABILITY CHAPTER LEARNING OBJECTIVES UNIT OVERVIEW
 CHAPTER 16 PROBABILITY LEARNING OBJECTIVES Concept of probability is used in accounting and finance to understand the likelihood of occurrence or non-occurrence of a variable. It helps in developing financial
CHAPTER 16 PROBABILITY LEARNING OBJECTIVES Concept of probability is used in accounting and finance to understand the likelihood of occurrence or non-occurrence of a variable. It helps in developing financial
Elementary Discrete Probability
 Elementary Discrete Probability MATH 472 Financial Mathematics J Robert Buchanan 2018 Objectives In this lesson we will learn: the terminology of elementary probability, elementary rules of probability,
Elementary Discrete Probability MATH 472 Financial Mathematics J Robert Buchanan 2018 Objectives In this lesson we will learn: the terminology of elementary probability, elementary rules of probability,
2.4. Conditional Probability
 2.4. Conditional Probability Objectives. Definition of conditional probability and multiplication rule Total probability Bayes Theorem Example 2.4.1. (#46 p.80 textbook) Suppose an individual is randomly
2.4. Conditional Probability Objectives. Definition of conditional probability and multiplication rule Total probability Bayes Theorem Example 2.4.1. (#46 p.80 textbook) Suppose an individual is randomly
Chance, too, which seems to rush along with slack reins, is bridled and governed by law (Boethius, ).
 Chapter 2 Probability Chance, too, which seems to rush along with slack reins, is bridled and governed by law (Boethius, 480-524). Blaise Pascal (1623-1662) Pierre de Fermat (1601-1665) Abraham de Moivre
Chapter 2 Probability Chance, too, which seems to rush along with slack reins, is bridled and governed by law (Boethius, 480-524). Blaise Pascal (1623-1662) Pierre de Fermat (1601-1665) Abraham de Moivre
Statistics for Managers Using Microsoft Excel/SPSS Chapter 4 Basic Probability And Discrete Probability Distributions
 Statistics for Managers Using Microsoft Excel/SPSS Chapter 4 Basic Probability And Discrete Probability Distributions 1999 Prentice-Hall, Inc. Chap. 4-1 Chapter Topics Basic Probability Concepts: Sample
Statistics for Managers Using Microsoft Excel/SPSS Chapter 4 Basic Probability And Discrete Probability Distributions 1999 Prentice-Hall, Inc. Chap. 4-1 Chapter Topics Basic Probability Concepts: Sample
F71SM STATISTICAL METHODS
 F71SM STATISTICAL METHODS RJG SUMMARY NOTES 2 PROBABILITY 2.1 Introduction A random experiment is an experiment which is repeatable under identical conditions, and for which, at each repetition, the outcome
F71SM STATISTICAL METHODS RJG SUMMARY NOTES 2 PROBABILITY 2.1 Introduction A random experiment is an experiment which is repeatable under identical conditions, and for which, at each repetition, the outcome
TOPIC 12 PROBABILITY SCHEMATIC DIAGRAM
 TOPIC 12 PROBABILITY SCHEMATIC DIAGRAM Topic Concepts Degree of Importance References NCERT Book Vol. II Probability (i) Conditional Probability *** Article 1.2 and 1.2.1 Solved Examples 1 to 6 Q. Nos
TOPIC 12 PROBABILITY SCHEMATIC DIAGRAM Topic Concepts Degree of Importance References NCERT Book Vol. II Probability (i) Conditional Probability *** Article 1.2 and 1.2.1 Solved Examples 1 to 6 Q. Nos
1 Probability Theory. 1.1 Introduction
 1 Probability Theory Probability theory is used as a tool in statistics. It helps to evaluate the reliability of our conclusions about the population when we have only information about a sample. Probability
1 Probability Theory Probability theory is used as a tool in statistics. It helps to evaluate the reliability of our conclusions about the population when we have only information about a sample. Probability
Intermediate Math Circles November 8, 2017 Probability II
 Intersection of Events and Independence Consider two groups of pairs of events Intermediate Math Circles November 8, 017 Probability II Group 1 (Dependent Events) A = {a sales associate has training} B
Intersection of Events and Independence Consider two groups of pairs of events Intermediate Math Circles November 8, 017 Probability II Group 1 (Dependent Events) A = {a sales associate has training} B
Lecture 1. Chapter 1. (Part I) Material Covered in This Lecture: Chapter 1, Chapter 2 ( ). 1. What is Statistics?
 Lecture 1 (Part I) Material Covered in This Lecture: Chapter 1, Chapter 2 (2.1 --- 2.6). Chapter 1 1. What is Statistics? 2. Two definitions. (1). Population (2). Sample 3. The objective of statistics.
Lecture 1 (Part I) Material Covered in This Lecture: Chapter 1, Chapter 2 (2.1 --- 2.6). Chapter 1 1. What is Statistics? 2. Two definitions. (1). Population (2). Sample 3. The objective of statistics.
Business Statistics MBA Pokhara University
 Business Statistics MBA Pokhara University Chapter 3 Basic Probability Concept and Application Bijay Lal Pradhan, Ph.D. Review I. What s in last lecture? Descriptive Statistics Numerical Measures. Chapter
Business Statistics MBA Pokhara University Chapter 3 Basic Probability Concept and Application Bijay Lal Pradhan, Ph.D. Review I. What s in last lecture? Descriptive Statistics Numerical Measures. Chapter
Probability and the Second Law of Thermodynamics
 Probability and the Second Law of Thermodynamics Stephen R. Addison January 24, 200 Introduction Over the next several class periods we will be reviewing the basic results of probability and relating probability
Probability and the Second Law of Thermodynamics Stephen R. Addison January 24, 200 Introduction Over the next several class periods we will be reviewing the basic results of probability and relating probability
Mathematical Foundations of Computer Science Lecture Outline October 18, 2018
 Mathematical Foundations of Computer Science Lecture Outline October 18, 2018 The Total Probability Theorem. Consider events E and F. Consider a sample point ω E. Observe that ω belongs to either F or
Mathematical Foundations of Computer Science Lecture Outline October 18, 2018 The Total Probability Theorem. Consider events E and F. Consider a sample point ω E. Observe that ω belongs to either F or
STAT Chapter 3: Probability
 Basic Definitions STAT 515 --- Chapter 3: Probability Experiment: A process which leads to a single outcome (called a sample point) that cannot be predicted with certainty. Sample Space (of an experiment):
Basic Definitions STAT 515 --- Chapter 3: Probability Experiment: A process which leads to a single outcome (called a sample point) that cannot be predicted with certainty. Sample Space (of an experiment):
Chapter 2. Conditional Probability and Independence. 2.1 Conditional Probability
 Chapter 2 Conditional Probability and Independence 2.1 Conditional Probability Probability assigns a likelihood to results of experiments that have not yet been conducted. Suppose that the experiment has
Chapter 2 Conditional Probability and Independence 2.1 Conditional Probability Probability assigns a likelihood to results of experiments that have not yet been conducted. Suppose that the experiment has
Basic notions of probability theory
 Basic notions of probability theory Contents o Boolean Logic o Definitions of probability o Probability laws Objectives of This Lecture What do we intend for probability in the context of RAM and risk
Basic notions of probability theory Contents o Boolean Logic o Definitions of probability o Probability laws Objectives of This Lecture What do we intend for probability in the context of RAM and risk
Origins of Probability Theory
 1 16.584: INTRODUCTION Theory and Tools of Probability required to analyze and design systems subject to uncertain outcomes/unpredictability/randomness. Such systems more generally referred to as Experiments.
1 16.584: INTRODUCTION Theory and Tools of Probability required to analyze and design systems subject to uncertain outcomes/unpredictability/randomness. Such systems more generally referred to as Experiments.
Example. What is the sample space for flipping a fair coin? Rolling a 6-sided die? Find the event E where E = {x x has exactly one head}
 Chapter 7 Notes 1 (c) Epstein, 2013 CHAPTER 7: PROBABILITY 7.1: Experiments, Sample Spaces and Events Chapter 7 Notes 2 (c) Epstein, 2013 What is the sample space for flipping a fair coin three times?
Chapter 7 Notes 1 (c) Epstein, 2013 CHAPTER 7: PROBABILITY 7.1: Experiments, Sample Spaces and Events Chapter 7 Notes 2 (c) Epstein, 2013 What is the sample space for flipping a fair coin three times?
Discrete Probability
 Discrete Probability Counting Permutations Combinations r- Combinations r- Combinations with repetition Allowed Pascal s Formula Binomial Theorem Conditional Probability Baye s Formula Independent Events
Discrete Probability Counting Permutations Combinations r- Combinations r- Combinations with repetition Allowed Pascal s Formula Binomial Theorem Conditional Probability Baye s Formula Independent Events
PROBABILITY.
 PROBABILITY PROBABILITY(Basic Terminology) Random Experiment: If in each trial of an experiment conducted under identical conditions, the outcome is not unique, but may be any one of the possible outcomes,
PROBABILITY PROBABILITY(Basic Terminology) Random Experiment: If in each trial of an experiment conducted under identical conditions, the outcome is not unique, but may be any one of the possible outcomes,
Probability Theory Review Reading Assignments
 Probability Theory Review Reading Assignments R. Duda, P. Hart, and D. Stork, Pattern Classification, John-Wiley, 2nd edition, 2001 (appendix A.4, hard-copy). "Everything I need to know about Probability"
Probability Theory Review Reading Assignments R. Duda, P. Hart, and D. Stork, Pattern Classification, John-Wiley, 2nd edition, 2001 (appendix A.4, hard-copy). "Everything I need to know about Probability"
Basic Probabilistic Reasoning SEG
 Basic Probabilistic Reasoning SEG 7450 1 Introduction Reasoning under uncertainty using probability theory Dealing with uncertainty is one of the main advantages of an expert system over a simple decision
Basic Probabilistic Reasoning SEG 7450 1 Introduction Reasoning under uncertainty using probability theory Dealing with uncertainty is one of the main advantages of an expert system over a simple decision
Introduction to Probability
 Introduction to Probability Content Experiments, Counting Rules, and Assigning Probabilities Events and Their Probability Some Basic Relationships of Probability Conditional Probability Bayes Theorem 2
Introduction to Probability Content Experiments, Counting Rules, and Assigning Probabilities Events and Their Probability Some Basic Relationships of Probability Conditional Probability Bayes Theorem 2
3.2 Probability Rules
 3.2 Probability Rules The idea of probability rests on the fact that chance behavior is predictable in the long run. In the last section, we used simulation to imitate chance behavior. Do we always need
3.2 Probability Rules The idea of probability rests on the fact that chance behavior is predictable in the long run. In the last section, we used simulation to imitate chance behavior. Do we always need
Random processes. Lecture 17: Probability, Part 1. Probability. Law of large numbers
 Random processes Lecture 17: Probability, Part 1 Statistics 10 Colin Rundel March 26, 2012 A random process is a situation in which we know what outcomes could happen, but we don t know which particular
Random processes Lecture 17: Probability, Part 1 Statistics 10 Colin Rundel March 26, 2012 A random process is a situation in which we know what outcomes could happen, but we don t know which particular
5.3 Conditional Probability and Independence
 28 CHAPTER 5. PROBABILITY 5. Conditional Probability and Independence 5.. Conditional Probability Two cubical dice each have a triangle painted on one side, a circle painted on two sides and a square painted
28 CHAPTER 5. PROBABILITY 5. Conditional Probability and Independence 5.. Conditional Probability Two cubical dice each have a triangle painted on one side, a circle painted on two sides and a square painted
ELEG 3143 Probability & Stochastic Process Ch. 1 Probability
 Department of Electrical Engineering University of Arkansas ELEG 3143 Probability & Stochastic Process Ch. 1 Probability Dr. Jingxian Wu wuj@uark.edu OUTLINE 2 Applications Elementary Set Theory Random
Department of Electrical Engineering University of Arkansas ELEG 3143 Probability & Stochastic Process Ch. 1 Probability Dr. Jingxian Wu wuj@uark.edu OUTLINE 2 Applications Elementary Set Theory Random
tossing a coin selecting a card from a deck measuring the commuting time on a particular morning
 2 Probability Experiment An experiment or random variable is any activity whose outcome is unknown or random upfront: tossing a coin selecting a card from a deck measuring the commuting time on a particular
2 Probability Experiment An experiment or random variable is any activity whose outcome is unknown or random upfront: tossing a coin selecting a card from a deck measuring the commuting time on a particular
Chapter 2. Conditional Probability and Independence. 2.1 Conditional Probability
 Chapter 2 Conditional Probability and Independence 2.1 Conditional Probability Example: Two dice are tossed. What is the probability that the sum is 8? This is an easy exercise: we have a sample space
Chapter 2 Conditional Probability and Independence 2.1 Conditional Probability Example: Two dice are tossed. What is the probability that the sum is 8? This is an easy exercise: we have a sample space
Lecture 10: Probability distributions TUESDAY, FEBRUARY 19, 2019
 Lecture 10: Probability distributions DANIEL WELLER TUESDAY, FEBRUARY 19, 2019 Agenda What is probability? (again) Describing probabilities (distributions) Understanding probabilities (expectation) Partial
Lecture 10: Probability distributions DANIEL WELLER TUESDAY, FEBRUARY 19, 2019 Agenda What is probability? (again) Describing probabilities (distributions) Understanding probabilities (expectation) Partial
Review of Basic Probability
 Review of Basic Probability Erik G. Learned-Miller Department of Computer Science University of Massachusetts, Amherst Amherst, MA 01003 September 16, 2009 Abstract This document reviews basic discrete
Review of Basic Probability Erik G. Learned-Miller Department of Computer Science University of Massachusetts, Amherst Amherst, MA 01003 September 16, 2009 Abstract This document reviews basic discrete
1 Combinatorial Analysis
 ECE316 Notes-Winter 217: A. K. Khandani 1 1 Combinatorial Analysis 1.1 Introduction This chapter deals with finding effective methods for counting the number of ways that things can occur. In fact, many
ECE316 Notes-Winter 217: A. K. Khandani 1 1 Combinatorial Analysis 1.1 Introduction This chapter deals with finding effective methods for counting the number of ways that things can occur. In fact, many
3 PROBABILITY TOPICS
 Chapter 3 Probability Topics 135 3 PROBABILITY TOPICS Figure 3.1 Meteor showers are rare, but the probability of them occurring can be calculated. (credit: Navicore/flickr) Introduction It is often necessary
Chapter 3 Probability Topics 135 3 PROBABILITY TOPICS Figure 3.1 Meteor showers are rare, but the probability of them occurring can be calculated. (credit: Navicore/flickr) Introduction It is often necessary
P (A B) P ((B C) A) P (B A) = P (B A) + P (C A) P (A) = P (B A) + P (C A) = Q(A) + Q(B).
 Lectures 7-8 jacques@ucsdedu 41 Conditional Probability Let (Ω, F, P ) be a probability space Suppose that we have prior information which leads us to conclude that an event A F occurs Based on this information,
Lectures 7-8 jacques@ucsdedu 41 Conditional Probability Let (Ω, F, P ) be a probability space Suppose that we have prior information which leads us to conclude that an event A F occurs Based on this information,
Lecture 8: Conditional probability I: definition, independence, the tree method, sampling, chain rule for independent events
 Lecture 8: Conditional probability I: definition, independence, the tree method, sampling, chain rule for independent events Discrete Structures II (Summer 2018) Rutgers University Instructor: Abhishek
Lecture 8: Conditional probability I: definition, independence, the tree method, sampling, chain rule for independent events Discrete Structures II (Summer 2018) Rutgers University Instructor: Abhishek
The set of all outcomes or sample points is called the SAMPLE SPACE of the experiment.
 Chapter 7 Probability 7.1 xperiments, Sample Spaces and vents Start with some definitions we will need in our study of probability. An XPRIMN is an activity with an observable result. ossing coins, rolling
Chapter 7 Probability 7.1 xperiments, Sample Spaces and vents Start with some definitions we will need in our study of probability. An XPRIMN is an activity with an observable result. ossing coins, rolling
Lecture Lecture 5
 Lecture 4 --- Lecture 5 A. Basic Concepts (4.1-4.2) 1. Experiment: A process of observing a phenomenon that has variation in its outcome. Examples: (E1). Rolling a die, (E2). Drawing a card form a shuffled
Lecture 4 --- Lecture 5 A. Basic Concepts (4.1-4.2) 1. Experiment: A process of observing a phenomenon that has variation in its outcome. Examples: (E1). Rolling a die, (E2). Drawing a card form a shuffled
Discrete Probability. Chemistry & Physics. Medicine
 Discrete Probability The existence of gambling for many centuries is evidence of long-running interest in probability. But a good understanding of probability transcends mere gambling. The mathematics
Discrete Probability The existence of gambling for many centuries is evidence of long-running interest in probability. But a good understanding of probability transcends mere gambling. The mathematics
Semester 2 Final Exam Review Guide for AMS I
 Name: Semester 2 Final Exam Review Guide for AMS I Unit 4: Exponential Properties & Functions Lesson 1 Exponent Properties & Simplifying Radicals Products of Powers: when two powers with the same base
Name: Semester 2 Final Exam Review Guide for AMS I Unit 4: Exponential Properties & Functions Lesson 1 Exponent Properties & Simplifying Radicals Products of Powers: when two powers with the same base
Event A: at least one tail observed A:
 Chapter 3 Probability 3.1 Events, sample space, and probability Basic definitions: An is an act of observation that leads to a single outcome that cannot be predicted with certainty. A (or simple event)
Chapter 3 Probability 3.1 Events, sample space, and probability Basic definitions: An is an act of observation that leads to a single outcome that cannot be predicted with certainty. A (or simple event)
The Geometric Distribution
 MATH 382 The Geometric Distribution Dr. Neal, WKU Suppose we have a fixed probability p of having a success on any single attempt, where p > 0. We continue to make independent attempts until we succeed.
MATH 382 The Geometric Distribution Dr. Neal, WKU Suppose we have a fixed probability p of having a success on any single attempt, where p > 0. We continue to make independent attempts until we succeed.
UNIT 5 ~ Probability: What Are the Chances? 1
 UNIT 5 ~ Probability: What Are the Chances? 1 6.1: Simulation Simulation: The of chance behavior, based on a that accurately reflects the phenomenon under consideration. (ex 1) Suppose we are interested
UNIT 5 ~ Probability: What Are the Chances? 1 6.1: Simulation Simulation: The of chance behavior, based on a that accurately reflects the phenomenon under consideration. (ex 1) Suppose we are interested
PROBABILITY VITTORIA SILVESTRI
 PROBABILITY VITTORIA SILVESTRI Contents Preface. Introduction 2 2. Combinatorial analysis 5 3. Stirling s formula 8 4. Properties of Probability measures Preface These lecture notes are for the course
PROBABILITY VITTORIA SILVESTRI Contents Preface. Introduction 2 2. Combinatorial analysis 5 3. Stirling s formula 8 4. Properties of Probability measures Preface These lecture notes are for the course
ENGI 4421 Introduction to Probability; Sets & Venn Diagrams Page α 2 θ 1 u 3. wear coat. θ 2 = warm u 2 = sweaty! θ 1 = cold u 3 = brrr!
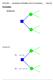 ENGI 4421 Introduction to Probability; Sets & Venn Diagrams Page 2-01 Probability Decision trees u 1 u 2 α 2 θ 1 u 3 θ 2 u 4 Example 2.01 θ 1 = cold u 1 = snug! α 1 wear coat θ 2 = warm u 2 = sweaty! θ
ENGI 4421 Introduction to Probability; Sets & Venn Diagrams Page 2-01 Probability Decision trees u 1 u 2 α 2 θ 1 u 3 θ 2 u 4 Example 2.01 θ 1 = cold u 1 = snug! α 1 wear coat θ 2 = warm u 2 = sweaty! θ
Motivation. Stat Camp for the MBA Program. Probability. Experiments and Outcomes. Daniel Solow 5/10/2017
 Stat Camp for the MBA Program Daniel Solow Lecture 2 Probability Motivation You often need to make decisions under uncertainty, that is, facing an unknown future. Examples: How many computers should I
Stat Camp for the MBA Program Daniel Solow Lecture 2 Probability Motivation You often need to make decisions under uncertainty, that is, facing an unknown future. Examples: How many computers should I
Probability (Devore Chapter Two)
 Probability (Devore Chapter Two) 1016-345-01: Probability and Statistics for Engineers Spring 2013 Contents 0 Preliminaries 3 0.1 Motivation..................................... 3 0.2 Administrata...................................
Probability (Devore Chapter Two) 1016-345-01: Probability and Statistics for Engineers Spring 2013 Contents 0 Preliminaries 3 0.1 Motivation..................................... 3 0.2 Administrata...................................
Statistics for Managers Using Microsoft Excel (3 rd Edition)
 Statistics for Managers Using Microsoft Excel (3 rd Edition) Chapter 4 Basic Probability and Discrete Probability Distributions 2002 Prentice-Hall, Inc. Chap 4-1 Chapter Topics Basic probability concepts
Statistics for Managers Using Microsoft Excel (3 rd Edition) Chapter 4 Basic Probability and Discrete Probability Distributions 2002 Prentice-Hall, Inc. Chap 4-1 Chapter Topics Basic probability concepts
Stat330 - Solution to Homework 2. 1 Kolmogorov. (c) For any two events A, B Ω, P (A B) = P (A) P (B). Because. and
 Stat330 - Solution to Homework 2 1 Kolmogorov (a For any two evens, B Ω, Because and P ( B = P ( P ( B. = ( B ( B, ( B ( B =, axiom iii implies that P ( = P ( B + P ( B. The statement follows from subtraction.
Stat330 - Solution to Homework 2 1 Kolmogorov (a For any two evens, B Ω, Because and P ( B = P ( P ( B. = ( B ( B, ( B ( B =, axiom iii implies that P ( = P ( B + P ( B. The statement follows from subtraction.
1. When applied to an affected person, the test comes up positive in 90% of cases, and negative in 10% (these are called false negatives ).
 CS 70 Discrete Mathematics for CS Spring 2006 Vazirani Lecture 8 Conditional Probability A pharmaceutical company is marketing a new test for a certain medical condition. According to clinical trials,
CS 70 Discrete Mathematics for CS Spring 2006 Vazirani Lecture 8 Conditional Probability A pharmaceutical company is marketing a new test for a certain medical condition. According to clinical trials,
Statistical Inference
 Statistical Inference Lecture 1: Probability Theory MING GAO DASE @ ECNU (for course related communications) mgao@dase.ecnu.edu.cn Sep. 11, 2018 Outline Introduction Set Theory Basics of Probability Theory
Statistical Inference Lecture 1: Probability Theory MING GAO DASE @ ECNU (for course related communications) mgao@dase.ecnu.edu.cn Sep. 11, 2018 Outline Introduction Set Theory Basics of Probability Theory
What is the probability of getting a heads when flipping a coin
 Chapter 2 Probability Probability theory is a branch of mathematics dealing with chance phenomena. The origins of the subject date back to the Italian mathematician Cardano about 1550, and French mathematicians
Chapter 2 Probability Probability theory is a branch of mathematics dealing with chance phenomena. The origins of the subject date back to the Italian mathematician Cardano about 1550, and French mathematicians
HW2 Solutions, for MATH441, STAT461, STAT561, due September 9th
 HW2 Solutions, for MATH44, STAT46, STAT56, due September 9th. You flip a coin until you get tails. Describe the sample space. How many points are in the sample space? The sample space consists of sequences
HW2 Solutions, for MATH44, STAT46, STAT56, due September 9th. You flip a coin until you get tails. Describe the sample space. How many points are in the sample space? The sample space consists of sequences
CSC Discrete Math I, Spring Discrete Probability
 CSC 125 - Discrete Math I, Spring 2017 Discrete Probability Probability of an Event Pierre-Simon Laplace s classical theory of probability: Definition of terms: An experiment is a procedure that yields
CSC 125 - Discrete Math I, Spring 2017 Discrete Probability Probability of an Event Pierre-Simon Laplace s classical theory of probability: Definition of terms: An experiment is a procedure that yields
 CHAPTER - 16 PROBABILITY Random Experiment : If an experiment has more than one possible out come and it is not possible to predict the outcome in advance then experiment is called random experiment. Sample
CHAPTER - 16 PROBABILITY Random Experiment : If an experiment has more than one possible out come and it is not possible to predict the outcome in advance then experiment is called random experiment. Sample
Example: Suppose we toss a quarter and observe whether it falls heads or tails, recording the result as 1 for heads and 0 for tails.
 Example: Suppose we toss a quarter and observe whether it falls heads or tails, recording the result as 1 for heads and 0 for tails. (In Mathematical language, the result of our toss is a random variable,
Example: Suppose we toss a quarter and observe whether it falls heads or tails, recording the result as 1 for heads and 0 for tails. (In Mathematical language, the result of our toss is a random variable,
Lecture notes for probability. Math 124
 Lecture notes for probability Math 124 What is probability? Probabilities are ratios, expressed as fractions, decimals, or percents, determined by considering results or outcomes of experiments whose result
Lecture notes for probability Math 124 What is probability? Probabilities are ratios, expressed as fractions, decimals, or percents, determined by considering results or outcomes of experiments whose result
Probability and Statistics Notes
 Probability and Statistics Notes Chapter One Jesse Crawford Department of Mathematics Tarleton State University (Tarleton State University) Chapter One Notes 1 / 71 Outline 1 A Sketch of Probability and
Probability and Statistics Notes Chapter One Jesse Crawford Department of Mathematics Tarleton State University (Tarleton State University) Chapter One Notes 1 / 71 Outline 1 A Sketch of Probability and
The probability of an event is viewed as a numerical measure of the chance that the event will occur.
 Chapter 5 This chapter introduces probability to quantify randomness. Section 5.1: How Can Probability Quantify Randomness? The probability of an event is viewed as a numerical measure of the chance that
Chapter 5 This chapter introduces probability to quantify randomness. Section 5.1: How Can Probability Quantify Randomness? The probability of an event is viewed as a numerical measure of the chance that
