136 Maths Quest 10 for Victoria

Transcription

1 Quadratic graphs 5 Barr is a basketball plaer. He passes the ball to a team mate. When the ball is thrown, the path traced b the ball is a parabola. Barr s throw follows the quadratic equation = Graph the path of the ball as it is passed and use our graph to calculate the distance of the pass and the maimum height reached b the ball. This chapter is concerned with graphing quadratic equations and this skill will enable ou to solve this problem and other similar problems that can be modelled b a quadratic equation.

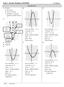
2 6 Maths Quest for Victoria Plotting parabolas A parabola is the graphical form of a quadratic equation. Its shape is seen in man everda situations, some of which are parts of nature and some are made b humans. If ou look at each of these pictures ou will notice that:. The are all smmetrical. For each one a line could be drawn down the middle to divide the parabola eactl in half.. The have either a maimum or a minimum turning point.. Some are wider or narrower than others but the have basicall the same shape. If the equation of the parabola is given, a table of values can be produced b substituting -values into the equation to obtain the corresponding -values. These - and - values provide the coordinates for points which can be plotted and joined to form the shape of the graph. When plotting graphs, use grid or graph paper for accurac.

3 Chapter 5 Quadratic graphs 7 Plot the graph of = for values of between and. State the equation of the ais of smmetr and the coordinates of the turning point. THINK WRITE WORKED Eample Write the equation. = Produce a table of values using -values from to. Draw a set of clearl labelled aes, plot the points and join them with a smooth curve. The scale on the -ais would be from to and from to on the -ais = 5 (, ) Write the equation of the line that The equation of the ais of smmetr is =. divides the parabola eactl in half. Write the coordinates of the turning point. The turning point is (, ). The graph of = is the basic graph of a quadratic equation or parabola. It has a minimum turning point at (, ). This parabola can be translated (moved horizontall and/or verticall), reflected (turned upside down) and dilated (made wider or narrower) to form other parabolas. How some of these transformations take place can be seen in the worked eample that follows. WORKED Eample Plot the graph of each of the following equations. In each case, use the values of shown as the values in our table. State the equation of the ais of smmetr, the coordinates of the turning point and the -intercept for each one. a = + for b = ( + ) for 6 c = for THINK WRITE a Write the equation. a = + Produce a table of values. 6 6 Draw a set of clearl labelled aes, plot the points and join them with a smooth curve. The scale on the -ais would be from to and to on the -ais. 9 6 = + (, ) Continued over page

4 8 Maths Quest for Victoria THINK Write the equation of the line that divides the parabola eactl in half. 5 Write the coordinates of the turning point. 6 Find the -coordinate of the point where the graph crosses the -ais. WRITE The equation of the ais of smmetr is =. The turning point is (, ). The -intercept is. b Write the equation. b = ( + ) Produce a table of values Draw a set of clearl labelled aes, plot the points and join them with a smooth curve. The scale on the -ais would be from to and 7 to on the -ais. = ( + ) (, ) (, 9) Write the equation of the line that divides the parabola eactl in half. Write the coordinates of the turning point. Find the -coordinate of the point where the graph crosses the -ais. The equation of the ais of smmetr is =. The turning point is (, ). The -intercept is 9. c Write the equation. c = Produce a table of values. 9 9 Draw a set of clearl labelled aes, plot the points and join them with a smooth curve. The scale on the -ais would be from 9 to and from to on the -ais. 9 = 5 6 Write the equation of the line that divides the parabola eactl in half. Write the coordinates of the turning point. Find the -coordinate of the point where the graph crosses the -ais. The equation of the ais of smmetr is =. The turning point is (, ). The -intercept is.

5 Chapter 5 Quadratic graphs 9 Graphics Calculator tip! Drawing graphs A graphics calculator can quickl provide ou with a graph of a parabola. Enter the equation in the Y= menu and press GRAPH. You ma need to adjust the WINDOW settings so that the shape of the parabola is clearl seen. (Note that the equation needs to be in the form =... so that ou enter onl the right side of the equation.) For comparison purposes, ou ma wish to see a number of graphs on the one set of aes. For eample, ou ma wish to compare the graphs of =, = + and =. Follow these steps:. Press Y=.. For Y enter b pressing X, T, θ, n (or ALPHA [X] ) ^.. For Y enter + b pressing X, T, θ, n ^ +.. For Y enter b pressing X, T, θ, n ^. 5. Adjust the WINDOW settings as shown in the screen. 6. Press GRAPH to see all three parabolas. Each parabola will be drawn in the order it was entered in the Y= menu so ou can match each with its equation. Note: You can press GRAPH after entering each equation to see the construction of each parabola on the same set of aes. 7. Once all parabolas are drawn, ou can press TRACE and use the arrow kes to move the flashing cursor along a curve. The up down arrow kes allow ou to move from one parabola to another with the appropriate equation displaed on the screen. The left right arrow kes move the cursor to trace the path of a particular parabola. The coordinates of the highlighted point are also displaed on the screen. (If ou want a particular point shown, enter the -value of the point and the displa will show the required point, the -value and the -value.)

6 Maths Quest for Victoria remember remember. Produce a table of values b substituting each integer value of into the equation.. Plot a graph b drawing and labelling a set of aes, plotting the points from the table and joining the points to form a smooth curve.. The ais of smmetr is the line that divides the parabola eactl in half.. The turning point is the point where the graph changes direction or turns. 5. The turning point is a maimum if it is the highest point on the graph and a minimum if it is the lowest point on the graph. 6. The -intercepts are the -coordinates of the points where the graph crosses the -ais. 7. The -intercept is the -coordinate of the point where the graph crosses the -ais. SkillSHEET SkillSHEET Mathcad Mathcad Parabolas of the form = + c Parabolas of the form = ( - b) WORKED Eample WORKED Eample a WORKED Eample b WORKED ORKED Eample c 5A Plotting parabolas You ma wish to use a graphics calculator for this eercise. Plot the graph of = for values of between and. State the equation of the ais of smmetr and the coordinates of the turning point. Plot the graph of each of the following for values of between and. State the equation of the ais of smmetr, the coordinates of the turning point and the -intercept for each one. a = + b = + c = d = Compare the graphs ou have drawn for question with that for = in question. Eplain how adding to or subtracting from affects the graph obtained. Plot the graph of each of the following equations. In each case, use the values of shown as the values in our table. State the equation of the ais of smmetr, the coordinates of the turning point and the -intercept for each one. a = ( + ) 5 b = ( + ) c = ( ) 5 d = ( ) 5 Compare the graphs ou have drawn for question with that for = in question. Eplain how adding to or subtracting from before squaring the result affects the graph obtained. 6 Plot the graph of each of the following equations. In each case, use the values of shown as the values in our table. State the equation of the ais of smmetr, the coordinates of the turning point and the -intercept for each one. a = + b = ( ) c = ( + ) d = 7 Compare the graphs ou have drawn for question 6 with that for = in question. Eplain how a negative sign in front of affects the graph obtained. Also compare the graphs obtained in question 6 with those in questions and. Which graphs have the same turning point? How are the different?

7 Chapter 5 Quadratic graphs 8 Plot the graph of each of the following, and state: i the equation of the ais of smmetr ii the coordinates of the turning point and whether it is a maimum or a minimum iii the -intercept. a = ( 5) + 6 b = ( + ) 5 c = ( ) + 6 d = ( ) + e = f = g = h = ( ) + 9 Use our graphs from question 8 a d to answer the following. a Eplain how ou can determine whether a parabola has a minimum or maimum turning point b looking onl at its equation. b Eplain how ou can determine the coordinates of the turning point of a parabola b looking onl at the equation. c Eplain how ou can obtain the equation of the ais of smmetr b looking onl at the equation of the parabola. multiple choice a For the graph of = ( ) + 5, the turning point is: A (5, ) B (, 5) C (, 5) D (, 5) E (, 5) b For the graph of = ( ) +, the turning point is: A (, ) B (, ) C (, ) D (, ) E (, ) c For the graph of = ( + ) 7, the -intercept is: A B 7 C D E 7 d Which of the following is true for the graph of = ( ) +? A Turning point (, ), -intercept 5 B Turning point (, ), -intercept 5 C Turning point (, ), -intercept 5 D Turning point (, ), -intercept 5 E Turning point (, ), -intercept A ball is thrown into the air. The height, h metres, of the ball at an time, t seconds, can be found b using the equation h = (t ) + 6. a Plot the graph for values of t between and 8. b Use the graph to find: i the maimum height of the ball ii how long it takes for the ball to fall back to the ground. From a crouching position in a ditch, an archer wants to fire an arrow over a horizontal tree branch, which is 5 metres above the ground. The height, in metres (h), of the arrow t seconds after it has been fired is given b the equation h = 8t(t ). a Plot the graph for t =,,.5,,. b From the graph find: i the maimum height the arrow reaches ii whether the arrow clears the branch and the distance b which it clears or falls short of the branch iii the time it takes to reach maimum height iv how long it takes for the arrow to hit the ground.

8 Maths Quest for Victoria Mathcad Parabolas of the form = + c Sketching parabolas using the basic graph of = (, ) Identifing the tpe of transformation which has occurred to the graph of = allows us to sketch rather than plot a parabola. A sketch graph is not drawn on grid or graph paper and there is no scale shown along each ais. We cannot read values from the line. However, a sketch graph allows us to see the relationship between and and the ke features of the graph such as the coordinates of the turning point and the - and -intercepts. The equation of a quadratic graph provides us with information as to whether the graphs are or, narrow or wide and whether the graphs have been translated verticall or horizontall compared with the graph of =. = The graph of = is shown. The turning point is (, ) and the graph is said to be upright or concave up. (, ) = + = Vertical translation Compare the graph of = + with that of =. The whole graph has been moved or translated units upwards. The turning point has become (, ). The -coordinate of the turning point has increased b units to show that the graph has been moved up units. Compare the graph of = with that of =. The whole graph has been moved or translated units downwards. The turning point has become (, ). The - coordinate of the turning point has decreased b units to show that the graph has been moved down units. WORKED Eample State the vertical translation and the coordinates of the turning point for the graphs of each of the following equations. a = + 5 b = THINK WRITE a Write the equation. a = means the graph is translated Vertical translation of 5 units up upwards 5 units. Translate the turning point of = The turning point becomes (, 5). which is (, ). The -coordinate of the turning point remains, and the -coordinate has 5 added to it. b Write the equation. b = means the graph is translated Vertical translation of units down downwards units. Translate the turning point of = which is (, ). The -coordinate of the turning point remains, and the -coordinate has subtracted from it. The turning point becomes (, ). (, ) = =

9 Chapter 5 Quadratic graphs Horizontal translation Compare the graph of = ( ) with that of =. The whole graph has been moved or translated units to the right. The turning point has become (, ). The -coordinate of the turning point has increased b units to show that the graph has been moved units to the right. Compare the graph of = ( + ) with that of =. The whole graph has been moved or translated unit left. The turning point has become (, ). The -coordinate of the turning point has decreased b unit to show that the graph has been moved left unit. WORKED Eample (, ) (, ) (, ) (, ) = = ( ) = ( + ) = State the horizontal translation and the coordinates of the turning point for the graphs of each of the following equations. a = ( ) b = ( + ) THINK WRITE a Write the equation. a = ( ) means the graph is translated to Horizontal translation of units to the right the right units. Translate the turning point of = The turning point becomes (, ). which is (, ). The -coordinate of the turning point remains, and the -coordinate has added to it. b Write the equation. b = ( + ) + means the graph is translated to Horizontal translation of units to the left the left units. Translate the turning point of = which is (, ). The -coordinate of the turning point remains, and the -coordinate has subtracted from it. The turning point becomes (, ). Parabolas of the form = ( - b) Mathcad Dilation Compare the graph of = with that of =. This graph is thinner or closer to the -ais. As the coefficient of increases, the graph becomes narrower and closer to the -ais. The turning point has not changed and is still (, ). Compare the graph of = -- with that of =. The graph is wider or closer to the -ais. The turning point has not changed and is still (, ). As the coefficient of decreases, the graph becomes wider or closer to the -ais. = = (, ) (, ) = = Parabolas of the form = a Mathcad

10 Maths Quest for Victoria WORKED Eample State whether each of the following graphs is wider or narrower than the graph of = and state the coordinates of the turning point of each one. a = -- b = THINK WRITE a Write the equation. a = -- Look at the coefficient of and decide -- <, so the graph is wider than whether it is greater than or less than. =. The dilation doesn t change the turning point. The turning point is (, ). b Write the equation. b = Look at the coefficient of and decide whether it is greater than or less than. >, so the graph is narrower than =. The dilation doesn t change the turning point. The turning point is (, ). 5 Reflection Compare the graph of = with that of =. In each case the ais of smmetr is the line = and the turning point is (, ). The onl difference between the equations is the sign in = and the difference between the graphs is that = sits on the -ais and = hangs from the -ais. (One is a reflection or mirror image of the other). = has a minimum turning point and = has a maimum turning point. = An quadratic graph where is positive has a shape and is said to be concave up or upright. Conversel if is negative the graph has a shape and is said to be concave down or inverted. WORKED Eample 6 (, ) For each of the following graphs give the coordinates of the turning point and state whether it is a maimum or a minimum. a = ( 7) b = 5 THINK WRITE a Write the equation. a = ( 7) It is a horizontal translation of 7 units to the right, The turning point is (7, ). so 7 units is added to the -coordinate of (, ). The sign in front of the term is negative, so it Maimum turning point is concave down. b Write the equation. b = 5 Rewrite the equation so that the term is first. = + 5 The vertical translation is 5 units up, so 5 units is The turning point is (, 5). added to the -coordinate of (, ). The sign in front of the term is negative, so it is concave down. Maimum turning point =

11 Chapter 5 Quadratic graphs 5 WORKED Eample 7 i State the appropriate dilation, reflection and translation of the graph of = needed to obtain the graph of each of the following quadratic equations. ii State the coordinates of the turning point for each. iii Hence, sketch the graph of each quadratic equation. a = ( + ) b = THINK WRITE a Write the quadratic equation. a = ( + ) Identif the transformation needed horizontal translation onl, no dilation or reflection. i Horizontal translation of units to the left Translate the turning point of = which is (, ), units to the left. ii The turning point is (, ). Sketch the graph of = ( + ). You ma iii = ( + ) find it helpful to lightl sketch the graph of = = on the same set of aes first. (, ) b Write the quadratic equation. b = Identif the transformations needed dilation ( in front of ) and reflection (negative in front of term), no translation. i Reflection so graph is concave down. As >, the graph is narrower than that of =. The turning point remains the same as there is no translation. ii The turning point is (, ). Sketch the graph of =. You ma find it iii helpful to lightl sketch the graph of = on the same set of aes first. = (, ) remember remember =. If the graph of = is translated c units verticall, the equation becomes = + c.. If the graph of = is translated b units horizontall, the equation becomes = ( b).. If the graph of = is dilated b factor a, the graph becomes narrower if a > and wider if < a <.. If the term is positive, the graph is upright (concave up), while if there is a negative sign in front of the term the graph is inverted (concave down).

12 6 Maths Quest for Victoria 5B Sketching parabolas using the basic graph of = WORKED Eample WORKED Eample WORKED Eample 5 WORKED Eample 6 WORKED Eample 7 State the vertical translation and the coordinates of the turning point for the graphs of each of the following equations. a = + b = c = 7 d = + -- e = f =. g = +.7 h = -- + State the horizontal translation and the coordinates of the turning point for the graphs of each of the following equations. a = ( ) b = ( ) c = ( + ) d = ( + ) e = ( -- ) f = ( + ) g = ( +.5) h = ( + ) -- 5 State whether each of the following graphs is wider or narrower than the graph of = and state the coordinates of the turning point of each one. a = 5 b = -- c = 7 d = e = f =.5 g =. h = -- 5 For each of the following graphs give the coordinates of the turning point and state whether it is a maimum or a minimum. a = + b = c = ( + ) d = e = f = g = ( 5) h = + 5 In each of the following state whether the graph is wider or narrower than = and whether it has a maimum or a minimum turning point. a = b = c = -- d = -- e = f =.5 g = 5 h =.6 i = -- j = k = 5 l = 6 i State the appropriate dilation, reflection and translation of the graph of = needed to obtain the graph of each of the following quadratic equations. ii State the coordinates of the turning point for each. iii Hence, sketch the graph of each quadratic equation. a = ( + ) b = c = + d = -- e = f = ( ) g = -- h = 5 i = + j = ( 6) 5 k = l = ( + ) WorkSHEET 5. 7 A vase 5 cm tall is positioned on a bench near a wall as shown. The shape of the vase follows the curve = ( ), where cm is the height of the vase and cm is the distance of the vase from the wall. a How far is the base of the vase from the wall? b What is the shortest distance from the top of the vase to the wall? c If the vase is moved so that the top just touches the wall, find the new distance from the wall to the base. d Find the new equation that follows the shape of the vase. Wall Bench

13 Chapter 5 Quadratic graphs 7 Sketching parabolas in turning point form So far, to sketch quadratic graphs we have looked at transforming the graph of = b dilation, reflection or translation. We can summarise this as follows: = a The graph of = is dilated b factor a. If a >, the graph becomes narrower and if < a <, the graph becomes wider. The turning point is (, ). = The graph of = is reflected in the -ais (turned upside down). The turning point is (, ). = ( b) The graph of = is translated b units horizontall. The turning point is (b, ). = + c The graph of = is translated c units verticall. The turning point is (, c). These transformations can be combined into what is called the turning point form of a quadratic equation: = a( b) + c. We can easil find some of the ke features of a parabola from the turning point form of a quadratic equation. These include: (i) the turning point, (b, c) (ii) whether the graph is concave up with a minimum turning point (positive term) or the graph is concave down with a maimum turning point (negative term) (iii) whether it is wider, narrower or the same width as the graph of = (size of the coefficient of the term). WORKED Eample 8 For each of the following equations state the coordinates of the turning point of the graph and whether it is a maimum or a minimum. a = ( 6) b = ( + ) + THINK WRITE a Write the equation. a = ( 6) Identif the transformations horizontal translation The turning point is (6, ). of 6 units to the right and a vertical translation of units down. The turning point (, ) of = changes to (6, ). As there is a positive sign in front of the term, the Minimum turning point graph is concave up with a minimum turning point. b Write the equation. b = ( + ) + Identif the transformations horizontal translation The turning point is (, ). of units to the left and a vertical translation of units up. The turning point of the basic graph changes to (, ). As there is a negative sign in front of the term, the graph is concave down with a maimum turning point. Maimum turning point Other ke features such as the - and -intercepts can also be determined from the equation of a parabola. The point(s) where the graph cuts or touches the -ais are called the -intercept(s). At these points, =. The point where the graph cuts the -ais is called the -intercept. At this point, =.

14 8 Maths Quest for Victoria WORKED Eample Determine i the -intercept and ii the -intercepts (where the eist) for the parabolas with equations: a = ( + ) b = ( ) c = ( + ). THINK WRITE a Write the equation. a = ( + ) Find the -intercept b substituting = into the equation. Find the -intercepts b substituting = into the equation and solving for. Use the difference of two squares rule to factorise the left side of the equation. Use the Null Factor Law to solve for. b Write the equation. b = ( ) Find the -intercept b substituting = into the equation. Find the -intercepts b substituting = into the equation and solving for. Note that there is onl one solution for and so there is onl one -intercept. (The graph touches the -ais.) -intercept: when =, = ( + ) = 9 = 5 The -intercept is 5. -intercepts: when = ( + ) = ( + ) = ( + + ) ( + ) = ( + 5) ( + ) = + 5 = or + = = 5 or The -intercepts are 5 and. -intercept: when = = ( ) = = The -intercept is. -intercepts: when =, ( ) = ( ) = = = + = The -intercept is. c Write the equation. c = ( + ) 9 Find the -intercept b substituting = into the equation. Find the -intercepts b substituting = into the equation and solving for. The difference of two squares rule cannot be used so we cannot solve for. -intercept: when = = ( + ) = = 5 The -intercept is 5. -intercepts: when = ( + ) = ( + ) + = There are no real solutions, so there are no -intercepts.

15 Chapter 5 Quadratic graphs 9 WORKED Eample For each of the following: i Write the coordinates of the turning point. ii State whether the graph has a maimum or a minimum turning point. iii State whether the graph is wider, narrower or the same width as the graph of =. iv Find the -intercept. v Find the -intercepts. vi Sketch the graph. a = ( ) + b = ( + ) + 6 THINK WRITE a Write the equation. a = ( ) + State the coordinates of the turning point from the equation. Use (b, c) since the equation is in the turning point form of = a( b) + c where a =, b = and c =. i The turning point is (, ). For the nature of the turning point, ii The graph has a minimum turning point. consider the sign in front of the term. As it is positive, the graph has a minimum turning point. For the dilation factor, consider the iii The graph has the same width as =. coefficient of the term. As the coefficient is, the width of the graph will be the same as that for =. 5 Find the -intercept b substituting = into the equation. iv -intercept: when = = ( ) + = + = 7 -intercept is 7. 6 Find the -intercepts b substituting v -intercepts: when = = into the equation and solving ( ) + = for. As we have the sum of two ( ) + ( ) = squares, we cannot solve for. There are no real solutions, and hence no -intercepts. 7 Sketch the graph, clearl showing vi the turning point and the -intercept. = ( ) + 7 (, ) Continued over page

16 5 Maths Quest for Victoria THINK WRITE b Write the equation. b = ( + ) + 6 State the coordinates of the turning point from the equation. Use (b, c) since the equation is in the turning point form of = a( b) + c where a =, b = and c = 6. i The turning point is (, 6). For the nature of the turning point, ii The graph has a maimum turning point. consider the sign in front of the term. As it is negative, the graph has a maimum turning point. For the dilation factor, consider the iii The graph is narrower than =. coefficient of the term. As >, the graph is narrower than the graph of =. 5 Find the -intercept b substituting = into the equation. iv -intercept: when = = ( + ) + 6 = + 6 = 6 7 Find the -intercepts b substituting = into the equation and solving for. Sketch the graph, clearl showing the turning point and the - and -intercepts. The -intercept is. v -intercepts: when = ( + ) + 6 = ( + ) = ( + ) ( ) = ( + + ) ( + ) = + + = or + = = or = + The -intercepts are and + (or approimatel.7 and.7). vi (, 6) 6 + = ( + ) + 6 Unless otherwise stated, eact values for the intercepts should be shown on sketch graphs. remember remember. If the equation of a parabola is in turning point form, = a( b) + c, then the turning point is (b, c).. If a is positive, the graph is concave up (upright) with a minimum turning point.. If a is negative, the graph is concave down (inverted) with a maimum turning point.. If the size of a is greater than, the graph is narrower than the graph of =. 5. If the size of a is between and, the graph is wider than the graph of =. 6. To find the -intercept, substitute = into the equation. 7. To find the -intercepts, substitute = into the equation and solve for.

17 Chapter 5 Quadratic graphs 5 WORKED Eample 8 5C Sketching parabolas in turning point form For each of the following equations state the coordinates of the turning point of the graph and whether it is a maimum or a minimum. a = ( ) + b = ( + ) c = ( + ) + d = ( ) + e = ( 5) + f = ( + ) 6 g = ( ) + 8 h = ( ) i = ( + 8) + j = ( + ) k = ( ) l = ( +.). m = (.6) +.7 n = ( + ) + 5 o = ( 7) + For each of the following state: i the coordinates of the turning point ii whether the graph has a maimum or a minimum turning point iii whether the graph is wider, narrower or the same width as that of =. a = ( + ) 5 b = ( ) + c = 5( + ) d = -- ( ) + e = -- ( + ) + 7 f =.( + -- ) Select the equation which best suits each of the following graphs. A B C 5 -- D E F a = ( ) b = ( ) + c = d = ( + ) + e = + f = ( + ) multiple choice a The translations required to change = into = ( ) are: A right --, up -- B left --, down -- C right --, down D left --, up -- E right --, up b For the graph -- ( -- ) + --, the effect of the -- on the graph is: A none C to make the graph wider E to translate the graph up a -- of a unit -- B to make the graph narrower D to invert the graph --

18 5 Maths Quest for Victoria EXCEL EXCEL WORKED Eample 9 Solving a( - b) + c = Spreadsheet Spreadsheet Mathcad Parabolas of the form = a( - b) + c Parabolas of the form = a( - b) + c WORKED Eample c d e Compared to the graph of =, = ( + ) is: A inverted and wider B inverted and narrower C upright and wider D upright and narrower E inverted and the same width A graph with maimum turning point (, 5) and which is narrower than the graph of = is: A = ( ) + 5 B = -- ( + ) + 5 C = ( ) + 5 D = ( + ) + 5 E = -- ( ) + 5 Compared to the graph of =, the graph of = ( ) has the following features. A Maimum TP at (, ), narrower B Maimum TP at (, ), narrower C Maimum TP at (, ), wider D Minimum TP at (, ), narrower E Minimum TP at (, ), wider 5 Determine i the -intercept and ii the -intercepts (where the eist) for the parabolas with equations: a = ( + ) b = ( ) c = ( + ) d = ( ) 9 e = + f = ( + ) 5 6 For each of the following: i Write the coordinates of the turning point. ii State whether the graph has a maimum or a minimum turning point. iii State whether the graph is wider, narrower or the same width as the graph of =. iv Find the -intercept. v Find the -intercepts. vi Sketch the graph. a = ( ) + b = ( ) c = ( + ) + d = ( + ) + e = ( + 5) f = ( + ) + g = ( ) + h = ( + ) i = ( + ) j = ( ) + k = ( + ) + 7 The price of shares in fledgling compan Lollies r us, after a breathtaking start, plunged dramaticall one afternoon following the breakout of a small fire on the premises. However, Ms Sarah Sava of Lollies Anonmous agreed to back the compan, and share prices began to rise. Sarah noted at the close of trade that afternoon that the compan s share price followed the curve: P =.(t ) + where $P is the price of shares t hours after noon. a What was the initial share price? b What was the lowest price of shares that afternoon? c At what time was the price at its lowest? d What was the final price of Lollies r us shares as trade closed at 5 pm? e Sketch a graph of the relationship between time and share price to represent the situation.

19 Chapter 5 Quadratic graphs 5 Designing our own water feature Have ou noticed that a jet or stream of water follows the path of a parabola? We can model the path of a water drop in a thin water stream b finding a quadratic equation of the form = a( b) + c which matches it. Consider a thin stream of water rising from an outlet at the surface of a pool that reaches a maimum height of m before hitting the surface of the pool again m awa. Draw a sketch of the path of a water drop in this stream of water. Assume that the surface of the pool lies along the -ais and that the path of the water drop starts from the origin (, ). Eplain what and represent in this situation. What are the coordinates of the turning point of our parabola? Eplain what this point represents. Using the turning point form for a parabola, = a( b) + c, substitute values for b and c. 5 Use another piece of information from our sketch to find the value for a. 6 Write the quadratic equation ou have found which represents the path of the water drop. 7 Now it is our turn to be creative. Imagine three water outlets clustered together in a single row, with water rising out at a different angle from each to form a spectacular water feature. (Assume the all start from the origin of a Cartesian plane.) Use the steps shown above to design our own water feature. Provide sketch graphs and accompaning quadratic equations to model each stream in our water feature. 8 Challenge: Tr to design a water feature where the streams don t start from the one point. Include all our calculations, equations and sketch graphs. (Keep our streams rising and falling in the one vertical plane. Wh is this?)

20 5 Maths Quest for Victoria Sketch the graph of =. Sketch the graph of = +. Sketch the graph of = ( ). Sketch the graph of = Sketch the graph of =. 6 State the coordinates of the turning point of the graph with equation = ( + ). 7 What is the nature of the turning point of the graph with equation = ( + )? (That is, does the parabola have a maimum or minimum turning point?) 8 Find the -intercept of the graph with equation = ( + ). 9 Find the -intercepts of the graph with equation = ( + ). Sketch the graph of = ( + ). MATHS MATHS QUEST C H A L LL E N G G E E Cop the rectangle shown below or use a piece of grid paper to show how to cut the rectangle into two pieces that will fit together to form a square. Trace the square shown below and cut along the dotted lines. Arrange the pieces to form a triangle. Draw our answer. A rectangle has the length of its sides increased b %. B what percentage will its area be increased?

21 Chapter 5 Quadratic graphs 55 Sketching parabolas of the form = a + b + c The standard form of a quadratic equation is = a + b + c where a, b and c are constants. (Note that the constants b and c in = a + b + c are different to the constants b and c in = a( b) + c.) As seen in the previous section, to sketch a parabola we need to know the - and -intercepts, the turning point and whether it is a maimum or a minimum turning point.. -intercept: substitute = into the equation.. -intercepts: substitute = into the equation and solve for. This will involve the factorisation and equation solving techniques ou learnt in chapter.. The nature of the turning point: check whether the term is positive or negative. If it is positive, the parabola is upright (or concave up) with a minimum turning point. If it is negative, the parabola is inverted (or concave down) with a maimum turning point.. The coordinates of the turning point: there are a number of methods to use if the equation is not in turning point form. Two methods are described below. Finding the turning point of a parabola when the equation is not in turning point form. Changing to turning point form As seen previousl, when an equation is written in turning point form the coordinates of the turning point can be read from the equation. That is, the coordinates of the turning point for = a( b) + c are (b, c). To change to turning point form we use the completing the square method. WORKED Eample Change each of the following equations into turning point form and hence state the coordinates of the turning point for each one. a = b = + 7 THINK WRITE a Write the equation. a = Use the first two terms on the righthand = ( ) 9 + side of the equation to create a new term to complete the square. Halve the coefficient of and square it. Add this new term to the righthand side of the equation. Balance the equation b subtracting the same term from the right-hand side of the equation. Factorise the perfect square and = ( + ) 9 + simplif the remaining terms. = ( + ) 7 State the coordinates of the turning The turning point is (, 7). point. Continued over page

22 56 Maths Quest for Victoria THINK WRITE b Write the equation. b = Take out a common factor. = [ ] Use the first two terms in the brackets to create a new term to complete the square. Halve the coefficient of and square it. Add this term to the right-hand side of the equation. Balance the equation b subtracting the same term from the right-hand side of the equation. Factorise the perfect square and simplif the remaining terms. Multipl the common factor b each term in the square brackets to have the epression in turning point form. State the coordinates of the turning point. 7 7 = [( ) ] 7 = [( -- ) ] 7 = ( -- ) The turning point is ( --, ) or ( --, -- ). Sketch the graph of = using the completing the square method to find the coordinates of the turning point. THINK WRITE Write the equation. = WORKED Eample Find the -intercept b substituting =. Find the -intercepts b substituting =. Factors cannot be easil found, so use the quadratic formula to solve for intercept: when = = = The -intercept is. -intercepts: when = = = ( ) = = b ± b = ac a where a =, b =, c = ± ( ) = ( )( ) ± 8 = The -intercepts are and + (appro.. and.). 8

23 Chapter 5 Quadratic graphs 57 THINK Use the completing the square method to change the equation into turning point form. (i) Take out a common factor so that the term has a coefficient of. (ii) Halve the coefficient of the -term and square it. Add this new term to the right-hand side to complete the square. Balance the equation b subtracting this value on the righthand side. (iii) Factorise the perfect square and simplif the remaining terms. (iv) Multipl the common factor b each term in the brackets to complete the turning point form. State the coordinates of the turning point. State the nature of the turning point. As the term is positive, the parabola has a minimum turning point. Sketch the graph. WRITE Turning point (TP): (i) = ( ) (ii) = [( + ) ] (iii) = [( ) ] (iv) = ( ) TP is (, ). The parabola has minimum TP. = + (, ). Using the -intercepts to find the -coordinate of the turning point A parabola is smmetrical, so the -intercepts are the same distance from the ais of smmetr (the line which divides the graph eactl in half). This means that the -coordinate of the turning point is halfwa between the -intercepts. =

24 58 Maths Quest for Victoria In this graph, the -intercepts are eactl unit from the -ais which is the ais of smmetr. One wa to find the -coordinate of the turning point is to calculate the + average of the two -intercepts. In this case, = is the -coordinate of the turning point. The -coordinate of the turning point can then be found b substituting the -coordinate into the equation. Sketch the graph of = +, using the -intercepts to find the coordinates of the turning point. THINK WRITE Write the equation. = WORKED Eample Find the -intercept b substituting =. Find the -intercepts b substituting =. Factorise and solve for b using the Null Factor Law. Find the -coordinate of the turning point b averaging the -intercepts, (This is halfwa between the -intercepts.) Find the -coordinate of the turning point b substituting the -coordinate into the equation and solving for. State the coordinates of the turning point. State the nature of the turning point. As the term is positive, the parabola has a minimum turning point. Sketch the graph. -intercept: when =, = + = The -intercept is. -intercepts: when =, + = ( 7)( ) = 7 = or = = 7 or = The -intercepts are and value of the turning point = = 5 When = 5, = 5 (5) + = The TP is (5, ). Parabola has a minimum TP. = (5, )

25 Chapter 5 Quadratic graphs 59 Which method is best for finding the turning point? You ma have a personal preference but ou can be guided b the -intercepts of the parabola. If the -intercepts are integer values, then finding the -coordinate halfwa between them will be the easier option. If there are no -intercepts or the -intercepts have surd or non-terminating decimal values, then changing the quadratic equation to turning point form will be our best option. Note that if there is onl one -intercept, then this point is the turning point of the parabola. remember remember. If the equation is in the form = a + b + c, the coordinates of the turning point can be found b: using the completing the square method to change the equation into turning point form finding the -coordinate of the point eactl halfwa between the two -intercepts. This is the -coordinate of the turning point. Then substitute the -value into the equation to find the -coordinate.. The graph should also show both the -intercept and the -intercepts of the parabola if the eist. 5D Sketching parabolas of the form = a + b + c WORKED Eample WORKED Eample Change each of the following equations into turning point form and write the coordinates of the turning point for each one. a = + b = + c = d = + e = + f = g = + + h = + i = j = k = + 6 l = Sketch the graph of each of the following using the completing the square method to find the coordinates of the turning point. a = + 5 b = + 7 c = + d = 5 + e = 5 + f = + g = + 8 h = i = + 8 j = + k = l = SkillSHEET SkillSHEET 5. 5.

26 6 Maths Quest for Victoria EXCEL SkillSHEET SkillSHEET Spreadsheet WORKED Eample Sketch the graph of each of the following, using the -intercepts to find the coordinates of the turning point. a = + b = + c = 8 9 d = 6 8 e = f = g = + h = 6 8 i = + 5 Sketch the graphs of each of the following. a = 7 9 b = + c = d = e = f = + + g = h = i = Solving a + b + c = 5 multiple choice a The equation that best suits the graph shown is: GC program EXCEL Solving a + b + c = Spreadsheet Parabolas of the form = a + b + c ( 6, ) 7 (, ) A = + B = C = D = 6 7 E = + 7 Mathcad Parabolas of the form = a + b + c b The equation = + 5 is best represented b: A B C D E 8 8

27 Chapter 5 Quadratic graphs 6 6 Match each of the following graphs with the appropriate equation. a b c 6 d e f g h i = ii = iii = + 9 iv = v = vi = + + vii = viii = The height, h metres, of a model rocket above the ground t seconds after launching is given b the equation h = t(5 t) for t 5. a Sketch the graph of the rocket s flight. b Find the height of the rocket when it is launched. c What is the greatest height the rocket reaches? d After how long does the rocket reach the greatest height? e How long is the rocket in the air? 8 A farmer decides to fence a new rectangular paddock with the greatest possible area, using an eisting fence for one side and metres of fencing to make the other three sides. Let the area of the paddock be defined as A m. a Write an equation using and to describe the area of the paddock. b Write an equation using and to describe the length of the new fence. Eisting fence c Rearrange the equation so that is the subject. d Substitute this value of into the equation for the area. e Using the intercept method find the coordinates of the turning point. f g Sketch the graph. Use the graph to find the maimum area of the paddock and its dimensions. New paddock m m m

28 6 Maths Quest for Victoria 9 A daring feat performed in Acapulco, Meico, is for a person to dive from a cliff into the ocean. Starting from about 7 metres above the water, the height, h (in metres), of a diver t seconds after he jumps can be represented b the equation h =.9t +.5t + 7. a Sketch a graph to represent the diver s height after jumping. b How long does it take for the diver to reach the water (to the nearest second)? c When does the diver reach his maimum height above the water? Give our answer correct to decimal places. d What is the diver s greatest height above the water? Give our answer correct to the nearest cm. GAMEtime WorkSHEET Quadratic graphs 5. A farmer has metres of fencing with which to fence sides of a rectangular paddock. a Using the method described in question 8, find an equation relating the area and the width of the paddock. b c Sketch the graph. Use the graph to find the greatest possible area for the paddock and its dimensions.

29 Find the fastest creatures. es. The features of the parabolas given give the puzzle answer code. Snake: 9 km/h Mammal: 55 km/h (in water) Mammal: km/h Chapter 5 Quadratic graphs 6 Insect: 58 km/h (7, ) 5 (, 6) (, 9) 5 5 (, ) 5 (, ) (, 9) (6, ) (7, ) (, 6) (6, ) Fish: 9 km/h 7 (6, ) (6, ) ( 6, ) 5 7 Bird: 5 km/h (6, ) (7, ) (6, ) (, 6) (7, ) (6, ) = A = -intercept = B = turning point = = 6 C = smaller -intercept = D = larger -intercept = = + 9 E = turning point = F= -intercept = = G = turning point = H = larger -intercept = = ( )( + ) I = -intercept = K = smaller -intercept = = ( ) + L = -intercept = M = turning point = = ( + ) 9 N = smaller -intercept = O = larger -intercept = = + 8 P = -intercept = R = turning point = = ( + ) S = -intercept = T = turning point = = ( )( + 7) W = turning point = Y= -intercept =

30 6 Maths Quest for Victoria Finding intercepts and turning points using a graphics calculator Information about the intercepts and the turning points of a parabola can be obtained from our graphics calculator. Consider the equation = + 6. Press Y= and enter the right side of the equation. Press WINDOW and enter the following settings. Press GRAPH to see a graph of the function. To find the -intercepts we use the CALCULATE menu. Press nd [CALC], then choose option : zero. 5 There are two zeros (-intercepts) for this parabola. We will first find the coordinates of the left intercept. The screen will now ask for a left bound as shown below. This asks for a lower possible limit for the intercept. Move the cursor with the arrow kes to a point on the left of the intercept as above and press ENTER. 6 The screen will now ask for a right bound. Move the cursor to the right of the intercept with the arrow kes and press ENTER.

31 Chapter 5 Quadratic graphs 65 7 You will now be asked to make a guess as shown below. Move the cursor with the arrow kes as close as possible to the intercept and press ENTER. 8 The coordinates of the zero will now be displaed. 9 Repeat steps 8 to find the coordinates of the second (right) zero. A similar process can be followed to find the coordinates of the turning point. Select the CALCULATE menu b pressing nd [CALC]. This graph has a minimum turning point and so we choose option : minimum. For concave down parabolas we would select : maimum. When the calculator asks for a lower limit, use the arrow kes to move the cursor to the left of the minimum and press ENTER. When the calculator asks for an upper limit, use the arrow kes to move the cursor to the right of the minimum and press ENTER. The calculator will then ask for a guess. Move the cursor as close as possible to the minimum and press ENTER. 5 The coordinates (in some cases approimate but ver close) of the minimum will then be displaed. Follow the eample above and use our graphics calculator to graph each of the following quadratics then find the -intercepts and the coordinates of the turning point. a = 7 b = + + c = 7 + d = 5 e = 9 7 f = 5

32 66 Maths Quest for Victoria Catch this! At the beginning of this chapter we met Barr who was a basketball plaer. Barr was passing a basketball and it followed the path given b the quadratic equation = Use a graphics calculator to graph the equation of the flight of the ball. Use the window function to set the Xmin and Ymin to as we onl need to consider positive values of and. Also set appropriate and maimums to see the tuning point and the intercept. Use the zero function on our graphics calculator to find the -intercept. This is the distance that the ball will travel if it is not caught. Alternativel, find this point b solving the equation using the quadratic formula. Use the turning point function on the graphics calculator to find the maimum height reached b the ball. Alternativel, use an appropriate method to find the coordinates of the turning point and hence the maimum height of the ball. Seichi is attempting to catch Barr s pass. If Seichi is. metres from Barr, at what height must she catch the ball? 5 Greg is an opponent who is standing. metres from Barr and in front of Seichi. Greg can catch a ball at a height of.8 metres. Will Greg intercept the pass from Barr to Seichi? 6 Use our graphics calculator and adjust the values of a, b and c in = a + b + c to find an equation that will pass over Greg and be caught b Seichi, whose maimum catch height is.6 metres. State the coordinates of the turning point of the parabola with equation = 5. State the coordinates of the turning point of the parabola with equation = ( + 7). Consider the equation = a. If a >, eplain the effect of increasing the value of a. In the equation = a, how does the graph differ if a <. 5 Write the equation = + 5 in turning point form. 6 Write the equation = in turning point form. 7 Sketch the graph of = ( + ) +. 8 Sketch the graph of = ( ). 9 Sketch the graph of = +. Sketch the graph of = + 5.

33 Chapter 5 Quadratic graphs 67 Solving quadratic inequations using sketch graphs Consider the sketch graph of the quadratic equation = + 6. = + 6 The -intercepts are and. This means that when =, = and. For what -values is <? In other words, for what -values is + 6 <? The graph below shows the section of the parabola (under the -ais) we are interested in (shown in green). = + 6 From the graph we can see that the solution to + 6 < is < <. This means that all -values between and give values for that are less than zero. For what values is >? In other words, for what -values is + 6 >? The graph below shows the sections of the parabola (above the -ais) in which we are interested (shown in green). = + 6 From the graph we can see that the solution to + 6 > is < and >. This means that all -values less than and all -values larger than give values for that are greater than zero. What would be the solution to + 6? What would be the solution to + 6? A quadratic inequation involves one of the inequalit signs <,, > or. We can solve a quadratic inequation b using a sketch graph of the matching quadratic equation. Notice that we need onl the -intercepts and the basic shape of the parabola to find the required solution.

34 68 Maths Quest for Victoria Solve the quadratic inequation + using a sketch graph. THINK Write the matching quadratic equation for which we need to sketch a graph. Find the -intercepts b substituting = and solving for. 5 6 Solve the quadratic inequation > using a sketch graph. THINK Write the matching quadratic equation for which we need to sketch a graph. Find the -intercepts b substituting = and solving for. (Factorise and use the Null Factor Law or use the quadratic formula.) 5 6 WORKED Eample WORKED Eample Identif whether the parabola is upright or inverted b checking whether the term is positive or negative. Sketch the required parabola. Identif which part of the parabola relates to. This is the part of the parabola on and above the -ais (shown in green). Locate the -values that match the parabola on and above the -ais. 5 Identif whether the parabola is upright or inverted b checking whether the term is positive or negative. Sketch the required parabola. Identif which part of the parabola relates to >. This is the part of the parabola above the -ais (shown in green). Locate the -values that match the parabola above the -ais. WRITE = + -intercepts: when =, + = ( )( ) = = or = = or The -intercepts are and. The parabola is upright as is positive. State the required solution. The solution to + is and. WRITE = intercepts: when =, = ( 7 ) = ( + )( ) = + = or = = -- or The -intercepts are -- and. The parabola is inverted as the term is negative. = State the required solution. The solution to > is -- < <. = +

35 remember remember Chapter 5 Quadratic graphs 69. To solve a quadratic inequation, sketch the graph of the matching quadratic equation.. The sketch graph needs to show onl the -intercepts.. Locate the -values which relate to the required parts of the parabola: < below the -ais = on the -ais > above the -ais. 5E Solving quadratic inequations using sketch graphs Use the given sketch graphs to solve the quadratic inequations. a > b < c + 9 = = SkillSHEET d 7 e < f 7 > = = + 9 = 7 7 WORKED Eample = 7 Solve the following quadratic inequations using a sketch graph. a + + < b > c + d + e + 6 > f 6 7 < SkillSHEET 5.5 WORKED Eample 5 Solve the following quadratic inequations using a sketch graph. a + > b + 5 < c + + d + 5 > e + f + 6 < SkillSHEET 5.6 multiple choice a The solution to the quadratic equation + > is: = + A < < B = C < and > D < E There is no solution. EXCEL Quadratic graphs Spreadsheet

36 7 Maths Quest for Victoria b The solution to the quadratic equation 6 9 is: = 6 9 A > B C = D all real values of E There is no solution. c The solution to the quadratic equation + < is: = + A > B C = D all real values of E There is no solution. 5 A tennis ball is hit over the net so that its height in metres t seconds after it is hit is modelled b the equation h = 6t + 9.6t when t.6. a b c d e f g Factorise the epression 6t + 9.6t. Use this factorised form to find the t-intercepts of the graph. Sketch the graph of the height of the tennis ball. When does the ball reach its maimum height? What is the maimum height of the ball? How long does it take before the height of the ball is zero again? Between what times is the tennis ball above the ground? That is, find when 6t + 9.6t >.

37 Chapter 5 Quadratic graphs 7 6 A football is kicked upwards in the air. The height, h, in metres, t seconds after the kick is modelled b the quadratic equation h = 5t + 5t. a Sketch the graph of this relationship. Quadratic graphs b For how man seconds is the ball in the air? That is, solve the quadratic inequation 5t + 5t >. c For how man seconds is the ball above a height of m? That is, solve the quadratic inequation 5t + 5t >. (Hint: Rearrange the inequation so that the righthand side is zero and sketch the new matching quadratic equation. Otherwise, solve > using the sketch in part a.) d For how man seconds is the ball below a height of m? Biccle helmets It is well known that, b law, all biccle riders are required to wear a helmet. But can wearing a helmet reall assist in preventing brain damage if a cclist s head hits the ground after a fall? Let s investigate what could happen if a helmet isn t worn. Suppose that the cclist falls from a stationar biccle. There is a formula we can use which links the distance travelled in m (d), time taken in s (t), initial speed in m/s (u) and acceleration in m/s (a). It is d = ut + at. For a vertical fall, the acceleration due to gravit is approimatel 9.8 m/s. If the initial speed is (stationar biccle), write an equation for the distance fallen in terms of the time b substituting the known values for u and a. Sketch the graph of this equation. For a person of average height sitting on a biccle, estimate how high a cclist s head would be above the ground. Use this height to estimate the time it takes for the cclist s head to hit the ground. 5 We can also work out the speed (v) at which the cclist s head hits the ground using the formula v = u + at. Write an equation for the speed in terms of time b substituting the known values for u and a. 6 Calculate the speed at which a cclist s head hits the ground in this situation. 7 It is believed that a cclist not wearing a helmet will generall have lasting brain damage if the cclist s head hits the ground at more than km/h. Compare this with the speed ou have calculated. Write a conclusion outlining our findings in this investigation. As an etension, ou ma like to find out more about how and wh helmets are constructed the wa the are to prevent serious head injuries. WorkSHEET GAMEtime 5.

38 7 Maths Quest for Victoria summar Cop the sentences below. Fill in the gaps b choosing the correct word or epression from the word list that follows. The graph of a parabola can be drawn b completing a table of values and the points generated. The divides the parabola eactl in half. The is where the graph changes direction or turns. If a parabola has the equation = + c, the graph of = is translated. 5 If a parabola has the equation = ( b), the graph of = is translated. 6 If a parabola has the equation = a and a >, the graph is than the graph of = while if < a < the graph is than the graph of =. 7 If the term of a parabola is positive, the graph is and has a turning point. If the term is negative, the graph is and has a turning point. 8 = a( b) + c is known as. The turning point is. 9 The -intercept is found b substituting into the equation. The -intercepts are found b substituting into the equation and solving for. The -coordinate of the turning point is between the -intercepts. To find the -coordinate of the turning point, add the two -intercepts together and the answer b. To find the -coordinate, substitute the -value into the original. The solution to a quadratic inequation can be read from a graph of the matching quadratic equation. > corresponds to the part of the parabola the -ais and < corresponds to the part of the parabola the -ais. WORD LIST plotting wider turning point above horizontall concave up = minimum maimum thinner equation verticall (a, b) turning point form concave down divide below = ais of smmetr halfwa sketch (b, c)

39 Chapter 5 Quadratic graphs 7 CHAPTER review For each of the following, produce a table of values for the stated -values and plot the graph. Show the -intercept and turning point. If ou can easil observe them from our graph, state the -intercepts. a =, for -values from 5 to b = , for -values from 9 to c = +, for -values from to Plot the graph of = ( + ) for values of between 6 and. From the graph, find the coordinates of the turning point. i State the appropriate dilation, reflection and translation of the graph of = needed to obtain the graph of each of the following quadratic equations. ii State the coordinates of the turning point for each. iii Hence, sketch the graph of each quadratic equation. a = b = ( + ) c = 5 For each of the following find the coordinates of the turning point and the - and -intercepts and sketch the graph. a = ( ) + b = ( + ) 5 c = ( ) + 5 Use the completing the square method to find the turning point for each of the following graphs. a = 8 + b = + 5 c = Sketch each of the graphs in question 5, clearl showing the intercepts and the turning point. 7 Sketch the graph of each of the following using the -intercepts to find the coordinates of the turning point. Clearl show the intercepts and turning point. a = b = c = a For the equation =, find: i the -intercept ii the -intercepts iii the coordinates of the turning point. b Use the information from part a to sketch the graph. 5A 5A 5B 5C 5D 5D 5D 5D

40 7 Maths Quest for Victoria 5D 9 The height, h, in metres of a golf ball t seconds after it is hit is given b the formula h = t t. 5E 5E test ourself CHAPTER 5 a b c d Sketch the graph of the path of the ball. What is the maimum height that the golf ball reaches? How long does it take for the ball to reach the maimum height? How long is it before the ball lands on the ground after it has been hit? Solve each of the following quadratic inequations b using a sketch graph. a > b + 5 c + 7 > A soccer ball is kicked upwards in the air. The height, h, in metres, t seconds after the kick is modelled b the quadratic equation h = 5t + t. a Sketch the graph of this relationship. b For how man seconds is the ball in the air? c For how man seconds is the ball above a height of 5 m? That is, solve the quadratic inequation 5t + t > 5. d For how man seconds is the ball above a height of m?