arxiv: v2 [math.fa] 9 Dec 2016
|
|
|
- Derrick Steven Casey
- 5 years ago
- Views:
Transcription
1 Eldan s Sochasc Localzaon and he KLS Hyperplane Conjecure: An Improved Lower Bound for Expanson Yn Ta Lee, Sanosh S Vempala arxv:60507v [mahfa] 9 Dec 06 December, 06 Absrac We show ha he KLS consan for n-dmensonal soropc logconcave measures s On /4 ), mprovng on he curren bes bound of On /3 logn) As corollares we oban he same mproved bound on he hn-shell esmae, Poncaré consan and exponenal concenraon consan and an alernave proof of hs bound for he soropc consan; also follows ha he ball walk for samplng from an soropc logconcave densy n R n converges n O n 5 ) seps from a warm sar Inroducon The sopermery of a subse s he rao of he measure of he boundary of he subse o he measure of he subse or s complemen, whchever s smaller The mnmum such rao over all subses s he Cheeger consan, also called expanson or sopermerc coeffcen Ths fundamenal consan appears n many sengs, eg, graphs and convex bodes and plays an essenal role n many lnes of sudy In he geomerc seng, he KLS hyperplane conjecure [] assers ha for any dsrbuon wh a logconcave densy, he mnmum expanson s approxmaed by ha of a halfspace, up o a unversal consan facor Thus, f he conjecure s rue, he Cheeger consan can be essenally deermned smply by examnng hyperplane cus More precsely, here s he saemen We use c,c for absolue consans, and A for he specral/operaor norm of a marx A Conjecure []) For any logconcave densy p n R n wh covarance marx A, def S = nf px)dx c { ψ p S R } n mn S ps)dx, R n\s px)dx A For an soropc logconcave densy all egenvalues of s covarance marx are equal o ), he conjecured sopermerc rao s an absolue consan Noe ha he sopermerc consan or KLS consanψ p s he recprocal of he mnmum expanson or Cheeger consan hs wll be more convenen for comparsons wh oher consans) Ths conjecure was formulaed by Kannan, Lovász and Smonovs n he course of her sudy of he convergence of a random process he ball walk) n a convex body and hey proved he followng weaker bound Theorem []) For any logconcave densy p n R n wh covarance marx A, he KLS consan sasfes ψ p C TrA) For an soropc dsrbuon, he heorem gves a bound of O n), whle he conjecure says O) The conjecure has several mporan consequences I mples ha he ball walk mxes n O n ) seps from a warm sar n any soropc convex body or logconcave densy) n R n ; hs s he bes possble bound, and s gh eg, for a hypercube The KLS conjecure has become cenral o modern asympoc convex geomery I s equvalen o a bound on he specral gap of soropc logconcave funcons [5] Alhough was formulaed due o an algorhmc movaon, mples several well-known conjecures n asympoc convex geomery We descrbe hese nex The hn-shell conjecure also known as he varance hypohess) [9, 6] says he followng Mcrosof Research and Unversy of Washngon, yle@mcrosofcom and yna@uwedu Georga Tech, vempala@gaechedu
2 Conjecure 3 Thn-shell) For a random pon X from an soropc logconcave densy p n R n, σ p def = E X n) ) = O) I mples ha a random pon X from an soropc logconcave densy les n a consan-wdh annulus a hn shell) wh consan probably Nong ha σ p = E X n) ) n Var X ) Cσ p, he conjecure s equvalen o asserng ha Var X ) = On) for an soropc logconcave densy The followng connecon s well-known: σ p Cψ p The curren bes bound s σ p n 3 by Guedon and Mlman [0], mprovng on a lne of work ha sared wh Klarag [3, 4, 8] Eldan [4] has shown ha he reverse nequaly holds approxmaely, n a wors-case sense, namely he wors possble KLS consan over all soropc logconcave denses n R n s bounded by he hn-shell esmae o whn roughly a logarhmc facor n he dmenson Ths resuls n he curren bes bound of ψ p n 3 logn A weaker nequaly was shown earler by Bobkov [5] see also [30]) The slcng conjecure, also called he hyperplane conjecure [8, 4] s he followng Conjecure 4 Slcng/Isoropc consan) Any convex body of un volume n R n conans a hyperplane secon of a leas consan volume Equvalenly, for any convex body K of un volume wh covarance marx L KI, he soropc consan L K = O) The soropc consan of a general soropc logconcave densy p wh covarance a mulple of he deny s defned as L p = p0) /n The bes curren bound s L p = On /4 ), due o Klarag [], mprovng on Bourgan s bound of L p = On /4 logn) [7] The sudy of hs conjecure has played an nfluenal role n he developmen of convex geomery over he pas several decades I was shown by Ball ha he KLS conjecure mples he slcng conjecure More recenly, Eldan and Klarag [5] showed ha he hn shell conjecure mples slcng, and herefore an alernave and sronger) proof ha KLS mples slcng: L p Cσ p The nex conjecure s a bound on he Poncaré consan for logconcave dsrbuons Conjecure 5 Poncaré consan) For any soropc logconcave densy p n R n, we have Q p def = sup g smooh Var p gx)) ) = O) E p gx) I was shown by Maz ja [34] and Cheeger [] ha hs Poncaré consan s bounded by wce he KLS consan Q p ψ p ) The curren bes bound s he same as he KLS bound Fnally, s conjecured ha Lpschz funcons concenrae over soropc logconcave denses Conjecure 6 Lpschz concenraon) For any L-Lpschz funcon g n R n, and soropc logconcave densy p, P x p gx) Eg > ) e /DpL) where D p = O) Gromov and Mlman [9] showed ha D p s also bounded by he KLS consan see Lemma??) For more background on hese conjecures, we refer he reader o [0,, 3] Resuls We prove he followng bound, conjecured n hs form n [33] Theorem 7 For any logconcave densy p n R n, wh covarance marx A, ψ p C Tr A )) /4 For soropc p, hs gves a bound of ψ p Cn 4, mprovng on he curren bes bound The followng corollary s mmedae Corollary 8 For any logconcave densy p n R n, he soropc slcng) consan L p, he Poncare consan Q p, he hn-shell consan σ p and he concenraon coeffcen D p are all bounded by O n /4) We menon an algorhmc consequence Corollary 9 The mxng me of he ball walk o sample from an soropc logconcave densy from a warm sar s O n 5)
3 Approach The KLS conjecure s rue for Gaussan dsrbuons More generally, for any dsrbuon whose densy funcon s he produc of he Gaussan densy for N0,σ I) and any logconcave funcon, s known ha he expanson s Ω/σ) Ths fac s used crucally n he Gaussan coolng algorhm of [3] for compung he volume of a convex body by sarng wh a sandard Gaussan resrced o a convex body and gradually makng he varance of he Gaussan large enough ha s effecvely unform over he convex body of neres Our overall sraegy s smlar n spr we sar wh an arbrary soropc logconcave densy and gradually nroduce a Gaussan erm n he densy of smaller and smaller varance The sopermery of he resulng dsrbuon afer suffcen me wll be very good snce has a large Gaussan facor And crucally, can be relaed o he sopermery of nal dsrbuon To acheve he laer, we would lke o manan he measure of a fxed subse close o s nal value as he dsrbuon changes For hs, our proof uses he localzaon approach o provng hgh-dmensonal nequales [7, ], and n parcular, he elegan sochasc verson nroduced by Eldan [4] and used n subsequen papers [7, 6] We fx a subse E of he orgnal space wh he orgnal logconcave measure of measure Ths s whou loss of generaly due o a resul of [30] In sandard localzaon we hen bsec space usng a hyperplane ha preserves he volume fracon of E The lm of hs process s -dmensonal logconcave measures needles ), for whch nequales are much easer o prove Ths approach runs no major dffcules for provng he KLS conjecure Whle he orgnal measure mgh be soropc, he -dmensonal measures could, n prncple, have varances roughly equal o he race of he orgnal covarance e, long hn needles), for whch only much weaker nequales hold Sochasc localzaon can be vewed as he connuous me verson of hs process, where a each sep, we pck a random drecon and mulply he curren densy wh a lnear funcon along he chosen drecon Over me, he dsrbuon can be vewed as a sphercal Gaussan mes a logconcave funcon, wh he Gaussan gradually reducng n varance When he Gaussan becomes suffcenly small n varance, hen he overall dsrbuon has good sopermerc coeffcen, deermned by he nverse of he Gaussan sandard devaon such an nequaly can be shown usng sandard localzaon, as n []) An mporan propery of he nfnesmal change a each sep s balance he densy a me s a marngale and herefore he expeced measure of any subse s he same as he orgnal measure Over me, he measure of a se E s a random quany ha devaes from s orgnal value of over me The man queson s hen wha drecon o use a each sep so ha a) he measure of E remans bounded and b) he Gaussan par of he densy has small varance We show ha he smples choce, namely a pure random drecon chosen from he unform dsrbuon suffces The analyss needs a poenal funcon ha grows slowly bu sll manans good conrol over he specral norm of he curren covarance marx The drec choce of A, where A s he covarance marx of he dsrbuon a me, s hard o conrol We use TrA ) Ths gves us he mproved bound of On/4 ) In he appendx, we show ha a hrd momen assumpon mples furher mprovemen va he same localzaon echnque Prelmnares In hs secon, we revew some basc defnons and heorems ha we use Sochasc calculus In hs paper, we only consder sochasc processes gven by sochasc dfferenal equaons Gven real-valued sochasc processes x and y, he quadrac varaons [x] and [x,y] are real-valued sochasc processes defned by [x] = lm [x,y] = lm P 0 n= P 0 n= ), xτn x τn ) ) xτn x τn yτn y τn, where P = {0 = τ 0 τ τ } s a sochasc paron of he non-negave real numbers, P = max n τ n τ n ) s called he mesh of P and he lm s defned usng convergence n probably Noe ha [x] In he frs arxv verson of hs paper, we ncorrecly clamed he assumpon as a lemma 3
4 s non-decreasng wh and [x,y] can be defned va polarzaon as [x,y] = 4 [x+y] [x y] ) For example, f he processes x and y sasfy he SDEs dx = µx )d+σx )dw and dy = νy )d+ηy )dw where W s a Wener process, we have ha [x] = 0 σ x s )ds and [x,y] = 0 σx s)ηy s )ds and d[x,y] = σx )ηy )d; for a vecor-valued SDE dx = µx )d + Σx )dw and dy = νy )d + My )dw, we have ha [x,x j ] = 0 Σx s)σ T x s )) j ds and d[x,y j ] = 0 Σx s)m T y s )) j ds Lemma 0 Iô s formula) Le x be a semmarngale and f be wce connuously dfferenable funcon, hen dfx ) = dfx ) dx dx + d fx ) dx dx j d[x,x j ],j The nex wo lemmas are well-known facs abou Wener processes; frs he reflecon prncple Lemma Reflecon prncple) Gven a Wener process W) and a, 0, hen we have ha P sup Ws) a) = PW) a) 0 s Second, a decomposon lemma for connuous marngales Theorem Dambs, Dubns-Schwarz heorem) Every connuous local marngale M s of he form where W s s a Wener process Logconcave funcons M = M 0 +W [M] for all 0 Lemma 3 Dnghas; Prékopa; Lendler) The convoluon of wo logconcave funcons s also logconcave; n parcular, any lnear ransformaon or any margnal of a logconcave densy s logconcave The nex lemma abou logconcave denses s folklore, see eg, [8] Lemma 4 Logconcave momens) Gven a logconcave densy p n R n, and any posve neger k, E x p x k k) k E x p x ) k/ The followng elemenary concenraon lemma s also well-known hs verson s from [8]) Lemma 5 Logconcave concenraon) For any soropc logconcave densy p n R n, and any > 0, P x p x > n ) e + A much sronger concenraon bound was shown by Paours [3] Lemma 6 [3]) For any soropc logconcave dsrbuon and any > C, P x p x n ) e c n The followng nequaly boundng he small ball probably s from [3] Lemma 7 [3, Thm 047]) For any soropc logconcave densy p, and any ǫ < ǫ 0, were ǫ 0,c are absolue consans P x p x ǫ n ) ǫ c n Defnon 8 We defne ψ n as he supremum of he KLS consan over all soropc logconcave dsrbuons n R n 4
5 The nex lemma follows from he fac ha he Poncaré consan s bounded by he KLS consan and Lemma 3 Lemma 9 For any marx A, and any soropc logconcave densy p, Var x p x T Ax ) Oψ r)e x p Ax ) where r = ranka+a T ) To prove a lower bound on he expanson, suffces o consder subses of measure / Ths follows from he concavy of he sopermerc profle We quoe a heorem from [30, Thm 8], whch apples even more generally o Remannan manfolds under suable convexy-ype assumpons Theorem 0 The Cheeger consan of any logconcave densy s acheved by a subse of measure / 3 Marx nequales For any symmerc marx B, we defne B = B, namely, he marx formed by akng absolue value of all egenvalues of B For any marx A, we defne RA) o be he span of he rows of A and NA) o be he null space of A For any vecor x and any posve sem-defne marx A, we defne x A = xt Ax Lemma Marx Hölder nequaly) Gven a symmerc marces A and B and any s, wh s + =, we have TrAB) Tr A s ) /s Tr B ) / Lemma Leb-Thrrng Inequaly [6]) Gven posve sem-defne marces A and B and r, we have TrB / AB / ) r ) TrB r/ A r B r/ ) Snce he followng lemma s saed dfferenly n [4, ], we show he proof from Eldan [4] here for compleeness Lemma 3 [4, ]) Gven a symmerc marx B, a posve sem-defne marx A and α [0,], we have TrA α BA α B) TrAB ) Proof Whou loss of generaly, we can assume A s dagonal Hence, we have ha TrA α BA α B) =,j A α A α jj B j,j αa + α)a jj )B j = α,j A B j + α),j A jj B j = TrAB ) 3 Eldan s sochasc localzaon In hs secon, we consder he sochasc localzaon scheme nroduced n [4] n slghly more general erms In dscree localzaon, he dea would be o resrc he dsrbuon wh a random halfspace and repea hs process In sochasc localzaon, hs dscree sep s replaced by nfnesmal seps, each of whch s a renormalzaon wh a lnear funcon n a random drecon One mgh vew hs nformally as an averagng over nfnesmal needles The dscree me equvalen would be p + x) = p x) + hx µ ) T w) for a suffcenly small h and random Gaussan vecor w Usng he approxmaon +y e y y, we see ha over me hs process nroduces a negave quadrac facor n he exponen, whch wll be he Gaussan facor As me ends o, he dsrbuon ends o a more and more concenraed Gaussan and evenually a dela funcon, a whch pon any subse has measure eher 0 or The dea of he proof s o sop a a me ha s large enough o have a srong Gaussan facor n he densy, bu small enough o ensure ha he measure of a se s no changed by more han a consan 5
6 3 The process and s basc properes Gven a dsrbuon wh logconcave densy px), we sar a me = 0 wh hs dsrbuon and a each me > 0, we apply an nfnesmal change o he densy Ths s done by pckng a random drecon from a Gaussan wh a ceran covarance marx C, called he conrol marx In Secon 4 and 6, we use hs process wh C = I In Secon 7, we use a varyng C o ge a bound for non-soropc dsrbuons In order o consruc he sochasc process, we assume ha he suppor of p s conaned n a ball of radus R > n There s only exponenally small probably ousde hs ball, a mos e cr by Lemma 6 Moreover, snce by Theorem 0, we only need o consder subses of measure /, hs runcaon does no affec he KLS consan of he dsrbuon Defnon 4 Gven a logconcave dsrbuon p, we defne he followng sochasc dfferenal equaon: c 0 = 0, dc = C / dw +C µ d, 3) B 0 = 0, db = C d, where he probably dsrbuon p, he mean µ and he covarance A are defned by p x) = e ct x x B px) R n e ct y y B py)dy, µ = E x p x, A = E x p x µ )x µ ) T, and he conrol marces C are symmerc marces o be specfed laer In Secon 4 and 6, we only consder he process wh C = I for all 0 In hs case, we have ha B = I, p x) = e ct x x px) R n e ct y y py)dy Also, snce µ s a bounded funcon ha s Lpschz wh respec o c and hence sandard exsence and unqueness heorems eg [3, Sec 5]) show he exsence and unqueness of he soluon on me [0,T] for any T > 0 In general, we have he followng resul: Lemma 5 Exsence and Unqueness) If px) has compac suppor and f C / funcons of A and B, he sochasc dfferenal equaon 3) has a unque soluon are bounded and Lpschz We defer all proofs for saemens n hs secon, consdered sandard n sochasc calculus, o Secon 5 Now we proceed o analyzng he process and how s parameers evolve Roughly speakng, he frs lemma below says ha he sochasc process s he same as connuously mulplyng p x) by a random nfnesmally small lnear funcon Lemma 6 [4, Lem ]) We have ha for any x R n dp x) = x µ ) T C / dw p x) By consderng he dervave dlogp x), we see ha applyng dp x) as n he lemma above resuls n he dsrbuon p x), wh he Gaussan erm n he densy: dlogp x) = dp x) p x) d[p x)] p x) = x µ ) T C / dw x µ ) T C x µ )d ) = x T C / dw +C µ d xt C xd µ T C/ dw + µt C µ d) = x T dc xt db xd+g) where he las erm s ndependen of x and he frs wo erms explan he form of p x) and he appearance of he Gaussan Nex we analyze he change of he covarance marx Lemma 7 [4]) We have ha da = x µ )x µ ) T R n x µ ) T C / dw )p x)dx A C A d 6
7 3 Boundng expanson Our plan s o bound he expanson by he specral norm of he covarance marx a me Frs, we bound he measure of a se of nal measure Lemma 8 For any se E R n wh E px)dx = and 0, we have ha P 4 p x)dx 3 4 ) 9 0 P Cs / A s Cs / ds 64 ) E Proof Le g = E p x)dx Then, we have ha dg = x µ ) T C / dw p x)dx E = x µ )p x)dx,c / dw E where he negral mgh no be 0 because s over he subse E and no all of R n Hence, we have, Hence, we have ha d[g] d d[g ] = C / x µ )p x)dx d E = max ζ T C / x µ )p x)dx) d ζ E p max ζ T C / x µ )) x)dx p x)dxd ζ R n R ) n = max ζ T C / A C / ζ d ζ = C / A C / d 0 C / A C / By he Dambs, Dubns-Schwarz heorem, here exss a Wener process W such ha g g 0 has he same dsrbuon as W [g] Usng g 0 =, we have ha P 4 g 3 4 ) = P 4 W [g] 4 ) P mn W s 0 s 4 and [g] 64 ) 64 P max 0 s 64 W s > 4 ) P[g] > 64 ) 4P W 64 > 4 ) P[g] > 64 ) 9 0 P[g] > 64 ) where we used reflecon prncple for -dmensonal Brownan moon n and he concenraon of normal dsrbuon n, namely P x N0,) x > ) 008 Theorem 9 Brascamp-Leb [9]) Le γ : R n R + be he sandard Gaussan densy n R n Le f : R n R + be any logconcave funcon Defne he densy funcon h as follows: hx) = fx)γx) R n fy)γy)dy Fx a un vecor v R n, le µ = E h x) Then, for any α, E h v T x µ) α ) E γ v T x α ) Usng hs we derve he followng well-known sopermerc nequaly ha was proved n [] and was also used n [4] 7
8 Theorem 30 [, Thm 44]) Le hx) = fx)e xtbx / fy)e ytby dy where f : R n R + s an negrable logconcave funcon and B s posve defne Then h s logconcave and for any measurable subse S of R n, { hx)dx = Ω B ) } mn hx)dx, hx)dx S R n \S B In oher words, he expanson of h s Ω ) Proof The proof uses he localzaon lemma o reduce he saemen o a -dmensonal saemen abou a Gaussan mes a logconcave densy, where he Gaussan s a projecon of he Gaussan N 0,B ) bu he logconcave funcon mgh be dfferen as he lm of localzaon s he orgnal funcon along an nerval mes an exponenal funcon) We hen apply he Brascamp-Leb nequaly n one dmenson Theorem 9) o prove ha for he resulng one-dmensonal dsrbuon, he varance s a mos ha of he Gaussan, herefore a mos B The sopermerc consan s bounded by he nverse of he sandard devaon mes a consan The complee proof, n more general erms, s carred ou n [, Thm 44] We can now prove a bound on he expanson Lemma 3 Gven a logconcave dsrbuon p Le A be defned by Defnon 4 usng nal dsrbuon p Suppose ha here s T > 0 such ha ) T P Cs / A s Cs / ds 64 and B T ui 3 4 Then, we have ha ψ p = Ω u /) 0 Proof By Mlman s heorem [30], suffces o consder subses of measure Consder any measurable subse E of R n of nal measure By Lemma 6, p s a marngale and herefore E px)dx = E S ) p 0 x)dx = E p x)dx E Nex, by he defnon ofp T 3), we have hap T x) e ct T x x B T px) and Theorem 30 shows ha he expanson of E s Ω λ mn B T ) /) Hence, we have E px)dx = E p T x)dx E = Ωu / )E BT ui mn p T x)dx, E Ē Ωu / )P B T ui and 4 p T x)dx 3 ) E 4 = Ωu / ) P 4 p T x)dx Ωu / ) 0 P = Ωu / ) E C / 0 )) p T x)dx ) PB T ui s false) s A s Cs / ds ) ) 64 ) PB T ui s false) where we used he assumpon a he end Usng Theorem 0, hs shows ha ψ p = Ω u /) 4 Conrollng A va he poenal TrA ) In hs secon, we only use C = I for he conrol marx Lem 8) 8
9 4 Thrd momen bounds Here are wo key lemmas abou he hrd-order ensor of a log-concave dsrbuon A specal case of he frs nequaly was used n [4] For our man heorem, we only he frs lemma wh B = I, bu we need he general case for he proof n Secon 7 Lemma 3 Gven a logconcave dsrbuon p wh mean µ and covarance A For any B 0, symmerc marx C, we have ha A E x p B / x µ)x µ) T Cx µ) = O / BA / / ) Tr A / CA / Proof We frs consder he case C = vv T Takng y = A / x µ) and w = A / v Then, y follows an soropc log concave dsrbuon p and he saemen becomes E y p B / A / y y T w ) A ) = O / BA / / w Then, we calculae ha E y p B / A / y y T w ) = max E y pb / A / y) T ζ y T w ) ζ max E y p B / A / y) T ζ ) E y p y T w) 4 = O ζ ) A / BA / w where we used he fac ha for a fxed w, y T w has a one-dmensonal logconcave dsrbuon Lemma 3) and hence Lemma 4 shows ha E y p y T w ) 4 = O) E y p y T w ) ) 4 = O w ) For a general symmerc marx C, we wre C = λ v v T where λ, v are egenvalues and egenvecors of C Hence, we have ha E x p B / x µ)x µ) T Cx µ) λ E x p B / x µ)x µ) T v v T x µ) O) λ A / BA / / A / v = O) A / BA / / Tr A / λ v v T A/) = O) A / BA / / Tr A / CA / Lemma 33 Gven a logconcave dsrbuon p wh mean µ and covarance A We have E x,y p x µ,y µ 3 = O Tr A ) ) 3/ Proof Whou loss of generaly, we assume µ = 0 For a fxed x and random y, x, y follows a one-dmensonal logconcave dsrbuon Lemma 3) and hence Lemma 4 shows ha E y p x,y 3 O) E y p x,y ) 3/ = O x T Ax ) 3/ Nex, we noe ha A / x follows a logconcave dsrbuon Lemma 3) and hence Lemma 4 shows ha E x,y p x,y 3 A = O)E / x p x 3 A O) E / x p x ) 3/ = O Tr A ) ) 3/ 9
10 4 Analyss of A Usng Iô s formula and Lemma 7, one can compue he dervaves of TrA Snce a smlar calculaon appears n Secons 4, 6 and 7, we prove a common generalzaon n Lemma 36 Lemma 34 Le A be defned by Defnon 4 We have ha dtra =E x p x µ ) T A x µ )x µ ) T dw TrA 3 )d+e x,y p x µ ) T y µ ) ) 3 d Lemma 35 Gven a logconcave dsrbuon p wh covarance marx A stra = n Le A defned by Defnon 4 usng nal dsrbuon p There s a unversal consan c such ha Proof Le Φ = TrA By Lemma 34, we have ha P max Tr A ) c 8n) 00 wh T = [0,T] n dφ = TrA 3 )d+e x,y p x µ ) T y µ ) ) 3 d+ex p x µ ) T A x µ )x µ ) T dw def =δ d+v T dw 4) For he drf erm δ d, Lemma 33 shows ha δ E x,y p x µ ) T y µ ) ) 3 = O Tr A ) 3/ ) C Φ 3/ 4) for some unversal consan C Noe ha we dropped he erm TrA 3 ) snce A s posve semdefne and herefore he erm s negave For he marngale erm v T dw, we noe ha v = Ex p x µ ) T A x µ )x µ ) A / Tr A Lem 3) OΦ 5/4 ) So he drf erm grows roughly as Φ 3/ whle he sochasc erm grows as Φ 5/4 Thus, boh bounds on he drf erm and he sochasc erm) sugges ha for up o O n ), he poenal Φ remans On) We now formalze hs, by decouplng he wo erms Le By 4) and Iô s formula, we have ha fa) = a+n v T dw dfφ ) = f Φ )dφ + f Φ )d[φ] ) δ = Φ +n) 3 v d+ v T dw 3/ 8Φ +n) 5/ Φ +n) 3/ C d+dy 43) where dy = Φ +n), Y 3/ = 0 and C s he unversal consan n 4) Noe ha d[y] = v d 4Φ +n) 3 = O) Φ 5/ Φ +n) 3 C n By Theorem, here exss a Wener process W such ha Y has he same dsrbuon as W [Y] Usng he reflecon prncple for -dmensonal Brownan moon, we have ha P max [0,T] Y γ) P max [0, C n T] W γ) = P W C n T γ) exp γ n CT ) 0
11 Snce Φ 0 = A p F = n, we have ha fφ 0) = n and herefore 43) shows ha P max fφ ) +C T +γ) exp γ n [0,T] n CT ) Pung T = 56C +C) n and γ = 4, we have ha n P max [0,T] fφ ) 3 n ) exp 8)) Noe ha fφ ) 3 n mples ha Φ 8n Hence, we have ha P max [0,T] Φ 8n) Proof of Theorem 7 Proof of Theorem 7 By rescalng, we can assume TrA = n By Lemma 35, we have ha Pmax Tr A ) c s 8n) 099 wh = s [0,] n Snce Tr A ) 8n mples ha A 8n, we have ha { where T = mn 64 8,c 5 Localzaon proofs T P A s ds 0 64 and B T T I) 099 } / n Now he heorem follows from Lemma 3 We begn wh he proof of exsence of a unque soluon for he SDE Proof of Lemma 5) We can wre he sochasc dfferenal equaon as dc = C / A,B )dw +CA,B )µc,b )d and db = CA,B )d where µc,b) = xqc,b,x)dx and A c,b) = x µc,b))x µc,b)) T qc,b,x)dx R n R n and qc,b,x) = e ct x x B px) R n e ct y y Bpy)dy Snce p has compac suppor, we have ha q s Lpschz n c and B varables, so are he funcons µ and A Nex, we noe ha boh µ and A are bounded snce p has compac suppor Snce C / s bounded and Lpschz funcon n c and B varables, so s C Therefore, we can use a sandard exsence and unqueness heorem eg [3, Sec 5]) o show he exsence and unqueness of he soluon on me [0,T] for any T > 0 Nex s he proof of he nfnesmal change n he densy Proof of Lemma 6) Le q x) = e ct x x B px) By Iô s formula, appled o fc,b) def = e ct x x B px), we have ha dq x) = dc T x db x,x + d[c T x] )) d[ B x,x ] q x)
12 Noe ha dc T x = C / dw +C µ d,x Hence, he quadrac varaons of c T x s d[c T x] = C x,x d Also, db s a predcable process namely, does no have a sochasc erm) and hence d[ B x,x ] = 0 Therefore, hs gves dq x) = C / dw +C µ d,x q x) 5) Le V = R n q y)dy Then, we have By Iô s formula, we have ha dv = dv = dq y)dy R n = C / dw +C µ d,y q y)dy R n = V C / dw +C µ d,µ V = V = V Combnng 5) and 5), we have ha dp x) =dv q x)) =q x)dv = q x)v =p x) +V dv + V 3 C / d[v] dq x)+d[v,q x)] C / dw,µ +V C / dw,x µ dw +C µ d,µ +V C µ,µ d C / dw,µ 5) C / dw +C µ d,x q x) V C / µ,c / x q x)d The nex proof s for he change n he covarance marx Proof of Lemma 7) Recall ha A = x µ )x µ ) T p x)dx R n Vewng A = fµ,p ), e, as a funcon of he varables µ and p, we apply Iô s formula In he dervaon below, we use [µ,µ T ] o denoe he marx whose,j coordnae s [µ,,µ,j ] Smlarly, [µ,p x)] s a column vecor and [µ T,p x)] s a row vecor da = x µ )x µ ) T dp x)dx R n dµ x µ ) T p x)dx x µ )dµ ) T p x)dx R n R n R x µ )d[µ T,p x)] dx d[µ,p x)] x µ ) T dx n R n + d[µ,µ T ] p x)dx R n
13 where he facor comes from he Hessans of x and xy Now he second erm vanshes because dµ x µ ) T p x)dx = dµ x µ )p x)dx) T = 0 R n R n Smlarly, he hrd erm also vanshes: R n x µ )dµ ) T p x)dx = 0 To compue he las 3 erms, we noe ha dµ = d xp x)dx R n = xx µ ) T C / dw p x)dx R n = x µ )x µ ) T C / dw p x)dx+ µ x µ ) T C / dw p x)dx R n R n = A C / dw Therefore, we have for he las erm d[µ,µ T ) ] j = ) A C / l l A C / whch we can smply wre as d[µ,µ T ] = A C A d Smlarly, we have ) jl d = A C / C / ) T A T ) j d = A C A ) j d d[µ,p x)] = p x)a C x µ )d Ths gves he fourh erm x µ )d[µ T,p x)] dx = x µ )x µ ) T C A p x)ddx = A C A d R n R n Smlarly, we have he ffh erm R d[µ n,p x)] x µ ) T dx = A C A d Combnng all he erms, we have ha da = x µ )x µ ) T dp x)dx A C A d R n Nex s he proof of sochasc dervave of he poenal Φ = TrA γi) q ) Lemma 36 Le A be defned by Defnon 4 For any neger q, we have ha dtra γi) q ) =qe x p x µ ) T A γi) q x µ )x µ ) T C / dw qtra γi) q A C )d + q E x,y p x µ ) T A γi) α y µ )x µ ) T A γi) β y µ )x µ ) T C y µ )d α+β=q Proof Le ΦX) = TrX γi) q ) Then he frs and second-order dreconal dervaves of Φ a X s gven by Φ X = qtrx γi) q H) and H Usng hese and Iô s formula, we have ha dtra γi) q ) = qtra γi) q da )+ q Φ q X X = q TrX γi) k H X γi) q k H ) H,H α+β=q jkl k=0 TrA γi) α e j A γi) β e kl )d[a j,a kl ] where e j s he marx ha s n he enry,j) and 0 oherwse, and A j s he real-valued sochasc process defned by he,j) h enry of A 3
14 Usng Lemma 7 and Lemma 6, we have ha da = E x p x µ )x µ ) T x µ ) T C / dw A C A d = E x p x µ )x µ ) T x µ ) T C / e z dw,z A C A d 53) where W,z s he z h coordnae of W Therefore, d[a j,a kl ] = ) E x p x µ ) x µ ) j x µ ) T C / e z E x p x µ ) k x µ ) l x µ ) T C / e z )d z = E x,y p x µ ) x µ ) j y µ ) k y µ ) l x µ ) T C y µ )d 54) Usng he formula for da 53) and d[a j,a kl ] 54), we have ha dtra γi) q ) =qe x p x µ ) T A γi) q x µ )x µ ) T C / dw qtra γi) q A C )d + q TrA γi) α e j A γi) β e kl )E x,y p x µ ) x µ ) j y µ ) k y µ ) l x µ ) T C y µ )d α+β=q jkl =qe x p x µ ) T A γi) q x µ )x µ ) T C / dw qtra γi) q A C )d + q E x,y p x µ ) T A γi) α y µ )x µ ) T A γi) β y µ )x µ ) T C y µ )d α+β=q Acknowledgemen We hank Rav Kannan, Lac Lovász, Assaf Naor and Nsheeh Vshno for her connuous suppor and encouragemen We also hank Sébasen Bubeck, Ben Cousns, Ronen Eldan, Bo az Klarag, Anup B Rao and Tng-Kam Leonard Wong for helpful dscussons References [] Zeyuan Allen-Zhu, Yn Ta Lee, and Lorenzo Oreccha Usng opmzaon o oban a wdh-ndependen, parallel, smpler, and faser posve sdp solver In Proceedngs of he Tweny-Sevenh Annual ACM-SIAM Symposum on Dscree Algorhms, pages SIAM, 06 [] Davd Alonso-Guérrez and Jesús Basero Approachng he Kannan-Lovász-Smonovs and varance conjecures, volume 3 Sprnger, 05 [3] Shr Arsen-Avdan, Aposolos Gannopoulos, and Val D Mlman Asympoc Geomerc Analyss, Par I, volume 0 05 [4] K M Ball Logarhmcally concave funcons and secons of convex ses n rn Suda Mahemaca, 88:69 84, 988 [5] S Bobkov On sopermerc consans for log-concave probably dsrbuons Geomerc aspecs of funconal analyss, Lec noes n Mah, 90:8 88, 007 [6] S G Bobkov and A Koldobsky On he Cenral Lm Propery of Convex Bodes, pages 44 5 Sprnger Berln Hedelberg, Berln, Hedelberg, 003 [7] J Bourgan On he dsrbuon of polynomals on hgh dmensonal convex ses 469:7 37, 99 [8] Jean Bourgan On hgh dmensonal maxmal funcons assocaed o convex bodes Amercan Journal of Mahemacs, 086): , 986 [9] H J Brascamp and E H Leb On exensons of he brunn-mnkowsk and prekopa-lendler heorems, ncludng nequales for log-concave funcons, and wh applcaon o he dffuson equaonslogarhmc concave measures and funcons J Funconal Anal, : , 976 4
15 [0] Slouanos Brazkos, Aposolos Gannopoulos, Peros Valeas, and Bearce-Helen Vrsou Geomery of soropc convex bodes, volume 96 Amercan Mahemacal Socey Provdence, 04 [] Jeff Cheeger A lower bound for he smalles egenvalue of he Laplacan, pages Prnceon Unv Press, 969 [] B Cousns and S Vempala A cubc algorhm for compung Gaussan volume In SODA, pages 5 8, 04 [3] B Cousns and S Vempala Bypassng KLS: Gaussan coolng and an O n 3 ) volume algorhm In STOC, pages , 05 [4] R Eldan Thn shell mples specral gap up o polylog va a sochasc localzaon scheme Geomerc and Funconal Analyss, 3:53 569, 03 [5] R Eldan and B Klarag Approxmaely gaussan margnals and he hyperplane conjecure Conermporary Mahemacs, 545, 0 [6] Ronen Eldan and James R Lee Talagrand s convoluon conjecure on gaussan space In IEEE 56h Annual Symposum on Foundaons of Compuer Scence, FOCS 05, Berkeley, CA, USA, 7-0 Ocober, 05, pages , 05 [7] Ronen Eldan and Joseph Lehec Boundng he norm of a log-concave vecor va hn-shell esmaes 03 [8] B Fleury Concenraon n a hn Eucldean shell for log-concave measures J Func Anal, 594):83 84, 00 [9] M Gromov and V D Mlman A opologcal applcaon of he sopermerc nequaly Amer J Mah, 054): , 983 [0] Olver Guedon and Emanuel Mlman Inerpolang hn-shell and sharp large-devaon esmaes for soropc log-concave measures Geomerc and Funconal Analyss, 5): , 0 [] R Kannan, L Lovász, and M Smonovs Isopermerc problems for convex bodes and a localzaon lemma Dscree & Compuaonal Geomery, 3:54 559, 995 [] B Klarag On convex perurbaons wh a bounded soropc consan Geom and Func Anal, 66):74 90, 006 [3] B Klarag A cenral lm heorem for convex ses Inven Mah, 68:9 3, 007 [4] B Klarag Power-law esmaes for he cenral lm heorem for convex ses J Func Anal, 45:84 30, 007 [5] M Ledoux Specral gap, logarhmc sobolev consan, and geomerc bounds In Surveys n Dff Geom, Vol IX, pages 9 40 In Press, 004 [6] E Leb and W Thrrng Inequales for he momens of he egenvalues of he Schrödnger equaon and her relaon o Sobolev nequales Sudes n Mahemacal Physcs: Essays n honor of Valenne Bargman, Leb, E, Smon, B, Wghman, AS eds), pages , 976 [7] L Lovász and M Smonovs Random walks n a convex body and an mproved volume algorhm In Random Srucures and Alg, volume 4, pages 359 4, 993 [8] L Lovász and S Vempala The geomery of logconcave funcons and samplng algorhms Random Srucures and Algorhms, 303): , 007 [9] Irn Perssnak Mlla Anla, Keh Ball The cenral lm problem for convex bodes Transacons of he Amercan Mahemacal Socey, 355): , 003 [30] E Mlman On he role of convexy n sopermery, specral gap and concenraon Inven Mah, 77): 43, 009 5
16 [3] Bern Oksendal Sochasc dfferenal equaons: an nroducon wh applcaons Sprnger Scence & Busness Meda, 03 [3] G Paours Concenraon of mass on convex bodes Geomerc and Funconal Analyss, 6:0 049, 006 [33] S S Vempala Algorhmc aspecs of convexy Lecure noes from he Insu Henr Poncare Wner School, January 9-3, 05 [34] VGMaz ja Classes of domans and mbeddng heorems for funcon spaces Dokl Acad Nauk SSSR Engl ransl Sove Mah Dokl, 96) ), 3:57 530, A reducon o a hrd momen assumpon In hs secon, we use he followng assumpon In he frs arxv verson of hs paper, we clamed hs assumpon as a lemma Whle mgh be rue, our proof was no correc Assumpon Thrd Momen) For an soropc logconcave dsrbuon p R n, E x,y p x,y 3) = Onψ n ) Noe ha E x,y p x,y 3) =,j,k E xx x j x k ) Under hs assumpon we prove he followng Theorem 37 Under he hrd momen assumpon above, any soropc logconcave densy p n R n, he KLS consan s ψ p = e O lognloglogn) The proof wll use he same process wh C = I, bu wh a more sensve poenal funcon Φ = TrA I) q ) for even negers q 6 Tensor bounds Defnon 38 3-Tensor) For any soropc logconcave dsrbuon p n R n and any symmerc marces A, B and C, we defne T p A,B,C) = E x,y p x T Ay)x T By)x T Cy) Ofen, we drop he subscrp p o ndcae he wors case bound TA,B,C) def = sup T p A,B,C) soropc logconcave p Remark I s clear from he defnon ha T s symmerc, namely TA,A,A 3 ) = TA σ),a σ),a σ3) ) for any permuaon σ We frs sar wh some smple equales abou a 3-ensor Here we repeaedly use he elemenary facs TrAB) = TrBA), x T Ay = Tr Ayx T) Lemma 39 For any soropc logconcave dsrbuon p and any symmerc marces A, B and C, we have ha T p A,B,I) = TrA B ) and T p A,B,I) =,j A j Tr B j ) where = E x p xx T x Proof Drec calculaon shows ha T p A,B,I) = E x,y p x T Ayx T Byx T y = E x,y p x T Ayx T Byx y = E x,y p Tr Axx T Byy T ) x y = TrA B ) 6
17 and T p A,B,I) = E x,y p x T Ayx T Byx T y = A j E x,y p x y j x T Byx T y,j = A j E x,y p Tr xx T Byy T ) x y j = A j Tr B j ),j,j Lemma 40 For any A,A,A 3 0, we have ha and for any symmerc marces B,B,B 3, we have ha TA,A,A 3 ) 0 TB,B,B 3 ) T B, B, B 3 ) Proof Fx any soropc logconcave dsrbuon p We defne = E x p xx T x T A / 3 e whch s well defned snce A 3 0 Then, we have ha T p A,A,A 3 ) =E x,y p x T A yx T A yx T A 3 y = TrA A ) Snce s symmerc and A,A 0, we have ha A / A A / 0 and TrA A ) 0 Therefore, TA,A,A 3 ) T p A,A,A 3 ) 0 For he second par, we wre B = B ) B ) where B ) 0, B ) 0 and B = B ) +B ) We defne B ),B),B) 3,B) 3 smlarly Noe ha TB,B,B 3 ) =TB ),B),B) 3 ) TB),B),B) 3 ) TB),B),B) 3 )+TB),B),B) 3 ) TB ),B),B) 3 )+TB),B),B) 3 )+TB),B),B) 3 ) TB),B),B) 3 ) Snce B ) j 0, he frs par of hs lemma shows ha every erm TB ),Bj),Bk) 3 ) 0 Hence, we have ha TB,B,B 3 ) TB ),B),B) 3 )+TB),B),B) 3 )+TB),B),B) 3 )+TB),B),B) 3 ) +TB ),B),B) 3 )+TB),B),B) 3 )+TB),B),B) 3 )+TB),B),B) 3 ) =T B, B, B 3 ) Lemma 4 Suppose ha ψ k αk β for all k n for some 0 β and α Gven an soropc logconcave dsrbuon p and an un vecor v, we defne = E x p xx T x T v Then, we have ha For any orhogonal projecon marx P wh rank r, we have ha For any symmerc marx A, we have ha Tr P ) Oψ mnr,n) ) Tr A ) Oα logn) Tr A /β)) β Proof We frs bound Tr P ) Ths par of he proof s generalzed from a proof by Eldan [4] Noe ha Tr P ) = E x p x T P xx T v Snce Ex T v = 0, we have ha Tr P ) Ex T v) Varx T P x) Lem 9 O ψ rankp + P) ) E x P x = O ψ rankp + P) ) Tr P ) 7
18 Ths gves Tr P ) Oψmnr,n) ) Now we bound Tr A ) Snce Tr A ) Tr A ), we can assume whou loss of generaly ha A 0 We wre A = A +B where each A has egenvalues beween A /n, A + /n] and B has egenvalues smaller han or equals o A /n Clearly, we only need a mos logn)+ many such A Le P be he orhogonal projecon from R n o he span of he range of A Usng A P A, we have ha ) Tr A ) A Tr P ) O ψmnranka ),n) A Oα ) ranka ) β A where we used he frs par of hs lemma n he las nequaly Smlarly, we have ha Tr B ) O ψ n) B On B ) O) A Combnng he bounds on Tr A ) and Tr B ), we have ha Tr A ) Oα ) ranka ) β A +O) A Oα ) Oα logn) ranka ) A /β) Tr A /β)) β ) β logn) β In he nex lemma, we collec ensor relaed nequales ha wll be useful Lemma 4 Suppose ha ψ k αk β for all k n for some 0 β dsrbuon p n R n and symmerc marces A and B, we have ha and α For any soropc logconcave E x x T Ax) O)Tr A ), E x p x T Ax TrA ) Oψ n )TrA, 3 TA,I,I) Oψ n ) A n, 4 TA,I,I) Oψ n )Tr A, 5 TA,B,I) Oψr ) B Tr A where r = mnrankb),n), 6 TA,B,I) Oα logn) Tr B /β)) β Tr A, 7 TA,B,I) T A s,i,i)) /s T B,I,I)) / for any s, wh s + = Proof Whou loss of generaly, we can assume A s dagonal by roang space In parcular, f we wan o prove somehng for TrA α A β ) where A, are symmerc marces, we use he specral decomposon A = UΣU T o rewre hs as Tr UΣ α U T UΣ β U T ) = Tr Σ α U T U)Σ β U T U) ) whch pus us back n he same suaon, bu wh a dagonal marx A Le = E x p xx T x For nequaly, we noe ha E x x T Ax) = j A A jj E x x x j j A A jj Ex 4 Lem 4 Ex4 j O) A ) For nequaly, we noe ha E x p x T Ax = TrA Hence, E x p x T Ax TrA ) = Var x T ) Lem 9 Ax Oψn )E x Ax = Oψn )TrA 8
19 For remanng nequales, suffces o upper bound T by upper boundng T p for any soropc logconcave dsrbuon p For nequaly 3, we noe ha T p A,I,I) Lem 39 = A Tr ) A Tr ) where he las nequaly s from he hrd momen assumpon For nequaly 4, we noe ha Lem 39 = A TI,I,I) Onψ n ) A T p A,I,I) Lem 39 = A Tr Lem 4 ) A Oψ n ) = Oψ n )Tr A For nequaly 5, we le P be he orhogonal projecon from R n o he span of he range of B Le r = rankp) Then, we have ha where we used ha B B P n For nequaly 6, we noe ha T p A,B,I) Lem 39 = T p A,B,I) T p A, B,I) Lem 40) A Tr B ) = A Tr B ) Lem 39) B A Tr P ) Oψr )Tr A B Lem 4) Lem 4 Oα logn)tr A Tr B /β)) β For nequaly 7, we noe ha T p A,B,I) T p A, B,I) Lem 40) = Tr A B ) Lem 39) = Tr A B ) Tr /s A /s / B / ) Tr /s A /s) s)) /s Tr / B /) )) / Lem ) = Tr A s )) /s / Tr B )) Lem ) Tr A s /s )) / )) Tr B Tr A s ) ) /s ) ) / Tr B = T p A s,i,i)) /s T p B,I,I)) / Lem 39) Lemma 43 For any posve sem-defne marces A,B,C and any α [0,], hen TB / A α B /,B / A α B /,C) TB / AB /,B,C) 9
20 Proof Fx any soropc logconcave dsrbuon p Le = E x p B / xx T B / x T C / e Then, we have ha T p B / A α B /,B / A α B /,C) = E x,y p x T B / A α B / yx T B / A α B / yx T Cy = ) ) E y T B / A α B / x x T B / A α B / y )x T C / e y T C / e = E Tr A α B / xx T B / A α B / yy T B /) )) x T C / e )y T C / e = TrA α A α ) Usng Lemma 3, we have ha TrA α A α ) TrA ) = E x,y px T B / AB / yx T Byx T Cy = T p B / AB /,B,C) Takng he supremum over all soropc logconcave dsrbuons p, we ge he resul 6 Dervaves of he poenal Lemma 44 Le A be defned by Defnon 4 For any neger q, we have ha dtra I) q ) =qe x p x µ ) T A I) q x µ )x µ ) T dw qtra I) q A )d + q E x,y p x µ ) T A I) α y µ )x µ ) T A I) β y µ )x µ ) T y µ )d α+β=q We gve he proof n Secon 5 The nex lemma bounds he sochasc process ha conrols hs poenal funcon Lemma 45 Le A and p be defned by Defnon 4 Le Φ = TrA I) q ) for some even neger q, hen we have ha dφ = δ d+v T dw wh and Proof By Lemma 44, we have δ qq )TA A I) q,a,a )+qφ + q +Φ q n q ) v q E x p x µ ) T A I) q x µ )x µ ) T dφ =qe x p x µ ) T A I) q x µ )x µ ) T dw qtra I) q A )d + q E x,y p x µ ) T A I) α y µ )x µ ) T A I) β y µ )x µ ) T y µ )d α+β=q =qe x p x µ ) T A I) q x µ )x µ ) T dw qtra I) q A )d + q E x,y p x T A A I) α yx T A A I) β yx T A yd α+β=q def =δ d+v T dw where p s he soropc verson of p defned by p x) = pa / x+µ ), δ d s he drf erm n dφ and v T dw s he marngale erm n dφ For he drf erm α d, we have δ q TA A I) α,a A I) β,a ) qtra I) q A ) α+β=q The frs erm n he drf s q TA A I) α,a A I) β,a ) q α+β=q q = α+β=q α+β=q TA A I α,a A I β,a ) Lem 40) TA A I q,a,a ) Lem 43) qq ) TA A I) q,a,a ) 0
21 For he second erm n drf, snce q s even, we have ha qtra I) q A ) = qtra I) q A I +I) ) qtra I) q+ ) qtra I) q ) qφ + q +qφ q n q For he marngale erm v T dw, we noe ha v = q E x p x µ ) T A I) q x µ )x µ ) T 63 Analyss of A We frs bound he drf erm from Lemma 44 Lemma 46 Suppose ha ψ k αk β for all k n for some 0 β and α Le Φ = TrA I)q ) for some even neger q and A 0 If βq, hen TAA I) q,a,a) O α )[ ] n β β q + q Φ q +n β β q + q Φ q +n β β βq+ Φ+logn)n β q Φ + q Proof We have ha TAA I) q,a,a) =TA I) q +A I) q,a I)+I,A I)+I) =TA I) q,a I,A I)+TA I) q,a I,I)+TA I) q,i,i) +TA I) q,a I,A I)+TA I) q,a I,I)+TA I) q,i,i) T A I q, A I, A I )+T A I q, A I,I)+T A I q,i,i) Lem 40) +TA I) q, A I, A I )+TA I) q, A I,I)+TA I) q,i,i) T A I q, A I, A I )+3T A I q, A I,I) 6) +3T A I q,i,i)+ta I) q,i,i) where we used Lemma 43 a he end For he frs erm n 6), we have ha T A I q, A I, A I ) T A I q, A I,I) Lem 43) Oα logn)φ Tr A I /β) β Lem 46) = Oα logn)φ Tr A I q ) /βq) n /βq)) β where we used βq a he las lne For he second erm n 6), we wre Oα logn)n β q Φ +/q A I = B +B where B consss of he egen-componens of A I wh egenvalues η and B s he remanng par where we wll pck η 0 laer Then, we have ha T A I q, A I,I) = TB q,b,i)+tb q,b,i)+tb q,b,i)+tb q,b,i) 6) For he frs erm n 6), we noe ha TB q,b,i) TB q,i,i) Lem 43) Oψ n n) B q Lem 43) Oη q ψ n n)
22 For he second erm n 6), we noe ha TB q,b,i) TB q,i,i)q q TB q,i,i) q Lem 47) Oη q ψ n n) q q Oψ n Φ) q Lem 43 and Lem 44) where we used B η and TrB q Tr A I q = Φ a he las lne For he hrd erm n 6), smlarly, we have TB q,b,i) TB q,i,i)q q TB q,i,i) q Lem 47) Oψ nφ) q q Oη q ψ n n) q Lem 43 and Lem 44) For he fourh erm n 6), we le P be he orhogonal projecon from R n o he range of B We have ha TB q,b,i) = TPB q P,PB P,I) TPB q P,P,I) Lem 43) Oψr )TrBq Lem 45) Oψ r)φ where r rankp) Φ η q Usng ψ k αk β and combnng all four erms, we have ha T A I q, A I,I) Oη q ψ n n)+oη q ψ n n) q q Oψ n Φ) q +Oψ n Φ) q Oα ) q Oη q ψ n n) q +Oψ r )Φ ] [ η q n +β +η q n q q +βq+) q Φ q +ηn q +β q ) Φ q q + Φ+β η βq Balancng he las wo erms and seng η = Φ q n q + qβq+), we ge ha [ ] T A I q, A I,I) Oα Φ) n β β q +βq +n β β q ) β +βq β +n +βq +n β β +βq where we used q and β 0 For he hrd erm n 6), we have ha Oα n β βq+) β Φ) β T A I q,i,i) = TB q,i,i)+tb q,i,i) O αη q n +β +α n βφ ) η Lem 43 and Lem 44) where we se η = n β q Φ q a he las lne For he fourh erm n 6), we have ha Oα n β q +β Φ q ) T A I q,i,i) = TB q,i,i)+tb q,i,i) where we se η = n β q Φ q a he las lne Combnng all erms, we have he resul Nex we bound he marngale erm Oαη q n +β +α n β Φ η) Lem 43 and Lem 44) Oα n β) q +β Φ q ) Lemma 47 Le p be a logconcave dsrbuon wh covarance marx A Le Φ = TrA I) q ) for some even neger q Then, E x p x µ ) T A I) q x µ )x µ ) T OΦ q n q +Φ + q +n q )
23 Proof Noe ha E x p x µ ) T A I) q x µ )x µ ) T O) A / Tr A / A I) q A / Lem 3) O) A / Tr A I q +O) A / Tr A I q O+Φ q )Φ q n q +O+Φ q )Φ OΦ q n q +Φ + q +n q ) Usng Lemma 46 and Lemma 47, we know ha Φ = TrA I) q ) sasfes he sochasc equaon dφ = δ d+v TdW wh δ O α q )[ ] n β β q + q Φ q +n β β q + q Φ β q β +n βq+ Φ +logn)n β + q Φ q +qφ + q +Φ q n q ) O α q )[ n β β q + q Φ q +n β β q + q Φ q +n β β βq+ Φ +logn)n β q Φ + q ] 63) and [ ] v Oq ) Φ q n + q +Φ q +n q 64) where we used α, βq and q n 63) Usng hese, one can bound he growh of Φ usng a sochasc Grönwall s nequaly For compleeness, we bound Φ drecly below Lemma 48 Suppose ha ψ k αk β for all k n for some 0 β and α Gven an soropc logconcave dsrbuon p Le A be defned by Defnon 4 usng nal dsrbuon p Le Φ = TrA I) q ) for some even neger q If βq and n q ηq for some large consan η, hen here s a unversal consan c such ha P max Φ n β log q cn β+ β q n) 00 wh T = [0,T] qα logn Proof The dea s o choose a a funcon Ψ = fφ,) so ha he resulng sochasc equaon for Ψ effecvely decouples he drf and marngale erms We use ) fa,) = a++e q +F q q wh By 45 and Iô s formula, we have ha E = q q α q n β+βq and F = q q α q n β+βq dψ = df df d+ d dφ dφ + d f dφdφ d[φ] df df d+ d dφ δ d+ df dφ vt dw where we used fa,) s concave n a n he las lne and dropped he second dervave erm The raonale for our choce of fa,) s ha +E q +F q s our guess for he soluon of he SDE for Φ, and he power /q s chosen so ha Φ can be elmnaed from he sochasc erm n he bound for Ψ above For he erm df dφ δ d, we use 63) and ge ha df dφ δ = δ q Φ ++E q +F q ) q Oqα ) n β β q + q Φ q + Φ ++E q +F q ) q +Oqα ) β β n βq+ Φ Φ ++E q +F q ) q n β β q + q Φ q Φ ++E q +F q ) q logn)n β + q Φ q + 65) Φ ++E q +F q ) q 3
24 For he frs erm n 65), we noe ha n β β q + q Φ q Φ ++E q +F q ) q n β β q + q Φ ++E q +F q ) β nβ q + q q q ) F q ) 3 q where we used F = q q α q n β+βq a he end For he second erm n 65), we noe ha n β β q + q Φ q Φ ++E q +F q ) q β nβ q + q E q ) q = E q qα = F q qα 3 4 where we used E = q q α q n β+βq a he end For he hrd erm n 65), assumng Φ n β log q n, we have ha β β β n βq+ Φ nβ /q β βq+ Φ nβ βq+ n q β β q nβ q + q = E q Φ ++E q +F q ) q E q ) q E q ) q E q ) q qα where we used ha qβ mples β β βq+ + q β q β β q + q a and E = qq α q n β+βq a For he fourh erm n 65), assumng Φ n β log q n, we have ha logn)n β q Φ + q Φ ++E q +F q ) q logn)nβ q Φ q E q ) q β nβ q + q E q ) q = E q qα where we used E = q q α q n β+βq a he end Combnng all four erms n 65), we have ha df ) dφ δ O E q +F q 3 4 For he erm df dd, we have ha df d = q qe q + q Fq Φ ++E q +F q ) q ) = O E q +F q 3 4 For he erm df dφ vt dw, usng 64) and assumng Φ n β log q n, we have ha [ ] v Oq ) Φ q n q +n q Hence, we have ha df dφ v 4q [ ] Oq ) Φ q n q +n q Φ ++E q +F q ) q On q ) Combnng he erms df dφ δ d, df df d d and dφ vt dw, we have ha, when Φ n β log q n, dψ = df df d+ d dφ dφ + d f dφdφ d[φ] C E q +F q 3 4 ) d+dy 66) where Y s a marngale wh Y 0 = 0 and d[y] d C n /q for some unversal consan C,C By Theorem, here exss a Wener process W such ha Y has he same dsrbuon as W [Y ] Usng he reflecon prncple for -dmensonal Brownan moon, we have ha P max Y γ) P [0,T] max [0,C n /q T] W γ) = P W Cn /q T γ) Oexp C n /q T )) γ Le Ψ u = n q β 4q log 4 n As long as Ψ Ψ u, he esmae 66) s vald and hence P max [0,T] Ψ Ψ u ) P max [0,T] Y Ψ u 4 T 0 ) C E q +F q 3 4 d)
25 where we used ha Ψ 0 = a he las lne Noe ha T 0 ) C E q +F q 3 4 d = C E q T +4C F q T /4 4C q β αn +β ) q T +q β 4 α n q +β T /4 β Seng T = n β+ q 6 C 4qα logn and usng n qηq for some large consan η, we have ha Hence, we have ha T 0 C E q +F q 3 4 )d < Ψu Noe ha P max [0,T] Ψ Ψ u ) P max [0,T] Y Ψu ) = Oexp Ψ u ) C n /q T )) Ψ u ) C n /q T = n q β q log n 8n /q C 6 C 4 qα logn n β+ β q = 3 C C4 qα n β +β q logn C nβ where we used qβ, 0 β, C, α, q a Usng he fac ha Ψ Φ q, we have ha P max Φ n β log q n) = Oexp C [0,T] nβ )) 00 where we used ha qβ and n q ηq for some large consan η Lemma 49 Suppose ha ψ k αk β for all k n for some 0 β βq, f n q ηq for some large consan η, we have ha and α For any even neger q wh ψ n Cα qlognn β β 4q for some unversal consan C β Proof By Lemma 48, for up o T = cn β+ q qα logn, wh probably 099, Assumng hs even, we have and TrA I) q ) = Φ n β log q n for all 0 T T 0 A +n q β q log n for all 0 T A d T +n q β q log n) c n q β qα log 3/ n whch s less han 64 when n s large enough Also, we have ha B T = T I Hence, we can apply Lemma 3 and ge ha ψ p = O α ) qlognn β β 4q Snce hs argumen holds for any soropc logconcave dsrbuon, hs gves he bound for ψ n Proof of Theorem 37 Fx a large enough n We sar wh a known bound: ψ k α k β for all k n where α s some unversal consan larger han and β = Now, we apply Lemma 49 for every k n wh q = Hence, we have ha β ψ k 4Cα β lognk β β 6 for all k n 5
26 Repeang hs process, we have ha ψ k α l k β l for all k n wh α l+ = 4Cα l β l logn, β l+ = β l β l 6 By nducon, we have ha α l = Ollogn) l/ and β l 6 l Hence, we have ha for all l Seng l = ψ n Ollogn) l n 6 l logn/loglogn, we have ha ) ψ n = n O log log n )) log n = exp O lognloglogn 7 Adapve localzaon for ansoropc dsrbuons In hs secon, we show ha he same hrd momen assumpon gves he followng bound on he KLS consan for arbrary logconcave dsrbuons Theorem 50 Under he hrd momen assumpon of Secon 6, for any logconcave densy p n R n wh covarance marx A, for any neger q, he KLS consan s bounded as 7 Conrolled sochasc localzaon ψ p Cq Oq) TrA q )) q Defnon 5 Gven a symmerc marx B, le E <u B) be he span of all egenvecors n B wh egenvalues less han u and Λ <u B) = dme <u B) We defne E u, Λ u, ec smlarly For hs reducon, we apply localzaon only n he subspace where he marx B conrollng he Gaussan has small egenvalues A me, he conrol marx s chosen so ha s he nverse of he projecon of he curren covarance marx A o he subspace of he small egenvalue of B Ths s capured n he nex defnon Defnon 5 Gven a logconcave dsrbuon p and a hreshold u, we defne he followng process: p 0 = p, c 0 = 0, B 0 = 0, τ 0 = 0 and for k, τ k = nf{ > τ k such ha Λ <u B ) Λ <u B τk )} p,c,b are defned by Defnon 4 on [τ k,τ k ) wh he nal daa c τk,b τk,p τk nsead of 0, 0 and p) and wh he conrol marx C gven by C = ψ r k) lm s I +A +sp k) ) where A s he covarance marx of p, r k) = Λ <u B τk ), P k) s he orhogonal projecon ono E u B τk ) and ψ r s any known bound on he KLS consan for soropc logconcave denses Le r = rankc ) The followng lemma gves an alernave defnon of C Lemma 53 For any A 0 and an orhogonal projecon marx P, we le T = lm s A + sp) Then, we have ha T = I P)AI P)) where denoes pseudonverse Furhermore, we have ha RP) = NT), e, he rowspace of P equals he nullspace of T 6
27 Proof By akng P = U T ΣU, we can see ha and lm s A+sP) = U T lm s UAUT +sσ) U I P)AI P)) = U T I Σ)UAU T I Σ) ) U Hence, suffces o prove he case P s a dagonal marx whose frs r dagonal enres are 0 and he remanng dagonal enres are Wre [ ] A A A = A T A 3 where A s a r r marx Then, we have ha [ ] A+sP) A A = = A 3 +si A T [ A +A A FA T A A FA T A F where F = A 3 +si A T A A ) As s, we have ha F 0 and hence [ ] A lm s A+sP) = 0 = I P)AI P)) 0 0 For any x RP), we have ha x s 0 n he frs r coordnaes and hence 0 x T Tx x T I +sp) x = x +s A F Takng s, we have ha x T Tx = 0 Usng T 0, hs shows ha RP) NT) On he anoher hand, we have ha A+sP A I P)+sP and hence A+sP) A I P)+s P Takng he lm, we have ha T A I P) Ths shows ha NT) RP) Hence, we have RP) = NT) The specfc formula above s no mporan and he reducon of hs secon uses only he followng properes of he conrol marx C Lemma 54 For any 0, we have ha Focus on small values n A ) 0 C ψ r A Focus on small values n B ) B ui and r = r k) = Λ <u B ) for [τ k,τ k ) 3 Large sep sze) TrC r + q /ψ r Φ /q +)) Proof For he frs par, snce I +A +sp k) A, we have ha ψ A r k) C 0 ForB ui n he second par, we prove by a connuous nducon Le = nf 0 {x T B x > u for some x = } Suppose ha < + By he defnon, we have ha B ui for Fx any [τ k,τ k ) Snce B ui, we can wre B = B +B where all egenvalues of B are u and B ] ui Snce db d = C 0 and snce he number of egenvalues beng u s unchanged durng [τ k,τ k ), we know ha B = B τ k By he defnon of P k), we have ha RP k) ) = E u B τ k ) = E u B ) For any x T B x u x, we have ha x E u B ) because B ui Hence, we have ha x RP k) ) and Lemma 53 shows ha RP k) ) = NC ) and hence x T C x = 0 Snce d d B = C, we have ha x T db d x = 0 for any xt B x u x and any 7
Part II CONTINUOUS TIME STOCHASTIC PROCESSES
 Par II CONTINUOUS TIME STOCHASTIC PROCESSES 4 Chaper 4 For an advanced analyss of he properes of he Wener process, see: Revus D and Yor M: Connuous marngales and Brownan Moon Karazas I and Shreve S E:
Par II CONTINUOUS TIME STOCHASTIC PROCESSES 4 Chaper 4 For an advanced analyss of he properes of he Wener process, see: Revus D and Yor M: Connuous marngales and Brownan Moon Karazas I and Shreve S E:
Relative controllability of nonlinear systems with delays in control
 Relave conrollably o nonlnear sysems wh delays n conrol Jerzy Klamka Insue o Conrol Engneerng, Slesan Techncal Unversy, 44- Glwce, Poland. phone/ax : 48 32 37227, {jklamka}@a.polsl.glwce.pl Keywor: Conrollably.
Relave conrollably o nonlnear sysems wh delays n conrol Jerzy Klamka Insue o Conrol Engneerng, Slesan Techncal Unversy, 44- Glwce, Poland. phone/ax : 48 32 37227, {jklamka}@a.polsl.glwce.pl Keywor: Conrollably.
ON THE WEAK LIMITS OF SMOOTH MAPS FOR THE DIRICHLET ENERGY BETWEEN MANIFOLDS
 ON THE WEA LIMITS OF SMOOTH MAPS FOR THE DIRICHLET ENERGY BETWEEN MANIFOLDS FENGBO HANG Absrac. We denfy all he weak sequenal lms of smooh maps n W (M N). In parcular, hs mples a necessary su cen opologcal
ON THE WEA LIMITS OF SMOOTH MAPS FOR THE DIRICHLET ENERGY BETWEEN MANIFOLDS FENGBO HANG Absrac. We denfy all he weak sequenal lms of smooh maps n W (M N). In parcular, hs mples a necessary su cen opologcal
. The geometric multiplicity is dim[ker( λi. number of linearly independent eigenvectors associated with this eigenvalue.
 Lnear Algebra Lecure # Noes We connue wh he dscusson of egenvalues, egenvecors, and dagonalzably of marces We wan o know, n parcular wha condons wll assure ha a marx can be dagonalzed and wha he obsrucons
Lnear Algebra Lecure # Noes We connue wh he dscusson of egenvalues, egenvecors, and dagonalzably of marces We wan o know, n parcular wha condons wll assure ha a marx can be dagonalzed and wha he obsrucons
John Geweke a and Gianni Amisano b a Departments of Economics and Statistics, University of Iowa, USA b European Central Bank, Frankfurt, Germany
 Herarchcal Markov Normal Mxure models wh Applcaons o Fnancal Asse Reurns Appendx: Proofs of Theorems and Condonal Poseror Dsrbuons John Geweke a and Gann Amsano b a Deparmens of Economcs and Sascs, Unversy
Herarchcal Markov Normal Mxure models wh Applcaons o Fnancal Asse Reurns Appendx: Proofs of Theorems and Condonal Poseror Dsrbuons John Geweke a and Gann Amsano b a Deparmens of Economcs and Sascs, Unversy
Solution in semi infinite diffusion couples (error function analysis)
 Soluon n sem nfne dffuson couples (error funcon analyss) Le us consder now he sem nfne dffuson couple of wo blocks wh concenraon of and I means ha, n a A- bnary sysem, s bondng beween wo blocks made of
Soluon n sem nfne dffuson couples (error funcon analyss) Le us consder now he sem nfne dffuson couple of wo blocks wh concenraon of and I means ha, n a A- bnary sysem, s bondng beween wo blocks made of
. The geometric multiplicity is dim[ker( λi. A )], i.e. the number of linearly independent eigenvectors associated with this eigenvalue.
![. The geometric multiplicity is dim[ker( λi. A )], i.e. the number of linearly independent eigenvectors associated with this eigenvalue. . The geometric multiplicity is dim[ker( λi. A )], i.e. the number of linearly independent eigenvectors associated with this eigenvalue.](/thumbs/78/77822798.jpg) Mah E-b Lecure #0 Noes We connue wh he dscusson of egenvalues, egenvecors, and dagonalzably of marces We wan o know, n parcular wha condons wll assure ha a marx can be dagonalzed and wha he obsrucons are
Mah E-b Lecure #0 Noes We connue wh he dscusson of egenvalues, egenvecors, and dagonalzably of marces We wan o know, n parcular wha condons wll assure ha a marx can be dagonalzed and wha he obsrucons are
Comparison of Differences between Power Means 1
 In. Journal of Mah. Analyss, Vol. 7, 203, no., 5-55 Comparson of Dfferences beween Power Means Chang-An Tan, Guanghua Sh and Fe Zuo College of Mahemacs and Informaon Scence Henan Normal Unversy, 453007,
In. Journal of Mah. Analyss, Vol. 7, 203, no., 5-55 Comparson of Dfferences beween Power Means Chang-An Tan, Guanghua Sh and Fe Zuo College of Mahemacs and Informaon Scence Henan Normal Unversy, 453007,
GENERATING CERTAIN QUINTIC IRREDUCIBLE POLYNOMIALS OVER FINITE FIELDS. Youngwoo Ahn and Kitae Kim
 Korean J. Mah. 19 (2011), No. 3, pp. 263 272 GENERATING CERTAIN QUINTIC IRREDUCIBLE POLYNOMIALS OVER FINITE FIELDS Youngwoo Ahn and Kae Km Absrac. In he paper [1], an explc correspondence beween ceran
Korean J. Mah. 19 (2011), No. 3, pp. 263 272 GENERATING CERTAIN QUINTIC IRREDUCIBLE POLYNOMIALS OVER FINITE FIELDS Youngwoo Ahn and Kae Km Absrac. In he paper [1], an explc correspondence beween ceran
Existence and Uniqueness Results for Random Impulsive Integro-Differential Equation
 Global Journal of Pure and Appled Mahemacs. ISSN 973-768 Volume 4, Number 6 (8), pp. 89-87 Research Inda Publcaons hp://www.rpublcaon.com Exsence and Unqueness Resuls for Random Impulsve Inegro-Dfferenal
Global Journal of Pure and Appled Mahemacs. ISSN 973-768 Volume 4, Number 6 (8), pp. 89-87 Research Inda Publcaons hp://www.rpublcaon.com Exsence and Unqueness Resuls for Random Impulsve Inegro-Dfferenal
CS434a/541a: Pattern Recognition Prof. Olga Veksler. Lecture 4
 CS434a/54a: Paern Recognon Prof. Olga Veksler Lecure 4 Oulne Normal Random Varable Properes Dscrmnan funcons Why Normal Random Varables? Analycally racable Works well when observaon comes form a corruped
CS434a/54a: Paern Recognon Prof. Olga Veksler Lecure 4 Oulne Normal Random Varable Properes Dscrmnan funcons Why Normal Random Varables? Analycally racable Works well when observaon comes form a corruped
CS286.2 Lecture 14: Quantum de Finetti Theorems II
 CS286.2 Lecure 14: Quanum de Fne Theorems II Scrbe: Mara Okounkova 1 Saemen of he heorem Recall he las saemen of he quanum de Fne heorem from he prevous lecure. Theorem 1 Quanum de Fne). Le ρ Dens C 2
CS286.2 Lecure 14: Quanum de Fne Theorems II Scrbe: Mara Okounkova 1 Saemen of he heorem Recall he las saemen of he quanum de Fne heorem from he prevous lecure. Theorem 1 Quanum de Fne). Le ρ Dens C 2
( ) () we define the interaction representation by the unitary transformation () = ()
 Hgher Order Perurbaon Theory Mchael Fowler 3/7/6 The neracon Represenaon Recall ha n he frs par of hs course sequence, we dscussed he chrödnger and Hesenberg represenaons of quanum mechancs here n he chrödnger
Hgher Order Perurbaon Theory Mchael Fowler 3/7/6 The neracon Represenaon Recall ha n he frs par of hs course sequence, we dscussed he chrödnger and Hesenberg represenaons of quanum mechancs here n he chrödnger
Density Matrix Description of NMR BCMB/CHEM 8190
 Densy Marx Descrpon of NMR BCMBCHEM 89 Operaors n Marx Noaon Alernae approach o second order specra: ask abou x magnezaon nsead of energes and ranson probables. If we say wh one bass se, properes vary
Densy Marx Descrpon of NMR BCMBCHEM 89 Operaors n Marx Noaon Alernae approach o second order specra: ask abou x magnezaon nsead of energes and ranson probables. If we say wh one bass se, properes vary
Mechanics Physics 151
 Mechancs Physcs 5 Lecure 9 Hamlonan Equaons of Moon (Chaper 8) Wha We Dd Las Tme Consruced Hamlonan formalsm H ( q, p, ) = q p L( q, q, ) H p = q H q = p H = L Equvalen o Lagrangan formalsm Smpler, bu
Mechancs Physcs 5 Lecure 9 Hamlonan Equaons of Moon (Chaper 8) Wha We Dd Las Tme Consruced Hamlonan formalsm H ( q, p, ) = q p L( q, q, ) H p = q H q = p H = L Equvalen o Lagrangan formalsm Smpler, bu
Mechanics Physics 151
 Mechancs Physcs 5 Lecure 9 Hamlonan Equaons of Moon (Chaper 8) Wha We Dd Las Tme Consruced Hamlonan formalsm Hqp (,,) = qp Lqq (,,) H p = q H q = p H L = Equvalen o Lagrangan formalsm Smpler, bu wce as
Mechancs Physcs 5 Lecure 9 Hamlonan Equaons of Moon (Chaper 8) Wha We Dd Las Tme Consruced Hamlonan formalsm Hqp (,,) = qp Lqq (,,) H p = q H q = p H L = Equvalen o Lagrangan formalsm Smpler, bu wce as
( t) Outline of program: BGC1: Survival and event history analysis Oslo, March-May Recapitulation. The additive regression model
 BGC1: Survval and even hsory analyss Oslo, March-May 212 Monday May 7h and Tuesday May 8h The addve regresson model Ørnulf Borgan Deparmen of Mahemacs Unversy of Oslo Oulne of program: Recapulaon Counng
BGC1: Survval and even hsory analyss Oslo, March-May 212 Monday May 7h and Tuesday May 8h The addve regresson model Ørnulf Borgan Deparmen of Mahemacs Unversy of Oslo Oulne of program: Recapulaon Counng
Linear Response Theory: The connection between QFT and experiments
 Phys540.nb 39 3 Lnear Response Theory: The connecon beween QFT and expermens 3.1. Basc conceps and deas Q: ow do we measure he conducvy of a meal? A: we frs nroduce a weak elecrc feld E, and hen measure
Phys540.nb 39 3 Lnear Response Theory: The connecon beween QFT and expermens 3.1. Basc conceps and deas Q: ow do we measure he conducvy of a meal? A: we frs nroduce a weak elecrc feld E, and hen measure
Lecture 6: Learning for Control (Generalised Linear Regression)
 Lecure 6: Learnng for Conrol (Generalsed Lnear Regresson) Conens: Lnear Mehods for Regresson Leas Squares, Gauss Markov heorem Recursve Leas Squares Lecure 6: RLSC - Prof. Sehu Vjayakumar Lnear Regresson
Lecure 6: Learnng for Conrol (Generalsed Lnear Regresson) Conens: Lnear Mehods for Regresson Leas Squares, Gauss Markov heorem Recursve Leas Squares Lecure 6: RLSC - Prof. Sehu Vjayakumar Lnear Regresson
CH.3. COMPATIBILITY EQUATIONS. Continuum Mechanics Course (MMC) - ETSECCPB - UPC
 CH.3. COMPATIBILITY EQUATIONS Connuum Mechancs Course (MMC) - ETSECCPB - UPC Overvew Compably Condons Compably Equaons of a Poenal Vecor Feld Compably Condons for Infnesmal Srans Inegraon of he Infnesmal
CH.3. COMPATIBILITY EQUATIONS Connuum Mechancs Course (MMC) - ETSECCPB - UPC Overvew Compably Condons Compably Equaons of a Poenal Vecor Feld Compably Condons for Infnesmal Srans Inegraon of he Infnesmal
On One Analytic Method of. Constructing Program Controls
 Appled Mahemacal Scences, Vol. 9, 05, no. 8, 409-407 HIKARI Ld, www.m-hkar.com hp://dx.do.org/0.988/ams.05.54349 On One Analyc Mehod of Consrucng Program Conrols A. N. Kvko, S. V. Chsyakov and Yu. E. Balyna
Appled Mahemacal Scences, Vol. 9, 05, no. 8, 409-407 HIKARI Ld, www.m-hkar.com hp://dx.do.org/0.988/ams.05.54349 On One Analyc Mehod of Consrucng Program Conrols A. N. Kvko, S. V. Chsyakov and Yu. E. Balyna
Mechanics Physics 151
 Mechancs Physcs 5 Lecure 0 Canoncal Transformaons (Chaper 9) Wha We Dd Las Tme Hamlon s Prncple n he Hamlonan formalsm Dervaon was smple δi δ Addonal end-pon consrans pq H( q, p, ) d 0 δ q ( ) δq ( ) δ
Mechancs Physcs 5 Lecure 0 Canoncal Transformaons (Chaper 9) Wha We Dd Las Tme Hamlon s Prncple n he Hamlonan formalsm Dervaon was smple δi δ Addonal end-pon consrans pq H( q, p, ) d 0 δ q ( ) δq ( ) δ
Density Matrix Description of NMR BCMB/CHEM 8190
 Densy Marx Descrpon of NMR BCMBCHEM 89 Operaors n Marx Noaon If we say wh one bass se, properes vary only because of changes n he coeffcens weghng each bass se funcon x = h< Ix > - hs s how we calculae
Densy Marx Descrpon of NMR BCMBCHEM 89 Operaors n Marx Noaon If we say wh one bass se, properes vary only because of changes n he coeffcens weghng each bass se funcon x = h< Ix > - hs s how we calculae
V.Abramov - FURTHER ANALYSIS OF CONFIDENCE INTERVALS FOR LARGE CLIENT/SERVER COMPUTER NETWORKS
 R&RATA # Vol.) 8, March FURTHER AALYSIS OF COFIDECE ITERVALS FOR LARGE CLIET/SERVER COMPUTER ETWORKS Vyacheslav Abramov School of Mahemacal Scences, Monash Unversy, Buldng 8, Level 4, Clayon Campus, Wellngon
R&RATA # Vol.) 8, March FURTHER AALYSIS OF COFIDECE ITERVALS FOR LARGE CLIET/SERVER COMPUTER ETWORKS Vyacheslav Abramov School of Mahemacal Scences, Monash Unversy, Buldng 8, Level 4, Clayon Campus, Wellngon
Online Supplement for Dynamic Multi-Technology. Production-Inventory Problem with Emissions Trading
 Onlne Supplemen for Dynamc Mul-Technology Producon-Invenory Problem wh Emssons Tradng by We Zhang Zhongsheng Hua Yu Xa and Baofeng Huo Proof of Lemma For any ( qr ) Θ s easy o verfy ha he lnear programmng
Onlne Supplemen for Dynamc Mul-Technology Producon-Invenory Problem wh Emssons Tradng by We Zhang Zhongsheng Hua Yu Xa and Baofeng Huo Proof of Lemma For any ( qr ) Θ s easy o verfy ha he lnear programmng
Tight results for Next Fit and Worst Fit with resource augmentation
 Tgh resuls for Nex F and Wors F wh resource augmenaon Joan Boyar Leah Epsen Asaf Levn Asrac I s well known ha he wo smple algorhms for he classc n packng prolem, NF and WF oh have an approxmaon rao of
Tgh resuls for Nex F and Wors F wh resource augmenaon Joan Boyar Leah Epsen Asaf Levn Asrac I s well known ha he wo smple algorhms for he classc n packng prolem, NF and WF oh have an approxmaon rao of
Epistemic Game Theory: Online Appendix
 Epsemc Game Theory: Onlne Appendx Edde Dekel Lucano Pomao Marcano Snscalch July 18, 2014 Prelmnares Fx a fne ype srucure T I, S, T, β I and a probably µ S T. Le T µ I, S, T µ, βµ I be a ype srucure ha
Epsemc Game Theory: Onlne Appendx Edde Dekel Lucano Pomao Marcano Snscalch July 18, 2014 Prelmnares Fx a fne ype srucure T I, S, T, β I and a probably µ S T. Le T µ I, S, T µ, βµ I be a ype srucure ha
Lecture 18: The Laplace Transform (See Sections and 14.7 in Boas)
 Lecure 8: The Lalace Transform (See Secons 88- and 47 n Boas) Recall ha our bg-cure goal s he analyss of he dfferenal equaon, ax bx cx F, where we emloy varous exansons for he drvng funcon F deendng on
Lecure 8: The Lalace Transform (See Secons 88- and 47 n Boas) Recall ha our bg-cure goal s he analyss of he dfferenal equaon, ax bx cx F, where we emloy varous exansons for he drvng funcon F deendng on
Lecture VI Regression
 Lecure VI Regresson (Lnear Mehods for Regresson) Conens: Lnear Mehods for Regresson Leas Squares, Gauss Markov heorem Recursve Leas Squares Lecure VI: MLSC - Dr. Sehu Vjayakumar Lnear Regresson Model M
Lecure VI Regresson (Lnear Mehods for Regresson) Conens: Lnear Mehods for Regresson Leas Squares, Gauss Markov heorem Recursve Leas Squares Lecure VI: MLSC - Dr. Sehu Vjayakumar Lnear Regresson Model M
FI 3103 Quantum Physics
 /9/4 FI 33 Quanum Physcs Aleander A. Iskandar Physcs of Magnesm and Phooncs Research Grou Insu Teknolog Bandung Basc Conces n Quanum Physcs Probably and Eecaon Value Hesenberg Uncerany Prncle Wave Funcon
/9/4 FI 33 Quanum Physcs Aleander A. Iskandar Physcs of Magnesm and Phooncs Research Grou Insu Teknolog Bandung Basc Conces n Quanum Physcs Probably and Eecaon Value Hesenberg Uncerany Prncle Wave Funcon
Dynamic Team Decision Theory. EECS 558 Project Shrutivandana Sharma and David Shuman December 10, 2005
 Dynamc Team Decson Theory EECS 558 Proec Shruvandana Sharma and Davd Shuman December 0, 005 Oulne Inroducon o Team Decson Theory Decomposon of he Dynamc Team Decson Problem Equvalence of Sac and Dynamc
Dynamc Team Decson Theory EECS 558 Proec Shruvandana Sharma and Davd Shuman December 0, 005 Oulne Inroducon o Team Decson Theory Decomposon of he Dynamc Team Decson Problem Equvalence of Sac and Dynamc
In the complete model, these slopes are ANALYSIS OF VARIANCE FOR THE COMPLETE TWO-WAY MODEL. (! i+1 -! i ) + [(!") i+1,q - [(!
 ANALYSIS OF VARIANCE FOR THE COMPLETE TWO-WAY MODEL The frs hng o es n wo-way ANOVA: Is here neracon? "No neracon" means: The man effecs model would f. Ths n urn means: In he neracon plo (wh A on he horzonal
ANALYSIS OF VARIANCE FOR THE COMPLETE TWO-WAY MODEL The frs hng o es n wo-way ANOVA: Is here neracon? "No neracon" means: The man effecs model would f. Ths n urn means: In he neracon plo (wh A on he horzonal
HEAT CONDUCTION PROBLEM IN A TWO-LAYERED HOLLOW CYLINDER BY USING THE GREEN S FUNCTION METHOD
 Journal of Appled Mahemacs and Compuaonal Mechancs 3, (), 45-5 HEAT CONDUCTION PROBLEM IN A TWO-LAYERED HOLLOW CYLINDER BY USING THE GREEN S FUNCTION METHOD Sansław Kukla, Urszula Sedlecka Insue of Mahemacs,
Journal of Appled Mahemacs and Compuaonal Mechancs 3, (), 45-5 HEAT CONDUCTION PROBLEM IN A TWO-LAYERED HOLLOW CYLINDER BY USING THE GREEN S FUNCTION METHOD Sansław Kukla, Urszula Sedlecka Insue of Mahemacs,
Notes on the stability of dynamic systems and the use of Eigen Values.
 Noes on he sabl of dnamc ssems and he use of Egen Values. Source: Macro II course noes, Dr. Davd Bessler s Tme Seres course noes, zarads (999) Ineremporal Macroeconomcs chaper 4 & Techncal ppend, and Hamlon
Noes on he sabl of dnamc ssems and he use of Egen Values. Source: Macro II course noes, Dr. Davd Bessler s Tme Seres course noes, zarads (999) Ineremporal Macroeconomcs chaper 4 & Techncal ppend, and Hamlon
Should Exact Index Numbers have Standard Errors? Theory and Application to Asian Growth
 Should Exac Index umbers have Sandard Errors? Theory and Applcaon o Asan Growh Rober C. Feensra Marshall B. Rensdorf ovember 003 Proof of Proposon APPEDIX () Frs, we wll derve he convenonal Sao-Vara prce
Should Exac Index umbers have Sandard Errors? Theory and Applcaon o Asan Growh Rober C. Feensra Marshall B. Rensdorf ovember 003 Proof of Proposon APPEDIX () Frs, we wll derve he convenonal Sao-Vara prce
Department of Economics University of Toronto
 Deparmen of Economcs Unversy of Torono ECO408F M.A. Economercs Lecure Noes on Heeroskedascy Heeroskedascy o Ths lecure nvolves lookng a modfcaons we need o make o deal wh he regresson model when some of
Deparmen of Economcs Unversy of Torono ECO408F M.A. Economercs Lecure Noes on Heeroskedascy Heeroskedascy o Ths lecure nvolves lookng a modfcaons we need o make o deal wh he regresson model when some of
TSS = SST + SSE An orthogonal partition of the total SS
 ANOVA: Topc 4. Orhogonal conrass [ST&D p. 183] H 0 : µ 1 = µ =... = µ H 1 : The mean of a leas one reamen group s dfferen To es hs hypohess, a basc ANOVA allocaes he varaon among reamen means (SST) equally
ANOVA: Topc 4. Orhogonal conrass [ST&D p. 183] H 0 : µ 1 = µ =... = µ H 1 : The mean of a leas one reamen group s dfferen To es hs hypohess, a basc ANOVA allocaes he varaon among reamen means (SST) equally
DEEP UNFOLDING FOR MULTICHANNEL SOURCE SEPARATION SUPPLEMENTARY MATERIAL
 DEEP UNFOLDING FOR MULTICHANNEL SOURCE SEPARATION SUPPLEMENTARY MATERIAL Sco Wsdom, John Hershey 2, Jonahan Le Roux 2, and Shnj Waanabe 2 Deparmen o Elecrcal Engneerng, Unversy o Washngon, Seale, WA, USA
DEEP UNFOLDING FOR MULTICHANNEL SOURCE SEPARATION SUPPLEMENTARY MATERIAL Sco Wsdom, John Hershey 2, Jonahan Le Roux 2, and Shnj Waanabe 2 Deparmen o Elecrcal Engneerng, Unversy o Washngon, Seale, WA, USA
( ) [ ] MAP Decision Rule
![( ) [ ] MAP Decision Rule ( ) [ ] MAP Decision Rule](/thumbs/82/84970741.jpg) Announcemens Bayes Decson Theory wh Normal Dsrbuons HW0 due oday HW o be assgned soon Proec descrpon posed Bomercs CSE 90 Lecure 4 CSE90, Sprng 04 CSE90, Sprng 04 Key Probables 4 ω class label X feaure
Announcemens Bayes Decson Theory wh Normal Dsrbuons HW0 due oday HW o be assgned soon Proec descrpon posed Bomercs CSE 90 Lecure 4 CSE90, Sprng 04 CSE90, Sprng 04 Key Probables 4 ω class label X feaure
Online Appendix for. Strategic safety stocks in supply chains with evolving forecasts
 Onlne Appendx for Sraegc safey socs n supply chans wh evolvng forecass Tor Schoenmeyr Sephen C. Graves Opsolar, Inc. 332 Hunwood Avenue Hayward, CA 94544 A. P. Sloan School of Managemen Massachuses Insue
Onlne Appendx for Sraegc safey socs n supply chans wh evolvng forecass Tor Schoenmeyr Sephen C. Graves Opsolar, Inc. 332 Hunwood Avenue Hayward, CA 94544 A. P. Sloan School of Managemen Massachuses Insue
Volatility Interpolation
 Volaly Inerpolaon Prelmnary Verson March 00 Jesper Andreasen and Bran Huge Danse Mares, Copenhagen wan.daddy@danseban.com brno@danseban.com Elecronc copy avalable a: hp://ssrn.com/absrac=69497 Inro Local
Volaly Inerpolaon Prelmnary Verson March 00 Jesper Andreasen and Bran Huge Danse Mares, Copenhagen wan.daddy@danseban.com brno@danseban.com Elecronc copy avalable a: hp://ssrn.com/absrac=69497 Inro Local
SELFSIMILAR PROCESSES WITH STATIONARY INCREMENTS IN THE SECOND WIENER CHAOS
 POBABILITY AD MATEMATICAL STATISTICS Vol., Fasc., pp. SELFSIMILA POCESSES WIT STATIOAY ICEMETS I TE SECOD WIEE CAOS BY M. M A E J I M A YOKOAMA AD C. A. T U D O LILLE Absrac. We sudy selfsmlar processes
POBABILITY AD MATEMATICAL STATISTICS Vol., Fasc., pp. SELFSIMILA POCESSES WIT STATIOAY ICEMETS I TE SECOD WIEE CAOS BY M. M A E J I M A YOKOAMA AD C. A. T U D O LILLE Absrac. We sudy selfsmlar processes
How about the more general "linear" scalar functions of scalars (i.e., a 1st degree polynomial of the following form with a constant term )?
 lmcd Lnear ransformaon of a vecor he deas presened here are que general hey go beyond he radonal mar-vecor ype seen n lnear algebra Furhermore, hey do no deal wh bass and are equally vald for any se of
lmcd Lnear ransformaon of a vecor he deas presened here are que general hey go beyond he radonal mar-vecor ype seen n lnear algebra Furhermore, hey do no deal wh bass and are equally vald for any se of
Ordinary Differential Equations in Neuroscience with Matlab examples. Aim 1- Gain understanding of how to set up and solve ODE s
 Ordnary Dfferenal Equaons n Neuroscence wh Malab eamples. Am - Gan undersandng of how o se up and solve ODE s Am Undersand how o se up an solve a smple eample of he Hebb rule n D Our goal a end of class
Ordnary Dfferenal Equaons n Neuroscence wh Malab eamples. Am - Gan undersandng of how o se up and solve ODE s Am Undersand how o se up an solve a smple eample of he Hebb rule n D Our goal a end of class
Chapter Lagrangian Interpolation
 Chaper 5.4 agrangan Inerpolaon Afer readng hs chaper you should be able o:. dere agrangan mehod of nerpolaon. sole problems usng agrangan mehod of nerpolaon and. use agrangan nerpolans o fnd deraes and
Chaper 5.4 agrangan Inerpolaon Afer readng hs chaper you should be able o:. dere agrangan mehod of nerpolaon. sole problems usng agrangan mehod of nerpolaon and. use agrangan nerpolans o fnd deraes and
On computing differential transform of nonlinear non-autonomous functions and its applications
 On compung dfferenal ransform of nonlnear non-auonomous funcons and s applcaons Essam. R. El-Zahar, and Abdelhalm Ebad Deparmen of Mahemacs, Faculy of Scences and Humanes, Prnce Saam Bn Abdulazz Unversy,
On compung dfferenal ransform of nonlnear non-auonomous funcons and s applcaons Essam. R. El-Zahar, and Abdelhalm Ebad Deparmen of Mahemacs, Faculy of Scences and Humanes, Prnce Saam Bn Abdulazz Unversy,
Comb Filters. Comb Filters
 The smple flers dscussed so far are characered eher by a sngle passband and/or a sngle sopband There are applcaons where flers wh mulple passbands and sopbands are requred Thecomb fler s an example of
The smple flers dscussed so far are characered eher by a sngle passband and/or a sngle sopband There are applcaons where flers wh mulple passbands and sopbands are requred Thecomb fler s an example of
arxiv: v2 [math.pr] 2 Nov 2015
![arxiv: v2 [math.pr] 2 Nov 2015 arxiv: v2 [math.pr] 2 Nov 2015](/thumbs/93/111427562.jpg) Weak and srong momens of l r -norms of log-concave vecors arxv:1501.01649v2 [mah.pr] 2 Nov 2015 Rafa l Laa la and Mara Srzelecka revsed verson Absrac We show ha for 1 and r 1 he -h momen of he l r -norm
Weak and srong momens of l r -norms of log-concave vecors arxv:1501.01649v2 [mah.pr] 2 Nov 2015 Rafa l Laa la and Mara Srzelecka revsed verson Absrac We show ha for 1 and r 1 he -h momen of he l r -norm
Appendix H: Rarefaction and extrapolation of Hill numbers for incidence data
 Anne Chao Ncholas J Goell C seh lzabeh L ander K Ma Rober K Colwell and Aaron M llson 03 Rarefacon and erapolaon wh ll numbers: a framewor for samplng and esmaon n speces dversy sudes cology Monographs
Anne Chao Ncholas J Goell C seh lzabeh L ander K Ma Rober K Colwell and Aaron M llson 03 Rarefacon and erapolaon wh ll numbers: a framewor for samplng and esmaon n speces dversy sudes cology Monographs
Advanced Machine Learning & Perception
 Advanced Machne Learnng & Percepon Insrucor: Tony Jebara SVM Feaure & Kernel Selecon SVM Eensons Feaure Selecon (Flerng and Wrappng) SVM Feaure Selecon SVM Kernel Selecon SVM Eensons Classfcaon Feaure/Kernel
Advanced Machne Learnng & Percepon Insrucor: Tony Jebara SVM Feaure & Kernel Selecon SVM Eensons Feaure Selecon (Flerng and Wrappng) SVM Feaure Selecon SVM Kernel Selecon SVM Eensons Classfcaon Feaure/Kernel
SOME NOISELESS CODING THEOREMS OF INACCURACY MEASURE OF ORDER α AND TYPE β
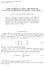 SARAJEVO JOURNAL OF MATHEMATICS Vol.3 (15) (2007), 137 143 SOME NOISELESS CODING THEOREMS OF INACCURACY MEASURE OF ORDER α AND TYPE β M. A. K. BAIG AND RAYEES AHMAD DAR Absrac. In hs paper, we propose
SARAJEVO JOURNAL OF MATHEMATICS Vol.3 (15) (2007), 137 143 SOME NOISELESS CODING THEOREMS OF INACCURACY MEASURE OF ORDER α AND TYPE β M. A. K. BAIG AND RAYEES AHMAD DAR Absrac. In hs paper, we propose
Variants of Pegasos. December 11, 2009
 Inroducon Varans of Pegasos SooWoong Ryu bshboy@sanford.edu December, 009 Youngsoo Cho yc344@sanford.edu Developng a new SVM algorhm s ongong research opc. Among many exng SVM algorhms, we wll focus on
Inroducon Varans of Pegasos SooWoong Ryu bshboy@sanford.edu December, 009 Youngsoo Cho yc344@sanford.edu Developng a new SVM algorhm s ongong research opc. Among many exng SVM algorhms, we wll focus on
TitleA random walk analogue of Levy's th. Studia scientiarum mathematicarum H Citation
 TleA random walk analogue of Levy's h Auhor(s) Fuja, Takahko Suda scenarum mahemacarum H Caon 3-33 Issue 008-06 Dae Type Journal Arcle Tex Verson auhor URL hp://hdlhandlene/10086/15876 Ths s an auhor's
TleA random walk analogue of Levy's h Auhor(s) Fuja, Takahko Suda scenarum mahemacarum H Caon 3-33 Issue 008-06 Dae Type Journal Arcle Tex Verson auhor URL hp://hdlhandlene/10086/15876 Ths s an auhor's
Fall 2010 Graduate Course on Dynamic Learning
 Fall 200 Graduae Course on Dynamc Learnng Chaper 4: Parcle Flers Sepember 27, 200 Byoung-Tak Zhang School of Compuer Scence and Engneerng & Cognve Scence and Bran Scence Programs Seoul aonal Unversy hp://b.snu.ac.kr/~bzhang/
Fall 200 Graduae Course on Dynamc Learnng Chaper 4: Parcle Flers Sepember 27, 200 Byoung-Tak Zhang School of Compuer Scence and Engneerng & Cognve Scence and Bran Scence Programs Seoul aonal Unversy hp://b.snu.ac.kr/~bzhang/
A NEW TECHNIQUE FOR SOLVING THE 1-D BURGERS EQUATION
 S19 A NEW TECHNIQUE FOR SOLVING THE 1-D BURGERS EQUATION by Xaojun YANG a,b, Yugu YANG a*, Carlo CATTANI c, and Mngzheng ZHU b a Sae Key Laboraory for Geomechancs and Deep Underground Engneerng, Chna Unversy
S19 A NEW TECHNIQUE FOR SOLVING THE 1-D BURGERS EQUATION by Xaojun YANG a,b, Yugu YANG a*, Carlo CATTANI c, and Mngzheng ZHU b a Sae Key Laboraory for Geomechancs and Deep Underground Engneerng, Chna Unversy
e-journal Reliability: Theory& Applications No 2 (Vol.2) Vyacheslav Abramov
 June 7 e-ournal Relably: Theory& Applcaons No (Vol. CONFIDENCE INTERVALS ASSOCIATED WITH PERFORMANCE ANALYSIS OF SYMMETRIC LARGE CLOSED CLIENT/SERVER COMPUTER NETWORKS Absrac Vyacheslav Abramov School
June 7 e-ournal Relably: Theory& Applcaons No (Vol. CONFIDENCE INTERVALS ASSOCIATED WITH PERFORMANCE ANALYSIS OF SYMMETRIC LARGE CLOSED CLIENT/SERVER COMPUTER NETWORKS Absrac Vyacheslav Abramov School
Scattering at an Interface: Oblique Incidence
 Course Insrucor Dr. Raymond C. Rumpf Offce: A 337 Phone: (915) 747 6958 E Mal: rcrumpf@uep.edu EE 4347 Appled Elecromagnecs Topc 3g Scaerng a an Inerface: Oblque Incdence Scaerng These Oblque noes may
Course Insrucor Dr. Raymond C. Rumpf Offce: A 337 Phone: (915) 747 6958 E Mal: rcrumpf@uep.edu EE 4347 Appled Elecromagnecs Topc 3g Scaerng a an Inerface: Oblque Incdence Scaerng These Oblque noes may
Chapter 6: AC Circuits
 Chaper 6: AC Crcus Chaper 6: Oulne Phasors and he AC Seady Sae AC Crcus A sable, lnear crcu operang n he seady sae wh snusodal excaon (.e., snusodal seady sae. Complee response forced response naural response.
Chaper 6: AC Crcus Chaper 6: Oulne Phasors and he AC Seady Sae AC Crcus A sable, lnear crcu operang n he seady sae wh snusodal excaon (.e., snusodal seady sae. Complee response forced response naural response.
THE PREDICTION OF COMPETITIVE ENVIRONMENT IN BUSINESS
 THE PREICTION OF COMPETITIVE ENVIRONMENT IN BUSINESS INTROUCTION The wo dmensonal paral dfferenal equaons of second order can be used for he smulaon of compeve envronmen n busness The arcle presens he
THE PREICTION OF COMPETITIVE ENVIRONMENT IN BUSINESS INTROUCTION The wo dmensonal paral dfferenal equaons of second order can be used for he smulaon of compeve envronmen n busness The arcle presens he
Lecture 11 SVM cont
 Lecure SVM con. 0 008 Wha we have done so far We have esalshed ha we wan o fnd a lnear decson oundary whose margn s he larges We know how o measure he margn of a lnear decson oundary Tha s: he mnmum geomerc
Lecure SVM con. 0 008 Wha we have done so far We have esalshed ha we wan o fnd a lnear decson oundary whose margn s he larges We know how o measure he margn of a lnear decson oundary Tha s: he mnmum geomerc
arxiv: v1 [math.pr] 6 Mar 2019
![arxiv: v1 [math.pr] 6 Mar 2019 arxiv: v1 [math.pr] 6 Mar 2019](/thumbs/94/118755942.jpg) Local law and Tracy Wdom lm for sparse sochasc block models Jong Yun Hwang J Oon Lee Wooseok Yang arxv:1903.02179v1 mah.pr 6 Mar 2019 March 7, 2019 Absrac We consder he specral properes of sparse sochasc
Local law and Tracy Wdom lm for sparse sochasc block models Jong Yun Hwang J Oon Lee Wooseok Yang arxv:1903.02179v1 mah.pr 6 Mar 2019 March 7, 2019 Absrac We consder he specral properes of sparse sochasc
Cubic Bezier Homotopy Function for Solving Exponential Equations
 Penerb Journal of Advanced Research n Compung and Applcaons ISSN (onlne: 46-97 Vol. 4, No.. Pages -8, 6 omoopy Funcon for Solvng Eponenal Equaons S. S. Raml *,,. Mohamad Nor,a, N. S. Saharzan,b and M.
Penerb Journal of Advanced Research n Compung and Applcaons ISSN (onlne: 46-97 Vol. 4, No.. Pages -8, 6 omoopy Funcon for Solvng Eponenal Equaons S. S. Raml *,,. Mohamad Nor,a, N. S. Saharzan,b and M.
J i-1 i. J i i+1. Numerical integration of the diffusion equation (I) Finite difference method. Spatial Discretization. Internal nodes.
 umercal negraon of he dffuson equaon (I) Fne dfference mehod. Spaal screaon. Inernal nodes. R L V For hermal conducon le s dscree he spaal doman no small fne spans, =,,: Balance of parcles for an nernal
umercal negraon of he dffuson equaon (I) Fne dfference mehod. Spaal screaon. Inernal nodes. R L V For hermal conducon le s dscree he spaal doman no small fne spans, =,,: Balance of parcles for an nernal
PHYS 705: Classical Mechanics. Canonical Transformation
 PHYS 705: Classcal Mechancs Canoncal Transformaon Canoncal Varables and Hamlonan Formalsm As we have seen, n he Hamlonan Formulaon of Mechancs,, are ndeenden varables n hase sace on eual foong The Hamlon
PHYS 705: Classcal Mechancs Canoncal Transformaon Canoncal Varables and Hamlonan Formalsm As we have seen, n he Hamlonan Formulaon of Mechancs,, are ndeenden varables n hase sace on eual foong The Hamlon
An introduction to Support Vector Machine
 An nroducon o Suppor Vecor Machne 報告者 : 黃立德 References: Smon Haykn, "Neural Neworks: a comprehensve foundaon, second edon, 999, Chaper 2,6 Nello Chrsann, John Shawe-Tayer, An Inroducon o Suppor Vecor Machnes,
An nroducon o Suppor Vecor Machne 報告者 : 黃立德 References: Smon Haykn, "Neural Neworks: a comprehensve foundaon, second edon, 999, Chaper 2,6 Nello Chrsann, John Shawe-Tayer, An Inroducon o Suppor Vecor Machnes,
FTCS Solution to the Heat Equation
 FTCS Soluon o he Hea Equaon ME 448/548 Noes Gerald Reckenwald Porland Sae Unversy Deparmen of Mechancal Engneerng gerry@pdxedu ME 448/548: FTCS Soluon o he Hea Equaon Overvew Use he forward fne d erence
FTCS Soluon o he Hea Equaon ME 448/548 Noes Gerald Reckenwald Porland Sae Unversy Deparmen of Mechancal Engneerng gerry@pdxedu ME 448/548: FTCS Soluon o he Hea Equaon Overvew Use he forward fne d erence
Robust and Accurate Cancer Classification with Gene Expression Profiling
 Robus and Accurae Cancer Classfcaon wh Gene Expresson Proflng (Compuaonal ysems Bology, 2005) Auhor: Hafeng L, Keshu Zhang, ao Jang Oulne Background LDA (lnear dscrmnan analyss) and small sample sze problem
Robus and Accurae Cancer Classfcaon wh Gene Expresson Proflng (Compuaonal ysems Bology, 2005) Auhor: Hafeng L, Keshu Zhang, ao Jang Oulne Background LDA (lnear dscrmnan analyss) and small sample sze problem
CHAPTER 10: LINEAR DISCRIMINATION
 CHAPER : LINEAR DISCRIMINAION Dscrmnan-based Classfcaon 3 In classfcaon h K classes (C,C,, C k ) We defned dscrmnan funcon g j (), j=,,,k hen gven an es eample, e chose (predced) s class label as C f g
CHAPER : LINEAR DISCRIMINAION Dscrmnan-based Classfcaon 3 In classfcaon h K classes (C,C,, C k ) We defned dscrmnan funcon g j (), j=,,,k hen gven an es eample, e chose (predced) s class label as C f g
NATIONAL UNIVERSITY OF SINGAPORE PC5202 ADVANCED STATISTICAL MECHANICS. (Semester II: AY ) Time Allowed: 2 Hours
 NATONAL UNVERSTY OF SNGAPORE PC5 ADVANCED STATSTCAL MECHANCS (Semeser : AY 1-13) Tme Allowed: Hours NSTRUCTONS TO CANDDATES 1. Ths examnaon paper conans 5 quesons and comprses 4 prned pages.. Answer all
NATONAL UNVERSTY OF SNGAPORE PC5 ADVANCED STATSTCAL MECHANCS (Semeser : AY 1-13) Tme Allowed: Hours NSTRUCTONS TO CANDDATES 1. Ths examnaon paper conans 5 quesons and comprses 4 prned pages.. Answer all
Lecture 2 M/G/1 queues. M/G/1-queue
 Lecure M/G/ queues M/G/-queue Posson arrval process Arbrary servce me dsrbuon Sngle server To deermne he sae of he sysem a me, we mus now The number of cusomers n he sysems N() Tme ha he cusomer currenly
Lecure M/G/ queues M/G/-queue Posson arrval process Arbrary servce me dsrbuon Sngle server To deermne he sae of he sysem a me, we mus now The number of cusomers n he sysems N() Tme ha he cusomer currenly
Robustness Experiments with Two Variance Components
 Naonal Insue of Sandards and Technology (NIST) Informaon Technology Laboraory (ITL) Sascal Engneerng Dvson (SED) Robusness Expermens wh Two Varance Componens by Ana Ivelsse Avlés avles@ns.gov Conference
Naonal Insue of Sandards and Technology (NIST) Informaon Technology Laboraory (ITL) Sascal Engneerng Dvson (SED) Robusness Expermens wh Two Varance Componens by Ana Ivelsse Avlés avles@ns.gov Conference
Testing a new idea to solve the P = NP problem with mathematical induction
 Tesng a new dea o solve he P = NP problem wh mahemacal nducon Bacground P and NP are wo classes (ses) of languages n Compuer Scence An open problem s wheher P = NP Ths paper ess a new dea o compare he
Tesng a new dea o solve he P = NP problem wh mahemacal nducon Bacground P and NP are wo classes (ses) of languages n Compuer Scence An open problem s wheher P = NP Ths paper ess a new dea o compare he
Graduate Macroeconomics 2 Problem set 5. - Solutions
 Graduae Macroeconomcs 2 Problem se. - Soluons Queson 1 To answer hs queson we need he frms frs order condons and he equaon ha deermnes he number of frms n equlbrum. The frms frs order condons are: F K
Graduae Macroeconomcs 2 Problem se. - Soluons Queson 1 To answer hs queson we need he frms frs order condons and he equaon ha deermnes he number of frms n equlbrum. The frms frs order condons are: F K
Clustering (Bishop ch 9)
 Cluserng (Bshop ch 9) Reference: Daa Mnng by Margare Dunham (a slde source) 1 Cluserng Cluserng s unsupervsed learnng, here are no class labels Wan o fnd groups of smlar nsances Ofen use a dsance measure
Cluserng (Bshop ch 9) Reference: Daa Mnng by Margare Dunham (a slde source) 1 Cluserng Cluserng s unsupervsed learnng, here are no class labels Wan o fnd groups of smlar nsances Ofen use a dsance measure
F-Tests and Analysis of Variance (ANOVA) in the Simple Linear Regression Model. 1. Introduction
 ECOOMICS 35* -- OTE 9 ECO 35* -- OTE 9 F-Tess and Analyss of Varance (AOVA n he Smple Lnear Regresson Model Inroducon The smple lnear regresson model s gven by he followng populaon regresson equaon, or
ECOOMICS 35* -- OTE 9 ECO 35* -- OTE 9 F-Tess and Analyss of Varance (AOVA n he Smple Lnear Regresson Model Inroducon The smple lnear regresson model s gven by he followng populaon regresson equaon, or
Supplementary Material to: IMU Preintegration on Manifold for E cient Visual-Inertial Maximum-a-Posteriori Estimation
 Supplemenary Maeral o: IMU Prenegraon on Manfold for E cen Vsual-Ineral Maxmum-a-Poseror Esmaon echncal Repor G-IRIM-CP&R-05-00 Chrsan Forser, Luca Carlone, Fran Dellaer, and Davde Scaramuzza May 0, 05
Supplemenary Maeral o: IMU Prenegraon on Manfold for E cen Vsual-Ineral Maxmum-a-Poseror Esmaon echncal Repor G-IRIM-CP&R-05-00 Chrsan Forser, Luca Carlone, Fran Dellaer, and Davde Scaramuzza May 0, 05
Math 128b Project. Jude Yuen
 Mah 8b Proec Jude Yuen . Inroducon Le { Z } be a sequence of observed ndependen vecor varables. If he elemens of Z have a on normal dsrbuon hen { Z } has a mean vecor Z and a varancecovarance marx z. Geomercally
Mah 8b Proec Jude Yuen . Inroducon Le { Z } be a sequence of observed ndependen vecor varables. If he elemens of Z have a on normal dsrbuon hen { Z } has a mean vecor Z and a varancecovarance marx z. Geomercally
M. Y. Adamu Mathematical Sciences Programme, AbubakarTafawaBalewa University, Bauchi, Nigeria
 IOSR Journal of Mahemacs (IOSR-JM e-issn: 78-578, p-issn: 9-765X. Volume 0, Issue 4 Ver. IV (Jul-Aug. 04, PP 40-44 Mulple SolonSoluons for a (+-dmensonalhroa-sasuma shallow waer wave equaon UsngPanlevé-Bӓclund
IOSR Journal of Mahemacs (IOSR-JM e-issn: 78-578, p-issn: 9-765X. Volume 0, Issue 4 Ver. IV (Jul-Aug. 04, PP 40-44 Mulple SolonSoluons for a (+-dmensonalhroa-sasuma shallow waer wave equaon UsngPanlevé-Bӓclund
Let s treat the problem of the response of a system to an applied external force. Again,
 Page 33 QUANTUM LNEAR RESPONSE FUNCTON Le s rea he problem of he response of a sysem o an appled exernal force. Agan, H() H f () A H + V () Exernal agen acng on nernal varable Hamlonan for equlbrum sysem
Page 33 QUANTUM LNEAR RESPONSE FUNCTON Le s rea he problem of he response of a sysem o an appled exernal force. Agan, H() H f () A H + V () Exernal agen acng on nernal varable Hamlonan for equlbrum sysem
Method of upper lower solutions for nonlinear system of fractional differential equations and applications
 Malaya Journal of Maemak, Vol. 6, No. 3, 467-472, 218 hps://do.org/1.26637/mjm63/1 Mehod of upper lower soluons for nonlnear sysem of fraconal dfferenal equaons and applcaons D.B. Dhagude1 *, N.B. Jadhav2
Malaya Journal of Maemak, Vol. 6, No. 3, 467-472, 218 hps://do.org/1.26637/mjm63/1 Mehod of upper lower soluons for nonlnear sysem of fraconal dfferenal equaons and applcaons D.B. Dhagude1 *, N.B. Jadhav2
The Finite Element Method for the Analysis of Non-Linear and Dynamic Systems
 Swss Federal Insue of Page 1 The Fne Elemen Mehod for he Analyss of Non-Lnear and Dynamc Sysems Prof. Dr. Mchael Havbro Faber Dr. Nebojsa Mojslovc Swss Federal Insue of ETH Zurch, Swzerland Mehod of Fne
Swss Federal Insue of Page 1 The Fne Elemen Mehod for he Analyss of Non-Lnear and Dynamc Sysems Prof. Dr. Mchael Havbro Faber Dr. Nebojsa Mojslovc Swss Federal Insue of ETH Zurch, Swzerland Mehod of Fne
3. OVERVIEW OF NUMERICAL METHODS
 3 OVERVIEW OF NUMERICAL METHODS 3 Inroducory remarks Ths chaper summarzes hose numercal echnques whose knowledge s ndspensable for he undersandng of he dfferen dscree elemen mehods: he Newon-Raphson-mehod,
3 OVERVIEW OF NUMERICAL METHODS 3 Inroducory remarks Ths chaper summarzes hose numercal echnques whose knowledge s ndspensable for he undersandng of he dfferen dscree elemen mehods: he Newon-Raphson-mehod,
ON THE ADDITION OF UNITS AND NON-UNITS IN FINITE COMMUTATIVE RINGS
 ROCKY MOUNTAIN JOURNAL OF MATHEMATICS Volume 45, Number 6, 2015 ON THE ADDITION OF UNITS AND NON-UNITS IN FINITE COMMUTATIVE RINGS DARIUSH KIANI AND MOHSEN MOLLAHAJIAGHAEI ABSTRACT. Le R be a fne commuave
ROCKY MOUNTAIN JOURNAL OF MATHEMATICS Volume 45, Number 6, 2015 ON THE ADDITION OF UNITS AND NON-UNITS IN FINITE COMMUTATIVE RINGS DARIUSH KIANI AND MOHSEN MOLLAHAJIAGHAEI ABSTRACT. Le R be a fne commuave
Approximate Analytic Solution of (2+1) - Dimensional Zakharov-Kuznetsov(Zk) Equations Using Homotopy
 Arcle Inernaonal Journal of Modern Mahemacal Scences, 4, (): - Inernaonal Journal of Modern Mahemacal Scences Journal homepage: www.modernscenfcpress.com/journals/jmms.aspx ISSN: 66-86X Florda, USA Approxmae
Arcle Inernaonal Journal of Modern Mahemacal Scences, 4, (): - Inernaonal Journal of Modern Mahemacal Scences Journal homepage: www.modernscenfcpress.com/journals/jmms.aspx ISSN: 66-86X Florda, USA Approxmae
Machine Learning 2nd Edition
 INTRODUCTION TO Lecure Sldes for Machne Learnng nd Edon ETHEM ALPAYDIN, modfed by Leonardo Bobadlla and some pars from hp://www.cs.au.ac.l/~aparzn/machnelearnng/ The MIT Press, 00 alpaydn@boun.edu.r hp://www.cmpe.boun.edu.r/~ehem/mle
INTRODUCTION TO Lecure Sldes for Machne Learnng nd Edon ETHEM ALPAYDIN, modfed by Leonardo Bobadlla and some pars from hp://www.cs.au.ac.l/~aparzn/machnelearnng/ The MIT Press, 00 alpaydn@boun.edu.r hp://www.cmpe.boun.edu.r/~ehem/mle
Bayes rule for a classification problem INF Discriminant functions for the normal density. Euclidean distance. Mahalanobis distance
 INF 43 3.. Repeon Anne Solberg (anne@f.uo.no Bayes rule for a classfcaon problem Suppose we have J, =,...J classes. s he class label for a pxel, and x s he observed feaure vecor. We can use Bayes rule
INF 43 3.. Repeon Anne Solberg (anne@f.uo.no Bayes rule for a classfcaon problem Suppose we have J, =,...J classes. s he class label for a pxel, and x s he observed feaure vecor. We can use Bayes rule
New M-Estimator Objective Function. in Simultaneous Equations Model. (A Comparative Study)
 Inernaonal Mahemacal Forum, Vol. 8, 3, no., 7 - HIKARI Ld, www.m-hkar.com hp://dx.do.org/.988/mf.3.3488 New M-Esmaor Objecve Funcon n Smulaneous Equaons Model (A Comparave Sudy) Ahmed H. Youssef Professor
Inernaonal Mahemacal Forum, Vol. 8, 3, no., 7 - HIKARI Ld, www.m-hkar.com hp://dx.do.org/.988/mf.3.3488 New M-Esmaor Objecve Funcon n Smulaneous Equaons Model (A Comparave Sudy) Ahmed H. Youssef Professor
On elements with index of the form 2 a 3 b in a parametric family of biquadratic elds
 On elemens wh ndex of he form a 3 b n a paramerc famly of bquadrac elds Bora JadrevĆ Absrac In hs paper we gve some resuls abou prmve negral elemens p(c p n he famly of bcyclc bquadrac elds L c = Q ) c;
On elemens wh ndex of he form a 3 b n a paramerc famly of bquadrac elds Bora JadrevĆ Absrac In hs paper we gve some resuls abou prmve negral elemens p(c p n he famly of bcyclc bquadrac elds L c = Q ) c;
P R = P 0. The system is shown on the next figure:
 TPG460 Reservor Smulaon 08 page of INTRODUCTION TO RESERVOIR SIMULATION Analycal and numercal soluons of smple one-dmensonal, one-phase flow equaons As an nroducon o reservor smulaon, we wll revew he smples
TPG460 Reservor Smulaon 08 page of INTRODUCTION TO RESERVOIR SIMULATION Analycal and numercal soluons of smple one-dmensonal, one-phase flow equaons As an nroducon o reservor smulaon, we wll revew he smples
A NUMERICAL SCHEME FOR BSDES. BY JIANFENG ZHANG University of Southern California, Los Angeles
 The Annals of Appled Probably 24, Vol. 14, No. 1, 459 488 Insue of Mahemacal Sascs, 24 A NUMERICAL SCHEME FOR BSDES BY JIANFENG ZHANG Unversy of Souhern Calforna, Los Angeles In hs paper we propose a numercal
The Annals of Appled Probably 24, Vol. 14, No. 1, 459 488 Insue of Mahemacal Sascs, 24 A NUMERICAL SCHEME FOR BSDES BY JIANFENG ZHANG Unversy of Souhern Calforna, Los Angeles In hs paper we propose a numercal
CHAPTER 5: MULTIVARIATE METHODS
 CHAPER 5: MULIVARIAE MEHODS Mulvarae Daa 3 Mulple measuremens (sensors) npus/feaures/arbues: -varae N nsances/observaons/eamples Each row s an eample Each column represens a feaure X a b correspons o he
CHAPER 5: MULIVARIAE MEHODS Mulvarae Daa 3 Mulple measuremens (sensors) npus/feaures/arbues: -varae N nsances/observaons/eamples Each row s an eample Each column represens a feaure X a b correspons o he
Econ107 Applied Econometrics Topic 5: Specification: Choosing Independent Variables (Studenmund, Chapter 6)
 Econ7 Appled Economercs Topc 5: Specfcaon: Choosng Independen Varables (Sudenmund, Chaper 6 Specfcaon errors ha we wll deal wh: wrong ndependen varable; wrong funconal form. Ths lecure deals wh wrong ndependen
Econ7 Appled Economercs Topc 5: Specfcaon: Choosng Independen Varables (Sudenmund, Chaper 6 Specfcaon errors ha we wll deal wh: wrong ndependen varable; wrong funconal form. Ths lecure deals wh wrong ndependen
2.1 Constitutive Theory
 Secon.. Consuve Theory.. Consuve Equaons Governng Equaons The equaons governng he behavour of maerals are (n he spaal form) dρ v & ρ + ρdv v = + ρ = Conservaon of Mass (..a) d x σ j dv dvσ + b = ρ v& +
Secon.. Consuve Theory.. Consuve Equaons Governng Equaons The equaons governng he behavour of maerals are (n he spaal form) dρ v & ρ + ρdv v = + ρ = Conservaon of Mass (..a) d x σ j dv dvσ + b = ρ v& +
On the numerical treatment ofthenonlinear partial differentialequation of fractional order
 IOSR Journal of Mahemacs (IOSR-JM) e-iss: 2278-5728, p-iss: 239-765X. Volume 2, Issue 6 Ver. I (ov. - Dec.26), PP 28-37 www.osrjournals.org On he numercal reamen ofhenonlnear paral dfferenalequaon of fraconal
IOSR Journal of Mahemacs (IOSR-JM) e-iss: 2278-5728, p-iss: 239-765X. Volume 2, Issue 6 Ver. I (ov. - Dec.26), PP 28-37 www.osrjournals.org On he numercal reamen ofhenonlnear paral dfferenalequaon of fraconal
@FMI c Kyung Moon Sa Co.
 Annals of Fuzzy Mahemacs and Informacs Volume 8, No. 2, (Augus 2014), pp. 245 257 ISSN: 2093 9310 (prn verson) ISSN: 2287 6235 (elecronc verson) hp://www.afm.or.kr @FMI c Kyung Moon Sa Co. hp://www.kyungmoon.com
Annals of Fuzzy Mahemacs and Informacs Volume 8, No. 2, (Augus 2014), pp. 245 257 ISSN: 2093 9310 (prn verson) ISSN: 2287 6235 (elecronc verson) hp://www.afm.or.kr @FMI c Kyung Moon Sa Co. hp://www.kyungmoon.com
Outline. Probabilistic Model Learning. Probabilistic Model Learning. Probabilistic Model for Time-series Data: Hidden Markov Model
 Probablsc Model for Tme-seres Daa: Hdden Markov Model Hrosh Mamsuka Bonformacs Cener Kyoo Unversy Oulne Three Problems for probablsc models n machne learnng. Compung lkelhood 2. Learnng 3. Parsng (predcon
Probablsc Model for Tme-seres Daa: Hdden Markov Model Hrosh Mamsuka Bonformacs Cener Kyoo Unversy Oulne Three Problems for probablsc models n machne learnng. Compung lkelhood 2. Learnng 3. Parsng (predcon
Sampling Procedure of the Sum of two Binary Markov Process Realizations
 Samplng Procedure of he Sum of wo Bnary Markov Process Realzaons YURY GORITSKIY Dep. of Mahemacal Modelng of Moscow Power Insue (Techncal Unversy), Moscow, RUSSIA, E-mal: gorsky@yandex.ru VLADIMIR KAZAKOV
Samplng Procedure of he Sum of wo Bnary Markov Process Realzaons YURY GORITSKIY Dep. of Mahemacal Modelng of Moscow Power Insue (Techncal Unversy), Moscow, RUSSIA, E-mal: gorsky@yandex.ru VLADIMIR KAZAKOV
[ ] 2. [ ]3 + (Δx i + Δx i 1 ) / 2. Δx i-1 Δx i Δx i+1. TPG4160 Reservoir Simulation 2018 Lecture note 3. page 1 of 5
![[ ] 2. [ ]3 + (Δx i + Δx i 1 ) / 2. Δx i-1 Δx i Δx i+1. TPG4160 Reservoir Simulation 2018 Lecture note 3. page 1 of 5 [ ] 2. [ ]3 + (Δx i + Δx i 1 ) / 2. Δx i-1 Δx i Δx i+1. TPG4160 Reservoir Simulation 2018 Lecture note 3. page 1 of 5](/thumbs/85/92299540.jpg) TPG460 Reservor Smulaon 08 page of 5 DISCRETIZATIO OF THE FOW EQUATIOS As we already have seen, fne dfference appromaons of he paral dervaves appearng n he flow equaons may be obaned from Taylor seres
TPG460 Reservor Smulaon 08 page of 5 DISCRETIZATIO OF THE FOW EQUATIOS As we already have seen, fne dfference appromaons of he paral dervaves appearng n he flow equaons may be obaned from Taylor seres
Normal Random Variable and its discriminant functions
 Noral Rando Varable and s dscrnan funcons Oulne Noral Rando Varable Properes Dscrnan funcons Why Noral Rando Varables? Analycally racable Works well when observaon coes for a corruped snle prooype 3 The
Noral Rando Varable and s dscrnan funcons Oulne Noral Rando Varable Properes Dscrnan funcons Why Noral Rando Varables? Analycally racable Works well when observaon coes for a corruped snle prooype 3 The
A New Generalized Gronwall-Bellman Type Inequality
 22 Inernaonal Conference on Image, Vson and Comung (ICIVC 22) IPCSIT vol. 5 (22) (22) IACSIT Press, Sngaore DOI:.7763/IPCSIT.22.V5.46 A New Generalzed Gronwall-Bellman Tye Ineualy Qnghua Feng School of
22 Inernaonal Conference on Image, Vson and Comung (ICIVC 22) IPCSIT vol. 5 (22) (22) IACSIT Press, Sngaore DOI:.7763/IPCSIT.22.V5.46 A New Generalzed Gronwall-Bellman Tye Ineualy Qnghua Feng School of
