2.9 Dirac Notation Vectors ji that are orthonormal hk ji = k,j span a vector space and express the identity operator I of the space as (1.
|
|
|
- Edwina Waters
- 5 years ago
- Views:
Transcription
1 14 Fourier Series 2.9 Dirac Notation Vectors ji that are orthonormal hk ji k,j san a vector sace and exress the identity oerator I of the sace as (1.132) I NX jihj. (2.99) Multilying from the right by any vector gi in the sace, we get j1 gi I gi NX jihj gi (2.1) which says that every vector gi in the sace has an exansion (1.133) in terms of the N orthonormal basis vectors ji. Thecoe cientshj gi of the exansion are inner roducts of the vector gi with the basis vectors ji. These roerties of finite-dimensional vector saces also are true of infinitedimensional vector saces of functions. We may use as basis vectors the hases ex(inx)/. They are orthonormal with inner roduct (2.1) (m, n) Z e imx j1 e inx Z dx e i(n m)x dx m,n (2.11) which in Dirac notation with hx ni ex(inx)/ and hm xi hx mi is hm ni Z hm xihx ni dx Z e i(n m)x The identity oerator for Fourier s sace of functions is I dx m,n. (2.12) nihn. (2.13) So we have fi I fi nihn f i (2.14) and hx fi hx I fi hx nihn fi hn fi (2.15) which with hn fi f n is the Fourier series (2.2). The coe cients hn fi f n
2 are the inner roducts (2.3) hn fi Z hn xihx fi dx 2.1 Dirac s Delta Function 15 Z hx fi dx Z f(x) dx. (2.16) 2.1 Dirac s Delta Function A Dirac delta function is a (continuous, linear) ma from a sace of functions into the real or comlex numbers. It is a functional that associates a number with each function in the function sace. Thus (x y) associates the number f(y) with the function f(x). We may write this association as Z f(y) f(x) (x y) dx. (2.17) Delta functions o u all over hysics. The inner roduct of two of the kets xi that aear in the Fourier-series formulas (2.15) and (2.16) is a delta function, hx yi (x y). The formula (2.16) for the coe cient hn fi becomes obvious if we write the identity oerator for functions defined on the interval [, ] as for then hn fi hn I fi Z I Z hn xihx fi dx xihx dx (2.18) Z hx fi dx. (2.19) The equation yi I yi with the identity oerator (2.18) gives yi I yi Z xihx yi dx. (2.11) Multilying (2.18) from the right by fi and from the left by hy, we get f(y) hy I fi Z hy xihx fi dx Z hy xif(x) dx. (2.111) These relations (2.11) and (2.111) say that the inner roduct hy xi is a delta function, hy xi hx yi (x y). The Fourier-series formulas (2.15) and (2.16) lead to a statement about the comleteness of the hases ex(inx)/ f(x) f n Z e iny f(y) einx dy. (2.112)
3 16 Fourier Series Interchanging and rearranging, we have Z e f(x) in(x y)! f(y) dy. (2.113) But f(x) and the hases are eriodic with eriod, so we also have Z! ein(x y) f(x +`) f(y) dy. (2.114) Thus we arrive at the Dirac comb ein(x y) ` 1 or more simly " # cos(nx) n1 (x y `) (2.115) ` 1 (x `). (2.116) Examle 2.13 (Dirac s Comb) The sum of the first 1, terms of this cosine series (2.116) for the Dirac comb is lotted for the interval ( 15, 15) in Fig Gibbs overshoots aear at the discontinuities. The integral of the first 1, terms from -15 to 15 is 5.. The stretched Dirac comb is e in(x y)/ ` 1 (x y `). (2.117) Examle 2.14 (Parseval s Identity) Using our formula (2.35) for the Fourier coe cients of a stretched interval, we can relate a sum of roducts fn g n of the Fourier coe cients of the functions f(x) and g(x) to an integral of the roduct f (x) g(x) Z Z fn g n dx einx/ f (x) dy e iny/ g(y). (2.118) This sum contains Dirac s comb (2.117) and so Z Z fn g n dx dy f (x) g(y) 1 Z dx Z dy f (x) g(y) ` 1 e in(x y)/ (x y `). (2.119)
4 2.1 Dirac s Delta Function x 14 Dirac Comb Sum of Series Figure 2.11 The sum of the first 1, terms of the series (2.116) for the Dirac comb is lotted for 15 ale x ale 15. Both Dirac sikes and Gibbs overshoots are visible. x But because only the ` tooth of the comb lies in the interval [,], we have more simly Z Z Z fn g n dx dy f (x) g(y) (x y) dx f (x) g(x). (2.12) In articular, if the two functions are the same, then Z f n 2 dx f(x) 2 (2.121) which is Parseval s identity. Thus if a function is square integrable on an interval, then the sum of the squares of the absolute values of its Fourier coe cients is the integral of the square of its absolute value. Examle 2.15 (Derivatives of Delta Functions) Delta functions and other generalized functions or distributions ma smooth functions that vanish at
5 18 Fourier Series infinity into numbers in ways that are linear and continuous. Derivatives of delta functions are defined so as to allow integrations by arts. Thus the nth derivative of the delta function (n) (x y) mas the function f(x) to ( 1) n times its nth derivative f (n) (y) at y Z Z (n) (x y) f(x) dx (x y)( 1) n f (n) (x) dx ( 1) n f (n) (y) (2.122) with no surface term. Examle 2.16 (The Equation xf(x) a) Dirac s delta function sometimes aears unexectedly. For instance, the general solution to the equation xf(x) a is f(x) a/x+b (x)wherebisan arbitrary constant (Dirac, 1967, sec. 15), (Waxman and Peck, 1998). Similarly, the general solution to the equation x 2 f(x) a is f(x) a/x 2 +b (x)/x+c (x)+d (x) inwhich (x) is the derivative of the delta function, and b, c, and d are arbitrary constants The Harmonic Oscillator The hamiltonian for the harmonic oscillator is H 2 2m m!2 q 2. (2.123) The commutation relation [q, ] q q i~ imlies that the lowering and raising oerators r m! a q + i r m! and a i q (2.124) 2~ m! 2~ m! obey the commutation relation [a, a ] 1. In terms of a and a, which also are called the annihilation and creation oerators, the hamiltonian H has the simle form H ~! a a (2.125) There is a unique state i that is annihilated by the oerator a, as may be seen by solving the di erential equation r m! hq a i 2~ hq q + i i. (2.126) m!
6 Since hq q q hq and 2.11 The Harmonic Oscillator 19 hq i ~ i the resulting di erential equation is dhq i dq (2.127) dhq i dq m! ~ q hq i. (2.128) Its suitably normalized solution is the wave function for the ground state of the harmonic oscillator m! 1/4 m!q hq 2 i ex. (2.129) ~ 2~ For n, 1, 2,...,thenth eigenstate of the hamiltonian H is ni 1 n! a n i (2.13) where n! n(n 1)...1isn-factorial and! 1. Its energy is H ni ~! n ni. (2.131) The identity oerator is I nihn. (2.132) n An arbitrary state i has an exansion in terms of the eigenstates ni i I i nihn i (2.133) and evolves in time like a Fourier series n X 1, ti e iht/~ i e iht/~ nihn i e i!t/2 with wave function n (q, t) hq, ti e i!t/2 1 X n 1 X n e in!t nihn i (2.134) e in!t hq nihn i. (2.135) The wave functions hq ni of the energy eigenstates are related to the Hermite olynomials (examle 8.6) H n (x) ( 1) n e x2 dn dx n e x2 (2.136)
7 11 Fourier Series by a change of variables x m!/~ q sq and a normalization factor se (sq) 2 /2 m! 1/4 e m!q 2 /2~ m! 1/2q hq ni 2 n n! H n(sq) H n. ~ 2 n n! ~ (2.137) The coherent state i i e 2 /2 e a i e 2 /2 n n n! ni (2.138) is an eigenstate a i i of the lowering (or annihilation) oerator a with eigenvalue. Its time evolution is simly, ti e i!t/2 e 2 /2 n e i!t n n! ni e i!t/2 e i!t i. (2.139) 2.12 Nonrelativistic Strings If we clam the ends of a nonrelativistic string at x and x, then the amlitude y(x, t) will obey the boundary conditions and the wave equation as long as y(x, t) remains small. The functions y n (x, t) sin n x y(,t)y(, t) (2.14) v 2 (2.141) f n sin n vt + d n cos n vt (2.142) satisfy this wave equation (2.141) and the boundary conditions (2.14). They reresent waves traveling along the x-axis with seed v. The sace S of functions f(x) that satisfy the boundary condition (2.14) is sanned by the functions sin(n x/). One may use the integral formula Z sin n x to derive for any function f 2 S the Fourier series f(x) f n sin n x m x sin dx 2 nm (2.143) n1 (2.144)
2 Fourier Series. 2.1 Complex Fourier Series The phases exp(inx)/ p 2, one for each integer n, are orthonormal on an interval of length 2 Z 2
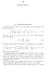 2 Fourier Series 2. Comlex Fourier Series The hases ex(inx)/, one for each integer n, are orthonormal on an interval of length e imx e inx e i(n m)x dx = dx = m,n (2.) where n,m =ifn = m, and n,m =ifn6=
2 Fourier Series 2. Comlex Fourier Series The hases ex(inx)/, one for each integer n, are orthonormal on an interval of length e imx e inx e i(n m)x dx = dx = m,n (2.) where n,m =ifn = m, and n,m =ifn6=
PHYS 301 HOMEWORK #9-- SOLUTIONS
 PHYS 0 HOMEWORK #9-- SOLUTIONS. We are asked to use Dirichlet' s theorem to determine the value of f (x) as defined below at x = 0, ± /, ± f(x) = 0, - < x
PHYS 0 HOMEWORK #9-- SOLUTIONS. We are asked to use Dirichlet' s theorem to determine the value of f (x) as defined below at x = 0, ± /, ± f(x) = 0, - < x
Elementary Analysis in Q p
 Elementary Analysis in Q Hannah Hutter, May Szedlák, Phili Wirth November 17, 2011 This reort follows very closely the book of Svetlana Katok 1. 1 Sequences and Series In this section we will see some
Elementary Analysis in Q Hannah Hutter, May Szedlák, Phili Wirth November 17, 2011 This reort follows very closely the book of Svetlana Katok 1. 1 Sequences and Series In this section we will see some
15 Functional Derivatives
 15 Functional Derivatives 15.1 Functionals A functional G[f] is a map from a space of functions to a set of numbers. For instance, the action functional S[q] for a particle in one imension maps the coorinate
15 Functional Derivatives 15.1 Functionals A functional G[f] is a map from a space of functions to a set of numbers. For instance, the action functional S[q] for a particle in one imension maps the coorinate
Introduction to Group Theory Note 1
 Introduction to Grou Theory Note July 7, 009 Contents INTRODUCTION. Examles OF Symmetry Grous in Physics................................. ELEMENT OF GROUP THEORY. De nition of Grou................................................
Introduction to Grou Theory Note July 7, 009 Contents INTRODUCTION. Examles OF Symmetry Grous in Physics................................. ELEMENT OF GROUP THEORY. De nition of Grou................................................
Periodic functions: simple harmonic oscillator
 Periodic functions: simple harmonic oscillator Recall the simple harmonic oscillator (e.g. mass-spring system) d 2 y dt 2 + ω2 0y = 0 Solution can be written in various ways: y(t) = Ae iω 0t y(t) = A cos
Periodic functions: simple harmonic oscillator Recall the simple harmonic oscillator (e.g. mass-spring system) d 2 y dt 2 + ω2 0y = 0 Solution can be written in various ways: y(t) = Ae iω 0t y(t) = A cos
1 Properties of Spherical Harmonics
 Proerties of Sherical Harmonics. Reetition In the lecture the sherical harmonics Y m were introduced as the eigenfunctions of angular momentum oerators lˆz and lˆ2 in sherical coordinates. We found that
Proerties of Sherical Harmonics. Reetition In the lecture the sherical harmonics Y m were introduced as the eigenfunctions of angular momentum oerators lˆz and lˆ2 in sherical coordinates. We found that
The oerators a and a obey the commutation relation Proof: [a a ] = (7) aa ; a a = ((q~ i~)(q~ ; i~) ; ( q~ ; i~)(q~ i~)) = i ( ~q~ ; q~~) = (8) As a s
![The oerators a and a obey the commutation relation Proof: [a a ] = (7) aa ; a a = ((q~ i~)(q~ ; i~) ; ( q~ ; i~)(q~ i~)) = i ( ~q~ ; q~~) = (8) As a s The oerators a and a obey the commutation relation Proof: [a a ] = (7) aa ; a a = ((q~ i~)(q~ ; i~) ; ( q~ ; i~)(q~ i~)) = i ( ~q~ ; q~~) = (8) As a s](/thumbs/78/77678205.jpg) They can b e used to exress q, and H as follows: 8.54: Many-body henomena in condensed matter and atomic hysics Last modied: Setember 4, 3 Lecture. Coherent States. We start the course with the discussion
They can b e used to exress q, and H as follows: 8.54: Many-body henomena in condensed matter and atomic hysics Last modied: Setember 4, 3 Lecture. Coherent States. We start the course with the discussion
Math 115 ( ) Yum-Tong Siu 1. Derivation of the Poisson Kernel by Fourier Series and Convolution
 Math 5 (006-007 Yum-Tong Siu. Derivation of the Poisson Kernel by Fourier Series and Convolution We are going to give a second derivation of the Poisson kernel by using Fourier series and convolution.
Math 5 (006-007 Yum-Tong Siu. Derivation of the Poisson Kernel by Fourier Series and Convolution We are going to give a second derivation of the Poisson kernel by using Fourier series and convolution.
3 The Harmonic Oscillator
 3 The Harmonic Oscillator What we ve laid out so far is essentially just linear algebra. I now want to show how this formalism can be used to do some physics. To do this, we ll study a simple system the
3 The Harmonic Oscillator What we ve laid out so far is essentially just linear algebra. I now want to show how this formalism can be used to do some physics. To do this, we ll study a simple system the
Fourier Series Tutorial
 Fourier Series Tutorial INTRODUCTION This document is designed to overview the theory behind the Fourier series and its alications. It introduces the Fourier series and then demonstrates its use with a
Fourier Series Tutorial INTRODUCTION This document is designed to overview the theory behind the Fourier series and its alications. It introduces the Fourier series and then demonstrates its use with a
FOURIER SERIES PART III: APPLICATIONS
 FOURIER SERIES PART III: APPLICATIONS We extend the construction of Fourier series to functions with arbitrary eriods, then we associate to functions defined on an interval [, L] Fourier sine and Fourier
FOURIER SERIES PART III: APPLICATIONS We extend the construction of Fourier series to functions with arbitrary eriods, then we associate to functions defined on an interval [, L] Fourier sine and Fourier
Math 489AB A Very Brief Intro to Fourier Series Fall 2008
 Math 489AB A Very Brief Intro to Fourier Series Fall 8 Contents Fourier Series. The coefficients........................................ Convergence......................................... 4.3 Convergence
Math 489AB A Very Brief Intro to Fourier Series Fall 8 Contents Fourier Series. The coefficients........................................ Convergence......................................... 4.3 Convergence
14 Fourier analysis. Read: Boas Ch. 7.
 14 Fourier analysis Read: Boas Ch. 7. 14.1 Function spaces A function can be thought of as an element of a kind of vector space. After all, a function f(x) is merely a set of numbers, one for each point
14 Fourier analysis Read: Boas Ch. 7. 14.1 Function spaces A function can be thought of as an element of a kind of vector space. After all, a function f(x) is merely a set of numbers, one for each point
Simplifications to Conservation Equations
 Chater 5 Simlifications to Conservation Equations 5.1 Steady Flow If fluid roerties at a oint in a field do not change with time, then they are a function of sace only. They are reresented by: ϕ = ϕq 1,
Chater 5 Simlifications to Conservation Equations 5.1 Steady Flow If fluid roerties at a oint in a field do not change with time, then they are a function of sace only. They are reresented by: ϕ = ϕq 1,
Math 118, Handout 4: Hermite functions and the Fourier transform. n! where D = d/dx, are a basis of eigenfunctions for the Fourier transform
 The Hermite functions defined by h n (x) = ( )n e x2 /2 D n e x2 where D = d/dx, are a basis of eigenfunctions for the Fourier transform f(k) = f(x)e ikx dx on L 2 (R). Since h 0 (x) = e x2 /2 h (x) =
The Hermite functions defined by h n (x) = ( )n e x2 /2 D n e x2 where D = d/dx, are a basis of eigenfunctions for the Fourier transform f(k) = f(x)e ikx dx on L 2 (R). Since h 0 (x) = e x2 /2 h (x) =
Lecture 3 Dynamics 29
 Lecture 3 Dynamics 29 30 LECTURE 3. DYNAMICS 3.1 Introduction Having described the states and the observables of a quantum system, we shall now introduce the rules that determine their time evolution.
Lecture 3 Dynamics 29 30 LECTURE 3. DYNAMICS 3.1 Introduction Having described the states and the observables of a quantum system, we shall now introduce the rules that determine their time evolution.
Fall f(x)g(x) dx. The starting place for the theory of Fourier series is that the family of functions {e inx } n= is orthonormal, that is
 18.103 Fall 2013 1. Fourier Series, Part 1. We will consider several function spaces during our study of Fourier series. When we talk about L p ((, π)), it will be convenient to include the factor 1/ in
18.103 Fall 2013 1. Fourier Series, Part 1. We will consider several function spaces during our study of Fourier series. When we talk about L p ((, π)), it will be convenient to include the factor 1/ in
On the irreducibility of a polynomial associated with the Strong Factorial Conjecture
 On the irreducibility of a olynomial associated with the Strong Factorial Conecture Michael Filaseta Mathematics Deartment University of South Carolina Columbia, SC 29208 USA E-mail: filaseta@math.sc.edu
On the irreducibility of a olynomial associated with the Strong Factorial Conecture Michael Filaseta Mathematics Deartment University of South Carolina Columbia, SC 29208 USA E-mail: filaseta@math.sc.edu
A construction of bent functions from plateaued functions
 A construction of bent functions from lateaued functions Ayça Çeşmelioğlu, Wilfried Meidl Sabancı University, MDBF, Orhanlı, 34956 Tuzla, İstanbul, Turkey. Abstract In this resentation, a technique for
A construction of bent functions from lateaued functions Ayça Çeşmelioğlu, Wilfried Meidl Sabancı University, MDBF, Orhanlı, 34956 Tuzla, İstanbul, Turkey. Abstract In this resentation, a technique for
Towards understanding the Lorenz curve using the Uniform distribution. Chris J. Stephens. Newcastle City Council, Newcastle upon Tyne, UK
 Towards understanding the Lorenz curve using the Uniform distribution Chris J. Stehens Newcastle City Council, Newcastle uon Tyne, UK (For the Gini-Lorenz Conference, University of Siena, Italy, May 2005)
Towards understanding the Lorenz curve using the Uniform distribution Chris J. Stehens Newcastle City Council, Newcastle uon Tyne, UK (For the Gini-Lorenz Conference, University of Siena, Italy, May 2005)
PHYS 502 Lecture 3: Fourier Series
 PHYS 52 Lecture 3: Fourier Series Fourier Series Introduction In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a (possibly infinite) set of simple oscillating
PHYS 52 Lecture 3: Fourier Series Fourier Series Introduction In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a (possibly infinite) set of simple oscillating
we get our formula for the saddle-point integral (5.294) h(w) e xf(w). (5.301) xf 00 (w) (w j )
 5.3 The Abel-Plana Formula and the Casimir E ect 9 and using f (w) = e i and + = to show that e i = e i i = e i = f (w) (5.3) we get our formula for the saddle-oint integral (5.94) I(x) / h(w) e xf(w).
5.3 The Abel-Plana Formula and the Casimir E ect 9 and using f (w) = e i and + = to show that e i = e i i = e i = f (w) (5.3) we get our formula for the saddle-oint integral (5.94) I(x) / h(w) e xf(w).
Daubechies orthonormal wavelet bases
 Daubechies orthonormal wavelet bases Teacher: Anatoliy Malyareno May 7, 04 Abstract Contents of the lecture. Construction of filters Calculating the scaling function in the frequency domain Calculating
Daubechies orthonormal wavelet bases Teacher: Anatoliy Malyareno May 7, 04 Abstract Contents of the lecture. Construction of filters Calculating the scaling function in the frequency domain Calculating
Participation Factors. However, it does not give the influence of each state on the mode.
 Particiation Factors he mode shae, as indicated by the right eigenvector, gives the relative hase of each state in a articular mode. However, it does not give the influence of each state on the mode. We
Particiation Factors he mode shae, as indicated by the right eigenvector, gives the relative hase of each state in a articular mode. However, it does not give the influence of each state on the mode. We
Physics 250 Green s functions for ordinary differential equations
 Physics 25 Green s functions for ordinary differential equations Peter Young November 25, 27 Homogeneous Equations We have already discussed second order linear homogeneous differential equations, which
Physics 25 Green s functions for ordinary differential equations Peter Young November 25, 27 Homogeneous Equations We have already discussed second order linear homogeneous differential equations, which
An interesting result concerning the lower bound to the energy in the Heisenberg picture
 Aeiron, Vol. 16, No. 2, Aril 29 191 An interesting result concerning the lower bound to the energy in the Heisenberg icture Dan Solomon Rauland-Borg Cororation 345 W Oakton Skokie, IL 676 USA Email: dan.solomon@rauland.com
Aeiron, Vol. 16, No. 2, Aril 29 191 An interesting result concerning the lower bound to the energy in the Heisenberg icture Dan Solomon Rauland-Borg Cororation 345 W Oakton Skokie, IL 676 USA Email: dan.solomon@rauland.com
08 Fourier Analysis. Utah State University. Charles G. Torre Department of Physics, Utah State University,
 Utah State University DigitalCommons@USU Foundations of Wave Phenomena ibrary Digital Monographs 8-04 08 Fourier Analysis Charles G. Torre Department of Physics, Utah State University, Charles.Torre@usu.edu
Utah State University DigitalCommons@USU Foundations of Wave Phenomena ibrary Digital Monographs 8-04 08 Fourier Analysis Charles G. Torre Department of Physics, Utah State University, Charles.Torre@usu.edu
Convergence for periodic Fourier series
 Chapter 8 Convergence for periodic Fourier series We are now in a position to address the Fourier series hypothesis that functions can realized as the infinite sum of trigonometric functions discussed
Chapter 8 Convergence for periodic Fourier series We are now in a position to address the Fourier series hypothesis that functions can realized as the infinite sum of trigonometric functions discussed
F(p) y + 3y + 2y = δ(t a) y(0) = 0 and y (0) = 0.
 Page 5- Chater 5: Lalace Transforms The Lalace Transform is a useful tool that is used to solve many mathematical and alied roblems. In articular, the Lalace transform is a technique that can be used to
Page 5- Chater 5: Lalace Transforms The Lalace Transform is a useful tool that is used to solve many mathematical and alied roblems. In articular, the Lalace transform is a technique that can be used to
DRAFT - Math 101 Lecture Note - Dr. Said Algarni
 2 Limits 2.1 The Tangent Problems The word tangent is derived from the Latin word tangens, which means touching. A tangent line to a curve is a line that touches the curve and a secant line is a line that
2 Limits 2.1 The Tangent Problems The word tangent is derived from the Latin word tangens, which means touching. A tangent line to a curve is a line that touches the curve and a secant line is a line that
Chapter 7: Bounded Operators in Hilbert Spaces
 Chapter 7: Bounded Operators in Hilbert Spaces I-Liang Chern Department of Applied Mathematics National Chiao Tung University and Department of Mathematics National Taiwan University Fall, 2013 1 / 84
Chapter 7: Bounded Operators in Hilbert Spaces I-Liang Chern Department of Applied Mathematics National Chiao Tung University and Department of Mathematics National Taiwan University Fall, 2013 1 / 84
Problem set 6 for Quantum Field Theory course
 Problem set 6 or Quantum Field Theory course 2018.03.13. Toics covered Scattering cross-section and decay rate Yukawa theory and Yukawa otential Scattering in external electromagnetic ield, Rutherord ormula
Problem set 6 or Quantum Field Theory course 2018.03.13. Toics covered Scattering cross-section and decay rate Yukawa theory and Yukawa otential Scattering in external electromagnetic ield, Rutherord ormula
Simple Harmonic Oscillator
 Classical harmonic oscillator Linear force acting on a particle (Hooke s law): F =!kx From Newton s law: F = ma = m d x dt =!kx " d x dt + # x = 0, # = k / m Position and momentum solutions oscillate in
Classical harmonic oscillator Linear force acting on a particle (Hooke s law): F =!kx From Newton s law: F = ma = m d x dt =!kx " d x dt + # x = 0, # = k / m Position and momentum solutions oscillate in
Mathematics (Course B) Lent Term 2005 Examples Sheet 2
 N12d Natural Sciences, Part IA Dr M. G. Worster Mathematics (Course B) Lent Term 2005 Examples Sheet 2 Please communicate any errors in this sheet to Dr Worster at M.G.Worster@damtp.cam.ac.uk. Note that
N12d Natural Sciences, Part IA Dr M. G. Worster Mathematics (Course B) Lent Term 2005 Examples Sheet 2 Please communicate any errors in this sheet to Dr Worster at M.G.Worster@damtp.cam.ac.uk. Note that
k and v = v 1 j + u 3 i + v 2
 ORTHOGONAL FUNCTIONS AND FOURIER SERIES Orthogonl functions A function cn e considered to e generliztion of vector. Thus the vector concets like the inner roduct nd orthogonlity of vectors cn e extended
ORTHOGONAL FUNCTIONS AND FOURIER SERIES Orthogonl functions A function cn e considered to e generliztion of vector. Thus the vector concets like the inner roduct nd orthogonlity of vectors cn e extended
Numerical Linear Algebra
 Numerical Linear Algebra Numerous alications in statistics, articularly in the fitting of linear models. Notation and conventions: Elements of a matrix A are denoted by a ij, where i indexes the rows and
Numerical Linear Algebra Numerous alications in statistics, articularly in the fitting of linear models. Notation and conventions: Elements of a matrix A are denoted by a ij, where i indexes the rows and
L p -CONVERGENCE OF THE LAPLACE BELTRAMI EIGENFUNCTION EXPANSIONS
 L -CONVERGENCE OF THE LAPLACE BELTRAI EIGENFUNCTION EXPANSIONS ATSUSHI KANAZAWA Abstract. We rovide a simle sufficient condition for the L - convergence of the Lalace Beltrami eigenfunction exansions of
L -CONVERGENCE OF THE LAPLACE BELTRAI EIGENFUNCTION EXPANSIONS ATSUSHI KANAZAWA Abstract. We rovide a simle sufficient condition for the L - convergence of the Lalace Beltrami eigenfunction exansions of
Phase velocity and group velocity (c) Zhengqing Yun,
 Phase velocity and grou velocity (c) Zhengqing Yun, 2011-2012 Objective: Observe the difference between hase and grou velocity; understand that the grou velocity can be less than, equal to, and greater
Phase velocity and grou velocity (c) Zhengqing Yun, 2011-2012 Objective: Observe the difference between hase and grou velocity; understand that the grou velocity can be less than, equal to, and greater
MA3H1 TOPICS IN NUMBER THEORY PART III
 MA3H1 TOPICS IN NUMBER THEORY PART III SAMIR SIKSEK 1. Congruences Modulo m In quadratic recirocity we studied congruences of the form x 2 a (mod ). We now turn our attention to situations where is relaced
MA3H1 TOPICS IN NUMBER THEORY PART III SAMIR SIKSEK 1. Congruences Modulo m In quadratic recirocity we studied congruences of the form x 2 a (mod ). We now turn our attention to situations where is relaced
Higher-order ordinary differential equations
 Higher-order ordinary differential equations 1 A linear ODE of general order n has the form a n (x) dn y dx n +a n 1(x) dn 1 y dx n 1 + +a 1(x) dy dx +a 0(x)y = f(x). If f(x) = 0 then the equation is called
Higher-order ordinary differential equations 1 A linear ODE of general order n has the form a n (x) dn y dx n +a n 1(x) dn 1 y dx n 1 + +a 1(x) dy dx +a 0(x)y = f(x). If f(x) = 0 then the equation is called
LECTURE 3 BASIC QUANTUM THEORY
 LECTURE 3 BASIC QUANTUM THEORY Matter waves and the wave function In 194 De Broglie roosed that all matter has a wavelength and exhibits wave like behavior. He roosed that the wavelength of a article of
LECTURE 3 BASIC QUANTUM THEORY Matter waves and the wave function In 194 De Broglie roosed that all matter has a wavelength and exhibits wave like behavior. He roosed that the wavelength of a article of
Math 104B: Number Theory II (Winter 2012)
 Math 104B: Number Theory II (Winter 01) Alina Bucur Contents 1 Review 11 Prime numbers 1 Euclidean algorithm 13 Multilicative functions 14 Linear diohantine equations 3 15 Congruences 3 Primes as sums
Math 104B: Number Theory II (Winter 01) Alina Bucur Contents 1 Review 11 Prime numbers 1 Euclidean algorithm 13 Multilicative functions 14 Linear diohantine equations 3 15 Congruences 3 Primes as sums
By following steps analogous to those that led to (20.177), one may show (exercise 20.30) that in Feynman s gauge, = 1, the photon propagator is
 20.2 Fermionic path integrals 74 factor, which cancels. But if before integrating over all gauge transformations, we shift so that 4 changes to 4 A 0, then the exponential factor is exp[ i 2 R ( A 0 4
20.2 Fermionic path integrals 74 factor, which cancels. But if before integrating over all gauge transformations, we shift so that 4 changes to 4 A 0, then the exponential factor is exp[ i 2 R ( A 0 4
About solving time dependent Schrodinger equation
 About solving time dependent Schrodinger equation (Griffiths Chapter 2 Time Independent Schrodinger Equation) Given the time dependent Schrodinger Equation: Ψ Ψ Ψ 2 1. Observe that Schrodinger time dependent
About solving time dependent Schrodinger equation (Griffiths Chapter 2 Time Independent Schrodinger Equation) Given the time dependent Schrodinger Equation: Ψ Ψ Ψ 2 1. Observe that Schrodinger time dependent
Math 205b Homework 2 Solutions
 Math 5b Homework Solutions January 5, 5 Problem (R-S, II.) () For the R case, we just expand the right hand side and use the symmetry of the inner product: ( x y x y ) = = ((x, x) (y, y) (x, y) (y, x)
Math 5b Homework Solutions January 5, 5 Problem (R-S, II.) () For the R case, we just expand the right hand side and use the symmetry of the inner product: ( x y x y ) = = ((x, x) (y, y) (x, y) (y, x)
PH 451/551 Quantum Mechanics Capstone Winter 201x
 These are the questions from the W7 exam presented as practice problems. The equation sheet is PH 45/55 Quantum Mechanics Capstone Winter x TOTAL POINTS: xx Weniger 6, time There are xx questions, for
These are the questions from the W7 exam presented as practice problems. The equation sheet is PH 45/55 Quantum Mechanics Capstone Winter x TOTAL POINTS: xx Weniger 6, time There are xx questions, for
Supplementary information I Hilbert Space, Dirac Notation, and Matrix Mechanics. EE270 Fall 2017
 Supplementary information I Hilbert Space, Dirac Notation, and Matrix Mechanics Properties of Vector Spaces Unit vectors ~xi form a basis which spans the space and which are orthonormal ( if i = j ~xi
Supplementary information I Hilbert Space, Dirac Notation, and Matrix Mechanics Properties of Vector Spaces Unit vectors ~xi form a basis which spans the space and which are orthonormal ( if i = j ~xi
2.2 The derivative as a Function
 2.2 The derivative as a Function Recall: The derivative of a function f at a fixed number a: f a f a+h f(a) = lim h 0 h Definition (Derivative of f) For any number x, the derivative of f is f x f x+h f(x)
2.2 The derivative as a Function Recall: The derivative of a function f at a fixed number a: f a f a+h f(a) = lim h 0 h Definition (Derivative of f) For any number x, the derivative of f is f x f x+h f(x)
10.2-3: Fourier Series.
 10.2-3: Fourier Series. 10.2-3: Fourier Series. O. Costin: Fourier Series, 10.2-3 1 Fourier series are very useful in representing periodic functions. Examples of periodic functions. A function is periodic
10.2-3: Fourier Series. 10.2-3: Fourier Series. O. Costin: Fourier Series, 10.2-3 1 Fourier series are very useful in representing periodic functions. Examples of periodic functions. A function is periodic
Further differentiation and integration
 7 Toic Further differentiation and integration Contents. evision exercise................................... 8. Introduction...................................... 9. Differentiation of sin x and cos x..........................
7 Toic Further differentiation and integration Contents. evision exercise................................... 8. Introduction...................................... 9. Differentiation of sin x and cos x..........................
NONRELATIVISTIC STRONG-FIELD APPROXIMATION (SFA)
 NONRELATIVISTIC STRONG-FIELD APPROXIMATION (SFA) Note: SFA will automatically be taken to mean Coulomb gauge (relativistic or non-diole) or VG (nonrelativistic, diole-aroximation). If LG is intended (rarely),
NONRELATIVISTIC STRONG-FIELD APPROXIMATION (SFA) Note: SFA will automatically be taken to mean Coulomb gauge (relativistic or non-diole) or VG (nonrelativistic, diole-aroximation). If LG is intended (rarely),
An Estimate For Heilbronn s Exponential Sum
 An Estimate For Heilbronn s Exonential Sum D.R. Heath-Brown Magdalen College, Oxford For Heini Halberstam, on his retirement Let be a rime, and set e(x) = ex(2πix). Heilbronn s exonential sum is defined
An Estimate For Heilbronn s Exonential Sum D.R. Heath-Brown Magdalen College, Oxford For Heini Halberstam, on his retirement Let be a rime, and set e(x) = ex(2πix). Heilbronn s exonential sum is defined
Quantum Mechanics Solutions
 Quantum Mechanics Solutions (a (i f A and B are Hermitian, since (AB = B A = BA, operator AB is Hermitian if and only if A and B commute So, we know that [A,B] = 0, which means that the Hilbert space H
Quantum Mechanics Solutions (a (i f A and B are Hermitian, since (AB = B A = BA, operator AB is Hermitian if and only if A and B commute So, we know that [A,B] = 0, which means that the Hilbert space H
ANALYTIC NUMBER THEORY AND DIRICHLET S THEOREM
 ANALYTIC NUMBER THEORY AND DIRICHLET S THEOREM JOHN BINDER Abstract. In this aer, we rove Dirichlet s theorem that, given any air h, k with h, k) =, there are infinitely many rime numbers congruent to
ANALYTIC NUMBER THEORY AND DIRICHLET S THEOREM JOHN BINDER Abstract. In this aer, we rove Dirichlet s theorem that, given any air h, k with h, k) =, there are infinitely many rime numbers congruent to
Dirac s Hole Theory and the Pauli Principle: Clearing up the Confusion
 Adv. Studies Theor. Phys., Vol. 3, 29, no. 9, 323-332 Dirac s Hole Theory and the Pauli Princile: Clearing u the Conusion Dan Solomon Rauland-Borg Cororation 82 W. Central Road Mount Prosect, IL 656, USA
Adv. Studies Theor. Phys., Vol. 3, 29, no. 9, 323-332 Dirac s Hole Theory and the Pauli Princile: Clearing u the Conusion Dan Solomon Rauland-Borg Cororation 82 W. Central Road Mount Prosect, IL 656, USA
FOURIER TRANSFORMS. At, is sometimes taken as 0.5 or it may not have any specific value. Shifting at
 Chapter 2 FOURIER TRANSFORMS 2.1 Introduction The Fourier series expresses any periodic function into a sum of sinusoids. The Fourier transform is the extension of this idea to non-periodic functions by
Chapter 2 FOURIER TRANSFORMS 2.1 Introduction The Fourier series expresses any periodic function into a sum of sinusoids. The Fourier transform is the extension of this idea to non-periodic functions by
In this appendix we show that the multidimensional Lyapunov exponents and
 Aendix A6 Lyaunov exonents Man who says it cannot be done should not interrut man doing it. Sayings of Vattay Gábor In this aendix we show that the multidimensional Lyaunov exonents and relaxation exonents
Aendix A6 Lyaunov exonents Man who says it cannot be done should not interrut man doing it. Sayings of Vattay Gábor In this aendix we show that the multidimensional Lyaunov exonents and relaxation exonents
DIVISIBILITY CRITERIA FOR CLASS NUMBERS OF IMAGINARY QUADRATIC FIELDS
 IVISIBILITY CRITERIA FOR CLASS NUMBERS OF IMAGINARY QUARATIC FIELS PAUL JENKINS AN KEN ONO Abstract. In a recent aer, Guerzhoy obtained formulas for certain class numbers as -adic limits of traces of singular
IVISIBILITY CRITERIA FOR CLASS NUMBERS OF IMAGINARY QUARATIC FIELS PAUL JENKINS AN KEN ONO Abstract. In a recent aer, Guerzhoy obtained formulas for certain class numbers as -adic limits of traces of singular
Solutions: Problem Set 3 Math 201B, Winter 2007
 Solutions: Problem Set 3 Math 201B, Winter 2007 Problem 1. Prove that an infinite-dimensional Hilbert space is a separable metric space if and only if it has a countable orthonormal basis. Solution. If
Solutions: Problem Set 3 Math 201B, Winter 2007 Problem 1. Prove that an infinite-dimensional Hilbert space is a separable metric space if and only if it has a countable orthonormal basis. Solution. If
An Inverse Problem for Two Spectra of Complex Finite Jacobi Matrices
 Coyright 202 Tech Science Press CMES, vol.86, no.4,.30-39, 202 An Inverse Problem for Two Sectra of Comlex Finite Jacobi Matrices Gusein Sh. Guseinov Abstract: This aer deals with the inverse sectral roblem
Coyright 202 Tech Science Press CMES, vol.86, no.4,.30-39, 202 An Inverse Problem for Two Sectra of Comlex Finite Jacobi Matrices Gusein Sh. Guseinov Abstract: This aer deals with the inverse sectral roblem
Use of Transformations and the Repeated Statement in PROC GLM in SAS Ed Stanek
 Use of Transformations and the Reeated Statement in PROC GLM in SAS Ed Stanek Introduction We describe how the Reeated Statement in PROC GLM in SAS transforms the data to rovide tests of hyotheses of interest.
Use of Transformations and the Reeated Statement in PROC GLM in SAS Ed Stanek Introduction We describe how the Reeated Statement in PROC GLM in SAS transforms the data to rovide tests of hyotheses of interest.
Principles of Computed Tomography (CT)
 Page 298 Princiles of Comuted Tomograhy (CT) The theoretical foundation of CT dates back to Johann Radon, a mathematician from Vienna who derived a method in 1907 for rojecting a 2-D object along arallel
Page 298 Princiles of Comuted Tomograhy (CT) The theoretical foundation of CT dates back to Johann Radon, a mathematician from Vienna who derived a method in 1907 for rojecting a 2-D object along arallel
ε i (E j )=δj i = 0, if i j, form a basis for V, called the dual basis to (E i ). Therefore, dim V =dim V.
 Covectors Definition. Let V be a finite-dimensional vector sace. A covector on V is real-valued linear functional on V, that is, a linear ma ω : V R. The sace of all covectors on V is itself a real vector
Covectors Definition. Let V be a finite-dimensional vector sace. A covector on V is real-valued linear functional on V, that is, a linear ma ω : V R. The sace of all covectors on V is itself a real vector
Matrix Representation
 Matrix Representation Matrix Rep. Same basics as introduced already. Convenient method of working with vectors. Superposition Complete set of vectors can be used to express any other vector. Complete set
Matrix Representation Matrix Rep. Same basics as introduced already. Convenient method of working with vectors. Superposition Complete set of vectors can be used to express any other vector. Complete set
SECTION 5: FIBRATIONS AND HOMOTOPY FIBERS
 SECTION 5: FIBRATIONS AND HOMOTOPY FIBERS In this section we will introduce two imortant classes of mas of saces, namely the Hurewicz fibrations and the more general Serre fibrations, which are both obtained
SECTION 5: FIBRATIONS AND HOMOTOPY FIBERS In this section we will introduce two imortant classes of mas of saces, namely the Hurewicz fibrations and the more general Serre fibrations, which are both obtained
PHYSICS 301/MATH 355 HOMEWORK #8
 PHYSICS 3/MATH 355 HOMEWORK #8 Solutions Question # We consider the integral : where m and n are both integers. We can evaluate this integral : Integrate@Cos@m xd Cos@n xd, 8x, π, π
PHYSICS 3/MATH 355 HOMEWORK #8 Solutions Question # We consider the integral : where m and n are both integers. We can evaluate this integral : Integrate@Cos@m xd Cos@n xd, 8x, π, π
Physics 215 Quantum Mechanics 1 Assignment 5
 Physics 15 Quantum Mechanics 1 Assignment 5 Logan A. Morrison February 10, 016 Problem 1 A particle of mass m is confined to a one-dimensional region 0 x a. At t 0 its normalized wave function is 8 πx
Physics 15 Quantum Mechanics 1 Assignment 5 Logan A. Morrison February 10, 016 Problem 1 A particle of mass m is confined to a one-dimensional region 0 x a. At t 0 its normalized wave function is 8 πx
Lecture 12. The harmonic oscillator
 Lecture 12 The harmonic oscillator 107 108 LECTURE 12. THE HARMONIC OSCILLATOR 12.1 Introduction In this chapter, we are going to find explicitly the eigenfunctions and eigenvalues for the time-independent
Lecture 12 The harmonic oscillator 107 108 LECTURE 12. THE HARMONIC OSCILLATOR 12.1 Introduction In this chapter, we are going to find explicitly the eigenfunctions and eigenvalues for the time-independent
E( x ) = [b(n) - a(n,m)x(m) ]
![E( x ) = [b(n) - a(n,m)x(m) ] E( x ) = [b(n) - a(n,m)x(m) ]](/thumbs/84/90638037.jpg) Exam #, EE5353, Fall 0. Here we consider MLPs with binary-valued inuts (0 or ). (a) If the MLP has inuts, what is the maximum degree D of its PBF model? (b) If the MLP has inuts, what is the maximum value
Exam #, EE5353, Fall 0. Here we consider MLPs with binary-valued inuts (0 or ). (a) If the MLP has inuts, what is the maximum degree D of its PBF model? (b) If the MLP has inuts, what is the maximum value
Problem. Set up the definite integral that gives the area of the region. y 1 = x 2 6x, y 2 = 0. dx = ( 2x 2 + 6x) dx.
 Wednesday, September 3, 5 Page Problem Problem. Set up the definite integral that gives the area of the region y x 6x, y Solution. The graphs intersect at x and x 6 and y is the uppermost function. So
Wednesday, September 3, 5 Page Problem Problem. Set up the definite integral that gives the area of the region y x 6x, y Solution. The graphs intersect at x and x 6 and y is the uppermost function. So
TRACES OF SCHUR AND KRONECKER PRODUCTS FOR BLOCK MATRICES
 Khayyam J. Math. DOI:10.22034/kjm.2019.84207 TRACES OF SCHUR AND KRONECKER PRODUCTS FOR BLOCK MATRICES ISMAEL GARCÍA-BAYONA Communicated by A.M. Peralta Abstract. In this aer, we define two new Schur and
Khayyam J. Math. DOI:10.22034/kjm.2019.84207 TRACES OF SCHUR AND KRONECKER PRODUCTS FOR BLOCK MATRICES ISMAEL GARCÍA-BAYONA Communicated by A.M. Peralta Abstract. In this aer, we define two new Schur and
t s (p). An Introduction
 Notes 6. Quadratic Gauss Sums Definition. Let a, b Z. Then we denote a b if a divides b. Definition. Let a and b be elements of Z. Then c Z s.t. a, b c, where c gcda, b max{x Z x a and x b }. 5, Chater1
Notes 6. Quadratic Gauss Sums Definition. Let a, b Z. Then we denote a b if a divides b. Definition. Let a and b be elements of Z. Then c Z s.t. a, b c, where c gcda, b max{x Z x a and x b }. 5, Chater1
First Order Differential Equations
 Chapter 2 First Order Differential Equations 2.1 9 10 CHAPTER 2. FIRST ORDER DIFFERENTIAL EQUATIONS 2.2 Separable Equations A first order differential equation = f(x, y) is called separable if f(x, y)
Chapter 2 First Order Differential Equations 2.1 9 10 CHAPTER 2. FIRST ORDER DIFFERENTIAL EQUATIONS 2.2 Separable Equations A first order differential equation = f(x, y) is called separable if f(x, y)
(Workshop on Harmonic Analysis on symmetric spaces I.S.I. Bangalore : 9th July 2004) B.Sury
 Is e π 163 odd or even? (Worksho on Harmonic Analysis on symmetric saces I.S.I. Bangalore : 9th July 004) B.Sury e π 163 = 653741640768743.999999999999.... The object of this talk is to exlain this amazing
Is e π 163 odd or even? (Worksho on Harmonic Analysis on symmetric saces I.S.I. Bangalore : 9th July 004) B.Sury e π 163 = 653741640768743.999999999999.... The object of this talk is to exlain this amazing
References: 1. Cohen Tannoudji Chapter 5 2. Quantum Chemistry Chapter 3
 Lecture #6 Today s Program:. Harmonic oscillator imortance. Quantum mechanical harmonic oscillations of ethylene molecule 3. Harmonic oscillator quantum mechanical general treatment 4. Angular momentum,
Lecture #6 Today s Program:. Harmonic oscillator imortance. Quantum mechanical harmonic oscillations of ethylene molecule 3. Harmonic oscillator quantum mechanical general treatment 4. Angular momentum,
I(n) = ( ) f g(n) = d n
 9 Arithmetic functions Definition 91 A function f : N C is called an arithmetic function Some examles of arithmetic functions include: 1 the identity function In { 1 if n 1, 0 if n > 1; 2 the constant
9 Arithmetic functions Definition 91 A function f : N C is called an arithmetic function Some examles of arithmetic functions include: 1 the identity function In { 1 if n 1, 0 if n > 1; 2 the constant
Linear Algebra in Hilbert Space
 Physics 342 Lecture 16 Linear Algebra in Hilbert Space Lecture 16 Physics 342 Quantum Mechanics I Monday, March 1st, 2010 We have seen the importance of the plane wave solutions to the potentialfree Schrödinger
Physics 342 Lecture 16 Linear Algebra in Hilbert Space Lecture 16 Physics 342 Quantum Mechanics I Monday, March 1st, 2010 We have seen the importance of the plane wave solutions to the potentialfree Schrödinger
Math 121A: Homework 6 solutions
 Math A: Homework 6 solutions. (a) The coefficients of the Fourier sine series are given by b n = π f (x) sin nx dx = x(π x) sin nx dx π = (π x) cos nx dx nπ nπ [x(π x) cos nx]π = n ( )(sin nx) dx + π n
Math A: Homework 6 solutions. (a) The coefficients of the Fourier sine series are given by b n = π f (x) sin nx dx = x(π x) sin nx dx π = (π x) cos nx dx nπ nπ [x(π x) cos nx]π = n ( )(sin nx) dx + π n
Syllabus Fourier analysis
 Syllabus Fourier analysis by T. H. Koornwinder, 1996 University of Amsterdam, Faculty of Science, Korteweg-de Vries Institute Last modified: 7 December 2005 Note This syllabus is based on parts of the
Syllabus Fourier analysis by T. H. Koornwinder, 1996 University of Amsterdam, Faculty of Science, Korteweg-de Vries Institute Last modified: 7 December 2005 Note This syllabus is based on parts of the
FOURIER TRANSFORMS. 1. Fourier series 1.1. The trigonometric system. The sequence of functions
 FOURIER TRANSFORMS. Fourier series.. The trigonometric system. The sequence of functions, cos x, sin x,..., cos nx, sin nx,... is called the trigonometric system. These functions have period π. The trigonometric
FOURIER TRANSFORMS. Fourier series.. The trigonometric system. The sequence of functions, cos x, sin x,..., cos nx, sin nx,... is called the trigonometric system. These functions have period π. The trigonometric
MPRI Cours I. Motivations. Lecture VI: continued fractions and applications. II. Continued fractions
 F Morain École olytechnique MPRI cours 222 200-20 3/25 F Morain École olytechnique MPRI cours 222 200-20 4/25 MPRI Cours 222 I Motivations F Morain Aroximate π by rationals Solve 009 = u 2 + v 2 Lecture
F Morain École olytechnique MPRI cours 222 200-20 3/25 F Morain École olytechnique MPRI cours 222 200-20 4/25 MPRI Cours 222 I Motivations F Morain Aroximate π by rationals Solve 009 = u 2 + v 2 Lecture
Chapter III. Quantum Computation. Mathematical preliminaries. A.1 Complex numbers. A.2 Linear algebra review
 Chapter III Quantum Computation These lecture notes are exclusively for the use of students in Prof. MacLennan s Unconventional Computation course. c 2017, B. J. MacLennan, EECS, University of Tennessee,
Chapter III Quantum Computation These lecture notes are exclusively for the use of students in Prof. MacLennan s Unconventional Computation course. c 2017, B. J. MacLennan, EECS, University of Tennessee,
be the set of complex valued 2π-periodic functions f on R such that
 . Fourier series. Definition.. Given a real number P, we say a complex valued function f on R is P -periodic if f(x + P ) f(x) for all x R. We let be the set of complex valued -periodic functions f on
. Fourier series. Definition.. Given a real number P, we say a complex valued function f on R is P -periodic if f(x + P ) f(x) for all x R. We let be the set of complex valued -periodic functions f on
Introduction to Banach Spaces
 CHAPTER 8 Introduction to Banach Saces 1. Uniform and Absolute Convergence As a rearation we begin by reviewing some familiar roerties of Cauchy sequences and uniform limits in the setting of metric saces.
CHAPTER 8 Introduction to Banach Saces 1. Uniform and Absolute Convergence As a rearation we begin by reviewing some familiar roerties of Cauchy sequences and uniform limits in the setting of metric saces.
Lecture 1. 1, 0 x < 1 2 1, 2. x < 1, 0, elsewhere. 1
 0 - - -3 Lecture Introductory mathematical ideas The term wavelet, meaning literally little wave, originated in the early 980s in its French version ondelette in the work of Morlet and some French seismologists.
0 - - -3 Lecture Introductory mathematical ideas The term wavelet, meaning literally little wave, originated in the early 980s in its French version ondelette in the work of Morlet and some French seismologists.
Final Exam May 4, 2016
 1 Math 425 / AMCS 525 Dr. DeTurck Final Exam May 4, 2016 You may use your book and notes on this exam. Show your work in the exam book. Work only the problems that correspond to the section that you prepared.
1 Math 425 / AMCS 525 Dr. DeTurck Final Exam May 4, 2016 You may use your book and notes on this exam. Show your work in the exam book. Work only the problems that correspond to the section that you prepared.
SEISMIC WAVE PROPAGATION. Lecture 2: Fourier Analysis
 SEISMIC WAVE PROPAGATION Lecture 2: Fourier Analysis Fourier Series & Fourier Transforms Fourier Series Review of trigonometric identities Analysing the square wave Fourier Transform Transforms of some
SEISMIC WAVE PROPAGATION Lecture 2: Fourier Analysis Fourier Series & Fourier Transforms Fourier Series Review of trigonometric identities Analysing the square wave Fourier Transform Transforms of some
2 Quantization of the Electromagnetic Field
 2 Quantization of the Electromagnetic Field 2.1 Basics Starting point of the quantization of the electromagnetic field are Maxwell s equations in the vacuum (source free): where B = µ 0 H, D = ε 0 E, µ
2 Quantization of the Electromagnetic Field 2.1 Basics Starting point of the quantization of the electromagnetic field are Maxwell s equations in the vacuum (source free): where B = µ 0 H, D = ε 0 E, µ
Solutions to Problems in Goldstein, Classical Mechanics, Second Edition. Chapter 9
 Solutions to Problems in Goldstein, Classical Mechanics, Second Edition Homer Reid October 29, 2002 Chater 9 Problem 9. One of the attemts at combining the two sets of Hamilton s equations into one tries
Solutions to Problems in Goldstein, Classical Mechanics, Second Edition Homer Reid October 29, 2002 Chater 9 Problem 9. One of the attemts at combining the two sets of Hamilton s equations into one tries
Exercise 11. Isao Sasano
 Exercise Isao Sasano Exercise Calculate the value of the following series by using the Parseval s equality for the Fourier series of f(x) x on the range [, π] following the steps ()-(5). () Calculate the
Exercise Isao Sasano Exercise Calculate the value of the following series by using the Parseval s equality for the Fourier series of f(x) x on the range [, π] following the steps ()-(5). () Calculate the
1 Review of di erential calculus
 Review of di erential calculus This chapter presents the main elements of di erential calculus needed in probability theory. Often, students taking a course on probability theory have problems with concepts
Review of di erential calculus This chapter presents the main elements of di erential calculus needed in probability theory. Often, students taking a course on probability theory have problems with concepts
ME scope Application Note 16
 ME scoe Alication Note 16 Integration & Differentiation of FFs and Mode Shaes NOTE: The stes used in this Alication Note can be dulicated using any Package that includes the VES-36 Advanced Signal Processing
ME scoe Alication Note 16 Integration & Differentiation of FFs and Mode Shaes NOTE: The stes used in this Alication Note can be dulicated using any Package that includes the VES-36 Advanced Signal Processing
MA4001 Engineering Mathematics 1 Lecture 15 Mean Value Theorem Increasing and Decreasing Functions Higher Order Derivatives Implicit Differentiation
 MA4001 Engineering Mathematics 1 Lecture 15 Mean Value Theorem Increasing and Decreasing Functions Higher Order Derivatives Implicit Differentiation Dr. Sarah Mitchell Autumn 2014 Rolle s Theorem Theorem
MA4001 Engineering Mathematics 1 Lecture 15 Mean Value Theorem Increasing and Decreasing Functions Higher Order Derivatives Implicit Differentiation Dr. Sarah Mitchell Autumn 2014 Rolle s Theorem Theorem
Hilbert Space Problems
 Hilbert Space Problems Prescribed books for problems. ) Hilbert Spaces, Wavelets, Generalized Functions and Modern Quantum Mechanics by Willi-Hans Steeb Kluwer Academic Publishers, 998 ISBN -7923-523-9
Hilbert Space Problems Prescribed books for problems. ) Hilbert Spaces, Wavelets, Generalized Functions and Modern Quantum Mechanics by Willi-Hans Steeb Kluwer Academic Publishers, 998 ISBN -7923-523-9
Beam-Beam Stability in Electron-Positron Storage Rings
 Beam-Beam Stability in Electron-Positron Storage Rings Bjoern S. Schmekel, Joseh T. Rogers Cornell University, Deartment of Physics, Ithaca, New York 4853, USA Abstract At the interaction oint of a storage
Beam-Beam Stability in Electron-Positron Storage Rings Bjoern S. Schmekel, Joseh T. Rogers Cornell University, Deartment of Physics, Ithaca, New York 4853, USA Abstract At the interaction oint of a storage
Research Article A Note on the Modified q-bernoulli Numbers and Polynomials with Weight α
 Abstract and Alied Analysis Volume 20, Article ID 54534, 8 ages doi:0.55/20/54534 Research Article A Note on the Modified -Bernoulli Numbers and Polynomials with Weight α T. Kim, D. V. Dolgy, 2 S. H. Lee,
Abstract and Alied Analysis Volume 20, Article ID 54534, 8 ages doi:0.55/20/54534 Research Article A Note on the Modified -Bernoulli Numbers and Polynomials with Weight α T. Kim, D. V. Dolgy, 2 S. H. Lee,
Chapter 7: Special Distributions
 This chater first resents some imortant distributions, and then develos the largesamle distribution theory which is crucial in estimation and statistical inference Discrete distributions The Bernoulli
This chater first resents some imortant distributions, and then develos the largesamle distribution theory which is crucial in estimation and statistical inference Discrete distributions The Bernoulli
i (H) 1 on the diagonal and W acts as Sn t on by permuting a j.)
 1 Introduction Let G be a comact connected Lie Grou with Lie algebra g. T a maximal torus of G with Lie Algebra t. Let W = N G (T )/T be the Weyl grou of T in G. W acts on t through the Ad reresentations.
1 Introduction Let G be a comact connected Lie Grou with Lie algebra g. T a maximal torus of G with Lie Algebra t. Let W = N G (T )/T be the Weyl grou of T in G. W acts on t through the Ad reresentations.
A QUATERNIONIC APPROACH to GEOMETRY of CURVES on SPACES of CONSTANT CURVATURE
 INTERNATIONAL JOURNAL OF GEOMETRY Vol. 3 (2014), No. 1, 53-65 A QUATERNIONIC APPROACH to GEOMETRY of CURVES on SPACES of CONSTANT CURVATURE TUNA BAYRAKDAR and A. A. ERG IN Abstract. We construct the Frenet-Serret
INTERNATIONAL JOURNAL OF GEOMETRY Vol. 3 (2014), No. 1, 53-65 A QUATERNIONIC APPROACH to GEOMETRY of CURVES on SPACES of CONSTANT CURVATURE TUNA BAYRAKDAR and A. A. ERG IN Abstract. We construct the Frenet-Serret
