Polynomial and Rational Functions
|
|
|
- Coleen Baker
- 5 years ago
- Views:
Transcription
1 pr0-6-7.i-hr /6/06 : PM Page 6 CHAPTER Polnomial and Rational Functions T HERE IS A FUNCTION THAT models the age in human ears, H, of a dog that is ears old: H = The function contains variables to powers that are whole numbers and is an eample of a polnomial function. In this chapter, we stud polnomial functions and functions that consist of quotients of polnomials, called rational functions. ONE OF THE JOYS OF YOUR LIFE IS YOUR dog, our ver special budd. Latel, however, ou ve noticed that our companion is slowing down a bit. He s now 8 ears old and ou wonder how this translates into human ears. You remember something about ever ear of a dog s life being equal to seven ears for a human. Is there a more accurate description? This problem appears as Eercises 6 6 in Eercise Set.. 6
2 66 Chapter Polnomial and Rational Functions SECTION. Objectives ❶ Add and subtract comple numbers. ❷ Multipl comple numbers. ❸ Divide comple numbers. ❹ Perform operations with square roots of negative numbers. ❺ Solve quadratic equations with comple imaginar solutions. Comple Numbers 00 Roz Chast from Cartoonbank.com. All rights reserved. The Imaginar Unit i Who is this kid warning us about our eeballs turning black if we attempt to find the square root of -9? Don t believe what ou hear on the street. Although square roots of negative numbers are not real numbers, the do pla a significant role in algebra. In this section, we move beond the real numbers and discuss square roots with negative radicands. In the net section, we will stud equations whose solutions ma involve the square roots of negative numbers. Because the square of a real number is never negative, there is no real number such that = -. To provide a setting in which such equations have solutions, mathematicians invented an epanded sstem of numbers, the comple numbers. The imaginar number i, defined to be a solution of the equation = -, is the basis of this new set. The Imaginar Unit i The imaginar unit i is defined as i = -, where i = -. Using the imaginar unit i, we can epress the square root of an negative number as a real multiple of i. For eample, - = - = i = i. We can check this result b squaring i and obtaining -. i = i = - = - A new sstem of numbers, called comple numbers, is based on adding multiples of i, such as i, to the real numbers. Real numbers a + bi with b = 0 Comple numbers a + bi Imaginar numbers a + bi with b 0 Figure. The comple number sstem Comple Numbers and Imaginar Numbers The set of all numbers in the form a + bi with real numbers a and b, and i, the imaginar unit, is called the set of comple numbers. The real number a is called the real part and the real number b is called the imaginar part of the comple number a + bi. If b Z 0, then the comple number is called an imaginar number (Figure.). An imaginar number in the form bi is called a pure imaginar number.
3 Section. Comple Numbers 67 Here are some eamples of comple numbers. Each number can be written in the form a + bi. +6i i=0+i =+0i a, the real part, is. b, the imaginar part, is 6. a, the real part, is 0. b, the imaginar part, is. a, the real part, is. b, the imaginar part, is 0. Can ou see that b, the imaginar part, is not zero in the first two comple numbers? Because b Z 0, these comple numbers are imaginar numbers. Furthermore, the imaginar number i is a pure imaginar number. B contrast, the imaginar part of the comple number on the right is zero. This comple number is not an imaginar number. The number, or + 0i, is a real number. A comple number is said to be simplified if it is epressed in the standard form a + bi. If b is a radical, we usuall write i before b. For eample, we write 7 + i rather than 7 + i, which could easil be confused with 7 + i. Epressed in standard form, two comple numbers are equal if and onl if their real parts are equal and their imaginar parts are equal. ❶ Add and subtract comple numbers. Equalit of Comple Numbers a + bi = c + di if and onl if a = c and b = d. Operations with Comple Numbers The form of a comple number a + bi is like the binomial a + b. Consequentl, we can add, subtract, and multipl comple numbers using the same methods we used for binomials, remembering that i = -. Adding and Subtracting Comple Numbers. a + bi + c + di = a + c + b + di In words, this sas that ou add comple numbers b adding their real parts, adding their imaginar parts, and epressing the sum as a comple number.. a + bi - c + di = a - c + b - di In words, this sas that ou subtract comple numbers b subtracting their real parts, subtracting their imaginar parts, and epressing the difference as a comple number. Stud Tip The following eamples, using the same integers as in Eample, show how operations with comple numbers are just like operations with polnomials. a = - 7 b = = EXAMPLE Adding and Subtracting Comple Numbers Perform the indicated operations, writing the result in standard form: a. - i i b. - + i i. Solution a. - i i = - i i = i + i = i Remove the parentheses. Group real and imaginar terms. Add real parts and add imaginar parts. b. = - 7i - + i i = - + i + + 6i = i + 6i = i = 6 + 7i Simplif. Remove the parentheses. Change signs of real and imaginar parts in the comple number being subtracted. Group real and imaginar terms. Add real parts and add imaginar parts. Simplif.
4 68 Chapter Polnomial and Rational Functions Check Point Add or subtract as indicated: a. - i + + i b. + 6i - - i. ❷Multipl comple numbers. Multiplication of comple numbers is performed the same wa as multiplication of polnomials, using the distributive propert and the FOIL method.after completing the multiplication, we replace an occurrences of i with -. This idea is illustrated in the net eample. EXAMPLE b. Multipling Comple Numbers Find the products: a. i - i b. 7 - i- - i. Solution a. i - i = i # - i # i = i - 0i = i - 0- = 0 + i 7 - i- - i Distribute i throughout the parentheses. Multipl. Replace i with. Simplif to i 0 and write in standard form. F O I L = -i+6i+i = - - i + 6i + - = i + 6i = -9-9i Use the FOIL method. i Group real and imaginar terms. Combine real and imaginar terms. ❸Divide comple numbers. Check Point Find the products: a. 7i - 9i b. + i6-7i. Comple Conjugates and Division It is possible to multipl comple numbers and obtain a real number. This occurs when we multipl a + bi and a - bi. F O I L a + bia - bi=a -abi+abi-b i Use the FOIL method. = a - b - i = a + b Notice that this product eliminates i. For the comple number a + bi, we define its comple conjugate to be a - bi. The multiplication of comple conjugates results in a real number. Conjugate of a Comple Number The comple conjugate of the number a + bi is a - bi, and the comple conjugate of a - bi is a + bi. The multiplication of comple conjugates gives a real number. a + bia - bi = a + b a - bia + bi = a + b Comple conjugates are used to divide comple numbers. B multipling the numerator and the denominator of the division b the comple conjugate of the denominator, ou will obtain a real number in the denominator.
5 EXAMPLE Using Comple Conjugates to Divide Comple Numbers Divide and epress the result in standard form: Section. Comple Numbers 69 Solution The comple conjugate of the denominator, - i, is + i. Multiplication of both the numerator and the denominator b + i will eliminate i from the denominator. 7 + i - i 7 + i + i = # - i + i F O I L +i+8i+0i = + = = = - + i i i 7 + i - i. Multipl the numerator and the denominator b the comple conjugate of the denominator. Use the FOIL method in the numerator and a bia bi a b in the denominator. Combine imaginar terms and replace Combine real terms in the numerator: Epress the answer in standard form. with. Observe that the quotient is epressed in the standard form a + bi, with a = - and b = 9. i 6 9 Check Point Divide and epress the result in standard form: + i - i. ❹ Perform operations with square roots of negative numbers. Roots of Negative Numbers The square of i and the square of -i both result in -6: i = 6i = 6- = -6 -i = 6i = 6- = -6. Consequentl, in the comple number sstem -6 has two square roots, namel, i and -i. We call i the principal square root of -6. Principal Square Root of a Negative Number For an positive real number b, the principal square root of the negative number -b is defined b -b = ib. Consider the multiplication problem i # i = 0i = 0(-) = -0. This problem can also be given in terms of principal square roots of negative numbers: - # -. Because the product rule for radicals onl applies to real numbers, multipling radicands is incorrect. When performing operations with square roots of negative numbers, begin b epressing all square roots in terms of i. Then perform the indicated operation.
6 70 Chapter Polnomial and Rational Functions Correct: Incorrect: - # - = i # i - # - = -- = i # i = 00 = 0i = 0- = -0 = 0 Comple Numbers on a Postage Stamp This stamp honors the work done b the German mathematician Carl Friedrich Gauss (777 8) with comple numbers. Gauss represented comple numbers as points in the plane. ❺ Solve quadratic equations with comple imaginar solutions. EXAMPLE Operations Involving Square Roots of Negative Numbers Perform the indicated operations and write the result in standard form: a b. A - + -B c. Solution Begin b epressing all square roots of negative numbers in terms of i. a = i8 - i8 = i9 # - i # b. c. Check Point i0 = - + i = = - + i = - + i (A + B) = A + A B + B ( + B =( +i B =( ) +( )(i B+(i B b ib 0 # Write the comple number in standard form. Simplif. = i - i = i = - i + i = - i + - = - - i Perform the indicated operations and write the result in standard form: a b. A - + -B c. Quadratic Equations with Comple Imaginar Solutions We have seen that a quadratic equation can be epressed in the general form a + b + c = 0, a Z All quadratic equations can be solved b the quadratic formula: Stud Tip If ou need to review quadratic equations and how to solve them, read Section P. 7, beginning on page 8. = -b ; b - ac. a Recall that the quantit b - ac, which appears under the radical sign in the quadratic formula, is called the discriminant. If the discriminant is negative, a quadratic equation has no real solutions. However, quadratic equations with negative discriminants do have two solutions. These solutions are imaginar numbers that are comple conjugates.
7 Section. Comple Numbers 7 EXAMPLE A Quadratic Equation with Imaginar Solutions Solve using the quadratic formula: - + = 0. Solution The given equation is in general form. Begin b identifing the values for a, b, and c. -+=0 a = b = c = = -b ; b - ac a = -- ; - - = ; = ; - 6 Use the quadratic formula. Substitute the values for a, b, and c: a, b, and c, and. Subtract under the radical. Because the number under the radical sign is negative, the solutions will not be real numbers. = ; i 6 i = A ; ib 6 Factor from the numerator. = ; i = ; i Divide numerator and denominator b. Write the comple numbers in standard form. The solutions are comple conjugates, and the solution set is e + i, - i f or e ; i f. Check Point Solve using the quadratic formula: - + = 0. EXERCISE SET. Practice Eercises In Eercises 8, add or subtract as indicated and write the result in standard form i + - i i + - i. + i - - 7i i i i i i i 7. 8i - - 9i 8. i - - i In Eercises 9 0, find each product and write the result in standard form. 9. -i7i ii i + i i + i. 7 - i- - i. 8 - i- + 9i. + i - i i - 7i i- - i i-7 + i 9. + i 0. - i
8 7 Chapter Polnomial and Rational Functions In Eercises 8, divide and epress the result in standard form... - i + i. i i. + i - i. 8i -6i 6. - i + i 7. + i - i 8. + i + i In Eercises 9, perform the indicated operations and write the result in standard form A - + -B. A B. A B 6. A - + -B A - - B. - A - - B. A-BA--B. A-7BA-8B In Eercises 0, solve each quadratic equation using the quadratic formula. Epress solutions in standard form = = = = 0 9. = = - 6 Practice Plus In Eercises 6, perform the indicated operation(s) and write the result in standard form.. - i - i - - i + i i - i - - i + i. + i - - i. - i - + i Evaluate - + for = + i. 8. Evaluate - + for = - i Evaluate for = i Evaluate for = i. - Application Eercises Comple numbers are used in electronics to describe the current in an electric circuit. Ohm s law relates the current in a circuit, I, in amperes, the voltage of the circuit, E, in volts, and the resistance of the circuit, R, in ohms, b the formula E = IR. Use this formula to solve Eercises Find E, the voltage of a circuit, if I = - i amperes and R = + 7i ohms. 6. Find E, the voltage of a circuit, if I = - i amperes and R = + i ohms. 6. The mathematician Girolamo Cardano is credited with the first use (in ) of negative square roots in solving the now-famous problem, Find two numbers whose sum is 0 and whose product is 0. Show that the comple numbers + i and - i satisf the conditions of the problem. (Cardano did not use the smbolism i or even -. He wrote R.m for -, meaning radi minus. He regarded the numbers + R.m and - R.m as fictitious or ghost numbers, and considered the problem manifestl impossible. But in a mathematicall adventurous spirit, he eclaimed, Nevertheless, we will operate. ) Writing in Mathematics 6. What is i? 6. Eplain how to add comple numbers. Provide an eample with our eplanation. 66. Eplain how to multipl comple numbers and give an eample. 67. What is the comple conjugate of + i? What happens when ou multipl this comple number b its comple conjugate? 68. Eplain how to divide comple numbers. Provide an eample with our eplanation. 69. Eplain each of the three jokes in the cartoon on page A stand-up comedian uses algebra in some jokes, including one about a telephone recording that announces You have just reached an imaginar number. Please multipl b i and dial again. Eplain the joke. Eplain the error in Eercises = - = i = i 7. A -9B = -9 # -9 = 8 = 9 Critical Thinking Eercises 7. Which one of the following is true? a. Some irrational numbers are not comple numbers. b. + 7i - 7i is an imaginar number. 7 + i c. + i = 7 d. In the comple number sstem, + (the sum of two squares) can be factored as + i - i. In Eercises 7 76, perform the indicated operations and write the result in standard form ( + i)( - i) i + i + i + - i - i
9 pr0-6-7.i-hr /6/06 : PM Page 7 Section. Quadratic Functions 7 SECTION. Quadratic Functions Objectives ❶ ❷ ❸ ❹ Recognize characteristics of parabolas. Graph parabolas. Determine a quadratic function s minimum or maimum value. Solve problems involving a quadratic function s minimum or maimum value. The Food Stamp Program is the first line of defense against hunger for millions of American families. The program provides benefits for eligible participants to purchase approved food items at approved food stores. Over half of all participants are children; one out of si is a low-income older adult. The function f = models the number of households, f, in millions, participating in the program ears after 999. For eample, to find the number of households receiving food stamps in 00, substitute 6 for because 00 is 6 ears after 999: f6 = =.6. Thus, in 00,.6 million households received food stamps. The function f = is an eample of a quadratic function. We have seen that a quadratic function is an function of the form f = a + b + c, where a, b, and c are real numbers, with a Z 0. A quadratic function is a polnomial function whose greatest eponent is. In this section, we stud quadratic functions and their graphs. ❶ Recognize characteristics of parabolas. Graphs of Quadratic Functions The graph of an quadratic function is called a parabola. Parabolas are shaped like cups, as shown in Figure.. If the coefficient of (the value of a in a + b + c) is positive, the parabola opens upward. If the coefficient of is negative, the graph opens downward.the verte (or turning point) of the parabola is the lowest point on the graph when it opens upward and the highest point on the graph when it opens downward. Ais of smmetr Verte (maimum point) f() = a + b + c (a > 0) f() = a + b + c (a < 0) Verte (minimum point) Ais of smmetr a > 0: Parabola opens upward. a < 0: Parabola opens downward. Figure. Characteristics of graphs of quadratic functions
10 7 Chapter Polnomial and Rational Functions Look at the unusual image of the word mirror shown below.the artist, Scott Kim, has created the image so that the two halves of the whole are mirror images of each other. A parabola shares this kind of smmetr, in which a line through the verte divides the figure in half. Parabolas are smmetric with respect to this line, called the ais of smmetr. If a parabola is folded along its ais of smmetr, the two halves match eactl. ❷Graph parabolas. Graphing Quadratic Functions in Standard Form In our earlier work with transformations, we applied a series of transformations to the graph of f =. The graph of this function is a parabola. The verte for this parabola is 0, 0. In Figure.(a), the graph of f = a for a 7 0 is shown in black; it opens upward. In Figure.(b), the graph of f = a for a 6 0 is shown in black; it opens downward. Ais of smmetr: = h Ais of smmetr: = h g() = a( h) + k Verte: (0, 0) Verte: (h, k) g() = a( h) + k f() = a f() = a Verte: (0, 0) Verte: (h, k) Figure.(a) a 7 0: Parabola opens upward. Figure.(b) a 6 0: Parabola opens downward. Transformations of f = a Figure.(a) and.(b) also show the graph of g = a - h + k in blue. Compare these graphs to those of f = a. Observe that h determines the horizontal shift and k determines the vertical shift of the graph of f = a : g()=a(-h) +k. If h > 0, the graph of f() = a is shifted h units to the right. If k > 0, the graph of = a( h) is shifted k units up. Consequentl, the verte 0, 0 on the black graph of f = a moves to the point h, k on the blue graph of g = a - h + k. The ais of smmetr is the vertical line whose equation is = h. The form of the epression for g is convenient because it immediatel identifies the verte of the parabola as h, k. This is the standard form of a quadratic function.
11 Section. Quadratic Functions 7 The Standard Form of a Quadratic Function The quadratic function f = a - h + k, a Z 0 is in standard form. The graph of f is a parabola whose verte is the point h, k. The parabola is smmetric with respect to the line = h. If a 7 0, the parabola opens upward; if a 6 0, the parabola opens downward. The sign of a in f = a - h + k determines whether the parabola opens upward or downward. Furthermore, if ƒaƒ is small, the parabola opens more flatl than if ƒaƒ is large. Here is a general procedure for graphing parabolas whose equations are in standard form: Graphing Quadratic Functions with Equations in Standard Form To graph f = a - h + k,. Determine whether the parabola opens upward or downward. If a 7 0, it opens upward. If a 6 0, it opens downward.. Determine the verte of the parabola. The verte is h, k.. Find an -intercepts b solving f = 0. The function s real zeros are the -intercepts.. Find the -intercept b computing f0.. Plot the intercepts, the verte, and additional points as necessar. Connect these points with a smooth curve that is shaped like a cup. In the graphs that follow, we will show each ais of smmetr as a dashed vertical line. Because this vertical line passes through the verte, h, k, its equation is = h. The line is dashed because it is not part of the parabola. EXAMPLE Graphing a Quadratic Function in Standard Form Graph the quadratic function f = Solution We can graph this function b following the steps in the preceding bo. We begin b identifing values for a, h, and k. Standard form f()=a(-h) +k Given function a = h = k = 8 f()= (-) +8 Step Determine how the parabola opens. Note that a, the coefficient of, is -. Thus, a 6 0; this negative value tells us that the parabola opens downward. Step Find the verte. The verte of the parabola is at h, k. Because h = and k = 8, the parabola has its verte at, 8. Step Find the -intercepts b solving f 0. Replace f with 0 in f = = 8 - = 0 = = or - = - - = - = - = = Find -intercepts, setting f equal to 0. Solve for. Add to both sides of the equation. Divide both sides b. Appl the square root propert. Add to both sides in each equation. The -intercepts are and. The parabola passes through, 0. and, 0.
12 76 Chapter Polnomial and Rational Functions intercept: intercept: 0 Figure. The graph of f = Verte: (, 8) -intercept: Ais of smmetr: = Step Find the -intercept b computing f0. Replace with 0 in f = The -intercept is -0. The parabola passes through 0, -0. Step Graph the parabola. With a verte at, 8, -intercepts at and, and a -intercept at -0, the graph of f is shown in Figure..The ais of smmetr is the vertical line whose equation is =. Check Point EXAMPLE f0 = = = = -0 Graph the quadratic function f = Graphing a Quadratic Function in Standard Form Graph the quadratic function f = + +. Solution We begin b finding values for a, h, and k. f()=a(-h) +k f()=(+) + f()=(-( )) + Standard form of quadratic function Given function a = h = k = Step Determine how the parabola opens. Note that a, the coefficient of, is. Thus, a 7 0; this positive value tells us that the parabola opens upward. Step Find the verte. The verte of the parabola is at h, k. Because h = - and k =, the parabola has its verte at -,. Step Find the -intercepts b solving f 0. Replace f with 0 in f = + +. Because the verte is at -,, which lies above the -ais, and the parabola opens upward, it appears that this parabola has no -intercepts. We can verif this observation algebraicall. Ais of smmetr: = Verte: (, ) Figure. The graph of f = + + -intercept: 0 0 = + + Find possible -intercepts, setting f equal to 0. - = + Solve for. Subtract from both sides. + = - or + = -- Appl the square root propert. + = i + = -i = - + i = - - i i The solutions are _i. Because this equation has no real solutions, the parabola has no -intercepts. Step Find the -intercept b computing f0. Replace with 0 in f = + +. f0 = = + = 9 + = 0 The -intercept is 0. The parabola passes through 0, 0. Step Graph the parabola. With a verte at -,, no -intercepts, and a -intercept at 0, the graph of f is shown in Figure.. The ais of smmetr is the vertical line whose equation is = -. Check Point Graph the quadratic function f = - +.
13 Section. Quadratic Functions 77 Graphing Quadratic Functions in the Form f a b c Quadratic functions are frequentl epressed in the form f = a + b + c. How can we identif the verte of a parabola whose equation is in this form? Completing the square provides the answer to this question. f = a + b + c = aa + b a b + c Factor out a from a b. =aa b b b + + b+c-aa b a a a Complete the square b adding the square of half the coefficient of. B completing the square, we added b a. To avoid changing the a function s equation, we must subtract this term. = a + b a + c - b a Write the trinomial as the square of a binomial and simplif the constant term. Compare this form of the equation with a quadratic function s standard form. Standard form f()=a(-h) +k h = b a k = c b a Equation under discussion f()=aa- a bb +cb a b a The important part of this observation is that h, the -coordinate of the verte, is - b b The -coordinate can be found b evaluating the function at - a. a. The Verte of a Parabola Whose Equation Is f a b c Consider the parabola defined b the quadratic function f = a + b + c. b The parabola s verte is a - a, fa - b a bb. We can appl our five-step procedure and graph parabolas in the form f = a + b + c. The onl step that is different is how we determine the verte. EXAMPLE Graphing a Quadratic Function in the Form f a b c Graph the quadratic function f = Use the graph to identif the function s domain and its range. Solution Step Determine how the parabola opens. Note that a, the coefficient of, is -. Thus, a 6 0; this negative value tells us that the parabola opens downward. b Step Find the verte. We know that the -coordinate of the verte is = - We identif a, b, and c in f = a + b + c. a. f()= -+ a = b = c =
14 78 Chapter Polnomial and Rational Functions Substitute - for a and - for b into the equation for the -coordinate: b = - a = = -a - - b = -. The -coordinate of the verte is - and the verte is at -, f-. We substitute - for in the equation of the function, f = - - +, to find the -coordinate: f- = = =. The verte is at -,. Step Find the -intercepts b solving f 0. Replace f with 0 in f = We obtain 0 = This equation cannot be solved b factoring. We will use the quadratic formula to solve it. -+=0 a = b = c = To locate the -intercepts, we need decimal approimations. Thus, there is no need to simplif the radical form of the solutions. b_ b -ac = = a Verte: (, ) -intercept:. + 8 =. or -intercept: -intercept: 0. ( )_ ( ) -( )() _ -( ) = ( ) - 8 = 0. The -intercepts are approimatel -. and 0.. The parabola passes through -., 0 and 0., 0. Step Find the -intercept b computing f0. Replace with 0 in f = f0 = -0 - # 0 + = The -intercept is. The parabola passes through 0,. Step Graph the parabola. With a verte at -,, -intercepts at approimatel -. and 0., and a -intercept at, the graph of f is shown in Figure.6(a). The ais of smmetr is the vertical line whose equation is = -. Domain: Inputs on -ais include all real numbers. Range: Outputs on -ais fall at or below. Stud Tip The domain of an quadratic function includes all real numbers. If the verte is the graph s highest point, the range includes all real numbers at or below the -coordinate of the verte. If the verte is the graph s lowest point, the range includes all real numbers at or above the -coordinate of the verte. Ais of smmetr: = Figure.6(a) The graph of f = Figure.6(b) Determining the domain and range of f = Now we are read to determine the domain and range of f = We can use the parabola, shown again in Figure.6(b), to do so.to find the domain, look for all the inputs on the -ais that correspond to points on the graph. As the graph widens and continues to fall at both ends, can ou see that these inputs include all real numbers? Domain of f is ƒ is a real number6 or - q, q. To find the range, look for all the outputs on the -ais that correspond to points on the graph. Figure.6(b) shows that the parabola s verte, -,, is the highest
15 Section. Quadratic Functions 79 point on the graph. Because the -coordinate of the verte is, outputs on the -ais fall at or below. Range of f is ƒ 6 or - q,. ❸ Determine a quadratic function s minimum or maimum value. Check Point Graph the quadratic function f = Use the graph to identif the function s domain and its range. Minimum and Maimum Values of Quadratic Functions Consider the quadratic function f = a + b + c. If a 7 0, the parabola opens upward and the verte is its lowest point. If a 6 0, the parabola opens downward b and the verte is its highest point.the -coordinate of the verte is - Thus, we can a. find the minimum or maimum value of f b evaluating the quadratic function at b = - a. Minimum and Maimum: Quadratic Functions Consider the quadratic function f = a + b + c.. If a 7 0, then f b has a minimum that occurs at = - This minimum b a. value is fa - a b.. If a 6 0, then f b has a maimum that occurs at = - This maimum b a. value is fa - a b. In each case, the value of gives the location of the minimum or maimum b value. The value of, or fa - gives that minimum or maimum value. a b, EXAMPLE Obtaining Information about a Quadratic Function from Its Equation Consider the quadratic function f = a. Determine, without graphing, whether the function has a minimum value or a maimum value. b. Find the minimum or maimum value and determine where it occurs. c. Identif the function s domain and its range. Solution We begin b identifing a, b, and c in the function s equation: f()= +6-. a = b = 6 c = a. Because a 6 0, the function has a maimum value. b. The maimum value occurs at = - b a = = The maimum value occurs at f = is = We see that the maimum is -0 at =. = -- =. and the maimum value of f = - # + 6 # - = = -0.
16 80 Chapter Polnomial and Rational Functions c. Like all quadratic functions, the domain is - q, q. Because the function s maimum value is -0, the range includes all real numbers at or below -0. The range is - q, -0. We can use the graph of f = to visualize the results of Eample. Figure.7 shows the graph in a -6, 6, b -0, 0, 0 viewing rectangle. The maimum function feature verifies that the function s maimum is -0 at =. Notice that gives the location of the maimum and gives the maimum value. Notice, too, that the maimum value is -0 and not the ordered pair, -0. Range is (, 0]. [ 6, 6, ] b [ 0, 0, 0] Figure.7 ❹ Solve problems involving a quadratic function s minimum or maimum value. Check Point Repeat parts (a) through (c) of Eample using the quadratic function f = Applications of Quadratic Functions When did the minimum number of households participate in the food stamp program? What is the age of a driver having the least number of car accidents? If ou throw a baseball verticall upward, after how man seconds will it reach its maimum height and what is that height? The answers to these questions involve finding the maimum or minimum value of a quadratic function, as well as where this value occurs. EXAMPLE Figure.8 shows the number of U.S. households, in millions, participating in the Food Stamp Program from 999 through 00. The function f = models the number of households, f, in millions, participating in the program ears after 999. According to this function, in which ear was the number of participants at a minimum? How man households received food stamps for that ear? How well does this model the data shown in Figure.8? The Food Stamp Program Number Receiving Food Stamps (millions) Figure Source: Food Stamp Program U.S. Households on Food Stamps Year Solution We begin b identifing a, b, and c in the function s equation: f()= a = 0. b = 0.0 c = 7.68 Because a 7 0, the function has a minimum value. The minimum value occurs at = - b a = = L.
17 Technolog Section. Quadratic Functions 8 This means that the number of households receiving food stamps was at a minimum approimatel ear after 999, in 000. Using the model f = , the number of households, in millions, for that ear was f = = 7.. In 000, the number of households receiving food stamps was at a minimum of 7. million. Because this is precisel what is shown in Figure.8 on the previous page, the function models the data etremel well. Because of the decreasing-increasing cuplike shape of the data in Figure.8, a quadratic function is an appropriate model. We entered the data Data: using (0, 7.7), (,7.), (, 7.), (number of ears after 999, millions of participants). (, 8.), (, 9.), (, 0.6) Upon entering the QUADratic REGression program, we obtain the results shown in the screen on the right. Thus, the quadratic function of best fit is f = , where represents the number of ears after 999 and f represents the number of U.S. households, in millions, on food stamps. Check Point The function f = models the number of accidents, f, per 0 million miles driven, for drivers ears old, where 6 7. What is the age of a driver having the least number of car accidents? What is the minimum number of car accidents per 0 million miles driven? Quadratic functions can also be modeled from verbal conditions. Once we have obtained a quadratic function, we can then use the -coordinate of the verte to determine its maimum or minimum value. Here is a step-b-step strateg for solving these kinds of problems: Strateg for Solving Problems Involving Maimizing or Minimizing Quadratic Functions. Read the problem carefull and decide which quantit is to be maimized or minimized.. Use the conditions of the problem to epress the quantit as a function in one variable.. Rewrite the function in the form f = a + b + c.. Calculate - b b If has a minimum at = - This minimum a. a 7 0, f a. value is fa - b b If a 6 0, f has a maimum at = - This maimum a b. a. b value is fa - a b.. Answer the question posed in the problem. EXAMPLE 6 Minimizing a Product Among all pairs of numbers whose difference is 0, find a pair whose product is as small as possible. What is the minimum product?
18 8 Chapter Polnomial and Rational Functions Solution Step Decide what must be maimized or minimized. We must minimize the product of two numbers. Calling the numbers and, and calling the product P,we must minimize P =. Step Epress this quantit as a function in one variable. In the formula P =, P is epressed in terms of two variables, and. However, because the difference of the numbers is 0, we can write - = 0. We can solve this equation for in terms of (or vice versa), substitute the result into P =, and obtain P as a function of one variable. - = = - 0 Subtract from both sides of 0. Multipl both sides of the equation b and solve for. Now we substitute - 0 for in P =. P = = - 0. Because P is now a function of, we can write P = - 0. Step Write the function in the form f a b c. We appl the distributive propert to obtain P()=(-0)= -0. a = b = 0 Technolog TABLE The feature of a graphing utilit can be used to verif our work in Eample 6. Enter = 0, the function for the product, when one of the numbers is. The product is a minimum,, when one of the numbers is. b Step Calculate If a>0, the function has a minimum at this value. The a. voice balloons show that a = and b = -0. = - b a = - -0 = -- = This means that the product, P, of two numbers whose difference is 0 is a minimum when one of the numbers,, is. Step Answer the question posed b the problem. The problem asks for the two numbers and the minimum product. We found that one of the numbers,, is. Now we must find the second number,. = - 0 = - 0 = - The number pair whose difference is 0 and whose product is as small as possible is, -. The minimum product is -, or -. Check Point6 Among all pairs of numbers whose difference is 8, find a pair whose product is as small as possible. What is the minimum product?
19 Section. Quadratic Functions 8 0 Figure.9 What value of will maimize the rectangle s area? EXAMPLE 7 Maimizing Area You have 00 ards of fencing to enclose a rectangular region. Find the dimensions of the rectangle that maimize the enclosed area. What is the maimum area? Solution Step Decide what must be maimized or minimized. We must maimize area. What we do not know are the rectangle s dimensions, and. Step Epress this quantit as a function in one variable. Because we must maimize area, we have A =. We need to transform this into a function in which A is represented b one variable. Because ou have 00 ards of fencing, the perimeter of the rectangle is 00 ards. This means that + = 00. We can solve this equation for in terms of, substitute the result into A =, and obtain A as a function in one variable. We begin b solving for. = 00 - Subtract from both sides = Divide both sides b. = 0 - Divide each term in the numerator b. Now we substitute 0 - for in A =. A = = 0 - The rectangle and its dimensions are illustrated in Figure.9. Because A is now a function of, we can write A = 0 -. This function models the area, A(), of an rectangle whose perimeter is 00 ards in terms of one of its dimensions,. Step Write the function in the form f a b c. We appl the distributive propert to obtain A()=(0-)=0- = +0. a = b = 0 Technolog The graph of the area function A = 0 - was obtained with a graphing utilit using a 0, 0, b 0, 700, viewing rectangle. The maimum function feature verifies that a maimum area of 6 square ards occurs when one of the dimensions is ards. b Step Calculate If a<0, the function has a maimum at this value. The a. voice balloons show that a = - and b = 0. = - b a = = This means that the area, A, of a rectangle with perimeter 00 ards is a maimum when one of the rectangle s dimensions,, is ards. Step Answer the question posed b the problem. We found that =. Figure.9 shows that the rectangle s other dimension is 0 - = 0 - =. The dimensions of the rectangle that maimize the enclosed area are ards b ards.the rectangle that gives the maimum area is actuall a square with an area of ards # ards, or 6 square ards. Check Point7 You have 0 feet of fencing to enclose a rectangular region. Find the dimensions of the rectangle that maimize the enclosed area. What is the maimum area? The abilit to epress a quantit to be maimized or minimized as a function in one variable plas a critical role in solving ma-min problems. In calculus, ou will learn a technique for maimizing or minimizing all functions, not onl quadratic functions.
20 8 Chapter Polnomial and Rational Functions EXERCISE SET. Practice Eercises In Eercises, the graph of a quadratic function is given. Write the function s equation, selecting from the following options. f = + - h = In Eercises 8, the graph of a quadratic function is given. Write the function s equation, selecting from the following options. f = + + h = g = + + j = g = - + j = - - In Eercises 9 6, find the coordinates of the verte for the parabola defined b the given quadratic function. 9. f = f = f = f = f = f = - +. f = f = In Eercises 7 8, use the verte and intercepts to sketch the graph of each quadratic function. Give the equation of the parabola s ais of smmetr. Use the graph to determine the function s domain and range. 7. f = f = f = f = = -. - = -. f = + -. f = - A - B. f = f = f = f = f = f = f = - +. f = - -. f = f = + -. f = f = f = f = In Eercises 9, an equation of a quadratic function is given. a. Determine, without graphing, whether the function has a minimum value or a maimum value. b. Find the minimum or maimum value and determine where it occurs. c. Identif the function s domain and its range. 9. f = f = f = f = f = -. f = 6-6 Practice Plus In Eercises 8, give the domain and the range of each quadratic function whose graph is described.. The verte is -, - and the parabola opens up. 6. The verte is -, - and the parabola opens down. 7. Maimum = -6 at = 0 8. Minimum = 8 at = -6 In Eercises 9, write an equation in standard form of the parabola that has the same shape as the graph of f =, but with the given point as the verte. 9., 0. 7,. -0, -. -8, -6 In Eercises 6, write an equation in standard form of the parabola that has the same shape as the graph of f = or g = -, but with the given maimum or minimum.. Maimum = at = -. Maimum = -7 at =. Minimum = 0 at = 6. Minimum = 0 at = 9
21 Section. Quadratic Functions 8 Number of Gang-Related Murders Per Capita Wine Consumption (gallons per person) Wine Consumption per U.S. Adult Source: Adams Business Media Application Eercises 7. The graph shows per capita U.S. adult wine consumption (in gallons per person) for selected ears from 980 through 00. The function models U.S. wine consumption, f, in gallons per person, ears after 980. According to this function, in which ear was wine consumption at a minimum? Round to the nearest ear. What does the function give for per capita consumption, to the nearest tenth of a gallon, for that ear? How well does this model the data shown in the graph? f = Year Gang-Related Homicides in the U.S After declining in the late 990s, the number of gang-related murders across the United States has increased in recent ears. The graph shows the number of gang-related homicides in the United States. The function f = models the number of gang-related homicides across the nation, f, ears after 99. According to this function, in which ear was the number of homicides at a minimum? Round to the nearest ear. What does the function give for the number of gang-related murders for that ear? How well does this model the data shown in the graph? 0 9. A person standing close to the edge on the top of a 00-foot building throws a baseball verticall upward. The quadratic function st = -6t + 6t + 00 models the ball s height above the ground, st, in feet, t seconds after it was thrown. a. After how man seconds does the ball reach its maimum height? What is the maimum height? b. How man seconds does it take until the ball finall hits the ground? Round to the nearest tenth of a second. c. Find s0 and describe what this means. d. Use our results from parts (a) through (c) to graph the quadratic function. Begin the graph with t = 0 and end with the value of t for which the ball hits the ground. 60. A person standing close to the edge on the top of a 60-foot building throws a baseball verticall upward. The quadratic function st = -6t + 6t + 60 models the ball s height above the ground, st, in feet, t seconds after it was thrown. a. After how man seconds does the ball reach its maimum height? What is the maimum height? b. How man seconds does it take until the ball finall hits the ground? Round to the nearest tenth of a second. c. Find s0 and describe what this means. d. Use our results from parts (a) through (c) to graph the quadratic function. Begin the graph with t = 0 and end with the value of t for which the ball hits the ground. 6. Among all pairs of numbers whose sum is 6, find a pair whose product is as large as possible. What is the maimum product? 6. Among all pairs of numbers whose sum is 0, find a pair whose product is as large as possible. What is the maimum product? 6. Among all pairs of numbers whose difference is 6, find a pair whose product is as small as possible. What is the minimum product? 6. Among all pairs of numbers whose difference is, find a pair whose product is as small as possible. What is the minimum product? 6. You have 600 feet of fencing to enclose a rectangular plot that borders on a river. If ou do not fence the side along the river, find the length and width of the plot that will maimize the area. What is the largest area that can be enclosed? 600 River Year Source: Professor James Alan Fo, Northeastern Universit You have 00 feet of fencing to enclose a rectangular plot that borders on a river. If ou do not fence the side along the
22 86 Chapter Polnomial and Rational Functions river, find the length and width of the plot that will maimize the area. What is the largest area that can be enclosed? You have 0 ards of fencing to enclose a rectangular region. Find the dimensions of the rectangle that maimize the enclosed area. What is the maimum area? 68. You have 80 ards of fencing to enclose a rectangular region. Find the dimensions of the rectangle that maimize the enclosed area. What is the maimum area? 69. A rectangular plaground is to be fenced off and divided in two b another fence parallel to one side of the plaground. Si hundred feet of fencing is used. Find the dimensions of the plaground that maimize the total enclosed area. What is the maimum area? 70. A rectangular plaground is to be fenced off and divided in two b another fence parallel to one side of the plaground. Four hundred feet of fencing is used. Find the dimensions of the plaground that maimize the total enclosed area. What is the maimum area? 7. A rain gutter is made from sheets of aluminum that are 0 inches wide b turning up the edges to form right angles. Determine the depth of the gutter that will maimize its cross-sectional area and allow the greatest amount of water to flow. What is the maimum cross-sectional area? 7. A rain gutter is made from sheets of aluminum that are inches wide b turning up the edges to form right angles. Determine the depth of the gutter that will maimize its cross-sectional area and allow the greatest amount of water to flow. What is the maimum cross-sectional area? If ou have difficult obtaining the functions to be maimized in Eercises 7 76, read Eample in Section.0 on pages. 7. On a certain route, an airline carries 8000 passengers per month, each paing $0. A market surve indicates that for each $ increase in the ticket price, the airline will lose 00 passengers. Find the ticket price that will maimize the airline s monthl revenue for the route. What is the maimum monthl revenue? 7. A car rental agenc can rent ever one of its 00 cars at $0 per da. Far each $ increase in rate, five fewer cars are rented. Find the rental amount that will maimize the agenc s dail revenue. What is the maimum dail revenue? 7. The annual ield per walnut tree is fairl constant at 60 pounds per tree when the number of trees per acre is 0 or fewer. For each additional tree over 0, the annual ield per tree for all trees on the acre decreases b pounds due to overcrowding. How man walnut trees should be planed per acre to maimize the annual ield for the acre? What is the maimum number of pounds of walnuts per acre? 76. The annual ield per cherr tree is fairl constant at 0 pounds per tree when the number of trees per acre is 0 or fewer. For each additional tree aver 0, the annual ield per tree for all trees on the acre decreases b pound due to overcrowding. How man cherr trees should be planted per acre to maimize the annual ield for the acre? What is the maimum number of pounds of cherries per acre? Writing in Mathematics 77. What is a quadratic function? 78. What is a parabola? Describe its shape. 79. Eplain how to decide whether a parabola opens upward or downward. 80. Describe how to find a parabola s verte if its equation is epressed in standard form. Give an eample. 8. Describe how to find a parabola s verte if its equation is in the form f = a + b + c. Use f = as an eample. 8. A parabola that opens upward has its verte at (, ). Describe as much as ou can about the parabola based on this information. Include in our discussion the number of -intercepts (if an) for the parabola. Technolog Eercises 8. Use a graphing utilit to verif an five of our hand-drawn graphs in Eercises a. Use a graphing utilit to graph = in a standard viewing rectangle. What do ou observe? b. Find the coordinates of the verte for the given quadratic function. c. The answer to part (b) is 0., -0.. Because the leading coefficient,, of the given function is positive, the verte is a minimum point on the graph. Use this fact to help find a viewing rectangle that will give a relativel complete picture of the parabola. With an ais of smmetr at = 0., the setting for should etend past this, so tr Xmin = 0 and Xma = 0. The setting for should include (and probabl go below) the -coordinate of the graph s minimum -value, so tr Ymin = -0. Eperiment with Yma until our utilit shows the parabola s major features. d. In general, eplain how knowing the coordinates of a parabola s verte can help determine a reasonable viewing rectangle on a graphing utilit for obtaining a complete picture of the parabola. In Eercises 8 88, find the verte for each parabola. Then determine a reasonable viewing rectangle on our graphing utilit and use it to graph the quadratic function. 8. = = = = The following data show fuel efficienc, in miles per gallon, for all U.S. automobiles in the indicated ear. (Average Number of Miles per Gallon (Years after 90) for U.S. Automobiles) 90: : : : : : : 60.0 Source: U.S. Department of Transportation
23 pr0-6-7.i-hr /6/06 : PM Page 87 Section. Polnomial Functions and Their Graphs a. Use a graphing utilit to draw a scatter plot of the data. Eplain wh a quadratic function is appropriate for modeling these data. b. Use the quadratic regression feature to find the quadratic function that best fits the data. c. Use the model in part (b) to determine the worst ear for automobile fuel efficienc. What was the average number of miles per gallon for that ear? d. Use a graphing utilit to draw a scatter plot of the data and graph the quadratic function of best fit on the scatter plot A 00-room hotel can rent ever one of its rooms at $80 per room. For each $ increase in rent, three fewer roams are rented. Each rented room costs the hotel $0 to service per da. How much should the hotel charge for each room to maimize its dail profit? What is the maimum dail profit? 97. A track and field area is to be constructed in the shape of a rectangle with semicircles at each end. The inside perimeter of the track is to be 0 ards. Find the dimensions of the rectangle that maimize the area of the rectangular portion of the field. Critical Thinking Eercises 90. Which one of the following is true? a. No quadratic functions have a range of - q, q. b. The verte of the parabola described b f = - - is at,. c. The graph of f = has one -intercept and two -intercepts. d. The maimum value of for the quadratic function f = is. In Eercises 9 9, find the ais of smmetr for each parabola whose equation is given. Use the ais of smmetr to find a second point on the parabola whose -coordinate is the same as the given point. 9. f = + - ; -, - 9. f = - + ; 6, In Eercises 9 9, write the equation of each parabola in standard form. 9. Verte: -, -; The graph passes through the point,. 9. Verte: -, -; The graph passes through the point -, Find the point on the line whose equation is + - = 0 that is closest to the origin. Hint: Minimize the distance function b minimizing the epression under the square root. Group Eercise 98. Each group member should consult an almanac, newspaper, magazine, or the Internet to find data that initiall increase and then decrease, or vice versa, and therefore can be modeled b a quadratic function. Group members should select the two sets of data that are most interesting and relevant. For each data set selected, a. Use the quadratic regression feature of a graphing utilit to find the quadratic function that best fits the data. b. Use the equation of the quadratic function to make a prediction from the data. What circumstances might affect the accurac of our prediction? c. Use the equation of the quadratic function to write and solve a problem involving maimizing or minimizing the function. SECTION. Polnomial Functions and Their Graphs Objectives ❶ ❷ ❸ ❹ ❺ ❻ ❼ ❽ Identif polnomial functions. Recognize characteristics of graphs of polnomial functions. Determine end behavior. Use factoring to find zeros of polnomial functions. Identif zeros and their multiplicities. Use the Intermediate Value Theorem. Understand the relationship between degree and turning points. Graph polnomial functions. Magnified 6000 times, this color-scanned image shows a T-lmphocte blood cell (green) infected with the HIV virus (red). Depletion of the number of T-cells causes destruction of the immune sstem. In 980, U.S. doctors diagnosed cases of a rare form of cancer, Kaposi s sarcoma, that involved skin lesions, pneumonia, and severe immunological deficiencies. All cases involved ga men ranging in age from 6 to. B the end of 00, approimatel 890,000 Americans, straight and ga, male and female, old and oung, were infected with the HIV virus.
24 88 Chapter Polnomial and Rational Functions Modeling AIDS-related data and making predictions about the epidemic s havoc is serious business. Figure.0 shows the number of AIDS cases diagnosed in the United States from 98 through 00. AIDS Cases Diagnosed in the U.S., Number of Cases Diagnosed 80,000 70,000 60,000 0,000 0,000 0,000 0,000 0, ,67 79,879 7,086 69,98 60,7 6, 9,6 9,79,99,,,9,7,6 6,6 9,0 9,0,0 ❶ Identif polnomial functions Year Figure.0 Source: Department of Health and Human Services Changing circumstances and unforeseen events can result in models for AIDS-related data that are not particularl useful over long periods of time. For eample, the function f = Cases Diagnosed 60, f() = Years after 98 [0, 8, ] b [0, 60,000, 000] Figure. The graph of a function modeling the number of AIDS cases from 98 through 99 models the number of AIDS cases diagnosed in the United States ears after 98. The model was obtained using a portion of the data shown in Figure.0, namel cases diagnosed from 98 through 99, inclusive. Figure. shows the graph of f from 98 through 99. This function is an eample of a polnomial function of degree. Definition of a Polnomial Function Let n be a nonnegative integer and let a n, a n -, Á, a, a, a 0 be real numbers, with a n Z 0. The function defined b f = a n n + a n - n - + Á + a + a + a 0 is called a polnomial function of degree n. The number a n, the coefficient of the variable to the highest power, is called the leading coefficient. A constant function f = c, where c Z 0, is a polnomial function of degree 0. A linear function f = m + b, where m Z 0, is a polnomial function of degree. A quadratic function f = a + b + c, where a Z 0, is a polnomial function of degree. In this section, we focus on polnomial functions of degree or higher. ❷ Recognize characteristics of graphs of polnomial functions. Smooth, Continuous Graphs Polnomial functions of degree or higher have graphs that are smooth and continuous. B smooth, we mean that the graphs contain onl rounded curves with no sharp corners. B continuous, we mean that the graphs have no breaks and can be drawn without lifting our pencil from the rectangular coordinate sstem. These ideas are illustrated in Figure. on the net page.
25 Section. Polnomial Functions and Their Graphs 89 Graphs of Polnomial Functions Not Graphs of Polnomial Functions Smooth rounded corner Smooth rounded corner Sharp corner Smooth rounded corner Smooth rounded corners Discontinuous; a break in the graph Sharp corner Figure. Recognizing graphs of polnomial functions ❸Determine end behavior. End Behavior of Polnomial Functions Figure. shows the graph of the function f = , which models the number of U.S. AIDS cases from 98 through 99. Look what happens to the graph when we etend the ear up through 00. B ear (00), the values of are negative and the function no longer models AIDS cases. We ve added an arrow to the graph at the far right to emphasize that it continues to decrease without bound. It is this far-right end behavior of the graph that makes it inappropriate for modeling AIDS cases into the future. 8,000 Cases Diagnosed Years after 98 [0,, ] b [ 0,000, 8,000, 000] Graph falls to the right. Figure. B etending the viewing rectangle, we see that is eventuall negative and the function no longer models the number of AIDS cases. Model breakdown occurs b 00. The behavior of a graph of a function to the far left or the far right is called its end behavior. Although the graph of a polnomial function ma have intervals where it increases or decreases, the graph will eventuall rise or fall without bound as it moves far to the left or far to the right. How can ou determine whether the graph of a polnomial function goes up or down at each end? The end behavior of a polnomial function f = a n n + a n - n - + Á + a + a 0 depends upon the leading term a n n, because when ƒƒ is large, the other terms are relativel insignificant in size. In particular, the sign of the leading coefficient, a n, and the degree, n, of the polnomial function reveal its end behavior. In terms of end behavior, onl the term of highest degree counts, as summarized b the Leading Coefficient Test. Stud Tip Odd-degree polnomial functions have graphs with opposite behavior at each end. Evendegree polnomial functions have graphs with the same behavior at each end.
26 90 Chapter Polnomial and Rational Functions The Leading Coefficient Test As increases or decreases without bound, the graph of the polnomial function f = a n n + a n - n - + a n - n - + Á + a + a 0 a n Z 0 eventuall rises or falls. In particular,. For n odd:. For n even: If the leading coefficient is positive, the graph falls to the left and rises to the right. If the leading coefficient is negative, the graph rises to the left and falls to the right. If the leading coefficient is positive, the graph rises to the left and to the right. If the leading coefficient is negative, the graph falls to the left and to the right. a n > 0 a n < 0 a n > 0 a n < 0 Rises right Rises left Rises right Rises left Falls right Falls left Falls left Falls right Odd degree; positive leading coefficient Odd degree; negative leading coefficient Even degree; positive leading coefficient Even degree; negative leading coefficient Falls left Rises right Figure. The graph of f = EXAMPLE Using the Leading Coefficient Test Use the Leading Coefficient Test to determine the end behavior of the graph of Solution We begin b identifing the sign of the leading coefficient and the degree of the polnomial. The degree of the function f is, which is odd. Odd-degree polnomial functions have graphs with opposite behavior at each end. The leading coefficient,, is positive. Thus, the graph falls to the left and rises to the right. The graph of f is shown in Figure.. Check Point f = f()= + -- The leading coefficient,, is positive. The degree of the polnomial,, is odd. Use the Leading Coefficient Test to determine the end behavior of the graph of f = -. EXAMPLE Using the Leading Coefficient Test Use end behavior to eplain wh f = is onl an appropriate model for AIDS cases for a limited time period.
27 Section. Polnomial Functions and Their Graphs 9 Solution We begin b identifing the sign of the leading coefficient and the degree of the polnomial. f()= The leading coefficient, 9, is negative. The degree of the polnomial,, is odd. The degree of f is, which is odd. Odd-degree polnomial functions have graphs with opposite behavior at each end. The leading coefficient, -9, is negative. Thus, the graph rises to the left and falls to the right. The fact that the graph falls to the right indicates that at some point the number of AIDS cases will be negative, an impossibilit. If a function has a graph that decreases without bound over time, it will not be capable of modeling nonnegative phenomena over long time periods. Model breakdown will eventuall occur. Check Point The polnomial function models the ratio of students to computers in U.S. public schools ears after 980. Use end behavior to determine whether this function could be an appropriate model for computers in the classroom well into the twentfirst centur. Eplain our answer. If ou use a graphing utilit to graph a polnomial function, it is important to select a viewing rectangle that accuratel reveals the graph s end behavior. If the viewing rectangle, or window, is too small, it ma not accuratel show the end behavior. EXAMPLE f = Using the Leading Coefficient Test The graph of f = was obtained with a graphing utilit using a -8, 8, b -0, 0, viewing rectangle. The graph is shown in Figure.(a). Does the graph show the end behavior of the function? [ 8, 8, ] b [ 0, 0, ] [ 0, 0, ] b [ 000, 70, 0] Figure.(a) Figure.(b) Solution We begin b identifing the sign of the leading coefficient and the degree of the polnomial. f()= The leading coefficient,, is negative. The degree of the polnomial,, is even. The degree of f is, which is even. Even-degree polnomial functions have graphs with the same behavior at each end. The leading coefficient, -, is negative. Thus, the graph should fall to the left and fall to the right. The graph in Figure.(a) is falling to the left, but it is not falling to the right. Therefore, the graph is not complete enough to show end behavior.a more complete graph of the function is shown in a larger viewing rectangle in Figure.(b).
28 9 Chapter Polnomial and Rational Functions ❹ Use factoring to find zeros of polnomial functions. Check Point The graph of f = is shown in a standard viewing rectangle in Figure.6. Use the Leading Coefficient Test to determine whether the graph shows the end behavior of the function. Eplain our answer. Figure.6 Zeros of Polnomial Functions If f is a polnomial function, then the values of for which f is equal to 0 are called the zeros of f. These values of are the roots, or solutions, of the polnomial equation f = 0. Each real root of the polnomial equation appears as an -intercept of the graph of the polnomial function. -intercept: -intercept: -intercept: Figure.7 Technolog EXAMPLE Finding Zeros of a Polnomial Function Find all zeros of f = Solution B definition, the zeros are the values of for which f is equal to 0. Thus, we set f equal to 0: f = = 0. We solve the polnomial equation = 0 for as follows: = 0 This is the equation needed to find the function s zeros = 0 Factor from the first two terms and from the last two terms. + - = 0 A common factor of is factored from the epression. + = 0 or - = 0 Set each factor equal to 0. = - = Solve for. = ; Remember that if d, then d. The zeros of f are -, -, and. The graph of f in Figure.7 shows that each zero is an -intercept. The graph passes through the points -, 0, -, 0, and, 0. A graphing utilit can be used to verif that -, -, and are the three real zeros of f = Numeric Check Graphic Check Displa a table for the function. Displa a graph for the function. The -intercepts indicate that -, -, and are the real zeros. is equal to 0 when =, =, and =. Enter = +.,, and are the real zeros. -intercept: -intercept: -intercept: [ 6, 6, ] b [ 6, 6, ] ZERO The utilit s feature on the graph of f also verifies that -, -, and are the function s real zeros.
29 Section. Polnomial Functions and Their Graphs 9 Check Point Find all zeros of f = intercept: 0 -intercept: Figure.8 The zeros of f = - + -, namel 0 and, are the -intercepts for the graph of f. EXAMPLE Finding Zeros of a Polnomial Function Find all zeros of f = Solution We find the zeros of f b setting f equal to 0 and solving the resulting equation = = = 0 - = 0 = 0 or - = 0 = 0 = We now have a polnomial equation. Multipl both sides b. This step is optional. Factor out. Factor completel. Set each factor equal to 0. Solve for. The zeros of f = are 0 and. The graph of f, shown in Figure.8, has -intercepts at 0 and.the graph passes through the points 0, 0 and, 0. ❺ Identif zeros and their multiplicities. Check Point Find all zeros of f = -. Multiplicities of Zeros We can use the results of factoring to epress a polnomial as a product of factors. For instance, in Eample, we can use our factoring to epress the function s equation as follows: f()= + - = ( - + )= (-). The factor occurs twice: =. The factor ( ) occurs twice: ( ) = ( )( ). Notice that each factor occurs twice. In factoring the equation for the polnomial function f, if the same factor - r occurs k times, but not k + times, we call r a zero with multiplicit k. For the polnomial function f = - -, 0 and are both zeros with multiplicit. Multiplicit provides another connection between zeros and graphs. The multiplicit of a zero tells us whether the graph of a polnomial function touches the -ais at the zero and turns around, or if the graph crosses the -ais at the zero. For eample, look again at the graph of f = in Figure.8. Each zero, 0 and, is a zero with multiplicit. The graph of f touches, but does not cross, the -ais at each of these zeros of even multiplicit. B contrast, a graph crosses the -ais at zeros of odd multiplicit. Multiplicit and -Intercepts If r is a zero of even multiplicit, then the graph touches the -ais and turns around at r. If r is a zero of odd multiplicit, then the graph crosses the -ais at r. Regardless of whether the multiplicit of a zero is even or odd, graphs tend to flatten out at zeros with multiplicit greater than one. If a polnomial function s equation is epressed as a product of linear factors, we can quickl identif zeros and their multiplicities.
30 9 Chapter Polnomial and Rational Functions EXAMPLE 6 Finding Zeros and Their Multiplicities Find the zeros of f = + - and give the multiplicit of each zero. State whether the graph crosses the -ais or touches the -ais and turns around at each zero. Solution We find the zeros of f b setting f equal to 0: + - = 0. Set each factor equal to 0. is a zero of odd multiplicit. Graph crosses -ais. + = 0 = This eponent is. Thus, the multiplicit of is. = 0 = (+) (-) =0 This eponent is. Thus, the multiplicit of is. is a zero of even multiplicit. Graph touches -ais, flattens, and turns around. [,, ] b [ 0, 0, ] Figure.9 The graph of f = + - The zeros of f = + - are -, with multiplicit, and, with multiplicit. Because the multiplicit of - is odd, the graph crosses the -ais at this zero. Because the multiplicit of is even, the graph touches the -ais and turns around at this zero. These relationships are illustrated b the graph of f in Figure.9. Check Point6 Find the zeros of f = -A + B - and give the multiplicit of each zero. State whether the graph crosses the -ais or touches the -ais and turns around at each zero. ❻ Use the Intermediate Value Theorem. (b, f(b)) f(b) > 0 The Intermediate Value Theorem The Intermediate Value Theorem tells us of the eistence of real zeros. The idea behind the theorem is illustrated in Figure.0. The figure shows that if a, fa lies below the -ais and b, fb lies above the -ais, the smooth, continuous graph of a polnomial function f must cross the -ais at some value c between a and b. This value is a real zero for the function. These observations are summarized in the Intermediate Value Theorem. f(c) = 0 a c (a, f(a)) f(a) < 0 Figure.0 The graph must cross the -ais at some value between a and b. b The Intermediate Value Theorem for Polnomials Let f be a polnomial function with real coefficients. If fa and fb have opposite signs, then there is at least one value of c between a and b for which fc = 0. Equivalentl, the equation f = 0 has at least one real root between a and b. EXAMPLE 7 Using the Intermediate Value Theorem Show that the polnomial function f = - - has a real zero between and. Solution Let us evaluate f at and at. If f and f have opposite signs, then there is at least one real zero between and. Using f = - -, we obtain f()= - -=8--= f() is negative.
31 = and Section. Polnomial Functions and Their Graphs 9 f()= - -=7-6-=6. f() is positive. Figure. ❼ Understand [,, ] b [ 0, 0, ] the relationship between degree and turning points. ❽Graph polnomial functions. Stud Tip Remember that, without calculus, it is often impossible to give the eact location of turning points. However, ou can obtain additional points satisfing the function to estimate how high the graph rises or how low it falls. To obtain these points, use values of between (and to the left and right of) the -intercepts. Because f = - and f = 6, the sign change shows that the polnomial function has a real zero between and. This zero is actuall irrational and is approimated using a graphing utilit s feature as.09 in Figure.. Check Point7 Show that the polnomial function f = has a real zero between - and -. Turning Points of Polnomial Functions The graph of f = is shown in Figure.. The graph has four smooth turning points. At each turning point, the graph changes direction from increasing to decreasing or vice versa. The given equation has as its greatest eponent and is therefore a polnomial function of degree. Notice that the graph has four turning points. In general, if f is a polnomial function of degree n, then the graph of f has at most n turning points. Figure. illustrates that the -coordinate of each turning point is either a relative maimum or a relative minimum of f. Without the aid of a graphing utilit or a knowledge of calculus, it is difficult and often impossible to locate turning points of polnomial functions with degrees greater than. If necessar, test values can be taken between the -intercepts to get a general idea of how high the graph rises or how low the graph falls. For the purpose of graphing in this section, a general estimate is sometimes appropriate and necessar. A Strateg for Graphing Polnomial Functions Here s a general strateg for graphing a polnomial function. A graphing utilit is a valuable complement, but not a necessar component, to this strateg. If ou are using a graphing utilit, some of the steps listed in the following bo will help ou to select a viewing rectangle that shows the important parts of the graph. Graphing a Polnomial Function ZERO Turning points: from increasing to decreasing f() = f = a n n + a n - n - + a n - n - + Á + a + a 0, a n Z 0. Use the Leading Coefficient Test to determine the graph s end behavior.. Find -intercepts b setting f = 0 and solving the resulting polnomial equation. If there is an -intercept at r as a result of - r k in the complete factorization of f, then a. If k is even, the graph touches the -ais at r and turns around. b. If k is odd, the graph crosses the -ais at r. c. If k 7, the graph flattens out at r, 0.. Find the -intercept b computing f0.. Use smmetr, if applicable, to help draw the graph: a. -ais smmetr: f- = f b. Origin smmetr: f- = -f.. Use the fact that the maimum number of turning points of the graph is n - to check whether it is drawn correctl. Turning points: from decreasing to increasing Figure. Graph with four turning points
32 96 Chapter Polnomial and Rational Functions EXAMPLE 8 Graphing a Polnomial Function Graph: f = - +. Solution Step Determine end behavior. Identif the sign of a n, the leading coefficient, and the degree, n, of the polnomial function. f()= - + The leading coefficient,, is positive. The degree of the polnomial function,, is even. Because the degree,, is even, the graph has the same behavior at each end.the leading coefficient,, is positive. Thus, the graph rises to the left and rises to the right. Rises left Rises right Step Find -intercepts (zeros of the function) b setting f = = = = 0 + = 0 or - = 0 = - = Factor. Factor completel. Epress the factorization in a more compact form. Set each factorization equal to 0. Solve for. We see that - and are both repeated zeros with multiplicit. Because of the even multiplicit, the graph touches the -ais at - and and turns around. Furthermore, the graph tends to flatten out at these zeros with multiplicit greater than one. Rises left Rises right Step Find the -intercept b computing f0. We use f = - + and compute f0. f0 = 0 - # 0 + = There is a -intercept at, so the graph passes through 0,. It appears that is a relative maimum, but we need more information to be certain.
33 Section. Polnomial Functions and Their Graphs 97 Figure. The graph of f = - + Step Use possible smmetr to help draw the graph. Our partial graph suggests -ais smmetr. Let s verif this b finding f-. f() = - + Replace with. f( )=( ) -( ) += - + Because f- = f, the graph of f is smmetric with respect to the -ais. Figure. shows the graph of f = - +. Step Use the fact that the maimum number of turning points of the graph is n to check whether it is drawn correctl. Because n =, the maimum number of turning points is -, or. Because the graph in Figure. has three turning points, we have not violated the maimum number possible. Can ou see how this verifies that is indeed a relative maimum and 0, is a turning point? If the graph rose above on either side of = 0, it would have to rise above on the other side as well because of smmetr. This would require additional turning points to smoothl curve back to the -intercepts. The graph alread has three turning points, which is the maimum number for a fourth-degree polnomial function. Check Point8 Use the five-step strateg to graph f = -. EXERCISE SET. Practice Eercises In Eercises 0, determine which functions are polnomial functions. For those that are, identif the degree.. f = + 6. f = g =. g = p p +. h = f = f = h = f = f = + 7 In Eercises, identif which graphs are not those of polnomial functions... f = - + In Eercises 8, use the Leading Coefficient Test to determine the end behavior of the graph of the given polnomial function. Then use this end behavior to match the polnomial function with. 6. f = - its graph. [The graphs are labeled (a) through d. ] f = - f = (a) (b) (c) (d) In Eercises 9, use the Leading Coefficient Test to determine the end behavior of the graph of the polnomial function. 9. f = f = f =
34 98 Chapter Polnomial and Rational Functions. f = f = f = f = f = In Eercises, find the zeros for each polnomial function and Practice Plus give the multiplicit for each zero. State whether the graph crosses In Eercises 6 7, complete graphs of polnomial the -ais, or touches the -ais and turns around, at each zero. functions whose zeros are integers are shown.. 6. f = - + f = + + a. Find the zeros and state whether the multiplicit of each zero is even or odd. 7. f = b. Write an equation, epressed as the product of factors, of a 8. f = -A + B - polnomial function that might have each graph. Use a leading coefficient of or -, and make the degree of f as f = - + f = + + f = small as possible. c. Use both the equation in part (b) and the graph to find the -intercept.. f = In Eercises 0, use the Intermediate Value Theorem to show that each polnomial has a real zero between the given integers.. f = - - ; between and. f = - + ; between 0 and. f = - + ; between - and 0 6. f = ; between and [,, ] b [,, ] 7. f = ; between - and f = - - ; between and 9. f = ; between - and - 0. f = ; between and In Eercises 6, a. Use the Leading Coefficient Test to determine the graph s end behavior. [ 6, 6, ] b [ 0, 0, 0] b. Find the -intercepts. State whether the graph crosses the -ais, or touches the -ais and turns around, at each intercept. 67. c. Find the -intercept. d. Determine whether the graph has -ais smmetr, origin smmetr, or neither. e. If necessar, find a few additional points and graph the function. Use the maimum number of turning points to check whether it is drawn correctl. [, 6, ] b [ 0, 0, ]. f = f = f = - 9. f = f = f = f = f = f = f = - +. f = f = f = -.. f = f = - [,, ] b [ 0, 0, ] f = f = - + f = + + f = f = f = f = [,, ] b [ 0,, ]
35 Section. Polnomial Functions and Their Graphs [,, ] b [ 0,, ] [,, ] b [, 0, ] 7. Use both functions to find the cumulative number of AIDS deaths in 00. Which function provides a better description for the actual number shown in the bar graph? 7. Use the Leading Coefficient Test to determine the end behavior to the right for the graph of f. Will this function be useful in modeling the cumulative number of AIDS deaths over an etended period of time? Eplain our answer. 76. Use the Leading Coefficient Test to determine the end behavior to the right for the graph of g. Will this function be useful in modeling the cumulative number of AIDS deaths over an etended period of time? Eplain our answer. 77. Although it has been more than 0 ears since the Supreme Court ruled against school segregation, data from the Civil Rights Project at Harvard Universit indicate that integration and academic equalit remain elusive. The graph shows the percentage of the average African-American student s classmates who were white for the period from 970 through 00. Cumulative Number of Deaths Application Eercises The bar graph shows the cumulative number of deaths from AIDS in the United States from 990 through 00. Cumulative Number of Deaths from AIDS in the U.S. 8,90 00,000 8, 0,000 00,000 0,000 00,000 0,000 00,000 0,000 00,000 [,, ] b [, 0, ] 0, Source: Centers for Disease Control Year The data in the bar graph can be modeled b the following second- and third-degree polnomial functions: Cumulative number of AIDS deaths ears after f()= +7,7+07, g()= ,609+,. Use these functions to solve Eercises Use both functions to find the cumulative number of AIDS deaths in 000. Which function provides a better description for the actual number shown in the bar graph? Percentage of White Classmates Percentage of the Average African-American Student s Classmates Who Were White Year 00 Source: Civil Rights Project, Harvard Universit a. For which ears was the percentage of white classmates increasing? b. For which ears was the percentage of white classmates decreasing? c. How man turning points (from increasing to decreasing or from decreasing to increasing) does the graph have for the period shown? d. Suppose that a polnomial function is used to model the data shown in the graph using (number of ears after 970, percentage of the average African-American student s classmates who were white). Use the number of turning points to determine the degree of the polnomial function of best fit. e. For the model in part (d), should the leading coefficient of the polnomial function be positive or negative? Eplain our answer.
36 00 Chapter Polnomial and Rational Functions Percentage Indicating Marriage Goes Well All the Time Stage Stage Stage Stage 78. The graphs show the percentage of husbands and wives with one or more children who said their marriage was going well all the time at various stages in their relationships. I: II: III: IV: I Marital Satisfaction for Families with Children Husbands II Wives Beginning families Child-bearing families Families with preschool children Families with school-age children III IV V VI Stage of Relationship Stage Stage Stage Stage VII VIII V: Families with teenagers VI: Families with adult children leaving home VII: Families in the middle ears VIII: Aging families Source: Rollins, B., & Feldman, H. (970), Marital satisfaction over the famil life ccle. Journal of Marriage and the Famil,, 0 8. a. Between which stages was marital satisfaction for wives decreasing? b. Between which stages was marital satisfaction for wives increasing? c. How man turning points (from decreasing to increasing or from increasing to decreasing) are shown in the graph for wives? d. Suppose that a polnomial function is used to model the data shown in the graph for wives using (stage in the relationship, percentage indicating that the marriage was going well all the time). Use the number of turning points to determine the degree of the polnomial function of best fit. e. For the model in part (d), should the leading coefficient of the polnomial function be positive or negative? Eplain our answer. 87. Eplain the relationship between the degree of a polnomial function and the number of turning points on its graph. 88. Can the graph of a polnomial function have no -intercepts? Eplain. 89. Can the graph of a polnomial function have no -intercept? Eplain. 90. Describe a strateg for graphing a polnomial function. In our description, mention intercepts, the polnomial s degree, and turning points. 9. The graphs shown in Eercise 78 indicate that marital satisfaction tends to be greatest at the beginning and at the end of the stages in the relationship, with a decline occurring in the middle. What eplanations can ou offer for this trend? Technolog Eercises 9. Use a graphing utilit to verif an five of the graphs that ou drew b hand in Eercises 6. Write a polnomial function that imitates the end behavior of each graph in Eercises The dashed portions of the graphs indicate that ou should focus onl on imitating the left and right behavior of the graph and can be fleible about what occurs between the left and right ends. Then use our graphing utilit to graph the polnomial function and verif that ou imitated the end behavior shown in the given graph Writing in Mathematics 79. What is a polnomial function? 80. What do we mean when we describe the graph of a polnomial function as smooth and continuous? 8. What is meant b the end behavior of a polnomial function? 8. Eplain how to use the Leading Coefficient Test to determine the end behavior of a polnomial function. 8. Wh is a third-degree polnomial function with a negative leading coefficient not appropriate for modeling nonnegative real-world phenomena over a long period of time? 8. What are the zeros of a polnomial function and how are the found? 8. Eplain the relationship between the multiplicit of a zero and whether or not the graph crosses or touches the -ais at that zero. 86. If f is a polnomial function, and fa and fb have opposite signs, what must occur between a and b? If fa and fb have the same sign, does it necessaril mean that this will not occur? Eplain our answer. In Eercises 97 00, use a graphing utilit with a viewing rectangle large enough to show end behavior to graph each polnomial function. 97. f = f = f = f = In Eercises 0 0, use a graphing utilit to graph f and g in the same viewing rectangle. Then use the ZOOM OUT feature to show that f and g have identical end behavior. 0. f = - 6 +, g = 0. f = , g = -
37 pr0-6-7.i-hr /6/06 : PM Page 0 Section. Dividing Polnomials; Remainder and Factor Theorems 0 Critical Thinking Eercises 0. Which one of the following is true? a. If f = - +, then the graph of f falls to the left and falls to the right. b. A mathematical model that is a polnomial of degree n whose leading term is ann, n odd and an 6 0, is ideall suited to describe nonnegative phenomena over unlimited periods of time. c. There is more than one third-degree polnomial function with the same three -intercepts. Use the descriptions in Eercises 0 0 to write an equation of a polnomial function with the given characteristics. Use a graphing utilit to graph our function to see if ou are correct. If not, modif the function s equation and repeat this process. 0. Crosses the -ais at -, 0, and ; lies above the -ais between - and 0; lies below the -ais between 0 and 0. Touches the -ais at 0 and crosses the -ais at ; lies below the -ais between 0 and d. The graph of a function with origin smmetr can rise to the left and to the right. SECTION. Dividing Polnomials; Remainder and Factor Theorems Objectives ❶ Use long division to divide polnomials. ❷ Use snthetic division to divide polnomials. Evaluate a polnomial using the Remainder Theorem. Use the Factor Theorem to solve a polnomial equation. ❸ ❹ A moth has moved into our closet. She appeared in our bedroom at night, but somehow her relativel stout bod escaped our clutches. Within a few weeks, swarms of moths in our tattered wardrobe suggest that Mama Moth was in the famil wa.there must be at least 00 critters nesting in ever crevice of our clothing. Two hundred plus moth-tkes from one female moth is this possible? Indeed it is. The number of eggs, f, in a female moth is a function of her abdominal width,, in millimeters, modeled b f = ,... Because there are 00 moths feasting on our favorite sweaters, Mama s abdominal width can be estimated b finding the solutions of the polnomial equation = 00. How can we solve such an equation? You might begin b subtracting 00 from both sides to obtain zero on one side. But then what? The factoring that we used in the previous section will not work in this situation. In Section., we will present techniques for solving certain kinds of polnomial equations. These techniques will further enhance our abilit to manipulate algebraicall the polnomial functions that model our world. Because these techniques are based on understanding polnomial division, in this section we look at two methods for dividing polnomials. (We ll return to Mama Moth s abdominal width in the eercise set.)
38 0 Chapter Polnomial and Rational Functions ❶ Use long division to divide polnomials. Long Division of Polnomials and the Division Algorithm We begin b looking at division b a polnomial containing more than one term, such as Divisor has two terms and is a binomial. The polnomial dividend has three terms and is a trinomial. When a divisor has more than one term, the four steps used to divide whole numbers divide, multipl, subtract, bring down the net term form the repetitive procedure for polnomial long division. EXAMPLE Divide Long Division of Polnomials b +. Solution The following steps illustrate how polnomial division is ver similar to numerical division. ( + ) = Arrange the terms of the dividend 0 and the divisor in descending powers of. Divide (the first term in the dividend) b (the first term in the divisor):. Align like terms. Multipl each term in the divisor b, aligning terms of the product under like terms in the dividend Change signs of the polnomial being subtracted p Subtract from 0 b changing the sign of each term in the lower epression and adding. Bring down from the original dividend and add algebraicall to form a new dividend. Find the second term of the quotient. Divide the first term of 7 b, the first term of the divisor: ( + ) = Remainder Multipl the divisor b 7, aligning under like terms in the new dividend. Then subtract to obtain the remainder of 0.
39 Section. Dividing Polnomials; Remainder and Factor Theorems 0 The quotient is + 7. Because the remainder is 0, we can conclude that + is a factor of and = Check Point Divide + + b + 9. Before considering additional eamples, let s summarize the general procedure for dividing one polnomial b another. Long Division of Polnomials. Arrange the terms of both the dividend and the divisor in descending powers of the variable.. Divide the first term in the dividend b the first term in the divisor. The result is the first term of the quotient.. Multipl ever term in the divisor b the first term in the quotient. Write the resulting product beneath the dividend with like terms lined up.. Subtract the product from the dividend.. Bring down the net term in the original dividend and write it net to the remainder to form a new dividend. 6. Use this new epression as the dividend and repeat this process until the remainder can no longer be divided. This will occur when the degree of the remainder (the highest eponent on a variable in the remainder) is less than the degree of the divisor. In our net long division, we will obtain a nonzero remainder. EXAMPLE Divide Long Division of Polnomials b -. Solution We begin b writing the dividend in descending powers of = ( ) = Change signs of the polnomial - being subtracted. 6 Divide: =. Multipl: (-)=6 -. Subtract 6 - from 6 - and bring down. Now we divide b to obtain, multipl and the divisor, and subtract. ( ) = Change signs of the polnomial being subtracted Divide: =. Multipl: (-)= -. Subtract - from - and bring down. Now we divide - b to obtain -, multipl - and the divisor, and subtract.
40 0 Chapter Polnomial and Rational Functions ( ) = Change signs of the polnomial being subtracted Remainder Divide: =. Multipl: (-)= +. Subtract + from +, leaving a remainder of. The quotient is + - and the remainder is. When there is a nonzero remainder, as in this eample, list the quotient, plus the remainder above the divisor. Thus, = Quotient Remainder above divisor An important propert of division can be illustrated b clearing fractions in the equation that concluded Eample. Multipling both sides of this equation b - results in the following equation: =(-)( +-)+. Dividend Divisor Quotient Remainder Polnomial long division is checked b multipling the divisor with the quotient and then adding the remainder. This should give the dividend. The process illustrates the Division Algorithm. The Division Algorithm If f and d are polnomials, with d Z 0, and the degree of d is less than or equal to the degree of f, then there eist unique polnomials q and r such that f() = d() q() + r(). Dividend Divisor Quotient Remainder The remainder, r, equals 0 or it is of degree less than the degree of d. If r = 0, we sa that d divides evenl into f and that d and q are factors of f. Check Point Divide b -. Epress the result in the form quotient, plus remainder divided b divisor. If a power of is missing in either a dividend or a divisor, add that power of with a coefficient of 0 and then divide. In this wa, like terms will be aligned as ou carr out the long division.
41 Section. Dividing Polnomials; Remainder and Factor Theorems 0 EXAMPLE Divide Long Division of Polnomials b -. Solution We write the dividend, , as to keep all like terms aligned. The division process is finished because the degree of 7 -, which is, is less than the degree of the divisor -, which is. The answer is Multipl ( ) = ( ) = ( ) = Remainder = ❷ Use snthetic division to divide polnomials. Check Point Divide b -. Dividing Polnomials Using Snthetic Division We can use snthetic division to divide polnomials if the divisor is of the form - c. This method provides a quotient more quickl than long division. Let s compare the two methods showing divided b -. Long Division Snthetic Division Divisor c; 7-7 c = Quotient Dividend Remainder Notice the relationship between the polnomials in the long division process and the numbers that appear in snthetic division. These are the coefficients of the dividend + +. The divisor is. This is, or c, in c These are the coefficients of the quotient This is the remainder.
42 06 Chapter Polnomial and Rational Functions Now let s look at the steps involved in snthetic division. Snthetic Division To divide a polnomial b - c:. Arrange the polnomial in descending powers, with a 0 coefficient for an missing term.. Write c for the divisor, To the right, write the coefficients of the dividend.. Write the leading coefficient of the dividend on the bottom row.. Multipl c (in this case, ) times the value just written on the bottom row. Write the product in the net column in the second row.. Add the values in this new column, writing the sum in the bottom row. 6. Repeat this series of multiplications and additions until all columns are filled in. Eample c. - - p Bring down. 7 Add. Multipl b : =. 7 6 Add. Multipl b : 7 = Add. Multipl b : 6 = Use the numbers in the last row to write the quotient, plus the remainder above the divisor. The degree of the first term of the quotient is one less than the degree of the first term of the dividend. The final value in this row is the remainder. Written from 7 6 the last row of the snthetic division EXAMPLE Using Snthetic Division Use snthetic division to divide b +. Solution The divisor must be in the form - c. Thus, we write + as - -. This means that c = -. Writing a 0 coefficient for the missing -term in the dividend, we can epress the division as follows: Now we are read to set up the problem so that we can use snthetic division. Use the coefficients of the dividend in descending powers of. This is c in ( )
43 Section. Dividing Polnomials; Remainder and Factor Theorems 07 We begin the snthetic division process b bringing down. This is followed b a series of multiplications and additions.. Bring down.. Multipl: 0.. Add: s Add. -0 Multipl b.. Multipl: Add: Multipl b s Add Multipl: Add: Multipl b s Add The numbers in the last row represent the coefficients of the quotient and the remainder. The degree of the first term of the quotient is one less than that of the dividend. Because the degree of the dividend, , is, the degree of the quotient is. This means that the in the last row represents The quotient is The remainder is. Thus, ❸ Evaluate a polnomial using the Remainder Theorem. Check Point Use snthetic division to divide b +. The Remainder Theorem Let s consider the Division Algorithm when the dividend, f, is divided b - c. In this case, the remainder must be a constant because its degree is less than one, the degree of - c. f() = ( -c)q() + r Dividend Divisor Quotient The remainder, r, is a constant when dividing b c.
44 08 Chapter Polnomial and Rational Functions Now let s evaluate f at c. fc = c - cqc + r fc = 0 # qc + r fc = r Find fc b letting c in f cq r. This will give an epression for r. c - c O O# qc O and O r r. What does this last equation mean? If a polnomial is divided b - c, the remainder is the value of the polnomial at c.this result is called the Remainder Theorem. The Remainder Theorem If the polnomial f is divided b - c, then the remainder is fc. Eample shows how we can use the Remainder Theorem to evaluate a polnomial function at. Rather than substituting for, we divide the function b -. The remainder is f. EXAMPLE Using the Remainder Theorem to Evaluate a Polnomial Function Given f = - + +, use the Remainder Theorem to find f. Solution B the Remainder Theorem, if f is divided b -, then the remainder is f. We ll use snthetic division to divide. Remainder The remainder,, is the value of f. Thus, f =. We can verif that this is correct b evaluating f directl. Using f = - + +, we obtain f = - # + # + = =. ❹ Use the Factor Theorem to solve a polnomial equation. Check Point Given f = + - +, use the Remainder Theorem to find f-. The Factor Theorem Let s look again at the Division Algorithm when the divisor is of the form - c. f() = ( -c)q() + r Dividend Divisor Quotient Constant remainder B the Remainder Theorem, the remainder r is fc, so we can substitute fc for r: f = - cq + fc. Notice that if fc = 0, then f = - cq so that - c is a factor of f.this means that for the polnomial function f, if fc = 0, then - c is a factor of f. Let s reverse directions and see what happens if - c is a factor of f. This means that f = - cq.
45 Section. Dividing Polnomials; Remainder and Factor Theorems 09 If we replace in f = - cq with c, we obtain Thus, if - c is a factor of f, then fc = 0. We have proved a result known as the Factor Theorem. The Factor Theorem Let f be a polnomial. a. If fc = 0, then - c is a factor of f. b. If - c is a factor of f, then fc = 0. The eample that follows shows how the Factor Theorem can be used to solve a polnomial equation. EXAMPLE 6 fc = c - cqc = 0 # qc = 0. Using the Factor Theorem Solve the equation = 0 f = given that is a zero of Solution We are given that is a zero of f = This means that f = 0. Because f = 0, the Factor Theorem tells us that - is a factor of f. We ll use snthetic division to divide f b -. Technolog Because the solution set of = 0 is E -,, F, this implies that the polnomial function f = has -intercepts (or zeros) at -,, and. This is verified b the graph of f. -intercept: -intercept: -intercept: [ 0, 0, ] b [,, ] The remainder, 0, verifies that is a factor of + 6. Now we can solve the polnomial equation = = = 0 - = 0 or - = 0 or + = 0 = = = - The solution set is E -,, F Equivalentl, = This is the given equation. Factor using the result from the snthetic division. Factor the trinomial. Set each factor equal to 0. Solve for. Based on the Factor Theorem, the following statements are useful in solving polnomial equations:. If f is divided b - c and the remainder is zero, then c is a zero of f and c is a root of the polnomial equation f = 0.. If f is divided b - c and the remainder is zero, then - c is a factor of f. Check Point6 Solve the equation = 0 given that - is a zero of f =
46 0 Chapter Polnomial and Rational Functions EXERCISE SET. Practice Eercises In Eercises 6, divide using long division. State the quotient, q, and the remainder, r , , , , , , , , In Eercises 7, divide using snthetic division , , , , , , , , , , In Eercises 0, use snthetic division and the Remainder Theorem to find the indicated function value.. f = ; f. f = ; f. f = ; f- 6. f = ; f- 7. f = ; f 8. f = ; f 9. f = ; fa - b 0. f = ; fa - b. Use snthetic division to divide Use the result to find all zeros of. Use snthetic division to divide Use the result to find all zeros of f.. Solve the equation = 0 given that is a zero of f = Solve the equation = 0 given that - is a zero of f = Solve the equation = 0 given that - is a root. 6. Solve the equation = 0 given that - is a root. Practice Plus In Eercises 7 0, use the graph or the table to determine a solution of each equation. Use snthetic division to verif that this number is a solution of the equation. Then solve the polnomial equation = = 0 f = b +. f = b +. 0 = + 6 [0,, ] b [,, ] = [, 0, ] b [,, ] = 0 = f. 0
47 Section. Dividing Polnomials; Remainder and Factor Theorems 0. Application Eercises. a. Use snthetic division to show that is a solution of the polnomial equation b. Use the solution from part (a) to solve this problem. The number of eggs, f, in a female moth is a function of her abdominal width,, in millimeters, modeled b What is the abdominal width when there are eggs?. a. Use snthetic division to show that is a solution of the polnomial equation b. Use the solution from part (a) to solve this problem. The width of a rectangular bo is twice the height and the length is 7 inches more than the height. If the volume is 7 cubic inches, find the dimensions of the bo. In Eercises, write a polnomial that represents the length of each rectangle = 0 = The area is square units. The area is square units = 0. f = h h + h - 7 = 0. h The width is + 0. units. The width is + units. h + 7 During the 980s, the controversial economist Arthur Laffer promoted the idea that ta increases lead to a reduction in government revenue. Called suppl-side economics, the theor uses functions such as f =, This function models the government ta revenue, f, in tens of billions of dollars, in terms of the ta rate,.the graph of the function is shown. It illustrates ta revenue decreasing quite dramaticall as the ta rate increases.at a ta rate of (gasp) 00%, the government takes all our mone and no one has an incentive to work. With no income earned, zero dollars in ta revenue is generated. fgovernment Ta Revenue (tens of billions of dollars) f() = At a 00% ta rate, $0 in ta revenue is generated Ta Rate Use function and its graph to solve Eercises 6.. a. Find and interpret f(0). Identif the solution as a point on the graph of the function. b. Rewrite the function b using long division to perform , - 0. Then use this new form of the function to find f(0). Do ou obtain the same answer as ou did in part (a)? c. Is f a polnomial function? Eplain our answer. 6. a. Find and interpret f0. Identif the solution as a point on the graph of the function. b. Rewrite the function b using long division to perform , - 0. Then use this new form of the function to find f0. Do ou obtain the same answer as ou did in part (a)? c. Is f a polnomial function? Eplain our answer. Writing in Mathematics Eplain how to perform long division of polnomials. Use divided b - in our eplanation. 8. In our own words, state the Division Algorithm. 9. How can the Division Algorithm be used to check the quotient and remainder in a long division problem? 60. Eplain how to perform snthetic division. Use the division problem in Eercise 7 to support our eplanation. 6. State the Remainder Theorem. 6. Eplain how the Remainder Theorem can be used to find f-6 if f = What advantage is there to using the Remainder Theorem in this situation rather than evaluating f-6 directl? 6. How can the Factor Theorem be used to determine if - is a factor of - - +? 80 00
48 Chapter Polnomial and Rational Functions 6. If ou know that - is a zero of f = , b. Snthetic division could not be used to find the quotient of and -. eplain how to solve the equation c. An problem that can be done b snthetic division can also be done b the method for long division of polnomials = 0. d. If a polnomial long-division problem results in a remainder that is a whole number, then the divisor is a factor of Technolog Eercise the dividend. 67. Find k so that + is a factor of 6. For each equation that ou solved in Eercises 6, use a graphing utilit to graph the polnomial function defined b the left side of the equation. Use end behavior to obtain a complete graph. Then use the graph s -intercepts to verif our solutions. Critical Thinking Eercises 66. Which one of the following is true? a. If a trinomial in of degree 6 is divided b a trinomial in of degree, the degree of the quotient is k. 68. When is divided b a polnomial, the quotient is - and the remainder is. Find the polnomial. 69. Find the quotient of n + and n Snthetic division is a process for dividing a polnomial b - c. The coefficient of is. How might snthetic division be used if ou are dividing b -? 7. Use snthetic division to show that is a solution of = 0. Then solve the polnomial equation. SECTION. Objectives ❶ Use the Rational Zero Theorem to find possible rational zeros. ❷ Find zeros of a polnomial function. ❸ Solve polnomial equations. ❹ Use the Linear Factorization Theorem to find polnomials with given zeros. ❺ Use Descartes s Rule of Signs. Zeros of Polnomial Functions You stole m formula! Tartaglia s Secret Formula for One Solution of m n = C - C B a n b + a m b + n B a n b + a m b - n Popularizers of mathematics are sharing bizarre stories that are giving math a secure place in popular culture. One episode, able to compete with the wildest fare served up b television talk shows and the tabloids, involves three Italian mathematicians and, of all things, zeros of polnomial functions. Tartaglia (99 7), poor and starving, has found a formula that gives a root for a third-degree polnomial equation. Cardano (0 76) begs Tartaglia to reveal the secret formula, wheedling it from him with the promise he will find the impoverished Tartaglia a patron. Then Cardano publishes his famous work Ars Magna, in which he presents Tartaglia s formula as his own. Cardano uses his most talented student, Ferrari ( 6), who derived a formula for a root of a fourthdegree polnomial equation, to falsel accuse Tartaglia of plagiarism. The dispute becomes violent and Tartaglia is fortunate to escape alive. The noise from this You Stole M Formula episode is quieted b the work of French mathematician Evariste Galois (8 8). Galois proved that there is no general formula for finding roots of polnomial equations of degree or higher. There are, however, methods for finding roots. In this section, we stud methods for finding zeros of polnomial functions. We begin with a theorem that plas an important role in this process.
49 Stud Tip Section. Zeros of Polnomial Functions Be sure ou are familiar with the various kinds of zeros of polnomial functions. Here s a quick eample: f()=(+)(-)(+ )(- )(-+i)(--i). Zeros:,,,, -i, +i Rational zeros Irrational zeros Comple imaginar zeros Real zeros Nonreal zeros ❶ Use the Rational Zero Theorem to find possible rational zeros. The Rational Zero Theorem The Rational Zero Theorem provides us with a tool that we can use to make a list of all possible rational zeros of a polnomial function. Equivalentl, the theorem gives all possible rational roots of a polnomial equation. Not ever number in the list will be a zero of the function, but ever rational zero of the polnomial function will appear somewhere in the list. The Rational Zero Theorem p If f = a n n + a n - n - + Á + a + a 0 has integer coefficients and p q (where is reduced to lowest terms) is a rational zero of f, then p is a q factor of the constant term, a 0, and q is a factor of the leading coefficient, a n. You can eplore the wh behind the Rational Zero Theorem in Eercise 90 of Eercise Set.. For now, let s see if we can figure out what the theorem tells us about possible rational zeros. To use the theorem, list all the integers that are factors of the constant term, a 0. Then list all the integers that are factors of the leading coefficient, a n. Finall list all possible rational zeros: EXAMPLE Possible rational zeros = Using the Rational Zero Theorem List all possible rational zeros of f = Solution The constant term is. We list all of its factors: ;, ;, ;. The leading coefficient is -. Its factors are ;. Factors of the constant term, : Factors of the leading coefficient, -: Factors of the constant term Factors of the leading coefficient. Because Factors of the constant term Possible rational zeros = Factors of the leading coefficient, we must take each number in the first row, ;, ;, ;, and divide b each number in the second row, ;. Factors of,, Possible rational zeros= = =,, Factors of ;, ; ;, ; Divide ± b ±. Divide ± b ±. Divide ± b ±.
50 Chapter Polnomial and Rational Functions Stud Tip Alwas keep in mind the relationship among zeros, roots, and -intercepts. The zeros of a function f are the roots, or solutions, of the equation f = 0. Furthermore, the real zeros, or real roots, are the -intercepts of the graph of f. There are si possible rational zeros, ;, ;, and ;. The graph of f = is shown in Figure.. The -intercepts are - and. Thus, - and are the actual rational zeros. Check Point List all possible rational zeros of f = is a rational zero. is a rational zero. Figure. The graph of f = shows that - and are rational zeros. EXAMPLE Using the Rational Zero Theorem List all possible rational zeros of f = Solution The constant term is - and the leading coefficient is. Possible rational zeros = Factors of the constant term, - Factors of the leading coefficient, = ;, ; ;, ;, ;, ; =,,,,,,, Divide ± and ± b ±. Divide ± and ± b ±. Divide ± and ± b ±. Divide ± and ± b ±. There are 6 possible rational zeros. The actual solution set of = 0 is E -, -, F, which contains three of the 6 possible zeros. ❷ Find zeros of a polnomial function. Check Point List all possible rational zeros of f = How do we determine which (if an) of the possible rational zeros are rational zeros of the polnomial function? To find the first rational zero, we can use a trial-and-error process involving snthetic division: If f is divided b - c and the remainder is zero, then c is a zero of f. After we identif the first rational zero, we use the result of the snthetic division to factor the original polnomial. Then we set each factor equal to zero to identif an additional rational zeros. EXAMPLE Finding Zeros of a Polnomial Function Find all zeros of f = Solution Possible rational zeros We begin b listing all possible rational zeros. Factors of the constant term, 6,,, 6 = = =,,, 6 Factors of the leading coefficient, Divide the eight numbers in the numerator b ±. Now we will use snthetic division to see if we can find a rational zero among the possible rational zeros ;, ;, ;, ;6. Keep in mind that if f is divided b
51 Section. Zeros of Polnomial Functions - c and the remainder is zero, then c is a zero of f. Let s start b testing. If is not a rational zero, then we will test other possible rational zeros. Possible rational zero Test. Coefficients of f() = The nonzero remainder shows that is not a zero. Possible rational zero Test. Coefficients of f() = The zero remainder shows that is a zero. The zero remainder tells us that is a zero of the polnomial function f = Equivalentl, is a solution, or root, of the polnomial equation = 0. Thus, - is a factor of the polnomial. The first three numbers in the bottom row of the snthetic division on the right,,, and, give the coefficients of the other factor. This factor is = 0 Finding the zeros of f 6 is the same as finding the roots of this equation = = 0 Factor using the result from the snthetic division. Factor completel. - = 0 = or + = 0 = - or + = 0 = - Set each factor equal to zero. Solve for. The solution set is -, -, 6. The zeros of f are -, -, and. Check Point Find all zeros of f = Our work in Eample involved finding zeros of a third-degree polnomial function. The Rational Zero Theorem is a tool that allows us to rewrite such functions as products of two factors, one linear and one quadratic. Zeros of the quadratic factor are found b factoring, the quadratic formula, or the square root propert. EXAMPLE Finding Zeros of a Polnomial Function Find all zeros of f = Solution We begin b listing all possible rational zeros. Possible rational zeros = Factors of the constant term, - Factors of the leading coefficient, = ;, ; ; = ;, ; Now we will use snthetic division to see if we can find a rational zero among the four possible rational zeros. Test. Test. Test. Test
52 6 Chapter Polnomial and Rational Functions The zero remainder in the final snthetic division on the previous page tells us that - is a zero of the polnomial function f = To find all zeros of f, we proceed as follows: = 0 Finding the zeros of f is the same thing as finding the roots of f = 0 This result is from the last snthetic division on the previous page. The first three numbers in the bottom row,,, and, give the coefficients of the second factor. + = 0 = - or + - = 0 Set each factor equal to 0. Solve the linear equation. We can use the quadratic formula to solve + - = 0. = -b ; b - ac a = - ; - - = - ; 0 = - ; = - ; We use the quadratic formula because cannot be factored. Let a, b, and c. Multipl and subtract under the radical: # Divide the numerator and the denominator b. The solution set is E -, - -, - + F. The zeros of f are -, - -, and - +. Among these three real zeros, one zero is rational and two are irrational. Check Point Find all zeros of f = If the degree of a polnomial function or equation is or higher, it is often necessar to find more than one linear factor b snthetic division. One wa to speed up the process of finding the first zero is to graph the function. An -intercept is a zero. ❸Solve polnomial equations. -intercept: Figure. The graph of f = in a [-,, ] b [-, 0, ] viewing rectangle EXAMPLE Solve: Solving a Polnomial Equation = 0. Solution Recall that we refer to the zeros of a polnomial function and the roots of a polnomial equation. Because we are given an equation, we will use the word roots, rather than zeros, in the solution process. We begin b listing all possible rational roots. Possible rational roots = = Factors of the constant term, Factors of the leading coefficient, ;, ;, ;, ;, ;6, ;8, ;, ; ; = ;, ;, ;, ;, ;6, ;8, ;, ; The graph of f = is shown in Figure.. Because the -intercept is, we will test b snthetic division and show that it is a root of the given equation. Without the graph, the procedure would be to start the
53 Section. Zeros of Polnomial Functions 7 trial-and-error snthetic division with and proceed until a zero remainder is found, as we did in Eample Careful! = The zero remainder indicates that is a root of = 0. Now we can rewrite the given equation in factored form = = 0 - = 0 or = 0 This is the given equation. This is the result obtained from the snthetic division. The first four numbers in the bottom row,,,, and, give the coefficients of the second factor. Set each factor equal to 0. We can use the same approach to look for rational roots of the polnomial equation = 0, listing all possible rational roots. Without the graph in Figure., the procedure would be to start testing possible rational roots b trial-and-error snthetic division. However, take a second look at the graph in Figure.. Because the graph turns around at, this means that is a root of even multiplicit. Thus, must also be a root of = 0, confirmed b the following snthetic division These are the coefficients of + = 0. The zero remainder indicates that is a root of + = 0. Now we can solve the original equation as follows: = = 0 This is the given equation. This factorization was obtained from the first snthetic division = 0 This factorization was obtained from the second snthetic division. The first three numbers in the bottom row,,, and 6, give the coefficients of the third factor. - = 0 = or - = 0 = or = 0 Set each factor equal to 0. Solve the linear equations. We can use the quadratic formula to solve = 0. We use the quadratic formula because = -b ; b - ac a 6 cannot be factored. = - ; - 6 = = - ; -8 - ; i = - ; i Let a, b, and c 6. Multipl and subtract under the radical: i Simplif.
54 8 Chapter Polnomial and Rational Functions The solution set of the original equation, = 0, is, - - i, - + i6. The graph of f = in Figure. illustrates that a graphing utilit does not reveal the two imaginar roots. -intercept: Figure. (repeated) In Eample, is a repeated root of the equation with multiplicit. The eample illustrates two general properties: Properties of Polnomial Equations. If a polnomial equation is of degree n, then counting multiple roots separatel, the equation has n roots.. If a + bi is a root of a polnomial equation with real coefficients b Z 0, then the comple imaginar number a - bi is also a root. Comple imaginar roots, if the eist, occur in conjugate pairs. Check Point Solve: = 0. The Fundamental Theorem of Algebra The fact that a polnomial equation of degree n has n roots is a consequence of a theorem proved in 799 b a -ear-old student named Carl Friedrich Gauss in his doctoral dissertation. His result is called the Fundamental Theorem of Algebra. The Fundamental Theorem of Algebra If f is a polnomial of degree n, where n Ú, then the equation f = 0 has at least one comple root. Suppose, for eample, that f = 0 represents a polnomial equation of degree n. B the Fundamental Theorem of Algebra, we know that this equation has at least one comple root; we ll call it c. B the Factor Theorem, we know that - c is a factor of f. Therefore, we obtain - c q = 0 - c = 0 or q = 0. The degree of the polnomial q is n. Set each factor equal to 0. If the degree of q is at least, b the Fundamental Theorem of Algebra, the equation q = 0 has at least one comple root. We ll call it c. The Factor Theorem gives us q = 0 - c q = 0 - c = 0 or q = 0. The degree of q is n. The degree of q is n. Set each factor equal to 0. Let s see what we have up to this point and then continue the process. f = 0 This is the original polnomial equation of degree n. - c q = 0 This is the result from our first application of the Fundamental Theorem. - c - c q = 0 This is the result from our second application of the Fundamental Theorem. B continuing this process, we will obtain the product of n linear factors. Setting each of these linear factors equal to zero results in n comple roots.thus, if f is a polnomial of degree n, where n Ú, then f = 0 has eactl n roots, where roots are counted according to their multiplicit.
55 ❹ Use the Linear Factorization Theorem to find polnomials with given zeros. Section. Zeros of Polnomial Functions 9 The Linear Factorization Theorem In Eample, we found that = 0 has E, - ; if as a solution set, where is a repeated root with multiplicit. The polnomial can be factored over the comple nonreal numbers as follows: f()= These are the four zeros. =[-( +i )][-( -i )](-)(-). This fourth-degree polnomial has four linear factors. Just as an nth-degree polnomial equation has n roots, an nth-degree polnomial has n linear factors. This is formall stated as the Linear Factorization Theorem. The Linear Factorization Theorem These are the linear factors. If f = a n n + a n - n - + Á + a + a 0, where n Ú and a n Z 0, then f = a n - c - c Á - cn, where c, c, Á, c n are comple numbers (possibl real and not necessaril distinct). In words: An nth-degree polnomial can be epressed as the product of a nonzero constant and n linear factors. Man of our problems involving polnomial functions and polnomial equations dealt with the process of finding zeros and roots. The Linear Factorization Theorem enables us to reverse this process, finding a polnomial function when the zeros are given. Technolog The graph of f = , shown in a [-,, ] b [-00, 0, 0] viewing rectangle, verifies that - and are real zeros. B tracing along the curve, we can check that f = -0. is a zero. is a zero. EXAMPLE 6 Finding a Polnomial Function with Given Zeros Find a fourth-degree polnomial function f with real coefficients that has -,, and i as zeros and such that f = -0. Solution Because i is a zero and the polnomial has real coefficients, the conjugate, -i, must also be a zero.we can now use the Linear Factorization Theorem. f = a n - c - c - c - c f = a n - - f = a n - # - = -0 Substituting - for in the formula for f, we obtain Equivalentl, = a n i + i = a n - + a n = -0 a n 0a n = -0 a n = - f = f = This is the linear factorization for a fourth-degree polnomial. Use the given zeros: c, c, c i, and, from above, c i. Multipl: i i - i. Complete the multiplication. To find a n, use the fact that f 0. Solve for a n. Simplif: Divide both sides b 0.
56 0 Chapter Polnomial and Rational Functions ❺Use Descartes s Rule of Sign. Check Point6 Find a third-degree polnomial function f with real coefficients that has - and i as zeros and such that f = 8. Descartes s Rule of Signs Because an nth-degree polnomial equation might have roots that are imaginar numbers, we should note that such an equation can have at most n real roots. Descartes s Rule of Signs provides even more specific information about the number of real zeros that a polnomial can have. The rule is based on considering variations in sign between consecutive coefficients.for eample,the function f = has three sign changes: f()= sign change sign change sign change An equation can have as man true [positive] roots as it contains changes of sign, from plus to minus or from minus to plus. René Descartes (96 60) in La Géométrie (67) Descartes s Rule of Signs Let f = a n n + a n - n - + Á + a + a + a 0 be a polnomial with real coefficients.. The number of positive real zeros of f is either a. the same as the number of sign changes of f or b. less than the number of sign changes of f b a positive even integer. If f has onl one variation in sign, then f has eactl one positive real zero.. The number of negative real zeros of f is either a. the same as the number of sign changes of f- or b. less than the number of sign changes of f- b a positive even integer. If f- has onl one variation in sign, then f has eactl one negative real zero. Stud Tip The number of real zeros given b Descartes s Rule of Signs includes rational zeros from a list of possible rational zeros, as well as irrational zeros not on the list. It does not include an imaginar zeros. Table. illustrates what Descartes s Rule of Signs tells us about the positive real zeros of various polnomial functions. Table. Descartes s Rule of Signs and Positive Real Zeros Polnomial Function Sign Changes Conclusion f()= sign change sign change sign change f()= sign change sign change f()= There are positive real zeros. or There is - = positive real zero. There are positive real zeros. or There are - = 0 positive real zeros. There is positive real zero. sign change
57 EXAMPLE 7 Section. Zeros of Polnomial Functions Using Descartes s Rule of Signs Determine the possible numbers of positive and negative real zeros of f = Solution. To find possibilities for positive real zeros, count the number of sign changes in the equation for f. Because all the coefficients are positive, there are no variations in sign. Thus, there are no positive real zeros.. To find possibilities for negative real zeros, count the number of sign changes in the equation for f-. We obtain this equation b replacing with - in the given function. Now count the sign changes. f() = Replace with. f( )=( ) +( ) +( )+ = + -+ f()= + -+ sign change sign change sign change There are three variations in sign. The number of negative real zeros of f is either equal to the number of sign changes,, or is less than this number b an even integer. This means that either there are negative real zeros or there is - = negative real zero. What do the results of Eample 7 mean in terms of solving Without using Descartes s Rule of Signs, we list the possible rational roots as follows: Possible rational roots = = 0? Factors of the constant term, Factors of the leading coefficient, = ;, ;, ; ; = ;, ;, ; However, Descartes s Rule of Signs informed us that f = has no positive real zeros. Thus, the polnomial equation = 0 has no positive real roots. This means that we can eliminate the positive numbers from our list of possible rational roots. Possible rational roots include onl -, -, and -. We can use snthetic division and test two of the three possible rational roots of = 0 as follows: Test. 0 Test The zero remainder shows that is a root. The nonzero remainder shows that is not a root. B solving the equation = 0, ou will find that this equation of degree has three roots. One root is - and the other two roots are imaginar numbers in a conjugate pair. Verif this b completing the solution process. Check Point7 Determine the possible numbers of positive and negative real zeros of f =
58 Chapter Polnomial and Rational Functions EXERCISE SET. Practice Eercises In Eercises 8, use the Rational Zero Theorem to list all possible rational zeros for each given function In Eercises 9 6, a. List all possible rational zeros. b. Use snthetic division to test the possible rational zeros and find an actual zero. c. Use the quotient from part (b) to find the remaining zeros of the polnomial function In Eercises 7, a. List all possible rational roots. b. Use snthetic division to test the possible rational roots and find an actual root. c. Use the quotient from part (b) to find the remaining roots and solve the equation = = = = f = f = f = f = f = f = f = f = f = f = f = f = f = f = f = f = = = = = 0 In Eercises 8, use Descartes s Rule of Signs to determine the possible number of positive and negative real zeros for each given function In Eercises 9, find all zeros of the polnomial function or solve the given polnomial equation. Use the Rational Zero Theorem, Descartes s Rule of Signs, and possibl the graph of the polnomial function shown b a graphing utilit as an aid in obtaining the first zero or the first root f = f = f = f = f = f = f = f = = = 0 f = f = = = 0 f = f = = = = = 0 Practice Plus Eercises 60, show incomplete graphs of given polnomial functions. a. Find all the zeros of each function. b. Without using a graphing utilit, draw a complete graph of the function.. f = In Eercises, find an nth-degree polnomial function with real coefficients satisfing the given conditions. If ou are using a graphing utilit, use it to graph the function and verif the real zeros and the given function value.. n = ; and i are zeros; f- = n = ; and i are zeros; f- = n = ; - and + i are zeros; f = 9 8. n = ; 6 and - + i are zeros; f = n = ; i and i are zeros; f- = 0 0. n = ; -, -, and i are zeros; f = 8. n = ; -,, and + i are zeros; f = -96. n = ; -,, and + i are zeros; f = 00. [, 0, ] b [ 0,, ] f = [, 0, ] b [ 0, 0, ]
59 . f = Section. Zeros of Polnomial Functions Application Eercises The graphs are based on a stud of the percentage of professional works completed in each age decade of life b 78 people who lived to be at least 79. Use the graphs to solve Eercises 6 6. Age Trends in Professional Productivit 6. [, 0, ] b [ 0, 0, ] f = Percentage of Works Completed Arts Sciences 0s 0s 0s 0s Age Decade 60s 70s [0,, Z] b [,, ] f = [0,, ~] b [ 0, 0, ] f = [0,, ] b [ 0, 0, 0] f = [0,, ] b [ 0,, ] f = [0,, ] b [ 0, 0, ] Source : Dennis, W. (966), Creative productivit between the ages of 0 and 80 ears. Journal of Gerontolog,, Suppose that a polnomial function f is used to model the data shown in the graph for the arts using (age decade, percentage of works completed). a. Use the graph to solve the polnomial equation f = 7. Describe what this means in terms of an age decade and productivit. b. Describe the degree and the leading coefficient of a function f that can be used to model the data in the graph. 6. Suppose that a polnomial function g is used to model the data shown in the graph for the sciences using (age decade, percentage of works completed). a. Use the graph to solve the polnomial equation g = 0. Find onl the meaningful value of and then describe what this means in terms of an age decade and productivit. b. Describe the degree and the leading coefficient of a function g that can be used to model the data in the graph. The polnomial function H = models the age in human ears, H, of a dog that is ears old, where Ú. Although the coefficients make it difficult to solve equations algebraicall using this function, a graph of the function makes approimate solutions possible. Use the graph shown to solve Eercises 6 6. Round all answers to the nearest ear. Age in Human Years Dog s Age in Human Years H() Age of Dog (ears) Source : U.C. Davis
60 Chapter Polnomial and Rational Functions (Be sure to turn back a page and refer to the graph to solve Eercises 6 6.) 6. If ou are, what is the equivalent age for dogs? 6. If ou are 90, what is the equivalent age for dogs? 6. Set up an equation to answer the question in either Eercise 6 or 6. Bring all terms to one side and obtain zero on the other side. What are some of the difficulties involved in solving this equation? Eplain how the Intermediate Value Theorem can be used to verif the approimate solution that ou obtained from the graph. 66. The concentration of a drug, in parts per million, in a patient s blood hours after the drug is administered is given b the function f = How man hours after the drug is administered will it be eliminated from the bloodstream? 67. A bo with an open top is formed b cutting squares out of the corners of a rectangular piece of cardboard 0 inches b 8 inches and then folding up the sides. If represents the length of the side of the square cut from each corner of the rectangle, what size square must be cut if the volume of the bo is to be 8 cubic inches? 8 0 Writing in Mathematics 68. Describe how to find the possible rational zeros of a polnomial function. 69. How does the linear factorization of f, that is, f = a n - c - c Á - c n, show that a polnomial equation of degree n has n roots? 70. Describe how to use Descartes s Rule of Signs to determine the possible number of positive real zeros of a polnomial function. 7. Describe how to use Descartes s Rule of Signs to determine the possible number of negative roots of a polnomial equation. 7. Wh must ever polnomial equation of degree have at least one real root? 7. Eplain wh the equation = 0 has no rational roots. 7. Suppose is a root of a polnomial equation. What does this tell us about the leading coefficient and the constant term in the equation? 7. Use the graphs for Eercises 6 6 to describe one similarit and one difference between age trends in professional productivit in the arts and the sciences. Technolog Eercises The equations in Eercises have real roots that are rational. Use the Rational Zero Theorem to list all possible rational roots. Then graph the polnomial function in the given viewing rectangle to determine which possible rational roots are actual roots of the equation = 0; -, 6, b -0, 0, = 0; 0,, b -,, = 0; -,, b -,, = 0; -,, b -,, 80. Use Descartes s Rule of Signs to determine the possible number of positive and negative real zeros of f = + +. What does this mean in terms of the graph of f? Verif our result b using a graphing utilit to graph f. 8. Use Descartes s Rule of Signs to determine the possible number of positive and negative real zeros of f = Verif our result b using a graphing utilit to graph f. 8. Write equations for several polnomial functions of odd degree and graph each function. Is it possible for the graph to have no real zeros? Eplain. Tr doing the same thing for polnomial functions of even degree. Now is it possible to have no real zeros? Use a graphing utilit to obtain a complete graph for each polnomial function in Eercises Then determine the number of real zeros and the number of imaginar zeros for each function. 8. f = f = f = f = 6-6 Critical Thinking Eercises 87. Which one of the following is true? a. The equation = 0 has one positive real root. b. Descartes s Rule of Signs gives the eact number of positive and negative real roots for a polnomial equation. c. Ever polnomial equation of degree has at least one rational root. d. None of the above is true. 88. Give an eample of a polnomial equation that has no real roots. Describe how ou obtained the equation. 89. If the volume of the solid shown in the figure is 08 cubic inches, find the value of In this eercise, we lead ou through the steps involved in the proof of the Rational Zero Theorem. Consider the polnomial equation a n n + a n - n - + a n - n - + Á + a + a 0 = 0, p where is a rational root reduced to lowest terms. q p a. Substitute for in the equation and show that the q equation can be written as a + a n - p n - q + Á + a pq n - = -a 0 q n n p n + a n - p n - q. b. Wh is p a factor of the left side of the equation? c. Because p divides the left side, it must also divide the right p side. However, because is reduced to lowest terms, p q cannot divide q. Thus, p and q have no common factors other than - and. Because p does divide the right side and it is not a factor of q n, what can ou conclude?
61 Mid-Chapter Check Point d. Rewrite the equation from part (a) with all terms containing q on the left and the term that does not have a factor of q on the right. Use an argument that parallels parts (b) and (c) to conclude that q is a factor of a n. In Eercises 9 9, the graph of a polnomial function is given. What is the smallest degree that each polnomial could have? Eplain wh a polnomial function of degree 0 cannot cross the -ais eactl once. CHAPTER MID-CHAPTER CHECK POINT What You Know: We performed operations with comple numbers and used the imaginar unit i i = -, where i =- to represent solutions of quadratic equations with negative discriminants. Onl real solutions correspond to -intercepts. We graphed quadratic functions using vertices, intercepts, and additional points, as necessar. We learned that the verte of f = a - h + k is and the verte of is A - b a, fa h, k f = a + b + c - abb. b We used the verte to solve problems that involved minimizing or maimizing quadratic functions. We learned a number of techniques for finding the zeros of a polnomial function f of degree or higher or, equivalentl, finding the roots, or solutions, of the equation f = 0. For some functions, the zeros were found b factoring f. For other functions, we listed possible rational zeros and used snthetic division and the Factor Theorem to determine the zeros. We saw that graphs cross the -ais at zeros of odd multiplicit and touch the -ais and turn around at zeros of even multiplicit. We learned to graph polnomial functions using zeros, the Leading Coefficient Test, intercepts, and smmetr. We checked graphs using the fact that a polnomial function of degree n has a graph with at most n - turning points. After finding zeros of polnomial functions, we reversed directions b using the Linear Factorization Theorem to find functions with given zeros. In Eercises 6, perform the indicated operations and write the result in standard form i i. i + i. + i - i. + i - i A - -B 7. Solve and epress solutions in standard form: - =-. In Eercises 8, graph the given quadratic function. Give each function s domain and range. 8. f = f = f = f = In Eercises 0, find all zeros of each polnomial function. Then graph the function.. f = - +. f = f = f = f = f = f = - 9. f = f = In Eercises 6, solve each polnomial equation = = = = = = 0 7. A compan manufactures and sells bath cabinets. The function P = models the compan s dail profit, P, when cabinets are manufactured and sold per da. How man cabinets should be manufactured and sold per da to maimize the compan s profit? What is the maimum dail profit? 8. Among all pairs of numbers whose sum is -8, find a pair whose product is as large as possible. What is the maimum product? 9. The base of a triangle measures 0 inches minus twice the measure of its height. For what measure of the height does the triangle have a maimum area? What is the maimum area? In Eercises 0, divide, using snthetic division if possible , , - In Eercises, find an nth-degree polnomial function with real coefficients satisfing the given conditions.. n = ; and i are zeros; f- = 8. n = ; (with multiplicit ) and i are zeros; f0 = 6. Does f = - - have a real zero between and?
62 pr0-6-7.i-hr 6 /6/06 : PM Page 6 Chapter Polnomial and Rational Functions SECTION.6 Rational Functions and Their Graphs Objectives ❶ ❷ ❸ ❹ ❺ ❻ ❼ ❽ Find the domain of rational functions. Use arrow notation. Identif vertical asmptotes. Identif horizontal asmptotes. Use transformations to graph rational functions. Graph rational functions. Identif slant asmptotes. Solve applied problems involving rational functions. ❶ Find the domain of rational functions. Technolog is now promising to bring light, fast, and beautiful wheelchairs to millions of disabled people. The cost of manufacturing these radicall different wheelchairs can be modeled b rational functions. In this section, we will see how graphs of these functions illustrate that low prices are possible with high production levels, which are urgentl needed in this situation. There are more than half a billion people with disabilities in developing countries; an estimated 0 million need wheelchairs right now. Rational Functions Rational functions are quotients of polnomial functions. This means that rational functions can be epressed as f = p, q where p and q are polnomial functions and q Z 0. The domain of a rational function is the set of all real numbers ecept the -values that make the denominator zero. For eample, the domain of the rational function +7+9 f()= (-)(+) This is p(). This is q(). is the set of all real numbers ecept 0,, and -. EXAMPLE Finding the Domain of a Rational Function Find the domain of each rational function: a. f = b. g = - 9 c. h = Solution Rational functions contain division. Because division b 0 is undefined, we must eclude from the domain of each function values of that cause the polnomial function in the denominator to be is 0 if =. Thus, cannot equal. - The domain of f consists of all real numbers ecept. We can epress the domain in set-builder or interval notation: a. The denominator of f = Domain of f = ƒ Z 6 Domain of f = - q,, q.
63 Section.6 Rational Functions and Their Graphs 7 Stud Tip Because the domain of a rational function is the set of all real numbers ecept those for which the denominator is 0, ou can identif such numbers b setting the denominator equal to 0 and solving for. Eclude the resulting real values of from the domain. b. The denominator of g = is 0 if = - or =. Thus, the domain - 9 of g consists of all real numbers ecept - and.we can epress the domain in set-builder or interval notation: Domain of g = ƒ Z -, Z 6 Domain of g = - q, - -,, q. c. No real numbers cause the denominator of h = + to equal 0. The domain of h consists of all real numbers. + 9 Domain of h = - q, q ❷Use arrow notation. Check Point Find the domain of each rational function: a. b. g = f = - c. - - h = + +. The most basic rational function is the reciprocal function, defined b f = The denominator of the reciprocal function is zero when = 0, so the. domain of f is the set of all real numbers ecept 0. Let s look at the behavior of f near the ecluded value 0.We start b evaluating f to the left of 0. approaches 0 from the left f Mathematicall, we sa that approaches 0 from the left. From the table and the accompaning graph, it appears that as approaches 0 from the left, the function values, f, decrease without bound. We sa that f approaches negative infinit. We use a special arrow notation to describe this situation smbolicall: As S 0, f() S q. As approaches 0 from the left, f() approaches negative infinit (that is, the graph falls). Observe that the minus - superscript on the 0 : 0 - is read from the left. Net, we evaluate f to the right of 0. approaches 0 from the right f Mathematicall, we sa that approaches 0 from the right. From the table and the accompaning graph, it appears that as approaches 0 from the right, the function values, f, increase without bound. We sa that f approaches infinit. We again use a special arrow notation to describe this situation smbolicall:
64 8 Chapter Polnomial and Rational Functions As S 0 ±, f() S q. As approaches 0 from the right, f() approaches infinit (that is, the graph rises). Observe that the plus + superscript on the 0 : 0 + is read from the right. Now let s see what happens to the function values, f, as gets farther awa from the origin. The following tables suggest what happens to f as increases or decreases without bound. increases without bound: decreases without bound: f f Figure.6 f approaches 0 as increases or decreases without bound. It appears that as increases or decreases without bound, the function values, f, are getting progressivel closer to 0. Figure.6 illustrates the end behavior of f = as increases or decreases without bound. The graph shows that the function values, f, are approaching 0. This means that as increases or decreases without bound, the graph of f is approaching the horizontal line = 0 (that is, the -ais). We use arrow notation to describe this situation: As S q, f() S 0 and as S q, f() S 0. As approaches infinit (that is, increases without bound), f() approaches 0. As approaches negative infinit (that is, decreases without bound), f() approaches 0. Stud Tip If is far from 0, then is close to 0. B contrast, if is close to 0, then is far from 0. Thus, as approaches infinit : q or as approaches negative infinit : - q, the function values are approaching zero: f : 0. The graph of the reciprocal function f = is shown in Figure.7. Unlike the graph of a polnomial function, the graph of the reciprocal function has a break and is composed of two distinct branches. The arrow notation used throughout our discussion of the reciprocal function is summarized in the following bo: Figure.7 The graph of the reciprocal function f = Arrow Notation Smbol : a + : a - : q : - q Meaning approaches a from the right. approaches a from the left. approaches infinit; that is, increases without bound. approaches negative infinit; that is, decreases without bound. In calculus, ou will use limits to conve ideas involving a function s end behavior or its possible asmptotic behavior. For eample, eamine the graph of f = in Figure.7 and its end behavior to the right. As : q, the values of f approach 0: f : 0. In calculus, this is smbolized b lim f = 0. This is read the limit of f as : q approaches infinit equals zero.
65 Section.6 Rational Functions and Their Graphs 9 Another basic rational function is f = The graph of this even function,. with -ais smmetr and positive function values, is shown in Figure.8. Like the reciprocal function, the graph has a break and is composed of two distinct branches. As S 0, f() S q. Function values increase without bound. As S 0 +, f() S q. Function values increase without bound. Figure.8 The graph of f = As S q (decreases without bound), f() S 0. As S q (increases without bound), f() S 0. ❸Identif vertical asmptotes. Vertical Asmptotes of Rational Functions Look again at the graph of f = in Figure.8.The curve approaches, but does not touch,the -ais. The -ais, or = 0, is said to be a vertical asmptote of the graph. A rational function ma have no vertical asmptotes, one vertical asmptote, or several vertical asmptotes. The graph of a rational function never intersects a vertical asmptote. We will use dashed lines to show asmptotes. Definition of a Vertical Asmptote The line = a is a vertical asmptote of the graph of a function f if f increases or decreases without bound as approaches a. f = a = a a = a f a = a a f f a As a +, f() q. As a, f() q. As a +, f() q. As a, f() q. lim f()=q lim f()=q lim f()= q lim f()= q Sa ± Sa Sa ± Sa Thus, as approaches a from either the left or the right, f : q or f : - q. If the graph of a rational function has vertical asmptotes, the can be located using the following theorem: Locating Vertical Asmptotes If f = p is a rational function in which p and q have no common q factors and a is a zero of q, the denominator, then = a is a vertical asmptote of the graph of f.
66 0 Chapter Polnomial and Rational Functions EXAMPLE Finding the Vertical Asmptotes of a Rational Function Find the vertical asmptotes, if an, of the graph of each rational function: a. f = b. g = + c. h = Solution Factoring is usuall helpful in identifing zeros of denominators. a. f()= = -9 (+)(-) This factor is 0 if =. This factor is 0 if =. There are no common factors in the numerator and the denominator. The zeros of the denominator are - and. Thus, the lines = - and = are the vertical asmptotes for the graph of f. [See Figure.9(a).] b. We will use factoring to see if there are common factors. + (+) g()= = = -9 (+)(-) - There is a common factor, +, so simplif. This denominator is 0 if =. The onl zero of the denominator of g in simplified form is. Thus, the line = is the onl vertical asmptote of the graph of g. [See Figure.9(b).] c. We cannot factor the denominator of h over the real numbers. + h()= +9 No real numbers make this denominator 0. The denominator has no real zeros. Thus, the graph of h has no vertical asmptotes. [See Figure.9(c).] There is a hole in the graph corresponding to = Vertical asmptote: = Vertical asmptote: = Vertical asmptote: = Figure.9(a) The graph of f = has two - 9 vertical asmptotes. Figure.9(b) The graph of g = + has one - 9 vertical asmptote. Figure.9(c) The graph of h = + has no + 9 vertical asmptotes. Check Point Find the vertical asmptotes, if an, of the graph of each rational function: a. f = b. g = - c. h =
67 Technolog Section.6 Rational Functions and Their Graphs The graph of the rational function f = drawn b hand in Figure.9(a), is - 9, graphed below in a -,, b -,, viewing rectangle. The graph is shown in connected mode and in dot mode. In connected mode, the graphing utilit plots man points and connects the points with curves. In dot mode, the utilit plots the same points, but does not connect them. Connected Mode Dot Mode This might appear to be the vertical asmptote =, but it is neither vertical nor an asmptote. This might appear to be the vertical asmptote =, but it is neither vertical nor an asmptote. The steep lines in connected mode that are almost the vertical asmptotes = - and = are not part of the graph and do not represent the vertical asmptotes. The graphing utilit has incorrectl connected the last point to the left of = - with the first point to the right of = -. It has also incorrectl connected the last point to the left of = with the first point to the right of =. The effect is to create two near-vertical segments that look like asmptotes. This erroneous effect does not appear using dot mode. A value where the denominator of a rational function is zero does not necessaril result in a vertical asmptote. There is a hole corresponding to = a, and not a vertical asmptote, in the graph of a rational function under the following conditions: The value a causes the denominator to be zero, but there is a reduced form of the function s equation in which a does not cause the denominator to be zero. Consider, for eample, the function f = - -. Because the denominator is zero when =, the function s domain is all real numbers ecept. However, there is a reduced form of the equation in which does not cause the denominator to be zero: - (+)(-) f()= = =+,. - - Denominator is zero at =. In this reduced form, does not result in a zero denominator. Figure.0 shows that the graph has a hole corresponding to utilities do not show this feature of the graph. =. Graphing f() = Hole corresponding to = Figure.0 A graph with a hole corresponding to the denominator s zero
68 Chapter Polnomial and Rational Functions ❹ Identif horizontal asmptotes. Horizontal Asmptotes of Rational Functions Figure.7, repeated at the left, shows the graph of the reciprocal function f =. As : q and as : - q, the function values are approaching 0: f : 0. The line = 0 (that is, the -ais) is a horizontal asmptote of the graph. Man, but not all, rational functions have horizontal asmptotes. Definition of a Horizontal Asmptote The line = b is a horizontal asmptote of the graph of a function f if f approaches b as increases or decreases without bound. = b = b f f f = b Figure.7 The graph of f = (repeated) As q, f() b. As q, f() b. As q, f() b. lim f()=b lim f()=b lim f()=b Sq Sq Sq Recall that a rational function ma have several vertical asmptotes. B contrast, it can have at most one horizontal asmptote. Although a graph can never intersect a vertical asmptote, it ma cross its horizontal asmptote. If the graph of a rational function has a horizontal asmptote, it can be located using the following theorem: Locating Horizontal Asmptotes Let f be the rational function given b f = a n n + a n - n - + Á + a + a 0 b m m + b m - m - + Á + b + b 0, a n Z 0, b m Z 0. The degree of the numerator is n. The degree of the denominator is m.. If n 6 m, the -ais, or = 0, is the horizontal asmptote of the graph of f.. If the line = a n n = m, is the horizontal asmptote of the graph of f. b m. If n 7 m, the graph of f has no horizontal asmptote. = 0 f() = + Figure.(a) The horizontal asmptote of the graph is = 0. EXAMPLE Finding the Horizontal Asmptote of a Rational Function Find the horizontal asmptote, if an, of the graph of each rational function: a. b. g = f = c. h = Solution a. f = + The degree of the numerator,, is less than the degree of the denominator,. Thus, the graph of f has the -ais as a horizontal asmptote. [See Figure.(a).] The equation of the horizontal asmptote is = 0.
69 b. c. Section.6 Rational Functions and Their Graphs g = + The degree of the numerator,, is equal to the degree of the denominator,. The leading coefficients of the numerator and denominator, and, are used to obtain the equation of the horizontal asmptote. The equation of the horizontal asmptote is = or =. [See Figure.(b).] h = + The degree of the numerator,, is greater than the degree of the denominator,. Thus, the graph of h has no horizontal asmptote. [See Figure.(c).] = f() = + f() = + Figure.(b) The horizontal asmptote of the graph is =. Figure.(c) The graph has no horizontal asmptote. Check Point Find the horizontal asmptote, if an, of the graph of each rational function: 9 a. b. g = 9 f = c. h = ❺ Use transformations to graph rational functions. Using Transformations to Graph Rational Functions Table. shows the graphs of two rational functions, f = and f = The dashed green lines indicate the asmptotes.. Table. Graphs of Common Rational Functions = 0 = 0 f() = (, q) (, ) ( q, ) (q, ) (, ) (, q) = 0 = 0 Odd function: f( ) = f() Origin smmetr ( q, ) f() = = 0 (q, ) (, ) (, ) (, ~) (, ~) = 0 = 0 Even function: f( ) = f() -ais smmetr Some rational functions can be graphed using transformations (horizontal shifting, stretching or shrinking, reflecting, vertical shifting) of these two common graphs.
70 Chapter Polnomial and Rational Functions EXAMPLE Using Transformations to Graph a Rational Function Use the graph of f = to graph g = Solution - +. Begin with f() =. We ve identified two points and the asmptotes. ( ) showing two points and the asmptotes The graph of = The graph of g() = + ( ) showing two points and the asmptotes = 0 Graph =. ( ) Graph g() = +. ( ) Shift units to the Shift unit up. Add right. Add to each = to each -coordinate. = -coordinate. (, ) (, ) (, ) (, ) (, ) (, ) = 0 = 0 = 0 = 0 = Check Point Use the graph of f = to graph g = + -. ❻Graph rational functions. Graphing Rational Functions Rational functions that are not transformations of f = or f = can be graphed using the following suggestions: Strateg for Graphing a Rational Function The following strateg can be used to graph f = p q, where p and q are polnomial functions with no common factors.. Determine whether the graph of f has smmetr. f- = f: -ais smmetr f- = -f: origin smmetr. Find the -intercept (if there is one) b evaluating f0.. Find the -intercepts (if there are an) b solving the equation p = 0.. Find an vertical asmptote(s) b solving the equation q = 0.. Find the horizontal asmptote (if there is one) using the rule for determining the horizontal asmptote of a rational function. 6. Plot at least one point between and beond each -intercept and vertical asmptote. 7. Use the information obtained previousl to graph the function between and beond the vertical asmptotes.
71 EXAMPLE Graph: Solution f = Section.6 Rational Functions and Their Graphs Graphing a Rational Function -. Step Determine smmetr. f- = = = + Because f- does not equal f or -f, the graph has neither -ais nor origin smmetr. Step Find the -intercept. Evaluate f0. f0 = # = 0 - = 0 The -intercept is 0, so the graph passes through the origin. Step Find -intercept(s). This is done b solving p = 0. = 0 = 0 Set the numerator equal to 0. Divide both sides b. There is onl one -intercept. This verifies that the graph passes through the origin. Step Find the vertical asmptote(s). Solve q = 0, thereb finding zeros of the denominator. - = 0 = Set the denominator equal to 0. Add to both sides. The equation of the vertical asmptote is =. Step Find the horizontal asmptote. Because the numerator and denominator of f = have the same degree,, the leading coefficients of the numerator - and denominator, and, respectivel, are used to obtain the equation of the horizontal asmptote. The equation is = =. Horizontal asmptote: = 7 6 -intercept and -intercept Vertical asmptote: = The equation of the horizontal asmptote is =. Step 6 Plot points between and beond each -intercept and vertical asmptote. With an -intercept at 0 and a vertical asmptote at =, we evaluate the function at -, -,,, and. - - f - 8 Figure. Preparing to graph the rational function f = - Figure. shows these points, the -intercept, the -intercept, and the asmptotes.
72 6 Chapter Polnomial and Rational Functions Technolog The graph of = -, obtained using the dot mode in a -6, 6, b -6, 6 viewing rectangle, verifies that our hand-drawn graph is correct. Step 7 Graph the function. The graph of f = is shown in Figure.. - Horizontal asmptote: = 7 6 -intercept and -intercept Vertical asmptote: = = 7 6 = Figure. (repeated) Preparing to graph the rational function f = - Figure. The graph of f = - Check Point Graph: f = -. EXAMPLE 6 Graphing a Rational Function Stud Tip Because the graph has -ais smmetr, it is not necessar to evaluate the even function at - and again at. f- = f = 7 This also applies to evaluation at - and. Graph: f = -. Solution - Step Determine smmetr. f- = The graph - - = - = f: of f is smmetric with respect to the -ais. Step Find the -intercept. f0 = # 0 The -intercept is 0, so 0 - = 0 - = 0: the graph passes through the origin. Step Find the -intercept(s). = 0, so = 0: The -intercept is 0, verifing that the graph passes through the origin. Step Find the vertical asmptote(s). Set q = 0. - = 0 Set the denominator equal to 0. = Add to both sides. = ; Use the square root propert. The vertical asmptotes are = - and =. Step Find the horizontal asmptote. Because the numerator and denominator of f = have the same degree,, their leading coefficients, and, are - used to determine the equation of the horizontal asmptote. The equation is = =. Step 6 Plot points between and beond each -intercept and vertical asmptote. With an -intercept at 0 and vertical asmptotes at = - and =, we evaluate the function at -, -,,, and. - - f 7 Figure. at the top of the net page shows these points, the -intercept, the -intercept, and the asmptotes
73 Section.6 Rational Functions and Their Graphs 7 Step 7 Graph the function. The graph of f = is shown in Figure.. The -ais smmetr is now obvious. - Technolog The graph of = -, generated b a graphing utilit, verifies that our hand-drawn graph is correct. Horizontal asmptote: = -intercept and -intercept 7 6 Vertical asmptote: = Vertical asmptote: = = 7 6 = = [ 6, 6, ] b [ 6, 6, ] Figure. (repeated) Preparing to graph f = - Figure. The graph of f = - Check Point6 Graph: f = - 9. Eample 7 illustrates that not ever rational function has vertical and horizontal asmptotes. EXAMPLE 7 Graph: Graphing a Rational Function Solution - Step Determine smmetr. f- = The graph - + = + = f: of f is smmetric with respect to the -ais. Step Find the -intercept. f0 = The -intercept is = 0 = 0: Step Find the -intercept(s). = 0, so = 0: The -intercept is 0. Step f = +. Find the vertical asmptote. Set q = = 0 = - Set the denominator equal to 0. Subtract from both sides. Although this equation has imaginar roots = ;i, there are no real roots. Thus, the graph of f has no vertical asmptotes. Step Find the horizontal asmptote. Because the degree of the numerator,, is greater than the degree of the denominator,, there is no horizontal asmptote. Step 6 Plot points between and beond each -intercept and vertical asmptote. With an -intercept at 0 and no vertical asmptotes, let s look at function values at
74 8 Chapter Polnomial and Rational Functions Figure.6 The graph of f = + ❼Identif slant asmptotes. Slant asmptote: = + 6 Vertical asmptote: = Figure.7 The graph of f = + with a slant asmptote - -, -,, and. You can evaluate the function at and. Use -ais smmetr to obtain function values at - and -: f- = f and f- = f. - - f 6 Step 7 Graph the function. Figure.6 shows the graph of f using the points obtained from the table and -ais smmetr. Notice that as approaches infinit or negative infinit ( : q or : - q), the function values, f, are getting larger without bound f : q. Check Point7 Graph: Slant Asmptotes Eamine the graph of f = + -, shown in Figure.7. Note that the degree of the numerator,, is greater than the degree of the denominator,. Thus, the graph of this function has no horizontal asmptote. However, the graph has a slant asmptote, = +. The graph of a rational function has a slant asmptote if the degree of the numerator is one more than the degree of the denominator. The equation of the slant asmptote can be found b division. For eample, to find the slant asmptote for the graph of f = + divide - into + : -, Observe that f = 0 +. Remainder + f()= = The equation of the slant asmptote is = +. As ƒƒ : q, the value of is approimatel 0. Thus, when ƒƒ is large, the - function is ver close to = This means that as : q or as : - q, the graph of f gets closer and closer to the line whose equation is = +. The line = + is a slant asmptote of the graph. In general, if f = p p and q have no common factors, and the degree of q, p is one greater than the degree of q, find the slant asmptote b dividing q into p. The division will take the form p() remainder =m+b+. q() q() Slant asmptote: = m + b The equation of the slant asmptote is obtained b dropping the term with the remainder. Thus, the equation of the slant asmptote is = m + b.
75 Section.6 Rational Functions and Their Graphs Slant asmptote: = Vertical asmptote: = EXAMPLE 8 Find the slant asmptote of Finding the Slant Asmptote of a Rational Function Solution Because the degree of the numerator,, is eactl one more than the degree of the denominator,, and - is not a factor of - -, the graph of f has a slant asmptote. To find the equation of the slant asmptote, divide - into - - : 8 Remainder f = Drop the remainder term and ou'll have the equation of the slant asmptote. Figure.8 The graph of f = The equation of the slant asmptote is = -. Using our strateg for graphing rational functions, the graph of f = - - is shown in Figure.8. - Check Point8 Find the slant asmptote of f = ❽ Solve applied problems involving rational functions. Applications There are numerous eamples of asmptotic behavior in functions that describe real-world phenomena. Let s consider an eample from the business world. The cost function, C, for a business is the sum of its fied and variable costs: C()=(fied cost)+c. Cost per unit times the number of units produced,. The average cost per unit for a compan to produce units is the sum of its fied and variable costs divided b the number of units produced. The average cost function is a rational function that is denoted b C. Thus, Cost of producing units: fied plus variable costs (fied cost)+c C()=. Number of units produced EXAMPLE 9 Average Cost of Producing a Wheelchair A compan is planning to manufacture wheelchairs that are light, fast, and beautiful. The fied monthl cost will be $00,000 and it will cost $00 to produce each radicall innovative chair. a. Write the cost function, C, of producing wheelchairs. b. Write the average cost function, C, of producing wheelchairs. c. Find and interpret C000, C0,000, and C00,000. d. What is the horizontal asmptote for the graph of the average cost function, C? Describe what this represents for the compan.
76 0 Chapter Polnomial and Rational Functions Solution a. The cost function of producing wheelchairs, C, is the sum of the fied cost and the variable costs. Fied cost is $00,000. Variable cost: $00 for each wheelchair produced b. The average cost function of producing wheelchairs, C, is the sum of the fied and variable costs divided b the number of wheelchairs produced. C = C()=00, , or C = ,000 Average Cost per Wheelchair for the Compan C() = 00 0,000 0,000 00,000 Number of Wheelchairs Produced per Month Figure.9 As production level increases, the average cost per wheelchair approaches $00: lim : q C = 00. c. We evaluate C at 000, 0,000, and 00,000, interpreting the results. C000 = The average cost per wheelchair of producing 000 wheelchairs per month is $900. C0,000 = The average cost per wheelchair of producing 0,000 wheelchairs per month is $ , ,000 C00,000 = = 0 00,000 The average cost per wheelchair of producing 00,000 wheelchairs per month is $0. Notice that with higher production levels, the cost of producing each wheelchair decreases. d. We developed the average cost function C = , , ,000 0, ,000 = 900 = 0 in which the degree of the numerator,, is equal to the degree of the denominator,. The leading coefficients of the numerator and denominator, 00 and, are used to obtain the equation of the horizontal asmptote. The equation of the horizontal asmptote is = 00 or = 00. The horizontal asmptote is shown in Figure.9. This means that the more wheelchairs produced per month, the closer the average cost per wheelchair for the compan comes to $00. The least possible cost per wheelchair is approaching $00. Competitivel low prices take place with high production levels, posing a major problem for small businesses. Check Point9 The time: the not-too-distant future. A new compan is hoping to replace traditional computers and two-dimensional monitors with its virtual realit sstem.the fied monthl cost will be $600,000 and it will cost $00 to produce each sstem. a. Write the cost function, C, of producing virtual realit sstems. b. Write the average cost function, C, of producing virtual realit sstems. c. Find and interpret C000, C0,000, and C00,000. d. What is the horizontal asmptote for the graph of the average cost function, C? Describe what this represents for the compan.
77 Section.6 Rational Functions and Their Graphs If an object moves at an average velocit v, the distance, s, covered in time t is given b the formula Thus, distance = velocit # time. Objects that move in accordance with this formula are said to be in uniform motion. In Eample 0, we use a rational function to model time, t, in uniform motion. Solving the uniform motion formula for t, we obtain Thus, time is the quotient of distance and average velocit. EXAMPLE 0 s = vt. t = s v. Time Involved in Uniform Motion Two commuters drove to work a distance of 0 miles and then returned again on the same route.the average velocit on the return trip was 0 miles per hour faster than the average velocit on the outgoing trip. Epress the total time required to complete the round trip, T, as a function of the average velocit on the outgoing trip,. Solution As specified, the average velocit on the outgoing trip is represented b. Because the average velocit on the return trip was 0 miles per hour faster than the average velocit on the outgoing trip, let + 0 = the average velocit on the return trip. The sentence that we use as a verbal model to write our rational function is Total time on the round trip equals time on the outgoing trip plus time on the return trip. 0 0 T() = ±. +0 This is outgoing distance, 0 miles, divided b outgoing velocit,. This is return distance, 0 miles, divided b return velocit, + 0. The function that epresses the total time required to complete the round trip is T = Figure.0 The graph of T = 0 As average velocit increases, time for the trip decreases: lim T = 0. : q Once ou have modeled a problem s conditions with a function, ou can use a graphing utilit to eplore the function s behavior. For eample let s graph the function in Eample 0. Because it seems unlikel that an average outgoing velocit eceeds 60 miles per hour with an average return velocit that is 0 miles per hour faster, we graph the function for Figure.0 shows the graph of T = 0 in a 0, 60, b 0, 0, viewing rectangle. Notice that the function is decreasing. This shows decreasing times with increasing average velocities. Can ou see that the vertical asmptote is = 0, or the -ais? This indicates that close to an outgoing average velocit of zero miles per hour, the round trip will take nearl forever: lim T = q. :0 Check Point 0 Two commuters drove to work a distance of 0 miles and then returned again on the same route. The average velocit on the return trip was 0 miles per hour slower than the average velocit on the outgoing trip. Epress the total time required to complete the round trip, T, as a function of the average velocit on the outgoing trip,.
78 Chapter Polnomial and Rational Functions EXERCISE SET.6 Practice Eercises In Eercises 8, find the domain of each rational function. 7. f =. f = g =. g = h = h = f = f = Use the graph of the rational function in the figure shown to complete each statement in Eercises 9. Vertical asmptote: = Horizontal asmptote: = 0 9. As : - -, f :. 0. As : - +, f :.. As : -, f :.. As : +, f :.. As : - q, f :.. As : q, f :. Use the graph of the rational function in the figure shown to complete each statement in Eercises 0. Vertical asmptote: = Horizontal asmptote: = 9. As : q, f :. 0. As : - q, f :. In Eercises 8, find the vertical asmptotes, if an, of the graph of each rational function.. f =. f = + +. g =. g = +. h = 6. h = + 7. r = 8. r = + + In Eercises 9 6, find the horizontal asmptote, if an, of the graph of each rational function. 9. f = 0. f = + +. g =. g = + +. h =. h = + +. f = In Eercises 7 8, use transformations of f = f = to graph each rational function. 7. g = 8. g = - 9. h = 0. h = + +. g =. g = f = g =. g = + +. h = 6. h = - - or h = h = - + Vertical asmptote: =. As : +, f :. 6. As : -, f :. 7. As : - +, f :. 8. As : - -, f :. Vertical asmptote: = In Eercises 9 70, follow the seven steps on page to graph each rational function. 9. f = 0. f = - -. f =. f = - -. f =. f = - - 9
79 Section.6 Rational Functions and Their Graphs -. f = f = - 8. f = f = 60. f = f = 6. f = f = 6. f = f = 66. f = f = f = f = In Eercises 7 78, a. Find the slant asmptote of the graph of each rational function and b. Follow the seven-step strateg and use the slant asmptote to graph each rational function. 7. f = f = f = f = Practice Plus In Eercises 79 8, the equation for f is given b the simplified epression that results after performing the indicated operation. Write the equation for f and then graph the function # , In Eercises 8 88, use long division to rewrite the equation for g in the form quotient, plus remainder divided b divisor. Then use this form of the function s equation and transformations of f = to graph g. 8. g = f = - + f = f = - f = + f = f = g = g = g = Application Eercises 89. A compan is planning to manufacture mountain bikes. The fied monthl cost will be $00,000 and it will cost $00 to produce each biccle. a. Write the cost function, C, of producing mountain bikes. b. Write the average cost function, C, of producing mountain bikes. c. Find and interpret C00, C000, C000, and C000. d. What is the horizontal asmptote for the graph of the average cost function, C? Describe what this means in practical terms. 90. A compan that manufactures running shoes has a fied monthl cost of $00,000. It costs $0 to produce each pair of shoes. a. Write the cost function, C, of producing pairs of shoes. b. Write the average cost function, C, of producing pairs of shoes. c. Find and interpret C000, C0,000, and C00,000. d. What is the horizontal asmptote for the graph of the average cost function, C? Describe what this represents for the compan. 9. The function f = models the ph level, f, of the human mouth minutes after a person eats food containing sugar. The graph of this function is shown in the figure. ph Level of the Human Mouth f() = Number of Minutes after Eating Food Containing Sugar a. Use the graph to obtain a reasonable estimate, to the nearest tenth, of the ph level of the human mouth minutes after a person eats food containing sugar. b. After eating sugar, when is the ph level the lowest? Use the function s equation to determine the ph level, to the nearest tenth, at this time. c. According to the graph, what is the normal ph level of the human mouth? d. What is the equation of the horizontal asmptote associated with this function? Describe what this means in terms of the mouth s ph level over time. e. Use the graph to describe what happens to the ph level during the first hour. 9. A drug is injected into a patient and the concentration of the drug in the bloodstream is monitored. The drug s concentration, Ct, in milligrams per liter, after t hours is modeled b t Ct = t +.
80 Chapter Polnomial and Rational Functions The graph of this rational function, obtained with a graphing utilit, is shown in the figure. a. Use the graph to obtain a reasonable estimate of the drug s concentration after hours. Then verif this estimate algebraicall. t b. Use the function s equation, Ct = to find the t +, horizontal asmptote for the graph. Describe what this means about the drug s concentration in the patient s bloodstream as time increases. Among all deaths from a particular disease, the percentage that are smoking related ( 9 cigarettes per da) is a function of the disease s incidence ratio. The incidence ratio describes the number of times more likel smokers are than nonsmokers to die from the disease. The following table shows the incidence ratios for heart disease and lung cancer for two age groups. Incidence Ratios Heart Disease Lung Cancer Ages Ages Source: Aleander M. Walker, Observations and Inference, Epidemiolog Resources Inc., 99. For eample, the incidence ratio of 9 in the table means that smokers between the ages of 6 and 7 are 9 times more likel than nonsmokers in the same age group to die from lung cancer. The rational function 00 - P = models the percentage of smoking-related deaths among all deaths from a disease, P, in terms of the disease s incidence ratio,. The graph of the rational function is shown. Use this function to solve Eercises Percentage of Deaths from the Disease That Are Smoking Related = + [0, 0, ] b [0,, ] P() = 00( ) The Disease s Incidence Ratio: The number of times more likel smokers are than nonsmokers to die from the disease 9. Find P0. Describe what this means in terms of the incidence ratio, 0, given in the table. Identif our solution as a point on the graph. 9. Find P9. Round to the nearest percent. Describe what this means in terms of the incidence ratio, 9, given in the table. Identif our solution as a point on the graph. 9. What is the horizontal asmptote of the graph? Describe what this means about the percentage of deaths caused b smoking with increasing incidence ratios. 96. According to the model and its graph, is there a disease for which all deaths are caused b smoking? Eplain our answer. 97. The graph shows the U.S. population, b gender, for selected ears from 90 through 00. Population (millions) Male Source: U.S. Census Bureau U.S. Population, b Gender Female Year a. Write a fraction that shows the ratio of males to females in 99.Then epress the fraction as a decimal, rounded to the nearest thousandth. How man males per 000 females were there in 99? b. How man males per 000 females were there in 00? c. The function p = models the male U.S. population, p, in millions, ears after 90. The function q = models the female U.S. population, q, in millions, ears after 90. Write a function that models the ratio of males to females ears after 90. d. Use the function that ou wrote in part (c) to find the number of males per 000 females in 99. How well does the function model the actual number that ou determined in part (a)? e. Use the function that ou wrote in part (c) to find the number of males per 000 females in 00. How well does the function model the actual number that ou determined in part (b)? f. What is the equation of the horizontal asmptote associated with the function in part (c)? Round to the nearest thousandth. What does this mean about the number of males per 000 females over time? Eercises 98 0 involve writing a rational function that models a problem s conditions. 98. You drive from our home to a vacation resort 600 miles awa. You return on the same highwa. The average velocit on the return trip is 0 miles per hour slower than the average velocit on the outgoing trip. Epress the total time required to complete the round trip, T, as a function of the average velocit on the outgoing trip,. 99. A tourist drives 90 miles along a scenic highwa and then takes a -mile walk along a hiking trail. The average velocit driving is nine times that while hiking. Epress the total time for driving and hiking, T, as a function of the average velocit on the hike,.
81 Section.6 Rational Functions and Their Graphs 00. A contractor is constructing the house shown in the figure. The cross section up to the roof is in the shape of a rectangle. The area of the rectangular floor of the house is 00 square feet. Epress the perimeter of the rectangular floor, P, as a function of the width of the rectangle,. Width: 0. The figure shows a page with -inch margins at the top and the bottom and half-inch side margins.a publishing compan is willing to var the page dimensions subject to the condition that the printed area of the page is 0 square inches. Epress the total area of the page, A, as a function of the width of the rectangle containing the print,. in. in. ere I encounter the most popular fallac of our times. It is not considered sufficient that the law should be just; it must be philanthropic. Nor is it sufficient that the law should guarantee to ever citizen the free and inoffensive use of his faculties for phsical, intellectual, and moral self-improvement. Instead, it is demanded that the law should directl etend welfare, education, and moralit throughout the nation. This is the seductive lure of socialism. And I repeat again: These two uses of the law are in direct contradiction to each other. We must choose between them. A citizen cannot at the same time be free and not free. Enforced Fraternit Destros Libert Mr. de Lamartine once wrote to me thusl: "Your doctrine is onl the half of m program. You have stopped at libert; I go on to fraternit." I answered him: "The second half of our program will destro the first." In fact, it is impossible for me to separate the word fraternit from the word voluntar. I cannot possibl understand how fraternit can be legall enforced without libert being legall destroed, and thus justice being legall trampled underfoot. Legal plunder has two roots: One of them, as I have said before, is in human greed; the other is in false philanthrop. At this point, I think that I should eplain eactl what I mean b the word plunder. Plunder Violates Ownership I do not, as is often done, use the word in an vague, uncertain, approimate, or metaphorical sense. I use it in its scientific acceptance as epressing the idea opposite to that of propert [wages, land, mone, or whatever]. When a portion of wealth is transferred from the person who owns it without his consent and q in. Writing in Mathematics Length q in. 0. What is a rational function? 0. Use everda language to describe the graph of a rational function f such that as : - q, f :. 0. Use everda language to describe the behavior of a graph near its vertical asmptote if f : q as : - - and f : - q as : If ou are given the equation of a rational function, eplain how to find the vertical asmptotes, if an, of the function s graph. 06. If ou are given the equation of a rational function, eplain how to find the horizontal asmptote, if an, of the function s graph. 07. Describe how to graph a rational function. 08. If ou are given the equation of a rational function, how can ou tell if the graph has a slant asmptote? If it does, how do ou find its equation? 09. Is ever rational function a polnomial function? Wh or wh not? Does a true statement result if the two adjectives rational and polnomial are reversed? Eplain. 0. Although our friend has a famil histor of heart disease, he smokes, on average, cigarettes per da. He sees the table showing incidence ratios for heart disease (see Eercises 9 96) and feels comfortable that the are less than, compared to 9 and 0 for lung cancer. He claims that all famil deaths have been from heart disease and decides not to give up smoking. Use the given function and its graph to describe some additional information not given in the table that might influence his decision. Technolog Eercises. Use a graphing utilit to verif an five of our hand-drawn graphs in Eercises Use a graphing utilit to graph = and in, =, the same viewing rectangle. For odd values of n, how does changing n affect the graph of = n?. Use a graphing utilit to graph = and =, =, 6 in the same viewing rectangle. For even values of n, how does changing n affect the graph of = n?. Use a graphing utilit to graph f = and g = What differences do ou observe between the graph of f and the graph of g? How do ou account for these differences?. The rational function 7,7 - f = models the number of arrests, f, per 00,000 drivers, for driving under the influence of alcohol, as a function of a driver s age,. a. Graph the function in a 0, 70, b 0, 00, 0 viewing rectangle. b. Describe the trend shown b the graph. c. Use the ZOOM and TRACE features or the maimum function feature of our graphing utilit to find the age that corresponds to the greatest number of arrests. How man arrests, per 00,000 drivers, are there for this age group? Critical Thinking Eercises 6. Which one of the following is true? a. The graph of a rational function cannot have both a vertical asmptote and a horizontal asmptote. b. It is not possible to have a rational function whose graph has no -intercept. c. The graph of a rational function can have three horizontal asmptotes. d. The graph of a rational function can never cross a vertical asmptote. 7. Which one of the following is true? a. The function f = is a rational function. - b. The -ais is a horizontal asmptote for the graph of f = - +. c. The number of televisions that a compan can produce per week after t weeks of production is given b Nt = 000t + 0,000t t + 0t +. Using this model, the compan will eventuall be able to produce 0,000 televisions in a single week. d. None of the given statements is true.
82 pr0-6-7.i-hr 6 /6/06 : PM Page 6 Chapter Polnomial and Rational Functions 9. f has vertical asmptotes given b = - and =, a horizontal asmptote =, -intercept at 9, -intercepts at - and, and -ais smmetr. In Eercises 8, write the equation of a rational function p having the indicated properties, in which the degrees f = q of p and q are as small as possible. More than one correct function ma be possible. Graph our function using a graphing utilit to verif that it has the required properties. 0. f has a vertical asmptote given b =, a slant asmptote whose equation is =, -intercept at, and -intercepts at - and. 8. f has a vertical asmptote given b =, a horizontal asmptote = 0, -intercept at -, and no -intercept.. f has no vertical, horizontal, or slant asmptotes, and no -intercepts. SECTION.7 Polnomial and Rational Inequalities Objectives ❶ ❷ ❸ Solve polnomial inequalities. Solve rational inequalities. Solve problems modeled b polnomial or rational inequalities. People are going to live longer in the twent-first centur. This will put added pressure on the Social Securit and Medicare sstems. The bar graph in Figure. shows the cost of Medicare, in billions of dollars, through 00. Medicare Spending Spending (billions of dollars) $00 Figure. Source: Congressional Budget Office $8 $6 00 $79 $ $78 $99 $9 $0 $6 $88 $ Year Medicare spending, f, in billions of dollars, ears after 99 can be modeled b the quadratic function f = To determine in which ears Medicare spending will eceed $00 billion, we must solve the inequalit.+.+8.>00. eceeds $00 billion. Medicare spending We begin b subtracting 00 from both sides. This will give us zero on the right:
83 Section.7 Polnomial and Rational Inequalities 7 The form of is a + b + c 7 0. Such an inequalit is called a polnomial inequalit. Definition of a Polnomial Inequalit A polnomial inequalit is an inequalit that can be put into one of the forms f 6 0, f 7 0, f 0, or f Ú 0, where f is a polnomial function. 7 6 Figure > 0 Boundar points < 0 ❶Solve polnomial inequalities. In this section, we establish the basic techniques for solving polnomial inequalities. We will use these techniques to solve inequalities involving rational functions. Solving Polnomial Inequalities Graphs can help us visualize the solutions of polnomial inequalities. For eample, the graph of f = is shown in Figure..The -intercepts, and, are boundar points between where the graph lies above the -ais, shown in blue, and where the graph lies below the -ais, shown in red. Locating the -intercepts of a polnomial function, f, is an important step in finding the solution set for polnomial inequalities in the form f 6 0 or f 7 0. We use the -intercepts of f as boundar points that divide the real number line into intervals. On each interval, the graph of f is either above the -ais f 7 0 or below the -ais f 6 0. For this reason, -intercepts pla a fundamental role in solving polnomial inequalities. The -intercepts are found b solving the equation f = 0. Procedure for Solving Polnomial Inequalities. Epress the inequalit in the form f 6 0 or f 7 0, where f is a polnomial function.. Solve the equation f = 0. The real solutions are the boundar points.. Locate these boundar points on a number line, thereb dividing the number line into intervals.. Choose one representative number, called a test value, within each interval and evaluate f at that number. a. If the value of f is positive, then f 7 0 for all numbers,, in the interval. b. If the value of f is negative, then f 6 0 for all numbers,, in the interval.. Write the solution set, selecting the interval or intervals that satisf the given inequalit. This procedure is valid if 6 is replaced b or 7 is replaced b Ú. However, if the inequalit involves or Ú, include the boundar points [the solutions of f = 0] in the solution set. EXAMPLE Solving a Polnomial Inequalit Solve and graph the solution set on a real number line: + 7. Solution Step Epress the inequalit in the form f<0 or f>0. We begin b rewriting the inequalit so that 0 is on the right side. + 7 This is the given inequalit Subtract from both sides Simplif. This inequalit is equivalent to the one we wish to solve. It is in the form f 7 0, where f = + -.
84 8 Chapter Polnomial and Rational Functions Step Solve the equation f 0. We find the -intercepts of f = + - b solving the equation + - = = 0 This polnomial equation is a quadratic equation. - + = 0 Factor. - = 0 or + = 0 Set each factor equal to 0. = = - Solve for. The -intercepts of f are - and. We will use these -intercepts as boundar points on a number line. Step Locate the boundar points on a number line and separate the line into intervals. The number line with the boundar points is shown as follows: 0 e The boundar points divide the number line into three intervals: - q, - A -, B A, q B. Step Choose one test value within each interval and evaluate f at that number. Substitute into Interval Test Value f Conclusion - q, - - f- = f 7 0 for all in - q, -. =, positive a -, b a, q b 0 f0 = # f 6 0 for all in a -, b. = -, negative f = # + - f 7 0 for all in a, q b. = 6, positive Technolog The solution set for + 7 or, equivalentl, can be verified with a graphing utilit. The graph of f = + - was obtained using a -0, 0, b -6, 6, viewing rectangle. The graph lies above the -ais, representing 7, for all in - q, - or A, q B. above -ais above -ais Step Write the solution set, selecting the interval or intervals that satisf the given inequalit. We are interested in solving , where f = + -. Based on our work in step, we see that f 7 0 for all in - q, - or A Thus, the solution set of the given inequalit,, q B. + 7, or, equivalentl, , is The graph of the solution set on a number line is shown as follows: Check Point - q, - A, q B or Eƒ 6 - or 7 F. Solve and graph the solution set: 0 e = = EXAMPLE Solving a Polnomial Inequalit Solve and graph the solution set on a real number line: + +. Solution Step Epress the inequalit in the form f 0 or f» 0. We begin b rewriting the inequalit so that 0 is on the right side.
85 Section.7 Polnomial and Rational Inequalities 9 Technolog The solution set for or, equivalentl, can be verified with a graphing utilit. The graph of f = lies on or below the -ais, representing, for all in - q, - or [-,. Below -ais = = Below -ais [,, ] b [ 7,, ] = This is the given inequalit. Subtract from both sides. Simplif. This inequalit is equivalent to the one we wish to solve. It is in the form f 0, where f = Step Solve the equation f 0. We find the -intercepts of f = b solving the equation = = = = 0 + = 0 or - = 0 = - = This polnomial equation is of degree. Factor from the first two terms and from the last two terms. A common factor of is factored from the epression. Set each factor equal to 0. Solve for. Use the square root propert. The -intercepts of f are -, -, and. We will use these -intercepts as boundar points on a number line. Step Locate the boundar points on a number line and separate the line into intervals. The number line with the boundar points is shown as follows: = ; The boundar points divide the number line into four intervals: 0 - q, - -, - -,, q. Step Choose one test value within each interval and evaluate f at that number. Substitute into Interval Test Value f Conclusion - q, - - f- = f 6 0 for = -0, negative all in - q, -. -, - -. f-. = f 7 0 for = 0.87, positive all in -, -. -, 0 f0 = # 0 - f 6 0 for = -, negative all in -,., q f = + - # - f 7 0 for = 0, positive all in, q. Step Write the solution set, selecting the interval or intervals that satisf the given inequalit. We are interested in solving , where f = Based on our work in step, we see that f 6 0 for all in - q, - or -,. However, because the inequalit involves (less than or equal to), we must also include the solutions of = 0, namel -, -, and, in the solution set. Thus, the solution set of the given inequalit, + +, or, equivalentl, , is - q, - -, or ƒ - or - 6. The graph of the solution set on a number line is shown as follows: 0
86 0 Chapter Polnomial and Rational Functions Check Point Solve and graph the solution set on a real number line: + +. ❷Solve rational inequalities. Above -ais Stud Tip Do not begin solving + + Ú b multipling both sides b +. We do not know if + is positive or negative. Thus, we do not know whether or not to change the sense of the inequalit. Above -ais Below -ais Figure. The graph of f = + + Solving Rational Inequalities A rational inequalit is an inequalit that can be put into one of the forms where f is a rational function. An eample of a rational inequalit is This inequalit is in the form f 7 0, where f is the rational function given b The graph of f is shown in Figure.. We can find the -intercept of f b setting the numerator equal to 0: We can determine where f is undefined b setting the denominator equal to 0: B setting both the numerator and the denominator of f equal to 0, we obtained - and -. These numbers separate the -ais into three intervals: - q, -, -, -, and -, q. On each interval, the graph of f is either above the -ais f 7 0 or below the -ais f 6 0. Eamine the graph in Figure. carefull. Can ou see that it is above the -ais for all in - q, - or -, q, shown in blue? Thus, the solution set of + is - q, - -, q. B contrast, the graph of f lies below the ais for all in -, -, + shown in red. Thus, the solution set of is -, The first step in solving a rational inequalit is to bring all terms to one side, obtaining zero on the other side. Then epress the rational function on the nonzero side as a single quotient. The second step is to set the numerator and the denominator of f equal to zero. The solutions of these equations serve as boundar points that separate the real number line into intervals. At this point, the procedure is the same as the one we used for solving polnomial inequalities. EXAMPLE f 6 0, f 7 0, f 0, or f Ú 0, +=0 = =. Solve and graph the solution set: +=0 = = f = + +. Solving a Rational Inequalit + + Ú. f has an -intercept at and passes through (, 0). f is undefined at. Figure. shows that the function s vertical asmptote is =. Solution Step Epress the inequalit so that one side is zero and the other side is a single quotient. We subtract from both sides to obtain zero on the right.
87 Section.7 Polnomial and Rational Inequalities Ú Ú Ú 0 Ú 0 Ú Ú 0 This is the given inequalit. Subtract from both sides, obtaining 0 on the right. The least common denominator is. Epress in terms of this denominator. Subtract rational epressions. Appl the distributive propert. Simplif. Stud Tip Never include the value that causes a rational function s denominator to equal zero in the solution set of a rational inequalit. Division b zero is undefined. This inequalit is equivalent to the one we wish to solve. It is in the form f Ú 0, where f = Step Set the numerator and the denominator of f equal to zero. The real solutions are the boundar points. - - = 0 + = 0 = - = - Set the numerator and denominator equal to 0. These are the values that make the previous quotient zero or undefined. Solve for. We will use these solutions as boundar points on a number line. Step Locate the boundar points on a number line and separate the line into intervals. The number line with the boundar points is shown as follows: The boundar points divide the number line into three intervals: - q, - -, - -, q. Step Choose one test value within each interval and evaluate f at that number. Substitute into Interval - q, - Test Value -6 f f-6 = = -, negative Conclusion f 6 0 for all in - q, -. -, - - f- = =, positive f 7 0 for all in -, -. -, q 0 f0 = f 6 0 for all = -, negative in -, q. Step Write the solution set, selecting the interval or intervals that satisf the - - given inequalit. We are interested in solving where f = Ú 0, +. Based on our work in step, we see that f 7 0 for all in -, -. However,
88 Chapter Polnomial and Rational Functions Discover Because + is positive, it is possible so solve + + Ú b first multipling both sides b + (where Z -). This will not change the sense of the inequalit and will clear the fraction. Tr using this solution method and compare it to the solution on pages 0. because the inequalit involves Ú (greater than or equal to), we must also include the solution of f = 0, namel the value that we obtained when we set the numerator of f equal to zero. Thus, we must include - in the solution set. The solution set of the given inequalit is The graph of the solution set on a number line is shown as follows: Technolog The solution set for or, equivalentl, Ú Ú 0 -, - or ƒ Graph lies on or above the -ais. = = can be verified with a graphing utilit. The graph of f = - - lies on or above the -ais, + representing Ú, for all in -, -. [ 8, 8, ] b [,, ] Check Point Solve and graph the solution set: + Ú. ❸ Solve problems modeled b polnomial or rational inequalities. Applications We are surrounded b evidence that the world is profoundl mathematical. For eample, did ou know that ever time ou throw an object verticall upward, its changing height above the ground can be described b a quadratic function? The same function can be used to describe objects that are falling, such as sk divers. The Position Function for a Free-Falling Object Near Earth s Surface An object that is falling or verticall projected into the air has its height above the ground, st, in feet, given b st = -6t + v 0 t + s 0, where v 0 is the original velocit (initial velocit) of the object, in feet per second, t is the time that the object is in motion, in seconds, and s 0 is the original height (initial height) of the object, in feet. In Eample, we solve a polnomial inequalit in a problem about the position of a free-falling object. EXAMPLE Using the Position Function A ball is thrown verticall upward from the top of the Leaning Tower of Pisa (90 feet high) with an initial velocit of 96 feet per second (Figure.). During which time period will the ball s height eceed that of the tower?
89 Section.7 Polnomial and Rational Inequalities t = 0 s 0 = 90 v 0 = 96 Solution st = -6t + v 0 t + s 0 st = -6t + 96t + 90 This is the position function for a free-falling object. Because v 0 initial velocit 96 and s 0 initial position 90, substitute these values into the formula. When will s(t), the ball s height, eceed that of the tower? 6t + 96t +90 > feet Figure. Throwing a ball from 90 feet with a velocit of 96 feet per second -6t + 96t t + 96t = 0-6tt - 6 = 0-6t = 0 or t - 6 = 0 0-6t + 96t 7 0 t = 0 t = This is the inequalit that models the problem s question. We must find t. Subtract 90 from both sides. This inequalit is in the form ft>0, where ft 6t 96t. Solve the equation ft 0. Factor. Set each factor equal to 0. Solve for t. The boundar points are 0 and 6. t Locate these values on a number line, with t» 0. The intervals are - q, 0, 0, 6, and 6, q. For our purposes, the mathematical model is useful onl from t = 0 until the ball hits the ground. (B setting -6t + 96t + 90 equal to zero, we find t L 7.7; the ball hits the ground after approimatel 7.7 seconds.) Thus, we use 0, 6 and 6, 7.7 for our intervals. Substitute into Interval Test Value ft 6t 96t Conclusion 0, 6 f = -6 # + 96 # ft 7 0 for all = 80, positive t in 0, 6. 6, f7 = -6 # # 7 ft 6 0 for all = -, negative t in 6, 7.7. We are interested in solving -6t + 96t 7 0, where ft = -6t + 96t. We see that ft 7 0 for all t in 0, 6. This means that the ball s height eceeds that of the tower between 0 and 6 seconds. Technolog The graphs of and = are shown in a [0, 8, ] b [0, 60, 6] seconds in motion = 90 height, in feet viewing rectangle. The graphs show that the ball s height eceeds that of the tower between 0 and 6 seconds. Height (feet) 60 Height of Ball: = Height of Tower: = Seconds in Motion [0, 8, ] b [0, 60, 6] Ball hits ground after 7.7 seconds.
90 Chapter Polnomial and Rational Functions Check Point An object is propelled straight up from ground level with an initial velocit of 80 feet per second. Its height at time t is modeled b st = -6t + 80t, where the height, st, is measured in feet and the time, t, is measured in seconds. In which time interval will the object be more than 6 feet above the ground? EXERCISE SET.7 Practice Eercises Solve each polnomial inequalit in Eercises 8 and graph the solution set on a real number line. Epress each solution set in interval notation Ú Ú 9. - Ú Ú Ú Ú Ú Ú Ú Ú Ú 9 8. Solve each rational inequalit in Eercises 9 6 and graph the solution set on a real number line. Epress each solution set in interval notation Ú Ú Practice Plus In Eercises 7 60, find the domain of each function. 7. f = f = f = 60. f = A + - A - - Solve each inequalit in Eercises 6 66 and graph the solution set on a real number line. 6. ƒ + - 6ƒ 7 6. ƒ ƒ In Eercises 67 68, use the graph of the polnomial function to solve each inequalit. f() = Ú Ú
91 Section.7 Polnomial and Rational Inequalities In Eercises 69 70, use the graph of the rational function to solve each inequalit. f() = + It s vacation time. You drive 90 miles along a scenic highwa and then take a -mile run along a hiking trail. Your driving rate is nine times that of our running rate. The graph shows the total time ou spend driving and running, f, as a function of our running rate,. Use the rational function and its graph to solve Eercises Time Driving and Running (hours) f() = 90 + = Running Rate (miles per hour) Application Eercises Use the position function st = -6t + v 0 t + s 0 v 0 = initial velocit, s 0 = initial position, t = time to answer Eercises Divers in Acapulco, Meico, dive headfirst at 8 feet per second from the top of a cliff 87 feet above the Pacific Ocean. During which time period will the diver s height eceed that of the cliff? 7. You throw a ball straight up from a rooftop 60 feet high with an initial velocit of 8 feet per second. During which time period will the ball s height eceed that of the rooftop? The bar graph in Figure. on page 6 shows the cost of Medicare, in billions of dollars, through 00. Using the regression feature of a graphing utilit, these data can be modeled b a linear function, f = 7 + 6; a quadratic function, g = In each function, represents the number of ears after 99. Use these functions to solve Eercises The graph indicates that Medicare spending reached $79 billion in 00. Find the amount predicted b each of the functions, f and g, for that ear. How well do the functions model the value in the graph? 7. The graph indicates that Medicare spending reached $8 billion in 00. Find the amount predicted b each of the functions, f and g, for that ear. How well do the functions model the value in the graph? Which function serves as a better model for that ear? 7. For which ears does the quadratic model indicate that Medicare spending will eceed $6.6 billion? 76. For which ears does the quadratic model indicate that Medicare spending will eceed $69. billion? 77. Describe our running rate if ou have no more than a total of hours for driving and running. Use a rational inequalit to solve the problem. Then eplain how our solution is shown on the graph. 78. Describe our running rate if ou have no more than a total of hours for driving and running. Use a rational inequalit to solve the problem. Then eplain how our solution is shown on the graph. 79. Describe the behavior of the graph as : q. What does this show about the time driving and running as a function of our running rate? 80. Describe the behavior of the graph as : 0 +. What does this show about the time driving and running as a function of our running rate? 8. Describe how to use the formula t = s and the problem s v verbal conditions to obtain the function s equation displaed in the voice balloon. 8. The perimeter of a rectangle is 0 feet. Describe the possible lengths of a side if the area of the rectangle is not to eceed square feet. 8. The perimeter of a rectangle is 80 feet. Describe the possible lengths of a side if the area of the rectangle is not to eceed 800 square feet. Writing in Mathematics 8. What is a polnomial inequalit? 8. What is a rational inequalit? 86. If f is a polnomial or rational function, eplain how the graph of f can be used to visualize the solution set of the inequalit f 6 0.
92 6 Chapter Polnomial and Rational Functions Technolog Eercises 87. Use a graphing utilit to verif our solution sets to an three of the polnomial inequalities that ou solved algebraicall in Eercises Use a graphing utilit to verif our solution sets to an three of the rational inequalities that ou solved algebraicall in Eercises 9 6. Solve each inequalit in Eercises 89 9 using a graphing utilit a. Use the graph to describe the solution set of b. Use the graph to describe the solution set of c. Use an algebraic approach to verif each of our descriptions in parts (a) and (b). 0. The graphing utilit screen shows the graph of = 7 -. Write and solve a quadratic inequalit that eplains wh the graph onl appears for -. = 7 [,, ] b [0, 6, ] Group Eercise Critical Thinking Eercises 9. Which one of the following is true? a. The solution set of 7 is, q. - b. The inequalit can be solved b multipling + 6 both sides b +, resulting in the equivalent inequalit c. + - Ú 0 and have the same - Ú 0 solution set. d. None of these statements is true. 96. Write a polnomial inequalit whose solution set is -,. 97. Write a rational inequalit whose solution set is - q, -, q. In Eercises 98 0, use inspection to describe each inequalit s solution set. Do not solve an of the inequalities The graphing utilit screen shows the graph of = This eercise is intended as a group learning eperience and is appropriate for groups of three to five people. Before working on the various parts of the problem, reread the description of the position function on page. a. Drop a ball from a height of feet, 6 feet, and feet. Record the number of seconds it takes for the ball to hit the ground. b. For each of the three initial positions, use the position function to determine the time required for the ball to hit the ground. c. What factors might result in differences between the times that ou recorded and the times indicated b the function? d. What appears to be happening to the time required for a free-falling object to hit the ground as its initial height is doubled? Verif this observation algebraicall and with a graphing utilit. e. Repeat part (a) using a sheet of paper rather than a ball. What differences do ou observe? What factor seems to be ignored in the position function? f. What is meant b the acceleration of gravit and how does this number appear in the position function for a free-falling object? = [, 6, ] b [, 8, ]
93 pr0-6-7.i-hr /6/06 : PM Page 7 Section.8 Modeling Using Variation 7 SECTION.8 Modeling Using Variation Objectives ❶ ❷ ❸ ❹ Solve direct variation problems. Solve inverse variation problems. Solve combined variation problems. Solve problems involving joint variation. Have ou ever wondered how telecommunication companies estimate the number of phone calls epected per da between two cities? The formula C = 0.0PP d shows that the dail number of phone calls, C, increases as the populations of the cities, P and P, in thousands, increase and decreases as the distance, d, between the cities increases. Certain formulas occur so frequentl in applied situations that the are given special names. Variation formulas show how one quantit changes in relation to other quantities. Quantities can var directl, inversel, or jointl. In this section, we look at situations that can be modeled b each of these kinds of variation. And think of this: The net time ou get one of those all-circuits-are-bus messages, ou will be able to use a variation formula to estimate how man other callers ou re competing with for those precious -cent minutes. ❶ Solve direct variation problems. Direct Variation When ou swim underwater, the pressure in our ears depends on the depth at which ou are swimming. The formula p = 0.d describes the water pressure, p, in pounds per square inch, at a depth of d feet. We can use this linear function to determine the pressure in our ears at various depths: If d = 0, p=0.(0)= 8.6. At a depth of 0 feet, water pressure is 8.6 pounds per square inch. Doubling the depth doubles the pressure. If d = 0, p=0.(0)=7.. At a depth of 0 feet, water pressure is 7. pounds per square inch. Doubling the depth doubles the pressure. If d = 80, p=0.(80)=.. At a depth of 80 feet, water pressure is. pounds per square inch. The formula p = 0.d illustrates that water pressure is a constant multiple of our underwater depth. If our depth is doubled, the pressure is doubled; if our depth is tripled, the pressure is tripled; and so on. Because of this, the pressure in our ears is said to var directl as our underwater depth. The equation of variation is p = 0.d.
94 8 Chapter Polnomial and Rational Functions Generalizing our discussion of pressure and depth on the previous page, we obtain the following statement: Direct Variation If a situation is described b an equation in the form = k, where k is a nonzero constant, we sa that varies directl as or is directl proportional to. The number k is called the constant of variation or the constant of proportionalit. Can ou see that the direct variation equation, k, is a special case of the linear function m b? When m = k and b = 0, = m + b becomes = k. Thus, the slope of a direct variation equation is k, the constant of variation. Because b, the -intercept, is 0, the graph of a direct variation equation is a line passing through the origin. This is illustrated in Figure., which shows the graph of p = 0.d: Water pressure varies directl as depth. Pressure in Diver's Ears (pounds per square inch) p p = 0.d Depth (feet) 0 Unsafe for amateur divers 0 60 d Figure. Water pressure at various depths Problems involving direct variation can be solved using the following procedure. This procedure applies to direct variation problems, as well as to the other kinds of variation problems that we will discuss. Solving Variation Problems. Write an equation that describes the given English statement.. Substitute the given pair of values into the equation in step and solve for k, the constant of variation.. Substitute the value of k into the equation in step.. Use the equation from step to answer the problem s question. EXAMPLE Solving a Direct Variation Problem Man areas of Northern California depend on the snowpack of the Sierra Nevada mountain range for their water suppl. The volume of water produced from melting snow varies directl as the volume of snow. Meteorologists have determined that 0 cubic centimeters of snow will melt to 8 cubic centimeters of water. How much water does 00 cubic centimeters of melting snow produce? Solution Step Write an equation. We know that varies directl as is epressed as = k. B changing letters, we can write an equation that describes the following English statement: Volume of water, W, varies directl as volume of snow, S. W = ks
95 Section.8 Modeling Using Variation 9 Step Use the given values to find k. We are told that 0 cubic centimeters of snow will melt to 8 cubic centimeters of water. Substitute 0 for S and 8 for W in the direct variation equation. Then solve for k. W = ks Volume of water varies directl as volume of melting snow. 8 = k0 0 cubic centimeters of snow melt to 8 cubic centimeters of water. 8 Divide both sides b 0. 0 = k = k Simplif. Step Substitute the value of k into the equation. W = ks This is the equation from step. W = 0.S Replace k, the constant of variation, with 0.. Step Answer the problem s question. How much water does 00 cubic centimeters of melting snow produce? Substitute 00 for S in W = 0.S and solve for W. W = 0.S Use the equation from step. W = 0.00 Substitute 00 for S. W =. Multipl. A snowpack measuring 00 cubic centimeters will produce. cubic centimeters of water. Check Point The number of gallons of water, W, used when taking a shower varies directl as the time, t, in minutes, in the shower.a shower lasting minutes uses 0 gallons of water. How much water is used in a shower lasting minutes? The direct variation equation k is a linear function. If k>0, then the slope of the line is positive. Consequentl, as increases, also increases. A direct variation situation can involve variables to higher powers. For eample, can var directl as = k or as = k. Direct Variation with Powers varies directl as the nth power of if there eists some nonzero constant k such that = k n. We also sa that is directl proportional to the nth power of. Direct variation with whole number powers is modeled b polnomial functions. In our net eample, the graph of the variation equation is the familiar parabola. EXAMPLE Solving a Direct Variation Problem The distance, s, that a bod falls from rest varies directl as the square of the time, t, of the fall. If skdivers fall 6 feet in seconds, how far will the fall in. seconds? Solution Step Write an equation. We know that varies directl as the square of is epressed as = k.
96 60 Chapter Polnomial and Rational Functions B changing letters, we can write an equation that describes the following English statement: Distance, s, varies directl as the square of time, t, of the fall. s = kt Step Use the given values to find k. Skdivers fall 6 feet in seconds. Substitute 6 for s and for t in the direct variation equation. Then solve for k. Distance the Skdivers Fall (feet) s(t) Distance Fallen b Skdivers over Time t 6 Time the Skdivers Fall (seconds) Figure.6 The graph of st = 6t ❷ Solve inverse variation problems. Step s = kt Distance varies directl as the square of time. 6 = k # Skdivers fall 6 feet in seconds. 6 = k Simplif:. 6 Divide both sides b. = k 6 = k Simplif. Substitute the value of k into the equation. s = kt Use the equation from step. s = 6t Replace k, the constant of variation, with 6. Step Answer the problem s question. How far will the skdivers fall in. seconds? Substitute. for t in s = 6t and solve for s. Thus, in. seconds, the skdivers will fall feet. We can epress the variation equation from Eample in function notation, writing st = 6t. The distance that a bod falls from rest is a function of the time, t, of the fall. The parabola that is the graph of this quadratic function is shown in Figure.6. The graph increases rapidl from left to right, showing the effects of the acceleration of gravit. Check Point The distance required to stop a car varies directl as the square of its speed. If 00 feet are required to stop a car traveling 60 miles per hour, how man feet are required to stop a car traveling 00 miles per hour? Inverse Variation The distance from San Francisco to Los Angeles is 0 miles. The time that it takes to drive from San Francisco to Los Angeles depends on the rate at which one drives and is given b Time = 0 Rate. For eample, if ou average 0 miles per hour, the time for the drive is Time = 0 0 =, or hours. If ou average 0 miles per hour, the time for the drive is Time = 0 0 = 8., s = 6. = 60. = or 8. hours. As our rate (or speed) increases, the time for the trip decreases and vice versa. This is illustrated b the graph in Figure.7. Time for Trip (hours) 0 0 t t = 0 r Averaging 0 mph, the trip takes hours. Averaging 0 mph, the trip takes 8. hours Driving Rate (miles per hour) Figure.7 r
97 Section.8 Modeling Using Variation 6 We can epress the time for the San Francisco Los Angeles trip using t for time and r for rate: t = 0 r. This equation is an eample of an inverse variation equation. Time, t, varies inversel as rate, r. When two quantities var inversel, one quantit increases as the other decreases and vice versa. Generalizing, we obtain the following statement: Inverse Variation If a situation is described b an equation in the form = k, k > 0 and > 0 = k, where k is a nonzero constant, we sa that varies inversel as or is inversel proportional to. The number k is called the constant of variation. Notice that the inverse variation equation Figure.8 The graph of the inverse variation equation = k, or f = k, is a rational function. For k 7 0 and 7 0, the graph of the function takes on the shape shown in Figure.8. We use the same procedure to solve inverse variation problems as we did to solve direct variation problems. Eample illustrates this procedure. P V P V Doubling the pressure halves the volume. EXAMPLE Solving an Inverse Variation Problem When ou use a spra can and press the valve at the top, ou decrease the pressure of the gas in the can. This decrease of pressure causes the volume of the gas in the can to increase. Because the gas needs more room than is provided in the can, it epands in spra form through the small hole near the valve. In general, if the temperature is constant, the pressure, P, of a gas in a container varies inversel as the volume, V, of the container. The pressure of a gas sample in a container whose volume is 8 cubic inches is pounds per square inch. If the sample epands to a volume of cubic inches, what is the new pressure of the gas? Solution Step Write an equation. We know that varies inversel as is epressed as = k. B changing letters, we can write an equation that describes the following English statement: The pressure, P, of a gas in a container varies inversel as the volume, V. P = k V. Step Use the given values to find k. The pressure of a gas sample in a container whose volume is 8 cubic inches is pounds per square inch. Substitute for P and 8 for V in the inverse variation equation. Then solve for k. P = k V = k 8 # k 8 = # = k Pressure varies inversel as volume. The pressure in an 8 cubic-inch container is pounds per square inch. Multipl both sides b 8. Simplif.
98 6 Chapter Polnomial and Rational Functions Step Substitute the value of k into the equation. P = k V P = 96 V Use the equation from step. Replace k, the constant of variation, with 96. Step Answer the problem s question. We need to find the pressure when the volume epands to cubic inches. Substitute for V and solve for P. P = 96 V = 96 = When the volume is cubic inches, the pressure of the gas is inch. pounds per square ❸ Solve combined variation problems. Check Point The length of a violin string varies inversel as the frequenc of its vibrations. A violin string 8 inches long vibrates at a frequenc of 60 ccles per second. What is the frequenc of a 0-inch string? Combined Variation In combined variation, direct and inverse variation occur at the same time. For eample, as the advertising budget, A, of a compan increases, its monthl sales, S, also increase. Monthl sales var directl as the advertising budget: S = ka. B contrast, as the price of the compan s product, P, increases, its monthl sales, S, decrease. Monthl sales var inversel as the price of the product: S = k P. We can combine these two variation equations into one combined equation: ka S=. P Monthl sales, S, var directl as the advertising budget, A, and inversel as the price of the product, P. The following eample illustrates an application of combined variation. EXAMPLE Solving a Combined Variation Problem The owners of Rollerblades Plus determine that the monthl sales, S, of its skates var directl as its advertising budget, A, and inversel as the price of the skates, P. When $60,000 is spent on advertising and the price of the skates is $0, the monthl sales are,000 pairs of rollerblades. a. Write an equation of variation that describes this situation. b. Determine monthl sales if the amount of the advertising budget is increased to $70,000. Solution a. Write an equation. ka S=. P Translate sales var directl as the advertising budget and inversel as the skates price.
99 Section.8 Modeling Using Variation 6 Use the given values to find k.,000 = k60,000 0 When $60,000 is spent on advertising A 60,000 and the price is $0 P 0, monthl sales are,000 units S,000.,000 = k # 00 Divide 60,000 b 0.,000 Divide both sides of the equation b = k # = k Simplif. Therefore, the equation of variation that describes monthl sales is S = 8A P. Substitute 8 for k in S ka P. b. The advertising budget is increased to $70,000, so A = 70,000. The skates price is still $0, so P = 0. S = 8A P This is the equation from part (a). S = 870,000 Substitute 70,000 for A and 0 for P. 0 S =,000 Simplif. With a $70,000 advertising budget and $0 price, the compan can epect to sell,000 pairs of rollerblades in a month (up from,000). Check Point The number of minutes needed to solve an eercise set of variation problems varies directl as the number of problems and inversel as the number of people working to solve the problems. It takes people minutes to solve 6 problems. How man minutes will it take 8 people to solve problems? ❹ Solve problems involving joint variation. Joint Variation Joint variation is a variation in which a variable varies directl as the product of two or more other variables. Thus, the equation = kz is read varies jointl as and z. Joint variation plas a critical role in Isaac Newton s formula for gravitation: The formula states that the force of gravitation, F, between two bodies varies jointl as the product of their masses, m and m, and inversel as the square of the distance between them, d. (G is the gravitational constant.) The formula indicates that gravitational force eists between an two objects in the universe, increasing as the distance between the bodies decreases. One practical result is that the pull of the moon on the oceans is greater on the side of Earth closer to the moon. This gravitational imbalance is what produces tides. EXAMPLE m m F = G d. Modeling Centrifugal Force The centrifugal force, C, of a bod moving in a circle varies jointl with the radius of the circular path, r, and the bod s mass, m, and inversel with the square of the time, t, it takes to move about one full circle.a 6-gram bod moving in a circle with radius 00 centimeters at a rate of revolution in seconds has a centrifugal force of 6000 dnes. Find the centrifugal force of an 8-gram bod moving in a circle with radius 00 centimeters at a rate of revolution in seconds.
100 6 Chapter Polnomial and Rational Functions Solution C = krm t 6000 = k = 0k 0 = k C = 0rm t C = 0008 = 8000 Translate Centrifugal force, C, varies jointl with radius, r, and mass, m, and inversel with the square of time, t. A 6-gram bod m 6 moving in a circle with radius 00 centimeters r 00 at revolution in seconds t has a centifugal force of 6000 dnes C Simplif. Divide both sides b 0 and solve for k. Substitute 0 for k in the model for centrifugal force. Find centifugal force, C, of an 8-gram bod m 8 moving in a circle with radius 00 centimeters r 00 at revolution in seconds t. Simplif. The centrifugal force is 8000 dnes. Check Point The volume of a cone, V, varies jointl as its height, h, and the square of its radius, r. A cone with a radius measuring 6 feet and a height measuring 0 feet has a volume of 0p cubic feet. Find the volume of a cone having a radius of feet and a height of feet. EXERCISE SET.8 Practice Eercises Use the four-step procedure for solving variation problems given on page 8 to solve Eercises 0.. varies directl as. = 6 when =. Find when =.. varies directl as. = when =. Find when =.. varies inversel as. = when =. Find when =.. varies inversel as. = 6 when =. Find when = 9.. varies directl as and inversel as the square of z. = 0 when = 0 and z =. Find when = and z = a varies directl as b and inversel as the square of c. a = 7 when b = 9 and c = 6. Find a when b = and c = varies jointl as and z. = when = and z =. Find when = 8 and z =. 8. C varies jointl as A and T. C = 7 when A = 00 and T =. Find C when A = 00 and T = varies jointl as a and b and inversel as the square root of c. = when a =, b =, and c =. Find when a =, b =, and c = varies jointl as m and the square of n and inversel as p. = when m =, n =, and p = 6. Find when m =, n =, and p = 0. Practice Plus In Eercises 0, write an equation that epresses each relationship. Then solve the equation for.. varies jointl as and z.. varies jointl as and the square of z.. varies directl as the cube of z and inversel as.. varies directl as the cube root of z and inversel as.. varies jointl as and z and inversel as the square root of w. 6. varies jointl as and z and inversel as the square of w. 7. varies jointl as z and the sum of and w. 8. varies jointl as z and the difference between and w. 9. varies directl as z and inversel as the difference between and w. 0. varies directl as z and inversel as the sum of and w.
101 pr0-6-7.i-hr /6/06 : PM Page 6 Section.8 Modeling Using Variation Application Eercises Use the four-step procedure for solving variation problems given on page 8 to solve Eercises 6.. An alligator s tail length, T, varies directl as its bod length, B. An alligator with a bod length of feet has a tail length of.6 feet. What is the tail length of an alligator whose bod length is 6 feet? Bod length, B 6 7. The figure shows that a bicclist tips the ccle when making a turn. The angle B, formed b the vertical direction and the biccle, is called the banking angle. The banking angle varies inversel as the ccle s turning radius. When the turning radius is feet, the banking angle is 8. What is the banking angle when the turning radius is. feet? Tail length, T. An object s weight on the moon, M, varies directl as its weight on Earth, E. Neil Armstrong, the first person to step on the moon on Jul 0, 969, weighed 60 pounds on Earth (with all of his equipment on) and 60 pounds on the moon. What is the moon weight of a person who weighs 86 pounds on Earth?. The height that a ball bounces varies directl as the height from which it was dropped. A tennis ball dropped from inches bounces 8. inches. From what height was the tennis ball dropped if it bounces 6 inches?. The distance that a spring will stretch varies directl as the force applied to the spring. A force of pounds is needed to stretch a spring 9 inches. What force is required to stretch the spring inches?. If all men had identical bod tpes, their weight would var directl as the cube of their height. Shown below is Robert Wadlow, who reached a record height of 8 feet inches (07 inches) before his death at age. If a man who is feet 0 inches tall (70 inches) with the same bod tpe as Mr. Wadlow weighs 70 pounds, what was Robert Wadlow s weight shortl before his death? 6. On a dr asphalt road, a car s stopping distance varies directl as the square of its speed. A car traveling at miles per hour can stop in 67. feet. What is the stopping distance for a car traveling at 60 miles per hour? B 8. The water temperature of the Pacific Ocean varies inversel as the water s depth. At a depth of 000 meters, the water temperature is. Celsius. What is the water temperature at a depth of 000 meters? 9. Radiation machines, used to treat tumors, produce an intensit of radiation that varies inversel as the square of the distance from the machine. At meters, the radiation intensit is 6. milliroentgens per hour. What is the intensit at a distance of. meters? 0. The illumination provided b a car s headlight varies inversel as the square of the distance from the headlight. A car s headlight produces an illumination of.7 footcandles at a distance of 0 feet. What is the illumination when the distance is 0 feet?. Bod-mass inde, or BMI, takes both weight and height into account when assessing whether an individual is underweight or overweight. BMI varies directl as one s weight, in pounds, and inversel as the square of one s height, in inches. In adults, normal values for the BMI are between 0 and, inclusive. Values below 0 indicate that an individual is underweight and values above 0 indicate that an individual is obese. A person who weighs 80 pounds and is feet, or 60 inches, tall has a BMI of.. What is the BMI, to the nearest tenth, for a 70 pound person who is feet 0 inches tall. Is this person overweight?. One s intelligence quotient, or IQ, varies directl as a person s mental age and inversel as that person s chronological age. A person with a mental age of and a chronological age of 0 has an IQ of. What is the chronological age of a person with a mental age of 0 and an IQ of 80?. The heat loss of a glass window varies jointl as the window s area and the difference between the outside and inside temperatures. A window feet wide b 6 feet long loses 00 Btu per hour when the temperature outside is 0 colder than the temperature inside. Find the heat loss through a glass window that is 6 feet wide b 9 feet long when the temperature outside is 0 colder than the temperature inside.
102 66 Chapter Polnomial and Rational Functions. Kinetic energ varies jointl as the mass and the square of the velocit. A mass of 8 grams and velocit of centimeters per second has a kinetic energ of 6 ergs. Find the kinetic energ for a mass of grams and velocit of 6 centimeters per second.. Sound intensit varies inversel as the square of the distance from the sound source. If ou are in a movie theater and ou change our seat to one that is twice as far from the speakers, how does the new sound intensit compare to that of our original seat? 6. Man people claim that as the get older, time seems to pass more quickl. Suppose that the perceived length of a period of time is inversel proportional to our age. How long will a ear seem to be when ou are three times as old as ou are now? 7. The average number of dail phone calls, C, between two cities varies jointl as the product of their populations, P and P, and inversel as the square of the distance, d, between them. a. Write an equation that epresses this relationship. b. The distance between San Francisco (population: 777,000) and Los Angeles (population:,69,000) is 0 miles. If the average number of dail phone calls between the cities is 6,000, find the value of k to two decimal places and write the equation of variation. c. Memphis (population: 60,000) is 00 miles from New Orleans (population: 90,000). Find the average number of dail phone calls, to the nearest whole number, between these cities. 8. The force of wind blowing on a window positioned at a right angle to the direction of the wind varies jointl as the area of the window and the square of the wind s speed. It is known that a wind of 0 miles per hour blowing on a window measuring feet b feet eerts a force of 0 pounds. During a storm with winds of 60 miles per hour, should hurricane shutters be placed on a window that measures feet b feet and is capable of withstanding 00 pounds of force? 9. The table shows the values for the current, I, in an electric circuit and the resistance, R, of the circuit. I (amperes) R (ohms) a. Graph the ordered pairs in the table of values, with values of I along the -ais and values of R along the -ais. Connect the eight points with a smooth curve. b. Does current var directl or inversel as resistance? Use our graph and eplain how ou arrived at our answer. c. Write an equation of variation for I and R, using one of the ordered pairs in the table to find the constant of variation. Then use our variation equation to verif the other seven ordered pairs in the table. Writing in Mathematics 0. What does it mean if two quantities var directl?. In our own words, eplain how to solve a variation problem.. What does it mean if two quantities var inversel?. Eplain what is meant b combined variation. Give an eample with our eplanation.. Eplain what is meant b joint variation. Give an eample with our eplanation. In Eercises 6, describe in words the variation shown b the given equation.. z = k 6. z = k 7. We have seen that the dail number of phone calls between two cities varies jointl as their populations and inversel as the square of the distance between them.this model, used b telecommunication companies to estimate the line capacities needed among various cities, is called the gravit model. Compare the model to Newton s formula for gravitation on page 6 and describe wh the name gravit model is appropriate. Technolog Eercise 8. Use a graphing utilit to graph an three of the variation equations in Eercises 0. Then TRACE along each curve and identif the point that corresponds to the problem s solution. Critical Thinking Eercises 9. In a hurricane, the wind pressure varies directl as the square of the wind velocit. If wind pressure is a measure of a hurricane s destructive capacit, what happens to this destructive power when the wind speed doubles? 0. The illumination from a light source varies inversel as the square of the distance from the light source. If ou raise a lamp from inches to 0 inches over our desk, what happens to the illumination?. The heat generated b a stove element varies directl as the square of the voltage and inversel as the resistance. If the voltage remains constant, what needs to be done to triple the amount of heat generated?. Galileo s telescope brought about revolutionar changes in astronom. A comparable leap in our abilit to observe the universe took place as a result of the Hubble Space Telescope. The space telescope was able to see stars and galaies whose brightness is 0 of the faintest objects observable using ground-based telescopes. Use the fact that the brightness of a point source, such as a star, varies inversel as the square of its distance from an observer to show that the space telescope was able to see about seven times farther than a ground-based telescope. Group Eercise. Begin b deciding on a product that interests the group because ou are now in charge of advertising this product. Members were told that the demand for the product varies directl as the amount spent on advertising and inversel as the price of the product. However, as more mone is spent on advertising, the price of our product rises. Under what conditions would members recommend an increased epense in advertising? Once ou ve determined what our product is, write formulas for the given conditions and eperiment with hpothetical numbers. What other factors might ou take into consideration in terms of our recommendation? How do these factor affect the demand for our product?
103 Summar, Review, and Test 67 Chapter Summar, Review, and Test Summar DEFINITIONS AND CONCEPTS. Comple Numbers a. The imaginar unit i is defined as i = -, where i = -. The set of numbers in the form a + bi is called the set of comple numbers; a is the real part and b is the imaginar part. If b = 0, the comple number is a real number. If b Z 0, the comple number is an imaginar number. Comple numbers in the form bi are called pure imaginar numbers. EXAMPLES b. Rules for adding and subtracting comple numbers are given in the bo on page 67. E., p. 67 c. To multipl comple numbers, multipl as if the are polnomials. After completing the multiplication, E., p. 68 replace i with - and simplif. d. The comple conjugate of a + bi is a - bi and vice versa. The multiplication of comple conjugates gives a real number: a + bia - bi = a + b. e. To divide comple numbers, multipl the numerator and the denominator b the comple conjugate of the denominator. f. When performing operations with square roots of negative numbers, begin b epressing all square roots in terms of i. The principal square root of -b is defined b -b = ib.. Quadratic Functions a. A quadratic function is of the form f = a + b + c, a Z 0. b. The standard form of a quadratic function is f = a - h + k, a Z 0. c. The graph of a quadratic function is a parabola. The verte is h, k b or a - A procedure for a, fa - b a bb. E., p. 7; E., p. 76; graphing a quadratic function is given in the bo on page 7. E., p. 77 d. See the bo on page 79 for minimum or maimum values of quadratic functions. E., p. 79; E., p. 80 e. A strateg for solving problems involving maimizing or minimizing quadratic functions is given in the bo on page 8.. Polnomial Functions and Their Graphs a. Polnomial Function of Degree n: f = a n n + a n - n - + Á + a + a + a 0, a n Z 0 E., p. 69 E., p. 70 g. Quadratic equations a + b + c = 0, a Z 0 with negative discriminants b - ac 6 0 have imaginar E., p. 7 solutions that are comple conjugates. E. 6, p. 8; E. 7, p. 8 b. The graphs of polnomial functions are smooth and continuous. Fig.., p. 89 c. The end behavior of the graph of a polnomial function depends on the leading term, given b the Leading Coefficient Test in the bo on page 90. E., p. 90; E., p. 90; E., p. 9 d. The values of for which f is equal to 0 are the zeros of the polnomial function f. These values are the E., p. 9; roots, or solutions, of the polnomial equation f = 0. E., p. 9 e. If - r occurs k times in a polnomial function s factorization, r is a repeated zero with multiplicit k. If k E. 6, p. 9 is even, the graph touches the -ais and turns around at r. If k is odd, the graph crosses the -ais at r. f. The Intermediate Value Theorem: If f is a polnomial function and fa and fb have opposite signs, E. 7, p. 9 there is at least one value of c between a and b for which fc = 0. g. If f is a polnomial of degree n, the graph of f has at most n - turning points. Fig.., p. 9 h. A strateg for graphing a polnomial function is given in the bo on page 9. E. 8, p. 96
104 68 Chapter Polnomial and Rational Functions DEFINITIONS AND CONCEPTS. Dividing Polnomials; Remainder and Factor Theorems a. Long division of polnomials is performed b dividing, multipling, subtracting, bringing down the net term, and repeating this process until the degree of the remainder is less than the degree of the divisor. The details are given in the bo on page 0. b. The Division Algorithm: f = dq + r. The dividend is the product of the divisor and the quotient plus the remainder. c. Snthetic division is used to divide a polnomial b - c. The details are given in the bo on page 06. EXAMPLES E., p. 0; E., p. 0; E., p. 0 E., p. 06 d. The Remainder Theorem: If a polnomial f is divided b - c, then the remainder is fc. E., p. 08 e. The Factor Theorem: If - c is a factor of a polnomial function f, then c is a zero of f and a root of E. 6, p. 09 f = 0. If c is a zero of f or a root of f = 0, then - c is a factor of f.. Zeros of Polnomial Functions a. The Rational Zero Theorem states that the possible rational zeros of a polnomial Factors of the constant term function = The theorem is stated in the bo on page. Factors of the leading coefficient. b. Number of roots: If f is a polnomial of degree n Ú, then, counting multiple roots separatel, the equation f = 0 has n roots. c. If a + bi is a root of f = 0, then a - bi is also a root. d. The Linear Factorization Theorem: An nth-degree polnomial can be epressed as the product of n linear factors. Thus, f = a n - c - c Á - c n. E., p. ; E., p. ; E., p. ; E., p. ; E., p. 6 E. 6, p. 9 e. Descartes s Rule of Signs:The number of positive real zeros of f equals the number of sign changes of f Table., p. 0; or is less than that number b an even integer. The number of negative real zeros of f applies a similar statement to f-. E. 7, p..6 Rational Functions and Their Graphs a. Rational function: f = p ; p and q are polnomial functions and q Z 0. The domain of f is the set q E., p. 6 of all real numbers ecluding values of that make q zero. b. Arrow notation is summarized in the bo on page 8. c. The line = a is a vertical asmptote of the graph of f if f increases or decreases without bound as E., p. 0 approaches a. Vertical asmptotes are identified using the location theorem in the bo on page 9. d. The line = b is a horizontal asmptote of the graph of f if f approaches b as increases or decreases E., p. without bound. Horizontal asmptotes are identified using the location theorem in the bo on page. e. Table. on page shows the graphs of f = and f = Some rational functions can be. graphed using transformations of these common graphs. E., p. f. A strateg for graphing rational functions is given in the bo on page. E., p. ; E. 6, p. 6; E. 7, p. 7 g. The graph of a rational function has a slant asmptote when the degree of the numerator is one more than the degree of the denominator. The equation of the slant asmptote is found using division and dropping the remainder term. E. 8, p. 9.7 Polnomial and Rational Inequalities a. A polnomial inequalit can be epressed as f 6 0, f 7 0, f 0, or f Ú 0, where f is a E., p. 7; polnomial function. A procedure for solving polnomial inequalities is given in the bo on page 7. E., p. 8
105 Review Eercises 69 DEFINITIONS AND CONCEPTS EXAMPLES b. A rational inequalit can be epressed as f 6 0, f 7 0, f 0, or f Ú 0, where f is a rational E., p. 0 function. The procedure for solving such inequalities begins with epressing them so that one side is zero and the other side is a single quotient. Find boundar points b setting the numerator and denominator equal to zero. Then follow a procedure similar to that for solving polnomial inequalities..8 Modeling Using Variation a. A procedure for solving variation problems is given in the lower bo on page 8. b. English Statement Equation varies directl as. = k E., p. 8 is directl proportional to. varies directl as n. = k n E., p. 9 is directl proportional to n. varies inversel as. E., p. 6; is inversel proportional to. E., p. 6 varies inversel as n. is inversel proportional to n. = k n varies jointl as and z. = kz E., p. 6 Review Eercises. In Eercises 0 perform the indicated operations and write the result in standard form i - 7-7i. ii i + i. - i i7-8i 6. + i i 9. A B i + -8 Ire Eercises, solve each quadratic equation using the quadratic formula. Epress solutions in standard form = = 0. In Eercises 6, use the verte and intercepts to sketch the graph of each quadratic function. Give the equation for the parabola s ais of smmetr. Use the graph to determine the function s domain and range.. f = f = + -. f = f = In Eercises 7 8, use the function s equation, and not its graph, to find a. the minimum or maimum value and where it occurs. b. the function s domain and its range. 7. f = f = The function models the earl growth of a oung redwood tree, f, in inches, with inches of rainfall per ear. How man inches of rainfall per ear result in maimum tree growth? What is the maimum earl growth? 0. Suppose that a quadratic function is used to model the data shown in the graph using Divorce Rate per 000 Population 6 f = U.S. Divorce Rate Year Source: National Center for Health Statistics (number of ears after 960, divorce rate per 000 population). Determine, without obtaining an actual quadratic function that models the data, the approimate coordinates of the verte for the function s graph. Describe what this means in practical terms.
106 70 Chapter Polnomial and Rational Functions. A field bordering a straight stream is to be enclosed.the side bordering the stream is not to be fenced. If 000 ards of fencing material is to be used, what are the dimensions of the largest rectangular field that can be fenced? What is the maimum area?. Among all pairs of numbers whose difference is, find a pair whose product is as small as possible. What is the minimum product?. You have 000 feet of fencing to construct si corrals, as shown in the figure. Find the dimensions that maimize the enclosed area. What is the maimum area?. The annual ield per fruit tree is fairl constant at 0 pounds per tree when the number of trees per acre is or fewer. For each additional tree over, the annual ield per tree for all trees on the acre decreases b pounds due to overcrowding. How man fruit trees should be planted per acre to maimize the annual ield for the acre? What is the maimum number of pounds of fruit per acre?. In Eercises 8, use the Leading Coefficient Test to determine the end behavior of the graph of the given polnomial function. Then use this end behavior to match the polnomial function with its graph. [The graphs are labeled (a) through (d).]. f = f = f = f = - + a. b. 0 A herd of 00 elk is introduced to a small island.the number of elk, f, after ears is modeled b the polnomial function f = Use the Leading Coefficient Test to determine the graph s end behavior to the right. What does this mean about what will eventuall happen to the elk population? In Eercises, find the zeros for each polnomial function and give the multiplicit of each zero. State whether the graph crosses the -ais, or touches the -ais and turns around, at each zero.. f = f = Show that f = - - has a real zero between and. In Eercises 9, a. Use the Leading Coefficient Test to determine the graph s end behavior. b. Determine whether the graph has -ais smmetr, origin smmetr, or neither. c. Graph the function.. f = f = - 6. f = f = f = f = - In Eercises 0, graph each polnomial function. 0. f = - +. f = c. d. 9. The polnomial function. In Eercises, divide using long division , , , + In Eercises 6, divide using snthetic division , , - 7. Given f = , use the Remainder Theorem to find f-. 8. Use snthetic division to divide f = b -. Use the result to find all zeros of f. 9. Solve the equation = 0 given that is a root. f = models the number of thefts, f, in thousands, in the United States ears after 987. Will this function be useful in modeling the number of thefts over an etended period of time? Eplain our answer.. In Eercises 0, use the Rational Zero Theorem to list all possible rational zeros for each given function. 0. f = f =
107 Review Eercises 7 In Eercises, use Descartes s Rule of Signs to determine the possible number of positive and negative real zeros for each given function... f = f = Use Descartes s Rule of Signs to eplain wh = 0 has no real roots. For Eercises 6, a. List all possible rational roots or rational zeros. b. Use Descartes s Rule of Signs to determine the possible number of positive and negative real roots or real zeros. c. Use snthetic division to test the possible rational roots or zeros and find an actual root or zero. d. Use the quotient from part (c) to find all the remaining zeros or roots.. f = f = = = = = 0 6. f = In Eercises 6 6, find an nth-degree polnomial function with real coefficients satisfing the given conditions. If ou are using a graphing utilit, graph the function and verif the real zeros and the given function value. 6. n = ; and - i are zeros; f = n = ; i is a zero; - is a zero of multiplicit ; f- = 6 In Eercises 6 6, find all the zeros of each polnomial function and write the polnomial as a product of linear factors. 6. f = g = In Eercises 66 69, graphs of fifth-degree polnomial functions are shown. In each case, specif the number of real zeros and the number of imaginar zeros. Indicate whether there are an real zeros with multiplicit other than In Eercises 70 7, use transformations of f = f = to graph each rational function. 70. g = 7. h = In Eercises 7 79, find the vertical asmptotes, if an, the horizontal asmptote, if one eists, and the slant asmptote, if there is one, of the graph of each rational function. Then graph the rational function. 7. f = 7. g = r = + + h = = + - = g = f = A compan is planning to manufacture affordable graphing calculators. The fied monthl cost will be $0,000 and it will cost $ to produce each calculator. a. Write the cost function, C, of producing graphing calculators. b. Write the average cost function, C, of producing graphing calculators. c. Find and interpret C0, C00, C000, and C00,000. d. What is the horizontal asmptote for the graph of this function and what does it represent? 8. In Palo Alto, California, a government agenc ordered computer-related companies to contribute to a monetar pool to clean up underground water supplies. (The companies had stored toic chemicals in leaking underground containers.) The rational function 00 C = 00 - models the cost, C, in tens of thousands of dollars, for removing percent of the contaminants. a. Find and interpret C90 - C0. b. What is the equation for the vertical asmptote? What does this mean in terms of the variables given b the function? Eercises 8 8 involve rational functions that model the given situations. In each case, find the horizontal asmptote as : q and then describe what this means in practical terms f = the number of bass, f, after ; months in a lake that was stocked with 0 bass 7, P = the percentage, P, of people in the ; United States with ears of education who are unemploed 8. The function p = models the number of nonviolent prisoners, p, in thousands, in New York State prisons ears after 980. The function q = models the total number of prisoners, q, in thousands, in New York State prisons ears after 980. or
108 7 Chapter Polnomial and Rational Functions a. Write a function that models the fraction of nonviolent prisoners in New York State prisons ears after 980. b. What is the equation of the horizontal asmptote associated with the function in part (a)? Describe what this means about the percentage, to the nearest tenth of a percent, of nonviolent prisoners in New York State prisons over time. c. Use our equation in part (b) to eplain wh, in 998, New York State implemented a strateg where more nonviolent offenders are granted parole and more violent offenders are denied parole. 8. A jogger ran miles and then walked miles. The average velocit running was miles per hour faster than the average velocit walking. Epress the total time for running and walking, T, as a function of the average velocit walking,. 86. The area of a rectangular floor is 000 square feet. Epress the perimeter of the floor, P, as a function of the width of the rectangle,..7 In Eercises 87 9, solve each inequalit and graph the solution set on a real number line Ú Ú Use the position function st = -6t + v 0 t + s 0.8 to solve this problem. A projectile is fired verticall upward from ground level with an initial velocit of 8 feet per second. During which time period will the projectile s height eceed feet? Solve the variation problems in Eercises An electric bill varies directl as the amount of electricit used. The bill for 00 kilowatts of electricit is $98. What is the bill for 00 kilowatts of electricit? 9. The distance that a bod falls from rest is directl proportional to the square of the time of the fall. If skdivers fall feet in seconds, how far will the fall in 0 seconds? 96. The time it takes to drive a certain distance is inversel proportional to the rate of travel. If it takes hours at 0 miles per hour to drive the distance, how long will it take at 0 miles per hour? 97. The loudness of a stereo speaker, measured in decibels, varies inversel as the square of our distance from the speaker. When ou are 8 feet from the speaker, the loudness is 8 decibels. What is the loudness when ou are feet from the speaker? 98. The time required to assemble computers varies directl as the number of computers assembled and inversel as the number of workers. If 0 computers can be assembled b 6 workers in 0 hours, how long would it take workers to assemble 0 computers? 99. The volume of a pramid varies jointl as its height and the area of its base.a pramid with a height of feet and a base with an area of square feet has a volume of 7 cubic feet. Find the volume of a pramid with a height of 0 feet and a base with an area of 0 square feet. Chapter Test In Eercises, perform the indicated operations and write the result in standard form.. 6-7i + i. - i Solve and epress solutions in standard form: = - 8. In Eercises 6, use the verte and intercepts to sketch the graph of each quadratic function. Give the equation for the parabola s ais of smmetr. Use the graph to determine the function s domain and range.. f = f = Determine, without graphing, whether the quadratic function f = has a minimum value or a maimum value. Then find a. the minimum or maimum value and where it occurs. b. the function s domain and its range. 8. The function f = models the dail profit, f, in hundreds of dollars, for a compan that manufactures computers dail. How man computers should be manufactured each da to maimize profit? What is the maimum dail profit? 9. Among all pairs of numbers whose sum is, find a pair whose product is as large as possible. What is the maimum product? 0. Consider the function f = a. Use factoring to find all zeros of f. b. Use the Leading Coefficient Test and the zeros of f to graph the function.. Use end behavior to eplain wh the graph shown below cannot be the graph of f = -. Then use intercepts to eplain wh the graph cannot represent f = -.
290 Chapter 1 Functions and Graphs
 90 Chapter Functions and Graphs 7. Studies show that teting while driving is as risk as driving with a 0.08 blood alcohol level, the standard for drunk driving. The bar graph shows the number of fatalities
90 Chapter Functions and Graphs 7. Studies show that teting while driving is as risk as driving with a 0.08 blood alcohol level, the standard for drunk driving. The bar graph shows the number of fatalities
Complex Numbers. The Imaginary Unit i
 292 Chapter 2 Polynomial and Rational Functions SECTION 2.1 Complex Numbers Objectives Add and subtract complex numbers. Multiply complex numbers. Divide complex numbers. Perform operations with square
292 Chapter 2 Polynomial and Rational Functions SECTION 2.1 Complex Numbers Objectives Add and subtract complex numbers. Multiply complex numbers. Divide complex numbers. Perform operations with square
83. 31x + 2x + 9 = 3. Review Exercises. 85. Divide using synthetic division: 86. Divide: 90. Rationalize the denominator: Complex Numbers
 718 CHAPTER 10 Radicals, Radical Functions, and Rational Exponents 76. Now that I know how to solve radical equations, I can use models that are radical functions to determine the value of the independent
718 CHAPTER 10 Radicals, Radical Functions, and Rational Exponents 76. Now that I know how to solve radical equations, I can use models that are radical functions to determine the value of the independent
Ready To Go On? Skills Intervention 5-1 Using Transformations to Graph Quadratic Functions
 Read To Go On? Skills Intervention 5-1 Using Transformations to Graph Quadratic Functions Find these vocabular words in Lesson 5-1 and the Multilingual Glossar. Vocabular quadratic function parabola verte
Read To Go On? Skills Intervention 5-1 Using Transformations to Graph Quadratic Functions Find these vocabular words in Lesson 5-1 and the Multilingual Glossar. Vocabular quadratic function parabola verte
Algebra 2 Unit 2 Practice
 Algebra Unit Practice LESSON 7-1 1. Consider a rectangle that has a perimeter of 80 cm. a. Write a function A(l) that represents the area of the rectangle with length l.. A rectangle has a perimeter of
Algebra Unit Practice LESSON 7-1 1. Consider a rectangle that has a perimeter of 80 cm. a. Write a function A(l) that represents the area of the rectangle with length l.. A rectangle has a perimeter of
For Thought. 3.1 Exercises 142 CHAPTER 3 POLYNOMIAL AND RATIONAL FUNCTIONS. 1. False, the range of y = x 2 is [0, ).
 CHAPTER POLYNOMIAL AND RATIONAL FUNCTIONS For Thought. False, the range of = is [0, ).. False, the verte is the point (, ). -5 -. True. True 5. True, since b a = 6 =. 6. True, the -intercept of = ( + )
CHAPTER POLYNOMIAL AND RATIONAL FUNCTIONS For Thought. False, the range of = is [0, ).. False, the verte is the point (, ). -5 -. True. True 5. True, since b a = 6 =. 6. True, the -intercept of = ( + )
Polynomial and Rational Functions
 Name Date Chapter Polnomial and Rational Functions Section.1 Quadratic Functions Objective: In this lesson ou learned how to sketch and analze graphs of quadratic functions. Important Vocabular Define
Name Date Chapter Polnomial and Rational Functions Section.1 Quadratic Functions Objective: In this lesson ou learned how to sketch and analze graphs of quadratic functions. Important Vocabular Define
Study Guide and Intervention
 6- NAME DATE PERID Stud Guide and Intervention Graphing Quadratic Functions Graph Quadratic Functions Quadratic Function A function defined b an equation of the form f () a b c, where a 0 b Graph of a
6- NAME DATE PERID Stud Guide and Intervention Graphing Quadratic Functions Graph Quadratic Functions Quadratic Function A function defined b an equation of the form f () a b c, where a 0 b Graph of a
150. a. Clear fractions in the following equation and write in. b. For the equation you wrote in part (a), compute. The Quadratic Formula
 75 CHAPTER Quadratic Equations and Functions Preview Eercises Eercises 8 50 will help you prepare for the material covered in the net section. 8. a. Solve by factoring: 8 + - 0. b. The quadratic equation
75 CHAPTER Quadratic Equations and Functions Preview Eercises Eercises 8 50 will help you prepare for the material covered in the net section. 8. a. Solve by factoring: 8 + - 0. b. The quadratic equation
3.1 Graph Quadratic Functions
 3. Graph Quadratic Functions in Standard Form Georgia Performance Standard(s) MMA3b, MMA3c Goal p Use intervals of increase and decrease to understand average rates of change of quadratic functions. Your
3. Graph Quadratic Functions in Standard Form Georgia Performance Standard(s) MMA3b, MMA3c Goal p Use intervals of increase and decrease to understand average rates of change of quadratic functions. Your
Ch 5 Alg 2 L2 Note Sheet Key Do Activity 1 on your Ch 5 Activity Sheet.
 Ch Alg L Note Sheet Ke Do Activit 1 on our Ch Activit Sheet. Chapter : Quadratic Equations and Functions.1 Modeling Data With Quadratic Functions You had three forms for linear equations, ou will have
Ch Alg L Note Sheet Ke Do Activit 1 on our Ch Activit Sheet. Chapter : Quadratic Equations and Functions.1 Modeling Data With Quadratic Functions You had three forms for linear equations, ou will have
LESSON #24 - POWER FUNCTIONS COMMON CORE ALGEBRA II
 1 LESSON #4 - POWER FUNCTIONS COMMON CORE ALGEBRA II Before we start to analze polnomials of degree higher than two (quadratics), we first will look at ver simple functions known as power functions. The
1 LESSON #4 - POWER FUNCTIONS COMMON CORE ALGEBRA II Before we start to analze polnomials of degree higher than two (quadratics), we first will look at ver simple functions known as power functions. The
CHAPTER 2 Polynomial and Rational Functions
 CHAPTER Polnomial and Rational Functions Section. Quadratic Functions..................... 9 Section. Polnomial Functions of Higher Degree.......... Section. Real Zeros of Polnomial Functions............
CHAPTER Polnomial and Rational Functions Section. Quadratic Functions..................... 9 Section. Polnomial Functions of Higher Degree.......... Section. Real Zeros of Polnomial Functions............
LESSON #28 - POWER FUNCTIONS COMMON CORE ALGEBRA II
 1 LESSON #8 - POWER FUNCTIONS COMMON CORE ALGEBRA II Before we start to analze polnomials of degree higher than two (quadratics), we first will look at ver simple functions known as power functions. The
1 LESSON #8 - POWER FUNCTIONS COMMON CORE ALGEBRA II Before we start to analze polnomials of degree higher than two (quadratics), we first will look at ver simple functions known as power functions. The
4 B. 4 D. 4 F. 3. How can you use the graph of a quadratic equation to determine the number of real solutions of the equation?
 3.1 Solving Quadratic Equations COMMON CORE Learning Standards HSA-SSE.A. HSA-REI.B.b HSF-IF.C.8a Essential Question Essential Question How can ou use the graph of a quadratic equation to determine the
3.1 Solving Quadratic Equations COMMON CORE Learning Standards HSA-SSE.A. HSA-REI.B.b HSF-IF.C.8a Essential Question Essential Question How can ou use the graph of a quadratic equation to determine the
Unit 10 - Graphing Quadratic Functions
 Unit - Graphing Quadratic Functions PREREQUISITE SKILLS: students should be able to add, subtract and multipl polnomials students should be able to factor polnomials students should be able to identif
Unit - Graphing Quadratic Functions PREREQUISITE SKILLS: students should be able to add, subtract and multipl polnomials students should be able to factor polnomials students should be able to identif
2.1 Evaluate and Graph Polynomial
 2. Evaluate and Graph Polnomial Functions Georgia Performance Standard(s) MM3Ab, MM3Ac, MM3Ad Your Notes Goal p Evaluate and graph polnomial functions. VOCABULARY Polnomial Polnomial function Degree of
2. Evaluate and Graph Polnomial Functions Georgia Performance Standard(s) MM3Ab, MM3Ac, MM3Ad Your Notes Goal p Evaluate and graph polnomial functions. VOCABULARY Polnomial Polnomial function Degree of
MATH 115: Review for Chapter 3
 MATH : Review for Chapter Can ou use the Zero-Product Propert to solve quadratic equations b factoring? () Solve each equation b factoring. 6 7 8 + = + ( ) = 8 7p ( p ) p ( p) = = c = c = + Can ou solve
MATH : Review for Chapter Can ou use the Zero-Product Propert to solve quadratic equations b factoring? () Solve each equation b factoring. 6 7 8 + = + ( ) = 8 7p ( p ) p ( p) = = c = c = + Can ou solve
Algebra II Notes Unit Six: Polynomials Syllabus Objectives: 6.2 The student will simplify polynomial expressions.
 Algebra II Notes Unit Si: Polnomials Sllabus Objectives: 6. The student will simplif polnomial epressions. Review: Properties of Eponents (Allow students to come up with these on their own.) Let a and
Algebra II Notes Unit Si: Polnomials Sllabus Objectives: 6. The student will simplif polnomial epressions. Review: Properties of Eponents (Allow students to come up with these on their own.) Let a and
Algebra II Notes Unit Five: Quadratic Functions. Syllabus Objectives: 5.1 The student will graph quadratic functions with and without technology.
 Sllabus Objectives:.1 The student will graph quadratic functions with and without technolog. Quadratic Function: a function that can be written in the form are real numbers Parabola: the U-shaped graph
Sllabus Objectives:.1 The student will graph quadratic functions with and without technolog. Quadratic Function: a function that can be written in the form are real numbers Parabola: the U-shaped graph
Chapter 5: Quadratic Equations and Functions 5.1 Modeling Data With Quadratic Functions Quadratic Functions and Their Graphs
 Ch 5 Alg Note Sheet Ke Chapter 5: Quadratic Equations and Functions 5.1 Modeling Data With Quadratic Functions Quadratic Functions and Their Graphs Definition: Standard Form of a Quadratic Function The
Ch 5 Alg Note Sheet Ke Chapter 5: Quadratic Equations and Functions 5.1 Modeling Data With Quadratic Functions Quadratic Functions and Their Graphs Definition: Standard Form of a Quadratic Function The
f(x) = 2x 2 + 2x - 4
 4-1 Graphing Quadratic Functions What You ll Learn Scan the tet under the Now heading. List two things ou will learn about in the lesson. 1. Active Vocabular 2. New Vocabular Label each bo with the terms
4-1 Graphing Quadratic Functions What You ll Learn Scan the tet under the Now heading. List two things ou will learn about in the lesson. 1. Active Vocabular 2. New Vocabular Label each bo with the terms
3.1-Quadratic Functions & Inequalities
 3.1-Quadratic Functions & Inequalities Quadratic Functions: Quadratic functions are polnomial functions of the form also be written in the form f ( ) a( h) k. f ( ) a b c. A quadratic function ma Verte
3.1-Quadratic Functions & Inequalities Quadratic Functions: Quadratic functions are polnomial functions of the form also be written in the form f ( ) a( h) k. f ( ) a b c. A quadratic function ma Verte
Essential Question How can you use a quadratic function to model a real-life situation?
 3. TEXAS ESSENTIAL KNOWLEDGE AND SKILLS A..A A..E A..A A..B A..C Modeling with Quadratic Functions Essential Question How can ou use a quadratic function to model a real-life situation? Work with a partner.
3. TEXAS ESSENTIAL KNOWLEDGE AND SKILLS A..A A..E A..A A..B A..C Modeling with Quadratic Functions Essential Question How can ou use a quadratic function to model a real-life situation? Work with a partner.
Summary, Review, and Test
 Summar, Review, and Test 79 56. Galileo s telescope brought about revolutionar changes in astronom. A comparable leap in our abilit to observe the universe took place as a result of the Hubble Space Telescope.
Summar, Review, and Test 79 56. Galileo s telescope brought about revolutionar changes in astronom. A comparable leap in our abilit to observe the universe took place as a result of the Hubble Space Telescope.
Lesson 7.1 Polynomial Degree and Finite Differences
 Lesson 7.1 Polnomial Degree and Finite Differences 1. Identif the degree of each polnomial. a. 1 b. 0. 1. 3. 3 c. 0 16 0. Determine which of the epressions are polnomials. For each polnomial, state its
Lesson 7.1 Polnomial Degree and Finite Differences 1. Identif the degree of each polnomial. a. 1 b. 0. 1. 3. 3 c. 0 16 0. Determine which of the epressions are polnomials. For each polnomial, state its
1.5. Analyzing Graphs of Functions. The Graph of a Function. What you should learn. Why you should learn it. 54 Chapter 1 Functions and Their Graphs
 0_005.qd /7/05 8: AM Page 5 5 Chapter Functions and Their Graphs.5 Analzing Graphs of Functions What ou should learn Use the Vertical Line Test for functions. Find the zeros of functions. Determine intervals
0_005.qd /7/05 8: AM Page 5 5 Chapter Functions and Their Graphs.5 Analzing Graphs of Functions What ou should learn Use the Vertical Line Test for functions. Find the zeros of functions. Determine intervals
Math Analysis Chapter 2 Notes: Polynomial and Rational Functions
 Math Analysis Chapter Notes: Polynomial and Rational Functions Day 13: Section -1 Comple Numbers; Sections - Quadratic Functions -1: Comple Numbers After completing section -1 you should be able to do
Math Analysis Chapter Notes: Polynomial and Rational Functions Day 13: Section -1 Comple Numbers; Sections - Quadratic Functions -1: Comple Numbers After completing section -1 you should be able to do
Unit 4 Practice Problem ANSWERS
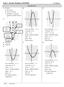 Unit Practice Problem ANSWERS SECTION.1A 1) Parabola ) a. Root, Zeros b. Ais of smmetr c. Substitute = 0 into the equation to find the value of. -int 6) 7 6 1 - - - - -1-1 1 - - - - -6-7 - ) ) Maimum )
Unit Practice Problem ANSWERS SECTION.1A 1) Parabola ) a. Root, Zeros b. Ais of smmetr c. Substitute = 0 into the equation to find the value of. -int 6) 7 6 1 - - - - -1-1 1 - - - - -6-7 - ) ) Maimum )
5.3 Polynomials and Polynomial Functions
 70 CHAPTER 5 Eponents, Polnomials, and Polnomial Functions 5. Polnomials and Polnomial Functions S Identif Term, Constant, Polnomial, Monomial, Binomial, Trinomial, and the Degree of a Term and of a Polnomial.
70 CHAPTER 5 Eponents, Polnomials, and Polnomial Functions 5. Polnomials and Polnomial Functions S Identif Term, Constant, Polnomial, Monomial, Binomial, Trinomial, and the Degree of a Term and of a Polnomial.
LESSON #42 - INVERSES OF FUNCTIONS AND FUNCTION NOTATION PART 2 COMMON CORE ALGEBRA II
 LESSON #4 - INVERSES OF FUNCTIONS AND FUNCTION NOTATION PART COMMON CORE ALGEBRA II You will recall from unit 1 that in order to find the inverse of a function, ou must switch and and solve for. Also,
LESSON #4 - INVERSES OF FUNCTIONS AND FUNCTION NOTATION PART COMMON CORE ALGEBRA II You will recall from unit 1 that in order to find the inverse of a function, ou must switch and and solve for. Also,
a. plotting points in Cartesian coordinates (Grade 9 and 10), b. using a graphing calculator such as the TI-83 Graphing Calculator,
 GRADE PRE-CALCULUS UNIT C: QUADRATIC FUNCTIONS CLASS NOTES FRAME. After linear functions, = m + b, and their graph the Quadratic Functions are the net most important equation or function. The Quadratic
GRADE PRE-CALCULUS UNIT C: QUADRATIC FUNCTIONS CLASS NOTES FRAME. After linear functions, = m + b, and their graph the Quadratic Functions are the net most important equation or function. The Quadratic
LESSON #11 - FORMS OF A LINE COMMON CORE ALGEBRA II
 LESSON # - FORMS OF A LINE COMMON CORE ALGEBRA II Linear functions come in a variet of forms. The two shown below have been introduced in Common Core Algebra I and Common Core Geometr. TWO COMMON FORMS
LESSON # - FORMS OF A LINE COMMON CORE ALGEBRA II Linear functions come in a variet of forms. The two shown below have been introduced in Common Core Algebra I and Common Core Geometr. TWO COMMON FORMS
Mini-Lecture 8.1 Solving Quadratic Equations by Completing the Square
 Mini-Lecture 8.1 Solving Quadratic Equations b Completing the Square Learning Objectives: 1. Use the square root propert to solve quadratic equations.. Solve quadratic equations b completing the square.
Mini-Lecture 8.1 Solving Quadratic Equations b Completing the Square Learning Objectives: 1. Use the square root propert to solve quadratic equations.. Solve quadratic equations b completing the square.
MATH 115: Final Exam Review. Can you find the distance between two points and the midpoint of a line segment? (1.1)
 MATH : Final Eam Review Can ou find the distance between two points and the midpoint of a line segment? (.) () Consider the points A (,) and ( 6, ) B. (a) Find the distance between A and B. (b) Find the
MATH : Final Eam Review Can ou find the distance between two points and the midpoint of a line segment? (.) () Consider the points A (,) and ( 6, ) B. (a) Find the distance between A and B. (b) Find the
Polynomial and Rational Functions
 Polnomial and Rational Functions Figure -mm film, once the standard for capturing photographic images, has been made largel obsolete b digital photograph. (credit film : modification of work b Horia Varlan;
Polnomial and Rational Functions Figure -mm film, once the standard for capturing photographic images, has been made largel obsolete b digital photograph. (credit film : modification of work b Horia Varlan;
Linear and Nonlinear Systems of Equations. The Method of Substitution. Equation 1 Equation 2. Check (2, 1) in Equation 1 and Equation 2: 2x y 5?
 3330_070.qd 96 /5/05 Chapter 7 7. 9:39 AM Page 96 Sstems of Equations and Inequalities Linear and Nonlinear Sstems of Equations What ou should learn Use the method of substitution to solve sstems of linear
3330_070.qd 96 /5/05 Chapter 7 7. 9:39 AM Page 96 Sstems of Equations and Inequalities Linear and Nonlinear Sstems of Equations What ou should learn Use the method of substitution to solve sstems of linear
Math 121. Practice Questions Chapters 2 and 3 Fall Find the other endpoint of the line segment that has the given endpoint and midpoint.
 Math 11. Practice Questions Chapters and 3 Fall 01 1. Find the other endpoint of the line segment that has the given endpoint and midpoint. Endpoint ( 7, ), Midpoint (, ). Solution: Let (, ) denote the
Math 11. Practice Questions Chapters and 3 Fall 01 1. Find the other endpoint of the line segment that has the given endpoint and midpoint. Endpoint ( 7, ), Midpoint (, ). Solution: Let (, ) denote the
LESSON #12 - FORMS OF A LINE COMMON CORE ALGEBRA II
 LESSON # - FORMS OF A LINE COMMON CORE ALGEBRA II Linear functions come in a variet of forms. The two shown below have been introduced in Common Core Algebra I and Common Core Geometr. TWO COMMON FORMS
LESSON # - FORMS OF A LINE COMMON CORE ALGEBRA II Linear functions come in a variet of forms. The two shown below have been introduced in Common Core Algebra I and Common Core Geometr. TWO COMMON FORMS
Secondary Mathematics 2 Table of Contents
 Secondar Mathematics Table of Contents Unit 1: Etending the Number Sstem Cluster 1: Etending Properties of Eponents (N.RN.1 and N.RN.)... 3 Cluster : Using Properties of Rational and Irrational Numbers
Secondar Mathematics Table of Contents Unit 1: Etending the Number Sstem Cluster 1: Etending Properties of Eponents (N.RN.1 and N.RN.)... 3 Cluster : Using Properties of Rational and Irrational Numbers
REVIEW KEY VOCABULARY REVIEW EXAMPLES AND EXERCISES
 Etra Eample. Graph.. 6. 7. (, ) (, ) REVIEW KEY VOCABULARY quadratic function, p. 6 standard form of a quadratic function, p. 6 parabola, p. 6 verte, p. 6 ais of smmetr, p. 6 minimum, maimum value, p.
Etra Eample. Graph.. 6. 7. (, ) (, ) REVIEW KEY VOCABULARY quadratic function, p. 6 standard form of a quadratic function, p. 6 parabola, p. 6 verte, p. 6 ais of smmetr, p. 6 minimum, maimum value, p.
LESSON #48 - INTEGER EXPONENTS COMMON CORE ALGEBRA II
 LESSON #8 - INTEGER EXPONENTS COMMON CORE ALGEBRA II We just finished our review of linear functions. Linear functions are those that grow b equal differences for equal intervals. In this unit we will
LESSON #8 - INTEGER EXPONENTS COMMON CORE ALGEBRA II We just finished our review of linear functions. Linear functions are those that grow b equal differences for equal intervals. In this unit we will
Polynomial Functions of Higher Degree
 SAMPLE CHAPTER. NOT FOR DISTRIBUTION. 4 Polynomial Functions of Higher Degree Polynomial functions of degree greater than 2 can be used to model data such as the annual temperature fluctuations in Daytona
SAMPLE CHAPTER. NOT FOR DISTRIBUTION. 4 Polynomial Functions of Higher Degree Polynomial functions of degree greater than 2 can be used to model data such as the annual temperature fluctuations in Daytona
Characteristics of Quadratic Functions
 . Characteristics of Quadratic Functions Essential Question What tpe of smmetr does the graph of f() = a( h) + k have and how can ou describe this smmetr? Parabolas and Smmetr Work with a partner. a. Complete
. Characteristics of Quadratic Functions Essential Question What tpe of smmetr does the graph of f() = a( h) + k have and how can ou describe this smmetr? Parabolas and Smmetr Work with a partner. a. Complete
2.3 Quadratic Functions
 88 Linear and Quadratic Functions. Quadratic Functions You ma recall studing quadratic equations in Intermediate Algebra. In this section, we review those equations in the contet of our net famil of functions:
88 Linear and Quadratic Functions. Quadratic Functions You ma recall studing quadratic equations in Intermediate Algebra. In this section, we review those equations in the contet of our net famil of functions:
2Polynomial and. Rational Functions
 Polnomial and Rational Functions A ballista was used in ancient times as a portable rock-throwing machine. Its primar function was to destro the siege weaponr of opposing forces. Skilled artiller men aimed
Polnomial and Rational Functions A ballista was used in ancient times as a portable rock-throwing machine. Its primar function was to destro the siege weaponr of opposing forces. Skilled artiller men aimed
Fair Game Review. Chapter 9. Find the square root(s) ± Find the side length of the square. 7. Simplify Simplify 63.
 Name Date Chapter 9 Find the square root(s). Fair Game Review... 9. ±. Find the side length of the square.. s. s s Area = 9 ft s Area = 0. m 7. Simplif 0. 8. Simplif. 9. Simplif 08. 0. Simplif 88. Copright
Name Date Chapter 9 Find the square root(s). Fair Game Review... 9. ±. Find the side length of the square.. s. s s Area = 9 ft s Area = 0. m 7. Simplif 0. 8. Simplif. 9. Simplif 08. 0. Simplif 88. Copright
review math0410 (1-174) and math 0320 ( ) aafinm mg
 Eam Name review math04 (1-174) and math 0320 (17-243) 03201700aafinm0424300 mg MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Simplif. 1) 7 2-3 A)
Eam Name review math04 (1-174) and math 0320 (17-243) 03201700aafinm0424300 mg MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Simplif. 1) 7 2-3 A)
Glossary. Also available at BigIdeasMath.com: multi-language glossary vocabulary flash cards. An equation that contains an absolute value expression
 Glossar This student friendl glossar is designed to be a reference for ke vocabular, properties, and mathematical terms. Several of the entries include a short eample to aid our understanding of important
Glossar This student friendl glossar is designed to be a reference for ke vocabular, properties, and mathematical terms. Several of the entries include a short eample to aid our understanding of important
Self- assessment 1010 (Intermediate Algebra)
 Self- assessment (Intermediate Algebra) If ou can work these problems using a scientific calculator, ou should have sufficient knowledge to demonstrate master of Intermediate Algebra and to succeed in
Self- assessment (Intermediate Algebra) If ou can work these problems using a scientific calculator, ou should have sufficient knowledge to demonstrate master of Intermediate Algebra and to succeed in
c) domain {x R, x 3}, range {y R}
 Answers Chapter 1 Functions 1.1 Functions, Domain, and Range 1. a) Yes, no vertical line will pass through more than one point. b) No, an vertical line between = 6 and = 6 will pass through two points..
Answers Chapter 1 Functions 1.1 Functions, Domain, and Range 1. a) Yes, no vertical line will pass through more than one point. b) No, an vertical line between = 6 and = 6 will pass through two points..
Unit 2 Notes Packet on Quadratic Functions and Factoring
 Name: Period: Unit Notes Packet on Quadratic Functions and Factoring Notes #: Graphing quadratic equations in standard form, verte form, and intercept form. A. Intro to Graphs of Quadratic Equations: a
Name: Period: Unit Notes Packet on Quadratic Functions and Factoring Notes #: Graphing quadratic equations in standard form, verte form, and intercept form. A. Intro to Graphs of Quadratic Equations: a
Mth 95 Module 4 Chapter 8 Spring Review - Solving quadratic equations using the quadratic formula
 Mth 95 Module 4 Chapter 8 Spring 04 Review - Solving quadratic equations using the quadratic formula Write the quadratic formula. The NUMBER of REAL and COMPLEX SOLUTIONS to a quadratic equation ( a b
Mth 95 Module 4 Chapter 8 Spring 04 Review - Solving quadratic equations using the quadratic formula Write the quadratic formula. The NUMBER of REAL and COMPLEX SOLUTIONS to a quadratic equation ( a b
 Eam Name algebra final eam review147 aam032020181t4highschool www.alvarezmathhelp.com MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Solve the equation.
Eam Name algebra final eam review147 aam032020181t4highschool www.alvarezmathhelp.com MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Solve the equation.
Polynomial and Rational Functions
 Polnomial and Rational Functions. Quadratic Functions and Models. Polnomial Functions of Higher Degree. Polnomial and Snthetic Division. Comple Numbers.5 Zeros of Polnomial Functions.6 Rational Functions.7
Polnomial and Rational Functions. Quadratic Functions and Models. Polnomial Functions of Higher Degree. Polnomial and Snthetic Division. Comple Numbers.5 Zeros of Polnomial Functions.6 Rational Functions.7
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
 Math 2 Stud Guide-Chapters 8 and 9 Name Date: Time: MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find all square roots of the number. ) 600 9,
Math 2 Stud Guide-Chapters 8 and 9 Name Date: Time: MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find all square roots of the number. ) 600 9,
= x. Algebra II Notes Quadratic Functions Unit Graphing Quadratic Functions. Math Background
 Algebra II Notes Quadratic Functions Unit 3.1 3. Graphing Quadratic Functions Math Background Previousl, ou Identified and graphed linear functions Applied transformations to parent functions Graphed quadratic
Algebra II Notes Quadratic Functions Unit 3.1 3. Graphing Quadratic Functions Math Background Previousl, ou Identified and graphed linear functions Applied transformations to parent functions Graphed quadratic
Additional Factoring Examples:
 Honors Algebra -3 Solving Quadratic Equations by Graphing and Factoring Learning Targets 1. I can solve quadratic equations by graphing. I can solve quadratic equations by factoring 3. I can write a quadratic
Honors Algebra -3 Solving Quadratic Equations by Graphing and Factoring Learning Targets 1. I can solve quadratic equations by graphing. I can solve quadratic equations by factoring 3. I can write a quadratic
f(x) Determine whether each function has a maximum or minimum value, and find that value. Then state the domain and range of the function.
 NAME DATE PERID 4-1 Practice Graphing Quadratic Functions Complete parts a c for each quadratic function. a. Find the -intercept, the equation of the ais of smmetr, and the -coordinate of the verte. b.
NAME DATE PERID 4-1 Practice Graphing Quadratic Functions Complete parts a c for each quadratic function. a. Find the -intercept, the equation of the ais of smmetr, and the -coordinate of the verte. b.
5. Determine the discriminant for each and describe the nature of the roots.
 4. Quadratic Equations Notes Day 1 1. Solve by factoring: a. 3 16 1 b. 3 c. 8 0 d. 9 18 0. Quadratic Formula: The roots of a quadratic equation of the form A + B + C = 0 with a 0 are given by the following
4. Quadratic Equations Notes Day 1 1. Solve by factoring: a. 3 16 1 b. 3 c. 8 0 d. 9 18 0. Quadratic Formula: The roots of a quadratic equation of the form A + B + C = 0 with a 0 are given by the following
Last modified Spring 2016
 Math 00 Final Review Questions In problems 6, perform the indicated operations and simplif if necessar.. 8 6 8. 7 6. ( i) ( 4 i) 4. (8 i). ( 9 i)( 7 i) 6. ( i)( i) In problems 7-, solve the following applications.
Math 00 Final Review Questions In problems 6, perform the indicated operations and simplif if necessar.. 8 6 8. 7 6. ( i) ( 4 i) 4. (8 i). ( 9 i)( 7 i) 6. ( i)( i) In problems 7-, solve the following applications.
QUADRATIC FUNCTIONS AND COMPLEX NUMBERS
 CHAPTER 86 5 CHAPTER TABLE F CNTENTS 5- Real Roots of a Quadratic Equation 5-2 The Quadratic Formula 5-3 The Discriminant 5-4 The Comple Numbers 5-5 perations with Comple Numbers 5-6 Comple Roots of a
CHAPTER 86 5 CHAPTER TABLE F CNTENTS 5- Real Roots of a Quadratic Equation 5-2 The Quadratic Formula 5-3 The Discriminant 5-4 The Comple Numbers 5-5 perations with Comple Numbers 5-6 Comple Roots of a
MATH 91 Final Study Package Name
 MATH 91 Final Stud Package Name Solve the sstem b the substitution method. If there is no solution or an infinite number of solutions, so state. Use set notation to epress the solution set. 1) - = 1 1)
MATH 91 Final Stud Package Name Solve the sstem b the substitution method. If there is no solution or an infinite number of solutions, so state. Use set notation to epress the solution set. 1) - = 1 1)
STANDARD FORM is a QUADRATIC FUNCTION and its graph is a PARABOLA. The domain of a quadratic function is the set of all real numbers.
 EXERCISE 2-3 Things to remember: 1. QUADRATIC FUNCTION If a, b, and c are real numbers with a 0, then the function f() = a 2 + b + c STANDARD FORM is a QUADRATIC FUNCTION and its graph is a PARABOLA. The
EXERCISE 2-3 Things to remember: 1. QUADRATIC FUNCTION If a, b, and c are real numbers with a 0, then the function f() = a 2 + b + c STANDARD FORM is a QUADRATIC FUNCTION and its graph is a PARABOLA. The
Northwest High School s Algebra 2/Honors Algebra 2
 Northwest High School s Algebra /Honors Algebra Summer Review Packet 0 DUE Frida, September, 0 Student Name This packet has been designed to help ou review various mathematical topics that will be necessar
Northwest High School s Algebra /Honors Algebra Summer Review Packet 0 DUE Frida, September, 0 Student Name This packet has been designed to help ou review various mathematical topics that will be necessar
3 Polynomial and Rational Functions
 3 Polnomial and Rational Functions 3.1 Quadratic Functions and Models 3.2 Polnomial Functions and Their Graphs 3.3 Dividing Polnomials 3.4 Real Zeros of Polnomials 3.5 Comple Zeros and the Fundamental
3 Polnomial and Rational Functions 3.1 Quadratic Functions and Models 3.2 Polnomial Functions and Their Graphs 3.3 Dividing Polnomials 3.4 Real Zeros of Polnomials 3.5 Comple Zeros and the Fundamental
math0320 FALL interactmath sections developmental mathematics sullivan 1e
 Eam final eam review 180 plus 234 TSI questions for intermediate algebra m032000 013014 NEW Name www.alvarezmathhelp.com math0320 FALL 201 1400 interactmath sections developmental mathematics sullivan
Eam final eam review 180 plus 234 TSI questions for intermediate algebra m032000 013014 NEW Name www.alvarezmathhelp.com math0320 FALL 201 1400 interactmath sections developmental mathematics sullivan
Quadratic Functions and Models
 Quadratic Functions and Models What ou should learn Analze graphs of quadratic functions. Write quadratic functions in standard form and use the results to sketch graphs of functions. Use quadratic functions
Quadratic Functions and Models What ou should learn Analze graphs of quadratic functions. Write quadratic functions in standard form and use the results to sketch graphs of functions. Use quadratic functions
Honors Pre-Calculus. Multiple Choice 1. An expression is given. Evaluate it at the given value
 Honors Pre-Calculus Multiple Choice. An epression is given. Evaluate it at the given value, (A) (B) 9 (C) 9 (D) (E). Simplif the epression. (A) + (B) (C) (D) (E) 7. Simplif the epression. (A) (B) (C) (D)
Honors Pre-Calculus Multiple Choice. An epression is given. Evaluate it at the given value, (A) (B) 9 (C) 9 (D) (E). Simplif the epression. (A) + (B) (C) (D) (E) 7. Simplif the epression. (A) (B) (C) (D)
C H A P T E R 3 Polynomial Functions
 C H A P T E R Polnomial Functions Section. Quadratic Functions and Models............. 9 Section. Polnomial Functions of Higher Degree......... Section. Polnomial and Snthetic Division............ 8 Section.
C H A P T E R Polnomial Functions Section. Quadratic Functions and Models............. 9 Section. Polnomial Functions of Higher Degree......... Section. Polnomial and Snthetic Division............ 8 Section.
One of your primary goals in mathematics should be to become a good problem solver. It helps to approach a problem with a plan.
 PROBLEM SOLVING One of our primar goals in mathematics should be to become a good problem solver. It helps to approach a problem with a plan. Step Step Step Step Understand the problem. Read the problem
PROBLEM SOLVING One of our primar goals in mathematics should be to become a good problem solver. It helps to approach a problem with a plan. Step Step Step Step Understand the problem. Read the problem
3.1 Graphing Quadratic Functions. Quadratic functions are of the form.
 3.1 Graphing Quadratic Functions A. Quadratic Functions Completing the Square Quadratic functions are of the form. 3. It is easiest to graph quadratic functions when the are in the form using transformations.
3.1 Graphing Quadratic Functions A. Quadratic Functions Completing the Square Quadratic functions are of the form. 3. It is easiest to graph quadratic functions when the are in the form using transformations.
Lesson #33 Solving Incomplete Quadratics
 Lesson # Solving Incomplete Quadratics A.A.4 Know and apply the technique of completing the square ~ 1 ~ We can also set up any quadratic to solve it in this way by completing the square, the technique
Lesson # Solving Incomplete Quadratics A.A.4 Know and apply the technique of completing the square ~ 1 ~ We can also set up any quadratic to solve it in this way by completing the square, the technique
Write each expression in terms of i : Add: (3 4i) (5 7i) (3 5) ( 4 7)i. 8 3i. Subtract: (3 4i) (5 7i) (3 4i) ( 5 7i) Find each product:
 7_Ch09_online 7// 0:7 AM Page 9-0 9-0 CHAPTER 9 Quadratic Equations SECTION 9. Comple Numbers DEFINITIONS AND CONCEPTS EXAMPLES The imaginar number i is defined as Write each epression in terms of i :
7_Ch09_online 7// 0:7 AM Page 9-0 9-0 CHAPTER 9 Quadratic Equations SECTION 9. Comple Numbers DEFINITIONS AND CONCEPTS EXAMPLES The imaginar number i is defined as Write each epression in terms of i :
x. 4. 2x 10 4x. 10 x
 CCGPS UNIT Semester 1 COORDINATE ALGEBRA Page 1 of Reasoning with Equations and Quantities Name: Date: Understand solving equations as a process of reasoning and eplain the reasoning MCC9-1.A.REI.1 Eplain
CCGPS UNIT Semester 1 COORDINATE ALGEBRA Page 1 of Reasoning with Equations and Quantities Name: Date: Understand solving equations as a process of reasoning and eplain the reasoning MCC9-1.A.REI.1 Eplain
d. 2x 3 7x 2 5x 2 2x 2 3x 1 x 2x 3 3x 2 1x 2 4x 2 6x 2 3. a. x 5 x x 2 5x 5 5x 25 b. x 4 2x 2x 2 8x 3 3x 12 c. x 6 x x 2 6x 6 6x 36
 Vertices: (.8, 5.), (.37, 3.563), (.6, 0.980), (5.373, 6.66), (.8, 7.88), (.95,.) Graph the equation for an value of P (the second graph shows the circle with P 5) and imagine increasing the value of P,
Vertices: (.8, 5.), (.37, 3.563), (.6, 0.980), (5.373, 6.66), (.8, 7.88), (.95,.) Graph the equation for an value of P (the second graph shows the circle with P 5) and imagine increasing the value of P,
P.4 Lines in the Plane
 28 CHAPTER P Prerequisites P.4 Lines in the Plane What ou ll learn about Slope of a Line Point-Slope Form Equation of a Line Slope-Intercept Form Equation of a Line Graphing Linear Equations in Two Variables
28 CHAPTER P Prerequisites P.4 Lines in the Plane What ou ll learn about Slope of a Line Point-Slope Form Equation of a Line Slope-Intercept Form Equation of a Line Graphing Linear Equations in Two Variables
8.4. If we let x denote the number of gallons pumped, then the price y in dollars can $ $1.70 $ $1.70 $ $1.70 $ $1.
 8.4 An Introduction to Functions: Linear Functions, Applications, and Models We often describe one quantit in terms of another; for eample, the growth of a plant is related to the amount of light it receives,
8.4 An Introduction to Functions: Linear Functions, Applications, and Models We often describe one quantit in terms of another; for eample, the growth of a plant is related to the amount of light it receives,
MATH 60 Review Problems for Final Exam
 MATH 60 Review Problems for Final Eam Scientific Calculators Onl - Graphing Calculators Not Allowed NO CLASS NOTES PERMITTED Evaluate the epression for the given values. m 1) m + 3 for m = 3 2) m 2 - n2
MATH 60 Review Problems for Final Eam Scientific Calculators Onl - Graphing Calculators Not Allowed NO CLASS NOTES PERMITTED Evaluate the epression for the given values. m 1) m + 3 for m = 3 2) m 2 - n2
Name Period Date. Practice FINAL EXAM Intro to Calculus (50 points) Show all work on separate sheet of paper for full credit!
 Name Period Date Practice FINAL EXAM Intro to Calculus (0 points) Show all work on separate sheet of paper for full credit! ) Evaluate the algebraic epression for the given value or values of the variable(s).
Name Period Date Practice FINAL EXAM Intro to Calculus (0 points) Show all work on separate sheet of paper for full credit! ) Evaluate the algebraic epression for the given value or values of the variable(s).
x c x c This suggests the following definition.
 110 Chapter 1 / Limits and Continuit 1.5 CONTINUITY A thrown baseball cannot vanish at some point and reappear someplace else to continue its motion. Thus, we perceive the path of the ball as an unbroken
110 Chapter 1 / Limits and Continuit 1.5 CONTINUITY A thrown baseball cannot vanish at some point and reappear someplace else to continue its motion. Thus, we perceive the path of the ball as an unbroken
Chapter 2 Polynomial, Power, and Rational Functions
 Section. Linear and Quadratic Functions and Modeling 6 Chapter Polnomial, Power, and Rational Functions Section. Linear and Quadratic Functions and Modeling Eploration. $000 per ear.. The equation will
Section. Linear and Quadratic Functions and Modeling 6 Chapter Polnomial, Power, and Rational Functions Section. Linear and Quadratic Functions and Modeling Eploration. $000 per ear.. The equation will
Vertex form of a quadratic equation
 Verte form of a quadratic equation Nikos Apostolakis Spring 017 Recall 1. Last time we looked at the graphs of quadratic equations in two variables. The upshot was that the graph of the equation: k = a(
Verte form of a quadratic equation Nikos Apostolakis Spring 017 Recall 1. Last time we looked at the graphs of quadratic equations in two variables. The upshot was that the graph of the equation: k = a(
Nonlinear Systems. No solution One solution Two solutions. Solve the system by graphing. Check your answer.
 8-10 Nonlinear Sstems CC.9-1.A.REI.7 Solve a simple sstem consisting of a linear equation and a quadratic equation in two variables algebraicall and graphicall. Objective Solve sstems of equations in two
8-10 Nonlinear Sstems CC.9-1.A.REI.7 Solve a simple sstem consisting of a linear equation and a quadratic equation in two variables algebraicall and graphicall. Objective Solve sstems of equations in two
UNCORRECTED SAMPLE PAGES. 3Quadratics. Chapter 3. Objectives
 Chapter 3 3Quadratics Objectives To recognise and sketch the graphs of quadratic polnomials. To find the ke features of the graph of a quadratic polnomial: ais intercepts, turning point and ais of smmetr.
Chapter 3 3Quadratics Objectives To recognise and sketch the graphs of quadratic polnomials. To find the ke features of the graph of a quadratic polnomial: ais intercepts, turning point and ais of smmetr.
FINAL EXAM REVIEW ITEMS Math 0312: Intermediate Algebra Name
 FINAL EXAM REVIEW ITEMS Math 0312: Intermediate Algebra Name 1) Find the SUM of the solutions of the equation. 82 + 0 = 16 Use the quadratic formula to solve the equation. (All solutions are real numbers.)
FINAL EXAM REVIEW ITEMS Math 0312: Intermediate Algebra Name 1) Find the SUM of the solutions of the equation. 82 + 0 = 16 Use the quadratic formula to solve the equation. (All solutions are real numbers.)
2 nd Semester Final Exam Review Block Date
 Algebra 1B Name nd Semester Final Eam Review Block Date Calculator NOT Allowed Graph each function. 1 (10-1) 1. (10-1). (10-1) 3. (10-1) 4. 3 Graph each function. Identif the verte, ais of smmetr, and
Algebra 1B Name nd Semester Final Eam Review Block Date Calculator NOT Allowed Graph each function. 1 (10-1) 1. (10-1). (10-1) 3. (10-1) 4. 3 Graph each function. Identif the verte, ais of smmetr, and
Chapter 13. Overview. The Quadratic Formula. Overview. The Quadratic Formula. The Quadratic Formula. Lewinter & Widulski 1. The Quadratic Formula
 Chapter 13 Overview Some More Math Before You Go The Quadratic Formula The iscriminant Multiplication of Binomials F.O.I.L. Factoring Zero factor propert Graphing Parabolas The Ais of Smmetr, Verte and
Chapter 13 Overview Some More Math Before You Go The Quadratic Formula The iscriminant Multiplication of Binomials F.O.I.L. Factoring Zero factor propert Graphing Parabolas The Ais of Smmetr, Verte and
CHAPTER 3 Polynomial Functions
 CHAPTER Polnomial Functions Section. Quadratic Functions and Models............. 7 Section. Polnomial Functions of Higher Degree......... 7 Section. Polnomial and Snthetic Division............ Section.
CHAPTER Polnomial Functions Section. Quadratic Functions and Models............. 7 Section. Polnomial Functions of Higher Degree......... 7 Section. Polnomial and Snthetic Division............ Section.
SECTION P.5. Factoring Polynomials. Objectives. Critical Thinking Exercises. Technology Exercises
 BLITMCPB.QXP.0599_48-74 2/0/02 0:4 AM Page 48 48 Chapter P Prerequisites: Fundamental Concepts of Algebra Technology Eercises 98. The common cold is caused by a rhinovirus. The polynomial -0.75 4 + + 5
BLITMCPB.QXP.0599_48-74 2/0/02 0:4 AM Page 48 48 Chapter P Prerequisites: Fundamental Concepts of Algebra Technology Eercises 98. The common cold is caused by a rhinovirus. The polynomial -0.75 4 + + 5
LESSON #1 - BASIC ALGEBRAIC PROPERTIES COMMON CORE ALGEBRA II
 1 LESSON #1 - BASIC ALGEBRAIC PROPERTIES COMMON CORE ALGEBRA II Mathematics has developed a language all to itself in order to clarif concepts and remove ambiguit from the analsis of problems. To achieve
1 LESSON #1 - BASIC ALGEBRAIC PROPERTIES COMMON CORE ALGEBRA II Mathematics has developed a language all to itself in order to clarif concepts and remove ambiguit from the analsis of problems. To achieve
Course 15 Numbers and Their Properties
 Course Numbers and Their Properties KEY Module: Objective: Rules for Eponents and Radicals To practice appling rules for eponents when the eponents are rational numbers Name: Date: Fill in the blanks.
Course Numbers and Their Properties KEY Module: Objective: Rules for Eponents and Radicals To practice appling rules for eponents when the eponents are rational numbers Name: Date: Fill in the blanks.
Unit 3. Expressions and Equations. 118 Jordan School District
 Unit 3 Epressions and Equations 118 Unit 3 Cluster 1 (A.SSE.): Interpret the Structure of Epressions Cluster 1: Interpret the structure of epressions 3.1. Recognize functions that are quadratic in nature
Unit 3 Epressions and Equations 118 Unit 3 Cluster 1 (A.SSE.): Interpret the Structure of Epressions Cluster 1: Interpret the structure of epressions 3.1. Recognize functions that are quadratic in nature
Quadratic Equations and Complex Numbers
 Quadratic Equations and Comple Numbers.1 Solving Quadratic Equations. Comple Numbers.3 Completing the Square. Using the Quadratic Formula.5 Solving Nonlinear Sstems. Quadratic Inequalities Robot-Building
Quadratic Equations and Comple Numbers.1 Solving Quadratic Equations. Comple Numbers.3 Completing the Square. Using the Quadratic Formula.5 Solving Nonlinear Sstems. Quadratic Inequalities Robot-Building
x Radical Sign: Radicand: the number beneath the radical sign
 Sllabus Objective: 9.4 The student will solve quadratic equations using graphic and algebraic techniques to include the quadratic formula, square roots, factoring, completing the square, and graphing.
Sllabus Objective: 9.4 The student will solve quadratic equations using graphic and algebraic techniques to include the quadratic formula, square roots, factoring, completing the square, and graphing.
Chapter 8 Vocabulary Check
 28 CHAPTER 8 Quadratic Equations and Functions d. What is the level of methane emissions for that ear? (Use our rounded answer from part (c).) (Round this answer to 2 decimals places.) Use a graphing calculator
28 CHAPTER 8 Quadratic Equations and Functions d. What is the level of methane emissions for that ear? (Use our rounded answer from part (c).) (Round this answer to 2 decimals places.) Use a graphing calculator
8.1 Exponents and Roots
 Section 8. Eponents and Roots 75 8. Eponents and Roots Before defining the net famil of functions, the eponential functions, we will need to discuss eponent notation in detail. As we shall see, eponents
Section 8. Eponents and Roots 75 8. Eponents and Roots Before defining the net famil of functions, the eponential functions, we will need to discuss eponent notation in detail. As we shall see, eponents
Copyrighted by Gabriel Tang B.Ed., B.Sc. Page 1.
 Chapter : Linear and Quadratic Functions Chapter : Linear and Quadratic Functions -: Points and Lines Sstem of Linear Equations: - two or more linear equations on the same coordinate grid. Solution of
Chapter : Linear and Quadratic Functions Chapter : Linear and Quadratic Functions -: Points and Lines Sstem of Linear Equations: - two or more linear equations on the same coordinate grid. Solution of
MATH 021 UNIT 1 HOMEWORK ASSIGNMENTS
 MATH 01 UNIT 1 HOMEWORK ASSIGNMENTS General Instructions You will notice that most of the homework assignments for a section have more than one part. Usuall, the part (A) questions ask for eplanations,
MATH 01 UNIT 1 HOMEWORK ASSIGNMENTS General Instructions You will notice that most of the homework assignments for a section have more than one part. Usuall, the part (A) questions ask for eplanations,
Unit 3 NOTES Honors Common Core Math 2 1. Day 1: Properties of Exponents
 Unit NOTES Honors Common Core Math Da : Properties of Eponents Warm-Up: Before we begin toda s lesson, how much do ou remember about eponents? Use epanded form to write the rules for the eponents. OBJECTIVE
Unit NOTES Honors Common Core Math Da : Properties of Eponents Warm-Up: Before we begin toda s lesson, how much do ou remember about eponents? Use epanded form to write the rules for the eponents. OBJECTIVE
