Statistical Methods in Particle Physics
|
|
|
- Samson Watson
- 5 years ago
- Views:
Transcription
1 Statistical Methods in Particle Physics Lecture 10 December 17, 01 Silvia Masciocchi, GSI Darmstadt Winter Semester 01 / 13
2 Method of least squares The method of least squares is a standard approach to the approximate solution of overdetermined systems, i.e., sets of equations in which there are more equations than unknowns. "Least squares" means that the overall solution minimizes the sum of the squares of the errors made in solving every single equation. The most important application is in data fitting. The best fit in the least-squares sense minimizes the sum of squared residuals, a residual being the difference between an observed value and the fitted value provided by a model. Least squares corresponds to the maximum likelihood criterion if the experimental errors have a normal distribution and can also be derived as a method of moments estimator. Statistical Methods, Lecture 10, December 17, 01
3 A bit of history Carl Friedrich Gauss is credited with developing the fundamentals of the basis for least-squares analysis in 1795 at the age of eighteen. Legendre was the first to publish the method, however. An early demonstration of the strength of Gauss's method came when it was used to predict the future location of the newly discovered asteroid Ceres. On January 1, 1801, the Italian astronomer Giuseppe Piazzi discovered Ceres and was able to track its path for 40 days before it was lost in the glare of the sun. Based on this data, astronomers desired to determine the location of Ceres after it emerged from behind the sun without solving the complicated Kepler's nonlinear equations of planetary motion. The only predictions that successfully allowed Hungarian astronomer Franz Xaver von Zach to relocate Ceres were those performed by the 4-year-old Gauss using least-squares analysis. Statistical Methods, Lecture 10, December 17, 01 3
4 Data fitting The method of least squares is often used to fit a function through a set of points by minimizing the distance between the points and the fitted function by the least squares But we need to define well the conditions under which the method can be applied Statistical Methods, Lecture 10, December 17, 01 4
5 Connection with the ML - 1 In many situations a measured value y can be regarded as a Gaussian random variable centered about the quantity's true value λ. This follows from the central theorem as long as the total error (i.e. the deviation from the true value) is the sum of a large number of small contributions. Extend to N measurements: N measurements yi related to another variable xi, assumed to be known without error The yi are N independent Gaussian random variables Each value yi has a different unknown mean λi, and..... a different but known variance σi Statistical Methods, Lecture 10, December 17, 01 5
6 Connection with the ML - The N measurements of yi can be equivalently regarded as a single measurement of an N-dimensional random vector, for which the joint pdf is the product of N Gaussians: 1 N g y 1,.., y N ; 1,.., N,,.., = N 1 i=1 i exp y i i i Suppose further that the true value is given as a function of x: λ = λ(x;θ) which depends on unknown parameters θ = (θ1,θ,..., θm) The aim of the method of least squares is to estimate the parameters θ. In addition, the method allows for a simple evaluation of the goodness-of-fit of the hypothesized function. Statistical Methods, Lecture 10, December 17, 01 6
7 Connection with the ML - 3 Illustration: x,.., x known 1 N Gaussian random variables yi E[yi] = λi = λ(xi;θ) V[yi] = σi known GOAL: Estimate the parameters θ fit the curve through the points Statistical Methods, Lecture 10, December 17, 01 7
8 Connection to the ML - 4 We take the logarithm of the joint pdf and drop the additive terms that do not depend on the parameters θ: We get the log-likelihood function N y x ; 1 i i log L = i i=1 This is maximized by finding the values of the parameters θ that minimize the quantity = N y x ; i i i=1 i Namely the quadratic sum of the differences between measured and hypothesized values, weighted by the inverse of the variances. This is the basis of the method of least squares. Statistical Methods, Lecture 10, December 17, 01 8
9 Definition of LS estimators If the N measurements are not independent but described by an Ndimensional Gaussian pdf with known covariance matrix V but unknown mean values, the joint pdf is: The log-likelihood is obtained (again dropping terms not depending on the parameters) as Statistical Methods, Lecture 10, December 17, 01 9
10 Definition of LS estimators - The log-likelihood is maximized by minimizing the quantity which reduces to the case on page 8 if the covariance matrix (and hence its inverse) are diagonal (and the variables are independent) The parameters which minimize the are called the least square (LS) estimators 1,..., m The minimization is most often done numerically. Example: program MINUIT (in ROOT) Statistical Methods, Lecture 10, December 17, 01 10
11 Example of a LS fit (polynomial) Fit a polynomial of order p: 0th order: 1 parameter 1st order: parameters 4th order: 5 parameters Statistical Methods, Lecture 10, December 17, 01 11
12 Linear least squares fit LS has particularly simple properties of the and of the LS estimators, for the case where λ(x;θ) is a linear function of the parameters θ m x ; = j=1 a j x j where the aj(x) are ANY linearly independent functions of x (they are just linearly independent from each other, i.e. one cannot be expressed as a linear combination of the others). For this case, when we calculate the variance, we obtain that is quadratic in θ and it follows that = 1 = min 1 Statistical Methods, Lecture 10, December 17, 01 1
13 Variance of least squares estimators = 1 = min 1 this yields the contours in parameter space whose tangents are at i± i corresponding to a one standard deviation departure from the LS estimates Example: polynomial fit, 0th order 1-parameter fit Obtain the variance: Statistical Methods, Lecture 10, December 17, 01 13
14 Two parameter LS fit 1st order polynomial fit, parameters (line with non-zero slope) Tangent lines, Angle of ellipse correlation (same as for ML) 0 1 Statistical Methods, Lecture 10, December 17, 01 14
15 Confidence region e d n mi e R r = 1 = min 1 this yields the contours in parameter space whose tangents are at i± i corresponding to a one standard deviation departure from the LS estimates If the function λ(x;θ) is NOT linear in the parameters, then the contour defined above is not in general elliptical, and one can no longer obtain the standard deviations from the tangents. It defines a region in parameter space, however, which can be interpreted as CONFIDENCE REGION, the size of which reflects the statistical uncertainty of the fitted parameters Next lecture!!! Statistical Methods, Lecture 10, December 17, 01 15
16 Five parameter LS fit 4th order polynomial fit, 5 parameters Curve goes through all points min = 0 Number of parameters = number of points The value of min reflects the level of agreement between data and hypothesis use as goodness-of-fit test statistics Statistical Methods, Lecture 10, December 17, 01 16
17 Goodness-of-fit with least squares The value of the X at its minimum is a measure of the level of agreement between the data and the fitted curve: min N = y i x i ; i=1 i It can therefore be employed as a goodness-of-fit statistic to test the hypothesized functional form λ(x;θ). We can show that if the hypothesis is correct, then the statistic t = min follows the chi-square pdf: f t ;nd = 1 n / 1 t / t e nd / d nd / where the number of degrees of freedom is: nd = number of data points number of fitted parameters Statistical Methods, Lecture 10, December 17, 01 17
18 Goodness-of-fit with least squares - The chi-square pdf has an expectation value equal to the number of degrees of freedom, so if min nd or min /nd 1 the fit is 'good'. Or more precisely: If min min /nd 1 all is as expected If /nd 1 then the fit is better than expected given the size of the measurement errors. This is not bad in the sense of providing evidence against the hypothesis, but it is usually grounds to check that the errors σi have not been overestimated or are not correlated If min /nd 1 then there is some reason to doubt the hypothesis Statistical Methods, Lecture 10, December 17, 01 18
19 Goodness-of-fit with least squares - 3 The chi-square pdf has an expectation value equal to the number of degrees of freedom, so if min nd the fit is 'good'. More generally, find the p-value: p = This is the probability of obtaining a higher, if the hypothesis is correct. min min f t ;nd dt as high as the one we got, or E.g. for the previous example with 1st order polynomial (straight line): min = 3.99 nd = 5 = 3 p = 0.63 That is: if the true function λ(x) were a straight line and if the experiment were repeated many times, each time yielding values for the parameters and the X, then one would expect... Statistical Methods, Lecture 10, December 17, 01 19
20 Goodness-of-fit with least squares - 4 the X values to be worse (i.e. higher) than the one actually obtained in 6.3% of the cases. Whereas for the 0th order polynomial (horizontal line) min = 45.5 nd = 5 1 = 4 9 p = 3.1x10 This hypothesis can be safely ruled out!!! Statistical Methods, Lecture 10, December 17, 01 0
21 Goodness-of-fit vs statistical errors Keep in mind the distinction between having SMALL STATISTICAL ERRORS and having a GOOD (small) X. The statistical errors are related to the change in X when the parameters are varied away from their fitted values, and not to the absolute value of X itself. The standard deviation of an estimator is a measure of how widely estimates would be distributed if the experiment were to be repeated many times. If the function form of the hypothesis is incorrect, however, then the estimate can still differ significantly from the true value. That is, if the form of the hypothesis is incorrect, then a small standard deviation is not sufficient to imply a small uncertainty in the estimate of the parameter. Statistical Methods, Lecture 10, December 17, 01 1
22 Goodness-of-fit vs statistical errors Example: horizontal line fit First case: page 16 0 =.66 ± 0.13 min = 45.5 Now keep x and the errors, move the data points wrt previous example New fit: 0 =.84 ± 0.13 min = 4.48 The variance is the same as before, but now the chi-square is good!! Statistical Methods, Lecture 10, December 17, 01
23 Least squares with binned data Suppose we have n observations of a random variable x from which one makes a histogram with N bins. Let yi be the number of entries in bin i, and f(x;θ) be a hypothesized pdf for which one would like to estimate the parameters θ = (θ1,.., θm). The number of entries predicted in bin i is: x max i i = E[y i ] = n x min where x i min i f x ; dx = npi max and x i are the bin limits and pi(θ) is the probability to have an entry in bin i. Statistical Methods, Lecture 10, December 17, 01 3
24 Least squares with binned data The parameters θ are found by minimizing the quantity: = N y i i i=1 i where σi=v[yi], here not known a priori. When the mean number of entries in each bin is small compared to the total number of entries, the contents of each bin are approximately Poisson distributed. The variance is therefore equal to the mean. In place of the true variance take either i = i LS method i = y i Modified LS method MLS sometimes easier computationally, but min no longer follows the chi-square pdf (or is undefined) if some bins have few or no entries. Statistical Methods, Lecture 10, December 17, 01 4
25 LS with binned data: normalization Appreciate the detail: f(x;θ) is a pdf and therefore normalized to 1. The function which is fitted to the histogram is λi(θ). Often, instead of using the observed total number of entries n to obtain λ i (see page 3), an additional adjustable parameter ν is introduced as normalization factor. The predicted number of entries in the bin i then becomes: x max i i, = x min i f x ; dx = pi ν is fitted along with θ. This might lead to an incorrect estimate of the total number of entries. Statistical Methods, Lecture 10, December 17, 01 5
26 LS with binned data: normalization is a bad estimator for n! Take the formula on the page before, take the derivative of X with respect to ν to 0, and we find: Since one expects a contribution to X on the order of 1 per bin, the relative error in the number of entries is typically N/n too high (LS) or N/n too low (MLS). If one takes as a rule of thumb that each bin should have at least five entries, one could have an (unnecessary) error in the normalization of 10-0%. general preference of maximum likelihood for histogram fitting Statistical Methods, Lecture 10, December 17, 01 6
27 LS with binned data: normalization Statistical Methods, Lecture 10, December 17, 01 7
28 Using LS to combine measurements Combine measurements of the same quantity: Suppose that a quantity of unknown true value λ has been measured N times (e.g. in N independent experiments) yielding independent values yi and estimated errors (standard deviations) σi for i = 1,.., N. Since the true value is the same for all the measurements, the value λ is a constant, i.e. the function λ(x) is a constant, and thus the variable x does not actually appear in the problem. yi = result of measurement i, i = 1,.., N σi = V[yi], assume known λ = true value (plays role of θ) For uncorrelated yi, minimize: = N y i i=1 i Statistical Methods, Lecture 10, December 17, 01 8
29 Using LS to combine measurements Set = 0 and solve to get the LS estimator for N = Variance: = V [ ] i=1 yi / i N 1/ j=1 j Weighted average 1 N i=1 1/ i The variance of the weighted average is smaller than any of the variances of the individual measurements. Furthermore, if one of the measured yi has a much smaller variance than the rest, then this measurement will dominate both in the value and variance of the weighted average. Statistical Methods, Lecture 10, December 17, 01 9
30 Using LS to combine measurements Generalization to the case where the measurements are not independent. This would occur, for example, if they are based at least in part on the same data. Covariance matrix: cov[yi, yj] = Vij. Minimize: LS has zero bias, minimum variance (Gauss-Markov theorem) Statistical Methods, Lecture 10, December 17, 01 30
31 Example: averaging two correlated measurements Suppose we have y1 and y, two measurements with the covariance matrix: 1 1 V = 1 where = V 1 / 1 is the correlation coefficient. The inverse covariance matrix is given by: V 1 1/ 1 / 1 1 = 1 / 1 1/ Statistical Methods, Lecture 10, December 17, 01 31
32 Example: averaging two correlated measurements Using the formulas on page 30, we determine the weighted average: = w y 1 1 w y with w = The variance is found to be: = V [ ] = Statistical Methods, Lecture 10, December 17, 01 3
33 Example: averaging two correlated measurements The change in the inverse variance due to the second measurement y is = This is always greater than or equal to zero, which is to say that the second measurement always helps to decrease σ, or at least it never hurts. If 1 / w 0!!! the weighted average does not lie between y1 and y!!!?? Cannot happen is correlation due to common data. But possible for shared random effect. Very unreliable if e.g., 1, incorrect Statistical Methods, Lecture 10, December 17, 01 33
34 Example We measure the length of an object with rulers made of different substances, so that the thermal expansion coefficients are different. Suppose both rulers have been calibrated to give accurate results at a temperature T0, but at any other temperature, a corrected estimate y of the true (unknown) length λ must be obtained using: y i = L i c i T T 0 i refers to ruler 1 or, Li is the uncorrected measurement, ci is the expansion coefficient, and T is the temperature, which must be measured. We will treat the measured temperature as a random variable with standard deviation σt, and we assume that T is the same for the measurements, i.e. they are carried out together. The uncorrected Li are treated as random variables, with standard deviation σli. Assume that ci, σli and σt are known. Statistical Methods, Lecture 10, December 17, 01 34
35 Example - Formulas Goal: determine the weighted average of y1 and y. We need their covariance matrix: Variances of the corrected measurements: = V [ y ] = c i i L i T i Diagonal term: if the measurements are unbiased is: E[ y i ] =, E[T ] = T true true (unknown) temperature E[Li ] = c i T true T 0 E[ T ] = T T true E[Li,L j ] = ij L i Therefore: cov [ y 1, y ] = V 1 = E[ y 1 y ] = c1 c T Statistical Methods, Lecture 10, December 17, 01 35
36 Example - Formulas The correlation coefficient is: V 1 = = 1 c1 c T L c1 T L c T 1 The weighted average is thus: = L c c 1 c T y 1 L c 1 c 1 c T y 1 L L c 1 c T 1 If σt is very small, then ρ goes to 0 and will lie between y1 and y. If σli are very small and σt is large, the weight becomes negative! In the extreme of ρ=1, the weighted average becomes: = c 1 c y1 y c 1 c c 1 c Statistical Methods, Lecture 10, December 17, 01 36
37 Example - Illustration The diagonal bands represent the possible values of the corrected length yi, given measured lengths Li, as a function of the temperature Suppose Li known very accurately, and yet y1 and y differ by quite a bit THEN the only available explanation is that the true temperature must be different from the measured value T!!!! The weighted average is thus pulled towards the point where the bands of y1(t) and y(t) cross. Statistical Methods, Lecture 10, December 17, 01 37
38 Example - Comments Always question the averaging of correlated quantities! The correlation here stems from the fact that the individual measurements are based in part on a common measurement, here the temperature, which itself is a random quantity. Averages of highly correlated quantities should be treated with caution, since a small error in the covariance matrix for the individual measurements can lead to a large error in the average, as well as an incorrect estimation of its variance. This is particularly true if the magnitudes of correlated uncertainties are overestimated. T In the example, if the correction to the temperature T = T turns out to be large compared to σt, then this means that our assumptions about the measurements are probably INCORRECT! This is reflected in a high min value, and a small p-value. Statistical Methods, Lecture 10, December 17, 01 38
39 Example More comments Here we would have to revise the model, perhaps reevaluating all standard deviations, or the relation between the measured and the corrected lengths. The correct conclusion is this example, would be that because of the large X the two measurements y1 and y are incompatible, and the average is therefore not reliable. Comments about under- and over-estimation of errors, PULLS Statistical Methods, Lecture 10, December 17, 01 39
40 ALICE data analysis January 14: ALICE master class at GSI 11:00 first arrival at GSI (registration at entrance) VISIT of GSI 1:00 lunch 13:00 introduction and analysis of ALICE data Please send to With subject 'SMIPP at GSI' With your full name, personal ID number, and the arrival time Statistical Methods, Lecture 10, December 17, 01 40
41 The next lectures January 7, 1, 8 + February 4 Statistical errors, confidence intervals and limits Higgs case Statistical and systematic errors Unfolding of distributions Don't forget to give me suggestions if you would like some topic to be discussed!!!! Statistical Methods, Lecture 10, December 17, 01 41
Lecture 3. G. Cowan. Lecture 3 page 1. Lectures on Statistical Data Analysis
 Lecture 3 1 Probability (90 min.) Definition, Bayes theorem, probability densities and their properties, catalogue of pdfs, Monte Carlo 2 Statistical tests (90 min.) general concepts, test statistics,
Lecture 3 1 Probability (90 min.) Definition, Bayes theorem, probability densities and their properties, catalogue of pdfs, Monte Carlo 2 Statistical tests (90 min.) general concepts, test statistics,
Statistical Methods in Particle Physics
 Statistical Methods in Particle Physics Lecture 11 January 7, 2013 Silvia Masciocchi, GSI Darmstadt s.masciocchi@gsi.de Winter Semester 2012 / 13 Outline How to communicate the statistical uncertainty
Statistical Methods in Particle Physics Lecture 11 January 7, 2013 Silvia Masciocchi, GSI Darmstadt s.masciocchi@gsi.de Winter Semester 2012 / 13 Outline How to communicate the statistical uncertainty
Statistical Data Analysis Stat 3: p-values, parameter estimation
 Statistical Data Analysis Stat 3: p-values, parameter estimation London Postgraduate Lectures on Particle Physics; University of London MSci course PH4515 Glen Cowan Physics Department Royal Holloway,
Statistical Data Analysis Stat 3: p-values, parameter estimation London Postgraduate Lectures on Particle Physics; University of London MSci course PH4515 Glen Cowan Physics Department Royal Holloway,
Modern Methods of Data Analysis - WS 07/08
 Modern Methods of Data Analysis Lecture VII (26.11.07) Contents: Maximum Likelihood (II) Exercise: Quality of Estimators Assume hight of students is Gaussian distributed. You measure the size of N students.
Modern Methods of Data Analysis Lecture VII (26.11.07) Contents: Maximum Likelihood (II) Exercise: Quality of Estimators Assume hight of students is Gaussian distributed. You measure the size of N students.
* Tuesday 17 January :30-16:30 (2 hours) Recored on ESSE3 General introduction to the course.
 Name of the course Statistical methods and data analysis Audience The course is intended for students of the first or second year of the Graduate School in Materials Engineering. The aim of the course
Name of the course Statistical methods and data analysis Audience The course is intended for students of the first or second year of the Graduate School in Materials Engineering. The aim of the course
Statistics for Data Analysis. Niklaus Berger. PSI Practical Course Physics Institute, University of Heidelberg
 Statistics for Data Analysis PSI Practical Course 2014 Niklaus Berger Physics Institute, University of Heidelberg Overview You are going to perform a data analysis: Compare measured distributions to theoretical
Statistics for Data Analysis PSI Practical Course 2014 Niklaus Berger Physics Institute, University of Heidelberg Overview You are going to perform a data analysis: Compare measured distributions to theoretical
Physics 403. Segev BenZvi. Propagation of Uncertainties. Department of Physics and Astronomy University of Rochester
 Physics 403 Propagation of Uncertainties Segev BenZvi Department of Physics and Astronomy University of Rochester Table of Contents 1 Maximum Likelihood and Minimum Least Squares Uncertainty Intervals
Physics 403 Propagation of Uncertainties Segev BenZvi Department of Physics and Astronomy University of Rochester Table of Contents 1 Maximum Likelihood and Minimum Least Squares Uncertainty Intervals
Modern Methods of Data Analysis - WS 07/08
 Modern Methods of Data Analysis Lecture VIc (19.11.07) Contents: Maximum Likelihood Fit Maximum Likelihood (I) Assume N measurements of a random variable Assume them to be independent and distributed according
Modern Methods of Data Analysis Lecture VIc (19.11.07) Contents: Maximum Likelihood Fit Maximum Likelihood (I) Assume N measurements of a random variable Assume them to be independent and distributed according
Statistics. Lent Term 2015 Prof. Mark Thomson. 2: The Gaussian Limit
 Statistics Lent Term 2015 Prof. Mark Thomson Lecture 2 : The Gaussian Limit Prof. M.A. Thomson Lent Term 2015 29 Lecture Lecture Lecture Lecture 1: Back to basics Introduction, Probability distribution
Statistics Lent Term 2015 Prof. Mark Thomson Lecture 2 : The Gaussian Limit Prof. M.A. Thomson Lent Term 2015 29 Lecture Lecture Lecture Lecture 1: Back to basics Introduction, Probability distribution
Physics 403. Segev BenZvi. Parameter Estimation, Correlations, and Error Bars. Department of Physics and Astronomy University of Rochester
 Physics 403 Parameter Estimation, Correlations, and Error Bars Segev BenZvi Department of Physics and Astronomy University of Rochester Table of Contents 1 Review of Last Class Best Estimates and Reliability
Physics 403 Parameter Estimation, Correlations, and Error Bars Segev BenZvi Department of Physics and Astronomy University of Rochester Table of Contents 1 Review of Last Class Best Estimates and Reliability
Statistical Methods in Particle Physics
 Statistical Methods in Particle Physics Lecture 3 October 29, 2012 Silvia Masciocchi, GSI Darmstadt s.masciocchi@gsi.de Winter Semester 2012 / 13 Outline Reminder: Probability density function Cumulative
Statistical Methods in Particle Physics Lecture 3 October 29, 2012 Silvia Masciocchi, GSI Darmstadt s.masciocchi@gsi.de Winter Semester 2012 / 13 Outline Reminder: Probability density function Cumulative
Systematic uncertainties in statistical data analysis for particle physics. DESY Seminar Hamburg, 31 March, 2009
 Systematic uncertainties in statistical data analysis for particle physics DESY Seminar Hamburg, 31 March, 2009 Glen Cowan Physics Department Royal Holloway, University of London g.cowan@rhul.ac.uk www.pp.rhul.ac.uk/~cowan
Systematic uncertainties in statistical data analysis for particle physics DESY Seminar Hamburg, 31 March, 2009 Glen Cowan Physics Department Royal Holloway, University of London g.cowan@rhul.ac.uk www.pp.rhul.ac.uk/~cowan
Non-linear least squares
 Non-linear least squares Concept of non-linear least squares We have extensively studied linear least squares or linear regression. We see that there is a unique regression line that can be determined
Non-linear least squares Concept of non-linear least squares We have extensively studied linear least squares or linear regression. We see that there is a unique regression line that can be determined
Brandon C. Kelly (Harvard Smithsonian Center for Astrophysics)
 Brandon C. Kelly (Harvard Smithsonian Center for Astrophysics) Probability quantifies randomness and uncertainty How do I estimate the normalization and logarithmic slope of a X ray continuum, assuming
Brandon C. Kelly (Harvard Smithsonian Center for Astrophysics) Probability quantifies randomness and uncertainty How do I estimate the normalization and logarithmic slope of a X ray continuum, assuming
The Common Factor Model. Measurement Methods Lecture 15 Chapter 9
 The Common Factor Model Measurement Methods Lecture 15 Chapter 9 Today s Class Common Factor Model Multiple factors with a single test ML Estimation Methods New fit indices because of ML Estimation method
The Common Factor Model Measurement Methods Lecture 15 Chapter 9 Today s Class Common Factor Model Multiple factors with a single test ML Estimation Methods New fit indices because of ML Estimation method
Introduction to Error Analysis
 Introduction to Error Analysis Part 1: the Basics Andrei Gritsan based on lectures by Petar Maksimović February 1, 2010 Overview Definitions Reporting results and rounding Accuracy vs precision systematic
Introduction to Error Analysis Part 1: the Basics Andrei Gritsan based on lectures by Petar Maksimović February 1, 2010 Overview Definitions Reporting results and rounding Accuracy vs precision systematic
Introduction to Statistics and Error Analysis II
 Introduction to Statistics and Error Analysis II Physics116C, 4/14/06 D. Pellett References: Data Reduction and Error Analysis for the Physical Sciences by Bevington and Robinson Particle Data Group notes
Introduction to Statistics and Error Analysis II Physics116C, 4/14/06 D. Pellett References: Data Reduction and Error Analysis for the Physical Sciences by Bevington and Robinson Particle Data Group notes
Statistics and Data Analysis
 Statistics and Data Analysis The Crash Course Physics 226, Fall 2013 "There are three kinds of lies: lies, damned lies, and statistics. Mark Twain, allegedly after Benjamin Disraeli Statistics and Data
Statistics and Data Analysis The Crash Course Physics 226, Fall 2013 "There are three kinds of lies: lies, damned lies, and statistics. Mark Twain, allegedly after Benjamin Disraeli Statistics and Data
STATISTICS OF OBSERVATIONS & SAMPLING THEORY. Parent Distributions
 ASTR 511/O Connell Lec 6 1 STATISTICS OF OBSERVATIONS & SAMPLING THEORY References: Bevington Data Reduction & Error Analysis for the Physical Sciences LLM: Appendix B Warning: the introductory literature
ASTR 511/O Connell Lec 6 1 STATISTICS OF OBSERVATIONS & SAMPLING THEORY References: Bevington Data Reduction & Error Analysis for the Physical Sciences LLM: Appendix B Warning: the introductory literature
LECTURE NOTES FYS 4550/FYS EXPERIMENTAL HIGH ENERGY PHYSICS AUTUMN 2013 PART I A. STRANDLIE GJØVIK UNIVERSITY COLLEGE AND UNIVERSITY OF OSLO
 LECTURE NOTES FYS 4550/FYS9550 - EXPERIMENTAL HIGH ENERGY PHYSICS AUTUMN 2013 PART I PROBABILITY AND STATISTICS A. STRANDLIE GJØVIK UNIVERSITY COLLEGE AND UNIVERSITY OF OSLO Before embarking on the concept
LECTURE NOTES FYS 4550/FYS9550 - EXPERIMENTAL HIGH ENERGY PHYSICS AUTUMN 2013 PART I PROBABILITY AND STATISTICS A. STRANDLIE GJØVIK UNIVERSITY COLLEGE AND UNIVERSITY OF OSLO Before embarking on the concept
Negative binomial distribution and multiplicities in p p( p) collisions
 Negative binomial distribution and multiplicities in p p( p) collisions Institute of Theoretical Physics University of Wroc law Zakopane June 12, 2011 Summary s are performed for the hypothesis that charged-particle
Negative binomial distribution and multiplicities in p p( p) collisions Institute of Theoretical Physics University of Wroc law Zakopane June 12, 2011 Summary s are performed for the hypothesis that charged-particle
Measurement And Uncertainty
 Measurement And Uncertainty Based on Guidelines for Evaluating and Expressing the Uncertainty of NIST Measurement Results, NIST Technical Note 1297, 1994 Edition PHYS 407 1 Measurement approximates or
Measurement And Uncertainty Based on Guidelines for Evaluating and Expressing the Uncertainty of NIST Measurement Results, NIST Technical Note 1297, 1994 Edition PHYS 407 1 Measurement approximates or
Introduction to Simple Linear Regression
 Introduction to Simple Linear Regression Yang Feng http://www.stat.columbia.edu/~yangfeng Yang Feng (Columbia University) Introduction to Simple Linear Regression 1 / 68 About me Faculty in the Department
Introduction to Simple Linear Regression Yang Feng http://www.stat.columbia.edu/~yangfeng Yang Feng (Columbia University) Introduction to Simple Linear Regression 1 / 68 About me Faculty in the Department
32. STATISTICS. 32. Statistics 1
 32. STATISTICS 32. Statistics 1 Revised April 1998 by F. James (CERN); February 2000 by R. Cousins (UCLA); October 2001, October 2003, and August 2005 by G. Cowan (RHUL). This chapter gives an overview
32. STATISTICS 32. Statistics 1 Revised April 1998 by F. James (CERN); February 2000 by R. Cousins (UCLA); October 2001, October 2003, and August 2005 by G. Cowan (RHUL). This chapter gives an overview
Statistical Methods for Astronomy
 Statistical Methods for Astronomy Probability (Lecture 1) Statistics (Lecture 2) Why do we need statistics? Useful Statistics Definitions Error Analysis Probability distributions Error Propagation Binomial
Statistical Methods for Astronomy Probability (Lecture 1) Statistics (Lecture 2) Why do we need statistics? Useful Statistics Definitions Error Analysis Probability distributions Error Propagation Binomial
Modern Methods of Data Analysis - WS 07/08
 Modern Methods of Data Analysis Lecture VIa (19.11.07) Contents: Uncertainties (II): Re: error propagation Correlated uncertainties Systematic uncertainties Re: Error Propagation (I) x = Vi,j and µi known
Modern Methods of Data Analysis Lecture VIa (19.11.07) Contents: Uncertainties (II): Re: error propagation Correlated uncertainties Systematic uncertainties Re: Error Propagation (I) x = Vi,j and µi known
A6523 Modeling, Inference, and Mining Jim Cordes, Cornell University
 A6523 Modeling, Inference, and Mining Jim Cordes, Cornell University Lecture 19 Modeling Topics plan: Modeling (linear/non- linear least squares) Bayesian inference Bayesian approaches to spectral esbmabon;
A6523 Modeling, Inference, and Mining Jim Cordes, Cornell University Lecture 19 Modeling Topics plan: Modeling (linear/non- linear least squares) Bayesian inference Bayesian approaches to spectral esbmabon;
32. STATISTICS. 32. Statistics 1
 32. STATISTICS 32. Statistics 1 Revised September 2007 by G. Cowan (RHUL). This chapter gives an overview of statistical methods used in High Energy Physics. In statistics, we are interested in using a
32. STATISTICS 32. Statistics 1 Revised September 2007 by G. Cowan (RHUL). This chapter gives an overview of statistical methods used in High Energy Physics. In statistics, we are interested in using a
Statistics. Lecture 2 August 7, 2000 Frank Porter Caltech. The Fundamentals; Point Estimation. Maximum Likelihood, Least Squares and All That
 Statistics Lecture 2 August 7, 2000 Frank Porter Caltech The plan for these lectures: The Fundamentals; Point Estimation Maximum Likelihood, Least Squares and All That What is a Confidence Interval? Interval
Statistics Lecture 2 August 7, 2000 Frank Porter Caltech The plan for these lectures: The Fundamentals; Point Estimation Maximum Likelihood, Least Squares and All That What is a Confidence Interval? Interval
Robot Mapping. Least Squares. Cyrill Stachniss
 Robot Mapping Least Squares Cyrill Stachniss 1 Three Main SLAM Paradigms Kalman filter Particle filter Graphbased least squares approach to SLAM 2 Least Squares in General Approach for computing a solution
Robot Mapping Least Squares Cyrill Stachniss 1 Three Main SLAM Paradigms Kalman filter Particle filter Graphbased least squares approach to SLAM 2 Least Squares in General Approach for computing a solution
9 Correlation and Regression
 9 Correlation and Regression SW, Chapter 12. Suppose we select n = 10 persons from the population of college seniors who plan to take the MCAT exam. Each takes the test, is coached, and then retakes the
9 Correlation and Regression SW, Chapter 12. Suppose we select n = 10 persons from the population of college seniors who plan to take the MCAT exam. Each takes the test, is coached, and then retakes the
Day By Day Notes for MATH 385/585 Fall 2013
 Day By Day Notes for MATH 385/585 Fall 2013 Day 1 Activity: Go over syllabus. Take roll. Guess some lines. Review course objectives: To model linear relationships, interpret the model estimates, and explore
Day By Day Notes for MATH 385/585 Fall 2013 Day 1 Activity: Go over syllabus. Take roll. Guess some lines. Review course objectives: To model linear relationships, interpret the model estimates, and explore
Lectures on Simple Linear Regression Stat 431, Summer 2012
 Lectures on Simple Linear Regression Stat 43, Summer 0 Hyunseung Kang July 6-8, 0 Last Updated: July 8, 0 :59PM Introduction Previously, we have been investigating various properties of the population
Lectures on Simple Linear Regression Stat 43, Summer 0 Hyunseung Kang July 6-8, 0 Last Updated: July 8, 0 :59PM Introduction Previously, we have been investigating various properties of the population
Statistical methods and data analysis
 Statistical methods and data analysis Teacher Stefano Siboni Aim The aim of the course is to illustrate the basic mathematical tools for the analysis and modelling of experimental data, particularly concerning
Statistical methods and data analysis Teacher Stefano Siboni Aim The aim of the course is to illustrate the basic mathematical tools for the analysis and modelling of experimental data, particularly concerning
Part IB Statistics. Theorems with proof. Based on lectures by D. Spiegelhalter Notes taken by Dexter Chua. Lent 2015
 Part IB Statistics Theorems with proof Based on lectures by D. Spiegelhalter Notes taken by Dexter Chua Lent 2015 These notes are not endorsed by the lecturers, and I have modified them (often significantly)
Part IB Statistics Theorems with proof Based on lectures by D. Spiegelhalter Notes taken by Dexter Chua Lent 2015 These notes are not endorsed by the lecturers, and I have modified them (often significantly)
Statistical Distribution Assumptions of General Linear Models
 Statistical Distribution Assumptions of General Linear Models Applied Multilevel Models for Cross Sectional Data Lecture 4 ICPSR Summer Workshop University of Colorado Boulder Lecture 4: Statistical Distributions
Statistical Distribution Assumptions of General Linear Models Applied Multilevel Models for Cross Sectional Data Lecture 4 ICPSR Summer Workshop University of Colorado Boulder Lecture 4: Statistical Distributions
Robustness and Distribution Assumptions
 Chapter 1 Robustness and Distribution Assumptions 1.1 Introduction In statistics, one often works with model assumptions, i.e., one assumes that data follow a certain model. Then one makes use of methodology
Chapter 1 Robustness and Distribution Assumptions 1.1 Introduction In statistics, one often works with model assumptions, i.e., one assumes that data follow a certain model. Then one makes use of methodology
Lecture 3: Multiple Regression
 Lecture 3: Multiple Regression R.G. Pierse 1 The General Linear Model Suppose that we have k explanatory variables Y i = β 1 + β X i + β 3 X 3i + + β k X ki + u i, i = 1,, n (1.1) or Y i = β j X ji + u
Lecture 3: Multiple Regression R.G. Pierse 1 The General Linear Model Suppose that we have k explanatory variables Y i = β 1 + β X i + β 3 X 3i + + β k X ki + u i, i = 1,, n (1.1) or Y i = β j X ji + u
[y i α βx i ] 2 (2) Q = i=1
![[y i α βx i ] 2 (2) Q = i=1 [y i α βx i ] 2 (2) Q = i=1](/thumbs/75/72005858.jpg) Least squares fits This section has no probability in it. There are no random variables. We are given n points (x i, y i ) and want to find the equation of the line that best fits them. We take the equation
Least squares fits This section has no probability in it. There are no random variables. We are given n points (x i, y i ) and want to find the equation of the line that best fits them. We take the equation
Lecture 3 - Least Squares
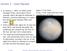 Lecture 3 - Least Squares In January 1, 1801, an Italian monk pages 1,2 are from Giuseppe Piazzi, discovered a faint, http://www.keplersdiscovery. nomadic object through his telescope in com/asteroid.html
Lecture 3 - Least Squares In January 1, 1801, an Italian monk pages 1,2 are from Giuseppe Piazzi, discovered a faint, http://www.keplersdiscovery. nomadic object through his telescope in com/asteroid.html
Economics 620, Lecture 2: Regression Mechanics (Simple Regression)
 1 Economics 620, Lecture 2: Regression Mechanics (Simple Regression) Observed variables: y i ; x i i = 1; :::; n Hypothesized (model): Ey i = + x i or y i = + x i + (y i Ey i ) ; renaming we get: y i =
1 Economics 620, Lecture 2: Regression Mechanics (Simple Regression) Observed variables: y i ; x i i = 1; :::; n Hypothesized (model): Ey i = + x i or y i = + x i + (y i Ey i ) ; renaming we get: y i =
FYST17 Lecture 8 Statistics and hypothesis testing. Thanks to T. Petersen, S. Maschiocci, G. Cowan, L. Lyons
 FYST17 Lecture 8 Statistics and hypothesis testing Thanks to T. Petersen, S. Maschiocci, G. Cowan, L. Lyons 1 Plan for today: Introduction to concepts The Gaussian distribution Likelihood functions Hypothesis
FYST17 Lecture 8 Statistics and hypothesis testing Thanks to T. Petersen, S. Maschiocci, G. Cowan, L. Lyons 1 Plan for today: Introduction to concepts The Gaussian distribution Likelihood functions Hypothesis
Chapter 5 continued. Chapter 5 sections
 Chapter 5 sections Discrete univariate distributions: 5.2 Bernoulli and Binomial distributions Just skim 5.3 Hypergeometric distributions 5.4 Poisson distributions Just skim 5.5 Negative Binomial distributions
Chapter 5 sections Discrete univariate distributions: 5.2 Bernoulli and Binomial distributions Just skim 5.3 Hypergeometric distributions 5.4 Poisson distributions Just skim 5.5 Negative Binomial distributions
Lecture 3 - Least Squares
 Lecture 3 - Least Squares In January 1, 1801, an Italian monk pages 1,2 are from Giuseppe Piazzi, discovered a faint, http://www.keplersdiscovery. nomadic object through his telescope in com/asteroid.html
Lecture 3 - Least Squares In January 1, 1801, an Italian monk pages 1,2 are from Giuseppe Piazzi, discovered a faint, http://www.keplersdiscovery. nomadic object through his telescope in com/asteroid.html
Review. December 4 th, Review
 December 4 th, 2017 Att. Final exam: Course evaluation Friday, 12/14/2018, 10:30am 12:30pm Gore Hall 115 Overview Week 2 Week 4 Week 7 Week 10 Week 12 Chapter 6: Statistics and Sampling Distributions Chapter
December 4 th, 2017 Att. Final exam: Course evaluation Friday, 12/14/2018, 10:30am 12:30pm Gore Hall 115 Overview Week 2 Week 4 Week 7 Week 10 Week 12 Chapter 6: Statistics and Sampling Distributions Chapter
Physics 509: Propagating Systematic Uncertainties. Scott Oser Lecture #12
 Physics 509: Propagating Systematic Uncertainties Scott Oser Lecture #1 1 Additive offset model Suppose we take N measurements from a distribution, and wish to estimate the true mean of the underlying
Physics 509: Propagating Systematic Uncertainties Scott Oser Lecture #1 1 Additive offset model Suppose we take N measurements from a distribution, and wish to estimate the true mean of the underlying
401 Review. 6. Power analysis for one/two-sample hypothesis tests and for correlation analysis.
 401 Review Major topics of the course 1. Univariate analysis 2. Bivariate analysis 3. Simple linear regression 4. Linear algebra 5. Multiple regression analysis Major analysis methods 1. Graphical analysis
401 Review Major topics of the course 1. Univariate analysis 2. Bivariate analysis 3. Simple linear regression 4. Linear algebra 5. Multiple regression analysis Major analysis methods 1. Graphical analysis
Regression Estimation - Least Squares and Maximum Likelihood. Dr. Frank Wood
 Regression Estimation - Least Squares and Maximum Likelihood Dr. Frank Wood Least Squares Max(min)imization Function to minimize w.r.t. β 0, β 1 Q = n (Y i (β 0 + β 1 X i )) 2 i=1 Minimize this by maximizing
Regression Estimation - Least Squares and Maximum Likelihood Dr. Frank Wood Least Squares Max(min)imization Function to minimize w.r.t. β 0, β 1 Q = n (Y i (β 0 + β 1 X i )) 2 i=1 Minimize this by maximizing
Physics 509: Error Propagation, and the Meaning of Error Bars. Scott Oser Lecture #10
 Physics 509: Error Propagation, and the Meaning of Error Bars Scott Oser Lecture #10 1 What is an error bar? Someone hands you a plot like this. What do the error bars indicate? Answer: you can never be
Physics 509: Error Propagation, and the Meaning of Error Bars Scott Oser Lecture #10 1 What is an error bar? Someone hands you a plot like this. What do the error bars indicate? Answer: you can never be
Sampling distribution of GLM regression coefficients
 Sampling distribution of GLM regression coefficients Patrick Breheny February 5 Patrick Breheny BST 760: Advanced Regression 1/20 Introduction So far, we ve discussed the basic properties of the score,
Sampling distribution of GLM regression coefficients Patrick Breheny February 5 Patrick Breheny BST 760: Advanced Regression 1/20 Introduction So far, we ve discussed the basic properties of the score,
Lecture 5. G. Cowan Lectures on Statistical Data Analysis Lecture 5 page 1
 Lecture 5 1 Probability (90 min.) Definition, Bayes theorem, probability densities and their properties, catalogue of pdfs, Monte Carlo 2 Statistical tests (90 min.) general concepts, test statistics,
Lecture 5 1 Probability (90 min.) Definition, Bayes theorem, probability densities and their properties, catalogue of pdfs, Monte Carlo 2 Statistical tests (90 min.) general concepts, test statistics,
p(z)
 Chapter Statistics. Introduction This lecture is a quick review of basic statistical concepts; probabilities, mean, variance, covariance, correlation, linear regression, probability density functions and
Chapter Statistics. Introduction This lecture is a quick review of basic statistical concepts; probabilities, mean, variance, covariance, correlation, linear regression, probability density functions and
Physics 509: Bootstrap and Robust Parameter Estimation
 Physics 509: Bootstrap and Robust Parameter Estimation Scott Oser Lecture #20 Physics 509 1 Nonparametric parameter estimation Question: what error estimate should you assign to the slope and intercept
Physics 509: Bootstrap and Robust Parameter Estimation Scott Oser Lecture #20 Physics 509 1 Nonparametric parameter estimation Question: what error estimate should you assign to the slope and intercept
Qualifying Exam CS 661: System Simulation Summer 2013 Prof. Marvin K. Nakayama
 Qualifying Exam CS 661: System Simulation Summer 2013 Prof. Marvin K. Nakayama Instructions This exam has 7 pages in total, numbered 1 to 7. Make sure your exam has all the pages. This exam will be 2 hours
Qualifying Exam CS 661: System Simulation Summer 2013 Prof. Marvin K. Nakayama Instructions This exam has 7 pages in total, numbered 1 to 7. Make sure your exam has all the pages. This exam will be 2 hours
ISQS 5349 Spring 2013 Final Exam
 ISQS 5349 Spring 2013 Final Exam Name: General Instructions: Closed books, notes, no electronic devices. Points (out of 200) are in parentheses. Put written answers on separate paper; multiple choices
ISQS 5349 Spring 2013 Final Exam Name: General Instructions: Closed books, notes, no electronic devices. Points (out of 200) are in parentheses. Put written answers on separate paper; multiple choices
Statistical Methods for Particle Physics Lecture 1: parameter estimation, statistical tests
 Statistical Methods for Particle Physics Lecture 1: parameter estimation, statistical tests http://benasque.org/2018tae/cgi-bin/talks/allprint.pl TAE 2018 Benasque, Spain 3-15 Sept 2018 Glen Cowan Physics
Statistical Methods for Particle Physics Lecture 1: parameter estimation, statistical tests http://benasque.org/2018tae/cgi-bin/talks/allprint.pl TAE 2018 Benasque, Spain 3-15 Sept 2018 Glen Cowan Physics
MS&E 226: Small Data. Lecture 11: Maximum likelihood (v2) Ramesh Johari
 MS&E 226: Small Data Lecture 11: Maximum likelihood (v2) Ramesh Johari ramesh.johari@stanford.edu 1 / 18 The likelihood function 2 / 18 Estimating the parameter This lecture develops the methodology behind
MS&E 226: Small Data Lecture 11: Maximum likelihood (v2) Ramesh Johari ramesh.johari@stanford.edu 1 / 18 The likelihood function 2 / 18 Estimating the parameter This lecture develops the methodology behind
Lecture 34: Properties of the LSE
 Lecture 34: Properties of the LSE The following results explain why the LSE is popular. Gauss-Markov Theorem Assume a general linear model previously described: Y = Xβ + E with assumption A2, i.e., Var(E
Lecture 34: Properties of the LSE The following results explain why the LSE is popular. Gauss-Markov Theorem Assume a general linear model previously described: Y = Xβ + E with assumption A2, i.e., Var(E
Hypothesis testing:power, test statistic CMS:
 Hypothesis testing:power, test statistic The more sensitive the test, the better it can discriminate between the null and the alternative hypothesis, quantitatively, maximal power In order to achieve this
Hypothesis testing:power, test statistic The more sensitive the test, the better it can discriminate between the null and the alternative hypothesis, quantitatively, maximal power In order to achieve this
Chapter 1 Linear Regression with One Predictor
 STAT 525 FALL 2018 Chapter 1 Linear Regression with One Predictor Professor Min Zhang Goals of Regression Analysis Serve three purposes Describes an association between X and Y In some applications, the
STAT 525 FALL 2018 Chapter 1 Linear Regression with One Predictor Professor Min Zhang Goals of Regression Analysis Serve three purposes Describes an association between X and Y In some applications, the
Statistical Models with Uncertain Error Parameters (G. Cowan, arxiv: )
 Statistical Models with Uncertain Error Parameters (G. Cowan, arxiv:1809.05778) Workshop on Advanced Statistics for Physics Discovery aspd.stat.unipd.it Department of Statistical Sciences, University of
Statistical Models with Uncertain Error Parameters (G. Cowan, arxiv:1809.05778) Workshop on Advanced Statistics for Physics Discovery aspd.stat.unipd.it Department of Statistical Sciences, University of
For more information about how to cite these materials visit
 Author(s): Kerby Shedden, Ph.D., 2010 License: Unless otherwise noted, this material is made available under the terms of the Creative Commons Attribution Share Alike 3.0 License: http://creativecommons.org/licenses/by-sa/3.0/
Author(s): Kerby Shedden, Ph.D., 2010 License: Unless otherwise noted, this material is made available under the terms of the Creative Commons Attribution Share Alike 3.0 License: http://creativecommons.org/licenses/by-sa/3.0/
First Year Examination Department of Statistics, University of Florida
 First Year Examination Department of Statistics, University of Florida August 20, 2009, 8:00 am - 2:00 noon Instructions:. You have four hours to answer questions in this examination. 2. You must show
First Year Examination Department of Statistics, University of Florida August 20, 2009, 8:00 am - 2:00 noon Instructions:. You have four hours to answer questions in this examination. 2. You must show
M2S2 Statistical Modelling
 UNIVERSITY OF LONDON BSc and MSci EXAMINATIONS (MATHEMATICS) May-June 2006 This paper is also taken for the relevant examination for the Associateship. M2S2 Statistical Modelling Date: Wednesday, 17th
UNIVERSITY OF LONDON BSc and MSci EXAMINATIONS (MATHEMATICS) May-June 2006 This paper is also taken for the relevant examination for the Associateship. M2S2 Statistical Modelling Date: Wednesday, 17th
The Gaussian distribution
 The Gaussian distribution Probability density function: A continuous probability density function, px), satisfies the following properties:. The probability that x is between two points a and b b P a
The Gaussian distribution Probability density function: A continuous probability density function, px), satisfies the following properties:. The probability that x is between two points a and b b P a
Summer School in Statistics for Astronomers V June 1 - June 6, Regression. Mosuk Chow Statistics Department Penn State University.
 Summer School in Statistics for Astronomers V June 1 - June 6, 2009 Regression Mosuk Chow Statistics Department Penn State University. Adapted from notes prepared by RL Karandikar Mean and variance Recall
Summer School in Statistics for Astronomers V June 1 - June 6, 2009 Regression Mosuk Chow Statistics Department Penn State University. Adapted from notes prepared by RL Karandikar Mean and variance Recall
Statistical Methods in Particle Physics
 Statistical Methods in Particle Physics Introduction October 15, 2012 Silvia Masciocchi, GSI Darmstadt s.masciocchi@gsi.de Niklaus Berger, University of Heidelberg nberger@physi.uni-heidelberg.de Winter
Statistical Methods in Particle Physics Introduction October 15, 2012 Silvia Masciocchi, GSI Darmstadt s.masciocchi@gsi.de Niklaus Berger, University of Heidelberg nberger@physi.uni-heidelberg.de Winter
statistical sense, from the distributions of the xs. The model may now be generalized to the case of k regressors:
 Wooldridge, Introductory Econometrics, d ed. Chapter 3: Multiple regression analysis: Estimation In multiple regression analysis, we extend the simple (two-variable) regression model to consider the possibility
Wooldridge, Introductory Econometrics, d ed. Chapter 3: Multiple regression analysis: Estimation In multiple regression analysis, we extend the simple (two-variable) regression model to consider the possibility
arxiv:hep-ex/ v1 2 Jun 2000
 MPI H - V7-000 May 3, 000 Averaging Measurements with Hidden Correlations and Asymmetric Errors Michael Schmelling / MPI for Nuclear Physics Postfach 03980, D-6909 Heidelberg arxiv:hep-ex/0006004v Jun
MPI H - V7-000 May 3, 000 Averaging Measurements with Hidden Correlations and Asymmetric Errors Michael Schmelling / MPI for Nuclear Physics Postfach 03980, D-6909 Heidelberg arxiv:hep-ex/0006004v Jun
Lecture 2: Linear Models. Bruce Walsh lecture notes Seattle SISG -Mixed Model Course version 23 June 2011
 Lecture 2: Linear Models Bruce Walsh lecture notes Seattle SISG -Mixed Model Course version 23 June 2011 1 Quick Review of the Major Points The general linear model can be written as y = X! + e y = vector
Lecture 2: Linear Models Bruce Walsh lecture notes Seattle SISG -Mixed Model Course version 23 June 2011 1 Quick Review of the Major Points The general linear model can be written as y = X! + e y = vector
EC212: Introduction to Econometrics Review Materials (Wooldridge, Appendix)
 1 EC212: Introduction to Econometrics Review Materials (Wooldridge, Appendix) Taisuke Otsu London School of Economics Summer 2018 A.1. Summation operator (Wooldridge, App. A.1) 2 3 Summation operator For
1 EC212: Introduction to Econometrics Review Materials (Wooldridge, Appendix) Taisuke Otsu London School of Economics Summer 2018 A.1. Summation operator (Wooldridge, App. A.1) 2 3 Summation operator For
Correlation 1. December 4, HMS, 2017, v1.1
 Correlation 1 December 4, 2017 1 HMS, 2017, v1.1 Chapter References Diez: Chapter 7 Navidi, Chapter 7 I don t expect you to learn the proofs what will follow. Chapter References 2 Correlation The sample
Correlation 1 December 4, 2017 1 HMS, 2017, v1.1 Chapter References Diez: Chapter 7 Navidi, Chapter 7 I don t expect you to learn the proofs what will follow. Chapter References 2 Correlation The sample
EEL 5544 Noise in Linear Systems Lecture 30. X (s) = E [ e sx] f X (x)e sx dx. Moments can be found from the Laplace transform as
![EEL 5544 Noise in Linear Systems Lecture 30. X (s) = E [ e sx] f X (x)e sx dx. Moments can be found from the Laplace transform as EEL 5544 Noise in Linear Systems Lecture 30. X (s) = E [ e sx] f X (x)e sx dx. Moments can be found from the Laplace transform as](/thumbs/85/92409620.jpg) L30-1 EEL 5544 Noise in Linear Systems Lecture 30 OTHER TRANSFORMS For a continuous, nonnegative RV X, the Laplace transform of X is X (s) = E [ e sx] = 0 f X (x)e sx dx. For a nonnegative RV, the Laplace
L30-1 EEL 5544 Noise in Linear Systems Lecture 30 OTHER TRANSFORMS For a continuous, nonnegative RV X, the Laplace transform of X is X (s) = E [ e sx] = 0 f X (x)e sx dx. For a nonnegative RV, the Laplace
Regression Models - Introduction
 Regression Models - Introduction In regression models there are two types of variables that are studied: A dependent variable, Y, also called response variable. It is modeled as random. An independent
Regression Models - Introduction In regression models there are two types of variables that are studied: A dependent variable, Y, also called response variable. It is modeled as random. An independent
1. The Multivariate Classical Linear Regression Model
 Business School, Brunel University MSc. EC550/5509 Modelling Financial Decisions and Markets/Introduction to Quantitative Methods Prof. Menelaos Karanasos (Room SS69, Tel. 08956584) Lecture Notes 5. The
Business School, Brunel University MSc. EC550/5509 Modelling Financial Decisions and Markets/Introduction to Quantitative Methods Prof. Menelaos Karanasos (Room SS69, Tel. 08956584) Lecture Notes 5. The
Applied Econometrics (QEM)
 Applied Econometrics (QEM) based on Prinicples of Econometrics Jakub Mućk Department of Quantitative Economics Jakub Mućk Applied Econometrics (QEM) Meeting #3 1 / 42 Outline 1 2 3 t-test P-value Linear
Applied Econometrics (QEM) based on Prinicples of Econometrics Jakub Mućk Department of Quantitative Economics Jakub Mućk Applied Econometrics (QEM) Meeting #3 1 / 42 Outline 1 2 3 t-test P-value Linear
Regression Estimation Least Squares and Maximum Likelihood
 Regression Estimation Least Squares and Maximum Likelihood Dr. Frank Wood Frank Wood, fwood@stat.columbia.edu Linear Regression Models Lecture 3, Slide 1 Least Squares Max(min)imization Function to minimize
Regression Estimation Least Squares and Maximum Likelihood Dr. Frank Wood Frank Wood, fwood@stat.columbia.edu Linear Regression Models Lecture 3, Slide 1 Least Squares Max(min)imization Function to minimize
Experiment 2. F r e e F a l l
 Suggested Reading for this Lab Experiment F r e e F a l l Taylor, Section.6, and standard deviation rule in Taylor handout. Review Chapters 3 & 4, Read Sections 8.1-8.6. You will also need some procedures
Suggested Reading for this Lab Experiment F r e e F a l l Taylor, Section.6, and standard deviation rule in Taylor handout. Review Chapters 3 & 4, Read Sections 8.1-8.6. You will also need some procedures
Estimation Theory. as Θ = (Θ 1,Θ 2,...,Θ m ) T. An estimator
 Estimation Theory Estimation theory deals with finding numerical values of interesting parameters from given set of data. We start with formulating a family of models that could describe how the data were
Estimation Theory Estimation theory deals with finding numerical values of interesting parameters from given set of data. We start with formulating a family of models that could describe how the data were
Recall the Basics of Hypothesis Testing
 Recall the Basics of Hypothesis Testing The level of significance α, (size of test) is defined as the probability of X falling in w (rejecting H 0 ) when H 0 is true: P(X w H 0 ) = α. H 0 TRUE H 1 TRUE
Recall the Basics of Hypothesis Testing The level of significance α, (size of test) is defined as the probability of X falling in w (rejecting H 0 ) when H 0 is true: P(X w H 0 ) = α. H 0 TRUE H 1 TRUE
Estimation theory. Parametric estimation. Properties of estimators. Minimum variance estimator. Cramer-Rao bound. Maximum likelihood estimators
 Estimation theory Parametric estimation Properties of estimators Minimum variance estimator Cramer-Rao bound Maximum likelihood estimators Confidence intervals Bayesian estimation 1 Random Variables Let
Estimation theory Parametric estimation Properties of estimators Minimum variance estimator Cramer-Rao bound Maximum likelihood estimators Confidence intervals Bayesian estimation 1 Random Variables Let
Linear Regression Linear Regression with Shrinkage
 Linear Regression Linear Regression ith Shrinkage Introduction Regression means predicting a continuous (usually scalar) output y from a vector of continuous inputs (features) x. Example: Predicting vehicle
Linear Regression Linear Regression ith Shrinkage Introduction Regression means predicting a continuous (usually scalar) output y from a vector of continuous inputs (features) x. Example: Predicting vehicle
Typing Equations in MS Word 2010
 CM3215 Fundamentals of Chemical Engineering Laboratory Typing Equations in MS Word 2010 https://www.youtube.com/watch?v=cenp9mehtmy Professor Faith Morrison Department of Chemical Engineering Michigan
CM3215 Fundamentals of Chemical Engineering Laboratory Typing Equations in MS Word 2010 https://www.youtube.com/watch?v=cenp9mehtmy Professor Faith Morrison Department of Chemical Engineering Michigan
32. STATISTICS. 32. Statistics 1
 32. STATISTICS 32. Statistics 1 Revised September 2009 by G. Cowan (RHUL). This chapter gives an overview of statistical methods used in high-energy physics. In statistics, we are interested in using a
32. STATISTICS 32. Statistics 1 Revised September 2009 by G. Cowan (RHUL). This chapter gives an overview of statistical methods used in high-energy physics. In statistics, we are interested in using a
Linear Regression Linear Regression with Shrinkage
 Linear Regression Linear Regression ith Shrinkage Introduction Regression means predicting a continuous (usually scalar) output y from a vector of continuous inputs (features) x. Example: Predicting vehicle
Linear Regression Linear Regression ith Shrinkage Introduction Regression means predicting a continuous (usually scalar) output y from a vector of continuous inputs (features) x. Example: Predicting vehicle
Lecture 2. G. Cowan Lectures on Statistical Data Analysis Lecture 2 page 1
 Lecture 2 1 Probability (90 min.) Definition, Bayes theorem, probability densities and their properties, catalogue of pdfs, Monte Carlo 2 Statistical tests (90 min.) general concepts, test statistics,
Lecture 2 1 Probability (90 min.) Definition, Bayes theorem, probability densities and their properties, catalogue of pdfs, Monte Carlo 2 Statistical tests (90 min.) general concepts, test statistics,
9. Model Selection. statistical models. overview of model selection. information criteria. goodness-of-fit measures
 FE661 - Statistical Methods for Financial Engineering 9. Model Selection Jitkomut Songsiri statistical models overview of model selection information criteria goodness-of-fit measures 9-1 Statistical models
FE661 - Statistical Methods for Financial Engineering 9. Model Selection Jitkomut Songsiri statistical models overview of model selection information criteria goodness-of-fit measures 9-1 Statistical models
Unit 10: Simple Linear Regression and Correlation
 Unit 10: Simple Linear Regression and Correlation Statistics 571: Statistical Methods Ramón V. León 6/28/2004 Unit 10 - Stat 571 - Ramón V. León 1 Introductory Remarks Regression analysis is a method for
Unit 10: Simple Linear Regression and Correlation Statistics 571: Statistical Methods Ramón V. León 6/28/2004 Unit 10 - Stat 571 - Ramón V. León 1 Introductory Remarks Regression analysis is a method for
Intelligent Embedded Systems Uncertainty, Information and Learning Mechanisms (Part 1)
 Advanced Research Intelligent Embedded Systems Uncertainty, Information and Learning Mechanisms (Part 1) Intelligence for Embedded Systems Ph. D. and Master Course Manuel Roveri Politecnico di Milano,
Advanced Research Intelligent Embedded Systems Uncertainty, Information and Learning Mechanisms (Part 1) Intelligence for Embedded Systems Ph. D. and Master Course Manuel Roveri Politecnico di Milano,
Lecture 5: Moment Generating Functions
 Lecture 5: Moment Generating Functions IB Paper 7: Probability and Statistics Carl Edward Rasmussen Department of Engineering, University of Cambridge February 28th, 2018 Rasmussen (CUED) Lecture 5: Moment
Lecture 5: Moment Generating Functions IB Paper 7: Probability and Statistics Carl Edward Rasmussen Department of Engineering, University of Cambridge February 28th, 2018 Rasmussen (CUED) Lecture 5: Moment
Data Analysis I. Dr Martin Hendry, Dept of Physics and Astronomy University of Glasgow, UK. 10 lectures, beginning October 2006
 Astronomical p( y x, I) p( x, I) p ( x y, I) = p( y, I) Data Analysis I Dr Martin Hendry, Dept of Physics and Astronomy University of Glasgow, UK 10 lectures, beginning October 2006 4. Monte Carlo Methods
Astronomical p( y x, I) p( x, I) p ( x y, I) = p( y, I) Data Analysis I Dr Martin Hendry, Dept of Physics and Astronomy University of Glasgow, UK 10 lectures, beginning October 2006 4. Monte Carlo Methods
Lecture 3. The Population Variance. The population variance, denoted σ 2, is the sum. of the squared deviations about the population
 Lecture 5 1 Lecture 3 The Population Variance The population variance, denoted σ 2, is the sum of the squared deviations about the population mean divided by the number of observations in the population,
Lecture 5 1 Lecture 3 The Population Variance The population variance, denoted σ 2, is the sum of the squared deviations about the population mean divided by the number of observations in the population,
Slides 12: Output Analysis for a Single Model
 Slides 12: Output Analysis for a Single Model Objective: Estimate system performance via simulation. If θ is the system performance, the precision of the estimator ˆθ can be measured by: The standard error
Slides 12: Output Analysis for a Single Model Objective: Estimate system performance via simulation. If θ is the system performance, the precision of the estimator ˆθ can be measured by: The standard error
1 Random and systematic errors
 1 ESTIMATION OF RELIABILITY OF RESULTS Such a thing as an exact measurement has never been made. Every value read from the scale of an instrument has a possible error; the best that can be done is to say
1 ESTIMATION OF RELIABILITY OF RESULTS Such a thing as an exact measurement has never been made. Every value read from the scale of an instrument has a possible error; the best that can be done is to say
Uncertainty and Bias UIUC, 403 Advanced Physics Laboratory, Fall 2014
 Uncertainty and Bias UIUC, 403 Advanced Physics Laboratory, Fall 2014 Liang Yang* There are three kinds of lies: lies, damned lies and statistics. Benjamin Disraeli If your experiment needs statistics,
Uncertainty and Bias UIUC, 403 Advanced Physics Laboratory, Fall 2014 Liang Yang* There are three kinds of lies: lies, damned lies and statistics. Benjamin Disraeli If your experiment needs statistics,
Maximum-Likelihood fitting
 CMP 0b Lecture F. Sigworth Maximum-Likelihood fitting One of the issues I want to address in this lecture is the fitting of distributions dwell times. We want to find the best curve to draw over a histogram,
CMP 0b Lecture F. Sigworth Maximum-Likelihood fitting One of the issues I want to address in this lecture is the fitting of distributions dwell times. We want to find the best curve to draw over a histogram,
Poisson distribution and χ 2 (Chap 11-12)
 Poisson distribution and χ 2 (Chap 11-12) Announcements: Last lecture today! Labs will continue. Homework assignment will be posted tomorrow or Thursday (I will send email) and is due Thursday, February
Poisson distribution and χ 2 (Chap 11-12) Announcements: Last lecture today! Labs will continue. Homework assignment will be posted tomorrow or Thursday (I will send email) and is due Thursday, February
Mathematical statistics
 October 1 st, 2018 Lecture 11: Sufficient statistic Where are we? Week 1 Week 2 Week 4 Week 7 Week 10 Week 14 Probability reviews Chapter 6: Statistics and Sampling Distributions Chapter 7: Point Estimation
October 1 st, 2018 Lecture 11: Sufficient statistic Where are we? Week 1 Week 2 Week 4 Week 7 Week 10 Week 14 Probability reviews Chapter 6: Statistics and Sampling Distributions Chapter 7: Point Estimation
Lecture 3: Linear Models. Bruce Walsh lecture notes Uppsala EQG course version 28 Jan 2012
 Lecture 3: Linear Models Bruce Walsh lecture notes Uppsala EQG course version 28 Jan 2012 1 Quick Review of the Major Points The general linear model can be written as y = X! + e y = vector of observed
Lecture 3: Linear Models Bruce Walsh lecture notes Uppsala EQG course version 28 Jan 2012 1 Quick Review of the Major Points The general linear model can be written as y = X! + e y = vector of observed
