FOURIER-BESSEL SERIES AND BOUNDARY VALUE PROBLEMS IN CYLINDRICAL COORDINATES
|
|
|
- Imogene Marsh
- 5 years ago
- Views:
Transcription
1 FOURIER-BESSE SERIES AND BOUNDARY VAUE PROBEMS IN CYINDRICA COORDINATES The paametic Bessel s equation appeas in connection with the aplace opeato in pola coodinates. The method of sepaation of vaiables fo poblem with cylindical geomety leads a singula Stum-iouville with the paametic Bessel s equation which in tun allows solutions to be epesented as seies involving Bessel functions.. The Paametic Bessel Equation The paametic Bessel s equation of ode α with α is the the second ode ODE x y + xy + λx α y =, with λ > a paamete, o equivalently, x y + xy + ν x α y =, whee ν = λ. We have the following lemma. emma. The geneal solution of equation in x > is yx = AJ α νx + BY α νx, whee J α and Y α ae, espectively, the Bessel functions of the fist and second kind of ode α and A, B ae constants. Moeove, lim x + yx is finite if and only if B = and so yx = AJ α νx. Poof. We tansfom equation into the standad Bessel equation of ode α by using the substitution t = νx. Indeed, we have dy dx = ν dy dt, and d y dx = ν d y dt. In tems of the vaiable t, equation becomes x ν d y dy + xν dt dt + x ν α y = t d y dt + tdy dt + t α y = which is the Bessel equation of ode α in the vaiable t. The geneal solution is theefoe, yt = AJ α t + BY α t. This is pecisely, yx = AJ α νx + BY α νx. Date: Apil 4, 6.
2 FOURIER-BESSE SERIES AND BOUNDARY VAUE PROBEMS IN CYINDRICA COORDINATES Note that J α = if α > and J =, while the second solution Y α satisfies lim x + Y α x =. Hence, if the solution yx is bounded in the inteval, ϵ with ϵ >, then necessaily B =. We can ewite equation in a self-adjoint fom by dividing by x and noticing that xy = xy + y to obtain xy + λx α y =. x We have hee with the notation of Note 9 that px = x, x = x, and qx = α /x. The point x = is a singula point. Any Stum-iouville poblem associated with this equation on the inteval [, R] is a singula S. As mentioned in Note 9, we can use use only the bounday condition at the endpoint x = R.. A Singula Stum-iouville Poblem We associate to the paametic Bessel equation the following S-poblem xy 3 + λx α y = x b yr + b y R = It is undestood in this poblem that yx is a bounded solution, o equivalently that lim x + yx exists and is finite. In the space Cp[, R], of piecewise continuous function on [, R], we conside the following inne poduct < f, g > x = R fxgxxdx. The poof given in Theoem of Note 9, can be caied out almost vebatim to establish the othogonality of the eigenfunctions of poblem 3. Thee is an exceptional case which occus when b = b α/r with b. In this case λ = is an eigenvalue of Poblem 3 with an eigenfunction x α. To simplify the discussion we will assume that b b α/r. By emma, we know that the bounded solutions of the ODE ae yx = J α νx with ν = λ. Note that y x = νj ανx In ode fo such a solution to satisfy the bounday condition, the paamete ν must satisfy 4 b J α νr + b νj ανr =. This means that λ = ν is an eigenvalue of Poblem 3 with eigenfunction J α νx. It can also be poved that these solutions fom a complete set basis in the space of piecewise continuous functions. This imply that any function f C p[, R] has a epesentation as a seies in these eigenfunctions. Denote by ν < ν < ν 3 < < ν j <, be the inceasing sequence of solutions of equation 4. The seies expansion is then fx C j J α ν j x, whee the coefficients ae given by, / C j = < f, J αν j x > R R x J α ν j x = fxj α ν j xxdx J α ν j x xdx x
3 FOURIER-BESSE SERIES ANDBOUNDARY VAUE PROBEMS INCYINDRICA COORDINATES3 It is of impotance to find the squae noms J α ν j x x. We have the lemma. emma. et ν j be a positive solution of 4, then we have the following: If b =, then J α ν j x x = R If b, let h = Rb/b, then we have J α ν j x x = R J α ν j x xdx = R J α+ν j R J α ν j x xdx = R νj α + h J α ν j R Poof. Since J α ν j x satisfies Poblem 3 with λ = ν j, then We multiply by J α ν j x to get ν j xxj α ν j x = α ν j x J α ν j x. xj α ν j x [xj α ν j x ] = α ν j x J α ν j xj α ν j x. By using ff = f, we obtain [ xj α ν j x ] = α ν j x J α ν j x Now we integate fom to R. The left side is R [xj α ν j x ] dx = [xj α ν j x ] x=r = RJ α ν j R. Fo the ight side we use integation by pats, R x= α ν j x J α ν j x dx = [ α ν j x J α ν j x ] R + ν j Afte equating the two sides, we get. R = ν j J αν j x x + α ν j R J α ν j R 5 ν j J α ν j x x = R J α ν j R + ν j R α J α ν j R We distinguish the two cases. If b =, then the condition is J α ν j R =, and elation 5 becomes J α ν j x x = R J α ν j R ν j. J α ν j x xdx We simplify this expession by using Popety 4 of Bessel junctions x α J α x = x α J α+ x in the fom J α x α x J αx = J α+ x. Fo x = ν j R, we have J α ν j R = and it follows that J α ν j x x = R J α+ ν j R ν j If b, then the bounday condition can be witten as ν j J αν j R = b b J α ν j R = h R J αν j R..
4 4FOURIER-BESSE SERIES AND BOUNDARY VAUE PROBEMS IN CYINDRICA COORDINATES Relation 5 becomes ν j J α ν j x x = h J α ν j R +ν j R α J α ν j R = R ν j +h α J α ν j R. Fom this we deduce that J α ν j x x = R νj + h α J α ν j R. ν j 3. Bessel Seies Expansions We summaize the above discussion in the following theoems. Theoem. Conside the S-poblem x y + xy + λx α y =, < x < R, yr = with bounded solutions yx. The eigenvalues values consist of the sequence λ j = ν j, with j Z + and whee ν j R is the j-th positive zeo of J α x. That is, ν < ν < ν 3 < < ν j < satisfy J α ν j R =. The coesponding j-th eigenfunction is y j x = J α ν j x. Futhemoe, the family of eigenfunctions J α ν j x is complete in Cp[, R]. The squae nom of the j-th eigenfunction is J α ν j x x = R Theoem. Conside the S-poblem J α ν j x xdx = R J α+ν j R x y + xy + λx α y =, < x < R, b yr + b y R =, b b αb /R with bounded solutions yx. The eigenvalues consist of the sequence λ j = ν j, with j Z +, such that, ν < ν < ν 3 < < ν j < satisfy the equation hj α ν j R + ν j RJ αν j R =, h = Rb b The coesponding j-th eigenfunction is y j x = J α ν j x. Futhemoe, the family of eigenfunctions J α ν j x is complete in Cp[, R]. The squae nom of the j-th eigenfunction is J α ν j x x = R J α ν j x xdx = R νj α + h J α ν j R Consequence of Theoem and. If f Cp[, R], then f has the expansion, f av x = fx+ + fx = C j J α ν j x, ν j
5 FOURIER-BESSE SERIES ANDBOUNDARY VAUE PROBEMS INCYINDRICA COORDINATES5 with C j = < fx, J αν j x > x J α ν j x x and whee the functions J α ν j x ae as in Theoem o as in Theoem. Remak. If we set z j = ν j R, then the above seies takes the fom fx + + fx x = C j J α z j R whee in the case of Theoem, the z j s ae the positive oots of J α, i.e., J α z j =, j =,, 3,, in the case of Theoem, the z j s ae the positive oots of the equation hj α z j + z j J αz j =, j =,, 3,. Remak. Since J α = fo α > and J =, then λ = is an eigenvalue of the S-poblem 3 only in the case of bounday condition y R = and the eigenfunction is J z j x/r, whee the z j s fom the sequence of positive zeos of J. We illustate this theoems with some examples. Example. Expand the function fx = on [, 3] into a J -Bessel seies with condition J z j =. This is the case of Theoem. We have zj x = C j J < x < 3, 3 Whee 3 C j = J z j x/3 J z j x/3xdx. x The squae noms ae J z j x/3 x = 9J z j / and to find the integal we use Popety 9 t α J α tdt = t α J α t + C and a substitution. 3 Hence, J z j x/3xdx = 9 z j and the seies expansion is = zj tj tdt = 9 z j C j = z j J z j J z j J z j zj x 3 z j J z j J = 9J z j z j. < x < 3. Now we give appoximations of the fist five tems of the seies j z j J z j /z j J z j
6 6FOURIER-BESSE SERIES AND BOUNDARY VAUE PROBEMS IN CYINDRICA COORDINATES The beginning of the seies expansion is.8j.8x.53j.84x +.46J.88x.365J 3.93x +.34J 4.98x + Example. An analogous calculation gives the expansion of fx = ove [, R] with espect J α with end point condition J α z j = as Whee C j = = R J α+ z j R zj x C j J α R J α z j x/rxdx = < x < R, zj zj J α+z j tj α tdt. Example 3. Expand fx = on [, ] in J α -Bessel seies with endpoint condition J αz j =. This is the case of Theoem with R = and h =. The squae noms ae J α z j x/ x = z j α zj J α z j and with C j = z j z j α J α z j = zj x C j J α, xj α z j x/dx = When α =, we get a moe compact fom of C j C j = z j J z j zj tj tdt = zj zj α J α z j tj α tdt z j J z j [tj t] z j = J z j z j J z j The expansion of fx = ove [, ] in a Bessel seies with endpoint J z j = is = J z j z j J z j J zj x. Example 4. Find the J -Bessel seies of fx = x ove [, ] with endpoint J z j =. We have fo < x <, x = C j J z j x, C j = < x, J z j x > x J z j x x We know that J z j x x = J z j see pevious calculations. To compute < x, J z j x > x, we use the substitution t = z j x in the integal and the.
7 FOURIER-BESSE SERIES ANDBOUNDARY VAUE PROBEMS INCYINDRICA COORDINATES7 popeties t α J α t = t α J α t and t α J α t = t α J α+ t: zj < x, J z j x > x = zj 4 zj t tj tdt = zj 4 zj t tj t dt [ z j t tj t ] z j = zj 4 + zj zj 4 t J tdt Hence the coefficient C j is = z 4 j zj = [ t J t ] z j zj 4 t J tdt = z 4 j zj zj + 4 zj 4 = 4 zj 4 [tj t] zj = 4J z j zj 3 C j = 4J z j /z 3 j J z j / = 8 z 3 j J z j. zj t J t dt tj tdt = 4 z 4 j The seies epesentation of x is x J z j x = 9 zj 3J, x,. z j zj tj tdt Example 5. The expansion of x m ove [, ] in J m -Bessel seies with endpoint condition J m z j = can be obtained by using simila aguments as befoe. x m = A calculation gives and the seies is C j J m z j x, x m = C j = C j = < xm, J m z j x > x J m z j x x z j J m+ z j J m z j x, x,. z j J m+ z j 4. Vibations of a Cicula Membane The following wave popagation poblem models the small vetical vibations of a cicula membane of adius whose bounday is held fixed. The initial position and velocity ae given by the functions f and g. whee u tt x, y, t = c ux, y, t x + y <, t >, ux, y, t = x + y =, t >, ux, y, = fx, y x + y <, u t x, y, = gx, y x + y <. = x + y
8 8FOURIER-BESSE SERIES AND BOUNDARY VAUE PROBEMS IN CYINDRICA COORDINATES is the -dimensional aplace opeato. Fo the pupose of using the method of sepaation of vaiables, this poblem is bette suited fo pola coodinates x = cos θ, y = sin θ. Recall the expession of the aplace opeato in pola coodinates is = + The expession of the BVP becomes u tt = c u + u + u θθ 6 + θ. <, θ π, t >, u, θ, t = θ π, t >, u, θ, = f, θ <, θ π, u t, θ, = g, θ <, θ π,. It is undestood that the sought solution u, θ, t and its deivatives need to be peiodic in θ: i.e., u, θ, t = u, θ + π, t and so on. Since in this fom the PDE has a singulaity at =, we impose that the solution u be continuous at the oigin. Befoe we conside the geneal case, we ae going to solve poblem 6 in the paticula case when f and g ae independent on θ invaiant unde otations. 4.. Rotationally invaiant case. Since f and g depend only on, we seek solution u that is also independent on θ. That is, at each time t the displacement, u = u, t depends only on the adius and not on the angle θ. In this case poblem 6 becomes a poblem in vaiables: u tt = c u + u <, t >, 7 u, t = t >, u, = f <, u t, = g <. We seek nontivial solutions with sepaated vaiables u = RT t of the homogeneous pat of the poblem: u tt = c u + u, u, t =. The sepaation of vaiables of the PDE leads to R R + R R = T t c = λ constant. T t This togethe with the bounday condition give the ODE poblems fo R and T t { R + R + λ R =, < < R, and R = T + c λt =. The R-poblem is the eigenvalue poblem. Its ODE is the paametic Bessel equation of ode. Since we ae seeking bounded solutions, then the eigenvalues and eigenfunctions ae λ j = z j, R zj j = J, j =,, 3, whee z j is the j-th positive oot of J x =.
9 FOURIER-BESSE SERIES ANDBOUNDARY VAUE PROBEMS INCYINDRICA COORDINATES9 Fo each j Z +, the T -equations becomes T +cz j / T = with independent solutions coscz j t/ and sincz j t/. Fo each j Z +, the homogeneous pat has two independent solutions with sepaated vaiables u czj t zj j, t = cos J and u czj t zj j, t = sin J. The geneal seies solution of the homogeneous pat is the linea combination of all the u j s and u j s: u, t = [ A j cos czj t + B j sin ] czj t zj J Now we use the nonhomogeneous conditions to find the constants A j and B j so that the seies solution satisfies the whole poblem. Fist we compute u t : [ ] cz j czj t czj t zj u t, t = A j sin + B j cos J. We have zj u, = f = A j J, cz j u t, = g = B zj jj. These ae, espectively, the J -Bessel seies of the functions f and g ove [, ] with endpoint condition J z j =. We have then, A j = < f, J z j / > J z j / = B j = cz j < g, J z j / > J z j / J z j = cz j J z j fj z j /d, gj z j /d. Example. The stuck dum head. Suppose that the above cicula membane, with = which was oiginally at equilibium is stuck at time t = at its cente in such a way that each point located at distance < fom the cente is given a velocity. The BVP in this case is we take c = u tt = u + u <, t >, u, t = t >, u, = u t, = g <. whee g = In this case the coefficients ae A j = and B j = { if < <, if < <. 5z j J z j gj z j /d.
10 FOURIER-BESSE SERIES AND BOUNDARY VAUE PROBEMS IN CYINDRICA COORDINATES Fo the last integal, we have We have theefoe and gj z j /d u, t = = = z j J z j /d = z j zj / [tj t] z j/ = z j J z j / B j = J z j / z j J z j J z j / z j J z j sin The following table list the appoximate values zj t j z j J z j J z j / B j We have then u, t zj J. tj tdt.53 sin.4tj.4.5 sin.55tj sin.86tj.86.3 sin.8tj.8.7 sin4.9tj Geneal case. Conside again BVP 6. This time we assume that the initial position f and initial velocity g depend effectively on θ and and also u = u, θ, t. We emphasize the π-peiodicity of u and its deivative u θ, with espect to θ, by adding it to the poblem. The poblem is theefoe u tt = c u + u + u θθ <, θ π, t >, u, θ, t = θ π, t >, 8 u, π, t = u, π, t < <, t >, u θ, π, t = u θ, π, t < <, t >, u, θ, = f, θ <, θ π, u t, θ, = g, θ <, θ π. We apply the method of sepaation of vaiables to the homogeneous pat. et u, θ, t = RΘθT t be a nontivial solution of the homogeneous pat. Fo such a function the wave equation can be witten as T t c T t = R R + R R + Θ θ = λ constant. Θθ Thus T t + c λt t = and R R + R R λ Θ θ Θθ =.
11 FOURIER-BESSE SERIES ANDBOUNDARY VAUE PROBEMS INCYINDRICA COORDINATES The last equation can be sepaated: R R + R R + λ = Θ θ Θθ = α constant. The ODEs fo R and Θ ae R + R + λ α R = and Θ + α Θ =. The homogeneous bounday conditions imply that R =, Θπ = Θ π and Θ π = Θ π. The thee ODE poblems ae Θ + α Θ = Θπ = Θ π Θ π = Θ π { R + R + λ α R = R = T t + c λt t = The Θ-poblem is the egula peiodic S-poblem and the R-poblem is the singula Bessel poblem of ode α with endpoint condition R =. The eigenvalues and eigenfunctions of the Θ-poblem ae. fo m Z +, α =, Θ θ = ; α m = m, Θ mθ = cosmθ, Θ mθ = sinmθ. We move to the R-poblem. Fo each α = m with m Z + {}, the eigenvalues and eigenfunctions of the R-poblem ae λ mj = z mj, R zmj mj = J m, whee {z mj } j is the inceasing sequence of zeos of J m. That is, < z m < z m < < z mj < satisfy J m z mj =. Now that we have the eigenvalues and eigenfunctions of the Θ- and R-poblems, we solve the T -poblem. Fo each m Z + {} and each j Z +, the coesponding T -equation is T czmj + T = with two independent solutions Tmj czmj t = cos and Tmj czmj t = sin. The collection of solutions with sepaated vaiables of the homogeneous pat of Poblem 8 consists of the following functions whee m =,,, and j =,, u zmj mj, θ, t = J m u mj, θ, t = J m zmj u 3 mj, θ, t = J m zmj u 4 mj, θ, t = J m zmj czmj t cosmθ cos, czmj t sinmθ cos, czmj t cosmθ sin, czmj t sinmθ sin.
12 FOURIER-BESSE SERIES AND BOUNDARY VAUE PROBEMS IN CYINDRICA COORDINATES These ae the m, j-modes of vibations of the membane. Up to a otation, the pofile of each mode is given by the gaph of the function zmj v mj, θ = J m cosmθ each m, j-mode is just v mj times a time-amplitude. Fo each m, j, the membane can be divided into egions whee v mj > and egions whee v mj <. The cuves whee v mj = ae called the nodal lines see figue. m,j=, m,j=, m,j=, m,j=, m,j=, m,j=, Some of the m, j-modes ae gaphed in the figue. m=, m=, m=, m=, j= m=, j= m=, j=
13 FOURIER-BESSE SERIES ANDBOUNDARY VAUE PROBEMS INCYINDRICA COORDINATES3 The geneal seies solution of the homogeneous pat is a linea combination of the solutions u k mj : zmj czmj t u, θ, t = J m cos A mj cosmθ + B mj sinmθ m= zmj czmj t +J m sin C mj cosmθ + D mj sinmθ and In ode fo such a solution to satisfy the nonhomogeneous condition, we need zmj u, θ, = f, θ = J m [A mj cosmθ + B mj sinmθ] u t, θ, = g, θ = m= m= cz mj t J m zmj [C mj cosmθ + D mj sinmθ] These ae the double Fouie-Bessel seies of f and g. To find the coefficients, we can poceed as follows. Expand f, θ into its Fouie seies view as a paamete, f, θ = A + A m cosmθ + B m sinmθ whee A m = π π π m= f, θ cosmθdθ, m =,,, B m = f, θ sinmθdθ, m =,, 3, π Now expand A m and B m into a J m -Bessel seies with end point condition J m z =. We get, zmj zmj A m = A mj J m, A mj = J m A m J m d and B m = zmj B mj J m, B mj = J m zmj B m J m d Afte substituting the expessions of A m and B m in tem of the integals of f, we obtain the coefficients A mj and B mj of the seies solution as: π zmj A mj = π J m z mj / f, θj m cosmθddθ, π zmj B mj = π J m z mj / f, θj m sinmθddθ. The othe coefficients C mj and D mj ae obtained in a simila way by using the second initial condition. Example Take =, c =, g, θ = and f, θ = + sin θ. In this situation C mj = D mj = fo m and j. Futhemoe, A mj = fo m
14 4 FOURIER-BESSE SERIES AND BOUNDARY VAUE PROBEMS IN CYINDRICA COORDINATES and B mj = fo m Hence, the solution has the fom u, θ, t = A j J z j cosz j t + B j J z j cosz j t sin θ, j j whee and B j = π J z j The squae noms ae A j = J z j π J z j = J z j J z j d J z j sin θ ddθ = J z j and J z j = J z j. J z j d. The integal involved in A j can be evaluated. Fist, notice that by using the popety t α J α t = t α J α t and integation by pats, we get t 3 J tdt = t tj t ttj tdt = t 3 J t t J t + C. Hence, by using the substitution t = z j, we get and so The solution u is u, θ, t = 4 J z j d = z 4 j = z 4 j zj = J z j z j A j = 4J z j z j J z j. J z j J z j z j J z j cosz j t + [ z j t t 3] J tdt [ z j t t 3 J t + t J t ] z j B j J z j cosz j t sin θ. 5. Heat Conduction in a Cicula Plate The following bounday value poblem models heat popagation in a thin cicula plate with insulated faces and with heat tansfe on the cicula bounday. In pola coodinates, the poblem is: u t = k u + u + u θθ 9 <, θ π, t >, hu, θ, t + u, θ, t = θ π, t >, u, θ, = f, θ <, θ π,
15 FOURIER-BESSE SERIES ANDBOUNDARY VAUE PROBEMS INCYINDRICA COORDINATES5 whee h is a constant. et us assume fo simplicity that f is otation invaiant f = f is independent on θ. We seek then a solution that is also independent on θ and the poblem becomes. u t = k u + u <, t >, hu, t + u, t = t >, u = f <. The solutions with sepaated vaiables: u, t = RT t of the homogeneous pat leads to the ODE poblems { R + R + λ R = hr + R and T + kλt =. = The R-equation is the paametic Bessel equation of ode. The values λ < cannot be eigenvalues. The case λ = is a paticula case. Remak about the case λ =. In this case, the R-equation is also a Cauchy- Eule equation with geneal solution A + B ln and the bounded solutions ae R = A. Such a solutions satisfies the bounday condition if and only if h =. This coespond to the situation whee the bounday is insulated The positive eigenvalues and eigenfunctions ae: λ j = z j, R zj j = J, j Z +, whee z j is the j-th positive oot of the equation A coesponding T -solution is hj z + zj z =. T j t = exp kz j t The seies solution of the homogeneous pat, when h >, is u, t = C j e kz j /t zj J and when h = is u, t = C + C j e kz j /t zj J In ode fo such a seies to satisfy the nonhomogeneous condition, we need zj u, = f = C + C j J with C = when h >. This is the J -Bessel seies of f with endpoint condition hj z + zj z =. We have then see Theoem, C j = J z j / fj zj d =. z j z j + h J z j fj zj d.
16 6 FOURIER-BESSE SERIES AND BOUNDARY VAUE PROBEMS IN CYINDRICA COORDINATES Remak. If instead of being independent on θ, the initial condition is of the fom f cosmθ, the solution u of poblem 9 can be put in the fom u, θ, t = v, t cosmθ, whee v solves the two vaiables poblem v t = k v + v v m <, t >, hv, t + v, t = t >, v = f <. This time the sepaation of vaiables of the v-poblem leads to the solution v of the fom v, t = C j e kz j /t zj J m 6. Helmholtz Equation in the Disk The Helmholtz equation in the disk is the following two-dimensional eigenvalue poblem: Find λ and nontivial functions u, θ defined in the disk of adius such that: { u, θ + λu, θ = < <, θ π, u, θ = θ π. The solutions with sepaated vaiables u, θ = RΘθ leads to the following one-dimensional eigenvalue poblems { Θ t + α Θt = Θ and Θ π peiodic and { R + R + λ α R = R =. The eigenvalues and eigenfunctions of the Θ-poblem ae α m = m, Θ mθ = cosmθ and Θ mθ = sinmθ m =,,, Fo each m, the R-poblem is an ode m Bessel type eigenvalues poblem with eigenvalues and eigenfunctions zj,m zj,m λ j,m =, Rj,m = J m. whee z j,m is the j-th positive oots of the equation J m z =. The eigenvalues and eigenfunctions of the Helmholtz equation ae λ j,m = z j,m, u zj,m j,m, θ = cosmθj m, u zj,m j,m, θ = sinmθj m, Eigenfunctions expansion fo a nonhomogeneous poblem. The eigenfunctions u j,m, u j,m can can be used to solve nonhomogeneous poblems such as the following { u, θ + au, θ = F, θ < <, θ π, 3 u, θ = θ π.
17 FOURIER-BESSE SERIES ANDBOUNDARY VAUE PROBEMS INCYINDRICA COORDINATES7 whee a is a constant. We expand F and u into these eigenfunctions Fouie-Bessel seies. We seek then a solution u of the fom u, θ = m= By using u, m,j = λ m,ju, m,j, we deduce that 4 u + au = m= zj,m [A m,j cosmθ + B m,j sinmθ] J m zj,m a λ m,j [A m,j cosmθ + B m,j sinmθ] J m The Fouie-Bessel seies of F is [ 5 F, θ = F m,j cosmθ + Fm,j sinmθ ] zj,m J m m= whee the coefficients F, m,j ae given by 6 F m,j F m,j } = π J m z m,j / π F, θj m zm,j By identifying the coefficients in the seies 4 and 5, we get { cosmθ d sinmθ dθ. A m,j = F m,j a λ m,j and B m,j = F m,j a λ m,j. povided that a λ m,j fo evey m, j nonesonant case. Example. Conside the poblem { u, θ u, θ = + sinθ < < 3, θ π, u3, θ = θ π. In this poblem, we have F, m,j =, fo evey m except when m = and m =. Futhemoe, F,j = fo evey j. Fo the emainde of the coefficients, we have F,j = J z,j /3 = z,j J z,j = z,j J z,j 3 z,j J z,j /3d tj tdt and F,j = J z,j /3 9 = z,j 4 J 3z,j 6 = z,j J 3 z,j 3 z,j 3 J z,j /3d t 3 J tdt
18 8 FOURIER-BESSE SERIES AND BOUNDARY VAUE PROBEMS IN CYINDRICA COORDINATES The coesponding coefficients of the solutions ae The solution of the poblem is u = 8 F,j A,j = z,j /9 = 8 z,j 9 + z,j J z,j B,j F,j = z,j /9 = 458 z,j 9 + z,j J 3z,j J z,j /3 z,j 9 + z,j J z,j Execises J z,j /3 sinθ z,j 9 + z,j J 3z,j In Execises to 9, find the J α -Bessel seies of the given function fx ove the given inteval and with espect to the given endpoint condition. Execise. fx = ove [, 5], and J z =. Execise. fx = x ove [, 7], and J z =. Execise 3. fx = 5 ove [, ], and J z =. { if x Execise 4. fx = if < x ove [, ], and J z =. Execise 5. fx = x ove [, 3], and J z = Execise 6. fx = ove [, 3], and J z + zj z =. Execise 7. fx = x ove [, 3], and J z = leave the coefficients in an integal fom. Execise 8. fx = x ove [, 3], and J 3 z = leave the coefficients in an integal fom. Execise 9. fx = x ove [, π], and J / z = use the explicit expession of J / and elate to Fouie seies. In execises to 4, solve the indicated bounday value poblem that deal with heat flow in a cicula domain. Execise. u t = u + u < <, t >, u, t = t >, u, = 5 < <. Execise. Execise 3. u t = u + u < <, t >, u, t = t >, u, = 5 < <. u t = u + u < <, t >, u, t u, t = t >, u, = 5 < <.
19 FOURIER-BESSE SERIES ANDBOUNDARY VAUE PROBEMS INCYINDRICA COORDINATES9 Execise 3. Find a solution u of the fom u, θ, t = v, t sinθ of the poblem. u t = u + u + u θθ < <, θ π, t >, u, θ, t = θ π, t >, u, θ, = 5 sinθ < <, θ π,. Execise 4. u t = u + u 9u < <, t >, u, t = t >, u, = 3 < <. In execises 5 to 8, solve the indicated bounday value poblem that deal with wave popagation in a cicula domain. Execise 5. u tt = u + u < < 3, t >, u3, t = t >, u, = 9 < < 3, u t, = < < 3. Execise 6. whee u tt = u + u < <, t >, u, t = t >, u, = < <, u t, = g < <. g = { if < < /, if / < <. Execise 7. Find a solution u of the fom u, θ, t = v, t cos θ u tt = u + u + u θθ < <, t >, u, t = t >, u, = < <, u t, = g cos θ < <. whee g = { if < < /, if / < <. Execise 8. Find a solution u of the fom u, θ, t = v, t cos θ u tt = u + u + u θθ < <, t >, u, t = t >, u, = J z, sin θ < <, u t, = g cos θ < <. whee z, is the fist positive zeo of J and whee { if < < /, g = if / < <.
20 FOURIER-BESSE SERIES AND BOUNDARY VAUE PROBEMS IN CYINDRICA COORDINATES In execises 9 to, solve the Helmholtz equation in the disk with adius Execise 9. = u u =, u, θ = Execise. = u = sin θ, u, θ = Execise. = 3 u + u = cos3θ, u3, θ = Execise. Solve the following Diichlet poblem in the cylinde with adius and height u + u + u zz = < <, < z <, u, z = < z <, u, = < <, u, = < <.
8 Separation of Variables in Other Coordinate Systems
 8 Sepaation of Vaiables in Othe Coodinate Systems Fo the method of sepaation of vaiables to succeed you need to be able to expess the poblem at hand in a coodinate system in which the physical boundaies
8 Sepaation of Vaiables in Othe Coodinate Systems Fo the method of sepaation of vaiables to succeed you need to be able to expess the poblem at hand in a coodinate system in which the physical boundaies
15 Solving the Laplace equation by Fourier method
 5 Solving the Laplace equation by Fouie method I aleady intoduced two o thee dimensional heat equation, when I deived it, ecall that it taes the fom u t = α 2 u + F, (5.) whee u: [0, ) D R, D R is the
5 Solving the Laplace equation by Fouie method I aleady intoduced two o thee dimensional heat equation, when I deived it, ecall that it taes the fom u t = α 2 u + F, (5.) whee u: [0, ) D R, D R is the
-Δ u = λ u. u(x,y) = u 1. (x) u 2. (y) u(r,θ) = R(r) Θ(θ) Δu = 2 u + 2 u. r = x 2 + y 2. tan(θ) = y/x. r cos(θ) = cos(θ) r.
 The Laplace opeato in pola coodinates We now conside the Laplace opeato with Diichlet bounday conditions on a cicula egion Ω {(x,y) x + y A }. Ou goal is to compute eigenvalues and eigenfunctions of the
The Laplace opeato in pola coodinates We now conside the Laplace opeato with Diichlet bounday conditions on a cicula egion Ω {(x,y) x + y A }. Ou goal is to compute eigenvalues and eigenfunctions of the
THE LAPLACE EQUATION. The Laplace (or potential) equation is the equation. u = 0. = 2 x 2. x y 2 in R 2
 THE LAPLACE EQUATION The Laplace (o potential) equation is the equation whee is the Laplace opeato = 2 x 2 u = 0. in R = 2 x 2 + 2 y 2 in R 2 = 2 x 2 + 2 y 2 + 2 z 2 in R 3 The solutions u of the Laplace
THE LAPLACE EQUATION The Laplace (o potential) equation is the equation whee is the Laplace opeato = 2 x 2 u = 0. in R = 2 x 2 + 2 y 2 in R 2 = 2 x 2 + 2 y 2 + 2 z 2 in R 3 The solutions u of the Laplace
Math 124B February 02, 2012
 Math 24B Febuay 02, 202 Vikto Gigoyan 8 Laplace s equation: popeties We have aleady encounteed Laplace s equation in the context of stationay heat conduction and wave phenomena. Recall that in two spatial
Math 24B Febuay 02, 202 Vikto Gigoyan 8 Laplace s equation: popeties We have aleady encounteed Laplace s equation in the context of stationay heat conduction and wave phenomena. Recall that in two spatial
x x2 2 B A ) v(0, t) = 0 and v(l, t) = 0. L 2. This is a familiar heat equation initial/boundary-value problem and has solution
 Hints to homewok 7 8.2.d. The poblem is u t ku xx + k ux fx u t A u t B. It has a souce tem and inhomogeneous bounday conditions but none of them depend on t. So as in example 3 of the notes we should
Hints to homewok 7 8.2.d. The poblem is u t ku xx + k ux fx u t A u t B. It has a souce tem and inhomogeneous bounday conditions but none of them depend on t. So as in example 3 of the notes we should
Exceptional regular singular points of second-order ODEs. 1. Solving second-order ODEs
 (May 14, 2011 Exceptional egula singula points of second-ode ODEs Paul Gaett gaett@math.umn.edu http://www.math.umn.edu/ gaett/ 1. Solving second-ode ODEs 2. Examples 3. Convegence Fobenius method fo solving
(May 14, 2011 Exceptional egula singula points of second-ode ODEs Paul Gaett gaett@math.umn.edu http://www.math.umn.edu/ gaett/ 1. Solving second-ode ODEs 2. Examples 3. Convegence Fobenius method fo solving
An Exact Solution of Navier Stokes Equation
 An Exact Solution of Navie Stokes Equation A. Salih Depatment of Aeospace Engineeing Indian Institute of Space Science and Technology, Thiuvananthapuam, Keala, India. July 20 The pincipal difficulty in
An Exact Solution of Navie Stokes Equation A. Salih Depatment of Aeospace Engineeing Indian Institute of Space Science and Technology, Thiuvananthapuam, Keala, India. July 20 The pincipal difficulty in
=0, (x, y) Ω (10.1) Depending on the nature of these boundary conditions, forced, natural or mixed type, the elliptic problems are classified as
 Chapte 1 Elliptic Equations 1.1 Intoduction The mathematical modeling of steady state o equilibium phenomena geneally esult in to elliptic equations. The best example is the steady diffusion of heat in
Chapte 1 Elliptic Equations 1.1 Intoduction The mathematical modeling of steady state o equilibium phenomena geneally esult in to elliptic equations. The best example is the steady diffusion of heat in
Do not turn over until you are told to do so by the Invigilator.
 UNIVERSITY OF EAST ANGLIA School of Mathematics Main Seies UG Examination 2015 16 FLUID DYNAMICS WITH ADVANCED TOPICS MTH-MD59 Time allowed: 3 Hous Attempt QUESTIONS 1 and 2, and THREE othe questions.
UNIVERSITY OF EAST ANGLIA School of Mathematics Main Seies UG Examination 2015 16 FLUID DYNAMICS WITH ADVANCED TOPICS MTH-MD59 Time allowed: 3 Hous Attempt QUESTIONS 1 and 2, and THREE othe questions.
Math 1105: Calculus I (Math/Sci majors) MWF 11am / 12pm, Campion 235 Written homework 3
 Math : alculus I Math/Sci majos MWF am / pm, ampion Witten homewok Review: p 94, p 977,8,9,6, 6: p 46, 6: p 4964b,c,69, 6: p 47,6 p 94, Evaluate the following it by identifying the integal that it epesents:
Math : alculus I Math/Sci majos MWF am / pm, ampion Witten homewok Review: p 94, p 977,8,9,6, 6: p 46, 6: p 4964b,c,69, 6: p 47,6 p 94, Evaluate the following it by identifying the integal that it epesents:
In the previous section we considered problems where the
 5.4 Hydodynamically Fully Developed and Themally Developing Lamina Flow In the pevious section we consideed poblems whee the velocity and tempeatue pofile wee fully developed, so that the heat tansfe coefficient
5.4 Hydodynamically Fully Developed and Themally Developing Lamina Flow In the pevious section we consideed poblems whee the velocity and tempeatue pofile wee fully developed, so that the heat tansfe coefficient
Geometry of the homogeneous and isotropic spaces
 Geomety of the homogeneous and isotopic spaces H. Sonoda Septembe 2000; last evised Octobe 2009 Abstact We summaize the aspects of the geomety of the homogeneous and isotopic spaces which ae most elevant
Geomety of the homogeneous and isotopic spaces H. Sonoda Septembe 2000; last evised Octobe 2009 Abstact We summaize the aspects of the geomety of the homogeneous and isotopic spaces which ae most elevant
LINEAR PLATE BENDING
 LINEAR PLATE BENDING 1 Linea plate bending A plate is a body of which the mateial is located in a small egion aound a suface in the thee-dimensional space. A special suface is the mid-plane. Measued fom
LINEAR PLATE BENDING 1 Linea plate bending A plate is a body of which the mateial is located in a small egion aound a suface in the thee-dimensional space. A special suface is the mid-plane. Measued fom
MATH 417 Homework 3 Instructor: D. Cabrera Due June 30. sin θ v x = v r cos θ v θ r. (b) Then use the Cauchy-Riemann equations in polar coordinates
 MATH 417 Homewok 3 Instucto: D. Cabea Due June 30 1. Let a function f(z) = u + iv be diffeentiable at z 0. (a) Use the Chain Rule and the fomulas x = cosθ and y = to show that u x = u cosθ u θ, v x = v
MATH 417 Homewok 3 Instucto: D. Cabea Due June 30 1. Let a function f(z) = u + iv be diffeentiable at z 0. (a) Use the Chain Rule and the fomulas x = cosθ and y = to show that u x = u cosθ u θ, v x = v
f(k) e p 2 (k) e iax 2 (k a) r 2 e a x a a 2 + k 2 e a2 x 1 2 H(x) ik p (k) 4 r 3 cos Y 2 = 4
 Fouie tansfom pais: f(x) 1 f(k) e p 2 (k) p e iax 2 (k a) 2 e a x a a 2 + k 2 e a2 x 1 2, a > 0 a p k2 /4a2 e 2 1 H(x) ik p 2 + 2 (k) The fist few Y m Y 0 0 = Y 0 1 = Y ±1 1 = l : 1 Y2 0 = 4 3 ±1 cos Y
Fouie tansfom pais: f(x) 1 f(k) e p 2 (k) p e iax 2 (k a) 2 e a x a a 2 + k 2 e a2 x 1 2, a > 0 a p k2 /4a2 e 2 1 H(x) ik p 2 + 2 (k) The fist few Y m Y 0 0 = Y 0 1 = Y ±1 1 = l : 1 Y2 0 = 4 3 ±1 cos Y
I. CONSTRUCTION OF THE GREEN S FUNCTION
 I. CONSTRUCTION OF THE GREEN S FUNCTION The Helmohltz equation in 4 dimensions is 4 + k G 4 x, x = δ 4 x x. In this equation, G is the Geen s function and 4 efes to the dimensionality. In the vey end,
I. CONSTRUCTION OF THE GREEN S FUNCTION The Helmohltz equation in 4 dimensions is 4 + k G 4 x, x = δ 4 x x. In this equation, G is the Geen s function and 4 efes to the dimensionality. In the vey end,
Tutorial Exercises: Central Forces
 Tutoial Execises: Cental Foces. Tuning Points fo the Keple potential (a) Wite down the two fist integals fo cental motion in the Keple potential V () = µm/ using J fo the angula momentum and E fo the total
Tutoial Execises: Cental Foces. Tuning Points fo the Keple potential (a) Wite down the two fist integals fo cental motion in the Keple potential V () = µm/ using J fo the angula momentum and E fo the total
Compactly Supported Radial Basis Functions
 Chapte 4 Compactly Suppoted Radial Basis Functions As we saw ealie, compactly suppoted functions Φ that ae tuly stictly conditionally positive definite of ode m > do not exist The compact suppot automatically
Chapte 4 Compactly Suppoted Radial Basis Functions As we saw ealie, compactly suppoted functions Φ that ae tuly stictly conditionally positive definite of ode m > do not exist The compact suppot automatically
Lecture 23. Representation of the Dirac delta function in other coordinate systems
 Lectue 23 Repesentation of the Diac delta function in othe coodinate systems In a geneal sense, one can wite, ( ) = (x x ) (y y ) (z z ) = (u u ) (v v ) (w w ) J Whee J epesents the Jacobian of the tansfomation.
Lectue 23 Repesentation of the Diac delta function in othe coodinate systems In a geneal sense, one can wite, ( ) = (x x ) (y y ) (z z ) = (u u ) (v v ) (w w ) J Whee J epesents the Jacobian of the tansfomation.
Green s Identities and Green s Functions
 LECTURE 7 Geen s Identities and Geen s Functions Let us ecall The ivegence Theoem in n-dimensions Theoem 7 Let F : R n R n be a vecto field ove R n that is of class C on some closed, connected, simply
LECTURE 7 Geen s Identities and Geen s Functions Let us ecall The ivegence Theoem in n-dimensions Theoem 7 Let F : R n R n be a vecto field ove R n that is of class C on some closed, connected, simply
PROBLEM SET #1 SOLUTIONS by Robert A. DiStasio Jr.
 POBLM S # SOLUIONS by obet A. DiStasio J. Q. he Bon-Oppenheime appoximation is the standad way of appoximating the gound state of a molecula system. Wite down the conditions that detemine the tonic and
POBLM S # SOLUIONS by obet A. DiStasio J. Q. he Bon-Oppenheime appoximation is the standad way of appoximating the gound state of a molecula system. Wite down the conditions that detemine the tonic and
Section 8.2 Polar Coordinates
 Section 8. Pola Coodinates 467 Section 8. Pola Coodinates The coodinate system we ae most familia with is called the Catesian coodinate system, a ectangula plane divided into fou quadants by the hoizontal
Section 8. Pola Coodinates 467 Section 8. Pola Coodinates The coodinate system we ae most familia with is called the Catesian coodinate system, a ectangula plane divided into fou quadants by the hoizontal
KOEBE DOMAINS FOR THE CLASSES OF FUNCTIONS WITH RANGES INCLUDED IN GIVEN SETS
 Jounal of Applied Analysis Vol. 14, No. 1 2008), pp. 43 52 KOEBE DOMAINS FOR THE CLASSES OF FUNCTIONS WITH RANGES INCLUDED IN GIVEN SETS L. KOCZAN and P. ZAPRAWA Received Mach 12, 2007 and, in evised fom,
Jounal of Applied Analysis Vol. 14, No. 1 2008), pp. 43 52 KOEBE DOMAINS FOR THE CLASSES OF FUNCTIONS WITH RANGES INCLUDED IN GIVEN SETS L. KOCZAN and P. ZAPRAWA Received Mach 12, 2007 and, in evised fom,
Math 2263 Solutions for Spring 2003 Final Exam
 Math 6 Solutions fo Sping Final Exam ) A staightfowad appoach to finding the tangent plane to a suface at a point ( x, y, z ) would be to expess the cuve as an explicit function z = f ( x, y ), calculate
Math 6 Solutions fo Sping Final Exam ) A staightfowad appoach to finding the tangent plane to a suface at a point ( x, y, z ) would be to expess the cuve as an explicit function z = f ( x, y ), calculate
Temporal-Difference Learning
 .997 Decision-Making in Lage-Scale Systems Mach 17 MIT, Sping 004 Handout #17 Lectue Note 13 1 Tempoal-Diffeence Leaning We now conside the poblem of computing an appopiate paamete, so that, given an appoximation
.997 Decision-Making in Lage-Scale Systems Mach 17 MIT, Sping 004 Handout #17 Lectue Note 13 1 Tempoal-Diffeence Leaning We now conside the poblem of computing an appopiate paamete, so that, given an appoximation
A method for solving dynamic problems for cylindrical domains
 Tansactions of NAS of Azebaijan, Issue Mechanics, 35 (7), 68-75 (016). Seies of Physical-Technical and Mathematical Sciences. A method fo solving dynamic poblems fo cylindical domains N.B. Rassoulova G.R.
Tansactions of NAS of Azebaijan, Issue Mechanics, 35 (7), 68-75 (016). Seies of Physical-Technical and Mathematical Sciences. A method fo solving dynamic poblems fo cylindical domains N.B. Rassoulova G.R.
Lecture 04: HFK Propagation Physical Optics II (Optical Sciences 330) (Updated: Friday, April 29, 2005, 8:05 PM) W.J. Dallas
 C:\Dallas\0_Couses\0_OpSci_330\0 Lectue Notes\04 HfkPopagation.doc: Page of 9 Lectue 04: HFK Popagation Physical Optics II (Optical Sciences 330) (Updated: Fiday, Apil 9, 005, 8:05 PM) W.J. Dallas The
C:\Dallas\0_Couses\0_OpSci_330\0 Lectue Notes\04 HfkPopagation.doc: Page of 9 Lectue 04: HFK Popagation Physical Optics II (Optical Sciences 330) (Updated: Fiday, Apil 9, 005, 8:05 PM) W.J. Dallas The
What Form of Gravitation Ensures Weakened Kepler s Third Law?
 Bulletin of Aichi Univ. of Education, 6(Natual Sciences, pp. - 6, Mach, 03 What Fom of Gavitation Ensues Weakened Keple s Thid Law? Kenzi ODANI Depatment of Mathematics Education, Aichi Univesity of Education,
Bulletin of Aichi Univ. of Education, 6(Natual Sciences, pp. - 6, Mach, 03 What Fom of Gavitation Ensues Weakened Keple s Thid Law? Kenzi ODANI Depatment of Mathematics Education, Aichi Univesity of Education,
( ) [ ] [ ] [ ] δf φ = F φ+δφ F. xdx.
![( ) [ ] [ ] [ ] δf φ = F φ+δφ F. xdx. ( ) [ ] [ ] [ ] δf φ = F φ+δφ F. xdx.](/thumbs/90/103689049.jpg) 9. LAGRANGIAN OF THE ELECTROMAGNETIC FIELD In the pevious section the Lagangian and Hamiltonian of an ensemble of point paticles was developed. This appoach is based on a qt. This discete fomulation can
9. LAGRANGIAN OF THE ELECTROMAGNETIC FIELD In the pevious section the Lagangian and Hamiltonian of an ensemble of point paticles was developed. This appoach is based on a qt. This discete fomulation can
POISSON S EQUATION 2 V 0
 POISSON S EQUATION We have seen how to solve the equation but geneally we have V V4k We now look at a vey geneal way of attacking this poblem though Geen s Functions. It tuns out that this poblem has applications
POISSON S EQUATION We have seen how to solve the equation but geneally we have V V4k We now look at a vey geneal way of attacking this poblem though Geen s Functions. It tuns out that this poblem has applications
3.1 Random variables
 3 Chapte III Random Vaiables 3 Random vaiables A sample space S may be difficult to descibe if the elements of S ae not numbes discuss how we can use a ule by which an element s of S may be associated
3 Chapte III Random Vaiables 3 Random vaiables A sample space S may be difficult to descibe if the elements of S ae not numbes discuss how we can use a ule by which an element s of S may be associated
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Physics Department Physics 8.07: Electromagnetism II September 15, 2012 Prof. Alan Guth PROBLEM SET 2
 MASSACHUSETTS INSTITUTE OF TECHNOLOGY Physics Depatment Physics 8.07: Electomagnetism II Septembe 5, 202 Pof. Alan Guth PROBLEM SET 2 DUE DATE: Monday, Septembe 24, 202. Eithe hand it in at the lectue,
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Physics Depatment Physics 8.07: Electomagnetism II Septembe 5, 202 Pof. Alan Guth PROBLEM SET 2 DUE DATE: Monday, Septembe 24, 202. Eithe hand it in at the lectue,
2 Governing Equations
 2 Govening Equations This chapte develops the govening equations of motion fo a homogeneous isotopic elastic solid, using the linea thee-dimensional theoy of elasticity in cylindical coodinates. At fist,
2 Govening Equations This chapte develops the govening equations of motion fo a homogeneous isotopic elastic solid, using the linea thee-dimensional theoy of elasticity in cylindical coodinates. At fist,
Right-handed screw dislocation in an isotropic solid
 Dislocation Mechanics Elastic Popeties of Isolated Dislocations Ou study of dislocations to this point has focused on thei geomety and thei ole in accommodating plastic defomation though thei motion. We
Dislocation Mechanics Elastic Popeties of Isolated Dislocations Ou study of dislocations to this point has focused on thei geomety and thei ole in accommodating plastic defomation though thei motion. We
THE CONE THEOREM JOEL A. TROPP. Abstract. We prove a fixed point theorem for functions which are positive with respect to a cone in a Banach space.
 THE ONE THEOEM JOEL A. TOPP Abstact. We pove a fixed point theoem fo functions which ae positive with espect to a cone in a Banach space. 1. Definitions Definition 1. Let X be a eal Banach space. A subset
THE ONE THEOEM JOEL A. TOPP Abstact. We pove a fixed point theoem fo functions which ae positive with espect to a cone in a Banach space. 1. Definitions Definition 1. Let X be a eal Banach space. A subset
Absorption Rate into a Small Sphere for a Diffusing Particle Confined in a Large Sphere
 Applied Mathematics, 06, 7, 709-70 Published Online Apil 06 in SciRes. http://www.scip.og/jounal/am http://dx.doi.og/0.46/am.06.77065 Absoption Rate into a Small Sphee fo a Diffusing Paticle Confined in
Applied Mathematics, 06, 7, 709-70 Published Online Apil 06 in SciRes. http://www.scip.og/jounal/am http://dx.doi.og/0.46/am.06.77065 Absoption Rate into a Small Sphee fo a Diffusing Paticle Confined in
RECTIFYING THE CIRCUMFERENCE WITH GEOGEBRA
 ECTIFYING THE CICUMFEENCE WITH GEOGEBA A. Matín Dinnbie, G. Matín González and Anthony C.M. O 1 Intoducction The elation between the cicumfeence and the adius of a cicle is one of the most impotant concepts
ECTIFYING THE CICUMFEENCE WITH GEOGEBA A. Matín Dinnbie, G. Matín González and Anthony C.M. O 1 Intoducction The elation between the cicumfeence and the adius of a cicle is one of the most impotant concepts
7.2.1 Basic relations for Torsion of Circular Members
 Section 7. 7. osion In this section, the geomety to be consideed is that of a long slende cicula ba and the load is one which twists the ba. Such poblems ae impotant in the analysis of twisting components,
Section 7. 7. osion In this section, the geomety to be consideed is that of a long slende cicula ba and the load is one which twists the ba. Such poblems ae impotant in the analysis of twisting components,
Math 209 Assignment 9 Solutions
 Math 9 Assignment 9 olutions 1. Evaluate 4y + 1 d whee is the fist octant pat of y x cut out by x + y + z 1. olution We need a paametic epesentation of the suface. (x, z). Now detemine the nomal vecto:
Math 9 Assignment 9 olutions 1. Evaluate 4y + 1 d whee is the fist octant pat of y x cut out by x + y + z 1. olution We need a paametic epesentation of the suface. (x, z). Now detemine the nomal vecto:
Chapter 2: Introduction to Implicit Equations
 Habeman MTH 11 Section V: Paametic and Implicit Equations Chapte : Intoduction to Implicit Equations When we descibe cuves on the coodinate plane with algebaic equations, we can define the elationship
Habeman MTH 11 Section V: Paametic and Implicit Equations Chapte : Intoduction to Implicit Equations When we descibe cuves on the coodinate plane with algebaic equations, we can define the elationship
KEPLER S LAWS OF PLANETARY MOTION
 EPER S AWS OF PANETARY MOTION 1. Intoduction We ae now in a position to apply what we have leaned about the coss poduct and vecto valued functions to deive eple s aws of planetay motion. These laws wee
EPER S AWS OF PANETARY MOTION 1. Intoduction We ae now in a position to apply what we have leaned about the coss poduct and vecto valued functions to deive eple s aws of planetay motion. These laws wee
F-IF Logistic Growth Model, Abstract Version
 F-IF Logistic Gowth Model, Abstact Vesion Alignments to Content Standads: F-IFB4 Task An impotant example of a model often used in biology o ecology to model population gowth is called the logistic gowth
F-IF Logistic Gowth Model, Abstact Vesion Alignments to Content Standads: F-IFB4 Task An impotant example of a model often used in biology o ecology to model population gowth is called the logistic gowth
Chapter 3 Optical Systems with Annular Pupils
 Chapte 3 Optical Systems with Annula Pupils 3 INTRODUCTION In this chapte, we discuss the imaging popeties of a system with an annula pupil in a manne simila to those fo a system with a cicula pupil The
Chapte 3 Optical Systems with Annula Pupils 3 INTRODUCTION In this chapte, we discuss the imaging popeties of a system with an annula pupil in a manne simila to those fo a system with a cicula pupil The
Homework # 3 Solution Key
 PHYSICS 631: Geneal Relativity Homewok # 3 Solution Key 1. You e on you hono not to do this one by hand. I ealize you can use a compute o simply look it up. Please don t. In a flat space, the metic in
PHYSICS 631: Geneal Relativity Homewok # 3 Solution Key 1. You e on you hono not to do this one by hand. I ealize you can use a compute o simply look it up. Please don t. In a flat space, the metic in
Chapter 2: Basic Physics and Math Supplements
 Chapte 2: Basic Physics and Math Supplements Decembe 1, 215 1 Supplement 2.1: Centipetal Acceleation This supplement expands on a topic addessed on page 19 of the textbook. Ou task hee is to calculate
Chapte 2: Basic Physics and Math Supplements Decembe 1, 215 1 Supplement 2.1: Centipetal Acceleation This supplement expands on a topic addessed on page 19 of the textbook. Ou task hee is to calculate
2. Plane Elasticity Problems
 S0 Solid Mechanics Fall 009. Plane lasticity Poblems Main Refeence: Theoy of lasticity by S.P. Timoshenko and J.N. Goodie McGaw-Hill New Yok. Chaptes 3..1 The plane-stess poblem A thin sheet of an isotopic
S0 Solid Mechanics Fall 009. Plane lasticity Poblems Main Refeence: Theoy of lasticity by S.P. Timoshenko and J.N. Goodie McGaw-Hill New Yok. Chaptes 3..1 The plane-stess poblem A thin sheet of an isotopic
transformation Earth V-curve (meridian) λ Conical projection. u,v curves on the datum surface projected as U,V curves on the projection surface
 . CONICAL PROJECTIONS In elementay texts on map pojections, the pojection sufaces ae often descibed as developable sufaces, such as the cylinde (cylindical pojections) and the cone (conical pojections),
. CONICAL PROJECTIONS In elementay texts on map pojections, the pojection sufaces ae often descibed as developable sufaces, such as the cylinde (cylindical pojections) and the cone (conical pojections),
Question Bank. Section A. is skew-hermitian matrix. is diagonalizable. (, ) , Evaluate (, ) 12 about = 1 and = Find, if
 Subject: Mathematics-I Question Bank Section A T T. Find the value of fo which the matix A = T T has ank one. T T i. Is the matix A = i is skew-hemitian matix. i. alculate the invese of the matix = 5 7
Subject: Mathematics-I Question Bank Section A T T. Find the value of fo which the matix A = T T has ank one. T T i. Is the matix A = i is skew-hemitian matix. i. alculate the invese of the matix = 5 7
(n 1)n(n + 1)(n + 2) + 1 = (n 1)(n + 2)n(n + 1) + 1 = ( (n 2 + n 1) 1 )( (n 2 + n 1) + 1 ) + 1 = (n 2 + n 1) 2.
 Paabola Volume 5, Issue (017) Solutions 151 1540 Q151 Take any fou consecutive whole numbes, multiply them togethe and add 1. Make a conjectue and pove it! The esulting numbe can, fo instance, be expessed
Paabola Volume 5, Issue (017) Solutions 151 1540 Q151 Take any fou consecutive whole numbes, multiply them togethe and add 1. Make a conjectue and pove it! The esulting numbe can, fo instance, be expessed
(read nabla or del) is defined by, k. (9.7.1*)
 9.7 Gadient of a scala field. Diectional deivative Some of the vecto fields in applications can be obtained fom scala fields. This is vey advantageous because scala fields can be handled moe easily. The
9.7 Gadient of a scala field. Diectional deivative Some of the vecto fields in applications can be obtained fom scala fields. This is vey advantageous because scala fields can be handled moe easily. The
c n ψ n (r)e ient/ h (2) where E n = 1 mc 2 α 2 Z 2 ψ(r) = c n ψ n (r) = c n = ψn(r)ψ(r)d 3 x e 2r/a0 1 πa e 3r/a0 r 2 dr c 1 2 = 2 9 /3 6 = 0.
 Poblem {a} Fo t : Ψ(, t ψ(e iet/ h ( whee E mc α (α /7 ψ( e /a πa Hee we have used the gound state wavefunction fo Z. Fo t, Ψ(, t can be witten as a supeposition of Z hydogenic wavefunctions ψ n (: Ψ(,
Poblem {a} Fo t : Ψ(, t ψ(e iet/ h ( whee E mc α (α /7 ψ( e /a πa Hee we have used the gound state wavefunction fo Z. Fo t, Ψ(, t can be witten as a supeposition of Z hydogenic wavefunctions ψ n (: Ψ(,
Introduction Common Divisors. Discrete Mathematics Andrei Bulatov
 Intoduction Common Divisos Discete Mathematics Andei Bulatov Discete Mathematics Common Divisos 3- Pevious Lectue Integes Division, popeties of divisibility The division algoithm Repesentation of numbes
Intoduction Common Divisos Discete Mathematics Andei Bulatov Discete Mathematics Common Divisos 3- Pevious Lectue Integes Division, popeties of divisibility The division algoithm Repesentation of numbes
B da = 0. Q E da = ε. E da = E dv
 lectomagnetic Theo Pof Ruiz, UNC Asheville, doctophs on YouTube Chapte Notes The Maxwell quations in Diffeential Fom 1 The Maxwell quations in Diffeential Fom We will now tansfom the integal fom of the
lectomagnetic Theo Pof Ruiz, UNC Asheville, doctophs on YouTube Chapte Notes The Maxwell quations in Diffeential Fom 1 The Maxwell quations in Diffeential Fom We will now tansfom the integal fom of the
As is natural, our Aerospace Structures will be described in a Euclidean three-dimensional space R 3.
 Appendix A Vecto Algeba As is natual, ou Aeospace Stuctues will be descibed in a Euclidean thee-dimensional space R 3. A.1 Vectos A vecto is used to epesent quantities that have both magnitude and diection.
Appendix A Vecto Algeba As is natual, ou Aeospace Stuctues will be descibed in a Euclidean thee-dimensional space R 3. A.1 Vectos A vecto is used to epesent quantities that have both magnitude and diection.
EFFECTS OF FRINGING FIELDS ON SINGLE PARTICLE DYNAMICS. M. Bassetti and C. Biscari INFN-LNF, CP 13, Frascati (RM), Italy
 Fascati Physics Seies Vol. X (998), pp. 47-54 4 th Advanced ICFA Beam Dynamics Wokshop, Fascati, Oct. -5, 997 EFFECTS OF FRININ FIELDS ON SINLE PARTICLE DYNAMICS M. Bassetti and C. Biscai INFN-LNF, CP
Fascati Physics Seies Vol. X (998), pp. 47-54 4 th Advanced ICFA Beam Dynamics Wokshop, Fascati, Oct. -5, 997 EFFECTS OF FRININ FIELDS ON SINLE PARTICLE DYNAMICS M. Bassetti and C. Biscai INFN-LNF, CP
Solution to HW 3, Ma 1a Fall 2016
 Solution to HW 3, Ma a Fall 206 Section 2. Execise 2: Let C be a subset of the eal numbes consisting of those eal numbes x having the popety that evey digit in the decimal expansion of x is, 3, 5, o 7.
Solution to HW 3, Ma a Fall 206 Section 2. Execise 2: Let C be a subset of the eal numbes consisting of those eal numbes x having the popety that evey digit in the decimal expansion of x is, 3, 5, o 7.
Graphs of Sine and Cosine Functions
 Gaphs of Sine and Cosine Functions In pevious sections, we defined the tigonometic o cicula functions in tems of the movement of a point aound the cicumfeence of a unit cicle, o the angle fomed by the
Gaphs of Sine and Cosine Functions In pevious sections, we defined the tigonometic o cicula functions in tems of the movement of a point aound the cicumfeence of a unit cicle, o the angle fomed by the
working pages for Paul Richards class notes; do not copy or circulate without permission from PGR 2004/11/3 10:50
 woking pages fo Paul Richads class notes; do not copy o ciculate without pemission fom PGR 2004/11/3 10:50 CHAPTER7 Solid angle, 3D integals, Gauss s Theoem, and a Delta Function We define the solid angle,
woking pages fo Paul Richads class notes; do not copy o ciculate without pemission fom PGR 2004/11/3 10:50 CHAPTER7 Solid angle, 3D integals, Gauss s Theoem, and a Delta Function We define the solid angle,
Brief summary of functional analysis APPM 5440 Fall 2014 Applied Analysis
 Bief summay of functional analysis APPM 5440 Fall 014 Applied Analysis Stephen Becke, stephen.becke@coloado.edu Standad theoems. When necessay, I used Royden s and Keyzsig s books as a efeence. Vesion
Bief summay of functional analysis APPM 5440 Fall 014 Applied Analysis Stephen Becke, stephen.becke@coloado.edu Standad theoems. When necessay, I used Royden s and Keyzsig s books as a efeence. Vesion
Vectors, Vector Calculus, and Coordinate Systems
 ! Revised Apil 11, 2017 1:48 PM! 1 Vectos, Vecto Calculus, and Coodinate Systems David Randall Physical laws and coodinate systems Fo the pesent discussion, we define a coodinate system as a tool fo descibing
! Revised Apil 11, 2017 1:48 PM! 1 Vectos, Vecto Calculus, and Coodinate Systems David Randall Physical laws and coodinate systems Fo the pesent discussion, we define a coodinate system as a tool fo descibing
Vector d is a linear vector function of vector d when the following relationships hold:
 Appendix 4 Dyadic Analysis DEFINITION ecto d is a linea vecto function of vecto d when the following elationships hold: d x = a xxd x + a xy d y + a xz d z d y = a yxd x + a yy d y + a yz d z d z = a zxd
Appendix 4 Dyadic Analysis DEFINITION ecto d is a linea vecto function of vecto d when the following elationships hold: d x = a xxd x + a xy d y + a xz d z d y = a yxd x + a yy d y + a yz d z d z = a zxd
Dymore User s Manual Two- and three dimensional dynamic inflow models
 Dymoe Use s Manual Two- and thee dimensional dynamic inflow models Contents 1 Two-dimensional finite-state genealized dynamic wake theoy 1 Thee-dimensional finite-state genealized dynamic wake theoy 1
Dymoe Use s Manual Two- and thee dimensional dynamic inflow models Contents 1 Two-dimensional finite-state genealized dynamic wake theoy 1 Thee-dimensional finite-state genealized dynamic wake theoy 1
Quantum theory of angular momentum
 Quantum theoy of angula momentum Igo Mazets igo.mazets+e141@tuwien.ac.at (Atominstitut TU Wien, Stadionallee 2, 1020 Wien Time: Fiday, 13:00 14:30 Place: Feihaus, Sem.R. DA gün 06B (exception date 18 Nov.:
Quantum theoy of angula momentum Igo Mazets igo.mazets+e141@tuwien.ac.at (Atominstitut TU Wien, Stadionallee 2, 1020 Wien Time: Fiday, 13:00 14:30 Place: Feihaus, Sem.R. DA gün 06B (exception date 18 Nov.:
Math 451: Euclidean and Non-Euclidean Geometry MWF 3pm, Gasson 204 Homework 9 Solutions
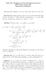 Math 451: Euclidean and Non-Euclidean Geomety MWF 3pm, Gasson 04 Homewok 9 Solutions Execises fom Chapte 3: 3.3, 3.8, 3.15, 3.19, 3.0, 5.11, 5.1, 5.13 Execise 3.3. Suppose that C and C ae two cicles with
Math 451: Euclidean and Non-Euclidean Geomety MWF 3pm, Gasson 04 Homewok 9 Solutions Execises fom Chapte 3: 3.3, 3.8, 3.15, 3.19, 3.0, 5.11, 5.1, 5.13 Execise 3.3. Suppose that C and C ae two cicles with
EM-2. 1 Coulomb s law, electric field, potential field, superposition q. Electric field of a point charge (1)
 EM- Coulomb s law, electic field, potential field, supeposition q ' Electic field of a point chage ( ') E( ) kq, whee k / 4 () ' Foce of q on a test chage e at position is ee( ) Electic potential O kq
EM- Coulomb s law, electic field, potential field, supeposition q ' Electic field of a point chage ( ') E( ) kq, whee k / 4 () ' Foce of q on a test chage e at position is ee( ) Electic potential O kq
arxiv: v1 [physics.pop-ph] 3 Jun 2013
![arxiv: v1 [physics.pop-ph] 3 Jun 2013 arxiv: v1 [physics.pop-ph] 3 Jun 2013](/thumbs/89/100795062.jpg) A note on the electostatic enegy of two point chages axiv:1306.0401v1 [physics.pop-ph] 3 Jun 013 A C Tot Instituto de Física Univesidade Fedeal do io de Janeio Caixa Postal 68.58; CEP 1941-97 io de Janeio,
A note on the electostatic enegy of two point chages axiv:1306.0401v1 [physics.pop-ph] 3 Jun 013 A C Tot Instituto de Física Univesidade Fedeal do io de Janeio Caixa Postal 68.58; CEP 1941-97 io de Janeio,
EM Boundary Value Problems
 EM Bounday Value Poblems 10/ 9 11/ By Ilekta chistidi & Lee, Seung-Hyun A. Geneal Desciption : Maxwell Equations & Loentz Foce We want to find the equations of motion of chaged paticles. The way to do
EM Bounday Value Poblems 10/ 9 11/ By Ilekta chistidi & Lee, Seung-Hyun A. Geneal Desciption : Maxwell Equations & Loentz Foce We want to find the equations of motion of chaged paticles. The way to do
1 Similarity Analysis
 ME43A/538A/538B Axisymmetic Tubulent Jet 9 Novembe 28 Similaity Analysis. Intoduction Conside the sketch of an axisymmetic, tubulent jet in Figue. Assume that measuements of the downsteam aveage axial
ME43A/538A/538B Axisymmetic Tubulent Jet 9 Novembe 28 Similaity Analysis. Intoduction Conside the sketch of an axisymmetic, tubulent jet in Figue. Assume that measuements of the downsteam aveage axial
ON THE TWO-BODY PROBLEM IN QUANTUM MECHANICS
 ON THE TWO-BODY PROBLEM IN QUANTUM MECHANICS L. MICU Hoia Hulubei National Institute fo Physics and Nuclea Engineeing, P.O. Box MG-6, RO-0775 Buchaest-Maguele, Romania, E-mail: lmicu@theoy.nipne.o (Received
ON THE TWO-BODY PROBLEM IN QUANTUM MECHANICS L. MICU Hoia Hulubei National Institute fo Physics and Nuclea Engineeing, P.O. Box MG-6, RO-0775 Buchaest-Maguele, Romania, E-mail: lmicu@theoy.nipne.o (Received
Chapter 5 Linear Equations: Basic Theory and Practice
 Chapte 5 inea Equations: Basic Theoy and actice In this chapte and the next, we ae inteested in the linea algebaic equation AX = b, (5-1) whee A is an m n matix, X is an n 1 vecto to be solved fo, and
Chapte 5 inea Equations: Basic Theoy and actice In this chapte and the next, we ae inteested in the linea algebaic equation AX = b, (5-1) whee A is an m n matix, X is an n 1 vecto to be solved fo, and
PHYS 110B - HW #7 Spring 2004, Solutions by David Pace Any referenced equations are from Griffiths Problem statements are paraphrased
 PHYS 0B - HW #7 Sping 2004, Solutions by David Pace Any efeenced euations ae fom Giffiths Poblem statements ae paaphased. Poblem 0.3 fom Giffiths A point chage,, moves in a loop of adius a. At time t 0
PHYS 0B - HW #7 Sping 2004, Solutions by David Pace Any efeenced euations ae fom Giffiths Poblem statements ae paaphased. Poblem 0.3 fom Giffiths A point chage,, moves in a loop of adius a. At time t 0
you of a spring. The potential energy for a spring is given by the parabola U( x)
 Small oscillations The theoy of small oscillations is an extemely impotant topic in mechanics. Conside a system that has a potential enegy diagam as below: U B C A x Thee ae thee points of stable equilibium,
Small oscillations The theoy of small oscillations is an extemely impotant topic in mechanics. Conside a system that has a potential enegy diagam as below: U B C A x Thee ae thee points of stable equilibium,
Σk=1. g r 3/2 z. 2 3-z. g 3 ( 3/2 ) g r 2. = 1 r = 0. () z = ( a ) + Σ. c n () a = ( a) 3-z -a. 3-z. z - + Σ. z 3, 5, 7, z ! = !
 09 Maclauin Seies of Completed Riemann Zeta 9. Maclauin Seies of Lemma 9.. ( Maclauin seies of gamma function ) When is the gamma function, n is the polygamma function and B n,kf, f, ae Bell polynomials,
09 Maclauin Seies of Completed Riemann Zeta 9. Maclauin Seies of Lemma 9.. ( Maclauin seies of gamma function ) When is the gamma function, n is the polygamma function and B n,kf, f, ae Bell polynomials,
So, if we are finding the amount of work done over a non-conservative vector field F r, we do that long ur r b ur =
 3.4 Geen s Theoem Geoge Geen: self-taught English scientist, 793-84 So, if we ae finding the amount of wok done ove a non-consevative vecto field F, we do that long u b u 3. method Wok = F d F( () t )
3.4 Geen s Theoem Geoge Geen: self-taught English scientist, 793-84 So, if we ae finding the amount of wok done ove a non-consevative vecto field F, we do that long u b u 3. method Wok = F d F( () t )
Physics 2A Chapter 10 - Moment of Inertia Fall 2018
 Physics Chapte 0 - oment of netia Fall 08 The moment of inetia of a otating object is a measue of its otational inetia in the same way that the mass of an object is a measue of its inetia fo linea motion.
Physics Chapte 0 - oment of netia Fall 08 The moment of inetia of a otating object is a measue of its otational inetia in the same way that the mass of an object is a measue of its inetia fo linea motion.
Euclidean Figures and Solids without Incircles or Inspheres
 Foum Geometicoum Volume 16 (2016) 291 298. FOUM GEOM ISSN 1534-1178 Euclidean Figues and Solids without Incicles o Insphees Dimitis M. Chistodoulou bstact. ll classical convex plana Euclidean figues that
Foum Geometicoum Volume 16 (2016) 291 298. FOUM GEOM ISSN 1534-1178 Euclidean Figues and Solids without Incicles o Insphees Dimitis M. Chistodoulou bstact. ll classical convex plana Euclidean figues that
INTRODUCTION. 2. Vectors in Physics 1
 INTRODUCTION Vectos ae used in physics to extend the study of motion fom one dimension to two dimensions Vectos ae indispensable when a physical quantity has a diection associated with it As an example,
INTRODUCTION Vectos ae used in physics to extend the study of motion fom one dimension to two dimensions Vectos ae indispensable when a physical quantity has a diection associated with it As an example,
Internet Appendix for A Bayesian Approach to Real Options: The Case of Distinguishing Between Temporary and Permanent Shocks
 Intenet Appendix fo A Bayesian Appoach to Real Options: The Case of Distinguishing Between Tempoay and Pemanent Shocks Steven R. Genadie Gaduate School of Business, Stanfod Univesity Andey Malenko Gaduate
Intenet Appendix fo A Bayesian Appoach to Real Options: The Case of Distinguishing Between Tempoay and Pemanent Shocks Steven R. Genadie Gaduate School of Business, Stanfod Univesity Andey Malenko Gaduate
Physics 161 Fall 2011 Extra Credit 2 Investigating Black Holes - Solutions The Following is Worth 50 Points!!!
 Physics 161 Fall 011 Exta Cedit Investigating Black Holes - olutions The Following is Woth 50 Points!!! This exta cedit assignment will investigate vaious popeties of black holes that we didn t have time
Physics 161 Fall 011 Exta Cedit Investigating Black Holes - olutions The Following is Woth 50 Points!!! This exta cedit assignment will investigate vaious popeties of black holes that we didn t have time
DonnishJournals
 DonnishJounals 041-1189 Donnish Jounal of Educational Reseach and Reviews. Vol 1(1) pp. 01-017 Novembe, 014. http:///dje Copyight 014 Donnish Jounals Oiginal Reseach Pape Vecto Analysis Using MAXIMA Savaş
DonnishJounals 041-1189 Donnish Jounal of Educational Reseach and Reviews. Vol 1(1) pp. 01-017 Novembe, 014. http:///dje Copyight 014 Donnish Jounals Oiginal Reseach Pape Vecto Analysis Using MAXIMA Savaş
7 Wave Equation in Higher Dimensions
 7 Wave Equation in Highe Dimensions We now conside the initial-value poblem fo the wave equation in n dimensions, u tt c u 0 x R n u(x, 0 φ(x u t (x, 0 ψ(x whee u n i u x i x i. (7. 7. Method of Spheical
7 Wave Equation in Highe Dimensions We now conside the initial-value poblem fo the wave equation in n dimensions, u tt c u 0 x R n u(x, 0 φ(x u t (x, 0 ψ(x whee u n i u x i x i. (7. 7. Method of Spheical
Chapter 10 Sample Exam
 Chapte Sample Exam Poblems maked with an asteisk (*) ae paticulaly challenging and should be given caeful consideation.. Conside the paametic cuve x (t) =e t, y (t) =e t, t (a) Compute the length of the
Chapte Sample Exam Poblems maked with an asteisk (*) ae paticulaly challenging and should be given caeful consideation.. Conside the paametic cuve x (t) =e t, y (t) =e t, t (a) Compute the length of the
Lecture 7: Angular Momentum, Hydrogen Atom
 Lectue 7: Angula Momentum, Hydogen Atom Vecto Quantization of Angula Momentum and Nomalization of 3D Rigid Roto wavefunctions Conside l, so L 2 2 2. Thus, we have L 2. Thee ae thee possibilities fo L z
Lectue 7: Angula Momentum, Hydogen Atom Vecto Quantization of Angula Momentum and Nomalization of 3D Rigid Roto wavefunctions Conside l, so L 2 2 2. Thus, we have L 2. Thee ae thee possibilities fo L z
On the integration of the equations of hydrodynamics
 Uebe die Integation de hydodynamischen Gleichungen J f eine u angew Math 56 (859) -0 On the integation of the equations of hydodynamics (By A Clebsch at Calsuhe) Tanslated by D H Delphenich In a pevious
Uebe die Integation de hydodynamischen Gleichungen J f eine u angew Math 56 (859) -0 On the integation of the equations of hydodynamics (By A Clebsch at Calsuhe) Tanslated by D H Delphenich In a pevious
PHYS 301 HOMEWORK #10 (Optional HW)
 PHYS 301 HOMEWORK #10 (Optional HW) 1. Conside the Legende diffeential equation : 1 - x 2 y'' - 2xy' + m m + 1 y = 0 Make the substitution x = cos q and show the Legende equation tansfoms into d 2 y 2
PHYS 301 HOMEWORK #10 (Optional HW) 1. Conside the Legende diffeential equation : 1 - x 2 y'' - 2xy' + m m + 1 y = 0 Make the substitution x = cos q and show the Legende equation tansfoms into d 2 y 2
Chapter 13 Gravitation
 Chapte 13 Gavitation In this chapte we will exploe the following topics: -Newton s law of gavitation, which descibes the attactive foce between two point masses and its application to extended objects
Chapte 13 Gavitation In this chapte we will exploe the following topics: -Newton s law of gavitation, which descibes the attactive foce between two point masses and its application to extended objects
3.6 Applied Optimization
 .6 Applied Optimization Section.6 Notes Page In this section we will be looking at wod poblems whee it asks us to maimize o minimize something. Fo all the poblems in this section you will be taking the
.6 Applied Optimization Section.6 Notes Page In this section we will be looking at wod poblems whee it asks us to maimize o minimize something. Fo all the poblems in this section you will be taking the
Lecture 8 - Gauss s Law
 Lectue 8 - Gauss s Law A Puzzle... Example Calculate the potential enegy, pe ion, fo an infinite 1D ionic cystal with sepaation a; that is, a ow of equally spaced chages of magnitude e and altenating sign.
Lectue 8 - Gauss s Law A Puzzle... Example Calculate the potential enegy, pe ion, fo an infinite 1D ionic cystal with sepaation a; that is, a ow of equally spaced chages of magnitude e and altenating sign.
$ i. !((( dv vol. Physics 8.02 Quiz One Equations Fall q 1 q 2 r 2 C = 2 C! V 2 = Q 2 2C F = 4!" or. r ˆ = points from source q to observer
 Physics 8.0 Quiz One Equations Fall 006 F = 1 4" o q 1 q = q q ˆ 3 4" o = E 4" o ˆ = points fom souce q to obseve 1 dq E = # ˆ 4" 0 V "## E "d A = Q inside closed suface o d A points fom inside to V =
Physics 8.0 Quiz One Equations Fall 006 F = 1 4" o q 1 q = q q ˆ 3 4" o = E 4" o ˆ = points fom souce q to obseve 1 dq E = # ˆ 4" 0 V "## E "d A = Q inside closed suface o d A points fom inside to V =
CHAPTER 3. Section 1. Modeling Population Growth
 CHAPTER 3 Section 1. Modeling Population Gowth 1.1. The equation of the Malthusian model is Pt) = Ce t. Apply the initial condition P) = 1. Then 1 = Ce,oC = 1. Next apply the condition P1) = 3. Then 3
CHAPTER 3 Section 1. Modeling Population Gowth 1.1. The equation of the Malthusian model is Pt) = Ce t. Apply the initial condition P) = 1. Then 1 = Ce,oC = 1. Next apply the condition P1) = 3. Then 3
MATH 220: SECOND ORDER CONSTANT COEFFICIENT PDE. We consider second order constant coefficient scalar linear PDEs on R n. These have the form
 MATH 220: SECOND ORDER CONSTANT COEFFICIENT PDE ANDRAS VASY We conside second ode constant coefficient scala linea PDEs on R n. These have the fom Lu = f L = a ij xi xj + b i xi + c i whee a ij b i and
MATH 220: SECOND ORDER CONSTANT COEFFICIENT PDE ANDRAS VASY We conside second ode constant coefficient scala linea PDEs on R n. These have the fom Lu = f L = a ij xi xj + b i xi + c i whee a ij b i and
Vectors, Vector Calculus, and Coordinate Systems
 Apil 5, 997 A Quick Intoduction to Vectos, Vecto Calculus, and Coodinate Systems David A. Randall Depatment of Atmospheic Science Coloado State Univesity Fot Collins, Coloado 80523. Scalas and vectos Any
Apil 5, 997 A Quick Intoduction to Vectos, Vecto Calculus, and Coodinate Systems David A. Randall Depatment of Atmospheic Science Coloado State Univesity Fot Collins, Coloado 80523. Scalas and vectos Any
Numerical approximation to ζ(2n+1)
 Illinois Wesleyan Univesity Fom the SelectedWoks of Tian-Xiao He 6 Numeical appoximation to ζ(n+1) Tian-Xiao He, Illinois Wesleyan Univesity Michael J. Dancs Available at: https://woks.bepess.com/tian_xiao_he/6/
Illinois Wesleyan Univesity Fom the SelectedWoks of Tian-Xiao He 6 Numeical appoximation to ζ(n+1) Tian-Xiao He, Illinois Wesleyan Univesity Michael J. Dancs Available at: https://woks.bepess.com/tian_xiao_he/6/
Doubling property for the Laplacian and its applications (Course Chengdu 2007)
 Doubling popety fo the Laplacian and its applications Couse Chengdu 007) K.-D. PHUNG The oiginal appoach of N. Gaofalo and F.H. Lin Fo simplicity, we epoduce the poof of N. Gaofalo and F.H. Lin in the
Doubling popety fo the Laplacian and its applications Couse Chengdu 007) K.-D. PHUNG The oiginal appoach of N. Gaofalo and F.H. Lin Fo simplicity, we epoduce the poof of N. Gaofalo and F.H. Lin in the
Analysis of simple branching trees with TI-92
 Analysis of simple banching tees with TI-9 Dušan Pagon, Univesity of Maibo, Slovenia Abstact. In the complex plane we stat at the cente of the coodinate system with a vetical segment of the length one
Analysis of simple banching tees with TI-9 Dušan Pagon, Univesity of Maibo, Slovenia Abstact. In the complex plane we stat at the cente of the coodinate system with a vetical segment of the length one
1 Spherical multipole moments
 Jackson notes 9 Spheical multipole moments Suppose we have a chage distibution ρ (x) wheeallofthechageiscontained within a spheical egion of adius R, as shown in the diagam. Then thee is no chage in the
Jackson notes 9 Spheical multipole moments Suppose we have a chage distibution ρ (x) wheeallofthechageiscontained within a spheical egion of adius R, as shown in the diagam. Then thee is no chage in the
Homework 7 Solutions
 Homewok 7 olutions Phys 4 Octobe 3, 208. Let s talk about a space monkey. As the space monkey is oiginally obiting in a cicula obit and is massive, its tajectoy satisfies m mon 2 G m mon + L 2 2m mon 2
Homewok 7 olutions Phys 4 Octobe 3, 208. Let s talk about a space monkey. As the space monkey is oiginally obiting in a cicula obit and is massive, its tajectoy satisfies m mon 2 G m mon + L 2 2m mon 2
Classical Mechanics Homework set 7, due Nov 8th: Solutions
 Classical Mechanics Homewok set 7, due Nov 8th: Solutions 1. Do deivation 8.. It has been asked what effect does a total deivative as a function of q i, t have on the Hamiltonian. Thus, lets us begin with
Classical Mechanics Homewok set 7, due Nov 8th: Solutions 1. Do deivation 8.. It has been asked what effect does a total deivative as a function of q i, t have on the Hamiltonian. Thus, lets us begin with
Unobserved Correlation in Ascending Auctions: Example And Extensions
 Unobseved Coelation in Ascending Auctions: Example And Extensions Daniel Quint Univesity of Wisconsin Novembe 2009 Intoduction In pivate-value ascending auctions, the winning bidde s willingness to pay
Unobseved Coelation in Ascending Auctions: Example And Extensions Daniel Quint Univesity of Wisconsin Novembe 2009 Intoduction In pivate-value ascending auctions, the winning bidde s willingness to pay
