SMALL SYMPLECTIC CALABI-YAU SURFACES AND EXOTIC 4-MANIFOLDS VIA GENUS-3 PENCILS. 1. Introduction
|
|
|
- Evelyn Phillips
- 5 years ago
- Views:
Transcription
1 SMALL SYMPLECTIC CALABI-YAU SURFACES AND EXOTIC 4-MANIFOLDS VIA GENUS-3 PENCILS R. İNANÇ BAYKUR Abstract. We explicitly produce symplectic genus-3 Lefschetz pencils (with base points), whose total spaces are homeomorphic but not diffeomorphic to rational surfaces CP #pcp for p = 7,8,9. We then give a new construction of an infinite family of symplectic Calabi-Yau surfaces with first Betti number b =,3, along with a surface with b = 4 homeomorphic to the 4-torus. These are presented as the total spaces of symplectic genus-3 Lefschetz pencils we construct via new positive factorizations in the mapping class group of a genus-3 surface. Our techniques in addition allow us to answer in the negative a question of Korkmaz regarding the upper bound on b of a genus-g fibration.. Introduction Since the advent of Gauge theory, many new construction techniques, such as rational blowdowns, generalized fiber sum, knot surgery and Luttinger surgery, have been introduced and successfully employed to produce symplectic 4-manifolds homeomorphic but not diffeomorphic to rational surfaces CP #pcp, for p. (e.g. [,, 7,, 8, 9, 3, 3, 36, 37, 46, 58, 57, 65].) All these 4-manifolds should admit symplectic Lefschetz pencils (which, by definition, always have base points) by the ground-breaking work of Donaldson []. Despite this a priori existence result, no explicit Lefschetz pencils on these small (as in small second homology) exotic 4-manifolds were known up to date. The main goal of this article is to introduce novel ways of constructing small positive factorizations (as in small number of positive Dehn twists) of the boundary multi-twist in the mapping class group Γ m g of a compact genus-g surface with m > 0 boundary components, which correspond to monodromy factorizations of genus-g Lefschetz pencils on small symplectic 4-manifolds. A first application yields the first explicit examples of pencils on exotic rational surfaces: Theorem. There are symplectic genus-3 Lefschetz pencils (X i,f i ) whose total spaces are homeomorphic but not diffeomorphic to CP #(6+i)CP for i =,,3. They realize the smallest possible genera pencils in these homeomorphism classes. A key result leading to Theorem is that CP #pcp, for p 9, does not admit a genus g Lefschetz fibration or a genus-g Lefschetz pencil with m < g base points (Lemma 7), which provides a new criterion to argue that the total spaces of such pencils/fibrations like the ones in Theorem are exotic. We moreover observe that g = 3 is the smallest possible genus for a Lefschetz pencil on these exotic 4-manifolds (Remark 9). We hope that the additional information on these exotic symplectic 4-manifolds we construct, namely the existence of genus-3 pencils on
2 R. İ. BAYKUR them, will help with understanding whether there are distinct minimal symplectic 4-manifolds in the homeomorphism classes CP #pcp, for p < 9 (a question which is still open as of today; see Remark ). To produce the positive factorizations for the pencils in Theorem, we employ a new way of deriving a positive factorization W in Γ m g, m 0 from a collection of positive factorizations W,...,W k of boundary twists in Γ n h, with h < g and n > 0. For(X,f)theLefschetzpencil/fibrationcorrespondingto W and(x i,f i )tow i, we say (X,f) is obtained by breeding (X,f ),...,(X k,f k ). This involves embedding the latter into Γ m g as factorizations for achiral Lefschetz pencils/fibrations, and then canceling matching pairs of positive and negative Dehn twists. The idea for this construction scheme comes from the smallest hyperelliptic genus-3 Lefschetz fibration Mustafa Korkmaz and the author produced in [4]. A careful variation of our construction of (X i,f i ) yield to our next theorem: Theorem. For any pair of non-negative integers M = (m,m ), there exists a symplectic genus-3 Lefschetz pencil (X i,m,f i,m ) with c (X i,m ) = 3 i, χ(x i,m ) =, and π (X i,m ) = (Z/m Z) (Z/m Z), for each i =,,3. Infinitely many of these pencils have total spaces homotopy inequivalent to a complex surface. In contrast, I know of only one explicit example of a non-holomorphic genus-3 Lefschetz pencil in the literature, due to Ivan Smith. ([6][Theorem.3]; see also Remark 3.) Our construction technique yielding the pencils in Theorem can be easily generalized to obtain many other non-holomorphic pencils. The second part of our article will deal with new constructions of symplectic Calabi-Yau surfaces. Recall that a symplectic 4-manifold (X, ω) is called a symplectic Calabi-Yau surface (SCY) if it has trivial canonical class K X H (X;Z), in obvious analogy with complex Calabi-Yau surfaces. As shown by Tian-Jun Li, any minimal symplectic 4-manifold with Kodaira dimension zero has torsion canonical class [47]. Up to date, the only known examples of symplectic Calabi-Yau surfaces that are not diffeomorphic to complex Calabi-Yau surfaces are torus bundles over tori (at least virtually), leading to the question [47, 4]: Question 3. Is every symplectic Calabi-Yau surface with b > 0 diffeomorphic to an oriented torus bundle over a torus? Works of Tian-Jun Li and Stefan Bauer independently established that any symplectic Calabi-Yau surface with b > 0 has the same rational homology as a torus bundle (and that of K3 and the Enriques surface when b = 0) [47, 49, 8]. All torus bundles over tori have solvmanifold fundamental groups [4], and notably, it was shown by Stefan Friedl and Stefano Vidussi that the homeomorphism type of a symplectic Calabi-Yau surface with a solvmanifold fundamental group is uniquely determined [34]. As stated by Tian-Jun Li in [50], what seems to commonly provide a posteriori reasoning for a positive answer to the Question 3 is the lack of any new constructions of symplectic 4-manifolds of Kodaira dimension zero. Surgical operations widely used to construct most interesting symplectic 4-manifolds in the A couple other examples of SCYs, such as symplectic S -bundles over T -bundles over S, although not known to be torus bundles themselves, are finitely covered by them [34].
3 SMALL SYMPLECTIC CALABI-YAUS AND EXOTIC 4-MANIFOLDS VIA PENCILS 3 past, such as Luttinger surgery, generalized fiber sums, knot surgery, or simplest rational blow-down operations, do not produce any new SCYs [40, 50, 7, 5]. WewillpresentanewconstructionofsymplecticCalabi-Yau surfaceswithb > 0 via Lefschetz pencils, where the genus of the pencil (X,f) versus c (X), building on the work of Cliff Taubes, will determine the Kodaira dimension of X (Lemma 5; also [60]). Once again, we will focus on generating the smallest genus examples: genus-3 pencils. To produce our examples, we will use a version of the aforementioned breeding technique for producing new positive factorizations in Γ m 3, which we will call inbreeding, where this time copies of the same positive factorization in Γ n will be embedded into Γ m 3 by identifying some of the boundary components of the fiber Σ n and introducing extra π -generators this way. The result is a family of positive factorizations W φ = t φ(b0)t φ(b)t φ(b)t φ(a0)t φ(a)t φ(a) 0 0 = inγ 3, whereφ Γ 3 isparametrizedbypairsofmappingclassesφ,φ Γ, andthe curves B j,a j are as shown in Figure 4. Here we inbreed the monodromy factorizations of Matsumoto s well-known genus- Lefschetz fibration [5], and using further lifts of it obtained by Noriyuki Hamada [39], we can even derive an explicit lift of W φ, whichisapositivefactorizationoftheboundarymulti-twist = t t t 3 t 4 in Γ 4 3. Letting (X φ,f φ ) denote the corresponding symplectic genus-3 Lefschetz pencil, we obtain (Theorem 6): Theorem 4. Positive factorizations W φ prescribe symplectic genus-3 Lefschetz pencils on a family of symplectic Calabi-Yau surfaces X φ in all rational homology classes of torus bundles over tori. This provides a first step towards analyzing the monodromies of pencils on a rich family of SCYs, as proposed by Simon Donaldson in [3][Problem 5]. The first question that arises here is whether or not all X φ are diffeomorphic to torus bundles over tori, in reference to Question 3. Torus bundles over tori with sections do admit symplectic genus-3 pencils [6]; however the uncanny freedom we have in the choice of φ appears to exceed that of a torus bundle with a section (see the discussion in Remark 8). The explicit nature of our construction allows us to derive explicit presentations for π (X φ ), which for instance yields an X (when φ is trivial) that is at least homeomorphic to the 4-torus. We will discuss this example in complete detail in Section 4.. It is not clear to us at this point whether or not all π (X φ ) are 4-dimensional solvmanifold groups (some of them certainly are), which we hope to understand in future work. On the other hand, we observe that all X φ are obtained from X, our SCY homeomorphic to the 4-torus, via fibered Luttinger surgeries along Lagrangian tori or Klein bottles (Remark 9). So if our family of X φ is equal to the family of torus bundles over tori, it immediately confirms an improved version of an interesting conjecture by Tian-Jun Li and Chung-I Ho [40][Conjecture 4.9]: Any smooth oriented torus bundle X possesses a symplectic structure ω such that (X,ω) can be obtained by applying Luttinger surgeries to (T 4,ω std ) (Remark 9). Only Luttinger surgeries along tori are considered in [40], but it is natural to include surgeries along Klein bottles, too.
4 4 R. İ. BAYKUR Finally, Theorem 4 implies that we have symplectic genus-3 pencils (X φ,f φ ) with H (X φ ) = Z (Z/m Z) (Z/m Z) for any m,m N. This yields further (infinitely many) examples of non-holomorphic genus-3 pencils, in the same fashion as in our earlier examples in Theorem. The techniques we employed to produce the genus-3 pencils in Theorems, and 4 can be easily adapted to produce higher genera pencils on similar 4-manifolds; we can in fact derive many of these by repeatedly breeding/inbreeding the same collection of positive factorizations used in this paper. This direction will be explored elsewhere. We will however discuss one immediate generalization of our construction of a genus-3 pencil to higher genera. It will allow us to address a problem raised by Mustafa Korkmaz [45][Problem.7], which we re-express here for pencils (which are even more constrained than fibrations): Question 5. Is b (X) g for any non-trivial genus-g Lefschetz pencil (X,f)? Is there an upper bound on b (X) linear in g, and sharper than g? In Section 4.3, generalizing our construction of a genus-3 pencil on X homeomorphic to the 4-torus, we will produce genus-g Lefschetz pencils violating the above bound for every odd g >. Though not much; we will indeed revamp Korkmaz s question by raising the upper bound to g + (Question 0). Acknowledgements. We would like to thank Weimin Chen, Bob Gompf, Jonathan Hillman, Tian-Jun Li, and Stefano Vidussi for helpful conversations related to our constructions in this paper. Thanks to Noriyuki Hamada for telling us about his preprint on the sections of the Matsumoto fibration. Our results on small symplectic Calabi-Yau surfaces via Lefschetz fibrations with exceptional sections were first presented at the Great Lakes Geometry Conference in Ann Arbor in March 05; we would like to thank the organizers for motivating discussions. Last but not least, we are grateful to Mustafa Korkmaz for his interest in our work and numerous stimulating discussions. The author was partially supported by the NSF Grant DMS Preliminaries Here we quickly review the definitions and basic properties of Lefschetz pencils and fibrations, Dehn twist factorizations in mapping class groups of surfaces, and symplectic Calabi-Yau surfaces. The reader can turn to [38, 48, 3] for more details... Lefschetz pencils and fibrations. A Lefschetz pencil on a closed, smooth, oriented 4-manifold X is a smooth surjective map f : X \ {b j } S, defined on the complement of a non-empty finite collection of points {b j }, such that around every base point b j and critical point p i there are local complex coordinates (compatible with the orientations on X and S ) withrespecttowhichthemapf takestheform(z,z ) z /z and(z,z ) z z, respectively. A Lefschetz fibration is defined similarly for {b j } =. Blowing-up all the base points b j in a pencil (X,f), one obtains a Lefschetz fibration ( X, f) with disjoint ( )-sphere sections S j corresponding to b j, and vice versa.
5 SMALL SYMPLECTIC CALABI-YAUS AND EXOTIC 4-MANIFOLDS VIA PENCILS 5 Wesay(X,f) is agenus g Lefschetz pencil or fibration for g thegenusof aregular fiber F of f. The fiber containing the critical point p i has a nodal singularity at p i, which locally arises from shrinking a simple loop c i on F, called the vanishing cycle. A singular fiber of (X,f) is called reducible if c i is separating. When c i is null-homotopic on F, one of the fiber components becomes an exceptional sphere, an embedded -sphere of self-intersection, which we can blow down without changing the rest of the fibration. In this paper we use the term Lefschetz fibration only when the set of critical points {p i } is non-empty, i.e. when the Lefschetz fibration is non-trivial. We moreover assume that the fibration is relatively minimal, i.e. it there are no exceptional spheres contained in the fibers, and also that the points p i lie in distinct singular fibers, which can be always achieved after a small perturbation. A widely used way of constructing Lefschetz fibrations is the fiber sum operation: if (X i,f i ) are genus-g Lefschetz fibrations with regular fiber F i for i =,, then their fiber sum is a genus-g Lefschetz fibration (X,f), where X is obtained by removing a fibered tubular neighborhood of each F i from X i and then identifying the resulting boundaries via a fiber-preserving, orientation-reversing selfdiffeomorphism, and where f restricts to f i on each X i \νf i. A Lefschetz fibration (X,f) that can be expressed in this way is called decomposable, and each (X i,f i ) are called its summands. Allowing local models (z,z ) z z around the critical points p i, called negative critical points, we can extend all of the above to achiral Lefschetz pencils and fibrations... Positive factorizations. Let Σ m g denote a compact, connected, oriented surface genus g with m boundary components. We denote by Γ m g its mapping class group; the group composed of orientation-preserving self homeomorphisms of Σ m g which restrict to the identity along Σ m g, modulo isotopies that also restrict to the identity along Σ m g. We write Σ g = Σ 0 g, and Γ g = Γ 0 g for simplicity. Denote by t c Σ m g the positive (righthanded) Dehn twist along the simple closed curve c Σ m g. The inverse t c denotes the negative (left-handed) Dehn twist along c. Let {c i } be a non-empty collection of simple closed curves on Σ m g, which do not become null-homotopic when Σ m g is capped off by disks, and let {δ j } be a collection of curves parallel to distinct boundary components of Σ m g. If the relation () t cl t c t c = t δ t δm holds in Γ m g, we call the word W on the left-hand side a positive factorization of the boundary multi-twist = t δ t δm in Γ n g. (We will also use i instead of δ i to denote boundary components at times when there are several surfaces with boundaries involved in our discussion.) Capping off Σ m g induces a homomorphism Γ m g Γ g, under which W maps to a similar positive factorization of the identity element Γ g. The positive factorization in () gives rise to a genus-g Lefschetz fibration ( X, f) with m disjoint ( )-sections S j, and equivalently a genus-g Lefschetz pencil (X,f)
6 6 R. İ. BAYKUR with m base points. Identifying the regular fiber F with Σ g, we can view the vanishing cycles as c i. In fact, every Lefschetz fibration or pencil can be described by a positive factorization W as in () [38, 4, 5], which is called the monodromy factorization of f or f. Let W be a positive factorization of the form W = PP in Γ m g, where P,P are products of positive Dehn twists along curves which do not become null-homotopic when Σ m g is capped off by disks. If P = t ci, as a mapping class, commutes with some φ Γ m g, we can produce a new positive factorization W φ = P φ P, where P φ denotes the conjugate factorization φpφ = (φt ci φ ) = t φ(ci). In this case, we say W φ is obtained from W by a partial conjugation φ along the factor P. When P,P Γ g are positive factorizations, W = PP is another positive factorization, Lefschetz fibration corresponding to which is a fiber sum of the fibrations corresponding to W and W. Allowing negative Dehn twists, which correspond to negative critical points, we can more generally work with factorizations for achiral Lefschetz fibrations and pencils. All of the above extend to this general case..3. Symplectic 4-manifolds and the Kodaira dimension. It was shown by Donaldson that every symplectic 4-manifold (X, ω) admits a symplectic Lefschetz pencil whose fibers are symplectic with respect to ω []. Conversely, generalizing a construction of Thurston, Gompf showed that the total space of a (nontrivial) Lefschetz fibration, and in particular blow-up of any pencil, always admits a symplectic form ω with respect to which all regular fibers and any preselected collection of disjoint sections are symplectic [38]. Whenever we take a symplectic form ω on a Lefschetz pencil or fibration (X,f) we will assume that it is of Thurston-Gompf type, with respect to which any explicitly discussed sections of f will always be assumed to be symplectic as well. The Kodaira dimension for projective surfaces can be extended to symplectic 4-manifolds as follows: Let K Xmin be the canonical class of a minimal model (X min,ω min ) of (X,ω). The symplectic Kodaira dimension of (X,ω), denoted by κ = κ(x,ω) is defined as κ(x,ω) = if K Xmin [ω min ] < 0 or K X min < 0 0 if K Xmin [ω min ] = K X min = 0 if K Xmin [ω min ] > 0 and K X min = 0 if K Xmin [ω min ] > 0 and K X min > 0 Remarkably, κ is not only independent of the minimal model (X min,ω min ) but also of the chosen symplectic form ω on X: it is a smooth invariant of the 4-manifold X [47]. Symplectic 4-manifolds with κ = are classified up to symplectomorphisms, which are precisely the rational and ruled surfaces[48]. Symplectic 4-manifolds with κ = 0 are the analogues of the Calabi-Yau surfaces that have torsion canonical class [47]. It has been shown by Tian-Jun Li, and independently by Stefan Bauer [47, 8], that the rational homology type of any minimal symplectic Calabi-Yau surface is that of either a torus bundle over a torus, the K3 surface, or the Enriques surface.
7 SMALL SYMPLECTIC CALABI-YAUS AND EXOTIC 4-MANIFOLDS VIA PENCILS 7 3. Exotic symplectic rational surfaces via genus-3 pencils Here we construct explicit positive factorizations for symplectic genus-3 Lefschetz pencils, whose total spaces are homeomorphic but not diffeomorphic to the complex rational surfaces. 3.. Breeding genus-3 Lefschetz pencils from genus- pencils. In [3], we have obtained the following relation in Γ which can be rewritten as t e t x t x t x3 t d t C t x4 = t δ, t e t x t x t x3 t d t B t C t δ =, where B = t c (x 4 ). Embed this relation into Γ 3 so that δ = Γ is mapped to c and the remaining curves are as in Figure, denoted by the same letters. (So, along with the embedding of x 4, the original curves on Γ can be all seen in the obvious subsurface of Γ 3 in Figure.) We thus get the following relation in Γ 3: () t e t x t x t x3 t d t B t C t C =, or P t C t C =, where we set P = t e t x t x t x3 t d t B. Note that P,t C and t C all commute with each other. Our second building block will be a positive factorization of the boundary multitwist in Γ, which is a lift of the monodromy factorization of Matsumoto s wellknown genus- Lefschetz fibration [5]. Such a lift to Γ was first found by Ozbagci and Stipsicz in [56] and a further lift to Γ by Korkmaz in [44]. We will however work with another lift discovered by Noriyuki Hamada, which yields the following relation in Γ [39]: (3) (t B0 t B t B t C ) = t δ t δ, where δ i are the boundary parallel curves, and the curves B i and C are as shown on the left-hand side of Figure. We can rewrite this relation in Γ as t B0 t B t B t A0 t A t A t Ct δ t δ =, where each A j = t C (B j ) for j = 0,, (Figure ). Let us first view this relation in Γ by capping off one of the boundary components, say δ. Embed the resulting relation into Γ 3, as induced by the same embedding of Γ into Γ 3 we used above so that the boundary is mapped to c, and all the other curves are as shown in Figure, once again denoted by the same letters for simplicity. So the following holds in Γ 3: (4) t B0 t B t B t A0 t A t A t Ct C =, or P t C t C =, where P = t B0 t B t B t A0 t A t A. Here P,t C and t C all commute with each other. Finally, we will embed the lat relation we had above in Γ into Γ 3 using an embedding of Σ into Σ 3 such that δ is mapped to c, δ is mapped to δ = Σ 3, and
8 8 R. İ. BAYKUR C C x B 0 B 0 x B B x 3 B B x 4 A 0 A 0 d A A e A A Figure. Curves C,x,x,x 3,x 4,d,e of the first embedding are given on the left. Curves B 0,B,B,A 0,A,A of the second embedding (along with the same C) and C,B 0,B,B,A 0,A,A of the third embedding are on the right.
9 SMALL SYMPLECTIC CALABI-YAUS AND EXOTIC 4-MANIFOLDS VIA PENCILS 9 the remaining curves are as shown in Figure, this time their labels are decorated by prime. This gives a third relation in Γ 3: (5) 0 0 t C t C = t δ, or P t C t C = t δ, where P = 0 0. Similar to the above, P,t C and t C all commute with each other. Now for φ = t b t a (where b,a are as in Figure 3), and in fact for any mapping class in Γ 3 that keeps C and C fixed, we have (P ) φ P P t C = (P ) φ t C t C P t C t C P t C t C = (P t C t C )φ t δ = t δ, where the first equality follows from the commutativity relations noted above, and the second equality follows from the relations () (5). So W = (P ) φ P P t C is a positive factorization of t δ in Γ 3. Similarly, we get two more positive factorizations W = (P ) φ P P t C and W 3 = (P ) φ P P t 3 C of t δ in Γ 3. Each W i prescribes a symplectic genus-3 Lefschetz fibration ( X i, f i ) with a ( )-section, which can be blown-down to arrive at a symplectic genus-3 Lefschetz pencil (X i,f i ) with one base point. They are all obtained by breeding the genus- Lefschetz pencils whose monodromies we have lifted to Γ Homeomorphism type of the pencils (X i,f i ). We will prove the following: Lemma 6. X i is homeomorphic to CP #(6+i)CP, for i =,,3. Proof. The proof will follow from Freedman s celebrated work [33], for which we will determine the Euler characteristic, the signature, and the spin type of X i, while showing that X i is simply-connected for all i =,,3. The Euler characteristic of X i is given by e(x i ) = e( X i ) = (4 4 3+l(W i )) = l(w i ) 9, where l(w i ) is the number of Dehn twists in the positive factorization W i. Since l(p ) = l(p ) = l(p ) = 6, we have l(w i ) = 8+i, and in turn, e(x i ) = 9+i. The signature of X i can be calculated as σ(x i ) = 5 i using Ozbagci s algorithm [54]. Here is a quick argument for this calculation: we have obtained the monodromy factorization of ( X, f ) after canceling a pair of t C and t C, and two pairs of t C and t C in the factorization (P t C t C )φ P t C t C P t C t C = in Γ 3 (where we capped off the boundary). The latter is a factorization of a genus-3 achiral Lefschetz fibration, which is a fiber sum of three achiral Lefschetz fibrations prescribed by P t C t C. P t C t C, and P t C t C. Each one of these three fibrations is obtained by a section sum of an achiral genus- Lefschetz fibration and a trivial torus fibration along a section of self-intersection zero, so by Novikov additivity, its signature is equal to that of the achiral genus- fibration. The hyperelliptic signature formula for genus- fibrations [5, 6] allows us to easily calculate these as,, and 3, which add up to give signature 7 for the original genus-3
10 0 R. İ. BAYKUR achiral Lefschetz fibration. The signature of ( X, f ) is the same as the signature of this achiral fibration, since canceling a pair of separating Dehn twists with opposite signs amounts to taking out a pair of ± contribution to the signature. Hence, we get σ(x ) = X + = 6. By identical arguments, we get σ(x ) = 7 and σ(x 3 ) = 8. Clearly each X i has an odd intersection form: this can be easily seen from the presence of the reducible fiber component split off by the separating vanishing cycle C and not hit by the ( )-sphere. (Alternatively, we can use Rokhlin s theorem after showing that π (X i ) =.) Lastly, we will show that π (X i ) = π ( X i ) =, by calculating the latter as the quotient of π (Σ 3 ) by the subgroup normally generated by the vanishing cycles of ( X i, f i ), for each i =,,3. It suffices to find enough relations that kill the generators a,b,a,b,a 3,b 3 of π (Σ 3 ) (which are as shown in Figure 3), so we do not need to work with the full presentation. Each positive factorization W i contains the factor P t C. So the following relations hold for the finite presentations we have for each π ( X i ): (6) (7) (8) (9) (0) [a,b ][a,b ][a 3,b 3 ] =, [a,b ] =, a a 3 =, a b a 3 b3 =, b 3 b =, where the relators (7) (0) come from the vanishing cycles C,B 0,B,B, respectively. We have a = ā 3 from (8) and b = b 3 from (0). Together with (9), these imply [a,b ] = [a 3,b 3 ] =. Together with (7), we conclude [a j,b j ] = for every j =,,3 (and (6) becomes a trivial relation). From the factor P, we get the following relations (among many others) () () (3) (4) a ( b a b ) =, a b3 a b a =, a b5 a [b,a ]b a =, b b [b 3,a 3 ] =, induced by the vanishing cycles x,x,x 3 and B, respectively. Adding these to the previous relators from the factor P, we immediately see that [a 3,b 3 ] = and (4) imply b = b. So () implies that a can be generated by a and b = b. From the factor P we get the following relations (again, among many others) (5) (6) a a =, b ā b ā [b 3,a 3 ] =, b b [b 3,a 3 ] =, induced by the vanishing cycles B 0,B and B, respectively. We get a = ā, and together with the relators from P we once again get b = b, since [a 3,b 3 ] =.
11 SMALL SYMPLECTIC CALABI-YAUS AND EXOTIC 4-MANIFOLDS VIA PENCILS Since the positive factorization W contains the factor P P t C and W,W 3 both contain the factor P P t C, the above discussion shows that every π ( X i ) is a factor of the abelian group Z generated by a and b. (In fact no additional relators come from the remaining twists in P,P or P.) For the remaining relators coming from the conjugated factors P φ or Pφ, it therefore suffices to look at the relators they induce in H (Σ 3 ). Moreover, this allows us to simply look at the homology classes of the vanishing cycles in these conjugated factors. (We haven t bothered to give explicitly for this very reason.) Without the conjugated factor, in each case we have the abelianized relations (7) a 3 = a and b 3 = b = b, and depending on whether W i contains the factor P or P, either (8) (9) where we used (7) to simplify. a +a +4b = 0 for W, or a +a = 0 for W and W 3, For our conjugation φ = t b t a, we easily check using the Picard-Lefschetz formula that we get the additional relator (0) b +a +b = 0, from both P φ and Pφ whereas, depending on whether it is Pφ or Pφ () () a +b +6a +4b = 0 for W and W, or a +b +a = 0 for W 3. we get either Therefore, (7) and (0), which hold for all π ( X i ), imply a = 0. The relators in (8), (9) and (), () involved in a given W i then easily give b = b = 0, for each i =,,3. Hence in all cases we have got π (X i ) = π ( X i ) =. By Freedman, we have X i homeomorphic to CP #(6+i)CP, for i =,, Diffeomorphism type of the pencils (X i,f i ). A quick amendment to the title: we will determine the non-diffeomorphism type of (X i,f i ), namely, we will prove that X i are not diffeomorphic to rational surfaces. This will follow from the next lemma. Lemma 7. The rational surface CP #pcp, for p 9, does not admit a genus g Lefschetz fibration or a genus-g Lefschetz pencil with m < g base points. Proof. It suffices to show this for X = CP #9CP, since we can always blow-up on the fibers to produce a genus-g Lefschetz fibration (resp. pencil) on X from a given genus-g Lefschetz fibration (resp. pencil) on CP #pcp, for any p < 9. Assume that X is equipped with a genus g Lefschetz fibration or a pencil with m < g base points. For our arguments to follow, it will be convenient to allow m to be non-negative so that m = 0 marks the fibration case.
12 R. İ. BAYKUR Let F = ah 9 i= c ie i be the fiber class, where H (X) is generated by H and E,...,E 9, with H =, E i E j = δ ij, and H E i = 0. Since F = m, we have 9 a = m+ c i. We can equip X with a Thurston-Gompf symplectic form ω which makes the fibers symplectic. Moreover, we can choose an ω-compatible almost complex structure J, even a generic one in the sense of Taubes (see e.g [70]), with respect to which f is J-holomorphic (for a suitable choice of almost complex structure on the base -sphere). It was shown by Li and Liu [5] that for a generic ω-compatible J, the class H in the rational surface X has a J-holomorphic representative. Hence, F and H both have J-holomorphic representatives, which implies that F H = a 0. There is a unique symplectic structure on X up to deformation and symplectomorphisms [5], so we can apply the adjunction formula to get g = F +K F = m+( 3H + E i ) (ah c i E i ) = m 3a+ c i. i= Since a,m 0, and g, from the above equalities we have 3a = 9 9a = 9(m+ c i ) 9 9( c i ) = 9 9 ( )( c i ) 9 c i, i= where the last inequality is by Cauchy-Schwartz, and in turn 9 9 3a c i = c i = g m+3a = g m+3a, i= i= i= implying m g. The contradiction shows that there exists no such symplectic surface F. In turn, there is no such fibration or pencil. In fact, if X is a symplectic 4-manifold in the homeomorphism class of a rational surface CP #pcp with p 9, X is exotic if and only if it admits a genus g pencil with m < g base points. This follows from Lemma 7 and Donaldson s result on the existence of Lefschetz pencils on symplectic 4-manifolds (together with the fact there is a unique genus- pencil, which is on CP). i= Combining the lemmas 6 and 7 we conclude: Theorem 8. (X i,f i ) are symplectic genus-3 Lefschetz pencils whose total spaces are homeomorphic but not diffeomorphic to CP #(6+i)CP for i =,,3. i= i= i= i= i= Remark 9. These are the smallest genera examples one can find. Any Lefschetz pencil of genus 0 or has a total space diffeomorphic to (a blow-up of) CP CP, CP #CP or E() = CP #9CP [4, 53]. After blowing-up all the base points of a genus- Lefschetz pencil we arrive at a genus- Lefschetz fibration on a nonminimal symplectic ( X, f). Now if X is an exotic rational surface, it cannot have the rational homology type of a(blow-up of a) symplectic Calabi-Yau surface either.
13 SMALL SYMPLECTIC CALABI-YAUS AND EXOTIC 4-MANIFOLDS VIA PENCILS 3 Thus there could be at most one base point, and as observed by Sato, ( X, f) has at most one reducible fiber; see Theorem 5-5(iii) and Theorem 5-(iii) in [60]. By Lemmas 4 and 5 in [3], there is no genus- Lefschetz fibration ( X, f) with at most one reducible fiber and say e( X) 3. In fact, in [3], we have constructed minimal genus- Lefschetz fibrations whose total spaces are homeomorphic to rational surfaces CP #pcp, for p = 7,8,9 [3]. These fibrations decompose as fiber sums, which implies their minimality [7, 9], and in turn why they are not diffeomorphic to blown-up rational surfaces. The above observation generalizes to any genus g 3 Lefschetz pencil (X,f) whose total space is an exotic CP #pcp, for p < 9, allowing us to conclude that f has at most g 4 base points. It follows from the following more general observation: A collection of exceptional classes in the corresponding Lefschetz fibration ( X, f) can be represented by disjoint multisections S j, so each one intersects the regular fiber F positively at least once. However, ( S j ) F g 3 implies that κ(x) = κ( X by the work of Sato [60]. Since X is not rational (nor can possibly be ruled), we already know that κ(x). Further, κ(x) = 0 or implies that the minimal model of X has c = 0, which is impossible for any X, as c (X) = c (CP #pcp ) = 9 p > 0 and blow-down increases c. Hence κ(x) = and has at most g 4 disjoint exceptional spheres. In particular we see that each X i in Theorem 8 is either minimal or it is only once blown-up of a minimal symplectic 4-manifold. Remark 0. Using a variation of our construction with 3 different embeddings of P into Γ 3, we can get a genus-3 Lefschetz fibration ( X 0, f 0 ) where X 0 is an exotic symplectic CP #7CP. I expect this monodromy lifts to Γ 3, and gives another pencil (X 0,f 0 ) whose total space is an exotic CP #6CP. Remark. The existence of exotic symplectic 4-manifolds in the homeomorphism classes in Theorem 8 was already established. The first example of an exotic symplectic CP #pcp, for p = 9, was the complex Dolgachev surface E(),3, as shown by Donaldson []. For p = 8, the first example was Barlow s complex surface, as proved by Kotschick [46]. For p = 7, the first examples were constructed via generalized rational blowdowns by Jongil Park [57], which are symplectic by the work of Symington [66]. Infinitely many distinct smooth structures in these homeomorphism classes were constructed using logarithmic transforms, knot surgeries and Luttinger surgeries [9, 35, 67, 30, ] (all of which are indeed instances of surgeries along tori [7].) Notably, onlyforp = 9itisknownthatthereisaninfinite familyofpairwisenondiffeomorphic symplectic 4-manifolds in the homeomorphism class of CP #pcp (e.g. [9]). Moreover, it was observed by Stipsicz and Szabo that Seiberg-Witten invariants cannot distinguish any two minimal symplectic 4-manifolds homeomorphic to CP #pcp for p < 9 [65][Corollary 4.4]. It remains an open question whether there are two distinct symplectic 4-manifolds in these homeomorphism classes [63][Problem ]. It is thus desirable to have examples with more structure in order to address this intriguing question. For instance, one can use other φ to obtain simply-connected symplectic genus-3 pencils in the same homeomorphism classes, possibly not isomorphic to the ones in Theorem 8.
14 4 R. İ. BAYKUR 3.4. An infinite family of genus-3 pencils with c = 0,, and χ h =. ByvaryingourconstructionofthepositivefactorizationsW i,wecanalsoproduce symplectic genus-3 Lefschetz pencils with any prescribed abelian group of rank at most. Let M = (m,m ), where m and m are nonnegative integers. For i =,,3, let ( X i,m, f i,m ) be the Lefschetz fibration prescribed by the positive factorization W i with φ i = t m b t m a, and (X i,m,f i,m ) be the corresponding pencil. Note that we still get a positive factorization W i since φ keeps C and C fixed. We claim that π ( X i,m ) = (Z/m Z) (Z/m Z). To verify it, let s go back to our fundamental group calculation via the finite presentation which has the generators a j,b j of π (Σ 3 ), and relators induced by the Dehn twist curves in W i. The arguments we gave in Section 3. for the relators coming from the factors P,P and P appearing in W i apply here as well. In particular, π ( X i,m )) is also a quotient of the abelian group Z generated by a and b, and the following abelianized relations hold: a 3 = a and b 3 = b = b for all W i, a +a +4b = 0 for W, a +a = 0 for W and W 3. Importantly, there are no other relations coming from the factors P,P and P : This is easy to see by abelianizing the relators ( 6) ( 6), which include all the relators induced by the curves x,x,x 3,B 0,B,B,B 0,B,B. Missing are the relators induced by the separating curves d,e from P, the curves A 0,A,A from P, and the curves A 0,A,A from P. The first two are trivial in homology, so they have no contribution to the list of relators we already have. On the other hand, for eachj = 0,,, A j ishomologoustob j, because[a j ] = [t C (B j )] = [B j ]+(C B j )[C] by the Picard-Lefschetz formula, where C is a separating cycle. Similarly each A j is homologous to B j. Therefore the abelianized relations they induce are identical to those we already had from B j,b j. (3) (4) (5) For our conjugation φ = t m b t m a, we get the additional relators b +m a +b = 0 = 0 for all W i, a +m b +(+4m )a +4b = 0 for W and W, a +m b +a = 0 for W 3. Similar to before, (3) and (5), which hold for all π ( X i,m ), imply m a = 0. The remaining relators involved in a given W i then easily give m b = m b = 0, for each i =,,3. Hence, π (X i,m ) = π ( X i,m ) = (Z/m Z) (Z/m Z), as claimed. Since the monodromy of each ( X i,m, f i,m ) is equivalent to that of ( X i, f i ) by a partial conjugation with t m+ b t m a, they have the same Euler characteristic and signature. So c (X i,m ) = 3 i and χ(x i,m ) =, for i =,,3. For each i, we clearly have an infinite family of symplectic genus-3 pencils among {(X i,m,f i,m ) M = (m,m ) N N }, with pairwise homotopy inequivalent total spaces easily distinguished by π (X i,m ). By Parshin and Arakelovs proofs of the Geometric Shafarevich Conjecture, there are
15 SMALL SYMPLECTIC CALABI-YAUS AND EXOTIC 4-MANIFOLDS VIA PENCILS 5 finitely many holomorphic fibrations with fixed fiber genus g and degeneracy [59, 4]. This implies that all but finitely many of these symplectic pencils are non-holomorphic. Furthermore, for M = (m,0) with m, we get an infinite subfamily of pencils, whose total spaces cannot be complex surfaces, since there is no complex surface Z with b (Z) = and b + (Z) > 0 (e.g. cf. [0][Lemma ]). (Note that the same argument applies to the infinite family of symplectic Calabi- Yau surfaces we will construct in the next section.) We have proved: Theorem. There exists a symplectic genus-3 Lefschetz pencil (X i,m,f i,m ) with c (X i,m ) = 3 i, χ(x i,m ) =, and π (X i,m ) = (Z/m Z) (Z/m Z), for any pair of non-negative integers M = (m,m ), and for each i =,,3. Infinitely many of these pencils have total spaces homotopy inequivalent to a complex surface. Remark 3. There is only one example of a non-holomorphic genus-3 Lefschetz pencil in the literature, which was given by Smith in [6][Theorem.3] without appealingtodonaldson stheorem. 3 (WelearnfromNaoyukiMondenthatinajoint work with Hamada and Kobayashi they produce two more examples.) Theorem improves the situation, at least quantitatively. Remark 4. Following the works of Donaldson [] and Gompf [37], every finitely presented group is the fundamental group of a symplectic Lefschetz pencil. (Also see [3] and [44].) An invariant of finitely presented group G is the m g (G), the minimal genusofagenus-g pencil(x,f) with π (X) = G, whichisnotaseasytocalculate in general. However, Theorem shows that for G = (Z/m Z) (Z/m Z), m(g) 3. Well-known examples of genus- and genus- pencils show that m g (G) = for G = (the pencil on CP ), and m g (G) = for G = Z (the pencil on the Enriques surface) or Z Z (e.g. Matsumoto s pencil on S T ). It seems likely that for all the other G as above, m g (G) = A new construction of symplectic Calabi-Yau surfaces with b > 0 Here we will give a new construction of an infinite family of symplectic Calabi- Yau surfaces with b = and 3, along with a symplectic Calabi-Yau surface with b = 4, homeomorphic to the 4-torus. This will follow from our construction of new positive factorization of boundary multi-twists in Γ 4 3 corresponding to symplectic genus-3 Lefschetz pencils. We find it more convenient for presentation purposes to discuss a special example first, and discuss the most general construction afterward. These will correspond to our examples with b = 4, and then the others with b = and 3. 3 In contrast, there are many non-holomorphic fibrations obtained by twisted fiber sums; e.g. [55, 43, 0]. However decomposable fibrations do not admit ( )-sections which could be blowndown to produce pencils [64].
16 6 R. İ. BAYKUR 4.. A symplectic Calabi-Yau homeomorphic to the 4-torus. (6) Our main building block will be the following relation in Γ [39]: (t B0 t B t B t C ) = t δ t δ, where δ i are the boundary parallel curves, and the curves B i and C are as shown on the left-hand side of Figure. The relation (6) can be rewritten as t B0 t B t B t A0 t A t A t Ct δ t δ =, where each A j = t C (B j ) for j = 0,, are given on the left-hand side Figure ). We can embed this relation into Γ 3 by gluing along the two boundary components δ and δ so that δ = δ is mapped to C and the curves C,B j,a j are as shown in Figure 4, denoted by the same letters for simplicity. Thus the following holds in Γ 3 : (7) t B0 t B t B t A0 t A t A t Ct C =, or P t C t C =, where P = t B 0 t B t B t A0 t A t A. Clearly P,t C and t C all commute with each other. A similar embedding into Γ 3 can be given by mapping δ = δ to C instead, where the curves C,B j,a j are now as shown in Figure 4, all decorated by a prime notation this time (so C indeed maps to C above). We thus get another relation in Γ 3 of the form: (8) 0 0 t C t C =, or P t C t C =, where P = 0 0. Similarly, P,t C and t C all commute with each other. Combining the above, we get a positive factorization W = PP in Γ 3, since PP = P t Ct C P t C t C =. Let ( X, f) be the genus-3 Lefschetz fibration prescribed by W. We can equip ( X, f) with a Gompf-Thurston symplectic form ω, in particular X is a symplectic 4-manifold. We will show that X is the 4 times blow-up of a symplectic Calabi-Yau surface X homeomorphic to the 4-torus. We will indeed show that it is a blow-up of a symplectic genus-3 pencil (X,f), which we will first argue implicitly below, and then explicitly in the next section. Lemma 5. Let ( X, f) be a genus g Lefschetz fibration and c ( X) = g. If X is not a rational or ruled surface, then ( X, f) is a blow-up of a symplectic Lefschetz pencil (X, f), where X is a (minimal) symplectic Calabi-Yau surface. Proof. We can equip ( X, f) with a Gompf-Thurston symplectic form ω. By the workoftaubes[68,69], anyminimal symplectic 4-manifold hasnon-negative c. So X = X 0 #mcp, where X 0 is a minimal model for X and m g, which means that X contains at least g disjoint exceptional spheres S j, j =,...,g. There is an ω-compatible almost complex structure J with respect to which both a regular fiber F of f and all Sj are J-holomorphic [60, 9], which implies that ( g j= S j) F g. By the work of Sato [60] (also see []), this is only
17 SMALL SYMPLECTIC CALABI-YAUS AND EXOTIC 4-MANIFOLDS VIA PENCILS 7 δ 3 δ δ C C C δ 4 B 0 B 0, B B, B B, A 0 B 0, A B, A B, Figure. Vanishing cycles B j,c,b j,i and C i in Hamada s lift of Matsumoto s fibration. On the left are the curves of the positive factorization in Γ, along with the curves A j we get after Hurwitz moves. On the right are the curves of the further lift in Γ 4.
18 8 R. İ. BAYKUR possible if the symplectic Kodaira dimension κ( X) 0. As we assumed X is not a rational or a ruled surface, we have κ( X) [47], leaving the only possibility as κ( X) = 0 and also that there are no other disjoint exceptional spheres than S j in X. Thus ( g j= S j) F = g, so one can blow-down these exceptional spheres (which can be assumed to be symplectic after deforming ω if needed [38]) to arrive at a symplectic genus-3 Lefschetz pencil (X,f), where X = X 0 is a minimal symplectic Calabi-Yau surface. We show that X satisfies the hypotheses of this lemma. The Euler characteristic of X is given by e( X) = l(w) = 4, where l(w) = is the number of Dehn twists in the factorization W. The signature of X can be calculated as σ( X) = 4 using the local signatures and Ozbagci s algorithm [54]. Since ( X, f) is not hyperelliptic, we do not have the luxury of employing Endo s closed formula for a direct calculation, however the following observation allows us to deduce the signature from a calculation in Γ, where any factorization is hyperelliptic: We have obtained W from the factorization which had two pairs of t C and t C with opposite signs. This is an achiral genus- 3 Lefschetz fibration, which is a fiber sum of two achiral fibrations prescribed by the factorizations P t C t C and P t C t C. Each one is a section sum of an achiral genus- Lefschetz fibration and a trivial torus fibration along a section of selfintersection zero, which, by Novikov additivity, has signature equals to that of the achiral genus- Lefschetz fibration. By the hyperelliptic signature formula for genus- fibrations [5, 6], the signature of the latter is. Invoking Novikov additivity again, we conclude that the decomposable achiral genus-3 fibration has signature 4, the sum of the signature of its summands. Lastly, we claim that canceling the pairs t ± C and t± C does not change the signature. This can be easily seen by splitting the fibration as t C t ) and the rest. The piece with C (or t C t C monodromy factorization t C t C has zero signature, which is easily calculated from the induced handle decomposition, or by observing that it can be further split into two identical fibrations whose total spaces have opposite orientations (and thus opposite signatures). By Novikov additivity once again, the rest of the fibration hasthesamesignatureasthetotalsignatureoftheachiralfibration. Soσ( X) = 4. It follows that c ( X) = e( X) + 3σ( X) = 4. Assuming π ( X) = Z 4 for the moment, let us complete our arguments regarding the homeomorphism type of the minimal model X of X. By Lemma 5 ( X, f) is a blow-up of a symplectic genus-3 Lefschetz pencil (X,f), where X is a symplectic Calabi-Yau surface. Since X is a symplectic Calabi-Yau surface with b (X) > 0, it has the rational homology type of a torus bundle over a torus [8, 47]. Moreover, since π (X) = Z 4 is a virtually poly-z group, the Borel conjecture holds in this case by the work of Farrell and Jones [7], and as observed by Friedl and Vidussi, this implies that a symplectic Calabi Yau surface with π (Z 4 ) is unique up to homeomorphism [34]. Hence X is homeomorphic to the well-known symplectic Calabi-Yau surface, the 4-torus. We now calculate π (X) = π ( X), which will constitute the rest of this section. Using the standard handlebody decomposition for ( X, f), we can obtain a finite presentation for π ( X) = π (Σ 3 )/N, where N denotes the subgroup of π (Σ 3 )
19 SMALL SYMPLECTIC CALABI-YAUS AND EXOTIC 4-MANIFOLDS VIA PENCILS 9 generated normally by the vanishing cycles of f. For {a j,b j } standard generators of π (Σ g ) as given in Figure 3, we get π (X) = a,b,a,b,a 3,b 3 [a,b ][a,b ][a 3,b 3 ],R,...,R, where each R i is a relation obtained by expressing a corresponding vanishing cycle (oriented arbitrarily) in {a j,b j }. Recall that ( X, f) has a section (in fact 4 ( )-sections), so the above presentation is complete, there is no other relation. b b b 3 a a a 3 Figure 3. Generators a j,b j of π (Σ 3 ) We have the following relations, the ones after the first one coming from Σ 3 all induced by the vanishing cycles B 0, B, B, A 0, A, A, B 0, B, B, A 0, A, A (which are all given in Figure 4, in the given order: (9) (30) (3) (3) (33) (34) (35) (36) (37) (38) (39) (40) (4) [a,b ][a,b ][a 3,b 3 ] =, a a 3 =, a b a b ā a 3 b3 =, b a b ā b3 =, a [b 3,a 3 ]b a 3 b [a 3,b 3 ] =, a 3 b3 b [a 3,b 3 ]a b ā [b 3,a 3 ]b [b 3,a 3 ]b =, a b ā [b 3,a 3 ]b [b 3,a 3 ]b b3 b [a 3,b 3 ] =, ā a a a 3 =, a b a a 3 b 3 ā 3 b ā =, b a b a 3 b 3 ā 3 ā =, a a b a 3 b ā =, a b a b a 3 b 3 ā 3 b ā =, b a b a 3 b3 ā 3 b ā =, Here x denotes the inverse of the element x in the group. Whenabelianized, therelationscomingfromeachoneofthetriples{b 0,B,B }, {A 0,A,A }, {B 0,B,B }, {A 0,A,A } give the same three relations a +a 3 = 0, a b +b +a 3 b 3 = 0, b +b b 3 = 0, where we identified the images of the generators with the same letters. Any of these relations imply the other. So we can eliminate a = a 3 and b = b b 3, and get a free abelian group of rank 4 generated by a,b,a 3 and b 3.
20 0 R. İ. BAYKUR C C B 0 B 0 B B B B A 0 A 0 A A A A Figure 4. Vanishing cycles B j,a j,b j,a j of the genus-3 fibration (X,f). On the left are the curves coming from the factorization P and on the right are those coming from the factorization P, which correspond to the two different embeddings of the factorization in Γ into Γ 3. (Dotted lines drawn on the surfaces on the top are the images of δ = δ under these embeddings.)
21 SMALL SYMPLECTIC CALABI-YAUS AND EXOTIC 4-MANIFOLDS VIA PENCILS Now, going back to the presentation we have above for π ( X), we easily see that it is also generated by a,b,a 3,b 3, since a = ā 3 by (30) and b = a b ā b3 by (3). To prove π ( X) = Z 4, it therefore suffices to show that a,b,a 3,b 3 all commute with each other. Replacing a with ā 3 in (36) gives [a 3,a ] =. From (3) we have b a b ā = b 3. Substitutingthisin(3), andreplacinga withā 3, weget[a 3,b 3 ] =. Witha = ā 3 and [a 3,b 3 ] =, the relation (33) simplifies to [a 3,b ] =. So a 3 commute with each one of a,b,b 3. We can rewrite (39) as a a b a 3 b ā = a b a 3 b ā =, since a = ā 3 and a 3 commutes with a and b. So [a,b ] =. It implies that b = a b ā b3 = b b3. Note that [a 3,b 3 ] = means a 3 b 3 ā 3 = b 3. Using these last two identities and (38) we derive b b3 a b b 3 ā =. So [b, b 3 a ] = [a, b b 3 ] =. These commuting relations, together with [a,b ] =, give us the last two commuting relations we need: [b,b 3 ] = [a,b 3 ] =. Hence π ( X) = Z 4, generated by a,b,a 3,b 3. This completes our claim that (X,f) is a symplectic genus-3 Lefschetz pencil, where X is a symplectic Calabi-Yau surface homeomorphic to the 4-torus. 4.. Symplectic Calabi-Yau surfaces with b = and 3 via pencils. We will now generalize the construction in the previous section, and construct an infinite family of examples of genus-3 Lefschetz pencils on symplectic Calabi- Yau surfaces with b = and 3. We will produce these pencils explicitly via positive factorizations of the boundary multi-twist = t t t 3 t 4 in Γ 4, where i are boundary parallel curves for distinct boundary components of Σ 4 3. For this, we will use a further lift of the monodromy factorization of Matsumoto s genus- fibrationtoγ 4 given byhamada, whichwill allow ustoobtain aniceandsymmetric presentation at the end. (4) The factorization (6) has a further lift to Γ 4 [39] of the form: t B0, t B, t B, t C t B0, t B, t B, t C = t δ t δ t δ3 t δ4, where again δ i are the boundary parallel curves, and the curves B j,i,c i are given on the right-hand side of Figure. When the two boundary components δ 3,δ 4, drawn in the middle of Σ 4 in Figure, are capped off, the curves B j,i descend to B j and C i to C for each j = 0,, and i =,. 4 C C 3 C C Figure 5. Curves involved in our embeddings of Σ 4 into Σ 4 3. The relation (4) can be rewritten as the following relation in Γ 4 : t B0, t B, t B, t A0, t A, t A, t C t C t δ t δ = t δ3 t δ4,
Exotic Lefschetz Fibrations and Stein Fillings with Arbitrary Fundamental Group
 Exotic Lefschetz Fibrations and Stein Fillings with Arbitrary Fundamental Group Anar Akhmedov University of Minnesota, Twin Cities February 19, 2015 Anar Akhmedov (University of Minnesota, Minneapolis)Exotic
Exotic Lefschetz Fibrations and Stein Fillings with Arbitrary Fundamental Group Anar Akhmedov University of Minnesota, Twin Cities February 19, 2015 Anar Akhmedov (University of Minnesota, Minneapolis)Exotic
SMALL EXOTIC 4-MANIFOLDS. 0. Introduction
 SMALL EXOTIC 4-MANIFOLDS ANAR AKHMEDOV Dedicated to Professor Ronald J. Stern on the occasion of his sixtieth birthday Abstract. In this article, we construct the first example of a simply-connected minimal
SMALL EXOTIC 4-MANIFOLDS ANAR AKHMEDOV Dedicated to Professor Ronald J. Stern on the occasion of his sixtieth birthday Abstract. In this article, we construct the first example of a simply-connected minimal
arxiv:math/ v2 [math.gt] 18 Apr 2007
![arxiv:math/ v2 [math.gt] 18 Apr 2007 arxiv:math/ v2 [math.gt] 18 Apr 2007](/thumbs/90/103896349.jpg) arxiv:math/0703480v2 [math.gt] 18 Apr 2007 CONSTRUCTING INFINITELY MANY SMOOTH STRUCTURES ON SMALL 4-MANIFOLDS ANAR AKHMEDOV, R. İNANÇ BAYKUR, AND B. DOUG PARK Abstract. The purpose of this article is
arxiv:math/0703480v2 [math.gt] 18 Apr 2007 CONSTRUCTING INFINITELY MANY SMOOTH STRUCTURES ON SMALL 4-MANIFOLDS ANAR AKHMEDOV, R. İNANÇ BAYKUR, AND B. DOUG PARK Abstract. The purpose of this article is
The topology of symplectic four-manifolds
 The topology of symplectic four-manifolds Michael Usher January 12, 2007 Definition A symplectic manifold is a pair (M, ω) where 1 M is a smooth manifold of some even dimension 2n. 2 ω Ω 2 (M) is a two-form
The topology of symplectic four-manifolds Michael Usher January 12, 2007 Definition A symplectic manifold is a pair (M, ω) where 1 M is a smooth manifold of some even dimension 2n. 2 ω Ω 2 (M) is a two-form
KODAIRA DIMENSION OF LEFSCHETZ FIBRATIONS OVER TORI
 KODAIRA DIMENSION OF LEFSCHETZ FIBRATIONS OVER TORI JOSEF G. DORFMEISTER Abstract. The Kodaira dimension for Lefschetz fibrations was defined in [1]. In this note we show that there exists no Lefschetz
KODAIRA DIMENSION OF LEFSCHETZ FIBRATIONS OVER TORI JOSEF G. DORFMEISTER Abstract. The Kodaira dimension for Lefschetz fibrations was defined in [1]. In this note we show that there exists no Lefschetz
Lefschetz pencils and the symplectic topology of complex surfaces
 Lefschetz pencils and the symplectic topology of complex surfaces Denis AUROUX Massachusetts Institute of Technology Symplectic 4-manifolds A (compact) symplectic 4-manifold (M 4, ω) is a smooth 4-manifold
Lefschetz pencils and the symplectic topology of complex surfaces Denis AUROUX Massachusetts Institute of Technology Symplectic 4-manifolds A (compact) symplectic 4-manifold (M 4, ω) is a smooth 4-manifold
THE CANONICAL PENCILS ON HORIKAWA SURFACES
 THE CANONICAL PENCILS ON HORIKAWA SURFACES DENIS AUROUX Abstract. We calculate the monodromies of the canonical Lefschetz pencils on a pair of homeomorphic Horikawa surfaces. We show in particular that
THE CANONICAL PENCILS ON HORIKAWA SURFACES DENIS AUROUX Abstract. We calculate the monodromies of the canonical Lefschetz pencils on a pair of homeomorphic Horikawa surfaces. We show in particular that
arxiv: v1 [math.gt] 8 Nov 2018
![arxiv: v1 [math.gt] 8 Nov 2018 arxiv: v1 [math.gt] 8 Nov 2018](/thumbs/88/117929434.jpg) Geography of Genus 2 Lefschetz Fibrations arxiv:1811.03708v1 [math.gt] 8 Nov 2018 Kai Nakamura November 12, 2018 Abstract Questions of geography of various classes of 4-manifolds have been a central motivating
Geography of Genus 2 Lefschetz Fibrations arxiv:1811.03708v1 [math.gt] 8 Nov 2018 Kai Nakamura November 12, 2018 Abstract Questions of geography of various classes of 4-manifolds have been a central motivating
Lefschetz Fibrations and Exotic Stein Fillings with Arbitrary Fundamental Group via Luttinger Surgery
 Lefschetz Fibrations and Exotic Stein Fillings with Arbitrary Fundamental Group via Luttinger Surgery Anar Akhmedov University of Minnesota, Twin Cities June 20, 2013, ESI, Vienna Anar Akhmedov (University
Lefschetz Fibrations and Exotic Stein Fillings with Arbitrary Fundamental Group via Luttinger Surgery Anar Akhmedov University of Minnesota, Twin Cities June 20, 2013, ESI, Vienna Anar Akhmedov (University
Symplectic 4-manifolds, singular plane curves, and isotopy problems
 Symplectic 4-manifolds, singular plane curves, and isotopy problems Denis AUROUX Massachusetts Inst. of Technology and Ecole Polytechnique Symplectic manifolds A symplectic structure on a smooth manifold
Symplectic 4-manifolds, singular plane curves, and isotopy problems Denis AUROUX Massachusetts Inst. of Technology and Ecole Polytechnique Symplectic manifolds A symplectic structure on a smooth manifold
An exotic smooth structure on CP 2 #6CP 2
 ISSN 1364-0380 (on line) 1465-3060 (printed) 813 Geometry & Topology Volume 9 (2005) 813 832 Published: 18 May 2005 G G G G T T T G T T T G T G T GG TT G G G G GG T T T TT An exotic smooth structure on
ISSN 1364-0380 (on line) 1465-3060 (printed) 813 Geometry & Topology Volume 9 (2005) 813 832 Published: 18 May 2005 G G G G T T T G T T T G T G T GG TT G G G G GG T T T TT An exotic smooth structure on
Classifying complex surfaces and symplectic 4-manifolds
 Classifying complex surfaces and symplectic 4-manifolds UT Austin, September 18, 2012 First Cut Seminar Basics Symplectic 4-manifolds Definition A symplectic 4-manifold (X, ω) is an oriented, smooth, 4-dimensional
Classifying complex surfaces and symplectic 4-manifolds UT Austin, September 18, 2012 First Cut Seminar Basics Symplectic 4-manifolds Definition A symplectic 4-manifold (X, ω) is an oriented, smooth, 4-dimensional
LANTERN SUBSTITUTION AND NEW SYMPLECTIC 4-MANIFOLDS WITH b 2 + = 3 arxiv: v2 [math.gt] 24 May 2014
![LANTERN SUBSTITUTION AND NEW SYMPLECTIC 4-MANIFOLDS WITH b 2 + = 3 arxiv: v2 [math.gt] 24 May 2014 LANTERN SUBSTITUTION AND NEW SYMPLECTIC 4-MANIFOLDS WITH b 2 + = 3 arxiv: v2 [math.gt] 24 May 2014](/thumbs/88/117929346.jpg) LANTERN SUBSTITUTION AND NEW SYMPLECTIC -MANIFOLDS WITH b 2 + = arxiv:207.068v2 [math.gt] 2 May 20 ANAR AKHMEDOV AND JUN-YONG PARK Abstract. Motivated by the construction of H. Endo and Y. Gurtas, changing
LANTERN SUBSTITUTION AND NEW SYMPLECTIC -MANIFOLDS WITH b 2 + = arxiv:207.068v2 [math.gt] 2 May 20 ANAR AKHMEDOV AND JUN-YONG PARK Abstract. Motivated by the construction of H. Endo and Y. Gurtas, changing
New symplectic 4-manifolds with nonnegative signature
 Journal of Gökova Geometry Topology Volume 2 2008) 1 13 New symplectic 4-manifolds with nonnegative signature Anar Akhmedov and B. Doug Park Abstract. We construct new families of symplectic 4-manifolds
Journal of Gökova Geometry Topology Volume 2 2008) 1 13 New symplectic 4-manifolds with nonnegative signature Anar Akhmedov and B. Doug Park Abstract. We construct new families of symplectic 4-manifolds
DIFFEOMORPHISMS OF SURFACES AND SMOOTH 4-MANIFOLDS
 DIFFEOMORPHISMS OF SURFACES AND SMOOTH 4-MANIFOLDS SDGLDTS FEB 18 2016 MORGAN WEILER Motivation: Lefschetz Fibrations on Smooth 4-Manifolds There are a lot of good reasons to think about mapping class
DIFFEOMORPHISMS OF SURFACES AND SMOOTH 4-MANIFOLDS SDGLDTS FEB 18 2016 MORGAN WEILER Motivation: Lefschetz Fibrations on Smooth 4-Manifolds There are a lot of good reasons to think about mapping class
Singular fibers in Lefschetz fibrations on manifolds with b + 2 = 1
 Topology and its Applications 117 (2002) 9 21 Singular fibers in Lefschetz fibrations on manifolds with b + 2 = 1 András I. Stipsicz a,b a Department of Analysis, ELTE TTK, 1088 Múzeum krt. 6-8, Budapest,
Topology and its Applications 117 (2002) 9 21 Singular fibers in Lefschetz fibrations on manifolds with b + 2 = 1 András I. Stipsicz a,b a Department of Analysis, ELTE TTK, 1088 Múzeum krt. 6-8, Budapest,
arxiv: v3 [math.gt] 4 Jun 2016
![arxiv: v3 [math.gt] 4 Jun 2016 arxiv: v3 [math.gt] 4 Jun 2016](/thumbs/95/124905073.jpg) ON THE MINIMAL NUMBER OF SINGULAR FIBERS IN LEFSCHETZ FIBRATIONS OVER THE TORUS arxiv:1604.04877v3 [math.gt] 4 Jun 2016 Abstract. We show that the minimal number of singular fibers N(g,1) in a genus-g
ON THE MINIMAL NUMBER OF SINGULAR FIBERS IN LEFSCHETZ FIBRATIONS OVER THE TORUS arxiv:1604.04877v3 [math.gt] 4 Jun 2016 Abstract. We show that the minimal number of singular fibers N(g,1) in a genus-g
arxiv: v1 [math.gt] 6 May 2007
![arxiv: v1 [math.gt] 6 May 2007 arxiv: v1 [math.gt] 6 May 2007](/thumbs/90/103241766.jpg) SIMPLY CONNECTED MINIMAL SYMPLECTIC 4-MANIFOLDS WITH SIGNATURE LESS THAN 1 arxiv:0705.0778v1 [math.gt] 6 May 2007 ANAR AKHMEDOV, SCOTT BALDRIDGE, R. İNANÇ BAYKUR, PAUL KIRK, AND B. DOUG PARK Abstract.
SIMPLY CONNECTED MINIMAL SYMPLECTIC 4-MANIFOLDS WITH SIGNATURE LESS THAN 1 arxiv:0705.0778v1 [math.gt] 6 May 2007 ANAR AKHMEDOV, SCOTT BALDRIDGE, R. İNANÇ BAYKUR, PAUL KIRK, AND B. DOUG PARK Abstract.
MINIMAL NUMBER OF SINGULAR FIBERS IN A LEFSCHETZ FIBRATION
 PROCEEDINGS OF THE AMERICAN MATHEMATICAL SOCIETY Volume 129, Number 5, Pages 1545 1549 S 0002-9939(00)05676-8 Article electronically published on October 20, 2000 MINIMAL NUMBER OF SINGULAR FIBERS IN A
PROCEEDINGS OF THE AMERICAN MATHEMATICAL SOCIETY Volume 129, Number 5, Pages 1545 1549 S 0002-9939(00)05676-8 Article electronically published on October 20, 2000 MINIMAL NUMBER OF SINGULAR FIBERS IN A
DIMENSION 4: GETTING SOMETHING FROM NOTHING
 DIMENSION 4: GETTING SOMETHING FROM NOTHING RON STERN UNIVERSITY OF CALIFORNIA, IRVINE MAY 6, 21 JOINT WORK WITH RON FINTUSHEL Topological n-manifold: locally homeomorphic to R n TOPOLOGICAL VS. SMOOTH
DIMENSION 4: GETTING SOMETHING FROM NOTHING RON STERN UNIVERSITY OF CALIFORNIA, IRVINE MAY 6, 21 JOINT WORK WITH RON FINTUSHEL Topological n-manifold: locally homeomorphic to R n TOPOLOGICAL VS. SMOOTH
A NOTE ON STEIN FILLINGS OF CONTACT MANIFOLDS
 A NOTE ON STEIN FILLINGS OF CONTACT MANIFOLDS ANAR AKHMEDOV, JOHN B. ETNYRE, THOMAS E. MARK, AND IVAN SMITH Abstract. In this note we construct infinitely many distinct simply connected Stein fillings
A NOTE ON STEIN FILLINGS OF CONTACT MANIFOLDS ANAR AKHMEDOV, JOHN B. ETNYRE, THOMAS E. MARK, AND IVAN SMITH Abstract. In this note we construct infinitely many distinct simply connected Stein fillings
arxiv: v1 [math.gt] 4 Aug 2008
![arxiv: v1 [math.gt] 4 Aug 2008 arxiv: v1 [math.gt] 4 Aug 2008](/thumbs/88/117701026.jpg) LANTERN RELATIONS AND RATIONAL BLOWDOWNS arxiv:0808.086v [math.gt] 4 Aug 2008 HISAAKI ENDO AND YUSUF Z. GURTAS Abstract. We discuss a connection between the lantern relation in mapping class groups and
LANTERN RELATIONS AND RATIONAL BLOWDOWNS arxiv:0808.086v [math.gt] 4 Aug 2008 HISAAKI ENDO AND YUSUF Z. GURTAS Abstract. We discuss a connection between the lantern relation in mapping class groups and
Broken pencils and four-manifold invariants. Tim Perutz (Cambridge)
 Broken pencils and four-manifold invariants Tim Perutz (Cambridge) Aim This talk is about a project to construct and study a symplectic substitute for gauge theory in 2, 3 and 4 dimensions. The 3- and
Broken pencils and four-manifold invariants Tim Perutz (Cambridge) Aim This talk is about a project to construct and study a symplectic substitute for gauge theory in 2, 3 and 4 dimensions. The 3- and
LECTURE 5: SOME BASIC CONSTRUCTIONS IN SYMPLECTIC TOPOLOGY
 LECTURE 5: SOME BASIC CONSTRUCTIONS IN SYMPLECTIC TOPOLOGY WEIMIN CHEN, UMASS, SPRING 07 1. Blowing up and symplectic cutting In complex geometry the blowing-up operation amounts to replace a point in
LECTURE 5: SOME BASIC CONSTRUCTIONS IN SYMPLECTIC TOPOLOGY WEIMIN CHEN, UMASS, SPRING 07 1. Blowing up and symplectic cutting In complex geometry the blowing-up operation amounts to replace a point in
CONSTRUCTING LEFSCHETZ FIBRATIONS VIA DAISY SUBSTITUTIONS arxiv: v3 [math.gt] 19 May 2015
![CONSTRUCTING LEFSCHETZ FIBRATIONS VIA DAISY SUBSTITUTIONS arxiv: v3 [math.gt] 19 May 2015 CONSTRUCTING LEFSCHETZ FIBRATIONS VIA DAISY SUBSTITUTIONS arxiv: v3 [math.gt] 19 May 2015](/thumbs/93/112734965.jpg) CONSTRUCTING LEFSCHETZ FIBRATIONS VIA DAISY SUBSTITUTIONS arxiv:1405.6669v3 [math.gt] 19 May 2015 ANAR AKHMEDOV AND NAOYUKI MONDEN Abstract. We construct new families of non-hyperelliptic Lefschetz fibrations
CONSTRUCTING LEFSCHETZ FIBRATIONS VIA DAISY SUBSTITUTIONS arxiv:1405.6669v3 [math.gt] 19 May 2015 ANAR AKHMEDOV AND NAOYUKI MONDEN Abstract. We construct new families of non-hyperelliptic Lefschetz fibrations
arxiv: v3 [math.gt] 26 Aug 2014
![arxiv: v3 [math.gt] 26 Aug 2014 arxiv: v3 [math.gt] 26 Aug 2014](/thumbs/94/121791915.jpg) ARBITRARILY LONG FACTORIZATIONS IN MAPPING CLASS GROUPS arxiv:309.3778v3 [math.gt] 6 Aug 0 ELİF DALYAN, MUSTAFA KORKMAZ AND MEHMETCİK PAMUK Abstract. Onacompact orientedsurface ofgenusg withn boundary
ARBITRARILY LONG FACTORIZATIONS IN MAPPING CLASS GROUPS arxiv:309.3778v3 [math.gt] 6 Aug 0 ELİF DALYAN, MUSTAFA KORKMAZ AND MEHMETCİK PAMUK Abstract. Onacompact orientedsurface ofgenusg withn boundary
arxiv:math/ v1 [math.gt] 14 Dec 2004
![arxiv:math/ v1 [math.gt] 14 Dec 2004 arxiv:math/ v1 [math.gt] 14 Dec 2004](/thumbs/86/93466553.jpg) arxiv:math/0412275v1 [math.gt] 14 Dec 2004 AN OPEN BOOK DECOMPOSITION COMPATIBLE WITH RATIONAL CONTACT SURGERY BURAK OZBAGCI Abstract. We construct an open book decomposition compatible with a contact
arxiv:math/0412275v1 [math.gt] 14 Dec 2004 AN OPEN BOOK DECOMPOSITION COMPATIBLE WITH RATIONAL CONTACT SURGERY BURAK OZBAGCI Abstract. We construct an open book decomposition compatible with a contact
The Classification of Nonsimple Algebraic Tangles
 The Classification of Nonsimple Algebraic Tangles Ying-Qing Wu 1 A tangle is a pair (B, T ), where B is a 3-ball, T is a pair of properly embedded arcs. When there is no ambiguity we will simply say that
The Classification of Nonsimple Algebraic Tangles Ying-Qing Wu 1 A tangle is a pair (B, T ), where B is a 3-ball, T is a pair of properly embedded arcs. When there is no ambiguity we will simply say that
STABILITY AND EXISTENCE OF SURFACES IN SYMPLECTIC 4-MANIFOLDS WITH b + = 1
 STABILITY AND EXISTENCE OF SURFACES IN SYMPLECTIC 4-MANIFOLDS WITH b + = 1 JOSEF G. DORFMEISTER, TIAN-JUN LI, AND WEIWEI WU Abstract. We establish various stability results for symplectic surfaces in symplectic
STABILITY AND EXISTENCE OF SURFACES IN SYMPLECTIC 4-MANIFOLDS WITH b + = 1 JOSEF G. DORFMEISTER, TIAN-JUN LI, AND WEIWEI WU Abstract. We establish various stability results for symplectic surfaces in symplectic
Introduction (Lecture 1)
 Introduction (Lecture 1) February 2, 2011 In this course, we will be concerned with variations on the following: Question 1. Let X be a CW complex. When does there exist a homotopy equivalence X M, where
Introduction (Lecture 1) February 2, 2011 In this course, we will be concerned with variations on the following: Question 1. Let X be a CW complex. When does there exist a homotopy equivalence X M, where
4-MANIFOLDS AS FIBER BUNDLES
 4-MANIFOLDS AS FIBER BUNDLES MORGAN WEILER Structures on 4-Manifolds I care about geometric structures on 4-manifolds because they allow me to obtain results about their smooth topology. Think: de Rham
4-MANIFOLDS AS FIBER BUNDLES MORGAN WEILER Structures on 4-Manifolds I care about geometric structures on 4-manifolds because they allow me to obtain results about their smooth topology. Think: de Rham
arxiv: v2 [math.gt] 11 Dec 2012
![arxiv: v2 [math.gt] 11 Dec 2012 arxiv: v2 [math.gt] 11 Dec 2012](/thumbs/88/117701025.jpg) NEW EXOTIC 4-MANIFOLDS VIA LUTTINGER SURGERY ON LEFSCHETZ FIBRATIONS arxiv:1212.1967v2 [math.gt] 11 Dec 2012 ANAR AKHMEDOV AND KADRIYE NUR SAGLAM Abstract. In [2], the first author constructed the first
NEW EXOTIC 4-MANIFOLDS VIA LUTTINGER SURGERY ON LEFSCHETZ FIBRATIONS arxiv:1212.1967v2 [math.gt] 11 Dec 2012 ANAR AKHMEDOV AND KADRIYE NUR SAGLAM Abstract. In [2], the first author constructed the first
B B. B g ... g 1 g ... c c. g b
 PROCEEDINGS OF THE AMERICAN MATHEMATICAL SOCIETY Volume 00, Number 0, Xxxx XXXX, Pages 000 000 S 0002-9939(XX)0000-0 CONTACT 3-MANIFOLDS WITH INFINITELY MANY STEIN FILLINGS BURAK OZBAGCI AND ANDRÁS I.
PROCEEDINGS OF THE AMERICAN MATHEMATICAL SOCIETY Volume 00, Number 0, Xxxx XXXX, Pages 000 000 S 0002-9939(XX)0000-0 CONTACT 3-MANIFOLDS WITH INFINITELY MANY STEIN FILLINGS BURAK OZBAGCI AND ANDRÁS I.
Scalar curvature and the Thurston norm
 Scalar curvature and the Thurston norm P. B. Kronheimer 1 andt.s.mrowka 2 Harvard University, CAMBRIDGE MA 02138 Massachusetts Institute of Technology, CAMBRIDGE MA 02139 1. Introduction Let Y be a closed,
Scalar curvature and the Thurston norm P. B. Kronheimer 1 andt.s.mrowka 2 Harvard University, CAMBRIDGE MA 02138 Massachusetts Institute of Technology, CAMBRIDGE MA 02139 1. Introduction Let Y be a closed,
A NOTE ON CONTACT SURGERY DIAGRAMS
 A NOTE ON CONTACT SURGERY DIAGRAMS BURAK OZBAGCI Abstract. We prove that for any positive integer the stabilization of a 1 -surgery curve in a contact surgery diagram induces an overtwisted contact structure.
A NOTE ON CONTACT SURGERY DIAGRAMS BURAK OZBAGCI Abstract. We prove that for any positive integer the stabilization of a 1 -surgery curve in a contact surgery diagram induces an overtwisted contact structure.
Mathematical Research Letters 2, (1995) A VANISHING THEOREM FOR SEIBERG-WITTEN INVARIANTS. Shuguang Wang
 Mathematical Research Letters 2, 305 310 (1995) A VANISHING THEOREM FOR SEIBERG-WITTEN INVARIANTS Shuguang Wang Abstract. It is shown that the quotients of Kähler surfaces under free anti-holomorphic involutions
Mathematical Research Letters 2, 305 310 (1995) A VANISHING THEOREM FOR SEIBERG-WITTEN INVARIANTS Shuguang Wang Abstract. It is shown that the quotients of Kähler surfaces under free anti-holomorphic involutions
Covering Invariants and Cohopficity of 3-manifold Groups
 Covering Invariants and Cohopficity of 3-manifold Groups Shicheng Wang 1 and Ying-Qing Wu 2 Abstract A 3-manifold M is called to have property C if the degrees of finite coverings over M are determined
Covering Invariants and Cohopficity of 3-manifold Groups Shicheng Wang 1 and Ying-Qing Wu 2 Abstract A 3-manifold M is called to have property C if the degrees of finite coverings over M are determined
DISTINGUISHING EMBEDDED CURVES IN RATIONAL COMPLEX SURFACES
 PROCEEDINGS OF THE AMERICAN MATHEMATICAL SOCIETY Volume 16, Number 1, January 1998, Pages 305 310 S 000-9939(98)04001-5 DISTINGUISHING EMBEDDED CURVES IN RATIONAL COMPLEX SURFACES TERRY FULLER (Communicated
PROCEEDINGS OF THE AMERICAN MATHEMATICAL SOCIETY Volume 16, Number 1, January 1998, Pages 305 310 S 000-9939(98)04001-5 DISTINGUISHING EMBEDDED CURVES IN RATIONAL COMPLEX SURFACES TERRY FULLER (Communicated
4-MANIFOLDS: CLASSIFICATION AND EXAMPLES. 1. Outline
 4-MANIFOLDS: CLASSIFICATION AND EXAMPLES 1. Outline Throughout, 4-manifold will be used to mean closed, oriented, simply-connected 4-manifold. Hopefully I will remember to append smooth wherever necessary.
4-MANIFOLDS: CLASSIFICATION AND EXAMPLES 1. Outline Throughout, 4-manifold will be used to mean closed, oriented, simply-connected 4-manifold. Hopefully I will remember to append smooth wherever necessary.
LECTURE 6: J-HOLOMORPHIC CURVES AND APPLICATIONS
 LECTURE 6: J-HOLOMORPHIC CURVES AND APPLICATIONS WEIMIN CHEN, UMASS, SPRING 07 1. Basic elements of J-holomorphic curve theory Let (M, ω) be a symplectic manifold of dimension 2n, and let J J (M, ω) be
LECTURE 6: J-HOLOMORPHIC CURVES AND APPLICATIONS WEIMIN CHEN, UMASS, SPRING 07 1. Basic elements of J-holomorphic curve theory Let (M, ω) be a symplectic manifold of dimension 2n, and let J J (M, ω) be
Exotic spheres. Overview and lecture-by-lecture summary. Martin Palmer / 22 July 2017
 Exotic spheres Overview and lecture-by-lecture summary Martin Palmer / 22 July 2017 Abstract This is a brief overview and a slightly less brief lecture-by-lecture summary of the topics covered in the course
Exotic spheres Overview and lecture-by-lecture summary Martin Palmer / 22 July 2017 Abstract This is a brief overview and a slightly less brief lecture-by-lecture summary of the topics covered in the course
Lagrangian knottedness and unknottedness in rational surfaces
 agrangian knottedness and unknottedness in rational surfaces Outline: agrangian knottedness Symplectic geometry of complex projective varieties, D 5, agrangian spheres and Dehn twists agrangian unknottedness
agrangian knottedness and unknottedness in rational surfaces Outline: agrangian knottedness Symplectic geometry of complex projective varieties, D 5, agrangian spheres and Dehn twists agrangian unknottedness
Rohlin s Invariant and 4-dimensional Gauge Theory. Daniel Ruberman Nikolai Saveliev
 Rohlin s Invariant and 4-dimensional Gauge Theory Daniel Ruberman Nikolai Saveliev 1 Overall theme: relation between Rohlin-type invariants and gauge theory, especially in dimension 4. Background: Recall
Rohlin s Invariant and 4-dimensional Gauge Theory Daniel Ruberman Nikolai Saveliev 1 Overall theme: relation between Rohlin-type invariants and gauge theory, especially in dimension 4. Background: Recall
arxiv: v2 [math.gt] 19 Oct 2014
![arxiv: v2 [math.gt] 19 Oct 2014 arxiv: v2 [math.gt] 19 Oct 2014](/thumbs/91/105493767.jpg) VIRTUAL LEGENDRIAN ISOTOPY VLADIMIR CHERNOV AND RUSTAM SADYKOV arxiv:1406.0875v2 [math.gt] 19 Oct 2014 Abstract. An elementary stabilization of a Legendrian knot L in the spherical cotangent bundle ST
VIRTUAL LEGENDRIAN ISOTOPY VLADIMIR CHERNOV AND RUSTAM SADYKOV arxiv:1406.0875v2 [math.gt] 19 Oct 2014 Abstract. An elementary stabilization of a Legendrian knot L in the spherical cotangent bundle ST
L E C T U R E N O T E S O N H O M O T O P Y T H E O R Y A N D A P P L I C AT I O N S
 L A U R E N T I U M A X I M U N I V E R S I T Y O F W I S C O N S I N - M A D I S O N L E C T U R E N O T E S O N H O M O T O P Y T H E O R Y A N D A P P L I C AT I O N S i Contents 1 Basics of Homotopy
L A U R E N T I U M A X I M U N I V E R S I T Y O F W I S C O N S I N - M A D I S O N L E C T U R E N O T E S O N H O M O T O P Y T H E O R Y A N D A P P L I C AT I O N S i Contents 1 Basics of Homotopy
Combinatorial Heegaard Floer Theory
 Combinatorial Heegaard Floer Theory Ciprian Manolescu UCLA February 29, 2012 Ciprian Manolescu (UCLA) Combinatorial HF Theory February 29, 2012 1 / 31 Motivation (4D) Much insight into smooth 4-manifolds
Combinatorial Heegaard Floer Theory Ciprian Manolescu UCLA February 29, 2012 Ciprian Manolescu (UCLA) Combinatorial HF Theory February 29, 2012 1 / 31 Motivation (4D) Much insight into smooth 4-manifolds
EXOTIC SMOOTH STRUCTURES ON SMALL 4-MANIFOLDS
 EXOTIC SMOOTH STRUCTURES ON SMALL 4-MANIFOLDS ANAR AKHMEDOV AND B. DOUG PARK Dedicated to Ronald J. Stern on the occasion of his sixtieth birthday Abstract. Let M be either CP 2 #3CP 2 or 3CP 2 #5CP 2.
EXOTIC SMOOTH STRUCTURES ON SMALL 4-MANIFOLDS ANAR AKHMEDOV AND B. DOUG PARK Dedicated to Ronald J. Stern on the occasion of his sixtieth birthday Abstract. Let M be either CP 2 #3CP 2 or 3CP 2 #5CP 2.
Scharlemann s manifold is standard
 Annals of Mathematics, 149 (1999), 497 510 Scharlemann s manifold is standard By Selman Akbulut* Dedicated to Robion Kirby on the occasion of his 60 th birthday Abstract In his 1974 thesis, Martin Scharlemann
Annals of Mathematics, 149 (1999), 497 510 Scharlemann s manifold is standard By Selman Akbulut* Dedicated to Robion Kirby on the occasion of his 60 th birthday Abstract In his 1974 thesis, Martin Scharlemann
Lecture XI: The non-kähler world
 Lecture XI: The non-kähler world Jonathan Evans 2nd December 2010 Jonathan Evans () Lecture XI: The non-kähler world 2nd December 2010 1 / 21 We ve spent most of the course so far discussing examples of
Lecture XI: The non-kähler world Jonathan Evans 2nd December 2010 Jonathan Evans () Lecture XI: The non-kähler world 2nd December 2010 1 / 21 We ve spent most of the course so far discussing examples of
arxiv:math/ v3 [math.sg] 20 Sep 2004
![arxiv:math/ v3 [math.sg] 20 Sep 2004 arxiv:math/ v3 [math.sg] 20 Sep 2004](/thumbs/86/93466565.jpg) arxiv:math/0404267v3 [math.sg] 20 Sep 2004 PLANAR OPEN BOOK DECOMPOSITIONS AND CONTACT STRUCTURES JOHN B. ETNYRE Abstract. In this note we observe that while all overtwisted contact structures on compact
arxiv:math/0404267v3 [math.sg] 20 Sep 2004 PLANAR OPEN BOOK DECOMPOSITIONS AND CONTACT STRUCTURES JOHN B. ETNYRE Abstract. In this note we observe that while all overtwisted contact structures on compact
arxiv:math/ v1 [math.gt] 14 Nov 2003
![arxiv:math/ v1 [math.gt] 14 Nov 2003 arxiv:math/ v1 [math.gt] 14 Nov 2003](/thumbs/93/111283059.jpg) AUTOMORPHISMS OF TORELLI GROUPS arxiv:math/0311250v1 [math.gt] 14 Nov 2003 JOHN D. MCCARTHY AND WILLIAM R. VAUTAW Abstract. In this paper, we prove that each automorphism of the Torelli group of a surface
AUTOMORPHISMS OF TORELLI GROUPS arxiv:math/0311250v1 [math.gt] 14 Nov 2003 JOHN D. MCCARTHY AND WILLIAM R. VAUTAW Abstract. In this paper, we prove that each automorphism of the Torelli group of a surface
arxiv: v1 [math.sg] 22 Nov 2011
![arxiv: v1 [math.sg] 22 Nov 2011 arxiv: v1 [math.sg] 22 Nov 2011](/thumbs/83/87621420.jpg) CONVEX PLUMBINGS AND LEFSCHETZ FIBRATIONS arxiv:1111.5327v1 [math.sg] 22 Nov 2011 DAVID GAY AND THOMAS E. MARK Abstract. We show that under appropriate hypotheses, a plumbing of symplectic surfaces in
CONVEX PLUMBINGS AND LEFSCHETZ FIBRATIONS arxiv:1111.5327v1 [math.sg] 22 Nov 2011 DAVID GAY AND THOMAS E. MARK Abstract. We show that under appropriate hypotheses, a plumbing of symplectic surfaces in
arxiv: v1 [math.gt] 11 Apr 2016
![arxiv: v1 [math.gt] 11 Apr 2016 arxiv: v1 [math.gt] 11 Apr 2016](/thumbs/93/114525127.jpg) FILLINGS OF GENUS 1 OPEN BOOKS AND 4 BRAIDS arxiv:1604.02945v1 [math.gt] 11 Apr 2016 R. İNANÇ BAYKUR AND JEREMY VAN HORN-MORRIS Abstract. We show that there are contact 3 manifolds of support genus one
FILLINGS OF GENUS 1 OPEN BOOKS AND 4 BRAIDS arxiv:1604.02945v1 [math.gt] 11 Apr 2016 R. İNANÇ BAYKUR AND JEREMY VAN HORN-MORRIS Abstract. We show that there are contact 3 manifolds of support genus one
arxiv:math/ v1 [math.gt] 26 Sep 2005
![arxiv:math/ v1 [math.gt] 26 Sep 2005 arxiv:math/ v1 [math.gt] 26 Sep 2005](/thumbs/93/113554162.jpg) EXPLICIT HORIZONTAL OPEN BOOKS ON SOME PLUMBINGS arxiv:math/0509611v1 [math.gt] 26 Sep 2005 TOLGA ETGÜ AND BURAK OZBAGCI ABSTRACT. We describe explicit open books on arbitrary plumbings of oriented circle
EXPLICIT HORIZONTAL OPEN BOOKS ON SOME PLUMBINGS arxiv:math/0509611v1 [math.gt] 26 Sep 2005 TOLGA ETGÜ AND BURAK OZBAGCI ABSTRACT. We describe explicit open books on arbitrary plumbings of oriented circle
Hyperelliptic Lefschetz fibrations and the Dirac braid
 Hyperelliptic Lefschetz fibrations and the Dirac braid joint work with Seiichi Kamada Hisaaki Endo (Tokyo Institute of Technology) Differential Topology 206 March 20, 206, University of Tsukuba March 20,
Hyperelliptic Lefschetz fibrations and the Dirac braid joint work with Seiichi Kamada Hisaaki Endo (Tokyo Institute of Technology) Differential Topology 206 March 20, 206, University of Tsukuba March 20,
Introduction to Poincare Conjecture and the Hamilton-Perelman program
 Introduction to Poincare Conjecture and the Hamilton-Perelman program David Glickenstein Math 538, Spring 2009 January 20, 2009 1 Introduction This lecture is mostly taken from Tao s lecture 2. In this
Introduction to Poincare Conjecture and the Hamilton-Perelman program David Glickenstein Math 538, Spring 2009 January 20, 2009 1 Introduction This lecture is mostly taken from Tao s lecture 2. In this
arxiv: v1 [math.gt] 23 Apr 2014
![arxiv: v1 [math.gt] 23 Apr 2014 arxiv: v1 [math.gt] 23 Apr 2014](/thumbs/75/72058242.jpg) THE NUMBER OF FRAMINGS OF A KNOT IN A 3-MANIFOLD PATRICIA CAHN, VLADIMIR CHERNOV, AND RUSTAM SADYKOV arxiv:1404.5851v1 [math.gt] 23 Apr 2014 Abstract. In view of the self-linking invariant, the number
THE NUMBER OF FRAMINGS OF A KNOT IN A 3-MANIFOLD PATRICIA CAHN, VLADIMIR CHERNOV, AND RUSTAM SADYKOV arxiv:1404.5851v1 [math.gt] 23 Apr 2014 Abstract. In view of the self-linking invariant, the number
FAKE PROJECTIVE SPACES AND FAKE TORI
 FAKE PROJECTIVE SPACES AND FAKE TORI OLIVIER DEBARRE Abstract. Hirzebruch and Kodaira proved in 1957 that when n is odd, any compact Kähler manifold X which is homeomorphic to P n is isomorphic to P n.
FAKE PROJECTIVE SPACES AND FAKE TORI OLIVIER DEBARRE Abstract. Hirzebruch and Kodaira proved in 1957 that when n is odd, any compact Kähler manifold X which is homeomorphic to P n is isomorphic to P n.
Lefschetz Fibrations of 4-Dimensional Manifolds
 Cubo A Mathematical Journal Vol.05/N ō 03 OCTOBER 2003 Lefschetz Fibrations of 4-Dimensional Manifolds Terry Fuller Department of Mathematics California State University, Northridge Northridge, CA 91330
Cubo A Mathematical Journal Vol.05/N ō 03 OCTOBER 2003 Lefschetz Fibrations of 4-Dimensional Manifolds Terry Fuller Department of Mathematics California State University, Northridge Northridge, CA 91330
Stein fillings of contact 3-manifolds obtained as Legendrian sur
 Stein fillings of contact 3-manifolds obtained as Legendrian surgeries Youlin Li (With Amey Kaloti) Shanghai Jiao Tong University A Satellite Conference of Seoul ICM 2014 Knots and Low Dimensional Manifolds
Stein fillings of contact 3-manifolds obtained as Legendrian surgeries Youlin Li (With Amey Kaloti) Shanghai Jiao Tong University A Satellite Conference of Seoul ICM 2014 Knots and Low Dimensional Manifolds
Topological rigidity for non-aspherical manifolds by M. Kreck and W. Lück
 Topological rigidity for non-aspherical manifolds by M. Kreck and W. Lück July 11, 2006 Abstract The Borel Conjecture predicts that closed aspherical manifolds are topological rigid. We want to investigate
Topological rigidity for non-aspherical manifolds by M. Kreck and W. Lück July 11, 2006 Abstract The Borel Conjecture predicts that closed aspherical manifolds are topological rigid. We want to investigate
Homological mirror symmetry via families of Lagrangians
 Homological mirror symmetry via families of Lagrangians String-Math 2018 Mohammed Abouzaid Columbia University June 17, 2018 Mirror symmetry Three facets of mirror symmetry: 1 Enumerative: GW invariants
Homological mirror symmetry via families of Lagrangians String-Math 2018 Mohammed Abouzaid Columbia University June 17, 2018 Mirror symmetry Three facets of mirror symmetry: 1 Enumerative: GW invariants
EXOTIC 4-MANIFOLDS OBTAINED BY AN INFINTE ORDER PLUG
 EXOTIC 4-MANIFOLDS OBTAINED BY AN INFINTE ORDER PLUG MOTOO TANGE Abstract. In the previous paper the author defined an infinite order plug (P, φ) which gives rise to infinite Fintushel-Stern s knot-surgeries.
EXOTIC 4-MANIFOLDS OBTAINED BY AN INFINTE ORDER PLUG MOTOO TANGE Abstract. In the previous paper the author defined an infinite order plug (P, φ) which gives rise to infinite Fintushel-Stern s knot-surgeries.
SYMPLECTIC 4-MANIFOLDS, SINGULAR PLANE CURVES, AND ISOTOPY PROBLEMS
 SYMPLECTIC 4-MANIFOLDS, SINGULAR PLANE CURVES, AND ISOTOPY PROBLEMS DENIS AUROUX Abstract. We give an overview of various recent results concerning the topology of symplectic 4-manifolds and singular plane
SYMPLECTIC 4-MANIFOLDS, SINGULAR PLANE CURVES, AND ISOTOPY PROBLEMS DENIS AUROUX Abstract. We give an overview of various recent results concerning the topology of symplectic 4-manifolds and singular plane
A PRESENTATION FOR THE MAPPING CLASS GROUP OF A NON-ORIENTABLE SURFACE FROM THE ACTION ON THE COMPLEX OF CURVES
 Szepietowski, B. Osaka J. Math. 45 (008), 83 36 A PRESENTATION FOR THE MAPPING CLASS GROUP OF A NON-ORIENTABLE SURFACE FROM THE ACTION ON THE COMPLEX OF CURVES BŁAŻEJ SZEPIETOWSKI (Received June 30, 006,
Szepietowski, B. Osaka J. Math. 45 (008), 83 36 A PRESENTATION FOR THE MAPPING CLASS GROUP OF A NON-ORIENTABLE SURFACE FROM THE ACTION ON THE COMPLEX OF CURVES BŁAŻEJ SZEPIETOWSKI (Received June 30, 006,
Invariants of knots and 3-manifolds: Survey on 3-manifolds
 Invariants of knots and 3-manifolds: Survey on 3-manifolds Wolfgang Lück Bonn Germany email wolfgang.lueck@him.uni-bonn.de http://131.220.77.52/lueck/ Bonn, 10. & 12. April 2018 Wolfgang Lück (MI, Bonn)
Invariants of knots and 3-manifolds: Survey on 3-manifolds Wolfgang Lück Bonn Germany email wolfgang.lueck@him.uni-bonn.de http://131.220.77.52/lueck/ Bonn, 10. & 12. April 2018 Wolfgang Lück (MI, Bonn)
CW-complexes. Stephen A. Mitchell. November 1997
 CW-complexes Stephen A. Mitchell November 1997 A CW-complex is first of all a Hausdorff space X equipped with a collection of characteristic maps φ n α : D n X. Here n ranges over the nonnegative integers,
CW-complexes Stephen A. Mitchell November 1997 A CW-complex is first of all a Hausdorff space X equipped with a collection of characteristic maps φ n α : D n X. Here n ranges over the nonnegative integers,
Part II. Algebraic Topology. Year
 Part II Year 2017 2016 2015 2014 2013 2012 2011 2010 2009 2008 2007 2006 2005 2017 Paper 3, Section II 18I The n-torus is the product of n circles: 5 T n = } S 1. {{.. S } 1. n times For all n 1 and 0
Part II Year 2017 2016 2015 2014 2013 2012 2011 2010 2009 2008 2007 2006 2005 2017 Paper 3, Section II 18I The n-torus is the product of n circles: 5 T n = } S 1. {{.. S } 1. n times For all n 1 and 0
EMBEDDING ALL CONTACT 3 MANIFOLDS IN A FIXED CONTACT 5 MANIFOLD
 EMBEDDING ALL CONTACT 3 MANIFOLDS IN A FIXED CONTACT 5 MANIFOLD JOHN B. ETNYRE AND YANKI LEKILI ABSTRACT. In this note we observe that one can contact embed all contact 3 manifolds into a Stein fillable
EMBEDDING ALL CONTACT 3 MANIFOLDS IN A FIXED CONTACT 5 MANIFOLD JOHN B. ETNYRE AND YANKI LEKILI ABSTRACT. In this note we observe that one can contact embed all contact 3 manifolds into a Stein fillable
Symmetries and exotic smooth structures on a K3 surface
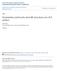 University of Massachusetts Amherst ScholarWorks@UMass Amherst Mathematics and Statistics Department Faculty Publication Series Mathematics and Statistics 2008 Symmetries and exotic smooth structures on
University of Massachusetts Amherst ScholarWorks@UMass Amherst Mathematics and Statistics Department Faculty Publication Series Mathematics and Statistics 2008 Symmetries and exotic smooth structures on
FAMILIES OF ALGEBRAIC CURVES AS SURFACE BUNDLES OF RIEMANN SURFACES
 FAMILIES OF ALGEBRAIC CURVES AS SURFACE BUNDLES OF RIEMANN SURFACES MARGARET NICHOLS 1. Introduction In this paper we study the complex structures which can occur on algebraic curves. The ideas discussed
FAMILIES OF ALGEBRAIC CURVES AS SURFACE BUNDLES OF RIEMANN SURFACES MARGARET NICHOLS 1. Introduction In this paper we study the complex structures which can occur on algebraic curves. The ideas discussed
Diffeomorphism Groups of Reducible 3-Manifolds. Allen Hatcher
 Diffeomorphism Groups of Reducible 3-Manifolds Allen Hatcher In a 1979 announcement by César de Sá and Rourke [CR] there is a sketch of an intuitively appealing approach to measuring the difference between
Diffeomorphism Groups of Reducible 3-Manifolds Allen Hatcher In a 1979 announcement by César de Sá and Rourke [CR] there is a sketch of an intuitively appealing approach to measuring the difference between
CONVEX PLUMBINGS AND LEFSCHETZ FIBRATIONS. David Gay and Thomas E. Mark
 JOURNAL OF SYMPLECTIC GEOMETRY Volume 11, Number 3, 363 375, 2013 CONVEX PLUMBINGS AND LEFSCHETZ FIBRATIONS David Gay and Thomas E. Mark We show that under appropriate hypotheses, a plumbing of symplectic
JOURNAL OF SYMPLECTIC GEOMETRY Volume 11, Number 3, 363 375, 2013 CONVEX PLUMBINGS AND LEFSCHETZ FIBRATIONS David Gay and Thomas E. Mark We show that under appropriate hypotheses, a plumbing of symplectic
3-manifolds and their groups
 3-manifolds and their groups Dale Rolfsen University of British Columbia Marseille, September 2010 Dale Rolfsen (2010) 3-manifolds and their groups Marseille, September 2010 1 / 31 3-manifolds and their
3-manifolds and their groups Dale Rolfsen University of British Columbia Marseille, September 2010 Dale Rolfsen (2010) 3-manifolds and their groups Marseille, September 2010 1 / 31 3-manifolds and their
DISSOLVING FOUR-MANIFOLDS AND POSITIVE SCALAR CURVATURE
 DISSOLVING FOUR-MANIFOLDS AND POSITIVE SCALAR CURVATURE B. HANKE, D. KOTSCHICK, AND J. WEHRHEIM ABSTRACT. We prove that many simply connected symplectic fourmanifolds dissolve after connected sum with
DISSOLVING FOUR-MANIFOLDS AND POSITIVE SCALAR CURVATURE B. HANKE, D. KOTSCHICK, AND J. WEHRHEIM ABSTRACT. We prove that many simply connected symplectic fourmanifolds dissolve after connected sum with
On the Diffeomorphism Group of S 1 S 2. Allen Hatcher
 On the Diffeomorphism Group of S 1 S 2 Allen Hatcher This is a revision, written in December 2003, of a paper of the same title that appeared in the Proceedings of the AMS 83 (1981), 427-430. The main
On the Diffeomorphism Group of S 1 S 2 Allen Hatcher This is a revision, written in December 2003, of a paper of the same title that appeared in the Proceedings of the AMS 83 (1981), 427-430. The main
CLASSIFICATION OF TIGHT CONTACT STRUCTURES ON SURGERIES ON THE FIGURE-EIGHT KNOT
 CLASSIFICATION OF TIGHT CONTACT STRUCTURES ON SURGERIES ON THE FIGURE-EIGHT KNOT JAMES CONWAY AND HYUNKI MIN ABSTRACT. Two of the basic questions in contact topology are which manifolds admit tight contact
CLASSIFICATION OF TIGHT CONTACT STRUCTURES ON SURGERIES ON THE FIGURE-EIGHT KNOT JAMES CONWAY AND HYUNKI MIN ABSTRACT. Two of the basic questions in contact topology are which manifolds admit tight contact
MONOPOLE CLASSES AND PERELMAN S INVARIANT OF FOUR-MANIFOLDS
 MONOPOLE CLASSES AND PERELMAN S INVARIANT OF FOUR-MANIFOLDS D. KOTSCHICK ABSTRACT. We calculate Perelman s invariant for compact complex surfaces and a few other smooth four-manifolds. We also prove some
MONOPOLE CLASSES AND PERELMAN S INVARIANT OF FOUR-MANIFOLDS D. KOTSCHICK ABSTRACT. We calculate Perelman s invariant for compact complex surfaces and a few other smooth four-manifolds. We also prove some
A NOTE ON E 8 -INTERSECTION FORMS AND CORRECTION TERMS
 A NOTE ON E 8 -INTERSECTION FORMS AND CORRECTION TERMS MOTOO TANGE Abstract. In this paper we construct families of homology spheres which bound 4-manifolds with intersection forms isomorphic to E 8. We
A NOTE ON E 8 -INTERSECTION FORMS AND CORRECTION TERMS MOTOO TANGE Abstract. In this paper we construct families of homology spheres which bound 4-manifolds with intersection forms isomorphic to E 8. We
Cobordant differentiable manifolds
 Variétés différentiables cobordant, Colloque Int. du C. N. R. S., v. LII, Géométrie différentielle, Strasbourg (1953), pp. 143-149. Cobordant differentiable manifolds By R. THOM (Strasbourg) Translated
Variétés différentiables cobordant, Colloque Int. du C. N. R. S., v. LII, Géométrie différentielle, Strasbourg (1953), pp. 143-149. Cobordant differentiable manifolds By R. THOM (Strasbourg) Translated
arxiv: v1 [math.gt] 21 Oct 2014
![arxiv: v1 [math.gt] 21 Oct 2014 arxiv: v1 [math.gt] 21 Oct 2014](/thumbs/74/71295167.jpg) BROKEN LEFSCHETZ FIBRATIONS AND MAPPING CLASS GROUPS arxiv:1410.5531v1 [math.gt] 21 Oct 2014 R. İNANÇ BAYKUR AND KENTA HAYANO Abstract. The purpose of this note is to explain a combinatorial description
BROKEN LEFSCHETZ FIBRATIONS AND MAPPING CLASS GROUPS arxiv:1410.5531v1 [math.gt] 21 Oct 2014 R. İNANÇ BAYKUR AND KENTA HAYANO Abstract. The purpose of this note is to explain a combinatorial description
Rational Curves On K3 Surfaces
 Rational Curves On K3 Surfaces Jun Li Department of Mathematics Stanford University Conference in honor of Peter Li Overview of the talk The problem: existence of rational curves on a K3 surface The conjecture:
Rational Curves On K3 Surfaces Jun Li Department of Mathematics Stanford University Conference in honor of Peter Li Overview of the talk The problem: existence of rational curves on a K3 surface The conjecture:
SURGERY ON A KNOT IN SURFACE I
 SURGERY ON A KNOT IN SURFACE I MARTIN SCHARLEMANN AND ABIGAIL THOMPSON Abstract. Suppose F is a compact orientable surface, K is a knot in F I, and (F I) surg is the 3-manifold obtained by some non-trivial
SURGERY ON A KNOT IN SURFACE I MARTIN SCHARLEMANN AND ABIGAIL THOMPSON Abstract. Suppose F is a compact orientable surface, K is a knot in F I, and (F I) surg is the 3-manifold obtained by some non-trivial
RESEARCH STATEMENT LUKE WILLIAMS
 RESEARCH STATEMENT LUKE WILLIAMS My research focuses on problems in smooth 4-dimensional topology. The primary goal of which is to understand smooth structures on 4-dimensional topological manifolds with
RESEARCH STATEMENT LUKE WILLIAMS My research focuses on problems in smooth 4-dimensional topology. The primary goal of which is to understand smooth structures on 4-dimensional topological manifolds with
AN EXPLICIT FAMILY OF EXOTIC CASSON HANDLES
 proceedings of the american mathematical society Volume 123, Number 4, April 1995 AN EXPLICIT FAMILY OF EXOTIC CASSON HANDLES 2ARKO BIZACA (Communicated by Ronald Stern) Abstract. This paper contains a
proceedings of the american mathematical society Volume 123, Number 4, April 1995 AN EXPLICIT FAMILY OF EXOTIC CASSON HANDLES 2ARKO BIZACA (Communicated by Ronald Stern) Abstract. This paper contains a
THE REPRESENTATION THEORY, GEOMETRY, AND COMBINATORICS OF BRANCHED COVERS
 THE REPRESENTATION THEORY, GEOMETRY, AND COMBINATORICS OF BRANCHED COVERS BRIAN OSSERMAN Abstract. The study of branched covers of the Riemann sphere has connections to many fields. We recall the classical
THE REPRESENTATION THEORY, GEOMETRY, AND COMBINATORICS OF BRANCHED COVERS BRIAN OSSERMAN Abstract. The study of branched covers of the Riemann sphere has connections to many fields. We recall the classical
Exercises for Algebraic Topology
 Sheet 1, September 13, 2017 Definition. Let A be an abelian group and let M be a set. The A-linearization of M is the set A[M] = {f : M A f 1 (A \ {0}) is finite}. We view A[M] as an abelian group via
Sheet 1, September 13, 2017 Definition. Let A be an abelian group and let M be a set. The A-linearization of M is the set A[M] = {f : M A f 1 (A \ {0}) is finite}. We view A[M] as an abelian group via
Definitions. Notations. Injective, Surjective and Bijective. Divides. Cartesian Product. Relations. Equivalence Relations
 Page 1 Definitions Tuesday, May 8, 2018 12:23 AM Notations " " means "equals, by definition" the set of all real numbers the set of integers Denote a function from a set to a set by Denote the image of
Page 1 Definitions Tuesday, May 8, 2018 12:23 AM Notations " " means "equals, by definition" the set of all real numbers the set of integers Denote a function from a set to a set by Denote the image of
arxiv:math/ v1 [math.gt] 22 Jan 2005
![arxiv:math/ v1 [math.gt] 22 Jan 2005 arxiv:math/ v1 [math.gt] 22 Jan 2005](/thumbs/88/117929326.jpg) arxiv:math/0501385v1 [math.gt] 22 Jan 2005 POSITIVE DEHN TWIST EXPRESSIONS FOR SOME ELEMENTS OF FINITE ORDER IN THE MAPPING CLASS GROUP YUSUF Z. GURTAS Abstract. Positive Dehn twist products for some elements
arxiv:math/0501385v1 [math.gt] 22 Jan 2005 POSITIVE DEHN TWIST EXPRESSIONS FOR SOME ELEMENTS OF FINITE ORDER IN THE MAPPING CLASS GROUP YUSUF Z. GURTAS Abstract. Positive Dehn twist products for some elements
SYMPLECTIC LEFSCHETZ FIBRATIONS ALEXANDER CAVIEDES CASTRO
 SYMPLECTIC LEFSCHETZ FIBRATIONS ALEXANDER CAVIEDES CASTRO. Introduction A Lefschetz pencil is a construction that comes from algebraic geometry, but it is closely related with symplectic geometry. Indeed,
SYMPLECTIC LEFSCHETZ FIBRATIONS ALEXANDER CAVIEDES CASTRO. Introduction A Lefschetz pencil is a construction that comes from algebraic geometry, but it is closely related with symplectic geometry. Indeed,
Math 6510 Homework 10
 2.2 Problems 9 Problem. Compute the homology group of the following 2-complexes X: a) The quotient of S 2 obtained by identifying north and south poles to a point b) S 1 (S 1 S 1 ) c) The space obtained
2.2 Problems 9 Problem. Compute the homology group of the following 2-complexes X: a) The quotient of S 2 obtained by identifying north and south poles to a point b) S 1 (S 1 S 1 ) c) The space obtained
J-holomorphic curves in symplectic geometry
 J-holomorphic curves in symplectic geometry Janko Latschev Pleinfeld, September 25 28, 2006 Since their introduction by Gromov [4] in the mid-1980 s J-holomorphic curves have been one of the most widely
J-holomorphic curves in symplectic geometry Janko Latschev Pleinfeld, September 25 28, 2006 Since their introduction by Gromov [4] in the mid-1980 s J-holomorphic curves have been one of the most widely
Bordism and the Pontryagin-Thom Theorem
 Bordism and the Pontryagin-Thom Theorem Richard Wong Differential Topology Term Paper December 2, 2016 1 Introduction Given the classification of low dimensional manifolds up to equivalence relations such
Bordism and the Pontryagin-Thom Theorem Richard Wong Differential Topology Term Paper December 2, 2016 1 Introduction Given the classification of low dimensional manifolds up to equivalence relations such
From symplectic deformation to isotopy
 From symplectic deformation to isotopy Dusa McDuff State University of New York at Stony Brook (dusa@math.sunysb.edu) May 15, 1996, revised Aug 4, 1997 Abstract Let X be an oriented 4-manifold which does
From symplectic deformation to isotopy Dusa McDuff State University of New York at Stony Brook (dusa@math.sunysb.edu) May 15, 1996, revised Aug 4, 1997 Abstract Let X be an oriented 4-manifold which does
Lecture VI: Projective varieties
 Lecture VI: Projective varieties Jonathan Evans 28th October 2010 Jonathan Evans () Lecture VI: Projective varieties 28th October 2010 1 / 24 I will begin by proving the adjunction formula which we still
Lecture VI: Projective varieties Jonathan Evans 28th October 2010 Jonathan Evans () Lecture VI: Projective varieties 28th October 2010 1 / 24 I will begin by proving the adjunction formula which we still
Characteristic classes in the Chow ring
 arxiv:alg-geom/9412008v1 10 Dec 1994 Characteristic classes in the Chow ring Dan Edidin and William Graham Department of Mathematics University of Chicago Chicago IL 60637 Let G be a reductive algebraic
arxiv:alg-geom/9412008v1 10 Dec 1994 Characteristic classes in the Chow ring Dan Edidin and William Graham Department of Mathematics University of Chicago Chicago IL 60637 Let G be a reductive algebraic
arxiv: v2 [math.gt] 26 Sep 2013
![arxiv: v2 [math.gt] 26 Sep 2013 arxiv: v2 [math.gt] 26 Sep 2013](/thumbs/88/115975443.jpg) HOMOLOGY CLASSES OF NEGATIVE SQUARE AND EMBEDDED SURFACES IN 4-MANIFOLDS arxiv:1301.3733v2 [math.gt] 26 Sep 2013 M. J. D. HAMILTON ABSTRACT. Let X be a simply-connected closed oriented 4-manifold and A
HOMOLOGY CLASSES OF NEGATIVE SQUARE AND EMBEDDED SURFACES IN 4-MANIFOLDS arxiv:1301.3733v2 [math.gt] 26 Sep 2013 M. J. D. HAMILTON ABSTRACT. Let X be a simply-connected closed oriented 4-manifold and A
Knot Homology from Refined Chern-Simons Theory
 Knot Homology from Refined Chern-Simons Theory Mina Aganagic UC Berkeley Based on work with Shamil Shakirov arxiv: 1105.5117 1 the knot invariant Witten explained in 88 that J(K, q) constructed by Jones
Knot Homology from Refined Chern-Simons Theory Mina Aganagic UC Berkeley Based on work with Shamil Shakirov arxiv: 1105.5117 1 the knot invariant Witten explained in 88 that J(K, q) constructed by Jones
arxiv: v1 [math.gt] 20 Dec 2017
![arxiv: v1 [math.gt] 20 Dec 2017 arxiv: v1 [math.gt] 20 Dec 2017](/thumbs/82/86068328.jpg) SYMPLECTIC FILLINGS, CONTACT SURGERIES, AND LAGRANGIAN DISKS arxiv:1712.07287v1 [math.gt] 20 Dec 2017 JAMES CONWAY, JOHN B. ETNYRE, AND BÜLENT TOSUN ABSTRACT. This paper completely answers the question
SYMPLECTIC FILLINGS, CONTACT SURGERIES, AND LAGRANGIAN DISKS arxiv:1712.07287v1 [math.gt] 20 Dec 2017 JAMES CONWAY, JOHN B. ETNYRE, AND BÜLENT TOSUN ABSTRACT. This paper completely answers the question
The Classification of Automorphism Groups of Rational Elliptic Surfaces With Section
 University of Pennsylvania ScholarlyCommons Publicly Accessible Penn Dissertations Spring 5-16-011 The Classification of Automorphism Groups of Rational Elliptic Surfaces With Section Tolga Karayayla tkarayay@math.upenn.edu
University of Pennsylvania ScholarlyCommons Publicly Accessible Penn Dissertations Spring 5-16-011 The Classification of Automorphism Groups of Rational Elliptic Surfaces With Section Tolga Karayayla tkarayay@math.upenn.edu
