Parabolic quasi-concavity for solutions to parabolic problems in convex rings
|
|
|
- Meredith Morgan
- 5 years ago
- Views:
Transcription
1 Math. Nachr. 283, No. 11, (2010) / DOI /mana Editor s Choice Parabolic quasi-concavity for solutions to parabolic problems in convex rings Kazuhiro Ishige 1 and Paolo Salani 2 1 Mathematical Institute, Tohoku University, Aoba, Sendai , Japan 2 Dipartimento di Matematica U. Dini, Università di Firenze, V. le Morgagni 67/A, Firenze, Italy Received 9 November 2009, revised 16 April 2010, accepted 4 May 2010 Published online 23 September 2010 Key words Parabolic equations, convexity, quasi-concavity MSC (2000) 35K05, 52A01, 35B05, 35B30 We investigate some geometric properties of level sets of the solutions of parabolic problems in convex rings. We introduce the notion of parabolic quasi-concavity, which involves time and space jointly and is a stronger property than the spatial quasi-concavity, and study the convexity of superlevel sets of the solutions. 1 Introduction Let u be a solution of the following parabolic problem t γ(u) =F (x, u, u, 2 u) in D (0, ), u(x, 0) = ϕ(x) 0 in D, u(x, t) =0 on Ω (0, ), u(x, t) =g(t) on K [0, ), (1.1) where t = / t, N 1, Ω and K are an open convex set and a closed convex set in R N, respectively, such that K Ω, D =Ω\ K, γ is a nonnegative convex function in [0, ) such that γ(0) = 0, g C 1 ([0, )) is a nonnegative bounded function with g 0 and g(0) ϕ(x) for x D, andf is a proper elliptic operator. Throughout the paper, by a solution u of (1.1), we mean a function u C 2,1 (D (0, )) C(D [0, ) \ D {0}) pointwise satisfying all of the conditions in (1.1). In this paper we investigate some convexity properties of the solutions of (1.1). The study of geometric properties (with special regard to concavity and quasi-concavity) of solutions of partial differential equations is a classical subject, especially in the field of elliptic equations, where it is hardly possible to compile a complete bibliography; then we just recall the classical monograph [19] and very recent related results like [1] and [2], and we refer to these for more references. For parabolic equations, fewer results are disposable, as far as we know, even if it is well-known (see for instance [5] and [12]) that log-concavity is preserved by the heat flow and it also seems to rule the large time behavior of solutions to parabolic equations in R N (see [25]). On the other hand, negative results are contained in [15] and [16], showing that in general one cannot expect the quasi-concavity of the initial datum to be preserved, even by the heat flow. Concavity properties of solutions to parabolic problems have been considered also in [3], [4], [8], [11], [21], [22], [23], [18], [26], for instance. See also references therein. Corresponding author: ishige@math.tohoku.ac.jp, Phone: , Fax: salani@math.unifi.it, Phone: , Fax:
2 Math. Nachr. 283, No. 11 (2010) / 1527 We recall that, roughly speaking, a function v : R N R {± }is said to be quasi-concave in R N if all its superlevel sets {x R N : v(x) l} are convex. More precisely, v is quasi-concave if v((1 λ)x 0 + λx 1 ) min{v(x 0 ),v(x 1 )} for every x 0,x 1 R N, λ (0, 1). If v is defined only in a proper subset Ω of R N,we extend it as outside Ω and we say that v is quasi-concave in Ω if such an extension is quasi-concave in R N. A solution u of (1.1) is said to be spatially quasi-concave if the function x u(x, t) is quasi-concave for every t 0,thatis, u((1 λ)x 0 + λx 1,t) min{u(x 0,t),u(x 1,t)} (1.2) for every x 0,x 1 Ω, t 0, λ (0, 1). A classical approach to study the spatial quasi-concavity of the solution u is based on the spatial quasi-concavity function Φ(x, y, t) =u((1 λ)x + λy, t) min{u(x, t),u(y, t)}, (x, y, t) Ω 2 [0, ). (1.3) Then u is spatially quasi-concave if and only if inf Φ 0 (1.4) Ω 2 [0, ) for any fixed λ (0, 1). Here we introduce a stronger quasi-concavity property, the parabolic quasi-concavity, which involves time and space jointly and seems to be more suitable for the parabolic framework. Precisely, inspired by Borell [4], who introduced the notion of parabolic convexity for subsets of R N [0, ), we give the following definition. Definition 1.1 A function u C(Ω [0, )) is called parabolically quasi-concave if u ((1 λ)x 0 + λx 1, ( (1 λ) t 0 + λ ) ) 2 t 1 min{u(x 0,t 0 ),u(x 1,t 1 )} (1.5) for every x 0,x 1 Ω, t 0,t 1 0, λ (0, 1). Clearly, if a function is parabolically quasi-concave, then it is spatially quasi-concave at every time; indeed, if we fix a time t 0, takingt 0 = t 1 = t, (1.5) coincides with (1.2). Roughly speaking, a function u is parabolically quasi-concave if all its superlevel sets {(x, t) : u(x, t) l} are parabolically convex in the sense of [4] (see Section 2.3 hereafter). An equivalent geometric characterization of parabolic quasi-concavity in terms of level sets is the following: u is parabolically quasi-concave if, for every l R, λ (0, 1), andt 0,t 1 0, there holds { x R N : u(x, t λ ) l } (1 λ) { x R N : u(x, t 0 ) l } + λ { x R N : u(x, t 1 ) l }, where t λ = ( (1 λ) t 0 + λ ) 2. t 1 Analogously to spatial quasi-concavity, to study the parabolic quasi-concavity of u, we can define a parabolic quasi-concavity function Π:Ω 2 [0, ) 2 R as follows ( Π(x, y, r, s) =u (1 λ)x + λy, ( (1 λ) r + λ s ) ) 2 min{u(x, r),u(y, s)}. (1.6) Then u is parabolically quasi-concave if and only if inf Π 0 (1.7) Ω 2 [0, ) 2 for any fixed λ (0, 1). The strategy here adopted is exactly to find suitable conditions such that (1.7) holds. Theorem 3.1 is a general theorem about minimum points of Π and it can be considered as the main result of this paper. As a consequence, we obtain Theorem 3.2, where we prove that, for the case of special initial and boundary data ϕ 0 in D and g 1 in [0, ), if the operator F satisfies a suitable convexity property, then u is parabolically quasi-concave. However, in order to state Theorems 3.1 and 3.2 in a clear and precise way, we need to introduce some notation. Therefore we postpone explicit statements of our main results to Section 3. Here we give a result on parabolic quasi-concavity for the heat equation with absorption, which is a typical application of our main theorems.
3 1528 K. Ishige and P. Salani: Parabolic quasi-concavity Proposition 1.2 Let D =Ω\ K, whereω is a bounded convex domain and K a compact convex set with nonempty interior, such that K Ω R N and Ω, K C 2,α for some α (0, 1). Letu be a solution of t u =Δu f(x, u) in D (0, ), u(x, 0) = 0 in D, u(x, t) =0 on Ω (0, ), u(x, t) =1 on K [0, ), where f = f(x, v) C 1 (Ω R) is a function such that Assume the following: f(x, 0) = 0 for x Ω and f(x, v) f(x, w) whenever v w. (1.9) the function x f(x, v) 1/2 is concave for every v (0, 1). (1.10) Then u is parabolically quasi-concave in Ω [0, ). If Ω is unbounded (and possibly also K is unbounded), by approximation with bounded convex sets, we see that there holds the conclusion of Proposition 1.2. Therefore, as a corollary, we also give the following result about the parabolic quasi-concavity of solutions to the heat equation with absorption in the exterior of a convex closed set. Corollary 1.3 Let D = R N \ K and K beaclosedconvexsetinr N with nonempty interior and K C 2,α for some α (0, 1). Letu be a bounded solution of t u =Δu f(x, u) in D (0, ), u(x, 0) = 0 in D, (1.11) u(x, t) =1 on K [0, ). If f C 1 (D R) satisfies (1.9) (1.10) with Ω replaced by R N,thenuisparabolically quasi-concave in R N [0, ). Notice that Theorem 3.2, Proposition 1.2 and Corollary 1.3 are the first results treating parabolic quasiconcavity in PDE s approach and they are new results even for the heat equation. In Section 3.3 we also give a general result about spatial quasi-concavity of solutions of problem (1.1), with a quasi-concave initial datum ϕ. We address the reader to Sections 3.3, 5 and 7 for more details and comparison with existing results. The paper is organized as follows. In Section 2 we introduce some notation and some basic results about quasi-concavity and parabolic quasi-concavity. In Section 3 we state and discuss our main results, Theorems 3.1 and 3.2, about parabolic quasi-concavity. Furthermore we state and discuss Theorems 3.3 and 3.4 about spatial quasi-concavity. Sections 4 and 5 are devoted to the proofs of Theorems 3.1 and 3.2 and Theorems 3.3 and 3.4, respectively. In Section 6 we prove Proposition 1.2 and we present some other explicit applications to relevant examples of parabolic equations. Section 7 contains some final remarks and comments. The paper ends with an Appendix, where we prove an interesting technical lemma regarding power concave functions, which is useful to simplify the application of our theorems. 2 Preliminaries In this section we introduce some notation and give some preliminary results about quasi-concavity and parabolic quasi-concavity. 2.1 Basic notation We denote by, the classical Euclidean scalar product and by the Euclidean norm in R N, N 1. Throughout this paper, if not otherwise specified, Ω is an open convex sets and K a nonempty compact convex set such that K Ω R N, while D denotes the convex ring Ω \ K. (1.8)
4 Math. Nachr. 283, No. 11 (2010) / 1529 Given a function v of class C 2,1, the time derivative of v is denoted by t v, while the i subscript means differentiation with respect to the space variable x i,i.e. v i = xi v, v ij = xi xj v, while v =(v 1,...,v N ) and 2 v =(v ij ) N denote the (spatial) gradient and the (spatial) Hessian matrix of v, respectively. The set of real symmetric N N matrices is denoted by M N,andM + N is the subset of M N of positive semidefinite matrices. For A, B M N,byA 0, we mean A M + N, and by A B, we mean B A 0, i.e. B A M + N. The transpose of the matrix A is denoted by AT. An operator F :Ω R R N M N R is said to be proper if F (x, u, q, A) F (x, v, q, A) whenever u v. (2.1) Furthermore the operator F is said to be strictly proper if F (x, u, q, A) <F(x, v, q, A) whenever u>v. (2.2) Let Γ be a convex cone in M N containing M + N and with vertex at the origin. Then F is degenerate elliptic in Γ if F (x, v, q, A) F (x, v, q, B), for every A, B Γ such that A B. (2.3) F is elliptic if the above inequality is strict whenever A>B. We put Γ F = Γ, where the union is extended to every cone Γ such that F is elliptic in Γ; whenwe say that F is elliptic, we mean that F is elliptic in Γ F. IfF is an elliptic operator, we say that a function v C 2 (D (0,T)) is admissible for F if 2 v(x, t) Γ F for every x D and for every t (0,T); equivalently, if F is sufficiently regular, v is admissible if the N N matrix with entries F ij (x, v(x, t), v(x, t), 2 v(x, t)) = F (x, v(x, t), v(x, t), 2 v(x, t)) v ij is positive definite for every x D and every t (0,T). A function u C 2,1 (D (0, )) C(D [0, )\ D {0}) is a subsolution of (1.1) if it satisfies (pointwise) t γ(u) F (x, u, u, 2 u) in D (0, ), u(x, 0) ϕ(x) in Ω, u(x, t) 0 on Ω (0, ), u(x, t) 1 on K (0, ). Analogously, u is a supersolution if the same holds with all the inequality signs reversed. We say that the Comparison Principle holds for (1.1) if, whenever u and v are a subsolution and a supersolution, then u v in D [0, ). 2.2 Power-concave and quasi-concave functions Given a 0,a 1 > 0, λ (0, 1),andα [, ], the quantity [(1 λ)a α 0 + λaα 1 ]1/α for α, 0,, a 1 λ 0 a λ 1 for α =0, M α (a 0,a 1,λ)= max{a 0,a 1 } for α =, min{a 0,a 1 } for α = (2.4) is the α-(weighted) mean of a 0,a 1, with ratio λ (for more details we refer to [13]). For a 0,a 1 0, wedefine M α (a 0,a 1,λ) as above if α 0 and M α (a 0,a 1,λ)=0 if α<0 and a 0 a 1 =0. It is easily seen that, for every λ (0, 1), lim α M α(a 0,a 1,λ)=max{a 0,a 1 }, lim M α(a 0,a 1,λ)=min{a 0,a 1 }. α
5 1530 K. Ishige and P. Salani: Parabolic quasi-concavity Definition 2.1 Let α [, ]. A nonnegative function v is called α-concave if v((1 λ)x + λy) M α (v(x),v(y),λ) for every x, y sprt(v), λ (0, 1). We say that v is strictly α-concave, if the inequality sign is strict whenever x y. Roughly speaking, v 0 is called α-concave if it has convex support sprt(v) andinsprt(v) it holds: (i) v α is concave, if α>0; (ii) log v is concave, if α =0; (iii) v α is convex, if α<0. Quasi-concavity corresponds to the case α = and it is the weakest concavity property one can imagine. Usual concavity corresponds to α =1, while log-concavity clearly corresponds to α =0. A simple consequence of Jensen s inequality is that M α (a 0,a 1,λ) M β (a 0,a 1,λ) if α β. (2.5) Therefore α-concavity is monotone with respect to α, thatis:ifv is α-concave, then it is β-concave for every β α (and in particular for β = ). 2.3 Parabolically quasi-concave functions In [4], Borell introduces the notion of parabolic convexity for sets. Definition 2.2 A subset E of R N [0, ) is said parabolically convex if, for every (x 0,t 0 ), (x 1,t 1 ) E, and λ (0, 1), there holds (x λ,t λ ) E, where x λ =(1 λ)x 0 + λx 1 and t λ = ( (1 λ) t 0 + λ ) 2. t 1 Borell [4] proves that the heat balls of a parabolically convex domain P R N [0, ) (i.e. the superlevel sets of the Green function of the heat operator in P, with the homogeneous Dirichlet boundary condition) are parabolically convex, while it is unknown whether heat balls are convex when P is convex. This suggests that parabolic convexity may be more suitable than usual convexity when dealing with solutions to parabolic equations. Then we introduce in Definition 1.1 the notion of parabolic quasi-concavity for functions. Of course, as expected, a function u C(Ω [0, )) is parabolically quasi-concave if and only if its superlevel sets {(x, t) Ω [0, ) : u(x, t) l} are parabolically convex, in the sense of Definition 2.2. This parallels the analogous characterization of quasi-concave functions, depending only on the space variable. By the way, it is not hard to see that parabolic quasi-concavity of a function u is also equivalent to the quasiconcavity with respect to (x, t) of v(x, t) =u(x, t 2 ) or of v(x, t) =u(x/t, 1/t 2 ). Notice that Definition 1.1 can also be expressed in the following way: u C(Ω [0, )) is parabolically quasi-concave if u(m 1 (x 0,x 1,λ),M 1/2 (t 0,t 1,λ)) M (u(x 0,t 0 ),u(x 1,t 1 ),λ) (2.6) for every x 0,x 1 Ω, t 0,t 1 0, λ (0, 1). Of course, one can easily imagine how to define analogous notions of parabolic power (and logarithmic) concavity by substituting M with M p in the right-hand side of (2.6). Other possible variations can be obtained by suitably changing the means M 1 and/or M 1/2 in (2.6) (see [17]). 3 Mainresults Throughout the rest of the paper we assume the following condition: γ = γ(v) C 1 ([0, )) is a convex function such that γ(0) = 0 and γ(v) > 0 for v>0; F = F (x, v, p, A) C 1 (Ω R R N M N : R) is a proper degenerate elliptic operator and the Comparison Principle holds for problem (1.1).
6 Math. Nachr. 283, No. 11 (2010) / t t=(x+1) 2 t=(x 1) x Fig. 1 (online colour at ) An example of parabolically convex set: the parabolically convex envelope of the segments [ 1, 1] {0} and [ 2, 2] {1}. We remark that the first condition implies γ (v) > 0 for v>0. (3.1) Moreover, for any fixed v (0, ) and θ S N 1, we define the functions F v,θ (x, p, A) and F + v,θ (x, p, A) on Ω (0, ) Γ F as follows: F v,θ (x, p, A) =F (x, v, p 1 θ, p 3 A), F + v,θ (x, p, A) =max{f v,θ(x, p, A), 0}. 3.1 Parabolic quasi-concavity Now we are ready to state our main result regarding the minimum points of the parabolical quasi-concavity function Π defined by (1.6). Theorem 3.1 Let D be an open subset of R N and let u C 2 (D (0, )) be an admissible nonnegative solution of such that t γ(u) =F (x, u, u, 2 u) in D (0, ) (3.2) t γ(u) 0 in D (0, ), (3.3) u > 0 in D (0, ). (3.4)
7 1532 K. Ishige and P. Salani: Parabolic quasi-concavity Assume that and (F 1 ) (F 1 ) { the function F + v,θ is ( 1/2)-concave in Ω (0, ) Γ F for any v (0, ) and θ S N 1 at least one of the following conditions holds: (i) γ is strictly convex and t γ(u) > 0 in D (0, ); (ii) F is strictly proper; (iii) F + v,θ is strictly ( 1/2)-concave with respect to the x variable (in its support). Then, for any λ (0, 1), the parabolic quasi-concavity function Π associated to u cannot attain a negative local minimum at any point (x, y, r, s) D 2 (0, ) 2 such that (1 λ)x + λy D. As a consequence of the above theorem, we can prove parabolic quasi-concavity of solutions to problems (1.1), but only in the case of vanishing initial datum. What we have to do is just to give conditions which exclude that Π becomes negative on the boundary of D 2 (0, ). In particular, to avoid that Π become negative as t, we need to link the large time behavior of u to the solution of the associated stationary problem, whose quasi-concavity has been studied in [2]. Moreover it is useful to introduce the following condition: (F ) for every x 0 K there exists δ>0such that F (x, v, w,a) ρ 2 F (ρ(x x 0 )+x 0,v,ρ 1 w,ρ 2 A) for ρ (1 δ, 1] for every fixed (x, v, w,a) D [0, 1] R n Γ F. Now we can state our main result about parabolic quasi-concavity. Theorem 3.2 Let D = Ω \ K, letg 1 in [0, ) and let ϕ 0 in D. Assume that Ω is a bounded convex domain in R N and that K is a convex compact set with nonempty interior such that K Ω. Letu be a nonnegative solution of problem (1.1) such that u C 2+β,1+β/2 (D [T, )) < for some β (0, 1) and T>0. (3.5) Assume that (3.3), (F 1 ), (F 1 ) and (F ) hold; moreover, assume that, either the strict inequality sign holds in (3.3) or (3.4) holds. Then u is parabolically quasi-concave in Ω [0, ). We conjecture that Theorem 3.2 holds not only for vanishing initial datum, but for every quasi-concave ϕ, satisfying suitable compatibility conditions. We explain in Remark 4.7 the technical difficulty to obtain the full result. Theorems 3.1 and 3.2 are proved in Section Assumptions of Theorems 3.1 and 3.2 In this section we discuss in detail the assumptions of Theorems 3.1 and 3.2. Some of them can be indeed weakened, substituted by explicit assumptions on the boundary and initial data or even neglected in many cases. We first discuss assumption (3.3). We easily see that it is equivalent to t u 0 in D (0, ). (3.6) Indeed, clearly t u(x, t) =0if u(x, t) =0,sinceu 0, while (3.6) is equivalent to (3.3) when u>0, thanks to (3.1). It is then worth to notice that, in many cases, for the problem (1.1), (3.6) can be easily obtained if the initial datum satisfies F (x, ϕ(x), ϕ(x), 2 ϕ(x)) 0. (3.7)
8 Math. Nachr. 283, No. 11 (2010) / 1533 Indeed, consider for instance the case γ(u) =u: if the operator F is regular enough and the boundary and initial data satisfy suitable compatibility conditions, the time derivative v = t u solves the following parabolic Dirichlet-Cauchy problem t v = F ij (x, u, u, 2 u)v ij + F ui v i + F u v in D (0, ), v(x, 0) = F (x, ϕ(x), ϕ(x), 2 ϕ(x)) in D, (3.8) v(x, t) =0 on Ω (0, ), v(x, t) =g (t) on K (0, ). Then (3.6) easily follows from the maximum principle and (3.7). Furthermore, if v(x, 0) 0 in D (or g (t) > 0 near t =0), by applying the strong maximum principle to the problem (3.8), we have t u>0, (x, t) D (0, ). (3.9) See also [8]. Regarding (3.4), we notice that (F ) yields the parabolic starshapedness of superlevel sets of u, see Lemma 4.4, which in turn implies (3.4), jointly with (3.9), see Remark 4.7. Then (3.4) can be reduced in Theorem 3.2, if we have a strict inequality sign in (3.3). About the possibility to neglect (3.4), see also Section 2 in [8] and [9], where the author proved a minimum principle for the starshapedness of the level sets of solutions to problem (1.1), which obviously implies u > 0. We also notice that (F ) can be in general removed thanks to (F 1 ), see the argument in the proof of Proposition 1.2, which could be generalized with some technical effort. Next we discuss assumption (F 1). If{u n } is a sequence of parabolically quasi-concave functions in the convex cylinder Ω (0, ), converging pointwise to the upper semicontinuous function u,thenu is also a parabolically quasi-concave function in Ω (0, ). Then parabolic quasi-concavity of solutions can be obtained by the use of approximate solutions, without the assumption (F 1). In fact, for any n =1, 2,...,letu n be a solution of the problem (1.1) with γ replaced by γ n (v) =γ(v)+n 1 v 2 or with the operator F replaced by F n (x, u, p, A) =F (x, u, p, A)+n 1 u or F n (x, u, p, A) =F (x, u, p, A)+n 1 f(x), where f(x) 0 is a strictly concave function in D, sothatγ n and F n satisfy (F 1 ). Then, if Theorem 3.1 (or Theorem 3.2) is applicable to the solutions u n and {u n } converges pointwise to u as n, we can prove the same conclusion as in Theorem 3.1 (or Theorem 3.2), without assumption (F 1 ). This consideration holds true in many relevant examples (see Proposition 1.2 for instance). Finally, we could say that the most important assumption of our theorems is the structure condition (F 1 ).We notice here that, by the properties of power concave functions recalled in Section 2.2, (F 1 ) is satisfied if F + v,θ is α-concave for some α 1/2, in particular, if it is concave or log-concave. Moreover, (F 1 ) could be also weakened, arguing as in Theorem 3.10 of [2] (see Remark 4.2). 3.3 Spatial quasi-concavity Arguing in a way similar to the one that takes us to the results of the previous section, we can state two theorems: one is related to the minimum points of the spatial quasi-concavity function Φ, defined by (1.3), and the other is related to spatial quasi-concavity of solutions of (1.1). Theorem 3.3 Let D be an open subset of R N and u C 2 (D (0, )) be an admissible nonnegative solution of (3.2), satisfying (3.3) and (3.4). Assume the following: (F 2 ) { the function (x, p, A) p F + v,θ (x, p, A) is concave in Ω (0, ) Γ F for any v (0, ) and θ S N 1 ;
9 1534 K. Ishige and P. Salani: Parabolic quasi-concavity and (F 2) at least one of the following conditions holds: (i) γ is strictly convex and t γ(u) > 0 in D (0, ); (ii) F is strictly proper; (iii) p F + v,θ is strictly concave with respect to the x variable (in its support). Then, for any λ (0, 1), the spatial quasi-concavity function Φ associated to u cannot attain a negative local minimum at any point (x, y, t) D 2 (0, ) such that (1 λ)x + λy D. As for the case of spatial quasi-concavity, the way from Theorem 3.3 to the spatial quasi-concavity of solutions to problem (1.1) is not very long. We have only to give conditions which exclude that Φ becomes negative on the boundary of D 2 (0, ). To this aim, we assume that (B) (i) g C 1 ([0, )), g(0) 0, g 0 and g = lim t g(t) < ; (ii) ϕ is a nonnegative, quasi-concave, continuous function in Ω such that ϕ =0on Ω and ϕ g(0) on K. As a consequence of Theorem 3.3, we can now state the following. Theorem 3.4 Let D =Ω\ K, whereω is a bounded convex domain in R N and K is a convex compact set with nonempty interior such that K Ω. Letu be a solution of problem (1.1) satisfying (3.5) and assume (B) and all the assumptions of Theorem 3.3 hold; then u(,t) is quasi-concave in Ω for every t 0. Theorems 3.3 and 3.4 will be proved in Section 4. Notice that analogous considerations as in Section 3.2 about the assumptions of Theorems 3.3 and 3.4 can be obviously done. The spatial quasi-concavity of solutions to problem (1.1) has been already considered in [8, Theorem 3]. Unfortunately, the proof of such theorem seems to be incomplete. Here we revisit and slightly improve the arguments in [8], obtaining Theorem 3.3. We must notice that Theorem 3.3 is valid for a general class of operators F, but it does not apply to the heat equation or to the operators considered in [8]. Then, while we conjecture that the claim of [8, Theorem 3] is true, it is very likely still unproved. See Section 7 for further details and comments. 4 Proof of Theorems 3.1 and 3.2 For any v [0,g ] and θ S N 1, we put H v,θ (x, t, p, A) =tf v,θ (x, p, A) ( = tf(x, v, p 1 θ, p 3 A) ), H + v,θ (x, p, A) =max{h v,θ(x, t, p, A), 0} = tf + v,θ (x, p, A), for any x Ω, t [0, ), p (0, ),anda Γ F. We first give the following lemma on the condition (F 1 ), which is a direct consequence of Lemma A.1 in Appendix. Lemma 4.1 The condition (F 1 ) is equivalent to the condition (H) { the function H + v,θ (x, t, p, D) is ( 1)-concave in Ω [0, ) (0, ) Γ F for any v (0, ) and θ S N 1. P r o o f. Applying Lemma A.1 with α = 1 and g(x, p, A) =F + v,θ (x, p, A) 1, we can easily obtain Lemma 4.1 (see also the definition of the power-concavity given in Section 1 and Section 2.2). Now we are ready to prove Theorem 3.1.
10 Math. Nachr. 283, No. 11 (2010) / 1535 Proof of Theorem 3.1. Letλ (0, 1) and assume that (x, y, r, s) is a local negative minimum point for Π in {(x, y, r, s) D 2 (0, ) 2 :(1 λ)x+λy D}, that is, there exist a neighborhood I = I x I y I r I s D 2 (0, ) 2 of (x, y, r, s) such that (1 λ)i x + λi y D and m := Π(x, y, r, s) =u(z, t ) min{u(x, r),u(y, s)} =infπ(x, y, r, s) < 0, (4.1) I where z =(1 λ)x + λy and t = ((1 λ) r + λ s ) 2.Thenwehave u(x, r) =u(y, s). (4.2) Indeed, assume by contradiction that u(x, r) <u(y, s); then there exists a neighborhood U I y of y such that u(x, r) <u(y, s) for y U, and we have Then (4.1) implies Π(x, y, r, s) =u((1 λ)x + λy, t ) u(x, r), y U. 0=( y Π)(x, y, r, s) =λ( u)(z,t ), which contradicts (3.4); hence we have u(x, r) u(y, s). Similarly we see u(x, r) u(y, s), and obtain (4.2). Next we consider the following minimum problem: minimize in I the function subject to Π(x, y, r, s) =u ( (1 λ)x + λy, ((1 λ) r + λ s) 2) u(x, r) u(x, r) =u(y, s). By (4.1) and (4.2), the minimum is attained at (x, y, r, s), and by the Lagrange multiplier theorem, it should be a free critical point of the Lagrangian function Hence we obtain w(x, y, r, s) = Π(x, y, r, s)+μ(u(x, r) u(y, s)). u(z, t )= 1 μ 1 λ u(x, r) = μ u(y, s), (4.3) λ so that either u(z,t ), u(x, r) and u(y, s) are all null or they are parallel. The first possibility is avoided by (3.4) and it is not hard to see that they must be also equally oriented (i.e. μ (0, 1)), otherwise we can move (x, r) and (y, s) so that u(x, r) and u(y, s) both increase, maintaining (z,t ) fixed, which contradicts the optimality of (x, y, r, s) for the function Π. Then we can set θ := Furthermore, by setting the equality (4.3) gives u(x, r) u(y, s) = u(x, r) u(y, s) = u(z, t ) u(z, t ). a 1 = u(x, r), b 1 = u(y, s), and c 1 = u(z, t ), c =(1 λ)a + λb. (4.4) Similarly we put A 1 = t u(x, r), B 1 = t u(y, s) and C 1 = t u(z,t ),
11 1536 K. Ishige and P. Salani: Parabolic quasi-concavity and obtain C = [ (1 λ) r + λ ] ( 1 λ s A + λ ) B, (4.5) r s if t u(x, r), t u(y, s),and t u(z, t ) do not vanish (simultaneously). Now let us consider the function u (z) =max { min{u(x, r),u(y, s)} : x Ω, y Ω, (1 λ)x + λy = z }, which corresponds to the function whose level sets are the λ-linear combination of the corresponding level sets of the functions v 0 (x) =u(x, r) and v 1 (y) =u(y, s). Then, by (4.1), the point z is also a minimum point for the function u(z,t ) u (z), hence, by [2] and [27], there holds 2 u(z, t ) u(z, t ) 3 (1 λ) 2 u(x, t ) u(x, t ) 3 + λ 2 u(y, s) u(y, s) 3. (4.6) We assume the condition (F 1)-(i), and continue the proof of Theorem 3.1. We put l = u(z, r), = u(x, t )= u(y, s), D 0 = 2 u(x, r), D 1 = 2 u(y, s), andd λ = 2 u(z, t ). Thenwehave 0 < rγ ( )A 1 = r t γ(u(x, r)) = rf(x,, a 1 θ, D 0 ) = H +,θ (x, r, a, a 3 D 0 ), 0 < sγ ( )B 1 = s t γ(u(y, s)) = sf (y,, b 1 θ, D 1 ) = H +,θ (y, s, b, b 3 D 1 ). (4.7) By (H) and (4.7), we have H +,θ ((1 λ)x + λy, (1 λ) r + λ s, λa +(1 λ)b, (1 λ)a 3 D 1 + λb 3 D 1 ) M 1 (H +,θ (x, r, a, a 3 D 0 ), H +,θ (y, ) s, b, b 3 D 1 ),λ > 0, and obtain ( F,θ (1 λ)x + λy, λa +(1 λ)b, (1 λ)a 3 D 1 + λb 3 ) D 1 > 0, (4.8) ((1 λ)x + λy, (1 λ) r + λ s, λa +(1 λ)b, (1 λ)a 3 D 1 + λb 3 D 1 ) 1 H +,θ (1 λ)h +,θ (x, r, a, a 3 D 0 ) 1 + λh +,θ (y, s, b, b 3 D 1 ) 1. (4.9) Furthermore, by (4.1), l<, and by (F 1)-(i), (1.1), (4.6), and (4.8), we have γ ( )C 1 >γ (l)c 1 = t γ(u(z, t )) = F (z,l,c 1 θ, D λ ) F ( z,, c 1 θ, c 3 ((1 λ)a 3 D 0 + λb 3 D 1 ) ) ( = F,θ (1 λ)x + λy,λa +(1 λ)b, (1 λ)a 3 D 1 + λb 3 ) D 1 > 0. This together with (4.5) and (4.7) implies
12 Math. Nachr. 283, No. 11 (2010) / 1537 H +,θ ((1 λ)x + λy, (1 λ) r + λ s, λa +(1 λ)b, (1 λ)a 3 D 1 + λb 3 D 1 ) 1 [ > (1 λ) r + λ ] 1 s γ ( ) 1 C = 1 λ γ ( ) 1 A + λ γ ( ) 1 B r s =(1 λ)h +,θ (x, r, a, a 3 D 0 ) 1 + λh +,θ (y, s, b, b 3 D 1 ) 1. This contradicts (4.9). Similarly we have a contradiction if there holds either (F 1 )-(ii) or (iii); thus the proof of Theorem 3.1 is complete. Remark 4.2 Inequality (4.6) can be substituted by an exact relation between the Hessian matrices 2 u(z, t ), 2 u(x, t ) and 2 u(y, t ), according to [2] and [27], in order to obtain a sharper theorem, where assumption (F 1 ) is replaced by a weaker one involving F ( x, t, θ/p, JBJ T /p ), like in Theorem 3.10 of [2]. On the other hand, such a theorem would be more involved and less immediate to apply than Theorem 3.1, hence we are not going to write here the explicit statement and we trust the interested reader can obtain it by following Section 3.2 of [2]. Next we prove Theorem 3.2. For this aim, we first prove the following lemmas. Lemma 4.3 Assume the same conditions as in Theorem 3.2. Then there exists a classical solution ū of such that F (x, u, u, 2 u)=0 in D, u =1 on K, u =0 on Ω (4.10) lim u(x, t) =ū(x), x Ω. (4.11) t P r o o f. By the comparison principle, we have 0 u(x, t) 1 (4.12) for all (x, t) D (0, ). Then, by (3.3), (3.6), and (4.12), for any fixed x Ω, u(x, t) is a bounded and monotone increasing function in the variable t, and there exists a function u on Ω such that lim u(x, t) =u (x), x Ω. t Let {t j } j=1 be such that t 1 > 0 and t j+1 >t j +2for j =1, 2,... Put u j (x, t) =u(x, t j + t) and Q = D ( 1, 1). By (3.5), the Ascoli-Arzelà Theorem, and the diagonal argument, taking a subsequence if necessary, we see that there exists a function ū =ū(x, t) C 2+β,1+β/2 (Q) such that lim u j ū C j 2+β,1+β/2 (R) =0 for any compact set R Q. Thenū(x, t) =u (x) for any (x, t) Q,andū is independent of the time variable t. Therefore, by (1.1), we see that ū is a classical solution of F (x, u, u, 2 u)=0 in D, ū =1 on K, ū =0 on Ω, and the proof of Lemma 4.3 is complete. Lemma 4.4 Assume that the origin 0 of R N belongs to K and let Ω and K be starshaped sets (with respect to 0). Let u be a solution of (1.1) with g 1 in (0, ) and assume that the initial datum ϕ has starshaped superlevel sets, i.e. ϕ(ρx) ϕ(x) if ρ 1, x Ω. Moreover, assume that there exists ɛ>0suchthat, for every fixed (x, v, w,a) Ω (0, 1) R N Γ F, it holds ρ 2 F (ρx, v, wρ, Aρ ) 2 F (x, v, w,a) for ρ (1 ɛ, 1). (4.13) Then it holds u(ρx, ρ 2 t) u(x, t) for 0 ρ 1, t > 0, x Ω. (4.14)
13 1538 K. Ishige and P. Salani: Parabolic quasi-concavity P r o o f. Following a similar argument as in [8], we consider the function v(x, t) =u(ρx, ρ 2 t), which satisfies t γ(v) =ρ 2 F (ρx,v,ρ 1 v, ρ 2 2 v) in ρ 1 D (0, ), v(x, 0) = ϕ(ρx) in ρ 1 Ω, v(x, t) =0 on ρ 1 Ω (0, ), v(x, t) =1 in ρ 1 K (0, ). Then, by applying the comparison principle between u and v in Ω \ (ρ 1 K) (0, ), wehave This yields (4.14). u(ρx, ρ 2 t) u(x, t) for ρ (1 ɛ, 1), t > 0, x Ω. Remark 4.5 When u satisfies (4.14), we say that u has parabolically starshaped level sets. Notice that (4.14) implies u(x, t),x +2tu t (x, t) 0. (4.15) As a consequence, if the strict sign holds in (3.3), then (3.4) is easily obtained whenever u>0, and hence it can be neglected in the assumptions of Theorem 3.2. Remark 4.6 Notice that if F is differentiable and we set g(ρ) =ρ 2 F (ρx,v,ρ 1 w,ρ 2 A), then (4.13) implies g (1) = 2F (x, v, w,a)+ x F (x, v, w,b),x w F (x, v, w,a),w 2F ij (x, v, w,a)a ij 0, (4.16) for every fixed (x, v, w,a) Ω (0, 1) R n Γ F,whereA =(a ij ) N. Vice versa, a strict inequality sign in (4.16) gives (4.13). We notice that (F ) coincides with (4.16) when the origin is in x 0 and that (F ) could be obtained, in general, from (F 1 ) with an argument similar to the one we will use in the proof of Proposition 1.2 for the special case F (x, v, w,a)=trace (A) f(x, v). We are ready to prove Theorem 3.2. Proof of Theorem 3.2. Itsufficestoprove { inf Π(x, y, r, s) :(x, y, r, s) D 2 [0, ) 2} 0 for any λ (0, 1). Let us argue by contradiction and assume that { m := inf Π(x, y, r, s) :(x, y, r, s) D 2 [0, ) 2} < 0 for some λ (0, 1) and let {(x j,y j,r j,s j )} j=1 be a minimizing sequence, i.e. lim j Π(x j,y j,r j,s j )= m. (4.17) By the compactness of Ω, we can obviously assume lim j x j = x and lim j y j = y with x, y Ω. First, let us consider the case Π approaches its infimum as time tends to infinity, that is assume that r j s j and lim j s j =. On the other hand, by [2], ū is quasi-concave in Ω, and by (3.3), (3.6), and (4.11), we see that ū(x) u(x, t), (x, t) Ω (0, ). Then we have
14 Math. Nachr. 283, No. 11 (2010) / 1539 lim Π(x j,y j,r j,s j ) lim [u((1 λ)x j + λy j,t j ) min{ū(x j ), ū(y j )}] j j =ū((1 λ)x + λy) min{ū(x), ū(y)} 0, where t j = ((1 λ) r j + λ s j ) 2. This contradicts (4.17). Therefore r j and s j must be bounded and there exist r, s [0, ) such that lim j r j = r and lim j s j = s. Since the case r =0and x K (or s =0 and y K ) is avoided thanks to Lemma 4.4, by the regularity of u,wehave Π(x, y, r, s) =u(z, t ) min{u(x, r),u(y, s)} = m <0, where z =(1 λ)x + λy and t = ((1 λ) r + λ s ) 2.Ifmin{r, s} =0, min{u(x, r),u(y, s)} =0,since ϕ 0 in D, andπ(x, y, r, s) 0. Thenwehave r>0, s>0. (4.18) Furthermore we easily see the following: (i) (ii) since u =0on Ω, by (3.3), Π(x, y, r, s) 0 if x Ω or y Ω (then we have x, y Ω); by the convexity of K, ifx K and y K, thenz K and Φ(x, y, r, s) =0(then we have x K or y K). Finally, if x K and y K, thenu(y, s) <u(x, r) =1, and we can exclude this case again due to (3.4). Therefore we have x, y K, and obtain (x, y, r, s) D 2 (0, ) 2, z D. This is excluded by Theorem 3.1, Lemma 4.4, and Remark 4.5. Thus we have a contradiction, and the proof of Theorem 3.2 is complete. Remark 4.7 In the case of a general (not identically vanishing) initial datum, we were not able to prove (4.18). Once one is able to prove (4.18) for the solution u of (1.1) with some initial datum ϕ, the proof of Theorem 3.2 remains true and the solution u is parabolicallyquasi-concavein Ω [0, ). 5 Proof of Theorems 3.3 and 3.4 Proof of Theorem 3.3. Let λ (0, 1) and assume that (x, y, t ) D 2 (0, ) is a local negative minimum point for Φ in {(x, y, t) D 2 (0, ) :(1 λ)x + λy D}, that is, there exist a neighborhood I = I x I y I t D 2 (0, ) of (x, y, t ) such that (1 λ)i x + λi y D and m := Φ(x, y, t )=u(z, t ) min{u(x, t ),u(y, t )} =infφ(x, y, t) < 0, (5.1) I where z =(1 λ)x + λy. First we prove u(x, t )=u(y, t ). (5.2) In order to prove (5.2) by contradiction, we assume u(x, t ) <u(y, t ). Then there exists a neighborhood U I y of y such that u(x, t ) <u(y, t ) for y U, and we have Then (5.1) implies Φ(x, y, t) =u((1 λ)x + λy, t ) u(x, t ), y U. 0=( y Φ)(x, y, t )=λ( u)(z,t ), which contradicts (3.4); hence we have u(x, t ) u(y, t ). Similarly we see u(x, t ) u(y, t ), and obtain (5.2).
15 1540 K. Ishige and P. Salani: Parabolic quasi-concavity Next we consider the following minimum problem: minimize in I the function subject to the constraint Φ(x, y, t) =u((1 λ)x + λy, t) u(x, t) u(x, t) =u(y, t). By (5.1) and (5.2), the minimum is attained at (x, y, t ), and by the Lagrange multiplier theorem, (x, y, t ) should be a free critical point of the Lagrangian function Hence we obtain w(x, y, t) = Φ(x, y, t)+μ(u(x, t) u(y, t)). u(z, t )= 1 μ 1 λ u(x, t )= μ u(y, t ), (5.3) λ so that either u(z, t ), u(x, t ) and u(y, t ) are all null or they are parallel. The first possibility is avoided by (3.3) and it is not hard to see that they must be also equally oriented (i.e. μ (0, 1)), otherwise we can move (x, t ) and (y, t ) so that u(x, t ) and u(y, t ) both increase, maintaining (z,t ) fixed, which contradicts the optimality of (x, y, t ) for the function v. Then we can set θ := u(x, t ) u(x, t ) = u(y, t ) u(y, t ) = u(z, t ) u(z, t ). Furthermore, by setting equality (5.3) gives a 1 = u(x, t ), b 1 = u(y, t ), and c 1 = u(z, t ), c =(1 λ)a + λb. (5.4) In the same way as above, we obtain that C =(1 μ)a + μb =(1 λ) aa c + λbb c, (5.5) where A = t u(x, t ), B = t u(y, t ) and C = t u(z, t ). Now let us consider the function u : Ω [0, ) R defined by ū (z) =max { min{u(x, t ),u(y, t )} : x D, y D, (1 λ)x + λy = z }, which corresponds to the function whose level sets are the λ-linear combination of the corresponding level sets of the functions v 0 (x) =u(x, t ) and v 1 (y) =u(y, t ). Then, by (5.1), the point z is also a minimum point for the function u(z,t ) u (z), hence 2 u(z, t ) 2 u (z) 0. On the other hand, we have (see [2], [27]) that is, 2 u(z, t ) u(z, t ) 3 (1 λ) 2 u(x, t ) u(x, t ) 3 + λ 2 u(y, t ) u(y, t ) 3, (5.6) c 3 2 u(z,t ) (1 λ)a 3 2 u(x, t )+λb 3 2 u(y, t ). (5.7)
16 Math. Nachr. 283, No. 11 (2010) / 1541 We assume the condition (F 1)-(i), and continue the proof of Theorem 3.4. Put l = u(z, t ), = u(x, t )= u(y, t ), D 0 = 2 u(x, t ), D 1 = 2 u(y, t ),andd λ = 2 u(z, t ), for simplicity. Then, by (F 1 )-(i), we have 0 <γ ( )A = t γ(u(x, t )) = F (x,, a 1 θ, D 0 )=F +,θ (x, a, a3 D 0 ), 0 <γ ( )B = t γ(u(y, t )) = F (y,, b 1 θ, D 1 )=F +,θ (y, b, b3 D 1 ). Furthermore, by (F 2 ) and (5.8), we have (λa +(1 λ)b)f + (,θ (1 λ)x + λy, (1 λ)a + λb, (1 λ)a 3 D 1 + λb 3 ) D 1 (1 λ)f +,θ (x, a, a3 D 0 )+λf +,θ (y, b, b3 D 1 ) > 0. (5.8) (5.9) On the other hand, by (5.1), l<, and by (F 1 )-(i), (1.1), and (5.7), we have γ ( )C >γ (l)c = t u(z, t ) = F (z, l, c 1 θ, D λ ) F ( z,, c 1 θ, c 3 ((1 λ)a 3 D 0 + λb 3 D 1 ) ) ( = F,θ (1 λ)x + λy, (1 λ)a + λb, (1 λ)a 3 D 1 + λb 3 ) D 1. Therefore, by (5.5)and (5.8) (5.10), we have (1 λ)af +,θ (x, a, a3 D 0 )+λbf +,θ (y, b, b3 D 1 ) = γ ( )cc ( (1 λ)x + λy, (1 λ)a + λb, (1 λ)a 3 D 1 + λb 3 ) D 1 >cf +,θ > 0. (5.10) This contradicts (F 2 ). Similarly we have a contradiction if there holds either (F 1 )-(ii) or (iii), and the proof of Theorem 3.3 is complete. Now we are ready to prove Theorem 3.4. Proof of Theorem 3.4. Itsufficestoprove { } inf Φ(x, y, t) :(x, y, t) Ω 2 [0, ) 0 for any λ (0, 1). Let us argue by contradiction and assume that { } m := inf Φ(x, y, t) :(x, y, t) Ω 2 [0, ) < 0 for some λ (0, 1). Then, thanks to Lemma 4.3, by the similar argument as in the proof of Theorem 3.2, we see that the infimum is attained at some point (x, y, t ) Ω Ω [0, ),thatis, Φ(x, y, t )=u(z, t ) min{u(x, t ),u(y, t )} = m <0, where z =(1 λ)x + λy. Then we easily see the following: (i) by the condition (B), the initial datum ϕ(x) is quasi-concavein Ω and Φ(x, y, 0) 0, hence we have t>0; (ii) since u =0on Ω, by (3.3), Φ(x, y, t) 0 if x Ω or y Ω, hence we have x, y Ω; (iii) by the convexity of K,ifx K and y K,thenz K and Φ(x, y, t) =0, hence x K or y K. Furthermore, if x K and y K, thenu(y, t ) <u(x, t )=g(t), and this is avoided thanks to (3.4). Therefore we have x, y K, and obtain (x, y, t ) D 2 (0, ) with (1 λ)x + λy D. This is excluded by Theorem 3.3, and the proof of Theorem 3.4 is complete.
17 1542 K. Ishige and P. Salani: Parabolic quasi-concavity 6 Selected examples The results of the previous sections can be applied to a very large class of parabolic equations. In this section we prove Proposition 1.2 and Corollary 1.3, regarding the heat equation with absorption, and we analyze some other relevant cases. 6.1 Proofs of Proposition 1.2 and Corollary 1.3 Proof of Proposition 1.2. Let n =1, 2,... Then, under the condition (1.9), there exists a classical solution u n of t u =Δu f n (x, u) in D (0, ), u(x, 0) = 0 in Ω, (6.1) u(x, t) =0 on Ω (0, ), u(x, t) 1 on K (0, ), where f n (x, u) =f(x, u)+n 1 u. (See for instance [24].) By the comparison principle and (1.9), we have 0 u n (x, t) u n+1 (x, t) 1, (x, t) D (0, ). (6.2) Then, by [24, Chapters III and IV], for any compact set R D [0, ) \ Ω {0},wehave sup u n C 2+β,1+β/2 (R) < for some β (0, 1). (6.3) n On the other hand, by (1.9), we apply similar arguments as in Section 3.2 to see that t u n > 0 in D (0, ). (6.4) By (1.9), the operator F (x, v, q, A) =tracea f n (x, v) is strictly proper and by (1.10), it satisfies the condition (F 1 )(see Section 6.2, use condition (F 3 ) and Lemma A.1). Furthermore, it is easily seen that (1.10) implies (4.13) in this case. Indeed, for any fixed value v (0, 1),leth(x) =fn 1/2 (x, v); then h(x) = f n(x, v) 2fn 3/2 (x, v), and, by a classical characterization of differentiable convex function (see for instance [29, Theorem (b)]), we have h(x 0 ) h(x)+ h(x),x 0 x for every x, x 0 Ω. The latter, thanks also to (1.9) which gives f n (x, v) > 0 in Ω, implies 2f n (x, v)+ f n (x, v),x x 0 > 0, x D, for every x 0 K, which coincides with (4.16) with the strict inequality for the case at hand. Then, by Lemmas 4.4 and Remark 4.6, we have x, u n +2t t u n 0 in D (0, ), and by (6.4), we obtain u n > 0 in D (0, ). Therefore, by Theorem 3.2, we see that u n is parabolically quasi-concave in Ω [0, ). On the other hand, by (6.2) and (6.3), we apply the Ascoli-Arzelá theorem to {u n }, and see that the limit function ũ(x, t) = lim n u n (x, t) is a solution of (1.8). Then, by the uniqueness property for parabolic equations (see [24]) and (6.2), we have ũ(x, t) =u(x, t) in Ω [0, ). Therefore, since u n is parabolically quasi-concave in Ω [0, ), u is also parabolically quasi-concave in Ω [0, ); thus the proof of Proposition 1.2 is complete.
18 Math. Nachr. 283, No. 11 (2010) / 1543 Proof of Corollary 1.3. Letn =1, 2,... and let K n be a compact convex set such that K n B(0,n)=K B(0,n), K n B(0,n+1), K n K n+1, K n C 2,α. Let u 0 0 in B(0,n+1)and let u n be a solution of (1.8) with Ω and K replaced by B(0,n+1)and K n, respectively. By the comparison principle, we have 0 <u n (x, t) u n+1 (x, t) 1, (x, t) B(0,n+1) (0, ). Then, by the same argument as in the proof of Proposition 1.2, there exists a solution ũ of (1.11) such that ũ(x, t) = lim n u n(x, t), (x, t) R N (0, ). Furthermore we see that ũ is parabolically quasi-concave in R N (0, ). Put w = u ũ. Thenw is a bounded solution of t w =Δw a(x, t)w in D (0, ) such that w(x, t) =0on D (0, ) and w(x, 0) = 0 in D, where f(x, u) f(x, ũ) if u ũ, a(x, t) = u ũ f u (x, u) if u =ũ. Since a L (D (0, )), by the uniqueness property for parabolic equations with the homogeneous Dirichlet boundary condition (see, for example, [14] and [28]), we have w 0 in D [0, ), thatis,u(x, t) =ũ(x, t) in R N [0, ); thus u is parabolically quasi-concave in R N [0, ), and the proof of Corollary 1.3 is complete. 6.2 Other examples Interesting generalizations of (1.8) are for instance obtained by replacing the Laplace operator with the q-laplacian (q >1), the mean curvature operator, or a Finsler Laplacian. Let us write explicitly what condition (F 1 ) becomes in these cases. We first consider the case of the q-laplacian. Let F (x, u, u, 2 u)=δ q u f(x, u, u), where Δ q u = div( u q 2 u) and q>1. Then the following condition (F 3 ) the function (x, p) p q+1 f(x, u, θ/p) is convex for every u (0, 1), θ S N 1 implies (F 1 ) if q 2. Indeed, since Δ q u = u q 2 ( Δu +(q 2) u 2 u u T u 2 ), we have F v,θ (x, p, A) = 1 p q+1 ( trace(a)+θaθ T ) f(x, v, θ/p). Let Λ= { (x, p, A) Ω (0, ) M N : trace(a)+θ T Aθ p q+1 f(x, v, θ/p) > 0 }.Then(F 1 ) requires the function p (q+1)/2 if (x, p, A) Λ, (x, p, A) trace(a)+θt Aθ p q+1 f(x, v, θ/p) + otherwise
19 1544 K. Ishige and P. Salani: Parabolic quasi-concavity to be convex. By Lemma A.1 with α =(q +1)/2, this happens if and only if the function G(x, A) =trace(a)+θ T Aθ p q+1 f(x, v, θ/p) is 1/(q 1)-concave in Λ. Since trace(a) +θ T Aθ is linear, if (F 3 ) holds, G is concave in Λ, sothatitis α-concave for every α 1, in particular, for α =(q 1) 1,ifq 2. For the possibility to substitute (3.3) with an explicit assumption on f, we refer again to [8] and [9]. Next we consider the case of the mean curvature operator. Let F (x, u, u, 2 u)=mu f(x, u, u), where ( ) Mu =(1+ u 2 ) 3/2 u div =(1+ u 2 )Δu u i u ij u j. 1+ u 2 Then, following [6, Section 4.2.2], we can see that the condition (F 3 ) with q 2 implies (F 1 ). Next we let F (x, u, u, 2 u)=δ H u f(x, u, u), where H is a norm on R N and Δ H u is the Finsler Laplacian associated to H,thatis Δ H u = div(h( u) ξ H( u)), where H is a positively homogeneous (of degree one) nonnegative convex function, which vanishes only at ξ =0. In this case the equation t u = F (x, u, u, 2 u) models the anisotropic diffusion dictated by the norm H. Then we can write Δ H u = ( ) u V ξiξ j u i,j, u ij where V (ξ) = 1 2 H2 (ξ), whichisa2-homogeneous convex function, and the condition (F 3 ) with q 2 can take the place of (F 1 ) again. Other examples can be obtained with Pucci extremal operators or any other operator F which can be treated with the methods of [2] (as the ones considered above). 7 Final remarks and comments In [8], Diaz and Kawohl investigated the starshapedness and spatial convexity of level sets of solutions to the following problem t γ(u) =Δ q u f(u) in (0, ) D, u =0 on (0, ) Ω, (7.1) u =1 on (0, ) K, u(x, 0) = ϕ(x) in Ω, where γ is continuous convex and nondecreasing, f is continuous and nondecreasing, γ(0) = f(0) = 0, q>1, D =Ω\ K a convex ring as usual. In particular, in [8, Theorem 3] they state that (under some reasonable regularity assumptions on the domain and u) if the initial datum ϕ is quasi-concave and Δ q ϕ 0, then the solution u is spatially quasi-concave for every t > 0. That would coincide with our Theorem 3.4 when F (x, u, u, 2 u)=δ q u f(u). Unfortunately their proof seems to contain a gap at the very last step. Indeed, at page 279 in [8], the authors proved the inequality 1 a q > [ α b q + 1 α c q ], (7.2)
20 Math. Nachr. 283, No. 11 (2010) / 1545 where α (0, 1),anda, b,andcare positive constants such that 1 a = 1 ( 1 2 b + 1 ). c Then they claimed that the inequality (7.2) contradicts the convexity of the map d d q.ifα =1/2, this claim would be true; however α is not necessarily equal to 1/2 in their argument. We remark that the proof of our Theorem 3.4 essentially follows the same scheme of the proof of [8, Theorem 3], up to the last step, where we had to recover the above explained gap. However, we regret to notice that Theorem 3.4 does not apply to problem (7.1), even when q =2and f 0. Indeed, assumption (F 2 ) would require (p, A) p 2 trace(a) to be convex, which is not satisfied. Although we conjecture that the statement of [8, Theorem 3] is actually true, we point out that the spatial quasi-concavity of solutions to (7.1) with quasiconcave initial datum is still an open problem, even in the case of the heat equation. We also remark here that some results strongly related to Proposition 1.2 are contained in [3] and in [7], an unpublished earlier version of [8], which we received during the completion of this paper from the authors through a personal communication. In both of these papers, the authors study the quasi-concavity with respect to (x, t) of solutions to parabolic problems, that is equivalent to the nonnegativity of the quasi-concavity function Υ(x, y, r, s) =u((1 λ)x + λy, (1 λ)r + λs) min{u(x, r),u(y, s)}. In [3] Borell considers problem (1.8) with f 0, that is the case of heat equation. In [7], the authors prove Υ 0 when u solves (7.1) with q =2and ϕ 0. We notice that, due to (2.5) and to u t 0, we trivially have Υ(x, y, r, s) Π(x, y, r, s) for every (x, y, r, s). Therefore parabolic quasi-concavity is a stronger property than the usual quasi-concavity and the results of both papers [3] and [7] are recovered by Theorem 3.2. A Appendix Here follows an interesting lemma regarding power concave functions. Lemma A.1 Let α 1, β =(1 α) 1, m 1. LetG : R m (0, ) R be defined by G(x, t) =t α g(x), where g C 2 (R m ) is a positive function. Then (i) in the case α 0, G is convex if and only if g β is convex; (ii) in the case 0 <α<1, G is concave if and only if g β is concave; (iii) in the case α>1, G is convex if and only if g β is concave. Proof. Set f(x) =g(x) β. For clarity of our proof, we will treat separately and first the one-dimensional case m =1. A straightforward calculation gives ( ) α(α 1)t 2 G = α 2 g(x) αt α 1 g (x) αt α 1 g (x) t α g (x) and f (x) =βg(x) β 2 [g(x)g (x)+(β 1)g (x) 2 ] [ g(x)g (x)+ = 1 2α 1 g(x) 1 α 1 α The matrix 2 G is semidefinite if and only if α 1 α g (x) 2 ]. det 2 G = αt 2α 2 [ (α 1)g(x)g (x) αg (x) 2] 0,
21 1546 K. Ishige and P. Salani: Parabolic quasi-concavity that is equivalent to g(x)g (x)+ α 1 α g (x) 2 0 for the cases (i) and (iii); g(x)g (x)+ α 1 α g (x) 2 0 for the case (ii). Comparing this with the sign of f and taking in account that case (i) if f is convex, then g is convex; case (ii) if f is concave, then g is concave; case (iii) if f is concave, then g is convex, we have Lemma A.1 for the case m =1. Let m 2 and let ξ =(ξ 0,ξ 1,...,ξ m ), ξ =(ξ 1,...,ξ m ).Thenf is convex if and only if 2 f(x) =βg(x) β 1 2 g(x)+β(β 1)g(x) β 2 g(x) g(x) 0, x R m. (A.1) We treat only the case (i) α 0, which implies β>0, and leave the other cases to the reader. Then (A.1) is equivalent to g(x) g ij (x)ξ i ξ j + α 1 α g i (x)g j (x)ξ i ξ j 0 (A.2) for all ξ R m and x R m. Analogously, the function G(x, t) is convex if and only if α(α 1)ξ 2 0 g(x)tα 2 +2αξ 0 t α 1 for all ξ R m and x R m ; this is equivalent to m g i (x)ξ i + t α m i=1 g ij (x)ξ i ξ j 0 α(α 1) ξ2 0 g(x) t 2 +2α ξ 0 t g i (x)ξ i + i=1 g ij (x)ξ i ξ j 0 (A.3) for all ξ R m and x R m. Therefore it suffices to prove that (A.2) is equivalent to (A.3). Assume g(x) satisfies (A.2). Then, since m 2 g i (x) ξ i ξ 0 = t 2 ξ0 g(x)(1 α) 1 m g i (x)ξ i t i=1 g(x)(1 α) i=1 (1 α)g(x)ξ2 0 1 t 2 + g i (x)g j (x)ξ i ξ j, (1 α)g(x) we obtain α(α 1) ξ2 0 g(x) t 2 +2α ξ 0 t α 1 α g(x) 1 0, g i (x)ξ i + i=1 g i (x)g j (x)ξ i ξ j + g ij (x)ξ i ξ j g ij (x)ξ i ξ j where the last inequality is due to (A.2). Thus g(x) satisfies (A.3).
22 Math. Nachr. 283, No. 11 (2010) / 1547 On the other hand, if g(x) satisfies (A.3), for any ξ R m, we put and obtain X = i=1 g i (x)ξ i, ξ 0 = 1 1 α tg(x) 1 X, α(α 1) ξ2 0 g(x) t 2 +2α ξ 0 t g i (x)ξ i + i=1 = α α 1 g(x) +2 α 1 α = 0. X 2 α (1 α)g(x) X g(x) g ij (x)ξ i ξ j g i (x)ξ i + i=1 g i (x)g j (x)ξ i ξ j + g ij (x)ξ i ξ j g ij (x)ξ i ξ j This implies (A.2). Therefore we see that (A.2) is equivalent to (A.3), and the proof of Lemma A.1 is complete. References [1] B. Bian and P. Guan, A microscopic convexity principle for nonlinear partial differential equations, Invent. Math. 177, (2009). [2] C. Bianchini, M. Longinetti, and P. Salani, Quasiconcave solutions to elliptic problems in convex rings, Indiana Univ. Math J. 58, (2009). [3] C. Borell, Brownian motion in a convex ring and quasiconcavity, Comm. Math. Phys. 86, (1982). [4] C. Borell, A note on parabolic convexity and heat conduction, Ann. Inst. H. Poincaré Probab. Statist. 32, (1996). [5] H. J. Brascamp and E. H. Lieb, On extensions of the Brunn-Minkowski and Prékopa-Leindler theorems, including inequalities for log concave functions, and with an application to the diffusion equation, J. Funct. Anal. 22, (1976). [6] A. Colesanti and P. Salani, Quasi-concave envelope of a function and convexity of level sets of Solutions to elliptic equations, Math. Nachr. 258, 3 15 (2003). [7] J. I. Diaz and B. Kawohl, On convexity and starshapedness of level sets for some nonlinear elliptic and parabolic problems on convex rings, Preprint No. 393, Sonderforschungsbereich Vol. 123 (Universität Heidelberg, 1986). Available at: kawohl. [8] J. I. Diaz and B. Kawohl, On convexity and starshapedness of level sets for some nonlinear elliptic and parabolic problems on convex rings, J. Math. Anal. Appl. 177, (1993). [9] E. Francini, Starshapedness of level sets for solutions of nonlinear parabolic equations, Rend. Ist. Mat. Univ. Trieste 28, (1996). [10] M. Gabriel, A result concerning convex level surfaces of three dimensional harmonic functions, London Math. Soc. J. 32, (1957). [11] Y. Giga, S. Goto, H. Ishi, and M.-H. Sato, Comparison principle and convexity preserving properties for singular degenerate parabolic equations on unbounded domains, Indiana Univ. Math. J. 40, (1991). [12] A. Greco and B. Kawohl, Log-concavity in some parabolic problems, Electron. J. Differential Equations 1999, 1 12 (1999). [13] G. H. Hardy, J. E. Littlewood, and G. Pólya, Inequalities (Cambridge Univ. Press, Cambridge, 1934). [14] K. Ishige, An intrinsic metric approach to uniqueness of the positive Dirichlet problem for parabolic equations in cylinders, J. Differential Equations 158, (1999). [15] K. Ishige and P. Salani, Is quasi-concavity preserved by heat flow?, Arch. Math. (Basel) 90, (2008). [16] K. Ishige and P. Salani, Convexity breaking of free boundary in porous medium equation, Interfaces Free Bound. 12, (2010). [17] K. Ishige and P. Salani, On a new kind of convexity for solutions of parabolic problems, Discrete Contin. Dyn. Syst. Ser. S, to appear. [18] S. Janson and J. Tysk, Preservation of convexity of solutions to parabolic equations, J. Differential Equations 206, (2004).
Convexity of level sets for solutions to nonlinear elliptic problems in convex rings. Paola Cuoghi and Paolo Salani
 Convexity of level sets for solutions to nonlinear elliptic problems in convex rings Paola Cuoghi and Paolo Salani Dip.to di Matematica U. Dini - Firenze - Italy 1 Let u be a solution of a Dirichlet problem
Convexity of level sets for solutions to nonlinear elliptic problems in convex rings Paola Cuoghi and Paolo Salani Dip.to di Matematica U. Dini - Firenze - Italy 1 Let u be a solution of a Dirichlet problem
VISCOSITY SOLUTIONS. We follow Han and Lin, Elliptic Partial Differential Equations, 5.
 VISCOSITY SOLUTIONS PETER HINTZ We follow Han and Lin, Elliptic Partial Differential Equations, 5. 1. Motivation Throughout, we will assume that Ω R n is a bounded and connected domain and that a ij C(Ω)
VISCOSITY SOLUTIONS PETER HINTZ We follow Han and Lin, Elliptic Partial Differential Equations, 5. 1. Motivation Throughout, we will assume that Ω R n is a bounded and connected domain and that a ij C(Ω)
Asymptotic behavior of infinity harmonic functions near an isolated singularity
 Asymptotic behavior of infinity harmonic functions near an isolated singularity Ovidiu Savin, Changyou Wang, Yifeng Yu Abstract In this paper, we prove if n 2 x 0 is an isolated singularity of a nonegative
Asymptotic behavior of infinity harmonic functions near an isolated singularity Ovidiu Savin, Changyou Wang, Yifeng Yu Abstract In this paper, we prove if n 2 x 0 is an isolated singularity of a nonegative
Brunn-Minkowski inequality for the 1-Riesz capacity and level set convexity for the 1/2-Laplacian
 Brunn-Minkowski inequality for the 1-Riesz capacity and level set convexity for the 1/2-Laplacian M. Novaga, B. Ruffini Abstract We prove that that the 1-Riesz capacity satisfies a Brunn-Minkowski inequality,
Brunn-Minkowski inequality for the 1-Riesz capacity and level set convexity for the 1/2-Laplacian M. Novaga, B. Ruffini Abstract We prove that that the 1-Riesz capacity satisfies a Brunn-Minkowski inequality,
Brunn-Minkowski inequalities for two functionals involving the p-laplace operator
 Brunn-Minkowski inequalities for two functionals involving the p-laplace operator Andrea Colesanti Paola Cuoghi Paolo Salani Abstract In the family of n-dimensional convex bodies, we prove a Brunn-Minkowski
Brunn-Minkowski inequalities for two functionals involving the p-laplace operator Andrea Colesanti Paola Cuoghi Paolo Salani Abstract In the family of n-dimensional convex bodies, we prove a Brunn-Minkowski
Brunn-Minkowski inequality for the 1-Riesz capacity and level set convexity for the 1/2-Laplacian
 Brunn-Minkowski inequality for the 1-Riesz capacity and level set convexity for the 1/2-Laplacian M. Novaga, B. Ruffini January 13, 2014 Abstract We prove that that the 1-Riesz capacity satisfies a Brunn-Minkowski
Brunn-Minkowski inequality for the 1-Riesz capacity and level set convexity for the 1/2-Laplacian M. Novaga, B. Ruffini January 13, 2014 Abstract We prove that that the 1-Riesz capacity satisfies a Brunn-Minkowski
A Brunn Minkowski inequality for the Hessian eigenvalue in three-dimensional convex domain
 Advances in Mathematics 5 010 1616 1633 www.elsevier.com/locate/aim A Brunn Minkowski inequality for the Hessian eigenvalue in three-dimensional convex domain Pan Liu a, Xi-Nan Ma b,,luxu c a Department
Advances in Mathematics 5 010 1616 1633 www.elsevier.com/locate/aim A Brunn Minkowski inequality for the Hessian eigenvalue in three-dimensional convex domain Pan Liu a, Xi-Nan Ma b,,luxu c a Department
A LOCALIZATION PROPERTY AT THE BOUNDARY FOR MONGE-AMPERE EQUATION
 A LOCALIZATION PROPERTY AT THE BOUNDARY FOR MONGE-AMPERE EQUATION O. SAVIN. Introduction In this paper we study the geometry of the sections for solutions to the Monge- Ampere equation det D 2 u = f, u
A LOCALIZATION PROPERTY AT THE BOUNDARY FOR MONGE-AMPERE EQUATION O. SAVIN. Introduction In this paper we study the geometry of the sections for solutions to the Monge- Ampere equation det D 2 u = f, u
On intermediate value theorem in ordered Banach spaces for noncompact and discontinuous mappings
 Int. J. Nonlinear Anal. Appl. 7 (2016) No. 1, 295-300 ISSN: 2008-6822 (electronic) http://dx.doi.org/10.22075/ijnaa.2015.341 On intermediate value theorem in ordered Banach spaces for noncompact and discontinuous
Int. J. Nonlinear Anal. Appl. 7 (2016) No. 1, 295-300 ISSN: 2008-6822 (electronic) http://dx.doi.org/10.22075/ijnaa.2015.341 On intermediate value theorem in ordered Banach spaces for noncompact and discontinuous
PERTURBATION THEORY FOR NONLINEAR DIRICHLET PROBLEMS
 Annales Academiæ Scientiarum Fennicæ Mathematica Volumen 28, 2003, 207 222 PERTURBATION THEORY FOR NONLINEAR DIRICHLET PROBLEMS Fumi-Yuki Maeda and Takayori Ono Hiroshima Institute of Technology, Miyake,
Annales Academiæ Scientiarum Fennicæ Mathematica Volumen 28, 2003, 207 222 PERTURBATION THEORY FOR NONLINEAR DIRICHLET PROBLEMS Fumi-Yuki Maeda and Takayori Ono Hiroshima Institute of Technology, Miyake,
Some Properties of the Augmented Lagrangian in Cone Constrained Optimization
 MATHEMATICS OF OPERATIONS RESEARCH Vol. 29, No. 3, August 2004, pp. 479 491 issn 0364-765X eissn 1526-5471 04 2903 0479 informs doi 10.1287/moor.1040.0103 2004 INFORMS Some Properties of the Augmented
MATHEMATICS OF OPERATIONS RESEARCH Vol. 29, No. 3, August 2004, pp. 479 491 issn 0364-765X eissn 1526-5471 04 2903 0479 informs doi 10.1287/moor.1040.0103 2004 INFORMS Some Properties of the Augmented
arxiv: v2 [math.ap] 12 Jan 2018
![arxiv: v2 [math.ap] 12 Jan 2018 arxiv: v2 [math.ap] 12 Jan 2018](/thumbs/80/82320809.jpg) CONVEXITY OF LEVEL SETS AND A TWO-POINT FUNCTION arxiv:1701.05820v2 [math.ap] 12 Jan 2018 BEN WEINKOVE Abstract. We establish a maximum principle for a two-point function in order to analyze the convexity
CONVEXITY OF LEVEL SETS AND A TWO-POINT FUNCTION arxiv:1701.05820v2 [math.ap] 12 Jan 2018 BEN WEINKOVE Abstract. We establish a maximum principle for a two-point function in order to analyze the convexity
Stationary isothermic surfaces and some characterizations of the hyperplane in the N-dimensional Euclidean space
 arxiv:081.165v1 [math.ap] 11 Dec 008 Stationary isothermic surfaces and some characterizations of the hyperplane in the N-dimensional Euclidean space Rolando Magnanini and Shigeru Sakaguchi October 6,
arxiv:081.165v1 [math.ap] 11 Dec 008 Stationary isothermic surfaces and some characterizations of the hyperplane in the N-dimensional Euclidean space Rolando Magnanini and Shigeru Sakaguchi October 6,
GEOMETRIC APPROACH TO CONVEX SUBDIFFERENTIAL CALCULUS October 10, Dedicated to Franco Giannessi and Diethard Pallaschke with great respect
 GEOMETRIC APPROACH TO CONVEX SUBDIFFERENTIAL CALCULUS October 10, 2018 BORIS S. MORDUKHOVICH 1 and NGUYEN MAU NAM 2 Dedicated to Franco Giannessi and Diethard Pallaschke with great respect Abstract. In
GEOMETRIC APPROACH TO CONVEX SUBDIFFERENTIAL CALCULUS October 10, 2018 BORIS S. MORDUKHOVICH 1 and NGUYEN MAU NAM 2 Dedicated to Franco Giannessi and Diethard Pallaschke with great respect Abstract. In
The Skorokhod reflection problem for functions with discontinuities (contractive case)
 The Skorokhod reflection problem for functions with discontinuities (contractive case) TAKIS KONSTANTOPOULOS Univ. of Texas at Austin Revised March 1999 Abstract Basic properties of the Skorokhod reflection
The Skorokhod reflection problem for functions with discontinuities (contractive case) TAKIS KONSTANTOPOULOS Univ. of Texas at Austin Revised March 1999 Abstract Basic properties of the Skorokhod reflection
SYMMETRY RESULTS FOR PERTURBED PROBLEMS AND RELATED QUESTIONS. Massimo Grosi Filomena Pacella S. L. Yadava. 1. Introduction
 Topological Methods in Nonlinear Analysis Journal of the Juliusz Schauder Center Volume 21, 2003, 211 226 SYMMETRY RESULTS FOR PERTURBED PROBLEMS AND RELATED QUESTIONS Massimo Grosi Filomena Pacella S.
Topological Methods in Nonlinear Analysis Journal of the Juliusz Schauder Center Volume 21, 2003, 211 226 SYMMETRY RESULTS FOR PERTURBED PROBLEMS AND RELATED QUESTIONS Massimo Grosi Filomena Pacella S.
Asymptotic Behavior of Infinity Harmonic Functions Near an Isolated Singularity
 Savin, O., and C. Wang. (2008) Asymptotic Behavior of Infinity Harmonic Functions, International Mathematics Research Notices, Vol. 2008, Article ID rnm163, 23 pages. doi:10.1093/imrn/rnm163 Asymptotic
Savin, O., and C. Wang. (2008) Asymptotic Behavior of Infinity Harmonic Functions, International Mathematics Research Notices, Vol. 2008, Article ID rnm163, 23 pages. doi:10.1093/imrn/rnm163 Asymptotic
From the Brunn-Minkowski inequality to a class of Poincaré type inequalities
 arxiv:math/0703584v1 [math.fa] 20 Mar 2007 From the Brunn-Minkowski inequality to a class of Poincaré type inequalities Andrea Colesanti Abstract We present an argument which leads from the Brunn-Minkowski
arxiv:math/0703584v1 [math.fa] 20 Mar 2007 From the Brunn-Minkowski inequality to a class of Poincaré type inequalities Andrea Colesanti Abstract We present an argument which leads from the Brunn-Minkowski
Helly's Theorem and its Equivalences via Convex Analysis
 Portland State University PDXScholar University Honors Theses University Honors College 2014 Helly's Theorem and its Equivalences via Convex Analysis Adam Robinson Portland State University Let us know
Portland State University PDXScholar University Honors Theses University Honors College 2014 Helly's Theorem and its Equivalences via Convex Analysis Adam Robinson Portland State University Let us know
A VARIATIONAL METHOD FOR THE ANALYSIS OF A MONOTONE SCHEME FOR THE MONGE-AMPÈRE EQUATION 1. INTRODUCTION
 A VARIATIONAL METHOD FOR THE ANALYSIS OF A MONOTONE SCHEME FOR THE MONGE-AMPÈRE EQUATION GERARD AWANOU AND LEOPOLD MATAMBA MESSI ABSTRACT. We give a proof of existence of a solution to the discrete problem
A VARIATIONAL METHOD FOR THE ANALYSIS OF A MONOTONE SCHEME FOR THE MONGE-AMPÈRE EQUATION GERARD AWANOU AND LEOPOLD MATAMBA MESSI ABSTRACT. We give a proof of existence of a solution to the discrete problem
Regularity estimates for fully non linear elliptic equations which are asymptotically convex
 Regularity estimates for fully non linear elliptic equations which are asymptotically convex Luis Silvestre and Eduardo V. Teixeira Abstract In this paper we deliver improved C 1,α regularity estimates
Regularity estimates for fully non linear elliptic equations which are asymptotically convex Luis Silvestre and Eduardo V. Teixeira Abstract In this paper we deliver improved C 1,α regularity estimates
A LOWER BOUND FOR THE GRADIENT OF -HARMONIC FUNCTIONS Edi Rosset. 1. Introduction. u xi u xj u xi x j
 Electronic Journal of Differential Equations, Vol. 1996(1996) No. 0, pp. 1 7. ISSN 107-6691. URL: http://ejde.math.swt.edu (147.6.103.110) telnet (login: ejde), ftp, and gopher access: ejde.math.swt.edu
Electronic Journal of Differential Equations, Vol. 1996(1996) No. 0, pp. 1 7. ISSN 107-6691. URL: http://ejde.math.swt.edu (147.6.103.110) telnet (login: ejde), ftp, and gopher access: ejde.math.swt.edu
VISCOSITY SOLUTIONS OF ELLIPTIC EQUATIONS
 VISCOSITY SOLUTIONS OF ELLIPTIC EQUATIONS LUIS SILVESTRE These are the notes from the summer course given in the Second Chicago Summer School In Analysis, in June 2015. We introduce the notion of viscosity
VISCOSITY SOLUTIONS OF ELLIPTIC EQUATIONS LUIS SILVESTRE These are the notes from the summer course given in the Second Chicago Summer School In Analysis, in June 2015. We introduce the notion of viscosity
GENERALIZED CONVEXITY AND OPTIMALITY CONDITIONS IN SCALAR AND VECTOR OPTIMIZATION
 Chapter 4 GENERALIZED CONVEXITY AND OPTIMALITY CONDITIONS IN SCALAR AND VECTOR OPTIMIZATION Alberto Cambini Department of Statistics and Applied Mathematics University of Pisa, Via Cosmo Ridolfi 10 56124
Chapter 4 GENERALIZED CONVEXITY AND OPTIMALITY CONDITIONS IN SCALAR AND VECTOR OPTIMIZATION Alberto Cambini Department of Statistics and Applied Mathematics University of Pisa, Via Cosmo Ridolfi 10 56124
Division of the Humanities and Social Sciences. Supergradients. KC Border Fall 2001 v ::15.45
 Division of the Humanities and Social Sciences Supergradients KC Border Fall 2001 1 The supergradient of a concave function There is a useful way to characterize the concavity of differentiable functions.
Division of the Humanities and Social Sciences Supergradients KC Border Fall 2001 1 The supergradient of a concave function There is a useful way to characterize the concavity of differentiable functions.
Optimization Theory. A Concise Introduction. Jiongmin Yong
 October 11, 017 16:5 ws-book9x6 Book Title Optimization Theory 017-08-Lecture Notes page 1 1 Optimization Theory A Concise Introduction Jiongmin Yong Optimization Theory 017-08-Lecture Notes page Optimization
October 11, 017 16:5 ws-book9x6 Book Title Optimization Theory 017-08-Lecture Notes page 1 1 Optimization Theory A Concise Introduction Jiongmin Yong Optimization Theory 017-08-Lecture Notes page Optimization
Chapter 1. Measure Spaces. 1.1 Algebras and σ algebras of sets Notation and preliminaries
 Chapter 1 Measure Spaces 1.1 Algebras and σ algebras of sets 1.1.1 Notation and preliminaries We shall denote by X a nonempty set, by P(X) the set of all parts (i.e., subsets) of X, and by the empty set.
Chapter 1 Measure Spaces 1.1 Algebras and σ algebras of sets 1.1.1 Notation and preliminaries We shall denote by X a nonempty set, by P(X) the set of all parts (i.e., subsets) of X, and by the empty set.
Chapter 2 Convex Analysis
 Chapter 2 Convex Analysis The theory of nonsmooth analysis is based on convex analysis. Thus, we start this chapter by giving basic concepts and results of convexity (for further readings see also [202,
Chapter 2 Convex Analysis The theory of nonsmooth analysis is based on convex analysis. Thus, we start this chapter by giving basic concepts and results of convexity (for further readings see also [202,
Laplace s Equation. Chapter Mean Value Formulas
 Chapter 1 Laplace s Equation Let be an open set in R n. A function u C 2 () is called harmonic in if it satisfies Laplace s equation n (1.1) u := D ii u = 0 in. i=1 A function u C 2 () is called subharmonic
Chapter 1 Laplace s Equation Let be an open set in R n. A function u C 2 () is called harmonic in if it satisfies Laplace s equation n (1.1) u := D ii u = 0 in. i=1 A function u C 2 () is called subharmonic
MINIMAL GRAPHS PART I: EXISTENCE OF LIPSCHITZ WEAK SOLUTIONS TO THE DIRICHLET PROBLEM WITH C 2 BOUNDARY DATA
 MINIMAL GRAPHS PART I: EXISTENCE OF LIPSCHITZ WEAK SOLUTIONS TO THE DIRICHLET PROBLEM WITH C 2 BOUNDARY DATA SPENCER HUGHES In these notes we prove that for any given smooth function on the boundary of
MINIMAL GRAPHS PART I: EXISTENCE OF LIPSCHITZ WEAK SOLUTIONS TO THE DIRICHLET PROBLEM WITH C 2 BOUNDARY DATA SPENCER HUGHES In these notes we prove that for any given smooth function on the boundary of
Equilibria with a nontrivial nodal set and the dynamics of parabolic equations on symmetric domains
 Equilibria with a nontrivial nodal set and the dynamics of parabolic equations on symmetric domains J. Földes Department of Mathematics, Univerité Libre de Bruxelles 1050 Brussels, Belgium P. Poláčik School
Equilibria with a nontrivial nodal set and the dynamics of parabolic equations on symmetric domains J. Földes Department of Mathematics, Univerité Libre de Bruxelles 1050 Brussels, Belgium P. Poláčik School
Homogenization and error estimates of free boundary velocities in periodic media
 Homogenization and error estimates of free boundary velocities in periodic media Inwon C. Kim October 7, 2011 Abstract In this note I describe a recent result ([14]-[15]) on homogenization and error estimates
Homogenization and error estimates of free boundary velocities in periodic media Inwon C. Kim October 7, 2011 Abstract In this note I describe a recent result ([14]-[15]) on homogenization and error estimates
On non negative solutions of some quasilinear elliptic inequalities
 On non negative solutions of some quasilinear elliptic inequalities Lorenzo D Ambrosio and Enzo Mitidieri September 28 2006 Abstract Let f : R R be a continuous function. We prove that under some additional
On non negative solutions of some quasilinear elliptic inequalities Lorenzo D Ambrosio and Enzo Mitidieri September 28 2006 Abstract Let f : R R be a continuous function. We prove that under some additional
Convex Functions and Optimization
 Chapter 5 Convex Functions and Optimization 5.1 Convex Functions Our next topic is that of convex functions. Again, we will concentrate on the context of a map f : R n R although the situation can be generalized
Chapter 5 Convex Functions and Optimization 5.1 Convex Functions Our next topic is that of convex functions. Again, we will concentrate on the context of a map f : R n R although the situation can be generalized
2 (Bonus). Let A X consist of points (x, y) such that either x or y is a rational number. Is A measurable? What is its Lebesgue measure?
 MA 645-4A (Real Analysis), Dr. Chernov Homework assignment 1 (Due 9/5). Prove that every countable set A is measurable and µ(a) = 0. 2 (Bonus). Let A consist of points (x, y) such that either x or y is
MA 645-4A (Real Analysis), Dr. Chernov Homework assignment 1 (Due 9/5). Prove that every countable set A is measurable and µ(a) = 0. 2 (Bonus). Let A consist of points (x, y) such that either x or y is
SYMMETRY OF POSITIVE SOLUTIONS OF SOME NONLINEAR EQUATIONS. M. Grossi S. Kesavan F. Pacella M. Ramaswamy. 1. Introduction
 Topological Methods in Nonlinear Analysis Journal of the Juliusz Schauder Center Volume 12, 1998, 47 59 SYMMETRY OF POSITIVE SOLUTIONS OF SOME NONLINEAR EQUATIONS M. Grossi S. Kesavan F. Pacella M. Ramaswamy
Topological Methods in Nonlinear Analysis Journal of the Juliusz Schauder Center Volume 12, 1998, 47 59 SYMMETRY OF POSITIVE SOLUTIONS OF SOME NONLINEAR EQUATIONS M. Grossi S. Kesavan F. Pacella M. Ramaswamy
Around the Brunn-Minkowski inequality
 Around the Brunn-Minkowski inequality Andrea Colesanti Technische Universität Berlin - Institut für Mathematik January 28, 2015 Summary Summary The Brunn-Minkowski inequality Summary The Brunn-Minkowski
Around the Brunn-Minkowski inequality Andrea Colesanti Technische Universität Berlin - Institut für Mathematik January 28, 2015 Summary Summary The Brunn-Minkowski inequality Summary The Brunn-Minkowski
g 2 (x) (1/3)M 1 = (1/3)(2/3)M.
 COMPACTNESS If C R n is closed and bounded, then by B-W it is sequentially compact: any sequence of points in C has a subsequence converging to a point in C Conversely, any sequentially compact C R n is
COMPACTNESS If C R n is closed and bounded, then by B-W it is sequentially compact: any sequence of points in C has a subsequence converging to a point in C Conversely, any sequentially compact C R n is
L p Spaces and Convexity
 L p Spaces and Convexity These notes largely follow the treatments in Royden, Real Analysis, and Rudin, Real & Complex Analysis. 1. Convex functions Let I R be an interval. For I open, we say a function
L p Spaces and Convexity These notes largely follow the treatments in Royden, Real Analysis, and Rudin, Real & Complex Analysis. 1. Convex functions Let I R be an interval. For I open, we say a function
Lecture Notes in Advanced Calculus 1 (80315) Raz Kupferman Institute of Mathematics The Hebrew University
 Lecture Notes in Advanced Calculus 1 (80315) Raz Kupferman Institute of Mathematics The Hebrew University February 7, 2007 2 Contents 1 Metric Spaces 1 1.1 Basic definitions...........................
Lecture Notes in Advanced Calculus 1 (80315) Raz Kupferman Institute of Mathematics The Hebrew University February 7, 2007 2 Contents 1 Metric Spaces 1 1.1 Basic definitions...........................
On the second differentiability of convex surfaces
 On the second differentiability of convex surfaces Gabriele Bianchi, Andrea Colesanti, Carlo Pucci Abstract Properties of pointwise second differentiability of real valued convex functions in IR n are
On the second differentiability of convex surfaces Gabriele Bianchi, Andrea Colesanti, Carlo Pucci Abstract Properties of pointwise second differentiability of real valued convex functions in IR n are
2 Statement of the problem and assumptions
 Mathematical Notes, 25, vol. 78, no. 4, pp. 466 48. Existence Theorem for Optimal Control Problems on an Infinite Time Interval A.V. Dmitruk and N.V. Kuz kina We consider an optimal control problem on
Mathematical Notes, 25, vol. 78, no. 4, pp. 466 48. Existence Theorem for Optimal Control Problems on an Infinite Time Interval A.V. Dmitruk and N.V. Kuz kina We consider an optimal control problem on
1 Directional Derivatives and Differentiability
 Wednesday, January 18, 2012 1 Directional Derivatives and Differentiability Let E R N, let f : E R and let x 0 E. Given a direction v R N, let L be the line through x 0 in the direction v, that is, L :=
Wednesday, January 18, 2012 1 Directional Derivatives and Differentiability Let E R N, let f : E R and let x 0 E. Given a direction v R N, let L be the line through x 0 in the direction v, that is, L :=
Exercises: Brunn, Minkowski and convex pie
 Lecture 1 Exercises: Brunn, Minkowski and convex pie Consider the following problem: 1.1 Playing a convex pie Consider the following game with two players - you and me. I am cooking a pie, which should
Lecture 1 Exercises: Brunn, Minkowski and convex pie Consider the following problem: 1.1 Playing a convex pie Consider the following game with two players - you and me. I am cooking a pie, which should
(convex combination!). Use convexity of f and multiply by the common denominator to get. Interchanging the role of x and y, we obtain that f is ( 2M ε
 1. Continuity of convex functions in normed spaces In this chapter, we consider continuity properties of real-valued convex functions defined on open convex sets in normed spaces. Recall that every infinitedimensional
1. Continuity of convex functions in normed spaces In this chapter, we consider continuity properties of real-valued convex functions defined on open convex sets in normed spaces. Recall that every infinitedimensional
SHARP BOUNDARY TRACE INEQUALITIES. 1. Introduction
 SHARP BOUNDARY TRACE INEQUALITIES GILES AUCHMUTY Abstract. This paper describes sharp inequalities for the trace of Sobolev functions on the boundary of a bounded region R N. The inequalities bound (semi-)norms
SHARP BOUNDARY TRACE INEQUALITIES GILES AUCHMUTY Abstract. This paper describes sharp inequalities for the trace of Sobolev functions on the boundary of a bounded region R N. The inequalities bound (semi-)norms
ON PARABOLIC HARNACK INEQUALITY
 ON PARABOLIC HARNACK INEQUALITY JIAXIN HU Abstract. We show that the parabolic Harnack inequality is equivalent to the near-diagonal lower bound of the Dirichlet heat kernel on any ball in a metric measure-energy
ON PARABOLIC HARNACK INEQUALITY JIAXIN HU Abstract. We show that the parabolic Harnack inequality is equivalent to the near-diagonal lower bound of the Dirichlet heat kernel on any ball in a metric measure-energy
Fractional convexity maximum principle
 Fractional convexity maximum principle Antonio Greco Department of Mathematics and Informatics via Ospedale 7, 0914 Cagliari, Italy E-mail: greco@unica.it Abstract We construct an anisotropic, degenerate,
Fractional convexity maximum principle Antonio Greco Department of Mathematics and Informatics via Ospedale 7, 0914 Cagliari, Italy E-mail: greco@unica.it Abstract We construct an anisotropic, degenerate,
CHAPTER 2: CONVEX SETS AND CONCAVE FUNCTIONS. W. Erwin Diewert January 31, 2008.
 1 ECONOMICS 594: LECTURE NOTES CHAPTER 2: CONVEX SETS AND CONCAVE FUNCTIONS W. Erwin Diewert January 31, 2008. 1. Introduction Many economic problems have the following structure: (i) a linear function
1 ECONOMICS 594: LECTURE NOTES CHAPTER 2: CONVEX SETS AND CONCAVE FUNCTIONS W. Erwin Diewert January 31, 2008. 1. Introduction Many economic problems have the following structure: (i) a linear function
Propagating terraces and the dynamics of front-like solutions of reaction-diffusion equations on R
 Propagating terraces and the dynamics of front-like solutions of reaction-diffusion equations on R P. Poláčik School of Mathematics, University of Minnesota Minneapolis, MN 55455 Abstract We consider semilinear
Propagating terraces and the dynamics of front-like solutions of reaction-diffusion equations on R P. Poláčik School of Mathematics, University of Minnesota Minneapolis, MN 55455 Abstract We consider semilinear
HARDY INEQUALITIES WITH BOUNDARY TERMS. x 2 dx u 2 dx. (1.2) u 2 = u 2 dx.
 Electronic Journal of Differential Equations, Vol. 003(003), No. 3, pp. 1 8. ISSN: 107-6691. UL: http://ejde.math.swt.edu or http://ejde.math.unt.edu ftp ejde.math.swt.edu (login: ftp) HADY INEQUALITIES
Electronic Journal of Differential Equations, Vol. 003(003), No. 3, pp. 1 8. ISSN: 107-6691. UL: http://ejde.math.swt.edu or http://ejde.math.unt.edu ftp ejde.math.swt.edu (login: ftp) HADY INEQUALITIES
REGULARITY RESULTS FOR THE EQUATION u 11 u 22 = Introduction
 REGULARITY RESULTS FOR THE EQUATION u 11 u 22 = 1 CONNOR MOONEY AND OVIDIU SAVIN Abstract. We study the equation u 11 u 22 = 1 in R 2. Our results include an interior C 2 estimate, classical solvability
REGULARITY RESULTS FOR THE EQUATION u 11 u 22 = 1 CONNOR MOONEY AND OVIDIU SAVIN Abstract. We study the equation u 11 u 22 = 1 in R 2. Our results include an interior C 2 estimate, classical solvability
Sébastien Chaumont a a Institut Élie Cartan, Université Henri Poincaré Nancy I, B. P. 239, Vandoeuvre-lès-Nancy Cedex, France. 1.
 A strong comparison result for viscosity solutions to Hamilton-Jacobi-Bellman equations with Dirichlet condition on a non-smooth boundary and application to parabolic problems Sébastien Chaumont a a Institut
A strong comparison result for viscosity solutions to Hamilton-Jacobi-Bellman equations with Dirichlet condition on a non-smooth boundary and application to parabolic problems Sébastien Chaumont a a Institut
On duality gap in linear conic problems
 On duality gap in linear conic problems C. Zălinescu Abstract In their paper Duality of linear conic problems A. Shapiro and A. Nemirovski considered two possible properties (A) and (B) for dual linear
On duality gap in linear conic problems C. Zălinescu Abstract In their paper Duality of linear conic problems A. Shapiro and A. Nemirovski considered two possible properties (A) and (B) for dual linear
3 (Due ). Let A X consist of points (x, y) such that either x or y is a rational number. Is A measurable? What is its Lebesgue measure?
 MA 645-4A (Real Analysis), Dr. Chernov Homework assignment 1 (Due ). Show that the open disk x 2 + y 2 < 1 is a countable union of planar elementary sets. Show that the closed disk x 2 + y 2 1 is a countable
MA 645-4A (Real Analysis), Dr. Chernov Homework assignment 1 (Due ). Show that the open disk x 2 + y 2 < 1 is a countable union of planar elementary sets. Show that the closed disk x 2 + y 2 1 is a countable
Perron method for the Dirichlet problem.
 Introduzione alle equazioni alle derivate parziali, Laurea Magistrale in Matematica Perron method for the Dirichlet problem. We approach the question of existence of solution u C (Ω) C(Ω) of the Dirichlet
Introduzione alle equazioni alle derivate parziali, Laurea Magistrale in Matematica Perron method for the Dirichlet problem. We approach the question of existence of solution u C (Ω) C(Ω) of the Dirichlet
MEAN VALUE PROPERTY FOR p-harmonic FUNCTIONS
 PROCEEDINGS OF THE AMERICAN MATHEMATICAL SOCIETY Volume 40, Number 7, July 0, Pages 453 463 S 000-9939(0)8-X Article electronically published on November, 0 MEAN VALUE PROPERTY FOR p-harmonic FUNCTIONS
PROCEEDINGS OF THE AMERICAN MATHEMATICAL SOCIETY Volume 40, Number 7, July 0, Pages 453 463 S 000-9939(0)8-X Article electronically published on November, 0 MEAN VALUE PROPERTY FOR p-harmonic FUNCTIONS
Foliations of hyperbolic space by constant mean curvature surfaces sharing ideal boundary
 Foliations of hyperbolic space by constant mean curvature surfaces sharing ideal boundary David Chopp and John A. Velling December 1, 2003 Abstract Let γ be a Jordan curve in S 2, considered as the ideal
Foliations of hyperbolic space by constant mean curvature surfaces sharing ideal boundary David Chopp and John A. Velling December 1, 2003 Abstract Let γ be a Jordan curve in S 2, considered as the ideal
On John type ellipsoids
 On John type ellipsoids B. Klartag Tel Aviv University Abstract Given an arbitrary convex symmetric body K R n, we construct a natural and non-trivial continuous map u K which associates ellipsoids to
On John type ellipsoids B. Klartag Tel Aviv University Abstract Given an arbitrary convex symmetric body K R n, we construct a natural and non-trivial continuous map u K which associates ellipsoids to
AN ASYMPTOTIC MEAN VALUE CHARACTERIZATION FOR p-harmonic FUNCTIONS. To the memory of our friend and colleague Fuensanta Andreu
 AN ASYMPTOTIC MEAN VALUE CHARACTERIZATION FOR p-harmonic FUNCTIONS JUAN J. MANFREDI, MIKKO PARVIAINEN, AND JULIO D. ROSSI Abstract. We characterize p-harmonic functions in terms of an asymptotic mean value
AN ASYMPTOTIC MEAN VALUE CHARACTERIZATION FOR p-harmonic FUNCTIONS JUAN J. MANFREDI, MIKKO PARVIAINEN, AND JULIO D. ROSSI Abstract. We characterize p-harmonic functions in terms of an asymptotic mean value
Problem Set 5: Solutions Math 201A: Fall 2016
 Problem Set 5: s Math 21A: Fall 216 Problem 1. Define f : [1, ) [1, ) by f(x) = x + 1/x. Show that f(x) f(y) < x y for all x, y [1, ) with x y, but f has no fixed point. Why doesn t this example contradict
Problem Set 5: s Math 21A: Fall 216 Problem 1. Define f : [1, ) [1, ) by f(x) = x + 1/x. Show that f(x) f(y) < x y for all x, y [1, ) with x y, but f has no fixed point. Why doesn t this example contradict
Symmetry of nonnegative solutions of elliptic equations via a result of Serrin
 Symmetry of nonnegative solutions of elliptic equations via a result of Serrin P. Poláčik School of Mathematics, University of Minnesota Minneapolis, MN 55455 Abstract. We consider the Dirichlet problem
Symmetry of nonnegative solutions of elliptic equations via a result of Serrin P. Poláčik School of Mathematics, University of Minnesota Minneapolis, MN 55455 Abstract. We consider the Dirichlet problem
Elliptic PDEs of 2nd Order, Gilbarg and Trudinger
 Elliptic PDEs of 2nd Order, Gilbarg and Trudinger Chapter 2 Laplace Equation Yung-Hsiang Huang 207.07.07. Mimic the proof for Theorem 3.. 2. Proof. I think we should assume u C 2 (Ω Γ). Let W be an open
Elliptic PDEs of 2nd Order, Gilbarg and Trudinger Chapter 2 Laplace Equation Yung-Hsiang Huang 207.07.07. Mimic the proof for Theorem 3.. 2. Proof. I think we should assume u C 2 (Ω Γ). Let W be an open
B. Appendix B. Topological vector spaces
 B.1 B. Appendix B. Topological vector spaces B.1. Fréchet spaces. In this appendix we go through the definition of Fréchet spaces and their inductive limits, such as they are used for definitions of function
B.1 B. Appendix B. Topological vector spaces B.1. Fréchet spaces. In this appendix we go through the definition of Fréchet spaces and their inductive limits, such as they are used for definitions of function
Applied Mathematics Letters
 Applied Mathematics Letters 25 (2012) 974 979 Contents lists available at SciVerse ScienceDirect Applied Mathematics Letters journal homepage: www.elsevier.com/locate/aml On dual vector equilibrium problems
Applied Mathematics Letters 25 (2012) 974 979 Contents lists available at SciVerse ScienceDirect Applied Mathematics Letters journal homepage: www.elsevier.com/locate/aml On dual vector equilibrium problems
PROD. TYPE: COM ARTICLE IN PRESS. Andrea Colesanti. Received 4 August 2003; accepted 8 June 2004 Communicated by Michael Hopkins
 YAIMA28.0. pp: - (col.fig.: nil) PROD. TYPE: COM ED: Suraina PAGN: Vidya -- SCAN: Girish Advances in Mathematics ( ) www.elsevier.com/locate/aim 2 2 Brunn Minkowski inequalities for variational functionals
YAIMA28.0. pp: - (col.fig.: nil) PROD. TYPE: COM ED: Suraina PAGN: Vidya -- SCAN: Girish Advances in Mathematics ( ) www.elsevier.com/locate/aim 2 2 Brunn Minkowski inequalities for variational functionals
Frequency functions, monotonicity formulas, and the thin obstacle problem
 Frequency functions, monotonicity formulas, and the thin obstacle problem IMA - University of Minnesota March 4, 2013 Thank you for the invitation! In this talk we will present an overview of the parabolic
Frequency functions, monotonicity formulas, and the thin obstacle problem IMA - University of Minnesota March 4, 2013 Thank you for the invitation! In this talk we will present an overview of the parabolic
Landesman-Lazer type results for second order Hamilton-Jacobi-Bellman equations
 Author manuscript, published in "Journal of Functional Analysis 258, 12 (2010) 4154-4182" Landesman-Lazer type results for second order Hamilton-Jacobi-Bellman equations Patricio FELMER, Alexander QUAAS,
Author manuscript, published in "Journal of Functional Analysis 258, 12 (2010) 4154-4182" Landesman-Lazer type results for second order Hamilton-Jacobi-Bellman equations Patricio FELMER, Alexander QUAAS,
EXISTENCE AND REGULARITY RESULTS FOR SOME NONLINEAR PARABOLIC EQUATIONS
 EXISTECE AD REGULARITY RESULTS FOR SOME OLIEAR PARABOLIC EUATIOS Lucio BOCCARDO 1 Andrea DALL AGLIO 2 Thierry GALLOUËT3 Luigi ORSIA 1 Abstract We prove summability results for the solutions of nonlinear
EXISTECE AD REGULARITY RESULTS FOR SOME OLIEAR PARABOLIC EUATIOS Lucio BOCCARDO 1 Andrea DALL AGLIO 2 Thierry GALLOUËT3 Luigi ORSIA 1 Abstract We prove summability results for the solutions of nonlinear
On a weighted total variation minimization problem
 On a weighted total variation minimization problem Guillaume Carlier CEREMADE Université Paris Dauphine carlier@ceremade.dauphine.fr Myriam Comte Laboratoire Jacques-Louis Lions, Université Pierre et Marie
On a weighted total variation minimization problem Guillaume Carlier CEREMADE Université Paris Dauphine carlier@ceremade.dauphine.fr Myriam Comte Laboratoire Jacques-Louis Lions, Université Pierre et Marie
USING FUNCTIONAL ANALYSIS AND SOBOLEV SPACES TO SOLVE POISSON S EQUATION
 USING FUNCTIONAL ANALYSIS AND SOBOLEV SPACES TO SOLVE POISSON S EQUATION YI WANG Abstract. We study Banach and Hilbert spaces with an eye towards defining weak solutions to elliptic PDE. Using Lax-Milgram
USING FUNCTIONAL ANALYSIS AND SOBOLEV SPACES TO SOLVE POISSON S EQUATION YI WANG Abstract. We study Banach and Hilbert spaces with an eye towards defining weak solutions to elliptic PDE. Using Lax-Milgram
REGULARITY FOR INFINITY HARMONIC FUNCTIONS IN TWO DIMENSIONS
 C,α REGULARITY FOR INFINITY HARMONIC FUNCTIONS IN TWO DIMENSIONS LAWRENCE C. EVANS AND OVIDIU SAVIN Abstract. We propose a new method for showing C,α regularity for solutions of the infinity Laplacian
C,α REGULARITY FOR INFINITY HARMONIC FUNCTIONS IN TWO DIMENSIONS LAWRENCE C. EVANS AND OVIDIU SAVIN Abstract. We propose a new method for showing C,α regularity for solutions of the infinity Laplacian
MATH MEASURE THEORY AND FOURIER ANALYSIS. Contents
 MATH 3969 - MEASURE THEORY AND FOURIER ANALYSIS ANDREW TULLOCH Contents 1. Measure Theory 2 1.1. Properties of Measures 3 1.2. Constructing σ-algebras and measures 3 1.3. Properties of the Lebesgue measure
MATH 3969 - MEASURE THEORY AND FOURIER ANALYSIS ANDREW TULLOCH Contents 1. Measure Theory 2 1.1. Properties of Measures 3 1.2. Constructing σ-algebras and measures 3 1.3. Properties of the Lebesgue measure
Math 341: Convex Geometry. Xi Chen
 Math 341: Convex Geometry Xi Chen 479 Central Academic Building, University of Alberta, Edmonton, Alberta T6G 2G1, CANADA E-mail address: xichen@math.ualberta.ca CHAPTER 1 Basics 1. Euclidean Geometry
Math 341: Convex Geometry Xi Chen 479 Central Academic Building, University of Alberta, Edmonton, Alberta T6G 2G1, CANADA E-mail address: xichen@math.ualberta.ca CHAPTER 1 Basics 1. Euclidean Geometry
ON THE EXISTENCE OF THREE SOLUTIONS FOR QUASILINEAR ELLIPTIC PROBLEM. Paweł Goncerz
 Opuscula Mathematica Vol. 32 No. 3 2012 http://dx.doi.org/10.7494/opmath.2012.32.3.473 ON THE EXISTENCE OF THREE SOLUTIONS FOR QUASILINEAR ELLIPTIC PROBLEM Paweł Goncerz Abstract. We consider a quasilinear
Opuscula Mathematica Vol. 32 No. 3 2012 http://dx.doi.org/10.7494/opmath.2012.32.3.473 ON THE EXISTENCE OF THREE SOLUTIONS FOR QUASILINEAR ELLIPTIC PROBLEM Paweł Goncerz Abstract. We consider a quasilinear
Some Remarks About the Density of Smooth Functions in Weighted Sobolev Spaces
 Journal of Convex nalysis Volume 1 (1994), No. 2, 135 142 Some Remarks bout the Density of Smooth Functions in Weighted Sobolev Spaces Valeria Chiadò Piat Dipartimento di Matematica, Politecnico di Torino,
Journal of Convex nalysis Volume 1 (1994), No. 2, 135 142 Some Remarks bout the Density of Smooth Functions in Weighted Sobolev Spaces Valeria Chiadò Piat Dipartimento di Matematica, Politecnico di Torino,
MATH COURSE NOTES - CLASS MEETING # Introduction to PDEs, Fall 2011 Professor: Jared Speck
 MATH 8.52 COURSE NOTES - CLASS MEETING # 6 8.52 Introduction to PDEs, Fall 20 Professor: Jared Speck Class Meeting # 6: Laplace s and Poisson s Equations We will now study the Laplace and Poisson equations
MATH 8.52 COURSE NOTES - CLASS MEETING # 6 8.52 Introduction to PDEs, Fall 20 Professor: Jared Speck Class Meeting # 6: Laplace s and Poisson s Equations We will now study the Laplace and Poisson equations
MATH COURSE NOTES - CLASS MEETING # Introduction to PDEs, Spring 2018 Professor: Jared Speck
 MATH 8.52 COURSE NOTES - CLASS MEETING # 6 8.52 Introduction to PDEs, Spring 208 Professor: Jared Speck Class Meeting # 6: Laplace s and Poisson s Equations We will now study the Laplace and Poisson equations
MATH 8.52 COURSE NOTES - CLASS MEETING # 6 8.52 Introduction to PDEs, Spring 208 Professor: Jared Speck Class Meeting # 6: Laplace s and Poisson s Equations We will now study the Laplace and Poisson equations
Contents: 1. Minimization. 2. The theorem of Lions-Stampacchia for variational inequalities. 3. Γ -Convergence. 4. Duality mapping.
 Minimization Contents: 1. Minimization. 2. The theorem of Lions-Stampacchia for variational inequalities. 3. Γ -Convergence. 4. Duality mapping. 1 Minimization A Topological Result. Let S be a topological
Minimization Contents: 1. Minimization. 2. The theorem of Lions-Stampacchia for variational inequalities. 3. Γ -Convergence. 4. Duality mapping. 1 Minimization A Topological Result. Let S be a topological
Recent developments in elliptic partial differential equations of Monge Ampère type
 Recent developments in elliptic partial differential equations of Monge Ampère type Neil S. Trudinger Abstract. In conjunction with applications to optimal transportation and conformal geometry, there
Recent developments in elliptic partial differential equations of Monge Ampère type Neil S. Trudinger Abstract. In conjunction with applications to optimal transportation and conformal geometry, there
COINCIDENCE SETS IN THE OBSTACLE PROBLEM FOR THE p-harmonic OPERATOR
 PROCEEDINGS OF THE AMERICAN MATHEMATICAL SOCIETY Volume 95, Number 3, November 1985 COINCIDENCE SETS IN THE OBSTACLE PROBLEM FOR THE p-harmonic OPERATOR SHIGERU SAKAGUCHI Abstract. We consider the obstacle
PROCEEDINGS OF THE AMERICAN MATHEMATICAL SOCIETY Volume 95, Number 3, November 1985 COINCIDENCE SETS IN THE OBSTACLE PROBLEM FOR THE p-harmonic OPERATOR SHIGERU SAKAGUCHI Abstract. We consider the obstacle
ON GAP FUNCTIONS OF VARIATIONAL INEQUALITY IN A BANACH SPACE. Sangho Kum and Gue Myung Lee. 1. Introduction
 J. Korean Math. Soc. 38 (2001), No. 3, pp. 683 695 ON GAP FUNCTIONS OF VARIATIONAL INEQUALITY IN A BANACH SPACE Sangho Kum and Gue Myung Lee Abstract. In this paper we are concerned with theoretical properties
J. Korean Math. Soc. 38 (2001), No. 3, pp. 683 695 ON GAP FUNCTIONS OF VARIATIONAL INEQUALITY IN A BANACH SPACE Sangho Kum and Gue Myung Lee Abstract. In this paper we are concerned with theoretical properties
Some lecture notes for Math 6050E: PDEs, Fall 2016
 Some lecture notes for Math 65E: PDEs, Fall 216 Tianling Jin December 1, 216 1 Variational methods We discuss an example of the use of variational methods in obtaining existence of solutions. Theorem 1.1.
Some lecture notes for Math 65E: PDEs, Fall 216 Tianling Jin December 1, 216 1 Variational methods We discuss an example of the use of variational methods in obtaining existence of solutions. Theorem 1.1.
PROBLEMS. (b) (Polarization Identity) Show that in any inner product space
 1 Professor Carl Cowen Math 54600 Fall 09 PROBLEMS 1. (Geometry in Inner Product Spaces) (a) (Parallelogram Law) Show that in any inner product space x + y 2 + x y 2 = 2( x 2 + y 2 ). (b) (Polarization
1 Professor Carl Cowen Math 54600 Fall 09 PROBLEMS 1. (Geometry in Inner Product Spaces) (a) (Parallelogram Law) Show that in any inner product space x + y 2 + x y 2 = 2( x 2 + y 2 ). (b) (Polarization
Set, functions and Euclidean space. Seungjin Han
 Set, functions and Euclidean space Seungjin Han September, 2018 1 Some Basics LOGIC A is necessary for B : If B holds, then A holds. B A A B is the contraposition of B A. A is sufficient for B: If A holds,
Set, functions and Euclidean space Seungjin Han September, 2018 1 Some Basics LOGIC A is necessary for B : If B holds, then A holds. B A A B is the contraposition of B A. A is sufficient for B: If A holds,
ON A LINEAR REFINEMENT OF THE PRÉKOPA-LEINDLER INEQUALITY
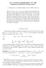 ON A LINEAR REFINEMENT OF TE PRÉKOPA-LEINDLER INEQUALITY A. COLESANTI, E. SAORÍN GÓMEZ, AND J. YEPES NICOLÁS Abstract. If f, g : R n R 0 are non-negative measurable functions, then the Prékopa-Leindler
ON A LINEAR REFINEMENT OF TE PRÉKOPA-LEINDLER INEQUALITY A. COLESANTI, E. SAORÍN GÓMEZ, AND J. YEPES NICOLÁS Abstract. If f, g : R n R 0 are non-negative measurable functions, then the Prékopa-Leindler
A Unified Analysis of Nonconvex Optimization Duality and Penalty Methods with General Augmenting Functions
 A Unified Analysis of Nonconvex Optimization Duality and Penalty Methods with General Augmenting Functions Angelia Nedić and Asuman Ozdaglar April 16, 2006 Abstract In this paper, we study a unifying framework
A Unified Analysis of Nonconvex Optimization Duality and Penalty Methods with General Augmenting Functions Angelia Nedić and Asuman Ozdaglar April 16, 2006 Abstract In this paper, we study a unifying framework
UNDERGROUND LECTURE NOTES 1: Optimality Conditions for Constrained Optimization Problems
 UNDERGROUND LECTURE NOTES 1: Optimality Conditions for Constrained Optimization Problems Robert M. Freund February 2016 c 2016 Massachusetts Institute of Technology. All rights reserved. 1 1 Introduction
UNDERGROUND LECTURE NOTES 1: Optimality Conditions for Constrained Optimization Problems Robert M. Freund February 2016 c 2016 Massachusetts Institute of Technology. All rights reserved. 1 1 Introduction
1 Lesson 1: Brunn Minkowski Inequality
 1 Lesson 1: Brunn Minkowski Inequality A set A R n is called convex if (1 λ)x + λy A for any x, y A and any λ [0, 1]. The Minkowski sum of two sets A, B R n is defined by A + B := {a + b : a A, b B}. One
1 Lesson 1: Brunn Minkowski Inequality A set A R n is called convex if (1 λ)x + λy A for any x, y A and any λ [0, 1]. The Minkowski sum of two sets A, B R n is defined by A + B := {a + b : a A, b B}. One
A note on the convex infimum convolution inequality
 A note on the convex infimum convolution inequality Naomi Feldheim, Arnaud Marsiglietti, Piotr Nayar, Jing Wang Abstract We characterize the symmetric measures which satisfy the one dimensional convex
A note on the convex infimum convolution inequality Naomi Feldheim, Arnaud Marsiglietti, Piotr Nayar, Jing Wang Abstract We characterize the symmetric measures which satisfy the one dimensional convex
On the infinity Laplace operator
 On the infinity Laplace operator Petri Juutinen Köln, July 2008 The infinity Laplace equation Gunnar Aronsson (1960 s): variational problems of the form S(u, Ω) = ess sup H (x, u(x), Du(x)). (1) x Ω The
On the infinity Laplace operator Petri Juutinen Köln, July 2008 The infinity Laplace equation Gunnar Aronsson (1960 s): variational problems of the form S(u, Ω) = ess sup H (x, u(x), Du(x)). (1) x Ω The
1. Introduction Boundary estimates for the second derivatives of the solution to the Dirichlet problem for the Monge-Ampere equation
 POINTWISE C 2,α ESTIMATES AT THE BOUNDARY FOR THE MONGE-AMPERE EQUATION O. SAVIN Abstract. We prove a localization property of boundary sections for solutions to the Monge-Ampere equation. As a consequence
POINTWISE C 2,α ESTIMATES AT THE BOUNDARY FOR THE MONGE-AMPERE EQUATION O. SAVIN Abstract. We prove a localization property of boundary sections for solutions to the Monge-Ampere equation. As a consequence
Radial Symmetry of Minimizers for Some Translation and Rotation Invariant Functionals
 journal of differential equations 124, 378388 (1996) article no. 0015 Radial Symmetry of Minimizers for Some Translation and Rotation Invariant Functionals Orlando Lopes IMECCUNICAMPCaixa Postal 1170 13081-970,
journal of differential equations 124, 378388 (1996) article no. 0015 Radial Symmetry of Minimizers for Some Translation and Rotation Invariant Functionals Orlando Lopes IMECCUNICAMPCaixa Postal 1170 13081-970,
The Dirichlet s P rinciple. In this lecture we discuss an alternative formulation of the Dirichlet problem for the Laplace equation:
 Oct. 1 The Dirichlet s P rinciple In this lecture we discuss an alternative formulation of the Dirichlet problem for the Laplace equation: 1. Dirichlet s Principle. u = in, u = g on. ( 1 ) If we multiply
Oct. 1 The Dirichlet s P rinciple In this lecture we discuss an alternative formulation of the Dirichlet problem for the Laplace equation: 1. Dirichlet s Principle. u = in, u = g on. ( 1 ) If we multiply
Convex Analysis and Economic Theory Winter 2018
 Division of the Humanities and Social Sciences Ec 181 KC Border Convex Analysis and Economic Theory Winter 2018 Topic 7: Quasiconvex Functions I 7.1 Level sets of functions For an extended real-valued
Division of the Humanities and Social Sciences Ec 181 KC Border Convex Analysis and Economic Theory Winter 2018 Topic 7: Quasiconvex Functions I 7.1 Level sets of functions For an extended real-valued
Convex Optimization Theory. Chapter 5 Exercises and Solutions: Extended Version
 Convex Optimization Theory Chapter 5 Exercises and Solutions: Extended Version Dimitri P. Bertsekas Massachusetts Institute of Technology Athena Scientific, Belmont, Massachusetts http://www.athenasc.com
Convex Optimization Theory Chapter 5 Exercises and Solutions: Extended Version Dimitri P. Bertsekas Massachusetts Institute of Technology Athena Scientific, Belmont, Massachusetts http://www.athenasc.com
Overview of normed linear spaces
 20 Chapter 2 Overview of normed linear spaces Starting from this chapter, we begin examining linear spaces with at least one extra structure (topology or geometry). We assume linearity; this is a natural
20 Chapter 2 Overview of normed linear spaces Starting from this chapter, we begin examining linear spaces with at least one extra structure (topology or geometry). We assume linearity; this is a natural
Example 1. Hamilton-Jacobi equation. In particular, the eikonal equation. for some n( x) > 0 in Ω. Here 1 / 2
 Oct. 1 0 Viscosity S olutions In this lecture we take a glimpse of the viscosity solution theory for linear and nonlinear PDEs. From our experience we know that even for linear equations, the existence
Oct. 1 0 Viscosity S olutions In this lecture we take a glimpse of the viscosity solution theory for linear and nonlinear PDEs. From our experience we know that even for linear equations, the existence
The local equicontinuity of a maximal monotone operator
 arxiv:1410.3328v2 [math.fa] 3 Nov 2014 The local equicontinuity of a maximal monotone operator M.D. Voisei Abstract The local equicontinuity of an operator T : X X with proper Fitzpatrick function ϕ T
arxiv:1410.3328v2 [math.fa] 3 Nov 2014 The local equicontinuity of a maximal monotone operator M.D. Voisei Abstract The local equicontinuity of an operator T : X X with proper Fitzpatrick function ϕ T
Chapter 13. Convex and Concave. Josef Leydold Mathematical Methods WS 2018/19 13 Convex and Concave 1 / 44
 Chapter 13 Convex and Concave Josef Leydold Mathematical Methods WS 2018/19 13 Convex and Concave 1 / 44 Monotone Function Function f is called monotonically increasing, if x 1 x 2 f (x 1 ) f (x 2 ) It
Chapter 13 Convex and Concave Josef Leydold Mathematical Methods WS 2018/19 13 Convex and Concave 1 / 44 Monotone Function Function f is called monotonically increasing, if x 1 x 2 f (x 1 ) f (x 2 ) It
