Chapter 13. Convex and Concave. Josef Leydold Mathematical Methods WS 2018/19 13 Convex and Concave 1 / 44
|
|
|
- Jacob Watts
- 5 years ago
- Views:
Transcription
1 Chapter 13 Convex and Concave Josef Leydold Mathematical Methods WS 2018/19 13 Convex and Concave 1 / 44
2 Monotone Function Function f is called monotonically increasing, if x 1 x 2 f (x 1 ) f (x 2 ) It is called strictly monotonically increasing, if f (x 2 ) f (x 1 ) x 1 < x 2 f (x 1 ) < f (x 2 ) x 1 x 2 Function f is called monotonically decreasing, if x 1 x 2 f (x 1 ) f (x 2 ) It is called strictly monotonically decreasing, if f (x 1 ) f (x 2 ) x 1 < x 2 f (x 1 ) > f (x 2 ) x 1 x 2 Josef Leydold Mathematical Methods WS 2018/19 13 Convex and Concave 2 / 44
3 Monotone Functions For differentiable functions we have f monotonically increasing f (x) 0 for all x D f f monotonically decreasing f (x) 0 for all x D f f strictly monotonically increasing f (x) > 0 for all x D f f strictly monotonically decreasing f (x) < 0 for all x D f Function f : (0, ), x ln(x) is strictly monotonically increasing, as f (x) = (ln(x)) = 1 x > 0 for all x > 0 Josef Leydold Mathematical Methods WS 2018/19 13 Convex and Concave 3 / 44
4 Locally Monotone Functions A function f can be monotonically increasing in some interval and decreasing in some other interval. For continuously differentiable functions (i.e., when f (x) is continuous) we can use the following procedure: 1. Compute first derivative f (x). 2. Determine all roots of f (x). 3. We thus obtain intervals where f (x) does not change sign. 4. Select appropriate points x i in each interval and determine the sign of f (x i ). Josef Leydold Mathematical Methods WS 2018/19 13 Convex and Concave 4 / 44
5 Example Locally Monotone Functions In which region is function f (x) = 2 x 3 12 x x 1 monotonically increasing? We have to solve inequality f (x) 0: 1. f (x) = 6 x 2 24 x Roots: x 2 4 x + 3 = 0 x 1 = 1, x 2 = 3 3. Obtain 3 intervals: (, 1], [1, 3], and [3, ) 4. Sign of f (x) at appropriate points in each interval: f (0) = 3 > 0, f (2) = 1 < 0, and f (4) = 3 > f (x) cannot change sign in each interval: f (x) 0 in (, 1] and [3, ). Function f (x) is monotonically increasing in (, 1] and in [3, ). Josef Leydold Mathematical Methods WS 2018/19 13 Convex and Concave 5 / 44
6 Monotone and Inverse Function If f is strictly monotonically increasing, then immediately implies That is, f is one-to-one. x 1 < x 2 f (x 1 ) < f (x 2 ) x 1 = x 2 f (x 1 ) = f (x 2 ) So if f is onto and strictly monotonically increasing (or decreasing), then f is invertible. Josef Leydold Mathematical Methods WS 2018/19 13 Convex and Concave 6 / 44
7 Convex Set A set D R n is called convex, if for any two points x, y D the straight line between these points also belongs to D, i.e., (1 h) x + h y D for all h [0, 1], and x, y D. convex: not convex: Josef Leydold Mathematical Methods WS 2018/19 13 Convex and Concave 7 / 44
8 Intersection of Convex Sets Let S 1,..., S k be convex subsets of R n. Then their intersection S 1... S k is also convex. The union of convex sets need not be convex. Josef Leydold Mathematical Methods WS 2018/19 13 Convex and Concave 8 / 44
9 Example Half-Space Let p R n and m R be fixed, p = 0. Then H = {x R n : p t x = m} is a so called hyper-plane which partitions the R n into two half-spaces H + = {x R n : p t x m}, H = {x R n : p t x m}. Sets H, H + and H are convex. Let x be a vector of goods, p the vector of prices and m the budget. Then the budget set is convex. {x R n : p t x m, x 0} = {x : p t x m} {x : x 1 0}... {x : x n 0} Josef Leydold Mathematical Methods WS 2018/19 13 Convex and Concave 9 / 44
10 Convex and Concave Functions Function f is called convex in domain D R n, if D is convex and f ((1 h) x 1 + h x 2 ) (1 h) f (x 1 ) + h f (x 2 ) for all x 1, x 2 D and all h [0, 1]. It is called concave, if f ((1 h) x 1 + h x 2 ) (1 h) f (x 1 ) + h f (x 2 ) x 1 x 2 x 1 x 2 convex concave Josef Leydold Mathematical Methods WS 2018/19 13 Convex and Concave 10 / 44
11 Concave Function f ( (1 h) x 1 + h x 2 ) (1 h) f (x1 ) + h f (x 2 ) f ( (1 h) x 1 + h x 2 ) (1 h) f (x 1 ) + h f (x 2 ) x 1 x 2 (1 h) x 1 + h x 2 Secant is below the graph of function f. Josef Leydold Mathematical Methods WS 2018/19 13 Convex and Concave 11 / 44
12 Strictly Convex and Concave Functions Function f is called strictly convex in domain D R n, if D is convex and f ((1 h) x 1 + h x 2 ) < (1 h) f (x 1 ) + h f (x 2 ) for all x 1, x 2 D with x 1 = x 2 and all h (0, 1). Function f is called strictly concave in domain D R n, if D is convex and f ((1 h) x 1 + h x 2 ) > (1 h) f (x 1 ) + h f (x 2 ) for all x 1, x 2 D with x 1 = x 2 and all h (0, 1). Josef Leydold Mathematical Methods WS 2018/19 13 Convex and Concave 12 / 44
13 Example Linear Function Let a R n be fixed. Then f (x) = a t x is a linear map and we find: f ((1 h) x 1 + h x 2 ) = a t ((1 h) x 1 + h x 2 ) = (1 h) a t x 1 + h a t x 2 = (1 h) f (x 1 ) + h f (x 2 ) That is, every linear function is both concave and convex. However, a linear function is neither strictly concave nor strictly convex, as the inequality is never strict. Josef Leydold Mathematical Methods WS 2018/19 13 Convex and Concave 13 / 44
14 Example Quadratic Univariate Function Function f (x) = x 2 is strictly convex: f ((1 h) x + h y) [ (1 h) f (x) + h f (y) ] = ((1 h) x + h y) 2 [ (1 h) x 2 + h y 2] = (1 h) 2 x 2 + 2(1 h)h xy + h 2 y 2 (1 h) x 2 h y 2 = h(1 h) x 2 + 2(1 h)h xy h(1 h) y 2 = h(1 h) (x y) 2 < 0 for x = y and 0 < h < 1. Thus f ((1 h) x + h y) < (1 h) f (x) + h f (y) for all x = y and 0 < h < 1, i.e., f (x) = x 2 is strictly convex, as claimed. Josef Leydold Mathematical Methods WS 2018/19 13 Convex and Concave 14 / 44
15 Properties If f (x) is (strictly) convex, then f (x) is (strictly) concave (and vice versa). If f 1 (x),..., f k (x) are convex (concave) functions and α 1,..., α k > 0, then is also convex (concave). g(x) = α 1 f 1 (x) + + α k f k (x) If (at least) one of the functions f i (x) is strictly convex (strictly concave), then g(x) is strictly convex (strictly concave). Josef Leydold Mathematical Methods WS 2018/19 13 Convex and Concave 15 / 44
16 Properties For a differentiable functions the following holds: Function f is concave if and only if f (x) f (x 0 ) f (x 0 ) (x x 0 ) i.e., the function graph is always below the tangent. x 0 Function f is strictly concave if and only if f (x) f (x 0 ) < f (x 0 ) (x x 0 ) for all x = x 0 Function f is convex if and only if f (x) f (x 0 ) f (x 0 ) (x x 0 ) (Analogous for strictly convex functions.) x 0 Josef Leydold Mathematical Methods WS 2018/19 13 Convex and Concave 16 / 44
17 Univariate Functions For two times differentiable functions we have f convex f (x) 0 for all x D f f concave f (x) 0 for all x D f Derivative f (x) is monotonically decreasing, thus f (x) 0. Josef Leydold Mathematical Methods WS 2018/19 13 Convex and Concave 17 / 44
18 Univariate Functions For two times differentiable functions we have f strictly convex f (x) > 0 for all x D f f strictly concave f (x) < 0 for all x D f Josef Leydold Mathematical Methods WS 2018/19 13 Convex and Concave 18 / 44
19 Example Convex Function Exponential function: f (x) = e x f (x) = e x f (x) = e x > 0 for all x R e exp(x) is (strictly) convex. 1 1 Josef Leydold Mathematical Methods WS 2018/19 13 Convex and Concave 19 / 44
20 Example Concave Function Logarithm function: (x > 0) f (x) = ln(x) 1 f (x) = 1 x f (x) = 1 x 2 < 0 for all x > 0 ln(x) is (strictly) concave. 1 e Josef Leydold Mathematical Methods WS 2018/19 13 Convex and Concave 20 / 44
21 Locally Convex Functions A function f may be convex in some interval and concave in some other interval. For two times continuously differentiable functions (i.e., when f (x) is continuous) we can use the following procedure: 1. Compute second derivative f (x). 2. Determine all roots of f (x). 3. We thus obtain intervals where f (x) does not change sign. 4. Select appropriate points x i in each interval and determine the sign of f (x i ). Josef Leydold Mathematical Methods WS 2018/19 13 Convex and Concave 21 / 44
22 Locally Concave Function In which region is f (x) = 2 x 3 12 x x 1 concave? We have to solve inequality f (x) f (x) = 12 x Roots: 12 x 24 = 0 x = 2 3. Obtain 2 intervals: (, 2] and [2, ) 4. Sign of f (x) at appropriate points in each interval: f (0) = 24 < 0 and f (4) = 24 > f (x) cannot change sign in each interval: f (x) 0 in (, 2] Function f (x) is concave in (, 2]. Josef Leydold Mathematical Methods WS 2018/19 13 Convex and Concave 22 / 44
23 Univariate Restrictions Notice, that by definition a (multivariate) function is convex if and only if every restriction of its domain to a straight line results in a convex univariate function. That is: Function f : D R n R is convex if and only if g(t) = f (x 0 + t h) is convex for all x 0 D and all non-zero h R n. x 0 h Josef Leydold Mathematical Methods WS 2018/19 13 Convex and Concave 23 / 44
24 Quadratic Form Let A be a symmetric matrix and q A (x) = x t Ax be the corresponding quadratic form. Matrix A can be diagonalized, i.e., if we use an orthonormal basis of its eigenvector, then A becomes a diagonal matrix with the eigenvalues of A as its elements: q A (x) = λ 1 x λ 2x λ n x 2 n. It is convex if all eigenvalues λ i 0 as it is the sum of convex functions. It is concave if all λ i 0 as it is the negative of a convex function. It is neither convex nor concave if we have eigenvalues with λ i > 0 and λ i < 0. Josef Leydold Mathematical Methods WS 2018/19 13 Convex and Concave 24 / 44
25 Quadratic Form We find for a quadratic form q A : strictly convex positive definite convex positive semidefinite strictly concave negative definite concave negative semidefinite neither indefinite We can determine the definiteness of A by means of the eigenvalues of A, or the (leading) principle minors of A. Josef Leydold Mathematical Methods WS 2018/19 13 Convex and Concave 25 / 44
26 Example Quadratic Form Let A = Leading principle minors: A 1 = 2 > A 2 = 1 3 = 5 > A 3 = A = = 8 > 0 A is thus positive definite. Quadratic form q A is strictly convex. Josef Leydold Mathematical Methods WS 2018/19 13 Convex and Concave 26 / 44
27 Example Quadratic Form Let A = Principle Minors: A 1 = 1 A 2 = 4 A 3 = A 1,2 = 0 4 = 4 A 1 1 1,3 = 1 2 = 1 A 4 2 2,3 = 2 2 = A i 0 A 1,2,3 = = 0 A i,j A 1,2,3 0 A is thus negative semidefinite. Quadratic form q A is concave (but not strictly concave). Josef Leydold Mathematical Methods WS 2018/19 13 Convex and Concave 27 / 44
28 Concavity of Differentiable Functions Le f : D R n R with Taylor series expansion f (x 0 + h) = f (x 0 ) + f (x 0 ) h ht H f (x 0 ) h + O( h 3 ) Hessian matrix H f (x 0 ) determines the concavity or convexity of f around expansion point x 0. H f (x 0 ) positive definite f strictly convex around x 0 H f (x 0 ) negative definite f strictly concave around x 0 H f (x) positive semidefinite for all x D f convex in D H f (x) negative semidefinite for all x D f concave in D Josef Leydold Mathematical Methods WS 2018/19 13 Convex and Concave 28 / 44
29 Recipe Strictly Convex 1. Compute Hessian matrix f x1 x 1 (x) f x1 x 2 (x) f x1 x n (x) f H f (x) = x2 x 1 (x) f x2 x 2 (x) f x2 x n (x) f xn x 1 (x) f xn x 2 (x) f xn x n (x) 2. Compute all leading principle minors H i. 3. f strictly convex all H k > 0 for (almost) all x D f strictly concave all ( 1) k H k > 0 for (almost) all x D [ ( 1) k H k > 0 implies: H 1, H 3,... < 0 and H 2, H 4,... > 0 ] 4. Otherwise f is neither strictly convex nor strictly concave. Josef Leydold Mathematical Methods WS 2018/19 13 Convex and Concave 29 / 44
30 Recipe Convex 1. Compute Hessian matrix f x1 x 1 (x) f x1 x 2 (x) f x1 x n (x) f H f (x) = x2 x 1 (x) f x2 x 2 (x) f x2 x n (x) f xn x 1 (x) f xn x 2 (x) f xn x n (x) 2. Check for strict convexity or concavity. 3. Compute all principle minors H i1,...,i k. (Only required if det(a) = 0) 4. f convex all H i1,...,i k 0 for all x D. f concave all ( 1) k H i1,...,i k 0 for all x D. 5. Otherwise f is neither convex nor concave. Josef Leydold Mathematical Methods WS 2018/19 13 Convex and Concave 30 / 44
31 Example Strict Convexity Is function f (strictly) concave or convex? f (x, y) = x 4 + x 2 2 x y + y 2 1. Hessian matrix: H f (x) = ( ) 12 x Leading principle minors: H 1 = 12 x > 0 H 2 = H f (x) = 24 x 2 > 0 for all x = All leading principle minors > 0 for almost all x f is strictly convex. (and thus convex, too) Josef Leydold Mathematical Methods WS 2018/19 13 Convex and Concave 31 / 44
32 Example Cobb-Douglas Function Let f (x, y) = x α y β with α, β 0 and α + β 1, and D = {(x, y) : x, y 0}. Hessian matrix at x: H f (x) = ( α(α 1) x α 2 y β αβ x α 1 y β 1 αβ x α 1 y β 1 β(β 1) x α y β 2 ) Principle Minors: H 1 = α }{{} 0 (α 1) }{{} 0 x α 2 y β }{{} 0 0 H 2 = β }{{} 0 (β 1) }{{} 0 x α y β 2 }{{} 0 0 Josef Leydold Mathematical Methods WS 2018/19 13 Convex and Concave 32 / 44
33 Example Cobb-Douglas Function H 1,2 = H f (x) = α(α 1) x α 2 y β β(β 1) x α y β 2 (αβ x α 1 y β 1 ) 2 = α(α 1) β(β 1) x 2α 2 y 2β 2 α 2 β 2 x 2α 2 y 2β 2 = αβ[(α 1)(β 1) αβ]x 2α 2 y 2β 2 = αβ }{{} 0 (1 α β) }{{} 0 x 2α 2 y 2β 2 }{{} 0 0 H 1 0 and H 2 0, and H 1,2 0 for all (x, y) D. f (x, y) thus is concave in D. For 0 < α, β < 1 and α + β < 1 we even find: H 1 = H 1 < 0 and H 2 = H f (x) > 0 for almost all (x, y) D. f (x, y) is then strictly concave. Josef Leydold Mathematical Methods WS 2018/19 13 Convex and Concave 33 / 44
34 Lower Level Sets of Convex Functions Assume that f is convex. Then the lower level sets of f {x D f : f (x) c} are convex. y x 2 Let x 1, x 2 {x D f : f (x) c}, i.e., f (x 1 ), f (x 2 ) c. x 1 Then for y = (1 h)x 1 + hx 2 where h [0, 1] we find f (y) = f ((1 h)x 1 + hx 2 ) (1 h) f (x 1 ) + h f (x 2 ) (1 h)c + hc = c That is, y {x D f : f (x) c}, too. Josef Leydold Mathematical Methods WS 2018/19 13 Convex and Concave 34 / 44
35 Upper Level Sets of Concave Functions Assume that f is concave. Then the upper level sets of f {x D f : f (x) c} are convex. c c upper level set lower level set Josef Leydold Mathematical Methods WS 2018/19 13 Convex and Concave 35 / 44
36 Extremum and Monotone Transformation Let T : R R be a strictly monotonically increasing function. If x is a maximum of f, then x is also a maximum of T f. As x is a maximum of f, we have f (x ) f (x) for all x. As T is strictly monotonically increasing,we have T(x 1 ) > T(x 2 ) falls x 1 > x 2. Thus we find (T f )(x ) = T( f (x )) > T( f (x)) = (T f )(x) for all x, i.e., x is a maximum of T f. As T is one-to-one we also get the converse statement: If x is a maximum of T f, then it also is a maximum of f. Josef Leydold Mathematical Methods WS 2018/19 13 Convex and Concave 36 / 44
37 Extremum and Monotone Transformation A strictly monotonically increasing Transformation T preserves the extrema of f. Transformation T also preserves the level sets of f : e 4 e 1 e 9 f (x, y) = x 2 y 2 T( f (x, y)) = exp( x 2 y 2 ) Josef Leydold Mathematical Methods WS 2018/19 13 Convex and Concave 37 / 44
38 Quasi-Convex and Quasi-Concave Function f is called quasi-convex in D R n, if D is convex and every lower level set {x D f : f (x) c} is convex. Function f is called quasi-concave in D R n, if D is convex and every upper level set {x D f : f (x) c} is convex. Josef Leydold Mathematical Methods WS 2018/19 13 Convex and Concave 38 / 44
39 Convex and Quasi-Convex Every concave (convex) function also is quasi-concave (and quasi-convex, resp.). However, a quasi-concave function need not be concave. Let T be a strictly monotonically increasing function. If function f (x) is concave (convex), then T f is quasi-concave (and quasi-convex, resp.). Function g(x, y) = e x2 y 2 is quasi-concave, as f (x, y) = x 2 y 2 is concave and T(x) = e x is strictly monotonically increasing. However, g = T f is not concave. Josef Leydold Mathematical Methods WS 2018/19 13 Convex and Concave 39 / 44
40 A Weaker Condition The notion of quasi-convex is weaker than that of convex in the sense that every convex function also is quasi-convex but not vice versa. There are much more quasi-convex functions than convex ones. The importance of such a weaker notions is based on the observation that a couple of propositions still hold if convex is replaced by quasi-convex. In this way we get a generalization of a theorem, where a stronger condition is replaced by a weaker one. Josef Leydold Mathematical Methods WS 2018/19 13 Convex and Concave 40 / 44
41 Quasi-Convex and Quasi-Concave II Function f is quasi-convex if and only if f ((1 h)x 1 + hx 2 ) max{ f (x 1 ), f (x 2 )} for all x 1, x 2 and h [0, 1]. Function f is quasi-concave if and only if f ((1 h)x 1 + hx 2 ) min{ f (x 1 ), f (x 2 )} for all x 1, x 2 and h [0, 1]. x 2 x 1 x 1 x 2 quasi-convex quasi-concave Josef Leydold Mathematical Methods WS 2018/19 13 Convex and Concave 41 / 44
42 Strictly Quasi-Convex and Quasi-Concave Function f is called strictly quasi-convex if f ((1 h)x 1 + hx 2 ) < max{ f (x 1 ), f (x 2 )} for all x 1, x 2, with x 1 = x 2, and h (0, 1). Function f is called strictly quasi-concave if f ((1 h)x 1 + hx 2 ) > min{ f (x 1 ), f (x 2 )} for all x 1, x 2, with x 1 = x 2, and h (0, 1). Josef Leydold Mathematical Methods WS 2018/19 13 Convex and Concave 42 / 44
43 Quasi-convex and Quasi-Concave III For a differentiable function f we find: Function f is quasi-convex if and only if f (x) f (x 0 ) f (x 0 ) (x x 0 ) 0 Function f is quasi-concave if and only if f (x) f (x 0 ) f (x 0 ) (x x 0 ) 0 Josef Leydold Mathematical Methods WS 2018/19 13 Convex and Concave 43 / 44
44 Summary Monotone function Convex set Convex and concave function Minors of Hessian matrix Quasi-convex and quasi-concave function Josef Leydold Mathematical Methods WS 2018/19 13 Convex and Concave 44 / 44
Monotone Function. Function f is called monotonically increasing, if. x 1 x 2 f (x 1 ) f (x 2 ) x 1 < x 2 f (x 1 ) < f (x 2 ) x 1 x 2
 Monotone Function Function f is called monotonically increasing, if Chapter 3 x x 2 f (x ) f (x 2 ) It is called strictly monotonically increasing, if f (x 2) f (x ) Convex and Concave x < x 2 f (x )
Monotone Function Function f is called monotonically increasing, if Chapter 3 x x 2 f (x ) f (x 2 ) It is called strictly monotonically increasing, if f (x 2) f (x ) Convex and Concave x < x 2 f (x )
September Math Course: First Order Derivative
 September Math Course: First Order Derivative Arina Nikandrova Functions Function y = f (x), where x is either be a scalar or a vector of several variables (x,..., x n ), can be thought of as a rule which
September Math Course: First Order Derivative Arina Nikandrova Functions Function y = f (x), where x is either be a scalar or a vector of several variables (x,..., x n ), can be thought of as a rule which
Chapter 11. Taylor Series. Josef Leydold Mathematical Methods WS 2018/19 11 Taylor Series 1 / 27
 Chapter 11 Taylor Series Josef Leydold Mathematical Methods WS 2018/19 11 Taylor Series 1 / 27 First-Order Approximation We want to approximate function f by some simple function. Best possible approximation
Chapter 11 Taylor Series Josef Leydold Mathematical Methods WS 2018/19 11 Taylor Series 1 / 27 First-Order Approximation We want to approximate function f by some simple function. Best possible approximation
7) Important properties of functions: homogeneity, homotheticity, convexity and quasi-convexity
 30C00300 Mathematical Methods for Economists (6 cr) 7) Important properties of functions: homogeneity, homotheticity, convexity and quasi-convexity Abolfazl Keshvari Ph.D. Aalto University School of Business
30C00300 Mathematical Methods for Economists (6 cr) 7) Important properties of functions: homogeneity, homotheticity, convexity and quasi-convexity Abolfazl Keshvari Ph.D. Aalto University School of Business
4) Univariate and multivariate functions
 30C00300 Mathematical Methods for Economists (6 cr) 4) Univariate and multivariate functions Simon & Blume chapters: 13, 15 Slides originally by: Timo Kuosmanen Slides amended by: Anna Lukkarinen Lecture
30C00300 Mathematical Methods for Economists (6 cr) 4) Univariate and multivariate functions Simon & Blume chapters: 13, 15 Slides originally by: Timo Kuosmanen Slides amended by: Anna Lukkarinen Lecture
Chapter 6. Eigenvalues. Josef Leydold Mathematical Methods WS 2018/19 6 Eigenvalues 1 / 45
 Chapter 6 Eigenvalues Josef Leydold Mathematical Methods WS 2018/19 6 Eigenvalues 1 / 45 Closed Leontief Model In a closed Leontief input-output-model consumption and production coincide, i.e. V x = x
Chapter 6 Eigenvalues Josef Leydold Mathematical Methods WS 2018/19 6 Eigenvalues 1 / 45 Closed Leontief Model In a closed Leontief input-output-model consumption and production coincide, i.e. V x = x
HW3 - Due 02/06. Each answer must be mathematically justified. Don t forget your name. 1 2, A = 2 2
 HW3 - Due 02/06 Each answer must be mathematically justified Don t forget your name Problem 1 Find a 2 2 matrix B such that B 3 = A, where A = 2 2 If A was diagonal, it would be easy: we would just take
HW3 - Due 02/06 Each answer must be mathematically justified Don t forget your name Problem 1 Find a 2 2 matrix B such that B 3 = A, where A = 2 2 If A was diagonal, it would be easy: we would just take
1 Overview. 2 A Characterization of Convex Functions. 2.1 First-order Taylor approximation. AM 221: Advanced Optimization Spring 2016
 AM 221: Advanced Optimization Spring 2016 Prof. Yaron Singer Lecture 8 February 22nd 1 Overview In the previous lecture we saw characterizations of optimality in linear optimization, and we reviewed the
AM 221: Advanced Optimization Spring 2016 Prof. Yaron Singer Lecture 8 February 22nd 1 Overview In the previous lecture we saw characterizations of optimality in linear optimization, and we reviewed the
Static Problem Set 2 Solutions
 Static Problem Set Solutions Jonathan Kreamer July, 0 Question (i) Let g, h be two concave functions. Is f = g + h a concave function? Prove it. Yes. Proof: Consider any two points x, x and α [0, ]. Let
Static Problem Set Solutions Jonathan Kreamer July, 0 Question (i) Let g, h be two concave functions. Is f = g + h a concave function? Prove it. Yes. Proof: Consider any two points x, x and α [0, ]. Let
Chapter 2: Unconstrained Extrema
 Chapter 2: Unconstrained Extrema Math 368 c Copyright 2012, 2013 R Clark Robinson May 22, 2013 Chapter 2: Unconstrained Extrema 1 Types of Sets Definition For p R n and r > 0, the open ball about p of
Chapter 2: Unconstrained Extrema Math 368 c Copyright 2012, 2013 R Clark Robinson May 22, 2013 Chapter 2: Unconstrained Extrema 1 Types of Sets Definition For p R n and r > 0, the open ball about p of
Equations and Inequalities
 Chapter 3 Equations and Inequalities Josef Leydold Bridging Course Mathematics WS 2018/19 3 Equations and Inequalities 1 / 61 Equation We get an equation by equating two terms. l.h.s. = r.h.s. Domain:
Chapter 3 Equations and Inequalities Josef Leydold Bridging Course Mathematics WS 2018/19 3 Equations and Inequalities 1 / 61 Equation We get an equation by equating two terms. l.h.s. = r.h.s. Domain:
Mathematical Economics: Lecture 16
 Mathematical Economics: Lecture 16 Yu Ren WISE, Xiamen University November 26, 2012 Outline 1 Chapter 21: Concave and Quasiconcave Functions New Section Chapter 21: Concave and Quasiconcave Functions Concave
Mathematical Economics: Lecture 16 Yu Ren WISE, Xiamen University November 26, 2012 Outline 1 Chapter 21: Concave and Quasiconcave Functions New Section Chapter 21: Concave and Quasiconcave Functions Concave
Symmetric Matrices and Eigendecomposition
 Symmetric Matrices and Eigendecomposition Robert M. Freund January, 2014 c 2014 Massachusetts Institute of Technology. All rights reserved. 1 2 1 Symmetric Matrices and Convexity of Quadratic Functions
Symmetric Matrices and Eigendecomposition Robert M. Freund January, 2014 c 2014 Massachusetts Institute of Technology. All rights reserved. 1 2 1 Symmetric Matrices and Convexity of Quadratic Functions
Paul Schrimpf. October 18, UBC Economics 526. Unconstrained optimization. Paul Schrimpf. Notation and definitions. First order conditions
 Unconstrained UBC Economics 526 October 18, 2013 .1.2.3.4.5 Section 1 Unconstrained problem x U R n F : U R. max F (x) x U Definition F = max x U F (x) is the maximum of F on U if F (x) F for all x U and
Unconstrained UBC Economics 526 October 18, 2013 .1.2.3.4.5 Section 1 Unconstrained problem x U R n F : U R. max F (x) x U Definition F = max x U F (x) is the maximum of F on U if F (x) F for all x U and
Math (P)refresher Lecture 8: Unconstrained Optimization
 Math (P)refresher Lecture 8: Unconstrained Optimization September 2006 Today s Topics : Quadratic Forms Definiteness of Quadratic Forms Maxima and Minima in R n First Order Conditions Second Order Conditions
Math (P)refresher Lecture 8: Unconstrained Optimization September 2006 Today s Topics : Quadratic Forms Definiteness of Quadratic Forms Maxima and Minima in R n First Order Conditions Second Order Conditions
ECON 5111 Mathematical Economics
 Test 1 October 1, 2010 1. Construct a truth table for the following statement: [p (p q)] q. 2. A prime number is a natural number that is divisible by 1 and itself only. Let P be the set of all prime numbers
Test 1 October 1, 2010 1. Construct a truth table for the following statement: [p (p q)] q. 2. A prime number is a natural number that is divisible by 1 and itself only. Let P be the set of all prime numbers
Convex Functions and Optimization
 Chapter 5 Convex Functions and Optimization 5.1 Convex Functions Our next topic is that of convex functions. Again, we will concentrate on the context of a map f : R n R although the situation can be generalized
Chapter 5 Convex Functions and Optimization 5.1 Convex Functions Our next topic is that of convex functions. Again, we will concentrate on the context of a map f : R n R although the situation can be generalized
MATH 5720: Unconstrained Optimization Hung Phan, UMass Lowell September 13, 2018
 MATH 57: Unconstrained Optimization Hung Phan, UMass Lowell September 13, 18 1 Global and Local Optima Let a function f : S R be defined on a set S R n Definition 1 (minimizers and maximizers) (i) x S
MATH 57: Unconstrained Optimization Hung Phan, UMass Lowell September 13, 18 1 Global and Local Optima Let a function f : S R be defined on a set S R n Definition 1 (minimizers and maximizers) (i) x S
Mathematical Economics (ECON 471) Lecture 3 Calculus of Several Variables & Implicit Functions
 Mathematical Economics (ECON 471) Lecture 3 Calculus of Several Variables & Implicit Functions Teng Wah Leo 1 Calculus of Several Variables 11 Functions Mapping between Euclidean Spaces Where as in univariate
Mathematical Economics (ECON 471) Lecture 3 Calculus of Several Variables & Implicit Functions Teng Wah Leo 1 Calculus of Several Variables 11 Functions Mapping between Euclidean Spaces Where as in univariate
Econ 101A Problem Set 1 Solution
 Econ 101A Problem Set 1 Solution Problem 1. Univariate unconstrained maximization. (10 points) Consider the following maximization problem: max x f(x; x 0)=exp( (x x 0 ) 2 ) 1. Write down the first order
Econ 101A Problem Set 1 Solution Problem 1. Univariate unconstrained maximization. (10 points) Consider the following maximization problem: max x f(x; x 0)=exp( (x x 0 ) 2 ) 1. Write down the first order
EC /11. Math for Microeconomics September Course, Part II Problem Set 1 with Solutions. a11 a 12. x 2
 LONDON SCHOOL OF ECONOMICS Professor Leonardo Felli Department of Economics S.478; x7525 EC400 2010/11 Math for Microeconomics September Course, Part II Problem Set 1 with Solutions 1. Show that the general
LONDON SCHOOL OF ECONOMICS Professor Leonardo Felli Department of Economics S.478; x7525 EC400 2010/11 Math for Microeconomics September Course, Part II Problem Set 1 with Solutions 1. Show that the general
1 Directional Derivatives and Differentiability
 Wednesday, January 18, 2012 1 Directional Derivatives and Differentiability Let E R N, let f : E R and let x 0 E. Given a direction v R N, let L be the line through x 0 in the direction v, that is, L :=
Wednesday, January 18, 2012 1 Directional Derivatives and Differentiability Let E R N, let f : E R and let x 0 E. Given a direction v R N, let L be the line through x 0 in the direction v, that is, L :=
CHAPTER 4: HIGHER ORDER DERIVATIVES. Likewise, we may define the higher order derivatives. f(x, y, z) = xy 2 + e zx. y = 2xy.
 April 15, 2009 CHAPTER 4: HIGHER ORDER DERIVATIVES In this chapter D denotes an open subset of R n. 1. Introduction Definition 1.1. Given a function f : D R we define the second partial derivatives as
April 15, 2009 CHAPTER 4: HIGHER ORDER DERIVATIVES In this chapter D denotes an open subset of R n. 1. Introduction Definition 1.1. Given a function f : D R we define the second partial derivatives as
Convex Functions. Daniel P. Palomar. Hong Kong University of Science and Technology (HKUST)
 Convex Functions Daniel P. Palomar Hong Kong University of Science and Technology (HKUST) ELEC5470 - Convex Optimization Fall 2017-18, HKUST, Hong Kong Outline of Lecture Definition convex function Examples
Convex Functions Daniel P. Palomar Hong Kong University of Science and Technology (HKUST) ELEC5470 - Convex Optimization Fall 2017-18, HKUST, Hong Kong Outline of Lecture Definition convex function Examples
Lecture 2 - Unconstrained Optimization Definition[Global Minimum and Maximum]Let f : S R be defined on a set S R n. Then
![Lecture 2 - Unconstrained Optimization Definition[Global Minimum and Maximum]Let f : S R be defined on a set S R n. Then Lecture 2 - Unconstrained Optimization Definition[Global Minimum and Maximum]Let f : S R be defined on a set S R n. Then](/thumbs/86/93291808.jpg) Lecture 2 - Unconstrained Optimization Definition[Global Minimum and Maximum]Let f : S R be defined on a set S R n. Then 1. x S is a global minimum point of f over S if f (x) f (x ) for any x S. 2. x S
Lecture 2 - Unconstrained Optimization Definition[Global Minimum and Maximum]Let f : S R be defined on a set S R n. Then 1. x S is a global minimum point of f over S if f (x) f (x ) for any x S. 2. x S
MATH529 Fundamentals of Optimization Unconstrained Optimization II
 MATH529 Fundamentals of Optimization Unconstrained Optimization II Marco A. Montes de Oca Mathematical Sciences, University of Delaware, USA 1 / 31 Recap 2 / 31 Example Find the local and global minimizers
MATH529 Fundamentals of Optimization Unconstrained Optimization II Marco A. Montes de Oca Mathematical Sciences, University of Delaware, USA 1 / 31 Recap 2 / 31 Example Find the local and global minimizers
ARE211, Fall 2005 CONTENTS. 5. Characteristics of Functions Surjective, Injective and Bijective functions. 5.2.
 ARE211, Fall 2005 LECTURE #18: THU, NOV 3, 2005 PRINT DATE: NOVEMBER 22, 2005 (COMPSTAT2) CONTENTS 5. Characteristics of Functions. 1 5.1. Surjective, Injective and Bijective functions 1 5.2. Homotheticity
ARE211, Fall 2005 LECTURE #18: THU, NOV 3, 2005 PRINT DATE: NOVEMBER 22, 2005 (COMPSTAT2) CONTENTS 5. Characteristics of Functions. 1 5.1. Surjective, Injective and Bijective functions 1 5.2. Homotheticity
CHAPTER 2: CONVEX SETS AND CONCAVE FUNCTIONS. W. Erwin Diewert January 31, 2008.
 1 ECONOMICS 594: LECTURE NOTES CHAPTER 2: CONVEX SETS AND CONCAVE FUNCTIONS W. Erwin Diewert January 31, 2008. 1. Introduction Many economic problems have the following structure: (i) a linear function
1 ECONOMICS 594: LECTURE NOTES CHAPTER 2: CONVEX SETS AND CONCAVE FUNCTIONS W. Erwin Diewert January 31, 2008. 1. Introduction Many economic problems have the following structure: (i) a linear function
Here each term has degree 2 (the sum of exponents is 2 for all summands). A quadratic form of three variables looks as
 Reading [SB], Ch. 16.1-16.3, p. 375-393 1 Quadratic Forms A quadratic function f : R R has the form f(x) = a x. Generalization of this notion to two variables is the quadratic form Q(x 1, x ) = a 11 x
Reading [SB], Ch. 16.1-16.3, p. 375-393 1 Quadratic Forms A quadratic function f : R R has the form f(x) = a x. Generalization of this notion to two variables is the quadratic form Q(x 1, x ) = a 11 x
EC /11. Math for Microeconomics September Course, Part II Lecture Notes. Course Outline
 LONDON SCHOOL OF ECONOMICS Professor Leonardo Felli Department of Economics S.478; x7525 EC400 20010/11 Math for Microeconomics September Course, Part II Lecture Notes Course Outline Lecture 1: Tools for
LONDON SCHOOL OF ECONOMICS Professor Leonardo Felli Department of Economics S.478; x7525 EC400 20010/11 Math for Microeconomics September Course, Part II Lecture Notes Course Outline Lecture 1: Tools for
14 Lecture 14 Local Extrema of Function
 14 Lecture 14 Local Extrema of Function 14.1 Taylor s Formula with Lagrangian Remainder Term Theorem 14.1. Let n N {0} and f : (a,b) R. We assume that there exists f (n+1) (x) for all x (a,b). Then for
14 Lecture 14 Local Extrema of Function 14.1 Taylor s Formula with Lagrangian Remainder Term Theorem 14.1. Let n N {0} and f : (a,b) R. We assume that there exists f (n+1) (x) for all x (a,b). Then for
E 600 Chapter 3: Multivariate Calculus
 E 600 Chapter 3: Multivariate Calculus Simona Helmsmueller August 21, 2017 Goals of this lecture: Know when an inverse to a function exists, be able to graphically and analytically determine whether a
E 600 Chapter 3: Multivariate Calculus Simona Helmsmueller August 21, 2017 Goals of this lecture: Know when an inverse to a function exists, be able to graphically and analytically determine whether a
Mathematical Economics. Lecture Notes (in extracts)
 Prof. Dr. Frank Werner Faculty of Mathematics Institute of Mathematical Optimization (IMO) http://math.uni-magdeburg.de/ werner/math-ec-new.html Mathematical Economics Lecture Notes (in extracts) Winter
Prof. Dr. Frank Werner Faculty of Mathematics Institute of Mathematical Optimization (IMO) http://math.uni-magdeburg.de/ werner/math-ec-new.html Mathematical Economics Lecture Notes (in extracts) Winter
A A x i x j i j (i, j) (j, i) Let. Compute the value of for and
 7.2 - Quadratic Forms quadratic form on is a function defined on whose value at a vector in can be computed by an expression of the form, where is an symmetric matrix. The matrix R n Q R n x R n Q(x) =
7.2 - Quadratic Forms quadratic form on is a function defined on whose value at a vector in can be computed by an expression of the form, where is an symmetric matrix. The matrix R n Q R n x R n Q(x) =
z = f (x; y) f (x ; y ) f (x; y) f (x; y )
 BEEM0 Optimization Techiniques for Economists Lecture Week 4 Dieter Balkenborg Departments of Economics University of Exeter Since the fabric of the universe is most perfect, and is the work of a most
BEEM0 Optimization Techiniques for Economists Lecture Week 4 Dieter Balkenborg Departments of Economics University of Exeter Since the fabric of the universe is most perfect, and is the work of a most
MATHEMATICS FOR ECONOMISTS. Course Convener. Contact: Office-Hours: X and Y. Teaching Assistant ATIYEH YEGANLOO
 INTRODUCTION TO QUANTITATIVE METHODS IN ECONOMICS MATHEMATICS FOR ECONOMISTS Course Convener DR. ALESSIA ISOPI Contact: alessia.isopi@manchester.ac.uk Office-Hours: X and Y Teaching Assistant ATIYEH YEGANLOO
INTRODUCTION TO QUANTITATIVE METHODS IN ECONOMICS MATHEMATICS FOR ECONOMISTS Course Convener DR. ALESSIA ISOPI Contact: alessia.isopi@manchester.ac.uk Office-Hours: X and Y Teaching Assistant ATIYEH YEGANLOO
Chapter 7. Extremal Problems. 7.1 Extrema and Local Extrema
 Chapter 7 Extremal Problems No matter in theoretical context or in applications many problems can be formulated as problems of finding the maximum or minimum of a function. Whenever this is the case, advanced
Chapter 7 Extremal Problems No matter in theoretical context or in applications many problems can be formulated as problems of finding the maximum or minimum of a function. Whenever this is the case, advanced
ECON2285: Mathematical Economics
 ECON2285: Mathematical Economics Yulei Luo Economics, HKU September 17, 2018 Luo, Y. (Economics, HKU) ME September 17, 2018 1 / 46 Static Optimization and Extreme Values In this topic, we will study goal
ECON2285: Mathematical Economics Yulei Luo Economics, HKU September 17, 2018 Luo, Y. (Economics, HKU) ME September 17, 2018 1 / 46 Static Optimization and Extreme Values In this topic, we will study goal
Lecture 8: Basic convex analysis
 Lecture 8: Basic convex analysis 1 Convex sets Both convex sets and functions have general importance in economic theory, not only in optimization. Given two points x; y 2 R n and 2 [0; 1]; the weighted
Lecture 8: Basic convex analysis 1 Convex sets Both convex sets and functions have general importance in economic theory, not only in optimization. Given two points x; y 2 R n and 2 [0; 1]; the weighted
Chapter 3: Constrained Extrema
 Chapter 3: Constrained Extrema Math 368 c Copyright 2012, 2013 R Clark Robinson May 22, 2013 Chapter 3: Constrained Extrema 1 Implicit Function Theorem For scalar fn g : R n R with g(x ) 0 and g(x ) =
Chapter 3: Constrained Extrema Math 368 c Copyright 2012, 2013 R Clark Robinson May 22, 2013 Chapter 3: Constrained Extrema 1 Implicit Function Theorem For scalar fn g : R n R with g(x ) 0 and g(x ) =
Lecture 2: Convex Sets and Functions
 Lecture 2: Convex Sets and Functions Hyang-Won Lee Dept. of Internet & Multimedia Eng. Konkuk University Lecture 2 Network Optimization, Fall 2015 1 / 22 Optimization Problems Optimization problems are
Lecture 2: Convex Sets and Functions Hyang-Won Lee Dept. of Internet & Multimedia Eng. Konkuk University Lecture 2 Network Optimization, Fall 2015 1 / 22 Optimization Problems Optimization problems are
1 Convexity, concavity and quasi-concavity. (SB )
 UNIVERSITY OF MARYLAND ECON 600 Summer 2010 Lecture Two: Unconstrained Optimization 1 Convexity, concavity and quasi-concavity. (SB 21.1-21.3.) For any two points, x, y R n, we can trace out the line of
UNIVERSITY OF MARYLAND ECON 600 Summer 2010 Lecture Two: Unconstrained Optimization 1 Convexity, concavity and quasi-concavity. (SB 21.1-21.3.) For any two points, x, y R n, we can trace out the line of
Announcements. Topics: Homework: - sections , 6.1 (extreme values) * Read these sections and study solved examples in your textbook!
 Announcements Topics: - sections 5.2 5.7, 6.1 (extreme values) * Read these sections and study solved examples in your textbook! Homework: - review lecture notes thoroughly - work on practice problems
Announcements Topics: - sections 5.2 5.7, 6.1 (extreme values) * Read these sections and study solved examples in your textbook! Homework: - review lecture notes thoroughly - work on practice problems
Constrained Optimization and Lagrangian Duality
 CIS 520: Machine Learning Oct 02, 2017 Constrained Optimization and Lagrangian Duality Lecturer: Shivani Agarwal Disclaimer: These notes are designed to be a supplement to the lecture. They may or may
CIS 520: Machine Learning Oct 02, 2017 Constrained Optimization and Lagrangian Duality Lecturer: Shivani Agarwal Disclaimer: These notes are designed to be a supplement to the lecture. They may or may
2.6 Logarithmic Functions. Inverse Functions. Question: What is the relationship between f(x) = x 2 and g(x) = x?
 Inverse Functions Question: What is the relationship between f(x) = x 3 and g(x) = 3 x? Question: What is the relationship between f(x) = x 2 and g(x) = x? Definition (One-to-One Function) A function f
Inverse Functions Question: What is the relationship between f(x) = x 3 and g(x) = 3 x? Question: What is the relationship between f(x) = x 2 and g(x) = x? Definition (One-to-One Function) A function f
MA102: Multivariable Calculus
 MA102: Multivariable Calculus Rupam Barman and Shreemayee Bora Department of Mathematics IIT Guwahati Differentiability of f : U R n R m Definition: Let U R n be open. Then f : U R n R m is differentiable
MA102: Multivariable Calculus Rupam Barman and Shreemayee Bora Department of Mathematics IIT Guwahati Differentiability of f : U R n R m Definition: Let U R n be open. Then f : U R n R m is differentiable
Week 4: Calculus and Optimization (Jehle and Reny, Chapter A2)
 Week 4: Calculus and Optimization (Jehle and Reny, Chapter A2) Tsun-Feng Chiang *School of Economics, Henan University, Kaifeng, China September 27, 2015 Microeconomic Theory Week 4: Calculus and Optimization
Week 4: Calculus and Optimization (Jehle and Reny, Chapter A2) Tsun-Feng Chiang *School of Economics, Henan University, Kaifeng, China September 27, 2015 Microeconomic Theory Week 4: Calculus and Optimization
1. Algebra and Functions
 1. Algebra and Functions 1.1.1 Equations and Inequalities 1.1.2 The Quadratic Formula 1.1.3 Exponentials and Logarithms 1.2 Introduction to Functions 1.3 Domain and Range 1.4.1 Graphing Functions 1.4.2
1. Algebra and Functions 1.1.1 Equations and Inequalities 1.1.2 The Quadratic Formula 1.1.3 Exponentials and Logarithms 1.2 Introduction to Functions 1.3 Domain and Range 1.4.1 Graphing Functions 1.4.2
x +3y 2t = 1 2x +y +z +t = 2 3x y +z t = 7 2x +6y +z +t = a
 UCM Final Exam, 05/8/014 Solutions 1 Given the parameter a R, consider the following linear system x +y t = 1 x +y +z +t = x y +z t = 7 x +6y +z +t = a (a (6 points Discuss the system depending on the
UCM Final Exam, 05/8/014 Solutions 1 Given the parameter a R, consider the following linear system x +y t = 1 x +y +z +t = x y +z t = 7 x +6y +z +t = a (a (6 points Discuss the system depending on the
where u is the decision-maker s payoff function over her actions and S is the set of her feasible actions.
 Seminars on Mathematics for Economics and Finance Topic 3: Optimization - interior optima 1 Session: 11-12 Aug 2015 (Thu/Fri) 10:00am 1:00pm I. Optimization: introduction Decision-makers (e.g. consumers,
Seminars on Mathematics for Economics and Finance Topic 3: Optimization - interior optima 1 Session: 11-12 Aug 2015 (Thu/Fri) 10:00am 1:00pm I. Optimization: introduction Decision-makers (e.g. consumers,
Review of Optimization Methods
 Review of Optimization Methods Prof. Manuela Pedio 20550 Quantitative Methods for Finance August 2018 Outline of the Course Lectures 1 and 2 (3 hours, in class): Linear and non-linear functions on Limits,
Review of Optimization Methods Prof. Manuela Pedio 20550 Quantitative Methods for Finance August 2018 Outline of the Course Lectures 1 and 2 (3 hours, in class): Linear and non-linear functions on Limits,
Section 3.9. The Geometry of Graphs. Difference Equations to Differential Equations
 Difference Equations to Differential Equations Section 3.9 The Geometry of Graphs In Section. we discussed the graph of a function y = f(x) in terms of plotting points (x, f(x)) for many different values
Difference Equations to Differential Equations Section 3.9 The Geometry of Graphs In Section. we discussed the graph of a function y = f(x) in terms of plotting points (x, f(x)) for many different values
Lecture 4: Optimization. Maximizing a function of a single variable
 Lecture 4: Optimization Maximizing or Minimizing a Function of a Single Variable Maximizing or Minimizing a Function of Many Variables Constrained Optimization Maximizing a function of a single variable
Lecture 4: Optimization Maximizing or Minimizing a Function of a Single Variable Maximizing or Minimizing a Function of Many Variables Constrained Optimization Maximizing a function of a single variable
March 25, 2010 CHAPTER 2: LIMITS AND CONTINUITY OF FUNCTIONS IN EUCLIDEAN SPACE
 March 25, 2010 CHAPTER 2: LIMIT AND CONTINUITY OF FUNCTION IN EUCLIDEAN PACE 1. calar product in R n Definition 1.1. Given x = (x 1,..., x n ), y = (y 1,..., y n ) R n,we define their scalar product as
March 25, 2010 CHAPTER 2: LIMIT AND CONTINUITY OF FUNCTION IN EUCLIDEAN PACE 1. calar product in R n Definition 1.1. Given x = (x 1,..., x n ), y = (y 1,..., y n ) R n,we define their scalar product as
Transpose & Dot Product
 Transpose & Dot Product Def: The transpose of an m n matrix A is the n m matrix A T whose columns are the rows of A. So: The columns of A T are the rows of A. The rows of A T are the columns of A. Example:
Transpose & Dot Product Def: The transpose of an m n matrix A is the n m matrix A T whose columns are the rows of A. So: The columns of A T are the rows of A. The rows of A T are the columns of A. Example:
Structural and Multidisciplinary Optimization. P. Duysinx and P. Tossings
 Structural and Multidisciplinary Optimization P. Duysinx and P. Tossings 2018-2019 CONTACTS Pierre Duysinx Institut de Mécanique et du Génie Civil (B52/3) Phone number: 04/366.91.94 Email: P.Duysinx@uliege.be
Structural and Multidisciplinary Optimization P. Duysinx and P. Tossings 2018-2019 CONTACTS Pierre Duysinx Institut de Mécanique et du Génie Civil (B52/3) Phone number: 04/366.91.94 Email: P.Duysinx@uliege.be
Computational Optimization. Mathematical Programming Fundamentals 1/25 (revised)
 Computational Optimization Mathematical Programming Fundamentals 1/5 (revised) If you don t know where you are going, you probably won t get there. -from some book I read in eight grade If you do get there,
Computational Optimization Mathematical Programming Fundamentals 1/5 (revised) If you don t know where you are going, you probably won t get there. -from some book I read in eight grade If you do get there,
STUDY MATERIALS. (The content of the study material is the same as that of Chapter I of Mathematics for Economic Analysis II of 2011 Admn.
 STUDY MATERIALS MATHEMATICAL TOOLS FOR ECONOMICS III (The content of the study material is the same as that of Chapter I of Mathematics for Economic Analysis II of 2011 Admn.) & MATHEMATICAL TOOLS FOR
STUDY MATERIALS MATHEMATICAL TOOLS FOR ECONOMICS III (The content of the study material is the same as that of Chapter I of Mathematics for Economic Analysis II of 2011 Admn.) & MATHEMATICAL TOOLS FOR
Nonlinear Programming (NLP)
 Natalia Lazzati Mathematics for Economics (Part I) Note 6: Nonlinear Programming - Unconstrained Optimization Note 6 is based on de la Fuente (2000, Ch. 7), Madden (1986, Ch. 3 and 5) and Simon and Blume
Natalia Lazzati Mathematics for Economics (Part I) Note 6: Nonlinear Programming - Unconstrained Optimization Note 6 is based on de la Fuente (2000, Ch. 7), Madden (1986, Ch. 3 and 5) and Simon and Blume
APPENDIX A. Background Mathematics. A.1 Linear Algebra. Vector algebra. Let x denote the n-dimensional column vector with components x 1 x 2.
 APPENDIX A Background Mathematics A. Linear Algebra A.. Vector algebra Let x denote the n-dimensional column vector with components 0 x x 2 B C @. A x n Definition 6 (scalar product). The scalar product
APPENDIX A Background Mathematics A. Linear Algebra A.. Vector algebra Let x denote the n-dimensional column vector with components 0 x x 2 B C @. A x n Definition 6 (scalar product). The scalar product
3. Convex functions. basic properties and examples. operations that preserve convexity. the conjugate function. quasiconvex functions
 3. Convex functions Convex Optimization Boyd & Vandenberghe basic properties and examples operations that preserve convexity the conjugate function quasiconvex functions log-concave and log-convex functions
3. Convex functions Convex Optimization Boyd & Vandenberghe basic properties and examples operations that preserve convexity the conjugate function quasiconvex functions log-concave and log-convex functions
Microeconomics I. September, c Leopold Sögner
 Microeconomics I c Leopold Sögner Department of Economics and Finance Institute for Advanced Studies Stumpergasse 56 1060 Wien Tel: +43-1-59991 182 soegner@ihs.ac.at http://www.ihs.ac.at/ soegner September,
Microeconomics I c Leopold Sögner Department of Economics and Finance Institute for Advanced Studies Stumpergasse 56 1060 Wien Tel: +43-1-59991 182 soegner@ihs.ac.at http://www.ihs.ac.at/ soegner September,
Math 117: Honours Calculus I Fall, 2002 List of Theorems. a n k b k. k. Theorem 2.1 (Convergent Bounded) A convergent sequence is bounded.
 Math 117: Honours Calculus I Fall, 2002 List of Theorems Theorem 1.1 (Binomial Theorem) For all n N, (a + b) n = n k=0 ( ) n a n k b k. k Theorem 2.1 (Convergent Bounded) A convergent sequence is bounded.
Math 117: Honours Calculus I Fall, 2002 List of Theorems Theorem 1.1 (Binomial Theorem) For all n N, (a + b) n = n k=0 ( ) n a n k b k. k Theorem 2.1 (Convergent Bounded) A convergent sequence is bounded.
Transpose & Dot Product
 Transpose & Dot Product Def: The transpose of an m n matrix A is the n m matrix A T whose columns are the rows of A. So: The columns of A T are the rows of A. The rows of A T are the columns of A. Example:
Transpose & Dot Product Def: The transpose of an m n matrix A is the n m matrix A T whose columns are the rows of A. So: The columns of A T are the rows of A. The rows of A T are the columns of A. Example:
AP Calculus Testbank (Chapter 9) (Mr. Surowski)
 AP Calculus Testbank (Chapter 9) (Mr. Surowski) Part I. Multiple-Choice Questions n 1 1. The series will converge, provided that n 1+p + n + 1 (A) p > 1 (B) p > 2 (C) p >.5 (D) p 0 2. The series
AP Calculus Testbank (Chapter 9) (Mr. Surowski) Part I. Multiple-Choice Questions n 1 1. The series will converge, provided that n 1+p + n + 1 (A) p > 1 (B) p > 2 (C) p >.5 (D) p 0 2. The series
, b = 0. (2) 1 2 The eigenvectors of A corresponding to the eigenvalues λ 1 = 1, λ 2 = 3 are
 Quadratic forms We consider the quadratic function f : R 2 R defined by f(x) = 2 xt Ax b T x with x = (x, x 2 ) T, () where A R 2 2 is symmetric and b R 2. We will see that, depending on the eigenvalues
Quadratic forms We consider the quadratic function f : R 2 R defined by f(x) = 2 xt Ax b T x with x = (x, x 2 ) T, () where A R 2 2 is symmetric and b R 2. We will see that, depending on the eigenvalues
MATH2070 Optimisation
 MATH2070 Optimisation Nonlinear optimisation with constraints Semester 2, 2012 Lecturer: I.W. Guo Lecture slides courtesy of J.R. Wishart Review The full nonlinear optimisation problem with equality constraints
MATH2070 Optimisation Nonlinear optimisation with constraints Semester 2, 2012 Lecturer: I.W. Guo Lecture slides courtesy of J.R. Wishart Review The full nonlinear optimisation problem with equality constraints
MATHEMATICAL ECONOMICS: OPTIMIZATION. Contents
 MATHEMATICAL ECONOMICS: OPTIMIZATION JOÃO LOPES DIAS Contents 1. Introduction 2 1.1. Preliminaries 2 1.2. Optimal points and values 2 1.3. The optimization problems 3 1.4. Existence of optimal points 4
MATHEMATICAL ECONOMICS: OPTIMIZATION JOÃO LOPES DIAS Contents 1. Introduction 2 1.1. Preliminaries 2 1.2. Optimal points and values 2 1.3. The optimization problems 3 1.4. Existence of optimal points 4
Functions of Several Variables
 Jim Lambers MAT 419/519 Summer Session 2011-12 Lecture 2 Notes These notes correspond to Section 1.2 in the text. Functions of Several Variables We now generalize the results from the previous section,
Jim Lambers MAT 419/519 Summer Session 2011-12 Lecture 2 Notes These notes correspond to Section 1.2 in the text. Functions of Several Variables We now generalize the results from the previous section,
Exponential Functions:
 Exponential Functions: An exponential function has the form f (x) = b x where b is a fixed positive number, called the base. Math 101-Calculus 1 (Sklensky) In-Class Work January 29, 2015 1 / 12 Exponential
Exponential Functions: An exponential function has the form f (x) = b x where b is a fixed positive number, called the base. Math 101-Calculus 1 (Sklensky) In-Class Work January 29, 2015 1 / 12 Exponential
Definitions & Theorems
 Definitions & Theorems Math 147, Fall 2009 December 19, 2010 Contents 1 Logic 2 1.1 Sets.................................................. 2 1.2 The Peano axioms..........................................
Definitions & Theorems Math 147, Fall 2009 December 19, 2010 Contents 1 Logic 2 1.1 Sets.................................................. 2 1.2 The Peano axioms..........................................
Tvestlanka Karagyozova University of Connecticut
 September, 005 CALCULUS REVIEW Tvestlanka Karagyozova University of Connecticut. FUNCTIONS.. Definition: A function f is a rule that associates each value of one variable with one and only one value of
September, 005 CALCULUS REVIEW Tvestlanka Karagyozova University of Connecticut. FUNCTIONS.. Definition: A function f is a rule that associates each value of one variable with one and only one value of
Preliminary draft only: please check for final version
 ARE211, Fall2012 CALCULUS4: THU, OCT 11, 2012 PRINTED: AUGUST 22, 2012 (LEC# 15) Contents 3. Univariate and Multivariate Differentiation (cont) 1 3.6. Taylor s Theorem (cont) 2 3.7. Applying Taylor theory:
ARE211, Fall2012 CALCULUS4: THU, OCT 11, 2012 PRINTED: AUGUST 22, 2012 (LEC# 15) Contents 3. Univariate and Multivariate Differentiation (cont) 1 3.6. Taylor s Theorem (cont) 2 3.7. Applying Taylor theory:
Week 3: Sets and Mappings/Calculus and Optimization (Jehle September and Reny, 20, 2015 Chapter A1/A2)
 Week 3: Sets and Mappings/Calculus and Optimization (Jehle and Reny, Chapter A1/A2) Tsun-Feng Chiang *School of Economics, Henan University, Kaifeng, China September 20, 2015 Week 3: Sets and Mappings/Calculus
Week 3: Sets and Mappings/Calculus and Optimization (Jehle and Reny, Chapter A1/A2) Tsun-Feng Chiang *School of Economics, Henan University, Kaifeng, China September 20, 2015 Week 3: Sets and Mappings/Calculus
7.4* General logarithmic and exponential functions
 7.4* General logarithmic and exponential functions Mark Woodard Furman U Fall 2010 Mark Woodard (Furman U) 7.4* General logarithmic and exponential functions Fall 2010 1 / 9 Outline 1 General exponential
7.4* General logarithmic and exponential functions Mark Woodard Furman U Fall 2010 Mark Woodard (Furman U) 7.4* General logarithmic and exponential functions Fall 2010 1 / 9 Outline 1 General exponential
Basics of Calculus and Algebra
 Monika Department of Economics ISCTE-IUL September 2012 Basics of linear algebra Real valued Functions Differential Calculus Integral Calculus Optimization Introduction I A matrix is a rectangular array
Monika Department of Economics ISCTE-IUL September 2012 Basics of linear algebra Real valued Functions Differential Calculus Integral Calculus Optimization Introduction I A matrix is a rectangular array
Fundamentals of Unconstrained Optimization
 dalmau@cimat.mx Centro de Investigación en Matemáticas CIMAT A.C. Mexico Enero 2016 Outline Introduction 1 Introduction 2 3 4 Optimization Problem min f (x) x Ω where f (x) is a real-valued function The
dalmau@cimat.mx Centro de Investigación en Matemáticas CIMAT A.C. Mexico Enero 2016 Outline Introduction 1 Introduction 2 3 4 Optimization Problem min f (x) x Ω where f (x) is a real-valued function The
Tangent spaces, normals and extrema
 Chapter 3 Tangent spaces, normals and extrema If S is a surface in 3-space, with a point a S where S looks smooth, i.e., without any fold or cusp or self-crossing, we can intuitively define the tangent
Chapter 3 Tangent spaces, normals and extrema If S is a surface in 3-space, with a point a S where S looks smooth, i.e., without any fold or cusp or self-crossing, we can intuitively define the tangent
Semi-definite representibility. For fun and profit
 Semi-definite representation For fun and profit March 9, 2010 Introduction Any convex quadratic constraint x T C T Cx a + b T x Can be recast as the linear matrix inequality (LMI): ( ) In Cx (Cx) T a +
Semi-definite representation For fun and profit March 9, 2010 Introduction Any convex quadratic constraint x T C T Cx a + b T x Can be recast as the linear matrix inequality (LMI): ( ) In Cx (Cx) T a +
Chapter 2: Preliminaries and elements of convex analysis
 Chapter 2: Preliminaries and elements of convex analysis Edoardo Amaldi DEIB Politecnico di Milano edoardo.amaldi@polimi.it Website: http://home.deib.polimi.it/amaldi/opt-14-15.shtml Academic year 2014-15
Chapter 2: Preliminaries and elements of convex analysis Edoardo Amaldi DEIB Politecnico di Milano edoardo.amaldi@polimi.it Website: http://home.deib.polimi.it/amaldi/opt-14-15.shtml Academic year 2014-15
Unconstrained optimization
 Chapter 4 Unconstrained optimization An unconstrained optimization problem takes the form min x Rnf(x) (4.1) for a target functional (also called objective function) f : R n R. In this chapter and throughout
Chapter 4 Unconstrained optimization An unconstrained optimization problem takes the form min x Rnf(x) (4.1) for a target functional (also called objective function) f : R n R. In this chapter and throughout
Module 7 : Applications of Integration - I. Lecture 20 : Definition of the power function and logarithmic function with positive base [Section 20.
 Module 7 : Applications of Integration - I Lecture 20 : Definition of the power function and logarithmic function with positive base [Section 201] Objectives In this section you will learn the following
Module 7 : Applications of Integration - I Lecture 20 : Definition of the power function and logarithmic function with positive base [Section 201] Objectives In this section you will learn the following
Lecture 4: Convex Functions, Part I February 1
 IE 521: Convex Optimization Instructor: Niao He Lecture 4: Convex Functions, Part I February 1 Spring 2017, UIUC Scribe: Shuanglong Wang Courtesy warning: These notes do not necessarily cover everything
IE 521: Convex Optimization Instructor: Niao He Lecture 4: Convex Functions, Part I February 1 Spring 2017, UIUC Scribe: Shuanglong Wang Courtesy warning: These notes do not necessarily cover everything
BEEM103 UNIVERSITY OF EXETER. BUSINESS School. January 2009 Mock Exam, Part A. OPTIMIZATION TECHNIQUES FOR ECONOMISTS solutions
 BEEM03 UNIVERSITY OF EXETER BUSINESS School January 009 Mock Exam, Part A OPTIMIZATION TECHNIQUES FOR ECONOMISTS solutions Duration : TWO HOURS The paper has 3 parts. Your marks on the rst part will be
BEEM03 UNIVERSITY OF EXETER BUSINESS School January 009 Mock Exam, Part A OPTIMIZATION TECHNIQUES FOR ECONOMISTS solutions Duration : TWO HOURS The paper has 3 parts. Your marks on the rst part will be
5 More on Linear Algebra
 14.102, Math for Economists Fall 2004 Lecture Notes, 9/23/2004 These notes are primarily based on those written by George Marios Angeletos for the Harvard Math Camp in 1999 and 2000, and updated by Stavros
14.102, Math for Economists Fall 2004 Lecture Notes, 9/23/2004 These notes are primarily based on those written by George Marios Angeletos for the Harvard Math Camp in 1999 and 2000, and updated by Stavros
Boston College. Math Review Session (2nd part) Lecture Notes August,2007. Nadezhda Karamcheva www2.bc.
 Boston College Math Review Session (2nd part) Lecture Notes August,2007 Nadezhda Karamcheva karamche@bc.edu www2.bc.edu/ karamche 1 Contents 1 Quadratic Forms and Definite Matrices 3 1.1 Quadratic Forms.........................
Boston College Math Review Session (2nd part) Lecture Notes August,2007 Nadezhda Karamcheva karamche@bc.edu www2.bc.edu/ karamche 1 Contents 1 Quadratic Forms and Definite Matrices 3 1.1 Quadratic Forms.........................
EC400 Math for Microeconomics Syllabus The course is based on 6 sixty minutes lectures and on 6 ninety minutes classes.
 London School of Economics Department of Economics Dr Francesco Nava Offi ce: 32L.3.20 EC400 Math for Microeconomics Syllabus 2016 The course is based on 6 sixty minutes lectures and on 6 ninety minutes
London School of Economics Department of Economics Dr Francesco Nava Offi ce: 32L.3.20 EC400 Math for Microeconomics Syllabus 2016 The course is based on 6 sixty minutes lectures and on 6 ninety minutes
Convex Optimization. Convex Analysis - Functions
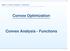 Convex Optimization Convex Analsis - Functions p. 1 A function f : K R n R is convex, if K is a convex set and x, K,x, λ (,1) we have f(λx+(1 λ)) λf(x)+(1 λ)f(). (x, f(x)) (,f()) x - strictl convex,
Convex Optimization Convex Analsis - Functions p. 1 A function f : K R n R is convex, if K is a convex set and x, K,x, λ (,1) we have f(λx+(1 λ)) λf(x)+(1 λ)f(). (x, f(x)) (,f()) x - strictl convex,
Introduction. Josef Leydold Mathematical Methods WS 2018/19 Introduction 1 / 27
 Introduction Josef Leydold Mathematical Methods WS 2018/19 Introduction 1 / 27 Literature ALPHA C. CHIANG, KEVIN WAINWRIGHT Fundamental Methods of Mathematical Economics McGraw-Hill, 2005. KNUT SYDSÆTER,
Introduction Josef Leydold Mathematical Methods WS 2018/19 Introduction 1 / 27 Literature ALPHA C. CHIANG, KEVIN WAINWRIGHT Fundamental Methods of Mathematical Economics McGraw-Hill, 2005. KNUT SYDSÆTER,
Session: 09 Aug 2016 (Tue), 10:00am 1:00pm; 10 Aug 2016 (Wed), 10:00am 1:00pm &3:00pm 5:00pm (Revision)
 Seminars on Mathematics for Economics and Finance Topic 2: Topics in multivariate calculus, concavity and convexity 1 Session: 09 Aug 2016 (Tue), 10:00am 1:00pm; 10 Aug 2016 (Wed), 10:00am 1:00pm &3:00pm
Seminars on Mathematics for Economics and Finance Topic 2: Topics in multivariate calculus, concavity and convexity 1 Session: 09 Aug 2016 (Tue), 10:00am 1:00pm; 10 Aug 2016 (Wed), 10:00am 1:00pm &3:00pm
MATH 1A, Complete Lecture Notes. Fedor Duzhin
 MATH 1A, Complete Lecture Notes Fedor Duzhin 2007 Contents I Limit 6 1 Sets and Functions 7 1.1 Sets................................. 7 1.2 Functions.............................. 8 1.3 How to define a
MATH 1A, Complete Lecture Notes Fedor Duzhin 2007 Contents I Limit 6 1 Sets and Functions 7 1.1 Sets................................. 7 1.2 Functions.............................. 8 1.3 How to define a
EC9A0: Pre-sessional Advanced Mathematics Course. Lecture Notes: Unconstrained Optimisation By Pablo F. Beker 1
 EC9A0: Pre-sessional Advanced Mathematics Course Lecture Notes: Unconstrained Optimisation By Pablo F. Beker 1 1 Infimum and Supremum Definition 1. Fix a set Y R. A number α R is an upper bound of Y if
EC9A0: Pre-sessional Advanced Mathematics Course Lecture Notes: Unconstrained Optimisation By Pablo F. Beker 1 1 Infimum and Supremum Definition 1. Fix a set Y R. A number α R is an upper bound of Y if
Chapter 2 Invertible Mappings
 Chapter 2 Invertible Mappings 2. Injective, Surjective and Bijective Mappings Given the map f : A B, and I A, theset f (I ) ={f (x) : x I } is called the image of I under f.ifi = A, then f (A) is called
Chapter 2 Invertible Mappings 2. Injective, Surjective and Bijective Mappings Given the map f : A B, and I A, theset f (I ) ={f (x) : x I } is called the image of I under f.ifi = A, then f (A) is called
3.5 Quadratic Approximation and Convexity/Concavity
 3.5 Quadratic Approximation and Convexity/Concavity 55 3.5 Quadratic Approximation and Convexity/Concavity Overview: Second derivatives are useful for understanding how the linear approximation varies
3.5 Quadratic Approximation and Convexity/Concavity 55 3.5 Quadratic Approximation and Convexity/Concavity Overview: Second derivatives are useful for understanding how the linear approximation varies
Math Matrix Algebra
 Math 44 - Matrix Algebra Review notes - (Alberto Bressan, Spring 7) sec: Orthogonal diagonalization of symmetric matrices When we seek to diagonalize a general n n matrix A, two difficulties may arise:
Math 44 - Matrix Algebra Review notes - (Alberto Bressan, Spring 7) sec: Orthogonal diagonalization of symmetric matrices When we seek to diagonalize a general n n matrix A, two difficulties may arise:
Logarithmic, Exponential, and Other Transcendental Functions
 5 Logarithmic, Exponential, and Other Transcendental Functions Copyright Cengage Learning. All rights reserved. 1 5.3 Inverse Functions Copyright Cengage Learning. All rights reserved. 2 Objectives Verify
5 Logarithmic, Exponential, and Other Transcendental Functions Copyright Cengage Learning. All rights reserved. 1 5.3 Inverse Functions Copyright Cengage Learning. All rights reserved. 2 Objectives Verify
The general programming problem is the nonlinear programming problem where a given function is maximized subject to a set of inequality constraints.
 1 Optimization Mathematical programming refers to the basic mathematical problem of finding a maximum to a function, f, subject to some constraints. 1 In other words, the objective is to find a point,
1 Optimization Mathematical programming refers to the basic mathematical problem of finding a maximum to a function, f, subject to some constraints. 1 In other words, the objective is to find a point,
Chapter 3 Prerequisite Skills. Chapter 3 Prerequisite Skills Question 1 Page 148. a) Let f (x) = x 3 + 2x 2 + 2x +1. b) Let f (z) = z 3 6z 4.
 Chapter 3 Curve Sketching Chapter 3 Prerequisite Skills Chapter 3 Prerequisite Skills Question 1 Page 148 a) Let f (x) = x 3 + 2x 2 + 2x +1. f (1) = 6 f (Ğ1) = 0 (x +1) is a factor. x 3 + 2x 2 + 2x +1
Chapter 3 Curve Sketching Chapter 3 Prerequisite Skills Chapter 3 Prerequisite Skills Question 1 Page 148 a) Let f (x) = x 3 + 2x 2 + 2x +1. f (1) = 6 f (Ğ1) = 0 (x +1) is a factor. x 3 + 2x 2 + 2x +1
LINEAR ALGEBRA (PMTH213) Tutorial Questions
 Tutorial Questions The tutorial exercises range from revision and routine practice, through lling in details in the notes, to applications of the theory. While the tutorial problems are not compulsory,
Tutorial Questions The tutorial exercises range from revision and routine practice, through lling in details in the notes, to applications of the theory. While the tutorial problems are not compulsory,
The Strong Largeur d Arborescence
 The Strong Largeur d Arborescence Rik Steenkamp (5887321) November 12, 2013 Master Thesis Supervisor: prof.dr. Monique Laurent Local Supervisor: prof.dr. Alexander Schrijver KdV Institute for Mathematics
The Strong Largeur d Arborescence Rik Steenkamp (5887321) November 12, 2013 Master Thesis Supervisor: prof.dr. Monique Laurent Local Supervisor: prof.dr. Alexander Schrijver KdV Institute for Mathematics
