2) case we obtained a zero determinant when one row was a multiple of the other (or is the same as the other), and this remains true of the (3 3)
|
|
|
- Osborn Gregory
- 5 years ago
- Views:
Transcription
1 Section 11 Rank and Linear Dependence In an early section, we learnt that the number of solutions in a system of linear equations depends on the number of independent equations in the system relative to the number of unknowns From Cramer s Rule, we learnt that a system of n -linear equations in n -unknowns will have a unique solution only when the determinant of the coefficient matrix is not zero When will the determinant of a matrix be zero? This has a lot to do with the linear dependence in the coefficient matrix The presence of any zero row or column will produce a zero determinant (this is easy to verify: just use the Laplace expansion along that zero row or column) In the (2 2) case we obtained a zero determinant when one row was a multiple of the other (or is the same as the other), and this remains true of the (33) case A more subtle case is when one row is a linear combination of the other two (ie, we can write one row as the sum of some multiple of a second row plus some multiple of the third) For instance, take the matrix Α which you can verify has a zero determinant Here the third row is equal to the first row plus half of the second row: (Alternatively, we can say that the first row is the third row minus half of the second or that the second row is two times the third row minus two times the first) We say that the three row vectors that make up the matrix are linearly dependent This linear dependence between the rows leads to a zero determinant because it means that row operations can be applied to ultimately create a zero row A (3 3) matrix will have a non-zero determinant only if it has three linearly independent rows (or columns) More generally, think of a (3 3) square matrix as a stack of three row vectors A
2 A a a 2 a21 a22 a23 a We say that three (column or row) vectors a 1, a 2, and a 3 there are constants c 1, c 2, and c 3, not all zero, such that c a c a c a are linearly dependent if If the only case where this is true is c1 c2 c3 0, then the vectors are said to be linearly independent For now, define the rank of the matrix is the number of linearly independent row vectors that it contains Examples 1 Let A Let a, a, and a Then these vectors are linearly dependent, since a1 a2 a 3 The second row is just twice that of the first row (or the first is half of the second) Removing one of the dependent vectors, say a , the remaining vectors a1 and a 3 are linearly independent: the only constants c1 and c2 such that c c are c 1 c 2 0 The matrix has two linear independent vectors, and is said to be of rank 2 If we imagine these three vectors in the usual representation as arrows in threedimensional co-ordinate space, we will see that the vector a2 is just an extension of a 1 Combinations of the three vectors are effectively combinations of only two vectors c a c a c a c a c 2( a c2) a c c a c a Different combinations of the three vectors will therefore result in new vectors that all lie on a plane (a two-dimensional space), and cannot span or cover the entire 3-d space 2 Let A Let a, a, and a Then these vectors are linearly dependent, since a1 a2 a 3 The second row depends on the other two in that it is the sum of a1 and a
3 (Equivalently, a 3 depends on a1 and a 2 because it is a2 a 1) Removing one of these dependent vectors (any one of them) leaves two independent vectors For instance, removing a 3, then the only constants c 1 and c 2 such that c a c a c c are c 1 c 2 0 The matrix has two linear independent vectors, and is said to be of rank 2 If we imagine these three vectors geometrically in three-dimensional co-ordinate space, we will see that although no one vector is an extension of another, all three vectors nonetheless lie in a single plane, so again combinations of the three vectors will create new vectors that also lie on that plane The three vectors cannot span, or cover, the entire 3-d space 3 Let A Let a, a, and a Then these vectors are linearly dependent, since In this case, there is only one linearly independent vector If we remove a 3, we find that the remaining two are still linearly dependent: a2 is twice that of a 1 The rank of this matrix is one: rank() A 1 Geometrically, all three vectors lie on a single line The vector a2 is twice that of a 1, and a3 is three times that of a 1 Combinations of these vectors therefore will only create new vectors that are also extensions of a 1 c a c a c a c a c 2a c 3( a 2 c 3) c c a Let A Let a, a, and a Then these vectors are linearly dependent, since c a 0 a 0 a for any c 1 Removing vector a1 leaves two linearly independent vectors The rank of this matrix is two 11-3
4 5 Let A Let a, a, and a Then all three row vectors are linearly independent; it is impossible to find c 1, c2 and c 3, not all zero, such that c1a 1 c2a2 c3a This matrix is of full rank A square matrix will have a non-zero determinant if and only if ( iff ) it has full rank There are many ways to determine the rank of a matrix One way is to do Gaussian Elimation ( the row operations) and see how many non-zero pivots you get (see Section 2 for pivots ) Other ways will be discussed in later sections, or in more advanced classes For the time being we will proceed by observation We conclude this section with several remarks regarding rank Earlier, we viewed a matrix as a stack of row vectors The rank concept that we discussed could be called row rank But we can also view a matrix as the concatenation (joining together) of three column vectors a a a a 21 a 22 a 23 a31 a23 a 33 A 1 Everything that we said here follows for column vectors as for row vectors, and in fact a matrix will have the same number of linearly independent column vectors as there are linearly independent row vectors: if A has two linearly independent row vectors, it will also have two linearly independent column vectors; if it has only one linearly independent row vector, then it will one have one linearly independent column vector, and so on A matrix s row rank is the same as its column rank 2 We can also speak of the rank of non-square matrices Take for example A This is in fact the last two rows of an earlier example we were looking at Looking at the rows, we see that these two rows are linearly independent (verify!) The row - rank is two What if we view this matrix as a concatenation of three two-dimensional vectors? Note that three two-dimensional vectors can only span a two-dimensional 11-4
5 space Draw three two dimensional vectors on a x - y co-ordinate space on a piece of paper Can you generate a three-dimensional space from this? (The answer is no) If we observe the three vectors we observe that these do span the entire two-dimensional plane So the column rank of this matrix is also 2 The principle that a matrix s row and column ranks are the same continues to hold, and holds generally As another illustration, consider A It is easy to see that the row rank of this matrix is one, and the column rank of this matrix is also one Because the row and column ranks are always the same, we can always speak unambiguously of the rank of a matrix Furthermore, 6 3 rank() A min(#rows, #columns) 3 Finally, we often need to find the rank of a product Here are two very useful results: 3a If A is ()m n and B is ()n p, then rank() AB min((),()) rank A rank B Proof Let C AB Every column of C is some linear combination of the columns of A, therefore the columns in C cannot span a space of dimension greater than the column rank of A Similarly, every row of C is some linear combination of the rows of B, therefore the rows in C cannot span a space of dimension greater than the row rank of B Since row rank and column rank are the same, we have our result 3b If A is ()m n and B is ()n n rank()() AB and full rank, then rank A 11-5
6 Proof If x min( a,) b, then obviously x a and x b are both true Since we have rank() AB min((),()) rank A rank B 1 1 rank()() A rank[ ABB exists since Bis full rank] B min((),) rank AB B rank() AB min((),()) rank A rank() A 1 rank This extends to the product CAB where both C and B are full rank: Exercises B rank()() CAB rank A 1 Find the determinants of the following matrices using the Laplace expansion If you find the determinant of a matrix to be zero, find out how many linear independent rows the matrix has (i) (ii) (iii) (vi) Show using the formula that the determinant of a (33) (i) one row is a multiple of another; matrix will be zero if (ii) one row is a linear combination of the other two 3 Show that T rank()() A A rank A 11-6
Linear Algebra Exam 1 Spring 2007
 Linear Algebra Exam 1 Spring 2007 March 15, 2007 Name: SOLUTION KEY (Total 55 points, plus 5 more for Pledged Assignment.) Honor Code Statement: Directions: Complete all problems. Justify all answers/solutions.
Linear Algebra Exam 1 Spring 2007 March 15, 2007 Name: SOLUTION KEY (Total 55 points, plus 5 more for Pledged Assignment.) Honor Code Statement: Directions: Complete all problems. Justify all answers/solutions.
Getting Started with Communications Engineering
 1 Linear algebra is the algebra of linear equations: the term linear being used in the same sense as in linear functions, such as: which is the equation of a straight line. y ax c (0.1) Of course, if we
1 Linear algebra is the algebra of linear equations: the term linear being used in the same sense as in linear functions, such as: which is the equation of a straight line. y ax c (0.1) Of course, if we
Department of Aerospace Engineering AE602 Mathematics for Aerospace Engineers Assignment No. 4
 Department of Aerospace Engineering AE6 Mathematics for Aerospace Engineers Assignment No.. Decide whether or not the following vectors are linearly independent, by solving c v + c v + c 3 v 3 + c v :
Department of Aerospace Engineering AE6 Mathematics for Aerospace Engineers Assignment No.. Decide whether or not the following vectors are linearly independent, by solving c v + c v + c 3 v 3 + c v :
MITOCW ocw f99-lec09_300k
 MITOCW ocw-18.06-f99-lec09_300k OK, this is linear algebra lecture nine. And this is a key lecture, this is where we get these ideas of linear independence, when a bunch of vectors are independent -- or
MITOCW ocw-18.06-f99-lec09_300k OK, this is linear algebra lecture nine. And this is a key lecture, this is where we get these ideas of linear independence, when a bunch of vectors are independent -- or
Linear Algebra. Preliminary Lecture Notes
 Linear Algebra Preliminary Lecture Notes Adolfo J. Rumbos c Draft date May 9, 29 2 Contents 1 Motivation for the course 5 2 Euclidean n dimensional Space 7 2.1 Definition of n Dimensional Euclidean Space...........
Linear Algebra Preliminary Lecture Notes Adolfo J. Rumbos c Draft date May 9, 29 2 Contents 1 Motivation for the course 5 2 Euclidean n dimensional Space 7 2.1 Definition of n Dimensional Euclidean Space...........
Math 33A Discussion Notes
 Math 33A Discussion Notes Jean-Michel Maldague October 21, 2017 Week 3 Incomplete! Will update soon. - A function T : R k R n is called injective, or one-to-one, if each input gets a unique output. The
Math 33A Discussion Notes Jean-Michel Maldague October 21, 2017 Week 3 Incomplete! Will update soon. - A function T : R k R n is called injective, or one-to-one, if each input gets a unique output. The
Linear Algebra. Preliminary Lecture Notes
 Linear Algebra Preliminary Lecture Notes Adolfo J. Rumbos c Draft date April 29, 23 2 Contents Motivation for the course 5 2 Euclidean n dimensional Space 7 2. Definition of n Dimensional Euclidean Space...........
Linear Algebra Preliminary Lecture Notes Adolfo J. Rumbos c Draft date April 29, 23 2 Contents Motivation for the course 5 2 Euclidean n dimensional Space 7 2. Definition of n Dimensional Euclidean Space...........
(II.B) Basis and dimension
 (II.B) Basis and dimension How would you explain that a plane has two dimensions? Well, you can go in two independent directions, and no more. To make this idea precise, we formulate the DEFINITION 1.
(II.B) Basis and dimension How would you explain that a plane has two dimensions? Well, you can go in two independent directions, and no more. To make this idea precise, we formulate the DEFINITION 1.
[Disclaimer: This is not a complete list of everything you need to know, just some of the topics that gave people difficulty.]
![[Disclaimer: This is not a complete list of everything you need to know, just some of the topics that gave people difficulty.] [Disclaimer: This is not a complete list of everything you need to know, just some of the topics that gave people difficulty.]](/thumbs/82/86615903.jpg) Math 43 Review Notes [Disclaimer: This is not a complete list of everything you need to know, just some of the topics that gave people difficulty Dot Product If v (v, v, v 3 and w (w, w, w 3, then the
Math 43 Review Notes [Disclaimer: This is not a complete list of everything you need to know, just some of the topics that gave people difficulty Dot Product If v (v, v, v 3 and w (w, w, w 3, then the
MATH SOLUTIONS TO PRACTICE PROBLEMS - MIDTERM I. 1. We carry out row reduction. We begin with the row operations
 MATH 2 - SOLUTIONS TO PRACTICE PROBLEMS - MIDTERM I. We carry out row reduction. We begin with the row operations yielding the matrix This is already upper triangular hence The lower triangular matrix
MATH 2 - SOLUTIONS TO PRACTICE PROBLEMS - MIDTERM I. We carry out row reduction. We begin with the row operations yielding the matrix This is already upper triangular hence The lower triangular matrix
Section 1.5. Solution Sets of Linear Systems
 Section 1.5 Solution Sets of Linear Systems Plan For Today Today we will learn to describe and draw the solution set of an arbitrary system of linear equations Ax = b, using spans. Ax = b Recall: the solution
Section 1.5 Solution Sets of Linear Systems Plan For Today Today we will learn to describe and draw the solution set of an arbitrary system of linear equations Ax = b, using spans. Ax = b Recall: the solution
3. Vector spaces 3.1 Linear dependence and independence 3.2 Basis and dimension. 5. Extreme points and basic feasible solutions
 A. LINEAR ALGEBRA. CONVEX SETS 1. Matrices and vectors 1.1 Matrix operations 1.2 The rank of a matrix 2. Systems of linear equations 2.1 Basic solutions 3. Vector spaces 3.1 Linear dependence and independence
A. LINEAR ALGEBRA. CONVEX SETS 1. Matrices and vectors 1.1 Matrix operations 1.2 The rank of a matrix 2. Systems of linear equations 2.1 Basic solutions 3. Vector spaces 3.1 Linear dependence and independence
ANALYTICAL MATHEMATICS FOR APPLICATIONS 2018 LECTURE NOTES 3
 ANALYTICAL MATHEMATICS FOR APPLICATIONS 2018 LECTURE NOTES 3 ISSUED 24 FEBRUARY 2018 1 Gaussian elimination Let A be an (m n)-matrix Consider the following row operations on A (1) Swap the positions any
ANALYTICAL MATHEMATICS FOR APPLICATIONS 2018 LECTURE NOTES 3 ISSUED 24 FEBRUARY 2018 1 Gaussian elimination Let A be an (m n)-matrix Consider the following row operations on A (1) Swap the positions any
NOTES FOR LINEAR ALGEBRA 133
 NOTES FOR LINEAR ALGEBRA 33 William J Anderson McGill University These are not official notes for Math 33 identical to the notes projected in class They are intended for Anderson s section 4, and are 2
NOTES FOR LINEAR ALGEBRA 33 William J Anderson McGill University These are not official notes for Math 33 identical to the notes projected in class They are intended for Anderson s section 4, and are 2
1 Matrices and Systems of Linear Equations
 Linear Algebra (part ) : Matrices and Systems of Linear Equations (by Evan Dummit, 207, v 260) Contents Matrices and Systems of Linear Equations Systems of Linear Equations Elimination, Matrix Formulation
Linear Algebra (part ) : Matrices and Systems of Linear Equations (by Evan Dummit, 207, v 260) Contents Matrices and Systems of Linear Equations Systems of Linear Equations Elimination, Matrix Formulation
Chapter 4. Solving Systems of Equations. Chapter 4
 Solving Systems of Equations 3 Scenarios for Solutions There are three general situations we may find ourselves in when attempting to solve systems of equations: 1 The system could have one unique solution.
Solving Systems of Equations 3 Scenarios for Solutions There are three general situations we may find ourselves in when attempting to solve systems of equations: 1 The system could have one unique solution.
Advanced Engineering Mathematics Prof. Pratima Panigrahi Department of Mathematics Indian Institute of Technology, Kharagpur
 Advanced Engineering Mathematics Prof. Pratima Panigrahi Department of Mathematics Indian Institute of Technology, Kharagpur Lecture No. # 02 Vector Spaces, Subspaces, linearly Dependent/Independent of
Advanced Engineering Mathematics Prof. Pratima Panigrahi Department of Mathematics Indian Institute of Technology, Kharagpur Lecture No. # 02 Vector Spaces, Subspaces, linearly Dependent/Independent of
Second Midterm Exam April 14, 2011 Answers., and
 Mathematics 34, Spring Problem ( points) (a) Consider the matrices all matrices. Second Midterm Exam April 4, Answers [ Do these matrices span M? ] [, ] [, and Lectures & (Wilson) ], as vectors in the
Mathematics 34, Spring Problem ( points) (a) Consider the matrices all matrices. Second Midterm Exam April 4, Answers [ Do these matrices span M? ] [, ] [, and Lectures & (Wilson) ], as vectors in the
Warm-up. True or false? Baby proof. 2. The system of normal equations for A x = y has solutions iff A x = y has solutions
 Warm-up True or false? 1. proj u proj v u = u 2. The system of normal equations for A x = y has solutions iff A x = y has solutions 3. The normal equations are always consistent Baby proof 1. Let A be
Warm-up True or false? 1. proj u proj v u = u 2. The system of normal equations for A x = y has solutions iff A x = y has solutions 3. The normal equations are always consistent Baby proof 1. Let A be
Linear transformations
 Linear Algebra with Computer Science Application February 5, 208 Review. Review: linear combinations Given vectors v, v 2,..., v p in R n and scalars c, c 2,..., c p, the vector w defined by w = c v +
Linear Algebra with Computer Science Application February 5, 208 Review. Review: linear combinations Given vectors v, v 2,..., v p in R n and scalars c, c 2,..., c p, the vector w defined by w = c v +
Linear Programming and its Extensions Prof. Prabha Shrama Department of Mathematics and Statistics Indian Institute of Technology, Kanpur
 Linear Programming and its Extensions Prof. Prabha Shrama Department of Mathematics and Statistics Indian Institute of Technology, Kanpur Lecture No. # 03 Moving from one basic feasible solution to another,
Linear Programming and its Extensions Prof. Prabha Shrama Department of Mathematics and Statistics Indian Institute of Technology, Kanpur Lecture No. # 03 Moving from one basic feasible solution to another,
Solution Set 4, Fall 12
 Solution Set 4, 18.06 Fall 12 1. Do Problem 7 from 3.6. Solution. Since the matrix is invertible, we know the nullspace contains only the zero vector, hence there does not exist a basis for this subspace.
Solution Set 4, 18.06 Fall 12 1. Do Problem 7 from 3.6. Solution. Since the matrix is invertible, we know the nullspace contains only the zero vector, hence there does not exist a basis for this subspace.
Linear Algebra (part 1) : Matrices and Systems of Linear Equations (by Evan Dummit, 2016, v. 2.02)
 Linear Algebra (part ) : Matrices and Systems of Linear Equations (by Evan Dummit, 206, v 202) Contents 2 Matrices and Systems of Linear Equations 2 Systems of Linear Equations 2 Elimination, Matrix Formulation
Linear Algebra (part ) : Matrices and Systems of Linear Equations (by Evan Dummit, 206, v 202) Contents 2 Matrices and Systems of Linear Equations 2 Systems of Linear Equations 2 Elimination, Matrix Formulation
can only hit 3 points in the codomain. Hence, f is not surjective. For another example, if n = 4
 .. Conditions for Injectivity and Surjectivity In this section, we discuss what we can say about linear maps T : R n R m given only m and n. We motivate this problem by looking at maps f : {,..., n} {,...,
.. Conditions for Injectivity and Surjectivity In this section, we discuss what we can say about linear maps T : R n R m given only m and n. We motivate this problem by looking at maps f : {,..., n} {,...,
Constrained and Unconstrained Optimization Prof. Adrijit Goswami Department of Mathematics Indian Institute of Technology, Kharagpur
 Constrained and Unconstrained Optimization Prof. Adrijit Goswami Department of Mathematics Indian Institute of Technology, Kharagpur Lecture - 01 Introduction to Optimization Today, we will start the constrained
Constrained and Unconstrained Optimization Prof. Adrijit Goswami Department of Mathematics Indian Institute of Technology, Kharagpur Lecture - 01 Introduction to Optimization Today, we will start the constrained
Finite Element Analysis Prof. Dr. B. N. Rao Department of Civil Engineering Indian Institute of Technology, Madras. Module - 01 Lecture - 11
 Finite Element Analysis Prof. Dr. B. N. Rao Department of Civil Engineering Indian Institute of Technology, Madras Module - 01 Lecture - 11 Last class, what we did is, we looked at a method called superposition
Finite Element Analysis Prof. Dr. B. N. Rao Department of Civil Engineering Indian Institute of Technology, Madras Module - 01 Lecture - 11 Last class, what we did is, we looked at a method called superposition
Math 3A Winter 2016 Midterm
 Math 3A Winter 016 Midterm Name Signature UCI ID # E-mail address There are 7 problems for a total of 115 points. Present your work as clearly as possible. Partial credit will be awarded, and you must
Math 3A Winter 016 Midterm Name Signature UCI ID # E-mail address There are 7 problems for a total of 115 points. Present your work as clearly as possible. Partial credit will be awarded, and you must
if b is a linear combination of u, v, w, i.e., if we can find scalars r, s, t so that ru + sv + tw = 0.
 Solutions Review # Math 7 Instructions: Use the following problems to study for Exam # which will be held Wednesday Sept For a set of nonzero vectors u v w} in R n use words and/or math expressions to
Solutions Review # Math 7 Instructions: Use the following problems to study for Exam # which will be held Wednesday Sept For a set of nonzero vectors u v w} in R n use words and/or math expressions to
GEOMETRY OF MATRICES x 1
 GEOMETRY OF MATRICES. SPACES OF VECTORS.. Definition of R n. The space R n consists of all column vectors with n components. The components are real numbers... Representation of Vectors in R n.... R. The
GEOMETRY OF MATRICES. SPACES OF VECTORS.. Definition of R n. The space R n consists of all column vectors with n components. The components are real numbers... Representation of Vectors in R n.... R. The
Volume in n Dimensions
 Volume in n Dimensions MA 305 Kurt Bryan Introduction You ve seen that if we have two vectors v and w in two dimensions then the area spanned by these vectors can be computed as v w = v 1 w 2 v 2 w 1 (where
Volume in n Dimensions MA 305 Kurt Bryan Introduction You ve seen that if we have two vectors v and w in two dimensions then the area spanned by these vectors can be computed as v w = v 1 w 2 v 2 w 1 (where
Sections 1.5, 1.7. Ma 322 Fall Ma 322. Sept
 Sections 1.5, 1.7 Ma 322 Fall 213 Ma 322 Sept. 9-13 Summary ˆ Solutions of homogeneous equations AX =. ˆ Using the rank. ˆ Parametric solution of AX = B. ˆ Linear dependence and independence of vectors
Sections 1.5, 1.7 Ma 322 Fall 213 Ma 322 Sept. 9-13 Summary ˆ Solutions of homogeneous equations AX =. ˆ Using the rank. ˆ Parametric solution of AX = B. ˆ Linear dependence and independence of vectors
M. Matrices and Linear Algebra
 M. Matrices and Linear Algebra. Matrix algebra. In section D we calculated the determinants of square arrays of numbers. Such arrays are important in mathematics and its applications; they are called matrices.
M. Matrices and Linear Algebra. Matrix algebra. In section D we calculated the determinants of square arrays of numbers. Such arrays are important in mathematics and its applications; they are called matrices.
1111: Linear Algebra I
 1111: Linear Algebra I Dr. Vladimir Dotsenko (Vlad) Lecture 13 Dr. Vladimir Dotsenko (Vlad) 1111: Linear Algebra I Lecture 13 1 / 8 The coordinate vector space R n We already used vectors in n dimensions
1111: Linear Algebra I Dr. Vladimir Dotsenko (Vlad) Lecture 13 Dr. Vladimir Dotsenko (Vlad) 1111: Linear Algebra I Lecture 13 1 / 8 The coordinate vector space R n We already used vectors in n dimensions
Fall Inverse of a matrix. Institute: UC San Diego. Authors: Alexander Knop
 Fall 2017 Inverse of a matrix Authors: Alexander Knop Institute: UC San Diego Row-Column Rule If the product AB is defined, then the entry in row i and column j of AB is the sum of the products of corresponding
Fall 2017 Inverse of a matrix Authors: Alexander Knop Institute: UC San Diego Row-Column Rule If the product AB is defined, then the entry in row i and column j of AB is the sum of the products of corresponding
18.06 Problem Set 3 Solution Due Wednesday, 25 February 2009 at 4 pm in Total: 160 points.
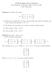 8.6 Problem Set 3 Solution Due Wednesday, 25 February 29 at 4 pm in 2-6. Total: 6 points. Problem : Consider the matrix A = 2 4 2 6 3 4 2 7 (a) Reduce A to echelon form U, find a special solution for each
8.6 Problem Set 3 Solution Due Wednesday, 25 February 29 at 4 pm in 2-6. Total: 6 points. Problem : Consider the matrix A = 2 4 2 6 3 4 2 7 (a) Reduce A to echelon form U, find a special solution for each
Homework Set #8 Solutions
 Exercises.2 (p. 19) Homework Set #8 Solutions Assignment: Do #6, 8, 12, 14, 2, 24, 26, 29, 0, 2, 4, 5, 6, 9, 40, 42 6. Reducing the matrix to echelon form: 1 5 2 1 R2 R2 R1 1 5 0 18 12 2 1 R R 2R1 1 5
Exercises.2 (p. 19) Homework Set #8 Solutions Assignment: Do #6, 8, 12, 14, 2, 24, 26, 29, 0, 2, 4, 5, 6, 9, 40, 42 6. Reducing the matrix to echelon form: 1 5 2 1 R2 R2 R1 1 5 0 18 12 2 1 R R 2R1 1 5
Math 54 HW 4 solutions
 Math 54 HW 4 solutions 2.2. Section 2.2 (a) False: Recall that performing a series of elementary row operations A is equivalent to multiplying A by a series of elementary matrices. Suppose that E,...,
Math 54 HW 4 solutions 2.2. Section 2.2 (a) False: Recall that performing a series of elementary row operations A is equivalent to multiplying A by a series of elementary matrices. Suppose that E,...,
Sections 1.5, 1.7. Ma 322 Spring Ma 322. Jan 24-28
 Sections 1.5, 1.7 Ma 322 Spring 217 Ma 322 Jan 24-28 Summary ˆ Text: Solution Sets of Linear Systems (1.5),Linear Independence (1.7) ˆ Solutions of homogeneous equations AX =. ˆ Using the rank. ˆ Parametric
Sections 1.5, 1.7 Ma 322 Spring 217 Ma 322 Jan 24-28 Summary ˆ Text: Solution Sets of Linear Systems (1.5),Linear Independence (1.7) ˆ Solutions of homogeneous equations AX =. ˆ Using the rank. ˆ Parametric
Working with Block Structured Matrices
 Working with Block Structured Matrices Numerical linear algebra lies at the heart of modern scientific computing and computational science. Today it is not uncommon to perform numerical computations with
Working with Block Structured Matrices Numerical linear algebra lies at the heart of modern scientific computing and computational science. Today it is not uncommon to perform numerical computations with
MTHSC 3110 Section 1.1
 MTHSC 3110 Section 1.1 Kevin James A system of linear equations is a collection of equations in the same set of variables. For example, { x 1 + 3x 2 = 5 2x 1 x 2 = 4 Of course, since this is a pair of
MTHSC 3110 Section 1.1 Kevin James A system of linear equations is a collection of equations in the same set of variables. For example, { x 1 + 3x 2 = 5 2x 1 x 2 = 4 Of course, since this is a pair of
MATH 2360 REVIEW PROBLEMS
 MATH 2360 REVIEW PROBLEMS Problem 1: In (a) (d) below, either compute the matrix product or indicate why it does not exist: ( )( ) 1 2 2 1 (a) 0 1 1 2 ( ) 0 1 2 (b) 0 3 1 4 3 4 5 2 5 (c) 0 3 ) 1 4 ( 1
MATH 2360 REVIEW PROBLEMS Problem 1: In (a) (d) below, either compute the matrix product or indicate why it does not exist: ( )( ) 1 2 2 1 (a) 0 1 1 2 ( ) 0 1 2 (b) 0 3 1 4 3 4 5 2 5 (c) 0 3 ) 1 4 ( 1
MATH 2331 Linear Algebra. Section 2.1 Matrix Operations. Definition: A : m n, B : n p. Example: Compute AB, if possible.
 MATH 2331 Linear Algebra Section 2.1 Matrix Operations Definition: A : m n, B : n p ( 1 2 p ) ( 1 2 p ) AB = A b b b = Ab Ab Ab Example: Compute AB, if possible. 1 Row-column rule: i-j-th entry of AB:
MATH 2331 Linear Algebra Section 2.1 Matrix Operations Definition: A : m n, B : n p ( 1 2 p ) ( 1 2 p ) AB = A b b b = Ab Ab Ab Example: Compute AB, if possible. 1 Row-column rule: i-j-th entry of AB:
Chapter 1: Linear Equations
 Chapter : Linear Equations (Last Updated: September, 7) The material for these notes is derived primarily from Linear Algebra and its applications by David Lay (4ed).. Systems of Linear Equations Before
Chapter : Linear Equations (Last Updated: September, 7) The material for these notes is derived primarily from Linear Algebra and its applications by David Lay (4ed).. Systems of Linear Equations Before
Mon Feb Matrix algebra and matrix inverses. Announcements: Warm-up Exercise:
 Math 2270-004 Week 5 notes We will not necessarily finish the material from a given day's notes on that day We may also add or subtract some material as the week progresses, but these notes represent an
Math 2270-004 Week 5 notes We will not necessarily finish the material from a given day's notes on that day We may also add or subtract some material as the week progresses, but these notes represent an
ARE211, Fall2012. Contents. 2. Linear Algebra (cont) Vector Spaces Spanning, Dimension, Basis Matrices and Rank 8
 ARE211, Fall2012 LINALGEBRA2: TUE, SEP 18, 2012 PRINTED: SEPTEMBER 27, 2012 (LEC# 8) Contents 2. Linear Algebra (cont) 1 2.6. Vector Spaces 1 2.7. Spanning, Dimension, Basis 3 2.8. Matrices and Rank 8
ARE211, Fall2012 LINALGEBRA2: TUE, SEP 18, 2012 PRINTED: SEPTEMBER 27, 2012 (LEC# 8) Contents 2. Linear Algebra (cont) 1 2.6. Vector Spaces 1 2.7. Spanning, Dimension, Basis 3 2.8. Matrices and Rank 8
Math 205, Summer I, Week 3a (continued): Chapter 4, Sections 5 and 6. Week 3b. Chapter 4, [Sections 7], 8 and 9
![Math 205, Summer I, Week 3a (continued): Chapter 4, Sections 5 and 6. Week 3b. Chapter 4, [Sections 7], 8 and 9 Math 205, Summer I, Week 3a (continued): Chapter 4, Sections 5 and 6. Week 3b. Chapter 4, [Sections 7], 8 and 9](/thumbs/88/117660928.jpg) Math 205, Summer I, 2016 Week 3a (continued): Chapter 4, Sections 5 and 6. Week 3b Chapter 4, [Sections 7], 8 and 9 4.5 Linear Dependence, Linear Independence 4.6 Bases and Dimension 4.7 Change of Basis,
Math 205, Summer I, 2016 Week 3a (continued): Chapter 4, Sections 5 and 6. Week 3b Chapter 4, [Sections 7], 8 and 9 4.5 Linear Dependence, Linear Independence 4.6 Bases and Dimension 4.7 Change of Basis,
MATH 1553, SPRING 2018 SAMPLE MIDTERM 2 (VERSION B), 1.7 THROUGH 2.9
 MATH 155, SPRING 218 SAMPLE MIDTERM 2 (VERSION B), 1.7 THROUGH 2.9 Name Section 1 2 4 5 Total Please read all instructions carefully before beginning. Each problem is worth 1 points. The maximum score
MATH 155, SPRING 218 SAMPLE MIDTERM 2 (VERSION B), 1.7 THROUGH 2.9 Name Section 1 2 4 5 Total Please read all instructions carefully before beginning. Each problem is worth 1 points. The maximum score
Chapter 3. Directions: For questions 1-11 mark each statement True or False. Justify each answer.
 Chapter 3 Directions: For questions 1-11 mark each statement True or False. Justify each answer. 1. (True False) Asking whether the linear system corresponding to an augmented matrix [ a 1 a 2 a 3 b ]
Chapter 3 Directions: For questions 1-11 mark each statement True or False. Justify each answer. 1. (True False) Asking whether the linear system corresponding to an augmented matrix [ a 1 a 2 a 3 b ]
MATH 221: SOLUTIONS TO SELECTED HOMEWORK PROBLEMS
 MATH 221: SOLUTIONS TO SELECTED HOMEWORK PROBLEMS 1. HW 1: Due September 4 1.1.21. Suppose v, w R n and c is a scalar. Prove that Span(v + cw, w) = Span(v, w). We must prove two things: that every element
MATH 221: SOLUTIONS TO SELECTED HOMEWORK PROBLEMS 1. HW 1: Due September 4 1.1.21. Suppose v, w R n and c is a scalar. Prove that Span(v + cw, w) = Span(v, w). We must prove two things: that every element
which are not all zero. The proof in the case where some vector other than combination of the other vectors in S is similar.
 It follows that S is linearly dependent since the equation is satisfied by which are not all zero. The proof in the case where some vector other than combination of the other vectors in S is similar. is
It follows that S is linearly dependent since the equation is satisfied by which are not all zero. The proof in the case where some vector other than combination of the other vectors in S is similar. is
We see that this is a linear system with 3 equations in 3 unknowns. equation is A x = b, where
 Practice Problems Math 35 Spring 7: Solutions. Write the system of equations as a matrix equation and find all solutions using Gauss elimination: x + y + 4z =, x + 3y + z = 5, x + y + 5z = 3. We see that
Practice Problems Math 35 Spring 7: Solutions. Write the system of equations as a matrix equation and find all solutions using Gauss elimination: x + y + 4z =, x + 3y + z = 5, x + y + 5z = 3. We see that
What is on this week. 1 Vector spaces (continued) 1.1 Null space and Column Space of a matrix
 Professor Joana Amorim, jamorim@bu.edu What is on this week Vector spaces (continued). Null space and Column Space of a matrix............................. Null Space...........................................2
Professor Joana Amorim, jamorim@bu.edu What is on this week Vector spaces (continued). Null space and Column Space of a matrix............................. Null Space...........................................2
1.2 Row Echelon Form EXAMPLE 1
 .2 Row Echelon Form 7. The two systems 2x + x 2 = 4x + x 2 = 5 and 2x + x 2 = 4x + x 2 = have the same coefficient matrix but different righthand sides. Solve both systems simultaneously by eliminating
.2 Row Echelon Form 7. The two systems 2x + x 2 = 4x + x 2 = 5 and 2x + x 2 = 4x + x 2 = have the same coefficient matrix but different righthand sides. Solve both systems simultaneously by eliminating
Contents. 1 Vectors, Lines and Planes 1. 2 Gaussian Elimination Matrices Vector Spaces and Subspaces 124
 Matrices Math 220 Copyright 2016 Pinaki Das This document is freely redistributable under the terms of the GNU Free Documentation License For more information, visit http://wwwgnuorg/copyleft/fdlhtml Contents
Matrices Math 220 Copyright 2016 Pinaki Das This document is freely redistributable under the terms of the GNU Free Documentation License For more information, visit http://wwwgnuorg/copyleft/fdlhtml Contents
Linear Equations in Linear Algebra
 1 Linear Equations in Linear Algebra 1.9 THE MATRIX OF A LINEAR TRANSFORMATION THE MATRIX OF A LINEAR TRANSFORMATION Theorem 10: Let T: R n R m be a linear transformation. Then there exists a unique matrix
1 Linear Equations in Linear Algebra 1.9 THE MATRIX OF A LINEAR TRANSFORMATION THE MATRIX OF A LINEAR TRANSFORMATION Theorem 10: Let T: R n R m be a linear transformation. Then there exists a unique matrix
Rank and Nullity. MATH 322, Linear Algebra I. J. Robert Buchanan. Spring Department of Mathematics
 Rank and Nullity MATH 322, Linear Algebra I J. Robert Buchanan Department of Mathematics Spring 2015 Objectives We have defined and studied the important vector spaces associated with matrices (row space,
Rank and Nullity MATH 322, Linear Algebra I J. Robert Buchanan Department of Mathematics Spring 2015 Objectives We have defined and studied the important vector spaces associated with matrices (row space,
Lecture 18: The Rank of a Matrix and Consistency of Linear Systems
 Lecture 18: The Rank of a Matrix and Consistency of Linear Systems Winfried Just Department of Mathematics, Ohio University February 28, 218 Review: The linear span Definition Let { v 1, v 2,..., v n }
Lecture 18: The Rank of a Matrix and Consistency of Linear Systems Winfried Just Department of Mathematics, Ohio University February 28, 218 Review: The linear span Definition Let { v 1, v 2,..., v n }
(v, w) = arccos( < v, w >
 MA322 F all206 Notes on Inner Products Notes on Chapter 6 Inner product. Given a real vector space V, an inner product is defined to be a bilinear map F : V V R such that the following holds: Commutativity:
MA322 F all206 Notes on Inner Products Notes on Chapter 6 Inner product. Given a real vector space V, an inner product is defined to be a bilinear map F : V V R such that the following holds: Commutativity:
Chapter 6 - Orthogonality
 Chapter 6 - Orthogonality Maggie Myers Robert A. van de Geijn The University of Texas at Austin Orthogonality Fall 2009 http://z.cs.utexas.edu/wiki/pla.wiki/ 1 Orthogonal Vectors and Subspaces http://z.cs.utexas.edu/wiki/pla.wiki/
Chapter 6 - Orthogonality Maggie Myers Robert A. van de Geijn The University of Texas at Austin Orthogonality Fall 2009 http://z.cs.utexas.edu/wiki/pla.wiki/ 1 Orthogonal Vectors and Subspaces http://z.cs.utexas.edu/wiki/pla.wiki/
EXAM 2 REVIEW DAVID SEAL
 EXAM 2 REVIEW DAVID SEAL 3. Linear Systems and Matrices 3.2. Matrices and Gaussian Elimination. At this point in the course, you all have had plenty of practice with Gaussian Elimination. Be able to row
EXAM 2 REVIEW DAVID SEAL 3. Linear Systems and Matrices 3.2. Matrices and Gaussian Elimination. At this point in the course, you all have had plenty of practice with Gaussian Elimination. Be able to row
Linear Algebra. Ben Woodruff. Compiled July 17, 2010
 Linear Algebra Ben Woodruff Compiled July 7, i c This work is licensed under the Creative Commons Attribution-Share Alike 3. United States License. You may copy, distribute, display, and perform this copyrighted
Linear Algebra Ben Woodruff Compiled July 7, i c This work is licensed under the Creative Commons Attribution-Share Alike 3. United States License. You may copy, distribute, display, and perform this copyrighted
Chapter 6. Orthogonality
 6.4 The Projection Matrix 1 Chapter 6. Orthogonality 6.4 The Projection Matrix Note. In Section 6.1 (Projections), we projected a vector b R n onto a subspace W of R n. We did so by finding a basis for
6.4 The Projection Matrix 1 Chapter 6. Orthogonality 6.4 The Projection Matrix Note. In Section 6.1 (Projections), we projected a vector b R n onto a subspace W of R n. We did so by finding a basis for
Linear Combination. v = a 1 v 1 + a 2 v a k v k
 Linear Combination Definition 1 Given a set of vectors {v 1, v 2,..., v k } in a vector space V, any vector of the form v = a 1 v 1 + a 2 v 2 +... + a k v k for some scalars a 1, a 2,..., a k, is called
Linear Combination Definition 1 Given a set of vectors {v 1, v 2,..., v k } in a vector space V, any vector of the form v = a 1 v 1 + a 2 v 2 +... + a k v k for some scalars a 1, a 2,..., a k, is called
c i r i i=1 r 1 = [1, 2] r 2 = [0, 1] r 3 = [3, 4].
![c i r i i=1 r 1 = [1, 2] r 2 = [0, 1] r 3 = [3, 4]. c i r i i=1 r 1 = [1, 2] r 2 = [0, 1] r 3 = [3, 4].](/thumbs/95/122836402.jpg) Lecture Notes: Rank of a Matrix Yufei Tao Department of Computer Science and Engineering Chinese University of Hong Kong taoyf@cse.cuhk.edu.hk 1 Linear Independence Definition 1. Let r 1, r 2,..., r m
Lecture Notes: Rank of a Matrix Yufei Tao Department of Computer Science and Engineering Chinese University of Hong Kong taoyf@cse.cuhk.edu.hk 1 Linear Independence Definition 1. Let r 1, r 2,..., r m
Singular Value Decomposition. 1 Singular Value Decomposition and the Four Fundamental Subspaces
 Singular Value Decomposition This handout is a review of some basic concepts in linear algebra For a detailed introduction, consult a linear algebra text Linear lgebra and its pplications by Gilbert Strang
Singular Value Decomposition This handout is a review of some basic concepts in linear algebra For a detailed introduction, consult a linear algebra text Linear lgebra and its pplications by Gilbert Strang
Linear Algebra 1 Exam 1 Solutions 6/12/3
 Linear Algebra 1 Exam 1 Solutions 6/12/3 Question 1 Consider the linear system in the variables (x, y, z, t, u), given by the following matrix, in echelon form: 1 2 1 3 1 2 0 1 1 3 1 4 0 0 0 1 2 3 Reduce
Linear Algebra 1 Exam 1 Solutions 6/12/3 Question 1 Consider the linear system in the variables (x, y, z, t, u), given by the following matrix, in echelon form: 1 2 1 3 1 2 0 1 1 3 1 4 0 0 0 1 2 3 Reduce
INVERSE OF A MATRIX [2.2] 8-1
![INVERSE OF A MATRIX [2.2] 8-1 INVERSE OF A MATRIX [2.2] 8-1](/thumbs/78/78101644.jpg) INVERSE OF A MATRIX [2.2] 8-1 The inverse of a matrix: Introduction We have a mapping from R n to R n represented by a matrix A. Can we invert this mapping? i.e. can we find a matrix (call it B for now)
INVERSE OF A MATRIX [2.2] 8-1 The inverse of a matrix: Introduction We have a mapping from R n to R n represented by a matrix A. Can we invert this mapping? i.e. can we find a matrix (call it B for now)
First of all, the notion of linearity does not depend on which coordinates are used. Recall that a map T : R n R m is linear if
 5 Matrices in Different Coordinates In this section we discuss finding matrices of linear maps in different coordinates Earlier in the class was the matrix that multiplied by x to give ( x) in standard
5 Matrices in Different Coordinates In this section we discuss finding matrices of linear maps in different coordinates Earlier in the class was the matrix that multiplied by x to give ( x) in standard
CONVERSION OF COORDINATES BETWEEN FRAMES
 ECS 178 Course Notes CONVERSION OF COORDINATES BETWEEN FRAMES Kenneth I. Joy Institute for Data Analysis and Visualization Department of Computer Science University of California, Davis Overview Frames
ECS 178 Course Notes CONVERSION OF COORDINATES BETWEEN FRAMES Kenneth I. Joy Institute for Data Analysis and Visualization Department of Computer Science University of California, Davis Overview Frames
INVERSE OF A MATRIX [2.2]
![INVERSE OF A MATRIX [2.2] INVERSE OF A MATRIX [2.2]](/thumbs/75/72004651.jpg) INVERSE OF A MATRIX [2.2] The inverse of a matrix: Introduction We have a mapping from R n to R n represented by a matrix A. Can we invert this mapping? i.e. can we find a matrix (call it B for now) such
INVERSE OF A MATRIX [2.2] The inverse of a matrix: Introduction We have a mapping from R n to R n represented by a matrix A. Can we invert this mapping? i.e. can we find a matrix (call it B for now) such
Solution Set 3, Fall '12
 Solution Set 3, 86 Fall '2 Do Problem 5 from 32 [ 3 5 Solution (a) A = Only one elimination step is needed to produce the 2 6 echelon form The pivot is the in row, column, and the entry to eliminate is
Solution Set 3, 86 Fall '2 Do Problem 5 from 32 [ 3 5 Solution (a) A = Only one elimination step is needed to produce the 2 6 echelon form The pivot is the in row, column, and the entry to eliminate is
2018 Fall 2210Q Section 013 Midterm Exam I Solution
 8 Fall Q Section 3 Midterm Exam I Solution True or False questions ( points = points) () An example of a linear combination of vectors v, v is the vector v. True. We can write v as v + v. () If two matrices
8 Fall Q Section 3 Midterm Exam I Solution True or False questions ( points = points) () An example of a linear combination of vectors v, v is the vector v. True. We can write v as v + v. () If two matrices
Vector Spaces and Dimension. Subspaces of. R n. addition and scalar mutiplication. That is, if u, v in V and alpha in R then ( u + v) Exercise: x
 Vector Spaces and Dimension Subspaces of Definition: A non-empty subset V is a subspace of if V is closed under addition and scalar mutiplication. That is, if u, v in V and alpha in R then ( u + v) V and
Vector Spaces and Dimension Subspaces of Definition: A non-empty subset V is a subspace of if V is closed under addition and scalar mutiplication. That is, if u, v in V and alpha in R then ( u + v) V and
8.4. Systems of Equations in Three Variables. Identifying Solutions 2/20/2018. Example. Identifying Solutions. Solving Systems in Three Variables
 8.4 Systems of Equations in Three Variables Copyright 2010 Pearson Education, Inc. Publishing as Pearson Addison- Wesley Identifying Solutions Solving Systems in Three Variables Dependency, Inconsistency,
8.4 Systems of Equations in Three Variables Copyright 2010 Pearson Education, Inc. Publishing as Pearson Addison- Wesley Identifying Solutions Solving Systems in Three Variables Dependency, Inconsistency,
ELEMENTARY LINEAR ALGEBRA
 ELEMENTARY LINEAR ALGEBRA DAVID MEREDITH These notes are about the application and computation of linear algebra objects in F n, where F is a field. I think everything here works over any field including
ELEMENTARY LINEAR ALGEBRA DAVID MEREDITH These notes are about the application and computation of linear algebra objects in F n, where F is a field. I think everything here works over any field including
18.02 Multivariable Calculus Fall 2007
 MIT OpenCourseWare http://ocw.mit.edu 18.02 Multivariable Calculus Fall 2007 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. M. Matrices and Linear Algebra
MIT OpenCourseWare http://ocw.mit.edu 18.02 Multivariable Calculus Fall 2007 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. M. Matrices and Linear Algebra
Linear Algebra March 16, 2019
 Linear Algebra March 16, 2019 2 Contents 0.1 Notation................................ 4 1 Systems of linear equations, and matrices 5 1.1 Systems of linear equations..................... 5 1.2 Augmented
Linear Algebra March 16, 2019 2 Contents 0.1 Notation................................ 4 1 Systems of linear equations, and matrices 5 1.1 Systems of linear equations..................... 5 1.2 Augmented
MH1200 Final 2014/2015
 MH200 Final 204/205 November 22, 204 QUESTION. (20 marks) Let where a R. A = 2 3 4, B = 2 3 4, 3 6 a 3 6 0. For what values of a is A singular? 2. What is the minimum value of the rank of A over all a
MH200 Final 204/205 November 22, 204 QUESTION. (20 marks) Let where a R. A = 2 3 4, B = 2 3 4, 3 6 a 3 6 0. For what values of a is A singular? 2. What is the minimum value of the rank of A over all a
NOTES on LINEAR ALGEBRA 1
 School of Economics, Management and Statistics University of Bologna Academic Year 207/8 NOTES on LINEAR ALGEBRA for the students of Stats and Maths This is a modified version of the notes by Prof Laura
School of Economics, Management and Statistics University of Bologna Academic Year 207/8 NOTES on LINEAR ALGEBRA for the students of Stats and Maths This is a modified version of the notes by Prof Laura
Math 3C Lecture 25. John Douglas Moore
 Math 3C Lecture 25 John Douglas Moore June 1, 2009 Let V be a vector space. A basis for V is a collection of vectors {v 1,..., v k } such that 1. V = Span{v 1,..., v k }, and 2. {v 1,..., v k } are linearly
Math 3C Lecture 25 John Douglas Moore June 1, 2009 Let V be a vector space. A basis for V is a collection of vectors {v 1,..., v k } such that 1. V = Span{v 1,..., v k }, and 2. {v 1,..., v k } are linearly
Linear Vector Spaces
 CHAPTER 1 Linear Vector Spaces Definition 1.0.1. A linear vector space over a field F is a triple (V, +, ), where V is a set, + : V V V and : F V V are maps with the properties : (i) ( x, y V ), x + y
CHAPTER 1 Linear Vector Spaces Definition 1.0.1. A linear vector space over a field F is a triple (V, +, ), where V is a set, + : V V V and : F V V are maps with the properties : (i) ( x, y V ), x + y
Lecture 14: The Rank-Nullity Theorem
 Math 108a Professor: Padraic Bartlett Lecture 14: The Rank-Nullity Theorem Week 6 UCSB 2013 In today s talk, the last before we introduce the concept of matrices, we prove what is arguably the strongest
Math 108a Professor: Padraic Bartlett Lecture 14: The Rank-Nullity Theorem Week 6 UCSB 2013 In today s talk, the last before we introduce the concept of matrices, we prove what is arguably the strongest
MTH Linear Algebra. Study Guide. Dr. Tony Yee Department of Mathematics and Information Technology The Hong Kong Institute of Education
 MTH 3 Linear Algebra Study Guide Dr. Tony Yee Department of Mathematics and Information Technology The Hong Kong Institute of Education June 3, ii Contents Table of Contents iii Matrix Algebra. Real Life
MTH 3 Linear Algebra Study Guide Dr. Tony Yee Department of Mathematics and Information Technology The Hong Kong Institute of Education June 3, ii Contents Table of Contents iii Matrix Algebra. Real Life
Kevin James. MTHSC 3110 Section 4.3 Linear Independence in Vector Sp
 MTHSC 3 Section 4.3 Linear Independence in Vector Spaces; Bases Definition Let V be a vector space and let { v. v 2,..., v p } V. If the only solution to the equation x v + x 2 v 2 + + x p v p = is the
MTHSC 3 Section 4.3 Linear Independence in Vector Spaces; Bases Definition Let V be a vector space and let { v. v 2,..., v p } V. If the only solution to the equation x v + x 2 v 2 + + x p v p = is the
Computational Fluid Dynamics Prof. Sreenivas Jayanti Department of Computer Science and Engineering Indian Institute of Technology, Madras
 Computational Fluid Dynamics Prof. Sreenivas Jayanti Department of Computer Science and Engineering Indian Institute of Technology, Madras Lecture 46 Tri-diagonal Matrix Algorithm: Derivation In the last
Computational Fluid Dynamics Prof. Sreenivas Jayanti Department of Computer Science and Engineering Indian Institute of Technology, Madras Lecture 46 Tri-diagonal Matrix Algorithm: Derivation In the last
b 1 b 2.. b = b m A = [a 1,a 2,...,a n ] where a 1,j a 2,j a j = a m,j Let A R m n and x 1 x 2 x = x n
![b 1 b 2.. b = b m A = [a 1,a 2,...,a n ] where a 1,j a 2,j a j = a m,j Let A R m n and x 1 x 2 x = x n b 1 b 2.. b = b m A = [a 1,a 2,...,a n ] where a 1,j a 2,j a j = a m,j Let A R m n and x 1 x 2 x = x n](/thumbs/90/102651734.jpg) Lectures -2: Linear Algebra Background Almost all linear and nonlinear problems in scientific computation require the use of linear algebra These lectures review basic concepts in a way that has proven
Lectures -2: Linear Algebra Background Almost all linear and nonlinear problems in scientific computation require the use of linear algebra These lectures review basic concepts in a way that has proven
Structural Analysis II Prof. P. Banerjee Department of Civil Engineering Indian Institute of Technology, Bombay Lecture 38
 Structural Analysis II Prof. P. Banerjee Department of Civil Engineering Indian Institute of Technology, Bombay Lecture 38 Good morning. We have been looking at influence lines for the last couple of lectures
Structural Analysis II Prof. P. Banerjee Department of Civil Engineering Indian Institute of Technology, Bombay Lecture 38 Good morning. We have been looking at influence lines for the last couple of lectures
Problem set #4. Due February 19, x 1 x 2 + x 3 + x 4 x 5 = 0 x 1 + x 3 + 2x 4 = 1 x 1 x 2 x 4 x 5 = 1.
 Problem set #4 Due February 19, 218 The letter V always denotes a vector space. Exercise 1. Find all solutions to 2x 1 x 2 + x 3 + x 4 x 5 = x 1 + x 3 + 2x 4 = 1 x 1 x 2 x 4 x 5 = 1. Solution. First we
Problem set #4 Due February 19, 218 The letter V always denotes a vector space. Exercise 1. Find all solutions to 2x 1 x 2 + x 3 + x 4 x 5 = x 1 + x 3 + 2x 4 = 1 x 1 x 2 x 4 x 5 = 1. Solution. First we
Gordon solutions. n=1 1. p n
 Gordon solutions 1. A positive integer is called a palindrome if its base-10 expansion is unchanged when it is reversed. For example, 121 and 7447 are palindromes. Show that if we denote by p n the nth
Gordon solutions 1. A positive integer is called a palindrome if its base-10 expansion is unchanged when it is reversed. For example, 121 and 7447 are palindromes. Show that if we denote by p n the nth
MTH 464: Computational Linear Algebra
 MTH 464: Computational Linear Algebra Lecture Outlines Exam 2 Material Prof. M. Beauregard Department of Mathematics & Statistics Stephen F. Austin State University March 2, 2018 Linear Algebra (MTH 464)
MTH 464: Computational Linear Algebra Lecture Outlines Exam 2 Material Prof. M. Beauregard Department of Mathematics & Statistics Stephen F. Austin State University March 2, 2018 Linear Algebra (MTH 464)
EXAM. Exam #2. Math 2360 Summer II, 2000 Morning Class. Nov. 15, 2000 ANSWERS
 EXAM Exam # Math 6 Summer II Morning Class Nov 5 ANSWERS i Problem Consider the matrix 6 pts A = 6 4 9 5 7 6 5 5 5 4 The RREF of A is the matrix R = A Find a basis for the nullspace of A Solve the homogeneous
EXAM Exam # Math 6 Summer II Morning Class Nov 5 ANSWERS i Problem Consider the matrix 6 pts A = 6 4 9 5 7 6 5 5 5 4 The RREF of A is the matrix R = A Find a basis for the nullspace of A Solve the homogeneous
Chapter 2 Subspaces of R n and Their Dimensions
 Chapter 2 Subspaces of R n and Their Dimensions Vector Space R n. R n Definition.. The vector space R n is a set of all n-tuples (called vectors) x x 2 x =., where x, x 2,, x n are real numbers, together
Chapter 2 Subspaces of R n and Their Dimensions Vector Space R n. R n Definition.. The vector space R n is a set of all n-tuples (called vectors) x x 2 x =., where x, x 2,, x n are real numbers, together
Linear Independence x
 Linear Independence A consistent system of linear equations with matrix equation Ax = b, where A is an m n matrix, has a solution set whose graph in R n is a linear object, that is, has one of only n +
Linear Independence A consistent system of linear equations with matrix equation Ax = b, where A is an m n matrix, has a solution set whose graph in R n is a linear object, that is, has one of only n +
MAT2342 : Introduction to Applied Linear Algebra Mike Newman, fall Projections. introduction
 MAT4 : Introduction to Applied Linear Algebra Mike Newman fall 7 9. Projections introduction One reason to consider projections is to understand approximate solutions to linear systems. A common example
MAT4 : Introduction to Applied Linear Algebra Mike Newman fall 7 9. Projections introduction One reason to consider projections is to understand approximate solutions to linear systems. A common example
Lecture 11: Finish Gaussian elimination and applications; intro to eigenvalues and eigenvectors (1)
 Lecture 11: Finish Gaussian elimination and applications; intro to eigenvalues and eigenvectors (1) Travis Schedler Tue, Oct 18, 2011 (version: Tue, Oct 18, 6:00 PM) Goals (2) Solving systems of equations
Lecture 11: Finish Gaussian elimination and applications; intro to eigenvalues and eigenvectors (1) Travis Schedler Tue, Oct 18, 2011 (version: Tue, Oct 18, 6:00 PM) Goals (2) Solving systems of equations
LS.1 Review of Linear Algebra
 LS. LINEAR SYSTEMS LS.1 Review of Linear Algebra In these notes, we will investigate a way of handling a linear system of ODE s directly, instead of using elimination to reduce it to a single higher-order
LS. LINEAR SYSTEMS LS.1 Review of Linear Algebra In these notes, we will investigate a way of handling a linear system of ODE s directly, instead of using elimination to reduce it to a single higher-order
SUMMARY OF MATH 1600
 SUMMARY OF MATH 1600 Note: The following list is intended as a study guide for the final exam. It is a continuation of the study guide for the midterm. It does not claim to be a comprehensive list. You
SUMMARY OF MATH 1600 Note: The following list is intended as a study guide for the final exam. It is a continuation of the study guide for the midterm. It does not claim to be a comprehensive list. You
Exam 1 - Definitions and Basic Theorems
 Exam 1 - Definitions and Basic Theorems One of the difficuliies in preparing for an exam where there will be a lot of proof problems is knowing what you re allowed to cite and what you actually have to
Exam 1 - Definitions and Basic Theorems One of the difficuliies in preparing for an exam where there will be a lot of proof problems is knowing what you re allowed to cite and what you actually have to
Chapter 1: Linear Equations
 Chapter : Linear Equations (Last Updated: September, 6) The material for these notes is derived primarily from Linear Algebra and its applications by David Lay (4ed).. Systems of Linear Equations Before
Chapter : Linear Equations (Last Updated: September, 6) The material for these notes is derived primarily from Linear Algebra and its applications by David Lay (4ed).. Systems of Linear Equations Before
MA 242 LINEAR ALGEBRA C1, Solutions to First Midterm Exam
 MA 242 LINEAR ALGEBRA C Solutions to First Midterm Exam Prof Nikola Popovic October 2 9:am - :am Problem ( points) Determine h and k such that the solution set of x + = k 4x + h = 8 (a) is empty (b) contains
MA 242 LINEAR ALGEBRA C Solutions to First Midterm Exam Prof Nikola Popovic October 2 9:am - :am Problem ( points) Determine h and k such that the solution set of x + = k 4x + h = 8 (a) is empty (b) contains
