= x. I (x,y ) Example: Translation. Operations depend on pixel s Coordinates. Context free. Independent of pixel values. I(x,y) Forward mapping:
|
|
|
- Todd Moody
- 5 years ago
- Views:
Transcription
1 Gomric Transormaion Oraions dnd on il s Coordinas. Con r. Indndn o il valus. (, ) ' (, ) ' I (, ) I ' ( (, ), ( ) ), (,) (, ) I(,) I (, ) Eaml: Translaion (, ) (, ) (, ) I(, ) I ' Forward Maing Forward maing: Sourc (, ) (, ) Targ Forward Maing (,) I(,) (, ) I (, ) Problms wih orward maing du o samling: Hols (som arg ils ar no oulad) Ovrlas (som arg ils assignd w colors)
2 Forward Maing ( ), Sourc Targ ( ), Invrs Maing Invrs maing: (, ) (, ) 4 Sourc Targ Invrs Maing ( ),. 7 Sourc? Targ ( ), Each arg il assignd a singl color. Color Inrolaion is ruird. Eaml: Scaling along X Inrolaion Forward maing: Sourc (,) ; Targ (,) Wha hans whn a maing uncion calculas a racional il locaion? Invrs maing: Sourc / ; Targ Inrolaion: gnras a nw il b analzing h surrounding ils.
3 Inrolaion Good inrolaion chnius am o ind an oimal balanc bwn hr undsirabl ariacs: aliasing, blurring, and dg halos. 4 scaling Nars Nighbor Inrolaion Th assign valu is akn rom h il closs o h gnrad locaion: I (, ) I round (, ) Advanag: Fas Disadvanag: Jaggd rsuls Aliasing nar dgs ( { }, round{ (, ) }) aliasing blurring halos 9 Original Imag Original Imag Nars N. Inrolaion Nars N. Inrolaion
4 Bilinar Inrolaion Linar Inrolaion Th assign valu is a wighd sum o h our nars ils. Each wigh is roorional o h disanc rom ach ising il. v v w v w w w v v v v w w Isolaing v in h abov uaion: ( α) w v αv v whr α w w Bilinar Inrolaion Bilinar Inrolaion NW V N NE NW V N NE SW S SE ( ) ( ) ( ) S SE SW N NE NW V N S SW S Th bilinar inrolaion is h bs i low-dgr olnomial o h orm: v(, ) SE Th il s boundaris ar C coninuous (coninuous valus across boundaris). i, j i a ij j 4
5 Bilinar aml 5 z5 z7 v 5 z z.5.5 Nars N. Inrolaion Bilinar Inrolaion Bicubic Inrolaion Th assign valu is a wighd sum o h 44 nars ils: v(, ) i, j i a ij j Nars N. Inrolaion Bilinar Inrolaion 5
6 How can w ind h righ coicins? Dno h il valus V {,..} Th unknown coicins ar a ij {i,j..} ij i, j v i a W hav a linar ssm o 6 uaions wih 6 coicins. j or, {.. },, [, ] s N.N Bilinar Bicubic Th il s boundaris ar C coninuous (coninuous drivaivs across boundaris). N.N Bilinar 6
7 Aling h Transormaion T % ransormaion mari [r,c] siz(img) % cra arra o dsinaion, coordinas [X,Y]mshgrid(:c,:r); % calcula sourc coordinas sourccoor inv(t) * [X(:) Y(:) ] ; % calcula nars nighbor inrolaion Xs round(sourccoor(,:)); Ys round(sourccoor(,:)); indind(xs< Xs>r); %ou o rang ils Xs(ind); Ys(ind); indind(ys< Ys>c); %ou o rang ils Xs(ind); Ys(ind); Bicubic % calcula nw imag nwimag img((xs-).*rys); nwimag(ind); nwimag(ind); nwimag rsha(nwimag,r,c); Ts o linar D ransormaions Rigid (Euclidan) ransormaion: Translaion Roaion (disanc rsrving). Similari ransormaion: Translaion Roaion Uniorm Scal (angl rsrving). Ain ransormaion: Translaion Roaion Scal Shar (aralllism rsrving). Projciv ransormaion Cross-raio rsrving All abov ransormaions ar grous whr Rigid Similari Ain Projciv Ts o linar D ransormaions All abov ransormaions ar grous whr Rigid Similari Ain Projciv 7
8 Mari Noaion Evr locaion (,) is rad as a column vcor: Coordina ransormaion is obaind b muliling wih a mari? a c b a b d c d Mari Noaion - Scal Scal(a,b): (,) (a,b) a I a or b ar ngaiv, w g rlcion. Invrs: S - (a,b)s(/a,/b) a a b b ' b' Mari Noaion - Shar Shar(a,b): (,) (a,b) b a a b a.5, b Mari Noaion - Roaion Roa(θ): (,) (cosθsinθ, -sinθ cosθ) cosθ sinθ Invrs: R - (θ)r T (θ)r(-θ) sinθ cosθ sinθ cosθ sinθ cosθ 8
9 9 Mari Noaion - Translaion Mari Noaion - Translaion Translaion(a,b): Canno rrsn ranslaion using marics. Invrs: b a b a Homognous Coordinas Homognous Coordinas Homognous Coordinas is a maing rom R n o R n : No: (,,) all corrsond o h sam nonhomognous oin (,). E.g. (,,) (6,9,) (4,6,). Invrs maing: ( ) ( ),,,, W Y W X W Y X ),, ( ),, ( ), ( W Y X Homognous Coordinas Homognous Coordinas (,) (,,) (,,) Som D Transormaions Som D Transormaions Translaion : Ain ransormaion: Projciv ransormaion: W Y X d c b a W Y X d c b a W Y X Ain
10 Hirarch o Linar D Transormaions Hirarch o Linar D Transormaions Global Transormaions Imag Rciicaion Global Transormaions Imag Rciicaion Global Transormaions Global Waring Global Transormaions Global Waring A Global Transormaions Global Waring Global Transormaions Global Waring oins i oins i mach A Y
11 Global Transormaions Global Waring Global Transormaions Global Waring oins i oins i mach A Y Invrs Maing: Global Transormaions Global Waring Global Transormaions Global Waring Solv or A - in rms o h las man suar. i.. ind A - which minimizs: i i i A Global Transormaions Global Waring Global Transormaions Global Waring soluion: ( ) ) ( T XX T X X inv Y inv A Global Transormaions Global Waring Global Transormaions Global Waring Alrnaiv rrsnaion: d c b a d c b a A Rarrang:
12 Global Transormaions Global Waring Global Transormaions Global Waring d cb a Global Transormaions Global Waring Global Transormaions Global Waring d cb a Global Transormaions Global Waring Global Transormaions Global Waring inv d c b a ' ( ) T T Q Q Q Q inv ) '( soluion: Global Transormaions Global Waring Global Transormaions Global Waring Wha abou Projciv Transormaions? h g d c b a Homogni mus b rsrvd! ' ; ' h g d c h g b a
13 Global Transormaions Global Waring Wha abou Projciv Transormaions? Global Transormaions Imag Rciicaion So who ARE w? a b ' g h ; c d ' g h ( ' ' ) And similarl or a b c d g h Local Transormaions Imag Waring Local Transormaions Imag Waring Ara o inlunc Ara o inlunc s d s d s sourc oin d dsinaion oin Dmo al
14 Local Transormaions Imag Waring Imag Morhing (Imag Mamorhosis) Ara o inlunc s s sourc oin d dsinaion oin d dsinaion d s s sourc d Dmo bw Cross Dissolv (il oraions) Waring Cross Dissolv War sourc imag owards inrmdia imag. War dsinaion imag owards inrmdia imag. Cross-dissolv h wo imags b aking h wighd avrag a ach il. Sourc Imag Dsinaion Imag sourc im cross dissolv I ( ) ( ) [,] S T Cross-dissolv war dissolv dsinaion waring imags 4
15 war Imag Mamorhosis war Cross-dissolv Cross-dissolv L S,T b h sourc and h arg imags L G() b h ransormaion rom S owards T, whr G()I (h idni) L [,] h im s o b snhsizd Algorihm:. War S owards T:. War T oward S:. Cross dissolv: S T ( ) G( ){ S} I ( ) G( ( ) ) { T} ( ) ( ) S( ) T( ) sours S()G( ){S} Faur Basd Morhing Morh on sha ino anohr sha Us local aurs o din h gomric waring I()(-) S() (T()) T()G((-) ) - {T} arg 5
16 Q Q Q Q P P P P Q Q Q Q P P P P 6
17 Q Q Q Q P P P P On Sgmn Waring Q u v β R α Sourc Imag Ds Imag α [,] is h rlaiv osiion along h sgmn (P,Q ). β is h acual rndicular disanc o h sgmn. (u,v ) is h local coordinas o h sgmn (P,Q ): u is a uni vcor aralll o Q -P v is h uni vcor rndicular o Q -P ( Q P) u u Q P v u u P Q u v β α R P Q u v β α Th oin R is mad ino (α,β) : ( R P ) u α ; β Q P whr R P ( R P ) v R' P' α Q' P' u' βv' 7
18 Q β u v R α P Q u v β α Sourc Imag Ds Imag Invrs Maing: R( α, β ) P α Q P u βv whr (u,v) is h local coordinas o h sgmn (P,Q): ( Q P) u u Q P v u u R P Mulil Sgmn Waring Q R β R P Q β P Q R β β P P Q In mulil sgmn waring h oin R is inluncd b mulil sgmns. Th inlunc srngh o ach sgmns is roorional o: Sgmn lngh Th disanc rom h oin R Th inlunc o ach sgmns is: Qi P i W i aβ i Th valu [,] conrols h inlunc o h lin lngh. Th valu a is a small numbr avoiding division b zro. Th valu b drmins how h rlaiv wigh diminish as h β incrass Th inal maing is: R k k W R k W k b k Eaml: Eaml imags rom: h:// For mor dails s: Thaddus Bir & Shawn Nl / Faur-Basd Imag Mamorhosis Siggrah '9 h:// 8
19 Anohr Eaml: Msh Waring From: h:// 7 -Pass Msh Waring Algorihm Th irs ass wars h rows o h imag: -Pass Msh Waring Algorihm Thn, ach row o h imag is ward individuall b linarl inrolaing ach sgmn bwn h -coordinas dind b h sourc msh o h siz o h corrsonding sgmn dind b h -coordinas o h dsinaion Msh. For ach column o h msh drmin h -coordinas a which h msh column crosss ach imag row. Th scond ass rorms h ac sam rocdur on h columns o h imag b inrolaing h -coordinas o h mshs. 9
20 VidMorh Fun Morh
Operations depend on pixel s Coordinates. Context free. Independent of pixel values. I(x,y) I (x,y )
 Geometric Transformation Operations depend on piel s Coordinates. Contet free. Independent of piel values. f f (, ) = ' (, ) = ' I(, ) = I' ( f (, ), f ( ) ), (,) (, ) I(,) I (, ) Eample: Translation =
Geometric Transformation Operations depend on piel s Coordinates. Contet free. Independent of piel values. f f (, ) = ' (, ) = ' I(, ) = I' ( f (, ), f ( ) ), (,) (, ) I(,) I (, ) Eample: Translation =
2. The Laplace Transform
 Th aac Tranorm Inroucion Th aac ranorm i a unamna an vry uu oo or uying many nginring robm To in h aac ranorm w conir a comx variab σ, whr σ i h ra ar an i h imaginary ar or ix vau o σ an w viw a a oin
Th aac Tranorm Inroucion Th aac ranorm i a unamna an vry uu oo or uying many nginring robm To in h aac ranorm w conir a comx variab σ, whr σ i h ra ar an i h imaginary ar or ix vau o σ an w viw a a oin
5. An object moving along an x-coordinate axis with its scale measured in meters has a velocity of 6t
 AP CALCULUS FINAL UNIT WORKSHEETS ACCELERATION, VELOCTIY AND POSITION In problms -, drmin h posiion funcion, (), from h givn informaion.. v (), () = 5. v ()5, () = b g. a (), v() =, () = -. a (), v() =
AP CALCULUS FINAL UNIT WORKSHEETS ACCELERATION, VELOCTIY AND POSITION In problms -, drmin h posiion funcion, (), from h givn informaion.. v (), () = 5. v ()5, () = b g. a (), v() =, () = -. a (), v() =
UNIT #5 EXPONENTIAL AND LOGARITHMIC FUNCTIONS
 Answr Ky Nam: Da: UNIT # EXPONENTIAL AND LOGARITHMIC FUNCTIONS Par I Qusions. Th prssion is quivaln o () () 6 6 6. Th ponnial funcion y 6 could rwrin as y () y y 6 () y y (). Th prssion a is quivaln o
Answr Ky Nam: Da: UNIT # EXPONENTIAL AND LOGARITHMIC FUNCTIONS Par I Qusions. Th prssion is quivaln o () () 6 6 6. Th ponnial funcion y 6 could rwrin as y () y y 6 () y y (). Th prssion a is quivaln o
Lecture 1: Numerical Integration The Trapezoidal and Simpson s Rule
 Lcur : Numrical ngraion Th Trapzoidal and Simpson s Rul A problm Th probabiliy of a normally disribud (man µ and sandard dviaion σ ) vn occurring bwn h valus a and b is B A P( a x b) d () π whr a µ b -
Lcur : Numrical ngraion Th Trapzoidal and Simpson s Rul A problm Th probabiliy of a normally disribud (man µ and sandard dviaion σ ) vn occurring bwn h valus a and b is B A P( a x b) d () π whr a µ b -
AR(1) Process. The first-order autoregressive process, AR(1) is. where e t is WN(0, σ 2 )
 AR() Procss Th firs-ordr auorgrssiv procss, AR() is whr is WN(0, σ ) Condiional Man and Varianc of AR() Condiional man: Condiional varianc: ) ( ) ( Ω Ω E E ) var( ) ) ( var( ) var( σ Ω Ω Ω Ω E Auocovarianc
AR() Procss Th firs-ordr auorgrssiv procss, AR() is whr is WN(0, σ ) Condiional Man and Varianc of AR() Condiional man: Condiional varianc: ) ( ) ( Ω Ω E E ) var( ) ) ( var( ) var( σ Ω Ω Ω Ω E Auocovarianc
CPSC 211 Data Structures & Implementations (c) Texas A&M University [ 259] B-Trees
![CPSC 211 Data Structures & Implementations (c) Texas A&M University [ 259] B-Trees CPSC 211 Data Structures & Implementations (c) Texas A&M University [ 259] B-Trees](/thumbs/74/70718364.jpg) CPSC 211 Daa Srucurs & Implmnaions (c) Txas A&M Univrsiy [ 259] B-Trs Th AVL r and rd-black r allowd som variaion in h lnghs of h diffrn roo-o-laf pahs. An alrnaiv ida is o mak sur ha all roo-o-laf pahs
CPSC 211 Daa Srucurs & Implmnaions (c) Txas A&M Univrsiy [ 259] B-Trs Th AVL r and rd-black r allowd som variaion in h lnghs of h diffrn roo-o-laf pahs. An alrnaiv ida is o mak sur ha all roo-o-laf pahs
Ma/CS 6a Class 15: Flows and Bipartite Graphs
 //206 Ma/CS 6a Cla : Flow and Bipari Graph By Adam Shffr Rmindr: Flow Nwork A flow nwork i a digraph G = V, E, oghr wih a ourc vrx V, a ink vrx V, and a capaciy funcion c: E N. Capaciy Sourc 7 a b c d
//206 Ma/CS 6a Cla : Flow and Bipari Graph By Adam Shffr Rmindr: Flow Nwork A flow nwork i a digraph G = V, E, oghr wih a ourc vrx V, a ink vrx V, and a capaciy funcion c: E N. Capaciy Sourc 7 a b c d
a dt a dt a dt dt If 1, then the poles in the transfer function are complex conjugates. Let s look at f t H t f s / s. So, for a 2 nd order system:
 Undrdamd Sysms Undrdamd Sysms nd Ordr Sysms Ouu modld wih a nd ordr ODE: d y dy a a1 a0 y b f If a 0 0, hn: whr: a d y a1 dy b d y dy y f y f a a a 0 0 0 is h naural riod of oscillaion. is h daming facor.
Undrdamd Sysms Undrdamd Sysms nd Ordr Sysms Ouu modld wih a nd ordr ODE: d y dy a a1 a0 y b f If a 0 0, hn: whr: a d y a1 dy b d y dy y f y f a a a 0 0 0 is h naural riod of oscillaion. is h daming facor.
Decline Curves. Exponential decline (constant fractional decline) Harmonic decline, and Hyperbolic decline.
 Dlin Curvs Dlin Curvs ha lo flow ra vs. im ar h mos ommon ools for forasing roduion and monioring wll rforman in h fild. Ths urvs uikly show by grahi mans whih wlls or filds ar roduing as xd or undr roduing.
Dlin Curvs Dlin Curvs ha lo flow ra vs. im ar h mos ommon ools for forasing roduion and monioring wll rforman in h fild. Ths urvs uikly show by grahi mans whih wlls or filds ar roduing as xd or undr roduing.
EXERCISE - 01 CHECK YOUR GRASP
 DIFFERENTIAL EQUATION EXERCISE - CHECK YOUR GRASP 7. m hn D() m m, D () m m. hn givn D () m m D D D + m m m m m m + m m m m + ( m ) (m ) (m ) (m + ) m,, Hnc numbr of valus of mn will b. n ( ) + c sinc
DIFFERENTIAL EQUATION EXERCISE - CHECK YOUR GRASP 7. m hn D() m m, D () m m. hn givn D () m m D D D + m m m m m m + m m m m + ( m ) (m ) (m ) (m + ) m,, Hnc numbr of valus of mn will b. n ( ) + c sinc
Double Slits in Space and Time
 Doubl Slis in Sac an Tim Gorg Jons As has bn ror rcnly in h mia, a am l by Grhar Paulus has monsra an inrsing chniqu for ionizing argon aoms by using ulra-shor lasr ulss. Each lasr uls is ffcivly on an
Doubl Slis in Sac an Tim Gorg Jons As has bn ror rcnly in h mia, a am l by Grhar Paulus has monsra an inrsing chniqu for ionizing argon aoms by using ulra-shor lasr ulss. Each lasr uls is ffcivly on an
Chap.3 Laplace Transform
 Chap. aplac Tranorm Tranorm: An opraion ha ranorm a uncion ino anohr uncion i Dirniaion ranorm: ii x: d dx x x Ingraion ranorm: x: x dx x c Now, conidr a dind ingral k, d,ha ranorm ino a uncion o variabl
Chap. aplac Tranorm Tranorm: An opraion ha ranorm a uncion ino anohr uncion i Dirniaion ranorm: ii x: d dx x x Ingraion ranorm: x: x dx x c Now, conidr a dind ingral k, d,ha ranorm ino a uncion o variabl
CSE 245: Computer Aided Circuit Simulation and Verification
 CSE 45: Compur Aidd Circui Simulaion and Vrificaion Fall 4, Sp 8 Lcur : Dynamic Linar Sysm Oulin Tim Domain Analysis Sa Equaions RLC Nwork Analysis by Taylor Expansion Impuls Rspons in im domain Frquncy
CSE 45: Compur Aidd Circui Simulaion and Vrificaion Fall 4, Sp 8 Lcur : Dynamic Linar Sysm Oulin Tim Domain Analysis Sa Equaions RLC Nwork Analysis by Taylor Expansion Impuls Rspons in im domain Frquncy
Chapter 12 Introduction To The Laplace Transform
 Chapr Inroducion To Th aplac Tranorm Diniion o h aplac Tranorm - Th Sp & Impul uncion aplac Tranorm o pciic uncion 5 Opraional Tranorm Applying h aplac Tranorm 7 Invr Tranorm o Raional uncion 8 Pol and
Chapr Inroducion To Th aplac Tranorm Diniion o h aplac Tranorm - Th Sp & Impul uncion aplac Tranorm o pciic uncion 5 Opraional Tranorm Applying h aplac Tranorm 7 Invr Tranorm o Raional uncion 8 Pol and
DEPARTMENT OF ELECTRICAL &ELECTRONICS ENGINEERING SIGNALS AND SYSTEMS. Assoc. Prof. Dr. Burak Kelleci. Spring 2018
 DEPARTMENT OF ELECTRICAL &ELECTRONICS ENGINEERING SIGNALS AND SYSTEMS Aoc. Prof. Dr. Burak Kllci Spring 08 OUTLINE Th Laplac Tranform Rgion of convrgnc for Laplac ranform Invr Laplac ranform Gomric valuaion
DEPARTMENT OF ELECTRICAL &ELECTRONICS ENGINEERING SIGNALS AND SYSTEMS Aoc. Prof. Dr. Burak Kllci Spring 08 OUTLINE Th Laplac Tranform Rgion of convrgnc for Laplac ranform Invr Laplac ranform Gomric valuaion
On the Speed of Heat Wave. Mihály Makai
 On h Spd of Ha Wa Mihály Maai maai@ra.bm.hu Conns Formulaion of h problm: infini spd? Local hrmal qulibrium (LTE hypohsis Balanc quaion Phnomnological balanc Spd of ha wa Applicaion in plasma ranspor 1.
On h Spd of Ha Wa Mihály Maai maai@ra.bm.hu Conns Formulaion of h problm: infini spd? Local hrmal qulibrium (LTE hypohsis Balanc quaion Phnomnological balanc Spd of ha wa Applicaion in plasma ranspor 1.
Midterm exam 2, April 7, 2009 (solutions)
 Univrsiy of Pnnsylvania Dparmn of Mahmaics Mah 26 Honors Calculus II Spring Smsr 29 Prof Grassi, TA Ashr Aul Midrm xam 2, April 7, 29 (soluions) 1 Wri a basis for h spac of pairs (u, v) of smooh funcions
Univrsiy of Pnnsylvania Dparmn of Mahmaics Mah 26 Honors Calculus II Spring Smsr 29 Prof Grassi, TA Ashr Aul Midrm xam 2, April 7, 29 (soluions) 1 Wri a basis for h spac of pairs (u, v) of smooh funcions
4.1 The Uniform Distribution Def n: A c.r.v. X has a continuous uniform distribution on [a, b] when its pdf is = 1 a x b
![4.1 The Uniform Distribution Def n: A c.r.v. X has a continuous uniform distribution on [a, b] when its pdf is = 1 a x b 4.1 The Uniform Distribution Def n: A c.r.v. X has a continuous uniform distribution on [a, b] when its pdf is = 1 a x b](/thumbs/71/65779443.jpg) 4. Th Uniform Disribuion Df n: A c.r.v. has a coninuous uniform disribuion on [a, b] whn is pdf is f x a x b b a Also, b + a b a µ E and V Ex4. Suppos, h lvl of unblivabiliy a any poin in a Transformrs
4. Th Uniform Disribuion Df n: A c.r.v. has a coninuous uniform disribuion on [a, b] whn is pdf is f x a x b b a Also, b + a b a µ E and V Ex4. Suppos, h lvl of unblivabiliy a any poin in a Transformrs
S.Y. B.Sc. (IT) : Sem. III. Applied Mathematics. Q.1 Attempt the following (any THREE) [15]
![S.Y. B.Sc. (IT) : Sem. III. Applied Mathematics. Q.1 Attempt the following (any THREE) [15] S.Y. B.Sc. (IT) : Sem. III. Applied Mathematics. Q.1 Attempt the following (any THREE) [15]](/thumbs/92/108666103.jpg) S.Y. B.Sc. (IT) : Sm. III Applid Mahmaics Tim : ½ Hrs.] Prlim Qusion Papr Soluion [Marks : 75 Q. Amp h following (an THREE) 3 6 Q.(a) Rduc h mari o normal form and find is rank whr A 3 3 5 3 3 3 6 Ans.:
S.Y. B.Sc. (IT) : Sm. III Applid Mahmaics Tim : ½ Hrs.] Prlim Qusion Papr Soluion [Marks : 75 Q. Amp h following (an THREE) 3 6 Q.(a) Rduc h mari o normal form and find is rank whr A 3 3 5 3 3 3 6 Ans.:
Phys463.nb Conductivity. Another equivalent definition of the Fermi velocity is
 39 Anohr quival dfiniion of h Fri vlociy is pf vf (6.4) If h rgy is a quadraic funcion of k H k L, hs wo dfiniions ar idical. If is NOT a quadraic funcion of k (which could happ as will b discussd in h
39 Anohr quival dfiniion of h Fri vlociy is pf vf (6.4) If h rgy is a quadraic funcion of k H k L, hs wo dfiniions ar idical. If is NOT a quadraic funcion of k (which could happ as will b discussd in h
XV Exponential and Logarithmic Functions
 MATHEMATICS 0-0-RE Dirnial Calculus Marin Huard Winr 08 XV Eponnial and Logarihmic Funcions. Skch h graph o h givn uncions and sa h domain and rang. d) ) ) log. Whn Sarah was born, hr parns placd $000
MATHEMATICS 0-0-RE Dirnial Calculus Marin Huard Winr 08 XV Eponnial and Logarihmic Funcions. Skch h graph o h givn uncions and sa h domain and rang. d) ) ) log. Whn Sarah was born, hr parns placd $000
( ) Geometric Operations and Morphing. Geometric Transformation. Forward v.s. Inverse Mapping. I (x,y ) Image Processing - Lesson 4 IDC-CG 1
 Img Procssing - Lsson 4 Gomtric Oprtions nd Morphing Gomtric Trnsformtion Oprtions dpnd on Pil s Coordints. Contt fr. Indpndnt of pil vlus. f f (, ) (, ) ( f (, ), f ( ) ) I(, ) I', (,) (, ) I(,) I (,
Img Procssing - Lsson 4 Gomtric Oprtions nd Morphing Gomtric Trnsformtion Oprtions dpnd on Pil s Coordints. Contt fr. Indpndnt of pil vlus. f f (, ) (, ) ( f (, ), f ( ) ) I(, ) I', (,) (, ) I(,) I (,
First Lecture of Machine Learning. Hung-yi Lee
 Firs Lcur of Machin Larning Hung-yi L Larning o say ys/no Binary Classificaion Larning o say ys/no Sam filring Is an -mail sam or no? Rcommndaion sysms rcommnd h roduc o h cusomr or no? Malwar dcion Is
Firs Lcur of Machin Larning Hung-yi L Larning o say ys/no Binary Classificaion Larning o say ys/no Sam filring Is an -mail sam or no? Rcommndaion sysms rcommnd h roduc o h cusomr or no? Malwar dcion Is
PERIODICAL SOLUTION OF SOME DIFFERENTIAL EQUATIONS UDC 517.9(045)=20. Julka Knežević-Miljanović
 FCT UNIVESITTIS Sri: chanic uomaic Conrol and oboic Vol. N o 7 5. 87-9 PEIODICL SOLUTION OF SOE DIFFEENTIL EQUTIONS UDC 57.95= Julka Knžvić-iljanović Facul o ahmaic Univri o lgrad E-mail: knzvic@oincar.ma.bg.ac.u
FCT UNIVESITTIS Sri: chanic uomaic Conrol and oboic Vol. N o 7 5. 87-9 PEIODICL SOLUTION OF SOE DIFFEENTIL EQUTIONS UDC 57.95= Julka Knžvić-iljanović Facul o ahmaic Univri o lgrad E-mail: knzvic@oincar.ma.bg.ac.u
where: u: input y: output x: state vector A, B, C, D are const matrices
 Sa pac modl: linar: y or in om : Sa q : f, u Oupu q : y h, u u Du F Gu y H Ju whr: u: inpu y: oupu : a vcor,,, D ar con maric Eampl " $ & ' " $ & 'u y " & * * * * [ ],, D H D I " $ " & $ ' " & $ ' " &
Sa pac modl: linar: y or in om : Sa q : f, u Oupu q : y h, u u Du F Gu y H Ju whr: u: inpu y: oupu : a vcor,,, D ar con maric Eampl " $ & ' " $ & 'u y " & * * * * [ ],, D H D I " $ " & $ ' " & $ ' " &
Applied Statistics and Probability for Engineers, 6 th edition October 17, 2016
 Applid Saisics and robabiliy for Enginrs, 6 h diion Ocobr 7, 6 CHATER Scion - -. a d. 679.. b. d. 88 c d d d. 987 d. 98 f d.. Thn, = ln. =. g d.. Thn, = ln.9 =.. -7. a., by symmry. b.. d...6. 7.. c...
Applid Saisics and robabiliy for Enginrs, 6 h diion Ocobr 7, 6 CHATER Scion - -. a d. 679.. b. d. 88 c d d d. 987 d. 98 f d.. Thn, = ln. =. g d.. Thn, = ln.9 =.. -7. a., by symmry. b.. d...6. 7.. c...
Wave Equation (2 Week)
 Rfrnc Wav quaion ( Wk 6.5 Tim-armonic filds 7. Ovrviw 7. Plan Wavs in Losslss Mdia 7.3 Plan Wavs in Loss Mdia 7.5 Flow of lcromagnic Powr and h Poning Vcor 7.6 Normal Incidnc of Plan Wavs a Plan Boundaris
Rfrnc Wav quaion ( Wk 6.5 Tim-armonic filds 7. Ovrviw 7. Plan Wavs in Losslss Mdia 7.3 Plan Wavs in Loss Mdia 7.5 Flow of lcromagnic Powr and h Poning Vcor 7.6 Normal Incidnc of Plan Wavs a Plan Boundaris
Math 221: Mathematical Notation
 Mah 221: Mahemaical Noaion Purpose: One goal in any course is o properly use he language o ha subjec. These noaions summarize some o he major conceps and more diicul opics o he uni. Typing hem helps you
Mah 221: Mahemaical Noaion Purpose: One goal in any course is o properly use he language o ha subjec. These noaions summarize some o he major conceps and more diicul opics o he uni. Typing hem helps you
Discussion 06 Solutions
 STAT Discussion Soluions Spring 8. Th wigh of fish in La Paradis follows a normal disribuion wih man of 8. lbs and sandard dviaion of. lbs. a) Wha proporion of fish ar bwn 9 lbs and lbs? æ 9-8. - 8. P
STAT Discussion Soluions Spring 8. Th wigh of fish in La Paradis follows a normal disribuion wih man of 8. lbs and sandard dviaion of. lbs. a) Wha proporion of fish ar bwn 9 lbs and lbs? æ 9-8. - 8. P
B) 25y e. 5. Find the second partial f. 6. Find the second partials (including the mixed partials) of
 Sampl Final 00 1. Suppos z = (, y), ( a, b ) = 0, y ( a, b ) = 0, ( a, b ) = 1, ( a, b ) = 1, and y ( a, b ) =. Thn (a, b) is h s is inconclusiv a saddl poin a rlaiv minimum a rlaiv maimum. * (Classiy
Sampl Final 00 1. Suppos z = (, y), ( a, b ) = 0, y ( a, b ) = 0, ( a, b ) = 1, ( a, b ) = 1, and y ( a, b ) =. Thn (a, b) is h s is inconclusiv a saddl poin a rlaiv minimum a rlaiv maimum. * (Classiy
CHAPTER 9 Compressible Flow
 CHPTER 9 Comrssibl Flow Char 9 / Comrssibl Flow Inroducion 9. c c cv + R. c kcv. c + R or c R k k Rk c k Sd of Sound 9.4 Subsiu Eq. 4.5.8 ino Eq. 4.5.7 and nglc onial nrgy chang: Q WS + + u~ u~. m ρ ρ
CHPTER 9 Comrssibl Flow Char 9 / Comrssibl Flow Inroducion 9. c c cv + R. c kcv. c + R or c R k k Rk c k Sd of Sound 9.4 Subsiu Eq. 4.5.8 ino Eq. 4.5.7 and nglc onial nrgy chang: Q WS + + u~ u~. m ρ ρ
Final Exam : Solutions
 Comp : Algorihm and Daa Srucur Final Exam : Soluion. Rcuriv Algorihm. (a) To bgin ind h mdian o {x, x,... x n }. Sinc vry numbr xcp on in h inrval [0, n] appar xacly onc in h li, w hav ha h mdian mu b
Comp : Algorihm and Daa Srucur Final Exam : Soluion. Rcuriv Algorihm. (a) To bgin ind h mdian o {x, x,... x n }. Sinc vry numbr xcp on in h inrval [0, n] appar xacly onc in h li, w hav ha h mdian mu b
Transfer function and the Laplace transformation
 Lab No PH-35 Porland Sa Univriy A. La Roa Tranfr funcion and h Laplac ranformaion. INTRODUTION. THE LAPLAE TRANSFORMATION L 3. TRANSFER FUNTIONS 4. ELETRIAL SYSTEMS Analyi of h hr baic paiv lmn R, and
Lab No PH-35 Porland Sa Univriy A. La Roa Tranfr funcion and h Laplac ranformaion. INTRODUTION. THE LAPLAE TRANSFORMATION L 3. TRANSFER FUNTIONS 4. ELETRIAL SYSTEMS Analyi of h hr baic paiv lmn R, and
3D Coordinate Systems. 3D Geometric Transformation Chapt. 5 in FVD, Chapt. 11 in Hearn & Baker. Right-handed coordinate system:
 3D Geomeric ransformaion Chap. 5 in FVD, Chap. in Hearn & Baker 3D Coordinae Ssems Righ-handed coordinae ssem: Lef-handed coordinae ssem: 2 Reminder: Vecor rodc U V UV VU sin ˆ V nu V U V U ˆ ˆ ˆ 3D oin
3D Geomeric ransformaion Chap. 5 in FVD, Chap. in Hearn & Baker 3D Coordinae Ssems Righ-handed coordinae ssem: Lef-handed coordinae ssem: 2 Reminder: Vecor rodc U V UV VU sin ˆ V nu V U V U ˆ ˆ ˆ 3D oin
Logistic equation of Human population growth (generalization to the case of reactive environment).
 Logisic quaion of Human populaion growh gnralizaion o h cas of raciv nvironmn. Srg V. Ershkov Insiu for Tim aur Exploraions M.V. Lomonosov's Moscow Sa Univrsi Lninski gor - Moscow 999 ussia -mail: srgj-rshkov@andx.ru
Logisic quaion of Human populaion growh gnralizaion o h cas of raciv nvironmn. Srg V. Ershkov Insiu for Tim aur Exploraions M.V. Lomonosov's Moscow Sa Univrsi Lninski gor - Moscow 999 ussia -mail: srgj-rshkov@andx.ru
Boyce/DiPrima 9 th ed, Ch 2.1: Linear Equations; Method of Integrating Factors
 Boc/DiPrima 9 h d, Ch.: Linar Equaions; Mhod of Ingraing Facors Elmnar Diffrnial Equaions and Boundar Valu Problms, 9 h diion, b William E. Boc and Richard C. DiPrima, 009 b John Wil & Sons, Inc. A linar
Boc/DiPrima 9 h d, Ch.: Linar Equaions; Mhod of Ingraing Facors Elmnar Diffrnial Equaions and Boundar Valu Problms, 9 h diion, b William E. Boc and Richard C. DiPrima, 009 b John Wil & Sons, Inc. A linar
Elements of Computer Graphics
 CS580: Compuer Graphics Min H. Kim KAIST School of Compuing Elemens of Compuer Graphics Geomery Maerial model Ligh Rendering Virual phoography 2 Foundaions of Compuer Graphics A PINHOLE CAMERA IN 3D 3
CS580: Compuer Graphics Min H. Kim KAIST School of Compuing Elemens of Compuer Graphics Geomery Maerial model Ligh Rendering Virual phoography 2 Foundaions of Compuer Graphics A PINHOLE CAMERA IN 3D 3
3(8 ) (8 x x ) 3x x (8 )
 Scion - CHATER -. a d.. b. d.86 c d 8 d d.9997 f g 6. d. d. Thn, = ln. =. =.. d Thn, = ln.9 =.7 8 -. a d.6 6 6 6 6 8 8 8 b 9 d 6 6 6 8 c d.8 6 6 6 6 8 8 7 7 d 6 d.6 6 6 6 6 6 6 8 u u u u du.9 6 6 6 6 6
Scion - CHATER -. a d.. b. d.86 c d 8 d d.9997 f g 6. d. d. Thn, = ln. =. =.. d Thn, = ln.9 =.7 8 -. a d.6 6 6 6 6 8 8 8 b 9 d 6 6 6 8 c d.8 6 6 6 6 8 8 7 7 d 6 d.6 6 6 6 6 6 6 8 u u u u du.9 6 6 6 6 6
Consider a system of 2 simultaneous first order linear equations
 Soluon of sysms of frs ordr lnar quaons onsdr a sysm of smulanous frs ordr lnar quaons a b c d I has h alrna mar-vcor rprsnaon a b c d Or, n shorhand A, f A s alrady known from con W know ha h abov sysm
Soluon of sysms of frs ordr lnar quaons onsdr a sysm of smulanous frs ordr lnar quaons a b c d I has h alrna mar-vcor rprsnaon a b c d Or, n shorhand A, f A s alrady known from con W know ha h abov sysm
Boyce/DiPrima 9 th ed, Ch 7.8: Repeated Eigenvalues
 Boy/DiPrima 9 h d Ch 7.8: Rpad Eignvalus Elmnary Diffrnial Equaions and Boundary Valu Problms 9 h diion by William E. Boy and Rihard C. DiPrima 9 by John Wily & Sons In. W onsidr again a homognous sysm
Boy/DiPrima 9 h d Ch 7.8: Rpad Eignvalus Elmnary Diffrnial Equaions and Boundary Valu Problms 9 h diion by William E. Boy and Rihard C. DiPrima 9 by John Wily & Sons In. W onsidr again a homognous sysm
Voltage v(z) ~ E(z)D. We can actually get to this wave behavior by using circuit theory, w/o going into details of the EM fields!
 Considr a pair of wirs idal wirs ngh >, say, infinily long olag along a cabl can vary! D olag v( E(D W can acually g o his wav bhavior by using circui hory, w/o going ino dails of h EM filds! Thr
Considr a pair of wirs idal wirs ngh >, say, infinily long olag along a cabl can vary! D olag v( E(D W can acually g o his wav bhavior by using circui hory, w/o going ino dails of h EM filds! Thr
Charging of capacitor through inductor and resistor
 cur 4&: R circui harging of capacior hrough inducor and rsisor us considr a capacior of capacianc is conncd o a D sourc of.m.f. E hrough a rsisr of rsisanc R, an inducor of inducanc and a y K in sris.
cur 4&: R circui harging of capacior hrough inducor and rsisor us considr a capacior of capacianc is conncd o a D sourc of.m.f. E hrough a rsisr of rsisanc R, an inducor of inducanc and a y K in sris.
Physics Notes - Ch. 2 Motion in One Dimension
 Physics Noes - Ch. Moion in One Dimension I. The naure o physical quaniies: scalars and ecors A. Scalar quaniy ha describes only magniude (how much), NOT including direcion; e. mass, emperaure, ime, olume,
Physics Noes - Ch. Moion in One Dimension I. The naure o physical quaniies: scalars and ecors A. Scalar quaniy ha describes only magniude (how much), NOT including direcion; e. mass, emperaure, ime, olume,
Microscopic Flow Characteristics Time Headway - Distribution
 CE57: Traffic Flow Thory Spring 20 Wk 2 Modling Hadway Disribuion Microscopic Flow Characrisics Tim Hadway - Disribuion Tim Hadway Dfiniion Tim Hadway vrsus Gap Ahmd Abdl-Rahim Civil Enginring Dparmn,
CE57: Traffic Flow Thory Spring 20 Wk 2 Modling Hadway Disribuion Microscopic Flow Characrisics Tim Hadway - Disribuion Tim Hadway Dfiniion Tim Hadway vrsus Gap Ahmd Abdl-Rahim Civil Enginring Dparmn,
Control System Engineering (EE301T) Assignment: 2
 Conrol Sysm Enginring (EE0T) Assignmn: PART-A (Tim Domain Analysis: Transin Rspons Analysis). Oain h rspons of a uniy fdack sysm whos opn-loop ransfr funcion is (s) s ( s 4) for a uni sp inpu and also
Conrol Sysm Enginring (EE0T) Assignmn: PART-A (Tim Domain Analysis: Transin Rspons Analysis). Oain h rspons of a uniy fdack sysm whos opn-loop ransfr funcion is (s) s ( s 4) for a uni sp inpu and also
ELEN E4830 Digital Image Processing
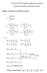 ELEN E48 Dgal Imag Procssng Mrm Eamnaon Sprng Soluon Problm Quanzaon and Human Encodng r k u P u P u r r 6 6 6 6 5 6 4 8 8 4 P r 6 6 P r 4 8 8 6 8 4 r 8 4 8 4 7 8 r 6 6 6 6 P r 8 4 8 P r 6 6 8 5 P r /
ELEN E48 Dgal Imag Procssng Mrm Eamnaon Sprng Soluon Problm Quanzaon and Human Encodng r k u P u P u r r 6 6 6 6 5 6 4 8 8 4 P r 6 6 P r 4 8 8 6 8 4 r 8 4 8 4 7 8 r 6 6 6 6 P r 8 4 8 P r 6 6 8 5 P r /
Copyright 2012 Pearson Education, Inc. Publishing as Prentice Hall.
 Chapr Rviw 0 6. ( a a ln a. This will qual a if an onl if ln a, or a. + k an (ln + c. Thrfor, a an valu of, whr h wo curvs inrsc, h wo angn lins will b prpnicular. 6. (a Sinc h lin passs hrough h origin
Chapr Rviw 0 6. ( a a ln a. This will qual a if an onl if ln a, or a. + k an (ln + c. Thrfor, a an valu of, whr h wo curvs inrsc, h wo angn lins will b prpnicular. 6. (a Sinc h lin passs hrough h origin
Southern Taiwan University
 Chaptr Ordinar Diffrntial Equations of th First Ordr and First Dgr Gnral form:., d +, d 0.a. f,.b I. Sparabl Diffrntial quations Form: d + d 0 C d d E 9 + 4 0 Solution: 9d + 4d 0 9 + 4 C E + d Solution:
Chaptr Ordinar Diffrntial Equations of th First Ordr and First Dgr Gnral form:., d +, d 0.a. f,.b I. Sparabl Diffrntial quations Form: d + d 0 C d d E 9 + 4 0 Solution: 9d + 4d 0 9 + 4 C E + d Solution:
Chapter 5 The Laplace Transform. x(t) input y(t) output Dynamic System
 EE 422G No: Chapr 5 Inrucor: Chung Chapr 5 Th Laplac Tranform 5- Inroducion () Sym analyi inpu oupu Dynamic Sym Linar Dynamic ym: A procor which proc h inpu ignal o produc h oupu dy ( n) ( n dy ( n) +
EE 422G No: Chapr 5 Inrucor: Chung Chapr 5 Th Laplac Tranform 5- Inroducion () Sym analyi inpu oupu Dynamic Sym Linar Dynamic ym: A procor which proc h inpu ignal o produc h oupu dy ( n) ( n dy ( n) +
1973 AP Calculus BC: Section I
 97 AP Calculus BC: Scio I 9 Mius No Calculaor No: I his amiaio, l dos h aural logarihm of (ha is, logarihm o h bas ).. If f ( ) =, h f ( ) = ( ). ( ) + d = 7 6. If f( ) = +, h h s of valus for which f
97 AP Calculus BC: Scio I 9 Mius No Calculaor No: I his amiaio, l dos h aural logarihm of (ha is, logarihm o h bas ).. If f ( ) =, h f ( ) = ( ). ( ) + d = 7 6. If f( ) = +, h h s of valus for which f
Elementary Differential Equations and Boundary Value Problems
 Elmnar Diffrnial Equaions and Boundar Valu Problms Boc. & DiPrima 9 h Ediion Chapr : Firs Ordr Diffrnial Equaions 00600 คณ ตศาสตร ว ศวกรรม สาขาว ชาว ศวกรรมคอมพ วเตอร ป การศ กษา /55 ผศ.ดร.อร ญญา ผศ.ดร.สมศ
Elmnar Diffrnial Equaions and Boundar Valu Problms Boc. & DiPrima 9 h Ediion Chapr : Firs Ordr Diffrnial Equaions 00600 คณ ตศาสตร ว ศวกรรม สาขาว ชาว ศวกรรมคอมพ วเตอร ป การศ กษา /55 ผศ.ดร.อร ญญา ผศ.ดร.สมศ
SOLUTIONS. 1. Consider two continuous random variables X and Y with joint p.d.f. f ( x, y ) = = = 15. Stepanov Dalpiaz
 STAT UIUC Pracic Problms #7 SOLUTIONS Spanov Dalpiaz Th following ar a numbr of pracic problms ha ma b hlpful for compling h homwor, and will lil b vr usful for suding for ams.. Considr wo coninuous random
STAT UIUC Pracic Problms #7 SOLUTIONS Spanov Dalpiaz Th following ar a numbr of pracic problms ha ma b hlpful for compling h homwor, and will lil b vr usful for suding for ams.. Considr wo coninuous random
Ratio-Product Type Exponential Estimator For Estimating Finite Population Mean Using Information On Auxiliary Attribute
 Raio-Produc T Exonnial Esimaor For Esimaing Fini Poulaion Man Using Informaion On Auxiliar Aribu Rajsh Singh, Pankaj hauhan, and Nirmala Sawan, School of Saisics, DAVV, Indor (M.P., India (rsinghsa@ahoo.com
Raio-Produc T Exonnial Esimaor For Esimaing Fini Poulaion Man Using Informaion On Auxiliar Aribu Rajsh Singh, Pankaj hauhan, and Nirmala Sawan, School of Saisics, DAVV, Indor (M.P., India (rsinghsa@ahoo.com
2.1. Differential Equations and Solutions #3, 4, 17, 20, 24, 35
 MATH 5 PS # Summr 00.. Diffrnial Equaions and Soluions PS.# Show ha ()C #, 4, 7, 0, 4, 5 ( / ) is a gnral soluion of h diffrnial quaion. Us a compur or calculaor o skch h soluions for h givn valus of h
MATH 5 PS # Summr 00.. Diffrnial Equaions and Soluions PS.# Show ha ()C #, 4, 7, 0, 4, 5 ( / ) is a gnral soluion of h diffrnial quaion. Us a compur or calculaor o skch h soluions for h givn valus of h
7.4 QUANTUM MECHANICAL TREATMENT OF FLUCTUATIONS *
 Andri Tokmakoff, MIT Dparmn of Chmisry, 5/19/5 7-11 7.4 QUANTUM MECANICAL TREATMENT OF FLUCTUATIONS * Inroducion and Prviw Now h origin of frquncy flucuaions is inracions of our molcul (or mor approprialy
Andri Tokmakoff, MIT Dparmn of Chmisry, 5/19/5 7-11 7.4 QUANTUM MECANICAL TREATMENT OF FLUCTUATIONS * Inroducion and Prviw Now h origin of frquncy flucuaions is inracions of our molcul (or mor approprialy
Lecture 4: Laplace Transforms
 Lur 4: Lapla Transforms Lapla and rlad ransformaions an b usd o solv diffrnial quaion and o rdu priodi nois in signals and imags. Basially, hy onvr h drivaiv opraions ino mulipliaion, diffrnial quaions
Lur 4: Lapla Transforms Lapla and rlad ransformaions an b usd o solv diffrnial quaion and o rdu priodi nois in signals and imags. Basially, hy onvr h drivaiv opraions ino mulipliaion, diffrnial quaions
Why Laplace transforms?
 MAE4 Linar ircui Why Lalac ranform? Firordr R cc v v v KVL S R inananou for ach Subiu lmn rlaion v S Ordinary diffrnial quaion in rm of caacior volag Lalac ranform Solv Invr LT V u, v Ri, i A R V A _ v
MAE4 Linar ircui Why Lalac ranform? Firordr R cc v v v KVL S R inananou for ach Subiu lmn rlaion v S Ordinary diffrnial quaion in rm of caacior volag Lalac ranform Solv Invr LT V u, v Ri, i A R V A _ v
MEM 355 Performance Enhancement of Dynamical Systems A First Control Problem - Cruise Control
 MEM 355 Prformanc Enhancmn of Dynamical Sysms A Firs Conrol Problm - Cruis Conrol Harry G. Kwany Darmn of Mchanical Enginring & Mchanics Drxl Univrsiy Cruis Conrol ( ) mv = F mg sinθ cv v +.2v= u 9.8θ
MEM 355 Prformanc Enhancmn of Dynamical Sysms A Firs Conrol Problm - Cruis Conrol Harry G. Kwany Darmn of Mchanical Enginring & Mchanics Drxl Univrsiy Cruis Conrol ( ) mv = F mg sinθ cv v +.2v= u 9.8θ
4.3 Design of Sections for Flexure (Part II)
 Prsrssd Concr Srucurs Dr. Amlan K Sngupa and Prof. Dvdas Mnon 4. Dsign of Scions for Flxur (Par II) This scion covrs h following opics Final Dsign for Typ Mmrs Th sps for Typ 1 mmrs ar xplaind in Scion
Prsrssd Concr Srucurs Dr. Amlan K Sngupa and Prof. Dvdas Mnon 4. Dsign of Scions for Flxur (Par II) This scion covrs h following opics Final Dsign for Typ Mmrs Th sps for Typ 1 mmrs ar xplaind in Scion
Let us start with a two dimensional case. We consider a vector ( x,
 Roaion marices We consider now roaion marices in wo and hree dimensions. We sar wih wo dimensions since wo dimensions are easier han hree o undersand, and one dimension is a lile oo simple. However, our
Roaion marices We consider now roaion marices in wo and hree dimensions. We sar wih wo dimensions since wo dimensions are easier han hree o undersand, and one dimension is a lile oo simple. However, our
The graph of y = x (or y = ) consists of two branches, As x 0, y + ; as x 0, y +. x = 0 is the
 Copyright itutcom 005 Fr download & print from wwwitutcom Do not rproduc by othr mans Functions and graphs Powr functions Th graph of n y, for n Q (st of rational numbrs) y is a straight lin through th
Copyright itutcom 005 Fr download & print from wwwitutcom Do not rproduc by othr mans Functions and graphs Powr functions Th graph of n y, for n Q (st of rational numbrs) y is a straight lin through th
This is an example to show you how SMath can calculate the movement of kinematic mechanisms.
 Dec :5:6 - Kinemaics model of Simple Arm.sm This file is provided for educaional purposes as guidance for he use of he sofware ool. I is no guaraeed o be free from errors or ommissions. The mehods and
Dec :5:6 - Kinemaics model of Simple Arm.sm This file is provided for educaional purposes as guidance for he use of he sofware ool. I is no guaraeed o be free from errors or ommissions. The mehods and
Laplace Transforms recap for ccts
 Lalac Tranform rca for cc Wha h big ida?. Loo a iniial condiion ron of cc du o caacior volag and inducor currn a im Mh or nodal analyi wih -domain imdanc rianc or admianc conducanc Soluion of ODE drivn
Lalac Tranform rca for cc Wha h big ida?. Loo a iniial condiion ron of cc du o caacior volag and inducor currn a im Mh or nodal analyi wih -domain imdanc rianc or admianc conducanc Soluion of ODE drivn
H is equal to the surface current J S
 Chapr 6 Rflcion and Transmission of Wavs 6.1 Boundary Condiions A h boundary of wo diffrn mdium, lcromagnic fild hav o saisfy physical condiion, which is drmind by Maxwll s quaion. This is h boundary condiion
Chapr 6 Rflcion and Transmission of Wavs 6.1 Boundary Condiions A h boundary of wo diffrn mdium, lcromagnic fild hav o saisfy physical condiion, which is drmind by Maxwll s quaion. This is h boundary condiion
Math 116 Practice for Exam 2
 Mah 6 Pracice for Exam Generaed Ocober 3, 7 Name: SOLUTIONS Insrucor: Secion Number:. This exam has 5 quesions. Noe ha he problems are no of equal difficuly, so you may wan o skip over and reurn o a problem
Mah 6 Pracice for Exam Generaed Ocober 3, 7 Name: SOLUTIONS Insrucor: Secion Number:. This exam has 5 quesions. Noe ha he problems are no of equal difficuly, so you may wan o skip over and reurn o a problem
Nikesh Bajaj. Fourier Analysis and Synthesis Tool. Guess.? Question??? History. Fourier Series. Fourier. Nikesh Bajaj
 Guss.? ourir Analysis an Synhsis Tool Qusion??? niksh.473@lpu.co.in Digial Signal Procssing School of Elcronics an Communicaion Lovly Profssional Univrsiy Wha o you man by Transform? Wha is /Transform?
Guss.? ourir Analysis an Synhsis Tool Qusion??? niksh.473@lpu.co.in Digial Signal Procssing School of Elcronics an Communicaion Lovly Profssional Univrsiy Wha o you man by Transform? Wha is /Transform?
Lecture #6: Continuous-Time Signals
 EEL5: Discree-Time Signals and Sysems Lecure #6: Coninuous-Time Signals Lecure #6: Coninuous-Time Signals. Inroducion In his lecure, we discussed he ollowing opics:. Mahemaical represenaion and ransormaions
EEL5: Discree-Time Signals and Sysems Lecure #6: Coninuous-Time Signals Lecure #6: Coninuous-Time Signals. Inroducion In his lecure, we discussed he ollowing opics:. Mahemaical represenaion and ransormaions
Lecture 2: Bayesian inference - Discrete probability models
 cu : Baysian infnc - Disc obabiliy modls Many hings abou Baysian infnc fo disc obabiliy modls a simila o fqunis infnc Disc obabiliy modls: Binomial samling Samling a fix numb of ials fom a Bnoulli ocss
cu : Baysian infnc - Disc obabiliy modls Many hings abou Baysian infnc fo disc obabiliy modls a simila o fqunis infnc Disc obabiliy modls: Binomial samling Samling a fix numb of ials fom a Bnoulli ocss
EE 315 Notes. Gürdal Arslan CLASS 1. (Sections ) What is a signal?
 EE 35 Noes Gürdal Arslan CLASS (Secions.-.2) Wha is a signal? In his class, a signal is some funcion of ime and i represens how some physical quaniy changes over some window of ime. Examples: velociy of
EE 35 Noes Gürdal Arslan CLASS (Secions.-.2) Wha is a signal? In his class, a signal is some funcion of ime and i represens how some physical quaniy changes over some window of ime. Examples: velociy of
1973 AP Calculus AB: Section I
 97 AP Calculus AB: Sction I 9 Minuts No Calculator Not: In this amination, ln dnots th natural logarithm of (that is, logarithm to th bas ).. ( ) d= + C 6 + C + C + C + C. If f ( ) = + + + and ( ), g=
97 AP Calculus AB: Sction I 9 Minuts No Calculator Not: In this amination, ln dnots th natural logarithm of (that is, logarithm to th bas ).. ( ) d= + C 6 + C + C + C + C. If f ( ) = + + + and ( ), g=
The Variance-Covariance Matrix
 Th Varanc-Covaranc Marx Our bggs a so-ar has bn ng a lnar uncon o a s o daa by mnmzng h las squars drncs rom h o h daa wh mnsarch. Whn analyzng non-lnar daa you hav o us a program l Malab as many yps o
Th Varanc-Covaranc Marx Our bggs a so-ar has bn ng a lnar uncon o a s o daa by mnmzng h las squars drncs rom h o h daa wh mnsarch. Whn analyzng non-lnar daa you hav o us a program l Malab as many yps o
Check in: 1 If m = 2(x + 1) and n = find y when. b y = 2m n 2
 7 Parameric equaions This chaer will show ou how o skech curves using heir arameric equaions conver arameric equaions o Caresian equaions find oins of inersecion of curves and lines using arameric equaions
7 Parameric equaions This chaer will show ou how o skech curves using heir arameric equaions conver arameric equaions o Caresian equaions find oins of inersecion of curves and lines using arameric equaions
Text: WMM, Chapter 5. Sections , ,
 Lcturs 6 - Continuous Probabilit Distributions Tt: WMM, Chaptr 5. Sctions 6.-6.4, 6.6-6.8, 7.-7. In th prvious sction, w introduc som of th common probabilit distribution functions (PDFs) for discrt sampl
Lcturs 6 - Continuous Probabilit Distributions Tt: WMM, Chaptr 5. Sctions 6.-6.4, 6.6-6.8, 7.-7. In th prvious sction, w introduc som of th common probabilit distribution functions (PDFs) for discrt sampl
Derivative Securities: Lecture 4 Introduction to option pricing
 Divaiv cuiis: Lcu 4 Inoducion o oion icing oucs: J. Hull 7 h diion Avllanda and Launc () Yahoo!Financ & assod wbsis Oion Picing In vious lcus w covd owad icing and h imoanc o cos-o cay W also covd Pu-all
Divaiv cuiis: Lcu 4 Inoducion o oion icing oucs: J. Hull 7 h diion Avllanda and Launc () Yahoo!Financ & assod wbsis Oion Picing In vious lcus w covd owad icing and h imoanc o cos-o cay W also covd Pu-all
Homework #2: CMPT-379 Distributed on Oct 2; due on Oct 16 Anoop Sarkar
 Homwork #2: CMPT-379 Disribud on Oc 2 du on Oc 16 Anoop Sarkar anoop@cs.su.ca Rading or his homwork includs Chp 4 o h Dragon book. I ndd, rr o: hp://ldp.org/howto/lx-yacc-howto.hml Only submi answrs or
Homwork #2: CMPT-379 Disribud on Oc 2 du on Oc 16 Anoop Sarkar anoop@cs.su.ca Rading or his homwork includs Chp 4 o h Dragon book. I ndd, rr o: hp://ldp.org/howto/lx-yacc-howto.hml Only submi answrs or
fiziks Institute for NET/JRF, GATE, IIT JAM, JEST, TIFR and GRE in PHYSICAL SCIENCES MATEMATICAL PHYSICS SOLUTIONS are
 MTEMTICL PHYSICS SOLUTIONS GTE- Q. Considr an ani-symmric nsor P ij wih indics i and j running from o 5. Th numbr of indpndn componns of h nsor is 9 6 ns: Soluion: Th numbr of indpndn componns of h nsor
MTEMTICL PHYSICS SOLUTIONS GTE- Q. Considr an ani-symmric nsor P ij wih indics i and j running from o 5. Th numbr of indpndn componns of h nsor is 9 6 ns: Soluion: Th numbr of indpndn componns of h nsor
Ali Karimpour Associate Professor Ferdowsi University of Mashhad. Reference: System Identification Theory For The User Lennart Ljung
 SYSEM IDEIFICAIO Ali Karimpour Associa Prossor Frdowsi Univrsi o Mashhad Rrnc: Ssm Idniicaion hor For h Usr Lnnar Ljung Lcur 7 lcur 7 Paramr Esimaion Mhods opics o b covrd includ: Guiding Principls Bhind
SYSEM IDEIFICAIO Ali Karimpour Associa Prossor Frdowsi Univrsi o Mashhad Rrnc: Ssm Idniicaion hor For h Usr Lnnar Ljung Lcur 7 lcur 7 Paramr Esimaion Mhods opics o b covrd includ: Guiding Principls Bhind
The transition:transversion rate ratio vs. the T-ratio.
 PhyloMah Lcur 8 by Dan Vandrpool March, 00 opics of Discussion ransiion:ransvrsion ra raio Kappa vs. ransiion:ransvrsion raio raio alculaing h xpcd numbr of subsiuions using marix algbra Why h nral im
PhyloMah Lcur 8 by Dan Vandrpool March, 00 opics of Discussion ransiion:ransvrsion ra raio Kappa vs. ransiion:ransvrsion raio raio alculaing h xpcd numbr of subsiuions using marix algbra Why h nral im
Circuits and Systems I
 Circuis and Sysms I LECTURE #3 Th Spcrum, Priodic Signals, and h Tim-Varying Spcrum lions@pfl Prof. Dr. Volan Cvhr LIONS/Laboraory for Informaion and Infrnc Sysms Licns Info for SPFirs Slids This wor rlasd
Circuis and Sysms I LECTURE #3 Th Spcrum, Priodic Signals, and h Tim-Varying Spcrum lions@pfl Prof. Dr. Volan Cvhr LIONS/Laboraory for Informaion and Infrnc Sysms Licns Info for SPFirs Slids This wor rlasd
Chapter 3 Common Families of Distributions
 Chaer 3 Common Families of Disribuions Secion 31 - Inroducion Purose of his Chaer: Caalog many of common saisical disribuions (families of disribuions ha are indeed by one or more arameers) Wha we should
Chaer 3 Common Families of Disribuions Secion 31 - Inroducion Purose of his Chaer: Caalog many of common saisical disribuions (families of disribuions ha are indeed by one or more arameers) Wha we should
Spring 2006 Process Dynamics, Operations, and Control Lesson 2: Mathematics Review
 Spring 6 Procss Dynamics, Opraions, and Conrol.45 Lsson : Mahmaics Rviw. conx and dircion Imagin a sysm ha varis in im; w migh plo is oupu vs. im. A plo migh imply an quaion, and h quaion is usually an
Spring 6 Procss Dynamics, Opraions, and Conrol.45 Lsson : Mahmaics Rviw. conx and dircion Imagin a sysm ha varis in im; w migh plo is oupu vs. im. A plo migh imply an quaion, and h quaion is usually an
Chapter 3 Linear Equations of Higher Order (Page # 144)
 Ma Modr Dirial Equaios Lcur wk 4 Jul 4-8 Dr Firozzama Darm o Mahmaics ad Saisics Arizoa Sa Uivrsi This wk s lcur will covr har ad har 4 Scios 4 har Liar Equaios o Highr Ordr Pag # 44 Scio Iroducio: Scod
Ma Modr Dirial Equaios Lcur wk 4 Jul 4-8 Dr Firozzama Darm o Mahmaics ad Saisics Arizoa Sa Uivrsi This wk s lcur will covr har ad har 4 Scios 4 har Liar Equaios o Highr Ordr Pag # 44 Scio Iroducio: Scod
Institute of Actuaries of India
 Insiu of Acuaris of India ubjc CT3 Probabiliy and Mahmaical aisics Novmbr Examinaions INDICATIVE OLUTION Pag of IAI CT3 Novmbr ol. a sampl man = 35 sampl sandard dviaion = 36.6 b for = uppr bound = 35+*36.6
Insiu of Acuaris of India ubjc CT3 Probabiliy and Mahmaical aisics Novmbr Examinaions INDICATIVE OLUTION Pag of IAI CT3 Novmbr ol. a sampl man = 35 sampl sandard dviaion = 36.6 b for = uppr bound = 35+*36.6
A MARCHING IN SPACE AND TIME (MAST) SOLVER OF THE SHALLOW WATER EQUATIONS
 XXX Convgno di Idraulica Cosruzioni Idraulich - IDRA 6 Masr Class: Modlli numrici di corrni luviali su ondo isso ondo mobil A MARCING IN SPACE AND TIME () SOLVER OF TE SALLOW WATER EQUATIONS Cosanza Aricò
XXX Convgno di Idraulica Cosruzioni Idraulich - IDRA 6 Masr Class: Modlli numrici di corrni luviali su ondo isso ondo mobil A MARCING IN SPACE AND TIME () SOLVER OF TE SALLOW WATER EQUATIONS Cosanza Aricò
2.1: What is physics? Ch02: Motion along a straight line. 2.2: Motion. 2.3: Position, Displacement, Distance
 Ch: Moion along a sraigh line Moion Posiion and Displacemen Average Velociy and Average Speed Insananeous Velociy and Speed Acceleraion Consan Acceleraion: A Special Case Anoher Look a Consan Acceleraion
Ch: Moion along a sraigh line Moion Posiion and Displacemen Average Velociy and Average Speed Insananeous Velociy and Speed Acceleraion Consan Acceleraion: A Special Case Anoher Look a Consan Acceleraion
Math 102. Rumbos Spring Solutions to Assignment #8. Solution: The matrix, A, corresponding to the system in (1) is
 Math 12. Rumbos Spring 218 1 Solutions to Assignmnt #8 1. Construct a fundamntal matrix for th systm { ẋ 2y ẏ x + y. (1 Solution: Th matrix, A, corrsponding to th systm in (1 is 2 A. (2 1 1 Th charactristic
Math 12. Rumbos Spring 218 1 Solutions to Assignmnt #8 1. Construct a fundamntal matrix for th systm { ẋ 2y ẏ x + y. (1 Solution: Th matrix, A, corrsponding to th systm in (1 is 2 A. (2 1 1 Th charactristic
Let s look again at the first order linear differential equation we are attempting to solve, in its standard form:
 Th Ingraing Facor Mhod In h prvious xampls of simpl firs ordr ODEs, w found h soluions by algbraically spara h dpndn variabl- and h indpndn variabl- rms, and wri h wo sids of a givn quaion as drivaivs,
Th Ingraing Facor Mhod In h prvious xampls of simpl firs ordr ODEs, w found h soluions by algbraically spara h dpndn variabl- and h indpndn variabl- rms, and wri h wo sids of a givn quaion as drivaivs,
NAME: ANSWER KEY DATE: PERIOD. DIRECTIONS: MULTIPLE CHOICE. Choose the letter of the correct answer.
 R A T T L E R S S L U G S NAME: ANSWER KEY DATE: PERIOD PREAP PHYSICS REIEW TWO KINEMATICS / GRAPHING FORM A DIRECTIONS: MULTIPLE CHOICE. Chs h r f h rr answr. Us h fgur bw answr qusns 1 and 2. 0 10 20
R A T T L E R S S L U G S NAME: ANSWER KEY DATE: PERIOD PREAP PHYSICS REIEW TWO KINEMATICS / GRAPHING FORM A DIRECTIONS: MULTIPLE CHOICE. Chs h r f h rr answr. Us h fgur bw answr qusns 1 and 2. 0 10 20
Math 2142 Exam 1 Review Problems. x 2 + f (0) 3! for the 3rd Taylor polynomial at x = 0. To calculate the various quantities:
 Mah 4 Eam Review Problems Problem. Calculae he 3rd Taylor polynomial for arcsin a =. Soluion. Le f() = arcsin. For his problem, we use he formula f() + f () + f ()! + f () 3! for he 3rd Taylor polynomial
Mah 4 Eam Review Problems Problem. Calculae he 3rd Taylor polynomial for arcsin a =. Soluion. Le f() = arcsin. For his problem, we use he formula f() + f () + f ()! + f () 3! for he 3rd Taylor polynomial
Homework: Introduction to Motion
 Homwork: Inroducon o Moon Dsanc vs. Tm Graphs Nam Prod Drcons: Answr h foowng qusons n h spacs provdd. 1. Wha do you do o cra a horzona n on a dsancm graph? 2. How do you wak o cra a sragh n ha sops up?
Homwork: Inroducon o Moon Dsanc vs. Tm Graphs Nam Prod Drcons: Answr h foowng qusons n h spacs provdd. 1. Wha do you do o cra a horzona n on a dsancm graph? 2. How do you wak o cra a sragh n ha sops up?
Vector autoregression VAR. Case 1
 Vecor auoregression VAR So far we have focused mosl on models where deends onl on as. More generall we migh wan o consider oin models ha involve more han one variable. There are wo reasons: Firs, we migh
Vecor auoregression VAR So far we have focused mosl on models where deends onl on as. More generall we migh wan o consider oin models ha involve more han one variable. There are wo reasons: Firs, we migh
EE 350 Signals and Systems Spring 2005 Sample Exam #2 - Solutions
 EE 35 Signals an Sysms Spring 5 Sampl Exam # - Soluions. For h following signal x( cos( sin(3 - cos(5 - T, /T x( j j 3 j 3 j j 5 j 5 j a -, a a -, a a - ½, a 3 /j-j -j/, a -3 -/jj j/, a 5 -½, a -5 -½,
EE 35 Signals an Sysms Spring 5 Sampl Exam # - Soluions. For h following signal x( cos( sin(3 - cos(5 - T, /T x( j j 3 j 3 j j 5 j 5 j a -, a a -, a a - ½, a 3 /j-j -j/, a -3 -/jj j/, a 5 -½, a -5 -½,
AP CALCULUS AB 2003 SCORING GUIDELINES (Form B)
 SCORING GUIDELINES (Form B) Quesion A blood vessel is 6 millimeers (mm) long Disance wih circular cross secions of varying diameer. x (mm) 6 8 4 6 Diameer The able above gives he measuremens of he B(x)
SCORING GUIDELINES (Form B) Quesion A blood vessel is 6 millimeers (mm) long Disance wih circular cross secions of varying diameer. x (mm) 6 8 4 6 Diameer The able above gives he measuremens of he B(x)
Partial Derivatives: Suppose that z = f(x, y) is a function of two variables.
 Chaptr Functions o Two Variabls Applid Calculus 61 Sction : Calculus o Functions o Two Variabls Now that ou hav som amiliarit with unctions o two variabls it s tim to start appling calculus to hlp us solv
Chaptr Functions o Two Variabls Applid Calculus 61 Sction : Calculus o Functions o Two Variabls Now that ou hav som amiliarit with unctions o two variabls it s tim to start appling calculus to hlp us solv
LaPlace Transform in Circuit Analysis
 LaPlac Tranform in Circui Analyi Obciv: Calcula h Laplac ranform of common funcion uing h dfiniion and h Laplac ranform abl Laplac-ranform a circui, including componn wih non-zro iniial condiion. Analyz
LaPlac Tranform in Circui Analyi Obciv: Calcula h Laplac ranform of common funcion uing h dfiniion and h Laplac ranform abl Laplac-ranform a circui, including componn wih non-zro iniial condiion. Analyz
On General Solutions of First-Order Nonlinear Matrix and Scalar Ordinary Differential Equations
 saartvlos mcnirbata rovnuli akadmiis moamb 3 #2 29 BULLTN OF TH ORN NTONL DMY OF SNS vol 3 no 2 29 Mahmaics On nral Soluions of Firs-Ordr Nonlinar Mari and Scalar Ordinary Diffrnial uaions uram L Kharaishvili
saartvlos mcnirbata rovnuli akadmiis moamb 3 #2 29 BULLTN OF TH ORN NTONL DMY OF SNS vol 3 no 2 29 Mahmaics On nral Soluions of Firs-Ordr Nonlinar Mari and Scalar Ordinary Diffrnial uaions uram L Kharaishvili
A THREE COMPARTMENT MATHEMATICAL MODEL OF LIVER
 A THREE COPARTENT ATHEATICAL ODEL OF LIVER V. An N. Ch. Paabhi Ramacharyulu Faculy of ahmaics, R D collgs, Hanamonda, Warangal, India Dparmn of ahmaics, Naional Insiu of Tchnology, Warangal, India E-ail:
A THREE COPARTENT ATHEATICAL ODEL OF LIVER V. An N. Ch. Paabhi Ramacharyulu Faculy of ahmaics, R D collgs, Hanamonda, Warangal, India Dparmn of ahmaics, Naional Insiu of Tchnology, Warangal, India E-ail:
Chapter 15: Phenomena. Chapter 15 Chemical Kinetics. Reaction Rates. Reaction Rates R P. Reaction Rates. Rate Laws
 Chaper 5: Phenomena Phenomena: The reacion (aq) + B(aq) C(aq) was sudied a wo differen emperaures (98 K and 35 K). For each emperaure he reacion was sared by puing differen concenraions of he 3 species
Chaper 5: Phenomena Phenomena: The reacion (aq) + B(aq) C(aq) was sudied a wo differen emperaures (98 K and 35 K). For each emperaure he reacion was sared by puing differen concenraions of he 3 species

 +
+