Chapter 2: Systems of Linear Equations and Matrices
|
|
|
- Franklin Nicholson
- 5 years ago
- Views:
Transcription
1 Chapter 2: Systems of Linear Equations and Matrices 2.1 Systems Linear Equations: An Introduction Example Find the solution to the system of equations 2x y = 2 3x + 5y = 15 Solve first equation for y : 1. The two lines intersect. Plug into the second equation Simplify 2. The two lines are the same. Solve for y 3. The two lines are parallel. Check by graphing: 2
2 Example - find the solution to the system of equations: x + 2y = -1 2x + 4y = -2 Solve first equation for x, Example Find the solution to the system of equations: x 2y = 1 -x + 2y = 4 Solve first equation for x, Plug into second equation, Plug into second equation, Write both in slope-intercept form: Write both in slope-intercept form: This system is called dependent. This system has no solution. The solution is a parametric solution (infinite). We can consider y as a parameter, Particular solutions: 3 4
3 EXAMPLE: Three Equations and 3 Linear Variables Applications Word Problems Example - An apartment complex is being developed that has small, large and luxury apartments. The developer has decided that there will be a total of 192 apartments. The number of bigger apartments (large and luxury) will equal the number of small apartments. Finally, the number of small apartments will be three times the number of luxury apartments. How many apartments of each type will there be? ONE SOLUTION Answer Define your variables first x = y = z = PARAMETRIC NO SOLUTION 5 6
4 Try a drawing: 2.2: Systems of Linear Equations: Unique Solutions You may: Interchange any two of the equations. Multiply an equation by a non-zero constant. Add a multiple of one equation to another. If the complex had 1 luxury apartment, it would have 3 small apartments, z = 1 (1 luxury apartment) what comes out for x? x = 3z = 3*1 = 3. 2x y = 6 x + 2y = -2 AUGMENTED MATRIX form Rules are Interchange any of the rows equations. Multiply a row by a non-zero constant. Add a multiple of one row to another. Goal is 7 8
5 Calculator can help with commands This form of the augmented matrix is called row-reduced echelon form (RREF). What is RREF form? rowswap(matrix, row A, row B) for R A R B *row(value, matrix, row) for R value*r *row+(value, matrix row A, row B) is value*r A + R B R B 2x y = 6 x + 2y = All rows consisting entirely of zeros are at the bottom of the matrix 2. The first non-zero entry in any row is a 1 (called a leading 1) 3. In any two successive non-zero rows the leading 1 in the lower row lies to the right of the leading 1 in the upper row. 4. If a column contains a leading 1, then the rest of the entries in that column are 0 s. PIVOT on an element make the element a 1 and the rest of the entries in that column 0 s. Gauss-Jordan Method Pivot until the augmented matrix is in RREF form. 9 10
6 Apartment Problem x + y + z = 192 y + z = x x = 3z 2.3: Systems of Linear Equations: Underdetermined and Overdetermined Systems Example: x + 2y + z = 2 2x 3y z = 1 2x + 4y + 2z = Use your calculator: Now check is this in RREF? Are the rows of all zeros is below the non-zero rows? Is the first non-zero entry in any row is a 1? Do the leading 1's go down in a diagonal? If a column has a leading 1 then does the rest of the column have zeros? 11 12
7 EXAMPLE: x + 0y z = 4 0x + y + z = 3 0x + 0y + 0z = 0 x + y 2z = 3 2x y + 3z = 7 x 2y + 5z = A column containing a leading 1 is called a unit column and the variable associated with the column is a basic variable. RREF form? Are the rows of all zeros below the non-zero rows? Is the first non-zero entry in any row is a 1? Do the leading 1's go down in a diagonal? If a column has a leading 1 then is the rest of the column is zero? 13 14
8 Number of Solutions Theorem Case 1: If the number of equations is greater than or equal to the number of variables in a linear system then one of the following is true: The system has no solution The system has exactly one solution The system has infinitely many solutions Case 2: If there are fewer equations than variables then the system has no solution or infinitely many solutions. Example: Solve the following system (Case 2) x1 + 2x2 + 4x3 = 2 x + x + 2x = Matrices A matrix is a compact way of organizing and displaying data. A matrix is often denoted by a capital letter M or A. A matrix having m rows and n columns is an m x n matrix M 1 1 = 1 is a 3x1 matrix 2 M 2 = [ 1 1 2] is a 1x3 matrix These two matrices are NOT EQUAL. A matrix is called square if it has the same number of rows and columns. 1 2 A = 3 4 is a 2 x 2 square matrix. Example: Solve the following system (Case 1): a ij is the element in the ith row and jth column of matrix A. 4x + 6y = 8 3x 2y = 7 x + 3y = 5 2x + 6y =
9 Example - There are three stores. In the first week store I sold 88 loaves of bread, 48 quarts of milk, 16 jars of peanut butter and 112 pounds of cold cuts. At the same time, store II sold 105 loaves of bread, 72 quarts of milk, 21 jars of peanut butter and 147 pounds of cold cuts. Store III sold 60 loaves of bread, 40 quarts of milk, 0 jars of peanut butter and 50 pounds of cold cuts. Organize this data in a 3 x 4 matrix. Transpose - The transpose of a matrix is found by switching the rows and columns of the matrix. If A is a 3x2 matrix then A T will be a 2x3 matrix. A MATRIX ALGEBRA Equality - two matrices are equal if and only if each pair of corresponding elements are equal. example - Find the values of a, b, c, d given 1 b a 3 0 = c 1 d Addition - two matrices are added by adding the pairs of elements in each location example - find A+B where A 0 5 and B Scalar multiplication A scalar is a number (NOT a matrix). Multiply a matrix by a scalar by multiplying every element in the matrix by the scalar. Example - find -2 A. Answer 17 18
10 2.5 Multiplication of Matrices Example - A flower shop sells 96 roses, 250 carnations and 130 daisies in a week. The roses sell for $2 each, the carnations for $1 each and the daisies for $0.50 each. Find the revenue of the shop during the week using matrices. Answer - Express the number of flowers in a 1x3 matrix: In general, If A is 1xn and B is nx1, the product AB is a 1x1 matrix: b 11 b 21 AB =[ a a a n ] b n1 = a b + a b + + a b [ ] n n 1 Even more general, Next express the price as a 3 x 1 matrix: If A is an mxn matrix and B is a nxp matrix, then the product matrix A B=C is mxp. We can think of this as a type x price matrix. The shop s revenue is $ b11 b12 a a a n b b AB = a a a n bn1 ( a11 b11 + a12 b21 + a1 b 1) ( ab) 12 n n = ( ab) 21 ( ab)
11 Matrix multiplication is not commutative. That means, in general, that AB BA Example: find the products AB and BA where 1 0 A= 2 3 Answer B= Example - Cost Analysis - The Mundo Candy Company makes three types of chocolate candy: cheery cherry (cc), mucho mocha (mm) and almond delight (ad). The company produces its candy in San Diego (SD), Mexico City (MC) and Managua (Ma) using two main ingredients, sugar (su) and chocolate (choc). (a) Each kilogram (kg) of cheery cherry requires.5 kg of sugar and.2 kg of chocolate. Each kilogram of mucho mocha requires.4 kg of sugar and.3 kg of chocolate. Each kilogram of almond delight requires.3 kg of sugar and.3 kg of chocolate. Put this information in a 2x3 matrix. Matching dimensions is not everything! Look back at the flower problem a (3x1)*(1x3) gives a 3x3, but does it mean anything?? One special matrix is called the identity matrix, I. It is a square matrix with 1's on the diagonal and zeros elsewhere, I = I 2 is a 2x2 identity matrix and I n is an nxn identity matrix. The identity matrix has the following property 21 22
12 (b) The cost of 1 kg of sugar is $3 in San Diego, $2 in Mexico City and $1 in Managua. The cost of 1 kg of chocolate is $3 in San Diego, $3 in Mexico City and $4 in Managua. Put this information into a matrix in such a way that when it is multiplied by the matrix in part (a) it will tell us the cost of producing each kind of candy in each city. Matrix multiplication and linear equations: We can express a system of linear equations as a matrix product, AX=B. Consider the system 2x 3y = 6 x+ 2y= 4 In matrix form this looks like 2 3 x 6 = 1 2 y
13 2.6 Inverse of a Square Matrix Solve the matrix equation D = X AX for X. For any non-zero real number r, the reciprocal (or inverse) is 1 r or 1 r Multiplicative identity: For matrices, the inverse is A -1 and it is defined by A matrix with no inverse is called singular. If needed, find the inverse with the x -1 function on the calculator. The one use of matrix inverses is to solve matrix equations. Solve the matrix equation AX = B for X 25 26
14 Matrix inverses can be use to encrypt messages. First, assign each letter of the alphabet a number: Decode the message, M = E -1 (EM) = 1 to A 2 to B 3 to C 4 to D 5 to E 6 to F 7 to G 8 to H 9 to I 10 to J 11 to K 12 to L 13 to M 14 to N 15 to O 16 to P 17 to Q 18 to R 19 to S 20 to T 21 to U 22 to V 23 to W 24 to X 25 to Y 26 to Z 27 to space So the word aggies would be written To make this more difficult to decode, we can put the letters in a message matrix. Our encoding matrix will be 3x3, so our message will need to have 3 rows: Decode the message below using the encryption matrix E M = And multiply by an encoding matrix E = EM = 27 28
15 2.7 Leontief Input-Output Model Consider the economy of small village that has two industries, farming and weaving. The villagers find that to produce $1.00 of food, they need $0.40 of food and $0.10 of cloth. To produce $1.00 of cloth, they need $0.30 of food and $0.20 of cloth. The local city is demanding $7200 worth of food and $2700 of cloth. How much food and cloth needs to be produced to meet the villagers internal need and have the necessary exports? Define your variables, x 1 = x 2 = x 1 = 0.40x x x 2 = 0.10x x Define the following matrices X = production matrix = A = I-O matrix = D = demand matrix = System can then be written as Solve this matrix equation Set up the system of equations 29 30
16 X = So the village must produce of food and of cloth to meet the internal and external demands. Given the following IO matrix, interpret the meaning of each element and find the amount each sector needs to produce to meet internal and external demand. auto energy transportation auto A = energy transportation auto 474 D = energy 948 in millions of dollars. transportation
Matrix Multiplication
 Matrix Multiplication Example (Cost Analysis, 45 in 2.4) The Mundo Candy Company makes three types of chocolate candy: Cheery Cherry, Mucho Mocha, and Almond Delight. The company produces its products
Matrix Multiplication Example (Cost Analysis, 45 in 2.4) The Mundo Candy Company makes three types of chocolate candy: Cheery Cherry, Mucho Mocha, and Almond Delight. The company produces its products
Finite Mathematics Chapter 2. where a, b, c, d, h, and k are real numbers and neither a and b nor c and d are both zero.
 Finite Mathematics Chapter 2 Section 2.1 Systems of Linear Equations: An Introduction Systems of Equations Recall that a system of two linear equations in two variables may be written in the general form
Finite Mathematics Chapter 2 Section 2.1 Systems of Linear Equations: An Introduction Systems of Equations Recall that a system of two linear equations in two variables may be written in the general form
3. Replace any row by the sum of that row and a constant multiple of any other row.
 Section. Solution of Linear Systems by Gauss-Jordan Method A matrix is an ordered rectangular array of numbers, letters, symbols or algebraic expressions. A matrix with m rows and n columns has size or
Section. Solution of Linear Systems by Gauss-Jordan Method A matrix is an ordered rectangular array of numbers, letters, symbols or algebraic expressions. A matrix with m rows and n columns has size or
5.1 Introduction to Matrices
 5.1 Introduction to Matrices Reminder: A matrix with m rows and n columns has size m x n. (This is also sometimes referred to as the order of the matrix.) The entry in the ith row and jth column of a matrix
5.1 Introduction to Matrices Reminder: A matrix with m rows and n columns has size m x n. (This is also sometimes referred to as the order of the matrix.) The entry in the ith row and jth column of a matrix
7.6 The Inverse of a Square Matrix
 7.6 The Inverse of a Square Matrix Copyright Cengage Learning. All rights reserved. What You Should Learn Verify that two matrices are inverses of each other. Use Gauss-Jordan elimination to find inverses
7.6 The Inverse of a Square Matrix Copyright Cengage Learning. All rights reserved. What You Should Learn Verify that two matrices are inverses of each other. Use Gauss-Jordan elimination to find inverses
DM559 Linear and Integer Programming. Lecture 2 Systems of Linear Equations. Marco Chiarandini
 DM559 Linear and Integer Programming Lecture Marco Chiarandini Department of Mathematics & Computer Science University of Southern Denmark Outline 1. Outline 1. 3 A Motivating Example You are organizing
DM559 Linear and Integer Programming Lecture Marco Chiarandini Department of Mathematics & Computer Science University of Southern Denmark Outline 1. Outline 1. 3 A Motivating Example You are organizing
Systems of Linear Equations in two variables (4.1)
 Systems of Linear Equations in two variables (4.1) 1. Solve by graphing 2. Solve using substitution 3. Solve by elimination by addition 4. Applications Opening example A restaurant serves two types of
Systems of Linear Equations in two variables (4.1) 1. Solve by graphing 2. Solve using substitution 3. Solve by elimination by addition 4. Applications Opening example A restaurant serves two types of
If A is a 4 6 matrix and B is a 6 3 matrix then the dimension of AB is A. 4 6 B. 6 6 C. 4 3 D. 3 4 E. Undefined
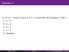 Question 1 If A is a 4 6 matrix and B is a 6 3 matrix then the dimension of AB is A. 4 6 B. 6 6 C. 4 3 D. 3 4 E. Undefined Quang T. Bach Math 18 October 18, 2017 1 / 17 Question 2 1 2 Let A = 3 4 1 2 3
Question 1 If A is a 4 6 matrix and B is a 6 3 matrix then the dimension of AB is A. 4 6 B. 6 6 C. 4 3 D. 3 4 E. Undefined Quang T. Bach Math 18 October 18, 2017 1 / 17 Question 2 1 2 Let A = 3 4 1 2 3
Math 140, c Benjamin Aurispa. 2.1 Matrices
 2.1 Matrices Reminder: A matrix with m rows and n columns has size m x n. (This is also sometimes referred to as the order of the matrix.) The entry in the ith row and jth column of a matrix A is denoted
2.1 Matrices Reminder: A matrix with m rows and n columns has size m x n. (This is also sometimes referred to as the order of the matrix.) The entry in the ith row and jth column of a matrix A is denoted
POLI270 - Linear Algebra
 POLI7 - Linear Algebra Septemer 8th Basics a x + a x +... + a n x n b () is the linear form where a, b are parameters and x n are variables. For a given equation such as x +x you only need a variable and
POLI7 - Linear Algebra Septemer 8th Basics a x + a x +... + a n x n b () is the linear form where a, b are parameters and x n are variables. For a given equation such as x +x you only need a variable and
Math 1314 Week #14 Notes
 Math 3 Week # Notes Section 5.: A system of equations consists of two or more equations. A solution to a system of equations is a point that satisfies all the equations in the system. In this chapter,
Math 3 Week # Notes Section 5.: A system of equations consists of two or more equations. A solution to a system of equations is a point that satisfies all the equations in the system. In this chapter,
Chapter 1. Vectors, Matrices, and Linear Spaces
 1.4 Solving Systems of Linear Equations 1 Chapter 1. Vectors, Matrices, and Linear Spaces 1.4. Solving Systems of Linear Equations Note. We give an algorithm for solving a system of linear equations (called
1.4 Solving Systems of Linear Equations 1 Chapter 1. Vectors, Matrices, and Linear Spaces 1.4. Solving Systems of Linear Equations Note. We give an algorithm for solving a system of linear equations (called
System of Linear Equations. Slide for MA1203 Business Mathematics II Week 1 & 2
 System of Linear Equations Slide for MA1203 Business Mathematics II Week 1 & 2 Function A manufacturer would like to know how his company s profit is related to its production level. How does one quantity
System of Linear Equations Slide for MA1203 Business Mathematics II Week 1 & 2 Function A manufacturer would like to know how his company s profit is related to its production level. How does one quantity
7.5 Operations with Matrices. Copyright Cengage Learning. All rights reserved.
 7.5 Operations with Matrices Copyright Cengage Learning. All rights reserved. What You Should Learn Decide whether two matrices are equal. Add and subtract matrices and multiply matrices by scalars. Multiply
7.5 Operations with Matrices Copyright Cengage Learning. All rights reserved. What You Should Learn Decide whether two matrices are equal. Add and subtract matrices and multiply matrices by scalars. Multiply
LINEAR SYSTEMS, MATRICES, AND VECTORS
 ELEMENTARY LINEAR ALGEBRA WORKBOOK CREATED BY SHANNON MARTIN MYERS LINEAR SYSTEMS, MATRICES, AND VECTORS Now that I ve been teaching Linear Algebra for a few years, I thought it would be great to integrate
ELEMENTARY LINEAR ALGEBRA WORKBOOK CREATED BY SHANNON MARTIN MYERS LINEAR SYSTEMS, MATRICES, AND VECTORS Now that I ve been teaching Linear Algebra for a few years, I thought it would be great to integrate
MATH 1003 Review: Part 2. Matrices. MATH 1003 Review: Part 2. Matrices
 Matrices (Ch.4) (i) System of linear equations in 2 variables (L.5, Ch4.1) Find solutions by graphing Supply and demand curve (ii) Basic ideas about Matrices (L.6, Ch4.2) To know a matrix Row operation
Matrices (Ch.4) (i) System of linear equations in 2 variables (L.5, Ch4.1) Find solutions by graphing Supply and demand curve (ii) Basic ideas about Matrices (L.6, Ch4.2) To know a matrix Row operation
Matrices. A matrix is a method of writing a set of numbers using rows and columns. Cells in a matrix can be referenced in the form.
 Matrices A matrix is a method of writing a set of numbers using rows and columns. 1 2 3 4 3 2 1 5 7 2 5 4 2 0 5 10 12 8 4 9 25 30 1 1 Reading Information from a Matrix Cells in a matrix can be referenced
Matrices A matrix is a method of writing a set of numbers using rows and columns. 1 2 3 4 3 2 1 5 7 2 5 4 2 0 5 10 12 8 4 9 25 30 1 1 Reading Information from a Matrix Cells in a matrix can be referenced
Linear Algebra: Lecture Notes. Dr Rachel Quinlan School of Mathematics, Statistics and Applied Mathematics NUI Galway
 Linear Algebra: Lecture Notes Dr Rachel Quinlan School of Mathematics, Statistics and Applied Mathematics NUI Galway November 6, 23 Contents Systems of Linear Equations 2 Introduction 2 2 Elementary Row
Linear Algebra: Lecture Notes Dr Rachel Quinlan School of Mathematics, Statistics and Applied Mathematics NUI Galway November 6, 23 Contents Systems of Linear Equations 2 Introduction 2 2 Elementary Row
Exam 3 Review Math 118 Sections 1 and 2
 Exam 3 Review Math 118 Sections 1 and 2 This exam will cover sections 5.3-5.6, 6.1-6.3 and 7.1-7.3 of the textbook. No books, notes, calculators or other aids are allowed on this exam. There is no time
Exam 3 Review Math 118 Sections 1 and 2 This exam will cover sections 5.3-5.6, 6.1-6.3 and 7.1-7.3 of the textbook. No books, notes, calculators or other aids are allowed on this exam. There is no time
Chapter 2 Notes, Linear Algebra 5e Lay
 Contents.1 Operations with Matrices..................................1.1 Addition and Subtraction.............................1. Multiplication by a scalar............................ 3.1.3 Multiplication
Contents.1 Operations with Matrices..................................1.1 Addition and Subtraction.............................1. Multiplication by a scalar............................ 3.1.3 Multiplication
Math Week in Review #7
 Math 166 Fall 2008 c Heather Ramsey Page 1 Math 166 - Week in Review #7 Section 4.3 - Gauss Elimination for Systems of Linear Equations When a system of linear equations has only two variables, each equation
Math 166 Fall 2008 c Heather Ramsey Page 1 Math 166 - Week in Review #7 Section 4.3 - Gauss Elimination for Systems of Linear Equations When a system of linear equations has only two variables, each equation
Chapter 1: Systems of linear equations and matrices. Section 1.1: Introduction to systems of linear equations
 Chapter 1: Systems of linear equations and matrices Section 1.1: Introduction to systems of linear equations Definition: A linear equation in n variables can be expressed in the form a 1 x 1 + a 2 x 2
Chapter 1: Systems of linear equations and matrices Section 1.1: Introduction to systems of linear equations Definition: A linear equation in n variables can be expressed in the form a 1 x 1 + a 2 x 2
1.3 Solving Systems of Linear Equations: Gauss-Jordan Elimination and Matrices
 1.3 Solving Systems of Linear Equations: Gauss-Jordan Elimination and Matrices We can represent a system of linear equations using an augmented matrix. In general, a matrix is just a rectangular arrays
1.3 Solving Systems of Linear Equations: Gauss-Jordan Elimination and Matrices We can represent a system of linear equations using an augmented matrix. In general, a matrix is just a rectangular arrays
September 23, Chp 3.notebook. 3Linear Systems. and Matrices. 3.1 Solve Linear Systems by Graphing
 3Linear Systems and Matrices 3.1 Solve Linear Systems by Graphing 1 Find the solution of the systems by looking at the graphs 2 Decide whether the ordered pair is a solution of the system of linear equations:
3Linear Systems and Matrices 3.1 Solve Linear Systems by Graphing 1 Find the solution of the systems by looking at the graphs 2 Decide whether the ordered pair is a solution of the system of linear equations:
All of my class notes can be found at
 My name is Leon Hostetler I am currently a student at Florida State University majoring in physics as well as applied and computational mathematics Feel free to download, print, and use these class notes
My name is Leon Hostetler I am currently a student at Florida State University majoring in physics as well as applied and computational mathematics Feel free to download, print, and use these class notes
Row Reduction and Echelon Forms
 Row Reduction and Echelon Forms 1 / 29 Key Concepts row echelon form, reduced row echelon form pivot position, pivot, pivot column basic variable, free variable general solution, parametric solution existence
Row Reduction and Echelon Forms 1 / 29 Key Concepts row echelon form, reduced row echelon form pivot position, pivot, pivot column basic variable, free variable general solution, parametric solution existence
Matrix Algebra. Learning Objectives. Size of Matrix
 Matrix Algebra 1 Learning Objectives 1. Find the sum and difference of two matrices 2. Find scalar multiples of a matrix 3. Find the product of two matrices 4. Find the inverse of a matrix 5. Solve a system
Matrix Algebra 1 Learning Objectives 1. Find the sum and difference of two matrices 2. Find scalar multiples of a matrix 3. Find the product of two matrices 4. Find the inverse of a matrix 5. Solve a system
1 - Systems of Linear Equations
 1 - Systems of Linear Equations 1.1 Introduction to Systems of Linear Equations Almost every problem in linear algebra will involve solving a system of equations. ü LINEAR EQUATIONS IN n VARIABLES We are
1 - Systems of Linear Equations 1.1 Introduction to Systems of Linear Equations Almost every problem in linear algebra will involve solving a system of equations. ü LINEAR EQUATIONS IN n VARIABLES We are
Matrix Multiplication
 3.2 Matrix Algebra Matrix Multiplication Example Foxboro Stadium has three main concession stands, located behind the south, north and west stands. The top-selling items are peanuts, hot dogs and soda.
3.2 Matrix Algebra Matrix Multiplication Example Foxboro Stadium has three main concession stands, located behind the south, north and west stands. The top-selling items are peanuts, hot dogs and soda.
[ ] 1 [ B] 7.2 Matrix Algebra Pre Calculus. 7.2 MATRIX ALGEBRA (Day 1)
![[ ] 1 [ B] 7.2 Matrix Algebra Pre Calculus. 7.2 MATRIX ALGEBRA (Day 1) [ ] 1 [ B] 7.2 Matrix Algebra Pre Calculus. 7.2 MATRIX ALGEBRA (Day 1)](/thumbs/72/66401904.jpg) 7. Matrix Algebra Pre Calculus 7. MATRIX ALGEBRA (Day 1) Learning Targets: 1. Use matrices to represent data.. Add or Subtract matrices without a calculator. 3. Multiply a scalar by a matrix without a
7. Matrix Algebra Pre Calculus 7. MATRIX ALGEBRA (Day 1) Learning Targets: 1. Use matrices to represent data.. Add or Subtract matrices without a calculator. 3. Multiply a scalar by a matrix without a
Glossary of Linear Algebra Terms. Prepared by Vince Zaccone For Campus Learning Assistance Services at UCSB
 Glossary of Linear Algebra Terms Basis (for a subspace) A linearly independent set of vectors that spans the space Basic Variable A variable in a linear system that corresponds to a pivot column in the
Glossary of Linear Algebra Terms Basis (for a subspace) A linearly independent set of vectors that spans the space Basic Variable A variable in a linear system that corresponds to a pivot column in the
ICS 6N Computational Linear Algebra Matrix Algebra
 ICS 6N Computational Linear Algebra Matrix Algebra Xiaohui Xie University of California, Irvine xhx@uci.edu February 2, 2017 Xiaohui Xie (UCI) ICS 6N February 2, 2017 1 / 24 Matrix Consider an m n matrix
ICS 6N Computational Linear Algebra Matrix Algebra Xiaohui Xie University of California, Irvine xhx@uci.edu February 2, 2017 Xiaohui Xie (UCI) ICS 6N February 2, 2017 1 / 24 Matrix Consider an m n matrix
Matrices (Ch.4) MATH 1003 Review: Part 2. Matrices. Matrices (Ch.4) Matrices (Ch.4)
 Matrices (Ch.4) Maosheng Xiong Department of Mathematics, HKUST (i) System of linear equations in 2 variables (L.5, Ch4.) Find solutions by graphing Supply and demand curve (ii) Basic ideas about Matrices
Matrices (Ch.4) Maosheng Xiong Department of Mathematics, HKUST (i) System of linear equations in 2 variables (L.5, Ch4.) Find solutions by graphing Supply and demand curve (ii) Basic ideas about Matrices
Systems of Linear Equations in Two Variables. Break Even. Example. 240x x This is when total cost equals total revenue.
 Systems of Linear Equations in Two Variables 1 Break Even This is when total cost equals total revenue C(x) = R(x) A company breaks even when the profit is zero P(x) = R(x) C(x) = 0 2 R x 565x C x 6000
Systems of Linear Equations in Two Variables 1 Break Even This is when total cost equals total revenue C(x) = R(x) A company breaks even when the profit is zero P(x) = R(x) C(x) = 0 2 R x 565x C x 6000
Linear Algebra. Solving Linear Systems. Copyright 2005, W.R. Winfrey
 Copyright 2005, W.R. Winfrey Topics Preliminaries Echelon Form of a Matrix Elementary Matrices; Finding A -1 Equivalent Matrices LU-Factorization Topics Preliminaries Echelon Form of a Matrix Elementary
Copyright 2005, W.R. Winfrey Topics Preliminaries Echelon Form of a Matrix Elementary Matrices; Finding A -1 Equivalent Matrices LU-Factorization Topics Preliminaries Echelon Form of a Matrix Elementary
2.1 Matrices. 3 5 Solve for the variables in the following matrix equation.
 2.1 Matrices Reminder: A matrix with m rows and n columns has size m x n. (This is also sometimes referred to as the order of the matrix.) The entry in the ith row and jth column of a matrix A is denoted
2.1 Matrices Reminder: A matrix with m rows and n columns has size m x n. (This is also sometimes referred to as the order of the matrix.) The entry in the ith row and jth column of a matrix A is denoted
Section Gaussian Elimination
 Section. - Gaussian Elimination A matrix is said to be in row echelon form (REF) if it has the following properties:. The first nonzero entry in any row is a. We call this a leading one or pivot one..
Section. - Gaussian Elimination A matrix is said to be in row echelon form (REF) if it has the following properties:. The first nonzero entry in any row is a. We call this a leading one or pivot one..
Basic Concepts in Linear Algebra
 Basic Concepts in Linear Algebra Grady B Wright Department of Mathematics Boise State University February 2, 2015 Grady B Wright Linear Algebra Basics February 2, 2015 1 / 39 Numerical Linear Algebra Linear
Basic Concepts in Linear Algebra Grady B Wright Department of Mathematics Boise State University February 2, 2015 Grady B Wright Linear Algebra Basics February 2, 2015 1 / 39 Numerical Linear Algebra Linear
Math 313 Chapter 1 Review
 Math 313 Chapter 1 Review Howard Anton, 9th Edition May 2010 Do NOT write on me! Contents 1 1.1 Introduction to Systems of Linear Equations 2 2 1.2 Gaussian Elimination 3 3 1.3 Matrices and Matrix Operations
Math 313 Chapter 1 Review Howard Anton, 9th Edition May 2010 Do NOT write on me! Contents 1 1.1 Introduction to Systems of Linear Equations 2 2 1.2 Gaussian Elimination 3 3 1.3 Matrices and Matrix Operations
Elementary Linear Algebra
 Elementary Linear Algebra Linear algebra is the study of; linear sets of equations and their transformation properties. Linear algebra allows the analysis of; rotations in space, least squares fitting,
Elementary Linear Algebra Linear algebra is the study of; linear sets of equations and their transformation properties. Linear algebra allows the analysis of; rotations in space, least squares fitting,
SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question.
 Assn.-.7 Name Perform the operation, if possible. ) Let A = 0 - - 0 and B = - 0 - -. Find AB. ) -6-9 ) Let A = - 5 and B = -5-7 - 6-8 - - - - - -. Find AB. ) 6-0 9 5-5 - -6-0 ) - 0 - - - 6-0 - 0 0 0 0
Assn.-.7 Name Perform the operation, if possible. ) Let A = 0 - - 0 and B = - 0 - -. Find AB. ) -6-9 ) Let A = - 5 and B = -5-7 - 6-8 - - - - - -. Find AB. ) 6-0 9 5-5 - -6-0 ) - 0 - - - 6-0 - 0 0 0 0
APPENDIX: MATHEMATICAL INDUCTION AND OTHER FORMS OF PROOF
 ELEMENTARY LINEAR ALGEBRA WORKBOOK/FOR USE WITH RON LARSON S TEXTBOOK ELEMENTARY LINEAR ALGEBRA CREATED BY SHANNON MARTIN MYERS APPENDIX: MATHEMATICAL INDUCTION AND OTHER FORMS OF PROOF When you are done
ELEMENTARY LINEAR ALGEBRA WORKBOOK/FOR USE WITH RON LARSON S TEXTBOOK ELEMENTARY LINEAR ALGEBRA CREATED BY SHANNON MARTIN MYERS APPENDIX: MATHEMATICAL INDUCTION AND OTHER FORMS OF PROOF When you are done
Fall Inverse of a matrix. Institute: UC San Diego. Authors: Alexander Knop
 Fall 2017 Inverse of a matrix Authors: Alexander Knop Institute: UC San Diego Row-Column Rule If the product AB is defined, then the entry in row i and column j of AB is the sum of the products of corresponding
Fall 2017 Inverse of a matrix Authors: Alexander Knop Institute: UC San Diego Row-Column Rule If the product AB is defined, then the entry in row i and column j of AB is the sum of the products of corresponding
Math Linear Algebra Final Exam Review Sheet
 Math 15-1 Linear Algebra Final Exam Review Sheet Vector Operations Vector addition is a component-wise operation. Two vectors v and w may be added together as long as they contain the same number n of
Math 15-1 Linear Algebra Final Exam Review Sheet Vector Operations Vector addition is a component-wise operation. Two vectors v and w may be added together as long as they contain the same number n of
Review of Basic Concepts in Linear Algebra
 Review of Basic Concepts in Linear Algebra Grady B Wright Department of Mathematics Boise State University September 7, 2017 Math 565 Linear Algebra Review September 7, 2017 1 / 40 Numerical Linear Algebra
Review of Basic Concepts in Linear Algebra Grady B Wright Department of Mathematics Boise State University September 7, 2017 Math 565 Linear Algebra Review September 7, 2017 1 / 40 Numerical Linear Algebra
Dependent ( ) Independent (1 or Ø) These lines coincide so they are a.k.a coincident.
 Notes #3- Date: 7.1 Solving Systems of Two Equations (568) The solution to a system of linear equations is the ordered pair (x, y) where the lines intersect! A solution can be substituted into both equations
Notes #3- Date: 7.1 Solving Systems of Two Equations (568) The solution to a system of linear equations is the ordered pair (x, y) where the lines intersect! A solution can be substituted into both equations
MTH 2032 Semester II
 MTH 232 Semester II 2-2 Linear Algebra Reference Notes Dr. Tony Yee Department of Mathematics and Information Technology The Hong Kong Institute of Education December 28, 2 ii Contents Table of Contents
MTH 232 Semester II 2-2 Linear Algebra Reference Notes Dr. Tony Yee Department of Mathematics and Information Technology The Hong Kong Institute of Education December 28, 2 ii Contents Table of Contents
7.2 Matrix Algebra. DEFINITION Matrix. D 21 a 22 Á a 2n. EXAMPLE 1 Determining the Order of a Matrix d. (b) The matrix D T has order 4 * 2.
 530 CHAPTER 7 Systems and Matrices 7.2 Matrix Algebra What you ll learn about Matrices Matrix Addition and Subtraction Matrix Multiplication Identity and Inverse Matrices Determinant of a Square Matrix
530 CHAPTER 7 Systems and Matrices 7.2 Matrix Algebra What you ll learn about Matrices Matrix Addition and Subtraction Matrix Multiplication Identity and Inverse Matrices Determinant of a Square Matrix
Finite Mathematics. Linear Equations (Chapter 4) Optimization (Chapter 5) Finite Probability (Chapter 6) Markov Chains (Chapter 9) Finite Mathematics
 Finite Mathematics Linear Equations (Chapter ) Optimization (Chapter ) Finite Probability (Chapter 6) Markov Chains (Chapter 9) Finite Mathematics Linear Algebra Probability Linear Equations Simple Method
Finite Mathematics Linear Equations (Chapter ) Optimization (Chapter ) Finite Probability (Chapter 6) Markov Chains (Chapter 9) Finite Mathematics Linear Algebra Probability Linear Equations Simple Method
MathQuest: Linear Algebra. 1. Which of the following operations on an augmented matrix could change the solution set of a system?
 MathQuest: Linear Algebra Gaussian Elimination 1. Which of the following operations on an augmented matrix could change the solution set of a system? (a) Interchanging two rows (b) Multiplying one row
MathQuest: Linear Algebra Gaussian Elimination 1. Which of the following operations on an augmented matrix could change the solution set of a system? (a) Interchanging two rows (b) Multiplying one row
Introduction to Matrices and Linear Systems Ch. 3
 Introduction to Matrices and Linear Systems Ch. 3 Doreen De Leon Department of Mathematics, California State University, Fresno June, 5 Basic Matrix Concepts and Operations Section 3.4. Basic Matrix Concepts
Introduction to Matrices and Linear Systems Ch. 3 Doreen De Leon Department of Mathematics, California State University, Fresno June, 5 Basic Matrix Concepts and Operations Section 3.4. Basic Matrix Concepts
LECTURES 4/5: SYSTEMS OF LINEAR EQUATIONS
 LECTURES 4/5: SYSTEMS OF LINEAR EQUATIONS MA1111: LINEAR ALGEBRA I, MICHAELMAS 2016 1 Linear equations We now switch gears to discuss the topic of solving linear equations, and more interestingly, systems
LECTURES 4/5: SYSTEMS OF LINEAR EQUATIONS MA1111: LINEAR ALGEBRA I, MICHAELMAS 2016 1 Linear equations We now switch gears to discuss the topic of solving linear equations, and more interestingly, systems
March 19 - Solving Linear Systems
 March 19 - Solving Linear Systems Welcome to linear algebra! Linear algebra is the study of vectors, vector spaces, and maps between vector spaces. It has applications across data analysis, computer graphics,
March 19 - Solving Linear Systems Welcome to linear algebra! Linear algebra is the study of vectors, vector spaces, and maps between vector spaces. It has applications across data analysis, computer graphics,
Linear Algebra March 16, 2019
 Linear Algebra March 16, 2019 2 Contents 0.1 Notation................................ 4 1 Systems of linear equations, and matrices 5 1.1 Systems of linear equations..................... 5 1.2 Augmented
Linear Algebra March 16, 2019 2 Contents 0.1 Notation................................ 4 1 Systems of linear equations, and matrices 5 1.1 Systems of linear equations..................... 5 1.2 Augmented
8.2 Systems of Linear Equations: Augmented Matrices
 8. Systems of Linear Equations: Augmented Matrices 567 8. Systems of Linear Equations: Augmented Matrices In Section 8. we introduced Gaussian Elimination as a means of transforming a system of linear
8. Systems of Linear Equations: Augmented Matrices 567 8. Systems of Linear Equations: Augmented Matrices In Section 8. we introduced Gaussian Elimination as a means of transforming a system of linear
Matrix & Linear Algebra
 Matrix & Linear Algebra Jamie Monogan University of Georgia For more information: http://monogan.myweb.uga.edu/teaching/mm/ Jamie Monogan (UGA) Matrix & Linear Algebra 1 / 84 Vectors Vectors Vector: A
Matrix & Linear Algebra Jamie Monogan University of Georgia For more information: http://monogan.myweb.uga.edu/teaching/mm/ Jamie Monogan (UGA) Matrix & Linear Algebra 1 / 84 Vectors Vectors Vector: A
Inverting Matrices. 1 Properties of Transpose. 2 Matrix Algebra. P. Danziger 3.2, 3.3
 3., 3.3 Inverting Matrices P. Danziger 1 Properties of Transpose Transpose has higher precedence than multiplication and addition, so AB T A ( B T and A + B T A + ( B T As opposed to the bracketed expressions
3., 3.3 Inverting Matrices P. Danziger 1 Properties of Transpose Transpose has higher precedence than multiplication and addition, so AB T A ( B T and A + B T A + ( B T As opposed to the bracketed expressions
10. Linear Systems of ODEs, Matrix multiplication, superposition principle (parts of sections )
 c Dr. Igor Zelenko, Fall 2017 1 10. Linear Systems of ODEs, Matrix multiplication, superposition principle (parts of sections 7.2-7.4) 1. When each of the functions F 1, F 2,..., F n in right-hand side
c Dr. Igor Zelenko, Fall 2017 1 10. Linear Systems of ODEs, Matrix multiplication, superposition principle (parts of sections 7.2-7.4) 1. When each of the functions F 1, F 2,..., F n in right-hand side
Matrix operations Linear Algebra with Computer Science Application
 Linear Algebra with Computer Science Application February 14, 2018 1 Matrix operations 11 Matrix operations If A is an m n matrix that is, a matrix with m rows and n columns then the scalar entry in the
Linear Algebra with Computer Science Application February 14, 2018 1 Matrix operations 11 Matrix operations If A is an m n matrix that is, a matrix with m rows and n columns then the scalar entry in the
Elementary maths for GMT
 Elementary maths for GMT Linear Algebra Part 2: Matrices, Elimination and Determinant m n matrices The system of m linear equations in n variables x 1, x 2,, x n a 11 x 1 + a 12 x 2 + + a 1n x n = b 1
Elementary maths for GMT Linear Algebra Part 2: Matrices, Elimination and Determinant m n matrices The system of m linear equations in n variables x 1, x 2,, x n a 11 x 1 + a 12 x 2 + + a 1n x n = b 1
TOPIC III LINEAR ALGEBRA
 [1] Linear Equations TOPIC III LINEAR ALGEBRA (1) Case of Two Endogenous Variables 1) Linear vs. Nonlinear Equations Linear equation: ax + by = c, where a, b and c are constants. 2 Nonlinear equation:
[1] Linear Equations TOPIC III LINEAR ALGEBRA (1) Case of Two Endogenous Variables 1) Linear vs. Nonlinear Equations Linear equation: ax + by = c, where a, b and c are constants. 2 Nonlinear equation:
MATRICES AND MATRIX OPERATIONS
 SIZE OF THE MATRIX is defined by number of rows and columns in the matrix. For the matrix that have m rows and n columns we say the size of the matrix is m x n. If matrix have the same number of rows (n)
SIZE OF THE MATRIX is defined by number of rows and columns in the matrix. For the matrix that have m rows and n columns we say the size of the matrix is m x n. If matrix have the same number of rows (n)
1.2 Row Echelon Form EXAMPLE 1
 .2 Row Echelon Form 7. The two systems 2x + x 2 = 4x + x 2 = 5 and 2x + x 2 = 4x + x 2 = have the same coefficient matrix but different righthand sides. Solve both systems simultaneously by eliminating
.2 Row Echelon Form 7. The two systems 2x + x 2 = 4x + x 2 = 5 and 2x + x 2 = 4x + x 2 = have the same coefficient matrix but different righthand sides. Solve both systems simultaneously by eliminating
is a 3 4 matrix. It has 3 rows and 4 columns. The first row is the horizontal row [ ]
![is a 3 4 matrix. It has 3 rows and 4 columns. The first row is the horizontal row [ ] is a 3 4 matrix. It has 3 rows and 4 columns. The first row is the horizontal row [ ]](/thumbs/82/86615780.jpg) Matrices: Definition: An m n matrix, A m n is a rectangular array of numbers with m rows and n columns: a, a, a,n a, a, a,n A m,n =...... a m, a m, a m,n Each a i,j is the entry at the i th row, j th column.
Matrices: Definition: An m n matrix, A m n is a rectangular array of numbers with m rows and n columns: a, a, a,n a, a, a,n A m,n =...... a m, a m, a m,n Each a i,j is the entry at the i th row, j th column.
Chapter 9: Systems of Equations and Inequalities
 Chapter 9: Systems of Equations and Inequalities 9. Systems of Equations Solve the system of equations below. By this we mean, find pair(s) of numbers (x, y) (if possible) that satisfy both equations.
Chapter 9: Systems of Equations and Inequalities 9. Systems of Equations Solve the system of equations below. By this we mean, find pair(s) of numbers (x, y) (if possible) that satisfy both equations.
Chapter 1 Matrices and Systems of Equations
 Chapter 1 Matrices and Systems of Equations System of Linear Equations 1. A linear equation in n unknowns is an equation of the form n i=1 a i x i = b where a 1,..., a n, b R and x 1,..., x n are variables.
Chapter 1 Matrices and Systems of Equations System of Linear Equations 1. A linear equation in n unknowns is an equation of the form n i=1 a i x i = b where a 1,..., a n, b R and x 1,..., x n are variables.
Linear Algebra Practice Problems
 Math 7, Professor Ramras Linear Algebra Practice Problems () Consider the following system of linear equations in the variables x, y, and z, in which the constants a and b are real numbers. x y + z = a
Math 7, Professor Ramras Linear Algebra Practice Problems () Consider the following system of linear equations in the variables x, y, and z, in which the constants a and b are real numbers. x y + z = a
3.4 Elementary Matrices and Matrix Inverse
 Math 220: Summer 2015 3.4 Elementary Matrices and Matrix Inverse A n n elementary matrix is a matrix which is obtained from the n n identity matrix I n n by a single elementary row operation. Elementary
Math 220: Summer 2015 3.4 Elementary Matrices and Matrix Inverse A n n elementary matrix is a matrix which is obtained from the n n identity matrix I n n by a single elementary row operation. Elementary
Chapter If M is the matrix 0 0 1, then M 100 is. (c) (a) (b) (d) (e) None of the above. (b) 2.
 Chapter 2. If M is the matrix, then M is (a) (b) (c) (d) (e) None of the above 3 6 2. If A is a 3 3 matrix such that A = and A 4 =, then the product A 7 is 2 5 8 (a) (b) 2 (c) 9 (d) (e) Not uniquely determined
Chapter 2. If M is the matrix, then M is (a) (b) (c) (d) (e) None of the above 3 6 2. If A is a 3 3 matrix such that A = and A 4 =, then the product A 7 is 2 5 8 (a) (b) 2 (c) 9 (d) (e) Not uniquely determined
MATH 1210 Assignment 4 Solutions 16R-T1
 MATH 1210 Assignment 4 Solutions 16R-T1 Attempt all questions and show all your work. Due November 13, 2015. 1. Prove using mathematical induction that for any n 2, and collection of n m m matrices A 1,
MATH 1210 Assignment 4 Solutions 16R-T1 Attempt all questions and show all your work. Due November 13, 2015. 1. Prove using mathematical induction that for any n 2, and collection of n m m matrices A 1,
Lecture 1 Systems of Linear Equations and Matrices
 Lecture 1 Systems of Linear Equations and Matrices Math 19620 Outline of Course Linear Equations and Matrices Linear Transformations, Inverses Bases, Linear Independence, Subspaces Abstract Vector Spaces
Lecture 1 Systems of Linear Equations and Matrices Math 19620 Outline of Course Linear Equations and Matrices Linear Transformations, Inverses Bases, Linear Independence, Subspaces Abstract Vector Spaces
Matrices and Systems of Equations
 M CHAPTER 3 3 4 3 F 2 2 4 C 4 4 Matrices and Systems of Equations Probably the most important problem in mathematics is that of solving a system of linear equations. Well over 75 percent of all mathematical
M CHAPTER 3 3 4 3 F 2 2 4 C 4 4 Matrices and Systems of Equations Probably the most important problem in mathematics is that of solving a system of linear equations. Well over 75 percent of all mathematical
Chapter 4. Solving Systems of Equations. Chapter 4
 Solving Systems of Equations 3 Scenarios for Solutions There are three general situations we may find ourselves in when attempting to solve systems of equations: 1 The system could have one unique solution.
Solving Systems of Equations 3 Scenarios for Solutions There are three general situations we may find ourselves in when attempting to solve systems of equations: 1 The system could have one unique solution.
MATH 2331 Linear Algebra. Section 2.1 Matrix Operations. Definition: A : m n, B : n p. Example: Compute AB, if possible.
 MATH 2331 Linear Algebra Section 2.1 Matrix Operations Definition: A : m n, B : n p ( 1 2 p ) ( 1 2 p ) AB = A b b b = Ab Ab Ab Example: Compute AB, if possible. 1 Row-column rule: i-j-th entry of AB:
MATH 2331 Linear Algebra Section 2.1 Matrix Operations Definition: A : m n, B : n p ( 1 2 p ) ( 1 2 p ) AB = A b b b = Ab Ab Ab Example: Compute AB, if possible. 1 Row-column rule: i-j-th entry of AB:
1300 Linear Algebra and Vector Geometry
 1300 Linear Algebra and Vector Geometry R. Craigen Office: MH 523 Email: craigenr@umanitoba.ca May-June 2017 Introduction: linear equations Read 1.1 (in the text that is!) Go to course, class webpages.
1300 Linear Algebra and Vector Geometry R. Craigen Office: MH 523 Email: craigenr@umanitoba.ca May-June 2017 Introduction: linear equations Read 1.1 (in the text that is!) Go to course, class webpages.
Lecture Notes in Mathematics. Arkansas Tech University Department of Mathematics. The Basics of Linear Algebra
 Lecture Notes in Mathematics Arkansas Tech University Department of Mathematics The Basics of Linear Algebra Marcel B. Finan c All Rights Reserved Last Updated November 30, 2015 2 Preface Linear algebra
Lecture Notes in Mathematics Arkansas Tech University Department of Mathematics The Basics of Linear Algebra Marcel B. Finan c All Rights Reserved Last Updated November 30, 2015 2 Preface Linear algebra
Chapter 3. Linear Equations. Josef Leydold Mathematical Methods WS 2018/19 3 Linear Equations 1 / 33
 Chapter 3 Linear Equations Josef Leydold Mathematical Methods WS 2018/19 3 Linear Equations 1 / 33 Lineares Gleichungssystem System of m linear equations in n unknowns: a 11 x 1 + a 12 x 2 + + a 1n x n
Chapter 3 Linear Equations Josef Leydold Mathematical Methods WS 2018/19 3 Linear Equations 1 / 33 Lineares Gleichungssystem System of m linear equations in n unknowns: a 11 x 1 + a 12 x 2 + + a 1n x n
Solutions of Linear system, vector and matrix equation
 Goals: Solutions of Linear system, vector and matrix equation Solutions of linear system. Vectors, vector equation. Matrix equation. Math 112, Week 2 Suggested Textbook Readings: Sections 1.3, 1.4, 1.5
Goals: Solutions of Linear system, vector and matrix equation Solutions of linear system. Vectors, vector equation. Matrix equation. Math 112, Week 2 Suggested Textbook Readings: Sections 1.3, 1.4, 1.5
Chapter 2: Matrix Algebra
 Chapter 2: Matrix Algebra (Last Updated: October 12, 2016) These notes are derived primarily from Linear Algebra and its applications by David Lay (4ed). Write A = 1. Matrix operations [a 1 a n. Then entry
Chapter 2: Matrix Algebra (Last Updated: October 12, 2016) These notes are derived primarily from Linear Algebra and its applications by David Lay (4ed). Write A = 1. Matrix operations [a 1 a n. Then entry
MTH Linear Algebra. Study Guide. Dr. Tony Yee Department of Mathematics and Information Technology The Hong Kong Institute of Education
 MTH 3 Linear Algebra Study Guide Dr. Tony Yee Department of Mathematics and Information Technology The Hong Kong Institute of Education June 3, ii Contents Table of Contents iii Matrix Algebra. Real Life
MTH 3 Linear Algebra Study Guide Dr. Tony Yee Department of Mathematics and Information Technology The Hong Kong Institute of Education June 3, ii Contents Table of Contents iii Matrix Algebra. Real Life
ECON 331 Homework #2 - Solution. In a closed model the vector of external demand is zero, so the matrix equation writes:
 ECON 33 Homework #2 - Solution. (Leontief model) (a) (i) The matrix of input-output A and the vector of level of production X are, respectively:.2.3.2 x A =.5.2.3 and X = y.3.5.5 z In a closed model the
ECON 33 Homework #2 - Solution. (Leontief model) (a) (i) The matrix of input-output A and the vector of level of production X are, respectively:.2.3.2 x A =.5.2.3 and X = y.3.5.5 z In a closed model the
ECON 186 Class Notes: Linear Algebra
 ECON 86 Class Notes: Linear Algebra Jijian Fan Jijian Fan ECON 86 / 27 Singularity and Rank As discussed previously, squareness is a necessary condition for a matrix to be nonsingular (have an inverse).
ECON 86 Class Notes: Linear Algebra Jijian Fan Jijian Fan ECON 86 / 27 Singularity and Rank As discussed previously, squareness is a necessary condition for a matrix to be nonsingular (have an inverse).
Mathematics 13: Lecture 10
 Mathematics 13: Lecture 10 Matrices Dan Sloughter Furman University January 25, 2008 Dan Sloughter (Furman University) Mathematics 13: Lecture 10 January 25, 2008 1 / 19 Matrices Recall: A matrix is a
Mathematics 13: Lecture 10 Matrices Dan Sloughter Furman University January 25, 2008 Dan Sloughter (Furman University) Mathematics 13: Lecture 10 January 25, 2008 1 / 19 Matrices Recall: A matrix is a
Perform the same three operations as above on the values in the matrix, where some notation is given as a shorthand way to describe each operation:
 SECTION 2.1: SOLVING SYSTEMS OF EQUATIONS WITH A UNIQUE SOLUTION In Chapter 1 we took a look at finding the intersection point of two lines on a graph. Chapter 2 begins with a look at a more formal approach
SECTION 2.1: SOLVING SYSTEMS OF EQUATIONS WITH A UNIQUE SOLUTION In Chapter 1 we took a look at finding the intersection point of two lines on a graph. Chapter 2 begins with a look at a more formal approach
MATH Mathematics for Agriculture II
 MATH 10240 Mathematics for Agriculture II Academic year 2018 2019 UCD School of Mathematics and Statistics Contents Chapter 1. Linear Algebra 1 1. Introduction to Matrices 1 2. Matrix Multiplication 3
MATH 10240 Mathematics for Agriculture II Academic year 2018 2019 UCD School of Mathematics and Statistics Contents Chapter 1. Linear Algebra 1 1. Introduction to Matrices 1 2. Matrix Multiplication 3
Exercise Sketch these lines and find their intersection.
 These are brief notes for the lecture on Friday August 21, 2009: they are not complete, but they are a guide to what I want to say today. They are not guaranteed to be correct. 1. Solving systems of linear
These are brief notes for the lecture on Friday August 21, 2009: they are not complete, but they are a guide to what I want to say today. They are not guaranteed to be correct. 1. Solving systems of linear
Definition of Equality of Matrices. Example 1: Equality of Matrices. Consider the four matrices
 IT 131: Mathematics for Science Lecture Notes 3 Source: Larson, Edwards, Falvo (2009): Elementary Linear Algebra, Sixth Edition. Matrices 2.1 Operations with Matrices This section and the next introduce
IT 131: Mathematics for Science Lecture Notes 3 Source: Larson, Edwards, Falvo (2009): Elementary Linear Algebra, Sixth Edition. Matrices 2.1 Operations with Matrices This section and the next introduce
Image Registration Lecture 2: Vectors and Matrices
 Image Registration Lecture 2: Vectors and Matrices Prof. Charlene Tsai Lecture Overview Vectors Matrices Basics Orthogonal matrices Singular Value Decomposition (SVD) 2 1 Preliminary Comments Some of this
Image Registration Lecture 2: Vectors and Matrices Prof. Charlene Tsai Lecture Overview Vectors Matrices Basics Orthogonal matrices Singular Value Decomposition (SVD) 2 1 Preliminary Comments Some of this
We could express the left side as a sum of vectors and obtain the Vector Form of a Linear System: a 12 a x n. a m2
 Week 22 Equations, Matrices and Transformations Coefficient Matrix and Vector Forms of a Linear System Suppose we have a system of m linear equations in n unknowns a 11 x 1 + a 12 x 2 + + a 1n x n b 1
Week 22 Equations, Matrices and Transformations Coefficient Matrix and Vector Forms of a Linear System Suppose we have a system of m linear equations in n unknowns a 11 x 1 + a 12 x 2 + + a 1n x n b 1
Algebra & Trig. I. For example, the system. x y 2 z. may be represented by the augmented matrix
 Algebra & Trig. I 8.1 Matrix Solutions to Linear Systems A matrix is a rectangular array of elements. o An array is a systematic arrangement of numbers or symbols in rows and columns. Matrices (the plural
Algebra & Trig. I 8.1 Matrix Solutions to Linear Systems A matrix is a rectangular array of elements. o An array is a systematic arrangement of numbers or symbols in rows and columns. Matrices (the plural
Math 220: Summer Midterm 1 Questions
 Math 220: Summer 2015 Midterm 1 Questions MOST questions will either look a lot like a Homework questions This lists draws your attention to some important types of HW questions. SOME questions will have
Math 220: Summer 2015 Midterm 1 Questions MOST questions will either look a lot like a Homework questions This lists draws your attention to some important types of HW questions. SOME questions will have
3. Vector spaces 3.1 Linear dependence and independence 3.2 Basis and dimension. 5. Extreme points and basic feasible solutions
 A. LINEAR ALGEBRA. CONVEX SETS 1. Matrices and vectors 1.1 Matrix operations 1.2 The rank of a matrix 2. Systems of linear equations 2.1 Basic solutions 3. Vector spaces 3.1 Linear dependence and independence
A. LINEAR ALGEBRA. CONVEX SETS 1. Matrices and vectors 1.1 Matrix operations 1.2 The rank of a matrix 2. Systems of linear equations 2.1 Basic solutions 3. Vector spaces 3.1 Linear dependence and independence
Matrix Algebra. Matrix Algebra. Chapter 8 - S&B
 Chapter 8 - S&B Algebraic operations Matrix: The size of a matrix is indicated by the number of its rows and the number of its columns. A matrix with k rows and n columns is called a k n matrix. The number
Chapter 8 - S&B Algebraic operations Matrix: The size of a matrix is indicated by the number of its rows and the number of its columns. A matrix with k rows and n columns is called a k n matrix. The number
Basic Linear Algebra in MATLAB
 Basic Linear Algebra in MATLAB 9.29 Optional Lecture 2 In the last optional lecture we learned the the basic type in MATLAB is a matrix of double precision floating point numbers. You learned a number
Basic Linear Algebra in MATLAB 9.29 Optional Lecture 2 In the last optional lecture we learned the the basic type in MATLAB is a matrix of double precision floating point numbers. You learned a number
Matrices 2. Slide for MA1203 Business Mathematics II Week 4
 Matrices 2 Slide for MA1203 Business Mathematics II Week 4 2.7 Leontief Input Output Model Input Output Analysis One important applications of matrix theory to the field of economics is the study of the
Matrices 2 Slide for MA1203 Business Mathematics II Week 4 2.7 Leontief Input Output Model Input Output Analysis One important applications of matrix theory to the field of economics is the study of the
Matrices. Ellen Kulinsky
 Matrices Ellen Kulinsky To learn the most (AKA become the smartest): Take notes. This is very important! I will sometimes tell you what to write down, but usually you will need to do it on your own. I
Matrices Ellen Kulinsky To learn the most (AKA become the smartest): Take notes. This is very important! I will sometimes tell you what to write down, but usually you will need to do it on your own. I
1. (7pts) Find the points of intersection, if any, of the following planes. 3x + 9y + 6z = 3 2x 6y 4z = 2 x + 3y + 2z = 1
 Math 125 Exam 1 Version 1 February 20, 2006 1. (a) (7pts) Find the points of intersection, if any, of the following planes. Solution: augmented R 1 R 3 3x + 9y + 6z = 3 2x 6y 4z = 2 x + 3y + 2z = 1 3 9
Math 125 Exam 1 Version 1 February 20, 2006 1. (a) (7pts) Find the points of intersection, if any, of the following planes. Solution: augmented R 1 R 3 3x + 9y + 6z = 3 2x 6y 4z = 2 x + 3y + 2z = 1 3 9
Chapter 7. Linear Algebra: Matrices, Vectors,
 Chapter 7. Linear Algebra: Matrices, Vectors, Determinants. Linear Systems Linear algebra includes the theory and application of linear systems of equations, linear transformations, and eigenvalue problems.
Chapter 7. Linear Algebra: Matrices, Vectors, Determinants. Linear Systems Linear algebra includes the theory and application of linear systems of equations, linear transformations, and eigenvalue problems.
GAUSSIAN ELIMINATION AND LU DECOMPOSITION (SUPPLEMENT FOR MA511)
 GAUSSIAN ELIMINATION AND LU DECOMPOSITION (SUPPLEMENT FOR MA511) D. ARAPURA Gaussian elimination is the go to method for all basic linear classes including this one. We go summarize the main ideas. 1.
GAUSSIAN ELIMINATION AND LU DECOMPOSITION (SUPPLEMENT FOR MA511) D. ARAPURA Gaussian elimination is the go to method for all basic linear classes including this one. We go summarize the main ideas. 1.
Section 9.2: Matrices.. a m1 a m2 a mn
 Section 9.2: Matrices Definition: A matrix is a rectangular array of numbers: a 11 a 12 a 1n a 21 a 22 a 2n A =...... a m1 a m2 a mn In general, a ij denotes the (i, j) entry of A. That is, the entry in
Section 9.2: Matrices Definition: A matrix is a rectangular array of numbers: a 11 a 12 a 1n a 21 a 22 a 2n A =...... a m1 a m2 a mn In general, a ij denotes the (i, j) entry of A. That is, the entry in
