Chapter 11. Parametric, Vector, and Polar Functions. aπ for any integer n. Section 11.1 Parametric Functions (pp ) cot
|
|
|
- Horace Cooper
- 5 years ago
- Views:
Transcription
1 Secion. 6 Chaper Parameric, Vecor, an Polar Funcions. an sec sec + an + Secion. Parameric Funcions (pp. 9) Eploraion Invesigaing Cclois 6. csc + co co cos cos cos [, ] b [, 8]. na for an ineger n.. a > an cos so. 8. sin cos sin. An arch is prouce b one complee urn of he wheel. Thus, he are congruen.. The maimum value of is a an occurs when ( n+ ) a for an ineger n. 6. The funcion represene b he ccloi is perioic wih perio a, an each arch represens one perio of he graph. In each arch, he graph is concave own, has an absolue maimum of a a he mipoin, an an absolue minimum of a he wo enpoins. Quick Review.. + ( ) cos + sin + since for.. cos + sin + since for. Secion. Eercises. Yes, is a funcion of. 9 (9, 9). sin cos cos + sin + (, ). sin sin cos Coprigh 6 Pearson Eucaion, Inc.
2 6 Secion.. Yes, is a funcion of. + 7 (, ) 6. No, is no a funcion of. sin ( ) (,.9) (, ). Yes, is a funcion of. + (, ) (, ). No, is no a funcion of. + (, ) (, ). Yes, is a funcion of. (, ) 7. (a) 8. (a) 9. (a) (, ) sin an cos cos sec cos sec 8 ( an ) sin sin ( ) sin / ( ) / ( )( + ) ( ) + / / ( )( + ) (, -). (a) ( ) Coprigh 6 Pearson Eucaion, Inc.
3 Secion. 6. (a) 7. (a) ( ) 6 8 ( ). (a) +. (a). (a) ( ) + + ( + ) sec an sin sec sin cos sec sin ( ) cos sin 8. (a) (.,.) (c) We seek o minimize as a funcion of, so we compue +, which is negaive for <. an posiive for. <. There is a relaive minimum a., where (, ) (.,.). ( cos ) sin. (a) ( ) 6. (a) ( ) e e ( e ) e + e 9. (a) (, 6) (c) We seek o minimize as a funcion of, so we compue +, which is negaive for < an posiive for <. There is a relaive minimum a, where (, ) (, 6). (, ) Coprigh 6 Pearson Eucaion, Inc.
4 6 Secion. (c) We seek o maimize as a funcion of, so we compue cos, which is posiive for < an negaive for <. There is a relaive maimum a, where (, ) (, ).. (a). (a) ( ln( ), ln()) (.9,.99) (, ) (c) We seek o minimize as a funcion of, so we compue secan, which is negaive for < an posiive for <. There is a relaive minimum a, where (, ) (, ).. (a) (, ) (c) We seek o maimize as a funcion of, so we compue sin( ), which is posiive for. < an negaive for <.. There is a relaive maimum a, where (, ) (, ). (c) We seek o maimize as a funcion of, so we compue, which is posiive for all >. There is an enpoin maimum a, where (, ) (ln(), ln()).. ( + sin ) cos an ( + cos ) sin. (a) Tangen is horizonal when an. If, hen cos, an + cos. If cos, hen sin ±, an + sin or. The poins are (, ) an (, ). Tangen is verical when an. If, hen sin, an + sin. If sin, hen cos ±, an + cos or. The poins are (, ) an (, ). Coprigh 6 Pearson Eucaion, Inc.
5 . (an ) sec an (sec ) sec an. Secion ( + sin ) cos an ( + cos ) sin. (a) Tangen is horizonal when an. Since sec > for all, here are no poins where he angen line is horizonal. (a) If, hen cos an + cos. If cos, hen sin ±, an + sin or. The poins are (, ) an (, ).. Tangen is verical when an. If, hen secan, so an. If an, hen sec ±. The poins are (, ) an (, ). ( ) an ( ). (a) If, hen an ±. Using he parameric formulas for an, he poins are 6, 6 an 9, + 9. (In ecimal form, he are (.8,.79) an (.,.79).) Tangen is verical when an. If, hen sin, an + cos. If sin, hen cos ±, an + cos or. The poins are (, ) an (, ). S ( sin ) + (cos ) S S S S ( cos ) + ( sin ) S 9 S S Tangen is verical when an. Since for all, here are no poins where he angen line is verical. Coprigh 6 Pearson Eucaion, Inc.
6 66 Secion. 9.. / / S (( 8sin + 8sin + 8cos ) + ( 8cos 8cos+ 8sin ) ) / / S (( 8cos ) + ( 8sin ) ) / S 8 / S S / ([ 6cos ()sin()] + [ 6sin ()cos()] ) 6 cos ()sin () + sin ()cos () 6 [cos ( ) + sin ( )][cos ( )sin ( )] 6 cos ( )sin ( ) / 6cos sin / sin / cos 6 [ ( )] / S + + ( + ) / S ( + + ) S. ( ) / S ( + ) 9 / S ( + + ) S. ( ). / (( ) + ( ) ) / S ( + ) S S Coprigh 6 Pearson Eucaion, Inc.
7 Secion. 67. / S (sec cos ) + ( sin ) / / ln an an ln cos /. (a) sin, cos, so / Lengh ( sin ) + ( cos ). cos, sin, so Lengh ( cos ) ( sin ) sin, cos, so Lengh.. ( sin ) ( cos ) which using NINT evaluaes o + 7. In he firs inegral, replace wih. Then becomes. 8. Parameerize he curve as g(),, c. The parameer is iself, so replace wih in he general formula. Then becomes. 9. a( cos ) (Noe: inegrae wih respec o from o a ; inegrae wih respec o from o.) a Area a( cos ) a( cos ) a ( cos+ cos ) a sin + + sin a Coprigh 6 Pearson Eucaion, Inc.
8 68 Secion.. a( cos ), so Volume [ a( cos )] a( cos ) a ( cos+ cos cos ) a sin + + sin sin sin a. a bsin an a b cos ( < b< a). a bsin an a b cos ( a < b< a).. S (( cos ) + ( sin ) ) S ( 9 cos+ cos + sin ) S ( cos ) S. S (( cos ) + ( sin )) S ( cos+ 9cos + 9sin ) S ( cos ) S.. False. Inee, ma no even be a funcion of. (See Eample.) 6. True. The orere pairs (, f()) an (, f()) are eacl he same. 7. B 8. C; if sin an csc, hen we can eliminae he parameer o ge. Since sin an csc are boh posiive for < <, he pah follows a porion of he curve in he firs quaran, where is ecreasing an concave up. 9. C; ln ( ) ln ( ). D e. (a) QP has lengh, so P can be obaine b saring a Q an moving sin unis righ an cos unis ownwar. (If eiher quani is negaive, he corresponing irecion is reverse.) Since Q (cos, sin ), he Coprigh 6 Pearson Eucaion, Inc.
9 Secion. 69 coorinaes of P are cos + sin an sin cos. Q sin cos P(, ) (, ) cos, sin, so Lengh (cos) + (sin). All isances are a imes as big as before. (a) a(co + sin ), a(sin cos ) Lengh a v For eercises 6, sin v cos an v sin, an for or. The maimum heigh 6 v sin v is aaine in mi-fligh a. sin / 6 To fin he pah lengh, evaluae ( vcos ) ( vsin ) + vsin vsin using NINT. To fin he maimum heigh, calculae ma ( v sin ) 6.. (a) The projecile his he groun when. ( sin 6) 7 or sin. 6 8 cos, sin ( 7sin )/ 8 Lengh ( cos ) + ( sin ) which, using NINT, evaluaes o 6.79 f The maimum heigh of he projecile occurs when, so. (a) 6.6 f 7 6 sin, 7 f 6 sin f 6. (a) 8. f Coprigh 6 Pearson Eucaion, Inc.
10 6 Secion. 6, f 6 6. (a) I is no necessar o use NINT Lengh ( ) [ 6 ] f 6. 6 f / (( sin ) cos ) S + S () ( + sin ) ( cos ) 8 / / / S (( ) + ( ) ) / S + / / / + + / ( + ). / S (( ) + ( ) ) / ( ) / ( )( ) S / / ((sec cos ) ( sin ) ) / / cos (sec ) / cosan / sin / ( cos ) S + S + Secion. Vecors in he Plane (pp. 6) Quick Review.. ( ) + ( ) 7. Solve b ; b.. Slope of PQ, so RQ an b. b. Slope of AB Slope of CD, so a an a. 6. Slope of AB Slope of CD, so b 6 8 an b v () (sin ) v () sin+ cos a () (sin+ cos) a () cos sin 8. () v () ( ) () 6 + C () 6() + C C ( ) 6( ) + 8 Coprigh 6 Pearson Eucaion, Inc.
11 Secion isance ( ) v () v ( ) + an, 8 v + cos, 9. ( cos ) + ( sin ) cos sin Secion. Eercises. (, ) (, ),. (, ) (, ),. (, ) (, ),. cos( 8 ) sin( 8 ),. 6cos( 7 ) 6sin( 7 ) 6, 6. cos( ). 868 sin( ) ,. 9. P +, (, ) (, ) (, ),. cos( ). 6 sin( ). 6. 6,. 6. v + 8 an, 6. v ( ) + 7. an, v + an, 8. ( ) v + an, cos 8 sin, 8 cos 6 8 sin 6, 7. (a) (), ( ) 9, ( 6) 7 8. (a) ( ), ( ), + ( ) (a) + ( ), +, Coprigh 6 Pearson Eucaion, Inc.
12 6 Secion. +. (a) ( ),, 7 + ( 7) 7. (a) u (), ( ) 6, v ( ), ( ) 6, u v 6 ( 6),, 9 + ( 9). (a) u (), ( ) 6,. (a). (a) v ( ), ( ), u+ v 6+ ( ), + 6, 9 ( 6) u (), ( ), 8 v ( ), ( ), u+ v +, +, 97 + u (), ( ), 6 v ( ), ( ), 6 u + v +, + 7, 7 6 ( ) +. Iniial veloci is 7 norh of eas: cos 7, sin 7. 7,.. Win veloci is norh of eas: cos, sin. 7,. 6. A he wo vecors o ge 8., 6.. The spee is he magniue, 6. 7 mph. 6. The irecion is an norh of eas, or. 66 eas of norh. 6. cos sin The rue veloci is,, so he rue angle is cos 6. an he rue spee is ( ) + ( ). 9mph () () v a 6, 6 6, r() v (), 6, 6 r() v () sin, cos cos, sin v() a () cos, sin sin, cos r() v () e, e e e, e v() a () e e, e e + e, e Coprigh 6 Pearson Eucaion, Inc.
13 Secion r() v () cos, sin 6sin, 8cos v() a() 6sin, 8cos 8cos, sin r() v () + sin, cos + cos, + sin v() a() + cos, + sin sin, + cos r() v () sin, cos sin + cos, cos sin v() a() sin + cos, cos sin cos sin, sin cos. (a) The posiion vecor of he ball a an ime is r () (), (), where () 9 cos an () 9sin 6. v (), 9cos, 9sin (c) Fin () when (). [, ] b [, ] No, he hi oes no clear he -foo fence. Coprigh 6 Pearson Eucaion, Inc.
14 6 Secion. () See he graph in par (c). The ball his he fence afer abou. secons. (e) Evaluae v() a.. v () ( 9cos ) + ( 9sin ) v (. ) ( 9cos ) + ( 9sin. ) 86. f/sec. (a) The posiion vecor of he ball a an ime is r () (), (), where () 8 cos 7 an () 8sin 7 6. Noe ha, is on he groun a he puner s posiion, ars 9 fee from he puner s goal line. v (), 8cos 7, 8sin 7 (c) Fin when () cos cos7 The ball is over he plaer afer abou.8 secons. () Fin () when.8. (. 8) 8(. 8)sin 7 6(. 8). 8 I is unlikel ha he plaer will be able o cach he ball wihou backing up.. r() v () cos, sin sin, cos v() a() sin, cos 9cos, sin [.6,.6] b [.,.] p Coprigh 6 Pearson Eucaion, Inc.
15 Secion r() v () sin, cos cos, sin v() a () cos, sin 6sin, 9cos [.6,.6] b [.,.] p 7. (a) v () sincos,sin cos cos sin sin, cos, Spee: ( / ) [, ] b [.,.] p (c) To he righ 8. (a) v () e + e, e e e e, e + e e e e lim lim lim e e e + + (c) For an, ( e + e ) ( e e ) e + + e ( e + e ) Coprigh 6 Pearson Eucaion, Inc.
16 66 Secion. () The veloci a is,. ( ) + ( + ) e e [ 9, 9] b [ 6, 6]. The parameric equaions are an + sin( ) (a). (a). (a). (a), + cos +, 6 ( ), + sin + 6, + 8, 6+, 9 ( ) + ( + cos ) 9. cos, sin + 7, sin, cos + 7, 7+, + 7, ( cos ) + ( sin ) 8. ( + ), ( + ) +, ln( + ), ( + ) +, + ln, 7. (( ) + ) + (( + ) ). 9 e, e + +, e e, + +, +. 86, ,. 86 [, ] b [, ]. The parameric equaions are 7 sin( ) + an cos( ) +. (Noe: The paricle raverses he Figure-8 hree imes, finishing where i sare.) [6, 8] b [., 6.]. (a) v () cos, sin 6 6 v() sin, cos v() sin + cos 7 v( ). 99 a () sin, cos a( ) cos, sin a( ), 7 Coprigh 6 Pearson Eucaion, Inc.
17 Secion. 67 (c) cos 6 sin (a) v () sec,an v secan, sec v, spee: + ( ) 6 ( ) / (sec ) (an ) (c) The upper par of he righ branch: [,.7] b [,.] < / 7. (a) v (), + + v (), ( + ) ( + ) No; he -componen of veloci is zero onl if, while he -componen of veloci is zero onl if. A no ime will he veloci be,. (c) lim,, (a) v () sin,cos v () cos, sin v ( ), where an. Coprigh 6 Pearson Eucaion, Inc.
18 68 Secion. (c) cos sin () [, ] b [.,.] p 9. (a) e sin, e cos e sin + e cos, e cos e sin e cos e sin m e sin + e cos e sin ( ) + e cos ( ), e cos( ) e sin ( ) 76., 87. v () ( 76. ) + ( 87. ) 8. (c). (a) (c). (a) ( e sin+ e cos ) + ( e cos e sin ).,, v( ) ( ( )) + ( ( ) ) v( ) / (( ) + ( ) ) / ( + ) / ( + ) + ( + sin( )) 9. m( ) 6 sin ( + ) (c) Spee ( + sin ) + ( 6) 6. 7 () 8cos 6, ( + sin 6) + 7( 8)cos ,. Coprigh 6 Pearson Eucaion, Inc.
19 Secion. 69. (a) m( ) cos ( ) sin 8 Spee (c) () ( cos ) + (sin 8). 96 ( cos( )) + (sin( )). 7 sin( ), cos( ) + + (., 7. ). False; for eample, u an (u) have opposie irecions.. False; for eample,, +,,, which has a irecion angle of.. E; +, ln( + ), +,, + ( + ) 6. D; + cos( ), 7+ sin( ) +. 6, , B; 7cos 6. 7sin. cos 6. sin. 7 ( ) + ( ) B; cos sin Spee 9. The veloci vecor is has slope is ( cos ) + ( sin ). 8,, which. The acceleraion vecor ( ),,,, which has slope. Since he slopes are negaive reciprocals of each oher, he vecors are orhogonal. 6. The posiion vecor is cos, sin, which has slope an. The veloci vecor is sin, cos, which has slope. The an acceleraion vecor is cos, sin, which has slope an. The veloci slope is he negaive reciprocal of he posiion an acceleraion slopes, so veloci is orhogonal o posiion an o acceleraion. 6. (a) Since also solves ( ), he paricles collie when. Firs paricle: v ( ),, so he irecion uni vecor is,. Secon paricle: v (),, so he irecion uni vecor is,. 6. (a) Referring o he figure, look a he circular arc from he poin where o he poin m. On he one han, his arc has lengh given b r, bu i also has lengh given b v. Seing hese wo quaniies equal gives he resul. () sin v v v v, vcos an r r v v v v a() cos, sin r r r r v v v cos, sin r r r Coprigh 6 Pearson Eucaion, Inc.
20 6 Secion. v (c) From par, a() r(). So, b Newon s secon law, r he law of graviaion gives he resul. v F m r. Subsiuing for F in r () Se vt r an solve for vt. (e) Subsiue r T r GM T r r GM T r GM T r T r GM for v in v GM an solve for T. r 6. Use he hin. TRACE unil Y is approimael 8. A closer view: The screens confirm ha he ball is a a heigh of 8 fee afer abou.869 secons when i is abou fee from home plae. 6. Le u a, b be one of he vecors. I has slope b a, so he perpenicular vecor v mus have slope a Thus v kb, ka for some nonzero scalar k, an he o prouc is ( ) u v a, b, kb, ka kab + kab. 6. (a) The iagram shows, b vecor aiion, ha v + w u, so w u v. This is jus he Law of Cosines applie o he riangle, he sies of which are he magniues of he vecors.. b Coprigh 6 Pearson Eucaion, Inc.
21 Secion. 6 (c) B he HMT Rule, w u v, u v.so u + v w ( u + u) + ( v + v) ( u v) + ( u v) u + u + v + v u uv+ v + u uv + v uv + uv ( uv + uv) () From par, w u + v u v cos, so u + v w u v cos. u + v w uv + uv. Subsiuing, we ge ( uv + uv ) uv cos, From par (c), ( ) so u v uv + uv u v cos. Secion. Polar Funcions (pp. 6 7) Quick Review.. cos sin,... A r () A r () Graph / an / ( sin ) ( cos ) cos sin co 76 co( ). Coprigh 6 Pearson Eucaion, Inc.
22 6 Secion. 8. co, so or cos cos sin sin (, ) an (, ). D C B A 9. sin, s or. cos cos sin sin (, ) an (, ). ( cos ) + ( sin ). 76 Secion. Eercises (a) cos 6 sin 6,. D C (a) cos sin (, ) B A cos() sin () (, ). cos an sin an (, ) (c) cos7 sin 7 (, ) () cos sin, ( ) (c) cos sin (, ) A D C B () cos sin (, ) (a) r ( ) + an,, an, Coprigh 6 Pearson Eucaion, Inc.
23 Secion. 6 r + ( ) ± (c) an,, an, r + ± an,, an, () r + ± an, (, ) an (, ).. () ( ) r + ± an, (, ) an (, ) 6. B A C D 7. r + ( ) ± (a) ( ) 7 an, 6 6 7, an, r + ± an, + an an, an (c) r +( ) ± an,,, an, Coprigh 6 Pearson Eucaion, Inc.
24 6 Secion. 9.. Limaçon 6 6 [.,.] b [, ] q p 6. Limaçon. [, ] b [, ] q p 7. Lemniscae. Carioi [, ] b [, ] p / q p / [, ] b [, ] q p 8. Lemniscae. Carioi [.,.] b [, ] q p / [ 6, 6] b [, ] q p 9. Circle. Rose [ 6, 6] b [, ] q p [, ] b [, ] q p. Circle. Rose [.,.] b [, ] q p [.,.] b [, ] q p Coprigh 6 Pearson Eucaion, Inc.
25 Secion. 6. r csc r sin, a horizonal line. r sec r cos avericalline,. I is a parabola. [ 6, 6] b [, ] q p. I is a parabola.. + aline, (slope, -inercep ).. 6. r +, a circle (cener (, ), raius ) r sin cos rsin rcos, a line (slope, -inercep ) r sin r ( sin cos ), a hperbola [ 6, 6] b [, ] q p. I is a parabola. [ 6, 6] b [, ] q p. I is a parabola. 7. rcos rsin, he union of wo lines: ± r rcos ( + ) +, a circle ( cener (, ), raius ) r 8 rsin + 8rsin ( ) 6, a circle ( cener (, ), raius ) [ 6, 6] b [, ] q p. I is a hperbola. [ 6, 6] b [, ] q p 6. I is an ellipse.. r cos + sin r rcos + r sin + + ( ) + ( ), acircle ( cener (, ), raius ) [ 6, 6] b [, ] q p Coprigh 6 Pearson Eucaion, Inc.
26 66 Secion. 7. I is an ellipse. [ 6, 6] b [, ] q p 8. I is a hperbola. [ 6, 6] b [, ] q p 9. r + sin (( + sin )sin ) (( + sin ) cos ) ( sin )cos cos sin sin A : A :. r cos (cos sin ) (cos cos ) cos cos sin sin sin cos cos sin A : unefine A : A : A : unefine. r sin ( sin )sin ( sin )cos ( 6sin )cos sin ( sin ) cos A (, ): A, : A (, ): A, :. r ( cos ) ( ( cos )sin ) ( ( cos ) cos ) 6cos + cos + sin ( cos ) A., : unefine A., : A (, 6 ): unefine A, :.. ( + cos ) 6 6 ( 8 8cos cos ) ( + cos + cos ) sin + sin 8 ( + sin ) ( 8 sin sin ) ( sin cos ) cos sin Coprigh 6 Pearson Eucaion, Inc.
27 (cos ) / / ( sin ) / ( cos ) / / 6 ( sin ) / cos ( ) / cos + / sin sin ( ) ( cos 8) sin 8 8 sin / / / cos ( ) ( cos ) ( 9 cos + cos ) 9 6 cos + + cos 6sin + sin /6 /6 ( sin ) /6 sin sin /6 + /6 cos sin /6 + /6 sin + cos / Secion. 67 / / ( sin ) sin / ( cos ) / [ sin ] + /6 / ( sin ) + ( ) /6 /6 / sin /6 /6 ( cos ) /6 + [ sin ] + / [ ( cos )] + ( ) / / ( cos + cos ) + / / ( 8cos + ( + cos )) + / [ 6 8sin + sin ] + 8 / ( ( cos )) / ( cos cos ) / [ 6sin / sin ] + ( 8 6cos + ( + cos )) The requese area is insie of he upper semicircle an ousie of he porion of he carioi ha is in Quarans I an II. ( ( sin )) ( sin + sin ) ( sin + cos ) + cos sin 8 Coprigh 6 Pearson Eucaion, Inc.
28 68 Secion (( cos ) ) /6 /6 /6 ( 6cos ) /6 (( 8 cos ) ) /6 ( 6 cos ) /6 [ 6 8sin ] [, ] b [, ] q p for he circle q p for he carioi / + / ( 8cos cos ) / + / [ + sin sin ] (( cos ) ( cos ) ) ( ( cos ) cos ) + 9. [, ] b [, ] q p ( sin ) sin 6. (a) ( cos 6) sin 6 6 ( sin sin ) Slope ( sin cos ) / 6sincos + cossin 6cos cos sin sin / + ln / / [ 6, 6] b [, ] q p ( ( ( sin )) ) ( + sin sin ) ( sin + cos ) cos + sin ( ) 8 (c) rcos rsin + r (cos sin ) r cos Le α an. Then he area is α. cos sin sin 6. True; polar coorinaes eermine a unique poin. Coprigh 6 Pearson Eucaion, Inc.
29 Secion False; inegraing from o raverses he curve wice, giving wice he area. The correc upper limi of inegraion is. 6. D 6. E 6. B 66. D 67. (a) [ 9, 9] b [ 6, 6] 68. (a) [ 9, 9] b [ 6, 6] (c) The graph of r is he graph of r roae counerclockwise abou he origin b angle α. 69. (a) [ 9, 9] b [ 6, 6] The graphs are ellipses. As e +, he graph approaches he circle of raius cenere a he origin. 7. (a) [ 6, ] b [, ] The graphs are ellipses ha srech ou o he righ. The ellipse wih eccenrici e is he reflecion across he -ais of he ellipse wih eccenrici e. [, ] b [, ] The graphs are hperbolas. + As e, he righ branch of he hperbola goes o infini an isappears. The lef branch approaches he parabola. Coprigh 6 Pearson Eucaion, Inc.
30 6 Secion. 7. (a) [ 9, 9] b [ 6, 6] The graphs are parabolas. + As c, he limi of he graph is he negaive -ais. 7. / / / [( ) + ( ) ] [( r cos r cos ) + ( r sin r sin ) ] [ r cos + r cos + r sin + r sin + rr cos cos + rr sin sin ] [ r + r rr cos( )] 7. (a) (c) a a( cos ) [ sin ] a a a [ ] a a a acos [ sin] ( ) ( f ( )cos f( )sin ) + ( f ( )sin + f( )cos ) ( f ( )cos ) + ( f( )sin ) + ( f ( )sin ) + ( f( )cos ) ( f( )) (cos + sin ) + ( f ( )) (cos + sin ) ( f( )) + ( f ( )) r r + ( + cos ) + ( sin ) cos + cos + cos 8sin (a) [, ] b [, ] You see boh branches of he hperbola as well as he lines ha appear o be he asmpoes. Coprigh 6 Pearson Eucaion, Inc.
31 Secion. 6 The branch on he lef correspons o cos < < cos... The branch on he righ correspons o cos < < cos... (c) Wha appear o be asmpoes are acuall lines pu in b he graphing calculaor o connec he las poin i fins on one branch of he hperbola o he firs poin i fins on he oher branch. 77. c r + ecos r+ recos c r c e( rcos ) Use rcos an r +. r + ( c e) c ce+ e + c ce+ e ( e ) + ce+ c ce Complee he square on b aing o boh sies. e ce c e c e ( e ) c + e ( e ) e ce c ( e ) + + e e ( e ) ce e + + c e c c c Le a an b. e e The las equaion becomes ( + ae) ( + ae) + or +. This is an ellipse wih cener a b a b ( ae, ). 78. The isance from he cener o one focus is a c c b ( e ) e ce ( e ) ce e This is ae, which is he isance from he cener of he ellipse in Eercise 77 o he origin. 79. The area swep ou from ime o ime is given b A K, we have r K K or. r () A r. Thus A r. Since Coprigh 6 Pearson Eucaion, Inc.
32 6 Secion. 8. From Eercise 79, r K, an since c K r, his gives. ( + ecos ) ( + ecos ) c csin ( + ecos ) c cos ( esin ) ( + ecos ) csin ( + ecos ) K csin c K sin c K K K cos cos c c r K cos cr c cos ( + ecos ) csin ( esin ) ( + ecos ) ce + c cos ( + ecos ) K ( ce + c cos ) c K ( e + cos ) c K K sin sin c cr K K K Thus he acceleraion vecor is cos, sin cos, sin which has magniue cr cr cr K cr an i poins owar he origin from he poin (, ) ( rcos, rsin ). Quick Quiz Secions... A ( ). C; ( ),. D Area + sin. 8. (a) ( ) r cos ( + sin ) cos 786. Coprigh 6 Pearson Eucaion, Inc.
33 Chaper Review 6 (c) The graph is geing closer o he origin as increases from o. () Maimize r + sin for. r + cos + cos cos r Since cos for an + > < < r cos for + < < <, here is a maimum of r when b he Firs Derivaive es. The curve is farhes from he origin when. Chaper Review Eercises (pp. 7 76). (a),, 7, ( 7) + ( ). (a), +,, sin 6 cos 6, r ( ) + ( ) 7 9. (a) 8,, ,, + ( sec ) ( an ) ( sin ) sec sin ( ) + ( ). (a), 6, ( 8). (a),,. + ( ) 7 9 sin cos,. (a) + ( ) ( + ) ( ) 6 Coprigh 6 Pearson Eucaion, Inc.
34 6 Chaper Review. (a) sec sec an Horizonal: an Also, an sec ± ± The poin are, an,. an sec Verical: sec ( impossible) There are no poins where he angens are verical. cos cos an sin an sin cos an cos (, ) an(, ). (a) ( sin ) sin sin an cos an cos sin an sin ( an, ) (, ) ( cos) 9 9cos 9cos an cos cos 9sin 9 9sin 9, 9 an, 9. (a) ( sin ) ( ) ( ) sin sin or cos, cos 9sin, 9sin (, ) an (, ) ( cos). Carioi [, ] b [, ] q p 6. Conve limaçon [.,.] b [, ] q p 7. -peale rose. (a) (cos ) sin cos cos sin cos sin a (, ) is never zero. There are no cos verical angens. [.,.] b [, ] q p 8. Verical line [, ] b [, ] p / q p / Coprigh 6 Pearson Eucaion, Inc.
35 Chaper Review 6 9. Lemniscae. Circle [.,.] b [, ] q p /. ( ( sin )sin ) ( sin )cos, ( ( sin )cos ) sin (sin ) cos, ± 98.. [.,.] b [, ] q p ( cos ) ( cos ) sin cos cos cos sin sin sin cos cos sin.. The ips of he peals are a he poins where r sin, which are he poins where,,, an 7. The slope is ( )(sin sin ) ( )(sin cos ) cos sin + sin cos. cos cos + sin sin. ( + cos ) ( + cos ) sin cos cos cos sin sin + cos sin cos cos sin sin. 6. cos sin ( ) sin sin cos cos + + cos, ±., ±. 79 cos cos cos sin ( ) sin cos sin +,. 67,. / (, ) ( ) (, ) (, ) 7 ( ) m Tangen line, + +, 6. The carioi crosses he -ais a he poins where an. The slope is ( )(( + sin )sin ) ( )(( + sin ) cos ) cossin + ( + sin ) cos. coscos + ( + sin ) sin Coprigh 6 Pearson Eucaion, Inc.
36 66 Chaper Review (, ) m Tangen line (, ) (, ). + 6 r cos + r sin 6, or 6 r cos + sin 7., a line r rcos +, a circle cener,, raius r sin r r cos cos cos rsin, a parabola. r cos cos sin sin cos sin or, a line r + r sin r sin + r r sin r sin.. ( + ) + ( ) 6 ( rcos + ) + ( rsin ) 6 ( cos ) (sin cos ( sin 9)) sin (sin cos ) 6 6. ( ) 7. / / ( + cos ) ( ) / + cos cos / + sin + sin + 6 sin + + sin + / Coprigh 6 Pearson Eucaion, Inc.
37 Chaper Review ( ( + sin )) ( sin ) ( + sin + sin ) sin + + ( sin cos ) ( cos ) cos sin sin (a) v () cos, sin v() sin, cos a() ( sin ), cos a() cos, sin cos, sin, ( ) ( ) Spee +. (a) v () sec, an v ( ) sec an, sec a( ) sec an, sec a ( ) (sec an + sec ), sec an sec( ) an( ), sec ( ), Spee + Coprigh 6 Pearson Eucaion, Inc.
38 68 Chaper Review. v (), + + v(), ( + ) ( + ) / / spee + / / ( ) ( ) + + spee + The maimum value of is, when +.. r( ) e cos, e sin, wih slope.. e sin an. e cos v( ) e cos e sin, e sin + e cos a( ) e sin, e cos, wih slope e cos. e sin Since he slopes are an negaive reciprocals, he angle is alwas 9. r() sin, cos r() cos,sin cos( ), sin( ), r() cos,sin + + C + C + C C + C C r (), + ( + ) + C + + C + C C + + C, C r() an, an, r() an +, +. v(), v(), + C () + C C So v(), r(), (), C C C r + + r(), 6. v (), 7. (a) v() +, r() ( + 6), ( + ) C C () C, C () C, C + 6+ C + + C 6 C C C C r(), () + () +, () + () +, r() + 6, + + ( ) sin cos cos ( ) sin sin ( ) cos ( ) + 7 Coprigh 6 Pearson Eucaion, Inc.
39 sin ( ) (c) 8. (a) cos 6 6 cos sin 6 6 ( ) ( ) ( ) cos an sin + 9 e sin + e cos e cos e sin cos+ sin cos sin (c) 9. (a) Disance v () e [ e ] e ( ) 6 () v,,, 96 v ( ) 8,, an 96 v ( ) 8 + Chaper Review 69 6 ( ) Disance ( + ) (c) +, so 6 +. e (sin + cos ), e (cos sin ) e (sin + sin cos + cos ) e ( + sin cos ) e (cos cos sin + sin ) e ( cos sin ) e e v() e v() Coprigh 6 Pearson Eucaion, Inc.
40 66 Chaper Review. egrees eas of norh is (9 ) egrees norh of eas. A he vecors: cos, sin + cos( ), sin( ) 9 cos, 8 sin 8. 96, Spee mph Direcion an 8. 8 eas of norh (a). (a) a v + + C () C + cos( + ) Posiion ( +,cos( + )) A his poin +, so. Spee ( ) + ( ( sin( + )). va(), anv B(), + ( ) 6. 6 (c) Seing A B, we fin ha. Plugging ino A an B, we fin ha boh values are he same (). Thus, he paricles collie when. (Noe: If ou graph boh pahs, he will cross a (, ). However, he paricles are here a ifferen imes.). (a) Area + sin The polar equaion is equivalen o r+ rsin. Thus, r rsin r ( rsin ) + ( ) (c) Area, 8 which, inee, is. Coprigh 6 Pearson Eucaion, Inc.
10.1 EXERCISES. y 2 t 2. y 1 t y t 3. y e
 66 CHAPTER PARAMETRIC EQUATINS AND PLAR CRDINATES SLUTIN We use a graphing device o produce he graphs for he cases a,,.5,.,,.5,, and shown in Figure 7. Noice ha all of hese curves (ecep he case a ) have
66 CHAPTER PARAMETRIC EQUATINS AND PLAR CRDINATES SLUTIN We use a graphing device o produce he graphs for he cases a,,.5,.,,.5,, and shown in Figure 7. Noice ha all of hese curves (ecep he case a ) have
15. Vector Valued Functions
 1. Vecor Valued Funcions Up o his poin, we have presened vecors wih consan componens, for example, 1, and,,4. However, we can allow he componens of a vecor o be funcions of a common variable. For example,
1. Vecor Valued Funcions Up o his poin, we have presened vecors wih consan componens, for example, 1, and,,4. However, we can allow he componens of a vecor o be funcions of a common variable. For example,
!!"#"$%&#'()!"#&'(*%)+,&',-)./0)1-*23)
 "#"$%&#'()"#&'(*%)+,&',-)./)1-*) #$%&'()*+,&',-.%,/)*+,-&1*#$)()5*6$+$%*,7&*-'-&1*(,-&*6&,7.$%$+*&%'(*8$&',-,%'-&1*(,-&*6&,79*(&,%: ;..,*&1$&$.$%&'()*1$$.,'&',-9*(&,%)?%*,('&5
"#"$%&#'()"#&'(*%)+,&',-)./)1-*) #$%&'()*+,&',-.%,/)*+,-&1*#$)()5*6$+$%*,7&*-'-&1*(,-&*6&,7.$%$+*&%'(*8$&',-,%'-&1*(,-&*6&,79*(&,%: ;..,*&1$&$.$%&'()*1$$.,'&',-9*(&,%)?%*,('&5
Answers to 1 Homework
 Answers o Homework. x + and y x 5 y To eliminae he parameer, solve for x. Subsiue ino y s equaion o ge y x.. x and y, x y x To eliminae he parameer, solve for. Subsiue ino y s equaion o ge x y, x. (Noe:
Answers o Homework. x + and y x 5 y To eliminae he parameer, solve for x. Subsiue ino y s equaion o ge y x.. x and y, x y x To eliminae he parameer, solve for. Subsiue ino y s equaion o ge x y, x. (Noe:
AP Calculus BC Chapter 10 Part 1 AP Exam Problems
 AP Calculus BC Chaper Par AP Eam Problems All problems are NO CALCULATOR unless oherwise indicaed Parameric Curves and Derivaives In he y plane, he graph of he parameric equaions = 5 + and y= for, is a
AP Calculus BC Chaper Par AP Eam Problems All problems are NO CALCULATOR unless oherwise indicaed Parameric Curves and Derivaives In he y plane, he graph of he parameric equaions = 5 + and y= for, is a
Physics 218 Exam 1. with Solutions Fall 2010, Sections Part 1 (15) Part 2 (20) Part 3 (20) Part 4 (20) Bonus (5)
 Physics 18 Exam 1 wih Soluions Fall 1, Secions 51-54 Fill ou he informaion below bu o no open he exam unil insruce o o so! Name Signaure Suen ID E-mail Secion # ules of he exam: 1. You have he full class
Physics 18 Exam 1 wih Soluions Fall 1, Secions 51-54 Fill ou he informaion below bu o no open he exam unil insruce o o so! Name Signaure Suen ID E-mail Secion # ules of he exam: 1. You have he full class
Chapters 6 & 7: Trigonometric Functions of Angles and Real Numbers. Divide both Sides by 180
 Algebra Chapers & : Trigonomeric Funcions of Angles and Real Numbers Chapers & : Trigonomeric Funcions of Angles and Real Numbers - Angle Measures Radians: - a uni (rad o measure he size of an angle. rad
Algebra Chapers & : Trigonomeric Funcions of Angles and Real Numbers Chapers & : Trigonomeric Funcions of Angles and Real Numbers - Angle Measures Radians: - a uni (rad o measure he size of an angle. rad
10.6 Parametric Equations
 0_006.qd /8/05 9:05 AM Page 77 Secion 0.6 77 Parameric Equaions 0.6 Parameric Equaions Wha ou should learn Evaluae ses of parameric equaions for given values of he parameer. Skech curves ha are represened
0_006.qd /8/05 9:05 AM Page 77 Secion 0.6 77 Parameric Equaions 0.6 Parameric Equaions Wha ou should learn Evaluae ses of parameric equaions for given values of he parameer. Skech curves ha are represened
WEEK-3 Recitation PHYS 131. of the projectile s velocity remains constant throughout the motion, since the acceleration a x
 WEEK-3 Reciaion PHYS 131 Ch. 3: FOC 1, 3, 4, 6, 14. Problems 9, 37, 41 & 71 and Ch. 4: FOC 1, 3, 5, 8. Problems 3, 5 & 16. Feb 8, 018 Ch. 3: FOC 1, 3, 4, 6, 14. 1. (a) The horizonal componen of he projecile
WEEK-3 Reciaion PHYS 131 Ch. 3: FOC 1, 3, 4, 6, 14. Problems 9, 37, 41 & 71 and Ch. 4: FOC 1, 3, 5, 8. Problems 3, 5 & 16. Feb 8, 018 Ch. 3: FOC 1, 3, 4, 6, 14. 1. (a) The horizonal componen of he projecile
Ground Rules. PC1221 Fundamentals of Physics I. Kinematics. Position. Lectures 3 and 4 Motion in One Dimension. A/Prof Tay Seng Chuan
 Ground Rules PC11 Fundamenals of Physics I Lecures 3 and 4 Moion in One Dimension A/Prof Tay Seng Chuan 1 Swich off your handphone and pager Swich off your lapop compuer and keep i No alking while lecure
Ground Rules PC11 Fundamenals of Physics I Lecures 3 and 4 Moion in One Dimension A/Prof Tay Seng Chuan 1 Swich off your handphone and pager Swich off your lapop compuer and keep i No alking while lecure
3.6 Derivatives as Rates of Change
 3.6 Derivaives as Raes of Change Problem 1 John is walking along a sraigh pah. His posiion a he ime >0 is given by s = f(). He sars a =0from his house (f(0) = 0) and he graph of f is given below. (a) Describe
3.6 Derivaives as Raes of Change Problem 1 John is walking along a sraigh pah. His posiion a he ime >0 is given by s = f(). He sars a =0from his house (f(0) = 0) and he graph of f is given below. (a) Describe
THE ESSENTIALS OF CALCULUS ANSWERS TO SELECTED EXERCISES
 Assignmen - page. m.. f 7 7.. 7..8 7..77 7. 87. THE ESSENTIALS OF CALCULUS ANSWERS TO SELECTED EXERCISES m.... no collinear 8...,,.,.8 or.,..78,.7 or.7,.8., 8.87 or., 8.88.,,, 7..7 Assignmen - page 7.
Assignmen - page. m.. f 7 7.. 7..8 7..77 7. 87. THE ESSENTIALS OF CALCULUS ANSWERS TO SELECTED EXERCISES m.... no collinear 8...,,.,.8 or.,..78,.7 or.7,.8., 8.87 or., 8.88.,,, 7..7 Assignmen - page 7.
a. Show that these lines intersect by finding the point of intersection. b. Find an equation for the plane containing these lines.
 Mah A Final Eam Problems for onsideraion. Show all work for credi. Be sure o show wha you know. Given poins A(,,, B(,,, (,, 4 and (,,, find he volume of he parallelepiped wih adjacen edges AB, A, and A.
Mah A Final Eam Problems for onsideraion. Show all work for credi. Be sure o show wha you know. Given poins A(,,, B(,,, (,, 4 and (,,, find he volume of he parallelepiped wih adjacen edges AB, A, and A.
3, so θ = arccos
 Mahemaics 210 Professor Alan H Sein Monday, Ocober 1, 2007 SOLUTIONS This problem se is worh 50 poins 1 Find he angle beween he vecors (2, 7, 3) and (5, 2, 4) Soluion: Le θ be he angle (2, 7, 3) (5, 2,
Mahemaics 210 Professor Alan H Sein Monday, Ocober 1, 2007 SOLUTIONS This problem se is worh 50 poins 1 Find he angle beween he vecors (2, 7, 3) and (5, 2, 4) Soluion: Le θ be he angle (2, 7, 3) (5, 2,
and v y . The changes occur, respectively, because of the acceleration components a x and a y
 Week 3 Reciaion: Chaper3 : Problems: 1, 16, 9, 37, 41, 71. 1. A spacecraf is raveling wih a veloci of v0 = 5480 m/s along he + direcion. Two engines are urned on for a ime of 84 s. One engine gives he
Week 3 Reciaion: Chaper3 : Problems: 1, 16, 9, 37, 41, 71. 1. A spacecraf is raveling wih a veloci of v0 = 5480 m/s along he + direcion. Two engines are urned on for a ime of 84 s. One engine gives he
Parametrics and Vectors (BC Only)
 Paramerics and Vecors (BC Only) The following relaionships should be learned and memorized. The paricle s posiion vecor is r() x(), y(). The velociy vecor is v(),. The speed is he magniude of he velociy
Paramerics and Vecors (BC Only) The following relaionships should be learned and memorized. The paricle s posiion vecor is r() x(), y(). The velociy vecor is v(),. The speed is he magniude of he velociy
Phys 221 Fall Chapter 2. Motion in One Dimension. 2014, 2005 A. Dzyubenko Brooks/Cole
 Phys 221 Fall 2014 Chaper 2 Moion in One Dimension 2014, 2005 A. Dzyubenko 2004 Brooks/Cole 1 Kinemaics Kinemaics, a par of classical mechanics: Describes moion in erms of space and ime Ignores he agen
Phys 221 Fall 2014 Chaper 2 Moion in One Dimension 2014, 2005 A. Dzyubenko 2004 Brooks/Cole 1 Kinemaics Kinemaics, a par of classical mechanics: Describes moion in erms of space and ime Ignores he agen
x i v x t a dx dt t x
 Physics 3A: Basic Physics I Shoup - Miderm Useful Equaions A y A sin A A A y an A y A A = A i + A y j + A z k A * B = A B cos(θ) A B = A B sin(θ) A * B = A B + A y B y + A z B z A B = (A y B z A z B y
Physics 3A: Basic Physics I Shoup - Miderm Useful Equaions A y A sin A A A y an A y A A = A i + A y j + A z k A * B = A B cos(θ) A B = A B sin(θ) A * B = A B + A y B y + A z B z A B = (A y B z A z B y
IB Physics Kinematics Worksheet
 IB Physics Kinemaics Workshee Wrie full soluions and noes for muliple choice answers. Do no use a calculaor for muliple choice answers. 1. Which of he following is a correc definiion of average acceleraion?
IB Physics Kinemaics Workshee Wrie full soluions and noes for muliple choice answers. Do no use a calculaor for muliple choice answers. 1. Which of he following is a correc definiion of average acceleraion?
CALCULUS EXPLORATION OF THE SECOND FUNDAMENTAL THEOREM OF CALCULUS. Second Fundamental Theorem of Calculus (Chain Rule Version):
 CALCULUS EXPLORATION OF THE SECOND FUNDAMENTAL THEOREM OF CALCULUS 6 cos Secon Funamenal Theorem of Calculus: f a 4 a f 6 cos Secon Funamenal Theorem of Calculus (Chain Rule Version): g f a E. Use he Secon
CALCULUS EXPLORATION OF THE SECOND FUNDAMENTAL THEOREM OF CALCULUS 6 cos Secon Funamenal Theorem of Calculus: f a 4 a f 6 cos Secon Funamenal Theorem of Calculus (Chain Rule Version): g f a E. Use he Secon
2.1: What is physics? Ch02: Motion along a straight line. 2.2: Motion. 2.3: Position, Displacement, Distance
 Ch: Moion along a sraigh line Moion Posiion and Displacemen Average Velociy and Average Speed Insananeous Velociy and Speed Acceleraion Consan Acceleraion: A Special Case Anoher Look a Consan Acceleraion
Ch: Moion along a sraigh line Moion Posiion and Displacemen Average Velociy and Average Speed Insananeous Velociy and Speed Acceleraion Consan Acceleraion: A Special Case Anoher Look a Consan Acceleraion
University Physics with Modern Physics 14th Edition Young TEST BANK
 Universi Phsics wih Modern Phsics 14h Ediion Young SOLUTIONS MANUAL Full clear download (no formaing errors) a: hps://esbankreal.com/download/universi-phsics-modern-phsics- 14h-ediion-oung-soluions-manual-/
Universi Phsics wih Modern Phsics 14h Ediion Young SOLUTIONS MANUAL Full clear download (no formaing errors) a: hps://esbankreal.com/download/universi-phsics-modern-phsics- 14h-ediion-oung-soluions-manual-/
KINEMATICS IN ONE DIMENSION
 KINEMATICS IN ONE DIMENSION PREVIEW Kinemaics is he sudy of how hings move how far (disance and displacemen), how fas (speed and velociy), and how fas ha how fas changes (acceleraion). We say ha an objec
KINEMATICS IN ONE DIMENSION PREVIEW Kinemaics is he sudy of how hings move how far (disance and displacemen), how fas (speed and velociy), and how fas ha how fas changes (acceleraion). We say ha an objec
Chapter 3 Kinematics in Two Dimensions
 Chaper 3 KINEMATICS IN TWO DIMENSIONS PREVIEW Two-dimensional moion includes objecs which are moing in wo direcions a he same ime, such as a projecile, which has boh horizonal and erical moion. These wo
Chaper 3 KINEMATICS IN TWO DIMENSIONS PREVIEW Two-dimensional moion includes objecs which are moing in wo direcions a he same ime, such as a projecile, which has boh horizonal and erical moion. These wo
Motion along a Straight Line
 chaper 2 Moion along a Sraigh Line verage speed and average velociy (Secion 2.2) 1. Velociy versus speed Cone in he ebook: fer Eample 2. Insananeous velociy and insananeous acceleraion (Secions 2.3, 2.4)
chaper 2 Moion along a Sraigh Line verage speed and average velociy (Secion 2.2) 1. Velociy versus speed Cone in he ebook: fer Eample 2. Insananeous velociy and insananeous acceleraion (Secions 2.3, 2.4)
Homework 2 Solutions
 Mah 308 Differenial Equaions Fall 2002 & 2. See he las page. Hoework 2 Soluions 3a). Newon s secon law of oion says ha a = F, an we know a =, so we have = F. One par of he force is graviy, g. However,
Mah 308 Differenial Equaions Fall 2002 & 2. See he las page. Hoework 2 Soluions 3a). Newon s secon law of oion says ha a = F, an we know a =, so we have = F. One par of he force is graviy, g. However,
Kinematics Vocabulary. Kinematics and One Dimensional Motion. Position. Coordinate System in One Dimension. Kinema means movement 8.
 Kinemaics Vocabulary Kinemaics and One Dimensional Moion 8.1 WD1 Kinema means movemen Mahemaical descripion of moion Posiion Time Inerval Displacemen Velociy; absolue value: speed Acceleraion Averages
Kinemaics Vocabulary Kinemaics and One Dimensional Moion 8.1 WD1 Kinema means movemen Mahemaical descripion of moion Posiion Time Inerval Displacemen Velociy; absolue value: speed Acceleraion Averages
( ) ( ) ( ) ( u) ( u) = are shown in Figure =, it is reasonable to speculate that. = cos u ) and the inside function ( ( t) du
 Porlan Communiy College MTH 51 Lab Manual The Chain Rule Aciviy 38 The funcions f ( = sin ( an k( sin( 3 38.1. Since f ( cos( k ( = cos( 3. Bu his woul imply ha k ( f ( = are shown in Figure =, i is reasonable
Porlan Communiy College MTH 51 Lab Manual The Chain Rule Aciviy 38 The funcions f ( = sin ( an k( sin( 3 38.1. Since f ( cos( k ( = cos( 3. Bu his woul imply ha k ( f ( = are shown in Figure =, i is reasonable
AP Calculus BC - Parametric equations and vectors Chapter 9- AP Exam Problems solutions
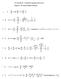 AP Calculus BC - Parameric equaions and vecors Chaper 9- AP Exam Problems soluions. A 5 and 5. B A, 4 + 8. C A, 4 + 4 8 ; he poin a is (,). y + ( x ) x + 4 4. e + e D A, slope.5 6 e e e 5. A d hus d d
AP Calculus BC - Parameric equaions and vecors Chaper 9- AP Exam Problems soluions. A 5 and 5. B A, 4 + 8. C A, 4 + 4 8 ; he poin a is (,). y + ( x ) x + 4 4. e + e D A, slope.5 6 e e e 5. A d hus d d
= + t ] can be used to calculate the angular
![= + t ] can be used to calculate the angular = + t ] can be used to calculate the angular](/thumbs/94/120776871.jpg) WEEK-7 Reciaion PHYS 3 Mar 8, 8 Ch. 8 FOC:, 4, 6,, 3 &5. () Using Equaion 8. (θ = Arc lengh / Raius) o calculae he angle (in raians) ha each objec subens a your eye shows ha θ Moon = 9. 3 ra, θ Pea = 7.
WEEK-7 Reciaion PHYS 3 Mar 8, 8 Ch. 8 FOC:, 4, 6,, 3 &5. () Using Equaion 8. (θ = Arc lengh / Raius) o calculae he angle (in raians) ha each objec subens a your eye shows ha θ Moon = 9. 3 ra, θ Pea = 7.
Lecture 2-1 Kinematics in One Dimension Displacement, Velocity and Acceleration Everything in the world is moving. Nothing stays still.
 Lecure - Kinemaics in One Dimension Displacemen, Velociy and Acceleraion Everyhing in he world is moving. Nohing says sill. Moion occurs a all scales of he universe, saring from he moion of elecrons in
Lecure - Kinemaics in One Dimension Displacemen, Velociy and Acceleraion Everyhing in he world is moving. Nohing says sill. Moion occurs a all scales of he universe, saring from he moion of elecrons in
Chapter 2 Trigonometric Functions
 Chaper Trigonomeric Funcions Secion.. 90 7 80 6. 90 70 89 60 70 9 80 79 60 70 70 09. 90 6 89 9 60 6 6 80 6 79 9 60 6 6 7. 9.. 0. 60 0 + 60 α is a quadran III angle coerminal wih an angle of measure 0..
Chaper Trigonomeric Funcions Secion.. 90 7 80 6. 90 70 89 60 70 9 80 79 60 70 70 09. 90 6 89 9 60 6 6 80 6 79 9 60 6 6 7. 9.. 0. 60 0 + 60 α is a quadran III angle coerminal wih an angle of measure 0..
SOLUTIONS TO CONCEPTS CHAPTER 3
 SOLUTIONS TO ONEPTS HPTER 3. a) Disance ravelled = 50 + 40 + 0 = 0 m b) F = F = D = 50 0 = 30 M His displacemen is D D = F DF 30 40 50m In ED an = DE/E = 30/40 = 3/4 = an (3/4) His displacemen from his
SOLUTIONS TO ONEPTS HPTER 3. a) Disance ravelled = 50 + 40 + 0 = 0 m b) F = F = D = 50 0 = 30 M His displacemen is D D = F DF 30 40 50m In ED an = DE/E = 30/40 = 3/4 = an (3/4) His displacemen from his
Check in: 1 If m = 2(x + 1) and n = find y when. b y = 2m n 2
 7 Parameric equaions This chaer will show ou how o skech curves using heir arameric equaions conver arameric equaions o Caresian equaions find oins of inersecion of curves and lines using arameric equaions
7 Parameric equaions This chaer will show ou how o skech curves using heir arameric equaions conver arameric equaions o Caresian equaions find oins of inersecion of curves and lines using arameric equaions
Physics 3A: Basic Physics I Shoup Sample Midterm. Useful Equations. x f. x i v x. a x. x i. v xi v xf. 2a x f x i. y f. a r.
 Physics 3A: Basic Physics I Shoup Sample Miderm Useful Equaions A y Asin A A x A y an A y A x A = A x i + A y j + A z k A * B = A B cos(θ) A x B = A B sin(θ) A * B = A x B x + A y B y + A z B z A x B =
Physics 3A: Basic Physics I Shoup Sample Miderm Useful Equaions A y Asin A A x A y an A y A x A = A x i + A y j + A z k A * B = A B cos(θ) A x B = A B sin(θ) A * B = A x B x + A y B y + A z B z A x B =
t A. 3. Which vector has the largest component in the y-direction, as defined by the axes to the right?
 Ke Name Insrucor Phsics 1210 Exam 1 Sepember 26, 2013 Please wrie direcl on he exam and aach oher shees of work if necessar. Calculaors are allowed. No noes or books ma be used. Muliple-choice problems
Ke Name Insrucor Phsics 1210 Exam 1 Sepember 26, 2013 Please wrie direcl on he exam and aach oher shees of work if necessar. Calculaors are allowed. No noes or books ma be used. Muliple-choice problems
d 1 = c 1 b 2 - b 1 c 2 d 2 = c 1 b 3 - b 1 c 3
 and d = c b - b c c d = c b - b c c This process is coninued unil he nh row has been compleed. The complee array of coefficiens is riangular. Noe ha in developing he array an enire row may be divided or
and d = c b - b c c d = c b - b c c This process is coninued unil he nh row has been compleed. The complee array of coefficiens is riangular. Noe ha in developing he array an enire row may be divided or
PHYSICS 149: Lecture 9
 PHYSICS 149: Lecure 9 Chaper 3 3.2 Velociy and Acceleraion 3.3 Newon s Second Law of Moion 3.4 Applying Newon s Second Law 3.5 Relaive Velociy Lecure 9 Purdue Universiy, Physics 149 1 Velociy (m/s) The
PHYSICS 149: Lecure 9 Chaper 3 3.2 Velociy and Acceleraion 3.3 Newon s Second Law of Moion 3.4 Applying Newon s Second Law 3.5 Relaive Velociy Lecure 9 Purdue Universiy, Physics 149 1 Velociy (m/s) The
Problem Set 7-7. dv V ln V = kt + C. 20. Assume that df/dt still equals = F RF. df dr = =
 20. Assume ha df/d sill equals = F + 0.02RF. df dr df/ d F+ 0. 02RF = = 2 dr/ d R 0. 04RF 0. 01R 10 df 11. 2 R= 70 and F = 1 = = 0. 362K dr 31 21. 0 F (70, 30) (70, 1) R 100 Noe ha he slope a (70, 1) is
20. Assume ha df/d sill equals = F + 0.02RF. df dr df/ d F+ 0. 02RF = = 2 dr/ d R 0. 04RF 0. 01R 10 df 11. 2 R= 70 and F = 1 = = 0. 362K dr 31 21. 0 F (70, 30) (70, 1) R 100 Noe ha he slope a (70, 1) is
The Natural Logarithm
 The Naural Logarihm 5-4-007 The Power Rule says n = n + n+ + C provie ha n. The formula oes no apply o. An anierivaive F( of woul have o saisfy F( =. Bu he Funamenal Theorem implies ha if > 0, hen Thus,
The Naural Logarihm 5-4-007 The Power Rule says n = n + n+ + C provie ha n. The formula oes no apply o. An anierivaive F( of woul have o saisfy F( =. Bu he Funamenal Theorem implies ha if > 0, hen Thus,
In this chapter the model of free motion under gravity is extended to objects projected at an angle. When you have completed it, you should
 Cambridge Universiy Press 978--36-60033-7 Cambridge Inernaional AS and A Level Mahemaics: Mechanics Coursebook Excerp More Informaion Chaper The moion of projeciles In his chaper he model of free moion
Cambridge Universiy Press 978--36-60033-7 Cambridge Inernaional AS and A Level Mahemaics: Mechanics Coursebook Excerp More Informaion Chaper The moion of projeciles In his chaper he model of free moion
CHAPTER 12 DIRECT CURRENT CIRCUITS
 CHAPTER 12 DIRECT CURRENT CIUITS DIRECT CURRENT CIUITS 257 12.1 RESISTORS IN SERIES AND IN PARALLEL When wo resisors are conneced ogeher as shown in Figure 12.1 we said ha hey are conneced in series. As
CHAPTER 12 DIRECT CURRENT CIUITS DIRECT CURRENT CIUITS 257 12.1 RESISTORS IN SERIES AND IN PARALLEL When wo resisors are conneced ogeher as shown in Figure 12.1 we said ha hey are conneced in series. As
Solutions from Chapter 9.1 and 9.2
 Soluions from Chaper 9 and 92 Secion 9 Problem # This basically boils down o an exercise in he chain rule from calculus We are looking for soluions of he form: u( x) = f( k x c) where k x R 3 and k is
Soluions from Chaper 9 and 92 Secion 9 Problem # This basically boils down o an exercise in he chain rule from calculus We are looking for soluions of he form: u( x) = f( k x c) where k x R 3 and k is
PROBLEMS FOR MATH 162 If a problem is starred, all subproblems are due. If only subproblems are starred, only those are due. SLOPES OF TANGENT LINES
 PROBLEMS FOR MATH 6 If a problem is sarred, all subproblems are due. If onl subproblems are sarred, onl hose are due. 00. Shor answer quesions. SLOPES OF TANGENT LINES (a) A ball is hrown ino he air. Is
PROBLEMS FOR MATH 6 If a problem is sarred, all subproblems are due. If onl subproblems are sarred, onl hose are due. 00. Shor answer quesions. SLOPES OF TANGENT LINES (a) A ball is hrown ino he air. Is
Linear Motion I Physics
 Linear Moion I Physics Objecives Describe he ifference beween isplacemen an isance Unersan he relaionship beween isance, velociy, an ime Describe he ifference beween velociy an spee Be able o inerpre a
Linear Moion I Physics Objecives Describe he ifference beween isplacemen an isance Unersan he relaionship beween isance, velociy, an ime Describe he ifference beween velociy an spee Be able o inerpre a
Some Basic Information about M-S-D Systems
 Some Basic Informaion abou M-S-D Sysems 1 Inroducion We wan o give some summary of he facs concerning unforced (homogeneous) and forced (non-homogeneous) models for linear oscillaors governed by second-order,
Some Basic Informaion abou M-S-D Sysems 1 Inroducion We wan o give some summary of he facs concerning unforced (homogeneous) and forced (non-homogeneous) models for linear oscillaors governed by second-order,
Kinematics in two dimensions
 Lecure 5 Phsics I 9.18.13 Kinemaics in wo dimensions Course websie: hp://facul.uml.edu/andri_danlo/teaching/phsicsi Lecure Capure: hp://echo36.uml.edu/danlo13/phsics1fall.hml 95.141, Fall 13, Lecure 5
Lecure 5 Phsics I 9.18.13 Kinemaics in wo dimensions Course websie: hp://facul.uml.edu/andri_danlo/teaching/phsicsi Lecure Capure: hp://echo36.uml.edu/danlo13/phsics1fall.hml 95.141, Fall 13, Lecure 5
AP CALCULUS AB 2003 SCORING GUIDELINES (Form B)
 SCORING GUIDELINES (Form B) Quesion A blood vessel is 6 millimeers (mm) long Disance wih circular cross secions of varying diameer. x (mm) 6 8 4 6 Diameer The able above gives he measuremens of he B(x)
SCORING GUIDELINES (Form B) Quesion A blood vessel is 6 millimeers (mm) long Disance wih circular cross secions of varying diameer. x (mm) 6 8 4 6 Diameer The able above gives he measuremens of he B(x)
Section 7.4 Modeling Changing Amplitude and Midline
 488 Chaper 7 Secion 7.4 Modeling Changing Ampliude and Midline While sinusoidal funcions can model a variey of behaviors, i is ofen necessary o combine sinusoidal funcions wih linear and exponenial curves
488 Chaper 7 Secion 7.4 Modeling Changing Ampliude and Midline While sinusoidal funcions can model a variey of behaviors, i is ofen necessary o combine sinusoidal funcions wih linear and exponenial curves
Giambattista, Ch 3 Problems: 9, 15, 21, 27, 35, 37, 42, 43, 47, 55, 63, 76
 Giambaisa, Ch 3 Problems: 9, 15, 21, 27, 35, 37, 42, 43, 47, 55, 63, 76 9. Sraeg Le be direced along he +x-axis and le be 60.0 CCW from Find he magniude of 6.0 B 60.0 4.0 A x 15. (a) Sraeg Since he angle
Giambaisa, Ch 3 Problems: 9, 15, 21, 27, 35, 37, 42, 43, 47, 55, 63, 76 9. Sraeg Le be direced along he +x-axis and le be 60.0 CCW from Find he magniude of 6.0 B 60.0 4.0 A x 15. (a) Sraeg Since he angle
x(m) t(sec ) Homework #2. Ph 231 Introductory Physics, Sp-03 Page 1 of 4
 Homework #2. Ph 231 Inroducory Physics, Sp-03 Page 1 of 4 2-1A. A person walks 2 miles Eas (E) in 40 minues and hen back 1 mile Wes (W) in 20 minues. Wha are her average speed and average velociy (in ha
Homework #2. Ph 231 Inroducory Physics, Sp-03 Page 1 of 4 2-1A. A person walks 2 miles Eas (E) in 40 minues and hen back 1 mile Wes (W) in 20 minues. Wha are her average speed and average velociy (in ha
PHYSICS 220 Lecture 02 Motion, Forces, and Newton s Laws Textbook Sections
 PHYSICS 220 Lecure 02 Moion, Forces, and Newon s Laws Texbook Secions 2.2-2.4 Lecure 2 Purdue Universiy, Physics 220 1 Overview Las Lecure Unis Scienific Noaion Significan Figures Moion Displacemen: Δx
PHYSICS 220 Lecure 02 Moion, Forces, and Newon s Laws Texbook Secions 2.2-2.4 Lecure 2 Purdue Universiy, Physics 220 1 Overview Las Lecure Unis Scienific Noaion Significan Figures Moion Displacemen: Δx
Chapter 7: Solving Trig Equations
 Haberman MTH Secion I: The Trigonomeric Funcions Chaper 7: Solving Trig Equaions Le s sar by solving a couple of equaions ha involve he sine funcion EXAMPLE a: Solve he equaion sin( ) The inverse funcions
Haberman MTH Secion I: The Trigonomeric Funcions Chaper 7: Solving Trig Equaions Le s sar by solving a couple of equaions ha involve he sine funcion EXAMPLE a: Solve he equaion sin( ) The inverse funcions
Physics 180A Fall 2008 Test points. Provide the best answer to the following questions and problems. Watch your sig figs.
 Physics 180A Fall 2008 Tes 1-120 poins Name Provide he bes answer o he following quesions and problems. Wach your sig figs. 1) The number of meaningful digis in a number is called he number of. When numbers
Physics 180A Fall 2008 Tes 1-120 poins Name Provide he bes answer o he following quesions and problems. Wach your sig figs. 1) The number of meaningful digis in a number is called he number of. When numbers
1. VELOCITY AND ACCELERATION
 1. VELOCITY AND ACCELERATION 1.1 Kinemaics Equaions s = u + 1 a and s = v 1 a s = 1 (u + v) v = u + as 1. Displacemen-Time Graph Gradien = speed 1.3 Velociy-Time Graph Gradien = acceleraion Area under
1. VELOCITY AND ACCELERATION 1.1 Kinemaics Equaions s = u + 1 a and s = v 1 a s = 1 (u + v) v = u + as 1. Displacemen-Time Graph Gradien = speed 1.3 Velociy-Time Graph Gradien = acceleraion Area under
k 1 k 2 x (1) x 2 = k 1 x 1 = k 2 k 1 +k 2 x (2) x k series x (3) k 2 x 2 = k 1 k 2 = k 1+k 2 = 1 k k 2 k series
 Final Review A Puzzle... Consider wo massless springs wih spring consans k 1 and k and he same equilibrium lengh. 1. If hese springs ac on a mass m in parallel, hey would be equivalen o a single spring
Final Review A Puzzle... Consider wo massless springs wih spring consans k 1 and k and he same equilibrium lengh. 1. If hese springs ac on a mass m in parallel, hey would be equivalen o a single spring
THE 2-BODY PROBLEM. FIGURE 1. A pair of ellipses sharing a common focus. (c,b) c+a ROBERT J. VANDERBEI
 THE 2-BODY PROBLEM ROBERT J. VANDERBEI ABSTRACT. In his shor noe, we show ha a pair of ellipses wih a common focus is a soluion o he 2-body problem. INTRODUCTION. Solving he 2-body problem from scrach
THE 2-BODY PROBLEM ROBERT J. VANDERBEI ABSTRACT. In his shor noe, we show ha a pair of ellipses wih a common focus is a soluion o he 2-body problem. INTRODUCTION. Solving he 2-body problem from scrach
( ) 2. Review Exercise 2. cos θ 2 3 = = 2 tan. cos. 2 x = = x a. Since π π, = 2. sin = = 2+ = = cotx. 2 sin θ 2+
 Review Eercise sin 5 cos sin an cos 5 5 an 5 9 co 0 a sinθ 6 + 4 6 + sin θ 4 6+ + 6 + 4 cos θ sin θ + 4 4 sin θ + an θ cos θ ( ) + + + + Since π π, < θ < anθ should be negaive. anθ ( + ) Pearson Educaion
Review Eercise sin 5 cos sin an cos 5 5 an 5 9 co 0 a sinθ 6 + 4 6 + sin θ 4 6+ + 6 + 4 cos θ sin θ + 4 4 sin θ + an θ cos θ ( ) + + + + Since π π, < θ < anθ should be negaive. anθ ( + ) Pearson Educaion
Solution: b All the terms must have the dimension of acceleration. We see that, indeed, each term has the units of acceleration
 PHYS 54 Tes Pracice Soluions Spring 8 Q: [4] Knowing ha in he ne epression a is acceleraion, v is speed, is posiion and is ime, from a dimensional v poin of view, he equaion a is a) incorrec b) correc
PHYS 54 Tes Pracice Soluions Spring 8 Q: [4] Knowing ha in he ne epression a is acceleraion, v is speed, is posiion and is ime, from a dimensional v poin of view, he equaion a is a) incorrec b) correc
Unit 1 Test Review Physics Basics, Movement, and Vectors Chapters 1-3
 A.P. Physics B Uni 1 Tes Reiew Physics Basics, Moemen, and Vecors Chapers 1-3 * In sudying for your es, make sure o sudy his reiew shee along wih your quizzes and homework assignmens. Muliple Choice Reiew:
A.P. Physics B Uni 1 Tes Reiew Physics Basics, Moemen, and Vecors Chapers 1-3 * In sudying for your es, make sure o sudy his reiew shee along wih your quizzes and homework assignmens. Muliple Choice Reiew:
AP CALCULUS BC 2016 SCORING GUIDELINES
 6 SCORING GUIDELINES Quesion A ime, he posiion of a paricle moving in he xy-plane is given by he parameric funcions ( x ( ), y ( )), where = + sin ( ). The graph of y, consising of hree line segmens, is
6 SCORING GUIDELINES Quesion A ime, he posiion of a paricle moving in he xy-plane is given by he parameric funcions ( x ( ), y ( )), where = + sin ( ). The graph of y, consising of hree line segmens, is
on the interval (x + 1) 0! x < ", where x represents feet from the first fence post. How many square feet of fence had to be painted?
 Calculus II MAT 46 Improper Inegrals A mahemaician asked a fence painer o complee he unique ask of paining one side of a fence whose face could be described by he funcion y f (x on he inerval (x + x
Calculus II MAT 46 Improper Inegrals A mahemaician asked a fence painer o complee he unique ask of paining one side of a fence whose face could be described by he funcion y f (x on he inerval (x + x
Section 3.8, Mechanical and Electrical Vibrations
 Secion 3.8, Mechanical and Elecrical Vibraions Mechanical Unis in he U.S. Cusomary and Meric Sysems Disance Mass Time Force g (Earh) Uni U.S. Cusomary MKS Sysem CGS Sysem fee f slugs seconds sec pounds
Secion 3.8, Mechanical and Elecrical Vibraions Mechanical Unis in he U.S. Cusomary and Meric Sysems Disance Mass Time Force g (Earh) Uni U.S. Cusomary MKS Sysem CGS Sysem fee f slugs seconds sec pounds
Chapter 2 The Derivative Applied Calculus 107. We ll need a rule for finding the derivative of a product so we don t have to multiply everything out.
 Chaper The Derivaive Applie Calculus 107 Secion 4: Prouc an Quoien Rules The basic rules will le us ackle simple funcions. Bu wha happens if we nee he erivaive of a combinaion of hese funcions? Eample
Chaper The Derivaive Applie Calculus 107 Secion 4: Prouc an Quoien Rules The basic rules will le us ackle simple funcions. Bu wha happens if we nee he erivaive of a combinaion of hese funcions? Eample
SMT 2014 Calculus Test Solutions February 15, 2014 = 3 5 = 15.
 SMT Calculus Tes Soluions February 5,. Le f() = and le g() =. Compue f ()g (). Answer: 5 Soluion: We noe ha f () = and g () = 6. Then f ()g () =. Plugging in = we ge f ()g () = 6 = 3 5 = 5.. There is a
SMT Calculus Tes Soluions February 5,. Le f() = and le g() =. Compue f ()g (). Answer: 5 Soluion: We noe ha f () = and g () = 6. Then f ()g () =. Plugging in = we ge f ()g () = 6 = 3 5 = 5.. There is a
Physics 101 Fall 2006: Exam #1- PROBLEM #1
 Physics 101 Fall 2006: Exam #1- PROBLEM #1 1. Problem 1. (+20 ps) (a) (+10 ps) i. +5 ps graph for x of he rain vs. ime. The graph needs o be parabolic and concave upward. ii. +3 ps graph for x of he person
Physics 101 Fall 2006: Exam #1- PROBLEM #1 1. Problem 1. (+20 ps) (a) (+10 ps) i. +5 ps graph for x of he rain vs. ime. The graph needs o be parabolic and concave upward. ii. +3 ps graph for x of he person
d = ½(v o + v f) t distance = ½ (initial velocity + final velocity) time
 BULLSEYE Lab Name: ANSWER KEY Dae: Pre-AP Physics Lab Projecile Moion Weigh = 1 DIRECTIONS: Follow he insrucions below, build he ramp, ake your measuremens, and use your measuremens o make he calculaions
BULLSEYE Lab Name: ANSWER KEY Dae: Pre-AP Physics Lab Projecile Moion Weigh = 1 DIRECTIONS: Follow he insrucions below, build he ramp, ake your measuremens, and use your measuremens o make he calculaions
AP Calculus BC 2004 Free-Response Questions Form B
 AP Calculus BC 200 Free-Response Quesions Form B The maerials included in hese files are inended for noncommercial use by AP eachers for course and exam preparaion; permission for any oher use mus be sough
AP Calculus BC 200 Free-Response Quesions Form B The maerials included in hese files are inended for noncommercial use by AP eachers for course and exam preparaion; permission for any oher use mus be sough
2001 November 15 Exam III Physics 191
 1 November 15 Eam III Physics 191 Physical Consans: Earh s free-fall acceleraion = g = 9.8 m/s 2 Circle he leer of he single bes answer. quesion is worh 1 poin Each 3. Four differen objecs wih masses:
1 November 15 Eam III Physics 191 Physical Consans: Earh s free-fall acceleraion = g = 9.8 m/s 2 Circle he leer of he single bes answer. quesion is worh 1 poin Each 3. Four differen objecs wih masses:
The Fundamental Theorems of Calculus
 FunamenalTheorems.nb 1 The Funamenal Theorems of Calculus You have now been inrouce o he wo main branches of calculus: ifferenial calculus (which we inrouce wih he angen line problem) an inegral calculus
FunamenalTheorems.nb 1 The Funamenal Theorems of Calculus You have now been inrouce o he wo main branches of calculus: ifferenial calculus (which we inrouce wih he angen line problem) an inegral calculus
MA 214 Calculus IV (Spring 2016) Section 2. Homework Assignment 1 Solutions
 MA 14 Calculus IV (Spring 016) Secion Homework Assignmen 1 Soluions 1 Boyce and DiPrima, p 40, Problem 10 (c) Soluion: In sandard form he given firs-order linear ODE is: An inegraing facor is given by
MA 14 Calculus IV (Spring 016) Secion Homework Assignmen 1 Soluions 1 Boyce and DiPrima, p 40, Problem 10 (c) Soluion: In sandard form he given firs-order linear ODE is: An inegraing facor is given by
Be able to sketch a function defined parametrically. (by hand and by calculator)
 Pre Calculus Uni : Parameric and Polar Equaions (7) Te References: Pre Calculus wih Limis; Larson, Hoseler, Edwards. B he end of he uni, ou should be able o complee he problems below. The eacher ma provide
Pre Calculus Uni : Parameric and Polar Equaions (7) Te References: Pre Calculus wih Limis; Larson, Hoseler, Edwards. B he end of he uni, ou should be able o complee he problems below. The eacher ma provide
Chapter Let. 1) k be a vector-valued function. (a) Evaluate f (0). (b) What is the domain of f () t? (c) Is f () t continuous at t = 1?
 Chaper. Le f() = sin i+ ( 3+ ) j ln( + ) k be a vecor-valued funcion. (a) Evaluae f (). (b) Wha is he domain of f ()? (c) Is f () coninuous a =? Chaper. Le f() = sin i+ ( 3+ ) j ln( + ) k be a vecor-valued
Chaper. Le f() = sin i+ ( 3+ ) j ln( + ) k be a vecor-valued funcion. (a) Evaluae f (). (b) Wha is he domain of f ()? (c) Is f () coninuous a =? Chaper. Le f() = sin i+ ( 3+ ) j ln( + ) k be a vecor-valued
Vector Calculus. Chapter 2
 Chaper Vecor Calculus. Elemenar. Vecor Produc. Differeniaion of Vecors 4. Inegraion of Vecors 5. Del Operaor or Nabla (Smbol 6. Polar Coordinaes Chaper Coninued 7. Line Inegral 8. Volume Inegral 9. Surface
Chaper Vecor Calculus. Elemenar. Vecor Produc. Differeniaion of Vecors 4. Inegraion of Vecors 5. Del Operaor or Nabla (Smbol 6. Polar Coordinaes Chaper Coninued 7. Line Inegral 8. Volume Inegral 9. Surface
Section 5: Chain Rule
 Chaper The Derivaive Applie Calculus 11 Secion 5: Chain Rule There is one more ype of complicae funcion ha we will wan o know how o iffereniae: composiion. The Chain Rule will le us fin he erivaive of
Chaper The Derivaive Applie Calculus 11 Secion 5: Chain Rule There is one more ype of complicae funcion ha we will wan o know how o iffereniae: composiion. The Chain Rule will le us fin he erivaive of
1. (16 points) Answer the following derivative-related questions. dx tan sec x. dx tan u = du d. dx du tan u. du tan u d v.
 Exam #2 Soluions. (6 poins) Answer he following eriaie-relae quesions. (a) (8 poins) If y an sec x, fin. This is an applicaion of he chain rule in wo sages, in which we shall le u sec x, an sec x: an sec
Exam #2 Soluions. (6 poins) Answer he following eriaie-relae quesions. (a) (8 poins) If y an sec x, fin. This is an applicaion of he chain rule in wo sages, in which we shall le u sec x, an sec x: an sec
MEI Mechanics 1 General motion. Section 1: Using calculus
 Soluions o Exercise MEI Mechanics General moion Secion : Using calculus. s 4 v a 6 4 4 When =, v 4 a 6 4 6. (i) When = 0, s = -, so he iniial displacemen = - m. s v 4 When = 0, v = so he iniial velociy
Soluions o Exercise MEI Mechanics General moion Secion : Using calculus. s 4 v a 6 4 4 When =, v 4 a 6 4 6. (i) When = 0, s = -, so he iniial displacemen = - m. s v 4 When = 0, v = so he iniial velociy
Math 116 Practice for Exam 2
 Mah 6 Pracice for Exam Generaed Ocober 3, 7 Name: SOLUTIONS Insrucor: Secion Number:. This exam has 5 quesions. Noe ha he problems are no of equal difficuly, so you may wan o skip over and reurn o a problem
Mah 6 Pracice for Exam Generaed Ocober 3, 7 Name: SOLUTIONS Insrucor: Secion Number:. This exam has 5 quesions. Noe ha he problems are no of equal difficuly, so you may wan o skip over and reurn o a problem
Math 2142 Exam 1 Review Problems. x 2 + f (0) 3! for the 3rd Taylor polynomial at x = 0. To calculate the various quantities:
 Mah 4 Eam Review Problems Problem. Calculae he 3rd Taylor polynomial for arcsin a =. Soluion. Le f() = arcsin. For his problem, we use he formula f() + f () + f ()! + f () 3! for he 3rd Taylor polynomial
Mah 4 Eam Review Problems Problem. Calculae he 3rd Taylor polynomial for arcsin a =. Soluion. Le f() = arcsin. For his problem, we use he formula f() + f () + f ()! + f () 3! for he 3rd Taylor polynomial
Homework sheet Exercises done during the lecture of March 12, 2014
 EXERCISE SESSION 2A FOR THE COURSE GÉOMÉTRIE EUCLIDIENNE, NON EUCLIDIENNE ET PROJECTIVE MATTEO TOMMASINI Homework shee 3-4 - Exercises done during he lecure of March 2, 204 Exercise 2 Is i rue ha he parameerized
EXERCISE SESSION 2A FOR THE COURSE GÉOMÉTRIE EUCLIDIENNE, NON EUCLIDIENNE ET PROJECTIVE MATTEO TOMMASINI Homework shee 3-4 - Exercises done during he lecure of March 2, 204 Exercise 2 Is i rue ha he parameerized
Integration Over Manifolds with Variable Coordinate Density
 Inegraion Over Manifolds wih Variable Coordinae Densiy Absrac Chrisopher A. Lafore clafore@gmail.com In his paper, he inegraion of a funcion over a curved manifold is examined in he case where he curvaure
Inegraion Over Manifolds wih Variable Coordinae Densiy Absrac Chrisopher A. Lafore clafore@gmail.com In his paper, he inegraion of a funcion over a curved manifold is examined in he case where he curvaure
Physics 221 Fall 2008 Homework #2 Solutions Ch. 2 Due Tues, Sept 9, 2008
 Physics 221 Fall 28 Homework #2 Soluions Ch. 2 Due Tues, Sep 9, 28 2.1 A paricle moving along he x-axis moves direcly from posiion x =. m a ime =. s o posiion x = 1. m by ime = 1. s, and hen moves direcly
Physics 221 Fall 28 Homework #2 Soluions Ch. 2 Due Tues, Sep 9, 28 2.1 A paricle moving along he x-axis moves direcly from posiion x =. m a ime =. s o posiion x = 1. m by ime = 1. s, and hen moves direcly
1. Kinematics I: Position and Velocity
 1. Kinemaics I: Posiion and Velociy Inroducion The purpose of his eperimen is o undersand and describe moion. We describe he moion of an objec by specifying is posiion, velociy, and acceleraion. In his
1. Kinemaics I: Posiion and Velociy Inroducion The purpose of his eperimen is o undersand and describe moion. We describe he moion of an objec by specifying is posiion, velociy, and acceleraion. In his
Announcements: Warm-up Exercise:
 Fri Apr 13 7.1 Sysems of differenial equaions - o model muli-componen sysems via comparmenal analysis hp//en.wikipedia.org/wiki/muli-comparmen_model Announcemens Warm-up Exercise Here's a relaively simple
Fri Apr 13 7.1 Sysems of differenial equaions - o model muli-componen sysems via comparmenal analysis hp//en.wikipedia.org/wiki/muli-comparmen_model Announcemens Warm-up Exercise Here's a relaively simple
Of all of the intellectual hurdles which the human mind has confronted and has overcome in the last fifteen hundred years, the one which seems to me
 Of all of he inellecual hurdles which he human mind has confroned and has overcome in he las fifeen hundred years, he one which seems o me o have been he mos amazing in characer and he mos supendous in
Of all of he inellecual hurdles which he human mind has confroned and has overcome in he las fifeen hundred years, he one which seems o me o have been he mos amazing in characer and he mos supendous in
Midterm Exam Review Questions Free Response Non Calculator
 Name: Dae: Block: Miderm Eam Review Quesions Free Response Non Calculaor Direcions: Solve each of he following problems. Choose he BEST answer choice from hose given. A calculaor may no be used. Do no
Name: Dae: Block: Miderm Eam Review Quesions Free Response Non Calculaor Direcions: Solve each of he following problems. Choose he BEST answer choice from hose given. A calculaor may no be used. Do no
1 1 + x 2 dx. tan 1 (2) = ] ] x 3. Solution: Recall that the given integral is improper because. x 3. 1 x 3. dx = lim dx.
![1 1 + x 2 dx. tan 1 (2) = ] ] x 3. Solution: Recall that the given integral is improper because. x 3. 1 x 3. dx = lim dx. 1 1 + x 2 dx. tan 1 (2) = ] ] x 3. Solution: Recall that the given integral is improper because. x 3. 1 x 3. dx = lim dx.](/thumbs/71/65799522.jpg) . Use Simpson s rule wih n 4 o esimae an () +. Soluion: Since we are using 4 seps, 4 Thus we have [ ( ) f() + 4f + f() + 4f 3 [ + 4 4 6 5 + + 4 4 3 + ] 5 [ + 6 6 5 + + 6 3 + ]. 5. Our funcion is f() +.
. Use Simpson s rule wih n 4 o esimae an () +. Soluion: Since we are using 4 seps, 4 Thus we have [ ( ) f() + 4f + f() + 4f 3 [ + 4 4 6 5 + + 4 4 3 + ] 5 [ + 6 6 5 + + 6 3 + ]. 5. Our funcion is f() +.
Multiple Choice Solutions 1. E (2003 AB25) () xt t t t 2. A (2008 AB21/BC21) 3. B (2008 AB7) Using Fundamental Theorem of Calculus: 1
 Paricle Moion Soluions We have inenionally included more maerial han can be covered in mos Suden Sudy Sessions o accoun for groups ha are able o answer he quesions a a faser rae. Use your own judgmen,
Paricle Moion Soluions We have inenionally included more maerial han can be covered in mos Suden Sudy Sessions o accoun for groups ha are able o answer he quesions a a faser rae. Use your own judgmen,
4.5 Constant Acceleration
 4.5 Consan Acceleraion v() v() = v 0 + a a() a a() = a v 0 Area = a (a) (b) Figure 4.8 Consan acceleraion: (a) velociy, (b) acceleraion When he x -componen of he velociy is a linear funcion (Figure 4.8(a)),
4.5 Consan Acceleraion v() v() = v 0 + a a() a a() = a v 0 Area = a (a) (b) Figure 4.8 Consan acceleraion: (a) velociy, (b) acceleraion When he x -componen of he velociy is a linear funcion (Figure 4.8(a)),
Displacement ( x) x x x
 Kinemaics Kinemaics is he branch of mechanics ha describes he moion of objecs wihou necessarily discussing wha causes he moion. 1-Dimensional Kinemaics (or 1- Dimensional moion) refers o moion in a sraigh
Kinemaics Kinemaics is he branch of mechanics ha describes he moion of objecs wihou necessarily discussing wha causes he moion. 1-Dimensional Kinemaics (or 1- Dimensional moion) refers o moion in a sraigh
Reading from Young & Freedman: For this topic, read sections 25.4 & 25.5, the introduction to chapter 26 and sections 26.1 to 26.2 & 26.4.
 PHY1 Elecriciy Topic 7 (Lecures 1 & 11) Elecric Circuis n his opic, we will cover: 1) Elecromoive Force (EMF) ) Series and parallel resisor combinaions 3) Kirchhoff s rules for circuis 4) Time dependence
PHY1 Elecriciy Topic 7 (Lecures 1 & 11) Elecric Circuis n his opic, we will cover: 1) Elecromoive Force (EMF) ) Series and parallel resisor combinaions 3) Kirchhoff s rules for circuis 4) Time dependence
Physics 235 Chapter 2. Chapter 2 Newtonian Mechanics Single Particle
 Chaper 2 Newonian Mechanics Single Paricle In his Chaper we will review wha Newon s laws of mechanics ell us abou he moion of a single paricle. Newon s laws are only valid in suiable reference frames,
Chaper 2 Newonian Mechanics Single Paricle In his Chaper we will review wha Newon s laws of mechanics ell us abou he moion of a single paricle. Newon s laws are only valid in suiable reference frames,
Let us start with a two dimensional case. We consider a vector ( x,
 Roaion marices We consider now roaion marices in wo and hree dimensions. We sar wih wo dimensions since wo dimensions are easier han hree o undersand, and one dimension is a lile oo simple. However, our
Roaion marices We consider now roaion marices in wo and hree dimensions. We sar wih wo dimensions since wo dimensions are easier han hree o undersand, and one dimension is a lile oo simple. However, our
23.5. Half-Range Series. Introduction. Prerequisites. Learning Outcomes
 Half-Range Series 2.5 Inroducion In his Secion we address he following problem: Can we find a Fourier series expansion of a funcion defined over a finie inerval? Of course we recognise ha such a funcion
Half-Range Series 2.5 Inroducion In his Secion we address he following problem: Can we find a Fourier series expansion of a funcion defined over a finie inerval? Of course we recognise ha such a funcion
1998 Calculus AB Scoring Guidelines
 AB{ / BC{ 1999. The rae a which waer ows ou of a pipe, in gallons per hour, is given by a diereniable funcion R of ime. The able above shows he rae as measured every hours for a {hour period. (a) Use a
AB{ / BC{ 1999. The rae a which waer ows ou of a pipe, in gallons per hour, is given by a diereniable funcion R of ime. The able above shows he rae as measured every hours for a {hour period. (a) Use a
- If one knows that a magnetic field has a symmetry, one may calculate the magnitude of B by use of Ampere s law: The integral of scalar product
 11.1 APPCATON OF AMPEE S AW N SYMMETC MAGNETC FEDS - f one knows ha a magneic field has a symmery, one may calculae he magniude of by use of Ampere s law: The inegral of scalar produc Closed _ pah * d
11.1 APPCATON OF AMPEE S AW N SYMMETC MAGNETC FEDS - f one knows ha a magneic field has a symmery, one may calculae he magniude of by use of Ampere s law: The inegral of scalar produc Closed _ pah * d
Math 2214 Solution Test 1A Spring 2016
 Mah 14 Soluion Tes 1A Spring 016 sec Problem 1: Wha is he larges -inerval for which ( 4) = has a guaraneed + unique soluion for iniial value (-1) = 3 according o he Exisence Uniqueness Theorem? Soluion
Mah 14 Soluion Tes 1A Spring 016 sec Problem 1: Wha is he larges -inerval for which ( 4) = has a guaraneed + unique soluion for iniial value (-1) = 3 according o he Exisence Uniqueness Theorem? Soluion
23.2. Representing Periodic Functions by Fourier Series. Introduction. Prerequisites. Learning Outcomes
 Represening Periodic Funcions by Fourier Series 3. Inroducion In his Secion we show how a periodic funcion can be expressed as a series of sines and cosines. We begin by obaining some sandard inegrals
Represening Periodic Funcions by Fourier Series 3. Inroducion In his Secion we show how a periodic funcion can be expressed as a series of sines and cosines. We begin by obaining some sandard inegrals
Week 1 Lecture 2 Problems 2, 5. What if something oscillates with no obvious spring? What is ω? (problem set problem)
 Week 1 Lecure Problems, 5 Wha if somehing oscillaes wih no obvious spring? Wha is ω? (problem se problem) Sar wih Try and ge o SHM form E. Full beer can in lake, oscillaing F = m & = ge rearrange: F =
Week 1 Lecure Problems, 5 Wha if somehing oscillaes wih no obvious spring? Wha is ω? (problem se problem) Sar wih Try and ge o SHM form E. Full beer can in lake, oscillaing F = m & = ge rearrange: F =
