Multivariate localization methods for ensemble Kalman filtering

Transcription

1 doi: /npg Author(s) CC Attribution 3.0 License. Multivariate localization methods for ensemble Kalman filtering S. Roh 1, M. Jun 1, I. Szunyogh 2, and M. G. Genton 3 1 Department of Statistics, Texas A&M University, College Station, TX , USA 2 Department of Atmospheric Sciences, Texas A&M University, College Station, TX , USA 3 CEMSE Division, King Abdullah University of Science and Technology, Thuwal , Saudi Arabia Correspondence to: M. Jun (mjun@stat.tamu.edu) Received: 14 April 2015 Published in Nonlin. Processes Geophys. Discuss.: 8 May 2015 Revised: 29 October 2015 Accepted: 18 November 2015 Published: 3 December 2015 Abstract. In ensemble Kalman filtering (EnKF), the small number of ensemble members that is feasible to use in a practical data assimilation application leads to sampling variability of the estimates of the background error covariances. The standard approach to reducing the effects of this sampling variability, which has also been found to be highly efficient in improving the performance of EnKF, is the localization of the estimates of the covariances. One family of localization techniques is based on taking the Schur (element-wise) product of the ensemble-based sample covariance matrix and a correlation matrix whose entries are obtained by the discretization of a distance-dependent correlation function. While the proper definition of the localization function for a single state variable has been extensively investigated, a rigorous definition of the localization function for multiple state variables that exist at the same locations has been seldom considered. This paper introduces two strategies for the construction of localization functions for multiple state variables. The proposed localization functions are tested by assimilating simulated observations experiments into the bivariate Lorenz 95 model with their help. 1 Introduction The components of the finite-dimensional state vector of a numerical model of the atmosphere are defined by the spatial discretization of the state variables considered in the model. An ensemble-based Kalman filter (EnKF) data assimilation scheme treats the finite-dimensional state vector as a multivariate random variable and estimates its probability distribution by an ensemble of samples from the distribution. To be precise, an EnKF scheme assumes that the probability distribution of the state is described by a multivariate normal distribution, and it estimates the mean and the covariance matrix of that distribution by the ensemble (sample) mean and the ensemble (sample) covariance matrix. The estimate of the mean and the estimate of the covariance matrix of the analysis distribution are obtained by updating the mean and the covariance matrix of a background (prior) distribution based on the latest observations. The background distribution is represented by an ensemble of short-term forecasts from the previous analysis time. This ensemble is called the background ensemble. Because the number of background ensemble members that is feasible to use in a realistic atmospheric model is small, the estimates of weak covariances (the entries with small absolute values in the background covariance matrix) tend to have large relative estimation errors. These large relative errors have a strong negative effect on the accuracy of an EnKF estimate of the analysis mean. The standard approach to alleviating this problem is to apply a physical-distancedependent localization to the sample background covariances before their use in the state update step of the EnKF. In essence, localization is a method to introduce the empirical understanding that the true background covariances tend to rapidly decrease with distance into the state estimation process. Data assimilation schemes treat the spatially discretized state vector, x, as a multivariate random variable. We use the conventional notation x b and x a for the background and the analysis state vectors, respectively. We also use the notation y for the vector of observations. In an EnKF scheme, the analysis mean, x a, is computed from the background mean, x b, by the update equation Published by Copernicus Publications on behalf of the European Geosciences Union & the American Geophysical Union.

2 724 S. Roh et al.: Multivariate localization methods for ensemble Kalman filtering ( x a = x b + K y h ( x b)). (1) The function h( ) is the observation function, which maps the finite-dimensional state vector into observables. Thus, h(x b ) is the ensemble mean of the prediction of the observations by the background. The matrix K = P b H T ( HP b H T + R) 1 (2) is the Kalman gain matrix, where P b is the background covariance matrix, H is the linearization of h about x b, and R is the observation error covariance matrix. EnKF schemes usually avoid the explicit computation of the linearized observation operator H by using approximations to P b H T and H P b H T that involve only the computation of h(x b ) and h(x b ) (e.g., Houtekamer and Mitchell, 1998). The entry K ij of K determines the effect of the jth observation on the ith component of the analysis mean, x a. Under the standard assumption that the observation errors are uncorrelated, the matrix, R, is diagonal. Hence, the way the effect of the observations is spread from the observations to the different locations and state variables is determined by P b and H. The sampling variability in the estimates of P b affects the accuracy of the information propagated in space and between the different state variables through the matrix products, P b H T and HP b H T. The goal of localization is to reduce the related effects of sampling variability on the estimates of K. Over the years, many different localization methods have been proposed. Hamill et al. (2001), Houtekamer and Mitchell (1998, 2001), Hunt et al. (2007), Ott et al. (2004), and Whitaker and Hamill (2002) used localization functions which set the covariance to zero beyond a certain distance (localization radius). Jun et al. (2011) proposed a nonparametric statistical method to estimate the covariance. Anderson (2007) used a hierarchical ensemble filter which estimates the covariance using an ensemble of ensemble filters. Bishop and Hodyss (2007, 2009a, b) adaptively determined the width of localization by computing powers of the sample correlations. Buehner and Charron (2007) examined the spectral and spatial localization of error covariance. Anderson and Lei (2013) and Lei and Anderson (2014) proposed an empirical localization function based on the output of an observing system simulation experiment. The focus of the present paper is on the family of schemes that localize the covariances by taking the Schur (Hadamard) product of the sample background covariance matrix and a correlation matrix of the same size, whose entries are obtained by the discretization of a distance-dependent correlation function with local (compact) support (e.g., Hamill et al., 2001; Houtekamer and Mitchell, 2001; Whitaker and Hamill, 2002). Such a correlation function is usually called a localization or taper function. The commonly used localization functions were introduced by Gaspari and Cohn (1999). Beyond a certain distance, all localization functions become zero, forcing the filtered estimates of the background covariance between state variables at locations that are far apart in space to zero. This property of the filtered background covariances can also be exploited to increase the computational efficiency of the EnKF schemes. A realistic atmospheric model has multiple scalar state variables (e.g., temperature, coordinates of the wind vector, surface pressure, humidity). If a univariate localization function, such as that described by Gaspari and Cohn (1999), is applied directly to a multivariate state vector (that is, the same localization function with the same localization parameters is applied to each state variables) when the crosscovariances of multiple state variables is not negligible, it may introduce a new undesirable form of rank deficiency, despite the general significant increase of rank. The resulting localized background covariance matrix may not be positive definite. Because P b is symmetric, its eigenvalues are real and non-negative, which implies that P b is invertible only if it is also positive definite. The matrix P b has non-negative eigenvalues and is invertible if it is positive definite. (An n n symmetric matrix A is defined to be positive definite if x T Ax > 0 for all nonzero vectors x R n.) Because the computation of the right-hand side of Eq. (2) does not require the invertibility of P b, the singularity of the localized P b usually does not lead to a breakdown of the computations in practice. An ill-conditioned estimate of P b, however, can degrade the conditioning (increase the condition number) of HP b H T +R, making the numerical computation of the righthand side of Eq. (2) less stable. This motivates us to seek rigorously derived multivariate localization functions for ensemble Kalman filtering. As will be demonstrated, such rigorously derived multivariate localization functions often produce more accurate analyses than those that apply the same univariate localization functions to each scalar component of the state vector. Kang et al. (2011) also introduced a multivariate localization method that zeros out covariances between physically unrelated variables. Their primary motivation for zeroing out such covariances, however, was to filter apparent spurious covariances, rather than to preserve the positive definiteness of the background error covariance matrix. In our search for proper multivariate localization functions, we take advantage of recent developments in the statistics literature. In particular, we use the localization functions developed in Porcu et al. (2013), who studied the radial basis functions to construct multivariate correlation functions with compact support. Note that Sect. 5 in Zhang and Du (2008) described a general methodology for covariance tapering in the case of multiple state variables. Du and Ma (2013) used a convolution approach and a mixture approach to derive covariance matrix functions with compactly supported covariances. Kleiber and Porcu (2015) constructed nonstationary correlation functions with compact support for multivariate random fields. Genton and Kleiber (2015) reviewed approaches to building models for covariances between two

3 S. Roh et al.: Multivariate localization methods for ensemble Kalman filtering 725 different variables such as compactly supported correlation functions for multivariate Gaussian random fields. The rest of the paper is organized as follows. Section 2 briefly describes EnKF and localization for the special case of two state variables. Section 3 describes the bivariate Lorenz 95 model we use to test our ideas. Section 4 summarizes the main results of the paper. 2 Methodology 2.1 Univariate localization In principle, localization can be implemented by using filtered estimates of the background covariances rather than the raw sample covariances to define the matrix, P b, used in the computation of K by Eq. (2). The filtered (localized) version of covariance matrix, P b, is obtained by computing the Schur (element-wise) product: P b = ˆP b C, (3) where C is a correlation matrix, which has the same dimensions as the sample covariance matrix, ˆP b. In practice, however, the localization is often done by taking advantage of the fact that localization affects the analysis through P b H T and H P b H T, or, ultimately, through K. In particular because a distance, d, can be defined for each entry, K ij, of K by the distance between the ith analyzed variable and the j th observation the simplest localization strategy is to set all entries, K ij, that are associated with a distance longer than a prescribed localization radius, R (d > R), to zero, while leaving the remaining entries unchanged (e.g., Houtekamer and Mitchell, 1998; Ott et al., 2004; Hunt et al., 2007). Another approach is to localize P b H T and H P b H T by a tapering function (e.g., Hamill et al., 2001; Houtekamer and Mitchell, 2001). The usual justification for this approach is that the localized matrix products provide good approximations of the products computed by using localized estimates of P b. Note that P b H T is the matrix of background covariances between the state variables at the model grid points and at the observation locations, while H P b H T is the matrix of background covariances between the state variables at the observation locations. Thus, a distance can be associated with each entry of the two matrix products, which makes the distance-dependent localization of the two products possible. The approach becomes problematic, however, when h( ) is not a local function, which is the typical case for remotely sensed observations (Campbell et al., 2010). We consider the situation where localization is applied directly to the background error covariance matrix, ˆP b. Recall that the localized covariance matrix is expressed as in Eq. (3). In particular, C is a positive-definite matrix with strictly positive eigenvalues, while the sample covariance matrix, ˆP b, may have zero eigenvalues (as it is only non-negative definite). The localization in Eq. (3) helps to eliminate those zero eigenvalues of ˆP b and alleviates the related large relative estimation errors. The positive definiteness of C ensures that localization does not introduce new zero eigenvalues in the process of eliminating the zero eigenvalues of ˆP b. The proper definition of the localization function that ensures that C is positive definite has been thoroughly investigated for the univariate case (N = 1) in the literature (e.g. Gaspari and Cohn, 1999). 2.2 Multivariate localization We now consider a model with multiple state variables (N > 1). For instance, we take a simple model based on the hydrostatic primitive equations. This model solves the equations for the two horizontal components of wind, the surface pressure, the virtual temperature and a couple of atmospheric constituents. The state of the model is represented by the state vector, x = (x 1, x 2,..., x N ), where x i, i = 1, 2,..., N, represents the spatially discretized state of the ith state variable in the model. The sample background covariance matrix, ˆP b, can be partitioned as ˆP b 11 ˆP b 12 ˆP b 1N ˆP b ˆP b 21 ˆP b 22 ˆP b 2N = (4) ˆP b N2 ˆP b NN ˆP b N1 The entries of the submatrices, ˆP b ii, i = 1,..., N, are called the marginal covariances for the ith state variable. In practical terms if the ith state variable is the virtual temperature, for instance, each diagonal entry of ˆP b ii represents the sample variance for the virtual temperature at a given model grid point, while each off-diagonal entry of ˆP b ii represents the sample covariances between the virtual temperatures at a pair of grid points. Likewise, the entries of ˆP b ij, i = j, are called the sample cross-covariances between the grid point values of the ith and the jth state variables at pairs of locations, where the two locations for an entry can be the same grid point. We thus consider matrix-valued localization functions, ρ(d) = {ρ ij (d)} i,j=1,...,n, which are continuous functions of d. The component ρ ij (d) of ρ(d) is the localization function used for the calculation of the covariances included in the submatrix P b ij of Pb. Each entry of the localization matrix C is computed by considering the value of the appropriate component of ρ(d) for a particular pair of state variables and the separation distance, d, associated with the related entry of ˆP b. In order to get a proper matrix-valued localization function, ρ, a seemingly obvious approach to extend the results of Gaspari and Cohn (1999) would be to compute the entries of C based on a univariate correlation function for a multivariate variable. That is, for the pair of state variables i and j, we localize the corresponding sample background covari

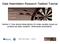
4 726 S. Roh et al.: Multivariate localization methods for ensemble Kalman filtering ance matrix, ˆP b ij, by multiplying a localization matrix from the same correlation function for all i and j. Formally, this would be possible because the distance d is uniquely defined for each entry of ˆP b the same way in the multivariate case as in the univariate case. This approach, however, cannot guarantee the positive definiteness of the resulting matrix, C. As a simple illustrative example, consider the situation where the discretized state vector has only two components that are defined by two different scalar state variables at the same location (e.g., the temperature and the pressure). In this case, if n is the number of locations, the localization matrix for the two state variables together can be written as ( ) C0 C C = 0 (5) C 0 C 0 independently of the particular choice of the localization function. Here C 0 is an n n localization matrix from a univariate localization function. From Eq. (5), it is clear that n eigenvalues of C are zero and the rank of C is n, while its dimensions are 2n 2n. As in Eq. (2), although C is rank-deficient and thus so is the localized covariance matrix P b (and thus P b may be rank-deficient as well), we may still be able to calculate the inverse of H P b H T +R, as R is a diagonal matrix. The smallest eigenvalue of H P b H T +R is the smallest (positive) value of R, and thus the matrix, H P b H T +R, is still invertible and has positive eigenvalues. However, unless the diagonal elements of R are large (which implies large observation error variance), the matrix H P b H T +R is seriously ill-conditioned and the computation of its inverse may be numerically unstable. Therefore, the numerical stability of the computation of the inverse of the matrix heavily relies on the observation error variance, which is an undesirable property. We therefore propose two approaches to construct positive-definite (full rank) matrix-valued localization functions, ρ(d). The first proposed method takes advantage of the knowledge of a proper univariate localization function, ρ. Instead of using the same correlation function to localize multiple state variables, for a certain distance lag, we let ρ = ρ B, where B is an N N symmetric, positive-definite matrix whose diagonal entries are 1. It can be easily verified that ρ is a matrix-valued positive-definite function, which makes it a valid multivariate localization function. For instance, in the hypothetical case where the two components of the state vector are two different state variables at the same location, making the choice ( ) 1 β B = (6) β 1 for β, with β < 1, leads to ( ) C0 βc C = 0 βc 0 C 0 rather than what is given in Eq. (5). Since the eigenvalues of the matrix B are 1 ± β > 0, it can be easily verified that (7) the matrix in Eq. (7) is positive definite. For the case with more than two state variables (N 3), the matrix B can be parametrized as B = LL T, where l 1,1 0 0 l 2,1 l 2,2 0 L =..... (8) 0 l N,1 l N,2 l N,N is a lower triangular matrix with the constraints that i l 2 i,j = 1 and l i,i > 0 for all i = 1,..., N. The constraints j=1 are used to have the diagonal entries of B be 1. Other than these constraints, the elements of L can vary freely in order to guarantee the positive definiteness of B. An attractive feature of this approach is that we can take advantage of any known univariate localization function to produce a multivariate localization function. However, the multivariate localization function from this approach is separable in the sense that the multivariate component (i.e., B) and the localization function (i.e., ρ) are factored. Another limitation of the approach is that the localization radius and decay rate are the same for each pair of state variables, leaving no flexibility to account for the potential differences in the correlation lengths and decay rate for the different state vector components. The second proposed method takes advantage of the availability of multivariate compactly supported functions from the spatial statistics literature. To the best of our knowledge, only a few papers have been published on this subject; one of them is Porcu et al. (2013). The function class they considered was essentially a multivariate extension of the function (, 1973), f (d; ν, c) = (1 d c )ν +, with c, ν > 0. Here, x + = max(x, 0) for x R. For instance, a bivariate function, which is a special case of the results of Porcu et al. (2013), is given by (i, j = 1, 2) ( ρ ij (d;ν,c) = β ij 1 d ) ν+µij, (9) c + where c > 0, µ 12 = µ (µ 11 +µ 22 ), ν [ 1 2 s]+2, β ii = 1 (i = 1, 2), β 12 = β 21, and β 12 Ɣ (1 + µ 12) Ɣ (1 + ν + µ 11 )Ɣ (1 + ν + µ 22 ). Ɣ (1 + ν + µ 12 ) Ɣ (1 + µ 11 )Ɣ (1 + µ 22 ) (10) Here, Ɣ( ) is the gamma function (e.g., Wilks, 2006) and s is the dimension of the Euclidean space where the state variable is defined. If the state is defined at a particular instant on a grid formed by latitude, longitude, and height, then s = 3. Here, [x] is the largest integer that is equal to or smaller than x. The function in Eq. (9) has the support c because it sets covariances beyond a distance c to zero. It can be seen

5 S. Roh et al.: Multivariate localization methods for ensemble Kalman filtering 727 Correlation Distance (ν=1) (ν=2) (ν=3) (ν=4) Figure 1. The Gaspari Cohn covariance function with a localization constant c = 25 (support of 50) and the covariance function f (d; ν, c) = (1 d c )ν +, with a support parameter c = 50 and various shape parameters. from Eq. (10) that, if the scalars, µ ij, are chosen to be the same for all values of i and j, the condition on β 12 for ρ to be valid is β (Note that the case of equality here, with the same µ ij s, reduces to the rank-deficient case where the multivariate localization matrix has zero eigenvalues, similarly to the case of β = 1 in Eq. 7.) For this choice, the second method is essentially the same as the first method with the function set to ρ. The localization function given by Eq. (9) is more flexible than the functions of the first method with the function set to ρ because µ ij can be chosen to be different for each pair of indexes, i and j. The localization length, however, is still the same for the different pairs of the state variables. The multivariate function is formed by ρ ij (d;ν,c) =c ν+1 B ( µ ij + 1,ν + 1 )( 1 d ) ν+µij +1, c d < c (11) and 0 otherwise, where ν (s + 1)/2, µ ij = (µ i + µ j )/2, and µ i > 0 for all i = 1,..., N. Here, B is the beta function (Porcu et al., 2013; Genton and Kleiber, 2015). To illustrate the differences between the shape of the Gaspari Cohn and the functions, we show the Gaspari Cohn function for c = 25 and the univariate function for c = 50 and ν = 1,..., 4 (Fig. 1). This figure shows that, for a given support, the functions are narrower. 3 Experiments 3.1 The EnKF scheme There are many different formulations of the EnKF update equations, which produce not only an updated estimate of the mean but also the ensemble of analysis perturbations that are added to the mean to obtain an ensemble of analyses. This ensemble of analyses serves as the ensemble of initial conditions for the model integration that produce the background ensemble. In our experiments, we use the method of perturbed observations. It obtains the analysis mean and the ensemble of analysis perturbations by the equations ( x a = x b + K y Hx b), (12) ( ) x a k = x b k + K y o k Hx b k, (13) where x k, k = 1, 2,..., M, are the ensemble perturbations and y o k, k = 1, 2,..., M, are random draws from the probability distribution of observation errors. As the notation suggests, we consider a linear observation function in our experiments. This choice is made for the sake of simplicity and limits the generality of our findings much less than the use of an idealized model of atmospheric dynamics. For the case of multiple state variables, the ensemble members are considered to be in a single ensemble, that is, not being grouped into distinct subensembles. 3.2 The bivariate Lorenz model Lorenz (1995) discussed the bivariate Lorenz 95 model, which mimics the nonlinear dynamics of two linearly coupled atmospheric state variables, X and Y, on a latitude circle. This model provides a simple and conceptually satisfying representation of basic atmospheric processes but is not suitable for some atmospheric processes. The model 3 in Lorenz (2005) made it more realistic and suitable with sacrifice of simplicity, by producing a rapidly varying small-scale activity superposed on the smooth large-scale waves. We use the Lorenz 95 model for simplicity in our following experiments. In the bivariate Lorenz 95 model, the variable X is a slow variable represented by K discrete values, X k, and Y is a fast variable represented by J K discrete values. The governing equations are dx k dt dy j,k dt = X k 1 (X k 2 X k+1 ) X k (ha/b) J Y j,k + F, j=1 = aby j+1,k ( Yj+2,k Y j 1,k ) ayj,k + (ha/b)x k, (14) (15) where Y j J,k = Y j,k 1 and Y j+j,k = Y j,k+1 for k = 1,..., K and j = 1,..., J. The boundary condition is periodic;

6 728 S. Roh et al.: Multivariate localization methods for ensemble Kalman filtering X k, Yk X Y X Y k (location) Figure 2. A snapshot of the variables X and Y from a numerical integration of the system of Eqs. (14) and (15) with K = 36, J = 10, F = 10, a = 10, b = 10, and h = 2. Figure 3. For the partially observed case, locations of observations of X and Y are indicated by the black dots and grey circles, respectively. that is, X k K = X k+k = X k, and Y j,k K = Y j,k+k = Y j,k. In our experiments, K = 36 and J = 10. The parameter h controls the strength of the coupling between X and Y, a is the ratio of the characteristic timescales of the slow motion of X to the fast motion of Y, b is the ratio of the characteristic amplitudes of X to Y, and F is a forcing term. We choose the parameters to be a = 10, b = 10, F = 10, and h = 2. These values of the model parameters are equal to those originally suggested by Lorenz (1995), except for the value of the coupling coefficient h, which is twice as large in our case. We made this change in h to increase the covariances between the errors in the estimates of X and Y, which makes the model more sensitive to the choices of the localization parameters. We use a fourth-order Runge Kutta time integration scheme with a time step of nondimensional units, as Lorenz (1995) did. We define the physical distances between X k1 and X k2, between Y j1,k 1 and Y j2,k 2, and between X k1 and Y j1,k 2 by 10(k 1 k 2 ), 10(k 1 k 2 ) + j 1 j 2, and 10(k 1 k 2 ) j 1, respectively. Figure 2 shows a typical state of the model for the selected parameters. The figure shows that X tends to drive the evolution of Y : the hypothetical process represented by Y is more active (its variability is higher) with higher values of X. 3.3 Experimental design Since the estimates of the cross-covariances play a particularly important role at locations where one of the variables is unobserved, we expect an improved treatment of the crosscovariances to lead to analysis improvements at locations where only one of the state variables is observed. This motivates us to consider an observation scenario in which X and Y are partially observed. The variable X is observed at 20 % of all locations, and Y is observed at 90 % of the locations where X is not observed. These observation locations for variables X and Y are randomly chosen. Spatial locations of the partially observed X and Y are illustrated in Fig. 3. The results from this experiment are compared to those from a control experiment, in which both X and Y are fully observed. We first generate a time series of true model states by a 2000-time-step integration of the model. We initialize an ensemble by adding the standard Gaussian noise to the true state; then we discard the first 3000 time steps. We then generate simulated observations by adding random observation noise of mean 0 and variance 0.02 to the the appropriate components of the true state of X at each time step. We use the same procedure to generate simulated observations of Y, except that the variance of the observation noise is Observations are assimilated at every time step by first using a 20-member ensemble with a constant covariance inflation factor of The error in the analysis at a given verification time is measured by the root-mean-square distance between the analysis mean and the true state. We refer to the resulting measure as the root-mean-square error (). The probability distribution of the for the last 1000 time steps of 50 different realizations of each experiment is shown by a box plot. The box plot is an effective way of displaying a summary of the distribution of numbers. The lower and upper bounds of the box respectively give the 25th and 75th percentiles. The thick line going across the interior of the box gives the median. The whisker depends on the interquartile range (IQR), which is precisely equal to the vertical length of the box. The whiskers extend to the extreme values, which are no more than 1.5 IQR from the box. Any values that fall outside of the end points of whiskers are considered outliers, and they are displayed as circles.

7 S. Roh et al.: Multivariate localization methods for ensemble Kalman filtering 729 In the box plot figures in the next section, we compare the for four different localization schemes. We use the following notation to distinguish between them in the figures: 1. S1 the bivariate sample background covariance is used without localization; 2. S2 same as S1 except that the cross-covariances between X and Y are replaced by zeros; 3. S3 a univariate localization function is used to filter the marginal covariances within X and Y, respectively, while the cross-covariances between X and Y are replaced by zeros; 4. S4 one of the bivariate localization methods described in Sect. 2.2 is used to filter both the marginal and the cross-covariances. In the experiments identified by S4, we consider two different bivariate localization functions: the first one is ρ (1) ( ) = {β ij ρ (1) ( )} i,j=1,2, with β ii = 1 (i = 1, 2) and β ij = β (i = j), for some β such that β < 1. We use the fifth-order piecewise-rational function of Gaspari and Cohn (1999) to define the univariate correlation function, ρ (1), in the following form: ρ (1) (d;c) = 1 4 ( d /c) (d/c) ( d /c)3 5 3 (d/c)2 + 1, 0 d c, 1 12 ( d /c)5 1 2 (d/c) ( d /c) (d/c)2 5( d /c) c/ d, c d 2c, 3 0, 2c d. (16) This correlation function attenuates the covariances with increasing distance, setting all the covariances to zero beyond distance 2c. So this function has the support 2c. If β < 1 and c is the same for both the marginal and the crosscovariances, the matrix-valued function, ρ (1), is positive definite and of full rank. We test various values of the localization parameters c and β, and present the test results in the next section. The second multivariate correlation function we consider, ρ (2), is the bivariate function described in Sect In particular, we use µ 11 = 0, µ 22 = 2, µ 12 = 1, and ν = 3. According to Eq. (10), for these choices of parameters, the one remaining parameter, β 12, must be chosen such that β Results Figure 4 shows the distribution of for variable X for different configurations of the localization scheme in the case where the state is only partially observed. This figure compares the function and Gaspari Cohn function which have the same support (localization radius), so setting all the covariances to zero beyond the same distance. We recall that, because X is much more sparsely observed than Y, we expect to see some sensitivity of the analyses of X to the treatment of the cross-covariance terms. The figure confirms this expectation. A comparison of the results for configurations S1 and S2 suggests that ignoring the cross-covariances is a better strategy than using them without localization. This conclusion does not hold once a univariate localization is applied to the marginal covariances, as using configuration S3 produces worse results than applying no localization at all (S1). Figure 4 also shows that the distribution of the state estimation error is less sensitive to the choice of localization strategy for the larger values of support. Of all localization schemes, S4 with β = 0.1 performs best regardless of the localization radius: the distribution of the state estimation error is narrow with a mean value that is lower than those for the other configurations of the localization scheme. For this choice of localization scheme and β, the function produces smaller errors than the Gaspari Cohn function, particularly for smaller localization radii. Figure 5 is the same as Fig. 4 but for variable Y rather than for variable X. A striking feature of the results shown in this figure is that the function clearly performs better than the Gaspari Cohn function. Another obvious conclusion is that using a smaller localization radius (a lower value of support) is clearly advantageous for the estimation of Y. This result is not surprising, considering that Y is densely observed and its spatial variability is much higher than that of X. In contrast to the results for variable X, configuration S3 produces much more accurate estimates of variable Y than do configurations S1 and S2. In addition, configuration S4 performs only slightly better, and only for the lowest value of support, than does configuration S3. The latter observations indicate that the marginal covariances play a more important role than do the cross-covariances in the estimation of the densely observed Y. The proper filtering of the marginal covariances can thus greatly increase the accuracy of the estimates of Y. In other words, the densely observed Y is primarily estimated based on observations of Y. Hence, the low signal-to-noise ratio for the sample estimate of the marginal covariances for Y greatly limits the value of the observations of Y at longer distances. Figure 6 is the same as Fig. 4 but for the case of a fully observed state. By comparing the two figures, we see that the analysis is far less sensitive to the localization radius in the fully observed case than in the partially observed case. As can be expected, the state estimates are also more accurate in the fully observed case. In the fully observed case, localization strategy S3 performs much better than do strategies S1 and S2 and similarly to S4. This result indicates that, in the fully observed case, X is primarily analyzed based on observations of X, making the analysis of X more sensitive to the localization of the marginal covariances than to the localization of the cross-covariances. Similar to the partially observed case, the function tends to perform better than the Gaspari Cohn function, but the differences between the accuracy of the state estimates for the two filter functions are negligible, except for the shortest localization radius.

8 730 S. Roh et al.: Multivariate localization methods for ensemble Kalman filtering Figure 4. The box plot of for variable X in the case when the system is only partially observed. Results are shown for different localization strategies. For the definitions of localization strategies S1, S2, S3 and S4, see the text. The title of each panel indicates the localization radius (length of support). The lower and upper bounds of the box respectively give the 25th and 75th percentiles. The thick line going across the interior of the box gives the median. The whisker depends on the interquartile range (IQR), which is precisely equal to the vertical length of the box. The whiskers extend to the extreme values, which are no more than 1.5 IQR from the box. Any values that fall outside of the end points of whiskers are considered outliers, and they are displayed as circles. The numbers below S4 indicate the value of β. There is no box plot for β = 1 for the S4 with the function, since the function is not defined with β = 1 ( β 0.79; see Sect. 3.3). Figure 7 shows the distribution of the errors for variable Y in the fully observed case. The best results are obtained by using a short localization radius with the function, even though the variability of the error is relatively large in that case. The fact that localization strategies S3 and S4 perform similarly well shows that the estimates of the crosscovariances do not play an important role in this case; that is, X is primarily estimated based on observations of X, and Y is dominantly estimated based on observations of Y. We also investigated the performance of EnKF with a 500- member ensemble. The results for the 500-member ensemble are shown in Figs. 8 to 11. We use an inflation factor of for 500 ensembles, because the optimal value of the inflation factor is typically smaller for a larger ensemble. The rank of the 500-member ensemble covariance matrix is significantly larger than that of the 20-member ensemble covariance matrix, as expected. Figures 8 to 11 show that, overall, S4 still performs better than the other localization schemes regardless of the choice of localization radius, as in the case of the 20-member ensemble. In particular, when observations are partially observed, S4 with β = 0.01 provides the smallest. The cross-correlation between X and Y, calculated using 500- member ensembles without assimilating any observation, varies from 0.4 to 0.4, which indicates that the crosscorrelation between the two variables are not negligible. Therefore, improved treatment of cross-covariance tends to lead to an improved accuracy in the state estimation. The results with the 500-member ensemble also show that the distribution of the state estimation error is in general less sensitive to the choice of the localization function or the localization radius, compared to the 20-member-ensemble case. Figure 8, however, shows that, for the estimation of sparsely observed X, the localization scheme S3 with smaller localization radius performs worse than that with larger localization radius. For variable Y in the partially observed case (Fig. 8) and both variables X and Y in the fully observed case (Figs. 10 and 11), the best results are obtained with S3 and S4 regardless of the localization radius. They also show

9 S. Roh et al.: Multivariate localization methods for ensemble Kalman filtering 731 Figure 5. Same as Fig. 4 but for variable Y Figure 6. Same as Fig. 4 but for the case when the system is fully observed.

10 732 S. Roh et al.: Multivariate localization methods for ensemble Kalman filtering Figure 7. Same as Fig. 6 but for variable Y Figure 8. Same as Fig. 4 but for 500 ensemble members.

11 S. Roh et al.: Multivariate localization methods for ensemble Kalman filtering 733 Figure 9. Same as Fig. 5 but for 500 ensemble members Figure 10. Same as Fig. 6 but for 500 ensemble members.

12 734 S. Roh et al.: Multivariate localization methods for ensemble Kalman filtering Figure 11. Same as Fig. 7 but for 500 ensemble members. that the state estimation error is not sensitive but stable to the choice of localization radius. Figures 10 and 11 show that the localization schemes S3 and S4 perform in a similar way, and obviously perform better than the other two localization schemes. This might imply that the cross-covariances do not have much influence on the state estimation in the fully observed case, once the covariances within each state variable are localized. 4 Discussion The central argument of this paper is that applying a single localization function for the localization of covariances between multiple state variables in an EnKF scheme may not sufficiently increase the rank of the estimate of the background covariance matrix. In the light of this, we suggested two different approaches for the construction of positivedefinite filtered estimates of the background covariance matrix. One of them takes advantage of the knowledge of a proper univariate localization function, whereas the other uses a multivariate extension of the function. The results of our numerical experiments show that a mathematically proper localization function often leads to improved state estimates. The results of the numerical experiments also suggest that, of the two approaches we introduced, the one based on the function produces more accurate state estimates than that based on the Gaspari Cohn function. This fact, however, does not mean that the function is always superior to the Gaspari Cohn function in other chaotic models or observation networks. Which correlation function is superior depends on what the true error correlation looks like. Acknowledgements. The authors are grateful to the reviewers for valuable comments that significantly improved presentation of the paper. M. Jun s research was supported by NSF grant DMS , while I. Szunyogh s research was supported by ONR Grant N This publication is based in part on work supported by Award No. KUS-C , made by King Abdullah University of Science and Technology (KAUST). Edited by: Z. Toth Reviewed by: two anonymous referees References Anderson, J. L.: Exploring the need for localization in ensemble data assimilation using a hierarchical ensemble filter, Physica D, 230, , Anderson, J. L. and Lei, L.: Empirical localization of observation impact in ensemble Kalman filters, Mon. Weather Rev., 142, , 2013.

13 S. Roh et al.: Multivariate localization methods for ensemble Kalman filtering 735, R.: Radial characteristic functions, technical report no. 1262, Mathematical Research Center, University of Wisconsin- Madison, Madison, Bishop, C. H. and Hodyss, D.: Flow adaptive moderation of spurious ensemble correlations and its use in ensemble based data assimilation, Q. J. Roy. Meteorol. Soc., 133, , Bishop, C. H. and Hodyss, D.: Ensemble covariances adaptively localized with ECO-RAP. Part 1: Tests on simple error models, Tellus A, 61, 84 96, 2009a. Bishop, C. H. and Hodyss, D.: Ensemble covariances adaptively localized with ECO-RAP. Part 2: A strategy for the atmosphere, Tellus A, 61, , 2009b. Buehner, M. and Charron, M.: Spectral and spatial localization of background-error correlations for data assimilation, Q. J. Roy. Meteorol. Soc., 133, , Campbell, W. F., Bishop, C. H., and Hodyss, D.: Vertical covariance localization for satellite radiances in ensemble Kalman filters, Mon. Weather Rev., 138, , Du, J. and Ma, C.: Vector random fields with compactly supported covariance matrix functions, J. Stat. Plan. Infer., 143, , Gaspari, G. and Cohn, S. E.: Construction of correlation functions in two and three dimensions, Q. J. Roy. Meteorol. Soc., 125, , Genton, M. G. and Kleiber, W.: Cross-covariance functions for multivariate geostatistics (with discussion), Stat. Sci., 30, , Hamill, T. M., Whitaker, J. S., and Snyder, C.: Distance-Dependent Filtering of Background Error Covariance Estimates in an Ensemble Kalman Filter, Mon. Weather Rev., 129, , Houtekamer, P. L. and Mitchell, H. L.: Data assimilation using an ensemble Kalman filter technique, Mon. Weather Rev., 126, , Houtekamer, P. L. and Mitchell, H. L.: A Sequential Ensemble Kalman Filter for Atmospheric Data Assimilation, Mon. Weather Rev., 129, , Hunt, B. R., Kostelich, E. J., and Szunyogh, I.: Efficient data assimilation for spatiotemporal chaos: A local ensemble transform Kalman filter, Physica D, 230, , Jun, M., Szunyogh, I., Genton, M. G., Zhang, F., and Bishop, C. H.: A Statistical Investigation of the Sensitivity of Ensemble-Based Kalman Filters to Covariance Filtering, Mon. Weather Rev., 139, , Kang, J.-S., Kalnay, E., Liu, J., Fung, I., Miyoshi, T., and Ide, K.: Variable localization in an ensemble Kalman filter: Application to the carbon cycle data assimilation, J. Geophys. Res., 116, D09110, doi: /2010jd014673, Kleiber, W. and Porcu, E.: Nonstationary Matrix Covariances: Compact Support, Long Range Dependence and Quasi-Arithmetic Constructions, Stoch. Env. Res. Risk. A., 29, , Lei, L. and Anderson, J.: Comparison of empirical localization techniques for serial ensemble Kalman filters in a simple atmospheric general circulation model, Mon. Weather Rev., 141, , Lorenz, E. N.: Predictability A problem partly solved, vol. 1, ECMWF, Reading, Berkshire, UK, Lorenz, E. N.: Designing chaotic models, J. Atmos. Sci., 62, , Ott, E., Hunt, B. R., Szunyogh, I., Zimin, A. V., Kostelich, E. J., Corazza, M., Kalnay, E., Patil, D. J., and Yorke, J. A.: A local ensemble Kalman filter for atmospheric data assimilation, Tellus A, 56, , Porcu, E., Daley, D. J., Buhmann, M., and Bevilacqua, M.: Radial basis functions with compact support for multivariate geostatistics, Stoch. Env. Res. Risk. A., 27, , Whitaker, J. S. and Hamill, T. M.: Ensemble data assimilation without perturbed observations, Mon. Weather Rev., 130, , Wilks, D. S.: Statistical methods in the atmospheric sciences, Academic Press, Amsterdam, Zhang, H. and Du, J.: Covariance Tapering in Spatial Statistics, edited by: Mateu, J. and Porcu, E., Graficas Casta ñ, s.l., Spain, 2008.