LOW-LYING ZEROS OF FAMILIES OF ELLIPTIC CURVES
|
|
|
- Noah Blaise Payne
- 5 years ago
- Views:
Transcription
1 LOW-LYING ZEROS OF FAMILIES OF ELLIPTIC CURVES MATTHEW P YOUNG Astrct Tr is groing ody of vidnc giving strong vidnc tt zros of fmilis of L-functions follo distriution ls of ignvlus of rndom mtrics Tis ilosoy is non s t rndom mtrix modl or t Ktz-Srn ilosoy T rndom mtrix modl ms rdictions for t vrg distriution of zros nr t cntrl oint for fmilis of L-functions W study t lo-lying zros for fmilis of llitic curv L-functions For ts L-functions tr is scil ritmtic intrst in ny zros t t cntrl oint y t conjctur of irc nd Sinnrton-Dyr nd t imrssiv rtil rsults tords rsolving t conjctur W clcult t dnsity of t lo-lying zros for vrious fmilis of llitic curvs Our min foci r t fmily of ll llitic curvs nd lrg fmily it ositiv rn A min cllng s n to otin rsults it tst functions tt r concntrtd clos to t origin sinc t cntrl oint is loction of grt intrst An liction is n imrovmnt on t ur ound of t vrg rn of t fmily of ll llitic curvs conditionl on t Gnrlizd Rimnn yotsis GRH T ur ound otind is lss tn 2, ic sos tt ositiv roortion of curvs in t fmily v lgric rn qul to nlytic rn nd finit Tt-Sfrvic grou W so tt tr is n xtr contriution to t dnsity of t lo-lying zros from t fmily it ositiv rn rsumly from t xtr zro t t cntrl oint 1
2 2 1 Introduction T rndom mtrix modl rdicts tt mny sttistics ssocitd to zros of fmily of L-functions cn modld or rdictd y t distriution of ignvlus of lrg rndom mtrics in on of t clssicl linr grous If t sttistics of fmily of L-functions r modld y t ignvlus of t grou G tn sy tt G is t symmtry grou or symmtry ty ssocitd to t fmily T sttistic of intrst to us in tis or is t dnsity of zros nr t cntrl oint lso non s t 1-lvl dnsity T rndom mtrix modl rdicts tt t distriution of ts zros sould modld y t ignnvlus nrst 1 for on of t symmtry tys G All of t diffrnt grous G v distinct vior in tis rgrd Trfor, comuting t 1-lvl dnsity givs torticl y to rdict t symmtry ty of fmily It is stndrd to ssum t Gnrlizd Rimnn Hyotsis GRH to study t 1-lvl dnsity nd do so trougout tis or In trut, t GRH is ncssry for only ndful of our rsults, ut it simlifis rgumnts in som non-ssntil lcs so us it frly vn n it could rmovd it xtr or It is scilly intrsting to invstigt t 1-lvl dnsity for fmilis of L-functions ttcd to llitic curvs ovr t rtionls sinc zros t t cntrl oint v imortnt ritmtic informtion y t conjctur of irc nd Sinnrton-Dyr Ts invstigtions v n t min focus of tis or 11 Acnoldgmnt Tis or constituts lrg ortion of my PD tsis I tn my dvisor, Hnry Inic, for suggsting tis rolm nd for is suort nd ncourgmnt il doing tis or 2 Prliminris W gin y collcting som fcts nd stting t nottion ill us W considr n llitic curv E/Q givn in gnrl Wirstrss form 1 E : y xy + 3 y = x x x + 6, r c i Z Undr cng of vrils E cn rougt into t simlr form 2 y 2 = x 3 + x +, r nd r intgrs T cnonicl cng of vrils cf [Si1], uss t rmtrs 2, 4, 6, c 4, nd c 6, r nd T curv 1 is tn quivlnt to 2 = , 4 = , 6 = , c 4 = , c 6 = y 2 = x 3 27c 4 x 54c 6 Wn givn y t form 2, E s discriminnt = ,
3 LOW-LYING ZEROS OF FAMILIES OF ELLIPTIC CURVES 3 ic is ncssrily non-zro for t curv E to llitic T Wirstrss qution for t llitic curv 1 is not uniqu Any to Wirstrss qutions for t sm curv r rltd y t dmissil cng of vrils 3 x = u 2 x + r y = u 3 y + su 2 x + t, r u, r, s, nd t r intgrs nd u 0 Undr tis cng of vrils t discriminnt trnsforms y u 12 = Liis, u 4 c 4 = c 4 nd u 6 c 6 = c 6 A stndrd tcniqu in studying E is to rduc t qution 1 mod for vry rim T qution 1 is miniml for t rim if t or of dividing cnnot dcrsd y n dmissil cng of vrils T qution 1 is glol miniml Wirstrss qution if it is miniml for ll rims simultnously For ny Wirstrss qution tr is n dmissil cng of vrils lcing it in glol miniml Wirstrss form cf [Si1], Corollry 83 W rcord r tt if t dmissil cng of vrils 3 lcs 1 in glol miniml Wirstrss form tn t only rims dividing u r tos for ic 1 is not miniml W rmr tt for > 3 if t qution 2 is not miniml t tn 4 nd 6 nd trfor 12 Suos E is givn y glol miniml Wirstrss qution 1 T conductor N of E is tn dfind y N = f r for > 3 f = { 1 if c 4, i E s multilictiv rduction t, 2 if c 4, i E s dditiv rduction t Wn = 2 or 3 t dfinition of f is mor comlictd cf [Si2], IV, 10, ut it ill usully noug for our uross tt N nd f 8 for ll rims If ncssry, t conductor cn comutd using Ogg s formul nd Tt s lgoritm Continuing to ssum 1 is glol miniml Wirstrss qution for E, t L-function of E is dfind y 4 Ls, E = 1 s + 1 2s 1 1 s 1, r 5 = #EF, nd #EF is t numr of ffin oints on E, n rducd mod T cntrl oint is t s = 1 Sinc 1 is miniml t cng of vrils ting 1 to 2 dos not ltr for > 3 Tus, for ny > 3, is givn y = x 3 + x + x mod W rmr tt for rims > 3 dividing t conductor v = ±1 if E s multilictiv rduction t nd = 0 if E s dditiv rduction t T infinit roduct 4 convrgs solutly nd uniformly for R s > 3 2, y Hss s stimt < 2 According
4 4 MATTHEW P YOUNG to t Simur-Tniym conjctur rovd y Wils t l [W], [TW], [CDT] tr xists igt to rimitiv cus form fz on Γ 0 N suc tt Ls, E = Ls, f Furtr, Ls, E s nlytic continution to t comlx ln nd stisfis t functionl qution s N Λs, E := ΓsLs, E = Λ2 s, E, 2π r = ±1 is t root numr of E Trougout tis or ill ssuming t Gnrlizd Rimnn Hyotsis olds, nmly tt ll t nontrivil zros of n ritmtic L-function li on its lin of symmtry Using t nottion of Inic-Luo-Srn [ILS] dfin for n L-function Ls, E t quntity DE; φ = γe φ 2π γ E r φ is n vn Scrtz clss tst function os Fourir trnsform 1 φ s comct suort, γ E runs troug t imginry rts of t nontrivil zros ρ E = 1 + iγ E of Ls, E countd it multilicity, nd X is rmtr t our disosl gnrlly of siz N E, t conductor of E; lloing X to only roximtly N E givs us mor frdom in vrging ovr fmily T scling fctor 2π 1 is insrtd to normliz t numr of zros countd y t tst function φ, so tt DE; φ sould tougt of s rrsnting t dnsity of zros of Ls, E nr t cntrl oint s = 1 W ill intrstd in vrging DE; φ ovr crtin fmilis of utomoric forms rising from llitic curvs Ec fmily study ill of t form F = {E d } r d rngs ovr st A, ic is sust of Z or Z Z, suc tt c d A nturlly dfins n llitic curv E D ovr Q T curv E d ill dfind y Wirstrss qution os cofficints r olynomils in d Our min fmily ill rmtrizd y d =, Z 2 r E d : y 2 = x 3 + x + It my n tt Ls, E d = Ls, E d for d d trivilly cus glol miniml Wirstrss qution for E d quls tt of E d or mor sutly cus E d is isognous to E d W t suc forms it multilicity W xct it sould m no sttisticl diffrnc tr on ts suc forms f it multilicity or not As gnrl rul, cn sily m rstrictions on d tt forc E d E to miniml, ut tis dos not cng ny sttistics t lst in t min trm s Sction 56 for mor toroug discussion W ill oftn surss t dndnc of F on A W study t igtd vrg DF; φ, = E F DE; φe, r E d := d is smoot, comctly suortd function cutoff function on R or R 2, icvr is rorit To void trivilitis ssum dos not v totl mss zro i ŵ0 0, nd in rticulr tt is not idnticlly zro W msur t igtd sum ginst t totl igt W F = E F E Sinc DE; φ dnds on X scl our cutoff function y X lso, in ic cs us t nottion X to dnot t scling of y X nd W X to t totl igt scld y 1 Trougout dnot fy = fx xydx, x = x2πix
5 LOW-LYING ZEROS OF FAMILIES OF ELLIPTIC CURVES 5 X T rcis scling dnds on t fmily nd is usd to ic out curvs it conductors N suc tt log N is symtoticlly on vrg Oftn simly t curvs it discriminnt X Usully in rndom mtrix tory on ts fmily it conductors rstrictd y cf X nd lt X tnd to infinity; for fmilis of llitic curvs tis is not rcticl sinc it is ncssry to v concrtly-givn st ovr ic to vrg Ktz nd Srn rdict tt for nturl fmily F t vrg dnsity sould stisfy DF; φ, X lim X W X F = φtwgtdt, r WG is t 1-lvl scling dnsity of ignvlus nr 1 for symmtry grou G W ill in gnrl distriution Suc rsult is clld t dnsity torm for t fmily F W v 1 if G = U sin 2πt 1 if G = S 2πt WGt = 1 + 1δ 2 0t if G = O sin 2πt 1 + if G = SOvn 2πt 1 + δ 0 t if G = SOodd, sin 2πt 2πt r δ 0 is t Dirc distriution [KS1] In rctic it is convnint to v t Fourir trnsforms of ts distriutions, ic rcord r δ 0 t if G = U δ 0 t 1ηt if G = S ŴGt = + δ 2 0t if G = O δ 0 t + 1ηt if G = SOvn δ 0 t 1 ηt if G = SOodd, 2 r 1 if t < 1, 1 ηt = if t = 1, 2 0 if y > 1 An imortnt ftur is tt t Fourir trnsforms of ŴOt, ŴSOvnt, nd ŴSOoddt ll gr for t < 1 ut r distinguisl for t > 1 Trfor, y t Plncrl Torm, to distinguis t dnsitis of ts tr symmtry tys on nds to ly tst functions φ os Fourir trnsforms r suortd outsid [ 1, 1] Inic, Luo, nd Srn rov tt t fmily H2N of rimitiv cus forms of igt 2 nd lvl N N squr-fr s symmtry ty O for tst functions φ rstrictd y su φ 2, 2 s [ILS] Ty lso rov t forms it root numr +1 v symmtry ty SOvn nd t forms it root numr 1 v symmtry ty SOodd in t sm rng Tis is rlvnt for our fmilis cus t fmily of ll llitic curvs forms sufmily of igt to rimitiv cus forms In rticulr, do not xct to dtct sttistics of t root numr of t fmily itout otining suort st 1, 1 Tis otntil cng in vior t 1 is not surrising in ligt of t roximt functionl qution, ic stts tt L1, E = 2πn 2πn n n 1/2 g + E n n 1/2 g U V n n
6 6 MATTHEW P YOUNG r g is tst function of crtin ind nd UV = N If t U > N 1+ε i sum t Fourir cofficints of lngt grtr tn N tn t first sum imlicitly cturs t root numr sinc t scond sum is tn smll rs if U N 1 ε tn t root numr xlicitly occurs in t scond sum Aftr dvloing t xlicit formul sll s t nlogy to tis drmtic sift in vior it similr sum xct ovr rims; going st suort 1, 1 is similr to ting U lrgr tn t conductor It is mor difficult to gin lrg suort for fmilis of llitic curvs tn for ll cus forms of igt to cus t forms coming from llitic curvs comos smll sufmily of t igt to cus forms Vry loosly sing, tr r roly round X 5/6 llitic curvs it conductors N X, rs tr r out X 2 igt to cus forms of lvls N X It is n on nd vry intrsting qustion to stimt t numr of llitic curvs tt v conductor N X Our figur of X 5/6 riss y simly counting t numr of ositiv intgrs nd suc tt = X Fouvry, Nir, nd Tnnum [FNT] v son tt t numr of non-isognous smi-stl llitic curvs it conductor N X is X 5/6 In t otr dirction, Du nd Kolsi [DK] uilding on or of rumr nd Silvrmn [S] v son tt t numr of llitic curvs it conductor N X is X 1+ε for ny ε > 0 Ny imrovmnt in t xonnt in tis ur ound ould vry intrsting cus it ould so tt for lmost ll lvls N tr is no llitic curvs it conductor N Not lso tt our lc of noldg in tis rgrd illustrts y cnnot vrg DE; φ ovr ll llitic curvs it N E X 3 Summry of Rsults 31 Min rsults Our min rsults r givn in tis sction Torm 31 Lt F t fmily of llitic curvs givn y t Wirstrss qutions E, : y 2 = x 3 + x + it nd ositiv intgrs Lt C 0 R + R + 2 nd st X E, = A,, r A = X 1/3, = X 1/2 X ositiv rl numr Tn for φ it su φ 7 9, 7 9 DF; φ, X [ φ φ0]w XF s X, Not tt W X F ŵ0, 0A s X so r ting out X 5/6 curvs from our fmily In t lngug of rndom mtrix tory tis torm sos tt t fmily of ll llitic curvs s symmtry ty O, insmuc s tis cn dtctd itout ving suort outsid 1, 1 Furtr, v Torm 32 Lt F t fmily of llitic curvs givn y t Wirstrss qutions E, : y 2 = x 3 + x + 2 it nd ositiv intgrs Lt C 0 R + R + nd st X E, = A,, r A = X 1/3, = X 1/4 X ositiv rl numr Tn for φ it su φ 23 48, DF; φ, X [ φ φ0]w XF s X, Hr r ting out X 7/12 curvs from our fmily Ts llitic curvs gnrlly v ositiv lgric rn if t oint 0, is torsion t Lutz-Ngll critrion imlis so instntly s tt t numr of curvs in tis fmily suc tt 0, is torsion is OX 1/3+ε, ic xlins t rsnc of t xtr φ0 contriution 2 For us R + = 0,
7 LOW-LYING ZEROS OF FAMILIES OF ELLIPTIC CURVES 7 Otining ts to torms it t sttd suort crucilly rquirs GRH for Diriclt L-functions S J Millr, in is doctorl tsis [Mil], s indndntly rovd dnsity torms for vrious fmilis of llitic curvs long it otr tings, ut mor rstrictd y t suort of φ rumr [], Ht-ron [H-], Micl [Mic], Silvrmn [Si3], nd otrs v rovd rsults on t vrg rn of crtin fmilis of llitic curvs tt cn no intrrtd to ssntilly dnsity torms Actully, in ordr to otin dnsity torm on must symtoticlly comut t vrg of log N ovr t fmily; in ordr to otin n ur ound on t vrg rn only trivil ur ound suc s N is rquird Not tt if on cn ly φ of lrg suort tn φ cn loclizd nr t origin, so t zros ρ E = 1 + iγ E r ld closr to t cntrl oint Trfor, on cllng for us s n to otin Torm 31 it t suort of φ s lrg s ossil ring suort 1, 1 ould of intrst, sinc it is t tt oint tt t Fourir trnsforms of t dnsitis of t grous O, SOvn, nd SOodd com distinguisl It rs tt t currnt tcnology is incl of roducing suc rsult vn ssuming GRH, ut v rsons to xrss t folloing Conjctur 33 Torm 31 olds for tst functions φ it no rstrictions on t suort W ill rovid som justifiction for tis conjctur in Sction 72 ftr rov Torms 31 nd 32 Tis conjctur grs it t follor conjctur tt t root numr is quidistriutd in t fmily of ll llitic curvs ut s [H] for n xtnsiv trtmnt of t vrition in sign of t root numr Millr lso rdicts t symmtry ty is O ut from n ntirly diffrnt dirction H considrs t 2-lvl dnsity of t fmily of ll llitic curvs nd uss conjcturs imlying quidistriution of root numrs to rdict symmtry ty O t 2-lvl dnsity cn distinguis tn t vrious ortogonl symmtry tys using tst functions it ritrrily smll suort ut it is ncssry to no t rcntg of curvs it givn root numr Our mtod is quit diffrnt nd rlis on sr stimts for t tr-vril crctr sum 26 for lrg vlus of P It is mystrious o t distriution of t root numr ssntilly controlld y t Möius function of t olynomil is cturd y suc crctr sum An sy consqunc of Torm 31 is t folloing Corollry 34 T fmily of ll llitic curvs ordrd y t discriminnt s in Torm 31 s vrg nlytic rn r 25/14 Conjctur 33 ing tru imlis tt r 1/2 T roof sos tt ny fmily it symmtry ty O nd suort u to ν s vrg rn oundd y Alying dnsity torm to otin n ur ound on t vrg 2 ν rn in tis fsion rquirs t Rimnn Hyotsis for ll L-functions in t fmily Using zro dnsity stimts Kolsi nd Micl [KM1], [KM2] otind n ur ound on t vrg ordr of vnising of ll igt 2 lvl q modulr L-functions, try rmoving t ssumtion of GRH for tir fmily T ound on t vrg rn is significntly lrgr tn tt ic is otind on GRH toug It ould intrsting to otin n unconditionl yt r ur ound for t vrg rn of t fmily of ll llitic curvs y mimicing tir mtods rumr [] sod tt t vrg rn r of ll llitic curvs stisfis r 23 nd Ht-ron [H-] rovd r 2, modulo f minor diffrncs in coic of tst functions nd siving of unlsnt curvs rumr s nd Ht-ron s rsults rquirs t GRH for llitic curv L-functions It is stndrd conjctur of rndom mtrix tory tt, onc t
8 8 MATTHEW P YOUNG symmtry ty G for t fmily s n idntifid, t dnsity torm sould old for tst function φ it ritrrily lrg suort Rndom mtrix tory rdicts tt Conjctur 33 imlis t quidistriution of root numrs vi t 2-lvl dnsity for instnc; it ould intrsting to s dirct numr-tortic rson for tis to so Using tt 25/14 = 178 < 2 nd t fmous torm tt sys tt if t nlytic rn is 1 tn t lgric rn nd nlytic rn r qul nd X is finit du in lrg rt to Kolyvgin [Ko] nd Gross-Zgir [GZ] otin Torm 35 Assum GRH Tn ositiv roortion of llitic curvs ordrd y igt v lgric rn qul to nlytic rn nd finit Tt-Sfrvic grou 32 Furtr rsults sids t rsults rcordd in t rvious sction, invstigt similr dnsity rsults for vrity of intrsting fmilis in Sctions 8-14 In rticulr invstigt numr of fmilis it roscrid torsion S [Ku], Tl 3 for t rmtriztions of t vrious torsion structurs Ts torsion fmilis v som surrisingly nic rortis For instnc, t fmily of curvs it torsion grou Z/4Z is rmtrizd y y 2 + xy y = x 3 x 2 it = As gnrl rul cnnot rov dnsity rsult for fmily r t dgr of t discriminnt is lrgr tn 3 Altoug t discriminnt s dgr 5 for tis fmily, it is sily trtd cus t irrducil fctors nd r linr In ddition t conductor is muc smllr tn t discriminnt N 2 rs 5 so tr r mny mor curvs in t fmily it conductor X tn on ould xct sd on t dgr of t discriminnt T otr torsion fmilis v similr crctristics tt m tir study xtrmly lsnt W study som oulr fmilis of curvs it comlx multiliction in Sction 13 Ts fmilis r rtr smll yt good rsults comrd it t sizs of t fmily r still otind cus of t siml ntur of t Fourir cofficints of t L-functions T rrir to otining ttr rsults it ts fmilis is lc of noldg on t oscilltion of ind of tistd cuic or qurtic, dnding on t fmily Guss sum In Sction 14 study tin squnc of qudrtic tists it ositiv rn Tis fmily is cllnging cus t conductor is ssntilly cuic olynomil Suc fmilis of qudrtic tists r studid y Ruin nd Silvrrg [RS] for xml 33 Structur of t r In Sction 4 st u t mcinry for roving dnsity rsult for fmily of llitic curvs W rov Torms 31 nd 32 in Sctions 5 nd 6; som of t mor tcnicl dtils r dfrrd to t Andics W rovid vidnc for Conjctur 33 in Sction 7 Tis conjctur nturlly follos from n ssumtion tt crtin crctr sum in tr vrils s squr-root cnclltion in c vril on of ic is summtion ovr rims W lnd crdnc to t conjctur y studying sum similr to t formntiond on ut r t summtion is xtndd to intgrs W otin strongr rsult it tis n sum; s Torm 72 In t rmining sctions rov dnsity rsults for t intrsting fmilis discussd in Sction 32 4 Gnrl Mtod of Proof In tis sction st u som mcinry to strmlin t roofs of our dnsity torms Suos r givn Wirstrss qution 1 not ncssrily miniml ic dfins n llitic curv E it conductor N nd L-function Ls, E To nlyz DE; φ ill
9 LOW-LYING ZEROS OF FAMILIES OF ELLIPTIC CURVES 9 mloy t xlicit formul for Ls, E, ic for cus forms of igt to nd lvl N ts t form s 425 in [ILS] log N 7 DE; φ = φ0 + 1 log log φ0 P E; φ + O 2 r P E; φ = log 2 log λ E φ >3 Hr is t discriminnt of t curv dfind y 1 gin, is not ssumd miniml, X is scling rmtr ny numr 2 t our disosl, nd 8 λ E = x 3 + x + x mod if t Wirstrss qution 1 dfining E is ut into t form 2 Actully, t sum P E; φ in [ILS] is rstrictd y N nd ssums λ E is t cofficint 5 of s in t Diriclt sris xnsion of Ls, E W clim t modifictions in P E; φ r cctl cus t discrncy in t formul 7 is sord y t rror trm To rov tis first not tt if nd 2 is in glol miniml Wirstrss form tn λ E is xctly t cofficint 5 Furtr, t crctr sum dfining t quntity λ E is lft uncngd y cng of vrils lcing 2 in glol miniml Wirstrss form Trfor t trms gr for On t otr nd, t trms r r sord y t rror trm It is ortil to not tt t rror trm in 7 is drivd y using t Rimnn Hyotsis for t symmtric-squr L-function Ls, sym 2 f to ndl trms of t form λ E 2 T formul 7 olds for individul E In rctic on could limint t us of t GRH y vrging ovr fmilis; v usd t Rimnn Hyotsis for simlicity nd rvity sinc r ssuming it for otr rsons nyys Nxt sum ovr t fmily W comut DF; φ, X = φ0 E F r log N E XE φ0w X F PF; φ, X + O PF; φ, X = E F P E; φ X E WX F,, nd W X F, = E F X E log log In gnrl log log ill log so tis ill tru rror trm Wit ll of our fmilis ill t X nd X so tt log N E 9 XE W X F s X E F It is gnrlly igly nontrivil to rov suc n symtotic olds; oftn it mounts to ving control on t squr divisors of olynomil of ig dgr Tis is significnt rrir to roducing dnsity torms it fmilis of ig rn W cll 9 t conductor condition for t fmily F T id in most css is to roximt N E it numrs R E ic v t sm rim divisors s N E ut r sir to comut oftn R E =, t discriminnt of t llitic
10 10 MATTHEW P YOUNG curv Tn X nd X ill cosn so tt X is roximtly R E for E in t suort of X For n xml, it t fmily y 2 = x 3 + x + givn in Torm 31 v X scld so tt X 1/3, X 1/2, X 5/6, nd t R E = T folloing lmm ill strmlin mny of our rgumnts to so 9 olds Lmm 41 Lt F = {E d } fmily of llitic curvs it nottion s in Sction 2 Lt d t discriminnt of t curv E d Suos tt tr xists n intgr olynomil Rd dividing d suc tt c irrducil fctor of d divids Rd Furtr suos 10 X E log α 1 + X E log W X F E F E F α R E α>0 R E 2 N E >3 uniformly in X, r v dfind R E = Rd for E = E d Suos Rd X for ll f in t suort of X Tn v log N E WX F XE = W X F + O E F Rmr ot sums in 10 v n intrrttion For t first sum to smll tr must not mny lrg squr divisors of R E i R E is not too lrg For t scond sum to smll it must rr for rim to divid R E to lor ordr tn N E i R E is not too smll In most lictions N E R E so t scond sum ill void In gnrl cn ndl t first sum s long s ll of t irrducil fctors of Rd r of dgr 3 or lss Proof Suos Rd is s ov Tn W X F E F log N E XE = E F logx/r E XE + E F logr E /N E XE Sinc r ssuming R E X t first sum is trivilly W X F 1 T scond sum is 1 X E log α β, E F α R E β N E y using t dditivity of t logritm to srt t rim fctors of R E nd N E ts rims v noting to do it t xlicit formul of cours First considr t trms it β > 0 y ting t trms it α > β nd α < β srtly it s clr t contriution is 1 E F α R E α>0 X E log α E F R E 2 N E >3 WX F X E log + O t rror trm coming from = 2 or 3 nd α < β in ic cs β my lrgr tn 2 No considr tos trms it β = 0 nd nc α > 0 Sinc ut N tis imlis t qution 1 dfind y d is not miniml t nd trfor α 12, so my sor ts trms into t first sum ic consists of α R E, α > 0 For ny individul fmily ill nd to stimt PF; φ, X using d oc tcniqus licl to t fmily In its vlution ill oftn m us of t folloing idntity Poisson Summtion mod l,
11 LOW-LYING ZEROS OF FAMILIES OF ELLIPTIC CURVES 11 Proosition 42 Lt Scrtz-clss function, D ositiv rl numr, nd n intgr Tn t folloing olds d 11 = D D ŵ D l l l d Z d mod l Z 5 Proof of Torm 31 y t discussion in Sction 4, to rov Torm 31 nd to so PF; φ, X W XF A nd to so t conductor condition 9 olds 51 T Conductor Condition In tis sction so 9 olds Lmm 51 Lt F, A,, nd s in Torm 31 Tn v { } log N E 1 XE = 1 + O W X F E F Proof W ly Lmm 41 W t t olynomil Rd for d =, to givn y Rd = Not Rd = d Rcll tt A = X 1/3 nd = X 1/2 so tt Rd X sinc A nd T sum X E log E F R E 2 N E is mty sinc N T otr trm is X E log α 1 = E F α R E α>0 α α>0 A, log α 1 y dfinition First suos > 3 Intrcng t ordr of summtion nd for c rim dfin γ y γ W first considr t trms r α < 3γ For ts css α 2 so α is ncssrily vn W mloy t cng of vrils = γ, = α/2 nd otin oftn us rims to indict tt summtion is crrid out it crtin corimlity conditions in lc ic sould rnt from contxt; in t nxt formul t rstriction is, =, = 1 α X α>0 α X α>0 α/3<γ log A α X α/3<γ log A α>0 log A + γ A, α/2 log α A 1 + log α 1 γ α/2 A log A + + [α/3]+1 α/2 A log α 1 α/2+[α/3]+1
12 12 MATTHEW P YOUNG Tis sum is cus X log A + A A X 5/6, α X α>0 α Z α>0 log α 1 Z, nd α 0 γ<α/3 α 3γ α>r log α 1 1 α/r No considr t trms it α 3γ In tis cs 3γ 2 so γ is ncssrily vn W mloy t cng of vrils γ, 3γ/2 nd otin γ A, 3γ/2 log α 1 W slit t summtion ovr into rogrssions mod α 3γ Sinc, =, = 1 gt tt for c t numr of solutions in mod to t congrunc mod α 3γ is oundd y 2 Trfor otin 1 + A 1 + 3γ/2 log α 1, γ α X α>0 α X α>0 0 γ<α/3 α + A + + α 3 2 [α/3] α 3γ A α 1 2 [α/3] log α 1 ic is oundd y X 5/6 y t sm ty of rsoning usd for t cs α > 3γ cc α = 2 nd α 3 srtly T rims 2 nd 3 r ndld in t sm y s ov it minor cngs For = 3 my ssum α 4 y trivilly stimting t trms it α 3 T stimtion for α < 3γ is t sm s for ftr t cng of vrils α α + 3 T stimtion for α 3γ is s for ftr t cng of vrils γ γ + 1 For = 2 my ssum α 6 Aftr cnclling 2 6 in t discriminnt congrunc r lft in vry similr cs to = 3 W omit t tdious yt lmntry dtils 52 T Cntrl Estimt W ill v rovd Torm 31 onc v rovd Lmm 52 St A = X 1/3 nd = X 1/2 Tn P E; φ rovidd su φ 7 9, 7 9 Tis lmm is t rt of t mttr Proof W clcult P E; φ A, = >3 A, 2 log φ log X5/6 λ, A, Aly Poisson summtion mod in t summtion ovr nd nd otin λ, A, = A α + β λ 2 α,β ŵ α mod β mod A,
13 LOW-LYING ZEROS OF FAMILIES OF ELLIPTIC CURVES 13 T summtion ovr α nd β is vlutd in Sction 53 t vlution is comltly strigtforrd Using Lmm 56 continu, otining 12 A 2 log log 3 2 A ε φ ŵ 3/2, >3 W rmr t tis oint tt if stimt tis sum trivilly gt ound of t ordr summing u to P, sy A log A + P 1/2 + P 3/2 1, 3/2 A P ic is O A 1 n P X 5/9 rumr ssntilly otind tis rsult [] To gt lrgr suort nd to rov tr is quit lot of cnclltion in t tr vril crctr sum 12 y xloiting som cnclltion in tis sum Ht-ron [H-] s imrovd rumr s rsult to t suort rng 2/3, 2/3 Not tt ny imrovmnt on Ht-ron s rsult sos tt t vrg rn is strictly lss tn to T first st is to limint t vrition in ε To do so sum srtly ovr t rogrssions 1 mod 4 nd 3 mod 4 Effctivly, it suffics to rlc ε y ψ 4, Diriclt crctr mod 4 No r u t summtion in 12 into dydic sgmnts using smoot rtition of unity It suffics to considr sums of t form 13 H <2H K <2K P <2P log 3/2 ψ φ log ŵ A, g,,, r g is smoot comctly suortd function rising from t rtition of unity W ssum tt t rstrictions on,, nd r rdundnt, folloing from t suort of g It suffics to so tt vry sum of ty 13 is X ε, it t imlid constnt dnding only on, g, g, tc In ddition v to ccount for t contriution to 12 of = 0, ut tis contriution is ngligil y trivil stimtions Lt SH, K, P t sum givn y 13 in t nottion surss t dndnc on t tst functions Using t ound ŵx, y M 1 + x M 1 + y M my ssum tt H ε P/A 1+ε nd K ε P/ 1+ε It ill ncssry to us diffrnt tcniqus of stimtion in diffrnt rngs As first st, v t ound H 3/4 P + HP 3/4 + H 1/4 P 5/4 HKP ε P <2P H <2H T roof is stndrd y Wyl s mtod If ly tis to 13 ftr using rtil summtion to srt t vrils gt t ound 15 SH, K, P H 3/4 KP 1/2 + HKP 3/4 + H 1/4 KP 1/4 X ε, ic is usful in som rngs To covr t rngs r 15 is insufficint continu it 13 W rfr to sum ovr rltivly rim nd so dfin d = 3, 2 nd lt d 0 to t lst ositiv intgr suc tt d d 3 0 Sinc d 0 my st = d 0 0 T condition
14 14 MATTHEW P YOUNG 3, 2 = d is quivlnt to 0, 2 /d = 1 nd d 3 0/d, 2 /d = 1 Tn 3 2 = 3 0d 3 0/d 2 /d d 2 0 0, 2 /d=1 d 3 0 /d,2 /d=1 T oint is tt vryting in t xonntil is corim it 2 /d sids ossily 2 /d No my mloy t folloing lmntry rcirocity formul ū 16 v + v u 1 mod 1, uv r u, v, ū, v r intgrs suc tt u, v = 1, uū 1 mod v, nd v v 1 mod u Tis rcirocity l s lso mloyd y [H-] in is or on tis rolm In our liction u = 2 /d nd v = No SH, K, P s trnsformd into 3 17 ψ 4 0 d 3 0/d 2 /d r K <2K P <2P d 2 H d 0 0 <2 H d 0 0, 2 d =1 d3 0 d, 2 d =1 0 d 0 A U 0, d 0,, = g 0 d 0,, ŵ, 3 0 d U 0, d 0,,, 2 log 3/2 φ log To srt t vrils us t folloing xnsion of dditiv crctrs into multilictiv crctrs vi Guss sums d 3 0/d 1 = τχχ 3 2 /d φ 2 /d 0d 3 0/d, χ mod 2 /d vlid cus of t corimlity conditions, otining t idntity 19 SH, K, P = 1 τχχd 3 φ 2 /d 0/dQd,, χ K <2K d 2 χ mod 2 /d r Qd,, χ = P <2P ψ 4 χ H d 0 <2 H 0 d 0 χ d 3 0 U 2 0, d 0,, Our gol is to gt good ound for Qd,, χ nd stimt t rst trivilly W is to ly Lmm 57 to Qd,, χ To do so must dfin numr of rmtrs nd cc tt t conditions of Lmm 57 r stisfid W st v 3/2 ud0 A 20 F u, v = gud0,, vŵ, log v φ P v v T crctr χu in Lmm 57 is rlcd y χ 3 u it modulus l 1 = 2 d crctr ψv in Lmm 57 is χvψ 4 v/v it modulus l 2 = lcm4,, 2 is t conductor of v, q = 2, U = min d 3 0 { H d 0, P d 0 A }, nd V = P W v d, il t, r
15 LOW-LYING ZEROS OF FAMILIES OF ELLIPTIC CURVES 15 Clim T tst function F u, v dfind y 20 stisfis t conditions of Lmm 57 it U = min {H/d 0, P/d 0 A} nd V = P Proof of clim T roof is strigtforrd clcultion T only sligtly torny issu is tt diffrntition of ŵ it rsct to v introducs fctor ud 0 A/v α Tis cn sord for M lrg noug y t ound of 1 + u/v/d 0 A M on ny rtil drivtiv of ŵ To ly Lmm 57 to Qd,, χ must first xtnd t summtion ovr to rim ors instd of just rims It s sy to s y trivil stimtions tt cn xtnd t summtion to rim ors itout cnging t ound for Qd,, χ Trfor v Corollry 53 If χψ 4 / nd χ 3 r nonrincil tn 1/2 H Qd,, χ P H3/2 X ε d 0 P 1/2 If χψ 4 / is rincil ut not χ 3 tn los fctor P 1/2 If χ 3 is rincil ut not χψ 4 / tn los fctor H/d 0 1/2 Hving otind t ound for Qd,, χ ly it to SH, K, P W v four css ccording to ic crctrs r rincil Lt S = S 1 +S 2 +S 3 +S 4, r S 1 corrsonds to t trms r ot crctrs r nonrincil, S 2 corrsonds to t trms r χ 3 is nonrincil ut χψ 4 / is not, S 3 corrsonds to t trms r ot crctrs r rincil, nd S 4 corrsonds to t rmining trms r χ = ψ 4 / is nonrincil Cs 1 To ound t sum S 1 ly Corollry 53 to 19, otining t ound S 1 K <2K 1 φ 2 /d d 2 χ mod 2 /d H 1/2 P H3/2 P 1/2 K P 1 H d 0 1/2 1 + H3/2 P 1/2 X ε K <2K H 1/2 P 1 K 2 + H 3/2 KP 1/2 X ε d 2 1 dd 0 1/2 X ε τχ W rquir tis ound to X ε Using H P/A 1+ε nd K P/ 1+ε sos t rquirmnt is P X 7/9 ε T xistnc of 7/9 r xiits t limit of our mtod T css r on or ot of t crctrs r rincil r tdious to crry out ut do not os significnt rrir to otining lrgr suort It rmins to ound t sum 19 n on or ot of t crctrs r rincil T loss of cnclltion in ts css ill md u for y t rrity of rincil crctrs First, χ 3 is trivil for ε crctrs χ T crctr χψ 4 / is trivil for only t crctr χ = ψ 4 / χ 0 Trfor t only y ot crctrs r trivil is if χ is trivil nd / ψ 4 is trivil ic limits to squr Cs 2 In cs χ 3 is trivil ut not χψ 4 / los H/d 0 1/2 from t loss of cnclltion ut sv φ 2 /d from t rrity of suc crctrs, ic givs t ound S 2 HP H3/2 P 1/2 K X ε 1 d 2 HP H3/2 K 1/3 X ε P 1/2 K d d 0
16 16 MATTHEW P YOUNG using only t ovious ound d 1 0 d 1/3 from d d 3 0 Using H P/A 1+ε nd 1 K P/ 1+ε nd rquiring tis X ε mns must rquir P X 5/6 ε Cs 3 In cs ot crctrs r trivil no is squr nd tt τχ 1 Using 19 nd ounding Qd,, χ trivilly y P H/d 0 sily gt t ound of S 3 HP 1/2 X ε = K <2K 2 d 2 d d 0 = HP 1/2 X ε K 1/2 l<2k 1/2 l 4 Notic tt if d tn / 0 d/d 0 loo t c rim srtly Trfor v S 3 HP 1/2 X ε 2 HP 1/2 K 1/2 X ε, K 1/2 l<2k 1/2 ic is X ε n K P X 2/3+ε To ndl K P X 2/3+ε simly ly Wyl s ound 14 n =, K < 2K W tus otin t ound S 3 H 3/4 P 1/2 + HP 3/4 + H 1/4 P 1/4 K 1/2 X ε, ic is X ε using H P/A 1+ε nd K P X 2/3+ε n P X 7/9 ε W xct tt us of currnt tcnology ould llo us to t P lrgr tn X 7/9 r ut sinc r rstrictd to 7/9 lsr do not ursu suc rsult Cs 4 In t lst cs r χψ 4 / is trivil ut χ 3 is not los P 1/2 ut sv φ 2 /d W gt furtr sving y noticing tt ψ 4 / s conductor qul to t squr-fr rt of u to fctor 2 or 4 Trfor 2 d 1 nd nc d 2 1 W gt t ound S 4 H 1/2 P 1/2 1 + H3/2 P 1/2 K X ε K <2K 1 l d 2 1 d l 4 1/2 d As for, d/d 0 1/2 is incrsing it rsct to divisiility so gt t ound S 4 H 1/2 P 1/2 1 + H3/2 X ε 1 P 1/2 K K <2K 2 H 1/2 P 1/2 X ε 1 + H3/2 P 1/2 K For tis ound to X ε it is ncssry nd sufficint tt 21 H 2 K 1 P X ε W us diffrnt mtod to stimt Qd,, χ ic ors ll for smll In our currnt cs v Qd,, χ = 3 0 d 3 0 χ U 0, d 0,, P <2P H/d 0 0 <2H/d 0 W xloit cnclltion in 0 c 0 3 0d 3 0/ 2 it ritrry comlx cofficints c n Prcisly, us t folloing d 0 d d 0
17 LOW-LYING ZEROS OF FAMILIES OF ELLIPTIC CURVES 17 Lmm 54 Lt c n comlx numrs stisfying c n 1 nd lt RN, P, d 0, = n 3 d 3 0 c 2 n Tn P <2P N n<2n RN, P, d 0, N 1/2 P + N 1/4 P 5/4 1/2 d 3/4 0 Tis is scil cs of mor gnrl rsult ic is sttd nd rovd in Andix ; scificlly, ly Lmm 1 it fx = x 3, gx = x 1, nd Y = N 3 d 3 0P 1 2 Alying Lmm 54 to Qd,, χ vi rtil summtion givs ctully on must srt t vrils 0 nd in U 0 d 0,, for lying Lmm 54, ic cn don in ny stndrd y it no cost Corollry 55 If χψ 4 / is rincil nd χ 3 is non-rincil tn 1/2 H Qd,, χ P 1/2 + P 1/4 H 1/4 1/2 d 1 0 X ε Alying Corollry 55 to S 4 givs t ound S 4 K <2K d 0 d 2 d 1/2 1 H 1/2 d 1/2 0 P 1/2 + H1/4 1/2 P 1/4 d 0 Using t sm tcniqus s for to stimt t sum ovr d givs t ound S 4 H1/2 K 1/2 X ε + H1/4 K 1/2 X ε P 1/2 P 1/4 Using only H P/A 1+ε nd K P/ 1+ε sos t first trm is X ε n P X 5/6 ε For t scond trm in t ov ound to sufficint must v K P 1/2 H 1/2 X ε Assuming 21 dos not old i H 2 K 1 P X ε nd using H P/A 1+ε s tt * olds n P X 5/6 ε Hving considrd ll ossil css t roof is comlt 53 A Comlt Crctr Sum In tis sction vlut crctr sum ic ros in our vrging St λ, = x 3 + x + x mod Not tt tis is λ E for t llitic curv givn y t qution y 2 = x 3 + x + Nxt, for ny intgrs nd dfin T, ; = α + β λ α,β α mod β mod Lmm 56 Lt > 2 rim nd dfind y 1 mod if, = 1 nd 0 = 0 Tn v T, ; = ε 3/2 r ε is t sign of t Guss sum 3 2, X ε
18 18 MATTHEW P YOUNG Proof y dfinition, T, ; = x mod α mod β mod x 3 + αx + β T cng of vrils β β x 3 αx givs x 3 α x T, ; = x mod α mod = ε 3/2 3 2 α + β β mod β β 54 An Estimt for n Incomlt Crctr Sum in To Vrils In tis sction stlis gnrl stimt for crctr sum in to vrils ic ill lid in our or Prcisly v Lmm 57 Lt F u, v smoot function stisfying 22 F α 1,α 2 u, vu α 1 v α 2 Cα 1, α u v 2 U V for ny α 1, α 2 0, t surscrit on F dnoting rtil diffrntition Tn u c χuψvλv F u, v ε U V U c 1/2 l 1 l 2 UV ε vq V q u v r χ nd ψ r nonrincil Diriclt crctrs to t moduli l 1 nd l 2, rsctivly, Λ is t von Mngoldt function, q is nonzro rtionl numr, c is ositiv intgr, nd ε is ny ositiv numr, t imlid constnt dnding only on ε, c, nd t numrs Cα 1, α 2 In cs χ is rincil ut not ψ t sm ound olds ut it U 1/2 lost In cs ψ is rincil ut not χ t sm ound olds ut it V 1/2 lost Rcll tt r ssuming t Rimnn Hyotsis for ll Diriclt L-functions; tis lmm, of cours, rlis vily on t GRH Proof First ssum χ nd ψ r nonrincil To gin, y Mllin invrsion, u c χuψvλv F u, v vq u v 2 1 = Ls 1, χ L 2πi L s 2, ψhs 1, s 2 ds 1 ds 2, r Hs 1, s 2 = Our gol is to otin t ound Hs 1, s 2 1/2+ε 1/2+ε 0 0 u c vq F u, vu s 1 v s 2 dudv uv U σ 1 V σ 2 s 1 /c + s 2 s 1 /c + s s 2 1+ε 1 + U c for R s 1 = σ 1, R s 2 = σ 2, σ j = 1/2 + ε or 1 + ε, nd us t GRH for t ound Ls 1, χ L s L 2, ψ s 1 s 2 l 1 l 2 ε/2 Putting ts to stimts togtr ill rov t dsird rsult T full dtils of t roof of t ound for Hs 1, s 2 r contind in Andix A V q 1/2
19 LOW-LYING ZEROS OF FAMILIES OF ELLIPTIC CURVES 19 In t css r on of t crctrs is rincil intgrt ovr t lin Rs j = 1+ε instd of R s j = 1/2 + ε for t rorit vril T ounds on t L-functions r t sm Tis ccounts for t squr-root loss T roof is no solly dndnt on t dtils of Andix A 55 Proof of Corollry 34 W follo n sy clcultion in [ILS] T 0 nd st 1 m X = X E W X F W dfin t vrg nlytic rn r y r = lim X m=1 E F ord s=1 Ls,f=m m m X, if t limit xists Our mtod rovids ound on t limsu of t ov quntity y ting tst function φ suc tt φx 0, φ0 = 1, nd suort of φ contind in [ ν, ν] driv y Torm 31 nd t Plncrl torm tt m m X g + ox, r m=1 g = φyŵoydy Tis uss GRH for ll llitic curv L-functions so tt y ositivity cn dro ll zros not t t cntrl oint y ting t Fourir ir 2 sinπνt 1 φt =, φy = 1 y πνt ν ν otin g = Ting ν lss tn 7/9 nd ltting X sos r 25/14 + ε for ν 2 ny ε > 0 An idnticl clcultion ors for ν < 1 + δ nd comlts t roof 56 A Not on Minimlity In tis sction invstigt t fmily givn in Torm 31 it t rstriction tt tr r no rims q suc tt ot q 4 nd q 6 Tis condition nsurs tt t qution E : y 2 = x 3 + x + is miniml for ll > 3 T rsult is t sm s tt sttd in Torm 31; omit t rcis sttmnt for rvity T conductor condition i t nlogu of Lmm 51 follos dirctly from Lmm 51 T sum ovr t Fourir cofficints is rdly comlictd y t divisiility rstrictions W sily v P E; φ q 4 q 6 = >3 A, = >3 2 log φ log 2 log φ log µd d q 4 q 6 λ, A, d 4 λ d 4,d 6 A, d6
20 20 MATTHEW P YOUNG = >3 2 log φ log d d,=1 µd Comlting t sum ovr nd mod lds to t sum r A >3 d d,=1 µd α β d 4 λ d 4,d 6 A, d6 λ αd 4,βd 6 α + β Φ,, = 2 log φ log A ŵ d 4, d 6 + oa Φ,, + oa, Alying t cng of vrils α αd 4, β βd 6 givs A 1 µd T d 4, d 6 ; Φ,, + oa, 2 d 10 >3 >3 d d,=1 r T is givn y Lmm 56 Alying Lmm 56 otin t sum A 2 log log µd 3 2 ε φ ŵ 3/2 d 10 d d,=1 A d 4, d 6 No simly rmov t rstriction d, = 1 nd mov t summtion ovr d to t outsid W r c to t rolm of stimting 12 xct it sligtly smllr A nd W cn simly us t sm ounds s for; t rsnc of d contriuts t orst oundd ors of Sinc sod tt c sum of ty 13 is X ε cn us t sm roof s for Lmm 52 It is ossil to imos minimlity rstrictions on t Wirstrss qutions for otr fmilis Sinc no intrsting fturs ris v limitd our discussions to tis rif not 6 Proof of t Dnsity Torm for t Min Rn On Fmily In tis sction rov Torm 32 T roof ill rocd muc t sm s Torm 31 ut t rgumnts ill mor intrict 61 T Conductor Condition To so 9 olds ill ly Lmm 41 W t Rd = Tn Rd = d X All nd to so is Proosition 61 r = α log α 1 A, X7/12 Proof W my ssum α = 2 cus similr rgumnt to tt usd in t roof of Lmm 51 it t rols of nd sitcd ill rovid t ncssry stimtion for α 3 W my furtr ssum > 3 nd tt, =, = 1 W no m to srt rgumnts to ndl rltivly smll nd rltivly lrg For t formr, v
21 Lmm 62 For P = X 1/3 LOW-LYING ZEROS OF FAMILIES OF ELLIPTIC CURVES 21 3< P,=1,=1 0 mod 2 t imlid constnt dnding only on For t lttr v Lmm 63 For P = X 11/36+ε P 2 t imlid constnt dnding only on ε nd log A, X7/12, log A, X7/12, Sinc 11/36 < 1/3 ts to lmms ill llo us to t ε smll nougt to clos t g nd comlt t roof of Proosition 61 Proof of Lmm 62 y ring t summtion ovr into congrunc clsssmod 2 sily otin t ound 1 + A log 2 A 1 + P, A P ic is sufficint rovidd P A = X 1/3, s climd Proof of Lmm 63 y mjorizing y smoot non-ngtiv function it sligtly lrgr suort my ssum 0 T conditions on imly tt if rit s d 2 l it l squrfr tn d P Trfor v log A, A, P d P 2 =d 2 l l squrfr l XP 2 l squrfr =d 2 l A, No dfin s =, l Sinc s is squrfr must v s Dfin l = sl, = s, nd = s Tn t condition on t discriminnt is 4s s 3 4 = d/4 2 l Sinc l is squrfr v s, l = 1, ic imlis s 4 1 d Tus t condition is rducd to s 4 = d/4s 2 l T imortnt ftur is tt, l = s, l = 1 nd, l = 1 or 2 St l = 2, l 3, l l, = 3,, = 2,, nd s = 2, ss Tn t discriminnt condition coms 4 3, 3 2, l 3, l , l 2, s2, 4 s 4 = d/4s 2 l 2, l y ting ll t ossil comintions of vlus for 2, l, 3, l, 3,,, r lft it finitly mny qutions of t form c c 2 s 4 = u 2 l it t condition c 1 c 2 s, l = 1
22 22 MATTHEW P YOUNG Trfor r rducd to stimting sums of t ty s L l L/s l squrfr c 1 3 +c 2 s 4 =u 2 l s A, s r L XP 2 nd t rims indict t summtion is rstrictd y c 1 c 2 s, l = 1 For squrfr l st s Ss, l = A, s c 1 3 +c 2 s 4 =u 2 l Lt Q st of rims q of siz q Q som fixd roortion, it Q t our disosl it ill cosn to X η for η smll W dtct t condition tt n intgr m is squr m y vluting t Lgndr symol for q Q ind of mlifiction tcniqu W q otin Ss, l = s A, s = Simlifying it coms 1 Q 2 1 Q 2 c 1 3 +c 2 s 4 =cl c= + 1 Q 2 c 1 3 +c 2 s 4 =cl c= c 1 3 +c 2 s 4 =cl c= q Q q Q c 1 3 +c 2 s 4 0 mod l + 1 Q 2 c 1 3 +c 2 s 4 =cl c= c q, 2 s A, s s {q Q : q c} 2 A, s c1 3 + c 2 s 4 l q 2 s A, s s {q Q : q cl} 2 A, s, sinc in t first sum v rlxd t condition tt c is squr For t scond sum, notic tt sinc q Q nd cl X {q Q : q cl} log Q Trfor t scond sum is / log Q 2 Q 2 Ss, l If lt S s, l t first sum ov, tn 1 Ss, l 1 log2 X Q 2 log 2 S s, l Q Our coics of Q nd Q ill so Ss, l S s, l so considr S s, l W xnd t summtion ovr q nd otin S s, l = 1 c1 3 + c 2 s 4 l s Q 2 q 1 q 2 A, s q 1 Q q 2 Q c 1 3 +c 2 s 4 0 mod l
23 LOW-LYING ZEROS OF FAMILIES OF ELLIPTIC CURVES 23 Lt S 2 = S 2 s, l, q 1, q 2 t ov summtion ovr nd St r = q 1 q 2 nd ly Poisson summtion in nd mod lr W gt S 2 = A c1 u 3 + c 2 sv 4 l u + v A ŵ l 2 r 2 s 2 r rl lrs, lrs u mod lr v mod lr c 1 u 3 +c 2 sv 4 0 mod l Using t Cins rmindr torm rit u = u 1 r + u 2 l it u 1 givn mod l nd u 2 givn mod r, nd similrly for v Tn gt S 2 = A A Ul, r, sŵ l 2 r 2 s 2 lrs, u1 + v 1, lrs l r Ul, r, s = u 2 mod r v 2 mod r u 1 v1 c 1 u 3 1 +c 2rsv1 4 0 mod l c1 u c 2 lsv 4 2 Aly t cng of vrils u 1 v 1 u 1 nd otin S 2 = A A Ul, r, sŵ l 2 r 2 s 2 lrs, lrs = A l 2 r 2 s 2 A Ul, r, sŵ lrs, lrs x mod r u2 + v 2 u 1 v1 c 1 u 3 1 +c 2rsv 1 0 mod l u 1 r v1 u 1 + l c1 c 2 rsu 3 1u 1 + sinc c 1 c 2 rs, l = 1 It s sy to s tt t xonntil sum ovr l fctors into xonntil sums of t form α x 3 x +, r l = nd α, = 1 A corollry of t Rimnn Hyotsis for curvs cf [Sc], Corollry 2F, g imlis tt t summtion ovr x is O 1/2 t imlid constnt solut, unlss ot nd r zro mod, in ic cs t sum is xctly 1 Trfor t summtion ovr u 1 is l 1/2,, l 1/2 τl, unlss = = 0, in ic cs t ound is l Clrly Ul, r, s r 3/2 + r 2 δ q1 q 2 so gt t ound S 2 A l 2 r r r 2 δ q1 q 2 l 1 2 +ε,, l A l lrs lrs Trfor, 0,0 A l 2 r 2 s r r 2 δ q1 q 2 l 12 +ε l2 r 2 s 2 A = r r 2 δ q1 q 2 + l 1 +ε lrs 2 l 1 2 +ε + l 1 2 +ε A rs + A lr 2 s 2 l + l S s, l Q Q l 1/2+ε + l 1/2+ε A Q sq + A 2 ls 2 Q 4,
24 24 MATTHEW P YOUNG On summtion ovr l Ls 1 nd s L gt S s, l 1 + Q Q s L l Ls 1 Q 3 L 3/2+ε + AQL 1/2+ε + A log L Q W t Q = X ε nd Q Q ic imlis Ss, l S s, l T ncssry ound on tis sum is X 7/12 ε, ic mns t rquirmnt on L is L X 7/18 ε Sinc L X/P 2 t rquirmnt on P is P X 11/36+ε No t roof of Lmm 63 is comlt 62 Estimting t Sum of t Fourir Cofficints In tis sction vlut PF; φ, X for t fmily givn in Torm 32 Tis is ccomlisd it Lmm 64 St A = X 1/3 nd = X 1/4 Tn P E; φ A, X 7/12 = φ0w X F + O rovidd su φ 23 48, W mimic t roof of Lmm 52 rgumnts Proof On Poisson summtion, r T dtils r similr so oftn condns our P E; φ A, = A 2 log 3 φ log T, ; ŵ >3 T, ; = α mod β mod α + β λ α,β 2 A, T comlt sum T cn vlutd xlicitly; t clcultion is md it Lmm 66 T δδ 2 trm in T givs t xtr φ0w X F y t Prim Numr Torm T trm is ngligil vi trivil stimtions W r lft it stimting t sum A 2 log ε 3/2 φ log A ŵ, >3 Estimting tis sum trivilly otins our rsult for suort u to 7/18 To gt lrgr suort nd to so tr is cnclltion in t sum W stimt it in xctly t sm y did in t roof of Lmm 52 First rlc ε y crctr ψ 4 mod 4 Tn r u t sum into dydic sgmnts using rtitions of unity It suffics to considr sums of t ty 23 ψ 4 H <2H K <2K P <2P log φ 3/2 log A ŵ,, g,,, r g is function rising from t rtitions of unity T contriution from = 0 is ngligil y trivil stimtions Lt SH, K, P t sum givn y 23 It suffics to so SH, K, P X ε
25 LOW-LYING ZEROS OF FAMILIES OF ELLIPTIC CURVES 25 Using t ound ŵx, y 1 + x M 1 + y M my ssum tt H P/A 1+ε nd K P/ 1+ε In ordr to sum ovr corim intgrs st d = 4, nd dfin d 0 to t lst ositiv intgr suc tt d d 4 0 Sinc d 0 my st = d 0 0 T condition 4, = d is quivlnt to t to conditions d 4 0/d, /d = 1 nd 0, /d = 1 Trfor SH, K, P is r H <2H d K P <2P d 0 <2 K 0 d d 4 0 d, =1 d 0,2 6 3 =1 d ψ 4 d 4 0/d /d U 0, d,,, A U 0, d,, = g, 0 d 0, ŵ, d 0 0 log log φ 3/2 W ly t lmntry rcirocity formul nd t xnsion of t xonntil into multilictiv crctrs s in t roof of Lmm 52 nd otin 24 SH, K, P = r Qd,, χ = P <2P H <2H 1 φ2 6 3 /d d χ mod /d ψ 4 χ K/d 0 0 <2K/d 0 τχ χd 4 0/dQd,, χ d χ U , d,, Sinc t rgumnts r no xtrmly similr to tos usd in t roof of Lmm 52 ill rif W ly Lmm 57 to Qd,, χ nd otin Lmm 65 If χψ 4 / nd χ 4 r nonrincil tn 1/2 Qd,, χ P 1 K 1/2 d 1/ K4 X ε P H 3 If χ 4 is rincil ut χψ 4 / is not rincil los fctor K 1/2 d 1/2 0 Lt S = S 1 + S 2 + S 3, r S 1 corrsonds to t trms r ot crctrs r nonrincil, S 2 corrsonds to t trms r χ 4 is rincil ut χψ 4 / is not rincil, nd S 3 corrsonds to t rmining trms r χψ 4 / is rincil nd ncssrily χ 4 is rincil Cs 1 W ly Lmm 65 to S 1 nd otin t ound 1/2 S 1 P 1 K 1/2 1 + K4 X ε 3/2 dd P H 3 0 1/2 H <2H d P 1 H 5/2 K 1 1/2 K 2 + X ε, P 1/2 H 3/2 ic is X ε n P X 23/48 ε
26 26 MATTHEW P YOUNG Cs 2 Alying Lmm 65 to S 2 givs S 2 1/2 P 1 K 1 + K4 X ε P H 3 P 1 K 2 K 1 + X ε P 1/2 H 3/2 H <2H 3/2 d 1/2 d 1 0 d Using only K P/ 1+ε nd H 1 sos tis is X ε n P X 1/2 ε Cs 3 No considr t cs r χψ 4 / nd nc χ 4 r rincil Sinc ψ 4 / s conductor qul to t squr fr rt of u to fctor of 2 or 4 gt xtr sving from t rstriction d Tus χ s conductor of siz so τχ 1/2 W trfor v t ound S 3 P 1/2 H 5/2 KX ε d d 0 H <2H d / P 1/2 KX ε 1 + 3/2 + ic is X ε n P X 1/2 ε sinc t infinit roduct convrgs Hving considrd ll ossil css t roof is comlt 63 A Comlt Crctr Sum As in t roof of Torm 31 nd to vlut comlt crctr sum W do tis no St T, ; = α + β λ α,β 2 W v α mod β mod Lmm 66 Lt > 2 rim nd dfind y 1 mod if, = 1 nd 0 = 0 Tn v T, ; = 2 δδ ε 3/2 6 +, r δ is t Kroncr dlt function mod Proof y dfinition, = α T, ; = β 2 sy W sily v β x mod α mod β mod x 3 + αx + β 2 α + β x 3 + αx + β 2 x 0 α β = T 1 + T 2, 1 if 0 mod, T 1 = if 0, 0 mod, 0 if 0 mod α + β α + β
27 LOW-LYING ZEROS OF FAMILIES OF ELLIPTIC CURVES 27 T sum T 2 is, ftr t linr cng of vrils α α x 2 β 2 x, givn y T 2 = x β2 x + β x 2 α α x 0 β α x x = ε 1/2 2 β2 x + β x 0 β x x = ε 1/2 2 xβ 2 + xβ from β xβ x 0 To vlut t summtion ovr β ly t formul x 2 + x ε ā 2 4 if, = 1, 25 = if 0 mod, x mod 0 otris W otin T 2 = ε x x x 0 Alying 25 gin otin T = ε Gtring trms nd simlifying finis t roof of t lmm β 1 7 Conjcturlly Enlrging t Suort for t Fmily of ll Ellitic Curvs 71 A Conjctur on t Siz of Crctr Sum In tis sction invstigt uristiclly t vior of DF; φ, X for t fmily givn in Torm 31 n xtnd t suort of φ outsid t rng 1, 1 Rcll tt tis is t slitting oint for t symmtry tys O, SOvn, nd SOodd W rdict tt t symmtry ty is O To rovid vidnc for tis conjctur, nd to rgu tt P E; φ A, = oa for φ it lrg suort From 12 nd 17 t rolm is siclly rducd to stimting t folloing crctr sum , 2 2 K H P it crtin rltions on t sizs of H, K, nd P On of t rltions is H 3 /P K 2 1 so for uross of tsting ignor t 3 / 2 trm Conjctur 71 Tr xists δ > 0 nd ε > 0 suc tt if P, is not squr i t crctr / is nonrincil, nd H = P 2/3+δ, tn 3 P 1 3δ/2 ε 2 H P
28 28 MATTHEW P YOUNG On summtion ovr P 1/2+3δ/2 tis conjctur ould indict tt Torm 31 rmins tru it tst functions os Fourir trnsforms φ v suort outsid of 1, 1 T xtnt to ic t suort could xcd 1, 1 ould dnd on t vlu of δ Prcisly, ould otin suort u to 1 3δ 1 T uristic usd in Sction 72 lnds suort to t vlu δ = 1/48, ic ould giv suort u to 16/15 72 Evidnc for Conjctur 71 To lnd suort for Conjctur 71 invstigt t sm sum ut it rnging ovr ositiv intgrs corim it instd of rims W v Torm 72 Lt H = P 2/3+δ, K = H 3/2 P 1/2 Tn for ny ε > 0 v m 3 m 2 H, m ε P 5/6+cδ+ε, P m r t rim indicts t summtion is rstrictd to, = 1 nd c is ositiv constnt t roof givs c = 13/2 Ting δ < 1 6 c nd ε smll noug ill so tt t sum is P 1 3δ/2 ε for ositiv δ nd ε T vlu c = 13/2 llos us to t ny δ < 1/48 Proof Lt S = S t sum to stimtd y Poisson summtion in m mod 2, S = m 3 m 2 H, m P m = P x 3 x + lx 2 2 H, lp, 2 l x mod 2 r t t ovr t scond vril indicts v tn t Fourir trnsform in tt vril only Rcll K 2 = H 3 /P = P 1+3δ so 2 /P P 3δ No rit x = y1 + z r y nd z rng ovr rrsnttivs mod Tn x = ȳ1 z r ȳ is t multilictiv invrs of ymod 2 W otin S = P 2 = P 2 = P l l H, lp 2 H, lp 2 l y mod ly 2 3 mod y y mod z mod y mod y 3ȳ + ly 2 y 3ȳ1 z + ly1 + z 3ȳ + ly 2 H, lp 2 z mod 2 z 3ȳ + ly Writ = r 0 H, 0, = 1, 1 H/, 0 ts vlus in n intrvl of lngt, nd 1 ts vlus in n intrvl of lngt H/ No xtnd t summtion ovr 0 to n intrvl of lngt H, so t sum is rtd H/ tims W otin ly S P H 0 l y mod ly mod 1 y 3 0 ȳ ȳ H, lp 2
29 LOW-LYING ZEROS OF FAMILIES OF ELLIPTIC CURVES 29 Alying t cng of vrils y 2 0ȳ givs S P y 2 0 lȳ H 2 l y mod y 2 l 0 mod y H, lp 2 Tr ill virtully no oscilltion in y/ 2 if y P ε 2 /H P 1/3+2δ+ε On t otr nd, if y P 1/3+2δ+ε tn it is sily son tt t summtion ovr 1 is ε,m P M Trfor v fixd 0 < y P ε K 2 /H Tus t sum is rducd to S P H 1 H/ 0 l 0<y P ε K 2 /H y 2 l 0 mod y 2 0 lȳ 2 1 0, 1,, l, y, r 1 is t n tst function otind y soring t non-oscilltory xonntil fctor into ny rocss of diffrntition of 1 it rsct to y introducs only fctors of siz P ε No ly t lmntry rcirocity l 16, otining S P H 1 H/ 0 l 0<y P ε K 2 /H y 2 l 0 mod y l y 2 0 l y 2 1 0, 1,, l, y T qulity y 2 = l 0 + s mns s P 2/3+4δ / 1+ε P 1/6+5δ/2+ε Tn t sum is rducd to S P y s2 l y 2 s 2 H y ly 2 1 0, 1,, l, y = P H 1 H 1 H/ 0 l 0<y P ε K2 H y 2 =l 0 +s s l 0<y P ε K 2 /H y 2 s mod l y s2ȳ l s2 ly + y2 s 2 ly 2 2 r 2 = 2 s, 1,, l, y, is t rlcmnt of 1 ftr t cng of vrils ic limints 0 nd introducs s No r t summtion ovr y into rogrssions mod l nd ly t Póly-Vinogrdov ound of y ly 1/2 log ly y Y y λ mod l to S vi rtil summtion Tis givs t finl ound of P 5/6+cδ+ε r c = 13/2 8 Curvs it Torsion Z/2Z Z/2Z In t folloing sctions study som intrsting fmilis of llitic curvs tt v torsion oints Ec fmily s its on intrsting fturs On common ftur is tt t squr divisors of t conductor r gnrlly rtr sy to control T sourc of tis s is tt t discriminnts fctor into olynomils of smllr dgr In ddition, t conductors r oftn muc smllr tn t discriminnt cus of ig multilicity in on or mor of ts olynomil fctors Tis fct cuss ts torsion fmilis to v rtr lrg numr of curvs it conductor N X
30 30 MATTHEW P YOUNG W rfr to t r of Kurt [Ku] s rfrnc for ts torsion fmilis In rticulr Tl 3 contins ssntilly ll t informtion us In tis sction invstigt rticulrly intrsting fmily of llitic curvs, givn in Wirstrss form y E s discriminnt E : y 2 = xx x + = T torsion grou is gnrtd y t oints 0, 0 nd, 0 nd λ = xx x + x mod Hlfgott s son tt t root numr in tis fmily is quidistriutd [H] W v t folloing Torm 81 Lt F t fmily of llitic curvs givn y t Wirstrss qutions E, : y 2 = xx x + it nd ositiv intgrs St A = = X 1/3, lt smoot comctly suortd function on R + R +, nd st X E, = A, Tn for φ it su φ 2 3, 2 3 DF; φ, X [ φ φ0]w XF s X, Tis fmily s rticulr intrst cus cn sum rims u to t siz of t fmily r ting A = X 2/3 curvs, nturl rrir for ny fmily sinc squr-root cnclltion coming solly from vrging ovr t fmily givs us tis suort; to go furtr rquirs dditionl cnclltion in t λ s s vris, t lst on vrg To rov Torm 81 nd to lmms For t conductor condition v Lmm 82 Lt F t fmily givn in Torm 81 Tn log N A, = W X F + O + 2 N, >3 A Proof W ill ly Lmm 41 W t Rd = + Tn it s clr tt Rd X nd tt t irrducil fctors of Rd ll divid d W first considr A, log Tis sum is mty cus 2 N imlis, sinc xx x + s tril root mod To stimt t sum A, log α 1 α + suos γ nd δ Tus α γ δ + W first suos γ δ y symmtry my ssum γ < δ ic imlis γ + nd γ < α/3 Sinc A = = X 1/3
31 LOW-LYING ZEROS OF FAMILIES OF ELLIPTIC CURVES 31 lys v X 1/3 Tn gt t ound α X α>0 X 1/3 γ α/3 α X α>0 X 1/3 1 + A γ 1 + α 2γ γ α/3 α 3γ + log α 1 X 2/3 In cs γ = δ ly t cng of vrils γ, γ nd gt t ound γ A, γ log α 1 For fixd, is dtrmind mod α 3γ so gt t ound 1 + A 1 + γ α 2γ α X α>0 X 1/3 γ α/3 log α 1, ic is t sm ound v for γ δ, so t roof is comlt T sum ovr t Fourir cofficints is ndld it Lmm 83 Lt F t fmily givn in Torm 81 Tn P E; φ A, X2/3 rovidd su φ 2 3, 2 3 Proof St so tt S = λ A, P E; φ A, = S 2 log φ log >3 Tn S = xx x + A, x mod = A xx ρx + σ ρ + σ 2 x,ρ,σ mod = A xρσ ρ + σ + x 2 x,ρ,σ mod = A ε A 1/2 ŵ, A ŵ ŵ, A, To gt furtr cnclltion sum ovr To ndl t vrition of ε introduc crctr ψ 4 mod 4 vlutd t For tos trms it / ψ 4 nontrivil
32 32 MATTHEW P YOUNG l to t Rimnn Hyotsis for Diriclt L-functions to otin t ound summing P A P P ε P 2 A = P 1+ε, ic is X 2/3 ε n P X 2/3 ε, i t rstriction on t suort of φ is 2/3 Wn / ψ 4 is trivil do not otin ny sving in t summtion ovr T crctr is trivil only if = ± so t rolm mounts to stimting t numr of suc solutions Tis is crrid out y t folloing Lmm 84 Lt Tn CY ε Y 1+ε CY = {, Z 2 : + Y, = ± } for roving t lmm ly it to our sum y t rid dcy of t Fourir trnsform my ssum, P A 1 1+ε Using t vlu Y = P A 1 1+ε in t lmm otin t ound A CY P 1/2+ε P 1/2 P on t contriution of t trms it trivil crctr / ψ 4 T contriution is X 2/3 ε n P X 2/3 ε, s dsird Tis ill comlt t roof of Lmm 83 nd nc Torm 81 onc rov Lmm 84 Proof of Lmm 84 Suos v solution = ± r + Y y ossily cnging t signs of nd nd sitcing t vlus of nd my ssum > 0, > 0, nd > t css r = 0 r trivil St g =, nd lt g = d 2 l r l is squrfr St = g nd = g Tn v l = Sinc, = 1 nd l is squrfr must v l = l 1 l 2 l 3 r l 1, l 2, l 3 nd nc c of l 1, l 2, nd l 3 must squr Tus = l 1, = l 2, nd = l 3 Tus vry solution to = is givn y r = d 2 l 2 1l 2 l 3 x 2, = d 2 l 1 l 2 2l 3 y 2, 27 l 1 x 2 = l 2 y 2 + l 3 z 2, it t rstrictions x, y = x, z = y, z = 1, l = l 1 l 2 l 3 is squrfr, nd c l i is ositiv ut no notic tt t solution 27 givs ris to t fctoriztion l 1 l 2 x 2 = l 2 y + l 2 l 3 zl 2 y l 2 l 3 z T numr of suc fctoriztions is clrly oundd y d Q l1 l 2 lx 2, t divisor function in t ring of intgrs of t fild Q l 2 l 3 It s ll-non tt d K n cε N K n ε r N K n is t norm in t numr fild K nd cε dos not dnd on t fild K Using = d 2 l 1 lx 2 d 2 lx 2 sily gt t ound CY Y 1+ε
Problem 1. Solution: = show that for a constant number of particles: c and V. a) Using the definitions of P
 rol. Using t dfinitions of nd nd t first lw of trodynis nd t driv t gnrl rltion: wr nd r t sifi t itis t onstnt rssur nd volu rstivly nd nd r t intrnl nrgy nd volu of ol. first lw rlts d dq d t onstnt
rol. Using t dfinitions of nd nd t first lw of trodynis nd t driv t gnrl rltion: wr nd r t sifi t itis t onstnt rssur nd volu rstivly nd nd r t intrnl nrgy nd volu of ol. first lw rlts d dq d t onstnt
Chapter 16. 1) is a particular point on the graph of the function. 1. y, where x y 1
 Prctic qustions W now tht th prmtr p is dirctl rltd to th mplitud; thrfor, w cn find tht p. cos d [ sin ] sin sin Not: Evn though ou might not now how to find th prmtr in prt, it is lws dvisl to procd
Prctic qustions W now tht th prmtr p is dirctl rltd to th mplitud; thrfor, w cn find tht p. cos d [ sin ] sin sin Not: Evn though ou might not now how to find th prmtr in prt, it is lws dvisl to procd
TOPIC 5: INTEGRATION
 TOPIC 5: INTEGRATION. Th indfinit intgrl In mny rspcts, th oprtion of intgrtion tht w r studying hr is th invrs oprtion of drivtion. Dfinition.. Th function F is n ntidrivtiv (or primitiv) of th function
TOPIC 5: INTEGRATION. Th indfinit intgrl In mny rspcts, th oprtion of intgrtion tht w r studying hr is th invrs oprtion of drivtion. Dfinition.. Th function F is n ntidrivtiv (or primitiv) of th function
SCHUR S THEOREM REU SUMMER 2005
 SCHUR S THEOREM REU SUMMER 2005 1. Combinatorial aroach Prhas th first rsult in th subjct blongs to I. Schur and dats back to 1916. On of his motivation was to study th local vrsion of th famous quation
SCHUR S THEOREM REU SUMMER 2005 1. Combinatorial aroach Prhas th first rsult in th subjct blongs to I. Schur and dats back to 1916. On of his motivation was to study th local vrsion of th famous quation
Integration Continued. Integration by Parts Solving Definite Integrals: Area Under a Curve Improper Integrals
 Intgrtion Continud Intgrtion y Prts Solving Dinit Intgrls: Ar Undr Curv Impropr Intgrls Intgrtion y Prts Prticulrly usul whn you r trying to tk th intgrl o som unction tht is th product o n lgric prssion
Intgrtion Continud Intgrtion y Prts Solving Dinit Intgrls: Ar Undr Curv Impropr Intgrls Intgrtion y Prts Prticulrly usul whn you r trying to tk th intgrl o som unction tht is th product o n lgric prssion
DISTRIBUTION OF DIFFERENCE BETWEEN INVERSES OF CONSECUTIVE INTEGERS MODULO P
 DISTRIBUTION OF DIFFERENCE BETWEEN INVERSES OF CONSECUTIVE INTEGERS MODULO P Tsz Ho Chan Dartmnt of Mathmatics, Cas Wstrn Rsrv Univrsity, Clvland, OH 4406, USA txc50@cwru.du Rcivd: /9/03, Rvisd: /9/04,
DISTRIBUTION OF DIFFERENCE BETWEEN INVERSES OF CONSECUTIVE INTEGERS MODULO P Tsz Ho Chan Dartmnt of Mathmatics, Cas Wstrn Rsrv Univrsity, Clvland, OH 4406, USA txc50@cwru.du Rcivd: /9/03, Rvisd: /9/04,
INTEGRALS. Chapter 7. d dx. 7.1 Overview Let d dx F (x) = f (x). Then, we write f ( x)
 Chptr 7 INTEGRALS 7. Ovrviw 7.. Lt d d F () f (). Thn, w writ f ( ) d F () + C. Ths intgrls r clld indfinit intgrls or gnrl intgrls, C is clld constnt of intgrtion. All ths intgrls diffr y constnt. 7..
Chptr 7 INTEGRALS 7. Ovrviw 7.. Lt d d F () f (). Thn, w writ f ( ) d F () + C. Ths intgrls r clld indfinit intgrls or gnrl intgrls, C is clld constnt of intgrtion. All ths intgrls diffr y constnt. 7..
The Angular Momenta Dipole Moments and Gyromagnetic Ratios of the Electron and the Proton
 Journl of Modrn hysics, 014, 5, 154-157 ublishd Onlin August 014 in SciRs. htt://www.scir.org/journl/jm htt://dx.doi.org/.436/jm.014.51415 Th Angulr Momnt Diol Momnts nd Gyromgntic Rtios of th Elctron
Journl of Modrn hysics, 014, 5, 154-157 ublishd Onlin August 014 in SciRs. htt://www.scir.org/journl/jm htt://dx.doi.org/.436/jm.014.51415 Th Angulr Momnt Diol Momnts nd Gyromgntic Rtios of th Elctron
Lecture 11 Waves in Periodic Potentials Today: Questions you should be able to address after today s lecture:
 Lctur 11 Wvs in Priodic Potntils Tody: 1. Invrs lttic dfinition in 1D.. rphicl rprsnttion of priodic nd -priodic functions using th -xis nd invrs lttic vctors. 3. Sris solutions to th priodic potntil Hmiltonin
Lctur 11 Wvs in Priodic Potntils Tody: 1. Invrs lttic dfinition in 1D.. rphicl rprsnttion of priodic nd -priodic functions using th -xis nd invrs lttic vctors. 3. Sris solutions to th priodic potntil Hmiltonin
Instructions for Section 1
 Instructions for Sction 1 Choos th rspons tht is corrct for th qustion. A corrct nswr scors 1, n incorrct nswr scors 0. Mrks will not b dductd for incorrct nswrs. You should ttmpt vry qustion. No mrks
Instructions for Sction 1 Choos th rspons tht is corrct for th qustion. A corrct nswr scors 1, n incorrct nswr scors 0. Mrks will not b dductd for incorrct nswrs. You should ttmpt vry qustion. No mrks
CIVL 8/ D Boundary Value Problems - Rectangular Elements 1/7
 CIVL / -D Boundr Vlu Prolms - Rctngulr Elmnts / RECANGULAR ELEMENS - In som pplictions, it m mor dsirl to us n lmntl rprsnttion of th domin tht hs four sids, ithr rctngulr or qudriltrl in shp. Considr
CIVL / -D Boundr Vlu Prolms - Rctngulr Elmnts / RECANGULAR ELEMENS - In som pplictions, it m mor dsirl to us n lmntl rprsnttion of th domin tht hs four sids, ithr rctngulr or qudriltrl in shp. Considr
Multi-Section Coupled Line Couplers
 /0/009 MultiSction Coupld Lin Couplrs /8 Multi-Sction Coupld Lin Couplrs W cn dd multipl coupld lins in sris to incrs couplr ndwidth. Figur 7.5 (p. 6) An N-sction coupld lin l W typiclly dsign th couplr
/0/009 MultiSction Coupld Lin Couplrs /8 Multi-Sction Coupld Lin Couplrs W cn dd multipl coupld lins in sris to incrs couplr ndwidth. Figur 7.5 (p. 6) An N-sction coupld lin l W typiclly dsign th couplr
Functions and Graphs 1. (a) (b) (c) (f) (e) (d) 2. (a) (b) (c) (d)
 Functions nd Grps. () () (c) - - - O - - - O - - - O - - - - (d) () (f) - - O - 7 6 - - O - -7-6 - - - - - O. () () (c) (d) - - - O - O - O - - O - -. () G() f() + f( ), G(-) f( ) + f(), G() G( ) nd G()
Functions nd Grps. () () (c) - - - O - - - O - - - O - - - - (d) () (f) - - O - 7 6 - - O - -7-6 - - - - - O. () () (c) (d) - - - O - O - O - - O - -. () G() f() + f( ), G(-) f( ) + f(), G() G( ) nd G()
Last time: introduced our first computational model the DFA.
 Lctur 7 Homwork #7: 2.2.1, 2.2.2, 2.2.3 (hnd in c nd d), Misc: Givn: M, NFA Prov: (q,xy) * (p,y) iff (q,x) * (p,) (follow proof don in clss tody) Lst tim: introducd our first computtionl modl th DFA. Tody
Lctur 7 Homwork #7: 2.2.1, 2.2.2, 2.2.3 (hnd in c nd d), Misc: Givn: M, NFA Prov: (q,xy) * (p,y) iff (q,x) * (p,) (follow proof don in clss tody) Lst tim: introducd our first computtionl modl th DFA. Tody
Floating Point Number System -(1.3)
 Floting Point Numbr Sstm -(.3). Floting Point Numbr Sstm: Comutrs rrsnt rl numbrs in loting oint numbr sstm: F,k,m,M 0. 3... k ;0, 0 i, i,...,k, m M. Nottions: th bs 0, k th numbr o igts in th bs xnsion
Floting Point Numbr Sstm -(.3). Floting Point Numbr Sstm: Comutrs rrsnt rl numbrs in loting oint numbr sstm: F,k,m,M 0. 3... k ;0, 0 i, i,...,k, m M. Nottions: th bs 0, k th numbr o igts in th bs xnsion
Floating Point Number System -(1.3)
 Floting Point Numbr Sstm -(.3). Floting Point Numbr Sstm: Comutrs rrsnt rl numbrs in loting oint numbr sstm: F,k,m,M 0. 3... k ;0, 0 i, i,...,k, m M. Nottions: th bs 0, k th numbr o igits in th bs xnsion
Floting Point Numbr Sstm -(.3). Floting Point Numbr Sstm: Comutrs rrsnt rl numbrs in loting oint numbr sstm: F,k,m,M 0. 3... k ;0, 0 i, i,...,k, m M. Nottions: th bs 0, k th numbr o igits in th bs xnsion
Elliptical motion, gravity, etc
 FW Physics 130 G:\130 lctur\ch 13 Elliticl motion.docx g 1 of 7 11/3/010; 6:40 PM; Lst rintd 11/3/010 6:40:00 PM Fig. 1 Elliticl motion, grvity, tc minor xis mjor xis F 1 =A F =B C - D, mjor nd minor xs
FW Physics 130 G:\130 lctur\ch 13 Elliticl motion.docx g 1 of 7 11/3/010; 6:40 PM; Lst rintd 11/3/010 6:40:00 PM Fig. 1 Elliticl motion, grvity, tc minor xis mjor xis F 1 =A F =B C - D, mjor nd minor xs
22.615, MHD Theory of Fusion Systems Prof. Freidberg Lecture 8: Effect of a Vertical Field on Tokamak Equilibrium
 .65, MHD Thory of usion Systms Prof. ridrg Lctur 8: Effct of Vrticl ild on Tokmk Equilirium Toroidl orc lnc y Mns of Vrticl ild. Lt us riw why th rticl fild is imortnt. 3. or ry short tims, th cuum chmr
.65, MHD Thory of usion Systms Prof. ridrg Lctur 8: Effct of Vrticl ild on Tokmk Equilirium Toroidl orc lnc y Mns of Vrticl ild. Lt us riw why th rticl fild is imortnt. 3. or ry short tims, th cuum chmr
INCOMPLETE KLOOSTERMAN SUMS AND MULTIPLICATIVE INVERSES IN SHORT INTERVALS. xy 1 (mod p), (x, y) I (j)
 INCOMPLETE KLOOSTERMAN SUMS AND MULTIPLICATIVE INVERSES IN SHORT INTERVALS T D BROWNING AND A HAYNES Abstract W invstigat th solubility of th congrunc xy (mod ), whr is a rim and x, y ar rstrictd to li
INCOMPLETE KLOOSTERMAN SUMS AND MULTIPLICATIVE INVERSES IN SHORT INTERVALS T D BROWNING AND A HAYNES Abstract W invstigat th solubility of th congrunc xy (mod ), whr is a rim and x, y ar rstrictd to li
Chapter 11 Calculation of
 Chtr 11 Clcultion of th Flow Fild OUTLINE 11-1 Nd for Scil Procdur 11-2 Som Rltd Difficultis 11-3 A Rmdy : Th stggrd Grid 11-4 Th Momntum Equtions 11-5 Th Prssur nd Vlocity Corrctions 11-6 Th Prssur-Corrction
Chtr 11 Clcultion of th Flow Fild OUTLINE 11-1 Nd for Scil Procdur 11-2 Som Rltd Difficultis 11-3 A Rmdy : Th stggrd Grid 11-4 Th Momntum Equtions 11-5 Th Prssur nd Vlocity Corrctions 11-6 Th Prssur-Corrction
The Theory of Small Reflections
 Jim Stils Th Univ. of Knss Dt. of EECS 4//9 Th Thory of Smll Rflctions /9 Th Thory of Smll Rflctions Rcll tht w nlyzd qurtr-wv trnsformr usg th multil rflction viw ot. V ( z) = + β ( z + ) V ( z) = = R
Jim Stils Th Univ. of Knss Dt. of EECS 4//9 Th Thory of Smll Rflctions /9 Th Thory of Smll Rflctions Rcll tht w nlyzd qurtr-wv trnsformr usg th multil rflction viw ot. V ( z) = + β ( z + ) V ( z) = = R
Ch 1.2: Solutions of Some Differential Equations
 Ch 1.2: Solutions of Som Diffrntil Equtions Rcll th fr fll nd owl/mic diffrntil qutions: v 9.8.2v, p.5 p 45 Ths qutions hv th gnrl form y' = y - b W cn us mthods of clculus to solv diffrntil qutions of
Ch 1.2: Solutions of Som Diffrntil Equtions Rcll th fr fll nd owl/mic diffrntil qutions: v 9.8.2v, p.5 p 45 Ths qutions hv th gnrl form y' = y - b W cn us mthods of clculus to solv diffrntil qutions of
, between the vertical lines x a and x b. Given a demand curve, having price as a function of quantity, p f (x) at height k is the curve f ( x,
 Clculus for Businss nd Socil Scincs - Prof D Yun Finl Em Rviw vrsion 5/9/7 Chck wbsit for ny postd typos nd updts Pls rport ny typos This rviw sht contins summris of nw topics only (This rviw sht dos hv
Clculus for Businss nd Socil Scincs - Prof D Yun Finl Em Rviw vrsion 5/9/7 Chck wbsit for ny postd typos nd updts Pls rport ny typos This rviw sht contins summris of nw topics only (This rviw sht dos hv
QUADRATIC RESIDUES MATH 372. FALL INSTRUCTOR: PROFESSOR AITKEN
 QUADRATIC RESIDUES MATH 37 FALL 005 INSTRUCTOR: PROFESSOR AITKEN When is n integer sure modulo? When does udrtic eution hve roots modulo? These re the uestions tht will concern us in this hndout 1 The
QUADRATIC RESIDUES MATH 37 FALL 005 INSTRUCTOR: PROFESSOR AITKEN When is n integer sure modulo? When does udrtic eution hve roots modulo? These re the uestions tht will concern us in this hndout 1 The
[ ] [ ] DFT: Discrete Fourier Transform ( ) ( ) ( ) ( ) Congruence (Integer modulo m) N-point signal
![[ ] [ ] DFT: Discrete Fourier Transform ( ) ( ) ( ) ( ) Congruence (Integer modulo m) N-point signal [ ] [ ] DFT: Discrete Fourier Transform ( ) ( ) ( ) ( ) Congruence (Integer modulo m) N-point signal](/thumbs/83/87440381.jpg) Congrunc (Intgr modulo m) : Discrt Fourir Transform In this sction, all lttrs stand for intgrs. gcd ( nm, ) th gratst common divisor of n and m Lt d gcd(n,m) All th linar combinations r n+ s m of n and
Congrunc (Intgr modulo m) : Discrt Fourir Transform In this sction, all lttrs stand for intgrs. gcd ( nm, ) th gratst common divisor of n and m Lt d gcd(n,m) All th linar combinations r n+ s m of n and
Chem 104A, Fall 2016, Midterm 1 Key
 hm 104A, ll 2016, Mitrm 1 Ky 1) onstruct microstt tl for p 4 configurtion. Pls numrt th ms n ml for ch lctron in ch microstt in th tl. (Us th formt ml m s. Tht is spin -½ lctron in n s oritl woul writtn
hm 104A, ll 2016, Mitrm 1 Ky 1) onstruct microstt tl for p 4 configurtion. Pls numrt th ms n ml for ch lctron in ch microstt in th tl. (Us th formt ml m s. Tht is spin -½ lctron in n s oritl woul writtn
Quadratic reciprocity
 Qudrtic recirocity Frncisc Bozgn Los Angeles Mth Circle Octoer 8, 01 1 Qudrtic Recirocity nd Legendre Symol In the eginning of this lecture, we recll some sic knowledge out modulr rithmetic: Definition
Qudrtic recirocity Frncisc Bozgn Los Angeles Mth Circle Octoer 8, 01 1 Qudrtic Recirocity nd Legendre Symol In the eginning of this lecture, we recll some sic knowledge out modulr rithmetic: Definition
CONTINUITY AND DIFFERENTIABILITY
 MCD CONTINUITY AND DIFFERENTIABILITY NCERT Solvd mpls upto th sction 5 (Introduction) nd 5 (Continuity) : Empl : Chck th continuity of th function f givn by f() = + t = Empl : Emin whthr th function f
MCD CONTINUITY AND DIFFERENTIABILITY NCERT Solvd mpls upto th sction 5 (Introduction) nd 5 (Continuity) : Empl : Chck th continuity of th function f givn by f() = + t = Empl : Emin whthr th function f
FSA. CmSc 365 Theory of Computation. Finite State Automata and Regular Expressions (Chapter 2, Section 2.3) ALPHABET operations: U, concatenation, *
 CmSc 365 Thory of Computtion Finit Stt Automt nd Rgulr Exprssions (Chptr 2, Sction 2.3) ALPHABET oprtions: U, conctntion, * otin otin Strings Form Rgulr xprssions dscri Closd undr U, conctntion nd * (if
CmSc 365 Thory of Computtion Finit Stt Automt nd Rgulr Exprssions (Chptr 2, Sction 2.3) ALPHABET oprtions: U, conctntion, * otin otin Strings Form Rgulr xprssions dscri Closd undr U, conctntion nd * (if
this is called an indeterninateformof-oior.fi?afleleitns derivatives can now differentiable and give 0 on on open interval containing I agree to.
 hl sidd r L Hospitl s Rul 11/7/18 Pronouncd Loh mtims splld Non p t mtims w wnt vlut limit ii m itn ) but irst indtrnintmori?lltns indtrmint t inn gl in which cs th clld n i 9kt ti not ncssrily snsign
hl sidd r L Hospitl s Rul 11/7/18 Pronouncd Loh mtims splld Non p t mtims w wnt vlut limit ii m itn ) but irst indtrnintmori?lltns indtrmint t inn gl in which cs th clld n i 9kt ti not ncssrily snsign
A physical solution for solving the zero-flow singularity in static thermal-hydraulics
 A ysicl solution for solving t zro-flow singulrity in sttic trml-ydrulics miing modls Dnil Bouskl Blig El Hfni EDF R&D 6, qui Wtir F-784 Ctou Cd, Frnc dnil.ouskl@df.fr lig.l-fni@df.fr Astrct For t D-D
A ysicl solution for solving t zro-flow singulrity in sttic trml-ydrulics miing modls Dnil Bouskl Blig El Hfni EDF R&D 6, qui Wtir F-784 Ctou Cd, Frnc dnil.ouskl@df.fr lig.l-fni@df.fr Astrct For t D-D
Lecture contents. Bloch theorem k-vector Brillouin zone Almost free-electron model Bands Effective mass Holes. NNSE 508 EM Lecture #9
 Lctur contnts Bloch thorm -vctor Brillouin zon Almost fr-lctron modl Bnds ffctiv mss Hols Trnsltionl symmtry: Bloch thorm On-lctron Schrödingr qution ch stt cn ccommo up to lctrons: If Vr is priodic function:
Lctur contnts Bloch thorm -vctor Brillouin zon Almost fr-lctron modl Bnds ffctiv mss Hols Trnsltionl symmtry: Bloch thorm On-lctron Schrödingr qution ch stt cn ccommo up to lctrons: If Vr is priodic function:
I. The Connection between Spectroscopy and Quantum Mechanics
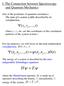 I. Th Connction twn Spctroscopy nd Quntum Mchnics On of th postults of quntum mchnics: Th stt of systm is fully dscrid y its wvfunction, Ψ( r1, r,..., t) whr r 1, r, tc. r th coordints of th constitunt
I. Th Connction twn Spctroscopy nd Quntum Mchnics On of th postults of quntum mchnics: Th stt of systm is fully dscrid y its wvfunction, Ψ( r1, r,..., t) whr r 1, r, tc. r th coordints of th constitunt
Trigonometric functions
 Robrto s Nots on Diffrntial Calculus Captr 5: Drivativs of transcndntal functions Sction 5 Drivativs of Trigonomtric functions Wat you nd to know alrady: Basic trigonomtric limits, t dfinition of drivativ,
Robrto s Nots on Diffrntial Calculus Captr 5: Drivativs of transcndntal functions Sction 5 Drivativs of Trigonomtric functions Wat you nd to know alrady: Basic trigonomtric limits, t dfinition of drivativ,
Lectures 2 & 3 - Population ecology mathematics refresher
 Lcturs & - Poultio cology mthmtics rrshr To s th mov ito vloig oultio mols, th olloig mthmtics crisht is suli I i out r mthmtics ttook! Eots logrithms i i q q q q q q ( tims) / c c c c ) ( ) ( Clculus
Lcturs & - Poultio cology mthmtics rrshr To s th mov ito vloig oultio mols, th olloig mthmtics crisht is suli I i out r mthmtics ttook! Eots logrithms i i q q q q q q ( tims) / c c c c ) ( ) ( Clculus
Recall that by Theorems 10.3 and 10.4 together provide us the estimate o(n2 ), S(q) q 9, q=1
 Chaptr 11 Th singular sris Rcall that by Thorms 10 and 104 togthr provid us th stimat 9 4 n 2 111 Rn = SnΓ 2 + on2, whr th singular sris Sn was dfind in Chaptr 10 as Sn = q=1 Sq q 9, with Sq = 1 a q gcda,q=1
Chaptr 11 Th singular sris Rcall that by Thorms 10 and 104 togthr provid us th stimat 9 4 n 2 111 Rn = SnΓ 2 + on2, whr th singular sris Sn was dfind in Chaptr 10 as Sn = q=1 Sq q 9, with Sq = 1 a q gcda,q=1
Continuous Random Variables: Basics
 Continuous Rndom Vrils: Bsics Brlin Chn Dprtmnt o Computr Scinc & Inormtion Enginring Ntionl Tiwn Norml Univrsit Rrnc: - D.. Brtss, J. N. Tsitsilis, Introduction to roilit, Sctions 3.-3.3 Continuous Rndom
Continuous Rndom Vrils: Bsics Brlin Chn Dprtmnt o Computr Scinc & Inormtion Enginring Ntionl Tiwn Norml Univrsit Rrnc: - D.. Brtss, J. N. Tsitsilis, Introduction to roilit, Sctions 3.-3.3 Continuous Rndom
The Matrix Exponential
 Th Matrix Exponntial (with xrciss) by Dan Klain Vrsion 28928 Corrctions and commnts ar wlcom Th Matrix Exponntial For ach n n complx matrix A, dfin th xponntial of A to b th matrix () A A k I + A + k!
Th Matrix Exponntial (with xrciss) by Dan Klain Vrsion 28928 Corrctions and commnts ar wlcom Th Matrix Exponntial For ach n n complx matrix A, dfin th xponntial of A to b th matrix () A A k I + A + k!
PH427/PH527: Periodic systems Spring Overview of the PH427 website (syllabus, assignments etc.) 2. Coupled oscillations.
 Dy : Mondy 5 inuts. Ovrviw of th PH47 wsit (syllus, ssignnts tc.). Coupld oscilltions W gin with sss coupld y Hook's Lw springs nd find th possil longitudinl) otion of such syst. W ll xtnd this to finit
Dy : Mondy 5 inuts. Ovrviw of th PH47 wsit (syllus, ssignnts tc.). Coupld oscilltions W gin with sss coupld y Hook's Lw springs nd find th possil longitudinl) otion of such syst. W ll xtnd this to finit
SOME ELEMENTARY PROPERTIES OF THE DISTRIBUTION OF THE NUMBERS OF POINTS ON ELLIPTIC CURVES OVER A FINITE PRIME FIELD
 SOME ELEMENTARY PROPERTIES OF THE DISTRIBUTION OF THE NUMBERS OF POINTS ON ELLIPTIC CURVES OVER A FINITE PRIME FIELD SAIYING HE AND J MC LAUGHLIN Abstract Lt 5 b a rim and for a, b F, lt E a,b dnot th
SOME ELEMENTARY PROPERTIES OF THE DISTRIBUTION OF THE NUMBERS OF POINTS ON ELLIPTIC CURVES OVER A FINITE PRIME FIELD SAIYING HE AND J MC LAUGHLIN Abstract Lt 5 b a rim and for a, b F, lt E a,b dnot th
CSE303 - Introduction to the Theory of Computing Sample Solutions for Exercises on Finite Automata
 CSE303 - Introduction to th Thory of Computing Smpl Solutions for Exrciss on Finit Automt Exrcis 2.1.1 A dtrministic finit utomton M ccpts th mpty string (i.., L(M)) if nd only if its initil stt is finl
CSE303 - Introduction to th Thory of Computing Smpl Solutions for Exrciss on Finit Automt Exrcis 2.1.1 A dtrministic finit utomton M ccpts th mpty string (i.., L(M)) if nd only if its initil stt is finl
CSE 373: AVL trees. Warmup: Warmup. Interlude: Exploring the balance invariant. AVL Trees: Invariants. AVL tree invariants review
 rmup CSE 7: AVL trs rmup: ht is n invrint? Mihl L Friy, Jn 9, 0 ht r th AVL tr invrints, xtly? Disuss with your nighor. AVL Trs: Invrints Intrlu: Exploring th ln invrint Cor i: xtr invrint to BSTs tht
rmup CSE 7: AVL trs rmup: ht is n invrint? Mihl L Friy, Jn 9, 0 ht r th AVL tr invrints, xtly? Disuss with your nighor. AVL Trs: Invrints Intrlu: Exploring th ln invrint Cor i: xtr invrint to BSTs tht
CBSE 2015 FOREIGN EXAMINATION
 CBSE 05 FOREIGN EXAMINATION (Sris SSO Cod No 65//F, 65//F, 65//F : Forign Rgion) Not tht ll th sts hv sm qustions Onl thir squnc of pprnc is diffrnt M Mrks : 00 Tim Allowd : Hours SECTION A Q0 Find th
CBSE 05 FOREIGN EXAMINATION (Sris SSO Cod No 65//F, 65//F, 65//F : Forign Rgion) Not tht ll th sts hv sm qustions Onl thir squnc of pprnc is diffrnt M Mrks : 00 Tim Allowd : Hours SECTION A Q0 Find th
PRIMES AND QUADRATIC RECIPROCITY
 PRIMES AND QUADRATIC RECIPROCITY ANGELICA WONG Abstrct We discuss number theory with the ultimte gol of understnding udrtic recirocity We begin by discussing Fermt s Little Theorem, the Chinese Reminder
PRIMES AND QUADRATIC RECIPROCITY ANGELICA WONG Abstrct We discuss number theory with the ultimte gol of understnding udrtic recirocity We begin by discussing Fermt s Little Theorem, the Chinese Reminder
Tangram Fractions Overview: Students will analyze standard and nonstandard
 ACTIVITY 1 Mtrils: Stunt opis o tnrm mstrs trnsprnis o tnrm mstrs sissors PROCEDURE Skills: Dsriin n nmin polyons Stuyin onrun Comprin rtions Tnrm Frtions Ovrviw: Stunts will nlyz stnr n nonstnr tnrms
ACTIVITY 1 Mtrils: Stunt opis o tnrm mstrs trnsprnis o tnrm mstrs sissors PROCEDURE Skills: Dsriin n nmin polyons Stuyin onrun Comprin rtions Tnrm Frtions Ovrviw: Stunts will nlyz stnr n nonstnr tnrms
Section 3: Antiderivatives of Formulas
 Chptr Th Intgrl Appli Clculus 96 Sction : Antirivtivs of Formuls Now w cn put th is of rs n ntirivtivs togthr to gt wy of vluting finit intgrls tht is ct n oftn sy. To vlut finit intgrl f(t) t, w cn fin
Chptr Th Intgrl Appli Clculus 96 Sction : Antirivtivs of Formuls Now w cn put th is of rs n ntirivtivs togthr to gt wy of vluting finit intgrls tht is ct n oftn sy. To vlut finit intgrl f(t) t, w cn fin
The Matrix Exponential
 Th Matrix Exponntial (with xrciss) by D. Klain Vrsion 207.0.05 Corrctions and commnts ar wlcom. Th Matrix Exponntial For ach n n complx matrix A, dfin th xponntial of A to b th matrix A A k I + A + k!
Th Matrix Exponntial (with xrciss) by D. Klain Vrsion 207.0.05 Corrctions and commnts ar wlcom. Th Matrix Exponntial For ach n n complx matrix A, dfin th xponntial of A to b th matrix A A k I + A + k!
OpenMx Matrices and Operators
 OpnMx Mtris n Oprtors Sr Mln Mtris: t uilin loks Mny typs? Dnots r lmnt mxmtrix( typ= Zro", nrow=, nol=, nm="" ) mxmtrix( typ= Unit", nrow=, nol=, nm="" ) mxmtrix( typ= Int", nrow=, nol=, nm="" ) mxmtrix(
OpnMx Mtris n Oprtors Sr Mln Mtris: t uilin loks Mny typs? Dnots r lmnt mxmtrix( typ= Zro", nrow=, nol=, nm="" ) mxmtrix( typ= Unit", nrow=, nol=, nm="" ) mxmtrix( typ= Int", nrow=, nol=, nm="" ) mxmtrix(
Linear Algebra Existence of the determinant. Expansion according to a row.
 Lir Algbr 2270 1 Existc of th dtrmit. Expsio ccordig to row. W dfi th dtrmit for 1 1 mtrics s dt([]) = (1) It is sy chck tht it stisfis D1)-D3). For y othr w dfi th dtrmit s follows. Assumig th dtrmit
Lir Algbr 2270 1 Existc of th dtrmit. Expsio ccordig to row. W dfi th dtrmit for 1 1 mtrics s dt([]) = (1) It is sy chck tht it stisfis D1)-D3). For y othr w dfi th dtrmit s follows. Assumig th dtrmit
MASSACHUSETTS INSTITUTE OF TECHNOLOGY HAYSTACK OBSERVATORY WESTFORD, MASSACHUSETTS
 VSRT MEMO #05 MASSACHUSETTS INSTITUTE OF TECHNOLOGY HAYSTACK OBSERVATORY WESTFORD, MASSACHUSETTS 01886 Fbrury 3, 009 Tlphon: 781-981-507 Fx: 781-981-0590 To: VSRT Group From: Aln E.E. Rogrs Subjct: Simplifid
VSRT MEMO #05 MASSACHUSETTS INSTITUTE OF TECHNOLOGY HAYSTACK OBSERVATORY WESTFORD, MASSACHUSETTS 01886 Fbrury 3, 009 Tlphon: 781-981-507 Fx: 781-981-0590 To: VSRT Group From: Aln E.E. Rogrs Subjct: Simplifid
1 Introduction to Modulo 7 Arithmetic
 1 Introution to Moulo 7 Arithmti Bor w try our hn t solvin som hr Moulr KnKns, lt s tk los look t on moulr rithmti, mo 7 rithmti. You ll s in this sminr tht rithmti moulo prim is quit irnt rom th ons w
1 Introution to Moulo 7 Arithmti Bor w try our hn t solvin som hr Moulr KnKns, lt s tk los look t on moulr rithmti, mo 7 rithmti. You ll s in this sminr tht rithmti moulo prim is quit irnt rom th ons w
Quadratic Residues. Chapter Quadratic residues
 Chter 8 Qudrtic Residues 8. Qudrtic residues Let n>be given ositive integer, nd gcd, n. We sy tht Z n is qudrtic residue mod n if the congruence x mod n is solvble. Otherwise, is clled qudrtic nonresidue
Chter 8 Qudrtic Residues 8. Qudrtic residues Let n>be given ositive integer, nd gcd, n. We sy tht Z n is qudrtic residue mod n if the congruence x mod n is solvble. Otherwise, is clled qudrtic nonresidue
SOLVED EXAMPLES. be the foci of an ellipse with eccentricity e. For any point P on the ellipse, prove that. tan
 LOCUS 58 SOLVED EXAMPLES Empl Lt F n F th foci of n llips with ccntricit. For n point P on th llips, prov tht tn PF F tn PF F Assum th llips to, n lt P th point (, sin ). P(, sin ) F F F = (-, 0) F = (,
LOCUS 58 SOLVED EXAMPLES Empl Lt F n F th foci of n llips with ccntricit. For n point P on th llips, prov tht tn PF F tn PF F Assum th llips to, n lt P th point (, sin ). P(, sin ) F F F = (-, 0) F = (,
(2) If we multiplied a row of B by λ, then the value is also multiplied by λ(here lambda could be 0). namely
 . DETERMINANT.. Dtrminnt. Introution:I you think row vtor o mtrix s oorint o vtors in sp, thn th gomtri mning o th rnk o th mtrix is th imnsion o th prlllppi spnn y thm. But w r not only r out th imnsion,
. DETERMINANT.. Dtrminnt. Introution:I you think row vtor o mtrix s oorint o vtors in sp, thn th gomtri mning o th rnk o th mtrix is th imnsion o th prlllppi spnn y thm. But w r not only r out th imnsion,
cycle that does not cross any edges (including its own), then it has at least
 W prov th following thorm: Thorm If a K n is drawn in th plan in such a way that it has a hamiltonian cycl that dos not cross any dgs (including its own, thn it has at last n ( 4 48 π + O(n crossings Th
W prov th following thorm: Thorm If a K n is drawn in th plan in such a way that it has a hamiltonian cycl that dos not cross any dgs (including its own, thn it has at last n ( 4 48 π + O(n crossings Th
A L A BA M A L A W R E V IE W
 A L A BA M A L A W R E V IE W Volume 52 Fall 2000 Number 1 B E F O R E D I S A B I L I T Y C I V I L R I G HT S : C I V I L W A R P E N S I O N S A N D TH E P O L I T I C S O F D I S A B I L I T Y I N
A L A BA M A L A W R E V IE W Volume 52 Fall 2000 Number 1 B E F O R E D I S A B I L I T Y C I V I L R I G HT S : C I V I L W A R P E N S I O N S A N D TH E P O L I T I C S O F D I S A B I L I T Y I N
Winter 2016 COMP-250: Introduction to Computer Science. Lecture 23, April 5, 2016
 Wintr 2016 COMP-250: Introduction to Computr Scinc Lctur 23, April 5, 2016 Commnt out input siz 2) Writ ny lgorithm tht runs in tim Θ(n 2 log 2 n) in wors cs. Explin why this is its running tim. I don
Wintr 2016 COMP-250: Introduction to Computr Scinc Lctur 23, April 5, 2016 Commnt out input siz 2) Writ ny lgorithm tht runs in tim Θ(n 2 log 2 n) in wors cs. Explin why this is its running tim. I don
Duke Math Meet
 Duke Mth Meet 01-14 Power Round Qudrtic Residues nd Prime Numers For integers nd, we write to indicte tht evenly divides, nd to indicte tht does not divide For exmle, 4 nd 4 Let e rime numer An integer
Duke Mth Meet 01-14 Power Round Qudrtic Residues nd Prime Numers For integers nd, we write to indicte tht evenly divides, nd to indicte tht does not divide For exmle, 4 nd 4 Let e rime numer An integer
MAT3707. Tutorial letter 201/1/2017 DISCRETE MATHEMATICS: COMBINATORICS. Semester 1. Department of Mathematical Sciences MAT3707/201/1/2017
 MAT3707/201/1/2017 Tutoril lttr 201/1/2017 DISCRETE MATHEMATICS: COMBINATORICS MAT3707 Smstr 1 Dprtmnt o Mtmtil Sins SOLUTIONS TO ASSIGNMENT 01 BARCODE Din tomorrow. univrsity o sout ri SOLUTIONS TO ASSIGNMENT
MAT3707/201/1/2017 Tutoril lttr 201/1/2017 DISCRETE MATHEMATICS: COMBINATORICS MAT3707 Smstr 1 Dprtmnt o Mtmtil Sins SOLUTIONS TO ASSIGNMENT 01 BARCODE Din tomorrow. univrsity o sout ri SOLUTIONS TO ASSIGNMENT
1 Input-Output Stability
 Inut-Outut Stability Inut-outut stability analysis allows us to analyz th stability of a givn syst without knowing th intrnal stat x of th syst. Bfor going forward, w hav to introduc so inut-outut athatical
Inut-Outut Stability Inut-outut stability analysis allows us to analyz th stability of a givn syst without knowing th intrnal stat x of th syst. Bfor going forward, w hav to introduc so inut-outut athatical
Math 61 : Discrete Structures Final Exam Instructor: Ciprian Manolescu. You have 180 minutes.
 Nm: UCA ID Numr: Stion lttr: th 61 : Disrt Struturs Finl Exm Instrutor: Ciprin nolsu You hv 180 minuts. No ooks, nots or lultors r llow. Do not us your own srth ppr. 1. (2 points h) Tru/Fls: Cirl th right
Nm: UCA ID Numr: Stion lttr: th 61 : Disrt Struturs Finl Exm Instrutor: Ciprin nolsu You hv 180 minuts. No ooks, nots or lultors r llow. Do not us your own srth ppr. 1. (2 points h) Tru/Fls: Cirl th right
Supplement 4 Permutations, Legendre symbol and quadratic reciprocity
 Sulement 4 Permuttions, Legendre symbol nd qudrtic recirocity 1. Permuttions. If S is nite set contining n elements then ermuttion of S is one to one ming of S onto S. Usully S is the set f1; ; :::; ng
Sulement 4 Permuttions, Legendre symbol nd qudrtic recirocity 1. Permuttions. If S is nite set contining n elements then ermuttion of S is one to one ming of S onto S. Usully S is the set f1; ; :::; ng
Kronecker-Jacobi symbol and Quadratic Reciprocity. Q b /Q p
 Kronecker-Jcoi symol nd Qudrtic Recirocity Let Q e the field of rtionl numers, nd let Q, 0. For ositive rime integer, the Artin symol Q /Q hs the vlue 1 if Q is the slitting field of in Q, 0 if is rmified
Kronecker-Jcoi symol nd Qudrtic Recirocity Let Q e the field of rtionl numers, nd let Q, 0. For ositive rime integer, the Artin symol Q /Q hs the vlue 1 if Q is the slitting field of in Q, 0 if is rmified
3-2-1 ANN Architecture
 ARTIFICIAL NEURAL NETWORKS (ANNs) Profssor Tom Fomby Dpartmnt of Economics Soutrn Mtodist Univrsity Marc 008 Artificial Nural Ntworks (raftr ANNs) can b usd for itr prdiction or classification problms.
ARTIFICIAL NEURAL NETWORKS (ANNs) Profssor Tom Fomby Dpartmnt of Economics Soutrn Mtodist Univrsity Marc 008 Artificial Nural Ntworks (raftr ANNs) can b usd for itr prdiction or classification problms.
Revisiting what you have learned in Advanced Mathematical Analysis
 Fourir sris Rvisiing wh you hv lrnd in Advncd Mhmicl Anlysis L f x b priodic funcion of priod nd is ingrbl ovr priod. f x cn b rprsnd by rigonomric sris, f x n cos nx bn sin nx n cos x b sin x cosx b whr
Fourir sris Rvisiing wh you hv lrnd in Advncd Mhmicl Anlysis L f x b priodic funcion of priod nd is ingrbl ovr priod. f x cn b rprsnd by rigonomric sris, f x n cos nx bn sin nx n cos x b sin x cosx b whr
Garnir Polynomial and their Properties
 Univrsity of Cliforni, Dvis Dprtmnt of Mthmtis Grnir Polynomil n thir Proprtis Author: Yu Wng Suprvisor: Prof. Gorsky Eugny My 8, 07 Grnir Polynomil n thir Proprtis Yu Wng mil: uywng@uvis.u. In this ppr,
Univrsity of Cliforni, Dvis Dprtmnt of Mthmtis Grnir Polynomil n thir Proprtis Author: Yu Wng Suprvisor: Prof. Gorsky Eugny My 8, 07 Grnir Polynomil n thir Proprtis Yu Wng mil: uywng@uvis.u. In this ppr,
Weighted Matching and Linear Programming
 Wightd Mtching nd Linr Progrmming Jonthn Turnr Mrch 19, 01 W v sn tht mximum siz mtchings cn b found in gnrl grphs using ugmnting pths. In principl, this sm pproch cn b pplid to mximum wight mtchings.
Wightd Mtching nd Linr Progrmming Jonthn Turnr Mrch 19, 01 W v sn tht mximum siz mtchings cn b found in gnrl grphs using ugmnting pths. In principl, this sm pproch cn b pplid to mximum wight mtchings.
I N A C O M P L E X W O R L D
 IS L A M I C E C O N O M I C S I N A C O M P L E X W O R L D E x p l o r a t i o n s i n A g-b eanste d S i m u l a t i o n S a m i A l-s u w a i l e m 1 4 2 9 H 2 0 0 8 I s l a m i c D e v e l o p m e
IS L A M I C E C O N O M I C S I N A C O M P L E X W O R L D E x p l o r a t i o n s i n A g-b eanste d S i m u l a t i o n S a m i A l-s u w a i l e m 1 4 2 9 H 2 0 0 8 I s l a m i c D e v e l o p m e
CSE 373: More on graphs; DFS and BFS. Michael Lee Wednesday, Feb 14, 2018
 CSE 373: Mor on grphs; DFS n BFS Mihl L Wnsy, F 14, 2018 1 Wrmup Wrmup: Disuss with your nighor: Rmin your nighor: wht is simpl grph? Suppos w hv simpl, irt grph with x nos. Wht is th mximum numr of gs
CSE 373: Mor on grphs; DFS n BFS Mihl L Wnsy, F 14, 2018 1 Wrmup Wrmup: Disuss with your nighor: Rmin your nighor: wht is simpl grph? Suppos w hv simpl, irt grph with x nos. Wht is th mximum numr of gs
u x A j Stress in the Ocean
 Strss in t Ocan T tratmnt of strss and strain in fluids is comlicatd and somwat bond t sco of tis class. Tos rall intrstd sould look into tis rtr in Batclor Introduction to luid Dnamics givn as a rfrnc
Strss in t Ocan T tratmnt of strss and strain in fluids is comlicatd and somwat bond t sco of tis class. Tos rall intrstd sould look into tis rtr in Batclor Introduction to luid Dnamics givn as a rfrnc
A Study of the Solutions of the Lotka Volterra. Prey Predator System Using Perturbation. Technique
 Inrnionl hmil orum no. 667-67 Sud of h Soluions of h o Volrr r rdor Ssm Using rurion Thniqu D.Vnu ol Ro * D. of lid hmis IT Collg of Sin IT Univrsi Vishnm.. Indi Y... Thorni D. of lid hmis IT Collg of
Inrnionl hmil orum no. 667-67 Sud of h Soluions of h o Volrr r rdor Ssm Using rurion Thniqu D.Vnu ol Ro * D. of lid hmis IT Collg of Sin IT Univrsi Vishnm.. Indi Y... Thorni D. of lid hmis IT Collg of
Case Study VI Answers PHA 5127 Fall 2006
 Qustion. A ptint is givn 250 mg immit-rls thophyllin tblt (Tblt A). A wk ltr, th sm ptint is givn 250 mg sustin-rls thophyllin tblt (Tblt B). Th tblts follow on-comprtmntl mol n hv first-orr bsorption
Qustion. A ptint is givn 250 mg immit-rls thophyllin tblt (Tblt A). A wk ltr, th sm ptint is givn 250 mg sustin-rls thophyllin tblt (Tblt B). Th tblts follow on-comprtmntl mol n hv first-orr bsorption
Introduction to Arithmetic Geometry Fall 2013 Lecture #20 11/14/2013
 18.782 Introduction to Arithmtic Gomtry Fall 2013 Lctur #20 11/14/2013 20.1 Dgr thorm for morphisms of curvs Lt us rstat th thorm givn at th nd of th last lctur, which w will now prov. Thorm 20.1. Lt φ:
18.782 Introduction to Arithmtic Gomtry Fall 2013 Lctur #20 11/14/2013 20.1 Dgr thorm for morphisms of curvs Lt us rstat th thorm givn at th nd of th last lctur, which w will now prov. Thorm 20.1. Lt φ:
C-Curves. An alternative to the use of hyperbolic decline curves S E R A F I M. Prepared by: Serafim Ltd. P. +44 (0)
 An ltntiv to th us of hypolic dclin cuvs Ppd y: Sfim Ltd S E R A F I M info@sfimltd.com P. +44 (02890 4206 www.sfimltd.com Contnts Contnts... i Intoduction... Initil ssumptions... Solving fo cumultiv...
An ltntiv to th us of hypolic dclin cuvs Ppd y: Sfim Ltd S E R A F I M info@sfimltd.com P. +44 (02890 4206 www.sfimltd.com Contnts Contnts... i Intoduction... Initil ssumptions... Solving fo cumultiv...
EEO 401 Digital Signal Processing Prof. Mark Fowler
 EEO 401 Digital Signal Procssing Prof. Mark Fowlr Dtails of th ot St #19 Rading Assignmnt: Sct. 7.1.2, 7.1.3, & 7.2 of Proakis & Manolakis Dfinition of th So Givn signal data points x[n] for n = 0,, -1
EEO 401 Digital Signal Procssing Prof. Mark Fowlr Dtails of th ot St #19 Rading Assignmnt: Sct. 7.1.2, 7.1.3, & 7.2 of Proakis & Manolakis Dfinition of th So Givn signal data points x[n] for n = 0,, -1
1 1D heat and wave equations on a finite interval
 1 1D het nd wve equtions on finite intervl In this section we consider generl method of seprtion of vribles nd its pplictions to solving het eqution nd wve eqution on finite intervl ( 1, 2. Since by trnsltion
1 1D het nd wve equtions on finite intervl In this section we consider generl method of seprtion of vribles nd its pplictions to solving het eqution nd wve eqution on finite intervl ( 1, 2. Since by trnsltion
Lecture 4. Conic section
 Lctur 4 Conic sction Conic sctions r locus of points whr distncs from fixd point nd fixd lin r in constnt rtio. Conic sctions in D r curvs which r locus of points whor position vctor r stisfis r r. whr
Lctur 4 Conic sction Conic sctions r locus of points whr distncs from fixd point nd fixd lin r in constnt rtio. Conic sctions in D r curvs which r locus of points whor position vctor r stisfis r r. whr
Split-plot Experiments and Hierarchical Data
 Split-plot Exprimnts nd Hirrchicl Dt Introduction Alx Stlzlni invstigtd th ffcts of fding rgim for bf nimls nd muscl typ on th tndrnss of mt. H ssignd ight nimls to ch of thr trtmnts. Th trtmnts wr th
Split-plot Exprimnts nd Hirrchicl Dt Introduction Alx Stlzlni invstigtd th ffcts of fding rgim for bf nimls nd muscl typ on th tndrnss of mt. H ssignd ight nimls to ch of thr trtmnts. Th trtmnts wr th
Chapter 10. The singular integral Introducing S(n) and J(n)
 Chaptr Th singular intgral Our aim in this chaptr is to rplac th functions S (n) and J (n) by mor convnint xprssions; ths will b calld th singular sris S(n) and th singular intgral J(n). This will b don
Chaptr Th singular intgral Our aim in this chaptr is to rplac th functions S (n) and J (n) by mor convnint xprssions; ths will b calld th singular sris S(n) and th singular intgral J(n). This will b don
k and v = v 1 j + u 3 i + v 2
 ORTHOGONAL FUNCTIONS AND FOURIER SERIES Orthogonl functions A function cn e considered to e generliztion of vector. Thus the vector concets like the inner roduct nd orthogonlity of vectors cn e extended
ORTHOGONAL FUNCTIONS AND FOURIER SERIES Orthogonl functions A function cn e considered to e generliztion of vector. Thus the vector concets like the inner roduct nd orthogonlity of vectors cn e extended
STEADY STATE ERRORS IN UNITY FEEDBACK CONTROL SYSTEMS
 VU -lrning Courwr Control Enginring (ME55) SEADY SAE ERRORS I UIY FEEDBAC COROL SYSEMS Error in control yt y ttriutd to ny fctor. Chng in th rfrnc inut will cu unoidl rror during trnint riod, nd lo cu
VU -lrning Courwr Control Enginring (ME55) SEADY SAE ERRORS I UIY FEEDBAC COROL SYSEMS Error in control yt y ttriutd to ny fctor. Chng in th rfrnc inut will cu unoidl rror during trnint riod, nd lo cu
McGill University Math 354: Honors Analysis 3 Fall 2012 Solutions to selected Exercises. g(x) 2 dx 1 2 a
 McGill University Mth 354: Honors Anlysis 3 Fll 2012 Assignment 1 Solutions to selected Exercises Exercise 1. (i) Verify the identity for ny two sets of comlex numers { 1,..., n } nd { 1,..., n } ( n )
McGill University Mth 354: Honors Anlysis 3 Fll 2012 Assignment 1 Solutions to selected Exercises Exercise 1. (i) Verify the identity for ny two sets of comlex numers { 1,..., n } nd { 1,..., n } ( n )
GUC (Dr. Hany Hammad) 9/28/2016
 U (r. Hny Hd) 9/8/06 ctur # 3 ignl flow grphs (cont.): ignl-flow grph rprsnttion of : ssiv sgl-port dvic. owr g qutions rnsducr powr g. Oprtg powr g. vill powr g. ppliction to Ntwork nlyzr lirtion. Nois
U (r. Hny Hd) 9/8/06 ctur # 3 ignl flow grphs (cont.): ignl-flow grph rprsnttion of : ssiv sgl-port dvic. owr g qutions rnsducr powr g. Oprtg powr g. vill powr g. ppliction to Ntwork nlyzr lirtion. Nois
LECTURE 10: JACOBI SYMBOL
 LECTURE 0: JACOBI SYMBOL The Jcobi symbol We wish to generlise the Legendre symbol to ccomodte comosite moduli Definition Let be n odd ositive integer, nd suose tht s, where the i re rime numbers not necessrily
LECTURE 0: JACOBI SYMBOL The Jcobi symbol We wish to generlise the Legendre symbol to ccomodte comosite moduli Definition Let be n odd ositive integer, nd suose tht s, where the i re rime numbers not necessrily
Families of Solutions to Bernoulli ODEs
 In the fmily of solutions to the differentil eqution y ry dx + = it is shown tht vrition of the initil condition y( 0 = cuses horizontl shift in the solution curve y = f ( x, rther thn the verticl shift
In the fmily of solutions to the differentil eqution y ry dx + = it is shown tht vrition of the initil condition y( 0 = cuses horizontl shift in the solution curve y = f ( x, rther thn the verticl shift
More Foundations. Undirected Graphs. Degree. A Theorem. Graphs, Products, & Relations
 Mr Funtins Grphs, Pruts, & Rltins Unirt Grphs An unirt grph is pir f 1. A st f ns 2. A st f gs (whr n g is st f tw ns*) Friy, Sptmr 2, 2011 Ring: Sipsr 0.2 ginning f 0.4; Stughtn 1.1.5 ({,,,,}, {{,}, {,},
Mr Funtins Grphs, Pruts, & Rltins Unirt Grphs An unirt grph is pir f 1. A st f ns 2. A st f gs (whr n g is st f tw ns*) Friy, Sptmr 2, 2011 Ring: Sipsr 0.2 ginning f 0.4; Stughtn 1.1.5 ({,,,,}, {{,}, {,},
#A27 INTEGERS 12 (2012) SUM-PRODUCTS ESTIMATES WITH SEVERAL SETS AND APPLICATIONS
 #A27 INTEGERS 12 (2012) SUM-PRODUCTS ESTIMATES WITH SEVERAL SETS AND APPLICATIONS Antal Balog Alfréd Rényi Institut of Mathmatics, Hungarian Acadmy of Scincs, Budast, Hungary balog@rnyihu Kvin A Broughan
#A27 INTEGERS 12 (2012) SUM-PRODUCTS ESTIMATES WITH SEVERAL SETS AND APPLICATIONS Antal Balog Alfréd Rényi Institut of Mathmatics, Hungarian Acadmy of Scincs, Budast, Hungary balog@rnyihu Kvin A Broughan
Fourier Transforms and the Wave Equation. Key Mathematics: More Fourier transform theory, especially as applied to solving the wave equation.
 Lur 7 Fourir Transforms and th Wav Euation Ovrviw and Motivation: W first discuss a fw faturs of th Fourir transform (FT), and thn w solv th initial-valu problm for th wav uation using th Fourir transform
Lur 7 Fourir Transforms and th Wav Euation Ovrviw and Motivation: W first discuss a fw faturs of th Fourir transform (FT), and thn w solv th initial-valu problm for th wav uation using th Fourir transform
Page 1. Question 19.1b Electric Charge II Question 19.2a Conductors I. ConcepTest Clicker Questions Chapter 19. Physics, 4 th Edition James S.
 ConTst Clikr ustions Chtr 19 Physis, 4 th Eition Jms S. Wlkr ustion 19.1 Two hrg blls r rlling h othr s thy hng from th iling. Wht n you sy bout thir hrgs? Eltri Chrg I on is ositiv, th othr is ngtiv both
ConTst Clikr ustions Chtr 19 Physis, 4 th Eition Jms S. Wlkr ustion 19.1 Two hrg blls r rlling h othr s thy hng from th iling. Wht n you sy bout thir hrgs? Eltri Chrg I on is ositiv, th othr is ngtiv both
The Z transform techniques
 h Z trnfor tchniqu h Z trnfor h th rol in dicrt yt tht th Lplc trnfor h in nlyi of continuou yt. h Z trnfor i th principl nlyticl tool for ingl-loop dicrt-ti yt. h Z trnfor h Z trnfor i to dicrt-ti yt
h Z trnfor tchniqu h Z trnfor h th rol in dicrt yt tht th Lplc trnfor h in nlyi of continuou yt. h Z trnfor i th principl nlyticl tool for ingl-loop dicrt-ti yt. h Z trnfor h Z trnfor i to dicrt-ti yt
# 1 ' 10 ' 100. Decimal point = 4 hundred. = 6 tens (or sixty) = 5 ones (or five) = 2 tenths. = 7 hundredths.
 How os it work? Pl vlu o imls rprsnt prts o whol numr or ojt # 0 000 Tns o thousns # 000 # 00 Thousns Hunrs Tns Ons # 0 Diml point st iml pl: ' 0 # 0 on tnth n iml pl: ' 0 # 00 on hunrth r iml pl: ' 0
How os it work? Pl vlu o imls rprsnt prts o whol numr or ojt # 0 000 Tns o thousns # 000 # 00 Thousns Hunrs Tns Ons # 0 Diml point st iml pl: ' 0 # 0 on tnth n iml pl: ' 0 # 00 on hunrth r iml pl: ' 0
set is not closed under matrix [ multiplication, ] and does not form a group.
![set is not closed under matrix [ multiplication, ] and does not form a group. set is not closed under matrix [ multiplication, ] and does not form a group.](/thumbs/78/78412113.jpg) Prolem 2.3: Which of the following collections of 2 2 mtrices with rel entries form groups under [ mtrix ] multipliction? i) Those of the form for which c d 2 Answer: The set of such mtrices is not closed
Prolem 2.3: Which of the following collections of 2 2 mtrices with rel entries form groups under [ mtrix ] multipliction? i) Those of the form for which c d 2 Answer: The set of such mtrices is not closed
Single Correct Type. cos z + k, then the value of k equals. dx = 2 dz. (a) 1 (b) 0 (c)1 (d) 2 (code-v2t3paq10) l (c) ( l ) x.
 IIT JEE/AIEEE MATHS y SUHAAG SIR Bhopl, Ph. (755)3 www.kolsss.om Qusion. & Soluion. In. Cl. Pg: of 6 TOPIC = INTEGRAL CALCULUS Singl Corr Typ 3 3 3 Qu.. L f () = sin + sin + + sin + hn h primiiv of f()
IIT JEE/AIEEE MATHS y SUHAAG SIR Bhopl, Ph. (755)3 www.kolsss.om Qusion. & Soluion. In. Cl. Pg: of 6 TOPIC = INTEGRAL CALCULUS Singl Corr Typ 3 3 3 Qu.. L f () = sin + sin + + sin + hn h primiiv of f()
Walk Like a Mathematician Learning Task:
 Gori Dprtmnt of Euction Wlk Lik Mthmticin Lrnin Tsk: Mtrics llow us to prform mny usful mthmticl tsks which orinrily rquir lr numbr of computtions. Som typs of problms which cn b on fficintly with mtrics
Gori Dprtmnt of Euction Wlk Lik Mthmticin Lrnin Tsk: Mtrics llow us to prform mny usful mthmticl tsks which orinrily rquir lr numbr of computtions. Som typs of problms which cn b on fficintly with mtrics
b. How many ternary words of length 23 with eight 0 s, nine 1 s and six 2 s?
 MATH 3012 Finl Exm, My 4, 2006, WTT Stunt Nm n ID Numr 1. All our prts o this prolm r onrn with trnry strings o lngth n, i.., wors o lngth n with lttrs rom th lpht {0, 1, 2}.. How mny trnry wors o lngth
MATH 3012 Finl Exm, My 4, 2006, WTT Stunt Nm n ID Numr 1. All our prts o this prolm r onrn with trnry strings o lngth n, i.., wors o lngth n with lttrs rom th lpht {0, 1, 2}.. How mny trnry wors o lngth
Lecture 12 Quantum chromodynamics (QCD) WS2010/11: Introduction to Nuclear and Particle Physics
 Lctur Quntum chromodynmics (QCD) WS/: Introduction to Nuclr nd Prticl Physics QCD Quntum chromodynmics (QCD) is thory of th strong intrction - bsd on color forc, fundmntl forc dscribing th intrctions of
Lctur Quntum chromodynmics (QCD) WS/: Introduction to Nuclr nd Prticl Physics QCD Quntum chromodynmics (QCD) is thory of th strong intrction - bsd on color forc, fundmntl forc dscribing th intrctions of
USA Mathematical Talent Search Round 1 Solutions Year 25 Academic Year
 1/1/5. Alex is trying to oen lock whose code is sequence tht is three letters long, with ech of the letters being one of A, B or C, ossibly reeted. The lock hs three buttons, lbeled A, B nd C. When the
1/1/5. Alex is trying to oen lock whose code is sequence tht is three letters long, with ech of the letters being one of A, B or C, ossibly reeted. The lock hs three buttons, lbeled A, B nd C. When the
CHAPTER 12. Finite-Volume (control-volume) Method-Introduction
 CHAPR 12 Finit-Volum (control-volum) Mthod-Introduction 12-1 Introduction (1) In dvloing ht hs bcom knon s th finit-volum mthod, th consrvtion rincils r lid to fixd rgion in sc knon s control volum, r
CHAPR 12 Finit-Volum (control-volum) Mthod-Introduction 12-1 Introduction (1) In dvloing ht hs bcom knon s th finit-volum mthod, th consrvtion rincils r lid to fixd rgion in sc knon s control volum, r
Minimum Spanning Trees
 Minimum Spnning Trs Minimum Spnning Trs Problm A town hs st of houss nd st of rods A rod conncts nd only houss A rod conncting houss u nd v hs rpir cost w(u, v) Gol: Rpir nough (nd no mor) rods such tht:
Minimum Spnning Trs Minimum Spnning Trs Problm A town hs st of houss nd st of rods A rod conncts nd only houss A rod conncting houss u nd v hs rpir cost w(u, v) Gol: Rpir nough (nd no mor) rods such tht:
Lagrangian Analysis of a Class of Quadratic Liénard-Type Oscillator Equations with Exponential-Type Restoring Force function
 agrangian Analysis of a Class of Quadratic iénard-ty Oscillator Equations wit Eonntial-Ty Rstoring Forc function J. Akand, D. K. K. Adjaï,.. Koudaoun,Y. J. F. Komaou,. D. onsia. Dartmnt of Pysics, Univrsity
agrangian Analysis of a Class of Quadratic iénard-ty Oscillator Equations wit Eonntial-Ty Rstoring Forc function J. Akand, D. K. K. Adjaï,.. Koudaoun,Y. J. F. Komaou,. D. onsia. Dartmnt of Pysics, Univrsity
