TechTest2014. Solutions Key. The Sierra Economics and Science Foundation
|
|
|
- Reginald Vincent Booth
- 5 years ago
- Views:
Transcription
1 TechTest014 Merit Scholarship Examination in the Sciences and Mathematics given on 5 April 014 and sponsored by The Sierra Economics and Science Foundation Solutions Key V8mar014 TechTest014 Solutions Key 1 / All Rights Reserved
2 Problem 1: Trigonometric Equation (5 points) Solve sin x + cos x = 1. Solution: Rewrite equation as sin x = 1 - cos x and square both sides. sin x1cos xcos x 1cos x1cos xcos x cos xcos xcos x cos x1 0. (50%) Then from cos x = 0 x = π/ 3π/. From cos x = 1 x = 0. Checking these solutions; For x = 0 sin x + cos x = = 1; for x = π/ sin x + cos x = = 1; for x = 3π/ sin x + cos x = = -1. Therefore the required solutions are x = 0 π/. The solution x = 3π/ is extraneous in that it arises from the squaring of both sides which does not satisfy the equation to be solved. (50%) Problem : ifferentiation (5 points) ax e Given y find dy. (Hint: express y as a function of subfunctions of x and use the 1 sin x dx appropriate derivative formula for that expression to simplify your work.) Solution: The most obvious re-expression of y is y = u(x)/v(x) giving dy 1du u dv 1 du dv v u dx u dx v dx v dx dx (33%) Substituting and taking the elementary derivatives du d ax ax dv d d e ae 1 sin x cos x cos xsin x dx dx dx dx dx dy 1 dx cos x ax ax dy e sin x cos x e a atan x. dx cos x cos x cos x ax ax then ae cos x e sin xcos x 4 (67%) V8mar014 TechTest014 Solutions Key / All Rights Reserved
3 3: Integration (15 points) It is easier to evaluate some definite integrals by using substitution to change the integration variable and then of course its commensurate limits. Consider the requirement to compute y b f ydy f ydy where now y = Φ(t). We presume that a simpler integration problem y1 a b would be to solve g t dt such that dy dy g t f y f t a dt noticing that substituting the dt new integrand g(t) into the integral would in effect cancel out the dt thereby computationally leaving the required dy of the original integral intact even though the new variable of integration is now t. The new limits a and b would be obtained from solving y 1 y = Φ(t). This approach also lets us integrate y mixed function integrals such as htdy where again y = Φ(t) which we now ask you to do in this y1 problem. (Hint: find dy and substitute in the integral.) Let y = 3t 4 t and calculate z 4t 1 dy. 0 Solution: First we reformulate the integrand and the integral s limits in terms of the single variable t. dy 6t 1 dt y t0 03t0 t0 t0 3t t yt1 43t 4 1 t1 3t1 t1 40 t (30%) 4 t1 The integral then becomes Working this out yields the four z 4t 1 dy 4t 1 6t 1 dt. 0 solutions to the integral for the two sets of upper and lower limits. (50%) t0 Then t t 1 zt t 4t t1 dt 8t t t z z t0 3 t t z 0 4 8t t t z t0 (0%) (We note that were such an integral encountered in a realworld problem then the solution set would most certainly be pruned by the problem s physical and/or temporal constraints.) V8mar014 TechTest014 Solutions Key 3 / All Rights Reserved
4 R Problem 4: Area of a Circle (10 points) erive the formula for the area of a circle of radius R given that its circumference C = πr. Solution: Student should draw picture to indicate understanding that the area of a circle is the sum of small isosceles triangles that becomes the integral of infinitesimal triangles as the apex angle Δθ is taken to the limit. (5%) The approximate area of the indicated triangle is R R A since for small Δθ the base and altitude of the triangle are approximately RΔθ and R and become the correct values in the limit. The concept here is to sum the small triangles to fill the circle by letting Δθ approach zero in Rd the limit. This is recognized as the integral over θ when the infinitesimal triangles of area fill the entire central angle of a circle from 0 to π radians. Performing the integration then gives the desired answer. Rd A lim Ai 0 0 (75%) R i R Problem 5: Volume of a Right Cone (10 points) r(h) R Δh h H erive the formula for the volume of a right cone of base radius R and height H. Solution: Again the student should draw the correct figure and indicate that the cone s volume is obtained in the limit from the sum of the volumes of circular discs of height Δh and decreasing radii which are a linear function r(h) of their perpendicular distance h from the base. (35%) V8mar014 TechTest014 Solutions Key 4 / All Rights Reserved
5 r h h R1 H H/ h H lim i h0 i 1 0 H 0 H h h R 1 H H 0 R H H V r h h r h dh R h 1 dh H dh H 3 3 R H (65%) Problem 6: The Price of a Bond (10 points) When issued a long term Treasury bond that yields (over its life) an annual coupon amount of C is sold for price P. This says that at issuance the bond has an interest percent yield of I = C/P. As interest rates go up and down the market price of the bond will change so that its coupon amount reflects the current market s interest rate. A 40%) If at a future time this interest rate becomes I + ΔI then what is the new market price of the bond? B 40%) Express the fractional (percent) change in a bond s price in terms of the fractional change in the interest rate. C 0%) If P = $10K C = $500 and I changes from 5% to 6% what is the percentage change in the market price of the bond? Solution: A) Let the new/changed price of the bond be P + ΔP. Then the new interest rate that the marketable bond must yield is I + ΔI = C/(P + ΔP). The new market price of the bond is then computed simply as P + ΔP = C/(I + ΔI). (40%) B) The fractional change in the interest rate is ΔI/I and the desired fractional change in the bond s price is ΔP /P. So using the solution to part A we want to find P I f P I PP C 1 I. P P I I I I P I I I I 1 P I I I I P I I I 1 P I I I I V8mar014 TechTest014 Solutions Key 5 / All Rights Reserved 1
6 From this we see the well-known fact that as interest rates rise bond prices fall and vice versa. (40%) C) Substituting the dollar amounts into the solution to part B gives I = $500/$10K = 0.05 and ΔI/I = 1%/5% = 0.0. Therefore 1 P I I % P I I (This says that the current market price of the face value $10K bond is now $ ) (0%) Problem 7: Galileo climbs the Tower of Pisa (5 points) Galileo is reputed to have climbed the leaning tower to settle once and for all Aristotle s claim that heavier objects fall to the ground faster. The experiment showed that neglecting air resistance both heavier and lighter masses were accelerated equally and hit the ground (almost) concurrently. Now Galileo did not have the benefit of Newton s laws but you do. Prove that in a vacuum masses m and 10m have the same acceleration profile and hit the ground at the same time when attracted by the mass of the earth m E >> m. Solution: Newton demonstrated that F = ma and that two masses attracted each other with the force of gravity that given by F = Gm 1 m /r where G is the gravitational constant and r the distance separating the masses. So if we calculate the acceleration of m due to the force of gravity we get GmmE GmE ma a r r and for the other mass of 10m we have G 10 mm Gm r r E E 10ma a showing that both masses accelerate equally therefore gain velocity equally and therefore hit the ground at the same time. Problem 8: Where to look when and for how long (0 points) Suppose you are charged to report on the whereabouts of a person who walks the same path every day at the same approximate time. As shown in the (not to scale) figure her walk takes her back and forth on a circuit between two points x 0 and x 5 over a straight path on which she is not visible to you the whole time because there are obstructing walls that will not let you see her V8mar014 TechTest014 Solutions Key 6 / All Rights Reserved
7 from your chosen vantage point. She walks at a constant speed of V = 4500 yards per hour. Her path is x 5 x 0 = 1500 yards long and defiladed by high walls as shown. She is known to walk at least one hour during her exercise session. Letting x 0 = 0 the coordinates of the other points along the path are x 1 = 500 yds x = 900 yds x 3 = 950 yds x 4 = 1150 yds x 5 = 1500 yds. x 0 x 1 x x 3 x 4 x 5 Your objective is to ascertain and report her presence or absence as quickly as possible. When you arrive at your observation point she is nowhere in sight. You note the time (t 0 ) and start scanning for her whereabouts. Since you cannot look concurrently at all points on the visible portions of her path your scanning is made up of a sequence of glimpses that cover a more narrow focus and of a duration enough to ascertain with high likelihood that the walker is there or not. escribe a reasonable scanning policy (sequence of glimpses) which will allow you to meet your objective. In short where will you look (focus your attention) when and for how long? (Hint: Your answer will be a written description with all additional assumptions clearly stated and appropriate numbers included as necessary.) Solution: This is a purely critical thinking problem with a little arithmetic added. The allocation of credit is here more arbitrary with the main thrust being to verify that the student did have certain critical insights but not necessarily in the order presented here. The student should first label and calculate the lengths of the three walls L 1 = 500 yds L = 50 yds L 3 = 350 yds and index all stated times from the start of scanning. Since the walker is not visible she must be walking behind one of the three walls and will eventually emerge at points x 1 through x 4 therefore all glimpses should be allocated to those four points. (15%) Since her position at t 0 can be anywhere behind the walls where she can be walking toward the right or left. And the probability that she is behind any of the walls is proportional to the time it takes her to disappear and then emerge from each of the walls. Since she walks at constant speed these probabilities should be proportional to the wall lengths divided by 900 yards the total length of the walls. But is that true since it takes a maximum of L 1 /V = 1000/4500 = 0. hr to walk behind wall #1; similarly a maximum of L 3 /V = 700/4500 = hr to walk behind wall #3. Wall # presents a problem because it has two points of entry and emergence and therefore for scanning purposes it s as if it is actually two walls with each wall having a maximum dwell time behind the wall of L /V = 50/4500 = hr. At this point the student should conclude that if the observer does not see the walker after scanning for 0. hr = 13.3 minutes then he can report that the walker is not on her walk. (30%) In a similar fashion the observer can eliminate scanning x and x 3 if the walker does not emerge within hr = 40 seconds of his arrival. And he can eliminate including x 4 in his scanning V8mar014 TechTest014 Solutions Key 7 / All Rights Reserved
8 after not seeing the walker past the hr = 9.36 minute mark of his arrival after which time all of his glimpses will be focused at x 1. (0%) Now comes the hard part how to allocate the glimpses between the four points being observed. Upon arrival where should he look? If she is still visible he will detect her if he glimpses her before she disappears behind a wall. The biggest penalty to be paid is if she is about to step behind one of the long walls because missing her then will result in a long delay until she emerges. So it seems that to glimpse first at x 1 and then x 4 would be a reasonable policy before quickly scanning the rest of the visible interval to ascertain her absence. This needs to be traded off against glimpsing at x 3 and x 4 because she will emerge soonest from behind wall # given that she was behind it when the observer arrived. But x 3 and x 4 can always be sequenced after eliminating the disappearance behind walls #1 and #3. So the initial glimpse sequence might be x 1 x 4 x 3 x. The remaining glimpses should then be allocated by the relative lengths of the four walls emergence points or the expected time to emergence from behind each of the walls of defilade dwell lengths L 1 L L L 3 which total 1800 yards. Then x 1 should get L 1 /1800 = fraction of the glimpses x 4 should get L 3 /1800 = of the glimpses and x and x 3 each should get L /1800 = 0.08 fraction of the glimpses. And this should continue only for the first 40 seconds after which time if the walker is not seen the glimpses will be allocated between x 1 and x 4 in proportion to their remaining dwell lengths of L 1 /1700 = and L3/1700 = 0.41 respectively. However after 9.36 minutes the observer will abandon scanning x 4 and concentrate his entire attention on x 1 until 13.3 minutes at which time scanning will be terminated with the report that She is not there. (35%) Problem 9: Rendezvous at Sea (10 points) Two ships are steaming abeam 50 miles apart on parallel courses and at the same speed of 15 knots. The ship A on the left is ordered to rendezvous with the ship B on the right as soon as possible. Ship B will maintain its course and speed. Ship A s maximum speed is 5 knots. A) What course and speed change will enable Ship A to comply with the minimum time to rendezvous requirement? B) What then is the course change and minimum time to rendezvous from the time that Ship A changes speed and course? (Hint: The speed of one knot equals one nautical mile per hour. 1 nautical mile = miles) Solution: A) The student should draw a figure representing the situation that looks something like the one given here. The critical geometry is indicated by the solid line triangle. Solving the triangle gives VT I VT T V V I V8mar014 TechTest014 Solutions Key 8 / All Rights Reserved
9 V V I T V Minimizing T will also minimize T. By inspection we see that maximizing V I will then minimize T. Therefore Ship A will accelerate to its maximum speed for the duration T. The course change θ is obtained from the triangle as θ VT VT 1 tan tan or for T V V I VT A B tan tan VT 1 1 V V I V Here we see that the course change for rendezvous does not depend on the separation distance between the ships. (75%) B) To obtain the numerical solution using the above relations we first convert the separation distance into nautical miles giving = 50/ = nautical miles. Then using V I = 5 knots we get T min hours hrs 10 min 3 sec. V V 5 15 I And Ship A s course change to starboard (right) is computed as 1 VI V tan tan degrees. (5%) V 15 Problem 10: Packing Loss (10 points) A large volume is divided into cubes with side length. Into each cube is placed a sphere of maximum volume. Then between these spheres are placed smaller spheres of maximum volume. What fraction of the large volume is consumed by such placement of spheres? (This is known as the packing density. The residual fraction is known as packing loss.) Solution: The student should draw a picture that looks something like the one nearby. Since a sphere s volume varies monotonically with its radius each cube contains a large (circumscribed) sphere of radius r L = /. The smaller spheres of radius r S centered on the vertices of the cubes are then placed between the larger spheres. An important insight here is that each smaller sphere contributes 1/8 of its volume to every cube in which it resides. This means that the eight corners of each cube together contribute the volume of one small sphere allowing the packing loss to be V8mar014 TechTest014 Solutions Key 9 / All Rights Reserved
10 computed simply as the difference between the volume of the cube and the volumes of the spheres divided by the volume of the cube. (30%) From the figure a is the length of the line connecting the centers of the large and small spheres. a / r = / a a 4 r ar S L. The volume of the cube is 3 and of a sphere is 4πr 3 /3. Therefore the packing loss PL is a straightforward calculation from 1 4 PL 3 r r L S (70%) V8mar014 TechTest014 Solutions Key 10 / All Rights Reserved
TechTest2018. Solutions Key. WIP Edit Copy. Merit Scholarship Examination in the Sciences and Mathematics given on 18 March 2018, and.
 TechTest08 Merit Scholarship Examination in the Sciences and Mathematics given on 8 March 08, and sponsored by The Sierra Economics and Science Foundation Solutions Key Vfeb8 TechTest08 Solutions Key /
TechTest08 Merit Scholarship Examination in the Sciences and Mathematics given on 8 March 08, and sponsored by The Sierra Economics and Science Foundation Solutions Key Vfeb8 TechTest08 Solutions Key /
TechTest2010. The Sierra Environmental Studies Foundation. Published Reference Version
 TechTest00 Merit Scholarship Examination in the Sciences and Mathematics given on 7 March 00 sponsored by The Sierra Environmental Studies Foundation Solution Key V9mar0 TechTest00 Solutions Key / 0 00
TechTest00 Merit Scholarship Examination in the Sciences and Mathematics given on 7 March 00 sponsored by The Sierra Environmental Studies Foundation Solution Key V9mar0 TechTest00 Solutions Key / 0 00
Lecture 9. Section 3.4 Derivative as a Rate of Change Section 3.8 Rates of Change per Unit Time. Jiwen He
 Review Section 3.4 Section 3.8 Lecture 9 Section 3.4 Derivative as a Rate of Change Section 3.8 Rates of Change per Unit Time Jiwen He Department of Mathematics, University of Houston jiwenhe@math.uh.edu
Review Section 3.4 Section 3.8 Lecture 9 Section 3.4 Derivative as a Rate of Change Section 3.8 Rates of Change per Unit Time Jiwen He Department of Mathematics, University of Houston jiwenhe@math.uh.edu
DIFFERENTIATION RULES
 3 DIFFERENTIATION RULES DIFFERENTIATION RULES If we are pumping air into a balloon, both the volume and the radius of the balloon are increasing and their rates of increase are related to each other. However,
3 DIFFERENTIATION RULES DIFFERENTIATION RULES If we are pumping air into a balloon, both the volume and the radius of the balloon are increasing and their rates of increase are related to each other. However,
DRAFT - Math 101 Lecture Note - Dr. Said Algarni
 3 Differentiation Rules 3.1 The Derivative of Polynomial and Exponential Functions In this section we learn how to differentiate constant functions, power functions, polynomials, and exponential functions.
3 Differentiation Rules 3.1 The Derivative of Polynomial and Exponential Functions In this section we learn how to differentiate constant functions, power functions, polynomials, and exponential functions.
3. On the grid below, sketch and label graphs of the following functions: y = sin x, y = cos x, and y = sin(x π/2). π/2 π 3π/2 2π 5π/2
 AP Physics C Calculus C.1 Name Trigonometric Functions 1. Consider the right triangle to the right. In terms of a, b, and c, write the expressions for the following: c a sin θ = cos θ = tan θ =. Using
AP Physics C Calculus C.1 Name Trigonometric Functions 1. Consider the right triangle to the right. In terms of a, b, and c, write the expressions for the following: c a sin θ = cos θ = tan θ =. Using
MAC Calculus II Spring Homework #6 Some Solutions.
 MAC 2312-15931-Calculus II Spring 23 Homework #6 Some Solutions. 1. Find the centroid of the region bounded by the curves y = 2x 2 and y = 1 2x 2. Solution. It is obvious, by inspection, that the centroid
MAC 2312-15931-Calculus II Spring 23 Homework #6 Some Solutions. 1. Find the centroid of the region bounded by the curves y = 2x 2 and y = 1 2x 2. Solution. It is obvious, by inspection, that the centroid
Guidelines for implicit differentiation
 Guidelines for implicit differentiation Given an equation with x s and y s scattered, to differentiate we use implicit differentiation. Some informal guidelines to differentiate an equation containing
Guidelines for implicit differentiation Given an equation with x s and y s scattered, to differentiate we use implicit differentiation. Some informal guidelines to differentiate an equation containing
1 The Derivative and Differrentiability
 1 The Derivative and Differrentiability 1.1 Derivatives and rate of change Exercise 1 Find the equation of the tangent line to f (x) = x 2 at the point (1, 1). Exercise 2 Suppose that a ball is dropped
1 The Derivative and Differrentiability 1.1 Derivatives and rate of change Exercise 1 Find the equation of the tangent line to f (x) = x 2 at the point (1, 1). Exercise 2 Suppose that a ball is dropped
See animations and interactive applets of some of these at. Fall_2009/Math123/Notes
 MA123, Chapter 7 Word Problems (pp. 125-153) Chapter s Goal: In this chapter we study the two main types of word problems in Calculus. Optimization Problems. i.e., max - min problems Related Rates See
MA123, Chapter 7 Word Problems (pp. 125-153) Chapter s Goal: In this chapter we study the two main types of word problems in Calculus. Optimization Problems. i.e., max - min problems Related Rates See
Calculus with Analytic Geometry 3 Fall 2018
 alculus with Analytic Geometry 3 Fall 218 Practice Exercises for the Final Exam I present here a number of exercises that could serve as practice for the final exam. Some are easy and straightforward;
alculus with Analytic Geometry 3 Fall 218 Practice Exercises for the Final Exam I present here a number of exercises that could serve as practice for the final exam. Some are easy and straightforward;
Derivatives and Rates of Change
 Sec.1 Derivatives and Rates of Change A. Slope of Secant Functions rise Recall: Slope = m = = run Slope of the Secant Line to a Function: Examples: y y = y1. From this we are able to derive: x x x1 m y
Sec.1 Derivatives and Rates of Change A. Slope of Secant Functions rise Recall: Slope = m = = run Slope of the Secant Line to a Function: Examples: y y = y1. From this we are able to derive: x x x1 m y
Unit 5 ICM/AB Applications of the Derivative Fall Nov 10 Learn Velocity and Acceleration: HW p P ,103 p.
 Unit 5 ICM/AB Applications of the Derivative Fall 2016 Nov 4 Learn Optimization, New PS up on Optimization, HW pg. 216 3,5,17,19,21,23,25,27,29,33,39,41,49,50 a,b,54 Nov 7 Continue on HW from Nov 4 and
Unit 5 ICM/AB Applications of the Derivative Fall 2016 Nov 4 Learn Optimization, New PS up on Optimization, HW pg. 216 3,5,17,19,21,23,25,27,29,33,39,41,49,50 a,b,54 Nov 7 Continue on HW from Nov 4 and
Math Exam 02 Review
 Math 10350 Exam 02 Review 1. A differentiable function g(t) is such that g(2) = 2, g (2) = 1, g (2) = 1/2. (a) If p(t) = g(t)e t2 find p (2) and p (2). (Ans: p (2) = 7e 4 ; p (2) = 28.5e 4 ) (b) If f(t)
Math 10350 Exam 02 Review 1. A differentiable function g(t) is such that g(2) = 2, g (2) = 1, g (2) = 1/2. (a) If p(t) = g(t)e t2 find p (2) and p (2). (Ans: p (2) = 7e 4 ; p (2) = 28.5e 4 ) (b) If f(t)
Integrals. D. DeTurck. January 1, University of Pennsylvania. D. DeTurck Math A: Integrals 1 / 61
 Integrals D. DeTurck University of Pennsylvania January 1, 2018 D. DeTurck Math 104 002 2018A: Integrals 1 / 61 Integrals Start with dx this means a little bit of x or a little change in x If we add up
Integrals D. DeTurck University of Pennsylvania January 1, 2018 D. DeTurck Math 104 002 2018A: Integrals 1 / 61 Integrals Start with dx this means a little bit of x or a little change in x If we add up
4.1 Implicit Differentiation
 4.1 Implicit Differentiation Learning Objectives A student will be able to: Find the derivative of variety of functions by using the technique of implicit differentiation. Consider the equation We want
4.1 Implicit Differentiation Learning Objectives A student will be able to: Find the derivative of variety of functions by using the technique of implicit differentiation. Consider the equation We want
WeBWorK demonstration assignment
 WeBWorK demonstration assignment The main purpose of this WeBWorK set is to familiarize yourself with WeBWorK. Here are some hints on how to use WeBWorK effectively: After first logging into WeBWorK change
WeBWorK demonstration assignment The main purpose of this WeBWorK set is to familiarize yourself with WeBWorK. Here are some hints on how to use WeBWorK effectively: After first logging into WeBWorK change
APPLICATIONS OF DERIVATIVES UNIT PROBLEM SETS
 APPLICATIONS OF DERIVATIVES UNIT PROBLEM SETS PROBLEM SET #1 Related Rates ***Calculators Allowed*** 1. An oil tanker spills oil that spreads in a circular pattern whose radius increases at the rate of
APPLICATIONS OF DERIVATIVES UNIT PROBLEM SETS PROBLEM SET #1 Related Rates ***Calculators Allowed*** 1. An oil tanker spills oil that spreads in a circular pattern whose radius increases at the rate of
= constant of gravitation is G = N m 2 kg 2. Your goal is to find the radius of the orbit of a geostationary satellite.
 Problem 1 Earth and a Geostationary Satellite (10 points) The earth is spinning about its axis with a period of 3 hours 56 minutes and 4 seconds. The equatorial radius of the earth is 6.38 10 6 m. The
Problem 1 Earth and a Geostationary Satellite (10 points) The earth is spinning about its axis with a period of 3 hours 56 minutes and 4 seconds. The equatorial radius of the earth is 6.38 10 6 m. The
HIGHER SCHOOL CERTIFICATE EXAMINATION MATHEMATICS 3 UNIT (ADDITIONAL) AND 3/4 UNIT (COMMON) Time allowed Two hours (Plus 5 minutes reading time)
 HIGHER SCHOOL CERTIFICATE EXAMINATION 000 MATHEMATICS UNIT (ADDITIONAL) AND /4 UNIT (COMMON) Time allowed Two hours (Plus 5 minutes reading time) DIRECTIONS TO CANDIDATES Attempt ALL questions. ALL questions
HIGHER SCHOOL CERTIFICATE EXAMINATION 000 MATHEMATICS UNIT (ADDITIONAL) AND /4 UNIT (COMMON) Time allowed Two hours (Plus 5 minutes reading time) DIRECTIONS TO CANDIDATES Attempt ALL questions. ALL questions
Almost all of the questions involving Related Rates will require one of the following relationships to link together the various changing rates:
 Related Rates All quantities that we meet in every-day life change with time, this is especially true in scientific investigations. Related Rate problems are those in which an equation epresses some relationship
Related Rates All quantities that we meet in every-day life change with time, this is especially true in scientific investigations. Related Rate problems are those in which an equation epresses some relationship
AP Calculus Free-Response Questions 1969-present AB
 AP Calculus Free-Response Questions 1969-present AB 1969 1. Consider the following functions defined for all x: f 1 (x) = x, f (x) = xcos x, f 3 (x) = 3e x, f 4 (x) = x - x. Answer the following questions
AP Calculus Free-Response Questions 1969-present AB 1969 1. Consider the following functions defined for all x: f 1 (x) = x, f (x) = xcos x, f 3 (x) = 3e x, f 4 (x) = x - x. Answer the following questions
Implicit Differentiation
 Week 6. Implicit Differentiation Let s say we want to differentiate the equation of a circle: y 2 + x 2 =9 Using the techniques we know so far, we need to write the equation as a function of one variable
Week 6. Implicit Differentiation Let s say we want to differentiate the equation of a circle: y 2 + x 2 =9 Using the techniques we know so far, we need to write the equation as a function of one variable
Time: 1 hour 30 minutes
 Paper Reference(s) 6666/0 Edecel GCE Core Mathematics C4 Gold Level (Harder) G Time: hour 0 minutes Materials required for eamination Mathematical Formulae (Green) Items included with question papers Nil
Paper Reference(s) 6666/0 Edecel GCE Core Mathematics C4 Gold Level (Harder) G Time: hour 0 minutes Materials required for eamination Mathematical Formulae (Green) Items included with question papers Nil
Answer Explanations for: ACT June 2012, Form 70C
 Answer Explanations for: ACT June 2012, Form 70C Mathematics 1) C) A mean is a regular average and can be found using the following formula: (average of set) = (sum of items in set)/(number of items in
Answer Explanations for: ACT June 2012, Form 70C Mathematics 1) C) A mean is a regular average and can be found using the following formula: (average of set) = (sum of items in set)/(number of items in
3.8 Exponential Growth and Decay
 3.8 Exponential Growth and Decay Suppose the rate of change of y with respect to t is proportional to y itself. So there is some constant k such that dy dt = ky The only solution to this equation is an
3.8 Exponential Growth and Decay Suppose the rate of change of y with respect to t is proportional to y itself. So there is some constant k such that dy dt = ky The only solution to this equation is an
Physics 20 Homework 2 SIMS 2016
 Physics 20 Homework 2 SIMS 2016 Due: Saturday, August 20 th 1. In class, we ignored air resistance in our discussion of projectile motion. Now, let s derive the relevant equation of motion in the case
Physics 20 Homework 2 SIMS 2016 Due: Saturday, August 20 th 1. In class, we ignored air resistance in our discussion of projectile motion. Now, let s derive the relevant equation of motion in the case
Lecture for Week 6 (Secs ) Derivative Miscellany I
 Lecture for Week 6 (Secs. 3.6 9) Derivative Miscellany I 1 Implicit differentiation We want to answer questions like this: 1. What is the derivative of tan 1 x? 2. What is dy dx if x 3 + y 3 + xy 2 + x
Lecture for Week 6 (Secs. 3.6 9) Derivative Miscellany I 1 Implicit differentiation We want to answer questions like this: 1. What is the derivative of tan 1 x? 2. What is dy dx if x 3 + y 3 + xy 2 + x
Math 121: Final Exam Review Sheet
 Exam Information Math 11: Final Exam Review Sheet The Final Exam will be given on Thursday, March 1 from 10:30 am 1:30 pm. The exam is cumulative and will cover chapters 1.1-1.3, 1.5, 1.6,.1-.6, 3.1-3.6,
Exam Information Math 11: Final Exam Review Sheet The Final Exam will be given on Thursday, March 1 from 10:30 am 1:30 pm. The exam is cumulative and will cover chapters 1.1-1.3, 1.5, 1.6,.1-.6, 3.1-3.6,
Solve for an unknown rate of change using related rates of change.
 Objectives: Solve for an unknown rate of change using related rates of change. 1. Draw a diagram. 2. Label your diagram, including units. If a quantity in the diagram is not changing, label it with a number.
Objectives: Solve for an unknown rate of change using related rates of change. 1. Draw a diagram. 2. Label your diagram, including units. If a quantity in the diagram is not changing, label it with a number.
MATH1013 Calculus I. Derivatives V ( 4.7, 4.9) 1
 1 Based on Stewart, James, Single Variable Calculus, Early Transcendentals, 7th edition, Brooks/Coles, 2012 Briggs, Cochran and Gillett: Calculus for Scientists and Engineers: Early Transcendentals, Pearson
1 Based on Stewart, James, Single Variable Calculus, Early Transcendentals, 7th edition, Brooks/Coles, 2012 Briggs, Cochran and Gillett: Calculus for Scientists and Engineers: Early Transcendentals, Pearson
Chapter 1: Trigonometric Functions 1. Find (a) the complement and (b) the supplement of 61. Show all work and / or support your answer.
 Trig Exam Review F07 O Brien Trigonometry Exam Review: Chapters,, To adequately prepare for the exam, try to work these review problems using only the trigonometry knowledge which you have internalized
Trig Exam Review F07 O Brien Trigonometry Exam Review: Chapters,, To adequately prepare for the exam, try to work these review problems using only the trigonometry knowledge which you have internalized
OPTIMATIZATION - MAXIMUM/MINIMUM PROBLEMS BC CALCULUS
 1 OPTIMATIZATION - MAXIMUM/MINIMUM PROBLEMS BC CALCULUS 1. Read each problem slowly and carefully. Read the problem at least three times before trying to solve it. Sometimes words can be ambiguous. It
1 OPTIMATIZATION - MAXIMUM/MINIMUM PROBLEMS BC CALCULUS 1. Read each problem slowly and carefully. Read the problem at least three times before trying to solve it. Sometimes words can be ambiguous. It
Basic Theory of Differential Equations
 page 104 104 CHAPTER 1 First-Order Differential Equations 16. The following initial-value problem arises in the analysis of a cable suspended between two fixed points y = 1 a 1 + (y ) 2, y(0) = a, y (0)
page 104 104 CHAPTER 1 First-Order Differential Equations 16. The following initial-value problem arises in the analysis of a cable suspended between two fixed points y = 1 a 1 + (y ) 2, y(0) = a, y (0)
Trigonometric ratios:
 0 Trigonometric ratios: The six trigonometric ratios of A are: Sine Cosine Tangent sin A = opposite leg hypotenuse adjacent leg cos A = hypotenuse tan A = opposite adjacent leg leg and their inverses:
0 Trigonometric ratios: The six trigonometric ratios of A are: Sine Cosine Tangent sin A = opposite leg hypotenuse adjacent leg cos A = hypotenuse tan A = opposite adjacent leg leg and their inverses:
Chapter 3.4 Practice Problems
 EXPECTED SKILLS: Chapter.4 Practice Problems Be able to solve related rates problems. It may be helpful to remember the following strategy:. Read the problem carefully. 2. Draw a diagram, if possible,
EXPECTED SKILLS: Chapter.4 Practice Problems Be able to solve related rates problems. It may be helpful to remember the following strategy:. Read the problem carefully. 2. Draw a diagram, if possible,
Mathematics Higher Level
 L.7/0 Pre-Leaving Certificate Examination, 07 Mathematics Higher Level Marking Scheme Paper Pg. Paper Pg. 4 Page of 68 exams Pre-Leaving Certificate Examination, 07 Mathematics Higher Level Paper Marking
L.7/0 Pre-Leaving Certificate Examination, 07 Mathematics Higher Level Marking Scheme Paper Pg. Paper Pg. 4 Page of 68 exams Pre-Leaving Certificate Examination, 07 Mathematics Higher Level Paper Marking
(a) The best linear approximation of f at x = 2 is given by the formula. L(x) = f(2) + f (2)(x 2). f(2) = ln(2/2) = ln(1) = 0, f (2) = 1 2.
 Math 180 Written Homework Assignment #8 Due Tuesday, November 11th at the beginning of your discussion class. Directions. You are welcome to work on the following problems with other MATH 180 students,
Math 180 Written Homework Assignment #8 Due Tuesday, November 11th at the beginning of your discussion class. Directions. You are welcome to work on the following problems with other MATH 180 students,
DIFFERENTIATION RULES
 3 DIFFERENTIATION RULES DIFFERENTIATION RULES Before starting this section, you might need to review the trigonometric functions. DIFFERENTIATION RULES In particular, it is important to remember that,
3 DIFFERENTIATION RULES DIFFERENTIATION RULES Before starting this section, you might need to review the trigonometric functions. DIFFERENTIATION RULES In particular, it is important to remember that,
PROBLEMS 13 - APPLICATIONS OF DERIVATIVES Page 1
 PROBLEMS - APPLICATIONS OF DERIVATIVES Page ( ) Water seeps out of a conical filter at the constant rate of 5 cc / sec. When the height of water level in the cone is 5 cm, find the rate at which the height
PROBLEMS - APPLICATIONS OF DERIVATIVES Page ( ) Water seeps out of a conical filter at the constant rate of 5 cc / sec. When the height of water level in the cone is 5 cm, find the rate at which the height
AH Mechanics Checklist (Unit 1) AH Mechanics Checklist (Unit 1) Rectilinear Motion
 Rectilinear Motion No. kill Done 1 Know that rectilinear motion means motion in 1D (i.e. along a straight line) Know that a body is a physical object 3 Know that a particle is an idealised body that has
Rectilinear Motion No. kill Done 1 Know that rectilinear motion means motion in 1D (i.e. along a straight line) Know that a body is a physical object 3 Know that a particle is an idealised body that has
( ) as a fraction. If both numerator and denominator are
 A. Limits and Horizontal Asymptotes What you are finding: You can be asked to find lim f x x a (H.A.) problem is asking you find lim f x x ( ) and lim f x x ( ). ( ) or lim f x x ± ( ). Typically, a horizontal
A. Limits and Horizontal Asymptotes What you are finding: You can be asked to find lim f x x a (H.A.) problem is asking you find lim f x x ( ) and lim f x x ( ). ( ) or lim f x x ± ( ). Typically, a horizontal
Interpreting Derivatives, Local Linearity, Newton s
 Unit #4 : Method Interpreting Derivatives, Local Linearity, Newton s Goals: Review inverse trigonometric functions and their derivatives. Create and use linearization/tangent line formulas. Investigate
Unit #4 : Method Interpreting Derivatives, Local Linearity, Newton s Goals: Review inverse trigonometric functions and their derivatives. Create and use linearization/tangent line formulas. Investigate
Days 3 & 4 Notes: Related Rates
 AP Calculus Unit 4 Applications of the Derivative Part 1 Days 3 & 4 Notes: Related Rates Implicitly differentiate the following formulas with respect to time. State what each rate in the differential equation
AP Calculus Unit 4 Applications of the Derivative Part 1 Days 3 & 4 Notes: Related Rates Implicitly differentiate the following formulas with respect to time. State what each rate in the differential equation
CHAPTER 3: DERIVATIVES
 (Exercises for Section 3.1: Derivatives, Tangent Lines, and Rates of Change) E.3.1 CHAPTER 3: DERIVATIVES SECTION 3.1: DERIVATIVES, TANGENT LINES, and RATES OF CHANGE In these Exercises, use a version
(Exercises for Section 3.1: Derivatives, Tangent Lines, and Rates of Change) E.3.1 CHAPTER 3: DERIVATIVES SECTION 3.1: DERIVATIVES, TANGENT LINES, and RATES OF CHANGE In these Exercises, use a version
Introduction to Calculus
 Introduction to Calculus Contents 1 Introduction to Calculus 3 11 Introduction 3 111 Origin of Calculus 3 112 The Two Branches of Calculus 4 12 Secant and Tangent Lines 5 13 Limits 10 14 The Derivative
Introduction to Calculus Contents 1 Introduction to Calculus 3 11 Introduction 3 111 Origin of Calculus 3 112 The Two Branches of Calculus 4 12 Secant and Tangent Lines 5 13 Limits 10 14 The Derivative
Solutions for the Practice Final - Math 23B, 2016
 olutions for the Practice Final - Math B, 6 a. True. The area of a surface is given by the expression d, and since we have a parametrization φ x, y x, y, f x, y with φ, this expands as d T x T y da xy
olutions for the Practice Final - Math B, 6 a. True. The area of a surface is given by the expression d, and since we have a parametrization φ x, y x, y, f x, y with φ, this expands as d T x T y da xy
= π + sin π = π + 0 = π, so the object is moving at a speed of π feet per second after π seconds. (c) How far does it go in π seconds?
 Mathematics 115 Professor Alan H. Stein April 18, 005 SOLUTIONS 1. Define what is meant by an antiderivative or indefinite integral of a function f(x). Solution: An antiderivative or indefinite integral
Mathematics 115 Professor Alan H. Stein April 18, 005 SOLUTIONS 1. Define what is meant by an antiderivative or indefinite integral of a function f(x). Solution: An antiderivative or indefinite integral
Related Rates. MATH 151 Calculus for Management. J. Robert Buchanan. Department of Mathematics. J. Robert Buchanan Related Rates
 Related Rates MATH 151 Calculus for Management J. Robert Buchanan Department of Mathematics 2014 Related Rates Problems Another common application of the derivative involved situations in which two or
Related Rates MATH 151 Calculus for Management J. Robert Buchanan Department of Mathematics 2014 Related Rates Problems Another common application of the derivative involved situations in which two or
Math 124 Final Examination Winter 2014 !!! READ...INSTRUCTIONS...READ!!!
 1 Math 124 Final Examination Winter 2014 Print Your Name Signature Student ID Number Quiz Section Professor s Name TA s Name!!! READ...INSTRUCTIONS...READ!!! 1. Your exam contains 8 questions and 10 pages;
1 Math 124 Final Examination Winter 2014 Print Your Name Signature Student ID Number Quiz Section Professor s Name TA s Name!!! READ...INSTRUCTIONS...READ!!! 1. Your exam contains 8 questions and 10 pages;
221 MATH REFRESHER session 3 SAT2015_P06.indd 221 4/23/14 11:39 AM
 Math Refresher Session 3 1 Area, Perimeter, and Volume Problems Area, Perimeter, and Volume 301. Formula Problems. Here, you are given certain data about one or more geometric figures, and you are asked
Math Refresher Session 3 1 Area, Perimeter, and Volume Problems Area, Perimeter, and Volume 301. Formula Problems. Here, you are given certain data about one or more geometric figures, and you are asked
Related Rates. da dt = 2πrdr dt. da, so = 2. I want to find. = 2π 3 2 = 12π
 Related Rates 9-22-2008 Related rates problems deal with situations in which several things are changing at rates which are related. The way in which the rates are related often arises from geometry, for
Related Rates 9-22-2008 Related rates problems deal with situations in which several things are changing at rates which are related. The way in which the rates are related often arises from geometry, for
Kinematics in Two-Dimensions
 Slide 1 / 92 Slide 2 / 92 Kinematics in Two-Dimensions www.njctl.org Slide 3 / 92 How to Use this File Each topic is composed of brief direct instruction There are formative assessment questions after
Slide 1 / 92 Slide 2 / 92 Kinematics in Two-Dimensions www.njctl.org Slide 3 / 92 How to Use this File Each topic is composed of brief direct instruction There are formative assessment questions after
A = 1 2 ab da dt = 1 da. We can find how fast the area is growing at 3 seconds by plugging everything into that differentiated equation: da
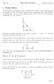 1 Related Rates In most related rates problems, we have an equation that relates a bunch of quantities that are changing over time. For example, suppose we have a right triangle whose base and height are
1 Related Rates In most related rates problems, we have an equation that relates a bunch of quantities that are changing over time. For example, suppose we have a right triangle whose base and height are
2.8 Linear Approximation and Differentials
 2.8 Linear Approximation Contemporary Calculus 1 2.8 Linear Approximation and Differentials Newton's method used tangent lines to "point toward" a root of the function. In this section we examine and use
2.8 Linear Approximation Contemporary Calculus 1 2.8 Linear Approximation and Differentials Newton's method used tangent lines to "point toward" a root of the function. In this section we examine and use
Math 125: Exam 3 Review
 Math 125: Exam 3 Review Since we re using calculators, to keep the playing field level between all students, I will ask that you refrain from using certain features of your calculator, including graphing.
Math 125: Exam 3 Review Since we re using calculators, to keep the playing field level between all students, I will ask that you refrain from using certain features of your calculator, including graphing.
Section 3.8 Related Rates
 Section 3.8 Related Rates Read and re-read the problem until you understand it. Draw and label a picture which gives the relevant information (if possible). Introduce notation. Assign a symbol to every
Section 3.8 Related Rates Read and re-read the problem until you understand it. Draw and label a picture which gives the relevant information (if possible). Introduce notation. Assign a symbol to every
Lecture 1a: Satellite Orbits
 Lecture 1a: Satellite Orbits Meteorological Satellite Orbits LEO view GEO view Two main orbits of Met Satellites: 1) Geostationary Orbit (GEO) 1) Low Earth Orbit (LEO) or polar orbits Orbits of meteorological
Lecture 1a: Satellite Orbits Meteorological Satellite Orbits LEO view GEO view Two main orbits of Met Satellites: 1) Geostationary Orbit (GEO) 1) Low Earth Orbit (LEO) or polar orbits Orbits of meteorological
RELATED RATE PROBLEMS
 MA123, Chapter 7a: Related Rates Word Problems (pp. 140-149, Gootman) Chapter Goals: In this Chapter we learn a general strategy on how to approach related rates problems, one of the main types of word
MA123, Chapter 7a: Related Rates Word Problems (pp. 140-149, Gootman) Chapter Goals: In this Chapter we learn a general strategy on how to approach related rates problems, one of the main types of word
AP Physics C Summer Homework. Questions labeled in [brackets] are required only for students who have completed AP Calculus AB
![AP Physics C Summer Homework. Questions labeled in [brackets] are required only for students who have completed AP Calculus AB AP Physics C Summer Homework. Questions labeled in [brackets] are required only for students who have completed AP Calculus AB](/thumbs/96/128301637.jpg) 1. AP Physics C Summer Homework NAME: Questions labeled in [brackets] are required only for students who have completed AP Calculus AB 2. Fill in the radian conversion of each angle and the trigonometric
1. AP Physics C Summer Homework NAME: Questions labeled in [brackets] are required only for students who have completed AP Calculus AB 2. Fill in the radian conversion of each angle and the trigonometric
(a) At what rate is the circumference of the circle changing when the radius is 10 inches? =2inches per minute and we want to find. c =2 r.
 3.11 Related Rates Problem 1 The radius of a circle is increasing at a rate of 2 inches per minute. (a) At what rate is the circumference of the circle changing when the radius is 10 inches? We know: dr
3.11 Related Rates Problem 1 The radius of a circle is increasing at a rate of 2 inches per minute. (a) At what rate is the circumference of the circle changing when the radius is 10 inches? We know: dr
MAT100 OVERVIEW OF CONTENTS AND SAMPLE PROBLEMS
 MAT100 OVERVIEW OF CONTENTS AND SAMPLE PROBLEMS MAT100 is a fast-paced and thorough tour of precalculus mathematics, where the choice of topics is primarily motivated by the conceptual and technical knowledge
MAT100 OVERVIEW OF CONTENTS AND SAMPLE PROBLEMS MAT100 is a fast-paced and thorough tour of precalculus mathematics, where the choice of topics is primarily motivated by the conceptual and technical knowledge
Workbook for Calculus I
 Workbook for Calculus I By Hüseyin Yüce New York 2007 1 Functions 1.1 Four Ways to Represent a Function 1. Find the domain and range of the function f(x) = 1 + x + 1 and sketch its graph. y 3 2 1-3 -2-1
Workbook for Calculus I By Hüseyin Yüce New York 2007 1 Functions 1.1 Four Ways to Represent a Function 1. Find the domain and range of the function f(x) = 1 + x + 1 and sketch its graph. y 3 2 1-3 -2-1
CALCULUS PROBLEMS Courtesy of Prof. Julia Yeomans. Michaelmas Term
 CALCULUS PROBLEMS Courtesy of Prof. Julia Yeomans Michaelmas Term The problems are in 5 sections. The first 4, A Differentiation, B Integration, C Series and limits, and D Partial differentiation follow
CALCULUS PROBLEMS Courtesy of Prof. Julia Yeomans Michaelmas Term The problems are in 5 sections. The first 4, A Differentiation, B Integration, C Series and limits, and D Partial differentiation follow
Forces and Motion in One Dimension
 Nicholas J. Giordano www.cengage.com/physics/giordano Forces and Motion in One Dimension Applications of Newton s Laws We will learn how Newton s Laws apply in various situations We will begin with motion
Nicholas J. Giordano www.cengage.com/physics/giordano Forces and Motion in One Dimension Applications of Newton s Laws We will learn how Newton s Laws apply in various situations We will begin with motion
Chapter 2 Derivatives
 Contents Chapter 2 Derivatives Motivation to Chapter 2 2 1 Derivatives and Rates of Change 3 1.1 VIDEO - Definitions................................................... 3 1.2 VIDEO - Examples and Applications
Contents Chapter 2 Derivatives Motivation to Chapter 2 2 1 Derivatives and Rates of Change 3 1.1 VIDEO - Definitions................................................... 3 1.2 VIDEO - Examples and Applications
Average rates of change May be used to estimate the derivative at a point
 Derivatives Big Ideas Rule of Four: Numerically, Graphically, Analytically, and Verbally Average rate of Change: Difference Quotient: y x f( a+ h) f( a) f( a) f( a h) f( a+ h) f( a h) h h h Average rates
Derivatives Big Ideas Rule of Four: Numerically, Graphically, Analytically, and Verbally Average rate of Change: Difference Quotient: y x f( a+ h) f( a) f( a) f( a h) f( a+ h) f( a h) h h h Average rates
AP Physics C: Mechanics 2005 Scoring Guidelines
 AP Physics C: Mechanics 005 Scoring Guidelines The College Board: Connecting Students to College Success The College Board is a not-for-profit membership association whose mission is to connect students
AP Physics C: Mechanics 005 Scoring Guidelines The College Board: Connecting Students to College Success The College Board is a not-for-profit membership association whose mission is to connect students
Math 106 Answers to Exam 3a Fall 2015
 Math 6 Answers to Exam 3a Fall 5.. Consider the curve given parametrically by x(t) = cos(t), y(t) = (t 3 ) 3, for t from π to π. (a) (6 points) Find all the points (x, y) where the graph has either a vertical
Math 6 Answers to Exam 3a Fall 5.. Consider the curve given parametrically by x(t) = cos(t), y(t) = (t 3 ) 3, for t from π to π. (a) (6 points) Find all the points (x, y) where the graph has either a vertical
Study Guide for Benchmark #1 Window of Opportunity: March 4-11
 Study Guide for Benchmark #1 Window of Opportunity: March -11 Benchmark testing is the department s way of assuring that students have achieved minimum levels of computational skill. While partial credit
Study Guide for Benchmark #1 Window of Opportunity: March -11 Benchmark testing is the department s way of assuring that students have achieved minimum levels of computational skill. While partial credit
For all questions, answer choice E. NOTA" means none of the above answers is correct.
 For all questions, answer choice " means none of the above answers is correct. 1. The sum of the integers 1 through n can be modeled by a quadratic polynomial. What is the product of the non-zero coefficients
For all questions, answer choice " means none of the above answers is correct. 1. The sum of the integers 1 through n can be modeled by a quadratic polynomial. What is the product of the non-zero coefficients
1. The accumulated net change function or area-so-far function
 Name: Section: Names of collaborators: Main Points: 1. The accumulated net change function ( area-so-far function) 2. Connection to antiderivative functions: the Fundamental Theorem of Calculus 3. Evaluating
Name: Section: Names of collaborators: Main Points: 1. The accumulated net change function ( area-so-far function) 2. Connection to antiderivative functions: the Fundamental Theorem of Calculus 3. Evaluating
2015 Canadian Team Mathematics Contest
 The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca 205 Canadian Team Mathematics Contest April 205 Solutions 205 University of Waterloo 205 CTMC Solutions Page 2 Individual Problems.
The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca 205 Canadian Team Mathematics Contest April 205 Solutions 205 University of Waterloo 205 CTMC Solutions Page 2 Individual Problems.
Multiple Choice. at the point where x = 0 and y = 1 on the curve
 Multiple Choice 1.(6 pts.) A particle is moving in a straight line along a horizontal axis with a position function given by s(t) = t 3 12t, where distance is measured in feet and time is measured in seconds.
Multiple Choice 1.(6 pts.) A particle is moving in a straight line along a horizontal axis with a position function given by s(t) = t 3 12t, where distance is measured in feet and time is measured in seconds.
Motion in 1 Dimension
 Motion in 1 Dimension Physics is all about describing motion. For now we are going to discuss motion in 1 dimension, which means either along the x axis or the y axis. To describe an object s motion, we
Motion in 1 Dimension Physics is all about describing motion. For now we are going to discuss motion in 1 dimension, which means either along the x axis or the y axis. To describe an object s motion, we
Notes on Radian Measure
 MAT 170 Pre-Calculus Notes on Radian Measure Radian Angles Terri L. Miller Spring 009 revised April 17, 009 1. Radian Measure Recall that a unit circle is the circle centered at the origin with a radius
MAT 170 Pre-Calculus Notes on Radian Measure Radian Angles Terri L. Miller Spring 009 revised April 17, 009 1. Radian Measure Recall that a unit circle is the circle centered at the origin with a radius
Physics 2514 Lecture 22
 Physics 2514 Lecture 22 P. Gutierrez Department of Physics & Astronomy University of Oklahoma Physics 2514 p. 1/15 Information Information needed for the exam Exam will be in the same format as the practice
Physics 2514 Lecture 22 P. Gutierrez Department of Physics & Astronomy University of Oklahoma Physics 2514 p. 1/15 Information Information needed for the exam Exam will be in the same format as the practice
Secondary School Certificate Examination Syllabus MATHEMATICS. Class X examination in 2011 and onwards. SSC Part-II (Class X)
 Secondary School Certificate Examination Syllabus MATHEMATICS Class X examination in 2011 and onwards SSC Part-II (Class X) 15. Algebraic Manipulation: 15.1.1 Find highest common factor (H.C.F) and least
Secondary School Certificate Examination Syllabus MATHEMATICS Class X examination in 2011 and onwards SSC Part-II (Class X) 15. Algebraic Manipulation: 15.1.1 Find highest common factor (H.C.F) and least
Final Exam. Monday March 19, 3:30-5:30pm MAT 21D, Temple, Winter 2018
 Name: Student ID#: Section: Final Exam Monday March 19, 3:30-5:30pm MAT 21D, Temple, Winter 2018 Show your work on every problem. orrect answers with no supporting work will not receive full credit. Be
Name: Student ID#: Section: Final Exam Monday March 19, 3:30-5:30pm MAT 21D, Temple, Winter 2018 Show your work on every problem. orrect answers with no supporting work will not receive full credit. Be
SUMMER KNOWHOW STUDY AND LEARNING CENTRE
 SUMMER KNOWHOW STUDY AND LEARNING CENTRE Differential Calculus 2 Contents Limits..5 Gradients, Tangents and Derivatives.6 Differentiation from First Principles.8 Rules for Differentiation..10 Chain Rule.12
SUMMER KNOWHOW STUDY AND LEARNING CENTRE Differential Calculus 2 Contents Limits..5 Gradients, Tangents and Derivatives.6 Differentiation from First Principles.8 Rules for Differentiation..10 Chain Rule.12
APPLICATIONS OF DERIVATIVES
 9 APPLICATIONS OF DERIVATIVES In the previous lesson, we have learnt that the slope of a line is the tangent of the angle which the line makes with the positive direction of x-axis. It is denoted by the
9 APPLICATIONS OF DERIVATIVES In the previous lesson, we have learnt that the slope of a line is the tangent of the angle which the line makes with the positive direction of x-axis. It is denoted by the
Prentice Hall Mathematics, Pre-Algebra 2007 Correlated to: Michigan Grade Level Content Expectations (Grades 8)
 NUMBER AND OPERATIONS Understand real number concepts N.ME.08.01 Understand the meaning SE/TE: Direct Instruction: 189 (Ex. 48), 588-591, of a square root of a number and its 593-596, 598-599, 603, 608,
NUMBER AND OPERATIONS Understand real number concepts N.ME.08.01 Understand the meaning SE/TE: Direct Instruction: 189 (Ex. 48), 588-591, of a square root of a number and its 593-596, 598-599, 603, 608,
PHY 141 Midterm 1 Oct 2, 2014 Version A
 PHY 141 Midterm 1 Oct 2, 2014 Version A Put FULL NAME, ID#, and EXAM VERSION on the front cover of the BLUE BOOKLET! To avoid problems in grading: do all problems in order, write legibly, and show all
PHY 141 Midterm 1 Oct 2, 2014 Version A Put FULL NAME, ID#, and EXAM VERSION on the front cover of the BLUE BOOKLET! To avoid problems in grading: do all problems in order, write legibly, and show all
KENDRIYA VIDYALAYA GACHIBOWLI, GPRA CAMPUS, HYD-32. SECTION A Questions 1 to 6 carry 1 mark each.
 KENDRIYA VIDYALAYA GACHIBOWLI, GPRA CAMPUS, HYD-32 SAMPLE PAPER TEST 03 (2018-19) (ANSWERS) SUBJECT: MATHEMATICS MAX. MARKS : 80 CLASS : X DURATION : 3 HRS General Instruction: (i) All questions are compulsory.
KENDRIYA VIDYALAYA GACHIBOWLI, GPRA CAMPUS, HYD-32 SAMPLE PAPER TEST 03 (2018-19) (ANSWERS) SUBJECT: MATHEMATICS MAX. MARKS : 80 CLASS : X DURATION : 3 HRS General Instruction: (i) All questions are compulsory.
MAC 2311 Calculus I Spring 2004
 MAC 2 Calculus I Spring 2004 Homework # Some Solutions.#. Since f (x) = d dx (ln x) =, the linearization at a = is x L(x) = f() + f ()(x ) = ln + (x ) = x. The answer is L(x) = x..#4. Since e 0 =, and
MAC 2 Calculus I Spring 2004 Homework # Some Solutions.#. Since f (x) = d dx (ln x) =, the linearization at a = is x L(x) = f() + f ()(x ) = ln + (x ) = x. The answer is L(x) = x..#4. Since e 0 =, and
PHYS101 Sec 001 Hour Exam No. 1 Page: 1
 PHYS101 Sec 001 Hour Exam No. 1 Page: 1 1 Galileo's experiments were designed to reveal the simple laws of motion by a. reproducing ordinary events. b. creating simplied events. c. adding to ordinary events.
PHYS101 Sec 001 Hour Exam No. 1 Page: 1 1 Galileo's experiments were designed to reveal the simple laws of motion by a. reproducing ordinary events. b. creating simplied events. c. adding to ordinary events.
II. Unit Speed Curves
 The Geometry of Curves, Part I Rob Donnelly From Murray State University s Calculus III, Fall 2001 note: This material supplements Sections 13.3 and 13.4 of the text Calculus with Early Transcendentals,
The Geometry of Curves, Part I Rob Donnelly From Murray State University s Calculus III, Fall 2001 note: This material supplements Sections 13.3 and 13.4 of the text Calculus with Early Transcendentals,
MAC 2311 Final Exam Review Fall Private-Appointment, one-on-one tutoring at Broward Hall
 Fall 2016 This review, produced by the CLAS Teaching Center, contains a collection of questions which are representative of the type you may encounter on the eam. Other resources made available by the
Fall 2016 This review, produced by the CLAS Teaching Center, contains a collection of questions which are representative of the type you may encounter on the eam. Other resources made available by the
Multiple Choice. Circle the best answer. No work needed. No partial credit available. is continuous.
 Multiple Choice. Circle the best answer. No work needed. No partial credit available. + +. Evaluate lim + (a (b (c (d 0 (e None of the above.. Evaluate lim (a (b (c (d 0 (e + + None of the above.. Find
Multiple Choice. Circle the best answer. No work needed. No partial credit available. + +. Evaluate lim + (a (b (c (d 0 (e None of the above.. Evaluate lim (a (b (c (d 0 (e + + None of the above.. Find
Circular motion. Aug. 22, 2017
 Circular motion Aug. 22, 2017 Until now, we have been observers to Newtonian physics through inertial reference frames. From our discussion of Newton s laws, these are frames which obey Newton s first
Circular motion Aug. 22, 2017 Until now, we have been observers to Newtonian physics through inertial reference frames. From our discussion of Newton s laws, these are frames which obey Newton s first
EDEXCEL NATIONAL CERTIFICATE UNIT 4 MATHEMATICS FOR TECHNICIANS OUTCOME 4 TUTORIAL 1 - INTEGRATION
 Learning outcomes EEXCEL NATIONAL CERTIFICATE UNIT MATHEMATICS FOR TECHNICIANS OUTCOME TUTORIAL 1 - INTEGRATION On completion of this unit a learner should: 1 Know how to use algebraic methods e able to
Learning outcomes EEXCEL NATIONAL CERTIFICATE UNIT MATHEMATICS FOR TECHNICIANS OUTCOME TUTORIAL 1 - INTEGRATION On completion of this unit a learner should: 1 Know how to use algebraic methods e able to
Math 8 Winter 2010 Midterm 2 Review Problems Solutions - 1. xcos 6xdx = 4. = x2 4
 Math 8 Winter 21 Midterm 2 Review Problems Solutions - 1 1 Evaluate xcos 2 3x Solution: First rewrite cos 2 3x using the half-angle formula: ( ) 1 + cos 6x xcos 2 3x = x = 1 x + 1 xcos 6x. 2 2 2 Now use
Math 8 Winter 21 Midterm 2 Review Problems Solutions - 1 1 Evaluate xcos 2 3x Solution: First rewrite cos 2 3x using the half-angle formula: ( ) 1 + cos 6x xcos 2 3x = x = 1 x + 1 xcos 6x. 2 2 2 Now use
MARLBORO CENTRAL SCHOOL DISTRICT CURRICULUM MAP. Unit 1: Integers & Rational Numbers
 Timeframe September/ October (5 s) What is an integer? What are some real life situations where integers are used? represent negative and positive numbers on a vertical and horizontal number line? What
Timeframe September/ October (5 s) What is an integer? What are some real life situations where integers are used? represent negative and positive numbers on a vertical and horizontal number line? What
Leaving Cert Applied Maths: Some Notes
 Leaving Cert Applied Maths: Some Notes Golden Rule of Applied Maths: Draw Pictures! Numbered equations are in the tables. Proportionality: Figure 1: Note that P = kq y = mx + c except c = 0 the line goes
Leaving Cert Applied Maths: Some Notes Golden Rule of Applied Maths: Draw Pictures! Numbered equations are in the tables. Proportionality: Figure 1: Note that P = kq y = mx + c except c = 0 the line goes
Implicit Differentiation and Related Rates
 Math 31A Discussion Session Week 5 Notes February 2 and 4, 2016 This week we re going to learn how to find tangent lines to curves which aren t necessarily graphs of functions, using an approach called
Math 31A Discussion Session Week 5 Notes February 2 and 4, 2016 This week we re going to learn how to find tangent lines to curves which aren t necessarily graphs of functions, using an approach called
L.41/42. Pre-Leaving Certificate Examination, Applied Mathematics. Marking Scheme. Ordinary Pg. 2. Higher Pg. 21.
 L./ Pre-Leaving Certificate Examination, 0 Applied Mathematics Marking Scheme Ordinary Pg. Higher Pg. Page of 6 exams Pre-Leaving Certificate Examination, 0 Applied Mathematics Ordinary Level Marking Scheme
L./ Pre-Leaving Certificate Examination, 0 Applied Mathematics Marking Scheme Ordinary Pg. Higher Pg. Page of 6 exams Pre-Leaving Certificate Examination, 0 Applied Mathematics Ordinary Level Marking Scheme
Lecture 6, September 1, 2017
 Engineering Mathematics Fall 07 Lecture 6, September, 07 Escape Velocity Suppose we have a planet (or any large near to spherical heavenly body) of radius R and acceleration of gravity at the surface of
Engineering Mathematics Fall 07 Lecture 6, September, 07 Escape Velocity Suppose we have a planet (or any large near to spherical heavenly body) of radius R and acceleration of gravity at the surface of
Sample Final Questions: Solutions Math 21B, Winter y ( y 1)(1 + y)) = A y + B
 Sample Final Questions: Solutions Math 2B, Winter 23. Evaluate the following integrals: tan a) y y dy; b) x dx; c) 3 x 2 + x dx. a) We use partial fractions: y y 3 = y y ) + y)) = A y + B y + C y +. Putting
Sample Final Questions: Solutions Math 2B, Winter 23. Evaluate the following integrals: tan a) y y dy; b) x dx; c) 3 x 2 + x dx. a) We use partial fractions: y y 3 = y y ) + y)) = A y + B y + C y +. Putting
Curriculum Scope & Sequence
 Subject/Grade Level: Mathematics/Grade 6 Curriculum Scope & Sequence BOE Approval 1.28.14 Course: Math 6 Above-Level Unit Duration NJ Common Core Standards / Unit Goals Transfer Goal(s) Enduring Understandings
Subject/Grade Level: Mathematics/Grade 6 Curriculum Scope & Sequence BOE Approval 1.28.14 Course: Math 6 Above-Level Unit Duration NJ Common Core Standards / Unit Goals Transfer Goal(s) Enduring Understandings
1985 AP Calculus AB: Section I
 985 AP Calculus AB: Section I 9 Minutes No Calculator Notes: () In this eamination, ln denotes the natural logarithm of (that is, logarithm to the base e). () Unless otherwise specified, the domain of
985 AP Calculus AB: Section I 9 Minutes No Calculator Notes: () In this eamination, ln denotes the natural logarithm of (that is, logarithm to the base e). () Unless otherwise specified, the domain of
