Related Rates. da dt = 2πrdr dt. da, so = 2. I want to find. = 2π 3 2 = 12π
|
|
|
- Michael Golden
- 5 years ago
- Views:
Transcription
1 Related Rates Related rates problems deal with situations in which several things are changing at rates which are related. The way in which the rates are related often arises from geometry, for example. Example. The radius of a circle increases at 2 light-years per fortnight. At what rate is the area increasing when the radius is 3 light-years? The area of a circle is A = πr 2, where r is the radius. Differentiate this equation with respect to t: da = 2πrdr. I want to know the rate of change of the area, which is da. The rate at which the radius increases is dr dr da, so = 2. I want to find da = 2π 3 2 = 12π The units should be square light-years per fortnight. when r = 3. Plug in: Notice that I don t plug r = 3 into the equation A = πr 2. I differentiate first, then plug in. In most related rates problems, you will perform the steps above: Differentiate a starting equation with respect to t (time), then plug in and answer the question. In most cases, the difficult part of the problem is obtaining the starting equation. Before I give some examples involving real-world situations, I ll do an example which just illustrates the kind of mathematics that is involved. Example. x and y are functions of t, and are related by x 3 y 3y = y y + x 2. Find the rate at which x is changing when x = 2 and y = 1, if y is decreasing at 3 units per second. I differentiate the given equation with respect to t. To save writing, I ll use x to denote dx and y to denote dy. (x 3 y + y 3x 2 x ) 3y = 2yy 1 y 2 y + x. ( ) Here s how I got some of the terms. x 3 y is a product, so I applied the Product Rule to get x 3 y + y 3x 2 x. Note that the derivative of y is dy = y, and by the Chain Rule, the derivative of x 3 is d x3 = 3x 2 dx = 3x2 x. 1
2 I differentiated y 2 using the Chain Rule: d dy y2 = 2y dy = 2yy. I differentiated 1 y = y 1 using the Chain Rule: I plug in x = 2, y = 1, and dy decreasing.) d y 1 2 dy = y = 1 y 2 y. = 3 into (*). (Note that dy (8)( 3) + (1)(12) x 3( 3) = 2(1)( 3) 1 1 ( 3) + x. is negative, because I was told that y is Simplify and solve for x : x = 3 + x, x = Example. Calvin and Phoebe elope in a hot air balloon, which rises at a constant rate of 3 meters per second. Five seconds after they cast off, Phoebe s jilted suitor Bonzo McTavish races up in his Porsche. He parks 50 meters from the launch pad, and runs toward the pad at 2 meters per second. At what rate is the distance between Bonzo and the balloon changing when the balloon is 30 meters above the ground? Here s a picture: balloon s y launch pad x Bonzo The triangle is a right triangle, and I ve labelled the three sides with variables. x is the distance from Bonzo to the launch pad, y is the height of the balloon, and s is the distance from Bonzo to the balloon. I use variables because the three sides are changing with time: The balloon rises (y changes), Bonzo runs toward the launch pad (x changes), and the distance between Bonzo and the balloon (s) changes. There is an obvious relationship among the variables Pythagoras theorem says s 2 + x 2 + y 2. 2s ds = 2xdx + 2ydy. 2
3 Cancel the 2 s: s ds = xdx + ydy. Now I plug in the numbers. Bonzo s velocity is dx = 2 negative, because the distance from Bonzo dy ds to the launch pad is decreasing. = 3 is the rate at which the balloon rises. I want to know what is when y = 30. I see that I still need x and s. The balloon was already 15 (3 5) meters high when Bonzo drove up. It has risen an additional = 15 meters. Since it s rising at 3 meters per second, 15 = 5 additional seconds elapse. 3 During these 5 seconds, Bonzo is running at 2 meters per second, so he travels 2 5 = 10 meters. That leaves him = 40 meters from the launch pad. In other words, x = 40. Finally, using the equation s 2 + x 2 + y 2, s = = 50. Plug all this stuff into the derivatives equation: 50 ds = (40)( 2) + (30)(3), ds = 0.2 meters/second. Here are some rules of thumb for setting up a related rates problem: 1. Draw a picture. Be sure you ve drawn it at an arbitrary instant. (In the previous example, it would be a bad idea to draw the picture with the balloon on the ground, or with Bonzo just getting out of his car.) 2. Label the quantities that are relevant to the problem. Quantities that are changing should be labelled with variables. 3. Don t put numbers on your picture unless they represent things which aren t changing. 4. Look for a relationship among the variables. Think of Pythagoras theorem, trigonometry, area or volume formulas, and similar triangles. 5. Once you have a starting equation, differentiate with respect to t, Then plug in the given values and solve for the appropriate rate. In the next example, I ll need the following facts from physics. The velocity of an object dropped from rest is 32t feet per second after t seconds. During that t seconds, it will have fallen 16t 2 feet. Example. A bowl of petunias is dropped from a point 12 feet above the ground, so that it will land 4 feet from the base of a 12 foot lamppost. At what rate is the shadow of the bowl moving along the ground when the bowl is 8 feet above the ground? 3
4 Here s a picture: light bowl 12 h 4 x - 4 shadow x x is the distance from the shadow to the post. (In order to measure the rate at which the shadow is moving, I have to measure its distance to some fixed object.) h is the height of the bowl above the ground. By similar triangles, x 4 = x h 12. (Notice that if you label the picture properly, it s usually obvious what mathematical formula you should use.) Clear denominators: 12x 48 = xh. Differentiate with respect to t, being careful to use the Product Rule on the right side: 12 dx = xdh + hdx. Now I plug the numbers in. I m trying to find dx, the rate at which the shadow is moving. When the bowl is 8 feet above the ground, h = 8, so the bowl has fallen 4 feet. By the physics fact I mentioned earlier, the bowl falls 16t 2 feet in t seconds; setting 16t 2 = 4, I get t = 1. The bowl has been 2 falling for 1 2 second. By the other physics fact I mentioned, its velocity is 32 1 dh = 16 feet per second. Thus, 2 = 16 negative, because h is decreasing. The only other thing I need is x. Set h = 8 in 12x 48 = xh: 12x 48 = 8x, x = 12. Substitute x, h, and dh : 12 dx = (12)( 16) + 8dx, dx = 48 feet/second. Example. Calvin and Bonzo drive on long parallel roads in opposite directions at 20 feet per second and 80 feet per second, respectively. The roads are 200 feet apart. How rapidly is the distance between them changing 5 seconds after they pass one another? 4
5 Here s a picture: Bonzo 200 s x Calvin x is the horizontal separation between Calvin and Bonzo. s is the distance between them. By Pythagoras, s 2 = x s ds = 2xdx, sds = xdx. I want ds. The rate of change of the distance between them is the same as it would be if Bonzo was moving at = 100 feet per second and Calvin was stationary. So dx = 100, and 5 second after they pass each other, x = = 500. To find s, plug x = 500 into s 2 = x : s = = Now plug everything in: ds = , ds = feet/second. 29 Example. A ferris wheel 50 feet in diameter makes 2 revolutions per minute. Assume that the wheel is tangent to the ground and let P be the point of tangency. At what rate is the distance between P and a rider changing, when she is 25 feet above the ground and going up? 5
6 Here s a picture: wheel q s rider ground θ is the angle between the vertical and a radius out to the rider. s is the distance between the bottom of the wheel and the rider. By the Law of Cosines, s 2 = cosθ. 2s ds = 1250 sin θdθ. Assuming that the wheel is turning counterclockwise in the picture, when the rider is 25 feet above the ground, she s on the far right hand side. At this point, θ = π 2, and s = 25 2 (since the triangle is then an isosceles right triangle). dθ is the rate at which the wheel is turning. I must be careful to express this in radians per minute: dθ ( = 2 rev ) ( 2π rad ) = 4π rad min rev min. Plug in: ds = 1250 sin π 2 4π, ds = 100π feet/minute. 2 Example. A spotlight on the top of a police cruiser makes one revolution per second. The spotlight is 40 feet from a long straight wall. At what rate is the spot of light moving across the wall at the instant when the beam makes a 30 angle with the wall? 6
7 Here s a picture: x spot 40 q police cruiser x is the distance from the spot to the point on the wall nearest the cruiser. θ is the angle between the beam and the altitude to the wall from the light. By basic trigonometry, tan θ = x 40. is (secθ) 2 dθ = 1 dx 40. When the beam makes a 30 angle with the wall, θ = 60 = π. The rate at which the beam is turning 3 Plug in: dθ ( = ( sec π ) 2 1 dx 2π = 3 40, 1 rev sec dx ) ( 2π rad ) = 2π rad rev sec. = 320π feet/second. Example. A helium balloon is released from ground level and rises at a constant rate of 2 feet per second. Calvin stands at the top of a 100-foot observation tower located 60 feet from the point where the balloon was released. At what rate is the distance between Calvin and the balloon changing when the balloon is 55 feet above the ground? Let y be the height of the balloon above the ground, and let r be the distance from Calvin to the balloon. 60 Calvin 100-y balloon 100 y 7
8 By Pythagoras, (100 y) 2 = r 2. 2(100 y)( 1) dy = 2rdr, (y 100)dy = rdr. I want dr. dy = 2 feet per second; when y = 55, (100 55) 2 = r 2, r = 75. Thus, (55 100)(2) = 75 dr, dr = 1.2 feet/second. c 2008 by Bruce Ikenaga 8
Section 3.8 Related Rates
 Section 3.8 Related Rates Read and re-read the problem until you understand it. Draw and label a picture which gives the relevant information (if possible). Introduce notation. Assign a symbol to every
Section 3.8 Related Rates Read and re-read the problem until you understand it. Draw and label a picture which gives the relevant information (if possible). Introduce notation. Assign a symbol to every
A = 1 2 ab da dt = 1 da. We can find how fast the area is growing at 3 seconds by plugging everything into that differentiated equation: da
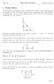 1 Related Rates In most related rates problems, we have an equation that relates a bunch of quantities that are changing over time. For example, suppose we have a right triangle whose base and height are
1 Related Rates In most related rates problems, we have an equation that relates a bunch of quantities that are changing over time. For example, suppose we have a right triangle whose base and height are
Review Problems for Test 2
 Review Problems for Test 2 Math 6-03/06 0 0/ 2007 These problems are provided to help you study. The fact that a problem occurs here does not mean that there will be a similar problem on the test. And
Review Problems for Test 2 Math 6-03/06 0 0/ 2007 These problems are provided to help you study. The fact that a problem occurs here does not mean that there will be a similar problem on the test. And
(x + 3)(x 1) lim(x + 3) = 4. lim. (x 2)( x ) = (x 2)(x + 2) x + 2 x = 4. dt (t2 + 1) = 1 2 (t2 + 1) 1 t. f(x) = lim 3x = 6,
 Math 140 MT1 Sample C Solutions Tyrone Crisp 1 (B): First try direct substitution: you get 0. So try to cancel common factors. We have 0 x 2 + 2x 3 = x 1 and so the it as x 1 is equal to (x + 3)(x 1),
Math 140 MT1 Sample C Solutions Tyrone Crisp 1 (B): First try direct substitution: you get 0. So try to cancel common factors. We have 0 x 2 + 2x 3 = x 1 and so the it as x 1 is equal to (x + 3)(x 1),
Chapter 3.4 Practice Problems
 EXPECTED SKILLS: Chapter.4 Practice Problems Be able to solve related rates problems. It may be helpful to remember the following strategy:. Read the problem carefully. 2. Draw a diagram, if possible,
EXPECTED SKILLS: Chapter.4 Practice Problems Be able to solve related rates problems. It may be helpful to remember the following strategy:. Read the problem carefully. 2. Draw a diagram, if possible,
Solve for an unknown rate of change using related rates of change.
 Objectives: Solve for an unknown rate of change using related rates of change. 1. Draw a diagram. 2. Label your diagram, including units. If a quantity in the diagram is not changing, label it with a number.
Objectives: Solve for an unknown rate of change using related rates of change. 1. Draw a diagram. 2. Label your diagram, including units. If a quantity in the diagram is not changing, label it with a number.
Trigonometric ratios:
 0 Trigonometric ratios: The six trigonometric ratios of A are: Sine Cosine Tangent sin A = opposite leg hypotenuse adjacent leg cos A = hypotenuse tan A = opposite adjacent leg leg and their inverses:
0 Trigonometric ratios: The six trigonometric ratios of A are: Sine Cosine Tangent sin A = opposite leg hypotenuse adjacent leg cos A = hypotenuse tan A = opposite adjacent leg leg and their inverses:
with dt. with 2. If x = u, find an equation relating du dt
 MATH 2250 Royal Section 3.10: Related Rates EXPANDED VERSION In this section, we consider two (or more) dependent variables that depend on a third variable (the independent variable). Usually, the independent
MATH 2250 Royal Section 3.10: Related Rates EXPANDED VERSION In this section, we consider two (or more) dependent variables that depend on a third variable (the independent variable). Usually, the independent
Trigonometry Final Exam Review
 Name Period Trigonometry Final Exam Review 2014-2015 CHAPTER 2 RIGHT TRIANGLES 8 1. Given sin θ = and θ terminates in quadrant III, find the following: 17 a) cos θ b) tan θ c) sec θ d) csc θ 2. Use a calculator
Name Period Trigonometry Final Exam Review 2014-2015 CHAPTER 2 RIGHT TRIANGLES 8 1. Given sin θ = and θ terminates in quadrant III, find the following: 17 a) cos θ b) tan θ c) sec θ d) csc θ 2. Use a calculator
DIFFERENTIATION RULES
 3 DIFFERENTIATION RULES DIFFERENTIATION RULES If we are pumping air into a balloon, both the volume and the radius of the balloon are increasing and their rates of increase are related to each other. However,
3 DIFFERENTIATION RULES DIFFERENTIATION RULES If we are pumping air into a balloon, both the volume and the radius of the balloon are increasing and their rates of increase are related to each other. However,
Review Problems for the Final
 Review Problems for the Final Math 6-3/6 3 7 These problems are intended to help you study for the final However, you shouldn t assume that each problem on this handout corresponds to a problem on the
Review Problems for the Final Math 6-3/6 3 7 These problems are intended to help you study for the final However, you shouldn t assume that each problem on this handout corresponds to a problem on the
Review Problems for Test 3
 Review Problems for Test 3 Math 6-3/6 7 These problems are provided to help you study. The presence of a problem on this handout does not imply that there will be a similar problem on the test. And the
Review Problems for Test 3 Math 6-3/6 7 These problems are provided to help you study. The presence of a problem on this handout does not imply that there will be a similar problem on the test. And the
(a) At what rate is the circumference of the circle changing when the radius is 10 inches? =2inches per minute and we want to find. c =2 r.
 3.11 Related Rates Problem 1 The radius of a circle is increasing at a rate of 2 inches per minute. (a) At what rate is the circumference of the circle changing when the radius is 10 inches? We know: dr
3.11 Related Rates Problem 1 The radius of a circle is increasing at a rate of 2 inches per minute. (a) At what rate is the circumference of the circle changing when the radius is 10 inches? We know: dr
SOLUTIONS FOR PRACTICE FINAL EXAM
 SOLUTIONS FOR PRACTICE FINAL EXAM ANDREW J. BLUMBERG. Solutions () Short answer questions: (a) State the mean value theorem. Proof. The mean value theorem says that if f is continuous on (a, b) and differentiable
SOLUTIONS FOR PRACTICE FINAL EXAM ANDREW J. BLUMBERG. Solutions () Short answer questions: (a) State the mean value theorem. Proof. The mean value theorem says that if f is continuous on (a, b) and differentiable
Find the length of an arc that subtends a central angle of 45 in a circle of radius 8 m. Round your answer to 3 decimal places.
 Chapter 6 Practice Test Find the radian measure of the angle with the given degree measure. (Round your answer to three decimal places.) 80 Find the degree measure of the angle with the given radian measure:
Chapter 6 Practice Test Find the radian measure of the angle with the given degree measure. (Round your answer to three decimal places.) 80 Find the degree measure of the angle with the given radian measure:
Show all work for full credit. Do NOT use trig to solve special right triangle problems (half credit).
 Chapter 8 Retake Review 1 The length of the hypotenuse of a 30 60 90 triangle is 4. Find the perimeter. 2 What similarity statement can you write relating the three triangles in the diagram? 5 Find the
Chapter 8 Retake Review 1 The length of the hypotenuse of a 30 60 90 triangle is 4. Find the perimeter. 2 What similarity statement can you write relating the three triangles in the diagram? 5 Find the
Implicit Differentiation
 Week 6. Implicit Differentiation Let s say we want to differentiate the equation of a circle: y 2 + x 2 =9 Using the techniques we know so far, we need to write the equation as a function of one variable
Week 6. Implicit Differentiation Let s say we want to differentiate the equation of a circle: y 2 + x 2 =9 Using the techniques we know so far, we need to write the equation as a function of one variable
Solution: It could be discontinuous, or have a vertical tangent like y = x 1/3, or have a corner like y = x.
 1. Name three different reasons that a function can fail to be differentiable at a point. Give an example for each reason, and explain why your examples are valid. It could be discontinuous, or have a
1. Name three different reasons that a function can fail to be differentiable at a point. Give an example for each reason, and explain why your examples are valid. It could be discontinuous, or have a
Section 6.2 Notes Page Trigonometric Functions; Unit Circle Approach
 Section Notes Page Trigonometric Functions; Unit Circle Approach A unit circle is a circle centered at the origin with a radius of Its equation is x y = as shown in the drawing below Here the letter t
Section Notes Page Trigonometric Functions; Unit Circle Approach A unit circle is a circle centered at the origin with a radius of Its equation is x y = as shown in the drawing below Here the letter t
6.3 More Sine Language
 6.3 More Sine Language A Solidify Understanding Task Clarita is helping Carlos calculate his height at different locations around a Ferris wheel. They have noticed when they use their formula h(t) = 30
6.3 More Sine Language A Solidify Understanding Task Clarita is helping Carlos calculate his height at different locations around a Ferris wheel. They have noticed when they use their formula h(t) = 30
V = π 3 r2 h. dv dt = π [ r 2dh dt r2. dv 3 dt +2rhdr dt
 9 Related Rates Related rates is the phrase used to describe the situation when two or more related variables are changing with respect to time. The rate of change, as mentioned earlier, is another expression
9 Related Rates Related rates is the phrase used to describe the situation when two or more related variables are changing with respect to time. The rate of change, as mentioned earlier, is another expression
Guidelines for implicit differentiation
 Guidelines for implicit differentiation Given an equation with x s and y s scattered, to differentiate we use implicit differentiation. Some informal guidelines to differentiate an equation containing
Guidelines for implicit differentiation Given an equation with x s and y s scattered, to differentiate we use implicit differentiation. Some informal guidelines to differentiate an equation containing
Math 113/114 Lecture 22
 Math 113/114 Lecture 22 Xi Chen 1 1 University of Alberta October 31, 2014 Outline 1 2 (Application of Implicit Differentiation) Given a word problem about related rates, we need to do: interpret the problem
Math 113/114 Lecture 22 Xi Chen 1 1 University of Alberta October 31, 2014 Outline 1 2 (Application of Implicit Differentiation) Given a word problem about related rates, we need to do: interpret the problem
UNIT 7: TRIGONOMETRY.
 UNIT 7: TRIGONOMETRY. Trigonometry: Trigonometry (from Greek trigonom triangle and metron measure ) is a branch of mathematics that studies triangles and the relationships between their sides and their
UNIT 7: TRIGONOMETRY. Trigonometry: Trigonometry (from Greek trigonom triangle and metron measure ) is a branch of mathematics that studies triangles and the relationships between their sides and their
4.6 Related Rates Notes RELATED RATES PROBLEMS --- IT S AS EASY AS 1 2-3!
 4.6 Related Rates Notes RELATED RATES PROBLEMS --- IT S AS EASY AS 1 2-3! 1) Draw a picture. Label all variables and constant values. Identify the given rate of change, the rate to be found, and when to
4.6 Related Rates Notes RELATED RATES PROBLEMS --- IT S AS EASY AS 1 2-3! 1) Draw a picture. Label all variables and constant values. Identify the given rate of change, the rate to be found, and when to
2. Find the side lengths of a square whose diagonal is length State the side ratios of the special right triangles, and
 1. Starting at the same spot on a circular track that is 80 meters in diameter, Hayley and Kendall run in opposite directions, at 300 meters per minute and 240 meters per minute, respectively. They run
1. Starting at the same spot on a circular track that is 80 meters in diameter, Hayley and Kendall run in opposite directions, at 300 meters per minute and 240 meters per minute, respectively. They run
Almost all of the questions involving Related Rates will require one of the following relationships to link together the various changing rates:
 Related Rates All quantities that we meet in every-day life change with time, this is especially true in scientific investigations. Related Rate problems are those in which an equation epresses some relationship
Related Rates All quantities that we meet in every-day life change with time, this is especially true in scientific investigations. Related Rate problems are those in which an equation epresses some relationship
Triangles and Vectors
 Chapter 3 Triangles and Vectors As was stated at the start of Chapter 1, trigonometry had its origins in the study of triangles. In fact, the word trigonometry comes from the Greek words for triangle measurement.
Chapter 3 Triangles and Vectors As was stated at the start of Chapter 1, trigonometry had its origins in the study of triangles. In fact, the word trigonometry comes from the Greek words for triangle measurement.
6.1 George W. Ferris Day Off
 6.1 George W. Ferris Day Off A Develop Understanding Task Perhaps you have enjoyed riding on a Ferris wheel at an amusement park. The Ferris wheel was invented by George Washington Ferris for the 1893
6.1 George W. Ferris Day Off A Develop Understanding Task Perhaps you have enjoyed riding on a Ferris wheel at an amusement park. The Ferris wheel was invented by George Washington Ferris for the 1893
Ch6prac 1.Find the degree measure of the angle with the given radian measure. (Round your answer to the nearest whole number.) -2
 Ch6prac 1.Find the degree measure of the angle with the given radian measure. (Round your answer to the nearest whole number.) -2 2. Find the degree measure of the angle with the given radian measure.
Ch6prac 1.Find the degree measure of the angle with the given radian measure. (Round your answer to the nearest whole number.) -2 2. Find the degree measure of the angle with the given radian measure.
AP Calculus AB Chapter 4 Packet Implicit Differentiation. 4.5: Implicit Functions
 4.5: Implicit Functions We can employ implicit differentiation when an equation that defines a function is so complicated that we cannot use an explicit rule to find the derivative. EXAMPLE 1: Find dy
4.5: Implicit Functions We can employ implicit differentiation when an equation that defines a function is so complicated that we cannot use an explicit rule to find the derivative. EXAMPLE 1: Find dy
Chapter 3. Radian Measure and Circular Functions. Copyright 2005 Pearson Education, Inc.
 Chapter 3 Radian Measure and Circular Functions Copyright 2005 Pearson Education, Inc. 3.1 Radian Measure Copyright 2005 Pearson Education, Inc. Measuring Angles Thus far we have measured angles in degrees
Chapter 3 Radian Measure and Circular Functions Copyright 2005 Pearson Education, Inc. 3.1 Radian Measure Copyright 2005 Pearson Education, Inc. Measuring Angles Thus far we have measured angles in degrees
MATH 2412 Sections Fundamental Identities. Reciprocal. Quotient. Pythagorean
 MATH 41 Sections 5.1-5.4 Fundamental Identities Reciprocal Quotient Pythagorean 5 Example: If tanθ = and θ is in quadrant II, find the exact values of the other 1 trigonometric functions using only fundamental
MATH 41 Sections 5.1-5.4 Fundamental Identities Reciprocal Quotient Pythagorean 5 Example: If tanθ = and θ is in quadrant II, find the exact values of the other 1 trigonometric functions using only fundamental
The Primary Trigonometric Ratios Word Problems
 The Primary Trigonometric Ratios Word Problems A. Determining the measures of the sides and angles of right triangles using the primary ratios When we want to measure the height of an inaccessible object
The Primary Trigonometric Ratios Word Problems A. Determining the measures of the sides and angles of right triangles using the primary ratios When we want to measure the height of an inaccessible object
APPLICATIONS OF DERIVATIVES UNIT PROBLEM SETS
 APPLICATIONS OF DERIVATIVES UNIT PROBLEM SETS PROBLEM SET #1 Related Rates ***Calculators Allowed*** 1. An oil tanker spills oil that spreads in a circular pattern whose radius increases at the rate of
APPLICATIONS OF DERIVATIVES UNIT PROBLEM SETS PROBLEM SET #1 Related Rates ***Calculators Allowed*** 1. An oil tanker spills oil that spreads in a circular pattern whose radius increases at the rate of
Math 131. Related Rates Larson Section 2.6
 Math 131. Related Rates Larson Section 2.6 There are many natural situations when there are related variables that are changing with respect to time. For example, a spherical balloon is being inflated
Math 131. Related Rates Larson Section 2.6 There are many natural situations when there are related variables that are changing with respect to time. For example, a spherical balloon is being inflated
Unit 3 Trigonometry Note Package. Name:
 MAT40S Unit 3 Trigonometry Mr. Morris Lesson Unit 3 Trigonometry Note Package Homework 1: Converting and Arc Extra Practice Sheet 1 Length 2: Unit Circle and Angles Extra Practice Sheet 2 3: Determining
MAT40S Unit 3 Trigonometry Mr. Morris Lesson Unit 3 Trigonometry Note Package Homework 1: Converting and Arc Extra Practice Sheet 1 Length 2: Unit Circle and Angles Extra Practice Sheet 2 3: Determining
Unit 5 ICM/AB Applications of the Derivative Fall Nov 10 Learn Velocity and Acceleration: HW p P ,103 p.
 Unit 5 ICM/AB Applications of the Derivative Fall 2016 Nov 4 Learn Optimization, New PS up on Optimization, HW pg. 216 3,5,17,19,21,23,25,27,29,33,39,41,49,50 a,b,54 Nov 7 Continue on HW from Nov 4 and
Unit 5 ICM/AB Applications of the Derivative Fall 2016 Nov 4 Learn Optimization, New PS up on Optimization, HW pg. 216 3,5,17,19,21,23,25,27,29,33,39,41,49,50 a,b,54 Nov 7 Continue on HW from Nov 4 and
MPE Review Section II: Trigonometry
 MPE Review Section II: Trigonometry Review similar triangles, right triangles, and the definition of the sine, cosine and tangent functions of angles of a right triangle In particular, recall that the
MPE Review Section II: Trigonometry Review similar triangles, right triangles, and the definition of the sine, cosine and tangent functions of angles of a right triangle In particular, recall that the
2.8 Linear Approximation and Differentials
 2.8 Linear Approximation Contemporary Calculus 1 2.8 Linear Approximation and Differentials Newton's method used tangent lines to "point toward" a root of the function. In this section we examine and use
2.8 Linear Approximation Contemporary Calculus 1 2.8 Linear Approximation and Differentials Newton's method used tangent lines to "point toward" a root of the function. In this section we examine and use
1. For Cosine Rule of any triangle ABC, b² is equal to A. a² - c² 4bc cos A B. a² + c² - 2ac cos B C. a² - c² + 2ab cos A D. a³ + c³ - 3ab cos A
 1. For Cosine Rule of any triangle ABC, b² is equal to A. a² - c² 4bc cos A B. a² + c² - 2ac cos B C. a² - c² + 2ab cos A D. a³ + c³ - 3ab cos A 2. For Cosine Rule of any triangle ABC, c² is equal to A.
1. For Cosine Rule of any triangle ABC, b² is equal to A. a² - c² 4bc cos A B. a² + c² - 2ac cos B C. a² - c² + 2ab cos A D. a³ + c³ - 3ab cos A 2. For Cosine Rule of any triangle ABC, c² is equal to A.
Precalculus: An Investigation of Functions. Student Solutions Manual for Chapter Solutions to Exercises
 Precalculus: An Investigation of Functions Student Solutions Manual for Chapter 5 5. Solutions to Exercises. D (5 ( )) + (3 ( 5)) (5 + ) + (3 + 5) 6 + 8 00 0 3. Use the general equation for a circle: (x
Precalculus: An Investigation of Functions Student Solutions Manual for Chapter 5 5. Solutions to Exercises. D (5 ( )) + (3 ( 5)) (5 + ) + (3 + 5) 6 + 8 00 0 3. Use the general equation for a circle: (x
TRIGONOMETRY RATIOS. LCOL and JCHL Revision
 TRIGONOMETRY RATIOS LCOL and JCHL Revision 2017 JCHL Paper 2 Question 8 (a) (i) The diagram below shows two right-angled triangles, ABC and ACD. They have right angles at B and D, respectively. AB = 10,
TRIGONOMETRY RATIOS LCOL and JCHL Revision 2017 JCHL Paper 2 Question 8 (a) (i) The diagram below shows two right-angled triangles, ABC and ACD. They have right angles at B and D, respectively. AB = 10,
MAC 2311 Calculus I Spring 2004
 MAC 2 Calculus I Spring 2004 Homework # Some Solutions.#. Since f (x) = d dx (ln x) =, the linearization at a = is x L(x) = f() + f ()(x ) = ln + (x ) = x. The answer is L(x) = x..#4. Since e 0 =, and
MAC 2 Calculus I Spring 2004 Homework # Some Solutions.#. Since f (x) = d dx (ln x) =, the linearization at a = is x L(x) = f() + f ()(x ) = ln + (x ) = x. The answer is L(x) = x..#4. Since e 0 =, and
Final practice, Math 31A - Lec 1, Fall 2013 Name and student ID: Question Points Score Total: 90
 Final practice, Math 31A - Lec 1, Fall 13 Name and student ID: Question Points Score 1 1 1 3 1 4 1 5 1 6 1 7 1 8 1 9 1 Total: 9 1. a) 4 points) Find all points x at which the function fx) x 4x + 3 + x
Final practice, Math 31A - Lec 1, Fall 13 Name and student ID: Question Points Score 1 1 1 3 1 4 1 5 1 6 1 7 1 8 1 9 1 Total: 9 1. a) 4 points) Find all points x at which the function fx) x 4x + 3 + x
AP Calculus. Applications of Derivatives. Table of Contents
 AP Calculus 2015 11 03 www.njctl.org Table of Contents click on the topic to go to that section Related Rates Linear Motion Linear Approximation & Differentials L'Hopital's Rule Horizontal Tangents 1 Related
AP Calculus 2015 11 03 www.njctl.org Table of Contents click on the topic to go to that section Related Rates Linear Motion Linear Approximation & Differentials L'Hopital's Rule Horizontal Tangents 1 Related
x f(x)
 1. Name three different reasons that a function can fail to be differential at a point. Give an example for each reason, and explain why your examples are valid. 2. Given the following table of values,
1. Name three different reasons that a function can fail to be differential at a point. Give an example for each reason, and explain why your examples are valid. 2. Given the following table of values,
x f(x)
 1. Name three different reasons that a function can fail to be differentiable at a point. Give an example for each reason, and explain why your examples are valid. 2. Given the following table of values,
1. Name three different reasons that a function can fail to be differentiable at a point. Give an example for each reason, and explain why your examples are valid. 2. Given the following table of values,
A = 1 2 ab da dt = 1 da. We can find how fast the area is growing at 3 seconds by plugging everything into that differentiated equation: da
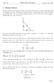 1 Related Rates In most related rates problems, we have an equation that relates a bunch of quantities that are changing over time. For example, suppose we have a right triangle whose base and height are
1 Related Rates In most related rates problems, we have an equation that relates a bunch of quantities that are changing over time. For example, suppose we have a right triangle whose base and height are
6.2 Related Rates Name: Notes
 Calculus Write your questions and thoughts here! 6.2 Related Rates Name: Notes Guidelines to solving related rate problems 1. Draw a picture. 2. Make a list of all known and unknown rates and quantities.
Calculus Write your questions and thoughts here! 6.2 Related Rates Name: Notes Guidelines to solving related rate problems 1. Draw a picture. 2. Make a list of all known and unknown rates and quantities.
Section 5.1 Exercises
 Section 5.1 Circles 79 Section 5.1 Exercises 1. Find the distance between the points (5,) and (-1,-5). Find the distance between the points (,) and (-,-). Write the equation of the circle centered at (8,
Section 5.1 Circles 79 Section 5.1 Exercises 1. Find the distance between the points (5,) and (-1,-5). Find the distance between the points (,) and (-,-). Write the equation of the circle centered at (8,
= π + sin π = π + 0 = π, so the object is moving at a speed of π feet per second after π seconds. (c) How far does it go in π seconds?
 Mathematics 115 Professor Alan H. Stein April 18, 005 SOLUTIONS 1. Define what is meant by an antiderivative or indefinite integral of a function f(x). Solution: An antiderivative or indefinite integral
Mathematics 115 Professor Alan H. Stein April 18, 005 SOLUTIONS 1. Define what is meant by an antiderivative or indefinite integral of a function f(x). Solution: An antiderivative or indefinite integral
Section 6.1. Standard position- the vertex of the ray is at the origin and the initial side lies along the positive x-axis.
 1 Section 6.1 I. Definitions Angle Formed by rotating a ray about its endpoint. Initial side Starting point of the ray. Terminal side- Position of the ray after rotation. Vertex of the angle- endpoint
1 Section 6.1 I. Definitions Angle Formed by rotating a ray about its endpoint. Initial side Starting point of the ray. Terminal side- Position of the ray after rotation. Vertex of the angle- endpoint
Department of Mathematical x 1 x 2 1
 Contents Limits. Basic Factoring Eample....................................... One-Sided Limit........................................... 3.3 Squeeze Theorem.......................................... 4.4
Contents Limits. Basic Factoring Eample....................................... One-Sided Limit........................................... 3.3 Squeeze Theorem.......................................... 4.4
1.1 Angles, Degrees, and Arcs
 MA140 Trig 2015 Homework p. 1 Name: 1.1 Angles, Degrees, and Arcs Find the fraction of a counterclockwise revolution that will form an angle with the indicated number of degrees. 3(a). 45 3(b). 150 3(c).
MA140 Trig 2015 Homework p. 1 Name: 1.1 Angles, Degrees, and Arcs Find the fraction of a counterclockwise revolution that will form an angle with the indicated number of degrees. 3(a). 45 3(b). 150 3(c).
Recall the following facts for the Ferris wheel Carlos is riding:
 In spite of his nervousness, Carlos enjoys his first ride on the amusement park Ferris wheel. He does, however, spend much of his time with his eyes fixed on the ground below him. After a while, he becomes
In spite of his nervousness, Carlos enjoys his first ride on the amusement park Ferris wheel. He does, however, spend much of his time with his eyes fixed on the ground below him. After a while, he becomes
AP Calculus Related Rates Worksheet
 AP Calculus Related Rates Worksheet 1. A small balloon is released at a point 150 feet from an observer, who is on level ground. If the balloon goes straight up at a rate of 8 feet per second, how fast
AP Calculus Related Rates Worksheet 1. A small balloon is released at a point 150 feet from an observer, who is on level ground. If the balloon goes straight up at a rate of 8 feet per second, how fast
Higher Mathematics Course Notes
 Higher Mathematics Course Notes Equation of a Line (i) Collinearity: (ii) Gradient: If points are collinear then they lie on the same straight line. i.e. to show that A, B and C are collinear, show that
Higher Mathematics Course Notes Equation of a Line (i) Collinearity: (ii) Gradient: If points are collinear then they lie on the same straight line. i.e. to show that A, B and C are collinear, show that
MATH 10550, EXAM 2 SOLUTIONS. 1. Find an equation for the tangent line to. f(x) = sin x cos x. 2 which is the slope of the tangent line at
 MATH 100, EXAM SOLUTIONS 1. Find an equation for the tangent line to at the point ( π 4, 0). f(x) = sin x cos x f (x) = cos(x) + sin(x) Thus, f ( π 4 ) = which is the slope of the tangent line at ( π 4,
MATH 100, EXAM SOLUTIONS 1. Find an equation for the tangent line to at the point ( π 4, 0). f(x) = sin x cos x f (x) = cos(x) + sin(x) Thus, f ( π 4 ) = which is the slope of the tangent line at ( π 4,
6.3 More Sine Language
 6.3 More Sine Language A Solidify Understanding Task Clarita is helping Carlos calculate his height at different locations around a Ferris wheel. They have noticed when they use their formula h(t) = 30
6.3 More Sine Language A Solidify Understanding Task Clarita is helping Carlos calculate his height at different locations around a Ferris wheel. They have noticed when they use their formula h(t) = 30
Arc Length We ve already defined radians and talked about a formula for how to calculate them. = s arc length. s r
 Arc Length We ve already defined radians and talked about a formula for how to calculate them. = s arc length = r radius From this it s not a huge leap to find a formula that will give us the arc length
Arc Length We ve already defined radians and talked about a formula for how to calculate them. = s arc length = r radius From this it s not a huge leap to find a formula that will give us the arc length
Vectors. Vector Practice Problems: Odd-numbered problems from
 Vectors Vector Practice Problems: Odd-numbered problems from 3.1-3.21 After today, you should be able to: Understand vector notation Use basic trigonometry in order to find the x and y components of a
Vectors Vector Practice Problems: Odd-numbered problems from 3.1-3.21 After today, you should be able to: Understand vector notation Use basic trigonometry in order to find the x and y components of a
Vectors. An Introduction
 Vectors An Introduction There are two kinds of quantities Scalars are quantities that have magnitude only, such as position speed time mass Vectors are quantities that have both magnitude and direction,
Vectors An Introduction There are two kinds of quantities Scalars are quantities that have magnitude only, such as position speed time mass Vectors are quantities that have both magnitude and direction,
Precalculus Honors Problem Set: Elementary Trigonometry
 Precalculus Honors Problem Set: Elementary Trigonometry Mr. Warkentin 03 Sprague Hall 017-018 Academic Year Directions: These questions are not presented in order of difficulty. Some of these questions
Precalculus Honors Problem Set: Elementary Trigonometry Mr. Warkentin 03 Sprague Hall 017-018 Academic Year Directions: These questions are not presented in order of difficulty. Some of these questions
Related Rates Example 1 Example 2 Example 3 Example 4 Example 5. Related Rates. Tamara Kucherenko
 Eample 1 Eample 2 Eample 3 Eample 4 Eample 5 Eample 1 Eample 2 Eample 3 Eample 4 Eample 5 In related rates problems we compute the rate of change of one quantity in terms of the rate of change of the other.
Eample 1 Eample 2 Eample 3 Eample 4 Eample 5 Eample 1 Eample 2 Eample 3 Eample 4 Eample 5 In related rates problems we compute the rate of change of one quantity in terms of the rate of change of the other.
AP Calculus Chapter 4 Testbank (Mr. Surowski)
 AP Calculus Chapter 4 Testbank (Mr. Surowski) Part I. Multiple-Choice Questions 1. Let f(x) = x 3 + 3x 2 45x + 4. Then the local extrema of f are (A) a local minimum of 179 at x = 5 and a local maximum
AP Calculus Chapter 4 Testbank (Mr. Surowski) Part I. Multiple-Choice Questions 1. Let f(x) = x 3 + 3x 2 45x + 4. Then the local extrema of f are (A) a local minimum of 179 at x = 5 and a local maximum
Section 6.1 Angles and Radian Measure Review If you measured the distance around a circle in terms of its radius, what is the unit of measure?
 Section 6.1 Angles and Radian Measure Review If you measured the distance around a circle in terms of its radius, what is the unit of measure? In relationship to a circle, if I go half way around the edge
Section 6.1 Angles and Radian Measure Review If you measured the distance around a circle in terms of its radius, what is the unit of measure? In relationship to a circle, if I go half way around the edge
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. C) dc. D) dr dt = 2πdC dt
 MAC 3 Chapter Review Materials (Part III) Topics Include Related Rates, Differentials, and Linear Approximations MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers
MAC 3 Chapter Review Materials (Part III) Topics Include Related Rates, Differentials, and Linear Approximations MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers
Name: Date: Period: Calculus Honors: 4-2 The Product Rule
 Name: Date: Period: Calculus Honors: 4- The Product Rule Warm Up: 1. Factor and simplify. 9 10 0 5 5 10 5 5. Find ' f if f How did you go about finding the derivative? Let s Eplore how to differentiate
Name: Date: Period: Calculus Honors: 4- The Product Rule Warm Up: 1. Factor and simplify. 9 10 0 5 5 10 5 5. Find ' f if f How did you go about finding the derivative? Let s Eplore how to differentiate
Algebra II Standard Term 4 Review packet Test will be 60 Minutes 50 Questions
 Algebra II Standard Term Review packet 2017 NAME Test will be 0 Minutes 0 Questions DIRECTIONS: Solve each problem, choose the correct answer, and then fill in the corresponding oval on your answer document.
Algebra II Standard Term Review packet 2017 NAME Test will be 0 Minutes 0 Questions DIRECTIONS: Solve each problem, choose the correct answer, and then fill in the corresponding oval on your answer document.
Bonus Homework and Exam Review - Math 141, Frank Thorne Due Friday, December 9 at the start of the final exam.
 Bonus Homework and Exam Review - Math 141, Frank Thorne (thornef@mailbox.sc.edu) Due Friday, December 9 at the start of the final exam. It is strongly recommended that you do as many of these problems
Bonus Homework and Exam Review - Math 141, Frank Thorne (thornef@mailbox.sc.edu) Due Friday, December 9 at the start of the final exam. It is strongly recommended that you do as many of these problems
Example 1 Give the degree measure of the angle shown on the circle.
 Section 5. Angles 307 Section 5. Angles Because many applications involving circles also involve q rotation of the circle, it is natural to introduce a measure for the rotation, or angle, between two rays
Section 5. Angles 307 Section 5. Angles Because many applications involving circles also involve q rotation of the circle, it is natural to introduce a measure for the rotation, or angle, between two rays
All work must be shown in this course for full credit. Unsupported answers may receive NO credit.
 AP Calculus.4 Worksheet All work must be shown in this course for full credit. Unsupported answers may receive NO credit.. What is a difference quotient?. How do you find the slope of a curve (aka slope
AP Calculus.4 Worksheet All work must be shown in this course for full credit. Unsupported answers may receive NO credit.. What is a difference quotient?. How do you find the slope of a curve (aka slope
Calculus I Review Solutions
 Calculus I Review Solutions. Compare and contrast the three Value Theorems of the course. When you would typically use each. The three value theorems are the Intermediate, Mean and Extreme value theorems.
Calculus I Review Solutions. Compare and contrast the three Value Theorems of the course. When you would typically use each. The three value theorems are the Intermediate, Mean and Extreme value theorems.
Chapter 3.5: Related Rates
 Expected Skills: Chapter.5: Related Rates Be able to solve related rates problems. It may be helpful to remember the following strategy:. Read the problem carefully. 2. Draw a diagram, if possible, representing
Expected Skills: Chapter.5: Related Rates Be able to solve related rates problems. It may be helpful to remember the following strategy:. Read the problem carefully. 2. Draw a diagram, if possible, representing
Review Questions, Exam 3
 Review Questions, Exam. A child is flying a kite. If the kite is 90 feet above the child s hand level and the wind is blowing it on a horizontal course at 5 feet per second, how fast is the child paying
Review Questions, Exam. A child is flying a kite. If the kite is 90 feet above the child s hand level and the wind is blowing it on a horizontal course at 5 feet per second, how fast is the child paying
Math 1710 Final Review 1 1
 Math 7 Final Review. Use the ɛ δ definition of it to prove 3 (2 2 +)=4. 2. Use the ɛ δ definition of it to prove +7 2 + =3. 3. Use the ɛ-δ definition of it to prove (32 +5 ) = 3. 4. Prove that if f() =
Math 7 Final Review. Use the ɛ δ definition of it to prove 3 (2 2 +)=4. 2. Use the ɛ δ definition of it to prove +7 2 + =3. 3. Use the ɛ-δ definition of it to prove (32 +5 ) = 3. 4. Prove that if f() =
5.1: Angles and Radian Measure Date: Pre-Calculus
 5.1: Angles and Radian Measure Date: Pre-Calculus *Use Section 5.1 (beginning on pg. 482) to complete the following Trigonometry: measurement of triangles An angle is formed by two rays that have a common
5.1: Angles and Radian Measure Date: Pre-Calculus *Use Section 5.1 (beginning on pg. 482) to complete the following Trigonometry: measurement of triangles An angle is formed by two rays that have a common
e x for x 0. Find the coordinates of the point of inflexion and justify that it is a point of inflexion. (Total 7 marks)
 Chapter 0 Application of differential calculus 014 GDC required 1. Consider the curve with equation f () = e for 0. Find the coordinates of the point of infleion and justify that it is a point of infleion.
Chapter 0 Application of differential calculus 014 GDC required 1. Consider the curve with equation f () = e for 0. Find the coordinates of the point of infleion and justify that it is a point of infleion.
4.5 Linearization Calculus 4.5 LINEARIZATION. Notecards from Section 4.5: Linearization; Differentials. Linearization
 4.5 Linearization Calculus 4.5 LINEARIZATION Notecards from Section 4.5: Linearization; Differentials Linearization The goal of linearization is to approximate a curve with a line. Why? Because it s easier
4.5 Linearization Calculus 4.5 LINEARIZATION Notecards from Section 4.5: Linearization; Differentials Linearization The goal of linearization is to approximate a curve with a line. Why? Because it s easier
PTF #AB 07 Average Rate of Change
 The average rate of change of f( ) over the interval following: 1. y dy d. f() b f() a b a PTF #AB 07 Average Rate of Change ab, can be written as any of the. Slope of the secant line through the points
The average rate of change of f( ) over the interval following: 1. y dy d. f() b f() a b a PTF #AB 07 Average Rate of Change ab, can be written as any of the. Slope of the secant line through the points
Implicit Differentiation and Related Rates
 Math 31A Discussion Session Week 5 Notes February 2 and 4, 2016 This week we re going to learn how to find tangent lines to curves which aren t necessarily graphs of functions, using an approach called
Math 31A Discussion Session Week 5 Notes February 2 and 4, 2016 This week we re going to learn how to find tangent lines to curves which aren t necessarily graphs of functions, using an approach called
( ) as a fraction. If both numerator and denominator are
 A. Limits and Horizontal Asymptotes What you are finding: You can be asked to find lim f x x a (H.A.) problem is asking you find lim f x x ( ) and lim f x x ( ). ( ) or lim f x x ± ( ). Typically, a horizontal
A. Limits and Horizontal Asymptotes What you are finding: You can be asked to find lim f x x a (H.A.) problem is asking you find lim f x x ( ) and lim f x x ( ). ( ) or lim f x x ± ( ). Typically, a horizontal
Review Problems for the Final
 Review Problems for the Final Math -3 5 7 These problems are provided to help you study. The presence of a problem on this handout does not imply that there will be a similar problem on the test. And the
Review Problems for the Final Math -3 5 7 These problems are provided to help you study. The presence of a problem on this handout does not imply that there will be a similar problem on the test. And the
Solutions to Math 41 Second Exam November 5, 2013
 Solutions to Math 4 Second Exam November 5, 03. 5 points) Differentiate, using the method of your choice. a) fx) = cos 03 x arctan x + 4π) 5 points) If u = x arctan x + 4π then fx) = fu) = cos 03 u and
Solutions to Math 4 Second Exam November 5, 03. 5 points) Differentiate, using the method of your choice. a) fx) = cos 03 x arctan x + 4π) 5 points) If u = x arctan x + 4π then fx) = fu) = cos 03 u and
Math 1131Q Section 10
 Math 1131Q Section 10 Section 3.9 and 3.10 Oct 19, 2010 Find the derivative of ln 3 5 e 2 ln 3 5 e 2 = ln 3 + ln 5/2 + ln e 2 = 3 ln + ( 5 ) ln + 2 2 (ln 3 5 e 2 ) = 3 + 5 2 + 2 Find the derivative of
Math 1131Q Section 10 Section 3.9 and 3.10 Oct 19, 2010 Find the derivative of ln 3 5 e 2 ln 3 5 e 2 = ln 3 + ln 5/2 + ln e 2 = 3 ln + ( 5 ) ln + 2 2 (ln 3 5 e 2 ) = 3 + 5 2 + 2 Find the derivative of
Section 6.1 Sinusoidal Graphs
 Chapter 6: Periodic Functions In the previous chapter, the trigonometric functions were introduced as ratios of sides of a right triangle, and related to points on a circle We noticed how the x and y values
Chapter 6: Periodic Functions In the previous chapter, the trigonometric functions were introduced as ratios of sides of a right triangle, and related to points on a circle We noticed how the x and y values
Old Math 120 Exams. David M. McClendon. Department of Mathematics Ferris State University
 Old Math 10 Exams David M. McClendon Department of Mathematics Ferris State University 1 Contents Contents Contents 1 General comments on these exams 3 Exams from Fall 016 4.1 Fall 016 Exam 1...............................
Old Math 10 Exams David M. McClendon Department of Mathematics Ferris State University 1 Contents Contents Contents 1 General comments on these exams 3 Exams from Fall 016 4.1 Fall 016 Exam 1...............................
Math 147 Exam II Practice Problems
 Math 147 Exam II Practice Problems This review should not be used as your sole source for preparation for the exam. You should also re-work all examples given in lecture, all homework problems, all lab
Math 147 Exam II Practice Problems This review should not be used as your sole source for preparation for the exam. You should also re-work all examples given in lecture, all homework problems, all lab
3. On the grid below, sketch and label graphs of the following functions: y = sin x, y = cos x, and y = sin(x π/2). π/2 π 3π/2 2π 5π/2
 AP Physics C Calculus C.1 Name Trigonometric Functions 1. Consider the right triangle to the right. In terms of a, b, and c, write the expressions for the following: c a sin θ = cos θ = tan θ =. Using
AP Physics C Calculus C.1 Name Trigonometric Functions 1. Consider the right triangle to the right. In terms of a, b, and c, write the expressions for the following: c a sin θ = cos θ = tan θ =. Using
Chapter 3 Homework Packet. Conceptual Questions
 Chapter 3 Homework Packet Conceptual Questions 1) Which one of the following is an example of a vector quantity? A) mass B) area C) distance D) velocity A vector quantity has both magnitude and direction.
Chapter 3 Homework Packet Conceptual Questions 1) Which one of the following is an example of a vector quantity? A) mass B) area C) distance D) velocity A vector quantity has both magnitude and direction.
Recall the following facts for the Ferris wheel Carlos is riding:
 SECONDARY MATH III // MODULE 6 In spite of his nervousness, Carlos enjoys his first ride on the amusement park Ferris wheel. He does, however, spend much of his time with his eyes fixed on the ground below
SECONDARY MATH III // MODULE 6 In spite of his nervousness, Carlos enjoys his first ride on the amusement park Ferris wheel. He does, however, spend much of his time with his eyes fixed on the ground below
Assignment 1 and 2: Complete practice worksheet: Simplifying Radicals and check your answers
 Geometry 0-03 Summary Notes Right Triangles and Trigonometry These notes are intended to be a guide and a help as you work through Chapter 8. These are not the only thing you need to read, however. Rely
Geometry 0-03 Summary Notes Right Triangles and Trigonometry These notes are intended to be a guide and a help as you work through Chapter 8. These are not the only thing you need to read, however. Rely
Trigonometry Unit 5. Reflect previous TEST mark, Overall mark now. Looking back, what can you improve upon?
 1 U n i t 5 11C Date: Name: Tentative TEST date Trigonometry Unit 5 Reflect previous TEST mark, Overall mark now. Looking back, what can you improve upon? Learning Goals/Success Criteria Use the following
1 U n i t 5 11C Date: Name: Tentative TEST date Trigonometry Unit 5 Reflect previous TEST mark, Overall mark now. Looking back, what can you improve upon? Learning Goals/Success Criteria Use the following
T.4 Applications of Right Angle Trigonometry
 424 section T4 T.4 Applications of Right Angle Trigonometry Solving Right Triangles Geometry of right triangles has many applications in the real world. It is often used by carpenters, surveyors, engineers,
424 section T4 T.4 Applications of Right Angle Trigonometry Solving Right Triangles Geometry of right triangles has many applications in the real world. It is often used by carpenters, surveyors, engineers,
Sample Examination VI 203
 Sample Examination VI 203 Section II Part A: Graphing Calculator MAY BE USED. 1. Two particles move in the xy-plane: Particle A moves along the graph of y = 1 + e- X and particle B moves along the graph
Sample Examination VI 203 Section II Part A: Graphing Calculator MAY BE USED. 1. Two particles move in the xy-plane: Particle A moves along the graph of y = 1 + e- X and particle B moves along the graph
Partial Fractions. June 27, In this section, we will learn to integrate another class of functions: the rational functions.
 Partial Fractions June 7, 04 In this section, we will learn to integrate another class of functions: the rational functions. Definition. A rational function is a fraction of two polynomials. For example,
Partial Fractions June 7, 04 In this section, we will learn to integrate another class of functions: the rational functions. Definition. A rational function is a fraction of two polynomials. For example,
Math Section 4.3 Unit Circle Trigonometry
 Math 10 - Section 4. Unit Circle Trigonometry An angle is in standard position if its vertex is at the origin and its initial side is along the positive x axis. Positive angles are measured counterclockwise
Math 10 - Section 4. Unit Circle Trigonometry An angle is in standard position if its vertex is at the origin and its initial side is along the positive x axis. Positive angles are measured counterclockwise
Section 6.5 Modeling with Trigonometric Functions
 Section 6.5 Modeling with Trigonometric Functions 441 Section 6.5 Modeling with Trigonometric Functions Solving right triangles for angles In Section 5.5, we used trigonometry on a right triangle to solve
Section 6.5 Modeling with Trigonometric Functions 441 Section 6.5 Modeling with Trigonometric Functions Solving right triangles for angles In Section 5.5, we used trigonometry on a right triangle to solve
10550 PRACTICE FINAL EXAM SOLUTIONS. x 2 4. x 2 x 2 5x +6 = lim x +2. x 2 x 3 = 4 1 = 4.
 55 PRACTICE FINAL EXAM SOLUTIONS. First notice that x 2 4 x 2x + 2 x 2 5x +6 x 2x. This function is undefined at x 2. Since, in the it as x 2, we only care about what happens near x 2 an for x less than
55 PRACTICE FINAL EXAM SOLUTIONS. First notice that x 2 4 x 2x + 2 x 2 5x +6 x 2x. This function is undefined at x 2. Since, in the it as x 2, we only care about what happens near x 2 an for x less than
