Modern Geometry Homework.
|
|
|
- Natalie Henry
- 5 years ago
- Views:
Transcription
1 Modern Geometry Homework. 1. One to one correspondences and the cardinality of sets. Definition 1. Let f : A B be a function between sets. (a) f is one-to-one (or injective) iff for all a 1, a 2 A with a 1 a 2 we have f(a 1 ) fa 2 ). (Or what is the same thing if a 1, a 2 A and f(a 1 ) = f(a 2 ) then a 1 = a 2.) (b) f is onto (or surjective) iff for all b B there is an a A with f(a) = b. (c) f is one-to-one and onto (or bijective, or a one-to-one correspondence) iff f both one-to-one and onto. Definition 2. If f : A B and g : B C, then the composition of g and f, denoted by g f is the function g f : A C given by g f(x) := g(f(x)). Proposition 3. Let f : A B and g : B C be functions. Then (a) If f and g are both one-to-one, then so is g g. (b) If f and g are both onto, then so is g f. (c) if f and g are both bijective, then so is g f. Problem 1. Prove this. Hint: Note that once you have done parts (a) and (b) you get part (c) for free. For parts (a) and (b) it is mostly a matter of writing down the definitions and following your nose. For example in (b) if c C, as g is onto, there is a b B with g(b) = c. But then as f is onto there is an a A with f(a) = b. Then what is (g f)(a) = g(f(a))? Definition 4. Let A and B be sets. Then A and B have the same number of elements (or have the same cardinality) iff there is a one-toone correspondence f : A B. Proposition 5. If A and B have the same cardinality and B and C have the same cardinality, then A and C have the same cardinality. Problem 2. Prove this. Hint: Proposition 3 part (c). Proposition 6. Let f : A B and g : B A be functions. Assume g(f(a)) = a for all a A, f(g(b)) = b for all b B. Then both f and g are one-to-one and onto. In this case we say that f is the inverse of g (and that g is the inverse of f). Problem 3. Prove this. Hint: As the hypothesis are symmetric in f and g it is enough to prove that f is bijective for, by reversing the roles of f and g, the same proof would show that g is bijective. To show that f is injective assume that f(a 1 ) = f(a 2 ). Then g(f(a 1 )) = g(f(a 2 )). But what are g(f(a 1 )) and g(f(a 1 ))? To show that f is onto, let b B. Then what is f(g(b))?
2 In this class many, if not most, of the one-one correspondences we well construct are based on drawing a line trough a point on one set and seeing where it interests anther set. We will use the notation P Q = the line through the points P and Q. and P Q = the ray starting at P and passing through Q. Here are a couple of examples of this idea. Problem 4. Let O be the origin in the plane R 2 (a) Draw the circle, C, defined by x 2 + y 2 = 1 and the ellipse, E, defined by x2 4 + y2 9 = 1 on the same axis. (b) Let P, P O be points such that P is on the ray OP. Draw a picture which shows why OP = OP. (c) Define a function f : C E be letting f(p ) by the point on the ray OP intersects E. That is f(p ) = E OP. Note by part (b) we have OP = Of(P ). Choose three points P 1, P 2 and P 3 on C and draw their images under f on E. (d) Define a function g : E C be letting g(q) by the point on the ray OQ intersects C, that is g(q) = C OQ. Again we can use part(b) to see that OQ = Og(Q) Choose three points Q 1, Q 2 and Q 3 on E and draw their images under g. (e) Explain why g(f(p )) = P for all P C and f(g(q)) = Q for all Q E. You can, and probably should, do a proof by picture on this. But here is a more formal version of showing f(g(p )) = P. f(g(q)) = E Og(Q) (Definition of f) = E OQ (As OQ = Og(Q)) ( ) As Q is on E so it is the point = Q of intersection of OQ and E Do a similar calculation to show g(f(p )) = P. (f) Conclude that f and g are bijections and therefore C and E have the same cardinality. Problem 5. Figure 1 shows the circle x 2 + y 2 = 1 where N = (0, 1) (the North Pole ). Let S be this circle with N removed (shown in blue). Let l be the x-axis (shown in red). Note for any downward pointing ray starting from N (three of these are shown in green) the ray will intersect both S and L in exactly one point. 2
3 N P 3 Q f(p ) g(q) Figure 1 (a) Let P, P N be points such that P is on the ray NP. Draw a picture which shows NP = NP. (b) If P is a point on S, then then the figure shows a corresponding point f(p ) on L. Give a verbal description of this function. In terms of a formula it is given by f(p ) = l NP. Note that by part (a) we have NP = Nf(P ). (c) If Q is a point on L, then then the figure shows a corresponding point g(q) on S. Give a verbal description. This time the formula is g(q) = S NQ. And by part (a) NQ = Ng(Q). (d) Show these functions are inverse to each other. Again proof by picture if accompanied by the correct English is fine, but we can be a bit more formal. Justify the following steps. g(f(p )) = S Nf(P ) = S NP = P (as P is on S and NP ). Do a similar calculation to show f(g(q)) = Q. 2. Axioms of Affine Geometry Affine geometry is the part of Euclidean geometry that is left over when all mention of distance and angles is removed. What is left are the ideas of incidence and parallelism. A surprise is that there are more examples than just the usual plane. We have some undefined notions. The first is point which you can think just as usual as a point in the plane. The collection of all points will be denote by A 2. The next undefined notation is line. These are special subsets of A 2 and again think of these as lines in the usual sense. Finally
4 there is the notion of incidence. This is a relation between points and lines. To say that the point P is incidence with the line l is just to say that the point P is on the line L. Other ways to say that the point P and the line l are incidence are to say that l goes through P, or that l is on P. The first axiom is just the familiar fact that two points determine a line. Affine Geometry: Axiom 1. If P and Q are distinct points of A 2 (that is P Q) then there is a unique line that passes through both of them. When we say that this line is unique we mean that there is exactly one of them. If P and Q are points of A 2 with P Q then we will use the notation P Q := The line through P and Q. Proposition 7. If l and m are distinct lines of A 2 then there is at most one point that is incident with both l and m. (Or a little more informally, two distinct lines meet in at most one point.) Thus if l and m are distinct lines in A 2 either they have no point incident with both of them, or there is exactly one point that is incident with both of them. Anther restatement would be that two distinct lines can not meet in two or more points. If l and m are lines we will use the notation l m = Point of intersection of l and m. Problem 6. Prove the last Proposition. Hint: Towards contradiction assume that the distinct lines l and m meet in two or more points and let P and Q be two of these points. Then by first axiom of affine geometry there is exactly one line through P and Q. If you think about it a bit this gives a contradiction. In Euclidian geometry we define two lines to be parallel if they have no point in common. But in some circumstances it is convenient to think of a line as being parallel to itself. Different text books have different conventions about this. I am going to assume that a line is parallel to itself. Definition 8. Two lines, l and m of A 2 are parallel iff either l = m or l and m have no points in common. Affine Geometry: Axiom 2 (Parallel Axiom). If l is a line of A 2 and P is a point that is not on l, then there is a unique line m that goes through P and is parallel to l. (See Figure 2.) Based on our definition of parallel lines we can give a slightly more general version of this. Proposition 9. If l is any line of A 2 and P any point, then there is a unique line m that goes through P and is parallel to l. Problem 7. Prove this. Hint: The only way this differs from the Parallel Axiom is that we allow the point P to be on the line l. If P is on l then you just need to find a line, m, through P parallel to l. 4
5 l 5 m P Figure 2. The Parallel Axiom tells us that given a line l (here in blue) and a point not on l (here in green) there is exactly one line m (here in red) through P that does not meet l. Proposition 10. If l 1 and l 2 are parallel lines and the line m l 1 intersects l 1, then it also intersects l 2. Figure 3. Proposition 10 tells us that if we have two parallel lines (in blue) then a third line (in red) meets one of these lines if and only if it meets the other one. Problem 8. Prove this. Hint: Let P be the point where l 1 and m meet. If m does not intersect l 2, then how many parallels does l 2 have that pass through P? Draw a picture. Problem 9. This is a special case of a slightly more general result we will prove later. Let l 1, l 2 and l 3 be distinct lines. Assume that l 1 is parallel to l 2 and that l 2 is parallel to l 3. Show that l 1 is parallel to l 3. The last axiom of affine geometry just ensures that we have more than one line. Affine Geometry: Axiom 3. There exists a set of four points in A 2 such that no three of which are all on the same line. We can give our first non-obvious example of an affine plane. In Figure 4 we have the four points A, B, C, D and the six lines a, b, c, d, e, f. We
6 only count the intersections at the labeled and shaded points (this the point at the center where you might think that a and d intersect does not count). Note that in this figure any two of the points determine a unique line. For any of the six lines and a point not on the line there is a unique parallel to the line through the point. For example the parallel to d through the points A is the line a. And no three of the points are all on the same line. Therefore this gives us an example of an affine geometry that only has four points and six lines. This is the smallest possible affine geometry. a b c d 6 e A B f D C Figure 4. This shows four points and the six lines they determine. We only count the lines as intersecting if they both pass through one of shaded circles. What determines the geometry of this plane is the sets of points, {A, B, C, D} and lines {a, b, c, d, e, f} and the incidence relations between them. In this case these are AB = e, and AC = a, AD = b, BC = c, BD = d, CD = b, (1) A = a b = a e = b e, B = c d = c e = d e, (2) C = a c = a f = c f, D = b d = b f = d f. These are what defines the geometry, not the particular picture that we draw of it. Figure 5 gives anther picture of the same geometry. Problem 10. Use Figure 4 or Figure 5 to find the following: (a) The line through C parallel to e. (b) The line through C parallel to d. Lemma 11. Let l 1 and l 2 be distinct lines of A 2. Assume that a third line m (not equal to either l 1 or l 2 intersects both l 1 and l 2 ). Then any line n parallel to m intersects each of l 1 and l 2 in exactly one point. (See figure 6.)
7 A 7 a b e C f D c Figure 5. This is anther model of the affine plane of Figue 4. The reason this is the same geometry is that the same set of incidence relations (1) and (2) hold. d B Figure 6. Some possible configurations of the lines in Lemma 11. Given two distinct lines (in blue) and a third line that intersects them both (in red) then any line parallel to the red line (such as the green line) also intersects each of the blue lines. Problem 11. Prove the last Proposition. Hint: Towards a contradiction assume that n does not intersect l 1. Let P be the point of intersection of l 1 and m. Then l 1 and m are parallel to n and both go through P. Theorem 12. Any two lines of A 2 have the same number of points. More precisely, for any two lines in A 2 there is a one-to-one correspondence between their points. Problem 12. Prove this along the following lines. Let l 1 and l 2 be lines of A 2. We wish to find a bijection between these two sets. If l 1 = l 2 then just use the identity map. So assume that l 1 l 2. (a) Show that there is a line m distinct from l 1 and l 2 that intersects both l 1 and l 2. Hint: As l 1 l 2, there is a point of l 1 that is not on l 2 and a point of l 2 that is not on l 1. Let m be line through these two points. (b) For each point P A 2 let n(p ) be the line of A 2 that passes through P and is parallel to m. Use Proposition 11 to show that each n(p ) intersects both l 1 and l 2. Draw a picture to illustrate this. (c) Define a function f that takes points on l 1 to points on l 2 as follows and a function g that takes points on l 2 to points on l 1 as follows. (See Figure 7.)
8 8 l 2 l 1 l 2 l P m f(p ) n(p ) g(q) Q m n(q) Figure 7. The construction of f is illustrated on the left. Given an input point P on l 1, draw the line n(p ) through P and parallel to m. The output, f(p ), is the point where n(p ) intersects l 2. The construction of g is illustrated on the right. Given an input point Q on l 2, draw the line n(q) through Q and parallel to m. Then g(q) is the point where n(q) intersects l 1. (i) If P is a point on l 1, then f(p ) is the point where n(p ) intersects l 2. That is f(p ) = n(p ) l 2. (ii) If Q is a point on l 2, then g(q) is the point where n(q) intersects l 1. That is g(q) = n(q) l 1 Explain why f and g are inverse to each other. Hint: It is enough to show that f(g(q)) = Q and g(f(p )) = P. Here is one of the two calculations f(g(q)) = n(g(q)) l 2 (definition of f) as n(q) = n(g(q) because = n(q) l n(q) and n(g(q)) are parallel 2 to m and contain Q and there is only one such parallel. = Q (as Q is on both n(q) and l 1.) Do a similar calculation so find show g(f(p )) = P. (d) Use Proposition 6 to finish the proof. Proposition 13. Each line of A 2 has at least two points on it. Problem 13. Prove this. Hint: By Theorem 12 all lines have the same number of points on them. So it is enough to show that there is at least one line with two or more points on it. You should be able to do this using Affine Axiom 3. Theorem 14. If some line of A 2 has a finite number of points on it, say n, then (a) Every line has exactly n points on it. (b) Each point has exactly n + 1 lines passing through it. (c) Each line has exactly n lines parallel to it (counting itself). (d) A 2 consists of exactly n 2 points.
9 y y(p ) Y (P ) P X(P ) x(p ) x 1 1 y y(x 0 ) Y 0 x(y 0 ) y(x 0 ) x(y 0 ) X 0 x 9 Figure 8. Start by choosing two intersecting lines x and y. Then for any point P of the plane let x(p ) be the line through P that is parallel to x and let y(p ) be the line through P parallel to y. Then let X(P ) = x y(p ) be the point where y(p ) intersects x and Y (P ) = y x(p ) be the point where x(p ) intersects y. This is illustrated in the figure on the left. Conversely given points X 0 on x and Y 0 on y by looking at the point of intersection of the line through X 0 and parallel to y and the line through Y 0 and parallel to x show there is a point P 0 = x(y 0) y(x 0) with X(P 0) = X 0 and Y (P 0) = Y 0. This is illustrated on the right. (e) There are exactly n 2 + n lines in A 2. Problem 14. Prove this. Hints: (a) This follows directly from Theorem 12. (b) Let P be a point of A 2 and l a line that does not go through P. Let m be the unique parallel to l through P. For any point Q of l let P Q be the line through P and Q. Draw a picture and explain why {m} { P Q : Q l} gives all the lines through P and why this shows that there are exactly n + 1 of them. (c) Let l be a line of A 2 and m a line that intersects l in exactly one point. Then any line n parallel to l will intersect m in a point. And given any point on m there is a line through this point parallel to l. These facts can be put together to find a bijection between the lines parallel to l and the points of m. Draw a picture. (d) You should be able to use the idea suggested by Figure 8 to find a bijection between the set of points P A 2 and the set of ordered pairs (X, Y ) with X ξ and Y η. (This should remind you of the construction of x-y coordinates in the plane.) (e) Let l be a line of A 2. Then any point l has n + 1 lines through it by part (b). If we throw out l itself, this gives that through each point of l there are n lines that are not parallel to l. Explain why this shows there are exactly n 2 lines of A 2 that are not parallel to l. This leaves the lines that are parallel to l and by part (c) there are n such lines. For anther example of an affine plane see Figure 9. In this example there are nine points, each line contains three points (so the n of Theorem 14 is n = 3) and there are n 2 + n = 12 lines.
10 In light of the couple of examples we have given so far, it is natural to ask for what number n is there an affine geometry where each line has n points. Definition 15. If A 2 is a an affine plane with only a finite number of points, then its order is the number of points on a line. Thus Theorem 14 tells us that an affine plane of order n has n 2 points and n 2 + n lines. For a positive result we have Theorem 16. If n = p k where p is a prime number and k is a positive integer, then there is an affine plane of order n. We will outline a proof of the above later in the term. But not every n can be the order of a finite plane. The most general known restriction is Theorem 17 (Bruck-Ryser theorem). If an affine plane of order n exists and n is of the form 4k + 1 or 4k + 2, then n is the sum of two squares. (That is n = x 2 + y 2 for some integers x and y.) For example 6 is of the form 4k+2 (where k = 1) but 6 can not be written as 6 = x 2 + y 2 (as you can see by a bit of trial trail and error). Thus there is no affine plane of order 6. Likewise 14 = 4(3) + 2 is of the form 4k + 2, and you can use trail an error to find that 14 can not be written as 14 = x 2 + y 2 (if x or y is 4 then x 2 + y = 16 is too large. So you only have to check the cases where x, y = 0, 1, 2, 3.) Therefore there is no affine plane of order 14. Problem 15. Use the Bruck-Ryser Theorem to show that there is no affine plane of order 22. The smallest number not covered by the last two theorems is 10. It is not a prime power, but it is the sum of two squares: 10 = It was a big deal in the 1980 s, when C. W. H. Lam, L. H. Thiel, and S. Swiercz Figure 9. An affine plane with 9 points and 12 lines and each line containing 3 points.
11 [2] proved that there is no plane of order 10. Even the New York Times had an article about the result (Dec. 20, 1988, Section 3, p. 1). If you want more information Lam has a article [1] describing the history of the result. A down side to this proof is that it is not directly human readable in that it relies on a large computer search to check a vast number of special cases. The next number not covered by the Bruck-Ryser Theorem is 12 which in not of either of the forms 4k + 1 or 4k + 2. If is still unknown if there is a affine plane of order 12 and this seems be be a vary hard question. References 1. C. W. H. Lam, The search for a finite projective plane of order 10, Amer. Math. Monthly 98 (1991), no. 4, MR (92b:513) 2. C. W. H. Lam, L. Thiel, and S. Swiercz, The nonexistence of finite projective planes of order 10, Canad. J. Math. 41 (1989), no. 6, MR (90j:51008) 11
ADVANCED CALCULUS - MTH433 LECTURE 4 - FINITE AND INFINITE SETS
 ADVANCED CALCULUS - MTH433 LECTURE 4 - FINITE AND INFINITE SETS 1. Cardinal number of a set The cardinal number (or simply cardinal) of a set is a generalization of the concept of the number of elements
ADVANCED CALCULUS - MTH433 LECTURE 4 - FINITE AND INFINITE SETS 1. Cardinal number of a set The cardinal number (or simply cardinal) of a set is a generalization of the concept of the number of elements
Theorem. For every positive integer n, the sum of the positive integers from 1 to n is n(n+1)
 Week 1: Logic Lecture 1, 8/1 (Sections 1.1 and 1.3) Examples of theorems and proofs Theorem (Pythagoras). Let ABC be a right triangle, with legs of lengths a and b, and hypotenuse of length c. Then a +
Week 1: Logic Lecture 1, 8/1 (Sections 1.1 and 1.3) Examples of theorems and proofs Theorem (Pythagoras). Let ABC be a right triangle, with legs of lengths a and b, and hypotenuse of length c. Then a +
Modern Geometry Homework.
 Modern Geometry Homework 1 Cramer s rule We now wish to become experts in solving two linear equations in two unknowns over our field F We first recall that a 2 2 matrix a b A = c b its determinant is
Modern Geometry Homework 1 Cramer s rule We now wish to become experts in solving two linear equations in two unknowns over our field F We first recall that a 2 2 matrix a b A = c b its determinant is
MATH 3300 Test 1. Name: Student Id:
 Name: Student Id: There are nine problems (check that you have 9 pages). Solutions are expected to be short. In the case of proofs, one or two short paragraphs should be the average length. Write your
Name: Student Id: There are nine problems (check that you have 9 pages). Solutions are expected to be short. In the case of proofs, one or two short paragraphs should be the average length. Write your
ABOUT THE CLASS AND NOTES ON SET THEORY
 ABOUT THE CLASS AND NOTES ON SET THEORY About the Class Evaluation. Final grade will be based 25%, 25%, 25%, 25%, on homework, midterm 1, midterm 2, final exam. Exam dates. Midterm 1: Oct 4. Midterm 2:
ABOUT THE CLASS AND NOTES ON SET THEORY About the Class Evaluation. Final grade will be based 25%, 25%, 25%, 25%, on homework, midterm 1, midterm 2, final exam. Exam dates. Midterm 1: Oct 4. Midterm 2:
Math 4603: Advanced Calculus I, Summer 2016 University of Minnesota Notes on Cardinality of Sets
 Math 4603: Advanced Calculus I, Summer 2016 University of Minnesota Notes on Cardinality of Sets Introduction In this short article, we will describe some basic notions on cardinality of sets. Given two
Math 4603: Advanced Calculus I, Summer 2016 University of Minnesota Notes on Cardinality of Sets Introduction In this short article, we will describe some basic notions on cardinality of sets. Given two
SETS AND FUNCTIONS JOSHUA BALLEW
 SETS AND FUNCTIONS JOSHUA BALLEW 1. Sets As a review, we begin by considering a naive look at set theory. For our purposes, we define a set as a collection of objects. Except for certain sets like N, Z,
SETS AND FUNCTIONS JOSHUA BALLEW 1. Sets As a review, we begin by considering a naive look at set theory. For our purposes, we define a set as a collection of objects. Except for certain sets like N, Z,
Definition: Let S and T be sets. A binary relation on SxT is any subset of SxT. A binary relation on S is any subset of SxS.
 4 Functions Before studying functions we will first quickly define a more general idea, namely the notion of a relation. A function turns out to be a special type of relation. Definition: Let S and T be
4 Functions Before studying functions we will first quickly define a more general idea, namely the notion of a relation. A function turns out to be a special type of relation. Definition: Let S and T be
Math 300 Introduction to Mathematical Reasoning Autumn 2017 Inverse Functions
 Math 300 Introduction to Mathematical Reasoning Autumn 2017 Inverse Functions Please read this pdf in place of Section 6.5 in the text. The text uses the term inverse of a function and the notation f 1
Math 300 Introduction to Mathematical Reasoning Autumn 2017 Inverse Functions Please read this pdf in place of Section 6.5 in the text. The text uses the term inverse of a function and the notation f 1
1 Take-home exam and final exam study guide
 Math 215 - Introduction to Advanced Mathematics Fall 2013 1 Take-home exam and final exam study guide 1.1 Problems The following are some problems, some of which will appear on the final exam. 1.1.1 Number
Math 215 - Introduction to Advanced Mathematics Fall 2013 1 Take-home exam and final exam study guide 1.1 Problems The following are some problems, some of which will appear on the final exam. 1.1.1 Number
Chapter 0. Introduction: Prerequisites and Preliminaries
 Chapter 0. Sections 0.1 to 0.5 1 Chapter 0. Introduction: Prerequisites and Preliminaries Note. The content of Sections 0.1 through 0.6 should be very familiar to you. However, in order to keep these notes
Chapter 0. Sections 0.1 to 0.5 1 Chapter 0. Introduction: Prerequisites and Preliminaries Note. The content of Sections 0.1 through 0.6 should be very familiar to you. However, in order to keep these notes
All numbered readings are from Beck and Geoghegan s The art of proof.
 MATH 301. Assigned readings and homework All numbered readings are from Beck and Geoghegan s The art of proof. Reading Jan 30, Feb 1: Chapters 1.1 1.2 Feb 6, 8: Chapters 1.3 2.1 Feb 13, 15: Chapters 2.2
MATH 301. Assigned readings and homework All numbered readings are from Beck and Geoghegan s The art of proof. Reading Jan 30, Feb 1: Chapters 1.1 1.2 Feb 6, 8: Chapters 1.3 2.1 Feb 13, 15: Chapters 2.2
MATH 220 (all sections) Homework #12 not to be turned in posted Friday, November 24, 2017
 MATH 220 (all sections) Homework #12 not to be turned in posted Friday, November 24, 2017 Definition: A set A is finite if there exists a nonnegative integer c such that there exists a bijection from A
MATH 220 (all sections) Homework #12 not to be turned in posted Friday, November 24, 2017 Definition: A set A is finite if there exists a nonnegative integer c such that there exists a bijection from A
MODEL ANSWERS TO THE SEVENTH HOMEWORK. (b) We proved in homework six, question 2 (c) that. But we also proved homework six, question 2 (a) that
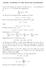 MODEL ANSWERS TO THE SEVENTH HOMEWORK 1. Let X be a finite set, and let A, B and A 1, A 2,..., A n be subsets of X. Let A c = X \ A denote the complement. (a) χ A (x) = A. x X (b) We proved in homework
MODEL ANSWERS TO THE SEVENTH HOMEWORK 1. Let X be a finite set, and let A, B and A 1, A 2,..., A n be subsets of X. Let A c = X \ A denote the complement. (a) χ A (x) = A. x X (b) We proved in homework
Homework has to be turned in this handout. For extra space, use the back pages, or blank pages between. due January 22/23
 Math 3181 Name: Dr. Franz Rothe January 15, 2014 All3181\3181_spr14h1.tex Homework has to be turned in this handout. For extra space, use the back pages, or blank pages between. due January 22/23 1 Homework
Math 3181 Name: Dr. Franz Rothe January 15, 2014 All3181\3181_spr14h1.tex Homework has to be turned in this handout. For extra space, use the back pages, or blank pages between. due January 22/23 1 Homework
Math 40510, Algebraic Geometry
 Math 40510, Algebraic Geometry Problem Set 1, due February 10, 2016 1. Let k = Z p, the field with p elements, where p is a prime. Find a polynomial f k[x, y] that vanishes at every point of k 2. [Hint:
Math 40510, Algebraic Geometry Problem Set 1, due February 10, 2016 1. Let k = Z p, the field with p elements, where p is a prime. Find a polynomial f k[x, y] that vanishes at every point of k 2. [Hint:
Written Homework # 4 Solution
 Math 516 Fall 2006 Radford Written Homework # 4 Solution 12/10/06 You may use results form the book in Chapters 1 6 of the text, from notes found on our course web page, and results of the previous homework.
Math 516 Fall 2006 Radford Written Homework # 4 Solution 12/10/06 You may use results form the book in Chapters 1 6 of the text, from notes found on our course web page, and results of the previous homework.
Chapter 1. Sets and Numbers
 Chapter 1. Sets and Numbers 1. Sets A set is considered to be a collection of objects (elements). If A is a set and x is an element of the set A, we say x is a member of A or x belongs to A, and we write
Chapter 1. Sets and Numbers 1. Sets A set is considered to be a collection of objects (elements). If A is a set and x is an element of the set A, we say x is a member of A or x belongs to A, and we write
CONSTRUCTION OF THE REAL NUMBERS.
 CONSTRUCTION OF THE REAL NUMBERS. IAN KIMING 1. Motivation. It will not come as a big surprise to anyone when I say that we need the real numbers in mathematics. More to the point, we need to be able to
CONSTRUCTION OF THE REAL NUMBERS. IAN KIMING 1. Motivation. It will not come as a big surprise to anyone when I say that we need the real numbers in mathematics. More to the point, we need to be able to
Lecture 3: Sizes of Infinity
 Math/CS 20: Intro. to Math Professor: Padraic Bartlett Lecture 3: Sizes of Infinity Week 2 UCSB 204 Sizes of Infinity On one hand, we know that the real numbers contain more elements than the rational
Math/CS 20: Intro. to Math Professor: Padraic Bartlett Lecture 3: Sizes of Infinity Week 2 UCSB 204 Sizes of Infinity On one hand, we know that the real numbers contain more elements than the rational
Sets and Functions. MATH 464/506, Real Analysis. J. Robert Buchanan. Summer Department of Mathematics. J. Robert Buchanan Sets and Functions
 Sets and Functions MATH 464/506, Real Analysis J. Robert Buchanan Department of Mathematics Summer 2007 Notation x A means that element x is a member of set A. x / A means that x is not a member of A.
Sets and Functions MATH 464/506, Real Analysis J. Robert Buchanan Department of Mathematics Summer 2007 Notation x A means that element x is a member of set A. x / A means that x is not a member of A.
Sets and Functions. (As we will see, in describing a set the order in which elements are listed is irrelevant).
 Sets and Functions 1. The language of sets Informally, a set is any collection of objects. The objects may be mathematical objects such as numbers, functions and even sets, or letters or symbols of any
Sets and Functions 1. The language of sets Informally, a set is any collection of objects. The objects may be mathematical objects such as numbers, functions and even sets, or letters or symbols of any
Chapter Summary. Sets The Language of Sets Set Operations Set Identities Functions Types of Functions Operations on Functions Computability
 Chapter 2 1 Chapter Summary Sets The Language of Sets Set Operations Set Identities Functions Types of Functions Operations on Functions Computability Sequences and Summations Types of Sequences Summation
Chapter 2 1 Chapter Summary Sets The Language of Sets Set Operations Set Identities Functions Types of Functions Operations on Functions Computability Sequences and Summations Types of Sequences Summation
Handout 2 (Correction of Handout 1 plus continued discussion/hw) Comments and Homework in Chapter 1
 22M:132 Fall 07 J. Simon Handout 2 (Correction of Handout 1 plus continued discussion/hw) Comments and Homework in Chapter 1 Chapter 1 contains material on sets, functions, relations, and cardinality that
22M:132 Fall 07 J. Simon Handout 2 (Correction of Handout 1 plus continued discussion/hw) Comments and Homework in Chapter 1 Chapter 1 contains material on sets, functions, relations, and cardinality that
POL502: Foundations. Kosuke Imai Department of Politics, Princeton University. October 10, 2005
 POL502: Foundations Kosuke Imai Department of Politics, Princeton University October 10, 2005 Our first task is to develop the foundations that are necessary for the materials covered in this course. 1
POL502: Foundations Kosuke Imai Department of Politics, Princeton University October 10, 2005 Our first task is to develop the foundations that are necessary for the materials covered in this course. 1
. As the binomial coefficients are integers we have that. 2 n(n 1).
 Math 580 Homework. 1. Divisibility. Definition 1. Let a, b be integers with a 0. Then b divides b iff there is an integer k such that b = ka. In the case we write a b. In this case we also say a is a factor
Math 580 Homework. 1. Divisibility. Definition 1. Let a, b be integers with a 0. Then b divides b iff there is an integer k such that b = ka. In the case we write a b. In this case we also say a is a factor
On Projective Planes
 C-UPPSATS 2002:02 TFM, Mid Sweden University 851 70 Sundsvall Tel: 060-14 86 00 On Projective Planes 1 2 7 4 3 6 5 The Fano plane, the smallest projective plane. By Johan Kåhrström ii iii Abstract It was
C-UPPSATS 2002:02 TFM, Mid Sweden University 851 70 Sundsvall Tel: 060-14 86 00 On Projective Planes 1 2 7 4 3 6 5 The Fano plane, the smallest projective plane. By Johan Kåhrström ii iii Abstract It was
Countability. 1 Motivation. 2 Counting
 Countability 1 Motivation In topology as well as other areas of mathematics, we deal with a lot of infinite sets. However, as we will gradually discover, some infinite sets are bigger than others. Countably
Countability 1 Motivation In topology as well as other areas of mathematics, we deal with a lot of infinite sets. However, as we will gradually discover, some infinite sets are bigger than others. Countably
Practice Test III, Math 314, Spring 2016
 Practice Test III, Math 314, Spring 2016 Dr. Holmes April 26, 2016 This is the 2014 test reorganized to be more readable. I like it as a review test. The students who took this test had to do four sections
Practice Test III, Math 314, Spring 2016 Dr. Holmes April 26, 2016 This is the 2014 test reorganized to be more readable. I like it as a review test. The students who took this test had to do four sections
Introduction to Proofs in Analysis. updated December 5, By Edoh Y. Amiran Following the outline of notes by Donald Chalice INTRODUCTION
 Introduction to Proofs in Analysis updated December 5, 2016 By Edoh Y. Amiran Following the outline of notes by Donald Chalice INTRODUCTION Purpose. These notes intend to introduce four main notions from
Introduction to Proofs in Analysis updated December 5, 2016 By Edoh Y. Amiran Following the outline of notes by Donald Chalice INTRODUCTION Purpose. These notes intend to introduce four main notions from
Name (print): Question 4. exercise 1.24 (compute the union, then the intersection of two sets)
 MTH299 - Homework 1 Question 1. exercise 1.10 (compute the cardinality of a handful of finite sets) Solution. Write your answer here. Question 2. exercise 1.20 (compute the union of two sets) Question
MTH299 - Homework 1 Question 1. exercise 1.10 (compute the cardinality of a handful of finite sets) Solution. Write your answer here. Question 2. exercise 1.20 (compute the union of two sets) Question
Math 127 Homework. Mary Radcliffe. Due 29 March Complete the following problems. Fully justify each response.
 Math 17 Homework Mary Radcliffe Due 9 March 018 Complete the following problems Fully justify each response NOTE: due to the Spring Break, this homework set is a bit longer than is typical You only need
Math 17 Homework Mary Radcliffe Due 9 March 018 Complete the following problems Fully justify each response NOTE: due to the Spring Break, this homework set is a bit longer than is typical You only need
MATH FINAL EXAM REVIEW HINTS
 MATH 109 - FINAL EXAM REVIEW HINTS Answer: Answer: 1. Cardinality (1) Let a < b be two real numbers and define f : (0, 1) (a, b) by f(t) = (1 t)a + tb. (a) Prove that f is a bijection. (b) Prove that any
MATH 109 - FINAL EXAM REVIEW HINTS Answer: Answer: 1. Cardinality (1) Let a < b be two real numbers and define f : (0, 1) (a, b) by f(t) = (1 t)a + tb. (a) Prove that f is a bijection. (b) Prove that any
MTH 299 In Class and Recitation Problems SUMMER 2016
 MTH 299 In Class and Recitation Problems SUMMER 2016 Last updated on: May 13, 2016 MTH299 - Examples CONTENTS Contents 1 Week 1 3 1.1 In Class Problems.......................................... 3 1.2 Recitation
MTH 299 In Class and Recitation Problems SUMMER 2016 Last updated on: May 13, 2016 MTH299 - Examples CONTENTS Contents 1 Week 1 3 1.1 In Class Problems.......................................... 3 1.2 Recitation
Discrete Mathematics for CS Spring 2007 Luca Trevisan Lecture 27
 CS 70 Discrete Mathematics for CS Spring 007 Luca Trevisan Lecture 7 Infinity and Countability Consider a function f that maps elements of a set A (called the domain of f ) to elements of set B (called
CS 70 Discrete Mathematics for CS Spring 007 Luca Trevisan Lecture 7 Infinity and Countability Consider a function f that maps elements of a set A (called the domain of f ) to elements of set B (called
Lecture Notes on DISCRETE MATHEMATICS. Eusebius Doedel
 Lecture Notes on DISCRETE MATHEMATICS Eusebius Doedel c Eusebius J. Doedel, 009 Contents Logic. Introduction............................................................................... Basic logical
Lecture Notes on DISCRETE MATHEMATICS Eusebius Doedel c Eusebius J. Doedel, 009 Contents Logic. Introduction............................................................................... Basic logical
WORKSHEET MATH 215, FALL 15, WHYTE. We begin our course with the natural numbers:
 WORKSHEET MATH 215, FALL 15, WHYTE We begin our course with the natural numbers: N = {1, 2, 3,...} which are a subset of the integers: Z = {..., 2, 1, 0, 1, 2, 3,... } We will assume familiarity with their
WORKSHEET MATH 215, FALL 15, WHYTE We begin our course with the natural numbers: N = {1, 2, 3,...} which are a subset of the integers: Z = {..., 2, 1, 0, 1, 2, 3,... } We will assume familiarity with their
Foundations of Mathematics MATH 220 FALL 2017 Lecture Notes
 Foundations of Mathematics MATH 220 FALL 2017 Lecture Notes These notes form a brief summary of what has been covered during the lectures. All the definitions must be memorized and understood. Statements
Foundations of Mathematics MATH 220 FALL 2017 Lecture Notes These notes form a brief summary of what has been covered during the lectures. All the definitions must be memorized and understood. Statements
Continuity. Chapter 4
 Chapter 4 Continuity Throughout this chapter D is a nonempty subset of the real numbers. We recall the definition of a function. Definition 4.1. A function from D into R, denoted f : D R, is a subset of
Chapter 4 Continuity Throughout this chapter D is a nonempty subset of the real numbers. We recall the definition of a function. Definition 4.1. A function from D into R, denoted f : D R, is a subset of
Homework 5. Solutions
 Homework 5. Solutions 1. Let (X,T) be a topological space and let A,B be subsets of X. Show that the closure of their union is given by A B = A B. Since A B is a closed set that contains A B and A B is
Homework 5. Solutions 1. Let (X,T) be a topological space and let A,B be subsets of X. Show that the closure of their union is given by A B = A B. Since A B is a closed set that contains A B and A B is
Section 7.5: Cardinality
 Section 7: Cardinality In this section, we shall consider extend some of the ideas we have developed to infinite sets One interesting consequence of this discussion is that we shall see there are as many
Section 7: Cardinality In this section, we shall consider extend some of the ideas we have developed to infinite sets One interesting consequence of this discussion is that we shall see there are as many
1. Decide for each of the following expressions: Is it a function? If so, f is a function. (i) Domain: R. Codomain: R. Range: R. (iii) Yes surjective.
 Homework 2 2/14/2018 SOLUTIONS Exercise 6. 1. Decide for each of the following expressions: Is it a function? If so, (i) what is its domain, codomain, and image? (iii) is it surjective? (ii) is it injective?
Homework 2 2/14/2018 SOLUTIONS Exercise 6. 1. Decide for each of the following expressions: Is it a function? If so, (i) what is its domain, codomain, and image? (iii) is it surjective? (ii) is it injective?
UMASS AMHERST MATH 300 SP 05, F. HAJIR HOMEWORK 8: (EQUIVALENCE) RELATIONS AND PARTITIONS
 UMASS AMHERST MATH 300 SP 05, F. HAJIR HOMEWORK 8: (EQUIVALENCE) RELATIONS AND PARTITIONS 1. Relations Recall the concept of a function f from a source set X to a target set Y. It is a rule for mapping
UMASS AMHERST MATH 300 SP 05, F. HAJIR HOMEWORK 8: (EQUIVALENCE) RELATIONS AND PARTITIONS 1. Relations Recall the concept of a function f from a source set X to a target set Y. It is a rule for mapping
INFINITY: CARDINAL NUMBERS
 INFINITY: CARDINAL NUMBERS BJORN POONEN 1 Some terminology of set theory N := {0, 1, 2, 3, } Z := {, 2, 1, 0, 1, 2, } Q := the set of rational numbers R := the set of real numbers C := the set of complex
INFINITY: CARDINAL NUMBERS BJORN POONEN 1 Some terminology of set theory N := {0, 1, 2, 3, } Z := {, 2, 1, 0, 1, 2, } Q := the set of rational numbers R := the set of real numbers C := the set of complex
RED. Name: Instructor: Pace Nielsen Math 290 Section 1: Winter 2014 Final Exam
 RED Name: Instructor: Pace Nielsen Math 290 Section 1: Winter 2014 Final Exam Note that the first 10 questions are true-false. Mark A for true, B for false. Questions 11 through 20 are multiple choice
RED Name: Instructor: Pace Nielsen Math 290 Section 1: Winter 2014 Final Exam Note that the first 10 questions are true-false. Mark A for true, B for false. Questions 11 through 20 are multiple choice
MATH 2200 Final Review
 MATH 00 Final Review Thomas Goller December 7, 01 1 Exam Format The final exam will consist of 8-10 proofs It will take place on Tuesday, December 11, from 10:30 AM - 1:30 PM, in the usual room Topics
MATH 00 Final Review Thomas Goller December 7, 01 1 Exam Format The final exam will consist of 8-10 proofs It will take place on Tuesday, December 11, from 10:30 AM - 1:30 PM, in the usual room Topics
Math 10850, fall 2017, University of Notre Dame
 Math 10850, fall 2017, University of Notre Dame Notes on first exam September 22, 2017 The key facts The first midterm will be on Thursday, September 28, 6.15pm-7.45pm in Hayes-Healy 127. What you need
Math 10850, fall 2017, University of Notre Dame Notes on first exam September 22, 2017 The key facts The first midterm will be on Thursday, September 28, 6.15pm-7.45pm in Hayes-Healy 127. What you need
Functions. Definition 1 Let A and B be sets. A relation between A and B is any subset of A B.
 Chapter 4 Functions Definition 1 Let A and B be sets. A relation between A and B is any subset of A B. Definition 2 Let A and B be sets. A function from A to B is a relation f between A and B such that
Chapter 4 Functions Definition 1 Let A and B be sets. A relation between A and B is any subset of A B. Definition 2 Let A and B be sets. A function from A to B is a relation f between A and B such that
(a) We need to prove that is reflexive, symmetric and transitive. 2b + a = 3a + 3b (2a + b) = 3a + 3b 3k = 3(a + b k)
 MATH 111 Optional Exam 3 lutions 1. (0 pts) We define a relation on Z as follows: a b if a + b is divisible by 3. (a) (1 pts) Prove that is an equivalence relation. (b) (8 pts) Determine all equivalence
MATH 111 Optional Exam 3 lutions 1. (0 pts) We define a relation on Z as follows: a b if a + b is divisible by 3. (a) (1 pts) Prove that is an equivalence relation. (b) (8 pts) Determine all equivalence
Logic and Mathematics:
 Logic and Mathematics: Mathematicians in Schools Program Lashi Bandara Mathematical Sciences Institute, Australian National University April 21, 2011 Contents 1 Russell s Paradox 1 2 Propositional Logic
Logic and Mathematics: Mathematicians in Schools Program Lashi Bandara Mathematical Sciences Institute, Australian National University April 21, 2011 Contents 1 Russell s Paradox 1 2 Propositional Logic
One-to-one functions and onto functions
 MA 3362 Lecture 7 - One-to-one and Onto Wednesday, October 22, 2008. Objectives: Formalize definitions of one-to-one and onto One-to-one functions and onto functions At the level of set theory, there are
MA 3362 Lecture 7 - One-to-one and Onto Wednesday, October 22, 2008. Objectives: Formalize definitions of one-to-one and onto One-to-one functions and onto functions At the level of set theory, there are
2 Lecture 2: Logical statements and proof by contradiction Lecture 10: More on Permutations, Group Homomorphisms 31
 Contents 1 Lecture 1: Introduction 2 2 Lecture 2: Logical statements and proof by contradiction 7 3 Lecture 3: Induction and Well-Ordering Principle 11 4 Lecture 4: Definition of a Group and examples 15
Contents 1 Lecture 1: Introduction 2 2 Lecture 2: Logical statements and proof by contradiction 7 3 Lecture 3: Induction and Well-Ordering Principle 11 4 Lecture 4: Definition of a Group and examples 15
The Fundamental Group and Covering Spaces
 Chapter 8 The Fundamental Group and Covering Spaces In the first seven chapters we have dealt with point-set topology. This chapter provides an introduction to algebraic topology. Algebraic topology may
Chapter 8 The Fundamental Group and Covering Spaces In the first seven chapters we have dealt with point-set topology. This chapter provides an introduction to algebraic topology. Algebraic topology may
How many elements does B have to have? At least one, since A is not empty. If
 15. Injective surjective and bijective The notion of an invertible function is very important and we would like to break up the property of being invertible into pieces. Definition 15.1. Let f : A B be
15. Injective surjective and bijective The notion of an invertible function is very important and we would like to break up the property of being invertible into pieces. Definition 15.1. Let f : A B be
Lecture Notes 1 Basic Concepts of Mathematics MATH 352
 Lecture Notes 1 Basic Concepts of Mathematics MATH 352 Ivan Avramidi New Mexico Institute of Mining and Technology Socorro, NM 87801 June 3, 2004 Author: Ivan Avramidi; File: absmath.tex; Date: June 11,
Lecture Notes 1 Basic Concepts of Mathematics MATH 352 Ivan Avramidi New Mexico Institute of Mining and Technology Socorro, NM 87801 June 3, 2004 Author: Ivan Avramidi; File: absmath.tex; Date: June 11,
5 Set Operations, Functions, and Counting
 5 Set Operations, Functions, and Counting Let N denote the positive integers, N 0 := N {0} be the non-negative integers and Z = N 0 ( N) the positive and negative integers including 0, Q the rational numbers,
5 Set Operations, Functions, and Counting Let N denote the positive integers, N 0 := N {0} be the non-negative integers and Z = N 0 ( N) the positive and negative integers including 0, Q the rational numbers,
3 FUNCTIONS. 3.1 Definition and Basic Properties. c Dr Oksana Shatalov, Fall
 c Dr Oksana Shatalov, Fall 2014 1 3 FUNCTIONS 3.1 Definition and Basic Properties DEFINITION 1. Let A and B be nonempty sets. A function f from A to B is a rule that assigns to each element in the set
c Dr Oksana Shatalov, Fall 2014 1 3 FUNCTIONS 3.1 Definition and Basic Properties DEFINITION 1. Let A and B be nonempty sets. A function f from A to B is a rule that assigns to each element in the set
Connectedness. Proposition 2.2. The following are equivalent for a topological space (X, T ).
 Connectedness 1 Motivation Connectedness is the sort of topological property that students love. Its definition is intuitive and easy to understand, and it is a powerful tool in proofs of well-known results.
Connectedness 1 Motivation Connectedness is the sort of topological property that students love. Its definition is intuitive and easy to understand, and it is a powerful tool in proofs of well-known results.
Metric spaces and metrizability
 1 Motivation Metric spaces and metrizability By this point in the course, this section should not need much in the way of motivation. From the very beginning, we have talked about R n usual and how relatively
1 Motivation Metric spaces and metrizability By this point in the course, this section should not need much in the way of motivation. From the very beginning, we have talked about R n usual and how relatively
Principles of Real Analysis I Fall I. The Real Number System
 21-355 Principles of Real Analysis I Fall 2004 I. The Real Number System The main goal of this course is to develop the theory of real-valued functions of one real variable in a systematic and rigorous
21-355 Principles of Real Analysis I Fall 2004 I. The Real Number System The main goal of this course is to develop the theory of real-valued functions of one real variable in a systematic and rigorous
1. A Little Set Theory
 . A Little Set Theory I see it, but I don t believe it. Cantor to Dedekind 29 June 877 Functions are the single most important idea pervading modern mathematics. We will assume the informal definition
. A Little Set Theory I see it, but I don t believe it. Cantor to Dedekind 29 June 877 Functions are the single most important idea pervading modern mathematics. We will assume the informal definition
Discrete dynamics on the real line
 Chapter 2 Discrete dynamics on the real line We consider the discrete time dynamical system x n+1 = f(x n ) for a continuous map f : R R. Definitions The forward orbit of x 0 is: O + (x 0 ) = {x 0, f(x
Chapter 2 Discrete dynamics on the real line We consider the discrete time dynamical system x n+1 = f(x n ) for a continuous map f : R R. Definitions The forward orbit of x 0 is: O + (x 0 ) = {x 0, f(x
Cardinality and ordinal numbers
 Cardinality and ordinal numbers The cardinality A of a finite set A is simply the number of elements in it. When it comes to infinite sets, we no longer can speak of the number of elements in such a set.
Cardinality and ordinal numbers The cardinality A of a finite set A is simply the number of elements in it. When it comes to infinite sets, we no longer can speak of the number of elements in such a set.
Finite and Infinite Sets
 Chapter 9 Finite and Infinite Sets 9. Finite Sets Preview Activity (Equivalent Sets, Part ). Let A and B be sets and let f be a function from A to B..f W A! B/. Carefully complete each of the following
Chapter 9 Finite and Infinite Sets 9. Finite Sets Preview Activity (Equivalent Sets, Part ). Let A and B be sets and let f be a function from A to B..f W A! B/. Carefully complete each of the following
WORKSHEET ON NUMBERS, MATH 215 FALL. We start our study of numbers with the integers: N = {1, 2, 3,...}
 WORKSHEET ON NUMBERS, MATH 215 FALL 18(WHYTE) We start our study of numbers with the integers: Z = {..., 2, 1, 0, 1, 2, 3,... } and their subset of natural numbers: N = {1, 2, 3,...} For now we will not
WORKSHEET ON NUMBERS, MATH 215 FALL 18(WHYTE) We start our study of numbers with the integers: Z = {..., 2, 1, 0, 1, 2, 3,... } and their subset of natural numbers: N = {1, 2, 3,...} For now we will not
Axioms for Set Theory
 Axioms for Set Theory The following is a subset of the Zermelo-Fraenkel axioms for set theory. In this setting, all objects are sets which are denoted by letters, e.g. x, y, X, Y. Equality is logical identity:
Axioms for Set Theory The following is a subset of the Zermelo-Fraenkel axioms for set theory. In this setting, all objects are sets which are denoted by letters, e.g. x, y, X, Y. Equality is logical identity:
ABSTRACT NONSINGULAR CURVES
 ABSTRACT NONSINGULAR CURVES Affine Varieties Notation. Let k be a field, such as the rational numbers Q or the complex numbers C. We call affine n-space the collection A n k of points P = a 1, a,..., a
ABSTRACT NONSINGULAR CURVES Affine Varieties Notation. Let k be a field, such as the rational numbers Q or the complex numbers C. We call affine n-space the collection A n k of points P = a 1, a,..., a
Topology. Xiaolong Han. Department of Mathematics, California State University, Northridge, CA 91330, USA address:
 Topology Xiaolong Han Department of Mathematics, California State University, Northridge, CA 91330, USA E-mail address: Xiaolong.Han@csun.edu Remark. You are entitled to a reward of 1 point toward a homework
Topology Xiaolong Han Department of Mathematics, California State University, Northridge, CA 91330, USA E-mail address: Xiaolong.Han@csun.edu Remark. You are entitled to a reward of 1 point toward a homework
Numbers, sets, and functions
 Chapter 1 Numbers, sets, and functions 1.1. The natural numbers, integers, and rational numbers We assume that you are familiar with the set of natural numbers the set of integers and the set of rational
Chapter 1 Numbers, sets, and functions 1.1. The natural numbers, integers, and rational numbers We assume that you are familiar with the set of natural numbers the set of integers and the set of rational
MATH 115, SUMMER 2012 LECTURE 4 THURSDAY, JUNE 21ST
 MATH 115, SUMMER 2012 LECTURE 4 THURSDAY, JUNE 21ST JAMES MCIVOR Today we enter Chapter 2, which is the heart of this subject. Before starting, recall that last time we saw the integers have unique factorization
MATH 115, SUMMER 2012 LECTURE 4 THURSDAY, JUNE 21ST JAMES MCIVOR Today we enter Chapter 2, which is the heart of this subject. Before starting, recall that last time we saw the integers have unique factorization
Introduction to Functions
 Mathematics for Economists Introduction to Functions Introduction In economics we study the relationship between variables and attempt to explain these relationships through economic theory. For instance
Mathematics for Economists Introduction to Functions Introduction In economics we study the relationship between variables and attempt to explain these relationships through economic theory. For instance
Research Methods in Mathematics Extended assignment 1
 Research Methods in Mathematics Extended assignment 1 T. PERUTZ Due: at the beginning of class, October 5. Choose one of the following assignments: (1) The circle problem (2) Complete ordered fields 2
Research Methods in Mathematics Extended assignment 1 T. PERUTZ Due: at the beginning of class, October 5. Choose one of the following assignments: (1) The circle problem (2) Complete ordered fields 2
NOTES ON FINITE FIELDS
 NOTES ON FINITE FIELDS AARON LANDESMAN CONTENTS 1. Introduction to finite fields 2 2. Definition and constructions of fields 3 2.1. The definition of a field 3 2.2. Constructing field extensions by adjoining
NOTES ON FINITE FIELDS AARON LANDESMAN CONTENTS 1. Introduction to finite fields 2 2. Definition and constructions of fields 3 2.1. The definition of a field 3 2.2. Constructing field extensions by adjoining
2) e = e G G such that if a G 0 =0 G G such that if a G e a = a e = a. 0 +a = a+0 = a.
 Chapter 2 Groups Groups are the central objects of algebra. In later chapters we will define rings and modules and see that they are special cases of groups. Also ring homomorphisms and module homomorphisms
Chapter 2 Groups Groups are the central objects of algebra. In later chapters we will define rings and modules and see that they are special cases of groups. Also ring homomorphisms and module homomorphisms
Discrete Mathematics. W. Ethan Duckworth. Fall 2017, Loyola University Maryland
 Discrete Mathematics W. Ethan Duckworth Fall 2017, Loyola University Maryland Contents 1 Introduction 4 1.1 Statements......................................... 4 1.2 Constructing Direct Proofs................................
Discrete Mathematics W. Ethan Duckworth Fall 2017, Loyola University Maryland Contents 1 Introduction 4 1.1 Statements......................................... 4 1.2 Constructing Direct Proofs................................
CHAPTER 8: EXPLORING R
 CHAPTER 8: EXPLORING R LECTURE NOTES FOR MATH 378 (CSUSM, SPRING 2009). WAYNE AITKEN In the previous chapter we discussed the need for a complete ordered field. The field Q is not complete, so we constructed
CHAPTER 8: EXPLORING R LECTURE NOTES FOR MATH 378 (CSUSM, SPRING 2009). WAYNE AITKEN In the previous chapter we discussed the need for a complete ordered field. The field Q is not complete, so we constructed
Math 309 Notes and Homework for Days 4-6
 Math 309 Notes and Homework for Days 4-6 Day 4 Read Section 1.2 and the notes below. The following is the main definition of the course. Definition. A vector space is a set V (whose elements are called
Math 309 Notes and Homework for Days 4-6 Day 4 Read Section 1.2 and the notes below. The following is the main definition of the course. Definition. A vector space is a set V (whose elements are called
MAT 417, Fall 2017, CRN: 1766 Real Analysis: A First Course
 MAT 47, Fall 207, CRN: 766 Real Analysis: A First Course Prerequisites: MAT 263 & MAT 300 Instructor: Daniel Cunningham What is Real Analysis? Real Analysis is the important branch of mathematics that
MAT 47, Fall 207, CRN: 766 Real Analysis: A First Course Prerequisites: MAT 263 & MAT 300 Instructor: Daniel Cunningham What is Real Analysis? Real Analysis is the important branch of mathematics that
Discussion Summary 10/16/2018
 Discussion Summary 10/16/018 1 Quiz 4 1.1 Q1 Let r R and r > 1. Prove the following by induction for every n N, assuming that 0 N as in the book. r 1 + r + r 3 + + r n = rn+1 r r 1 Proof. Let S n = Σ n
Discussion Summary 10/16/018 1 Quiz 4 1.1 Q1 Let r R and r > 1. Prove the following by induction for every n N, assuming that 0 N as in the book. r 1 + r + r 3 + + r n = rn+1 r r 1 Proof. Let S n = Σ n
Automata Theory and Formal Grammars: Lecture 1
 Automata Theory and Formal Grammars: Lecture 1 Sets, Languages, Logic Automata Theory and Formal Grammars: Lecture 1 p.1/72 Sets, Languages, Logic Today Course Overview Administrivia Sets Theory (Review?)
Automata Theory and Formal Grammars: Lecture 1 Sets, Languages, Logic Automata Theory and Formal Grammars: Lecture 1 p.1/72 Sets, Languages, Logic Today Course Overview Administrivia Sets Theory (Review?)
Equivalent Forms of the Axiom of Infinity
 Equivalent Forms of the Axiom of Infinity Axiom of Infinity 1. There is a set that contains each finite ordinal as an element. The Axiom of Infinity is the axiom of Set Theory that explicitly asserts that
Equivalent Forms of the Axiom of Infinity Axiom of Infinity 1. There is a set that contains each finite ordinal as an element. The Axiom of Infinity is the axiom of Set Theory that explicitly asserts that
Introduction to Real Analysis
 Introduction to Real Analysis Joshua Wilde, revised by Isabel Tecu, Takeshi Suzuki and María José Boccardi August 13, 2013 1 Sets Sets are the basic objects of mathematics. In fact, they are so basic that
Introduction to Real Analysis Joshua Wilde, revised by Isabel Tecu, Takeshi Suzuki and María José Boccardi August 13, 2013 1 Sets Sets are the basic objects of mathematics. In fact, they are so basic that
Homework #5 Solutions
 Homework #5 Solutions p 83, #16. In order to find a chain a 1 a 2 a n of subgroups of Z 240 with n as large as possible, we start at the top with a n = 1 so that a n = Z 240. In general, given a i we will
Homework #5 Solutions p 83, #16. In order to find a chain a 1 a 2 a n of subgroups of Z 240 with n as large as possible, we start at the top with a n = 1 so that a n = Z 240. In general, given a i we will
Midterm Exam. There are 6 problems. Your 5 best answers count. Please pay attention to the presentation of your work! Best 5
 Department of Mathematical Sciences Instructor: Daiva Pucinskaite Modern Algebra June 22, 2017 Midterm Exam There are 6 problems. Your 5 best answers count. Please pay attention to the presentation of
Department of Mathematical Sciences Instructor: Daiva Pucinskaite Modern Algebra June 22, 2017 Midterm Exam There are 6 problems. Your 5 best answers count. Please pay attention to the presentation of
Week Some Warm-up Questions
 1 Some Warm-up Questions Week 1-2 Abstraction: The process going from specific cases to general problem. Proof: A sequence of arguments to show certain conclusion to be true. If... then... : The part after
1 Some Warm-up Questions Week 1-2 Abstraction: The process going from specific cases to general problem. Proof: A sequence of arguments to show certain conclusion to be true. If... then... : The part after
Sets, Structures, Numbers
 Chapter 1 Sets, Structures, Numbers Abstract In this chapter we shall introduce most of the background needed to develop the foundations of mathematical analysis. We start with sets and algebraic structures.
Chapter 1 Sets, Structures, Numbers Abstract In this chapter we shall introduce most of the background needed to develop the foundations of mathematical analysis. We start with sets and algebraic structures.
Peter Kahn. Spring 2007
 MATH 304: CONSTRUCTING THE REAL NUMBERS Peter Kahn Spring 2007 Contents 1 The Natural Numbers 1 1.1 The Peano Axioms............................ 2 1.2 Proof by induction............................ 4 1.3
MATH 304: CONSTRUCTING THE REAL NUMBERS Peter Kahn Spring 2007 Contents 1 The Natural Numbers 1 1.1 The Peano Axioms............................ 2 1.2 Proof by induction............................ 4 1.3
LECTURE NOTES DISCRETE MATHEMATICS. Eusebius Doedel
 LECTURE NOTES on DISCRETE MATHEMATICS Eusebius Doedel 1 LOGIC Introduction. First we introduce some basic concepts needed in our discussion of logic. These will be covered in more detail later. A set is
LECTURE NOTES on DISCRETE MATHEMATICS Eusebius Doedel 1 LOGIC Introduction. First we introduce some basic concepts needed in our discussion of logic. These will be covered in more detail later. A set is
2. Two binary operations (addition, denoted + and multiplication, denoted
 Chapter 2 The Structure of R The purpose of this chapter is to explain to the reader why the set of real numbers is so special. By the end of this chapter, the reader should understand the difference between
Chapter 2 The Structure of R The purpose of this chapter is to explain to the reader why the set of real numbers is so special. By the end of this chapter, the reader should understand the difference between
Chapter One. The Real Number System
 Chapter One. The Real Number System We shall give a quick introduction to the real number system. It is imperative that we know how the set of real numbers behaves in the way that its completeness and
Chapter One. The Real Number System We shall give a quick introduction to the real number system. It is imperative that we know how the set of real numbers behaves in the way that its completeness and
Sets, Functions and Relations
 Chapter 2 Sets, Functions and Relations A set is any collection of distinct objects. Here is some notation for some special sets of numbers: Z denotes the set of integers (whole numbers), that is, Z =
Chapter 2 Sets, Functions and Relations A set is any collection of distinct objects. Here is some notation for some special sets of numbers: Z denotes the set of integers (whole numbers), that is, Z =
Topology, Math 581, Fall 2017 last updated: November 24, Topology 1, Math 581, Fall 2017: Notes and homework Krzysztof Chris Ciesielski
 Topology, Math 581, Fall 2017 last updated: November 24, 2017 1 Topology 1, Math 581, Fall 2017: Notes and homework Krzysztof Chris Ciesielski Class of August 17: Course and syllabus overview. Topology
Topology, Math 581, Fall 2017 last updated: November 24, 2017 1 Topology 1, Math 581, Fall 2017: Notes and homework Krzysztof Chris Ciesielski Class of August 17: Course and syllabus overview. Topology
2.2 Some Consequences of the Completeness Axiom
 60 CHAPTER 2. IMPORTANT PROPERTIES OF R 2.2 Some Consequences of the Completeness Axiom In this section, we use the fact that R is complete to establish some important results. First, we will prove that
60 CHAPTER 2. IMPORTANT PROPERTIES OF R 2.2 Some Consequences of the Completeness Axiom In this section, we use the fact that R is complete to establish some important results. First, we will prove that
MORE EXERCISES FOR SECTIONS II.1 AND II.2. There are drawings on the next two pages to accompany the starred ( ) exercises.
 Math 133 Winter 2013 MORE EXERCISES FOR SECTIONS II.1 AND II.2 There are drawings on the next two pages to accompany the starred ( ) exercises. B1. Let L be a line in R 3, and let x be a point which does
Math 133 Winter 2013 MORE EXERCISES FOR SECTIONS II.1 AND II.2 There are drawings on the next two pages to accompany the starred ( ) exercises. B1. Let L be a line in R 3, and let x be a point which does
Math 3140 Fall 2012 Assignment #3
 Math 3140 Fall 2012 Assignment #3 Due Fri., Sept. 21. Remember to cite your sources, including the people you talk to. My solutions will repeatedly use the following proposition from class: Proposition
Math 3140 Fall 2012 Assignment #3 Due Fri., Sept. 21. Remember to cite your sources, including the people you talk to. My solutions will repeatedly use the following proposition from class: Proposition
3 The language of proof
 3 The language of proof After working through this section, you should be able to: (a) understand what is asserted by various types of mathematical statements, in particular implications and equivalences;
3 The language of proof After working through this section, you should be able to: (a) understand what is asserted by various types of mathematical statements, in particular implications and equivalences;
Section 4.4 Functions. CS 130 Discrete Structures
 Section 4.4 Functions CS 130 Discrete Structures Function Definitions Let S and T be sets. A function f from S to T, f: S T, is a subset of S x T where each member of S appears exactly once as the first
Section 4.4 Functions CS 130 Discrete Structures Function Definitions Let S and T be sets. A function f from S to T, f: S T, is a subset of S x T where each member of S appears exactly once as the first
MATH 215 Sets (S) Definition 1 A set is a collection of objects. The objects in a set X are called elements of X.
 MATH 215 Sets (S) Definition 1 A set is a collection of objects. The objects in a set X are called elements of X. Notation 2 A set can be described using set-builder notation. That is, a set can be described
MATH 215 Sets (S) Definition 1 A set is a collection of objects. The objects in a set X are called elements of X. Notation 2 A set can be described using set-builder notation. That is, a set can be described
Cosets and Lagrange s theorem
 Cosets and Lagrange s theorem These are notes on cosets and Lagrange s theorem some of which may already have been lecturer. There are some questions for you included in the text. You should write the
Cosets and Lagrange s theorem These are notes on cosets and Lagrange s theorem some of which may already have been lecturer. There are some questions for you included in the text. You should write the
EUCLIDEAN AND HYPERBOLIC CONDITIONS
 EUCLIDEAN AND HYPERBOLIC CONDITIONS MATH 410. SPRING 2007. INSTRUCTOR: PROFESSOR AITKEN The first goal of this handout is to show that, in Neutral Geometry, Euclid s Fifth Postulate is equivalent to the
EUCLIDEAN AND HYPERBOLIC CONDITIONS MATH 410. SPRING 2007. INSTRUCTOR: PROFESSOR AITKEN The first goal of this handout is to show that, in Neutral Geometry, Euclid s Fifth Postulate is equivalent to the
