Math 127 Homework. Mary Radcliffe. Due 29 March Complete the following problems. Fully justify each response.
|
|
|
- Amie Skinner
- 5 years ago
- Views:
Transcription
1 Math 17 Homework Mary Radcliffe Due 9 March 018 Complete the following problems Fully justify each response NOTE: due to the Spring Break, this homework set is a bit longer than is typical You only need to turn in those problems marked with (*) 1 In lecture we defined a finite set X to be of size n if there exists a bijection f : [n] X Prove that if X, Y are finite, and there exists a bijection f : X Y, then X = Y Suppose X and Y are finite, so that there exists bijections g : X [n] and h : Y [m] for some n, m N Now, let f : X Y Note that we can construct a function w : [n] [m] by w( = h f g 1 ( Moreover, since h and g are bijections, such a function w is bijective if and only if f is bijective Hence, if there exists a bijection f : X Y, then there exists a bijection w : [n] [m], and hence n = m On the other hand, suppose that X = Y, so n = m Then we can construct a bijection f : X Y by f(x) = h 1 g(x) (*) Let X be a finite set, and suppose there is a surjection f : X Y Prove that X Y 3 (*) Let and Let f : X Y be surjective, and X finite Define a function g : Y X so that for each y Y, g(y) f 1 (y); note that this may not be uniquely defined, but since f is surjective, there always exists such a choice of g(y) for all y Moreover, as f is well-defined, it must be the case that g(y) g(z) whenever y z Therefore, g is injective, and as proved in lecture, this implies that Y X Determine X X 3 X 4 X = {n 1 n 00, n = k k Z}, X 3 = {n 1 n 00, n = k 3 k Z}, X 4 = {n 1 n 00, n = k 4 k Z} We have X = {1, 4, 9, 16, 5, 36, 49, 64, 81, 100, 11, 144, 169, 196} 1
2 and Therefore, we obtain X 3 = {1, 8, 7, 64, 15} X 4 = {1, 16, 81} X X 3 X 4 = {1, 4, 8, 9, 16, 5, 7, 36, 49, 64, 81, 100, 11, 15, 144, 169, 196}, and hence X X 3 X 4 = 17 4 Prove Theorem 41: De Morgan s Law for sets (finite version) The theorem we wish to prove is stated as follows: Let n N For each i [n] let X i be a set, and let Z be a set Then (a) Z\ ( n i=1 X i) = n i=1 (Z\X i) (b) Z\ ( n i=1 X i) = n i=1 (Z\X i) Proof (a) Suppose that z Z\ ( n i=1 X i) Then z Z, and z / n i=1 X i Note that this implies that for all X i, we must have z / X i, as otherwise z would be in the union Therefore, z Z\X i for all i, and hence z n i=1 (Z\X i) Hence, Z\ ( n i=1 X i) n i=1 (Z\X i) For the other containment, suppose that z n i=1 (Z\X i) Then by definition, it must be the case that z Z\X i for all i, so z Z and z / X i for all i Therefore, as z is not a member of any X i, it is also true that z / n i=1 X i Therefore, as z Z, we have z Z\ n i=1 X i Hence, Z\ ( n i=1 X i) n i=1 (Z\X i) By double containment, Z\ ( n i=1 X i) = n i=1 (Z\X i) (b) Suppose that z \ ( n i=1 X i) Then z Z, and z / n i=1 X i Note that if z were a member of X i for all i, then we would necessarily have that z would be a member of the intersection; thus there must exist some choice of i such that z / X i For this choice of i, then, we have z Z\X i Therefore, by definition z n i=1 (Z\X i), and thus Z\ ( n i=1 X i) n i=1 (Z\X i) For the opposite containment, suppose that z n i=1 (Z\X i) Then there exists some i such that z Z\X i, and hence z Z, and z / X i for this specific i Therefore, z / n i=1 X i, since in order to belong to the intersection, z would need to belong to each set But then z Z\ n i=1 X i, and hence Z\ ( n i=1 X i) n i=1 (Z\X i) By double containment, then, Z\ ( n i=1 X i) = n i=1 (Z\X i) 5 You decide to go to Chipotle for a burrito Chipotle has many options: choices of rice, choices of beans, 5 choices of meat, 4 choices of salsa, and 5 other toppings (including queso and guacamole) How many different burritos could you order having exactly 1 rice, 1 bean, 1 meat, salsas, and other toppings? 5 (4 ) ( 5 ) 6 (*) Let X = {(a 1, a,, a n ) a i {0, 1} i} = {0, 1} n These are sometimes called bitstrings of length n
3 (a) Show that there is a bijection between X and {f : [n] {0, 1}}, the set of functions from [n] to {0, 1} (b) Show that there is a bijection between X and P([n]) (c) Determine X (a) Let A = (a 1, a,, a n ) X Define a function F : X {f : [n] {0, 1}} by F (A)( = a k We show that F is injective and surjective To avoid confusing the notation, we will write F A in place of F (A) injective: Let A, B X, with A B Then there must exist some k for which a k b k But then F A ( = a k b k = F B (, and hence F A and F B are not the same function Thus, F is injective surjective: Let f : [n] {0, 1} be a function Define a sequence A by A = (f(1), f(),, f(n)) Clearly F A = f, and hence F is surjective As F is both injective and surjective, it is a bijection (b) Let G : X P([n]) be given by G(A) = {k [n] a k = 1} Note that if A, B X, with A B, then there exists some k such that a k b k ; wlog suppose a k = 1 and b k = 0 Then k G(A) and k / G(B), so G(A) G(B) Hence G is injective For surjectivity, let S [n] Define a sequence A by a k = 1 if k S and a k = 0 elsewise Then G(A) = S by definition, and hence G is surjective Therefore, G is a bijection (c) As we have seen before, P([n]) = n As G : X P([n]) is a bijection, we have X = P([n]) = n 7 (*) Let X and Y be finite sets Define X Y = {f : Y X}, the set of functions from Y to X Prove that X Y = X Y Let S = X X X, where there are Y copies of X As Y is finite, there exists some n so that we can write Y = {y 1, y,, y n } Define a function F : X Y S by F (f) = (f(y 1 ), f(y ),, f(y n )) For the same reason as in the previous problem, F is a bijection, and hence X Y = S Moreover, S is a finite Cartesian product of finite sets, so S = X X X, where there are Y copies of X Hence X Y = X Y 8 (*) Let n, k N with n k Prove, by counting in ways, that k ( n = (n k + 1) ( n Suppose we have n people We form a committee of size k from these people, and then select a leader from that committee Note that there are ( n ways to select the k people, and then k choices of leader, and hence there are k ( n ways to form this committee On the other hand, we could first select k 1 people to be nonleaders, in ( n ways, and then from the remaining n (k 1) = n k + 1 people, choose the leader, which can be done in n k + 1 ways Hence, there are (n k + 1) ( n ways to form this committee Therefore, k ( n k ) = (n k + 1) ( n 3
4 9 Let n, m N with m n Prove that n ( )( ) ( ) n k n = n m k m m k=m Suppose we have a collection of n people We wish to choose m of these people to be Kings, and from the remaining people, we will choose any number to be Queens Everybody else is a Joker We can have any number of Queens, from 0 to n m We can first do this by selecting the m Kings, in ( n ways Then, the remaining people will each be assigned Queen or Joker There are choices for each of these people, so there are n m ways to assign Queens and Jokers Hence, this can be done in n m( n ways On the other hand, we could select a set of k m people from the n people to be Queens or Kings Then we assign m of these k people to be Kings, and the remaining will be Queens For each k m, this can be done in ( n k ( ways, and hence in total there are n ( n k k=m ( such assignments Therefore, n ( n k ) k=m ( ( m = n m n 10 (*) How many subsets of [0] contain a multiple of 4? Prove that your answer is correct In order to contain a multiple of 4, we wish to count subsets that contain either 4, 8, 1, 16, or 0 Given S [0], define X S to be the subsets of [0] that contain S as a subset Notice that X S = 0 S, as we can choose for each element of [0] that is not in S whether to put it in each subset in X S Hence, we wish to count X {4,8,1,16,0} Further, note that X S1 X S = X S1 S, as any element of both will contain all elements in S 1 and all elements in S Hence we have X {4,8,1,16,0} = X 4 X 8 X 1 X 16 X 0 By Inclusion/Exclusion, we obtain X {4,8,1,16,0} = = 5 ( 1) i+1 i=1 i=1 J {4,8,1,16,0} 5 ( ) 5 ( 1) i+1 0 i i X J = = 15 ( ) = (*) Let f : X Y be a bijection Prove that X is countably infinite if and only if Y is countably infinite For the first direction, suppose that Y is countably infinite Let g : Y N be a bijection Then g f : X N is a composition of bijections, so g is also a bijection, and hence X is countably infinite For the opposite direction, repeat the above argument using f 1 : Y X in place of f 4
5 1 Show directly (without using Proposition 4310) that N N is countably infinite (If you cannot derive a bijection, you may look to Problem 438 for one) Define f : N N N by f(a, b) = a (b + 1) 1 We will show that f is bijective For injectivity, suppose that f(a, b) = f(c, d) Then a (b+1) 1 = c (d + 1) 1, so a (b + 1) = c (d + 1) Define this value as k, and consider the unique prime decomposition of k Note that b + 1 and d + 1 are both odd, so the number of times that appears in the unique prime decomposition of k must be c, and also must be a Hence, a = c But if a = c, clearly b + 1 = d + 1, and hence b = d Therefore, (a, b) = (c, d), and f is injective For surjectivity, let k N If k is even, write k = m Then f(0, = 0 (m+1) 1 = m = k, and hence k is in the image of f If k is odd, then k + 1 is even Let a be the number of times that appears in the unique prime decomposition of k+1 Then k+1 is an odd integer, and hence there exists b such that a k+1 = b + 1 But then f(a, b) = a (b + 1) 1 = k = k, a and thus k is in the image of f Therefore, as f is both injective and surjective, it is bijective, so N N is countably infinite 13 (*) Let X be a finite set Show that N X = {f : X N} is countably infinite We work by induction on X If X = 1, so X = {x}, then all the functions on X are of the form f : X N, where f(x) = k We note that there is a bijection, F : N X N, by F (f) = f(x) Hence, X = N Now, suppose the result holds when X = n 1 Let X = n Let x X, and let X = X\{x}, so write X = {x} X and X = n 1 Given a function f : X N, define a function g : {x} N and h : X N by g(x) = f(x) and h(x ) = f(x ) Clearly, every f defines a unique g and h, and every choice of g and h correspond to exactly one f Hence, if we let F : N X (N {x} ) (N X ) by F (f) = (g, h), F is bijective Moreover, by the inductive hypothesis and the base case, we have that both N {x} and N X are countably infinite As finite products of countable sets are countable, we therefore have that N X is countably infinite By induction, then, the result holds for all possible X 5
MATH 13 SAMPLE FINAL EXAM SOLUTIONS
 MATH 13 SAMPLE FINAL EXAM SOLUTIONS WINTER 2014 Problem 1 (15 points). For each statement below, circle T or F according to whether the statement is true or false. You do NOT need to justify your answers.
MATH 13 SAMPLE FINAL EXAM SOLUTIONS WINTER 2014 Problem 1 (15 points). For each statement below, circle T or F according to whether the statement is true or false. You do NOT need to justify your answers.
MATH 220 (all sections) Homework #12 not to be turned in posted Friday, November 24, 2017
 MATH 220 (all sections) Homework #12 not to be turned in posted Friday, November 24, 2017 Definition: A set A is finite if there exists a nonnegative integer c such that there exists a bijection from A
MATH 220 (all sections) Homework #12 not to be turned in posted Friday, November 24, 2017 Definition: A set A is finite if there exists a nonnegative integer c such that there exists a bijection from A
Sets and Functions. MATH 464/506, Real Analysis. J. Robert Buchanan. Summer Department of Mathematics. J. Robert Buchanan Sets and Functions
 Sets and Functions MATH 464/506, Real Analysis J. Robert Buchanan Department of Mathematics Summer 2007 Notation x A means that element x is a member of set A. x / A means that x is not a member of A.
Sets and Functions MATH 464/506, Real Analysis J. Robert Buchanan Department of Mathematics Summer 2007 Notation x A means that element x is a member of set A. x / A means that x is not a member of A.
MATH 3300 Test 1. Name: Student Id:
 Name: Student Id: There are nine problems (check that you have 9 pages). Solutions are expected to be short. In the case of proofs, one or two short paragraphs should be the average length. Write your
Name: Student Id: There are nine problems (check that you have 9 pages). Solutions are expected to be short. In the case of proofs, one or two short paragraphs should be the average length. Write your
3 FUNCTIONS. 3.1 Definition and Basic Properties. c Dr Oksana Shatalov, Fall
 c Dr Oksana Shatalov, Fall 2014 1 3 FUNCTIONS 3.1 Definition and Basic Properties DEFINITION 1. Let A and B be nonempty sets. A function f from A to B is a rule that assigns to each element in the set
c Dr Oksana Shatalov, Fall 2014 1 3 FUNCTIONS 3.1 Definition and Basic Properties DEFINITION 1. Let A and B be nonempty sets. A function f from A to B is a rule that assigns to each element in the set
Functions. Definition 1 Let A and B be sets. A relation between A and B is any subset of A B.
 Chapter 4 Functions Definition 1 Let A and B be sets. A relation between A and B is any subset of A B. Definition 2 Let A and B be sets. A function from A to B is a relation f between A and B such that
Chapter 4 Functions Definition 1 Let A and B be sets. A relation between A and B is any subset of A B. Definition 2 Let A and B be sets. A function from A to B is a relation f between A and B such that
MATH 215 Sets (S) Definition 1 A set is a collection of objects. The objects in a set X are called elements of X.
 MATH 215 Sets (S) Definition 1 A set is a collection of objects. The objects in a set X are called elements of X. Notation 2 A set can be described using set-builder notation. That is, a set can be described
MATH 215 Sets (S) Definition 1 A set is a collection of objects. The objects in a set X are called elements of X. Notation 2 A set can be described using set-builder notation. That is, a set can be described
3 FUNCTIONS. 3.1 Definition and Basic Properties. c Dr Oksana Shatalov, Spring
 c Dr Oksana Shatalov, Spring 2016 1 3 FUNCTIONS 3.1 Definition and Basic Properties DEFINITION 1. Let A and B be nonempty sets. A function f from A to B is a rule that assigns to each element in the set
c Dr Oksana Shatalov, Spring 2016 1 3 FUNCTIONS 3.1 Definition and Basic Properties DEFINITION 1. Let A and B be nonempty sets. A function f from A to B is a rule that assigns to each element in the set
REVIEW FOR THIRD 3200 MIDTERM
 REVIEW FOR THIRD 3200 MIDTERM PETE L. CLARK 1) Show that for all integers n 2 we have 1 3 +... + (n 1) 3 < 1 n < 1 3 +... + n 3. Solution: We go by induction on n. Base Case (n = 2): We have (2 1) 3 =
REVIEW FOR THIRD 3200 MIDTERM PETE L. CLARK 1) Show that for all integers n 2 we have 1 3 +... + (n 1) 3 < 1 n < 1 3 +... + n 3. Solution: We go by induction on n. Base Case (n = 2): We have (2 1) 3 =
Chapter-2 Relations and Functions. Miscellaneous
 1 Chapter-2 Relations and Functions Miscellaneous Question 1: The relation f is defined by The relation g is defined by Show that f is a function and g is not a function. The relation f is defined as It
1 Chapter-2 Relations and Functions Miscellaneous Question 1: The relation f is defined by The relation g is defined by Show that f is a function and g is not a function. The relation f is defined as It
0 Sets and Induction. Sets
 0 Sets and Induction Sets A set is an unordered collection of objects, called elements or members of the set. A set is said to contain its elements. We write a A to denote that a is an element of the set
0 Sets and Induction Sets A set is an unordered collection of objects, called elements or members of the set. A set is said to contain its elements. We write a A to denote that a is an element of the set
SETS AND FUNCTIONS JOSHUA BALLEW
 SETS AND FUNCTIONS JOSHUA BALLEW 1. Sets As a review, we begin by considering a naive look at set theory. For our purposes, we define a set as a collection of objects. Except for certain sets like N, Z,
SETS AND FUNCTIONS JOSHUA BALLEW 1. Sets As a review, we begin by considering a naive look at set theory. For our purposes, we define a set as a collection of objects. Except for certain sets like N, Z,
Cartesian Products and Relations
 Cartesian Products and Relations Definition (Cartesian product) If A and B are sets, the Cartesian product of A and B is the set A B = {(a, b) : (a A) and (b B)}. The following points are worth special
Cartesian Products and Relations Definition (Cartesian product) If A and B are sets, the Cartesian product of A and B is the set A B = {(a, b) : (a A) and (b B)}. The following points are worth special
MAT115A-21 COMPLETE LECTURE NOTES
 MAT115A-21 COMPLETE LECTURE NOTES NATHANIEL GALLUP 1. Introduction Number theory begins as the study of the natural numbers the integers N = {1, 2, 3,...}, Z = { 3, 2, 1, 0, 1, 2, 3,...}, and sometimes
MAT115A-21 COMPLETE LECTURE NOTES NATHANIEL GALLUP 1. Introduction Number theory begins as the study of the natural numbers the integers N = {1, 2, 3,...}, Z = { 3, 2, 1, 0, 1, 2, 3,...}, and sometimes
Mathematics 220 Workshop Cardinality. Some harder problems on cardinality.
 Some harder problems on cardinality. These are two series of problems with specific goals: the first goal is to prove that the cardinality of the set of irrational numbers is continuum, and the second
Some harder problems on cardinality. These are two series of problems with specific goals: the first goal is to prove that the cardinality of the set of irrational numbers is continuum, and the second
Chapter 1. Sets and Mappings
 Chapter 1. Sets and Mappings 1. Sets A set is considered to be a collection of objects (elements). If A is a set and x is an element of the set A, we say x is a member of A or x belongs to A, and we write
Chapter 1. Sets and Mappings 1. Sets A set is considered to be a collection of objects (elements). If A is a set and x is an element of the set A, we say x is a member of A or x belongs to A, and we write
MATH FINAL EXAM REVIEW HINTS
 MATH 109 - FINAL EXAM REVIEW HINTS Answer: Answer: 1. Cardinality (1) Let a < b be two real numbers and define f : (0, 1) (a, b) by f(t) = (1 t)a + tb. (a) Prove that f is a bijection. (b) Prove that any
MATH 109 - FINAL EXAM REVIEW HINTS Answer: Answer: 1. Cardinality (1) Let a < b be two real numbers and define f : (0, 1) (a, b) by f(t) = (1 t)a + tb. (a) Prove that f is a bijection. (b) Prove that any
Definition: Let S and T be sets. A binary relation on SxT is any subset of SxT. A binary relation on S is any subset of SxS.
 4 Functions Before studying functions we will first quickly define a more general idea, namely the notion of a relation. A function turns out to be a special type of relation. Definition: Let S and T be
4 Functions Before studying functions we will first quickly define a more general idea, namely the notion of a relation. A function turns out to be a special type of relation. Definition: Let S and T be
ADVANCED CALCULUS - MTH433 LECTURE 4 - FINITE AND INFINITE SETS
 ADVANCED CALCULUS - MTH433 LECTURE 4 - FINITE AND INFINITE SETS 1. Cardinal number of a set The cardinal number (or simply cardinal) of a set is a generalization of the concept of the number of elements
ADVANCED CALCULUS - MTH433 LECTURE 4 - FINITE AND INFINITE SETS 1. Cardinal number of a set The cardinal number (or simply cardinal) of a set is a generalization of the concept of the number of elements
Sets and Functions. (As we will see, in describing a set the order in which elements are listed is irrelevant).
 Sets and Functions 1. The language of sets Informally, a set is any collection of objects. The objects may be mathematical objects such as numbers, functions and even sets, or letters or symbols of any
Sets and Functions 1. The language of sets Informally, a set is any collection of objects. The objects may be mathematical objects such as numbers, functions and even sets, or letters or symbols of any
Review 3. Andreas Klappenecker
 Review 3 Andreas Klappenecker Final Exam Friday, May 4, 2012, starting at 12:30pm, usual classroom Topics Topic Reading Algorithms and their Complexity Chapter 3 Logic and Proofs Chapter 1 Logic and Proofs
Review 3 Andreas Klappenecker Final Exam Friday, May 4, 2012, starting at 12:30pm, usual classroom Topics Topic Reading Algorithms and their Complexity Chapter 3 Logic and Proofs Chapter 1 Logic and Proofs
Final Exam Review. 2. Let A = {, { }}. What is the cardinality of A? Is
 1. Describe the elements of the set (Z Q) R N. Is this set countable or uncountable? Solution: The set is equal to {(x, y) x Z, y N} = Z N. Since the Cartesian product of two denumerable sets is denumerable,
1. Describe the elements of the set (Z Q) R N. Is this set countable or uncountable? Solution: The set is equal to {(x, y) x Z, y N} = Z N. Since the Cartesian product of two denumerable sets is denumerable,
2.1 Sets. Definition 1 A set is an unordered collection of objects. Important sets: N, Z, Z +, Q, R.
 2. Basic Structures 2.1 Sets Definition 1 A set is an unordered collection of objects. Important sets: N, Z, Z +, Q, R. Definition 2 Objects in a set are called elements or members of the set. A set is
2. Basic Structures 2.1 Sets Definition 1 A set is an unordered collection of objects. Important sets: N, Z, Z +, Q, R. Definition 2 Objects in a set are called elements or members of the set. A set is
MTH 299 In Class and Recitation Problems SUMMER 2016
 MTH 299 In Class and Recitation Problems SUMMER 2016 Last updated on: May 13, 2016 MTH299 - Examples CONTENTS Contents 1 Week 1 3 1.1 In Class Problems.......................................... 3 1.2 Recitation
MTH 299 In Class and Recitation Problems SUMMER 2016 Last updated on: May 13, 2016 MTH299 - Examples CONTENTS Contents 1 Week 1 3 1.1 In Class Problems.......................................... 3 1.2 Recitation
Chapter 1 : The language of mathematics.
 MAT 200, Logic, Language and Proof, Fall 2015 Summary Chapter 1 : The language of mathematics. Definition. A proposition is a sentence which is either true or false. Truth table for the connective or :
MAT 200, Logic, Language and Proof, Fall 2015 Summary Chapter 1 : The language of mathematics. Definition. A proposition is a sentence which is either true or false. Truth table for the connective or :
Mathematics Course 111: Algebra I Part I: Algebraic Structures, Sets and Permutations
 Mathematics Course 111: Algebra I Part I: Algebraic Structures, Sets and Permutations D. R. Wilkins Academic Year 1996-7 1 Number Systems and Matrix Algebra Integers The whole numbers 0, ±1, ±2, ±3, ±4,...
Mathematics Course 111: Algebra I Part I: Algebraic Structures, Sets and Permutations D. R. Wilkins Academic Year 1996-7 1 Number Systems and Matrix Algebra Integers The whole numbers 0, ±1, ±2, ±3, ±4,...
MATH 433 Applied Algebra Lecture 14: Functions. Relations.
 MATH 433 Applied Algebra Lecture 14: Functions. Relations. Cartesian product Definition. The Cartesian product X Y of two sets X and Y is the set of all ordered pairs (x,y) such that x X and y Y. The Cartesian
MATH 433 Applied Algebra Lecture 14: Functions. Relations. Cartesian product Definition. The Cartesian product X Y of two sets X and Y is the set of all ordered pairs (x,y) such that x X and y Y. The Cartesian
Principles of Real Analysis I Fall I. The Real Number System
 21-355 Principles of Real Analysis I Fall 2004 I. The Real Number System The main goal of this course is to develop the theory of real-valued functions of one real variable in a systematic and rigorous
21-355 Principles of Real Analysis I Fall 2004 I. The Real Number System The main goal of this course is to develop the theory of real-valued functions of one real variable in a systematic and rigorous
In N we can do addition, but in order to do subtraction we need to extend N to the integers
 Chapter 1 The Real Numbers 1.1. Some Preliminaries Discussion: The Irrationality of 2. We begin with the natural numbers N = {1, 2, 3, }. In N we can do addition, but in order to do subtraction we need
Chapter 1 The Real Numbers 1.1. Some Preliminaries Discussion: The Irrationality of 2. We begin with the natural numbers N = {1, 2, 3, }. In N we can do addition, but in order to do subtraction we need
3 FUNCTIONS. 3.1 Definition and Basic Properties. c Dr Oksana Shatalov, Fall
 c Dr Oksana Shatalov, Fall 2016 1 3 FUNCTIONS 3.1 Definition and Basic Properties DEFINITION 1. Let A and B be nonempty sets. A function f from the set A to the set B is a correspondence that assigns to
c Dr Oksana Shatalov, Fall 2016 1 3 FUNCTIONS 3.1 Definition and Basic Properties DEFINITION 1. Let A and B be nonempty sets. A function f from the set A to the set B is a correspondence that assigns to
Selected problems from past exams
 Discrete Structures CS2800 Prelim 1 s Selected problems from past exams 1. True/false. For each of the following statements, indicate whether the statement is true or false. Give a one or two sentence
Discrete Structures CS2800 Prelim 1 s Selected problems from past exams 1. True/false. For each of the following statements, indicate whether the statement is true or false. Give a one or two sentence
MATH 201 Solutions: TEST 3-A (in class)
 MATH 201 Solutions: TEST 3-A (in class) (revised) God created infinity, and man, unable to understand infinity, had to invent finite sets. - Gian Carlo Rota Part I [5 pts each] 1. Let X be a set. Define
MATH 201 Solutions: TEST 3-A (in class) (revised) God created infinity, and man, unable to understand infinity, had to invent finite sets. - Gian Carlo Rota Part I [5 pts each] 1. Let X be a set. Define
Foundations Revision Notes
 oundations Revision Notes hese notes are designed as an aid not a substitute for revision. A lot of proofs have not been included because you should have them in your notes, should you need them. Also,
oundations Revision Notes hese notes are designed as an aid not a substitute for revision. A lot of proofs have not been included because you should have them in your notes, should you need them. Also,
Sets, Functions and Relations
 Chapter 2 Sets, Functions and Relations A set is any collection of distinct objects. Here is some notation for some special sets of numbers: Z denotes the set of integers (whole numbers), that is, Z =
Chapter 2 Sets, Functions and Relations A set is any collection of distinct objects. Here is some notation for some special sets of numbers: Z denotes the set of integers (whole numbers), that is, Z =
Review 1. Andreas Klappenecker
 Review 1 Andreas Klappenecker Summary Propositional Logic, Chapter 1 Predicate Logic, Chapter 1 Proofs, Chapter 1 Sets, Chapter 2 Functions, Chapter 2 Sequences and Sums, Chapter 2 Asymptotic Notations,
Review 1 Andreas Klappenecker Summary Propositional Logic, Chapter 1 Predicate Logic, Chapter 1 Proofs, Chapter 1 Sets, Chapter 2 Functions, Chapter 2 Sequences and Sums, Chapter 2 Asymptotic Notations,
Countability. 1 Motivation. 2 Counting
 Countability 1 Motivation In topology as well as other areas of mathematics, we deal with a lot of infinite sets. However, as we will gradually discover, some infinite sets are bigger than others. Countably
Countability 1 Motivation In topology as well as other areas of mathematics, we deal with a lot of infinite sets. However, as we will gradually discover, some infinite sets are bigger than others. Countably
Week Some Warm-up Questions
 1 Some Warm-up Questions Week 1-2 Abstraction: The process going from specific cases to general problem. Proof: A sequence of arguments to show certain conclusion to be true. If... then... : The part after
1 Some Warm-up Questions Week 1-2 Abstraction: The process going from specific cases to general problem. Proof: A sequence of arguments to show certain conclusion to be true. If... then... : The part after
1.4 Cardinality. Tom Lewis. Fall Term Tom Lewis () 1.4 Cardinality Fall Term / 9
 1.4 Cardinality Tom Lewis Fall Term 2006 Tom Lewis () 1.4 Cardinality Fall Term 2006 1 / 9 Outline 1 Functions 2 Cardinality 3 Cantor s theorem Tom Lewis () 1.4 Cardinality Fall Term 2006 2 / 9 Functions
1.4 Cardinality Tom Lewis Fall Term 2006 Tom Lewis () 1.4 Cardinality Fall Term 2006 1 / 9 Outline 1 Functions 2 Cardinality 3 Cantor s theorem Tom Lewis () 1.4 Cardinality Fall Term 2006 2 / 9 Functions
5 Set Operations, Functions, and Counting
 5 Set Operations, Functions, and Counting Let N denote the positive integers, N 0 := N {0} be the non-negative integers and Z = N 0 ( N) the positive and negative integers including 0, Q the rational numbers,
5 Set Operations, Functions, and Counting Let N denote the positive integers, N 0 := N {0} be the non-negative integers and Z = N 0 ( N) the positive and negative integers including 0, Q the rational numbers,
Exam Practice Problems
 Math 231 Exam Practice Problems WARNING: This is not a sample test. Problems on the exams may or may not be similar to these problems. These problems are just intended to focus your study of the topics.
Math 231 Exam Practice Problems WARNING: This is not a sample test. Problems on the exams may or may not be similar to these problems. These problems are just intended to focus your study of the topics.
Extension of continuous functions in digital spaces with the Khalimsky topology
 Extension of continuous functions in digital spaces with the Khalimsky topology Erik Melin Uppsala University, Department of Mathematics Box 480, SE-751 06 Uppsala, Sweden melin@math.uu.se http://www.math.uu.se/~melin
Extension of continuous functions in digital spaces with the Khalimsky topology Erik Melin Uppsala University, Department of Mathematics Box 480, SE-751 06 Uppsala, Sweden melin@math.uu.se http://www.math.uu.se/~melin
Discrete Mathematics. Spring 2017
 Discrete Mathematics Spring 2017 Previous Lecture Principle of Mathematical Induction Mathematical Induction: rule of inference Mathematical Induction: Conjecturing and Proving Climbing an Infinite Ladder
Discrete Mathematics Spring 2017 Previous Lecture Principle of Mathematical Induction Mathematical Induction: rule of inference Mathematical Induction: Conjecturing and Proving Climbing an Infinite Ladder
Lecture Notes on Discrete Mathematics. October 15, 2018 DRAFT
 Lecture Notes on Discrete Mathematics October 15, 2018 2 Contents 1 Basic Set Theory 5 1.1 Basic Set Theory....................................... 5 1.1.1 Union and Intersection of Sets...........................
Lecture Notes on Discrete Mathematics October 15, 2018 2 Contents 1 Basic Set Theory 5 1.1 Basic Set Theory....................................... 5 1.1.1 Union and Intersection of Sets...........................
Introduction to Functions
 Mathematics for Economists Introduction to Functions Introduction In economics we study the relationship between variables and attempt to explain these relationships through economic theory. For instance
Mathematics for Economists Introduction to Functions Introduction In economics we study the relationship between variables and attempt to explain these relationships through economic theory. For instance
Homework 5. Solutions
 Homework 5. Solutions 1. Let (X,T) be a topological space and let A,B be subsets of X. Show that the closure of their union is given by A B = A B. Since A B is a closed set that contains A B and A B is
Homework 5. Solutions 1. Let (X,T) be a topological space and let A,B be subsets of X. Show that the closure of their union is given by A B = A B. Since A B is a closed set that contains A B and A B is
Topology. Xiaolong Han. Department of Mathematics, California State University, Northridge, CA 91330, USA address:
 Topology Xiaolong Han Department of Mathematics, California State University, Northridge, CA 91330, USA E-mail address: Xiaolong.Han@csun.edu Remark. You are entitled to a reward of 1 point toward a homework
Topology Xiaolong Han Department of Mathematics, California State University, Northridge, CA 91330, USA E-mail address: Xiaolong.Han@csun.edu Remark. You are entitled to a reward of 1 point toward a homework
(1) Which of the following are propositions? If it is a proposition, determine its truth value: A propositional function, but not a proposition.
 Math 231 Exam Practice Problem Solutions WARNING: This is not a sample test. Problems on the exams may or may not be similar to these problems. These problems are just intended to focus your study of the
Math 231 Exam Practice Problem Solutions WARNING: This is not a sample test. Problems on the exams may or may not be similar to these problems. These problems are just intended to focus your study of the
6 CARDINALITY OF SETS
 6 CARDINALITY OF SETS MATH10111 - Foundations of Pure Mathematics We all have an idea of what it means to count a finite collection of objects, but we must be careful to define rigorously what it means
6 CARDINALITY OF SETS MATH10111 - Foundations of Pure Mathematics We all have an idea of what it means to count a finite collection of objects, but we must be careful to define rigorously what it means
Logical Connectives and Quantifiers
 Chapter 1 Logical Connectives and Quantifiers 1.1 Logical Connectives 1.2 Quantifiers 1.3 Techniques of Proof: I 1.4 Techniques of Proof: II Theorem 1. Let f be a continuous function. If 1 f(x)dx 0, then
Chapter 1 Logical Connectives and Quantifiers 1.1 Logical Connectives 1.2 Quantifiers 1.3 Techniques of Proof: I 1.4 Techniques of Proof: II Theorem 1. Let f be a continuous function. If 1 f(x)dx 0, then
In N we can do addition, but in order to do subtraction we need to extend N to the integers
 Chapter The Real Numbers.. Some Preliminaries Discussion: The Irrationality of 2. We begin with the natural numbers N = {, 2, 3, }. In N we can do addition, but in order to do subtraction we need to extend
Chapter The Real Numbers.. Some Preliminaries Discussion: The Irrationality of 2. We begin with the natural numbers N = {, 2, 3, }. In N we can do addition, but in order to do subtraction we need to extend
CHAPTER 10: POLYNOMIALS (DRAFT)
 CHAPTER 10: POLYNOMIALS (DRAFT) LECTURE NOTES FOR MATH 378 (CSUSM, SPRING 2009). WAYNE AITKEN The material in this chapter is fairly informal. Unlike earlier chapters, no attempt is made to rigorously
CHAPTER 10: POLYNOMIALS (DRAFT) LECTURE NOTES FOR MATH 378 (CSUSM, SPRING 2009). WAYNE AITKEN The material in this chapter is fairly informal. Unlike earlier chapters, no attempt is made to rigorously
UMASS AMHERST MATH 300 SP 05, F. HAJIR HOMEWORK 8: (EQUIVALENCE) RELATIONS AND PARTITIONS
 UMASS AMHERST MATH 300 SP 05, F. HAJIR HOMEWORK 8: (EQUIVALENCE) RELATIONS AND PARTITIONS 1. Relations Recall the concept of a function f from a source set X to a target set Y. It is a rule for mapping
UMASS AMHERST MATH 300 SP 05, F. HAJIR HOMEWORK 8: (EQUIVALENCE) RELATIONS AND PARTITIONS 1. Relations Recall the concept of a function f from a source set X to a target set Y. It is a rule for mapping
Math Fall 2014 Final Exam Solutions
 Math 2001-003 Fall 2014 Final Exam Solutions Wednesday, December 17, 2014 Definition 1. The union of two sets X and Y is the set X Y consisting of all objects that are elements of X or of Y. The intersection
Math 2001-003 Fall 2014 Final Exam Solutions Wednesday, December 17, 2014 Definition 1. The union of two sets X and Y is the set X Y consisting of all objects that are elements of X or of Y. The intersection
447 HOMEWORK SET 1 IAN FRANCIS
 7 HOMEWORK SET 1 IAN FRANCIS For each n N, let A n {(n 1)k : k N}. 1 (a) Determine the truth value of the statement: for all n N, A n N. Justify. This statement is false. Simply note that for 1 N, A 1
7 HOMEWORK SET 1 IAN FRANCIS For each n N, let A n {(n 1)k : k N}. 1 (a) Determine the truth value of the statement: for all n N, A n N. Justify. This statement is false. Simply note that for 1 N, A 1
Sets, Proofs and Functions. Anton Velinov
 Sets, Proofs and Functions Anton Velinov DIW WS 2018 Takeaways Sets and set operations. De Morgan s laws. Logical quantifiers and operators. Implication. Methods of proof, deduction, induction, contradiction.
Sets, Proofs and Functions Anton Velinov DIW WS 2018 Takeaways Sets and set operations. De Morgan s laws. Logical quantifiers and operators. Implication. Methods of proof, deduction, induction, contradiction.
RED. Fall 2016 Student Submitted Sample Questions
 RED Fall 2016 Student Submitted Sample Questions Name: Last Update: November 22, 2016 The questions are divided into three sections: True-false, Multiple Choice, and Written Answer. I will add questions
RED Fall 2016 Student Submitted Sample Questions Name: Last Update: November 22, 2016 The questions are divided into three sections: True-false, Multiple Choice, and Written Answer. I will add questions
POL502: Foundations. Kosuke Imai Department of Politics, Princeton University. October 10, 2005
 POL502: Foundations Kosuke Imai Department of Politics, Princeton University October 10, 2005 Our first task is to develop the foundations that are necessary for the materials covered in this course. 1
POL502: Foundations Kosuke Imai Department of Politics, Princeton University October 10, 2005 Our first task is to develop the foundations that are necessary for the materials covered in this course. 1
Functions and cardinality (solutions) sections A and F TA: Clive Newstead 6 th May 2014
 Functions and cardinality (solutions) 21-127 sections A and F TA: Clive Newstead 6 th May 2014 What follows is a somewhat hastily written collection of solutions for my review sheet. I have omitted some
Functions and cardinality (solutions) 21-127 sections A and F TA: Clive Newstead 6 th May 2014 What follows is a somewhat hastily written collection of solutions for my review sheet. I have omitted some
Math 300: Final Exam Practice Solutions
 Math 300: Final Exam Practice Solutions 1 Let A be the set of all real numbers which are zeros of polynomials with integer coefficients: A := {α R there exists p(x) = a n x n + + a 1 x + a 0 with all a
Math 300: Final Exam Practice Solutions 1 Let A be the set of all real numbers which are zeros of polynomials with integer coefficients: A := {α R there exists p(x) = a n x n + + a 1 x + a 0 with all a
Solutions to Homework Set 1
 Solutions to Homework Set 1 1. Prove that not-q not-p implies P Q. In class we proved that A B implies not-b not-a Replacing the statement A by the statement not-q and the statement B by the statement
Solutions to Homework Set 1 1. Prove that not-q not-p implies P Q. In class we proved that A B implies not-b not-a Replacing the statement A by the statement not-q and the statement B by the statement
Lecture Notes 1 Basic Concepts of Mathematics MATH 352
 Lecture Notes 1 Basic Concepts of Mathematics MATH 352 Ivan Avramidi New Mexico Institute of Mining and Technology Socorro, NM 87801 June 3, 2004 Author: Ivan Avramidi; File: absmath.tex; Date: June 11,
Lecture Notes 1 Basic Concepts of Mathematics MATH 352 Ivan Avramidi New Mexico Institute of Mining and Technology Socorro, NM 87801 June 3, 2004 Author: Ivan Avramidi; File: absmath.tex; Date: June 11,
Notes on ordinals and cardinals
 Notes on ordinals and cardinals Reed Solomon 1 Background Terminology We will use the following notation for the common number systems: N = {0, 1, 2,...} = the natural numbers Z = {..., 2, 1, 0, 1, 2,...}
Notes on ordinals and cardinals Reed Solomon 1 Background Terminology We will use the following notation for the common number systems: N = {0, 1, 2,...} = the natural numbers Z = {..., 2, 1, 0, 1, 2,...}
Foundations of Mathematics MATH 220 FALL 2017 Lecture Notes
 Foundations of Mathematics MATH 220 FALL 2017 Lecture Notes These notes form a brief summary of what has been covered during the lectures. All the definitions must be memorized and understood. Statements
Foundations of Mathematics MATH 220 FALL 2017 Lecture Notes These notes form a brief summary of what has been covered during the lectures. All the definitions must be memorized and understood. Statements
Definitions. Notations. Injective, Surjective and Bijective. Divides. Cartesian Product. Relations. Equivalence Relations
 Page 1 Definitions Tuesday, May 8, 2018 12:23 AM Notations " " means "equals, by definition" the set of all real numbers the set of integers Denote a function from a set to a set by Denote the image of
Page 1 Definitions Tuesday, May 8, 2018 12:23 AM Notations " " means "equals, by definition" the set of all real numbers the set of integers Denote a function from a set to a set by Denote the image of
1 Basic Combinatorics
 1 Basic Combinatorics 1.1 Sets and sequences Sets. A set is an unordered collection of distinct objects. The objects are called elements of the set. We use braces to denote a set, for example, the set
1 Basic Combinatorics 1.1 Sets and sequences Sets. A set is an unordered collection of distinct objects. The objects are called elements of the set. We use braces to denote a set, for example, the set
Written Homework # 4 Solution
 Math 516 Fall 2006 Radford Written Homework # 4 Solution 12/10/06 You may use results form the book in Chapters 1 6 of the text, from notes found on our course web page, and results of the previous homework.
Math 516 Fall 2006 Radford Written Homework # 4 Solution 12/10/06 You may use results form the book in Chapters 1 6 of the text, from notes found on our course web page, and results of the previous homework.
Notes for Math 290 using Introduction to Mathematical Proofs by Charles E. Roberts, Jr.
 Notes for Math 290 using Introduction to Mathematical Proofs by Charles E. Roberts, Jr. Chapter : Logic Topics:. Statements, Negation, and Compound Statements.2 Truth Tables and Logical Equivalences.3
Notes for Math 290 using Introduction to Mathematical Proofs by Charles E. Roberts, Jr. Chapter : Logic Topics:. Statements, Negation, and Compound Statements.2 Truth Tables and Logical Equivalences.3
Midterm Exam. There are 6 problems. Your 5 best answers count. Please pay attention to the presentation of your work! Best 5
 Department of Mathematical Sciences Instructor: Daiva Pucinskaite Modern Algebra June 22, 2017 Midterm Exam There are 6 problems. Your 5 best answers count. Please pay attention to the presentation of
Department of Mathematical Sciences Instructor: Daiva Pucinskaite Modern Algebra June 22, 2017 Midterm Exam There are 6 problems. Your 5 best answers count. Please pay attention to the presentation of
One-to-one functions and onto functions
 MA 3362 Lecture 7 - One-to-one and Onto Wednesday, October 22, 2008. Objectives: Formalize definitions of one-to-one and onto One-to-one functions and onto functions At the level of set theory, there are
MA 3362 Lecture 7 - One-to-one and Onto Wednesday, October 22, 2008. Objectives: Formalize definitions of one-to-one and onto One-to-one functions and onto functions At the level of set theory, there are
A Readable Introduction to Real Mathematics
 Solutions to selected problems in the book A Readable Introduction to Real Mathematics D. Rosenthal, D. Rosenthal, P. Rosenthal Chapter 10: Sizes of Infinite Sets 1. Show that the set of all polynomials
Solutions to selected problems in the book A Readable Introduction to Real Mathematics D. Rosenthal, D. Rosenthal, P. Rosenthal Chapter 10: Sizes of Infinite Sets 1. Show that the set of all polynomials
Practice Midterm Exam
 CS/MATH320L - Applied Discrete Math Spring 2013 Instructor: Marc Pomplun Practice Midterm Exam Sample Solutions Question 1: out of points Question 2: out of points Question 3: out of points Question 4:
CS/MATH320L - Applied Discrete Math Spring 2013 Instructor: Marc Pomplun Practice Midterm Exam Sample Solutions Question 1: out of points Question 2: out of points Question 3: out of points Question 4:
Functions as Relations
 Functions as Relations Definition Recall that if A and B are sets, then a relation from A to B is a subset of A B. A function from A to B is a relation f from A to B with the following properties (i) The
Functions as Relations Definition Recall that if A and B are sets, then a relation from A to B is a subset of A B. A function from A to B is a relation f from A to B with the following properties (i) The
Discrete Mathematics for CS Spring 2007 Luca Trevisan Lecture 27
 CS 70 Discrete Mathematics for CS Spring 007 Luca Trevisan Lecture 7 Infinity and Countability Consider a function f that maps elements of a set A (called the domain of f ) to elements of set B (called
CS 70 Discrete Mathematics for CS Spring 007 Luca Trevisan Lecture 7 Infinity and Countability Consider a function f that maps elements of a set A (called the domain of f ) to elements of set B (called
Maths 212: Homework Solutions
 Maths 212: Homework Solutions 1. The definition of A ensures that x π for all x A, so π is an upper bound of A. To show it is the least upper bound, suppose x < π and consider two cases. If x < 1, then
Maths 212: Homework Solutions 1. The definition of A ensures that x π for all x A, so π is an upper bound of A. To show it is the least upper bound, suppose x < π and consider two cases. If x < 1, then
Math 320: Real Analysis MWF 1pm, Campion Hall 302 Homework 8 Solutions Please write neatly, and in complete sentences when possible.
 Math 320: Real Analysis MWF pm, Campion Hall 302 Homework 8 Solutions Please write neatly, and in complete sentences when possible. Do the following problems from the book: 4.3.5, 4.3.7, 4.3.8, 4.3.9,
Math 320: Real Analysis MWF pm, Campion Hall 302 Homework 8 Solutions Please write neatly, and in complete sentences when possible. Do the following problems from the book: 4.3.5, 4.3.7, 4.3.8, 4.3.9,
MATH 13 FINAL EXAM SOLUTIONS
 MATH 13 FINAL EXAM SOLUTIONS WINTER 2014 Problem 1 (15 points). For each statement below, circle T or F according to whether the statement is true or false. You do NOT need to justify your answers. T F
MATH 13 FINAL EXAM SOLUTIONS WINTER 2014 Problem 1 (15 points). For each statement below, circle T or F according to whether the statement is true or false. You do NOT need to justify your answers. T F
Section 4.4 Functions. CS 130 Discrete Structures
 Section 4.4 Functions CS 130 Discrete Structures Function Definitions Let S and T be sets. A function f from S to T, f: S T, is a subset of S x T where each member of S appears exactly once as the first
Section 4.4 Functions CS 130 Discrete Structures Function Definitions Let S and T be sets. A function f from S to T, f: S T, is a subset of S x T where each member of S appears exactly once as the first
MODEL ANSWERS TO THE SEVENTH HOMEWORK. (b) We proved in homework six, question 2 (c) that. But we also proved homework six, question 2 (a) that
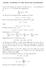 MODEL ANSWERS TO THE SEVENTH HOMEWORK 1. Let X be a finite set, and let A, B and A 1, A 2,..., A n be subsets of X. Let A c = X \ A denote the complement. (a) χ A (x) = A. x X (b) We proved in homework
MODEL ANSWERS TO THE SEVENTH HOMEWORK 1. Let X be a finite set, and let A, B and A 1, A 2,..., A n be subsets of X. Let A c = X \ A denote the complement. (a) χ A (x) = A. x X (b) We proved in homework
Algebraic Cryptography Exam 2 Review
 Algebraic Cryptography Exam 2 Review You should be able to do the problems assigned as homework, as well as problems from Chapter 3 2 and 3. You should also be able to complete the following exercises:
Algebraic Cryptography Exam 2 Review You should be able to do the problems assigned as homework, as well as problems from Chapter 3 2 and 3. You should also be able to complete the following exercises:
MATH 102 INTRODUCTION TO MATHEMATICAL ANALYSIS. 1. Some Fundamentals
 MATH 02 INTRODUCTION TO MATHEMATICAL ANALYSIS Properties of Real Numbers Some Fundamentals The whole course will be based entirely on the study of sequence of numbers and functions defined on the real
MATH 02 INTRODUCTION TO MATHEMATICAL ANALYSIS Properties of Real Numbers Some Fundamentals The whole course will be based entirely on the study of sequence of numbers and functions defined on the real
9 FUNCTIONS. 9.1 The Definition of Function. c Dr Oksana Shatalov, Fall
 c Dr Oksana Shatalov, Fall 2018 1 9 FUNCTIONS 9.1 The Definition of Function DEFINITION 1. Let X and Y be nonempty sets. A function f from the set X to the set Y is a correspondence that assigns to each
c Dr Oksana Shatalov, Fall 2018 1 9 FUNCTIONS 9.1 The Definition of Function DEFINITION 1. Let X and Y be nonempty sets. A function f from the set X to the set Y is a correspondence that assigns to each
Introduction to Proofs
 Introduction to Proofs Notes by Dr. Lynne H. Walling and Dr. Steffi Zegowitz September 018 The Introduction to Proofs course is organised into the following nine sections. 1. Introduction: sets and functions
Introduction to Proofs Notes by Dr. Lynne H. Walling and Dr. Steffi Zegowitz September 018 The Introduction to Proofs course is organised into the following nine sections. 1. Introduction: sets and functions
18.S097 Introduction to Proofs IAP 2015 Lecture Notes 1 (1/5/2015)
 18.S097 Introduction to Proofs IAP 2015 Lecture Notes 1 (1/5/2015) 1. Introduction The goal for this course is to provide a quick, and hopefully somewhat gentle, introduction to the task of formulating
18.S097 Introduction to Proofs IAP 2015 Lecture Notes 1 (1/5/2015) 1. Introduction The goal for this course is to provide a quick, and hopefully somewhat gentle, introduction to the task of formulating
1 Take-home exam and final exam study guide
 Math 215 - Introduction to Advanced Mathematics Fall 2013 1 Take-home exam and final exam study guide 1.1 Problems The following are some problems, some of which will appear on the final exam. 1.1.1 Number
Math 215 - Introduction to Advanced Mathematics Fall 2013 1 Take-home exam and final exam study guide 1.1 Problems The following are some problems, some of which will appear on the final exam. 1.1.1 Number
Axioms for Set Theory
 Axioms for Set Theory The following is a subset of the Zermelo-Fraenkel axioms for set theory. In this setting, all objects are sets which are denoted by letters, e.g. x, y, X, Y. Equality is logical identity:
Axioms for Set Theory The following is a subset of the Zermelo-Fraenkel axioms for set theory. In this setting, all objects are sets which are denoted by letters, e.g. x, y, X, Y. Equality is logical identity:
Solutions to Homework Problems
 Solutions to Homework Problems November 11, 2017 1 Problems II: Sets and Functions (Page 117-118) 11. Give a proof or a counterexample of the following statements: (vi) x R, y R, xy 0; (x) ( x R, y R,
Solutions to Homework Problems November 11, 2017 1 Problems II: Sets and Functions (Page 117-118) 11. Give a proof or a counterexample of the following statements: (vi) x R, y R, xy 0; (x) ( x R, y R,
Chapter Summary. Sets The Language of Sets Set Operations Set Identities Functions Types of Functions Operations on Functions Computability
 Chapter 2 1 Chapter Summary Sets The Language of Sets Set Operations Set Identities Functions Types of Functions Operations on Functions Computability Sequences and Summations Types of Sequences Summation
Chapter 2 1 Chapter Summary Sets The Language of Sets Set Operations Set Identities Functions Types of Functions Operations on Functions Computability Sequences and Summations Types of Sequences Summation
There are seven questions, of varying point-value. Each question is worth the indicated number of points.
 Final Exam MAT 200 Solution Guide There are seven questions, of varying point-value. Each question is worth the indicated number of points. 1. (15 points) If X is uncountable and A X is countable, prove
Final Exam MAT 200 Solution Guide There are seven questions, of varying point-value. Each question is worth the indicated number of points. 1. (15 points) If X is uncountable and A X is countable, prove
Induction. Induction. Induction. Induction. Induction. Induction 2/22/2018
 The principle of mathematical induction is a useful tool for proving that a certain predicate is true for all natural numbers. It cannot be used to discover theorems, but only to prove them. If we have
The principle of mathematical induction is a useful tool for proving that a certain predicate is true for all natural numbers. It cannot be used to discover theorems, but only to prove them. If we have
1. Decide for each of the following expressions: Is it a function? If so, f is a function. (i) Domain: R. Codomain: R. Range: R. (iii) Yes surjective.
 Homework 2 2/14/2018 SOLUTIONS Exercise 6. 1. Decide for each of the following expressions: Is it a function? If so, (i) what is its domain, codomain, and image? (iii) is it surjective? (ii) is it injective?
Homework 2 2/14/2018 SOLUTIONS Exercise 6. 1. Decide for each of the following expressions: Is it a function? If so, (i) what is its domain, codomain, and image? (iii) is it surjective? (ii) is it injective?
Handout 2 (Correction of Handout 1 plus continued discussion/hw) Comments and Homework in Chapter 1
 22M:132 Fall 07 J. Simon Handout 2 (Correction of Handout 1 plus continued discussion/hw) Comments and Homework in Chapter 1 Chapter 1 contains material on sets, functions, relations, and cardinality that
22M:132 Fall 07 J. Simon Handout 2 (Correction of Handout 1 plus continued discussion/hw) Comments and Homework in Chapter 1 Chapter 1 contains material on sets, functions, relations, and cardinality that
4.1 Real-valued functions of a real variable
 Chapter 4 Functions When introducing relations from a set A to a set B we drew an analogy with co-ordinates in the x-y plane. Instead of coming from R, the first component of an ordered pair comes from
Chapter 4 Functions When introducing relations from a set A to a set B we drew an analogy with co-ordinates in the x-y plane. Instead of coming from R, the first component of an ordered pair comes from
Cardinality and ordinal numbers
 Cardinality and ordinal numbers The cardinality A of a finite set A is simply the number of elements in it. When it comes to infinite sets, we no longer can speak of the number of elements in such a set.
Cardinality and ordinal numbers The cardinality A of a finite set A is simply the number of elements in it. When it comes to infinite sets, we no longer can speak of the number of elements in such a set.
REAL VARIABLES: PROBLEM SET 1. = x limsup E k
 REAL VARIABLES: PROBLEM SET 1 BEN ELDER 1. Problem 1.1a First let s prove that limsup E k consists of those points which belong to infinitely many E k. From equation 1.1: limsup E k = E k For limsup E
REAL VARIABLES: PROBLEM SET 1 BEN ELDER 1. Problem 1.1a First let s prove that limsup E k consists of those points which belong to infinitely many E k. From equation 1.1: limsup E k = E k For limsup E
Induction, sequences, limits and continuity
 Induction, sequences, limits and continuity Material covered: eclass notes on induction, Chapter 11, Section 1 and Chapter 2, Sections 2.2-2.5 Induction Principle of mathematical induction: Let P(n) be
Induction, sequences, limits and continuity Material covered: eclass notes on induction, Chapter 11, Section 1 and Chapter 2, Sections 2.2-2.5 Induction Principle of mathematical induction: Let P(n) be
Thus, X is connected by Problem 4. Case 3: X = (a, b]. This case is analogous to Case 2. Case 4: X = (a, b). Choose ε < b a
![Thus, X is connected by Problem 4. Case 3: X = (a, b]. This case is analogous to Case 2. Case 4: X = (a, b). Choose ε < b a Thus, X is connected by Problem 4. Case 3: X = (a, b]. This case is analogous to Case 2. Case 4: X = (a, b). Choose ε < b a](/thumbs/93/112528193.jpg) Solutions to Homework #6 1. Complete the proof of the backwards direction of Theorem 12.2 from class (which asserts the any interval in R is connected). Solution: Let X R be a closed interval. Case 1:
Solutions to Homework #6 1. Complete the proof of the backwards direction of Theorem 12.2 from class (which asserts the any interval in R is connected). Solution: Let X R be a closed interval. Case 1:
Sets. We discuss an informal (naive) set theory as needed in Computer Science. It was introduced by G. Cantor in the second half of the nineteenth
 Sets We discuss an informal (naive) set theory as needed in Computer Science. It was introduced by G. Cantor in the second half of the nineteenth century. Most students have seen sets before. This is intended
Sets We discuss an informal (naive) set theory as needed in Computer Science. It was introduced by G. Cantor in the second half of the nineteenth century. Most students have seen sets before. This is intended
CSCE 222 Discrete Structures for Computing. Review for the Final. Hyunyoung Lee
 CSCE 222 Discrete Structures for Computing Review for the Final! Hyunyoung Lee! 1 Final Exam Section 501 (regular class time 8:00am) Friday, May 8, starting at 1:00pm in our classroom!! Section 502 (regular
CSCE 222 Discrete Structures for Computing Review for the Final! Hyunyoung Lee! 1 Final Exam Section 501 (regular class time 8:00am) Friday, May 8, starting at 1:00pm in our classroom!! Section 502 (regular
Example: Use a direct argument to show that the sum of two even integers has to be even. Solution: Recall that an integer is even if it is a multiple
 Use a direct argument to show that the sum of two even integers has to be even. Solution: Recall that an integer is even if it is a multiple of 2, that is, an integer x is even if x = 2y for some integer
Use a direct argument to show that the sum of two even integers has to be even. Solution: Recall that an integer is even if it is a multiple of 2, that is, an integer x is even if x = 2y for some integer
and problem sheet 6
 2-28 and 5-5 problem sheet 6 Solutions to the following seven exercises and optional bonus problem are to be submitted through gradescope by 2:0AM on Thursday 9th October 207. There are also some practice
2-28 and 5-5 problem sheet 6 Solutions to the following seven exercises and optional bonus problem are to be submitted through gradescope by 2:0AM on Thursday 9th October 207. There are also some practice
