Landau Damping. W. E. Drummond. Department of Physics & Institute for Fusion Studies. The University of Texas, Austin, TX 78712
|
|
|
- Quentin Bradley
- 5 years ago
- Views:
Transcription
1 Landau Damping W. E. Drummond Department of Physics & Institute for Fusion Studies The University of Texas, Austin, TX The damping of a longitudinal plasma wave of finite amplitude is considered. It is shown that the Landau result is the first term in a systematic expansion in a small parameter, and the corrections for finite wave amplitude are shown to be 5 th order in the small parameter. The contributions to the damping from particles with different velocities near the phase velocity are explicitly calculated and this leads to a simple physical picture of the damping process.
2 2 I. INTRODUCTION Landau [1] predicted the damping of small amplitude longitudinal plasma oscillations in a collisionless plasma. There is little doubt that this is correct in the limit of small amplitude waves, however the Landau derivation does not tell us just how small these waves must be. The purpose of the present paper is to give an alternate derivation of the Landau results that provides a simple picture of the damping process, together with a bound on the wave amplitude. The starting point is the Vlasov-Poisson equation set: F t +v F x + e m E F = (1) E x =4πe F (x, v,t)dv 4πn e (2) Landau set F (x, v,t)=f (v)+f (x, v,t) where f (v) is the unperturbed distribution function which he too to be a Maxwellian, f (v) = n / 2πv exp{ (1/2)(v/v) 2 }, and f (x, v,t)is a perturbation. The Vlasov equation thus becomes f t +v f x + e m E f = e m E f, (3) and he linearized this equation by dropping the term (e/m)e f /, which is bilinear in the small quantities. He then considered the initial value problem: For t<, f (x, v, t) and E are zero, and at t = there is a small perturbation, f (v) cos(x) which provides a perturbed electric field. Using Fourier transforms in space and Laplace transforms in time, Landau then integrated the linearized equation to find a solution of the form E = E exp( γt) sin(x ωt) + transients which decay rapidly (4) where: ω 2 ( ) 2 v = ωp ; (5) ω p γ ω = π 2 γ ω ( ) ωp 2 1 n f v= ω ; ( ) 2 v 1. (6) ω p
3 3 Since the Landau result was derived from the linearized Vlasov equation it provides no information on the effect of finite amplitude on the damping. The Landau derivation also provides little insight into the wave particle interactions that produce the damping. Plainly, from the form of the damping coefficient, it is the particles with velocities near the phase velocity which lead to the damping, but how the particles with different velocities in this range contribute to the damping is not clear. Our objective is to rederive the Landau result in a way that addresses these questions. II. PHASE SPACE PICTURE In his treatment of the linearized theory, Landau divided F (x, v,t) into two terms, f (v), the unperturbed distribution function, and f (x, v,t), the perturbation. The following considerations suggest a somewhat different division of F (x, v, t) for the nonlinear initial value problem. At t = we have the unperturbed distribution function, f (v), and the initial perturbation, f (v) cos x, which provides an initial electric field. This field causes the unperturbed distribution function, f (v), which represents the bul of the particles, to change, leading to an electric field from these particles. It is this motion of the bul of the particles which then evolves into the plasma wave. It thus seems natural to brea up F (x, v,t) into f(x, v,t)+ f(x, v,t) where f(x, v,t) is the distribution which evolves from f (v), and f(x, v,t) is the distribution which evolves from f (v) cos x, i.e. f(x, v, ) = f (v), and f(x, v, ) = f (v) cos x. Both f(x, v,t) and f(x, v,t) obey the Vlasov equation, and thus, in particular, f(x, v,t)=f(x, v, ) = f (v ), where x and v are the phase space coordinates of a particle which was at x and v at t =. If we now x = x(x, v,t) and v=v(x, v,t) and if we can invert these to find x =x (x, v,t) and v =v (v, x,t) we can solve for f(x, v,t)=f [v (x, v,t)]. If we write v =v (v v ) and expand f (v ) we have f(x, v,t) = f (v) (v v ) f =f (v) δv f (7) where δv =v v. This approximation requires only (δv)/v (v/v) 2. As discussed in Sec. VI, this is easily satisfied even when nonlinear effects are important for particles moving with velocities near the phase velocity.
4 4 Similarly, we can write f(x, v,t)=f [v (x, v,t)] cos[x (x, v,t)]. However, as shown in Sec. III, this term phase mixes and does not contribute to the damping. To mae use of this we need to find the orbit of a particle moving in an electric field, E = E exp( γt) sin(x ωt). Since it is the particles with velocities near the phase velocity, ω/, that produce the damping, we move to the wave frame, v =v ω/, x =x (ω/)t, E(x, t) =E exp( γt) sin x. In the wave frame we have v = e m E exp( γt) sin(x) (8) ẋ = v. (9) Introducing the dimensionless variables where ω = ee m we have v = v ω, x = x, t = ω t, Γ= γ ω v = exp( Γt) sin x (1) ẋ = v. (11) For large amplitude waves in the sense that Γ 1, O Neil [2] has addressed this problem and finds that after an initial transient, the damping stops. In the Landau limit E, and thus Γ. We see the solution for small but finite amplitude waves for which Γ 1, and proceed by expanding in powers of ( 1 ) eeping terms up through the fifth order in 1. Γ Γ t Integrating Eq. (1) we note that (v v )= dt exp( Γt ) sin x is bounded by ( 1 ). Γ We are interested in times, t, for which γt O(1). Thus, since Γt = γt, and Γ 1, t is of order ( 1 ). Integrating Eq. (11) this gives Γ and x x = (v v )= ( ( dt [v + O = v t + O Γ)] Γ) ( 1 3 dt exp( Γt ) sin(x + v t )+O Γ) From the above x +v t = x v (t t )+O( 1 Γ )2 = x (v+o( 1 Γ )(t t )=x v(t t )+O( 1 Γ )2. Inserting this in the integral for v v we have ( ) 1 3 δv = v v = dt exp( γt )sin(x v(t t )) + O (12) Γ
5 5 which is just the linearized limit. The corrections to this up through terms of order ( 1 Γ )5 are calculated in the appendix. As will be discussed, the first correction to the Landau damping result is of order ( 1 Γ )5. Integrating Eq. (12) and expressing the result in terms of dimensional variables in the wave frame gives δv = v v = ee m 1 {exp( γt)[v cos x + γ sin x] [v cos(x vt)+γsin(x vt)]}. (v) 2 + γ2 Letting t yields the time asymptotic change in the velocity δv = e { } v cos(x vt)+γsin(x vt) m E (v) 2 + γ 2 which is sometimes called the ballistic term since it represents particles traveling with constant velocity. It is δv which leads to plasma wave echos. III. THE ENERGY TRANSFER At a point, x, v, in phase space in the laboratory frame, the rate of energy transfer between the field and the particles is given by P (x, v) = ee(x,t)vf(x, v,t) and since f(x, v,t)= f δv f, the spatially-averaged power transfer is P (v) = ee exp( γt)v f 2π/ dx sin(x ωt)δv. 2π Expressing this in wave frame coordinates and carrying out the integration gives P (v) = e2 E 2 { 2m exp( γt) (ω/ + v) f [ ]} γ exp( γt) v sin(vt) γ cos(vt). (13) (v) 2 + γ 2 Consider the terms in curly bracets. The term proportional to γ exp( γt) is negative (since f / < ) and leads to energy transfer from particles of all velocities to the electric field. The velocity dependence has a resonance, γ/((v) 2 + γ 2 ), at v = with a half-width of γ/. Since the width of the resonance is small compared to the range over which the term (ω/ + v) f / < varies, this term will be evaluated at the pea of the resonance and treated as a constant in the resonance region. Integrating v over the resonance yields π/ exp( γt)(ω/) f / v=. For the main part of the velocity spectrum, away from the resonance, this term is given by ( ) γ ω exp( γt) (v) 2 +(γ 2 ) + v f γ = exp( γt) (ω v) v f /, 2
6 6 which, as shown in Sec. V, simply leads to the loss of particle sloshing energy as the wave damps. The terms, vsin(vt), and γ cos(vt), after integrating over the resonance, each give (π/) exp( γt) f / v=. The resonant contribution from these two terms thus leads to an energy transfer from the field to the particles which is twice the energy transfer in the opposite direction from the γ exp( γt) term. If we integrate these terms over the broad spectrum of the particle velocities, excluding the resonance, phase mixing leads to a rapid decay in time, and this nonresonant contribution can be neglected. The net energy transfer from all of the terms is thus to the particles in the resonance region and from the particles in the bul of the plasma. The total power transfer is thus given by: t 2π dx E2 8π = where P means principal part. dvp (v) = e2 E 2 exp( 2γt) 2m { πω f 2 + γ P v= ω } dv v f (v ω) 2 (14) Carrying out the integral, the sloshing energy term on the right-hand side of Eq. (14) has the same size but opposite sign as the field energy term on the left-hand side. This yields the Landau result γ = π ( ) ωp 2 1 f. 2 n v= ω Returning to Eq. (13), we note that since ω/ + v and f / are essentially constant over the narrow resonance, and since f/ is negative, the velocity dependence of P (v) is proportional to { } γ exp( γt) v sin(vt) γ cos(vt) P (v). (15) (v) 2 + γ 2 We thus have a simple picture of the energy transfer as a function of the particle velocity. The velocity dependence of Eq. (15) is shown in Fig. 1 for various values of γt. From this we conclude. 1. The bul of the energy transfer comes from particles for which v < γ/, and almost all of these gain energy. 2. The energy transfer is an even function of v. 3. δv /(γ/) < 1/Γ 2 so the mixing of velocities is very local.
7 7 4. The distance these particles move in a time, t, is(vt) < γt, so they travel only a fraction of a wavelength in one damping time. Qualitatively, the contribution of the resonant particles to the damping arises from the increase in energy of almost all of the particles without significant mixing: the particles moving more slowly than the wave contribute exactly the same both in size and sign as the particles moving faster than the wave; and during the damping, these particles move less than a wavelength. The decay of the contribution from f(x, v,t) follows from similar considerations. [ ] f(x, v,t) = f (v) (v v ) f (v) cos[(x vt)]. The first term phase mixes in time when integrated over v unless there is a sharp resonance in f (v) and the second term is out of phase with E sin(x ωt) when integrated over a wavelength. IV. THE DISPERSION RELATION The charge density in the wave frame is given by e dvδf = e dv δv f. Writing δv as Im(eE /m) exp( γt)e ix { e i(v+iγ)t 1} where Im means imaginary part, i(v+iγ) and then moving bac to the laboratory frame we have δf(x, v, t) = e m E exp( γt)ime i(x ωt) { e i(v ω+iγ)t 1 i[(v ω)+iγ] } f. The charge density is thus e δf(x, v, t)dv = e2 m E exp( γt) Im e i(x ωt) dv { 1 e i(v ω+iγ)t i[(v ω)+iγ] } f. (16) The integrand has a pole in the lower half plane at v = ω/ i(γ/), and for the first term in the bracet in the integrand we choose the contour shown in Fig. 2(a), which gives e 2 { m E exp( γt) P dv f ( ) (v ω) cos x + γ sin x π } f sin x, (17) (v ω) 2 v=ω/ where P means principal part. For the second term we choose the contour shown in Fig. 2(b). For this contour the phase-mixing term, e i(v ω)t, exp( Mt) along the lower leg of the
8 8 contour, and we choose M sufficiently large so that this part can be neglected. The remaining part is + e2 m E exp( γt) 2π Combining the contributions the result is: E = E exp( γt) cos x =4πe f sin x. (18) v= ω f(x, v,t)dv 4πen { = ωpe 2 exp( γt) P dv f (v ω) cos x + γ sin x) + π } f (v ω) 2 + γ 2 sin x. (19) v=ω/ Equating the coefficients of cos x, and sin x separately to zero respectively gives the Landau dispersion relation and damping: ( ) 2 v ω 2 = ωp 2 1+3, ω p γ ω = π 2 ( ωp ) 2 ) 1 f. n v=ω/ V. THE AVERAGE DISTRIBUTION FUNCTION As discussed above the energy exchange between the electric field and the particles in the resonance region is a function of position and time. However, the spatial average of f(x, v, t) can be used to provide a simple description of the energy exchange. 2π Integrating df/dt = over x gives 2π dx df (x, v, t) = dt 2π 2π dx f t + 2π 2π dx e { E exp( γt) sin x f δv f }. m (2) Denoting the first term on the right-hand side of Eq. (28) as df /dt this gives df dt = 1 2 (ee ) 2 /m exp( γt) {[ ] } γ exp( γt) (v ω) sin[(v ω)t] γ cos[(v ω)t] f, (ω v) 2 + γ 2 (21) Let E be the plasma inetic energy, then {[ de dt = dv 1 df ( 2 mv2 e 2 ) dt = 1 2 m E exp( γt) dv 1 2 mv2 ] f γ exp( iγt) (v ω) sin[(v ω)t]+γcos[(v ω)t]. (22) (ω v) 2 + γ 2 The integral over the bul of the particles give γ(e 2 /8π) exp( 2γt) and the integral over the resonance gives 2γ(E 2 /8π) exp( 2γt). The net of these two terms gives de dt = E 2 exp( 2γt) (23) t 16π }
9 9 which just balances the rate of decrease of the field energy, (E 2 /16π) exp( 2γt). As is well nown, the wave energy of a plasma wave is ( )( ɛ(ω) E 2 ) ω ω 16π = 2 E 2 16π where ɛ(ω) is the dielectric function. This is shared equally by the electric field and the sloshing energy of the particles. Equation (21) describes the flow of this energy to the resonant particles as the wave decays. VI. FINITE E CONSIDERATIONS The effect of finite values of E can be determined by continuing the expansion which led to the order (1/Γ) results above. This is done in the appendix. The result is that there are contributions to δv from terms of order (1/Γ) 3 and (1/Γ) 5. The terms of order ( 1 Γ )3 are spatial harmonics, e.g. sin(2x), sin x cos(x vt), etc., and are thus out of phase with E sin(x), and do not lead to net energy transfer. The terms of order (1/Γ) 5, give a contribution to the energy transfer, which is equal to the contribution from the terms of order 1/Γ times the factor γt 51γ 2 t γ 3 t 3 768Γ 4 + exp( 2γt)( γt +96γ2 t γ 3 t 3 ) 768Γ 4. For Γ 4 1, these nonlinear corrections to δv thus produce a negligible change in the damping for times of physical interest. Similarly, the diffusion of f (v, t) is equally negligible. The flattening of f (v) can be estimated from Eq. (2). Writing this as f t = D f (24) and approximating D as ( ) ee 2 1 D m γ ( v)2 t where ( v) 2 is the range of the flattening in a time, t, yields ( v) 2 ( (γ/) = ee ) m Γ (γt) = 1 4 Γ (γt). 4 Thus for γt O(1), the flattening is negligible.
10 1 Here we note that the approximation leading to Eq. (7) can be written as: which gives 1 Γ 2 δv v = ee mγ ω = ( ω γ ) 2 ( ) γ v 2 ω = v ω γ ( v ω )2, and this is easily satisfied. ( ) 2 v ω VII. EARLIER WORK Landau damping is discussed in many papers and in most plasma physics textboos, however, since it maes use of the linearized Vlasov equation, Landau s paper does not provide any information about the effect of finite wave amplitude. With respect to the nonlinear effects several authors have suggested that the nonlinear corrections should depend on the smallness of 1/Γ =ω /γ. However these wors have been largely qualitative in nature and there appears to be no systematic calculation which leads to a specific dependence on this parameter. Similarly, the Landau paper does not provide a physical picture of the contribution of particles of different velocities to the damping. Aside from a detailed calculation by Dawson [3], the earlier discussions of the energy transfer to or from particles of different velocities are mostly of a qualitative nature and lead to similarly qualitative descriptions of the origin of the damping. One such description, sometimes called the surfer picture [3 6] is that in a damping wave, particles moving slightly slower than the wave tend to be speeded up, and particles moving slightly faster than the wave tend to be slowed down. The damping then results from the fact that since f / < there are more particles gaining energy from the wave than there are particles losing energy to the wave. This is in direct contradiction to the results given in Sec. III where it is shown that both the particles with velocity less than the wave velocity and the particles with velocity greater than the wave velocity gain energy. Something ain to the surfer picture is, however meaningful for large amplitude plasma waves. As discussed in Sec. II, O Neil [2] has considered the damping of large amplitude plasma waves, i.e., the limit, γ/ω 1. In this limit particles with v <ω / are trapped. The physical picture developed by O Neil is that the bul of the energy loss of the wave is due to the net increase in energy of these particles as their phase space orbits in the
11 11 wave frame change from straight-line orbits to rotational orbits, and then phase mix. In this process particles initially going slower than the wave are speeded up and particles going faster than the wave are slowed, which is consistent with the surfer picture. By contrast, in the present paper we are dealing with the limit γ/ω, i.e., the limit of E, and there are no trapped particles. A similar picture [7] envisions a mixing of the slower and faster particles. This is in direct contradiction to the results in Sec. III where it is shown that there is virtually no mixing of the slower and faster particles. Another picture [8, 9] is that the damping results from the oscillation of trapped particles in a damping wave. This is in direct contradiction to the results of Sec. III where it is shown that the particles which contribute to the damping do not oscillate and move much less that a wavelength during a damping time 1/γ. Dawson s calculation involves an integration along the linearized particle orbit, however he does not include the damping in these orbits. In effect, he finds for the in-phase terms v sin vt δv, rather than δv (v) 2 resonance of the form sin(vt) v γ form (v) 2 +γ 2 than πee m γ exp( γt)+v sin(vt)+γ cos(vt). The result is that he finds a (v) 2 +γ 2 which has a half-width of π/t, rather than a resonance of the with a half-width of γ/. The integral over velocity of this gives πee m exp( γt). rather It was shown in Sec. II that for (1/Γ) 4 1, the linearized theory is correct and the orbits are essentially straight lines in phase space. But for Γ, the orbits of particles with small velocity in the wave frame are oscillatory, i.e. there are trapped particles, and the linearized theory is not applicable. Thus Dawson s use of the linearized theory with Γ is inconsistent with the equations of motion for the particles with velocities near the wave velocity. VIII. GROWING WAVES In the foregoing only the case of damping was considered. However, it is well nown that if the distribution function has a gentle bump on the tail, i.e., a range of velocities in which f / >, plasma waves will grow. Although the growth rate is given by the same formula there is a significant difference in the physical interactions. In particular, in Eq. (13), if the sign of γ is negative, the γ exp( γt) term will have a growing exponential
12 12 coefficient, whereas the vsin vt and γ cos vt terms cancel each other when integrated over the resonance. This is reflected in the calculation of the dispersion relation. For γ< the pole is above the axis and the contour of integration of the first term [Fig. 2(a)] must be a semi-circle going under the pole. For the second term [Fig. 2(b)], γ< leads to the entire contour being along the line v = im, and this entire term drops out. This removes the oscillatory time dependence from f(x, v, t) and from the averaged distribution function, f. The result is that Eq. (2) becomes a simple diffusion equation as in the quasilinear theory [1] leading to a flattening of the velocity distribution for a growing wave. f t = D(v) f where D(v) = 1 2 ( )2 ee m exp( γt) ( γ) (ω v) 2 + γ. (25) 2 IX. EXPERIMENTAL RESULTS Predictions based on the Landau theory for both damping and growth of plasma waves have been experimentally tested by Malmberg et al. [11] and by Roberson et al. [12] The results show good agreement over a wide range of parameters. The amplitude bound, ( 1 Γ )4 1, is not very restrictive but should be measurable. Both of these experiments were done with plasma temperatures of about 1eV and waves for which ω/v was in the range of 3.5 to 4. From ( 1 Γ )4 1, which can be written as ( ) 2 [ ( ) ] ev π ω 8 2 e ( ω v )2 κt 8 v where T is the plasma temperature and κ is the Boltzman constant, this would require that 2 millivolt <V < 2 millivolt. If the criterion 1/Γ 1, suggested in the literature, had been used, these bounds would be reduced by an order of magnitude. Unfortunately neither of these experimental papers report on the size of V, although it was estimated in Ref. [8] to be in the 1 MeV range. X. SUMMARY The two principal results are the bound on E, given by ( 1 Γ )4 1, and the energy exchange picture developed in Sec. III. It is worth noting that the pedagogical steps leading to these results are both simple and few. To obtain the energy bound requires three steps: 1) recognize that the well-nown result, f(x, v,t)=f (x, v ), when applied to the initial
13 13 value problem at hand, leads to the nonlinear result: δf = (v v ) δf ; 2) recognize that dv v v depends on the constants,, ee /m, and γ, only through the ratio, γ/ω = Γ, and note that Γ 1 for the Landau problem; and 3) show that the corrections to v v are of fifth order in 1 Γ insofar as they affect the damping, a simple matter if this term is not explicity evaluated. Since this shows that the linearized theory is correct for (1/Γ) 4 1, the energy exchange picture is obtained by simply integrating the linearized equations and examining the energy transfer. The result, discussed in detail in Sect. III, is that essentially all the particles with velocities near the phase velocity gain energy during the damping without significant mixing of the particles in phase space. This energy comes equally from the electric field and the sloshing energy of the bul of the particles moving in the field. The remaining sections simply fill out this physical picture, and attempt to put this wor in perspective. Acnowledgment The author would lie to than the students in his plasma seminar course whose persistent questions led to the present wor. This wor was supported by a grant from The Texas Atomic Energy Research Foundation.
14 14 Appendix Evaluation of the Higher-Order Terms We wish to solve Eqs. (a-1) and (a-1) by expanding in powers of 1/Γ, where Γ 1 v = exp( Γt) sin x (a-1) ẋ = v. Let v = v + δv, x = x + v t + δx. Then δ v = exp( Γt) sin(x + v t + δx) (a-2) δẋ = δv. We anticipate that δv will have terms of order (1/Γ), (1/Γ) 3, (1/Γ) and set δv = δv 1 + δv 3 + δv Similarly we anticipate that δx = δx 2 + δx From (a-2) δx = dt δv = dt (δv 1 + δv ) =δx 2 + δx where δx 2 = dt δv 1 and δx 4 = dt δv 3. From (a-2) δv = dt exp( Γt )sin[x + v t + δx 2 + δx 4 ] t )+ = dt exp( Γt ) sin(x + v t dt exp( Γt )(δx 2 + δx 4 ) cos(x + v t ) 1 dt exp( Γt )(δx 2 + δx 4 ) 2 cos(x + v t ), which gives 2 δv 1 = dt exp( Γt ) sin(x + v t ), (a-3) δv 3 = δv 5 = dt exp( Γt )δx 2 cos(x + v t ) t ( dt exp( Γt ) δx 4 cos(x + v t ) 1 ) 2 (δx 2) 2 sin(x + v t ). Using δv 1 we find which gives δx 2 = dt dt exp( Γt ) sin(t + v t ) δv 3 = dt exp( Γt ) dt dt (3) exp( Γt (3) ) sin(x + v t (3) ) cos(x + v t )). (a-4)
15 15 this gives δx 4 δx 4 = dt and δv 5 = (3) dt exp( Γt ) dt (3) dt (4) exp( Γt (4) ) sin(x +v t ( 4)) cos(x +v t ) (3) (4) dt exp( Γt ) dt dt (3) exp( Γt (3) ) dt (4) dt (4) exp(γt (4) ) sin(x + v t (5) cos(x + v t (3) ) cos(x + v t ) 1 { t 2 dt exp( Γt ) dt dt (3) exp( Γt (3) ) sin(y 2 + v t )} (3) sin(x + v t ) (a-5) We now must express δv in terms of x and v, rather than x and v.wehave Thus (x + v t )=x v(t t ) η, where x = x + v t + x 2 + x 4 v = v + v 1 + v 3 + v 5. η = {x 2 + x 4 (v 1 + v 2 )(t t )}. (a-6) Toget(x + v t ) to 4th-order x 2 and v 1 must be expressed in terms of x and v which gives x 2 = x 2 x 2 dt dt exp( Γ/x t ) cos(x v(t t ) + ṽ 1 dt dt exp( Γ/x t (t t ) cos(x v(t t )) and v 1 = ṽ 1 x 2 dt exp( Γ/γ t ) cos(x v(t t )) + v 1 dt exp( Γ/γ t )(t t ) cos(x v(t t )) where x 2, ṽ 1 denote x 2 and v 2, expressed in terms of x and v, and x 4 = x 4, v 3 = ṽ 3 to the same order. Proceeding in this way we get about a dozen terms of order ( 1 Γ )3 and ( 1 Γ )5. The 3rd-order terms involve the product of two sine or cosine functions equations, e.g.: dt x 2 dt exp( γt ) cos(x v(t t )) dt exp(γt ) sin(x v(t t )) dt exp( γt ) cos(x v(t t ). is
16 16 We are interested in the energy transfer, 2π 2π E sin(x)δvdx and for the above terms sinx sin(x v(t t )) cos(t v(t t ))dx =. This is true for all δṽ terms of 3rd order. Only the 1st- and 5th-order terms remain. The 5th-order terms can be evaluated in a straightforward manner. To see this, consider the term: (3) (4) δ v 5 = dt exp( Γt ) dt dt (3) exp( Γt (3) ) dt (4) dt (5) exp( Γt (5) ) sin ( x v(t t (5)) cos ( x v(t t (3)) cos ( x v(t t ) ). Multiplying this by sin(x) and integrating over x the trigonometric terms gives π { [ cos v(t + t t) (3) t (5)] + cos [ v(t t + t) (3) t (5)] + cos [ v(t t t (3) + t (5)]}. 4 The remaining integrals are straightforward; however, there are a large numbers of terms. These, however, can be simply handled by the use of Mathematica. A typical term is e itv π (2v 5 2iv 4 Γ v 3 Γ 2 3iv 2 3iv 2 Γ 3 + vγ 4 +3iΓ 5 ) 16(iv Γ) 3 (v iγ) 4 (v 3iΓ)Γ 2 which has a strong resonance of v = with a half-width of Γ. These can also be evaluated with the use of Mathematica and the result for δ v 5 is 3π 2 exp( 3γt)+π 2 exp( γt)( 3+6γt 6(γt) 2 +4(γt) 3 ) 96Γ 4. Here we see that when integrated over v, the term, which is of order ( 1 Γ )5 is lowered to the order ( 1 Γ )4. The numerator contains only powers of exp[ γt] and of γt. This is true of all such terms. Evaluating and adding all of the 5th-order terms leads to a factor ( ( γt 51γ 2 t γ 3 t 3 π exp( γt) + exp( 2γt)( γt +96γ2 t γ 3 t 3 ) 768Γ 4 768Γ 4 which is to be compared with the 1st-order result, π exp( γt).
17 17 [1] L. Landau, J. Phys. 45 (1946). [2] T. O Neil, Phys. Fluids 8, 2255 (1965). [3] J. Dawson, Phys. Fluids 4, 869 (1961). [4] F. Chen, Introduction to Plasma Physics and Controlled Fusion (Plenum Press, 1984), p [5] G. Schmidt, Physics of High Temperature Plasmas (Academic Press, 1966), p [6] N. Krall and A. Trivelpiece, Principles of Plasma Physics (San Francisco Press, 1986), p [7] R. D. Hazeltine and F. Waelbroec, The Framewor of Plasma Physics (Persus Boos, 1998), p [8] J. D. Jacson, J. Nucl. Energy 1, 171 (196). [9] V. D. Shafranov, Reviews of Plasma Physics, ed. M. A. Leontovich (Consultants Bureau, 1967), Vol. 3, p. 42. [1] W. E. Drummond, and D. Pines, Nucl. Fusion (1962); Suppl. Part 3, p. 149 (1962). A. Vedenov, E. Velihov, and R. E. Sagdeev, Nucl. Fusion 1, 82 (1961). [11] J. H. Malmberg, C. B. Wharton, and W. E. Drummond, (International Atomic Energy Agency Conference, Culham, 1965), Vol. 1, p [12] C. Roberson, K. W. Gentle, and P. Nielson, Phys. Rev. Lett. 26, 226 (1971); C. Roberson and K. W. Gentle, Phys. Fluids 14, 2962 (1971).
18 18 FIGURE CAPTIONS FIG. 1. Relative power transfer in the resonant region as a function of v/γ for γt =.1,.5, 1. FIG. 2. (a)-(b) Contours for evaluation of the integrals leading to Eqs. (16) and (17).
19 γ t= γ t=.5 γ t= Fig. 1 u/γ
20 2
21 21
Non-Linear Plasma Wave Decay to Longer Wavelength
 Non-Linear Plasma Wave Decay to Longer Wavelength F. Anderegg 1, a), M. Affolter 1, A. Ashourvan 1, D.H.E. Dubin 1, F. Valentini 2 and C.F. Driscoll 1 1 University of California San Diego Physics Department
Non-Linear Plasma Wave Decay to Longer Wavelength F. Anderegg 1, a), M. Affolter 1, A. Ashourvan 1, D.H.E. Dubin 1, F. Valentini 2 and C.F. Driscoll 1 1 University of California San Diego Physics Department
4. Complex Oscillations
 4. Complex Oscillations The most common use of complex numbers in physics is for analyzing oscillations and waves. We will illustrate this with a simple but crucially important model, the damped harmonic
4. Complex Oscillations The most common use of complex numbers in physics is for analyzing oscillations and waves. We will illustrate this with a simple but crucially important model, the damped harmonic
Influence of Generalized (r, q) Distribution Function on Electrostatic Waves
 Commun. Theor. Phys. (Beijing, China) 45 (2006) pp. 550 554 c International Academic Publishers Vol. 45, No. 3, March 15, 2006 Influence of Generalized (r, q) istribution Function on Electrostatic Waves
Commun. Theor. Phys. (Beijing, China) 45 (2006) pp. 550 554 c International Academic Publishers Vol. 45, No. 3, March 15, 2006 Influence of Generalized (r, q) istribution Function on Electrostatic Waves
Landau damping in space plasmas with generalized r, q distribution function
 PHYSICS OF PLASMAS 12, 122902 2005 Landau damping in space plasmas with generalized r, q distribution function M. N. S. Qureshi Key Laboratory of Space Weather, CSSAR, Chinese Academy of Sciences, Beijing
PHYSICS OF PLASMAS 12, 122902 2005 Landau damping in space plasmas with generalized r, q distribution function M. N. S. Qureshi Key Laboratory of Space Weather, CSSAR, Chinese Academy of Sciences, Beijing
Chapter 1. Harmonic Oscillator. 1.1 Energy Analysis
 Chapter 1 Harmonic Oscillator Figure 1.1 illustrates the prototypical harmonic oscillator, the mass-spring system. A mass is attached to one end of a spring. The other end of the spring is attached to
Chapter 1 Harmonic Oscillator Figure 1.1 illustrates the prototypical harmonic oscillator, the mass-spring system. A mass is attached to one end of a spring. The other end of the spring is attached to
Lecture 4: Oscillators to Waves
 Matthew Schwartz Lecture 4: Oscillators to Waves Review two masses Last time we studied how two coupled masses on springs move If we take κ=k for simplicity, the two normal modes correspond to ( ) ( )
Matthew Schwartz Lecture 4: Oscillators to Waves Review two masses Last time we studied how two coupled masses on springs move If we take κ=k for simplicity, the two normal modes correspond to ( ) ( )
Lectures on basic plasma physics: Kinetic approach
 Lectures on basic plasma physics: Kinetic approach Department of applied physics, Aalto University April 30, 2014 Motivation Layout 1 Motivation 2 Boltzmann equation (a nasty bastard) 3 Vlasov equation
Lectures on basic plasma physics: Kinetic approach Department of applied physics, Aalto University April 30, 2014 Motivation Layout 1 Motivation 2 Boltzmann equation (a nasty bastard) 3 Vlasov equation
Fourier transforms, Generalised functions and Greens functions
 Fourier transforms, Generalised functions and Greens functions T. Johnson 2015-01-23 Electromagnetic Processes In Dispersive Media, Lecture 2 - T. Johnson 1 Motivation A big part of this course concerns
Fourier transforms, Generalised functions and Greens functions T. Johnson 2015-01-23 Electromagnetic Processes In Dispersive Media, Lecture 2 - T. Johnson 1 Motivation A big part of this course concerns
Fundamentals of wave kinetic theory
 Fundamentals of wave kinetic theory Introduction to the subject Perturbation theory of electrostatic fluctuations Landau damping - mathematics Physics of Landau damping Unmagnetized plasma waves The plasma
Fundamentals of wave kinetic theory Introduction to the subject Perturbation theory of electrostatic fluctuations Landau damping - mathematics Physics of Landau damping Unmagnetized plasma waves The plasma
Damped harmonic motion
 Damped harmonic motion March 3, 016 Harmonic motion is studied in the presence of a damping force proportional to the velocity. The complex method is introduced, and the different cases of under-damping,
Damped harmonic motion March 3, 016 Harmonic motion is studied in the presence of a damping force proportional to the velocity. The complex method is introduced, and the different cases of under-damping,
Lecture XXVI. Morris Swartz Dept. of Physics and Astronomy Johns Hopkins University November 5, 2003
 Lecture XXVI Morris Swartz Dept. of Physics and Astronomy Johns Hopins University morris@jhu.edu November 5, 2003 Lecture XXVI: Oscillations Oscillations are periodic motions. There are many examples of
Lecture XXVI Morris Swartz Dept. of Physics and Astronomy Johns Hopins University morris@jhu.edu November 5, 2003 Lecture XXVI: Oscillations Oscillations are periodic motions. There are many examples of
The dynamics of small particles whose size is roughly 1 µmt or. smaller, in a fluid at room temperature, is extremely erratic, and is
 1 I. BROWNIAN MOTION The dynamics of small particles whose size is roughly 1 µmt or smaller, in a fluid at room temperature, is extremely erratic, and is called Brownian motion. The velocity of such particles
1 I. BROWNIAN MOTION The dynamics of small particles whose size is roughly 1 µmt or smaller, in a fluid at room temperature, is extremely erratic, and is called Brownian motion. The velocity of such particles
Plasma heating in stellarators at the fundamental ion cyclotron frequency
 PHYSICS OF PLASMAS VOLUME 7, NUMBER FEBRUARY 000 Plasma heating in stellarators at the fundamental ion cyclotron frequency V. A. Svidzinski and D. G. Swanson Department of Physics, Auburn University, Auburn,
PHYSICS OF PLASMAS VOLUME 7, NUMBER FEBRUARY 000 Plasma heating in stellarators at the fundamental ion cyclotron frequency V. A. Svidzinski and D. G. Swanson Department of Physics, Auburn University, Auburn,
Observations on the ponderomotive force
 Observations on the ponderomotive force D.A. Burton a, R.A. Cairns b, B. Ersfeld c, A. Noble c, S. Yoffe c, and D.A. Jaroszynski c a University of Lancaster, Physics Department, Lancaster LA1 4YB, UK b
Observations on the ponderomotive force D.A. Burton a, R.A. Cairns b, B. Ersfeld c, A. Noble c, S. Yoffe c, and D.A. Jaroszynski c a University of Lancaster, Physics Department, Lancaster LA1 4YB, UK b
Experimental observations of nonlinear effects in waves in a nonneutral plasma
 Experimental observations of nonlinear effects in waves in a nonneutral plasma Grant W. Hart, Ross L. Spencer, and Bryan G. Peterson Citation: AIP Conference Proceedings 498, 182 (1999); doi: 10.1063/1.1302118
Experimental observations of nonlinear effects in waves in a nonneutral plasma Grant W. Hart, Ross L. Spencer, and Bryan G. Peterson Citation: AIP Conference Proceedings 498, 182 (1999); doi: 10.1063/1.1302118
2.3 Damping, phases and all that
 2.3. DAMPING, PHASES AND ALL THAT 107 2.3 Damping, phases and all that If we imagine taking our idealized mass on a spring and dunking it in water or, more dramatically, in molasses), then there will be
2.3. DAMPING, PHASES AND ALL THAT 107 2.3 Damping, phases and all that If we imagine taking our idealized mass on a spring and dunking it in water or, more dramatically, in molasses), then there will be
13.1 Ion Acoustic Soliton and Shock Wave
 13 Nonlinear Waves In linear theory, the wave amplitude is assumed to be sufficiently small to ignore contributions of terms of second order and higher (ie, nonlinear terms) in wave amplitude In such a
13 Nonlinear Waves In linear theory, the wave amplitude is assumed to be sufficiently small to ignore contributions of terms of second order and higher (ie, nonlinear terms) in wave amplitude In such a
As is well known, the general solution of the linearized equations for plasma oscillations1 >
 SOVIET PHYSICS JETP VOLUME 24, NUMBER 3 MARCH, 1967 "SINGULAR" SOLUTIONS OF THE EQUATIONS FOR PLASMA OSCILLATIONS V. I. KARPMAN Novosibirs State University Submitted to JETP editor April 7, 1966 J. Exptl.
SOVIET PHYSICS JETP VOLUME 24, NUMBER 3 MARCH, 1967 "SINGULAR" SOLUTIONS OF THE EQUATIONS FOR PLASMA OSCILLATIONS V. I. KARPMAN Novosibirs State University Submitted to JETP editor April 7, 1966 J. Exptl.
1 (2n)! (-1)n (θ) 2n
 Complex Numbers and Algebra The real numbers are complete for the operations addition, subtraction, multiplication, and division, or more suggestively, for the operations of addition and multiplication
Complex Numbers and Algebra The real numbers are complete for the operations addition, subtraction, multiplication, and division, or more suggestively, for the operations of addition and multiplication
Boundary. DIFFERENTIAL EQUATIONS with Fourier Series and. Value Problems APPLIED PARTIAL. Fifth Edition. Richard Haberman PEARSON
 APPLIED PARTIAL DIFFERENTIAL EQUATIONS with Fourier Series and Boundary Value Problems Fifth Edition Richard Haberman Southern Methodist University PEARSON Boston Columbus Indianapolis New York San Francisco
APPLIED PARTIAL DIFFERENTIAL EQUATIONS with Fourier Series and Boundary Value Problems Fifth Edition Richard Haberman Southern Methodist University PEARSON Boston Columbus Indianapolis New York San Francisco
Report submitted to Prof. P. Shipman for Math 540, Fall 2009
 Dynamics at the Horsetooth Volume 1, 009. Three-Wave Interactions of Spin Waves Aaron Hagerstrom Department of Physics Colorado State University aaronhag@rams.colostate.edu Report submitted to Prof. P.
Dynamics at the Horsetooth Volume 1, 009. Three-Wave Interactions of Spin Waves Aaron Hagerstrom Department of Physics Colorado State University aaronhag@rams.colostate.edu Report submitted to Prof. P.
= k, (2) p = h λ. x o = f1/2 o a. +vt (4)
 Traveling Functions, Traveling Waves, and the Uncertainty Principle R.M. Suter Department of Physics, Carnegie Mellon University Experimental observations have indicated that all quanta have a wave-like
Traveling Functions, Traveling Waves, and the Uncertainty Principle R.M. Suter Department of Physics, Carnegie Mellon University Experimental observations have indicated that all quanta have a wave-like
Superposition of electromagnetic waves
 Superposition of electromagnetic waves February 9, So far we have looked at properties of monochromatic plane waves. A more complete picture is found by looking at superpositions of many frequencies. Many
Superposition of electromagnetic waves February 9, So far we have looked at properties of monochromatic plane waves. A more complete picture is found by looking at superpositions of many frequencies. Many
AST 553. Plasma Waves and Instabilities. Course Outline. (Dated: December 4, 2018)
 AST 553. Plasma Waves and Instabilities Course Outline (Dated: December 4, 2018) I. INTRODUCTION Basic concepts Waves in plasmas as EM field oscillations Maxwell s equations, Gauss s laws as initial conditions
AST 553. Plasma Waves and Instabilities Course Outline (Dated: December 4, 2018) I. INTRODUCTION Basic concepts Waves in plasmas as EM field oscillations Maxwell s equations, Gauss s laws as initial conditions
A Propagating Wave Packet The Group Velocity
 Lecture 7 A Propagating Wave Pacet The Group Velocity Phys 375 Overview and Motivation: Last time we looed at a solution to the Schrödinger equation (SE) with an initial condition (,) that corresponds
Lecture 7 A Propagating Wave Pacet The Group Velocity Phys 375 Overview and Motivation: Last time we looed at a solution to the Schrödinger equation (SE) with an initial condition (,) that corresponds
Linear and Nonlinear Oscillators (Lecture 2)
 Linear and Nonlinear Oscillators (Lecture 2) January 25, 2016 7/441 Lecture outline A simple model of a linear oscillator lies in the foundation of many physical phenomena in accelerator dynamics. A typical
Linear and Nonlinear Oscillators (Lecture 2) January 25, 2016 7/441 Lecture outline A simple model of a linear oscillator lies in the foundation of many physical phenomena in accelerator dynamics. A typical
Modeling ionization by helicon waves
 Modeling ionization by helicon waves Space Plasma & Plasma Processing Group, Plasma Research Laboratory, Research School of Physical Sciences and Engineering, Australian National University, Australian
Modeling ionization by helicon waves Space Plasma & Plasma Processing Group, Plasma Research Laboratory, Research School of Physical Sciences and Engineering, Australian National University, Australian
Answers to Problem Set Number MIT (Fall 2005).
 Answers to Problem Set Number 6. 18.305 MIT (Fall 2005). D. Margetis and R. Rosales (MIT, Math. Dept., Cambridge, MA 02139). December 12, 2005. Course TA: Nikos Savva, MIT, Dept. of Mathematics, Cambridge,
Answers to Problem Set Number 6. 18.305 MIT (Fall 2005). D. Margetis and R. Rosales (MIT, Math. Dept., Cambridge, MA 02139). December 12, 2005. Course TA: Nikos Savva, MIT, Dept. of Mathematics, Cambridge,
A.1 Introduction & Rant
 Scott Hughes 1 March 004 A.1 Introduction & Rant Massachusetts Institute of Technology Department of Physics 8.0 Spring 004 Supplementary notes: Complex numbers Complex numbers are numbers that consist
Scott Hughes 1 March 004 A.1 Introduction & Rant Massachusetts Institute of Technology Department of Physics 8.0 Spring 004 Supplementary notes: Complex numbers Complex numbers are numbers that consist
PHYSICS OF HOT DENSE PLASMAS
 Chapter 6 PHYSICS OF HOT DENSE PLASMAS 10 26 10 24 Solar Center Electron density (e/cm 3 ) 10 22 10 20 10 18 10 16 10 14 10 12 High pressure arcs Chromosphere Discharge plasmas Solar interior Nd (nω) laserproduced
Chapter 6 PHYSICS OF HOT DENSE PLASMAS 10 26 10 24 Solar Center Electron density (e/cm 3 ) 10 22 10 20 10 18 10 16 10 14 10 12 High pressure arcs Chromosphere Discharge plasmas Solar interior Nd (nω) laserproduced
Transient Phenomena in Quantum Bound States Subjected to a Sudden Perturbation
 Symmetry, Integrability and Geometry: Methods and Applications Vol. (5), Paper 3, 9 pages Transient Phenomena in Quantum Bound States Subjected to a Sudden Perturbation Marcos MOSHINSKY and Emerson SADURNÍ
Symmetry, Integrability and Geometry: Methods and Applications Vol. (5), Paper 3, 9 pages Transient Phenomena in Quantum Bound States Subjected to a Sudden Perturbation Marcos MOSHINSKY and Emerson SADURNÍ
Damped Oscillation Solution
 Lecture 19 (Chapter 7): Energy Damping, s 1 OverDamped Oscillation Solution Damped Oscillation Solution The last case has β 2 ω 2 0 > 0. In this case we define another real frequency ω 2 = β 2 ω 2 0. In
Lecture 19 (Chapter 7): Energy Damping, s 1 OverDamped Oscillation Solution Damped Oscillation Solution The last case has β 2 ω 2 0 > 0. In this case we define another real frequency ω 2 = β 2 ω 2 0. In
2/8/16 Dispersive Media, Lecture 5 - Thomas Johnson 1. Waves in plasmas. T. Johnson
 2/8/16 Dispersive Media, Lecture 5 - Thomas Johnson 1 Waves in plasmas T. Johnson Introduction to plasma physics Magneto-Hydro Dynamics, MHD Plasmas without magnetic fields Cold plasmas Transverse waves
2/8/16 Dispersive Media, Lecture 5 - Thomas Johnson 1 Waves in plasmas T. Johnson Introduction to plasma physics Magneto-Hydro Dynamics, MHD Plasmas without magnetic fields Cold plasmas Transverse waves
Bohr & Wheeler Fission Theory Calculation 4 March 2009
 Bohr & Wheeler Fission Theory Calculation 4 March 9 () Introduction The goal here is to reproduce the calculation of the limiting Z /A against spontaneous fission Z A lim a S. (.) a C as first done by
Bohr & Wheeler Fission Theory Calculation 4 March 9 () Introduction The goal here is to reproduce the calculation of the limiting Z /A against spontaneous fission Z A lim a S. (.) a C as first done by
Tutorial on obtaining Taylor Series Approximations without differentiation
 Tutorial on obtaining Taylor Series Approximations without differentiation Professor Henry Greenside February 2, 2018 1 Overview An important mathematical technique that is used many times in physics,
Tutorial on obtaining Taylor Series Approximations without differentiation Professor Henry Greenside February 2, 2018 1 Overview An important mathematical technique that is used many times in physics,
Dispersive Media, Lecture 7 - Thomas Johnson 1. Waves in plasmas. T. Johnson
 2017-02-14 Dispersive Media, Lecture 7 - Thomas Johnson 1 Waves in plasmas T. Johnson Introduction to plasmas as a coupled system Magneto-Hydro Dynamics, MHD Plasmas without magnetic fields Cold plasmas
2017-02-14 Dispersive Media, Lecture 7 - Thomas Johnson 1 Waves in plasmas T. Johnson Introduction to plasmas as a coupled system Magneto-Hydro Dynamics, MHD Plasmas without magnetic fields Cold plasmas
Lecture 2 Notes, Electromagnetic Theory II Dr. Christopher S. Baird, faculty.uml.edu/cbaird University of Massachusetts Lowell
 Lecture Notes, Electromagnetic Theory II Dr. Christopher S. Baird, faculty.uml.edu/cbaird University of Massachusetts Lowell 1. Dispersion Introduction - An electromagnetic wave with an arbitrary wave-shape
Lecture Notes, Electromagnetic Theory II Dr. Christopher S. Baird, faculty.uml.edu/cbaird University of Massachusetts Lowell 1. Dispersion Introduction - An electromagnetic wave with an arbitrary wave-shape
kg meter ii) Note the dimensions of ρ τ are kg 2 velocity 2 meter = 1 sec 2 We will interpret this velocity in upcoming slides.
 II. Generalizing the 1-dimensional wave equation First generalize the notation. i) "q" has meant transverse deflection of the string. Replace q Ψ, where Ψ may indicate other properties of the medium that
II. Generalizing the 1-dimensional wave equation First generalize the notation. i) "q" has meant transverse deflection of the string. Replace q Ψ, where Ψ may indicate other properties of the medium that
Mathematical Modeling and response analysis of mechanical systems are the subjects of this chapter.
 Chapter 3 Mechanical Systems A. Bazoune 3.1 INRODUCION Mathematical Modeling and response analysis of mechanical systems are the subjects of this chapter. 3. MECHANICAL ELEMENS Any mechanical system consists
Chapter 3 Mechanical Systems A. Bazoune 3.1 INRODUCION Mathematical Modeling and response analysis of mechanical systems are the subjects of this chapter. 3. MECHANICAL ELEMENS Any mechanical system consists
Computational Methods in Plasma Physics
 Computational Methods in Plasma Physics Richard Fitzpatrick Institute for Fusion Studies University of Texas at Austin Purpose of Talk Describe use of numerical methods to solve simple problem in plasma
Computational Methods in Plasma Physics Richard Fitzpatrick Institute for Fusion Studies University of Texas at Austin Purpose of Talk Describe use of numerical methods to solve simple problem in plasma
dx n a 1(x) dy
 HIGHER ORDER DIFFERENTIAL EQUATIONS Theory of linear equations Initial-value and boundary-value problem nth-order initial value problem is Solve: a n (x) dn y dx n + a n 1(x) dn 1 y dx n 1 +... + a 1(x)
HIGHER ORDER DIFFERENTIAL EQUATIONS Theory of linear equations Initial-value and boundary-value problem nth-order initial value problem is Solve: a n (x) dn y dx n + a n 1(x) dn 1 y dx n 1 +... + a 1(x)
LINEAR RESPONSE THEORY
 MIT Department of Chemistry 5.74, Spring 5: Introductory Quantum Mechanics II Instructor: Professor Andrei Tokmakoff p. 8 LINEAR RESPONSE THEORY We have statistically described the time-dependent behavior
MIT Department of Chemistry 5.74, Spring 5: Introductory Quantum Mechanics II Instructor: Professor Andrei Tokmakoff p. 8 LINEAR RESPONSE THEORY We have statistically described the time-dependent behavior
2.3 Oscillation. The harmonic oscillator equation is the differential equation. d 2 y dt 2 r y (r > 0). Its solutions have the form
 2. Oscillation So far, we have used differential equations to describe functions that grow or decay over time. The next most common behavior for a function is to oscillate, meaning that it increases and
2. Oscillation So far, we have used differential equations to describe functions that grow or decay over time. The next most common behavior for a function is to oscillate, meaning that it increases and
Impurity problem, relation to doping, densities of state
 Impurity problem, relation to doping, densities of state Sohrab Ismail-Beigi June 8, 2015 The basic motivation is to see what happens when we have a dopant/impurity in a metallic system where the Fermi
Impurity problem, relation to doping, densities of state Sohrab Ismail-Beigi June 8, 2015 The basic motivation is to see what happens when we have a dopant/impurity in a metallic system where the Fermi
How many initial conditions are required to fully determine the general solution to a 2nd order linear differential equation?
 How many initial conditions are required to fully determine the general solution to a 2nd order linear differential equation? (A) 0 (B) 1 (C) 2 (D) more than 2 (E) it depends or don t know How many of
How many initial conditions are required to fully determine the general solution to a 2nd order linear differential equation? (A) 0 (B) 1 (C) 2 (D) more than 2 (E) it depends or don t know How many of
Multiple scale methods
 Multiple scale methods G. Pedersen MEK 3100/4100, Spring 2006 March 13, 2006 1 Background Many physical problems involve more than one temporal or spatial scale. One important example is the boundary layer
Multiple scale methods G. Pedersen MEK 3100/4100, Spring 2006 March 13, 2006 1 Background Many physical problems involve more than one temporal or spatial scale. One important example is the boundary layer
Time-asymptotic wave propagation in collisionless plasmas
 PHYSICAL EVIEW E 68, 646 3 Time-asymptotic wave propagation in collisionless plasmas Carlo Lancellotti Department of Mathematics, City University of New York CSI, Staten Island, New Yor34, USA J. J. Dorning
PHYSICAL EVIEW E 68, 646 3 Time-asymptotic wave propagation in collisionless plasmas Carlo Lancellotti Department of Mathematics, City University of New York CSI, Staten Island, New Yor34, USA J. J. Dorning
Macroscopic dielectric theory
 Macroscopic dielectric theory Maxwellʼs equations E = 1 c E =4πρ B t B = 4π c J + 1 c B = E t In a medium it is convenient to explicitly introduce induced charges and currents E = 1 B c t D =4πρ H = 4π
Macroscopic dielectric theory Maxwellʼs equations E = 1 c E =4πρ B t B = 4π c J + 1 c B = E t In a medium it is convenient to explicitly introduce induced charges and currents E = 1 B c t D =4πρ H = 4π
1D Wave PDE. Introduction to Partial Differential Equations part of EM, Scalar and Vector Fields module (PHY2064) Richard Sear.
 Introduction to Partial Differential Equations part of EM, Scalar and Vector Fields module (PHY2064) November 12, 2018 Wave equation in one dimension This lecture Wave PDE in 1D Method of Separation of
Introduction to Partial Differential Equations part of EM, Scalar and Vector Fields module (PHY2064) November 12, 2018 Wave equation in one dimension This lecture Wave PDE in 1D Method of Separation of
1) SIMPLE HARMONIC MOTION/OSCILLATIONS
 1) SIMPLE HARMONIC MOTION/OSCILLATIONS 1.1) OSCILLATIONS Introduction: - An event or motion that repeats itself at regular intervals is said to be periodic. Periodicity in Space is the regular appearance
1) SIMPLE HARMONIC MOTION/OSCILLATIONS 1.1) OSCILLATIONS Introduction: - An event or motion that repeats itself at regular intervals is said to be periodic. Periodicity in Space is the regular appearance
Waves in plasma. Denis Gialis
 Waves in plasma Denis Gialis This is a short introduction on waves in a non-relativistic plasma. We will consider a plasma of electrons and protons which is fully ionized, nonrelativistic and homogeneous.
Waves in plasma Denis Gialis This is a short introduction on waves in a non-relativistic plasma. We will consider a plasma of electrons and protons which is fully ionized, nonrelativistic and homogeneous.
Chapter 4. Oscillatory Motion. 4.1 The Important Stuff Simple Harmonic Motion
 Chapter 4 Oscillatory Motion 4.1 The Important Stuff 4.1.1 Simple Harmonic Motion In this chapter we consider systems which have a motion which repeats itself in time, that is, it is periodic. In particular
Chapter 4 Oscillatory Motion 4.1 The Important Stuff 4.1.1 Simple Harmonic Motion In this chapter we consider systems which have a motion which repeats itself in time, that is, it is periodic. In particular
Plasmas as fluids. S.M.Lea. January 2007
 Plasmas as fluids S.M.Lea January 2007 So far we have considered a plasma as a set of non intereacting particles, each following its own path in the electric and magnetic fields. Now we want to consider
Plasmas as fluids S.M.Lea January 2007 So far we have considered a plasma as a set of non intereacting particles, each following its own path in the electric and magnetic fields. Now we want to consider
B2.III Revision notes: quantum physics
 B.III Revision notes: quantum physics Dr D.M.Lucas, TT 0 These notes give a summary of most of the Quantum part of this course, to complement Prof. Ewart s notes on Atomic Structure, and Prof. Hooker s
B.III Revision notes: quantum physics Dr D.M.Lucas, TT 0 These notes give a summary of most of the Quantum part of this course, to complement Prof. Ewart s notes on Atomic Structure, and Prof. Hooker s
Final 09/14/2017. Notes and electronic aids are not allowed. You must be seated in your assigned row for your exam to be valid.
 Final 09/4/207 Name: Problems -5 are each worth 8 points. Problem 6 is a bonus for up to 4 points. So a full score is 40 points and the max score is 44 points. The exam has 6 pages; make sure you have
Final 09/4/207 Name: Problems -5 are each worth 8 points. Problem 6 is a bonus for up to 4 points. So a full score is 40 points and the max score is 44 points. The exam has 6 pages; make sure you have
Notes on the Periodically Forced Harmonic Oscillator
 Notes on the Periodically orced Harmonic Oscillator Warren Weckesser Math 38 - Differential Equations 1 The Periodically orced Harmonic Oscillator. By periodically forced harmonic oscillator, we mean the
Notes on the Periodically orced Harmonic Oscillator Warren Weckesser Math 38 - Differential Equations 1 The Periodically orced Harmonic Oscillator. By periodically forced harmonic oscillator, we mean the
Problem 1: Lagrangians and Conserved Quantities. Consider the following action for a particle of mass m moving in one dimension
 105A Practice Final Solutions March 13, 01 William Kelly Problem 1: Lagrangians and Conserved Quantities Consider the following action for a particle of mass m moving in one dimension S = dtl = mc dt 1
105A Practice Final Solutions March 13, 01 William Kelly Problem 1: Lagrangians and Conserved Quantities Consider the following action for a particle of mass m moving in one dimension S = dtl = mc dt 1
QUANTUM MECHANICS I PHYS 516. Solutions to Problem Set # 5
 QUANTUM MECHANICS I PHYS 56 Solutions to Problem Set # 5. Crossed E and B fields: A hydrogen atom in the N 2 level is subject to crossed electric and magnetic fields. Choose your coordinate axes to make
QUANTUM MECHANICS I PHYS 56 Solutions to Problem Set # 5. Crossed E and B fields: A hydrogen atom in the N 2 level is subject to crossed electric and magnetic fields. Choose your coordinate axes to make
Space Plasma Physics Thomas Wiegelmann, 2012
 Space Plasma Physics Thomas Wiegelmann, 2012 1. Basic Plasma Physics concepts 2. Overview about solar system plasmas Plasma Models 3. Single particle motion, Test particle model 4. Statistic description
Space Plasma Physics Thomas Wiegelmann, 2012 1. Basic Plasma Physics concepts 2. Overview about solar system plasmas Plasma Models 3. Single particle motion, Test particle model 4. Statistic description
nonlinear oscillators. method of averaging
 Physics 4 Spring 7 nonlinear oscillators. method of averaging lecture notes, spring semester 7 http://www.phys.uconn.edu/ rozman/courses/p4_7s/ Last modified: April, 7 Oscillator with nonlinear friction
Physics 4 Spring 7 nonlinear oscillators. method of averaging lecture notes, spring semester 7 http://www.phys.uconn.edu/ rozman/courses/p4_7s/ Last modified: April, 7 Oscillator with nonlinear friction
Final Review Solutions
 Final Review Solutions Jared Pagett November 30, 206 Gassed. Rapid Fire. We assume several things when maing the ideal gas approximation. With inetic molecular theory, we model gas molecules as point particles
Final Review Solutions Jared Pagett November 30, 206 Gassed. Rapid Fire. We assume several things when maing the ideal gas approximation. With inetic molecular theory, we model gas molecules as point particles
MATH 205C: STATIONARY PHASE LEMMA
 MATH 205C: STATIONARY PHASE LEMMA For ω, consider an integral of the form I(ω) = e iωf(x) u(x) dx, where u Cc (R n ) complex valued, with support in a compact set K, and f C (R n ) real valued. Thus, I(ω)
MATH 205C: STATIONARY PHASE LEMMA For ω, consider an integral of the form I(ω) = e iωf(x) u(x) dx, where u Cc (R n ) complex valued, with support in a compact set K, and f C (R n ) real valued. Thus, I(ω)
Atomic cross sections
 Chapter 12 Atomic cross sections The probability that an absorber (atom of a given species in a given excitation state and ionziation level) will interact with an incident photon of wavelength λ is quantified
Chapter 12 Atomic cross sections The probability that an absorber (atom of a given species in a given excitation state and ionziation level) will interact with an incident photon of wavelength λ is quantified
Summer College on Plasma Physics. 30 July - 24 August, The particle-in-cell simulation method: Concept and limitations
 1856-30 2007 Summer College on Plasma Physics 30 July - 24 August, 2007 The particle-in-cell M. E. Dieckmann Institut fuer Theoretische Physik IV, Ruhr-Universitaet, Bochum, Germany The particle-in-cell
1856-30 2007 Summer College on Plasma Physics 30 July - 24 August, 2007 The particle-in-cell M. E. Dieckmann Institut fuer Theoretische Physik IV, Ruhr-Universitaet, Bochum, Germany The particle-in-cell
Problem Set 1 October 30, 2017
 1. e π can be calculated from e x = x n. But that s not a good approximation method. The n! reason is that π is not small compared to 1. If you want O(0.1) accuracy, then the last term you need to include
1. e π can be calculated from e x = x n. But that s not a good approximation method. The n! reason is that π is not small compared to 1. If you want O(0.1) accuracy, then the last term you need to include
Energetic particle modes: from bump on tail to tokamak plasmas
 Energetic particle modes: from bump on tail to tokamak plasmas M. K. Lilley 1 B. N. Breizman 2, S. E. Sharapov 3, S. D. Pinches 3 1 Physics Department, Imperial College London, London, SW7 2AZ, UK 2 IFS,
Energetic particle modes: from bump on tail to tokamak plasmas M. K. Lilley 1 B. N. Breizman 2, S. E. Sharapov 3, S. D. Pinches 3 1 Physics Department, Imperial College London, London, SW7 2AZ, UK 2 IFS,
Gyrokinetic simulations of magnetic fusion plasmas
 Gyrokinetic simulations of magnetic fusion plasmas Tutorial 2 Virginie Grandgirard CEA/DSM/IRFM, Association Euratom-CEA, Cadarache, 13108 St Paul-lez-Durance, France. email: virginie.grandgirard@cea.fr
Gyrokinetic simulations of magnetic fusion plasmas Tutorial 2 Virginie Grandgirard CEA/DSM/IRFM, Association Euratom-CEA, Cadarache, 13108 St Paul-lez-Durance, France. email: virginie.grandgirard@cea.fr
Lecture #8: Quantum Mechanical Harmonic Oscillator
 5.61 Fall, 013 Lecture #8 Page 1 Last time Lecture #8: Quantum Mechanical Harmonic Oscillator Classical Mechanical Harmonic Oscillator * V(x) = 1 kx (leading term in power series expansion of most V(x)
5.61 Fall, 013 Lecture #8 Page 1 Last time Lecture #8: Quantum Mechanical Harmonic Oscillator Classical Mechanical Harmonic Oscillator * V(x) = 1 kx (leading term in power series expansion of most V(x)
Chapter 1. Introduction to Nonlinear Space Plasma Physics
 Chapter 1. Introduction to Nonlinear Space Plasma Physics The goal of this course, Nonlinear Space Plasma Physics, is to explore the formation, evolution, propagation, and characteristics of the large
Chapter 1. Introduction to Nonlinear Space Plasma Physics The goal of this course, Nonlinear Space Plasma Physics, is to explore the formation, evolution, propagation, and characteristics of the large
Chapter 16 Waves in One Dimension
 Chapter 16 Waves in One Dimension Slide 16-1 Reading Quiz 16.05 f = c Slide 16-2 Reading Quiz 16.06 Slide 16-3 Reading Quiz 16.07 Heavier portion looks like a fixed end, pulse is inverted on reflection.
Chapter 16 Waves in One Dimension Slide 16-1 Reading Quiz 16.05 f = c Slide 16-2 Reading Quiz 16.06 Slide 16-3 Reading Quiz 16.07 Heavier portion looks like a fixed end, pulse is inverted on reflection.
KEELE UNIVERSITY PHYSICS/ASTROPHYSICS MODULE PHY OSCILLATIONS AND WAVES PRACTICE EXAM
 KEELE UNIVERSITY PHYSICS/ASTROPHYSICS MODULE PHY-10012 OSCILLATIONS AND WAVES PRACTICE EXAM Candidates should attempt ALL of PARTS A and B, and TWO questions from PART C. PARTS A and B should be answered
KEELE UNIVERSITY PHYSICS/ASTROPHYSICS MODULE PHY-10012 OSCILLATIONS AND WAVES PRACTICE EXAM Candidates should attempt ALL of PARTS A and B, and TWO questions from PART C. PARTS A and B should be answered
Kinetic theory of Jeans instability
 PHYSICAL REVIEW E 69, 066403 (2004) Kinetic theory of Jeans instability S. A. Trigger, 1, * A. I. Ershkovich, 2 G. J. F. van Heijst, 3 and P. P. J. M. Schram 3 1 Joint Institute for High Temperatures,
PHYSICAL REVIEW E 69, 066403 (2004) Kinetic theory of Jeans instability S. A. Trigger, 1, * A. I. Ershkovich, 2 G. J. F. van Heijst, 3 and P. P. J. M. Schram 3 1 Joint Institute for High Temperatures,
MAGNETIC NOZZLE PLASMA EXHAUST SIMULATION FOR THE VASIMR ADVANCED PROPULSION CONCEPT
 MAGNETIC NOZZLE PLASMA EXHAUST SIMULATION FOR THE VASIMR ADVANCED PROPULSION CONCEPT ABSTRACT A. G. Tarditi and J. V. Shebalin Advanced Space Propulsion Laboratory NASA Johnson Space Center Houston, TX
MAGNETIC NOZZLE PLASMA EXHAUST SIMULATION FOR THE VASIMR ADVANCED PROPULSION CONCEPT ABSTRACT A. G. Tarditi and J. V. Shebalin Advanced Space Propulsion Laboratory NASA Johnson Space Center Houston, TX
4. The interaction of light with matter
 4. The interaction of light with matter The propagation of light through chemical materials is described by a wave equation similar to the one that describes light travel in a vacuum (free space). Again,
4. The interaction of light with matter The propagation of light through chemical materials is described by a wave equation similar to the one that describes light travel in a vacuum (free space). Again,
Second harmonic autoresonant control of the lä1 diocotron mode in pure-electron plasmas
 PHYSICAL REVIEW E VOLUME 62, NUMBER 3 SEPTEMBER 2000 Second harmonic autoresonant control of the lä1 diocotron mode in pure-electron plasmas J. Fajans, 1 E. Gilson, 1 and L. Friedland 2 1 Department of
PHYSICAL REVIEW E VOLUME 62, NUMBER 3 SEPTEMBER 2000 Second harmonic autoresonant control of the lä1 diocotron mode in pure-electron plasmas J. Fajans, 1 E. Gilson, 1 and L. Friedland 2 1 Department of
Formation and Long Term Evolution of an Externally Driven Magnetic Island in Rotating Plasmas )
 Formation and Long Term Evolution of an Externally Driven Magnetic Island in Rotating Plasmas ) Yasutomo ISHII and Andrei SMOLYAKOV 1) Japan Atomic Energy Agency, Ibaraki 311-0102, Japan 1) University
Formation and Long Term Evolution of an Externally Driven Magnetic Island in Rotating Plasmas ) Yasutomo ISHII and Andrei SMOLYAKOV 1) Japan Atomic Energy Agency, Ibaraki 311-0102, Japan 1) University
f(x)e ikx dx. (1) f(k)e ikx dk. (2) e ikx dx = 2sinak. k f g(x) = g f(x) = f(s)e iks ds
 Mathematical Methods: Page 15 2 Fourier transforms 2.1 Integral transforms The Fourier transform is studied in this chapter and the Laplace transform in the next. They are both integral transforms that
Mathematical Methods: Page 15 2 Fourier transforms 2.1 Integral transforms The Fourier transform is studied in this chapter and the Laplace transform in the next. They are both integral transforms that
Time dependent perturbation theory 1 D. E. Soper 2 University of Oregon 11 May 2012
 Time dependent perturbation theory D. E. Soper University of Oregon May 0 offer here some background for Chapter 5 of J. J. Sakurai, Modern Quantum Mechanics. The problem Let the hamiltonian for a system
Time dependent perturbation theory D. E. Soper University of Oregon May 0 offer here some background for Chapter 5 of J. J. Sakurai, Modern Quantum Mechanics. The problem Let the hamiltonian for a system
Damped Oscillations *
 OpenStax-CNX module: m58365 1 Damped Oscillations * OpenStax This wor is produced by OpenStax-CNX and licensed under the Creative Commons Attribution License 4.0 By the end of this section, you will be
OpenStax-CNX module: m58365 1 Damped Oscillations * OpenStax This wor is produced by OpenStax-CNX and licensed under the Creative Commons Attribution License 4.0 By the end of this section, you will be
Frequency- and Time-Domain Spectroscopy
 Frequency- and Time-Domain Spectroscopy We just showed that you could characterize a system by taking an absorption spectrum. We select a frequency component using a grating or prism, irradiate the sample,
Frequency- and Time-Domain Spectroscopy We just showed that you could characterize a system by taking an absorption spectrum. We select a frequency component using a grating or prism, irradiate the sample,
= qe cos(kz ωt). ω sin(αt) This is further averaged over the distribution of initial ( ) α + ω. = 2m k P g(α) sin(αt) g(α) = g(0) + αg (0) + α2 2 g +
 6 Landau Damping 61 Physical Picture of Landau Damping Consider a 1-dimensional electrostatic (longitudinal) wave with k E in the absence of magnetic field Taking v = ẑv and E = ẑe cos(kz ωt), the singleparticle
6 Landau Damping 61 Physical Picture of Landau Damping Consider a 1-dimensional electrostatic (longitudinal) wave with k E in the absence of magnetic field Taking v = ẑv and E = ẑe cos(kz ωt), the singleparticle
MIT Weakly Nonlinear Things: Oscillators.
 18.385 MIT Weakly Nonlinear Things: Oscillators. Department of Mathematics Massachusetts Institute of Technology Cambridge, Massachusetts MA 02139 Abstract When nonlinearities are small there are various
18.385 MIT Weakly Nonlinear Things: Oscillators. Department of Mathematics Massachusetts Institute of Technology Cambridge, Massachusetts MA 02139 Abstract When nonlinearities are small there are various
Finite difference modelling, Fourier analysis, and stability
 Finite difference modelling, Fourier analysis, and stability Peter M. Manning and Gary F. Margrave ABSTRACT This paper uses Fourier analysis to present conclusions about stability and dispersion in finite
Finite difference modelling, Fourier analysis, and stability Peter M. Manning and Gary F. Margrave ABSTRACT This paper uses Fourier analysis to present conclusions about stability and dispersion in finite
221B Lecture Notes on Resonances in Classical Mechanics
 1B Lecture Notes on Resonances in Classical Mechanics 1 Harmonic Oscillators Harmonic oscillators appear in many different contexts in classical mechanics. Examples include: spring, pendulum (with a small
1B Lecture Notes on Resonances in Classical Mechanics 1 Harmonic Oscillators Harmonic oscillators appear in many different contexts in classical mechanics. Examples include: spring, pendulum (with a small
APPLIED PARTIM DIFFERENTIAL EQUATIONS with Fourier Series and Boundary Value Problems
 APPLIED PARTIM DIFFERENTIAL EQUATIONS with Fourier Series and Boundary Value Problems Fourth Edition Richard Haberman Department of Mathematics Southern Methodist University PEARSON Prentice Hall PEARSON
APPLIED PARTIM DIFFERENTIAL EQUATIONS with Fourier Series and Boundary Value Problems Fourth Edition Richard Haberman Department of Mathematics Southern Methodist University PEARSON Prentice Hall PEARSON
Waves in plasmas. S.M.Lea
 Waves in plasmas S.M.Lea 17 1 Plasma as an example of a dispersive medium We shall now discuss the propagation of electromagnetic waves through a hydrogen plasm an electrically neutral fluid of protons
Waves in plasmas S.M.Lea 17 1 Plasma as an example of a dispersive medium We shall now discuss the propagation of electromagnetic waves through a hydrogen plasm an electrically neutral fluid of protons
03. Simple Dynamical Systems
 University of Rhode Island DigitalCommons@URI Classical Dynamics Physics Course Materials 2015 03. Simple Dynamical Systems Gerhard Müller University of Rhode Island, gmuller@uri.edu Creative Commons License
University of Rhode Island DigitalCommons@URI Classical Dynamics Physics Course Materials 2015 03. Simple Dynamical Systems Gerhard Müller University of Rhode Island, gmuller@uri.edu Creative Commons License
Perturbation theory for anharmonic oscillations
 Perturbation theory for anharmonic oscillations Lecture notes by Sergei Winitzki June 12, 2006 Contents 1 Introduction 1 2 What is perturbation theory 1 21 A first example 1 22 Limits of applicability
Perturbation theory for anharmonic oscillations Lecture notes by Sergei Winitzki June 12, 2006 Contents 1 Introduction 1 2 What is perturbation theory 1 21 A first example 1 22 Limits of applicability
Academic and Research Staff. Prof. T. H. Dupree Prof. L. M. Lidsky Prof. N. L. Oleson. Graduate Students
 XV. INTERACTION OF LASER RADIATION WITH PLASMAS AND NONADIABATIC MOTION OF PARTICLES IN MAGNETIC FIELDS Academic and Research Staff Prof. T. H. Dupree Prof. L. M. Lidsy Prof. N. L. Oleson Graduate Students
XV. INTERACTION OF LASER RADIATION WITH PLASMAS AND NONADIABATIC MOTION OF PARTICLES IN MAGNETIC FIELDS Academic and Research Staff Prof. T. H. Dupree Prof. L. M. Lidsy Prof. N. L. Oleson Graduate Students
Lab 1: Damped, Driven Harmonic Oscillator
 1 Introduction Lab 1: Damped, Driven Harmonic Oscillator The purpose of this experiment is to study the resonant properties of a driven, damped harmonic oscillator. This type of motion is characteristic
1 Introduction Lab 1: Damped, Driven Harmonic Oscillator The purpose of this experiment is to study the resonant properties of a driven, damped harmonic oscillator. This type of motion is characteristic
Electrodynamics I Final Exam - Part A - Closed Book KSU 2005/12/12 Electro Dynamic
 Electrodynamics I Final Exam - Part A - Closed Book KSU 2005/12/12 Name Electro Dynamic Instructions: Use SI units. Short answers! No derivations here, just state your responses clearly. 1. (2) Write an
Electrodynamics I Final Exam - Part A - Closed Book KSU 2005/12/12 Name Electro Dynamic Instructions: Use SI units. Short answers! No derivations here, just state your responses clearly. 1. (2) Write an
1 Simple Harmonic Oscillator
 Physics 1a Waves Lecture 3 Caltech, 10/09/18 1 Simple Harmonic Oscillator 1.4 General properties of Simple Harmonic Oscillator 1.4.4 Superposition of two independent SHO Suppose we have two SHOs described
Physics 1a Waves Lecture 3 Caltech, 10/09/18 1 Simple Harmonic Oscillator 1.4 General properties of Simple Harmonic Oscillator 1.4.4 Superposition of two independent SHO Suppose we have two SHOs described
UNIVERSITY OF SOUTHAMPTON. A foreign language dictionary (paper version) is permitted provided it contains no notes, additions or annotations.
 UNIVERSITY OF SOUTHAMPTON MATH055W SEMESTER EXAMINATION 03/4 MATHEMATICS FOR ELECTRONIC & ELECTRICAL ENGINEERING Duration: 0 min Solutions Only University approved calculators may be used. A foreign language
UNIVERSITY OF SOUTHAMPTON MATH055W SEMESTER EXAMINATION 03/4 MATHEMATICS FOR ELECTRONIC & ELECTRICAL ENGINEERING Duration: 0 min Solutions Only University approved calculators may be used. A foreign language
Seminar 6: COUPLED HARMONIC OSCILLATORS
 Seminar 6: COUPLED HARMONIC OSCILLATORS 1. Lagrangian Equations of Motion Let consider a system consisting of two harmonic oscillators that are coupled together. As a model, we will use two particles attached
Seminar 6: COUPLED HARMONIC OSCILLATORS 1. Lagrangian Equations of Motion Let consider a system consisting of two harmonic oscillators that are coupled together. As a model, we will use two particles attached
Lab 1: damped, driven harmonic oscillator
 Lab 1: damped, driven harmonic oscillator 1 Introduction The purpose of this experiment is to study the resonant properties of a driven, damped harmonic oscillator. This type of motion is characteristic
Lab 1: damped, driven harmonic oscillator 1 Introduction The purpose of this experiment is to study the resonant properties of a driven, damped harmonic oscillator. This type of motion is characteristic
Light in Matter (Hecht Ch. 3)
 Phys 531 Lecture 3 9 September 2004 Light in Matter (Hecht Ch. 3) Last time, talked about light in vacuum: Maxwell equations wave equation Light = EM wave 1 Today: What happens inside material? typical
Phys 531 Lecture 3 9 September 2004 Light in Matter (Hecht Ch. 3) Last time, talked about light in vacuum: Maxwell equations wave equation Light = EM wave 1 Today: What happens inside material? typical
Solution for Problem Set 21
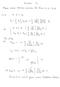 Solution for Problem Set 21 (compiled by Nate Bode April 24, 2009 A 21.1 Non-resonant Particle Energy in Wave [by Keith Matthews adapted from Chris Hirata] The rate of change of the non-resonant electron
Solution for Problem Set 21 (compiled by Nate Bode April 24, 2009 A 21.1 Non-resonant Particle Energy in Wave [by Keith Matthews adapted from Chris Hirata] The rate of change of the non-resonant electron
Lecture 4. Diffusing photons and superradiance in cold gases
 Lecture 4 Diffusing photons and superradiance in cold gases Model of disorder-elastic mean free path and group velocity. Dicke states- Super- and sub-radiance. Scattering properties of Dicke states. Multiple
Lecture 4 Diffusing photons and superradiance in cold gases Model of disorder-elastic mean free path and group velocity. Dicke states- Super- and sub-radiance. Scattering properties of Dicke states. Multiple
MET 4301 LECTURE SEP17
 ------------------------------------------------------------------------------------------------------------------------------------ Objectives: To review essential mathematics for Meteorological Dynamics
------------------------------------------------------------------------------------------------------------------------------------ Objectives: To review essential mathematics for Meteorological Dynamics
I. Impulse Response and Convolution
 I. Impulse Response and Convolution 1. Impulse response. Imagine a mass m at rest on a frictionless track, then given a sharp kick at time t =. We model the kick as a constant force F applied to the mass
I. Impulse Response and Convolution 1. Impulse response. Imagine a mass m at rest on a frictionless track, then given a sharp kick at time t =. We model the kick as a constant force F applied to the mass
