1 MathematicalPreliminaries
|
|
|
- Alannah Conley
- 5 years ago
- Views:
Transcription
1 1 MathematicalPeliminaies The enomous usefulness of mathematics in the natual sciences is something bodeing on the mysteious. Eugene Wigne ( Intoduction This chapte pesents a collection of mathematical notation, definitions, identities, theoems, and tansfomations that play an impotant ole in the study of electomagnetism. A bief discussion accompanies some of the less familia topics and only a few poofs ae given in detail. Fo moe details and complete poofs, the eade should consult the books and papes listed in ouces, Refeences, and Additional Reading at the end of the chapte. Appendix C at the end of the book summaizes the popeties of Legende polynomials, spheical hamonics, and Bessel functions. 1.2 ectos A vecto is a geometical object chaacteized by a magnitude and diection. 1 Although not necessay, it is convenient to discuss an abitay vecto using its components defined with espect to a given coodinate system. An example is the ight-handed coodinate system with othogonal unit basis vectos (ê 1, ê 2, ê 3 shown in Figue 1.1, whee ê 1 ê 1 = 1 ê 2 ê 2 = 1 ê 3 ê 3 = 1 (1.1 ê 1 ê 2 = 0 ê 2 ê 3 = 0 ê 3 ê 1 = 0 (1.2 ê 1 ê 2 = ê 3 ê 2 ê 3 = ê 1 ê 3 ê 1 = ê 2. (1.3 We expess an abitay vecto in this basis using components k = ê k, A vecto can be decomposed in any coodinate system we please, so = 1 ê ê ê 3. (1.4 3 k ê k = k=1 3 k=1 kê k. (1.5 1 A moe pecise definition of a vecto is given in ection 1.8.
2 2 MATHEMATICAL PRELIMINARIE: DEFINITION, IDENTITIE, AND THEOREM ê 3 ê 1 Figue 1.1: An othonomal set of unit vectos ê 1, ê 2, ê 3. is an abitay vecto. ê 2 z z z y y x (a Cylindical x (b pheical Figue 1.2: Two cuvilinea coodinate systems Catesian Coodinates Ou notation fo Catesian components and unit vectos is = x ˆx + y ŷ + z ẑ. (1.6 In paticula, k always denotes the Catesian components of the position vecto, = x ˆx + yŷ + zẑ. (1.7 It is not obvious geometically (see Example 1.7 in ection 1.8, but the gadient opeato is a vecto with the Catesian epesentation The divegence, cul, and Laplacian opeations ae, espectively, = ( z y y z =ˆx x + ŷ y + ẑ z. (1.8 = x x + y y + z z ˆx + ( x z z x ŷ + (1.9 ( y x x ẑ (1.10 y 2 A = 2 A x A y A z 2. ( Cylindical Coodinates Figue 1.2(a defines cylindical coodinates (ρ,φ,z. Ou notation fo the components and unit vectos in this system is The tansfomation to Catesian coodinates is = ρ ˆρ + φ ˆφ + z ẑ. (1.12 x = ρ cosφ y = ρ sin φ z= z. (1.13
3 1.2 ectos 3 The volume element in cylindical coodinates is d 3 = ρdρdφdz. The unit vectos ( ˆρ, ˆφ, ẑ foma ight-handed othogonal tiad. ẑ is the same as in Catesian coodinates. Othewise, ˆρ = ˆx cosφ + ŷ sin φ ˆx = ˆρ cosφ ˆφ sin φ (1.14 ˆφ = ˆx sin φ + ŷ cosφ ŷ = ˆρ sin φ + ˆφ cosφ. (1.15 The gadient opeato in cylindical coodinates is The divegence, cul, and Laplacian opeations ae, espectively, = [ 1 z ρ φ ] φ ˆρ + z 2 A = 1 ρ pheical Coodinates = ˆρ ρ + ˆφ ρ φ + ẑ z. (1.16 = 1 (ρ ρ + 1 φ ρ ρ ρ φ + z z [ ρ z ] z ˆφ + 1 [ (ρφ ρ ρ ρ ( ρ A ρ ρ (1.17 ] ρ ẑ (1.18 φ + 1 ρ 2 2 A φ A z 2. (1.19 Figue 1.2(b defines spheical coodinates (, θ, φ. Ou notation fo the components and unit vectos in this system is The tansfomation to Catesian coodinates is = ˆ + θ ˆθ + φ ˆφ. (1.20 x = sin θ cos φ y = sin θ sin φ z= cosθ. (1.21 The volume element in spheical coodinates is d 3 = 2 sinθddθdφ. The unit vectos ae elated by ˆ = ˆx sin θ cosφ + ŷ sin θ sin φ + ẑ cosθ ˆx = ˆ sin θ cosφ + ˆθ cosθ cosφ ˆφ sin φ (1.22 ˆθ = ˆx cosθ cos φ + ŷ cosθ sin φ ẑ sin θ ŷ = ˆ sin θ sin φ + ˆθ cosθ sin φ + ˆφ cosφ (1.23 ˆφ = ˆx sin φ + ŷ cosφ ẑ = ˆ cosθ ˆθ sin θ. (1.24 The gadient opeato in spheical coodinates is =ˆ + ˆθ θ + ˆφ sin θ The divegence, cul, and Laplacian opeations ae, espectively, = 1 ( (sin θ θ + 1 φ 2 sin θ θ sin θ φ = 1 [ (sin θφ ] θ ˆ sin θ θ φ + 1 [ 1 sin θ φ ( ] φ ˆθ + 1 [ (θ 2 A = 1 2 ( 2 A sin θ ( sin θ A θ θ φ. ( ] ˆφ θ (1.26 ( A 2 sin 2 θ φ. (1.28 2
4 4 MATHEMATICAL PRELIMINARIE: DEFINITION, IDENTITIE, AND THEOREM he Einstein ummation Convention Einstein (1916 intoduced the following convention. An index which appeas exactly twice in a single tem of a mathematical expession is implicitly summed ove all possible values fo that index. The ange of this dummy index must be clea fom context and the index cannot be used elsewhee in the same expession fo anothe pupose. In this book, the ange fo a oman index like i is fom 1 to 3, indicating a sum ove the Catesian indices x, y, andz. Thus, in (1.6 and its dot poduct with anothe vecto F ae witten = 3 k ê k k ê k F = k=1 3 k F k k F k. (1.29 In a Catesian basis, the gadient of a scala ϕ and the divegence of a vecto D can be vaiously witten k=1 ϕ = ê k k ϕ = ê k k ϕ = ê k ϕ k (1.30 D = k D k = k D k = D k k. (1.31 If an N N matix C is the poduct of an N M matix A and an M N matix B, C ik = M A ij B jk = A ij B jk. (1.32 j= hekonecke and Levi-Civitàymbols The Konecke delta symbol δ ij and Levi-Cività pemutation symbol ǫ ijk have oman indices i, j,and k which take on the Catesian coodinate values x, y, andz. They ae defined by and δ ij = { 1 i = j, 0 i j, 1 ijk = xyz yzx zxy, ǫ ijk = 1 ijk = xzy yxz zyx, 0 othewise. ome useful Konecke delta and Levi-Cività symbol identities ae (1.33 (1.34 ê i ê j = δ ij δ kk = 3 (1.35 k j = δ jk k δ kj = j (1.36 [ F] i = ǫ ijk j F k [ A] i = ǫ ijk j A k (1.37 δ ij ǫ ijk = 0 ǫ ijk ǫ ijk = 6. (1.38 A paticulaly useful identity involves a single sum ove the epeated index i: ǫ ijk ǫ ist = δ js δ kt δ jt δ ks. (1.39 A genealization of (1.39 when thee ae no epeated indices to sum ove is the deteminant δ km δ im δ lm ǫ kil ǫ mpq = δ kp δ ip δ lp δ kq δ iq δ lq. (1.40
5 1.2 ectos 5 Finally, let C bea3 3 matix with matix elements C 11,C 12, etc. The deteminant of C can be witten using eithe an expansion by columns, o an expansion by ows, A closely elated identity we will use in ection is det C = ǫ ijk C i1 C j2 C k3, (1.41 det C = ǫ ijk C 1i C 2j C 3k. (1.42 ǫ lmn det C = ǫ ijk C li C mj C nk. ( ecto Identities in Catesian Components The Konecke and Levi-Cività symbols simplify the poof of vecto identities. An example is Using the left side of (1.37, the ith component of a (b cis a (b c = b(a c c(a b. (1.44 [a (b c] i = ǫ ijk a j (b c k = ǫ ijk a j ǫ klm b l c m. (1.45 The definition (1.34 tells us that ǫ ijk = ǫ kij. Theefoe, the identity (1.39 gives [a (b c] i = ǫ kij ǫ klm a j b l c m = (δ il δ jm δ im δ jl a j b l c m = a j b i c j a j b j c i. (1.46 The final esult, b i (a c c i (a b, is indeed the ith component of the ight side of (1.44. The same method of poof applies to gadient-, divegence-, and cul-type vecto identities because the components of the opeato tansfom like the components of a vecto [see above (1.8]. The next thee examples illustate this point. Example 1.1 Pove that ( g = 0. olution: Begin with ( g = i ǫ ijk j g k = 1 2 i j g k ǫ ijk i j g k ǫ ijk. Exchanging the dummy indices i and j in the last tem gives g = 1 2 i j g k ǫ ijk j i g k ǫ jik = 1 2 {ǫ ijk + ǫ jik } i j g k = 0. The final zeo comes fom ǫ ijk = ǫ jik, which is a consequence of (1.34. Example 1.2 Pove that (A B = A B (A B + (B A B A. olution: Focus on the ith Catesian component and use the left side of (1.37 to wite [ (A B] i = ǫ ijk j (A B k = ǫ ijk ǫ kst j (A s B t. The cyclic popeties of the Levi-Cività symbol and the identity (1.39 give [ (A B] i = ǫ kij ǫ kst j (A s B t = (δ is δ jt δ it δ js (A s j B t + B t j A s. Theefoe, [ (A B] i = A i j B j A j j B i + B j j A i B i j A j. This poves the identity because the choice of i is abitay.
6 6 MATHEMATICAL PRELIMINARIE: DEFINITION, IDENTITIE, AND THEOREM Example 1.3 Pove the double-cul identity ( A = ( A 2 A. olution: Conside the ith Catesian component. The identity on the left side of (1.37 and the invaiance of the Levi-Cività symbol with espect to cyclic pemutations of its indices give [ ( A] i = ǫ ijk j ( A k = ǫ ijk j ǫ kpq p A q = ǫ kij ǫ kpq j p A q. Now apply the identity (1.39 to get [ ( A] i = (δ ip δ jq δ iq δ jp j p A q = i j A j j j A i = i ( A 2 A i. The double-cul identity follows because 2 A = 2 (A x ˆx + A y ŷ + A z ẑ = ˆx 2 A x + ŷ 2 A y + ẑ 2 A z ecto Identities in Cuvilinea Components Cae is needed to intepet the vecto identities in Examples 1.2 and 1.3 when the vectos in question ae decomposed into spheical o cylindical components such as A = A ˆ + A θ ˆθ + A φ ˆφ. This can be seen fom Example 1.3 whee the final step is no longe valid because ˆ, ˆθ, and ˆφ ae not constant vectos. In othe wods, 2 A = (A ˆ + A θ ˆθ + A φ ˆφ ˆ 2 A + ˆθ 2 A θ + ˆφ 2 A φ. (1.47 One way to poceed is to wok out the components of (A ˆ, (A θ ˆθ, and (A φ ˆφ. Altenatively, we may simply define the meaning of the opeation 2 A when A is expessed using cuvilinea components. Fo example, [ 2 A] φ φ ( A [ ( A] φ, (1.48 and similaly fo ( 2 A and ( 2 A θ. Exactly the same issue aises when we examine the last step in Example 1.2, namely [ (A B] i = A i B (A B i + (B A i B i A. (1.49 By constuction, this equation makes sense when i stands fo x, y, oz. It does not make sense if i stands fo, say,, θ, oφ. On the othe hand, the full vecto vesion of the identity is coect as long as we etain the, θ,andφ vaiations of ˆ, ˆθ,and ˆφ. Fo example, (A B = [ A + A θ θ + A φ sin θ φ ] (B ˆ + B θ ˆθ + B φ ˆφ. (1.50 Application 1.1 Two Identities fo L The h = 1 vesion of the quantum mechanical angula momentum opeato, L = i,playsa useful ole in the analysis of classical spheical systems. In this Application, we pove two opeato identities which will appea late in the text: (A L = i 2 + ( i (1 + 1 (B L = (ˆ L + ˆ i L2.
7 1.3 Deivatives 7 Poof of Identity (A: We use (1.37, (1.39, and the cyclic popety of the Levi-Cività symbol to evaluate the kth component of L acting on a scala function φ: [ L] k φ = i[ ( ] k φ = iǫ mkl ǫ mst l s t φ = i[ l k l φ l l k φ]. (1.51 Because l l = 3and l k = δ lk, Howeve, Lφ = [ i 2 + i2 +i( ]φ. (1.52 k [ l l φ] = k φ + l l k φ, (1.53 which is the kth component of ( φ = φ + ( φ. ubstituting the latte into (1.53 gives Identity (A. Poof of Identity (B: We decompose the gadient opeato into its adial and angula pieces: =ˆ(ˆ ˆ (ˆ = ˆ i ˆ L. (1.54 Equation (1.54 and the Levi-Cività fomalism poduce the intemediate esult L = (ˆ L i (ˆ L L = (ˆ L i [ˆk LL k ˆL 2]. (1.55 Howeve, the angula momentum opeato obeys commutation elations which can be summaized as L L = il. Theefoe, ˆ (L L = iˆ L ˆ k LL k ˆ k L k L = iˆ L. (1.56 On the othe hand, k L k = 0 because L is pependicula to both and. Theefoe, ˆ k LL k = iˆ L, which we can substitute into (1.55. The esult is identity (B because, fo any scala function φ, [ ] 1 (φ = φ + φ. ( Deivatives Functions of and The position vecto is = ˆ with = x 2 + y 2 + z 2.Iff ( is a scala function and f ( = df/d, = ˆ = 0 (1.58 f = f ˆ 2 f = (2 f 2 (1.59 (f = (3 f 2 (f = 0. (1.60 imilaly, if g( is a vecto function and c is a constant vecto, g = g ˆ g = ˆ g (1.61 (g = g ( g = g (1.62
8 8 MATHEMATICAL PRELIMINARIE: DEFINITION, IDENTITIE, AND THEOREM ( g = g + ( g (g = 2g + g ( g (g = 0 (1.63 (c = c. ( Functions of Let R = = (x x ˆx + (y y ŷ + (z z ẑ. Then, Moeove, because f (R = f (R ˆR g(r = g (R ˆR g(r = ˆR g (R. (1.65 =ˆx x + ŷ y + ẑ z it it staightfowad to confim that heconvective Deivative and = ˆx x + ŷ y + ẑ z, (1.66 f (R = f (R. (1.67 Let φ(,t be a scala function of space and time. An obseve who epeatedly samples the value of φ at a fixed point in space,, ecods the time ate of change of φ as the patial deivative φ/t. Howeve, the same obseve who epeatedly samples φ along a tajectoy in space (t that moves with velocity υ(t = ṙ(t ecods the time ate of change of φ as the convective deivative, dφ = φ t + dx φ x + dy φ y + dz φ z = φ + (υ φ. (1.68 t Fo a vecto function g(,t, the coesponding convective deivative is Taylo s heoem dg = g t + (υ g. (1.69 Taylo s theoem in one dimension is f (x = f (a + (x a df dx + 1 x=a 2! (x d2 f a2 dx 2 +. (1.70 x=a An altenative fom follows fom (1.70 if x x + ǫ and a x: Equivalently, f (x + ǫ = [ f (x + ǫ = f (x + ǫ df dx + 1 d2 f 2! ǫ2 +. (1.71 dx2 1 + ǫ d dx + 1 2! This genealizes fo a function of thee vaiables to ( f (x + ǫ x,y+ ǫ y,z+ ǫ z = exp ǫ x x o f ( + ǫ = exp (ǫ f( = ( ǫ d 2 ( + ] f (x = exp ǫ d f (x. (1.72 dx dx exp ( ( ǫ y exp ǫ z f (x,y,z, (1.73 y z [ 1 + ǫ + 1 ] 2! (ǫ 2 + f (. (1.74
9 1.4 Integals Integals Jacobian Deteminant The deteminant of the Jacobian matix J elates volume elements when changing vaiables in an integal. Fo example, suppose x and y ae N-dimensional space vectos in two diffeent coodinate systems, e.g., Catesian and spheical. The volume elements d N x and d N y ae elated by x 1 x 1 x 1 y 1 y 2 y N d N x = J(x, y d N y = d N y. (1.75 x N x N x N y 1 y 2 y N hedivegenceheoem Let F( be a vecto function defined in a volume enclosed by a suface with an outwad nomal ˆn.Ifd = dˆn, the divegence theoem is d 3 F = d F. (1.76 pecial choices fo the vecto function F( poduce vaious integal identities based on (1.76. Fo example, if c is an abitay constant vecto, the eade can confim that the choices F( = cψ(and F( = A( c substituted into (1.76 espectively yield d 3 ψ = dψ ( Geen s Identities d 3 A = d A. (1.78 The choice F( = φ( ψ( in (1.76 leads to Geen s fist identity, d 3 [φ 2 ψ + φ ψ] = d φ ψ. (1.79 Witing (1.79 with the oles of φ and ψ exchanged and subtacting that equation fom (1.79 itself gives Geen s second identity, d 3 [φ 2 ψ ψ 2 φ] = d [φ ψ ψ φ]. (1.80 The choice F = P Qin (1.76 and the identity (A B = B A A Bpoduces a vecto analog of Geen s fist identity: d 3 [ P Q P Q] = d (P Q. (1.81
10 10 MATHEMATICAL PRELIMINARIE: DEFINITION, IDENTITIE, AND THEOREM Witing (1.81 with P and Q intechanged and subtacting that equation fom (1.81 gives a vecto analog of Geen s second identity: d 3 [Q P P Q] = d [P Q Q P]. ( tokes heoem tokes theoem applies to a vecto function F( definedonanopensuface bounded by a closed cuve C. Ifdl is a line element of C, d F = dl F. (1.83 The cuve C in (1.83 is tavesed in the diection given by the ight-hand ule when the thumb points in the diection of d. As with the divegence theoem, vaiations of (1.83 follow fom the choices F = cψ and F = A c: d ψ = dlψ (1.84 C C dl A = C d k A k hetime Deivative ofaflux Integal Leibniz Rule fo the time deivative of a one-dimensional integal is d x 2(t x 1(t dxb(x,t = b(x 2,t dx 2 b(x 1,t dx 1 d( A. ( x 2(t x 1(t dx b t. (1.86 This fomula genealizes to integals ove cicuits, sufaces, and volumes which move though space. Ou teatment of Faaday s law makes use of the time deivative of a suface integal whee the suface (t moves because its individual aea elements move with velocity υ(,t. In that case, d (t d B = (t Poof: We calculate the change in flux fom [ ] δ B d = [ d υ( B (υ B + B ]. (1.87 t δb d + B δ(ˆnd. (1.88 The fist tem on the ight comes fom time vaiations of B. The second tem comes fom time vaiations of the suface. Multiplication of evey tem in (1.88 by 1/δt gives d B B d = d + 1 B δ(ˆnd. (1.89 t δt We can focus on the second tem on the ight-hand side of (1.89 because the fist tem appeas aleady as the last tem in (1.87. Figue 1.3 shows an open suface(t with local nomal ˆn(t which moves and/o distots to the suface (t + δt with local nomal ˆn(t + δt in time δt.
As is natural, our Aerospace Structures will be described in a Euclidean three-dimensional space R 3.
 Appendix A Vecto Algeba As is natual, ou Aeospace Stuctues will be descibed in a Euclidean thee-dimensional space R 3. A.1 Vectos A vecto is used to epesent quantities that have both magnitude and diection.
Appendix A Vecto Algeba As is natual, ou Aeospace Stuctues will be descibed in a Euclidean thee-dimensional space R 3. A.1 Vectos A vecto is used to epesent quantities that have both magnitude and diection.
Appendix A. Appendices. A.1 ɛ ijk and cross products. Vector Operations: δ ij and ɛ ijk
 Appendix A Appendices A1 ɛ and coss poducts A11 Vecto Opeations: δ ij and ɛ These ae some notes on the use of the antisymmetic symbol ɛ fo expessing coss poducts This is an extemely poweful tool fo manipulating
Appendix A Appendices A1 ɛ and coss poducts A11 Vecto Opeations: δ ij and ɛ These ae some notes on the use of the antisymmetic symbol ɛ fo expessing coss poducts This is an extemely poweful tool fo manipulating
3 VECTOR CALCULUS I. 3.1 Divergence and curl of vector fields. 3.2 Important identities
 3 VECTOR CALCULU I 3.1 Divegence and cul of vecto fields Let = ( x, y, z ). eveal popeties of φ fo scala φ wee intoduced in section 1.2. The gadient opeato may also be applied to vecto fields. Let F =
3 VECTOR CALCULU I 3.1 Divegence and cul of vecto fields Let = ( x, y, z ). eveal popeties of φ fo scala φ wee intoduced in section 1.2. The gadient opeato may also be applied to vecto fields. Let F =
(read nabla or del) is defined by, k. (9.7.1*)
 9.7 Gadient of a scala field. Diectional deivative Some of the vecto fields in applications can be obtained fom scala fields. This is vey advantageous because scala fields can be handled moe easily. The
9.7 Gadient of a scala field. Diectional deivative Some of the vecto fields in applications can be obtained fom scala fields. This is vey advantageous because scala fields can be handled moe easily. The
J. N. R E DDY ENERGY PRINCIPLES AND VARIATIONAL METHODS APPLIED MECHANICS
 J. N. E DDY ENEGY PINCIPLES AND VAIATIONAL METHODS IN APPLIED MECHANICS T H I D E DI T IO N JN eddy - 1 MEEN 618: ENEGY AND VAIATIONAL METHODS A EVIEW OF VECTOS AND TENSOS ead: Chapte 2 CONTENTS Physical
J. N. E DDY ENEGY PINCIPLES AND VAIATIONAL METHODS IN APPLIED MECHANICS T H I D E DI T IO N JN eddy - 1 MEEN 618: ENEGY AND VAIATIONAL METHODS A EVIEW OF VECTOS AND TENSOS ead: Chapte 2 CONTENTS Physical
Vector d is a linear vector function of vector d when the following relationships hold:
 Appendix 4 Dyadic Analysis DEFINITION ecto d is a linea vecto function of vecto d when the following elationships hold: d x = a xxd x + a xy d y + a xz d z d y = a yxd x + a yy d y + a yz d z d z = a zxd
Appendix 4 Dyadic Analysis DEFINITION ecto d is a linea vecto function of vecto d when the following elationships hold: d x = a xxd x + a xy d y + a xz d z d y = a yxd x + a yy d y + a yz d z d z = a zxd
PHZ 3113 Fall 2017 Homework #5, Due Friday, October 13
 PHZ 3113 Fall 2017 Homewok #5, Due Fiday, Octobe 13 1. Genealize the poduct ule (fg) = f g +f g to wite the divegence Ö (Ù Ú) of the coss poduct of the vecto fields Ù and Ú in tems of the cul of Ù and
PHZ 3113 Fall 2017 Homewok #5, Due Fiday, Octobe 13 1. Genealize the poduct ule (fg) = f g +f g to wite the divegence Ö (Ù Ú) of the coss poduct of the vecto fields Ù and Ú in tems of the cul of Ù and
Math 124B February 02, 2012
 Math 24B Febuay 02, 202 Vikto Gigoyan 8 Laplace s equation: popeties We have aleady encounteed Laplace s equation in the context of stationay heat conduction and wave phenomena. Recall that in two spatial
Math 24B Febuay 02, 202 Vikto Gigoyan 8 Laplace s equation: popeties We have aleady encounteed Laplace s equation in the context of stationay heat conduction and wave phenomena. Recall that in two spatial
DonnishJournals
 DonnishJounals 041-1189 Donnish Jounal of Educational Reseach and Reviews. Vol 1(1) pp. 01-017 Novembe, 014. http:///dje Copyight 014 Donnish Jounals Oiginal Reseach Pape Vecto Analysis Using MAXIMA Savaş
DonnishJounals 041-1189 Donnish Jounal of Educational Reseach and Reviews. Vol 1(1) pp. 01-017 Novembe, 014. http:///dje Copyight 014 Donnish Jounals Oiginal Reseach Pape Vecto Analysis Using MAXIMA Savaş
Vectors, Vector Calculus, and Coordinate Systems
 Apil 5, 997 A Quick Intoduction to Vectos, Vecto Calculus, and Coodinate Systems David A. Randall Depatment of Atmospheic Science Coloado State Univesity Fot Collins, Coloado 80523. Scalas and vectos Any
Apil 5, 997 A Quick Intoduction to Vectos, Vecto Calculus, and Coodinate Systems David A. Randall Depatment of Atmospheic Science Coloado State Univesity Fot Collins, Coloado 80523. Scalas and vectos Any
ECE 3318 Applied Electricity and Magnetism. Spring Prof. David R. Jackson ECE Dept. Notes 13
 ECE 338 Applied Electicity and Magnetism ping 07 Pof. David R. Jackson ECE Dept. Notes 3 Divegence The Physical Concept Find the flux going outwad though a sphee of adius. x ρ v0 z a y ψ = D nˆ d = D ˆ
ECE 338 Applied Electicity and Magnetism ping 07 Pof. David R. Jackson ECE Dept. Notes 3 Divegence The Physical Concept Find the flux going outwad though a sphee of adius. x ρ v0 z a y ψ = D nˆ d = D ˆ
Lecture 23. Representation of the Dirac delta function in other coordinate systems
 Lectue 23 Repesentation of the Diac delta function in othe coodinate systems In a geneal sense, one can wite, ( ) = (x x ) (y y ) (z z ) = (u u ) (v v ) (w w ) J Whee J epesents the Jacobian of the tansfomation.
Lectue 23 Repesentation of the Diac delta function in othe coodinate systems In a geneal sense, one can wite, ( ) = (x x ) (y y ) (z z ) = (u u ) (v v ) (w w ) J Whee J epesents the Jacobian of the tansfomation.
Geometry of the homogeneous and isotropic spaces
 Geomety of the homogeneous and isotopic spaces H. Sonoda Septembe 2000; last evised Octobe 2009 Abstact We summaize the aspects of the geomety of the homogeneous and isotopic spaces which ae most elevant
Geomety of the homogeneous and isotopic spaces H. Sonoda Septembe 2000; last evised Octobe 2009 Abstact We summaize the aspects of the geomety of the homogeneous and isotopic spaces which ae most elevant
Vectors, Vector Calculus, and Coordinate Systems
 ! Revised Apil 11, 2017 1:48 PM! 1 Vectos, Vecto Calculus, and Coodinate Systems David Randall Physical laws and coodinate systems Fo the pesent discussion, we define a coodinate system as a tool fo descibing
! Revised Apil 11, 2017 1:48 PM! 1 Vectos, Vecto Calculus, and Coodinate Systems David Randall Physical laws and coodinate systems Fo the pesent discussion, we define a coodinate system as a tool fo descibing
Math 2263 Solutions for Spring 2003 Final Exam
 Math 6 Solutions fo Sping Final Exam ) A staightfowad appoach to finding the tangent plane to a suface at a point ( x, y, z ) would be to expess the cuve as an explicit function z = f ( x, y ), calculate
Math 6 Solutions fo Sping Final Exam ) A staightfowad appoach to finding the tangent plane to a suface at a point ( x, y, z ) would be to expess the cuve as an explicit function z = f ( x, y ), calculate
Analytic Evaluation of two-electron Atomic Integrals involving Extended Hylleraas-CI functions with STO basis
 Analytic Evaluation of two-electon Atomic Integals involving Extended Hylleaas-CI functions with STO basis B PADHY (Retd.) Faculty Membe Depatment of Physics, Khalikote (Autonomous) College, Behampu-760001,
Analytic Evaluation of two-electon Atomic Integals involving Extended Hylleaas-CI functions with STO basis B PADHY (Retd.) Faculty Membe Depatment of Physics, Khalikote (Autonomous) College, Behampu-760001,
Review: Electrostatics and Magnetostatics
 Review: Electostatics and Magnetostatics In the static egime, electomagnetic quantities do not vay as a function of time. We have two main cases: ELECTROSTATICS The electic chages do not change postion
Review: Electostatics and Magnetostatics In the static egime, electomagnetic quantities do not vay as a function of time. We have two main cases: ELECTROSTATICS The electic chages do not change postion
THE LAPLACE EQUATION. The Laplace (or potential) equation is the equation. u = 0. = 2 x 2. x y 2 in R 2
 THE LAPLACE EQUATION The Laplace (o potential) equation is the equation whee is the Laplace opeato = 2 x 2 u = 0. in R = 2 x 2 + 2 y 2 in R 2 = 2 x 2 + 2 y 2 + 2 z 2 in R 3 The solutions u of the Laplace
THE LAPLACE EQUATION The Laplace (o potential) equation is the equation whee is the Laplace opeato = 2 x 2 u = 0. in R = 2 x 2 + 2 y 2 in R 2 = 2 x 2 + 2 y 2 + 2 z 2 in R 3 The solutions u of the Laplace
Physics 235 Chapter 5. Chapter 5 Gravitation
 Chapte 5 Gavitation In this Chapte we will eview the popeties of the gavitational foce. The gavitational foce has been discussed in geat detail in you intoductoy physics couses, and we will pimaily focus
Chapte 5 Gavitation In this Chapte we will eview the popeties of the gavitational foce. The gavitational foce has been discussed in geat detail in you intoductoy physics couses, and we will pimaily focus
EM Boundary Value Problems
 EM Bounday Value Poblems 10/ 9 11/ By Ilekta chistidi & Lee, Seung-Hyun A. Geneal Desciption : Maxwell Equations & Loentz Foce We want to find the equations of motion of chaged paticles. The way to do
EM Bounday Value Poblems 10/ 9 11/ By Ilekta chistidi & Lee, Seung-Hyun A. Geneal Desciption : Maxwell Equations & Loentz Foce We want to find the equations of motion of chaged paticles. The way to do
Compactly Supported Radial Basis Functions
 Chapte 4 Compactly Suppoted Radial Basis Functions As we saw ealie, compactly suppoted functions Φ that ae tuly stictly conditionally positive definite of ode m > do not exist The compact suppot automatically
Chapte 4 Compactly Suppoted Radial Basis Functions As we saw ealie, compactly suppoted functions Φ that ae tuly stictly conditionally positive definite of ode m > do not exist The compact suppot automatically
Quantum theory of angular momentum
 Quantum theoy of angula momentum Igo Mazets igo.mazets+e141@tuwien.ac.at (Atominstitut TU Wien, Stadionallee 2, 1020 Wien Time: Fiday, 13:00 14:30 Place: Feihaus, Sem.R. DA gün 06B (exception date 18 Nov.:
Quantum theoy of angula momentum Igo Mazets igo.mazets+e141@tuwien.ac.at (Atominstitut TU Wien, Stadionallee 2, 1020 Wien Time: Fiday, 13:00 14:30 Place: Feihaus, Sem.R. DA gün 06B (exception date 18 Nov.:
Qualifying Examination Electricity and Magnetism Solutions January 12, 2006
 1 Qualifying Examination Electicity and Magnetism Solutions Januay 12, 2006 PROBLEM EA. a. Fist, we conside a unit length of cylinde to find the elationship between the total chage pe unit length λ and
1 Qualifying Examination Electicity and Magnetism Solutions Januay 12, 2006 PROBLEM EA. a. Fist, we conside a unit length of cylinde to find the elationship between the total chage pe unit length λ and
ENGI 4430 Non-Cartesian Coordinates Page xi Fy j Fzk from Cartesian coordinates z to another orthonormal coordinate system u, v, ˆ i ˆ ˆi
 ENGI 44 Non-Catesian Coodinates Page 7-7. Conesions between Coodinate Systems In geneal, the conesion of a ecto F F xi Fy j Fzk fom Catesian coodinates x, y, z to anothe othonomal coodinate system u,,
ENGI 44 Non-Catesian Coodinates Page 7-7. Conesions between Coodinate Systems In geneal, the conesion of a ecto F F xi Fy j Fzk fom Catesian coodinates x, y, z to anothe othonomal coodinate system u,,
SUPPLEMENTARY MATERIAL CHAPTER 7 A (2 ) B. a x + bx + c dx
 SUPPLEMENTARY MATERIAL 613 7.6.3 CHAPTER 7 ( px + q) a x + bx + c dx. We choose constants A and B such that d px + q A ( ax + bx + c) + B dx A(ax + b) + B Compaing the coefficients of x and the constant
SUPPLEMENTARY MATERIAL 613 7.6.3 CHAPTER 7 ( px + q) a x + bx + c dx. We choose constants A and B such that d px + q A ( ax + bx + c) + B dx A(ax + b) + B Compaing the coefficients of x and the constant
working pages for Paul Richards class notes; do not copy or circulate without permission from PGR 2004/11/3 10:50
 woking pages fo Paul Richads class notes; do not copy o ciculate without pemission fom PGR 2004/11/3 10:50 CHAPTER7 Solid angle, 3D integals, Gauss s Theoem, and a Delta Function We define the solid angle,
woking pages fo Paul Richads class notes; do not copy o ciculate without pemission fom PGR 2004/11/3 10:50 CHAPTER7 Solid angle, 3D integals, Gauss s Theoem, and a Delta Function We define the solid angle,
3D-Central Force Problems I
 5.73 Lectue #1 1-1 Roadmap 1. define adial momentum 3D-Cental Foce Poblems I Read: C-TDL, pages 643-660 fo next lectue. All -Body, 3-D poblems can be educed to * a -D angula pat that is exactly and univesally
5.73 Lectue #1 1-1 Roadmap 1. define adial momentum 3D-Cental Foce Poblems I Read: C-TDL, pages 643-660 fo next lectue. All -Body, 3-D poblems can be educed to * a -D angula pat that is exactly and univesally
COORDINATE TRANSFORMATIONS - THE JACOBIAN DETERMINANT
 COORDINATE TRANSFORMATIONS - THE JACOBIAN DETERMINANT Link to: phsicspages home page. To leave a comment o epot an eo, please use the auilia blog. Refeence: d Inveno, Ra, Intoducing Einstein s Relativit
COORDINATE TRANSFORMATIONS - THE JACOBIAN DETERMINANT Link to: phsicspages home page. To leave a comment o epot an eo, please use the auilia blog. Refeence: d Inveno, Ra, Intoducing Einstein s Relativit
3D-Central Force Problems II
 5.73 ectue # - 1 3D-Cental Foce Poblems II ast time: [x,p] vecto commutation ules: genealize fom 1-D to 3-D conugate position and momentum components in Catesian coodinates Coespondence Pinciple Recipe
5.73 ectue # - 1 3D-Cental Foce Poblems II ast time: [x,p] vecto commutation ules: genealize fom 1-D to 3-D conugate position and momentum components in Catesian coodinates Coespondence Pinciple Recipe
AE301 Aerodynamics I UNIT B: Theory of Aerodynamics
 AE301 Aeodynamics I UNIT B: Theoy of Aeodynamics ROAD MAP... B-1: Mathematics fo Aeodynamics B-2: Flow Field Repesentations B-3: Potential Flow Analysis B-4: Applications of Potential Flow Analysis AE301
AE301 Aeodynamics I UNIT B: Theoy of Aeodynamics ROAD MAP... B-1: Mathematics fo Aeodynamics B-2: Flow Field Repesentations B-3: Potential Flow Analysis B-4: Applications of Potential Flow Analysis AE301
= e2. = 2e2. = 3e2. V = Ze2. where Z is the atomic numnber. Thus, we take as the Hamiltonian for a hydrogenic. H = p2 r. (19.4)
 Chapte 9 Hydogen Atom I What is H int? That depends on the physical system and the accuacy with which it is descibed. A natual stating point is the fom H int = p + V, (9.) µ which descibes a two-paticle
Chapte 9 Hydogen Atom I What is H int? That depends on the physical system and the accuacy with which it is descibed. A natual stating point is the fom H int = p + V, (9.) µ which descibes a two-paticle
Homework # 3 Solution Key
 PHYSICS 631: Geneal Relativity Homewok # 3 Solution Key 1. You e on you hono not to do this one by hand. I ealize you can use a compute o simply look it up. Please don t. In a flat space, the metic in
PHYSICS 631: Geneal Relativity Homewok # 3 Solution Key 1. You e on you hono not to do this one by hand. I ealize you can use a compute o simply look it up. Please don t. In a flat space, the metic in
dq 1 (5) q 1 where the previously mentioned limit has been taken.
 1 Vecto Calculus And Continuum Consevation Equations In Cuvilinea Othogonal Coodinates Robet Maska: Novembe 25, 2008 In ode to ewite the consevation equations(continuit, momentum, eneg) to some cuvilinea
1 Vecto Calculus And Continuum Consevation Equations In Cuvilinea Othogonal Coodinates Robet Maska: Novembe 25, 2008 In ode to ewite the consevation equations(continuit, momentum, eneg) to some cuvilinea
2. Electrostatics. Dr. Rakhesh Singh Kshetrimayum 8/11/ Electromagnetic Field Theory by R. S. Kshetrimayum
 2. Electostatics D. Rakhesh Singh Kshetimayum 1 2.1 Intoduction In this chapte, we will study how to find the electostatic fields fo vaious cases? fo symmetic known chage distibution fo un-symmetic known
2. Electostatics D. Rakhesh Singh Kshetimayum 1 2.1 Intoduction In this chapte, we will study how to find the electostatic fields fo vaious cases? fo symmetic known chage distibution fo un-symmetic known
6 Vector Operators. 6.1 The Gradient Operator
 6 Vecto Opeatos 6. The Gadient Opeato In the B2 couse ou wee intoduced to the gadient opeato in Catesian coodinates. Fo an diffeentiable scala function f(x,, z), we can define a vecto function though (
6 Vecto Opeatos 6. The Gadient Opeato In the B2 couse ou wee intoduced to the gadient opeato in Catesian coodinates. Fo an diffeentiable scala function f(x,, z), we can define a vecto function though (
APPENDIX. For the 2 lectures of Claude Cohen-Tannoudji on Atom-Atom Interactions in Ultracold Quantum Gases
 APPENDIX Fo the lectues of Claude Cohen-Tannoudji on Atom-Atom Inteactions in Ultacold Quantum Gases Pupose of this Appendix Demonstate the othonomalization elation(ϕ ϕ = δ k k δ δ )k - The wave function
APPENDIX Fo the lectues of Claude Cohen-Tannoudji on Atom-Atom Inteactions in Ultacold Quantum Gases Pupose of this Appendix Demonstate the othonomalization elation(ϕ ϕ = δ k k δ δ )k - The wave function
A Relativistic Electron in a Coulomb Potential
 A Relativistic Electon in a Coulomb Potential Alfed Whitehead Physics 518, Fall 009 The Poblem Solve the Diac Equation fo an electon in a Coulomb potential. Identify the conseved quantum numbes. Specify
A Relativistic Electon in a Coulomb Potential Alfed Whitehead Physics 518, Fall 009 The Poblem Solve the Diac Equation fo an electon in a Coulomb potential. Identify the conseved quantum numbes. Specify
1 Spherical multipole moments
 Jackson notes 9 Spheical multipole moments Suppose we have a chage distibution ρ (x) wheeallofthechageiscontained within a spheical egion of adius R, as shown in the diagam. Then thee is no chage in the
Jackson notes 9 Spheical multipole moments Suppose we have a chage distibution ρ (x) wheeallofthechageiscontained within a spheical egion of adius R, as shown in the diagam. Then thee is no chage in the
Question 1: The dipole
 Septembe, 08 Conell Univesity, Depatment of Physics PHYS 337, Advance E&M, HW #, due: 9/5/08, :5 AM Question : The dipole Conside a system as discussed in class and shown in Fig.. in Heald & Maion.. Wite
Septembe, 08 Conell Univesity, Depatment of Physics PHYS 337, Advance E&M, HW #, due: 9/5/08, :5 AM Question : The dipole Conside a system as discussed in class and shown in Fig.. in Heald & Maion.. Wite
3. Electromagnetic Waves II
 Lectue 3 - Electomagnetic Waves II 9 3. Electomagnetic Waves II Last time, we discussed the following. 1. The popagation of an EM wave though a macoscopic media: We discussed how the wave inteacts with
Lectue 3 - Electomagnetic Waves II 9 3. Electomagnetic Waves II Last time, we discussed the following. 1. The popagation of an EM wave though a macoscopic media: We discussed how the wave inteacts with
Lecture 7: Angular Momentum, Hydrogen Atom
 Lectue 7: Angula Momentum, Hydogen Atom Vecto Quantization of Angula Momentum and Nomalization of 3D Rigid Roto wavefunctions Conside l, so L 2 2 2. Thus, we have L 2. Thee ae thee possibilities fo L z
Lectue 7: Angula Momentum, Hydogen Atom Vecto Quantization of Angula Momentum and Nomalization of 3D Rigid Roto wavefunctions Conside l, so L 2 2 2. Thus, we have L 2. Thee ae thee possibilities fo L z
Energy Levels Of Hydrogen Atom Using Ladder Operators. Ava Khamseh Supervisor: Dr. Brian Pendleton The University of Edinburgh August 2011
 Enegy Levels Of Hydogen Atom Using Ladde Opeatos Ava Khamseh Supeviso: D. Bian Pendleton The Univesity of Edinbugh August 11 1 Abstact The aim of this pape is to fist use the Schödinge wavefunction methods
Enegy Levels Of Hydogen Atom Using Ladde Opeatos Ava Khamseh Supeviso: D. Bian Pendleton The Univesity of Edinbugh August 11 1 Abstact The aim of this pape is to fist use the Schödinge wavefunction methods
Preliminary Exam: Quantum Physics 1/14/2011, 9:00-3:00
 Peliminay Exam: Quantum Physics /4/ 9:-: Answe a total of SIX questions of which at least TWO ae fom section A and at least THREE ae fom section B Fo you answes you can use eithe the blue books o individual
Peliminay Exam: Quantum Physics /4/ 9:-: Answe a total of SIX questions of which at least TWO ae fom section A and at least THREE ae fom section B Fo you answes you can use eithe the blue books o individual
f(k) e p 2 (k) e iax 2 (k a) r 2 e a x a a 2 + k 2 e a2 x 1 2 H(x) ik p (k) 4 r 3 cos Y 2 = 4
 Fouie tansfom pais: f(x) 1 f(k) e p 2 (k) p e iax 2 (k a) 2 e a x a a 2 + k 2 e a2 x 1 2, a > 0 a p k2 /4a2 e 2 1 H(x) ik p 2 + 2 (k) The fist few Y m Y 0 0 = Y 0 1 = Y ±1 1 = l : 1 Y2 0 = 4 3 ±1 cos Y
Fouie tansfom pais: f(x) 1 f(k) e p 2 (k) p e iax 2 (k a) 2 e a x a a 2 + k 2 e a2 x 1 2, a > 0 a p k2 /4a2 e 2 1 H(x) ik p 2 + 2 (k) The fist few Y m Y 0 0 = Y 0 1 = Y ±1 1 = l : 1 Y2 0 = 4 3 ±1 cos Y
The Poisson bracket and magnetic monopoles
 FYST420 Advanced electodynamics Olli Aleksante Koskivaaa Final poject ollikoskivaaa@gmail.com The Poisson backet and magnetic monopoles Abstact: In this wok magnetic monopoles ae studied using the Poisson
FYST420 Advanced electodynamics Olli Aleksante Koskivaaa Final poject ollikoskivaaa@gmail.com The Poisson backet and magnetic monopoles Abstact: In this wok magnetic monopoles ae studied using the Poisson
-Δ u = λ u. u(x,y) = u 1. (x) u 2. (y) u(r,θ) = R(r) Θ(θ) Δu = 2 u + 2 u. r = x 2 + y 2. tan(θ) = y/x. r cos(θ) = cos(θ) r.
 The Laplace opeato in pola coodinates We now conside the Laplace opeato with Diichlet bounday conditions on a cicula egion Ω {(x,y) x + y A }. Ou goal is to compute eigenvalues and eigenfunctions of the
The Laplace opeato in pola coodinates We now conside the Laplace opeato with Diichlet bounday conditions on a cicula egion Ω {(x,y) x + y A }. Ou goal is to compute eigenvalues and eigenfunctions of the
Magnetic field due to a current loop.
 Example using spheical hamonics Sp 18 Magnetic field due to a cuent loop. A cicula loop of adius a caies cuent I. We place the oigin at the cente of the loop, with pola axis pependicula to the plane of
Example using spheical hamonics Sp 18 Magnetic field due to a cuent loop. A cicula loop of adius a caies cuent I. We place the oigin at the cente of the loop, with pola axis pependicula to the plane of
2 Governing Equations
 2 Govening Equations This chapte develops the govening equations of motion fo a homogeneous isotopic elastic solid, using the linea thee-dimensional theoy of elasticity in cylindical coodinates. At fist,
2 Govening Equations This chapte develops the govening equations of motion fo a homogeneous isotopic elastic solid, using the linea thee-dimensional theoy of elasticity in cylindical coodinates. At fist,
PHYS 110B - HW #7 Spring 2004, Solutions by David Pace Any referenced equations are from Griffiths Problem statements are paraphrased
 PHYS 0B - HW #7 Sping 2004, Solutions by David Pace Any efeenced euations ae fom Giffiths Poblem statements ae paaphased. Poblem 0.3 fom Giffiths A point chage,, moves in a loop of adius a. At time t 0
PHYS 0B - HW #7 Sping 2004, Solutions by David Pace Any efeenced euations ae fom Giffiths Poblem statements ae paaphased. Poblem 0.3 fom Giffiths A point chage,, moves in a loop of adius a. At time t 0
Lecture 8 - Gauss s Law
 Lectue 8 - Gauss s Law A Puzzle... Example Calculate the potential enegy, pe ion, fo an infinite 1D ionic cystal with sepaation a; that is, a ow of equally spaced chages of magnitude e and altenating sign.
Lectue 8 - Gauss s Law A Puzzle... Example Calculate the potential enegy, pe ion, fo an infinite 1D ionic cystal with sepaation a; that is, a ow of equally spaced chages of magnitude e and altenating sign.
MODULE 5a and 5b (Stewart, Sections 12.2, 12.3) INTRO: In MATH 1114 vectors were written either as rows (a1, a2,..., an) or as columns a 1 a. ...
 MODULE 5a and 5b (Stewat, Sections 2.2, 2.3) INTRO: In MATH 4 vectos wee witten eithe as ows (a, a2,..., an) o as columns a a 2... a n and the set of all such vectos of fixed length n was called the vecto
MODULE 5a and 5b (Stewat, Sections 2.2, 2.3) INTRO: In MATH 4 vectos wee witten eithe as ows (a, a2,..., an) o as columns a a 2... a n and the set of all such vectos of fixed length n was called the vecto
Chapter 5 Linear Equations: Basic Theory and Practice
 Chapte 5 inea Equations: Basic Theoy and actice In this chapte and the next, we ae inteested in the linea algebaic equation AX = b, (5-1) whee A is an m n matix, X is an n 1 vecto to be solved fo, and
Chapte 5 inea Equations: Basic Theoy and actice In this chapte and the next, we ae inteested in the linea algebaic equation AX = b, (5-1) whee A is an m n matix, X is an n 1 vecto to be solved fo, and
CALCULUS II Vectors. Paul Dawkins
 CALCULUS II Vectos Paul Dawkins Table of Contents Peface... ii Vectos... 3 Intoduction... 3 Vectos The Basics... 4 Vecto Aithmetic... 8 Dot Poduct... 13 Coss Poduct... 21 2007 Paul Dawkins i http://tutoial.math.lama.edu/tems.aspx
CALCULUS II Vectos Paul Dawkins Table of Contents Peface... ii Vectos... 3 Intoduction... 3 Vectos The Basics... 4 Vecto Aithmetic... 8 Dot Poduct... 13 Coss Poduct... 21 2007 Paul Dawkins i http://tutoial.math.lama.edu/tems.aspx
S7: Classical mechanics problem set 2
 J. Magoian MT 9, boowing fom J. J. Binney s 6 couse S7: Classical mechanics poblem set. Show that if the Hamiltonian is indepdent of a genealized co-odinate q, then the conjugate momentum p is a constant
J. Magoian MT 9, boowing fom J. J. Binney s 6 couse S7: Classical mechanics poblem set. Show that if the Hamiltonian is indepdent of a genealized co-odinate q, then the conjugate momentum p is a constant
A Bijective Approach to the Permutational Power of a Priority Queue
 A Bijective Appoach to the Pemutational Powe of a Pioity Queue Ia M. Gessel Kuang-Yeh Wang Depatment of Mathematics Bandeis Univesity Waltham, MA 02254-9110 Abstact A pioity queue tansfoms an input pemutation
A Bijective Appoach to the Pemutational Powe of a Pioity Queue Ia M. Gessel Kuang-Yeh Wang Depatment of Mathematics Bandeis Univesity Waltham, MA 02254-9110 Abstact A pioity queue tansfoms an input pemutation
Scattering in Three Dimensions
 Scatteing in Thee Dimensions Scatteing expeiments ae an impotant souce of infomation about quantum systems, anging in enegy fom vey low enegy chemical eactions to the highest possible enegies at the LHC.
Scatteing in Thee Dimensions Scatteing expeiments ae an impotant souce of infomation about quantum systems, anging in enegy fom vey low enegy chemical eactions to the highest possible enegies at the LHC.
I. CONSTRUCTION OF THE GREEN S FUNCTION
 I. CONSTRUCTION OF THE GREEN S FUNCTION The Helmohltz equation in 4 dimensions is 4 + k G 4 x, x = δ 4 x x. In this equation, G is the Geen s function and 4 efes to the dimensionality. In the vey end,
I. CONSTRUCTION OF THE GREEN S FUNCTION The Helmohltz equation in 4 dimensions is 4 + k G 4 x, x = δ 4 x x. In this equation, G is the Geen s function and 4 efes to the dimensionality. In the vey end,
Question Bank. Section A. is skew-hermitian matrix. is diagonalizable. (, ) , Evaluate (, ) 12 about = 1 and = Find, if
 Subject: Mathematics-I Question Bank Section A T T. Find the value of fo which the matix A = T T has ank one. T T i. Is the matix A = i is skew-hemitian matix. i. alculate the invese of the matix = 5 7
Subject: Mathematics-I Question Bank Section A T T. Find the value of fo which the matix A = T T has ank one. T T i. Is the matix A = i is skew-hemitian matix. i. alculate the invese of the matix = 5 7
New problems in universal algebraic geometry illustrated by boolean equations
 New poblems in univesal algebaic geomety illustated by boolean equations axiv:1611.00152v2 [math.ra] 25 Nov 2016 Atem N. Shevlyakov Novembe 28, 2016 Abstact We discuss new poblems in univesal algebaic
New poblems in univesal algebaic geomety illustated by boolean equations axiv:1611.00152v2 [math.ra] 25 Nov 2016 Atem N. Shevlyakov Novembe 28, 2016 Abstact We discuss new poblems in univesal algebaic
A New Approach to General Relativity
 Apeion, Vol. 14, No. 3, July 7 7 A New Appoach to Geneal Relativity Ali Rıza Şahin Gaziosmanpaşa, Istanbul Tukey E-mail: aizasahin@gmail.com Hee we pesent a new point of view fo geneal elativity and/o
Apeion, Vol. 14, No. 3, July 7 7 A New Appoach to Geneal Relativity Ali Rıza Şahin Gaziosmanpaşa, Istanbul Tukey E-mail: aizasahin@gmail.com Hee we pesent a new point of view fo geneal elativity and/o
AST 121S: The origin and evolution of the Universe. Introduction to Mathematical Handout 1
 Please ead this fist... AST S: The oigin and evolution of the Univese Intoduction to Mathematical Handout This is an unusually long hand-out and one which uses in places mathematics that you may not be
Please ead this fist... AST S: The oigin and evolution of the Univese Intoduction to Mathematical Handout This is an unusually long hand-out and one which uses in places mathematics that you may not be
is the instantaneous position vector of any grid point or fluid
 Absolute inetial, elative inetial and non-inetial coodinates fo a moving but non-defoming contol volume Tao Xing, Pablo Caica, and Fed Sten bjective Deive and coelate the govening equations of motion in
Absolute inetial, elative inetial and non-inetial coodinates fo a moving but non-defoming contol volume Tao Xing, Pablo Caica, and Fed Sten bjective Deive and coelate the govening equations of motion in
IX INDUCTANCE AND MAGNETIC FIELDS
 IX INDUCTNCE ND MGNETIC FIELDS 9. Field in a solenoid vaying cuent in a conducto will poduce a vaying magnetic field. nd this vaying magnetic field then has the capability of inducing an EMF o voltage
IX INDUCTNCE ND MGNETIC FIELDS 9. Field in a solenoid vaying cuent in a conducto will poduce a vaying magnetic field. nd this vaying magnetic field then has the capability of inducing an EMF o voltage
B da = 0. Q E da = ε. E da = E dv
 lectomagnetic Theo Pof Ruiz, UNC Asheville, doctophs on YouTube Chapte Notes The Maxwell quations in Diffeential Fom 1 The Maxwell quations in Diffeential Fom We will now tansfom the integal fom of the
lectomagnetic Theo Pof Ruiz, UNC Asheville, doctophs on YouTube Chapte Notes The Maxwell quations in Diffeential Fom 1 The Maxwell quations in Diffeential Fom We will now tansfom the integal fom of the
Transformation of the Navier-Stokes Equations in Curvilinear Coordinate Systems with Maple
 Global Jounal of Pue and Applied Mathematics. ISSN 0973-1768 Volume 12, Numbe 4 2016, pp. 3315 3325 Reseach India Publications http://www.ipublication.com/gjpam.htm Tansfomation of the Navie-Stokes Equations
Global Jounal of Pue and Applied Mathematics. ISSN 0973-1768 Volume 12, Numbe 4 2016, pp. 3315 3325 Reseach India Publications http://www.ipublication.com/gjpam.htm Tansfomation of the Navie-Stokes Equations
FI 2201 Electromagnetism
 FI Electomagnetim Aleande A. Ikanda, Ph.D. Phyic of Magnetim and Photonic Reeach Goup ecto Analyi CURILINEAR COORDINAES, DIRAC DELA FUNCION AND HEORY OF ECOR FIELDS Cuvilinea Coodinate Sytem Cateian coodinate:
FI Electomagnetim Aleande A. Ikanda, Ph.D. Phyic of Magnetim and Photonic Reeach Goup ecto Analyi CURILINEAR COORDINAES, DIRAC DELA FUNCION AND HEORY OF ECOR FIELDS Cuvilinea Coodinate Sytem Cateian coodinate:
Physics 506 Winter 2006 Homework Assignment #9 Solutions
 Physics 506 Winte 2006 Homewok Assignment #9 Solutions Textbook poblems: Ch. 12: 12.2, 12.9, 12.13, 12.14 12.2 a) Show fom Hamilton s pinciple that Lagangians that diffe only by a total time deivative
Physics 506 Winte 2006 Homewok Assignment #9 Solutions Textbook poblems: Ch. 12: 12.2, 12.9, 12.13, 12.14 12.2 a) Show fom Hamilton s pinciple that Lagangians that diffe only by a total time deivative
On a quantity that is analogous to potential and a theorem that relates to it
 Su une quantité analogue au potential et su un théoème y elatif C R Acad Sci 7 (87) 34-39 On a quantity that is analogous to potential and a theoem that elates to it By R CLAUSIUS Tanslated by D H Delphenich
Su une quantité analogue au potential et su un théoème y elatif C R Acad Sci 7 (87) 34-39 On a quantity that is analogous to potential and a theoem that elates to it By R CLAUSIUS Tanslated by D H Delphenich
15 Solving the Laplace equation by Fourier method
 5 Solving the Laplace equation by Fouie method I aleady intoduced two o thee dimensional heat equation, when I deived it, ecall that it taes the fom u t = α 2 u + F, (5.) whee u: [0, ) D R, D R is the
5 Solving the Laplace equation by Fouie method I aleady intoduced two o thee dimensional heat equation, when I deived it, ecall that it taes the fom u t = α 2 u + F, (5.) whee u: [0, ) D R, D R is the
ON INDEPENDENT SETS IN PURELY ATOMIC PROBABILITY SPACES WITH GEOMETRIC DISTRIBUTION. 1. Introduction. 1 r r. r k for every set E A, E \ {0},
 ON INDEPENDENT SETS IN PURELY ATOMIC PROBABILITY SPACES WITH GEOMETRIC DISTRIBUTION E. J. IONASCU and A. A. STANCU Abstact. We ae inteested in constucting concete independent events in puely atomic pobability
ON INDEPENDENT SETS IN PURELY ATOMIC PROBABILITY SPACES WITH GEOMETRIC DISTRIBUTION E. J. IONASCU and A. A. STANCU Abstact. We ae inteested in constucting concete independent events in puely atomic pobability
Stress, Cauchy s equation and the Navier-Stokes equations
 Chapte 3 Stess, Cauchy s equation and the Navie-Stokes equations 3. The concept of taction/stess Conside the volume of fluid shown in the left half of Fig. 3.. The volume of fluid is subjected to distibuted
Chapte 3 Stess, Cauchy s equation and the Navie-Stokes equations 3. The concept of taction/stess Conside the volume of fluid shown in the left half of Fig. 3.. The volume of fluid is subjected to distibuted
Classical Mechanics Homework set 7, due Nov 8th: Solutions
 Classical Mechanics Homewok set 7, due Nov 8th: Solutions 1. Do deivation 8.. It has been asked what effect does a total deivative as a function of q i, t have on the Hamiltonian. Thus, lets us begin with
Classical Mechanics Homewok set 7, due Nov 8th: Solutions 1. Do deivation 8.. It has been asked what effect does a total deivative as a function of q i, t have on the Hamiltonian. Thus, lets us begin with
PROBLEM SET #1 SOLUTIONS by Robert A. DiStasio Jr.
 POBLM S # SOLUIONS by obet A. DiStasio J. Q. he Bon-Oppenheime appoximation is the standad way of appoximating the gound state of a molecula system. Wite down the conditions that detemine the tonic and
POBLM S # SOLUIONS by obet A. DiStasio J. Q. he Bon-Oppenheime appoximation is the standad way of appoximating the gound state of a molecula system. Wite down the conditions that detemine the tonic and
BASIC ALGEBRA OF VECTORS
 Fomulae Fo u Vecto Algeba By Mi Mohammed Abbas II PCMB 'A' Impotant Tems, Definitions & Fomulae 01 Vecto - Basic Intoduction: A quantity having magnitude as well as the diection is called vecto It is denoted
Fomulae Fo u Vecto Algeba By Mi Mohammed Abbas II PCMB 'A' Impotant Tems, Definitions & Fomulae 01 Vecto - Basic Intoduction: A quantity having magnitude as well as the diection is called vecto It is denoted
CHAPTER 25 ELECTRIC POTENTIAL
 CHPTE 5 ELECTIC POTENTIL Potential Diffeence and Electic Potential Conside a chaged paticle of chage in a egion of an electic field E. This filed exets an electic foce on the paticle given by F=E. When
CHPTE 5 ELECTIC POTENTIL Potential Diffeence and Electic Potential Conside a chaged paticle of chage in a egion of an electic field E. This filed exets an electic foce on the paticle given by F=E. When
Solution to HW 3, Ma 1a Fall 2016
 Solution to HW 3, Ma a Fall 206 Section 2. Execise 2: Let C be a subset of the eal numbes consisting of those eal numbes x having the popety that evey digit in the decimal expansion of x is, 3, 5, o 7.
Solution to HW 3, Ma a Fall 206 Section 2. Execise 2: Let C be a subset of the eal numbes consisting of those eal numbes x having the popety that evey digit in the decimal expansion of x is, 3, 5, o 7.
1 Equations of linear elasticity
 C5.2 Elasticity & Plasticity Daft date: 17 Januay 2017 1 1 1 Equations of linea elasticity 1.1 Hooke s law Robet Hooke (1678 wote... it is... evident that the ule o law of natue in evey spinging body is
C5.2 Elasticity & Plasticity Daft date: 17 Januay 2017 1 1 1 Equations of linea elasticity 1.1 Hooke s law Robet Hooke (1678 wote... it is... evident that the ule o law of natue in evey spinging body is
Vector Calculus Identities
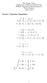 The Coope Union Depatment of Electical Engineeing ECE135 Engineeing Electomagnetics Vecto Analysis Mach 8, 2012 Vecto Calculus Identities A B B A A B C B C A C A B A B C B A C C A B fg f g + g f fg f G
The Coope Union Depatment of Electical Engineeing ECE135 Engineeing Electomagnetics Vecto Analysis Mach 8, 2012 Vecto Calculus Identities A B B A A B C B C A C A B A B C B A C C A B fg f g + g f fg f G
Math 209 Assignment 9 Solutions
 Math 9 Assignment 9 olutions 1. Evaluate 4y + 1 d whee is the fist octant pat of y x cut out by x + y + z 1. olution We need a paametic epesentation of the suface. (x, z). Now detemine the nomal vecto:
Math 9 Assignment 9 olutions 1. Evaluate 4y + 1 d whee is the fist octant pat of y x cut out by x + y + z 1. olution We need a paametic epesentation of the suface. (x, z). Now detemine the nomal vecto:
Class #16 Monday, March 20, 2017
 D. Pogo Class #16 Monday, Mach 0, 017 D Non-Catesian Coodinate Systems A point in space can be specified by thee numbes:, y, and z. O, it can be specified by 3 diffeent numbes:,, and z, whee = cos, y =
D. Pogo Class #16 Monday, Mach 0, 017 D Non-Catesian Coodinate Systems A point in space can be specified by thee numbes:, y, and z. O, it can be specified by 3 diffeent numbes:,, and z, whee = cos, y =
ESCI 342 Atmospheric Dynamics I Lesson 3 Fundamental Forces II
 Reading: Matin, Section. ROTATING REFERENCE FRAMES ESCI 34 Atmospheic Dnamics I Lesson 3 Fundamental Foces II A efeence fame in which an object with zeo net foce on it does not acceleate is known as an
Reading: Matin, Section. ROTATING REFERENCE FRAMES ESCI 34 Atmospheic Dnamics I Lesson 3 Fundamental Foces II A efeence fame in which an object with zeo net foce on it does not acceleate is known as an
ON THE TWO-BODY PROBLEM IN QUANTUM MECHANICS
 ON THE TWO-BODY PROBLEM IN QUANTUM MECHANICS L. MICU Hoia Hulubei National Institute fo Physics and Nuclea Engineeing, P.O. Box MG-6, RO-0775 Buchaest-Maguele, Romania, E-mail: lmicu@theoy.nipne.o (Received
ON THE TWO-BODY PROBLEM IN QUANTUM MECHANICS L. MICU Hoia Hulubei National Institute fo Physics and Nuclea Engineeing, P.O. Box MG-6, RO-0775 Buchaest-Maguele, Romania, E-mail: lmicu@theoy.nipne.o (Received
Why Professor Richard Feynman was upset solving the Laplace equation for spherical waves? Anzor A. Khelashvili a)
 Why Pofesso Richad Feynman was upset solving the Laplace equation fo spheical waves? Anzo A. Khelashvili a) Institute of High Enegy Physics, Iv. Javakhishvili Tbilisi State Univesity, Univesity St. 9,
Why Pofesso Richad Feynman was upset solving the Laplace equation fo spheical waves? Anzo A. Khelashvili a) Institute of High Enegy Physics, Iv. Javakhishvili Tbilisi State Univesity, Univesity St. 9,
sinγ(h y > ) exp(iωt iqx)dωdq
 Lectue 9/28/5 Can we ecove a ay pictue fom the above G fo a membane stip? Such a pictue would be complementay to the above expansion in a seies of integals along the many banches of the dispesion elation.
Lectue 9/28/5 Can we ecove a ay pictue fom the above G fo a membane stip? Such a pictue would be complementay to the above expansion in a seies of integals along the many banches of the dispesion elation.
transformation Earth V-curve (meridian) λ Conical projection. u,v curves on the datum surface projected as U,V curves on the projection surface
 . CONICAL PROJECTIONS In elementay texts on map pojections, the pojection sufaces ae often descibed as developable sufaces, such as the cylinde (cylindical pojections) and the cone (conical pojections),
. CONICAL PROJECTIONS In elementay texts on map pojections, the pojection sufaces ae often descibed as developable sufaces, such as the cylinde (cylindical pojections) and the cone (conical pojections),
MATH 417 Homework 3 Instructor: D. Cabrera Due June 30. sin θ v x = v r cos θ v θ r. (b) Then use the Cauchy-Riemann equations in polar coordinates
 MATH 417 Homewok 3 Instucto: D. Cabea Due June 30 1. Let a function f(z) = u + iv be diffeentiable at z 0. (a) Use the Chain Rule and the fomulas x = cosθ and y = to show that u x = u cosθ u θ, v x = v
MATH 417 Homewok 3 Instucto: D. Cabea Due June 30 1. Let a function f(z) = u + iv be diffeentiable at z 0. (a) Use the Chain Rule and the fomulas x = cosθ and y = to show that u x = u cosθ u θ, v x = v
Chapter 1: Vector Analysis
 Chapte 1: Vecto Analysis Campos Electomagnéticos 2º Cuso Ingenieía Industial Dpto.Física Aplicada III Cuso 2007/2008 Dpto. Física Aplicada III - Univ. de Sevilla Joaquín Benal Méndez 1 Chapte 1: Index
Chapte 1: Vecto Analysis Campos Electomagnéticos 2º Cuso Ingenieía Industial Dpto.Física Aplicada III Cuso 2007/2008 Dpto. Física Aplicada III - Univ. de Sevilla Joaquín Benal Méndez 1 Chapte 1: Index
4. Electrodynamic fields
 4. Electodynamic fields D. Rakhesh Singh Kshetimayum 1 4.1 Intoduction Electodynamics Faaday s law Maxwell s equations Wave equations Lenz s law Integal fom Diffeential fom Phaso fom Bounday conditions
4. Electodynamic fields D. Rakhesh Singh Kshetimayum 1 4.1 Intoduction Electodynamics Faaday s law Maxwell s equations Wave equations Lenz s law Integal fom Diffeential fom Phaso fom Bounday conditions
Temporal-Difference Learning
 .997 Decision-Making in Lage-Scale Systems Mach 17 MIT, Sping 004 Handout #17 Lectue Note 13 1 Tempoal-Diffeence Leaning We now conside the poblem of computing an appopiate paamete, so that, given an appoximation
.997 Decision-Making in Lage-Scale Systems Mach 17 MIT, Sping 004 Handout #17 Lectue Note 13 1 Tempoal-Diffeence Leaning We now conside the poblem of computing an appopiate paamete, so that, given an appoximation
TheWaveandHelmholtzEquations
 TheWaveandHelmholtzEquations Ramani Duaiswami The Univesity of Mayland, College Pak Febuay 3, 2006 Abstact CMSC828D notes (adapted fom mateial witten with Nail Gumeov). Wok in pogess 1 Acoustic Waves 1.1
TheWaveandHelmholtzEquations Ramani Duaiswami The Univesity of Mayland, College Pak Febuay 3, 2006 Abstact CMSC828D notes (adapted fom mateial witten with Nail Gumeov). Wok in pogess 1 Acoustic Waves 1.1
B. Spherical Wave Propagation
 11/8/007 Spheical Wave Popagation notes 1/1 B. Spheical Wave Popagation Evey antenna launches a spheical wave, thus its powe density educes as a function of 1, whee is the distance fom the antenna. We
11/8/007 Spheical Wave Popagation notes 1/1 B. Spheical Wave Popagation Evey antenna launches a spheical wave, thus its powe density educes as a function of 1, whee is the distance fom the antenna. We
MATH 220: SECOND ORDER CONSTANT COEFFICIENT PDE. We consider second order constant coefficient scalar linear PDEs on R n. These have the form
 MATH 220: SECOND ORDER CONSTANT COEFFICIENT PDE ANDRAS VASY We conside second ode constant coefficient scala linea PDEs on R n. These have the fom Lu = f L = a ij xi xj + b i xi + c i whee a ij b i and
MATH 220: SECOND ORDER CONSTANT COEFFICIENT PDE ANDRAS VASY We conside second ode constant coefficient scala linea PDEs on R n. These have the fom Lu = f L = a ij xi xj + b i xi + c i whee a ij b i and
3.1 Random variables
 3 Chapte III Random Vaiables 3 Random vaiables A sample space S may be difficult to descibe if the elements of S ae not numbes discuss how we can use a ule by which an element s of S may be associated
3 Chapte III Random Vaiables 3 Random vaiables A sample space S may be difficult to descibe if the elements of S ae not numbes discuss how we can use a ule by which an element s of S may be associated
The Divergence Theorem
 13.8 The ivegence Theoem Back in 13.5 we ewote Geen s Theoem in vecto fom as C F n ds= div F x, y da ( ) whee C is the positively-oiented bounday cuve of the plane egion (in the xy-plane). Notice this
13.8 The ivegence Theoem Back in 13.5 we ewote Geen s Theoem in vecto fom as C F n ds= div F x, y da ( ) whee C is the positively-oiented bounday cuve of the plane egion (in the xy-plane). Notice this
EFFECTS OF FRINGING FIELDS ON SINGLE PARTICLE DYNAMICS. M. Bassetti and C. Biscari INFN-LNF, CP 13, Frascati (RM), Italy
 Fascati Physics Seies Vol. X (998), pp. 47-54 4 th Advanced ICFA Beam Dynamics Wokshop, Fascati, Oct. -5, 997 EFFECTS OF FRININ FIELDS ON SINLE PARTICLE DYNAMICS M. Bassetti and C. Biscai INFN-LNF, CP
Fascati Physics Seies Vol. X (998), pp. 47-54 4 th Advanced ICFA Beam Dynamics Wokshop, Fascati, Oct. -5, 997 EFFECTS OF FRININ FIELDS ON SINLE PARTICLE DYNAMICS M. Bassetti and C. Biscai INFN-LNF, CP
18.06 Problem Set 4 Solution
 8.6 Poblem Set 4 Solution Total: points Section 3.5. Poblem 2: (Recommended) Find the lagest possible numbe of independent vectos among ) ) ) v = v 4 = v 5 = v 6 = v 2 = v 3 =. Solution (4 points): Since
8.6 Poblem Set 4 Solution Total: points Section 3.5. Poblem 2: (Recommended) Find the lagest possible numbe of independent vectos among ) ) ) v = v 4 = v 5 = v 6 = v 2 = v 3 =. Solution (4 points): Since
What Form of Gravitation Ensures Weakened Kepler s Third Law?
 Bulletin of Aichi Univ. of Education, 6(Natual Sciences, pp. - 6, Mach, 03 What Fom of Gavitation Ensues Weakened Keple s Thid Law? Kenzi ODANI Depatment of Mathematics Education, Aichi Univesity of Education,
Bulletin of Aichi Univ. of Education, 6(Natual Sciences, pp. - 6, Mach, 03 What Fom of Gavitation Ensues Weakened Keple s Thid Law? Kenzi ODANI Depatment of Mathematics Education, Aichi Univesity of Education,
Solutions to Exercises in Notes 1., multiplying byg kl, and using [ ]
![Solutions to Exercises in Notes 1., multiplying byg kl, and using [ ] Solutions to Exercises in Notes 1., multiplying byg kl, and using [ ]](/thumbs/96/127738252.jpg) Fo any vecto fields X, Y and Z that Solutions to Execises in Notes. 2g ( X Y, Z) = X (g (Y, Z)) + Y (g (X, Z)) Z (g (X, Y )) () + g ([X, Y ], Z) g ([X, Z], Y ) g ([Y, Z], X). Applying this to X =, Y =,
Fo any vecto fields X, Y and Z that Solutions to Execises in Notes. 2g ( X Y, Z) = X (g (Y, Z)) + Y (g (X, Z)) Z (g (X, Y )) () + g ([X, Y ], Z) g ([X, Z], Y ) g ([Y, Z], X). Applying this to X =, Y =,
arxiv: v1 [physics.pop-ph] 3 Jun 2013
![arxiv: v1 [physics.pop-ph] 3 Jun 2013 arxiv: v1 [physics.pop-ph] 3 Jun 2013](/thumbs/89/100795062.jpg) A note on the electostatic enegy of two point chages axiv:1306.0401v1 [physics.pop-ph] 3 Jun 013 A C Tot Instituto de Física Univesidade Fedeal do io de Janeio Caixa Postal 68.58; CEP 1941-97 io de Janeio,
A note on the electostatic enegy of two point chages axiv:1306.0401v1 [physics.pop-ph] 3 Jun 013 A C Tot Instituto de Física Univesidade Fedeal do io de Janeio Caixa Postal 68.58; CEP 1941-97 io de Janeio,
Do not turn over until you are told to do so by the Invigilator.
 UNIVERSITY OF EAST ANGLIA School of Mathematics Main Seies UG Examination 2015 16 FLUID DYNAMICS WITH ADVANCED TOPICS MTH-MD59 Time allowed: 3 Hous Attempt QUESTIONS 1 and 2, and THREE othe questions.
UNIVERSITY OF EAST ANGLIA School of Mathematics Main Seies UG Examination 2015 16 FLUID DYNAMICS WITH ADVANCED TOPICS MTH-MD59 Time allowed: 3 Hous Attempt QUESTIONS 1 and 2, and THREE othe questions.
