Journal of Geoscience Education, v. 47, n. 1, p , 1999, January 1999 (edits, June 2005)
|
|
|
- Jeffry Norman
- 5 years ago
- Views:
Transcription
1 Journal of Geoscience Education, v. 47, n. 1, p , 1999, January 1999 (edits, June 005) Computational Geology 4 Mapping with Vectors H.L. Vacher, Department of Geology, University of South Florida, 40 E. Fowler Ave., Tampa FL 3360 Introduction Vectors Who needs them? If you have had a course in physics, you know that physicists can't live without them. The reason is that key quantities such as velocity and force have direction, and vectors deal explicitly with direction. But geologists, too, need to think about direction all geologists, not only geodynamicists who deal explicitly with forces and enjoy physics. For geologists, no matter what else they may think about, must think about location, and thinking about location in a quantitative way quickly brings a person to direction. As an example, consider your present location. Now think about some other location, say the location of your book that tells about maps (it might come in handy soon). What is the location of that book relative to you? Let's say that it is,730 m in a direction NNE. Now, think of yourself as the origin of a planar coordinate system (on a planar world); then, the position of the book can be stipulated by two numbers, r and θ. The r is the distance,,730 m. The θ is an angle defining the direction and requires a little explanation. In order for θ to mean anything it must be measured from a reference line that is understood by everyone. This agreed-upon direction is the direction of positive x, which, for map work, is taken as due east. By convention, θ is measured counterclockwise from the x-axis. So when θ = 90, the point stipulated by r and θ lies on the y-axis in the direction of positive y, which means it lies due north of the origin (the x- and y-axes form a right-handed, Cartesian coordinate system). The r,θ coordinates are probably familiar to you; they are the polar coordinates of the point in question. The polar coordinates of your book, then, are: r =,730 m and θ = 67.5 (recall, you are the origin of the coordinate system). If you are uncertain where the value of θ came from, get that book on maps and look up bearing and azimuth. The bearing of NNE is N. 5 E, and the Azimuth is.5. Then, θ is E or Now, back to vectors, which have both magnitude and direction. The position of the book relative to you (or, in general, the origin of the coordinate system), can be thought of as a vector: the magnitude is,730 m, and the direction is θ = 67.5 counterclockwise from the x- axis. This vector is known as the position vector, which can be thought of as a directed distance from the center of a coordinate system to a point under examination. Think of it as an arrow starting at the origin of the coordinate system and ending at the point. Vectors are generally written in a way that distinguishes them from mere directionless numbers (scalars). Sometimes the vectors are written with an arrow over the letter; sometimes they are represented in bold font. We will use bold letters here. The position vector is denoted by r. This essay is about r and how it can help you deal
2 with positions on the surface of the Earth that is, geographic location as represented on maps. Components of r. Thinking of vectors in terms of magnitude and direction is intuitive for geologists. For purposes of calculation, however, it is generally more useful to think of them in terms of components along the axes of a Cartesian coordinate system: x,y for two-dimensional problems. The vector describing a distance of,730 m in a direction 67.5 north of east can be thought of as the vector sum of two vectors, one along the x-axis and the other along the y-axis; specifically, the first is a vector with magnitude 1,045 m in the direction of due east, and the second is a vector with magnitude,5 m in the direction of due north (assuming the original data are good to four significant figures). Saying that they are combined by a vector sum means that the tail of one is placed at the origin of the coordinate system, and the tail of the second is placed at the arrowhead of the first; then the original position vector, r, is the vector that extends from the origin of the coordinate system to the arrowhead of the second (along the hypotenuse of the right triangle defined by the west-to-east and the south-to-north vectors). You can think of this vector sum as the result of walking 1,045 m to the east and then,5 m to the north; you wind up at a distance of,730 m in a direction of θ = 67.5 from where you started. Note that you get to the same place by walking,5 m north first and then 1,045 m east. In other words, the order of terms in the vector sum does not matter. In the language of mathematics, vector addition is commutative. This vector sum that produces r can be succinctly written as: r = 1045 i + 5 j (1) where the numbers are in meters, and i and j are, themselves, vectors. The i and j are unit vectors, meaning that the magnitude of each of them is exactly 1, and they are dimensionless; all they do is indicate direction. The unit vector i extends in the positive x-direction, and j extends in the positive y-direction. The first term, 1,045i, is a vector extending 1,045 m in the direction of due east; the second term,,5j, is a vector of,5 m in the direction of due north. Because x and y (and i and j) are at right angles to each other, the vector sum expressed in Equation 1 can be thought of as a right triangle with the west-east leg being 1,045 m, and the south-north leg being,5 m. So, by the Pythagorean Theorem, the magnitude of r in meters or the length of the hypotenuse is: r = , () where the vertical lines on the sides of r (i.e., the absolute value of r) denote the magnitude of the vector. Also (remembering your trig), the angle counterclockwise from east is: θ = arctan (5/1045) = arctan (.413) = 67.5 (3) Where did the numbers 1,045 and,5 in Equations 1 and come from? The first is r cos(67.5 ), and the second is r sin(67.5 ). You should note that converting between the two forms of the position vector the distance-and-direction form, and the xy-components form is the same as converting between
3 polar and Cartesian coordinates of the point at the end of the position vector. For, if you are given the polar coordinates (r,θ) of a point relative to an origin, then the Cartesian coordinates of the point relative to the same origin are x = rcosθ and y = rsinθ. (4) This is the same as saying that to walk from the origin to the point (r,θ), you can walk a distance r*cos(θ) in the x-direction and then walk a distance r*sin(θ) in the y-direction. The vector r, then, can be expressed by: r = r cos(θ ) i + r sin(θ ) j (5) To transform the location of a point from Cartesian to polar coordinates, you use r = x + y and θ = arctan( y / x ). (6) These quantities give the magnitude and direction, respectively, of the position vector from the origin of the coordinate system to the point in question. Equations and 3 are simply applications of Equations 6. Finding yourself One of the most basic problems in field geology is finding your location on a map; there's no point in making a serious observation if you can't record where it is. If you are on land, you generally can be guided by the contours on your map to figure out where you are. If it is totally hopeless, then the old-fashioned way you can sight on two landmarks that are on the map and triangulate your location. (The new-fashioned way is to use your GPS system, which, for the purpose of this column, we will say has dead batteries). If you are on the sea and close to shore, you can triangulate on two lighthouses to find the location of your boat before it locates a reef. The routine way of solving this triangulation problem is graphically, as follows. First, find the two landmarks on the map: let's call them A and B. Second, in the field, determine the direction from you to each of the landmarks (with a compass); let's say the direction to A is N0E (or Azimuth 0 ), and the direction to B is S60E (or Azimuth 10 ). Third, on the map, draw a line through A with a direction of N0E, and a line through B with a direction of S60E. Where the two lines cross is your location on the map. Now here is another way you can solve the problem. Think of your unknown location as the origin of a coordinate system, with the positive x-axis going due east and the positive y-axis going due north. The vector r A gives the position of A, and the vector r B gives the position of B. We do not know the length of these vectors, but we do know their direction. Because we do not know the length of r A and r B, let's forget about these vectors and their length for the moment and focus on unit vectors, e A and e B, corresponding to r A and r B, respectively. A unit vector, as you know, is a vector with a magnitude of 1; you can think of it as a vector that is of interest only because of its direction. The unit vectors i and j are the bestknown examples, but there are others. Whereas i and j necessarily point in the direction of coordinate axes, the unit vectors e A and e B point in other specific directions: parallel to r A and r B, respectively. So r A can be written as r A e A, where r A (note, not bold) denotes the magnitude of
4 r A, and e A denotes the direction of r A. Similarly, r B can be written as r B e B. Now resolve e A and e B into their component vectors. Because e A has the same direction as r A, the direction of e A is N0E. The counterclockwise angle between the x-axis and e A, therefore, is θ = 70. Because e A = 1 (e A is a unit vector), then: e A = cos(70 ) i + sin(70 ) j = i j, (7) again assuming that the measured directions are good to four significant figures. Similarly, from the direction of e B (S60E), the counterclockwise angle between the x-axis and e B is 30, and so e B = cos(-30 ) i + sin(-30 ) j = i j, (8) Having established vectors giving the direction to the landmarks, you now bring in information about the location of the landmarks on your map. Given the map location of the landmarks and the measured directions to them in the field, you can determine your location on your map by use of similar triangles. Suppose, for example, the coordinates of Landmark A are (x A,y A ), relative to the origin of the map's coordinate system; these map coordinates can be as simple as the number of centimeters east and north, respectively, from the lower-left (southwest) corner of the map sheet. Then letting (x,y) be the map coordinates of your location relative to the same origin, the lower-left corner of the map the distance that Landmark A is east of you on the map is x A x, and the distance that Landmark A is north of you on the map is y A y. The ratio of these two distances is the same as the ratio of the corresponding components of e A : y x A A y x = = , (9) where the numbers and come from Equation 7. Similarly, letting (x B,y B ) be the map coordinates of Landmark B, y x B B y x = = , (10) from Equation 8. Equations 9 and 10 are two equations in the two unknowns, x and y. They are your map coordinates. Solve Equations 9 and 10 for x and y, and you have found where you are on the map. Without intending to go far into the subject of solving simultaneous equations, I would like to point out that there is a very easy way of proceeding to an answer. First, get Equations 9 and 10 into the following form: ax 1 + by 1 = c ax + by = c Then, the solution is given by: 1. (11)
5 x = cb ab cb ab and ac a c y = 1 1. (1) ab 1 a1 b Equations 1 are an application of Cramer's Rule, which you may have encountered in an algebra course in connection with determinants. The technique is named for Gabriel Cramer ( ), a contemporary and countryman of the Swiss mathematician, Leonhard Euler (see the Computational Geology columns of the preceding two issues). To illustrate how easy the computation is, let's complete the problem by assuming that Landmark A is located at x A = 5.5 cm and y A = 4.3 cm from the lower left corner of the map, and that Landmark B is located at x B = 3.3 cm and y B = 9.6 cm from the lower left corner. From these coordinates, and carrying four digits, Equations 9 and 10 in the form of Equations 11 are:.748x y = x y = 8.4 (13) Plugging the coefficients in Equations 13 into Equations 1, you have: (7.77)( 1) ( 8.4)( 1) x = (.748)( 1) ( )( 1) (14) (.748)( 8.4) ( )(7.77) y = (.748)( 1) ( )( 1) Chug out the arithmetic of Equations 14, and you get x = 16.8 and y = 18.5, which means that your location on the map is 16.8 cm to the right and 18.5 cm up from the lower left corner of the map sheet. Calculating distances Now that you know where you are on your map, you can easily calculate your distance to each of the two landmarks. Your map coordinates are (16.8,18.5). The map coordinates of Landmark A are (5.5, 4.3), and the map coordinates of Landmark B are (3.3, 9.6). All these coordinates are in centimeters on the map. In general, the distance between two points (x 1,y 1 ) and (x,y ) is given by the Pythagorean sum: distance = ( x y. (15) x1) + ( y 1) This is the general form of the relation that we used way back at Equation. For the cases here (and with an extra digit),
6 r A = ( ) + ( ) = and r B = ( ) + ( ) = (16) in centimeters on the map. These distances on the map can be easily converted to distances in the field by consideration of the scale of the map. Let's say that the scale of the map is 1:100,000. Then every centimeter on the map corresponds to 100,000 cm in the field. Converting the centimeters to kilometers, 10 5 cm = (10 5 cm) (10 - m/cm) (10-3 km/m) = 1 km, (17) you see that your distances in the field to Locations A and B are 5.3 km and 17.9 km, respectively. (Notice, too, how convenient metric units are.) These distances are the magnitudes r A and r B, respectively, of position vectors r A and r B from you to Locations A and B. We also have the directions of r A and r B from the unit vectors e A and e B (Equations 7 and 8). Recalling that a vector is its magnitude multiplied by its unit vector, you have: r A = r A e A = 5.34 (0.340 i j) and r B = r B e B = ( i j). (18) Complete the multiplication, and you get the position vectors from you to A and to B: r A = 8.7 i j and r B = 15.5 i 8.9 j, (19) where the numbers are in kilometers. The same result can be obtained a more direct way. You have the coordinates of your location and the two landmarks in centimeters on the map. Convert these to coordinates on the ground in kilometers by using the map scale. This gives (16.8, 18.5) for your location, (5.5, 4.3) for Location A, and (3.3, 9.6) for Location B, all in kilometers. Then you can use a general equation for the position vector from Point 1 at (x 1, y 1 ) to Point at (x, y ): r = (x x 1 ) i + (y y 1 ) j. (0) For the position vector from you to the two locations, Equation 0 gives r A = ( ) i + ( ) j = 8.7 i j and r B = ( ) i + ( ) j = 15.5 i 8.9 j, (1) which is the same result as Equations 19. Some other calculations Before proceeding with a three-dimensional problem, it is useful to discuss some vector operations in the context of our two-dimensional position vectors of Equations 19.
7 We have already noted that vectors can be added. In Equation 1, for example, the terms stating the vector components of r are added together vectorally. Similarly, if we were to add r A and r B together we would get a vector with the length and direction that would take you directly from your position at (16.8, 18.5) to a point that you could also reach by walking N0E for 5.34 km and then S60E for km. This vector is obtained by adding the x-components together and the y-components together: Thus (from Equation 19): r 1 + r = (x 1 i + y 1 j ) + (x i + y j ) = (x 1 + x ) i + (y 1 + y ) j. () r A + r B = (8.7 i j ) + (15.5 i 8.9 j ) = 4. i j. (3) The length and direction of this vector can be found from the Pythagorean sum and the arctangent, respectively: r A + r B = = 8.4 km 14.9 θ = arctan = 3. (4) 4. Then, to find where this would get you, simply add the vector (Equation 3) to the coordinates of your original location: (16.8, 18.5) + (4., 14.9) = (41.0, 33.4). (5) Similarly, two vectors can be subtracted: r r 1 = (x i + y j ) (x 1 i + y 1 j ) = (x x 1 ) i + (y y 1 ) j. (6) This results in a vector r r 1 that extends from the arrowhead of r 1 to the arrowhead of r. In the case of our position vectors, r A and r B, the vector r B r A extends from Landmark A at (5.5, 4.3) to Landmark B at (3.3, 9.6). From Equation 6, this vector is: r B r A = (15.5 i 8.9 j ) (8.7 i 3.8 j ) = 6.8 i 3.7 j. (7) This vector can also be obtained from the coordinates of the two landmarks: r B r A = ( ) i + ( ) j = 6.8 i 3.7 j. (8)
8 No matter how the vector is obtained, its length and direction is easily found from the Pythagorean sum and arctangent, respectively: r B r A = ( 3.7) = 33.4 km, and 3.8 θ = arctan = 78, (9) 6.8 where θ indicates a direction of 78 south of east (Azimuth 168, or S1E). Thus if you start at (16.8, 18.5), walk 5.3 km in a direction of N0E to Landmark A, and then turn and walk 33.4 km in a direction S1E, you will arrive at Landmark B (3.3, 9.6), which you could have walked to in 17.9 km in a direction of S60E. In other words: r A + (r B r A ) = r B. (30) There are two ways of multiplying vectors together: the dot product and the crossproduct. We will not need the cross-product here (see CG-14), but the dot product is very useful now because it can supply the angle between vectors. The dot product of two vectors is defined as the product of their magnitudes times the cosine of the angle between them: r 1 r = r 1 r cos (λ), (31) where λ is the angle between r 1 and r. The dot product results in a scalar, and so it is also called the scalar product. From Equation 31, it can be shown (we won't do it) that the dot product is numerically the same as the sum of the product of the two x-components and the product of the two y-components. That is: r 1 r = (x 1 i + y 1 j ) (x i + y j ) = x 1 y 1 + x y. (3) Combining Equations 31 and 3 gives you a means of calculating the angle: (33) cos (λ) = (x 1 y 1 + x y ) / ( r 1 r ). For the two position vectors we have been considering: cos (λ) = (8.7 i j ) (15.5 i 8.9 j ) / ( 8.7 i j 15.5 i 8.9 j ) (8.7)(15.5) + (3.8)( 8.9) or, cos λ = = ( 8.9) and so, λ = 100. (34)
9 The answer, 100, is obviously the angle between a vector going N0E (Az 0 ) and another going S60E (Az 10 ). For position vectors in three dimensions, however, the answer is not so obvious. A three-dimensional problem Vectors earn their keep in three-dimensional problems for example, in working out the relative position of locations on multi-level maps. As an illustration, consider the following cave. You enter the cave along an inclined shaft that runs in a direction N43W for a distance of 48 m with a plunge (the slope down from the horizontal) of 38. At a distance of 8 m down the shaft, a tunnel goes off in a direction of N48E and up an incline of 3. Call this Level A, and let Point A1 be the start of the tunnel at the shaft. At the bottom of the shaft (48 m down from the entrance), a second tunnel goes off from the shaft. This second tunnel heads in a direction of N1W and up an incline of 6. Call this Level B, and let Point B1 be the start of the tunnel at the shaft. You explore both tunnels. Starting at A1, the tunnel at Level A continues at a constant bearing and incline for 49 m, where it turns (Point A). The new direction is S70W, and the tunnel descends at a plunge of 1 for 36 m to Point A3, where the tunnel ends. Starting at Point B1, the tunnel at Level B continues at a constant bearing and incline for a distance of 55 m, and then it turns (Point B) and goes for 47 m in a direction of S40E and up an incline of 4. At this point, Point B3, the tunnel ends. You can probably guess the questions. Where are A3 and B3 relative to the entrance of the cave and relative to each other? How far away are they from each other? You start by defining an origin of an xyz-coordinate system. An obvious choice is the entrance to the cave. Let x be due east, y be due north, and z be straight up. The procedure then is to convert all of the given information into point-to-point vectors; then add appropriate segments to get the position vectors to A3 and B3; then subtract the two position vectors to get the vector between A3 and B3. Let v be a general vector for which you know its length v, its azimuth (AZ) in the horizontal plane, and its plunge (PL) downward from the horizontal plane. Then, with a little trig, you can show: (1) The projection of v onto the z-axis is v z = v cos (90 + PL) ; (35) () The projection of v onto the xy-plane (horizontal) is v H = v sin (90 + PL); (36) (3) The projection of v onto the positive y-axis is v y = v H cos (AZ) = v cos (AZ) sin (90 + PL) ; and (37) (4) The projection of v onto the positive x-axis is: v x = v H cos (90 AZ) = v cos (90 AZ) sin (90 + PL). (38)
10 We start with the inclined shaft. Let v O A1 be the vector from the entrance (Origin) to A1. Then (carrying more digits than we want in the end), the three components are: (v O A1 ) x = 8 cos( ) sin ( ) = 15.0 (v O A1 ) y = 8 cos(317 ) sin ( ) = 16.1 (v O A1 ) z = 8 cos( ) = 17., (39) where all the lengths are in meters. Combining the components, the vector is: v O A1 = 15.1 i j 17. k, (40) where k is the unit vector along the positive z-axis. Similarly, the vector from the entrance to B1 is: v O B1 = 5.8 i j 9.6 k. (41) You can check these results by checking that the components produce the known magnitude. For example, from the general relation, v = v + v + v, (4) x y z you have v O B1 = ( 58) ( 9.6), (43) which checks. By the same process, you can determine the vectors from A1 to A and from A to A3: Similarly: v A1 A = 36.4 i j +.6 k, and v A A3 = 33.1 i 1.0 j 7.5 k. (44) v B1 B = 19.6 i j +5.8 k, and v B B3 = 30.1 i 36.0 j +3.3 k. (45) Now add up the appropriate vectors. For the position vector r A3 from the origin at the entrance of the cave to A3: r A3 = v O A1 + v A1 A + v A A3 = ( ) i + ( ) j + ( ) k, = 11.7 i j.1 k, (46)
11 which means that A3 is 11.7 m west of the cave entrance, 36.8 m north of it, and.1 m below it. By similar arithmetic, the position vector r B3 is: r B3 = 15.3 i j 0.5 k. (47) The vector from A3 to B3 is found by subtracting r A3 from r B3. Thus: v A3 B3 = r B3 r A3 = 3.6 i j k, (48) which means that B3 is 4 m west, 6 m north, and m up(!) from A3 (so much for the two "levels"). The straight-line distance between the two points is: v A3 B3 = ( + 3.6) = 7. (49) or 7 m. The direction θ (in the horizontal plane, clockwise from the x-axis) is found from the ratio of the y- and x-components: 6.0 θ = arctan = arctan( 1.667). (50) 3.6 The two possible answers are θ = 59 and θ = 39 corresponding to AZ = 149 (S31E) and AZ = 39 (N31W), respectively. The latter is the appropriate choice. Finally, the plunge is found from the dot product of v A3 B3 and the projection of v A3 B3 onto the xy-plane (you get this projection by simply omitting the z-component of the sloping vector): cos (λ) = (-3.6i + 6.0j + 1.6k) (-3.6i + 6.0j) / ( -3.6i + 6.0j + 1.6k -3.6i + 6.0j ), (51) from which the plunge works out to be 13. Vectors from the center of the Earth As our last example, we will consider a question that you might not think to solve with vectors: How far is it between, say, Seattle and Miami? Here, "how far" means the shortest distance on, as opposed to through, the sphere of the Earth. In other words, what is the length of the great-circle arc between the two points? All you need to know is the radius of the Earth (6,370 km, to three significant digits), the latitude and longitude of Seattle (47.35N, 1.0W) and Miami (5.45N, 80.15W), the meaning of latitude and longitude in terms of coordinates, and a little about vectors. Specifically, what you need to know about vectors is that the dot product gives you the angle between two vectors. Conceptually, the key to the problem is that the latitude and longitude of a point on the globe allow you to define a position vector from the center of the Earth to the point. You merely need to convert the latitude and longitude information to Cartesian coordinates. To do this, define a (right-handed) coordinate system with the origin at the center of the Earth (i.e., a geocentric coordinate system that rotates with the Earth). Let the z-axis run up through the North Pole; let the x-axis pass through the equator at the Prime (or Greenwich) Meridian (i.e., where latitude = 0 and longitude = 0); and let the y-axis pass through the equator at longitude 90
12 E (so that the y-axis is 90 counterclockwise from the x-axis as viewed looking down the z-axis). By the convention that angles in the xy-plane are positive counterclockwise from the x-axis: east longitude is positive, and west longitude is negative. Similarly, latitude is positive in the Northern Hemisphere and negative in the Southern Hemisphere. Then, the angular information together with the radius of the Earth gives three coordinates that specify the location of points on the surface of the Earth. For our two points of interest: Seattle: r = 6,370 km, Θ lat = o, Θ long = 1.0 o W Miami: r = 6,370 km, Θ lat = 5.45 o, Θ long = o W How do these latitudes and longitudes translate into the geocentric Cartesian coordinates? The z-coordinate is the projection of the position vector (from the center of the Earth) onto the z-axis and is given by z = r sin (Θ lat ). (5) The projection of the position vector onto the equatorial plane (the xy-plane) of the Earth is r H = r cos (Θ lat ). (53) Then, the x-coordinate is the projection of this equatorial projection (r H ) onto the x-axis: x = r cos (Θ lat ) cos (Θ lat ). (54) Similarly, the y-coordinate is the projection of r H onto the y-axis: y = r cos (Θ lat ) sin (Θ lat ). (55) With these equations, the geocentric Cartesian coordinates of the two points are: Seattle: x =,300, y = 3,65, z = 4,685 Miami: x = 984, y = 5,667, z =,737, all in kilometers. So, you can immediately write down the two position vectors: r Seattle = 300 i 365 j k r Miami = 984 i 5667 j +737 k. (56) The question now is: What is the angle between the two vectors of equations 56? The equation to use is equation 33, which for this problem becomes: cos (λ) = (r Seattle r Miami ) / r Earth. (57) Then, multiplying out as in equations 34, we get: cos (λ) = [( 300)(984) + ( 365)( 5667) + (4685)(737)] / 6370 = 0.770
13 λ = (58) To complete the solution, we need only to calculate the length on a spherical Earth that corresponds to a geocentric angle of In other words: How long is 39.6/360 (or 11.0%) of the Earth's circumference? The Earth's circumference is 40,000 to three significant figures. So, the great-circle distance from Seattle to Miami is 11% of 40,000 km, or 4,400 km to three significant figures. Not that there would be any reason other than simple curiosity, but we can also calculate the straight-line distance from Seattle to Miami (i.e., the length of the shortest tunnel between them). First, subtract the two position vectors to obtain the vector that runs from Seattle straight to Miami: r Mia r Sea = ( ) i + ( ) j + ( ) k = 384 i 015 j 1948 k. (59) Then apply equation 4 (the three-dimensional Pythagorean relation) to find the magnitude of the vector of equation 59: r Mia r Sea = ( 015) + ( 1948) = 4317, (60) or 4,30 km to three significant figures. In passing, a historical note is appropriate. It is no coincidence that the circumference of the spherical Earth came out to be the nice round number, 40,000 km. The 40,000-km circumference makes the length of a quadrant of a meridian (i.e., the great-circle distance from the pole to the equator) equal to 10,000 km. It is that length, because the meter was defined to make it so. The commission that defined the metric system was interested in units that related to what were perceived as natural, fundamental quantities. For length, they selected the circumference of the Earth as a fundamental quantity and defined the meter to be 1/10 6 of a quadrant of that length. This was shortly after the French Revolution, and the panel included such historical figures as Legendre and Laplace, of mathematical fame, and Lavoisier, the socalled father of chemistry. This definition set into motion efforts to determine the length of a meridian (or the length of a degree of latitude), which in turn led to discoveries about the shape of the Earth and the deflection of plum bobs near large masses (i.e., isostasy). As a result of this original metric-scale definition of the meter, it is easy to remember the size of the Earth. The circumference is 4 10,000 km; the radius is this value divided by π (or km to three significant figures). Concluding remarks You learn vectors in your freshman physics course. But don't leave them there. They can help you with the most basic of geography and geology problems. For example, how else would you get the shortest distance between two points on the surface of the Earth? Don't say, "use a map", because that won't work (unless you mean a globe). Most people I ask don't know; some tell me there are places on the Web to go, and some mention their GPS system. But if you
14 need an answer to this or any other problem involving distance and direction, use the trusty vectors.
9.4 Polar Coordinates
 9.4 Polar Coordinates Polar coordinates uses distance and direction to specify a location in a plane. The origin in a polar system is a fixed point from which a ray, O, is drawn and we call the ray the
9.4 Polar Coordinates Polar coordinates uses distance and direction to specify a location in a plane. The origin in a polar system is a fixed point from which a ray, O, is drawn and we call the ray the
Notes: Vectors and Scalars
 A particle moving along a straight line can move in only two directions and we can specify which directions with a plus or negative sign. For a particle moving in three dimensions; however, a plus sign
A particle moving along a straight line can move in only two directions and we can specify which directions with a plus or negative sign. For a particle moving in three dimensions; however, a plus sign
Vectors and 2D Kinematics. AIT AP Physics C
 Vectors and 2D Kinematics Coordinate Systems Used to describe the position of a point in space Coordinate system consists of a fixed reference point called the origin specific axes with scales and labels
Vectors and 2D Kinematics Coordinate Systems Used to describe the position of a point in space Coordinate system consists of a fixed reference point called the origin specific axes with scales and labels
Vectors a vector is a quantity that has both a magnitude (size) and a direction
 Vectors In physics, a vector is a quantity that has both a magnitude (size) and a direction. Familiar examples of vectors include velocity, force, and electric field. For any applications beyond one dimension,
Vectors In physics, a vector is a quantity that has both a magnitude (size) and a direction. Familiar examples of vectors include velocity, force, and electric field. For any applications beyond one dimension,
SECTION 6.3: VECTORS IN THE PLANE
 (Section 6.3: Vectors in the Plane) 6.18 SECTION 6.3: VECTORS IN THE PLANE Assume a, b, c, and d are real numbers. PART A: INTRO A scalar has magnitude but not direction. We think of real numbers as scalars,
(Section 6.3: Vectors in the Plane) 6.18 SECTION 6.3: VECTORS IN THE PLANE Assume a, b, c, and d are real numbers. PART A: INTRO A scalar has magnitude but not direction. We think of real numbers as scalars,
Physics 2A Chapter 1 - Vectors Fall 2017
 These notes are eight pages. That includes some diagrams, but I realize reading them could get a bit tedious. So here is a quick summary: A vector quantity is one for which direction is relevant, like
These notes are eight pages. That includes some diagrams, but I realize reading them could get a bit tedious. So here is a quick summary: A vector quantity is one for which direction is relevant, like
FORCE TABLE INTRODUCTION
 FORCE TABLE INTRODUCTION All measurable quantities can be classified as either a scalar 1 or a vector 2. A scalar has only magnitude while a vector has both magnitude and direction. Examples of scalar
FORCE TABLE INTRODUCTION All measurable quantities can be classified as either a scalar 1 or a vector 2. A scalar has only magnitude while a vector has both magnitude and direction. Examples of scalar
A SCALAR is ANY quantity in physics that has MAGNITUDE, but NOT a direction associated with it. Magnitude A numerical value with units.
 Vectors and Scalars A SCALAR is ANY quantity in physics that has MAGNITUDE, but NOT a direction associated with it. Magnitude A numerical value with units. Scalar Example Speed Distance Age Heat Number
Vectors and Scalars A SCALAR is ANY quantity in physics that has MAGNITUDE, but NOT a direction associated with it. Magnitude A numerical value with units. Scalar Example Speed Distance Age Heat Number
Coordinate Systems. Chapter 3. Cartesian Coordinate System. Polar Coordinate System
 Chapter 3 Vectors Coordinate Systems Used to describe the position of a point in space Coordinate system consists of a fixed reference point called the origin specific axes with scales and labels instructions
Chapter 3 Vectors Coordinate Systems Used to describe the position of a point in space Coordinate system consists of a fixed reference point called the origin specific axes with scales and labels instructions
Notes on multivariable calculus
 Notes on multivariable calculus Jonathan Wise February 2, 2010 1 Review of trigonometry Trigonometry is essentially the study of the relationship between polar coordinates and Cartesian coordinates in
Notes on multivariable calculus Jonathan Wise February 2, 2010 1 Review of trigonometry Trigonometry is essentially the study of the relationship between polar coordinates and Cartesian coordinates in
VECTORS. 3-1 What is Physics? 3-2 Vectors and Scalars CHAPTER
 CHAPTER 3 VECTORS 3-1 What is Physics? Physics deals with a great many quantities that have both size and direction, and it needs a special mathematical language the language of vectors to describe those
CHAPTER 3 VECTORS 3-1 What is Physics? Physics deals with a great many quantities that have both size and direction, and it needs a special mathematical language the language of vectors to describe those
Halliday/Resnick/Walker 7e Chapter 3
 HRW 7e Chapter 3 Page 1 of 7 Halliday/Resnick/Walker 7e Chapter 3 1. The x and the y components of a vector a lying on the xy plane are given by a = acos θ, a = asinθ x y where a = a is the magnitude and
HRW 7e Chapter 3 Page 1 of 7 Halliday/Resnick/Walker 7e Chapter 3 1. The x and the y components of a vector a lying on the xy plane are given by a = acos θ, a = asinθ x y where a = a is the magnitude and
Vectors. In kinematics, the simplest concept is position, so let s begin with a position vector shown below:
 Vectors Extending the concepts of kinematics into two and three dimensions, the idea of a vector becomes very useful. By definition, a vector is a quantity with both a magnitude and a spatial direction.
Vectors Extending the concepts of kinematics into two and three dimensions, the idea of a vector becomes very useful. By definition, a vector is a quantity with both a magnitude and a spatial direction.
Chapter 3 Vectors. 3.1 Vector Analysis
 Chapter 3 Vectors 3.1 Vector nalysis... 1 3.1.1 Introduction to Vectors... 1 3.1.2 Properties of Vectors... 1 3.2 Coordinate Systems... 6 3.2.1 Cartesian Coordinate System... 6 3.2.2 Cylindrical Coordinate
Chapter 3 Vectors 3.1 Vector nalysis... 1 3.1.1 Introduction to Vectors... 1 3.1.2 Properties of Vectors... 1 3.2 Coordinate Systems... 6 3.2.1 Cartesian Coordinate System... 6 3.2.2 Cylindrical Coordinate
Module 3: Cartesian Coordinates and Vectors
 Module 3: Cartesian Coordinates and Vectors Philosophy is written in this grand book, the universe which stands continually open to our gaze. But the book cannot be understood unless one first learns to
Module 3: Cartesian Coordinates and Vectors Philosophy is written in this grand book, the universe which stands continually open to our gaze. But the book cannot be understood unless one first learns to
Energy Efficiency, Acoustics & Daylighting in building Prof. B. Bhattacharjee Department of Civil Engineering Indian Institute of Technology, Delhi
 Energy Efficiency, Acoustics & Daylighting in building Prof. B. Bhattacharjee Department of Civil Engineering Indian Institute of Technology, Delhi Lecture - 05 Introduction & Environmental Factors (contd.)
Energy Efficiency, Acoustics & Daylighting in building Prof. B. Bhattacharjee Department of Civil Engineering Indian Institute of Technology, Delhi Lecture - 05 Introduction & Environmental Factors (contd.)
Chapter 3 Models of the Earth. 3.1 Finding Locations on the Earth. 3.1 Objectives
 Chapter 3 Models of the Earth 3.1 Finding Locations on the Earth 3.1 Objectives Explain latitude and longitude. How can latitude and longitude be used to find locations on Earth? How can a magnetic compass
Chapter 3 Models of the Earth 3.1 Finding Locations on the Earth 3.1 Objectives Explain latitude and longitude. How can latitude and longitude be used to find locations on Earth? How can a magnetic compass
Vectors Part 1: Two Dimensions
 Vectors Part 1: Two Dimensions Last modified: 20/02/2018 Links Scalars Vectors Definition Notation Polar Form Compass Directions Basic Vector Maths Multiply a Vector by a Scalar Unit Vectors Example Vectors
Vectors Part 1: Two Dimensions Last modified: 20/02/2018 Links Scalars Vectors Definition Notation Polar Form Compass Directions Basic Vector Maths Multiply a Vector by a Scalar Unit Vectors Example Vectors
Chapter 5 Trigonometric Functions of Angles
 Chapter 5 Trigonometric Functions of Angles Section 3 Points on Circles Using Sine and Cosine Signs Signs I Signs (+, +) I Signs II (+, +) I Signs II (, +) (+, +) I Signs II (, +) (+, +) I III Signs II
Chapter 5 Trigonometric Functions of Angles Section 3 Points on Circles Using Sine and Cosine Signs Signs I Signs (+, +) I Signs II (+, +) I Signs II (, +) (+, +) I Signs II (, +) (+, +) I III Signs II
Mathematical review trigonometry vectors Motion in one dimension
 Mathematical review trigonometry vectors Motion in one dimension Used to describe the position of a point in space Coordinate system (frame) consists of a fixed reference point called the origin specific
Mathematical review trigonometry vectors Motion in one dimension Used to describe the position of a point in space Coordinate system (frame) consists of a fixed reference point called the origin specific
Trigonometric ratios:
 0 Trigonometric ratios: The six trigonometric ratios of A are: Sine Cosine Tangent sin A = opposite leg hypotenuse adjacent leg cos A = hypotenuse tan A = opposite adjacent leg leg and their inverses:
0 Trigonometric ratios: The six trigonometric ratios of A are: Sine Cosine Tangent sin A = opposite leg hypotenuse adjacent leg cos A = hypotenuse tan A = opposite adjacent leg leg and their inverses:
The Essentials to the Mathematical world
 The Essentials to the Mathematical world There is nothing that is unachievable, any person can start the journey to you are starting, never give into hopelessness and always push on because nothing is
The Essentials to the Mathematical world There is nothing that is unachievable, any person can start the journey to you are starting, never give into hopelessness and always push on because nothing is
Math Refresher Answer Sheet (NOTE: Only this answer sheet and the following graph will be evaluated)
 Name: Score: / 50 Math Refresher Answer Sheet (NOTE: Only this answer sheet and the following graph will be evaluated) 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. MAKE SURE CALCULATOR
Name: Score: / 50 Math Refresher Answer Sheet (NOTE: Only this answer sheet and the following graph will be evaluated) 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. MAKE SURE CALCULATOR
Unit IV: Introduction to Vector Analysis
 Unit IV: Introduction to Vector nalysis s you learned in the last unit, there is a difference between speed and velocity. Speed is an example of a scalar: a quantity that has only magnitude. Velocity is
Unit IV: Introduction to Vector nalysis s you learned in the last unit, there is a difference between speed and velocity. Speed is an example of a scalar: a quantity that has only magnitude. Velocity is
Problem Set 1: Solutions 2
 UNIVERSITY OF ALABAMA Department of Physics and Astronomy PH 125 / LeClair Spring 2009 Problems due 15 January 2009. Problem Set 1: Solutions 2 1. A person walks in the following pattern: 3.1 km north,
UNIVERSITY OF ALABAMA Department of Physics and Astronomy PH 125 / LeClair Spring 2009 Problems due 15 January 2009. Problem Set 1: Solutions 2 1. A person walks in the following pattern: 3.1 km north,
11.8 Vectors Applications of Trigonometry
 00 Applications of Trigonometry.8 Vectors As we have seen numerous times in this book, Mathematics can be used to model and solve real-world problems. For many applications, real numbers suffice; that
00 Applications of Trigonometry.8 Vectors As we have seen numerous times in this book, Mathematics can be used to model and solve real-world problems. For many applications, real numbers suffice; that
CHAPTER II THE COORDINATES SYSTEM AND FORMULARIES
 CHAPTER II THE COORDINATES SYSTEM AND FORMULARIES www.loxodrome.org/ Introduction to Celestial Navigation/Chapter II THE CO-ORDINATES SYSTEMS AND FORMULARIES In previous section we had a purely geometrical
CHAPTER II THE COORDINATES SYSTEM AND FORMULARIES www.loxodrome.org/ Introduction to Celestial Navigation/Chapter II THE CO-ORDINATES SYSTEMS AND FORMULARIES In previous section we had a purely geometrical
Vector components and motion
 Vector components and motion Objectives Distinguish between vectors and scalars and give examples of each. Use vector diagrams to interpret the relationships among vector quantities such as force and acceleration.
Vector components and motion Objectives Distinguish between vectors and scalars and give examples of each. Use vector diagrams to interpret the relationships among vector quantities such as force and acceleration.
6. Vectors. Given two points, P 0 = (x 0, y 0 ) and P 1 = (x 1, y 1 ), a vector can be drawn with its foot at P 0 and
 6. Vectors For purposes of applications in calculus and physics, a vector has both a direction and a magnitude (length), and is usually represented as an arrow. The start of the arrow is the vector s foot,
6. Vectors For purposes of applications in calculus and physics, a vector has both a direction and a magnitude (length), and is usually represented as an arrow. The start of the arrow is the vector s foot,
Chapter 2 A Mathematical Toolbox
 Chapter 2 Mathematical Toolbox Vectors and Scalars 1) Scalars have only a magnitude (numerical value) Denoted by a symbol, a 2) Vectors have a magnitude and direction Denoted by a bold symbol (), or symbol
Chapter 2 Mathematical Toolbox Vectors and Scalars 1) Scalars have only a magnitude (numerical value) Denoted by a symbol, a 2) Vectors have a magnitude and direction Denoted by a bold symbol (), or symbol
Vector Spaces. Chapter 1
 Chapter 1 Vector Spaces Linear algebra is the study of linear maps on finite-dimensional vector spaces. Eventually we will learn what all these terms mean. In this chapter we will define vector spaces
Chapter 1 Vector Spaces Linear algebra is the study of linear maps on finite-dimensional vector spaces. Eventually we will learn what all these terms mean. In this chapter we will define vector spaces
Transforming from Geographic to Celestial Coordinates
 Transforming from Geographic to Celestial Coordinates Michael McEllin 1 Introduction The simplest astronomical observation of all is that the stars appear to move around the Earth (which, of course is
Transforming from Geographic to Celestial Coordinates Michael McEllin 1 Introduction The simplest astronomical observation of all is that the stars appear to move around the Earth (which, of course is
Physics 12. Chapter 1: Vector Analysis in Two Dimensions
 Physics 12 Chapter 1: Vector Analysis in Two Dimensions 1. Definitions When studying mechanics in Physics 11, we have realized that there are two major types of quantities that we can measure for the systems
Physics 12 Chapter 1: Vector Analysis in Two Dimensions 1. Definitions When studying mechanics in Physics 11, we have realized that there are two major types of quantities that we can measure for the systems
Latitude and Longitude:
 Latitude and Longitude: Finding Locations on Planet Earth. With thanks and credit to Step.com Typical Graph This is an example of a typical graph. It is made up of points that are connected by a line.
Latitude and Longitude: Finding Locations on Planet Earth. With thanks and credit to Step.com Typical Graph This is an example of a typical graph. It is made up of points that are connected by a line.
+ 35º 53ʹ 16ʺ 84º 09ʹ 35ʺ
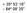 + 35º 53ʹ 16ʺ 84º 09ʹ 35ʺ 35º 53ʹ 16ʺ N 84º 09ʹ 35ʺ W (the precise location of Farragut High School!) Spherical Coordinates Mapping a Sphere The student will be able to: HW: 1 Utilize and convert SI units
+ 35º 53ʹ 16ʺ 84º 09ʹ 35ʺ 35º 53ʹ 16ʺ N 84º 09ʹ 35ʺ W (the precise location of Farragut High School!) Spherical Coordinates Mapping a Sphere The student will be able to: HW: 1 Utilize and convert SI units
AP Physics 1 Summer Assignment 2016
 AP Physics 1 Summer Assignment 2016 You need to do this assignment on your own paper AND YOU MUST SHOW ALL OF YOUR WORK TO RECEIVE CREDIT. You can put the answers on this assignment sheet or you can put
AP Physics 1 Summer Assignment 2016 You need to do this assignment on your own paper AND YOU MUST SHOW ALL OF YOUR WORK TO RECEIVE CREDIT. You can put the answers on this assignment sheet or you can put
The choice of origin, axes, and length is completely arbitrary.
 Polar Coordinates There are many ways to mark points in the plane or in 3-dim space for purposes of navigation. In the familiar rectangular coordinate system, a point is chosen as the origin and a perpendicular
Polar Coordinates There are many ways to mark points in the plane or in 3-dim space for purposes of navigation. In the familiar rectangular coordinate system, a point is chosen as the origin and a perpendicular
Vectors. Vectors are a very important type of quantity in science, but what is it? A simple definition might be:
 Vectors Vectors are a very important type of quantity in science, but what is it? A simple definition might be: Vector: A quantity that has magnitude, unit, and direction; and is commonly represented by
Vectors Vectors are a very important type of quantity in science, but what is it? A simple definition might be: Vector: A quantity that has magnitude, unit, and direction; and is commonly represented by
Kinematics in Two Dimensions; 2D- Vectors
 Kinematics in Two Dimensions; 2D- Vectors Addition of Vectors Graphical Methods Below are two example vector additions of 1-D displacement vectors. For vectors in one dimension, simple addition and subtraction
Kinematics in Two Dimensions; 2D- Vectors Addition of Vectors Graphical Methods Below are two example vector additions of 1-D displacement vectors. For vectors in one dimension, simple addition and subtraction
Chapter 8: Further Applications of Trigonometry
 308 Chapter 8 Chapter 8: Further Applications of Trigonometry In this chapter, we will eplore additional applications of trigonometry. We will begin with an etension of the right triangle trigonometry
308 Chapter 8 Chapter 8: Further Applications of Trigonometry In this chapter, we will eplore additional applications of trigonometry. We will begin with an etension of the right triangle trigonometry
Chapter 3. Vectors and. Two-Dimensional Motion Vector vs. Scalar Review
 Chapter 3 Vectors and Two-Dimensional Motion Vector vs. Scalar Review All physical quantities encountered in this text will be either a scalar or a vector A vector quantity has both magnitude (size) and
Chapter 3 Vectors and Two-Dimensional Motion Vector vs. Scalar Review All physical quantities encountered in this text will be either a scalar or a vector A vector quantity has both magnitude (size) and
Vectors. Introduction. Prof Dr Ahmet ATAÇ
 Chapter 3 Vectors Vectors Vector quantities Physical quantities that have both n u m e r i c a l a n d d i r e c t i o n a l properties Mathematical operations of vectors in this chapter A d d i t i o
Chapter 3 Vectors Vectors Vector quantities Physical quantities that have both n u m e r i c a l a n d d i r e c t i o n a l properties Mathematical operations of vectors in this chapter A d d i t i o
Precalculus Notes: Unit 6 Vectors, Parametrics, Polars, & Complex Numbers. A: Initial Point (start); B: Terminal Point (end) : ( ) ( )
 Syllabus Objectives: 5.1 The student will explore methods of vector addition and subtraction. 5. The student will develop strategies for computing a vector s direction angle and magnitude given its coordinates.
Syllabus Objectives: 5.1 The student will explore methods of vector addition and subtraction. 5. The student will develop strategies for computing a vector s direction angle and magnitude given its coordinates.
Section 2. Locating Astronomical Objects in the Night Sky What Do You See? What Do You See? Think About It. Investigate.
 Section 2 Locating Astronomical Objects in the Night Sky Section 2 Locating Astronomical Objects in the Night Sky What Do You See? What Do You See? Learning Outcomes In this section, you will Construct
Section 2 Locating Astronomical Objects in the Night Sky Section 2 Locating Astronomical Objects in the Night Sky What Do You See? What Do You See? Learning Outcomes In this section, you will Construct
2 VECTORS. Introduction. Chapter Outline. 2.1 Scalars and Vectors
 Chapter 2 Vectors 43 2 VECTORS Figure 2.1 A signpost gives information about distances and directions to towns or to other locations relative to the location of the signpost. Distance is a scalar quantity.
Chapter 2 Vectors 43 2 VECTORS Figure 2.1 A signpost gives information about distances and directions to towns or to other locations relative to the location of the signpost. Distance is a scalar quantity.
Relative and Absolute Directions
 Relative and Absolute Directions Purpose Learning about latitude and longitude Developing math skills Overview Students begin by asking the simple question: Where Am I? Then they learn about the magnetic
Relative and Absolute Directions Purpose Learning about latitude and longitude Developing math skills Overview Students begin by asking the simple question: Where Am I? Then they learn about the magnetic
Chapter 3 Vectors 3-1
 Chapter 3 Vectors Chapter 3 Vectors... 2 3.1 Vector Analysis... 2 3.1.1 Introduction to Vectors... 2 3.1.2 Properties of Vectors... 2 3.2 Cartesian Coordinate System... 6 3.2.1 Cartesian Coordinates...
Chapter 3 Vectors Chapter 3 Vectors... 2 3.1 Vector Analysis... 2 3.1.1 Introduction to Vectors... 2 3.1.2 Properties of Vectors... 2 3.2 Cartesian Coordinate System... 6 3.2.1 Cartesian Coordinates...
GPS Measurement Protocol
 GPS Measurement Protocol Purpose To determine the latitude, longitude, and elevation of your school and of all your GLOBE sites Overview The GPS receiver will be used to determine the latitude, longitude
GPS Measurement Protocol Purpose To determine the latitude, longitude, and elevation of your school and of all your GLOBE sites Overview The GPS receiver will be used to determine the latitude, longitude
Projectile Motion and 2-D Dynamics
 Projectile Motion and 2-D Dynamics Vector Notation Vectors vs. Scalars In Physics 11, you learned the difference between vectors and scalars. A vector is a quantity that includes both direction and magnitude
Projectile Motion and 2-D Dynamics Vector Notation Vectors vs. Scalars In Physics 11, you learned the difference between vectors and scalars. A vector is a quantity that includes both direction and magnitude
Journal of Geoscience Education, v. 46, n. 3, p , May 1998 (edits, June 2005)
 Journal of Geoscience Education, v. 46, n. 3, p. 292-295, May 1998 (edits, June 2005) Computational Geology 1 Significant Figures! H.L. Vacher, Department of Geology, University of South Florida, 4202
Journal of Geoscience Education, v. 46, n. 3, p. 292-295, May 1998 (edits, June 2005) Computational Geology 1 Significant Figures! H.L. Vacher, Department of Geology, University of South Florida, 4202
Section 8.2 Vector Angles
 Section 8.2 Vector Angles INTRODUCTION Recall that a vector has these two properties: 1. It has a certain length, called magnitude 2. It has a direction, indicated by an arrow at one end. In this section
Section 8.2 Vector Angles INTRODUCTION Recall that a vector has these two properties: 1. It has a certain length, called magnitude 2. It has a direction, indicated by an arrow at one end. In this section
General Physics I, Spring Vectors
 General Physics I, Spring 2011 Vectors 1 Vectors: Introduction A vector quantity in physics is one that has a magnitude (absolute value) and a direction. We have seen three already: displacement, velocity,
General Physics I, Spring 2011 Vectors 1 Vectors: Introduction A vector quantity in physics is one that has a magnitude (absolute value) and a direction. We have seen three already: displacement, velocity,
SiRF White Paper. Great Circle Distances Computing the distance between two points on the surface of the Earth
 SiRF White Paper Great Circle Distances Computing the distance between two points on the surface of the Earth Carl Carter May 17, 2002 Introduction The distance between two points on the Earth is computed
SiRF White Paper Great Circle Distances Computing the distance between two points on the surface of the Earth Carl Carter May 17, 2002 Introduction The distance between two points on the Earth is computed
DATE: MATH ANALYSIS 2 CHAPTER 12: VECTORS & DETERMINANTS
 NAME: PERIOD: DATE: MATH ANALYSIS 2 MR. MELLINA CHAPTER 12: VECTORS & DETERMINANTS Sections: v 12.1 Geometric Representation of Vectors v 12.2 Algebraic Representation of Vectors v 12.3 Vector and Parametric
NAME: PERIOD: DATE: MATH ANALYSIS 2 MR. MELLINA CHAPTER 12: VECTORS & DETERMINANTS Sections: v 12.1 Geometric Representation of Vectors v 12.2 Algebraic Representation of Vectors v 12.3 Vector and Parametric
Vector Addition and Subtraction: Graphical Methods
 Vector Addition and Subtraction: Graphical Methods Bởi: OpenStaxCollege Displacement can be determined graphically using a scale map, such as this one of the Hawaiian Islands. A journey from Hawai i to
Vector Addition and Subtraction: Graphical Methods Bởi: OpenStaxCollege Displacement can be determined graphically using a scale map, such as this one of the Hawaiian Islands. A journey from Hawai i to
Trig Identities. or (x + y)2 = x2 + 2xy + y 2. Dr. Ken W. Smith Other examples of identities are: (x + 3)2 = x2 + 6x + 9 and
 Trig Identities An identity is an equation that is true for all values of the variables. Examples of identities might be obvious results like Part 4, Trigonometry Lecture 4.8a, Trig Identities and Equations
Trig Identities An identity is an equation that is true for all values of the variables. Examples of identities might be obvious results like Part 4, Trigonometry Lecture 4.8a, Trig Identities and Equations
Introduction to Vectors
 Introduction to Vectors Why Vectors? Say you wanted to tell your friend that you re running late and will be there in five minutes. That s precisely enough information for your friend to know when you
Introduction to Vectors Why Vectors? Say you wanted to tell your friend that you re running late and will be there in five minutes. That s precisely enough information for your friend to know when you
Lesson 6 Plane Geometry Practice Test Answer Explanations
 Lesson 6 Plane Geometry Practice Test Answer Explanations Question 1 One revolution is equal to one circumference: C = r = 6 = 1, which is approximately 37.68 inches. Multiply that by 100 to get 3,768
Lesson 6 Plane Geometry Practice Test Answer Explanations Question 1 One revolution is equal to one circumference: C = r = 6 = 1, which is approximately 37.68 inches. Multiply that by 100 to get 3,768
Lecture 1 - Vectors. A Puzzle... Introduction. Vectors: The quest begins! TA s Information. Vectors
 Lecture 1 - Vectors Puzzle... The sum starts at 0. Players alternate by choosing an integer from 1 to 10 and then adding it to the sum. The player who gets to 100 wins. You go first. What is the winning
Lecture 1 - Vectors Puzzle... The sum starts at 0. Players alternate by choosing an integer from 1 to 10 and then adding it to the sum. The player who gets to 100 wins. You go first. What is the winning
Significant Figures & Vectors
 You have to complete this reading Booklet before you attempt the Substantive Assignment. Significant Figures Significant Figures & Vectors There are two kinds of numbers in the world Exact: o Example:
You have to complete this reading Booklet before you attempt the Substantive Assignment. Significant Figures Significant Figures & Vectors There are two kinds of numbers in the world Exact: o Example:
VECTORS REVIEW. ii. How large is the angle between lines A and B? b. What is angle C? 45 o. 30 o. c. What is angle θ? d. How large is θ?
 VECTOS EVIEW Solve the following geometric problems. a. Line touches the circle at a single point. Line etends through the center of the circle. i. What is line in reference to the circle? ii. How large
VECTOS EVIEW Solve the following geometric problems. a. Line touches the circle at a single point. Line etends through the center of the circle. i. What is line in reference to the circle? ii. How large
Be prepared to take a test covering the whole assignment in September. MATH REVIEW
 P- Physics Name: Summer 013 ssignment Date Period I. The attached pages contain a brief review, hints, and example problems. It is hoped that combined with your previous math knowledge this assignment
P- Physics Name: Summer 013 ssignment Date Period I. The attached pages contain a brief review, hints, and example problems. It is hoped that combined with your previous math knowledge this assignment
Chapter 7.4: Vectors
 Chapter 7.4: Vectors In many mathematical applications, quantities are determined entirely by their magnitude. When calculating the perimeter of a rectangular field, determining the weight of a box, or
Chapter 7.4: Vectors In many mathematical applications, quantities are determined entirely by their magnitude. When calculating the perimeter of a rectangular field, determining the weight of a box, or
HOW TO THINK ABOUT POINTS AND VECTORS WITHOUT COORDINATES. Math 225
 HOW TO THINK ABOUT POINTS AND VECTORS WITHOUT COORDINATES Math 225 Points Look around. What do you see? You see objects: a chair here, a table there, a book on the table. These objects occupy locations,
HOW TO THINK ABOUT POINTS AND VECTORS WITHOUT COORDINATES Math 225 Points Look around. What do you see? You see objects: a chair here, a table there, a book on the table. These objects occupy locations,
Definitions In physics we have two types of measurable quantities: vectors and scalars.
 1 Definitions In physics we have two types of measurable quantities: vectors and scalars. Scalars: have magnitude (magnitude means size) only Examples of scalar quantities include time, mass, volume, area,
1 Definitions In physics we have two types of measurable quantities: vectors and scalars. Scalars: have magnitude (magnitude means size) only Examples of scalar quantities include time, mass, volume, area,
GEOMATICS ENGINEERING / SURVEYING
 1 GEOMATICS ENGINEERING / SURVEYING CHAPTER 1 Dr. Muhammad Ashraf Javid Assistant Professor Department of Civil and Environmental Engineering Email: muhammad.javid@unizwa.edu.om 2 Geomatics Engineering
1 GEOMATICS ENGINEERING / SURVEYING CHAPTER 1 Dr. Muhammad Ashraf Javid Assistant Professor Department of Civil and Environmental Engineering Email: muhammad.javid@unizwa.edu.om 2 Geomatics Engineering
Coordinate Systems. Location on earth is defined by coordinates
 Coordinate Systems We think of the earth as a sphere It is actually a spheroid (ellipsoid), slightly larger in radius at the equator than at the poles Shape of the Earth Location on earth is defined by
Coordinate Systems We think of the earth as a sphere It is actually a spheroid (ellipsoid), slightly larger in radius at the equator than at the poles Shape of the Earth Location on earth is defined by
2. Find the side lengths of a square whose diagonal is length State the side ratios of the special right triangles, and
 1. Starting at the same spot on a circular track that is 80 meters in diameter, Hayley and Kendall run in opposite directions, at 300 meters per minute and 240 meters per minute, respectively. They run
1. Starting at the same spot on a circular track that is 80 meters in diameter, Hayley and Kendall run in opposite directions, at 300 meters per minute and 240 meters per minute, respectively. They run
MATH 103 Pre-Calculus Mathematics Dr. McCloskey Fall 2008 Final Exam Sample Solutions
 MATH 103 Pre-Calculus Mathematics Dr. McCloskey Fall 008 Final Exam Sample Solutions In these solutions, FD refers to the course textbook (PreCalculus (4th edition), by Faires and DeFranza, published by
MATH 103 Pre-Calculus Mathematics Dr. McCloskey Fall 008 Final Exam Sample Solutions In these solutions, FD refers to the course textbook (PreCalculus (4th edition), by Faires and DeFranza, published by
Latitude and Longitude Pre Test
 Name Date Latitude and Longitude Pre Test Multiple Choice Directions: For questions, 1 10 circle the answer that letter that best answers the question. Each question is worth 1 point each. 1. To locate
Name Date Latitude and Longitude Pre Test Multiple Choice Directions: For questions, 1 10 circle the answer that letter that best answers the question. Each question is worth 1 point each. 1. To locate
Physics 40 Chapter 3: Vectors
 Physics 40 Chapter 3: Vectors Cartesian Coordinate System Also called rectangular coordinate system x-and y- axes intersect at the origin Points are labeled (x,y) Polar Coordinate System Origin and reference
Physics 40 Chapter 3: Vectors Cartesian Coordinate System Also called rectangular coordinate system x-and y- axes intersect at the origin Points are labeled (x,y) Polar Coordinate System Origin and reference
CHAPTER 24 THE SAILINGS
 CHAPTER 24 THE SAILINGS INTRODUCTION 2400. Introduction Dead reckoning involves the determination of one s present or future position by projecting the ship s course and distance run from a known position.
CHAPTER 24 THE SAILINGS INTRODUCTION 2400. Introduction Dead reckoning involves the determination of one s present or future position by projecting the ship s course and distance run from a known position.
SB Ch 6 May 15, 2014
 Warm Up 1 Chapter 6: Applications of Trig: Vectors Section 6.1 Vectors in a Plane Vector: directed line segment Magnitude is the length of the vector Direction is the angle in which the vector is pointing
Warm Up 1 Chapter 6: Applications of Trig: Vectors Section 6.1 Vectors in a Plane Vector: directed line segment Magnitude is the length of the vector Direction is the angle in which the vector is pointing
ES 111 Mathematical Methods in the Earth Sciences Lecture Outline 3 - Thurs 5th Oct 2017 Vectors and 3D geometry
 ES 111 Mathematical Methods in the Earth Sciences Lecture Outline 3 - Thurs 5th Oct 2017 Vectors and 3D geometry So far, all our calculus has been two-dimensional, involving only x and y. Nature is threedimensional,
ES 111 Mathematical Methods in the Earth Sciences Lecture Outline 3 - Thurs 5th Oct 2017 Vectors and 3D geometry So far, all our calculus has been two-dimensional, involving only x and y. Nature is threedimensional,
PHYSICS - CLUTCH CH 01: UNITS & VECTORS.
 !! www.clutchprep.com Physics is the study of natural phenomena, including LOTS of measurements and equations. Physics = math + rules. UNITS IN PHYSICS We measure in nature. Measurements must have. - For
!! www.clutchprep.com Physics is the study of natural phenomena, including LOTS of measurements and equations. Physics = math + rules. UNITS IN PHYSICS We measure in nature. Measurements must have. - For
Vectors and their uses
 Vectors and their uses Sharon Goldwater Institute for Language, Cognition and Computation School of Informatics, University of Edinburgh DRAFT Version 0.95: 3 Sep 2015. Do not redistribute without permission.
Vectors and their uses Sharon Goldwater Institute for Language, Cognition and Computation School of Informatics, University of Edinburgh DRAFT Version 0.95: 3 Sep 2015. Do not redistribute without permission.
Chapter 2 One-Dimensional Kinematics
 Review: Chapter 2 One-Dimensional Kinematics Description of motion in one dimension Copyright 2010 Pearson Education, Inc. Review: Motion with Constant Acceleration Free fall: constant acceleration g =
Review: Chapter 2 One-Dimensional Kinematics Description of motion in one dimension Copyright 2010 Pearson Education, Inc. Review: Motion with Constant Acceleration Free fall: constant acceleration g =
Section 6.1 Sinusoidal Graphs
 Chapter 6: Periodic Functions In the previous chapter, the trigonometric functions were introduced as ratios of sides of a right triangle, and related to points on a circle We noticed how the x and y values
Chapter 6: Periodic Functions In the previous chapter, the trigonometric functions were introduced as ratios of sides of a right triangle, and related to points on a circle We noticed how the x and y values
HOW TO TRAVEL ON EARTH WITHOUT GETTING LOST
 HOW TO TRAVEL ON EARTH WITHOUT GETTING LOST Using a globe to learn how a position on Earth can be described. Rui Dilão, Instituto Superior Técnico Curriculum topic latitude, longitude, coordinate system
HOW TO TRAVEL ON EARTH WITHOUT GETTING LOST Using a globe to learn how a position on Earth can be described. Rui Dilão, Instituto Superior Técnico Curriculum topic latitude, longitude, coordinate system
Vectors. Chapter 3. Arithmetic. Resultant. Drawing Vectors. Sometimes objects have two velocities! Sometimes direction matters!
 Vectors Chapter 3 Vector and Vector Addition Sometimes direction matters! (vector) Force Velocity Momentum Sometimes it doesn t! (scalar) Mass Speed Time Arithmetic Arithmetic works for scalars. 2 apples
Vectors Chapter 3 Vector and Vector Addition Sometimes direction matters! (vector) Force Velocity Momentum Sometimes it doesn t! (scalar) Mass Speed Time Arithmetic Arithmetic works for scalars. 2 apples
Welcome to IB Math - Standard Level Year 2
 Welcome to IB Math - Standard Level Year 2 Why math? Not So Some things to know: Good HW Good HW Good HW www.aleimath.blogspot.com Example 1. Lots of info at Example Example 2. HW yup. You know you love
Welcome to IB Math - Standard Level Year 2 Why math? Not So Some things to know: Good HW Good HW Good HW www.aleimath.blogspot.com Example 1. Lots of info at Example Example 2. HW yup. You know you love
Preliminary Physics. Moving About. DUXCollege. Week 2. Student name:. Class code:.. Teacher name:.
 Week 2 Student name:. Class code:.. Teacher name:. DUXCollege Week 2 Theory 1 Present information graphically of: o Displacement vs time o Velocity vs time for objects with uniform and non-uniform linear
Week 2 Student name:. Class code:.. Teacher name:. DUXCollege Week 2 Theory 1 Present information graphically of: o Displacement vs time o Velocity vs time for objects with uniform and non-uniform linear
COORDINATE SYSTEMS: LOCATING YOURSELF ON A SPHERE
 NAME DATE PARTNER(S) COORDINATE SYSTEMS: LOCATING YOURSELF ON A SPHERE Activity 1: Getting Your Bearings 1. Close your eyes and point to the north. Did you point up? Why or why not? Up is the #1 answer.
NAME DATE PARTNER(S) COORDINATE SYSTEMS: LOCATING YOURSELF ON A SPHERE Activity 1: Getting Your Bearings 1. Close your eyes and point to the north. Did you point up? Why or why not? Up is the #1 answer.
Vectors. For physics and calculus students. Prepared by Larry Friesen and Anne Gillis
 Vectors For physics and calculus students Prepared by Larry Friesen and Anne Gillis Butler Community College http://www.butlercc.edu Vectors This project is a direct result of math/physics instructional
Vectors For physics and calculus students Prepared by Larry Friesen and Anne Gillis Butler Community College http://www.butlercc.edu Vectors This project is a direct result of math/physics instructional
Chapter 1 Test on Geography Skills
 Name Score Chapter 1 Test on Geography Skills Part 1 Matching (14 pts.) Match each term in Column B with its correct definition in Column A by clearly writing the number in the blank space provided. Two
Name Score Chapter 1 Test on Geography Skills Part 1 Matching (14 pts.) Match each term in Column B with its correct definition in Column A by clearly writing the number in the blank space provided. Two
AP-1 Physics. Summer 2016 Assignment Date Period. Name: What is due the first day of school? When is this assignment due? MATH REVIEW =
 P- Physics Name: Summer 06 ssignment Date Period I. The attached pages contain a brief review, hints, and example problems. It is hoped that combined with your previous math knowledge this assignment is
P- Physics Name: Summer 06 ssignment Date Period I. The attached pages contain a brief review, hints, and example problems. It is hoped that combined with your previous math knowledge this assignment is
Shape e o f f the e Earth
 1 Coordinate Systems & Projections Coordinate Systems Two map layers are not going to register spatially unless they are based on the same coordinate system. 2 Contents Shape of the earth Datum Projections
1 Coordinate Systems & Projections Coordinate Systems Two map layers are not going to register spatially unless they are based on the same coordinate system. 2 Contents Shape of the earth Datum Projections
Kinematics in Two Dimensions; Vectors
 Kinematics in Two Dimensions; Vectors Vectors & Scalars!! Scalars They are specified only by a number and units and have no direction associated with them, such as time, mass, and temperature.!! Vectors
Kinematics in Two Dimensions; Vectors Vectors & Scalars!! Scalars They are specified only by a number and units and have no direction associated with them, such as time, mass, and temperature.!! Vectors
If the pull is downward (Fig. 1), we want C to point into the page. If the pull is upward (Fig. 2), we want C to point out of the page.
 11.5 Cross Product Contemporary Calculus 1 11.5 CROSS PRODUCT This section is the final one about the arithmetic of vectors, and it introduces a second type of vector vector multiplication called the cross
11.5 Cross Product Contemporary Calculus 1 11.5 CROSS PRODUCT This section is the final one about the arithmetic of vectors, and it introduces a second type of vector vector multiplication called the cross
MAC 1114: Trigonometry Notes
 MAC 1114: Trigonometry Notes Instructor: Brooke Quinlan Hillsborough Community College Section 7.1 Angles and Their Measure Greek Letters Commonly Used in Trigonometry Quadrant II Quadrant III Quadrant
MAC 1114: Trigonometry Notes Instructor: Brooke Quinlan Hillsborough Community College Section 7.1 Angles and Their Measure Greek Letters Commonly Used in Trigonometry Quadrant II Quadrant III Quadrant
Vectors 1. The METRIC Project, Imperial College. Imperial College of Science Technology and Medicine, 1996.
 Vectors 1 The METRIC Project, Imperial College. Imperial College of Science Technology and Medicine, 1996. Launch Mathematica. Type
Vectors 1 The METRIC Project, Imperial College. Imperial College of Science Technology and Medicine, 1996. Launch Mathematica. Type
Chapter 3. Vectors. 3.1 Coordinate Systems 3.2 Vector and Scalar Quantities 3.3 Some Properties of Vectors 3.4 Components of a Vector and Unit Vectors
 Chapter 3 Vectors 3.1 Coordinate Systems 3.2 Vector and Scalar Quantities 3.3 Some Properties of Vectors 3.4 Components of a Vector and Unit Vectors 1 Vectors Vector quantities Physical quantities that
Chapter 3 Vectors 3.1 Coordinate Systems 3.2 Vector and Scalar Quantities 3.3 Some Properties of Vectors 3.4 Components of a Vector and Unit Vectors 1 Vectors Vector quantities Physical quantities that
(arrows denote positive direction)
 12 Chapter 12 12.1 3-dimensional Coordinate System The 3-dimensional coordinate system we use are coordinates on R 3. The coordinate is presented as a triple of numbers: (a,b,c). In the Cartesian coordinate
12 Chapter 12 12.1 3-dimensional Coordinate System The 3-dimensional coordinate system we use are coordinates on R 3. The coordinate is presented as a triple of numbers: (a,b,c). In the Cartesian coordinate
Name. Welcome to AP Physics. I am very excited that you have signed up to take the AP Physics class.
 Name P Physics Summer ssignment Fall 013-014 Welcome to P Physics. I am very excited that you have signed up to take the P Physics class. You may ask I sure would why a summer packet? There is so much
Name P Physics Summer ssignment Fall 013-014 Welcome to P Physics. I am very excited that you have signed up to take the P Physics class. You may ask I sure would why a summer packet? There is so much
Chapter 3: Vectors and Projectile Motion
 Chapter 3: Vectors and Projectile Motion Vectors and Scalars You might remember from math class the term vector. We define a vector as something with both magnitude and direction. For example, 15 meters/second
Chapter 3: Vectors and Projectile Motion Vectors and Scalars You might remember from math class the term vector. We define a vector as something with both magnitude and direction. For example, 15 meters/second
Chapter 3 Vectors Prof. Raymond Lee, revised
 Chapter 3 Vectors Prof. Raymond Lee, revised 9-2-2010 1 Coordinate systems Used to describe a point s position in space Coordinate system consists of fixed reference point called origin specific axes with
Chapter 3 Vectors Prof. Raymond Lee, revised 9-2-2010 1 Coordinate systems Used to describe a point s position in space Coordinate system consists of fixed reference point called origin specific axes with
DuVal High School Summer Review Packet AP Calculus
 DuVal High School Summer Review Packet AP Calculus Welcome to AP Calculus AB. This packet contains background skills you need to know for your AP Calculus. My suggestion is, you read the information and
DuVal High School Summer Review Packet AP Calculus Welcome to AP Calculus AB. This packet contains background skills you need to know for your AP Calculus. My suggestion is, you read the information and
Chapter 5. Forces in Two Dimensions
 Chapter 5 Forces in Two Dimensions Chapter 5 Forces in Two Dimensions In this chapter you will: Represent vector quantities both graphically and algebraically. Use Newton s laws to analyze motion when
Chapter 5 Forces in Two Dimensions Chapter 5 Forces in Two Dimensions In this chapter you will: Represent vector quantities both graphically and algebraically. Use Newton s laws to analyze motion when
Introduction to Vectors
 Introduction to Vectors K. Behrend January 31, 008 Abstract An introduction to vectors in R and R 3. Lines and planes in R 3. Linear dependence. 1 Contents Introduction 3 1 Vectors 4 1.1 Plane vectors...............................
Introduction to Vectors K. Behrend January 31, 008 Abstract An introduction to vectors in R and R 3. Lines and planes in R 3. Linear dependence. 1 Contents Introduction 3 1 Vectors 4 1.1 Plane vectors...............................
AP PHYSICS B SUMMER ASSIGNMENT: Calculators allowed! 1
 P PHYSICS SUMME SSIGNMENT: Calculators allowed! 1 The Metric System Everything in physics is measured in the metric system. The only time that you will see English units is when you convert them to metric
P PHYSICS SUMME SSIGNMENT: Calculators allowed! 1 The Metric System Everything in physics is measured in the metric system. The only time that you will see English units is when you convert them to metric
