Chapter 4 Lecture. Populations with Age and Stage structures. Spring 2013
|
|
|
- Hillary Arnold
- 5 years ago
- Views:
Transcription
1 Chapter 4 Lecture Populations with Age and Stage structures Spring 2013
2 4.1 Introduction Life Table- approach to quantify age specific fecundity and survivorship data Age (or Size Class) structured populations Stage structured populations Plant: seed, seedling, pre-reproductive, reproductive, nonreproductive Genet = Ramet = Animals: if age is not available, pre-reproductive, reproductive, post- reproductive Phenotypic plasticity =
3 Organism s phenotypic trait Organism s phenotypic trait Phenotypic Plasticity Concepts Organism s phenotypic trait Organism s fitness environment Phenotypic plasticity environment Genetic variation environment Genotype by environment interaction environment *Each line is a genetic unit
4 4.2 Survivorship l x 1 st Approach: Cohort = individuals born at the same time (year) Advantage: Know exact age of each individual Disadvantage: lacks generality, cohorts born in different years may not respond the same way If organisms live a LONG time one investigator could spend their whole life studying one cohort Called a Fixed-cohort, Dynamic or Horizontal life table Table 4.3 we will examine shortly
5 4.2 Survivorship l x 2 nd Approach: Static, Vertical or Time-specific life table Locate all dead individuals during some time period. This approach assumes that rates of survival within a population are ~ constant Ex., Table 4.1 OR more likely done with living organisms.. Collect life history data from several cohorts over one time period Thus cohorts are not followed in time but reconstructed using one-time observations. Assumes that mortality is constant across age. 3 rd Approach: Collect vertical data across as many years as possible to produce a more realistic estimate of survivorship and reproduction. GOAL: to produce an estimate of age specific survivorship and fertility
6 4.2 Survivorship curves l x Type I Type II Type III Why would survivorship curves vary across years and cohorts? Age-specific survivorship= birth living to a given age or age class
7 4.3 Fertility Fertility m x column Table 4.2 Pre-reproductive Reproductive Post-reproductive GRR = Gross reproductive rate = m x (not taking survivorship into account) Survivorship = l x l x m x = R 0 = Net Reproductive Rate Again assume that lx and mx remains constant. Realistic? Thoughts? Figs. 4.8: human fertility and 4.9:cactus ground finch
8 Table 4.3 Life Table of gray squirrel population, pg 87 Age l x m x p x q x l x m x GRR = R 0 = l x = prob. at birth of surviving to a given age m x = age specific fertility p x = l x+1 /l x = age specific prob. of surviving to the next age class q x = proportion of pop survived until x, but will die in next age class Thus q x = 1- p x
9 4.4 Mortality Curves Mortality Rates (1000 q x ) Mortality Curves Fig Impala and 4.11 Humans - often exhibit U shaped distributions females males Age in years
10 4.5 Expectation of Life Expectations of Life = e x L x = mean survivorship for any particular age interval & assumes that on avg. an individual dies half-way between the two age classes. Standard practical approach w/ discrete age classes: L x = l x + l x+1 /2 T x = area under survivorship curve for indiv. of a given age (x) to the age (w) when oldest indiv. dies = l x + l x+1 /2 (eq.4.6) w x See Table 4.4 for ex.: Expectation of life = e x = T x /l x (eq.4.7)
11 4.6 Net reproductive rate (R 0 ), generation time (G) and intrinsic rate of increase (r) R 0 = l x m x Net Reproductive Rate (eq. 4.8) The standard approach to compare populations is to compare intrinsic rate of increase (r ) or finite rate of increase (λ)because both are estimated for a specific unit of time. Using the Characteristic equation of demography (Lotka, Euhler) l x m x e -rx = 1 Excellent approximation for r, assuming a stable age distribution: Intrinsic rate of increase = r = ln R 0 / G (eq. 4.10) G = Generation time = x l x m x / R 0 = xl x m x / l x m x (eq. 4.12) = mean age of mothers at time of their daughter s births
12 Table 4.3 Life Table of gray squirrel population, pg 87 Age l x m x p x q x l x m x GRR = R 0 = l x = prob. at birth of surviving to a given age m x = age specific fertility p x = l x+1 /l x = age specific prob. of surviving to the next age class q x = proportion of pop survived until x, but will die in next age class Thus q x = 1- p x
13 4.7 Age structure and stable age distribution c x = Age distribution of a population = proportion of population belonging to various age classes at a given point in time Proportion of population belonging to a given category, c x and n x equals the number of individuals in that age category. c x = n x /N = n x / n x (eq. 4.13) Stable age distribution occurs when survivorship and fertility remain constant for a period of time. The population will grow or decline at a stable state = λ If popln has stable age distr. Then N t+1 /N t = λ And r = ln λ Formula predicting stable age distr.: c x = e -rx l x / e -rx l x (eq. 4.14)
14 4.8 Projection of population growth in age structured populations Table 4.5 Review of life table components Table 4.6 Projection of population growth how to Assignment: Work through math to project population growth for next class
15 Table 4.5 Review of life table components, pg 94 Age, x lx mx px qx lxmx Sums GRR=4 R 0 = 1.3 mx = lx= px= qx= lxmx = GRR =? R 0 =? Table 4.6 how to growth projection utilizing life history table 4.5 Please review Example 4.1 for homework (pg. 96)
16 Table 4.6 Projected population growth based on Table 4.5: starting with 200 individuals at age 0 Age, x n x, t=0 c x, t=o n x, t=1 c x, t=1 n x, t=2 c x, t=2 n x, t=3 c x, t=3 C x =Calc. SAD Sums λ from t=0 to t=1 = 300/200 = 1.5 λ from t=1 to t=2 = 300/200 = 1.27 λ from t=2 to t=3 = 300/200 = 1.26 λ from t=3 to t=4 = 300/200 = 1.22 SAD reached
17 4.8 Projection of population growth in age structured populations Observations from this example: 1) in the short term, population growth is greatly influenced by age distribution of the population 2) a popln with a short generation time can rapidly reach a stable age distribution (SAD) 3) finite rate of increase (λ)is influenced by age distribution, but quickly settles into the predicted value from the life history table (e r ) as pop reaches SAD.
18 4.9 Age structure, 1 st version of Leslie projection matrix Leslie (1945) demonstrated that one could readily project population growth utilizing matrix algebra (please see Appendix 2 for an overview) Table 4.7 This approach allows one to rapidly quantify changes in the age structure & population size and can calculate λ when there is a SAD. Matrix models allow one to describe behavior of poplns with overlapping generations of which indiv. fall into different age (Leslie) or stage/size classes (Lefkovitch). Matrix approach commonly used now with computer programs to estimate λ. Excel Program posted on Website for your exploration
19 Table 4.7 General matrix format Age classes A Matrix t=0 t=1 0 p 0 m 1 p 1 m 2 p 2 m 3 p 3 m 4 0 n 0 n 0 1 p n 1 n p n 2 n p n 3 n p 3 0 n 4 n 4 - Off diagonal = p x = prob (surv. from age x to age x+1 ) or aij -Surv. and fert. columns placed in matrix form A - top row - population itself considered a column vector, thus when: N t+1 = A N t x =
20 4.9 Age structure, 1 st version of Leslie projection matrix From pg 97, Tables 4.7 & 4.8 and Assume year begins with repro. season Population is a column vector (@ t = 0) Multiply Popln Matrix, A by column vector (@ t=0) -> t=1 Popln Matrix A p x = probability of surviving from age x to x+1 in OFF diagonal First row = p x x (m x+1 ) = Fertilities in top row (some refs use fecundity) Matrix must be square with final column consisting of zeros
21 How to construct a matrix w/ comparable notation Individuals present in each stage (or age class) are entered in column matrix: A column matrix of 3 classes (Lefkovitch): Ns Nr Nf Transition probability from one stage/age to the next = a ij
22 Transition matrix = projection matrix, perennial plant (t) Seeds N s Rosettes N r Flowering N f a fs a ss a a rr sr a rf a ff a fr (t+1) Seeds N s Rosettes N r Flowering N f Matrix elements ~ a ij t Seed rosette flower t+1 Seed a ss a a rs fs rosette a sr a a rr fr flower a sf a a rf ff
23 How to matrix cont. Some coefficients have no biological meaning = 0 (see below) Each number in matrix is an element Ordinary single number is a called a scalar Single row of numbers = row vector Single column of numbers = column vector A (projection matrix) Seed rosette flower x B t Column matrix) = B t+1 Seed rosette flower 0 a ss 0 a fs N s a sr a a rr fr x a a rf ff N r N f =
24 Transition matrix iterated = repeatedly multiplied A x B 1 = B 2 ; A x B 2 = B 3 ; A x B 3 = B 4 Then the age or stage structure of a popln eventually stabilizes at a constant ratio of classes, reach SAD, then per year rate of increase λ = R 0 /t t= generation time; R 0 = net repro. Rate = N t+1 /N t A (projection matrix) Seed rosette flower x B t Column matrix) = B t+1 Seed rosette flower 0 a ss 0 a fs N s a sr a rr a fr x a a rf ff N r N f =
25 4.9 Age structure, 1 st version of Leslie projection matrix Table 4.7 Age classes Matrix t=0 t=1 0 p 0 m 1 p 1 m 2 p 2 m 3 p 3 m 4 0 n 0 n 0 1 p n 1 n p n 2 n p n 3 n p 3 0 n 4 n 4 x =
26 nd version of Leslie projection matrix Now assume: 1) Able to count individuals completed at least 1 st year of life 2) NO count of newborn individuals, too difficult, as with seeds 3) It is possible to estimate fertility & survivorship by individuals in yr 1 onwards Results the same!! Individuals in age class 0 do NOT reproduce, thus λ is identical. Resulting in much simpler Life Table and matrix! Table 4.9 (based on Table 4.5) where NO count is made on zero-year age class t=2 t=3 t=2 t=3 m 1 p 0 m 2 p 0 m 3 p 0 m 4 p 0 n 1 n p n 2 n x = => = 0 p n 3 n p 3 0 n 4 n
27 4.11 Stage structure or Lefkovitch projection matrix Noted that once indiv. becoming reproductive both their survivorship and fertility remained relatively constant Stage classes: juvenile, young adult, adult OR Pre-reproductive, reproductive, post-reproductive Lefkovitch demonstrated that in spite of lumping the age classes the finite rate of growth, λ, was conserved. This is because these repro. indiv. were recycled back into the SAME stage as the year before for many years (iteroparous repro.)
28 4.11 Stage structure or Lefkovitch projection matrix Table 4.10 : Simplified life table of ground squirrel Age/Stage class m x p x Y = young adult A = mature adult Table 4.11: Projection of gray squirrel popln (2x2 matrix) Stage class Matrix t=0 t=1 t=2 t=3 Y A =140 =180 =230 =294
29 4.12 Dominant latent roots & the characteristic equation If lx and mx remain constant, then able to project forward Nt = A t N 0 And can also project backward in time but requires Identity matrix (I): I A = A I = A Recall, in algebra each number has an inverse except zero A A -1 = I (Identity matrix) If the inverse of a square matrix A is B then A B = I (Identity matrix) Then square matrix has a determinant (D), which is a scalar that determines the dependency among the equations that a matrix represents When D=0 then the # of equations is NOT equal to the # of unknowns and the equations have no unique solution
30 4.12 Dominant latent roots & characteristic equation If popln is in SAD then each group grows at the same rate as the popln as a whole ~ λ Characteristic Equation for a matrix A - λi = 0 Only exists for square matrices λ is known as the latent root, characteristic root, or Eigenvalue of equation. Leslie matrix has only ONE positive, primary or dominant latent root = λ Leslie has also shown: λ = e r Please try out the Projection matrix program online at my website.
31 4.12 Eigenvalue of square projection matrix Recall: λ is the dominant and most POSITIVE eigenvalue from projection matrix and it will grow exponentially with rate = λ The stable age distribution and λ are independent of the initial age distribution; they depend on the projection matrix. A row eigenvector is NOT transpose of column vector, thus have left and right eigenvectors AND they have different roles in the projection matrix.
32 4.12 Eigenvectors of square projection matrix: Vectors denoted by x and transition matrix by A A right eigenvector, x R (right side of A) solves for SAD (stable age/stage distr.) Eq 1: A(x R ) = λ(x) or (x) λ same since λ is scalar A left eigenvector, x L (left side of A) is defined and solves for the V, Reproductive Value (exp. contribution of each stage to pop growth): Eq 2: (x L )A = (x) λ or λ(x) same since λ is scalar FYI: The only difference is in the actual form of A. Depending on what kind of object A is, left or right eigenvectors might not be allowed; or they might both equal each other, or be different. For example: (x R )A = undefined, as is A(x L ) = undefined.
33 4.13 Reproductive value (V x ) V x =A measure of which group of individuals within the population will contribute the greatest to future reproduction. Approach 1: Weighted avg. of present and future repro of indiv. at age x Approach 2: Ignores current repro., and only estimates future repro. V x is normalized (scaled) such that the value for the first age class is 1.0. Approach 3: Ignores current repro., via a computer generated program, Populus with same assumptions as Approach 2. z V x = e -rx l x m x /e -rx l x x Fig Equation 4.21 (data are normally provided by computer program) Ex. 4.2
34 4.14 Sensitivity Analysis How sensitive is a poplulation s growth (or extinction) to a particular demographic change? Examine how changing vital rates (survivorship or fertility) alters λ Table 4.12 and Fig Vital rates = factors that have a direct impact on survival & reproduction. This type of examination = perturbation or sensitivity analysis Survivorship scales from 0 to 1, but reproduction can range from s This approach makes it difficult to compare different poplns of the same species or to compare species
35 4.14 Sensitivity Analysis Each transition, a ij (or p) has a sensitivity, s ij Calculate sensitivity of λ between classes of ij. SA Requires: 1) SAD 2) Repro. Value, V x of indiv in each stage or age class 3) All transition probabilities equally likely**** likely NOT true in nature SA = (V i ) x (% indiv in size class j)
36 Why perform Sensitivity Analysis? 1) Measure importance of vital rates 2) Evaluate effects of error in estimation 3) Quantify effects of environmental perturbations 4) Evaluate alternative management strategies 5) Predict intensity of natural selection Be able to compare populations across a species range to determine vulnerability, need another metric.
37 Elasticity Analysis To facilitate being able to compare changes in vital rate with changes in λ across populations and species => elasticity analysis Utilize proportional changes in λ as a proportion of change in the vital rates ~ matrix coefficients (a ij ) (sum to 100%). Standardized sensitivity = Elasticity Elasticities reveal the effect of the perturbations in vital rates that are all the same relative magnitude. Elasticity is a refined SA e ij = a ij /λ = δ λ/ δ a ij δ log λ/ δ log a ij
38 Elasticity Analysis Thus -> provides a proportional change in λ resulting from a proportional change in a ij. e ij s sum to 1.0 e ij = (a ij /λ) x (s ij ) e ij = (transition probability/ λ) x (sensitivity of particular transition) Therefore one could be given these values (a ij, λ, and s ij ) and calculate e ij for a given matrix. AND compare across populations and species as well.
39 Example: Comparison of SA and EA Transitions Sensitivity Elasticity a ss a sr a rf a rr ~ 1.00
40 Highlights An understanding of: Survivorship Fertility Mortality curves Expectation of life Net Reproductive rate, generation time, r Age structure and stable age distribution Projecting popln growth in age-structured poplns Leslie or population projection matrix Reproductive value Sensitivity analysis Elasticity analysis
41 Questions? Reference information on website related to a refresher of matrix algebra to be able to appreciate how computer programs can project population growth. Readings Problem set and answer key Excel program that you can manipulate to gain an understanding of how important age and stage structure is in estimating future population growth.
Introduction to course: BSCI 462 of BIOL 708 R
 Introduction to course: BSCI 462 of BIOL 708 R Population Ecology: Fundamental concepts in plant and animal systems Spring 2013 Introduction The biology of a population = Population Ecology Issue of scale,
Introduction to course: BSCI 462 of BIOL 708 R Population Ecology: Fundamental concepts in plant and animal systems Spring 2013 Introduction The biology of a population = Population Ecology Issue of scale,
Chapter 6 Lecture. Life History Strategies. Spring 2013
 Chapter 6 Lecture Life History Strategies Spring 2013 6.1 Introduction: Diversity of Life History Strategies Variation in breeding strategies, fecundity, and probability of survival at different stages
Chapter 6 Lecture Life History Strategies Spring 2013 6.1 Introduction: Diversity of Life History Strategies Variation in breeding strategies, fecundity, and probability of survival at different stages
Leslie Matrix II Formal Demography Stanford Spring Workshop in Formal Demography May 2008
 Leslie Matrix II Formal Demography Stanford Spring Workshop in Formal Demography May 2008 James Holland Jones Department of Anthropology Stanford University May 2, 2008 1 Outline 1. Spectral Decomposition
Leslie Matrix II Formal Demography Stanford Spring Workshop in Formal Demography May 2008 James Holland Jones Department of Anthropology Stanford University May 2, 2008 1 Outline 1. Spectral Decomposition
A Note on the Eigenvalues and Eigenvectors of Leslie matrices. Ralph Howard Department of Mathematics University of South Carolina
 A Note on the Eigenvalues and Eigenvectors of Leslie matrices Ralph Howard Department of Mathematics University of South Carolina Vectors and Matrices A size n vector, v, is a list of n numbers put in
A Note on the Eigenvalues and Eigenvectors of Leslie matrices Ralph Howard Department of Mathematics University of South Carolina Vectors and Matrices A size n vector, v, is a list of n numbers put in
SENSITIVITY AND ELASTICITY ANALYSES
 1 SENSITIVITY AND ELASTICITY ANALYSES Objectives Using the stage-based matrix model for a sea turtle population, conduct a sensitivity analysis of model parameters to determine the absolute contribution
1 SENSITIVITY AND ELASTICITY ANALYSES Objectives Using the stage-based matrix model for a sea turtle population, conduct a sensitivity analysis of model parameters to determine the absolute contribution
Section 9.2: Matrices. Definition: A matrix A consists of a rectangular array of numbers, or elements, arranged in m rows and n columns.
 Section 9.2: Matrices Definition: A matrix A consists of a rectangular array of numbers, or elements, arranged in m rows and n columns. That is, a 11 a 12 a 1n a 21 a 22 a 2n A =...... a m1 a m2 a mn A
Section 9.2: Matrices Definition: A matrix A consists of a rectangular array of numbers, or elements, arranged in m rows and n columns. That is, a 11 a 12 a 1n a 21 a 22 a 2n A =...... a m1 a m2 a mn A
Properties of Linear Transformations from R n to R m
 Properties of Linear Transformations from R n to R m MATH 322, Linear Algebra I J. Robert Buchanan Department of Mathematics Spring 2015 Topic Overview Relationship between the properties of a matrix transformation
Properties of Linear Transformations from R n to R m MATH 322, Linear Algebra I J. Robert Buchanan Department of Mathematics Spring 2015 Topic Overview Relationship between the properties of a matrix transformation
From Lay, 5.4. If we always treat a matrix as defining a linear transformation, what role does diagonalisation play?
 Overview Last week introduced the important Diagonalisation Theorem: An n n matrix A is diagonalisable if and only if there is a basis for R n consisting of eigenvectors of A. This week we ll continue
Overview Last week introduced the important Diagonalisation Theorem: An n n matrix A is diagonalisable if and only if there is a basis for R n consisting of eigenvectors of A. This week we ll continue
Eigenvalue and Eigenvector Homework
 Eigenvalue and Eigenvector Homework Olena Bormashenko November 4, 2 For each of the matrices A below, do the following:. Find the characteristic polynomial of A, and use it to find all the eigenvalues
Eigenvalue and Eigenvector Homework Olena Bormashenko November 4, 2 For each of the matrices A below, do the following:. Find the characteristic polynomial of A, and use it to find all the eigenvalues
9 Demography. 9.1 Survival. last revised: 25 February 2009
 last revised: 25 February 2009 9 Demography We have already considered population dynamics and growth using the differential reproduction model in Chapter 3. For simplicity, that model assumed that the
last revised: 25 February 2009 9 Demography We have already considered population dynamics and growth using the differential reproduction model in Chapter 3. For simplicity, that model assumed that the
Chapter 2 Lecture. Density dependent growth and intraspecific competition ~ The Good, The Bad and The Ugly. Spring 2013
 Chapter 2 Lecture Density dependent growth and intraspecific competition ~ The Good, The Bad and The Ugly Spring 2013 2.1 Density dependence, logistic equation and carrying capacity dn = rn K-N Dt K Where
Chapter 2 Lecture Density dependent growth and intraspecific competition ~ The Good, The Bad and The Ugly Spring 2013 2.1 Density dependence, logistic equation and carrying capacity dn = rn K-N Dt K Where
Ecology 302: Lecture VI. Evolution of Life Histories
 Ecology 302: Lecture VI. Evolution of Life Histories (Ricklefs, Chapter 7; Life Histories, pp.46-48; Knowledge Project.) Spawning sockeye salmon (Oncorhyncus nerka). The adaptive significance (if any)
Ecology 302: Lecture VI. Evolution of Life Histories (Ricklefs, Chapter 7; Life Histories, pp.46-48; Knowledge Project.) Spawning sockeye salmon (Oncorhyncus nerka). The adaptive significance (if any)
Further Mathematical Methods (Linear Algebra) 2002
 Further Mathematical Methods (Linear Algebra) 2002 Solutions For Problem Sheet 4 In this Problem Sheet, we revised how to find the eigenvalues and eigenvectors of a matrix and the circumstances under which
Further Mathematical Methods (Linear Algebra) 2002 Solutions For Problem Sheet 4 In this Problem Sheet, we revised how to find the eigenvalues and eigenvectors of a matrix and the circumstances under which
Multiple choice 2 pts each): x 2 = 18) Essay (pre-prepared) / 15 points. 19) Short Answer: / 2 points. 20) Short Answer / 5 points
 P 1 Biology 217: Ecology Second Exam Fall 2004 There should be 7 ps in this exam - take a moment and count them now. Put your name on the first p of the exam, and on each of the ps with short answer questions.
P 1 Biology 217: Ecology Second Exam Fall 2004 There should be 7 ps in this exam - take a moment and count them now. Put your name on the first p of the exam, and on each of the ps with short answer questions.
Main Points. Note: Tutorial #1, help session, and due date have all been pushed back 1 class period. Will send Tutorial #1 by end of day.
 1) Demographic PVA -- age- and stage-structured matrices Main Points Pre-reading: Thursday 21 September: Marris Tuesday 26 September: NA Note: Tutorial #1, help session, and due date have all been pushed
1) Demographic PVA -- age- and stage-structured matrices Main Points Pre-reading: Thursday 21 September: Marris Tuesday 26 September: NA Note: Tutorial #1, help session, and due date have all been pushed
APPM 2360 Project 2: Exploring Stage-Structured Population Dynamics with Loggerhead Sea Turtles
 APPM 2360 Project 2: Exploring Stage-Structured Population Dynamics with Loggerhead Sea Turtles Due: March 22, 2018 by 11:59 PM Submit to the Dropbox on D2L as a PDF 1 Introduction In this lab, you will
APPM 2360 Project 2: Exploring Stage-Structured Population Dynamics with Loggerhead Sea Turtles Due: March 22, 2018 by 11:59 PM Submit to the Dropbox on D2L as a PDF 1 Introduction In this lab, you will
Lecture 15, 16: Diagonalization
 Lecture 15, 16: Diagonalization Motivation: Eigenvalues and Eigenvectors are easy to compute for diagonal matrices. Hence, we would like (if possible) to convert matrix A into a diagonal matrix. Suppose
Lecture 15, 16: Diagonalization Motivation: Eigenvalues and Eigenvectors are easy to compute for diagonal matrices. Hence, we would like (if possible) to convert matrix A into a diagonal matrix. Suppose
Section 9.2: Matrices.. a m1 a m2 a mn
 Section 9.2: Matrices Definition: A matrix is a rectangular array of numbers: a 11 a 12 a 1n a 21 a 22 a 2n A =...... a m1 a m2 a mn In general, a ij denotes the (i, j) entry of A. That is, the entry in
Section 9.2: Matrices Definition: A matrix is a rectangular array of numbers: a 11 a 12 a 1n a 21 a 22 a 2n A =...... a m1 a m2 a mn In general, a ij denotes the (i, j) entry of A. That is, the entry in
Chapter 3. Determinants and Eigenvalues
 Chapter 3. Determinants and Eigenvalues 3.1. Determinants With each square matrix we can associate a real number called the determinant of the matrix. Determinants have important applications to the theory
Chapter 3. Determinants and Eigenvalues 3.1. Determinants With each square matrix we can associate a real number called the determinant of the matrix. Determinants have important applications to the theory
Mathematical Methods in Biology Part 3: Vectors and matrices
 Mathematical Methods in Biology Part 3: Vectors and matrices Eva Kisdi Department of Mathematics and Statistics University of Helsinki c Eva Kisdi. Any part of this material may be copied or re-used only
Mathematical Methods in Biology Part 3: Vectors and matrices Eva Kisdi Department of Mathematics and Statistics University of Helsinki c Eva Kisdi. Any part of this material may be copied or re-used only
Stage-structured Populations
 Department of Biology New Mexico State University Las Cruces, New Mexico 88003 brook@nmsu.edu Fall 2009 Age-Structured Populations All individuals are not equivalent to each other Rates of survivorship
Department of Biology New Mexico State University Las Cruces, New Mexico 88003 brook@nmsu.edu Fall 2009 Age-Structured Populations All individuals are not equivalent to each other Rates of survivorship
Chapter 9 Population Dynamics, Carrying Capacity, and Conservation Biology
 Chapter 9 Population Dynamics, Carrying Capacity, and Conservation Biology 9-1 Population Dynamics & Carrying Capacity Populations change in response to enviromental stress or changes in evironmental conditions
Chapter 9 Population Dynamics, Carrying Capacity, and Conservation Biology 9-1 Population Dynamics & Carrying Capacity Populations change in response to enviromental stress or changes in evironmental conditions
5. DISCRETE DYNAMICAL SYSTEMS
 5 DISCRETE DYNAMICAL SYSTEMS In Chapter 5, we considered the dynamics of systems consisting of a single quantity in either discrete or continuous time Here we consider the dynamics of certain systems consisting
5 DISCRETE DYNAMICAL SYSTEMS In Chapter 5, we considered the dynamics of systems consisting of a single quantity in either discrete or continuous time Here we consider the dynamics of certain systems consisting
Recall : Eigenvalues and Eigenvectors
 Recall : Eigenvalues and Eigenvectors Let A be an n n matrix. If a nonzero vector x in R n satisfies Ax λx for a scalar λ, then : The scalar λ is called an eigenvalue of A. The vector x is called an eigenvector
Recall : Eigenvalues and Eigenvectors Let A be an n n matrix. If a nonzero vector x in R n satisfies Ax λx for a scalar λ, then : The scalar λ is called an eigenvalue of A. The vector x is called an eigenvector
CS 246 Review of Linear Algebra 01/17/19
 1 Linear algebra In this section we will discuss vectors and matrices. We denote the (i, j)th entry of a matrix A as A ij, and the ith entry of a vector as v i. 1.1 Vectors and vector operations A vector
1 Linear algebra In this section we will discuss vectors and matrices. We denote the (i, j)th entry of a matrix A as A ij, and the ith entry of a vector as v i. 1.1 Vectors and vector operations A vector
Chapter 53 POPULATION ECOLOGY
 Ch. 53 Warm-Up 1. Sketch an exponential population growth curve and a logistic population growth curve. 2. What is an ecological footprint? 3. What are ways that you can reduce your ecological footprint?
Ch. 53 Warm-Up 1. Sketch an exponential population growth curve and a logistic population growth curve. 2. What is an ecological footprint? 3. What are ways that you can reduce your ecological footprint?
MATH 423 Linear Algebra II Lecture 33: Diagonalization of normal operators.
 MATH 423 Linear Algebra II Lecture 33: Diagonalization of normal operators. Adjoint operator and adjoint matrix Given a linear operator L on an inner product space V, the adjoint of L is a transformation
MATH 423 Linear Algebra II Lecture 33: Diagonalization of normal operators. Adjoint operator and adjoint matrix Given a linear operator L on an inner product space V, the adjoint of L is a transformation
The Leslie Matrix Part II
 The Leslie Matrix Part II Math 45 Linear Algebra David Arnold and Kevin Yokoyama David-Arnold@Eurekaredwoodscccaus Abstract The Leslie Model is a powerful tool used to determine the growth of a population
The Leslie Matrix Part II Math 45 Linear Algebra David Arnold and Kevin Yokoyama David-Arnold@Eurekaredwoodscccaus Abstract The Leslie Model is a powerful tool used to determine the growth of a population
STUDY GUIDE SECTION 16-1 Genetic Equilibrium
 STUDY GUIDE SECTION 16-1 Genetic Equilibrium Name Period Date Multiple Choice-Write the correct letter in the blank. 1. The smallest unit in which evolution occurs is a. an individual organism. c. a species
STUDY GUIDE SECTION 16-1 Genetic Equilibrium Name Period Date Multiple Choice-Write the correct letter in the blank. 1. The smallest unit in which evolution occurs is a. an individual organism. c. a species
Further Mathematical Methods (Linear Algebra)
 Further Mathematical Methods (Linear Algebra) Solutions For The Examination Question (a) To be an inner product on the real vector space V a function x y which maps vectors x y V to R must be such that:
Further Mathematical Methods (Linear Algebra) Solutions For The Examination Question (a) To be an inner product on the real vector space V a function x y which maps vectors x y V to R must be such that:
7.5 Operations with Matrices. Copyright Cengage Learning. All rights reserved.
 7.5 Operations with Matrices Copyright Cengage Learning. All rights reserved. What You Should Learn Decide whether two matrices are equal. Add and subtract matrices and multiply matrices by scalars. Multiply
7.5 Operations with Matrices Copyright Cengage Learning. All rights reserved. What You Should Learn Decide whether two matrices are equal. Add and subtract matrices and multiply matrices by scalars. Multiply
Further Mathematical Methods (Linear Algebra)
 Further Mathematical Methods (Linear Algebra) Solutions For The 2 Examination Question (a) For a non-empty subset W of V to be a subspace of V we require that for all vectors x y W and all scalars α R:
Further Mathematical Methods (Linear Algebra) Solutions For The 2 Examination Question (a) For a non-empty subset W of V to be a subspace of V we require that for all vectors x y W and all scalars α R:
Changing Planet: Changing Mosquito Genes
 Changing Planet: Changing Mosquito Genes Name Background As the climate changes around the globe, organisms will need to adapt in order to survive. But what does it mean to adapt? When you put on a sweater
Changing Planet: Changing Mosquito Genes Name Background As the climate changes around the globe, organisms will need to adapt in order to survive. But what does it mean to adapt? When you put on a sweater
Math 520 Exam 2 Topic Outline Sections 1 3 (Xiao/Dumas/Liaw) Spring 2008
 Math 520 Exam 2 Topic Outline Sections 1 3 (Xiao/Dumas/Liaw) Spring 2008 Exam 2 will be held on Tuesday, April 8, 7-8pm in 117 MacMillan What will be covered The exam will cover material from the lectures
Math 520 Exam 2 Topic Outline Sections 1 3 (Xiao/Dumas/Liaw) Spring 2008 Exam 2 will be held on Tuesday, April 8, 7-8pm in 117 MacMillan What will be covered The exam will cover material from the lectures
Life History Evolution
 Life history evolution References Stearns (1992) The Evolution of Life Histories Roff (2002) Review Partridge & Harvey (1988) Science 241: 1449-1455 1 Overview Life history traits Life history : how individuals
Life history evolution References Stearns (1992) The Evolution of Life Histories Roff (2002) Review Partridge & Harvey (1988) Science 241: 1449-1455 1 Overview Life history traits Life history : how individuals
Chapter 13- Reproduction, Meiosis, and Life Cycles. Many plants and other organisms depend on sexual reproduction.
 Chapter 13- Reproduction, Meiosis, and Life Cycles Many plants and other organisms depend on sexual reproduction. Flowers are the sexual reproductive organ systems of angiosperms. Sexual reproduction gametes
Chapter 13- Reproduction, Meiosis, and Life Cycles Many plants and other organisms depend on sexual reproduction. Flowers are the sexual reproductive organ systems of angiosperms. Sexual reproduction gametes
7.6 The Inverse of a Square Matrix
 7.6 The Inverse of a Square Matrix Copyright Cengage Learning. All rights reserved. What You Should Learn Verify that two matrices are inverses of each other. Use Gauss-Jordan elimination to find inverses
7.6 The Inverse of a Square Matrix Copyright Cengage Learning. All rights reserved. What You Should Learn Verify that two matrices are inverses of each other. Use Gauss-Jordan elimination to find inverses
Grand-daughters, Great Granddaughters, Daughters. : Σ lx m x e r (Tmax - x )
 Basic reproductive rate, R o = Σ l x m x umber of offspring produced by an individual female in her lifetime, can be used as multiplier to compute population growth rate if generations don t overlap. If
Basic reproductive rate, R o = Σ l x m x umber of offspring produced by an individual female in her lifetime, can be used as multiplier to compute population growth rate if generations don t overlap. If
The Leslie Matrix. The Leslie Matrix (/2)
 The Leslie Matrix The Leslie matrix is a generalization of the above. It describes annual increases in various age categories of a population. As above we write p n+1 = Ap n where p n, A are given by:
The Leslie Matrix The Leslie matrix is a generalization of the above. It describes annual increases in various age categories of a population. As above we write p n+1 = Ap n where p n, A are given by:
A.P. Biology CH Population Ecology. Name
 1 A.P. Biology CH. 53 - Population Ecology Name How many ants (shown below - 6 ants / cm 2 ) would there be in an ant colony that is flat and one meter long on each side? Dispersion Patterns Matching A
1 A.P. Biology CH. 53 - Population Ecology Name How many ants (shown below - 6 ants / cm 2 ) would there be in an ant colony that is flat and one meter long on each side? Dispersion Patterns Matching A
1. The characteristic time of exponential growth/decline for this population is A. 5 years B. 20 years C. 5 per year D. 20 per year T c = 1/r
 Use this information for the next four questions. A reintroduced population of wolves, starting with 20 individuals in year 0, is growing continuously at a rate of 5%/year. The instantaneous growth rate
Use this information for the next four questions. A reintroduced population of wolves, starting with 20 individuals in year 0, is growing continuously at a rate of 5%/year. The instantaneous growth rate
MATH 315 Linear Algebra Homework #1 Assigned: August 20, 2018
 Homework #1 Assigned: August 20, 2018 Review the following subjects involving systems of equations and matrices from Calculus II. Linear systems of equations Converting systems to matrix form Pivot entry
Homework #1 Assigned: August 20, 2018 Review the following subjects involving systems of equations and matrices from Calculus II. Linear systems of equations Converting systems to matrix form Pivot entry
Math 2331 Linear Algebra
 5. Eigenvectors & Eigenvalues Math 233 Linear Algebra 5. Eigenvectors & Eigenvalues Shang-Huan Chiu Department of Mathematics, University of Houston schiu@math.uh.edu math.uh.edu/ schiu/ Shang-Huan Chiu,
5. Eigenvectors & Eigenvalues Math 233 Linear Algebra 5. Eigenvectors & Eigenvalues Shang-Huan Chiu Department of Mathematics, University of Houston schiu@math.uh.edu math.uh.edu/ schiu/ Shang-Huan Chiu,
2 Discrete-Time Markov Chains
 2 Discrete-Time Markov Chains Angela Peace Biomathematics II MATH 5355 Spring 2017 Lecture notes follow: Allen, Linda JS. An introduction to stochastic processes with applications to biology. CRC Press,
2 Discrete-Time Markov Chains Angela Peace Biomathematics II MATH 5355 Spring 2017 Lecture notes follow: Allen, Linda JS. An introduction to stochastic processes with applications to biology. CRC Press,
History and meaning of the word Ecology A. Definition 1. Oikos, ology - the study of the house - the place we live
 History and meaning of the word Ecology A. Definition 1. Oikos, ology - the study of the house - the place we live B. Etymology study of the origin and development of a word 1. Earliest - Haeckel (1869)
History and meaning of the word Ecology A. Definition 1. Oikos, ology - the study of the house - the place we live B. Etymology study of the origin and development of a word 1. Earliest - Haeckel (1869)
Solutions: 6.2 FE 1: If f is linear what is f( Solution: ) = FE 6: The fuction g : R 2 R 2 is linear Since = what is g( Solution:
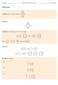 Solutions: 6 FE : If f is linear what is f(? f( 6 FE 6: The fuction g : R R is linear ( 5 ( g( g( Since ( 5 ( + ( what is g( (? 5g ( + g( ( ( + ( 5 8 5 + 5 ( g( g(5 6 FE 9: Multiply: (a (b (c [ ] ( [ ]
Solutions: 6 FE : If f is linear what is f(? f( 6 FE 6: The fuction g : R R is linear ( 5 ( g( g( Since ( 5 ( + ( what is g( (? 5g ( + g( ( ( + ( 5 8 5 + 5 ( g( g(5 6 FE 9: Multiply: (a (b (c [ ] ( [ ]
Math 115 Spring 11 Written Homework 10 Solutions
 Math 5 Spring Written Homework 0 Solutions. For following its, state what indeterminate form the its are in and evaluate the its. (a) 3x 4x 4 x x 8 Solution: This is in indeterminate form 0. Algebraically,
Math 5 Spring Written Homework 0 Solutions. For following its, state what indeterminate form the its are in and evaluate the its. (a) 3x 4x 4 x x 8 Solution: This is in indeterminate form 0. Algebraically,
Math 3191 Applied Linear Algebra
 Math 9 Applied Linear Algebra Lecture 9: Diagonalization Stephen Billups University of Colorado at Denver Math 9Applied Linear Algebra p./9 Section. Diagonalization The goal here is to develop a useful
Math 9 Applied Linear Algebra Lecture 9: Diagonalization Stephen Billups University of Colorado at Denver Math 9Applied Linear Algebra p./9 Section. Diagonalization The goal here is to develop a useful
n α 1 α 2... α m 1 α m σ , A =
 The Leslie Matrix The Leslie matrix is a generalization of the above. It is a matrix which describes the increases in numbers in various age categories of a population year-on-year. As above we write p
The Leslie Matrix The Leslie matrix is a generalization of the above. It is a matrix which describes the increases in numbers in various age categories of a population year-on-year. As above we write p
Eigenspaces. (c) Find the algebraic multiplicity and the geometric multiplicity for the eigenvaules of A.
 Eigenspaces 1. (a) Find all eigenvalues and eigenvectors of A = (b) Find the corresponding eigenspaces. [ ] 1 1 1 Definition. If A is an n n matrix and λ is a scalar, the λ-eigenspace of A (usually denoted
Eigenspaces 1. (a) Find all eigenvalues and eigenvectors of A = (b) Find the corresponding eigenspaces. [ ] 1 1 1 Definition. If A is an n n matrix and λ is a scalar, the λ-eigenspace of A (usually denoted
TMA Calculus 3. Lecture 21, April 3. Toke Meier Carlsen Norwegian University of Science and Technology Spring 2013
 TMA4115 - Calculus 3 Lecture 21, April 3 Toke Meier Carlsen Norwegian University of Science and Technology Spring 2013 www.ntnu.no TMA4115 - Calculus 3, Lecture 21 Review of last week s lecture Last week
TMA4115 - Calculus 3 Lecture 21, April 3 Toke Meier Carlsen Norwegian University of Science and Technology Spring 2013 www.ntnu.no TMA4115 - Calculus 3, Lecture 21 Review of last week s lecture Last week
Chapter 2: Time Series Modelling. Chapter 3: Discrete Models. Notes. Notes. Intro to the Topic Time Series Discrete Models Growth and Decay
 Chapter 2: Modelling 6 / 71 Chapter 3: 7 / 71 Glossary of Terms Here are some of the types of symbols you will see in this section: Name Symbol Face Examples Vector Lower-case bold u, v, p Matrix Upper-case
Chapter 2: Modelling 6 / 71 Chapter 3: 7 / 71 Glossary of Terms Here are some of the types of symbols you will see in this section: Name Symbol Face Examples Vector Lower-case bold u, v, p Matrix Upper-case
IB 153 Fall 2006 Life histories and population regulation 9/21/2006. Life history classification schemes. r/k selection (MacArthur and Wilson 1967)
 IB 153 Fall 26 Life histories and 9/21/26 Today's lecture: 1. Finish discussion on life histories 2. Review exponential and logistic growth equations 3. Effects of density on vital rates and consequences
IB 153 Fall 26 Life histories and 9/21/26 Today's lecture: 1. Finish discussion on life histories 2. Review exponential and logistic growth equations 3. Effects of density on vital rates and consequences
Maths for Signals and Systems Linear Algebra in Engineering
 Maths for Signals and Systems Linear Algebra in Engineering Lectures 13 15, Tuesday 8 th and Friday 11 th November 016 DR TANIA STATHAKI READER (ASSOCIATE PROFFESOR) IN SIGNAL PROCESSING IMPERIAL COLLEGE
Maths for Signals and Systems Linear Algebra in Engineering Lectures 13 15, Tuesday 8 th and Friday 11 th November 016 DR TANIA STATHAKI READER (ASSOCIATE PROFFESOR) IN SIGNAL PROCESSING IMPERIAL COLLEGE
Lecture 10: Powers of Matrices, Difference Equations
 Lecture 10: Powers of Matrices, Difference Equations Difference Equations A difference equation, also sometimes called a recurrence equation is an equation that defines a sequence recursively, i.e. each
Lecture 10: Powers of Matrices, Difference Equations Difference Equations A difference equation, also sometimes called a recurrence equation is an equation that defines a sequence recursively, i.e. each
Linear Algebra review Powers of a diagonalizable matrix Spectral decomposition
 Linear Algebra review Powers of a diagonalizable matrix Spectral decomposition Prof. Tesler Math 283 Fall 2018 Also see the separate version of this with Matlab and R commands. Prof. Tesler Diagonalizing
Linear Algebra review Powers of a diagonalizable matrix Spectral decomposition Prof. Tesler Math 283 Fall 2018 Also see the separate version of this with Matlab and R commands. Prof. Tesler Diagonalizing
MATH3200, Lecture 31: Applications of Eigenvectors. Markov Chains and Chemical Reaction Systems
 Lecture 31: Some Applications of Eigenvectors: Markov Chains and Chemical Reaction Systems Winfried Just Department of Mathematics, Ohio University April 9 11, 2018 Review: Eigenvectors and left eigenvectors
Lecture 31: Some Applications of Eigenvectors: Markov Chains and Chemical Reaction Systems Winfried Just Department of Mathematics, Ohio University April 9 11, 2018 Review: Eigenvectors and left eigenvectors
Elementary Matrices. MATH 322, Linear Algebra I. J. Robert Buchanan. Spring Department of Mathematics
 Elementary Matrices MATH 322, Linear Algebra I J. Robert Buchanan Department of Mathematics Spring 2015 Outline Today s discussion will focus on: elementary matrices and their properties, using elementary
Elementary Matrices MATH 322, Linear Algebra I J. Robert Buchanan Department of Mathematics Spring 2015 Outline Today s discussion will focus on: elementary matrices and their properties, using elementary
Chapter 6 Population and Community Ecology. Thursday, October 19, 17
 Chapter 6 Population and Community Ecology Module 18 The Abundance and Distribution of After reading this module you should be able to explain how nature exists at several levels of complexity. discuss
Chapter 6 Population and Community Ecology Module 18 The Abundance and Distribution of After reading this module you should be able to explain how nature exists at several levels of complexity. discuss
Environmental Influences on Adaptation
 Have you ever noticed how the way you feel sometimes mirrors the emotions of the people with whom you spend a lot of time? For example, when you re around happy people, do you tend to become happy? Since
Have you ever noticed how the way you feel sometimes mirrors the emotions of the people with whom you spend a lot of time? For example, when you re around happy people, do you tend to become happy? Since
Age (x) nx lx. Population dynamics Population size through time should be predictable N t+1 = N t + B + I - D - E
 Population dynamics Population size through time should be predictable N t+1 = N t + B + I - D - E Time 1 N = 100 20 births 25 deaths 10 immigrants 15 emmigrants Time 2 100 + 20 +10 25 15 = 90 Life History
Population dynamics Population size through time should be predictable N t+1 = N t + B + I - D - E Time 1 N = 100 20 births 25 deaths 10 immigrants 15 emmigrants Time 2 100 + 20 +10 25 15 = 90 Life History
Darwin, Mendel, and Genetics
 Darwin, Mendel, and Genetics The age old questions Who am I? In particular, what traits define me? How (and why) did I get to be who I am, that is, how were these traits passed on to me? Pre-Science (and
Darwin, Mendel, and Genetics The age old questions Who am I? In particular, what traits define me? How (and why) did I get to be who I am, that is, how were these traits passed on to me? Pre-Science (and
Chapter 5 Lecture. Metapopulation Ecology. Spring 2013
 Chapter 5 Lecture Metapopulation Ecology Spring 2013 5.1 Fundamentals of Metapopulation Ecology Populations have a spatial component and their persistence is based upon: Gene flow ~ immigrations and emigrations
Chapter 5 Lecture Metapopulation Ecology Spring 2013 5.1 Fundamentals of Metapopulation Ecology Populations have a spatial component and their persistence is based upon: Gene flow ~ immigrations and emigrations
population size at time t, then in continuous time this assumption translates into the equation for exponential growth dn dt = rn N(0)
 Appendix S1: Classic models of population dynamics in ecology and fisheries science Populations do not grow indefinitely. No concept is more fundamental to ecology and evolution. Malthus hypothesized that
Appendix S1: Classic models of population dynamics in ecology and fisheries science Populations do not grow indefinitely. No concept is more fundamental to ecology and evolution. Malthus hypothesized that
BIOS 3010: Ecology Lecture 14: Life Histories: 2. Components of life histories: Growth, fecundity and survivorship. 3. Components of life histories:
 BIOS 3010: Ecology Lecture 14: Life Histories: Lecture summary: Components of life histories: Growth. Fecundity. Survivorship. Reproductive value. Trade-offs. r- and K-selection. Habitat templates. Clutch
BIOS 3010: Ecology Lecture 14: Life Histories: Lecture summary: Components of life histories: Growth. Fecundity. Survivorship. Reproductive value. Trade-offs. r- and K-selection. Habitat templates. Clutch
Math 4377/6308 Advanced Linear Algebra
 2.3 Composition Math 4377/6308 Advanced Linear Algebra 2.3 Composition of Linear Transformations Jiwen He Department of Mathematics, University of Houston jiwenhe@math.uh.edu math.uh.edu/ jiwenhe/math4377
2.3 Composition Math 4377/6308 Advanced Linear Algebra 2.3 Composition of Linear Transformations Jiwen He Department of Mathematics, University of Houston jiwenhe@math.uh.edu math.uh.edu/ jiwenhe/math4377
Linear Algebra review Powers of a diagonalizable matrix Spectral decomposition
 Linear Algebra review Powers of a diagonalizable matrix Spectral decomposition Prof. Tesler Math 283 Fall 2016 Also see the separate version of this with Matlab and R commands. Prof. Tesler Diagonalizing
Linear Algebra review Powers of a diagonalizable matrix Spectral decomposition Prof. Tesler Math 283 Fall 2016 Also see the separate version of this with Matlab and R commands. Prof. Tesler Diagonalizing
Singular Value Decomposition
 Singular Value Decomposition Motivatation The diagonalization theorem play a part in many interesting applications. Unfortunately not all matrices can be factored as A = PDP However a factorization A =
Singular Value Decomposition Motivatation The diagonalization theorem play a part in many interesting applications. Unfortunately not all matrices can be factored as A = PDP However a factorization A =
MATH 423 Linear Algebra II Lecture 20: Geometry of linear transformations. Eigenvalues and eigenvectors. Characteristic polynomial.
 MATH 423 Linear Algebra II Lecture 20: Geometry of linear transformations. Eigenvalues and eigenvectors. Characteristic polynomial. Geometric properties of determinants 2 2 determinants and plane geometry
MATH 423 Linear Algebra II Lecture 20: Geometry of linear transformations. Eigenvalues and eigenvectors. Characteristic polynomial. Geometric properties of determinants 2 2 determinants and plane geometry
Linear Algebra Section 2.6 : LU Decomposition Section 2.7 : Permutations and transposes Wednesday, February 13th Math 301 Week #4
 Linear Algebra Section. : LU Decomposition Section. : Permutations and transposes Wednesday, February 1th Math 01 Week # 1 The LU Decomposition We learned last time that we can factor a invertible matrix
Linear Algebra Section. : LU Decomposition Section. : Permutations and transposes Wednesday, February 1th Math 01 Week # 1 The LU Decomposition We learned last time that we can factor a invertible matrix
A time discrete linear model of an age and time of residence structured population in a patchy environment
 Biological Modelling South African Journal of Science 104 May/June 2008 203 A time discrete linear model of an age and time of residence structured population in a patchy environment A. Moussaoui ab* P.Auger
Biological Modelling South African Journal of Science 104 May/June 2008 203 A time discrete linear model of an age and time of residence structured population in a patchy environment A. Moussaoui ab* P.Auger
Speciation and Patterns of Evolution
 Speciation and Patterns of Evolution What is a species? Biologically, a species is defined as members of a population that can interbreed under natural conditions Different species are considered reproductively
Speciation and Patterns of Evolution What is a species? Biologically, a species is defined as members of a population that can interbreed under natural conditions Different species are considered reproductively
Linear Algebra (MATH ) Spring 2011 Final Exam Practice Problem Solutions
 Linear Algebra (MATH 4) Spring 2 Final Exam Practice Problem Solutions Instructions: Try the following on your own, then use the book and notes where you need help. Afterwards, check your solutions with
Linear Algebra (MATH 4) Spring 2 Final Exam Practice Problem Solutions Instructions: Try the following on your own, then use the book and notes where you need help. Afterwards, check your solutions with
Homework For each of the following matrices, find the minimal polynomial and determine whether the matrix is diagonalizable.
 Math 5327 Fall 2018 Homework 7 1. For each of the following matrices, find the minimal polynomial and determine whether the matrix is diagonalizable. 3 1 0 (a) A = 1 2 0 1 1 0 x 3 1 0 Solution: 1 x 2 0
Math 5327 Fall 2018 Homework 7 1. For each of the following matrices, find the minimal polynomial and determine whether the matrix is diagonalizable. 3 1 0 (a) A = 1 2 0 1 1 0 x 3 1 0 Solution: 1 x 2 0
EXAMPLES OF CLASSICAL ITERATIVE METHODS
 EXAMPLES OF CLASSICAL ITERATIVE METHODS In these lecture notes we revisit a few classical fixpoint iterations for the solution of the linear systems of equations. We focus on the algebraic and algorithmic
EXAMPLES OF CLASSICAL ITERATIVE METHODS In these lecture notes we revisit a few classical fixpoint iterations for the solution of the linear systems of equations. We focus on the algebraic and algorithmic
Levels of Ecological Organization. Biotic and Abiotic Factors. Studying Ecology. Chapter 4 Population Ecology
 Chapter 4 Population Ecology Lesson 4.1 Studying Ecology Levels of Ecological Organization Biotic and Abiotic Factors The study of how organisms interact with each other and with their environments Scientists
Chapter 4 Population Ecology Lesson 4.1 Studying Ecology Levels of Ecological Organization Biotic and Abiotic Factors The study of how organisms interact with each other and with their environments Scientists
Chapter 4 Population Ecology
 Chapter 4 Population Ecology Lesson 4.1 Studying Ecology Levels of Ecological Organization The study of how organisms interact with each other and with their environments Scientists study ecology at various
Chapter 4 Population Ecology Lesson 4.1 Studying Ecology Levels of Ecological Organization The study of how organisms interact with each other and with their environments Scientists study ecology at various
SEMELPAROUS PERIODICAL INSECTS
 SEMELPROUS PERIODICL INSECTS BRENDN FRY Honors Thesis Spring 2008 Chapter Introduction. History Periodical species are those whose life cycle has a fixed length of n years, and whose adults do not appear
SEMELPROUS PERIODICL INSECTS BRENDN FRY Honors Thesis Spring 2008 Chapter Introduction. History Periodical species are those whose life cycle has a fixed length of n years, and whose adults do not appear
Matrix Models for Evolutionary Population Dynamics: Studies of the Effects of Climate Change on Seabirds
 Matrix Models for Evolutionary Population Dynamics: Studies of the Effects of Climate Change on Seabirds J. M. Cushing Department of Mathematics & Interdisciplinary Program in Applied Mathematics University
Matrix Models for Evolutionary Population Dynamics: Studies of the Effects of Climate Change on Seabirds J. M. Cushing Department of Mathematics & Interdisciplinary Program in Applied Mathematics University
Math 345 Intro to Math Biology Lecture 1: Biological Models using Difference Equations
 Math 345 Intro to Math Biology Lecture 1: Biological Models using Difference Equations Junping Shi College of William and Mary, USA Population of James City County, Virginia Population is often recorded
Math 345 Intro to Math Biology Lecture 1: Biological Models using Difference Equations Junping Shi College of William and Mary, USA Population of James City County, Virginia Population is often recorded
NOTES Ch 17: Genes and. Variation
 NOTES Ch 17: Genes and Vocabulary Fitness Genetic Drift Punctuated Equilibrium Gene flow Adaptive radiation Divergent evolution Convergent evolution Gradualism Variation 17.1 Genes & Variation Darwin developed
NOTES Ch 17: Genes and Vocabulary Fitness Genetic Drift Punctuated Equilibrium Gene flow Adaptive radiation Divergent evolution Convergent evolution Gradualism Variation 17.1 Genes & Variation Darwin developed
Chapter 6 Meiosis and Mendel
 UNIT 3 GENETICS Chapter 6 Meiosis and Mendel 1 hairy ears (hypertrichosis)- due to holandric gene. (Y chromosome)-only occurs in males. Appears in all sons. 2 Polydactyly- having extra fingers Wendy the
UNIT 3 GENETICS Chapter 6 Meiosis and Mendel 1 hairy ears (hypertrichosis)- due to holandric gene. (Y chromosome)-only occurs in males. Appears in all sons. 2 Polydactyly- having extra fingers Wendy the
JUST THE MATHS SLIDES NUMBER 9.6. MATRICES 6 (Eigenvalues and eigenvectors) A.J.Hobson
 JUST THE MATHS SLIDES NUMBER 96 MATRICES 6 (Eigenvalues and eigenvectors) by AJHobson 96 The statement of the problem 962 The solution of the problem UNIT 96 - MATRICES 6 EIGENVALUES AND EIGENVECTORS 96
JUST THE MATHS SLIDES NUMBER 96 MATRICES 6 (Eigenvalues and eigenvectors) by AJHobson 96 The statement of the problem 962 The solution of the problem UNIT 96 - MATRICES 6 EIGENVALUES AND EIGENVECTORS 96
Kontakt: (Verantwortlicher Dozent): Part 3 of Hauptvorlesung Evolutionsbiologie
 There is strong variation among species and taxonomic groups in life history traits. Why? There is also strong variation within clades in life history traits. 3 4 The evolution of life histories Outline:
There is strong variation among species and taxonomic groups in life history traits. Why? There is also strong variation within clades in life history traits. 3 4 The evolution of life histories Outline:
LIFE HISTORY STRATEGIES
 LIFE HISTORY STRATEGIES LIFE HISTORY STRATEGIES What characteristics help a population survive and grow? What are the dominant species in an ecosystem? Why doesn't a dominant species (of plant or animal)
LIFE HISTORY STRATEGIES LIFE HISTORY STRATEGIES What characteristics help a population survive and grow? What are the dominant species in an ecosystem? Why doesn't a dominant species (of plant or animal)
Chapter 6 Population and Community Ecology
 Chapter 6 Population and Community Ecology Friedland and Relyea Environmental Science for AP, second edition 2015 W.H. Freeman and Company/BFW AP is a trademark registered and/or owned by the College Board,
Chapter 6 Population and Community Ecology Friedland and Relyea Environmental Science for AP, second edition 2015 W.H. Freeman and Company/BFW AP is a trademark registered and/or owned by the College Board,
Ch. 4 - Population Ecology
 Ch. 4 - Population Ecology Ecosystem all of the living organisms and nonliving components of the environment in an area together with their physical environment How are the following things related? mice,
Ch. 4 - Population Ecology Ecosystem all of the living organisms and nonliving components of the environment in an area together with their physical environment How are the following things related? mice,
Linear Algebra Primer
 Introduction Linear Algebra Primer Daniel S. Stutts, Ph.D. Original Edition: 2/99 Current Edition: 4//4 This primer was written to provide a brief overview of the main concepts and methods in elementary
Introduction Linear Algebra Primer Daniel S. Stutts, Ph.D. Original Edition: 2/99 Current Edition: 4//4 This primer was written to provide a brief overview of the main concepts and methods in elementary
Matrix Solutions to Linear Systems of ODEs
 Matrix Solutions to Linear Systems of ODEs James K. Peterson Department of Biological Sciences and Department of Mathematical Sciences Clemson University November 3, 216 Outline 1 Symmetric Systems of
Matrix Solutions to Linear Systems of ODEs James K. Peterson Department of Biological Sciences and Department of Mathematical Sciences Clemson University November 3, 216 Outline 1 Symmetric Systems of
Section 1.1 Algorithms. Key terms: Algorithm definition. Example from Trapezoidal Rule Outline of corresponding algorithm Absolute Error
 Section 1.1 Algorithms Key terms: Algorithm definition Example from Trapezoidal Rule Outline of corresponding algorithm Absolute Error Approximating square roots Iterative method Diagram of a general iterative
Section 1.1 Algorithms Key terms: Algorithm definition Example from Trapezoidal Rule Outline of corresponding algorithm Absolute Error Approximating square roots Iterative method Diagram of a general iterative
Charles Darwin became a naturalist, a scientist who studies nature, during a voyage on the British ship HMS Beagle.
 Theory of Evolution Darwin s Voyage What did Darwin observe? Charles Darwin became a naturalist, a scientist who studies nature, during a voyage on the British ship HMS Beagle. On his journey, Darwin observed
Theory of Evolution Darwin s Voyage What did Darwin observe? Charles Darwin became a naturalist, a scientist who studies nature, during a voyage on the British ship HMS Beagle. On his journey, Darwin observed
2.3.6 Exercises NS-3. Q 1.1: What condition(s) must hold for p and q such that a, b, and c are always positive 10 and nonzero?
 .3. LECTURE 4: (WEEK 3) APPLICATIONS OF PRIME NUMBER 67.3.6 Exercises NS-3 Topic of this homework: Pythagorean triples, Pell s equation, Fibonacci sequence Deliverable: Answers to problems 5 Pythagorean
.3. LECTURE 4: (WEEK 3) APPLICATIONS OF PRIME NUMBER 67.3.6 Exercises NS-3 Topic of this homework: Pythagorean triples, Pell s equation, Fibonacci sequence Deliverable: Answers to problems 5 Pythagorean
Math 4377/6308 Advanced Linear Algebra
 3.1 Elementary Matrix Math 4377/6308 Advanced Linear Algebra 3.1 Elementary Matrix Operations and Elementary Matrix Jiwen He Department of Mathematics, University of Houston jiwenhe@math.uh.edu math.uh.edu/
3.1 Elementary Matrix Math 4377/6308 Advanced Linear Algebra 3.1 Elementary Matrix Operations and Elementary Matrix Jiwen He Department of Mathematics, University of Houston jiwenhe@math.uh.edu math.uh.edu/
Evolution of Populations
 Evolution of Populations Gene Pools 1. All of the genes in a population - Contains 2 or more alleles (forms of a gene) for each trait 2. Relative frequencies - # of times an allele occurs in a gene pool
Evolution of Populations Gene Pools 1. All of the genes in a population - Contains 2 or more alleles (forms of a gene) for each trait 2. Relative frequencies - # of times an allele occurs in a gene pool
Vectors and Matrices Statistics with Vectors and Matrices
 Vectors and Matrices Statistics with Vectors and Matrices Lecture 3 September 7, 005 Analysis Lecture #3-9/7/005 Slide 1 of 55 Today s Lecture Vectors and Matrices (Supplement A - augmented with SAS proc
Vectors and Matrices Statistics with Vectors and Matrices Lecture 3 September 7, 005 Analysis Lecture #3-9/7/005 Slide 1 of 55 Today s Lecture Vectors and Matrices (Supplement A - augmented with SAS proc
Math 16A Discussion Worksheet January 23, 2018
 1 Reminders 1. A quiz will be given every other week starting next week. So a quiz will be given on January 0, February 1, February 27, March 1, March 27, April 10, and April 24. 2. Section Grade (a) Homework
1 Reminders 1. A quiz will be given every other week starting next week. So a quiz will be given on January 0, February 1, February 27, March 1, March 27, April 10, and April 24. 2. Section Grade (a) Homework
On the Fundamental Bifurcation Theorem for Semelparous Leslie Models
 On the Fundamental Bifurcation Theorem for Semelparous Leslie Models J M Cushing May 11, 215 Abstract This brief survey of nonlinear Leslie models focuses on the fundamental bifurcation that occurs when
On the Fundamental Bifurcation Theorem for Semelparous Leslie Models J M Cushing May 11, 215 Abstract This brief survey of nonlinear Leslie models focuses on the fundamental bifurcation that occurs when
Examples: u = is a vector in 2. is a vector in 5.
 3 Vectors and vector equations We'll carefully define vectors, algebraic operations on vectors and geometric interpretations of these operations, in terms of displacements These ideas will eventually give
3 Vectors and vector equations We'll carefully define vectors, algebraic operations on vectors and geometric interpretations of these operations, in terms of displacements These ideas will eventually give
In this lab, you and your partners will try to devise a strategy that will allow your plant to thrive and reproduce (make flowers).
 The Plant Game credit: Elena DiMuzio at the Cornell Institute for Plant Biology Teachers I rewrote some of the explanatory material but the game idea is hers. Rules: First of all, to win at any game, players
The Plant Game credit: Elena DiMuzio at the Cornell Institute for Plant Biology Teachers I rewrote some of the explanatory material but the game idea is hers. Rules: First of all, to win at any game, players
spring, math 204 (mitchell) list of theorems 1 Linear Systems Linear Transformations Matrix Algebra
 spring, 2016. math 204 (mitchell) list of theorems 1 Linear Systems THEOREM 1.0.1 (Theorem 1.1). Uniqueness of Reduced Row-Echelon Form THEOREM 1.0.2 (Theorem 1.2). Existence and Uniqueness Theorem THEOREM
spring, 2016. math 204 (mitchell) list of theorems 1 Linear Systems THEOREM 1.0.1 (Theorem 1.1). Uniqueness of Reduced Row-Echelon Form THEOREM 1.0.2 (Theorem 1.2). Existence and Uniqueness Theorem THEOREM
