Differentially Private Empirical Risk Minimization
|
|
|
- Janice Summers
- 5 years ago
- Views:
Transcription
1 Differentially Private Empirical Risk Minimization Kamalika Chaudhuri, Claire Monteleoni, Anand D. Sarwate June 1, 2010 Abstract Privacy-preserving machine learning algorithms are crucial for the increasingly common setting in which personal data, such as medical or financial records, are analyzed. We provide general techniques to produce privacy-preserving approximations of classifiers learned via (regularized) empirical risk minimization (ERM). These algorithms are private under the ǫ-differential privacy definition due to Dwork et al. (2006). First we apply the output perturbation ideas of Dwork et al. (2006), to ERM classification. Then we propose a new method, objective perturbation, for privacy-preserving machine learning algorithm design. This method entails perturbing the objective function before optimizing over classifiers. We prove theoretical results showing that our algorithms preserve privacy and give generalization bounds for linear and nonlinear kernels. We further present a privacy-preserving technique for tuning the parameters in general machine learning algorithms, thereby providing end-to-end privacy guarantees for the training process. We apply these results to produce privacy-preserving analogues of regularized logistic regression and support vector machines. We obtain encouraging results from evaluating their performance on real demographic and benchmark data sets. Our results show that both theoretically and empirically, objective perturbation is superior to the previous state-of-the-art, output perturbation, in managing the inherent tradeoff between privacy and learning performance. 1 Introduction Privacy has become a growing concern, due to the massive increase in personal information stored in electronic databases, such as medical records, financial records, web search histories, and social network data. Machine learning can be employed to discover novel population-wide patterns, however the results of such algorithms may reveal certain individuals sensitive information, thereby violating their privacy. Thus, an emerging challenge for machine learning is how to learn from datasets that contain sensitive personal information. At the first glance, it may appear that simple anonymization of private information is enough to preserve privacy. However, this is often not the case; even if obvious identifiers, such as names and addresses, are removed from the data, the remaining fields can still form unique signatures that can help re-identify individuals. Such attacks have been demonstrated by various works, and are Department of Computer Science and Engineering, University of California, San Diego, La Jolla, CA 92093, USA. kchaudhuri@ucsd.edu Center for Computational Learning Systems, Columbia University, New York, NY 10115, USA. cmontel@ccls.columbia.edu Information Theory and Applications Center, University of California, San Diego, La Jolla, CA , USA. asarwate@ucsd.edu 1
2 possible in many realistic settings, such as when an adversary has side information [Sweeney, 1997, Narayanan and Shmatikov, 2008, Ganta et al., 2008], and when the data has structural properties [Backstrom et al., 2007], among others. Moreover, even releasing statistics on a sensitive dataset may not be sufficient to preserve privacy, as illustrated on genetic data [Homer et al., 2008, Wang et al., 2009]. Thus, there is a great need for designing machine learning algorithms, that also preserve the privacy of individuals on the datasets they train and operate on. In this paper, we focus on the problem of classification, one of the fundamental problems of machine learning, when the training data consists of sensitive information of individuals. Our work addresses the Empirical risk minimization (ERM) framework for classification, in which a classifier is chosen by minimizing the average over the training data of the prediction loss (with respect to the label) of the classifier in predicting each training data point. In this work, we focus on regularized ERM in which there is an additional term in the optimization, called the regularizer, which penalizes the complexity of the classifier, with respect to some metric. Regularized ERM methods are widely used in practice, for example logistic regression and SVM, and many also have theoretical justification in the form of generalization error bounds with respect to independently, identically distributed (i.i.d.) data (see Vapnik [1998] for further details). For our privacy measure, we use a definition due to Dwork et al. [2006b], who have proposed a measure of quantifying the privacy-risk associated with computing functions of sensitive data. Their ǫ-differential privacy model is a strong, cryptographically-motivated definition of privacy that has recently received a significant amount of research attention for its robustness to known attacks, such as those involving side information [Ganta et al., 2008]. Algorithms satisfying ǫ-differential privacy are randomized; the output is a random variable whose distribution is conditioned on the data set. A statistical procedure satisfies ǫ-differential privacy if changing a single data point does not shift the output distribution by too much. Therefore, from looking at the output the algorithm, it is difficult to infer the value of any particular data point. In this paper, we develop methods for approximating empirical risk minimization (ERM) while guaranteeing ǫ-differential privacy. We develop methods for end-to-end privacy; each step in the learning process can cause additional risk of privacy violation, and we provide algorithms with quantifiable privacy guarantees for training as well as parameter tuning. For training, we provide two privacy-preserving approximations to ERM. The first is output perturbation, based on the sensitivity method proposed by Dwork et al. [2006b]. In this method noise is added to the output of the standard ERM algorithm. The second method is novel, and involves adding noise to the regularized ERM objective function prior to minimizing. We call this second method objective perturbation. We show theoretical bounds for both procedures; the theoretical performance of objective perturbation is superior to that of output perturbation for most problems. We validate these theoretical results on data sets from the UCI repository. In practice, parameters in learning algorithms are chosen via a holdout data set. In the context of privacy, we must guarantee the privacy of the holdout data as well. We exploit results from the theory of differential privacy to develop a privacy-preserving parameter tuning algorithm, and demonstrate its use in practice. Together with our training algorithms, this parameter tuning algorithm guarantees privacy to all data used in the learning process. Guaranteeing privacy incurs a cost in performance; because the algorithms must cause some uncertainty in the output, they increase the loss of the output predictor. Because the ǫ-differential privacy model requires robustness against all data sets, we make no assumptions on the underlying data for the purposes of making privacy guarantees. However, to prove the impact of privacy 2
3 constraints on the generalization error, we assume the data is i.i.d. according to a fixed but unknown distribution. Although many of our results hold for ERM in general, we provide specific results for classification using logistic regression and support vector machines. Some of the former results were reported in Chaudhuri and Monteleoni [2008]; here we generalize them to ERM and extend the results to kernel methods, and provide experiments on real datasets. More specifically, the contributions of this paper are as follows: We derive a computationally efficient algorithm for ERM classification, based on the sensitivity method due to Dwork et al. [2006b]. We analyze the accuracy of this algorithm, and provide an upper bound on the number of training samples required by this algorithm to achieve a fixed generalization error. We provide a general technique, objective perturbation, for providing computationally efficient, differentially private approximations to regularized ERM algorithms. This extends the work of Chaudhuri and Monteleoni [2008], which follows as a special case. We specialize the results on the sensitivity method and objective perturbation to logistic regression and support vector machine classifiers. In addition to privacy guarantees, we also provide generalization bounds for this algorithm. For kernel methods with nonlinear kernel functions, the optimal classifier is a linear combination of kernel functions centered at the training points. This form is inherently non-private because it reveals the training data. We adapt a random projection method due to Rahimi and Recht Rahimi and Recht [2007, 2008b], to develop privacy-preserving kernel-erm algorithms. We provide theoretical results on generalization performance. Because the holdout data is used in the process of training and releasing a classifier, we provide a privacy-preserving parameter tuning algorithm based on a randomized selection procedure [McSherry and Talwar, 2007] applicable to general machine learning algorithms. This guarantees end-to-end privacy during the learning procedure. We validate our results using experiments on two datasets from the UCI Machine Learning repositories (Asuncion and Newman [2007]) and KDDCup (Hettich and Bay [1999]). Our results show that objective perturbation is generally superior to output perturbation. We also demonstrate the impact of end-to-end privacy on generalization error. 1.1 Related Work There has been a significant amount of literature on the ineffectiveness of simple anonymization procedures. For example, Narayanan and Shmatikov [2008] show that a small amount of auxiliary information (knowledge of a few movie-ratings, and approximate dates) is sufficient for an adversary to re-identify an individual in the Netflix dataset, which consists of anonymized data about Netflix users and their movie ratings. The same phenomenon has been observed in other kinds of data, such as social network graphs (Backstrom et al. [2007]), search query logs (Jones et al. [2007]) and others. Releasing statistics computed on sensitive data can also be problematic; for example, Wang et al. [2009] show that releasing R 2 -values computed on high-dimensional genetic data can lead to privacy breaches by an adversary who is armed with a small amount of auxiliary information. There has also been a significant amount of work on privacy-preserving data mining [Agrawal and Srikant, 2000, Evfimievski et al., 2003, Sweeney, 2002, Machanavajjhala et al., 2006], spanning 3
4 several communities, that uses privacy models other than differential privacy. Many of the models used have been shown to be susceptible to composition attacks, attacks in which the adversary has some reasonable amount of prior knowledge [Ganta et al., 2008]. Other work [Mangasarian et al., 2008] considers the problem of privacy-preserving SVM classification when separate agents have to share private data, and provides a solution that uses random kernels, but does provide any formal privacy guarantee. An alternative line of privacy work is in the Secure Multiparty Computation setting due to Yao [1982], where the sensitive data is split across multiple hostile databases, and the goal is to compute a function on the union of these databases. Zhan and Matwin [2007] and Laur et al. [2006] consider computing privacy-preserving SVMs in this setting, and their goal is to design a distributed protocol to learn a classifier. This is in contrast with our work, which deals with a setting where the algorithm has access to the entire dataset. Differential privacy, the formal privacy definition used in our paper, was proposed by the seminal work of Dwork et al. [2006b], and has been used since in numerous works on privacy for example, Chaudhuri and Mishra [2006], McSherry and Talwar [2007], Nissim et al. [2007], Barak et al. [2007], Chaudhuri and Monteleoni [2008], Machanavajjhala et al. [2008]. Unlike many other privacy definitions, such as those mentioned above, differential privacy has been shown to be resistant to composition attacks (attacks involving side-information) [Ganta et al., 2008]. Some follow-up work on differential privacy includes work on differentially-private combinatorial optimization, due to Gupta et al. [2010], and differentially-private contingency tables, due to Barak et al. [2007] and Kasivishwanathan et al. [2010]. Wasserman and Zhou [2010] provide a more statistical view of differential privacy, and Zhou et al. [2009b] provide a technique of generating synthetic data using compression via random linear or affine transformations. Previous literature has also considered learning with differential privacy. One of the first such works is Kasiviswanathan et al. [2008], which presents a general, although computationally inefficient, method for PAC-learning finite concept classes. Blum et al. [2008] presents a method for releasing a database in a differentially-private manner, so that certain fixed classes of queries can be answered accurately, provided the class of queries has a bounded VC-dimension. Their methods can also be used to learn classifiers with a fixed VC-dimension see Kasiviswanathan et al. [2008]; however the resulting algorithm is also computationally inefficient. Some sample complexity lower bounds in this setting have been provided by Beimel et al. [2010]. In addition, Dwork and Lei [2009] explore a connection between differential privacy and robust statistics, and provide an algorithm for privacy-preserving regression using ideas from robust statistics. However, their algorithm also requires a running time which is exponential in the data dimension, and is hence computationally inefficient. This work builds on our preliminary work in Chaudhuri and Monteleoni [2008]. We first show how to extend the sensitivity method, a form of output perturbation, due to Dwork et al. [2006b], to classification algorithms. In general, output perturbation methods alter the output of the function computed on the database, before releasing it; in particular the sensitivity method makes an algorithm differentially private by adding noise to its output. In the classification setting, the noise protects the privacy of the training data, but increases the prediction error of the classifier. 1 In 1 Recently, independent work by Rubinstein et al. [2009] has reported an extension of the sensitivity method to linear and kernel SVMs. Their utility analysis differs from ours, and thus the analogous generalization bounds are not comparable. Because Rubinstein et al. use techniques from algorithmic stability, their utility bounds compare the private and non-private classifiers using the same value for the regularization parameter. In contrast, our approach takes into account how the value of the regularization parameter might change due to privacy constraints. 4
5 contrast, we propose the objective perturbation method, in which noise is added to the objective function before optimizing over the space classifiers. Both the sensitivity method and objective perturbation result in computationally efficient algorithms, for our specific case. In general, our theoretical bounds on sample requirement are incomparable with the bounds of Kasiviswanathan et al. [2008] because of the difference between their setting and ours. 2 Model We will use x, x, and x H to denote the l 2 -norm, l -norm, and norm in a Hilbert space H, respectively. For an integer n we will use [n] to denote the set {1, 2,..., n}. Vectors will typically be written in boldface and sets in calligraphic type. For a matrix A, we will use the notation A 2 to denote the L 2 norm of A. 2.1 Empirical Risk Minimization In this paper we develop privacy-preserving algorithms for regularized empirical risk minimization, a special case of which is learning a classifier from labeled examples. We will phrase our problem in terms of classification and indicate when more general results hold. Our algorithms take as input training data D = {(x i,y i ) X Y : i = 1,2,...,n} of n data-label pairs. In the case of binary classification the data space X = R d and the label set Y = { 1,+1}. We will assume throughout that X is the unit ball so that x i 2 1. We would like to produce a predictor f : X Y. We measure the quality of our predictor on the training data via a nonnegative loss function l : Y Y R. In regularized empirical risk minimization (ERM), we choose a predictor f that minimizes the regularized empirical loss: J(f) = 1 n n l(f(x i ),y i ) + ΛN(f). (1) i=1 This minimization is performed over f in an hypothesis class H. The regularizer N( ) prevents over-fitting. For the first part of this paper we will restrict our attention to linear predictors and with some abuse of notation we will write f(x) = f T x. 2.2 Assumptions on loss and regularizer The conditions under which we can prove results on privacy and generalization error depend on analytic properties of the loss and regularizer. In particular, we will require certain forms of convexity (see Rockafellar and Wets [1998]). Definition 1. A function H(f) over f R d is said to be strictly convex if for all α (0,1), f, and g, H (αf + (1 α)g) < αh(f) + (1 α)h(g). (2) It is said to be λ-strongly convex if for all α (0,1), f, and g, H(f) + H(g) H (αf + (1 α)g) α λ α(1 α) f g 2 2. (3) 5
6 A strictly convex function has a unique minimum see Boyd and Vandenberghe [2004]. Strong convexity plays a role in guaranteeing our privacy and generalization requirements. For our privacy results to hold we will also require that the regularizer N( ) and loss function l(, ) be differentiable functions of f. This excludes certain classes of regularizers, such as the l 1 -norm regularizer N(f) = f 1, and classes of loss functions such as the hinge loss l SVM (f T x,y) = (1 yf T x) +. In some cases we can prove privacy guarantees for approximations to these non-differentiable functions. 2.3 Privacy model We are interested in producing a classifier in a manner that preserves the privacy of individual entries of the dataset D that is used in training the classifier. The notion of privacy we use is the ǫ-differential privacy model, developed by Dwork et al. [2006b], Dwork [2006], which defines a notion of privacy for a randomized algorithm A(D). Suppose A(D) produces a classifier, and let D be another dataset that differs from D in one entry (which we assume is the private value of one person). That is, D and D have n 1 points (x i,y i ) in common. The algorithm A provides differential privacy if for any set S, the likelihood that A(D) S is close to the likelihood A(D ) S, (where the likelihood is over the randomness in the algorithm). That is, any single entry of the dataset does not affect the output distribution of the algorithm by much; dually, this means that an adversary, who knows all but one entry of the dataset, cannot gain much additional information about the last entry by observing the output of the algorithm. The following definition of differential privacy is due to Dwork et al. [2006b], paraphrased from Wasserman and Zhou [2010]. Definition 2. An algorithm A(B) taking values in a set T provides ǫ p -differential privacy if sup S µ (S B = D) sup D,D µ (S B = D ) eǫp, (4) where the first supremum is over all measurable S T, the second is over all datasets D and D differing in a single entry, and µ( B) is the conditional distribution (measure) on T induced by the output A(B) given a dataset B. The ratio is interpreted to be 1 whenever the numerator and denominator are both 0. Note that if S is a set of measure 0 under the conditional measures induced by D and D, the ratio is automatically 1. A more measure-theoretic definition is given in Zhou et al. [2009a]. An illustration of the definition is given in Figure 1. The following form of the definition is due to Dwork et al. [2006a]. Definition 3. An algorithm A provides ǫ p -differential privacy if for any two datasets D and D that differ in a single entry and for any set S, exp( ǫ p )P(A(D ) S) P(A(D) S) exp(ǫ p )P(A(D ) S), (5) where A(D) (resp. A(D )) is the output of A on input D (resp. D ). We observe that an algorithm A that satisfies Equation 4 also satisfies Equation 5, and as a result, Definition 2 is stronger than Definition 3. From this definition, it is clear that the A(D) that outputs the minimizer of the ERM objective (1) does not provide ǫ p -differential privacy for any ǫ p. This is because an ERM solution is a linear 6
7 (x i, y i ) D D A( ) (x i, y i) S Figure 1: An algorithm which is differentially private. When datasets which are identical except for a single entry are input to the algorithm A, the two distributions on the algorithm s output are close. For a fixed measurable S the ratio of the measures (or densities) should be bounded. combination of some selected training samples near the decision boundary. If D and D differ in one of these samples, then the classifier will change completely, making the likelihood ratio in (5) infinite. Regularization helps by bounding the L 2 norm of the change, but does not completely solve the problem. Dwork et al. [2006b] also provide a standard recipe for computing privacy-preserving approximations to functions by adding noise with a particular distribution to the output of the function. We call this recipe the sensitivity method. Let g : (R m ) n R be a scalar function of z 1,...,z n, where z i R m corresponds to the private value of individual i; then the sensitivity of g is defined as follows. Definition 4. The sensitivity of a function g : (R m ) n R is maximum difference between the values of the function when one input changes. More formally, the sensitivity S(g) of g is defined as: S(g) = max i max z 1,...,z n,z i g(z1,...,z i 1,z i,z i+1,...,z n ) g(z 1,...,z i 1,z i,z i+1,...,z n ). (6) To compute a function g on a dataset D = {z 1,...,z n }, the sensitivity method outputs g(z 1,...,z n ) + η, where η is a random variable drawn according to the Laplace distribution, with mean 0 and standard deviation S(g) ǫ p. It is shown in Dwork et al. [2006b] that such a procedure is ǫ p -differentially private. 3 Privacy-preserving ERM Here we describe two approaches for creating privacy-preserving algorithms from (1). 3.1 Output perturbation : the sensitivity method Algorithm 1 is derived from the sensitivity method of Dwork et al. [2006b], a general method for generating a privacy-preserving approximation to any function A( ). In this section the norm 7
8 is the L 2 -norm unless otherwise specified. For the function A(D) = argmin J(f, D), Algorithm 1 outputs a vector A(D) + b, where b is random noise with density ν(b) = 1 α e β b, (7) where α is a normalizing constant. The parameter β is a function of ǫ p, and the L 2 -sensitivity of A( ), which is defined as follows. Definition 5. The L 2 -sensitivity of a vector-valued function is defined as the maximum change in the L 2 norm of the value of the function when one input changes. More formally, S(A) = max max A(z 1,...,z i,...) A(z 1,...,z i,...). (8) i z 1,...,z n,z i The interested reader is referred to Dwork et al. [2006b] for further details. Adding noise to the output of A( ) has the effect of masking the effect of any particular data point. However, in some applications the sensitivity of the minimizer argmin J(f, D) may be quite high, which would require the sensitivity method to add noise with high variance. Algorithm 1 ERM with output perturbation (sensitivity) Inputs: Data D = {z i }, parameters ǫ p, Λ. Output: Approximate minimizer f priv. Draw a vector b according to (7) with β = nλǫp 2. Compute f priv = argmin J(f, D) + b. 3.2 Objective perturbation A different approach, first proposed by Chaudhuri and Monteleoni [2008], is to add noise to the objective function itself and then produce the minimizer of the perturbed objective. That is, we can minimize J priv (f, D) = J(f, D) + 1 n bt f, (9) where b has density given by (7), with β = ǫ p. Note that the privacy parameter here does not depend on the sensitivity of the of the classification algorithm. Algorithm 2 ERM with objective perturbation Inputs: Data D = {z i }, parameters ǫ p, Λ, c. Output: Approximate minimizer f priv. Let ǫ p = ǫ p log(1 + 2c nλ + c2 ). n 2 Λ 2 If ǫ c p > 0, then = 0, else = Λ, and n(e ǫp/4 1) ǫ p = ǫ p/2. Draw a vector b according to (7) with β = ǫ p /2. Compute f priv = argmin J priv (f, D) f 2. The algorithm requires a certain slack, log(1 + 2c nλ + c2 ), in the privacy parameter. This is n 2 Λ 2 due to additional factors in bounding the ratio of the densities. 8
9 3.3 Privacy guarantees In this section, we establish the conditions under which Algorithms 1 and 2 provide ǫ p -differential privacy. First, we establish guarantees for Algorithm Privacy Guarantees for Output Perturbation Theorem 1. If N( ) is differentiable, and 1-strongly convex, and l is convex and differentiable, with l (z) 1 for all z, then, Algorithm 1 provides ǫ p -differential privacy. The proof of Theorem 1 follows from Corollary 1, and Dwork et al. [2006b]. The proof is provided here for completeness. Proof. From Corollary 1, if the conditions on N( ) and l hold, then the L 2 -sensivity of ERM with regularization parameter Λ is at most 2 nλ. We observe that when we pick b from the distribution in Algorithm 1, for a specific vector b 0 R d, the density at b 0 is proportional to e nλǫp b 2 0. Let D and D be any two datasets that differ in the value of one individual. Then, for any f, g(f D) g(f D ) = ν(b 1) ν(b 2 ) = nλǫp e ( b 2 1 b 2 ), (10) where b 1 and b 2 are the corresponding noise vectors chosen in Step 1 of Algorithm 1, and g(f D) (g(f D ) resp.) is the density of the output of Algorithm 1 at f, when the input is D (D resp.). If f 1 and f 2 are the solutions respectively to non-private regularized ERM when the input is D and D, then, b 2 b 1 = f 2 f 1. From Corollary 1, and using a triangle inequality, b 1 b 2 b 1 b 2 = f 2 f 1 2 nλ. (11) Moreover, by symmetry, the density of the directions of b 1 and b 2 are uniform. Therefore, by construction, ν(b 1) ν(b 2 ) eǫp. The theorem follows. The main ingredient of the proof of Theorem 1 is a result about the sensitivity of regularized ERM, which is provided below. Lemma 1. Let G(f) and g(f) be two vector-valued functions, which are continuous, and differentiable at all points. Moreover, let G(f) and G(f) + g(f) be λ-strongly convex. If f 1 = argmin f G(f) and f 2 = argmin f G(f) + g(f), then f 1 f 2 1 λ max g(f). (12) f Proof. Using the definition of f 1 and f 2, and the fact that G and g are continuous and differentiable everywhere, G(f 1 ) = G(f 2 ) + g(f 2 ) = 0. (13) As G(f) is λ-strongly convex, it follows from Lemma 14 of (Shalev-Shwartz [2007]) that: ( G(f 1 ) G(f 2 )) T (f 1 f 2 ) λ f 1 f 2 2. (14) Combining this with (13) and the Cauchy-Schwartz inequality, we get that f 1 f 2 g(f 2 ) (f 1 f 2 ) T g(f 2 ) = ( G(f 1 ) G(f 2 )) T (f 1 f 2 ) λ f 1 f 2 2. (15) The conclusion follows from dividing both sides by λ f 1 f 2. 9
10 Corollary 1. If N( ) is differentiable and 1-strongly convex, and l is convex and differentiable with l (z) 1 for all z, then, the L 2 -sensitivity of J(f, D) is at most 2 nλ. Proof. Let D = {(x 1,y 1 ),...,(x n,y n )} and D = {(x 1,y 1 ),...,(x n,y n)} be two datasets that differ in the value of the n-th individual. Moreover, we let G(f) = J(f, D), g(f) = J(f, D ) J(f, D), f 1 = argmin f J(f, D), and f 2 = argmin f J(f, D ). Finally, we set g(f) = 1 n (l(y nf T x n) l(y n f T x n )). We observe that due to the convexity of l, and 1-strong convexity of N( ), G(f) = J(f, D) is Λ-strongly convex. Moreover, G(f) + g(f) = J(f, D ) is also Λ-strongly convex. Finally, due to the differentiability of N( ) and l, G(f) and g(f) are also differentiable at all points. We have: g(f) = 1 n (y nl (y n f T x n )x n y n l (y n ft x n )x n ). (16) As y i [ 1,1], l (z) 1, for all z, and x i 1, for any f, g(f) 1 n ( x n x n ) 1 n ( x n + x n ) 2 n. The proof now follows by an application of Lemma Privacy Guarantees for Objective Perturbation In this section, we show that Algorithm 2 is ǫ p -differentially private. Theorem 2. If N( ) is 1-strongly convex and doubly differentiable, and l( ) is convex and doubly differentiable, with l (z) 1 and l (z) c for all z, then Algorithm 2 is ǫ p -differentially private. Proof. Consider an f priv output by Algorithm 2. We observe that given any fixed f priv and a fixed dataset D, there always exists a b such that Algorithm 2 outputs f priv on input D. Because l is differentiable and convex, and N( ) is differentiable, we can take the gradient of the objective function and set it to 0 at f priv. Therefore, b = nλ N(f priv ) n y i l (y i fpriv T x i)x i n f priv. (17) i=1 Note that (17) holds because for any f, l(f T x) = l (f T x)x. We claim that as l is differentiable and J(f, D) + 2 f 2 is strongly convex, given a dataset D = (x 1,y 1 ),...,(x n,y n ), there is a bijection between b and f priv. The relation (17) shows that two different b values cannot result in the same f priv. Furthermore, since the objective is strictly convex, for a fixed b and D, there is a unique f priv ; therefore the map from b to f priv is injective. The relation (17) also shows that for any f priv there exists a b for which f priv is the minimizer, so the map from b to f priv is surjective. To show ǫ p -differential privacy, we need to compute the ratio g(f priv D)/g(f priv D ) of the densities of f priv under the two datasets D and D. This ratio can be written as [Billingsley, 1995] g(f priv D) g(f priv D ) = µ(b D) µ(b D ) det(j(f priv b D)) 1 det(j(f priv b D )) 1, (18) where J(f priv b D), J(f priv b D ) are the Jacobian matrices of the mappings from f priv to b, and µ(b D) and µ(b D ) are the densities of the unique bs given output f priv, when the datasets are D and D respectively. 10
11 First, we bound the ratio of the Jacobian determinants. Let b (j) denote the j-th coordinate of b. From (17) we have b (j) = nλ N(f priv ) (j) n i=1 l (y i f T priv x i)x (j) i Given a dataset D, the (j,k)-th entry of the Jacobian matrix J(f b D) is n f (j) priv. (19) b (j) f (k) priv = nλ 2 N(f priv ) (j,k) i yi 2 l (y i fpriv T x i)x (j) i x (k) i n 1(j = k), (20) where 1( ) is the indicator function. We note that the Jacobian is defined for all f priv because N( ) and l are globally doubly differentiable. Let D and D be two datasets which differ in the value of the n-th item such that D = {(x 1,y 1 ),...,(x n 1,y n 1 ),(x n,y n )} and D = {(x 1,y 1 ),...,(x n 1,y n 1 ),(x n,y n)}. Moreover, we define matrices A and E as follows: n A = nλ 2 N(f priv ) + yi 2 l (y i fprivx T i )x i x T i + n I d i=1 E = y 2 nl (y n f T privx n )x n x T n + (y n) 2 l (y nf T privx n)x nx T n. Then, J(f priv b D) = A, and J(f priv b D ) = (A + E). As E has rank at most 2, from Lemma 2, det(j(f priv b D )) det(j(f priv b D)) = det(a + E) det A = 1 + λ 1 (A 1 E) + λ 2 (A 1 E) + λ 1 (A 1 E)λ 2 (A 1 E). (21) For a 1-strongly convex function N, the Hessian 2 N(f priv ) has eigenvalues greater than 1 (Boyd and Vandenberghe [2004]). Since we have assumed l is doubly differentiable and convex, any eigenvalue of A is therefore at least nλ + n ; therefore, for j = 1,2, λ j (A 1 E) λ j(e) n(λ+ ). Applying Lemma 3, with w 1 = y 2 n l (y n f T priv x n), x 1 = x n, and w 2 = (y n )2 l (y n ft priv x n ), x 2 = x n, and upper bounds on y i and x i and l (z), Therefore, λ 1 (E) λ 2 (E) c 2, and det(a + E) det(a) 1 + λ 1 (E) + λ 2 (E) 2c. (22) 2c n(λ + ) + c 2 ( ) n 2 (Λ + ) 2 = c (23) n(λ + ) We now consider two cases. In the first case, = 0, and by definition, in that case, 1+ 2c nλ + c2 n 2 Λ 2 e ǫp ǫ p. In the second case, > 0, and in this case, by definition of, (1+ c n(λ+ ) )2 = e ǫp/2 = e ǫp ǫ p. Next, we bound the ratio of the densities of b. We observe that as l (z) 1, for any z and y i, x i 1, for datasets D and D which differ by one value, b b = y n l (y n f T privx n )x n y nl (y n f T privx n)x n. (24) 11
12 This implies that: We can write: µ(b D) µ(b D ) b b b b 2. (25) b d 1e ǫ p b /2 1 surf( b ) = b d 1 e ǫ p b /2 1 surf( b ) e ǫ p ( b b )/2 e ǫ p, (26) where surf(x) denotes the surface area of the sphere in d dimensions with radius x. Here the last step follows from the fact that surf(x) = s(1)x d 1, where s(1) is the surface area of the unit sphere in R d. Finally, we are ready to bound the ratio of densities: Thus, Algorithm 2 satisfies Definition 2. g(f priv D) g(f priv D ) = µ(b D) µ(b D ) det(j(f priv b D )) det(j(f priv b D)) = µ(b D) det(a + E) µ(b D ) det A Lemma 2. If A is full rank, and if E has rank at most 2, then, (27) (28) e ǫ p e ǫp ǫ p (29) e ǫp. (30) det(a + E) det(a) det(a) = λ 1 (A 1 E) + λ 2 (A 1 E) + λ 1 (A 1 E)λ 2 (A 1 E), (31) where λ j (Z) is the j-th eigenvalue of matrix Z. Proof. To show this we use some recent results of Ipsen and Rehman [2008]. Theorem 2.13 in their paper gives an expansion det(a + E) det(a) det A n 1 = det(a 1 E) + k=1 1 i i <i 2 < <i k n det ( (A 1 E) i1,...,i k ), (32) where (B) i1,...,i k is the submatrix of matrix B formed by removing rows i 1,...,i k and columns i 1,...,i k from B. Turning to the other terms, note that the computation should not depend on the basis in which the matrices are expressed. In particular, we can write out the expansion as if A 1 E has been diagonalized. Since the matrices are positive semidefinite, diagonalizing A 1 E puts the eigenvalues on the diagonal. Therefore det((a 1 E) i1,...,i k ) is the product of the eigenvalues of A 1 E for indices not equal to i 1,...,i k. Thus det ( (A 1 ) E) i1,...,i k = 1 i i <i 2 < <i k n = 1 i i <i 2 < <i k n S {1,2,...,n}: S =k k λ ij (A 1 E) (33) j=1 λ j (A 1 E). (34) j S 12
13 This is just the k-th symmetric polynomial in the eigenvalues of A 1 E, which is the sum of all products of size-k subsets of the eigenvalues. But since E has rank at most 2, the matrix A 1 E has rank at most 2, so at most 2 of the eigenvalues are non-zero. Thus for k 2 all of those terms are 0 since they are products of 3 or more eigenvalues. Thus we have det(a + E) det(a) deta = λ 1 (A 1 E) + λ 2 (A 1 E) + λ 1 (A 1 E)λ 2 (A 1 E). (35) Lemma 3. Let A = j w jx j x T j, for d 1 vectors x j. Then, d λ i (A) j i=1 w j x j 2. (36) Proof. Let u 1,...,u d be the singular vectors of A. Recall that the u i s form an orthonormal basis of R d. Now, d λ i (A) = i=1 d u T i Au i = i=1 i=1 d u T i ( j d w j (u T i x j) 2 = j i=1 j w j x j x T j )u i = d w j (u T i x j ) 2 j i=1 d w j i=1(u T i x j) 2 = w j x j 2, j where the last step follows because u i s form an orthonormal basis of R d. 3.4 Application to classification In this section, we show how to use our results to provide privacy-preserving versions of logistic regression and support vector machines Logistic Regression One popular ERM classification algorithm is regularized logistic regression. In this case, N(f) = 1 2 f 2, and the loss function is l LR (z) = log(1 + e z ). Taking derivatives and double derivatives, l LR (z) = 1 (1 + e z ) l 1 LR(z) = (1 + e z )(1 + e z ). Note that l LR is continuous, differentiable and doubly differentiable, with c 1 4. Therefore, we can plug in logistic loss directly to Theorems 1 and 2 to get the following result. Corollary 2. The output of Algorithm 1 with N(f) = 1 2 f 2, l = l LR is an ǫ p -differentially private approximation to logistic regression. The output of Algorithm 2 with N(f) = 1 2 f 2, c = 1 4, and l = l LR, is an ǫ p -differentially private approximation to logistic regression. We quantify how well the outputs of Algorithms 1 and 2 approximate (non-private) logistic regression in Section 4. 13
14 3.4.2 Support Vector Machines Another very commonly used classifier is L 2 -regularized support vector machines. In this case, again, N(f) = 1 2 f 2, and l SVM (z) = max(0,1 z). (37) Notice that this loss function is continuous, but not differentiable, and thus it does not satisfy conditions in Theorems 1 and 2. There are two alternative solutions to this. First, we can approximate l SVM by a different loss function, which is doubly differentiable, as follows. This is motivated by Chapelle [2007]. 0 if z > 1 + h l s (z) = (1 z)4 + 3(1 z)2 16h 3 8h + 1 z 2 + 3h 16 if 1 z h 1 z if z < 1 h (38) As h 0, this loss approaches the hinge loss. Taking derivatives, we observe that: 0 if z > 1 + h l (1 z) s(z) = 3 3(1 z) 4h 3 4h 1 2 if 1 z h 1 if z < 1 h (39) Moreover, l s(z) = 0 if z > 1 + h if 1 z h 0 if z < 1 h 3(1 z) h 3 4h (40) Observe that this implies that l s(z) 3 4h for all h and z. Moreover, l s is convex, as l s(z) 0 for all z. Therefore, l s can be used in Theorems 1 and 2, which gives us privacy-preserving approximations to regularized support vector machines. Corollary 3. The output of Algorithm 1 with N(f) = 1 2 f 2, and l = l s is an ǫ p -differentially private approximation to support vector machines. The output of Algorithm 2 with N(f) = 1 2 f 2, c = 3 4h, and l = l s is an ǫ p -differentially private approximation to support vector machines. The second solution is to use Huber Loss, as suggested by Chapelle [2007], which is defined as follows: 0 if z > 1 + h 1 l Huber (z) = 4h (1 + h z)2 if 1 z h (41) 1 z if z < 1 h Observe that Huber loss is convex and differentiable, and piecewise doubly-differentiable, with c = 1 2h. However, it is not globally doubly differentiable, and hence the Jacobian in the proof of Theorem 2 is undefined for certain values of f. However, we can show that in this case, Algorithm 2, when run with c = 1 2h satisfies Definition 3. Let G denote the map from f priv to b in (17) under B = D, and H denote the map under B = D. By definition, the probability P(f priv S B = D) = P b (b G(S)). 14
15 Corollary 4. Let f priv be the output of Algorithm 2 with l = l Huber, c = 1 2h, and N(f) = 1 2 f 2 2. For any set S of possible values of f priv, and any pair of datasets D, D which differ in the private value of one person (x n,y n ), e ǫp P(S B = D ) P(S B = D) e ǫp P(S B = D ). (42) Proof. Consider the event f priv S. Let T = G(S) and T = H(S). Because G is a bijection, we have P(f priv S B = D) = P b (b T B = D), (43) and a similar expression when B = D. Now note that l Huber (z) is only non-differentiable for a finite number of values of z. Let Z be the set of these values of z. C = {f : yf T x = z Z, (x,y) D D }. (44) Pick a tuple (z,(x,y)) Z (D D ). The set of f such that yf T x = z is a hyperplane in R d. Since N(f) = f/2 and l is piecewise linear, from (17) we see that the set of corresponding b s is also piecewise linear, and hence has Lebesgue measure 0. Since the measure corresponding to b is absolutely continuous with respect to the Lebesgue measure, this hyperplane has probability 0 under b as well. Since C is a finite union of such hyperplanes, we have P(b G(C)) = 0. Thus we have P b (T B = D) = P b (G(S \ C) B = D), and similarly for D. From the definition of G and H, for f S \ C, H(f) = G(f) + y n l (y n f T x n )x n y nl (y nf T x n)x n. (45) since f / C, this mapping shows that if P b (G(S \ C) B = D) = 0 then we must have P b (H(S \ C) B = D) = 0. Thus the result holds for sets of measure 0. If S \ C has positive measure we can calculate the ratio of the probabilities for f priv for which the loss is twice-differentiable. For such f priv the Jacobian is also defined, and we can use a method similar to Theorem 2 to prove the result. Remark: Because the privacy proof for Algorithm 1 does not require the analytic properties of 2, we can also use Huber loss in Algorithm 1 to get an ǫ g -differentially private approximation to the SVM. We quantify how well the outputs of Algorithms 1 and 2 approximate private support vector machines in Section 4. 4 Generalization performance In this section, we provide guarantees on the performance of privacy-preserving ERM algorithms in Section 3. We provide these bounds for L 2 -regularization. To quantify this performance, we will assume that the n entries in the dataset D are drawn i.i.d. according to a fixed distribution P(x,y). We measure the performance of these algorithms by the number of samples n required to acheive error L + ǫ g, where L is the loss of the best ERM predictor. 15
16 Given a distribution P the expected loss L(f) for a classifier f is L(f) = E (x,y) P [ l(f T x,y) ]. (46) The sample complexity for generalization error ǫ g against a classifier f 0 is number of samples n required to achieve error L(f 0 ) + ǫ g under any data distribution P. We would like the sample complexity to be low. For a fixed P we define the following function, which will be useful in our analysis: J(f) = L(f) + Λ 2 f 2. (47) The function J(f) is the expectation (over P) of the non-private L 2 -regularized ERM objective evaluated at f. For non-private ERM, Shalev-Shwartz and Srebro [2008] show that for a given f 0 with loss L(f 0 ) = L, if the number of data points n > C f 0 2 log( 1 δ ) ǫ 2 g (48) for some constant C, then the excess loss of the SVM solution f svm satisfies L(f svm ) L(f 0 ) + ǫ g. This order growth will hold for our results as well. It also serves as a reference against which we can compare the additional burden on the sample complexity imposed by the privacy constraints. For most learning problems, we require the generalization error ǫ g < 1. Moreover, it is also typically the case that for more difficult learning problems, f 0 is higher. For example, for regularized SVM, 1 f 0 is the margin of classification, and as a result, f 0 is higher for learning problems with smaller margin. From the bounds provided in this section, we note that the dominating term in the sample requirement for objective perturbation has a better dependence on f 0 as well as 1 ǫ g ; as a result, for more difficult learning problems, we expect objective perturbation to perform better than output perturbation. 4.1 Output perturbation First, we provide performance guarantees for Algorithm 1, by providing a bound on the number of samples required for Algorithm 1 to produce a classifier with low error. Definition 6. A function g(z) : R R is c-lipschitz if g(z 1 ) g(z 2 ) c z 1 z 2, for all pairs z 1, z 2. Recall that if a function g(z) is differentiable, with g (z) r for all z, then g(z) is also r-lipschitz. Theorem 3. Let N(f) = 1 2 f 2, and let f 0 be a classifier such that L(f 0 ) = L. If l is differentiable and continuous, the derivative l is c-lipschitz, the data D is drawn i.i.d. according to P, and the number of training samples satisfies ( f0 2 log( 1 δ n > C max ), dlog(d δ ) f ) 0, dlog(d δ )c1/2 f 0 2, (49) ǫ g ǫ p for some constant C, then the output f priv of Algorithm 1 satisfies ǫ 2 g ǫ 3/2 g ǫ p P (L(f priv ) L + ǫ g ) 1 2δ. (50) 16
17 Proof. Let f rtr = argmin J(f) f f = argmin J(f, D), f and f priv denote the output of Algorithm 1. Using the analysis method of Shalev-Shwartz and Srebro [2008] shows L(f priv ) = L(f 0 ) + ( J(f priv ) J(f rtr )) + ( J(f rtr ) J(f 0 )) + Λ 2 f 0 2 Λ 2 f priv 2. (51) We will bound the terms on the right-hand side of (51). For a regularizer N(f) = 1 2 f 2 the Hessian satisfies 2 N(f) 2 1. Therefore, from Lemma 4, with probability 1 δ over the privacy mechanism, J(f priv, D) J(f, D) 8d2 log 2 (d/δ)(c + Λ) Λ 2 n 2 ǫ 2. (52) p Furthermore, the results of Sridharan et al. [2008] show that with probability 1 δ over the choice of the data distribution, ( ) J(f priv ) J(f log(1/δ) rtr ) 2(J(f priv, D) J(f, D)) + O. (53) Λn Combining the preceding two statements, with probability 1 2δ over the noise in the privacy mechanism and the data distribution, the second term in the right-hand-side of (51) is at most: J(f priv ) J(f rtr ) 16d2 log 2 (d/δ)(c + Λ) Λ 2 n 2 ǫ 2 p ( log(1/δ) + O Λn ). (54) By definition of f rtr, the difference ( J(f rtr ) J(f 0 )) 0. Setting Λ = ǫg f 0 in (51) and using (54), 2 we obtain L(f priv ) L(f 0 ) + 16 f 0 4 d 2 log 2 (d/δ)(c + ǫ g / f 0 2 ) n 2 ǫ 2 g ǫ2 p Solving for n to make the total excess error equal to ǫ g yields (49). ( + O f 0 2log(1/δ) ) + ǫ g nǫ g 2. (55) Lemma 4. Suppose N( ) is doubly differentiable with 2 N(f) 2 η for all f, and suppose that l is differentiable and has continuous and c-lipschitz derivatives. Given training data D, let f be a classifier that minimizes J(f, D) and let f priv be the classifier output by Algorithm 1. Then ( P b J(f priv, D) J(f, D) + 2d2 (c + Λη)log 2 ) (d/δ) Λ 2 n 2 ǫ 2 1 δ, (56) p where the probability is taken over the randomness in the noise b of Algorithm 1. Note that when l is doubly differentiable, c is an upper bound on the double derivative of l, and is the same as the constant c in Theorem 2. 17
18 Proof. Let D = {(x 1,y 1 ),...,(x n,y n )}, and recall that x i 1, and y i 1. As N( ) and l are differentiable, we use the Mean Value Theorem to show that for some t between 0 and 1, J(f priv, D) J(f, D) = (f priv f ) T J(tf + (1 t)f priv ) (57) f priv f J(tf + (1 t)f priv ), (58) where the second step follows by an application of the Cauchy-Schwartz inequality. Recall that J(f, D) = Λ N(f) + 1 y i l (y i f T x i )x i. (59) n Moreover, recall that J(f, D) = 0, from the optimality of f. Therefore, J(tf + (1 t)f priv, D) = J(f, D) Λ( N(f ) N(tf + (1 t)f priv )) 1 ( y i l (y i (f ) T x i ) l (y i (tf + (1 t)f priv ) T x i ) ) x i. (60) n i Now, from the Lipschitz condition on l, for each i we can upper bound each term in the summation above: yi ( l (y i (f ) T x i ) l (y i (tf + (1 t)f priv ) T x i ) ) x i i y i x i l (y i (f ) T x i ) l (y i (tf + (1 t)f priv ) T x i ) y i x i c y i (1 t)(f f priv ) T x i c(1 t) y i 2 x i 2 f f priv c(1 t) f f priv. (61) The third step follows because l is c-lipschitz and the last step follows from the bounds on y i and x i. Because N is doubly differentiable, we can apply the Mean Value Theorem again to conclude that N(tf + (1 t)f priv ) N(f ) (1 t) f priv f 2 N(f ) 2 (62) for some f R d. As 0 t 1, we can combine (60), (61), and (62) to obtain J(tf + (1 t)f priv, D) Λ( N(f ) N(tf + (1 t)f priv )) 1 + y i (l (y i (f ) T x i ) l (y i (tf + (1 t)f priv ) T x i ))x i n i (1 t) f priv f (Λη + 1n ) n c f priv f (Λη + c). (63) From the definition of Algorithm 1, f priv f = b, where b is the noise vector. Now we can apply Lemma 5 to f priv f, with parameters k = d, and θ = 2 Λnǫ p. From Lemma 5, with probability 1 δ, f priv f 2d log( d δ ) Λnǫ p. The Lemma follows by combining this with Equations 63 and
19 Lemma 5. Let X be a random variable drawn from the distribution Γ(k,θ), where k is an integer. Then, ( ( )) k P X < kθ log 1 δ. (64) δ Proof. Since k is an integer, we can decompose X distributed according to Γ(k, θ) as a summation X = X X k, (65) where X 1,X 2,...,X k are independent exponential random variables with mean θ. For each i we have P(X i θ log(k/δ)) = δ/k. Now, P(X < kθ log(k/δ)) P(X i < θ log(k/δ) i = 1,2,...,k) (66) = (1 δ/k) k (67) 1 δ. (68) 4.2 Objective perturbation We now establish performance bounds on Algorithm 2. The bound can be summarized as follows. Theorem 4. Let N(f) = 1 2 f 2, and let f 0 be a classifier with expected loss L(f 0 ) = L. Let l be convex, doubly differentiable, and let its derivatives satisfy l (z) 1 and l (z) c for all z. If the n training samples in D are drawn i.i.d. accoding to P, and if n > C max ( f 0 2 log(1/δ) ǫ 2, c f 0 2, dlog(d δ ) f 0 g ǫ g ǫ p ǫ g ǫ p for some constant C, then, the output f priv of Algorithm 2 satisfies ) (69) P (L(f priv ) L + ǫ g ) 1 2δ. (70) Proof. Let f rtr = argmin J(f) f f = argmin J(f, D), f and f priv denote the output of Algorithm 1. As in Theorem 3, the analysis of Shalev-Shwartz and Srebro [2008] shows L(f priv ) = L(f 0 ) + ( J(f priv ) J(f rtr )) + ( J(f rtr ) J(f 0 )) + Λ 2 f 0 2 Λ 2 f priv 2. (71) We will bound each of the terms on the right-hand-side. 19
20 If n > c f 0 2 ǫ gǫ p and Λ > ǫg 4 f 0, then nλ > c 2 4ǫ p, so from the definition of ǫ p in Algorithm 2, ) ( ) ǫ p = ǫ p 2log ( 1 + c nλ = ǫ p 2log 1 + ǫ p 4 ǫ p ǫ p 2, (72) where the last step follows because log(1 + x) x for x [0, 1]. Note that for these values of Λ we have ǫ p > 0. Therefore, we can apply Lemma 6 to conclude that with probability at least 1 δ over the privacy mechanism, J(f priv, D) J(f, D) 4d2 log 2 (d/δ) Λn 2 ǫ 2. (73) p From Sridharan et al. [2008], ( ) J(f priv ) J(f log(1/δ) rtr ) 2(J(f priv, D) J(f, D)) + O (74) Λn 8d2 log 2 ( ) (d/δ) log(1/δ) Λn 2 ǫ 2 + O. (75) p Λn By definition of f, we have J(f rtr ) J(f 0 ) 0. If Λ is set to be in Equation 71 is at most ǫg 2. The theorem follows. ǫ g f 0 2, then, the fourth quantity The following lemma is analogous to Lemma 4, and it establishes a bound on the distance between the output of Algorithm 2, and non-private regularized ERM. We note that this bound holds when Algorithm 2 has ǫ p > 0, that is, when = 0. Ensuring that = 0 requires an additional condition on n, which is stated in Theorem 4. Lemma 6. Let ǫ p > 0. Let f = argmin J(f, D), and let f priv be the classifier output by Algorithm 2. If N( ) is 1-strongly convex and globally differentiable, and if l is convex and differentiable at all points, with l (z) 1 for all z, then ( P b J(f priv, D) J(f, D) + 4d2 log 2 ) (d/δ) Λn 2 ǫ 2 1 δ, (76) p where the probability is taken over the randomness in the noise b of Algorithm 2. Proof. By the assumption ǫ p > 0, the classifier f priv minimizes the objective function J(f, D)+ 1 n bt f, and therefore J(f priv, D) J(f, D) + 1 n bt (f f priv ). (77) First, we try to bound f f priv. Recall that ΛN( ) is Λ-strongly convex and globally differentiable, and l is convex and differentiable. We can therefore apply Lemma 1 with G(f) = J(f, D) and g(f) = 1 n bt f to obtain the bound f f priv 1 Λ (1 n bt f) b nλ. (78) 20
21 Therefore by the Cauchy-Schwartz inequality, J(f priv, D) J(f, D) b 2 n 2 Λ. (79) Since b is drawn from a Γ(d, 2 ǫ p ) distribution, from Lemma 5, with probability 1 δ, b. The Lemma follows by plugging this in to the previous equation. 2d log(d/δ) ǫ p 4.3 Applications In this section, we examine the sample requirement of privacy-preserving regularized logistic regression and support vector machines. Recall that in both these cases, N(f) = 1 2 f 2. Corollary 5 (Logistic Regression). Let training data D be generated i.i.d. accoding to a distribution P and let f 0 be a classifier with expected loss L(f 0 ) = L. Let the loss function l = l LR. 1. There exists a C 1 such that if ( f0 2 log( 1 δ n > C 1 max ), dlog(d δ ) f 0, dlog(d δ ) f ) 0 2 ǫ g ǫ p ǫ 2 g ǫ 3/2 g ǫ p (80) then the output f priv of Algorithm 1 satisfies P (L(f priv ) L + ǫ g ) 1 δ. (81) 2. There exists a C 2 such that if n > C max ( f 0 2 log(1/δ) ǫ 2, f 0 2, dlog(d δ ) f ) 0 g ǫ g ǫ p ǫ g ǫ p (82) then the output f priv of Algorithm 2 with c = 1 4 satisfies P (L(f priv ) L + ǫ g ) 1 δ. (83) Proof. Since l LR is convex and doubly differentiable for any z 1, z 2, l LR(z 1 ) l LR(z 2 ) l LR(z )(z 1 z 2 ) (84) for some z [z 1,z 2 ]. Moreover, l LR (z ) c = 1 4, so l is 1 4-Lipschitz. The corollary now follows from Theorems 3 and 4. For SVMs we state results with l = l Huber, but a similar bound can be shown for l s as well. Corollary 6 (Huber Support Vector Machines). Let training data D be generated i.i.d. accoding to a distribution P and let f 0 be a classifier with expected loss L(f 0 ) = L. Let the loss function l = l Huber. 21
Differentially Private Empirical Risk Minimization
 Journal of Machine Learning Research 12 2011 1069-1109 Submitted 6/10; Revised 2/11; Published 3/11 Differentially Private Empirical Risk Minimization Kamalika Chaudhuri Department of Computer Science
Journal of Machine Learning Research 12 2011 1069-1109 Submitted 6/10; Revised 2/11; Published 3/11 Differentially Private Empirical Risk Minimization Kamalika Chaudhuri Department of Computer Science
Privacy-preserving logistic regression
 Privacy-preserving logistic regression Kamalika Chaudhuri Information Theory and Applications University of California, San Diego kamalika@soe.ucsd.edu Claire Monteleoni Center for Computational Learning
Privacy-preserving logistic regression Kamalika Chaudhuri Information Theory and Applications University of California, San Diego kamalika@soe.ucsd.edu Claire Monteleoni Center for Computational Learning
Sample complexity bounds for differentially private learning
 Sample complexity bounds for differentially private learning Kamalika Chaudhuri University of California, San Diego Daniel Hsu Microsoft Research Outline 1. Learning and privacy model 2. Our results: sample
Sample complexity bounds for differentially private learning Kamalika Chaudhuri University of California, San Diego Daniel Hsu Microsoft Research Outline 1. Learning and privacy model 2. Our results: sample
What Can We Learn Privately?
 What Can We Learn Privately? Sofya Raskhodnikova Penn State University Joint work with Shiva Kasiviswanathan Homin Lee Kobbi Nissim Adam Smith Los Alamos UT Austin Ben Gurion Penn State To appear in SICOMP
What Can We Learn Privately? Sofya Raskhodnikova Penn State University Joint work with Shiva Kasiviswanathan Homin Lee Kobbi Nissim Adam Smith Los Alamos UT Austin Ben Gurion Penn State To appear in SICOMP
Near-optimal Differentially Private Principal Components
 Near-optimal Differentially Private Principal Components Kamalika Chaudhuri UC San Diego kchaudhuri@ucsd.edu Anand D. Sarwate TTI-Chicago asarwate@ttic.edu Kaushik Sinha UC San Diego ksinha@cs.ucsd.edu
Near-optimal Differentially Private Principal Components Kamalika Chaudhuri UC San Diego kchaudhuri@ucsd.edu Anand D. Sarwate TTI-Chicago asarwate@ttic.edu Kaushik Sinha UC San Diego ksinha@cs.ucsd.edu
Generalization theory
 Generalization theory Daniel Hsu Columbia TRIPODS Bootcamp 1 Motivation 2 Support vector machines X = R d, Y = { 1, +1}. Return solution ŵ R d to following optimization problem: λ min w R d 2 w 2 2 + 1
Generalization theory Daniel Hsu Columbia TRIPODS Bootcamp 1 Motivation 2 Support vector machines X = R d, Y = { 1, +1}. Return solution ŵ R d to following optimization problem: λ min w R d 2 w 2 2 + 1
Introduction to Machine Learning (67577) Lecture 3
 Introduction to Machine Learning (67577) Lecture 3 Shai Shalev-Shwartz School of CS and Engineering, The Hebrew University of Jerusalem General Learning Model and Bias-Complexity tradeoff Shai Shalev-Shwartz
Introduction to Machine Learning (67577) Lecture 3 Shai Shalev-Shwartz School of CS and Engineering, The Hebrew University of Jerusalem General Learning Model and Bias-Complexity tradeoff Shai Shalev-Shwartz
Lecture 3: Introduction to Complexity Regularization
 ECE90 Spring 2007 Statistical Learning Theory Instructor: R. Nowak Lecture 3: Introduction to Complexity Regularization We ended the previous lecture with a brief discussion of overfitting. Recall that,
ECE90 Spring 2007 Statistical Learning Theory Instructor: R. Nowak Lecture 3: Introduction to Complexity Regularization We ended the previous lecture with a brief discussion of overfitting. Recall that,
Lecture 20: Introduction to Differential Privacy
 6.885: Advanced Topics in Data Processing Fall 2013 Stephen Tu Lecture 20: Introduction to Differential Privacy 1 Overview This lecture aims to provide a very broad introduction to the topic of differential
6.885: Advanced Topics in Data Processing Fall 2013 Stephen Tu Lecture 20: Introduction to Differential Privacy 1 Overview This lecture aims to provide a very broad introduction to the topic of differential
Reproducing Kernel Hilbert Spaces
 9.520: Statistical Learning Theory and Applications February 10th, 2010 Reproducing Kernel Hilbert Spaces Lecturer: Lorenzo Rosasco Scribe: Greg Durrett 1 Introduction In the previous two lectures, we
9.520: Statistical Learning Theory and Applications February 10th, 2010 Reproducing Kernel Hilbert Spaces Lecturer: Lorenzo Rosasco Scribe: Greg Durrett 1 Introduction In the previous two lectures, we
Reproducing Kernel Hilbert Spaces Class 03, 15 February 2006 Andrea Caponnetto
 Reproducing Kernel Hilbert Spaces 9.520 Class 03, 15 February 2006 Andrea Caponnetto About this class Goal To introduce a particularly useful family of hypothesis spaces called Reproducing Kernel Hilbert
Reproducing Kernel Hilbert Spaces 9.520 Class 03, 15 February 2006 Andrea Caponnetto About this class Goal To introduce a particularly useful family of hypothesis spaces called Reproducing Kernel Hilbert
Class 2 & 3 Overfitting & Regularization
 Class 2 & 3 Overfitting & Regularization Carlo Ciliberto Department of Computer Science, UCL October 18, 2017 Last Class The goal of Statistical Learning Theory is to find a good estimator f n : X Y, approximating
Class 2 & 3 Overfitting & Regularization Carlo Ciliberto Department of Computer Science, UCL October 18, 2017 Last Class The goal of Statistical Learning Theory is to find a good estimator f n : X Y, approximating
Machine Learning. Lecture 9: Learning Theory. Feng Li.
 Machine Learning Lecture 9: Learning Theory Feng Li fli@sdu.edu.cn https://funglee.github.io School of Computer Science and Technology Shandong University Fall 2018 Why Learning Theory How can we tell
Machine Learning Lecture 9: Learning Theory Feng Li fli@sdu.edu.cn https://funglee.github.io School of Computer Science and Technology Shandong University Fall 2018 Why Learning Theory How can we tell
Midterm exam CS 189/289, Fall 2015
 Midterm exam CS 189/289, Fall 2015 You have 80 minutes for the exam. Total 100 points: 1. True/False: 36 points (18 questions, 2 points each). 2. Multiple-choice questions: 24 points (8 questions, 3 points
Midterm exam CS 189/289, Fall 2015 You have 80 minutes for the exam. Total 100 points: 1. True/False: 36 points (18 questions, 2 points each). 2. Multiple-choice questions: 24 points (8 questions, 3 points
1 Differential Privacy and Statistical Query Learning
 10-806 Foundations of Machine Learning and Data Science Lecturer: Maria-Florina Balcan Lecture 5: December 07, 015 1 Differential Privacy and Statistical Query Learning 1.1 Differential Privacy Suppose
10-806 Foundations of Machine Learning and Data Science Lecturer: Maria-Florina Balcan Lecture 5: December 07, 015 1 Differential Privacy and Statistical Query Learning 1.1 Differential Privacy Suppose
Lecture Notes 1: Vector spaces
 Optimization-based data analysis Fall 2017 Lecture Notes 1: Vector spaces In this chapter we review certain basic concepts of linear algebra, highlighting their application to signal processing. 1 Vector
Optimization-based data analysis Fall 2017 Lecture Notes 1: Vector spaces In this chapter we review certain basic concepts of linear algebra, highlighting their application to signal processing. 1 Vector
Privacy-Preserving Data Mining
 CS 380S Privacy-Preserving Data Mining Vitaly Shmatikov slide 1 Reading Assignment Evfimievski, Gehrke, Srikant. Limiting Privacy Breaches in Privacy-Preserving Data Mining (PODS 2003). Blum, Dwork, McSherry,
CS 380S Privacy-Preserving Data Mining Vitaly Shmatikov slide 1 Reading Assignment Evfimievski, Gehrke, Srikant. Limiting Privacy Breaches in Privacy-Preserving Data Mining (PODS 2003). Blum, Dwork, McSherry,
Mark your answers ON THE EXAM ITSELF. If you are not sure of your answer you may wish to provide a brief explanation.
 CS 189 Spring 2015 Introduction to Machine Learning Midterm You have 80 minutes for the exam. The exam is closed book, closed notes except your one-page crib sheet. No calculators or electronic items.
CS 189 Spring 2015 Introduction to Machine Learning Midterm You have 80 minutes for the exam. The exam is closed book, closed notes except your one-page crib sheet. No calculators or electronic items.
Machine Learning And Applications: Supervised Learning-SVM
 Machine Learning And Applications: Supervised Learning-SVM Raphaël Bournhonesque École Normale Supérieure de Lyon, Lyon, France raphael.bournhonesque@ens-lyon.fr 1 Supervised vs unsupervised learning Machine
Machine Learning And Applications: Supervised Learning-SVM Raphaël Bournhonesque École Normale Supérieure de Lyon, Lyon, France raphael.bournhonesque@ens-lyon.fr 1 Supervised vs unsupervised learning Machine
Machine Learning. VC Dimension and Model Complexity. Eric Xing , Fall 2015
 Machine Learning 10-701, Fall 2015 VC Dimension and Model Complexity Eric Xing Lecture 16, November 3, 2015 Reading: Chap. 7 T.M book, and outline material Eric Xing @ CMU, 2006-2015 1 Last time: PAC and
Machine Learning 10-701, Fall 2015 VC Dimension and Model Complexity Eric Xing Lecture 16, November 3, 2015 Reading: Chap. 7 T.M book, and outline material Eric Xing @ CMU, 2006-2015 1 Last time: PAC and
Generalization, Overfitting, and Model Selection
 Generalization, Overfitting, and Model Selection Sample Complexity Results for Supervised Classification Maria-Florina (Nina) Balcan 10/03/2016 Two Core Aspects of Machine Learning Algorithm Design. How
Generalization, Overfitting, and Model Selection Sample Complexity Results for Supervised Classification Maria-Florina (Nina) Balcan 10/03/2016 Two Core Aspects of Machine Learning Algorithm Design. How
FORMULATION OF THE LEARNING PROBLEM
 FORMULTION OF THE LERNING PROBLEM MIM RGINSKY Now that we have seen an informal statement of the learning problem, as well as acquired some technical tools in the form of concentration inequalities, we
FORMULTION OF THE LERNING PROBLEM MIM RGINSKY Now that we have seen an informal statement of the learning problem, as well as acquired some technical tools in the form of concentration inequalities, we
SVMs: Non-Separable Data, Convex Surrogate Loss, Multi-Class Classification, Kernels
 SVMs: Non-Separable Data, Convex Surrogate Loss, Multi-Class Classification, Kernels Karl Stratos June 21, 2018 1 / 33 Tangent: Some Loose Ends in Logistic Regression Polynomial feature expansion in logistic
SVMs: Non-Separable Data, Convex Surrogate Loss, Multi-Class Classification, Kernels Karl Stratos June 21, 2018 1 / 33 Tangent: Some Loose Ends in Logistic Regression Polynomial feature expansion in logistic
Statistical Data Mining and Machine Learning Hilary Term 2016
 Statistical Data Mining and Machine Learning Hilary Term 2016 Dino Sejdinovic Department of Statistics Oxford Slides and other materials available at: http://www.stats.ox.ac.uk/~sejdinov/sdmml Naïve Bayes
Statistical Data Mining and Machine Learning Hilary Term 2016 Dino Sejdinovic Department of Statistics Oxford Slides and other materials available at: http://www.stats.ox.ac.uk/~sejdinov/sdmml Naïve Bayes
Statistical Methods for Data Mining
 Statistical Methods for Data Mining Kuangnan Fang Xiamen University Email: xmufkn@xmu.edu.cn Support Vector Machines Here we approach the two-class classification problem in a direct way: We try and find
Statistical Methods for Data Mining Kuangnan Fang Xiamen University Email: xmufkn@xmu.edu.cn Support Vector Machines Here we approach the two-class classification problem in a direct way: We try and find
Accuracy First: Selecting a Differential Privacy Level for Accuracy-Constrained Empirical Risk Minimization
 Accuracy First: Selecting a Differential Privacy Level for Accuracy-Constrained Empirical Risk Minimization Katrina Ligett HUJI & Caltech joint with Seth Neel, Aaron Roth, Bo Waggoner, Steven Wu NIPS 2017
Accuracy First: Selecting a Differential Privacy Level for Accuracy-Constrained Empirical Risk Minimization Katrina Ligett HUJI & Caltech joint with Seth Neel, Aaron Roth, Bo Waggoner, Steven Wu NIPS 2017
Learning Theory. Piyush Rai. CS5350/6350: Machine Learning. September 27, (CS5350/6350) Learning Theory September 27, / 14
 Learning Theory Piyush Rai CS5350/6350: Machine Learning September 27, 2011 (CS5350/6350) Learning Theory September 27, 2011 1 / 14 Why Learning Theory? We want to have theoretical guarantees about our
Learning Theory Piyush Rai CS5350/6350: Machine Learning September 27, 2011 (CS5350/6350) Learning Theory September 27, 2011 1 / 14 Why Learning Theory? We want to have theoretical guarantees about our
Introduction to Support Vector Machines
 Introduction to Support Vector Machines Shivani Agarwal Support Vector Machines (SVMs) Algorithm for learning linear classifiers Motivated by idea of maximizing margin Efficient extension to non-linear
Introduction to Support Vector Machines Shivani Agarwal Support Vector Machines (SVMs) Algorithm for learning linear classifiers Motivated by idea of maximizing margin Efficient extension to non-linear
Machine Learning Practice Page 2 of 2 10/28/13
 Machine Learning 10-701 Practice Page 2 of 2 10/28/13 1. True or False Please give an explanation for your answer, this is worth 1 pt/question. (a) (2 points) No classifier can do better than a naive Bayes
Machine Learning 10-701 Practice Page 2 of 2 10/28/13 1. True or False Please give an explanation for your answer, this is worth 1 pt/question. (a) (2 points) No classifier can do better than a naive Bayes
Kernel Methods. Machine Learning A W VO
 Kernel Methods Machine Learning A 708.063 07W VO Outline 1. Dual representation 2. The kernel concept 3. Properties of kernels 4. Examples of kernel machines Kernel PCA Support vector regression (Relevance
Kernel Methods Machine Learning A 708.063 07W VO Outline 1. Dual representation 2. The kernel concept 3. Properties of kernels 4. Examples of kernel machines Kernel PCA Support vector regression (Relevance
Stochastic optimization in Hilbert spaces
 Stochastic optimization in Hilbert spaces Aymeric Dieuleveut Aymeric Dieuleveut Stochastic optimization Hilbert spaces 1 / 48 Outline Learning vs Statistics Aymeric Dieuleveut Stochastic optimization Hilbert
Stochastic optimization in Hilbert spaces Aymeric Dieuleveut Aymeric Dieuleveut Stochastic optimization Hilbert spaces 1 / 48 Outline Learning vs Statistics Aymeric Dieuleveut Stochastic optimization Hilbert
Short Course Robust Optimization and Machine Learning. 3. Optimization in Supervised Learning
 Short Course Robust Optimization and 3. Optimization in Supervised EECS and IEOR Departments UC Berkeley Spring seminar TRANSP-OR, Zinal, Jan. 16-19, 2012 Outline Overview of Supervised models and variants
Short Course Robust Optimization and 3. Optimization in Supervised EECS and IEOR Departments UC Berkeley Spring seminar TRANSP-OR, Zinal, Jan. 16-19, 2012 Outline Overview of Supervised models and variants
Foundations of Machine Learning
 Introduction to ML Mehryar Mohri Courant Institute and Google Research mohri@cims.nyu.edu page 1 Logistics Prerequisites: basics in linear algebra, probability, and analysis of algorithms. Workload: about
Introduction to ML Mehryar Mohri Courant Institute and Google Research mohri@cims.nyu.edu page 1 Logistics Prerequisites: basics in linear algebra, probability, and analysis of algorithms. Workload: about
Reproducing Kernel Hilbert Spaces
 Reproducing Kernel Hilbert Spaces Lorenzo Rosasco 9.520 Class 03 February 11, 2009 About this class Goal To introduce a particularly useful family of hypothesis spaces called Reproducing Kernel Hilbert
Reproducing Kernel Hilbert Spaces Lorenzo Rosasco 9.520 Class 03 February 11, 2009 About this class Goal To introduce a particularly useful family of hypothesis spaces called Reproducing Kernel Hilbert
Warm up: risk prediction with logistic regression
 Warm up: risk prediction with logistic regression Boss gives you a bunch of data on loans defaulting or not: {(x i,y i )} n i= x i 2 R d, y i 2 {, } You model the data as: P (Y = y x, w) = + exp( yw T
Warm up: risk prediction with logistic regression Boss gives you a bunch of data on loans defaulting or not: {(x i,y i )} n i= x i 2 R d, y i 2 {, } You model the data as: P (Y = y x, w) = + exp( yw T
18.9 SUPPORT VECTOR MACHINES
 744 Chapter 8. Learning from Examples is the fact that each regression problem will be easier to solve, because it involves only the examples with nonzero weight the examples whose kernels overlap the
744 Chapter 8. Learning from Examples is the fact that each regression problem will be easier to solve, because it involves only the examples with nonzero weight the examples whose kernels overlap the
Learning symmetric non-monotone submodular functions
 Learning symmetric non-monotone submodular functions Maria-Florina Balcan Georgia Institute of Technology ninamf@cc.gatech.edu Nicholas J. A. Harvey University of British Columbia nickhar@cs.ubc.ca Satoru
Learning symmetric non-monotone submodular functions Maria-Florina Balcan Georgia Institute of Technology ninamf@cc.gatech.edu Nicholas J. A. Harvey University of British Columbia nickhar@cs.ubc.ca Satoru
SYMMETRIC MATRIX PERTURBATION FOR DIFFERENTIALLY-PRIVATE PRINCIPAL COMPONENT ANALYSIS. Hafiz Imtiaz and Anand D. Sarwate
 SYMMETRIC MATRIX PERTURBATION FOR DIFFERENTIALLY-PRIVATE PRINCIPAL COMPONENT ANALYSIS Hafiz Imtiaz and Anand D. Sarwate Rutgers, The State University of New Jersey ABSTRACT Differential privacy is a strong,
SYMMETRIC MATRIX PERTURBATION FOR DIFFERENTIALLY-PRIVATE PRINCIPAL COMPONENT ANALYSIS Hafiz Imtiaz and Anand D. Sarwate Rutgers, The State University of New Jersey ABSTRACT Differential privacy is a strong,
Improved Bounds on the Dot Product under Random Projection and Random Sign Projection
 Improved Bounds on the Dot Product under Random Projection and Random Sign Projection Ata Kabán School of Computer Science The University of Birmingham Birmingham B15 2TT, UK http://www.cs.bham.ac.uk/
Improved Bounds on the Dot Product under Random Projection and Random Sign Projection Ata Kabán School of Computer Science The University of Birmingham Birmingham B15 2TT, UK http://www.cs.bham.ac.uk/
The exam is closed book, closed notes except your one-page (two sides) or two-page (one side) crib sheet.
 CS 189 Spring 013 Introduction to Machine Learning Final You have 3 hours for the exam. The exam is closed book, closed notes except your one-page (two sides) or two-page (one side) crib sheet. Please
CS 189 Spring 013 Introduction to Machine Learning Final You have 3 hours for the exam. The exam is closed book, closed notes except your one-page (two sides) or two-page (one side) crib sheet. Please
Announcements. Proposals graded
 Announcements Proposals graded Kevin Jamieson 2018 1 Bayesian Methods Machine Learning CSE546 Kevin Jamieson University of Washington November 1, 2018 2018 Kevin Jamieson 2 MLE Recap - coin flips Data:
Announcements Proposals graded Kevin Jamieson 2018 1 Bayesian Methods Machine Learning CSE546 Kevin Jamieson University of Washington November 1, 2018 2018 Kevin Jamieson 2 MLE Recap - coin flips Data:
COMS 4771 Introduction to Machine Learning. Nakul Verma
 COMS 4771 Introduction to Machine Learning Nakul Verma Announcements HW2 due now! Project proposal due on tomorrow Midterm next lecture! HW3 posted Last time Linear Regression Parametric vs Nonparametric
COMS 4771 Introduction to Machine Learning Nakul Verma Announcements HW2 due now! Project proposal due on tomorrow Midterm next lecture! HW3 posted Last time Linear Regression Parametric vs Nonparametric
The Power of Linear Reconstruction Attacks
 The Power of Linear Reconstruction Attacks Shiva Prasad Kasiviswanathan Mark Rudelson Adam Smith Abstract We consider the power of linear reconstruction attacks in statistical data privacy, showing that
The Power of Linear Reconstruction Attacks Shiva Prasad Kasiviswanathan Mark Rudelson Adam Smith Abstract We consider the power of linear reconstruction attacks in statistical data privacy, showing that
Private Empirical Risk Minimization, Revisited
 Private Empirical Risk Minimization, Revisited Raef Bassily Adam Smith Abhradeep Thakurta April 10, 2014 Abstract In this paper, we initiate a systematic investigation of differentially private algorithms
Private Empirical Risk Minimization, Revisited Raef Bassily Adam Smith Abhradeep Thakurta April 10, 2014 Abstract In this paper, we initiate a systematic investigation of differentially private algorithms
Machine Learning. Support Vector Machines. Fabio Vandin November 20, 2017
 Machine Learning Support Vector Machines Fabio Vandin November 20, 2017 1 Classification and Margin Consider a classification problem with two classes: instance set X = R d label set Y = { 1, 1}. Training
Machine Learning Support Vector Machines Fabio Vandin November 20, 2017 1 Classification and Margin Consider a classification problem with two classes: instance set X = R d label set Y = { 1, 1}. Training
Introduction to Machine Learning
 Introduction to Machine Learning Vapnik Chervonenkis Theory Barnabás Póczos Empirical Risk and True Risk 2 Empirical Risk Shorthand: True risk of f (deterministic): Bayes risk: Let us use the empirical
Introduction to Machine Learning Vapnik Chervonenkis Theory Barnabás Póczos Empirical Risk and True Risk 2 Empirical Risk Shorthand: True risk of f (deterministic): Bayes risk: Let us use the empirical
Improved Algorithms for Confidence-Rated Prediction with Error Guarantees
 Improved Algorithms for Confidence-Rated Prediction with Error Guarantees Kamalika Chaudhuri Chicheng Zhang Department of Computer Science and Engineering University of California, San Diego 95 Gilman
Improved Algorithms for Confidence-Rated Prediction with Error Guarantees Kamalika Chaudhuri Chicheng Zhang Department of Computer Science and Engineering University of California, San Diego 95 Gilman
Discriminative Models
 No.5 Discriminative Models Hui Jiang Department of Electrical Engineering and Computer Science Lassonde School of Engineering York University, Toronto, Canada Outline Generative vs. Discriminative models
No.5 Discriminative Models Hui Jiang Department of Electrical Engineering and Computer Science Lassonde School of Engineering York University, Toronto, Canada Outline Generative vs. Discriminative models
Lecture 2 Machine Learning Review
 Lecture 2 Machine Learning Review CMSC 35246: Deep Learning Shubhendu Trivedi & Risi Kondor University of Chicago March 29, 2017 Things we will look at today Formal Setup for Supervised Learning Things
Lecture 2 Machine Learning Review CMSC 35246: Deep Learning Shubhendu Trivedi & Risi Kondor University of Chicago March 29, 2017 Things we will look at today Formal Setup for Supervised Learning Things
Convex optimization COMS 4771
 Convex optimization COMS 4771 1. Recap: learning via optimization Soft-margin SVMs Soft-margin SVM optimization problem defined by training data: w R d λ 2 w 2 2 + 1 n n [ ] 1 y ix T i w. + 1 / 15 Soft-margin
Convex optimization COMS 4771 1. Recap: learning via optimization Soft-margin SVMs Soft-margin SVM optimization problem defined by training data: w R d λ 2 w 2 2 + 1 n n [ ] 1 y ix T i w. + 1 / 15 Soft-margin
Qualifying Exam in Machine Learning
 Qualifying Exam in Machine Learning October 20, 2009 Instructions: Answer two out of the three questions in Part 1. In addition, answer two out of three questions in two additional parts (choose two parts
Qualifying Exam in Machine Learning October 20, 2009 Instructions: Answer two out of the three questions in Part 1. In addition, answer two out of three questions in two additional parts (choose two parts
Statistical learning theory, Support vector machines, and Bioinformatics
 1 Statistical learning theory, Support vector machines, and Bioinformatics Jean-Philippe.Vert@mines.org Ecole des Mines de Paris Computational Biology group ENS Paris, november 25, 2003. 2 Overview 1.
1 Statistical learning theory, Support vector machines, and Bioinformatics Jean-Philippe.Vert@mines.org Ecole des Mines de Paris Computational Biology group ENS Paris, november 25, 2003. 2 Overview 1.
Sharp Generalization Error Bounds for Randomly-projected Classifiers
 Sharp Generalization Error Bounds for Randomly-projected Classifiers R.J. Durrant and A. Kabán School of Computer Science The University of Birmingham Birmingham B15 2TT, UK http://www.cs.bham.ac.uk/ axk
Sharp Generalization Error Bounds for Randomly-projected Classifiers R.J. Durrant and A. Kabán School of Computer Science The University of Birmingham Birmingham B15 2TT, UK http://www.cs.bham.ac.uk/ axk
Understanding Generalization Error: Bounds and Decompositions
 CIS 520: Machine Learning Spring 2018: Lecture 11 Understanding Generalization Error: Bounds and Decompositions Lecturer: Shivani Agarwal Disclaimer: These notes are designed to be a supplement to the
CIS 520: Machine Learning Spring 2018: Lecture 11 Understanding Generalization Error: Bounds and Decompositions Lecturer: Shivani Agarwal Disclaimer: These notes are designed to be a supplement to the
Efficient Private ERM for Smooth Objectives
 Efficient Private ERM for Smooth Objectives Jiaqi Zhang, Kai Zheng, Wenlong Mou, Liwei Wang Key Laboratory of Machine Perception, MOE, School of Electronics Engineering and Computer Science, Peking University,
Efficient Private ERM for Smooth Objectives Jiaqi Zhang, Kai Zheng, Wenlong Mou, Liwei Wang Key Laboratory of Machine Perception, MOE, School of Electronics Engineering and Computer Science, Peking University,
Perceptron Revisited: Linear Separators. Support Vector Machines
 Support Vector Machines Perceptron Revisited: Linear Separators Binary classification can be viewed as the task of separating classes in feature space: w T x + b > 0 w T x + b = 0 w T x + b < 0 Department
Support Vector Machines Perceptron Revisited: Linear Separators Binary classification can be viewed as the task of separating classes in feature space: w T x + b > 0 w T x + b = 0 w T x + b < 0 Department
The Learning Problem and Regularization
 9.520 Class 02 February 2011 Computational Learning Statistical Learning Theory Learning is viewed as a generalization/inference problem from usually small sets of high dimensional, noisy data. Learning
9.520 Class 02 February 2011 Computational Learning Statistical Learning Theory Learning is viewed as a generalization/inference problem from usually small sets of high dimensional, noisy data. Learning
Online Learning and Sequential Decision Making
 Online Learning and Sequential Decision Making Emilie Kaufmann CNRS & CRIStAL, Inria SequeL, emilie.kaufmann@univ-lille.fr Research School, ENS Lyon, Novembre 12-13th 2018 Emilie Kaufmann Online Learning
Online Learning and Sequential Decision Making Emilie Kaufmann CNRS & CRIStAL, Inria SequeL, emilie.kaufmann@univ-lille.fr Research School, ENS Lyon, Novembre 12-13th 2018 Emilie Kaufmann Online Learning
Support Vector Machines
 Support Vector Machines Le Song Machine Learning I CSE 6740, Fall 2013 Naïve Bayes classifier Still use Bayes decision rule for classification P y x = P x y P y P x But assume p x y = 1 is fully factorized
Support Vector Machines Le Song Machine Learning I CSE 6740, Fall 2013 Naïve Bayes classifier Still use Bayes decision rule for classification P y x = P x y P y P x But assume p x y = 1 is fully factorized
Day 4: Classification, support vector machines
 Day 4: Classification, support vector machines Introduction to Machine Learning Summer School June 18, 2018 - June 29, 2018, Chicago Instructor: Suriya Gunasekar, TTI Chicago 21 June 2018 Topics so far
Day 4: Classification, support vector machines Introduction to Machine Learning Summer School June 18, 2018 - June 29, 2018, Chicago Instructor: Suriya Gunasekar, TTI Chicago 21 June 2018 Topics so far
Learning with Rejection
 Learning with Rejection Corinna Cortes 1, Giulia DeSalvo 2, and Mehryar Mohri 2,1 1 Google Research, 111 8th Avenue, New York, NY 2 Courant Institute of Mathematical Sciences, 251 Mercer Street, New York,
Learning with Rejection Corinna Cortes 1, Giulia DeSalvo 2, and Mehryar Mohri 2,1 1 Google Research, 111 8th Avenue, New York, NY 2 Courant Institute of Mathematical Sciences, 251 Mercer Street, New York,
Statistical Methods for SVM
 Statistical Methods for SVM Support Vector Machines Here we approach the two-class classification problem in a direct way: We try and find a plane that separates the classes in feature space. If we cannot,
Statistical Methods for SVM Support Vector Machines Here we approach the two-class classification problem in a direct way: We try and find a plane that separates the classes in feature space. If we cannot,
1 Directional Derivatives and Differentiability
 Wednesday, January 18, 2012 1 Directional Derivatives and Differentiability Let E R N, let f : E R and let x 0 E. Given a direction v R N, let L be the line through x 0 in the direction v, that is, L :=
Wednesday, January 18, 2012 1 Directional Derivatives and Differentiability Let E R N, let f : E R and let x 0 E. Given a direction v R N, let L be the line through x 0 in the direction v, that is, L :=
Class Prior Estimation from Positive and Unlabeled Data
 IEICE Transactions on Information and Systems, vol.e97-d, no.5, pp.1358 1362, 2014. 1 Class Prior Estimation from Positive and Unlabeled Data Marthinus Christoffel du Plessis Tokyo Institute of Technology,
IEICE Transactions on Information and Systems, vol.e97-d, no.5, pp.1358 1362, 2014. 1 Class Prior Estimation from Positive and Unlabeled Data Marthinus Christoffel du Plessis Tokyo Institute of Technology,
Constrained Optimization and Lagrangian Duality
 CIS 520: Machine Learning Oct 02, 2017 Constrained Optimization and Lagrangian Duality Lecturer: Shivani Agarwal Disclaimer: These notes are designed to be a supplement to the lecture. They may or may
CIS 520: Machine Learning Oct 02, 2017 Constrained Optimization and Lagrangian Duality Lecturer: Shivani Agarwal Disclaimer: These notes are designed to be a supplement to the lecture. They may or may
CS60021: Scalable Data Mining. Large Scale Machine Learning
 J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 1 CS60021: Scalable Data Mining Large Scale Machine Learning Sourangshu Bhattacharya Example: Spam filtering Instance
J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 1 CS60021: Scalable Data Mining Large Scale Machine Learning Sourangshu Bhattacharya Example: Spam filtering Instance
Machine Learning. Linear Models. Fabio Vandin October 10, 2017
 Machine Learning Linear Models Fabio Vandin October 10, 2017 1 Linear Predictors and Affine Functions Consider X = R d Affine functions: L d = {h w,b : w R d, b R} where ( d ) h w,b (x) = w, x + b = w
Machine Learning Linear Models Fabio Vandin October 10, 2017 1 Linear Predictors and Affine Functions Consider X = R d Affine functions: L d = {h w,b : w R d, b R} where ( d ) h w,b (x) = w, x + b = w
Reducing Multiclass to Binary: A Unifying Approach for Margin Classifiers
 Reducing Multiclass to Binary: A Unifying Approach for Margin Classifiers Erin Allwein, Robert Schapire and Yoram Singer Journal of Machine Learning Research, 1:113-141, 000 CSE 54: Seminar on Learning
Reducing Multiclass to Binary: A Unifying Approach for Margin Classifiers Erin Allwein, Robert Schapire and Yoram Singer Journal of Machine Learning Research, 1:113-141, 000 CSE 54: Seminar on Learning
Convex Optimization M2
 Convex Optimization M2 Lecture 8 A. d Aspremont. Convex Optimization M2. 1/57 Applications A. d Aspremont. Convex Optimization M2. 2/57 Outline Geometrical problems Approximation problems Combinatorial
Convex Optimization M2 Lecture 8 A. d Aspremont. Convex Optimization M2. 1/57 Applications A. d Aspremont. Convex Optimization M2. 2/57 Outline Geometrical problems Approximation problems Combinatorial
Discriminative Models
 No.5 Discriminative Models Hui Jiang Department of Electrical Engineering and Computer Science Lassonde School of Engineering York University, Toronto, Canada Outline Generative vs. Discriminative models
No.5 Discriminative Models Hui Jiang Department of Electrical Engineering and Computer Science Lassonde School of Engineering York University, Toronto, Canada Outline Generative vs. Discriminative models
SYMMETRIC MATRIX PERTURBATION FOR DIFFERENTIALLY-PRIVATE PRINCIPAL COMPONENT ANALYSIS. Hafiz Imtiaz and Anand D. Sarwate
 SYMMETRIC MATRIX PERTURBATION FOR DIFFERENTIALLY-PRIVATE PRINCIPAL COMPONENT ANALYSIS Hafiz Imtiaz and Anand D. Sarwate Rutgers, The State University of New Jersey ABSTRACT Differential privacy is a strong,
SYMMETRIC MATRIX PERTURBATION FOR DIFFERENTIALLY-PRIVATE PRINCIPAL COMPONENT ANALYSIS Hafiz Imtiaz and Anand D. Sarwate Rutgers, The State University of New Jersey ABSTRACT Differential privacy is a strong,
Support Vector Machines
 Wien, June, 2010 Paul Hofmarcher, Stefan Theussl, WU Wien Hofmarcher/Theussl SVM 1/21 Linear Separable Separating Hyperplanes Non-Linear Separable Soft-Margin Hyperplanes Hofmarcher/Theussl SVM 2/21 (SVM)
Wien, June, 2010 Paul Hofmarcher, Stefan Theussl, WU Wien Hofmarcher/Theussl SVM 1/21 Linear Separable Separating Hyperplanes Non-Linear Separable Soft-Margin Hyperplanes Hofmarcher/Theussl SVM 2/21 (SVM)
Differential Privacy and Pan-Private Algorithms. Cynthia Dwork, Microsoft Research
 Differential Privacy and Pan-Private Algorithms Cynthia Dwork, Microsoft Research A Dream? C? Original Database Sanitization Very Vague AndVery Ambitious Census, medical, educational, financial data, commuting
Differential Privacy and Pan-Private Algorithms Cynthia Dwork, Microsoft Research A Dream? C? Original Database Sanitization Very Vague AndVery Ambitious Census, medical, educational, financial data, commuting
Support'Vector'Machines. Machine(Learning(Spring(2018 March(5(2018 Kasthuri Kannan
 Support'Vector'Machines Machine(Learning(Spring(2018 March(5(2018 Kasthuri Kannan kasthuri.kannan@nyumc.org Overview Support Vector Machines for Classification Linear Discrimination Nonlinear Discrimination
Support'Vector'Machines Machine(Learning(Spring(2018 March(5(2018 Kasthuri Kannan kasthuri.kannan@nyumc.org Overview Support Vector Machines for Classification Linear Discrimination Nonlinear Discrimination
A Magiv CV Theory for Large-Margin Classifiers
 A Magiv CV Theory for Large-Margin Classifiers Hui Zou School of Statistics, University of Minnesota June 30, 2018 Joint work with Boxiang Wang Outline 1 Background 2 Magic CV formula 3 Magic support vector
A Magiv CV Theory for Large-Margin Classifiers Hui Zou School of Statistics, University of Minnesota June 30, 2018 Joint work with Boxiang Wang Outline 1 Background 2 Magic CV formula 3 Magic support vector
Convex Optimization and Modeling
 Convex Optimization and Modeling Introduction and a quick repetition of analysis/linear algebra First lecture, 12.04.2010 Jun.-Prof. Matthias Hein Organization of the lecture Advanced course, 2+2 hours,
Convex Optimization and Modeling Introduction and a quick repetition of analysis/linear algebra First lecture, 12.04.2010 Jun.-Prof. Matthias Hein Organization of the lecture Advanced course, 2+2 hours,
Part of the slides are adapted from Ziko Kolter
 Part of the slides are adapted from Ziko Kolter OUTLINE 1 Supervised learning: classification........................................................ 2 2 Non-linear regression/classification, overfitting,
Part of the slides are adapted from Ziko Kolter OUTLINE 1 Supervised learning: classification........................................................ 2 2 Non-linear regression/classification, overfitting,
Machine Learning Basics Lecture 2: Linear Classification. Princeton University COS 495 Instructor: Yingyu Liang
 Machine Learning Basics Lecture 2: Linear Classification Princeton University COS 495 Instructor: Yingyu Liang Review: machine learning basics Math formulation Given training data x i, y i : 1 i n i.i.d.
Machine Learning Basics Lecture 2: Linear Classification Princeton University COS 495 Instructor: Yingyu Liang Review: machine learning basics Math formulation Given training data x i, y i : 1 i n i.i.d.
1 Machine Learning Concepts (16 points)
 CSCI 567 Fall 2018 Midterm Exam DO NOT OPEN EXAM UNTIL INSTRUCTED TO DO SO PLEASE TURN OFF ALL CELL PHONES Problem 1 2 3 4 5 6 Total Max 16 10 16 42 24 12 120 Points Please read the following instructions
CSCI 567 Fall 2018 Midterm Exam DO NOT OPEN EXAM UNTIL INSTRUCTED TO DO SO PLEASE TURN OFF ALL CELL PHONES Problem 1 2 3 4 5 6 Total Max 16 10 16 42 24 12 120 Points Please read the following instructions
Name (NetID): (1 Point)
 CS446: Machine Learning (D) Spring 2017 March 16 th, 2017 This is a closed book exam. Everything you need in order to solve the problems is supplied in the body of this exam. This exam booklet contains
CS446: Machine Learning (D) Spring 2017 March 16 th, 2017 This is a closed book exam. Everything you need in order to solve the problems is supplied in the body of this exam. This exam booklet contains
Advanced Introduction to Machine Learning CMU-10715
 Advanced Introduction to Machine Learning CMU-10715 Risk Minimization Barnabás Póczos What have we seen so far? Several classification & regression algorithms seem to work fine on training datasets: Linear
Advanced Introduction to Machine Learning CMU-10715 Risk Minimization Barnabás Póczos What have we seen so far? Several classification & regression algorithms seem to work fine on training datasets: Linear
Perceptron Mistake Bounds
 Perceptron Mistake Bounds Mehryar Mohri, and Afshin Rostamizadeh Google Research Courant Institute of Mathematical Sciences Abstract. We present a brief survey of existing mistake bounds and introduce
Perceptron Mistake Bounds Mehryar Mohri, and Afshin Rostamizadeh Google Research Courant Institute of Mathematical Sciences Abstract. We present a brief survey of existing mistake bounds and introduce
Machine Learning
 Machine Learning 10-601 Tom M. Mitchell Machine Learning Department Carnegie Mellon University October 11, 2012 Today: Computational Learning Theory Probably Approximately Coorrect (PAC) learning theorem
Machine Learning 10-601 Tom M. Mitchell Machine Learning Department Carnegie Mellon University October 11, 2012 Today: Computational Learning Theory Probably Approximately Coorrect (PAC) learning theorem
Learning Theory. Ingo Steinwart University of Stuttgart. September 4, 2013
 Learning Theory Ingo Steinwart University of Stuttgart September 4, 2013 Ingo Steinwart University of Stuttgart () Learning Theory September 4, 2013 1 / 62 Basics Informal Introduction Informal Description
Learning Theory Ingo Steinwart University of Stuttgart September 4, 2013 Ingo Steinwart University of Stuttgart () Learning Theory September 4, 2013 1 / 62 Basics Informal Introduction Informal Description
12. Structural Risk Minimization. ECE 830 & CS 761, Spring 2016
 12. Structural Risk Minimization ECE 830 & CS 761, Spring 2016 1 / 23 General setup for statistical learning theory We observe training examples {x i, y i } n i=1 x i = features X y i = labels / responses
12. Structural Risk Minimization ECE 830 & CS 761, Spring 2016 1 / 23 General setup for statistical learning theory We observe training examples {x i, y i } n i=1 x i = features X y i = labels / responses
Differential Privacy in an RKHS
 Differential Privacy in an RKHS Rob Hall (with Larry Wasserman and Alessandro Rinaldo) 2/20/2012 rjhall@cs.cmu.edu http://www.cs.cmu.edu/~rjhall 1 Overview Why care about privacy? Differential Privacy
Differential Privacy in an RKHS Rob Hall (with Larry Wasserman and Alessandro Rinaldo) 2/20/2012 rjhall@cs.cmu.edu http://www.cs.cmu.edu/~rjhall 1 Overview Why care about privacy? Differential Privacy
Nearest Neighbor. Machine Learning CSE546 Kevin Jamieson University of Washington. October 26, Kevin Jamieson 2
 Nearest Neighbor Machine Learning CSE546 Kevin Jamieson University of Washington October 26, 2017 2017 Kevin Jamieson 2 Some data, Bayes Classifier Training data: True label: +1 True label: -1 Optimal
Nearest Neighbor Machine Learning CSE546 Kevin Jamieson University of Washington October 26, 2017 2017 Kevin Jamieson 2 Some data, Bayes Classifier Training data: True label: +1 True label: -1 Optimal
The sample complexity of agnostic learning with deterministic labels
 The sample complexity of agnostic learning with deterministic labels Shai Ben-David Cheriton School of Computer Science University of Waterloo Waterloo, ON, N2L 3G CANADA shai@uwaterloo.ca Ruth Urner College
The sample complexity of agnostic learning with deterministic labels Shai Ben-David Cheriton School of Computer Science University of Waterloo Waterloo, ON, N2L 3G CANADA shai@uwaterloo.ca Ruth Urner College
Reproducing Kernel Hilbert Spaces
 Reproducing Kernel Hilbert Spaces Lorenzo Rosasco 9.520 Class 03 February 12, 2007 About this class Goal To introduce a particularly useful family of hypothesis spaces called Reproducing Kernel Hilbert
Reproducing Kernel Hilbert Spaces Lorenzo Rosasco 9.520 Class 03 February 12, 2007 About this class Goal To introduce a particularly useful family of hypothesis spaces called Reproducing Kernel Hilbert
Course Notes for EE227C (Spring 2018): Convex Optimization and Approximation
 Course Notes for EE7C (Spring 08): Convex Optimization and Approximation Instructor: Moritz Hardt Email: hardt+ee7c@berkeley.edu Graduate Instructor: Max Simchowitz Email: msimchow+ee7c@berkeley.edu October
Course Notes for EE7C (Spring 08): Convex Optimization and Approximation Instructor: Moritz Hardt Email: hardt+ee7c@berkeley.edu Graduate Instructor: Max Simchowitz Email: msimchow+ee7c@berkeley.edu October
BINARY CLASSIFICATION
 BINARY CLASSIFICATION MAXIM RAGINSY The problem of binary classification can be stated as follows. We have a random couple Z = X, Y ), where X R d is called the feature vector and Y {, } is called the
BINARY CLASSIFICATION MAXIM RAGINSY The problem of binary classification can be stated as follows. We have a random couple Z = X, Y ), where X R d is called the feature vector and Y {, } is called the
Lecture Support Vector Machine (SVM) Classifiers
 Introduction to Machine Learning Lecturer: Amir Globerson Lecture 6 Fall Semester Scribe: Yishay Mansour 6.1 Support Vector Machine (SVM) Classifiers Classification is one of the most important tasks in
Introduction to Machine Learning Lecturer: Amir Globerson Lecture 6 Fall Semester Scribe: Yishay Mansour 6.1 Support Vector Machine (SVM) Classifiers Classification is one of the most important tasks in
Machine Learning
 Machine Learning 10-601 Tom M. Mitchell Machine Learning Department Carnegie Mellon University October 11, 2012 Today: Computational Learning Theory Probably Approximately Coorrect (PAC) learning theorem
Machine Learning 10-601 Tom M. Mitchell Machine Learning Department Carnegie Mellon University October 11, 2012 Today: Computational Learning Theory Probably Approximately Coorrect (PAC) learning theorem
Linear Regression and Its Applications
 Linear Regression and Its Applications Predrag Radivojac October 13, 2014 Given a data set D = {(x i, y i )} n the objective is to learn the relationship between features and the target. We usually start
Linear Regression and Its Applications Predrag Radivojac October 13, 2014 Given a data set D = {(x i, y i )} n the objective is to learn the relationship between features and the target. We usually start
9 Classification. 9.1 Linear Classifiers
 9 Classification This topic returns to prediction. Unlike linear regression where we were predicting a numeric value, in this case we are predicting a class: winner or loser, yes or no, rich or poor, positive
9 Classification This topic returns to prediction. Unlike linear regression where we were predicting a numeric value, in this case we are predicting a class: winner or loser, yes or no, rich or poor, positive
PAC-learning, VC Dimension and Margin-based Bounds
 More details: General: http://www.learning-with-kernels.org/ Example of more complex bounds: http://www.research.ibm.com/people/t/tzhang/papers/jmlr02_cover.ps.gz PAC-learning, VC Dimension and Margin-based
More details: General: http://www.learning-with-kernels.org/ Example of more complex bounds: http://www.research.ibm.com/people/t/tzhang/papers/jmlr02_cover.ps.gz PAC-learning, VC Dimension and Margin-based
Machine Learning 4771
 Machine Learning 477 Instructor: Tony Jebara Topic 5 Generalization Guarantees VC-Dimension Nearest Neighbor Classification (infinite VC dimension) Structural Risk Minimization Support Vector Machines
Machine Learning 477 Instructor: Tony Jebara Topic 5 Generalization Guarantees VC-Dimension Nearest Neighbor Classification (infinite VC dimension) Structural Risk Minimization Support Vector Machines
Course Summary Math 211
 Course Summary Math 211 table of contents I. Functions of several variables. II. R n. III. Derivatives. IV. Taylor s Theorem. V. Differential Geometry. VI. Applications. 1. Best affine approximations.
Course Summary Math 211 table of contents I. Functions of several variables. II. R n. III. Derivatives. IV. Taylor s Theorem. V. Differential Geometry. VI. Applications. 1. Best affine approximations.
Differential Privacy
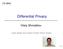 CS 380S Differential Privacy Vitaly Shmatikov most slides from Adam Smith (Penn State) slide 1 Reading Assignment Dwork. Differential Privacy (invited talk at ICALP 2006). slide 2 Basic Setting DB= x 1
CS 380S Differential Privacy Vitaly Shmatikov most slides from Adam Smith (Penn State) slide 1 Reading Assignment Dwork. Differential Privacy (invited talk at ICALP 2006). slide 2 Basic Setting DB= x 1
Differentially-private Learning and Information Theory
 Differentially-private Learning and Information Theory Darakhshan Mir Department of Computer Science Rutgers University NJ, USA mir@cs.rutgers.edu ABSTRACT Using results from PAC-Bayesian bounds in learning
Differentially-private Learning and Information Theory Darakhshan Mir Department of Computer Science Rutgers University NJ, USA mir@cs.rutgers.edu ABSTRACT Using results from PAC-Bayesian bounds in learning
