Some results about the index of matrix and Drazin inverse
|
|
|
- Gary Underwood
- 5 years ago
- Views:
Transcription
1 Mathematical Sciences Vol. 4, No. 3 (2010) Some results about the index of matrix and Drazin inverse M. Nikuie a,1, M.K. Mirnia b, Y. Mahmoudi b a Member of Young Researchers Club, Islamic Azad University-Tabriz Branch b Islamic Azad University-Tabriz Branch Abstract In this paper, some results about the index of matrix and Drazin inverse are given. We then explain applications of them in solving singular linear system of equations. Keywords: Index, Drazin inverse, Singular linear system, Jordan normal form. c 2010 Published by Islamic Azad University-Karaj Branch. 1 Introduction Let C n n denote the space comprising those matrices of order n, over the complex field. Any matrix A C n n have an index that we get Drazin inverse of A to make use of it. On the contrary to our expectation, for any matrix A C n n, even singular matrices, index and Drazin inverse of matrix A exists and is unique[10]. According to this truth, the aim of this paper is to give the new results of them. The Drazin inverse has various applications in the theory of finite Markov chains, the study of singular differentail and difference equations, the investigation of Cesaro-Neumann iterations, cryptograph, iterative methods in numerical analysis, multibody system dynamics and others[4,8,9]. Computing the Drazin inverse is a current issue in recent years[3,10]. Section 2 provides preliminaries for index of matrix and Drazin inverse. Applications 1 Corresponding Author. Address: nikoie m@yahoo.com
2 284 Mathematical Sciences Vol. 4, No. 3 (2010) of them in solving singular linear system of equations is also explained. Some new results on the index of matrix and Drazin inverse are given in section 3. Numerical examples to illustrate previous sections are given in section 4. 2 Preliminaries and Basic Definitions We first present some definitions and theorems about the index of matrix and Drazin inverse which are needed in this paper. Definition 2.1 Let A C n n. We say the nonnegative integer number k to be the index of matrix A, if k is the smallest nonnegative integer number such that rank(a k+1 ) = rank(a k ) (1) It is equivalent to the dimension of largest Jordan block corresponding to the zero eigenvalue of A [9]. The index of matrix A, is denoted by ind(a). For any matrix A C n n the unique Jordan normal form of a matrix A can be built [6]. Therefore for any matrix A C n n the index of A exists and is unique. Definition 2.2 A number λ C, is called an eigenvalue of the matrix A if there is a vector x 0 such that Ax = λx. Any such vector is called an eigenvector of A associated to the eigenvalue λ. The set L(λ) = {x (A λi)x = 0} forms a linear subspace of C n, of dimension ρ(λ) = n rank(a λi) The integer ρ(λ) = diml(λ) specifies the maximum number of linearly independent eigenvectors associated with the eigenvalue λ. It is easily seen that ϕ(µ) = det(a µi) is a nth-degree polynomial of the form ϕ(µ) = ( 1) n (µ n + α n 1 µ n α 0 ) (2)
3 M. Nikuie et al. 285 It is called the characteristic polynomial of the matrix A. Its zeros are the eigenvalues of A. If λ 1,, λ k are the distinct zeros of ϕ(µ), then ϕ can be represented in the form ϕ(µ) = ( 1) n (µ λ 1 ) σ 1 (µ λ 2 ) σ2 (µ λ k ) σ k The integer σ i, which we also denote by σ(λ i ) = σ i, is called the multiplicity of the eigenvalue λ i. Theorem 2.3. If λ be an eigenvalue of matrix A C n n, then 1 ρ(λ) σ(λ) n (3) Proof See [6]. Definition 2.4 Let A C n n, with ind(a) = k. The matrix X of order n is the Drazin inverse of A,denoted by A D, if X satisfies the following conditions AX = XA, XAX = X, A k XA = A k (4) When ind(a) = 1, A D is called the group inverse of A, and denoted by A g. For any matrix A C n n, the Drazin inverse A D of A exists and is unique [3,10]. Theorem 2.5 Let A C n n, with ind(a) = k, rank(a k ) = r. We may assume that the Jordan normal form of A has the form as follows ( ) D 0 A = P P 1 0 N where P is a nonsingular matrix, D is a nonsingular matrix of order r, and N is a nilpotent matrix that N k = ō. Then we can write the Drazin inverse of A in the form ( D 1 ) 0 A D = P P 1 0 N When ind(a) = 1, it is obvious that N = ō [3,10]. Corollary 2.6. Let ind(a) = 1 and D = I. It is clear that D 1 = I, thus A = A g.
4 286 Mathematical Sciences Vol. 4, No. 3 (2010) Theorem 2.7 If Ax = b be a consistent or inconsistent singular linear system where ind(a) = k,then the linear system of equations A k Ax = A k b (5) is consistent. Proof The linear system Ax = b has solution if and only if rank(a) = rank[a b] [8]. From (1) we have rank(a k+1 ) = rank[a k+1 A k b]. Therefore (5) is consistent. According to[5]and properties of the Drazin inverse, in order to obtain the Drazin inverse the projection method solves consistent or inconsistent singular linear system Ax = b where ind(a) = k through solving the consistent singular linear system (5)[9]. Theorem 2.8 A D b is a solution of Ax = b, k = ind(a) (6) if and only if b R(A k ), and A D b is an unique solution of (6) provided that x R(A k ). We now explain applications of the index of matrix and Drazin inverse in solving singular linear system of equations. Singular linear system of equations arise in many different scientific applications. Notably, partial differential equations discretized with finite difference or finite element methods yield singular linear systems of equations. Large singular linear systems can be solved with either sparse decompositions techniques or with iterative methods. For consistent singular linear systems, these two approaches can be also combined into a method that uses approximate decomposition preconditioning for an iterative method. However, we cannot use preconditioned iterative method for inconsistent singular linear systems[9]. A cramer rule for A D b was given in [7]. Singular linear systems with index one arises in many applications, such as Markov chain modelling and numerical experiment on the perturbed Navier-Stokes equation. Therefore, for the singular linear system with unit index, we must solve the system AAx = Ab (7)
5 M. Nikuie et al. 287 which is consistent. So we can choose all kinds of preconditioned methods, such as PCG, PGMRES, etc., to solve system (7). In [9] Wei proposed a two step algorithm for solving singular linear system with index one. In an implementation we first solve the system Ay = Ab, the inner iteration, and then we solve Ax = y, the outer iteration. 3 Some Results In this section, we give some results about the index of matrix and Drazin inverse. Theorem 3.1 If A C n n be a nonsingular matrix, then ind(a) = 0. Proof. Let A C n n be nonsingular matrix, we know that rank(a) = rank(i n ) = n. Thus ind(a) = 0. Moreover the eigenvalues of A are nonzero. Therefore if A be a nonsingular matrix then ind(a) = 0 and A D = A 1, which satisfies the conditions (4). Theorem 3.2 If A C n n be a matrix with index one, then rank(a) = rank(a g ). Proof. From rank(a g ) = rank(a g AA g ) rank(aa g ) rank(a) we have rank(a g ) rank(a) (8) Since rank(a) = rank(aa g A) rank(a g A) rank(a g ) rank(a) rank(a g ) (9) Thus of (8), (9) we have rank(a) = rank(a g ). Corollary 3.3 Let A C n n where ind(a) > 1. We have rank(a D ) < rank(a). Theorem 3.4 Let A C n n,then A g exists if and only if rank(a) = rank(a 2 )[1]. Corollary 3.5 The index of any idempotent matrix equal one. The converse of this statement is not true always.
6 288 Mathematical Sciences Vol. 4, No. 3 (2010) Theorem 3.6 If A C n n be a symmetric matrix with index one, then A g = (A g ) T. Proof Since A g be group inverse of A we have AA g = A g A, A g AA g = A g, AA g A = A From A = A T we have (A g ) T A = A(A g ) T, (A g ) T A(A g ) T = (A g ) T, A(A g ) T A = A (10) From (10) by Definition (2.4), (A g ) T is group inverse of A. The group inverse of matrix A is unique. Therefore A g = (A g ) T. Corollary 3.7 For any matrix A C n n with index one, (A g ) g = A. Theorem 3.8. If A C n n where ind(a) = k,then ind(a) = ind(a T ). Proof Since ind(a) = k, by Definition(2.1) we have rank(a k+1 ) = rank(a k ). From (A n ) T = (A T ) n. We have (A k+1 ) T = (A T ) k+1, (A k ) T = (A T ) k Since rank(a) = rank(a T ) we have rank(a k+1 ) = rank((a T ) k+1 ), rank(a k ) = rank((a T ) k ) Thus, we have rank((a T ) k+1 ) = rank((a T ) k ). Therefore ind(a) = ind(a T ). Theorem 3.9. If λ be an eigenvalue of A C n n, then 1 λ is an eigenvalue of AD. Proof From Ax = λx, (x 0) we have AA D x = λa D x A D AA D x = λa D A D x From (4) we can get A D x = λa D A D x. Now if we set A D x = y we have 1 λ y = AD y. Therefore 1 λ is an eigenvalue of AD.
7 M. Nikuie et al. 289 Theorem If A C n n be a nilpotent matrix that A k = ō, then ind(a) = k. Proof From A k = ō we have rank(a k ) = rank(ō) From A k+n = ō, n N we can get rank(a k+1 ) = rank(a k ). Therefore ind(a) = k. Corollary 3.11 Let A C n n be a nilpotent matrix of index n, so ind(a) = n and rank(a n ) = 0. Thus in Theorem 1.2, D = ō. Therefore A D = ō. Theorem If A C n n, then 0 ind(a) n. Proof By Theorem 3.1, ind(a) = 0 for a nonsingular matrix A. By Theorem 3.10 ind(a) = n for a nilpotent matrix A such that A n = ō. Let λ 1,, λ k are the distinct zeros of the characteristic polynomial of the matrix A C n n, and λ 1 = 0 with multiplicity σ(λ 1 ) = k < n. From (2) any matrix A C n n has exactly n eigenvalue. By Theorem 2.3 ρ(λ 1 ) σ(λ 1 ) < n. From Definition 2.1 we can get 0 < ind(a) < n. Therefore 0 ind(a) n. 4 Numerical Examples We now give the following examples to explain the present results. Example 4.1 Determine the index and Drazin inverse of the following matrix A = It is obvious that rank(a) = rank(a 2 ), so ind(a) = 1. Moreover the matrix A has the eigenvalues λ 1 = 0, λ 2 = 1 with multiplicity σ(λ 1 ) = 1, ρ(λ 1 ) = 1
8 290 Mathematical Sciences Vol. 4, No. 3 (2010) σ(λ 2 ) = 2, ρ(λ 2 ) = 2 Thus Jordan normal form of matrix A has the following form [1] J = P AP 1 = 0 [1] 0, P = (11) 0 0 [0] P is a nonsingular matrix. The dimension of largest Jordan block corresponding to the zero eigenvalue of (11) is equal to one. Moreover A = A 2,then A is an idempotent matrix, by Corollary 3.5 ind(a) = 1. From Theorem 2.5 we have ( ) D 0 A = P 1 P = N ( 1 ) 0 wherein D = 0 1, is a nonsingular matrix of order 2, and N = ō, is a nilpotent matrix. Therefore the group inverse of A is ( ) D 0 A g = P 1 P = N Moreover D = I, so of Corollary 2.6, we have A = A g. A,A g satisfies the conditions (4), thus A g is group inverse of A. The system 2x 1 x 2 + x 3 = 1 3x 1 + 4x 2 3x 3 = 1 5x 1 + 5x 2 4x 3 = 2 is inconsistent. Ind(A T ) = 1, it is clear that the following system is consistent. 2x 1 x 2 + x 3 = 3 3x 1 + 4x 2 3x 3 5x 1 + 5x 2 4x 3 = 5 = 8
9 M. Nikuie et al. 291 Example 4.2 Determine the index and Drazin inverse of the following matrix B = It is obvious that rank(b 3 ) = rank(b 4 ), so ind(b) = 3. Moreover the matrix B has the eigenvalues λ = 0 with multiplicity σ(λ) = 3, ρ(λ) = 1 So Jordan normal form of matrix B has the following form J = P BP 1 = 0 0 1, P = (12) P is a nonsingular matrix. The dimension of largest Jordan block corresponding to the zero eigenvalue of (12) equal to 3. Moreover B 3 = ō,then ind(b) = 3 By Theorem 2.5 we have B = P P = Therefore the Drazin inverse of B is B D = P P = Moreover B C 3 3 is a nilpotent matrix of index 3, so of Corollary 3.11 we have B D = ō. B, B D fulfills the conditions (4), thus B D is Drazin inverse of B. Example 4.3 Consider the following symmetric matrix C =
10 292 Mathematical Sciences Vol. 4, No. 3 (2010) The matrix C has the eigenvalues λ 1 = 0, λ 2 = 1, λ 3 = 8 3. The index of matrix C is equal to one, because rank(c) = rank(c 2 ). So Jordan normal form of matrix C has the following form [1] 0 0 J = P CP 1 = 0 [ 8 3 ] 0, P = 0 0 [0] (13) P is a nonsingular matrix. The dimension of largest Jordan block corresponding to the zero eigenvalue of (13) is equal to one. By Theorem 2.5 we have C g = P 1 JP = C, C g satisfies the conditions (4) thus C g is group inverse of C. It is clear that rank(c) = rank(c g ) and (C g ) g = C. Consider the following singular linear system of equation with index one x 1 x 2 x 3 = 3 x x 2 x 3 = 1 x 1 x 2 x 3 = 3 3 Since b = 1 R(C), the solution of (14) is 3 5 Conclusions x = C g b = = (14) In this paper, we prove some properties of index of matrix and Drazin inverse and give some examples.
11 M. Nikuie et al. 293 Acknowledgment This paper is outcome of the project (No ) that is supported by Young Researchers Club, Islamic Azad University-Tabriz Branch. The authors thank the Young Researchers Club, Islamic Azad University-Tabriz Branch for its supports. References [1] Bhaskara K., Meyer C., The Theory of Generalized inverse over commutative Rings, London and New York, [2] Campbell S.L., Meyer C., Generalized inverse of Linear Transformations, Pitman London, [3] Chen J., Xu Z. (2008) Comment on condition number of Drazin inverse and their condition number of singular systems, Applied Mathematics and Computation, 199, [4] Chen J., Xu Z. (2008) Comment on condition number of Drazin inverse and their condition number of singular systems, Applied Mathematics and Computation, 199, [5] Lin L., Wei Y., Zhang N. (2008) Convergence and quotient convergence of iterative methods for solving singular linear equations with index one, Linear Algebra and its Applications, 203, [6] Stoer J., Bulirsch R., Introduction to Numerical Analysis, Springer, [7] Wang G. (1989) A cramer rule for finding the solution of a class of singular equations, Linear Algebra and its Applications, 1, [8] Wei Y. (1998) Index splitting for the Drazin inverse and the singular linear system, Applied Mathematics and Computation, 95,
12 294 Mathematical Sciences Vol. 4, No. 3 (2010) [9] Wei Y., Zhou J. (2006) A two-step algorithm for solving singular linear systems with index one, Applied Mathematics and Computation, 175, [10] Zheng L. (2001) A characterization of the Drazin inverse, Linear Algebra and its Applications, 335,
Group inverse for the block matrix with two identical subblocks over skew fields
 Electronic Journal of Linear Algebra Volume 21 Volume 21 2010 Article 7 2010 Group inverse for the block matrix with two identical subblocks over skew fields Jiemei Zhao Changjiang Bu Follow this and additional
Electronic Journal of Linear Algebra Volume 21 Volume 21 2010 Article 7 2010 Group inverse for the block matrix with two identical subblocks over skew fields Jiemei Zhao Changjiang Bu Follow this and additional
Chapter 1. Matrix Algebra
 ST4233, Linear Models, Semester 1 2008-2009 Chapter 1. Matrix Algebra 1 Matrix and vector notation Definition 1.1 A matrix is a rectangular or square array of numbers of variables. We use uppercase boldface
ST4233, Linear Models, Semester 1 2008-2009 Chapter 1. Matrix Algebra 1 Matrix and vector notation Definition 1.1 A matrix is a rectangular or square array of numbers of variables. We use uppercase boldface
Applied Matrix Algebra Lecture Notes Section 2.2. Gerald Höhn Department of Mathematics, Kansas State University
 Applied Matrix Algebra Lecture Notes Section 22 Gerald Höhn Department of Mathematics, Kansas State University September, 216 Chapter 2 Matrices 22 Inverses Let (S) a 11 x 1 + a 12 x 2 + +a 1n x n = b
Applied Matrix Algebra Lecture Notes Section 22 Gerald Höhn Department of Mathematics, Kansas State University September, 216 Chapter 2 Matrices 22 Inverses Let (S) a 11 x 1 + a 12 x 2 + +a 1n x n = b
Multiplicative Perturbation Bounds of the Group Inverse and Oblique Projection
 Filomat 30: 06, 37 375 DOI 0.98/FIL67M Published by Faculty of Sciences Mathematics, University of Niš, Serbia Available at: http://www.pmf.ni.ac.rs/filomat Multiplicative Perturbation Bounds of the Group
Filomat 30: 06, 37 375 DOI 0.98/FIL67M Published by Faculty of Sciences Mathematics, University of Niš, Serbia Available at: http://www.pmf.ni.ac.rs/filomat Multiplicative Perturbation Bounds of the Group
The Drazin inverses of products and differences of orthogonal projections
 J Math Anal Appl 335 7 64 71 wwwelseviercom/locate/jmaa The Drazin inverses of products and differences of orthogonal projections Chun Yuan Deng School of Mathematics Science, South China Normal University,
J Math Anal Appl 335 7 64 71 wwwelseviercom/locate/jmaa The Drazin inverses of products and differences of orthogonal projections Chun Yuan Deng School of Mathematics Science, South China Normal University,
The Jordan Normal Form and its Applications
 The and its Applications Jeremy IMPACT Brigham Young University A square matrix A is a linear operator on {R, C} n. A is diagonalizable if and only if it has n linearly independent eigenvectors. What happens
The and its Applications Jeremy IMPACT Brigham Young University A square matrix A is a linear operator on {R, C} n. A is diagonalizable if and only if it has n linearly independent eigenvectors. What happens
The DMP Inverse for Rectangular Matrices
 Filomat 31:19 (2017, 6015 6019 https://doi.org/10.2298/fil1719015m Published by Faculty of Sciences Mathematics, University of Niš, Serbia Available at: http://.pmf.ni.ac.rs/filomat The DMP Inverse for
Filomat 31:19 (2017, 6015 6019 https://doi.org/10.2298/fil1719015m Published by Faculty of Sciences Mathematics, University of Niš, Serbia Available at: http://.pmf.ni.ac.rs/filomat The DMP Inverse for
Some additive results on Drazin inverse
 Linear Algebra and its Applications 322 (2001) 207 217 www.elsevier.com/locate/laa Some additive results on Drazin inverse Robert E. Hartwig a, Guorong Wang a,b,1, Yimin Wei c,,2 a Mathematics Department,
Linear Algebra and its Applications 322 (2001) 207 217 www.elsevier.com/locate/laa Some additive results on Drazin inverse Robert E. Hartwig a, Guorong Wang a,b,1, Yimin Wei c,,2 a Mathematics Department,
Formulas for the Drazin Inverse of Matrices over Skew Fields
 Filomat 30:12 2016 3377 3388 DOI 102298/FIL1612377S Published by Faculty of Sciences and Mathematics University of Niš Serbia Available at: http://wwwpmfniacrs/filomat Formulas for the Drazin Inverse of
Filomat 30:12 2016 3377 3388 DOI 102298/FIL1612377S Published by Faculty of Sciences and Mathematics University of Niš Serbia Available at: http://wwwpmfniacrs/filomat Formulas for the Drazin Inverse of
Linear Algebra Practice Problems
 Linear Algebra Practice Problems Math 24 Calculus III Summer 25, Session II. Determine whether the given set is a vector space. If not, give at least one axiom that is not satisfied. Unless otherwise stated,
Linear Algebra Practice Problems Math 24 Calculus III Summer 25, Session II. Determine whether the given set is a vector space. If not, give at least one axiom that is not satisfied. Unless otherwise stated,
Key words. Index, Drazin inverse, group inverse, Moore-Penrose inverse, index splitting, proper splitting, comparison theorem, monotone iteration.
 The Electronic Journal of Linear Algebra. A publication of the International Linear Algebra Society. Volume 8, pp. 83-93, June 2001. ISSN 1081-3810. http://math.technion.ac.il/iic/ela ELA ADDITIONAL RESULTS
The Electronic Journal of Linear Algebra. A publication of the International Linear Algebra Society. Volume 8, pp. 83-93, June 2001. ISSN 1081-3810. http://math.technion.ac.il/iic/ela ELA ADDITIONAL RESULTS
Recall the convention that, for us, all vectors are column vectors.
 Some linear algebra Recall the convention that, for us, all vectors are column vectors. 1. Symmetric matrices Let A be a real matrix. Recall that a complex number λ is an eigenvalue of A if there exists
Some linear algebra Recall the convention that, for us, all vectors are column vectors. 1. Symmetric matrices Let A be a real matrix. Recall that a complex number λ is an eigenvalue of A if there exists
Chap 3. Linear Algebra
 Chap 3. Linear Algebra Outlines 1. Introduction 2. Basis, Representation, and Orthonormalization 3. Linear Algebraic Equations 4. Similarity Transformation 5. Diagonal Form and Jordan Form 6. Functions
Chap 3. Linear Algebra Outlines 1. Introduction 2. Basis, Representation, and Orthonormalization 3. Linear Algebraic Equations 4. Similarity Transformation 5. Diagonal Form and Jordan Form 6. Functions
ICS 6N Computational Linear Algebra Eigenvalues and Eigenvectors
 ICS 6N Computational Linear Algebra Eigenvalues and Eigenvectors Xiaohui Xie University of California, Irvine xhx@uci.edu Xiaohui Xie (UCI) ICS 6N 1 / 34 The powers of matrix Consider the following dynamic
ICS 6N Computational Linear Algebra Eigenvalues and Eigenvectors Xiaohui Xie University of California, Irvine xhx@uci.edu Xiaohui Xie (UCI) ICS 6N 1 / 34 The powers of matrix Consider the following dynamic
Computational Methods. Eigenvalues and Singular Values
 Computational Methods Eigenvalues and Singular Values Manfred Huber 2010 1 Eigenvalues and Singular Values Eigenvalues and singular values describe important aspects of transformations and of data relations
Computational Methods Eigenvalues and Singular Values Manfred Huber 2010 1 Eigenvalues and Singular Values Eigenvalues and singular values describe important aspects of transformations and of data relations
arxiv: v1 [math.ra] 14 Apr 2018
![arxiv: v1 [math.ra] 14 Apr 2018 arxiv: v1 [math.ra] 14 Apr 2018](/thumbs/92/110340597.jpg) Three it representations of the core-ep inverse Mengmeng Zhou a, Jianlong Chen b,, Tingting Li c, Dingguo Wang d arxiv:180.006v1 [math.ra] 1 Apr 018 a School of Mathematics, Southeast University, Nanjing,
Three it representations of the core-ep inverse Mengmeng Zhou a, Jianlong Chen b,, Tingting Li c, Dingguo Wang d arxiv:180.006v1 [math.ra] 1 Apr 018 a School of Mathematics, Southeast University, Nanjing,
c c c c c c c c c c a 3x3 matrix C= has a determinant determined by
 Linear Algebra Determinants and Eigenvalues Introduction: Many important geometric and algebraic properties of square matrices are associated with a single real number revealed by what s known as the determinant.
Linear Algebra Determinants and Eigenvalues Introduction: Many important geometric and algebraic properties of square matrices are associated with a single real number revealed by what s known as the determinant.
ALGEBRA QUALIFYING EXAM PROBLEMS LINEAR ALGEBRA
 ALGEBRA QUALIFYING EXAM PROBLEMS LINEAR ALGEBRA Kent State University Department of Mathematical Sciences Compiled and Maintained by Donald L. White Version: August 29, 2017 CONTENTS LINEAR ALGEBRA AND
ALGEBRA QUALIFYING EXAM PROBLEMS LINEAR ALGEBRA Kent State University Department of Mathematical Sciences Compiled and Maintained by Donald L. White Version: August 29, 2017 CONTENTS LINEAR ALGEBRA AND
Math Bootcamp An p-dimensional vector is p numbers put together. Written as. x 1 x =. x p
 Math Bootcamp 2012 1 Review of matrix algebra 1.1 Vectors and rules of operations An p-dimensional vector is p numbers put together. Written as x 1 x =. x p. When p = 1, this represents a point in the
Math Bootcamp 2012 1 Review of matrix algebra 1.1 Vectors and rules of operations An p-dimensional vector is p numbers put together. Written as x 1 x =. x p. When p = 1, this represents a point in the
Properties of Matrices and Operations on Matrices
 Properties of Matrices and Operations on Matrices A common data structure for statistical analysis is a rectangular array or matris. Rows represent individual observational units, or just observations,
Properties of Matrices and Operations on Matrices A common data structure for statistical analysis is a rectangular array or matris. Rows represent individual observational units, or just observations,
Elementary linear algebra
 Chapter 1 Elementary linear algebra 1.1 Vector spaces Vector spaces owe their importance to the fact that so many models arising in the solutions of specific problems turn out to be vector spaces. The
Chapter 1 Elementary linear algebra 1.1 Vector spaces Vector spaces owe their importance to the fact that so many models arising in the solutions of specific problems turn out to be vector spaces. The
Chapters 5 & 6: Theory Review: Solutions Math 308 F Spring 2015
 Chapters 5 & 6: Theory Review: Solutions Math 308 F Spring 205. If A is a 3 3 triangular matrix, explain why det(a) is equal to the product of entries on the diagonal. If A is a lower triangular or diagonal
Chapters 5 & 6: Theory Review: Solutions Math 308 F Spring 205. If A is a 3 3 triangular matrix, explain why det(a) is equal to the product of entries on the diagonal. If A is a lower triangular or diagonal
Econ Slides from Lecture 7
 Econ 205 Sobel Econ 205 - Slides from Lecture 7 Joel Sobel August 31, 2010 Linear Algebra: Main Theory A linear combination of a collection of vectors {x 1,..., x k } is a vector of the form k λ ix i for
Econ 205 Sobel Econ 205 - Slides from Lecture 7 Joel Sobel August 31, 2010 Linear Algebra: Main Theory A linear combination of a collection of vectors {x 1,..., x k } is a vector of the form k λ ix i for
STAT200C: Review of Linear Algebra
 Stat200C Instructor: Zhaoxia Yu STAT200C: Review of Linear Algebra 1 Review of Linear Algebra 1.1 Vector Spaces, Rank, Trace, and Linear Equations 1.1.1 Rank and Vector Spaces Definition A vector whose
Stat200C Instructor: Zhaoxia Yu STAT200C: Review of Linear Algebra 1 Review of Linear Algebra 1.1 Vector Spaces, Rank, Trace, and Linear Equations 1.1.1 Rank and Vector Spaces Definition A vector whose
Generalized core inverses of matrices
 Generalized core inverses of matrices Sanzhang Xu, Jianlong Chen, Julio Benítez and Dingguo Wang arxiv:179.4476v1 [math.ra 13 Sep 217 Abstract: In this paper, we introduce two new generalized inverses
Generalized core inverses of matrices Sanzhang Xu, Jianlong Chen, Julio Benítez and Dingguo Wang arxiv:179.4476v1 [math.ra 13 Sep 217 Abstract: In this paper, we introduce two new generalized inverses
Eigenvalues, Eigenvectors, and Diagonalization
 Week12 Eigenvalues, Eigenvectors, and Diagonalization 12.1 Opening Remarks 12.1.1 Predicting the Weather, Again Let us revisit the example from Week 4, in which we had a simple model for predicting the
Week12 Eigenvalues, Eigenvectors, and Diagonalization 12.1 Opening Remarks 12.1.1 Predicting the Weather, Again Let us revisit the example from Week 4, in which we had a simple model for predicting the
Remark 1 By definition, an eigenvector must be a nonzero vector, but eigenvalue could be zero.
 Sec 5 Eigenvectors and Eigenvalues In this chapter, vector means column vector Definition An eigenvector of an n n matrix A is a nonzero vector x such that A x λ x for some scalar λ A scalar λ is called
Sec 5 Eigenvectors and Eigenvalues In this chapter, vector means column vector Definition An eigenvector of an n n matrix A is a nonzero vector x such that A x λ x for some scalar λ A scalar λ is called
Linear Algebra: Matrix Eigenvalue Problems
 CHAPTER8 Linear Algebra: Matrix Eigenvalue Problems Chapter 8 p1 A matrix eigenvalue problem considers the vector equation (1) Ax = λx. 8.0 Linear Algebra: Matrix Eigenvalue Problems Here A is a given
CHAPTER8 Linear Algebra: Matrix Eigenvalue Problems Chapter 8 p1 A matrix eigenvalue problem considers the vector equation (1) Ax = λx. 8.0 Linear Algebra: Matrix Eigenvalue Problems Here A is a given
MATH 240 Spring, Chapter 1: Linear Equations and Matrices
 MATH 240 Spring, 2006 Chapter Summaries for Kolman / Hill, Elementary Linear Algebra, 8th Ed. Sections 1.1 1.6, 2.1 2.2, 3.2 3.8, 4.3 4.5, 5.1 5.3, 5.5, 6.1 6.5, 7.1 7.2, 7.4 DEFINITIONS Chapter 1: Linear
MATH 240 Spring, 2006 Chapter Summaries for Kolman / Hill, Elementary Linear Algebra, 8th Ed. Sections 1.1 1.6, 2.1 2.2, 3.2 3.8, 4.3 4.5, 5.1 5.3, 5.5, 6.1 6.5, 7.1 7.2, 7.4 DEFINITIONS Chapter 1: Linear
Linear Algebra 1. M.T.Nair Department of Mathematics, IIT Madras. and in that case x is called an eigenvector of T corresponding to the eigenvalue λ.
 Linear Algebra 1 M.T.Nair Department of Mathematics, IIT Madras 1 Eigenvalues and Eigenvectors 1.1 Definition and Examples Definition 1.1. Let V be a vector space (over a field F) and T : V V be a linear
Linear Algebra 1 M.T.Nair Department of Mathematics, IIT Madras 1 Eigenvalues and Eigenvectors 1.1 Definition and Examples Definition 1.1. Let V be a vector space (over a field F) and T : V V be a linear
Eigenvalues, Eigenvectors, and Diagonalization
 Week12 Eigenvalues, Eigenvectors, and Diagonalization 12.1 Opening Remarks 12.1.1 Predicting the Weather, Again View at edx Let us revisit the example from Week 4, in which we had a simple model for predicting
Week12 Eigenvalues, Eigenvectors, and Diagonalization 12.1 Opening Remarks 12.1.1 Predicting the Weather, Again View at edx Let us revisit the example from Week 4, in which we had a simple model for predicting
Linear Algebra and its Applications
 Linear Algebra and its Applications 432 21 1691 172 Contents lists available at ScienceDirect Linear Algebra and its Applications journal homepage: www.elsevier.com/locate/laa Drazin inverse of partitioned
Linear Algebra and its Applications 432 21 1691 172 Contents lists available at ScienceDirect Linear Algebra and its Applications journal homepage: www.elsevier.com/locate/laa Drazin inverse of partitioned
OHSx XM511 Linear Algebra: Solutions to Online True/False Exercises
 This document gives the solutions to all of the online exercises for OHSx XM511. The section ( ) numbers refer to the textbook. TYPE I are True/False. Answers are in square brackets [. Lecture 02 ( 1.1)
This document gives the solutions to all of the online exercises for OHSx XM511. The section ( ) numbers refer to the textbook. TYPE I are True/False. Answers are in square brackets [. Lecture 02 ( 1.1)
TMA Calculus 3. Lecture 21, April 3. Toke Meier Carlsen Norwegian University of Science and Technology Spring 2013
 TMA4115 - Calculus 3 Lecture 21, April 3 Toke Meier Carlsen Norwegian University of Science and Technology Spring 2013 www.ntnu.no TMA4115 - Calculus 3, Lecture 21 Review of last week s lecture Last week
TMA4115 - Calculus 3 Lecture 21, April 3 Toke Meier Carlsen Norwegian University of Science and Technology Spring 2013 www.ntnu.no TMA4115 - Calculus 3, Lecture 21 Review of last week s lecture Last week
Ir O D = D = ( ) Section 2.6 Example 1. (Bottom of page 119) dim(v ) = dim(l(v, W )) = dim(v ) dim(f ) = dim(v )
 Section 3.2 Theorem 3.6. Let A be an m n matrix of rank r. Then r m, r n, and, by means of a finite number of elementary row and column operations, A can be transformed into the matrix ( ) Ir O D = 1 O
Section 3.2 Theorem 3.6. Let A be an m n matrix of rank r. Then r m, r n, and, by means of a finite number of elementary row and column operations, A can be transformed into the matrix ( ) Ir O D = 1 O
The Eigenvalue Problem: Perturbation Theory
 Jim Lambers MAT 610 Summer Session 2009-10 Lecture 13 Notes These notes correspond to Sections 7.2 and 8.1 in the text. The Eigenvalue Problem: Perturbation Theory The Unsymmetric Eigenvalue Problem Just
Jim Lambers MAT 610 Summer Session 2009-10 Lecture 13 Notes These notes correspond to Sections 7.2 and 8.1 in the text. The Eigenvalue Problem: Perturbation Theory The Unsymmetric Eigenvalue Problem Just
AMS526: Numerical Analysis I (Numerical Linear Algebra)
 AMS526: Numerical Analysis I (Numerical Linear Algebra) Lecture 16: Eigenvalue Problems; Similarity Transformations Xiangmin Jiao Stony Brook University Xiangmin Jiao Numerical Analysis I 1 / 18 Eigenvalue
AMS526: Numerical Analysis I (Numerical Linear Algebra) Lecture 16: Eigenvalue Problems; Similarity Transformations Xiangmin Jiao Stony Brook University Xiangmin Jiao Numerical Analysis I 1 / 18 Eigenvalue
AN ELEMENTARY PROOF OF THE SPECTRAL RADIUS FORMULA FOR MATRICES
 AN ELEMENTARY PROOF OF THE SPECTRAL RADIUS FORMULA FOR MATRICES JOEL A. TROPP Abstract. We present an elementary proof that the spectral radius of a matrix A may be obtained using the formula ρ(a) lim
AN ELEMENTARY PROOF OF THE SPECTRAL RADIUS FORMULA FOR MATRICES JOEL A. TROPP Abstract. We present an elementary proof that the spectral radius of a matrix A may be obtained using the formula ρ(a) lim
Lecture Notes: Eigenvalues and Eigenvectors. 1 Definitions. 2 Finding All Eigenvalues
 Lecture Notes: Eigenvalues and Eigenvectors Yufei Tao Department of Computer Science and Engineering Chinese University of Hong Kong taoyf@cse.cuhk.edu.hk 1 Definitions Let A be an n n matrix. If there
Lecture Notes: Eigenvalues and Eigenvectors Yufei Tao Department of Computer Science and Engineering Chinese University of Hong Kong taoyf@cse.cuhk.edu.hk 1 Definitions Let A be an n n matrix. If there
Remark By definition, an eigenvector must be a nonzero vector, but eigenvalue could be zero.
 Sec 6 Eigenvalues and Eigenvectors Definition An eigenvector of an n n matrix A is a nonzero vector x such that A x λ x for some scalar λ A scalar λ is called an eigenvalue of A if there is a nontrivial
Sec 6 Eigenvalues and Eigenvectors Definition An eigenvector of an n n matrix A is a nonzero vector x such that A x λ x for some scalar λ A scalar λ is called an eigenvalue of A if there is a nontrivial
Problem Set (T) If A is an m n matrix, B is an n p matrix and D is a p s matrix, then show
 MTH 0: Linear Algebra Department of Mathematics and Statistics Indian Institute of Technology - Kanpur Problem Set Problems marked (T) are for discussions in Tutorial sessions (T) If A is an m n matrix,
MTH 0: Linear Algebra Department of Mathematics and Statistics Indian Institute of Technology - Kanpur Problem Set Problems marked (T) are for discussions in Tutorial sessions (T) If A is an m n matrix,
Dragan S. Djordjević. 1. Introduction
 UNIFIED APPROACH TO THE REVERSE ORDER RULE FOR GENERALIZED INVERSES Dragan S Djordjević Abstract In this paper we consider the reverse order rule of the form (AB) (2) KL = B(2) TS A(2) MN for outer generalized
UNIFIED APPROACH TO THE REVERSE ORDER RULE FOR GENERALIZED INVERSES Dragan S Djordjević Abstract In this paper we consider the reverse order rule of the form (AB) (2) KL = B(2) TS A(2) MN for outer generalized
Mathematical Foundations of Applied Statistics: Matrix Algebra
 Mathematical Foundations of Applied Statistics: Matrix Algebra Steffen Unkel Department of Medical Statistics University Medical Center Göttingen, Germany Winter term 2018/19 1/105 Literature Seber, G.
Mathematical Foundations of Applied Statistics: Matrix Algebra Steffen Unkel Department of Medical Statistics University Medical Center Göttingen, Germany Winter term 2018/19 1/105 Literature Seber, G.
ELE/MCE 503 Linear Algebra Facts Fall 2018
 ELE/MCE 503 Linear Algebra Facts Fall 2018 Fact N.1 A set of vectors is linearly independent if and only if none of the vectors in the set can be written as a linear combination of the others. Fact N.2
ELE/MCE 503 Linear Algebra Facts Fall 2018 Fact N.1 A set of vectors is linearly independent if and only if none of the vectors in the set can be written as a linear combination of the others. Fact N.2
Lecture Summaries for Linear Algebra M51A
 These lecture summaries may also be viewed online by clicking the L icon at the top right of any lecture screen. Lecture Summaries for Linear Algebra M51A refers to the section in the textbook. Lecture
These lecture summaries may also be viewed online by clicking the L icon at the top right of any lecture screen. Lecture Summaries for Linear Algebra M51A refers to the section in the textbook. Lecture
Matrix Algebra, part 2
 Matrix Algebra, part 2 Ming-Ching Luoh 2005.9.12 1 / 38 Diagonalization and Spectral Decomposition of a Matrix Optimization 2 / 38 Diagonalization and Spectral Decomposition of a Matrix Also called Eigenvalues
Matrix Algebra, part 2 Ming-Ching Luoh 2005.9.12 1 / 38 Diagonalization and Spectral Decomposition of a Matrix Optimization 2 / 38 Diagonalization and Spectral Decomposition of a Matrix Also called Eigenvalues
Math Camp Lecture 4: Linear Algebra. Xiao Yu Wang. Aug 2010 MIT. Xiao Yu Wang (MIT) Math Camp /10 1 / 88
 Math Camp 2010 Lecture 4: Linear Algebra Xiao Yu Wang MIT Aug 2010 Xiao Yu Wang (MIT) Math Camp 2010 08/10 1 / 88 Linear Algebra Game Plan Vector Spaces Linear Transformations and Matrices Determinant
Math Camp 2010 Lecture 4: Linear Algebra Xiao Yu Wang MIT Aug 2010 Xiao Yu Wang (MIT) Math Camp 2010 08/10 1 / 88 Linear Algebra Game Plan Vector Spaces Linear Transformations and Matrices Determinant
Eigenvalues and Eigenvectors
 November 3, 2016 1 Definition () The (complex) number λ is called an eigenvalue of the n n matrix A provided there exists a nonzero (complex) vector v such that Av = λv, in which case the vector v is called
November 3, 2016 1 Definition () The (complex) number λ is called an eigenvalue of the n n matrix A provided there exists a nonzero (complex) vector v such that Av = λv, in which case the vector v is called
Math 315: Linear Algebra Solutions to Assignment 7
 Math 5: Linear Algebra s to Assignment 7 # Find the eigenvalues of the following matrices. (a.) 4 0 0 0 (b.) 0 0 9 5 4. (a.) The characteristic polynomial det(λi A) = (λ )(λ )(λ ), so the eigenvalues are
Math 5: Linear Algebra s to Assignment 7 # Find the eigenvalues of the following matrices. (a.) 4 0 0 0 (b.) 0 0 9 5 4. (a.) The characteristic polynomial det(λi A) = (λ )(λ )(λ ), so the eigenvalues are
CS 143 Linear Algebra Review
 CS 143 Linear Algebra Review Stefan Roth September 29, 2003 Introductory Remarks This review does not aim at mathematical rigor very much, but instead at ease of understanding and conciseness. Please see
CS 143 Linear Algebra Review Stefan Roth September 29, 2003 Introductory Remarks This review does not aim at mathematical rigor very much, but instead at ease of understanding and conciseness. Please see
Math 240 Calculus III
 Generalized Calculus III Summer 2015, Session II Thursday, July 23, 2015 Agenda 1. 2. 3. 4. Motivation Defective matrices cannot be diagonalized because they do not possess enough eigenvectors to make
Generalized Calculus III Summer 2015, Session II Thursday, July 23, 2015 Agenda 1. 2. 3. 4. Motivation Defective matrices cannot be diagonalized because they do not possess enough eigenvectors to make
Here is an example of a block diagonal matrix with Jordan Blocks on the diagonal: J
 Class Notes 4: THE SPECTRAL RADIUS, NORM CONVERGENCE AND SOR. Math 639d Due Date: Feb. 7 (updated: February 5, 2018) In the first part of this week s reading, we will prove Theorem 2 of the previous class.
Class Notes 4: THE SPECTRAL RADIUS, NORM CONVERGENCE AND SOR. Math 639d Due Date: Feb. 7 (updated: February 5, 2018) In the first part of this week s reading, we will prove Theorem 2 of the previous class.
Computational Methods CMSC/AMSC/MAPL 460. Eigenvalues and Eigenvectors. Ramani Duraiswami, Dept. of Computer Science
 Computational Methods CMSC/AMSC/MAPL 460 Eigenvalues and Eigenvectors Ramani Duraiswami, Dept. of Computer Science Eigen Values of a Matrix Recap: A N N matrix A has an eigenvector x (non-zero) with corresponding
Computational Methods CMSC/AMSC/MAPL 460 Eigenvalues and Eigenvectors Ramani Duraiswami, Dept. of Computer Science Eigen Values of a Matrix Recap: A N N matrix A has an eigenvector x (non-zero) with corresponding
Lecture 1: Review of linear algebra
 Lecture 1: Review of linear algebra Linear functions and linearization Inverse matrix, least-squares and least-norm solutions Subspaces, basis, and dimension Change of basis and similarity transformations
Lecture 1: Review of linear algebra Linear functions and linearization Inverse matrix, least-squares and least-norm solutions Subspaces, basis, and dimension Change of basis and similarity transformations
MOORE-PENROSE INVERSE IN AN INDEFINITE INNER PRODUCT SPACE
 J. Appl. Math. & Computing Vol. 19(2005), No. 1-2, pp. 297-310 MOORE-PENROSE INVERSE IN AN INDEFINITE INNER PRODUCT SPACE K. KAMARAJ AND K. C. SIVAKUMAR Abstract. The concept of the Moore-Penrose inverse
J. Appl. Math. & Computing Vol. 19(2005), No. 1-2, pp. 297-310 MOORE-PENROSE INVERSE IN AN INDEFINITE INNER PRODUCT SPACE K. KAMARAJ AND K. C. SIVAKUMAR Abstract. The concept of the Moore-Penrose inverse
Linear System Theory
 Linear System Theory Wonhee Kim Lecture 4 Apr. 4, 2018 1 / 40 Recap Vector space, linear space, linear vector space Subspace Linearly independence and dependence Dimension, Basis, Change of Basis 2 / 40
Linear System Theory Wonhee Kim Lecture 4 Apr. 4, 2018 1 / 40 Recap Vector space, linear space, linear vector space Subspace Linearly independence and dependence Dimension, Basis, Change of Basis 2 / 40
Recall : Eigenvalues and Eigenvectors
 Recall : Eigenvalues and Eigenvectors Let A be an n n matrix. If a nonzero vector x in R n satisfies Ax λx for a scalar λ, then : The scalar λ is called an eigenvalue of A. The vector x is called an eigenvector
Recall : Eigenvalues and Eigenvectors Let A be an n n matrix. If a nonzero vector x in R n satisfies Ax λx for a scalar λ, then : The scalar λ is called an eigenvalue of A. The vector x is called an eigenvector
The Singular Value Decomposition
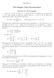 CHAPTER 6 The Singular Value Decomposition Exercise 67: SVD examples (a) For A =[, 4] T we find a matrixa T A =5,whichhastheeigenvalue =5 Thisprovidesuswiththesingularvalue =+ p =5forA Hence the matrix
CHAPTER 6 The Singular Value Decomposition Exercise 67: SVD examples (a) For A =[, 4] T we find a matrixa T A =5,whichhastheeigenvalue =5 Thisprovidesuswiththesingularvalue =+ p =5forA Hence the matrix
Eigenvalues, Eigenvectors. Eigenvalues and eigenvector will be fundamentally related to the nature of the solutions of state space systems.
 Chapter 3 Linear Algebra In this Chapter we provide a review of some basic concepts from Linear Algebra which will be required in order to compute solutions of LTI systems in state space form, discuss
Chapter 3 Linear Algebra In this Chapter we provide a review of some basic concepts from Linear Algebra which will be required in order to compute solutions of LTI systems in state space form, discuss
Diagonalization of Matrix
 of Matrix King Saud University August 29, 2018 of Matrix Table of contents 1 2 of Matrix Definition If A M n (R) and λ R. We say that λ is an eigenvalue of the matrix A if there is X R n \ {0} such that
of Matrix King Saud University August 29, 2018 of Matrix Table of contents 1 2 of Matrix Definition If A M n (R) and λ R. We say that λ is an eigenvalue of the matrix A if there is X R n \ {0} such that
EIGENVALUE PROBLEMS. Background on eigenvalues/ eigenvectors / decompositions. Perturbation analysis, condition numbers..
 EIGENVALUE PROBLEMS Background on eigenvalues/ eigenvectors / decompositions Perturbation analysis, condition numbers.. Power method The QR algorithm Practical QR algorithms: use of Hessenberg form and
EIGENVALUE PROBLEMS Background on eigenvalues/ eigenvectors / decompositions Perturbation analysis, condition numbers.. Power method The QR algorithm Practical QR algorithms: use of Hessenberg form and
Chapter 3 Transformations
 Chapter 3 Transformations An Introduction to Optimization Spring, 2014 Wei-Ta Chu 1 Linear Transformations A function is called a linear transformation if 1. for every and 2. for every If we fix the bases
Chapter 3 Transformations An Introduction to Optimization Spring, 2014 Wei-Ta Chu 1 Linear Transformations A function is called a linear transformation if 1. for every and 2. for every If we fix the bases
Introduction to Numerical Linear Algebra II
 Introduction to Numerical Linear Algebra II Petros Drineas These slides were prepared by Ilse Ipsen for the 2015 Gene Golub SIAM Summer School on RandNLA 1 / 49 Overview We will cover this material in
Introduction to Numerical Linear Algebra II Petros Drineas These slides were prepared by Ilse Ipsen for the 2015 Gene Golub SIAM Summer School on RandNLA 1 / 49 Overview We will cover this material in
Eigenvalue and Eigenvector Problems
 Eigenvalue and Eigenvector Problems An attempt to introduce eigenproblems Radu Trîmbiţaş Babeş-Bolyai University April 8, 2009 Radu Trîmbiţaş ( Babeş-Bolyai University) Eigenvalue and Eigenvector Problems
Eigenvalue and Eigenvector Problems An attempt to introduce eigenproblems Radu Trîmbiţaş Babeş-Bolyai University April 8, 2009 Radu Trîmbiţaş ( Babeş-Bolyai University) Eigenvalue and Eigenvector Problems
Lecture 10 - Eigenvalues problem
 Lecture 10 - Eigenvalues problem Department of Computer Science University of Houston February 28, 2008 1 Lecture 10 - Eigenvalues problem Introduction Eigenvalue problems form an important class of problems
Lecture 10 - Eigenvalues problem Department of Computer Science University of Houston February 28, 2008 1 Lecture 10 - Eigenvalues problem Introduction Eigenvalue problems form an important class of problems
Linear Algebra review Powers of a diagonalizable matrix Spectral decomposition
 Linear Algebra review Powers of a diagonalizable matrix Spectral decomposition Prof. Tesler Math 283 Fall 2016 Also see the separate version of this with Matlab and R commands. Prof. Tesler Diagonalizing
Linear Algebra review Powers of a diagonalizable matrix Spectral decomposition Prof. Tesler Math 283 Fall 2016 Also see the separate version of this with Matlab and R commands. Prof. Tesler Diagonalizing
UCSD ECE269 Handout #18 Prof. Young-Han Kim Monday, March 19, Final Examination (Total: 130 points)
 UCSD ECE269 Handout #8 Prof Young-Han Kim Monday, March 9, 208 Final Examination (Total: 30 points) There are 5 problems, each with multiple parts Your answer should be as clear and succinct as possible
UCSD ECE269 Handout #8 Prof Young-Han Kim Monday, March 9, 208 Final Examination (Total: 30 points) There are 5 problems, each with multiple parts Your answer should be as clear and succinct as possible
Knowledge Discovery and Data Mining 1 (VO) ( )
 Knowledge Discovery and Data Mining 1 (VO) (707.003) Review of Linear Algebra Denis Helic KTI, TU Graz Oct 9, 2014 Denis Helic (KTI, TU Graz) KDDM1 Oct 9, 2014 1 / 74 Big picture: KDDM Probability Theory
Knowledge Discovery and Data Mining 1 (VO) (707.003) Review of Linear Algebra Denis Helic KTI, TU Graz Oct 9, 2014 Denis Helic (KTI, TU Graz) KDDM1 Oct 9, 2014 1 / 74 Big picture: KDDM Probability Theory
(a) If A is a 3 by 4 matrix, what does this tell us about its nullspace? Solution: dim N(A) 1, since rank(a) 3. Ax =
 . (5 points) (a) If A is a 3 by 4 matrix, what does this tell us about its nullspace? dim N(A), since rank(a) 3. (b) If we also know that Ax = has no solution, what do we know about the rank of A? C(A)
. (5 points) (a) If A is a 3 by 4 matrix, what does this tell us about its nullspace? dim N(A), since rank(a) 3. (b) If we also know that Ax = has no solution, what do we know about the rank of A? C(A)
A Note on the Group Inverses of Block Matrices Over Rings
 Filomat 31:1 017, 3685 369 https://doiorg/1098/fil171685z Published by Faculty of Sciences and Mathematics, University of Niš, Serbia Available at: http://wwwpmfniacrs/filomat A Note on the Group Inverses
Filomat 31:1 017, 3685 369 https://doiorg/1098/fil171685z Published by Faculty of Sciences and Mathematics, University of Niš, Serbia Available at: http://wwwpmfniacrs/filomat A Note on the Group Inverses
Eigenvalues and Eigenvectors
 Chapter 1 Eigenvalues and Eigenvectors Among problems in numerical linear algebra, the determination of the eigenvalues and eigenvectors of matrices is second in importance only to the solution of linear
Chapter 1 Eigenvalues and Eigenvectors Among problems in numerical linear algebra, the determination of the eigenvalues and eigenvectors of matrices is second in importance only to the solution of linear
Jim Lambers MAT 610 Summer Session Lecture 1 Notes
 Jim Lambers MAT 60 Summer Session 2009-0 Lecture Notes Introduction This course is about numerical linear algebra, which is the study of the approximate solution of fundamental problems from linear algebra
Jim Lambers MAT 60 Summer Session 2009-0 Lecture Notes Introduction This course is about numerical linear algebra, which is the study of the approximate solution of fundamental problems from linear algebra
Linear Algebra Highlights
 Linear Algebra Highlights Chapter 1 A linear equation in n variables is of the form a 1 x 1 + a 2 x 2 + + a n x n. We can have m equations in n variables, a system of linear equations, which we want to
Linear Algebra Highlights Chapter 1 A linear equation in n variables is of the form a 1 x 1 + a 2 x 2 + + a n x n. We can have m equations in n variables, a system of linear equations, which we want to
New concepts: rank-nullity theorem Inverse matrix Gauss-Jordan algorithm to nd inverse
 Lesson 10: Rank-nullity theorem, General solution of Ax = b (A 2 R mm ) New concepts: rank-nullity theorem Inverse matrix Gauss-Jordan algorithm to nd inverse Matrix rank. matrix nullity Denition. The
Lesson 10: Rank-nullity theorem, General solution of Ax = b (A 2 R mm ) New concepts: rank-nullity theorem Inverse matrix Gauss-Jordan algorithm to nd inverse Matrix rank. matrix nullity Denition. The
Linear Algebra Formulas. Ben Lee
 Linear Algebra Formulas Ben Lee January 27, 2016 Definitions and Terms Diagonal: Diagonal of matrix A is a collection of entries A ij where i = j. Diagonal Matrix: A matrix (usually square), where entries
Linear Algebra Formulas Ben Lee January 27, 2016 Definitions and Terms Diagonal: Diagonal of matrix A is a collection of entries A ij where i = j. Diagonal Matrix: A matrix (usually square), where entries
1. Linear systems of equations. Chapters 7-8: Linear Algebra. Solution(s) of a linear system of equations (continued)
 1 A linear system of equations of the form Sections 75, 78 & 81 a 11 x 1 + a 12 x 2 + + a 1n x n = b 1 a 21 x 1 + a 22 x 2 + + a 2n x n = b 2 a m1 x 1 + a m2 x 2 + + a mn x n = b m can be written in matrix
1 A linear system of equations of the form Sections 75, 78 & 81 a 11 x 1 + a 12 x 2 + + a 1n x n = b 1 a 21 x 1 + a 22 x 2 + + a 2n x n = b 2 a m1 x 1 + a m2 x 2 + + a mn x n = b m can be written in matrix
This operation is - associative A + (B + C) = (A + B) + C; - commutative A + B = B + A; - has a neutral element O + A = A, here O is the null matrix
 1 Matrix Algebra Reading [SB] 81-85, pp 153-180 11 Matrix Operations 1 Addition a 11 a 12 a 1n a 21 a 22 a 2n a m1 a m2 a mn + b 11 b 12 b 1n b 21 b 22 b 2n b m1 b m2 b mn a 11 + b 11 a 12 + b 12 a 1n
1 Matrix Algebra Reading [SB] 81-85, pp 153-180 11 Matrix Operations 1 Addition a 11 a 12 a 1n a 21 a 22 a 2n a m1 a m2 a mn + b 11 b 12 b 1n b 21 b 22 b 2n b m1 b m2 b mn a 11 + b 11 a 12 + b 12 a 1n
CS 246 Review of Linear Algebra 01/17/19
 1 Linear algebra In this section we will discuss vectors and matrices. We denote the (i, j)th entry of a matrix A as A ij, and the ith entry of a vector as v i. 1.1 Vectors and vector operations A vector
1 Linear algebra In this section we will discuss vectors and matrices. We denote the (i, j)th entry of a matrix A as A ij, and the ith entry of a vector as v i. 1.1 Vectors and vector operations A vector
Online Exercises for Linear Algebra XM511
 This document lists the online exercises for XM511. The section ( ) numbers refer to the textbook. TYPE I are True/False. Lecture 02 ( 1.1) Online Exercises for Linear Algebra XM511 1) The matrix [3 2
This document lists the online exercises for XM511. The section ( ) numbers refer to the textbook. TYPE I are True/False. Lecture 02 ( 1.1) Online Exercises for Linear Algebra XM511 1) The matrix [3 2
Linear Algebra in Actuarial Science: Slides to the lecture
 Linear Algebra in Actuarial Science: Slides to the lecture Fall Semester 2010/2011 Linear Algebra is a Tool-Box Linear Equation Systems Discretization of differential equations: solving linear equations
Linear Algebra in Actuarial Science: Slides to the lecture Fall Semester 2010/2011 Linear Algebra is a Tool-Box Linear Equation Systems Discretization of differential equations: solving linear equations
Lecture notes: Applied linear algebra Part 1. Version 2
 Lecture notes: Applied linear algebra Part 1. Version 2 Michael Karow Berlin University of Technology karow@math.tu-berlin.de October 2, 2008 1 Notation, basic notions and facts 1.1 Subspaces, range and
Lecture notes: Applied linear algebra Part 1. Version 2 Michael Karow Berlin University of Technology karow@math.tu-berlin.de October 2, 2008 1 Notation, basic notions and facts 1.1 Subspaces, range and
arxiv: v1 [math.ra] 27 Jul 2013
![arxiv: v1 [math.ra] 27 Jul 2013 arxiv: v1 [math.ra] 27 Jul 2013](/thumbs/81/82700357.jpg) Additive and product properties of Drazin inverses of elements in a ring arxiv:1307.7229v1 [math.ra] 27 Jul 2013 Huihui Zhu, Jianlong Chen Abstract: We study the Drazin inverses of the sum and product
Additive and product properties of Drazin inverses of elements in a ring arxiv:1307.7229v1 [math.ra] 27 Jul 2013 Huihui Zhu, Jianlong Chen Abstract: We study the Drazin inverses of the sum and product
HOMEWORK PROBLEMS FROM STRANG S LINEAR ALGEBRA AND ITS APPLICATIONS (4TH EDITION)
 HOMEWORK PROBLEMS FROM STRANG S LINEAR ALGEBRA AND ITS APPLICATIONS (4TH EDITION) PROFESSOR STEVEN MILLER: BROWN UNIVERSITY: SPRING 2007 1. CHAPTER 1: MATRICES AND GAUSSIAN ELIMINATION Page 9, # 3: Describe
HOMEWORK PROBLEMS FROM STRANG S LINEAR ALGEBRA AND ITS APPLICATIONS (4TH EDITION) PROFESSOR STEVEN MILLER: BROWN UNIVERSITY: SPRING 2007 1. CHAPTER 1: MATRICES AND GAUSSIAN ELIMINATION Page 9, # 3: Describe
A Little Necessary Matrix Algebra for Doctoral Studies in Business & Economics. Matrix Algebra
 A Little Necessary Matrix Algebra for Doctoral Studies in Business & Economics James J. Cochran Department of Marketing & Analysis Louisiana Tech University Jcochran@cab.latech.edu Matrix Algebra Matrix
A Little Necessary Matrix Algebra for Doctoral Studies in Business & Economics James J. Cochran Department of Marketing & Analysis Louisiana Tech University Jcochran@cab.latech.edu Matrix Algebra Matrix
Massachusetts Institute of Technology Department of Economics Statistics. Lecture Notes on Matrix Algebra
 Massachusetts Institute of Technology Department of Economics 14.381 Statistics Guido Kuersteiner Lecture Notes on Matrix Algebra These lecture notes summarize some basic results on matrix algebra used
Massachusetts Institute of Technology Department of Economics 14.381 Statistics Guido Kuersteiner Lecture Notes on Matrix Algebra These lecture notes summarize some basic results on matrix algebra used
Section 3.3. Matrix Rank and the Inverse of a Full Rank Matrix
 3.3. Matrix Rank and the Inverse of a Full Rank Matrix 1 Section 3.3. Matrix Rank and the Inverse of a Full Rank Matrix Note. The lengthy section (21 pages in the text) gives a thorough study of the rank
3.3. Matrix Rank and the Inverse of a Full Rank Matrix 1 Section 3.3. Matrix Rank and the Inverse of a Full Rank Matrix Note. The lengthy section (21 pages in the text) gives a thorough study of the rank
City Suburbs. : population distribution after m years
 Section 5.3 Diagonalization of Matrices Definition Example: stochastic matrix To City Suburbs From City Suburbs.85.03 = A.15.97 City.15.85 Suburbs.97.03 probability matrix of a sample person s residence
Section 5.3 Diagonalization of Matrices Definition Example: stochastic matrix To City Suburbs From City Suburbs.85.03 = A.15.97 City.15.85 Suburbs.97.03 probability matrix of a sample person s residence
Practice Problems for the Final Exam
 Practice Problems for the Final Exam Linear Algebra. Matrix multiplication: (a) Problem 3 in Midterm One. (b) Problem 2 in Quiz. 2. Solve the linear system: (a) Problem 4 in Midterm One. (b) Problem in
Practice Problems for the Final Exam Linear Algebra. Matrix multiplication: (a) Problem 3 in Midterm One. (b) Problem 2 in Quiz. 2. Solve the linear system: (a) Problem 4 in Midterm One. (b) Problem in
CHAPTER 3. Matrix Eigenvalue Problems
 A SERIES OF CLASS NOTES FOR 2005-2006 TO INTRODUCE LINEAR AND NONLINEAR PROBLEMS TO ENGINEERS, SCIENTISTS, AND APPLIED MATHEMATICIANS DE CLASS NOTES 3 A COLLECTION OF HANDOUTS ON SYSTEMS OF ORDINARY DIFFERENTIAL
A SERIES OF CLASS NOTES FOR 2005-2006 TO INTRODUCE LINEAR AND NONLINEAR PROBLEMS TO ENGINEERS, SCIENTISTS, AND APPLIED MATHEMATICIANS DE CLASS NOTES 3 A COLLECTION OF HANDOUTS ON SYSTEMS OF ORDINARY DIFFERENTIAL
LINEAR ALGEBRA BOOT CAMP WEEK 2: LINEAR OPERATORS
 LINEAR ALGEBRA BOOT CAMP WEEK 2: LINEAR OPERATORS Unless otherwise stated, all vector spaces in this worksheet are finite dimensional and the scalar field F has characteristic zero. The following are facts
LINEAR ALGEBRA BOOT CAMP WEEK 2: LINEAR OPERATORS Unless otherwise stated, all vector spaces in this worksheet are finite dimensional and the scalar field F has characteristic zero. The following are facts
Linear Algebra. Matrices Operations. Consider, for example, a system of equations such as x + 2y z + 4w = 0, 3x 4y + 2z 6w = 0, x 3y 2z + w = 0.
 Matrices Operations Linear Algebra Consider, for example, a system of equations such as x + 2y z + 4w = 0, 3x 4y + 2z 6w = 0, x 3y 2z + w = 0 The rectangular array 1 2 1 4 3 4 2 6 1 3 2 1 in which the
Matrices Operations Linear Algebra Consider, for example, a system of equations such as x + 2y z + 4w = 0, 3x 4y + 2z 6w = 0, x 3y 2z + w = 0 The rectangular array 1 2 1 4 3 4 2 6 1 3 2 1 in which the
Glossary of Linear Algebra Terms. Prepared by Vince Zaccone For Campus Learning Assistance Services at UCSB
 Glossary of Linear Algebra Terms Basis (for a subspace) A linearly independent set of vectors that spans the space Basic Variable A variable in a linear system that corresponds to a pivot column in the
Glossary of Linear Algebra Terms Basis (for a subspace) A linearly independent set of vectors that spans the space Basic Variable A variable in a linear system that corresponds to a pivot column in the
ELA ON THE GROUP INVERSE OF LINEAR COMBINATIONS OF TWO GROUP INVERTIBLE MATRICES
 ON THE GROUP INVERSE OF LINEAR COMBINATIONS OF TWO GROUP INVERTIBLE MATRICES XIAOJI LIU, LINGLING WU, AND JULIO BENíTEZ Abstract. In this paper, some formulas are found for the group inverse of ap +bq,
ON THE GROUP INVERSE OF LINEAR COMBINATIONS OF TWO GROUP INVERTIBLE MATRICES XIAOJI LIU, LINGLING WU, AND JULIO BENíTEZ Abstract. In this paper, some formulas are found for the group inverse of ap +bq,
Chapter 5. Linear Algebra. A linear (algebraic) equation in. unknowns, x 1, x 2,..., x n, is. an equation of the form
 Chapter 5. Linear Algebra A linear (algebraic) equation in n unknowns, x 1, x 2,..., x n, is an equation of the form a 1 x 1 + a 2 x 2 + + a n x n = b where a 1, a 2,..., a n and b are real numbers. 1
Chapter 5. Linear Algebra A linear (algebraic) equation in n unknowns, x 1, x 2,..., x n, is an equation of the form a 1 x 1 + a 2 x 2 + + a n x n = b where a 1, a 2,..., a n and b are real numbers. 1
Eigenvalues and Eigenvectors
 Contents Eigenvalues and Eigenvectors. Basic Concepts. Applications of Eigenvalues and Eigenvectors 8.3 Repeated Eigenvalues and Symmetric Matrices 3.4 Numerical Determination of Eigenvalues and Eigenvectors
Contents Eigenvalues and Eigenvectors. Basic Concepts. Applications of Eigenvalues and Eigenvectors 8.3 Repeated Eigenvalues and Symmetric Matrices 3.4 Numerical Determination of Eigenvalues and Eigenvectors
The matrix will only be consistent if the last entry of row three is 0, meaning 2b 3 + b 2 b 1 = 0.
 ) Find all solutions of the linear system. Express the answer in vector form. x + 2x + x + x 5 = 2 2x 2 + 2x + 2x + x 5 = 8 x + 2x + x + 9x 5 = 2 2 Solution: Reduce the augmented matrix [ 2 2 2 8 ] to
) Find all solutions of the linear system. Express the answer in vector form. x + 2x + x + x 5 = 2 2x 2 + 2x + 2x + x 5 = 8 x + 2x + x + 9x 5 = 2 2 Solution: Reduce the augmented matrix [ 2 2 2 8 ] to
Math 489AB Exercises for Chapter 2 Fall Section 2.3
 Math 489AB Exercises for Chapter 2 Fall 2008 Section 2.3 2.3.3. Let A M n (R). Then the eigenvalues of A are the roots of the characteristic polynomial p A (t). Since A is real, p A (t) is a polynomial
Math 489AB Exercises for Chapter 2 Fall 2008 Section 2.3 2.3.3. Let A M n (R). Then the eigenvalues of A are the roots of the characteristic polynomial p A (t). Since A is real, p A (t) is a polynomial
Displacement rank of the Drazin inverse
 Available online at www.sciencedirect.com Journal of Computational and Applied Mathematics 167 (2004) 147 161 www.elsevier.com/locate/cam Displacement rank of the Drazin inverse Huaian Diao a, Yimin Wei
Available online at www.sciencedirect.com Journal of Computational and Applied Mathematics 167 (2004) 147 161 www.elsevier.com/locate/cam Displacement rank of the Drazin inverse Huaian Diao a, Yimin Wei
MAT Linear Algebra Collection of sample exams
 MAT 342 - Linear Algebra Collection of sample exams A-x. (0 pts Give the precise definition of the row echelon form. 2. ( 0 pts After performing row reductions on the augmented matrix for a certain system
MAT 342 - Linear Algebra Collection of sample exams A-x. (0 pts Give the precise definition of the row echelon form. 2. ( 0 pts After performing row reductions on the augmented matrix for a certain system
Final Review Written by Victoria Kala SH 6432u Office Hours R 12:30 1:30pm Last Updated 11/30/2015
 Final Review Written by Victoria Kala vtkala@mathucsbedu SH 6432u Office Hours R 12:30 1:30pm Last Updated 11/30/2015 Summary This review contains notes on sections 44 47, 51 53, 61, 62, 65 For your final,
Final Review Written by Victoria Kala vtkala@mathucsbedu SH 6432u Office Hours R 12:30 1:30pm Last Updated 11/30/2015 Summary This review contains notes on sections 44 47, 51 53, 61, 62, 65 For your final,
