On a Generalization of the Master Cyclic Group Polyhedron
|
|
|
- Garry Perry
- 6 years ago
- Views:
Transcription
1 O a Geeralizatio of the Master Cyclic Group Polyhedro Sajeeb Dash IBM Research Ricardo Fukasawa Georgia Ist. Tech. October 21, 2008 Oktay Guluk IBM Research Abstract We study the Master Equality Polyhedro (MEP) which geeralizes the Master Cyclic Group Polyhedro ad the Master Kapsack Polyhedro. We preset a explicit characterizatio of the polar of the otrivial facet-deig iequalities for MEP. This result geeralizes similar results for the Master Cyclic Group Polyhedro by Gomory [10] ad for the Master Kapsack Polyhedro by Araoz [1]. Furthermore, this characterizatio gives a polyomial time algorithm for separatig a arbitrary poit from MEP. We describe how facet-deig iequalities for the Master Cyclic Group Polyhedro ca be lifted to obtai facet-deig iequalities for MEP, ad also preset facet-deig iequalities for MEP that caot be obtaied i such a way. Fially, we study the mixed-iteger extesio of MEP ad preset a iterpolatio theorem that produces valid iequalities for geeral mixed iteger programmig problems usig facets of MEP. 1 Itroductio We study the Master Equality Polyhedro (MEP), which we dee as: ( K(; r) = cov (x; y) 2 Z + Z + : X ix i X iy i = r ) (1) where ; r 2 Z ad > 0. Without loss of geerality we assume that r 0. To the best of our kowledge, K(; r) was rst itroduced by Uchoa [17] i a slightly dieret form. Its polyhedral structure was however ot studied i that paper. Two well-kow families of polyhedra are lower dimesioal faces of MEP: the Master Cyclic Group Polyhedro (MCGP), which is deed as P (; r) = cov ( (x; y) 2 Z 1 + Z + : X1 ix i y = r ) ; (2) where r; 2 Z, ad > r > 0; ad the Master Kapsack Polyhedro (MKP), which is deed as K(r) = cov ( x 2 Z r + : 1 rx ix i = r ) ; (3)
2 where r 2 Z ad r > 0. Facets of P (; r) ca be used to obtai cuttig plaes for geeral MIPs. For example, the Gomory mixed-iteger cut (also kow as the mixed-iteger roudig (MIR) iequality) ca be derived from a facet of P (; r) [11]. See [2, 5, 6, 7, 8, 9, 12, 13, 14] for work o properties ad facets of the Master Cyclic Group Polyhedro. I particular, see [2] for the relatioship betwee facet-deig iequalities of MCGP ad facet-deig iequalities of MKP. The Master Cyclic Group Polyhedro is usually preseted as P 0 (; r) = cov ( x 2 Z 1 + : X1 ix i r mod which is the projectio of P (; r) i the space of x variables. We use (2) as it makes the compariso to K(; r) simpler. Gomory [10] ad Araoz [1] give a explicit characterizatio of the polar of the otrivial facets of MCGP ad MKP. I this paper, we give a similar descriptio of the otrivial facets of MEP for r 0. Usig this result, we obtai a polyomial time algorithm to separate over MEP for all r 0 (icludig r > ). We also aalyze some structural properties of MEP ad relate it to MCGP. For > r > 0, it is easy to obtai valid (facet-deig) iequalities for MEP usig valid (facet-deig) iequalities for MCGP. Notice that X ix i X iy i = r () X1 i(x i + y i ) ( X ) y i x ) = r: (4) Furthermore, P y i x 0 for all (x; y) 2 K(; r). Therefore, ay valid iequality P 1 ix i + y for P (; r) leads to a valid iequality X1 X 1 i x i + ( i + )y i + y x for K(; r). I fact, as MCGP is a lower dimesioal face of MEP, ay facet-deig iequality for MCGP ca lead to oe or more facet-deig iequalities (icludig the iequality preseted above) for MEP via liftig. We study lifted iequalities from MCGP ad show that ot all facets of MEP ca be obtaied i this way. I additio, we describe how to obtai valid iequalities for geeral MIPs usig facet-deig iequalities for MEP. Aother motivatio to study MEP is that it also arises as a atural structure i a reformulatio of the Fixed-Charge Network Flow problem. Such reformulatio gives rise to the followig polyhedro, almost idetical to MEP: cov ( y 2 Z C + ; z 2 ZC 1 + : CX d=1 C X1 dy d d=1 dz d = d(s) I [18], simple rouded Chvatal-Gomory cuts for the above polyhedro were used to reduce the itegrality gap o istaces of the Capacitated Miimum Spaig Tree Problem by more tha 2 ) :
3 50% o average. Therefore, the study of MEP will allow the derivatio of strog iequalities for this ad other related problems such as the Capacitated Vehicle Routig Problem. I the ext sectio, we preset a characterizatio of the polar of the otrivial facets of K(; r), for ay > 0 ad ay r satisfyig 0 < r. I Sectio 3 we discuss how to lift facets of P (; r) to obtai facets of K(; r) ad i Sectio 4, we show that ot all facets of K(; r) ca be obtaied by liftig. I Sectio 5, we study K(; r) whe r = 0. I Sectio 6, we describe how to separate a arbitrary poit from K(; r) for ay r, icludig the case r >. Sectio 7 is dedicated to extedig the results of K(; r) to the mixed-iteger case. I Sectio 8, we follow the approach of Gomory ad Johso [11] to derive valid iequalities for mixed-iteger programs from facets of K(; r) via iterpolatio. We coclude i Sectio 9 with some remarks o directios for further research o K(; r). 2 Polyhedral aalysis of K(; r) whe 0 < r Throughout this sectio, we assume 0 < r. The case r = 0 is studied i Sectio 5. We start with some otatio ad some basic polyhedral properties of K(; r). Let e i 2 R 2 be the uit vector with a oe i the compoet correspodig to x i ad let f i 2 R 2 be the uit vector with a oe i the compoet correspodig to y i, for i = 1; : : : ;. Lemma 2.1 dim(k(; r)) = 2 1. Proof. P P Clearly dim(k(; r)) 2 1 as all poits i K(; r) satisfy ix i iy i = r. Let U be the set of 2 poits p 1 = re 1, p i = re 1 + e i + if 1 for i = 2; : : : ;, ad q i = (r + i)e 1 + f i for i = 1; : : : ;. The vectors of U are aely idepedet, as fu p 1 : u 2 U; u 6= p 1 g is a set of liearly idepedet vectors. As U K(; r), dim(k(; r)) 2 1. Lemma 2.2 The oegativity costraits of K(; r) are facet-deig if 2. Proof. Let U be deed as i the proof of Lemma 2.1. For ay i 6= 1, the vectors i U fp i g ad U fq i g are aely idepedet, ad satisfy x i = 0 ad y i = 0, respectively. Therefore x i 0 ad y i 0 dee facets of K(; r) for i 2. To see that y 1 0 is facet-deig, replace p i (2 i ) i U by p 0 i = re 1 + e i + if to obtai a set of aely idepedet vectors U 0 K(; r). All poits i U 0 other tha q 1 satisfy y 1 = 0. Fially, let V be the set of poits t 0 = e + ( r)f 1, t i = t 0 + ie + f i for i = 1; : : : ;, ad s i = t 0 + e i + if 1 for i = 2; : : : ; K(; r), ad its elemets are aely idepedet vectors as fv liearly idepedet vectors. The poits i V also satisfy x 1 = V is cotaied i t 0 : v 2 V; v 6= t 0 g is a set of Clearly, K(; r) is a ubouded polyhedro. We ext characterize all the extreme rays (oedimesioal faces of the recessio coe) of K(; r). We represet a extreme ray fu + v : u; v 2 R 2 + ; 0g of K(; r) simply by the vector v. Let r ij = je i + if j for ay i; j 2 f1; : : : ; g. Lemma 2.3 The set of extreme rays of K(; r) is give by R = fr ij : 1 i; j g. 3
4 Proof. P P Let (c; d) be a extreme ray of K(; r), that is, ic i j=1 jd j = 0. Sice (c; d) is a oe-dimesioal face of the recessio coe, at least 2 2 of the oegativity costraits hold as equality. As (c; d) ca ot have a sigle ozero compoet, P it must have exactly two ozero P compoets. Thus, (c; d) is of the form e i + f j ad sice ic i j=1 jd j = 0, we have that i j = 0 ) = j. Sice (c; d) is a ray, we may scale it so that = i, ad we have show that i R cotais all extreme rays of K(; r). To complete the proof, assume that oe of the rays i R is ot extreme. The it must be a coic combiatio of 2 or more (extreme) rays i R. As coic combiatio of the rays i R have at least 3 ozero etries, we have a cotradictio. As K(; r) is ot a full-dimesioal polyhedro, ay valid iequality x + y o for K(; r) has a equivalet represetatio with = 0. If a valid P iequality does ot satisfy this coditio, P oe ca add a appropriate multiple of the equatio ix i iy i = r to it. We state this formally i Observatio 2.4, ad subsequetly assume all valid iequalities have = 0. This is oe of may possible choices of ormalizatio ad it was chose to make the relatio to facets of P (; r) easier, sice Gomory's characterizatio also satises that property. Observatio 2.4 If x + y o dees a valid iequality for K(; r), we may assume = 0. We classify the facets of K(; r) as trivial ad otrivial facets. Deitio 2.5 The followig facet-deig iequalities of K(; r) are called trivial: x i 0; 8i = 1; : : : ; ; (5) All other facet-deig iequalities of K(; r) are called otrivial. y i 0; 8i = 1; : : : ; 1: (6) Accordig to this deitio, the iequality y 0 dees a otrivial facet. There is othig special about the y 0 iequality except that it is the oly oegativity costrait that does ot comply directly with the = 0 assumptio. With this distictio betwee y 0 ad the other trivial facets, our results are easier to state ad prove. 2.1 Characterizatio of the otrivial facets Let N = f1; : : : ; g. We ext state our mai result, the proof of which requires several prelimiary results which will be preseted later i this sectio. Theorem 2.6 Cosider a iequality x + y o with = 0. It dees a otrivial facet of K(; r) if ad oly if the followig coditios hold: (i) o > 0, ad, (ii) (; ; o )= o is a extreme 4
5 poit of T R 2+1 where T is deed by the followig liear equatios ad iequalities: i + j i j ; 8i; j 2 N; i > j; (SA1) i + j i+j ; 8i; j 2 N; i + j ; (SA2) k + i + j i+j k ; 8i; j; k 2 N; 1 i + j k ; (SA3) i + r i = o ; 8i 2 N; i < r; (EP1) r = o ; (EP2) i + i r = o ; 8i 2 N i > r; (EP3) = 0; o = 1: (NC1) (NC2) We ote that = 0 is ot a restrictive assumptio i the above theorem as ay valid iequality has a equivalet represetatio with = 0. We call costraits (SA1)-(SA3) relaxed subadditivity coditios as they are implied by the rst four of the followig pairwise subadditivity coditios: i + i 0; 8i 2 N; (SA0) i + j i j ; 8i; j 2 N; i > j; (SA1) i + j j i ; 8i; j 2 N; i < j; (SA1') i + j i+j ; 8i; j 2 N; i + j ; (SA2) i + j i+j ; 8i; j 2 N; i + j < : (SA2') i + j i+j ; 8i; j 2 N; i + j = : (SA2") We distiguish the cases i (SA2') ad (SA2") as (SA2") is ot satised by the oegativity costrait o y ad we will eed this distictio to establish certai structural properties later o. Lemma 2.7 Let (; ) 2 R 2 satisfy the pairwise subadditivity coditios (SA0), (SA1), (SA1'), ad (SA2), the (; ) satises (SA3) as well. Proof. Let i; j; k 2 N be such that 1 i + j k ad without loss of geerality assume that i j. If i + j, the usig (SA2) ad (SA1) we have k + i + j k + i+j i+j k : If, o the other had, i + j >, we cosider three cases: Case 1: k < j. Usig (SA1) ad (SA2), we have: k + i + j j k + i i+j k : Case 2: k > i. Usig (SA1') ad (SA1), we have: k + i + j k i + j i+j k : Case 3: k = i = j. Usig (SA0), we have: k + k 0 () k + k + k k : As we show later, ay otrivial facet-deig iequality x + y o for K(; r) satises (SA1)-(SA3) as well as (SA0), (SA1') ad (SA2'). Based o Gomory's characterizatio of MCGP usig pairwise subadditivity coditio, it would seem more atural to characterize the otrivial 5
6 facets usig the pairwise subadditivity coditios above istead of the relaxed subadditivity coditios. We show i Sectio 2.4 that Theorem 2.6 does ot hold if (SA3) is replaced with (SA0), (SA1') ad (SA2'). The equatios (EP1)-(EP3) essetially state that the followig poits, which we call the elemetary poits of K(; r), fe i + e r i : 1 i < rg [ e r [ fe i + f i r ; : r < i g r 1 2 aely idepedet lie o every otrivial facet of K(; r). I other words, K(; r) has a face of dimesio at least r where all otrivial facets itersect. The last two costraits (NC1) ad (NC2) are ormalizatio costraits that are ecessary to have a uique represetatio of otrivial facets. Note that the deitio of T i Theorem 2.6 is similar to that of a polar. However, T is ot the polar of K(; r), as it does ot cotai extreme poits of the polar that correspod to the trivial iequalities. It is possible to iterpret T as a importat subset of the polar that cotais all extreme poits of the polar besides the oes that lead to the trivial iequalities. I the rest of this sectio we develop the required aalysis to prove Theorem Basic properties of T We start with a basic observatio which states that ay valid iequality for K(; r) has to be valid for its extreme rays ad elemetary poits. Observatio 2.8 Let x + y o be a valid iequality for K(; r), the the followig holds: j i + i j 0; 8i; j 2 N (R1) i + r i o ; 8i 2 N; i < r; (P1) r o ; (P2) i + i r o ; 8i 2 N; i > r: (P3) We ext show that otrivial facet-deig iequalities satisfy the relaxed subadditivity coditios ad they are tight at the elemetary poits of K(; r). Lemma 2.9 Let x + y o be a otrivial facet-deig iequality of K(; r), the it satises (SA1)-(SA3) as well as (SA0), (SA1'), (SA2') ad (EP1)-(EP3). Proof. Due to Observatio 2.8, i i + i i 0 for all i 2 N ad therefore (SA0) holds. Next, let (x ; y ) 2 K(; r) be such that x + y = o ad x i j > 0. Such a poit exists because the facet-deig iequality we cosider is otrivial. The (x ; y ) + (e i + f j e i j ) is also cotaied i K(; r). Therefore, (SA1) holds. Proofs for (SA2), (SA3), (SA1') ad (SA2') are aalogous. 6
7 Fially, let (x 0 ; y 0 ) ad (x 00 ; y 00 ) be itegral poits i K(; r) lyig o the facet deed by x + y o such that x 0 i Therefore > 0 ad x00 r i > 0. The (x; y) = (x0 ; y 0 ) + (x 00 ; y 00 ) e i e r i 2 K(; r). x + y = x 0 + y 0 + x 00 + y 00 i r i = 2 o i r i o : The last iequality above implies that i + r (EP2) ad (EP3) are aalogous. i o ad therefore (P1) ) (EP1). The proofs of Observatio 2.10 If x + y o is a facet-deig iequality of K(; r) which is ot a oegativity costrait, the it also satises (SA2"). We ext show that the ormalizatio coditio (NC2) does ot elimiate ay otrivial facets. Lemma 2.11 Let x + y o be a otrivial facet-deig iequality of K(; r), that satises = 0. The o > 0. Proof. By (R1), we have, for all i 2 N, i + i 0 ad therefore i 0 sice = 0. Also by (EP2), we have o = r which implies that o 0. that Assume o = 0. As 0, usig (EP1) we have i = 0 for i = 1; : : : ; r. But the, (SA2) implies 0 + i 1 i 0; for i = 2; : : : ; : Startig with i = r + 1, we ca iductively show that i = 0 for all i 2 N. This also implies that k = 0 for 1 k r by (EP3). I additio k 0 for r + 1 k by (SA3). Therefore, if o = 0, the = 0, 0 ad therefore x + y 0 ca be writte as a coic combiatio of the oegativity facets, which is a cotradictio. Thus o > 0. Combiig Lemmas 2.9 ad 2.11 we have therefore established the followig. Corollary 2.12 Let x + y o be a otrivial facet-deig iequality of K(; r), that satises = 0. The 1 o (; ; o ) 2 T: I the followig result, we show that a subset of the coditios preseted i Theorem 2.6 suces to esure validity of a iequality for K(; r). Lemma 2.13 Let (; ; o ) satisfy (SA1), (SA2), (SA3) ad (EP2). The x + y o dees a valid iequality for K(; r). Proof. We will prove this by cotradictio. Assume that x + y o satises (EP2), (SA1), (SA2) ad (SA3) but x + y o does ot dee a valid iequality for K(; r), r > 0. Let (x ; y ) be a iteger poit i K(; r) that has miimum L 1 orm amog all poits violated by x + y o. Clearly, (x ; y ) 6= 0 ad therefore jj(x ; y )jj 1 > 0. If jj(x ; y )jj 1 = 1, the x = e r ad y = 0, ad as r = o, (x ; y ) does ot violate the iequality yieldig a cotradictio. Therefore jj(x ; y )jj 1 2. We ext cosider three cases. 7
8 Case 1: Assume that y = 0. The P ix i o > X i x i X = r. By successively applyig (SA2), we obtai ix i P ix i = r which cotradicts (EP2). Case 2: Assume that there exists i > j such that x i > 0 ad y j > 0. Let (x 0 ; y 0 ) = (x ; y ) + (e i j e i f j ). Clearly, (x 0 ; y 0 ) 2 K(; r), ad jj(x 0 ; y 0 )jj 1 = jj(x ; y )jj 1 1. Moreover, as x + y o satises (SA1), x 0 + y 0 = x + y + i j i j x + y < o, which cotradicts the choice of (x ; y ) as a solutio with miimum support. Case 3: Assume that for ay i; k 2 N, x i > 0 ad y k > 0 imply that i k. Let i 2 N be such that x i > 0, the either there exists aother idex j 6= i such that x j > 0, or, x i 2 (i which case, let j = i). If i + j, let (x 0 ; y 0 ) = (x ; y ) + (e i+j e i e j ). If i + j >, as y 6= 0, there exists k such that y k > 0 ad k i, ad therefore 1 i + j k. The let (x0 ; y 0 ) = (x ; y ) + (e i+j k e i e j f k ). I either case, (x 0 ; y 0 ) 2 K(; r) ad jj(x 0 ; y 0 )jj 1 < jj(x ; y )jj 1. Moreover, as (; ; o ) satisfy (SA2) ad (SA3), i either case x 0 + y 0 x + y < o, which cotradicts the choice of (x ; y ). Corollary 2.14 Let (; ; o ) 2 T, the x + y o is a valid iequality for K(; r). Note that by Lemma 2.7 a iequality satisfyig pairwise subadditivity coditios ad (EP2) is valid for K(; r). We ext determie the extreme rays of T. Lemma 2.15 The extreme rays of T are (f k ; 0) 2 R 2+1 for r < k <. Proof. First ote that (f k ; 0) is ideed a extreme ray of T for r < k <. Let (; ; o ) be a extreme ray of T that is ot equivalet to (f k ; 0) for some r < k <. Clearly o = 0. I this case, x+y 0 is a valid iequality for K(; r). Usig the same argumets preseted i the proof of Lemma 2.11, it is straightforward to establish that i = 0 for all i 2 N, k = 0 for 1 k r ad k 0 for r + 1 k. But the, (; ; o ) ca be writte as a coic combiatio of the rays (f k ; 0) for r < k <, a cotradictio. 2.3 Facet characterizatio Let F = o M ( k ; k ; k o ) k=1 be the set of coeciets of otrivial facets of K(; r) with = 0 ad o = 1. Note that by Lemma 2.11 these two assumptios do ot elimiate otrivial facets. Also, as y 0 is a otrivial facet, F 6= ;. By Lemma 2.9, F T. We ow proceed to prove Theorem 2.6 i two steps. Lemma 2.16 If (; ; o ) 2 F, the (; ; o ) is a extreme poit of T. 8
9 Proof. Assume that (; ; o ) 2 F but is ot a extreme poit of T. It ca be writte as a covex combiatio of two distict poits i T. The ormalizatio coditios = 0 ad o = 1 imply that ay two distict poits i T represet two distict valid iequalities for K(; r) i the sese that either P iequality ca be obtaied from the other by scalig or by addig multiples of the P equatio ix i iy i = r. Therefore x + y o ca be writte as a combiatio of two distict valid iequalities for K(; r), ad therefore does ot dee a facet of K(; r). Lemma 2.17 If (; ; o ) is a extreme poit of T, the (; ; o ) 2 F. Proof. Let (^; ^; 1) be a extreme poit of T. By Lemma 2.13, (^; ^; 1) dees a valid iequality for K(; r) ad therefore it ca P be obtaied as a coic combiatio of facet-deig iequalities P plus a multiple of the equatio ix i iy i = r. I other words, there exists multipliers 2 R M + ad 2 R such that ^ i ^ i ^ = 1 MX k=1 MX k=1 MX k=1 MX k=1 k k i + i; 8 i 2 N (7) k k i i; 8 i 2 N fg (8) k k ; (9) k + r (10) hold. The iequalities i (7) follow from the fact that ^ i = P M k=1 k k i + i + ie i, where i 0, for i = 1; : : : ;. The term i e i correspods to addig i times the trivial facet-deig iequality x i 0. The iequalities i (8) ca be derived i a similar maer, from the fact that y i 0 for i = 1; : : : ; 1 are trivial facet-deig iequalities. The equality i (9) is due to the fact that y 0 is cosidered to be otrivial. As ^ = 0 ad k = 0 for all otrivial facet-deig iequalities, (9) implies that = 0. Furthermore, ^ r = 1 ad k r = 1, for all k, ad combiig (8) ad (10) we ca coclude that P M k=1 k = 1. For ay i < r, iequality (7) for i ad r i combied with the equatio (EP1) implies that 1 = ^ i + ^ r i MX k ( k i + k r i) = 1 which ca hold oly if ^ i = P M k k i for all i < r. Similarly, for i > r, we use the equatio (EP3) to observe that 1 = ^ i + ^ i r MX 9 k ( k i + k i r) = 1
10 P P M ad therefore ^ i = ki k M ad ^ i r = k k i r for all i > r,. P M Fially as ^ i k k i for i > r, we ca write (^; ^; 1) as a covex combiatio of poits of F plus a coic combiatio of extreme rays of T. This ca oly be possible if (^; ^; 1) 2 F. Thus, (^; ^; 1) is a otrivial facet. As a al remark, it is iterestig to ote that coditios (R1) do ot appear i the descriptio of T eve though they are ecessary for ay valid iequality. This is because coditios (R1) are implied by (SA1), (SA2) ad (SA3). The proof is aalogous to the proof of Lemma 2.13, so we just state it as a observatio. Observatio 2.18 Let (; ; o ) 2 T. The j i + i j 0; 8i; j 2 N. We ext show that coeciets of facet-deig iequalities are bouded by small umbers. Lemma 2.19 Let (; ; o ) be a extreme poit of T, the for all k 2 N. 0 k dk=re ad dk=re k d=re Proof. Usig Observatio 2.18 with j = ad the fact that = 0, we have 0. For k < r, combiig iequality (EP1) k + r k 1 with 0 gives k 1 = dk=re. For k > r, let k = bk=rc r + q, where 0 q < r. If q = 0, by (SA2) we have k bk=rc r = dk=re sice k is iteger. Similarly, if r q > 0 we have k bk=rc r + q = bk=rc + q, where q 1. Therefore, 0 k dk=re. The iequality (SA3) with i = 1 ad j = k implies that k k ad therefore k dk=re for all k 2 N. If k r, (EP3) implies that k = r k+r 1 d=re. If k > r, the as (; ; o ) is a extreme poit of T, at least oe of (SA1) ad (SA3) must hold with equality, i which case, k i, for some i 2 N. Thus k d=re. 2.4 Pairwise subadditivity coditios Next we give a example that demostrates that usig pairwise subadditivity coditios istead of the relaxed subadditivity coditios i the descriptio of the coeciet polyhedro T leads to extreme poits that do ot give facet-deig iequalities for K(; r). To geerate this example, we used PORTA [4]. Example 2.20 Cosider K(3; 2) ad deote a extreme poit of T as p = ( 1 ; 2 ; 3 ; 1 ; 2 ; 3 ). We do ot iclude o i the descriptio of p sice o = 1 for all poits i T. It ca be checked that T has the followig two extreme poits: p 1 = (1=2; 1; 0; 1; 1=2; 0) ad p 2 = (1=2; 1; 3=2; 1=2; 1; 0). Poit p 2 correspods to the oegativity costrait for y. Let T 0 be a restrictio of T obtaied by replacig (SA3) with the missig pairwise subadditivity coditios (SA0) ad (SA1'). It ca be checked that i additio to p 1 ad p 2, the set T 0 has the followig extreme poit: p 3 = (1=2; 1; 3=2; 1=2; 1=2; 0). 10
11 Note that p 2 p 3 ad p 2 6= p 3. Therefore p T 3 (x; y) 1 is strictly implied by pt 2 (x; y) 1. Therefore T 0 ideed has extreme poits that do ot correspod to facets of K(3; 2). Oe could thik that by usig (SA2') ad/or (SA2") it might be possible to obtai a characterizatio of either otrivial facets or all facets except oegativity costraits. However this is ot the case, as usig (SA2') ad/or (SA2") i additio to (SA0) ad (SA1'), we obtai couterexamples similar to the oe preseted above. 3 Liftig facets of P (; r) whe > r > 0 Liftig is a geeral priciple for costructig valid (facet-deig) iequalities for higher dimesioal sets usig valid (facet-deig) iequalities for lower dimesioal sets. Startig with the early work of Gomory [10], the liftig approach was geeralized by Wolsey [19], Balas ad Zemel [3] ad Gu et. al [15], amog others. For ay > r > 0, P (; r) is a 1 dimesioal face of K(; r) obtaied by settig variables to their lower bouds. Therefore, ay facet-deig iequality for P (; r) X1 i x i 1 (11) ca be lifted to obtai oe or more facet-deig iequalities of the form X1 X 1 i x i + 0 x + 0 i y i 1 (12) for K(; r). We call iequality (12) a lifted iequality. I this sectio we study properties of the lifted iequality (12) whe the iitial iequality (11) dees a facet of P (; r). The purpose of this study is to uderstad whe ad how facets of K(; r) ca be obtaied by liftig facets of P (; r). This will allow us to obtai ew facet-deig iequalities for K(; r) from kow facet-deig iequalities for P (; r) ad also to aswer a very atural questio: Ca all facets of K(; r) be obtaied by liftig facets of P (; r)? We aswer this questio i the followig sectio ad show that K(; r) ideed has facets that ca ot be obtaied via liftig. Note that we oly eed to focus o liftig otrivial facet-deig iequalities of P (; r). Accordig to our deitio, ay trivial facet-deig iequality of P (; r) has the form x i 0. Let x i + x + P 1 j=1 jy j 0 be a lifted facet-deig iequality for K(; r). As k = 0 for some k 6= i, the iequality (R1) of Observatio 2.8 implies that 0. I additio, as = 0, we ca also coclude that 0. Therefore, a (trivial) facet of P (; r) deed by a oegativity iequality ca oly yield a coic combiatio of oegativity iequalities for K(; r) whe lifted. 3.1 The restricted coeciet polyhedro T We start with a result of Gomory [10] that gives a complete characterizatio of the otrivial facets (i.e., excludig the oegativity iequalities) of P (; r). I this descriptio facet-deig iequalities are ormalized so that y has a coeciet of zero ad the right-had side is 1. 11
12 Theorem 3.1 (Gomory [10]) The iequality x 1 dees a otrivial facet of P (; r), for > r > 0, if ad oly if 2 R Q = 8 >< >: 1 is a extreme poit of i + j (i+j) mod 8i; j 2 f1; : : : ; 1g; i + j = r 8i; j such that r = (i + j) mod ; j 0 8j 2 f1; : : : ; 1g; r = 1: Clearly otrivial facets of P (; r) would give otrivial facets of K(; r) whe lifted. Usig Gomory's characterizatio above, the liftig of otrivial facets of P (; r) ca be see as a way of extedig a extreme poit of Q to obtai a extreme poit (; 0 ; 0 ; 0) of T. Let p = (; 0 ; 0 ; 0) be a extreme poit of T. The, p also has to be a extreme poit of the lower dimesioal polyhedro T = T \ Let L = f r + 1; : : : ; 1g. o i = i ; 8i 2 f1; : : : ; 1g : Lemma 3.2 If (11) dees a otrivial facet of P (; r), the T 6= ; ad has the form T = 8 >< >: 0 k l k 8 k 2 L k + t k 8 k 2 L k f k 8 k 2 L + r = 1 = 0 k = k 8k 2 f1; : : : ; r 1g i = i 8i 2 f1; : : : ; 1g where umbers l k ; t k ; f k ad ca be computed easily usig. Proof. First ote that 2 Q ad therefore satises iequality (SA2) as well as equatios (EP1) ad (EP2). I additio, as i + j = 1 for all i; j such that r = (i + j) mod, equality (EP3) ca be rewritte as i = i for all 1 i r. Further, as is subadditive (i the modular sese), iequalities (SA1) ad (SA3) are satised for all k 2 f1; : : : ; r 1g. Therefore, settig = 0 ad k = 8 < : k if k 2 f1; : : : ; r 1g; 1 otherwise; produces a feasible poit for T, establishig that the set is ot empty. We ext show that T has the proposed form, ad also compute the values of l k ; t k ; f k ad. Iequality (SA1): If i =, (SA1) becomes + k k. If i 6=, it becomes k i k i, ad therefore k l 1 k = max >i>kf i k i g. 12
13 Iequality (SA2): The oly relevat case is i+j = whe (SA2) becomes i + i. Whe combied, these iequalities simply become 1 = mi >i>0 f i + i g. Iequality (SA3): Without loss of geerality assume i j. We cosider 3 cases. Case 1, k = : I this case the iequality reduces to i + j i+j i; j <. For i =, this iequality simply becomes 0. which is satised by whe Case 2, k < ad i + j k = : I this case the iequality becomes k i j. If i; j < these iequalities ca be combied to obtai k f 1 = max k 1i;j<; k=i+j i =, the j = k ad the iequality becomes k k. i j. If, Case 3, k < ad i + j k < : If i; j < the iequality becomes k i+j k i j. These iequalities ca be combied to obtai k l 2 k = max 1i;j<: k<i+j<+k i+j k i j. If i = the j <, so the iequality becomes + k +j k j, implyig + k t 1 k = max k>j +j k j. Therefore, combiig these observatios, it is easy to see that T has form give i Lemma 3.2 where l k ; t k ; f k ad are computed as follows: l k = max l 1 k ; l2 k ; k ; t k = max t 1 k ; k = k ; f k = f 1 k ; = mi 1 ; 1 l r ; (1 f r )=2 : The secod equality i the descriptio of t k states that t k = k comes from the fact that is subadditive ad therefore k + j +j k for all j < k. The 1 l r ad (1 f r )=2 terms i the last equatio come from usig the bouds o of T to obtai implied bouds for. r together with the equatios ad iequalities We ext make a simple observatio that will help us show that T has a polyomial umber of extreme poits. Lemma 3.3 If p = (; 0 ; 0 ; 0) is a extreme poit of T, the for all k 2 L. 0 k = max l k ; t k 0 ; f k + 0 Proof. Assume that the claim does ot hold for some k 2 L ad let = max l k ; t k 0 ; f k + 0. As p 2 T, 0 k ad therefore = 0 k > 0. I this case, two distict poits i T ca be geerated by icreasig ad decreasig the associated coordiate of p by, establishig that p is ot a extreme poit, a cotradictio. We ext characterize the set of possible values 0 ca take at a extreme poit of T. 13
14 Lemma 3.4 Let p = (; 0 ; 0 ; 0) be a extreme poit of T, if 0 62 f0; g, the 0 2 := [ k2l1 t k l k ; l k f k o 1 A [ where L 1 = fk 2 L : t k + f k < 2l k g ad L 2 = L L 1. k2l2 (t k f k )=2o 1 A Proof. Note that the descriptio of T cosists of 3(r 1) iequalities that ivolve k variables ad upper ad lower boud iequalities for. 0 Beig a extreme poit, p has to satisfy r of these iequalities as equality. Therefore, if 0 62 f0; g the, there exists a idex k 2 L for which at least two of the followig iequalities k l k (a) k + t k (b) k f k (c) hold as equality. Clearly, this uiquely determies the value of 0 ad therefore [ o = t k l k ; l k f k ; (t k f k )=2 : k2l Furthermore, for ay xed k 2 L, addig iequalities (b) ad (c) gives 2 k t k + f k. Therefore if t k + f k > 2l k iequality (a) is implied by iequalities (b) ad (c) ad it caot hold as equality. Similarly, if t k +f k < 2l k, iequalities (b) ad (c) caot hold simultaeously. Fially, if t k +f k = 2l k the it is easy to see that t k l k = l k f k = (t k f k )=2. Therefore lettig L 1 = fk 2 S : t k + f k < 2l k g; L 2 = L L 1 proves the claim. Combiig the previous lemmas, we have the followig result: Theorem 3.5 Give a otrivial facet-deig iequality (11) for P (; r), there are at most 2r lifted iequalities that dee facets of K(; r). Proof. The set L has r 1 members ad therefore together with 0 ad, there are at most 2r possible values for 0 i a facet-deig lifted iequality (12). As the value of 0 uiquely determies the remaiig coeciets i the lifted iequality, by Lemma 3.3, the claim follows. I geeral, determiig all possible lifted iequalities is a hard task. However, the above results show that obtaiig all possible facet-deig iequalities lifted from a facet of P (; r) is straightforward ad ca be performed i polyomial time. I Figure 1, we display two facets of K(16; 13) obtaied by liftig the same facet of P (16; 13). The facet coeciet of each variable is a fuctio of its coeciet i K(; r), that is, variable x i will have a facet coeciet f(i) ad variable y i will have a facet coeciet f( i). We marked all of these coeciets as discs i the 14
15 gure. Also, ote that the displayed fuctios are obtaied by iterpolatig the facet coeciets; we explai their sigicace i Sectio 8. Note that the secod facet has the same coeciet values for x i ; i = 1; : : : ; 1 as the rst, ad a larger coeciet for x, ad therefore it has coeciet values for the y variables which are less tha (sometimes strictly less tha) the correspodig coeciets for the rst facet. To make compariso easier, we plot the rst facet i dashed lies behid the secod facet. Later, i Figure 2, we display facets of K(16; 13) which caot be obtaied by liftig. f(a) 1 f(a) 1 a a Figure 1: Example of two facets of K(16; 13) obtaied by liftig 3.2 Sequetial liftig Sequetial liftig is a procedure that itroduces the variables xed at 0 oe at a time to obtai the lifted iequality. Depedig o the order i which missig variables are lifted, oe obtais dieret iequalities. We ote that ot all lifted facets ca be obtaied by sequetial liftig, see [16]. I Lemma 3.2 we have established that (regardless of the liftig sequece) 0 = k k for k 2 K 0 = f1; : : : ; r 1g. Furthermore, i Lemma 3.3 we established that the coeciet of variable x determies the coeciets of the remaiig variables. Therefore, give a liftig sequece, if K 00 deotes the set of idices of y k variables that are lifted after either oe of x or y r, the the lifted iequality does ot deped o the order i which variables y k for k 2 K 0 or k 2 K 00 are lifted. We ext preset a result adapted from Wolsey [19]. Lemma 3.6 (Wolsey [19]) Give a facet-deig iequality (11) for P (; r) ad a liftig sequece for the variables x ad y i for i = 1; : : : ; 1, the sequetial liftig procedure produces a facet-deig iequality for K(; r). Furthermore, whe a variable is lifted, it is assiged the smallest value amog all coeciets for that variable i lifted iequalities havig the same coeciets for previously lifted variables. Therefore, give a otrivial facet-deig iequality x 1, for P (; r), the liftig coeciet of the variable curretly beig lifted ca simply be computed by solvig a liear program that miimizes the coeciet of that variable subject to the costrait that T has a poit cosistet with the coeciets of the variables that have already bee lifted. 15
16 We coclude this sectio by showig that the simple mappig discussed i the Itroductio (see iequality (4)) leads to a particular lifted iequality. Lemma 3.7 If variable x is lifted before all y k for k 2 f r; : : : ; 1g, the idepedet of the rest of the liftig sequece the lifted iequality is X1 X 1 i x i + i y i 1: Proof. By Lemma 3.6, we kow that variable x will be assiged the smallest possible coeciet i the lifted iequality. As 0 i the descriptio of T ad as T does cotai a poit with = 0 (as described i the proof of Lemma 3.2), we coclude that = 0 i the lifted iequality. Therefore, by Lemma 3.3, 0 k = mi l k ; k ; f k ad we eed to show that k l k ; t k for all k 2 f1; : : : ; 1g. First, observe that 0 t k ad therefore k t k for all k 2 f1; : : : ; 1g. Fially, recall that is subadditive (i the modular sese), ad therefore k + i i k for all > i > k ad k + i + j i+j k for all > i; j ad + k > i + j > k. The rst facet i Figure 1 has the form give i the previous lemma; it is obtaied from a facet of P (; r) by rst liftig x. 4 Mixed iteger roudig iequalities for K(; r) whe r > 0 I this sectio we study MIR iequalities i the cotext of K(; r). Our aalysis also provides a example that shows that liftig facets of P (; r) caot give all facets of K(; r). Throughout, we will use the otatio ^x := x bxc ad (x) + = maxfx; 0g. Recall that, for a geeral sigle row system of the form: w P 2 Z p p + : a iw i = b where ^b > 0, the MIR iequality is: px ba i c + mi ^a i =^b; 1 w i dbe : We dee the 1-MIR (for t t 2 Z +) to be the MIR iequality obtaied from the followig equivalet represetatio of K(; r) = (x; P y) 2 Z + Z P + : (i=t)x i (i=t)y i = r=t. Lemma 4.1 Give t 2 Z such that 2 t, the 1 -MIR iequality t X i i mod t X i (t i) t + mi r mod t ; 1 x i + is facet-deig for K(; r) provided that r=t 62 Z. t + mi r mod t mod t ; 1 y i Proof. Let x + y o deote the 1 -MIR iequality ad let F deote the set of poits t that are o the face deed by this iequality. Also let q i deote (i mod t). Usig this deitio i = q i + bi=tc t. l r t m 16
17 For i 2 N f1; tg, cosider the poit w i = e i + (br=tc bi=tc) + e t + (bi=tc br=tc) + f t + (q r q i ) + e 1 + (q i q r ) + f 1 ad observe that w i 2 K(; r). Moreover, (; ) T w i = (bi=tc + mifq i =q r ; 1g) + (br=tc bi=tc) + (qr q i ) + q r = br=tc + 1 = o ad therefore w i 2 F. Similarly, let i = di=te + m i, with 0 m i < t ad cosider the poit z i = f i + (br=tc + di=te)e t + (q r m i ) + e 1 + (m i q r ) + f 1 for i 2 N f1; tg. Clearly x i 2 K(; r). Furthermore, (; ) T z i = ( di=te + mifm=q r ; 1g) + (br=tc + di=te) + (qr m) + q r = br=tc + 1 = o ad therefore z i 2 F. Additioally the followig three poits are also i K(; r) \ F : u 1 = br=tc e t + q r e 1, u 2 = (br=tc+1)e t +(t q r )f 1, u 3 = (br=tc+1)e t +f t +q r e 1. Therefore, fu i g 3 [fwi g i2n f1;tg [fz i g i2n f1;tg is a set of 2 1 aely idepedet poits i F. We ext show that 1 -MIR iequalities are ot facet-deig uless they satisfy the coditios t of Theorem 4.1. First, observe that the iequality is ot deed if t divides r. Next, we show that 1=-MIR iequality domiates all 1 -MIR iequalities with t >. t Lemma 4.2 If t >, the 1 -MIR iequality is ot facet-deig for K(; r). t Proof. Whe t >, 1 -MIR iequality becomes t X i2n mifi=r; 1gx i X i:i>t r 1 t i r y i 1 ad is domiated by the 1=-MIR: X i2n mifi=r; 1gx i X i:i> r 1 i r y i 1: We coclude this sectio by showig that 1 -MIR iequalities give facets that caot be obtaied t by liftig facets of P (; r). Theorem 4.3 For 9 ad caot be obtaied by liftig facet-deig iequalities for P (; r). 2 r > 0, there are facet-deig iequalities for K(; r) that 17
18 1 Proof. Whe 0 < r 4, cosider the facet iduced by the -MIR iequality x + y 2 o where 4 = 2 + mi ; 1 = 1: P r We subtract 1 times P ix i iy i = r to the iequality to obtai 0 x + 0 y o 0 where 0 = 0 ad therefore it satises the ormalizatio coditio (NC1). Notice that 0 r r = 1 + = 1 r + 1 r r whereas r 0 = 1 r= < 0 + r This proves the claim for 0 < r 4 as all facet-deig iequalities for P (; r) have to satisfy 0 + r+1 0 = 1 0 r. 1 For r 2 f 3; 2g, the -MIR provides such a example. r 1 For r = 1, all poits i T automatically satisfy all equatios i Q. Therefore, ay give facet-deig iequality of K(; r) ca be obtaied by liftig a poit i Q. However, this poit is ot ecessarily a extreme poit of Q. Usig PORTA [4], we also determied that for 4, all otrivial facets of K(; r) ca be obtaied from liftig otrivial facets of P (; r). This is ot the case for = 7; 8 ad for some values of r for = 5; 6. 5 Polyhedral aalysis of K(; 0) Observe that LK(; 0), the liear relaxatio of K(; 0), is a poited coe (as it is cotaied i the oegative orthat) ad has a sigle extreme poit (x; y) = (0; 0). Therefore LK(; 0) equals its iteger hull, i.e., LK(; 0) = K(; 0). I Lemma 2.3, we characterized the extreme rays of K(; r) ad thereby showed that the recessio coe of K(; r) is geerated by the vectors fr ij g. But the recessio coe of K(; r) for some r > 0 is just K(; 0). Therefore, LK(; 0) is geerated by the vectors fr ij g, ad the ext result follows. Theorem 5.1 The iequality x + y o is facet-deig for K(; 0) if ad oly if (; ; o ) is a miimal face of T o = ( j i + i j 0 ; 8i; j 2 N; o = 0: I his work o MCGP, Gomory also studied P (; 0), the covex hull of o-zero itegral solutios that satisfy P 1 ix i y = 0, ad showed that Theorem 3.1 also holds for r = 0. For the sake of completeess, we ow cosider a similar modicatio of K(; 0) ad study the set: K(; 0) = cov ( (x; y) 2 Z + Z + : X ix i X iy i = 0; (x; y) 6= 0 ) : 18
19 For this case it will be more coveiet to cosider all oegativity iequalities (icludig y 0) as trivial. We will ext prove that all otrivial facet-deig iequalities for K(; 0) are give by the extreme poits of To deed below. Deitio 5.2 We dee To R 2+1 as the set of poits that satisfy the followig liear equalities ad iequalities: i + j i j ; 8i; j 2 N; i > j; (SA1) i + j j i ; 8i; j 2 N; i < j; (SA1') i + i = o ; 8i 2 N; (EP1-R0) o = 1; = 0: (N1-R0) (N2-R0) It is easy to see that the coditios (SA1), (SA1'), ad (EP1-R0) are together equivalet to the coditios (SA2), (SA2'), (SA2") ad (EP1-R0). For example, replacig i by o i ad i j by o i j i (SA1), we get (SA2'). Therefore, a poit i To satises all the pairwise subadditivity coditios give i the previous sectio. Also ote that To is a bouded polyhedro. To see this otice that after swappig idices i ad j i iequality (SA1') ad usig equatio (EP1-R0) to substitute out variables i (SA1) ad (SA1') we obtai 1 j + i j i 0 8i; j 2 N; i > j: Therefore, ay ray i the recessio coe of To must have d j + d i j d i = 0 where d deotes the compoets of the ray correspodig to variables (ote that, by equatio (EP1-R0), d gives the compoets of the ray for the variables). Takig j = 1, it is easy to see that d i = id 1 for all i 2 N. As d = 0 by equatio (N2-R0), each d i has to be zero. Lemma 5.3 If (; ; o ) 2 To the x + y o is a valid iequality for K(; 0). Proof. Suppose x + y o is ot valid for K(; 0). The, let (x ; y ) 2 K(; 0) be the iteger poit i K(; 0) with smallest L1 orm such that x + y < o. Note that ay poit i K(; 0) has L 1 orm 2 or more. If jj(x ; y )jj 1 = 2, the (x ; y ) = e i + f i for some i 2 N, but by (EP1-R0), x + y = o, which is a cotradictio. So we may assume that jj(x ; y )jj 1 > 2. As (x ; y ) 2 K(; 0), there exists i; j 2 N such that x i > 0 ad y j (x 0 ; y 0 ) = (x ; y ) e i f j + 8 >< >: f j i if i < j; 0 if i = j; e i j if i > j: > 0. Let Clearly, (x 0 ; y 0 ) is a iteger poit i K(; 0) ad jj(x 0 ; y 0 )jj 1 jj(x ; y )jj 1 1. Furthermore, as (; ; o ) satises (SA1), (SA1') ad (EP1-R0), we also have x 0 + y 0 x + x < o, which cotradicts the choice of (x ; y ). 19
20 Theorem 5.4 Cosider a iequality x + y o with = 0. It dees a otrivial facet of K(; 0) if ad oly if it the followig coditios hold: (i) o > 0, ad, (ii) (; ; o )= o is a extreme poit of To. Proof. ()): Let x + y o dee a otrivial facet of K(; 0). We rst show that (; ; o ) satises (SA1), (SA1') ad (EP1-R0), ad ca be assumed to satisfy (N1-R0) ad (N2-R0). (SA1) - (SA1'): Let i; j be idices such that i; j 2 N ad i > j. Let z = (x ; y ) be a itegral poit lyig o the above facet such that x i j > 0. As z + (e i + f j e i j ) belogs to K(; 0), (SA1) is true. The proof of (SA1') is similar. (EP1-R0): Let = (; ). Let z 1 = (x 1 ; y 1 ) ad z 2 = (x 2 ; y 2 ) be itegral poits lyig o the facet such that x 1 i > 0 ad y 2 i > 0. The z = z 1 + z 2 e i f i 2 K(; 0), ad therefore z = z 1 + z 2 i i = 2 o i i o ) i + i o. But as e i + f i 2 K(; 0), i + i o ad the result follows. (N1-R0): Assume o < 0, ad let (x ; y ) be a itegral poit i K(; 0) satisfyig x +y = o. As (x ; y ) 2 K(; 0) for ay positive iteger, whereas x + y = o < o, we obtai a cotradictio to the fact that poits i K(; 0) satisfy x + y o. If o = 0, the (EP1-R0) implies that i = i for all i 2 N. This fact, alog with (SA1) ad (SA1') P implies that i = i 1 ad i = i 1 for all i 2 N. But the x + y o is the same as P 1 ( ix i iy i) 0, ad therefore caot dee a proper face of K(; 0). Therefore, for ay otrivial facet, o > 0 ad ca be assumed to be 1 by P scalig. P We ca assume, by subtractig appropriate multiples of ix i iy i = 0 from x+y o, that (N2-R0) holds. Therefore (; ; o ) ca be assumed to be cotaied i To. If it is ot a extreme poit of To, it ca be writte as a covex combiatio of two distict poits of To, dieret from itself, each of which dees a valid iequality for K(; 0) (by Lemma 5.3). As the ormalizatio coditios (N1-R0) ad (N2-R0) mea that each otrivial facet-deig iequality correspods to a uique poit i To, this implies that (; ; o ) is a extreme poit of To. ((): Let F = ( k ; k ; o k M ) be the set of all otrivial facets of k=1 K(; 0) such that k = 0 ad o k = 1. Let (; ; 1) be a extreme poit of To. By Lemma 5.3, (; ; 1) dees a valid iequality for K(; 0), ad therefore there exist umbers k ad such that i + P M k=1 k k i i ; 8i 2 N i + P M k=1 k k i i ; 8i 2 N P M k=1 k 1 0; free P M (EP1-R0) implies that for all i 2 N, 1 = i + i P k=1 k(i k + k i ) ad sice all otrivial M facets also satisfy (EP1-R0), we ca coclude that k=1 k = 1. Therefore, 1 = i + i 20
21 P M k=1 k( k i P P + k) = 1 ad hece i M i = k=1 ki k M ad i = k=1 k k i. I other words, (; ; 1) ca be expressed as a covex combiatio of the elemets of F, each of which is cotaied i To. This is possible oly if (; ; 1) is itself a elemet of F, i.e., it dees a otrivial facet of K(; 0). As P (; 0) is a lower dimesioal face of K(; 0), it is possible to lift facet-deig iequalities of P (; 0) to obtai facet-deig iequalities for K(; 0). From the descriptio of To, ay otrivial facet-deig iequality x + y o of K(; 0) satises i = 1 i. Thus, if P 1 i x i 1 dees a otrivial facet of P (; 0), there is a uique way to lift this iequality to obtai a facet-deig iequality for K(; 0), amely: X 1 x + X 1 i x i + (1 i )y i 1: Next, we show that whe = 3 ot all facet-deig iequalities for K(; 0) ca be obtaied via liftig. Remember that, after ormalizatio, coeciets of all facet-deig iequalities for P (; 0) are betwee 0 ad 1. Example 5.5 Cosider K(3; 0) ad ote that all (x; y) 2 K(3; 0) satisfy P 3 x i P 3 ix i P 3 iy i = 0 to this iequality yields 1: Addig 2x 1 + 3x 2 + 4x 3 y 1 2y 2 3y 3 1: (13) Dividig (13) by 2 ad writig the MIR iequality gives x 1 + 2x 2 + 2x 3 y 2 y 3 1 which becomes 2 3 x x 2 + x y y 2 1 (14) after ormalizatio. Deotig feasible poits p 2 K(3; 0) as p = (x 1 ; x 2 ; x 3 ; y 1 ; y 2 ; y 3 ), ote that the followig 5 aely idepedet poits satisfy (14) as equality: p 1 = (1; 0; 0; 1; 0; 0), p 2 = (0; 1; 0; 0; 1; 0), p 3 = (0; 0; 1; 0; 0; 1), p 4 = (2; 0; 0; 0; 1; 0) ad p 5 = (0; 0; 1; 1; 1; 0) ad therefore (14) dees a facet of K(3; 0). Notice that (14) caot be obtaied via liftig as the coeciet of x 2 is greater tha 1. Lemma 5.6 For ay 3, K(; 0) has at least oe facet that caot be obtaied by liftig a facet of P (; 0). Proof. For = 3 the example above proves the claim so we cosider 4. Let i = ( i+2 if i < 1 if i = i = ( i 2 if i < 0 if i = ad otice that 1 > 1. We ext show that p = (; ; 1) 2 To. Clearly p satises equatios (EP1-R0), (N1-R0) ad (N2-R0). Usig (i + 2)= i i= ad ( i)= i ( i 2)= for all i 2 N, ote that i + j i j i= + ( j 2)= (i j + 2)= 1 4= 0 21
22 ad therefore p satises iequality (SA1). Fially, if we have that i; j 2 N ad j > i, the j i < which implies that j i = ( j + i 2)= ad hece: i + j j i i= + ( j 2)= ( j + i 2)= 0 Therefore p satises iequality (SA1') as well ad it is ideed cotaied i T o. As T o is a bouded polyhedro, it must therefore have a extreme poit (; ; 1) that has 1 > 1. Clearly, the iequality correspodig to this extreme poit caot be obtaied by liftig a facet of P (; 0). 6 Separatig from K(; r) Let LK(; r) be the liear relaxatio of K(; r). We dee the separatio problem over K(; r) as follows: give (x ; y ) 2 LK(; r), either verify that (x ; y ) 2 K(; r) or d a violated valid iequality for K(; r). Note that the coditio that (x ; y ) 2 LK(; r) is easy to satisfy. From Theorems 2.6, 5.1 ad 5.4, it follows that ay poit (x ; y ) 2 LK(; r), with 0 < r, ca be separated from K(; r) by miimizig x +y over T. Therefore, i this case the separatio problem ca be solved i polyomial-time usig a LP with O() variables ad O( 3 ) costraits. Similarly, by Theorem 5.4, oe ca separate a poit from K(; 0) usig a LP with O() variables ad O( 2 ) costraits. We ext show that the separatio problem over K(; r) ca also be solved for ay r > 0 usig a LP with O( 2 ) costraits. Theorem 6.1 Give (x ; y ) 2 LK(; r), where r > 0, the separatio problem over K(; r) ca be solved i time polyomial i maxf; rg usig a LP with O(maxf; rg) variables ad O(maxf; rg 2 ) costraits. Proof. First we cosider the case r. Let T 0 be a restrictio of T obtaied by replacig the relaxed subadditivity coditios (SA1)-(SA3) with the pairwise subadditivity coditios (SA0), (SA1), (SA1'), (SA2), ad (SA2'). Due to Lemma 2.7, T 0 T ad therefore if (; ) 2 T 0, the x + y 1 is a valid iequality for K(; r). I additio, by Lemma 2.9, if x + y 1 dees a otrivial facet of K(; r), the (; ) 2 T 0. Let ( 0 ; 0 ) be a optimal solutio of z = mifx + y : (; ) 2 T 0 g: If z < 1 the 0 x + 0 y 1 is a violated valid iequality. If, o the other had, z 1, the (x ; y ) satises all facet-deig iequalities ad therefore belogs to K(; r). Next, assume that r >. Dee (x 0 ; y 0 ) 2 R r R r such that x 0 = i x ; i y0 = i y i ; for i = 1; : : : ; ad x 0 = i y0 = i 0; for i = + 1; : : : ; r. As (x ; y ) 2 K(; r) () (x 0 ; y 0 ) 2 K(r; r), separatio ca be doe usig K(r; r). If a violated iequality is foud, the it ca simply be tured ito a valid iequality for K(; r) by droppig the extra coeciets. 22
23 7 Mixed-iteger extesio Cosider the mixed-iteger extesio of K(; r): K 0 (; r) = cov ( (v + ; v ; x; y) 2 R 2 + Z 2 + : v + v + X ix i X iy i = r ) where ; r 2 Z ad r > 0. As i the case of the mixed-iteger extesio of MCGP studied by Gomory ad Johso [11], the facets of K 0 (; r) ca easily be derived from the facets of K(; r) whe r is a iteger. To prove such a result, we itroduce a few deitios, ad also state some easy results without proof. The dimesio of K 0 (; r) is 2 + 1, i.e., oe less tha the umber of variables. The iequalities x i 0 ad y i 0, for i = 1; : : : ;, ad v + 0 ad v 0 dee facets of K 0 (; r). We refer to the facets above { other tha y 0 { as trivial facets, ad refer to the remaiig facets of K 0 (; r) as otrivial. Fially, ote that the recessio coe of K 0 (; r) cotais the vectors je i + if j, for all i; j satisfyig 1 i; j. For K 0 (; r), let e + ad e be the uit vectors i R 2+2 with oes i, respectively, the v + compoet, ad the v compoet, ad zeros elsewhere. For a vector i the K 0 (; r) space, dee its restrictio to the K(; r) space by removig the v + ad v ad deote it by re. Propositio 7.1 All otrivial facet-deig iequalities for K 0 (; r) have the form 1 v v + X i x i + X compoets, i y i o : (15) Furthermore, iequality (15) is facet-deig if ad oly if x + y o dees a otrivial facet of K(; r). Proof. Let x + y o dee a otrivial facet of K(; r). We rst show that the iequality (15) is valid for K 0 (; r). Assume (15) is violated by some itegral poit 2 K 0 (; r) (the x ad y compoets of are itegral). The the left-had-side of (15) evaluated at equals a umber z less tha o. Let v 0 + = e T + ad v0 = e T. The property (R1) i Observatio 2.8 implies that Therefore, if mifv 0 + ; v0 g = > 0, the (15) is also violated by the poit (e + + e ) 2 K 0 (; r). We ca thus assume that satises mifv 0 + ; v0 g = 0. But mifv 0 + ; v0 g = 0 combied with the itegrality of implies that v 0 + ad v 0 are both itegers. Therefore 0 = re + v 0 + e 1 + v 0 f 1 is a itegral poit cotaied i K(; r), ad (; ) T 0 = z < o, which cotradicts the fact that x + y o is satised by all poits i K(; r). To see that (15) dees a facet of K 0 (; r), let 1 ; : : : 2 1 be aely idepedet itegral poits i K(; r) which satisfy (; ) T i = o. As the facet deed by x + y o does ot equal the facet deed by either x 1 0 or y 1 0, there are idices j; k such that e T 1 j = s > 0 ad f T 1 k = t > 0. Dee aely idepedet poits i R 2+2 as follows: i = (0; 0; i ) for i = 1; : : : ; 2 1; 23
24 + = j + se + se 1 ; = k + te tf 1 : These poits satisfy (15) at equality, ad therefore (15) dees a facet of K 0 (; r). We ow show that every otrivial facet of K 0 (; r) has the form i (15). Assume T (v + ; v ; x; y) o dees a otrivial facet F of K 0 (; r). Let = ( + ; ; ; ), where + ; 2 R, ad ; 2 R. There exists a poit 2 K 0 (; r) lyig o the above facet such that T e 1 > 0. As e 1 + e + 2 K 0 (; r), we coclude that + 1. We ca similarly coclude that 1 ad therefore The last iequality is implied by the fact that e 1 + f 1 is cotaied i the recessio coe of K 0 (; r). If + + = 0, the clearly + = 1 ad = 1. Assume + + > 0. As F is ot the same as the facet v + 0, there exists a itegral poit = (v 0 + ; v0 ; x 0 ; y 0 ) 2 K 0 (; r) lyig o F such that v 0 + > 0. If v0 > 0, let mifv 0 + ; v0 g = > 0. The 1 = (e + + e ) 2 K 0 (; r), but T 1 = o ( + + ) < o. This cotradicts the fact that (; o ) dees a valid iequality for K 0 (; r). We ca therefore assume that v 0 v 0 + = t, for some positive iteger t. Dee 2 as = 0 ad te + + te 1. As 2 2 K 0 (; r), it follows that T 2 o ) + 1. We coclude that + = 1 ; a similar argumet shows that = 1. Fially, we show that if (15) dees a facet of K 0 (; r), the the iequality x + y o dees a facet of K(; r). Firstly, this dees a valid iequality for K(; r) as ay poit i K(; r) ca be mapped to a poit i K 0 (; r) by appedig zeros i the v + ad v compoets. If it does ot dee a facet, the (; ) P i i( i ; i ) ad o P i i i o for some otrivial facetdeig iequalities i x + i y i o of K(; r), ad some umbers i 0. But that would imply that ( 1 ; 1 ; ; ) P i i( i 1 ; i 1 ; i ; i ). i 1 v + + i 1 v By the rst part of the proof, the iequalities + i x + i y i o dee facets of K 0 (; r), ad this cotradicts the assumptio that (15) dees a facet of K 0 (; r). 8 Usig K(; r) to geerate valid iequalities for MIP Gomory ad Johso [11, 12] show how to derive subadditive fuctios, or fuctios which satisfy f(u) + f(v) f(u + v) for all u; v 2 R, from facets of P (; r) via iterpolatio of facet coeciets. These fuctios yield valid iequalities for o-egative iteger solutios w of of a kapsack costrait P p a iw i = b. We ext derive valid iequalities for such kapsack sets from facets of K(; r) via iterpolatio. As a rst step, we iterpolate coeciets of facet-deig iequalities of K(; r) to obtai fuctios which are subadditive over a iterval. Subsequetly, we use earlier results to prove Theorem 8.5, which states that such fuctios yield valid iequalities for kapsack sets, (ad thus for geeral MIPs). A importat cosequece of our results is that we ca use a wider class of subadditive fuctios to get valid iequalities for MIPs tha implied by the results of Gomory ad Johso. For a real umber v, we dee ^v as v bvc. Deitio 8.1 Give a facet-deig iequality x+y o for K(; r), let f z : Z\[ ; ]! R 24
w (1) ˆx w (1) x (1) /ρ and w (2) ˆx w (2) x (2) /ρ.
 2 5. Weighted umber of late jobs 5.1. Release dates ad due dates: maximimizig the weight of o-time jobs Oce we add release dates, miimizig the umber of late jobs becomes a sigificatly harder problem. For
2 5. Weighted umber of late jobs 5.1. Release dates ad due dates: maximimizig the weight of o-time jobs Oce we add release dates, miimizig the umber of late jobs becomes a sigificatly harder problem. For
Math 61CM - Solutions to homework 3
 Math 6CM - Solutios to homework 3 Cédric De Groote October 2 th, 208 Problem : Let F be a field, m 0 a fixed oegative iteger ad let V = {a 0 + a x + + a m x m a 0,, a m F} be the vector space cosistig
Math 6CM - Solutios to homework 3 Cédric De Groote October 2 th, 208 Problem : Let F be a field, m 0 a fixed oegative iteger ad let V = {a 0 + a x + + a m x m a 0,, a m F} be the vector space cosistig
ACO Comprehensive Exam 9 October 2007 Student code A. 1. Graph Theory
 1. Graph Theory Prove that there exist o simple plaar triagulatio T ad two distict adjacet vertices x, y V (T ) such that x ad y are the oly vertices of T of odd degree. Do ot use the Four-Color Theorem.
1. Graph Theory Prove that there exist o simple plaar triagulatio T ad two distict adjacet vertices x, y V (T ) such that x ad y are the oly vertices of T of odd degree. Do ot use the Four-Color Theorem.
15.083J/6.859J Integer Optimization. Lecture 3: Methods to enhance formulations
 15.083J/6.859J Iteger Optimizatio Lecture 3: Methods to ehace formulatios 1 Outlie Polyhedral review Slide 1 Methods to geerate valid iequalities Methods to geerate facet defiig iequalities Polyhedral
15.083J/6.859J Iteger Optimizatio Lecture 3: Methods to ehace formulatios 1 Outlie Polyhedral review Slide 1 Methods to geerate valid iequalities Methods to geerate facet defiig iequalities Polyhedral
Seunghee Ye Ma 8: Week 5 Oct 28
 Week 5 Summary I Sectio, we go over the Mea Value Theorem ad its applicatios. I Sectio 2, we will recap what we have covered so far this term. Topics Page Mea Value Theorem. Applicatios of the Mea Value
Week 5 Summary I Sectio, we go over the Mea Value Theorem ad its applicatios. I Sectio 2, we will recap what we have covered so far this term. Topics Page Mea Value Theorem. Applicatios of the Mea Value
Beurling Integers: Part 2
 Beurlig Itegers: Part 2 Isomorphisms Devi Platt July 11, 2015 1 Prime Factorizatio Sequeces I the last article we itroduced the Beurlig geeralized itegers, which ca be represeted as a sequece of real umbers
Beurlig Itegers: Part 2 Isomorphisms Devi Platt July 11, 2015 1 Prime Factorizatio Sequeces I the last article we itroduced the Beurlig geeralized itegers, which ca be represeted as a sequece of real umbers
Infinite Sequences and Series
 Chapter 6 Ifiite Sequeces ad Series 6.1 Ifiite Sequeces 6.1.1 Elemetary Cocepts Simply speakig, a sequece is a ordered list of umbers writte: {a 1, a 2, a 3,...a, a +1,...} where the elemets a i represet
Chapter 6 Ifiite Sequeces ad Series 6.1 Ifiite Sequeces 6.1.1 Elemetary Cocepts Simply speakig, a sequece is a ordered list of umbers writte: {a 1, a 2, a 3,...a, a +1,...} where the elemets a i represet
The Method of Least Squares. To understand least squares fitting of data.
 The Method of Least Squares KEY WORDS Curve fittig, least square GOAL To uderstad least squares fittig of data To uderstad the least squares solutio of icosistet systems of liear equatios 1 Motivatio Curve
The Method of Least Squares KEY WORDS Curve fittig, least square GOAL To uderstad least squares fittig of data To uderstad the least squares solutio of icosistet systems of liear equatios 1 Motivatio Curve
Machine Learning Theory Tübingen University, WS 2016/2017 Lecture 12
 Machie Learig Theory Tübige Uiversity, WS 06/07 Lecture Tolstikhi Ilya Abstract I this lecture we derive risk bouds for kerel methods. We will start by showig that Soft Margi kerel SVM correspods to miimizig
Machie Learig Theory Tübige Uiversity, WS 06/07 Lecture Tolstikhi Ilya Abstract I this lecture we derive risk bouds for kerel methods. We will start by showig that Soft Margi kerel SVM correspods to miimizig
Math 155 (Lecture 3)
 Math 55 (Lecture 3) September 8, I this lecture, we ll cosider the aswer to oe of the most basic coutig problems i combiatorics Questio How may ways are there to choose a -elemet subset of the set {,,,
Math 55 (Lecture 3) September 8, I this lecture, we ll cosider the aswer to oe of the most basic coutig problems i combiatorics Questio How may ways are there to choose a -elemet subset of the set {,,,
6.3 Testing Series With Positive Terms
 6.3. TESTING SERIES WITH POSITIVE TERMS 307 6.3 Testig Series With Positive Terms 6.3. Review of what is kow up to ow I theory, testig a series a i for covergece amouts to fidig the i= sequece of partial
6.3. TESTING SERIES WITH POSITIVE TERMS 307 6.3 Testig Series With Positive Terms 6.3. Review of what is kow up to ow I theory, testig a series a i for covergece amouts to fidig the i= sequece of partial
Chapter Vectors
 Chapter 4. Vectors fter readig this chapter you should be able to:. defie a vector. add ad subtract vectors. fid liear combiatios of vectors ad their relatioship to a set of equatios 4. explai what it
Chapter 4. Vectors fter readig this chapter you should be able to:. defie a vector. add ad subtract vectors. fid liear combiatios of vectors ad their relatioship to a set of equatios 4. explai what it
6 Integers Modulo n. integer k can be written as k = qn + r, with q,r, 0 r b. So any integer.
 6 Itegers Modulo I Example 2.3(e), we have defied the cogruece of two itegers a,b with respect to a modulus. Let us recall that a b (mod ) meas a b. We have proved that cogruece is a equivalece relatio
6 Itegers Modulo I Example 2.3(e), we have defied the cogruece of two itegers a,b with respect to a modulus. Let us recall that a b (mod ) meas a b. We have proved that cogruece is a equivalece relatio
Definition 4.2. (a) A sequence {x n } in a Banach space X is a basis for X if. unique scalars a n (x) such that x = n. a n (x) x n. (4.
 4. BASES I BAACH SPACES 39 4. BASES I BAACH SPACES Sice a Baach space X is a vector space, it must possess a Hamel, or vector space, basis, i.e., a subset {x γ } γ Γ whose fiite liear spa is all of X ad
4. BASES I BAACH SPACES 39 4. BASES I BAACH SPACES Sice a Baach space X is a vector space, it must possess a Hamel, or vector space, basis, i.e., a subset {x γ } γ Γ whose fiite liear spa is all of X ad
Definitions and Theorems. where x are the decision variables. c, b, and a are constant coefficients.
 Defiitios ad Theorems Remember the scalar form of the liear programmig problem, Miimize, Subject to, f(x) = c i x i a 1i x i = b 1 a mi x i = b m x i 0 i = 1,2,, where x are the decisio variables. c, b,
Defiitios ad Theorems Remember the scalar form of the liear programmig problem, Miimize, Subject to, f(x) = c i x i a 1i x i = b 1 a mi x i = b m x i 0 i = 1,2,, where x are the decisio variables. c, b,
Chapter 4. Fourier Series
 Chapter 4. Fourier Series At this poit we are ready to ow cosider the caoical equatios. Cosider, for eample the heat equatio u t = u, < (4.) subject to u(, ) = si, u(, t) = u(, t) =. (4.) Here,
Chapter 4. Fourier Series At this poit we are ready to ow cosider the caoical equatios. Cosider, for eample the heat equatio u t = u, < (4.) subject to u(, ) = si, u(, t) = u(, t) =. (4.) Here,
62. Power series Definition 16. (Power series) Given a sequence {c n }, the series. c n x n = c 0 + c 1 x + c 2 x 2 + c 3 x 3 +
 62. Power series Defiitio 16. (Power series) Give a sequece {c }, the series c x = c 0 + c 1 x + c 2 x 2 + c 3 x 3 + is called a power series i the variable x. The umbers c are called the coefficiets of
62. Power series Defiitio 16. (Power series) Give a sequece {c }, the series c x = c 0 + c 1 x + c 2 x 2 + c 3 x 3 + is called a power series i the variable x. The umbers c are called the coefficiets of
Chapter 6 Infinite Series
 Chapter 6 Ifiite Series I the previous chapter we cosidered itegrals which were improper i the sese that the iterval of itegratio was ubouded. I this chapter we are goig to discuss a topic which is somewhat
Chapter 6 Ifiite Series I the previous chapter we cosidered itegrals which were improper i the sese that the iterval of itegratio was ubouded. I this chapter we are goig to discuss a topic which is somewhat
Optimally Sparse SVMs
 A. Proof of Lemma 3. We here prove a lower boud o the umber of support vectors to achieve geeralizatio bouds of the form which we cosider. Importatly, this result holds ot oly for liear classifiers, but
A. Proof of Lemma 3. We here prove a lower boud o the umber of support vectors to achieve geeralizatio bouds of the form which we cosider. Importatly, this result holds ot oly for liear classifiers, but
DIVISIBILITY PROPERTIES OF GENERALIZED FIBONACCI POLYNOMIALS
 DIVISIBILITY PROPERTIES OF GENERALIZED FIBONACCI POLYNOMIALS VERNER E. HOGGATT, JR. Sa Jose State Uiversity, Sa Jose, Califoria 95192 ad CALVIN T. LONG Washigto State Uiversity, Pullma, Washigto 99163
DIVISIBILITY PROPERTIES OF GENERALIZED FIBONACCI POLYNOMIALS VERNER E. HOGGATT, JR. Sa Jose State Uiversity, Sa Jose, Califoria 95192 ad CALVIN T. LONG Washigto State Uiversity, Pullma, Washigto 99163
Chapter IV Integration Theory
 Chapter IV Itegratio Theory Lectures 32-33 1. Costructio of the itegral I this sectio we costruct the abstract itegral. As a matter of termiology, we defie a measure space as beig a triple (, A, µ), where
Chapter IV Itegratio Theory Lectures 32-33 1. Costructio of the itegral I this sectio we costruct the abstract itegral. As a matter of termiology, we defie a measure space as beig a triple (, A, µ), where
Product measures, Tonelli s and Fubini s theorems For use in MAT3400/4400, autumn 2014 Nadia S. Larsen. Version of 13 October 2014.
 Product measures, Toelli s ad Fubii s theorems For use i MAT3400/4400, autum 2014 Nadia S. Larse Versio of 13 October 2014. 1. Costructio of the product measure The purpose of these otes is to preset the
Product measures, Toelli s ad Fubii s theorems For use i MAT3400/4400, autum 2014 Nadia S. Larse Versio of 13 October 2014. 1. Costructio of the product measure The purpose of these otes is to preset the
Hoggatt and King [lo] defined a complete sequence of natural numbers
![Hoggatt and King [lo] defined a complete sequence of natural numbers Hoggatt and King [lo] defined a complete sequence of natural numbers](/thumbs/96/128001016.jpg) REPRESENTATIONS OF N AS A SUM OF DISTINCT ELEMENTS FROM SPECIAL SEQUENCES DAVID A. KLARNER, Uiversity of Alberta, Edmoto, Caada 1. INTRODUCTION Let a, I deote a sequece of atural umbers which satisfies
REPRESENTATIONS OF N AS A SUM OF DISTINCT ELEMENTS FROM SPECIAL SEQUENCES DAVID A. KLARNER, Uiversity of Alberta, Edmoto, Caada 1. INTRODUCTION Let a, I deote a sequece of atural umbers which satisfies
Math 451: Euclidean and Non-Euclidean Geometry MWF 3pm, Gasson 204 Homework 3 Solutions
 Math 451: Euclidea ad No-Euclidea Geometry MWF 3pm, Gasso 204 Homework 3 Solutios Exercises from 1.4 ad 1.5 of the otes: 4.3, 4.10, 4.12, 4.14, 4.15, 5.3, 5.4, 5.5 Exercise 4.3. Explai why Hp, q) = {x
Math 451: Euclidea ad No-Euclidea Geometry MWF 3pm, Gasso 204 Homework 3 Solutios Exercises from 1.4 ad 1.5 of the otes: 4.3, 4.10, 4.12, 4.14, 4.15, 5.3, 5.4, 5.5 Exercise 4.3. Explai why Hp, q) = {x
(A sequence also can be thought of as the list of function values attained for a function f :ℵ X, where f (n) = x n for n 1.) x 1 x N +k x N +4 x 3
 MATH 337 Sequeces Dr. Neal, WKU Let X be a metric space with distace fuctio d. We shall defie the geeral cocept of sequece ad limit i a metric space, the apply the results i particular to some special
MATH 337 Sequeces Dr. Neal, WKU Let X be a metric space with distace fuctio d. We shall defie the geeral cocept of sequece ad limit i a metric space, the apply the results i particular to some special
Solutions for the Exam 9 January 2012
 Mastermath ad LNMB Course: Discrete Optimizatio Solutios for the Exam 9 Jauary 2012 Utrecht Uiversity, Educatorium, 15:15 18:15 The examiatio lasts 3 hours. Gradig will be doe before Jauary 23, 2012. Studets
Mastermath ad LNMB Course: Discrete Optimizatio Solutios for the Exam 9 Jauary 2012 Utrecht Uiversity, Educatorium, 15:15 18:15 The examiatio lasts 3 hours. Gradig will be doe before Jauary 23, 2012. Studets
TEACHER CERTIFICATION STUDY GUIDE
 COMPETENCY 1. ALGEBRA SKILL 1.1 1.1a. ALGEBRAIC STRUCTURES Kow why the real ad complex umbers are each a field, ad that particular rigs are ot fields (e.g., itegers, polyomial rigs, matrix rigs) Algebra
COMPETENCY 1. ALGEBRA SKILL 1.1 1.1a. ALGEBRAIC STRUCTURES Kow why the real ad complex umbers are each a field, ad that particular rigs are ot fields (e.g., itegers, polyomial rigs, matrix rigs) Algebra
Optimization Methods MIT 2.098/6.255/ Final exam
 Optimizatio Methods MIT 2.098/6.255/15.093 Fial exam Date Give: December 19th, 2006 P1. [30 pts] Classify the followig statemets as true or false. All aswers must be well-justified, either through a short
Optimizatio Methods MIT 2.098/6.255/15.093 Fial exam Date Give: December 19th, 2006 P1. [30 pts] Classify the followig statemets as true or false. All aswers must be well-justified, either through a short
4 The Sperner property.
 4 The Sperer property. I this sectio we cosider a surprisig applicatio of certai adjacecy matrices to some problems i extremal set theory. A importat role will also be played by fiite groups. I geeral,
4 The Sperer property. I this sectio we cosider a surprisig applicatio of certai adjacecy matrices to some problems i extremal set theory. A importat role will also be played by fiite groups. I geeral,
Convergence of random variables. (telegram style notes) P.J.C. Spreij
 Covergece of radom variables (telegram style otes).j.c. Spreij this versio: September 6, 2005 Itroductio As we kow, radom variables are by defiitio measurable fuctios o some uderlyig measurable space
Covergece of radom variables (telegram style otes).j.c. Spreij this versio: September 6, 2005 Itroductio As we kow, radom variables are by defiitio measurable fuctios o some uderlyig measurable space
Supplemental Material: Proofs
 Proof to Theorem Supplemetal Material: Proofs Proof. Let be the miimal umber of traiig items to esure a uique solutio θ. First cosider the case. It happes if ad oly if θ ad Rak(A) d, which is a special
Proof to Theorem Supplemetal Material: Proofs Proof. Let be the miimal umber of traiig items to esure a uique solutio θ. First cosider the case. It happes if ad oly if θ ad Rak(A) d, which is a special
Mathematical Induction
 Mathematical Iductio Itroductio Mathematical iductio, or just iductio, is a proof techique. Suppose that for every atural umber, P() is a statemet. We wish to show that all statemets P() are true. I a
Mathematical Iductio Itroductio Mathematical iductio, or just iductio, is a proof techique. Suppose that for every atural umber, P() is a statemet. We wish to show that all statemets P() are true. I a
Problem Set 2 Solutions
 CS271 Radomess & Computatio, Sprig 2018 Problem Set 2 Solutios Poit totals are i the margi; the maximum total umber of poits was 52. 1. Probabilistic method for domiatig sets 6pts Pick a radom subset S
CS271 Radomess & Computatio, Sprig 2018 Problem Set 2 Solutios Poit totals are i the margi; the maximum total umber of poits was 52. 1. Probabilistic method for domiatig sets 6pts Pick a radom subset S
CSE 1400 Applied Discrete Mathematics Number Theory and Proofs
 CSE 1400 Applied Discrete Mathematics Number Theory ad Proofs Departmet of Computer Scieces College of Egieerig Florida Tech Sprig 01 Problems for Number Theory Backgroud Number theory is the brach of
CSE 1400 Applied Discrete Mathematics Number Theory ad Proofs Departmet of Computer Scieces College of Egieerig Florida Tech Sprig 01 Problems for Number Theory Backgroud Number theory is the brach of
CHAPTER I: Vector Spaces
 CHAPTER I: Vector Spaces Sectio 1: Itroductio ad Examples This first chapter is largely a review of topics you probably saw i your liear algebra course. So why cover it? (1) Not everyoe remembers everythig
CHAPTER I: Vector Spaces Sectio 1: Itroductio ad Examples This first chapter is largely a review of topics you probably saw i your liear algebra course. So why cover it? (1) Not everyoe remembers everythig
Economics 241B Relation to Method of Moments and Maximum Likelihood OLSE as a Maximum Likelihood Estimator
 Ecoomics 24B Relatio to Method of Momets ad Maximum Likelihood OLSE as a Maximum Likelihood Estimator Uder Assumptio 5 we have speci ed the distributio of the error, so we ca estimate the model parameters
Ecoomics 24B Relatio to Method of Momets ad Maximum Likelihood OLSE as a Maximum Likelihood Estimator Uder Assumptio 5 we have speci ed the distributio of the error, so we ca estimate the model parameters
CALCULATION OF FIBONACCI VECTORS
 CALCULATION OF FIBONACCI VECTORS Stuart D. Aderso Departmet of Physics, Ithaca College 953 Daby Road, Ithaca NY 14850, USA email: saderso@ithaca.edu ad Dai Novak Departmet of Mathematics, Ithaca College
CALCULATION OF FIBONACCI VECTORS Stuart D. Aderso Departmet of Physics, Ithaca College 953 Daby Road, Ithaca NY 14850, USA email: saderso@ithaca.edu ad Dai Novak Departmet of Mathematics, Ithaca College
Measure and Measurable Functions
 3 Measure ad Measurable Fuctios 3.1 Measure o a Arbitrary σ-algebra Recall from Chapter 2 that the set M of all Lebesgue measurable sets has the followig properties: R M, E M implies E c M, E M for N implies
3 Measure ad Measurable Fuctios 3.1 Measure o a Arbitrary σ-algebra Recall from Chapter 2 that the set M of all Lebesgue measurable sets has the followig properties: R M, E M implies E c M, E M for N implies
1 Outline. 2 Kakeya in Analysis. Kakeya Sets: The Paper: The Talk. I aim to cover roughly the following things:
 Kakeya Sets: The Paper: The Talk 1 Outlie I aim to cover roughly the followig thigs: 1 Brief history of the Kakeya problem i aalysis 2 The ite-eld Kakeya problem >> Dvir's solutio 3 Kakeya over o-archimedea
Kakeya Sets: The Paper: The Talk 1 Outlie I aim to cover roughly the followig thigs: 1 Brief history of the Kakeya problem i aalysis 2 The ite-eld Kakeya problem >> Dvir's solutio 3 Kakeya over o-archimedea
If a subset E of R contains no open interval, is it of zero measure? For instance, is the set of irrationals in [0, 1] is of measure zero?
![If a subset E of R contains no open interval, is it of zero measure? For instance, is the set of irrationals in [0, 1] is of measure zero? If a subset E of R contains no open interval, is it of zero measure? For instance, is the set of irrationals in [0, 1] is of measure zero?](/thumbs/89/99848926.jpg) 2 Lebesgue Measure I Chapter 1 we defied the cocept of a set of measure zero, ad we have observed that every coutable set is of measure zero. Here are some atural questios: If a subset E of R cotais a
2 Lebesgue Measure I Chapter 1 we defied the cocept of a set of measure zero, ad we have observed that every coutable set is of measure zero. Here are some atural questios: If a subset E of R cotais a
Chapter 3. Strong convergence. 3.1 Definition of almost sure convergence
 Chapter 3 Strog covergece As poited out i the Chapter 2, there are multiple ways to defie the otio of covergece of a sequece of radom variables. That chapter defied covergece i probability, covergece i
Chapter 3 Strog covergece As poited out i the Chapter 2, there are multiple ways to defie the otio of covergece of a sequece of radom variables. That chapter defied covergece i probability, covergece i
M A T H F A L L CORRECTION. Algebra I 1 4 / 1 0 / U N I V E R S I T Y O F T O R O N T O
 M A T H 2 4 0 F A L L 2 0 1 4 HOMEWORK ASSIGNMENT #4 CORRECTION Algebra I 1 4 / 1 0 / 2 0 1 4 U N I V E R S I T Y O F T O R O N T O P r o f e s s o r : D r o r B a r - N a t a Correctio Homework Assigmet
M A T H 2 4 0 F A L L 2 0 1 4 HOMEWORK ASSIGNMENT #4 CORRECTION Algebra I 1 4 / 1 0 / 2 0 1 4 U N I V E R S I T Y O F T O R O N T O P r o f e s s o r : D r o r B a r - N a t a Correctio Homework Assigmet
Stochastic Matrices in a Finite Field
 Stochastic Matrices i a Fiite Field Abstract: I this project we will explore the properties of stochastic matrices i both the real ad the fiite fields. We first explore what properties 2 2 stochastic matrices
Stochastic Matrices i a Fiite Field Abstract: I this project we will explore the properties of stochastic matrices i both the real ad the fiite fields. We first explore what properties 2 2 stochastic matrices
Math 104: Homework 2 solutions
 Math 04: Homework solutios. A (0, ): Sice this is a ope iterval, the miimum is udefied, ad sice the set is ot bouded above, the maximum is also udefied. if A 0 ad sup A. B { m + : m, N}: This set does
Math 04: Homework solutios. A (0, ): Sice this is a ope iterval, the miimum is udefied, ad sice the set is ot bouded above, the maximum is also udefied. if A 0 ad sup A. B { m + : m, N}: This set does
Simple Polygons of Maximum Perimeter Contained in a Unit Disk
 Discrete Comput Geom (009) 1: 08 15 DOI 10.1007/s005-008-9093-7 Simple Polygos of Maximum Perimeter Cotaied i a Uit Disk Charles Audet Pierre Hase Frédéric Messie Received: 18 September 007 / Revised:
Discrete Comput Geom (009) 1: 08 15 DOI 10.1007/s005-008-9093-7 Simple Polygos of Maximum Perimeter Cotaied i a Uit Disk Charles Audet Pierre Hase Frédéric Messie Received: 18 September 007 / Revised:
MASSACHUSETTS INSTITUTE OF TECHNOLOGY 6.436J/15.085J Fall 2008 Lecture 19 11/17/2008 LAWS OF LARGE NUMBERS II THE STRONG LAW OF LARGE NUMBERS
 MASSACHUSTTS INSTITUT OF TCHNOLOGY 6.436J/5.085J Fall 2008 Lecture 9 /7/2008 LAWS OF LARG NUMBRS II Cotets. The strog law of large umbers 2. The Cheroff boud TH STRONG LAW OF LARG NUMBRS While the weak
MASSACHUSTTS INSTITUT OF TCHNOLOGY 6.436J/5.085J Fall 2008 Lecture 9 /7/2008 LAWS OF LARG NUMBRS II Cotets. The strog law of large umbers 2. The Cheroff boud TH STRONG LAW OF LARG NUMBRS While the weak
Algebra of Least Squares
 October 19, 2018 Algebra of Least Squares Geometry of Least Squares Recall that out data is like a table [Y X] where Y collects observatios o the depedet variable Y ad X collects observatios o the k-dimesioal
October 19, 2018 Algebra of Least Squares Geometry of Least Squares Recall that out data is like a table [Y X] where Y collects observatios o the depedet variable Y ad X collects observatios o the k-dimesioal
SOME TRIBONACCI IDENTITIES
 Mathematics Today Vol.7(Dec-011) 1-9 ISSN 0976-38 Abstract: SOME TRIBONACCI IDENTITIES Shah Devbhadra V. Sir P.T.Sarvajaik College of Sciece, Athwalies, Surat 395001. e-mail : drdvshah@yahoo.com The sequece
Mathematics Today Vol.7(Dec-011) 1-9 ISSN 0976-38 Abstract: SOME TRIBONACCI IDENTITIES Shah Devbhadra V. Sir P.T.Sarvajaik College of Sciece, Athwalies, Surat 395001. e-mail : drdvshah@yahoo.com The sequece
ON THE LEHMER CONSTANT OF FINITE CYCLIC GROUPS
 ON THE LEHMER CONSTANT OF FINITE CYCLIC GROUPS NORBERT KAIBLINGER Abstract. Results of Lid o Lehmer s problem iclude the value of the Lehmer costat of the fiite cyclic group Z/Z, for 5 ad all odd. By complemetary
ON THE LEHMER CONSTANT OF FINITE CYCLIC GROUPS NORBERT KAIBLINGER Abstract. Results of Lid o Lehmer s problem iclude the value of the Lehmer costat of the fiite cyclic group Z/Z, for 5 ad all odd. By complemetary
A Simplified Binet Formula for k-generalized Fibonacci Numbers
 A Simplified Biet Formula for k-geeralized Fiboacci Numbers Gregory P. B. Dresde Departmet of Mathematics Washigto ad Lee Uiversity Lexigto, VA 440 dresdeg@wlu.edu Zhaohui Du Shaghai, Chia zhao.hui.du@gmail.com
A Simplified Biet Formula for k-geeralized Fiboacci Numbers Gregory P. B. Dresde Departmet of Mathematics Washigto ad Lee Uiversity Lexigto, VA 440 dresdeg@wlu.edu Zhaohui Du Shaghai, Chia zhao.hui.du@gmail.com
The Boolean Ring of Intervals
 MATH 532 Lebesgue Measure Dr. Neal, WKU We ow shall apply the results obtaied about outer measure to the legth measure o the real lie. Throughout, our space X will be the set of real umbers R. Whe ecessary,
MATH 532 Lebesgue Measure Dr. Neal, WKU We ow shall apply the results obtaied about outer measure to the legth measure o the real lie. Throughout, our space X will be the set of real umbers R. Whe ecessary,
A REMARK ON A PROBLEM OF KLEE
 C O L L O Q U I U M M A T H E M A T I C U M VOL. 71 1996 NO. 1 A REMARK ON A PROBLEM OF KLEE BY N. J. K A L T O N (COLUMBIA, MISSOURI) AND N. T. P E C K (URBANA, ILLINOIS) This paper treats a property
C O L L O Q U I U M M A T H E M A T I C U M VOL. 71 1996 NO. 1 A REMARK ON A PROBLEM OF KLEE BY N. J. K A L T O N (COLUMBIA, MISSOURI) AND N. T. P E C K (URBANA, ILLINOIS) This paper treats a property
Optimization Methods: Linear Programming Applications Assignment Problem 1. Module 4 Lecture Notes 3. Assignment Problem
 Optimizatio Methods: Liear Programmig Applicatios Assigmet Problem Itroductio Module 4 Lecture Notes 3 Assigmet Problem I the previous lecture, we discussed about oe of the bech mark problems called trasportatio
Optimizatio Methods: Liear Programmig Applicatios Assigmet Problem Itroductio Module 4 Lecture Notes 3 Assigmet Problem I the previous lecture, we discussed about oe of the bech mark problems called trasportatio
Sequences. Notation. Convergence of a Sequence
 Sequeces A sequece is essetially just a list. Defiitio (Sequece of Real Numbers). A sequece of real umbers is a fuctio Z (, ) R for some real umber. Do t let the descriptio of the domai cofuse you; it
Sequeces A sequece is essetially just a list. Defiitio (Sequece of Real Numbers). A sequece of real umbers is a fuctio Z (, ) R for some real umber. Do t let the descriptio of the domai cofuse you; it
Sequences A sequence of numbers is a function whose domain is the positive integers. We can see that the sequence
 Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece 1, 1, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet
Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece 1, 1, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet
CHAPTER 10 INFINITE SEQUENCES AND SERIES
 CHAPTER 10 INFINITE SEQUENCES AND SERIES 10.1 Sequeces 10.2 Ifiite Series 10.3 The Itegral Tests 10.4 Compariso Tests 10.5 The Ratio ad Root Tests 10.6 Alteratig Series: Absolute ad Coditioal Covergece
CHAPTER 10 INFINITE SEQUENCES AND SERIES 10.1 Sequeces 10.2 Ifiite Series 10.3 The Itegral Tests 10.4 Compariso Tests 10.5 The Ratio ad Root Tests 10.6 Alteratig Series: Absolute ad Coditioal Covergece
A 2nTH ORDER LINEAR DIFFERENCE EQUATION
 A 2TH ORDER LINEAR DIFFERENCE EQUATION Doug Aderso Departmet of Mathematics ad Computer Sciece, Cocordia College Moorhead, MN 56562, USA ABSTRACT: We give a formulatio of geeralized zeros ad (, )-discojugacy
A 2TH ORDER LINEAR DIFFERENCE EQUATION Doug Aderso Departmet of Mathematics ad Computer Sciece, Cocordia College Moorhead, MN 56562, USA ABSTRACT: We give a formulatio of geeralized zeros ad (, )-discojugacy
Complex Analysis Spring 2001 Homework I Solution
 Complex Aalysis Sprig 2001 Homework I Solutio 1. Coway, Chapter 1, sectio 3, problem 3. Describe the set of poits satisfyig the equatio z a z + a = 2c, where c > 0 ad a R. To begi, we see from the triagle
Complex Aalysis Sprig 2001 Homework I Solutio 1. Coway, Chapter 1, sectio 3, problem 3. Describe the set of poits satisfyig the equatio z a z + a = 2c, where c > 0 ad a R. To begi, we see from the triagle
1. By using truth tables prove that, for all statements P and Q, the statement
 Author: Satiago Salazar Problems I: Mathematical Statemets ad Proofs. By usig truth tables prove that, for all statemets P ad Q, the statemet P Q ad its cotrapositive ot Q (ot P) are equivalet. I example.2.3
Author: Satiago Salazar Problems I: Mathematical Statemets ad Proofs. By usig truth tables prove that, for all statemets P ad Q, the statemet P Q ad its cotrapositive ot Q (ot P) are equivalet. I example.2.3
Lecture XVI - Lifting of paths and homotopies
 Lecture XVI - Liftig of paths ad homotopies I the last lecture we discussed the liftig problem ad proved that the lift if it exists is uiquely determied by its value at oe poit. I this lecture we shall
Lecture XVI - Liftig of paths ad homotopies I the last lecture we discussed the liftig problem ad proved that the lift if it exists is uiquely determied by its value at oe poit. I this lecture we shall
Introduction to Machine Learning DIS10
 CS 189 Fall 017 Itroductio to Machie Learig DIS10 1 Fu with Lagrage Multipliers (a) Miimize the fuctio such that f (x,y) = x + y x + y = 3. Solutio: The Lagragia is: L(x,y,λ) = x + y + λ(x + y 3) Takig
CS 189 Fall 017 Itroductio to Machie Learig DIS10 1 Fu with Lagrage Multipliers (a) Miimize the fuctio such that f (x,y) = x + y x + y = 3. Solutio: The Lagragia is: L(x,y,λ) = x + y + λ(x + y 3) Takig
The Discrete Fourier Transform
 The Discrete Fourier Trasform Complex Fourier Series Represetatio Recall that a Fourier series has the form a 0 + a k cos(kt) + k=1 b k si(kt) This represetatio seems a bit awkward, sice it ivolves two
The Discrete Fourier Trasform Complex Fourier Series Represetatio Recall that a Fourier series has the form a 0 + a k cos(kt) + k=1 b k si(kt) This represetatio seems a bit awkward, sice it ivolves two
Chapter 6 Principles of Data Reduction
 Chapter 6 for BST 695: Special Topics i Statistical Theory. Kui Zhag, 0 Chapter 6 Priciples of Data Reductio Sectio 6. Itroductio Goal: To summarize or reduce the data X, X,, X to get iformatio about a
Chapter 6 for BST 695: Special Topics i Statistical Theory. Kui Zhag, 0 Chapter 6 Priciples of Data Reductio Sectio 6. Itroductio Goal: To summarize or reduce the data X, X,, X to get iformatio about a
An Introduction to Randomized Algorithms
 A Itroductio to Radomized Algorithms The focus of this lecture is to study a radomized algorithm for quick sort, aalyze it usig probabilistic recurrece relatios, ad also provide more geeral tools for aalysis
A Itroductio to Radomized Algorithms The focus of this lecture is to study a radomized algorithm for quick sort, aalyze it usig probabilistic recurrece relatios, ad also provide more geeral tools for aalysis
September 2012 C1 Note. C1 Notes (Edexcel) Copyright - For AS, A2 notes and IGCSE / GCSE worksheets 1
 September 0 s (Edecel) Copyright www.pgmaths.co.uk - For AS, A otes ad IGCSE / GCSE worksheets September 0 Copyright www.pgmaths.co.uk - For AS, A otes ad IGCSE / GCSE worksheets September 0 Copyright
September 0 s (Edecel) Copyright www.pgmaths.co.uk - For AS, A otes ad IGCSE / GCSE worksheets September 0 Copyright www.pgmaths.co.uk - For AS, A otes ad IGCSE / GCSE worksheets September 0 Copyright
Lecture Notes for Analysis Class
 Lecture Notes for Aalysis Class Topological Spaces A topology for a set X is a collectio T of subsets of X such that: (a) X ad the empty set are i T (b) Uios of elemets of T are i T (c) Fiite itersectios
Lecture Notes for Aalysis Class Topological Spaces A topology for a set X is a collectio T of subsets of X such that: (a) X ad the empty set are i T (b) Uios of elemets of T are i T (c) Fiite itersectios
Week 5-6: The Binomial Coefficients
 Wee 5-6: The Biomial Coefficiets March 6, 2018 1 Pascal Formula Theorem 11 (Pascal s Formula For itegers ad such that 1, ( ( ( 1 1 + 1 The umbers ( 2 ( 1 2 ( 2 are triagle umbers, that is, The petago umbers
Wee 5-6: The Biomial Coefficiets March 6, 2018 1 Pascal Formula Theorem 11 (Pascal s Formula For itegers ad such that 1, ( ( ( 1 1 + 1 The umbers ( 2 ( 1 2 ( 2 are triagle umbers, that is, The petago umbers
Linear Regression Demystified
 Liear Regressio Demystified Liear regressio is a importat subject i statistics. I elemetary statistics courses, formulae related to liear regressio are ofte stated without derivatio. This ote iteds to
Liear Regressio Demystified Liear regressio is a importat subject i statistics. I elemetary statistics courses, formulae related to liear regressio are ofte stated without derivatio. This ote iteds to
Support vector machine revisited
 6.867 Machie learig, lecture 8 (Jaakkola) 1 Lecture topics: Support vector machie ad kerels Kerel optimizatio, selectio Support vector machie revisited Our task here is to first tur the support vector
6.867 Machie learig, lecture 8 (Jaakkola) 1 Lecture topics: Support vector machie ad kerels Kerel optimizatio, selectio Support vector machie revisited Our task here is to first tur the support vector
4.3 Growth Rates of Solutions to Recurrences
 4.3. GROWTH RATES OF SOLUTIONS TO RECURRENCES 81 4.3 Growth Rates of Solutios to Recurreces 4.3.1 Divide ad Coquer Algorithms Oe of the most basic ad powerful algorithmic techiques is divide ad coquer.
4.3. GROWTH RATES OF SOLUTIONS TO RECURRENCES 81 4.3 Growth Rates of Solutios to Recurreces 4.3.1 Divide ad Coquer Algorithms Oe of the most basic ad powerful algorithmic techiques is divide ad coquer.
Resolution Proofs of Generalized Pigeonhole Principles
 Resolutio Proofs of Geeralized Pigeohole Priciples Samuel R. Buss Departmet of Mathematics Uiversity of Califoria, Berkeley Győrgy Turá Departmet of Mathematics, Statistics, ad Computer Sciece Uiversity
Resolutio Proofs of Geeralized Pigeohole Priciples Samuel R. Buss Departmet of Mathematics Uiversity of Califoria, Berkeley Győrgy Turá Departmet of Mathematics, Statistics, ad Computer Sciece Uiversity
Bertrand s Postulate
 Bertrad s Postulate Lola Thompso Ross Program July 3, 2009 Lola Thompso (Ross Program Bertrad s Postulate July 3, 2009 1 / 33 Bertrad s Postulate I ve said it oce ad I ll say it agai: There s always a
Bertrad s Postulate Lola Thompso Ross Program July 3, 2009 Lola Thompso (Ross Program Bertrad s Postulate July 3, 2009 1 / 33 Bertrad s Postulate I ve said it oce ad I ll say it agai: There s always a
Lecture 3 The Lebesgue Integral
 Lecture 3: The Lebesgue Itegral 1 of 14 Course: Theory of Probability I Term: Fall 2013 Istructor: Gorda Zitkovic Lecture 3 The Lebesgue Itegral The costructio of the itegral Uless expressly specified
Lecture 3: The Lebesgue Itegral 1 of 14 Course: Theory of Probability I Term: Fall 2013 Istructor: Gorda Zitkovic Lecture 3 The Lebesgue Itegral The costructio of the itegral Uless expressly specified
Square-Congruence Modulo n
 Square-Cogruece Modulo Abstract This paper is a ivestigatio of a equivalece relatio o the itegers that was itroduced as a exercise i our Discrete Math class. Part I - Itro Defiitio Two itegers are Square-Cogruet
Square-Cogruece Modulo Abstract This paper is a ivestigatio of a equivalece relatio o the itegers that was itroduced as a exercise i our Discrete Math class. Part I - Itro Defiitio Two itegers are Square-Cogruet
IP Reference guide for integer programming formulations.
 IP Referece guide for iteger programmig formulatios. by James B. Orli for 15.053 ad 15.058 This documet is iteded as a compact (or relatively compact) guide to the formulatio of iteger programs. For more
IP Referece guide for iteger programmig formulatios. by James B. Orli for 15.053 ad 15.058 This documet is iteded as a compact (or relatively compact) guide to the formulatio of iteger programs. For more
Integer Linear Programming
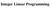 Iteger Liear Programmig Itroductio Iteger L P problem (P) Mi = s. t. a = b i =,, m = i i 0, iteger =,, c Eemple Mi z = 5 s. t. + 0 0, 0, iteger F(P) = feasible domai of P Itroductio Iteger L P problem
Iteger Liear Programmig Itroductio Iteger L P problem (P) Mi = s. t. a = b i =,, m = i i 0, iteger =,, c Eemple Mi z = 5 s. t. + 0 0, 0, iteger F(P) = feasible domai of P Itroductio Iteger L P problem
On Random Line Segments in the Unit Square
 O Radom Lie Segmets i the Uit Square Thomas A. Courtade Departmet of Electrical Egieerig Uiversity of Califoria Los Ageles, Califoria 90095 Email: tacourta@ee.ucla.edu I. INTRODUCTION Let Q = [0, 1] [0,
O Radom Lie Segmets i the Uit Square Thomas A. Courtade Departmet of Electrical Egieerig Uiversity of Califoria Los Ageles, Califoria 90095 Email: tacourta@ee.ucla.edu I. INTRODUCTION Let Q = [0, 1] [0,
subject to A 1 x + A 2 y b x j 0, j = 1,,n 1 y j = 0 or 1, j = 1,,n 2
 Additioal Brach ad Boud Algorithms 0-1 Mixed-Iteger Liear Programmig The brach ad boud algorithm described i the previous sectios ca be used to solve virtually all optimizatio problems cotaiig iteger variables,
Additioal Brach ad Boud Algorithms 0-1 Mixed-Iteger Liear Programmig The brach ad boud algorithm described i the previous sectios ca be used to solve virtually all optimizatio problems cotaiig iteger variables,
1 Introduction. 1.1 Notation and Terminology
 1 Itroductio You have already leared some cocepts of calculus such as limit of a sequece, limit, cotiuity, derivative, ad itegral of a fuctio etc. Real Aalysis studies them more rigorously usig a laguage
1 Itroductio You have already leared some cocepts of calculus such as limit of a sequece, limit, cotiuity, derivative, ad itegral of a fuctio etc. Real Aalysis studies them more rigorously usig a laguage
U8L1: Sec Equations of Lines in R 2
 MCVU U8L: Sec. 8.9. Equatios of Lies i R Review of Equatios of a Straight Lie (-D) Cosider the lie passig through A (-,) with slope, as show i the diagram below. I poit slope form, the equatio of the lie
MCVU U8L: Sec. 8.9. Equatios of Lies i R Review of Equatios of a Straight Lie (-D) Cosider the lie passig through A (-,) with slope, as show i the diagram below. I poit slope form, the equatio of the lie
Feedback in Iterative Algorithms
 Feedback i Iterative Algorithms Charles Byre (Charles Byre@uml.edu), Departmet of Mathematical Scieces, Uiversity of Massachusetts Lowell, Lowell, MA 01854 October 17, 2005 Abstract Whe the oegative system
Feedback i Iterative Algorithms Charles Byre (Charles Byre@uml.edu), Departmet of Mathematical Scieces, Uiversity of Massachusetts Lowell, Lowell, MA 01854 October 17, 2005 Abstract Whe the oegative system
A Note on the Symmetric Powers of the Standard Representation of S n
 A Note o the Symmetric Powers of the Stadard Represetatio of S David Savitt 1 Departmet of Mathematics, Harvard Uiversity Cambridge, MA 0138, USA dsavitt@mathharvardedu Richard P Staley Departmet of Mathematics,
A Note o the Symmetric Powers of the Stadard Represetatio of S David Savitt 1 Departmet of Mathematics, Harvard Uiversity Cambridge, MA 0138, USA dsavitt@mathharvardedu Richard P Staley Departmet of Mathematics,
5 Birkhoff s Ergodic Theorem
 5 Birkhoff s Ergodic Theorem Amog the most useful of the various geeralizatios of KolmogorovâĂŹs strog law of large umbers are the ergodic theorems of Birkhoff ad Kigma, which exted the validity of the
5 Birkhoff s Ergodic Theorem Amog the most useful of the various geeralizatios of KolmogorovâĂŹs strog law of large umbers are the ergodic theorems of Birkhoff ad Kigma, which exted the validity of the
Math 220A Fall 2007 Homework #2. Will Garner A
 Math 0A Fall 007 Homewor # Will Garer Pg 3 #: Show that {cis : a o-egative iteger} is dese i T = {z œ : z = }. For which values of q is {cis(q): a o-egative iteger} dese i T? To show that {cis : a o-egative
Math 0A Fall 007 Homewor # Will Garer Pg 3 #: Show that {cis : a o-egative iteger} is dese i T = {z œ : z = }. For which values of q is {cis(q): a o-egative iteger} dese i T? To show that {cis : a o-egative
A sequence of numbers is a function whose domain is the positive integers. We can see that the sequence
 Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece,, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet as
Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece,, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet as
THE ASYMPTOTIC COMPLEXITY OF MATRIX REDUCTION OVER FINITE FIELDS
 THE ASYMPTOTIC COMPLEXITY OF MATRIX REDUCTION OVER FINITE FIELDS DEMETRES CHRISTOFIDES Abstract. Cosider a ivertible matrix over some field. The Gauss-Jorda elimiatio reduces this matrix to the idetity
THE ASYMPTOTIC COMPLEXITY OF MATRIX REDUCTION OVER FINITE FIELDS DEMETRES CHRISTOFIDES Abstract. Cosider a ivertible matrix over some field. The Gauss-Jorda elimiatio reduces this matrix to the idetity
The natural exponential function
 The atural expoetial fuctio Attila Máté Brookly College of the City Uiversity of New York December, 205 Cotets The atural expoetial fuctio for real x. Beroulli s iequality.....................................2
The atural expoetial fuctio Attila Máté Brookly College of the City Uiversity of New York December, 205 Cotets The atural expoetial fuctio for real x. Beroulli s iequality.....................................2
Riesz-Fischer Sequences and Lower Frame Bounds
 Zeitschrift für Aalysis ud ihre Aweduge Joural for Aalysis ad its Applicatios Volume 1 (00), No., 305 314 Riesz-Fischer Sequeces ad Lower Frame Bouds P. Casazza, O. Christese, S. Li ad A. Lider Abstract.
Zeitschrift für Aalysis ud ihre Aweduge Joural for Aalysis ad its Applicatios Volume 1 (00), No., 305 314 Riesz-Fischer Sequeces ad Lower Frame Bouds P. Casazza, O. Christese, S. Li ad A. Lider Abstract.
On Involutions which Preserve Natural Filtration
 Proceedigs of Istitute of Mathematics of NAS of Ukraie 00, Vol. 43, Part, 490 494 O Ivolutios which Preserve Natural Filtratio Alexader V. STRELETS Istitute of Mathematics of the NAS of Ukraie, 3 Tereshchekivska
Proceedigs of Istitute of Mathematics of NAS of Ukraie 00, Vol. 43, Part, 490 494 O Ivolutios which Preserve Natural Filtratio Alexader V. STRELETS Istitute of Mathematics of the NAS of Ukraie, 3 Tereshchekivska
7 Sequences of real numbers
 40 7 Sequeces of real umbers 7. Defiitios ad examples Defiitio 7... A sequece of real umbers is a real fuctio whose domai is the set N of atural umbers. Let s : N R be a sequece. The the values of s are
40 7 Sequeces of real umbers 7. Defiitios ad examples Defiitio 7... A sequece of real umbers is a real fuctio whose domai is the set N of atural umbers. Let s : N R be a sequece. The the values of s are
The Borel hierarchy classifies subsets of the reals by their topological complexity. Another approach is to classify them by size.
 Lecture 7: Measure ad Category The Borel hierarchy classifies subsets of the reals by their topological complexity. Aother approach is to classify them by size. Filters ad Ideals The most commo measure
Lecture 7: Measure ad Category The Borel hierarchy classifies subsets of the reals by their topological complexity. Aother approach is to classify them by size. Filters ad Ideals The most commo measure
Integrable Functions. { f n } is called a determining sequence for f. If f is integrable with respect to, then f d does exist as a finite real number
 MATH 532 Itegrable Fuctios Dr. Neal, WKU We ow shall defie what it meas for a measurable fuctio to be itegrable, show that all itegral properties of simple fuctios still hold, ad the give some coditios
MATH 532 Itegrable Fuctios Dr. Neal, WKU We ow shall defie what it meas for a measurable fuctio to be itegrable, show that all itegral properties of simple fuctios still hold, ad the give some coditios
Random Walks on Discrete and Continuous Circles. by Jeffrey S. Rosenthal School of Mathematics, University of Minnesota, Minneapolis, MN, U.S.A.
 Radom Walks o Discrete ad Cotiuous Circles by Jeffrey S. Rosethal School of Mathematics, Uiversity of Miesota, Mieapolis, MN, U.S.A. 55455 (Appeared i Joural of Applied Probability 30 (1993), 780 789.)
Radom Walks o Discrete ad Cotiuous Circles by Jeffrey S. Rosethal School of Mathematics, Uiversity of Miesota, Mieapolis, MN, U.S.A. 55455 (Appeared i Joural of Applied Probability 30 (1993), 780 789.)
Linear Programming and the Simplex Method
 Liear Programmig ad the Simplex ethod Abstract This article is a itroductio to Liear Programmig ad usig Simplex method for solvig LP problems i primal form. What is Liear Programmig? Liear Programmig is
Liear Programmig ad the Simplex ethod Abstract This article is a itroductio to Liear Programmig ad usig Simplex method for solvig LP problems i primal form. What is Liear Programmig? Liear Programmig is
Axioms of Measure Theory
 MATH 532 Axioms of Measure Theory Dr. Neal, WKU I. The Space Throughout the course, we shall let X deote a geeric o-empty set. I geeral, we shall ot assume that ay algebraic structure exists o X so that
MATH 532 Axioms of Measure Theory Dr. Neal, WKU I. The Space Throughout the course, we shall let X deote a geeric o-empty set. I geeral, we shall ot assume that ay algebraic structure exists o X so that
CHAPTER 5. Theory and Solution Using Matrix Techniques
 A SERIES OF CLASS NOTES FOR 2005-2006 TO INTRODUCE LINEAR AND NONLINEAR PROBLEMS TO ENGINEERS, SCIENTISTS, AND APPLIED MATHEMATICIANS DE CLASS NOTES 3 A COLLECTION OF HANDOUTS ON SYSTEMS OF ORDINARY DIFFERENTIAL
A SERIES OF CLASS NOTES FOR 2005-2006 TO INTRODUCE LINEAR AND NONLINEAR PROBLEMS TO ENGINEERS, SCIENTISTS, AND APPLIED MATHEMATICIANS DE CLASS NOTES 3 A COLLECTION OF HANDOUTS ON SYSTEMS OF ORDINARY DIFFERENTIAL
Lecture Overview. 2 Permutations and Combinations. n(n 1) (n (k 1)) = n(n 1) (n k + 1) =
 COMPSCI 230: Discrete Mathematics for Computer Sciece April 8, 2019 Lecturer: Debmalya Paigrahi Lecture 22 Scribe: Kevi Su 1 Overview I this lecture, we begi studyig the fudametals of coutig discrete objects.
COMPSCI 230: Discrete Mathematics for Computer Sciece April 8, 2019 Lecturer: Debmalya Paigrahi Lecture 22 Scribe: Kevi Su 1 Overview I this lecture, we begi studyig the fudametals of coutig discrete objects.
(3) If you replace row i of A by its sum with a multiple of another row, then the determinant is unchanged! Expand across the i th row:
 Math 5-4 Tue Feb 4 Cotiue with sectio 36 Determiats The effective way to compute determiats for larger-sized matrices without lots of zeroes is to ot use the defiitio, but rather to use the followig facts,
Math 5-4 Tue Feb 4 Cotiue with sectio 36 Determiats The effective way to compute determiats for larger-sized matrices without lots of zeroes is to ot use the defiitio, but rather to use the followig facts,
10-701/ Machine Learning Mid-term Exam Solution
 0-70/5-78 Machie Learig Mid-term Exam Solutio Your Name: Your Adrew ID: True or False (Give oe setece explaatio) (20%). (F) For a cotiuous radom variable x ad its probability distributio fuctio p(x), it
0-70/5-78 Machie Learig Mid-term Exam Solutio Your Name: Your Adrew ID: True or False (Give oe setece explaatio) (20%). (F) For a cotiuous radom variable x ad its probability distributio fuctio p(x), it
REVISION SHEET FP1 (MEI) ALGEBRA. Identities In mathematics, an identity is a statement which is true for all values of the variables it contains.
 The mai ideas are: Idetities REVISION SHEET FP (MEI) ALGEBRA Before the exam you should kow: If a expressio is a idetity the it is true for all values of the variable it cotais The relatioships betwee
The mai ideas are: Idetities REVISION SHEET FP (MEI) ALGEBRA Before the exam you should kow: If a expressio is a idetity the it is true for all values of the variable it cotais The relatioships betwee
