Two Applications of the Generalized Ptolemy Theorem
|
|
|
- Alvin Hodges
- 5 years ago
- Views:
Transcription
1 Two Applications of the Generalized Ptolemy Theorem Shay Gueron 1. INTRODUCTION. The classical theorem of Ptolemy (used for computations by Claudius Ptolemaeus of Alexandria, 2nd century AD, but probably known even before him [7, pp ) states that if A, B, C, D are, in this order, four points on the circle 0, then IABI x lcdi + ladl x lbcl = lacl x IBDl. This result includes Pythagoras' Theorem when applied to a rectangle, and yields other important trigonometric identities when applied to special cyclic quadrilaterals A BCD. For example, if the diagonal AC is a diameter, lacl = 1, idac = a, and ibac = P, then Ptolemy's Theorem gives sin(a + P) = sin a cos /3 + sin /3 cos a. In a more gen- eral context, Ptolemy's Theorem is the inequality labl x lcdl + ladl x I BCI > lacl x I BDI, where equality occurs if and only if A, B, C, D lie (in this order) on a circle or on a line. This formulation of the theorem can be viewed as the "image under inversion7' of the triangle inequality [ll, p Ptolemy's Theorem can be generalized to the situation where the points A, B, C, D are replaced by four circles that touch 0. Our goal is to show how the Generalized Ptolemy Theorem can be used to prove two results in plane geometry. The first result, Theorem 1, is a generalization of a theorem that was originally proposed in 1938, as a MONTHLY problem, by the French geometer Victor ThCbault [15]. ThCbault's Theorem remained an open problem (allegedly a tough one, see [lo, p ) for some 45 years, until it was proved in 1983 by Taylor [16]. Taylor's proof used analytic geometry and involved lengthy computations. It was therefore cited only in abbreviated form. A shorter (trigonometric) proof for ThCbault's Theorem was found in 1986 by Tuwald [17], and a synthetic proof (which also generalizes the problem) was found by Stark in 1989 [14]. Another (still lengthy) proof based on analytic geometry, in which computer algebra software is employed for carrying out the computations, was recently proposed by Shail [12]. Our generalization of Thkbault's Theorem is the following. Theorem 1 (Exteal ThCbault Theorem). Let AABC be a triangle, let (0, R) be its circumcircle, and let D be a point on BC such that ibda = 0; see Figure 2b. Let (01, rl) be a circle touching BC (produced) at P, toztching AD (produced) at M, and touching 0 (exteally). Let (02, r2) be a circle touching BC (produced) at Q, touching AD (produced) at N, and touching 0 (exteally). Let (I,, r,) be the excircle of AA BC, touching the side BC and the sides A B, AC (produced). Then: (a) r, = rl cos2(0/2) + r2 sin2(0/2). (b) The lines ll and 12 passing through P and Q, respectively, parallel to AD, are tangent to the excircle (I,,r,). (c) 01,02,and I, are collinear. (d) O1Ia/021a= tan2(0/2). Theorem 1 is a dual (an exteal form) of ThCbault's Theorem. In the latter, (01, rl) and (02, r2) touch the sides BD and CD (at inteal points on the respective sides) THE MATHEMATICAL ASSOCIATION OF AMERICA [Monthly 109
2 and touch 0 inteally; see Figure 2a. (I,r) is the incircle of AABC, and the statement claims that r = rl cos2(q/2) + r2 sin2(q/2); 01, 02, and I are collinear; and O1I/O2I = tan2 (812). Part of the original formulation of the problem in [15] (namely, that rl + r2 = r2 sec2(q/2)) was erroneous. Special cases of ThCbault's Theorem have appeared as problems. The case in which the touching points M and N coincide was discussed in [13]. The author used the Generalized Ptolemy Theorem to prove this simplified version of ThCbault's Theorem, noticed the natural relation to the more general case, and stated that he was not able to extend this technique to prove it. The case in which AABC is isosceles and 0 = 90" appeared in [3, problem The case in which Q = 90" appeared in [4]. The solutions [5] and [6] considered the general case and gave references to proofs of ThCbault's Theorem published (in Dutch) prior to Taylor's proof. Our second result generalizes the following well-known property: Let the circles cl, c2 touch each other exteally and touch the circle c inteally, and let their common inteal tangent intersect c at the point X. Then, the tangent to c that passes through X is parallel to the common exteal tangent of cl and c2 that lies on the same side of cl, c2 as X. We extend this geometric situation to the case where cl and c:! are disjoint. Theorem 2 (The Parallel Tangent Theorem). Let c be a given circle, and let cl and c2 be two disjoint circles touching c: (a) inteally (as in Figure 3a); (b) exteally (as in Figure 3b); (c) from different sides (as in Figure 3c). Denote the common (a) inteal; (b) inteal; (c) exteal tangents of cl and c2 by L1 and L2, respectively, and denote their points of intersection with c by B and A, respectively. Let L3 be a common (a) exteal; (b) exteal; (c) inteal tangent to cl and c2 that lies on the same side as A and B. Then AB is parallel to L3. Before proving Theorems 1 and 2, we first review the Generalized Ptolemy Theorem. 2. ON THE THE GENERALIZED PTOLEMY THEOREM. The Generalized Ptolemy Theorem was first stated by John Casey as early as 1881 [I] (in [3, p. 1201, the statement is dated 1857), although there is some indication [3, p that it was known in Japan even before Casey. The complete statement of the Generalized Ptolemy Theorem involves several cases, and Casey's original statement did not sufficiently restrict the discussion of these cases; see [I, p and remarks in [2, Theorem 45, pp ]. On the other hand, other authors only partially formulate the Generalized Ptolemy Theorem. For example, see [2] and the related comments in [8, p and [7, p The first complete discussion of the Generalized Ptolemy Theorem is probably due to Johnson [8, pp Notations: We identify circles by giving their center, or by giving their center and radius. Suppose that 0 is a nondegenerate circle and that the two circles O1 andx2, neither of which includes the other, touch 0 at two distinct points. The notation O1 0 2 denotes the length of (1) the common exteal tangent of O1 and O2 (i.e., O1 and 02 lie on the same side of this tangent) if both of circles touch 0 from the same side; (2) the common inteal tangent of O1 and O2 (i.e., O1 and O2 lie on opposite sides of this tangent) if O1 and O2 touch 0 from opposite sides; (3) the tangent to 0 2, extended from 01, if the circle O1 is degenerate (i.e., zero radius); or (4) the line segment O1 0 2 if both O1 and O2 are degenerate circles. April TWO APPLICATIONS OF THE GENERALIZED PTOLEMY THEOREM 363
3 Theorem 3 (The Generalized Ptolemy Theorem). Let 0 be a nondegenerate circle, and let A, B, C, D be, in this order; four distinct points on 0.Let (01, Rl), (02, R2), (03, R3), (04, R4) be four circles touching 0 at the points A, B, C, D, respectively. Then A proof based on inversion is found in [S, pp , We give an elementary proof in the Appendix. Remarks: 1. The Generalized Ptolemy Theorem involves six configurations, depending on the relative positions of the four circles with respect to the circle 0, i.e., depending on whether they touch 0 exteally or inteally; see Figure 1. An additional configuration arises when the four circles 01, 02, 03,o4include 0 (i.e., when 0 touches them inteally). The analogous result remains true in this case as well. However, it is not true when some but not all of the four circles include The theorem is valid with any combination of degenerate circles. In particular, Ptolemy's Theorem is the special case in which the circles 01, 02, 03, 0 4 are degenerate. A different generalization of the Ptolemy theorem involves four circles 01, 02, 03, and O4 that touch the fifth circle 0 exteally, and also touch a sixth circle inteally [9]. 3. Relation (1) remains true (but is less interesting) when 0 is a line or a point. 4. The converse of the Generalized Ptolemy Theorem is also true: if the relation (1) holds for four circles 01,02, 03, and 04, then there exists a fifth circle 0 that touches all of them (with the appropriate combination of inteallexteal tangency). Figure 1. The six configurations of inteal/exteal tangency for thc Ccneralized Ptolemy Theorem THE MATHEMATICAL ASSOCIATION OF AMERICA [Monthly 109
4 (a) Figure 2. (a) Thtbault's Theorem; (b) Exteal Thtbault Theorem. (b) 3. PROOF OF THEOREM 1 (EXTERNAL THEBAULT'S THEOREM). Denote labl = c, lbcl = a, lcal = b, ldpl = x, ldql = y. Use the Generalized Ptolemy Theorem with A, B, 01,C, and the identity 1 DM1 = 1 D P I to obtain which, after rearranging, reduces to c(lcd1 + x) + b(x - 1 BDI) = a(ladi + x), Similarly, using the Generalized Ptolemy Theorem with A, B, 02, C, we get Adding (2) and (3) gives Since cot(q/2) = rl/x and tan(q/2) = r2/y, we obtain Multiplying (4) by sin(q/2) cos(q/2) gives = a 1 AD 1 sin 8 = 2SABC April TWO APPLICATIONS OF THE GENERALIZED PTOLEMY THEOREM 365
5 and, finally, rl cos 2 - Q + r2 sin2 8 = ~SABC- - r,. 2 2 c+b-a This completes part (a) of Theorem 1. To prove (b) we denote the intersection point of the line l1 with AB (produced) by R (not shown in Figure 2). Using the Generalized Ptolemy Theorem with A, B, 01, C gives or, after rearranging, bibpi +c(a + IBPI) = a(lad1 + x + IBPI), Since ABPR -- ABDA, we have IPRI/IADI = IBPI/IBDI = IBRIIIBAI, and therefore We denote the exradius of APBR, with respect to the side BR, by rj,. To complete the proof of (b), it is sufficient to show that r: = r,. To this end, we note that Now, On the other hand, SABD/SABc= xla, which implies Finally, we get which completes our proof of part (b). Let T be the foot of the perpendicular from I, to BC. From (b), we have IT PI, = (n- Q)/2,and i T QI, = 812. Thus, to prove (c), it is enough to show that We have 1 PT 1 = r, tan(q/2) and / QT 1 = r, cot(q/2), and finally, using (a), we obtain 2 8 r - r rl cos2 $ +rl sin 2. - ra (rl- r2) sin2 : Q lptl = tan - = - r, - 2 r, - r2sin2 - r2 cos2 $ (r1- r2) cos2 2 IQTI' The verification of (d) is straightforward. THE MATHEMATICAL ASSOCIATION OF AMERICA [Monthly 109
6 Remark: This method of proof can be used to prove ThCbault's Theorem (compare with [5] or [6]). It then adds the following propetry (analogous to part (b) of Theorem 2), which extends the original ThCbault's Theorem: the lines l1 and l2 that are parallel to AD and pass through the tangency points P and Q, respectively, are tangent to the incircle (I,r);see Figure 2b. 4. PROOF OF THEOREM 2 (THE PARALLEL TANGENT THEOREM). We prove here case (a) (Figure 3a), in which the two circles el and c2 touch c inteally. Proofs for the other two cases (Figures 3b, 3c) are similar. Let K1 and Tl denote the points where L1 touches el and c2,respectively. Let K2 and T2denote the points where L2 touches el and c2, respectively. (c) Figure 3. Parallel Tangent Theore. Lemma 1. Let X be the point where c intersects the radical axis (dotted lines in Figure 3) of cl and c2. Then the tangent to c that passes through X (clashed lines in April TWO APPLICATIONS OF THE GENERALIZED PTOLEMY THEOREM 367
7 Figure 3) is parallel to the exteal tangent to cl and c2 that lies on the same side of AB as X. (The radical axis of two circles is the geometric locus of the points from which the tangents to these two circles have equal lengths). Proot Since X lies on the radical axis of cl and c2,there exists an inversion through X as a center under which cl and c2 are invariant. Since c is tangent to both cl and c2, its image under the inversion (which is a line) is also tangent to cl and c2. Hence this image is the common tangent of cl and c2 that lies on the same side as X. The tangent to c that passes through X is invariant under this inversion. Since it is tangent to c, it is parallel to the image of c, namely, to the common tangent of cl and c2. Remark: To handle the two remaining configurations, we need to modify Lemma 1. For the case illustrated in Figure 3b, the exteal tangent lies on the opposite side of X. For the case illustrated in Figure 3c, we need to consider the inteal tangent that lies on the same side of A B as X. Proof of the Theorem: Denote the common length of the tangents from X to cl and to c2by t. Using the Generalized Ptolemy Theorem with A, X, B, cl gives Using the Generalized Ptolemy Theorem with A, X, B, c2 gives Subtracting (5) from (6), and using the identity I TIKII = I T2 K2 1, we get 1 AX 1 = IBX I. Hence, the tangent to c that passes through X is parallel to AB. Finally, invoking Lemma 1 completes the proof. Because the Generalized Ptolemy Theorem includes the various configurations detailed in the statement of Theorem 3 (see Figure I), the proof of Theorem 2 holds also for the cases where cl and c2 touch c exteally or from different sides. Appendix: a Proof of Theorem 3 (Generalized Ptolemy Theorem). Lemma 2. Suppose that (01, R1) and (02, R2) are two given circles, not containing one another: Then the length of their common exteal tangent is If the circles are disjoint, the length of their common inteal tangent is Prooj The exteal tangents indeed exist, since neither circle contains the other. The inteal tangents exist when the circles are disjoint. The required expression for the length of the common tangents follows from Pythagoras' Theorem. The statement holds when one or both circles are degenerate. Lemma 3. Let (0, R) be a non-degenerate circle, and suppose the two circles (01, R1) and (02, R2) touch it at the distinct points PI and P2, respectively. Suppose that 01and 02do not include 0. Then: THE MATHEMATICAL ASSOCIATION OF AMERICA [Monthly 109
8 (a) If Ol and O2 touch 0 exteally, then (6) If O1and 0 2 touch 0 inteally, then (c) If 01 touches 0 inteally and O2 touches 0 exteally, then Proofi Apply the cosine law to the triangles A0 O1 O2 and A0 PL2, and use Lemma 2. The given conditions guarantee that the expressions for O1 O2 are well defined. A proof of the Generalized Ptolemy Theorem. We need to consider six cases, according to the various configurations of exteal and inteal tangency of the four circles illustrated in Figure 1. We demonstrate the case in which two adjacent circles touch 0 exteally and the other two touch it inteally. Ptolemy's Theorem ensures that Multiply both sides of (7)by J(R + R1) (R + R2)(R- R3)(R- R~)/R~. The desired equality (1)follows from Lemma 3. Proofs of (1) for the other cases can be constructed in a similar fashion: apply Ptolemy's Theorem to the cyclic quadrilateral ABC D, multiply the resulting expression by the appropriate combination of J(R fri) (R& R2) (R& R3) (R fr4)/ R2, and use Lemma 3. REFERENCES 1. J. Casey,A Sequel to Euclid, Hodges, Figgis, and Co., Dublin, J. L. Coolidge, A Treatise on the Geometry of the Circle and the Sphere, Chelsea Publishing Company, New York, H. Fukagawa and D. Pedoe, Sun Gaku-Japanese Temple Geometry Problems, The Charles Babbage Research Center, Winnipeg, Canada, H. Fukagawa, Problem 1260, Crux Math. 13 (1987) Solution to Problem 1260, editor's comment, Crux Math. 14 (1988) Solution to Problem 1260, comment by G. R. Veldkamp Crux Math. 15 (1989) H. W. Eves, Fundamentals of Geometry, Allyn and Bacon, Boston, R. A. Johnson, Advanced Euclidean Geometry. Mode Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle, Dover, New York, Y. Michiwaki and M. Oyama, An invariant relation in chains of tangent circles, Math. Mag. 48 (1975) C. S. Ogilvy, Tomorrow's Math; Unsolved Problems for the Amateur, Oxford University Press, New York, D. Pedoe, Geometry. A Comprehensive Course, Dover, New York, R. Shail, A proof of ThBbault's theorem, Amel: Math. Monthly 108 (2001) S. Shirali, On the generalized Ptoley theorem, Crux Math. 22 (1989) R. Stiirk. Eine weitere Losung der ThCbault'schen Aufgabe, Elem. Math. 44 (1989) V. ThBbault, Problem 3887, Three circles with collinear centers, Amel: Math. Monthly 45 (1938) April TWO APPLICATIONS OF THE GENERALIZED PTOLEMY THEOREM 369
9 16. K. B. Taylor, Solution to Problem 3887, Amer Math. Monthly 90 (1983) G. Tuwald, Kleine Mitteilungen, Elem. Math. 41 (1986) SHAY GUERON is a faculty member of the department of mathematics at the University of Haifa, Israel. His research interests are in applied mathematics (mathematical biology, and computations). He is also interested in problem solving and mathematical competitions, and has been the Israeli Team Leader for the Inteational Mathematical Olympiad since Universiv of Ha@, Haifa, 31905, Israel A Short Proof of the Lebesgue Number Theorem Lebesgue Number Theorem. For each open cover U = {U,},,I of a compact set A in a metric space (X, d)there exists a number S > 0 with the following property: corresponding to each point 1, of A there is a member U of Zi that contains the open metric ball B(p. 8). (Such a nuniber 6 is called a Lehesglre iluher for U.) I! Proof: For each point p of,4, let e,, > 0 be chosen so that B(p. E,) lies in some U,. Let {B(pi,e,,,)),,,,,,,,,, be a finite subcover of A by tnembers of {B(p.e,,) : p E A). Then {B(p,, E,,, - kp')},=l,,,, r,:~=~,~.3... is an open cover of A. This cover has a finite subcuver (B(p,>E,,- k;l))i,i,,,,. Clearly is a Lebespue number for C'. 1 Submitted by Michael Starbird University of Texas at THE MATHEMATICAL ASSOCIATION OF AMERICA [Monthly 109
About the Japanese theorem
 188/ ABOUT THE JAPANESE THEOREM About the Japanese theorem Nicuşor Minculete, Cătălin Barbu and Gheorghe Szöllősy Dedicated to the memory of the great professor, Laurenţiu Panaitopol Abstract The aim of
188/ ABOUT THE JAPANESE THEOREM About the Japanese theorem Nicuşor Minculete, Cătălin Barbu and Gheorghe Szöllősy Dedicated to the memory of the great professor, Laurenţiu Panaitopol Abstract The aim of
Symmetry: The Quarterly of the International Society for the Interdisciplinary Study of Symmetry (ISIS-Symmetry) Volume 8, Number 1, 1997
 Symmetry: The Quarterly of the International Society for the Interdisciplinary Study of Symmetry (ISIS-Symmetry) Volume 8, Number 1, 1997 Symmetry: Culture and Science Vol. 8, No. 1, 55-57, 1997 AN INCORRECT
Symmetry: The Quarterly of the International Society for the Interdisciplinary Study of Symmetry (ISIS-Symmetry) Volume 8, Number 1, 1997 Symmetry: Culture and Science Vol. 8, No. 1, 55-57, 1997 AN INCORRECT
arxiv: v1 [math.ho] 29 Nov 2017
![arxiv: v1 [math.ho] 29 Nov 2017 arxiv: v1 [math.ho] 29 Nov 2017](/thumbs/78/76977765.jpg) The Two Incenters of the Arbitrary Convex Quadrilateral Nikolaos Dergiades and Dimitris M. Christodoulou ABSTRACT arxiv:1712.02207v1 [math.ho] 29 Nov 2017 For an arbitrary convex quadrilateral ABCD with
The Two Incenters of the Arbitrary Convex Quadrilateral Nikolaos Dergiades and Dimitris M. Christodoulou ABSTRACT arxiv:1712.02207v1 [math.ho] 29 Nov 2017 For an arbitrary convex quadrilateral ABCD with
A NEW PROOF OF PTOLEMY S THEOREM
 A NEW PROOF OF PTOLEMY S THEOREM DASARI NAGA VIJAY KRISHNA Abstract In this article we give a new proof of well-known Ptolemy s Theorem of a Cyclic Quadrilaterals 1 Introduction In the Euclidean geometry,
A NEW PROOF OF PTOLEMY S THEOREM DASARI NAGA VIJAY KRISHNA Abstract In this article we give a new proof of well-known Ptolemy s Theorem of a Cyclic Quadrilaterals 1 Introduction In the Euclidean geometry,
PTOLEMY S THEOREM A New Proof
 PTOLEMY S THEOREM A New Proof Dasari Naga Vijay Krishna Abstract: In this article we present a new proof of Ptolemy s theorem using a metric relation of circumcenter in a different approach.. Keywords:
PTOLEMY S THEOREM A New Proof Dasari Naga Vijay Krishna Abstract: In this article we present a new proof of Ptolemy s theorem using a metric relation of circumcenter in a different approach.. Keywords:
2013 Sharygin Geometry Olympiad
 Sharygin Geometry Olympiad 2013 First Round 1 Let ABC be an isosceles triangle with AB = BC. Point E lies on the side AB, and ED is the perpendicular from E to BC. It is known that AE = DE. Find DAC. 2
Sharygin Geometry Olympiad 2013 First Round 1 Let ABC be an isosceles triangle with AB = BC. Point E lies on the side AB, and ED is the perpendicular from E to BC. It is known that AE = DE. Find DAC. 2
INVERSION IN THE PLANE BERKELEY MATH CIRCLE
 INVERSION IN THE PLANE BERKELEY MATH CIRCLE ZVEZDELINA STANKOVA MILLS COLLEGE/UC BERKELEY SEPTEMBER 26TH 2004 Contents 1. Definition of Inversion in the Plane 1 Properties of Inversion 2 Problems 2 2.
INVERSION IN THE PLANE BERKELEY MATH CIRCLE ZVEZDELINA STANKOVA MILLS COLLEGE/UC BERKELEY SEPTEMBER 26TH 2004 Contents 1. Definition of Inversion in the Plane 1 Properties of Inversion 2 Problems 2 2.
Berkeley Math Circle, May
 Berkeley Math Circle, May 1-7 2000 COMPLEX NUMBERS IN GEOMETRY ZVEZDELINA STANKOVA FRENKEL, MILLS COLLEGE 1. Let O be a point in the plane of ABC. Points A 1, B 1, C 1 are the images of A, B, C under symmetry
Berkeley Math Circle, May 1-7 2000 COMPLEX NUMBERS IN GEOMETRY ZVEZDELINA STANKOVA FRENKEL, MILLS COLLEGE 1. Let O be a point in the plane of ABC. Points A 1, B 1, C 1 are the images of A, B, C under symmetry
Radical axes revisited Darij Grinberg Version: 7 September 2007
 Radical axes revisited Darij Grinberg Version: 7 September 007 1. Introduction In this note we are going to shed new light on some aspects of the theory of the radical axis. For a rather complete account
Radical axes revisited Darij Grinberg Version: 7 September 007 1. Introduction In this note we are going to shed new light on some aspects of the theory of the radical axis. For a rather complete account
Chapter 4. Feuerbach s Theorem
 Chapter 4. Feuerbach s Theorem Let A be a point in the plane and k a positive number. Then in the previous chapter we proved that the inversion mapping with centre A and radius k is the mapping Inv : P\{A}
Chapter 4. Feuerbach s Theorem Let A be a point in the plane and k a positive number. Then in the previous chapter we proved that the inversion mapping with centre A and radius k is the mapping Inv : P\{A}
1. Suppose that a, b, c and d are four different integers. Explain why. (a b)(a c)(a d)(b c)(b d)(c d) a 2 + ab b = 2018.
 New Zealand Mathematical Olympiad Committee Camp Selection Problems 2018 Solutions Due: 28th September 2018 1. Suppose that a, b, c and d are four different integers. Explain why must be a multiple of
New Zealand Mathematical Olympiad Committee Camp Selection Problems 2018 Solutions Due: 28th September 2018 1. Suppose that a, b, c and d are four different integers. Explain why must be a multiple of
chapter 1 vector geometry solutions V Consider the parallelogram shown alongside. Which of the following statements are true?
 chapter vector geometry solutions V. Exercise A. For the shape shown, find a single vector which is equal to a)!!! " AB + BC AC b)! AD!!! " + DB AB c)! AC + CD AD d)! BC + CD!!! " + DA BA e) CD!!! " "
chapter vector geometry solutions V. Exercise A. For the shape shown, find a single vector which is equal to a)!!! " AB + BC AC b)! AD!!! " + DB AB c)! AC + CD AD d)! BC + CD!!! " + DA BA e) CD!!! " "
Classical Theorems in Plane Geometry 1
 BERKELEY MATH CIRCLE 1999 2000 Classical Theorems in Plane Geometry 1 Zvezdelina Stankova-Frenkel UC Berkeley and Mills College Note: All objects in this handout are planar - i.e. they lie in the usual
BERKELEY MATH CIRCLE 1999 2000 Classical Theorems in Plane Geometry 1 Zvezdelina Stankova-Frenkel UC Berkeley and Mills College Note: All objects in this handout are planar - i.e. they lie in the usual
The Apollonius Circle as a Tucker Circle
 Forum Geometricorum Volume 2 (2002) 175 182 FORUM GEOM ISSN 1534-1178 The Apollonius Circle as a Tucker Circle Darij Grinberg and Paul Yiu Abstract We give a simple construction of the circular hull of
Forum Geometricorum Volume 2 (2002) 175 182 FORUM GEOM ISSN 1534-1178 The Apollonius Circle as a Tucker Circle Darij Grinberg and Paul Yiu Abstract We give a simple construction of the circular hull of
1966 IMO Shortlist. IMO Shortlist 1966
 IMO Shortlist 1966 1 Given n > 3 points in the plane such that no three of the points are collinear. Does there exist a circle passing through (at least) 3 of the given points and not containing any other
IMO Shortlist 1966 1 Given n > 3 points in the plane such that no three of the points are collinear. Does there exist a circle passing through (at least) 3 of the given points and not containing any other
SMT Power Round Solutions : Poles and Polars
 SMT Power Round Solutions : Poles and Polars February 18, 011 1 Definition and Basic Properties 1 Note that the unit circles are not necessary in the solutions. They just make the graphs look nicer. (1).0
SMT Power Round Solutions : Poles and Polars February 18, 011 1 Definition and Basic Properties 1 Note that the unit circles are not necessary in the solutions. They just make the graphs look nicer. (1).0
IMO Training Camp Mock Olympiad #2
 IMO Training Camp Mock Olympiad #2 July 3, 2008 1. Given an isosceles triangle ABC with AB = AC. The midpoint of side BC is denoted by M. Let X be a variable point on the shorter arc MA of the circumcircle
IMO Training Camp Mock Olympiad #2 July 3, 2008 1. Given an isosceles triangle ABC with AB = AC. The midpoint of side BC is denoted by M. Let X be a variable point on the shorter arc MA of the circumcircle
IMO Training Camp Mock Olympiad #2 Solutions
 IMO Training Camp Mock Olympiad #2 Solutions July 3, 2008 1. Given an isosceles triangle ABC with AB = AC. The midpoint of side BC is denoted by M. Let X be a variable point on the shorter arc MA of the
IMO Training Camp Mock Olympiad #2 Solutions July 3, 2008 1. Given an isosceles triangle ABC with AB = AC. The midpoint of side BC is denoted by M. Let X be a variable point on the shorter arc MA of the
36th United States of America Mathematical Olympiad
 36th United States of America Mathematical Olympiad 1. Let n be a positive integer. Define a sequence by setting a 1 = n and, for each k > 1, letting a k be the unique integer in the range 0 a k k 1 for
36th United States of America Mathematical Olympiad 1. Let n be a positive integer. Define a sequence by setting a 1 = n and, for each k > 1, letting a k be the unique integer in the range 0 a k k 1 for
Theorem 1.2 (Converse of Pythagoras theorem). If the lengths of the sides of ABC satisfy a 2 + b 2 = c 2, then the triangle has a right angle at C.
 hapter 1 Some asic Theorems 1.1 The ythagorean Theorem Theorem 1.1 (ythagoras). The lengths a b < c of the sides of a right triangle satisfy the relation a + b = c. roof. b a a 3 b b 4 b a b 4 1 a a 3
hapter 1 Some asic Theorems 1.1 The ythagorean Theorem Theorem 1.1 (ythagoras). The lengths a b < c of the sides of a right triangle satisfy the relation a + b = c. roof. b a a 3 b b 4 b a b 4 1 a a 3
Calgary Math Circles: Triangles, Concurrency and Quadrilaterals 1
 Calgary Math Circles: Triangles, Concurrency and Quadrilaterals 1 1 Triangles: Basics This section will cover all the basic properties you need to know about triangles and the important points of a triangle.
Calgary Math Circles: Triangles, Concurrency and Quadrilaterals 1 1 Triangles: Basics This section will cover all the basic properties you need to know about triangles and the important points of a triangle.
(D) (A) Q.3 To which of the following circles, the line y x + 3 = 0 is normal at the point ? 2 (A) 2
 CIRCLE [STRAIGHT OBJECTIVE TYPE] Q. The line x y + = 0 is tangent to the circle at the point (, 5) and the centre of the circles lies on x y = 4. The radius of the circle is (A) 3 5 (B) 5 3 (C) 5 (D) 5
CIRCLE [STRAIGHT OBJECTIVE TYPE] Q. The line x y + = 0 is tangent to the circle at the point (, 5) and the centre of the circles lies on x y = 4. The radius of the circle is (A) 3 5 (B) 5 3 (C) 5 (D) 5
RMT 2014 Geometry Test Solutions February 15, 2014
 RMT 014 Geometry Test Solutions February 15, 014 1. The coordinates of three vertices of a parallelogram are A(1, 1), B(, 4), and C( 5, 1). Compute the area of the parallelogram. Answer: 18 Solution: Note
RMT 014 Geometry Test Solutions February 15, 014 1. The coordinates of three vertices of a parallelogram are A(1, 1), B(, 4), and C( 5, 1). Compute the area of the parallelogram. Answer: 18 Solution: Note
Inversion in the Plane. Part II: Radical Axes 1
 BERKELEY MATH CIRCLE, October 18 1998 Inversion in the Plane. Part II: Radical Axes 1 Zvezdelina Stankova-Frenkel, UC Berkeley Definition 2. The degree of point A with respect to a circle k(o, R) is defined
BERKELEY MATH CIRCLE, October 18 1998 Inversion in the Plane. Part II: Radical Axes 1 Zvezdelina Stankova-Frenkel, UC Berkeley Definition 2. The degree of point A with respect to a circle k(o, R) is defined
The circumcircle and the incircle
 hapter 4 The circumcircle and the incircle 4.1 The Euler line 4.1.1 nferior and superior triangles G F E G D The inferior triangle of is the triangle DEF whose vertices are the midpoints of the sides,,.
hapter 4 The circumcircle and the incircle 4.1 The Euler line 4.1.1 nferior and superior triangles G F E G D The inferior triangle of is the triangle DEF whose vertices are the midpoints of the sides,,.
XX Asian Pacific Mathematics Olympiad
 XX Asian Pacific Mathematics Olympiad March, 008 Problem 1. Let ABC be a triangle with A < 60. Let X and Y be the points on the sides AB and AC, respectively, such that CA + AX = CB + BX and BA + AY =
XX Asian Pacific Mathematics Olympiad March, 008 Problem 1. Let ABC be a triangle with A < 60. Let X and Y be the points on the sides AB and AC, respectively, such that CA + AX = CB + BX and BA + AY =
Name Date Period Notes Formal Geometry Chapter 8 Right Triangles and Trigonometry 8.1 Geometric Mean. A. Definitions: 1.
 Name Date Period Notes Formal Geometry Chapter 8 Right Triangles and Trigonometry 8.1 Geometric Mean A. Definitions: 1. Geometric Mean: 2. Right Triangle Altitude Similarity Theorem: If the altitude is
Name Date Period Notes Formal Geometry Chapter 8 Right Triangles and Trigonometry 8.1 Geometric Mean A. Definitions: 1. Geometric Mean: 2. Right Triangle Altitude Similarity Theorem: If the altitude is
Recognise the Equation of a Circle. Solve Problems about Circles Centred at O. Co-Ordinate Geometry of the Circle - Outcomes
 1 Co-Ordinate Geometry of the Circle - Outcomes Recognise the equation of a circle. Solve problems about circles centred at the origin. Solve problems about circles not centred at the origin. Determine
1 Co-Ordinate Geometry of the Circle - Outcomes Recognise the equation of a circle. Solve problems about circles centred at the origin. Solve problems about circles not centred at the origin. Determine
The Geometry of The Arbelos
 The Geometry of The Arbelos Brian Mortimer, Carleton University April, 1998 The basic figure of the arbelos (meaning shoemaker s knife ) is formed by three semicircles with diameters on the same line.
The Geometry of The Arbelos Brian Mortimer, Carleton University April, 1998 The basic figure of the arbelos (meaning shoemaker s knife ) is formed by three semicircles with diameters on the same line.
Collinearity/Concurrence
 Collinearity/Concurrence Ray Li (rayyli@stanford.edu) June 29, 2017 1 Introduction/Facts you should know 1. (Cevian Triangle) Let ABC be a triangle and P be a point. Let lines AP, BP, CP meet lines BC,
Collinearity/Concurrence Ray Li (rayyli@stanford.edu) June 29, 2017 1 Introduction/Facts you should know 1. (Cevian Triangle) Let ABC be a triangle and P be a point. Let lines AP, BP, CP meet lines BC,
RMT 2013 Geometry Test Solutions February 2, = 51.
 RMT 0 Geometry Test Solutions February, 0. Answer: 5 Solution: Let m A = x and m B = y. Note that we have two pairs of isosceles triangles, so m A = m ACD and m B = m BCD. Since m ACD + m BCD = m ACB,
RMT 0 Geometry Test Solutions February, 0. Answer: 5 Solution: Let m A = x and m B = y. Note that we have two pairs of isosceles triangles, so m A = m ACD and m B = m BCD. Since m ACD + m BCD = m ACB,
Syllabus. + + x + n 1 n. + x + 2
 1. Special Functions This class will cover problems involving algebraic functions other than polynomials, such as square roots, the floor function, and logarithms. Example Problem: Let n be a positive
1. Special Functions This class will cover problems involving algebraic functions other than polynomials, such as square roots, the floor function, and logarithms. Example Problem: Let n be a positive
Maharashtra Board Class X Mathematics - Geometry Board Paper 2014 Solution. Time: 2 hours Total Marks: 40
 Maharashtra Board Class X Mathematics - Geometry Board Paper 04 Solution Time: hours Total Marks: 40 Note: - () All questions are compulsory. () Use of calculator is not allowed.. i. Ratio of the areas
Maharashtra Board Class X Mathematics - Geometry Board Paper 04 Solution Time: hours Total Marks: 40 Note: - () All questions are compulsory. () Use of calculator is not allowed.. i. Ratio of the areas
Trigonometrical identities and inequalities
 Trigonometrical identities and inequalities Finbarr Holland January 1, 010 1 A review of the trigonometrical functions These are sin, cos, & tan. These are discussed in the Maynooth Olympiad Manual, which
Trigonometrical identities and inequalities Finbarr Holland January 1, 010 1 A review of the trigonometrical functions These are sin, cos, & tan. These are discussed in the Maynooth Olympiad Manual, which
Homework Assignments Math /02 Fall 2017
 Homework Assignments Math 119-01/02 Fall 2017 Assignment 1 Due date : Wednesday, August 30 Section 6.1, Page 178: #1, 2, 3, 4, 5, 6. Section 6.2, Page 185: #1, 2, 3, 5, 6, 8, 10-14, 16, 17, 18, 20, 22,
Homework Assignments Math 119-01/02 Fall 2017 Assignment 1 Due date : Wednesday, August 30 Section 6.1, Page 178: #1, 2, 3, 4, 5, 6. Section 6.2, Page 185: #1, 2, 3, 5, 6, 8, 10-14, 16, 17, 18, 20, 22,
Review Exercise 2. , æ. ç ø. ç ø. ç ø. ç ø. = -0.27, 0 x 2p. 1 Crosses y-axis when x = 0 at sin 3p 4 = 1 2. ö ø. æ Crosses x-axis when sin x + 3p è
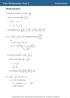 Review Exercise 1 Crosses y-axis when x 0 at sin p 4 1 Crosses x-axis when sin x + p 4 ö 0 x + p 4 -p, 0, p, p x - 7p 4, - p 4, p 4, 5p 4 So coordinates are 0, 1 ö, - 7p 4,0 ö, - p 4,0 ö, p 4,0 ö, 5p 4,0
Review Exercise 1 Crosses y-axis when x 0 at sin p 4 1 Crosses x-axis when sin x + p 4 ö 0 x + p 4 -p, 0, p, p x - 7p 4, - p 4, p 4, 5p 4 So coordinates are 0, 1 ö, - 7p 4,0 ö, - p 4,0 ö, p 4,0 ö, 5p 4,0
Definitions, Axioms, Postulates, Propositions, and Theorems from Euclidean and Non-Euclidean Geometries by Marvin Jay Greenberg ( )
 Definitions, Axioms, Postulates, Propositions, and Theorems from Euclidean and Non-Euclidean Geometries by Marvin Jay Greenberg (2009-03-26) Logic Rule 0 No unstated assumptions may be used in a proof.
Definitions, Axioms, Postulates, Propositions, and Theorems from Euclidean and Non-Euclidean Geometries by Marvin Jay Greenberg (2009-03-26) Logic Rule 0 No unstated assumptions may be used in a proof.
Exercises for Unit V (Introduction to non Euclidean geometry)
 Exercises for Unit V (Introduction to non Euclidean geometry) V.1 : Facts from spherical geometry Ryan : pp. 84 123 [ Note : Hints for the first two exercises are given in math133f07update08.pdf. ] 1.
Exercises for Unit V (Introduction to non Euclidean geometry) V.1 : Facts from spherical geometry Ryan : pp. 84 123 [ Note : Hints for the first two exercises are given in math133f07update08.pdf. ] 1.
REQUIRED MATHEMATICAL SKILLS FOR ENTERING CADETS
 REQUIRED MATHEMATICAL SKILLS FOR ENTERING CADETS The Department of Applied Mathematics administers a Math Placement test to assess fundamental skills in mathematics that are necessary to begin the study
REQUIRED MATHEMATICAL SKILLS FOR ENTERING CADETS The Department of Applied Mathematics administers a Math Placement test to assess fundamental skills in mathematics that are necessary to begin the study
Homework Assignments Math /02 Fall 2014
 Homework Assignments Math 119-01/02 Fall 2014 Assignment 1 Due date : Friday, September 5 6th Edition Problem Set Section 6.1, Page 178: #1, 2, 3, 4, 5, 6. Section 6.2, Page 185: #1, 2, 3, 5, 6, 8, 10-14,
Homework Assignments Math 119-01/02 Fall 2014 Assignment 1 Due date : Friday, September 5 6th Edition Problem Set Section 6.1, Page 178: #1, 2, 3, 4, 5, 6. Section 6.2, Page 185: #1, 2, 3, 5, 6, 8, 10-14,
First selection test
 First selection test Problem 1. Let ABC be a triangle right at C and consider points D, E on the sides BC, CA, respectively such that BD = AE = k. Lines BE and AC CD AD intersect at point O. Show that
First selection test Problem 1. Let ABC be a triangle right at C and consider points D, E on the sides BC, CA, respectively such that BD = AE = k. Lines BE and AC CD AD intersect at point O. Show that
( 1 ) Show that P ( a, b + c ), Q ( b, c + a ) and R ( c, a + b ) are collinear.
 Problems 01 - POINT Page 1 ( 1 ) Show that P ( a, b + c ), Q ( b, c + a ) and R ( c, a + b ) are collinear. ( ) Prove that the two lines joining the mid-points of the pairs of opposite sides and the line
Problems 01 - POINT Page 1 ( 1 ) Show that P ( a, b + c ), Q ( b, c + a ) and R ( c, a + b ) are collinear. ( ) Prove that the two lines joining the mid-points of the pairs of opposite sides and the line
Chapter (Circle) * Circle - circle is locus of such points which are at equidistant from a fixed point in
 Chapter - 10 (Circle) Key Concept * Circle - circle is locus of such points which are at equidistant from a fixed point in a plane. * Concentric circle - Circle having same centre called concentric circle.
Chapter - 10 (Circle) Key Concept * Circle - circle is locus of such points which are at equidistant from a fixed point in a plane. * Concentric circle - Circle having same centre called concentric circle.
Definitions, Axioms, Postulates, Propositions, and Theorems from Euclidean and Non-Euclidean Geometries by Marvin Jay Greenberg
 Definitions, Axioms, Postulates, Propositions, and Theorems from Euclidean and Non-Euclidean Geometries by Marvin Jay Greenberg Undefined Terms: Point, Line, Incident, Between, Congruent. Incidence Axioms:
Definitions, Axioms, Postulates, Propositions, and Theorems from Euclidean and Non-Euclidean Geometries by Marvin Jay Greenberg Undefined Terms: Point, Line, Incident, Between, Congruent. Incidence Axioms:
NEW YORK CITY INTERSCHOLASTIC MATHEMATICS LEAGUE Senior A Division CONTEST NUMBER 1
 Senior A Division CONTEST NUMBER 1 PART I FALL 2011 CONTEST 1 TIME: 10 MINUTES F11A1 Larry selects a 13-digit number while David selects a 10-digit number. Let be the number of digits in the product of
Senior A Division CONTEST NUMBER 1 PART I FALL 2011 CONTEST 1 TIME: 10 MINUTES F11A1 Larry selects a 13-digit number while David selects a 10-digit number. Let be the number of digits in the product of
Objective Mathematics
 . In BC, if angles, B, C are in geometric seq- uence with common ratio, then is : b c a (a) (c) 0 (d) 6. If the angles of a triangle are in the ratio 4 : :, then the ratio of the longest side to the perimeter
. In BC, if angles, B, C are in geometric seq- uence with common ratio, then is : b c a (a) (c) 0 (d) 6. If the angles of a triangle are in the ratio 4 : :, then the ratio of the longest side to the perimeter
Figure 1: Problem 1 diagram. Figure 2: Problem 2 diagram
 Geometry A Solutions 1. Note that the solid formed is a generalized cylinder. It is clear from the diagram that the area of the base of this cylinder (i.e., a vertical cross-section of the log) is composed
Geometry A Solutions 1. Note that the solid formed is a generalized cylinder. It is clear from the diagram that the area of the base of this cylinder (i.e., a vertical cross-section of the log) is composed
ON CIRCLES TOUCHING THE INCIRCLE
 ON CIRCLES TOUCHING THE INCIRCLE ILYA I. BOGDANOV, FEDOR A. IVLEV, AND PAVEL A. KOZHEVNIKOV Abstract. For a given triangle, we deal with the circles tangent to the incircle and passing through two its
ON CIRCLES TOUCHING THE INCIRCLE ILYA I. BOGDANOV, FEDOR A. IVLEV, AND PAVEL A. KOZHEVNIKOV Abstract. For a given triangle, we deal with the circles tangent to the incircle and passing through two its
Problems First day. 8 grade. Problems First day. 8 grade
 First day. 8 grade 8.1. Let ABCD be a cyclic quadrilateral with AB = = BC and AD = CD. ApointM lies on the minor arc CD of its circumcircle. The lines BM and CD meet at point P, thelinesam and BD meet
First day. 8 grade 8.1. Let ABCD be a cyclic quadrilateral with AB = = BC and AD = CD. ApointM lies on the minor arc CD of its circumcircle. The lines BM and CD meet at point P, thelinesam and BD meet
20th Bay Area Mathematical Olympiad. BAMO 2018 Problems and Solutions. February 27, 2018
 20th Bay Area Mathematical Olympiad BAMO 201 Problems and Solutions The problems from BAMO- are A E, and the problems from BAMO-12 are 1 5. February 27, 201 A Twenty-five people of different heights stand
20th Bay Area Mathematical Olympiad BAMO 201 Problems and Solutions The problems from BAMO- are A E, and the problems from BAMO-12 are 1 5. February 27, 201 A Twenty-five people of different heights stand
Power Round: Geometry Revisited
 Power Round: Geometry Revisited Stobaeus (one of Euclid s students): But what shall I get by learning these things? Euclid to his slave: Give him three pence, since he must make gain out of what he learns.
Power Round: Geometry Revisited Stobaeus (one of Euclid s students): But what shall I get by learning these things? Euclid to his slave: Give him three pence, since he must make gain out of what he learns.
The Cauchy-Schwarz inequality
 The Cauchy-Schwarz inequality Finbarr Holland, f.holland@ucc.ie April, 008 1 Introduction The inequality known as the Cauchy-Schwarz inequality, CS for short, is probably the most useful of all inequalities,
The Cauchy-Schwarz inequality Finbarr Holland, f.holland@ucc.ie April, 008 1 Introduction The inequality known as the Cauchy-Schwarz inequality, CS for short, is probably the most useful of all inequalities,
PRACTICE TEST 1 Math Level IC
 SOLID VOLUME OTHER REFERENCE DATA Right circular cone L = cl V = volume L = lateral area r = radius c = circumference of base h = height l = slant height Sphere S = 4 r 2 V = volume r = radius S = surface
SOLID VOLUME OTHER REFERENCE DATA Right circular cone L = cl V = volume L = lateral area r = radius c = circumference of base h = height l = slant height Sphere S = 4 r 2 V = volume r = radius S = surface
2009 Math Olympics Level II Solutions
 Saginaw Valley State University 009 Math Olympics Level II Solutions 1. f (x) is a degree three monic polynomial (leading coefficient is 1) such that f (0) 3, f (1) 5 and f () 11. What is f (5)? (a) 7
Saginaw Valley State University 009 Math Olympics Level II Solutions 1. f (x) is a degree three monic polynomial (leading coefficient is 1) such that f (0) 3, f (1) 5 and f () 11. What is f (5)? (a) 7
Concurrency and Collinearity
 Concurrency and Collinearity Victoria Krakovna vkrakovna@gmail.com 1 Elementary Tools Here are some tips for concurrency and collinearity questions: 1. You can often restate a concurrency question as a
Concurrency and Collinearity Victoria Krakovna vkrakovna@gmail.com 1 Elementary Tools Here are some tips for concurrency and collinearity questions: 1. You can often restate a concurrency question as a
Two applications of the theorem of Carnot
 Annales Mathematicae et Informaticae 40 (2012) pp. 135 144 http://ami.ektf.hu Two applications of the theorem of Carnot Zoltán Szilasi Institute of Mathematics, MTA-DE Research Group Equations, Functions
Annales Mathematicae et Informaticae 40 (2012) pp. 135 144 http://ami.ektf.hu Two applications of the theorem of Carnot Zoltán Szilasi Institute of Mathematics, MTA-DE Research Group Equations, Functions
TWO THEOREMS ON THE FOCUS-SHARING ELLIPSES: A THREE-DIMENSIONAL VIEW
 TWO THEOREMS ON THE FOCUS-SHARING ELLIPSES: A THREE-DIMENSIONAL VIEW ILYA I. BOGDANOV Abstract. Consider three ellipses each two of which share a common focus. The radical axes of the pairs of these ellipses
TWO THEOREMS ON THE FOCUS-SHARING ELLIPSES: A THREE-DIMENSIONAL VIEW ILYA I. BOGDANOV Abstract. Consider three ellipses each two of which share a common focus. The radical axes of the pairs of these ellipses
Q.1 If a, b, c are distinct positive real in H.P., then the value of the expression, (A) 1 (B) 2 (C) 3 (D) 4. (A) 2 (B) 5/2 (C) 3 (D) none of these
 Q. If a, b, c are distinct positive real in H.P., then the value of the expression, b a b c + is equal to b a b c () (C) (D) 4 Q. In a triangle BC, (b + c) = a bc where is the circumradius of the triangle.
Q. If a, b, c are distinct positive real in H.P., then the value of the expression, b a b c + is equal to b a b c () (C) (D) 4 Q. In a triangle BC, (b + c) = a bc where is the circumradius of the triangle.
Math 1230, Notes 2. Aug. 28, Math 1230, Notes 2 Aug. 28, / 17
 Math 1230, Notes 2 Aug. 28, 2014 Math 1230, Notes 2 Aug. 28, 2014 1 / 17 This fills in some material between pages 10 and 11 of notes 1. We first discuss the relation between geometry and the quadratic
Math 1230, Notes 2 Aug. 28, 2014 Math 1230, Notes 2 Aug. 28, 2014 1 / 17 This fills in some material between pages 10 and 11 of notes 1. We first discuss the relation between geometry and the quadratic
1. Matrices and Determinants
 Important Questions 1. Matrices and Determinants Ex.1.1 (2) x 3x y Find the values of x, y, z if 2x + z 3y w = 0 7 3 2a Ex 1.1 (3) 2x 3x y If 2x + z 3y w = 3 2 find x, y, z, w 4 7 Ex 1.1 (13) 3 7 3 2 Find
Important Questions 1. Matrices and Determinants Ex.1.1 (2) x 3x y Find the values of x, y, z if 2x + z 3y w = 0 7 3 2a Ex 1.1 (3) 2x 3x y If 2x + z 3y w = 3 2 find x, y, z, w 4 7 Ex 1.1 (13) 3 7 3 2 Find
2001 Higher Maths Non-Calculator PAPER 1 ( Non-Calc. )
 001 PAPER 1 ( Non-Calc. ) 1 1) Find the equation of the straight line which is parallel to the line with equation x + 3y = 5 and which passes through the point (, 1). Parallel lines have the same gradient.
001 PAPER 1 ( Non-Calc. ) 1 1) Find the equation of the straight line which is parallel to the line with equation x + 3y = 5 and which passes through the point (, 1). Parallel lines have the same gradient.
Geometry. Class Examples (July 3) Paul Yiu. Department of Mathematics Florida Atlantic University. Summer 2014
 Geometry lass Examples (July 3) Paul Yiu Department of Mathematics Florida tlantic University c b a Summer 2014 Example 11(a): Fermat point. Given triangle, construct externally similar isosceles triangles
Geometry lass Examples (July 3) Paul Yiu Department of Mathematics Florida tlantic University c b a Summer 2014 Example 11(a): Fermat point. Given triangle, construct externally similar isosceles triangles
XI Geometrical Olympiad in honour of I.F.Sharygin Final round. Grade 8. First day. Solutions Ratmino, 2015, July 30.
 XI Geometrical Olympiad in honour of I.F.Sharygin Final round. Grade 8. First day. Solutions Ratmino, 2015, July 30. 1. (V. Yasinsky) In trapezoid D angles and are right, = D, D = + D, < D. Prove that
XI Geometrical Olympiad in honour of I.F.Sharygin Final round. Grade 8. First day. Solutions Ratmino, 2015, July 30. 1. (V. Yasinsky) In trapezoid D angles and are right, = D, D = + D, < D. Prove that
The 3rd Olympiad of Metropolises
 The 3rd Olympiad of Metropolises Day 1. Solutions Problem 1. Solve the system of equations in real numbers: (x 1)(y 1)(z 1) xyz 1, Answer: x 1, y 1, z 1. (x )(y )(z ) xyz. (Vladimir Bragin) Solution 1.
The 3rd Olympiad of Metropolises Day 1. Solutions Problem 1. Solve the system of equations in real numbers: (x 1)(y 1)(z 1) xyz 1, Answer: x 1, y 1, z 1. (x )(y )(z ) xyz. (Vladimir Bragin) Solution 1.
0114ge. Geometry Regents Exam 0114
 0114ge 1 The midpoint of AB is M(4, 2). If the coordinates of A are (6, 4), what are the coordinates of B? 1) (1, 3) 2) (2, 8) 3) (5, 1) 4) (14, 0) 2 Which diagram shows the construction of a 45 angle?
0114ge 1 The midpoint of AB is M(4, 2). If the coordinates of A are (6, 4), what are the coordinates of B? 1) (1, 3) 2) (2, 8) 3) (5, 1) 4) (14, 0) 2 Which diagram shows the construction of a 45 angle?
1 / 23
 CBSE-XII-017 EXAMINATION CBSE-X-008 EXAMINATION MATHEMATICS Series: RLH/ Paper & Solution Code: 30//1 Time: 3 Hrs. Max. Marks: 80 General Instuctions : (i) All questions are compulsory. (ii) The question
CBSE-XII-017 EXAMINATION CBSE-X-008 EXAMINATION MATHEMATICS Series: RLH/ Paper & Solution Code: 30//1 Time: 3 Hrs. Max. Marks: 80 General Instuctions : (i) All questions are compulsory. (ii) The question
Chapter 3. The angle bisectors. 3.1 The angle bisector theorem
 hapter 3 The angle bisectors 3.1 The angle bisector theorem Theorem 3.1 (ngle bisector theorem). The bisectors of an angle of a triangle divide its opposite side in the ratio of the remaining sides. If
hapter 3 The angle bisectors 3.1 The angle bisector theorem Theorem 3.1 (ngle bisector theorem). The bisectors of an angle of a triangle divide its opposite side in the ratio of the remaining sides. If
Geometry - An Olympiad Approach
 Geometry - An Olympiad Approach Manjil P. Saikia Department of Mathematical Sciences Tezpur University manjil@gonitsora.com April 19, 2013 UGC Sponsored Workshop for High School Students and Teachers Women
Geometry - An Olympiad Approach Manjil P. Saikia Department of Mathematical Sciences Tezpur University manjil@gonitsora.com April 19, 2013 UGC Sponsored Workshop for High School Students and Teachers Women
The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca Euclid Contest. Wednesday, April 15, 2015
 The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca 015 Euclid Contest Wednesday, April 15, 015 (in North America and South America) Thursday, April 16, 015 (outside of North America
The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca 015 Euclid Contest Wednesday, April 15, 015 (in North America and South America) Thursday, April 16, 015 (outside of North America
Chapter 1. Some Basic Theorems. 1.1 The Pythagorean Theorem
 hapter 1 Some asic Theorems 1.1 The ythagorean Theorem Theorem 1.1 (ythagoras). The lengths a b < c of the sides of a right triangle satisfy the relation a 2 + b 2 = c 2. roof. b a a 3 2 b 2 b 4 b a b
hapter 1 Some asic Theorems 1.1 The ythagorean Theorem Theorem 1.1 (ythagoras). The lengths a b < c of the sides of a right triangle satisfy the relation a 2 + b 2 = c 2. roof. b a a 3 2 b 2 b 4 b a b
UNCC 2001 Comprehensive, Solutions
 UNCC 2001 Comprehensive, Solutions March 5, 2001 1 Compute the sum of the roots of x 2 5x + 6 = 0 (A) (B) 7/2 (C) 4 (D) 9/2 (E) 5 (E) The sum of the roots of the quadratic ax 2 + bx + c = 0 is b/a which,
UNCC 2001 Comprehensive, Solutions March 5, 2001 1 Compute the sum of the roots of x 2 5x + 6 = 0 (A) (B) 7/2 (C) 4 (D) 9/2 (E) 5 (E) The sum of the roots of the quadratic ax 2 + bx + c = 0 is b/a which,
XIII GEOMETRICAL OLYMPIAD IN HONOUR OF I.F.SHARYGIN The correspondence round. Solutions
 XIII GEOMETRIL OLYMPID IN HONOUR OF I.F.SHRYGIN The correspondence round. Solutions 1. (.Zaslavsky) (8) Mark on a cellular paper four nodes forming a convex quadrilateral with the sidelengths equal to
XIII GEOMETRIL OLYMPID IN HONOUR OF I.F.SHRYGIN The correspondence round. Solutions 1. (.Zaslavsky) (8) Mark on a cellular paper four nodes forming a convex quadrilateral with the sidelengths equal to
In this article we examine a famous and important result in
 How to Prove It In this episode of How To Prove It, we prove a striking theorem first discovered by Ptolemy. We then discuss some nice applications of the theorem. lassroom In this article we examine a
How to Prove It In this episode of How To Prove It, we prove a striking theorem first discovered by Ptolemy. We then discuss some nice applications of the theorem. lassroom In this article we examine a
EHRMANN S THIRD LEMOINE CIRCLE
 EHRMNN S THIRD EMOINE IRE DRIJ GRINERG bstract. The symmedian point of a triangle is known to give rise to two circles, obtained by drawing respectively parallels and antiparallels to the sides of the
EHRMNN S THIRD EMOINE IRE DRIJ GRINERG bstract. The symmedian point of a triangle is known to give rise to two circles, obtained by drawing respectively parallels and antiparallels to the sides of the
Definitions, Axioms, Postulates, Propositions, and Theorems from Euclidean and Non-Euclidean Geometries by Marvin Jay Greenberg ( )
 Definitions, Axioms, Postulates, Propositions, and Theorems from Euclidean and Non-Euclidean Geometries by Marvin Jay Greenberg (2005-02-16) Logic Rules (Greenberg): Logic Rule 1 Allowable justifications.
Definitions, Axioms, Postulates, Propositions, and Theorems from Euclidean and Non-Euclidean Geometries by Marvin Jay Greenberg (2005-02-16) Logic Rules (Greenberg): Logic Rule 1 Allowable justifications.
Complex numbers in the realm of Euclidean Geometry
 Complex numbers in the realm of Euclidean Geometry Finbarr Holland February 7, 014 1 Introduction Before discussing the complex forms of lines and circles, we recall some familiar facts about complex numbers.
Complex numbers in the realm of Euclidean Geometry Finbarr Holland February 7, 014 1 Introduction Before discussing the complex forms of lines and circles, we recall some familiar facts about complex numbers.
THE CYCLIC QUADRANGLE IN THE ISOTROPIC PLANE
 SARAJEVO JOURNAL OF MATHEMATICS Vol.7 (0) (011), 65 75 THE CYCLIC QUADRANGLE IN THE ISOTROPIC PLANE V. VOLENEC, J. BEBAN-BRKIĆ AND M. ŠIMIĆ Abstract. In [15], [] we focused on the geometry of the non-tangential
SARAJEVO JOURNAL OF MATHEMATICS Vol.7 (0) (011), 65 75 THE CYCLIC QUADRANGLE IN THE ISOTROPIC PLANE V. VOLENEC, J. BEBAN-BRKIĆ AND M. ŠIMIĆ Abstract. In [15], [] we focused on the geometry of the non-tangential
Vectors - Applications to Problem Solving
 BERKELEY MATH CIRCLE 00-003 Vectors - Applications to Problem Solving Zvezdelina Stankova Mills College& UC Berkeley 1. Well-known Facts (1) Let A 1 and B 1 be the midpoints of the sides BC and AC of ABC.
BERKELEY MATH CIRCLE 00-003 Vectors - Applications to Problem Solving Zvezdelina Stankova Mills College& UC Berkeley 1. Well-known Facts (1) Let A 1 and B 1 be the midpoints of the sides BC and AC of ABC.
This class will demonstrate the use of bijections to solve certain combinatorial problems simply and effectively.
 . Induction This class will demonstrate the fundamental problem solving technique of mathematical induction. Example Problem: Prove that for every positive integer n there exists an n-digit number divisible
. Induction This class will demonstrate the fundamental problem solving technique of mathematical induction. Example Problem: Prove that for every positive integer n there exists an n-digit number divisible
22 SAMPLE PROBLEMS WITH SOLUTIONS FROM 555 GEOMETRY PROBLEMS
 22 SPL PROLS WITH SOLUTIOS FRO 555 GOTRY PROLS SOLUTIOS S O GOTRY I FIGURS Y. V. KOPY Stanislav hobanov Stanislav imitrov Lyuben Lichev 1 Problem 3.9. Let be a quadrilateral. Let J and I be the midpoints
22 SPL PROLS WITH SOLUTIOS FRO 555 GOTRY PROLS SOLUTIOS S O GOTRY I FIGURS Y. V. KOPY Stanislav hobanov Stanislav imitrov Lyuben Lichev 1 Problem 3.9. Let be a quadrilateral. Let J and I be the midpoints
Inversion. Contents. 1 General Properties. 1 General Properties Problems Solutions... 3
 c 007 The Author(s) and The IMO Compendium Group Contents Inversion Dušan Djukić 1 General Properties................................... 1 Problems........................................ 3 Solutions........................................
c 007 The Author(s) and The IMO Compendium Group Contents Inversion Dušan Djukić 1 General Properties................................... 1 Problems........................................ 3 Solutions........................................
1999 Solutions Fermat Contest (Grade 11)
 Canadian Mathematics Competition n activity of The Centre for Education in Mathematics and Computing, University of Waterloo, Waterloo, Ontario 999 s Fermat Contest (Grade ) for the wards 999 Waterloo
Canadian Mathematics Competition n activity of The Centre for Education in Mathematics and Computing, University of Waterloo, Waterloo, Ontario 999 s Fermat Contest (Grade ) for the wards 999 Waterloo
COORDINATE GEOMETRY BASIC CONCEPTS AND FORMULAE. To find the length of a line segment joining two points A(x 1, y 1 ) and B(x 2, y 2 ), use
 COORDINATE GEOMETRY BASIC CONCEPTS AND FORMULAE I. Length of a Line Segment: The distance between two points A ( x1, 1 ) B ( x, ) is given b A B = ( x x1) ( 1) To find the length of a line segment joining
COORDINATE GEOMETRY BASIC CONCEPTS AND FORMULAE I. Length of a Line Segment: The distance between two points A ( x1, 1 ) B ( x, ) is given b A B = ( x x1) ( 1) To find the length of a line segment joining
UNC Charlotte 2005 Comprehensive March 7, 2005
 March 7, 2005 1. The numbers x and y satisfy 2 x = 15 and 15 y = 32. What is the value xy? (A) 3 (B) 4 (C) 5 (D) 6 (E) none of A, B, C or D Solution: C. Note that (2 x ) y = 15 y = 32 so 2 xy = 2 5 and
March 7, 2005 1. The numbers x and y satisfy 2 x = 15 and 15 y = 32. What is the value xy? (A) 3 (B) 4 (C) 5 (D) 6 (E) none of A, B, C or D Solution: C. Note that (2 x ) y = 15 y = 32 so 2 xy = 2 5 and
IYGB. Special Paper U. Time: 3 hours 30 minutes. Created by T. Madas. Created by T. Madas
 IYGB Special Paper U Time: 3 hours 30 minutes Candidates may NOT use any calculator Information for Candidates This practice paper follows the Advanced Level Mathematics Core Syllabus Booklets of Mathematical
IYGB Special Paper U Time: 3 hours 30 minutes Candidates may NOT use any calculator Information for Candidates This practice paper follows the Advanced Level Mathematics Core Syllabus Booklets of Mathematical
Exercise 2.1. Identify the error or errors in the proof that all triangles are isosceles.
 Exercises for Chapter Two He is unworthy of the name of man who is ignorant of the fact that the diagonal of a square is incommensurable with its side. Plato (429 347 B.C.) Exercise 2.1. Identify the error
Exercises for Chapter Two He is unworthy of the name of man who is ignorant of the fact that the diagonal of a square is incommensurable with its side. Plato (429 347 B.C.) Exercise 2.1. Identify the error
LLT Education Services
 8. The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle. (a) 4 cm (b) 3 cm (c) 6 cm (d) 5 cm 9. From a point P, 10 cm away from the
8. The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle. (a) 4 cm (b) 3 cm (c) 6 cm (d) 5 cm 9. From a point P, 10 cm away from the
Chapter 6. Basic triangle centers. 6.1 The Euler line The centroid
 hapter 6 asic triangle centers 6.1 The Euler line 6.1.1 The centroid Let E and F be the midpoints of and respectively, and G the intersection of the medians E and F. onstruct the parallel through to E,
hapter 6 asic triangle centers 6.1 The Euler line 6.1.1 The centroid Let E and F be the midpoints of and respectively, and G the intersection of the medians E and F. onstruct the parallel through to E,
Geometry JWR. Monday September 29, 2003
 Geometry JWR Monday September 29, 2003 1 Foundations In this section we see how to view geometry as algebra. The ideas here should be familiar to the reader who has learned some analytic geometry (including
Geometry JWR Monday September 29, 2003 1 Foundations In this section we see how to view geometry as algebra. The ideas here should be familiar to the reader who has learned some analytic geometry (including
A TAXICAB VERSION OF A TRIANGLE S APOLLONIUS CIRCLE
 A TAXICAB VERSION OF A TRIANGLE S APOLLONIUS CIRCLE TEMEL ERMİŞ*, ÖZCAN GELİŞGEN AND AYBÜKE EKİCİ DEPARTMENT OF MATHEMATICS AND COMPUTER SCIENCES, ESKİŞEHİR OSMANGAZİ UNIVERSITY, TÜRKİYE E-MAILS: TERMIS@OGU.EDU.TR,
A TAXICAB VERSION OF A TRIANGLE S APOLLONIUS CIRCLE TEMEL ERMİŞ*, ÖZCAN GELİŞGEN AND AYBÜKE EKİCİ DEPARTMENT OF MATHEMATICS AND COMPUTER SCIENCES, ESKİŞEHİR OSMANGAZİ UNIVERSITY, TÜRKİYE E-MAILS: TERMIS@OGU.EDU.TR,
XIV GEOMETRICAL OLYMPIAD IN HONOUR OF I.F.SHARYGIN The correspondence round. Solutions
 XIV GEOMETRIL OLYMPI IN HONOUR OF I.F.SHRYGIN The correspondence round. Solutions 1. (L.Shteingarts, grade 8) Three circles lie inside a square. Each of them touches externally two remaining circles. lso
XIV GEOMETRIL OLYMPI IN HONOUR OF I.F.SHRYGIN The correspondence round. Solutions 1. (L.Shteingarts, grade 8) Three circles lie inside a square. Each of them touches externally two remaining circles. lso
Singapore International Mathematical Olympiad Training Problems
 Singapore International athematical Olympiad Training Problems 18 January 2003 1 Let be a point on the segment Squares D and EF are erected on the same side of with F lying on The circumcircles of D and
Singapore International athematical Olympiad Training Problems 18 January 2003 1 Let be a point on the segment Squares D and EF are erected on the same side of with F lying on The circumcircles of D and
Higher Geometry Problems
 Higher Geometry Problems (1) Look up Eucidean Geometry on Wikipedia, and write down the English translation given of each of the first four postulates of Euclid. Rewrite each postulate as a clear statement
Higher Geometry Problems (1) Look up Eucidean Geometry on Wikipedia, and write down the English translation given of each of the first four postulates of Euclid. Rewrite each postulate as a clear statement
Abstract The symmedian point of a triangle is known to give rise to two circles, obtained by drawing respectively parallels and antiparallels to the
 bstract The symmedian point of a triangle is known to give rise to two circles, obtained by drawing respectively parallels and antiparallels to the sides of the triangle through the symmedian point. In
bstract The symmedian point of a triangle is known to give rise to two circles, obtained by drawing respectively parallels and antiparallels to the sides of the triangle through the symmedian point. In
arxiv: v1 [math.nt] 10 Dec 2009
![arxiv: v1 [math.nt] 10 Dec 2009 arxiv: v1 [math.nt] 10 Dec 2009](/thumbs/96/128277757.jpg) Ford circles, continued fractions, and best approximation of the second kind arxiv:092.997v [math.nt] 0 Dec 2009 Ian Short Centre for Mathematical Sciences Wilberforce Road Cambridge CB3 0WB United Kingdom
Ford circles, continued fractions, and best approximation of the second kind arxiv:092.997v [math.nt] 0 Dec 2009 Ian Short Centre for Mathematical Sciences Wilberforce Road Cambridge CB3 0WB United Kingdom
Complex Numbers in Geometry
 Complex Numers in Geometry Seastian Jeon Decemer 3, 206 The Complex Plane. Definitions I assume familiarity with most, if not all, of the following definitions. Some knowledge of linear algera is also
Complex Numers in Geometry Seastian Jeon Decemer 3, 206 The Complex Plane. Definitions I assume familiarity with most, if not all, of the following definitions. Some knowledge of linear algera is also
Two applications of the theorem of Carnot
 Two applications of the theorem of Carnot Zoltán Szilasi Abstract Using the theorem of Carnot we give elementary proofs of two statements of C Bradley We prove his conjecture concerning the tangents to
Two applications of the theorem of Carnot Zoltán Szilasi Abstract Using the theorem of Carnot we give elementary proofs of two statements of C Bradley We prove his conjecture concerning the tangents to
Seul Lee, Dong-Soo Kim and Hyeon Park
 Honam Mathematical J. 39 (2017), No. 2, pp. 247 258 https://doi.org/10.5831/hmj.2017.39.2.247 VARIOUS CENTROIDS OF QUADRILATERALS Seul Lee, Dong-Soo Kim and Hyeon Park Abstract. For a quadrilateral P,
Honam Mathematical J. 39 (2017), No. 2, pp. 247 258 https://doi.org/10.5831/hmj.2017.39.2.247 VARIOUS CENTROIDS OF QUADRILATERALS Seul Lee, Dong-Soo Kim and Hyeon Park Abstract. For a quadrilateral P,
Plane geometry Circles: Problems with some Solutions
 The University of Western ustralia SHL F MTHMTIS & STTISTIS UW MY FR YUNG MTHMTIINS Plane geometry ircles: Problems with some Solutions 1. Prove that for any triangle, the perpendicular bisectors of the
The University of Western ustralia SHL F MTHMTIS & STTISTIS UW MY FR YUNG MTHMTIINS Plane geometry ircles: Problems with some Solutions 1. Prove that for any triangle, the perpendicular bisectors of the
Grade XI Mathematics
 Grade XI Mathematics Exam Preparation Booklet Chapter Wise - Important Questions and Solutions #GrowWithGreen Questions Sets Q1. For two disjoint sets A and B, if n [P ( A B )] = 32 and n [P ( A B )] =
Grade XI Mathematics Exam Preparation Booklet Chapter Wise - Important Questions and Solutions #GrowWithGreen Questions Sets Q1. For two disjoint sets A and B, if n [P ( A B )] = 32 and n [P ( A B )] =
