ELEMENTS OF ACOUSTIC WAVES IN POROUS MEDIA
|
|
|
- Maude Powers
- 6 years ago
- Views:
Transcription
1 ELEMENTS OF ACOSTIC WAVES IN POROS MEDIA By George F FREIHA niversiy of Balamand (Spervised y Dr Elie HNEIN) niversié de Valenciennes e d Haina Camrésis (Spervised y Dr Berrand NONGAILLARD & Dr George NASSAR) Sppored y: CNRS (Comié Naional de Recherche Scienifiqe de France)
2 Plan of he Presenaion Theory of homogeneiy & heerogeneiy Inrodcion o poros media and is properies 3 Inrodcion o acosic wave propagaion 4 Lagrangian formalism of he Bio Theory 5 Solion of he eqaion of celeriy and coefficien of aenaion of he differen acosic waves in he Bio Theory 6 Graph presenaion and discssion of he ehavior of he celeriy and aenaion coefficien in fncion of differen parameers
3 HOMOGENEITY & HETEROGENEITY - Homogeneos Medim: Physical Properies Independen of Posiion - Heerogeneos Medim: Change in Properies when Passing from Poin o Poin in he Medim W W According o W, he medim is homogeneos, according o W, i is heerogeneos Two ypes of heerogeneos medim: -Coninos heerogeneos medim -Discree heerogeneos medim
4 INTRODCTION TO POROS MEDIM ( I ) In general, a poros medim has wo phases: The solid phase which can e elasic or rigid The flid phase which can e a viscos and compressile liqid Fier form Grain form Cone form
5 INTRODCTION TO POROS MEDIM ( II ) A microscopic mahemaical descripion of sch medim is impossile ecase of he mechanical and hermal ineracion eween he flid and solid, dring heir displacemen In he macroscopic approach, he size of he elemenary volme ms follow wo essenial condiions If: L he characerisic size of he medim R he size of he elemenary volme ha we are working on d he characerisic dimension of he pores we ms have d << R << L
6 INTRODCTION TO POROS MEDIM ( III ) Characerisics of a poros medim ( I ) Porosiy: β v v flide oal v v f v s v f v f Types of porosiy: -Non conneced porosiy: oflid medim conaining solid inclsions osolid medim conaining flid inclsions -Conneced porosiy: pores are conneced ogeher -Semi-conneced porosiy: pores are conneced o ohers y a very small common srface
7 INTRODCTION TO POROS MEDIM ( IV ) Characerisics of a poros medim ( II ) In mos of he poros medims, he semi-conneced and non-conneced pores are negligile while doing measremens Or sdy will concenrae on he conneced porosiy ype where acosic waves can ravel and where he flid circlaion is possile
8 INTRODCTION TO POROS MEDIM ( V ) Characerisics of a poros medim ( III ) Permeailiy: a facor ha inflences he energeic dissipaion eween solid and flid dring heir displacemen Torosiy: a facor ha gives an idea ao ways of he flid inside he solid medim and i is considered as a facor of he size and geomery of he pores The eqaion of porosiy is given y α v f v f v vdv dv
9 INTRODCTION TO ACOSTIC WAVE ( I ) Acosic waves are resls of mechanical perraion There are wo kinds of waves: - Longidinal waves where he mechanical perraion is done in a direcion parallel o he propagaion - Transversal waves where he mechanical perraion is done in a direcion perpendiclar o he propagaion The medim is considered isoropic so he characerisics of propagaion are independen of he direcion of propagaion
10 INTRODCTION TO ACOSTIC WAVE ( II ) x3 Displacemen vecors are r AA' A' A AA' and B he deformaion of he solid will e he ensor E where he elemens E are defined as BB' A B r BB' B' x E i x j x i j Where i is he direcion of vecor r x in x i direcion e E represens he dilaion of he solid E E33
11 INTRODCTION TO ACOSTIC WAVE ( III ) Force eqaions: a force df j is applied on a elemenary ni of srface ds j This force can e projeced giving s he sress componens τ ds lim j df ds Hooke s law: Hooke s law gives s he relaion eween sress and j srain in he volme τ c kl E kl xj For isoropic solid τ λ eδ μe where λ and μ are he Lame coefficiens τ r ik df jk e is he dilaion of he solid k r r j i r r τ r τ jk xi E is he ensor of srain xk
12 INTRODCTION TO ACOSTIC WAVE ( IV ) Eqaion of propagaion of a harmonic plane wave( I ) The fndamenal eqaion of dynamics gives s he firs relaionship eween force and he local displacemen in he medim ρ i Having τ τ x in isoropic medim j c where ρ is he mass per ni volme of he medim kl E kl ρ i c kl x jxk ( ) ( ) [ ( )] λ μ grad div μro ro ρ Helmholz heorem ( ) gradφ ro ψ r φ r Ψ Δφ and ΔΨ v v L T wo propagaion eqaions
13 Lagrange fncion : A Λ() d Λ Ω L r, ( r ) dv Assming ha he exciaion done on he medim is A, we will have The mos general Lagrangian densiy fncion ms e r & r, & are he emporal derivaives i, j, k, LAGRANGIAN FORMALISM OF BIOT THEORY( I ) Inrodcion o Lagrangian formalism: x i are he spaial derivaives of he field, k j i j r & r & r r (,,,, &,, i ) L, j, k, x x
14 r & r r r r r L (,,,, i, j ) L(,,,, i, j ) r LAGRANGIAN FORMALISM OF BIOT THEORY( II ) Condiions of invariance of he Lagrangian fncion L Since we are dealing wih a homogenos and isoropic medim he fncion L ms e invarian according o roaion and ranslaion r r & ( A B, A, A ) L(, ) L i, j, i, j The Lagrangian is only fncion of he speed and he gradiens of he deformaions r r & r & r e i, j
15 BIOT THEORY ( I ) Condiions of he heory: Small srain for he solid and flid We ms deal wih conneced ype of porosiy The wave lengh ms e o imes greaer hen he dimensions of pores A insan he Lagrangian fncion of he fields (srain of he solid) and r r, ( r ) cominaion of he wo fields r r, (srain of he liqid) is a linear ( r ) r r, ( r ) r r, ( r ), and heir derivaives
16 [ ( ) ( ), L jj ii jj ii jj ii γ ω ω γ ε ε γ ε ε γ ε ε γ ε ε γ ε ε γ ε ε γ ρ ρ ρ ( )( ) ( )( ) ( )( ) ( )( ) a a a a a a a a a a a a jj a ii A o A e,,,, ε ε ω ω ε ε General Lagrangian fncion: BIOT THEORY ( II )
17 ( ) [ ( ) ( ) ( )( ) ( ) ( )]}, A L T α α α α α α α ρ ρ ρ a a a T A A A A, 6, 5, 4 γ γ γ BIOT THEORY ( III ) Wih α γ γ 4 ; α γ γ 5 ; α 3 γ 3 γ 6 ; α 4 γ 4 γ 7 ; α 5 γ 5 - γ 7 ; α 6 γ 6 γ 7 ; α 8 γ 8
18 [ ] ( ) ω d L r d A Ω Ω,, ;, a A a i δ δ a i 3 j a i j j a i a i L x L L BIOT THEORY ( IV ) For a small variaion on any of he fields he exciaion done on he medim ms e saionary Eler Lagrange eqaions for each of he srain fields : exciaion:
19 ( ) ( ) ( ) ( ) ( ), α α α α α ρ ρ ( ) ( ) ( ) ( ) ( ) α α α α α ρ ρ ( ) ( ) ( ) 4 α α α ρ ρ ( ) ( ) 3 α α ρ ρ BIOT THEORY ( V ) and and
20 , M ( ) ( ) ( ) Ρ Q μ ρ ρ Dissipaion can e he variaion of emperare from poin o poin which leads o an irreversile hermo condcion process The dissipaion sress noed M are a linear eqaions of he relaive velociy eween he wo phases ( ) ( ) Q R ρ ρ and BIOT THEORY ( VI )
21 BIOT THEORY ( VII ) The componens of he sress ensors can e fond sing he following eqaion which leads s o a relaionship eween sress and srain in or medim L a τ, a i, j τ s Ρ ( ) ( ) ( ) Q N ( ) ( ) ( ) f τ i p f hδ R Q δ R Q P,Q,R,N are considered as phenomenological parameers in he BIOT heory and are know as coefficien of BIOT They can e fond y doing 3 special physical experimens known as BIOT and WILLIS experimens
22 f s s s s K K h K K h hk K K h Q, f s s s K K h K K h K h R, ( ) N K K h K K h K K K h K K K h h P f s s f s s s 3 4, BIOT THEORY ( VIII )
23 BIOT THEORY ( IX ) Copling in BIOT heory ( I ) The ineracions eween he solid and flid phases are deermined in he eqaions y cerain copling consans The mos imporan wo ypes of copling consan are he mass copling and viscos copling omass copling : sing Lagrangian expression we can define he kineic energy of he medim E c ρ ρ ρ,
24 BIOT THEORY ( X ) Copling in BIOT heory ( II ) Viscos copling: I represens he relaive moion eween he wo phases: F ( ) ( κ) κt κ 4 T iκ ( κ) T ( ) κ er ' ( κ ) i ei '( κ) ( κ ) i ei( κ) Where: κ is a facor of he geomery and dimensions of he pores er and ei are he real and imaginary pars of he Kelvin fncion κ and ( ) ( ) ( 3 ) er κ i ei κ J i κ J is he Bessel fncion of order zero Ber and ei are he real and imaginary pars of he derivaive of he Kelvin fncion ha can e calclaed as following: er ( 3 ) κ ( κ ) ( κ) J i x x dx i er ' i ei '
25 ( ) ( ) ( ) Λ Λ N P Q ρ ρ ( ) ( ) Q R ρ ρ Λ w φ ΛW ψ We already fond he eqaion of wave propagaion in he medim SOLTION OF EQATIONS OF WAVE PROPAGATION IN BIOT THEORY ( I )
26 SOLTION OF EQATIONS OF WAVE PROPAGATION IN BIOT THEORY ( II ) Longidinal waves eqaions ( I ) We sar working on he scalar par alone firs y replacing φ y heir vales:, ψ and φ ρ ψ P ( ) ( ) ψ φ φ Q ψ ρ, ψ ρ ρ ω ~ ρ ω ~ ρ φ ω ~ ρ φ R Harmonic plan waves Wih ψ ω ~ ρ ~ ρ ψ φ ψ φ ( ) ( ) ψ Q φ f r r e ( ) ( ) jω P R, φ Q ψ Q ρ j ; ~ ρ ρ j ; ~ ρ ρ ω ω f ψ φ j ω
27 ~ ~ ~ ~ ρ ρ ρ ρ ω A Ψ Ψ A M Longidinal waves eqaions ( II ) A is he complex densiy marix: R Q Q P M M is he BIOT coefficien marix: Ψ ψ φ Ψ is he poenial vecor : Mliplying he eqaion y M - we will ge: φ φ φ φ δ δ, SOLTION OF EQATIONS OF WAVE PROPAGATION IN BIOT THEORY ( III ) Ψ Ψ M A Marix form
28 SOLTION OF EQATIONS OF WAVE PROPAGATION IN BIOT THEORY ( IV ) Longidinal waves eqaions ( III ) Wih δ and δ he eigen vales of he eigen vecors represening he consan of propagaion of he waves Φ Φ and δ δ ω [ ~ ~ ~ Δ ] ( ) ( Pρ ) Rρ Qρ PR Q ω [ ~ ~ ~ Δ ] ( ) ( Pρ ) Rρ Qρ PR Q Wih Δ ( P ~ ρ R ~ ρ Q ~ ρ ) 4( PR Q )( ~ ρ ~ ρ ~ ρ )
29 SOLTION OF EQATIONS OF WAVE PROPAGATION IN BIOT THEORY ( V ) Longidinal waves eqaions ( IV ) We will ge modes of propagaion associaed o wo longidinal P ~ ρ R ~ ρ ~ Qρ waves one rapid wih phase velociy : v ~ ~ ~ ρ ρ ρ And a slow longidinal wave wih phase velociy: v P ~ ρ R ~ ρ Q ~ ρ ~ ( ~ ρ ~ ρ ρ ) Δ ( ) Δ Normalizaion: P R Q,, H H H σ σ σ H P R Q ρ ρ ρ γ, γ, γ ρ ρ ρ and z V v c L, wih, wih ( ) ρρ ρ ρ ρ ρ βρ β ρ f s
30 SOLTION OF EQATIONS OF WAVE PROPAGATION IN BIOT THEORY ( VI ) Longidinal waves eqaions ( V ) Afer sdying differen geomery of pores, BIOT inrodced a characerisic freqency δ f c πρ πρ γ γ ( ) 6 varying eween and 3 f, and noiced ha κ δ, wih f So he phase velociies of he waves will e:, ~ V s r Re The aenaion coefficiens per cycle of he waves are: ( z ) Ac s r c Im π Re ( z ) ( z ) The aenaion coefficiens per disance of he waves are: Ad s r ( ) π Im z
31 SOLTION OF EQATIONS OF WAVE PROPAGATION IN BIOT THEORY ( VII ) Transversal wave eqaions Now we will work on he vecorial par alone and y heir vales: Λω Λ Ω r r Δω ρ ωρ Ω κ ωω r r r N r r r ( ) F( ) ( ) r r ( ) ( ) ( ) F ρ ωρ Ω κ ωω
32 SOLTION OF EQATIONS OF WAVE PROPAGATION IN BIOT THEORY ( VIII ) Transversal wave eqaions (II) N Having V R we can calclae he velociy of ransversal wave sing: ρ f c ( ) i V γ γ γ ( γ γ ) R f T v f c γ i ( γ γ ) f So he phase velociies of he waves will e:, ~ V Re The aenaion coefficiens per cycle of he waves are: ( T ) Ac Im π Re ( T ) ( T ) The aenaion coefficiens per disance of he waves are: Ad π Im( T )
33 Graphs of he Variaion of he Velociy and Coefficien of Aenaion for he Transversal and Longidinal (Slow & Rapid) Wave
34 Resls in he asence of copling (I) Inflence of he srcral facor δ δ σ σ σ γ γ γ 6/3 8
35 Phase Velociy of he wave in fncion of δ Slow Longidinal Wave Rapid Longidinal Wave Transversal Wave
36 Aenaion per Cycle of he wave in fncion of δ Slow Longidinal Wave Rapid Longidinal Wave Transversal Wave
37 Aenaion per Disance ni of he wave in fncion of δ Slow Longidinal Wave Rapid Longidinal Wave Transversal Wave
38 Resls in he asence of copling (II) Inflence of he raio σ / σ δ σ σ σ γ γ γ σσ 8,,9, 8 8,9, 9
39 Phase Velociy of he wave in fncion of σ σ Slow Longidinal Wave Rapid Longidinal Wave Transversal Wave
40 Aenaion per Cycle of he wave in fncion of σ σ Slow Longidinal Wave Rapid Longidinal Wave Transversal Wave
41 Aenaion per Disance ni of he wave in fncion of σ σ Slow Longidinal Wave Rapid Longidinal Wave Transversal Wave
42 Resls in he asence of copling (III) Inflence of he raio γ / γ δ σ σ σ γ γ γ γγ 8,,9, 8 8,9, 9
43 Phase Velociy of he wave in fncion of γ γ Slow Longidinal Wave Rapid Longidinal Wave Transversal Wave
44 Aenaion per Cycle of he wave in fncion of γ γ Slow Longidinal Wave Rapid Longidinal Wave Transversal Wave
45 Aenaion per Disance ni of he wave in fncion of γ γ Slow Longidinal Wave Rapid Longidinal Wave Transversal Wave
46 Resls wih copling effec Inflence of he coefficien of elasic copling σ δ σ σ σ γ γ γ 8 8,3, 8,,
47 Phase Velociy of he wave in fncion of σ Slow Longidinal Wave Rapid Longidinal Wave Transversal Wave
48 Aenaion per Cycle of he wave in fncion of σ Slow Longidinal Wave Rapid Longidinal Wave Transversal Wave
49 Aenaion per Disance of he wave in fncion of σ Slow Longidinal Wave Rapid Longidinal Wave Transversal Wave
50 THANK YO Qesions???
Earthquake, Volcano and Tsunami
 A. Merapi Volcano Erpion Earhqake, Volcano and Tsnami Qesion Answer Marks A. Using Black s Principle he eqilibrim emperare can be obained Ths,.5 A. For ideal gas, pv e e RTe, hs.3 A.3 The relaive velociy
A. Merapi Volcano Erpion Earhqake, Volcano and Tsnami Qesion Answer Marks A. Using Black s Principle he eqilibrim emperare can be obained Ths,.5 A. For ideal gas, pv e e RTe, hs.3 A.3 The relaive velociy
Lecture 4 Kinetics of a particle Part 3: Impulse and Momentum
 MEE Engineering Mechanics II Lecure 4 Lecure 4 Kineics of a paricle Par 3: Impulse and Momenum Linear impulse and momenum Saring from he equaion of moion for a paricle of mass m which is subjeced o an
MEE Engineering Mechanics II Lecure 4 Lecure 4 Kineics of a paricle Par 3: Impulse and Momenum Linear impulse and momenum Saring from he equaion of moion for a paricle of mass m which is subjeced o an
Lecture 10: Wave equation, solution by spherical means
 Lecure : Wave equaion, soluion by spherical means Physical modeling eample: Elasodynamics u (; ) displacemen vecor in elasic body occupying a domain U R n, U, The posiion of he maerial poin siing a U in
Lecure : Wave equaion, soluion by spherical means Physical modeling eample: Elasodynamics u (; ) displacemen vecor in elasic body occupying a domain U R n, U, The posiion of he maerial poin siing a U in
Method of Moment Area Equations
 Noe proided b JRR Page-1 Noe proided b JRR Page- Inrodcion ehod of omen rea qaions Perform deformaion analsis of flere-dominaed srcres eams Frames asic ssmpions (on.) No aial deformaion (aiall rigid members)
Noe proided b JRR Page-1 Noe proided b JRR Page- Inrodcion ehod of omen rea qaions Perform deformaion analsis of flere-dominaed srcres eams Frames asic ssmpions (on.) No aial deformaion (aiall rigid members)
Finite Element Analysis of Structures
 KAIT OE5 Finie Elemen Analysis of rucures Mid-erm Exam, Fall 9 (p) m. As shown in Fig., we model a russ srucure of uniform area (lengh, Area Am ) subjeced o a uniform body force ( f B e x N / m ) using
KAIT OE5 Finie Elemen Analysis of rucures Mid-erm Exam, Fall 9 (p) m. As shown in Fig., we model a russ srucure of uniform area (lengh, Area Am ) subjeced o a uniform body force ( f B e x N / m ) using
Ch1: Introduction and Review
 //6 Ch: Inroducion and Review. Soli and flui; Coninuum hypohesis; Transpor phenomena (i) Solid vs. Fluid No exernal force : An elemen of solid has a preferred shape; fluid does no. Under he acion of a
//6 Ch: Inroducion and Review. Soli and flui; Coninuum hypohesis; Transpor phenomena (i) Solid vs. Fluid No exernal force : An elemen of solid has a preferred shape; fluid does no. Under he acion of a
Lecture 2-1 Kinematics in One Dimension Displacement, Velocity and Acceleration Everything in the world is moving. Nothing stays still.
 Lecure - Kinemaics in One Dimension Displacemen, Velociy and Acceleraion Everyhing in he world is moving. Nohing says sill. Moion occurs a all scales of he universe, saring from he moion of elecrons in
Lecure - Kinemaics in One Dimension Displacemen, Velociy and Acceleraion Everyhing in he world is moving. Nohing says sill. Moion occurs a all scales of he universe, saring from he moion of elecrons in
1. VELOCITY AND ACCELERATION
 1. VELOCITY AND ACCELERATION 1.1 Kinemaics Equaions s = u + 1 a and s = v 1 a s = 1 (u + v) v = u + as 1. Displacemen-Time Graph Gradien = speed 1.3 Velociy-Time Graph Gradien = acceleraion Area under
1. VELOCITY AND ACCELERATION 1.1 Kinemaics Equaions s = u + 1 a and s = v 1 a s = 1 (u + v) v = u + as 1. Displacemen-Time Graph Gradien = speed 1.3 Velociy-Time Graph Gradien = acceleraion Area under
Navneet Saini, Mayank Goyal, Vishal Bansal (2013); Term Project AML310; Indian Institute of Technology Delhi
 Creep in Viscoelasic Subsances Numerical mehods o calculae he coefficiens of he Prony equaion using creep es daa and Herediary Inegrals Mehod Navnee Saini, Mayank Goyal, Vishal Bansal (23); Term Projec
Creep in Viscoelasic Subsances Numerical mehods o calculae he coefficiens of he Prony equaion using creep es daa and Herediary Inegrals Mehod Navnee Saini, Mayank Goyal, Vishal Bansal (23); Term Projec
Unsteady laminar flow of visco-elastic fluid of second order type between two parallel plates
 Indian Jornal of Engineering & Maerials Sciences Vol., Febrary 5, pp. 5-57 Unseady laminar flow of visco-elasic flid of second order ype beween wo parallel plaes Ch V Ramana Mrhy & S B Klkarni Deparmen
Indian Jornal of Engineering & Maerials Sciences Vol., Febrary 5, pp. 5-57 Unseady laminar flow of visco-elasic flid of second order ype beween wo parallel plaes Ch V Ramana Mrhy & S B Klkarni Deparmen
Traveling Waves. Chapter Introduction
 Chaper 4 Traveling Waves 4.1 Inroducion To dae, we have considered oscillaions, i.e., periodic, ofen harmonic, variaions of a physical characerisic of a sysem. The sysem a one ime is indisinguishable from
Chaper 4 Traveling Waves 4.1 Inroducion To dae, we have considered oscillaions, i.e., periodic, ofen harmonic, variaions of a physical characerisic of a sysem. The sysem a one ime is indisinguishable from
Structural Dynamics and Earthquake Engineering
 Srucural Dynamics and Earhquae Engineering Course 1 Inroducion. Single degree of freedom sysems: Equaions of moion, problem saemen, soluion mehods. Course noes are available for download a hp://www.c.up.ro/users/aurelsraan/
Srucural Dynamics and Earhquae Engineering Course 1 Inroducion. Single degree of freedom sysems: Equaions of moion, problem saemen, soluion mehods. Course noes are available for download a hp://www.c.up.ro/users/aurelsraan/
Modelling Traffic Flow with Constant Speed using the Galerkin Finite Element Method
 Proceedings of he World Congress on Engineering 29 Vol II WCE 29, Jly - 3, 29, London, U.K. Modelling Traffic Flow wih Consan Speed sing he Galerin Finie Elemen Mehod Wesley Celemans, Magd A. Wahab, Kr
Proceedings of he World Congress on Engineering 29 Vol II WCE 29, Jly - 3, 29, London, U.K. Modelling Traffic Flow wih Consan Speed sing he Galerin Finie Elemen Mehod Wesley Celemans, Magd A. Wahab, Kr
Theory of! Partial Differential Equations-I!
 hp://users.wpi.edu/~grear/me61.hml! Ouline! Theory o! Parial Dierenial Equaions-I! Gréar Tryggvason! Spring 010! Basic Properies o PDE!! Quasi-linear Firs Order Equaions! - Characerisics! - Linear and
hp://users.wpi.edu/~grear/me61.hml! Ouline! Theory o! Parial Dierenial Equaions-I! Gréar Tryggvason! Spring 010! Basic Properies o PDE!! Quasi-linear Firs Order Equaions! - Characerisics! - Linear and
MECHANICS OF MATERIALS Poisson s Ratio
 Poisson s Raio For a slender bar subjeced o axial loading: ε x x y 0 The elongaion in he x-direcion i is accompanied by a conracion in he oher direcions. Assuming ha he maerial is isoropic (no direcional
Poisson s Raio For a slender bar subjeced o axial loading: ε x x y 0 The elongaion in he x-direcion i is accompanied by a conracion in he oher direcions. Assuming ha he maerial is isoropic (no direcional
Theory of! Partial Differential Equations!
 hp://www.nd.edu/~gryggva/cfd-course/! Ouline! Theory o! Parial Dierenial Equaions! Gréar Tryggvason! Spring 011! Basic Properies o PDE!! Quasi-linear Firs Order Equaions! - Characerisics! - Linear and
hp://www.nd.edu/~gryggva/cfd-course/! Ouline! Theory o! Parial Dierenial Equaions! Gréar Tryggvason! Spring 011! Basic Properies o PDE!! Quasi-linear Firs Order Equaions! - Characerisics! - Linear and
2.1: What is physics? Ch02: Motion along a straight line. 2.2: Motion. 2.3: Position, Displacement, Distance
 Ch: Moion along a sraigh line Moion Posiion and Displacemen Average Velociy and Average Speed Insananeous Velociy and Speed Acceleraion Consan Acceleraion: A Special Case Anoher Look a Consan Acceleraion
Ch: Moion along a sraigh line Moion Posiion and Displacemen Average Velociy and Average Speed Insananeous Velociy and Speed Acceleraion Consan Acceleraion: A Special Case Anoher Look a Consan Acceleraion
DESIGN OF TENSION MEMBERS
 CHAPTER Srcral Seel Design LRFD Mehod DESIGN OF TENSION MEMBERS Third Ediion A. J. Clark School of Engineering Deparmen of Civil and Environmenal Engineering Par II Srcral Seel Design and Analysis 4 FALL
CHAPTER Srcral Seel Design LRFD Mehod DESIGN OF TENSION MEMBERS Third Ediion A. J. Clark School of Engineering Deparmen of Civil and Environmenal Engineering Par II Srcral Seel Design and Analysis 4 FALL
Asymptotic Solution of the Anti-Plane Problem for a Two-Dimensional Lattice
 Asympoic Solion of he Ani-Plane Problem for a Two-Dimensional Laice N.I. Aleksandrova N.A. Chinakal Insie of Mining, Siberian Branch, Rssian Academy of Sciences, Krasnyi pr. 91, Novosibirsk, 6391 Rssia,
Asympoic Solion of he Ani-Plane Problem for a Two-Dimensional Laice N.I. Aleksandrova N.A. Chinakal Insie of Mining, Siberian Branch, Rssian Academy of Sciences, Krasnyi pr. 91, Novosibirsk, 6391 Rssia,
first-order circuit Complete response can be regarded as the superposition of zero-input response and zero-state response.
 Experimen 4:he Sdies of ransiional processes of 1. Prpose firs-order circi a) Use he oscilloscope o observe he ransiional processes of firs-order circi. b) Use he oscilloscope o measre he ime consan of
Experimen 4:he Sdies of ransiional processes of 1. Prpose firs-order circi a) Use he oscilloscope o observe he ransiional processes of firs-order circi. b) Use he oscilloscope o measre he ime consan of
Key Chemistry 102 Discussion #4, Chapter 11 and 12 Student name TA name Section. ; u= M. and T(red)=2*T(yellow) ; t(yellow)=4*t(red) or
 Key Chemisry 0 Discssion #4, Chaper and Sden name TA name Secion. Two idenical conainers, one red and one yellow, are inflaed wih differen gases a he same volme and pressre. Boh conainers have an idenically
Key Chemisry 0 Discssion #4, Chaper and Sden name TA name Secion. Two idenical conainers, one red and one yellow, are inflaed wih differen gases a he same volme and pressre. Boh conainers have an idenically
Kinematics Vocabulary. Kinematics and One Dimensional Motion. Position. Coordinate System in One Dimension. Kinema means movement 8.
 Kinemaics Vocabulary Kinemaics and One Dimensional Moion 8.1 WD1 Kinema means movemen Mahemaical descripion of moion Posiion Time Inerval Displacemen Velociy; absolue value: speed Acceleraion Averages
Kinemaics Vocabulary Kinemaics and One Dimensional Moion 8.1 WD1 Kinema means movemen Mahemaical descripion of moion Posiion Time Inerval Displacemen Velociy; absolue value: speed Acceleraion Averages
Physics 235 Chapter 2. Chapter 2 Newtonian Mechanics Single Particle
 Chaper 2 Newonian Mechanics Single Paricle In his Chaper we will review wha Newon s laws of mechanics ell us abou he moion of a single paricle. Newon s laws are only valid in suiable reference frames,
Chaper 2 Newonian Mechanics Single Paricle In his Chaper we will review wha Newon s laws of mechanics ell us abou he moion of a single paricle. Newon s laws are only valid in suiable reference frames,
Solution to Theoretical Question 2. A Piezoelectric Crystal Resonator under an Alternating Voltage Part A
 Solion o eoreical Qesion A Piezoelecric Crysal Resonaor ner an Alernaing olage Par A a Refer o Figre A e lef face of e ro oves a isance v wile e ressre wave ravels a isance wi / ρ e srain a e lef face
Solion o eoreical Qesion A Piezoelecric Crysal Resonaor ner an Alernaing olage Par A a Refer o Figre A e lef face of e ro oves a isance v wile e ressre wave ravels a isance wi / ρ e srain a e lef face
New effective moduli of isotropic viscoelastic composites. Part I. Theoretical justification
 IOP Conference Series: Maerials Science and Engineering PAPE OPEN ACCESS New effecive moduli of isoropic viscoelasic composies. Par I. Theoreical jusificaion To cie his aricle: A A Sveashkov and A A akurov
IOP Conference Series: Maerials Science and Engineering PAPE OPEN ACCESS New effecive moduli of isoropic viscoelasic composies. Par I. Theoreical jusificaion To cie his aricle: A A Sveashkov and A A akurov
Mat 267 Engineering Calculus III Updated on 04/30/ x 4y 4z 8x 16y / 4 0. x y z x y. 4x 4y 4z 24x 16y 8z.
 Ma 67 Engineering Calcls III Updaed on 04/0/0 r. Firoz Tes solion:. a) Find he cener and radis of he sphere 4 4 4z 8 6 0 z ( ) ( ) z / 4 The cener is a (, -, 0), and radis b) Find he cener and radis of
Ma 67 Engineering Calcls III Updaed on 04/0/0 r. Firoz Tes solion:. a) Find he cener and radis of he sphere 4 4 4z 8 6 0 z ( ) ( ) z / 4 The cener is a (, -, 0), and radis b) Find he cener and radis of
where the coordinate X (t) describes the system motion. X has its origin at the system static equilibrium position (SEP).
 Appendix A: Conservaion of Mechanical Energy = Conservaion of Linear Momenum Consider he moion of a nd order mechanical sysem comprised of he fundamenal mechanical elemens: ineria or mass (M), siffness
Appendix A: Conservaion of Mechanical Energy = Conservaion of Linear Momenum Consider he moion of a nd order mechanical sysem comprised of he fundamenal mechanical elemens: ineria or mass (M), siffness
( ) ( ) if t = t. It must satisfy the identity. So, bulkiness of the unit impulse (hyper)function is equal to 1. The defining characteristic is
 UNIT IMPULSE RESPONSE, UNIT STEP RESPONSE, STABILITY. Uni impulse funcion (Dirac dela funcion, dela funcion) rigorously defined is no sricly a funcion, bu disribuion (or measure), precise reamen requires
UNIT IMPULSE RESPONSE, UNIT STEP RESPONSE, STABILITY. Uni impulse funcion (Dirac dela funcion, dela funcion) rigorously defined is no sricly a funcion, bu disribuion (or measure), precise reamen requires
Wall. x(t) f(t) x(t = 0) = x 0, t=0. which describes the motion of the mass in absence of any external forcing.
 MECHANICS APPLICATIONS OF SECOND-ORDER ODES 7 Mechanics applicaions of second-order ODEs Second-order linear ODEs wih consan coefficiens arise in many physical applicaions. One physical sysems whose behaviour
MECHANICS APPLICATIONS OF SECOND-ORDER ODES 7 Mechanics applicaions of second-order ODEs Second-order linear ODEs wih consan coefficiens arise in many physical applicaions. One physical sysems whose behaviour
Let us start with a two dimensional case. We consider a vector ( x,
 Roaion marices We consider now roaion marices in wo and hree dimensions. We sar wih wo dimensions since wo dimensions are easier han hree o undersand, and one dimension is a lile oo simple. However, our
Roaion marices We consider now roaion marices in wo and hree dimensions. We sar wih wo dimensions since wo dimensions are easier han hree o undersand, and one dimension is a lile oo simple. However, our
IB Physics Kinematics Worksheet
 IB Physics Kinemaics Workshee Wrie full soluions and noes for muliple choice answers. Do no use a calculaor for muliple choice answers. 1. Which of he following is a correc definiion of average acceleraion?
IB Physics Kinemaics Workshee Wrie full soluions and noes for muliple choice answers. Do no use a calculaor for muliple choice answers. 1. Which of he following is a correc definiion of average acceleraion?
Ground Rules. PC1221 Fundamentals of Physics I. Kinematics. Position. Lectures 3 and 4 Motion in One Dimension. A/Prof Tay Seng Chuan
 Ground Rules PC11 Fundamenals of Physics I Lecures 3 and 4 Moion in One Dimension A/Prof Tay Seng Chuan 1 Swich off your handphone and pager Swich off your lapop compuer and keep i No alking while lecure
Ground Rules PC11 Fundamenals of Physics I Lecures 3 and 4 Moion in One Dimension A/Prof Tay Seng Chuan 1 Swich off your handphone and pager Swich off your lapop compuer and keep i No alking while lecure
MEI Mechanics 1 General motion. Section 1: Using calculus
 Soluions o Exercise MEI Mechanics General moion Secion : Using calculus. s 4 v a 6 4 4 When =, v 4 a 6 4 6. (i) When = 0, s = -, so he iniial displacemen = - m. s v 4 When = 0, v = so he iniial velociy
Soluions o Exercise MEI Mechanics General moion Secion : Using calculus. s 4 v a 6 4 4 When =, v 4 a 6 4 6. (i) When = 0, s = -, so he iniial displacemen = - m. s v 4 When = 0, v = so he iniial velociy
Speed and Velocity. Overview. Velocity & Speed. Speed & Velocity. Instantaneous Velocity. Instantaneous and Average
 Overview Kinemaics: Descripion of Moion Posiion and displacemen velociy»insananeous acceleraion»insananeous Speed Velociy Speed and Velociy Speed & Velociy Velociy & Speed A physics eacher walks 4 meers
Overview Kinemaics: Descripion of Moion Posiion and displacemen velociy»insananeous acceleraion»insananeous Speed Velociy Speed and Velociy Speed & Velociy Velociy & Speed A physics eacher walks 4 meers
Oscillations. Periodic Motion. Sinusoidal Motion. PHY oscillations - J. Hedberg
 Oscillaions PHY 207 - oscillaions - J. Hedberg - 2017 1. Periodic Moion 2. Sinusoidal Moion 3. How do we ge his kind of moion? 4. Posiion - Velociy - cceleraion 5. spring wih vecors 6. he reference circle
Oscillaions PHY 207 - oscillaions - J. Hedberg - 2017 1. Periodic Moion 2. Sinusoidal Moion 3. How do we ge his kind of moion? 4. Posiion - Velociy - cceleraion 5. spring wih vecors 6. he reference circle
Differential Equations
 Mah 21 (Fall 29) Differenial Equaions Soluion #3 1. Find he paricular soluion of he following differenial equaion by variaion of parameer (a) y + y = csc (b) 2 y + y y = ln, > Soluion: (a) The corresponding
Mah 21 (Fall 29) Differenial Equaions Soluion #3 1. Find he paricular soluion of he following differenial equaion by variaion of parameer (a) y + y = csc (b) 2 y + y y = ln, > Soluion: (a) The corresponding
INSTABILITY REGIONS DUE TO INTERNAL DAMPING ON ROTORS IN WOUNDING-SHAFT
 NSTABTY RGONS DU TO NTRNA DAMPNG ON ROTORS N WOUNDNG-SHAFT José C. Pereira and Márcio. Silveira Deparameno de ngenharia Mecânica Universidade Federal de Sana Caarina Caixa Posal 476 - Camps Universiário
NSTABTY RGONS DU TO NTRNA DAMPNG ON ROTORS N WOUNDNG-SHAFT José C. Pereira and Márcio. Silveira Deparameno de ngenharia Mecânica Universidade Federal de Sana Caarina Caixa Posal 476 - Camps Universiário
Finite element method for structural dynamic and stability analyses
 Finie elemen mehod for srucural dynamic and sabiliy analyses Module- Nonlinear FE Models Lecure-39 Toal and updaed Lagrangian formulaions Prof C Manohar Deparmen of Civil Engineering IIc, Bangalore 56
Finie elemen mehod for srucural dynamic and sabiliy analyses Module- Nonlinear FE Models Lecure-39 Toal and updaed Lagrangian formulaions Prof C Manohar Deparmen of Civil Engineering IIc, Bangalore 56
Parametrics and Vectors (BC Only)
 Paramerics and Vecors (BC Only) The following relaionships should be learned and memorized. The paricle s posiion vecor is r() x(), y(). The velociy vecor is v(),. The speed is he magniude of he velociy
Paramerics and Vecors (BC Only) The following relaionships should be learned and memorized. The paricle s posiion vecor is r() x(), y(). The velociy vecor is v(),. The speed is he magniude of he velociy
ψ(t) = V x (0)V x (t)
 .93 Home Work Se No. (Professor Sow-Hsin Chen Spring Term 5. Due March 7, 5. This problem concerns calculaions of analyical expressions for he self-inermediae scaering funcion (ISF of he es paricle in
.93 Home Work Se No. (Professor Sow-Hsin Chen Spring Term 5. Due March 7, 5. This problem concerns calculaions of analyical expressions for he self-inermediae scaering funcion (ISF of he es paricle in
Relaxation. T1 Values. Longitudinal Relaxation. dm z dt. = " M z T 1. (1" e "t /T 1 ) M z. (t) = M 0
 Relaxaion Bioengineering 28A Principles of Biomedical Imaging Fall Quarer 21 MRI Lecure 2 An exciaion pulse roaes he magneiaion vecor away from is equilibrium sae (purely longiudinal). The resuling vecor
Relaxaion Bioengineering 28A Principles of Biomedical Imaging Fall Quarer 21 MRI Lecure 2 An exciaion pulse roaes he magneiaion vecor away from is equilibrium sae (purely longiudinal). The resuling vecor
KINEMATICS IN ONE DIMENSION
 KINEMATICS IN ONE DIMENSION PREVIEW Kinemaics is he sudy of how hings move how far (disance and displacemen), how fas (speed and velociy), and how fas ha how fas changes (acceleraion). We say ha an objec
KINEMATICS IN ONE DIMENSION PREVIEW Kinemaics is he sudy of how hings move how far (disance and displacemen), how fas (speed and velociy), and how fas ha how fas changes (acceleraion). We say ha an objec
The Maxwell Equations, the Lorentz Field and the Electromagnetic Nanofield with Regard to the Question of Relativity
 The Maxwell Equaions, he Lorenz Field and he Elecromagneic Nanofield wih Regard o he Quesion of Relaiviy Daniele Sasso * Absrac We discuss he Elecromagneic Theory in some main respecs and specifically
The Maxwell Equaions, he Lorenz Field and he Elecromagneic Nanofield wih Regard o he Quesion of Relaiviy Daniele Sasso * Absrac We discuss he Elecromagneic Theory in some main respecs and specifically
Flow-Induced Vibration Analysis of Supported Pipes with a Crack
 Flow-Induced Vibraion Analsis of Suppored Pipes wih a Crack Jin-Huk Lee, Samer Masoud Al-Said Deparmen of Mechanical Engineering American Universi of Sharjah, UAE Ouline Inroducion and Moivaion Aeroacousicall
Flow-Induced Vibraion Analsis of Suppored Pipes wih a Crack Jin-Huk Lee, Samer Masoud Al-Said Deparmen of Mechanical Engineering American Universi of Sharjah, UAE Ouline Inroducion and Moivaion Aeroacousicall
Summary of shear rate kinematics (part 1)
 InroToMaFuncions.pdf 4 CM465 To proceed o beer-designed consiuive equaions, we need o know more abou maerial behavior, i.e. we need more maerial funcions o predic, and we need measuremens of hese maerial
InroToMaFuncions.pdf 4 CM465 To proceed o beer-designed consiuive equaions, we need o know more abou maerial behavior, i.e. we need more maerial funcions o predic, and we need measuremens of hese maerial
Some Basic Information about M-S-D Systems
 Some Basic Informaion abou M-S-D Sysems 1 Inroducion We wan o give some summary of he facs concerning unforced (homogeneous) and forced (non-homogeneous) models for linear oscillaors governed by second-order,
Some Basic Informaion abou M-S-D Sysems 1 Inroducion We wan o give some summary of he facs concerning unforced (homogeneous) and forced (non-homogeneous) models for linear oscillaors governed by second-order,
0 time. 2 Which graph represents the motion of a car that is travelling along a straight road with a uniformly increasing speed?
 1 1 The graph relaes o he moion of a falling body. y Which is a correc descripion of he graph? y is disance and air resisance is negligible y is disance and air resisance is no negligible y is speed and
1 1 The graph relaes o he moion of a falling body. y Which is a correc descripion of he graph? y is disance and air resisance is negligible y is disance and air resisance is no negligible y is speed and
Scalar Conservation Laws
 MATH-459 Nmerical Mehods for Conservaion Laws by Prof. Jan S. Heshaven Solion se : Scalar Conservaion Laws Eercise. The inegral form of he scalar conservaion law + f ) = is given in Eq. below. ˆ 2, 2 )
MATH-459 Nmerical Mehods for Conservaion Laws by Prof. Jan S. Heshaven Solion se : Scalar Conservaion Laws Eercise. The inegral form of he scalar conservaion law + f ) = is given in Eq. below. ˆ 2, 2 )
CSE-4303/CSE-5365 Computer Graphics Fall 1996 Take home Test
 Comper Graphics roblem #1) A bi-cbic parameric srface is defined by Hermie geomery in he direcion of parameer. In he direcion, he geomery ecor is defined by a poin @0, a poin @0.5, a angen ecor @1 and
Comper Graphics roblem #1) A bi-cbic parameric srface is defined by Hermie geomery in he direcion of parameer. In he direcion, he geomery ecor is defined by a poin @0, a poin @0.5, a angen ecor @1 and
THE MYSTERY OF STOCHASTIC MECHANICS. Edward Nelson Department of Mathematics Princeton University
 THE MYSTERY OF STOCHASTIC MECHANICS Edward Nelson Deparmen of Mahemaics Princeon Universiy 1 Classical Hamilon-Jacobi heory N paricles of various masses on a Euclidean space. Incorporae he masses in he
THE MYSTERY OF STOCHASTIC MECHANICS Edward Nelson Deparmen of Mahemaics Princeon Universiy 1 Classical Hamilon-Jacobi heory N paricles of various masses on a Euclidean space. Incorporae he masses in he
Symmetric form of governing equations for capillary fluids
 Symmeric form of governing eqaions for capillary flids Sergey Gavrilyk, Henri Goin To cie his version: Sergey Gavrilyk, Henri Goin. Symmeric form of governing eqaions for capillary flids. Gerard Iooss,
Symmeric form of governing eqaions for capillary flids Sergey Gavrilyk, Henri Goin To cie his version: Sergey Gavrilyk, Henri Goin. Symmeric form of governing eqaions for capillary flids. Gerard Iooss,
Chapter 6 Differential Analysis of Fluid Flow
 57:00 Mechanics of Flids and Transpor Processes Chaper 6 Professor Fred Sern Fall 006 1 Chaper 6 Differenial Analysis of Flid Flow Flid Elemen Kinemaics Flid elemen moion consiss of ranslaion, linear deformaion,
57:00 Mechanics of Flids and Transpor Processes Chaper 6 Professor Fred Sern Fall 006 1 Chaper 6 Differenial Analysis of Flid Flow Flid Elemen Kinemaics Flid elemen moion consiss of ranslaion, linear deformaion,
From Particles to Rigid Bodies
 Rigid Body Dynamics From Paricles o Rigid Bodies Paricles No roaions Linear velociy v only Rigid bodies Body roaions Linear velociy v Angular velociy ω Rigid Bodies Rigid bodies have boh a posiion and
Rigid Body Dynamics From Paricles o Rigid Bodies Paricles No roaions Linear velociy v only Rigid bodies Body roaions Linear velociy v Angular velociy ω Rigid Bodies Rigid bodies have boh a posiion and
PHYSICS 220 Lecture 02 Motion, Forces, and Newton s Laws Textbook Sections
 PHYSICS 220 Lecure 02 Moion, Forces, and Newon s Laws Texbook Secions 2.2-2.4 Lecure 2 Purdue Universiy, Physics 220 1 Overview Las Lecure Unis Scienific Noaion Significan Figures Moion Displacemen: Δx
PHYSICS 220 Lecure 02 Moion, Forces, and Newon s Laws Texbook Secions 2.2-2.4 Lecure 2 Purdue Universiy, Physics 220 1 Overview Las Lecure Unis Scienific Noaion Significan Figures Moion Displacemen: Δx
Diffusion & Viscosity: Navier-Stokes Equation
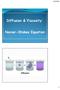 4/5/018 Diffusion & Viscosiy: Navier-Sokes Equaion 1 4/5/018 Diffusion Equaion Imagine a quaniy C(x,) represening a local propery in a fluid, eg. - hermal energy densiy - concenraion of a polluan - densiy
4/5/018 Diffusion & Viscosiy: Navier-Sokes Equaion 1 4/5/018 Diffusion Equaion Imagine a quaniy C(x,) represening a local propery in a fluid, eg. - hermal energy densiy - concenraion of a polluan - densiy
PROJECTS WITH APPLICATIONS OF DIFFERENTIAL EQUATIONS AND MATLAB
 PROJECTS WITH APPLICATIONS OF DIFFERENTIAL EQUATIONS AND MATLAB David Szrley Francis Marion Universiy Deparmen of Mahemaics PO Box 1547 Florence, SC 95 dszrley@fmarion.ed I. INTRODUCTION Differenial eqaions
PROJECTS WITH APPLICATIONS OF DIFFERENTIAL EQUATIONS AND MATLAB David Szrley Francis Marion Universiy Deparmen of Mahemaics PO Box 1547 Florence, SC 95 dszrley@fmarion.ed I. INTRODUCTION Differenial eqaions
Modified one dimensional elastic wave equations that retain time synchronization under spatial coordinate transformations
 Modified one dimensional elasic wave equaions ha reain ime synchronizaion under spaial coordinae ransformaions Ruiwen Yao, Zhihai Xiang * AML, Deparmen of Engineering Mechanics, Tsinghua Universiy, Beijing
Modified one dimensional elasic wave equaions ha reain ime synchronizaion under spaial coordinae ransformaions Ruiwen Yao, Zhihai Xiang * AML, Deparmen of Engineering Mechanics, Tsinghua Universiy, Beijing
Problem Set #1. i z. the complex propagation constant. For the characteristic impedance:
 Problem Se # Problem : a) Using phasor noaion, calculae he volage and curren waves on a ransmission line by solving he wave equaion Assume ha R, L,, G are all non-zero and independen of frequency From
Problem Se # Problem : a) Using phasor noaion, calculae he volage and curren waves on a ransmission line by solving he wave equaion Assume ha R, L,, G are all non-zero and independen of frequency From
Numerical Dispersion
 eview of Linear Numerical Sabiliy Numerical Dispersion n he previous lecure, we considered he linear numerical sabiliy of boh advecion and diffusion erms when approimaed wih several spaial and emporal
eview of Linear Numerical Sabiliy Numerical Dispersion n he previous lecure, we considered he linear numerical sabiliy of boh advecion and diffusion erms when approimaed wih several spaial and emporal
The motions of the celt on a horizontal plane with viscous friction
 The h Join Inernaional Conference on Mulibody Sysem Dynamics June 8, 18, Lisboa, Porugal The moions of he cel on a horizonal plane wih viscous fricion Maria A. Munisyna 1 1 Moscow Insiue of Physics and
The h Join Inernaional Conference on Mulibody Sysem Dynamics June 8, 18, Lisboa, Porugal The moions of he cel on a horizonal plane wih viscous fricion Maria A. Munisyna 1 1 Moscow Insiue of Physics and
Module 3: The Damped Oscillator-II Lecture 3: The Damped Oscillator-II
 Module 3: The Damped Oscillaor-II Lecure 3: The Damped Oscillaor-II 3. Over-damped Oscillaions. This refers o he siuaion where β > ω (3.) The wo roos are and α = β + α 2 = β β 2 ω 2 = (3.2) β 2 ω 2 = 2
Module 3: The Damped Oscillaor-II Lecure 3: The Damped Oscillaor-II 3. Over-damped Oscillaions. This refers o he siuaion where β > ω (3.) The wo roos are and α = β + α 2 = β β 2 ω 2 = (3.2) β 2 ω 2 = 2
TIME-SPACE DEPENDENT FRACTIONAL VISCOELASTIC MHD FLUID FLOW AND HEAT TRANSFER OVER ACCELERATING PLATE WITH SLIP BOUNDARY
 HERMAL SCIENCE: Year 7, Vol., No. A, pp. 7-7 IME-SPACE DEPENDEN FRACIONAL VISCOELASIC MHD FLUID FLOW AND HEA RANSFER OVER ACCELERAING PLAE WIH SLIP BOUNDARY b Shenging CHEN a, Liancn ZHENG a*, Chnri LI
HERMAL SCIENCE: Year 7, Vol., No. A, pp. 7-7 IME-SPACE DEPENDEN FRACIONAL VISCOELASIC MHD FLUID FLOW AND HEA RANSFER OVER ACCELERAING PLAE WIH SLIP BOUNDARY b Shenging CHEN a, Liancn ZHENG a*, Chnri LI
ME 425: Aerodynamics
 ME 45: Aerodnamics Dr. A.B.M. Toiqe Hasan Proessor Deparmen o Mechanical Engineering Bangladesh Uniersi o Engineering & Technolog BUET, Dhaka Lecre-7 Fndamenals so Aerodnamics oiqehasan.be.ac.bd oiqehasan@me.be.ac.bd
ME 45: Aerodnamics Dr. A.B.M. Toiqe Hasan Proessor Deparmen o Mechanical Engineering Bangladesh Uniersi o Engineering & Technolog BUET, Dhaka Lecre-7 Fndamenals so Aerodnamics oiqehasan.be.ac.bd oiqehasan@me.be.ac.bd
Questions 1 and 2 refer to the graph below. The graph is a displacement-time graph for a runner. Displacement / m. Time / s
 Quesions 1 and 2 refer o he graph below. The graph is a displacemen-ime graph for a runner. 80 isplacemen / m 60 40 0 0 4 6 8 / s 1 The velociy of he runner a 5 s is approximaely 8 m s 9 m s C 40 m s 2
Quesions 1 and 2 refer o he graph below. The graph is a displacemen-ime graph for a runner. 80 isplacemen / m 60 40 0 0 4 6 8 / s 1 The velociy of he runner a 5 s is approximaely 8 m s 9 m s C 40 m s 2
Effects of Hall Current and Rotation in Modified Couple Stress Generalized Thermoelastic Half Space due to Ramp-Type Heating
 Journal of Solid Mechanics Vol. 9, No. (7) pp. 57-54 Effecs of Hall Curren and Roaion in Modified Couple Sress Generalized Thermoelasic Half Space due o Ramp-Type Heaing R. Kumar, *, Sh. Devi, V. Sharma
Journal of Solid Mechanics Vol. 9, No. (7) pp. 57-54 Effecs of Hall Curren and Roaion in Modified Couple Sress Generalized Thermoelasic Half Space due o Ramp-Type Heaing R. Kumar, *, Sh. Devi, V. Sharma
Solution: b All the terms must have the dimension of acceleration. We see that, indeed, each term has the units of acceleration
 PHYS 54 Tes Pracice Soluions Spring 8 Q: [4] Knowing ha in he ne epression a is acceleraion, v is speed, is posiion and is ime, from a dimensional v poin of view, he equaion a is a) incorrec b) correc
PHYS 54 Tes Pracice Soluions Spring 8 Q: [4] Knowing ha in he ne epression a is acceleraion, v is speed, is posiion and is ime, from a dimensional v poin of view, he equaion a is a) incorrec b) correc
Acceleration. Part I. Uniformly Accelerated Motion: Kinematics & Geometry
 Acceleraion Team: Par I. Uniformly Acceleraed Moion: Kinemaics & Geomery Acceleraion is he rae of change of velociy wih respec o ime: a dv/d. In his experimen, you will sudy a very imporan class of moion
Acceleraion Team: Par I. Uniformly Acceleraed Moion: Kinemaics & Geomery Acceleraion is he rae of change of velociy wih respec o ime: a dv/d. In his experimen, you will sudy a very imporan class of moion
Class Meeting # 10: Introduction to the Wave Equation
 MATH 8.5 COURSE NOTES - CLASS MEETING # 0 8.5 Inroducion o PDEs, Fall 0 Professor: Jared Speck Class Meeing # 0: Inroducion o he Wave Equaion. Wha is he wave equaion? The sandard wave equaion for a funcion
MATH 8.5 COURSE NOTES - CLASS MEETING # 0 8.5 Inroducion o PDEs, Fall 0 Professor: Jared Speck Class Meeing # 0: Inroducion o he Wave Equaion. Wha is he wave equaion? The sandard wave equaion for a funcion
We just finished the Erdős-Stone Theorem, and ex(n, F ) (1 1/(χ(F ) 1)) ( n
 Lecure 3 - Kövari-Sós-Turán Theorem Jacques Versraëe jacques@ucsd.edu We jus finished he Erdős-Sone Theorem, and ex(n, F ) ( /(χ(f ) )) ( n 2). So we have asympoics when χ(f ) 3 bu no when χ(f ) = 2 i.e.
Lecure 3 - Kövari-Sós-Turán Theorem Jacques Versraëe jacques@ucsd.edu We jus finished he Erdős-Sone Theorem, and ex(n, F ) ( /(χ(f ) )) ( n 2). So we have asympoics when χ(f ) 3 bu no when χ(f ) = 2 i.e.
THE EFFECT OF SUCTION AND INJECTION ON UNSTEADY COUETTE FLOW WITH VARIABLE PROPERTIES
 Kragujevac J. Sci. 3 () 7-4. UDC 53.5:536. 4 THE EFFECT OF SUCTION AND INJECTION ON UNSTEADY COUETTE FLOW WITH VARIABLE PROPERTIES Hazem A. Aia Dep. of Mahemaics, College of Science,King Saud Universiy
Kragujevac J. Sci. 3 () 7-4. UDC 53.5:536. 4 THE EFFECT OF SUCTION AND INJECTION ON UNSTEADY COUETTE FLOW WITH VARIABLE PROPERTIES Hazem A. Aia Dep. of Mahemaics, College of Science,King Saud Universiy
, u denotes uxt (,) and u. mean first partial derivatives of u with respect to x and t, respectively. Equation (1.1) can be simply written as
 Proceedings of he rd IMT-GT Regional Conference on Mahemaics Saisics and Applicaions Universii Sains Malaysia ANALYSIS ON () + () () = G( ( ) ()) Jessada Tanhanch School of Mahemaics Insie of Science Sranaree
Proceedings of he rd IMT-GT Regional Conference on Mahemaics Saisics and Applicaions Universii Sains Malaysia ANALYSIS ON () + () () = G( ( ) ()) Jessada Tanhanch School of Mahemaics Insie of Science Sranaree
Kinematics Motion in 1 Dimension and Graphs
 Kinemaics Moion in 1 Dimension and Graphs Lana Sheridan De Anza College Sep 27, 2017 Las ime moion in 1-dimension some kinemaic quaniies graphs Overview velociy and speed acceleraion more graphs Kinemaics
Kinemaics Moion in 1 Dimension and Graphs Lana Sheridan De Anza College Sep 27, 2017 Las ime moion in 1-dimension some kinemaic quaniies graphs Overview velociy and speed acceleraion more graphs Kinemaics
- If one knows that a magnetic field has a symmetry, one may calculate the magnitude of B by use of Ampere s law: The integral of scalar product
 11.1 APPCATON OF AMPEE S AW N SYMMETC MAGNETC FEDS - f one knows ha a magneic field has a symmery, one may calculae he magniude of by use of Ampere s law: The inegral of scalar produc Closed _ pah * d
11.1 APPCATON OF AMPEE S AW N SYMMETC MAGNETC FEDS - f one knows ha a magneic field has a symmery, one may calculae he magniude of by use of Ampere s law: The inegral of scalar produc Closed _ pah * d
CLASS XI SET A PHYSICS. 1. If and Let. The correct order of % error in. (a) (b) x = y > z (c) x < z < y (d) x > z < y
 PHYSICS 1. If and Le. The correc order of % error in (a) (b) x = y > z x < z < y x > z < y. A hollow verical cylinder of radius r and heigh h has a smooh inernal surface. A small paricle is placed in conac
PHYSICS 1. If and Le. The correc order of % error in (a) (b) x = y > z x < z < y x > z < y. A hollow verical cylinder of radius r and heigh h has a smooh inernal surface. A small paricle is placed in conac
Chapter 12: Velocity, acceleration, and forces
 To Feel a Force Chaper Spring, Chaper : A. Saes of moion For moion on or near he surface of he earh, i is naural o measure moion wih respec o objecs fixed o he earh. The 4 hr. roaion of he earh has a measurable
To Feel a Force Chaper Spring, Chaper : A. Saes of moion For moion on or near he surface of he earh, i is naural o measure moion wih respec o objecs fixed o he earh. The 4 hr. roaion of he earh has a measurable
Dynamic Response of Inclined Isotropic Elastic Damped Rectangular Mindlin Plate resting on Pasternak Foundation under a Moving Load
 Proceedings of he Inernaional MliConference of Engineers and Comper Scieniss 016 Vol II, IMECS 016, March 16-18, 016, Hong Kong Dnamic Response of Inclined Isoropic Elasic Damped Recanglar Mindlin Plae
Proceedings of he Inernaional MliConference of Engineers and Comper Scieniss 016 Vol II, IMECS 016, March 16-18, 016, Hong Kong Dnamic Response of Inclined Isoropic Elasic Damped Recanglar Mindlin Plae
Chapter Q1. We need to understand Classical wave first. 3/28/2004 H133 Spring
 Chaper Q1 Inroducion o Quanum Mechanics End of 19 h Cenury only a few loose ends o wrap up. Led o Relaiviy which you learned abou las quarer Led o Quanum Mechanics (1920 s-30 s and beyond) Behavior of
Chaper Q1 Inroducion o Quanum Mechanics End of 19 h Cenury only a few loose ends o wrap up. Led o Relaiviy which you learned abou las quarer Led o Quanum Mechanics (1920 s-30 s and beyond) Behavior of
L p -L q -Time decay estimate for solution of the Cauchy problem for hyperbolic partial differential equations of linear thermoelasticity
 ANNALES POLONICI MATHEMATICI LIV.2 99) L p -L q -Time decay esimae for soluion of he Cauchy problem for hyperbolic parial differenial equaions of linear hermoelasiciy by Jerzy Gawinecki Warszawa) Absrac.
ANNALES POLONICI MATHEMATICI LIV.2 99) L p -L q -Time decay esimae for soluion of he Cauchy problem for hyperbolic parial differenial equaions of linear hermoelasiciy by Jerzy Gawinecki Warszawa) Absrac.
Voltage/current relationship Stored Energy. RL / RC circuits Steady State / Transient response Natural / Step response
 Review Capaciors/Inducors Volage/curren relaionship Sored Energy s Order Circuis RL / RC circuis Seady Sae / Transien response Naural / Sep response EE4 Summer 5: Lecure 5 Insrucor: Ocavian Florescu Lecure
Review Capaciors/Inducors Volage/curren relaionship Sored Energy s Order Circuis RL / RC circuis Seady Sae / Transien response Naural / Sep response EE4 Summer 5: Lecure 5 Insrucor: Ocavian Florescu Lecure
Acceleration. Part I. Uniformly Accelerated Motion: Kinematics & Geometry
 Acceleraion Team: Par I. Uniformly Acceleraed Moion: Kinemaics & Geomery Acceleraion is he rae of change of velociy wih respec o ime: a dv/d. In his experimen, you will sudy a very imporan class of moion
Acceleraion Team: Par I. Uniformly Acceleraed Moion: Kinemaics & Geomery Acceleraion is he rae of change of velociy wih respec o ime: a dv/d. In his experimen, you will sudy a very imporan class of moion
Analytic nonlinear elasto-viscosity of two types of BN and PI rubbers at large deformations
 Bulgarian Chemical Communicaions, Volume 48, Special Issue E (pp. 59-64) 016 Analyic nonlinear elaso-viscosiy of wo ypes of BN and PI rubbers a large deformaions K. B. Hadjov, A. S. Aleksandrov, M. P.
Bulgarian Chemical Communicaions, Volume 48, Special Issue E (pp. 59-64) 016 Analyic nonlinear elaso-viscosiy of wo ypes of BN and PI rubbers a large deformaions K. B. Hadjov, A. S. Aleksandrov, M. P.
Curling Stress Equation for Transverse Joint Edge of a Concrete Pavement Slab Based on Finite-Element Method Analysis
 TRANSPORTATION RESEARCH RECORD 155 35 Curling Sress Equaion for Transverse Join Edge of a Concree Pavemen Slab Based on Finie-Elemen Mehod Analysis TATSUO NISHIZAWA, TADASHI FUKUDA, SABURO MATSUNO, AND
TRANSPORTATION RESEARCH RECORD 155 35 Curling Sress Equaion for Transverse Join Edge of a Concree Pavemen Slab Based on Finie-Elemen Mehod Analysis TATSUO NISHIZAWA, TADASHI FUKUDA, SABURO MATSUNO, AND
MOMENTUM CONSERVATION LAW
 1 AAST/AEDT AP PHYSICS B: Impulse and Momenum Le us run an experimen: The ball is moving wih a velociy of V o and a force of F is applied on i for he ime inerval of. As he resul he ball s velociy changes
1 AAST/AEDT AP PHYSICS B: Impulse and Momenum Le us run an experimen: The ball is moving wih a velociy of V o and a force of F is applied on i for he ime inerval of. As he resul he ball s velociy changes
Exam I. Name. Answer: a. W B > W A if the volume of the ice cubes is greater than the volume of the water.
 Name Exam I 1) A hole is punched in a full milk caron, 10 cm below he op. Wha is he iniial veloci of ouflow? a. 1.4 m/s b. 2.0 m/s c. 2.8 m/s d. 3.9 m/s e. 2.8 m/s Answer: a 2) In a wind unnel he pressure
Name Exam I 1) A hole is punched in a full milk caron, 10 cm below he op. Wha is he iniial veloci of ouflow? a. 1.4 m/s b. 2.0 m/s c. 2.8 m/s d. 3.9 m/s e. 2.8 m/s Answer: a 2) In a wind unnel he pressure
AP Calculus BC Chapter 10 Part 1 AP Exam Problems
 AP Calculus BC Chaper Par AP Eam Problems All problems are NO CALCULATOR unless oherwise indicaed Parameric Curves and Derivaives In he y plane, he graph of he parameric equaions = 5 + and y= for, is a
AP Calculus BC Chaper Par AP Eam Problems All problems are NO CALCULATOR unless oherwise indicaed Parameric Curves and Derivaives In he y plane, he graph of he parameric equaions = 5 + and y= for, is a
Solutions from Chapter 9.1 and 9.2
 Soluions from Chaper 9 and 92 Secion 9 Problem # This basically boils down o an exercise in he chain rule from calculus We are looking for soluions of he form: u( x) = f( k x c) where k x R 3 and k is
Soluions from Chaper 9 and 92 Secion 9 Problem # This basically boils down o an exercise in he chain rule from calculus We are looking for soluions of he form: u( x) = f( k x c) where k x R 3 and k is
A Direct Method for Solving Nonlinear PDEs and. New Exact Solutions for Some Examples
 In. J. Conemp. Mah. Sciences, Vol. 6, 011, no. 46, 83-90 A Direc Mehod for Solving Nonlinear PDEs and New Eac Solions for Some Eamples Ameina S. Nseir Jordan Universiy of Science and Technology Deparmen
In. J. Conemp. Mah. Sciences, Vol. 6, 011, no. 46, 83-90 A Direc Mehod for Solving Nonlinear PDEs and New Eac Solions for Some Eamples Ameina S. Nseir Jordan Universiy of Science and Technology Deparmen
CSE 5365 Computer Graphics. Take Home Test #1
 CSE 5365 Comper Graphics Take Home Tes #1 Fall/1996 Tae-Hoon Kim roblem #1) A bi-cbic parameric srface is defined by Hermie geomery in he direcion of parameer. In he direcion, he geomery ecor is defined
CSE 5365 Comper Graphics Take Home Tes #1 Fall/1996 Tae-Hoon Kim roblem #1) A bi-cbic parameric srface is defined by Hermie geomery in he direcion of parameer. In he direcion, he geomery ecor is defined
!!"#"$%&#'()!"#&'(*%)+,&',-)./0)1-*23)
 "#"$%&#'()"#&'(*%)+,&',-)./)1-*) #$%&'()*+,&',-.%,/)*+,-&1*#$)()5*6$+$%*,7&*-'-&1*(,-&*6&,7.$%$+*&%'(*8$&',-,%'-&1*(,-&*6&,79*(&,%: ;..,*&1$&$.$%&'()*1$$.,'&',-9*(&,%)?%*,('&5
"#"$%&#'()"#&'(*%)+,&',-)./)1-*) #$%&'()*+,&',-.%,/)*+,-&1*#$)()5*6$+$%*,7&*-'-&1*(,-&*6&,7.$%$+*&%'(*8$&',-,%'-&1*(,-&*6&,79*(&,%: ;..,*&1$&$.$%&'()*1$$.,'&',-9*(&,%)?%*,('&5
Non-uniform circular motion *
 OpenSax-CNX module: m14020 1 Non-uniform circular moion * Sunil Kumar Singh This work is produced by OpenSax-CNX and licensed under he Creaive Commons Aribuion License 2.0 Wha do we mean by non-uniform
OpenSax-CNX module: m14020 1 Non-uniform circular moion * Sunil Kumar Singh This work is produced by OpenSax-CNX and licensed under he Creaive Commons Aribuion License 2.0 Wha do we mean by non-uniform
A Special Hour with Relativity
 A Special Hour wih Relaiviy Kenneh Chu The Graduae Colloquium Deparmen of Mahemaics Universiy of Uah Oc 29, 2002 Absrac Wha promped Einsen: Incompaibiliies beween Newonian Mechanics and Maxwell s Elecromagneism.
A Special Hour wih Relaiviy Kenneh Chu The Graduae Colloquium Deparmen of Mahemaics Universiy of Uah Oc 29, 2002 Absrac Wha promped Einsen: Incompaibiliies beween Newonian Mechanics and Maxwell s Elecromagneism.
4 3 a b (C) (a 2b) (D) (2a 3b)
 * A balloon is moving verically pwards wih a velociy of 9 m/s. A sone is dropped from i and i reaches he grond in 10 sec. The heigh of he balloon when he sone was dropped is (ake g = 9.8 ms - ) (a) 100
* A balloon is moving verically pwards wih a velociy of 9 m/s. A sone is dropped from i and i reaches he grond in 10 sec. The heigh of he balloon when he sone was dropped is (ake g = 9.8 ms - ) (a) 100
Variable acceleration, Mixed Exercise 11
 Variable acceleraion, Mixed Exercise 11 1 a v 1 P is a res when v 0. 0 1 b s 0 0 v d (1 ) 1 0 1 0 7. The disance ravelled by P is 7. m. 1 a v 6+ a d v 6 + When, a 6+ 0 The acceleraion of P when is 0 m
Variable acceleraion, Mixed Exercise 11 1 a v 1 P is a res when v 0. 0 1 b s 0 0 v d (1 ) 1 0 1 0 7. The disance ravelled by P is 7. m. 1 a v 6+ a d v 6 + When, a 6+ 0 The acceleraion of P when is 0 m
Phys 221 Fall Chapter 2. Motion in One Dimension. 2014, 2005 A. Dzyubenko Brooks/Cole
 Phys 221 Fall 2014 Chaper 2 Moion in One Dimension 2014, 2005 A. Dzyubenko 2004 Brooks/Cole 1 Kinemaics Kinemaics, a par of classical mechanics: Describes moion in erms of space and ime Ignores he agen
Phys 221 Fall 2014 Chaper 2 Moion in One Dimension 2014, 2005 A. Dzyubenko 2004 Brooks/Cole 1 Kinemaics Kinemaics, a par of classical mechanics: Describes moion in erms of space and ime Ignores he agen
Course II. Lesson 7 Applications to Physics. 7A Velocity and Acceleration of a Particle
 Course II Lesson 7 Applicaions o Physics 7A Velociy and Acceleraion of a Paricle Moion in a Sraigh Line : Velociy O Aerage elociy Moion in he -ais + Δ + Δ 0 0 Δ Δ Insananeous elociy d d Δ Δ Δ 0 lim [ m/s
Course II Lesson 7 Applicaions o Physics 7A Velociy and Acceleraion of a Paricle Moion in a Sraigh Line : Velociy O Aerage elociy Moion in he -ais + Δ + Δ 0 0 Δ Δ Insananeous elociy d d Δ Δ Δ 0 lim [ m/s
3, so θ = arccos
 Mahemaics 210 Professor Alan H Sein Monday, Ocober 1, 2007 SOLUTIONS This problem se is worh 50 poins 1 Find he angle beween he vecors (2, 7, 3) and (5, 2, 4) Soluion: Le θ be he angle (2, 7, 3) (5, 2,
Mahemaics 210 Professor Alan H Sein Monday, Ocober 1, 2007 SOLUTIONS This problem se is worh 50 poins 1 Find he angle beween he vecors (2, 7, 3) and (5, 2, 4) Soluion: Le θ be he angle (2, 7, 3) (5, 2,
An Introduction to Malliavin calculus and its applications
 An Inroducion o Malliavin calculus and is applicaions Lecure 5: Smoohness of he densiy and Hörmander s heorem David Nualar Deparmen of Mahemaics Kansas Universiy Universiy of Wyoming Summer School 214
An Inroducion o Malliavin calculus and is applicaions Lecure 5: Smoohness of he densiy and Hörmander s heorem David Nualar Deparmen of Mahemaics Kansas Universiy Universiy of Wyoming Summer School 214
dt = C exp (3 ln t 4 ). t 4 W = C exp ( ln(4 t) 3) = C(4 t) 3.
 Mah Rahman Exam Review Soluions () Consider he IVP: ( 4)y 3y + 4y = ; y(3) = 0, y (3) =. (a) Please deermine he longes inerval for which he IVP is guaraneed o have a unique soluion. Soluion: The disconinuiies
Mah Rahman Exam Review Soluions () Consider he IVP: ( 4)y 3y + 4y = ; y(3) = 0, y (3) =. (a) Please deermine he longes inerval for which he IVP is guaraneed o have a unique soluion. Soluion: The disconinuiies
Two Coupled Oscillators / Normal Modes
 Lecure 3 Phys 3750 Two Coupled Oscillaors / Normal Modes Overview and Moivaion: Today we ake a small, bu significan, sep owards wave moion. We will no ye observe waves, bu his sep is imporan in is own
Lecure 3 Phys 3750 Two Coupled Oscillaors / Normal Modes Overview and Moivaion: Today we ake a small, bu significan, sep owards wave moion. We will no ye observe waves, bu his sep is imporan in is own
