SIMPLE METHOD FOR THE SOLUTION OF INCOMPRESSIBLE FLOWS ON NON-STAGGERED GRIDS
|
|
|
- Kelly McKinney
- 6 years ago
- Views:
Transcription
1 SIML MTHOD FOR TH SOLUTION OF INCOMRSSIBL FLOWS ON NON-STAGGRD GRIDS I. Szai - astr Mditrraa Uivrsity, Mchaical girig Dpartmt, Mrsi 10 -Trky 1. Itrdcti Thr ar sally t kids f grid arragmts sd t slv th flid fl prblms: staggrd grids ad -staggrd grids. Fr th staggrd grids, vctr variabls ad scalar variabls ar strd at th sam lcatis, hil fr th staggrd grids, vctr cmpts ad scalar variabls ar strd at diffrt lcatis, shiftd half ctrl vlm i ach crdiat dircti. Staggrd grids ar pplar bcas f thir ability t prvt chckrbard prssr i th fl slti as discssd i Chaptr 6. Hvr, prgrammig f th staggrd grid mthd is tdis sic ad v-mmtm qatis ar discrtizd at diffrt ctrl vlms shiftd i diffrt dirctis frm th mai ctrl vlms. Th prgrammig difficltis icras h dals ith crviliar r strctrd grids. As a rslt, arly all cds ritt crviliar r strctrd grids s -staggrd grid arragmt fr th slti f flid fl prblms. O th thr had -staggrd grids ar pr t prdc a fals prssr fild - chckrbard prssr if spcial prcatis is t tak. Fr this ras, i th arly 1980s ad bfr, -staggrd r rarly sd fr icmprssibl fl. Hvr, sic 1983 th staggrd grid (r cllcatd grid has b sd mr idly, aftr Rhi ad Ch (1983 prpsd a mmtm itrplati mthd t limiat th chckrbard prssr prblm. 1. Mathmatical Frmlati Th gvrig qatis fr t dimsial icmprssibl lamiar hat ad flid fl i Cartsia crdiats ith cstat prprtis ar: ctiity qati + v y = 0 (1 1
2 -mmtm qati ( ρ ( ρ ( ρ v p μ = + + μ + S t y y y v-mmtm qati ( ρ ( ρ ( ρ v v vv p v v μ = + + μ + S t y y y y rgy qati ( ρt ( ρt ( ρvt T T = k + k + ST t y y y qatis (2 (4 ca b prssd i a gral frm as: ( ( v ρφ ρ φ ρ φ φ φ = Γ + Γ + Sφ + f( p t y y y (5 hr ad v ar th vlcity cmpts, T is tmpratr ad φ is ay dpdt variabl (i.., v ad T, ad t, ρ, Γ, ad S φ ar tim, dsity, diffsi cfficit, ad src trm, rspctivly. Als f ( p = p/ fr -mmtm qati f ( p = p/ y fr y-mmtm qati Nt that fr th ctiity qati, φ = 1, Γ = 0, ad S φ = 0. Th gvrig qatis ar discrtizd by sig th fiit-vlm mthd a staggrd grid systm i hich all variabls ar strd at th ctr f th ctrl vlm (Figr 1. Itgratig q. (5 vr th ctrl vlm ith bdd cll facs,,, ad s srrdig ctr, hav ρδδy ( φ φ + ( ρφ ( ρφ Δ y+ ( ρvφ ( ρvφ Δ = s Δt Γ Γ Γ Γ s ( φ φ ( φ φw Δ y+ ( φn φ ( φ φs Δ (6 δ δ δ y δ ys + S ΔΔ y+ S φ ΔΔ y+ f( p ΔΔy c hr th sprscript rfrs t th prvis tim lvl ad Δ, Δ y, δ, δ, δy ad δ y s ar gmtric lgths as sh i Figr 1. v (2 (3 (4 2
3 Figr 1. Nstaggrd Grid Arragmt Th discrtizd ctiity qati fr icmprssibl fl is ( ρ Δy ( ρ Δ y+ ( ρv Δ ( ρvs Δ = 0 (7 Th cll fac vals φ, φ tc ar calclatd sig QUICK r ay thr high rdr schm i a dfrrd crrcti mar. Sbstittig ths vals it q. (6 ad rarragig, btai th fial discrtizd qati fr ay gral variabl φ as flls: aφ aφ awφw anφn asφs aφ b φ = (8 hr 3
4 ΓΔ y a = + ma ( ρ Δy, 0 Δ ΓΔ y aw = + ma ( ρ Δy, 0 Δ ΓΔ an = + ma ( ρv Δ, 0 Δy ΓΔ s as = + ma ( ρv Δ, 0 s Δy s ρδδ y a = Δt a = a + a + a + a + a S ΔΔ y+δf W N S ( ρ ( ρ ( ρ ( ρ Δ F = Δy Δ y+ v Δ v Δ b = S ΔΔ y+ b c dc s ( ρ ( φ φ + ma ρ Δy, 0 φ φ ( ρ y ( φ φ ( ρ y ( φ φ b = ma Δy, 0 dc ma Δ, 0 + ma Δ, 0 ( ρv ( φ φ ( ρv ( φ φ ma Δ, 0 + ma Δ, 0 ( ρv ( φ φ ( ρv ( φ φ ma Δ, 0 ma, 0 s + Δ s = ( p p Δy fr -mmtm qati φ φ = ( ps p Δ fr v-mmtm qati φ = 0 fr all thr qatis W N s s S (9 hr th trm b dc rslts frm th adpti f th dfrrd-crrcti prcdr i hich th fac vals f th idpdt variabl, φ, φ, φ, φ s ar calclatd frm a sitabl high rdr schm sch as QUICK. φ is th val f φ frm th prvis tim stp. It ca b bsrvd that th cfficits f th discrtizd - ad y-mmtm qatis ar th sam i cllcatd grid systm, prvidd that th diffsi cfficits ar th sam i ad y-dirctis. I rdr t sl d th chags f dpdt variabls i csctiv sltis, a drrlaati factr is itrdcd it th discrtizd qati as flls: α φ = φ + φ + φ + φ + φ + α φ ( a a a a b φ a ( 1 φ φ 1 W W N N S S a αφ = + a ( aφ awφw anφn asφs B φ (10 4
5 hr th sprscript -1 rfrs t th prvis itrati ad ( 1 αφ 1 B = b + a φ + a φ (11 αφ Nt that th trm b i qatis (8 ad (9 shld b rplacd by B if th qatis ar rlad. 4. Mmtm Itrplati 4.1. Mmtm itrplati fr stady-stat prblm B = b + 1 α α a [q.(11]. Fr th 1 Nt that fr th stady prblms vlcity cmpt at ds ad, q.(10 ca b ritt as α i a i i + Bp α Δy p p = (12 α i a i i + Bp α Δy p p = (13 Mimickig th frmlati f ad, ca btai fllig prssi fr th itrfac vlcity at th cll fac. α i a i i + Bp α Δy p p = (14 hr th trms th right-had sid ith sbscript shld b itrplatd i a apprpriat mar. Th itrfac vlcity at cll facs,, ad s ca b btaid similarly. I Rhi ad Ch s mmtm itrplati, th first trm ad 1 i scd trm f th q. (14 ar liarly itrplatd frm thir ctrparts i qs. (12 ad (13: a + B a + B a + B ( 1 f i i i p + i i i p + i i i p = f + a a a = f + (16 a a a ( 1 f (15 5
6 hr f + is a liar itrplati factr dfis as f = (17 2δ + Δ I rdr t hav a bttr drstadig f q. (14, sbstittig ( a B a q. (15 ad ( a + B a, ( a B a i i i p (14 ad mittig th trm a, btai i i i p + frm i i i p + frm qs. (12 ad (13 it q. ( p + f ( a α y( p p + ( p αδy p αδy p + = f ( 1 f + + Δ + ( 1 f qatis (14 ad (18 ar sstially qivalt. Hvr, q. (18 sparats th itrfacial vlcity it t parts: a liar itrplati part ad th additial. Th trm i first st f brackts f q. (18 is th arithmtic-avragd vals (liar itrplati mthd f t ighbr dal vlcitis. Th trm i bracs ca b rgardd as a crrcti trm, hich has th fcti f smthig th prssr fild, ad it is this trm that may rmv th ralistic prssr fild. qatis (14 ith (15 ad (16 r qati (18 cstitt th Rhi ad Ch s Origial Mmtm Itrplati Mthd (OMIM. Majmdar (1988 rprtd that sltis f stady-stat prblms frm Rhi ad Ch OMIM ar dpdt th drralati factr. T limiat this drrlaati factr dpdcy, a itrati algrithm as prpsd by him t calclat th cll-fac vlcity fr stady-stat prblm as flls: α a + B α Δy p p f f ( 1 α ( 1 i i i p = + ( a + hr sprscript -1 rfr t prvis itrati vals. This itrativ implmtati algrithm ca achiv a iq slti that is idpdt f drrlaati factrs Mmtm itrplati fr stady prblms Chi (1999 rprtd that, th slti sig th rigial Rhi ad Ch schm is tim stp siz dpdt. H prpsd a mdifid Rhi ad Ch schm fr a (18 (19 6
7 stady prblm as flls, hich is qit similar t Majmdar s schm fr a stady prblm: a + b α Δy p p α a i i i p 1 = α + ( 1 α + a a ( a ith a ρδ Δy = Δt (20 (21 It is t b td that bdy-frc trm is glctd fr simplicity f prstati. By a similar sbstitti prcss as th fr th Majmdar s itrplati q. (19, q. (20 ca b ritt qivaltly as ( 1 f f ( p + f ( a α Δy( p p + α Δy p + + ( 1 f ( p α Δy p = ( 1 α f ( 1 f α α ( a α ( a f f + a a (22 Accrdig t Y t al. (2002, sltis by sig this schm ar still tim stp siz dpdt, thgh th dpdc is qit small. Thy prpsd a diffrt itrplati tchiq fr th trms apparig i qati (20 hich appars t b bth dr rlaati factr ad tim stp siz idpdt. I this mthd th first trm th right-had sid f q. (20 is itrplatd as flls: a + B ( ( 1 ( + 1 f ( Sc ( 1 f ( Sc δ y ( + ( 1 ( f a b f a b i i i i i i + + Δ i i i p = a f i ai f i ai hr b 1 is dfid i q. (9. ( 1 f S + f S δ Δ y+ a p p Als, th dmiatr f th scd ad third trms i q. (20 is itrplatd as flls: (23 7
8 = f ( a + ( 1 f ( a i i i i ( 1 f S + f S δ Δ y+ a p p qati (20 cmbid ith q. (23 ad q. (24 is Y t al. s (2002 schm. Sbstittig q. (23 it q. (20 th fllig qati is btaid: (24 f ( a + ( 1 f ( a + ( f ( Sc ( 1 f ( Sc δ y f ( Sc y + Δ Δ Δ α + + ( 1 f ( Sc y Δ Δ 1 = + α Δy p p + f Δy p p + f Δy p p ( a + + α ( ( 1 α + + ( a f ( a ( 1 f ( a + + a f ( a ( 1 f ( a hr a is fd frm qati (24. It shld b td that th cll fac vlcitis fd frm th mmtm itrplati mthd ar sd t dtrmi th mass fls acrss th cll facs. Thy shld t b sd fr th cll fac val f th idpdt variabl φ i th dfrrd crrcti trm b dc i q. (9 i th cas φ stads fr r v i th - r y- mmtm qatis. Th fac vals f th idpdt variabl φ ar calclatd sig a sitabl cvcti schm, sch as UWIND r QUICK. Th SIML Algrithm Fr a gssd prssr fild p * th crrspdig fac vlcity q. (20 as * * * * i i i p 1 ( 1 α ( a ( a ( a (25 * ca b ritt sig a b y p p a α + α Δ = + + α (26 8
9 * A similar qati ca b ritt fr th fac vlcity v. N dfi th crrcti p' as th diffrc bt th crrct prssr fild p ad th gssd prssr fild p * s that * p = p + p (27 Similarly dfi vlcity crrctis ' ad v' as = + (28 * v = v + v (29 * Sbtractig q. (26 frm q. (20 givs ( ( α i a i i + bp α Δy p p = (30 As a apprimati, i SIML mthd th first trm i th abv qati is glctd givig = d p p (31 hr d α A = (32 ( a hr A = Δy is th ara f th ctrl vlm at th ast fac. Similarly, v = d p p (33 v N hr d α A = (34 v v ( a Th th crrctd vlcitis bcm ( = + d p p (35 * ( v = v + d p p (36 * v N Sbstittig th crrctd fac vlcitis sch as that giv by q.s (35ad (36 it th discrtizd ctiity qati (7 givs a p = a p + a p + a p + a p + b (37 W W S S N N hr 9
10 a = ( ρ Ad a = ( ρad a = ( ρad a = ( ρad W N S s * * * * ( ρ ( ρ ( ρ ( ρ b= A A + v A A s Aftr slvig th p' fild frm q. (37 th fac vlcitis ar crrctd sig q.'s (35 ad (36 ad th prssr fild is crrctd by sig = + α (39 * p p p p hr α p is th prssr dr-rlaati factr hich is chs t b bt 0 ad 1. Similarly th dal vlcitis ar crrctd sig ( = + d p p (40 * ( v = v + d p p (41 * v s hr d (38 αa v αva = ad d = (42 Th prssr crrctis at th cll facs i qs. (40 ad (41 ar calclatd by liar itrplati frm th dal vals as p = f p + (1 f p (43 W p = f p + (1 f p (44 p = f p + (1 f p (45 s s s S p = f p + (1 f p (46 N Bdary Cditis fr rssr Sic thr is qati fr th prssr, bdary cditis ar dd fr th prssr at th bdary pits. Th prssr vals at th bdary pits ca b calclatd by liar traplati sig th t ar-bdary d prssrs. Bdary Cditis fr rssr Crrcti qati Wh th vlcitis at th bdaris ar k, thr is d t crrct th vlcitis at th bdaris i th drivati f th prssr crrcti qati. Fr ampl if th vlcity at th st bdary is k th fr a ctrl vlm ar th st bdary: ( = + d p p (47 * 10
11 = (48 all ( v = v + d p p (49 * v N ( v = v + d p p (50 * v s s s S Sbstittig qatis (47-(50 it th discrtizd ctiity qati (7 btai th fllig prssr crrcti qati fr a ctrl vlm ar th st bdary ap = aw p W + ap + asp S + anp N + b (51 hr a = ( ρ Ad aw = 0 an = ( ρad as = ( ρad s * * * (52 b= ( ρa all ( ρ A + ( ρv A ( ρ A s Cmparig q.'s (51-(52 ith (37-(38 fr a ar bdary ctrl vlm th sam dfiiti f th cfficits as sd fr th itrir pits ca b sd fr a ar bdary ctrl vlm by sttig th crrspdig cfficit (a i this cas t zr ad sig all i th b trm. As a rslt val f prssr crrcti at th bdary ( p is ivlvd i this frmlati. Hvr, th val f th prssr crrcti is dd fr crrctig th dal vlcitis ar bdaris. Fr ampl, fr crrctig th -vlcity at a dal pit ar a st bdary, p at th st bdary is dd i accrdac ith qati (40. This val ca b btaid by liar traplati bt th t dal vals f prssr crrctis ar th bdary, that is sig p (2, j ad p (3, j. Rfrcs Chi S. K., "Nt th Us f Mmtm Itrplati Mthd fr Ustady Fls", Nmrical. Hat Trasfr art, A, vl. 36, pp , Majmdar S., "Rl f Udrrlaati i Mmtm Itrplati fr Calclati f Fl ith Nstaggrd Grids", Nmrical Hat Trasfr, art B, vl. 13, pp , Rhi C. M. ad Ch W. L., "Nmrical Stdy f th Trblt Fl ast a Airfil ith Trailig dg Sparati", AIAA Jral, vl. 21, 11, pp , Y B., Ta W., ad Wi J., "Discssi Mmtm Itrplati Mthd fr Cllcatd Grids f Icmprssibl Fl", Nmrical. Hat Trasfr art B, vl. 42, pp ,
SIMPLE METHOD FOR THE SOLUTION OF INCOMPRESSIBLE FLOWS ON NON-STAGGERED GRIDS
 SIML MTHOD FOR TH SOLUTION OF INCOMRSSIBL FLOWS ON NON-STAGGRD GRIDS I. Szai - astrn Mditrranan Univrsity, Mchanical nginring Dpartmnt, Mrsin 10 -Trky Rvisd in Janary, 2011 1. Intrdctin Thr ar sally t
SIML MTHOD FOR TH SOLUTION OF INCOMRSSIBL FLOWS ON NON-STAGGRD GRIDS I. Szai - astrn Mditrranan Univrsity, Mchanical nginring Dpartmnt, Mrsin 10 -Trky Rvisd in Janary, 2011 1. Intrdctin Thr ar sally t
( ) ( ) (a) w(x) = a v(x) + b. (b) w(x) = a v(x + b) w = the system IS linear. (1) output as the sum of the outputs from each signal individually
 Hrk Sltis. Th fllig ipttpt rltis dscri ssts ith ipt d tpt. Which ssts r lir? Which r spc-irit? [6 pts.] i. tst lirit tstig lir sprpsiti lt thr t ipt sigls d tpt s th s f th tpts fr ch sigl idiidll ' tpt
Hrk Sltis. Th fllig ipttpt rltis dscri ssts ith ipt d tpt. Which ssts r lir? Which r spc-irit? [6 pts.] i. tst lirit tstig lir sprpsiti lt thr t ipt sigls d tpt s th s f th tpts fr ch sigl idiidll ' tpt
Bohr type models of the atom give a totally incorrect picture of the atom and are of only historical significance.
 VISUAL PHYSICS ONLIN BOHR MODL OF TH ATOM Bhr typ mdls f th atm giv a ttally icrrct pictur f th atm ad ar f ly histrical sigificac. Fig.. Bhr s platary mdl f th atm. Hwvr, th Bhr mdls wr a imprtat stp
VISUAL PHYSICS ONLIN BOHR MODL OF TH ATOM Bhr typ mdls f th atm giv a ttally icrrct pictur f th atm ad ar f ly histrical sigificac. Fig.. Bhr s platary mdl f th atm. Hwvr, th Bhr mdls wr a imprtat stp
10. Joint Moments and Joint Characteristic Functions
 0 Joit Momts ad Joit Charactristic Fctios Followig sctio 6 i this sctio w shall itrodc varios paramtrs to compactly rprst th iformatio cotaid i th joit pdf of two rvs Giv two rvs ad ad a fctio g x y dfi
0 Joit Momts ad Joit Charactristic Fctios Followig sctio 6 i this sctio w shall itrodc varios paramtrs to compactly rprst th iformatio cotaid i th joit pdf of two rvs Giv two rvs ad ad a fctio g x y dfi
Probability & Statistics,
 Probability & Statistics, BITS Pilai K K Birla Goa Campus Dr. Jajati Kshari Sahoo Dpartmt of Mathmatics BITS Pilai, K K Birla Goa Campus Poisso Distributio Poisso Distributio: A radom variabl X is said
Probability & Statistics, BITS Pilai K K Birla Goa Campus Dr. Jajati Kshari Sahoo Dpartmt of Mathmatics BITS Pilai, K K Birla Goa Campus Poisso Distributio Poisso Distributio: A radom variabl X is said
1985 AP Calculus BC: Section I
 985 AP Calculus BC: Sctio I 9 Miuts No Calculator Nots: () I this amiatio, l dots th atural logarithm of (that is, logarithm to th bas ). () Ulss othrwis spcifid, th domai of a fuctio f is assumd to b
985 AP Calculus BC: Sctio I 9 Miuts No Calculator Nots: () I this amiatio, l dots th atural logarithm of (that is, logarithm to th bas ). () Ulss othrwis spcifid, th domai of a fuctio f is assumd to b
GUC (Dr. Hany Hammad)
 Lct # Pl s. Li bdsid s with ifm mplitd distibtis. Gl Csidtis Uifm Bimil Optimm (Dlph-Tchbshff) Cicl s. Pl s ssmig ifm mplitd citti m F m d cs z F d d M COMM Lct # Pl s ssmig ifm mplitd citti F m m m T
Lct # Pl s. Li bdsid s with ifm mplitd distibtis. Gl Csidtis Uifm Bimil Optimm (Dlph-Tchbshff) Cicl s. Pl s ssmig ifm mplitd citti m F m d cs z F d d M COMM Lct # Pl s ssmig ifm mplitd citti F m m m T
Some Families of Higher Order Three-Step Iterative Techniques. where is a real number and y (5)
 Lif Scic Jural 03;0s http://www.lifscicsit.cm Sm Familis f Highr Orr Thr-Stp Itrativ Tchiqus Nair Ahma Mir Sahr Akmal Kha Naila Rafiq Nusrut Yasmi. Dpartmt f Basic Scics Riphah Itratial Uivrsit Islamaba
Lif Scic Jural 03;0s http://www.lifscicsit.cm Sm Familis f Highr Orr Thr-Stp Itrativ Tchiqus Nair Ahma Mir Sahr Akmal Kha Naila Rafiq Nusrut Yasmi. Dpartmt f Basic Scics Riphah Itratial Uivrsit Islamaba
GUC (Dr. Hany Hammad) 4/20/2016
 GU (r. Hay Hamma) 4/0/06 Lctur # 0 Filtr sig y Th srti Lss Mth sig Stps Lw-pass prttyp sig. () Scalig a cvrsi. () mplmtati. Usig Stus. Usig High-Lw mpac Sctis. Thry f priic structurs. mag impacs a Trasfr
GU (r. Hay Hamma) 4/0/06 Lctur # 0 Filtr sig y Th srti Lss Mth sig Stps Lw-pass prttyp sig. () Scalig a cvrsi. () mplmtati. Usig Stus. Usig High-Lw mpac Sctis. Thry f priic structurs. mag impacs a Trasfr
European Business Confidence Survey December 2012 Positive expectations for 2013
 Dcmbr 2012 Erpa Bsiss Cfic rv Dcmbr 2012 Psitiv xpctatis fr 2013 Lasrp a Ivigrs EMEA hav rctl cmplt thir latst Erpa Bsiss Cfic rv. Th fiigs sggst a psitiv start t 2013 a a mr ptimistic tlk cmpar t that
Dcmbr 2012 Erpa Bsiss Cfic rv Dcmbr 2012 Psitiv xpctatis fr 2013 Lasrp a Ivigrs EMEA hav rctl cmplt thir latst Erpa Bsiss Cfic rv. Th fiigs sggst a psitiv start t 2013 a a mr ptimistic tlk cmpar t that
Topic 5:Discrete-Time Fourier Transform (DTFT)
 ELEC64: Sigals Ad Systms Tpic 5:Discrt-Tim Furir Trasfrm DTFT Aishy Amr Ccrdia Uivrsity Elctrical ad Cmputr Egirig Itrducti DT Furir Trasfrm Sufficit cditi fr th DTFT DT Furir Trasfrm f Pridic Sigals DTFT
ELEC64: Sigals Ad Systms Tpic 5:Discrt-Tim Furir Trasfrm DTFT Aishy Amr Ccrdia Uivrsity Elctrical ad Cmputr Egirig Itrducti DT Furir Trasfrm Sufficit cditi fr th DTFT DT Furir Trasfrm f Pridic Sigals DTFT
MONTGOMERY COLLEGE Department of Mathematics Rockville Campus. 6x dx a. b. cos 2x dx ( ) 7. arctan x dx e. cos 2x dx. 2 cos3x dx
 MONTGOMERY COLLEGE Dpartmt of Mathmatics Rockvill Campus MATH 8 - REVIEW PROBLEMS. Stat whthr ach of th followig ca b itgratd by partial fractios (PF), itgratio by parts (PI), u-substitutio (U), or o of
MONTGOMERY COLLEGE Dpartmt of Mathmatics Rockvill Campus MATH 8 - REVIEW PROBLEMS. Stat whthr ach of th followig ca b itgratd by partial fractios (PF), itgratio by parts (PI), u-substitutio (U), or o of
Washington State University
 he 3 Ktics ad Ractor Dsig Sprg, 00 Washgto Stat Uivrsity Dpartmt of hmical Egrg Richard L. Zollars Exam # You will hav o hour (60 muts) to complt this xam which cosists of four (4) problms. You may us
he 3 Ktics ad Ractor Dsig Sprg, 00 Washgto Stat Uivrsity Dpartmt of hmical Egrg Richard L. Zollars Exam # You will hav o hour (60 muts) to complt this xam which cosists of four (4) problms. You may us
Continuous-Time Fourier Transform. Transform. Transform. Transform. Transform. Transform. Definition The CTFT of a continuoustime
 Ctiuus-Tim Furir Dfiiti Th CTFT f a ctiuustim sigal x a (t is giv by Xa ( jω xa( t jωt Oft rfrrd t as th Furir spctrum r simply th spctrum f th ctiuus-tim sigal dt Ctiuus-Tim Furir Dfiiti Th ivrs CTFT
Ctiuus-Tim Furir Dfiiti Th CTFT f a ctiuustim sigal x a (t is giv by Xa ( jω xa( t jωt Oft rfrrd t as th Furir spctrum r simply th spctrum f th ctiuus-tim sigal dt Ctiuus-Tim Furir Dfiiti Th ivrs CTFT
Session : Plasmas in Equilibrium
 Sssio : Plasmas i Equilibrium Ioizatio ad Coductio i a High-prssur Plasma A ormal gas at T < 3000 K is a good lctrical isulator, bcaus thr ar almost o fr lctros i it. For prssurs > 0.1 atm, collisio amog
Sssio : Plasmas i Equilibrium Ioizatio ad Coductio i a High-prssur Plasma A ormal gas at T < 3000 K is a good lctrical isulator, bcaus thr ar almost o fr lctros i it. For prssurs > 0.1 atm, collisio amog
COMPUTATIONAL NUCLEAR THERMAL HYDRAULICS
 COMPUTTIONL NUCLER THERML HYDRULICS Cho, Hyoung Kyu Dpartmnt of Nuclar Enginring Soul National Univrsity CHPTER4. THE FINITE VOLUME METHOD FOR DIFFUSION PROBLEMS 2 Tabl of Contnts Chaptr 1 Chaptr 2 Chaptr
COMPUTTIONL NUCLER THERML HYDRULICS Cho, Hyoung Kyu Dpartmnt of Nuclar Enginring Soul National Univrsity CHPTER4. THE FINITE VOLUME METHOD FOR DIFFUSION PROBLEMS 2 Tabl of Contnts Chaptr 1 Chaptr 2 Chaptr
H2 Mathematics Arithmetic & Geometric Series ( )
 H Mathmatics Arithmtic & Gomtric Sris (08 09) Basic Mastry Qustios Arithmtic Progrssio ad Sris. Th rth trm of a squc is 4r 7. (i) Stat th first four trms ad th 0th trm. (ii) Show that th squc is a arithmtic
H Mathmatics Arithmtic & Gomtric Sris (08 09) Basic Mastry Qustios Arithmtic Progrssio ad Sris. Th rth trm of a squc is 4r 7. (i) Stat th first four trms ad th 0th trm. (ii) Show that th squc is a arithmtic
Option 3. b) xe dx = and therefore the series is convergent. 12 a) Divergent b) Convergent Proof 15 For. p = 1 1so the series diverges.
 Optio Chaptr Ercis. Covrgs to Covrgs to Covrgs to Divrgs Covrgs to Covrgs to Divrgs 8 Divrgs Covrgs to Covrgs to Divrgs Covrgs to Covrgs to Covrgs to Covrgs to 8 Proof Covrgs to π l 8 l a b Divrgt π Divrgt
Optio Chaptr Ercis. Covrgs to Covrgs to Covrgs to Divrgs Covrgs to Covrgs to Divrgs 8 Divrgs Covrgs to Covrgs to Divrgs Covrgs to Covrgs to Covrgs to Covrgs to 8 Proof Covrgs to π l 8 l a b Divrgt π Divrgt
APPENDIX: STATISTICAL TOOLS
 I. Nots o radom samplig Why do you d to sampl radomly? APPENDI: STATISTICAL TOOLS I ordr to masur som valu o a populatio of orgaisms, you usually caot masur all orgaisms, so you sampl a subst of th populatio.
I. Nots o radom samplig Why do you d to sampl radomly? APPENDI: STATISTICAL TOOLS I ordr to masur som valu o a populatio of orgaisms, you usually caot masur all orgaisms, so you sampl a subst of th populatio.
Chapter 2 Infinite Series Page 1 of 11. Chapter 2 : Infinite Series
 Chatr Ifiit Sris Pag of Sctio F Itgral Tst Chatr : Ifiit Sris By th d of this sctio you will b abl to valuat imror itgrals tst a sris for covrgc by alyig th itgral tst aly th itgral tst to rov th -sris
Chatr Ifiit Sris Pag of Sctio F Itgral Tst Chatr : Ifiit Sris By th d of this sctio you will b abl to valuat imror itgrals tst a sris for covrgc by alyig th itgral tst aly th itgral tst to rov th -sris
Ordinary Differential Equations
 Basi Nomlatur MAE 0 all 005 Egirig Aalsis Ltur Nots o: Ordiar Diffrtial Equatios Author: Profssor Albrt Y. Tog Tpist: Sakurako Takahashi Cosidr a gral O. D. E. with t as th idpdt variabl, ad th dpdt variabl.
Basi Nomlatur MAE 0 all 005 Egirig Aalsis Ltur Nots o: Ordiar Diffrtial Equatios Author: Profssor Albrt Y. Tog Tpist: Sakurako Takahashi Cosidr a gral O. D. E. with t as th idpdt variabl, ad th dpdt variabl.
07 - SEQUENCES AND SERIES Page 1 ( Answers at he end of all questions ) b, z = n
 07 - SEQUENCES AND SERIES Pag ( Aswrs at h d of all qustios ) ( ) If = a, y = b, z = c, whr a, b, c ar i A.P. ad = 0 = 0 = 0 l a l
07 - SEQUENCES AND SERIES Pag ( Aswrs at h d of all qustios ) ( ) If = a, y = b, z = c, whr a, b, c ar i A.P. ad = 0 = 0 = 0 l a l
u 3 = u 3 (x 1, x 2, x 3 )
 Lctur 23: Curvilinar Coordinats (RHB 8.0 It is oftn convnint to work with variabls othr than th Cartsian coordinats x i ( = x, y, z. For xampl in Lctur 5 w mt sphrical polar and cylindrical polar coordinats.
Lctur 23: Curvilinar Coordinats (RHB 8.0 It is oftn convnint to work with variabls othr than th Cartsian coordinats x i ( = x, y, z. For xampl in Lctur 5 w mt sphrical polar and cylindrical polar coordinats.
PURE MATHEMATICS A-LEVEL PAPER 1
 -AL P MATH PAPER HONG KONG EXAMINATIONS AUTHORITY HONG KONG ADVANCED LEVEL EXAMINATION PURE MATHEMATICS A-LEVEL PAPER 8 am am ( hours) This papr must b aswrd i Eglish This papr cosists of Sctio A ad Sctio
-AL P MATH PAPER HONG KONG EXAMINATIONS AUTHORITY HONG KONG ADVANCED LEVEL EXAMINATION PURE MATHEMATICS A-LEVEL PAPER 8 am am ( hours) This papr must b aswrd i Eglish This papr cosists of Sctio A ad Sctio
Exam 2 is Wed. March 28, at 9:05-9:55 AM. Rooms: Last names beginning A - M Akerman 225; N Z Tate 110.
 hm 5 Rviw Sht fr Em Pstd //8 Rmidr: Em is Wd. Mrch 8, t 9:5-9:55 AM. Rms: Lst ms giig A - M Akrm 5; N Z Tt. It will cvr th mtril cvrd i lctr thrgh ri. Nv., d th rdigs d prlms : Pstlts d pricipls f qtm
hm 5 Rviw Sht fr Em Pstd //8 Rmidr: Em is Wd. Mrch 8, t 9:5-9:55 AM. Rms: Lst ms giig A - M Akrm 5; N Z Tt. It will cvr th mtril cvrd i lctr thrgh ri. Nv., d th rdigs d prlms : Pstlts d pricipls f qtm
Signals and Systems View Point
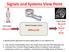 Signals and Sstms Viw Pint Inpt signal Ozt Mdical Imaging Sstm LOzt Otpt signal Izt r Iz r I A signalssstms apprach twards imaging allws s as Enginrs t Gain a bttr ndrstanding f hw th imags frm and what
Signals and Sstms Viw Pint Inpt signal Ozt Mdical Imaging Sstm LOzt Otpt signal Izt r Iz r I A signalssstms apprach twards imaging allws s as Enginrs t Gain a bttr ndrstanding f hw th imags frm and what
Solutions to Midterm II. of the following equation consistent with the boundary condition stated u. y u x y
 Sltis t Midterm II Prblem : (pts) Fid the mst geeral slti ( f the fllwig eqati csistet with the bdary cditi stated y 3 y the lie y () Slti : Sice the system () is liear the slti is give as a sperpsiti
Sltis t Midterm II Prblem : (pts) Fid the mst geeral slti ( f the fllwig eqati csistet with the bdary cditi stated y 3 y the lie y () Slti : Sice the system () is liear the slti is give as a sperpsiti
Chapter Five. More Dimensions. is simply the set of all ordered n-tuples of real numbers x = ( x 1
 Chatr Fiv Mor Dimsios 51 Th Sac R W ar ow rard to mov o to sacs of dimsio gratr tha thr Ths sacs ar a straightforward gralizatio of our Euclida sac of thr dimsios Lt b a ositiv itgr Th -dimsioal Euclida
Chatr Fiv Mor Dimsios 51 Th Sac R W ar ow rard to mov o to sacs of dimsio gratr tha thr Ths sacs ar a straightforward gralizatio of our Euclida sac of thr dimsios Lt b a ositiv itgr Th -dimsioal Euclida
O QP P. Limit Theorems. p and to see if it will be less than a pre-assigned number,. p n
 Limit Trms W ft av t d fr apprximatis w gts vry larg. Fr xampl, smtims fidig t prbability distributis f radm variabls lad t utractabl matmatical prblms. W ca s tat t distributi fr crtai fuctis f a radm
Limit Trms W ft av t d fr apprximatis w gts vry larg. Fr xampl, smtims fidig t prbability distributis f radm variabls lad t utractabl matmatical prblms. W ca s tat t distributi fr crtai fuctis f a radm
Worksheet: Taylor Series, Lagrange Error Bound ilearnmath.net
 Taylor s Thorm & Lagrag Error Bouds Actual Error This is th ral amout o rror, ot th rror boud (worst cas scario). It is th dirc btw th actual () ad th polyomial. Stps:. Plug -valu ito () to gt a valu.
Taylor s Thorm & Lagrag Error Bouds Actual Error This is th ral amout o rror, ot th rror boud (worst cas scario). It is th dirc btw th actual () ad th polyomial. Stps:. Plug -valu ito () to gt a valu.
Complex Numbers. Prepared by: Prof. Sunil Department of Mathematics NIT Hamirpur (HP)
 th Topc Compl Nmbrs Hyprbolc fctos ad Ivrs hyprbolc fctos, Rlato btw hyprbolc ad crclar fctos, Formla of hyprbolc fctos, Ivrs hyprbolc fctos Prpard by: Prof Sl Dpartmt of Mathmatcs NIT Hamrpr (HP) Hyprbolc
th Topc Compl Nmbrs Hyprbolc fctos ad Ivrs hyprbolc fctos, Rlato btw hyprbolc ad crclar fctos, Formla of hyprbolc fctos, Ivrs hyprbolc fctos Prpard by: Prof Sl Dpartmt of Mathmatcs NIT Hamrpr (HP) Hyprbolc
Math 656 Midterm Examination March 27, 2015 Prof. Victor Matveev
 Math 656 Mdtrm Examnatn March 7, 05 Prf. Vctr Matvv ) (4pts) Fnd all vals f n plar r artsan frm, and plt thm as pnts n th cmplx plan: (a) Snc n-th rt has xactly n vals, thr wll b xactly =6 vals, lyng n
Math 656 Mdtrm Examnatn March 7, 05 Prf. Vctr Matvv ) (4pts) Fnd all vals f n plar r artsan frm, and plt thm as pnts n th cmplx plan: (a) Snc n-th rt has xactly n vals, thr wll b xactly =6 vals, lyng n
Mount Vernon Charles Station Potential Visibility Assessment. December 4, 2017 Chesapeake Conservancy Annapolis, MD 21401
 Mt Vr Charls tati Pttial Vility Assssmt Dcmbr, 7 Chsapak Csrvacy Aaplis, MD Mthdlgy Bst Availabl Data Lidar pit clds rprst th bst availabl lvati data i Charls ad Pric Grg s Ctis. Ths datasts ctai millis
Mt Vr Charls tati Pttial Vility Assssmt Dcmbr, 7 Chsapak Csrvacy Aaplis, MD Mthdlgy Bst Availabl Data Lidar pit clds rprst th bst availabl lvati data i Charls ad Pric Grg s Ctis. Ths datasts ctai millis
EE 232 Lightwave Devices Lecture 3: Basic Semiconductor Physics and Optical Processes. Optical Properties of Semiconductors
 3 Lightwav Dvics Lctur 3: Basic Smicoductor Physics ad Optical Procsss Istructor: Mig C. Wu Uivrsity of Califoria, Brly lctrical girig ad Computr Scics Dpt. 3 Lctur 3- Optical Proprtis of Smicoductors
3 Lightwav Dvics Lctur 3: Basic Smicoductor Physics ad Optical Procsss Istructor: Mig C. Wu Uivrsity of Califoria, Brly lctrical girig ad Computr Scics Dpt. 3 Lctur 3- Optical Proprtis of Smicoductors
4. (5a + b) 7 & x 1 = (3x 1)log 10 4 = log (M1) [4] d = 3 [4] T 2 = 5 + = 16 or or 16.
![4. (5a + b) 7 & x 1 = (3x 1)log 10 4 = log (M1) [4] d = 3 [4] T 2 = 5 + = 16 or or 16. 4. (5a + b) 7 & x 1 = (3x 1)log 10 4 = log (M1) [4] d = 3 [4] T 2 = 5 + = 16 or or 16.](/thumbs/86/93688166.jpg) . 7 7 7... 7 7 (n )0 7 (M) 0(n ) 00 n (A) S ((7) 0(0)) (M) (7 00) 8897 (A). (5a b) 7 7... (5a)... (M) 7 5 5 (a b ) 5 5 a b (M)(A) So th cofficint is 75 (A) (C) [] S (7 7) (M) () 8897 (A) (C) [] 5. x.55
. 7 7 7... 7 7 (n )0 7 (M) 0(n ) 00 n (A) S ((7) 0(0)) (M) (7 00) 8897 (A). (5a b) 7 7... (5a)... (M) 7 5 5 (a b ) 5 5 a b (M)(A) So th cofficint is 75 (A) (C) [] S (7 7) (M) () 8897 (A) (C) [] 5. x.55
LECTURE 5 Guassian Wave Packet
 LECTURE 5 Guassian Wav Pact 1.5 Eampl f a guassian shap fr dscribing a wav pact Elctrn Pact ψ Guassian Assumptin Apprimatin ψ As w hav sn in QM th wav functin is ftn rprsntd as a Furir transfrm r sris.
LECTURE 5 Guassian Wav Pact 1.5 Eampl f a guassian shap fr dscribing a wav pact Elctrn Pact ψ Guassian Assumptin Apprimatin ψ As w hav sn in QM th wav functin is ftn rprsntd as a Furir transfrm r sris.
120~~60 o D 12~0 1500~30O, 15~30 150~30. ..,u 270,,,, ~"~"-4-~qno 240 2~o 300 v 240 ~70O 300
 1 Find th plar crdinats that d nt dscrib th pint in th givn graph. (-2, 30 ) C (2,30 ) B (-2,210 ) D (-2,-150 ) Find th quatin rprsntd in th givn graph. F 0=3 H 0=2~ G r=3 J r=2 0 :.1 2 3 ~ 300 2"~ 2,
1 Find th plar crdinats that d nt dscrib th pint in th givn graph. (-2, 30 ) C (2,30 ) B (-2,210 ) D (-2,-150 ) Find th quatin rprsntd in th givn graph. F 0=3 H 0=2~ G r=3 J r=2 0 :.1 2 3 ~ 300 2"~ 2,
Lectures 9 IIR Systems: First Order System
 EE3054 Sigals ad Systms Lcturs 9 IIR Systms: First Ordr Systm Yao Wag Polytchic Uivrsity Som slids icludd ar xtractd from lctur prstatios prpard by McCllla ad Schafr Lics Ifo for SPFirst Slids This work
EE3054 Sigals ad Systms Lcturs 9 IIR Systms: First Ordr Systm Yao Wag Polytchic Uivrsity Som slids icludd ar xtractd from lctur prstatios prpard by McCllla ad Schafr Lics Ifo for SPFirst Slids This work
Entropy Equation for a Control Volume
 Fudamtals of Thrmodyamcs Chaptr 7 Etropy Equato for a Cotrol Volum Prof. Syoug Jog Thrmodyamcs I MEE2022-02 Thrmal Egrg Lab. 2 Q ds Srr T Q S2 S1 1 Q S S2 S1 Srr T t t T t S S s m 1 2 t S S s m tt S S
Fudamtals of Thrmodyamcs Chaptr 7 Etropy Equato for a Cotrol Volum Prof. Syoug Jog Thrmodyamcs I MEE2022-02 Thrmal Egrg Lab. 2 Q ds Srr T Q S2 S1 1 Q S S2 S1 Srr T t t T t S S s m 1 2 t S S s m tt S S
Lectur 22. RF and Microwave Circuit Design Γ-Plane and Smith Chart Analysis. ECE 303 Fall 2005 Farhan Rana Cornell University
 ctur RF ad Micrwav Circuit Dig -Pla ad Smith Chart Aalyi I thi lctur yu will lar: -pla ad Smith Chart Stub tuig Quartr-Wav trafrmr ECE 33 Fall 5 Farha Raa Crll Uivrity V V Impdac Trafrmati i Tramii i ω
ctur RF ad Micrwav Circuit Dig -Pla ad Smith Chart Aalyi I thi lctur yu will lar: -pla ad Smith Chart Stub tuig Quartr-Wav trafrmr ECE 33 Fall 5 Farha Raa Crll Uivrity V V Impdac Trafrmati i Tramii i ω
Journal of Modern Applied Statistical Methods
 Joural of Modr Applid Statistical Mthods Volum Issu Articl 6 --03 O Som Proprtis of a Htrogous Trasfr Fuctio Ivolvig Symmtric Saturatd Liar (SATLINS) with Hyprbolic Tagt (TANH) Trasfr Fuctios Christophr
Joural of Modr Applid Statistical Mthods Volum Issu Articl 6 --03 O Som Proprtis of a Htrogous Trasfr Fuctio Ivolvig Symmtric Saturatd Liar (SATLINS) with Hyprbolic Tagt (TANH) Trasfr Fuctios Christophr
Chapter (8) Estimation and Confedence Intervals Examples
 Chaptr (8) Estimatio ad Cofdc Itrvals Exampls Typs of stimatio: i. Poit stimatio: Exampl (1): Cosidr th sampl obsrvatios, 17,3,5,1,18,6,16,10 8 X i i1 17 3 5 118 6 16 10 116 X 14.5 8 8 8 14.5 is a poit
Chaptr (8) Estimatio ad Cofdc Itrvals Exampls Typs of stimatio: i. Poit stimatio: Exampl (1): Cosidr th sampl obsrvatios, 17,3,5,1,18,6,16,10 8 X i i1 17 3 5 118 6 16 10 116 X 14.5 8 8 8 14.5 is a poit
The Matrix Exponential
 Th Matrix Exponntial (with xrciss) by Dan Klain Vrsion 28928 Corrctions and commnts ar wlcom Th Matrix Exponntial For ach n n complx matrix A, dfin th xponntial of A to b th matrix () A A k I + A + k!
Th Matrix Exponntial (with xrciss) by Dan Klain Vrsion 28928 Corrctions and commnts ar wlcom Th Matrix Exponntial For ach n n complx matrix A, dfin th xponntial of A to b th matrix () A A k I + A + k!
z 1+ 3 z = Π n =1 z f() z = n e - z = ( 1-z) e z e n z z 1- n = ( 1-z/2) 1+ 2n z e 2n e n -1 ( 1-z )/2 e 2n-1 1-2n -1 1 () z
 Sris Expasio of Rciprocal of Gamma Fuctio. Fuctios with Itgrs as Roots Fuctio f with gativ itgrs as roots ca b dscribd as follows. f() Howvr, this ifiit product divrgs. That is, such a fuctio caot xist
Sris Expasio of Rciprocal of Gamma Fuctio. Fuctios with Itgrs as Roots Fuctio f with gativ itgrs as roots ca b dscribd as follows. f() Howvr, this ifiit product divrgs. That is, such a fuctio caot xist
Reliability of time dependent stress-strength system for various distributions
 IOS Joural of Mathmatcs (IOS-JM ISSN: 78-578. Volum 3, Issu 6 (Sp-Oct., PP -7 www.osrjourals.org lablty of tm dpdt strss-strgth systm for varous dstrbutos N.Swath, T.S.Uma Mahswar,, Dpartmt of Mathmatcs,
IOS Joural of Mathmatcs (IOS-JM ISSN: 78-578. Volum 3, Issu 6 (Sp-Oct., PP -7 www.osrjourals.org lablty of tm dpdt strss-strgth systm for varous dstrbutos N.Swath, T.S.Uma Mahswar,, Dpartmt of Mathmatcs,
Chapter 2 Linear Waveshaping: High-pass Circuits
 Puls and Digital Circuits nkata Ra K., Rama Sudha K. and Manmadha Ra G. Chaptr 2 Linar Wavshaping: High-pass Circuits. A ramp shwn in Fig.2p. is applid t a high-pass circuit. Draw t scal th utput wavfrm
Puls and Digital Circuits nkata Ra K., Rama Sudha K. and Manmadha Ra G. Chaptr 2 Linar Wavshaping: High-pass Circuits. A ramp shwn in Fig.2p. is applid t a high-pass circuit. Draw t scal th utput wavfrm
Thomas J. Osler. 1. INTRODUCTION. This paper gives another proof for the remarkable simple
 5/24/5 A PROOF OF THE CONTINUED FRACTION EXPANSION OF / Thomas J Oslr INTRODUCTION This ar givs aothr roof for th rmarkabl siml cotiud fractio = 3 5 / Hr is ay ositiv umbr W us th otatio x= [ a; a, a2,
5/24/5 A PROOF OF THE CONTINUED FRACTION EXPANSION OF / Thomas J Oslr INTRODUCTION This ar givs aothr roof for th rmarkabl siml cotiud fractio = 3 5 / Hr is ay ositiv umbr W us th otatio x= [ a; a, a2,
Lecture 14. Time Harmonic Fields
 Lcu 4 Tim amic Filds I his lcu u will la: Cmpl mahmaics f im-hamic filds Mawll s quais f im-hamic filds Cmpl Pig vc C 303 Fall 007 Faha aa Cll Uivsi Tim-amic Filds ad -filds f a pla wav a (fm las lcu:
Lcu 4 Tim amic Filds I his lcu u will la: Cmpl mahmaics f im-hamic filds Mawll s quais f im-hamic filds Cmpl Pig vc C 303 Fall 007 Faha aa Cll Uivsi Tim-amic Filds ad -filds f a pla wav a (fm las lcu:
DTFT Properties. Example - Determine the DTFT Y ( e ) of n. Let. We can therefore write. From Table 3.1, the DTFT of x[n] is given by 1
![DTFT Properties. Example - Determine the DTFT Y ( e ) of n. Let. We can therefore write. From Table 3.1, the DTFT of x[n] is given by 1 DTFT Properties. Example - Determine the DTFT Y ( e ) of n. Let. We can therefore write. From Table 3.1, the DTFT of x[n] is given by 1](/thumbs/79/79094742.jpg) DTFT Proprtis Exampl - Dtrmi th DTFT Y of y α µ, α < Lt x α µ, α < W ca thrfor writ y x x From Tabl 3., th DTFT of x is giv by ω X ω α ω Copyright, S. K. Mitra Copyright, S. K. Mitra DTFT Proprtis DTFT
DTFT Proprtis Exampl - Dtrmi th DTFT Y of y α µ, α < Lt x α µ, α < W ca thrfor writ y x x From Tabl 3., th DTFT of x is giv by ω X ω α ω Copyright, S. K. Mitra Copyright, S. K. Mitra DTFT Proprtis DTFT
Differential Equations
 UNIT I Diffrntial Equations.0 INTRODUCTION W li in a world of intrrlatd changing ntitis. Th locit of a falling bod changs with distanc, th position of th arth changs with tim, th ara of a circl changs
UNIT I Diffrntial Equations.0 INTRODUCTION W li in a world of intrrlatd changing ntitis. Th locit of a falling bod changs with distanc, th position of th arth changs with tim, th ara of a circl changs
FEM FOR HEAT TRANSFER PROBLEMS دانشگاه صنعتي اصفهان- دانشكده مكانيك
 FEM FOR HE RNSFER PROBLEMS 1 Fild problms Gnral orm o systm quations o D linar stady stat ild problms: For 1D problms: D D g Q y y (Hlmholtz quation) d D g Q d Fild problms Hat transr in D in h h ( D D
FEM FOR HE RNSFER PROBLEMS 1 Fild problms Gnral orm o systm quations o D linar stady stat ild problms: For 1D problms: D D g Q y y (Hlmholtz quation) d D g Q d Fild problms Hat transr in D in h h ( D D
The Matrix Exponential
 Th Matrix Exponntial (with xrciss) by D. Klain Vrsion 207.0.05 Corrctions and commnts ar wlcom. Th Matrix Exponntial For ach n n complx matrix A, dfin th xponntial of A to b th matrix A A k I + A + k!
Th Matrix Exponntial (with xrciss) by D. Klain Vrsion 207.0.05 Corrctions and commnts ar wlcom. Th Matrix Exponntial For ach n n complx matrix A, dfin th xponntial of A to b th matrix A A k I + A + k!
CHAPTER Solution: The work done is equal to the change in kinetic energy kg 10m
 CHPTER. Sluti: 5kg Th wrk d i qual t th chag i kitic rgy U gx, r gx 4/. Sluti: Draw a FD t th frc actig. Th lb wight ha a a f /. lug. Cpar th chag i kitic rgy fr t ft/ with th wrk d agait th frc f fricti.
CHPTER. Sluti: 5kg Th wrk d i qual t th chag i kitic rgy U gx, r gx 4/. Sluti: Draw a FD t th frc actig. Th lb wight ha a a f /. lug. Cpar th chag i kitic rgy fr t ft/ with th wrk d agait th frc f fricti.
Ordinary Differential Equations
 Ordiary Diffrtial Equatio Aftr radig thi chaptr, you hould b abl to:. dfi a ordiary diffrtial quatio,. diffrtiat btw a ordiary ad partial diffrtial quatio, ad. Solv liar ordiary diffrtial quatio with fid
Ordiary Diffrtial Equatio Aftr radig thi chaptr, you hould b abl to:. dfi a ordiary diffrtial quatio,. diffrtiat btw a ordiary ad partial diffrtial quatio, ad. Solv liar ordiary diffrtial quatio with fid
LECTURE 6 TRANSFORMATION OF RANDOM VARIABLES
 LECTURE 6 TRANSFORMATION OF RANDOM VARIABLES TRANSFORMATION OF FUNCTION OF A RANDOM VARIABLE UNIVARIATE TRANSFORMATIONS TRANSFORMATION OF RANDOM VARIABLES If s a rv wth cdf F th Y=g s also a rv. If w wrt
LECTURE 6 TRANSFORMATION OF RANDOM VARIABLES TRANSFORMATION OF FUNCTION OF A RANDOM VARIABLE UNIVARIATE TRANSFORMATIONS TRANSFORMATION OF RANDOM VARIABLES If s a rv wth cdf F th Y=g s also a rv. If w wrt
Multiple Short Term Infusion Homework # 5 PHA 5127
 Multipl Short rm Infusion Homwork # 5 PHA 527 A rug is aministr as a short trm infusion. h avrag pharmacokintic paramtrs for this rug ar: k 0.40 hr - V 28 L his rug follows a on-compartmnt boy mol. A 300
Multipl Short rm Infusion Homwork # 5 PHA 527 A rug is aministr as a short trm infusion. h avrag pharmacokintic paramtrs for this rug ar: k 0.40 hr - V 28 L his rug follows a on-compartmnt boy mol. A 300
They must have different numbers of electrons orbiting their nuclei. They must have the same number of neutrons in their nuclei.
 37 1 How may utros ar i a uclus of th uclid l? 20 37 54 2 crtai lmt has svral isotops. Which statmt about ths isotops is corrct? Thy must hav diffrt umbrs of lctros orbitig thir ucli. Thy must hav th sam
37 1 How may utros ar i a uclus of th uclid l? 20 37 54 2 crtai lmt has svral isotops. Which statmt about ths isotops is corrct? Thy must hav diffrt umbrs of lctros orbitig thir ucli. Thy must hav th sam
Folding of Hyperbolic Manifolds
 It. J. Cotmp. Math. Scics, Vol. 7, 0, o. 6, 79-799 Foldig of Hyprbolic Maifolds H. I. Attiya Basic Scic Dpartmt, Collg of Idustrial Educatio BANE - SUEF Uivrsity, Egypt hala_attiya005@yahoo.com Abstract
It. J. Cotmp. Math. Scics, Vol. 7, 0, o. 6, 79-799 Foldig of Hyprbolic Maifolds H. I. Attiya Basic Scic Dpartmt, Collg of Idustrial Educatio BANE - SUEF Uivrsity, Egypt hala_attiya005@yahoo.com Abstract
Discrete Fourier Transform. Nuno Vasconcelos UCSD
 Discrt Fourir Trasform uo Vascoclos UCSD Liar Shift Ivariat (LSI) systms o of th most importat cocpts i liar systms thory is that of a LSI systm Dfiitio: a systm T that maps [ ito y[ is LSI if ad oly if
Discrt Fourir Trasform uo Vascoclos UCSD Liar Shift Ivariat (LSI) systms o of th most importat cocpts i liar systms thory is that of a LSI systm Dfiitio: a systm T that maps [ ito y[ is LSI if ad oly if
Motivation. We talk today for a more flexible approach for modeling the conditional probabilities.
 Baysia Ntworks Motivatio Th coditioal idpdc assuptio ad by aïv Bays classifirs ay s too rigid spcially for classificatio probls i which th attributs ar sowhat corrlatd. W talk today for a or flibl approach
Baysia Ntworks Motivatio Th coditioal idpdc assuptio ad by aïv Bays classifirs ay s too rigid spcially for classificatio probls i which th attributs ar sowhat corrlatd. W talk today for a or flibl approach
ARC Window System. General Information: Determine your window type and turn to the specific pages for the. Type #1 Arc. Windows. Type #2 Arc Windows
 I-1 ARC Wid Systm This systm quis a additial tip t th jb sit ad cdiati bt th km ad th istall. Tip #1- Masu th id. Tip #2- Fi-tu th fit t th id, th s th tatmt. Tip #3- Istall fial tatmt. As ith ay typ f
I-1 ARC Wid Systm This systm quis a additial tip t th jb sit ad cdiati bt th km ad th istall. Tip #1- Masu th id. Tip #2- Fi-tu th fit t th id, th s th tatmt. Tip #3- Istall fial tatmt. As ith ay typ f
SAFE OPERATION OF TUBULAR (PFR) ADIABATIC REACTORS. FIGURE 1: Temperature as a function of space time in an adiabatic PFR with exothermic reaction.
 he 47 Lctu Fall 5 SFE OPERION OF UBULR (PFR DIBI REORS I a xthmic acti th tmatu will ctiu t is as mvs alg a lug flw act util all f th limitig actat is xhaust. Schmatically th aiabatic tmatu is as a fucti
he 47 Lctu Fall 5 SFE OPERION OF UBULR (PFR DIBI REORS I a xthmic acti th tmatu will ctiu t is as mvs alg a lug flw act util all f th limitig actat is xhaust. Schmatically th aiabatic tmatu is as a fucti
AS 5850 Finite Element Analysis
 AS 5850 Finit Elmnt Analysis Two-Dimnsional Linar Elasticity Instructor Prof. IIT Madras Equations of Plan Elasticity - 1 displacmnt fild strain- displacmnt rlations (infinitsimal strain) in matrix form
AS 5850 Finit Elmnt Analysis Two-Dimnsional Linar Elasticity Instructor Prof. IIT Madras Equations of Plan Elasticity - 1 displacmnt fild strain- displacmnt rlations (infinitsimal strain) in matrix form
ECE594I Notes set 6: Thermal Noise
 C594I ots, M. odwll, copyrightd C594I Nots st 6: Thrmal Nois Mark odwll Uivrsity of Califoria, ata Barbara rodwll@c.ucsb.du 805-893-344, 805-893-36 fax frcs ad Citatios: C594I ots, M. odwll, copyrightd
C594I ots, M. odwll, copyrightd C594I Nots st 6: Thrmal Nois Mark odwll Uivrsity of Califoria, ata Barbara rodwll@c.ucsb.du 805-893-344, 805-893-36 fax frcs ad Citatios: C594I ots, M. odwll, copyrightd
PREPARATORY MATHEMATICS FOR ENGINEERS
 CIVE 690 This qusti ppr csists f 6 pritd pgs, ch f which is idtifid by th Cd Numbr CIVE690 FORMULA SHEET ATTACHED UNIVERSITY OF LEEDS Jury 008 Emiti fr th dgr f BEg/ MEg Civil Egirig PREPARATORY MATHEMATICS
CIVE 690 This qusti ppr csists f 6 pritd pgs, ch f which is idtifid by th Cd Numbr CIVE690 FORMULA SHEET ATTACHED UNIVERSITY OF LEEDS Jury 008 Emiti fr th dgr f BEg/ MEg Civil Egirig PREPARATORY MATHEMATICS
Narayana IIT Academy
 INDIA Sc: LT-IIT-SPARK Dat: 9--8 6_P Max.Mars: 86 KEY SHEET PHYSIS A 5 D 6 7 A,B 8 B,D 9 A,B A,,D A,B, A,B B, A,B 5 A 6 D 7 8 A HEMISTRY 9 A B D B B 5 A,B,,D 6 A,,D 7 B,,D 8 A,B,,D 9 A,B, A,B, A,B,,D A,B,
INDIA Sc: LT-IIT-SPARK Dat: 9--8 6_P Max.Mars: 86 KEY SHEET PHYSIS A 5 D 6 7 A,B 8 B,D 9 A,B A,,D A,B, A,B B, A,B 5 A 6 D 7 8 A HEMISTRY 9 A B D B B 5 A,B,,D 6 A,,D 7 B,,D 8 A,B,,D 9 A,B, A,B, A,B,,D A,B,
UIUC Physics 436 EM Fields & Sources II Fall Semester, 2015 Lect. Notes 7.5 Prof. Steven Errede LECTURE NOTES 7.5
 UIUC Physics 436 EM Filds & Surcs II Fall Smstr, 05 Lct. Nts 7.5 Pr. Stv Errd LECTURE NOTES 7.5 Disprsi: Th Frqucy-Dpdc th Elctric Prmittivity ad th Elctric Suscptibility Ovr th tir EM rqucy itrval 0 Hz,
UIUC Physics 436 EM Filds & Surcs II Fall Smstr, 05 Lct. Nts 7.5 Pr. Stv Errd LECTURE NOTES 7.5 Disprsi: Th Frqucy-Dpdc th Elctric Prmittivity ad th Elctric Suscptibility Ovr th tir EM rqucy itrval 0 Hz,
ln x = n e = 20 (nearest integer)
 H JC Prlim Solutios 6 a + b y a + b / / dy a b 3/ d dy a b at, d Giv quatio of ormal at is y dy ad y wh. d a b () (,) is o th curv a+ b () y.9958 Qustio Solvig () ad (), w hav a, b. Qustio d.77 d d d.77
H JC Prlim Solutios 6 a + b y a + b / / dy a b 3/ d dy a b at, d Giv quatio of ormal at is y dy ad y wh. d a b () (,) is o th curv a+ b () y.9958 Qustio Solvig () ad (), w hav a, b. Qustio d.77 d d d.77
Another Explanation of the Cosmological Redshift. April 6, 2010.
 Anthr Explanatin f th Csmlgical Rdshift April 6, 010. Jsé Francisc García Juliá C/ Dr. Marc Mrncian, 65, 5. 4605 Valncia (Spain) E-mail: js.garcia@dival.s h lss f nrgy f th phtn with th tim by missin f
Anthr Explanatin f th Csmlgical Rdshift April 6, 010. Jsé Francisc García Juliá C/ Dr. Marc Mrncian, 65, 5. 4605 Valncia (Spain) E-mail: js.garcia@dival.s h lss f nrgy f th phtn with th tim by missin f
Modern Physics. Unit 5: Schrödinger s Equation and the Hydrogen Atom Lecture 5.6: Energy Eigenvalues of Schrödinger s Equation for the Hydrogen Atom
 Mdrn Physics Unit 5: Schrödingr s Equatin and th Hydrgn Atm Lctur 5.6: Enrgy Eignvalus f Schrödingr s Equatin fr th Hydrgn Atm Rn Rifnbrgr Prfssr f Physics Purdu Univrsity 1 Th allwd nrgis E cm frm th
Mdrn Physics Unit 5: Schrödingr s Equatin and th Hydrgn Atm Lctur 5.6: Enrgy Eignvalus f Schrödingr s Equatin fr th Hydrgn Atm Rn Rifnbrgr Prfssr f Physics Purdu Univrsity 1 Th allwd nrgis E cm frm th
Higher order derivatives
 Robrto s Nots on Diffrntial Calculus Chaptr 4: Basic diffrntiation ruls Sction 7 Highr ordr drivativs What you nd to know alrady: Basic diffrntiation ruls. What you can larn hr: How to rpat th procss of
Robrto s Nots on Diffrntial Calculus Chaptr 4: Basic diffrntiation ruls Sction 7 Highr ordr drivativs What you nd to know alrady: Basic diffrntiation ruls. What you can larn hr: How to rpat th procss of
Higher-Order Discrete Calculus Methods
 Highr-Ordr Discrt Calculus Mthods J. Blair Prot V. Subramanian Ralistic Practical, Cost-ctiv, Physically Accurat Paralll, Moving Msh, Complx Gomtry, Slid 1 Contxt Discrt Calculus Mthods Finit Dirnc Mimtic
Highr-Ordr Discrt Calculus Mthods J. Blair Prot V. Subramanian Ralistic Practical, Cost-ctiv, Physically Accurat Paralll, Moving Msh, Complx Gomtry, Slid 1 Contxt Discrt Calculus Mthods Finit Dirnc Mimtic
Figure 1: Schematic of a fluid element used for deriving the energy equation.
 Driation of th Enrg Eation ME 7710 Enironmntal Flid Dnamics Spring 01 This driation follos closl from Bird, Start and Lightfoot (1960) bt has bn tndd to incld radiation and phas chang. W can rit th 1 st
Driation of th Enrg Eation ME 7710 Enironmntal Flid Dnamics Spring 01 This driation follos closl from Bird, Start and Lightfoot (1960) bt has bn tndd to incld radiation and phas chang. W can rit th 1 st
Thomas Whitham Sixth Form
 Thomas Whitham Sith Form Pur Mathmatics Unit C Algbra Trigonomtr Gomtr Calculus Vctor gomtr Pag Algbra Molus functions graphs, quations an inqualitis Graph of f () Draw f () an rflct an part of th curv
Thomas Whitham Sith Form Pur Mathmatics Unit C Algbra Trigonomtr Gomtr Calculus Vctor gomtr Pag Algbra Molus functions graphs, quations an inqualitis Graph of f () Draw f () an rflct an part of th curv
The phenomenon of nonlinear optical birefringence in uniaxial crystals
 Th phmf liar ptical birfrigc i uiaial crstals Timtr Pascal, Adam Usma, J. C. Odd Dpartmt f Phsics, Fdral Uivrsit f Tchlg, Yla. P.M.B. 2076 Yla. Adamawa Stat, Nigria. E-mail: ptimtr@ah.cm; aausma@ah.c.uk
Th phmf liar ptical birfrigc i uiaial crstals Timtr Pascal, Adam Usma, J. C. Odd Dpartmt f Phsics, Fdral Uivrsit f Tchlg, Yla. P.M.B. 2076 Yla. Adamawa Stat, Nigria. E-mail: ptimtr@ah.cm; aausma@ah.c.uk
Solution to 1223 The Evil Warden.
 Solutio to 1 Th Evil Ward. This is o of thos vry rar PoWs (I caot thik of aothr cas) that o o solvd. About 10 of you submittd th basic approach, which givs a probability of 47%. I was shockd wh I foud
Solutio to 1 Th Evil Ward. This is o of thos vry rar PoWs (I caot thik of aothr cas) that o o solvd. About 10 of you submittd th basic approach, which givs a probability of 47%. I was shockd wh I foud
International Journal of Mathematical Archive-7(5), 2016, Available online through ISSN
 Itratial Jural f athmatial Arhiv-7(5), 06, 60-70 Availabl li thrugh wwwimaif ISSN 9 5046 IDEALS IN ALOST SEILATTICE G NANAJI RAO, TEREFE GETACHEW BEYENE*,Dpartmt f athmatis, Adhra Uivrsity, Visakhpataam,
Itratial Jural f athmatial Arhiv-7(5), 06, 60-70 Availabl li thrugh wwwimaif ISSN 9 5046 IDEALS IN ALOST SEILATTICE G NANAJI RAO, TEREFE GETACHEW BEYENE*,Dpartmt f athmatis, Adhra Uivrsity, Visakhpataam,
N J of oscillators in the three lowest quantum
 . a) Calculat th fractinal numbr f scillatrs in th thr lwst quantum stats (j,,,) fr fr and Sl: ( ) ( ) ( ) ( ) ( ).6.98. fr usth sam apprach fr fr j fr frm q. b) .) a) Fr a systm f lcalizd distinguishabl
. a) Calculat th fractinal numbr f scillatrs in th thr lwst quantum stats (j,,,) fr fr and Sl: ( ) ( ) ( ) ( ) ( ).6.98. fr usth sam apprach fr fr j fr frm q. b) .) a) Fr a systm f lcalizd distinguishabl
Discrete Fourier Transform (DFT)
 Discrt Fourir Trasorm DFT Major: All Egirig Majors Authors: Duc guy http://umricalmthods.g.us.du umrical Mthods or STEM udrgraduats 8/3/29 http://umricalmthods.g.us.du Discrt Fourir Trasorm Rcalld th xpotial
Discrt Fourir Trasorm DFT Major: All Egirig Majors Authors: Duc guy http://umricalmthods.g.us.du umrical Mthods or STEM udrgraduats 8/3/29 http://umricalmthods.g.us.du Discrt Fourir Trasorm Rcalld th xpotial
Elements of Statistical Thermodynamics
 24 Elmnts of Statistical Thrmodynamics Statistical thrmodynamics is a branch of knowldg that has its own postulats and tchniqus. W do not attmpt to giv hr vn an introduction to th fild. In this chaptr,
24 Elmnts of Statistical Thrmodynamics Statistical thrmodynamics is a branch of knowldg that has its own postulats and tchniqus. W do not attmpt to giv hr vn an introduction to th fild. In this chaptr,
THESEUS ARRIVES MARY JANE LEACH. Mixed Chorus (SSAATB) and String Quartet. Ariadne Press Duration: ca. 2:30
 HESEUS ARRIVES Mixd hors (SSAA) and String Qartt Dration: ca. 2:30 MARY JANE LEAH Ariadn rss 00034 Soprano 1 Soprano 2 Vocal rangs: & & b Alto 1 & Alto 2 & b nor V b ass b In a pic sch as this, in hich
HESEUS ARRIVES Mixd hors (SSAA) and String Qartt Dration: ca. 2:30 MARY JANE LEAH Ariadn rss 00034 Soprano 1 Soprano 2 Vocal rangs: & & b Alto 1 & Alto 2 & b nor V b ass b In a pic sch as this, in hich
Thomas Whitham Sixth Form
 Thomas Whitham Sith Form Pur Mathmatics Cor rvision gui Pag Algbra Moulus functions graphs, quations an inqualitis Graph of f () Draw f () an rflct an part of th curv blow th ais in th ais. f () f () f
Thomas Whitham Sith Form Pur Mathmatics Cor rvision gui Pag Algbra Moulus functions graphs, quations an inqualitis Graph of f () Draw f () an rflct an part of th curv blow th ais in th ais. f () f () f
5. B To determine all the holes and asymptotes of the equation: y = bdc dced f gbd
 1. First you chck th domain of g x. For this function, x cannot qual zro. Thn w find th D domain of f g x D 3; D 3 0; x Q x x 1 3, x 0 2. Any cosin graph is going to b symmtric with th y-axis as long as
1. First you chck th domain of g x. For this function, x cannot qual zro. Thn w find th D domain of f g x D 3; D 3 0; x Q x x 1 3, x 0 2. Any cosin graph is going to b symmtric with th y-axis as long as
Types of Communication
 Tps f Cmmunicatin Analg: cntinuus ariabls with nis {rrr 0} 0 (imprfct) Digital: dcisins, discrt chics, quantizd, nis {rrr} 0 (usuall prfct) Mssag S, S, r S M Mdulatr (t) channl; adds nis and distrtin M-ar
Tps f Cmmunicatin Analg: cntinuus ariabls with nis {rrr 0} 0 (imprfct) Digital: dcisins, discrt chics, quantizd, nis {rrr} 0 (usuall prfct) Mssag S, S, r S M Mdulatr (t) channl; adds nis and distrtin M-ar
The graph of y = x (or y = ) consists of two branches, As x 0, y + ; as x 0, y +. x = 0 is the
 Copyright itutcom 005 Fr download & print from wwwitutcom Do not rproduc by othr mans Functions and graphs Powr functions Th graph of n y, for n Q (st of rational numbrs) y is a straight lin through th
Copyright itutcom 005 Fr download & print from wwwitutcom Do not rproduc by othr mans Functions and graphs Powr functions Th graph of n y, for n Q (st of rational numbrs) y is a straight lin through th
INTEGRATION BY PARTS
 Mathmatics Rvision Guids Intgration by Parts Pag of 7 MK HOME TUITION Mathmatics Rvision Guids Lvl: AS / A Lvl AQA : C Edcl: C OCR: C OCR MEI: C INTEGRATION BY PARTS Vrsion : Dat: --5 Eampls - 6 ar copyrightd
Mathmatics Rvision Guids Intgration by Parts Pag of 7 MK HOME TUITION Mathmatics Rvision Guids Lvl: AS / A Lvl AQA : C Edcl: C OCR: C OCR MEI: C INTEGRATION BY PARTS Vrsion : Dat: --5 Eampls - 6 ar copyrightd
Mathematical Statistics. Chapter VIII Sampling Distributions and the Central Limit Theorem
 Mahmacal ascs 8 Chapr VIII amplg Dsrbos ad h Cral Lm Thorm Fcos of radom arabls ar sall of rs sascal applcao Cosdr a s of obsrabl radom arabls L For ampl sppos h arabls ar a radom sampl of s from a poplao
Mahmacal ascs 8 Chapr VIII amplg Dsrbos ad h Cral Lm Thorm Fcos of radom arabls ar sall of rs sascal applcao Cosdr a s of obsrabl radom arabls L For ampl sppos h arabls ar a radom sampl of s from a poplao
CDS 101: Lecture 5.1 Reachability and State Space Feedback
 CDS, Lctur 5. CDS : Lctur 5. Rachability ad Stat Spac Fdback Richard M. Murray 7 Octobr 3 Goals: Di rachability o a cotrol systm Giv tsts or rachability o liar systms ad apply to ampls Dscrib th dsig o
CDS, Lctur 5. CDS : Lctur 5. Rachability ad Stat Spac Fdback Richard M. Murray 7 Octobr 3 Goals: Di rachability o a cotrol systm Giv tsts or rachability o liar systms ad apply to ampls Dscrib th dsig o
STRUCTURES IN MIKE 21. Flow over sluice gates A-1
 A-1 STRUCTURES IN MIKE 1 Fl ver luice gate Fr a give gemetry f the luice gate ad k ater level uptream ad dtream f the tructure, the fl rate, ca be determied thrugh the equati f eergy ad mmetum - ee B Pedere,
A-1 STRUCTURES IN MIKE 1 Fl ver luice gate Fr a give gemetry f the luice gate ad k ater level uptream ad dtream f the tructure, the fl rate, ca be determied thrugh the equati f eergy ad mmetum - ee B Pedere,
That is, we start with a general matrix: And end with a simpler matrix:
 DIAGON ALIZATION OF THE STR ESS TEN SOR INTRO DUCTIO N By th us of Cauchy s thorm w ar abl to rduc th numbr of strss componnts in th strss tnsor to only nin valus. An additional simplification of th strss
DIAGON ALIZATION OF THE STR ESS TEN SOR INTRO DUCTIO N By th us of Cauchy s thorm w ar abl to rduc th numbr of strss componnts in th strss tnsor to only nin valus. An additional simplification of th strss
a 1and x is any real number.
 Calcls Nots Eponnts an Logarithms Eponntial Fnction: Has th form y a, whr a 0, a an is any ral nmbr. Graph y, Graph y ln y y Th Natral Bas (Elr s nmbr): An irrational nmbr, symboliz by th lttr, appars
Calcls Nots Eponnts an Logarithms Eponntial Fnction: Has th form y a, whr a 0, a an is any ral nmbr. Graph y, Graph y ln y y Th Natral Bas (Elr s nmbr): An irrational nmbr, symboliz by th lttr, appars
Signals & Systems - Chapter 3
 .EgrCS.cm, i Sigls d Sysms pg 9 Sigls & Sysms - Chpr S. Ciuus-im pridic sigl is rl vlud d hs fudml prid 8. h zr Furir sris cfficis r -, - *. Eprss i h m. cs A φ Slui: 8cs cs 8 8si cs si cs Eulrs Apply
.EgrCS.cm, i Sigls d Sysms pg 9 Sigls & Sysms - Chpr S. Ciuus-im pridic sigl is rl vlud d hs fudml prid 8. h zr Furir sris cfficis r -, - *. Eprss i h m. cs A φ Slui: 8cs cs 8 8si cs si cs Eulrs Apply
2617 Mark Scheme June 2005 Mark Scheme 2617 June 2005
 Mark Schm 67 Ju 5 GENERAL INSTRUCTIONS Marks i th mark schm ar plicitly dsigatd as M, A, B, E or G. M marks ("mthod" ar for a attmpt to us a corrct mthod (ot mrly for statig th mthod. A marks ("accuracy"
Mark Schm 67 Ju 5 GENERAL INSTRUCTIONS Marks i th mark schm ar plicitly dsigatd as M, A, B, E or G. M marks ("mthod" ar for a attmpt to us a corrct mthod (ot mrly for statig th mthod. A marks ("accuracy"
Lecture 37 (Schrödinger Equation) Physics Spring 2018 Douglas Fields
 Lctur 37 (Schrödingr Equation) Physics 6-01 Spring 018 Douglas Filds Rducd Mass OK, so th Bohr modl of th atom givs nrgy lvls: E n 1 k m n 4 But, this has on problm it was dvlopd assuming th acclration
Lctur 37 (Schrödingr Equation) Physics 6-01 Spring 018 Douglas Filds Rducd Mass OK, so th Bohr modl of th atom givs nrgy lvls: E n 1 k m n 4 But, this has on problm it was dvlopd assuming th acclration
Vr Vr
 F rt l Pr nt t r : xt rn l ppl t n : Pr nt rv nd PD RDT V t : t t : p bl ( ll R lt: 00.00 L n : n L t pd t : 0 6 20 8 :06: 6 pt (p bl Vr.2 8.0 20 8.0. 6 TH N PD PPL T N N RL http : h b. x v t h. p V l
F rt l Pr nt t r : xt rn l ppl t n : Pr nt rv nd PD RDT V t : t t : p bl ( ll R lt: 00.00 L n : n L t pd t : 0 6 20 8 :06: 6 pt (p bl Vr.2 8.0 20 8.0. 6 TH N PD PPL T N N RL http : h b. x v t h. p V l
ELEG 413 Lecture #6. Mark Mirotznik, Ph.D. Professor The University of Delaware
 LG 43 Lctur #6 Mrk Mirtnik, Ph.D. Prfssr Th Univrsity f Dlwr mil: mirtni@c.udl.du Wv Prpgtin nd Plritin TM: Trnsvrs lctrmgntic Wvs A md is prticulr fild cnfigurtin. Fr givn lctrmgntic bundry vlu prblm,
LG 43 Lctur #6 Mrk Mirtnik, Ph.D. Prfssr Th Univrsity f Dlwr mil: mirtni@c.udl.du Wv Prpgtin nd Plritin TM: Trnsvrs lctrmgntic Wvs A md is prticulr fild cnfigurtin. Fr givn lctrmgntic bundry vlu prblm,
Iterative Methods of Order Four for Solving Nonlinear Equations
 Itrativ Mods of Ordr Four for Solvig Noliar Equatios V.B. Kumar,Vatti, Shouri Domii ad Mouia,V Dpartmt of Egirig Mamatis, Formr Studt of Chmial Egirig Adhra Uivrsity Collg of Egirig A, Adhra Uivrsity Visakhapatam
Itrativ Mods of Ordr Four for Solvig Noliar Equatios V.B. Kumar,Vatti, Shouri Domii ad Mouia,V Dpartmt of Egirig Mamatis, Formr Studt of Chmial Egirig Adhra Uivrsity Collg of Egirig A, Adhra Uivrsity Visakhapatam
CDS 101: Lecture 5.1 Reachability and State Space Feedback
 CDS, Lctur 5. CDS : Lctur 5. Rachability ad Stat Spac Fdback Richard M. Murray ad Hido Mabuchi 5 Octobr 4 Goals: Di rachability o a cotrol systm Giv tsts or rachability o liar systms ad apply to ampls
CDS, Lctur 5. CDS : Lctur 5. Rachability ad Stat Spac Fdback Richard M. Murray ad Hido Mabuchi 5 Octobr 4 Goals: Di rachability o a cotrol systm Giv tsts or rachability o liar systms ad apply to ampls
LECTURE 13 Filling the bands. Occupancy of Available Energy Levels
 LUR 3 illig th bads Occupacy o Availabl rgy Lvls W hav dtrmid ad a dsity o stats. W also d a way o dtrmiig i a stat is illd or ot at a giv tmpratur. h distributio o th rgis o a larg umbr o particls ad
LUR 3 illig th bads Occupacy o Availabl rgy Lvls W hav dtrmid ad a dsity o stats. W also d a way o dtrmiig i a stat is illd or ot at a giv tmpratur. h distributio o th rgis o a larg umbr o particls ad
How many neutrino species?
 ow may utrio scis? Two mthods for dtrmii it lium abudac i uivrs At a collidr umbr of utrio scis Exasio of th uivrs is ovrd by th Fridma quatio R R 8G tot Kc R Whr: :ubblcostat G :Gravitatioal costat 6.
ow may utrio scis? Two mthods for dtrmii it lium abudac i uivrs At a collidr umbr of utrio scis Exasio of th uivrs is ovrd by th Fridma quatio R R 8G tot Kc R Whr: :ubblcostat G :Gravitatioal costat 6.
