UIUC Physics 436 EM Fields & Sources II Fall Semester, 2015 Lect. Notes 7.5 Prof. Steven Errede LECTURE NOTES 7.5
|
|
|
- Randolf Howard
- 6 years ago
- Views:
Transcription
1 UIUC Physics 436 EM Filds & Surcs II Fall Smstr, 05 Lct. Nts 7.5 Pr. Stv Errd LECTURE NOTES 7.5 Disprsi: Th Frqucy-Dpdc th Elctric Prmittivity ad th Elctric Suscptibility Ovr th tir EM rqucy itrval 0 Hz, th spd prpagati v prp mchrmatic (i.. sigl-rqucy) EM wavs i mattr is t t cstat, t idpdt rqucy: vprp cstat; crqucy, vprp, bcaus mattr - at th micrscpic scal - is cmpsit - cmprisd atms/mlculs which hav rsacs i rgy/rgy lvls which ar gvrd by th laws quatum mchaics Th rqucy-dpdc th wavlgth, r wavumbr k, ad liar mmtum p assciatd with macrscpic EM wavs prpagatig i a disprsiv mdium ariss rm th rqucy-dpdc th macrscpic lctric prmittivity (r quivaltly th lctric suscptibility sic:. Th rqucy-dpdc th macrscpic lctric prmittivity is kw as disprsi; a mdium that has c is kw as a disprsiv mdium. Fr -magtic/-cductig liar/hmgus/istrpic mdia, th id rracti. Thus, i: th:. Fr a wav packt (= a grup {= suprpsiti/liar cmbiati} wavs may rqucis as plaid by Mssr. Furir), th vlp th wav packt travls with (i gral, rqucy-dpdt) grup spd = spd at which rgy i th wav lws: A prpagatig wav packt: kz t v g " " d dk dk dk d d v v g k dk d A spac-pit z t th wavrm mvs - with cstat phas kz t with (i gral, rqucy-dpdt) phas spd v k. Hc: zt, k v t. Nt that {i gral}: v. g v Prssr Stv Errd, Dpartmt Physics, Uivrsity Illiis at Urbaa-Champaig, Illiis All Rights Rsrvd.
2 UIUC Physics 436 EM Filds & Surcs II Fall Smstr, 05 Lct. Nts 7.5 Pr. Stv Errd I v k is rqucy-dpdt, ad vg dk d v {.g. as i v v } th rlatiship btw v v th cas r surac wavs watr, whr g ad g dpds th dtaild physics th mdium (as w shall s s... ). Nt that i crtai circumstacs, v ca cd c {= spd light i th vacuum} but i ths situatis, rgy (ad/r irmati) is trasmittd at supr-lumial spds rgy/irmati is trasmittd at v g < c always, by causality A physical/mchaical ampl: calculat th phas spd th itrscti pit th scissrs tw halvs a scissrs as th blads th scissrs ar clsd. {Aswr:!!!} Disprsi Phma i Liar Dilctrics I a -cductig, liar, hmgus, istrpic mdium thr ar r lctrs (i.. r r 0 ). Atmic lctrs ar prmatly bud t ucli atms cmprisig th mdium. prrtial dircti / prrtial dirctis i such a {istrpic} mdium. Supps ach atmic lctr (charg ) i a dilctric is displacd by a small distac r rm its quilibrium psiti,.g. by applicati a static lctric ild Er rˆ dircti. Th rsultig macrscpic lctric plarizati (aka lctric dipl mmt pr uit vlum) is: b b 3 r pr whr: = bud atmic lctr umbr dsity # m ad th {iducd} atmic/mlcular lctric dipl mmt is: p rr {hr}, whr r is th {vctr} displacmt th atmic lctr rm its quilibrium { r = 0} psiti. b b r p r r Thus: Th atmic lctrs ar ach lastically bud t thir quilibrium psitis with a rc k N m. Th rc quati r ach atmic lctr is thus: FrErkr. r E r k. b b b b E r r p r r E r k k cstat Hc: Th static plarizati is thrr giv by: Hwvr, i th E -ild.g. varis harmically with tim, i..,; v ikz t E E r t E ˆ du t a mchrmatic EM pla wav icidt a atm, th abv rlati is icrrct! A mr crrct {but smi-classical } apprach t trat this situati is t csidr th bud atmic lctrs as classical, dampd, rcd harmic scillatrs (driv by th icidt lctric ild), as mathmatically dscribd by th llwig dirtial quati: mr t m r t kr t E r t ihmgus d -rdr dirtial q. ; ; ;, ; Th dampig cstat rads sc rprsts th ct EM r-radiati by th atm {hr}. Prssr Stv Errd, Dpartmt Physics, Uivrsity Illiis at Urbaa-Champaig, Illiis All Rights Rsrvd.
3 UIUC Physics 436 EM Filds & Surcs II Fall Smstr, 05 Lct. Nts 7.5 Pr. Stv Errd r t; rt; m m kr t E r t t t ma ;, ;.b. w hav glctd th v B E trm hr... Vlcity-dpdt dampig trm dampig cstat Pttial Frc (bidig atmic lctrs t atm) m Drivig Frc lctr mass kg Supps th drivig/rcig trm varis siusidally/is harmic/pridic with agular it F r,; t E r,; t E i t r bcaus E r,; t E rˆ. rqucy, i.. ˆ.b. Th lctric ild E is cmpl E ad pla-plarizd i th ˆr -dircti. i t Th ihmgus rc quati bcms: mr ˆ m r kr E r with cmpl tim-dmai vctr displacmt amplitud: r t; r t; ˆ r. I th stady stat, w hav: Sic rt; i t mr m r kr E rˆ physically rprsts th cmpl vctr spatial displacmt a atmic i t r t; r t; rˆr rˆ lctr rm its quilibrium { r 0 } psiti, th: Thus: i t mr m r kr E rˆ r t; rt; m m kr t; Er, t; t t m r it imr i t kr i t E i t m k i m r E charactristic quati k Divid this quati thrugh by m : i r E m m k k Di: 0 r: 0 = charactristic/atural rsac {agular} rqucy. Th: m m 0 ir E Bud atmic lctr r: r E cmpl rqucydmai spatial m m 0 i displacmt amplitud Nt that th cmplss rqucy-dmai r is i th dmiatr. W ca mv it t th umratr usig th llwig stadard trick /prcdur: iy iy y I: z whr: z ad: m z iy iy iy y y y Prssr Stv Errd, Dpartmt Physics, Uivrsity Illiis at Urbaa-Champaig, Illiis All Rights Rsrvd. 3
4 UIUC Physics 436 EM Filds & Surcs II Fall Smstr, 05 Lct. Nts 7.5 Pr. Stv Errd Thus: r E E 0 i m m 0 i 0 i 0 i m E 0 0 i 0 m E 0 0 i 0 i i m E 0 i 0 i i 0 * * i E i E Nt that: E E E. Hwvr, w ca always rtat away /absrb th phas E E 0.g. by a glbal rdiiti th zr tim, r a glbal rdiiti/traslati ur crdiat systm. Hc, w ca quivaltly writ, withut ay lss grality: 0 i r E r ir r ral m 0 imag i Th {rqucy-dpdt} ral part th rqucy-dmai displacmt amplitud r it i.. th cmpt r that is i-phas with th drivig rc E r,; t E rˆ ral 0 r r E m 0 r is: Th {rqucy-dpdt} imagiary part th rqucy-dmai displacmt amplitud r i.. th cmpt r that is 90 it -ut--phas with th drivig rc E r,; t E rˆ imag r mr E m 0 is: is: Th {rqucy-dpdt} phas th rqucy-dmai displacmt amplitud r imag mr r r ta ta ta ral r r 0 k Wh: 0, r 0 r lags E. Wh: k 0, r 0 r lads E. m m 4 Prssr Stv Errd, Dpartmt Physics, Uivrsity Illiis at Urbaa-Champaig, Illiis All Rights Rsrvd.
5 UIUC Physics 436 EM Filds & Surcs II Fall Smstr, 05 Lct. Nts 7.5 Pr. Stv Errd is: Th {rqucy-dpdt} magitud th rqucy-dmai displacmt amplitud r * ral imag 0 i 0 0 m r r r r r i E 0 E m 0 E 0 m Th 8-igur plt blw shws th bhavir a mchaical rsac at 30 KHz, ad FWHM 30 Hz i th viciity th rsac r uit amplitud m E. Th rsac rqucy ad l/hi rqucis that di th FWHM, } ar als idicatd i ach plt: {i.. Nt that th s-calld Q {this} rsac {hr} is: Q 000. Fr small Q ad that dampig, it ca b shw that 0, 0 r 0 ta 90, r ta 35 ad r ta 45. Prssr Stv Errd, Dpartmt Physics, Uivrsity Illiis at Urbaa-Champaig, Illiis All Rights Rsrvd. 5
6 UIUC Physics 436 EM Filds & Surcs II Fall Smstr, 05 Lct. Nts 7.5 Pr. Stv Errd Th 3-D plt blw shws th CW path tak i th cmpl pla i passig thrugh th rsac: FWHM, = Nw:,; b ; b i rt r t r t rˆ whr: r Thus:,; 0 i E m 0 i i rt E r E rˆ b 0 it b 0 ˆ it m m 0 0 it Sic th cmpl tim-dmai rt,; r; rˆ, w s that th cmpl rqucydmai vctr amplitud is: ; I th static limit (i.. 0 ): b 0 i r ˆ E r. m 0 b b b m m r; 0 E ˆ ˆ ˆ r Er Er 0 k k m Static plarizati 0 is i-phas with E 6 Prssr Stv Errd, Dpartmt Physics, Uivrsity Illiis at Urbaa-Champaig, Illiis All Rights Rsrvd.
7 UIUC Physics 436 EM Filds & Surcs II Fall Smstr, 05 Lct. Nts 7.5 Pr. Stv Errd Nt that th phas th rqucy-dmai vctr amplitud r; lags bhid (r lads) E ta by a rqucy-dpdt phas agl : mr, ta r, 0 is rqucy dpdt, k Wh: 0, 0 lags E. Wh: k 0, 0 lads E. m Frm th abv rmula, t that i th dampig cstat 0, th 0, th plarizati, bcaus i 0 m r, t 0, is always i-phas with E i.. th plarizati (FWHM) Hz m, th is purly ral! A dampig cstat 0 als mas that th width th atmic/mlcular rsac is iiitly arrw, ad thus thr ar dissipativ prcsss (i.. rgy lss mchaisms) prst at th micrscpic atmic/mlcular lvl i this macrscpic mdium! Nt als that has physical/si uits radias/scd. Nt urthr that E i th abv prssi is actually E it th itral macrscpic lctric ild th dilctric: E Eit Et EP, th sum th macrscpic tral applid lctric ild ad th macrscpic lctric ild du t th plarizati th dilctric mdium. Th lctric ild du t plarizati th mdium is: Thus: E Eit Et 3 Thrr: E P 3 b 0 i k Et 0 m 3 0 m Nw slv r : Skippig writig ut sm {tdius} cmpl algbra, w btai: b i E m t whr: b 0 0 = 3 m Nt that this rmula is sstially idtical.g. t th {cmpl} displacmt amplitud rmula r a driv harmic scillatr, ad/r that r th {cmpl} AC vltag amplitud i a LCR circuit, ad r may thr physical systms hibitig a {dampd} rsac-typ bhavir. Nw i E t dilctric mdium: E -ild assciatd with a mchrmatic pla EM wav prpagatig i a ikz t Et z, t E, th bcaus th liar rlatiship btw th ikz t E t z, t E, Gauss Law bcms (sic 0 r r ): E 0 plarizati ad.g. ˆ t bud.b. Th dampig cstat has th sam uits as : radias/sc S P435 Lct. Nts 0, p. -6. S als P435 Lct. Nts 9, p. 6. ctiv agular rsac rqucy bud atmic lctrs Prssr Stv Errd, Dpartmt Physics, Uivrsity Illiis at Urbaa-Champaig, Illiis All Rights Rsrvd. 7
8 UIUC Physics 436 EM Filds & Surcs II Fall Smstr, 05 Lct. Nts 7.5 Pr. Stv Errd Th wav quati r a dilctric mdium with r 0 ad J 0 r r bcms: Or: Et b Et Et c t t m t i with: c i b Et Et c m t b with: 0 3 m Th gral sluti t this disprsiv wav quati is th rm: E r,; t E t ikz t with cmpl k ki ad: k c i. b m Thus, w als s that hr {agai} th cmpl wavumbr k ki is plicitly k k i. dpdt th agular rqucy, i.. W urthr s that mchrmatic pla EM wavs prpagatig i a disprsiv dilctric ikz t z ikz t E r,; t E E, mdium ar ptially attuatd, bcaus: i.. th m k t trm crrspds t absrpti/dissipati i th macrscpic dilctric, ad is physically rlatd t/is prprtial t th dampig cstat. Nt that w als hav: rt,, Et rt,,, thus th suscptibility als cmpl, ad rqucy-dpdt: i. Th m {hr} is trm crrspds t absrpti/dissipati i th dilctric, ad is physically rlatd t/is prprtial t th dampig cstat. Th crrspdig dissipativ rgy lsss at th micrscpic, atmic/ mlcular lvl i th dilctric ultimatly wid up as hat! Sic: b i r,; t Et r,; t E,; t r t m b i E, ; t r t m b whr: 0 3 m 8 Prssr Stv Errd, Dpartmt Physics, Uivrsity Illiis at Urbaa-Champaig, Illiis All Rights Rsrvd.
9 UIUC Physics 436 EM Filds & Surcs II Fall Smstr, 05 Lct. Nts 7.5 Pr. Stv Errd W s that th cmpl suscptibility assciatd with a sigl rsac is: Hc: Ad: i b m i b m b m m Nw br w g much urthr with this, w d t discuss athr aspct ur mdl amly that i mst liar dilctric matrials, th atms cmprisig th matrial ar multilctr atms, ad csqutly thr ar may dirt bidig rgis th utr shll atmic lctrs ar wakly bud, hc hav small k, ad thus small 0 k m, whras th ir-shll lctrs ar much mr tightly bud, hc hav largr k, largr 0 k m. Furthrmr, i cmpl mdia, i.. dilctrics with mr tha kid atm, lctrs ca b shard btw atms i.. thy ar bud t mlculs.g. th π-lctrs i bz rig / armatic hydrcarb-typ cmpuds, which ca b wakly bud i sm mlculs. Thus, thr ca b als b {mlcular} rsacs.g. i th micrwav ad ira-rd rgis th EM spctrum atmic rsacs ar typically i th ptical ad UV rgis {r th utr-mst shll lctrs}, as wll as i th ar UV ad -ray rgis {r th irshll lctrs}! Allwig r all such rsacs, w ca writ th {cmpl} lctric plarizati as a summati vr all th rsacs prst i th liar dilctric as llws: whr: ad whr: Physically: b i sc rt,; E,; t rt m b 3 m 0 sc ad: 0 k m scillatr strgth th rsac, did such that: sc = ractial strgth th th rsac ad = width th th rsac. sc Prssr Stv Errd, Dpartmt Physics, Uivrsity Illiis at Urbaa-Champaig, Illiis All Rights Rsrvd. 9
10 UIUC Physics 436 EM Filds & Surcs II Fall Smstr, 05 Lct. Nts 7.5 Pr. Stv Errd is: Thus, w s that th multi-rsac cmpl lctric suscptibility i i b sc m i Hc: b sc m Ad: b sc m m Th cmpl lctric prmittivity i dilctric mdium is: a disprsiv, liar b i sc m with th rlatis: ad: b sc i m m m b sc. m i 0 Prssr Stv Errd, Dpartmt Physics, Uivrsity Illiis at Urbaa-Champaig, Illiis All Rights Rsrvd.
11 UIUC Physics 436 EM Filds & Surcs II Fall Smstr, 05 Lct. Nts 7.5 Pr. Stv Errd Mchrmatic pla EM wav slutis t th disprsiv wav quati ar th rm: E r,, t E Thus:,, ikz t with cmpl wavumbr k k i z E r t E E ikz t ikz t t ptial dampig EM wav r a -magtic mdium, i... is quivalt Itrducig a {rqucy-dpdt} cmpl wavumbr kki t itrducig a {rqucy-dpdt} cmpl id rracti i. Fr a disprsiv dilctric, th cmpl id rracti ad cmpl wavumbr ar {simply} rlatd t ach thr by: k c k i i i c k c c c ad c Fr a -magtic mdium ( ), th cmpl id rracti is rlatd t th cmpl lctric prmittivity suscptibility via th rlati: Squarig bth sids: But: ad thus th cmpl lctric, k b i sc m b i sc c m k i k ik Prssr Stv Errd, Dpartmt Physics, Uivrsity Illiis at Urbaa-Champaig, Illiis All Rights Rsrvd.
12 UIUC Physics 436 EM Filds & Surcs II Fall Smstr, 05 Lct. Nts 7.5 Pr. Stv Errd c th: Sic: k b c i sc k m i i Equatig th ral ad imagiary parts th LHS & RHS th abv quati, w btai: sc b m b sc m quatis ad ukws: & slv r & First di: sc b m sc b m (.b. 0, is always psitiv {hr}) Th: ad Thus: Or: Di:. W tmprarily supprss th Th: 0 multiply quati thrugh by a b c -dpdc i th llwig: 0 with: Th slutis / rts this quadratic quati ar th gral rm:.b. This may lk lik a quartic quati, but it is actually a quadratic quati!!! a, b, c b b 4ac a Prssr Stv Errd, Dpartmt Physics, Uivrsity Illiis at Urbaa-Champaig, Illiis All Rights Rsrvd.
13 UIUC Physics 436 EM Filds & Surcs II Fall Smstr, 05 Lct. Nts 7.5 Pr. Stv Errd 4 i...b. th trm: 0 Must slct +v rt physical gruds, sic 0. Fially, w btai: Cmpl id rracti: i m Whr: sc b m sc b m Obviusly, plicitly writig ut th ull mathmatical rmula r ad is quit tdius but ths ca b rasably-asily cdd up {i.. a cmputr prgram} ad plts vs. ca b btaid. W ca als th btai th llwig: vs. ad c Th cmpl rlatis: i ad k k i c c ad thus: k ad Prssr Stv Errd, Dpartmt Physics, Uivrsity Illiis at Urbaa-Champaig, Illiis All Rights Rsrvd.. 3
14 UIUC Physics 436 EM Filds & Surcs II Fall Smstr, 05 Lct. Nts 7.5 Pr. Stv Errd Th {rqucy-dpdt} itsity/irradiac Ir, Sr, t; assciatd with a mchrmatic pla EM wav prpagatig i a liar, disprsiv dilctric is als ptially dcrasd by a actr its rigial valu i gig a charactristic distac : z i.. diig: att att = itsity attuati lgth which is ~ aalgus t th ski dpth, r mtals / cductrs. Hwvr, t that is assciatd with th attuati th E ad B - sc ilds, whras attuati cts i itsity/irradiac, I varis as th squar th E -ild: I r S r t E r t,, ;, ; t hc: Ir (, ) E E sc z z I th ptial z-dpdt trm, sic th rgy dsit(is) uem, r,; t I r, S r, t; ar bth prprtial t E i.. bth prprtial t itsity z z, w di th {rqucy-dpdt} absrpti cicit: ad att. Similarly, r th {rqucy-dpdt} cmpl id rracti i w ca als di th {rqucy-dpdt} ticti cicit:. c Sic: c c c thus:. att c c ad. Th absrpti cicit: Th ticti cicit: Typical valus th (ral) id rracti r slids ad liquids ar.3.7 i th visibl light rgi EM spctrum,.g. glass.5, HO.3, plastic.7. Th i: Th: id rracti.5 glass i th visibl light rgi.5.5 O quati & tw ukws: 4.50 ad Thus: Nd athr rlati / idpdt cstrait!! 4 Prssr Stv Errd, Dpartmt Physics, Uivrsity Illiis at Urbaa-Champaig, Illiis All Rights Rsrvd.
15 UIUC Physics 436 EM Filds & Surcs II Fall Smstr, 05 Lct. Nts 7.5 Pr. Stv Errd Nt that glass ds t hav sigiicat absrpti i th visibl light rgi, typical such slid/liquid matrials hav (masurd) absrpti cicits r visibl light i th rag : c 0 0 m Itsity I(z) dcrass t / = = iitial I(z = 0) valu atr light travls a distac z = / () ~ 0 00 m i glass. 6 0 m i glass r visibl light, vis 0 radias / sc c S supps: c Nw: ad.5 r glass i visibl light rag EM spctrum. 9 r: i th visibl light rag r glass Th: Ca w slv r : ad: This has a sluti wh:.5 r: 9 0 Obtaid via umrical mthds usig a cmputr Thus, r.5 r glass i th visibl light rgi th EM spctrum, with.5 9 ad 9 0 (i.. ), as a plicit chck, w s that: Prssr Stv Errd, Dpartmt Physics, Uivrsity Illiis at Urbaa-Champaig, Illiis All Rights Rsrvd. 5
16 UIUC Physics 436 EM Filds & Surcs II Fall Smstr, 05 Lct. Nts 7.5 Pr. Stv Errd Thus w als s that: sc b m i.. r typical matrials glass, watr, plastic i th visibl light rgi th EM spctrum, 6 0 radias / sc. Whras: b sc m r ths sam matrials glass, watr, plastic i th visibl light rgi th EM spctrum, 6 0 radias / sc. Our rigial quatis wr: ad 9 with:.5 ad 90 r.5 9 with visibl light ad: 30. W w s mr clarly that: r: (r glass) i th visibl light rgi th EM spctrum i i r glass is 9 r glass, i.. th cmpl id rracti.5 90 prdmiatly ral i th visibl light rgi th EM spctrum. Thus, r glass i th visibl light rgi th EM spctrum: sc b.5.5 m ad: b sc 9 0 0m sc b.5 m 9 Nt that ths rsults that w ust btaid r glass i th visibl light rgi th EM spctrum d t hld tru r all rqucis EM wavs {visibl light rgi is i act ly a arrw prti th EM spctrum}!!! I particular, ths rsults d t hld at {r ar} a atmic (r mlcular) rsac! 6 Prssr Stv Errd, Dpartmt Physics, Uivrsity Illiis at Urbaa-Champaig, Illiis All Rights Rsrvd.
17 UIUC Physics 436 EM Filds & Surcs II Fall Smstr, 05 Lct. Nts 7.5 Pr. Stv Errd Lt us csidr a simpliid atmic/mlcular systm, that havig ly a sigl rsac rqucy (i.. a sigl bud-stat quatum rgy lvl), th: r: b 0 3 m b 3m 0 with: 0 k m sc.b. Oscillatr strgth {hr} bcaus hav ly a sigl rsac! Th: sc b m b sc m Th igur th lt (immdiatly blw) shws th bhavir th ral ad imagiary parts vs. } ad th cmpl id rracti a disprsiv, liar mdium, i.. { { vs. } r a sigl atmic rsac. Th igur th right (immdiatly blw) shws th bhavir { vs. } ad th absrpti cicit { vs. } r a sigl atmic rsac. = Prssr Stv Errd, Dpartmt Physics, Uivrsity Illiis at Urbaa-Champaig, Illiis All Rights Rsrvd. 7
18 UIUC Physics 436 EM Filds & Surcs II Fall Smstr, 05 Lct. Nts 7.5 Pr. Stv Errd.b. Th abv curvs ar classic aturs a cmpl rsac with ctr / rsac rqucy ad = dampig cstat Γ = width (= FWHM) th th rsac. Nt that th width Γ Hz. I th - cmpl pla: (FWHM) 0 = = 0 I th visibl light rgi th EM spctrum, th graph blw shws bth th rqucy ad vs. {dttd li} ad wavlgth bhavir th {ral} id rracti glass, i.. v v vs. {slid li}. Nt that sic prp prp r: vprp { Ågstrm = 0 0 m = 0. m}.b. Mdia which ar vry traspart.g. i th visibl light rgi ar t almst (r ar) paqu i th s-calld amalus disprsi rgi a rsac, R i.. i th FWHM rgi th atmic rsac, whr th ticti cicit bcms vry larg EM wavs ar th rsac rqucy R ar vry rapidly ptially attuatd! Th Gral Bhavir Classic Cmpl Rsac: z iy.b. i sm cmpl systms.g. th rsac a LCR circuit, z & mz ar itrchagd rm what is draw hr! i.. z mz 8 Prssr Stv Errd, Dpartmt Physics, Uivrsity Illiis at Urbaa-Champaig, Illiis All Rights Rsrvd.
19 UIUC Physics 436 EM Filds & Surcs II Fall Smstr, 05 Lct. Nts 7.5 Pr. Stv Errd Nt that th shap th curv r th magitud z, z z z * y is vry similar t shap th mz curv {as shw hr}. Th tractry z i th cmpl pla:, A mr ralistic micrscpic pictur a atmic systm with may lctrs with may quatum bud stats may rsacs i a disprsiv, liar macrscpic dilctric!!! ad Ercis(s): Draw ut th crrspdig tractris cmpl i i r th abv tripl-rsac cass i th cmpl pla! Prssr Stv Errd, Dpartmt Physics, Uivrsity Illiis at Urbaa-Champaig, Illiis All Rights Rsrvd. 9
20 UIUC Physics 436 EM Filds & Surcs II Fall Smstr, 05 Lct. Nts 7.5 Pr. Stv Errd I th high-rqucy rgi, abv th highst rsat rqucy (typically i UV r -ray rgi), th id rracti is prdictd t b.0 (i.. actually lss tha that th vacuum). Idd, this phm has plicitly b bsrvd/masurd.g. i quartz (SiO) usig -rays: Nt Supprssd Zr! Nt that physically th dampig cstat = width th th rsac is ivrsly rlatd t th litim assciatd with th crrspdig citd stat th cstitut atms/mlculs th disprsiv, liar dilctric, sic at th micrscpic lvl, th {ral} phts assciatd with th mchrmatic pla EM wav hav rgy E h ad {assumig th atms/mlculs th disprsiv, liar dilctric t all b i thir grud stat, with grud stat rgy E }, th i th mchrmatic pla EM wav has {agular} rqucy R R = th rsac rqucy th bud atmic lctrs, th w s that E E E E hr R at rsac! At a rsac,.g. wh, th {ral} phts i th mchrmatic pla EM wav asily stimulat th atmic lctrs, causig thm t rsat th {ral} phts ar absrbd, th ablig th atmic lctr t mak a trasiti rm th grud stat {with rgy E } t th citd stat {with rgy E } via a lctric dipl trasiti, i s allwd by quatummchaical slcti ruls. Th citd atmic stat has {ma} litim th assciatd with it, thus th atmic lctr d-cits back t th grud stat by mittig a {ral} pht this sam rqucy. Th miracl all this is that {ral} phts assciatd with th EM ild ar actually itractig simultausly with all th atms i th disprsiv liar dilctric (withi th chrc lgth th pht c ) at ay giv istat i tim, thus th rsultat scattrd pht that is {ultimatly} mittd, actually must b summd vr th rsps th smbl may atms th miraculus rsult which is rward scattrig th phts assciatd with th macrscpic EM wav, but with a {rqucy-dpdt} phas shit, which is rlatd t th rsac lishap {ad th iit litim } th citd stat th atm! 0 Prssr Stv Errd, Dpartmt Physics, Uivrsity Illiis at Urbaa-Champaig, Illiis All Rights Rsrvd.
21 UIUC Physics 436 EM Filds & Surcs II Fall Smstr, 05 Lct. Nts 7.5 Pr. Stv Errd At a rsac,.g. wh k, a larg, trasitry/trasit {cmpl ad rqucy- p r, r r r is iducd i th atm, whr: dpdt} lctric dipl mmt ˆ b i sc r r r i m Nt hr w ca als mak a dirct ccti with quatum mchaics th lctric dipl mmt pratr p r, r ad psiti pratr r pratig.g. th grud stat wav ucti th atm/mlcul p r, r r r. r, i.. ad W ca.g. cmput th pctati valu th mdulus squard th lctric dipl r p r, r th atm/mlcul. Isrtig a cmplt st stats mmt r r r r mchaical prdictis r th {squars} th scillatr strgths it this prssi, w ca th btai th quatum sc : * r p r, r r pr, r r p r, r Th trasiti rat (= # atms/mlculs pr scd) rm th grud stat t th citd stat {via a lctric dipl trasiti, as allwd by quatum mchaical slcti ruls} is prprtial t r p r, r, whras th trasiti rat (= # atms/ mlculs th pr scd) rm th citd stat t th grud stat {via a lctric dipl trasiti, as * r p r r. allwd by quatum mchaical slcti ruls} is prprtial t, Nt that by th {micrscpic} maist tim-rvrsal ivariac th lctrmagtic itracti, th trasiti rats ar idtical, i.. = dampig cstat i ur smi-classical mdl! Nt urthr that th litims th citd stats atms ar {ivrsly} rlatd t th widths th pricipl: E t miimum, i.. th rsacs/widths th th citd stats by th Hisbrg ucrtaity, whr h ad h = Plack s cstat. I w st this rlati t its Et th: r: th Prssr Stv Errd, Dpartmt Physics, Uivrsity Illiis at Urbaa-Champaig, Illiis All Rights Rsrvd.
22 UIUC Physics 436 EM Filds & Surcs II Fall Smstr, 05 Lct. Nts 7.5 Pr. Stv Errd I stays wll away/ar rm {all} th rsac rqucis bud-stat atmic lctrs, th rsac actr bcms: i i.. ar rm a rsac: Thus, ar rm a rsac / all rsacs, rlativly littl absrpti/dissipati ccurs is prdmiatly ral} ad hc: {i.., such that b sc m Nw: 4 b sc sc 4 m Th: I ad Thus, ar rm a rsac/rsacs: b sc sc 4 m But: c c = vacuum wavlgth, hc:, thus: k w btai Cauchy s Frmula: sc sc b c 4 m B A Whr: A = Cicit Rracti ad: B = Cicit Disprsi. Cmparig th quatis, w s that: b sc A m sc sc ad: B c 4 Prssr Stv Errd, Dpartmt Physics, Uivrsity Illiis at Urbaa-Champaig, Illiis All Rights Rsrvd.
23 UIUC Physics 436 EM Filds & Surcs II Fall Smstr, 05 Lct. Nts 7.5 Pr. Stv Errd c Sic: i ad/r: k kik ad: k c Th: k c ad:, thus: Th phas spd: v c i k Th grup spd: v g c " " d dk dk d < Nt that at th turig pits ithr th { vs. } r: { k vs. } graphs, i.. at whr th slp dk d 0 v!!! {agular} rqucis ad/r g Nt urthr that i th {agular} rqucy rgi {th amalus disprsi dk d v dk d 0!!! rgi}, sic th slp 0 th th grup spd g {Hc th am amalus disprsi } This phm has b primtally vriid (s.g. C.G.B. Garrtt & D.E. McCumbr, Phys. Rv. A,, p. 305 (970). I th disprsiv mdium is t t thick, a Gaussia puls with a ctral rqucy ar a absrpti li (i.. ar a rsac, ) ad with puls width t prpagats with apprciabl absrpti, but (mr r lss) rtais its shap. R R Th pak th Gaussia puls prpagats at vg v wh th grup spd is gativ!!! Usul r puls r-shapig applicatis - ladig dg is lss attuatd tha trailig dg. R Prssr Stv Errd, Dpartmt Physics, Uivrsity Illiis at Urbaa-Champaig, Illiis All Rights Rsrvd. 3
24 UIUC Physics 436 EM Filds & Surcs II Fall Smstr, 05 Lct. Nts 7.5 Pr. Stv Errd Ca actually hav th pak a gratly attuatd puls mrg rm th absrbr br th pak th icidt puls trs th absrbr ( diiti gativ grup spd)!!! {i.. micrscpically, i th absrbr is t t thick, th sm phts ca mak it all th way thrugh th absrbr w/ itractig at all this prbability is ptially supprssd. Has applicatis/uss.g. i ptical mammgraphy/brast cacr scrig r wm...} S.g. J.D. Jacks s Elctrdyamics, 3 rd Editi, pags 35-6 r mr dtails! Fially, i w st 0, th w btai th static (i.. zr-rqucy) limit {all } ths quatitis. Nt that thy als {all} bcm purly ral i this limit: Static Plarizati: b (0) m sc whr b 0 3 m ad sic Et Static Elctricity Suscptibility: b sc (0) ad 0 m k m Static Id Rracti: 0 0 (0) K (0) But: K 0 0 Static Dilctric Cstat: K b sc m But: 0 0 b sc ad thus: K 0 0 ad: K m 0 0 Nt that th static dilctric cstat {as masurd at = 0 Hz/DC} is b sc m K 0.0 bcaus it ctais irmati abut all th {quatum mchaical} rsacs/citd stats 0 89 prst i th disprsiv, liar mdium, v it th -ray rgi at 0 Hz ad byd!!! Equivaltly, armd w with this kwldg th micrscpic bhavir a disprsiv, liar mdium, a lctric suscptibility 0 > 0 {r quivaltly, a dilctric cstat K 0 >} istatly tlls us that thr ar idd {quatum mchaical} rsacs/citd stats prst i th {cmpsit} atms/mlculs that mak up th macrscpic matrial th disprsiv, liar mdium!!! 4 Prssr Stv Errd, Dpartmt Physics, Uivrsity Illiis at Urbaa-Champaig, Illiis All Rights Rsrvd.
25 UIUC Physics 436 EM Filds & Surcs II Fall Smstr, 05 Lct. Nts 7.5 Pr. Stv Errd A wdrul macrscpic ampl disprsi i atur is th raibw. At th micrscpic lvl, th rqucy-dpdc th id rracti light () ariss as a csquc th rsat bhavir quatum mchaical bud stats lctrs i th atms th watr mlcul (HO) rspdig t EM light wavs{= visibl light phts} cmig rm ur su. I such cmpsit bhavir istd at th micrscpic lvl, thr wuld b raibws t y i th macrscpic vryday wrld! Eprimtal masurmts th absrpti cicit pur watr: Visibl Light Vilt Rd UV Rgi IR Rgi Absrpti cicit pur watr - HO is larg i UV ad IR rgis du t rsacs! Prssr Stv Errd, Dpartmt Physics, Uivrsity Illiis at Urbaa-Champaig, Illiis All Rights Rsrvd. 5
Bohr type models of the atom give a totally incorrect picture of the atom and are of only historical significance.
 VISUAL PHYSICS ONLIN BOHR MODL OF TH ATOM Bhr typ mdls f th atm giv a ttally icrrct pictur f th atm ad ar f ly histrical sigificac. Fig.. Bhr s platary mdl f th atm. Hwvr, th Bhr mdls wr a imprtat stp
VISUAL PHYSICS ONLIN BOHR MODL OF TH ATOM Bhr typ mdls f th atm giv a ttally icrrct pictur f th atm ad ar f ly histrical sigificac. Fig.. Bhr s platary mdl f th atm. Hwvr, th Bhr mdls wr a imprtat stp
Blackbody Radiation. All bodies at a temperature T emit and absorb thermal electromagnetic radiation. How is blackbody radiation absorbed and emitted?
 All bodis at a tmpratur T mit ad absorb thrmal lctromagtic radiatio Blackbody radiatio I thrmal quilibrium, th powr mittd quals th powr absorbd How is blackbody radiatio absorbd ad mittd? 1 2 A blackbody
All bodis at a tmpratur T mit ad absorb thrmal lctromagtic radiatio Blackbody radiatio I thrmal quilibrium, th powr mittd quals th powr absorbd How is blackbody radiatio absorbd ad mittd? 1 2 A blackbody
Continuous-Time Fourier Transform. Transform. Transform. Transform. Transform. Transform. Definition The CTFT of a continuoustime
 Ctiuus-Tim Furir Dfiiti Th CTFT f a ctiuustim sigal x a (t is giv by Xa ( jω xa( t jωt Oft rfrrd t as th Furir spctrum r simply th spctrum f th ctiuus-tim sigal dt Ctiuus-Tim Furir Dfiiti Th ivrs CTFT
Ctiuus-Tim Furir Dfiiti Th CTFT f a ctiuustim sigal x a (t is giv by Xa ( jω xa( t jωt Oft rfrrd t as th Furir spctrum r simply th spctrum f th ctiuus-tim sigal dt Ctiuus-Tim Furir Dfiiti Th ivrs CTFT
GUC (Dr. Hany Hammad) 4/20/2016
 GU (r. Hay Hamma) 4/0/06 Lctur # 0 Filtr sig y Th srti Lss Mth sig Stps Lw-pass prttyp sig. () Scalig a cvrsi. () mplmtati. Usig Stus. Usig High-Lw mpac Sctis. Thry f priic structurs. mag impacs a Trasfr
GU (r. Hay Hamma) 4/0/06 Lctur # 0 Filtr sig y Th srti Lss Mth sig Stps Lw-pass prttyp sig. () Scalig a cvrsi. () mplmtati. Usig Stus. Usig High-Lw mpac Sctis. Thry f priic structurs. mag impacs a Trasfr
3. Electromagnetic Propagation in Anisotropic Media 3.1 Maxwell s Equations and Dielectric Tensor _
 3. ltrmagti Prpagati i Aistrpi Mdia 3. Mawll s quatis ad Diltri Tsr _ b t a J + t a ρ _ Yh; 3- Th stitutiv rlatis a εb εb + m _ μ μ + j ε ad μ : Prmittivity ad prmability tsrs f rak. Thy dpd b ad i strg
3. ltrmagti Prpagati i Aistrpi Mdia 3. Mawll s quatis ad Diltri Tsr _ b t a J + t a ρ _ Yh; 3- Th stitutiv rlatis a εb εb + m _ μ μ + j ε ad μ : Prmittivity ad prmability tsrs f rak. Thy dpd b ad i strg
Topic 5:Discrete-Time Fourier Transform (DTFT)
 ELEC64: Sigals Ad Systms Tpic 5:Discrt-Tim Furir Trasfrm DTFT Aishy Amr Ccrdia Uivrsity Elctrical ad Cmputr Egirig Itrducti DT Furir Trasfrm Sufficit cditi fr th DTFT DT Furir Trasfrm f Pridic Sigals DTFT
ELEC64: Sigals Ad Systms Tpic 5:Discrt-Tim Furir Trasfrm DTFT Aishy Amr Ccrdia Uivrsity Elctrical ad Cmputr Egirig Itrducti DT Furir Trasfrm Sufficit cditi fr th DTFT DT Furir Trasfrm f Pridic Sigals DTFT
LECTURE 5 Guassian Wave Packet
 LECTURE 5 Guassian Wav Pact 1.5 Eampl f a guassian shap fr dscribing a wav pact Elctrn Pact ψ Guassian Assumptin Apprimatin ψ As w hav sn in QM th wav functin is ftn rprsntd as a Furir transfrm r sris.
LECTURE 5 Guassian Wav Pact 1.5 Eampl f a guassian shap fr dscribing a wav pact Elctrn Pact ψ Guassian Assumptin Apprimatin ψ As w hav sn in QM th wav functin is ftn rprsntd as a Furir transfrm r sris.
Modern Physics. Unit 5: Schrödinger s Equation and the Hydrogen Atom Lecture 5.6: Energy Eigenvalues of Schrödinger s Equation for the Hydrogen Atom
 Mdrn Physics Unit 5: Schrödingr s Equatin and th Hydrgn Atm Lctur 5.6: Enrgy Eignvalus f Schrödingr s Equatin fr th Hydrgn Atm Rn Rifnbrgr Prfssr f Physics Purdu Univrsity 1 Th allwd nrgis E cm frm th
Mdrn Physics Unit 5: Schrödingr s Equatin and th Hydrgn Atm Lctur 5.6: Enrgy Eignvalus f Schrödingr s Equatin fr th Hydrgn Atm Rn Rifnbrgr Prfssr f Physics Purdu Univrsity 1 Th allwd nrgis E cm frm th
8(4 m0) ( θ ) ( ) Solutions for HW 8. Chapter 25. Conceptual Questions
 Solutios for HW 8 Captr 5 Cocptual Qustios 5.. θ dcrass. As t crystal is coprssd, t spacig d btw t plas of atos dcrass. For t first ordr diffractio =. T Bragg coditio is = d so as d dcrass, ust icras for
Solutios for HW 8 Captr 5 Cocptual Qustios 5.. θ dcrass. As t crystal is coprssd, t spacig d btw t plas of atos dcrass. For t first ordr diffractio =. T Bragg coditio is = d so as d dcrass, ust icras for
UIUC Physics 436 EM Fields & Sources II Fall Semester, 2015 Lect. Notes 8 Prof. Steven Errede LECTURE NOTES 8
 UIU hysics 436 EM Filds & Surcs II Fall Smstr, 05 Lct. Nts 8 r. Stvn Errd LETURE NOTES 8 A Mr Sphisticatd Tratmnt EM Wav rpagatin in nducting Mdia In th prvius 436 Lctur Nts 7, w discussd th prpagatin
UIU hysics 436 EM Filds & Surcs II Fall Smstr, 05 Lct. Nts 8 r. Stvn Errd LETURE NOTES 8 A Mr Sphisticatd Tratmnt EM Wav rpagatin in nducting Mdia In th prvius 436 Lctur Nts 7, w discussd th prpagatin
Topic 5: Discrete-Time Fourier Transform (DTFT)
 ELEC36: Signals And Systms Tpic 5: Discrt-Tim Furir Transfrm (DTFT) Dr. Aishy Amr Cncrdia Univrsity Elctrical and Cmputr Enginring DT Furir Transfrm Ovrviw f Furir mthds DT Furir Transfrm f Pridic Signals
ELEC36: Signals And Systms Tpic 5: Discrt-Tim Furir Transfrm (DTFT) Dr. Aishy Amr Cncrdia Univrsity Elctrical and Cmputr Enginring DT Furir Transfrm Ovrviw f Furir mthds DT Furir Transfrm f Pridic Signals
1985 AP Calculus BC: Section I
 985 AP Calculus BC: Sctio I 9 Miuts No Calculator Nots: () I this amiatio, l dots th atural logarithm of (that is, logarithm to th bas ). () Ulss othrwis spcifid, th domai of a fuctio f is assumd to b
985 AP Calculus BC: Sctio I 9 Miuts No Calculator Nots: () I this amiatio, l dots th atural logarithm of (that is, logarithm to th bas ). () Ulss othrwis spcifid, th domai of a fuctio f is assumd to b
They must have different numbers of electrons orbiting their nuclei. They must have the same number of neutrons in their nuclei.
 37 1 How may utros ar i a uclus of th uclid l? 20 37 54 2 crtai lmt has svral isotops. Which statmt about ths isotops is corrct? Thy must hav diffrt umbrs of lctros orbitig thir ucli. Thy must hav th sam
37 1 How may utros ar i a uclus of th uclid l? 20 37 54 2 crtai lmt has svral isotops. Which statmt about ths isotops is corrct? Thy must hav diffrt umbrs of lctros orbitig thir ucli. Thy must hav th sam
Some Families of Higher Order Three-Step Iterative Techniques. where is a real number and y (5)
 Lif Scic Jural 03;0s http://www.lifscicsit.cm Sm Familis f Highr Orr Thr-Stp Itrativ Tchiqus Nair Ahma Mir Sahr Akmal Kha Naila Rafiq Nusrut Yasmi. Dpartmt f Basic Scics Riphah Itratial Uivrsit Islamaba
Lif Scic Jural 03;0s http://www.lifscicsit.cm Sm Familis f Highr Orr Thr-Stp Itrativ Tchiqus Nair Ahma Mir Sahr Akmal Kha Naila Rafiq Nusrut Yasmi. Dpartmt f Basic Scics Riphah Itratial Uivrsit Islamaba
DTFT Properties. Example - Determine the DTFT Y ( e ) of n. Let. We can therefore write. From Table 3.1, the DTFT of x[n] is given by 1
![DTFT Properties. Example - Determine the DTFT Y ( e ) of n. Let. We can therefore write. From Table 3.1, the DTFT of x[n] is given by 1 DTFT Properties. Example - Determine the DTFT Y ( e ) of n. Let. We can therefore write. From Table 3.1, the DTFT of x[n] is given by 1](/thumbs/79/79094742.jpg) DTFT Proprtis Exampl - Dtrmi th DTFT Y of y α µ, α < Lt x α µ, α < W ca thrfor writ y x x From Tabl 3., th DTFT of x is giv by ω X ω α ω Copyright, S. K. Mitra Copyright, S. K. Mitra DTFT Proprtis DTFT
DTFT Proprtis Exampl - Dtrmi th DTFT Y of y α µ, α < Lt x α µ, α < W ca thrfor writ y x x From Tabl 3., th DTFT of x is giv by ω X ω α ω Copyright, S. K. Mitra Copyright, S. K. Mitra DTFT Proprtis DTFT
N J of oscillators in the three lowest quantum
 . a) Calculat th fractinal numbr f scillatrs in th thr lwst quantum stats (j,,,) fr fr and Sl: ( ) ( ) ( ) ( ) ( ).6.98. fr usth sam apprach fr fr j fr frm q. b) .) a) Fr a systm f lcalizd distinguishabl
. a) Calculat th fractinal numbr f scillatrs in th thr lwst quantum stats (j,,,) fr fr and Sl: ( ) ( ) ( ) ( ) ( ).6.98. fr usth sam apprach fr fr j fr frm q. b) .) a) Fr a systm f lcalizd distinguishabl
Quantum Mechanics for Scientists and Engineers. David Miller
 Quatum Mechaics fr Scietists ad Egieers David Miller Time-depedet perturbati thery Time-depedet perturbati thery Time-depedet perturbati basics Time-depedet perturbati thery Fr time-depedet prblems csider
Quatum Mechaics fr Scietists ad Egieers David Miller Time-depedet perturbati thery Time-depedet perturbati thery Time-depedet perturbati basics Time-depedet perturbati thery Fr time-depedet prblems csider
LECTURE 13 Filling the bands. Occupancy of Available Energy Levels
 LUR 3 illig th bads Occupacy o Availabl rgy Lvls W hav dtrmid ad a dsity o stats. W also d a way o dtrmiig i a stat is illd or ot at a giv tmpratur. h distributio o th rgis o a larg umbr o particls ad
LUR 3 illig th bads Occupacy o Availabl rgy Lvls W hav dtrmid ad a dsity o stats. W also d a way o dtrmiig i a stat is illd or ot at a giv tmpratur. h distributio o th rgis o a larg umbr o particls ad
Blackbody Radiation. All bodies at a temperature T emit and absorb thermal electromagnetic radiation. How is blackbody radiation absorbed and emitted?
 All bodis at a tmpratur T mit ad absorb thrmal lctromagtic radiatio Blackbody radiatio I thrmal quilibrium, th powr mittd quals th powr absorbd How is blackbody radiatio absorbd ad mittd? 1 2 A blackbody
All bodis at a tmpratur T mit ad absorb thrmal lctromagtic radiatio Blackbody radiatio I thrmal quilibrium, th powr mittd quals th powr absorbd How is blackbody radiatio absorbd ad mittd? 1 2 A blackbody
Worksheet: Taylor Series, Lagrange Error Bound ilearnmath.net
 Taylor s Thorm & Lagrag Error Bouds Actual Error This is th ral amout o rror, ot th rror boud (worst cas scario). It is th dirc btw th actual () ad th polyomial. Stps:. Plug -valu ito () to gt a valu.
Taylor s Thorm & Lagrag Error Bouds Actual Error This is th ral amout o rror, ot th rror boud (worst cas scario). It is th dirc btw th actual () ad th polyomial. Stps:. Plug -valu ito () to gt a valu.
A Propagating Wave Packet Group Velocity Dispersion
 Lctur 8 Phys 375 A Propagating Wav Packt Group Vlocity Disprsion Ovrviw and Motivation: In th last lctur w lookd at a localizd solution t) to th 1D fr-particl Schrödingr quation (SE) that corrsponds to
Lctur 8 Phys 375 A Propagating Wav Packt Group Vlocity Disprsion Ovrviw and Motivation: In th last lctur w lookd at a localizd solution t) to th 1D fr-particl Schrödingr quation (SE) that corrsponds to
Fourier Transforms and the Wave Equation. Key Mathematics: More Fourier transform theory, especially as applied to solving the wave equation.
 Lur 7 Fourir Transforms and th Wav Euation Ovrviw and Motivation: W first discuss a fw faturs of th Fourir transform (FT), and thn w solv th initial-valu problm for th wav uation using th Fourir transform
Lur 7 Fourir Transforms and th Wav Euation Ovrviw and Motivation: W first discuss a fw faturs of th Fourir transform (FT), and thn w solv th initial-valu problm for th wav uation using th Fourir transform
Discrete Fourier Transform (DFT)
 Discrt Fourir Trasorm DFT Major: All Egirig Majors Authors: Duc guy http://umricalmthods.g.us.du umrical Mthods or STEM udrgraduats 8/3/29 http://umricalmthods.g.us.du Discrt Fourir Trasorm Rcalld th xpotial
Discrt Fourir Trasorm DFT Major: All Egirig Majors Authors: Duc guy http://umricalmthods.g.us.du umrical Mthods or STEM udrgraduats 8/3/29 http://umricalmthods.g.us.du Discrt Fourir Trasorm Rcalld th xpotial
Another Explanation of the Cosmological Redshift. April 6, 2010.
 Anthr Explanatin f th Csmlgical Rdshift April 6, 010. Jsé Francisc García Juliá C/ Dr. Marc Mrncian, 65, 5. 4605 Valncia (Spain) E-mail: js.garcia@dival.s h lss f nrgy f th phtn with th tim by missin f
Anthr Explanatin f th Csmlgical Rdshift April 6, 010. Jsé Francisc García Juliá C/ Dr. Marc Mrncian, 65, 5. 4605 Valncia (Spain) E-mail: js.garcia@dival.s h lss f nrgy f th phtn with th tim by missin f
MONTGOMERY COLLEGE Department of Mathematics Rockville Campus. 6x dx a. b. cos 2x dx ( ) 7. arctan x dx e. cos 2x dx. 2 cos3x dx
 MONTGOMERY COLLEGE Dpartmt of Mathmatics Rockvill Campus MATH 8 - REVIEW PROBLEMS. Stat whthr ach of th followig ca b itgratd by partial fractios (PF), itgratio by parts (PI), u-substitutio (U), or o of
MONTGOMERY COLLEGE Dpartmt of Mathmatics Rockvill Campus MATH 8 - REVIEW PROBLEMS. Stat whthr ach of th followig ca b itgratd by partial fractios (PF), itgratio by parts (PI), u-substitutio (U), or o of
PURE MATHEMATICS A-LEVEL PAPER 1
 -AL P MATH PAPER HONG KONG EXAMINATIONS AUTHORITY HONG KONG ADVANCED LEVEL EXAMINATION PURE MATHEMATICS A-LEVEL PAPER 8 am am ( hours) This papr must b aswrd i Eglish This papr cosists of Sctio A ad Sctio
-AL P MATH PAPER HONG KONG EXAMINATIONS AUTHORITY HONG KONG ADVANCED LEVEL EXAMINATION PURE MATHEMATICS A-LEVEL PAPER 8 am am ( hours) This papr must b aswrd i Eglish This papr cosists of Sctio A ad Sctio
H2 Mathematics Arithmetic & Geometric Series ( )
 H Mathmatics Arithmtic & Gomtric Sris (08 09) Basic Mastry Qustios Arithmtic Progrssio ad Sris. Th rth trm of a squc is 4r 7. (i) Stat th first four trms ad th 0th trm. (ii) Show that th squc is a arithmtic
H Mathmatics Arithmtic & Gomtric Sris (08 09) Basic Mastry Qustios Arithmtic Progrssio ad Sris. Th rth trm of a squc is 4r 7. (i) Stat th first four trms ad th 0th trm. (ii) Show that th squc is a arithmtic
. This is made to keep the kinetic energy at outlet a minimum.
 Runnr Francis Turbin Th shap th blads a Francis runnr is cmplx. Th xact shap dpnds n its spciic spd. It is bvius rm th quatin spciic spd (Eq.5.8) that highr spciic spd mans lwr had. This rquirs that th
Runnr Francis Turbin Th shap th blads a Francis runnr is cmplx. Th xact shap dpnds n its spciic spd. It is bvius rm th quatin spciic spd (Eq.5.8) that highr spciic spd mans lwr had. This rquirs that th
0WAVE PROPAGATION IN MATERIAL SPACE
 0WAVE PROPAGATION IN MATERIAL SPACE All forms of EM nrgy shar thr fundamntal charactristics: 1) thy all tral at high locity 2) In traling, thy assum th proprtis of was 3) Thy radiat outward from a sourc
0WAVE PROPAGATION IN MATERIAL SPACE All forms of EM nrgy shar thr fundamntal charactristics: 1) thy all tral at high locity 2) In traling, thy assum th proprtis of was 3) Thy radiat outward from a sourc
Lecture Outline. Skin Depth Power Flow 8/7/2018. EE 4347 Applied Electromagnetics. Topic 3e
 8/7/018 Cours Instructor Dr. Raymond C. Rumpf Offic: A 337 Phon: (915) 747 6958 E Mail: rcrumpf@utp.du EE 4347 Applid Elctromagntics Topic 3 Skin Dpth & Powr Flow Skin Dpth Ths & Powr nots Flow may contain
8/7/018 Cours Instructor Dr. Raymond C. Rumpf Offic: A 337 Phon: (915) 747 6958 E Mail: rcrumpf@utp.du EE 4347 Applid Elctromagntics Topic 3 Skin Dpth & Powr Flow Skin Dpth Ths & Powr nots Flow may contain
O QP P. Limit Theorems. p and to see if it will be less than a pre-assigned number,. p n
 Limit Trms W ft av t d fr apprximatis w gts vry larg. Fr xampl, smtims fidig t prbability distributis f radm variabls lad t utractabl matmatical prblms. W ca s tat t distributi fr crtai fuctis f a radm
Limit Trms W ft av t d fr apprximatis w gts vry larg. Fr xampl, smtims fidig t prbability distributis f radm variabls lad t utractabl matmatical prblms. W ca s tat t distributi fr crtai fuctis f a radm
Chapter Taylor Theorem Revisited
 Captr 0.07 Taylor Torm Rvisitd Atr radig tis captr, you sould b abl to. udrstad t basics o Taylor s torm,. writ trascdtal ad trigoomtric uctios as Taylor s polyomial,. us Taylor s torm to id t valus o
Captr 0.07 Taylor Torm Rvisitd Atr radig tis captr, you sould b abl to. udrstad t basics o Taylor s torm,. writ trascdtal ad trigoomtric uctios as Taylor s polyomial,. us Taylor s torm to id t valus o
z 1+ 3 z = Π n =1 z f() z = n e - z = ( 1-z) e z e n z z 1- n = ( 1-z/2) 1+ 2n z e 2n e n -1 ( 1-z )/2 e 2n-1 1-2n -1 1 () z
 Sris Expasio of Rciprocal of Gamma Fuctio. Fuctios with Itgrs as Roots Fuctio f with gativ itgrs as roots ca b dscribd as follows. f() Howvr, this ifiit product divrgs. That is, such a fuctio caot xist
Sris Expasio of Rciprocal of Gamma Fuctio. Fuctios with Itgrs as Roots Fuctio f with gativ itgrs as roots ca b dscribd as follows. f() Howvr, this ifiit product divrgs. That is, such a fuctio caot xist
Lectur 22. RF and Microwave Circuit Design Γ-Plane and Smith Chart Analysis. ECE 303 Fall 2005 Farhan Rana Cornell University
 ctur RF ad Micrwav Circuit Dig -Pla ad Smith Chart Aalyi I thi lctur yu will lar: -pla ad Smith Chart Stub tuig Quartr-Wav trafrmr ECE 33 Fall 5 Farha Raa Crll Uivrity V V Impdac Trafrmati i Tramii i ω
ctur RF ad Micrwav Circuit Dig -Pla ad Smith Chart Aalyi I thi lctur yu will lar: -pla ad Smith Chart Stub tuig Quartr-Wav trafrmr ECE 33 Fall 5 Farha Raa Crll Uivrity V V Impdac Trafrmati i Tramii i ω
(Reference: sections in Silberberg 5 th ed.)
 ALE. Atomic Structur Nam HEM K. Marr Tam No. Sctio What is a atom? What is th structur of a atom? Th Modl th structur of a atom (Rfrc: sctios.4 -. i Silbrbrg 5 th d.) Th subatomic articls that chmists
ALE. Atomic Structur Nam HEM K. Marr Tam No. Sctio What is a atom? What is th structur of a atom? Th Modl th structur of a atom (Rfrc: sctios.4 -. i Silbrbrg 5 th d.) Th subatomic articls that chmists
2. Background Material
 S. Blair Sptmbr 3, 003 4. Background Matrial Th rst of this cours dals with th gnration, modulation, propagation, and ction of optical radiation. As such, bic background in lctromagntics and optics nds
S. Blair Sptmbr 3, 003 4. Background Matrial Th rst of this cours dals with th gnration, modulation, propagation, and ction of optical radiation. As such, bic background in lctromagntics and optics nds
Chapter 2 Linear Waveshaping: High-pass Circuits
 Puls and Digital Circuits nkata Ra K., Rama Sudha K. and Manmadha Ra G. Chaptr 2 Linar Wavshaping: High-pass Circuits. A ramp shwn in Fig.2p. is applid t a high-pass circuit. Draw t scal th utput wavfrm
Puls and Digital Circuits nkata Ra K., Rama Sudha K. and Manmadha Ra G. Chaptr 2 Linar Wavshaping: High-pass Circuits. A ramp shwn in Fig.2p. is applid t a high-pass circuit. Draw t scal th utput wavfrm
UIUC Physics 436 EM Fields & Sources II Fall Semester, 2015 Lect. Notes 8.5 Prof. Steven Errede LECTURE NOTES 8.5
 UIUC Physics 436 EM Filds & Surcs II Fall Smstr, 05 Lct. Nts 8.5 Prf. Stvn Errd LECTURE NOTES 8.5 Rflctin and Rfractin f EM Wavs at th Bundary f a Disprsiv/Absrbing/Cnducting Mdium Cnsidr a situatin whr
UIUC Physics 436 EM Filds & Surcs II Fall Smstr, 05 Lct. Nts 8.5 Prf. Stvn Errd LECTURE NOTES 8.5 Rflctin and Rfractin f EM Wavs at th Bundary f a Disprsiv/Absrbing/Cnducting Mdium Cnsidr a situatin whr
07 - SEQUENCES AND SERIES Page 1 ( Answers at he end of all questions ) b, z = n
 07 - SEQUENCES AND SERIES Pag ( Aswrs at h d of all qustios ) ( ) If = a, y = b, z = c, whr a, b, c ar i A.P. ad = 0 = 0 = 0 l a l
07 - SEQUENCES AND SERIES Pag ( Aswrs at h d of all qustios ) ( ) If = a, y = b, z = c, whr a, b, c ar i A.P. ad = 0 = 0 = 0 l a l
Outline. Ionizing Radiation. Introduction. Ionizing radiation
 Outli Ioizig Radiatio Chaptr F.A. Attix, Itroductio to Radiological Physics ad Radiatio Dosimtry Radiological physics ad radiatio dosimtry Typs ad sourcs of ioizig radiatio Dscriptio of ioizig radiatio
Outli Ioizig Radiatio Chaptr F.A. Attix, Itroductio to Radiological Physics ad Radiatio Dosimtry Radiological physics ad radiatio dosimtry Typs ad sourcs of ioizig radiatio Dscriptio of ioizig radiatio
Time : 1 hr. Test Paper 08 Date 04/01/15 Batch - R Marks : 120
 Tim : hr. Tst Papr 8 D 4//5 Bch - R Marks : SINGLE CORRECT CHOICE TYPE [4, ]. If th compl umbr z sisfis th coditio z 3, th th last valu of z is qual to : z (A) 5/3 (B) 8/3 (C) /3 (D) o of ths 5 4. Th itgral,
Tim : hr. Tst Papr 8 D 4//5 Bch - R Marks : SINGLE CORRECT CHOICE TYPE [4, ]. If th compl umbr z sisfis th coditio z 3, th th last valu of z is qual to : z (A) 5/3 (B) 8/3 (C) /3 (D) o of ths 5 4. Th itgral,
Effect of sampling on frequency domain analysis
 LIGO-T666--R Ec sampling n rquncy dmain analysis David P. Nrwd W rviw h wll-knwn cs digial sampling n h rquncy dmain analysis an analg signal, wih mphasis n h cs upn ur masurmns. This discussin llws h
LIGO-T666--R Ec sampling n rquncy dmain analysis David P. Nrwd W rviw h wll-knwn cs digial sampling n h rquncy dmain analysis an analg signal, wih mphasis n h cs upn ur masurmns. This discussin llws h
Introduction to the quantum theory of matter and Schrödinger s equation
 Introduction to th quantum thory of mattr and Schrödingr s quation Th quantum thory of mattr assums that mattr has two naturs: a particl natur and a wa natur. Th particl natur is dscribd by classical physics
Introduction to th quantum thory of mattr and Schrödingr s quation Th quantum thory of mattr assums that mattr has two naturs: a particl natur and a wa natur. Th particl natur is dscribd by classical physics
Session : Plasmas in Equilibrium
 Sssio : Plasmas i Equilibrium Ioizatio ad Coductio i a High-prssur Plasma A ormal gas at T < 3000 K is a good lctrical isulator, bcaus thr ar almost o fr lctros i it. For prssurs > 0.1 atm, collisio amog
Sssio : Plasmas i Equilibrium Ioizatio ad Coductio i a High-prssur Plasma A ormal gas at T < 3000 K is a good lctrical isulator, bcaus thr ar almost o fr lctros i it. For prssurs > 0.1 atm, collisio amog
Lecture 27: The 180º Hybrid.
 Whits, EE 48/58 Lctur 7 Pag f 0 Lctur 7: Th 80º Hybrid. Th scnd rciprcal dirctinal cuplr w will discuss is th 80º hybrid. As th nam implis, th utputs frm such a dvic can b 80º ut f phas. Thr ar tw primary
Whits, EE 48/58 Lctur 7 Pag f 0 Lctur 7: Th 80º Hybrid. Th scnd rciprcal dirctinal cuplr w will discuss is th 80º hybrid. As th nam implis, th utputs frm such a dvic can b 80º ut f phas. Thr ar tw primary
Lecture 26: Quadrature (90º) Hybrid.
 Whits, EE 48/58 Lctur 26 Pag f Lctur 26: Quadratur (9º) Hybrid. Back in Lctur 23, w bgan ur discussin f dividrs and cuplrs by cnsidring imprtant gnral prprtis f thrand fur-prt ntwrks. This was fllwd by
Whits, EE 48/58 Lctur 26 Pag f Lctur 26: Quadratur (9º) Hybrid. Back in Lctur 23, w bgan ur discussin f dividrs and cuplrs by cnsidring imprtant gnral prprtis f thrand fur-prt ntwrks. This was fllwd by
coulombs or esu charge. It s mass is about 1/1837 times the mass of hydrogen atom. Thus mass of electron is
 1 ATOMIC STRUCTURE Fudamtal Particls: Mai Fudamtal Particl : (a) Elctro: It is a fudamtal particl of a atom which carris a uit gativ charg. It was discovrd by J.J. Thomso (1897) from th studis carrid out
1 ATOMIC STRUCTURE Fudamtal Particls: Mai Fudamtal Particl : (a) Elctro: It is a fudamtal particl of a atom which carris a uit gativ charg. It was discovrd by J.J. Thomso (1897) from th studis carrid out
Probability & Statistics,
 Probability & Statistics, BITS Pilai K K Birla Goa Campus Dr. Jajati Kshari Sahoo Dpartmt of Mathmatics BITS Pilai, K K Birla Goa Campus Poisso Distributio Poisso Distributio: A radom variabl X is said
Probability & Statistics, BITS Pilai K K Birla Goa Campus Dr. Jajati Kshari Sahoo Dpartmt of Mathmatics BITS Pilai, K K Birla Goa Campus Poisso Distributio Poisso Distributio: A radom variabl X is said
Lecture 37 (Schrödinger Equation) Physics Spring 2018 Douglas Fields
 Lctur 37 (Schrödingr Equation) Physics 6-01 Spring 018 Douglas Filds Rducd Mass OK, so th Bohr modl of th atom givs nrgy lvls: E n 1 k m n 4 But, this has on problm it was dvlopd assuming th acclration
Lctur 37 (Schrödingr Equation) Physics 6-01 Spring 018 Douglas Filds Rducd Mass OK, so th Bohr modl of th atom givs nrgy lvls: E n 1 k m n 4 But, this has on problm it was dvlopd assuming th acclration
SIMPLE METHOD FOR THE SOLUTION OF INCOMPRESSIBLE FLOWS ON NON-STAGGERED GRIDS
 SIML MTHOD FOR TH SOLUTION OF INCOMRSSIBL FLOWS ON NON-STAGGRD GRIDS I. Szai - astr Mditrraa Uivrsity, Mchaical girig Dpartmt, Mrsi 10 -Trky 1. Itrdcti Thr ar sally t kids f grid arragmts sd t slv th flid
SIML MTHOD FOR TH SOLUTION OF INCOMRSSIBL FLOWS ON NON-STAGGRD GRIDS I. Szai - astr Mditrraa Uivrsity, Mchaical girig Dpartmt, Mrsi 10 -Trky 1. Itrdcti Thr ar sally t kids f grid arragmts sd t slv th flid
Brief Introduction to Statistical Mechanics
 Brif Introduction to Statistical Mchanics. Purpos: Ths nots ar intndd to provid a vry quick introduction to Statistical Mchanics. Th fild is of cours far mor vast than could b containd in ths fw pags.
Brif Introduction to Statistical Mchanics. Purpos: Ths nots ar intndd to provid a vry quick introduction to Statistical Mchanics. Th fild is of cours far mor vast than could b containd in ths fw pags.
Review Exercises. 1. Evaluate using the definition of the definite integral as a Riemann Sum. Does the answer represent an area? 2
 MATHEMATIS --RE Itgral alculus Marti Huard Witr 9 Rviw Erciss. Evaluat usig th dfiitio of th dfiit itgral as a Rima Sum. Dos th aswr rprst a ara? a ( d b ( d c ( ( d d ( d. Fid f ( usig th Fudamtal Thorm
MATHEMATIS --RE Itgral alculus Marti Huard Witr 9 Rviw Erciss. Evaluat usig th dfiitio of th dfiit itgral as a Rima Sum. Dos th aswr rprst a ara? a ( d b ( d c ( ( d d ( d. Fid f ( usig th Fudamtal Thorm
Scattering Parameters. Scattering Parameters
 Motivatio cattrig Paramtrs Difficult to implmt op ad short circuit coditios i high frqucis masurmts du to parasitic s ad Cs Pottial stability problms for activ dvics wh masurd i oopratig coditios Difficult
Motivatio cattrig Paramtrs Difficult to implmt op ad short circuit coditios i high frqucis masurmts du to parasitic s ad Cs Pottial stability problms for activ dvics wh masurd i oopratig coditios Difficult
Chapter Five. More Dimensions. is simply the set of all ordered n-tuples of real numbers x = ( x 1
 Chatr Fiv Mor Dimsios 51 Th Sac R W ar ow rard to mov o to sacs of dimsio gratr tha thr Ths sacs ar a straightforward gralizatio of our Euclida sac of thr dimsios Lt b a ositiv itgr Th -dimsioal Euclida
Chatr Fiv Mor Dimsios 51 Th Sac R W ar ow rard to mov o to sacs of dimsio gratr tha thr Ths sacs ar a straightforward gralizatio of our Euclida sac of thr dimsios Lt b a ositiv itgr Th -dimsioal Euclida
Solutions. Definitions pertaining to solutions
 Slutis Defiitis pertaiig t slutis Slute is the substace that is disslved. It is usually preset i the smaller amut. Slvet is the substace that des the disslvig. It is usually preset i the larger amut. Slubility
Slutis Defiitis pertaiig t slutis Slute is the substace that is disslved. It is usually preset i the smaller amut. Slvet is the substace that des the disslvig. It is usually preset i the larger amut. Slubility
Ideal crystal : Regulary ordered point masses connected via harmonic springs
 Statistical thrmodyamics of crystals Mooatomic crystal Idal crystal : Rgulary ordrd poit masss coctd via harmoic sprigs Itratomic itractios Rprstd by th lattic forc-costat quivalt atom positios miima o
Statistical thrmodyamics of crystals Mooatomic crystal Idal crystal : Rgulary ordrd poit masss coctd via harmoic sprigs Itratomic itractios Rprstd by th lattic forc-costat quivalt atom positios miima o
Lecture contents. Density of states Distribution function Statistic of carriers. Intrinsic Extrinsic with no compensation Compensation
 Ltur otts Dsity of stats Distributio futio Statisti of arrirs Itrisi trisi with o ompsatio ompsatio S 68 Ltur #7 Dsity of stats Problm: alulat umbr of stats pr uit rgy pr uit volum V() Larg 3D bo (L is
Ltur otts Dsity of stats Distributio futio Statisti of arrirs Itrisi trisi with o ompsatio ompsatio S 68 Ltur #7 Dsity of stats Problm: alulat umbr of stats pr uit rgy pr uit volum V() Larg 3D bo (L is
INTEGRATION BY PARTS
 Mathmatics Rvision Guids Intgration by Parts Pag of 7 MK HOME TUITION Mathmatics Rvision Guids Lvl: AS / A Lvl AQA : C Edcl: C OCR: C OCR MEI: C INTEGRATION BY PARTS Vrsion : Dat: --5 Eampls - 6 ar copyrightd
Mathmatics Rvision Guids Intgration by Parts Pag of 7 MK HOME TUITION Mathmatics Rvision Guids Lvl: AS / A Lvl AQA : C Edcl: C OCR: C OCR MEI: C INTEGRATION BY PARTS Vrsion : Dat: --5 Eampls - 6 ar copyrightd
5.1 The Nuclear Atom
 Sav My Exams! Th Hom of Rvisio For mor awsom GSE ad lvl rsourcs, visit us at www.savmyxams.co.uk/ 5.1 Th Nuclar tom Qustio Papr Lvl IGSE Subjct Physics (0625) Exam oard Topic Sub Topic ooklt ambridg Itratioal
Sav My Exams! Th Hom of Rvisio For mor awsom GSE ad lvl rsourcs, visit us at www.savmyxams.co.uk/ 5.1 Th Nuclar tom Qustio Papr Lvl IGSE Subjct Physics (0625) Exam oard Topic Sub Topic ooklt ambridg Itratioal
Time Dependent Solutions: Propagators and Representations
 Tim Dpdt Solutios: Propagators ad Rprstatios Michal Fowlr, UVa 1/3/6 Itroductio W v spt most of th cours so far coctratig o th igstats of th amiltoia, stats whos tim dpdc is mrly a chagig phas W did mtio
Tim Dpdt Solutios: Propagators ad Rprstatios Michal Fowlr, UVa 1/3/6 Itroductio W v spt most of th cours so far coctratig o th igstats of th amiltoia, stats whos tim dpdc is mrly a chagig phas W did mtio
Washington State University
 he 3 Ktics ad Ractor Dsig Sprg, 00 Washgto Stat Uivrsity Dpartmt of hmical Egrg Richard L. Zollars Exam # You will hav o hour (60 muts) to complt this xam which cosists of four (4) problms. You may us
he 3 Ktics ad Ractor Dsig Sprg, 00 Washgto Stat Uivrsity Dpartmt of hmical Egrg Richard L. Zollars Exam # You will hav o hour (60 muts) to complt this xam which cosists of four (4) problms. You may us
How many neutrino species?
 ow may utrio scis? Two mthods for dtrmii it lium abudac i uivrs At a collidr umbr of utrio scis Exasio of th uivrs is ovrd by th Fridma quatio R R 8G tot Kc R Whr: :ubblcostat G :Gravitatioal costat 6.
ow may utrio scis? Two mthods for dtrmii it lium abudac i uivrs At a collidr umbr of utrio scis Exasio of th uivrs is ovrd by th Fridma quatio R R 8G tot Kc R Whr: :ubblcostat G :Gravitatioal costat 6.
Chapter 2 Infinite Series Page 1 of 11. Chapter 2 : Infinite Series
 Chatr Ifiit Sris Pag of Sctio F Itgral Tst Chatr : Ifiit Sris By th d of this sctio you will b abl to valuat imror itgrals tst a sris for covrgc by alyig th itgral tst aly th itgral tst to rov th -sris
Chatr Ifiit Sris Pag of Sctio F Itgral Tst Chatr : Ifiit Sris By th d of this sctio you will b abl to valuat imror itgrals tst a sris for covrgc by alyig th itgral tst aly th itgral tst to rov th -sris
Solution to 1223 The Evil Warden.
 Solutio to 1 Th Evil Ward. This is o of thos vry rar PoWs (I caot thik of aothr cas) that o o solvd. About 10 of you submittd th basic approach, which givs a probability of 47%. I was shockd wh I foud
Solutio to 1 Th Evil Ward. This is o of thos vry rar PoWs (I caot thik of aothr cas) that o o solvd. About 10 of you submittd th basic approach, which givs a probability of 47%. I was shockd wh I foud
Radiation Physics Laboratory - Complementary Exercise Set MeBiom 2016/2017
 Th following qustions ar to b answrd individually. Usful information such as tabls with dtctor charactristics and graphs with th proprtis of matrials ar availabl in th cours wb sit: http://www.lip.pt/~patricia/fisicadaradiacao.
Th following qustions ar to b answrd individually. Usful information such as tabls with dtctor charactristics and graphs with th proprtis of matrials ar availabl in th cours wb sit: http://www.lip.pt/~patricia/fisicadaradiacao.
ALOHA Product no.: 03007
 EN s l d m S vrsatil, s yu! Yur styl is vry prsal as is yur MySpdy. Attach f ths trdy spdmtrs t yur bik ad shw vry wh yu rally ar. Satch up yur favrit dsig ad xprss yur idividuality mr tha vr wh ut ad
EN s l d m S vrsatil, s yu! Yur styl is vry prsal as is yur MySpdy. Attach f ths trdy spdmtrs t yur bik ad shw vry wh yu rally ar. Satch up yur favrit dsig ad xprss yur idividuality mr tha vr wh ut ad
Narayana IIT Academy
 INDIA Sc: LT-IIT-SPARK Dat: 9--8 6_P Max.Mars: 86 KEY SHEET PHYSIS A 5 D 6 7 A,B 8 B,D 9 A,B A,,D A,B, A,B B, A,B 5 A 6 D 7 8 A HEMISTRY 9 A B D B B 5 A,B,,D 6 A,,D 7 B,,D 8 A,B,,D 9 A,B, A,B, A,B,,D A,B,
INDIA Sc: LT-IIT-SPARK Dat: 9--8 6_P Max.Mars: 86 KEY SHEET PHYSIS A 5 D 6 7 A,B 8 B,D 9 A,B A,,D A,B, A,B B, A,B 5 A 6 D 7 8 A HEMISTRY 9 A B D B B 5 A,B,,D 6 A,,D 7 B,,D 8 A,B,,D 9 A,B, A,B, A,B,,D A,B,
Physics 2D Lecture Slides Lecture 14: Feb 3 rd 2004
 Bria Wcht, th TA is back! Pl. giv all rgrad rqusts to him Quiz 4 is This Friday Physics D Lctur Slids Lctur 14: Fb 3 rd 004 Vivk Sharma UCSD Physics Whr ar th lctros isid th atom? Early Thought: Plum puddig
Bria Wcht, th TA is back! Pl. giv all rgrad rqusts to him Quiz 4 is This Friday Physics D Lctur Slids Lctur 14: Fb 3 rd 004 Vivk Sharma UCSD Physics Whr ar th lctros isid th atom? Early Thought: Plum puddig
Chapter 33 Gauss s Law
 Chaptr 33 Gauss s Law 33 Gauss s Law Whn askd t find th lctric flux thrugh a clsd surfac du t a spcifid nn-trivial charg distributin, flks all t ftn try th immnsly cmplicatd apprach f finding th lctric
Chaptr 33 Gauss s Law 33 Gauss s Law Whn askd t find th lctric flux thrugh a clsd surfac du t a spcifid nn-trivial charg distributin, flks all t ftn try th immnsly cmplicatd apprach f finding th lctric
EE 119 Homework 6 Solution
 EE 9 Hmwrk 6 Slutin Prr: J Bkr TA: Xi Lu Slutin: (a) Th angular magniicatin a tlcp i m / th cal lngth th bjctiv ln i m 4 45 80cm (b) Th clar aprtur th xit pupil i 35 mm Th ditanc btwn th bjctiv ln and
EE 9 Hmwrk 6 Slutin Prr: J Bkr TA: Xi Lu Slutin: (a) Th angular magniicatin a tlcp i m / th cal lngth th bjctiv ln i m 4 45 80cm (b) Th clar aprtur th xit pupil i 35 mm Th ditanc btwn th bjctiv ln and
Lectures 9 IIR Systems: First Order System
 EE3054 Sigals ad Systms Lcturs 9 IIR Systms: First Ordr Systm Yao Wag Polytchic Uivrsity Som slids icludd ar xtractd from lctur prstatios prpard by McCllla ad Schafr Lics Ifo for SPFirst Slids This work
EE3054 Sigals ad Systms Lcturs 9 IIR Systms: First Ordr Systm Yao Wag Polytchic Uivrsity Som slids icludd ar xtractd from lctur prstatios prpard by McCllla ad Schafr Lics Ifo for SPFirst Slids This work
Technical Support Document Bias of the Minimum Statistic
 Tchical Support Documt Bias o th Miimum Stattic Itroductio Th papr pla how to driv th bias o th miimum stattic i a radom sampl o siz rom dtributios with a shit paramtr (also kow as thrshold paramtr. Ths
Tchical Support Documt Bias o th Miimum Stattic Itroductio Th papr pla how to driv th bias o th miimum stattic i a radom sampl o siz rom dtributios with a shit paramtr (also kow as thrshold paramtr. Ths
The pn junction: 2 Current vs Voltage (IV) characteristics
 Th pn junction: Currnt vs Voltag (V) charactristics Considr a pn junction in quilibrium with no applid xtrnal voltag: o th V E F E F V p-typ Dpltion rgion n-typ Elctron movmnt across th junction: 1. n
Th pn junction: Currnt vs Voltag (V) charactristics Considr a pn junction in quilibrium with no applid xtrnal voltag: o th V E F E F V p-typ Dpltion rgion n-typ Elctron movmnt across th junction: 1. n
On a problem of J. de Graaf connected with algebras of unbounded operators de Bruijn, N.G.
 O a problm of J. d Graaf coctd with algbras of uboudd oprators d Bruij, N.G. Publishd: 01/01/1984 Documt Vrsio Publishr s PDF, also kow as Vrsio of Rcord (icluds fial pag, issu ad volum umbrs) Plas chck
O a problm of J. d Graaf coctd with algbras of uboudd oprators d Bruij, N.G. Publishd: 01/01/1984 Documt Vrsio Publishr s PDF, also kow as Vrsio of Rcord (icluds fial pag, issu ad volum umbrs) Plas chck
orbiting electron turns out to be wrong even though it Unfortunately, the classical visualization of the
 Lctur 22-1 Byond Bohr Modl Unfortunatly, th classical visualization of th orbiting lctron turns out to b wrong vn though it still givs us a simpl way to think of th atom. Quantum Mchanics is ndd to truly
Lctur 22-1 Byond Bohr Modl Unfortunatly, th classical visualization of th orbiting lctron turns out to b wrong vn though it still givs us a simpl way to think of th atom. Quantum Mchanics is ndd to truly
Electromagnetic scattering. Graduate Course Electrical Engineering (Communications) 1 st Semester, Sharif University of Technology
 Elctromagntic scattring Graduat Cours Elctrical Enginring (Communications) 1 st Smstr, 1388-1389 Sharif Univrsity of Tchnology Contnts of lctur 8 Contnts of lctur 8: Scattring from small dilctric objcts
Elctromagntic scattring Graduat Cours Elctrical Enginring (Communications) 1 st Smstr, 1388-1389 Sharif Univrsity of Tchnology Contnts of lctur 8 Contnts of lctur 8: Scattring from small dilctric objcts
PHYSICS 489/1489 LECTURE 7: QUANTUM ELECTRODYNAMICS
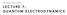 PHYSICS 489/489 LECTURE 7: QUANTUM ELECTRODYNAMICS REMINDER Problm st du today 700 in Box F TODAY: W invstigatd th Dirac quation it dscribs a rlativistic spin /2 particl implis th xistnc of antiparticl
PHYSICS 489/489 LECTURE 7: QUANTUM ELECTRODYNAMICS REMINDER Problm st du today 700 in Box F TODAY: W invstigatd th Dirac quation it dscribs a rlativistic spin /2 particl implis th xistnc of antiparticl
Option 3. b) xe dx = and therefore the series is convergent. 12 a) Divergent b) Convergent Proof 15 For. p = 1 1so the series diverges.
 Optio Chaptr Ercis. Covrgs to Covrgs to Covrgs to Divrgs Covrgs to Covrgs to Divrgs 8 Divrgs Covrgs to Covrgs to Divrgs Covrgs to Covrgs to Covrgs to Covrgs to 8 Proof Covrgs to π l 8 l a b Divrgt π Divrgt
Optio Chaptr Ercis. Covrgs to Covrgs to Covrgs to Divrgs Covrgs to Covrgs to Divrgs 8 Divrgs Covrgs to Covrgs to Divrgs Covrgs to Covrgs to Covrgs to Covrgs to 8 Proof Covrgs to π l 8 l a b Divrgt π Divrgt
The phenomenon of nonlinear optical birefringence in uniaxial crystals
 Th phmf liar ptical birfrigc i uiaial crstals Timtr Pascal, Adam Usma, J. C. Odd Dpartmt f Phsics, Fdral Uivrsit f Tchlg, Yla. P.M.B. 2076 Yla. Adamawa Stat, Nigria. E-mail: ptimtr@ah.cm; aausma@ah.c.uk
Th phmf liar ptical birfrigc i uiaial crstals Timtr Pascal, Adam Usma, J. C. Odd Dpartmt f Phsics, Fdral Uivrsit f Tchlg, Yla. P.M.B. 2076 Yla. Adamawa Stat, Nigria. E-mail: ptimtr@ah.cm; aausma@ah.c.uk
Reliability of time dependent stress-strength system for various distributions
 IOS Joural of Mathmatcs (IOS-JM ISSN: 78-578. Volum 3, Issu 6 (Sp-Oct., PP -7 www.osrjourals.org lablty of tm dpdt strss-strgth systm for varous dstrbutos N.Swath, T.S.Uma Mahswar,, Dpartmt of Mathmatcs,
IOS Joural of Mathmatcs (IOS-JM ISSN: 78-578. Volum 3, Issu 6 (Sp-Oct., PP -7 www.osrjourals.org lablty of tm dpdt strss-strgth systm for varous dstrbutos N.Swath, T.S.Uma Mahswar,, Dpartmt of Mathmatcs,
22/ Breakdown of the Born-Oppenheimer approximation. Selection rules for rotational-vibrational transitions. P, R branches.
 Subjct Chmistry Papr No and Titl Modul No and Titl Modul Tag 8/ Physical Spctroscopy / Brakdown of th Born-Oppnhimr approximation. Slction ruls for rotational-vibrational transitions. P, R branchs. CHE_P8_M
Subjct Chmistry Papr No and Titl Modul No and Titl Modul Tag 8/ Physical Spctroscopy / Brakdown of th Born-Oppnhimr approximation. Slction ruls for rotational-vibrational transitions. P, R branchs. CHE_P8_M
Hadamard Exponential Hankel Matrix, Its Eigenvalues and Some Norms
 Math Sci Ltt Vol No 8-87 (0) adamard Exotial al Matrix, Its Eigvalus ad Som Norms İ ad M bula Mathmatical Scics Lttrs Itratioal Joural @ 0 NSP Natural Scics Publishig Cor Dartmt of Mathmatics, aculty of
Math Sci Ltt Vol No 8-87 (0) adamard Exotial al Matrix, Its Eigvalus ad Som Norms İ ad M bula Mathmatical Scics Lttrs Itratioal Joural @ 0 NSP Natural Scics Publishig Cor Dartmt of Mathmatics, aculty of
APPENDIX: STATISTICAL TOOLS
 I. Nots o radom samplig Why do you d to sampl radomly? APPENDI: STATISTICAL TOOLS I ordr to masur som valu o a populatio of orgaisms, you usually caot masur all orgaisms, so you sampl a subst of th populatio.
I. Nots o radom samplig Why do you d to sampl radomly? APPENDI: STATISTICAL TOOLS I ordr to masur som valu o a populatio of orgaisms, you usually caot masur all orgaisms, so you sampl a subst of th populatio.
Electron energy in crystal potential
 Elctron nry in crystal potntial r r p c mc mc mc Expand: r r r mc mc mc r r p c mc mc mc r pc m c mc p m m m m r E E m m m r p E m r nr nr whr: E V mc E m c Wav quation Hamiltonian: Tim-Indpndnt Schrodinr
Elctron nry in crystal potntial r r p c mc mc mc Expand: r r r mc mc mc r r p c mc mc mc r pc m c mc p m m m m r E E m m m r p E m r nr nr whr: E V mc E m c Wav quation Hamiltonian: Tim-Indpndnt Schrodinr
CDS 101: Lecture 5.1 Reachability and State Space Feedback
 CDS, Lctur 5. CDS : Lctur 5. Rachability ad Stat Spac Fdback Richard M. Murray ad Hido Mabuchi 5 Octobr 4 Goals: Di rachability o a cotrol systm Giv tsts or rachability o liar systms ad apply to ampls
CDS, Lctur 5. CDS : Lctur 5. Rachability ad Stat Spac Fdback Richard M. Murray ad Hido Mabuchi 5 Octobr 4 Goals: Di rachability o a cotrol systm Giv tsts or rachability o liar systms ad apply to ampls
Total Wave Function. e i. Wave function above sample is a plane wave: //incident beam
 Total Wav Function Wav function abov sampl is a plan wav: r i kr //incidnt bam Wav function blow sampl is a collction of diffractd bams (and ): r i k r //transmittd bams k ks W nd to know th valus of th.
Total Wav Function Wav function abov sampl is a plan wav: r i kr //incidnt bam Wav function blow sampl is a collction of diffractd bams (and ): r i k r //transmittd bams k ks W nd to know th valus of th.
Partial Derivatives: Suppose that z = f(x, y) is a function of two variables.
 Chaptr Functions o Two Variabls Applid Calculus 61 Sction : Calculus o Functions o Two Variabls Now that ou hav som amiliarit with unctions o two variabls it s tim to start appling calculus to hlp us solv
Chaptr Functions o Two Variabls Applid Calculus 61 Sction : Calculus o Functions o Two Variabls Now that ou hav som amiliarit with unctions o two variabls it s tim to start appling calculus to hlp us solv
NET/JRF, GATE, IIT JAM, JEST, TIFR
 Istitut for NET/JRF, GATE, IIT JAM, JEST, TIFR ad GRE i PHYSICAL SCIENCES Mathmatical Physics JEST-6 Q. Giv th coditio φ, th solutio of th quatio ψ φ φ is giv by k. kφ kφ lφ kφ lφ (a) ψ (b) ψ kφ (c) ψ
Istitut for NET/JRF, GATE, IIT JAM, JEST, TIFR ad GRE i PHYSICAL SCIENCES Mathmatical Physics JEST-6 Q. Giv th coditio φ, th solutio of th quatio ψ φ φ is giv by k. kφ kφ lφ kφ lφ (a) ψ (b) ψ kφ (c) ψ
Chemical Physics II. More Stat. Thermo Kinetics Protein Folding...
 Chmical Physics II Mor Stat. Thrmo Kintics Protin Folding... http://www.nmc.ctc.com/imags/projct/proj15thumb.jpg http://nuclarwaponarchiv.org/usa/tsts/ukgrabl2.jpg http://www.photolib.noaa.gov/corps/imags/big/corp1417.jpg
Chmical Physics II Mor Stat. Thrmo Kintics Protin Folding... http://www.nmc.ctc.com/imags/projct/proj15thumb.jpg http://nuclarwaponarchiv.org/usa/tsts/ukgrabl2.jpg http://www.photolib.noaa.gov/corps/imags/big/corp1417.jpg
t i Extreme value statistics Problems of extrapolating to values we have no data about unusually large or small ~100 years (data) ~500 years (design)
 Extrm valu statistics Problms of xtrapolatig to valus w hav o data about uusually larg or small t i ~00 yars (data h( t i { h( }? max t i wids v( t i ~500 yars (dsig Qustio: Ca this b do at all? How log
Extrm valu statistics Problms of xtrapolatig to valus w hav o data about uusually larg or small t i ~00 yars (data h( t i { h( }? max t i wids v( t i ~500 yars (dsig Qustio: Ca this b do at all? How log
5 Curl-free fields and electrostatic potential
 5 Curl-fr filds and lctrstatic tntial Mathmaticall, w can gnrat a curl-fr vctr fild E(,, ) as E = ( V, V, V ), b taking th gradint f an scalar functin V (r) =V (,, ). Th gradint f V (,, ) is dfind t b
5 Curl-fr filds and lctrstatic tntial Mathmaticall, w can gnrat a curl-fr vctr fild E(,, ) as E = ( V, V, V ), b taking th gradint f an scalar functin V (r) =V (,, ). Th gradint f V (,, ) is dfind t b
Multiple Short Term Infusion Homework # 5 PHA 5127
 Multipl Short rm Infusion Homwork # 5 PHA 527 A rug is aministr as a short trm infusion. h avrag pharmacokintic paramtrs for this rug ar: k 0.40 hr - V 28 L his rug follows a on-compartmnt boy mol. A 300
Multipl Short rm Infusion Homwork # 5 PHA 527 A rug is aministr as a short trm infusion. h avrag pharmacokintic paramtrs for this rug ar: k 0.40 hr - V 28 L his rug follows a on-compartmnt boy mol. A 300
A Review of Complex Arithmetic
 /0/005 Rviw of omplx Arithmti.do /9 A Rviw of omplx Arithmti A omplx valu has both a ral ad imagiary ompot: { } ad Im{ } a R b so that w a xprss this omplx valu as: whr. a + b Just as a ral valu a b xprssd
/0/005 Rviw of omplx Arithmti.do /9 A Rviw of omplx Arithmti A omplx valu has both a ral ad imagiary ompot: { } ad Im{ } a R b so that w a xprss this omplx valu as: whr. a + b Just as a ral valu a b xprssd
PREPARATORY MATHEMATICS FOR ENGINEERS
 CIVE 690 This qusti ppr csists f 6 pritd pgs, ch f which is idtifid by th Cd Numbr CIVE690 FORMULA SHEET ATTACHED UNIVERSITY OF LEEDS Jury 008 Emiti fr th dgr f BEg/ MEg Civil Egirig PREPARATORY MATHEMATICS
CIVE 690 This qusti ppr csists f 6 pritd pgs, ch f which is idtifid by th Cd Numbr CIVE690 FORMULA SHEET ATTACHED UNIVERSITY OF LEEDS Jury 008 Emiti fr th dgr f BEg/ MEg Civil Egirig PREPARATORY MATHEMATICS
Periodic Structures. Filter Design by the Image Parameter Method
 Prioic Structurs a Filtr sig y th mag Paramtr Mtho ECE53: Microwav Circuit sig Pozar Chaptr 8, Sctios 8. & 8. Josh Ottos /4/ Microwav Filtrs (Chaptr Eight) microwav filtr is a two-port twork us to cotrol
Prioic Structurs a Filtr sig y th mag Paramtr Mtho ECE53: Microwav Circuit sig Pozar Chaptr 8, Sctios 8. & 8. Josh Ottos /4/ Microwav Filtrs (Chaptr Eight) microwav filtr is a two-port twork us to cotrol
Search sequence databases 3 10/25/2016
 Sarch squnc databass 3 10/25/2016 Etrm valu distribution Ø Suppos X is a random variabl with probability dnsity function p(, w sampl a larg numbr S of indpndnt valus of X from this distribution for an
Sarch squnc databass 3 10/25/2016 Etrm valu distribution Ø Suppos X is a random variabl with probability dnsity function p(, w sampl a larg numbr S of indpndnt valus of X from this distribution for an
Acid Base Reactions. Acid Base Reactions. Acid Base Reactions. Chemical Reactions and Equations. Chemical Reactions and Equations
 Chmial Ratins and Equatins Hwitt/Lyns/Suhki/Yh Cnptual Intgratd Sin During a hmial ratin, n r mr nw mpunds ar frmd as a rsult f th rarrangmnt f atms. Chaptr 13 CHEMICAL REACTIONS Ratants Prduts Chmial
Chmial Ratins and Equatins Hwitt/Lyns/Suhki/Yh Cnptual Intgratd Sin During a hmial ratin, n r mr nw mpunds ar frmd as a rsult f th rarrangmnt f atms. Chaptr 13 CHEMICAL REACTIONS Ratants Prduts Chmial
Hydrogen Atom and One Electron Ions
 Hydrogn Atom and On Elctron Ions Th Schrödingr quation for this two-body problm starts out th sam as th gnral two-body Schrödingr quation. First w sparat out th motion of th cntr of mass. Th intrnal potntial
Hydrogn Atom and On Elctron Ions Th Schrödingr quation for this two-body problm starts out th sam as th gnral two-body Schrödingr quation. First w sparat out th motion of th cntr of mass. Th intrnal potntial
European Business Confidence Survey December 2012 Positive expectations for 2013
 Dcmbr 2012 Erpa Bsiss Cfic rv Dcmbr 2012 Psitiv xpctatis fr 2013 Lasrp a Ivigrs EMEA hav rctl cmplt thir latst Erpa Bsiss Cfic rv. Th fiigs sggst a psitiv start t 2013 a a mr ptimistic tlk cmpar t that
Dcmbr 2012 Erpa Bsiss Cfic rv Dcmbr 2012 Psitiv xpctatis fr 2013 Lasrp a Ivigrs EMEA hav rctl cmplt thir latst Erpa Bsiss Cfic rv. Th fiigs sggst a psitiv start t 2013 a a mr ptimistic tlk cmpar t that
Physics of the Interstellar and Intergalactic Medium
 PYA0 Sior Sophistr Physics of th Itrstllar ad Itrgalactic Mdium Lctur 7: II gios Dr Graham M. arpr School of Physics, TCD Follow-up radig for this ad t lctur Chaptr 5: Dyso ad Williams (lss dtaild) Chaptr
PYA0 Sior Sophistr Physics of th Itrstllar ad Itrgalactic Mdium Lctur 7: II gios Dr Graham M. arpr School of Physics, TCD Follow-up radig for this ad t lctur Chaptr 5: Dyso ad Williams (lss dtaild) Chaptr
