Modeling with First-Order Equations
|
|
|
- Madlyn Bradford
- 5 years ago
- Views:
Transcription
1 Modeling with First-Order Equations MATH 365 Ordinary Differential Equations J. Robert Buchanan Department of Mathematics Spring 2018
2 Radioactive Decay Radioactive decay takes place continuously. The number of atoms decaying at any instant is proportional to the number of un-decayed atoms present. Let Q represent the number of un-decayed atoms and t represent time. A first-order ODE describing radioactive decay is dq dt = k Q. The proportionality constant k is called the decay constant and is assumed to be positive.
3 Radioactive Decay Radioactive decay takes place continuously. The number of atoms decaying at any instant is proportional to the number of un-decayed atoms present. Let Q represent the number of un-decayed atoms and t represent time. A first-order ODE describing radioactive decay is dq dt = k Q. The proportionality constant k is called the decay constant and is assumed to be positive. This ODE is both linear and separable.
4 Radioactive Decay Radioactive decay takes place continuously. The number of atoms decaying at any instant is proportional to the number of un-decayed atoms present. Let Q represent the number of un-decayed atoms and t represent time. A first-order ODE describing radioactive decay is dq dt = k Q. The proportionality constant k is called the decay constant and is assumed to be positive. This ODE is both linear and separable. If Q(t 0 ) = Q 0, then the solution to the IVP is Q(t) = Q 0 e k(t t 0).
5 Half-Life Definition The half-life (denoted t 1/2 ) of the radioactive substance is the time required for half of the initial amount to decay.
6 Half-Life Definition The half-life (denoted t 1/2 ) of the radioactive substance is the time required for half of the initial amount to decay. Find the relationship between the half-life t 1/2 and the decay constant k.
7 Half-Life Definition The half-life (denoted t 1/2 ) of the radioactive substance is the time required for half of the initial amount to decay. Find the relationship between the half-life t 1/2 and the decay constant k. Assuming t 0 = 0 then Q 0 2 = Q 0 e k t 1/2 1 2 = e k t 1/2 ln 1 2 = k t 1/2 ln 2 = k t 1/2 t 1/2 = ln 2 k.
8 Continuous Infusion Suppose that a chemical is eliminated from the blood stream of an animal at a rate proportional to the amount of the chemical present (similar to radioactive decay). The chemical enters the animal s blood stream at a rate given by the function F(t). A first order differential equation describing the amount of chemical in the blood stream is then dq dt = k Q + F(t).
9 Continuous Infusion Suppose that a chemical is eliminated from the blood stream of an animal at a rate proportional to the amount of the chemical present (similar to radioactive decay). The chemical enters the animal s blood stream at a rate given by the function F(t). A first order differential equation describing the amount of chemical in the blood stream is then dq dt = k Q + F(t). This equation is first-order linear.
10 Example (1 of 2) Suppose the chemical has a half-life of 2.5 hours in the blood stream and enters the blood stream at a constant rate C. If the chemical is a beneficial medicine whose effective dose is 50 ± 2.5 mg, what should the infusion rate be?
11 Example (1 of 2) Suppose the chemical has a half-life of 2.5 hours in the blood stream and enters the blood stream at a constant rate C. If the chemical is a beneficial medicine whose effective dose is 50 ± 2.5 mg, what should the infusion rate be? We must solve the first-order, linear IVP: dq dt + k Q = C Q(0) = 0. Since t 1/2 = 2.5 then k = ln
12 Example (1 of 2) If the infusion is constant and never ceases, then the ODE in addition to being first-order and linear is autonomous. The beneficial equilibrium solution is an amount of 50 mg. We can find the value of C for which Q(t) = 50 is an equilibrium solution. dq dt + k Q = C 0 + ln (50) = C C = 20 ln mg/hr.
13 Example (1 of 2) If the infusion is constant and never ceases, then the ODE in addition to being first-order and linear is autonomous. The beneficial equilibrium solution is an amount of 50 mg. We can find the value of C for which Q(t) = 50 is an equilibrium solution. dq dt + k Q = C 0 + ln (50) = C C = 20 ln mg/hr. Now we may solve the IVP for a non-constant solution.
14 Example (1 of 2) (ln 2)t The integrating factor is µ(t) = e 2.5. d [µ(t)q(t)] = (20 ln 2)µ(t) dt d [µ(t)q(t)] dt = (20 ln 2) µ(t) dt dt µ(t)q(t) = (20 ln 2)µ(t) 2.5 ln 2 + D (ln 2)t Q(t) = 50 + De = 50 + D D = 50 (ln 2)t Q(t) = 50 50e 2.5
15 Example (1 of 2) (ln 2)t The integrating factor is µ(t) = e 2.5. d [µ(t)q(t)] = (20 ln 2)µ(t) dt d [µ(t)q(t)] dt = (20 ln 2) µ(t) dt dt µ(t)q(t) = (20 ln 2)µ(t) 2.5 ln 2 + D (ln 2)t Q(t) = 50 + De = 50 + D D = 50 (ln 2)t Q(t) = 50 50e e t
16 Graph Q t t
17 Graph Q t t How long after the infusion is started will it take until the effective dose is achieved?
18 Effective Dose The medicine becomes effective when the dose is = 47.5 mg.
19 Effective Dose The medicine becomes effective when the dose is = 47.5 mg. Thus we must solve the equation: Q(t) = 47.5 (ln 2)t 50 50e 2.5 = 47.5 (ln 2)t 50e 2.5 = 2.5 (ln 2)t e (ln 2)t = 0.05 = ln 0.05 t = 2.5 ln 0.05 ln 2
20 Effective Dose The medicine becomes effective when the dose is = 47.5 mg. Thus we must solve the equation: Q(t) = 47.5 (ln 2)t 50 50e 2.5 = 47.5 (ln 2)t 50e 2.5 = 2.5 (ln 2)t e (ln 2)t = 0.05 = ln ln 0.05 t = hr. ln 2
21 Example (2 of 2) Suppose the chemical has a half-life of 3 hours in the blood stream and enters the blood stream at a rate given by 10(1 + sin(2πt)). Initially 50 mg of the chemical is in the blood stream. How much of the chemical is in the blood stream at time t > 0?
22 Example (2 of 2) Suppose the chemical has a half-life of 3 hours in the blood stream and enters the blood stream at a rate given by 10(1 + sin(2πt)). Initially 50 mg of the chemical is in the blood stream. How much of the chemical is in the blood stream at time t > 0? We must solve the IVP: dq dt = kq + 10(1 + sin(2πt)) Q(0) = 50.
23 Example (2 of 2) Suppose the chemical has a half-life of 3 hours in the blood stream and enters the blood stream at a rate given by 10(1 + sin(2πt)). Initially 50 mg of the chemical is in the blood stream. How much of the chemical is in the blood stream at time t > 0? We must solve the IVP: dq dt = kq + 10(1 + sin(2πt)) Q(0) = 50. This is another first-order linear ODE. The decay constant can be found from the half-life.
24 Example (2 of 2) Suppose the chemical has a half-life of 3 hours in the blood stream and enters the blood stream at a rate given by 10(1 + sin(2πt)). Initially 50 mg of the chemical is in the blood stream. How much of the chemical is in the blood stream at time t > 0? We must solve the IVP: dq dt = kq + 10(1 + sin(2πt)) Q(0) = 50. This is another first-order linear ODE. The decay constant can be found from the half-life. k = ln hr 1
25 Solution The integrating factor is µ(t) = e kt.
26 Solution The integrating factor is µ(t) = e kt. t 0 dq + kq = 10(1 + sin(2πt)) dt d [ ] e kt Q(t) = 10e kt (1 + sin(2πt)) dt d [ ] t e ks Q(s) ds = 10 e ku (1 + sin(2πu)) du ds e kt Q(t) Q(0) = 0 20π k 2 + 4π (ekt 1) k + 10ekt k 2 (k sin(2πt) 2π cos(2πt)) + 4π2 Q(t) = 50e kt + 20πe kt k 2 + 4π (1 e kt ) k 10 + k 2 (k sin(2πt) 2π cos(2πt)) + 4π2
27 Graph Q t t
28 Stirred/Mixed Tanks (1 of 3) Suppose a tank (or some other vessel) has a constant volume V and is being fed a solution of water and a chemical in concentration γ g/l at a rate of r L/min. The tank is well stirred so that the chemical is evenly distributed throughout the tank. The well-stirred mixture flows out of the tank also at rate r L/min. If the tank is initially filled completely with pure water, find the concentration of the chemical in the well-stirred tank as a function of time.
29 Stirred/Mixed Tanks (2 of 3) The amount of chemical in the incoming stream is the product of the incoming concentration and the incoming flow rate, γ r g/min.
30 Stirred/Mixed Tanks (2 of 3) The amount of chemical in the incoming stream is the product of the incoming concentration and the incoming flow rate, γ r g/min. We can express the concentration of the chemical in the tank C(t) as the amount of chemical in the tank Q(t) divided by the volume of the tank V, C(t) = 1 Q(t) g/l. V Since the concentration of the chemical in the outflow is the same as the concentration of the chemical in the tank (recall that the tank is well-stirred), the amount of chemical leaving the tank per minute is the product of the concentration in the tank and the outgoing flow rate, r Q(t) V = r C(t) g/min.
31 Stirred/Mixed Tanks (3 of 3) The rate of change in the amount of the chemical in the tank Q(t) is the difference between the inflow rate and the outflow rate, then an ODE describing the amount of chemical in the tank is dq = γ r r Q dt V.
32 Stirred/Mixed Tanks (3 of 3) The rate of change in the amount of the chemical in the tank Q(t) is the difference between the inflow rate and the outflow rate, then an ODE describing the amount of chemical in the tank is dq = γ r r Q dt V. The concentration of the chemical in the tank C(t) is just the amount of chemical in the tank divided by the volume of the tank. An ODE for the concentration is 1 dq V dt dc dt = γ r V r V Q V = γ r V r V C.
33 Example Suppose a 500 L tank initially containing 500 L of pure water is fed with a solution of saline and water at a rate of 2 L/min with a concentration of 1/2 g/l of saline. Set up an IVP describing the concentration of saline in the tank as a function of time. Solve the IVP for t > 0. Find the lim t C(t).
34 Example Suppose a 500 L tank initially containing 500 L of pure water is fed with a solution of saline and water at a rate of 2 L/min with a concentration of 1/2 g/l of saline. Set up an IVP describing the concentration of saline in the tank as a function of time. Solve the IVP for t > 0. Find the lim t C(t). The appropriate IVP: dc dt dc dt = (1/2)(2) C = C(0) = C The ODE is first-order, linear with an integrating factor of µ(t) = e t/250.
35 Solution t 0 d ds dc + 1 dt 250 C = d [ ] e t/250 1 C(t) = dt [ ] t e s/250 C(s) ds = 500 et/ eu/250 du e t/250 C(t) C(0) = 1 2 (et/250 1) C(t) = 1 2 (1 e t/250 )
36 Solution t 0 d ds dc + 1 dt 250 C = d [ ] e t/250 1 C(t) = dt [ ] t e s/250 C(s) ds = 500 et/ eu/250 du e t/250 C(t) C(0) = 1 2 (et/250 1) C(t) = 1 2 (1 e t/250 ) ( ) 1 lim C(t) = lim t t 2 (1 e t/250 ) = 1 2
37 Graph C t t
38 Newton s Law of Cooling Suppose the temperature of an object is θ and the temperature of the environment in which the object sits is T. Furthermore assume the temperature of the environment is constant. Newton s Law of Cooling states that the rate of change in the temperature of the object is proportional to the difference between the temperature of the object and the temperature of the environment.
39 Newton s Law of Cooling Suppose the temperature of an object is θ and the temperature of the environment in which the object sits is T. Furthermore assume the temperature of the environment is constant. Newton s Law of Cooling states that the rate of change in the temperature of the object is proportional to the difference between the temperature of the object and the temperature of the environment. A first-order, linear ODE describing the change in θ is dθ dt = k(θ T ).
40 Newton s Law of Cooling Suppose the temperature of an object is θ and the temperature of the environment in which the object sits is T. Furthermore assume the temperature of the environment is constant. Newton s Law of Cooling states that the rate of change in the temperature of the object is proportional to the difference between the temperature of the object and the temperature of the environment. A first-order, linear ODE describing the change in θ is dθ dt = k(θ T ). If we assume the proportionality constant k > 0, why does the right-hand side of the ODE possess a minus " sign?
41 Example Suppose a cup of coffee is initially 200 degrees Fahrenheit and one minute later is at 190 degrees Fahrenheit in a room whose temperature is 70 degrees Fahrenheit. When will the temperature of the coffee be 150 degrees Fahrenheit?
42 Example Suppose a cup of coffee is initially 200 degrees Fahrenheit and one minute later is at 190 degrees Fahrenheit in a room whose temperature is 70 degrees Fahrenheit. When will the temperature of the coffee be 150 degrees Fahrenheit? An IVP describing this situation is dθ dt = k(θ 70) θ(0) = 200. We should also use the observation that θ(1) = 190 degrees Fahrenheit.
43 Solution Re-writing the ODE in standard form as dθ dt + k θ = 70k we see that the integrating factor is µ(t) = e k t.
44 Solution Re-writing the ODE in standard form as dθ dt + k θ = 70k we see that the integrating factor is µ(t) = e k t. t 0 d [ ] e k t θ(t) = 70ke k t dt d [ ] t e k s θ(s) ds = 70ke k u du ds e k t θ(t) θ(0) = 70(e k t 1) 0 θ(t) = 200e k t + 70(1 e k t ) θ(t) = e k t
45 Solution Re-writing the ODE in standard form as dθ dt + k θ = 70k we see that the integrating factor is µ(t) = e k t. t 0 d [ ] e k t θ(t) = 70ke k t dt d [ ] t e k s θ(s) ds = 70ke k u du ds e k t θ(t) θ(0) = 70(e k t 1) Question: how do we find k? 0 θ(t) = 200e k t + 70(1 e k t ) θ(t) = e k t
46 Determining the Value of k Recall that θ(1) = 190 so that we have the equation, θ(1) = e k(1)
47 Determining the Value of k Recall that θ(1) = 190 so that we have the equation, θ(1) = e k(1) 190 = e k e k = k = ln k = ln 13 12
48 Determining the Value of k Recall that θ(1) = 190 so that we have the equation, θ(1) = e k(1) 190 = e k e k = k = ln k = ln
49 Determining the Value of k Recall that θ(1) = 190 so that we have the equation, θ(1) = e k(1) 190 = e k e k = k = ln k = ln t ln(13/12) θ(t) = e
50 When is the Coffee s Temperature 150 F? 150 = t ln(13/12) e 80 = t ln(13/12) 130e e t ln(13/12) = 8 ( ) t ln = ln 12 ( 8 13 ) t = ln(8/13) ln(12/13)
51 When is the Coffee s Temperature 150 F? 150 = t ln(13/12) e 80 = t ln(13/12) 130e e t ln(13/12) = 8 ( ) t ln = ln 12 ( 8 13 ) t = ln(8/13) min. ln(12/13)
52 Graph 200 Θ t t
53 Escape Velocity (1 of 2) An object of mass m is launched perpendicularly from the surface of the earth with initial velocity v 0. Question: what is the minimum initial velocity that will allow the object to escape the earth s gravitational attraction?
54 Escape Velocity (1 of 2) An object of mass m is launched perpendicularly from the surface of the earth with initial velocity v 0. Question: what is the minimum initial velocity that will allow the object to escape the earth s gravitational attraction? Assumptions: The only force on the object is gravity which varies inversely with the square of the distance separating the centers of mass of the object and the earth. The radius of the earth is R. The distance from the object to the surface of the earth is x.
55 Escape Velocity (2 of 2) Recall Newton s Second Law of Motion, F = m a, then Comments: a = dv dt = d 2 x dt 2 m a = m g R 2 (R + x) 2. The right-hand side of the equation captures the effect that the gravitational attraction of the earth decreases as x increases. We can treat x as the independent variable and v as the dependent variable using relationship (justified by the Chain Rule for Derivatives) a = dv dt = dv dx dx dt = dv dx v.
56 Solution (1 of 3) We now have the IVP: m v dv R 2 = m g dx (R + x) 2 v(0) = v 0. The ODE is first-order, separable.
57 Solution (1 of 3) We now have the IVP: m v dv R 2 = m g dx (R + x) 2 v(0) = v 0. The ODE is first-order, separable. v v dv dx = g R 2 (R + x) 2 R 2 v dv = g (R + x) 2 dx v 0 u du = x 1 2 (v 2 v 2 0 ) = g R2 R + x g R 0 g R 2 (R + z) 2 dz
58 Solution (2 of 3) Solving for v(x) yields v(x) = v 2 0 2g R + 2g R R + x.
59 Solution (2 of 3) Solving for v(x) yields v(x) = v 2 0 2g R + 2g R R + x. As the object travels upward, its velocity decreases toward 0 at its maximum altitude (apogee). Solving the equation v(x) = 0 produces 2g R 2g R R + x 2g R R + x R + x = = v 2 0 = 2g R v 2 0 2g R 2g R v 2 0 x = R v 2 0 2g R v 2 0
60 Solution (3 of 3) R v0 2 x max = 2g R v0 2 If the object has achieved escape velocity, the maximum altitude is +, so we need an initial velocity v 0 for which 2g R v 2 0 = 0 v 0 = 2g R. If we use R 6, 378, 140 m and g m/s 2 then v m/s 6.95 mi/s!
61 Homework Read Section 2.3 Exercises: 1, 3, 15, 19, 31, 32
Modeling with First-Order Equations
 Modeling with First-Order Equations MATH 365 Ordinary Differential Equations J. Robert Buchanan Department of Mathematics Fall 2018 Radioactive Decay Radioactive decay takes place continuously. The number
Modeling with First-Order Equations MATH 365 Ordinary Differential Equations J. Robert Buchanan Department of Mathematics Fall 2018 Radioactive Decay Radioactive decay takes place continuously. The number
Mathematical Models. MATH 365 Ordinary Differential Equations. J. Robert Buchanan. Fall Department of Mathematics
 Mathematical Models MATH 365 Ordinary Differential Equations J. Robert Buchanan Department of Mathematics Fall 2018 Ordinary Differential Equations The topic of ordinary differential equations (ODEs) is
Mathematical Models MATH 365 Ordinary Differential Equations J. Robert Buchanan Department of Mathematics Fall 2018 Ordinary Differential Equations The topic of ordinary differential equations (ODEs) is
Mathematical Models. MATH 365 Ordinary Differential Equations. J. Robert Buchanan. Spring Department of Mathematics
 Mathematical Models MATH 365 Ordinary Differential Equations J. Robert Buchanan Department of Mathematics Spring 2018 Ordinary Differential Equations The topic of ordinary differential equations (ODEs)
Mathematical Models MATH 365 Ordinary Differential Equations J. Robert Buchanan Department of Mathematics Spring 2018 Ordinary Differential Equations The topic of ordinary differential equations (ODEs)
Modeling with First Order ODEs (cont). Existence and Uniqueness of Solutions to First Order Linear IVP. Second Order ODEs
 Modeling with First Order ODEs (cont). Existence and Uniqueness of Solutions to First Order Linear IVP. Second Order ODEs September 18 22, 2017 Mixing Problem Yuliya Gorb Example: A tank with a capacity
Modeling with First Order ODEs (cont). Existence and Uniqueness of Solutions to First Order Linear IVP. Second Order ODEs September 18 22, 2017 Mixing Problem Yuliya Gorb Example: A tank with a capacity
MA 214 Calculus IV (Spring 2016) Section 2. Homework Assignment 2 Solutions
 MA 214 Calculus IV (Spring 2016) Section 2 Homework Assignment 2 Solutions 1 Boyce and DiPrima, p 60, Problem 2 Solution: Let M(t) be the mass (in grams) of salt in the tank after t minutes The initial-value
MA 214 Calculus IV (Spring 2016) Section 2 Homework Assignment 2 Solutions 1 Boyce and DiPrima, p 60, Problem 2 Solution: Let M(t) be the mass (in grams) of salt in the tank after t minutes The initial-value
Homework 2 Solutions Math 307 Summer 17
 Homework 2 Solutions Math 307 Summer 17 July 8, 2017 Section 2.3 Problem 4. A tank with capacity of 500 gallons originally contains 200 gallons of water with 100 pounds of salt in solution. Water containing
Homework 2 Solutions Math 307 Summer 17 July 8, 2017 Section 2.3 Problem 4. A tank with capacity of 500 gallons originally contains 200 gallons of water with 100 pounds of salt in solution. Water containing
(1 2t), y(1) = 2 y. dy dt = t. e t y, y(0) = 1. dr, r(1) = 2 (r = r(θ)) y = t(t2 + 1) 4y 3, y(0) = 1. 2t y + t 2 y, y(0) = 2. 2t 1 + 2y, y(2) = 0
 MATH 307 Due: Problem 1 Text: 2.2.9-20 Solve the following initial value problems (this problem should mainly be a review of MATH 125). 1. y = (1 2t)y 2, y(0) = 1/6 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12.
MATH 307 Due: Problem 1 Text: 2.2.9-20 Solve the following initial value problems (this problem should mainly be a review of MATH 125). 1. y = (1 2t)y 2, y(0) = 1/6 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12.
4. Some Applications of first order linear differential
 September 9, 2012 4-1 4. Some Applications of first order linear differential Equations The modeling problem There are several steps required for modeling scientific phenomena 1. Data collection (experimentation)
September 9, 2012 4-1 4. Some Applications of first order linear differential Equations The modeling problem There are several steps required for modeling scientific phenomena 1. Data collection (experimentation)
MTH 3311 Test #2 Solutions
 Pat Rossi MTH 3311 Test #2 Solutions S 2018 Name Directions: Do two of the three exercises. 1. A paratrooper and parachute weigh 160 lb. At the instant the parachute opens, she is traveling vertically
Pat Rossi MTH 3311 Test #2 Solutions S 2018 Name Directions: Do two of the three exercises. 1. A paratrooper and parachute weigh 160 lb. At the instant the parachute opens, she is traveling vertically
Math 308 Exam I Practice Problems
 Math 308 Exam I Practice Problems This review should not be used as your sole source of preparation for the exam. You should also re-work all examples given in lecture and all suggested homework problems..
Math 308 Exam I Practice Problems This review should not be used as your sole source of preparation for the exam. You should also re-work all examples given in lecture and all suggested homework problems..
Practice Midterm 1 Solutions Written by Victoria Kala July 10, 2017
 Practice Midterm 1 Solutions Written by Victoria Kala July 10, 2017 1. Use the slope field plotter link in Gauchospace to check your solution. 2. (a) Not linear because of the y 2 sin x term (b) Not linear
Practice Midterm 1 Solutions Written by Victoria Kala July 10, 2017 1. Use the slope field plotter link in Gauchospace to check your solution. 2. (a) Not linear because of the y 2 sin x term (b) Not linear
MATH 251 Examination I October 8, 2015 FORM A. Name: Student Number: Section:
 MATH 251 Examination I October 8, 2015 FORM A Name: Student Number: Section: This exam has 14 questions for a total of 100 points. Show all you your work! In order to obtain full credit for partial credit
MATH 251 Examination I October 8, 2015 FORM A Name: Student Number: Section: This exam has 14 questions for a total of 100 points. Show all you your work! In order to obtain full credit for partial credit
Math 308 Exam I Practice Problems
 Math 308 Exam I Practice Problems This review should not be used as your sole source for preparation for the exam. You should also re-work all examples given in lecture and all suggested homework problems..
Math 308 Exam I Practice Problems This review should not be used as your sole source for preparation for the exam. You should also re-work all examples given in lecture and all suggested homework problems..
Math 31S. Rumbos Fall Solutions to Exam 1
 Math 31S. Rumbos Fall 2011 1 Solutions to Exam 1 1. When people smoke, carbon monoxide is released into the air. Suppose that in a room of volume 60 m 3, air containing 5% carbon monoxide is introduced
Math 31S. Rumbos Fall 2011 1 Solutions to Exam 1 1. When people smoke, carbon monoxide is released into the air. Suppose that in a room of volume 60 m 3, air containing 5% carbon monoxide is introduced
2. (12 points) Find an equation for the line tangent to the graph of f(x) =
 November 23, 2010 Name The total number of points available is 153 Throughout this test, show your work Throughout this test, you are expected to use calculus to solve problems Graphing calculator solutions
November 23, 2010 Name The total number of points available is 153 Throughout this test, show your work Throughout this test, you are expected to use calculus to solve problems Graphing calculator solutions
Modeling using ODEs: Mixing Tank Problem. Natasha Sharma, Ph.D.
 Reference W. Boyce and R. DiPrima, Elementary Differential Equations and Boundary Value s 8th Edition, John Wiley and Sons, 2005. First-Order Ordinary Differential Equation Definition (First Order Ordinary
Reference W. Boyce and R. DiPrima, Elementary Differential Equations and Boundary Value s 8th Edition, John Wiley and Sons, 2005. First-Order Ordinary Differential Equation Definition (First Order Ordinary
1.5. Applications. Theorem The solution of the exponential decay equation with N(0) = N 0 is N(t) = N 0 e kt.
 6 Section Objective(s): The Radioactive Decay Equation Newton s Cooling Law Salt in a Water Tanks 151 Exponential Decay 15 Applications Definition 151 The exponential decay equation for N is N = k N, k
6 Section Objective(s): The Radioactive Decay Equation Newton s Cooling Law Salt in a Water Tanks 151 Exponential Decay 15 Applications Definition 151 The exponential decay equation for N is N = k N, k
Math 116 Practice for Exam 2
 Math 116 Practice for Exam 2 Generated February 25, 2016 Name: SOLUTIONS Instructor: Section Number: 1. This exam has 5 questions. Note that the problems are not of equal difficulty, so you may want to
Math 116 Practice for Exam 2 Generated February 25, 2016 Name: SOLUTIONS Instructor: Section Number: 1. This exam has 5 questions. Note that the problems are not of equal difficulty, so you may want to
The most up-to-date version of this collection of homework exercises can always be found at bob/math365/mmm.pdf.
 Millersville University Department of Mathematics MATH 365 Ordinary Differential Equations January 23, 212 The most up-to-date version of this collection of homework exercises can always be found at http://banach.millersville.edu/
Millersville University Department of Mathematics MATH 365 Ordinary Differential Equations January 23, 212 The most up-to-date version of this collection of homework exercises can always be found at http://banach.millersville.edu/
A population is modeled by the differential equation
 Math 2, Winter 2016 Weekly Homework #8 Solutions 9.1.9. A population is modeled by the differential equation dt = 1.2 P 1 P ). 4200 a) For what values of P is the population increasing? P is increasing
Math 2, Winter 2016 Weekly Homework #8 Solutions 9.1.9. A population is modeled by the differential equation dt = 1.2 P 1 P ). 4200 a) For what values of P is the population increasing? P is increasing
LECTURE 4-1 INTRODUCTION TO ORDINARY DIFFERENTIAL EQUATIONS
 130 LECTURE 4-1 INTRODUCTION TO ORDINARY DIFFERENTIAL EQUATIONS DIFFERENTIAL EQUATIONS: A differential equation (DE) is an equation involving an unknown function and one or more of its derivatives. A differential
130 LECTURE 4-1 INTRODUCTION TO ORDINARY DIFFERENTIAL EQUATIONS DIFFERENTIAL EQUATIONS: A differential equation (DE) is an equation involving an unknown function and one or more of its derivatives. A differential
Solving differential equations (Sect. 7.4) Review: Overview of differential equations.
 Solving differential equations (Sect. 7.4 Previous class: Overview of differential equations. Exponential growth. Separable differential equations. Review: Overview of differential equations. Definition
Solving differential equations (Sect. 7.4 Previous class: Overview of differential equations. Exponential growth. Separable differential equations. Review: Overview of differential equations. Definition
Sample Questions, Exam 1 Math 244 Spring 2007
 Sample Questions, Exam Math 244 Spring 2007 Remember, on the exam you may use a calculator, but NOT one that can perform symbolic manipulation (remembering derivative and integral formulas are a part of
Sample Questions, Exam Math 244 Spring 2007 Remember, on the exam you may use a calculator, but NOT one that can perform symbolic manipulation (remembering derivative and integral formulas are a part of
MATH 251 Examination I July 1, 2013 FORM A. Name: Student Number: Section:
 MATH 251 Examination I July 1, 2013 FORM A Name: Student Number: Section: This exam has 12 questions for a total of 100 points. Show all your work! In order to obtain full credit for partial credit problems,
MATH 251 Examination I July 1, 2013 FORM A Name: Student Number: Section: This exam has 12 questions for a total of 100 points. Show all your work! In order to obtain full credit for partial credit problems,
MAT 285: Introduction to Differential Equations. James V. Lambers
 MAT 285: Introduction to Differential Equations James V. Lambers April 2, 27 2 Contents Introduction 5. Some Basic Mathematical Models............................. 5.2 Solutions of Some Differential Equations.........................
MAT 285: Introduction to Differential Equations James V. Lambers April 2, 27 2 Contents Introduction 5. Some Basic Mathematical Models............................. 5.2 Solutions of Some Differential Equations.........................
VANDERBILT UNIVERSITY. MATH 2610 ORDINARY DIFFERENTIAL EQUATIONS Practice for test 1 solutions
 VANDERBILT UNIVERSITY MATH 2610 ORDINARY DIFFERENTIAL EQUATIONS Practice for test 1 solutions The first test will cover all material discussed up to (including) section 4.5. Important: The solutions below
VANDERBILT UNIVERSITY MATH 2610 ORDINARY DIFFERENTIAL EQUATIONS Practice for test 1 solutions The first test will cover all material discussed up to (including) section 4.5. Important: The solutions below
Exponential Growth (Doubling Time)
 Exponential Growth (Doubling Time) 4 Exponential Growth (Doubling Time) Suppose we start with a single bacterium, which divides every hour. After one hour we have 2 bacteria, after two hours we have 2
Exponential Growth (Doubling Time) 4 Exponential Growth (Doubling Time) Suppose we start with a single bacterium, which divides every hour. After one hour we have 2 bacteria, after two hours we have 2
FINAL EXAM CALCULUS 2. Name PRACTICE EXAM SOLUTIONS
 FINAL EXAM CALCULUS MATH 00 FALL 08 Name PRACTICE EXAM SOLUTIONS Please answer all of the questions, and show your work. You must explain your answers to get credit. You will be graded on the clarity of
FINAL EXAM CALCULUS MATH 00 FALL 08 Name PRACTICE EXAM SOLUTIONS Please answer all of the questions, and show your work. You must explain your answers to get credit. You will be graded on the clarity of
Differential Equation (DE): An equation relating an unknown function and one or more of its derivatives.
 Lexicon Differential Equation (DE): An equation relating an unknown function and one or more of its derivatives. Ordinary Differential Equation (ODE): A differential equation that contains only ordinary
Lexicon Differential Equation (DE): An equation relating an unknown function and one or more of its derivatives. Ordinary Differential Equation (ODE): A differential equation that contains only ordinary
Graded and supplementary homework, Math 2584, Section 4, Fall 2017
 Graded and supplementary homework, Math 2584, Section 4, Fall 2017 (AB 1) (a) Is y = cos(2x) a solution to the differential equation d2 y + 4y = 0? dx2 (b) Is y = e 2x a solution to the differential equation
Graded and supplementary homework, Math 2584, Section 4, Fall 2017 (AB 1) (a) Is y = cos(2x) a solution to the differential equation d2 y + 4y = 0? dx2 (b) Is y = e 2x a solution to the differential equation
Chapter1. Ordinary Differential Equations
 Chapter1. Ordinary Differential Equations In the sciences and engineering, mathematical models are developed to aid in the understanding of physical phenomena. These models often yield an equation that
Chapter1. Ordinary Differential Equations In the sciences and engineering, mathematical models are developed to aid in the understanding of physical phenomena. These models often yield an equation that
Math Applied Differential Equations
 Math 256 - Applied Differential Equations Notes Existence and Uniqueness The following theorem gives sufficient conditions for the existence and uniqueness of a solution to the IVP for first order nonlinear
Math 256 - Applied Differential Equations Notes Existence and Uniqueness The following theorem gives sufficient conditions for the existence and uniqueness of a solution to the IVP for first order nonlinear
The Fundamental Theorem of Calculus: Suppose f continuous on [a, b]. 1.) If G(x) = x. f(t)dt = F (b) F (a) where F is any antiderivative
![The Fundamental Theorem of Calculus: Suppose f continuous on [a, b]. 1.) If G(x) = x. f(t)dt = F (b) F (a) where F is any antiderivative The Fundamental Theorem of Calculus: Suppose f continuous on [a, b]. 1.) If G(x) = x. f(t)dt = F (b) F (a) where F is any antiderivative](/thumbs/96/128959530.jpg) 1 Calulus pre-requisites you must know. Derivative = slope of tangent line = rate. Integral = area between curve and x-axis (where area can be negative). The Fundamental Theorem of Calculus: Suppose f
1 Calulus pre-requisites you must know. Derivative = slope of tangent line = rate. Integral = area between curve and x-axis (where area can be negative). The Fundamental Theorem of Calculus: Suppose f
Integration by Substitution
 Integration by Substitution MATH 151 Calculus for Management J. Robert Buchanan Department of Mathematics Fall 2018 Objectives After this lesson we will be able to use the method of integration by substitution
Integration by Substitution MATH 151 Calculus for Management J. Robert Buchanan Department of Mathematics Fall 2018 Objectives After this lesson we will be able to use the method of integration by substitution
MATH 312 Section 3.1: Linear Models
 MATH 312 Section 3.1: Linear Models Prof. Jonathan Duncan Walla Walla College Spring Quarter, 2007 Outline 1 Population Growth 2 Newton s Law of Cooling 3 Kepler s Law Second Law of Planetary Motion 4
MATH 312 Section 3.1: Linear Models Prof. Jonathan Duncan Walla Walla College Spring Quarter, 2007 Outline 1 Population Growth 2 Newton s Law of Cooling 3 Kepler s Law Second Law of Planetary Motion 4
Math 2300 Calculus II University of Colorado Final exam review problems
 Math 300 Calculus II University of Colorado Final exam review problems. A slope field for the differential equation y = y e x is shown. Sketch the graphs of the solutions that satisfy the given initial
Math 300 Calculus II University of Colorado Final exam review problems. A slope field for the differential equation y = y e x is shown. Sketch the graphs of the solutions that satisfy the given initial
Laplace Transform Problems
 AP Calculus BC Name: Laplace Transformation Day 3 2 January 206 Laplace Transform Problems Example problems using the Laplace Transform.. Solve the differential equation y! y = e t, with the initial value
AP Calculus BC Name: Laplace Transformation Day 3 2 January 206 Laplace Transform Problems Example problems using the Laplace Transform.. Solve the differential equation y! y = e t, with the initial value
Solutions to Math 53 First Exam April 20, 2010
 Solutions to Math 53 First Exam April 0, 00. (5 points) Match the direction fields below with their differential equations. Also indicate which two equations do not have matches. No justification is necessary.
Solutions to Math 53 First Exam April 0, 00. (5 points) Match the direction fields below with their differential equations. Also indicate which two equations do not have matches. No justification is necessary.
Separable Differential Equations
 Separable Differential Equations MATH 6 Calculus I J. Robert Buchanan Department of Mathematics Fall 207 Background We have previously solved differential equations of the forms: y (t) = k y(t) (exponential
Separable Differential Equations MATH 6 Calculus I J. Robert Buchanan Department of Mathematics Fall 207 Background We have previously solved differential equations of the forms: y (t) = k y(t) (exponential
Chapter 2: First Order ODE 2.4 Examples of such ODE Mo
 Chapter 2: First Order ODE 2.4 Examples of such ODE Models 28 January 2018 First Order ODE Read Only Section! We recall the general form of the First Order DEs (FODE): dy = f (t, y) (1) dt where f (t,
Chapter 2: First Order ODE 2.4 Examples of such ODE Models 28 January 2018 First Order ODE Read Only Section! We recall the general form of the First Order DEs (FODE): dy = f (t, y) (1) dt where f (t,
Lecture Notes for Math 251: ODE and PDE. Lecture 6: 2.3 Modeling With First Order Equations
 Lecture Notes for Math 251: ODE and PDE. Lecture 6: 2.3 Modeling With First Order Equations Shawn D. Ryan Spring 2012 1 Modeling With First Order Equations Last Time: We solved separable ODEs and now we
Lecture Notes for Math 251: ODE and PDE. Lecture 6: 2.3 Modeling With First Order Equations Shawn D. Ryan Spring 2012 1 Modeling With First Order Equations Last Time: We solved separable ODEs and now we
Chapters 8.1 & 8.2 Practice Problems
 EXPECTED SKILLS: Chapters 8.1 & 8. Practice Problems Be able to verify that a given function is a solution to a differential equation. Given a description in words of how some quantity changes in time
EXPECTED SKILLS: Chapters 8.1 & 8. Practice Problems Be able to verify that a given function is a solution to a differential equation. Given a description in words of how some quantity changes in time
Solutions to Homework 1, Introduction to Differential Equations, 3450: , Dr. Montero, Spring y(x) = ce 2x + e x
 Solutions to Homewor 1, Introduction to Differential Equations, 3450:335-003, Dr. Montero, Spring 2009 problem 2. The problem says that the function yx = ce 2x + e x solves the ODE y + 2y = e x, and ass
Solutions to Homewor 1, Introduction to Differential Equations, 3450:335-003, Dr. Montero, Spring 2009 problem 2. The problem says that the function yx = ce 2x + e x solves the ODE y + 2y = e x, and ass
Applications of First Order Differential Equation
 Dr Mansoor Alshehri King Saud University MATH204-Differential Equations Center of Excellence in Learning and Teaching 1 / 39 Orthogonal Trajectories How to Find Orthogonal Trajectories Growth and Decay
Dr Mansoor Alshehri King Saud University MATH204-Differential Equations Center of Excellence in Learning and Teaching 1 / 39 Orthogonal Trajectories How to Find Orthogonal Trajectories Growth and Decay
APPM 2360: Midterm exam 1 February 15, 2017
 APPM 36: Midterm exam 1 February 15, 17 On the front of your Bluebook write: (1) your name, () your instructor s name, (3) your recitation section number and () a grading table. Text books, class notes,
APPM 36: Midterm exam 1 February 15, 17 On the front of your Bluebook write: (1) your name, () your instructor s name, (3) your recitation section number and () a grading table. Text books, class notes,
DIFFERENTIAL EQUATIONS
 Mr. Isaac Akpor Adjei (MSc. Mathematics, MSc. Biostats) isaac.adjei@gmail.com April 7, 2017 ORDINARY In many physical situation, equation arise which involve differential coefficients. For example: 1 The
Mr. Isaac Akpor Adjei (MSc. Mathematics, MSc. Biostats) isaac.adjei@gmail.com April 7, 2017 ORDINARY In many physical situation, equation arise which involve differential coefficients. For example: 1 The
Integral Curve (generic name for a member of the collection of known as the general solution)
 Section 1.2 Solutions of Some Differential Equations Key Terms/Ideas: Phase Line (This topic is not in this section of the book.) Classification of Equilibrium Solutions: Source, Sink, Node SPECIAL CASE:
Section 1.2 Solutions of Some Differential Equations Key Terms/Ideas: Phase Line (This topic is not in this section of the book.) Classification of Equilibrium Solutions: Source, Sink, Node SPECIAL CASE:
Math 2214 Solution Test 1D Spring 2015
 Math 2214 Solution Test 1D Spring 2015 Problem 1: A 600 gallon open top tank initially holds 300 gallons of fresh water. At t = 0, a brine solution containing 3 lbs of salt per gallon is poured into the
Math 2214 Solution Test 1D Spring 2015 Problem 1: A 600 gallon open top tank initially holds 300 gallons of fresh water. At t = 0, a brine solution containing 3 lbs of salt per gallon is poured into the
Modeling with first order equations (Sect. 2.3). The mathematical modeling of natural processes.
 Modeling with first order equations (Sect. 2.3). The mathematical modeling of natural processes. Main example: Salt in a water tank. The experimental device. The main equations. Analysis of the mathematical
Modeling with first order equations (Sect. 2.3). The mathematical modeling of natural processes. Main example: Salt in a water tank. The experimental device. The main equations. Analysis of the mathematical
Math 2930 Worksheet Introduction to Differential Equations
 Math 2930 Worksheet Introduction to Differential Equations Week 2 February 1st, 2019 Learning Goals Solve linear first order ODEs analytically. Solve separable first order ODEs analytically. Questions
Math 2930 Worksheet Introduction to Differential Equations Week 2 February 1st, 2019 Learning Goals Solve linear first order ODEs analytically. Solve separable first order ODEs analytically. Questions
Math Spring 2014 Homework 2 solution
 Math 3-00 Spring 04 Homework solution.3/5 A tank initially contains 0 lb of salt in gal of weater. A salt solution flows into the tank at 3 gal/min and well-stirred out at the same rate. Inflow salt concentration
Math 3-00 Spring 04 Homework solution.3/5 A tank initially contains 0 lb of salt in gal of weater. A salt solution flows into the tank at 3 gal/min and well-stirred out at the same rate. Inflow salt concentration
2.4 Differences Between Linear and Nonlinear Equations 75
 .4 Differences Between Linear and Nonlinear Equations 75 fying regions of the ty-plane where solutions exhibit interesting features that merit more detailed analytical or numerical investigation. Graphical
.4 Differences Between Linear and Nonlinear Equations 75 fying regions of the ty-plane where solutions exhibit interesting features that merit more detailed analytical or numerical investigation. Graphical
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
 Chapter Practice Test Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find the general solution to the eact differential equation. ) dy dt =
Chapter Practice Test Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find the general solution to the eact differential equation. ) dy dt =
Math 308, Sections 301, 302, Summer 2008 Review before Test I 06/09/2008
 Math 308, Sections 301, 302, Summer 2008 Review before Test I 06/09/2008 Chapter 1. Introduction Section 1.1 Background Definition Equation that contains some derivatives of an unknown function is called
Math 308, Sections 301, 302, Summer 2008 Review before Test I 06/09/2008 Chapter 1. Introduction Section 1.1 Background Definition Equation that contains some derivatives of an unknown function is called
Practice Final Exam Solutions
 Important Notice: To prepare for the final exam, study past exams and practice exams, and homeworks, quizzes, and worksheets, not just this practice final. A topic not being on the practice final does
Important Notice: To prepare for the final exam, study past exams and practice exams, and homeworks, quizzes, and worksheets, not just this practice final. A topic not being on the practice final does
Goals: To develop skills needed to find the appropriate differential equations to use as mathematical models.
 Unit #16 : Differential Equations Goals: To develop skills needed to find the appropriate differential equations to use as mathematical models. Differential Equation Modelling - 1 Differential Equation
Unit #16 : Differential Equations Goals: To develop skills needed to find the appropriate differential equations to use as mathematical models. Differential Equation Modelling - 1 Differential Equation
Solution. It is evaluating the definite integral r 1 + r 4 dr. where you can replace r by any other variable.
 Solutions of Sample Problems for First In-Class Exam Math 246, Fall 202, Professor David Levermore () (a) Give the integral being evaluated by the following MATLAB command. int( x/(+xˆ4), x,0,inf) Solution.
Solutions of Sample Problems for First In-Class Exam Math 246, Fall 202, Professor David Levermore () (a) Give the integral being evaluated by the following MATLAB command. int( x/(+xˆ4), x,0,inf) Solution.
Section , #5. Let Q be the amount of salt in oz in the tank. The scenario can be modeled by a differential equation.
 Section.3.5.3, #5. Let Q be the amount of salt in oz in the tank. The scenario can be modeled by a differential equation dq = 1 4 (1 + sin(t) ) + Q, Q(0) = 50. (1) 100 (a) The differential equation given
Section.3.5.3, #5. Let Q be the amount of salt in oz in the tank. The scenario can be modeled by a differential equation dq = 1 4 (1 + sin(t) ) + Q, Q(0) = 50. (1) 100 (a) The differential equation given
2.3: Modeling with Differential Equations
 2.3: Modeling with Differential Equations Some General Comments: A mathematical model is an equation or set of equations that mimic the behavior of some phenomenon under certain assumptions/approximations.
2.3: Modeling with Differential Equations Some General Comments: A mathematical model is an equation or set of equations that mimic the behavior of some phenomenon under certain assumptions/approximations.
Mathematics 256 a course in differential equations for engineering students
 Mathematics 256 a course in differential equations for engineering students Chapter 1. How things cool off One physical system in which many important phenomena occur is that where an initial uneven temperature
Mathematics 256 a course in differential equations for engineering students Chapter 1. How things cool off One physical system in which many important phenomena occur is that where an initial uneven temperature
Practice Exam 1 Solutions
 Practice Exam 1 Solutions 1a. Let S be the region bounded by y = x 3, y = 1, and x. Find the area of S. What is the volume of the solid obtained by rotating S about the line y = 1? Area A = Volume 1 1
Practice Exam 1 Solutions 1a. Let S be the region bounded by y = x 3, y = 1, and x. Find the area of S. What is the volume of the solid obtained by rotating S about the line y = 1? Area A = Volume 1 1
It is convenient to think that solutions of differential equations consist of a family of functions (just like indefinite integrals ).
 Section 1.1 Direction Fields Key Terms/Ideas: Mathematical model Geometric behavior of solutions without solving the model using calculus Graphical description using direction fields Equilibrium solution
Section 1.1 Direction Fields Key Terms/Ideas: Mathematical model Geometric behavior of solutions without solving the model using calculus Graphical description using direction fields Equilibrium solution
2.5 Linear Applications
 2.5 Linear Applications 111 2.5 Linear Applications This collection of applications for the linear equation y + p(x)y = r(x) includes mixing problems, especially brine tanks in single and multiple cascade,
2.5 Linear Applications 111 2.5 Linear Applications This collection of applications for the linear equation y + p(x)y = r(x) includes mixing problems, especially brine tanks in single and multiple cascade,
weebly.com/ Core Mathematics 3 Exponentials and Natural Logarithms
 http://kumarmaths. weebly.com/ Core Mathematics 3 Exponentials and Natural Logarithms Core Maths 3 Exponentials and natural Logarithms Page 1 Ln and Exponentials C3 Content By the end of this unit you
http://kumarmaths. weebly.com/ Core Mathematics 3 Exponentials and Natural Logarithms Core Maths 3 Exponentials and natural Logarithms Page 1 Ln and Exponentials C3 Content By the end of this unit you
Homogeneous Equations with Constant Coefficients
 Homogeneous Equations with Constant Coefficients MATH 365 Ordinary Differential Equations J. Robert Buchanan Department of Mathematics Spring 2018 General Second Order ODE Second order ODEs have the form
Homogeneous Equations with Constant Coefficients MATH 365 Ordinary Differential Equations J. Robert Buchanan Department of Mathematics Spring 2018 General Second Order ODE Second order ODEs have the form
= 2e t e 2t + ( e 2t )e 3t = 2e t e t = e t. Math 20D Final Review
 Math D Final Review. Solve the differential equation in two ways, first using variation of parameters and then using undetermined coefficients: Corresponding homogenous equation: with characteristic equation
Math D Final Review. Solve the differential equation in two ways, first using variation of parameters and then using undetermined coefficients: Corresponding homogenous equation: with characteristic equation
Goals: To develop skills needed to find the appropriate differential equations to use as mathematical models.
 Unit #17 : Differential Equations Goals: To develop skills needed to find the appropriate differential equations to use as mathematical models. Reading: Sections 11.5-11.7. In workingwiththemodels insections11.5
Unit #17 : Differential Equations Goals: To develop skills needed to find the appropriate differential equations to use as mathematical models. Reading: Sections 11.5-11.7. In workingwiththemodels insections11.5
Practice Final Exam Solutions
 Important Notice: To prepare for the final exam, one should study the past exams and practice midterms (and homeworks, quizzes, and worksheets), not just this practice final. A topic not being on the practice
Important Notice: To prepare for the final exam, one should study the past exams and practice midterms (and homeworks, quizzes, and worksheets), not just this practice final. A topic not being on the practice
Section 11.1 What is a Differential Equation?
 1 Section 11.1 What is a Differential Equation? Example 1 Suppose a ball is dropped from the top of a building of height 50 meters. Let h(t) denote the height of the ball after t seconds, then it is known
1 Section 11.1 What is a Differential Equation? Example 1 Suppose a ball is dropped from the top of a building of height 50 meters. Let h(t) denote the height of the ball after t seconds, then it is known
AP Calculus Testbank (Chapter 6) (Mr. Surowski)
 AP Calculus Testbank (Chapter 6) (Mr. Surowski) Part I. Multiple-Choice Questions 1. Suppose that f is an odd differentiable function. Then (A) f(1); (B) f (1) (C) f(1) f( 1) (D) 0 (E). 1 1 xf (x) =. The
AP Calculus Testbank (Chapter 6) (Mr. Surowski) Part I. Multiple-Choice Questions 1. Suppose that f is an odd differentiable function. Then (A) f(1); (B) f (1) (C) f(1) f( 1) (D) 0 (E). 1 1 xf (x) =. The
Core Mathematics 3 Exponentials and Natural Logarithms
 Edexcel past paper questions Core Mathematics 3 Exponentials and Natural Logarithms Edited by: K V kumaran Email: kvkumaran@gmail.com Core Maths 3 Exponentials and natural Logarithms Page Ln and Exponentials
Edexcel past paper questions Core Mathematics 3 Exponentials and Natural Logarithms Edited by: K V kumaran Email: kvkumaran@gmail.com Core Maths 3 Exponentials and natural Logarithms Page Ln and Exponentials
Motion in Space. MATH 311, Calculus III. J. Robert Buchanan. Fall Department of Mathematics. J. Robert Buchanan Motion in Space
 Motion in Space MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Fall 2011 Background Suppose the position vector of a moving object is given by r(t) = f (t), g(t), h(t), Background
Motion in Space MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Fall 2011 Background Suppose the position vector of a moving object is given by r(t) = f (t), g(t), h(t), Background
Ordinary Differential Equations
 Ordinary Differential Equations Swaroop Nandan Bora swaroop@iitg.ernet.in Department of Mathematics Indian Institute of Technology Guwahati Guwahati-781039 A first-order differential equation is an equation
Ordinary Differential Equations Swaroop Nandan Bora swaroop@iitg.ernet.in Department of Mathematics Indian Institute of Technology Guwahati Guwahati-781039 A first-order differential equation is an equation
The acceleration of gravity is constant (near the surface of the earth). So, for falling objects:
 1. Become familiar with a definition of and terminology involved with differential equations Calculus - Santowski. Solve differential equations with and without initial conditions 3. Apply differential
1. Become familiar with a definition of and terminology involved with differential equations Calculus - Santowski. Solve differential equations with and without initial conditions 3. Apply differential
Final Exam Review Part I: Unit IV Material
 Final Exam Review Part I: Unit IV Material Math114 Department of Mathematics, University of Kentucky April 26, 2017 Math114 Lecture 37 1/ 11 Outline 1 Conic Sections Math114 Lecture 37 2/ 11 Outline 1
Final Exam Review Part I: Unit IV Material Math114 Department of Mathematics, University of Kentucky April 26, 2017 Math114 Lecture 37 1/ 11 Outline 1 Conic Sections Math114 Lecture 37 2/ 11 Outline 1
MATH 151, Fall 2013, Week 10-2, Section 4.5, 4.6
 MATH 151, Fall 2013, Week 10-2, Section 4.5, 4.6 Recall the derivative of logarithmic and exponential functions. Theorem 1 (ln x) = (ln f(x)) = (log a x) = (log a f(x)) = Theorem 2 (a x ) = (a f(x) ) =
MATH 151, Fall 2013, Week 10-2, Section 4.5, 4.6 Recall the derivative of logarithmic and exponential functions. Theorem 1 (ln x) = (ln f(x)) = (log a x) = (log a f(x)) = Theorem 2 (a x ) = (a f(x) ) =
Three major steps in modeling: Construction of the Model Analysis of the Model Comparison with Experiment or Observation
 Section 2.3 Modeling : Key Terms: Three major steps in modeling: Construction of the Model Analysis of the Model Comparison with Experiment or Observation Mixing Problems Population Example Continuous
Section 2.3 Modeling : Key Terms: Three major steps in modeling: Construction of the Model Analysis of the Model Comparison with Experiment or Observation Mixing Problems Population Example Continuous
Tangent and Normal Vectors
 Tangent and Normal Vectors MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Fall 2011 Navigation When an observer is traveling along with a moving point, for example the passengers in
Tangent and Normal Vectors MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Fall 2011 Navigation When an observer is traveling along with a moving point, for example the passengers in
Old Math 330 Exams. David M. McClendon. Department of Mathematics Ferris State University
 Old Math 330 Exams David M. McClendon Department of Mathematics Ferris State University Last updated to include exams from Fall 07 Contents Contents General information about these exams 3 Exams from Fall
Old Math 330 Exams David M. McClendon Department of Mathematics Ferris State University Last updated to include exams from Fall 07 Contents Contents General information about these exams 3 Exams from Fall
3.8 Exponential Growth and Decay
 October 15, 2010 Population growth Population growth If y = f (t) is the number of individuals in a population of animals or humans at time t, then it seems reasonable to expect that the rate of growth
October 15, 2010 Population growth Population growth If y = f (t) is the number of individuals in a population of animals or humans at time t, then it seems reasonable to expect that the rate of growth
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. D) u = - x15 cos (x15) + C
 AP Calculus AB Exam Review Differential Equations and Mathematical Modelling MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find the general solution
AP Calculus AB Exam Review Differential Equations and Mathematical Modelling MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find the general solution
MATH 1231 MATHEMATICS 1B Calculus Section 3A: - First order ODEs.
 MATH 1231 MATHEMATICS 1B 2010. For use in Dr Chris Tisdell s lectures. Calculus Section 3A: - First order ODEs. Created and compiled by Chris Tisdell S1: What is an ODE? S2: Motivation S3: Types and orders
MATH 1231 MATHEMATICS 1B 2010. For use in Dr Chris Tisdell s lectures. Calculus Section 3A: - First order ODEs. Created and compiled by Chris Tisdell S1: What is an ODE? S2: Motivation S3: Types and orders
CHAPTER 3. Mathematical Models and Numerical Methods Involving First-Order Equations
 CHAPTER 3 Mathematical Models and Numerical Methods Involving First-Order Equations 2. Compartmental Analysis The asic one-compartment system consists of a function x(t) that represents the amount of a
CHAPTER 3 Mathematical Models and Numerical Methods Involving First-Order Equations 2. Compartmental Analysis The asic one-compartment system consists of a function x(t) that represents the amount of a
Math 116 Practice for Exam 2
 Math 116 Practice for Exam 2 Generated November 11, 2016 Name: SOLUTIONS Instructor: Section Number: 1. This exam has 9 questions. Note that the problems are not of equal difficulty, so you may want to
Math 116 Practice for Exam 2 Generated November 11, 2016 Name: SOLUTIONS Instructor: Section Number: 1. This exam has 9 questions. Note that the problems are not of equal difficulty, so you may want to
MATH165 Homework 7. Solutions
 MATH165 Homework 7. Solutions March 23. 2010 Problem 1. 3.7.9 The stone is thrown with speed of 10m/s, and height is given by h = 10t 0.83t 2. (a) To find the velocity after 3 seconds, we first need to
MATH165 Homework 7. Solutions March 23. 2010 Problem 1. 3.7.9 The stone is thrown with speed of 10m/s, and height is given by h = 10t 0.83t 2. (a) To find the velocity after 3 seconds, we first need to
Math 116 Practice for Exam 3
 Math 116 Practice for Exam 3 Generated November 30, 2017 Name: SOLUTIONS Instructor: Section Number: 1. This exam has 6 questions. Note that the problems are not of equal difficulty, so you may want to
Math 116 Practice for Exam 3 Generated November 30, 2017 Name: SOLUTIONS Instructor: Section Number: 1. This exam has 6 questions. Note that the problems are not of equal difficulty, so you may want to
Lecture Notes in Mathematics. Arkansas Tech University Department of Mathematics
 Lecture Notes in Mathematics Arkansas Tech University Department of Mathematics Introductory Notes in Ordinary Differential Equations for Physical Sciences and Engineering Marcel B. Finan c All Rights
Lecture Notes in Mathematics Arkansas Tech University Department of Mathematics Introductory Notes in Ordinary Differential Equations for Physical Sciences and Engineering Marcel B. Finan c All Rights
Basic Theory of Differential Equations
 page 104 104 CHAPTER 1 First-Order Differential Equations 16. The following initial-value problem arises in the analysis of a cable suspended between two fixed points y = 1 a 1 + (y ) 2, y(0) = a, y (0)
page 104 104 CHAPTER 1 First-Order Differential Equations 16. The following initial-value problem arises in the analysis of a cable suspended between two fixed points y = 1 a 1 + (y ) 2, y(0) = a, y (0)
DIFFERENTIATION RULES
 3 DIFFERENTIATION RULES DIFFERENTIATION RULES If we are pumping air into a balloon, both the volume and the radius of the balloon are increasing and their rates of increase are related to each other. However,
3 DIFFERENTIATION RULES DIFFERENTIATION RULES If we are pumping air into a balloon, both the volume and the radius of the balloon are increasing and their rates of increase are related to each other. However,
Lecture 6, September 1, 2017
 Engineering Mathematics Fall 07 Lecture 6, September, 07 Escape Velocity Suppose we have a planet (or any large near to spherical heavenly body) of radius R and acceleration of gravity at the surface of
Engineering Mathematics Fall 07 Lecture 6, September, 07 Escape Velocity Suppose we have a planet (or any large near to spherical heavenly body) of radius R and acceleration of gravity at the surface of
ISLAMIYA ENGLISH SCHOOL ABU DHABI U. A. E.
 ISLAMIYA ENGLISH SCHOOL ABU DHABI U. A. E. MATHEMATICS ASSIGNMENT-1 GRADE-A/L-II(Sci) CHAPTER.NO.1,2,3(C3) Algebraic fractions,exponential and logarithmic functions DATE:18/3/2017 NAME.------------------------------------------------------------------------------------------------
ISLAMIYA ENGLISH SCHOOL ABU DHABI U. A. E. MATHEMATICS ASSIGNMENT-1 GRADE-A/L-II(Sci) CHAPTER.NO.1,2,3(C3) Algebraic fractions,exponential and logarithmic functions DATE:18/3/2017 NAME.------------------------------------------------------------------------------------------------
Chapter 3. Periodic functions
 Chapter 3. Periodic functions Why do lights flicker? For that matter, why do they give off light at all? They are fed by an alternating current which turns into heat because of the electrical resistance
Chapter 3. Periodic functions Why do lights flicker? For that matter, why do they give off light at all? They are fed by an alternating current which turns into heat because of the electrical resistance
Solutions to Homework Assignment #2
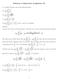 Solutions to Homework Assignment #. [4 marks] Evaluate each of the following limits. n i a lim n. b lim c lim d lim n i. sin πi n. a i n + b, where a and b are constants. n a There are ways to do this
Solutions to Homework Assignment #. [4 marks] Evaluate each of the following limits. n i a lim n. b lim c lim d lim n i. sin πi n. a i n + b, where a and b are constants. n a There are ways to do this
XXIX Applications of Differential Equations
 MATHEMATICS 01-BNK-05 Advanced Calculus Martin Huard Winter 015 1. Suppose that the rate at which a population of size yt at time t changes is proportional to the amount present. This gives rise to the
MATHEMATICS 01-BNK-05 Advanced Calculus Martin Huard Winter 015 1. Suppose that the rate at which a population of size yt at time t changes is proportional to the amount present. This gives rise to the
Solutions for homework 1. 1 Introduction to Differential Equations
 Solutions for homework 1 1 Introduction to Differential Equations 1.1 Differential Equation Models The phrase y is proportional to x implies that y is related to x via the equation y = kx, where k is a
Solutions for homework 1 1 Introduction to Differential Equations 1.1 Differential Equation Models The phrase y is proportional to x implies that y is related to x via the equation y = kx, where k is a
Heat Equation on Unbounded Intervals
 Heat Equation on Unbounded Intervals MATH 467 Partial Differential Equations J. Robert Buchanan Department of Mathematics Fall 28 Objectives In this lesson we will learn about: the fundamental solution
Heat Equation on Unbounded Intervals MATH 467 Partial Differential Equations J. Robert Buchanan Department of Mathematics Fall 28 Objectives In this lesson we will learn about: the fundamental solution
Mathematics 132 Calculus for Physical and Life Sciences 2 Exam 3 Review Sheet April 15, 2008
 Mathematics 32 Calculus for Physical and Life Sciences 2 Eam 3 Review Sheet April 5, 2008 Sample Eam Questions - Solutions This list is much longer than the actual eam will be (to give you some idea of
Mathematics 32 Calculus for Physical and Life Sciences 2 Eam 3 Review Sheet April 5, 2008 Sample Eam Questions - Solutions This list is much longer than the actual eam will be (to give you some idea of
Arc Length and Surface Area in Parametric Equations
 Arc Length and Surface Area in Parametric Equations MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2011 Background We have developed definite integral formulas for arc length
Arc Length and Surface Area in Parametric Equations MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2011 Background We have developed definite integral formulas for arc length
y0 = F (t0)+c implies C = y0 F (t0) Integral = area between curve and x-axis (where I.e., f(t)dt = F (b) F (a) wheref is any antiderivative 2.
 Calulus pre-requisites you must know. Derivative = slope of tangent line = rate. Integral = area between curve and x-axis (where area can be negative). The Fundamental Theorem of Calculus: Suppose f continuous
Calulus pre-requisites you must know. Derivative = slope of tangent line = rate. Integral = area between curve and x-axis (where area can be negative). The Fundamental Theorem of Calculus: Suppose f continuous
MATH 251 Examination I October 10, 2013 FORM A. Name: Student Number: Section:
 MATH 251 Examination I October 10, 2013 FORM A Name: Student Number: Section: This exam has 13 questions for a total of 100 points. Show all you your work! In order to obtain full credit for partial credit
MATH 251 Examination I October 10, 2013 FORM A Name: Student Number: Section: This exam has 13 questions for a total of 100 points. Show all you your work! In order to obtain full credit for partial credit
